勾股定理练习题(含答案)
勾股定理练习题目及问题详解(共6套)

勾股定理课时练(1)1. 在直角三角形ABC中,斜边AB=1,则AB222ACBC++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰AB的长是______ cm(结果不取近似值).3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m,旗杆在断裂之前高多少m?5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.6. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7. 如图所示,无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度. 8. 一个零件的形状如图所示,已知AC=3cm,AB=4cm,BD=12cm。
求CD的长.9. 如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.10. 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?11如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12. 甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?“路”4m3m第2题图第5题图第7题图第9题图第8题图5m13m第11题第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC,所以AB 222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360 ,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+ ,再利用面积法得,1360,132112521=⨯⨯=⨯⨯x x ;4. 解:依题意,AB=16m ,AC=12m ,在直角三角形ABC 中,由勾股定理,222222201216=+=+=AC AB BC ,所以BC=20m ,20+12=32(m ), 故旗杆在断裂之前有32m 高. 5.86. 解:如图,由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC=30004000500022=-(米),所以飞机飞行的速度为5403600203=(千米/小时) 7. 解:将曲线沿AB 展开,如图所示,过点C 作CE ⊥AB 于E. 在R 90,=∠∆CEF CEF t ,EF=18-1-1=16(cm ),CE=)(3060.21cm =⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得254322222=+=+=AB AC BC在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13.9. 解:延长BC 、AD 交于点E.(如图所示)∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
勾股定理典型练习题(含答案)
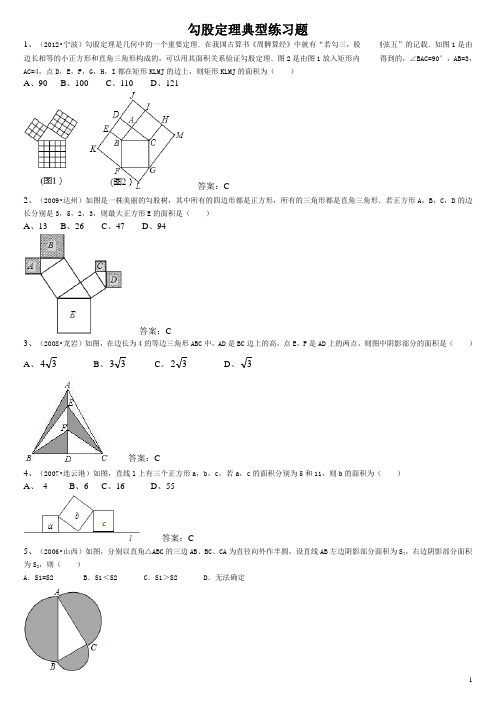
勾股定理典型练习题 1、(2012•宁波)勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则矩形KLMJ 的面积为( ) A 、90 B 、100 C 、110 D 、121答案:C2、(2009•达州)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A ,B ,C ,D 的边长分别是3,5,2,3,则最大正方形E 的面积是( )A 、13B 、26C 、47D 、94答案:C3、(2008•龙岩)如图,在边长为4的等边三角形ABC 中,AD 是BC 边上的高,点E ,F 是AD 上的两点,则图中阴影部分的面积是( )A 、34B 、33C 、32D 、3答案:C4、(2007•连云港)如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为5和11,则b 的面积为( )A 、 4B 、6C 、16D 、55答案:C5、(2006•山西)如图,分别以直角△ABC 的三边AB 、BC 、CA 为直径向外作半圆,设直线AB 左边阴影部分面积为S 1,右边阴影部分面积为S 2,则( )A .S1=S2B .S1<S2C .S1>S2D .无法确定▲6、如图,Rt△ABC 中,∠ACB=90°.在AB 的同侧分别以AB 、BC 、AC 为直径作三个半圆.图中阴影部分的面积分别记作为S1和S2.(1)求证:S1+S2=S△ABC;(2)若Rt△ABC 的周长是 62+,斜边长为2,求图中阴影部分面积的和.答案:21 ▲7、如图,直角三角形ABC 中,∠ABC=90°,AB=6,以AB 为直径画半圆,若阴影部分的面积S1-S2= 2π,则BC= _____。
勾股定理练习题及答案(共6套)

勾股定理课时练(1)1.在直角三角形ABC中,斜边AB=1,则AB222ACBC++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰AB的长是______ cm(结果不取近似值).3.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16m,旗杆在断裂之前高多少m?5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.6.飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米?7.如图所示,无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口1cm的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,所走的最短路线的长度. 8.一个零件的形状如图所示,已知AC=3cm,AB=4cm,BD=12cm。
求CD的长.9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长.10.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?11如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC,所以AB 222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360 ,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+ ,再利用面积法得,1360,132112521=⨯⨯=⨯⨯x x ;4. 解:依题意,AB=16m ,AC=12m ,在直角三角形ABC 中,由勾股定理,222222201216=+=+=AC AB BC ,所以BC=20m ,20+12=32(m ), 故旗杆在断裂之前有32m 高. 5.86. 解:如图,由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC=30004000500022=-(米),所以飞机飞行的速度为5403600203=(千米/小时) 7. 解:将曲线沿AB 展开,如图所示,过点C 作CE ⊥AB 于E. 在R 90,=∠∆CEF CEF t ,EF=18-1-1=16(cm ),CE=)(3060.21cm =⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得254322222=+=+=AB AC BC在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13.9. 解:延长BC 、AD 交于点E.(如图所示)∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
勾股定理练习题及答案解析

勾股定理练习题及答案解析一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+1 4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形 5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定 6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33 7.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )(A 2d (B d(C )2d (D )d8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3B :4C :5D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17 B.3 C.17或3 D.以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则三角形的形状是( )A :底与边不相等的等腰三角形B :等边三角形C :钝角三角形D :直角三角形 11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为 14.一个三角形三边之比是6:8:10,则按角分类它是 三角形. 15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___.16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.17.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .18.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .19. 一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 .二、综合发展:1.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.ACB2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?3.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?AECDB15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长. 答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解. 答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角. 8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.小汽车小汽车观测点10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5. 答案:cm 5. 二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解. 答案:6.5s . 15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h . 答案:这辆小汽车超速了. 附:如何掌握好每学期应掌握的知识如何掌握好每学期应掌握的知识,每学期对知识归纳总结是打好基础的好方式, 可以遵循以下方式进行:一、地毯式扫荡。
勾股定理练习题及答案

勾股定理练习题及答案1. 直角三角形1.1 已知直角三角形的两个直角边分别为3cm和4cm,求斜边的长度。
解答:根据勾股定理,斜边的长度可以通过以下公式计算:c = √(a^2 + b^2)其中,a和b分别为两个直角边的长度。
代入已知值,可以得到:c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5cm所以,斜边的长度为5cm。
1.2 已知直角三角形的斜边长度为10cm,其中一条直角边的长度为6cm,求另一条直角边的长度。
解答:同样根据勾股定理,可以得到以下公式:c^2 = a^2 + b^2将已知值代入,可以得到:10^2 = 6^2 + b^2100 = 36 + b^2b^2 = 100 - 36b^2 = 64b = √64 = 8cm所以,另一条直角边的长度为8cm。
2. 直角三角形的应用2.1 一根长度为12cm的电话线在地面上拉出了一个直角三角形,其中一条直角边长为9cm,求另一条直角边和斜边的长度。
解答:根据勾股定理,可以得到以下公式:c^2 = a^2 + b^2已知直角边的长度为9cm,将已知值代入公式,可以得到:c^2 = 9^2 + b^2c^2 = 81 + b^2又已知三角形的斜边是长为12cm的电话线,所以可以得到另一个公式:c = 12将这两个公式结合,可以得到以下方程:81 + b^2 = 12^281 + b^2 = 144b^2 = 144 - 81b^2 = 63b = √63 ≈ 7.94cm所以,另一条直角边的长度约为7.94cm,斜边的长度为12cm。
2.2 一根高度为10m的电线杆倒在地面上形成了一个直角三角形,其中一条直角边长为8m,求另一条直角边和斜边的长度。
解答:同样根据勾股定理,可以得到以下公式:c^2 = a^2 + b^2已知直角边的长度为8m,将已知值代入公式,可以得到:c^2 = 8^2 + b^2c^2 = 64 + b^2又已知三角形的斜边是高度为10m的电线杆,所以可以得到另一个公式:c = 10将这两个公式结合,可以得到以下方程:64 + b^2 = 10^264 + b^2 = 100b^2 = 100 - 64b^2 = 36b = √36 = 6m所以,另一条直角边的长度为6m,斜边的长度为10m。
勾股定理练习题及答案

勾股定理练习题及答案一、选择题1、直角三角形的两直角边分别为 5 厘米、12 厘米,则斜边长是()A 13 厘米B 14 厘米C 15 厘米D 16 厘米答案:A解析:根据勾股定理,直角三角形的两直角边的平方和等于斜边的平方。
所以斜边的平方= 5²+ 12²= 25 + 144 = 169,斜边长为 13 厘米。
2、以下列各组数为边长,能组成直角三角形的是()A 3,4,6B 5,12,13C 5,11,12D 2,3,4答案:B解析:对于选项 A,3²+ 4²= 9 + 16 = 25,6²= 36,因为25 ≠ 36,所以不能组成直角三角形;对于选项 B,5²+ 12²= 25 + 144 =169,13²= 169,因为 169 = 169,所以能组成直角三角形;对于选项C,5²+ 11²= 25 + 121 = 146,12²= 144,因为146 ≠ 144,所以不能组成直角三角形;对于选项 D,2²+ 3²= 4 + 9 = 13,4²= 16,因为13 ≠ 16,所以不能组成直角三角形。
3、一个直角三角形的三边长分别为 2,3,x,则 x 的值为()A √13B √5C √13 或√5D 无法确定答案:C解析:当 x 为斜边时,x =√(2²+ 3²) =√13;当 3 为斜边时,x =√(3² 2²) =√5。
所以 x 的值为√13 或√5 。
4、已知直角三角形的两条边长分别是 5 和 12,则第三边的长为()A 13B √119C 13 或√119D 不能确定答案:C解析:当 12 为斜边时,第三边的长为√(12² 5²) =√119;当 5 和12 为直角边时,第三边的长为√(5²+ 12²) = 13。
(完整版)勾股定理测试题及参考答案

勾股定理测试题一、选择题(每小题4分,共40分)1.以下列各组数为边长能组成直角三角形的是( )A .567,,B .1084,,C .91517,,D .72425,,2. 直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长( )(A )4 cm (B )8 cm (C )10 cm(D )12 cm3. 已知一个Rt △的两边长分别为3和4,则第三边长的平方是( ) (A)25(B )14 (C )7 (D )7或254.已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A 。
直角三角形B.等腰三角形C 。
等腰直角三角形D.等腰三角形或直角三角形5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )715242520715202425157252024257202415(A)(B)(C)(D)6.如图,一个梯子AB 长2.5米,顶端A 靠在墙AC 上,这时梯子下端B 与墙角C 距离为1.5米,梯子滑动后停在DE 的位置上,测得BD 长为0.5米,则梯子顶端A 下落了( )米EA BCDA .0.5B .1C .1.5D .2DCBA5米3米7.一只蚂蚁沿如图所示折线从A点爬到D点,共爬行了()(图中方格边长为1cm)A.12cm B.10cmC.14cm D.以上答案都不对8.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a元计算,那么共需要资金().(A)50a元(B)600a元(C)1200a元(D)1500a元9.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行()米A.8米B.10米C.12米D.14米10.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,B C/交AD于E,AD=8,AB=4,则DE的长为().A.3 B.4 C.5 D.6二、填空题(每小题4分,共16分)11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12. 在直角三角形ABC中,斜边AB=2,则222AB AC BC++=______。
勾股定理练习(含答案)

勾股定理练习一、单选题(共12题;共24分)1.如图,长为8cm 的橡皮筋放置在x 轴上,固定两端A和B,然后把中点C向上拉升3cm 至D点,则橡皮筋被拉长了()A. 2cmB. 3cmC. 4cmD. 5cm2.如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于()A. B. 3 C. 4 D. 53.在下列的线段中,能组成直角三角形的是( )A. 1,2,3B. 2,3,4C. 3,4,5D. 4,5,64.如果梯子的底端离建筑物5 米,13 米长的梯子可以达到该建筑物的高度是()A. 12 米B. 13 米C. 14 米D. 15 米5.一直角三角形两边分别为3和5,则第三边为()A. 4B.C. 4或D. 26.在△ABC中,∠C=90°,若AC=3,BC=4,则AB=()A. B. 5 C. D. 77.如图,一个梯子AB长2.5 米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.9米,则梯子顶端A下落了()A. 0.9米B. 1.3米C. 1.5米D. 2米8.若直角三角形的三边长分别为2、4、x,则x的可能值有()A. 1个B. 2个C. 3个D. 4个9.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A. 25海里B. 30海里C. 40海里D. 50海里10.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为()A. 20cmB. 50cmC. 40cmD. 45cm11.如图所示:某商场有一段楼梯,高BC=6m,斜边AC是10米,如果在楼梯上铺上地毯,那么需要地毯的长度是()A. 8mB. 10mC. 14mD. 24m12.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB=2米,则树高为()A. 米B. 米C. (米D. 3 米二、填空题(共8题;共8分)13.在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.14.若直角三角形两直角边长分别为6和8,则它的斜边长为________.15.直角三角形两直角边长分别为,,则斜边长为________.16.如图,作一个长方形,以数轴的原点为中心,长方形对角线为半径,交数轴于点A,则点A表示的数是________.17.如图,小华将升旗的绳子拉到竖直旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,此时绳子末端距离地面2m,则绳子的总长度为________ m.18.已知一个直角三角形的两条直角边的差为2,两条直角边的平方和为8,则这个直角三角形的面积是________19.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于________ cm2.20.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!三、作图题(共1题;共5分)21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点,①在图1中画出边长分别为:3,2 ,的三角形(不写画法);②在图2中画出边长分别为,4,,4的平行四边形(不写画法).四、计算题(共1题;共5分)22.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.23.有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多什么米?24.如图,梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图所示。
勾股定理全章练习题含答案

勾股定理课堂学习检测—、填空题:! •若是直角三角形的两直角边长别离为a、b,斜边长为c,那么 _______ 二3 ;这必然理在我国被称为 ______ ・2・厶中,zC二90°, a、b、c别离是乙B、/U的对边・(1) ____________________________ 假设a=5, b = 12t那么c二;⑵假设c 41, ”40,那么0二____________ ;(3) 假设z»=30\ a",那么c二 _________ . b二____ :(4) 假设z/l二45°,日二丄,那么" ______ , c二____ ・3•如图是由边长为lm的正方形地砖铺设的地面示用意,小明沿图中所示的折线从XB-C所走的路程为4 •等腰直角三角形的斜边为10,那么腰长为_______ ,斜边上的高为______ •5 •在直角三角形中,一条直角边为11cm ,另两边是两个持续自探数,那么此直角三角形的周长为二瞬题6 • R^ABC中#斜边BC二2 .那么+ BO的值为()•(A)8 (B)4 (C)6 (D)无法计算7 •如图,L ABC中f AB二AC^ 10 , BD是边上的高线.DC=2 ,那么SQ等于().(A)4 (B)6 (C)8 (D) 2 価8 •如图,M^ABC中,zC 90°,假设AB二15cm #那么正方形"比和正方形BCFG的面积和为().(A)l 50cm2(B )200cm2(C)225cm2(D)无法计算三、解答题9.在RtZUBC 中,ZC=90° , ZA> ZB. ZC 的对边别离为a、b. c.(1)假设a : b=3 : 4, c=75cm,求a、b;(2)假设a : c = 15 : 17, b=2A,求AABC 的面积;(3)假设c—a=4, b = 16f求a、c;(4)假设ZA=30。
勾股定理练习题含答案

一、选择题1.如图,点A 的坐标是(2)2,,若点P 在x 轴上,且APO △是等腰三角形,则点P 的坐标不可能是( )A .(2,0)B .(4,0)C .(-22,0)D .(3,0)2.如图,OP =1,过点P 作PP 1⊥OP ,且PP 1=1,得OP 1=2;再过点P 1作P 1P 2⊥OP 1且P 1P 2=1,得OP 2=3;又过点P 2作P 2P 3⊥OP 2且P 2P 3=1,得OP 3=2……依此法继续作下去,得OP 2018的值为( )A .2016B .2017C .2018D .2019 3.如图,在四边形ABCD 中,∠ABC =∠ACB =∠ADC =45︒,若AD =4,CD =2,则BD 的长为( )A .6B .27C .5D .254.如图,在ABC 中,13AB =,10BC =,BC 边上的中线12AD =,请试着判定ABC 的形状是( )A .直角三角形B .等边三角形C .等腰三角形D .以上都不对 5.以下列各组数为边长,不能构成直角三角形的是( )A .3,4,5B .1,12C.8,12,13 D.2、3、56.《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)()A.3 B.5 C.4.2 D.47.将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则 h 的取值范围是()A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm 8.已知三组数据:①2,3,4;②3,4,5;③1,25三角形的三边长,能构成直角三角形的是()A.②B.①②C.①③D.②③9.已知一个直角三角形的两边长分别为3和5,则第三边长是()A.5 B.4 C34D.43410.由下列条件不能判定△ABC为直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:3:2C.a=2,b=3,c=4 D.(b+c)(b-c)=a²二、填空题11.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.12.如图,RT ABC ,90ACB ∠=︒,6AC =,8BC =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B '处,两条折痕与斜边AB 分别交于点E 、F ,则B FC '△的面积为______.13.如图,这是由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为 1S ,2S ,3S ,若123144S S S ++=,则2S 的值是__________.14.如图,等腰梯形ABCD 中,//AD BC ,1AB DC ==,BD 平分ABC ∠,BD CD ⊥,则AD BC +等于_________.15.如图,△ABC 是一个边长为1的等边三角形,BB 1是△ABC 的高,B 1B 2是△ABB 1的高,B 2B 3是△AB 1B 2的高,……B n-1B n 是△AB n-2B n-1的高,则B 4B 5的长是________,猜想B n-1B n 的长是________.16.若ABC ∆为直角三角形,90B ∠=︒,6AB =,8BC =,点D 在斜边AC 上,且2AC BD =,则AD 的长为__________.17.如图,在△ABC 中,AB =AC ,∠BAC =120°,AC 的垂直平分线交 BC 于 F ,交 AC 于 E ,交 BA 的延长线于 G ,若 EG =3,则 BF 的长是______.18.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,AD=4,AB=3,则CD=_________19.如图,30AOB ∠=︒,点,M N 分别在,OA OB 上,且6,8OM ON ==,点,P Q 分别在,OB OA 上运动,则PM PQ QN ++的最小值为______.20.已知,在△ABC 中,BC=3,∠A=22.5°,将△ABC 翻折使得点B 与点A 重合,折痕与边AC 交于点P ,如果AP=4,那么AC 的长为_______三、解答题21.定义:有一组邻边均和一条对角线相等的四边形叫做邻和四边形.(1)如图1,四边形ABCD 中,∠ABC =70°,∠BAC =40°,∠ACD =∠ADC =80°,求证:四边形ABCD 是邻和四边形.(2)如图2,是由50个小正三角形组成的网格,每个小正三角形的顶点称为格点,已知A 、B 、C 三点的位置如图,请在网格图中标出所有的格点.......D .,使得以A 、B 、C 、D 为顶点的四边形为邻和四边形.(3)如图3,△ABC 中,∠ABC =90°,AB =2,BC =3D ,使四边形ABCD 是邻和四边形,求邻和四边形ABCD 的面积.22.定义:如图1,平面上两条直线AB 、CD 相交于点O ,对于平面内任意一点M ,点M 到直线AB 、CD 的距离分别为p 、q ,则称有序实数对(p ,q )是点M 的“距离坐标”,根据上述定义,“距离坐标”为(0,0)的点有1个,即点O .(1)“距离坐标”为(1,0)的点有 个;(2)如图2,若点M 在过点O 且与直线AB 垂直的直线l 上时,点M 的“距离坐标”为(p ,q ),且∠BOD = 150︒,请写出p 、q 的关系式并证明;(3)如图3,点M 的“距离坐标”为(1,3),且∠DOB = 30︒,求OM 的长.23.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB =∠ECD =90°,点D 在边AB 上,点E 在边AC 的左侧,连接AE .(1)求证:AE =BD ;(2)试探究线段AD 、BD 与CD 之间的数量关系;(3)过点C 作CF ⊥DE 交AB 于点F ,若BD :AF =1:2,CD 36,求线段AB 的长.24.已知ABC ∆中,AB AC =.(1)如图1,在ADE ∆中,AD AE =,连接BD 、CE ,若DAE BAC ∠=∠,求证:BD CE =(2)如图2,在ADE ∆中,AD AE =,连接BE 、CE ,若60DAE BAC ∠=∠=,CE AD ⊥于点F ,4AE =,5EC =,求BE 的长;(3)如图3,在BCD ∆中,45CBD CDB ∠=∠=,连接AD ,若45CAB ∠=,求AD AB的值.25.如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为k . (1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?(2)已知ABC 为优三角形,AB c =,AC b =,BC a =,①如图1,若90ACB ∠=︒,b a ≥,6b =,求a 的值.②如图2,若c b a ≥≥,求优比k 的取值范围.(3)已知ABC 是优三角形,且120ABC ∠=︒,4BC =,求ABC 的面积.26.在ABC ∆中,AB AC =,CD 是AB 边上的高,若10,45AB BC ==.(1)求CD 的长.(2)动点P 在边AB 上从点A 出发向点B 运动,速度为1个单位/秒;动点Q 在边AC 上从点A 出发向点C 运动,速度为v 个单位秒()v>1,设运动的时间为()0t t >,当点Q 到点C 时,两个点都停止运动.①若当2v =时,CP BQ =,求t 的值.②若在运动过程中存在某一时刻,使CP BQ =成立,求v 关于t 的函数表达式,并写出自变量t 的取值范围.27.定义:在△ABC 中,若BC =a ,AC =b ,AB =c ,若a ,b ,c 满足ac +a 2=b 2,则称这个三角形为“类勾股三角形”,请根据以上定义解决下列问题:(1)命题“直角三角形都是类勾股三角形”是 命题(填“真”或“假”);(2)如图1,若等腰三角形ABC 是“类勾股三角形”,其中AB =BC ,AC >AB ,请求∠A 的度数;(3)如图2,在△ABC 中,∠B =2∠A ,且∠C >∠A .①当∠A =32°时,你能把这个三角形分成两个等腰三角形吗?若能,请在图2中画出分割线,并标注被分割后的两个等腰三角形的顶角的度数;若不能,请说明理由; ②请证明△ABC 为“类勾股三角形”.28.如图1, △ABC 和△CDE 均为等腰三角形,AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a ,且点A 、D 、E 在同一直线上,连结BE.(1)求证: AD=BE.(2)如图2,若a=90°,CM ⊥AE 于E.若CM=7, BE=10, 试求AB 的长.(3)如图3,若a=120°, CM ⊥AE 于E, BN ⊥AE 于N, BN=a, CM=b,直接写出AE 的值(用a, b 的代数式表示).29.如图,在平面直角坐标系中,点O 是坐标原点,ABC ∆,ADE ∆,AFO ∆均为等边三角形,A 在y 轴正半轴上,点0()6,B -,点(6,0)C ,点D 在ABC ∆内部,点E 在ABC ∆的外部,32=AD 30DOE ∠=︒,OF 与AB 交于点G ,连接DF ,DG ,DO ,OE .(1)求点A 的坐标;(2)判断DF 与OE 的数量关系,并说明理由;(3)直接写出ADG ∆的周长.30.如图1,点E 是正方形ABCD 边CD 上任意一点,以DE 为边作正方形DEFG ,连接BF ,点M 是线段BF 中点,射线EM 与BC 交于点H ,连接CM .(1)请直接写出CM 和EM 的数量关系和位置关系.(2)把图1中的正方形DEFG 绕点D 顺时针旋转45︒,此时点F 恰好落在线段CD 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.(3)把图1中的正方形DEFG 绕点D 顺时针旋转90︒,此时点E 、G 恰好分别落在线段AD 、CD 上,连接CE ,如图3,其他条件不变,若2DG =,6AB =,直接写出CM 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【详解】解:(1)当点P 在x 轴正半轴上,①以OA 为腰时,∵A的坐标是(2,2),∴∠AOP=45°,OA=22,∴P的坐标是(4,0)或(22,0);②以OA为底边时,∵点A的坐标是(2,2),∴当点P的坐标为:(2,0)时,OP=AP;(2)当点P在x轴负半轴上,③以OA为腰时,∵A的坐标是(2,2),∴OA= 22∴OA=AP=2∴P的坐标是(-220).故选D.2.D解析:D【解析】【分析】由勾股定理求出各边,再观察结果的规律.【详解】∵OP=1,OP12OP23OP34=2,∴OP45…,OP20182019故选D【点睛】本题考查了勾股定理,读懂题目信息,理解定理并观察出被开方数比相应的序数大1是解题的关键.3.A解析:A【解析】【分析】作AD′⊥AD ,AD′=AD ,连接C D′,DD′,根据等式的性质,可得∠BAD 与∠CAD′的关系,根据SAS ,可得△BAD 与△CAD′的关系,根据全等三角形的性质,可得BD 与CD′的关系,根据勾股定理,可得答案.【详解】作AD′⊥AD ,AD′=AD ,连接CD′,DD′,则有∠AD′D=∠D′AD=45︒,∵∠BAC+∠CAD=∠DAD′+∠CAD ,即∠BAD=∠CAD′,在△BAD 与△CAD′中,''BC CA BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAD′(SAS ),∴BD=CD′,∠DAD′=90°,由勾股定理得DD′=22'AD AD +=42,∠D′DA+∠ADC=90°,由勾股定理得CD′=22DC DD +'=()22422+=6,故选 A.【点睛】本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,勾股定理,添加辅助线作出全等图形是解题关键.4.C解析:C【分析】利用勾股定理的逆定理可以推导出ABD △是直角三角形.再利用勾股定理求出A C ,可得出AB=AC ,即可判断.【详解】解:由已知可得CD=BD=5,22251213+=即222BD AD AB +=,ABD ∴是直角三角形,90ADB ∠=︒,90ADC ∴∠=︒222AD CD AC ∴+= 2251213AC ∴=+=13AB AC ∴==故ABC 是等腰三角形.故选C【点睛】本题考查了勾股定理和它的逆定理,熟练掌握定理是解题关键.5.C解析:C【分析】根据勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可作出判断.【详解】A. 32+42=52,能构成直角三角形,故不符合题意;B. 12+12=(2)2,能构成直角三角形,故不符合题意;C. 82+122≠132,不能构成直角三角形,故符合题意;D.(2)2+(3)2=(5)2,能构成直角三角形,故不符合题意,故选C.【点睛】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.6.C解析:C【分析】根据题意可设折断处离地面的高度OA 是x 尺,折断处离竹梢AB 是(10-x )尺,结合勾股定理即可得出折断处离地面的高度.【详解】设折断处离地面的高度OA 是x 尺,则折断处离竹梢AB 是(10-x )尺,由勾股定理可得:222=OA OB AB +即:()2224=10x x +-,解得:x =4.2故折断处离地面的高度OA 是4.2尺.故答案选:C .本题主要考查直角三角形勾股定理的应用,解题的关键是熟练运用勾股定理.7.C解析:C【分析】筷子浸没在水中的最短距离为水杯高度,最长距离如下图,是筷子斜卧于杯中时,利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时,筷子浸没水中距离最短,为杯高=8cmAD 是筷子,AB 长是杯子直径,BC 是杯子高,当筷子如下图斜卧于杯中时,浸没在水中的距离最长由题意得:AB=15cm ,BC=8cm ,△ABC 是直角三角形∴在Rt △ABC 中,根据勾股定理,AC=17cm∴8cm≤h≤17cm故选:C【点睛】本题考查勾股定理在实际生活中的应用,解题关键是将题干中生活实例抽象成数学模型,然后再利用相关知识求解.8.D解析:D【分析】根据三角形勾股定理的逆定理符合222a b c +=即为直角三角形 ,所以将数据分别代入,符合即为能构成直角三角形.【详解】由题意得:①2222+3=134≠ ;②2223+4=25=5 ;③2221+2=5=5 , 所以能构成直角三角形的是②③.故选D .【点睛】考查直角三角形的构成,学生熟悉掌握勾股定理的逆定理是本题解题的关键,利用勾股定理的逆定理判断是否能够成直角三角形.解析:D【详解】解:∵一个直角三角形的两边长分别为3和5,∴①当5是此直角三角形的斜边时,设另一直角边为x,则由勾股定理得到:x;②当5是此直角三角形的直角边时,设另一直角边为x,则由勾股定理得到:x故选:D10.C解析:C【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可.【详解】A、∠A+∠B=∠C,可得∠C=90°,是直角三角形,错误;B、∠A:∠B:∠C=1:3:2,可得∠B=90°,是直角三角形,错误;C、∵22+32≠42,故不能判定是直角三角形,正确;D、∵(b+c)(b﹣c)=a2,∴b2﹣c2=a2,即a2+c2=b2,故是直角三角形,错误;故选C.【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.二、填空题11.103.【解析】试题解析:将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10,故3x+12y=10,x+4y=103,所以S2=x+4y=103.考点:勾股定理的证明.12.96 25【分析】将△B´CF的面积转化为求△BCF的面积,由折叠的性质可得CD=AC=6,∠ACE=∠DCE,∠BCF=∠B´CF,CE⊥AB,可证得△ECF是等腰直角三角形,EF=CE,∠EFC=45°,由等面积法可求CE的长,由勾股定理可求AE的长,进而求得BF的长,即可求解.【详解】根据折叠的性质可知,CD=AC=6,∠ACE=∠DCE,∠BCF=∠B´CF,CE⊥AB,∴∠DCE+∠B´CF=∠ACE+∠BCF,∵∠ACB=90°,∴∠ECF=45°,且CE⊥AB,∴△ECF是等腰直角三角形,∴EF=CE,∠EFC=45°,∵S△ABC=12AC•BC=12AB•CE,∴AC•BC=AB•CE,∵根据勾股定理求得AB=10,∴CE=245,∴EF=245,∵AE 185,∴BF=AB−AE−EF=10-185-245=85,∴S△CBF=12×BF×CE=12×85×245=9625,∴S△CB´F=96 25,故填:96 25.【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等知识,根据折叠的性质求得相等的角是解决本题的关键.13.48【分析】用a和b表示直角三角形的两个直角边,然后根据勾股定理列出正方形面积的式子,求出2S的面积.【详解】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a ,较短的长度为b ,即图中的AE a =,AH b =,则()221S AB a b ==+,2222S HE a b ==+,()223S TM a b ==-, ∵123144S S S ++=,∴()()2222144a b a b a b ++++-= 22222222144a b ab a b a b ab ++++++-=2233144a b +=2248a b +=,∴248S =.故答案是:48.【点睛】本题考查勾股定理,解题的关键是要熟悉赵爽弦图中勾股定理的应用.14.3【分析】由//AD BC ,BD 平分ABC ∠,易证得ABD ∆是等腰三角形,即可求得1AD AB ==,又由四边形ABCD 是等腰梯形,易证得2C DBC ∠=∠,然后由BD CD ⊥,根据直角三角形的两锐角互余,即可求得30DBC ∠=︒,则可求得BC 的值,继而求得AD BC +的值.【详解】解:∵//AD BC ,AB DC =,∴C ABC ∠=∠,ADB DBC ∠=∠,∵BD 平分ABC ∠,∴2ABC DBC ∠=∠,ABD DBC ∠=∠,∴ABD ADB ∠=∠,∴1AD AB ==,∴2C DBC ∠=∠,∵BD CD ⊥,∴90BDC ∠=︒,∵三角形内角和为180°,∴90DBC C ∠+∠=︒,∴260C DBC ∠=∠=︒,∴2212BC CD ==⨯=,∴123AD BC +=+=.故答案为:3.【点睛】本题主要考查对勾股定理,含30度角的直角三角形,等腰三角形的性质和判定,平行线的性质,等腰梯形的性质等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键.15 【分析】 根据等边三角形性质得出AB 1=CB 1=12,∠AB 1B =∠BB 1C =90°,由勾股定理求出BB 1=ABC 113ABB BCB S S ==B 1B 2,由勾股定理求出BB 2,根据11221ABB BB B AB B S S S =+代入求出B 2B 3=,B 3B 4=B 4B 5=,推出B n ﹣1B n =2n . 【详解】解:∵△ABC 是等边三角形,∴BA =AC ,∵BB 1是△ABC 的高,∴AB 1=CB 1=12,∠AB 1B =∠BB 1C =90°,由勾股定理得:BB 1=;∴△ABC 的面积是12×1=;∴1112ABB BCB SS ==⨯,12=×1×B 1B 2,B 1B 2,由勾股定理得:BB 234=, ∵11221ABB BB B AB B S S S =+,2313112422B B =⨯⨯⨯,B 2B 3,B 3B 4=16,B 4B 5=332, …, B n ﹣1B n =32n .故答案为:332,32n . 【点睛】 本题考查了等边三角形的性质,勾股定理,三角形的面积等知识点的应用,关键是能根据计算结果得出规律.16.5【分析】 在直角ABC 中,依据勾股定理求出AC 的长度,再算出BD ,过点B 作BE AC ⊥于点E ,通过等面积法求出BE ,得到两个直角三角形,分别运用勾股定理算出AE ED 、,两者相加即为AD 的长.【详解】解:如图,过点B 作BE AC ⊥于点E ,则90BEA ∠=︒,90BED ∠=︒,∵直角ABC 中,90B ∠=︒,6AB =,8BC =,∴22=10AC AB BC +=,又∵2ABC S AB BC AC BE =⋅=⋅,2AC BD =∴6810BE ⨯=,5BD =,∴=4.8BE ,∵90BEA ∠=︒,90BED ∠=︒∴22= 3.6AE AB BE -=,22= 1.4ED BD BE -=,∴5AD AE ED =+=.故答案为:5.【点睛】本题考查了勾股定理,通过作直角三角形斜边上的高,既构造了两个直角三角形求位置线段,又通过等面积法求出了一条直角边的长度,为运用勾股定理求线段创造了条件;故在求线段长时,可以考虑构造直角三角形.17.4【分析】根据线段垂直平分线得出AE=EC,∠AEG=∠AEF=90°,求出∠B=∠C=∠G=30°,根据勾股定理和含30°角的直角三角形性质求出AE和EF,即可求出FG,再求出BF=FG即可【详解】∵AC的垂直平分线FG,∴AE=EC,∠AEG=∠AEF=90°,∵∠BAC=120°,∴∠G=∠BAC-∠AEG=120°-90°=30°,∵∠BAC=120°,AB=AC,∴∠B=∠C=12(180°-∠BAC)=30°,∴∠B=∠G,∴BF=FG,∵在Rt△AEG中,∠G=30°,EG=3,∴AG=2AE,即(2AE)2=AE2+32,∴AE=3(负值舍去)即CE=3,同理在Rt△CEF中,∠C=30°,CF=2EF,(2EF)2=EF2+(3)2,∴EF=1(负值舍去),∴BF=GF=EF+CE=1+3=4,故答案为4.【点睛】本题考查了勾股定理,含30°角的直角三角形性质,等腰三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.18.【解析】【分析】延长BC,AD交于E点,在直角三角形ABE和直角三角形CDE中,根据30°角所对的直角边等于斜边的一半和勾股定理即可解答.【详解】如图,延长AD、BC相交于E,∵∠A=60°,∠B=∠ADC=90°,∴∠E=30°∴AE=2AB,CE=2CD∵AB=3,AD=4,∴AE=6, DE=2设CD=x,则CE=2x,DE=x即x=2x=即CD=故答案为:【点睛】本题考查了勾股定理的运用,含30°角所对的直角边是斜边的一半的性质,本题中构建直角△ABE和直角△CDE,是解题的关键.19.10【分析】首先作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN 的最小值,易得△ONN′为等边三角形,△OMM′为等边三角形,∠N′OM′=90°,继而可以求得答案.【详解】作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,OM′=OM=6,ON′=ON=8,∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°.在Rt△M′ON′中,M′N′=22+=10.OM ON''故答案为10.【点睛】本题考查了最短路径问题,根据轴对称的定义,找到相等的线段,得到直角三角形是解题的关键.20.522,32++【分析】过B作BF⊥CA于F,构造直角三角形,分两种情况讨论,利用勾股定理以及等腰直角三角形的性质,即可得到AC的长.【详解】分两种情况:①当∠C为锐角时,如图所示,过B作BF⊥AC于F,由折叠可得,折痕PE垂直平分AB,∴AP=BP=4,∴∠BPC=2∠A=45°,∴△BFP是等腰直角三角形,∴BF=DF=22,又∵BC=3,∴Rt△BFC中,CF=221-=,BC BF∴AC=AP+PF+CF=5+22;②当∠ACB为钝角时,如图所示,过B作BF⊥AC于F,同理可得,△BFP是等腰直角三角形,∴BF=FP=22又∵BC=3,∴Rt△BCF中,221-=,BC BF∴AC=AF-CF=3+22故答案为:5+223+22【点睛】本题主要考查了折叠问题以及勾股定理的运用,解决问题的关键是分两种情况画出图形进行求解.解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三、解答题21.(1)见解析;(2)见解析;(3)363【分析】(1)先由三角形的内角和为180°求得∠ACB的度数,从而根据等腰三角形的判定证得AB=AC=AD ,按照邻和四边形的定义即可得出结论.(2)以点A 为圆心,AB 长为半径画圆,与网格的交点,以及△ABC 外侧与点B 和点C 组成等边三角形的网格点即为所求.(3)先根据勾股定理求得AC 的长,再分类计算即可:①当DA=DC=AC 时;②当CD=CB=BD 时;③当DA=DC=DB 或AB=AD=BD 时.【详解】(1)∵∠ACB =180°﹣∠ABC ﹣∠BAC =70°,∴∠ACB =∠ABC ,∴AB =AC .∵∠ACD =∠ADC ,∴AC =AD ,∴AB =AC =AD .∴四边形ABCD 是邻和四边形;(2)如图,格点D 、D'、D''即为所求作的点;(3)∵在△ABC 中,∠ABC =90°,AB =2,BC =23,∴AC =()22222234AB BC +=+=,显然AB ,BC ,AC 互不相等.分两种情况讨论:①当DA =DC =AC=4时,如图所示:∴△ADC 为等边三角形,过D 作DG ⊥AC 于G ,则∠ADG =160302⨯︒=︒, ∴122AG AD ==,22224223DG AD AG =-=-=,∴S △ADC =1423432⨯⨯=,S △ABC =12AB×BC =23, ∴S 四边形ABCD =S △ADC +S △ABC =63;②当CD =CB =BD =23时,如图所示:∴△BDC 为等边三角形,过D 作DE ⊥BC 于E ,则∠BDE =160302⨯︒=︒, ∴132BE BD == ()()22222333DE BD BE =-=-=, ∴S △BDC =1233332⨯= 过D 作DF ⊥AB 交AB 延长线于F , ∵∠FBD=∠FBC -∠DBC =90︒-60︒=30︒,∴DF=123 S △ADB =12332⨯=, ∴S 四边形ABCD =S △BDC +S △ADB =3;③当DA =DC =DB 或AB =AD =BD 时,邻和四边形ABCD 不存在.∴邻和四边形ABCD 的面积是3或3【点睛】本题属于四边形的新定义综合题,考查了等腰三角形的判定和性质、勾股定理、三角形的面积计算等知识点,数形结合并读懂定义是解题的关键.22.(1)2;(2)32q p =;(3)27OM =【分析】(1)根据“距离坐标”的定义结合图形判断即可;(2)过M 作MN ⊥CD 于N ,根据已知得出MN q =,OM p =,求出∠MON =60°,根据含30度直角三角形的性质和勾股定理求出2232MN MO NO p =-=即可解决问题; (3)分别作点M 关于AB 、CD 的对称点F 、E ,连接EF 、OE 、OF ,连接MF 、ME 分别交AB 、CD 于P 点、Q 点,首先证明OM OE OF EF ===,求出2MF =,23ME =,然后过F 作FG QM ⊥,交QM 延长线于G ,根据含30度直角三角形的性质求出1FG =,3MG =,再利用勾股定理求出EF 即可.【详解】解:(1)由题意可知,在直线CD 上,且在点O 的两侧各有一个,共2个,故答案为:2;(2)过M 作MN CD ⊥于N ,∵直线l AB ⊥于O ,150BOD ∠=︒,∴60MON ∠=︒,∵MN q =,OM p =,∴1122NO MO p ==, ∴223MN MO NO p =-=, ∴32q p =; (3)分别作点M 关于AB 、CD 的对称点F 、E ,连接EF 、OE 、OF ,连接MF 、ME 分别交AB 、CD 于P 点、Q 点.∴OFP OMP △≌△,OEQ OMQ △≌△,∴FOP MOP ∠=∠,EOQ MOQ ∠=∠,OM OE OF ==,∴260EOF BOD ∠=∠=︒,∴△OEF 是等边三角形,∴OM OE OF EF ===,∵1MP =,3MQ =∴2MF =,23ME =, ∵30BOD ∠=︒,∴150PMQ ∠=︒,过F 作FG QM ⊥,交QM 延长线于G ,∴30FMG ∠=︒, 在Rt FMG △中,112FG MF ==,则3MG =,在Rt EGF 中,1FG =,33EG ME MG =+=,∴22(33)127EF =+=,∴27OM =.【点睛】本题考查了轴对称的应用,含30度直角三角形的性质,勾股定理以及等边三角形的判定和性质等,正确理解题目中的新定义是解答本题的关键.23.(1)见解析;(2)BD 2+AD 2=2CD 2;(3)AB =2+4.【分析】(1)根据等腰直角三角形的性质证明△ACE ≌△BCD 即可得到结论;(2)利用全等三角形的性质及勾股定理即可证得结论;(3)连接EF ,设BD =x ,利用(1)、(2)求出EF=3x ,再利用勾股定理求出x ,即可得到答案.【详解】(1)证明:∵△ACB 和△ECD 都是等腰直角三角形∴AC =BC ,EC =DC ,∠ACB =∠ECD =90°∴∠ACB ﹣∠ACD =∠ECD ﹣∠ACD∴∠ACE =∠BCD ,∴△ACE ≌△BCD (SAS ),∴AE =BD .(2)解:由(1)得△ACE ≌△BCD ,∴∠CAE =∠CBD ,又∵△ABC 是等腰直角三角形,∴∠CAB =∠CBA =∠CAE =45°,∴∠EAD =90°,在Rt △ADE 中,AE 2+AD 2=ED 2,且AE =BD ,∴BD 2+AD 2=ED 2,∵ED =2CD ,∴BD 2+AD 2=2CD 2,(3)解:连接EF ,设BD =x ,∵BD :AF =1:2AF =2x ,∵△ECD 都是等腰直角三角形,CF ⊥DE ,∴DF =EF ,由 (1)、(2)可得,在Rt △FAE 中,EF 22AF AE +22(22)x x +3x , ∵AE 2+AD 2=2CD 2,∴222(223)2(36)x x x ++=,解得x =1,∴AB =2+4.【点睛】此题考查三角形全等的判定及性质,等腰直角三角形的性质,勾股定理.24.(1)详见解析;(241;(33【分析】 (1)证∠EAC=∠DAB.利用SAS 证△ACE ≌△ABD 可得;(2)连接BD ,证1302FEA AED ∠=∠=,证△ACE ≌△ABD 可得30FEA BDA ∠=∠=,CE=BD=5,利用勾股定理求解;(3)作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=,利用勾股定理得AE 2AB =,3AB ,根据(1)思路得3AB .【详解】(1) 证明:∵∠DAE=∠BAC ,∴∠DAE+∠CAD=∠BAC+∠CAD ,即∠EAC=∠DAB.在△ACE 与△ABD 中,AD AE EAC BAB AC AB =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△ABD(SAS),∴BD CE =;(2)连接BD因为AD AE =, 60DAE BAC ∠=∠=,所以ADE ∆是等边三角形因为60DAE DEA EDA ∠=∠=∠=,ED=AD=AE=4因为CE AD ⊥ 所以1302FEA AED ∠=∠= 同(1)可知△ACE ≌△ABD(SAS),所以30FEA BDA ∠=∠=,CE=BD=5所以90BDE BDA ADE ∠=∠+∠=所以BE=22225441BD DE +=+=(3)作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=所以222AB AC AC +因为AB AC =所以AE 2=又因为45CAB ∠=所以90ABE ∠= 所以()222223BE AE AB AB AB AB =+=+= 因为45CBD CDB ∠=∠=所以BC=CD, 90BCD ∠=因为同(1)可得△ACD ≌△ECB(SAS)所以3AB所以33AD AB AB ==【点睛】考核知识点:等边三角形;勾股定理.构造全等三角形和直角三角形是关键.25.(1)该命题是真命题,理由见解析;(2)①a 的值为92;②k 的取值范围为13k ≤<;(3)ABC ∆203123. 【分析】 (1)根据等边三角形的性质、优三角形和优比的定义即可判断;(2)①先利用勾股定理求出c 的值,再根据优三角形的定义列出,,a b c 的等式,然后求解即可;②类似①分三种情况分析,再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系,然后根据优比的定义求解即可;(3)如图(见解析),设BD x =,先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式,再类似(2),根据优三角形的定义分三种情况分别列出等式,然后解出x 的值,即可得出ABC ∆的面积.【详解】(1)该命题是真命题,理由如下:设等边三角形的三边边长为a则其中两条边的和为2a ,恰好是第三边a 的2倍,满足优三角形的定义,即等边三角形为优三角形又因该两条边相等,则这两条边的比为1,即其优比为1故该命题是真命题;(2)①90,6CB b A ∠=︒=22236c a b a ∴=++根据优三角形的定义,分以下三种情况:当2a b c +=时,26236a a +=+,整理得24360a a -+=,此方程没有实数根 当2a c b +=时,23612a a +=,解得92a = 当2bc a +=时,26362a a +=,解得86a =>,不符题意,舍去综上,a 的值为92; ②由题意得:,,a b c 均为正数 根据优三角形的定义,分以下三种情况:(c b a ≥≥)当2a b c +=时,则1b k a=≥ 由三角形的三边关系定理得b a c a b -<<+ 则2a b b a a b +-<<+,解得3b a <,即3b k a=< 故此时k 的取值范围为13k ≤< 当2a c b +=时,则1c k a =≥ 由三角形的三边关系定理得c a b a c -<<+ 则2a c c a a c +-<<+,解得3c a <,即3c k a=< 故此时k 的取值范围为13k ≤< 当2b c a +=时,则1c k b =≥ 由三角形的三边关系定理得c b a b c -<<+ 则2b c c b b c +-<<+,解得3c b <,即3c k b=< 故此时k 的取值范围为13k ≤<综上,k 的取值范围为13k ≤<;(3)如图,过点A 作AD BC ⊥,则180********ABC ABD ∠=︒-︒∠-==︒︒ 设BD x =22,AB BD x AD ∴====AC ===11422ABC S BC AD ∆=⋅=⨯= ABC ∆是优三角形,分以下三种情况:当2AC BC AB +=时,即44x =,解得103x =则103ABC S ∆===当2AC AB BC +=时,即28x =,解得65x =则655ABC S ∆===当2BC AB AC +=时,即242424x x x +=++,整理得234120x x ++=,此方程没有实数根综上,ABC ∆的面积为2033或1235.【点睛】本题考查了等边三角形的性质、直角三角形的性质、勾股定理、三角形的三边关系定理等知识点,理解题中的新定义,正确分多种情况讨论是解题关键.26.(1)CD=8;(2)t=4;(3)12-=t v t (26t ≤<) 【分析】(1)作AE ⊥BC 于E ,根据等腰三角形三线合一的性质可得BE=12BC ,然后利用勾股定理求出AE ,再用等面积法可求出CD 的长;(2)①过B 作BF ⊥AC 于F ,易得BF=CD ,分别讨论Q 点在AF 和FC 之间时,根据△BQF ≌△CPD ,得到PD=QF ,建立方程即可求出t 的值;(3)同(2)建立等式关系即可得出关系式,再根据Q 在FC 之间求出t 的取值范围即可.【详解】解:(1)如图,作AE ⊥BC 于E ,∵AB=AC ,∴BE=12BC=25在Rt △ABE 中,()2222AE=AB BE =1025=45--∵△ABC 的面积=11BC AE=AB CD 22⋅⋅∴BC AE4545 CD===8AB10⋅⨯(2)过B作BQ⊥AC,当Q在AF之间时,如图所示,∵△ABC的面积=11AC BF=AB CD22⋅⋅,AB=AC∴BF=CD在Rt△CPD和Rt△BQF中∵CP=BQ,CD=BF,∴Rt△CPD≌Rt△BQF(HL)∴PD=QF在Rt△ACD中,CD=8,AC=AB=10∴22AD=AC CD=6-同理可得AF=6∴PD=AD=AP=6-t,QF=AF-AQ=6-2t由PD=QF得6-t=6-2t,解得t=0,∵t>0,∴此种情况不符合题意,舍去;当Q点在FC之间时,如图所示,此时PD=6-t,QF=2t-6由PD=QF得6-t=2t-6,解得t=4,综上得t的值为4.(3)同(2)可知v>1时,Q在AF之间不存在CP=BQ,Q在FC之间存在CP=BQ,Q在F点时,显然CP ≠BQ ,∵运动时间为t ,则AP=t ,AQ=vt ,∴PD=6-t ,QF=vt-6,由PD=QF 得6-t=vt-6, 整理得12-=t v t, ∵Q 在FC 之间,即AF <AQ ≤AC∴610<≤vt ,代入12-=t v t得 61210<-≤t ,解得26t ≤<所以答案为12-=t v t (26t ≤<) 【点睛】本题考查三角形中的动点问题,熟练掌握勾股定理求出等腰三角形的高,利用全等三角形对应边相等建立方程是解题的关键.27.(1)假;(2)∠A =45°;(3)①不能,理由见解析,②见解析【分析】(1)先由直角三角形是类勾股三角形得出ab+a 2=c 2,再由勾股定理得a 2+b 2=c 2,即可判断出此直角三角形是等腰直角三角形;(2)由类勾股三角形的定义判断出此三角形是等腰直角三角形,即可得出结论; (3)①分三种情况,利用等腰三角形的性质即可得出结论;②先求出CD=CB=a ,AD=CD=a ,DB=AB-AD=c-a ,DG=BG=12(c-a ),AG=12(a+c ),两个直角三角形中利用勾股定理建立方程即可得出结论.【详解】解:(1)如图1,假设Rt △ABC 是类勾股三角形,∴ab +a 2=c 2,在Rt △ABC 中,∠C =90°,根据勾股定理得,a 2+b 2=c 2,∴ab +b 2=a 2+b 2,∴ab =a 2,∴a =b ,∴△ABC 是等腰直角三角形,∴等腰直角三角形是类勾股三角形,即:原命题是假命题,故答案为:假;(2)∵AB=BC,AC>AB,∴a=c,b>c,∵△ABC是类勾股三角形,∴ac+a2=b2,∴c2+a2=b2,∴△ABC是等腰直角三角形,∴∠A=45°,(3)①在△ABC中,∠ABC=2∠BAC,∠BAC=32°,∴∠ABC=64°,根据三角形的内角和定理得,∠ACB=180°﹣∠BAC﹣∠ABC=84°,∵把这个三角形分成两个等腰三角形,∴(Ⅰ)、当∠BCD=∠BDC时,∵∠ABC=64°,∴∠BCD=∠BDC=58°,∴∠ACD=∠ACB﹣∠BCD=84°﹣58°=26°,∠ADC=∠ABC+∠BCD=122°∴△ACD不是等腰三角形,此种情况不成立;(Ⅱ)、当∠BCD=∠ABC=64°时,∴∠BDC=52°,∴∠ACD=20°,∠ADC=128°,∴△ACD是等腰三角形,此种情况不成立;(Ⅲ)、当∠BDC=∠ABC=64°时,∴∠BCD=52°,∴∠ACD=∠ACB﹣BCD=32°=∠BAC,∴△ACD是等腰三角形,即:分割线和顶角标注如图2所示,Ⅱ、分∠ABC,同(Ⅰ)的方法,判断此种情况不成立;Ⅲ、分∠BAC,同(Ⅱ)的方法,判断此种情况不成立;②如图3,在AB边上取点D,连接CD,使∠ACD=∠A。
勾股定理经典例题(含答案)

经典例题透析类型一:勾股定理的直接用法1、在Rt△ABC中,∠C=90° (1)已知a=6, c=10,求b, (2)已知a=40,b=9,求c; (3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b=(2) 在△ABC中,∠C=90°,a=40,b=9,c=(3) 在△ABC中,∠C=90°,c=25,b=15,a=举一反三【变式】:如图∠B=∠ACD=90°,AD=13,CD=12,BC=3,则AB的长是多少? 【答案】∵∠ACD=90°AD=13, CD=12∴AC=AD-CD=13-12=25 ∴AC=5又∵∠ABC=90°且BC=3∴由勾股定理可得 AB=AC-BC=5-3=16 ∴AB= 4∴AB的长是4.类型二:勾股定理的构造应用2、如图,已知:在中,,,. 求:BC的长.思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有,,再由勾股定理计算出AD、DC的长,进而求出BC的长.解析:作于D,则因,∴(的两个锐角互余)∴(在中,如果一个锐角等于,那么它所对的直角边等于斜边的一半).根据勾股定理,在中,.根据勾股定理,在中,.∴.举一反三【变式1】如图,已知:,,于P.求证:.解析:连结BM,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又∵(已知),∴.在中,根据勾股定理有,∴.【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。
解析:延长AD、BC交于E。
勾股定理练习题及答案(共6套)

勾股定理课时练(1)1.在直角三角形ABC 中,斜边AB=1,则AB 222AC BC ++的值是()A.2B.4C.6D.82.如图18-2-4所示,有一个形状为直角梯形的零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm ,∠D=120°,则该零件另一腰AB 的长是______cm (结果不取近似值).3.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.4.一根旗杆于离地面12m 处断裂,犹如装有铰链那样倒向地6.飞机在空中水平飞行上方4000米处,过了209.如图,在四边形CD=3,求AB 的长10.如图,一个牧童在小河的南的小屋B 的西8km 2m 的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗? 第一课时答案:1.A ,提示:根据勾股定理得122=+AC BC ,所以AB222AC BC ++=1+1=2;2.4,提示:由勾股定理可得斜边的长为5m ,而3+4-5=2m ,所以他们少走了4步.3.1360,提示:设斜边的高为x ,根据勾股定理求斜边为1316951222==+,再利用面积法得,136011米,由勾所以飞机飞行的速度为CE=60.2⨯,由勾股定理,得CF=)(3416302222cm EF CE =+=+8.解:在直角三角形ABC 中,根据勾股定理,得在直角三角形CBD 中,根据勾股定理,得CD 2=BC 2+BD 2=25+122=169,所以CD=13. 9.解:延长BC 、AD 交于点E.(如图所示)第5题图第8题∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8, 设AB=x ,则AE=2x ,由勾股定理。
勾股定理练习题精华(含答案)

勾股定理练习题一、填空题1、若直角三角形的两边长分别是3、4,则第三边的长为 ;2、若等腰三角形的一边长为6,则另两边的长分别是3、如图:AC ⊥BC 于C ,CD ⊥AB 于D (1)若BC=8,AC=15,则CD= (2)若AB=29,AC=21,则CD=4、如图∠C=30°,AD ⊥BC ,AB ⊥AC ,BE=EC (1)若AE=4,则AD=(2)若DE=3,则BC= ;AB=;AC=5、如图,正方形ABCD ,若OD=3,OC ⊥OD ,OC=OD ,则BD= ,正方形ABCD 的面积=6、直角三角形ABC 中,若周长为30,斜边上中线长为6.5,则该三角形的面积为7、若两条线段长分别是20,25,则当第三条线段的长为时,这三条线段首尾连结可以组成直角三角形。
8、若2224618a b c a c ++=++-,则△ABC 的形状是 二、写出下列命题的逆命题,并判断真假。
1、两条直线平行,同旁内角互补。
2、若x=-3,则2230x x +-=。
3、直角三角形中,30°锐角所对直角边等于斜边的一半。
4、若一个整数的末位数字是0,则这个数能被5整除。
三、解答题1、如图:RtABC中,CA=,AM=AC=12, BN=BC=5, 求MN的长。
2、RtABC中,C=,AD平分C,AC=10cm,AB=26cm,求BD长。
3、RtABC中,C=,AC=BC, BDAB,,AD=12,求BC长。
4、直角三角形中,两条直角边的差为cm,斜边长为。
5.如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=17,BD=9,AD=10,求AC的长B6.在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,且CD=1.5,BD=2.5,求AC的长A7.如图,在Rt△ABC中,∠C=90°,AD=AC且DE∥AC,BE=,求AC,AB的长C8.在△ABC 中,AB=15,AC=13,高AD=12,求△ABC 的周长9、已知:如图四边形ABCD 中对角线AC 、BD 互相平分,相交于O ,且AC ⊥BD 。
勾股定理练习卷(含答案)

勾股定理学习要点1、认识勾股定理。
2、勾股定理公式=a2+b2=c2基础练习例题:已知直角三角形高米,底边米,求斜边的长度是多少?解:勾股定理公式=a2+b2=c21、如图,这个正方形的对角线的长度是5cm.求圆的半径、直径、面积、周长(第1题图)勾股定理测试卷(完卷时间60分钟,满分120分)一、填空题(每小题3分,24分)1. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要_________米.2. 在直角三角形中,斜边 =2,则 =_____.3. 直角三角形的三边长为连续偶数,则其周长为 .4. 如图,在△ABC中,∠C=90°,BC=3,AC=4.以斜边AB为直径作半圆,则这个半圆的面积是________.(保留π)5. 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞_________米.6. 如图,△ABC中,∠C=90°,AB垂直平分线交BC于D若BC=8,AD=5,则AC等于___________.7. 如图,四边形是正方形,垂直于,且 =3, =4,阴影部分的面积是___19___.8. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A,B,C,D的面积之和为___________cm2.二、选择题(每小题3分,共30分)9. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( ).(A)30 (B)28 (C)56 (D)不能确定10. 直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( ) (A)4 cm (B)8 cm (C)10 cm (D)12 cm11. 已知一个Rt△的两边长分别为3和4,则第三边长的平方是()(A)25 (B)14 (C)7 (D)7或2512. 等腰三角形的腰长为10,底长为12,则其底边上的高为( )(A)13 (B)8 (C)25 (D)6413. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是()14. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )(A)钝角三角形(B)锐角三角形(C)直角三角形(D)等腰三角形. 15. 如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )(A) 25 (B)(C) 9 (D)16. 三角形的三边长为 ,则这个三角形是( )(A)等边三角形(B)钝角三角形(C)直角三角形(D)锐角三角形.17.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮元计算,那么共需要资金(). (A)50 元(B)600 元(C)1200 元(D)1500 元18.如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC 的长为().(A)12 (B)7 (C)5 (D)13三、解答题(每小题8分,共40分)19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远?20. 如图,已知一等腰三角形的周长是16,底边上的高是4.求这个三角形各边的长.21. 如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?22. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积。
勾股定理练习题(含答案)_初二数学_数学_初中教育_教育专区

勾股定理练习题一、基础达标:1. 下列说法正确的是( )A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2.2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )A .c b a =+ B. c b a >+ C. c b a <+ D.222c b a =+3. 如果Rt △的两直角边长分别为k 2-1,2k (k>1),那么它的斜边长是( )A 、2kB 、k+1C 、k 2-1D 、k 2+14.已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形5.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A .121B .120C .90D .不能确定6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( )A .42B .32C .42 或 32D .37 或 337.※直角三角形的面积为,斜边上的中线长为,则这个三角形周S d 长为( )(A (B2d +d -(C ) (D )2d +d +8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为()A :3 B :4 C :5 D :79.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )A .17 B.3 C.17或3 D.以上都不对10.已知a 、b 、c 是三角形的三边长,如果满足则三角形的形状是()2(6)100a -=A :底与边不相等的等腰三角形 B :等边三角形 C :钝角三角形 D :直角三角形11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 .12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为14.一个三角形三边之比是6:8:10,则按角分类它是 三角形.15.一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___. 16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.17.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 .18.如图,已知ABC ∆中,︒=∠90C ,15=BA ,12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .19.一长方形的一边长为cm 3,面积为212cm ,那么它的一条对角线长是 .二、综合发展:1.如图,一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条,求木条的长.2、有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗? 3.一个三角形三条边的长分别为cm 15,cm 20,cm 25,这个三角形最长边上的高是多少?AE B4.如图,要修建一个育苗棚,棚高h=3m ,棚宽a=4m ,棚的长为12m ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?5.如图,有一只小鸟在一棵高13m 的大树树梢上捉虫子,它的伙伴在离该树12m ,高8m 的一棵小树树梢上发出友好的叫声,它立刻以2m/s 的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m 处,过了2s 后,测得小汽车与车速检测仪间距离为50m ,这辆小汽车超速了吗?小汽车小汽车观测点答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.答案: D.2. 解析:本题考察三角形的三边关系和勾股定理.答案:B.3.解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然后再求它的周长.答案:C .4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角形的外部,有两种情况,分别求解.答案:C.5. 解析: 勾股定理得到:22215817=-,另一条直角边是15,所求直角三角形面积为21158602cm ⨯⨯=.答案: 260cm .6.解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.答案:222c b a =+,c ,直角,斜,直角.7. 解析:本题由边长之比是6:8:10可知满足勾股定理,即是直角三角形.答案:直角.8.解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、︒90,3.9. 解析:由勾股定理知道:22222291215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5.答案:cm 5.二、综合发展11. 解析:木条长的平方=门高长的平方+门宽长的平方.答案:5m .12解析:因为222252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为xcm ,由直角三角形面积关系,可得1115202522x ⨯⨯=⨯⋅,∴12=x .答案:12cm13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助勾股定理求出.答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是:5×20=100(m 2) .14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解.答案:6.5s .15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h .答案:这辆小汽车超速了.卡祖玛咖,卡祖玛咖官网 lxMQovlLvRTh。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理练习题
张颐甜
一、基础达标:
1. 下列说法正确的是( )
A.若 a 、b 、c 是△ABC 的三边,则a 2+b 2=c 2;
B.若 a 、b 、c 是Rt△ABC 的三边,则a 2+b 2=c 2;
C.若 a 、b 、c 是Rt△ABC 的三边, 90=∠A ,则a 2+b 2=c 2;
D.若 a 、b 、c 是Rt△ABC 的三边, 90=∠C ,则a 2+b 2=c 2. 2. Rt △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( )
A .c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+ 3. 如果Rt △的两直角边长分别为k 2-1,2k (k >1),那么它的斜边长是( )
A 、2k
B 、k+1
C 、k 2-1
D 、k 2+1
4. 已知a ,b ,c 为△ABC 三边,且满足(a 2-b 2)(a 2+b 2-c 2)=0,则它的形状为( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
5. 直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A .121
B .120
C .90
D .不能确定
6. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42 或 32 D .37 或 33
7.※直角三角形的面积为S ,斜边上的中线长为d ,则这个三角形周长为( )
(A 2d (B d -
(C )2d (D )d
8、在平面直角坐标系中,已知点P 的坐标是(3,4),则OP 的长为( )A :3
B :4
C :5
D :7
9.若△ABC 中,AB=25cm ,AC=26cm 高AD=24,则BC 的长为( )
A .17 B.3 C.17或3 D.以上都不对
10.已知a 、b 、c 是三角形的三边长,如果满足2(6)100a c --=则
三角形的形状是( )
A :底与边不相等的等腰三角形
B :等边三角形
C :钝角三角形
D :直角三角形
11.斜边的边长为cm 17,一条直角边长为cm 8的直角三角形的面积是 . 12. 等腰三角形的腰长为13,底边长为10,则顶角的平分线为__. 13. 一个直角三角形的三边长的平方和为200,则斜边长为 14.一个三角形三边之比是6:8:10,则按角分类它是 三角形.
15. 一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是___. 16. 在Rt △ABC 中,斜边AB=4,则AB 2+BC 2+AC 2=_____.
17.若三角形的三个内角的比是3:2:1,最短边长为cm 1,最长边长为cm 2,则这个三角形三个角度数分别是 ,另外一边的平方是 . 18.如图,已知ABC ∆中,︒=∠90C ,15=BA ,
12=AC ,以直角边BC 为直径作半圆,则这个半圆的面积是 .
19. 一长方形的一边长为cm 3,面积为2
12cm ,那
么它的一条对角线长是 .
20. 一个直角三角形的三边分别是6、8、x ,则x= 。
二、综合发展:
1、已知,如图,在Rt △ABC 中,∠C=90°,∠1=∠2,CD=1.5,BD=2.5,求AC 的
长.
3、已知,△ABC 中,AB=17cm ,BC=16cm ,BC 边上的中线AD=15cm ,试说明
△ABC 是等腰三角形。
A
C
B
C D
A
B
第1题图
2、
(1)求AD 的长。
(2)求AE 的长。
(3)求EC 的长。
(4)求点E 到AC 的距离。
4、如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过
的知识说明:AB2-AP2=PB×PC。
7、如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B。
现在要在铁路AB上建一个土特产品收购站E。
已知DA=15km,CB=10km。
(1)若使得C、D两村到E站的距离相等,则E站应建在离A站多少km处?并求一下此时DE的长。
(2)若使得E站到C、D两村距离最短,则E站应建在离A站多少km处?并求一下此时CE的长。
(3)若连接CD,假设点E是AB上一个动点,从点A出发,到点B停止运动。
设AE=x,S
△DEC =y。
请写出y关于x的函数解析式(0≤x≤25)并求出S
△DEC的
最大
值和最小值以及相应的DE的长。
A
B
P
C
第4题图
A
D
E B
C
7题图
5、
6、
1 3
答案:
一、基础达标
1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角.
答案: D.
2. 解析:本题考察三角形的三边关系和勾股定理.
答案:B.
3. 解析:设另一条直角边为x ,则斜边为(x+1)利用勾股定理可得方程,可以求出x .然
后再求它的周长. 答案:C .
4.解析:解决本题关键是要画出图形来,作图时应注意高AD 是在三角形的内部还是在三角
形的外部,有两种情况,分别求解. 答案:C.
5. 解析: 勾股定理得到:2
2215817=-,另一条直角边是15,
所求直角三角形面积为2
1
158602cm ⨯⨯=.答案: 2
60cm .
6. 解析:本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立.
答案:222c b a =+,c ,直角,斜,直角.
7. 解析:本题由边长之比是6:8:10 可知满足勾股定理,即是直角三角形.答案:直角. 8. 解析:由三角形的内角和定理知三个角的度数,断定是直角三角形.答案:︒30、︒60、
︒90,3. 9. 解析:由勾股定理知道:2
2
2
2
2
2
91215=-=-=AC AB BC ,所以以直角边9=BC 为直径的半圆面积为10.125π.答案:10.125π.
10. 解析:长方形面积长×宽,即12长×3,长4=,所以一条对角线长为5. 答案:cm 5. 二、综合发展
11. 解析:木条长的平方=门高长的平方+门宽长的平方.
答案:5m .
12解析:因为2
22252015=+,所以这三角形是直角三角形,设最长边(斜边)上的高为
xcm ,由直角三角形面积关系,可得1115202522
x ⨯⨯=⨯⋅,∴12=x .答案:12cm
13.解析:透阳光最大面积是塑料薄膜的面积,需要求出它的另一边的长是多少,可以借助
勾股定理求出.
答案:在直角三角形中,由勾股定理可得:直角三角形的斜边长为5m,
所以矩形塑料薄膜的面积是:5×20=100(m 2
) .
14.解析:本题的关键是构造直角三角形,利用勾股定理求斜边的值是13m ,也就是两树树梢之间的距离是13m ,两再利用时间关系式求解. 答案:6.5s . 15.解析:本题和14题相似,可以求出BC 的值,再利用速度等于路程除以时间后比较.BC=40米,时间是2s ,可得速度是20m/s=72km/h >70km/h . 答案:这辆小汽车超速了.。
