珠算乘方和开方
数学知识:关于珠算的口诀

数学知识:关于珠算的口诀【导语】珠算是以算盘为工具进行数字计算的一种方法,被誉为中国的第五大发明。
下面是无忧考网分享的数学知识:关于珠算的口诀。
欢迎阅读参考!【口诀】珠算四则运算皆用一套口诀指导拨珠完成。
加减法﹐明代称“上法”和“退法”﹐其口诀为珠算所特有﹐最早见于吴敬《九章算法比类大全》(1450)。
乘法所用的“九九”口诀﹐起源甚早﹐春秋战国时已在筹算中应用。
北宋科学家沈括在其《梦溪笔谈》卷十八中介绍“增成法”时说:“唯增成一法稍异﹐其术都不用乘除﹐但补亏就盈而已。
假如欲九除者增一便是﹐八除者增二便是﹐但一位一因之”。
“九除者增一”﹐后来变为“九一下加一”﹐“八除者增二”后来变为“八一下加二”等口诀。
可见“增成法”就是“归除法”的前身。
杨辉在《乘除通变算宝》中﹐叙述了“九归”﹐他在当时流传的四句“古括”上﹐添注了新的口诀三十二句﹐与现今口诀接近。
元代朱世杰的《算学启蒙》(1299﹐卷上)载有九归口诀三十六句﹐和现今通行的口诀大致相同。
14世纪中丁巨撰算法八卷(1355)﹐内有“撞归口诀”。
总之﹐归除口诀的全部完成在元代。
有了四则口诀﹐珠算的算法就形成了一个体系﹐长期沿用了下来。
中国珠算﹐从明代以来﹐极为盛行﹐先后传到日本﹑朝鲜﹑东南亚各国﹐后在美洲也渐流行。
由于算盘不但是一种极简便的计算工具﹐而且具有独特的教育职能﹐所以仍盛行不衰。
【加法口诀表】不进位的加进位的加直加满五加进十加破五进十加加一:一上一,一下五去四,一去九进一加二:二上二,二下五去三,二去八进一加三:三上三,三下五去二,三去七进一加四:四上四,四下五去一,四去六进一加五:五上五,五去五进一加六:六上六,六去四进一,六上一去五进一加七:七上七,七去三进一,七上二去五进一加八:八上八,八去二进一,八上三去五进一加九:九上九,九去一进一,九上四去五进一【减法口诀表】不退位的减退位的减直减破五减退位减退十补五的减减一:一下一,一上四去五,一退一还九减二:二下二,二上三去五,二退一还八减三:三下三,三上二去五,三退一还七减四:四下四,四上一去五,四退一还六减五:五下五,五退一还五减六:六下六,六退一还四,六退一还五去一减七:七下七,七退一还三,七退一还五去二减八:八下八,八退一还二,八退一还五去三减九:九下九,九退一还一,九退一还五去四【乘法九九口诀】在春秋战国时已在筹算中得到应用;归除口诀,首见杨辉《乘除通变算宝》(1274)。
关于珠心算口诀表及学习方法

关于珠心算口诀表及学习方法关于珠心算口诀表及学习方法珠心算是通过思维作数的计算而得出结果的活动。
是在大脑中以算珠表象作为载体,运用珠算法则所进行的计算。
下面小编为大家带来珠心算口诀表及学习方法,希望对您有所帮助!珠心算口诀表一、珠心2113算加法口诀表:一上一、二上二、三5261上三、四上四4102、五上五、六上六、七上七、八上八、九上1653九;二下五去三、三下五去二、四下五去一;一去九进一、二去八进一、三去七进一、四去六进一、五去五进一、六去四进一、七去三进一、八去二进一、九去一进一;二、珠心算减法口诀表:一下一、二下二、三下三、四下四、五下五、六下六、七下七、八下八、九下九;一上四去五、二上三去五、三上二去五、四上一去五;一退一还九、二退一还八、三退一还七、四退一还六、五退一还五、六退一还四、八退一还二、九退一还一。
三、珠心算除法九归口诀:逢一进一,逢二进二,逢三进三,逢四进四,逢五进五,逢六进六,逢七进七,逢八进八,逢九进九。
四、珠心算除法退商口诀:无除退一下还一,无除退一下还二,无除退一下还三,无除退一下还四,无除退一下还五,无除退一下还六,无除退一下还七,无除退一下还八,无除退一下还九。
五、珠心算除法商九口诀:见一无除作九一,见二无除作九二,见三无除作九三,见四无除作九四,见五无除作九五,见六无除作九六,见七无除作九七,见八无除作九八,见九无除作九九。
珠心算学习如何入门珠心算教学方2113法不同普通的教学方法,当然也不能5261用普通心理学规范珠4102心算教学。
同样也不能用普通的心理规1653律指导珠心算教学。
哲学有云,要用不同质的方法解决不同质的矛盾。
为了搞好珠心算教学,一个有效办法是学习探究珠心算入门的基本规律。
把视觉后象变成强化的视觉后象在相对会打算盘的基础上,利用视觉后象进行强化视觉后象的训练。
训练的办法是:先看清楚算盘,然后把眼睛闭上,“看”自己视觉后象的脑算盘形象。
“看”该形象的算盘框是什么颜色、珠是什么颜色、珠的样式、珠的数量与位置。
珠心算口诀表 全面详解
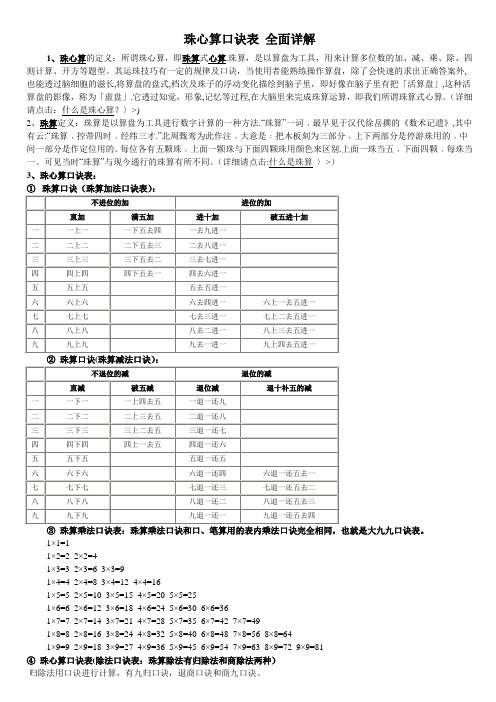
九归口诀共61句:一归(用1除):逢一进一,逢二进二,逢三进三,逢四进四,逢五进五,逢六进六,逢七进七,逢八进八,逢九进九。
二归(用2除):逢二进一,逢四进二,逢六进三,逢八进四, 二一添作五。
三归(用3除):逢三进一,逢六进二,逢九进三,三一三余一,三二六余二。
四归(用4除):逢四进一,逢八进二,四二添作五,四一二余二,四三七余二。
五归(用5除):逢五进一,五一倍作二,五二倍作四,五三倍作六,五四倍作八。
六归(用6除):逢六进一,逢十二进二,六三添作五,六一下加四,六二三余二,六四六余四,六五八余二.七归(用7除):逢七进一,逢十四进二,七一下加三,七二下加六,七三四余二,七四五余五,七五七余一,七六八余四.八归(用8除):逢八进一,八四添作五,八一下加二,八二下加四,八三下加六,八五六余二,八六七余四,八七八余六。
九归(用9除):逢九进一,九一下加一,九二下加二,九三下加三,九四下加四,九五下加五,九六下加六,九七下加七,九八下加八.退商口诀共9句:无除退一下还一,无除退一下还二,无除退一下还三无除退一下还四,无除退一下还五,无除退一下还六无除退一下还七,无除退一下还八,无除退一下还九商九口诀共9句:见一无除作九一,见二无除作九二,见三无除作九三见四无除作九四,见五无除作九五,见六无除作九六见七无除作九七,见八无除作九八,见九无除作九九除数是一位数的除法叫“单归”;除数是两位或两位以上的除法叫“归除”,除数的首位叫“归”,以下各位叫“除”。
如,除数是534的归除,叫“五归三四除",即用五归口诀求商后,再用34除。
幼儿珠心算口诀加一请拨双下九,我们都是好朋友;加二请拨双下八,开心时候笑哈哈;加三请拨双下七,有时也会生生气;加四请拨双下六,快乐时候蹦又跳。
减一请拨双上九,唱歌要学百灵鸟;减二请拨双上八,做事不要太拖拉;减三请拨双上七,排队做操要整齐;减四请拨双上六,早上不要睡懒觉。
从上表的”加”来看共26个动珠码,”减"只是反向拨珠,加与减是一上一下和一去一回的还原关系,是一种动作相对形态.手指拨打到后来已在脑中形成条件反射,珠动数出,这是完成的”内化”的一种表现.训练珠心算从实拨到空拨,再到想拨,或同步进行等等,从心理上讲也是经过"珠算的动珠码映象"的形成,完成珠算的内化过程.由于动静结合一次成象,珠心算的运算过程实际上是每码至多3种模型的不断转换过程。
再谈珠算_开方_1_2_

◆朱阳生笔者在2011年本刊上曾发表过类似的文章,今天再谈珠算开方,旨在让人们了解珠算能开任意次方,在数理化、工程技术方面也有应用的空间,这也是珠算作为文化遗产的价值之一。
但要用珠算开方,首先要熟悉珠算多位乘、除法的运算,在多位数乘法方面要用破头乘法;其次就是要有耐心、细心,在学会基本方法后,勤加练习,就会得心应手;算盘应选用档位多的,如十七档算盘。
一、珠算开平方运算什么是开平方?也就是开二次方。
通俗来讲,如果已知一个数,求出一个数,自己乘自己可得这个已知数,那么这个数是已知数的平方根,而求这个数的运算就是开平方。
如25的平方根是5,64的平方根是8。
当然,能开得尽的数,也就是完全平方数是极少数。
2的平方根是多少?这不是整数,而是无限不循环小数—无理数:1.4142……。
下面就讨论珠算的开平方运算。
如,求767376的平方根是多少。
首先在算盘上拨出这个数,从个位向前每二位一节分节第一节76,其含最大平方数是64,82=64,首位根是8(图中8的头上标上“·”号,其意是根位),从第一节中减去64得:,整个后面数除以2(用二归除法),用首位根8去除6,八六七余四,得出第二位7(并标7688。
7的平方是49,再紧接下位减去49的一半24.5得位根6(图上6标上·号)8觶7觶6觶4380。
按除数是二位的除法运算则减去,6×6觶018,依次、依位减去6的平方一半18,000,于是开尽了:姨767376π的平方根是多少?取π=3.1415926535,这里π取小数点后十位,以所用的算盘档数,或需要精确度来取小数点后位数,如只取小数点后五位亦也。
整数只一位3,3的前一位空上(0)占一位,凑成一节。
小数点后面依次从前到后,整数3含最大平方数是1:12=1,首位根1拨在03前面,。
第一节.021*********,注意小数点位置,整数节只有一节(图上1标上·号)。
后面所有法)1觶.107079632675,以首位根1去除下一位1,见一无除作九一,除商过大,退二还二,得出第觶37079632675(图上7标·号),减,1觶.7觶12579632675,以17去除下位1,又是见一无除作九一,除商过大退二还二,得出,依二位除数除法运算减去7×7=49,依次依位减去7的平方一半24.5, 1觶 .7觶 7觶 0434632675 以177去除下面的数, 逢二进,再 用87去 除 后 一 位5,八 五 六 余 二 ,确 定二 , 得 出 第 四 位 根 2, ( 图 上 2珠算与珠心算 2014.225号),依三位数除数除法运算减去:7×2=14,7×2=14,再依次依位减去2的平方一半2;以1772去除下面的数,逢四进四,得出第五位根4(图上4标4觶40432675,依四位数除数除法运算28,7×4=28,2×4=8,再依次依位减去4的平方一半8得,……因篇幅所限只能介绍到这里,读若耐心照上面的方法进行计算可得姨π=1.772453850905。
珠算乘法

的空盘前乘法两种。
第二节 乘积的定位
一、公式定位法 二、固定个位定位法
• 用珠算计算,定位很重要,如果算盘上没 有固定的位数,同样的数就不能确定它数值的 大小,如3、0.3、300等,因此,我们就先 给盘上的各档定位。
•
4380
一位乘法
• 【例2】239×0.0004=0.0956
• 根据固定个位定位法定位:p=m+n=3+(-3) =0
• 置被乘数首位在0位档:
•
•
•
239
• 运算9×4 3 6
• 3×4 1 2
• 2×4 0 8
•
0.0 9 5 6
一位乘法
• 【例3】0.08×1093=87.44
• 根据固定个位定位法定位:p=m+n=(-1) +4=3
乘法的运算定律
• 乘法交换律:根据计算数字的特点交换 实法位置而乘积不变的规律;
• 乘法结合律:对几个乘数相乘可以将容 易相乘的数据结合起来,其积不变的规 律;
• 乘法分配律:是指在被乘数上增加或减 少一个补数,其代数和与乘数相乘的积 数等于各个加数与乘数相乘的代数和的 规律。
二、乘法口诀
• 顺九九(小九九)口诀:乘法口诀中,两 因数小数在前,大数在后及两因数相同的 口诀,叫顺九九,亦称小九九,共45句。
• 积的首位数与被乘数或乘数首位数是相 同,比较第2位属“偏小”,用公式1定 位:1+1=2,结果为95.06。
• 【例8】12×0.014得积数有效数字168
• 积的首位数与被乘数或乘数首位数相同, 比较第2位属“偏大”,用公式2定位: 2+(-1)-1=0,结果为0.168。
珠心算技巧

珠心算技巧珠心算技巧-------------------------------------------------------------------------------- 告诉朋友来自状园培训网2010-04-20 被关注了220次珠心算一、一种做多位乘法不用竖式的方法。
我们都可以口算1X1 10X1,但是,11X12 12X13 12X14呢?这时候,大家一般都会用竖式,通过竖式计算,得数是132、156、168。
其中有趣的规律:积个位上的数字正好是两个因数个位数字的积。
十位上的数字是两个数字个位上的和。
百位上的数字是两个因数十位数字的积。
例如:12X14=168 1=1X1 6=2+4 8=2X4如果有进位怎么办呢?这个定律对有进位的情况同样适用,在竖式时只要~满几时,就向下一位进几。
~例如:14X16=224 4=4X6的个位2=2+4+6 2=1+1X1试着做做看下面的题:12X15= 11X13= 15X18= 17X19=二、几十一乘以几十一的速算方法例如:21×61=41×91=41×91= 51×61= 81×91= 41×51= 41×81= 71×81=这些算式有什么特点呢?是“几十一乘以几十一”的乘法算式,我们可以用:先写十位积,再写十位和(和满10 进1),后写个位积。
“先写十位积,再写十位和(和满10 进1),后写个位积”就是一见到几十一乘以几十一的乘法算式,如果十位数的和是一位数,我们先直接写十位数的积,再接着写十位数的和,最后写上1 就一定正确;如果十位数的和是两位数,我们先直接写十位数的积加1 的和,再接着写十位数的和的个位数,最后写一个 1 就一定正确。
我们来看两个算式:21×61=41×91=用“先写十位积,再写十位和(和满10 进1),后写个位积”这种速算方法直接写得数时的思维过程。
乘方和开方认识乘方和开方的概念和计算方法

乘方和开方认识乘方和开方的概念和计算方法乘方和开方:认识乘方和开方的概念和计算方法乘方和开方是数学中常见的概念和计算方法,在各个领域的应用广泛。
本文将详细介绍乘方和开方的概念、计算方法以及一些实例,帮助读者深入了解并掌握这两个数学运算。
一、乘方的概念和计算方法乘方,也称为指数运算,是将一个数称为底数,另一个数称为指数,在指数上方标注一个小的数字,表示底数连乘的次数。
例如,a的n次方表示a连乘自己n次,即a^n。
其中,n为正整数时,表示乘方;n为负整数时,表示倒数的乘方;n为0时,结果为1。
计算乘方的方法有多种,常见的有以下几种:1. 重复乘法法:将底数连乘n次。
例如,2的3次方可以表示为2 ×2 × 2 = 8。
2. 公式法:应用乘方的性质,如a的n次方可以表示为a^n。
3. 递归法:通过递归方式计算乘方,将问题分解为更小规模的乘方计算。
除了整数乘方外,还存在分数乘方、小数乘方等复杂的情况。
在实际应用中,我们可以借助计算器或电子设备进行计算,提高计算效率。
二、开方的概念和计算方法开方是乘方的逆运算,将一个数的乘方结果转化为底数。
开方运算的结果称为根,常用符号为√。
例如,√9 = 3,表示9的平方根为3。
开方运算的计算方法主要有以下几种:1. 试探法:从可能的结果中进行尝试,找到一个数使得其平方等于给定数。
例如,√49 = 7,因为7的平方等于49。
2. 牛顿迭代法:通过逼近法不断逼近给定数的平方根,直到满足一定精度要求。
3. 查表法:利用已经计算好的平方根表,查询给定数的平方根。
类似于乘方,开方也存在复杂情况,如分数开方、小数开方等。
在实际应用中,我们可以利用计算器或电子设备进行开方运算。
三、乘方和开方的应用乘方和开方在各个领域都有广泛的应用,以下是几个常见的应用示例:1. 计算面积和体积:乘方可以简化面积和体积的计算。
例如,矩形的面积可以表示为长乘以宽(A = l × w),立方体的体积可以表示为边长的三次方(V = a^3)。
珠心算的乘法运算

珠心算的乘法运算学习目标:掌握珠算乘法的乘算原理,了解不同类型乘法的基本乘算方法,熟练掌握空盘前乘法学习内容:珠算乘法的算理算法一位数和多位数的空盘前乘法小数乘法1、珠算乘法是在加法的基础上,根据乘法口诀进行的运算,乘法是加法的简便运算。
2、珠算乘法的种类很多,按不同的分类方法,可有置数乘法、空盘乘法、前乘法、后乘法、隔位乘法、不隔位乘法等等,在这些方法中,最简便、最容易掌握的还是空盘前乘法,我们要学习的也是这种方法。
3、空盘前乘法:“空盘”是指被乘数和乘数均不置在算盘上,而将两者的乘积直接拨在算盘上;“前乘”是指乘数首先同被乘数的首位相乘,随后自左向右逐位相乘,直至乘完为止。
4、空盘前乘法的优点是:乘数和被乘数事先均不步入算盘,节约了拨珠布数的时间,尤其在求多笔乘积之和的算题时,可边乘边加,不必把各个乘积算得后再相加,节约了运算时间,提高了运算速度。
5、要学习空盘前乘法,需要有一些预备知识:(1)必须使用大九九口诀大九九口诀:大数在前小数在后,如:9×2=18 8×7=56小九九口诀:小数在前大数在后,如:2×9=18 7×8=56大九九口诀一律四字一句,有利于避免错位,提高计算速度。
(2)每个单积必须使用两位数记积法“单积”:两个1位数相乘所得的积即单积,如:3×5=15,15即为单积。
“两位数记积法”:每两个1位数相乘的积必须是两位数,没有数都要用0补齐。
如:6×4=24 1×5=05 3×0=00多位数乘法多位数乘法是指乘数和被乘数都在二位或二位以上的数字相乘的乘法。
空盘前乘的多位数乘法方法是:用乘数的首位数从左向右去乘被乘数的各位,把各单积依次退位叠加,结果为“第一分积”;再用乘数的次字位从左向右遍乘被乘数的各位,从第一分积的第二位起依次退位叠加,结果为“第一、第二分积”之和;若乘数还有第三位,方法同上,第一个单积从一、二分积之和的第三位起退位叠加即可。
小学生乘法口诀表、除法口诀表、珠算口诀表【范本模板】
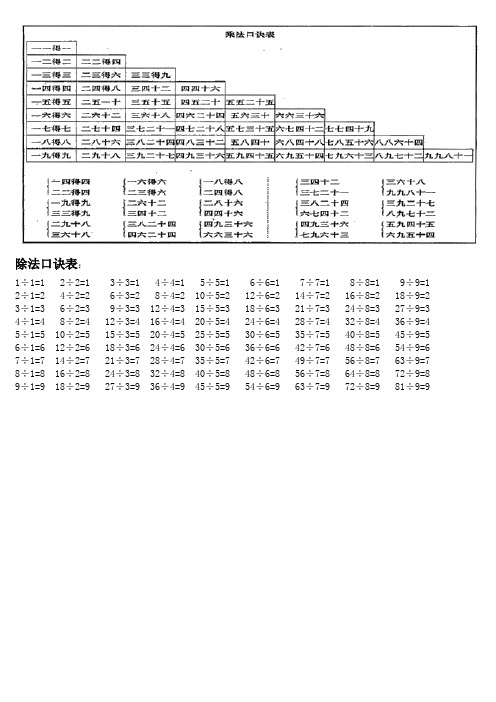
除法口诀表:1÷1=1 2÷2=1 3÷3=1 4÷4=1 5÷5=1 6÷6=1 7÷7=1 8÷8=1 9÷9=1 2÷1=2 4÷2=2 6÷3=2 8÷4=2 10÷5=2 12÷6=2 14÷7=2 16÷8=2 18÷9=2 3÷1=3 6÷2=3 9÷3=3 12÷4=3 15÷5=3 18÷6=3 21÷7=3 24÷8=3 27÷9=3 4÷1=4 8÷2=4 12÷3=416÷4=4 20÷5=4 24÷6=4 28÷7=4 32÷8=4 36÷9=4 5÷1=5 10÷2=5 15÷3=5 20÷4=5 25÷5=5 30÷6=5 35÷7=5 40÷8=5 45÷9=5 6÷1=6 12÷2=6 18÷3=6 24÷4=6 30÷5=6 36÷6=6 42÷7=6 48÷8=6 54÷9=6 7÷1=7 14÷2=7 21÷3=7 28÷4=7 35÷5=7 42÷6=7 49÷7=7 56÷8=7 63÷9=7 8÷1=8 16÷2=8 24÷3=8 32÷4=8 40÷5=8 48÷6=8 56÷7=8 64÷8=8 72÷9=8 9÷1=9 18÷2=9 27÷3=9 36÷4=9 45÷5=9 54÷6=9 63÷7=9 72÷8=9 81÷9=91+ 1= 21+ 2= 3 2+ 2= 41+ 3= 4 2+ 3= 5 3+ 3= 61+ 4= 5 2+ 4= 6 3+ 4= 7 4+ 4= 81+ 5= 6 2+ 5= 7 3+ 5= 8 4+ 5= 9 5+ 5=101+ 6= 7 2+ 6= 8 3+ 6= 9 4+ 6=10 5+ 6=11 6+ 6=121+ 7= 8 2+ 7= 9 3+ 7=10 4+ 7=11 5+ 7=12 6+ 7=13 7+ 7=141+ 8= 9 2+ 8= 10 3+ 8=11 4+ 8=12 5+ 8=13 6+ 8=14 7+ 8=15 8+ 8=161+ 9= 10 2+ 9= 11 3+ 9=12 4+ 9=13 5+ 9=14 6+ 9=15 7+ 9=16 8+ 9=17 9+ 9=18 1+ 10=11 2+ 10=12 3+10=13 4+10=14 5+10=15 6+10=16 7+10=17 8+10=18 9+10=19 10+10=2020以内加法口诀:1+11=12 2+11=13 3+11=14 4+11=15 5+11=16 6+11=17 7+11=18 8+11=19 9+11=201+12=13 2+12=14 3+12=15 4+12=16 5+12=17 6+12=18 7+12=19 8+12=201+13=14 2+13=15 3+13=16 4+13=17 5+13=18 6+13=19 7+13=201+14=15 2+14=16 3+14=17 4+14=18 5+14=19 6+14=201+15=16 2+15=17 3+15=18 4+15=19 5+15=201+16=17 2+16=18 3+16=19 4+16=201+17=18 2+17=19 3+17=201+18=19 2+18=201+19=2010以内减法口诀:9-9=0 9-8=1 9-7=2 9—6=3 9-5=4 9-4=5 9—3=6 9—2=7 9-1=88-8=0 8—7=1 8—6=2 8—5=3 8-4=4 8—3=5 8—2=6 8-1=77—7=0 7-6=1 7—5=2 7—4=3 7-3=4 7—2=5 7—1=66-6=0 6—5=1 6—4=2 6-3=3 6—2=4 6-1=55-5=0 5-4=1 5—3=2 5-2=3 5—1=44-4=0 4—3=1 4-2=2 4—1=33-3=0 3—2=1 3—1=22-2=0 2-1=11-1=0不进位的加进位的加直加满五加进十加破五进十加加一:一上一,一下五去四,一去九进一加二:二上二,二下五去三,二去八进一加三:三上三,三下五去二,三去七进一加四:四上四,四下五去一,四去六进一加五:五上五,五去五进一加六:六上六,六去四进一,六上一去五进一加七:七上七,七去三进一,七上二去五进一加八:八上八,八去二进一,八上三去五进一加九:九上九,九去一进一,九上四去五进一珠算减法口诀表:不退位的减退位的减直减破五减退位减退十补五的减减一:一下一,一上四去五,一退一还九减二:二下二,二上三去五,二退一还八减三:三下三,三上二去五,三退一还七减四:四下四,四上一去五,四退一还六减五:五下五,五退一还五减六:六下六,六退一还四,六退一还五去一减七:七下七,七退一还三,七退一还五去二减八:八下八,八退一还二,八退一还五去三减九:九下九,九退一还一,九退一还五去四珠算乘法「九九」口诀:在春秋战国时已在筹算中得到应用;归除口诀,首见杨辉《乘除通变算宝》〔1274〕,朱世杰《算学启蒙》〔1299〕所载九归口诀已与现代基本相同.有了四则口诀,珠算的算法就形成一个体系,长期沿用下来。
珠算基本乘法

演示
学生练习:
839×504= 317×6002= 694×308= 692×4001= 216×108= 9254×60005=
答案:
839×504=422856 317×6002=1902634 694×308=213752 692×4001= 2768692 216×108=23328 9254×60005=555286270
1068×70 07 00 42 56 07476 02 00 12 16 076896
1068×2
学生练习:
809×54= 307×62= 604×38= 5008×79= 6004×786= 90001×4295=
答案:
809×54=43686 307×62= 19034 604×38=22952 5008×79= 395632 6004×786=4719144 90001×4295=386554295
积的定位方法 公式:
第一单积十位数拨入档位=被乘数位数+乘数位数
3
2
[例1] 624×90.7=
定位:3+2=+5 9×6=54的5,从+5位拨入
3 1
[例2] 624×9.07=
定位:3+1=+4 9×6=54的5,从+4位拨入
3
0
[例3] 624×0.907=
定位:3+0=+3 9×6=54的5,从+3位拨入
前面我们已经学习了乘数为一位数的 乘法,空盘前乘法的基本方法已经掌握. 今天我们要学习的是第二节——多位数乘 法,它是对一位数乘法的一个扩展.我们 所要讲的多位数乘法是指乘数和被乘数都 在二位或二位以上的数字相乘的乘法.
第二节 多位数乘法
珠心算教程:乘法的运算法则

珠心算教程:乘法的运算法则
朋友们,没有学习珠心算的时候,意味珠心算真的很简单,等到我们开始投入,用心的学习的时候才发现原来还有这么多的文章,下面我们就来看看如何解除乘法的运算法则的吧。
首积:当每个乘数与被乘数相乘时,所得乘积的第一个数字,即积的首位数。
简称“首积”。
首积进位:积的首位数比被乘数的首位数小时,称为首积进位。
简称“积首<被首”。
首积不进:积的首位数比被乘数的首位数大时,称为首积进位。
“积首>被首”。
如果出现完全相等的现象,也就当乘数中有“1”的时候。
又该如何处理?
什么是本档?什么是退档?要结合算盘进行对比指导。
它的位置主要是由乘数所在的位置来决定的。
在乘数中从左向右数起,每个乘数在第几位上,那么它的本档就在算盘左起的第几个档位上。
即当乘数在第一位时,那么算盘的第一档就是它的本档、第二档就是它的退档。
……
什么是本档加?什么是退档加?即当乘数在第一位时,有进位(积首<被首),那么就在算盘的第一档(本档)加、没有进位(积首>被首),那么就在第二档(退档)加。
……。
算盘 开方 微积分

算盘开方微积分
算盘是一种古老的计算工具,它由珠子和棒子组成,可以用来
进行基本的数学运算,如加减乘除。
使用算盘进行开方运算需要一
定的技巧和熟练度,通常需要将被开方数按位拆分,然后通过移动
珠子和棒子来进行计算。
开方在数学中是一个重要的运算,它表示
一个数的平方根,即一个数乘以自身等于被开方数。
微积分是数学
中的一个重要分支,它研究的是变化和运动的规律,包括函数、极限、导数、积分等概念。
微积分在物理、工程、经济等领域都有着
广泛的应用,可以用来描述和分析各种变化和运动的规律。
微积分
的概念和方法对于理解自然界和人类活动中的各种现象具有重要意义,它是现代科学和技术发展的重要基础之一。
从历史角度看,微
积分的概念最早可以追溯到古希腊的亚里士多德和阿基米德,而算
盘则可以追溯到中国古代。
现代数学和物理学的发展离不开微积分
的方法和思想,它对于推动科学技术的进步发挥着不可或缺的作用。
因此,算盘、开方和微积分都是数学领域中非常重要的概念和工具,它们在不同的历史背景和文化传统中都有着深远的影响。
希望这些
信息能够对你有所帮助。
珠算的一般公式法

珠⼼算的公式是⼤家更好的了解珠⼼算的⽅法,那么珠⼼算公式是什么呢?珠⼼算公式为将简捷乘算法统⼀于⼗字相乘公式之中,进⽽运⽤多种⽅法,简化运算过程,提⾼计算速度。
下⾯就来看看吧! 前⾯提到,如:27×964、1998×778、999992应怎样计算,才会更为快捷、⽅便。
根据以上原理,笔者研究出补数乘法的⼀般公式法,暂定为魏⽒公式法: (1)设被乘数的最末⼀位数的补数为a,乘数的补数为b,那么在被乘数的末位的下位加a×b(a×b有进位者,要进到本位); (2)设被乘数去掉尾数后的数为n,那么应从被乘数⾸位的下位减去(n+1)×b。
注意(n+1)×b有进位,从⾸位减,b前有0位,有⼏个零应移档向后⼏位再减,就是:先从尾后加a×b,再在次档减(n+1)×b,这就是补数乘法的⼀般公式法。
利⽤此公式可以解决以下类别的数乘以任意数的快速计算问题: 1、被乘数是两位数的例题; 2、被乘数是两位以上的数时,n+1等于齐数或强数的例题。
如:例1:27×964=26028(补数036) (1)先在被乘数个位7的下位加上(a×b),即3×036=108,得27.108; (2)再从被乘数的次⾼档7的本位减去(n+1)×b,即(2+1)×036,得26028,即是积数。
例2:19998×778=15558444(补数222) (1)先在被乘数个位8的下位加上(a×b)即2×222,得19998.444; (2)再从被乘数的次⾼档减去(n+1)×b即(1999+1)×222,得15558444,即得积。
注:实际上,(n+1)×b⽐原数少了10倍,把(n+1)再扩⼤10倍后,就是实际需要减的数。
如例2:第1步尾下加上444后,可看作 19998444;达到千万位;(1999+1)×222×10=4440000,达到百万位;从19998444中减去 4440000=15558444。
珠心算技巧

珠心算技巧-------------------------------------------------------------------------------- 告诉朋友来自状园培训网2010-04-20 被关注了220次珠心算一、一种做多位乘法不用竖式的方法。
我们都可以口算1X1 10X1,但是,11X12 12X13 12X14呢?这时候,大家一般都会用竖式,通过竖式计算,得数是132、156、168。
其中有趣的规律:积个位上的数字正好是两个因数个位数字的积。
十位上的数字是两个数字个位上的和。
百位上的数字是两个因数十位数字的积。
例如:12X14=168 1=1X1 6=2+4 8=2X4如果有进位怎么办呢?这个定律对有进位的情况同样适用,在竖式时只要~满几时,就向下一位进几。
~例如:14X16=224 4=4X6的个位2=2+4+6 2=1+1X1试着做做看下面的题:12X15= 11X13= 15X18= 17X19=二、几十一乘以几十一的速算方法例如:21×61=41×91=41×91= 51×61= 81×91= 41×51= 41×81= 71×81=这些算式有什么特点呢?是“几十一乘以几十一”的乘法算式,我们可以用:先写十位积,再写十位和(和满10 进1),后写个位积。
“先写十位积,再写十位和(和满10 进1),后写个位积”就是一见到几十一乘以几十一的乘法算式,如果十位数的和是一位数,我们先直接写十位数的积,再接着写十位数的和,最后写上1 就一定正确;如果十位数的和是两位数,我们先直接写十位数的积加1 的和,再接着写十位数的和的个位数,最后写一个 1 就一定正确。
我们来看两个算式:21×61=41×91=用“先写十位积,再写十位和(和满10 进1),后写个位积”这种速算方法直接写得数时的思维过程。
珠算开方的一种简捷算法

珠算开方的一种简捷算法
唐松林
【期刊名称】《黑龙江珠算》
【年(卷),期】1996(000)005
【摘要】开方是乘方的逆运算,也是一种特殊除法。
据有关珠算书刊介绍,珠算开平方有多种方法,但简单易学的不多。
笔者经过反复比较探索,对珠算开平方的简捷算法,有以下一点体会,介绍出来,就教于专家学者。
【总页数】2页(P32-33)
【作者】唐松林
【作者单位】安徽省珠算协会
【正文语种】中文
【中图分类】O121.5
【相关文献】
1.一种基于汇编语言实现的快速开方算法设计 [J], 崔磊
2.王文素《算学宝鉴》筹算开方新法——传统筹算开方到珠算开方的过渡形态 [J], 牛腾;邹大海
3.开拓珠算算法新天地——介绍一种珠算加积除法 [J], 安季平
4.《算海说详》中珠算开方新增法及其特点——兼与《算法统宗》开方法的比较[J], 牛腾
5.N次乘方与开方简捷验算法 [J], 方有昆
因版权原因,仅展示原文概要,查看原文内容请购买。
