]初中的数学定理证明
初中数学公式定理大全

初中数学公式定理大全1点的定理:过两点有且只有一条直线;两点之间线段最短角的定理:同角或等角的补角相等;同角或等角的余角相等直线定理:过一点有且只有一条直线和已知直线垂直;直线外一点与直线上各点连接的所有线段中,垂线段最短2平行定理:经过直线外一点,有且只有一条直线与这条直线平行推论:如果两条直线都和第三条直线平行,这两条直线也互相平行证明两直线平行定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行两直线平行推论:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补3定理:三角形两边的和大于第三边推论:三角形两边的差小于第三边三角形内角和定理:三角形三个内角的和等于180°4定理:全等三角形的对应边、对应角相等边角边定理(SAS):有两边和它们的夹角对应相等的两个三角形全等;有两角和它们的夹边对应相等的两个三角形全等推论(AAS):有两角和其中一角的对边对应相等的两个三角形全等边边边定理(SSS):有三边对应相等的两个三角形全等斜边、直角边定理(HL):有斜边和一条直角边对应相等的两个直角三角形全等5定理1:在角的平分线上的点到这个角的两边的距离相等定理2:到一个角的两边的距离相同的点,在这个角的平分线上;角的平分线是到角的两边距离相等的所有点的集合6等腰三角形的性质定理:等腰三角形的两个底角相等(即等边对等角)推论1:等腰三角形顶角的平分线平分底边并且垂直于底边;等腰三角形顶角平分线、底边上的中线和底边上的高互相重合等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)7定理:线段垂直平分线上的点和这条线段两个端点的距离相等逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;线段的垂直平分线可看作和线段两端点距离相等的所有点的集合定理1:关于某条直线对称的两个图形是全等形定理2:如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线定理3:两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上逆定理:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称8定理:在直角三角形中,如果一个锐角等于30°那它所对的直角边等于斜边的一半判定定理:直角三角形斜边上的中线等于斜边上的一半勾股定理:直角三角形两直角边a、b的平方和、等于斜边c的平方,a^2+b^2=c^2勾股定理的逆定理:如果三角形的三边长a、b、c有关系a^2+b^2=c^2,那么这个三角形是直角三角形9定理:四边形的内角和等于360°;四边形的外角和等于360°多边形内角和定理:n边形的内角和等于(n-2)×180°推论:任意多边的外角和等于360°10平行四边形性质定理:1.平行四边形的对角相等2.平行四边形的对边相等3.平行四边形的对角线互相平分推论:夹在两条平行线间的平行线段相等平行四边形判定定理 1.两组对角分别相等的四边形是平行四边形 2.两组对边分别相等的四边形是平行四边形 3.对角线互相平分的四边形是平行四边形 4.一组对边平行相等的四边形是平行四边形11矩形性质定理:矩形的四个角都是直角;矩形的对角线相等矩形判定定理1:有三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形12菱形性质定理1:菱形的四条边都相等菱形性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1:四边都相等的四边形是菱形菱形判定定理2:对角线互相垂直的平行四边形是菱形13正方形性质定理1:正方形的四个角都是直角,四条边都相等正方形性质定理2:正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角14定理:关于中心对称的两个图形是全等的;关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分逆定理:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称15等腰梯形性质定理:1.等腰梯形在同一底上的两个角相等2.等腰梯形的两条对角线相等等腰梯形判定定理:1. 在同一底上的两个角相等的梯形是等腰梯形2.对角线相等的梯形是等腰梯形平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边16三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半:L=(a+b)÷2S=L×h17相似三角形定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似相似三角形判定定理:1. 两角对应相等,两三角形相似(ASA)2. 两边对应成比例且夹角相等,两三角形相似(SAS)3. 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似判定定理3:三边对应成比例,两三角形相似(SSS)相似直角三角形定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似性质定理:1.相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比2.相似三角形周长的比等于相似比3.相似三角形面积的比等于相似比的平方18定理1:任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值定理2:任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值19定理:过不共线的三个点,可以作且只可以作一个圆;垂直于弦的直径平分这条弦,并且评分弦所对的两条弧推论1:平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧推论2:弦的垂直平分弦经过圆心,并且平分弦所对的两条弧推论3:平分弦所对的一条弧的直径,垂直评分弦,并且平分弦所对的另一条弧定理3:1.在同圆或等圆中,相等的弧所对的弦相等,所对的弦的弦心距相等2.经过圆的半径外端点,并且垂直于这条半径的直线是这个圆的切线3.圆的切线垂直经过切点的半径4.三角形的三个内角平分线交于一点,这点是三角形的内心5.从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角6.圆的外切四边形的两组对边的和相等7.如果四边形两组对边的和相等,那么它必有内切圆8.两圆的两条外公切线的长相等;两圆的两条内公切线的长也相等20比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b。
初中数学-勾股定理16种证明方法
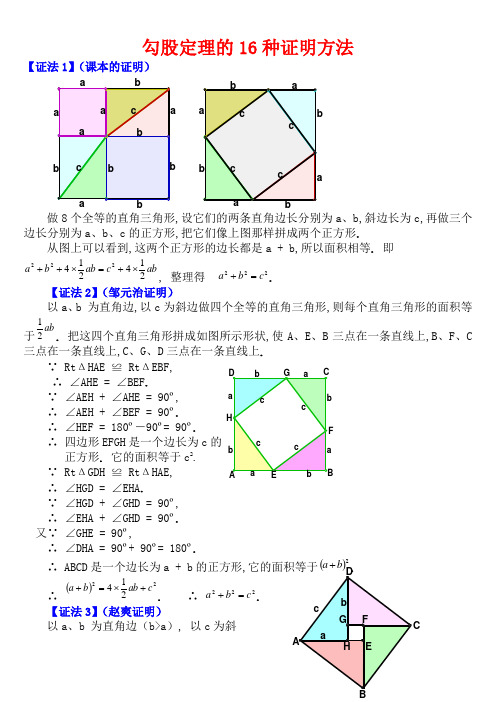
勾股定理的16种证明方法【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b,斜边长为c,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜D 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +.∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P . ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED,C∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC,交AC 于点P . 过点B 作BM ⊥PQ,垂足为M;再过点F 作FN ⊥PQ,垂足为N .∵ ∠BCA = 90º,QP ∥BC, ∴ ∠MPC = 90º, ∵ BM ⊥PQ, ∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c, ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE,交AB 于点M,交DE 于点L . ∵ AF = AC,AB = AD,∠FAB = ∠GAD, ∴ ΔFAB ≌ ΔGAD,∵ ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC, ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB, 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC,AF 交GT 于F,AF 交DT 于R . 过B 作BP ⊥AF,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c,∴ Rt ΔDHA ≌ Rt ΔBCA .K∴ DH = BC = a,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b,AP= a,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a,下底BP= b,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 = ab b 212-, 985S S S +=,∴824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º,∴ ∠TBH = ∠ABE .又∵ ∠BTH = ∠BEA = 90º,BT = BE = b, ∴ Rt ΔHBT ≌ Rt ΔABE .∴ HT = AE = a . ∴ GH = GT ―HT = b ―a . 又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º,∴ ∠GHF = ∠DBC.R∵ DB = EB ―ED = b ―a, ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM,而AB = AQ = c,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM,又得QM = AE = a,∠AQM = ∠BAE . ∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE, ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC •=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a cb -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c (如图). 过点A 作AD ∥CB,过点B 作BD ∥CA,则ACBD为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•, ∵ AB = DC = c,AD = BC = a, AC = BD = b,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法13】(作直角三角形的内切圆证明)在Rt ΔABC 中,设直角边BC = a,AC = b,斜边AB = c . 作Rt ΔABC 的内切圆⊙O,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF,BF = BD,CD = CE,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AO C BO CAO B ABC S S S S ∆∆∆∆++= = brar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c,过点C 作CD ⊥AB,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A,∴ 若 AD :AC ≠AC :AB,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B, ∴ 若BD :BC ≠BC :AB,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a,连结DA 、DC,则 AD = c .∵ EM = EH + HM = b + a , ED = a, ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a, ∠AED = 90º, AE = b, ∴ Rt ΔAED ≌ Rt ΔDMC . ∴ ∠EAD = ∠MDC,DC = AD = c .∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC,CB ∥DA,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º,D D∴ ∠BAF=∠DAE .连结FB,在ΔABF 和ΔADE 中,∵ AB =AD = c,AE = AF = b,∠BAF=∠DAE, ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中, ∵ AB = BC = c,BF = CG = a, ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
初中几何证明的所有公理和定理

初中几何证明的所有公理和定理几何学是数学的一个分支,研究平面和空间中的图形、形状、大小以及它们之间的关系。
在几何学中,有一些基本的公理和定理被广泛应用于证明其他几何结论。
以下是初中几何中常用的公理和定理。
一、公理1.尺规公理:任意两点可以用直尺连接,任意一点可以用剪刀间距来复原。
2.同位角公理:同位角互等。
3.平行公理:通过点外一条直线的直线,与这条直线平行的直线只有唯一一条。
4.直线偏转公理:过直线和不在直线上的一点,有且只有一条直线与该直线相交。
二、定理1.垂直平分线定理:平分一条线段的直线必垂直于该线段。
2.三角形内角和定理:三角形内角的和为180°。
3.直角三角形定理:在直角三角形中,两个直角三角形的边长和斜边相等。
4.点到直线的距离定理:点到直线的距离等于点到该直线上垂线的距离。
5.等腰三角形定理:等腰三角形的底边中点到顶点的距离等于底边的一半。
6.等边三角形定理:等边三角形的三条边相等。
7.三角形外角定理:三角形外角等于其对应内角的和。
8.直角三角形的勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
9.海伦公式:已知三角形的三边长,可以通过海伦公式求解其面积。
10.等周定理:等周的两角相等,反之亦成立。
11.三角形中位线定理:三角形两边中点连线中位线,且平分第三边。
12.周长定理:四边形周长等于各边长的和。
13.三角形周长定理:三角形的周长等于三边长的和。
14.三角形中线定理:三角形中线等分中位线,且平分第三边。
15.三角形终边定理:一个角的终边上的点,到另一个角所在的直线的距离永远相等。
16.五边形内角和定理:五边形的内角和是540°。
17.钝角三角形的边长关系:钝角三角形两边长的平方和小于斜边长的平方。
18.三角形的相似性定理:对应角等价、对应边成比例的两个三角形为相似三角形。
19.平行线的性质定理:平行条边分别过枚角且长度成正比,则连线为平行线。
20.重叠三角形定理:如果两个角和一个边分别相等,则两个三角形相等。
初中数学定理及推论的证明

初中数学定理及推论的证明证明一:等腰三角形的定理定理:如果一个三角形的两条边等长,那么这个三角形是等腰三角形。
证明:假设三角形ABC的两条边AB和AC等长,即AB=AC。
由等量减法原理,我们可以得到:AB-AC=0。
再根据减法交换律,我们可以得到:AC-AB=0。
根据减法结合律,上述两式可以合并为:AC-AB+AB-AC=0。
通过合并同类项,我们可以得到:AC-AC+AB-AB=0。
根据零元素的性质,我们可以得到:0+0=0。
根据加法恒等性质,上述两式可以合并为:0=0。
根据等式传递律,我们可以得到:AC-AB=AB-AC。
根据相反数的性质,上式可以变为:AC+(-AB)=AB+(-AC)。
根据加法逆元的定义,我们可以将上式简化为:AC-AB=AB-AC=0。
由于AC-AB=0,所以AC=AB。
这就证明了三角形ABC是等腰三角形。
证明二:三角形内角和定理定理:三角形的内角和等于180度。
证明:假设三角形ABC的三个内角分别为∠A、∠B、∠C。
我们可以通过以下步骤来证明内角和定理:1.根据直角三角形的性质,直角三角形的内角和等于90度。
所以∠A+∠B+∠C=90度。
2.将三角形ABC划分为两个直角三角形,其中一个直角三角形的两个内角分别为∠A和∠B。
3.根据直角三角形内角和定理,我们可以得到∠A+∠B=90度。
4.将上述结果代入第一步的等式中,我们可以得到90度+∠C=90度。
5.根据加法逆元的定义,我们可以将上述结果简化为∠C=0度。
6.根据零元素的性质,0度+0度+0度=0度。
结合第一步的等式,我们可以得到∠A+∠B+∠C=0度。
因此,三角形ABC的内角和等于180度。
证明三:略以上是初中数学中的两个重要定理及其证明。
这些证明基于基本的数学概念和运算法则,通过逻辑推理和数学运算的方法,从已知条件推导出结论。
这些证明过程旨在培养学生的逻辑思维能力和数学推理能力,加深对数学定理的理解和应用。
同时,这些定理的证明也为后续数学知识的学习和应用奠定了基础。
初中数学几何定理大全

( 2)N边形的内角和:( n -2)× 180° .
( 3)任意多边形的外角和都为 360°
28、平行四边形的性质:
( 1)平行四边形的对边平行且相等;
( 2)平行四边形的对角相等;
( 3)平行四边形的对角线互相平分。
-可编辑修改 -
29、平行四边形的判定 : ( 1)两组对边分别平行的四边形是平行四边形; ( 2)一组对边平行且相等的四边形是平行四边形; ( 3)两组对边分别相等的四边形是平行四边形; ( 4)两组对角分别相等的四边形是平行四边形; ( 5)对角线互相平分的四边形是平行四边形 . 30、矩形的性质: ( 1)具有平行四边形的所有性质 ( 2)矩形的四个角都是直角; ( 3)矩形的对角线相等且互相平分 . 31、矩形的判定: ( 1)有一个角是直角的平行四边形是矩形。 ( 2)有三个角是直角的四边形是矩形 . ( 3)对角线相等的平行四边形是矩形。 32、菱形的性质: ( 1)具有平行四边形的所有性质 ( 2)菱形的四条边都相等; ( 3)菱形的对角线互相垂直平分,并且每一条对角线平分 一组对角 . 33、菱形的判定: ( 1)四条边相等的四边形是菱形 . ( 2)一组邻边相等的平行四边形是菱形。 ( 3)对角线互相垂直的平行四边形是菱形。 34、正方形的性质: ( 1)具有矩形、菱形的所有性质 ( 2)正方形的四个角都是直角; ( 3)正方形的四条边都相等; ( 4)正方形的两条对角线相等,且互相垂直平分,每一条 对角线平分一组对角 . 35、正方形的判定:(证明既是矩形又是菱形) ( 1)有一个角是直角的菱形是正方形; ( 2)有一组邻边相等的矩形是正方形 . ( 3)对角线相等的菱形是正方形 ( 4)对角线互相垂直的矩形是正方形 36、等腰梯形的判定: ( 1)同一条底边上的两个内角相等的梯形是等腰梯形; ( 2)两条对角线相等的梯形是等腰梯形 . 37、等腰梯形的性质: ( 1)等腰梯形的同一条底边上的两个内角相等; ( 2)等腰梯形的两条对角线相等 . 38、梯形的中位线平行于梯形的两底边,并且等于两底和 的一半 . 四、相似形与全等形 39、全等多边形的对应边、对应角分别相等 . 40、全等三角形的判定: ( 1)如果两个三角形的三条边分别对应相等,那么这两个 三角形全等( SSS.) . ( 2)如果两个三角形有两边及其夹角分别对应相等,那么 这两个三角形全等.( SAS.) ( 3)如果两个三角形的两个角及其夹边分别对应相等,那 么这两个三角形全等 (ASA). ( 4)有两个角及其中一个角的对边分别对应相等的两个三 角形全等( AAS.) ( 5)如果两个直角三角形的斜边及一条直角边分别对应相 等,那么这两个直角三角形全等 . ( H.L. ) 41、相似三角形的性质:对应边、周长、对应线段的比均 等于相似比,面积比等于相似比的平方 42、相似三角形的判定:(类似于全等判定) ( 1)平行于三角形的一边的直线和其他两边相交所构成的 三角形与原三角形相似。 ( 2)如果一个三角形的两角分别与另一个三角形的两角对 应相等,那么这两个三角形相似;
初中数学几何定理大全

初中数学公理和定理一、公理(不需证明)1、两直线被第三条直线所截,如果同位角相等,那么这两条直线平行;2、两条平行线被第三条直线所截,同位角相等;3、两边和夹角对应相等的两个三角形全等; (SAS)4、角及其夹边对应相等的两个三角形全等; (ASA)5、三边对应相等的两个三角形全等; (SSS)6、全等三角形的对应边相等,对应角相等.7、线段公理:两点之间,线段最短。
8、直线公理:过两点有且只有一条直线。
9、平行公理:过直线外一点有且只有一条直线与已知直线平行10、垂直性质:经过直线外或直线上一点,有且只有一条直线与已知直线垂直以下对初中阶段所学的公理、定理进行分类:一、直线与角1、两点之间,线段最短。
2、经过两点有一条直线,并且只有一条直线。
3、同角或等角的补角相等,同角或等角的余角相等。
4、对顶角相等二、平行与垂直5、经过直线外或直线上一点,有且只有一条直线与已知直线垂直。
6、经过已知直线外一点,有且只有一条直线与已知直线平行。
7、连接直线外一点与直线上各点的所有线段中,垂线段最短。
8、夹在两平行线间的平行线段相等9、平行线的判定:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行;(4)垂直于同一条直线的两条的直线互相平行.(5)如果两条直线都和第三条直线平行,那么这两条直线也平行10、平行线的性质:(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
三、角平分线、垂直平分线、图形的变化(轴对称、平称、旋转)11、角平分线的性质:角平分线上的点到这个角的两边的距离相等.12、角平分线的判定:到一个角的两边距离相等的点在这个角的平分线上.13、线段垂直平分线的性质:线段的垂直平分线上的点到这条线段的两个端点的距离相等.14、线段垂直平分线的判定:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.15、轴对称的性质:(1)如果图形关于某一直线对称,那么连结对应点的线段被对称轴垂直平分.(2)对应线段相等、对应角相等。
初中数学定理最全整理归纳

初中数学定理大全初中数学点、线、角的定理点的定理:过两点有且只有一条直线点的定理:两点之间线段最短角的定理:同角或等角的补角相等角的定理:同角或等角的余角相等直线定理:过一点有且只有一条直线和已知直线垂直直线定理:直线外一点与直线上各点连接的所有线段中,垂线段最短几何平行定理平行定理:经过直线外一点,有且只有一条直线与这条直线平行推论:如果两条直线都和第三条直线平行,这两条直线也互相平行证明两直线平行定理:同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行两直线平行推论:两直线平行,同位角相等初中数学定理:三角形内角定理定理:三角形两边的和大于第三边推论:三角形两边的差小于第三边三角形内角和定理:三角形三个内角的和等于180°推论1:直角三角形的两个锐角互余推论2:三角形的一个外角等于和它不相邻的两个内角的和推论3:三角形的一个外角大于任何一个和它不相邻的内角全等三角形判定定理定理:全等三角形的对应边、对应角相等边角边定理(SAS):有两边和它们的夹角对应相等的两个三角形全等角边角定理(ASA):有两角和它们的夹边对应相等的两个三角形全等推论(AAS):有两角和其中一角的对边对应相等的两个三角形全等边边边定理(SSS):有三边对应相等的两个三角形全等斜边、直角边定理(HL):有斜边和一条直角边对应相等的两个直角三角形全等角的平分线定理定理1:在角的平分线上的点到这个角的两边的距离相等定理2:到一个角的两边的距离相同的点,在这个角的平分线上角的平分线是到角的两边距离相等的所有点的集合等腰三角形性质定理等腰三角形的性质定理:等腰三角形的两个底角相等(即等边对等角)推论1:等腰三角形顶角的平分线平分底边并且垂直于底边等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合推论3:等边三角形的各角都相等,并且每一个角都等于60°等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)推论1:三个角都相等的三角形是等边三角形推论2有一个角等于60°的等腰三角形是等边三角形初中数学公式定理对称定理定理:线段垂直平分线上的点和这条线段两个端点的距离相等逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上线段的垂直平分线可看作和线段两端点距离相等的所有点的集合定理1:关于某条直线对称的两个图形是全等形定理2:如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线定理3:两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上逆定理:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称直角三角形定理定理:在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半判定定理:直角三角形斜边上的中线等于斜边上的一半勾股定理:直角三角形两直角边a、b的平方和、等于斜边c 的平方,即a^2+b^2=c^2勾股定理的逆定理:如果三角形的三边长a、b、c有关系a^2+b^2=c^2,那么这个三角形是直角三角形多边形内角和定理定理:四边形的内角和等于360°四边形的外角和等于360°多边形内角和定理:n边形的内角的和等于(n-2)×180°推论:任意多边的外角和等于360°平行四边形定理平行四边形性质定理1:平行四边形的对角相等平行四边形性质定理2:平行四边形的对边相等推论:夹在两条平行线间的平行线段相等平行四边形性质定理3:平行四边形的对角线互相平分平行四边形判定定理1:两组对角分别相等的四边形是平行四边形平行四边形判定定理2:两组对边分别相等的四边形是平行四边形平行四边形判定定理3:对角线互相平分的四边形是平行四边形平行四边形判定定理4:一组对边平行相等的四边形是平行四边形矩形的定理矩形性质定理1:矩形的四个角都是直角矩形性质定理2:矩形的对角线相等矩形判定定理1:有三个角是直角的四边形是矩形矩形判定定理2:对角线相等的平行四边形是矩形菱形定理菱形性质定理1:菱形的四条边都相等菱形性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1:四边都相等的四边形是菱形菱形判定定理2:对角线互相垂直的平行四边形是菱形正方形定理正方形性质定理1:正方形的四个角都是直角,四条边都相等正方形性质定理2:正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角中心对称定理定理1:关于中心对称的两个图形是全等的定理2:关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分逆定理:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称等腰梯形性质定理等腰梯形性质定理:1.等腰梯形在同一底上的两个角相等2.等腰梯形的两条对角线相等等腰梯形判定定理:1.在同一底上的两个角相等的梯形是等腰梯形2.对角线相等的梯形是等腰梯形平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边中位线定理三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2S=L×h相似三角形定理相似三角形定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似相似三角形判定定理1:两角对应相等,两三角形相似(ASA)直角三角形被斜边上的高分成的两个直角三角形和原三角形相似判定定理2:两边对应成比例且夹角相等,两三角形相似(SAS)判定定理3:三边对应成比例,两三角形相似(SSS)相似直角三角形定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似性质定理1:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比性质定理2:相似三角形周长的比等于相似比性质定理3:相似三角形面积的比等于相似比的平方三角函数定理任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值初中数学圆的定理1.2不共线的三点确定一个圆经过一点可以作无数个圆经过两点也可以作无数个圆,且圆心都在连结这两点的线段的垂直平分线上定理:过不共线的三个点,可以作且只可以作一个圆推论:三角形的三边垂直平分线相交于一点,这个点就是三角形的外心三角形的三条高线的交点叫三角形的垂心1.3垂径定理圆是中心对称图形;圆心是它的对称中心圆是周对称图形,任一条通过圆心的直线都是它的对称轴定理:垂直于弦的直径平分这条弦,并且评分弦所对的两条弧推论1:平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧推论2:弦的垂直平分弦经过圆心,并且平分弦所对的两条弧推论3:平分弦所对的一条弧的直径,垂直评分弦,并且平分弦所对的另一条弧1.4弧、弦和弦心距定理:在同圆或等圆中,相等的弧所对的弦相等,所对的弦的弦心距相等圆与直线的位置关系2.1圆与直线的位置关系如果一条直线和一个圆没有公共点,我们就说这条直线和这个圆相离如果一条直线和一个圆只有一个公共点,我们就说这条直线和这个圆相切,这条直线叫做圆的切线,这个公共点叫做它们的切点定理:经过圆的半径外端点,并且垂直于这条半径的直线是这个圆的切线定理:圆的切线垂直经过切点的半径推论1:经过圆心且垂直于切线的直线必经过切点推论2:经过切点且垂直于切线的直线必经过圆心如果一条直线和一个圆有两个公共点,我们就说,这条直线和这个圆相交,这条直线叫这个圆的割线,这两个公共点叫做它们的交点直线和圆的位置关系只能由相离、相切和相交三种2.2三角形的内切圆如果一个多边形的各边所在的直线,都和一个圆相切,这个多边形叫做圆的外切多边形,这个圆叫做多边形的内切圆定理:三角形的三个内角平分线交于一点,这点是三角形的内心三角形一内角评分线和其余两内角的外角评分线交于一点,这一点叫做三角形的旁心。
中学数学竞赛中常用的几个重要定理
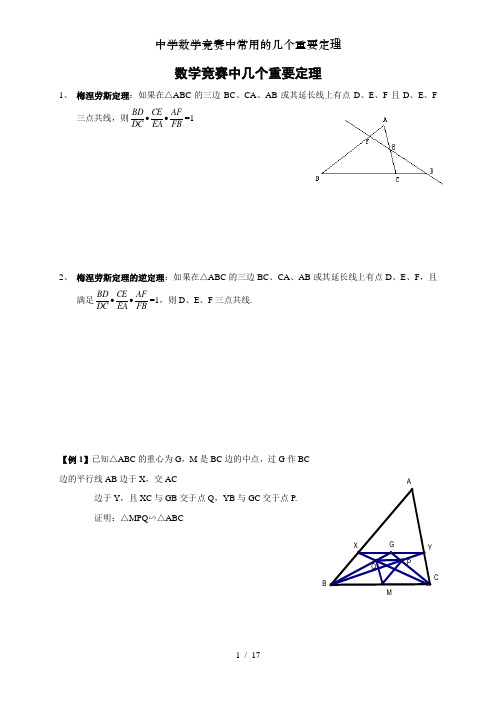
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学定义、定理、公理、公式汇编直线、线段、射线七上p128 1. 过两点有且只有一条直线. (简:两点决定一条直线)七上p132 2.两点之间线段最短七上p142 3.同角或等角的补角相等.同角或等角的余角相等.七下p44. 过一点有且只有一条直线和已知直线垂直七下p65. 直线外一点与直线上各点连接的所有线段中,垂线段最短. (简:垂线段最短)平行线的判断七下p131.平行公理经过直线外一点,有且只有一条直线与这条直线平行.七下p132.如果两条直线都和第三条直线平行,这两条直线也互相平行(简:平行于同一直线的两直线平行)七下p143.同位角相等,两直线平行.七下p144.内错角相等,两直线平行.七下p155.同旁内角互补,两直线平行.平行线的性质七下p201.两直线平行,同位角相等.2.两直线平行,内错角相等.3.两直线平行,同旁内角互补.三角形三边的关系七下p641.三角形两边的和大于第三边、三角形两边的差小于第三边.三角形角的关系七下p731. 三角形内角和定理三角形三个内角的和等于180°.2.直角三角形的两个锐角互余.已知:Rt ABC,∠C=90°求证:∠A+∠B=90°证明:∵∠C=90°,∠A+∠B+∠C=180°∴∠A+∠B=90°七下p753.三角形的一个外角等于和它不相邻的两个内角的和.4. 三角形的一个外角大于任何一个和它不相邻的内角.全等三角形的性质、判定八上p31.全等三角形的对应边、对应角相等.八上p92.边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等.八上p113.角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等.八上p124.推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等.八上p75. 边边边公理(SSS)有三边对应相等的两个三角形全等.八上p146.斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等.角的平分线的性质、判定八上p20性质:在角的平分线上的点到这个角的两边的距离相等.八上p21判定:到一个角的两边的距离相同的点,在这个角的平分线上.等腰三角形的性质八上p501.等腰三角形的性质定理等腰三角形的两个底角相等 (即等边对等角).2.推论 1 等腰三角形顶角的平分线平分底边并且垂直于底边 .已知:ABC中,AB=AC,AD是∠BAC的角平分线求证:AD平分BC,AD⊥BC.证明:∵AB=AC,AD是∠BAC的角平分线∴AD平分BC,AD⊥BC.(三线合一)八上p503.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.八上p544.推论 3 等边三角形的各角都相等,并且每一个角都等于60° .等腰三角形判定八上p521等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)八上p542.三个角都相等的三角形是等边三角形.八上p543.有一个角等于60°的等腰三角形是等边三角形.线段垂直平分线的性质、判定八上p331. 定理:线段垂直平分线上的点和这条线段两个端点的距离相等 .八上p332.逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.3.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合.轴对称、中心对称、平移、旋转八上p301. 关于某条直线对称的两个图形是全等形八上p32 八上p322.如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线八上p333.两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上八上p324.若两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称. 九上p645.关于中心对称的两个图形是全等的.关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分.九上p646. 若两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点成中心对称.九上p57 p627.平移或旋转前后的图形是不变的.中心对称是旋转的特殊形式。
八下p65勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a2+b2=c2 .八下p73勾股定理的逆定理如果三角形的三边长a、b、c有关系a2+b2=c2 ,那么这个三角形是直角八上p55①直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半.八下p95②直角三角形斜边上的中线等于斜边上的一半. n边形、四边形的内角和、外角和七下p821.四边形的内角和等于360°.七下p832.四边形的外角和等于360°七下p823.多边形内角和定理 n边形的内角的和等于(n-2)180°.abABCD七下p834.推论任意多边的外角和等于360°.平行四边形性质八下p841.平行四边形的对角相等.八下p842.平行四边形的对边相等.3.夹在两条平行线间的平行线段相等.已知:直线a∥b,线段AB∥CD.求证:AB=CD.证明:∵a∥b, AB∥CD,∴四边形ABDC是平行四边形∴AB=CD八下p854.平行四边形的对角线互相平分.平行四边形判定八下p831.两组对边分别平行的四边形是平行四边形.八下p872.两组对角分别相等的四边形是平行四边形.八下p873.两组对边分别相等的四边形是平行四边形.八下p874.对角线互相平分的四边形是平行四边形.八下p885. 一组对边平行相等的四边形是平行四边形八下p94矩形性质1. 矩形的四个角都是直角 .2. 矩形的对角线相等.矩形判定八下p951.有一个角是直角的平行四边形是矩形.八下p962.有三个角是直角的四边形是矩形.八下p963. 对角线相等的平行四边形是矩形 .八下p98菱形性质1、菱形的四条边都相等.2. 菱形的对角线互相垂直,并且每一条对角线平分一组对角.3、菱形面积=对角线乘积的一半,即abs21证明:菱形被两条对角线分成四个全等的直角三角形,且菱形对角线互相平分设菱形对角线长为x,y则S菱形=4×1/2×(x/2×y/2)==1/2×xy所以菱形的面积等于其对角线乘积的一半八下p99菱形判定1.有一组邻边相等的平行四边形是菱形2.四边都相等的四边形是菱形3.对角线互相垂直的平行四边形是菱形.八下p100正方形性质1.正方形的四个角都是直角,四条边都相等.2.正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角.正方形判定八下p1001.四个角都是直角,四条边都相等的四边形是正方形2.对角线互相垂直平分且相等的四边形是正方形.证明:对角线互相平分→平行四边形;对角线互相垂直的平行四边形→菱形;对角线相等的平行四边形→矩形形;菱形+矩形→正方形八下p107等腰梯形性质1.等腰梯形在同一底上的两个角相等.2.等腰梯形的两条对角线相等.等腰梯形判定八下p1081.同一底上的两个角相等的梯形是等腰梯形D DE AC BC E AD BCACED AC=DE,ACB=DEB BD=AC BD=DEDBC=DEB DBC=ACB AC=BD,BC=CB ABC DCB AB=DCABCD ∴∴∠∠∴∴∠∠∴∠∠∴∆≅∆∴∴过点作∥交延长线与点,∥四边形是平行四边形梯形是等腰梯形 2.对角线相等的梯形是等腰梯形. 已知:梯形ABCD 中,AD ∥BC,AC=BD. 求证:梯形ABCD 是等腰梯形。
证明:① 经过梯形一腰的中点与底平行的直线,必平分另一腰.已知:梯形ABCD 中,AD ∥BC ∥EF ,其中E 是AB 中点。
求证:F 是CD 中点 证明:连接AC 交EF 于点G ∵AD ∥BC ∥EF ∴△AEG ∽△ABC∵E 是AB 中点∴12AEAG AB AC == ∴12CGAC= 同理可证12CF CG CD AC == ∴F 是CD 中点.② 经过三角形一边的中点与另一边平行的直线,必平分第三边. (证法参照上题) 八下p89三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半.梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半 )(21b a l +=,S=Lh已知:梯形ABCD 中,AD ∥BC, EF 是梯形的中位线,设AD=a,BC=b,EF=l,梯形高为h 。
求证:)(21b a l += S=Lh证明:连接AF 交BC 延长线与G 点ABCD DF=CFAD BCG=DAG,D=DCG ADF GCFAD=CG=,ABG 1EF BG,EF=BG21()21=BG 212ABG EF a AF FG EF l a b S S hS Lh∆∴∴∠∠∠∠∴∆≅∆∴=∴∆∴∴=+=⨯∴=梯形是中位线是的中位线1k OB OA AC OE OD ED ===1k OC OA AC OF OD FD ===1kAC BA BC OA FD ED EF OD ∴==== 九下p36比例的基本性质 如果相似三角形判定 九下p42 1.定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似. 九下p462.两角对应相等,两三角形相似. 九下p443.两边对应成比例且夹角相等,两三角形相似 九下p434.三边对应成比例,两三角形相似 九下p475.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 已知:RT △ABC 和RT △DEF ,AC 与DF 为ABCRT =AC:DF=AB :DE∴三边对应成比例∴RT △ABC RT △DEF相似三角形性质 九下p521. 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.2.相似三角形周长的比等于相似比.3.相似三角形面积的比等于相似比的平方. 九下p59-604.位似图形是相似图形的特殊形式。
位似比等于相似比。
以三角形为例:已知:ABC ∆与DEF ∆是以O 为位似中心的位似图形,位似比为1:k求证:ABC ∆与DEF ∆的相似比为1:k ABC ∆与DEF ∆是以O 为位似中心的位似图形]理可得 ,ABC DEF ∴,ABC ∆与DEF ∆的相似比为1:k1k BC EF OBC OEF OB OC BC OE OF EF ∴∴∴===,OA OB AD BD OD AB CD AB==∴⊥⊥又,11,22()BA CD OE AB OF CD AE AB CF CDAE CF OAE OCF AE CF OA OC OAE OCF HL OE OF=⊥⊥∴==∴==⎧⎨=⎩∴≅∴=在Rt 和Rt 中Rt Rt 圆九上p791.圆是到定点的距离等于定长的点的集合. 九上p902.圆的内部可以看作是到圆心的距离小于半径.的点的集合.3.圆的外部可以看作是到圆心的距离大于半径的点的集合. 九上p794.同圆或等圆的半径相等. 九上p925.不在同一直线上的三点确定一个圆。
