高等数学知识地图
高等数学知识地图

函数映射函数保序性数列极限唯一性联系→性质有界性微积分学函数极限保号性e^x理论基础无穷小→无穷小的比较→等价无穷小sin(x)、cos(x)——极限无穷及常用代换微分学ln(1+x)、(1+x)^n 函数、无穷大极限运算法则麦克劳林中值定理→佩亚诺型余项和连续存在法则→重要极限↑↑定义四则运算复合函数连续性反函数连续初等函数端点间断点第一类——可去、跳跃↓第二类——无穷、振荡鞍点最值点←间断点、不可导点最值定理函数↑↑介值定理y’=0原理基本概念零点基本定理拐点y=0可分离变量的微分方程y’’=0 一阶微分方程齐次微分方程→可化为齐次微分方程的方程线性微分方程常微分伯努利方程方程全微分方程可降阶的y^(n)=f(x)高阶微分方程y’’=f(x,y’)、y’’=f(y,y’) 函数高阶微分方程常系数线性齐次方程微分方程非齐次方程Pn(x)e^ax差分欧拉方程(Pl(x)cos(bx) 弧长方程其他解法幂级数解法+Pn(x)sin(bx))e^ax 几何应用平面面积、回转体侧面积微分方程组的解法物理应用体积概念、性质条件收敛比较定义几何级数绝对收敛比值极限最值定理p级数审敛法根值连续介值定理常数项级数正项级数极限定义、计算交错级数高阶偏导数无穷级数概念线性性质收敛区间幂级数性质微分积分性收敛域敛散性收敛半径→求法向量值函数→方向导数→梯度grad 函数项级数泰勒级数→函数展开式几何曲线——切线与法平面应用近似计算曲面——法线与切平面解微分方程极值、最值→条件极值→拉格朗日乘数法三角级数→正交性泰勒公式→拉格朗日中值定理↓定义定义、性质→中值定理傅立叶级数敛散性→狄利克雷收敛定理计算直角坐标→X、Y型函数展开二重积分极坐标→R、θ型无界区域上的二重积分定义、坐标表示重积分换元法概念模方向角定义、性质截面法方向方向余弦多元函数三重积分柱坐标面积投影法向量运算加减法方向数积分学球坐标乘法→数乘、数量积、向量积、混合积及应用应用几何相互关系平行、垂直物理夹角、投影第一类曲线积分——定义、性质、计算空间方程——一般式、点法式、截距式、三点式↓联系↑解析几何面平面关系——平行、垂直、相交、夹角曲线积分第二类曲线积分——定义、性质、计算与距离——点面、线面、面面线面积分格林公式→平面曲线积分与路径无关的条件向量代数二次曲面——九种常见曲面及方程斯托克斯公式→空间曲线积分与路径无关的条件曲面法线与切平面第一类曲面积分——定义、性质、计算方程——一般式、点向式、参数式、两点式曲面积分↓联系↑直线关系——平行、垂直、相交、异面、夹角——平面束第二类曲面积分——定义、性质、计算线距离——点线、线线概念→数量场、矢量场高斯公式→延任意闭曲面的曲面积分为零的条件方程方向导数→梯度grad曲线投射——投影柱面、投影曲线场论通量→散度div 哈密顿算子▽→拉普拉斯算子△切线与法平面环量→旋度rot学习必备欢迎下载。
高等数学知识地图
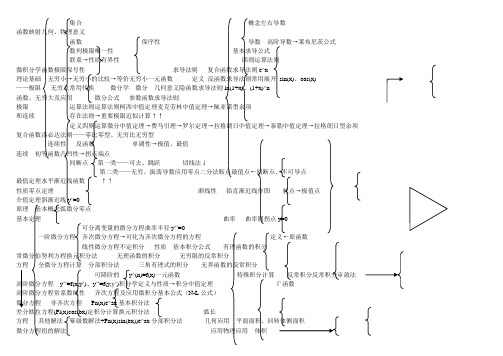
集合概念左右导数函数映射几何、物理意义函数保序性导数高阶导数→莱布尼茨公式数列极限唯一性基本求导公式联系→性质有界性四则运算法则微积分学函数极限保号性求导法则复合函数求导法则e^x理论基础无穷小→无穷小的比较→等价无穷小一元函数定义反函数求导法则常用展开sin(x)、cos(x)——极限无穷及常用代换微分学微分几何意义隐函数求导法则ln(1+x)、(1+x)^n函数、无穷大及应用微分公式参数函数求导法则极限运算法则运算法则柯西中值定理麦克劳林中值定理→佩亚诺型余项和连续存在法则→重要极限近似计算↑↑定义四则运算微分中值定理→费马引理→罗尔定理→拉格朗日中值定理→泰勒中值定理→拉格朗日型余项复合函数洛必达法则——零比零型、无穷比无穷型连续性反函数单调性→极值、最值连续初等函数凸凹性→拐点端点间断点第一类——可去、跳跃切线法↓第二类——无穷、振荡导数应用零点二分法鞍点最值点←间断点、不可导点最值定理水平渐近线函数↑↑性质零点定理渐线性铅直渐近线作图驻点→极值点介值定理斜渐近线y’=0原理基本概念弧微分零点基本定理曲率曲率圆拐点y=0可分离变量的微分方程曲率半径y’’=0一阶微分方程齐次微分方程→可化为齐次微分方程的方程定义←原函数线性微分方程不定积分性质基本积分公式有理函数的积分常微分伯努利方程换元积分法无理函数的积分无穷限的反常积分方程全微分方程计算分部积分法三角有理式的积分无界函数的反常积分可降阶的y^(n)=f(x)一元函数特殊积分计算反常积分反常积分审敛法高阶微分方程y’’=f(x,y’)、y’’=f(y,y’)积分学定义与性质→积分中值定理Γ函数高阶微分方程常系数线性齐次方程及应用微积分基本公式(N-L公式)微分方程非齐次方程Pn(x)e^ax基本积分法差分欧拉方程(Pl(x)cos(bx)定积分计算换元积分法弧长方程其他解法幂级数解法+Pn(x)sin(bx))e^ax分部积分法几何应用平面面积、回转体侧面积微分方程组的解法应用物理应用体积概念、性质条件收敛比较平面点集定义几何级数绝对收敛比值理论基础极限最值定理p级数审敛法根值多元函数连续介值定理常数项级数正项级数极限偏导数定义、计算交错级数多元函数高阶偏导数无穷级数线性性质收敛区间微分学微分法全微分微分积分性收敛域及应用求导法则——复合函数、隐函数敛散性收敛半径→求法应用grad 函数项级数近似计算解微分方程三角级数→正交性↓定义傅立叶级数敛散性→狄利克雷收敛定理X、Y型函数展开R、θ型定义、坐标表示重积分概念模方向角截面法方向方向余弦多元函数三重积分柱坐标面积投影法向量运算加减法方向数积分学球坐标乘法→数乘、数量积、向量积、混合积及应用应用相互关系平行、垂直夹角、投影第一类曲线积分——定义、性质、计算空间方程——一般式、点法式、截距式、三点式↓联系↑解析几何面平面关系——平行、垂直、相交、夹角曲线积分第二类曲线积分——定义、性质、计算与距离——点面、线面、面面线面积分格林公式→平面曲线积分与路径无关的条件向量代数二次曲面——九种常见曲面及方程斯托克斯公式→空间曲线积分与路径无关的条件曲面法线与切平面第一类曲面积分——定义、性质、计算方程——一般式、点向式、参数式、两点式曲面积分↓联系↑直线关系——平行、垂直、相交、异面、夹角——平面束第二类曲面积分——定义、性质、计算线距离——点线、线线概念→数量场、矢量场高斯公式→延任意闭曲面的曲面积分为零的条件方程方向导数→梯度grad曲线投射——投影柱面、投影曲线场论通量→散度div 哈密顿算子▽→拉普拉斯算子△切线与法平面环量→旋度rot。
数学有意思11 为什么世界地图是平的

11 为什么世界地图是平的?本集覆盖基础课程知识点三年级数学 | 测量六年级数学 | 比例尺七年级地理 | 认识地图九年级数学 | 中心投影与平行投影高等数学 | 数学模型——————————————这一集,我来告诉你怎么选择合适的数学模型。
| 如何选择世界地图?我先问你个问题,你知道世界地图的缺点吗?在我们最常见的世界地图里,国家的大小被严重扭曲了,越靠近两极的国家面积显得越大。
比如我们看地图,会觉得俄罗斯的面积和非洲差不多大,其实非洲比俄罗斯大了一倍半都多。
也就是说我们平时使用的世界地图把真实的世界严重扭曲了。
你要是光看这张世界地图,你会得出很多错误的结论,要想得不出错误的结论也很容易,使用地球仪就行了。
地球仪是球形的,它上面的各国面积就没有被歪曲,可是在现实中往往是世界地图比地球仪更常见。
i那么,现在的问题是,明明地球仪比世界地图更准确,为什么大部分人还会去用地图?这需要用模型的思想来回答。
你记不记得我们前两次讲过建立模型的思想?所谓建立模型,简单地说,就是我们从一个现实问题中筛选出一些关键的信息,用一个规律描述出这些信息之间的关系,这个抽象的规律就叫做模型。
我们还举过原始人数水果的例子,原始人想记住水果的数量,可是水果有很多属性,有大小、重量、颜色,太复杂了。
于是这个原始人就把所有他觉得不重要的信息全都抛弃掉,只抓住一个他认为最重要的信息,就是个数。
他利用个数这个信息,建立了一个数学模型叫做“正整数”,然后就可以用这个模型来确定他到底有多少水果了。
我们说过,数学是一门追求精确的学科,可是在刚才那个原始人建立模型的过程中,他有一步其实并不精确,就是他在选择哪些信息重要,哪些信息可以忽略掉的那一步。
原始人并没有经过一个严谨的逻辑推理来证明,他凭什么选择“个数”这个信息,凭什么抛弃掉了其他信息?所以,他建立的这个数学模型其实不是绝对精确的。
| 什么是好用的模型?我们可以想像另外一个场景:假设我现在不是原始人,是一个水果公司的经理,我要管理库存的水果,那么这个时候,我用来描述水果的数学模型就不能是水果的个数。
不同角度下高等数学知识的思维导图绘制

不同角度下高等数学知识的思维导图绘制摘要:本文根据高等数学学科的特点,从不同视角,阐释知识概念、计算方法和逻辑推理,形成特色的思维导图,使得抽象概念、复杂公式、严谨理论直观化和可视化,有助于学生提升学习质量和效率,并锻炼学生的逻辑和创新思维能力。
1.引言对于理工科专业学生,高等数学是一门重要的公共基础必修课程。
课程内容庞大复杂分散,不仅有着高度的抽象性和概括性,而且具有严密的逻辑性和连贯性。
对于大一学生,高等数学课程难度和学习进度相比高中情形明显难且快,且课程课时学习短。
因此,在高等数学课程中,如何在有限的时间内使学生理解并掌握庞大复杂分散的知识体系,是高等数学课程中教师所面临的教育难题。
随着教育教学改革的不断深入,根据人类大脑的放射性工作机制,教师在教学活动中越来越广泛地综合应用思维导图方法。
思维导图(Mind Mapping)又称心智图, 是享有“世界大脑先生”美誉的英国著名心理学家、教育学家东尼·博赞 (Tony Busan) 于20世纪60年代所创[1]。
思维导图呈现了思维的自然表达过程,以图示的方式向人们展现看不见、摸不着的思维结构。
一张思维导图是一张很好的知识地图。
随着颜色、位置、图像、符号、逻辑等元素的加入,思维导图的呈现变得更加鲜活和丰富,能够有效地激发学生的学习兴趣和参与积极性,在培养学生自主学习、创新思维能力方面具有巨大的作用与价值。
在文献[2-5]中,分别研究了思维导图在高等数学课堂中的应用、提高学生学习效率等方面的研究。
本文根据高等数学的知识体系和思维导图的特征,从填空、知识的联系与区别以及分类汇总角度出发,将具体概念、定理、计算等内容的知识逻辑结构化,通过不断研发、实践和优化,形成特色思维导图,使得数学逻辑更为直观可视化。
这将有助于更好地展现数学教学的新颖性,引导学生建构系统的知识体系,掌握知识之间的逻辑性,拓展学生思维和视野,培养学生的数学素养和创新思维能力。
高等数学场论基本概念

数学物理基础梯度、散度和旋度梯度、散度和旋度是矢量分析里的重要概念。
之所以是“分析”,因为三者是三种偏导数计算形式。
这里假设读者已经了解了三者的定义。
它们的符号分别记作如下:从符号中可以获得这样的信息:①求梯度是针对一个标量函数,求梯度的结果是得到一个矢量函数。
这里φ称为势函数;②求散度则是针对一个矢量函数,得到的结果是一个标量函数,跟求梯度是反一下的;③求旋度是针对一个矢量函数,得到的还是一个矢量函数。
这三种关系可以从定义式很直观地看出,因此可以求“梯度的散度”、“散度的梯度”、“梯度的旋度”、“旋度的散度”和“旋度的旋度”,只有旋度可以连续作用两次,而一维波动方程具有如下的形式(1)其中a为一实数,于是可以设想,对于一个矢量函数来说,要求得它的波动方程,只有求它的“旋度的旋度”才能得到。
下面先给出梯度、散度和旋度的计算式:(2)(3)(4)旋度公式略显复杂。
这里结合麦克斯韦电磁场理论,来讨论前面几个“X度的X度”。
I.梯度的散度:根据麦克斯韦方程有:而(5)则电势的梯度的散度为这是一个三维空间上的标量函数,常记作(6)称为泊松方程,而算符▽2称为拉普拉斯算符。
事实上因为定义所以有当然,这只是一种记忆方式。
当空间内无电荷分布时,即ρ=0,则称为拉普拉斯方程当我们仅需要考虑一维情况时,比如电荷均匀分布的无限大平行板电容器之间(不包含极板)的电场,我们知道该电场只有一个指向,场强处处相等,于是该电场满足一维拉普拉斯方程,即这就是说如果那边平行板电容器的负极板接地,则板间一点处的电压与该点距负极板的距离呈线性关系。
II.散度的梯度:散度的梯度,从上面的公式中可以看到结果会比较复杂,但是它的物理意义却是很明确的,因为从麦克斯韦方程可以看出空间某点处电场的散度是该点处的电荷密度,那么再求梯度就是空间中电荷密度的梯度。
这就好比说清水中滴入一滴红墨水,起初水面红色浓度最高,杯底浓度最低,这样水面与杯底形成一个浓度梯度,红墨水由水面向杯底扩散,最后均匀。
考研高等数学知识点总结

高等数学知识点总结导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
高数基础知识自学方法

高数基础知识自学方法在数学的世界里,高等数学像是一个神秘的迷宫,吸引着那些渴望探险的心灵。
为了在这个迷宫中找到出口,你需要一个系统而有效的自学方法。
首先,你必须了解高等数学的基本概念和结构。
将复杂的理论分解成易于消化的部分就像是给迷宫中的每个角落贴上标签,让你能更清晰地辨认方向。
选择合适的教材是关键。
教材不仅是知识的容器,更是引导你走向知识深处的地图。
选择那些内容清晰、讲解详细且配有丰富例题的教材,可以大大提高你的学习效率。
记住,基础知识的掌握是成功的前提,因此,细致地阅读教材中的每一个定义和定理,不应跳过任何一个看似简单的步骤。
实践是检验理论的最佳方式。
通过做大量的习题,你可以在实际应用中加深对理论的理解。
每一道题目都像是迷宫中的一扇门,打开它,你会发现更多的知识和技巧。
不要害怕错误,错误是探索过程中的宝贵经验,它们指引你找出自己的不足,并不断修正。
另外,制定一个合理的学习计划至关重要。
设定明确的学习目标和时间表,可以帮助你保持专注,并逐步完成学习任务。
像规划一场探险旅程一样,设定每一天的学习目标,并定期回顾自己的进度,能够让你在不断前行的同时保持方向感。
求助于外部资源也是一种有效的学习方法。
网络上有大量的学习资源,如在线课程、论坛和学术文章,这些都能为你提供额外的视角和解释。
通过与他人讨论问题,你可以更全面地理解复杂的概念,就像是在迷宫中遇到的指引者,帮助你找到正确的路径。
保持积极的学习态度同样重要。
在高等数学的学习过程中,难题和挫折是难以避免的。
要学会以平常心对待这些挑战,相信每一次的失败都是通向最终成功的垫脚石。
持续的努力和坚持将是你通向高等数学精通的关键。
最后,定期复习已学的内容,巩固基础知识。
就像是不断回顾地图上的每一个细节,你需要时不时地回到之前学过的部分,以确保自己对知识的掌握牢固且准确。
通过不断地复习和练习,你将能够逐渐构建起高等数学的完整知识体系,最终在这个知识的迷宫中自如地穿行。
专升本高数全知识点

专升本高数全知识点一、知识概述《专升本高数全知识点》①基本定义:高等数学就是大学数学,主要研究函数、极限、导数、积分这些东西。
函数就像是一个有输入和输出的“魔法盒子”,你给它一个数,它按照一定规则给你一个结果。
极限有点像你一直朝着一个地方走,快到目的地但还没到那个确切的点时候的情况。
导数呢,就是函数在某一点变化的快慢程度,就像汽车在某个瞬间的速度。
积分和导数相反,就像是知道速度求路程这样。
②重要程度:在专升本学科里那可是相当重要的。
很多专业都要考,而且是筛选人才的重要部分。
高数好的话,在理工科专业学习起来就会很顺利。
③前置知识:你得对基本的代数知识很熟悉,像一元二次方程这些。
还有函数的概念也要清楚,比如一次函数、二次函数的图像性质等。
④应用价值:在工程领域可以用来计算结构强度,在经济领域可以做成本效益分析之类的。
比如说盖房子的时候,通过高数能算出怎么设计结构能承受更大压力。
二、知识体系①知识图谱:整个高数体系像一棵大树,函数是树根,极限是树干,导数和积分就是树枝和树叶。
导数和积分又各自有很多分支。
②关联知识:函数和极限密切相关,有函数才有极限概念。
导数是从极限发展来的,积分又和导数是逆运算关系。
③重难点分析:重难点有极限的计算(有时候要用到很多复杂技巧)、导数的复合函数求导、积分的换元积分法。
关键是要理解概念然后多做练习才能掌握。
④考点分析:在考试里每个部分都可能考。
选择题会考查基本概念,计算题就着重极限、导数、积分的计算等。
应用题可能会把高数知识用在实际场景下考查。
三、详细讲解【理论概念类- 函数】①概念辨析:函数就是一种对应关系,一个自变量x能通过某种法则找到唯一对应的因变量y。
就像每个人(x)对应着自己唯一的身份证号(y)。
②特征分析:主要特征就是有定义域(x能取的值的范围)和值域(y 能取的值的范围)。
单值性是很重要的一点,就是一个x只能对应一个y。
③分类说明:有初等函数像多项式函数(如y = x²+1)、三角函数(如y = sinx)等,还有分段函数,就是在不同区间有不同表达式的函数。
高等数学模型—微积分模型(数学建模课件)

2、假设易拉罐是一个正圆柱体,什么是它的最优设计?其结果是
否可以合理地说明你们所测量地易拉罐地形状和尺寸。
二、数据测量
罐直径、罐高、罐壁厚、顶盖厚、圆台高、
顶盖直径、圆柱体高、罐底厚、罐内体积等。
该如何测量?
二、数据测量
1、直接测量
①用软皮尺环绕易拉罐相关部位一圈
(罐桶直径、罐
测得周长。
高、圆台高、顶
速度、出手角度和出手高度)
作定性和定量研究并得到明
确结论。
森林救火问题
微积分模型
知识点
一、问题的提出
二、模型分析与假设
三、模型建立与求解
四、模型应用
一、问题的提出
一、问题的提出
森林失火了!消防站接到火警后,立即决定派消防队员前去救火。队
员多,火被扑灭的快,森林损失小,但救援费用大;队员少,救援费用小,
118.0 123.5 136.5 142.0 146.0 150.0 157.0 158.0];
y1=[44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68];
y2=[44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86
四、模型建立与求解
一、问题的提出
运动员单手托住铅球,在投掷圆内将铅球掷出并使铅
球落入有效区内,以铅球投掷的远度评定运动员的成绩。
问题:
建模分析如何使铅球投掷的最远?
二、问题分析
• 铅球投掷中,影响投掷距离的因素有哪些?
伯努利效应用到的高等数学知识

伯努利效应用到的高等数学知识伯努利效应在生活中可真是个神奇的存在呢。
那它用到了哪些高等数学知识呢?咱先得知道啥是伯努利效应。
就好比你拿着两张纸,往中间吹气,你会发现两张纸竟然贴在一起了,这就是伯努利效应在捣鬼。
从数学的角度看,这背后可有不少门道。
微积分在伯努利效应里可是个重要角色。
你想啊,流体的运动是很复杂的,速度在不同位置是不一样的。
这就像一群小蚂蚁在搬家,有的地方蚂蚁走得快,有的地方走得慢。
那怎么描述这种速度的变化呢?这就用到微积分里的导数概念了。
导数就像是一个放大镜,能把速度在某一点的变化趋势给揪出来。
在伯努利效应里,流体速度的这种变化和压力的变化是紧密相关的。
速度变了,压力也跟着变,这就像是一个连锁反应。
要是没有微积分这个强大的工具,咱们可很难精确地描述这种关系呢。
你说是不是?再说说多元函数吧。
在实际的流体情况中,可不是只有一个变量在起作用。
就好比做菜,你不能只放盐或者只放酱油,很多因素都得考虑。
流体的压力、速度、密度这些量可都是相互影响的。
这就像一个复杂的人际关系网,每个人都和其他人有着千丝万缕的联系。
多元函数就可以把这些变量之间的关系用一种数学的方式表示出来。
在伯努利效应里,通过多元函数,我们能更好地理解压力、速度、密度这些量是怎么相互作用的。
这就好比有了一张地图,我们能清楚地看到各个地方之间的联系。
向量分析也在伯努利效应里露了脸。
流体的流动是有方向的,这就像风往哪儿吹是有方向的一样。
向量就能很好地描述这种有方向的量。
在伯努利效应里,流体的速度、力这些都是向量。
我们要研究流体在不同方向上的表现,向量分析就派上用场了。
如果把流体比作一群奔跑的马,那向量就像是缰绳,能控制着马往哪个方向跑,能描述马跑的力量大小和方向。
要是没有向量分析,我们就只能模糊地知道流体在动,却不知道它具体怎么动的。
还有微分方程呢。
伯努利效应中的各种关系可不会是一成不变的。
随着时间和空间的变化,这些关系也在变。
这就像天气一样,一会儿晴一会儿雨的。
高数学习中的思维导图与总结技巧

高数学习中的思维导图与总结技巧
在高等数学学习中,思维导图与总结技巧扮演着重要角色。
它们如同一位引导者,带领着学生们在广袤的数学知识海洋中航行,找到宝贵的知识珍珠并将它们串联成精巧的项链。
首先,思维导图可以比喻为一张引导地图。
当学生们面对复杂的数学概念和公式时,这张地图为他们指明方向,帮助他们理清头绪。
通过将各个概念、定理、公式用节点和链接连接起来,思维导图呈现出数学知识的结构和逻辑关系。
就像一位热心的导游,它们把学生们从迷失的迷宫中带出来,让他们能够更清晰地看到整个数学学科的全景图。
其次,总结技巧像是一位智者,帮助学生们从学习的浩瀚中提炼精华。
通过总结,学生们可以把学到的知识归纳概括,从而更深刻地理解和记忆。
就像一个精巧的工匠,总结技巧帮助学生们将零散的数学知识点打磨成统一的整体。
它们教导学生们如何从细节中抽丝剥茧,发现并把握住数学问题的核心。
在实际运用中,思维导图与总结技巧相辅相成。
思维导图提供了一个构建知识结构的框架,而总结技巧则在这个框架上填充内容,使其更加丰富和有力。
通过将两者结合运用,学生们可以
在高等数学学习中事半功倍,既提高学习效率又加深对数学内容的理解。
总之,高等数学学习中的思维导图和总结技巧如同学习之路上的得力助手。
它们不仅指引着学生们前行的方向,还帮助他们在广袤的数学知识海洋中留下深刻的足迹。
通过不断地练习和应用,学生们能够将这些技巧内化成为自己学习的一部分,从而在数学学习的旅程中获得更多的收获和成长。
大学高等数学知识点

大学高等数学知识点整理公式,用法合集极限与连续一.数列函数: 1.类型:(1)数列:*()n a f n =;*1()n n a f a += (2)初等函数:(3)分段函数:*0102()(),()x x f x F x x x f x ≤⎧=⎨>⎩;*0()(),x x f x F x x x a ≠⎧=⎨=⎩;* (4)复合(含f )函数:(),()y f u u x ϕ== (5)隐式(方程):(,)0F x y =(6)参式(数一,二):()()x x t y y t =⎧⎨=⎩(7)变限积分函数:()(,)xa F x f x t dt =⎰(8)级数和函数(数一,三):0(),n n n S x a x x ∞==∈Ω∑2.特征(几何):(1)单调性与有界性(判别);(()f x 单调000,()(()())x x x f x f x ⇒∀--定号) (2)奇偶性与周期性(应用).3.反函数与直接函数:11()()()y f x x f y y f x --=⇔=⇒= 二.极限性质:1.类型:*lim n n a →∞;*lim ()x f x →∞(含x →±∞);*0lim ()x x f x →(含0x x ±→) 2.无穷小与无穷大(注:无穷量):3.未定型:000,,1,,0,0,0∞∞∞-∞⋅∞∞∞4.性质:*有界性,*保号性,*归并性 三.常用结论:11n n →,1(0)1n a a >→,1()max(,,)nnn na b c a b c ++→,()00!na a n >→1(0)x x→→∞,0lim1xx x +→=,lim 0n x x x e →+∞=,ln lim 0n x x x →+∞=, 0lim ln 0nx x x +→=,0,xx e x →-∞⎧→⎨+∞→+∞⎩四.必备公式:1.等价无穷小:当()0u x →时,sin ()()u x u x :;tan ()()u x u x :;211cos ()()2u x u x -:; ()1()u x e u x -:;ln(1())()u x u x +:;(1())1()u x u x αα+-:;arcsin ()()u x u x :;arctan ()()u x u x :2.泰勒公式:(1)2211()2!x e x x o x =+++; (2)221ln(1)()2x x x o x +=-+;(3)341sin ()3!x x x o x =-+;(4)24511cos 1()2!4!x x x o x =-++;(5)22(1)(1)1()2!x x x o x αααα-+=+++. 五.常规方法:前提:(1)准确判断0,,1,0M α∞∞∞(其它如:00,0,0,∞-∞⋅∞∞);(2)变量代换(如:1t x=)1.抓大弃小()∞∞,2.无穷小与有界量乘积(M α⋅)(注:1sin 1,x x≤→∞) 3.1∞处理(其它如:000,∞) 4.左右极限(包括x →±∞):(1)1(0)x x→;(2)()x e x →∞;1(0)x e x →;(3)分段函数:x ,[]x ,max ()f x5.无穷小等价替换(因式中的无穷小)(注:非零因子)6.洛必达法则(1)先”处理”,后法则(00最后方法);(注意对比:1ln lim1x x x x →-与0ln lim 1x x xx→-) (2)幂指型处理:()()ln ()()v x v x u x u x e=(如:1111111(1)x x x x xee e e-++-=-)(3)含变限积分; (4)不能用与不便用7.泰勒公式(皮亚诺余项):处理和式中的无穷小 8.极限函数:()lim (,)n f x F x n →∞=(⇒分段函数) 六.非常手段 1.收敛准则: (1)()lim ()n x a f n f x →+∞=⇒ (2)双边夹:*?n n n b a c ≤≤,*,?n n b c a →(3)单边挤:1()n n a f a +=*21?a a ≥*?n a M ≤*'()0?f x >2.导数定义(洛必达):00lim '()x ff x x→=VV V 3.积分和:10112lim[()()()]()n nf f f f x dx n n n n →∞+++=⎰L , 4.中值定理:lim[()()]lim '()x x f x a f x a f ξ→+∞→+∞+-=5.级数和(数一三):(1)1n n a ∞=∑收敛lim 0n n a →∞⇒=,(如2!lim n n n n n →∞)(2)121lim()n n n n a a a a ∞→∞=+++=∑L , (3){}n a 与11()n n n a a ∞-=-∑同敛散七.常见应用:1.无穷小比较(等价,阶):*(),(0)?n f x kx x →: (1)(1)()(0)'(0)(0)0,(0)n n f f f f a -=====⇔L ()()!!n n na a f x x x x n n α=+: (2)00()xxn f t dt kt dt ⎰⎰:2.渐近线(含斜):(1)()lim,lim[()]x x f x a b f x ax x→∞→∞==-()f x ax b α⇒++: (2)()f x ax b α=++,(10x→)3.连续性:(1)间断点判别(个数);(2)分段函数连续性(附:极限函数,'()f x 连续性) 八.[,]a b 上连续函数性质1.连通性:([,])[,]f a b m M =(注:01λ∀<<,“平均”值:0()(1)()()f a f b f x λλ+-=)2.介值定理:(附:达布定理)(1)零点存在定理:()()0f a f b <0()0f x ⇒=(根的个数); (2)()0(())'0xa f x f x dx =⇒=⎰.第二讲:导数及应用(一元)(含中值定理)一.基本概念:1.差商与导数:'()f x =0()()limx f x x f x x→+-V V V ;0'()f x =000()()lim x x f x f x x x →--(1)0()(0)'(0)limx f x f f x →-=(注:0()lim (x f x A f x→=连续)(0)0,'(0)f f A ⇒==) (2)左右导:''00(),()f x f x -+;(3)可导与连续;(在0x =处,x 连续不可导;x x 可导) 2.微分与导数:()()'()()'()f f x x f x f x x o x df f x dx =+-=+⇒=V V V V (1)可微⇔可导;(2)比较,f df ∆与"0"的大小比较(图示); 二.求导准备:1.基本初等函数求导公式;(注:(())'f x )2.法则:(1)四则运算;(2)复合法则;(3)反函数1'dx dy y = 三.各类求导(方法步骤):1.定义导:(1)'()f a 与'()x a f x =;(2)分段函数左右导;(3)0()()limh f x h f x h h→+--(注:0()(),x x F x f x x x a ≠⎧=⎨=⎩,求:0'(),'()f x f x 及'()f x 的连续性) 2.初等导(公式加法则): (1)[()]u f g x =,求:0'()u x (图形题);(2)()()xa F x f t dt =⎰,求:'()F x (注:((,))',((,))',(())'xbba a a f x t dt f x t dt f t dt ⎰⎰⎰)(3)0102(),()x x f x y x x f x <⎧=⎨≥⎩,求''00(),()f x f x -+及0'()f x (待定系数) 3.隐式((,)0f x y =)导:22,dy d ydx dx(1)存在定理;(2)微分法(一阶微分的形式不变性). (3)对数求导法.4.参式导(数一,二):()()x x t y y t =⎧⎨=⎩,求:22,dy d ydx dx5.高阶导()()n f x 公式:()()ax n n axe a e =;()11!()()n n n b n a bx a bx +=--; ()(sin )sin()2n n ax a ax n π=+⨯;()(cos )cos()2n n ax a ax n π=+⨯注:()(0)n f与泰勒展式:2012()nn f x a a x a x a x =+++++L L ()(0)!n n f a n ⇒=四.各类应用:1.斜率与切线(法线);(区别:()y f x =上点0M 和过点0M 的切线)2.物理:(相对)变化率-速度;3.曲率(数一二):ρ=曲率半径,曲率中心,曲率圆)4.边际与弹性(数三):(附:需求,收益,成本,利润) 五.单调性与极值(必求导) 1.判别(驻点0'()0f x =):(1)'()0()f x f x ≥⇒Z ;'()0()f x f x ≤⇒]; (2)分段函数的单调性(3)'()0f x >⇒零点唯一;"()0f x >⇒驻点唯一(必为极值,最值). 2.极值点:(1)表格('()f x 变号);(由0002'()'()''()lim0,lim 0,lim 00x x x x x x f x f x f x x x x x→→→≠≠≠⇒=的特点)(2)二阶导(0'()0f x =)注(1)f 与',"f f 的匹配('f 图形中包含的信息);(2)实例:由'()()()()f x x f x g x λ+=确定点“0x x =”的特点. (3)闭域上最值(应用例:与定积分几何应用相结合,求最优) 3.不等式证明(()0f x ≥)(1)区别:*单变量与双变量*[,]x a b ∈与[,),(,)x a x ∈+∞∈-∞+∞ (2)类型:*'0,()0f f a ≥≥;*'0,()0f f b ≤≥ *"0,(),()0f f a f b ≤≥;*00"()0,'()0,()0f x f x f x ≥=≥ (3)注意:单调性⊕端点值⊕极值⊕凹凸性.(如:max ()()f x M f x M ≤⇔=) 4.函数的零点个数:单调⊕介值 六.凹凸与拐点(必求导!): 1."y ⇒表格;(0"()0f x =)2.应用:(1)泰勒估计;(2)'f 单调;(3)凹凸. 七.罗尔定理与辅助函数:(注:最值点必为驻点) 1.结论:()()'()()0F b F a F f ξξ=⇒== 2.辅助函数构造实例: (1)()f ξ⇒()()xa F x f t dt =⎰(2)'()()()'()0()()()f g f g F x f x g x ξξξξ+=⇒= (3)()'()()()'()0()()f x fg f g F x g x ξξξξ-=⇒= (4)'()()()0f f ξλξξ+=⇒()()()x dxF x e f x λ⎰=;3.()()0()n f f x ξ=⇔有1n +个零点(1)()n f x -⇔有2个零点4.特例:证明()()n f a ξ=的常规方法:令()()()n F x f x P x =-有1n +个零点(()n P x 待定)5.注:含12,ξξ时,分家!(柯西定理)6.附(达布定理):()f x 在[,]a b 可导,['(),'()]c f a f b ∀∈,[,]a b ξ∃∈,使:'()f c ξ=八.拉格朗日中值定理1.结论:()()'()()f b f a f b a ξ-=-;(()(),'()0a b ϕϕξϕξ<⇒∃∍>)2.估计:'()f f x ξ=V V九.泰勒公式(连接,',"f f f 之间的桥梁) 1.结论:2300000011()()'()()"()()"'()()2!3!f x f x f x x x f x x x f x x ξ=+-+-+-; 2.应用:在已知()f a 或()f b 值时进行积分估计十.积分中值定理(附:广义):[注:有定积分(不含变限)条件时使用]第三讲:一元积分学一.基本概念: 1.原函数()F x :(1)'()()F x f x =;(2)()()f x dx dF x =;(3)()()f x dx F x c =+⎰ 注(1)()()xa F x f t dt =⎰(连续不一定可导); (2)()()()()xxa a x t f t dt f t dt f x -⇒⇒⎰⎰(()f x 连续) 2.不定积分性质:(1)(())'()f x dx f x =⎰;(())()d f x dx f x dx =⎰ (2)'()()f x dx f x c =+⎰;()()df x f x c =+⎰ 二.不定积分常规方法 1.熟悉基本积分公式 2.基本方法:拆(线性性)3.凑微法(基础):要求巧,简,活(221sin cos x x =+) 如:211(),,ln ,2dxdx d ax b xdx dx d x ax=+==2= 4.变量代换:(1)常用(三角代换,根式代换,倒代换):1sin ,,,x t t t t x====(2)作用与引伸(化简x t = 5.分部积分(巧用):(1)含需求导的被积函数(如ln ,arctan ,()xa x x f t dt ⎰); (2)“反对幂三指”:,ln ,n ax n x e dx x xdx ⎰⎰(3)特别:()xf x dx ⎰(*已知()f x 的原函数为()F x ;*已知'()()f x F x =) 6.特例:(1)11sin cos sin cos a x b xdx a x b x++⎰;(2)(),()sin kx p x e dx p x axdx ⎰⎰快速法;(3)()()n v x dx u x ⎰三.定积分: 1.概念性质:(1)积分和式(可积的必要条件:有界,充分条件:连续) (2)几何意义(面积,对称性,周期性,积分中值)*20(0)8a a π>=⎰;*()02ba a bx dx +-=⎰ (3)附:()()b a f x dx M b a ≤-⎰,()()()bba a f x g x dx M g x dx ≤⎰⎰) (4)定积分与变限积分,反常积分的区别联系与侧重 2:变限积分()()xa x f t dt Φ=⎰的处理(重点) (1)f 可积⇒Φ连续,f 连续⇒Φ可导(2)(())'x a f t dt ⎰()f x =;(()())'()x x a a x t f t dt f t dt -=⎰⎰;()()()xa f x dt x a f x =-⎰ (3)由函数()()xa F x f t dt =⎰参与的求导,极限,极值,积分(方程)问题 3.N L -公式:()()()ba f x dx Fb F a =-⎰(()F x 在[,]a b 上必须连续!) 注:(1)分段积分,对称性(奇偶),周期性 (2)有理式,三角式,根式 (3)含()ba f t dt ⎰的方程.4.变量代换:()(())'()ba f x dx f u t u t dt βα=⎰⎰ (1)00()()()aa f x dx f a x dx x a t =-=-⎰⎰,(2)0()()()[()()]aaaa a f x dx f x dx x t f x f x dx --=-=-=+-⎰⎰⎰(如:4411sin dx x ππ-+⎰)(3)2201sin n n n n I xdx I nπ--==⎰, (4)2200(sin )(cos )f x dx f x dx ππ=⎰⎰;200(sin )2(sin )f x dx f x dx ππ=⎰⎰, (5)00(sin )(sin )2xf x dx f x dx πππ=⎰⎰,5.分部积分(1)准备时“凑常数”(2)已知'()f x 或()xa f x =⎰时,求()ba f x dx ⎰ 6.附:三角函数系的正交性: 四.反常积分: 1.类型:(1)(),(),()aaf x dx f x dx f x dx +∞+∞-∞-∞⎰⎰⎰(()f x 连续)(2)()ba f x dx ⎰:(()f x 在,,()x a xb xc a c b ===<<处为无穷间断) 2.敛散;3.计算:积分法⊕N L -公式⊕极限(可换元与分部)4.特例:(1)11pdx x +∞⎰;(2)101p dx x ⎰ 五.应用:(柱体侧面积除外) 1.面积,(1)[()()];ba S f x g x dx =-⎰(2)1()dc S f y dy -=⎰; (3)21()2S rd βαθθ=⎰;(4)侧面积:2(b a S f x π=⎰ 2.体积:(1)22[()()]b x a V f x g x dx π=-⎰;(2)12[()]2()d by c a V f y dy xf x dx ππ-==⎰⎰ (3)0x x V =与0y y V =3.弧长:ds(1)(),[,]y f x x a b =∈a s =⎰ (2)12(),[,]()x x t t t t y y t =⎧∈⎨=⎩21t t s =⎰ (3)(),[,]r r θθαβ=∈:s βαθ=⎰ 4.物理(数一,二)功,引力,水压力,质心, 5.平均值(中值定理): (1)1[,]()ba f ab f x dx b a=-⎰; (2)0()[0)lim x x f t dt f x→+∞+∞=⎰,(f 以T 为周期:0()Tf t dt fT=⎰)第四讲:微分方程一.基本概念1.常识:通解,初值问题与特解(注:应用题中的隐含条件)2.变换方程:(1)令()'""x x t y Dy =⇒=(如欧拉方程)(2)令(,)(,)'u u x y y y x u y =⇒=⇒(如伯努利方程) 3.建立方程(应用题)的能力 二.一阶方程:1.形式:(1)'(,)y f x y =;(2)(,)(,)0M x y dx N x y dy +=;(3)()y a b =2.变量分离型:'()()y f x g y = (1)解法:()()()()dyf x dx G y F x Cg y =⇒=+⎰⎰(2)“偏”微分方程:(,)zf x y x∂=∂; 3.一阶线性(重点):'()()y p x y q x += (1)解法(积分因子法):0()01()[()()]()x x p x dxx x M x e y M x q x dx y M x ⎰=⇒=+⎰ (2)变化:'()()x p y x q y +=;(3)推广:伯努利(数一)'()()y p x y q x y α+= 4.齐次方程:'()y y x=Φ (1)解法:'(),()y du dxu u xu u x u u x =⇒+=Φ=Φ-⎰⎰(2)特例:111222a xb yc dy dx a x b y c ++=++ 5.全微分方程(数一):(,)(,)0M x y dx N x y dy +=且N Mx y∂∂=∂∂ 6.一阶差分方程(数三):1*()()x x x x x n xx y ca y ay b p x y x Q x b+=⎧-=⇒⎨=⎩ 三.二阶降阶方程1."()y f x =:12()y F x c x c =++2."(,')y f x y =:令'()"(,)dpy p x y f x p dx=⇒==3."(,')y f y y =:令'()"(,)dpy p y y pf y p dy=⇒== 四.高阶线性方程:()"()'()()a x y b x y c x y f x ++= 1.通解结构:(1)齐次解:01122()()()y x c y x c y x =+(2)非齐次特解:1122()()()*()y x c y x c y x y x =++ 2.常系数方程:"'()ay by cy f x ++= (1)特征方程与特征根:20a b c λλ++=(2)非齐次特解形式确定:待定系数;(附:()ax f x ke =的算子法) (3)由已知解反求方程.3.欧拉方程(数一):2"'()ax y bxy cy f x ++=,令2"(1),'t x e x y D D y xy Dy =⇒=-=五.应用(注意初始条件):1.几何应用(斜率,弧长,曲率,面积,体积); 注:切线和法线的截距2.积分等式变方程(含变限积分); 可设()(),()0xa f x dx F x F a ==⎰ 3.导数定义立方程:含双变量条件()f x y +=L 的方程 4.变化率(速度)5.22dv d xF ma dt dt===6.路径无关得方程(数一):Q Px y∂∂=∂∂7.级数与方程:(1)幂级数求和;(2)方程的幂级数解法:201201,(0),'(0)y a a x a x a y a y =+++==L 8.弹性问题(数三)第五讲:多元微分与二重积分一.二元微分学概念1.极限,连续,单变量连续,偏导,全微分,偏导连续(必要条件与充分条件),(1)000000(,),(,),(,)x y f f x x y y f f x x y f f x y y ∆=++∆=+∆=+V V V V(2)lim ,lim ,lim y x x y f ff f f x y∆∆∆==∆∆(3),x y f x f y df +V V @(判别可微性)注:(0,0)点处的偏导数与全微分的极限定义: 2.特例:(1)22(0,0)(,)0,(0,0)xyx y f x y ⎧≠⎪+=⎨⎪=⎩:(0,0)点处可导不连续;(2)(0,0)(,)0,(0,0)f x y ≠==⎩:(0,0)点处连续可导不可微;二.偏导数与全微分的计算: 1.显函数一,二阶偏导:(,)z f x y = 注:(1)y x 型;(2)0(,)x x y z ;(3)含变限积分2.复合函数的一,二阶偏导(重点):[(,),(,)]z f u x y v x y =熟练掌握记号''"""12111222,,,,f f f f f 的准确使用3.隐函数(由方程或方程组确定): (1)形式:*(,,)0F x y z =;*(,,)0(,,)0F x y z G x y z =⎧⎨=⎩(存在定理)(2)微分法(熟练掌握一阶微分的形式不变性):0x y z F dx F dy F dz ++=(要求:二阶导)(3)注:00(,)x y 与0z 的及时代入 (4)会变换方程. 三.二元极值(定义); 1.二元极值(显式或隐式): (1)必要条件(驻点); (2)充分条件(判别)2.条件极值(拉格朗日乘数法)(注:应用)(1)目标函数与约束条件:(,)(,)0z f x y x y ϕ=⊕=,(或:多条件) (2)求解步骤:(,,)(,)(,)L x y f x y x y λλϕ=+,求驻点即可. 3.有界闭域上最值(重点).(1)(,){(,)(,)0}z f x y M D x y x y ϕ=⊕∈=≤ (2)实例:距离问题 四.二重积分计算:1.概念与性质(“积”前工作): (1)Dd σ⎰⎰,(2)对称性(熟练掌握):*D 域轴对称;*f 奇偶对称;*字母轮换对称;*重心坐标;(3)“分块”积分:*12D D D =U ;*(,)f x y 分片定义;*(,)f x y 奇偶 2.计算(化二次积分):(1)直角坐标与极坐标选择(转换):以“D ”为主; (2)交换积分次序(熟练掌握). 3.极坐标使用(转换):22()f x y +附:222:()()D x a y b R -+-≤;2222:1x y D a b+≤;双纽线222222()()x y a x y +=-:1D x y +≤ 4.特例:(1)单变量:()f x 或()f y(2)利用重心求积分:要求:题型12()Dk x k y dxdy +⎰⎰,且已知D 的面积D S 与重心(,)x y5.无界域上的反常二重积分(数三)五:一类积分的应用(():;;;;f M d D L σΩ⇒ΩΩΓ∑⎰):1.“尺寸”:(1)D Dd S σ⇔⎰⎰;(2)曲面面积(除柱体侧面);2.质量,重心(形心),转动惯量;3.为三重积分,格林公式,曲面投影作准备.第六讲:无穷级数(数一,三)一.级数概念1.定义:(1){}n a ,(2)12n n S a a a =+++L ;(3)lim n n S →∞(如1(1)!n nn ∞=+∑) 注:(1)lim n n a →∞;(2)n q ∑(或1na ∑);(3)“伸缩”级数:1()n n a a +-∑收敛{}n a ⇔收敛.2.性质:(1)收敛的必要条件:lim 0n n a →∞=;(2)加括号后发散,则原级数必发散(交错级数的讨论); (3)221,0n n n n s s a s s s s +→→⇒→⇒→; 二.正项级数1.正项级数:(1)定义:0n a ≥;(2)特征:n S Z ;(3)收敛n S M ⇔≤(有界)2.标准级数:(1)1p n ∑,(2)ln k n n α∑,(3)1ln k n n∑3.审敛方法:(注:222ab a b ≤+,ln ln b a a b =)(1)比较法(原理):n p ka n:(估计),如10()n f x dx ⎰;()()P n Q n ∑(2)比值与根值:*1limn n n u u +→∞*n 应用:幂级数收敛半径计算) 三.交错级数(含一般项):1(1)n n a +-∑(0n a >)1.“审”前考察:(1)0?n a >(2)0?n a →;(3)绝对(条件)收敛 注:若1lim1n n na a ρ+→∞=>,则n u ∑发散 2.标准级数:(1)11(1)n n +-∑;(2)11(1)n p n +-∑;(3)11(1)ln n p n+-∑ 3.莱布尼兹审敛法(收敛)(1)前提:n a ∑发散;(2)条件:,0n n a a →];(3)结论:1(1)n n a +-∑条件收敛. 4.补充方法:(1)加括号后发散,则原级数必发散;(2)221,0n n n n s s a s s s s +→→⇒→⇒→.5.注意事项:对比n a ∑;(1)n n a -∑;n a ∑;2n a ∑之间的敛散关系四.幂级数: 1.常见形式:(1)n n a x ∑,(2)0()n n a x x -∑,(3)20()n n a x x -∑ 2.阿贝尔定理:(1)结论:*x x =敛*0R x x ⇒≥-;*x x =散*0R x x ⇒≤- (2)注:当*x x =条件收敛时*R x x ⇒=- 3.收敛半径,区间,收敛域(求和前的准备) 注(1),n n n n a na x x n∑∑与n n a x ∑同收敛半径 (2)n n a x ∑与20()n n a x x -∑之间的转换 4.幂级数展开法:(1)前提:熟记公式(双向,标明敛域)3511sin ,3!5!x x x x R =-+-Ω=L 2411cos 1,2!4!x x x R =-++Ω=L ; 211,(1,1)1x x x x =+++∈--L ;211,(1,1)1x x x x=-+-∈-+L (2)分解:()()()f x g x h x =+(注:中心移动)(特别:021,x x ax bx c =++)(3)考察导函数:()'()g x f x @0()()(0)xf xg x dx f ⇒=+⎰ (4)考察原函数:0()()xg x f x dx ⎰@()'()f x g x ⇒= 5.幂级数求和法(注:*先求收敛域,*变量替换): (1)(),S x =+∑∑(2)'()S x =L ,(注意首项变化) (3)()()'S x =∑,(4)()"()"S x S x ⇒的微分方程(5)应用:()(1)n n n n a a x S x a S ⇒=⇒=∑∑∑.6.方程的幂级数解法7.经济应用(数三):(1)复利:(1)n A p +;(2)现值:(1)n A p -+ 五.傅里叶级数(数一):(2T π=)1.傅氏级数(三角级数):01()cos sin 2n n n a S x a nx b nx ∞==++∑2.Dirichlet 充分条件(收敛定理): (1)由()()f x S x ⇒(和函数) (2)1()[()()]2S x f x f x =-++3.系数公式:01()cos 1(),,1,2,3,1()sin n na f x nxdx a f x dx nb f x nxdx πππππππππ---⎧=⎪⎪==⎨⎪=⎪⎩⎰⎰⎰L4.题型:(注:()(),?f x S x x =∈)(1)2T π=且(),(,]f x x ππ=∈-L (分段表示) (2)(,]x ππ∈-或[0,2]x π∈ (3)[0,]x π∈正弦或余弦 *(4)[0,]x π∈(T π=) *5.2T l =6.附产品:()f x ⇒01()cos sin 2n n n a S x a nx b nx ∞==++∑第七讲:向量,偏导应用与方向导(数一)一.向量基本运算1.12k a k b +r r ;(平行b a λ⇔=v v )2.a r;(单位向量(方向余弦)01(cos ,cos ,cos )a a aαβγ=u u v v @v )3.a b ⋅r r ;(投影:()aa b b a ⋅=v v vv v ;垂直:0a b a b ⊥⇔⋅=v v v v ;夹角:(,)a b a b a b⋅=v v v v S v v ) 4.a b ⨯r r ;(法向:,n a b a b =⨯⊥v v v v v ;面积:S a b =⨯Y v v )二.平面与直线 1.平面∏(1)特征(基本量):0000(,,)(,,)M x y z n A B C ⊕=v(2)方程(点法式):000:()()()00A x x B y y C z z Ax By Cz D π-+-+-=⇒+++= (3)其它:*截距式1x y z abc++=;*三点式 2.直线L(1)特征(基本量):0000(,,)(,,)M x y z s m n p ⊕=v(2)方程(点向式):000:x x y y z z L m n p---== (3)一般方程(交面式):111122220A xB yC zD A x B y C z D +++=⎧⎨+++=⎩(4)其它:*二点式;*参数式;(附:线段AB 的参数表示:121121121()(),[0,1]()x a a a t y b b b t t z c c c t=+-⎧⎪=+-∈⎨⎪=+-⎩)3.实用方法:(1)平面束方程:11112222:()0A x B y C z D A x B y C z D πλ+++++++= (2)距离公式:如点000(,)M x y到平面的距离d =(3)对称问题;(4)投影问题.三.曲面与空间曲线(准备)1.曲面(1)形式∑:(,,)0F x y z =或(,)z f x y =;(注:柱面(,)0f x y =)(2)法向(,,)(cos ,cos ,cos )x y z n F F F αβγ=⇒v (或(,1)x y n z z =--v )2.曲线(1)形式():()()x x t y y t z z t =⎧⎪Γ=⎨⎪=⎩,或(,,)0(,,)0F x y z G x y z =⎧⎨=⎩; (2)切向:{'(),'(),'()}s x t y t z t =r (或12s n n =⨯v u v u u v )3.应用(1)交线,投影柱面与投影曲线;(2)旋转面计算:参式曲线绕坐标轴旋转;(3)锥面计算.四.常用二次曲面1.圆柱面:222x y R +=2.球面:2222x y z R ++=变形:2222x y R z +=-,z =,2222x y z az ++=,2222000()()()x x y y z z R -+-+-=3.锥面:z =变形:222x y z +=,z a =4.抛物面:22z x y =+,变形:22x y z +=,22()z a x y =-+5.双曲面:2221x y z +=±6.马鞍面:22z x y =-,或z xy =五.偏导几何应用1.曲面(1)法向:(,,)0(,,)x y z F x y z n F F F =⇒=v ,注:(,)(,1)x y z f x y n f f =⇒=-v(2)切平面与法线:2.曲线(1)切向:(),(),()(',',')x x t y y t z z t s x y z ===⇒=v(2)切线与法平面3.综合::Γ00F G =⎧⎨=⎩,12s n n =⨯v u v u u v 六.方向导与梯度(重点)1.方向导(l v 方向斜率):(1)定义(条件):(,,)(cos ,cos ,cos )l m n p αβγ=⇒v(2)计算(充分条件:可微):cos cos cos x y z u u u u l αβγ∂=++∂ 附:0(,),{cos ,sin }z f x y l θθ==u r cos sin x y z f f lθθ∂⇒=+∂r (3)附:2222cos 2sin cos sin xx xy yy f f f f lθθθθ∂=++∂ 2.梯度(取得最大斜率值的方向)G u r :(1)计算:()(,)(,)x y a z f x y G gradz f f =⇒==u v ;(2)结论()a u l ∂∂0G l =⋅u r u r ; ()b 取l G =u r v 为最大变化率方向;()c 0()G M u r 为最大方向导数值.第八讲:三重积分与线面积分(数一)一.三重积分(fdV Ω⎰⎰⎰)1.Ω域的特征(不涉及复杂空间域):(1)对称性(重点):含:关于坐标面;关于变量;关于重心(2)投影法:22212{(,)}(,)(,)xy D x y x y R z x y z z x y =+≤⊕≤≤(3)截面法:222(){(,)()}D z x y x y R z a z b =+≤⊕≤≤(4)其它:长方体,四面体,椭球2.f 的特征:(1)单变量()f z ,(2)22()f x y +,(3)222()f x y z ++,(4)f ax by cz d =+++3.选择最适合方法:(1)“积”前:*dv Ω⎰⎰⎰;*利用对称性(重点)(2)截面法(旋转体):()ba D z I dz fdxdy =⎰⎰⎰(细腰或中空,()f z ,22()f x y +) (3)投影法(直柱体):21(,)(,)xy z x y z x y D I dxdy fdz =⎰⎰⎰ (4)球坐标(球或锥体):22000sin ()RI d d f d παθϕϕρρ=⋅⋅⋅⎰⎰⎰,(5)重心法(f ax by cz d =+++):()I ax by cz d V Ω=+++4.应用问题:(1)同第一类积分:质量,质心,转动惯量,引力(2)Gauss 公式二.第一类线积分(Lfds ⎰)1.“积”前准备:(1)Lds L =⎰;(2)对称性;(3)代入“L ”表达式2.计算公式:()[,]((),(()b a Lx x t t a b fds f x t y t y y t =⎧∈⇒=⎨=⎩⎰⎰ 3.补充说明:(1)重心法:()()Lax by c ds ax by c L ++=++⎰;(2)与第二类互换:L L A ds A dr τ⋅=⋅⎰⎰u v v u v v4.应用范围(1)第一类积分(2)柱体侧面积(),Lz x y ds ⎰三.第一类面积分(fdS ∑⎰⎰)1.“积”前工作(重点):(1)dS ∑=∑⎰⎰;(代入:(,,)0F x y z ∑=)(2)对称性(如:字母轮换,重心)(3)分片2.计算公式:(1)(,),(,)(,,(,xyxy D z z x y x y D I f x y z x y =∈⇒=⎰⎰ (2)与第二类互换:A ndS A d S ∑∑⋅=⋅⎰⎰⎰⎰u v v u v u v四:第二类曲线积分(1):(,)(,)LP x y dx Q x y dy +⎰(其中L 有向)1.直接计算:()()x x t y y t =⎧⎨=⎩,2112:['()'()]t t t t t I Px t Qy t dt →⇒=+⎰ 常见(1)水平线与垂直线;(2)221x y +=2.Green 公式: (1)()L D Q P Pdx Qdy dxdy x y∂∂+=-∂∂⎰⎰⎰Ñ; (2)()L A B →⎰:*P Q y y ∂∂=⇒∂∂换路径;*P Q y y∂∂≠⇒∂∂围路径 (3)L ⎰Ñ(x y Q P =但D 内有奇点)*L L =⎰⎰蜒(变形)3.推广(路径无关性):P Q y y∂∂=∂∂ (1)Pdx Qdy du +=(微分方程)()BA L AB u →⇔=⎰(道路变形原理) (2)(,)(,)LP x y dx Q x y dy +⎰与路径无关(f 待定):微分方程.4.应用功(环流量):I F dr Γ=⋅⎰u v v (Γ有向τv ,(,,)F P Q R =u v ,(,,)d r ds dx dy dz τ==v v )五.第二类曲面积分:1.定义:Pdydz Qdzdx Rdxdy ∑++⎰⎰,或(,,)R x y z dxdy ∑⎰⎰(其中∑含侧)2.计算:(1)定向投影(单项):(,,)R x y z dxdy ∑⎰⎰,其中:(,)z z x y ∑=(特别:水平面);注:垂直侧面,双层分隔(2)合一投影(多项,单层):(,,1)x y n z z =--v(3)化第一类(∑不投影):(cos ,cos ,cos )n αβγ=v3.Gauss 公式及其应用:(1)散度计算:P Q R divA x y z∂∂∂=++∂∂∂u v (2)Gauss 公式:∑封闭外侧,Ω内无奇点(3)注:*补充“盖”平面:0∑∑+⎰⎰⎰⎰;*封闭曲面变形∑⎰⎰Ò(含奇点)4.通量与积分:A d S ∑Φ=⋅⎰⎰u v u v (∑有向n v ,(),,A P Q R =u v ,(,,)d S ndS dydz dzdx dxdy ==u v v )六:第二类曲线积分(2):(,,)(,,)(,,)P x y z dx Q x y z dy R x y z dz Γ++⎰1.参数式曲线Γ:直接计算(代入)注(1)当0rot A =u v v 时,可任选路径;(2)功(环流量):I F dr Γ=⋅⎰u v v2.Stokes 公式:(要求:Γ为交面式(有向),所张曲面∑含侧)(1)旋度计算:(,,)(,,)R A P Q R x y z∂∂∂=∇⨯=⨯∂∂∂u v u v (2)交面式(一般含平面)封闭曲线:00F G =⎧⇒⎨=⎩同侧法向{,,}x y z n F F F =v 或{,,}x y z G G G ;(3)Stokes 公式(选择):()A dr A ndS Γ∑⋅=∇⨯⋅⎰⎰⎰u v v u v v Ñ(a )化为Pdydz Qdzdx Rdxdy ∑++⎰⎰;(b )化为(,,)R x y z dxdy ∑⎰⎰;(c )化为fdS ∑⎰⎰。
数学14章知识树

数学14章知识树全文共四篇示例,供读者参考第一篇示例:数学作为一门重要的学科,被广泛地运用于各个领域。
而在数学的学习过程中,很多时候我们往往会感觉有些知识点相互关联,但却无法构建出一个系统性的框架,难以将其融会贯通。
为了帮助大家更好地理解数学的知识体系,我们可以通过绘制“知识树”的形式,将各个知识点串联起来,形成一个有机的整体。
在本文中,我将为大家介绍一份关于数学的14章知识树,希望可以帮助大家更好地理解数学知识的结构和内在联系。
第一章:基本概念在这一章中,我们将学习到数学的起源和基本概念,包括数的分类、数的性质、集合的概念等。
这是数学学习的基础,建立在这些基本概念之上,我们才能更深入地探索数学的世界。
第二章:初等代数在这一章中,我们将学习关于代数的基本概念和技巧,包括多项式的运算、方程的解法、因式分解等。
初等代数是数学学习的重要阶段,它为我们打下了解决各种数学问题的基础。
第三章:几何学几何学是研究空间和形状的科学,它包括点、线、面、体等基本概念,以及几何图形的性质和相互关系。
通过学习几何学,我们可以更好地理解空间结构,解决与形状和大小相关的问题。
第四章:三角学三角学是研究三角形和三角函数的学科,它包括三角函数的定义、图像、性质和应用等内容。
三角学是数学中一个重要的分支,它在解决各种实际问题中扮演着至关重要的角色。
第五章:微积分微积分是研究变化的数学,它包括导数、微分、积分等概念和技巧。
微积分被广泛地应用于科学、工程、经济等领域,它为我们提供了解决变化和尺度问题的数学工具。
第六章:概率论概率论是研究随机事件的概率和规律的学科,它包括概率的定义、性质、分布等内容。
概率论在各种实际问题中都有着广泛的应用,它帮助我们了解随机现象的规律性和规律。
第七章:数论数论是研究整数的性质和规律的学科,它包括素数、同余、数论函数等内容。
数论在密码学、编码理论等领域有着重要的应用,它帮助我们理解整数之间的关系和规律。
数学map

数学map数学Map:用地图梳理数学知识数学是一门抽象的学科,常常让学生感到头疼。
尤其是高等数学,难以理解和记忆。
许多人可能记得做题的步骤,但对于知识点的梳理却很模糊。
这时候,一个好的数学Map可以帮助我们更好地理解和记忆数学知识。
什么是数学Map?数学Map,又称知识图谱,是指将一门学科中的知识点、定义、公式和概念等元素按照一定的逻辑关系进行组织和呈现的一种图形表达方式。
数学Map主要有两种类型:一种是线性Map,即将知识点按照章节顺序排列;另一种是非线性Map,即将知识点按照它们之间的关系进行组织,构成一种网状结构。
如何制作数学Map?制作数学Map需要以下步骤:1.确定主题:确定数学Map的主题,以及确定使用线性还是非线性结构。
2.收集知识点:根据主题列出与之相关的知识点,包括定义、公式、定理等。
3.建立框架:按照知识点之间的逻辑关系构建框架,建立一个初步的数学Map。
4.补充细节:在框架的基础上,逐渐补充和细化每一个知识点,增加详细解释和示例。
5.精心设计:利用合适的图标、颜色和排版等元素设计数学Map,让其更加易于理解和记忆。
学习数学Map的好处1.梳理思路:数学Map能够清晰地展示知识点之间的逻辑关系,帮助学生更好地理解和记忆数学知识。
2.备考利器:数学Map可以使学生清楚地了解考试的考点和考点之间的关系,帮助备考更加有针对性。
3.知识框架:数学Map可以帮助学生建立清晰的知识框架,方便他们在学习中不断深入和拓展知识。
总之,数学Map是一种强大的学习工具,帮助学生更加清晰地理解和记忆数学知识。
希望大家在学习数学的过程中能够尝试一下数学Map的制作,让数学之路更加畅通。
新疆高一月考重要知识点

新疆高一月考重要知识点一、高等数学1. 函数与极限- 一元函数的极限- 常用极限的计算与性质- 极限存在准则2. 导数与微分- 导数的定义与计算- 高等导数的应用- 微分的应用3. 不定积分与定积分- 不定积分的基本公式与计算方法- 定积分的计算与性质- 积分中值定理4. 函数与导数的应用- 曲线的切线与法线- 函数的单调性与极值- 最值问题与最优化问题5. 微分方程与数列- 一阶常微分方程的解法- 高阶线性常微分方程的解法- 数列的极限与常用数列的性质二、物理1. 力学- 物理量与单位制- 物体的运动学描述- 牛顿定律与运动方程- 万有引力与行星运动2. 热学- 温度与热量- 热传递与热平衡- 理想气体的状态方程与分子速率- 热力学第一、二定律3. 光学- 光的反射与折射- 光的波动性质- 几何光学与光仪器- 光的衍射与干涉4. 电学- 电荷与电场- 静电场与电势- 电流与电阻- 电路与电能三、化学1. 物质的结构与性质- 原子结构与元素周期表 - 化学键与分子结构- 氧化还原与电负性- 物质的相态与溶液2. 化学变化与能量- 化学方程式与化学平衡- 化学反应的速率与化学平衡常数 - 热力学与化学反应- 扩散与溶解热3. 电化学与电解- 电解质与非电解质- 电化学平衡与电解过程- 电池与电解池原理4. 物质量的关系与计算- 反应物与生成物的量比关系- 摩尔质量与化学计量计算- 溶液的浓度计算与稀释计算- 化学反应速率与化学平衡计算四、生物1. 细胞与遗传- 细胞的基本结构与功能- 遗传物质DNA的结构与复制 - 基因与蛋白质合成- 遗传与进化2. 生物的发展与调节- 植物的生长与发育- 动物的生长与发育- 激素与内环境稳态- 生物钟与生物行为3. 生物体的结构与功能- 植物体与植物器官- 动物组织与器官系统- 组织工程与器官移植- 生物膜与运输4. 生态系统与生物多样性- 生态系统的结构与功能- 生态平衡与生态位- 物种多样性与生态保护 - 生物圈与地球环境五、地理1. 自然地理- 地球与环境- 大气环流与气候- 水文循环与水资源- 地貌与地球内部结构2. 人文地理- 人口与城市- 农业与工业- 交通与通信- 区域发展与可持续性3. 地理信息技术与调查- 地理信息系统与遥感技术- 地理数据的收集与分析- 地图制作与空间信息展示- 地理调查与实地考察以上是新疆高一月考的重要知识点,掌握这些知识将有助于你在考试中取得好成绩。
高等数学基本函数及图像

第一节 初等函数1、基本初等函数及图形基本初等函数为以下五类函数:(1) 幂函数 μx y =,μ是常数;(2) 指数函数 x a y = (a 是常数且01a a >≠,),),(+∞-∞∈x ;(3) 对数函数 x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞;(4) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;(5) 反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .我现在就付诸行动[美]奥格.曼狄诺著安辽我的幻想毫无价值,我的计划渺如尘埃,我的目标不可能达到。
一切的一切毫无意义——除非我们付诸行动。
我现在就付诸行动。
一张地图,不论多么详尽,比例多么精确,它永远不可能带着它的主人在地面上移动半步。
一个国家的法律,不论多么公正,永远不可能防止罪恶的发生。
任何宝典,即使我手中的羊皮卷,永远不可能创造财富。
只有行动才能使地图、法律、宝典、梦想、计划、目标具有现实意义。
行动像食物和水一样,能滋润我,使我成功。
我现在就付诸行动。
拖延使我裹足不前,它来自恐惧。
现在我从所有勇敢的心灵深处,体会到这一秘密。
我知道,要想克服恐惧,必须毫不犹豫,起而行动,惟其如此,心中的慌乱方得以平定。
现在我知道,行动会使猛狮般的恐惧减缓为蚂蚁般的平静。
高等数学复习98024

第三步 确 定 在 这 些 部 分 区 间 内 f'(x)和 f"(x)的 符 号 , 并 由 此 确 定 函 数 的 增 减 性 与 极 值 及 曲 线 的 凹 凸 与 拐 点 ( 可 列 表 进 行 讨 论 ) ;
(3)如l果 im kC (C0,k0)就 , 是 说 是 k阶的 无穷 . 小
等价无穷小的性质
定理(等价无穷小替换定理)
设 ~ , ~ 且 li m 存 ,则 l在 i m li m .
两个重要极限
(1) lim six n1 x 0 x
连续定义
limy0
x0
x l ix0m f(x)f(x0)
左右连续
连续的 充要条件
间断点定义
第一类 可跳 去跃 间间 断断 点点
第二类 无振 穷荡 间间 断断 点点
x2 1 x 0
7)讨论 f (x) x
0 x 1
2 x 1 x 2
在x=0和x=1处的连续性。
医用高等数学知识概要
一、极限与连续
1)函数的极限 2)无穷小 3)函数的连续性
数列极限
函数极限
ln im xn a
lim f(x)A
x
limf(x)A
xx0
极限存在的 充要条件
左右极限 无穷小的比较
等价无穷小 及其性质
无穷小
limf (x) 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集合
函数映射
函数保序性
数列极限唯一性
联系→性质有界性
微积分学函数极限保号性e^x
理论基础无穷小→无穷小的比较→等价无穷小一元函数sin(x)、cos(x)
——极限无穷及常用代换微分学微分ln(1+x)、(1+x)^n 函数、无穷大及应用
极限运算法则柯西中值定理麦克劳林中值定理→佩亚诺型余项
和连续存在法则→重要极限↑↑
定义四则运算微分中值定理→费马引理→罗尔定理→拉格朗日中值定理→泰勒中值定理→拉格朗日型余项复合函数洛必达法则——零比零型、无穷比无穷型
连续性反函数单调性→极值、最值
连续初等函数凸凹性→拐点端点
间断点第一类——可去、跳跃切线法↓
第二类——无穷、振荡导数应用零点二分法鞍点最值点←间断点、不可导点
最值定理水平渐近线函数↑↑
性质零点定理渐线性铅直渐近线作图驻点→极值点
介值定理斜渐近线y’=0 原理基本概念弧微分零点基本定理曲率曲率圆拐点y=0 可分离变量的微分方程曲率半径y’’=0 一阶微分方程齐次微分方程→可化为齐次微分方程的方程定义←原函数
线性微分方程不定积分性质基本积分公式有理函数的积分
常微分伯努利方程换元积分法
方程全微分方程计算分部积分法
可降阶的y^(n)=f(x) 一元函数特殊积分计算
高阶微分方程y’’=f(x,y’)、y’’=f(y,y’) 积分学定义与性质→积分中值定理函数高阶微分方程常系数线性齐次方程及应用微积分基本公式(
微分方程非齐次方程Pn(x)e^ax
差分欧拉方程(Pl(x)cos(bx) 定积分计算弧长
方程其他解法幂级数解法+Pn(x)sin(bx))e^ax 几何应用平面面积、回转体侧面积微分方程组的解法应用物理应用体积
概念、性质条件收敛比较平面点集定义
几何级数绝对收敛比值理论基础极限最值定理
p级数审敛法根值多元函数连续介值定理
常数项级数正项级数极限偏导数定义、计算
交错级数高阶偏导数
无穷级数概念线性性质收敛区间全微分
幂级数性质微分积分性收敛域求导法则——复合函数、隐函数
敛散性收敛半径→求法应用向量值函数→方向导数→梯度grad 函数项级数泰勒级数→函数展开式几何曲线——切线与法平面
应用近似计算曲面——法线与切平面
解微分方程极值、最值→条件极值→拉格朗日乘数法三角级数→正交性泰勒公式→拉格朗日中值定理
↓定义定义、性质→中值定理
傅立叶级数敛散性→狄利克雷收敛定理计算直角坐标→X、Y型
函数展开二重积分极坐标→R、θ型
无界区域上的二重积分
定义、坐标表示重积分换元法
概念模方向角定义、性质截面法
方向方向余弦多元函数三重积分柱坐标面积投影法向量运算加减法方向数积分学球坐标
乘法→数乘、数量积、向量积、混合积及应用应用几何
相互关系平行、垂直
夹角、投影第一类曲线积分——定义、性质、计算
空间方程——一般式、点法式、截距式、三点式↓联系↑
解析几何面平面关系——平行、垂直、相交、夹角曲线积分第二类曲线积分——定义、性质、计算
与距离——点面、线面、面面线面积分格林公式→平面曲线积分与路径无关的条件
向量代数二次曲面——九种常见曲面及方程斯托克斯公式→空间曲线积分与路径无关的条件曲面法线与切平面第一类曲面积分——定义、性质、计算方程——一般式、点向式、参数式、两点式曲面积分↓联系↑
直线关系——平行、垂直、相交、异面、夹角——平面束第二类曲面积分——定义、性质、计算线距离——点线、线线概念→数量场、矢量场高斯公式→延任意闭曲面的曲面积分为零的条件方程方向导数→梯度grad
曲线投射——投影柱面、投影曲线场论通量→散度div 哈密顿算子▽→拉普拉斯算子△
切线与法平面环量→旋度rot。
