组合梁自动计算程序
midas操作例题资料-钢箱梁

Civil&Civil Designer一、钢箱梁操作例题资料1概要钢桥是高强、轻型薄壁结构,截面和自重比混凝土桥小,跨越能力大,因而在实际工程中有广泛应用。
钢桥按形式可大致分为钢箱梁、钢板梁(工字钢)、钢桁梁、组合梁桥等类型。
钢桥在使用时不仅要求钢材具有较高的强度,而且还要求具有良好的塑性。
钢桥的刚度相对比较小,变形和振动比混凝土桥大。
为了保证车辆行驶安全和舒适性、避免过大的变形和振动对钢桥结构产生不利的影响,钢桥必须有足够的整体刚度[2] 。
钢桥缺点除容易腐蚀影响耐久性外,另一缺点是疲劳。
影响疲劳的因素很多,除钢材品质、连接的构造与方法等外,与荷载性质、疲劳细节关系也很大。
钢箱梁除钢材等力学特性外,还具有箱梁的受力特点,广泛应用于市政高架、匝道、大跨度斜拉桥、悬索桥、拱桥加劲梁、大跨连续钢箱梁及人行桥钢箱梁等方面。
本专题将通过介绍工程概况、结合规范构造检查、midas Civil详细建模过程以及midas Civil Designer设计平台及结果查看等操作流程,希望能为读者结合实际项目学习程序,通过程序了解钢箱梁提供帮助。
钢箱梁操作例题资料2 钢桥概况及构造检查2.1 钢桥概况主梁为20+30+40+30m单箱单室正交钢箱梁,钢材为Q345;桥面宽8m,梁高2.335m,翼缘板长1.8m;顶板、腹板、翼缘板均厚16mm,底板标准段厚16mm,支座两侧3~3.5m范围内加厚为24mm;顶板设置闭口U型加劲肋;翼缘板、腹板均设置板型加劲肋;底板标准段设置板型加劲肋,桥墩两侧5~7m范围内设置T型加劲肋;横隔板等设置距离详见图1~图3所示。
建模之前,应按照《公路钢结构桥梁设计规范》(JTG D64—2015)[1] (以下简称规范)对钢桥面板、加劲肋、翼缘板及腹板等尺寸进行构造检查。
2.2构造检查2.2.1钢桥面板近年来正交异性钢桥面板出现疲劳和桥面铺装损伤的现象较为普遍,为保证钢桥面板具有足够的刚度,需对最小厚度有要求;为减小应力集中和避免采用疲劳等级过低的构造细节,需对纵向闭口加劲肋尺寸进行规定[1]。
钢结构设计应用常见问题

.
9
节点归并真的做不好么
专家相伴、设计梦想
.
9
节点归并真的做不好么
专家相伴、设计梦想
.
9
型钢混凝土组合梁设计的注意事项
专家相伴、设计梦想
.
10
型钢混凝土组合梁设计的注意事项
PKPM软件中组合梁设计的两种途径: 1 在SATWE前处理特殊构件补充定义中定义组合梁,软件自动按照 组合构件的刚度来进行分析,并按组合梁进行承载力验算。如下图:
两种方法的异同:
方法1:SATWE定义组合梁构件计算
1 2
SATWE中组合梁不考虑施工阶段的验算。 1 只能按完全抗剪计算,不能对连接件经行 2 验算。 1 SATWE分析计算结果中的梁挠度输出,对 1 于组合梁为短期刚度下的弹性挠度,没有 考虑钢与混凝土剪切面滑移的影响,也没 有考虑混凝土长期效应徐变下的挠度计算 1 1 负弯矩区段,混凝土板退出工作,记入等 效翼板宽度范围内的板钢筋作用,SATWE 中是按构造的最小配筋面积记入,钢筋级 别为Ⅰ级钢
高钢规 6.3.2:
高钢规 5.5.2:
专家相伴、设计梦想
3
有侧移还是无侧移
新版本的软件,可以两个方向分别计算:
专家相伴、设计梦想
4
连廊和空间桁架注意事项
一个连廊,上下弦杆都没有轴力,软件算错了 么?
专家相伴、设计梦想
4
连廊和空间桁架注意事项
1 楼板设置成弹性板 2 调整模拟施工次序
专家相伴、设计梦想
专家相伴、设计梦想
5
新版本的“强柱梁”计算
为了验证是否是 起到了作用,可以选取上面超 限的柱子做一下简单的验算。柱子的截面尺寸: B*H*U*T*D*F=0.350*0.350*0.000*0.012*0.000*0.012 ; 钢号 Q235 ,计算长度 6.82 , 5.5 ,稳定系数: 0.89;构件的轴力如下图: 。
钢桥、组合梁桥-《公路钢结构桥梁设计规范》(JTG D64-2015)功能介绍

12p
《公路钢结构桥梁设计规范》JTG D64-2015 功能展示
前处理-构件参数
We Analyze and Design the Future
1、在工作树构件右键“构件列表”可统一查看、修改所有构件参数。 2、在工作树参数右键“显示表格”可查看、修改对应的构件参数。
Copyright ⓒ since 1989 MIDAS Information Technology Co., Ltd. All rights reserved.
Copyright ⓒ since 1989 MIDAS Information Technology Co., Ltd. All rights reserved.
20p
《公路钢结构桥梁设计规范》JTG D64-2015 功能展示
验算项-轴心受压构件整体稳定验算
We Analyze and Design the Future
13p
《公路钢结构桥梁设计规范》JTG D64-2015 功能展示
前处理-倾覆
We Analyze and Design the Future
1、自动生成倾覆边界条件。 2、自动生成空间倾覆轴。 3、用户可手动输入支座反力。 4、用户可手动输入倾覆轴。
Copyright ⓒ since 1989 MIDAS Information Technology Co., Ltd. All rights reserved.
8p
《公路钢结构桥梁设计规范》JTG D64-2015 功能展示
“设置” 界面
前处理-设置
We Analyze and Design the Future
1、程序自动生成设置界面默认值。
Copyright ⓒ since 1989 MIDAS Information Technology Co., Ltd. All rights reserved.
pkpm-波浪腹板H型钢设计工具使用说明
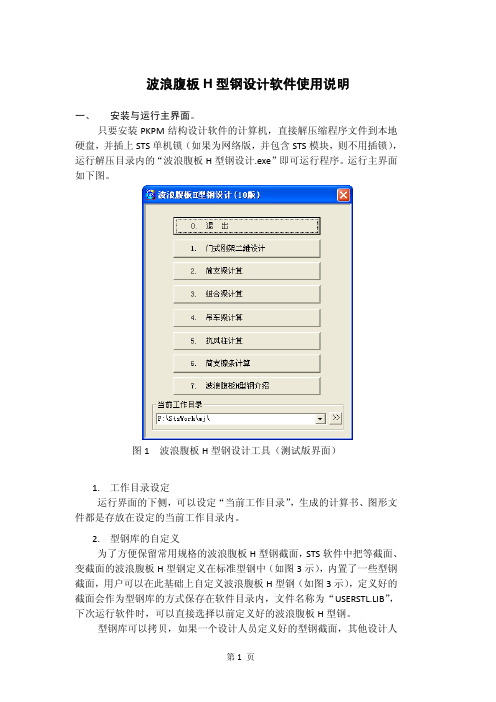
波浪腹板H型钢设计软件使用说明一、安装与运行主界面。
只要安装PKPM结构设计软件的计算机,直接解压缩程序文件到本地硬盘,并插上STS单机锁(如果为网络版,并包含STS模块,则不用插锁),运行解压目录内的“波浪腹板H型钢设计.exe”即可运行程序。
运行主界面如下图。
图1 波浪腹板H型钢设计工具(测试版界面)1.工作目录设定运行界面的下侧,可以设定“当前工作目录”,生成的计算书、图形文件都是存放在设定的当前工作目录内。
2.型钢库的自定义为了方便保留常用规格的波浪腹板H型钢截面,STS软件中把等截面、变截面的波浪腹板H型钢定义在标准型钢中(如图3示),内置了一些型钢截面,用户可以在此基础上自定义波浪腹板H型钢(如图3示),定义好的截面会作为型钢库的方式保存在软件目录内,文件名称为“USERSTL.LIB”,下次运行软件时,可以直接选择以前定义好的波浪腹板H型钢。
型钢库可以拷贝,如果一个设计人员定义好的型钢截面,其他设计人员需要使用,可以把“USERSTL.LIB”拷贝到对方的程序目录内,再进入程序就可以使用了。
图2波浪腹板H型钢截面图3自定义波浪腹板H型钢截面二、门式刚架二维设计。
门式刚架建模与荷载输入,同普通H型钢门式刚架设计。
波浪腹板H 型钢截面定义中指定,并且可以自定义。
图4截面定义入口图5翼缘与腹板可以定义不同钢号图6定义波浪腹板门式刚架图7计算简图波浪腹板门式刚架计算长度确定方式同门规CECS102:2002,梁、柱构件都考虑轴力影响按压弯计算,承载力计算按《波浪腹板钢结构应用技术规程》(CECS 290:2011)。
图8应力图与计算书表达STS软件可以完成波浪腹板门式刚架的施工图设计,连接计算按《波浪腹板钢结构应用技术规程》(CECS 290:2011)。
主要处理技术点如下图:图9门式刚架施工图处理图10部分图纸图11节点计算书输出图12节点区域处理参数选择三、简支梁计算工具。
波浪腹板H型钢简支梁计算工具运行界面如下图所示。
钢结构自动计算工具表格

钢筋混凝土结构
钢结构
矩形截面单双筋--抗弯抗剪验算
单筋T形截面--抗弯验算
深梁与短梁--抗弯验算
矩形截面受弯剪扭--抗扭验算
雨蓬板配筋裂缝计算
雨蓬梁配筋裂缝计算
软弱下卧层验算
地下室外墙计算 单(双)柱锥形基础计算 墙高厚比验算 灌注桩单桩竖向承载力计算 柱体积配箍率计算 筏基底板冲切计算 楼面荷载计算 楼梯间荷载计算 砌体梁端局部受压计算 双柱条基计算 螺旋楼梯计算 板式楼梯计算 一字形剪力墙配箍计算 L形剪力墙配箍计算 无翼墙L形剪力墙配箍计算 牛腿计算
常用资料
双吊钩桥式起重机参数资料 LH型电动葫芦起重机参数资料
支撑系统Байду номын сангаас--ST梁,墙面斜撑,风拉杆计算
工型拉(压)弯构件强度及稳定性校核计算
箱形拉(压)弯构件强度及稳定性校核计算
工字型、T型、箱型截面斜撑计算
框架柱计算长度(有侧移及无侧移)
砼-钢组合梁计算
钢梁(工字型、箱型)受扭计算
工型梁加劲肋计算 地震反映谱 高强度螺栓连接计算 格构式双工截面参数计算(I I) 实腹式双工截面参数计算(十字) 实腹式工型组合截面参数计算(|—I) 箱型(工型帖板)截面参数计算 简支梁温度变化引起内力 钢梁受扭计算 梁柱固结计算 次梁与主梁铰接计算程式 钢管混凝土柱计算 摩擦型高强螺栓拉剪连接计算
06钢混组合梁教程文档

桥梁博士V4.0案例教程 钢混组合梁上海同豪土木工程咨询有限公司2019年2月目 录1工程概述 (1)2总体信息 (2)3结构建模 (3)4钢筋设计 (12)5加劲设计 (13)6施工分析 (15)7横向分布计算 (18)8运营分析 (21)9结果查询 (24)10计算报告 (26)1工程概述计算的内容为一个钢板组合连续梁。
跨径2*30m,计算跨径29.4m。
桥面全宽12m,单向3车道,单片主梁宽3m,主梁间距3m,防撞墙宽0.5m。
组合梁全高为1.95m,其中桥面板高0.28m,钢梁1.67m。
设计规范:2018公路规范;结构重要性系数:1.1;环境相对湿度:80%;环境类别:I类;钢梁材料:Q345;混凝土桥面板材料:C50;钢筋:HRB400,直径25mm;焊钉:电弧螺柱焊用圆柱头焊钉;桥面铺装:沥青混凝土,100mm。
图1-1 横断面布置图图1-2单梁断面图打开同豪桥梁博士V4软件,在【开始】下选择【新建】,弹出“新建项目”对话框,修改项目名称为“钢板组合梁”,指定保存路径,其余默认,如图1-3所示。
图1-2单梁断面图2总体信息1)在操作树上双击【总体信息】。
默认进入到总体信息的【基本】标签页。
2)在【常规】中,【计算规范】选择“2018公路规范”,其余信息采用默认值,如图2-1所示。
图2-1常规信息设置3)在【计算内容】中,勾选计算收缩,徐变,活载,自振、验算,图2-2所示。
图2-2 计算内容设置4)在【材料定义】中,定义本例用到的材料。
桥面板-混凝土-C50,钢板-普通钢筋(高)HRB400,普通钢筋(低)HPB300,删除其余材料,如图2-3所示。
图2-3 材料定义3结构建模3.1截面设计1)在操作树上双击【结构件模】。
进入到结构件模界面,然后在图形区右侧单击【截面】标签,进入截面设计窗口。
2)导入桥面板。
右击下方【截面1】修改截面名称为组合梁截面,使用【导入区域】命令,弹出导入区域对话框,依次指定导入的cad目录位置、图层名称以及CAD单位,先将桥面板进行导入,导入后如图3-1所示。
组合梁计算自动计算程序

组基本数据输入:组合梁跨度:l=6000mm 梁间距a=2000组合梁截面总高:h=500mm 砼等级:C 20f c=10N/mm 2E c = 2.55E+04楼承板型号:YX76楼承板特性:h c1=100mm h c 2=150mm h c =250b 0=300mm S 0=1700mm1.截面特性计算:(1)钢梁BH 250x200x6x10钢材:Q345下翼缘:b 1=200mm t 1=10mm 上翼缘:b 2=100mm t 2=10mm 腹 板:h w =230mmt w =6mm钢梁截面:A s=4380mm 2 重量34.4钢梁中和轴的位置:y s =98mm钢梁截面惯性矩:I s =4.60E+07mm 4钢梁上翼缘的弹性抵抗矩:W s2=3.02E+05mm 3钢梁下翼缘的弹性抵抗矩:W s1=4.72E+05mm 3本表格已经设计好所有函数公式,只需在表格中填入相关的数据即可自动进行计算(2)组合梁钢与砼弹性模量比:αE=8.08钢筋砼翼缘板计算宽度:b e=l/6+l/6+b0=2300mmb e=S0/2+S/2+b=2000mmb e=6hc1+6hc1+b=1500mm取b e=1500mm b e,eq=185.7mm 钢筋砼翼缘板的截面面积:A ce=150000mm2换算成钢截面的组合梁截面面积:A0=22948mm2钢梁至组合梁截面中和轴的距离:y x=383mm钢筋砼翼缘板的截面惯性矩:I ce= 1.25E+08mm4组合梁换算成钢截面时的惯性矩:I0== 5.02E+08mm4组合梁换算截面中的钢筋砼板顶边(点4)的截面抵抗矩:W=4.28E+06mm304组合梁换算截面中的钢筋砼板顶边(点3)的截面抵抗矩:=2.91E+07mm3W03组合梁换算截面中的钢筋砼板顶边(点2)的截面抵抗矩:=3.78E+06mm3W02组合梁换算截面中的钢筋砼板顶边(点1)的截面抵抗矩:W=1.31E+06mm301(3)考虑砼的徐变影响时,组合梁的截面特性换算钢截面组合梁的面积:A'0=13664mm2钢筋砼翼板顶面至组合截面中和轴的距离:y'x=337mm 换算钢截面组合梁的惯性矩:I'0=4.23E+08mm4组合梁换算截面中的钢筋砼板顶边(点4)的截面抵抗矩:=2.60E+06mm3W'04组合梁换算截面中的钢筋砼板顶边(点3)的截面抵抗矩:W'=6.72E+06mm303组合梁换算截面中的钢筋砼板顶边(点2)的截面抵抗矩:=4.86E+06mm3W'02组合梁换算截面中的钢筋砼板顶边(点1)的截面抵抗矩:W'=1.26E+06mm301p2k=4863659.94KN/m p2=########KN/m 弯矩:=########KN·mM1剪力:=########KNV1(2)钢梁的强度、稳定和挠度的验算:钢梁上翼缘应力:σ1=########N/mm2钢梁下翼缘应力:σ2=########N/mm2钢梁剪应力:τ=########N/mm2挠度:w=########mmw/l=1/0。
远盛水工计算说明书

远盛水工计算说明书(总55页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第六章计算菜单组结构及简介计算的菜单结构如图3-1所示。
图 6-1 菜单结构功能简介:计算菜单组提供了很多方便工程师计算的实用工具,同时把计算得结果绘制出来,把许多重复繁琐的操作交给程序处理,简化了很多设计中常用的操作步骤。
菜单组各命令详细说明一、桁架计算117[命令]:HJJS[菜单位置]:计算桁架计算功能:对各种桁架结构进行内力计算并绘制轴力图和变形图,同时生成计算书。
您使用AutoCAD的命令绘制出如图所示桁架结构的单线图以后,即可对该桁架结构进行计算。
桁架单线图须以毫米为单位绘制。
在“基本工具”菜单列的“初始设置”中将“出图比例”和“绘图比例”进行正确设置,出图比例除以绘图比例的比值等于单线图的缩放比例。
例如,如果一根梁的实际长度为2000mm,而您在CAD上绘制长度为20单位长,也就是说,图形相对结构缩小了20/2000倍。
那么,如果您设置出图比例为1,则须设置绘图比例=2000/20×1=100;如果您设置出图比例为2,则须设置绘图比例=2000/20×2=200。
桁架单线图执行此命令,弹出如图所示对话框。
桁架计算主对话框在“工程”菜单列点击“新建”,按照程序要求输入工程名“桁架计算例题一”,此时就创建了一个桁架计算工程。
点击“节点处理”菜单列中“添加节点”,程序将自动在单线图中线段的顶点和交点位置添加节点。
点击“节点设置”,可以对图中的节点大小和颜色进行调整。
如果在某些交点位置不需要节点,请执行“删除节点”将这个节点删除,而不要使用“erase”命令直接删除。
点击“编号”中“杆件、节点编号”,选择桁架结构的所有单线图和节点,程序将自动对杆件和节点进行编号。
点击“材料库”中“定义材料库”,将弹出如图所示对话框。
118材料库管理在图中右侧录入框中输入适当的数值后,点击“入库”,则将这种名为“bar”的材料存入材料库;如果该桁架中有几种不同截面积或材质的材料,则可以分别定义不同的材料名,并存入材料库。
MIDAS在钢混组合截面计算中的应用

·工 程 结 构 ·
M IDAS在钢混组合截面计算中的应用
基于以上假定 ,将结合截面特性 ,如面积 、惯性矩等换算 为同种材料 (钢材 )的特性 ,然后在此基础上按照普通截面的 计算原理进行受力分析和内力计算 。换算关系为 :
Eeq
= Es , Aeq
=As
+
Ac n
,
Ieq
= Is
+
Ic n
式中 : Eeq为等效截面弹性模量 ; Es , Ec 分别为钢材和混 凝土的弹性模量 ; A s , Ac 分别为钢材和混凝土的截面积 ; Is , Ic 分别为钢材和混凝土对自身形心轴的惯性矩 ; Ec、Es 分别表 示混凝土和钢梁的弹性模量 , n = Es / Ec 为弹模比 。
2 算例
211 M IDAS计算 采用软件的施工阶段联合截面功能计算组合梁 。在程
序中定义四个施工阶段 : CS1 为架设钢梁 ; CS2 为现浇混凝 土 ; CS3为施加集中力 。钢梁自重由程序自动考虑 ,混凝土 自重按均布荷载施加 ,不考虑收缩徐变的影响 。20 m 简支梁 纵向单元分段为 40 ×015 m。
人工算结果见表 1。
[收稿日期 ]2009 - 02 - 25 [作者简介 ]杜振华 (1984~) ,男 ,硕士研究生 。
150
四川建筑 第 3 0 卷 1 期 20 10. 02
© 1994-2011 China Academic Journal Electronic Publishing House. All rights reserved.
弯扭组合梁主应力大小及方向的测定

弯扭组合梁主应力大小及方向的测定1 实验目的⑴、用电测方法测定弯扭组合变形梁主应力大小及方向。
⑵、掌握主应力大小及方向的理论和实测计算公式,并进行比较计算其误差值。
⑶、掌握电阻应变花的应用。
2 仪器和设备⑴、50KN微机控制电子万能试验机。
⑵、TS3861静态电阻应变仪。
⑶、游标卡尺。
3 实验原理及装置图8-1 弯扭组合梁示意图图8-2 Ⅰ-Ⅰ截面弯扭组合梁为一空心薄壁园轴,材料为45号钢,其弹性常数为:E=210GPa,μ=0.28,横截面尺寸,外经D=30mm,内径d=26mm。
其一端固定,另一端装一固定加力臂端,轴与力臂端的轴线相互垂直,并且在同一水平面内。
离悬臂端加载点的垂直距离135mm处I-I截面为被测位置,如图1。
在此处园轴表面的前后、上下(图8-2)所示的A、C、B、D四个被测位置上,每处粘贴一枚三轴直角应变花,如图8-3所示。
共计12片应变片,供不同的测试目的选用。
当加力臂端作用载荷P后,园轴发生扭转与变形的组合变形,薄壁园轴横截面上便有内力素:弯矩、扭矩和剪力。
在I-I 截面的A 、C 、B 、D 被测四点上,其单元体上应力状态如图8-4所示。
一.实验测定主应力大小及方向弯扭组合变形构件表面上一点处于平面应力状态,由应力-应变广义胡克定律可知,为了确定一点处的主应力,可在该点处粘贴一直角应变花,该直角应变花由三个应变片组成,既由+45o方向的应变片、O o方向的应变片和-45o方向的应变片组成。
只要用静态电阻应变仪将这三个方向上的线应变测出,代入公式既可计算出主应变的大小和方向。
为了兼测其它实验值,本实验采用直角应变花,并使中间的应变片方向与园轴母线一致,另外两片分别与母线成±45o角,在A 、B 、C 、D 四个测点分别粘贴四枚应变花。
根据被测点三个方向应变值ε45°、ε0°、ε-45° ,计算主应力大小和方向公式分别为:245020454545maxmin )()()1(2)()1(2o o o o o o EE εεεεμεεμσ-+-+⋅±++=-- ……(8—1)Tan2ɑ0=oooo o 4545454502εεεεε----- ……… (8—2)式中ɑ。
midas操作例题资料-钢箱梁

Civil&Civil Designer一、钢箱梁操作例题资料1概要钢桥是高强、轻型薄壁结构,截面和自重比混凝土桥小,跨越能力大,因而在实际工程中有广泛应用。
钢桥按形式可大致分为钢箱梁、钢板梁(工字钢)、钢桁梁、组合梁桥等类型。
钢桥在使用时不仅要求钢材具有较高的强度,而且还要求具有良好的塑性。
钢桥的刚度相对比较小,变形和振动比混凝土桥大。
为了保证车辆行驶安全和舒适性、避免过大的变形和振动对钢桥结构产生不利的影响,钢桥必须有足够的整体刚度[2] 。
钢桥缺点除容易腐蚀影响耐久性外,另一缺点是疲劳。
影响疲劳的因素很多,除钢材品质、连接的构造与方法等外,与荷载性质、疲劳细节关系也很大。
钢箱梁除钢材等力学特性外,还具有箱梁的受力特点,广泛应用于市政高架、匝道、大跨度斜拉桥、悬索桥、拱桥加劲梁、大跨连续钢箱梁及人行桥钢箱梁等方面。
本专题将通过介绍工程概况、结合规范构造检查、midas Civil详细建模过程以及midas Civil Designer设计平台及结果查看等操作流程,希望能为读者结合实际项目学习程序,通过程序了解钢箱梁提供帮助。
钢箱梁操作例题资料2 钢桥概况及构造检查2.1 钢桥概况主梁为20+30+40+30m单箱单室正交钢箱梁,钢材为Q345;桥面宽8m,梁高2.335m,翼缘板长1.8m;顶板、腹板、翼缘板均厚16mm,底板标准段厚16mm,支座两侧3~3.5m范围内加厚为24mm;顶板设置闭口U型加劲肋;翼缘板、腹板均设置板型加劲肋;底板标准段设置板型加劲肋,桥墩两侧5~7m范围内设置T型加劲肋;横隔板等设置距离详见图1~图3所示。
建模之前,应按照《公路钢结构桥梁设计规范》(JTG D64—2015)[1] (以下简称规范)对钢桥面板、加劲肋、翼缘板及腹板等尺寸进行构造检查。
2.2构造检查2.2.1钢桥面板近年来正交异性钢桥面板出现疲劳和桥面铺装损伤的现象较为普遍,为保证钢桥面板具有足够的刚度,需对最小厚度有要求;为减小应力集中和避免采用疲劳等级过低的构造细节,需对纵向闭口加劲肋尺寸进行规定[1]。
TD-温度荷载-梁截面温度设置

midas Civil 技术资料----温度荷载-梁截面温度设置目录midas Civil 技术资料1 ----温度荷载-梁截面温度设置 1 1概述2 2梁截面温度设置 2 3梁截面温度设置举例3 3.1预应力混凝土箱梁温度梯度输入(一般截面) 3 3.2预应力混凝土箱梁温度梯度输入(PSC/组合截面) 5 3.2联合截面-梁截面温度设置 6 4梁截面温度计算结果对比 7 5总结 10 参考文献12北京迈达斯技术有限公司 桥梁部2013/04/221概述midas Civil模拟截面内部温度变化而引起的效应有两种方式:温度梯度和梁截面温度。
可沿截面高度和宽度方向分段输入温度。
温度梯度适用:1、截面温度呈线性变化;2、截面材料特性(弹性模量、热膨胀系数)无变化,即单一材料。
梁截面温度适用:1、截面温度呈非线性变化,如图1-1所示的钢混叠合梁、预应力混凝土箱型梁等。
2、截面内材料特性(弹性模量、热膨胀系数)发生变化,如组合截面。
a)实际的温度分布b)简化的温度分布图1-1 温度分布示意图2梁截面温度设置执行命令:荷载>温度荷载>梁截面温度。
如图2-1。
定义梁截面温度梯度荷载工况,因其在成桥阶段考虑,故,荷载组可不设置。
在“截面类型”中,可以选择“一般截面”或“PSC/组合”:1)选择“一般截面”,需自定义输入B值和H值以及相应的温度数据,根据B值或H 值变化,可分割多个温度点输入,如图2-1 a、b。
定义沿截面宽度方向的温度时,B值相当于定义沿高度方向变化时的H值,H值相当于定义沿高度方向的B值。
两者定义方式类似,故本文只介绍沿截面高度方向的梁截面温度设置。
2)选择“PSC/组合”后,选择“截面”,程序将自动考虑截面宽度B值,也可自定义输入B值,如图2-1c、d。
温度变化点的位置H1、H2和对应温度值T1、T2,需根据设计情况进行输入。
a)一般截面(高度)b)一般截面(宽度)c)PSC/组合截面(自动)d)PSC/组合截面(手动)图2-1 梁截面温度定义关于“一般截面”和“PSC/组合”适用范围,详见本文5.2所述。
框架梁组合梁计算自动计算程序
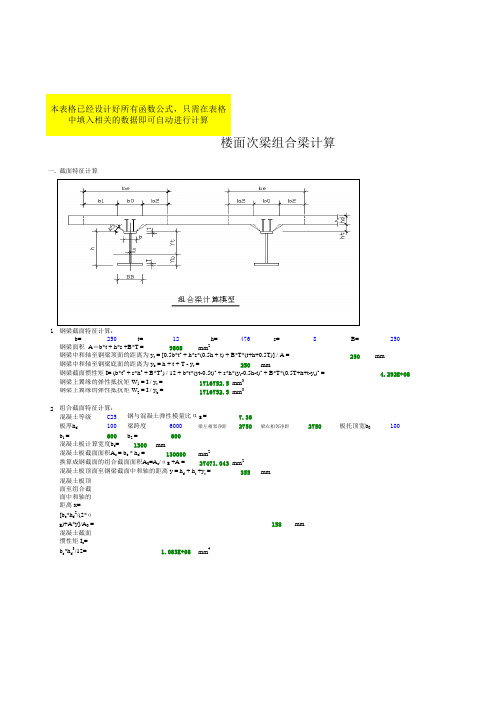
2.2 考虑混凝土徐变在垂直荷载作用下的正应力
混凝土板顶面应力:
σ0ctc=-(M2g/W0ctc+M2q/W0ct)=
-2.09
混凝土板底面应力:
σ0cbc=-(M2g/W0cbc+M2q/W0cb)=
-0.81
钢梁上翼缘应力
σ0tc = -M1/W1+(M2g/W0tc+M2q/W0t)=
钢梁下翼缘应力
24 mm
PASS!
使用阶段的 三 验算 1 弯矩及剪力
找平层重:
3.6 kN/m
活荷载:
19.5
使用阶段弯矩设计值M
使用阶段剪力设计值V
kN/m 103.95 kN.m 69.30 kN
(活荷 载:
5 kn/m2)
2 组合梁的抗弯强度
2.1 在垂直荷载作用下的正应力
混凝土板顶面应力σ0ct=-M/W0ct=
σ0bc = -M1/W2+(M2g/W0bc+M2q/W0b)=
N/mm2
<
N/mm2
<
-32.55 N/mm2 71.51 N/mm2
12.5 N/mm2
12.5 N/mm2
<
315
<
315
2.3 温度差产生的应力 (略)
2.4 组合梁中由于混凝土收缩引起的内力 (略)
钢梁的剪应
3力
钢梁腹板顶面处对钢梁中和轴的面积矩S1=
2.20 mm
< L/250 =
24 mm
四 。 材料统计:
钢材重量:
G=
461.9568 kg
N/mm2 N/mm2
N/mm2 N/mm2
钢桥、组合梁桥-midas操作例题资料-钢混组合梁

钢桥、组合梁桥-midas操作例题资料-钢混组合梁Civil&Civil Designer⼆、钢混组合梁操作例题资料1⼯程概况本桥为某⾼速路联络线匝道桥中的⼀联,桥宽6m。
上部结构采⽤38+33.5+37.5m钢混组合连续梁,下部结构桥墩为柱式。
主梁为单箱单室,梁⾼3.5m,预制⾼3.1m,钢箱底板厚50mm,上翼缘板厚50mm,腹板厚20mm,布置加劲肋。
钢材均采⽤Q345,分4段预制后现场采⽤⾼强螺栓拼接。
钢箱顶部混凝⼟桥⾯板厚0.2m,承托⾼0.2m,抗剪界⾯为c-c,采⽤C50混凝⼟现浇;横隔板等设置距离详见图2所⽰。
图1.1-1 钢箱梁构造图(⼀)钢混组合梁操作例题资料图1.1-2 钢箱梁构造图(⼆)2 建模步骤2.1定义材料特性>材料特性值>材料图2.1-1 材料定义图2.1-2 材料数据《公路钢混组合桥梁设计与施⼯规范》(JTG/T D64-01-2015)桥梁设计,需要定义组合材料,选择规范“JTG D64-2015(S)”。
2.2定义截⾯特性>截⾯特性值>组合梁截⾯组合梁截⾯⽀持“钢-箱型(Type1)”、“钢-I 型(Type1)、“钢-槽型(Type1)” 、“钢-箱型(Type2)、“钢-I 型(Type2)、“钢-槽型(Type2),共六种。
截⾯中可任意设置纵向加劲肋,⽀持“平板”、“T 形”、“U 肋”三种类型,截⾯特性值考虑了纵向加劲肋的影响。
图2.2-1 截⾯数据按照界⾯内辅助⽰意图,输⼊混凝⼟板和钢箱梁各段距离,顶底板、腹板厚度等。
输⼊Es/Ec(钢与混凝⼟弹性模量之⽐)、Ds/Dc(钢与混凝⼟容重之⽐)、Ps(钢梁泊松⽐)、Pc(混凝⼟板泊松⽐)、Ts/Tc(钢与混凝⼟线膨胀系数之⽐)。
点击“截⾯加劲肋”,进⾏加劲肋设置。
点击“定义加劲肋”,定义加劲肋尺⼨,设置加劲肋布置位置及间距。
图2.2-2 加劲肋布置数据图2.2-3加劲肋截⾯数据2.3 建⽴结构模型导⼊DXF⽂件:Civil图标>导⼊>AutoCAD DXF⽂件曲线桥梁可以通过导⼊CAD线形的⽅法建⽴单元节点。
远盛水工计算说明书

第六章计算◆菜单组结构及简介计算的菜单结构如图3-1所示。
图6-1 菜单结构功能简介:计算菜单组提供了很多方便工程师计算的实用工具,同时把计算得结果绘制出来,把许多重复繁琐的操作交给程序处理,简化了很多设计中常用的操作步骤。
◆菜单组各命令详细说明一、桁架计算[命令]:HJJS[菜单位置]:计算→桁架计算功能:对各种桁架结构进行内力计算并绘制轴力图和变形图,同时生成计算书。
您使用AutoCAD的命令绘制出如图6-1.1所示桁架结构的单线图以后,即可对该桁架结构进行计算。
桁架单线图须以毫米为单位绘制。
在“基本工具”菜单列的“初始设置”中将“出图比例”和“绘图比例”进行正确设置,出图比例除以绘图比例的比值等于单线图的缩放比例。
例如,如果一根梁的实际长度为2000mm,而您在CAD上绘制长度为20单位长,也就是说,图形相对结构缩小了20/2000倍。
那么,如果您设置出图比例为1,则须设置绘图比例=2000/20×1=100;如果您设置出图比例为2,则须设置绘图比例=2000/20×2=200。
6-1.1 桁架单线图执行此命令,弹出如图6-1.2所示对话框。
6-1.2桁架计算主对话框在“工程”菜单列点击“新建”,按照程序要求输入工程名“桁架计算例题一”,此时就创建了一个桁架计算工程。
点击“节点处理”菜单列中“添加节点”,程序将自动在单线图中线段的顶点和交点位置添加节点。
点击“节点设置”,可以对图中的节点大小和颜色进行调整。
如果在某些交点位置不需要节点,请执行“删除节点”将这个节点删除,而不要使用“erase”命令直接删除。
点击“编号”中“杆件、节点编号”,选择桁架结构的所有单线图和节点,程序将自动对杆件和节点进行编号。
点击“材料库”中“定义材料库”,将弹出如图6-1.3所示对话框。
6-1.3材料库管理在图中右侧录入框中输入适当的数值后,点击“入库”,则将这种名为“bar”的材料存入材料库;如果该桁架中有几种不同截面积或材质的材料,则可以分别定义不同的材料名,并存入材料库。
ETABS常见问题_bywxh5330

ETABS常见问题_bywxh53301问:定义⾯截⾯时,怎样选择其类型?“壳”、“膜”、“板”的含义是什么?答:ETABS中把楼板、墙都抽象为⾯对象,⾯对象的类型有三种,即“壳”、“膜”、“板”。
“壳”具有平⾯内以及平⾯外刚度,⼀般⽤于定义墙单元。
“膜”仅具有平⾯内刚度,⼀般⽤于定义楼板单元,起传递荷载的作⽤。
“板”仅具有平⾯外刚度,仅存在平⾯外变形。
对于⾯截⾯类型的选择,⼀定程度上要靠⼯程师根据⼯程情况作出选择。
2问:请问输⼊楼⾯恒荷载时⽤不⽤考虑楼板⾃重?答:ETABS中考虑⾃重的⽅法⾮常简单,即在定义静⼒荷载⼯况时设定⾃重系数为1,ETABS 会⾃动计算结构中所有结构构件的⾃重,因此在输⼊楼板上的⾯荷载时不⽤再考虑楼板的⾃重。
3问:安装了ETABS,但启动程序时提⽰“LicenseNotFound”,该怎么办?答:这是由于电脑没有识别道加密锁或许可证⽂件。
解决办法请详见《ETABS中⽂版使⽤指南》附录A.3。
4问:竖向地震荷载怎么加不上?答:请注意在质量源的定义中有⼀个复选项“仅包括侧向质量”,默认情况下,该项是勾选的。
若定义了竖向地震荷载,要去掉这个勾。
另外,设计时需要添加⾃定义组合来考虑有竖向荷载参与的组合。
5问:ETABS如何判断薄弱层?能否输出薄弱层的相关信息?答:ETABS可根据规范规定⾃动判断结构薄弱层。
关于层刚度的计算,ETABS是按照GB50011第3.4.2条及其条⽂说明的⽅法进⾏。
另外,程序也允许对薄弱层进⾏⾃定义。
也就是在结构总信息对话框中对“结构不规则层”的定义,当此项定义为零时,代表结构薄弱层由程序⾃动判断,若此项定义为某⾃然数,对话框中将出现相应数量的不规则层层号定义项,这时程序将不会⾃动判断薄弱层。
关于薄弱层判断及其地震剪⼒调整的信息可以在结构总体信息中输出。
6问:License到期了如何更新?答:⾸先与⾦⼟⽊公司客服联系:010********-401,获取更新license。
第五讲 实例演示-钢混组合梁1

第五讲实例演示-钢混组合梁1 第五讲实例演示,钢混组合梁桥的计算一、结构尺寸:某桥为34米简支钢混组合梁桥,如下图所示,横桥向由多片梁组成,梁中到中间距7.3米,取其中一片梁计算。
钢梁裸梁高1.4米,顶板(含翼缘)宽5.5米,底板4.374米,底板厚0.025米,腹板厚0.016~0.02米。
二次浇注混凝土厚0.20米。
图1钢混组合箱梁桥构造图二、设计计算参数:1. 设计荷载:城 - A级。
2. 车道数:2车道。
3. 结构重力:一期恒载:结构自重混凝土γ=25KN/m3;钢γ=100KN/m3二期恒载:桥面铺装(t=100mm)防撞栏杆: 8 KN/m(一侧)5.温度影响力:温度条件考虑按规范取值(JTGD60—2004 4.3.10条)整体均匀温差+15?、-30?。
梯度温度正温差A=400mm,T1=16.4?,T2=6?;负温差A=400mm, T1= -8.2?,T2=-3?。
7.收缩徐变影响力:按新设计规范取用。
三、计算方法选用1本系统包含三种算法 :1. 平面梁单元算法。
2. 梁格法。
3(膜、板、八节点非协调块单元算法。
这里我们选用第三种算法。
模型的建立主要有两大步骤:(1)和建立梁单元计算模型类似,通过输入单元集、材料、截面、积分方法等参数建立网格划分控制信息;(2)执行网格划分。
网格划分控制信息的建立分以下几种情况:1、当桥的内横梁及边横梁垂直于桥中线(对于弯桥横梁沿径向),开始建模时,可完全按单根梁模型来建,建完后定义一下每个梁单元的积分方法,再执行网格划分,基本的空间块单元模型便可建立。
在建立单根梁模型时,梁可以位于桥的中线,此时需定义梁为中纵梁;梁也可定位于桥的边缘,此时需定义梁为边纵梁。
2、对于其它异型桥,网格划分控制信息建立有两种方式:(1)梁边缘控制法;(2)腹板节点控制法。
具体可参照说明书。
在本例题中,由于桥为直桥且等宽,因此建立起单根梁模型后就可以执行网格划分。
总体建模思路是:(1)不考虑横隔板将主梁模型建立起来;(2)按基本类似的步骤在主梁模型上增加横隔板或先单独建立横隔板模型文件再将该文件合并到主梁模型中。
Midas Gen 1.8.2版本新功能说明解析

版本号:Release 2016 1.8.X发行日期:2017-1-23YJK1.8.2版本新增功能目录YJK1.8.2版本新增功能 (1)一、建模部分的改进 (3)(一)大体量模型时仍保持建模操作的顺畅 (3)(二)转AutoCAD平面图时可以识别梁的截面尺寸 (3)(三)转AutoCAD平面图时对构件的图素指定可以按图素单选 (3)(四)空间菜单下导到楼层的导到1层选项可不受层高限制 (4)(五)蒙皮导荷时对梁构件导成均布荷载 (4)(六)改进了荷载菜单下的构件荷载显示 (4)(七)构件荷载布置时对当前层布置的构件衬出底色 (4)(八)屏幕右下角增加三维快速浏览菜单 (5)二、外包钢板混凝土剪力墙设计 (6)三、单拉杆件设计 (8)四、计算前处理 (10)五、计算后处理 (12)六、弹塑性动力时程分析软件YJK-EP的改进 (21)(一)计算加速 (21)(二)改进了墙的二维本构计算 (22)(三)改进了损伤的计算效果 (23)(四)完善了送审报告 (26)(五)完善了多塔结构后处理 (26)(六)PushOver改进说明 (27)七、梁平法施工图增加读取AutoCAD图钢筋数据 (29)1.目的 (29)2.方法 (30)3.菜单 (30)4.操作步骤 (30)5.具体实现规则 (35)八、楼板施工图中导入AutoCAD楼板钢筋 (37)1.目的 (37)2.选择DWG绘制方法和设置未标注钢筋信息 (37)3.钢筋导入前的分组 (38)4.菜单 (40)5.操作步骤 (40)6.其他说明 (43)九、装配式软件 (44)1.预制构件参数修改对话框改进 (44)2.增加导入构件库数据画详图菜单 (45)3.预制墙吊装验算的图面表达 (45)4.单排套筒 (46)5.三维图中增加后浇节点 (46)6.碰撞检测。
(46)7.详图的双线间距参数 (46)8.预制叠合板改进 (46)9.预制楼梯改进 (48)十、钢结构计算 (49)1.梁的整体稳定计算考虑隅撑刚度 (49)2.门刚柱计算长度按照《门刚规范》GB51022-2015附录A实现; (50)3.增加了新增热轧无缝钢管的设计验算及优化设计 (51)4.组合梁放开施工荷载参数 (52)5.支持闭口压型钢板组合楼盖计算 (52)十一、钢结构施工图 (55)1.对于梁柱节点的短梁连接节点补充了节点表画图方式下的变量图 (55)2.放开了支撑参数中支撑实际轴力小于等强内力的1/x时内力取承载力的x 倍 (56)3.对于梁柱短梁拼接翼缘焊接的情况对腹板承担的弯矩给予0.4的折减 (56)4.增加了门刚中间柱与斜梁节点方式的选择 (56)5.变截面梁设计增加设计参数节点抗震验算时梁截面取值系数 (58)6.屋面檩条计算修正为《门刚规范》9.1.5条 (58)7.网架施工图增加了节点编号布置图等 (59)十二、基础设计 (60)(一)防水板计算增加“不考虑恒载活载组合”功能选项参数 (60)(二)可以按EP曲线输入地质资料孔点的压缩模量 (61)(三)条基按相连组加权平均计算重叠面积 (65)(四)增加承台、拉梁、地基梁、条基汇总计算书 (66)(五)其他改进 (66)(六)修正1.8.1存在的BUG (67)一、建模部分的改进(一)大体量模型时仍保持建模操作的顺畅大体量模型是指层数较多、塔数较多的多塔结构、超大规模平面、带有较大体量空间模型的结构等等,新版使大体量模型的操作仍保持顺畅,在切换菜单、构件布置荷载布置、选择构件等的操作仍与普通规模的模型相同。
Sap2000与etabs功能比较

Sap2000与etabs功能比较ETABS功能1)有限元库:框架单元(梁柱单元)、壳单元(薄壳/厚壳、膜单元)、弹簧单元、塑性铰单元、阻尼器、缝隙单元、钩单元、塑性单元、滞回隔振器、摩擦隔振器2)线性分析:静力分析(线性静力分析、温度应力分析、风荷载自动施加、可以指定任意复杂立面风荷载体型系数等等)、反应谱分析(反应谱函数可编辑)、线弹性时程分析(可导入人工波)3)非线性分析:P-delta 分析、静力弹塑性分析(Pushover分析) 、非线性时程分析、施工顺序加载分析(刚度逐层形成、荷载逐层施加)4)其他功能:相似层、截面设计器(自定义任意复杂几何形状、材料组成的截面形式,程序自动计算该截面的所有力学指标)、增强的OpenGL三维透视图、自动边束缚、刚性隔板定义、准刚性隔板用于楼板开大洞5)初始化模型模板(钢楼板、交错桁架、无梁楼盖、带边梁的无梁楼盖、井字梁楼盖、双向板或肋板)6)数据接口(基于IFC建筑信息交互、导入SATWE模型与荷载、导入/导出CAD的DXF 文件、导入/导出RevitStructure、导入/导出Prosteel.mdb文件、导入/导出Xsteel、导入StaadPro、导入GT Strudl、导出SAP2000.s2k、导出Safe.s2k、导出ADABS.a2k、导出Perform3D、导出Access数据库)7)设计(钢筋混凝土结构、钢结构、组合结构、组合梁/钢桁架梁)及详细计算书输出功能、修改覆盖项快速修改模型各种参数、结构总信息文本打印输出、后处理平法施工图模块cksDetailer8)钢结构优化设计(周期、位移控制)、截面自动选择列表功能9)规范:中国02规范、美国规范、加拿大规范、墨西哥规范、欧洲规范、英国规范、意大利规范、印度规范、新加坡规范、香港规范、韩国规范、新西兰规范。
SAP2000功能1)有限元库:框架单元(梁柱单元)、壳单元(薄壳/厚壳、膜单元)、实体单元、索单元、钢束单元、平面应力单元、平面应变单元、只拉/压弹簧单元、塑性铰单元、纤维铰、阻尼器、缝隙单元、钩单元、多段线弹性连接单元、多段线塑性连接单元、Wen塑性单元、摩擦隔振器2)线性分析:静力分析(线性静力分析、温度应力分析、风荷载自动施加、任意复杂立面风荷载体型系数)、反应谱分析、线弹性时程分析(可考虑多基激烈,行波效应)3)无应力变形几何(考虑初始缺陷)、预应力分析、线性屈曲分析、多步静力分析、稳态分析、功率谱密度分析、波浪模块(适用于大坝、池壁或水工模型,水的速度和加速度由拖拉和惯性力计算得到,并将其转化为分布荷载自动施加在结构上)4)非线性分析:P-delta 分析、大位移、非线性屈曲分析、静力弹塑性分析(Pushover分析) 、非线性时程分析、阻尼隔振分析、施工顺序分析(可考虑混凝土的收缩,徐变、预应力钢筋松弛、构件和荷载及边界的多次变化)5)其他功能:截面设计器(自定义任意复杂几何形状、材料组成的截面形式,程序自动计算该截面的所有力学指标)、增强的OpenGL三维透视图、动画模拟、自动边束缚、刚体束缚、刚性隔板、杆束缚.......等等6)初始化模型模板(梁、二维桁架、三维桁架、二维框架、三维框架、墙、无梁楼盖、壳体、楼梯、储藏结构、地下混凝土、实体模型、索桥、Caltrans-BAG、快速桥梁信息模型、管和板)7)完整的数据库格式,电子表格交互式编辑、开放的应用程序接口OAPI,为用户提供二次开发的平台8)数据接口(基于IFC建筑信息交互、导入/导出CAD的DXF文件、导入/导出Prosteel.mdb 文件、导入/导出Xsteel、导入StaadPro、导入GT Strudl、导出Perform3D、导出Access 数据库、导出excel电子表格)9)设计(钢筋混凝土框架结构、钢结构、组合结构、组合梁/钢桁架梁、铝框架设计、冷弯薄壁框架设计)10)钢结构优化设计(周期、位移控制)、截面自动选择列表功能11)规范:中国02规范、美国规范、加拿大规范、墨西哥规范、欧洲规范、英国规范、意大利规范、印度规范、新加坡规范、香港规范、韩国规范、新西兰规范...........12)桥梁模块加入中国桥梁规范。
【桥梁设计】桥梁伸缩缝宽度计算程序自动生成计算书(原版)

计算条件:1、跨径组合=25m2、L=25m3、温度变化范围-15~+40°C4、砼线膨胀系数a=5、∈∞=6、δc=7、Ec=MPa8、β=9、бp=MPa10、Tset=°C计算:1、13.8mm2、5mm3、8.75mm4、 1.5mm5、 2.0mm6、 1.0mm温度降低引起的缩短量:温度升高引起的伸长量:梁体因温度变化产生的伸缩量为:R=0.04L=△ls=бp/Ec×δc×L×β×1000=因车辆荷载作用使梁体挠曲使伸缩装置开口产生的位移:砼徐变引起的梁体缩短量:砼收缩引起的缩短量:预应力截面平均应力伸缩装置的安装温度 4.6202.0E-042徐变系数3.45E+040.3收缩徐变的折减系数桥头伸缩量计算△lt +=a×(t2-Test)×L×1000=△lt -=a×(Test-t1)×L×1000=△l s =∈∞×L×β×1000=△lt=a ×(t2-t1)×L×1000=1×251.0E-05弹性模量收缩应变伸缩梁长(1/2桥长)=5mm =12.3mm所以:=17mm 22mm同样=6.5mm=15.9mm1、选用D6050~110则:53.5>5075.9<1102、选用D6050~110则:53.5>5075.9<110B 0-梁端设计闭口量=B 0-梁端设计闭口量=B 0-梁端设计开口量=伸缩装置所选伸缩缝型号满足要求伸缩装置所选伸缩缝型号满足要求变形范围f 为B 0-梁端设计开口量=总伸长量=△lt +总缩短量=△lt -+△l s +△ls基本伸缩量=总伸长量+总缩短量提高30%后为注:提高系数β可取1.2~1.4。
变形范围f 为梁端设计开口量=总伸长量×1.3梁端设计闭口量=总缩短量×1.3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
302773 mm3
钢梁上翼缘的弹性抵抗矩 W2 = I / yb =
469607 mm3
4.6E+07 mm4
2 组合截面特征计
混凝土等
级
C20
钢与混凝土弹性模量比αE =
8.08
板厚hd
100 梁跨度
梁左相邻净
梁右相邻净
板托顶宽
板托高度
6000 距
1800 距
1800
b0
300 ht
150
b混1 =凝土板计算宽60度0 b2 =
2000 6000
mm) 7.31
mm)
kN/m
钢梁抗弯
2 强度设计
钢梁上翼缘应力 M / rx*W1 = 143.14 N/mm2
<
215 N/mm2
钢梁下翼缘应力 M / rx*W2 =
92.29 N/mm2
<
215 N/mm2
PASS! PASS!
钢梁剪应
3 力计算
面积矩 S= 207492 mm3
施工阶段 二 的验算
弯矩和剪 1力
钢梁自 重: 板自重: 板托重:
0.41 6.00 0.90
自重标准值 g1k:
施工荷
载:
2.80
施工阶段
弯矩设计
值M
施工阶段
剪力设计
值V
kN/m kN/m kN/m
6.09
(平台梁间距:
kN/m
自重标准 值 g1:
kN/m
45.51 kN.m
(梁跨 度:
30.34 kN
2.3 温度差产生的应力 (略)
2.4 组合梁中由于混凝土收缩引起的内力 (略)
钢梁的剪
3 应 钢力 梁腹板顶面处对钢梁中和轴的面积矩
S钢1=梁腹板顶面以外的砼及钢梁上翼缘对组合1截47面00中0 和m轴m的3 面
积矩So=
两个受力阶段的荷载对组合梁的钢梁产生的剪应力
τ=V1S1/Itw+V2So/IoTw=
混凝土板
顶面至组
合截面中
和轴的距
离xc=
[be*hd2/(4* α
E)+A*y]/A
c 0
=
162 mm
换算成钢截面的组合截面惯性矩 I0c = Ic/(2*αE) + Ac*(xc-0.5hd)2/(2*αE) + I + A(y-
对混凝土板顶面的组合截面弹性抵抗矩 w0ctc = 2αE*I0c / xc= 4.2E+07 mm4
19.35 N/mm2
<
1105812 mm3 125 N/mm2
组合梁的 4 挠度
△=5qkl4/384EIo+5gkl4/384EIoc= 3.46 mm
< L/400 =
15 mm
PASS! PASS! PASS! PASS! PASS! PASS! PASS! PASS!
PASS!
PASS!
本表格已经设计好所有函数公式,只需在表 格中填入相关的数据即可自动进行计算
一. 截面特征计算
组合梁计算
1 钢梁截面特征计
b=
100
t=
10
h=
230
s=
6
B=
200
T=
10
钢梁面积 A=b*t + h*s +B*T = 4380 mm2 钢梁中和轴至钢梁顶面的距离为 yt = [0.5b*t2 + h*s*(0.5h + t) + B*T*(t+h+0.5T)] / A
152 mm
钢梁中和轴至钢梁顶面的距离为 yb = h + t + T - yt = 98 mm
钢梁截面惯性矩 I= (b*t3 + s*h3 + B*T3) / 12 + b*t*(yt-0.5t)2 + s*h*(yt-0.5h-t)2 + B*T*(0.5T+h+t-
钢梁上翼缘的弹性抵抗矩 W1 = I / yt =
对混凝土板底面的组合截面弹性抵抗矩 w0cbc=2αE*I0c / (x c- hd 1.1E+08 mm4
对钢梁上翼缘的组合截面弹性抵抗矩 w0tc = I0c / (d- 4800913 mm4
对钢梁下翼缘的组合截面弹性抵抗矩 w0bc = I0c / (H- 1249942 mm4
4.2E+08 mm4
kN/m 78.84 52.56
kN.m kN
(活荷 载:
6 kn/m2)
2 组合梁的抗弯强度
2.1 在垂直荷载作用下的正应力
混凝土板顶面应力σ0ct=-
-2.28
混凝土板底面应力σ0cb=-
-0.33
钢梁上翼缘应力σ0t = -M1/W1+M2/W0t=
钢梁下翼缘应力σ0b = -M1/W2+M2/W0b=
E)+A*y]/A
0= 混凝土截 面惯性矩
117 mm
Ic= be*hd3/12= 换算成钢 截面的组 合截面惯 性矩 I0 = Ic/αE +
Ac*(x0.5hd)2/αE
+ I + A(y-
1.3E+08 mm4
x)2 =
5E+08 mm4
对混凝土板顶面的组合截面弹性抵抗矩 w0ct = α 3.5E+07 mm4
钢梁剪应力τ1max = v1*s1/I*tw = 22.80 N/mm2
<
125 N/mm2
PASS!
4 挠度计算 △ =5*g*l4/(3
84*E*I)=
10.8 mm
< L/400 =
15 mm
SS!
使用阶段 三 的验算
弯矩及剪 1力
找平层 重:
1.9 kN/m
活荷载: 15.6 使用阶段弯矩设计 使用阶段剪力设计
对混凝土板底面的组合截面弹性抵抗矩 w0cb=αE*I0 / (x - hd ) = 2.4E+08 mm4
对钢梁上翼缘的组合截面弹性抵抗矩 w0t = I0 / (d-x) 3763855 mm4
对钢梁下翼缘的组合截面弹性抵抗矩 w0b = I0 / (H-x) 1307031 mm4
3 考虑混凝土徐变的组合截面特征计算 换算成钢截面的组合截面面积 A0c = Ac / 2αE + A = 13662.2 mm2
-0.37
钢梁上翼缘应力
σ0tc = -M1/W1+(M2g/W0tc+M2q/W0t)=
钢梁下翼缘应力
σ0bc = -M1/W2+(M2g/W0bc+M2q/W0b)=
N/mm2
<
N/mm2
<
-88.23 N/mm2
130.69 N/mm2
10 N/mm2
10 N/mm2
<
215 N/mm2
<
215 N/mm2
600
be=
1500 mm
混凝土板截面面积Ac = be * hd = 150000 mm2
换算成钢截面的组合截面面积A0=Ac/αE 22944.4 mm2
混凝土板顶面至钢梁截面中和轴的距离 y = hd + ht
402 mm
混凝土板 顶面至组 合截面中 和轴的距 离 x=
[be*hd2/(2* α
N/mm2 N/mm2
-87.74 130.39
<
< N/mm2 N/mm2
10 N/mm2
10 N/mm2
<
215 N/mm2
<
215 N/mm2
2.2 考虑混凝土徐变在垂直荷载作用下的正
混凝土板顶面应力:
σ0ctc=-(M2g/W0ctc+M2q/W0ct)=
-2.24
混凝土板底面应力:
σ0cbc=-(M2g/W0cbc+M2q/W0cb)=
