与圆有关的压轴题(提高)

合集下载

2022-2023学年人教版中考数学复习圆综合压轴题专题提升训练

2022-2023学年人教版中考数学复习《圆综合压轴题》专题提升训练（附答案）1．锐角三角形△ABC的外心为O，外接圆直径为d，延长AO，BO，CO，分别与对边BC，CA，AB交于D，E，F．（1）求的值；（2）求证：．2．如图，AB是⊙O的直径，点C在⊙O上，CP是⊙O的切线．点P在AB的延长线上．（1）求证：∠COB＝2∠PCB；（2）若M是弧AB的中点，CM交AB于点N，若AB＝6．求MC•MN的值．3．如图，AC为⊙O的直径，CF切⊙O于点C，AF交⊙O于点D，点B在DF上，BC交⊙O于点E，且∠CAF＝2∠BCF，BG⊥CF于点G，连接AE．（1）求∠AEB的度数；（2）求证：△CBG∽△ABE；（3）若∠F＝60°，GF＝2，求⊙O的半径长．4．如图，△ABC内接于⊙O，BC是⊙O的直径，E是上一点，弦BE交AC于点F，弦AD⊥BE于点G，连接CD、CG，且∠CBE＝∠ACG．（1）求证：∠CAG＝∠ABE；（2）求证：CG＝CD；（3）若AB＝4，BC＝2，求GF的长．5．如图，△ABC为⊙O的内接三角形，AD⊥BC，垂足为D，直径AE平分∠BAD，交BC于点F，连结BE．（1）求证：∠AEB＝∠AFD；（2）若AB＝10，BF＝5，求DF的长；（3）若点G为AB的中点，连结DG，若点O在DG上，求BF：FC的值．6．如图，△ABC为⊙O的内接等腰三角形，AB＝AC，CD为⊙O的直径，DF∥AC交AB、BC于点E、F．（1）求证：DE＝EF；（2）若sin∠B＝，⊙O的半径为5，求CF的长．7．如图，⊙O为△ABC的外接圆，AB为⊙O直径，AC＝BC，点D在劣弧BC上，CE⊥CD交AD于E，连接BD．（1）求证：△ACE≌△BCD．（2）若CD＝2，BD＝3，求⊙O的半径．8．如图，在△ABC中，∠ACB＝90°，点D在BC边上（不包括端点B，C），过A，C，D三点的⊙O交AB于另一点E，连接AD，DE，CE，且CE⊥AD于点G，过点C作CF∥DE交AD于点F，连接EF．（1）求证：四边形DCFE是菱形；（2）当tan∠AEF＝，AC＝4时，求⊙O的直径长．9．如图，在△ABC中，以AB为直径的⊙O交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，且DH是⊙O的切线，连接DE交AB于点F，连接BE．（1）求证：DC＝DE；（2）若AE＝4，．求：①BE的长；②cos∠BDF的值．10．如图，AB是半圆的直径，AC为半圆的切线，AC＝AB、在半圆上任取一点D，作DE⊥CD，交直线AB 于点F，BF⊥AB，交线段AD的延长线于点F．（1）设是x°的弧，并要使点E在线段BA的延长线上，则x的取值范围是；（2）不论D点取在半圆什么位置，图中除AB＝AC外，还有两条线段一定相等，指出这两条相等的线段，并予证明．11．如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接P A，PB，AB，已知∠PBA＝∠C．（1）求证：PB是⊙O的切线；（2）连接OP，若OP∥BC，且OP＝8，⊙O的半径为2，求BC的长．12．如图，点C是以AB为直径的圆O上一点，直线AC与过B点的切线相交于D，点E是BD的中点，直线CE交直线AB于点F．（1）求证：CF是⊙O的切线；（2）若ED＝3，cos F＝，求⊙O的半径．13．如图①，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE＝CB．（1）求证：BC为⊙O的切线；（2）连接AE并延长与BC的延长线交于点G（如图②所示）．若AB＝，CD＝9，求线段BC和EG 的长．14．如图，AB为⊙O的直径，AB＝10，C为⊙O上一点，AD⊥CD，垂足为D，且交⊙O于E，C是的中点．（1）求证：DC是⊙O的切线；（2）若AC＝8，请直接写出CD的长．（3）若DC+DE＝6，求AE的长．15．如图，AB为⊙O的直径，点P是⊙O外一点，PD与⊙O相切于点C，与BA的延长线交于点D，DE ⊥PO，交PO的延长线于点E，连接PB，∠EDB＝∠EPB．（1）求证：PB是⊙O的切线；（2）若PB＝3，DB＝4，求⊙O的半径．16．如图，点P是⊙O外一点，P A切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O 于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD＝cm，AC＝8cm，点E是的中点，连接CE，求CE的长．17．如图，点O是等腰△ABC的外心，AD是圆O的切线，切点为A，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M，连接AD，交过点C的直线于点P，且∠BCP＝∠ACD．（1）判断直线PC与⊙O的位置关系，并说明理由；（2）若AB＝12，BC＝8．求PC的长．18．如图，在Rt△ABC中，∠C＝90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．（1）求证：ED为⊙O的切线；（2）如果⊙O的半径为，ED＝2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．19．如图1，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且∠PDA＝∠PBD．延长PD交圆的切线BE于点E（1）判断直线PD是否为⊙O的切线，并说明理由；（2）如图2，如果∠BED＝60°，PD＝，求P A的长．20．如图，AB是⊙O的直径，点C是的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且＝，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．（1）求证：BD是⊙O的切线；（2）当OB＝2时，求BH的长．21．如图，AB是⊙O的直径，延长BA至点P，过点P作⊙O的切线PC，切点为C，过点B向PC的延长线作垂线BE交该延长线于点E，BE交⊙O于点D，已知P A＝1，PC＝OC，（1）求BE的长；（2）连接DO，延长DO交⊙O于F，连接PF，①求DE的长；②求证：PF是⊙O的切线．参考答案1．（1）解：由于AD，BE，CF交于点O，∴＝，＝，＝，∴++＝1；（2）证明：如图，延长AD交⊙O于M，设R为△ABC的外接圆半径，AD，BE，CF交于点O．∵＝＝1﹣＝1﹣，同理有：＝1﹣，＝1﹣，代入++＝1，得（1﹣）+（1﹣）+（1﹣）＝1，∴++＝2，∴++＝＝．2．（1）证明：∵CP是⊙O的切线，∴OC⊥CP，∴∠PCB+∠OCB＝90°，∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°，∴∠ACO＝∠PCB，∵OA＝OC，∴∠A＝∠ACO，∵∠PCB＝∠A，∴∠COB＝2∠A＝2∠PCB；（2）解：如图2中，连接MA．∵点M是弧AB的中点，∴＝，∴∠ACM＝∠BAM，∵∠AMC＝∠AMN，∴△AMC∽△NMA，∴＝，∴AM2＝MC•MN，∵AB是⊙O的直径，∴∠AMB＝90°，∵AM＝BM，AB＝6．∴2AM2＝62，∴AM2＝18，∴MC•MN＝18．3．解：（1）如图，∵AC是⊙O的直径，∴∠AEC＝∠AEB＝90°．（2）如图∵CF与⊙O相切，∴∠ACF＝90°．∴∠BCF＝90°﹣∠ACE＝∠CAE．∵∠CAF＝2∠BCF．∴∠CAF＝2∠CAE．∴∠CAE＝∠BAE．∴∠BCF＝∠BAE．∵BG⊥BF，AE⊥BC，∴∠CGB＝∠AEB＝90°．∵∠BCF＝∠BAE，∠CGB＝∠AEB，∴△CBG∽△ABE．（3）连接BD，如图2所示．∵∠DAE＝∠DCE，∠DAE＝∠BCF，∴∠DCE＝∠BCF．∵AC是⊙O的直径，∴∠ADC＝90°．∴CD⊥AF．∵∠DCB＝∠BCF，CD⊥AF，BGCBF，∴BD＝BG．∵∠F＝60°，GF＝2，∠BGF＝90°，∴tan∠F＝＝BG＝tan60°＝，∵BG＝2，∴BD＝BG＝2．∵∠AFC＝60°，∠ACF＝90°，∴∠CAF＝30°．∵∠ADC＝90°，∠CAF＝30°，∴AC＝2CD．∵∠CAE＝∠BAE，∠AEC＝∠AEB，∴∠ACE＝∠ABE．∴AB＝AC．设⊙O的半径为r，则AC＝AB＝2r，CD＝r．∵∠ADC＝90°，∴AD＝r．∴DB＝AB﹣AD＝2r﹣r＝（2﹣）r＝2．∴r＝4+6．∴⊙O的半径长为4+6．4．（1）证明：∵BC是⊙O的直径，∴∠CAB＝90°，∴∠CAG+∠BAG＝90°，∵AD⊥BE，∴∠AGB＝90°，∴∠BAG+∠ABE＝90°，∴∠CAG＝∠ABE；（2）证明：∵∠CGD＝∠CAG+∠ACG，∠ABC＝∠ABE+∠CBE，由（1）知，∠CAG＝∠ABE，∵∠CBE＝∠ACG，∴∠CGD＝∠ABC，∵∠ABC＝∠D，∴∠DGC＝∠D，∴CG＝CD；（3）解：连接AE、CE，∵BC是直径，∴∠BEC＝90°，∴∠AGE＝∠BEC，∴AD∥CE，∵∠CAE＝∠EBC，∠ACG＝∠EBC，∴∠CAE＝∠ACG，∴AE∥CG，∴四边形AGCE是平行四边形，∴AF＝AC，∵AC2＝BC2﹣AB2，∴AC2＝﹣42，∴AC＝6，∴AF＝×6＝3，∵BF2＝AF2+AB2，∴BF2＝32+42，∴BF＝5，∵∠ABG＝∠ABF，∠AGB＝∠BAF，∴△BAG∽△BF A，∴BA：BF＝BG：BA，∴4：5＝BG：4，∴BG＝，∵FG＝BF﹣BG，∴FG＝5﹣＝．5．（1）证明：∵AE为⊙O的直径，∴∠ABE＝90°，∴∠BAE+∠AEB＝90°，∵AD⊥BC，∴∠ADF＝90°，∴∠AFD+∠F AD＝90°，∵AE平分∠BAD，∴∠BAE＝∠F AD，∴∠AEB＝∠AFD；（2）解：如图1，过点F作BM⊥AB于点M．则∠AMF＝90°，∵∠AFD＝∠BFE，∠AFD＝∠AEB，∴∠BFE＝∠AEB，∴BF＝BE＝5，∵∠ABE＝∠AMF＝90°，∠BAE＝∠MAF，∴△AMF∽△ABE，∴，即，设MF＝x，则AM＝2x，∴BM＝10﹣2x，∵BM2+MF2＝BF2，∴（10﹣2x）2+x2＝52，解得x＝3，即MF＝3，∵AE平分∠ABD，AD⊥BC，∴DF＝MF＝3；（3）解：∵∠ADB＝90°，G为AB的中点，∴AG＝DG＝BG，OG⊥AB，∴∠BGD＝∠AGD＝90°，∴△ADG为等腰直角三角形，∴∠GAD＝45°，∴∠ABD＝45°，过点F作FH⊥AB于点H，如图2，∵AF平分∠BAD，∴FD＝FH，∵∠ABD＝45°，∴BF＝FH＝FD，∵∠AFD＝∠AEB，∠AEB＝∠C，∴∠AFD＝∠C，∴AF＝AC，又∵AD⊥BC，∴FD＝DC，设FD＝DC＝x，则BF＝x，∴．6．（1）证明：如图，连接DB，∵CD为⊙O的直径，∴∠DBC＝90°，∵DF∥AC，AB＝AC，∴∠ABC＝∠ACB＝∠DFB，∴EB＝EF，∵∠DBF＝90°，∴∠DBE+∠EBF＝∠EDB+∠EFB，∴∠DBE＝∠EDB，∴DE＝EB，∴DE＝EF；（2）解：如图，连接AO，EO，延长AO交BC于点G，∵AB＝AC，∴AG⊥BC，∵OC＝OD，DE＝EF，∴OE∥FC，FC＝2OE，∴∠AEO＝∠B，∵OE⊥OA，在Rt△AEO中，sin∠AEO＝，∵sin∠B＝，⊙O的半径为5，∴＝，∴AE＝，∴OE＝＝＝．∴CF＝2OE＝．7．解：（1）证明：∵AB为⊙O直径，∴∠ACB＝90°，∵CE⊥CD，∴∠ECD＝90°，∴∠ACE＝90°﹣∠ECB＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（ASA）；（2）∵△ACE≌△BCD，∴CE＝CD，AE＝BD，∵CE⊥CD，∴△ECD是等腰直角三角形，∵CD＝2，BD＝3,∴DE＝2，AE＝3，∴AD＝5，∵AB为⊙O直径，∴∠ADB＝90°，∴AB＝＝2，∴⊙O的半径为．8．解：（1）证明：∵CE⊥AD，∴EG＝CG，∵CF∥DE，∴∠DEG＝∠FCG，∵∠FGC＝∠DGE，∴△DEG≌△FCG（ASA），∴ED＝FC，∴四边形DCFE为平行四边形，又∵CE⊥DF，∴四边形DCFE是菱形；（2）∵AG⊥EC，EG＝CG，∴AE＝AC＝4，∵四边形AEDC内接于⊙O，∴∠BED＝∠BCA＝90°，∵四边形DCFE是菱形，∴EF∥DC，DE＝DC，∴∠AEF＝∠ABC，∴tan∠ABC＝tan∠AEF＝，在Rt△BED中，设DE＝3a，则BE＝4a，∴DC＝3a，BD＝＝5a，∵BC2+AC2＝AB2，∴（5a+3a）2+42＝（4a+4）2，解得a＝或a＝0（舍去），∴DE＝DC＝2，∴AD＝＝＝2．即⊙O的直径长为2．9．解：（1）证明：连接OD，BE，∵OD⊥AC，且DH是⊙O的切线，∴∠ODH＝∠DHA＝90°，∴OD∥CA，∴∠C＝∠ODB，∵OD＝OB，∴∠OBD＝∠ODB，∴∠OBD＝∠C，∵∠OBD＝∠DEC，∴∠C＝∠DEC，∴DC＝DE；（2）①由（1）可知：OD∥AC，∴∠AEF＝∠ODF，∴∠AFE＝∠OFD，∴△AFE∽△OFD，∴，∵AE＝4，∴OD＝6，∵AB为⊙O的直径，∴；∴BE的长为8；②在Rt△AEB中，，∵∠BDF＝∠BAE，∴．10．解：（1）0＜x＜90，（2）连接BD，可证△BDF∽△ADB，得＝，∵∠DBE＝∠DAC，∴∠BDE＝∠ADC＝90°﹣∠ADE，∴△BDE∽△ADC，∴＝，∴＝，∴BE＝BF．11．（1）证明：连接OB，如图所示：∵AC是⊙O的直径，∴∠ABC＝90°，∴∠C+∠BAC＝90°，∵OA＝OB，∴∠BAC＝∠OBA，∵∠PBA＝∠C，∴∠PBA+∠OBA＝90°，即PB⊥OB，∴PB是⊙O的切线；（2）解：∵⊙O的半径为2，∴OB＝2，AC＝4，∵OP∥BC，∴∠C＝∠BOP，又∵∠ABC＝∠PBO＝90°，∴△ABC∽△PBO，∴＝，即＝，∴BC＝2．12．（1）证明：连CB、OC，如图，∵BD为⊙O的切线，∴DB⊥AB，∴∠ABD＝90°，∵AB是直径，∴∠ACB＝90°，∴∠BCD＝90°，∵E为BD的中点，∴CE＝BE，∴∠BCE＝∠CBE，而∠OCB＝∠OBC，∴∠OBC+∠CBE＝∠OCB+∠BCE＝90°，∴OC⊥CF，∴CF是⊙O的切线；（2）解：CE＝BE＝DE＝3，在Rt△BFE中，cos F＝，tan F＝＝，∴BF＝4，∴EF＝＝5，∴CF＝CE+EF＝8，在Rt△OCF中，tan F＝＝，∴OC＝6，即⊙O的半径为6．13．（1）证明：如图1，连接OE，OC；∵CB＝CE，OB＝OE，OC＝OC∴△OEC≌△OBC（SSS）∴∠OBC＝∠OEC又∵DE与⊙O相切于点E∴∠OEC＝90°∴∠OBC＝90°∴BC为⊙O的切线．（2）解：如图2，过点D作DF⊥BC于点F，则四边形ABFD是矩形，∵AD，DC，BG分别切⊙O于点A，E，B∴DA＝DE，CE＝CB，在Rt△DFC中，CF＝＝1，设AD＝DE＝BF＝x，则x+x+1＝9，x＝4，∵AD∥BG，∴∠DAE＝∠EGC，∵DA＝DE，∴∠DAE＝∠AED；∵AD∥BG，∵∠AED＝∠CEG，∴∠EGC＝∠CEG，∴CG＝CE＝CB＝5，∴BG＝10，在Rt△ABG中，AG＝＝6，∵AD∥CG，∴＝＝，∴EG＝×6＝．14．（1）证明：连接OC．∵C是的中点，∴AC平分∠DAB，∴∠DAC＝∠OAC，∵OA＝OC，∴∠OCA＝∠OAC，∴∠DAC＝∠OCA，∴DA∥OC，∵AD⊥DC，∴∠ADC＝90°，∴∠OCD＝90°，即OC⊥DC，∵OC为半径，∴DC为⊙O的切线．（2）解：∵AB是⊙O的直径，∴AB＝10，∠ACB＝90°＝∠ADC，∴BC＝＝6，又∵∠DAC＝∠OAC，∴△ACD∽△ABC，∴＝，即＝，解得：CD＝4.8．（3）如图，连接EC，作CF⊥AB于F．∵CA平分∠BAD，CD⊥AD，CF⊥AB，∴CD＝CF，∵＝，∴CE＝BC，∴Rt△CDE≌Rt△CFB，∴DE＝BF，∴CF+BF＝CD+DE＝6，设BF＝x，则CF＝6﹣x，由△ACF∽△CBF，可得CF2＝AF•BF，∴（6﹣x）2＝（10﹣x）•x，解得x＝2或9（舍弃），∴BF＝DE＝2，CD＝CF＝4，易证AF＝AD＝8，∴AE＝AD﹣DE＝6．15．（1）证明：∵∠EDB＝∠EPB，∠DOE＝∠POB，∴∠DEO＝∠PBO，∵DE⊥PE，∴∠DEO＝90°，∴∠PBO＝90°，∴PB是⊙O的切线；（2）由（1）知，PB是⊙O的切线，∴∠PBD＝90°，∵PB＝3，DB＝4，∴PD＝5，∵PC和PB都是⊙O的切线，∴PC＝PB＝3，∠OCD＝90°，∴CD＝2，设⊙O的半径为x，则OC＝x，OD＝4﹣x，则22+x2＝（4﹣x）2，解得，x＝，即⊙O的半径是．16．（1）证明：如图，连接OC，∵P A切⊙O于A．∴OA⊥P A，∴∠P AO＝90°，∵OP∥BC，∴∠AOP＝∠OBC，∠COP＝∠OCB，∵OC＝OB，∴∠OBC＝∠OCB，∴∠AOP＝∠COP，在△P AO和△PCO中，∴△P AO≌△PCO（SAS），∴∠P AO＝∠PCO＝90°，∴OC⊥PC，∴PC是⊙O的切线；（2）解：连接EA、EB，作BH⊥CE于H，如图，∵AB是⊙O的直径，∴∠ACB＝∠AEB＝90°，∵OP∥BC，∴PO⊥AC，∴AD＝CD＝AC＝4，在Rt△P AD中，P A＝＝＝，∵∠APO＝∠DP A，∴Rt△P AD∽Rt△POA，∴P A：PO＝PD：P A，即：PO＝：，解得PO＝，∴OD＝PO﹣PD＝3，∵AO＝BO，OD∥BC，∴BC＝2OD＝6，在Rt△ACB中，AB＝＝10，∵点E是的中点，∴∠BCE＝∠ACE＝∠ACB＝45°，∴AE＝BE，∴△BCH和△ABE都是等腰直角三角形，∴CH＝BH＝BC＝3，BE＝AB＝5，在Rt△BEH中，EH＝＝4，∴CE＝CH+EH＝3+4＝7．17．解：（1）直线PC与圆O相切，理由为：过C点作直径CE，连接EB，如图，∵CE为直径，∴∠EBC＝90°，即∠E+∠BCE＝90°，∵AB∥DC，∴∠ACD＝∠BAC，∵∠BAC＝∠E，∠BCP＝∠ACD．∴∠E＝∠BCP，∴∠BCP+∠BCE＝90°，即∠PCE＝90°，∴CE⊥PC，∴PC与圆O相切；（2）∵AD是⊙O的切线，切点为A，∴OA⊥AD，∵BC∥AD，∴AM⊥BC，∴BM＝CM＝BC＝4，∴AC＝AB＝12，在Rt△AMC中，AM＝＝8，设圆O的半径为r，则OC＝r，OM＝AM﹣r＝8﹣r，在Rt△OCM中，OM2+CM2＝OC2，即42+（8﹣r）2＝r2，解得：r＝，∴CE＝2r＝＝9，OM＝8﹣＝，∴BE＝2OM＝7，∵∠E＝∠MCP，∴Rt△PCM∽Rt△CEB，∴＝，即＝∴PC＝．18．解：（1）证明：连接OD，∵OE∥AB，∴∠COE＝∠CAD，∠EOD＝∠ODA，∵OA＝OD，∴∠OAD＝∠ODA，∴∠COE＝∠DOE，在△COE和△DOE中，，∴△COE≌△DOE（SAS），∴∠ODE＝∠OCE＝90°，∴ED⊥OD，∴ED是圆O的切线；（2）连接CD，交OE于M，在Rt△ODE中，∵OD＝，DE＝2，∴OE＝＝＝，∵OE∥AB，∴△COE∽△CAB，∴＝，∴AB＝5，∵AC是直径，∴∠ADC＝90°，∴cos∠BAC＝＝＝，∴AD＝，∴CD＝＝，∵EF∥AB，∴，∴CM＝DM＝CD＝，∴EF＝OE+OF＝4，BD＝AB﹣AD＝5﹣＝，∴S△ADF＝S梯形ABEF﹣S梯形DBEF＝（AB+EF）•DM﹣（BD+EF）•DM＝×（5+4）×﹣×（+4）×＝．∴△ADF的面积为．19．解：（1）直线PD是否为⊙O的切线．理由如下：连接OD，如图1，∵OD＝OB，∴∠1＝∠OBD，∵∠PDA＝∠PBD，∴∠1＝∠PDA，∵AB为直径，∴∠ADB＝90°，即∠2+∠1＝90°，∴∠PDA+∠2＝90°，即∠PDO＝90°，∴OD⊥PD，∴PD为⊙O的切线；（2）如图2，连接OD，∵ED和EB为⊙O的切线，∴ED＝EB，而∠BED＝60°，∴△EDB为等边三角形，∴∠EBD＝60°，∴∠PBD＝30°，∴∠PDA＝30°，而∠ADB＝90°，∴∠P＝30°，在Rt△OAD中，OD＝PD＝×＝1，OP＝2OD＝2，∴P A＝PO﹣OA＝2﹣1＝1．20．证明：（1）连接OC，∵AB是⊙O的直径，点C是的中点，∴∠AOC＝90°，∵OA＝OB，CD＝AC，∴OC是△ABD是中位线，∴OC∥BD，∴∠ABD＝∠AOC＝90°，∴AB⊥BD，∵点B在⊙O上，∴BD是⊙O的切线；解：（2）由（1）知，OC∥BD，∴△OCE∽△BFE，∴，∵OB＝2，∴OC＝OB＝2，AB＝4，，∴，∴BF＝3，在Rt△ABF中，∠ABF＝90°，根据勾股定理得，AF＝5，∵S△ABF＝AB•BF＝AF•BH，∴AB•BF＝AF•BH，∴4×3＝5BH，∴BH＝．21．解：（1）设圆的半径是r，则OP＝P A+r＝1+r，OC＝r，PC＝r．∵PC是圆的切线，∴∠PCO＝90°，∴在直角△PCO中，PC2+OC2＝OP2，即（r）2+r2＝（1+r）2，解得：r＝1或r＝﹣（舍去负值）．在直角△OPC中，cos∠POC＝＝，∴∠POC＝60°，∵∠PCO＝90°，BE⊥BC，∴BE∥OC，∴△OPC∽△BPE，∠B＝∠POC＝60°，∴＝＝，∴BE＝OC＝；（2）①在△OBD中，OB＝OD，∠B＝60°，∴△OBD是等边三角形，BD＝OB＝1，∠BOD＝60°．∴DE＝BE﹣BD＝﹣1＝；②∵在△OPC和△OPF中，，∴△OPC≌△OPF（SAS），∴∠OFP＝∠OCP＝90°，∴PF是⊙O的切线．。

中考数学压轴题之圆的综合(中考题型整理,突破提升)及答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．在⊙O 中，点C是AB上的一个动点(不与点A，B重合)，∠ACB=120°，点I是∠ABC的内心，CI的延长线交⊙O于点D，连结AD,BD．（1）求证：AD=BD．（2）猜想线段AB与DI的数量关系，并说明理由．（3）若⊙O的半径为2，点E，F是AB的三等分点，当点C从点E运动到点F时，求点I 随之运动形成的路径长．23【答案】（1）证明见解析；（2）AB=DI，理由见解析（3【解析】分析：（1）根据内心的定义可得CI平分∠ACB，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I 随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE是直径∴DE=4，∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，∴∠ADB=60°∴弧AB的度数为120°，∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.2．如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，交BC的延长线于点E，使得∠DAC=∠B．（1）求证：DA是⊙O切线；（2）求证：△CED∽△ACD；（3）若OA=1，sinD=13，求AE的长．【答案】（1）证明见解析；（22【解析】分析：（1）由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线；（2）由∠DAC=∠DCE，∠D=∠D可知△DEC∽△DCA；（3）由题意可知AO=1，OD=3，DC=2，由勾股定理可知AD=2，故此可得到DC2=DE•AD，故此可求得DE的长，于是可求得AE的长．详解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°．∵∠DAC=∠B，∴∠CAB+∠DAC=90°，∴AD⊥AB．∵OA是⊙O半径，∴DA为⊙O的切线；（2）∵OB=OC，∴∠OCB=∠B．∵∠DCE=∠OCB，∴∠DCE=∠B．∵∠DAC=∠B，∴∠DAC=∠DCE．∵∠D=∠D，∴△CED∽△ACD；（3）在Rt△AOD中，OA=1，sin D=13，∴OD=OAsinD=3，∴CD=OD﹣OC=2．∵AD=22OD OA-=22．又∵△CED∽△ACD，∴AD CDCD DE=，∴DE=2CDAD=2，∴AE=AD﹣DE=22﹣2=2．点睛：本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定，证得△DEC∽△DCA是解题的关键．3．如图，已知AB为⊙O直径，D是BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．（1）求证：直线DE与⊙O相切；（2）已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．【答案】（1）证明见解析；（2）2．【解析】试题分析：（1）连接BC、OD，由D是弧BC的中点，可知：OD⊥BC；由OB为⊙O的直径，可得：BC⊥AC，根据DE⊥AC，可证OD⊥DE，从而可证DE是⊙O的切线；（2）直接利用勾股定理得出GO的长，再利用锐角三角函数关系得出tan∠F的值．试题解析：解：（1）证明：连接OD，BC，∵D是弧BC的中点，∴OD垂直平分BC，∵AB 为⊙O的直径，∴AC⊥BC，∴OD∥AE．∵DE⊥AC，∴OD⊥DE，∵OD为⊙O的半径，∴DE 是⊙O的切线；（2）解：∵D是弧BC的中点，∴DC DB=，∴∠EAD=∠BAD，∵DE⊥AC，DG⊥AB且DE=4，∴DE=DG=4，∵DO=5，∴GO=3，∴AG=8，∴tan∠ADG=84=2，∵BF是⊙O的切线，∴∠ABF=90°，∴DG∥BF，∴tan∠F=tan∠ADG=2．点睛：此题主要考查了切线的判定与性质以及勾股定理等知识，正确得出AG，DG的长是解题关键．4．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA 的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．（1）求证：BF=EF：（2）求证：PA是⊙O的切线；（3）若FG=BF，且⊙O的半径长为32，求BD的长度.【答案】(1)证明见解析；(2) 证明见解析；（3）2【解析】分析：（1）利用平行线截三角形得相似三角形，得△BFC∽△DGC且△FEC∽△GAC，得到对应线段成比例，再结合已知条件可得BF=EF；（2）利用直角三角形斜边上的中线的性质和等边对等角，得到∠FAO=∠EBO，结合BE是圆的切线，得到PA⊥OA，从而得到PA是圆O的切线；（3）点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性质即可以求出BD 的长度．详解：证明：(1)∵BC是圆O的直径，BE是圆O的切线，∴EB⊥BC.又∵AD⊥BC，∴AD∥BE.∴△BFC∽△DGC，△FEC∽△GAC，∴BFDG=CFCG，EFAG=CFCG，∴BFDG=EFAG，∵G是AD的中点，∴BF=EF；(2)连接AO，AB.∵BC是圆O的直径，∴∠BAC=90°，由(1)得：在Rt△BAE中，F是斜边BE的中点，∴AF=FB=EF，可得∠FBA=∠FAB，又∵OA=OB，∴∠ABO=∠BAO，∵BE是圆O的切线，∴∠EBO=90°，∴∠FBA+∠ABO=90°，∴∠FAB+∠BAO=90°，即∠FAO=90°，∴PA⊥OA，∴PA是圆O的切线；（3）过点F作FH⊥AD于点H，∵BD⊥AD，FH⊥AD，∴FH∥BC，由(2)，知∠FBA=∠BAF，∴BF=AF.∵BF=FG，∴AF=FG，∴△AFG是等腰三角形.∵FH⊥AD，∴AH=GH，∴DG =2HG . 即12HG DG =， ∵FH ∥BD ，BF ∥AD ，∠FBD =90°，∴四边形BDHF 是矩形，∴BD =FH ，∵FH ∥BC∴△HFG ∽△DCG ，∴12FH HG CD DG ==，即12BD CD =， ∴23 2.153≈， ∵O 的半径长为32，∴BC =62，∴BD =13BC ＝22. 点睛：本题考查了切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质.结合已知条件准确对图形进行分析并应用相应的图形性质是解题的关键.5．如图，正三角形ABC 内接于⊙O ，P 是BC 上的一点，且PB ＜PC ，PA 交BC 于E ，点F 是PC 延长线上的点，CF=PB ，AB=13，PA=4．（1）求证：△ABP ≌△ACF ；（2）求证：AC 2=PA•AE ；（3）求PB 和PC 的长．【答案】（1）证明见解析；（2）证明见解析；（3）PB=1，PC=3．【解析】试题分析：（1）先根据等边三角形的性质得到AB=AC ，再利用圆的内接四边形的性质得∠ACF=∠ABP ，于是可根据“SAS”判断△ABP ≌△ACF ；（2）先根据等边三角形的性质得到∠ABC=∠ACB=60°，再根据圆周角定理得∠APC=∠ABB=60°，加上∠CAE=∠PAC ，于是可判断△ACE ∽△APC ，然后利用相似比即可得到结论；（3）先利用AC 2=PA •AE 计算出AE=134 ，则PE=AP-AE=34，再证△APF 为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP ∽△CEP ，得到PB•PC=PE•A=3，然后根据根与系数的关系，可把PB 和PC 看作方程x 2-4x+3=0的两实数解，再解此方程即可得到PB 和PC 的长．试题解析：（1）∵∠ACP+∠ABP=180°，又∠ACP+∠ACF=180°，∴∠ABP=∠ACF在ABP ∆和ACF ∆中，∵AB=AC ，∠ABP=∠ACF ， CF PB =∴ABP ∆≌ACF ∆．(2)在AEC ∆和ACP ∆中，∵∠APC=∠ABC ，而ABC ∆是等边三角形，故∠ACB=∠ABC=60º，∴∠ACE =∠APC .又∠CAE =∠PAC ，∴AEC ∆∽ACP ∆ ∴AC AE AP AC=,即2AC PA AE =⋅. 由（1）知ABP ∆≌ACF ∆，∴∠BAP=∠CAF ， CF PB =∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°，又∠APC ＝∠ABC ＝60°.∴APF ∆是等边三角形∴AP=PF∴4PB PC PC CF PF PA +=+===在PAB ∆与CEP ∆中，∵∠BAP=∠ECP ，又∠APB=∠EPC=60°，∴PAB ∆∽CEP ∆ ∴PB PA PE PC=,即PB PC PA PE ⋅=⋅ 由（2）2AC PA AE =⋅， ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+= ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴22222243PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解．解这个方程，得11x =， 23x =．∵PB<PB ，∴PB=11x =，PC=23x =，∴PB 和PC 的长分别是1和3。

中考数学压轴题提升训练：圆中证明及计算问题

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学压轴题提升训练：圆中证明及计算问题【例1】如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：AB•CP＝BD•CD；（3）当AB＝5 cm，AC＝12 cm时，求线段PC的长．【答案】见解析.【解析】（1）证明：连接OD．∵∠BAD＝∠CAD，∴弧BD=弧CD，∴∠BOD＝∠COD＝90°，∵BC∥P A，∴∠ODP＝∠BOD＝90°，即OD⊥P A，∴PD是⊙O的切线．（2）证明：∵BC∥PD，∴∠PDC＝∠BCD．∵∠BCD＝∠BAD，∴∠BAD＝∠PDC，∵∠ABD+∠ACD＝180°，∠ACD+∠PCD＝180°，∴∠ABD＝∠PCD，∴△BAD∽△CDP，∴AB BD CD CP，∴AB•CP＝BD•CD．（3）∵BC是直径，∴∠BAC＝∠BDC＝90°，∵AB＝5，AC＝12，由勾股定理得：BC＝13，由（1）知，△BCD是等腰直角三角形，∴BD＝CD，∵AB•CP＝BD•CD．∴PC＝169 10．【变式1-1】如图，△ABC内接于⊙O，且AB=AC，延长BC到点D，使CD=CA，连接AD交⊙O于点E．（1）求证：△ABE≌△CDE；（2）填空：①当∠ABC的度数为时，四边形AOCE是菱形；②若AE=6，BE=8，则EF的长为．【答案】（1）见解析；（2）60；9 2 .【解析】（1）证明：连接CE，∵AB=AC，CD=CA，∴∠ABC=∠ACB，AB=CD，∵四边形ABCE是圆内接四边形，∴∠ECD+∠BCE=∠BAE +∠BCE=180°，∴∠ECD=∠BAE，同理，∠CED=∠ABC，∵∠ABC=∠ACB=∠AEB，∴∠CED=∠AEB，∴△ABE≌△CDE；（2）①60；连接AO、OC，∵四边形ABCE是圆内接四边形，∴∠ABC+∠AEC=180°，∵∠ABC=60，∴∠AEC=∠AOC=120°，∵OA=OC，∴∠OAC=∠OCA=30°，∵AB=AC，∴△ABC是等边三角形，∴∠ACB=60°，∵∠ACB=∠CAD+∠D，AC=CD，∴∠CAD=∠D=30°，∴∠ACE =30°， ∴∠OAE =∠OCE =60°，即四边形AOCE 是平行四边形， ∵OA =OC ，∴四边形AOCE 是菱形； ②由（1）得：△ABE ≌△CDE ， ∴BE =DE =8，AE =CE =6，∠D =∠EBC ，由∠CED =∠ABC =∠ACB ，得△ECD ∽△CFB ， ∴CE CF DE BC ==68， ∵∠AFE =∠BFC ，∠AEB =∠FCB ， ∴△AEF ∽△BCF ，∴EF CFAE BC =，即668EF =，∴EF =92．【例2】如图，AB 为⊙O 的直径，点C 为AB 上方的圆上一动点，过点C 作⊙O 的切线l ，过点A 作直线l 的垂线AD ，交⊙O 于点D ，连接OC ，CD ，BC ，BD ，且BD 与OC 交于点E ．（1）求证：△CDE ≌△CBE ；（2）若AB ＝4，填空：①当弧CD 的长度是时，△OBE 是等腰三角形； ②当BC ＝时，四边形OADC 为菱形．【答案】（1）见解析；（2）2π；2．【解析】（1）证明：延长AD 交直线l 于点F ，∵AD垂直于直线l，∴∠AFC＝90°，∵直线l为⊙O切线，∴∠OCF＝90°，∴∠AFC＝∠OCF＝90°，∴AD∥OC，∵AB为⊙O直径，∴∠ADB＝90°，∴∠OEB＝90°，∴OC⊥DB，∴DE＝BE，∠DEC＝∠BEC＝90°，∵CE＝CE，∴△CDE≌△CBE；（2）①如图2，连接OD，由（1）知∠OEB＝90°，当△OBE是等腰三角形时，则△OEB为等腰直角三角形，∴∠BOE＝∠OBE=45°，∵OD＝OB，OE⊥BD，∴∠DOC＝∠BOE＝45°，∵AB ＝4， ∴OD ＝2， ∴弧CD 的长=452180π⨯=2π； ②当四边形OADC 为菱形时，则AD ＝DC ＝OC ＝AO ＝2，由（1）知，BC ＝DC ， ∴BC ＝2.【变式2-1】（2019·河南南阳一模）如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为2，∠B =135°，则弧AC 的长为（）A. 2πB. πC.2πD.3π【分析】根据弧长公式180n rl π=，需先确定弧AC 所对的圆心角∠AOC 的度数，再根据同弧所对的圆心角是圆周角的2倍得到∠AOC =2∠D ，根据圆内接四边形对角互补，求出∠D =180°－∠B =45°，再代入弧长公式求解即可.【解析】解：∵四边形ABCD 是⊙O 的内接四边形， ∴∠D =180°－∠B =45°，∴弧AC 所对圆心角的度数为：2×45°=90°， ∵⊙O 的半径为2， ∴弧AC 的长为：902180180n r l ππ⨯===π，故选B .1.如图，在Rt △ABC 中，∠ACB =90°，以AC 为直径的⊙O ，与斜边AB 交于点D ，E 为BC 边的中点，连接DE .（1）求证：DE 是⊙O 的切线；（2）填空：①若∠B=30°，AC=BD=②当∠B=时，以O、D、E、C为顶点的四边形是正方形.【答案】见解析.【解析】解：（1）连接OD，∵AC为直径，∴∠ADC=90°，∠CDB=90°，∵E是BC的中点，∴DE=CE=BE，∴∠DCE=∠EDC，∵OD=OC，∴∠OCD=∠ODC，∴∠ODC+∠CDE=∠OCD+∠DCE=90°，即∠ODE=90°，∴DE是⊙O的切线；（2）3；45°，理由如下：①∵∠B=30°，AC=BCA=90°，∴BC= AC÷tan30°=6，∴DE=3，②由∠B=∠A=45°，OA=OD，得∠ADO=∠AOD=45°，∴∠AOD=90°，∴∠DOC=90°，又∠ODE=90°，∴四边形ODEC是矩形，∵OD=OC，∴四边形ODEC是正方形.2.已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA∶AB=1∶2．（1）求∠CDB的度数；（2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明．【答案】见解析.【解析】解：（1）如图，连接OC，∵CD是⊙O的切线，∴∠OCD=90°．∵DA：AB=1：2，∴DA=OC，DO=2OC．在Rt△DOC中，sin∠CDO=12，∴∠CDO=30°，即∠CDB=30°．（2）直线EB与⊙O相切．证明：连接OC，由（1）可知∠CDO=30°，∴∠COD=60°，∵OC=OB，∴∠OBC=∠OCB=30°，∴∠CBD=∠CDB，∴CD=CB，∵CD是⊙O的切线，∴∠OCE=90°，∴∠ECB=60°，又∵CD=CE，∴CB=CE，∴△CBE为等边三角形，∴∠EBA=∠EBC+∠CBD=90°，∴EB是⊙O的切线．3.如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与斜边AB交于点D，E为BC边上一点，且DE是⊙O的切线．（1）求证：BE=EC；（2）填空：①若∠B=30°，AC DE=；②当∠B=°时，以O，D，E，C为顶点的四边形是正方形．【答案】（1）见解析；（2）①3；②45.【解析】解：（1）证明：如图，连接OD，∵∠ACB=90°，AC为⊙O的直径，∴EC为⊙O的切线，∵DE为⊙O的切线，∴EC=ED，∵∠EDO=90°，∴∠BDE+∠ADO=90°，∵OD=OA，∴∠ADO=∠A，∴∠BDE+∠A=90°，∵∠A+∠B=90°，∴∠BDE=∠B，∴BE=EC；（2）①3；②45，理由如下：①在Rt△ABC中，∠B=30°，AC，∴BC=6，由（1）知，E是BC中点，∴DE=12BC=3；②∵ODEC为正方形，∴∠DEC=90°，DE=CE=BE，∴∠B=45°，故答案为：3；45.4.如图，AB为⊙O的直径，C为半圆上一动点，过点C作⊙O的切线l的垂线BD，垂足为D，BD与⊙O交于点E，连接OC，CE，AE，AE交OC于点F．（1）求证：△CDE≌△EFC；（2）若AB=4，连接AC．①当AC= 时，四边形OBEC为菱形；②当AC= 时，四边形EDCF为正方形．【答案】见解析．【解析】（1）证明：如图，∵BD⊥CD，∴∠CDE=90°，∵AB是直径，∴∠AEB=90°，∵CD是切线，∴∠FCD=90°，∴四边形CFED矩形，∴CF=DE，EF=CD，∵CE=CE，∴△CDE≌△EFC．（2）解：①当AC=2时，四边形OCEB是菱形．理由：连接OE．∵AC=OA=OC=2，∴△ACO是等边三角形，∴∠CAO=∠AOC=60°，∵∠AFO=90°，∴∠EAB=30°，∵∠AEB=90°，∴∠B=60°，∵OE=OB，∴△OEB是等边三角形，∴∠EOB=60°，∴∠COE=180°﹣60°﹣60°=60°，∵CO=OE，∴△COE是等边三角形，∴CE=CO=OB=EB，∴四边形OCEB是菱形．故答案为2．②当四边形DEFC是正方形时，∵CF=FE，∴∠CEF=∠FCE=45°，∵OC⊥AE，∴弧AC=弧CE，∴∠CAE=∠CEA=45°，∴∠ACE=90°，∴AE是⊙O的直径，∴△AOC是等腰直角三角形，∴AC．∴AC时，四边形DEFC是正方形．故答案为．5.如图，AB是半圆O的直径，D为半圆上的一个动点（不与点A，B重合），连接AD，过点O作AD 的垂线，交半圆O的切线AC于点C，交半圆O于点E．连接BE，DE．（1）求证：∠BED＝∠C．（2）连接BD，OD，CD．填空：①当∠ACO的度数为时，四边形OBDE为菱形；②当∠ACO的度数为时，四边形AODC为正方形．【答案】（1）见解析；（2）30；45．【解析】解：（1）证明：设AD，OC交于点P，∵OC⊥AD，∴∠APC＝90°．∴∠C+∠CAP＝90°∵AC是半圆O的切线，∴∠CAO＝∠CAP+∠BAD＝90°，∴∠BAD＝∠C，∵∠BED＝∠BAD，∴∠BED＝∠C；（2）①30，理由如下：连接BD，如图：∵AB是半圆O的直径，∴∠ADB＝90°，∵∠DAB＝∠ACO＝30°，∴∠DBA＝60°，∵OE⊥AD，∴弧AE=弧AD，∴∠DBE＝∠ABE＝30°∵∠DEB＝∠DAB＝30°，∴∠DEB＝∠ABE，DE∥AB∵∠ADB＝90°，即BD⊥AD，OE⊥AD，∴OE∥BD，∴四边形OBDE是平行四边形∵OB＝OE∴四边形OBDE是菱形；故答案为30°；②45，理由如下：连接CD、OD，∵∠BED＝∠ACO＝45°，∴∠BOD＝2∠BED＝90°，∴∠AOD＝90°，∵OC⊥AD，∴OC垂直平分AD，∴∠OCD＝∠OCA＝45°，∴∠ACD＝90°，∵∠ACO＝90°，∴四边形AODC 是矩形， ∵OA ＝OD ，∴四边形AODC 是正方形，故答案为45°．6.如图，CD 是⊙O 的直径，且CD ＝2cm ，点P 为CD 的延长线上一点，过点P 作⊙O 的切线P A 、PB ，切点分别为A 、B ．（1）连接AC ，若∠APO ＝30°，试证明△ACP 是等腰三角形；（2）填空：①当弧AB 的长为 cm 时，四边形AOBD 是菱形； ②当DP ＝ cm 时，四边形AOBP 是正方形．【答案】（1）见解析；（2）23π1. 【解析】解：（1）连接AO ，∵P A 是⊙O 的切线， ∴∠P AO ＝90°， ∵∠APO ＝30°， ∴∠AOP ＝60°， ∵OA ＝OC ，∴∠C ＝∠CAO ＝30°， ∴∠C ＝∠APO =30°， ∴△ACP 是等腰三角形；（2）①若四边形AOBD 是菱形，则AO ＝AD ，∵AO＝OD，∴△AOD是等边三角形，∠AOD＝60°，∴∠AOB＝120°，∵CD=2，∴圆O的半径为1，∴弧AB的长为：21201180π⨯=23π.②若四边形AOBP为正方形时，则P A＝AO＝1，则OP，∵OD=1，∴PD－1，－1．7.如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交弧AC于点D，过点D作⊙O的切线，交BA的延长线于点E．（1）求证：AC∥DE；（2）连接CD，若OA=AE=2时，求出四边形ACDE的面积．【答案】见解析．【解析】证明：（1）∵F为弦AC（不是直径）的中点，∴AF=CF，OD⊥AC，∵DE是⊙O的切线，∴OD⊥DE，∴AC∥DE．（2）连接CD，∵AC∥DE，OA=AE=2，∴OF=FD，∵AF=CF，∠AFO=∠CFD，∴△AFO≌△CFD，∴S△AFO=S△CFD，∴S四边形ACDE=S△ODE∵OD=OA=AE=2，∴OE=4，由勾股定理得：DE∴S四边形ACDE=S△ODE= 12×OD×OE=12×2×．8.已知：如图，△ABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．（1）求证：∠DAC＝∠DBA；（2）求证：P是线段AF的中点；（3）连接CD，若CD＝3，BD＝4，求⊙O的半径和DE的长．【答案】见解析．【解析】（1）证明：∵BD平分∠CBA，∴∠CBD＝∠DBA，∵∠DAC与∠CBD是弧CD所对的圆周角，∴∠DAC＝∠CBD，∴∠DAC＝∠DBA；（2）证明：∵AB为直径，∴∠ADB＝90°，∵DE⊥AB于E，∴∠DEB＝90°，∴∠ADE+∠BDE＝∠DBE+∠BDE＝90°，∴∠ADE＝∠DBE＝∠DAC，∴PD＝P A，∵∠DF A+∠DAF＝∠ADE+∠BDE＝90°，∴∠PDF＝∠PFD，∴PD＝PF，∴P A＝PF，即P是线段AF的中点；（3）解：∵∠CBD＝∠DBA，CD＝3，∴CD＝AD＝3，由勾股定理得：AB＝5，即⊙O的半径为2.5，由DE×AB＝AD×BD，即：5DE＝3×4，∴DE＝2.4．即DE的长为2.4．9.如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD，AC分别交于点E，F，且∠ACB＝∠DCE．（1）判断直线CE与⊙O的位置关系，并证明你的结论；（2）若tan∠ACB＝12，BC＝4，求⊙O的半径．【答案】见解析．【解析】（1）直线CE与⊙O相切，证明：连接OE，∵OA＝OE，∴∠EAO＝∠AEO，∵∠ACB＝∠DCE，∴∠AEO＝∠ACB＝∠DCE，∵四边形ABCD是矩形，∴BC∥AD，∴∠ACB＝∠DAC，∵∠ACB＝∠DCE，∴∠DAC＝∠DCE，由∠D＝90°，得：∠DCE+∠DEC＝90°，∴∠AEO+∠DEC＝90°，∴∠OEC＝90°，即OE⊥EC，∵OE为半径，∴直线CE与⊙O相切；（2）解：在Rt△ACB中，AB＝tan∠ACB×BC=12×4＝2，由勾股定理得：AC＝，∵∠ACB＝∠DCE，∴tan∠DCE＝tan∠ACB＝12，在Rt△DCE中，CD＝AB＝2，DE＝DC×tan∠DCE＝2×12＝1，由勾股定理得：CE，在Rt△COE中，CO2＝CE2+OE2，OE=OA，（OA）2＝OA2+）2，解得：OA，即⊙O．10.如图，在△ABC中，AC＝BC，AB是⊙C的切线，切点为点D，直线AC交⊙C于点E、F，且CF=12AC，（1）求证：△ABF是直角三角形；（2）若AC＝6，则直接回答BF的长是多少．【答案】见解析.【解析】（1）证明：连接CD，则CF＝CD，∵AB是⊙C的切线．∴CD⊥AB，∠ADC＝∠BDC＝90°，在Rt△ACD中，CF=12 AC，∴CD＝CF=12AC，∴∠A＝30°∵AC＝BC，∴∠ABC＝∠A＝30°，∴∠ACB＝120°，∠BCD＝∠BCF＝60°，∵BC＝BC，∴△BCD≌△BCF，∴∠BFC＝∠BDC＝90°，∴△ABF是直角三角形．（2）解：由（1）知：AC＝BC，CD⊥AB，∴AD＝BD＝BF，在Rt△ACD中，∠A＝30°，AC＝6，∴CD＝3，∴AD＝．∴BF＝金榜题名前程似锦21。

压轴题圆的五种考法(解析版)--九年级数学常考压轴题

压轴题圆的五种考法目录解题知识必备压轴题型讲练类型一、四点共圆类型二、圆中最值问题类型三、定点定长构造辅助圆类型四、定弦定角构造辅助圆类型五、对角互补构造辅助圆压轴能力测评(10题)类型一、四点共圆一．填空题1.(2022秋•大丰区期中)如图，ΔABC中，AD⊥BC，∠B=45°，∠C=30°．以AD为弦的圆分别交AB、AC于E、F两点．点G在AC边上，且满足∠EDG=120°．若CD=4+22，则ΔDEG的面积的最小值是．【分析】连接EF，利用四点共圆和同弧所对的圆周角相等证明EF⎳DG，从而得到SΔEDG=S△EDG，当FG最小时，ΔDFG的面积就最小，作ΔDFG的外接圆O，过O点作OH⊥FG交于点H，连接OF、OG，DO+OH=12+22FG，当DO+OH最小时，FG就最小，当D、O、H三点共线时，DO+OH最小，此时DH⊥FG，在RtΔFHO中，(2FH)2=FH2+(2+2-2FH)2，求出FH=2，可得FG的最小值为22，再求SΔDFG =22+2，即ΔDEG的面积的最小值为22+2．【解答】解：连接EF，AD⊥BC，∠B=45°，∠C=30°，∴∠B=45°，∠DAC=60°，∵∠BAC=105°，∵A、E、F、D四点共圆，∴∠EDF=75°，∵∠EDG=120°，∴∠FDG=45°，∵ED =ED ，∴∠EFD =∠FDG ，∴EF ⎳DG ，∴S ΔEDG =S △EDG ，∵CD =4+22，∠C =30°，∴AC =833+463，AD =433+263，∴AC 边上的高=AD ⋅DC AC=2+2，∴当FG 最小时，ΔDFG 的面积就最小，作ΔDFG 的外接圆O ，过O 点作OH ⊥FG 交于点H ，连接OF 、OG ，∵∠FDG =45°，∴∠FOG =90°，∵OF =GO ，∴ΔFOG 是等腰直角三角形，∵∠FOH =12∠FOG =45°，∴ΔFOH 是等腰直角三角形，∴FH =OH =12FG ，FO =2FH ，∴DO +OH =22FG +12FG =12+22FG ，∴当DO +OH 最小时，FG 就最小，∵DO +OH ≥DH ，∴当D 、O 、H 三点共线时，DO +OH 最小，此时DH ⊥FG ，∴DH =2+2，在Rt ΔFHO 中，(2FH )2=FH 2+(2+2-2FH )2，解得FH =2或FH =4+32，∵OH =2+2=FH +FO ，∴FH =2，∴FG 的最小值为22，∴S ΔDFG =12×22×(2+2)=22+2，∴ΔDEG 的面积的最小值为22+2，故答案为：22+2．【点评】本题考查圆的综合应用，熟练掌握圆心角与圆周角的关系，四点共圆的性质，三角形外接圆的性质是解题的关键．二．解答题2.(2022秋•建湖县期中)如图，在⊙O 的内接四边形ABCD 中，DB =DC ，∠DAE 是四边形ABCD 的一个外角．(1)若∠DAE =75°，则∠DAC =°；(2)过点D 作DE ⊥AB 于E ，判断AB 、AE 、AC 之间的数量关系并证明；(3)若AB =6、AE =2，求BD 2-AD 2的值．【分析】(1)根据四边形外接圆的性质，同弧所对的圆周角相等，可得∠DCB=∠DBC=∠DAC=75°；(2)过点D作DF⊥AC于点F，可证明ΔBDE≅ΔCDF(AAS)，ΔADE≅ΔADF(AAS)，则AC=AF+FC= AE+BE=AE+AE+AB=2AE+AB；(3)在RtΔBDE中，BD2=64+DE2，在RtΔAED中，AD2=4+ED2，再求解即可．【解答】解：(1)∵四边形ABCD是圆O的内接四边形，∴∠BCD+∠BAD=180°，∵∠DAE是四边形ABCD的一个外角，∴∠DAE=∠BCD，∵BD=CD，∴∠CBD=∠DCB，∵弧CD所对的圆周角分别为∠CAD、∠CBD，∴∠CBD=∠CAD，∵∠DAE=75°，∴∠DCB=∠DBC=∠DAC=75°，故答案为：75；(2)过点D作DF⊥AC于点F，∵DE⊥AB，∴∠DEA=90°，∵∠ABD=∠ACD，BD=CD，∠E=∠DFC=90°，∴ΔBDE≅ΔCDF(AAS)，∴DE=DF，AE=CF，∴∠ADE=∠ADF，又∵∠E=∠AFD，AD=AD，∴ΔADE≅ΔADF(AAS)，∴AE=AF，∴AC=AF+FC=AE+BE=AE+AE+AB=2AE+AB，即AC=2AE+AB；(3)在RtΔBDE中，BD2=BE2+DE2，在RtΔAED中，AD2=AE2+ED2，∵AB=6，AE=2，∴BE=8，∴BD2=64+DE2，AD2=4+ED2，∴BD2-AD2=60．【点评】本题考查圆的综合应用，熟练掌握同弧所对的圆周角相等，四点共圆的性质，直角三角形勾股定理，三角形全等的判定及性质是解题的关键．3.(2023秋•鄞州区期中)如图，在△ABC 中，点D ，E 为AB ，AC 上的点，BE =CD ，DC ，BE 交于F ，△BDF 与△CEF 的外接圆相交于点G (异于F )，H 1，H 2分别为△ABC 和△ADE 的垂心．证明：(1)GF 平分∠BFC ；(2)H 1，H 2，G 三点共线．(注：利用坐标系、复数解题者不给分)【分析】(1)通过证明△BGE ≅△DGC 得出DG =BG ，然后由BG =DG 推导出∠BFG +∠DFG =180°，再由邻补角的性质得出∠BFG =∠GFC ，即可证明结论；(2)根据题意构造B 、E 、B ′、E ′四点共⊙P ，以及D 、C 、D ′、C ′四点共⊙Q ，然后由相似三角形推导出点H 1、H 2对于⊙P 和⊙Q 等幂，再由根轴的性质得出H 1H 2是PQ 的垂直平分线，最后根据GP =GQ 得到GM ⊥PQ ，进而证得三点共线．【解答】(1)证明：在△BGE 和△DGC 中，∠GBE =∠GDC ，BE =CD ，∠GEB =∠GCD ，∴△BGE ≅△DGC (ASA )．∴DG =BG ，∴BG =DG ，∵DBG +DG =2πR (R 为△BDF 的外接圆半径)．∴∠BFG +∠DFG =180°．又∵∠GFC +∠DFG =180°，∴∠BFG =∠GFC ，∴GF 平分∠BFC ．(2)证明：连接BH 1、DH 2并延长分别交AC 于B ′、D ′，连接CH 1、EH 2并延长交AB 于C ′、E ′．BE 中点为P ，CD 中点为Q .∵BB ′⊥AC ，EE ′⊥AB ，∴B 、E 、B ′、E ′四点共⊙P ．∵DD ′⊥AC ，CC ′⊥AB ，∴D 、C 、D ′、C ′四点共⊙Q ．∵∠DE ′H 2=∠ED ′H 2，∠DH 2E ′∽△EH 2D ′，∴△DE ′H2∽△ED ′H 2，∴DH 2:EH 2=E ′H 2:D ′H 2，∴DH 2⋅D ′H 2=EH 2⋅E ′H 2．同理得CH 1⋅C ′H 1=BH 1⋅B ′H 1．∴H 1，H 2在⊙P 和⊙Q 的根轴上．∵⊙P 和⊙Q 的根轴是过两圆的交点的直线．∴H 1，H 2在⊙P 和⊙Q 的公共弦JK 上．又∵BE =CD ，即⊙P 和⊙Q 是等圆，∴四边形PJQK 为菱形．∴H 1H 2是PQ 的垂直平分线，M 为PQ 中点．由(1)知△BGE ≅△DGC ，∵GP 、GQ 分别为△BGE 和△DGC 的对应边上的中线，∴GP =GQ ，∴点G 在PQ 的垂直平分线上．∴H 1，H 2，G 三点共线．【点评】本题考查了全等三角形的判定和性质，圆周角定理，圆幂定理，菱形的性质，等腰三角形的性质等．本题辅助线繁多，综合性强，通过四点共圆判断出H 1、H 2两点对于⊙P 和⊙Q 等幂是解答本题的关键．4.(2022秋•沙坪坝区校级期中)在ΔABC 中，已知AB =AC ，作AM ⊥BC ，D 是AM 上一点，∠DBC =30°，连接BD 、CD ，在BD 上截取DE =AD ，连接AE ．(1)如图1所示，若∠BAC =90°，AD =3，求ΔABE 的周长；(2)如图2所示，若分别取AE 、AC 的中点N 、H ，连接MN 、MH ，求证：MN =MH ；(3)如图3所示，∠BAC =90°，BC =2，将AC 沿着直线AP 翻折得到AQ ，连接BQ ，直线BQ 交AP 于点P ，N 为AE 中点，当PN 取得最小值时，请直接写出ΔAPN 的面积．【分析】(1)过点D 作DL ⊥AE 于L ，则∠ALD =∠ELD =90°，由∠DBC =30°，可得BD =2DM ，设DM =x ，则BD =2x ，由勾股定理可得BM =3x ，AM =x +3，可得BM =CM =AM =33+32，AB =2BM =2×33+32=36+322，利用勾股定理可得AL =AD 2-DL 2=(3)2-32 2=32，进而可得AE =2AL =2×32=3，即可求得答案；(2)延长AM 至F ，使MF =AM ，在DF 上截取DT =DE ，连接EF ，ET ，设∠ABM =α，则∠BAM =90°-α，可证得ΔDET 是等边三角形，得出：DT =ET =DE =AD ，∠DTE =60°，再证得ΔABD ≅ΔEFT (SAS )，可得AB =EF =AC ，利用三角形中位线定理可得MN =12EF ，再由直角三角形性质可得MH =12AC ，即可证得结论；(3)连接CP ，先证得点P 在ΔABC 的外接圆⊙M 上，当且仅当点P 为半径MP 经过点N 时，PN 取得最小值，连接DN ，过点N 作NG ⊥AM 于G ，利用解直角三角形可得DM =BM ⋅tan30°=33，AD =DE =1-33，AN =EN =32AD =321-33 ，NG =12AN =12×321-33 =3-14，AG =3NG =3-34，GM =AM -AG =1-3-34=1+34，由勾股定理可得MN =GM 2+NG 2=1+34 2+3-14 2=22，PN =MP -MN =1-22，再利用S ΔAPN S ΔAMN =PN MN=2-1，即可求得答案．【解答】(1)解：过点D 作DL ⊥AE 于L ，则∠ALD =∠ELD =90°，∵∠BAC =90°，AB =AC ，AM ⊥BC ，∴AM =BM =CM ，∠BMD =90°，∠ABM =∠BAM =45°，∵∠DBC =30°，∴BD =2DM ，设DM =x ，则BD =2x ，∴BM =BD 2-DM 2=(2x )2-x 2=3x ，AM =x +3，∴3x =x +3，∴x =3+32，∴BM =CM =AM =33+32，∴AB =2BM =2×33+32=36+322，∵DE =AD ，∴∠DAE =∠DEA ，∵∠DAE +∠DEA =∠BDM =90°-30°=60°，∴∠DAE =∠DEA =30°，∴∠BAE =∠BAM -∠DAE =45°-30°=15°，∵∠ABD =∠ABM -∠DBC =45°-30°=15°，∴∠BAE =∠ABD ，∴AE =BE ，在Rt ΔADL 中，DL =12AD =32，∴AL =AD 2-DL 2=(3)2-322=32，∵DE =AD ，DL ⊥AE ，∴AE =2AL =2×32=3，∴ΔABE 的周长=AB +AE +BE =36+322+3+3=36+32+122；(2)证明：延长AM 至F ，使MF =AM ，在DF 上截取DT =DE ，连接EF ，ET ，设∠ABM =α，则∠BAM =90°-α，∵∠DBC =30°，∴∠BDT =60°，∠ABD =α-30°，BD =2DM ，∵DE =AD ，∴∠AED =∠DAE =30°，∴ΔDET 是等边三角形，∴DT =ET =DE =AD ，∠DTE=60°，∵AF =2(AD +DM )=AT +FT ，∴FT =2DM =BD ，∵∠EDT =∠ETD =60°，∴∠ADB =180°-60°=120°=∠ETF ，在ΔABD 和ΔEFT 中，AD =ET∠ADB =∠ETF BD =FT，∴ΔABD ≅ΔEFT (SAS )，∴AB =EF ，∵AB =AC ，∴EF =AC ，∵N 、M 分别是AE 、AF 的中点，∴MN =12EF ，∵点H 是Rt ΔACM 斜边AC 的中点，∴MH =12AC ，∴MN =MH ；(3)解：如图，连接CP ，由翻折得：∠ACP =∠AQP ，AC =AQ ，∵AB =AC ，∠BAC =90°，BC =2，AM ⊥BC ，∴AB =AQ ，AM =BM =CM =1，∴∠ABP =∠AQB ，∵∠AQB +∠AQP =180°，∴∠ABP +∠ACP =180°，∴点P 在ΔABC 的外接圆⊙M 上，当且仅当点P 为半径MP 经过点N 时，PN 取得最小值，如图，连接DN ，过点N 作NG ⊥AM 于G ，∵∠DBC =30°，∴DM =BM ⋅tan30°=33，∴AD =DE =1-33，∴AN =EN =32AD =321-33，∵∠AGN =90°，∠NAG =30°，∴NG =12AN =12×321-33 =3-14，∴AG =3NG =3-34，∴GM =AM -AG =1-3-34=1+34，在Rt ΔMNG 中，MN =GM 2+NG 2=1+342+3-14 2=22，∴PN =MP -MN =1-22，∴SΔAPNSΔAMN=PNMN=1-2222=2-1，∵SΔAMN=12AM⋅NG=12×1×3-14=3-18，∴SΔAPN=(2-1)SΔAMN=(2-1)×3-18=6-3-2+18．【点评】本题是几何综合题，考查了等腰三角形性质，等腰直角三角形性质，直角三角形性质，等边三角形性质，全等三角形的判定和性质，勾股定理，圆内接四边形的判定，三角形面积等，涉及知识点多，难度大，添加适当的辅助线是解题的关键与难点．5.(2022秋•鼓楼区期中)以下是“四点共圆”的几个结论，你能证明并运用它们吗？Ⅰ．若两个直角三角形有公共斜边，则这两个三角形的4个顶点共圆(图1、2)；Ⅱ．若四边形的一组对角互补，则这个四边形的4个顶点共圆(图3)；Ⅲ．若线段同侧两点与线段两端点连线的夹角相等，则这两点和线段两端点共圆(图4)．(1)在图1、2中，取AC的中点O，根据得OA=OB=OC=OD，即A，B，C，D共圆；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得=180°，所以∠BED=，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．(3)利用四点共圆证明锐角三角形的三条高交于一点．已知：如图6，锐角三角形ABC的高BD，CE相交于点H，射线AH交BC于点F．求证：AF是ΔABC的高．(补全以下证明框图，并在图上作必要标注)(4)如图7，点P是ΔABC外部一点，过P作直线AB，BC，CA的垂线，垂足分别为E，F，D，且点D，E，F在同一条直线上．求证：点P在ΔABC的外接圆上．【分析】(1)根据直角三角形斜边中线的性质可得结论；(2)由圆周角的性质可得∠BED+∠A=180°，再结合题干条件，得出矛盾，由此可得出结论；(3)如图，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，从而证明∠BAF+∠ABF=90°即可；(4)连接BP和CP，由点A，E，P，F四点共圆可得，∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF =∠CPF，再由外角的性质及角的和差可得∠BAC=∠BPC，由此可得点A，B，C，P四点共圆，即点P在ΔABC的外接圆上．【解答】解：(1)在图1、2中，取AC的中点O，根据直角三角形斜边上的中线等于斜边的一半，得OA=OB= OC=OD，即A，B，C，D共圆；故答案为：直角三角形斜边上的中线等于斜边的一半；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得∠BED+∠A=180°，∴∠BED=180°-∠A，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．故答案为：∠BED+∠A；180°-∠A；(3)如图6，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，∴∠ECB=∠BAF，∵∠BEC=90°，∴∠ECB+∠ABF=90°，∴∠BAF+∠ABF=90°，∴∠BFA=90°，∴AF为ΔABC的边BC上的高．(4)如图7，连接BP和CP，由点A，E，P，F四点共圆可得∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF=∠CPF，∵∠ADE=∠CDF，∴∠ADE=∠CPF，∵∠BAC=∠BEF+∠ADE，∠BPC=∠BPF+∠CPF，∴∠BAC=∠BPC，∴点A，B，C，P四点共圆，即点P在ΔABC的外接圆上．【点评】本题考查了圆的定义，直角三角形斜边上的中线等于斜边一半，圆内接四边形对角互补，圆周角定理，内心的定义．第(3)(4)题解题关键是选取适当的四点证明共圆，再利用圆周角定理证明角相等．类型二、圆中最值问题一．填空题6.(2022秋•长沙期中)如图，⊙O 的半径为1，P A ，PB 为⊙O 的切线，切点为A ，B ，∠APB =60°，点M 为劣弧AB 上一动点，过点M 作⊙O 的切线，分别交P A ，PB 于点E ，F ，EF 的最小值是．【分析】由切线的性质定理，全等三角形的判定和性质，三角形外心的性质，可以求解．【解答】解：连接OA ，OE ，OM ，OF ，OB ，∵P A ，PB 为⊙O 的切线，EF 切⊙O 于M ，∴OA ⊥P A ，OB ⊥PB ，OM ⊥EF ，∵四边形PBOA 内角和是360°，∴∠P +∠AOB =360°-∠P AB -∠PBA =180°，∴∠AOB =180°-∠P =120°，∵OE =OE ，OA =OM ，∴Rt ΔOAE ≅Rt ΔOME (HL )，∴∠AOE =∠MOE ，同理：∠MOF =∠BOF ，∴∠EOF =∠EOM +∠FOM =12∠AOB =60°，设ΔOEF 的外心是点C ，作CH ⊥EF 于H ，连接CO ，CE ，CF ，OM ，∵点C 是ΔOEF 的外心，∴OC =EC =FC ，∴∠CEF =∠CFE ，EH =FH ，∵∠ECF =2∠EOF =120°，∴∠CEF =30°，∴CH =12CE =12OC ，∵OC +CH ≥OM ，∴3CH ≥1，∴CH ≥13，∵tan ∠CEH =CH EH，∴EH =3CH ，∴EF =2EH =23CH ，∴EF ≥233，∴EF 的最小值是233，故答案为：233．【点评】本题考查有关圆的最值问题，关键是掌握切线的性质定理，全等三角形的判定和性质，三角形外心的性二．解答题7.(2022秋•东城区校级期中)对于平面直角坐标系xOy中的图形G和点P给出如下定义；Q为图形G上任意一点，若P，Q两点间距离的最大值和最小值都存在，且最大值是最小值的k倍，则称点P为图形G 的“k分点”．已知点N(3,0)，A(1,0)，B(0,3)，C(1,-1)．(1)①在点A，B，C中，线段ON的“2分点”是；②点D(a,0)，若点C为线段OD的“二分点”，求a的值；(2)以点O为圆心，r为半径画图，若线段AN上存在⊙O的“二分点”，直接写出r的取值范围．【分析】(1)①分别求出点A、B、C到线段ON的最小值和最大值，看是否满足“2分点”定义即可，②对a的取值分情况讨论：0<a≤1，1<a≤2，a>2和a<0，根据“二分点”的定义可求解，(2)设线段AN上存在⊙O的“二分点”为M(m，0)(1≤m≤3)．对r的取值分情况讨论0<r≤1，1<r<3且m<r，1<r<3且m>r，r≥3，根据二分点的定义可求解．【解答】(1)解：①如图，∵点A在ON上，故最小值为0，不符合题意，点B到ON的最小值为OB=3，最大值为BN=32+32=32，∴点B是线段ON的“2分点”，点C到ON的最小值为1，最大值为CN=22+12=5∴点C不是线段ON的“2分点”，故答案为：点B；②当0<a≤1时，点C到OD的最小值为CD=(1-a)2+(-1)2=2-2a+a2，点C到OD的最大值为CO=12+(-1)2=2，∴2=22-2a+a2，即2a2-4a+3=0，∵△<0，故无解，舍去；当1<a≤2时，点C到OD的最小值为1，点C到OD的最大值为CO=12+(-1)2=2，最大值不是最小值的2倍，所以舍去，当a>2时，点C到OD的最小值为1，点C到OD的最大值为CD=(a-1)2+(0-1)2=a2-2a+2，∵点C为线段OD的“二分点”，∴a2-2a+2=2×1，a1=1+3,a2=1-3(舍去)，当a<0时，点C到OD的最小值为CO=12+(-1)2=2，点C到OD的最大值为CD=(1-a)2+(-1-0)2=a2-2a+2，∵点C为线段OD的“二分点”，同0<a≤1时，无解，舍去；综上，a=1+3．(2)如图所示，设线段AN上存在⊙O的“二分点”为M(m，0)(1≤m≤3)，当0<r≤1时，最小值为：m-r，最大值为：m+r，m，∴2(m-r)=m+r，即r=13∵1≤m≤3，≤r≤1，∴13当1<r<3且m<r时，最小值为：r-m，最大值为r+m，∴2(r-m)=r+m，即r=3m，∵1≤m≤3，∴3≤r≤9，∵1<r<3，∴r不存在，当1<r<3且m>r时，最小值为：m-r，最大值为：m+r，m，∴2(m-r)=r+m，即r=13≤r≤1，∴13∵1<r<3，∴r 不存在．当r ≥3时，最小值为：r -m ，最大值为：m +r ，∴2(r -m )=r +m ，即r =3m ，∴3≤r ≤9．综上所述，r 的取值范围为13≤r ≤1或3≤r ≤9．【点评】本题考查坐标上的两点距离，勾股定理，点到圆的距离．根据题目所给条件，掌握“k 分点”的定义是解题的关键．8.(2022秋•江阴市期中)如图，在平面直角坐标系中，点A 的坐标为(-3，0)，点B 在y 轴的正半轴上，且∠ABO =30°，以点B 为圆心，1为半径画⊙B ，与y 轴交于点C (点C 在点B 的下方)，点Q 是AB 的中点，点P 是⊙B 上的一个动点，从点C 开始以5度/秒的速度沿圆周逆时针运动一周，设运动时间为t 秒．(1)如图1，连接OQ ，当OQ ⎳BP 时，求t 的值；(2)如图2，点P 在运动过程中，连接AP ，以AP 为边在左侧作等边ΔAPD ，①当t =12秒时，求点D 的坐标；②连接DQ ，当DQ 最大时，求此时t 的值和这个最大值．【分析】(1)如图，过点B 作BP ⎳OQ ，交⊙B 于点P 1，P 2，由平行得出点P 的旋转角，进而可得出时间t ；(2)①将线段AB 绕点A 逆时针旋转60°到线段AB ′，连接B ′D ，易证△AB ′D ≅ΔABP (SAS )，所以B ′D =BP =1，∠AB ′D =∠ABP =90°；过点B ′作B ′N ⊥x 轴于点N ，过点D 作DM ⊥B ′N 于点M ，所以∠M =∠ANB ′=90°，由互余可知，∠MBD ′=∠B ′AN ，所以∠B ′AB =60°，∠BAO =60°，所以∠B ′AN =60°，AN =3，B ′N =3，则MB ′=12，MD =32，进而可得点D 的坐标；②由旋转可知，点D 在以点B ′为圆心，1长为半径的圆上运动，当DQ 最大时，点D ，B ′，Q 三点共线，设⊙B与y 轴的另一个交点为C ′，则C ′(0,4)，OC ′=4，由点Q 是AB 的中点可知，Q -32，32，B ′(-23，3)，进而可得B ′Q =3，所以DQ =4，易证△AB ′Q ≅ΔABO (SSS )，进而可得ΔADQ ≅△AC ′O (SAS )，所以AD =AC ′，即此时点P 与点C ′重合，所以t =180°5°=36．【解答】解：(1)如图：∵ΔABO 是直角三角形，Q 是AB 中点，∴OQ =QA =QB ，∴∠BOQ =∠ABO =30°，又∵OQ ⎳BP 1，∴∠OBP 1=∠BOQ =30°，∴点P 的轨迹是⊙B 中30°圆心角所对的弧，∴t =30°5°=6，∵当点P 运动到P 1B 延长线与⊙B 的交点P 2时，点P 的轨迹是⊙B 中180°+30°=210°圆心角所对的弧，∴t =210°5°=42．故t 的值为6或42；(2)①如图，∵∠ABO =30°，OA =3，∴OB =3，AB =23，当t =12时，∠CBP =60°，∴∠ABP =90°，将线段AB 绕点A 逆时针旋转60°到线段AB ′，连接B ′D ，由旋转可知，∠BAB ′=60°，AB =AB ′=23，∵ΔADP 是等边三角形，∴∠DAP =60°，AD =AP ，∴∠B ′AD =∠BAP ，∴△AB ′D ≅ΔABP (SAS )，∴B ′D =BP =1，∠AB ′D =∠ABP =90°，过点B ′作B ′N ⊥x 轴于点N ，过点D 作DM ⊥B ′N 于点M ，∴∠M =∠ANB ′=90°，∴∠AB ′N +∠B ′AN =90°，∠MB ′D +∠AB ′N =90°，∴∠MB ′D =∠B ′AN ，∵∠B ′AB =60°，∠BAO =60°，∴∠B ′AN =60°，AN =3，B ′N =3，∴∠MB ′D =60°，∴MB ′=12，MD =32，∴MN =72．∴D -332，72；②由旋转可知，点D 在以点B ′为圆心，1长为半径的圆上运动，∴当DQ 最大时，点D ，B ′，Q 三点共线，如图所示，设⊙B 与y 轴的另一个交点为C ′，∴C ′(0,4)，∴OC ′=4，∵点Q 为AB 的中点，∴AQ =BQ =3，AB ′=AB =23，由①可知，B (0,3)，∴Q -32，32，B ′(-23，3)，∴DQ =4，∴B ′Q =BO ，AQ =BQ =3，AB ′=AB =23，∴△AB ′Q ≅ΔABO (SSS )，∴∠AQB ′=∠AOB =90°，∵DQ =OC ′，AQ =AO ，∴ΔADQ ≅△AC ′O (SAS )，∴AD =AC ′，即此时点P 与点C ′重合，∴t =180°5°=36．综上，t =36，DQ 最大值是4．【点评】本题属于圆的综合题，涉及考查旋转的性质，等边三角形的性质，全等三角形的性质与判定，相似三角形的相似与判定，含30°的直角三角形的三边关系，根据题意得出点D 的轨迹是解题关键．类型三、定点定长构造辅助圆一．填空题9.(2023秋•常州期中)如图，点A ，B 的坐标分别为A (4,0)，B (0,4)，C 为坐标平面内一点，BC =2，点M 为线段AC 的中点，连接OM ，OM 的最大值为．【分析】先判断出点C 的运动轨迹是在半径为2的⊙B 上，再取OD =OA =4，连接OD ，则OM 是ΔACD 的中位线，OM =12CD ，进而可得OM 最大值时，CD 取最大值，此时D 、B 、C 三点共线，计算即可求出结果．【解答】解：∵C 为坐标平面内一点，BC =2，∴点C 的运动轨迹是在半径为2的⊙B 上，如图，取OD =OA =4，连接OD ，∵点M 为线段AC 的中点，∴OM 是ΔACD 的中位线，∴OM =12CD ，∴OM 最大值时，CD 取最大值，此时D 、B 、C 三点共线，此时在Rt ΔOBD 中，BD =42+42=42，∴CD =2+42，∴OM 的最大值是1+22．故答案为：1+22．【点评】本题考查了坐标和三角形的中位线，定点定长构造辅助圆等，解题关键是确定点C 的运动轨迹．二．解答题10.(2022秋•秀洲区期中)如图，ΔABC 中，AC =BC =4，∠ACB =90°，过点C 任作一条直线CD ，将线段BC 沿直线CD 翻折得线段CE ，直线AE 交直线CD 于点F ．(1)小智同学通过思考推得当点E 在AB 上方时，∠AEB 的角度是不变的，请按小智的思路帮助小智完成以下推理过程：∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上．∴∠AEB =∠ACB =°．(2)若BE =2，求CF 的长．(3)线段AE 最大值为；若取BC 的中点M ，则线段MF 的最小值为．【分析】(1)根据AC =BC =EC ，得A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，根据圆周角定理可知∠AEB 的度数；(2)由ΔEFG 是等腰三角形可求出FG =1，利用勾股定理求出CG 的长，从而得出答案；(3)根据直径是圆中最大的弦知当AE 经过圆心C 时，线段AE 的最大值为2AC =8，取AB 的中点O ，连接OF ，可证∠AFB =90°，则点F 在以AB 为直径的圆O 上，当OF 经过点M 时，MF 最短，此时OF ⊥BC ，从而解决问题．【解答】解：(1)∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，∴∠AEB =12∠ACB =45°，故答案为：12，45；(2)由折叠可知，CD 垂直平分BE ，∴BE ⊥CD ，设CD 、BE 交于点G ，则GE =BG =12BE =1，∴∠FGE =90°，∵∠AEB =45°，∴FG =GE =1，在Rt ΔCEG 中，由勾股定理得，CG =CE 2-DE 2=15，∴CF =CG -FG =15-1；当点E 在AB 的下方时，如图，∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，∴∠EAB +∠EBA =12∠ACB =45°，即∠BEF =45°，由翻折可知，∠EGF=90°，EG=GB 12BE=1，∴ΔEGF是等腰直角三角形，∴GF=EG=1，在RtΔCEG中，CG=CE2-EG2=42-12=15，∴CF=15+1，综上所述，CF的长为15-1或15+1；(3)∵A，B，E，三点在以C为圆心，以AC为半径的圆上，∴当AE经过圆心C时，线段AE的最大值为2AC=8，在RtΔABC中，AC=BC=4，∠ACB=90°，∴AB=AC2+BC2=42，BM=CM=12BC=2，∠ABC=∠BAC=45°，连接BF，取AB的中点O，连接OF，如图，∵CD垂直平分BE，∠AEB=45°，∴BF=EF，∴∠EBF=∠AEB=45°，∴∠EFB=90°，∴∠AFB=90°，∴OF=12AB=OA=OB=22，∴点F在以点O为圆心，AB为直径的圆上，∵∠ACB=90°，∴点C在⊙O上，∴当OF经过点M时，MF最短，此时OF⊥BC，∴OM=BM⋅tan∠ABC=2×1=2，∴MF=OF-OM=22-2，即线段MF的最小值为22-2，故答案为：8；22-2．【点评】本题是圆的综合题，主要考查了等腰直角三角形的性质，线段垂直平分线的性质，圆周角定理，利用定点定长构造辅助圆是解题的关键．类型四、定弦定角构造辅助圆一．填空题11.(2023春•梁子湖区期中)如图，矩形ABCD的边AB=8，AD=6，M为BC的中点，P是矩形内部一动点，且满足∠ADP=∠P AB，N为边CD上的一个动点，连接PN，MN，则PN+MN的最小值为．【分析】先找出点P 的运动路线为以AD 为直径的圆，设圆心为O ，作点M 关于直线DC 的对称点M ′，连接OM ′交⊙O 于点P ′，可推出M ′P ′的长即为PN +MN 的最小值，再求出M ′P ′的长即可．【解答】解：∵四边形ABCD 是矩形，∴∠BAD =90°，∵∠ADP =∠P AB ，∴∠ADP +∠P AD =∠P AB +∠P AD =∠BAD =90°，∴点P 的运动路线为以AD 为直径的圆，作以AD 为直径的⊙O ，作点M 关于直线DC 的对称点M ′，连接OM ′交⊙O 于点P ′，连接M ′N ，OP ，则OP =OP ′=3，M ′N =MN ，∴PN +MN =PN +M ′N =PN +M ′N +OP -OP ′≥OM ′-OP ′=OM ′-3，∴PN +MN 的最小值为OM ′-3；连接OM ，∵四边形ABCD 是矩形，点O 是AD 的中点，点M 为BC 的中点，∴OD =12AD =12BC =CM =3，OD ⎳CM ，∠ODC =90°，∴四边形OMCD 是矩形，∴OM =DC =AB =8，∵点M 关于直线DC 的对称点M ′，∴M ′M =2MC =6，在Rt △M ′OM 中，由勾股定理，得OM ′=OM 2+M ′M 2=82+62=10，∴PN +MN 的最小值为OM ′-3=10-3=7，故答案为：7．【点评】本题考查轴对称-最短路线问题，矩形的性质，勾股定理，能利用一条线段的长表示两线段的和的最小值是解题的关键．二．解答题小赵同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．我们把这个过程称为“化隐圆为显圆”．①已知：如图1，OA =OB =OC ，若∠AOB =50°，求∠ACB 的度数．解：若以点O 为圆心，OA 为半径作辅助圆，∠AOB 是⊙O 的圆心角，而∠ACB 是圆周角，从而可容易得到∠ACB = °．②如图2，点P 为正方形ABCD 内一点，且∠BPC =90°，若AB =4，求AP 的最小值．解：∵BC =4，∠BPC =90°，∴点P 在以BC 为直径的圆上，设圆心为点O ，则O 、P 、A 三点共线时AP 最小，最小值为．(2)【问题解决】①如图3，在平行四边形ABCD 中，已知AB =4，BC =6，∠ABC =60°，点P 是BC 边上一动点(点P 不与B ，C 重合)，连接AP ，作点B 关于直线AP 的对称点Q ，则线段QC 的最小值为．②如图4，△ABC 中，∠BAC =90°，AB =4，AC =3，D 为AC 上一动点，以AD 为直径的⊙O 交BD 于E ，求线段CE 的最小值．(3)【问题拓展】如图5，在平面直角坐标系中，已知两点A (2,3)，B (6,7)，x 轴上有一动点P ，当∠APB 最大时，直接写出点P 的坐标．【分析】(1)①利用圆周角定理即可求得答案；②由正方形性质可得：∠ABC =90°，BC =AB =4，OB =12BC =2，由勾股定理得：AO =25，推出点P 在以BC 为直径的⊙O 上，则O 、P 、A 三点共线时AP 最小，即可求得答案；(2)①过点A 作AH ⊥BC 于H ，利用解直角三角形得AH =AB ⋅sin ∠ABC =23，BH =AB ⋅cos ∠ABC =2，CH =BC -BH =4，由勾股定理得AC =27，再由AQ =AB =4，可得点Q 在以A 为圆心AB 为半径的⊙A 上，即当C 、Q 、A 三点共线时QC 最小，QC 的最小值=AC -AQ =27-4；②连接AE ，由AD 是⊙O 的直径，可得∠AED =90°，推出∠AEB =90°，即点E 在以AB 为直径的圆上，进而可得当C 、E 、Q 三点共线时，CE 最小，运用勾股定理即可求得答案；(3)当∠APB 最大时，过A 、B 两点的⊙O ′与x 轴相切，利用待定系数法可得直线AB 的解析式为y =x +1，线段AB 的垂直平分线为y =-x +9，设O ′(m ,-m +9)，根据O ′A =O ′B =O ′P ，建立方程求解即可得出答【解答】解：(1)①如图1，以点O为圆心，OA为半径作辅助圆⊙O，∵AB =AB ，∠AOB=50°，∠AOB=25°，∴∠ACB=12故答案为：25．②点P为正方形ABCD内一点，且∠BPC=90°，若AB=4，求AP的最小值．如图②，以BC为直径作⊙O，∵四边形ABCD是正方形，∴∠ABC=90°，BC=AB=4，BC=2，∴OB=12在Rt△ABO中，AO=AB2+OB2=42+22=25，∵BC=4，∠BPC=90°，∴点P在以BC为直径的⊙O上，则O、P、A三点共线时AP最小，∴AP的最小值=AO-OP=25-2，故答案为：25-2．(2)①如图3，过点A作AH⊥BC于H，∵AB=4，BC=6，∠ABC=60°，则AH=AB⋅sin∠ABC=4sin60°=23，BH=AB⋅cos∠ABC=4cos60°=2，∴CH=BC-BH=6-2=4，在Rt△ACH中，AC=AH2+CH2=(23)2+42=27，∵点B与点Q关于直线AP对称，∴AQ=AB=4，∴点Q在以A为圆心AB为半径的⊙A上，∴当C、Q、A三点共线时QC最小，QC的最小值=AC-AQ=27-4，故答案为：27-4．②如图4，连接AE，∵AD是⊙O的直径，∴∠AED=90°，∴∠AEB=180°-∠AED=90°，以AB 为直径作⊙Q ，交⊙O 于E ，当C 、E 、Q 三点共线时，CE 最小，∵△ABC 中，∠BAC =90°，AB =4，AC =3，∴QE =AQ =12AB =2，∴CQ =AC 2+AQ 2=32+22=13，∴CE =CQ -QE =13-2，故线段CE 的最小值为13-2．(3)当∠APB 最大时，过A 、B 两点的⊙O ′与x 轴相切，设直线AB 的解析式为y =kx +b ，把A (2,3)，B (6,7)代入，得：2k +b =36k +b =7 ，解得：k =1b =1 ，∴直线AB 的解析式为y =x +1，∵线段AB 的中点坐标为(4,5)，圆心O ′在AB 的垂直平分线上，∴线段AB 的垂直平分线为y =-x +9，设O ′(m ,-m +9)，∵O ′A =O ′B =O ′P ，∴(m -2)2+(-m +9-3)2=(-m +9)2，解得：m =42-1或m =-42-1(舍去)，∴点P 的坐标为(42-1，0)，故答案为：42-1．【点评】本题是圆的综合题，考查了圆的有关知识，正方形的性质，平行四边形的性质，解直角三角形等知识，灵活运用这些性质解决问题是解题的关键．13.(2022秋•泗洪县期中)已知：⊙O 和⊙O 外一点P ．(1)如图甲，P A 和PB 是⊙O 的两条切线，A 、B 分别为切点，求证：P A =PB ．(2)尺规作图：在图乙中，过P 点画⊙O 的两条切线PE 、PF ，E 、F 为切点(要求：保留作图痕迹，不写作法)．【分析】(1)如图，连接OP、OA、OB．只要证明RtΔP AO≅RtΔPBO(HL)，可得P A=PB．(2)以OP为直径作⊙O′，两圆交于点E、F，直线PE、PF即为所求；【解答】解：(1)如图，连接OP、OA、OB．∵P A、PB是切线，∴P A⊥OA，PB⊥OB，∴∠P AO=∠PBO=90°，在RtΔP AO和RtΔPBO中，OP=OP，OA=OB∴RtΔP AO≅RtΔPBO，∴P A=PB．(2)以OP为直径作⊙O′，两圆交于点E、F，直线PE、PF即为所求；【点评】本题考查切线的性质、全等三角形的判定和性质，直径的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用辅助圆解决问题，属于中考常考题型．类型五、对角互补构造辅助圆14.(2021秋•越秀区校级期中)如图1，在ΔABC中，∠ACB=90°，CD平分∠ACB，且AD⊥BD于点D．(1)判断ΔABD的形状；(2)如图2，在(1)的结论下，若BQ=22，DQ=3，∠BQD=75°，求AQ的长；(3)如图3，在(1)的结论下，若将DB绕着点D顺时针旋转α(0°<α<90°)得到DP，连接BP，作DE⊥BP交AP于点F．试探究AF与DE的数量关系，并说明理由．【分析】(1)由∠ACB+∠ADB=90°+90°=180°，知点A、C、B、D上四点共圆，则∠ACD=∠ABD=45°，即可得出结论；(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE，连接EQ，过点B作EQ的垂线，交EQ的延长线于H，得ΔQDE是等腰直角三角形，从而可解直角三角形BQH，在RtΔBEH中，利用勾股定理得可求出BE的长度，从而解决问题；(3)在AF上截取AM=PF，利用SAS证明ΔADM≅ΔPDF，得∠ADM=∠PDE，DM=DF，可证明ΔMDF、ΔPEF是等腰直角三角形，从而解决问题．【解答】解：(1)∵∠ACB=90°，CD平分∠ACB，∴∠ACD=45°，∵∠ACB+∠ADB=90°+90°=180°，∴点A、C、B、D上四点共圆，∴∠ACD=∠ABD=45°，∴∠BAD=∠ABD=45°，∴ΔABD是等腰直角三角形；(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE，连接EQ，过点B作EQ的垂线，交EQ的延长线于H，∴DQ=DE，∠QDE=90°，AQ=BE，∴ΔQDE是等腰直角三角形，∴∠DQE=45°，∴QE=2DQ=32，∵∠BQD=75°，∴∠BQE=∠BQD+∠DQE=120°，∴∠BQH=60°，BQ=2，BH=6，∴QH=12在RtΔBEH中，由勾股定理得BE=BH2+EH2=(42)2+(6)2=38，∴AQ=BE=38；(3)AF=2DE．，理由如下：如图，在AF上截取AM=PF，∵DA=DP，∴∠DAM=∠DPF，∴ΔADM≅ΔPDF(SAS)，∴∠ADM=∠PDE，DM=DF，∵BD=DP，DE⊥BP，∴∠BDE=∠PDE，∴∠ADM=∠BDE，∴ΔMDF是等腰直角三角形，∴∠MFD=45°，MF=2DF，∴∠EFP=45°，∴ΔPEF是等腰直角三角形，∴PF=2EF，∴AF=2DE．【点评】本题主要考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，等腰三角形的性质，含30°角的直角三角形的性质，勾股定理，四点共圆等知识，作辅助线构造全等三角形是解题的关键．15.(2021秋•西城区校级期中)如图，ΔABC为等边三角形，点P是线段AC上一动点(点P不与A，C重合)，连接BP，过点A作直线BP的垂线段，垂足为点D，将线段AD绕点A逆时针旋转60°得到线段AE，连接DE，CE．(1)求证：BD=CE；(2)延长ED交BC于点F，求证：F为BC的中点；(3)若ΔABC的边长为1，直接写出EF的最大值．【分析】(1)利用SAS证明ΔBAD≅ΔCAE，即可得出结论；(2)过点C作CG⎳BP交DF的延长线于点G，利用等角对等边可得CG=CE，由(1)ΔBAD≅ΔCAE，得BD=CE，再利用AAS证明ΔBDF≅ΔCGF，从而解决问题；(3)由(2)知∠AFC=∠AEC=90°，则点A，F，C，E四点在以AC为直径的圆上，故EF的最大值为直径．【解答】(1)证明：∵线段AD绕点A逆时针旋转60°得到线段AE，∴ΔADE是等边三角形，∴AD=AE，∠DAE=60°，∵ΔABC是等边三角形，∴AB=AC，∠BAC=60°，∴∠BAC=∠DAE，∴∠BAD=∠CAE，在ΔBAD和ΔCAE中，AB=AC∠BAD=∠CAE AD=AE，∴ΔBAD≅ΔCAE(SAS)，∴BD=CE；(2)证明：如图，过点C作CG⎳BP交DF的延长线于点G，∴∠G=∠BDF，∴∠G =30°，由(1)可知，BD =CE ，∠CEA =∠BDA ，∵AD ⊥BP ，∴∠BDA =90°，∴∠CEA =90°，∵∠AED =60°，∴∠CED =30°=∠G ，∴CE =CG ，∴BD =CG ，在ΔBDF 和ΔCGF 中，∠BDF =∠G∠BFD =∠CFG BD =CG，∴ΔBDF ≅ΔCGF (AAS )，∴BF =FC ，即F 为BC 的中点；(3)解：如图，连接AF ，∵ΔABC 是等边三角形，BF =FC ，∴AF ⊥BC ，∴∠AFC =90°，∴∠AFC =∠AEC =90°，∴点A ，F ，C ，E 四点在以AC 为直径的圆上，∴EF 的最大值为直径，即最大值为1．【点评】本题主要考查了等边三角形的性质，全等三角形的判定与性质，四点共圆等知识，作辅助线构造全等三角形是解题的关键．16.(2023秋•东城区校级期中)如图1，在Rt ΔABC 中，∠ABC =90°，BA =BC ，直线MN 是过点A 的直线CD ⊥MN 于点D ，连接BD ．(1)观察猜想张老师在课堂上提出问题：线段DC ，AD ，BD 之间有什么数量关系．经过观察思考，小明出一种思路：如图1，过点B 作BE ⊥BD ，交MN 于点E ，进而得出：DC +AD =BD ．(2)探究证明将直线MN 绕点A 顺时针旋转到图2的位置写出此时线段DC ，AD ，BD之间的数量关系，并证明(3)拓展延伸在直线MN 绕点A 旋转的过程中，当ΔABD 面积取得最大值时，若CD 长为1，请直接写BD 的长．【分析】(1)由题意：ΔBAE≅ΔBCD，推出AE=CD，BE=BD，推出CD+AD=AD+AE=DE，ΔBDE是等腰直角三角形，推出DE=2BD，可得DC+AD=2BD；(2)结论：AD-DC=2BD．过点B作BE⊥BD，交MN于点E．AD交BC于O．只要证明ΔCDB≅ΔAEB，即可解决问题；(3)如图3中，当点D在线段AB的垂直平分线上且在AB的右侧时，ΔABD的面积最大．【解答】解：(1)如图1中，由题意：ΔBAE≅ΔBCD，∴AE=CD，BE=BD，∴CD+AD=AD+AE=DE，∵ΔBDE是等腰直角三角形，∴DE=2BD，∴DC+AD=2BD，故答案为2．(2)AD-DC=2BD．证明：如图，过点B作BE⊥BD，交MN于点E．AD交BC于O．∵∠ABC=∠DBE=90°，∴∠ABE+∠EBC=∠CBD+∠EBC，∴∠ABE=∠CBD．∵∠BAE+∠AOB=90°，∠BCD+∠COD=90°，∠AOB=∠COD，∴∠BAE=∠BCD，∴∠ABE=∠DBC．又∵AB=CB，∴ΔCDB≅ΔAEB，∴CD=AE，EB=BD，∴△BD为等腰直角三角形，DE=2BD．∵DE=AD-AE=AD-CD，∴AD-CD=2BD．(3)如图3中，易知A、B、C、D四点共圆，当点D在线段AB的垂直平分线上且在AB的右侧时，ΔABD的面积最大．。

2021年九年级数学中考一轮复习圆综合填空压轴题提升专题训练

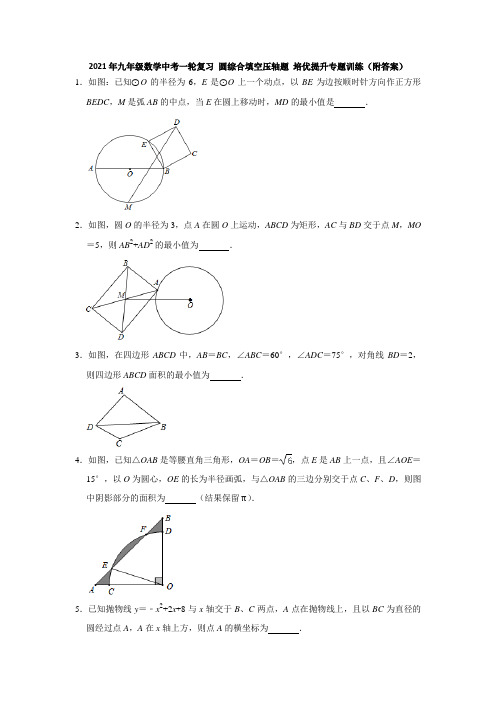
2021年九年级数学中考一轮复习圆综合填空压轴题培优提升专题训练（附答案）1．如图：已知⊙O的半径为6，E是⊙O上一个动点，以BE为边按顺时针方向作正方形BEDC，M是弧AB的中点，当E在圆上移动时，MD的最小值是．2．如图，圆O的半径为3，点A在圆O上运动，ABCD为矩形，AC与BD交于点M，MO ＝5，则AB2+AD2的最小值为．3．如图，在四边形ABCD中，AB＝BC，∠ABC＝60°，∠ADC＝75°，对角线BD＝2，则四边形ABCD面积的最小值为．4．如图，已知△OAB是等腰直角三角形，OA＝OB＝，点E是AB上一点，且∠AOE＝15°，以O为圆心，OE的长为半径画弧，与△OAB的三边分别交于点C、F、D，则图中阴影部分的面积为（结果保留π）．5．已知抛物线y＝﹣x2+2x+8与x轴交于B、C两点，A点在抛物线上，且以BC为直径的圆经过点A，A在x轴上方，则点A的横坐标为．6．如图，在矩形ABCD中，AB＞BC，以点B为圆心，AB的长为半径的圆分别交CD边于点M，交BC边的延长线于点E．若DM＝CE，的长为2π，则CE的长．7．如图，过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，作直线BC，连接AB，AC，若∠P＝80°，则∠C＝°．8．已知⊙O的直径AB为4cm，点C是⊙O上的动点，点D是BC的中点，AD延长线交⊙O 于点E，则BE的最大值为．9．如图，等腰△ABC中，AC＝BC＝2．∠ACB＝120°，以AB为直径在△ABC另一侧作半圆，圆心为O，点D为半圆上的动点，将半圆沿AD所在直线翻叠，翻折后的弧AD 与直径AB交点为F，当弧AD与BC边相切时，AF的长为．10．如图，△ABC中，∠ACB＝90°，BC＝3，cos∠B＝，将△ABC绕点C顺时针旋转90°得到△AB'C，P为线段AB上的动点，以点P为圆心，P A长为半径作⊙P，当⊙P与△A′B′C的一边所在的直线相切时，⊙P的半径为．11．如图，四边形ABDC内接于半圆O，AB为直径，AD平分∠CAB，AB﹣AC＝4，AD＝3，作DE⊥AB于点E，则BE的长为，AC的长为．12．已知：如图，四边形ABCD中，AD∥BC，AB＝BC＝4，∠B＝60°，∠C＝105°，点E为BC的中点，以CE为弦作圆，设该圆与四边形ABCD的一边的交点为P，若∠CPE ＝30°，则EP的长为．13．已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO＝，以线段BC为直径作⊙M交线段AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y＝ax2+bx+e，直线与抛物线和⊙M的另一个交点分别是E，F，当EF＝BD时，则m的值为．14．Rt△ABC中，∠ACB＝90°，CD为AB边上的高，P为AC的中点，连接PD，BC＝6，DP＝4．O为边BA上一点，以O为圆心，OB为半径作⊙O，当⊙O与△PDC的一边所在直线相切时，⊙O的半径等于．15．如图，⊙O的直径AB的长12，长度为4的弦DF在半圆上滑动，DE⊥AB于点E，OC ⊥DF于点C，连接CE，AF，则sin∠AEC的值是，当CE的长取得最大值时AF 的长是．16．如图，在平面直角坐标系中，⊙P与x轴相切于原点O，平行于y轴的直线交⊙P于E，F两点，若点E的坐标是（﹣3，﹣1），则点F的坐标是．17．如图，已知在Rt△ABC中，∠ACB＝90°，cos B＝，BC＝3，P是射线AB上的一个动点，以P为圆心，P A为半径的⊙P与射线AC的另一个交点为D，直线PD交直线BC 于点E．设线段BE的中点为Q，射线PQ与⊙P相交于点F，点P在运动过程中，当PE ∥CF时，则AP的长为．18．矩形ABCD的边AB＝4，边AD上有一点M，连接BM，将MB绕M点逆时针旋转90°得MN，N恰好落在CD上，过M、D、N作⊙O，⊙O与BC相切，Q为⊙O上的动点，连BQ，P为BQ中点，连AP，则AP的最小值为．19．如图，矩形ABCD中，AB＝，BC＝AB2，E为射线BA上一动点，连接CE交以BE 为直径的圆于点H，则线段DH长度的最小值为．20．如图，抛物线y＝x2﹣x﹣1与x轴交于A、B两点，与y轴交于C点，⊙B的圆心为B，半径是1，点P是直线AC上的动点，过点P作⊙B的切线，切点是Q，则切线长PQ的最小值是．21．平面直角坐标系中，⊙O交x轴正负半轴于点A、B，点P为⊙O外y轴正半轴上一点，C为第三象限内⊙O上一点，PH⊥CB交CB延长线于点H，已知∠BPH＝2∠BPO，PH ＝15，CH＝24，则tan∠BAC的值为．22．如图，AB是以点O为圆心的圆形纸片的直径，弦CD⊥AB于点E，AB＝10，BE＝3．将阴影部分沿着弦AC翻折压平，翻折后，弧AC对应的弧为G，则点O与弧G所在圆的位置关系为．23．如图，在平行四边形ABCD中，以对角线AC为直径的圆O分别交BC，CD于点E，F．若AB＝13，BC＝14，CE＝9，则线段EF的长为．24．如图，在扇形OAB中，∠AOB＝90°，OA＝OB＝2，将扇形OAB绕边OB的中点D 顺时针旋转90°得到扇形O'A'B'，弧A'B′交OA于点E，则图中阴影部分的面积为．25．如图所示，已知AB＝10，点P是线段AB上的动点，以AP为边作正六边形APCDEF，以PB为底作等腰三角形BPN，连接PD，DN，则△PDN的面积的最大值是．26．如图，已知扇形AOB的圆心角为120°，点C是半径OA上一点，点D是弧AB上一点．将扇形AOB沿CD对折，使得折叠后的图形恰好与半径OB相切于点E．若∠OCD ＝45°，OC＝+1，则扇形AOB的半径长是．27．如图，在矩形ABCD中，AB＝6，AD＝8，点M，N分别为AD，AC上的动点（不含端点），AN＝DM，连接点M与矩形的一个顶点，以该线段为直径作⊙O，当点N和矩形的另一个顶点也在⊙O上时，线段DM的长为．参考答案1．解：如图，连接MO，延长MO交⊙O于T，连接BT，OE，BD．∵M是弧AB的中点，AB是直径，∴MT⊥AB，∵OB＝OT＝6，∴∠OBT＝∠OTB＝45°，∴BT＝OB，∵四边形BCDE是正方形，∴∠EBD＝∠OBT＝45°，BD＝BE，∴∠OBE＝∠TBD，＝＝，∴△TBD∽△OBE，∴＝＝，∴TD＝OE＝6，∵DM≥TM﹣TD，∴DM≥12﹣6，∴DM的最小值为12﹣6．故答案为：12﹣6．2．解：如图，连接OA．∵四边形ABCD是矩形，∴AC＝BD，AM＝MC＝BM＝MD，∠BAD＝90°，∴AB2+AD2＝BD2，∴BD的值最小时，AB2+AD2的值最小，∵AM≥OM﹣OA，OM＝5，OA＝3，∴AM≥2，∴AM的最小值为2，∴BD的最小值为4，∴AB2+AD2的最小值为16，故答案为16．3．解：如图，连接AC，∵AB＝CB，∠ABC＝60°，∴△ABC是等边三角形，将△DBC绕点B顺时针旋转60°得△HBA，连接DH，则BD＝BH＝2，∠HBD＝60°，∴△HBD是等边三角形，∴S四边形ABCD＝S△ABD+S△BCD＝S△BDH﹣S△ADH，∵BD＝2，是定值，∴S△BDH是定值，∴当△ADH的面积最大时，四边形ABCD的面积最小，∵∠ADC＝75°，∠ABC＝60°，∴∠BAD+∠BCD＝360°﹣75°﹣60°＝225°，∴∠DAH＝360°﹣∠BAD﹣∠HAB＝360°﹣225°＝135°，∵点A在定圆⊙O（△ADH的外接圆）上运动，当O、A、B共线时，△ADH的面积最大，此时，OB⊥DH，设OA交DH于K，则HK＝KD＝1，∵AH＝AD，∴∠AHD＝∠ADH＝22.5°，在HK上取一点F，使FH＝AF，则△AKF是等腰直角三角形，设AK＝FK＝x，则AF＝FH＝x，∴1＝x+x，∴x＝﹣1，∴△ADH面积的最大值＝×2×（﹣1）＝﹣1，∴四边形ABCD的面积的最小值＝×22﹣（2﹣2）＝﹣+1．故答案为：﹣+1．4．解：如图，连接OF．作OH⊥EF于H．由题意：∠AOE＝∠FOB＝15°，∠EOF＝90°﹣15°﹣15°＝60°，∵∠AOB＝90°，OA＝OB＝，∴AB＝2，∵OH⊥AB，OA＝OB，∴AH＝BH，∴OH＝AB＝，∠EOH＝∠FOH＝30°，∴OF＝＝2，∴S阴＝（S△AOB﹣2•S扇形EOC﹣S△EOF）+（S扇形OEF﹣S△OEF）＝××﹣2×﹣×22+﹣×22＝3+﹣2．故答案为3+﹣2．5．解：对于抛物线y＝﹣x2+2x+8，令y＝0，得到x2﹣2x﹣8＝0，解得x＝﹣2或4，不妨设B（﹣2，0），C（4，0），A（m，﹣m2+2m+8），由题意（m﹣1）2+（﹣m2+2m+8）2＝9，∴（m﹣1）2﹣32+（m+2）2•（m﹣4）2＝0，∴（m﹣4）（m+2）+（m+2）2•（m﹣4）2＝0，∴（m+2）（m﹣4）[1+（m+2）（m﹣4）]＝0，∴（m+2）（m﹣4）（m2﹣2m﹣7）＝0，解得m＝﹣2或4或1±2，∵点A在x轴的上方，∴点A的横坐标为1±2．6．解：连接BM，则AB＝BE＝BM，设BM＝R，∵四边形ABCD是矩形，∴AB＝CD＝BE，∠B＝∠BCD＝90°，∵DM＝VE，∴CM＝BC，∵的长为2π，∴＝2π，解得：R＝4，即BM＝BE＝CD＝AB＝4，在Rt△BCM中，由勾股定理得：BC2+CM2＝BM2，BC＝CM＝2，∴CE＝4﹣2，故答案为：4﹣2．7．解：连接OA，∵过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，∴∠P AO＝∠PBO＝90°，∵∠P＝80°，∴∠AOB＝360°﹣90°﹣90°﹣80°＝100°，∴∠C＝AOB＝50°，故答案为：50．8．解：如图，以OB为直径作⊙K，当直线AE切⊙K于D时，BE的值最大．∵AE是⊙K的切线，∴DK⊥AE，∴∠ADK＝90°，∵AB是直径，∴∠AEB＝90°，∴∠ADK＝∠AEB，∴DK∥BE，∴＝，∴＝，∴BE＝，故答案为．9．解：如图，作点O关于AD的对称点O′，连接O′A，∵AC＝BC＝2．∠ACB＝120°，∴AB＝6，∴O′A＝OA＝3，延长BC交⊙O于点E，∵AB是⊙O的直径，∴∠E＝90°，设⊙O′与BC相切于点G，则∠O′GB＝90°，∴∠E＝∠O′GB，∴AE∥O′G，∵∠ABC＝30°，AB＝6，∴AE＝O′G＝3，∴四边形O′AEG为平行四边形，∴AO′∥BE，∴∠O′AB＝∠ABC＝30°，作O′M⊥AF于M∵O′A＝3，∠O′AB＝30°，∴AM＝MF＝，∴AF＝2AM＝．故答案为：．10．解：①当⊙P与△A′B′C的A′B′边所在的直线相切时，即：⊙P′所在的位置，设切点为H点，圆的半径为R，BC＝3，cos∠B＝，则sin∠B＝＝sin∠AB′H，则AC＝A′C＝4，BC＝CB′＝3，AB′＝AC﹣B′C＝1，sin∠AB′H＝＝＝，则R＝，②当⊙P与△A′B′C的A′C边所在的直线相切时，即：⊙P′′所在的位置，同理，可得：R＝；故：答案为：或．11．解：如图，作DF⊥AC交AC的延长线于F．∵AD平分∠CAB，DF⊥AC，DE⊥AB，∴DE＝DF，∵∠DAC＝∠DAB，∴＝，∴CD＝DB，∵∠F＝∠DEB＝90°，∴Rt△DFC≌Rt△DEB（HL），∴CF＝BE，∵∠F＝∠AED＝90°，AD＝AD．DF＝DE，∴Rt△ADF≌Rt△ADE（HL），∴AF＝AE，∵AB﹣AC＝AE+EB﹣（AF﹣CF）＝2BE＝4，∴BE＝2，∵AB是直径，∴∠ADB＝90°，∵∠DAE＝∠BAD，∠AED＝∠ADB＝90°，∴△ADE∽△ABD，∴＝，∴AD2＝AE•AB，设AE＝x，则有：63＝x（x+2），解得x＝7或﹣9（舍弃），∴AE＝7，∴AB＝AE+BE＝9，∵AB﹣AC＝4，∴AC＝5，故答案为2，5．12．解：如图，连接AC，AE，∵AB＝BC＝4，∠B＝60°，∴△ABC是等边三角形，∵点E为BC的中点，∴BE＝CE＝2，AE⊥BC，∠EAC＝30°，∴AC是以CE为弦的圆的直径，设圆心为O，当⊙O与CD边交于P1，则∠EP1C＝30°，∵∠ECP1＝105°，∴∠P1EC＝45°，过C作CH⊥P1E于H，∴EH＝CH＝CE＝，∴P1H＝HC＝，∴P1E＝+；当⊙O与AD交于P2，A（P3），∵AD∥CE，∴∠ECP2＝∠AP2C＝90°，∴四边形AECP2是矩形，∴P2E＝AC＝4，P3E＝P2C＝2，当⊙O与AB交于P4，∵∠AP4C＝90°，∠EP4C＝30°，∴∠BP4E＝60°，∴△BP4E是等边三角形，∴P4E＝BE＝2，综上所述，若∠CPE＝30°，则EP的长为或4或2或2，故答案为：或4或2或2．13．解：∵tan∠ABO＝＝，且A（1，0），∴OB＝2，即：点B的坐标为（0，2）．点C（m，0），A（1，0），B（0，2）在抛物线y＝ax2+bx+e上，∴，解得：b＝﹣，a＝，∴x＝﹣＝．∵EB＝﹣（1+m），FB＝﹣m，EF＝FB﹣EB＝1，∴线段EF的长是定值1．∴BD＝EF＝1．如图所示，连接CD∵BC为直径∴∠CDB＝90°∴∠CDA＝∠AOB＝90°，∠CAD＝∠BAO∴△CAD∽△BAO∴＝A（1，0），B（0，2），C（m，0），∴AB＝，AC＝1﹣m，AO＝1∵BD＝1∴AD＝﹣1∴＝∴1﹣m＝5﹣∴m＝故答案为：．14．解：∵∠ADC＝90°，P是AC中点，∴AC＝2DP＝8，又∵BC＝6，∴AB＝10，则CD＝＝＝，∴BD＝＝，如图1，若⊙O与CD相切，则⊙O的半径r＝BD＝；如图2，若⊙O与CP相切，则BO＝OE＝r，AO＝10﹣r，由OE⊥AC知OE∥BC，∴△AOE∽△ABC，∴＝，即＝，解得r＝；如图3，若⊙O与DP所在直线相切，切点F，则OF⊥DP，即∠OFD＝∠ACB＝90°，OB＝OF＝r，∴OD＝BD﹣BO＝﹣r，∵∠ODF＝∠ADP＝∠A，∴△ODF∽△BAC，∴＝，即＝，解得r＝；综上，当⊙O与△PDC的一边所在直线相切时，⊙O的半径等于或或，故答案为：或或．15．解：如图1，连接OD，∴DO＝AB＝6，∵OC⊥DF，∴∠OCD＝90°，CD＝CF＝DF＝2，在Rt△OCD中，根据勾股定理得，OC＝＝4，∴sin∠ODC＝＝＝，∵DE⊥AB，∴∠DEO＝90°＝∠OCD，∴点O，C，D，E是以OD为直径的圆上，∴∠AEC＝∠ODC，∴sin∠AEC＝sin∠ODC＝，如图2，∵CE是以OD为直径的圆中的弦，CE要最大，即：CE是以OD为直径的圆的直径，∴CE＝OD＝6，∠COE＝90°，∵∠OCD＝∠OED＝90°，∴四边形OCDE是矩形，∴DF∥AB，过点F作FG⊥AB于G，易知，四边形OCFG是矩形，∴OG＝CF＝2，FG＝OC＝4，∴AG＝OA﹣OG＝4连接AF，在Rt△AFG中，根据勾股定理得，AF＝＝4，故答案为，4．16．解：过点P作AP⊥EF交EF于点A，连接PE，设OP＝x，∵⊙P与x轴相切于原点O，∴OP⊥OE，∵平行于y轴的直线交⊙P于E，F两点，∴四边形APOB是矩形，∴AB＝OP＝x，∵点E的坐标是（﹣3，﹣1），∴AP＝OB＝3，AE＝AB﹣BE＝x﹣1，在Rt△ABE中，32+（x﹣1）2＝x2，解得x＝5，∴AE＝4，∵AF＝AE，∴EF＝8，∴BF＝EF+BE＝9，∴点F的坐标是（﹣3，﹣9）．故答案为（﹣3，﹣9）．17．解：如图，连接CF，过点P作PG⊥AC于G，设P A＝x．在Rt∠ACB中，∵ACB＝90°，BC＝3，cos B＝＝，∴AB＝5，AC＝＝＝4，∵PG⊥AD，∴AG＝DG＝P A•cos∠BAC＝x，∴AD＝x，CD＝4﹣x，∵∠ABC+∠A＝90°，∠PEC+∠CDE＝90°，∵∠A＝∠PDA，∴∠ABC＝∠PEC，∵∠ABC＝∠EBP，∴∠PEC＝∠EBP，∴PB＝PE，∵点Q为线段BE的中点，∴PQ⊥BC，∴PQ∥AC∴当PE∥CF时，四边形PDCF是平行四边形，∴PF＝CD，当点P在边AB的上时，x＝4﹣x，x＝，当点P在边AB的延长线上时，x＝x﹣4，x＝，综上所述，当PE∥CF时，AP的长为或．18．解：设⊙O与BC的交点为F，连接OB、OF，如图1所示．∵△MDN为直角三角形，∴MN为⊙O的直径，∵BM与⊙O相切，∴MN⊥BM，∵将MB绕M点逆时针旋转90°得MN，∴MB＝MN，∴△BMN为等腰直角三角形，∵∠AMB+∠NMD＝180°﹣∠AMN＝90°，∠MBA+∠AMB＝90°，∴∠NMD＝∠MBA，且BM＝NP，∠A＝∠NMD＝90°，∴△ABM≌△DMN（AAS），∴DM＝AB＝4，DN＝AM，设DN＝2a，则AM＝2a，OF＝4﹣a，BM＝＝2，∵BM＝MP＝2OF，∴2＝2×（4﹣a），解得：a＝，∴DN＝2a＝3，OF＝4﹣＝，∴⊙O半径为，如图2，延长BA，使AH＝AB＝4，连接HQ，OH，过O作OG⊥AB于G，∵AB＝AH，BP＝PQ，∴AP＝HQ，HQ∥AP，∴当HQ取最小值时，AP有最小值，∴当点Q在HO时，HQ的值最小，∵HG＝4+4﹣＝，GO＝3+4﹣2＝5，∴OH＝＝＝，∴HQ的最小值＝﹣＝，∴AP的最小值为，故答案为：．19．解：取BC的中点G，连接BH，HG，DG．∵四边形ABCD是矩形，∴AB＝CD＝，BC＝AB2＝，∠DCG＝90°，∵CG＝BG＝，∴DG＝＝＝，∵BE是直径，∴∠BHE＝∠BHC＝90°，∵BG＝GC，∴HG＝BC＝，∵DH≥DG﹣HG，∴DH≥﹣＝，∴DH的最小值为．故答案为．20．解：对于抛物线y＝x2﹣x﹣1，令x＝0，得到y＝﹣1，∴C（0，﹣1），令y＝0，x2﹣x﹣1＝0，解得x＝5或﹣，∴A（﹣，0），B（5，0），∵PQ是切线，∴PQ⊥BQ，∴∠PQB＝90°，∴PQ＝＝，∴PB的值最小时，PQ的值最小，根据垂线段最短可知，当BP′⊥AC于P′时，BP′的值最小，∵OA＝，OC＝1，∴tan∠OAC＝＝，∴∠OAC＝30°，∴BP′＝AB•sin30°＝6×＝3，∴PQ的最小值＝＝，故答案为．21．解：设PB交⊙O于点N，连接P A，延长PB、AC交于点M，∵AB是直径，PH⊥CB∴∠ANP＝90°＝∠ACB＝∠H，∴MC∥PH，由圆的对称性可得，P A＝PB，∠BPO＝∠APO＝∠APB，∵∠BPH＝2∠BPO，∴∠BPH＝∠APB，∴△PHB≌△PNA（AAS），∴PN＝PH＝15，由MC∥PH得，∠HPB＝∠M＝∠APM，∴AM＝AP＝PB，∵AN⊥PM，∴PM＝2PN＝30，由△PHB∽△MCB，∴＝＝，设MC＝a，BC＝b，MB＝c，则HB＝24﹣b，PB＝30﹣c，∴＝＝，∴＝＝sin M＝sin∠HPB，∴cos∠HPB＝在Rt△PHB中，PH＝15，∴PB＝＝＝25，HB＝sin∠HPB•PH＝20，∴BC＝24﹣20＝4，MB＝30﹣25＝5，则MC＝＝3，在Rt△ABC中，BC＝4，AC＝AM﹣MC＝25﹣3＝22，∴tan∠BAC＝＝＝，故答案为：．22．解：过O作OM⊥AC，交⊙O于F，交弧G于H，连接OC，∵AB为⊙O的直径，AB＝10，∴OA＝OB＝OG＝OD＝5，∵BE＝3，∴OE＝2，在Rt△OED中，由勾股定理得：CE＝＝＝，在Rt△AEC中，AC＝＝＝，∵OF⊥AC，∴AM＝AC＝，由勾股定理得：OM＝＝＝，由折叠得：弧G所在圆与圆O是等圆，∴弧G所在圆的半径为5，∴MH＝FM＝5﹣，∵5﹣＜，∴FM＜OM，∴O在G所在圆外，故答案为：点在圆外．23．解：如图，连接AE，AF．∵BC＝14，CE＝9，∴BE＝BC﹣EC＝14﹣9＝5，∵AC是直径，∴∠AEC＝∠AEB＝90°，∴AE＝＝＝12，∴AC＝＝＝15，∵四边形ABCD是平行四边形，∴AD∥BC，AB＝CD＝13，∴∠DAC＝∠ACB，∵∠AFE＝∠ACB，∴∠AFE＝∠DAC，∵∠AEF＝∠ACD，∴△AFE∽△DAC，∴＝，∴＝，∴EF＝，故答案为．24．解：延长EO交O'A'于P，则由∠AOB＝90°，OA＝OB＝2，D为OB中点，可得S阴影OPO′＝12﹣＝1﹣；∵O′P＝OE，∠EPO'＝90°，∴cos∠EO'P＝，∴∠EO'P＝60°，EP＝∴S阴影A′PE＝S扇形O′A′E﹣S△O′PE＝﹣××1＝﹣∴S阴影═1﹣+﹣＝1﹣+．故答案为1﹣+．25．解：连接AD，作NM⊥PB于M，∵六边形APCDEF是正六边形，∴EF∥AD，DP⊥AB，DP⊥ED，正六边形的每一个内角为120°，∴∠ADE＝60°，∴∠ADP＝30°∴PD＝P A，∵DP⊥AB，NM⊥PB∴PD∥MN，∴PM就是△PDN的PD边的高，设P A＝x．则PB＝10﹣x，∵在等腰△BPN中，MN⊥PB，∴PM＝PB＝（10﹣x），∴S△PDN＝PD•PM＝×x×（10﹣x）＝﹣（x﹣5）2+（0＜x＜10），∴△PDN的面积的最大值为：．故答案为：．26．解：作O关于CD的对称点F，连接CF、EF，如图1所示：则EF为扇形AOB的半径，由折叠的性质得：∠FCD＝∠OCD＝45°，FC＝OC＝+1，∴∠OCF＝90°，∴△OCF是等腰直角三角形，∴∠COF＝45°，OF＝OC＝+，∴∠EOF＝∠AOB﹣∠COF＝75°，∵折叠后的图形恰好与半径OB相切于点E，∴∠OEF＝90°，∴∠OFE＝15°，∵cos∠OFE＝＝cos15°＝，如图2所示：∴EF＝OF×cos15°＝（）×＝2+；故答案为：2+．27．解：如图1中，当点N在CM为直径的圆上时，设DM＝AN＝x．∵四边形ABCD是矩形，∴∠ADC＝90°，AB＝CD＝6，BC＝AD＝8，∴AC＝＝＝10，∵∠MAN＝∠DAC，∠ANM＝∠ADC＝90°，∴△ANM∽△ADC，∴＝，∴＝，解得x＝，∴DM＝如图2中，当点N在BM为直径的圆上时，设BC与圆的交点为H，连接MH，NH．设DM＝AN＝y．∵BM是直径，∴∠MHB＝90°，∴∠MHC＝∠D＝∠DCH＝90°，∴四边形CDMH是矩形，∴CH＝DM＝y，∵∠NCH＝∠BCA，∠CHN＝∠CAB，∴△CNH∽△CBA，∴＝，∴＝，解得y＝，∴DM＝，故答案为或。

中考数学压轴题-圆的压轴题含解析

圆的压轴题（1）1、如图，BF 为⊙O 的直径，直线AC 交⊙O 于A ，B 两点，点D 在⊙O 上，BD 平分∠OBC ，DE ⊥AC 于点E 。

（1）求证：直线DE 是⊙O 的切线；（2）若 BF=10，sin ∠BDE=，求DE 的长。

2、如图，AN 是M ⊙的直径，NB x ∥轴，AB 交M ⊙于点C .(1)若点()0,6A ，()0,2N ，30ABN =∠°，求点B 的坐标；(2)若D 为线段NB 的中点，求证：直线CD 是M ⊙的切线.x y C D M O B NA3、如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．4、已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，若=，如图1，．（1）判断△ABC的形状，并证明你的结论；（2）设AE与DF相交于点M，如图2，AF=2FC=4，求AM的长．5、如图，AB是⊙O的直径，AC是上半圆的弦，过点C作⊙O的切线DE交AB的延长线于点E，过点A作切线DE的垂线，垂足为D，且与⊙O交于点F，设∠DAC，∠CEA的度数分别是α，β．（1）用含α的代数式表示β，并直接写出α的取值范围；（2）连接OF与AC交于点O′，当点O′是AC的中点时，求α，β的值．6、如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．7、如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．（1）求证：∠FEB=∠ECF；（2）若BC=6，DE=4，求EF的长．8、如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）设OE交⊙O于点F，若DF=1，BC=2 ，求阴影部分的面积．9、如图，已知⊙O的直径CD=6，A，B为圆周上两点，且四边形OABC是平行四边形，过A点作直线EF∥BD，分别交CD，CB的延长线于点E，F，AO与BD交于G点．（1）求证：EF是⊙O的切线；（2）求AE的长．10、如图，C、D是半圆O上的三等分点，直径AB=4，连接AD、AC，DE⊥AB，垂足为E，DE交AC于点F．（1）求∠AFE的度数；（2）求阴影部分的面积（结果保留π和根号）．11、如图，MN是⊙O的直径，MN=4，点A在⊙O上，∠AMN=30°，B为的中点，P是直径MN上一动点．（1）利用尺规作图，确定当PA+PB最小时P点的位置（不写作法，但要保留作图痕迹）．（2）求PA+PB的最小值．12、如图，已知直线PT与⊙O相切于点T，直线PO与⊙O相交于A，B两点．（1）求证：PT2=PA•PB；（2）若PT=TB=，求图中阴影部分的面积．13、如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．（1）求证：四边形ACBP是菱形；（2）若⊙O半径为1，求菱形ACBP的面积．14、如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC边于点D，过点C作CF ∥AB，与过点B的切线交于点F，连接BD．（1）求证：BD=BF；（2）若AB=10，CD=4，求BC的长．15、如图，梯形ABCD中，AD∥BC，AE⊥BC于E，∠ADC的平分线交AE于点O，以点O为圆心，OA为半径的圆经过点B，交BC于另一点F．（1）求证：CD与⊙O相切；（2）若BF=24，OE=5，求tan∠ABC的值．16、已知：如图，MN为⊙O的直径，ME是⊙O的弦，MD垂直于过点E的直线DE，垂足为点D，且ME平分∠DMN．求证：（1）DE是⊙O的切线；（2）ME2=MD•MN．参考答案1、【解答】解：（1）如图所示，连接OD，∵OD=OB，∴∠ODB=∠OBD，∵BD平分∠OBC，∴∠OBD=∠DBE，∴∠ODB=∠DBE，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∵OD是⊙O的半径，∴直线DE是⊙O的切线；（2）如图，连接DF，∵BF是⊙O的直径，∴∠FDB=90°，∴∠F+∠OBD=90°，∵∠OBD=∠DBE，∠BDE+∠DBE=90°，∴∠F=∠BDE，在Rt△BDF中，=sinF=sin∠BDE=，∴BD=10×=2，∴在Rt△BDE中，sin∠BDE==，∴BE=2×=2，∴在Rt△BDE中，DE===4。

人教版数学九年级上册第二十四章《圆》压轴题综合培优训练(包含答案)

《圆》压轴题综合培优训练1．如图，以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D，过点D作⊙O的切线与BC 交于点E，弦DM与AB垂直，垂足为H．（1）求证：E为BC的中点；（2）若⊙O的面积为12π，两个三角形△AHD和△BMH的外接圆面积之比为3，求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比．2．如图，在△ABC中，CA＝CB，E是边BC上一点，以AE为直径的⊙O经过点C，并交AB 于点D，连结ED．（1）判断△BDE的形状并证明．（2）连结CO并延长交AB于点F，若BE＝CE＝3，求AF的长．3．如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．（1）求证：AD平分∠BAC；（2）若∠BAC＝60°，OA＝2，求阴影部分的面积（结果保留π）．4．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD 的延长线于点E．（1）求证：∠BDC＝∠A；（2）若CE＝2，DE＝2，求AD的长．（3）在（2）的条件下，求弧BD的长．5．如图，在△ABC中，AB＝AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．（1）求证：DE是⊙O的切线；（2）当⊙O半径为3，CE＝2时，求BD长．6．如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF＝DA，AE∥BC交CF于E．（1）求证：EA是⊙O的切线；（2）求证：BD＝CF．7．如图，AH是圆O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．（1）求证：直线FG是⊙O的切线；（2）若AD＝8，EB＝5，求⊙O的直径．8．如图，AB是⊙O的直径，弦CD垂直平分OA，垂足为点M，连接并延长CO交⊙O于点E，分别连接DE，BE，DB，其中∠EDB＝30°，∠CDE的平分线DN交CE于点G，交⊙O于点N，延长CE至点F，使FG＝FD．（1）求证：DF是⊙O的切线；（2）若⊙O半径r为8，求线段DB，BE与劣弧DE所围成的阴影部分的面积．9．如图，∠BAC的平分线交△ABC的外接圆于点D，交BC于点F，∠ABC的平分线交AD于点E．（1）求证：DE＝DB：（2）若∠BAC＝90°，BD＝4，求△ABC外接圆的半径；（3）若BD＝6，DF＝4，求AD的长10．在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，过点B作⊙O的切线BF交CD的延长线于点F．（I）如图①，若∠F＝50°，求∠BGF的大小；（II）如图②，连接BD，AC，若∠F＝36°，AC∥BF，求∠BDG的大小．11．如图，AB是圆O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交圆O于点F，且CE＝CB．（1）求证：BC是⊙O的切线；（2）连接AF，BF，求∠ABF的度数；（3）如果OA＝3，求AE•AB的值．12．Rt△ABC中，∠ACB＝90°，AC：BC＝4：3，O是BC上一点，⊙O交AB于点D，交BC 延长线于点E．连接ED，交AC于点G，且AG＝AD．（1）求证：AB与⊙O相切；（2）设⊙O与AC的延长线交于点F，连接EF，若EF∥AB，且EF＝5，求BD的长．13．Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC边于点D，E是边BC的中点，连接DE，OD．（Ⅰ）如图①，求∠ODE的大小；（Ⅱ）如图②，连接OC交DE于点F，若OF＝CF，求∠A的大小．14．如图，已知圆O是△ABC的外接圆，AB是圆O的直径，C是圆上的一点，D是AB延长线上的一点，AE⊥CD交DC的延长线于点E，且AC平分∠EAB．（1）求证：DE是圆O的切线．（2）若AB＝6，AE＝4.8，求BD和BC的长．15．已知AB是半圆O的直径，M，N是半圆不与A，B重合的两点，且点N在弧BM上．（1）如图1，MA＝6，MB＝8，∠NOB＝60°，求NB的长；（2）如图2，过点M作MC⊥AB于点C，点P是MN的中点，连接MB、NA、PC，试探究∠MCP、∠NAB、∠MBA之间的数量关系，并证明．参考答案一．解答题1．解：（1）连接BD、OE，∵AB是直径，则∠ADB＝90°＝∠ADO+∠ODB，∵DE是切线，∴∠ODE＝90°＝∠EDB+∠BDO，∴∠EDB＝∠ADO＝∠CAB，∵∠ABC＝90°，即BC是圆的切线，∴∠DBC＝∠CAB，∴∠EDB＝∠EBD，则∠BDC＝90°，∴E为BC的中点；（2）△AHD和△BMH的外接圆面积之比为3，则两个三角形的外接圆的直径分别为AD、BM，∴AD：BM＝，而△ADH∽△MBH，∴DH：BH＝，则DH＝HM，∴HM：BH＝，∴∠BMH＝30°＝∠BAC，∴∠C＝60°，E是直角三角形的中线，∴DE＝CE，∴△DEC为等边三角形，⊙O的面积：12π＝（AB）2π，则AB＝4，∠CAB＝30°，∴BD＝2，BC＝4，AC＝8，而OE＝AC＝4，四边形OBED的外接圆面积S2＝π（2）2＝4π，等边三角形△DEC边长为2，则其内切圆的半径为：，面积为，故△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比为：．2．（1）证明：△BDE是等腰直角三角形．∵AE是⊙O的直径∴∠ACB＝∠ADE＝90°，∴∠BDE＝180°﹣90°＝90°．∵CA＝CB，∴∠B＝45°，∴△BDE是等腰直角三角形．（2）过点F作FG⊥AC于点G，则△AFG是等腰直角三角形，且AG＝FG．∵OA＝OC，∴∠EAC＝∠FCG．∵BE＝CE＝3，∴AC＝BC＝2CE＝6，∴tan∠FCG＝tan∠EAC＝．∴CG＝2FG＝2AG．∴FG＝AG＝2，∴AF＝2．3．【解答】（1）证明：∵⊙O切BC于D，∴OD⊥BC，∵AC⊥BC，∴AC∥OD，∴∠CAD＝∠ADO，∵OA＝OD，∴∠OAD＝∠ADO，∴∠OAD＝∠CAD，即AD平分∠CAB；（2）设EO与AD交于点M，连接ED．∵∠BAC＝60°，OA＝OE，∴△AEO是等边三角形，∴AE＝OA，∠AOE＝60°，∴AE＝AO＝OD，又由（1）知，AC∥OD即AE∥OD，∴四边形AEDO是菱形，则△AEM≌△DMO，∠EOD＝60°，∴S△AEM ＝S△DMO，∴S阴影＝S扇形EOD＝＝π．4．（1）证明：连接OD，∵CD是⊙O切线，∴∠ODC＝90°，即∠ODB+∠BDC＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，即∠ODB+∠ADO＝90°，∴∠BDC＝∠ADO，∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A；（2）∵CE⊥AE，∴∠E＝∠ADB＝90°，∴DB∥EC，∴∠DCE＝∠BDC，∵∠BDC＝∠A，∴∠A＝∠DCE，∵∠E＝∠E，∴△AEC∽△CED，∴＝，∴EC2＝DE•AE，∴（2）2＝2（2+AD），∴AD＝4．（3）∵直角△CDE中，tan∠DCE＝＝＝，∴∠DCE＝30°，又∵△AEC∽△CED，∴∠A＝∠DCE＝30°，∴∠DOB＝2∠A＝60°，BD＝AD•tan A＝4×＝，∴△OBD是等边三角形，则OD＝BD＝，则弧BD的长是＝．5．（1）证明：连接OD，如图，∵AB为⊙0的直径，∴∠ADB＝90°，∴AD⊥BC，∵AB＝AC，∴AD平分BC，即DB＝DC，∵OA＝OB，∴OD为△ABC的中位线，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∴DE是⊙0的切线；（2）证明：∵∠B＝∠C，∠CED＝∠BDA＝90°，∴△DEC∽△ADB，∴，∴BD•CD＝AB•CE，∵BD＝CD，∴BD2＝AB•CE，∵⊙O半径为3，CE＝2，∴BD＝＝2．6．证明：（1）连接OA，∵⊙O是等边三角形ABC的外接圆，∴∠OAC＝30°，∠BCA＝60°，∵AE∥BC，∴∠EAC＝∠BCA＝60°，∴∠OAE＝∠OAC+∠EAC＝30°+60°＝90°，∴AE是⊙O的切线；（2）∵△ABC是等边三角形，∴AB＝AC，∠BAC＝∠ABC＝60°，∵A、B、C、D四点共圆，∴∠ADF＝∠ABC＝60°，∵AD＝DF，∴△ADF是等边三角形，∴AD＝AF，∠DAF＝60°，∴∠BAC+∠CAD＝∠DAF+∠CAD，即∠BAD＝∠CAF，在△BAD和△CAF中，∵，∴△BAD≌△CAF，∴BD＝CF．7．解：（1）如图1，连接OE，∵OA＝OE，∴∠EAO＝∠AEO，∵AE平分∠FAH，∴∠EAO＝∠FAE，∴∠FAE＝∠AEO，∴AF∥OE，∴∠AFE+∠OEF＝180°，∵AF⊥GF，∴∠AFE＝∠OEF＝90°，∴OE⊥GF，∵点E在圆上，OE是半径，∴GF是⊙O的切线．（2）设AB＝x，∵四边形ABCD是矩形，∴AB＝CD＝x，BC＝AD＝8，∴CE＝BC﹣BE＝3，∵AE是∠BAF的角平分线，BE⊥AB，EF⊥AF，∴EF＝BE＝5，在Rt△CEF中，根据勾股定理得，CF＝4，∴DF＝CD﹣CF＝x﹣4，在Rt△ABE和Rt△AFE中，，∴Rt△ABE≌Rt△AFE（HL），∴AF＝AB＝x，在Rt△ADF中，x2﹣（x﹣4）2＝64，∴x＝10，∴AB＝10，设⊙O的半径为r，∴OB＝10﹣r，在Rt△BOE中，r2﹣（10﹣r）2＝25，∴r＝，∴⊙O的直径为．8．（1）证明：连接OD，∵CD垂直平分OA，∴OM＝OA＝OD，∴∠ODC＝30°，∵CE为⊙O的直径，∴∠CDE＝90°，∵DN平分∠CDE，∴∠CDN＝45°，∴∠ODN＝45°﹣30°＝15°，∵OD＝OC，∴∠DCO＝∠ODC＝30°，∴∠FGD＝45°+30°＝75°，∵FD＝FG，∴∠FDG＝∠FGD＝75°，∴∠ODF＝∠ODN+∠FDG＝15°+75°＝90°，∴DF是⊙O的切线；（2）解：∵∠EDB＝30°，∴∠EOB＝60°，Rt△CDE中，∠DEC＝60°，∴∠DEC＝∠EOB＝60°，∴DE∥AB，∴S△DOE ＝S△ODE，∴S阴影＝S扇形ODE＝＝；答：线段DB，BE与劣弧DE所围成的阴影部分的面积是，9．（1）证明：∵AD平分∠BAC，BE平分∠ABD，∴∠1＝∠2，∠3＝∠4，∴∠BED＝∠1+∠3＝∠2+∠4＝∠5+∠4＝∠DBE，∴DB＝DE；（2）解：连接CD，如图，∵∠BAC＝90°，∴BC为直径，∴∠BDC＝90°，∵∠1＝∠2，∴DB＝BC，∴△DBC为等腰直角三角形，∴BC＝BD＝4，∴△ABC外接圆的半径为2；（3）解：∵∠5＝∠2＝∠1，∠FDB＝∠BDA，∴△DBF∽△ADB，∴＝，即＝，∴AD＝9．10．解：（I）如图①，连接OB，∵BF为⊙O的切线，∴OB⊥BF，∴∠OBF＝90°，∵OA⊥CD，∴∠OED＝90°，∴∠AOB＝180°﹣∠F＝180°﹣50°＝130°，∵OA＝OB，∴∠1＝∠A＝（180°﹣130°）＝25°，∴∠2＝90°﹣∠1＝65°，∴∠BGF＝180°﹣∠2﹣∠F＝180°﹣65°﹣50°＝65°；（II）如图②，连接OB，BO的延长线交AC于H，∵BF为⊙O的切线，∴OB⊥BF，∵AC∥BF，∴BH⊥AC，与（Ⅰ）方法可得到∠AOB＝180°﹣∠F＝180°﹣36°＝144°，∵OA＝OB，∴∠OBA＝∠OAB＝（180°﹣144°）＝18°，∵∠AOB＝∠OHA+∠OAH，∴∠OAH＝144°﹣90°＝54°，∴∠BAC＝∠OAH+∠OAB＝54°+18°＝72°，∴∠BDG＝∠BAC＝72°．11．（1）证明：连接OB．∵CD⊥OA，∴∠ADE＝90°，∴∠DAE+∠AED＝90°，∵OA＝OB，∴∠A＝∠OBA，∵CE＝CB，∴∠CBE＝∠CEB＝∠AED，∴∠ABO+∠CBE＝90°，∴∠OBC＝90°，∴OB⊥BC．（2）解：连接OF．∵AD＝OD，FD⊥OA，∴FA＝FO＝AO，∴△AOF是等边三角形，∴∠AOF＝60°，∴∠ABF＝∠AOF＝30°．（3）解：延长AO交⊙O于H，连接BH．∵AH是直径，∴∠ABH＝∠ADE＝90°，∵∠DAE＝∠HAB，∴△DAE∽△BAH，∴＝，∴AE•AB＝AD•AH＝×6＝9．12．（1）证明：连结OD，∵∠ACB＝90°，∴∠OED+∠EGC＝90°，∵OD＝OE，∴∠ODE＝∠OED，∵AG＝AD，∴∠ADG＝∠AGD，∵∠AGD＝∠EGC，∴∠OED+∠EGC＝∠ADG+∠ODE＝∠ADO＝90°，∴OD⊥AB，∵OD为半径，∴AB是⊙O的切线；（2）解：连接OF，∵EF∥AB，AC：BC＝4：3，∴CF：CE＝4：3，又∵EF＝5，∴CF＝4，CE＝3，设半径＝r，则OF＝r，CF＝4，CO＝r﹣3．在Rt△OCF中，由勾股定理，可得r＝，∵EF∥AB，∴∠CEF＝∠B，∵∠ECF＝∠ODB＝90°，∴△CEF∽△DBO，∴＝，∴＝，∴BD＝．13．证明：（Ⅰ）连接OE，BD，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠CDB＝90°，∵E点是BC的中点，∴DE＝BC＝BE，∵OD＝OB，OE＝OE，∴△ODE≌△OBE，∴∠ODE＝∠OBE，∵∠ABC＝90°，∴∠ODE＝90°；（Ⅱ）∵CF＝OF，CE＝EB，∴FE是△COB的中位线，∴FE∥OB，∴∠AOD＝∠ODE，由（Ⅰ）得∠ODE＝90°，∴∠AOD＝90°，∵OA＝OD，∴∠A＝∠ADO＝．14．解：（1）如图，连接OC，∵AC平分∠EAB，∴∠EAC＝∠BA C；又在圆中OA＝OC，∴∠ACO＝∠BAC，∴∠EAC＝∠ACO，∴OC∥AE，由AE⊥DC知OC⊥DC，∴DE是⊙O的切线．（2）∵∠D＝∠D，∠E＝∠OCD＝90°，∴△DCO∽△DEA，∴＝，∴＝，∴＝，∴BD＝2；∵Rt△EAC∽Rt△CAB，∴＝，∴＝∴AC2＝，由勾股定理得：BC＝＝．15．解：（1）如图1，∵AB是半圆O的直径，∴∠M＝90°，在Rt△AMB中，AB＝，∴AB＝10．∴OB＝5，∵OB＝ON，又∵∠NOB＝60°，∴△NOB是等边三角形，∴NB＝OB＝5．（2）结论：∠MCP+∠MBA+∠NAB＝90°．理由：方法一：如图2中，画⊙O，延长MC交⊙O于点Q，连接NQ，NB．∵MC⊥AB，又∵OM＝OQ，∴MC＝CQ，即C是MQ的中点，又∵P是MQ的中点，∴CP是△MQN的中位线，∴CP∥QN，∴∠MCP＝∠MQN，∵∠MQN＝∠MON，∠MBN＝∠MON，∴∠MQN＝∠MBN，∴∠MCP＝∠MBN，∵AB是直径，∴∠ANB＝90°，∴在△ANB中，∠NBA+∠NAB＝90°，∴∠MBN+∠MBA+∠NAB＝90°，即∠MCP+∠MBA+∠NAB＝90°．方法二：如图2﹣1中，连接MO，OP，NO，BN．∵P是MN中点，又∵OM＝ON，∴OP⊥MN，且∠MOP＝∠MON，∵MC⊥AB，∴∠MCO＝∠MPO＝90°，∴设OM的中点为Q，则QM＝QO＝QC＝QP，∴点C，P在以OM为直径的圆上，在该圆中，∠MCP＝∠MOP＝∠MQP，又∵∠MOP＝∠MON，∴∠MCP＝∠MON，在半圆O中，∠NBM＝∠MON，∴∠MCP＝∠NBM，∵AB是直径，∴∠ANB＝90°，∴在△ANB中，∠NBA+∠NAB＝90°，∴∠NBM+∠MBA+∠NAB＝90°，即∠MCP+∠MBA+∠NAB＝90°．。

备战中考数学压轴题之圆的综合(备战中考题型整理,突破提升)含答案解析

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，已知△ABC内接于⊙O，AB是⊙O的直径，点F在⊙O上，且点C是的中点，过点C作⊙O的切线交AB的延长线于点D，交AF的延长线于点E．（1）求证：AE⊥DE；（2）若∠BAF=60°，AF=4，求CE的长．【答案】（1）证明见解析；（2）【解析】试题分析：（1）首先连接OC，由OC=OA，，易证得OC∥AE，又由DE切⊙O于点C，易证得AE⊥DE；（2）由AB是⊙O的直径，可得△ABC是直角三角形，易得△AEC为直角三角形，根据AE=3求得AC的长，然后连接OF，可得△OAF为等边三角形，知AF=OA=AB，在△ACB 中，利用已知条件求得答案．试题解析：（1）证明：连接OC，∵OC=OA，∴∠BAC=∠OCA，∵∴∠BAC=∠EAC，∴∠EAC=∠OCA，∴OC∥AE，∵DE切⊙O于点C，∴OC⊥DE，∴AE⊥DE；（2）解：∵AB是⊙O的直径，∴△ABC是直角三角形，∵∠CBA=60°，∴∠BAC=∠EAC=30°，∵△AEC为直角三角形，AE=3，∴AC=2，连接OF，∵OF=OA，∠OAF=∠BAC+∠EAC=60°，∴△OAF为等边三角形，∴AF=OA=AB，在Rt△ACB中，AC=2，tan∠CBA=，∴BC=2，∴AB=4，∴AF=2．考点：切线的性质．2．如图1，将长为10的线段OA绕点O旋转90°得到OB，点A的运动轨迹为AB，P是半径OB上一动点，Q是AB上的一动点，连接PQ.发现：∠POQ＝________时，PQ有最大值，最大值为________；思考：（1）如图2，若P是OB中点，且QP⊥OB于点P，求BQ的长；（2）如图3，将扇形AOB沿折痕AP折叠，使点B的对应点B′恰好落在OA的延长线上，求阴影部分面积；探究：如图4，将扇形OAB沿PQ折叠，使折叠后的弧QB′恰好与半径OA相切，切点为C，若OP＝6，求点O到折痕PQ的距离．【答案】发现： 90°，2；思考：（1）103π=；（2）2+100；（3）点O到折痕PQ30【解析】分析：发现：先判断出当PQ取最大时，点Q与点A重合，点P与点B重合，即可得出结论；思考：（1）先判断出∠POQ=60°，最后用弧长用弧长公式即可得出结论；（2）先在Rt△B'OP中，OP22−10)2=（10-OP）2，解得2−10，最后用面积的和差即可得出结论．探究：先找点O 关于PQ 的对称点O′，连接OO′、O′B 、O′C 、O′P ，证明四边形OCO′B 是矩形，由勾股定理求O′B ，从而求出OO′的长，则OM=12OO′=30．详解：发现：∵P 是半径OB 上一动点，Q 是AB 上的一动点，∴当PQ 取最大时，点Q 与点A 重合，点P 与点B 重合，此时，∠POQ=90°，PQ=22OA OB +=102；思考：（1）如图，连接OQ ，∵点P 是OB 的中点，∴OP=12OB=12OQ ． ∵QP ⊥OB ，∴∠OPQ=90° 在Rt △OPQ 中，cos ∠QOP=12OP OQ =， ∴∠QOP=60°，∴l BQ =6010101803ππ⨯=；（2）由折叠的性质可得，BP ＝B ′P ，AB ′＝AB ＝102，在Rt △B'OP 中，OP 2+(102−10)2=（10-OP ）2解得OP=102−10，S 阴影=S 扇形AOB -2S △AOP =290101210(10210)3602π⨯-⨯⨯⨯- ＝25π−1002+100；探究：如图2，找点O 关于PQ 的对称点O′，连接OO′、O′B 、O′C 、O′P ，则OM=O′M ，OO′⊥PQ ，O′P=OP=3，点O′是B Q '所在圆的圆心，∴O′C=OB=10，∵折叠后的弧QB′恰好与半径OA 相切于C 点，∴O′C ⊥AO ，∴O′C ∥OB ，∴四边形OCO′B 是矩形，在Rt △O′BP 中，O′B=226425-=，在Rt △OBO′K ，OO′=2210(25)=230-，∴OM=12OO′=12×230=30，即O 到折痕PQ 的距离为30．点睛：本题考查了折叠问题和圆的切线的性质、矩形的性质和判定，熟练掌握弧长公式l=180n R π（n 为圆心角度数，R 为圆半径），明确过圆的切线垂直于过切点的半径，这是常考的性质；对称点的连线被对称轴垂直平分．3．如图，△ABC 的内接三角形，P 为BC 延长线上一点，∠PAC=∠B ，AD 为⊙O 的直径，过C 作CG ⊥AD 于E ，交AB 于F ，交⊙O 于G ．（1）判断直线PA 与⊙O 的位置关系，并说明理由；（2）求证：AG 2=AF·AB ；（3）若⊙O 的直径为10，AC=25，AB=45，求△AFG 的面积.【答案】（1）PA 与⊙O 相切，理由见解析；（2）证明见解析；（3）3.【解析】试题分析：（1）连接CD ，由AD 为⊙O 的直径，可得∠ACD=90°，由圆周角定理，证得∠B=∠D ，由已知∠PAC=∠B ，可证得DA ⊥PA ，继而可证得PA 与⊙O 相切．（2）连接BG ，易证得△AFG ∽△AGB ，由相似三角形的对应边成比例，证得结论.（3）连接BD ，由AG 2=AF•AB ，可求得AF 的长，易证得△AEF ∽△ABD ，即可求得AE 的长，继而可求得EF 与EG 的长，则可求得答案．试题解析：解：（1）PA 与⊙O 相切．理由如下：如答图1，连接CD ，∵AD 为⊙O 的直径，∴∠ACD=90°.∴∠D+∠CAD=90°.∵∠B=∠D ，∠PAC=∠B ，∴∠PAC=∠D.∴∠PAC+∠CAD=90°，即DA ⊥PA.∵点A 在圆上，∴PA 与⊙O 相切．（2）证明：如答图2，连接BG ，∵AD 为⊙O 的直径，CG ⊥AD ，∴AC AD =.∴∠AGF=∠ABG.∵∠GAF=∠BAG ，∴△AGF ∽△ABG.∴AG ：AB=AF ：AG. ∴AG 2=AF•AB.（3）如答图3，连接BD ，∵AD 是直径，∴∠ABD=90°.∵AG 2=AF•AB ，55∴5∵CG ⊥AD ，∴∠AEF=∠ABD=90°.∵∠EAF=∠BAD ，∴△AEF ∽△ABD. ∴AE AF AB AD =545=，解得：AE=2. ∴221EF AF AE =-=. ∵224EG AG AE =-=，∴413FG EG EF =-=-=.∴1132322AFG S FG AE ∆=⋅⋅=⨯⨯=．考点：1. 圆周角定理；2.直角三角形两锐角的关系；3. 相切的判定；4.垂径定理；5.相似三角形的判定和性质；6.勾股定理；7.三角形的面积.4．如图，在⊙O 中，直径AB ⊥弦CD 于点E ，连接AC ，BC ，点F 是BA 延长线上的一点，且∠FCA ＝∠B .(1)求证：CF 是⊙O 的切线；(2)若AE ＝4，tan ∠ACD ＝33，求FC 的长．【答案】（1）见解析【解析】分析：（1）利用圆周角定理以及等腰三角形的性质得出∠OCF=90°，进而得出答案；（2）根据正切的性质求出EC 的长，然后利用垂径定理求出圆的半径，再根据等边三角形的性质，利用勾股定理求出即可．详解：(1)证明：连接OC.∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴∠OCB ＋∠ACO ＝90°.∵OB ＝OC ，∴∠B ＝∠OCB.又∵∠FCA ＝∠B ，∴∠FCA ＝∠OCB ，∴∠FCA ＋∠ACO ＝90°，即∠FCO ＝90°，∴FC ⊥OC ，∴FC 是⊙O 切线．(2)解：∵AB⊥CD，∴∠AEC＝90°，∴EC=AE43 tan ACE33∠==，设OA＝OC＝r，则OE＝OA－AE＝r－4.在Rt△OEC中，OC2＝OE2＋CE2，即r2＝(r－4)2＋(43)2，解得r＝8.∴OE＝r－4＝4＝AE.∵CE⊥OA，∴CA＝CO＝8，∴△AOC是等边三角形，∴∠FOC＝60°，∴∠F＝30°.在Rt△FOC中，∵∠OCF＝90°，OC＝8，∠F＝30°，∴OF＝2OC＝16，∴FC＝22OF OC83-=.点睛：此题主要考查了切线的判定、垂径定理的推论以及勾股定理等知识，得出BC的长是解题关键．5．函数是描述客观世界运动变化的重要模型，理解函数的本质是重要的任务。

人教版数学九年级上册第二十四章《圆》压轴题综合培优训练(含答案)

《圆》压轴题综合培优训练1．如图，以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D，过点D作⊙O的切线与BC 交于点E，弦DM与AB垂直，垂足为H．（1）求证：E为BC的中点；（2）若⊙O的面积为12π，两个三角形△AHD和△BMH的外接圆面积之比为3，求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比．2．如图，在△ABC中，CA＝CB，E是边BC上一点，以AE为直径的⊙O经过点C，并交AB 于点D，连结ED．（1）判断△BDE的形状并证明．（2）连结CO并延长交AB于点F，若BE＝CE＝3，求AF的长．3．如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．（1）求证：AD平分∠BAC；（2）若∠BAC＝60°，OA＝2，求阴影部分的面积（结果保留π）．4．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD 的延长线于点E．（1）求证：∠BDC＝∠A；（2）若CE＝2，DE＝2，求AD的长．（3）在（2）的条件下，求弧BD的长．5．如图，在△ABC中，AB＝AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．（1）求证：DE是⊙O的切线；（2）当⊙O半径为3，CE＝2时，求BD长．6．如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF＝DA，AE∥BC交CF于E．（1）求证：EA是⊙O的切线；（2）求证：BD＝CF．7．如图，AH是圆O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．（1）求证：直线FG是⊙O的切线；（2）若AD＝8，EB＝5，求⊙O的直径．8．如图，AB是⊙O的直径，弦CD垂直平分OA，垂足为点M，连接并延长CO交⊙O于点E，分别连接DE，BE，DB，其中∠EDB＝30°，∠CDE的平分线DN交CE于点G，交⊙O于点N，延长CE至点F，使FG＝FD．（1）求证：DF是⊙O的切线；（2）若⊙O半径r为8，求线段DB，BE与劣弧DE所围成的阴影部分的面积．9．如图，∠BAC的平分线交△ABC的外接圆于点D，交BC于点F，∠ABC的平分线交AD于点E．（1）求证：DE＝DB：（2）若∠BAC＝90°，BD＝4，求△ABC外接圆的半径；（3）若BD＝6，DF＝4，求AD的长10．在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，过点B作⊙O的切线BF交CD的延长线于点F．（I）如图①，若∠F＝50°，求∠BGF的大小；（II）如图②，连接BD，AC，若∠F＝36°，AC∥BF，求∠BDG的大小．11．如图，AB是圆O的弦，D为半径OA的中点，过D作CD⊥OA交弦AB于点E，交圆O于点F，且CE＝CB．（1）求证：BC是⊙O的切线；（2）连接AF，BF，求∠ABF的度数；（3）如果OA＝3，求AE•AB的值．12．Rt△ABC中，∠ACB＝90°，AC：BC＝4：3，O是BC上一点，⊙O交AB于点D，交BC 延长线于点E．连接ED，交AC于点G，且AG＝AD．（1）求证：AB与⊙O相切；（2）设⊙O与AC的延长线交于点F，连接EF，若EF∥AB，且EF＝5，求BD的长．13．Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC边于点D，E是边BC的中点，连接DE，OD．（Ⅰ）如图①，求∠ODE的大小；（Ⅱ）如图②，连接OC交DE于点F，若OF＝CF，求∠A的大小．14．如图，已知圆O是△ABC的外接圆，AB是圆O的直径，C是圆上的一点，D是AB延长线上的一点，AE⊥CD交DC的延长线于点E，且AC平分∠EAB．（1）求证：DE是圆O的切线．（2）若AB＝6，AE＝4.8，求BD和BC的长．15．已知AB是半圆O的直径，M，N是半圆不与A，B重合的两点，且点N在弧BM上．（1）如图1，MA＝6，MB＝8，∠NOB＝60°，求NB的长；（2）如图2，过点M作MC⊥AB于点C，点P是MN的中点，连接MB、NA、PC，试探究∠MCP、∠NAB、∠MBA之间的数量关系，并证明．参考答案一．解答题1．解：（1）连接BD、OE，∵AB是直径，则∠ADB＝90°＝∠ADO+∠ODB，∵DE是切线，∴∠ODE＝90°＝∠EDB+∠BDO，∴∠EDB＝∠ADO＝∠CAB，∵∠ABC＝90°，即BC是圆的切线，∴∠DBC＝∠CAB，∴∠EDB＝∠EBD，则∠BDC＝90°，∴E为BC的中点；（2）△AHD和△BMH的外接圆面积之比为3，则两个三角形的外接圆的直径分别为AD、BM，∴AD：BM＝，而△ADH∽△MBH，∴DH：BH＝，则DH＝HM，∴HM：BH＝，∴∠BMH＝30°＝∠BAC，∴∠C＝60°，E是直角三角形的中线，∴DE＝CE，∴△DEC为等边三角形，⊙O 的面积：12π＝（AB ）2π，则AB ＝4，∠CAB ＝30°，∴BD ＝2，BC ＝4，AC ＝8，而OE ＝AC ＝4，四边形OBED 的外接圆面积S 2＝π（2）2＝4π，等边三角形△DEC 边长为2，则其内切圆的半径为：，面积为，故△DEC 的内切圆面积S 1和四边形OBED 的外接圆面积S 2的比为：． 2．（1）证明：△BDE 是等腰直角三角形．∵AE 是⊙O 的直径∴∠ACB ＝∠ADE ＝90°，∴∠BDE ＝180°﹣90°＝90°．∵CA ＝CB ，∴∠B ＝45°，∴△BDE 是等腰直角三角形．（2）过点F 作FG ⊥AC 于点G ，则△AFG 是等腰直角三角形，且AG ＝FG ．∵OA ＝OC ，∴∠EAC ＝∠FCG ．∵BE ＝CE ＝3，∴AC ＝BC ＝2CE ＝6，∴tan ∠FCG ＝tan ∠EAC ＝．∴CG ＝2FG ＝2AG ．∴FG ＝AG ＝2，∴AF ＝2． 3．【解答】（1）证明：∵⊙O 切BC 于D ，∴OD ⊥BC ，∵AC⊥BC，∴AC∥OD，∴∠CAD＝∠ADO，∵OA＝OD，∴∠OAD＝∠ADO，∴∠OAD＝∠CAD，即AD平分∠CAB；（2）设EO与AD交于点M，连接ED．∵∠BAC＝60°，OA＝OE，∴△AEO是等边三角形，∴AE＝OA，∠AOE＝60°，∴AE＝AO＝OD，又由（1）知，AC∥OD即AE∥OD，∴四边形AEDO是菱形，则△AEM≌△DMO，∠EOD＝60°，∴S△AEM ＝S△DMO，∴S阴影＝S扇形EOD＝＝π．4．（1）证明：连接OD，∵CD是⊙O切线，∴∠ODC＝90°，即∠ODB+∠BDC＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，即∠ODB+∠ADO＝90°，∴∠BDC＝∠ADO，∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A；（2）∵CE⊥AE，∴∠E＝∠ADB＝90°，∴DB∥EC，∴∠DCE＝∠BDC，∵∠BDC＝∠A，∴∠A＝∠DCE，∵∠E＝∠E，∴△AEC∽△CED，∴＝，∴EC2＝DE•AE，∴（2）2＝2（2+AD），∴AD＝4．（3）∵直角△CDE中，tan∠DCE＝＝＝，∴∠DCE＝30°，又∵△AEC∽△CED，∴∠A＝∠DCE＝30°，∴∠DOB＝2∠A＝60°，BD＝AD•tan A＝4×＝，∴△OBD是等边三角形，则OD＝BD＝，则弧BD的长是＝．5．（1）证明：连接OD，如图，∵AB为⊙0的直径，∴∠ADB＝90°，∴AD⊥BC，∵AB＝AC，∴AD平分BC，即DB＝DC，∵OA＝OB，∴OD为△ABC的中位线，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∴DE是⊙0的切线；（2）证明：∵∠B＝∠C，∠CED＝∠BDA＝90°，∴△DEC∽△ADB，∴，∴BD•CD＝AB•CE，∵BD＝CD，∴BD2＝AB•CE，∵⊙O半径为3，CE＝2，∴BD＝＝2．6．证明：（1）连接OA，∵⊙O是等边三角形ABC的外接圆，∴∠OAC＝30°，∠BCA＝60°，∵AE∥BC，∴∠EAC＝∠BCA＝60°，∴∠OAE＝∠OAC+∠EAC＝30°+60°＝90°，∴AE是⊙O的切线；（2）∵△ABC是等边三角形，∴AB＝AC，∠BAC＝∠ABC＝60°，∵A、B、C、D四点共圆，∴∠ADF＝∠ABC＝60°，∵AD＝DF，∴△ADF是等边三角形，∴AD＝AF，∠DAF＝60°，∴∠BAC+∠CAD＝∠DAF+∠CAD，即∠BAD＝∠CAF，在△BAD和△CAF中，∵，∴△BAD≌△CAF，∴BD＝CF．7．解：（1）如图1，连接OE，∵OA＝OE，∴∠EAO＝∠AEO，∵AE平分∠FAH，∴∠EAO＝∠FAE，∴∠FAE＝∠AEO，∴AF∥OE，∴∠AFE+∠OEF＝180°，∵AF⊥GF，∴∠AFE＝∠OEF＝90°，∴OE⊥GF，∵点E在圆上，OE是半径，∴GF是⊙O的切线．（2）设AB＝x，∵四边形ABCD是矩形，∴AB＝CD＝x，BC＝AD＝8，∴CE＝BC﹣BE＝3，∵AE是∠BAF的角平分线，BE⊥AB，EF⊥AF，∴EF＝BE＝5，在Rt△CEF中，根据勾股定理得，CF＝4，∴DF＝CD﹣CF＝x﹣4，在Rt△ABE和Rt△AFE中，，∴Rt△ABE≌Rt△AFE（HL），∴AF＝AB＝x，在Rt△ADF中，x2﹣（x﹣4）2＝64，∴x＝10，∴AB＝10，设⊙O的半径为r，∴OB＝10﹣r，在Rt△BOE中，r2﹣（10﹣r）2＝25，∴r＝，∴⊙O的直径为．8．（1）证明：连接OD，∵CD垂直平分OA，∴OM＝OA＝OD，∴∠ODC＝30°，∵CE为⊙O的直径，∴∠CDE＝90°，∵DN平分∠CDE，∴∠CDN＝45°，∴∠ODN＝45°﹣30°＝15°，∵OD＝OC，∴∠DCO＝∠ODC＝30°，∴∠FGD＝45°+30°＝75°，∵FD＝FG，∴∠FDG＝∠FGD＝75°，∴∠ODF＝∠ODN+∠FDG＝15°+75°＝90°，∴DF是⊙O的切线；（2）解：∵∠EDB＝30°，∴∠EOB＝60°，Rt△CDE中，∠DEC＝60°，∴∠DEC＝∠EOB＝60°，∴DE∥AB，∴S△DOE ＝S△ODE，∴S阴影＝S扇形ODE＝＝；答：线段DB，BE与劣弧DE所围成的阴影部分的面积是，9．（1）证明：∵AD平分∠BAC，BE平分∠ABD，∴∠1＝∠2，∠3＝∠4，∴∠BED＝∠1+∠3＝∠2+∠4＝∠5+∠4＝∠DBE，∴DB＝DE；（2）解：连接CD，如图，∵∠BAC＝90°，∴BC为直径，∴∠BDC＝90°，∵∠1＝∠2，∴DB＝BC，∴△DBC为等腰直角三角形，∴BC＝BD＝4，∴△ABC外接圆的半径为2；（3）解：∵∠5＝∠2＝∠1，∠FDB＝∠BDA，∴△DBF∽△ADB，∴＝，即＝，∴AD＝9．10．解：（I）如图①，连接OB，∵BF为⊙O的切线，∴OB⊥BF，∴∠OBF＝90°，∵OA⊥CD，∴∠OED＝90°，∴∠AOB＝180°﹣∠F＝180°﹣50°＝130°，∵OA＝OB，∴∠1＝∠A＝（180°﹣130°）＝25°，∴∠2＝90°﹣∠1＝65°，∴∠BGF＝180°﹣∠2﹣∠F＝180°﹣65°﹣50°＝65°；（II）如图②，连接OB，BO的延长线交AC于H，∵BF为⊙O的切线，∴OB⊥BF，∵AC∥BF，∴BH⊥AC，与（Ⅰ）方法可得到∠AOB＝180°﹣∠F＝180°﹣36°＝144°，∵OA＝OB，∴∠OBA＝∠OAB＝（180°﹣144°）＝18°，∵∠AOB＝∠OHA+∠OAH，∴∠OAH＝144°﹣90°＝54°，∴∠BAC＝∠OAH+∠OAB＝54°+18°＝72°，∴∠BDG＝∠BAC＝72°．11．（1）证明：连接OB．∵CD⊥OA，∴∠ADE＝90°，∴∠DAE+∠AED＝90°，∵OA＝OB，∴∠A＝∠OBA，∵CE＝CB，∴∠CBE＝∠CEB＝∠AED，∴∠ABO+∠CBE＝90°，∴∠OBC＝90°，∴OB⊥BC．（2）解：连接OF．∵AD＝OD，FD⊥OA，∴FA＝FO＝AO，∴△AOF是等边三角形，∴∠AOF＝60°，∴∠ABF＝∠AOF＝30°．（3）解：延长AO交⊙O于H，连接BH．∵AH是直径，∴∠ABH＝∠ADE＝90°，∵∠DAE＝∠HAB，∴△DAE∽△BAH，∴＝，∴AE•AB＝AD•AH＝×6＝9．12．（1）证明：连结OD，∵∠ACB＝90°，∴∠OED+∠EGC＝90°，∵OD＝OE，∴∠ODE＝∠OED，∵AG＝AD，∴∠ADG＝∠AGD，∵∠AGD＝∠EGC，∴∠OED+∠EGC＝∠ADG+∠ODE＝∠ADO＝90°，∴OD⊥AB，∵OD为半径，∴AB是⊙O的切线；（2）解：连接OF，∵EF∥AB，AC：BC＝4：3，∴CF：CE＝4：3，又∵EF＝5，∴CF＝4，CE＝3，设半径＝r，则OF＝r，CF＝4，CO＝r﹣3．在Rt△OCF中，由勾股定理，可得r＝，∵EF∥AB，∴∠CEF＝∠B，∵∠ECF＝∠ODB＝90°，∴△CEF∽△DBO，∴＝，∴＝，∴BD＝．13．证明：（Ⅰ）连接OE，BD，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠CDB＝90°，∵E点是BC的中点，∴DE＝BC＝BE，∵OD＝OB，OE＝OE，∴△ODE≌△OBE，∴∠ODE＝∠OBE，∵∠ABC＝90°，∴∠ODE＝90°；（Ⅱ）∵CF＝OF，CE＝EB，∴FE是△COB的中位线，∴FE∥OB，∴∠AOD＝∠ODE，由（Ⅰ）得∠ODE＝90°，∴∠AOD＝90°，∵OA＝OD，∴∠A＝∠ADO＝．14．解：（1）如图，连接OC，∵AC平分∠EAB，∴∠EAC＝∠BA C；又在圆中OA＝OC，∴∠ACO＝∠BAC，∴∠EAC＝∠ACO，∴OC∥AE，由AE⊥DC知OC⊥DC，∴DE是⊙O的切线．（2）∵∠D＝∠D，∠E＝∠OCD＝90°，∴△DCO∽△DEA，∴＝，∴＝，∴＝，∴BD＝2；∵Rt△EAC∽Rt△CAB，∴＝，∴＝∴AC2＝，由勾股定理得：BC＝＝．15．解：（1）如图1，∵AB是半圆O的直径，∴∠M＝90°，在Rt△AMB中，AB＝，∴AB＝10．∴OB＝5，∵OB＝ON，又∵∠NOB＝60°，∴△NOB是等边三角形，∴NB＝OB＝5．（2）结论：∠MCP+∠MBA+∠NAB＝90°．理由：方法一：如图2中，画⊙O，延长MC交⊙O于点Q，连接NQ，NB．∵MC⊥AB，又∵OM＝OQ，∴MC＝CQ，即C是MQ的中点，又∵P是MQ的中点，∴CP是△MQN的中位线，∴CP∥QN，∴∠MCP＝∠MQN，∵∠MQN＝∠MON，∠MBN＝∠MON，∴∠MQN＝∠MBN，∴∠MCP＝∠MBN，∵AB是直径，∴∠ANB＝90°，∴在△ANB中，∠NBA+∠NAB＝90°，∴∠MBN+∠MBA+∠NAB＝90°，即∠MCP+∠MBA+∠NAB＝90°．方法二：如图2﹣1中，连接MO，OP，NO，BN．∵P是MN中点，又∵OM＝ON，∴OP⊥MN，且∠MOP＝∠MON，∵MC⊥AB，∴∠MCO＝∠MPO＝90°，∴设OM的中点为Q，则QM＝QO＝QC＝QP，∴点C，P在以OM为直径的圆上，在该圆中，∠MCP＝∠MOP＝∠MQP，又∵∠MOP＝∠MON，∴∠MCP＝∠MON，在半圆O中，∠NBM＝∠MON，∴∠MCP＝∠NBM，∵AB是直径，∴∠ANB＝90°，∴在△ANB中，∠NBA+∠NAB＝90°，∴∠NBM+∠MBA+∠NAB＝90°，即∠MCP+∠MBA+∠NAB＝90°．。

2020-2021中考数学压轴题之圆的综合(中考题型整理,突破提升)含答案

2020-2021中考数学压轴题之圆的综合(中考题型整理,突破提升)含答案一、圆的综合1．如图，在⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，在AB的延长线上有点E，且EF=ED．（1）求证：DE是⊙O的切线；（2）若tan A=12，探究线段AB和BE之间的数量关系，并证明；（3）在（2）的条件下，若OF=1，求圆O的半径．【答案】（1）答案见解析；（2）AB=3BE；（3）3．【解析】试题分析：（1）先判断出∠OCF+∠CFO=90°，再判断出∠OCF=∠ODF，即可得出结论；（2）先判断出∠BDE=∠A，进而得出△EBD∽△EDA，得出AE=2DE，DE=2BE，即可得出结论；（3）设BE=x，则DE=EF=2x，AB=3x，半径OD=32x，进而得出OE=1+2x，最后用勾股定理即可得出结论．试题解析：（1）证明：连结OD，如图．∵EF=ED，∴∠EFD=∠EDF．∵∠EFD=∠CFO，∴∠CFO=∠EDF．∵OC⊥OF，∴∠OCF+∠CFO=90°．∵OC=OD，∴∠OCF=∠ODF，∴∠ODC+∠EDF=90°，即∠ODE=90°，∴OD⊥DE．∵点D在⊙O上，∴DE是⊙O的切线；（2）线段AB、BE之间的数量关系为：AB=3BE．证明如下：∵AB为⊙O直径，∴∠ADB=90°，∴∠ADO=∠BDE．∵OA=OD，∴∠ADO=∠A，∴∠BDE=∠A，而∠BED=∠DEA，∴△EBD∽△EDA，∴DE BE BDAE DE AD==．∵Rt△ABD中，tan A=BDAD=12，∴DE BEAE DE==12，∴AE=2DE，DE=2BE，∴AE=4BE，∴AB=3BE；（3）设BE=x，则DE=EF=2x，AB=3x，半径OD=32x．∵OF=1，∴OE=1+2x．在Rt△ODE中，由勾股定理可得：（32x）2+（2x）2=（1+2x）2，∴x=﹣29（舍）或x=2，∴圆O的半径为3．点睛：本题是圆的综合题，主要考查了切线的判定和性质，等腰三角形的性质，锐角三角函数，相似三角形的判定和性质，勾股定理，判断出△EBD∽△EDA是解答本题的关键．2．如图，A、B两点的坐标分别为（0，6），（0，3），点P为x轴正半轴上一动点，过点A作AP的垂线，过点B作BP的垂线，两垂线交于点Q，连接PQ，M为线段PQ的中点．（1）求证：A、B、P、Q四点在以M为圆心的同一个圆上；（2）当⊙M与x轴相切时，求点Q的坐标；（3）当点P从点（2，0）运动到点（3，0）时，请直接写出线段QM扫过图形的面积．【答案】(1)见解析;(2) Q的坐标为（32，9）;(3)63 8.【解析】（1）解：连接AM、BM，∵AQ⊥AP，BQ⊥BP∵△APQ和△BPQ都是直角三角形，M是斜边PQ的中点∴AM＝BM＝PM=QM= 12 PQ，∴A、B、P、Q四点在以M为圆心的同一个圆上。

人教中考数学(圆的综合提高练习题)压轴题训练附答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙O是△ABC的外接圆，点E为△ABC内切圆的圆心，连接AE的延长线交BC于点F，交⊙O于点D；连接BD，过点D作直线DM，使∠BDM=∠DAC．（1）求证：直线DM是⊙O的切线；（2）若DF=2，且AF=4，求BD和DE的长．【答案】（1）证明见解析（2）23【解析】【分析】（1）根据垂径定理的推论即可得到OD⊥BC，再根据∠BDM=∠DBC，即可判定BC∥DM，进而得到OD⊥DM，据此可得直线DM是⊙O的切线；（2）根据三角形内心的定义以及圆周角定理，得到∠BED=∠EBD，即可得出DB=DE，再判定△DBF∽△DAB，即可得到DB2=DF•DA，据此解答即可．【详解】（1）如图所示，连接OD．∵点E是△ABC的内心，∴∠BAD=∠CAD，∴BD CD=，∴OD⊥BC．又∵∠BDM=∠DAC，∠DAC=∠DBC，∴∠BDM=∠DBC，∴BC∥DM，∴OD⊥DM．又∵OD为⊙O半径，∴直线DM是⊙O的切线．（2）连接BE．∵E为内心，∴∠ABE=∠CBE．∵∠BAD=∠CAD，∠DBC=∠CAD，∴∠BAD=∠DBC，∴∠BAE+∠ABE=∠CBE+∠DBC，即∠BED=∠DBE，∴BD=DE．又∵∠BDF=∠ADB（公共角），∴△DBF∽△DAB，∴DF DBDB DA=，即DB2=DF•DA．∵DF=2，AF=4，∴DA=DF+AF=6，∴DB2=DF•DA=12，∴DB=DE=23．【点睛】本题主要考查了三角形的内心与外心，圆周角定理以及垂径定理的综合应用，解题时注意：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．2．已知：如图，在矩形ABCD 中，点O 在对角线BD 上，以OD 的长为半径的⊙O 与AD ，BD 分别交于点E 、点F ，且∠ABE=∠DBC ．（1）判断直线BE 与⊙O 的位置关系，并证明你的结论；（2）若sin ∠ABE=33，CD=2，求⊙O 的半径．【答案】（1）直线BE 与⊙O 相切，证明见解析；（2）⊙O 的半径为3．【解析】分析：（1）连接OE ，根据矩形的性质，可证∠BEO =90°，即可得出直线BE 与⊙O 相切；（2）连接EF ，先根据已知条件得出BD 的值，再在△BEO 中，利用勾股定理推知BE 的长，设出⊙O 的半径为r ，利用切线的性质，用勾股定理列出等式解之即可得出r 的值．详解：（1）直线BE 与⊙O 相切．理由如下：连接OE ，在矩形ABCD 中，AD ∥BC ，∴∠ADB =∠DBC ． ∵OD =OE ，∴∠OED =∠ODE ．又∵∠ABE =∠DBC ，∴∠ABE =∠OED ， ∵矩形ABDC ，∠A =90°，∴∠ABE +∠AEB =90°，∴∠OED +∠AEB =90°，∴∠BEO =90°，∴直线BE 与⊙O 相切；（2）连接EF ，方法1：∵四边形ABCD 是矩形，CD =2，∴∠A =∠C =90°，AB =CD =2． ∵∠ABE =∠DBC ，∴sin ∠CBD =3sin ABE ∠= ∴23DCBD sin CBD∠==在Rt △AEB 中，∵CD =2，∴22BC =．∵tan ∠CBD =tan ∠ABE ，∴2222DC AE AEAE BC AB ，，=∴=∴=，由勾股定理求得6BE =．在Rt △BEO 中，∠BEO =90°，EO 2+EB 2=OB 2．设⊙O 的半径为r ，则222623r r +=-（）（），∴r =3，方法2：∵DF 是⊙O 的直径，∴∠DEF =90°． ∵四边形ABCD 是矩形，∴∠A =∠C =90°，AB =CD =2． ∵∠ABE =∠DBC ，∴sin ∠CBD =33sin ABE ∠=．设3DC x BD x ==，，则2BC x =．∵CD =2，∴22BC =． ∵tan ∠CBD =tan ∠ABE ，∴2222DC AE AEAE BC AB ，，=∴=∴=， ∴E 为AD 中点．∵DF 为直径，∠FED =90°，∴EF ∥AB ，∴132DF BD ==，∴⊙O 的半径为3．点睛：本题综合考查了切线的性质、勾股定理以及三角函数的应用等知识点，具有较强的综合性，有一定的难度．3．已知：如图，△ABC 中，AC=3，∠ABC=30°．（1）尺规作图：求作△ABC 的外接圆，保留作图痕迹，不写作法；（2）求（1）中所求作的圆的面积．【答案】（1）作图见解析；（2）圆的面积是9π．【解析】试题分析：（1）按如下步骤作图：①作线段AB 的垂直平分线；②作线段BC 的垂直平分线；③以两条垂直平分线的交点O 为圆心，OA 长为半圆画圆，则圆O 即为所求作的圆．如图所示（2）要求外接圆的面积，需求出圆的半径，已知AC ＝3，如图弦AC 所对的圆周角是∠ABC=30°，所以圆心角∠AOC=60°，所以∆AOC是等边三角形，所以外接圆的半径是3故可求得外接圆的面积．（2）连接OA，OB．∵AC=3，∠ABC=30°，∴∠AOC=60°，∴△AOC是等边三角形，∴圆的半径是3，∴圆的面积是S=πr2=9π．4．如图，△ABC中，∠A=45°，D是AC边上一点，⊙O经过D、A、B三点，OD∥BC．（1）求证：BC与⊙O相切；（2）若OD=15，AE=7，求BE的长．【答案】(1)见解析;(2)18.【解析】分析：（1）连接OB，求出∠DOB度数，根据平行线性质求出∠CBO=90°，根据切线判定得出即可；（2）延长BO交⊙O于点F，连接AF，求出∠ABF，解直角三角形求出BE．详解：（1）证明：连接OB．∵∠A=45°，∴∠DOB=90°．∵OD∥BC，∴∠DOB+∠CBO=180°．∴∠CBO=90°．∴直线BC是⊙O的切线．（2）解：连接BD．则△ODB是等腰直角三角形，∴∠ODB=45°，BD=OD=15，∵∠ODB=∠A，∠DBE=∠DBA，∴△DBE∽△ABD，∴BD2=BE•BA，∴（15）2=（7+BE）BE，∴BE=18或﹣25（舍弃），∴BE=18．点睛：本题考查了切线的判定，圆周角定理，解直角三角形等知识点，能综合运用定理进行推理和计算是解此题的关键，题目综合性比较强，难度偏大．5．如图，已知AB为⊙O直径，D是BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．（1）求证：直线DE与⊙O相切；（2）已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．【答案】（1）证明见解析；（2）2．【解析】试题分析：（1）连接BC、OD，由D是弧BC的中点，可知：OD⊥BC；由OB为⊙O的直径，可得：BC⊥AC，根据DE⊥AC，可证OD⊥DE，从而可证DE是⊙O的切线；（2）直接利用勾股定理得出GO的长，再利用锐角三角函数关系得出tan∠F的值．试题解析：解：（1）证明：连接OD，BC，∵D是弧BC的中点，∴OD垂直平分BC，∵AB 为⊙O的直径，∴AC⊥BC，∴OD∥AE．∵DE⊥AC，∴OD⊥DE，∵OD为⊙O的半径，∴DE 是⊙O的切线；（2）解：∵D是弧BC的中点，∴DC DB，∴∠EAD=∠BAD，∵DE⊥AC，DG⊥AB且DE=4，∴DE=DG=4，∵DO=5，∴GO=3，∴AG=8，∴tan∠ADG=84=2，∵BF是⊙O的切线，∴∠ABF=90°，∴DG∥BF，∴tan∠F=tan∠ADG=2．点睛：此题主要考查了切线的判定与性质以及勾股定理等知识，正确得出AG，DG的长是解题关键．6．阅读：圆是最完美的图形，它具有一些特殊的性质：同弧或等弧所对的圆周角相等，一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”，再利用圆的性质将问题进行转化，往往能化隐为显、化难为易。

2024年中考数学压轴题型-专题03 与圆有关问题的压轴题之五大题型(解析版)

专题03与圆有关问题的压轴题之五大题型目录【题型一与圆中三角形全等的有关问题】 (1)【题型二与圆中三角形相似问题的有关问题】 (5)【题型三与圆中证明直线是切线的有关问题】 (29)【题型四与圆中求弧长、扇形面积的有关问题】 (40)【题型五与圆中求函数表达式的有关问题】 (50)【题型一与圆中三角形全等的有关问题】【变式训练】(1)求证：CD BF =．(2)若14BE BF ==，，求GE 的长．(3)连结GO OF ，，如图2，求证：122+EOG AOF ∠∠=【答案】(1)见解析(2)的长为3，由（1）得： CFBD =，FBC BCD ∴∠=∠，BG CG ∴=，AB 为O 的直径，CD 12DE CE CD ∴===，，AF AF =，12AOF OBF ∴∠=∠，在OCG 和OBG △中，OC OB =⎧⎪【题型二与圆中三角形相似问题的有关问题】例题：（2023·浙江宁波·校考一模）如图，已知BC 是O 的直径，点D 为BC 延长线上的一点，点A 为圆上一点，且AB AD =，AC CD =．(1)求证：ACD BAD ∽ ；(2)求证：AD 是O 的切线．【答案】(1)见解析(2)见解析【分析】（1）根据等腰三角形的性质得到CAD B ∠=∠，由于D D ∠=∠，于是得到ACD BAD ∽ ；（2）连接OA ，根据等腰三角形的性质得到B OAB ∠=∠，得到OAB CAD ∠=∠，由BC 是O 的直径，得到90BAC ∠=︒，即可得到结论．【详解】（1）证明：（1）∵AB AD =，∴B D ∠=∠，∵AC CD =，∴CAD D ∠=∠，∴CAD B ∠=∠，∵D D ∠=∠，∴ACD BAD ∽ ；（2）连接OA ，∵OA OB =，∴B OAB ∠=∠，∴OAB CAD ∠=∠，∵BC 是O 的直径，∴90BAC ∠=︒，∴OA ⊥AD ，∴AD 是O 的切线．【点睛】本题考查了相似三角形的判定和性质，切线的判定，等腰三角形的性质，圆周角定理，正确的作出辅助线是解题的关键．【变式训练】(1)求证：BDE DCE △∽△．(2)若2,DE C =为BE 中点，求【答案】(1)见解析(2)3AC =【分析】（1）根据CD 平分∠BDE DCE △∽△；（2）由BDE DCE △∽△得BE DE 在由Rt DCE V 中，cos ACD ∠【详解】（1）∵CD 平分ACE ∠∴ACD DCE∠=∠∵AB DE ∥，（2）∵BDE DCE △∽△，∴BE DE DE CE=，∵点C 为BE 中点，设BC =则2a DE DE a=，∴22D E a ==，即1a =∵90ABC ∠=︒，∴90E ADC ∠=∠=︒在Rt DCE V 中，1CE CD =，∴cos cos ACD DCE ∠=∠=∴3AC =．【点睛】此题主要考查了相似三角形的判定和性质，三角形的外接圆等，解答此题的关键是熟练掌握相似三角形的判定方法，理解相似三角形的对应边成比例，难点是正确的作出辅助线．2．（2023·浙江杭州·杭州市公益中学校考三模）如图，AC ，BD 交于点E ，P 为DB(1)求证：ABE DBA∽；的切线；(2)求证：PA是O(3)若E为BD的中点，求tan 【答案】(1)见解析(2)见解析(3)2(1)求B D ∠-∠的值．(2)当75B ∠=︒时，求(3)若BC CE =，DOE 【答案】(1)45︒∵AB是O的直径，半径∴OAD ODA∠=∠=∵ AC AC=，∴ABC ADC∠=∠，（3）解：如图所示，连接∵ BDBD =，∴12BCD BOD =∠∠∵BC CE =，∴B CEB ∠=∠67.5=(1)求BGC ∠的度数．(2)①求证：AF BC =．②若AG DF =，求tan GBC ∠的值，(3)如图2，当点O 恰好在BG 上且1OG =时，求AC 的长．【答案】(1)90︒(2)①证明见解析；②15tan 5GBC ∠=；(3)3172+∵OB OC =，∴CBE OBC OCB ∠=∠=∠，∴OC BE ∥，∵BD CD =，BDE CDN ∠=∠∴EBD NCD ≌，∴BE CN =，DB DG = ，DBG DGB ∠=∠∴．又,DBG CAG BGD ∠=∠∠=∠ CAG AGM ∴∠=∠，MA MG ∴=．OB OC = ，OBC OCB ∴∠=∠，(1)求ACB ∠的大小（用α，β表示）；(2)连接CF ，交AB 于H （如图2）．若45β=︒，且BC EF AE CF ⨯=⨯．求证：(3)在（2）的条件下，取CH 中点M ，连接OM 、GM （如图3），若OGM ∠①求证：GM BC ∥，12GM BC =；②OM∵AF AG =，∴AFG AGF ∠∠==∴ACF AGF ∠∠==∵FAB ∠β=，∴ACB ACF ∠=∠+∠∵AF AG =，45β=︒，∴AFG G ACH ∠=∠=∠∵EAF FAC ∠=∠，∴EAF FAC ∽，∴EF AE CF FA=，∴AE CF EF FA ⨯=⨯，∵BC EF AE CF ⨯=⨯，∴BC EF EF AF ⨯=⨯，∴BC AF =，∴ AF BC=，∴45BAC AGF ∠=∠=︒，∴180454590AHC ∠=︒-︒-︒=︒，∴2AHC BAC ∠=∠；（3）①证明：如图3中，连接CG ，延长GM 交AB 于点I ．∵245OGM α∠=-︒，45AGF ∠=︒，∴2AGM α∠=，∵45AFG G ACH ∠=∠=∠=︒，∴90FAG ∠=︒，∴FG 是直径，∴90FCG ∠=︒，∵90AHC ∠=︒，∴180AHC GCH ∠+∠=︒，∴AB CG ∥，∴MHI MCG ∠=∠，∵MH MC =，HMI CMG ∠∠=，∴ASA MHI MCG ≌（），∴MI MG =，HI CG =，MGC HIM ∠=∠，∵90FAG ∠=︒，∴90FAG BAF BAG BAG α∠=∠+∠=+∠=︒，在AIG V 中，180AGM BAG HIM ∠+∠+∠=︒，∴2180BAG HIM α+∠+∠=︒即()22BAG HIM BAG αα+∠+∠=+∠，∴HIM BAG ∠=∠，又45BAC ∠=︒，【点睛】本题属于圆综合题，考查了圆周角定理，相似三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是正确寻找相似三角形或全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．6．（2023·浙江·统考中考真题）如图，在径CE 交AB 于点F ，连结(1)求证：AD HC ∥；(2)若2OG GC=，求tan FAG ∠的值；(3)连结BC 交AD 于点N ，若O ①若52OF =，求BC 的长；②若10AH =，求ANB 的周长；∠=∠．∴BAD CAD∴52CF =．∴54CG FG ==，∴154OG =，∴22574AG OA OG =-=．∵CE AD ⊥，∴5272AD AG ==．∵ ==AC CDDB ，∴ AD CB=，∵,AD HC FG GC =∥，∴AH AF =．∵90HCF ∠=︒，∴10AC AH AF ===．设CG x =，则,5FG x OG ==-由勾股定理得222AG AO OG =-2225(5)10x x --=-，设CG x =，则,5FG x OG x ==-由勾股定理得222AG AO OG =-2222210AF AG FG x x x =+=-+∵,AD HC FG GC =∥，∴12AH AF HF ==，∴12AG HC =．(1)设E ∠为α，请用α表示BAC ∠的度数．(2)如图1，当BE AD ⊥时，①求证：DE BG =．②当3tan ,54ABE BG ∠==时，求半径的长．(3)如图2，当BE 过圆心O 时，若tan ABE k ∠=90 ABC ADC∴∠=∠=又AB AD=，AC=∴ABC ADC△≌△．∴12 BAC CAD∠=∠=∠E BADα∠=∠=，3tan 4ABE ∠=，BG =∴3tan 4FDE ∠=，DE 3EF FG ∴==，FD =8BF BG GF ∴=+=．AB AD = ，BAC ∠AC BD ∴⊥，【题型三与圆中证明直线是切线的有关问题】(1)求证：DE 为圆O 的切线；(2)连接OC 交DE 于点F ，若cos ABC ∠O为AB中点，D为BC中点，OD AC∴∥．DE AC⊥，DE OD∴⊥，且点D在O上，DE∴是O的切线；OD AC∥，∴OF OD FC EC=．AB为O的直径，90ADB ADC∴∠=∠=︒．又D为BC的中点，【变式训练】1．（2023·浙江台州·台州市书生中学统考一模）如图，直线AB 经过O 上的点M ，并且,OA OB MA MB ==，OA 交O 于点N ．(1)求证：直线AB 是O 的切线；(2)当ON AN =时，求AOB ∠的度数．【答案】(1)见解析(2)120AOB ∠=︒【分析】（1）连接OM ，根据等腰三角形的性质与判定推出OM AB ⊥，即可证明结论；（2）连接MN ，根据直角三角形的性质和圆的基本性质得出OMN 是等边三角形，从而得到60MON ∠=︒，即可求解．【详解】（1）连接OM ，∵OA OB =，∴OAB 是等腰三角形，∵MA MB =，∴OM AB ⊥，又点M 在O 上，∴直线AB 是O 的切线；（2）连接MN ，∵,OM AB ON AN ⊥=，∴MN AN ON ==，又OM ON =，∴OMN 是等边三角形，∴60MON ∠=︒，∴906030A B ==︒-︒=︒∠∠，∴120AOB ∠=︒．【点睛】本题考查了圆的性质，圆的切线证明，等腰三角形的性质与判定，等边三角形的性质与判定，直角三角形的性质等知识点，熟练掌握相关知识点是解题的关键．2．（2023·浙江金华·校联考模拟预测）如图，BC 是O 的直径，PB 是O 的切线，切点为B ，连接PO ，过点C 作AC PO 交O 于点A ，连接PA ．(1)求证：AP是O的切线；(2)若4cos5APO∠=，O的半径为∵OA OC=，∴OAC OCA∠=∠．∵O 的半径为3，∴3,6OA BC ==．∵POB POA △≌△，(1)求证：DG 是O 的切线．(2)已知3DG =，1EG =，求【答案】(1)见解析(2)O 的半径为5【分析】（1）连接OD ，根据（2）解：∵OD DG ⊥∴四边形ODGF 为矩形，∴3OF DG ==，OD 设O 的半径为r ，即∵1EG =，(1)求证：DC 为O 的切线；(2)若ACB ∠的角平分线CE 交线段AB 于点F ，交O 于点E ，连接BE ，求CF CE ⋅．OA OC，=∴∠=∠，OAC OCA ，DCB OAC ∠=∠∴∠=∠，OCA DCB 是直径，AB(1)求证：直线AB 是O 的切线；(2)若2BC OC =，①求tan ADB ∠的值；②作CAD ∠的平分线AP 交O 于点P 的代数式表示）．∴90OAC OAD ∠+∠=︒，又∵OA OD =，∴OAD ODA ∠=∠，∵BAC ADB ∠=∠，∴OAD BAC ∠=∠，∴90BAC OAC ∠+∠=°，即90BAO ∠=∴AB OA ⊥，又∵OA 为半径，∴直线AB 是O 的切线；（2）解：①解：∵BAC ADB ∠=∠，∴BCA BAD △∽△，∴AC BC AD BA=，2②在Rt CAD △中，22AC AD =，2AC +∴()()222222AC AC CD r +==解得233AC r =，263AD r =，∵AP 平分CAD ∠，∴CAP EAD ∠=∠，又∵APC ADE ∠=∠，∴CAP EAD △∽△，∴AC AP AE AD=，∴2423AE AP AC AD r ⋅=⋅=，∵22AB r k ==，∴24r k =，∴224212386AE AP k k ⋅=⋅=．【点睛】本题考查圆周角定理、切线的判定、等腰三角形的性质、相似三角形的判定与性质、勾股定理、角平分线的定义等知识，熟练掌握相关知识的联系与运用，会利用相似三角形的性质求解是解答的关键．【题型四与圆中求弧长、扇形面积的有关问题】(1)求证：BC BD =．(2)若,2OB OA AE ==．①求半圆O 的半径．②求图中阴影部分的面积．【变式训练】1．（2023·浙江绍兴·校联考三模）如图，已知，在ABC 中，4AB =，以AB 为直径作O ，交边BC 的中点D ．DE AC ⊥于点E ，连结AD ．(1)求证：DE 是O 的切线．(2)请你给ABC 添加一个条件，并求弧【答案】(1)证明过程见详解(2)添加条件为：60DAB ∠=︒（添加条件不唯一）【分析】（1）如图所示，连接OD 由此即可求证；（2）根据圆周角的性质，可求出∵点D 是BC 的中点，点O 是∴12BD BO BC BA ==，∴OD AC ∥，∴ADO DAE ∠=∠，∵DE AC ⊥，∴90ADE DAE ∠+∠=︒，∴90ADE ADO ∠+∠=︒，∴OD DE ⊥，点D 在O 上，∥；(1)求证：OD ACAB=，求阴影部分的面积．(2)若6【答案】(1)见解析393∵OA OC =，60A ∠=︒，∴AOC 是等边三角形，过点C 作CF AO ⊥，(1)证明： BDCE =；(2)若60A ∠=︒，2BC =，求阴影部分面积．【答案】(1)证明见解析∵AB AC =，∴A ABC CB =∠∠，∵BC 为O 的直径，∵AB AC =，60BAC ∠=︒，OB ∴ABC 为等边三角形，AO ∴60ABC ACB ∠=∠=︒，OB(1)求证:DE AB ⊥．(2)若3DE =，30C ∠=︒，求阴影部分面积．【答案】(1)见解析(2)332π23-∵AC 为直径，∴AD BC ⊥，∵AB AC =，(1)求证：ACD E∠=∠；(2)若3AC=，1AD=，求弧【答案】(1)见解析(2)π3∵直线AC与O相切于点C ∴OC CA⊥，∴190ACD︒∠+∠=，∵ED为直径，【题型五与圆中求函数表达式的有关问题】(1)求CD 的长；(2)如图2，当90PQD ∠=︒时，求PEC 的正切值；(3)如图1，设PE x DF y ==，．①求y 关于x 的函数解析式；②若20PF DQ ⨯=，求y 的值．【答案】(1)8(2)322x 73。

2023年中考真题与圆有关的压轴题汇编(附详解)

2023年中考真题与圆有关的压轴题汇编(附详解)1.(2023·安徽)已知四边形ABCD 内接于O ,对角线BD 是O 的直径．（1）如图1,连接,OA CA ,若OA BD ⊥,求证;CA 平分BCD ∠;（2）如图2,E 为O 内一点,满足,AE BC CE AB ⊥⊥,若33BD =,3AE =,求弦BC的长． 2.(2023·北京)如图,圆内接四边形ABCD 的对角线AC ,BD 交于点E ,BD 平分ABC ∠,BAC ADB ∠=∠．（1）求证DB 平分ADC ∠,并求BAD ∠的大小;（2）过点C 作CF AD ∥交AB 的延长线于点F ．若AC AD =,2BF =,求此圆半径的长．3.(2023·福建)如图,已知ABC ∆内接于,O CO 的延长线交AB 于点D ,交O 于点E ,交O 的切线AF 于点F ,且AF BC ∥．（1）求证：AO BE ∥;（2）求证：AO 平分BAC ∠．4.(2023·广东)综合探究如图1,在矩形ABCD 中()AB AD >,对角线AC BD ，相交于点O ,点A 关于BD 的对称点为A ',连接AA '交BD 于点E ,连接CA '．（1）求证：AA CA '⊥';（2）以点O 为圆心,OE 为半径作圆．①如图2,O 与CD 相切,求证：3AA CA '='; ①如图3,O 与CA '相切,1AD =,求O 的面积．5.(2023·广西) 如图,PO 平分APD ∠,PA 与O 相切于点A ,延长AO 交PD 于点C ,过点O 作OB PD ⊥,垂足为B ．（1）求证：PB 是O 的切线; （2）若O 的半径为4,5OC =,求PA 的长．6.(2023·贵州) 如图,已知O 是等边三角形ABC 的外接圆,连接CO 并延长交AB 于点D ,交O 于点E ,连接EA ,EB ．（1）写出图中一个度数为30︒的角：_______,图中与ΔACD 全等的三角形是_______; （2）求证：AED CEB ∽△△;（3）连接OA ,OB ,判断四边形OAEB 的形状,并说明理由．7.(2023·河北)如图,点18~P P 是O 的八等分点．若137PP P ,四边形3467P P P P 的周长分别为a ,b ,则下列正确的是( )A. a b <B. a b =C. a b >D. a ,b 大小无法比较8.(2023·河北)装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,50cm AB =,如图1和图2所示,MN 为水面截线,GH 为台面截线,MN GH ∥．计算：在图1中,已知48cm MN =,作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动,使水流出一部分,当30ANM ∠=︒时停止滚动,如图2．其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D ．探究：在图2中（2）操作后水面高度下降了多少？（3）连接OQ 并延长交GH 于点F ,求线段EF 与EQ 的长度,并比较大小．9.(2023·河南)如图,PA 与O 相切于点A ,PO 交O 于点B ,点C 在PA 上,且CB CA =．若5OA =,12PA =,则CA 的长为______．10.(2023·上海)在ABC ∆中7,3,90AB BC C ==∠=︒,点D 在边AC 上,点E 在CA 延长线上,且CD DE =,如果B 过点A ,E 过点D ,若B 与E 有公共点,那么E 半径r 的取值范围是________．11.(2023·上海)如图,在O 中,弦AB 的长为8,点C 在BO 延长线上,且41cos ,52ABC OC OB ∠==．（1）求O 的半径;（2）求BAC ∠的正切值．12.(2023·苏州)如图,AB 是半圆O 的直径,点,C D 在半圆上,CD DB =,连接,,OC CA OD ,过点B 作EB AB ⊥,交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ,若1223S S =,则tan ACO ∠的值为（）A.2 B. 223 C. 75 D. 32∆是O的内接三角形,AB是O的直径, 13.(2023·苏州)如图,ABC==,点F在AB上,连接CF并延长,交O于点D,连接BD,作AC BC5,25⊥,垂足为E．BE CD△∽△;（1）求证：DBE ABCAF=,求ED的长．（2）若214.(2023·天津)如图,在每个小正方形的边长为1的网格中,等边三角形ABC内接于圆,且顶点A,B均在格点上．（1）线段AB的长为________;（2）若点D在圆上,AB与CD相交于点P．请用无刻度．．．的直尺,在如图所示的网格中,画出∆为等边三角形,并简要说明点Q的位置是如何找到的（不要求证明）________．点Q,使CPQ15.(2023·天津)在O 中,半径OC 垂直于弦AB ,垂足为D ,60AOC ∠=︒,E 为弦AB 所对的优弧上一点．（1）如图①,求AOB ∠和CEB ∠的大小;（2）如图②,CE 与AB 相交于点F ,EF EB =,过点E 作O 的切线,与CO 的延长线相交于点G ,若3OA =,求EG 的长． 16.(2023·无锡)如图,AB 是O 的直径,CD 与AB 相交于点E ．过点D 的圆O 的切线DF AB ∥,交CA 的延长线于点F ,CF CD =．（1）求F ∠的度数;（2）若8DE DC ⋅=,求O 的半径．17.(2023·武汉)如图,,,OA OB OC 都是O 的半径,2ACB BAC ∠=∠．（1）求证：2AOB BOC ∠=∠;（2）若4,5AB BC ==,求O 的半径．18.(2023·杭州) 如图,在O 中,直径AB 垂直弦CD 于点E ,连接,,AC AD BC ,作CF AD ⊥于点F ,交线段OB 于点G （不与点,O B 重合）,连接OF ．（1）若1BE =,求GE 的长．（2）求证：2BC BG BO =⋅．（3）若FO FG =,猜想CAD ∠的度数,并证明你的结论．19.(2023·宜宾)如图,以AB 为直径的O 上有两点E ,F ,BE EF =,过点E 作直线CD AF ⊥交AF 的延长线于点D ,交AB 的延长线于点C ,过C 作CM 平分ACD ∠交AE 于点M ,交BE 于点N ．（1）求证：CD 是O 的切线;（2）求证：EM EN =;（3）如果N 是CM 的中点,且95AB =,求EN 的长．20.(2023·内江)如图,以线段AB 为直径作O ,交射线AC 于点C ,AD 平分CAB ∠交O 于点D ,过点D 作直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F ．连接BD 并延长交AC 的延长线于点M ．（1）求证：直线DE 是O 的切线;（2）当30F ∠=︒时,判断ABM 的形状,并说明理由;（3）在（2）的条件下,1ME =,连接BC 交AD 于点P ,求AP 的长．21.(2023·乐山)如图,在平面直角坐标系xOy 中,直线2y x =--与x 轴,y 轴分别交于A ,B 两点,C ,D 是半径为1的O 上两动点,且2CD =,P 为弦CD 的中点．当C ,D 两点在圆上运动时,PAB 面积的最大值是（）A. 8B. 6C. 4D. 322.(2023·乐山)如图,已知O 是Rt ABC △的外接圆,90ACB ∠=︒,D 是圆上一点,E 是DC 延长线上一点,连结AD AE ，,且AD AE CA CE ==，．（1）求证：直线AE 是O 是的切线; （2）若2sin 3E =,O 的半径为3,求AD 的长．23.(2023·广元) 如图,45ACB ∠=︒,半径为2的O 与角的两边相切,点P 是⊙O 上任意一点,过点P 向角的两边作垂线,垂足分别为E ,F ,设2t PE PF =+,则t 的取值范围是 _____．24.(2023·广元)如图,AB 为O 的直径,C 为O 上一点,连接AC BC ，,过点C 作O 的切线交AB 延长线于点D ,OF BC ⊥于点E ,交CD 于点F ．（1）求证：BCD BOE ∠=∠;（2）若3sin 5CAB ∠=,10AB =,求BD 的长．25.(2023·滨州) 如图,点E 是ABC ∆的内心,AE 的延长线与边BC 相交于点F ,与ABC ∆的外接圆相交于点D ．（1）求证：::ABF ACF S S AB AC =△△;（2）求证：::AB AC BF CF =;（3）求证：2AF AB AC BF CF =⋅-⋅;（4）猜想：线段,,DF DE DA 三者之间存在的等量关系．（直接写出,不需证明．）26.(2023·东营) 如图,在ABC 中,AB AC =,以AB 为直径的O 交BC 于点D ,DE AC ⊥,垂足为E ．（1）求证：DE 是O 的切线;（2）若30C ∠=︒,23CD =,求BD 的长．27.(2023·济宁) 如图,已知AB 是O 的直径,CD CB =,BE 切O 于点B ,过点C 作CF OE ⊥交BE 于点F ,若2EF BF =．（1）如图1,连接BD ,求证：ADB OBE △≌△;（2）如图2,N 是AD 上一点,在AB 上取一点M ,使60MCN ∠=︒,连接MN ．请问：三条线段MN BM DN ，，有怎样的数量关系？并证明你的结论．28.(2023·烟台)如图,在菱形ABCD 中,对角线,AC BD 相交于点,E O 经过,A D 两点,交对角线AC 于点F ,连接OF 交AD 于点G ,且AG GD =．（1）求证：AB 是O 的切线; （2）已知O 的半径与菱形的边长之比为5:8,求tan ADB ∠的值．29.(2023·临沂)如图,O 是ABC 的外接圆,BD 是O 的直径,,AB AC AE BC =∥,E 为BD 的延长线与AE 的交点．（1）求证：AE 是O 的切线;（2）若75,2ABC BC ∠=︒=,求CD 的长．30.(2023·聊城) 如图,在Rt ABC △中,90ACB ∠=︒,BAC ∠的平分线AD 交BC 于点D ,ADC ∠的平分线DE 交AC 于点E ．以AD 上的点O 为圆心,OD 为半径作O ,恰好过点E ．（1）求证：AC 是O 的切线;（2）若12CD =,3tan 4ABC ∠=,求O 的半径．2023年中考真题与圆有关的压轴题汇编详解1.(2023·安徽)已知四边形ABCD 内接于O ,对角线BD 是O 的直径．（1）如图1,连接,OA CA ,若OA BD ⊥,求证;CA 平分BCD ∠;（2）如图2,E 为O 内一点,满足,AE BC CE AB ⊥⊥,若33BD =,3AE =,求弦BC 的长．【答案】（1）见解析（2）32BC =【小问1详解】∵对角线BD 是O 的直径,OA BD ⊥ ∴AB AD =.∴BCA DCA ∠=∠.∴CA 平分BCD ∠．【小问2详解】∵对角线BD 是O 的直径.∴90BAD BCD ∠=∠=︒.∴,DC BC DA AB ⊥⊥∵,AE BC CE AB ⊥⊥.∴，，CE DA AE DC ////∴四边形AECD 平行四边形.∴DC AE =.∵33BD =,3AE =.∴33BD =,3DC =.∴BC ==2.(2023·北京)如图,圆内接四边形ABCD 的对角线AC ,BD 交于点E ,BD 平分ABC ∠,BAC ADB ∠=∠．（1）求证DB 平分ADC ∠,并求BAD ∠的大小;（2）过点C 作CF AD ∥交AB 的延长线于点F ．若AC AD =,2BF =,求此圆半径的长．【答案】（1）见解析,90BAD ∠=︒（2）4【小问1详解】解：①BAC ADB ∠=∠∴AB BC =.∴ADB CDB ∠=∠,即DB 平分ADC ∠．∵BD 平分ABC ∠.①ABD CBD ∠=∠.①AD CD =.①AB AD BC CD +=+,即BAD BCD =.①BD 是直径.①90BAD ∠=︒;【小问2详解】解：∵90BAD ∠=︒,CF AD ∥.①180F BAD ∠+∠=︒,则90F ∠=︒．①AD CD =.①AD DC =．①AC AD =.∴AC AD CD ==.∴ADC △是等边三角形,则60ADC ∠=︒．∵BD 平分ADC ∠. ∴1302CDB ADC ∠=∠=︒． ∵BD 是直径. ∴90BCD ∠=︒,则12BC BD =． ∵四边形ABCD 是圆内接四边形.∴180ADC ABC ∠+∠=︒,则120ABC ∠=︒.∴60FBC ∠=︒.∴906030FCB ∠=︒-︒=︒. ∴12FB BC =． ∵2BF =.∴4BC =.∴28BD BC ==．∵BD 是直径. ∴此圆半径的长为142BD =． 3.(2023·福建)如图,已知ABC 内接于,O CO 的延长线交AB 于点D ,交O 于点E ,交O 的切线AF 于点F ,且AF BC ∥．（1）求证：AO BE ∥;（2）求证：AO 平分BAC ∠．【答案】（1）见解析（2）见解析【小问1详解】证明AF 是O 的切线.AF OA ∴⊥,即90OAF ∠=︒． CE 是O 的直径.90CBE ∴∠=︒．∴90OAF CBE ∠=∠=︒．AF BC ∥.BAF ABC ∴∠=∠.OAF BAF CBE ABC ∴∠-∠=∠-∠,即OAB ABE ∠=∠.AO BE ∴∥．【小问2详解】解：ABE ∠与ACE ∠都是AE 所对的圆周角.ABE ACE ∴∠=∠．OA OC =.ACE OAC ∴∠=∠.ABE OAC ∴∠=∠．由（1）知OAB ABE ∠=∠.OAB OAC ∴∠=∠.AO ∴平分BAC ∠．4.(2023·广东)综合探究如图1,在矩形ABCD 中()AB AD >,对角线AC BD ，相交于点O ,点A 关于BD 的对称点为A ',连接AA '交BD 于点E ,连接CA '．（1）求证：AA CA '⊥';（2）以点O 为圆心,OE 为半径作圆．①如图2,O 与CD 相切,求证：3AA CA '='; ①如图3,O 与CA '相切,1AD =,求O 的面积．【答案】（1）见解析（2）①见解析;①224π+. 【小问1详解】∵点A 关于BD 的对称点为A '.∴点E 是AA '的中点,90AEO ∠=︒.又∵四边形ABCD 是矩形.∴O 是AC 的中点.∴OE 是ACA '的中位线.∴OE A C '∥∴90AAC AEO ∠'=∠=︒.∴AA CA '⊥'【小问2详解】①过点O 作OF AB ⊥于点F ,延长FO 交CD 于点G ,则90OFA ∠=︒.∵四边形ABCD 是矩形.∴AB CD ,AO BO CO DO ===.∴OCG OAF ∠=∠,90OGC OFA ∠=∠=︒．∵OCG OAF ∠=∠,90OGC OFA ∠=∠=︒,AO CO =.∴()AAS OCG OAF ≌.∴OG OF =．∵O 与CD 相切,OE 为半径,90OGC ∠=︒.∴OG OE =.∴OE OF =又∵90AEO ∠=︒即OE AE ⊥,OF AB ⊥.∴AO 是EAF ∠的角平分线,即OAE OAF ∠=∠.设OAE OAF x ∠=∠=,则OCG OAF x ∠=∠=.又∵CO DO =∴OCG ODG x ∠=∠=∴2AOE OCG ODG x ∠=∠+∠=又∵90AEO ∠=︒,即AEO △是直角三角形.∴90AOE OAE ∠+∠=︒,即290x x +=︒解得：30x =︒.∴30OAE ∠=︒,即30A AC '∠=︒.在Rt A AC '△中,30A AC '∠=︒,90AA C '∠=︒.∴2AC CA '=. ∴()222223AA AC CA CA CA CA ''''=-=-=';①过点O 作OH A C '⊥于点H .∵O 与CA '相切.∴OE OH =,90A HO '∠=︒∵90AAC AEO A EO A HO ''∠'=∠=∠=∠=︒∴四边形A EOH '是矩形.又∵OE OH =.∴四边形A EOH '是正方形.∴OE OH A H '==.又∵OE 是ACA '的中位线. ∴12OE A C '= ∴12A H CH A C ''==∴OH CH = 又∵90A HO '∠=︒.∴45OCH ∠=︒又∵OE A C '∥.∴45AOE ∠=︒又∵90AEO ∠=︒.∴AEO △是等腰直角三角形,AE OE =.设AE OE r ==,则AO DO ==∴)1DE DO OE r r =-=-= 在Rt ADE △中,222AE DE AD +=,1AD =即)222211r r +=∴()2212411r ===+∴O 的面积为：224S r π==. 5.(2023·广西) 如图,PO 平分APD ∠,PA 与O 相切于点A ,延长AO 交PD 于点C ,过点O 作OB PD ⊥,垂足为B ．（1）求证：PB 是O 的切线; （2）若O 的半径为4,5OC =,求PA 的长．【答案】（1）见解析（2）12AP =【小问1详解】①PA 与O 相切于点A .①OA PA ⊥.①PO 平分APD ∠,OB PD ⊥.①OA OB =.①PB 是O 的切线;【小问2详解】①O 的半径为4.①4OA OB ==.①OB PD ⊥,5OC =. ①223BC OC OB =-=,459AC OA OC =+=+=.①BCO ACP ∠=∠.①tan tan BCO ACP ∠=∠.①BO AP BC AC =,即439AP =. ①12AP =．6.(2023·贵州) 如图,已知O 是等边三角形ABC 的外接圆,连接CO 并延长交AB 于点D ,交O 于点E ,连接EA ,EB ．（1）写出图中一个度数为30︒的角：_______,图中与ACD 全等的三角形是_______; （2）求证：AED CEB ∽△△;（3）连接OA ,OB ,判断四边形OAEB 的形状,并说明理由．【答案】（1）1∠,2∠,3∠,4∠;BCD △;（2）证明见详解; （3）四边形OAEB 是菱形;【小问1详解】解：∵O 是等边三角形ABC 的外接圆.∴CO 是ACB ∠的角平分线,60ACB ABC CAB ∠=∠=∠=︒.∴1230∠=∠=︒.∵CE 是O 的直径.∴90CAE CBE ∠=∠=︒.∴3430∠=∠=︒.∴30︒的角有：1∠,2∠,3∠,4∠.∵CO 是ACB ∠的角平分线.∴90ADC BDC ∠=∠=︒,56903060∠=∠=︒-︒=︒.在ACD 与BCD △中.∵1290CD CD ADC BDC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩.∴ACD BCD ≌.故答案为：1∠,2∠,3∠,4∠,BCD △;【小问2详解】证明：∵56∠=∠,3=230∠∠=︒.∴AED CEB ∽△△;【小问3详解】解：连接OA ,OB .∵OA OE OB r ===,5660∠=∠=︒.∴OAE △ ,OBE △是等边三角形.∴OA OB AE EB r ====.∴四边形OAEB 是菱形．7.(2023·河北)如图,点18~P P 是O 的八等分点．若137PP P ,四边形3467P P P P 的周长分别为a ,b ,则下列正确的是( )A. a b <B. a b =C. a b >D. a ,b 大小无法比较【答案】A【详解】连接1223,PP P P .∵点18~P P 是O 的八等分点,即1223345566778148PP P P P P P P P P P P P P P P ======= ∴12233467PP P P P P P P ===,464556781178P P P P P P P P P P PP =+=+= ∴4617P P PP =又∵137PP P 的周长为131737a PPPP P P ++=.四边形3467P P P P 的周长为34466737b PP P P P P P P ++=+. ∴()()34466737131737b a P P P P P P P P PP PP P P ++-++=+-()()12172337131737PP PP P P P P PP PP P P =+++-++122313PP P P PP =-+在123PP P 中有122313PPP P PP >+ ∴1223130b a PP P P PP -=+>-故选A ．8.(2023·河北)装有水的水槽放置在水平台面上,其横截面是以AB 为直径的半圆O ,50cm AB =,如图1和图2所示,MN 为水面截线,GH 为台面截线,MN GH ∥．计算：在图1中,已知48cm MN =,作OC MN ⊥于点C ．（1）求OC 的长．操作：将图1中的水面沿GH 向右作无滑动的滚动,使水流出一部分,当30ANM ∠=︒时停止滚动,如图2．其中,半圆的中点为Q ,GH 与半圆的切点为E ,连接OE 交MN 于点D ．探究：在图2中（2）操作后水面高度下降了多少？（3）连接OQ 并延长交GH 于点F ,求线段EF 与EQ 的长度,并比较大小．【答案】（1）7cm ;（2）11cm 2;（3）253cm 3EF =,25π=cm 6EQ ,EF EQ >．【详解】解：（1）连接OM .∵O 为圆心,OC MN ⊥于点C ,48cm MN =.∴124cm 2MC MN ==. ∵50cm AB =. ∴125cm 2OM AB ==. ∴在Rt OMC 中.222225247cm OC OM MC =-=-=．（2）∵GH 与半圆的切点为E .∴OE GH ⊥∵MN GH ∥∴OE MN ⊥于点D .∵30ANM ∠=︒,25cm ON =.∴125cm 22OD ON ==. ∴操作后水面高度下降高度为：25117cm 22-=．（3）∵OE MN ⊥于点D ,30ANM ∠=︒∴60DOB ∠=︒.∵半圆的中点为Q .∴AQ QB =.∴90QOB ∠=︒.∴30QOE ∠=︒.∴tan EF QOE OE =∠⋅=. 30π2525π==cm 1806EQ ⨯⨯.()25π25π066==>.∴EF EQ >．9.(2023·河南)如图,PA 与O 相切于点A ,PO 交O 于点B ,点C 在PA 上,且CB CA =．若5OA =,12PA =,则CA 的长为______．【答案】103【详解】如图,连接OC .∵PA 与O 相切于点A .∴90OAC ∠=︒;∵OA OB CA CB OC OC =⎧⎪=⎨⎪=⎩.∴OAC OBC ≌.∴90OAC OBC ∠=∠=︒.∴90PAO PBC ∠=∠=︒.∵P P ∠=∠.∴PAO PBC ∽. ∴PO AO PC BC=. ∵5OA =,12PA =.∴13PO =.设CB CA x ==,则12PC PA CA x =-=-. ∴13512x x=-. 解得103x =. 故CA 的长为103. 故答案为：103． 10.(2023·上海)在ABC 中7,3,90AB BC C ==∠=︒,点D 在边AC 上,点E 在CA 延长线上,且CD DE =,如果B 过点A ,E 过点D ,若B 与E 有公共点,那么E 半径r 的取值范围是________．【答案】10210r <≤【详解】解：由题意画出图形如下：连接BE .B 过点A ,且7AB =.B 的半径为7. E 过点D ,它的半径为r ,且CD DE =.2CE CD DE r ∴=+=.3,90BC C =∠=︒. 22294BE BC CE r ∴=+=+,22210AC AB BC =-=.D 在边AC 上,点E 在CA 延长线上.CD AC CE AC ≤⎧∴⎨>⎩,即2102210r r ⎧≤⎪⎨>⎪⎩. 10210r ∴<≤.B 与E 有公共点.AB DE BE AB DE ∴-≤≤+,即22947794r r r r ⎧+≤+⎪⎨-≤+⎪⎩①②. 不等式①可化为2314400r r --≤.解方程2314400r r --=得：2r =-或203r =. 画出函数231440y r r =--的大致图象如下：由函数图象可知,当0y ≤时,2023r -≤≤. 即不等式①的解集为2023r -≤≤.同理可得：不等式②的解集为2r ≥或203r ≤-. 则不等式组的解集为2023r ≤≤.又10r <≤①①r r <≤.r <≤11.(2023·上海)如图,在O 中,弦AB 的长为8,点C 在BO 延长线上,且41cos ,52ABC OC OB ∠==．（1）求O 的半径;（2）求BAC ∠的正切值．【答案】（1）5 （2）94 【小问1详解】解：如图,延长BC ,交O 于点D ,连接AD .由圆周角定理得：90BAD ∠=︒.弦AB 的长为8,且4cos 5ABC ∠=. 845AB BD BD ∴==. 解得10BD =.O ∴的半径为152BD =．【小问2详解】解：如图,过点C 作CE AB ⊥于点E .O 的半径为5.5OB ∴=.12OC OB =. 31522BC OB ∴==. 4cos 5ABC ∠=. 45BE BC ∴=,即41552BE =. 解得6BE =.2AE AB BE ∴=-=,2292CE BC BE =-=. 则BAC ∠的正切值为99224CE AE ==． 12.(2023·苏州)如图,AB 是半圆O 的直径,点,C D 在半圆上,CD DB =,连接,,OC CA OD ,过点B 作EB AB ⊥,交OD 的延长线于点E ．设OAC 的面积为1,S OBE △的面积为2S ,若1223S S =,则tan ACO ∠的值为（）A. 2B. 223 C . 75 D. 32 【答案】A【详解】解：如图,过C 作CH AO ⊥于H .∵CD BD =.∴COD BOE CAO ∠=∠=∠.∵1223S S =,即122132OA CH OB BE =. ∴23CH BE =. ∵A BOE ∠=∠.∴tan tan A BOE ∠=∠.∴CH BE AH OB =,即23CH AH BE OB ==. 设2AH m =,则3BO m AO CO ===.∴32OH m m m =-=.∴22922CH m m m =-=.∴22tan 22CH m A AH m∠===.∵OA OC =.∴A ACO ∠=∠.∴tan ACO ∠=; 故选A.13.(2023·苏州)如图,ABC 是O 的内接三角形,AB 是O 的直径,5,25AC BC ==,点F 在AB 上,连接CF 并延长,交O 于点D ,连接BD ,作BE CD ⊥,垂足为E ．（1）求证：DBE ABC △∽△;（2）若2AF =,求ED 的长．【答案】（1）证明见解析（2）355【小问1详解】证明：∵AB 是O 的直径,BE CD ⊥.∴90ACB BED ∠=︒=∠.∵CAB CDB ∠=∠.∴DBE ABC △∽△．【小问2详解】∵5,25AC BC ==,90ACB ∠=︒. ∴225AB AC BC =+=,1tan 2AC ABC BC ∠==. ∵2AF =.∴3BF =.∵DBE ABC △∽△.∴ABC DBE ∠=∠. ∴1tan tan 2DE ABC DBE BE ∠=∠==.设DE x =,则2BE x =,BD =. ∵AFC BFD ∠=∠,CAB CDB ∠=∠.∴ACF DBF ∽. ∴AC AF CF BD DF BF==.2DF=,则2DF x =. ∴EF x DE ==.∴3BD BF ==.∴5DE =． 14.(2023·天津)如图,在每个小正方形的边长为1的网格中,等边三角形ABC 内接于圆,且顶点A ,B 均在格点上．（1）线段AB 的长为________;（2）若点D 在圆上,AB 与CD 相交于点P ．请用无刻度．．．的直尺,在如图所示的网格中,画出点Q ,使CPQ 为等边三角形,并简要说明点Q 的位置是如何找到的（不要求证明）________．【答案】（1）29（2）画图见解析;如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求【小问1详解】解：222529AB =+=;故答案为：29．【小问2详解】解：如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求;连接PQ ,,AD BK ,过点E 作ET ⊥网格线,过点G 作GS ⊥网格线.由图可得：∵AJF BLF ∠=∠,AFJ BFL ∠=∠,AJ BL =.①()Rt Rt AAS AJF BLF ≌.①FJ FL =,AF BF =.①MJ NL =.①FJ MJ FL NL -=-,即FM FN =.①IMF HNF ∠=∠,IFM HFN ∠=∠.①()Rt Rt ASA IMF HNF ≌.①FI FH =.①AFI BFH ∠=∠,AF BF =.①()SAS AIF BHF ≌.①FAI FBH ∠=∠.①AD BK =.①12∠=∠.①ABC 是等边三角形.①60ACB ∠=︒,即1+60PCB ∠∠=︒.①2+60PCB ∠∠=︒,即60PCQ ∠=︒.①ET GS =,ETF GSF ∠=∠,EFT GFS ∠=∠.①()Rt Rt AAS ETF GSF ≌.①EF GF =.①AF BF =,AFE BFG ∠=∠.①()SAS AFE BFG ≌.①EAF GBF ∠=∠.①60GBF EAF CBA ∠=∠=∠=︒.①18060CBQ CBA GBF ∠=︒-∠-∠=︒.①CBQ CAB ∠=∠.①CA CB =.①()ASA CAP CBQ ≌.①CQ CP =.①60PCQ ∠=︒.①PCQ △是等边三角形,此时点Q 即为所求;故答案为：如图,取,AC AB 与网格线的交点E ,F ,连接EF 并延长与网格线相交于点G ;连接DB 与网格线相交于点H ,连接HF 并延长与网格线相交于点I ,连接AI 并延长与圆相交于点K ,连接CK 并延长与GB 的延长线相交于点Q ,则点Q 即为所求．15.(2023·天津)在O 中,半径OC 垂直于弦AB ,垂足为D ,60AOC ∠=︒,E 为弦AB 所对的优弧上一点．（1）如图①,求AOB ∠和CEB ∠的大小;（2）如图②,CE 与AB 相交于点F ,EF EB =,过点E 作O 的切线,与CO 的延长线相交于点G ,若3OA =,求EG 的长．【答案】（1）120AOB ∠=︒,30CEB ∠=︒ （2）3 【小问1详解】解：在O 中,半径OC 垂直于弦AB .∴AC BC =,得AOC BOC ∠=∠．∵60AOC ∠=︒.∴2120AOB AOC ∠=∠=︒．∵1122CEB BOC AOC ∠=∠=∠. ∴30CEB ∠=︒．【小问2详解】解：如图,连接OE ．同（1）得30CEB ∠=︒．∵在BEF △中,EF EB =.∴75EBF EFB ∠=∠=︒．∴2150AOE EBA ∠=∠=︒．又180120AOG AOC ∠=︒-∠=︒.∴30GOE AOE AOG ∠=∠-∠=︒．∵GE 与O 相切于点E .∴OE GE ⊥,即90OEG ∠=︒．在Rt OEG △中,tan ,3EG GOE OE OA OE∠===. ∴3tan 303EG =⨯︒=．16.(2023·无锡)如图,AB 是O 的直径,CD 与AB 相交于点E ．过点D 的圆O 的切线DF AB ∥,交CA 的延长线于点F ,CF CD =．（1）求F ∠的度数;（2）若8DE DC ⋅=,求O 的半径．【答案】（1）67.5︒（2）2【小问1详解】如图,连接OD ．FD 为O 的切线.∴90ODF ∠=︒．DF AB ∥.∴90AOD ∠=︒．AD AD =. ∴1452ACD AOD ∠=∠=︒． CF CD =.∴1(180)67.52F ACD ∠∠=⨯-=︒．【小问2详解】如图,连接AD .AO OD =,90AOD ∠=︒.∴45EAD ∠=︒．45ACD ∠=︒.∴ACD EAD ∠=∠,且ADE CDA ∠=∠.∴DAE DCA ∽.∴DE DA DA DC=,即28DA DE DC =⋅=. ∴22DA =.∴222OA OD AD ===,即半径为2． 17.(2023·武汉)如图,,,OA OB OC 都是O 的半径,2ACB BAC ∠=∠．（1）求证：2AOB BOC ∠=∠;（2）若4,5AB BC ==,求O 的半径．【答案】（1）见解析（2）52 【小问1详解】证明：∵AB AB =.∴12ACB AOB ∠=∠. ∵BC BC =.∴12BAC BOC ∠=∠. 2ACB BAC ∠=∠.2AOB BOC ∴∠=∠．【小问2详解】解：过点O 作半径OD AB ⊥于点E ,则1,2∠=∠=DOB AOB AE BE . BOC AOB ∠=∠2 .∴DOB BOC ∠=∠.BD BC ∴=.4,5==AB BC .2,5∴==BE DB .在Rt BDE △中,90DEB =︒∠221∴=-=DE BD BE .在Rt BOE 中,90OEB ∠=︒.222(1)2∴=-+OB OB .52OB ∴=,即O 的半径是52．18.(2023·杭州) 如图,在O 中,直径AB 垂直弦CD 于点E ,连接,,AC AD BC ,作CF AD ⊥于点F ,交线段OB 于点G （不与点,O B 重合）,连接OF ．（1）若1BE =,求GE 的长．（2）求证：2BC BG BO =⋅．（3）若FO FG =,猜想CAD ∠的度数,并证明你的结论．【答案】（1）1 （2）见解析（3）45CAD ∠=︒,证明见解析【小问1详解】解：直径AB 垂直弦CD .∴90AED ∠=︒.∴90DAE D ∠+∠=︒.CF AD ⊥.∴90FCD D ∠+∠=︒.∴DAE FCD ∠=∠.由圆周角定理得：DAE BCD ∠=∠.∴BCD FCD ∠=∠.在BCE 和GCE 中.BCE GCE CE CEBEC GEC ∠=∠⎧⎪=⎨⎪∠=∠⎩. ∴BCE GCE≌()ASA .∴1GE BE ==; 【小问2详解】证明：AB 是O 的直径.∴90ACB ∠=︒.在ACB △和CEB 中.90ACB CEB ABC CBE∠=∠=︒⎧⎨∠=∠⎩. ∴ACB △CEB ∽.∴BC BA BE BC=. ∴2BC BA BE =⋅.由（1）知GE BE =.∴12BE BG =. 又2AB BO =. ∴2122BC BA BE BO BG BG BO =⋅=⋅=⋅; 【小问3详解】解：45CAD ∠=︒,证明如下：如图,连接OC .FO FG=.∴FOG FGO∠=∠.直径AB垂直弦CD.∴CE DE=,90AED AEC∠=∠=︒,又AE AE=.∴ACE△ADE≌()SAS.∴DAE CAE∠=∠.设DAE CAEα∠=∠=,FOG FGOβ∠=∠=.则FCD BCD DAEα∠=∠=∠=,OA OC=.∴OCA OACα∠=∠=.又90ACB∠=︒.∴903OCF ACB OCA FCD BCDα∠=∠-∠-∠-∠=︒-.CGE OGFβ∠=∠=,GCEα∠=,90CGE GCE∠+∠=︒∴90βα+=︒.∴90αβ=︒-.2COG OAC OCAααα∠=∠+∠=+=.∴()2290180 COF COG GOFαββββ∠=∠+∠=+=︒-+=︒-. ∴COF AOF∠=∠.COF和AOF中.CO AOCOF AOFOF OF=⎧⎪∠=∠⎨⎪=⎩∴()SASCOF AOF≌,∴OCF OAF∠=∠.即903αα︒-=.∴22.5α=︒.∴245CADα∠==︒．19.(2023·宜宾)如图,以AB 为直径的O 上有两点E ,F ,BE EF =,过点E 作直线CD AF ⊥交AF 的延长线于点D ,交AB 的延长线于点C ,过C 作CM 平分ACD ∠交AE 于点M ,交BE 于点N ．（1）求证：CD 是O 的切线;（2）求证：EM EN =;（3）如果N 是CM 的中点,且95AB =,求EN 的长．【答案】（1）见解析（2）见解析（3）6【小问1详解】证明：如图所示.①BE EF =.∴12∠=∠.∵OA OE =∴13∠=∠.∴23∠∠=.∴OE AF ∥∵CD AF ⊥.∴OE CD ⊥.∴CD 是O 的切线;【小问2详解】证明：如图所示.①CM 平分ACD ∠ ∴1562DCA ∠=∠=∠ 又∵1122DAC ∠=∠=∠,AD CD ⊥ 则90ADC ∠=︒.∴EMC =∠()()11151804522DAC DCA ADC ∠+∠=∠+∠=︒-∠=︒. ∵AB 是O 的直径.∴90MEN AEB ∠=∠=︒.∴45ENM EMN ∠=∠=︒.∴EM EN =;【小问3详解】解：如图所示,取EC 的中点P ,连接PN .①CD 是O 的切线.∴90CEB OEB ∠+∠=︒.∵90AEB AEO OEB ∠=∠+∠=︒.∴AEO BEC ∠=∠.又OAE OEA ∠=∠.∴BEC OAE ∠=∠.∵N 是MC 的中点,P 是EC 的中点. ∴11,22PN EM PN EM EN ==∥. ∵AE EB ⊥.∴PN EB ⊥.在Rt PEN △中,1tan 2PN PEN EN ∠==. ∵BEC OAE ∠=∠. ∴1tan tan 2EB EAB PEN AE ∠==∠= 设BE b =,则2AE b =.∴AB =∵AB =∴9b =∴18AE =,9EB =.∵BEC EAC ∠=∠,ECB ACE ∠=∠.∴ECB ACE ∽. ∴2AE CE EB CB==. ∵CM 是ACD ∠的角平分线.∴N 到,CD AC 的距离相等,设为d ,在EBC ,设点C 到EB 的距离为h . ∴11221122ENC BNC EC d EN h S S BC d BN h ⨯⨯==⨯⨯. ∴2EN EC BN BC==. ∴263EN EB ==．20.(2023·内江)如图,以线段AB 为直径作O ,交射线AC 于点C ,AD 平分CAB ∠交O 于点D ,过点D 作直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F ．连接BD 并延长交AC 的延长线于点M ．（1）求证：直线DE 是O 的切线;（2）当30F ∠=︒时,判断ABM 的形状,并说明理由;（3）在（2）的条件下,1ME =,连接BC 交AD 于点P ,求AP 的长．【答案】（1）见解析（2）ABM 是等边三角形,理由见解析（3）433AP =．【小问1详解】证明：连接OD .∵AD 平分CAB ∠.∴12∠=∠.∵OA OD =.∴32∠=∠.∴31∠=∠.∴OD AC ∥.∵DE AC ⊥.∴OD DE ⊥.∵OD 是O 的半径.。

初中八年级圆形拔高题综合题压轴题(含答案)

初中八年级圆形拔高题综合题压轴题
(含答案)
本文档提供了一份初中八年级的圆形拔高题综合题压轴题，包
括题目和答案。

以下是题目及其对应的答案：
1. 题目一
- 题目描述：有一个半径为5cm的圆，求其周长和面积。

- 答案：周长为31.42cm，面积为78.54cm^2。

2. 题目二
- 题目描述：有一个半径为8cm的圆，求其直径、周长和面积。

- 答案：直径为16cm，周长为50.24cm，面积为201.06cm^2。

3. 题目三
- 题目描述：有一个圆的直径为12cm，求其半径、周长和面积。

- 答案：半径为6cm，周长为37.68cm，面积为113.04cm^2。

4. 题目四
- 题目描述：有一个圆的面积为50.24cm^2，求其半径和周长。

- 答案：半径为4cm，周长为25.12cm。

5. 题目五
- 题目描述：有一个圆的周长为18.84cm，求其直径和面积。

- 答案：直径为6cm，面积为28.26cm^2。

这些题目涵盖了圆的基本概念和计算方法，旨在帮助学生巩固
和应用所学的知识。

请学生根据题目描述和答案进行练和自我检查，以加深对圆形的理解和掌握。

祝学习愉快！。

高中数学-直线、圆与方程压轴题(培优、提高)汇编

高二数学第3讲直线与圆综合1.已知圆C ：x 2+y 2+2x -3=0．（1）求圆的圆心C 的坐标和半径长；（2）直线l 经过坐标原点且不与y 轴重合，l 与圆C 相交于A （x 1，y 1）、B （x 2，y 2）两点，求证：2111x x 为定值；（3）斜率为1的直线m 与圆C 相交于D 、E 两点，求直线m 的方程，使△CDE 的面积最大．2.已知点G （5，4），圆C 1：（x -1）2+（x -4）2=25，过点G 的动直线l 与圆C 1相交于E 、F 两点，线段EF 的中点为C ．（1）求点C 的轨迹C 2的方程；（2）若过点A （1，0）的直线l 1与C 2相交于P 、Q 两点，线段PQ 的中点为M ；又l 1与l 2：x +2y +2=0的交点为N ，求证|AM|•|AN|为定值．3.已知点C （1，0），点A ，B 是⊙O ：x2+y2=9上任意两个不同的点，且满足0=⋅BC AC ，设M 为弦AB 的中点．求点M 的轨迹T 的方程；4.已知平面直角坐标系上一动点(,)P x y 到点(2,0)A -的距离是点P 到点(1,0)B 的距离的2倍。

（1）求点P 的轨迹方程；（2）若点P 与点Q 关于点(2,1)对称，点(3,0)C ，求22||||QA QC +的最大值和最小值；（3）过点A 的直线l 与点P 的轨迹C 相交于,E F 两点，点(2,0)M ，则是否存在直线l ，使EFM S △取得最大值，若存在，求出此时l 的方程，若不存在，请说明理由。

5.已知圆22:4O x y +=和点(1,)M a ．（1）若过点M 有且只有一条直线与圆O 相切，求正数a 的值，并求出切线方程；（2）若a =M 的圆的两条弦AC ，BD 互相垂直．①求四边形ABCD 面积的最大值；②求||||AC BD +的最大值．6.已知过原点的动直线l 与圆C 1：x 2+y 2-6x +5=0相交于不同的两点A ，B ．（1）求圆C 1的圆心坐标；（2）求线段AB 的中点M 的轨迹C 的方程；（3）是否存在实数k ，使得直线L ：y =k （x -4）与曲线C 只有一个交点？若存在，求出k 的取值范围；若不存在，说明理由．7.已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交于M、N两点，Q是MN的中点，直线l与l1相交于点P．（I）求圆A的方程；2时，求直线l的方程；（Ⅱ）当MN＝19（Ⅲ）BPBQ 是否为定值，如果是，求出定值；如果不是，请说明理由．8.已知直线l：4x+3y+10=0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方（1）求圆C的方程；（2）过点M（1，0）的直线与圆C交于A，B两点（A在x轴上方），问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．9.平面直角坐标系xoy中，直线x-y+1=0截以原点O为圆心的圆所得的弦长为6.（1）求圆O的方程；（2）若直线l与圆O切于第一象限，且与坐标轴交于D，E，当DE长最小时，求直线l的方程；（3）设M，P是圆O上任意两点，点M关于x轴的对称点为N，若直线MP、NP分别交于x轴于点（m，0）和（n，0），问mn是否为定值？若是，请求出该定值；若不是，请说明理由．10.已知圆M：x2+（y-4）2=4，点P是直线l：x-2y=0上的一动点，过点P作圆M的切线PA、PB，切点为A、B．（Ⅰ）当切线PA的长度为23时，求点P的坐标；（Ⅱ）若△PAM的外接圆为圆N，试问：当P运动时，圆N是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由；（Ⅲ）求线段AB长度的最小值．11.已知一动圆经过点M（2，0），且在y轴上截得的弦长为4，设动圆圆心的轨迹为曲线C．（1）求曲线C的方程；（2）过点N（1，0）任意作相互垂直的两条直线l1，l2，分别交曲线C于不同的两点A，B和不同的两点D，E．设线段AB，DE的中点分别为P，Q．①求证：直线PQ过定点R，并求出定点R的坐标；②求|PQ|的最小值．。

2021年九年级中考数学复习《中考压轴题：圆的综合应用》经典题型提升练习(四)

2021年中考数学复习《中考压轴题：圆的综合应用》经典题型提升练习（四）1．如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE 平分∠BAC交边BC与点E，经过A、D、E三点的即的圆心F恰好在y轴上，⊙F与y轴交于另一点G．（1）求证：BC是⊙F的切线；（2）试探究线段AG、AD、CD之间的关系，并证明；（3）若点A（O，﹣1）、D（2，0），求AB的长．2．如图，在Rt△ABC中，∠ABC＝90°，⊙O（圆心O在△ABC内部）经过B，C两点，交线段AC于点D，直径BH交AC于点E，点A关于直线BD的对称点F落在⊙O上．连结BF．（1）求证：∠C＝45°；（2）在圆心O的运动过程中；①若tan∠EDF＝，AB＝6，求CE的长；②若点F关于AC的对称点落在△BFE边上时，求点的值．（直接写出答案）；（3）令⊙O与边AB的另一个交点为P，连结PC，交BD于点Q，若PC⊥BF，垂足为点G，求证：BD＝AD+CE．3．如图①，△ABC和△CDE都是等腰直角三角形，∠ACB＝∠DCE＝90°，且点A在ED的延长线上，以DE为直径的⊙O与AB交于G、H两点，连接BE．（1）求证：BE是⊙O的切线；（2）如图②，连接OB、OC，若tan∠CAD＝，试判断四边形BECO的形状，请说明理由；（3）在（2）的条件下，若BF＝，请你求出HG的长．4．如图1，AB为半圆O的直径，半径OP⊥AB，过劣弧AP上一点D作DC⊥AB于点C．连接DB，交OP于点E，∠DBA＝22.5°．（1）若OC＝2，则AC的长为；（2）试写出AC与PE之间的数量关系，并说明理由；（3）连接AD并延长，交OP的延长线于点G，设DC＝x，GP＝y，请求出x与y之间的等量关系式．（请先补全图形，再解答）．5．如图，在△ABC中，AB＝AC＝4，以AB为直径的⊙O交BC于点D，交AC于点E，点P是AB的延长线上一点，且∠PDB＝∠A，连接DE、OE．（1）求证：PD是⊙O的切线；（2）填空：①当∠P的度数为时，四边形OBDE是菱形；②当∠BAC＝45°时，△CDE的面积为．6．如图，△OAB中，OA＝OB＝5cm，AB长为8cm，以点O为圆心6cm为直径的⊙O交线段OA 于点C，交直线OB于点E、D，连接CD，EC．（1）求证：△OCD∽△OAB；（2）求证：AB为⊙O的切线；（3）在（2）的结论下，连接点E和切点，交OA于点F求证：OF•CE＝OD•CF．7．已知：在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点，以CD为直径的⊙Q分别交BC、BA于点F、E，点E位于点D下方，连接EF交CD于点G．（1）如图1，如果BC＝2，求DE的长；（2）如图2，设BC＝x，＝y，求y关于x的函数关系式及其定义域；（3）如图3，连接CE，如果CG＝CE，求BC的长．8．已知：在矩形ABCD中，AB＝a（a为定值），连接AC，点O是AC上的一个动点，以AO 为半径的⊙O与AD交于点P．（1）如图（a），当∠DCP＝∠DAC时，求证：PC是⊙O的切线；（2）在（1）的条件下，若△APC是等腰三角形，①请你判断⊙O与BC的位置关系，并说明理由；②求⊙O的半径（用含a的代数式表示）；（3）如图（b），若BC＝AB＝a，且点O运动到AC与BD的交点处，在弧CD上任取一点Q，连接AQ、BQ分别交BD、AC于M，N．求证：四边形ABNM的面积为定值．9．如图，△ABC内接于⊙O，AB＝BC，AO⊥BC于D．（1）求证：△ABC是等边三角形；（2）若AB＝1，P是劣弧上一个动点，∠APC＝60°（点P与B、C不重合），PA交BC于点E，设AE＝x，EP＝y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3）在（2）的前提下，令∠PAC＝α，∠APC＝β，当y取何值时，sin2α+sin2β＝1．10．如图①，已知A、B是⊙O1上的两点，直线l与⊙O1相交于B、C两点，过A点作⊙O1的切线AO，AO⊥l交于点O，已知BC＝8，⊙O1的半径为5．（1）证明：∠ABO1＝∠ABO．（2）求AB的长．（3）如图②，以AO所在直线为x轴，以直线l为y轴，建立如图所示的直角坐标系，过A、B两点作⊙O2与y轴的正半轴交于点M，与O1B的延长线交于点N，当⊙O2的大小变化时，BM﹣BN的值是否改变？若改变，请说明理由．若不变，请求出该值．参考答案1．（1）证明：连接EF，如图1所示：∵AE平分∠BAC，∴∠FAE＝∠CAE，∵FA＝FE，∴∠FAE＝∠FEA，∴∠FEA＝∠EAC，∴FE∥AC，∴∠FEB＝∠C＝90°，即BC是⊙F的切线；（2）解：AG＝AD+2CD；理由如下：作FR⊥AD于R，连接DF，如图2所示：则∠FRC＝90°，又∠FEC＝∠C＝90°，∴四边形RCEF是矩形，∴EF＝RC＝RD+CD，∠EFR＝90°，∵FR⊥AD，∴AR＝RD＝AD，∴EF＝RD+CD＝AD+CD，∵AF＝EF，∴AF＝AD+CD，∴AG＝2AF＝AD+2CD；（3）解：设⊙F的半径为r，则r2＝（r﹣1）2+22，解得，r＝，∴FA＝FG＝FE＝，∵点A（O，﹣1）、D（2，0），∴AD＝＝，∴AR＝，∵∠EFR＝90°，∴∠BFE+∠AFR＝90°，∵∠BFE+∠EBF＝90°，∴∠EBF＝∠AFR，∵∠BEF＝∠FRA＝90°，∴△BEF∽△FRA，∴＝，即＝，解得：BF＝，∴AB＝AF+BF＝+＝．2．（1）证明：∵点A，F关于直线BD对称，∵∠BFD＝∠C，∴∠A＝∠C，∵∠ABC＝90°，∴∠C＝45°；（2）①解：∵点A，F关于直线BD对称，∴AD＝DF，AB＝FB，∵∠A＝∠C＝45°，∴AB＝BC＝FB＝6，∴，∵BH是直径，∴由圆的对称性可知，△BFE≌△BCE，∴∠BFE＝∠C＝∠BFD＝45°，FE＝CE，∴∠DFE＝90°，∵tan∠EDF＝，AB＝6，∴设DF＝AD＝3a，则EF＝CE＝4a，DE＝5a，∵AC＝＝6，∴AC＝3a+4a+5a＝6，解得，a＝，∴CE＝4a＝2；②如图1，当点F关于AC的对称点落在BF边上时，连接DO，设FF'交AC于点M，则AC垂直平分FF'，由（1）知，∠A＝∠C＝45°，∠ABC＝90°，∴BA＝BC，∠ABM＝∠CBM＝×90°＝45°，∵点A，F关于直线BD对称，∴AD＝DF，AB＝FB，∴△ABD≌△FBD（SSS），∴∠ABD＝∠FBD，由（2）知，△BFE≌△BCE，∴∠FBE＝∠CBE，∴∠ABD＝∠FBD＝∠FBE＝∠CBE＝22.5°，∴∠DBE＝∠DBF+∠EBF＝45°，∵OD＝OB，∴∠OBD＝∠ODB＝45°，∴∠DOB＝90°，在△BDM与△BEM中，∠BDM＝∠BEM＝90°﹣22.5°＝67.5°，∴BD＝BE，在等腰Rt△BOD中，设OB＝OD＝r，则BD＝r，∴BE＝r，OE＝（﹣1）r，∴＝＝﹣1；如图2，当点F关于AC的对称点落在BE边上时，∵∠DF'E＝∠DOE＝90°，∴点F'与点O重合，连接OF，则OD＝OF＝DF，∴△DOF为等边三角形，∴∠ODF＝60°，由对称性知，∠ODE＝∠FDE＝30°，在Rt△DOE中，tan∠ODE＝＝tan30°＝，∴＝；综上所述，的值为﹣1或；（3）如图3，连接PD，FC，FC交BH于点M，∵∠ABC＝90°，∴PC⊥BF，∴CF＝BC＝BF，∴△FBC是等边三角形，∴BG＝CM＝BF，∠QGB＝∠CME＝90°，∠DBF＝∠DCF，∴△QBG≌△ECM（ASA），∴BQ＝CE，∵∠PDA＝90°，∠A＝45°，∴DP＝DA＝DF，∴，∵∠DPC＝（），∠DQP＝∠QDC+∠QCP＝（），∴∠DPC＝∠DQP，∴DQ＝DP＝AD，∴BD＝AD+CE．3．（1）证明：∵△ABC和△CDE都是等腰直角三角形，∴BC＝AC，EC＝DC，∴∠DCE＝∠ACB＝90°，∴∠DCE﹣∠FCD＝∠ACB﹣∠FCD，∴∠BCE＝∠ACD，∴△BCE≌△ACD（SAS），∴∠CBE＝∠CAD，∴∠ABE+∠BAE＝90°，∴∠AEB＝90°，∴BE⊥OE，又∵OE是⊙O的半径，∴BE是⊙O的切线；（2）四边形BECO是平行四边形，理由如下：∵点O是ED的中点，∴CO是DE边上的中线，∵△CDE是等腰三角形，∴CO是DE边上的高线，∴CO⊥DE，∴∠COE＝∠AOC＝90°，∵∠AEB＝90°，∴∠AEB＝COE，∴CO∥BE，∵在Rt△AOC中，tan∠CAD＝，∴＝，∴AO＝2CO，∴DO＝CO，∴AD＝CO，∵△BCE≌△ACD，∴BE＝AD，∴BE＝CO，∴四边形BECO是平行四边形；（3）∵四边形BECO是平行四边形，∴CF＝BF＝，∴BC＝2，∴AC＝BC＝2，∴AB＝＝2，设OC＝x，则AO＝2x，∵在Rt△AOC中，OC2+AO2＝AC2，∴x2+（2x）2＝（2）2，解得，x＝2（取正值），∴OC＝BE＝2，AO＝4，如图3，过点O作OM⊥AB于点M，连接OG，∴∠AMO＝90°，HG＝2MG，∴∠AMO＝∠AEB＝90°，∵∠MAO＝∠BAE，∴△MAO∽△BAE，∴＝，∴＝，∴OM＝，在Rt△MOG中，OM2+MG2＝OG2，∴（）2+MG2＝22，∴MG＝（取正值），∴HG＝2MG＝．4．解：（1）．∵∠DBA＝22.5°∴∠DOC＝45°∵OC＝2∴OD＝∴AC＝OA﹣OC＝（2）连接AD，DP，OD，过点D作DF⊥OP，垂足为点F．∵∠DCA＝∠DFP＝90°，AD＝DP，CD＝DF∴Rt△ACD≌Rt△DFP（HL）∴AC＝PF∵∠A＝∠CDB＝∠OEB＝∠DEF，∠ACD＝∠DFE＝90°，CD＝DF ∴Rt△ACD≌Rt△DEF（HL）∴AC＝EF∴PE＝2AC（3）如图所示，由∠DCO＝90°，∠DOC＝45°得OD＝＝∵∠ADB＝90°，点O是AB中点∴AB＝2OD＝∵∠A＝∠GED，∠GDE＝∠ADB，AD＝DE∴△DGE≌△DBA（ASA）∴GE＝AB＝x∵PE＝2AC∴PE＝2（）∴GP＝GE﹣PE＝即：y＝2x5．解：（1）如图，连接OD∵OB＝OD，∠PDB＝∠A∴∠ODB＝∠ABD＝90°﹣∠A＝90°﹣∠PDB ∴∠ODB+∠PDB＝90°∴∠ODP＝90°又∵OD是⊙O的半径∴PD是⊙O的切线（2）①30°若四边形OBDE为菱形，则OB＝BD＝DE＝EO＝OD ∴△OBD为等边三角形∴∠ABD＝∠A＝60°∴∠PDB＝30°∴∠P＝30°即当∠P为30°时，四边形OBDE为菱形②如图所示∵AO＝OE＝2，∠AOE＝90°∴AE＝∴EC＝4﹣∵∠BAC＝45°∴∠EDB＝135°∴∠EDC＝45°设DF＝EF＝b，FC＝a∵△EFC∽△ADC∴∴∵a2+b2＝（4﹣）2解得a＝（）b，b2＝4﹣2S＝＝＝b2＝△CDE6．证明：（1）∵OC＝OD，OA＝OB，∴＝，又∵∠COD＝∠AOB，∴△OCD∽△OAB；（2）过点O作OG⊥AB，垂足为G，∴∠OGA＝∠OGB＝90，∵OA＝OB，∴AG＝BG＝4，在Rt△AOG中，OA＝5，AG＝4，∴OG＝＝3，∵⊙O的直径为6，∴半径r为3，∴OG＝r＝3，又OG⊥AB，∴AB为⊙O的切线；（3）∵OA＝OB，AG＝BG，∴∠AOG＝∠BOG，∵OE＝OC，∴∠OEC＝∠OCE，∵∠AOB＝∠OEC+∠OCE，∴∠AOG＝∠OCE，∴OG∥EC，∴△FOG∽△FCE，∴＝，∴OF•CE＝OD•CF，∵OG＝OD，∴OF•CE＝OD•CF．7．解：（1）如图1中，连接CE．在Rt△ACB中，∵∠ACB＝90°，AC＝1，BC＝2，∴AB＝＝，∵CD是⊙Q的直径，∴∠CED＝90°，∴CE⊥AB，∵BD＝AD，∴CD＝AB＝，∵•AB•CE＝•BC•AC，∴CE＝，在Rt△CDE中，DE＝＝＝．（2）如图2中，连接CE，设AC交⊙Q于K，连接FK，DF，DK．∵∠FCK＝90°，∴FK是⊙Q的直径，∴直线FK经过点Q，∵CD是⊙Q的直径，∴∠CFD＝∠CKD＝90°，∴DF⊥BC，DK⊥AC，∵DC＝DB＝DA，∴BF＝CF，CK＝AK，∴FK∥AB，∴＝，∵BC＝x，AC＝1，∴AB＝，∴DC＝DB＝DA＝，∵△ACE∽△ABC，∴可得AE＝，∴DE＝AD﹣AE＝﹣，∴＝，∴＝，∴y＝（x＞1）．（3）如图3中，连接FK．∵CE＝CG，∴∠CEG＝∠CGE，∵∠FKC＝∠CEG，∵FK∥AB，∴∠FKC＝∠A，∵DC＝DA，∴∠A＝∠DCA，∴∠A＝∠DCA＝∠CEG＝∠CGE，∴∠CDA＝∠ECG，∴EC＝DE，由（2）可知：＝﹣，整理得：x2﹣2x﹣1＝0，∴x＝1+或1﹣（舍弃），∴BC＝1+．8．解：（1）证明：连接OP，如图a，∵OA＝OP，∴∠DAC＝∠APO，∵∠DCP＝∠DAC，∴∠DCP＝∠APO，∵四边形ABCD是矩形，∴∠D＝90°，CD＝AB＝a，∴∠DCP+∠DPC＝90°，∴∠OPC＝180°﹣∠DPC﹣∠APO＝180°﹣∠DPC﹣∠DCP＝90°，∴OP⊥PC，∴PC是⊙O的切线；（2）①BC是⊙O的切线，理由如下：如图a﹣1，过点O作OE⊥BC于E，∵△APC是等腰三角形，∴AP＝PC，∴∠PAC＝∠PCA，∵AD∥BC，∴∠PAC＝∠ACE＝∠PCA，又∵∠OPC＝∠OEC＝90°，OC＝OC，∴△OPC≌△OEC（AAS），∴OP＝OE，又∵OE⊥BC，∴BC是⊙O的切线；②∵AP＝PC，∴∠DAC＝∠ACP，∵∠DAC+∠ACD＝∠DAC+∠ACP+∠DCP＝90°，∴∠DAC＝∠DCP＝∠ACP＝30°，∵在Rt△CDP中，cos∠DCP＝＝，∴PC＝＝a，∵Rt△OPC中，tan∠OCP＝＝，∴OP＝PC＝，∴⊙O半径为；（3）连接DQ、CQ，如图b，∵矩形ABCD中，BC＝AB＝a，∴矩形ABCD是正方形，∴AB＝AD＝BC＝a，∠AOB＝∠AOM＝∠BON＝90°，∠ADM＝∠BCN＝45°，∴AC＝BD＝a，OA＝OB＝a，AC、BD为⊙O直径，∵Q在弧CD上运动，∴∠AQB＝∠AOB＝45°，∵∠ADM＝∠AQB＝45°，∠DAM＝∠QBM，∴△ADM∽△BQM，∴，∴BM＝，∵∠BCN＝∠AQB＝45°，∠CBN＝∠QAN，∴△BCN∽△AQN，∴，∴AN＝，∵AC、BD为⊙O直径，∴∠AQC＝∠BQD＝90°，∵∠AOM＝∠AQC＝90°，∠OAM＝∠QAC，∴△AOM∽△AQC，∴，∴AM•AQ＝AO•AC＝a2，∵∠BON＝∠BQD＝90°，∠OBN＝∠QBD，∴△BON∽△BQD，∴，∴BN•BQ＝BO•BD＝a2，∴S四边形AMNB ＝S△AMB+S△NMB＝MB•OA+MB•ON＝MB（OA+ON）＝MB•AN＝••＝•＝•＝a2，∴四边形AMNB的面积为定值．9．（1）证明：∵△ABC内接于⊙O，AO⊥BC，∴BD＝CD＝BC，∴AB＝AC，∵AB＝BC，∴AB＝BC＝AC，∴△ABC是等边三角形；（2）解：由（1）得：△ABC是等边三角形，∴AC＝AB＝BC＝1，∠ABC＝∠ACB＝60°，∴BD＝CD＝，AD＝BD＝，∵∠APC＝∠ABC，∴∠ACB＝∠APC，又∵∠CAE＝∠PAC，∴△ACE∽△APC，∴＝，∴AE×AP＝AC2＝1，即x（x+y）＝1，∴y＝又∵AD＜AE＜AB，∴＜x＜1；（3）解：∵∠APC＝∠B＝60°，∠PAC＝α，∠APC＝β，∴sin2α＝sin2∠APC＝（）2＝，∵sin2α+sin2β＝1．∴sin2β＝1﹣＝，∴sinβ＝，∴∠PAC＝30°，∴点E与D重合，如图所示：连接OB，则OB平分∠ABC，∴∠OBD＝30°，∵AD⊥BC，∴OD＝BD＝，OP＝OA＝OB＝2OD＝，∴PD＝PE＝OP﹣OD＝﹣＝；即y取时，sin2α+sin2β＝1．10．解：（1）连接O1A，过O1作EO1⊥BC于E，∵EO1⊥BC，∴BE＝BC＝4，∵O1B＝5，∴O1E＝＝＝3，∵过A点作⊙O1的切线AO，∴AO1⊥AO，且AO⊥l，EO1⊥BC，∴四边形OEO1A是矩形，∴AO＝O1E＝3，AO1∥OE，AO1＝EO＝5，∴∠O1AB＝∠ABO，∵O1A＝O1B，∴∠O1AB＝∠O1BA，∴∠ABO1＝∠ABO；（2）∵OB＝OE﹣BE＝5﹣4＝1，∴AB＝＝＝；（3）在MB上截取MG＝NB，连接AM，AN，AG，MN，∵四边形ABNM是圆内接四边形，＝∠NMA，∴∠ABO1＝∠ABO，∠ABO＝∠ANM∵∠ABO1∴∠AMN＝∠ANM，∴AM＝AN，∵＝，∴∠AMG＝∠ANB，且AM＝AN，MG＝NB，∴△AMG≌△ANB（SAS）∴AG＝AB，且AO⊥BC，∴BO＝GO＝1，∴BG＝2，∴BM﹣BN＝BM﹣MG＝BG＝2，∴BM﹣BN的值不变．。

与圆有关的压轴题(提高)

2022-2023学年人教版中考数学复习 圆综合压轴题 专题提升训练

中考数学压轴题之圆的综合(中考题型整理,突破提升)及答案

中考数学压轴题提升训练：圆中证明及计算问题

压轴题 圆的五种考法(解析版)--九年级数学常考压轴题

2021年九年级数学中考一轮复习 圆综合填空压轴题 提升专题训练

中考数学压轴题-圆的压轴题 含解析

人教版数学九年级上册 第二十四章 《圆》 压轴题综合培优训练(包含答案)