jacobi迭代法和Gauss-Seidel迭代法
雅可比迭代法和高斯塞德尔迭代法对比

雅可比迭代法和高斯塞德尔迭代法对比引言雅可比迭代法和高斯塞德尔迭代法是数值分析中常用的迭代求解线性方程组的方法。
它们都是通过迭代更新变量的值,逐渐逼近方程组的真实解。
本文将详细讨论这两种迭代法的原理、特点和适用情况,并给出一些比较和应用实例。
雅可比迭代法(Jacobi Iteration)雅可比迭代法是一种逐个更新变量的值的迭代方法。
对于线性方程组Ax = b,雅可比迭代法的更新公式如下:x i(k+1)=1a ii(b i−∑a ijnj=1j≠ix j(k))其中,aii表示系数矩阵A的第i行第i列的元素,而bi表示方程组的第i个方程的右侧常数。
特点1.雅可比迭代法的计算过程简单,容易理解和实现。
2.每次迭代只更新一个变量的值,相邻两次迭代之间没有数据依赖关系,可以并行计算。
3.雅可比迭代法收敛的条件是系数矩阵A满足严格对角占优条件或对称正定条件。
优缺点•优点:简单易懂,在一些特定情况下收敛速度较快。
•缺点:收敛速度相对较慢,尤其是在系数矩阵A的条件数较大时;不适用于对角占优条件较弱的问题。
高斯塞德尔迭代法(Gauss-Seidel Iteration)高斯塞德尔迭代法是一种逐个更新变量的值,并立即使用最新的值进行下一个变量的更新的迭代方法。
对于线性方程组Ax = b,高斯塞德尔迭代法的更新公式如下:x i(k+1)=1a ii(b i−∑a iji−1j=1x j(k+1)−∑a ijnj=i+1x j(k))特点1.高斯塞德尔迭代法相较于雅可比迭代法,每次迭代可以使用当前迭代步骤中已更新的变量值,因此收敛速度更快。
2.如果系数矩阵A是严格对角占优或对称正定的,高斯塞德尔迭代法一定收敛。
优缺点•优点:相较于雅可比迭代法,收敛速度更快,对于条件数较大的问题也有较好的效果。
•缺点:实现稍微复杂一些,每次迭代的计算依赖于之前已更新的变量值,无法并行计算。
雅可比迭代法和高斯塞德尔迭代法的比较收敛速度在一些特定的问题中,雅可比迭代法可以比高斯塞德尔迭代法更快地收敛。
Jacobi迭代法与GaussSeidel迭代法算法比较

Jacobi 迭代法与Gauss-Seidel迭代法算法比较目录1 引言 (1)1.1Jacobi迭代法 (2)1.2Gauss-Seidel迭代法 (2)1.3逐次超松弛(SOR)迭代法 (3)2算法分析 (3)3 结论 (5)4 附录程序 (5)参考文献 (8)Jacobi 迭代法与Gauss-Seidel 迭代法比较1 引言解线性方程组的方法分为直接法和迭代法,直接法是在没有舍入误差的假设下,能在预定的运算次数内求得精确解,而迭代法是构造一定的递推格式,产生逼近精确值的序列。
这两种方法各有优缺点,直接法普遍适用,但要求计算机有较大的存储量,迭代法要求的存储量较小,但必须在收敛性得以保证的情况下才能使用。
对于高阶方程组,如一些偏微分方程数值求解中出现的方程组,采用直接法计算代价比较高,迭代法则简单又实用,所以比较受工程人员青睐。
迭代法求解方程组就是构造一个无限的向量序列,使它的极限是方程组的解向量。
即使计算机过程是精确的,迭代法也不能通过有限次算术运算求得方程组的精确解,而只能逐步逼近它。
因此迭代法存在收敛性与精度控制的问题。
迭代法是常用于求解大型稀疏线性方程组(系数矩阵阶数较高且0元素较多),特别是某些偏微分方程离散化后得到的大型稀疏方程组的重要方法。
设n 元线性微分方程组b Ax = (1)的系数矩阵A 非奇异,右端向量0≠b ,因而方程组有唯一的非零解向量。
而对于这种线性方程组的近似解,前辈们发展研究了许多种有效的方法,有Jacobi 迭代法、Gauss —Seidel 迭代法,逐次超松弛迭代法(SOR 法),这几种迭代方法均属一阶线性定常迭代法,即若系数矩阵A 分解成两个矩阵N 和P 的差,即P N A -=;其中N 为可逆矩阵,线性方程组(1)化为:b x P N =-)(b Px Nx +=b N Px N x 11--+=可得到迭代方法的一般公式:d Gx xk k +=+))1(( (2)其中:P N G 1-=,b N d 1-=,对任取一向量)0(x 作为方程组的初始近似解,按递推公式产生一个向量序列)1(x ,)2(x ,...,)k x(,...,当k 足够大时,此序列就可以作为线性方程组的近似解。
数值分析5-用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组
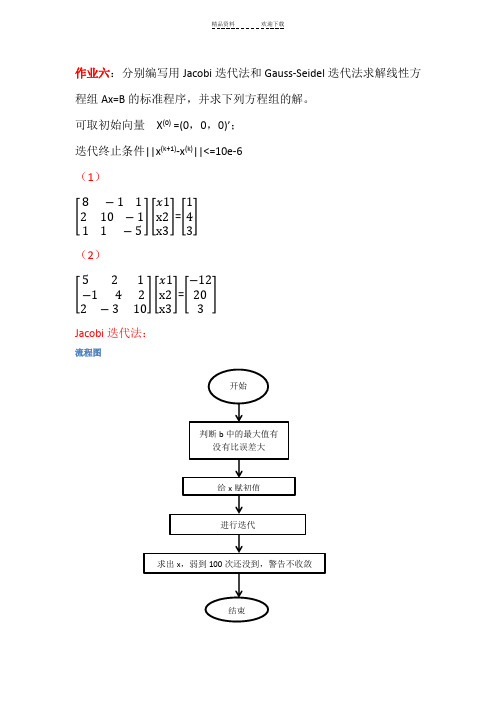
作业六:分别编写用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组Ax=B的标准程序,并求下列方程组的解。
可取初始向量X(0) =(0,0,0)’;迭代终止条件||x(k+1)-x(k)||<=10e-6(1)=(2)=Jacobi迭代法:流程图程序clear;clc;A=[8,-1,1;2,10,01;1,1,-5];b=[1;4;3];e=1e-6;x0=[0;0;0]';n=length(A);x=zeros(n,1);k=0;r=max(abs(b));while r>efor i=1:nd=A(i,i);if abs(d)<ewarning('矩阵A输入有误');return;endsum=0;for j=1:nif j~=isum=sum+A(i,j)*x0(j);endendx1(i)=(b(i)-sum)/A(i,i);endk=k+1;r=max(abs(x1-x0));x0=x1;fprintf('第%d次迭代:',k)fprintf('\n与上次计算结果的距离:%f \n',r)disp(x1);if k>100warning('不收敛');endendx=x0;程序结果(1)(2)Gauss-Seidel迭代法:程序clear;clc;%A=[8,-1,1;2,10,01;1,1,-5];%b=[1;4;3];A=[5,2,1;-1,4,2;2,-3,10];b=[-12;20;3];m=size(A);if m(1)~=m(2)error('矩阵A不是方阵');endn=length(b);%初始化N=0;%迭代次数L=zeros(n);%分解A=D+L+U,D是对角阵,L是下三角阵,U是上三角阵U=zeros(n);D=zeros(n);G=zeros(n);%G=-inv(D+L)*Ud=zeros(n,1);%d=inv(D+L)*bx=zeros(n,1);for i=1:n%初始化L和Ufor j=1:nif i<jL(i,j)=A(i,j);endif i>jU(i,j)=A(i,j);endendendfor i=1:n%初始化DD(i,i)=A(i,i);endG=-inv(D+L)*U;%初始化Gd=(D+L)\b;%初始化d%迭代开始x1=x;x2=G*x+d;while norm(x2-x1,inf)>10^(-6)x1=x2;x2=G*x2+d;N=N+1;endx=x2;程序结果(1)(2)。
分别用 jacobi 迭代法和 gauss-seidel 迭代法,求解方程组

分别用 jacobi 迭代法和 gauss-seidel 迭代法,求解方程组【jacobi 迭代法和 gauss-seidel 迭代法分别应用于方程组的求解】1. 引言在数学领域中,方程组的求解一直是一个重要的课题。
为了解决复杂的线性方程组,人们提出了各种迭代方法,其中 jacobi 迭代法和gauss-seidel 迭代法是两种常见的方法。
本文将探讨这两种迭代方法在求解方程组中的应用。
2. jacobi 迭代法的原理和应用jacobi 迭代法是一种基于逐次逼近的迭代方法。
对于线性方程组AX=B,其中 A 是系数矩阵,X 是未知数向量,B 是已知向量。
我们可以通过以下公式进行逐次逼近:X(k+1) = D^(-1)*(B - (L+U)X(k))其中,D、L、U 分别是 A 的对角线、下三角和上三角矩阵。
jacobi 迭代法的优点在于易于理解和实现,但在收敛速度上较慢,需要进行多次迭代才能得到精确解。
在实际应用中,需要根据实际情况选择合适的迭代次数。
3. gauss-seidel 迭代法的原理和应用与 jacobi 迭代法类似,gauss-seidel 迭代法也是一种基于逐次逼近的迭代方法。
不同之处在于,gauss-seidel 迭代法在计算 X(k+1) 时利用了已经得到的 X(k) 的信息,即:X(k+1)_i = (B_i - Σ(A_ij*X(k+1)_j,j≠i))/A_ii这种方式使得 gauss-seidel 迭代法的收敛速度较快,通常比 jacobi 迭代法更快,尤其是对于对角占优的方程组。
4. 分别用 jacobi 迭代法和 gauss-seidel 迭代法求解方程组为了更具体地说明 jacobi 迭代法和 gauss-seidel 迭代法的应用,我们分别用这两种方法来求解以下方程组:2x1 + x2 = 9x1 + 3x2 = 11我们将该方程组写成矩阵形式 AX=B:|2 1| |x1| |9||1 3| * |x2| = |11|我们根据 jacobi 迭代法和 gauss-seidel 迭代法的原理,依次进行迭代计算,直到满足收敛条件。
Jacobi 迭代法与Gauss-Seidel迭代法算法比较

Jacobi 迭代法与Gauss-Seidel迭代法算法比较目录1 引言 (1)1.1 Jacobi迭代法 (2)1.2 Gauss-Seidel迭代法 (2)1.3 逐次超松弛(SOR)迭代法 (3)2算法分析 (4)3 结论 (5)4 附录程序 (6)参考文献 (10)Jacobi 迭代法与Gauss-Seidel 迭代法比较1 引言解线性方程组的方法分为直接法和迭代法,直接法是在没有舍入误差的假设下,能在预定的运算次数内求得精确解,而迭代法是构造一定的递推格式,产生逼近精确值的序列。
这两种方法各有优缺点,直接法普遍适用,但要求计算机有较大的存储量,迭代法要求的存储量较小,但必须在收敛性得以保证的情况下才能使用。
对于高阶方程组,如一些偏微分方程数值求解中出现的方程组,采用直接法计算代价比较高,迭代法则简单又实用,所以比较受工程人员青睐。
迭代法求解方程组就是构造一个无限的向量序列,使它的极限是方程组的解向量。
即使计算机过程是精确的,迭代法也不能通过有限次算术运算求得方程组的精确解,而只能逐步逼近它。
因此迭代法存在收敛性与精度控制的问题。
迭代法是常用于求解大型稀疏线性方程组(系数矩阵阶数较高且0元素较多),特别是某些偏微分方程离散化后得到的大型稀疏方程组的重要方法。
设n 元线性微分方程组b Ax = (1)的系数矩阵A 非奇异,右端向量0≠b ,因而方程组有唯一的非零解向量。
而对于这种线性方程组的近似解,前辈们发展研究了许多种有效的方法,有Jacobi 迭代法、Gauss —Seidel 迭代法,逐次超松弛迭代法(SOR 法),这几种迭代方法均属一阶线性定常迭代法,即若系数矩阵A 分解成两个矩阵N 和P 的差,即P N A -=;其中N 为可逆矩阵,线性方程组(1)化为:b x P N =-)(b Px Nx +=b N Px N x 11--+=可得到迭代方法的一般公式:2 算法分析例1 用雅可比迭代法求解下列方程组⎪⎩⎪⎨⎧=+--=-+-=--2453821027210321321321.x x x .x x x .x x x解 将方程组按雅可比方法写成⎪⎪⎩⎪⎪⎨⎧++=++=++=8402020830201072020*******2321.x .x .x .x .x .x .x .x .x取初始值()()()()()()T T,,,x ,x ,x x 0000302010==按迭代公式()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=++=++=+++840202083020107202010211331123211.x .x .x .x .x .x .x .x .x k k k k k k k k k例2 用高斯——塞德尔迭代法求解例1.解 取初始值()()()()()()TT,,,x ,x ,x x 0000302010==,按迭代公式()()()()()()()()()⎪⎩⎪⎨⎧++=++=++=++++++840202083020107202010121113311123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如下表23 结论使用Gauss-Seidel 迭代法迭代法,7次就可以求出方程的解,收敛速度要比Jacobi迭代法收敛快(达到同样的精度所需迭代次数少);但是这个结论,在一定条件下才是对的,甚至有这样的方程组,雅可比方法收敛,而高斯—塞德尔迭代法却是发散的.4 附录程序/* 求解线性方程组--Gauss-Seidel迭代法*/#include <iostream>#include <cmath>using namespace std;/* 二维数组动态分配模板*/template <class T>T** Allocation2D(int m, int n){T **a;a = new T*[m];for (int i=0; i<m; i++){a[i] = new T[n];}return a;}/* 一维数组动态分配模板*/template <class T>T* Allocation1D(int n){T *a;a = new T[n];return a;}/* 求矩阵的一范数*/float matrix_category(float* x, int n){float temp = 0;for(int i=0; i<n; i++){temp = temp + fabs(x[i]);}return temp;}int main(){const int MAX = 1000; // 最大迭代次数int i,j,k; // 循环变量int n; // 矩阵阶数float** a; // 增广矩阵float* x_0; // 初始向量float* x_k; // 迭代向量float precision; // 精度cout<<"输入精度e:";cin>>precision;/* 动态生成增广矩阵*/cout<<endl<<"输入系数矩阵的阶数,N:";cin>>n;a = Allocation2D<float>(n, n+1);/* 输入增广矩阵的各值*/cout<<endl<<"输入增广矩阵的各值:\n";for(i=0; i<n; i++){for(j=0; j<n+1; j++){cin>>a[i][j];}}/* 生成并初始化初始向量*/x_0 = Allocation1D<float>(n);cout<<endl<<"输入初始向量:\n";for(i=0; i<n; i++){cin>>x_0[i];}/* 生成迭代向量*/x_k = Allocation1D<float>(n);float temp;/* 迭代过程*/for(k=0; k<MAX; k++){for(i=0; i<n; i++){temp = 0;for(j=0; j<i; j++){temp = temp + a[i][j] * x_k[j];}x_k[i] = a[i][n] - temp;temp = 0;for(j=i+1; j<n; j++){temp = temp + a[i][j] * x_0[j];}x_k[i] = (x_k[i] - temp) / a[i][i];}/* 求两解向量的差的范数*/for(i=0; i<n; i++){x_0[i] = x_k[i] - x_0[i];}if(matrix_category(x_0,n) < precision){break;}else{for(i=0; i<n; i++){x_0[i] = x_k[i];}}}/* 输出过程*/if(MAX == k){cout<<"迭代不收敛\n";}cout<<"迭代次数为:"<<k<<endl;cout<<"解向量为:\n";for(i=0; i<n; i++){cout<<"x"<<i<<": "<<x_k[i]<<endl;}return 0;}参考文献[1]颜庆津. 数值分析[M]. 北京:航空航天大学出版社,1999.[2]黎建玲,简金宝,李群宏.数值分析与实验[M].北京:科学出版社,2012.[3]宋叶志.MATLAB数值分析与应用[M].北京:机械工业出版社,2013.。
第八节 雅可比迭代法与高斯-塞德尔迭代法综述

第八节 雅可比迭代法与高斯—塞德尔迭代法一 雅可比迭代法设线性方程组b Ax = (1) 的系数矩阵A 可逆且主对角元素nn a ,...,a ,a 2211均不为零,令()nna ,...,a ,a diag D 2211=并将A 分解成()D D A A +-= (2)从而(1)可写成 ()b x A D Dx +-=令11f x B x +=其中b D f ,A D I B 1111--=-=. (3) 以1B 为迭代矩阵的迭代法(公式)()()111f x B x k k +=+ (4)称为雅可比(Jacobi)迭代法(公式),用向量的分量来表示,(4)为⎩⎨⎧[],...,,k ,n ,...,i x a ba xnij j )k (j j i iii)k (i21021111==∑-=≠=+ (5)其中()()()()()Tn x ,...x ,x x 002010=为初始向量.由此看出,雅可比迭代法公式简单,每迭代一次只需计算一次矩阵和向量的乘法.在电算时需要两组存储单元,以存放()k x 及()1+k x . 例1 例1 用雅可比迭代法求解下列方程组⎪⎩⎪⎨⎧=+--=-+-=--2453821027210321321321.x x x .x x x .x x x解 将方程组按雅可比方法写成⎪⎪⎩⎪⎪⎨⎧++=++=++=8402020830201072020*******2321.x .x .x .x .x .x .x .x .x取初始值()()()()()()T T ,,,x ,x ,x x 0000302010==按迭代公式()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=++=++=+++840202083020107202010211331123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如表1所示表1二 高斯—塞德尔迭代法由雅可比迭代公式可知,在迭代的每一步计算过程中是用()k x的全部分量来计算()1+k x的所有分量,显然在计算第i 个分量()1+k i x 时,已经计算出的最新分量()()1111+-+k i k x ,...,x 没有被利用,从直观上看,最新计算出的分量可能比旧的分量要好些.因此,对这些最新计算出来的第1+k 次近似()1+k x的分量()1+k jx 加以利用,就得到所谓解方程组的高斯—塞德(Gauss-Seidel )迭代法.把矩阵A 分解成U L D A --= (6)其中()nn a ,...,a ,a diag D 2211=,U ,L --分别为A 的主对角元除外的下三角和上三角部分,于是,方程组(1)便可以写成 ()b Ux x L D +=-即 22f x B x +=其中()()b L D f ,U L D B 1212---=-= (7)以2B 为迭代矩阵构成的迭代法(公式)()()221f x B x k k +=+ (8)称为高斯—塞德尔迭代法(公式),用 量表示的形式为⎩⎨⎧[],...,,k ,n ,,i x a x a b a xi j n i j )k (j ij )k (j ij i ii)k (i21021111111==∑∑--=-=+=++ (9)由此看出,高斯—塞德尔迭代法的一个明显的优点是,在电算时,只需一组存储单元(计算出()1+k ix 后()k ix 不再使用,所以用()1+k i x 冲掉()k ix ,以便存放近似解.例2 例2 用高斯——塞德尔迭代法求解例1.解 取初始值()()()()()()TT,,,x ,x ,x x 0000302010==,按迭代公式()()()()()()()()()⎪⎩⎪⎨⎧++=++=++=++++++840202083020107202010121113311123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如下表2从此例看出,高斯—塞德尔迭代法比雅可比迭代法收敛快(达到同样的精度所需迭代次数少),但这个结论,在一定条件下才是对的,甚至有这样的方程组,雅可比方法收敛,而高斯—塞德尔迭代法却是发散的.三 迭代收敛的充分条件定理1 在下列任一条件下,雅可比迭代法(5)收敛.①111<∑=≠=∞nij j iiij ia a max B ;②1111<∑=≠=nij i iiij ja a max B ;③ 111<∑=-≠=∞-nji i jjij jTa a max AD I定理2 设21B B ,分别为雅可比迭代矩阵与高斯—塞德尔迭代矩阵,则∞∞≤12B B (10)从而,当111<∑=≠=∞nij j iiij ia a max B时,高斯—塞德尔迭代法(8)收敛. 证明 由21B B ,的定义,它们可表示成()U L D B +=-11()()U D L D I U L D B 11112-----=-=用e 表示n 维向量()T,...,,e 111=,则有不等式eB e B ∞≤11UD L D B 111--+=这里,记号|·|表示其中矩阵的元素都取绝对值,而不等式是对相应元素来考虑的,于是()()()Ie B L D I eL D B e U D ∞------≤-=111111容易验证()11==--nnL D L D所以,L D I 1--及L D I 1--可逆,且()()()1111111111-----------=++≤+++=-L D I LD ...L D I L D ...L D I LD I n n()I L D I ≥---11从而有()()((){}e I B L D I L D I eU D LD I e B ∞----------≤⋅-≤111111121{()()}eB eL D I I B I ∞--∞≤-⋅--=11111因此必有∞∞≤12B B因为已知11<∞B 所以12<∞B .即高斯—塞德尔迭代法收敛.若矩阵A 为对称,我们有定理3 若矩阵A 正定,则高斯—塞德尔迭代法收敛.证明 把实正定对称矩阵A 分解为T L L D A --=()TL U =,则D 为正定的,迭代矩阵()T L L D B 12--=设λ是2B 的任一特征值,x 为相应的特征向量,则()()x x L L D T λ=--1以L D -左乘上式两端,并由TL L D A --=有()Ax x L T λλ=-1用向量x 的共轭转置左乘上式两端,得()Ax x x L xTTT--=-λλ1 (11)求上式左右两端的共轭转置,得Ax x x L x T T ----=⎪⎭⎫ ⎝⎛-λλ1以λ--1和λ-1分别乘以上二式然后相加,得()()Axx x L L x T T T -----⎪⎭⎫ ⎝⎛-+=+⎪⎭⎫ ⎝⎛--λλλλλλ211 由TL L D A --=,得()()Axx x A D x T T -----⎪⎭⎫ ⎝⎛-+=-⎪⎭⎫ ⎝⎛--λλλλλλ211即()Ax x x L x TT---=-λλλ2211 (12)因为A 和D 都是正定的,且x 不是零向量,所以由(11)式得1≠λ,而由(12)式得012>-λ, 即1<λ,从而()12<B ρ,因而高斯—塞德尔迭代法收敛.定义1 设()nn ij a A ⨯=为n 阶矩阵.① ①如果n,...,i ,a a nij i j ij ii 21=∑>≠= (13)即A 的每一行对角元素的绝对值都严格大于同行其他元素绝对值之和,则称A 为严格对角优势矩阵.② ②如果n,...,i ,a a nij i j ij ii 21=∑≥≠=且至少有一个不等式严格成立,则称A 为弱对角优势矩阵.例如⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-310131012是严格对角优势矩阵,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--310121011是弱对角优势矩阵. 定义2 设()nn ij a A ⨯=是n 阶矩阵,如果经过行的互换及相应列的互换可化为⎥⎦⎤⎢⎣⎡2212110A A A ,即存在n 阶排列矩阵P,使⎥⎦⎤⎢⎣⎡=2212110A A A AP P T其中2211A ,A 为方阵,则称A 是可约的,否则称A 为不可约的.A 是可约矩阵,意味着b Ax =可经过若干次行列重排,化为两个低阶方程组,事实上,b Ax =可化为 ()b P x P AP P TT T =,记()()()()⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡==2121d d d b P ,y y y x P TT于是,求解b Ax =化为求解()()()()()⎪⎩⎪⎨⎧=+=+22221212111d y A d y A y A可以证明,如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则A 是非奇异的.定理4 如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则对任意()0x ,雅可比迭代法(4)与高斯—塞德尔迭代法(8)均为收敛的.证明 下面我们以A 为不可约弱对角优势矩阵为例,证明雅可比迭代法收敛,其他证明留给读者.要证明雅可比迭代法收敛,只要证()11<B ρ,1B 是迭代矩阵.用反证法,设矩阵1B 有某个特征值μ,使得1≥μ,则()01=-B I det μ,由于A 不可约,且具有弱对角优势,所以1-D 存在,且 ()()D A D D A D I I B I -+=--=---μμμ111从而()0=-+D A D detμ另一方面,矩阵()D A D -+μ与矩阵A 的非零元素的位置是完全相同的,所以()D A D -+μ也是不可约的,又由于1≥μ,且A 弱对角优势,所以n,...,i ,a a a nij i j ij ii ii 21=∑≥≥≠=μ并且至少有一个i 使不等号严格成立.因此,矩阵()D A D -+μ弱对角优势,故()D A D -+μ为不可约弱对角优势矩阵.从而()0≠-+D A D det μ矛盾,故1B 的特征值不能大于等于1,定理得证.。
数值分析5-用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组

数值分析5-⽤Jacobi迭代法和Gauss-Seidel迭代法求解线性⽅程组作业六:分别编写⽤Jacobi迭代法和Gauss-Seidel迭代法求解线性⽅程组Ax⼆B的标准程序,并求下列⽅程组的解。
可取初始向量X(o)=(O, 0, Of;迭代终⽌条件||x(k+1,-x(k)||<=10e-6(1)」521X1-12-14 2x2⼆20.2-310 .x3 -.3 .Jacobi迭代法:流程图进⾏迭代程序clear;clc;A ⽃&?:U;2J0,01;:L,:L,?5];e=le-6;x0=[0;0;0]1; n=length(A); x=zeros(n/l);k=0;r=max(abs(b));while r>efor i=l:nd=A(iJ);if abs(d)waming('矩阵A输⼊有误'); return; endsum=0;forj=l:nif j"=isum=sum+A(iJ)*xO(j);endendxl(i)=(b(i)-sum)/A(iJ);endk=k+l;r=max(abs(xl-xO));xO=xl;fprintff第%(1 次迭代:fprintf('\n与上次计算结果的距离56f \n',r) disp(xl); if k>100warningf 不收敛,);endendx=xO;程序结果(1)第1次迭代;与上次计算结果的3^:0.6000000. 1250 0.4000 -0. 6000第2次迭代;与上次计算结果的距誇:0. 1250000.2500 0.4350 -0. 4950第3次迭代;与上次计茸结果的距^:0. 0355000.2412 0.3995 -0. 4630与上次计算结果的距S:0. 0088500.2328 0. 3981 -0. 4718第5次迭代;与上次计算结果的3^:0.0025720.2337 0.4006 -0. 4738策6次迭代:与上次计算结果的距^:0. 0006990.2343 0.4006 -0.4731第:次迭代:与上次计算结果的距离;0. 00Q1840.2342 0.4005 -0.4730第8次迭代;勻上次计算结果的距离:0. 0000540.2342 0.4005 -0.4731第9次迭代:与上次计算结果的距离:0. 0000130.2342 0.4005 -0.4731第10次迭代:与上次计算结果的距离:0. 0000040.2342 0.4005 -0. 4731第11次迭代;与上次计算结果的距离;0?0000010.2342 0.4005 -0.4731(2)第i次迭代:与上次计算结果的距离:5. 000000 -2.4000 5.0000 0.3000第2次迭代:与上次计尊结果的3^:2. 060000 ⼀4?4600 4.2500 2.2800第3次迭代:与上次计算结果的距离:1?505000 -4.5560 2.7450 2.4670第4次迭代:与上次计算结累的距离;0.564600 -3.9914 2.6275 2.0347第5次迭代;与上次计算结果的距离:0?357300 -3. 8579 2.9848 1.8865与上次计算结果的距⾼:0?1 13286 -3.9712 3.0922 1.9670第13次迭代:与上次计算结果的距^:0. 001023 -4.0002 2.99922.0002第14次迭代:与上次计算结果的距离;0?000626 -3.9997 2.99981.9998第15次迭代:与上次计算结果的距离:0. 000341 -3.9999 3.00021.9999第16次迭代:与上次计茸结果的距离:0. 000155 -4.0000 3.00012.0000第订次迭代;与上次计算结果的距离:o. 000106 ?4.0000 3.00002.0000第18次迭代:与上次计算结果的距离:0. 000041 -4.0000 3.00032.0000第;次迭代:与上次计算结果的距离:0. 068570 -4. 0303 3.0237 2.0219第8次迭代:与上次计算结果的匪离;0. 042216 -4.0139 2.9815 2.0132第9次迭代:与上次计算结果的距离:0. 018637 -3.9952 2.9900 1.9972第10次迭代:与上次计算结果的范离:0. 0L2637 -3. 9954 3.0026 1.9960第⼝次迭代:与上次计算结果的徒离:0. 004819 -4.0002 3. 0031 1.9999第12次迭代;与上次计聲结果的施禹:0. 003121 -£ 0012 3.0000 2.0010第19次迭代:与上次计算结果的昵离:3. 000027 -4.0000 3.0000 2.0000第如次迭代;与上次i+算结果的柜胡:3. 000009 -4.0000 3.0000 2.0000第21次迭代:与上次i+算结果的距韶:1 000006 -4.0000 3.0000 2.0000錮22次送代:与上次计算结果的捱离:1 000003 ?4.0000 3.0000 2.0000第23次迭代:与上次计算结果的距离:3. OOOOOL-4.0000 3.0000 2.0000籠加次逑代:与上次计算结果的拒离:3. OOOOOL -4.0000 3.0000 2.0000 Gauss-Seidel 迭代法:SJ?%A=[8r14;240,01;14z-5];%b=[l;4;3];A=[5,24;-l/4,2;2,-340];b=[-12;20;3];m=size(A);if m(l)r'=m(2) errorC矩阵A不是⽅阵J;endn=length(b);%初始化N=0,%迭代次数L=zeros(n)^6分解A=D+L+U,D是对⾓阵,L是下三⾓阵,U是上三⾓阵U=zeros(n); D=zeros(n);G=zeros(n)^6G=-inv(D+L)*Ud=zeros(n/l)56d=inv(D+L)w,bx=zeros(n4);for i=l:n%初始化L和Uforj=l:nif iL(iJ)=A(iJ);endif i>jU(iJ)=A(iJ);endendendfori=l:n%初始化 DD(iJ)=A(iJ);endG=-inv(D+L)*U^6初始化Gd=(D+L)\b56初始化 d%迭代开始xl=x;x2=G*x+d;while norm(x2-xljnf)>10A(-6)。
3.2Jacobi迭代法和Gauss-Seidel迭代法.

步骤1 输入系数矩阵A,右端向量b,以及初始向量 x0 ,
精度 , 最大迭代次数 N .令 k 1.
步骤2 当k N时,执行步骤2.1 2.2.
步骤2.1 对i 1, 2, , n,计算
x k 1 i
1 aii
n
aij xkj
j1, ji
bi
.
aii 0 (i 1, 2, , n)
下面考虑一般的情形:
Ax b,
(3.2.1)
其中A是n阶非奇异矩阵. 且其主对角元素 aii 0 (i 1, 2, , n).
方程组(3.2.1)的分量形式为
n
aij x j bi , i 1, 2, , n.
j 1
因aii 0, 所以有
卡尔.雅可比
以上迭代法称为Jacobi迭代法.
卡尔 雅可比(Carl Gustav Jacobi, 1804--1851) 是一位德国数学家. 1804年生于波茨坦.
Jacobi是历史上最伟大的数学家之一,他在数学 方面的突出成就是和挪威数学家 Abel 相互独立地奠 定了椭圆函数论的基础.Jacobi的工作还包括代数学、 变分法、复变函数论、微分方程和数学史等方面. Jacobi 在数值计算方面的主要贡献是提出求解线性方程组的 迭代法以及求解矩阵的特征值和特征向量的方法等.
计算结果见下表:
k
x1k
00
x2k
x3k
0
0
k
x1k
x2k
x3k
3 0.9950 0.9850 0.9900
1 0.9000 0.7000 0.8000 4 0.9985 0.9975 0.9970
jacobi迭代法和Gauss-Seidel迭代法

数值计算方法实验报告(五)班级:地信10801 序号:姓名:一、实验题目:jacobi迭代法和Gauss-Seidel迭代法二、实验学时: 2学时三、实验目的和要求:1.掌握迭代法的基础原理。
2.掌握jacobi迭代法和Gauss-Seidel迭代法的步骤。
3.能用程序语言对jacobi迭代法和Gauss-Seidel迭代法进行编程实现。
四、实验过程代码及结果1、代码:#include<iostream.h>#include<math.h>float x[100],xk[100];float e;int N,M=1000;float a[100][101];void initdata(){cout<<"输入方程阶数:";cin>>N;cout<<"输入误差限e:";cin>>e;cout<<"输入方程系数:"<<endl;for(int i=1;i<=N;i++)for(int j=1;j<=N+1;j++)cin>>a[i][j];cout<<"输入初始解向量x0:"<<endl;for(i=1;i<=N;i++)cin>>xk[i];}void jocobi(){int Nx=0,times=0;while(Nx<N){times++; Nx=0;if(times>=M){cout<<"发散"<<endl; break;}for(int i=1;i<=N;i++){float sum=0;for(int j=1;j<=N;j++)if(i!=j)sum+=xk[j]*a[i][j];x[i]=(a[i][N+1]-sum)/a[i][i];if(fabs(x[i]-xk[i])<e)Nx++;}for(i=1;i<=N;i++)xk[i]=x[i];}cout<<"times="<<times<<endl;for(int i=1;i<=N;i++)cout<<"x["<<i<<"]="<<x[i]<<endl;}void guass_seidel(){int Nx=0,times=0;while(Nx<N){times++;Nx=0;if(times>=M){cout<<"发散"<<endl;break;}for(int i=1;i<=N;i++){float sum1=0;float sum2=0;for( int j=i+1;j<=N;j++){sum1+=xk[j]*a[i][j];}for( j=1;j<=i-1;j++){sum2+=a[i][j]*xk[j];}x[i]=(a[i][N+1]-sum1-sum2)/a[i][i];if(fabs(x[i]-xk[i])<e)Nx++;}for(i=1;i<=N;i++)xk[i]=x[i];}cout<<"times="<<times<<endl;for(int i=1;i<=N;i++)cout<<"x["<<i<<"]="<<x[i]<<endl;}void main(){char ch;initdata();cout<<"请选择解方程的方法:\n";cout<<"A:jocobi B:guass_seidel \n";cin>>ch;if(ch=='A')jocobi();else if(ch=='B')guass_seidel();}2.结果:欢迎您的下载,资料仅供参考!。
实验4 Jacobi迭代法和GS迭代2

实验题目 1. Jacobi 迭代法用Jacobi 迭代法求解线性方程组AX b =,保留四位有效数字(err =1e-4),其中A=[8 -1 1;2 10 -1;1 1 -5]; b=[1 ;4; 3]。
2.Gauss-Seidel 迭代法用Gauss-Seidel 迭代法求解线性方程组AX b =,保留四位有效数字(err =1e-4),其中A=[8 -1 1;2 10 -1;1 1 -5]; b=[1 ;4; 3]。
3.分别用Jacobi 迭代法和Gauss-Seidel 迭代法求解方程组12345641010001410105014001010041060101412010146x x x x x x ⎡⎤--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦⎣⎦ 要求精度0.00001ε=,初始00=x ,最大迭代次数N=25,试比较这几种迭代法的迭代次数和收敛速度。
1.程序: #include<math.h> #include<stdio.h> int main(){int n=3,i,k,j,mm=1000;//最大迭代次数; float t,x[mm][n],dx[n],dx_max=1,err=1e-4;//精度 for(i=0;i<n;i++) x[0][i]=0;float a[3][3]={8,-1,1,2,10,-1,1,1,-5}; float b[3]={1,4,3}; for(i=0;i<n;i++){ b[i]=b[i]/a[i][i]; }for(i=0;i<n;i++){ for(j=0;j<n;j++) if(j!=i)a[i][j]=a[i][j]/a[i][i];a[i][i]=0;}printf("精度1e-4时,解x'[%d]=\n",n); for(k=0;dx_max>1e-8;k++){dx_max=0;for(i=0;i<n;i++){t=0;for(j=0;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;printf("%0.4f ",x[k+1][i]);dx[i]=x[k+1][i]-x[k][i];dx_max+=pow(dx[i],2);}printf(" %d",k+1);printf("\n");} printf("\n");}程序结果:精度1e-4时,解x'[3]=0.1250 0.4000 -0.6000 10.2500 0.3150 -0.4950 20.2262 0.3005 -0.4870 30.2234 0.3061 -0.4947 40.2251 0.3058 -0.4941 50.2250 0.3056 -0.4938 60.2249 0.3056 -0.4939 70.2249 0.3056 -0.4939 82.程序:#include<math.h>#include<stdio.h>int main(){int n=3,i,k,j,mm=1000;//最大迭代次数;float t,x[mm][n],dx[n],dx_max=1,err=1e-4;//精度for(i=0;i<n;i++)x[0][i]=0;float a[3][3]={8,-1,1,2,10,-1,1,1,-5};float b[3]={1,4,3};for(i=0;i<n;i++){b[i]=b[i]/a[i][i];}for(i=0;i<n;i++){for(j=0;j<n;j++)if(j!=i)a[i][j]=a[i][j]/a[i][i];a[i][i]=0;}printf("精度1e-4时,解x'[%d]=\n",n);for(k=0;dx_max>1e-8;k++){dx_max=0;for(i=0;i<n;i++){if(i==0){t=0;for(j=i+1;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;}else{t=0;for(j=0;j<=i-1;j++)t+=a[i][j]*x[k+1][j];for(j=i+1;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;}printf("%0.4f ",x[k+1][i]);dx[i]=x[k+1][i]-x[k][i];dx_max+=pow(dx[i],2);}printf("\n");} printf("\n");}程序结果:精度1e-4时,解x'[3]=0.1250 0.3750 -0.50000.2344 0.3031 -0.49250.2245 0.3059 -0.49390.2250 0.3056 -0.49390.2249 0.3056 -0.49393.Jacobi迭代法程序:#include<math.h>#include<stdio.h>int main(){int n=6,i,k,j,mm=1000;//最大迭代次数;float t,x[mm][n],dx[n],dx_max=1,err=1e-5;//精度for(i=0;i<n;i++)x[0][i]=0;float a[6][6]={4,-1,0,-1,0,0,-1,4,-1,0,-1,0,0 ,-1 ,4 ,0 ,0 ,-1,-1, 0, 0 ,4 ,-1 ,0, 0 ,-1 ,0 ,-1, 4 ,-1,0 ,0 ,-1, 0, -1 ,4};float b[6]={0 ,5 ,0 ,6 ,-2, 6};for(i=0;i<n;i++){b[i]=b[i]/a[i][i];}for(i=0;i<n;i++){for(j=0;j<n;j++)if(j!=i)a[i][j]=a[i][j]/a[i][i];a[i][i]=0;}printf("精度1e-4时,解x'[%d]=\n",n);for(k=0;dx_max>pow(err,2);k++){dx_max=0;for(i=0;i<n;i++){t=0;for(j=0;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;printf("%0.4f ",x[k+1][i]);dx[i]=x[k+1][i]-x[k][i];dx_max+=pow(dx[i],2);}printf(" %d",k+1);printf("\n");} printf("\n");}程序结果:a的对角变0处理后的(a[6][6],b[6])=0.0000 -0.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 -0.2500 0.0000 1.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 1.5000 0.0000 -0.2500 0.0000 -0.2500 0.0000 -0.2500 -0.5000 0.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 1.5000 精度1e-005时,解x'[6]=0.0000 1.2500 0.0000 1.5000 -0.5000 1.5000 1 0.6875 1.1250 0.6875 1.3750 0.5625 1.3750 20.6250 1.7344 0.6250 1.8125 0.4688 1.8125 30.8867 1.6797 0.8867 1.7734 0.8398 1.7734 40.8633 1.9033 0.8633 1.9316 0.8066 1.9316 50.9587 1.8833 0.9587 1.9175 0.9417 1.9175 60.9502 1.9648 0.9502 1.9751 0.9296 1.9751 70.9850 1.9575 0.9850 1.9699 0.9787 1.9699 80.9819 1.9872 0.9819 1.9909 0.9743 1.9909 90.9945 1.9845 0.9945 1.9890 0.9923 1.9890 100.9934 1.9953 0.9934 1.9967 0.9907 1.9967 110.9980 1.9944 0.9980 1.9960 0.9972 1.9960 120.9976 1.9983 0.9976 1.9988 0.9966 1.9988 130.9993 1.9979 0.9993 1.9985 0.9990 1.9985 140.9991 1.9994 0.9991 1.9996 0.9988 1.9996 150.9997 1.9993 0.9997 1.9995 0.9996 1.9995 160.9997 1.9998 0.9997 1.9998 0.9995 1.9998 170.9999 1.9997 0.9999 1.9998 0.9999 1.9998 180.9999 1.9999 0.9999 1.9999 0.9998 1.9999 191.0000 1.9999 1.0000 1.9999 1.0000 1.9999 201.00002.0000 1.0000 2.0000 0.9999 2.0000 211.00002.0000 1.0000 2.0000 1.0000 2.0000 221.00002.0000 1.0000 2.0000 1.0000 2.0000 231.00002.0000 1.0000 2.0000 1.0000 2.0000 241.00002.0000 1.0000 2.0000 1.0000 2.0000 25Gauss-Seidel迭代法程序:#include<math.h>#include<stdio.h>int main(){int n=6,i,k,j,mm=25;//最大迭代次数;float t,x[mm][n],dx[n],dx_max=1,err=1e-5;//精度for(i=0;i<n;i++)x[0][i]=0;float a[6][6]={4,-1,0,-1,0,0,-1,4,-1,0,-1,0,0 ,-1 ,4 ,0 ,0 ,-1,-1, 0, 0 ,4 ,-1 ,0, 0 ,-1 ,0 ,-1, 4 ,-1,0 ,0 ,-1, 0, -1 ,4};float b[6]={0 ,5 ,0 ,6 ,-2, 6};for(i=0;i<n;i++){b[i]=b[i]/a[i][i];}for(i=0;i<n;i++){for(j=0;j<n;j++)if(j!=i)a[i][j]=a[i][j]/a[i][i];a[i][i]=0;}printf("精度1e-4时,解x'[%d]=\n",n);for(k=0;dx_max>pow(err,2)&&k<mm;k++){dx_max=0;for(i=0;i<n;i++){if(i==0){t=0;for(j=i+1;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;}else{t=0;for(j=0;j<=i-1;j++)t+=a[i][j]*x[k+1][j];for(j=i+1;j<n;j++)t+=a[i][j]*x[k][j];x[k+1][i]=b[i]-t;}printf("%0.4f ",x[k+1][i]);dx[i]=x[k+1][i]-x[k][i];dx_max+=pow(dx[i],2);}printf(" %d\n",k+1);} printf("\n");}程序结果:a对角0化处理后的(a[6][6],b[6][1])=0.0000 -0.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 -0.2500 0.0000 1.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 0.0000 0.0000 -0.2500 0.0000 1.5000 0.0000 -0.2500 0.0000 -0.2500 0.0000 -0.2500 -0.50000.0000 0.0000 -0.2500 0.0000 -0.2500 0.0000 1.5000精度1e-005时,解x'[6]=0.0000 1.2500 0.3125 1.5000 0.1875 1.6250 1 0.6875 1.5469 0.7930 1.7188 0.7227 1.8789 2 0.8164 1.8330 0.9280 1.8848 0.8992 1.9568 3 0.9294 1.9391 0.9740 1.9572 0.9633 1.9843 4 0.9741 1.9778 0.9905 1.9843 0.9866 1.9943 5 0.9905 1.9919 0.9966 1.9943 0.9951 1.9979 6 0.9966 1.9971 0.9987 1.9979 0.9982 1.9992 7 0.9987 1.9989 0.9995 1.9992 0.9994 1.9997 8 0.9995 1.9996 0.9998 1.9997 0.9998 1.9999 9 0.9998 1.9999 0.9999 1.9999 0.9999 2.0000 100.9999 1.9999 1.0000 2.0000 1.0000 2.0000 111.00002.0000 1.0000 2.0000 1.0000 2.0000 12 1.0000 2.0000 1.0000 2.0000 1.0000 2.0000 13 1.0000 2.0000 1.0000 2.0000 1.0000 2.0000 14。
数值研究分析5-用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组

数值分析5-用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组————————————————————————————————作者:————————————————————————————————日期:作业六:分别编写用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组Ax=B的标准程序,并求下列方程组的解。
可取初始向量X(0) =(0,0,0)’;迭代终止条件||x(k+1)-x(k)||<=10e-6(1)[8 −1 12 10 −11 1 −5][x1x2x3]=[143](2)[5 2 1−1 4 22 −3 10][x1x2x3]=[−12203]Jacobi迭代法:流程图开判断b中的最大值有没给x赋初值进行迭代结求出x,弱到100次还程序clear;clc;A=[8,-1,1;2,10,01;1,1,-5];b=[1;4;3];e=1e-6;x0=[0;0;0]';n=length(A);x=zeros(n,1);k=0;r=max(abs(b));while r>efor i=1:nd=A(i,i);if abs(d)<ewarning('矩阵A输入有误');return;endsum=0;for j=1:nif j~=isum=sum+A(i,j)*x0(j);endendx1(i)=(b(i)-sum)/A(i,i);endk=k+1;r=max(abs(x1-x0));x0=x1;fprintf('第%d次迭代:',k)fprintf('\n与上次计算结果的距离:%f \n',r)disp(x1);if k>100warning('不收敛');endendx=x0;程序结果(1)(2)Gauss-Seidel迭代法:程序clear;clc;%A=[8,-1,1;2,10,01;1,1,-5];%b=[1;4;3];A=[5,2,1;-1,4,2;2,-3,10];b=[-12;20;3];m=size(A);if m(1)~=m(2)error('矩阵A不是方阵');endn=length(b);%初始化N=0;%迭代次数L=zeros(n);%分解A=D+L+U,D是对角阵,L是下三角阵,U是上三角阵U=zeros(n);D=zeros(n);G=zeros(n);%G=-inv(D+L)*Ud=zeros(n,1);%d=inv(D+L)*bx=zeros(n,1);for i=1:n%初始化L和Ufor j=1:nif i<jL(i,j)=A(i,j);endif i>jU(i,j)=A(i,j);endendendfor i=1:n%初始化DD(i,i)=A(i,i);endG=-inv(D+L)*U;%初始化Gd=(D+L)\b;%初始化d%迭代开始x1=x;x2=G*x+d;while norm(x2-x1,inf)>10^(-6)x1=x2;x2=G*x2+d;N=N+1;endx=x2;程序结果(1)(2)。
Jacobi迭代法和Gauss-Seidel迭代法解线性方程组

实验四线性方程组的迭代解法一、实验目的(1) 学会用Jacobi迭代法、Gauss- Seidel迭代法和超松弛迭代法求线性方程组解(2) 学会对各种迭代法作收敛性分析,研究求方程组解的最优迭代方法.(3) 按照题目要求完成实验内容,写出相应的Matlab程序,给出实验结果.(4) 对实验结果进行分析讨论.(5) 写出相应的实验报告.二、实验内容1.熟悉Jacobi迭代法,并编写Matlab程序matlab程序按照算法(Jacobi迭代法)编写Matlab程序(Jacobi.m)function [x,k,index]=Jacobi(A,b,ep,it_max)if nargin<4it_max=100;endif nargin<3ep=1e-5;endn=length(A);k=0;x=zeros(n,1);y=x;index=1;while 1for i=1:ny(i)=b(i);for j=1:nif j~=iy(i)=y(i)-A(i,j)*x(j);endendif abs(A(i,i))<1e-10||k==it_maxindex=0;return;endy(i)=y(i)/A(i,i);endif norm(y-x,inf)<ep;break;endx=y;k=k+1;end2. 熟悉Gauss-Seidel 迭代法,并编写Matlab 程序3.练习练习题1. 用Jacobi 迭代法求方程组123430243313001424x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦的解。
练习题2. 用Gauss-Seidel 迭代法求解上题的线性方程组,取(0)5(0,0,0),10T x ε-==。
function [x,k,index]=Gauss_Seidel(A,b,ep,it_max) if nargin<4it_max=100;endif nargin<3ep=1e-5;endn=length(A);k=0;x=zeros(n,1);y=x;y1=y;index=1;while 1for i=1:ny(i)=b(i);for j=1:nif j>iy(i)=y(i)-A(i,j)*y1(j);endif j<iy(i)=y(i)-A(i,j)*x(j);endendif abs(A(i,i))<1e-10||k==it_maxindex=0;return ;endy(i)=y(i)/A(i,i);y1(i)=y(i);endif norm(y-x,inf)<ep;break ;endx=y;k=k+1;end三、实验要求要求在实验前必须预习,将实验内容事先准备好,否则不允许上机。
Jacobi迭代法_Gauss-Seidel迭代法

Matlab线性方程组的迭代解法(Jacobi迭代法Gauss-Seidel迭代法)实验报告2008年11月09日星期日12:49Jacobi迭代法,并编写Matlab程序matlab程序按照算法(Jacobi迭代法)编写Matlab程序(Jacobi.m)function [x, k, index]=Jacobi(A, b, ep, it_max)%求解线性方程组的Jacobi迭代法,其中% A ---方程组的系数矩阵% b ---方程组的右端项% ep ---精度要求。
省缺为1e-5% it_max ---最大迭代次数,省缺为100% x ---方程组的解% k ---迭代次数% index --- index=1表示迭代收敛到指定要求;% index=0表示迭代失败if nargin <4 it_max=100; endif nargin <3 ep=1e-5; endn=length(A); k=0;x=zeros(n,1); y=zeros(n,1); index=1;while 1for i=1:ny(i)=b(i);for j=1:nif j~=iy(i)=y(i)-A(i,j)*x(j);endendif abs(A(i,i))<1e-10 | k==it_maxindex=0; return;endy(i)=y(i)/A(i,i);endif norm(y-x,inf)<epbreak;endx=y; k=k+1;end用Jacobi迭代法求方程组的解。
输入:A=[4 3 0;3 3 -1;0 -1 4];b=[24;30;-24];[x, k, index]=Jacobi(A, b, 1e-5, 100)输出:x =k =100index =Gauss-Seidel迭代法,并编写Matlab程序function [v,sN,vChain]=gaussSeidel(A,b,x0,errorBound,maxSp)%Gauss-Seidel迭代法求解线性方程组%A-系数矩阵b-右端向量x0-初始迭代点errorBound-近似精度maxSp-最大迭代次数%v-近似解sN-迭代次数vChain-迭代过程的所有值step=0;error=inf;s=size(A);D=zeros(s(1));vChain=zeros(15,3);%最多能记录15次迭代次数k=1;fx0=x0;for i=1:s(1)D(i,i)=A(i,i);end;L=-tril(A,-1);U=-triu(A,1);while error>=errorBound & step<maxSpx0=inv(D)*(L+U)*x0+inv(D)*b;vChain(k,:)=x0';k=k+1;error=norm(x0-fx0);fx0=x0;step=step+1;endv=x0;sN=step;用Gauss-Seidel迭代法求解上题的线性方程组,取。
计算物理学:第二章 方程的数值解法 3 Jacobi和Gauss-Seidel迭代法

0 0
⎪ ⎩
x30
=
0
⎧ ⎪
x11
⎪
=
b1 a11
⎪ ⎨ x21 ⎪
=
b2 a22
⎪ ⎪ x31 ⎩
=
b3 a33
j-1:上一步迭代 j:当前迭代
xij
−
x j−1 i
xij
×100% ≤ ε
ε = 10−4 ,ε = 10−6 ,ε = 10−8
§2.1.4 迭代解法/*Iterative Method */
迭代法是一种逐次逼近的方法,与直接法比较, 具有: 程序简单,存储量小的优点。特别适用于求解系数 矩阵为大型稀疏矩阵 的方程组
优点
1. 迭代公式的构造
¾迭代法的一般迭代格式:
x(k +1) = Fk ( x(k ) ) k = 0,1,L
如果Fk 是线性的,称之为线性迭代法,即
x(k +1) = gk x(k ) + dk k = 0,1,L
−
x3(k ) ) 10
Jacobi
迭 代 格
x(k +1) 2
=
(−5 −
2 x1(k )
− 3x3(k ) ) (−10)
式
x(k +1) 3
=
(14 −
x(k) 1
− 3x2(k ) ) 10
二、 Gauss-Seidel迭代法
在J迭代公式中,计算
x
( i
k
+
1时) ,利用已经算出来的新的
x1( k
则方程组化为 (M − N )x = b
⇒ x = M −1Nx + M −1b
⇒ x = gx + d
雅克比迭代法和高斯-塞德尔迭代法

一、 向量范数
定义:设 f ( x是) Rn的一R个映射,若对
x Rn
存在唯一实数 x与之对应,且满足
非负性: x 0,x Rn 且 x 0 x 0
❖齐次性: x x ,x Rn , R
三角不等性:x y x y , x, y Rn
则称 x为 中Rn向量 的x范数。
A Rnn,存在唯一实数 A与之对应,且满足
非负性:A 0,A Rnn且 A 0 A 0
❖齐次性: A A , A Rnn , R
三角不等性: A B A B , A, B Rnn AB A B A, B Rnn
则称 A为 R中n矩n 阵 的范A数。
➢常用的几种矩阵范数: 记 A (aij )nn
非负实值 函数
➢常用的几种向量范数:
n
设
x
( x1,
x2 ,
, xn )T
1-范数: x 1
xi
i 1
❖ 2-范数:
n
x ( 2
xi2
)
1 2
(x, x)i 1 Nhomakorabea-范数:
x
max
1 i n
xi
上述3种向量范数统称为P-范数
n
x ( p
xi p ) 1 p
1 p
i 1
二、 矩阵范数
定义:设 f ( A是) Rnn的一个R映射,若对
x3(k ) ) 10
x ( k 1) 2
(5
2 x1(k1)
3x3(k) ) (10)
x ( k 1) 3
(14
x ( k 1) 1
3x2(k1) ) 10
雅克比迭代法 取初值 x (0 0 0)T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级:地信10801序号:姓名:
一、实验题目:jacobi迭代法和Gauss-Seidel迭代法
二、实验学时: 2学时
三、实验目的和要求:
1.掌握迭代法的基础原理。
2.掌握jacobi迭代法和Gauss-Seidel迭代法的步骤。
3.能用程序语言对jacobi迭代法和Gauss-Seidel迭代法进行编程实现。
cout<<"x["<<i<<"]="<<x[i]<<endl;
}
void guass_seidel()
{
int Nx=0,times=0;
while(Nx<N)
{
times++;
Nx=0;
if(times>=M)
{
cout<<"发散"<<endl;
break;
}
for(int i=1;i<=N;i++)
四、实验过程代码及结果
1、代码:
#include<iostream.h>
#include<math.h>
float x[100],xk[100];
float e;
int N,M=1000;
float a[100][101];
void t;"输入方程阶数:";
cin>>N;
cout<<"输入误差限e:";
cin>>e;
cout<<"输入方程系数:"<<endl;
for(int i=1;i<=N;i++)
for(int j=1;j<=N+1;j++)
cin>>a[i][j];
cout<<"输入初始解向量x0:"<<endl;
for(i=1;i<=N;i++)cin>>xk[i];
if(i!=j)sum+=xk[j]*a[i][j];
x[i]=(a[i][N+1]-sum)/a[i][i];
if(fabs(x[i]-xk[i])<e)Nx++;
}
for(i=1;i<=N;i++)xk[i]=x[i];
}
cout<<"times="<<times<<endl;
for(int i=1;i<=N;i++)
{
char ch;
initdata();
cout<<"请选择解方程的方法:\n";
cout<<"A:jocobi B:guass_seidel \n";
cin>>ch;
if(ch=='A')
jocobi();
else if(ch=='B')
guass_seidel();
}
2.结果:
}
void jocobi()
{
int Nx=0,times=0;
while(Nx<N)
{
times++; Nx=0;
if(times>=M){cout<<"发散"<<endl; break;}
for(int i=1;i<=N;i++)
{
float sum=0;
for(int j=1;j<=N;j++)
if(fabs(x[i]-xk[i])<e)
Nx++;
}
for(i=1;i<=N;i++)xk[i]=x[i];
}
cout<<"times="<<times<<endl;
for(int i=1;i<=N;i++)
cout<<"x["<<i<<"]="<<x[i]<<endl;
}
void main()
{
float sum1=0;
float sum2=0;
for( int j=i+1;j<=N;j++)
{sum1+=xk[j]*a[i][j];}
for( j=1;j<=i-1;j++)
{sum2+=a[i][j]*xk[j];}
x[i]=(a[i][N+1]-sum1-sum2)/a[i][i];
