2017年小学数学竞赛决赛试题及答案
加拿大国家中小学数学竞赛( kangaroo math 袋鼠竞赛)2017年五六年级(含答案)

I N T ER N A T I ON A L CO N T E S T-GA M EM A TH KA N GA RO OC A N A DA, 2017INSTRUCTIONSGRADE 5-61.You have 75 minutes to solve 30 multiple choice problems. For each problem, circle onlyone of the proposed five choices. If you circle more than one choice, your response will be marked as wrong.2.Record your answers in the response form. Remember that this is the only sheet that ismarked, so make sure you have all your answers transferred here by the end of the contest.3.The problems are arranged in three groups. A correct answer of the first 10 problems isworth 3 points. A correct answer of problems 11-20 is worth 4 points. A correct answer of problems 21-30 is worth 5 points. For each incorrect answer, one point is deducted from your score. Each unanswered question is worth 0 points. To avoid negative scores, you start from 30 points. The maximum score possible is 150.4.Calculators and graph paper are not permitted. You are allowed to use rough paper for draftwork.5.The figures are not drawn to scale. They should be used only for illustration.6.Remember, you have about 2-3 minutes for each problem; hence, if a problem appears tobe too difficult, save it for later and move on to the other problems.7.At the end of the allotted time, please submit the response form to the contest supervisor.Please do not forget to pick up your Certificate of Participation!Good luck! Canadian Math Kangaroo Contest team2017 CMKC locations: Algoma University; Bishop's University; Brandon University; Brock University; Carlton University; Concordia University; Concordia University of Edmonton; Coquitlam City Library; Dalhousie University; Evergreen Park School; F.H. Sherman Recreation & Learning Centre; GAD Elementary School; Grande Prairie Regional College; Humber College; Lakehead University (Orillia and Thunder Bay); Laurentian University; MacEwan University; Memorial University of Newfoundland; Mount Allison University; Mount Royal University; Nipissing University; St. Mary’s University (Calgary); St. Peter’s College; The Renert School at Royal Vista; Trent University; University of Alberta-Augustana Campus; University of British Columbia (Okanagan); University of Guelph; University of Lethbridge; University of New Brunswick; University of Prince Edward Island; University of Quebec at Chicoutimi; University of Quebec at Rimouski; University of Regina; University of Toronto Mississauga; University of Toronto Scarborough; University of Toronto St. George; University of Windsor; The University of Western Ontario; University of Winnipeg; Vancouver Island University; Walter Murray Collegiate, Wilfrid Laurier University; YES Education Centre; York University; Yukon College.2017 CMKC supporters: Laurentian University; Canadian Mathematical Society; IEEE; PIMS.Canadian Math Kangaroo ContestPart A: Each correct answer is worth 3 points1.A fly has 6 legs, a spider has 8 legs. Together, 3 flies and 2 spiders have as many legs as 9 chickens andseveral cats. How many cats are there?(A) 2 cats (B) 3 cats (C) 4 cats (D) 5 cats (E) 6 cats2.Alice has 4 pieces of this shape: . Which picture can she not make from these four pieces?(A) (B) (C)(D) (E)3.Kalle knows that 1111 × 1111 = 1234321. What is the answer of 1111 × 2222?(A) 3456543 (B) 2346642 (C)2457642 (D) 2468642 (E) 43212344.There are 10 islands and 12 bridges, as depicted in the figure. All bridgesare open for traffic right now. What is the smallest number of bridges thatmust be closed in order to stop the traffic between A and B?(A) 1 (B) 2 (C) 3 (D) 4 (E) 55.Martin wants to colour the squares of the rectangle so that 1/3 of allsquares are blue and half of all squares are yellow. The rest of the squaresare to be coloured red.How many squares will he colour red?(A) 1 (B) 2 (C) 3 (D) 4 (E) 56.When the car wheels make one full rotation the car moves forward by about 1.8 meters. Approximatelyhow many kilometres will the car move forward after 10,000 full rotations of the wheels?(A) 1.8 (B) 18 (C) 180 (D) 1 800 (E) 18 0007.There are 32 students in Mrs. Vicky’s class. Part of the students took one pencil each from the box withpencils on the teacher’s desk. Then a third of the remaining students took 3 pencils each, and there were no more pencils left in the box. How many pencils were there in the box at first?(A) 16 (B) 24 (C) 32 (D) 43 (E) 648.Three rhinoceroses Jane, Kate and Lynn go for a walk: Jane first, Kate in the middle, and Lynn – last. Janeweighs 500 kg more than Kate. Kate weighs 1000 kg less than Lynn. Which of the following pictures may show Jane, Kate and Lynn in the order they walked?(A) (B)(C) (D)(E)9.Peter and Nick are both working on "Kangaroo" contest problems. For every two problems that Petersolves, Nick manages to solve three problems. In total, the boys solved 30 problems. How many problems did Nick solve more than Peter?(A) 5 (B) 6 (C) 7 (D) 8 (E) 910.Bob folded a piece of paper, used a hole puncher and punched exactly one hole in the folded paper.Then, he unfolded the piece of paper, which looked as shown below.Which of the following pictures shows the lines along which Bob folded the piece of paper?(A) (B) (C) (D) (E)Part B: Each correct answer is worth 4 points11.A special die has a number on each of its six faces. The sums of the numbers on opposite faces are all equal. Five of the numbers are 5, 6, 9, 11 and 14. What number is on the sixth face? (A) 4 (B) 7 (C) 8 (D) 13 (E) 15 12.Tom wrote all the numbers from 1 to 20 in a row and obtained the 31‐digit number1234567891011121314151617181920.Then he deleted 24 of the 31 digits, so that the remaining number was as large as possible. Which number was it? (A) 9671819 (B) 9567892 (C) 9781920 (D) 9912345 (E) 981819213.Peter went hiking in the mountains for 5 days. He started on Monday and his last trip was on Friday. Each day he walked 2km more than the day before. The total distance he walked during the five days was 70km. What distance did Peter walk on Thursday? (A) 12 km (B) 13 km (C) 14 km (D) 15 km (E) 16 km14.In a chocolate store, one chocolate costs $3. One day the store had a deal: “Buy two and get a third one free” and Adam decided to take 49 chocolates. How much did he pay for the chocolates? (A) $75 (B) $98 (C) $99 (D) $102 (E) $14715.Eight kangaroos stood in a line as shown in the diagram.At some point, two kangaroos standing side by side and facing each other exchanged places by jumping past each other. This was repeated until no further jumps were possible. How many exchanges were made? (A) 2 (B) 10 (C) 12 (D) 13 (E) 1616.The Modern Furniture store is selling sofas, loveseats, and chairs made from identical modular pieces as shown in the picture. Including the armrests, the width of the sofa is 220 cm and the width of the loveseat is 160 cm.What is the width of the chair? (A) 60 cm (B) 80 cm (C) 90 cm(D) 100 cm(E) 120 cmsofa loveseatchair220 cm160cm17.There are five padlocks and 5 keys – one for each of them (see the figure). The number code on each key has been modified into a letter code on the corresponding padlock. Equal digits have been replaced by the same letter, and different digits – by different letters. What is the number code on the fifth key?(A) 382(B) 282 (C) 284 (D) 823 (E) 82418.Boris has an amount of money and three magic wands that he can use only once. Wand A adds $1. Wand S subtracts $1. Wand D doubles the amount. In which order must he use these wands to obtain the largest amount of money? (A) DAS (B) ASD (C) DSA (D) ADS (E) SAD19.A vase weighs 600 g when one third of it is filled with water. The same vase weighs 800 g when two thirds of it are filled with water. What is the weight of the vase when it is empty? (A) 100 g (B) 200 g (C) 300 g (D) 400 g (E) 500 g20.Rafael has three squares. The first one has side length 2 cm. The second one has side length 4 cm and a vertex is placed in the centre of the first square. The last one has side length 6 cm and a vertex is placed in the centre of the second square, as shown in the picture. What is the area of the figure? (A) 32 cm 2 (B) 51 cm 2 (C) 27 cm 2 (D) 16 cm 2 (E) 6 cm 2Part C: Each correct answer is worth 5 points21.The natural numbers are arranged in the form of a triangle: 1 is in the first row, 2 and 3 are in the second row, 4, 5 and 6 are in the third row, and so on. What is the sum of the numbers written in the 10‐th row?(A) 490(B) 495 (C) 500(D) 505 (E) 5101 2 3 456.. .22.There are eight balls numbered with the numbers 40, 80, 100, 101, 190, 200, 260 and 292 in a bag.Martina takes four balls out of the bag and calculates the sum of the numbers on these balls. It appears that this sum is half of the sum of the numbers on the balls that remain in the bag. What is the greatest number written on the balls taken out?(A) 101 (B) 200 (C) 260 (D) 190 (E) 29223.The structure on the figure is made of unit cubes glued together. Morten wants toput it into a rectangular box. What are the dimensions (length, width and height)of the smallest box he can use?(A) 3 × 3 × 4 (B) 3 × 5 × 5 (C) 3 × 4 × 5 (D) 4 × 4 × 4 (E) 4 × 4 × 524.Four players scored goals in a handball game. All of them scored a different number of goals. One of theplayers, Mike, scored the least number of goals. The other three players scored 20 goals in total. What is the largest number of goals Mike could have scored?(A) 2 (B) 3 (C) 4 (D) 5 (E) 625.Ala likes even numbers, Beata likes numbers divisible by 3, Celina likes numbers divisible by 5. Each ofthese three girls went separately to a basket containing 8 balls with numbers written on them, and took all the balls with numbers she liked. It turned out that Ala collected balls with numbers 32 and 52, Beata ‐ 24,33 and 45, Celina ‐ 20, 25 and 35. In what order did the girls approach the basket?(A) Ala, Celina, Beata (B) Celina, Beata, Ala (C) Beata, Ala, Celina(D) Beata, Celina, Ala (E) Celina, Ala, Beata26.The picture of a kangaroo in the first (leftmost) triangle was reflected across the dotted lines, as in mirrors.The first two reflections are shown.What does the reflection look like in the shaded triangle?(A) (B) (C) (D) (E)27.The numbers 1, 2, 3, 4, and 5 must be written in the five cells in the figure, respecting the following rules:-If a number is just below another number, it must be greater.-If a number is just to the right of another number, it must be greater.In how many ways can this be done?(A) 3 (B) 4 (C) 5 (D) 6 (E) 828.John wrote a natural number in each of the four boxes in the bottom row of the diagram. Then he wrote ineach of the other boxes the sum of the two numbers in the boxes immediately underneath. What is the largest number of odd numbers that could appear in the completed diagram?(A) 4 (B) 5 (C) 6 (D) 7 (E) 829.Julia has four pencils of different colours and wants to use some or all of them to paint the map of anisland divided into four countries, as in the picture. Any two countries with a common border must be coloured differently on the map. How many different colourings of this map are possible? (Twocolourings are considered different if at least one of the countries is coloured differently).(A) 12 (B) 18 (C) 24 (D) 36 (E) 4830.A bar consists of two grey cubes and one white cube glued together as shown in the figure.Which cube can be built from nine such bars?(A) (B) (C) (D) (E)International Contest-GameMath Kangaroo Canada, 2017Answer KeyGrade 5-61 A B C D E 11 A B C D E21 A B C D E2 A B C D E12 A B C D E 22 A B C D E3 A B C D E 13 A B C D E23 A B C D E4 A B C D E 14 A B C D E 24 A B C D E5 A B C D E 15 A B C D E 25 A B C D E6 A B C D E 16 A B C D E 26 A B C D E7 A B C D E 17 A B C D E 27 A B C D E8 A B C D E 18 A B C D E 28 A B C D E9 A B C D E 19 A B C D E 29 A B C D E10 A B C D E 20 A B C D E 30 A B C D E。
2017年小学数学竞赛决赛试题及答案

2017年小学数学竞赛决赛试题2017年4月9日下午2:00--3:301.计算:=⎪⎭⎫ ⎝⎛⨯+-+51315.644.38585.441______。
2.计算:=+++++4211230111201712156132______。
3.四位数b a 31能被33整除。
那么,b a +的最大值是_____。
4.小华每月的1号将2000元存入银行,月利率为0.5%,如果不计复利(利息不再产生利息),存足一年时,小华的本息和为_____元。
5.把一个长方体的木条左右两端切去长度分别为5厘米的一段和4厘米的一段后,得到一个正方体,如果正方体的表面积比原长方体的表面积减少360平分厘米,那么,原长方体的体积是______立方厘米。
6.有B A ,两堆乒乓球,A 堆有橙色球36个,白色球50个;B 堆球有橙色球40个,白色球10个。
小唐从B 堆中取出一些橙色球和白色球放入A 堆,使得A 堆中的橙色球和白色球个数相等,且B 堆剩下的球中,橙色球个数占B 堆剩下球总数的四分之三。
那么,从B 堆拿到A 堆得橙色球有_____个。
7.已知算式cf cf eef c ab ⨯==+19中f e c b a ,,,,代表从1到5的不同数字,那么=abcef _____。
8.果园的35个工人用8小时摘水蜜桃,共摘4400千克。
在最热的两小时中,男工每人一小时摘15千克,女工每人一小时摘11千克;其余6小时,男工每人一小时摘19千克,女工每人一小时摘15千克。
那么,果园共有女工_____人。
9.如图,三角形ABC 的面积为1,且BE CE BD AD 2,==。
那么,四边形DBEF 的面积等于_____。
10.金球合唱团共有50人,年龄均按整数计算,平均值为63.4,且合唱团成员之间任意两人的年龄差均不超过7岁。
若至少有一名成员年龄达到70岁,那么合唱团中年龄大于63岁的人最多有_____名。
11.495名学生从左到右排成一排,按如下规则从左到右报出整数:若学生报出的整数是一位数,他右边的同学就报这个一位数与9的和,若某学生报出的整数是两位数,他右边的同学就报这个两位数的个位数与5的和。
2017年第22届华杯总决赛小高组一试及详解

么甲第 10 次到达山顶前,有 2 次(第 3 次和第 9 次)当甲到达山顶时,乙正爬向
山顶,且距离山脚 5 处(小于 1 ).
18
3
(法 2): v甲上 : v乙上 : v甲下 : v乙下 6 : 5 : 6 1.5 : 5 1.5 =12 :10 :18 :15
易求: t甲上 : t乙上 : t甲下 : t乙下 15 :18 :10 :12
20174 20172 12 2 20162 2
20174 20174 2 20172 1 20162 2
2 20172 20162 1
2 2017 2016 2017 2016 1
2 4033 1 8065
2017kb b 2016kb 2016k kb b 2016k
k 1b 2016k
匠人之心 精致教学 5
当
k
1 时,无解.当
k
1
时,
b
2016k
k 1
.
k 1,k 1 , b 是整数,所以 k 1 是 2016 的因数.
2016 25 32 7
20174 20162 20172 2 2017 3 20174 20162 20172 2 2017 12 2
20174 20162 2017 12 20162 2 20174 2017 1 2017 12 20162 2
即 a 与 b 有 36 种不同的数值. 综上所述,有 36 种不同的方法.
6. 甲、乙锻炼身体,从山脚爬到山顶,再从山顶跑回山脚,来回往返不断运动.己知甲、 乙下山速度都是上山速度的 1.5 倍,甲的速度与乙的速度之比是 6 : 5 .两人同时从山脚 开始爬山,经过一段时间后,甲第 10 次到达山顶.问:在此之前,甲在山顶上有多少 次看到乙正爬向山顶,且此时乙距离山顶尚有多于从山脚到山顶路程的三分之二?
2017-2018年“海都杯”数学竞赛五年级决赛试卷及解答

第3届“海都杯”数学竞赛五年级决赛试卷1、早晨4:20的时候,钟面上长针与短针所夹的锐角的角度是()度。
2、已知2※3=2+3+4,5※2=5+6,2※5=2+3+4+5+6,则5※5=()。
3、一个正方形的边长增加5厘米,它的面积就会增加225平方厘米,原来的正方形的面积是()平方厘米。
4、一个正三角形的周长与一个正六边形的周长相等。
若此正三角形的面积为4,则这个正六边形的面积为()。
5、某超市为庆祝元旦,准备将毛巾类商品做促销:儿童毛巾5元3条,大人毛巾4元1条。
明明的妈妈花了39元购买了15条毛巾。
那么他购买了()条儿童毛巾和()条大人毛巾。
6、有三个质数的和是50,则这三个质数的积最大是()。
7、在一个纸盒中装有红色、绿色及黄色的弹珠。
已知盒子里的弹珠除了38颗之外都是红色的弹珠,除了33颗之外都是绿色的弹珠,除了35颗之外都是黄色的弹珠。
那么盒子中总共装有()颗弹珠。
8、有A、B、C、D四个点从左向右依次排在一条直线上,以这四个点为端点,可以数出6条线段。
已知这6条线段的长度分别是12、18、30、32、44、62(单位:厘米),那么线段BC的长度是()厘米。
9、如下图,甲、乙两图形都是正方形,它们的边长分别是20厘米和12厘米,则三角形AEG的面积为()平方厘米。
10、通信班举行10分钟汉字输入大赛,全班平均成绩为每分钟120字,男生平均成绩比全班平均成绩少18字,女生平均成绩比男生平均成绩多27字,则这个班女生的人数是男生的()倍。
11、一个整数,如果它的各位上的数字之和再加上它的各位数字之积,恰好等于这个数,我们就称这个数为“海都数”,例如39=3+9+3×9就是一个“海都数”。
两位数中这样的“海都数”一共有()个。
12、依次写下整数1,2,3,4,…,998,999,则得到的整数123456789101112…998999,这个整数左起第2018位上的数字是()。
13、在桌面上摆有一些大小一样的正方体木块,从正面看如下(图1),从右面看如下(图2),要摆出这样的图形至少需要()块正方体木块。
2017年第十六届“春蕾杯”小学数学竞赛试卷及答案(五年级决赛)

第 1 页 共 10 页 2017年第十六届“春蕾杯”小学数学竞赛试卷(五年级决赛)一、基础题(每题6分,共60分)1.(6分)计算①(4.8×7.5×8.4)÷(2.1×1.6×1.5)= .②(0.125+34)÷(75−0.7)×16125= . ③(1−12)×(1−13)×(1−14)×(1+15)×(1+16)×(1+17)= .2.(6分)一张足够大的纸的厚度是0.01厘米,对折一次就是0.02厘米,再对折就是0.04厘米,继续对折下去,一共对折15次,这张纸的厚度是 厘米.3.(6分)有3个连续的三位数,分别能被7、8、9整除,这3个连续的三位数的总和是 .4.(6分)有四个孩子,他们的年龄之积是3024,且一个比一个大一岁,这四个孩子的平均年龄是 岁.5.(6分)把57化为循环小数,小数部分前2017个数字的和是 . 6.(6分)从2,2,4,4,5,5,6,6,8,8中取出5个数字,要求其中至少有4个数字不相同,且这五个数字乘积的末位数字是6.用这5个数字组成一个最大的五位数和一个最小的五位数,它们的差是 .7.(6分)有一堆水果糖,如果按8粒一份来分,最后剩下2粒;如果按9粒一份来分,最后剩下3粒;如果按10粒一份来分,最后剩下4粒,这堆糖至少有 粒.8.(6分)有一个长方体,它的正面和底面的面积之和是117,如果它的长、宽、高都是素数,那么它的体积是 .9.(6分)如图所示,在一条400米的环形跑道上,A 、B 两点相距100米.甲、乙两人分别从A 、B 两点同时出发,按逆时针方向跑步.甲每秒跑5米,乙每秒跑4米,每人每跑100米都要停10秒钟,那么甲追上乙需要 秒.10.(6分)如图所示,圆周上共有八个点,每相邻两点的距离不全相等.若以任意三个点为顶点作三角形,一共可以作出 个三角形.。
2017年小学五年级数学竞赛试题及参考答案

2017年小学五年级数学竞赛试题及参考答案2017年小学数学学校姓名成绩:一、填空题(每小题4分,共40分)1、一个三位数,它的数字之和正好是18,而十位数字是个位数字的2倍,百位数字是个位数字的3倍,这个三位数是()。
2、100个馒头100个和尚吃,大和尚每人吃3个,小和尚3人吃一个,则大和尚有()个,小和尚有()个。
3、15年前父亲年龄是儿子的7倍,10年后,父亲年龄是儿子的2倍。
今年父亲()岁,儿子()岁。
4、差是减数的4倍,差与减数的差是150。
被减数是()。
5、平面上有30个点,任意三点都不在同一条直线上,若每两点间连一条线段,共可连出()条线段。
6、有人民币5元一张、2元一张、1元三张、5角一张、2角三张、1角一张。
要从中拿出8.6元,有()种分歧的拿法。
7、1×2×3×……×49×50的积的末尾继续有()个零。
8、午餐时,甲有4包点心,乙带有3包点心,(7包点心价钱一样),丙没食物。
他们把点心平分食用,吃完算账丙要给甲和乙共7元钱,那么,乙()元。
9、3247—1630的尾数是()。
10、在右面的乘法中,A、B表示不同的数字,其中A表示(),B表示()。
二、挑选题(每题2分,共10分)1、全班35位同学排成一行,从左边数小明是第20个,从右边数小刚是第21个,小明与小刚之间有()人。
A.6 B.5 C.4D.31应得2、右图中共有()个三角形。
A.8B.11C.14D.173、小华今年12岁,5年后爷爷是他年龄的5倍,爷爷现在的年龄是()。
A.80 B.81 C.82D.844、566除以一个数所得的商是12,而且除数与余数的差是6,余数是()。
A.40 B.38C.36D.345、现有30克和5克的砝码和一台天平,要把300克盐均分成3等份,至少要称()次。
A.2 B.3C.4D.5三、简便计算(每题5分,共20分)(1)2010×—2009×(2)6.8×0.1+0.5×68+0.049×680(3)5.3÷9+3.7÷9(4)1-3+5-7+9-11+…-1999+2001四、解答题(每小题10分,共30分)。
2017年全国迎春杯小学中年级决赛A卷竞赛数学试卷(解析)

价格减少90x + 2(a − 90) 元,两次变化都是两只山羊的价钱,应该相等,那么
,解得 . 60x + 2(a + 60) = 90x + 2(a − 90)
x = 10
9. 现有A、B、C 、D、E 五名诚实的安保在2016年12月1日~5日各值班3天,每天恰有3位安保值班,每位安保值班安排5天
E :圣诞节(12月25日)那天我和A都值班了.
那么,安保A在1 2 月份中第2 次、第6 次、第1 0 次值班日期顺次排列组成的五位数是
.
(如A第2次、第6次、第10次值班分别在12月3、12、17日,则答案为31217 )
答案
41016
解 析 12月份值班表如下:
由E 说的话可知,2 日 5 A 和E 都值班,又由D的话可知D和E 永远在一起,那么可以判断5日这一竖列值班人为 A ,D和E . 由C 的话可知,3日他不值班,由于每天必须有3人值班,所以D和E 中必须有一个,又因 为D和E 一起,所以3日这一竖列,D和E 都值班. 通过A 的话判断,A 和B 在周末值班的日子比C ,D和E 多,统计出每一列中的周末数量,为2,1,2,2,2 .每人都要在三列中值班,若要A 和B 比其他人多,那么1那一列必须是C ,D和E 值班. 每天都要有3人值班,D和E 现在已经排满,因此第1列,第4列为A ,B 和C 值班. 还剩第3列没有排完,B 要跟每个人都搭配过,因此此处为B . A 在12月份中第2 次、第6 次、第10次值班日期日期依次为4 ,10,16,五位数为41016.
得每个格子中都恰好放了一枚棋子,那么共有
名同学.
答案 7
解 析 由题意可知,若相邻两枚棋子之间有偶数个空格子,刖无法再往其中放棋子,那么若想要在每个格子中都放 上棋子,每次放完相邻两棋子间空格教应为奇教.第一轮只能在最中间放1 枚棋子,此时将格子分为了前半
2017年数学竞赛小学五年级试题(含答案)

2017年小学五年级数学竞赛试题( 完成时间:60分钟 满分:100分。
)班级 姓名1.计算: 5.62×49-5.62×39+43.8= 。
2. 早读课从7时30分开始,到8时下课,一节早读课,钟面上的分针正好旋转了( )( ) 周,时针旋转了( )( )周。
3. 观察右图,“?”代表的数是 。
4.某市市内出租车收费标准如表:(1)张叔叔乘出租车行了1.5千米,应付 元。
(2)李叔叔乘出租车行了4千米,应付 元。
(3)李叔叔乘出租车行了 千米,付9元.5.五(1)班有学生48人。
在学校运动会上,参加比赛的女生占全班人数的61,参加比赛的男生占全班人数的41,参加比赛的男生人数比女生人数多( )( ) 。
6. 五年级一班共有36人,每人参加一个兴趣小组,共有A,B,C,D,E 五个小组,若参加A 组的有15人,参加B 组的仅次于A 组,参加C 组、D 组的人数相同。
参加E 组的人数最少,只有4人,那么,参加B 组的有 人。
7. 从甲地到乙地,原来每隔45米装一根电线杆,加上两端的两根有53根,现改成每隔60米装一根电线杆,除两端两根不移动外,中间还有 根不必移动。
8. 盒子里放有编号为1至10的十个球,小明先后三次从盒中共取出九个球。
如果从第二次开始,每次取出的球的编号之和都是前一次的2倍,那么未取出的球的编号是。
9. 王叔叔开车从甲地到乙地,以每小时40千米的速度行进,下午1点到;以每小时60千米的速度行进,上午11点到。
如果王叔叔希望中午12点到乙地,那么行使的速度是每小时千米。
10.沿如图的虚线折叠,可以围成一个长方体。
这个长方体的体积是立方厘米,表面积是平方厘米。
11.歌德巴赫猜想:任何不小于7的奇数都可以写成三个质数的和。
如7=2+2+3。
请把31写成三个质数的和。
(在下面写出所有式子)12. 有两个长方体水箱,甲水箱里有水,乙水箱空着。
从里面量,甲水箱长40厘米,宽32厘米,水面高20厘米;乙水箱长30厘米,宽24厘米,深25厘米。
2017年第十六届“春蕾杯”小学数学竞赛试卷(五年级初赛)

所以最终结论是:乙是第一名,丙是第2名,甲是第3名,丁是第4名.
【解答】解:2017去7、0得到21.
21×2=42(岁)
故答案为:42.
9.(6分)如果如图(1)是常见的一副七巧板的图,图(2)是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的 .
【解答】解:
1÷8
即第2块板的面积等于整幅图的面积的 .
故答案为: .
10.(5分)甲、乙两个工程队分别从道路的两端同时开工修路.甲队每天修路20米,乙队每天修路25米.开工若干天后,两队离这条路的中点50米的地方汇合.这条马路的长度是900米.
【解答】解:①375+625÷25×4﹣10
=375+25×4﹣10
=375+100﹣10
=465
②[110﹣(56+1.1÷0.25)]×0.01÷0.125
=[110﹣(56+4.4)]×0.01÷0.125
=[110﹣60.4]×0.01÷0.125
=49.6×0.01÷0.125
=0.496÷0.125
故答案为:2,197.
6.(4分)有一堆水果糖,如果按8粒一份来分,最后剩下2粒;如果按9粒一份来分,最后剩下3粒;如果按10粒一份来分,最后剩下4粒,这堆糖至少有354粒.
【解答】解:8﹣2=9﹣3=10﹣4=6
8=2×2×2
9=3×3
10=2×5
2×2×2×3×3×5=360(粒)
360﹣6=354(粒)
4+3+2=9(周).
即三人共走了9周.
故答案为:9.
5.(4分)质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的数.例如:3的因数只有1和它本身;5的因数也只有1和它本身;3和5都是质数.若把199分解成2个质数,那么这两个质数是2,197.
word完整版)2017小学五年级数学竞赛题及答案解析

word完整版)2017小学五年级数学竞赛题及答案解析1、XXX家住在三楼,他每上一层楼要走14级台阶,XXX从一楼走到三楼要走(28)级台阶。
2、请你在算式:。
1+2×3+4×5+6中添上适当的一个小括号,使算式的得数最大,最大的得数是(71)。
3、一件毛衣102元,比一副手套的5倍还多12元,一副手套(18)元。
4、简算:7.29×4.6+46×1.271=50.934+58.366=109.3.5、XXX有2元和5元的人民币共34张,总值110元,问2元的人民币有(22)张;5元的人民币有(12)张。
6、在爷爷是父亲现在的年龄时候,父亲才12岁。
等父亲到爷爷现在这么大的年龄时,爷爷84岁。
爷爷现在(72)岁;父亲现在(60)岁。
7、幼儿园的老师给小朋友发苹果,每位小朋友4个,就多出12个,每个小朋友6个,就少12个,共有苹果(180)个。
8、XXX4次语文测验的平均成绩是89分,第5次测验得了94分。
她5次测验的平均成绩是(90)分。
9、用5、5、5、1四个数字组成一个算式,使其结果为24.算式是5×5-1-5=24.10、已知三个连续偶数的和比其中最大的一个偶数的2倍还多2,这三个偶数分别是(8、10、12)。
应用题:1、一架飞机从甲地到乙地,原计划每分钟飞行9千米,现在按每分钟12千米的速度飞行,结果比原计划提前半小时到达。
甲、乙两地相距多少千米?解:假设原计划需要x分钟到达,那么原计划的速度为9千米/分钟,飞行距离为9x千米。
现在的速度为12千米/分钟,飞行距离为12(x-30)千米。
根据题意得到方程9x=12(x-30)+9x,解得x=180,即原计划需要3小时到达,飞行距离为9×180=1620千米。
2.有19人到旅馆住宿,住3人间和2人间(每个房间不能有空床位),有多少种不同的安排?解:设住3人间x个,住2人间y个,则x+y=19,3x+2y=57.解得x=12,y=7.所以有12个3人间,7个2人间,共有12+7=19种不同的安排。
2017年第十五届小学“希望杯”全国数学邀请赛试卷(六年级第1试)

二、以下每题6分,共120分2017年第十五届小学“希望杯”全国数学邀请赛试卷(六年级第1试))1.(6分)计算:2017×+=.2.(6分)计算:0.4285×6.3﹣0.2857×1=.3.(6分)定义:a ☆b =,则2☆(3☆4)=.4.(6分)如图所示的点阵图中,图①中有3个点,图②中有7个点,图③中有13个点,图④中有21个点,按此规律,图⑩中有个点.5.(6分)已知A 是B 的,B 是C 的,若A +C =55,则A =.6.(6分)如图所示的圆周上有12个数字,按顺时针方向可以组成只有一位整数的循环小数,如: 1.9579, 3.5791.在所有这样只有一位整数的循环小数中,最大的是.7.(6分)甲、乙两人拥有邮票张数的比是5:4,如果甲给乙5张邮票,则甲、乙两人邮票张数的比变成4:5.两人共有邮票张.8.(6分)从1,2,3,…,2016中任意取出n 个数,若取出的数中至少有两个数互质,则n 最小是.9.(6分)等腰△ABC 中,有两个内角的度数比是1:2,则△ABC 的内角中,角度最大可以是度.10.(6分)能被5和6整除,并且数字中至少有一个6的三位数有个.11.(6分)小红买1支钢笔和3个笔记本共用了36.45元,其中每个笔记本售价的与每支钢笔的售价相等,则1支钢笔的售价是元.12.(6分)已知x是最简真分数,若它的分子加a,化简得;若它的分母加a,化简得,则x=.13.(6分)a,b,c是三个互不相等的自然数,且a+b+c=48,那么a,b,c的乘积最大是.14.(6分)小丽做一份希望杯练习题,第一小时做完了全部的,第二小时做完了余下的,第三小时做完了余下的,这时,余下24道题没有做,则这份练习题共有道.15.(6分)如图,将正方形纸片ABCD折叠,使点A、B重合于点O,则∠EFO=度.16.(6分)如图,由七巧板拼成的兔子图形中,兔子耳朵(阴影部分)的面积是10平方厘米,则兔子图形的面积是平方厘米.17.(6分)如图,将一根长10米的长方体木块锯成6段,表面积比原来增加了100平方分米,这根长方体木块原来的体积是立方分米.18.(6分)将浓度为40%的100克糖水倒入浓度为20%的a克糖水中,得到浓度为25%的糖水,则a=.19.(6分)张强晚上六点多外出锻炼身体,此时时针与分针的夹角是110°;回家时还未到七点,此时时针与分针的夹角仍是110°,则张强外出锻炼身体用了分钟.20.(6分)甲、乙两人分别从A、B两地同时出发,相向而行,在C点相遇,若在出发时,甲将速度提高,乙将速度每小时提高10千米,二人依然在C点相遇,则乙原来每小时行千米.2017年第十五届小学“希望杯”全国数学邀请赛试卷(六年级第1试)参考答案与试题解析二、以下每题6分,共120分)1.(6分)计算:2017×+=2016.【解答】解:2017×+=(2016+1)×+=2016×++=2015+(+)=2015+1=2016;故答案为:2016.2.(6分)计算:0.4285×6.3﹣0.2857×1=.【解答】解:因为0.4285=,0.2857=,所以0.4285×6.3﹣0.2857×1=×6.3﹣×1=﹣=﹣=.故答案为:3.(6分)定义:a☆b=,则2☆(3☆4)=2.【解答】解:3☆4==2☆(3☆4)=2☆()==2;故答案为:2.4.(6分)如图所示的点阵图中,图①中有3个点,图②中有7个点,图③中有13个点,图④中有21个点,按此规律,图⑩中有111个点.【解答】解:根据分析得出的规律我们可以得到:图⑩中有3+(4+6+8+10+12+14+16+18+20)=3+(4+20)×9÷2=111;故答案为:111.5.(6分)已知A是B的,B是C的,若A+C=55,则A=15.【解答】解:A是C的×=,即A=C,A+C=55,则:C+C=55C=55C=55÷C=40A=40×=15故答案为:15.6.(6分)如图所示的圆周上有12个数字,按顺时针方向可以组成只有一位整数的循环小数,如:1.9579,3.5791.在所有这样只有一位整数的循环小数中,最大的是.【解答】解:根据分析,先确定整数部分的数,显然9是最大的,再确定小数点后第一位的数,9后面最大的为5,再确定第三位,因为是按顺时针排列,7为最大,故此数可以确定为:故答案是:7.(6分)甲、乙两人拥有邮票张数的比是5:4,如果甲给乙5张邮票,则甲、乙两人邮票张数的比变成4:5.两人共有邮票45张.【解答】解:5÷()=5=45(张)答:两人共有邮票45张.故答案为:45.8.(6分)从1,2,3,…,2016中任意取出n个数,若取出的数中至少有两个数互质,则n最小是1009.【解答】解:根据分析,1~2016数中,有奇数1008个,偶数1008个,因为偶数和偶数之间不能互质,故:①n<1008时,有可能取的n个数都是偶数,就不能出现至少有两个数互质的情况;②n=1008时,若取的数都是偶数,也不能出现至少有两个数互质的情况;③n≥1009时,则取的n个数里至少有一个为奇数,取出的这个奇数和它相邻的偶数一定互质,综上,n最小是1009.故答案是:1009.9.(6分)等腰△ABC中,有两个内角的度数比是1:2,则△ABC的内角中,角度最大可以是90度.【解答】解:180°×=180°×=90°答:角度最大可以是90度.故答案为:90.10.(6分)能被5和6整除,并且数字中至少有一个6的三位数有6个.【解答】解:根据分析,分解质因数6=2×3∴这个三位数能同时被2、3、5整除,而且数字中至少含有一个6∴这个三位数的个位数必须为偶数或0,因被5整除的数个位数必须是0或5,故个位数为0,设此三位数为,按题意a、b中至少有一个数字为6,①a=6时,则6+b+0是3的倍数,则b=0,3,6,9,符合的三位数为:600、630、660、690②b=6时,则6+a+0是3的倍数,则a=3,6,9,符合的三位数为:360、660、960综上所述,符合题意的三位数为:360、660、960、600、630、690故答案为:6.11.(6分)小红买1支钢笔和3个笔记本共用了36.45元,其中每个笔记本售价的与每支钢笔的售价相等,则1支钢笔的售价是20.25元.【解答】解:36.45÷(3+)=36.45=5.45.4×=20.25(元)答:1支钢笔的售价是20.25元.故答案为:20.25.12.(6分)已知x是最简真分数,若它的分子加a,化简得;若它的分母加a,化简得,则x=.【解答】解:设原来的分数x是,则:=则:b=3(c+a)=3c+3a①=则:4c=a+b②①代入②可得:4c=a+3c+3a4c=4a+3c则:c=4a③③代入①可得:b=3c+3a=3×4a+3a=15a所以==即x=.故答案为:.13.(6分)a,b,c是三个互不相等的自然数,且a+b+c=48,那么a,b,c的乘积最大是4080.【解答】解:48÷3=16,16﹣1=15,16+1=17,所以,a,b,c的乘积最大是:15×16×17=4080.故答案为:4080.14.(6分)小丽做一份希望杯练习题,第一小时做完了全部的,第二小时做完了余下的,第三小时做完了余下的,这时,余下24道题没有做,则这份练习题共有60道.【解答】解:24÷(1﹣)÷(1﹣)÷(1﹣)=24÷=60(道)答:这份练习题共有60道.故答案为:60.15.(6分)如图,将正方形纸片ABCD折叠,使点A、B重合于点O,则∠EFO=30度.【解答】解:沿DE折叠,所以AD=OD,同理可得BC=OC,则:OD=DC=OC,△OCD是等边三角形,所以∠DCO=60°,∠OCB=90°﹣60°=30°;由于是对折,所以CF平分∠OCB,∠BCF=30°÷2=15°∠BFC=180°﹣90°﹣15°=75°所以∠EFO=180°﹣75°×2=30°.故答案为:30.16.(6分)如图,由七巧板拼成的兔子图形中,兔子耳朵(阴影部分)的面积是10平方厘米,则兔子图形的面积是80平方厘米.【解答】解:10=80(平方厘米)答:兔子图形的面积是80平方厘米.故答案为:80.17.(6分)如图,将一根长10米的长方体木块锯成6段,表面积比原来增加了100平方分米,这根长方体木块原来的体积是1000立方分米.【解答】解:依题意可知:将一根长10米的长方体木块锯成6段,表面积比原来增加了100平方分米,变面积增加了10个面,那么每一个面的面积为100÷10=10平方分米.10米=100分米.体积为:10×100=1000(立方分米).故答案为:100018.(6分)将浓度为40%的100克糖水倒入浓度为20%的a克糖水中,得到浓度为25%的糖水,则a=300.【解答】解:依题意可知:根据浓度是十字交叉法可知:浓度差的比等于溶液质量比即1:3=100:a,所以a=300克故答案为:30019.(6分)张强晚上六点多外出锻炼身体,此时时针与分针的夹角是110°;回家时还未到七点,此时时针与分针的夹角仍是110°,则张强外出锻炼身体用了40分钟.【解答】解:依题意可知:分针开始落后时针共格;后来分针领先格,路程差为格.锻炼身体的时间为:=40(分);故答案为:40.20.(6分)甲、乙两人分别从A、B两地同时出发,相向而行,在C点相遇,若在出发时,甲将速度提高,乙将速度每小时提高10千米,二人依然在C点相遇,则乙原来每小时行40千米.【解答】解:依题意可知:根据甲乙两人的相遇点相同,那么他们的速度比例是不变的.当甲提高时,乙也同样需要提高,而乙提高的是每小时10千米.即10÷=40千米/小时.故答案为:40第11页(共11页)。
重点小学新五年级数学竞赛试题答卷及参考答案2017.5

小学五年级数学知识竞赛测试卷(60分钟完卷)1、简算: 8888×89+2222×44=( )(2+4+6+…+100)–(1+3+5+…+99)=( )2、把1—10这10个数填在圆圈里,使两个大圆圈上3124)只。
5、有 )7、( )89、从10、在一条长200米的公路两旁,每隔5米栽一棵树(两端都栽),一共要栽( )棵树。
(背面还有试题)11、布袋里有红、绿、黄三种颜色、大小相同的球各6个,一次至少摸出( )个才能保证有3个颜色不同的球。
12、某月中,星期四的天数比星期一的天数多,星期二的天数比星期日的天数多,这个月的2日是星期()。
13、一个长30厘米、宽20厘米、高15厘米的长方体木块,最多能切成()个棱长4厘米的小正方体木块。
14、用1—8这八个数字分别组成两个四位数,使这两个四位数的乘积最大,这15181617、本笔记本和3)1840千1920分钟行90米,甲骑车到B地后立即返回,在离B地3.6千米处与乙相遇。
A、B两地间的距离是()千米。
五年级数学知识竞赛测试卷2017.5.24(60分钟完卷)1、简算:8888×89+2222×44=(888800 )(2+4+6+…+100)–(1+3+5+…+99)=(50 )2、把1—10这10个数填在圆圈里,使两个大圆圈上六个数的和都等于37。
3、一条毛毛虫由幼虫长成成虫,每天长大一倍,12天能长到2厘米,长到8厘米共要(14 )天。
4)只。
5、有 4 )67、31 )89、从1011、布袋里有红、绿、黄三种颜色、大小相同的球各6个,一次至少摸出(13 )个才能保证有3个颜色不同的球。
12、某月中,星期四的天数比星期一的天数多,星期二的天数比星期日的天数多,这个月的2日是星期(三)。
13、一个长30厘米、宽20厘米、高15厘米的长方体木块,最多能切成(105 )个棱长4厘米的小正方体木块。
14、用1—8这八个数字分别组成两个四位数,使这两个四位数的乘积最大,这两个数分别是(8531 )和(7642 )。
湖州市2017年第十届“期望杯”小学数学竞赛试题及参考答案(五年级)

湖州市第十届“期望杯”小学数学竞赛试题(五年级)(2017年12月30日下午1:30—3:00;满分120分)考点:_______________________ 考场号:___________ 座位号:_________________学校:_______________________ 班级:____________姓名:_________________题号一(1~11)二(12~16)得分得分一、填空(第1~2题每题6分,第3~11题每题7分,共75分)1. 计算:0.37×1.9+0.81×3.7=()2. 计算:15.9÷1.1-3.8÷1.1=()3. 2017个7连乘,积的个位数字是()。
4. 把循环小数2.71828·1·,移动循环节的第一个圆点,使新产生的循环小数尽可能大,最大是()。
5. 左下图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔。
如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入()号袋。
6. 排一本400页的书的页码,共需要()个数码“0”。
7. 右上图中每个小正方形的边长都是1,图中阴影部分的面积是()。
8. 把15把椅子放成一排,客人随时来到,并在空椅子上就坐,而每当此时,与他相邻的客人就起身离去。
如果开始时所有椅子都是空的,那么椅子上客人最多时坐()人。
9. 下图中共有12个小图形,每一个不同的小图形表示1-9中的一个数码,每三个图形表示1个三位数。
共有4个三位数:146,521,658和692。
请问,第2幅图表示的三位数是()。
(1)(2)(3)(4)10.从1~9这9个数字中取出三个,组成六个不同的三位数。
如果六个三位数的和是3330,那么这六个三位数中最大的是()11.如右图,1个三角形把平面分成了A、B两部分,那么用3个三角形最多可以把平面分成()部分。
2017联合杯决赛(数学)试题及答案
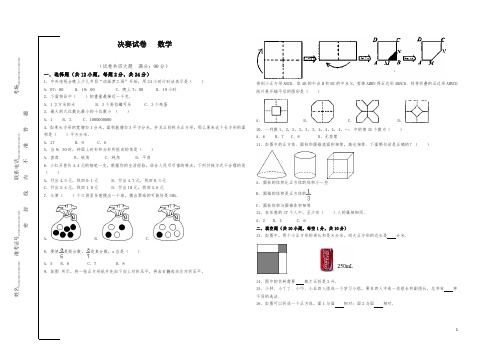
决赛试卷 数学(试卷共四大题 满分:90分)一.选择题(共12小题,每题2分,共24分)1.中央电视台晚上少儿节目“动画梦工场”开始,用24小时计时法表示是( ) A .07:00 B .19:00 C .晚上7:00 D .19小时2.下面物品中( )的重量最接近一千克.A .1立方米的水B .3个易拉罐可乐C .3个鸡蛋3.最大的九位数比最小的十位数小 ( ) A .1 B .2 C .10000000004.如果长方形的宽增加1分米,面积就增加3平方分米,并且正好称为正方形,那么原来这个长方形的面积是( )平方分米. A .27B .9C .65.当9:30时,钟面上时针和分针所组成的角是( ) A .直角 B .锐角 C .钝角 D .平角6.小红买售价4.4元的钢笔一支,根据你的生活经验,结合人民币币值的特点,下列付钱方式不合理的是( )A .付出4.5元,找回0.1元B .付出4.7元,找回0.3元C .付出5.4元,找回1.0元D .付出10元,找回5.6元 7.从第( )个口袋里任意摸出一个球,摸出黑球的可能性是50%.A .B .C .8.要使是假分数,是真分数,a 应是( )A .5B .6C .7D .89.如图 所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD .取AB 的中点M 和BC 的中点N ,剪掉AMBN 得五边形AMNCD .则将折叠的五边形AMNCD 纸片展开铺平后的图形是( )A .B .C .D .10.一列数1,2,2,3,3,3,4,4,4,4,….中的第35个数为( ) A .6 B .7 C .8D .无答案11.如图中的正方体、圆柱和圆锥底面积相等,高也相等.下面哪句话是正确的?( )A .圆柱的体积比正方体的体积小一些B .圆锥的体积是正方体的C .圆柱体积与圆锥体积相等12.在任意的37个人中,至少有( )人的属相相同. A .2 B .4C .6二.填空题(共10小题,每空1分,共10分)13.如图中,两个小正方形的周长和是8分米,则大正方形的边长是 分米.14.图中的饮料需要 瓶才正好是2升.15.小胖、小丁丁、小巧、小亚四人组成一个学习小组,要在四人中选一名组长和副组长,总共有 种不同的选法.16.如图可以折成一个正方体,面1与面 相对;面2与面 相对.姓名__________ 准考证号__________ 联系电话__________ 考场___________密 封 线 内 不 准 答 题17.爷爷患了感冒,医生给他开了感冒药,如图是该药品的部分说明,请根据说明书回答问题:(1)爷爷一天最多可服药克.(2)这种药片的保质期是年.18.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是平方厘米.(18题图)(19题图)(20题图)19.如图,围绕礼品盒绳子的长度是厘米.20.小明统计了自己装有125个硬币的储蓄罐的情况如图,则储蓄罐内共有元钱.21.如图,甲、乙、丙三个图形面积的比是.22.一群人开舞会,每人头上都戴着一顶帽子.帽子只有黑白两种,黑的至少有一顶.每个人都能看到其它人帽子的颜色,却看不到自己的.主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍手.第一次关灯,没有声音.于是再开灯,大家再看一遍,关灯时仍然鸦雀无声.一直到第三次关灯,才有劈劈啪啪手的声音响起.则有人戴着黑帽子.三.计算题(共2小题,23、24题各12分,共24分)23.直接写出下面各题的得数.+== ﹣﹣= ÷=24.能简算的要简算(1)2.5×12.5×32 =(2)1375+450÷18×25=(3)=(4)=四.解答题(共5题,25题7分,26、27题各8分,28题9分)25.王大娘家菜地里的西红柿获得了丰收,收下全部的时,装满了5筐还多48千克,收完其余的部分时,又刚好装满10筐,求王大娘共收获西红柿多少千克?26.图形计算(1)如图1,计算图形的体积.(得数保留两位小数,单位:米)(2)如图2,求阴影部分的面积.(单位:米)27.甲、乙和丙同时由东、西两城出发,甲、乙两人由东城到西城,甲步行每小时走5千米,乙骑自行车每小时行15千米,丙也骑自行车每小时20千米,已知丙在途中遇到乙后,又经过1小时才遇到甲,求东、西城相距多少千米?28.期六下午,城关二小王明同学骑自行车到6千米远的六郎镇姥姥家去玩,请根据下面折线统计图回答下列问题:(1)王明在姥姥家玩了多少时间?(2)如果王明从出发起一直骑自行车走不休息,下午几时几分可到达姥姥家?(3)求出王明骑自行车的往返的平均速度?2017年小升初学业水平测试数学试卷参考答案与试题解析一.选择题(共12小题)1-5 B.B.A.C.C.6-10 B.B.B.D.C.11-12 B.B.二.填空题(共12小题)13. 2.14. 8.15. 12.16. 6,4.17. 2.4,2.18. 6419. 340.20. 67.5.21. 1:5:4.22. 3三.计算题(共2小题)23.+==0.6=7﹣=÷=24.解:(1)2.5×12.5×32=(2.5×4)×(12.5×8),=10×100,=1000;(2)1375+450÷18×25=1375+25×25,=1375+625,=2000;(3)×0.25+×=0.25×(+),=0.25;(4)×[(+0.75)÷]=×[÷+÷],=×[1+],=×,=.四.解答题(共2小题)25. 【解答】解:48÷[1﹣÷10×(5+10)]=48÷[1﹣×15]=48÷[1﹣]=48=288(千克)答:王大娘共收获西红柿288千克.26.【解答】解:(1) 3.14×102×10+4.14×102×10 =≈1046.67+3140=4186.67(立方米);答:它的体积是4186.67立方米.(2)8÷2=4(米),答:王明骑自行车的往返的平均速度是千米/时.3.14×42×4×4÷2=3.14×16÷2=12.56﹣8=4.56(平方米);答:阴影部分的面积是4.56平方米.27.【解答】解:乙丙经过x小时相遇,根据总路程相等列出方程:(15+20)x=(5+20)(x+1)35x=25x+25x=2.5总路程:(15+20)×2.5=35×2.5=87.5(千米)答:东、西城相距87.5千米.28.【解答】解:(1)王明在姥姥家是从下午2时到2时30分;2时30分﹣2时=30分;答:王明在姥姥家玩了30分.(2)王明中间休息了20分钟;否则他会提前20分钟到姥姥家.2时﹣20分=1时40分;答:下午1时40分可到达姥姥家.(3)20+20=40(分);3时﹣2时30分=30分;40+30=70(分);70分=时;6×2÷,=12÷,=(千米/时);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年小学数学竞赛决赛试题
2017年4月9日下午2:00--3:30
1.计算:=⎪⎭⎫ ⎝⎛⨯+-+51315.644.38585.441______。
2.计算:=+++++42
11230111201712156132______。
3.四位数b a 31能被33整除。
那么,b a +的最大值是_____。
4.小华每月的1号将2000元存入银行,月利率为%,如果不计复利(利息不再产生利息),存足一年时,小华的本息和为_____元。
5.把一个长方体的木条左右两端切去长度分别为5厘米的一段和4厘米的一段后,得到一个正方体,如果正方体的表面积比原长方体的表面积减少360平分厘米,那么,原长方体的体积是______立方厘米。
6.有
B A ,两堆乒乓球,A 堆有橙色球36个,白色球50个;B 堆球有橙色球40个,白色球10个。
小唐从B 堆中取出一些橙色球和白色球放入A 堆,使得A 堆中的橙色球和白色球个数相等,且B 堆剩下的球中,橙色球个数占B 堆剩下球总数的四分之三。
那么,从B 堆拿到A 堆得橙色球有_____个。
7.已知算式cf cf eef c ab ⨯==+19中f e c b a ,,,,代表从1到5的不同数字,那么=abcef _____。
8.果园的35个工人用8小时摘水蜜桃,共摘4400千克。
在最热的两小时中,男工每人一小时摘15千克,女工每人一小时摘11千克;其余6小时,男工每人一小时摘19千克,女工每人一小时摘15千克。
那么,果园共有女工_____人。
9.如图,三角形ABC 的面积为1,且BE CE BD AD 2,==。
那么,四边形DBEF 的面积等于_____。
10.金球合唱团共有50人,年龄均按整数计算,平均值为,且合唱团成员之间任意两人的年龄
差均不超过7岁。
若至少有一名成员年龄达到70岁,那么合唱团中年龄大于63岁的人最多
有_____名。
11.495名学生从左到右排成一排,按如下规则从左到右报出整数:若学生报出的整数是一位
数,他右边的同学就报这个一位数与9的和,若某学生报出的整数是两位数,他右边的同学就
报这个两位数的个位数与5的和。
如果第一名同学报出的整数是1,那
么,最后一名同学报出的整数是_____。
12.一块三角形绿地,第一边的长度是第二边长度的倍,是第三边长度的三分之二。
第三边比第二边长320米。
现在计划在三边上按相同的等距离植树,并在三角形的三个顶点各种一棵树。
那么,至少需要种树_____颗。
13.(此题为解答题,需写出解答过程)B A ,两地相距125千米,甲、乙、丙同时从A 地出发前往B 地,甲与丙以每小时25千米的速度乘车前进,乙以每小时5千米的速度步行前进。
甲与丙的车行到途中C 地时,丙下车以每小时5千米的速度步行前进,甲则以原速度返回,他和乙在途中D 地相遇,立即将乙载上车开往B 地。
甲乙到达B 地时,丙距离B 地还有4千米。
那么,甲到达B 地共用时间______小时。
14.(此题为解答题,需写出解答过程)B A ,两项工程分别由甲、乙两个工程队来承担。
不是雨天时,甲队完成A 工程需要15天,乙队完成B 工程需要18天;在雨天,甲队的工作效率降低40%,乙队的工作效率降低10%。
若两队完成自己承担的工程用了相同的天数,那么,在施工期间共有______个雨天。
15.(此题为解答题,需写出解答过程)有一个空的蓄水池,装有一个进水管和一个出水管。
如果单独开进水管,2小时可以将空池注满;如果单独开出水管,3小时可以将满池水放完。
现在按进水管开1小时、出水管开1小时、进水管开1小时、出水管开1小时、······,进水管和出水管不能同时打开,只能按照这样的顺序轮流打开。
那么将蓄水池的水蓄满至少要_______小时。
