材料力学 第十四章 静不定问题分析
合集下载
第14章 静不定问题

+
FS l 2
)
⋅(
l 2)dx2 ]
=
0
∫ ∫ Δ1/1' =
2 l/2 M [(
EI 0 2
+ Fs x1 )(x1) ⋅dx1 +
lM 0 (s 2
+
FS l 2
)
⋅(
l 2
)dx2
]
=
0
FS
=
− 15M 14l
求C截面转角
M/2
M/2
x2
xF1 S F
M (x1) =
M 2
+ Fs x1
=
q
1
2
3
A
B
αα
A
F
二、静不定结构分类
q
q
q
FAx A
FAy
B FBx
A
FBy
B
FAx A
FAy
FBx
B
FBy
外力静不定结构
内力静不定结构
混合型静不定结构
仅在结构外部存在多 仅在结构内部存在多 在结构外部和内部均
余约束
余约束
存在多余约束
¾ 外力静不定
F
q
F
q
外1度
外3度(平面)
外6度(空间)
约束力分量个数:
例1(教材例14-2)图示刚架,承受载荷F,
求刚架的最大弯矩。EI为常数。
B
C
解:沿CC’将刚架切开,由载
F
F
荷的对称性,截面C和C’上
A
A’
的剪力等于零,只有轴力FN 和弯矩M
利用平衡条件求出FN=F/2, 只有 M 为多余约束力
材料力学(单辉组)第十四章静不定问题分析

FBy F
B
F A xA
Rj
F Ay
MA
Rj
A
静定基
解:4个反力,3个平衡方程,1次外力静不定
认为B处为多余约束,移去B支座,加反力
变形协调条件: DBy=0
11
FBy F 利用截面法求弯矩
M
B
Rj
A
M j FR1 cosj FByRsinj
利用卡氏第二定理求位移
静定基
曲杆弯矩正号 使曲率增大
静定基
A
B
Dcy
V Fcy
M2
M 2 Fcy
EI dx AB
2
M1
M1 Fcx
EI dx BC
1
a2 EI
1 2
Fcx
1 3
Fcy
3 8
qa2
C
Fcx
Fcy 利用变形协调条件求支反力
由
D D
cx cy
0 0
4
3
1
2
根据多余的约束条件
几何方程 物理方程
补充方程
当杆件外形、载荷较复杂或材料为非线性弹 性时,问题难于求解
由于能量方法可较容易给出载荷与位移关系, 从而采用能量法比较容易处理静不定问题
9
EX1
F
B
Rj
A
已知:小曲率杆,半径R
不计剪力和轴力对曲杆变形影响
求解:支反力和内力?
10
FBy F
B
4
有缝 q
F Ax A F A y (a)
刚架
B
FBy
材料力学(18)第十四章-3

A C’
x3
2 a M ( x1 ) M ( x1 )d x1 EI 0
2a 0
M ( x 2 ) M ( x 2 )d x 2
a 0
M ( x 3 ) M ( x 3 )d x 3
Page8
BUAA
MECHANICS OF MATERIALS
x2
x1
C A’
60° 60°
B’
P
A’
M ( ) M M
B
F NB R ( 1 cos ) 3 3
( 2 3 9)
A/O
/3
0
1 V 3 P
M ( )
2
B
PR ( 1 cos )
M
PR 6
B
V 6
Rd
2 EI
Page22
BUAA
MECHANICS OF MATERIALS
MECHANICS OF MATERIALS
A B FNB MB
1、解静不定问题:
C MC P FNC
利用对称性减少未知力的数目
F SB F SC 0 B C 0
F NB F NC
B C 0
3 3 P
A FNB MB B
根据平衡方程:
C
剩余一个未知力MB
P
B M C l/2 A MC FNC FSC A l/2 F
D
解: 三度外力静不定 对称结构,反对称受载
F N C= 0 M C= M / 2 f C / C = 0 f C= 0
l
B
剩余一个多余内力——剪力
协调条件: f C / C 0
材料力学课件:静不定问题分析-1

是否是原结构静力 许可场?
Page20
例2:图示桁架,各杆EA相同,求各杆轴力
a
a
4
2
a 57
8 3
1
6
解: 判断静不定度: P 存在1个多余内部约束
内力静不定度: 8 - 25 + 3 = 1
4
m
5 N7m’N7 8 3
2 1
6
1、 去除多余约束,建立相当系统
P
2、 建立补充方程(找变形协调条件)
内力静定
5度
5度
4度
Page6
➢ 混合(一般)静不定
2度
6度
➢ 组合梁或梁杆结构的静不定度分析
Page7
➢ 组合梁或梁杆结构的静不定度分析
安装法 2度
拆卸法
2度
Page8
拆卸法
1度
安装法 两杆多余,2度内力静不定
Page9
➢ 静不定问题的分析方法: 力法: 以多余未知力为待定量,利用变形 协调条件列方程。 位移法: 以位移为待定量,利用平衡条件求解。
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
平面刚架: 三度内力静不定
断开:内力静定
刚性连接:多了三 个约束
两度内力静不定
六度内力静不定
四度内力静不定
封闭框架三内,加一铰减一,加一刚接杆加三,加一铰支杆加一
Page5
平面曲杆:
三度内力静不定 两度内力静不定 ➢ 例:判断内力静不定度
l
B
l
B
l
l
A RC
l
C
HC
材料力学:ch14静不定问题分析
,
FN3
F 2
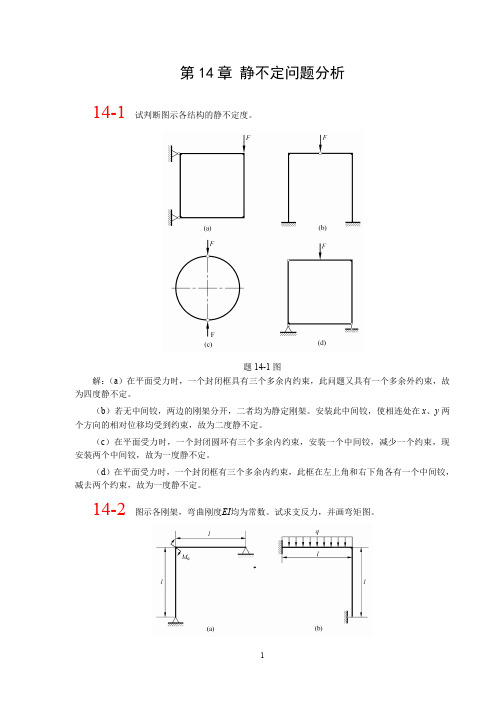
2. 角位移计算
施加单位力偶如图 d 所示,并同样以刚性杆 BC 与 DG 为研究对象,则由平衡方程
11
M B 0, 1 F N2 2a F N3 3a 0
M G 0, F N2 2a F N3 a 0
得
F
N2
1 4a
,
F
N3
1 2a
于是得杆 BC 的转角为
F 2
(负号代表压力)
15
MC
MD
π2 2π
FR
,
MA
MB
FR π
由 F 引起的 Δ C D 可根据图 14-12(a)和(b)来算。
弯矩方程为
图 14-12
M
π2 2π
FR
F 2
R1
cos
M Rsin
将其代入 积分后,得
C/ D
2 EI
π2 M M Rd
0
C/ D
4 πFR3
2πEI
ΔBy
1 EI
π/2 0
(Rsin ) qR2 ( sin ) FBy Rsin Rd
由此得
ΔBy
R3 4EI
qR(4 π) FBy π
代入式(a),得补充方程为
qR(4 π) FBy π 0
由此得
FBy
qR(4 π
π)
2. 计算水平位移
多余未知力确定后,将其代入式(b),得曲杆的弯矩方程为
解:此为一度静不定问题。
题 14-5 图
7
选杆 BC 为多余杆,求切口处相对位移 Δe / e' 的载荷状态及单位状态分别如图 14-5(a)和(b)
所示。
求相对位移 Δe / e' 的过程列于下表:
17__第十四章__静不定问题分析

结构关于BD对称,载荷反对称
沿45度方向切开B截面
对称面处: F 0
M MB 2
F’
F
沿BD方向的线位移为零 构造相当系统:
RA H A M 2l
12
第十四章 例2:弯曲刚度EI为常数。 解法1:
F
M F x x dx
a/2 0 s 1 1 1 a a/2
x1
A 单位载荷状态 M/2 M/28
M FSC x1 2 M l M ( x2 ) FSC 2 2 M ( x1 )
M ( x1 ) x1 l M ( x2 ) 2
相当系统
FSC
15 M 14 l
M/28
27
第十四章 求C点载荷与铅垂位移
F
C
a 2 a 2
静不定问题分析
24
第十四章
FSC 0 FN C
A’ C’
M ( x1 )
静不定问题分析
F 2 MC Fa 8
x2
x1
C
F
A
F
画弯矩图——只画1/4部分即可
Fa 8 M ( x2 ) Fa Fx2 8 2
Fa/8 Fa/8
3Fa/8
3Fa/8
25
第十四章 例6:EI为常数,画弯矩图。
a a
静不定问题分析
C
a
F
a
A C’ FNA MA
A’
F
F FSA FSA ' 2 A A' 0 A A' 0
FNA FNA '
FNA’
FSA’ FNA MA
M A M A'
第十四章 静不定问题分析ppt课件

B端的水平位移为
1
BH EI
0
1
2cos
3
M0
Rsin
Rd
M0R2 sinsin2Rd
3EI 0
A
2M0R2 3EI
R
O
图(一)
M0
B 2M 0
3R
R
1
O
B
图(1)
. 24
第十四章 静不定问题分析
4. 计算B端水平位移(2)
方法2
M123cosM0 A
R
O
图(二)
M '4R1cosRsin
对称载荷
载荷作用点(或 面)、大小、方 位与指向(或转 向)均对称
反对称载荷
载荷作用点(面) 、 大小与方位均对称, 但指向(转向)反对 称
. 38
第十四章 静不定问题分析
对称问题的内力与变形特点
Fa a F C C
A
B
Fa a F C
MC
MC
FNC
A
FNC B
变形特征: C 0 , C 0
.2
第十四章 静不定问题分析
目录
§1 引言 §2 用力法分析静不定问题 §3 对称与反对称静不定问题分析 §4 平面刚架空间受力分析 §5 连续梁与三弯矩方程式 §6 位移法概念
.3
第十四章 静不定问题分析
§1 引 言
静不定问题类型 静不定度判断
.4
第十四章 静不定问题分析
静不定问题类型
•配置单位载荷系统
FN2
FN1 2
LFN 5
2FFN 1, 2
FN 6FN 21
FN1 1,FN2 1 L
1 FN6
材料力学第14章(静不定)-06分析

F
A
j2
j1 B
O
F 2
F 2
M (j1 ) Rsinj1
1 A j2
j1
1
O
M (j2 ) Rsinj2
11
2
2 0
M(j1)M(j1)Rdj1
EI
2 R3 EI
2 0
sin2
j1dj1
R3
2 EI
11X1 1F 0
X1
F
[例3] 求解图示超静定结构中拉杆CD的轴力。设刚架ABC的 抗弯刚度为EI,拉杆CD的抗拉刚度为EA。
1
1
X1
F 4
2
F
a
a A
X1
F 4
a
B
1 Fa 4
X1
3qa4 8EI
0
X
1
9qa 16
A
q
X1
9qa 16
q
qa 16
A
X1
9qa 16
B
B
7qa
qa 16
16
qa
16
qa 2
A
X1
9qa 16
16
q
qa 2
B
7qa
qa 16
49qa2 16 512
16
[例5] 试画出图示刚架弯矩图,刚架EI为常数。 F
解:①刚架有一个多余约束。
a
a
A
②选取并去除多余约束,代以多
∴变形协调方程
1F 11X1 0 或:11X1 1F 0
——力法正则方程
系数11和Δ1F可由莫尔定理求得 A
(积分或图乘)
F
B
1F
1X1 X1
高等教育大学本科课件 材料力学 第14章 静不定问题分析

M
l
A
B
HA RA HC
相当系统
x1 l
A
l x2 C RC B
l x2 1C
单位载荷状态
真实载荷状态(相当系统):
HA HC
RA
M l
HC
M ( x1 )
(
M l
HC
) x1
M ( x2 ) HC x2
C 0
单位载荷状态:
M( x1 ) x1 M( x2 ) x2
C
1 EI
[
l
0 M( x1 ) M( x1 )dx1
§14-2 用力法分析静不定问题
➢ 几个概念: 基本系统: 解除多余约束后的静定结构(静定基)
相当系统: 作用有载荷和多余反力的基本系统。
Page11
BUAA
MECHANICS OF MATERIALS
➢ 第一类静不定问题:存在多余的外部约束
解除多余的外部约束,代之以支反力
相当系统
在解除约束处,建立变形协调条件
Page3
BUAA
➢ 内力静不定
MECHANICS OF MATERIALS
存在多余内部约束 平面桁架:
内力静不定度 = m - 2n + 3 m: 杆数 n: 节点数
外力静定 内力静不定(一度)
几何可变
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
例1:已知EI为常数,求A
A
M l
B
解: 解静不定,求解多余未知力
l
存在1个多余外部约束:
一度外力静不定
C
材料力学(单辉祖)第十四章静不定问题分析

求解上式可得
X1
=
1−
π2
π
4⋅ −1
P 2
=
4−π π2 −8
P
,8X2来自=π π−3
2
−1
⋅
PR 4
=
2(π
π2
− 3)
−8
PR
8
27
Example-7
在平面xy内,由k根等直杆组 y
成的杆系,在结点A处用铰连 接在一起,并受到水平载荷P1 和垂直载荷P2的作用。已知各 杆的材料相同,其拉压弹性模
∂X 1
∂X 2
Rϕ
25
Example-6
由对称截面处的约束条件, 可得变形相容性条件
Δ = ∂Uc = 0, θ = ∂Uc = 0
∂X 1
∂X 2
P/2 X2
X1 X3
Rϕ
即
∫ − 1
EI
π 2
0
⎜⎛ ⎝
PR 2
sin
ϕ
−
X 1R(1 −
cos ϕ )
−
X
2
⎟⎞ ⎠
⋅
R(1 −
cosϕ )Rdϕ
F
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
π
∫ Δ By
=
∂Vε ∂FBy
=
2
[M
0
(ϕ ) ∂M (ϕ )][EI ]−1Rdϕ
∂FBy
8
Example-1
π
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
∫ Δ By
=
∂Vε ∂FBy
=
2
[EI ]−1 ⎡⎣FR (1− cosϕ ) − FBy R sinϕ ⎤⎦ (−R sinϕ ) Rdϕ
材料力学第14章(静不定)

a
qa4 8EI
( M1 M1) ( M1 M2) ( M2 M2)
( MF M1)
(MF M2)
⑤代入力法正则方程:
4a3
a3
qa4
3EI
X1 2EI
X2
6EI
0
a3 2EI
X1
a3 3EI
X
2
qa4 8EI
0
X1
1 7
qa
X2
5 28
qa
⑥画弯矩图
A 5qa
28
q
qa
7
B
qa2 qa2 7
1 6
2
B
A
应用叠加法求桁架各杆的内力
( P78)
表14.1
杆件 编号 FNi FNi
1 -F 1
2 -F 1
3
01
401
5 2F 2
6 0 2
FNPi FNi FNi X1
-F/2 -F/2 F/2 F/2
F/ 2 -F/ 2
[题2-43] 求三杆的轴力,各杆的EA相等。 解:
1
2
3
l
a
a
1
A
q
MF图
B
1 2
qa
2
a
a
A
1
B M1图
A
1
M2图
Ba
11
1 EI
1 2
a
2
2 3
a
a
2
a
4a3
3EI
12
1 EI
1 2
a2
a
a3 2EI
22
1 EI
1 2
a2
2 3
a
材料力学-第14章 静不定问题分析

材料力学
第十四章 静不定问题分析
材料力学- 材料力学-第14章 静不定问题分析 章
本章主要研究如何运用能量方法求解一次静 不定问题。 不定问题。
材料力学- 材料力学-第14章 静不定问题分析 章
g 静不定次数 g 相当系统 g 能量法求解静不定系统 g 对称与反对称性
材料力学- 材料力学-第14章 静不定问题分析 章
Fa
x1
A F
a
q
x2
C
qa 横梁弯矩 M ( x1 ) = − F x1 2 1 2 竖梁弯矩 M ( x2 ) = − qx2 − ( F − qa ) x2 2
M ( x1 ) = 1 ⋅ ( − x1 ) = − x1
M ( x2 ) = 1 ⋅ ( − x2 ) = − x2
g 静不定次数
材料力学- 材料力学-第14章 静不定问题分析 章
静定问题与静定结构——未知力 内力或外力) 未知力( 静定问题与静定结构——未知力(内力或外力)个数 等于独立的平衡方程数
F FAx FAy
三个): 平衡方程 (三个): M(x)
q
FAx FBy
= 0,
FAy
三个): 平衡方程 (三个):
单位载荷法
1 qx 2 M ( x) ∂M ( x) ∆B = ∫ dx = ∫l ( FB − 2 )xdx = 0 l EI EI ∂FB 1 qx 2 1 ∆B = ∫l M ( x)M ( x)dx = EI ∫l ( FB − 2 ) xdx = 0 EI q Fl FB l M C1
q
B
q
例如: 例如:
相当系统 FBy
额外的约束方程: 额外的约束方程:∆ By = 0
第十四章 静不定问题分析
材料力学- 材料力学-第14章 静不定问题分析 章
本章主要研究如何运用能量方法求解一次静 不定问题。 不定问题。
材料力学- 材料力学-第14章 静不定问题分析 章
g 静不定次数 g 相当系统 g 能量法求解静不定系统 g 对称与反对称性
材料力学- 材料力学-第14章 静不定问题分析 章
Fa
x1
A F
a
q
x2
C
qa 横梁弯矩 M ( x1 ) = − F x1 2 1 2 竖梁弯矩 M ( x2 ) = − qx2 − ( F − qa ) x2 2
M ( x1 ) = 1 ⋅ ( − x1 ) = − x1
M ( x2 ) = 1 ⋅ ( − x2 ) = − x2
g 静不定次数
材料力学- 材料力学-第14章 静不定问题分析 章
静定问题与静定结构——未知力 内力或外力) 未知力( 静定问题与静定结构——未知力(内力或外力)个数 等于独立的平衡方程数
F FAx FAy
三个): 平衡方程 (三个): M(x)
q
FAx FBy
= 0,
FAy
三个): 平衡方程 (三个):
单位载荷法
1 qx 2 M ( x) ∂M ( x) ∆B = ∫ dx = ∫l ( FB − 2 )xdx = 0 l EI EI ∂FB 1 qx 2 1 ∆B = ∫l M ( x)M ( x)dx = EI ∫l ( FB − 2 ) xdx = 0 EI q Fl FB l M C1
q
B
q
例如: 例如:
相当系统 FBy
额外的约束方程: 额外的约束方程:∆ By = 0
材料力学课件:静不定问题分析
1
C
l
A
B
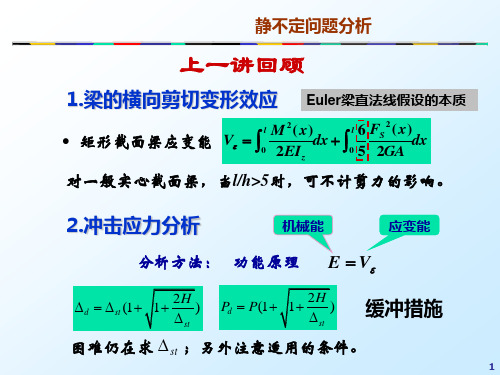
1、以相当系统为真实载荷状态
l
2、单位载荷法的本质
C
1A
1 EI
[
l
0 M( x1)M( x1 )dx1
l
0 M( x2 )M( x2 )dx2]
M
l
A
B
3、分解式的证明
l
C
21
3、分解式的证明
M
l
A
B
A
l
C
静不定问题分析
M l
B l HC C
x1 l
A 1
B l x2 C
静不定问题分析
上一讲回顾
1.梁的横向剪切变形效应 Euler梁直法线假设的本质
•
矩形截面梁应变能
V
l M2(x) dx
0 2EIz
l 6 FS2( x)dx 0 5 2GA
对一般实心截面梁,当l/h>5时,可不计剪力的影响。
2.冲击应力分析
机械能
应变能
分析方法: 功能原理 E V
d st (1
➢ 分析要点: 1、 去除多余约束,建立相当系统 2、 建立补充方程(找变形协调条件) 3、 确定多余未知力(多余内力和多余外力)
14
静不定问题分析
一、 外力静不定结构分析 解除多余的外部约束,代之以支反力
相当系统
在解除约束处,建立变形协调条件
建立补充方程
M
A
l
BA
l
B
l
B
l
l
A RC
l
C
HC
RC
2、 位移法: 以位移为待定量,利用平衡条件求解。
KU F 刚度法,平衡法
课件:静不定问题分析(3rd)

ai2q
Fa
0
3. 要点
用q 表示li 与FNi
由平衡方程确定q
31
位移法简介
以位移作为基本未知量进行求解的方法-位移法
位移法的求解方法与步骤 选择确定结构变形状态的位移为基本未知量 利用变形几何关系与物理关系,用所选位移表 示构件的变形与内力 建立用所选位移表示的平衡方程,并由此求出 该位移 由已确定的位移,求各构件的变形与内力
第 14 章 静不定问题分析 单辉祖编著:材料力学 Ⅱ
第 14 章 静不定问题分析
本章主要研究:
用力法分析静不定问题 对称与反对称静不定问题分析 平面刚架空间受力分析 位移法概念简介
单辉祖:材料力学Ⅱ
2
§1 引言 §2 用力法分析静不定问题 §3 对称与反对称静不定问题分析 §4 平面刚架空间受力分析 §5 位移法概念简介
FAy
2F
MA
1
2
FR
j
j 11
内静不定问题分析
分析图示桁架的内力与qAB ,各杆各截面的EA相同
1. 问题分析 一度内力静不定 ❖ 选杆 1 为多余约束,FN为多余未知力 变形协调条件: m / m' 0
截面m与m’间沿轴线方向的相对线位移为零
单辉祖:材料力学Ⅱ
12
2. 内力分析
结论:惟一未知多余力-FSC
单辉祖:材料力学Ⅱ
20
2. 求解静不定
S,C- /C 0
S,C
/ C
2 EI
l/2
0 M (x1)M (x1)dx1
l 0
M
(
x2
)M
(
x2
)dx2
M
(
x1
材料力学(17)第十四章-3PPT课件

反对称载荷作用时
对称面上:
M z 0 M y 0 FN 0 fz 0 fy 0 0
T
FSy FSz
T
具有反对称性质的内力分量
Page10
BUAA
MECHANICS OF MATERIALS
平面刚架空间受力时的对称与反对称问题
H F
y z x
A
结构与载荷均关于CH 铅垂面对称,对称面上无集 中力
FN
z Bx
截面上只存在对称性的内力分量 Mz , My, FN
载荷关于AB对称
My=Me/2, FN=0 载荷作用面垂直于圆环平面 Mz=0 可直接写出圆环的内力分布
Page13
BUAA C My Me y D M My z Bx
MECHANICS OF MATERIALS
求圆环的内力分布(1/4圆弧)
RD
C D A B 0 A B 0 1
R
C B
B
相当系统
C B 0
单位载荷状态
Page5
BUAA
MECHANICS OF MATERIALS
例:EI为常数,求A截面相对于O点的位移
P
120° C
A B R
O
解: 问题分析:
三度内力静不定 结构轴对称,载荷具有三个 对称轴
P
60° 60°
B’
A’
A截面相对于O点的位移是载荷 P的相应位移 利用卡氏定理求位移
M ( ) M B FNB R(1 cos ) 3 MB PR(1 cos ) 3
MB PR ( 2 3 9) 6
A/O
V 6
16__第十四章__静不定问题分析
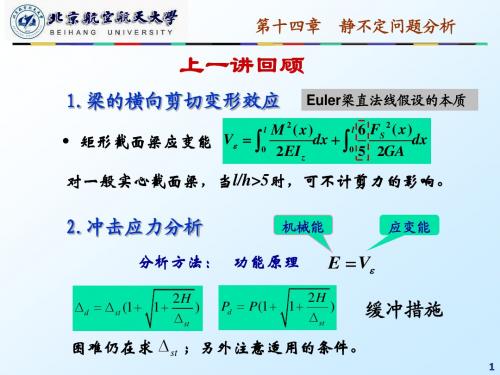
A
l
M
B l
C 0
利用单位载荷法建立补充方程
HC
C
17
第十四章
x1 A HA RA HC l M B l x2
静不定问题分析
真实载荷状态(相当系统):
H A HC RA M HC l
C 0
C
RC B l x2
相当系统
x1 A l
M M ( x1 ) ( H C ) x1 l M ( x2 ) H C x2
内2度
m : 杆数;n :节点数
9
第十四章 内力静不定 (刚架)
F F
静不定问题分析
FS M
FN
确定静不定度
内3度 单闭口的平面刚架或曲杆,3度内静不定。 F F F
F
5度内力静不定,加一中间铰减 6度内力静不定 少一度静不定
4度内力静不定,加一根二力杆 增加一度静不定
10
第十四章
静不定问题分析
20
第十四章 1
A
l B l 1 A C l B l
静不定问题分析
有关单位载荷状态的选择问题 为什么可以使用基本系统进行分析? 1、以相当系统为真实载荷状态 2、单位载荷法的本质
l 1 l 1 A [ M ( x1 ) M ( x1 )dx1 M ( x2 ) M ( x2 )dx2 ] 0 EI 0
H
EI
P
1、 去除多余约束,建立相当系统 2、 建立补充方程(找变形协调条件) m / m 0 D
B
N
C
N
A
H
利用单位载荷法建立补充方程
24
P
第十四章
x2 B
材料力学14章-3静不定结构中对称与反对称性质

材料力学14章-3静不定结 构中对称与反对称性质
在材料力学的14章-3中,我们将探讨静不定结构中的对称与反对称性质。了 解这些性质对于理解结构的力学行为至关重要。
对称性与反对称性
对称性和反对称性是结构力学中重要的概念。它们可以帮助我们分析和预测 结构的行为,并提供简化问题的方法。
静Hale Waihona Puke 定结构介绍静不定结构是指需要使用静力学和弹性力学的原理进行分析的结构。它们在工程中非常常见,需要特殊的技巧 来解决。
对称性的定义和特点
对称性是指一个结构在某种变换下保持不变的特性。它可以简化结构分析, 并揭示结构的关键特点和行为。
反对称性的定义和特点
反对称性是指一个结构在特定条件下会发生变化的特性。它可以帮助我们理 解结构的变形和应力分布。
对称性与反对称性在结构中的应用
对称性和反对称性在结构设计和分析中具有广泛的应用。它们能够帮助我们优化结构设计、降低成本,并提高 结构的可靠性和稳定性。
对称性与反对称性的优劣比较
对称性和反对称性各自具有优劣势,根据结构的具体需求和约束条件,选择适合的性质可以使结构更加高效和 可靠。
结论和要点
通过研究材料力学14章-3中的对称与反对称性质,我们可以更好地理解和分析静不定结构的行为。这些概念在 结构设计和分析中起着重要的作用。
在材料力学的14章-3中,我们将探讨静不定结构中的对称与反对称性质。了 解这些性质对于理解结构的力学行为至关重要。
对称性与反对称性
对称性和反对称性是结构力学中重要的概念。它们可以帮助我们分析和预测 结构的行为,并提供简化问题的方法。
静Hale Waihona Puke 定结构介绍静不定结构是指需要使用静力学和弹性力学的原理进行分析的结构。它们在工程中非常常见,需要特殊的技巧 来解决。
对称性的定义和特点
对称性是指一个结构在某种变换下保持不变的特性。它可以简化结构分析, 并揭示结构的关键特点和行为。
反对称性的定义和特点
反对称性是指一个结构在特定条件下会发生变化的特性。它可以帮助我们理 解结构的变形和应力分布。
对称性与反对称性在结构中的应用
对称性和反对称性在结构设计和分析中具有广泛的应用。它们能够帮助我们优化结构设计、降低成本,并提高 结构的可靠性和稳定性。
对称性与反对称性的优劣比较
对称性和反对称性各自具有优劣势,根据结构的具体需求和约束条件,选择适合的性质可以使结构更加高效和 可靠。
结论和要点
通过研究材料力学14章-3中的对称与反对称性质,我们可以更好地理解和分析静不定结构的行为。这些概念在 结构设计和分析中起着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C
D
Page21
2 B 2a
第十三章
静不定问题分析
§13-3
基本概念
对称与反对称静不定问题分析
对称结构: 形状、截面尺寸、材料、支持 方式沿对称面对称。 P M F P P M F F M P M P M F
对称载荷
反对称载荷
Page22
第十三章
静不定问题分析
对称问题的内力与变形特点
A
1
o
Page26
第十三章 (3)计算 B D (i)利用整圆环
1 sin M FR 2 1 sin M R 2
静不定问题分析
B A R
F
C
D
F 1
C
B D
4 EI
2 0
2 0
M M Rd
内力静不定结构
混合型静不定结构
Page 2
第十三章 外力静不定
F q
静不定问题分析
F q
外 1度 外3度(平面) 外6度(空间)
约束力分量个数: 平面固定铰 2 平面活动铰 1 空间球形铰 3
平面固定端
3
空间固定端
6
Page 3
第十三章 内力静不定 (桁架)
F
静不定问题分析
F
内 1度 内 2度
F 2FN cos45 FN FN F ( 2 1)F 1 2
F F
静不定问题分析
F
D O 1 3 A
C
B
2
FN
F
FN FN
F
Page34
第十三章
静不定问题分析
改错 : 求C点支反力与铅垂位移 cv
F
C
a 2 a 2
F 2
1 1 8 3 6
Page20
思考:若求加载点的水平位移,如何选择单位载荷状态
4 5
6 8 3
2 1
4 5
2 1
第十三章 思考:求BD杆的转角,正确 的单位载荷系统是_______ 答:C、D
D
1 a
静不定问题分析
D
1 a
A
C
1 B a
A
A
2 2a
D
A
2 2a 2 B 2a
D
A
C
B
1 a
C
C
F
F
4度内力静不定,加一根二力杆增加一 度静不定
Page 6
第十三章 混合静不定
F
静不定问题分析
F
1(内)+1(外)= 2 度
3(内)+3(外)= 6 度
F
圆环
梁:外3 环:内3 梁环接触:1 3+3+1=7 度
圆环在水平方向有一自由度
Page 7
第十三章
静不定问题分析
混合静不定(梁杆结构)
A
1
1
B
Page30
第十三章 例:对称还是反对称问题? 双对称轴问题 双反对称轴问题
F
a 2 a 2
静不定问题分析
F
F
a2
a2
2FS 2F cos45 0 2 FS F 2
F S
F F
F
一类双反对称轴问题可仅用平衡条件求解
F S
Page31
第十三章 结构对称、载荷不对称的问题
静不定问题分析
A
FS
F S
B FR
F 2
1 M ( ) FS R sin FR(1 cos ) 2 M ( ) R sin
1 M ( ) M ( ) Rd 0 A B EI 0 1 1 3 3 ( FS R FR 2) 0 EI 2 2 2F FS
第十三章
静不定问题分析
第十三章
§13-1 §13-2 §13-3 §13-4
静不定问题分析
引言 用力法分析静不定问题 对称与反对称静不定问题分析 平面刚架空间受力分析
Page 1
第十三章
静不定问题分析
§13-1
引言
q
q
q
FAx A
B FBx
FBy
A
B
FAx
A
FAy
B
FBx
FBy
FAy
外力静不定结构
静不定度 = m - ( 2n – 3 )
m : 杆数;n :节点数
Page 4
第十三章 内力静不定 (刚架)
q
静不定问题分析
q
FS
M
FN
内 3度
F
F
单闭口的平面 刚架或曲杆, 3度内静不定
内6度(外3自由度)
Page 5
第十三章
静不定问题分析
F
F
6度内力静不定,外3自由度
F
F
5度内力静不定,加一中间铰减 少一度静不定
Page28
第十三章
静不定问题分析
例:小曲率圆环,已知R,EI.求A截面内力.
F
A R
F 2
A
F 2
R
B
2FR
F 2
F
F B 2 2FR
F 2
A
FS
F S
B FR
F 2
反对称轴AB 内力特征
M A 0, FNA 0,
A/ B 0
Page29
未知力 FS
变形特征
第十三章
F 2
静不定问题分析
第十三章
静不定问题分析
思考:计算 BH ,下图相当系统选取是否正确?
M0 3R M0 3R
R A
M0
o
B
对应的单位载荷系统:
R A
o
B
1
Page16
第十三章 例:求B 端反力
q A
l l
静不定问题分析
q A B
FBx
A B 1 B FBy
单位载荷系统 1
相当系统
A B 1
单位载荷系统 2
Page17
F
=
F 2
F 2
+
F 2
F 2
结论: 结构对称、载荷不对称的平面结构问题可 分解为一个对称与一个反对称问题。
Page32
第十三章 中心对称问题
m
E
静不定问题分析
M C
C
o
D
m
C
O
m
F B
M
M
A
30
m
C
m
A
关于原点O 中心对称
M
M
3 M m A C 3
Page33
A
第十三章 例:正方形行架杆,各杆EI, O点固结。 (1)几度静不定? (2)求各杆内力。 解: (1)4度静不定 (2)中心对称 各杆应变相同,FN 相同
M R 1 cos
A
静不定问题分析
R O
FB (a)
M0 B
变形协调条件 BV=0 单位载荷法
BV
A R O 1 (b)
B
1 FB R 1 cos M 0 R 1 cos Rd 0 EI 2M0 1 3 3 2 F R M R 0 F B 0 B EI 2 3R
2、 建立补充方程(找变形协调条件) 3、 确定多余未知力(多余内力和多余外力)
Page 9
第十三章 一、 外力静不定结构分析
静不定问题分析
解除多余的外部约束,代之以支反力
相当系统 建立补充方程
M
在解除约束处,建立变形协调条件
A
l
B
l C
A
l
B l
l
B
l
A RC
HC
C
RC
C 0 fC 0
F M M B R sin 2
静不定问题分析
F 2
B
MB
M 1
A
o
B
1 B EI
2 0
F M B 2 R sin Rd 0
R 1 M FR 0 B EI 2 2
MB FR 1 sin , M FR 2
P
6
2、 建立补充方程(找变形协调条件)
m / m 0
Page18
第十三章
4
5
N7 N7
静不定问题分析
利用单位载荷法建立补充方程
8 2 1
3
P
li 1 2 3 4
2a
Ni
2P
Ni 0 0
2 2 2 2 2 2 2 2
6
a a a a
P
2 N7 P 2 2 N7 2 2 N7 2 2 N7 P 2
Page24
第十三章
静不定问题分析
B A R D
例:已知圆环EI,求B、D相对位移d
解:(1)利用对称性,选取相当系统
F
C
F
F
B
B R
F
R A
C
B
A
MA
o
F 2
A
MA
C
MA
MA
F 2
FN A
FN A
A 0
A 0
1 FN A F 2 A C 0
Page25
第十三章 解:(2)利用单位载荷法,计算MB
(a)
(b) (a): 内2度
(b): 1度
