测量学导线测量常用计算公式
闭合导线坐标增量改正数公式

闭合导线坐标增量改正数公式闭合导线坐标增量改正数公式是测量学中一套相当重要的公式,它用于测量坐标计算中,对测量坐标进行预先改正和终点改正的计算公式。
这是一种计算包含两个坐标系上的两个点的坐标增量的计算方法,以及闭合坐标的记录与回算。
闭合导线坐标增量改正数公式的定义和应用要求都很复杂,所以有必要详细介绍一下。
闭合导线坐标增量改正数公式是以导线坐标起点终点的各改正增量为分析对象,运用空间三角法和点坐标排列的原理,结合坐标的空间相邻关系,以外点的实测值及前点的预先改正值和后点的终点改正值,计算当前点的预先改正值和终点改正值。
计算的主要步骤有以下几个:1.导线上各点的空间相邻关系:取测量点ai和后点a(i+1),求出各个空间方位角及里程差,即:αi=αi+1-Δασi=σi+1-Δσ2.先改正值和终点改正值的计算:根据起点a1处的实测点坐标,以及中间点ai处的实测点坐标和前点a(i-1)处的终点改正值,按照三角形角平分比例原理,计算当前点ai处的预先改正值、终点改正值以及依据前点a(i-1)处的终点改正值,依据当前点ai处的预先改正值,按照正方形对称原理,计算后点a(i+1)处的终点改正值、前点a(i-1)处的预先改正值等。
3.算点坐标:根据前点的预先改正值和后点的终点改正值,即可求出各点的终点改正坐标经测量值,即闭合点。
由以上所述,我们可以得出闭合导线坐标增量改正数公式的有效性和重要性,它可以帮助测量人员实现准确的测量和精确的结果,比如地形测量和精密测量。
闭合导线坐标增量改正数公式还可以用于土地所有制和房地产测量,其中一些在勘测前就完成了,这在很大程度上提高了工作效率,提升了土地调查和评估质量。
因此,闭合导线坐标增量改正数公式具有广泛的应用前景,只有通过正确的使用,才能实现测量和精确结果的高质量和高精度。
工程测量基础知识

1基础知识测量学是研究地球的形状和大小以及确定地球表面(包括空中、地面和海底)点位关系的一门科学。
工程建设三阶段:勘测设计、施工建设、运营管理。
一、建筑工程测量的任务及作用:(1) 地形测图,亦称测定(测绘)它是利用各种测量仪器和工具,将地面上局部区域的地物和地面起伏得形状、大小,按一定的比例尺缩小测绘成地形图,为工程建设的规划、设计和施工提供服务。
(2) 施工放样,亦称测设(放样)它是将图纸上规划、设计好的建筑物位置、尺寸测设于地面,作为施工依据,并在施工过程中,配合工程进度进行一系列测量工作,以保证工程质量。
(3) 变形测量对于一些大型或重要的建筑物,在施工和运营期间,要定期进行变形观测,了解其变形规律,以确保建筑物的安全。
二、地面点位的确定:确定地面上一点的空间位置,需要用三个量来表示,在测量工作中,是用地面点在基准面(参考椭球面)上的投影位置坐标和该点沿投影方向到基准面(大地水准面)的距离来表示的。
三、用水平面代替水准面的限度(1)地球曲率对水平距离的影响:在半径为10km 的范围内,地球曲率对水平距离的影响可以忽略不计,即可以用水平面代替水准面。
(2)地球曲率对高程的影响:当距离为100m 时,在高程方面的误差就接近1mm ,这对高程测量的影响是很大的,所以地球曲率对高程的影响是必须予以考虑的,即尽管距离很短,也不能以水平面代替水准面。
四、测量基本工作:角度测量、距离测量、高程测量。
五、测量工作应遵循的基本原则:“从整体到局部”“先控制后碎部”。
其目的是:防止测量误差的积累,保证测量精度;同时由于建立了统一的控制网,把碎部测量划分成几部分来进行,可以加快测量进度。
测量工作的基准线是:铅垂线测量工作的基准面是:水准面测量计算的基准面是:参考椭球面水准面:设想由一个静止的海水面向陆地延伸而形成一个封闭的曲面,曲面上处处和铅锤方向相垂直,这个静止的海水面称为水准面。
大地水准面:海水受潮汐影响,时涨时落,所以水准面有无数个,其中与平均海水面重合的水准面称为大地水准面,是测量工作中点位投影和计算点位高度得基准面。
《测量学》第5章距离测量

距离测量是传统测量的三种基本测量工作之一, 导线测量、碎部点测量等一般需要进行距离测量。 传统距离的测量方法有钢尺量距、光电测距仪测距 和光学视距法测距等。
《测量学》第5章距离测量
5.1 钢尺量距
5.1.1 量距的工具
1. 钢尺
• 钢尺分划类型 • 零分划位置
《测量学》第5章距离测量
钢尺长度尺长会随着拉力的变化而改变,如果 测量时拉力不等于标准拉力,也会产生长度误差:
lP
P •l EA
例,某钢尺长30m,标准拉力是10kg,弹性模量 为2×106kg/cm2,其横截面积为0.03cm2,测量时 拉力为20kg,则拉力产生的长度误差为
lp E p•lA 2 16 2 k 0 k /g c 0 g 1 2 m k 0 0 .0 g c3 2 m 3m 0 0 .0m 05
《测量学》第5章距离测量
1 定线误差
ldll222l2l2
《测量学》第5章距离测量
例:使用30米钢尺量距时,如果测量某尺段时, 尺端两端的定向误差均为0.2米,定向误差引起的距 离误差为:
22 20.22
ll
2.6m 7 m 30
当尺长为50米,为使定线误差产生的量距误差小 于1/10000时,应使ε≤0.3536m
2. 其它工具
《测量学》第5章距离测量
5.1.2 直线的定线
要点:
甲在A点后1米左右处指挥,甲从在A点沿标杆的同一侧 看到A、2、B三支标杆成一条线为止。
两点间定线,一般应由远到近,即先定1点,再定2点。 乙所持标杆应竖直,利用食指和姆指夹住标杆的上部,稍 微提起,利用重心使标杆自《测然量学》竖第5章直距离。测量
如果钢尺长为50m,其它条件同上,则拉力产生 《测量学》第5章距离测量
工程测量放线常用公式
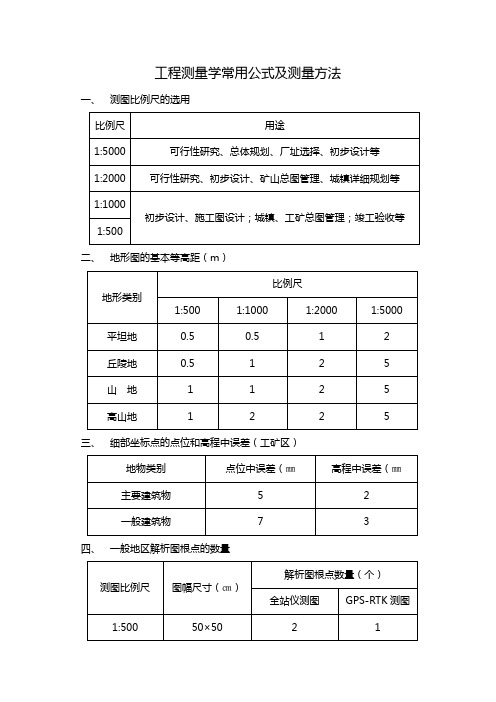
工程测量学常用公式及测量方法一、测图比例尺的选用二、地形图的基本等高距(m)三、细部坐标点的点位和高程中误差(工矿区)四、一般地区解析图根点的数量五、图根导线测量的主要技术要求六、图根水准测量的主要技术要求七、图根电磁波测距三角高程的主要技术要求注:D为电磁波测距边的长度(㎞)。
八、铁路隧道贯通的允许偏差九、矿山井巷贯通的允许偏差十、符号A──GPS接收机标称的固定误差;a──电磁波测距仪器标称的固定误差;B──GPS接收机标称的比例误差系数、隧道开挖面宽度;b──电磁波测距仪器标称的比例误差系数;C──照准差;D──电磁波测距边长度、GPS-RTK参考站到检查点的距离、送变电线路档距;D g──测距边在高斯投影面上的长度;D h──测区平均高程面上的测距边长度;D p──测线的水平距离;D o──归算到参考椭球面上的测距边长度;d──GPS网相邻点间的距离;DS05、DS1、DS3──水准仪型号;fβ──方位角闭合差;H──水深、高;H m──测距边两端点的平均高程;H p──测区的平均高程;h──高差、建筑施工的沉井高度、地下管线的埋深、隧道的高度;h d──基本等高距;h m──测区大地水准面高出参考椭球的高差;ι──水准仪视准轴与水准管轴的夹角;K──大气折光系数;L──水准测段或路线长度、长度;l──测点至线路中桩的水平距离、桥梁所跨越的江河的宽度;M──测图比例尺的分母、中误差;M w──高差全中误差;M△──高差偶然中误差;m──中误差;m D──测距中误差;m H──地形管线重复探测的平面中误差;m v──地下管线重复探测的埋深中误差;mα──方位角的中误差;mβ──测角中误差;N──符合路线或闭合环的个数;n──测站数、测段数、边数、基线数、三角形个数、建筑物结构的跨数;P──测量的权;R──地球平均曲率半径;R A──参考椭球体在测距边方向法截弧的曲率半径;R m──测距边中点处在参考椭球面上的平均曲率半径;S──边长、斜距、两相邻细部点间的距离、转点桩至中桩的距离;T──边长相对中误差分母;W──闭合差;W x、W y、W z──坐标分量闭合差;W f、W g、W j、W b—分别为方位角条件、角-级条件、边(基线)条件自由项的限差;Уm──测距边两端点横坐标的平均值;α──垂直角、地面倾斜角、比例系数;δh──对向观测的高差较差;δ1、2──测站点1向照准点2观测方向的方向改化值;△──测段往返高差不符值;△d──长度较差;△H──复查点位与原点位的埋深较差;△S──复查点位与原点位间的平面位置偏差;△α──补偿式自动安平水准仪的补偿误差;μ──单位权中误差;σ──基线长度中误差、度盘和测微器位置变换值。
5.1导线测量

§5-2
一、导线测量
导线测量
1、导线:测区内选定一系列控制点,标定后构成闭合
多边形或折线形。
2、导线点:构成导线的控制点。
3、导线转折角:导线点上的水平角。(左角、右角) 4、导线边长:相邻两导线点间的水平距离。
5、外业观测:所有导线转折角,并测量所有导线
边长,则导线点之间的相对位置得
以确定。
1536.86 837.54 B -107.27 -17.89 +30.91 -0.59 -13.00 -64.83 1429.59 772.71 1 +97.10 1411.70 869.81 2 +141.27 1442.61 1011.08 3 +116.42 1442.02 1127.50 4 +155.67 1429.02 1283.17 C D
辅 助 计 算
f 始 测 n 180 终
f 容 60 6
fx fy
f f x2 f y2
K
K容 1 2000
观测角
点 号 A B 205 36 48 1 2 290 40 54 (右角) °´"
改 正 数
˝
改正角 °´"
3、测角 经纬仪测导线的转折角: 附合导线测右角 闭合导线测内角。
4、联测
• 测区内有高级控制点时,应将导线与高级控制
点进行联系测量,简称联测。这样既可以使导
线计算时获得起算方向和坐标,又可使导线和
高级控制点连成一整体,检核导线观测成果。
A 2 4 D
B
3
C
• 附近无高级控制点时, 可用罗盘仪测定导线 2 起始边的磁方位角作 2 为起算方向,并假定 3 起始点的坐标为起算 1 1 坐标,建立独立控制 4 5 网系统。
浅述光电测距高程导线测量的方法及应用

浅述光电测距高程导线测量的方法及应用摘要:本文主要论述了三角高程测量原理以及光电测距高程导线中常用的每点设站法和隔点设站法。
并比较两种方法的优缺点及实际应用。
关键词:光电测距高程导线;每点设站法;隔点设站法0 前言随着高精度电子全站仪的不断普及,光电测距三角高程测量以其快捷的优点逐渐被广泛应用。
为了消除地球弯曲差和大气垂直折光差的影响,用此方法传递高程一般采取每点设站和隔点设站法进行。
1 三角高程测量原理在不考虑垂线偏差情况下,如图1所示,A为测站点,仪器高为。
B为照准点,觇标高为。
S为A、B两点的实地水平距离。
为P点的水准面,为P点的水平视线,CE为地球弯曲差。
为目标N的光程曲线,为P点望远镜照准目标N时视准轴所指的方向,MN为大气垂直折光差。
为P点望远镜观测目标N的垂直角。
AF为A点的水准面,BF为B点对A点的高差。
在平面三角形PCM中,∠PCM≈90°,PC≈,故MC≈,由图1可看出:== (1)式中K为大气垂直折光系数。
上式为三角高程测量单向观测高差的基本计算公式。
同样可得在B点观测A 点的高差计算公式:(2)如果三角高程的边长由电磁波测距仪直接观测,则电磁波测距三角高程测量可按斜距由下列公式计算高差(3)式中,为测站与镜站之间的高差;为垂直角;为经气象改正后的斜距;为大气折光系数;为经纬仪水平轴到地面点的高度;为反光镜瞄准中心到地面点的高度。
该计算公式为光电测距三角高程测量单向观测高差的基本计算公式。
由(1)、(2)、(3)式可看出,如不考虑垂线偏差影响,则三角高程测量的主要误差来源是边长、垂直角、仪器高、觇标高的测量误差,以及球曲差和大气垂直折光差的影响。
属于人或仪器影响的误差一般都可以通过提高仪器精度,选择有利的观测条件及认真作业等加以消除。
关于球曲差,在同一测区,可认为其地球平均曲率半径相同,可通过对向观测或控制前后边长差加以消除。
大气垂直折光由大气密度的分布不均匀引起,它随大气压、温度、湿度、风场、植被、海拔等的变化而变化,具有不稳定性。
导线测量中坐标方位角的推算

第43卷第12期2020年12月测绘与空间地理信息GEOMATICS&SPATIALINFORMATIONTECHNOLOGYVol.43ꎬNo.12Dec.ꎬ2020收稿日期:2019-12-02基金项目:陕西铁路工程职业技术学院科学研究基金项目 BRB加固震后框架梁柱节点抗剪设计(KY2016-46)资助作者简介:王㊀婷(1990-)ꎬ女ꎬ山西运城人ꎬ助教ꎬ硕士ꎬ2016年毕业于西安建筑科技大学防灾减灾及防护工程专业ꎬ主要从事工程测量㊁抗震减灾等方面的教学与科研工作ꎮ导线测量中坐标方位角的推算王㊀婷ꎬ张㊀磊(陕西铁路工程职业技术学院ꎬ陕西渭南714000)摘要:导线测量是平面控制测量的一种常见方法ꎬ坐标方位角的推算是导线内业计算中起承接作用的一步ꎬ是后续坐标增量计算以及未知导线点坐标计算的基础ꎮ本文通过相邻导线间4种不同的位置关系ꎬ推导出沿着导线前进方向ꎬ根据后一条导线边坐标方位角求解前一条导线边坐标方位角的通用计算公式及其应用方法ꎬ为导线内业计算中方便㊁快速地计算各边坐标方位角提供了理论依据ꎮ关键词:导线测量ꎻ坐标方位角ꎻ位置关系ꎻ通用计算公式ꎻ应用方法中图分类号:P209㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1672-5867(2020)12-0035-03CalculationofCoordinateAzimuthinTraverseSurveyWANGTingꎬZHANGLei(ShaanxiRailwayInstituteꎬWeinan714000ꎬChina)Abstract:Traversesurveyisacommonmethodofplanecontrolsurvey.Thecalculationofcoordinateazimuthisastepwhichplaystheroleofconnectiontransitionintraversesurvey.Itisthebasisofsubsequentcoordinateincrementcalculationandunknowntraversepointcoordinatecalculation.Basedonfourdifferentpositionrelationsbetweenadjacenttraverseꎬthegeneralformulaofcalculatingthecoordinateazimuthoftheprevioustraverseaccordingtothecoordinateazimuthoflattertraverseisderivedandtheapplicationmethodoftheformulaisconcluded.Itprovidesatheoreticalbasisfortheconvenientandrapidcalculationofthecoordinateazimuthinofficecalculationoftraverse.Keywords:traversesurveyꎻcoordinateazimuthꎻpositionrelationsꎻthegeneralformulaꎻapplicationmethod0㊀引㊀言在工程建设中ꎬ为减小各项测量工作误差的累积ꎬ需在测区内选定若干具有控制意义的控制点ꎬ将其按一定规律和要求组成连续多边形或连续折线ꎬ构成控制网ꎬ作为各种细部测量的基准ꎮ测定控制网平面坐标的工作称为平面控制测量ꎬ平面控制测量常见的方法有导线测量㊁三角测量㊁三边测量㊁GNSS测量等[1-3]ꎮ导线测量布置灵活ꎬ满足相邻控制点间通视即可ꎬ尤其适用于建筑物或障碍物较多的区域ꎬ随着电磁波测距技术的发展ꎬ导线测量已成为小区域平面控制测量的主要方法ꎮ导线测量是根据起算边的方位角㊁起算点的坐标ꎬ结合外业观测的相邻导线边水平夹角和导线边长ꎬ计算控制网中各未知导线点的坐标ꎮ在导线内业计算中ꎬ涉及相邻导线边之间坐标方位角的推算ꎬ本文针对坐标方位角的推算[4-7]进行探讨ꎬ推导其通用的计算公式以及公式的应用方法ꎮ1㊀正反坐标方位角的关系坐标方位角是指从直线一端的坐标纵轴方向的北端起ꎬ顺时针旋转到该直线所形成的水平夹角ꎮ由于一条直线具有起点和终点两个端点ꎬ分别过这两个端点可以做出两个坐标方位角ꎬ它们互为正反方位角ꎮ如图1(a)所示ꎬαAB和αBA互为正反方位角ꎮ做出直线AB的延长线以及αAB的同位角(如图1(b)所示)ꎬ从图中可以看出ꎬαAB=αBA-180ʎ或αBA=αAB+180ʎꎬ由于αAB和αBA互为正反方位角ꎬ将上述两式合并可得α反=α正ʃ180ʎꎬ式中ꎬ ʃ 取决于α正的大小ꎬ当α正>180ʎ时取 - 号ꎬ当α正<180ʎ时取+ 号ꎬ以保证计算所得α反的角值大小介于0ʎ 360ʎ区间内ꎮ图1㊀正反坐标方位角Fig.1㊀Coordinateazimuth2㊀相邻导线边坐标方位角的推算沿着导线前进方向ꎬ根据后一条导线边推算前一条导线边的坐标方位角可按以下两个步骤进行ꎮ2.1㊀推算后一条导线的反方位角1)当直线AB的方位角αAB<180ʎꎬ即对应于测量中平面直角坐标系中的Ⅰ㊁Ⅱ象限(如图2所示)ꎬ此时αBA=αAB+180ʎ(1)2)当直线AB的方位角αAB>180ʎꎬ即对应于Ⅲ㊁Ⅳ象限(如图3所示)ꎬ此时αBA=αAB-180ʎ(2)图2㊀αAB<180ʎ示意图Fig.2㊀SchematicofαAB<180ʎ图3㊀αAB>180ʎ示意图Fig.3㊀SchematicofαAB>180ʎ2.2㊀推算前一条导线的方位角1)如图4所示ꎬ当后一条导线AB的方位角小于180ʎ且前一条导线BC的方位角小于AB的反方位角ꎬ即当αAB<180ʎ且αBC<αBA时ꎬαBC=αBA-β右ꎬ将公式(1)带入得αBC=αAB-β右+180ʎ或αBC=αAB+β左-180ʎ(3)2)如图5所示ꎬ当后一条导线AB的方位角小于180ʎ且前一条导线BC的方位角大于AB的反方位角ꎬ即当αAB<180ʎ且αBC>αBA时ꎬαBC=αBA+β左ꎬ将公式(1)带入得αBC=αAB+β左+180ʎ或αBC=(αAB-β右+180ʎ)+360ʎ(4)3)如图6所示ꎬ当后一条导线AB的方位角大于180ʎ且前一条导线BC的方位角大于AB的反方位角ꎬ即当αAB>180ʎ且αBC>αBA时ꎬαBC=αBA+β左ꎬ将公式(2)带入得αBC=αAB+β左-180ʎ或αBC=αAB-β右+180ʎ(5)4)如图7所示ꎬ当后一条导线AB的方位角大于180ʎ且前一条导线BC的方位角小于AB的反方位角ꎬ即当αAB>180ʎ且αBC<αBA时ꎬαBC=αBA-β右ꎬ将公式(2)带入得αBC=αAB-β右-180ʎ或αBC=(αAB+β左-180ʎ)-360ʎ(6)图4㊀公式(3)的推导Fig.4㊀Derivationofformula(3)图5㊀公式(4)的推导Fig.5㊀Derivationofformula(4)图6㊀公式(5)的推导Fig.6㊀Derivationofformula(5)图7㊀公式(6)的推导Fig.7㊀Derivationofformula(6)3㊀方位角推算公式的简化及应用在导线内业计算中ꎬ为合理有效地利用上述公式(3) (6)推算方位角ꎬ现将这几个公式进行合并简化ꎮ由于沿着导线前进方向(箭头方向)ꎬAB边在后ꎬCD边在前ꎬ因此将αAB记为α后ꎬ将αCD记为α前ꎮ考虑到导线外业测量中所测水平角统一为左角或者右角ꎬ分两种情形63㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀测绘与空间地理信息㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2020年讨论ꎮ1)水平角为左角β左将公式(3) (5)中的左角计算公式合并为α前=α后+β左ʃ180ʎꎬ公式中 ʃ 号取决于 α后+β左 的大小ꎮ当α后+β左<180ʎ时取 + 号ꎬ当α后+β左>180ʎ时取 - 号ꎬ这样可保证所求α前的角值大小介于0ʎ 360ʎ区间ꎮ公式(6)中的左角计算公式α前=(α后+β左-180ʎ)-360ʎꎬ即当前后导线间位置关系如图7所示情形时ꎬα后+β左-180ʎ计算的角值大于360ʎꎬ此时需在计算结果基础上再减360ʎ作为最终结果α前ꎮ2)水平角为右角β右公式(3)㊁(5)㊁(6)中的右角计算公式合并为α前=α后-β右ʃ180ʎꎬ公式中 ʃ 号取决于 α后-β右 的大小ꎮ当α后-β右<180ʎ时取 + 号ꎬ当α后-β右>180ʎ时取 - 号ꎬ这样可保证所求α前的角值大小介于0ʎ 360ʎ区间ꎮ公式(4)中的右角计算公式α前=(α后-β右+180ʎ)+360ʎꎬ即当前后导线间位置关系如图5所示情形时ꎬα后-β右+180ʎ计算的角值小于0ʎꎬ此时需在计算结果基础上再加360ʎ作为最终结果α前ꎮ4㊀结束语本文通过相邻导线间的4种不同的位置关系ꎬ推导出沿着导线前进方向ꎬ根据后一条导线边坐标方位角求解前一条导线边坐标方位角的通用计算公式α前=α后+β-βʃ180ʎ[ʃ360ʎ](7)公式的应用方法归结如下:1)根据已知数据α后以及外业观测数据β左(或β右)计算α后+β左(或α后-β右)ꎮ2)当α后+β左<180ʎ(或α后-β右<180ʎ)时ꎬ利用公式α前=α后+β左+180ʎ(或α前=α后-β右+180ʎ)计算α前ꎻ当α后+β左>180ʎ(或α后-β右>180ʎ)时ꎬ利用公式α前=α后+β左-180ʎ(或α前=α后-β右-180ʎ)计算α前ꎮ3)若2)中计算结果为大于360ʎ的数值ꎬ在其基础上减360ʎ作为所求前一条导线边坐标方位角的最终结果ꎬ若2)中计算结果为小于0ʎ的数值ꎬ在其基础上加360ʎ作为所求前一条导线边坐标方位角的最终结果ꎮ参考文献:[1]㊀黄雅.高密度建筑区图根控制测量方法探讨[J].智能建筑与智慧城市ꎬ2019(5):121-123.[2]㊀张继贤ꎬ肖雨彤.仙泉煤矿井下导线网设计与测量成果分析[J].煤炭工程ꎬ2019ꎬ51(5):163-167.[3]㊀梁继利.导线测量在东乌珠穆沁旗矿区的应用[J].内蒙古煤炭经济ꎬ2015(7):200-201.[4]㊀杨朝辉.导线测量中起始坐标方位角的计算新方法[J].测绘与空间地理信息ꎬ2012ꎬ35(6):13-14ꎬ18.[5]㊀陈伟标ꎬ陈树镇.测量学教材中存在的若干问题探讨[J].广东水利电力职业技术学院学报ꎬ2011ꎬ9(3):67-69.[6]㊀王金玲.方位角推算问题的探讨[J].长江水利教育ꎬ1995(1):25-27.[7]㊀李福纪.坐标方位角推算公式新议[J].中州大学学报ꎬ1991(Z1):84-85.[编辑:张㊀曦](上接第34页)3㊀结束语此次试验利用ArcGIS10.2平台ꎬ采用空间统计分析全国参评地级城市土地集约利用综合指数的空间分异特征ꎬ经过Box-Cox变换的克里金插值分析其变化规律ꎬ并进行评估预测全国参评地级城市的土地集约利用潜力ꎬ实现了属性数据与空间数据的链接ꎬ证明并探讨了中国城市土地集约利用水平的空间分布特征ꎮ但是对GIS在城市土地集约利用作用研究还不够深入ꎬ未来研究还应选取一个城市区域进行实证研究与分析ꎬ以构建GIS支持下的城市土地集约利用水平评价标准与系统ꎬ实现一键操作ꎬ图表并进(属性数据关联空间数据)的可行性ꎬ更好地为城市规划合理配置城市土地资源ꎬ提供直观㊁可靠的依据ꎮ参考文献:[1]㊀孙英君ꎬ王劲峰ꎬ柏延臣ꎬ等.地统计学的GIS空间分析功能扩展[J].华侨大学学报(自然科学版)ꎬ2004ꎬ25(4):435-439.[2]㊀李俊晓ꎬ李朝奎ꎬ殷智慧.基于ArcGIS的克里金插值方法及其应用[J].测绘通报ꎬ2013(9):87-97.[3]㊀王婷ꎬ钱晓霞ꎬ张雪ꎬ等.基于GIS与地统计的庄浪县土壤养分空间变异研究[J].河南农业ꎬ2019(14):57-59.[4]㊀阿依妮尕尔 艾尔肯.喀什市耕地集约利用时空变化特征分析[D].乌鲁木齐:新疆大学ꎬ2019.[5]㊀殷绪华ꎬ朱亮ꎬ陈琳ꎬ等.ArcGIS在水源地污染源强度空间分析中的应用[J].河海大学学报(自然科学版)ꎬ2018ꎬ46(5):395-401.[6]㊀庞晓兰ꎬ叶宗达ꎬ韦燕飞ꎬ等.广西国家级贫困县土地集约利用空间分异特征研究[J].大众科技ꎬ2017ꎬ19(8):35-39.[7]㊀成洁.基于地统计学的陕西县域耕地质量空间变异研究[D].西安:长安大学ꎬ2017.[8]㊀路振华.城市土地集约利用评价研究综述[J].国土资源科技管理ꎬ2017ꎬ34(6):44-53.[9]㊀郭安廷ꎬ崔锦霞ꎬ许鑫ꎬ等.基于GIS与地统计的土壤养分空间变异研究[J].中国农学通报ꎬ2018ꎬ34(23):72-79.[10]㊀胡江霞ꎬ文传浩.基于地统计分析的三峡库区农业发展的空间分布特征研究[J].河南农业大学学报ꎬ2016ꎬ50(2):248-253.[11]㊀陈真ꎬ刘辉.福州市住宅价格空间分布趋势及其特征研究[J].亚热带资源与环境学报ꎬ2015ꎬ10(4):58-62.[12]㊀董大伟.基于空间数据挖掘和地统计学的土地集约利用时空分异研究[D].武汉:华中师范大学ꎬ2011.[13]㊀苏斌.GIS支持下的城市地价空间分布与土地集约利用研究[D].郑州:信息工程大学ꎬ2010.[编辑:刘莉鑫]73第12期王㊀婷等:导线测量中坐标方位角的推算。
工程测量学基础知识

3)控制网:由控制点分布和测量方法决定所组成的图形。 4)控制测量:为建立控制网所进行的测量工作。 ⑶.控制测量分类 1)按内容分:平面控制测量、高程控制测量 2)按精度分:一等、二等、三等、四等;一级、二级、三级 3)按方法分:三角测量、导线测量、水准测量、GPS卫星定位测量 4)按区域分:国家控制测量、城市控制测量、小区域工程控制测量
⒈高程点放样的方法
在已知水准点(BM)和待放样高程点P中间位置附近架 仪,后视BM点,读后视读数a ,得视线高Hi=HBM+a,上、 下移动水准尺,使前视读数b=Hi-HP,并沿尺底画线, 得P点。
完整编辑ppt
6
⑵ 点平面位置的测设 正拨、反拨的概念: 水平角正拨——顺时针测设;水平角反拨——逆时针测设。 点平面位置的测设方法 1)直角坐标法 ⒈适用:有彼此垂直的主轴线时。 ⒉方法: O点架仪,瞄准A,量取y,定出过渡点C;C点架仪,瞄准A,反拨90°,
征点与控制点之间的距离、角度、高差等测设数据,以控制点为根据, 将各特征点在实地桩定出来。
⒉测设的基本工作——水平距离、水平角和高程(称为测设工作三要 素)。
2)水平距离的测设 ⒈直接法——从起点A直接用钢尺或测距仪在给定方向上,丈量待放样
的水平距离,得B点。
⒉归化法 用直接法测设出B点——精密丈量其距离——根据差值,实地改正。
完整编辑ppt
33
五、道路中线测量
完整编辑ppt
34
完整编辑ppt
35
例:某圆曲线半径R为1500m,转向角α为20°30′40″,JD的里程为DK15+108.086,计算圆曲线各主点的里 程。
根据公式计算而得:T=271.394;L=536.980;E=24.354;q=5.809。
【测量学】导线测量常用计算公式

一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的国家坐标:X ″=U+T cos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角 L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°)边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°)Y b =Y m +Bsin(O+MW+90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW+90°) Y b =Y m +Bsin(A+MD-MW+90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
测量学闭合导线坐标计算

测量学闭合导线坐标计算
测量学闭合导线坐标计算是测量学中的一种方法,适用于闭合导线的测量。
下面是详细的步骤:
1. 根据测量现场的实际情况,选择适当的测量仪器,比如全站仪、经纬仪等。
2. 在测量现场设置控制点和测量站点,控制点要尽可能地散布在要测区域的四周,以保证测量的准确性。
3. 在控制点和测量站点上测量出所有需要的距离和角度,并记录下来。
4. 根据测量数据,计算出每个控制点和测量站点的坐标值,这些坐标值表示了地面上点的位置。
5. 对于闭合导线,需要对起点和终点的坐标值进行闭合差计算,以验证测量数据的准确性。
如果闭合差过大,需要重新进行测量。
6. 最后,将所有的坐标值进行整理和汇总,形成闭合导线的坐标值表。
需要注意的是,测量学闭合导线坐标计算需要准确的仪器和严密的计算方法,以确保测量数据的准确性,因此在实际的测量工作中应当非常谨慎。
6平面控制测量、导线测量

现 代 测 量 技 术 室
土木工程测量学
点 名
观测角 方位角 真方位角 边长
160 35 42
i
yi
M A 1
2 3 B N fβ = -10″
+ 02 80 04 52
60 40 34
60 40 36
281.457 269.974 315.345 392.121
+ 02 247 27 32 128 08 06 128 08 10 + 02 91 12 43 39 20 49 39 20 55 + 02 255 03 51 114 24 40 114 24 48 + 02 219 58 55 154 23 45
2. 计算坐标方位角的通用公式
AB
M o d e r n
X AB 180 90 sgn(YAB ) arctan Y AB
S u r v e y
现 代 测 量 技 术 室
土木工程测量学
§6-4
aAB = a Δ YAB > 0 Δ XAB >0 a a A AB B
单导线的近似平差计算
二、双定向附(闭)合导线计算 1.方位角闭合差及其配赋
M o d e r n
S u r v e y
现 代 测 量 技 术 室
土木工程测量学
§6-5 单导线的近似平差计算
β
n
M β A
β
2
Pn P2
1
N
Sn β n+1
S1
S2 P 3
B
1 MA 1 180
2 1 2 180
x B
αBA
【测量学】导线测量常用计算公式

一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、方位角的计算公式1. 字母所代表的意义:x1:QD的X坐标y1:QD的Y坐标x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+T sin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosOY m =V+Tsin (A+180°)+G sinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW +90°) Y b =Y m +Bsin(A+MW +90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2 中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW +90°) Y b =Y m +Bsin(O+MW +90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW +90°) Y b =Y m +Bsin(A+MD-MW +90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD +90°) Y b =Y m +Bsin(A+MD +90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
导线测量实习报告5篇

导线测量实习报告5篇导线测量实习报告1首先感谢学校和老师给以了我这次参加工程实践的机会,在这次20多天的实习过程中,经过这次实习,无论在心理上还是在生理上都得到了很好的锻炼。
学生现在学习的内容是为以后的发展奠定基础,是丰富自己的文化知识,是自己能够成为一个对社会,对国家有用的人才,但是现在我们所学的知识大多只是理论上的东西,为此我们应该将理论和实际联系起来,积极参加实际工程,这次为期20天的实习教会了我们如何将自己所学的知识应用于实际工程项目之中,懂得了解决一些实际问题的方法,对增加自己的生活和工作经历有很大益处。
同时也可以说这次工作是对同学的一次考念,在实习过程中有的同学虽然生病但是依然坚持工作,可以说着种精神是相当高贵的。
通过这次野外工程实习,加强了自身掌握数字测图外业数据采集方法与内业作图方法,更加深刻的理解了数字测图在野外的运用,数字测图带来的不但是数据采集速度的提高,工作效率的增加,更加减轻了工作人员的工作强度;明白了在数据采集过程中应该注意的问题,使自己在课堂上学到的知识得到了在实际中的运用首先,通过实习,让我发现我在平时学习中存在的很多知识漏洞。
课本上介绍仪器使用的知识都比较抽象,到了真正实践中的时候,我们未能很好把书本知识应用到实践中,还需要老师再次进行指导。
在近距离的接触这些实物,能我更牢固的掌握相关的知识点;也能令我提高对仪器的操作的熟练、精准程度(比如能够迅速对中整平)。
__是由上传的:全站仪测量实习报告。
首先感谢学校和老师给以了我这次参加工程实践的机会,在这次20多天的实习过程中,经过这次实习,无论在心理上还是在生理上都得到了很好的锻炼。
学生现在学习的内容是为以后的发展奠定基础,是丰富自己的文化知识,是自己能够成为一个对社会,对国家有用的人才,但是现在我们所学的知识大多只是理论上的东西,为此我们应该将理论和实际联系起来,积极参加实际工程,这次为期20天的实习教会了我们如何将自己所学的知识应用于实际工程项目之中,懂得了解决一些实际问题的方法,对增加自己的生活和工作经历有很大益处。
经纬仪导线测量与导线坐标计算

实验四、经纬仪导线测量与导线坐标计算一、实验目的1.学会在地面上用经纬仪标定直线及用普通钢尺精密丈量距离方法。
2.学会导线外业的基本测量工作。
3.学会用罗盘仪测定直线的磁方位角。
二、实验计划1. 实验时数4学时。
2. 每实验小组由4到5人组成。
1人观测,1人记录,2人扶尺,依次轮流进行。
3. 每组在实验场地上选定4到5个导线点,组成闭合导线,进行量距、测角。
4. 用罗盘仪测定起始直线的磁方位角,进行导线坐标计算。
雅安地区磁偏角为西偏2度24分。
据此推算起始边方位角。
三、仪器与工具1. 由仪器室借领:电子经纬仪1台、50 m钢尺1把、测钎2根、水泥钉6个、钉锤1把、记录板1个、计算器一个,罗盘仪1台。
2. 自备:、铅笔、小刀、计算用纸、测角与测距记录纸。
四、实验方法与步骤1. 指导教师讲解本次实习的内容和方法。
2. 在实习场地上选定比较平坦、相距60 m ~ 80 m的边长的多边形,构成一闭合导线,打入小铁钉(或油漆绘标记)。
3. 进行直线定线。
欲精密丈量直线AB的距离,首先清除直线上的障碍物,然后安置经纬仪于A点上,瞄准B点,用经纬仪进行定线。
用钢尺进行概量,在视线上依次定出此钢尺一整尺略短的A1、12、23……等尺段。
在各尺段端点粉笔绘标记,4.丈量距离用检定过的钢尺丈量相邻两点之间的距离。
丈量组一般由5入组成,2人拉尺,2人读数,1人指挥兼记录。
丈量时,拉伸钢尺置于相邻两点,并使钢尺有刻划线一侧贴近标志。
拉平、拉紧、拉直。
两端的读尺员同时根据点位读取读数,估读到0.1mm记入手簿。
每尺段要移动钢尺位置丈量三次,三次测得的结果的较差视不同要求而定,一般不得超过5mm,否则要重量。
如在限差以内,则取三次结果的平均值,作为此尺段的往测观测成果。
本次实习不考虑三项改正问题,每个尺段相加即为总边长。
每个边应往返丈量。
在记录表中进行成果整理和精度计算。
直线丈量相对误差要小于1/2000。
如果丈量成果超限,要分析原因并进行重量,直至符合要求为止。
测量学基本公式

测 量 员 手 簿一、测量工作的基本原则布局上:由整体到局部精度上:由高级到低级次序上:先控制后细部所有测量工作都必须遵循以上原则,也是测量的工作次序。
二、控制测量的程序由整体到局部由高级到低级先控制后细部三、确定地面点位的三个基本要素水平距离:S水平夹角:β高 差:h称为三个基本观测量在测量过程中应遵循“随时检查、杜绝错误”的原则。
测量的三项基本工作:距离测量、角度测量、高差测量。
坐标系统:国家三角测量采用1980年西安坐标系统。
平面坐标系统:国家三角测量平面坐标系统采用高斯--克吕格平面坐标系统.三 角 函 数邻边与斜边的比叫做余弦,记作cos cos=邻边/斜边对边与邻边的比叫做正切,记作tan tan=对边/邻边对边与斜边的比叫做正弦,记作sin sin=对边/斜边弧 度(rad)已知弧度计算弧长的公式: 已知弧度÷(180°÷π)³半径已知弧长计算弧度的公式: 已知弧长÷半径³(180°÷π)象限角(R)及方位角(α)象限角:直线与X轴的夹角(R=0~90°)象限角R AB=arctan(ΔX AB2+ΔY AB2)方位角:从标准方向起,顺时针量到直线所成的夹角。
从0°~360°方位角αAB=该角所在的象限加上相应的数值(如下)当增量x正;y正,那就是在第一象限控 制 测 量小地区控制测量1.相关的概念:控制网:就是在测区内选择一些有控制意义的点(称为控制点)构成的几何图形。
按功能分为:平面控制网、高程控制网。
按规模分为: 国家控制网、城市控制网、小区域控制网和图根控制网。
国家控制网分为:一、二、三、四等4个级别。
小地区控制网:是指在面积小于15m2 范围内建立的控制网。
2.平面控制导线测量就是测量导线各边长和各转折角,然后根据已知数据和观测值计算各导线点的平面坐标。
(1)附合导线:起始于一个高级控制点,最后附和到另一个高级控制点的导线,称为附和导线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、方位角的计算公式二、平曲线转角点偏角计算公式三、平曲线直缓、缓直点的坐标计算公式四、平曲线上任意点的坐标计算公式五、竖曲线上点的高程计算公式六、超高计算公式七、地基承载力计算公式八、标准差计算公式九、坐标中线测量与计算十、全站仪的使用方法和坐标测量步骤一、方位角的计算公式1. 字母所代表的意义:x1:QD的X坐标y1:QD的Y坐标x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α 2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+T cos(A+180°)Y ′=V+T sin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C-T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosOY m =V+Tsin (A+180°)+G sinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW +90°) Y b =Y m +Bsin(A+MW +90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2 中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW +90°) Y b =Y m +Bsin(O+MW +90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD-MW +90°) Y b =Y m +Bsin(A+MD-MW +90°)5)当P>K 时中桩坐标:X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD +90°) Y b =Y m +Bsin(A+MD +90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
五、 竖曲线上点的高程计算公式1. 字母所代表的意义:R :曲线半径i 1:ZY ~JD 方向的坡度 i 2:JD ~YZ 方向的坡度 T :曲线的切线长 E :外失距x :竖曲线上的点到直圆或圆直的距离 y :竖曲线上点的高程修正值2. 计算公式:212i i RT -=R T E 22=Rx y 22= 六、 超高计算公式1. 字母所代表的意义:i 0:路拱坡度 i b :超高坡度 L s :缓和曲线长b 1:所求点~路中线距离x 0:从直缓开始,到路左右坡度一致的距离,即图中C---C x :所求点~直缓或缓直的距离 h b :超高值X0LC=LS×i bb 1HY(YH)ZH(HZ)超高计算公式1相对于路中线超高值行车道外侧边缘行车道内侧边缘X0=2×i0/(i0+ib)×LsX≤x0hb=b1×(i0+ib)×X/Ls-b1×i0hb=-(b1+bx)×i0X≥x0hb=-(b1+bx)×X/LS×ib行车道外侧边缘行车道内侧边缘hb=(-i0+(i0+ib)×X/Ls)×bhb=(-i0-(ib-i0)×X/Ls)×bi0:路拱坡度ib:超高坡度L s :缓和曲线长b:到路中线距离X:所求点到ZH(HZ)距离超高计算公式22. 计算公式(公式1):(绕中线旋转)()b si i Li x +=0002 1)当x ≤x 0时 行车道外侧边缘:()0101i b L xi i b h s b b -+=行车道内侧边缘:()01i b b h x b +-=2)当x ≥x0时 行车道外侧边缘:()0101i b L xi i b h s b b -+= 行车道内侧边缘:()b sx b i L xb b h +-=13. 计算公式(公式2):行车道外侧边缘:()100b L x i i i h sb b ⎪⎪⎭⎫⎝⎛++-= 行车道内侧边缘:()100b L x i i i h sb b ⎪⎪⎭⎫⎝⎛---= 七、 地基承载力计算公式1. 字母所代表的意义:N :锤击数 M :地基承载力2. 计算公式(公式1):(绕中线旋转)()1002785.0-⨯=N M注:贯入深度为30cm ,单位为MPa八、 标准差计算公式1. 字母所代表的意义:X :样本平均值S :样本标准差2. 计算公式:基于整个样本总体的标准差:()221212nXXnnXXSnii nii∑∑∑⎪⎭⎫⎝⎛-=-===基于样本估算标准差:()()1121212-⎪⎭⎫⎝⎛-=--=∑∑∑==nnXXnnXXSnii nii九、坐标中线测量与计算采用全站仪测量线路中线,其基本的原理就是:利用假定坐标系或大地坐标系,测量各交点的坐标,并计算中线上的任意一点的坐标,利用坐标放样的原理,把各中桩在地面上确定(打桩),以备后续测量。
(一)控制点测设由于线路通常较长,为确保测量各交点坐标的准确性,通常在线路的全长,每隔一定的距离设置一个坐标控制点,该控制点的坐标是测量该段线路交点的坐标基准点。
因此,坐标中线测量的第一步就是进行控制点的测量。
一、控制点的布设控制点布置在线路沿线两侧,点位尽量放置在较高的位置上,能够看见越长的线路越图5-1好。
点位要固定,不能有移动的现象。
尽量设置在建筑物的顶上等位置,若在没有建筑物的地区,则应在地上打入大木桩,在桩顶上订小钢钉。
两相邻的控制点能够相互通视,距离在50m —500m 的范围之内。
如图5-1,控制点为D1、D2、D3。
二、控制点坐标测量控制点坐标测量可以分成两类,其一是有提供大地坐标系的,即提供地上固定的两可通视点及其坐标。
其二是不能提供大地坐标系统的,可以自己假定坐标系统。
(一)无已知的大地坐标,坐标系统是假定的假定坐标时应注意坐标的起点位置最好数据能大,以免中线测量的时候出现负坐标。
如第一点的坐标假定为(10000,10000)。
(二)有已知的大地坐标,坐标系统是已知的大地坐标系统是已知的,必须提供已知的两点坐标和实地的点位。
其测量出来的坐标均是大地坐标。
如提供两点点位与坐标,S1、S2。
实训项图5-2 控制点测量程序1图5-3 控制点测量程序2目:在实训场地进行三个控制点的测量,假定坐标系统。
实训时间:2课时。
(二)坐标计算1、已知某点的坐标,求另一点的坐标 置罗盘仪于D1,后视D2,瞄准JD 1,得方位角β0,测JD 1—D1的距离L 1得 X JD1 = X D1 +L 1cos β0Y JD1 = Y D1 +L 1sinβ0 同理测JD 2、JD 3……的坐标。
2、已知二点坐标,求方位角与距离。
已知 JD A (X A 、Y A ) JD B (X B 、Y B )用L AB = 22)()(A B A B Y Y X X -+- βAB =arctgAB AB X X Y Y --+n*1800注意:计算βAB 的时候必须是B 点坐标减A 点坐标。
当 △Y 、△X>0,n=0△Y>0、△X<0,n=1 △Y<0、△X<0,n=1 △Y<0、△X>0,n=2 同理得 L BC ,βBCаB =βB C -βAB 当а>0时为右偏,а<0时为左偏。
3、计算线路中桩坐标 (1)直线段已知:方位角аAB ,JD A (X A ,Y A ), 直线上P 1点到JD A 的距离为D 则P 1的坐标为: X P1=X A +D ·cos аAB Y P1=Y A +D ·sin аAB图5-4 交点坐标计算图5-5 直线段坐标计算注意:距离D=P1的桩号—JDA 的YZ 桩桩号+JDA 的切线长T 。
