(新)方差分析操作步骤详解
方差分析(单因素、多因素方差分析)

单因素方差分析1.基本理解方差分析:是一种利用实验获取数据并进行分析的统计方法,经常用于研究不同效应对指定实验的影响是否显著。
方差分析用于检验连续型随机变量在三及以上分类数据不同水平上的差异情况。
方差分析包括:单因素方差分析、多元素方差分析、多元方差分析、协方差分析、重复测量方差分析。
在问卷数据中:单因素方差分析使用较多。
单因素方差分析:用于检验单个因素取不同水平是某因变量的均值是否有显著的变化,也可进一步用于因变量均值的多重比较(检验某些水平下的实验结果具体区别于其他水平的显著差异)。
图1检验步骤2.单因素方差分析操作步骤操作步骤第一步:首先将数据导入spss中并进行赋值后,点击分析、比较平均值、单因素ANOVA检验。
图2单因素方差分析第一步操作步骤第二步:进入图中对话框后将需检验的变量放入因变量列表中,在因子中放入分类变量,点击事后比较勾选假定等方差(LSD),不假定等方差(塔姆黑泥T2)点击继续。
图3单因素方差分析事后比较勾选3.当因素方差分析结果后点击线性进入图中下方选项框、勾选描述、方差齐性检验点击继续、确定。
图4单因素方差分析选项勾选然后单因素方差分析的描述、方差齐性、假设检验就出来了。
图5单因素方差分析结果单因素方差分析事后两两比较结果。
图6事后比较结果4.结果整理将首先将描述统计的结果粘贴复制到Excel表格中进行整理,保留均值和标准差及前面的内容,后在后面加入ANOVA表中的F和p值,将整理好的两两比较结果粘贴到表格的最后,最后将整理好的结果粘贴到Word文档中进行整理。
可参考图中结果整理。
(注:一般在看结果时首先看ANOVA表的结果,看显著情况,显著(p<0.05)看方差齐性检验的结果,若方差齐性检验的结果方差齐(p>0.05),然后再看事后比较的结果,方差齐看LSD,方差不齐看塔姆黑泥的结果,同样差异的显著看事后比较每行对应的显著性(若p<0.05,代表比较的对象显著。
方差分析minitab操作流程

方差分析minitab操作流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!方差分析在Minitab中的操作流程详解方差分析(ANOVA)是一种统计方法,用于确定两个或更多个组间的差异是否显著。
方差分析SPSS操作流程PPT课件

ANOVA
WEIGHT
Sum of Squares Betwee2n05G3r8o.u7p0s Within G6r5o2u.p1s59 Total 21190.86
dfMean Square F 36846.231357.467
15 43.477 18
Sig. .000
• 第一栏:方差来源
• 第二栏:离均差平方和
.;
22
• Homogeneity of variance复选项,要求进行方差齐次性检验 ,并输出检验结果。
• Brown-Forsythe:检验各组均数相等,当不能确定方差齐性 检验时,该统计量优于F统计量。
• Welch:检验各组均数相等,当不能确定方差齐性检验时,该 统计量优于F统计量。
• Mean plot复选项,即均数分布图,横轴为分类变量,纵轴为 反应变量的均数线图;
重比较对每个水平的均值逐对进行比较,以判断具体是哪些水
平间存在显著差异。
• 常用方法备选:
– LSD法:t检验的变形,在变异和自由度的计算上利用了整个样本信息
。
– Duncan 新复极差测验法
– Tukey 固定极差测验法
– Dunnett最小显著差数测验法 等
• 实现手段:
– 方差分析菜单中的“Post ho. c test…”按钮
• One-Way ANOVA过程要求:
因(分析)变量属于正态分布总体,若因(分析 )变量的分布明显的是非正态,应该用非参数分 析过程。
对被观测对象的实验不是随机分组的,而是进行 的重复测量形成几个彼此不独立的变量,应该用 Repeated Measure菜. 单项,进行重复测量方差8
• analyze→compare means→one-way ANVOA
方差分析基本原理与步骤

知识回顾…
知识回顾…
自变量:由实验者操纵的,对被试的反应产生 影响的变量,又称因素。
水平:自变量的每个特定的值。 实验处理:指实验中一个特定的、独特的实验
条件。 在单因素实验设计中,自变量的每一个水平相 当于一个实验处理。 在多因素实验设计中,实验处理是各自变量不 同水平的组合。 因变量:由操纵自变量而引起的被试的某种特 定反应。
若F>1且落入F分布的临界区域,表明数据的 总变异基本上由不同的实验处理造成,或者说 不同的实验处理的效果之间存在显著差异。
所以,方差分析又称作变异分析(analysis of variance, ANOVA),是对数据样本变异量的 分析。其主要功能在于分析实验数据中不用来 源的变异对总变异的贡献大小,从而确定实验 中的自变量是否对因变量有重要影响。
MS B
SSB dfB
9-6
MSW
SSW dfW
9-7
MSB表示组间均方,或称组间方差;dfB为组间自由度。 MSW表示组内均方或称组内方差;dfW为组内自由度。
自由度是任何变量中可以自由变化的数目。
组间自由度:dfB k 1(即组数减1)
组内自由度:dfW=K(n-1)
总自由度: dfT nk 1
10性检验提出假设提出假设求平方和总平方和组间平方和组内平方和求平方和总平方和组间平方和组内平方和计算自由度总自由度组间自由度组内自由计算自由度总自由度组间自由度组内自由度度计算均方计算均方组间均方组内均方组间均方组内均方计算计算ff值值查查ff值表进行值表进行ff检验并做出决断检验并做出决断陈列方差分析表陈列方差分析表方差齐性检验方差齐性检验提出假设提出假设计算计算f值值平方和自由度均方平方和自由度均方f查表并作出决断查表并作出决断陈列方差分析表陈列方差分析表nxnx222tbxxss2ttxxssnxx222xxsswnxx
Excel教程方差分析(共41张)

表7-1 不同水平(shuǐpíng)下的样本观测值
第6页,共41页。
表7-2 各组销售人员(rényuán)销售业绩
第7页,共41页。
在Excel中具体的操作步骤如下:
(1)建立“方差分析”工作表,如图7-1所示。
(2)在单元格A7中输入“样本均值”,在单元格A8中输 入“总体均值”。
第2页,共41页。
7.1 单因素(yīn sù)方差分析
7.1.1 单因素方差分析的构想 7.1.2 检验模型 7.1.3 方差分析表
第3页,共41页。
返回首页
方差分析最简单的形式就是(jiùshì)单因素方差分析。单因素 方差分析可用于检验两个或两个以上总体均值相等的原假 设。方差分析有三个基本假设:
第33页,共41页。
(2)选择“工具”菜单中的“数据分析”选 项,弹出“数据分析”对话框,选择“方差分 析:可重复双因素分析”选项,单击“确定 (quèdìng)”按钮,进入“方差分析:可重复双因素 分析”对话框。
(3)在“输入区域”中输入“$A$1: $D$7”, 在“每一样本的行数”中输入2,在“”区域 中输入0.05,表明显著性水平。
第8页,共41页。
(6)分别将单元格A2~A6、A7~A11、A12~A16合并,并分别输
入“第一组”、“第二组”、“第三组”,表示样本的组数。
(7)将“方差分析”工作表中B2~B6、C2~C6、D2~D6区
域内的数据复制到“计算(jìsuàn)表”的B2~B16区域中。 (8)在“方差分析”工作表中选择单元格B7,单击“复制” 按钮,切换到“计算表”工作表,选定单元格C2~C6,右击 选择“选择性粘贴”选项,打开“选择性粘贴”对话框,单
第5章 方差分析

F检验
若实际计算的F值大于 F 0 . 0 5 ( d f , d f ) ,则 F 值在 α=0.05的水平上显著,我们以95% 的可靠性推断 2 2 St代表的处理间方差大于Se 代表的处理内方差。
1 2
这种用F值出现概率的大小推断两个总体方差 是否相等的方法称为 F检验。
F检验时,是将由试验资料所算得的F值与根 ,F 据df1=dft 和df2=dfe查表所得的临界F值F 相比较作出统计推断的。
1 1
k
n
x ) n (x i x )
2 2 1
k
(x
1 1
k
n
xi )
2
上式可简写成:SST=SSt+SSe 分别表示总 平方和,处理间平方和,处理内平方和。 即:总平方和=处理间平方和+处理内平
方和。
C=T2/kn:
SST
x C
2
1 2 SS t Ti C n SS e SS T SS t
P ( F F ) 1 F ( F )
F
f (F )d F
F表列出的是不同df1和df2下, P(F≥Fα)=0.05和P(F≥Fα)=0.01时的F值, 即右尾概率α=0.05和α=0.01时的临界F 值,一般记作F0.05(df1,df2), F0.01(df1,df2) 。
所以 d f T d f t d f e 综合以上各式得:
df T kn 1 df t k 1 df e df T df t
均方差,均方(mean square,MS)
变异程度除与离均差平方和的大小有关外, 还与其自由度有关,由于各部分自由度不相等, 因此各部分离均差平方和不能直接比较,须将 各部分离均差平方和除以相应自由度,其比值 称为均方差,简称均方 (mean square , MS )。组 间均方和组内均方的计算公式为 :
方差分析(ANOVA)(转)

⽅差分析(ANOVA)(转)转⾃:⽅差分析(analysis of variance,ANOVA),即变量分析,是对多个样本平均数差异显著性检验的⽅法。
在⼀个多处理试验中,可以得到⼀系列不同的观测值。
造成观测值不同的原因是多⽅⾯的,有的是不同的处理引起的,即处理效应;有的是试验过程中偶然性因素的⼲扰和测量误差造成的,即误差效应。
⽅差分析的基本思想就是将测量数据的总变异按变异原因不同分解为处理效应和试验误差,并作出其数量估计。
要正确认识观测值的变异是由处理效应还是误差效应引起的,我们可以计算出处理效应的均⽅和误差效应的均⽅,在⼀定意义下进⾏⽐较,从⽽检验处理间的差异显著性。
假设⼀个试验有k个处理,每个处理有n个观测数据,则总共有nk的观测值。
⽤表⽰第i个处理的第j个观测值,其中i=1,2,3,...,k;j=1,2,3,...,n。
表⽰第i个处理观测值的总体平均数,表⽰试验误差,则有:,即第i个处理的第j个观测值是由该处理的总体平均数加上不可避免的试验误差组成的。
⽽对于总体平均数(所有nk个观测数据的平均数),则有。
若将各⾃处理⽔平上的总体平均数视为在总体平均数的基础上施加了不同的处理效应造成了,则有。
综上,,即任⼀个观测数据都是由总体平均数加上处理效应以及试验误差组成的。
同理,对于由样本估计的线性模型为:,为样本平均数,为第i个处理的效应,为试验误差。
根据的不同假定,上述模型可分为: 固定模型(fixed model):各个处理的效应值是固定的,即除去随机误差外每个处理所产⽣的效应是固定的,是个常量且之和为0。
此时的试验处理⽔平常是根据⽬的事先主观选定的,如⼏种不同温度下⼩麦籽粒的发芽情况。
随机模型(random model):各个处理的效应值不是固定的,⽽是由随机因素所引起的效应。
是从期望均值为0,⽅差为的正态总体中得到的随机变量。
如调查不同⽣境下某物种的⽣长状况时,不同⽣境的⽓候、⼟壤条件及⽔分条件等属于⽆法认为控制的因素,就要⽤随机模型来处理。
第一节-方差分析的基本原理与步骤

第一节方差分析的基本原理与步骤方差分析有很多类型,无论简单与否,其基本原理与步骤是相同的。
本节结合单因素试验结果的方差分析介绍其原理与步骤。
一、线性模型与基本假定假设某单因素试验有k个处理,每个处理有n次重复,共有nk个观测值。
这类试验资料的数据模式如表6-1所示。
表6-1k个处理每个处理有n个观测值的数据模式处理观测值合计平均A1 x11 x12 …x1j …x 1nA2 x21 x22 …x2j …x 2n……A i x i1 x i2 …x ij …x in……A k x k1 x k2 …x kj …x kn xk .合计表中表示第i个处理的第j个观测值(i=1,2,…,k;j=1,2,…,n);表示第i个处理n 个观测值的和;表示全部观测值的总和;表示第i 个处理的平均数;表示全部观测值的总平均数;可以分解为(6-1)表示第i个处理观测值总体的平均数。
为了看出各处理的影响大小,将再进行分解,令(6-2)(6-3)则(6-4)其中μ表示全试验观测值总体的平均数,是第i个处理的效应(treatmenteffects)表示处理i对试验结果产生的影响。
显然有(6-5)εij是试验误差,相互独立,且服从正态分布N(0,σ2)。
(6-4)式叫做单因素试验的线性模型(linearmodel)亦称数学模型。
在这个模型中表示为总平均数μ、处理效应αi、试验误差εij之和。
由εij相互独立且服从正态分布N(0,σ2),可知各处理Ai(i=1,2,…,k)所属总体亦应具正态性,即服从正态分布N(μi,σ2)。
尽管各总体的均数可以不等或相等,σ2则必须是相等的。
所以,单因素试验的数学模型可归纳为:效应的可加性(additivity)、分布的正态性(normality)、方差的同质性(homogeneity)。
这也是进行其它类型方差分析的前提或基本假定。
若将表(6-1)中的观测值xij(i=1,2,…,k;j=1,2,…,n)的数据结构(模型)用样本符号来表示,则(6-6)与(6-4)式比较可知,、、分别是μ、(μi-μ)=、(xij-)=的估计值。
方差分析

a ni j
a
ni
(Yij Y i )
i 1
2
称为就是组内离均差平方和,用 SS组内 表示;
n (Y i Y ) 称为组间离均差平方和,用 SS组间 表示。
2 i 1 i
a
自由度
总离均差平方和的自由度
总 =N-1
组间离均差平方和的自由度
组间 =a-1,
为研究铅对儿童神经行为的影 响,研究者在某铅矿区对儿童的血铅水平及 神经行为评价指标手指敲击测验进行了测定, 第一年和第二年儿童的血铅水平均大于等于 40 mg/dl的17名,为暴露组(group=2),第一 年儿童的血铅水平均大于等于40mg/dl、第 二年儿童的血铅水平小于40mg/dl的15名, 为既往暴露组(group=3),第一年和第二年儿 童的血铅水平均小于40mg/dl的15名,为对 照组(group=1),神经行为评价指标为第二年 的手指敲击测验得分。
=0.05。
2. 计算每一组的均数 Yi ,然后计算每一测量值与组内均数差 值的绝对值 Zij
Z ij Yij Yi
方差齐性检验
计算 L 统计量
a 2 1 ni Z i Z a 1 i 1 L a ni 2 1 Z ij Z n a i 1 j 1
例9.1
表 9.1 某铅矿区儿童不同铅表露水平的手指敲击测验结果 对照组 手指敲击 No 1 2 3 4 16 17 18 19 group 1 1 1 1 1 1 1 1 测验得分 72 51 57 53 56 54 57 50 No group 20 21 22 23 35 36 2 2 2 2 2 2 暴露组 手指敲击 测验得分 54 57 48 41 44 48 No group 37 38 39 40 3 3 3 3 既往暴露组 手指敲击 测验得分 62 37 46 59
生物统计——方差分析的基本原理与步骤

方差分析的基本原理与步骤
一、线性模型与基本假定
假设某单因素试验有k个处理,n次重 复,完全随机设计,则共有nk个观察值, 其数据结构和符号如表5-1所示。
xij可以表示为
xij i ij
其中, i
ij
为第i个处理观测值总体平均数;
为试验误差、相互独立、且 服从正态分布N(0,σ2)。
SSe SST SSt
(二)总自由度的分解 在计算总平方和时,资料中kn个观测值
的离均差 ( xij x ) 要受
( x
i 1 j 1
k
n
ij
x )0
这一条件的约束,故总自由度等于资料中观
测值的总个数减一, 即kn-1。总自由度记为
dfT,dfT=kn-1。
在计算处理间平方和时,k个处理均数的
统计学上,这种分解是通过将总均方
的分子──称为总离均差平方和,简称为总
平方和,分解为处理间平方和与处理内平
方和两部分;将总均方的分母──称为总自
由度,分解为处理间自由度与处理内自由
度两部分来实现的。
(一)总平方和的分解
在表5-1中,反映全部观测值总变异的总 平方和是各观测值xij与总平均数 x .. 的离均 差平方和,记为SST。即
离均差 ( xi x ) 要受
(x
i 1
k
i
x )0
这一条件的约束,故处理间自由度为处理数 减一,即k-1。处理间自由度记为dft,dft=k-1
在计算处理内平方和时,kn个离均差
( xij xi ) 要受k个条件的约束,即
(x
j 1
n
ij
xi ) 0 (i=1,2,…,k)
最新SPSS单因素方差分析步骤

spss教程:单因素方差分析用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。
方差分析前提:不同水平下,各总体均值服从方差相同的正态分布。
所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。
统计推断方法是计算F统计量,进行F检验,总的变异平方和 SST,控制变量引起的离差SSA(Between Group离差平方和),另一部分随机变量引起的SSE(组内Within Group离差平方和),SST=SSA+SSE。
方法/步骤1.计算检验统计量的观察值和概率P_值:Spss自动计算F统计值,如果相伴概率P小于显著性水平a,拒绝零假设,认为控制变量不同水平下各总体均值有显著差异,反之,则相反,即没有差异。
2.方差齐性检验:控制变量不同水平下各观察变量总体方差是否相等进行分析。
采用方差同质性检验方法(Homogeneity of variance),原假设“各水平下观察变量总体的方差无显著差异,思路同spss两独立样本t检验中的方差分析”。
图中相伴概率0.515大于显著性水平0.05,故认为总体方差相等。
趋势检验:趋势检验可以分析随着控制变量水平的变化,观测变量值变化的总体趋势是怎样的,线性变化,二次、三次等多项式。
趋势检验可以帮助人们从另一个角度把握控制变量不同水平对观察变量总体作用的程度。
图中线性相伴概率为0小于显著性水平0.05,故不符合线性关系。
3.多重比较检验:单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响,多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何,那个水平显著,哪个不显著。
常用LSD、S-N-K方法。
LSD方法检测灵敏度是最高的,但也容易导致第一类错误(弃真)增大,观察图中结果,在LSD项中,报纸与广播没有显著差异,但在别的方法中,广告只与宣传有显著差异。
4. 相似性子集:由图可知,划分的子集结果是一样的。
通常在相似性子集划分时多采用S-N-K 方法的结论。
方差分析的基本原理及分析过程

三 方差分析的步骤
步骤三:
计算各变异源引起数据变异的方差,即均方MS
均方等于变异平方和除以自由度
MS = SS / df
MSb = SSb / dfb MSw = SSw / dfw
三 方差分析的步骤
步骤四:
计算各效应是否显著的检验统计量 F 比率
方差分析中关心的是MSb是否显著大于MSw ,如果经步骤三 发现MSb小于MSw ,则无需进行是否小到显著性水平;反之, 则进行单侧检验,所以总是将MSb放在分子的位置。
断多个总体均数有无 差异,所以又叫变异 分析。
二 方差分析的基本思想
依据An的al基ysi本s 原of理Va是ri变an异ce的(可AN加OVA ) 性,不同来源的变异只有可加 时,才能保证变异分解的可能。
将所有测量值间的总变异按照其变异的 来源分解为多个部份,然后进行比较,评价 由某种因素所引起的变异是否具有统计学意 义。
处理因素
组间变异
随机误差
组内变异
总变异
方差分析的主要功能是 分析因变量的总变异中不同来源的变异,或者说是分析
实验数据中不同来源的变异对总变异的贡献大小, 以确定自变量是否对因变量有重要影响。
F检验是 计算组间变异与组内变异的比率F = MSb / MSw
三 方差分析的步骤
步骤一: 计算数据总变异量并对总变异进行分解
一组数据的变异量是用该组数据与平均数离差的平方和来计 算的,也叫平方和(sum of square),平方和的通用公式:
SS=∑(X﹣ ¯X)2 = ∑X2 ﹣ (∑X)2/ N
SSt = SSb ﹢SSw
三 方差分析的步骤
• 总平方和
一组数据的观测数据与平均数离差的平方总和,代表该组数据 总体的变异程度。计算方式:每个观测值与该组数据的总平均 数相减的平方之和。
方差分析方法的实施步骤

方差分析方法的实施步骤1. 简介方差分析是一种常用的统计方法,用于比较两个或多个组之间的均值差异是否显著。
它是通过分解总方差为组内方差和组间方差,并进行推断的方法。
2. 数据准备在实施方差分析之前,我们需要准备一些数据。
这些数据可以是实验、观察或调查得到的,通常是连续的数值型数据。
我们需要将数据分成两个或多个组,每个组包含一组相关的数据。
确保数据的采样是随机的,并且每个组的样本量大致相等,以保证结果的准确性。
3. 假设检验在进行方差分析之前,我们需要明确我们要检验的假设。
对于方差分析,我们通常关心以下两个假设: - 原假设(H0):各组间的均值相等,即组间差异不显著。
- 备择假设(H1):各组间的均值不相等,即至少存在一组的均值与其他组存在显著差异。
4. 方差分析模型选择在实施方差分析之前,我们需要选择适当的方差分析模型。
根据数据的特性和实验设计的不同,我们可以选择以下几种常见的方差分析模型: - 单因素方差分析:适用于只有一个分类变量的情况,用于比较不同组别之间的均值差异。
- 双因素方差分析:适用于两个分类变量的情况,用于比较不同组别之间的均值差异,并探究两个分类变量的交互作用。
- 多因素方差分析:适用于多个分类变量的情况,用于比较不同组别之间的均值差异,并探究多个分类变量的交互作用。
5. 数据分析接下来,我们需要进行实际的数据分析。
在这一步骤中,我们需要计算各个组别的均值、总均值以及方差。
5.1 组内方差首先,我们需要计算各个组内的方差。
通过计算每个组别中各数据与该组别均值的差的平方和来计算组内方差。
然后将所有组别的组内方差相加得到总的组内方差。
5.2 组间方差接下来,我们需要计算组间方差。
通过计算每个组别均值与总均值的差的平方和再乘以各组别的样本量来计算组间方差。
5.3 F统计量最后,通过计算组间方差与组内方差的比值,得到F统计量。
F统计量的计算公式为:F = (组间方差 / 自由度1) / (组内方差 / 自由度2)。
统计学方差分析ppt课件

水平
水平指因素的具体表现,如销售的 四种方式就是因素的不同取值等级。有 时水平是人为划分的,比如质量被评定 为好、中、差。
单元
单元指因素水平之间的组合。如销 售方式一下有五种不同的销售业绩,就 是五个单元。方差分析要求的方差齐就 是指的各个单元间的方差齐性。
元素
元素指用于测量因变量的最小单 位。一个单元里可以只有一个元素, 也可以有多个元素。
均衡
如果一个试验设计中任一因素各水 平在所有单元格中出现的次数相同,且 每个单元格内的元素数相同,则称该试 验是为均衡,否则,就被称为不均衡。 不均衡试验中获得的数据在分析时较为 复杂。
交互作用
如果一个因素的效应大小在另一 个因素不同水平下明显不同,则称为 两因素间存在交互作用。当存在交互 作用时,单纯研究某个因素的作用是 没有意义的,必须分另一个因素的不 同水平研究该因素的作用大小。如果 所有单元格内都至多只有一个元素, 则交互作用无法测出。
地点一 地点二 地点三 地点四 地点五
方式一
77
86
81
88
83
方式二
95
92
78
96
89
方式三
71
76
68
81
74
方式四
80
84
79
70
82
【解】设这四种方式的销售量的均值分别用 1•, 2•, 3•, 4• 表示,四 个销售地点的平均销售量用 •1, •2, •3, •4 表示;则要检验的假设为
例题
Excel操作
构造F统计量
判断与结论
例题
Excel操作
方差分析概述
因素和水平
单元和元素
均衡
交互作用
方差分析

2
2. 组间变异
3. 组内变异
SS组内 (ni - 1 )Si
i
2
11
均方差,均方(mean square,MS)
变异程度除与离均差平方和的大小有关 外,还与其自由度有关,由于各部分自由度 不相等,因此各部分离均差平方和不能直接 比较,须将各部分离均差平方和除以相应自 由度,其比值称为均方差,简称均方(mean square,MS)。组间均方和组内均方的计算 公式为:
因变量 (Dependent variable)
24
完全随机设计(单因素)方差分析
在评价某药物耐受性及安全性的I期临床试
验中,对符合纳入标准的30名健康自愿者 随机分为3组每组10名,各组注射剂量分别 为0.5U、1U、2U,观察48小时部分凝血活 酶时间(s)试问不同剂量的部分凝血活酶 时间有无不同?
17
例题:比较不同人种的肝体比值
Table Comparison of liver/body proportion (%) A B C D 2.62 2.82 2.91 3.92 2.76 3.02 3.00 Y 2.23 2.36 2.43 3.28 3.32 2.40 2.73 3.18 3.04
32
如果多组样本均数的比较用t检验会怎样?
当有k个均数需作两两比较时,比较的次数共有 c= k = k!/(2!(k-2)!)=k(k-1)/2
2
设每次检验所用Ⅰ类错误的概率水准为α,累积Ⅰ类 错误的概率为α’,则在对同一实验资料进行c次检验时 ,在样本彼此独立的条件下,根据概率乘法原理,其累 积Ⅰ类错误概率α’与c有下列关系: α’=1-(1-α)c
X
Y 2. 组间变异( between group variation ):各 组的均数 X i 与全部观察值的均数 X 间的差
全流程总结方差分析
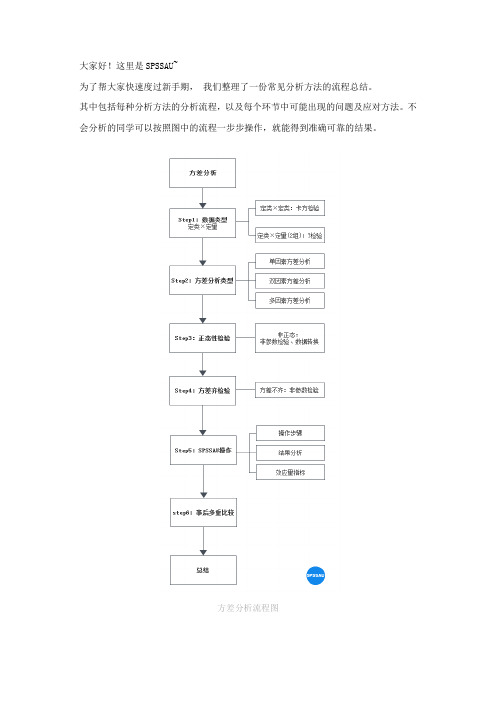
大家好!这里是SPSSAU~为了帮大家快速度过新手期,我们整理了一份常见分析方法的流程总结。
其中包括每种分析方法的分析流程,以及每个环节中可能出现的问题及应对方法。
不会分析的同学可以按照图中的流程一步步操作,就能得到准确可靠的结果。
方差分析流程图方差分析是一种分析调查或试验结果是否有差异的统计分析方法,也就是检验各组别间是否有差异。
本文我们就一起来梳理下方差分析的分析流程。
1.数据类型方差分析用于分析定类数据与定量数据之间的关系情况,可以比较2组或多组数据的差异。
分析前首先应根据数据类型判断使用的方法是否正确。
●如果X是定类数据,Y是定类数据,则应该使用卡方分析。
●如果X是定类数据,Y是定量数据,且X组别仅为两组,则应该使用T检验。
2.方差分析的类型方差分析按照自变量个数的不同,可以分为单因素方差分析、双因素方差分析、以及多因素方差分析。
单因素方差分析可以比较一个自变量(比如品牌);而双因素方差可以比较两个自变量(品牌和销售地区);多因素方差可比较三个及以上的自变量。
单因素方差分析在问卷研究中常用于分析个人背景信息对核心研究变量的影响(比如不同性别人群对工作满意度是否有显著差异)。
同时也可用于对聚类分析效果的判断。
在得到聚类类别之后,通过方差分析去对比不同类别的差异,如果全部呈现出显著性差异,以及研究人员结合专业知识可以对类别进行命名时,则说明聚类效果较好。
而双因素和多因素方差分析,可以研究多个自变量对因变量Y的交互影响。
通常只有在实验研究中才会使用,一般的问卷数据很少使用。
本文将主要针对单因素方差分析说明。
3.正态性检验方差分析要求Y项满足需要正态性,SPSSAU提供多种检验正态性的方法,选择其中一种方法检验即可。
问卷数据很难保证数据的正态性,而正态性检验的判断标准较为严格,因为更推荐使用正态图或P-P/Q-Q图查看正态性,当数据基本满足正态性特征即可接受为正态分布。
P-P图P-P图中散点近似呈现为一条对角直线,则说明数据呈现出正态分布。
(新)方差分析操作步骤详解
SPSS 11.0 单因素方差分析步骤1.数据输入后点击“分析”(analyze)菜单2.进入“Compare Means”(均值比较)→One-Way ANOVA(单因素方差分析)3.点击“One-Way ANOVA”:4.确定“Dependent List”(相关要分析的组)(图中分别为低糖St和高糖St),左侧匡中选中点击箭头键:5.确定“Factor”(因素)(图中为group):5. Contrast子对话框:该对话框有两个用途:对均数的变动趋势进行趋势检验:定义根据研究目的需要进行的某些精确两两比较。
由于该对话框太专业,也较少用,这里只做简单介绍,在综合实例中会结合具体例题讲解。
1). Polynomial:定义是否在方差分析中进行趋势检验,即随着组别的变化,各组均数是否呈现某种变化趋势。
2).Degree下拉列表:和Polynomial复选框配合使用,用于定义需检验的趋势曲线的最高次方项,可选择从线性趋势一直到五次方曲线。
如果你选择了高次方曲线,系统会给出所有相应各低次方曲线的拟合优度检验结果(比如选择3次方曲线时,系统会给出线性、二次方、三次方三个结果),以供你选择。
3).Coefficients框:精确定义某些组间均数的比较。
这里按照分组变量升序给每组一个系数值,注意最终所有系数值相加应为o。
比如说在上例中要对第一、三组进行单独比较,则在这里给三组分配系数为1、0、-1,就会在结果中给出相应的检验内容。
6.点击“Post Hoc…”确定两两比较方法(当各组方差齐时适用):equal variances assume复选框:方差齐时比较结果有效,根据需要选择,通常选LSD、Tukey 等, 点击“Contimue”返回。
EqualVariancesNotAssumed复选框组:提供了方差不齐时可以采用的两两比较方法,共有四种可以选择,一般认为是Games-Howell法稍好一些,推荐使用。
第三章 方差分析

N 报纸 广播 宣传品 体验 Total 36 36 36 36 144
Mean 73.2222 70.8889 56.5556 66.6111 66.8194
Std. Error 1.62232 2.16127 1.93647 2.24961 1.12732
Minimum 54.00 33.00 33.00 37.00 33.00
df1 3
df2 140
Sig. .515
分析:统计量值为0.765, P=0.515>0.5, 不拒绝原假设, 即可以认为方差齐的。
(因为已证明了各水平既服从正态分布又是方差齐的,所以可以进 行方差分析)
方差分析表
A N OV A 销售额 Sum of Squares 5866.083 20303.222 26169.306 df 3 140 143 Mean Square 1955.361 145.023 F 13.483 Sig. .000
√
勾选“Descriptive”、 “Homogeneity-of-variance”、 “Means plot”三项。 点击“Continue”钮返回
点击“OK”钮输出结果
结果输出和讨论:
D e sc r i p ti v e s 销售额 Std. Deviation 9.73392 12.96760 11.61881 13.49768 13.52783 95% Confidence Interval for Mean Lower Bound Upper Bound 69.9287 76.5157 66.5013 75.2765 52.6243 60.4868 62.0442 71.1781 64.5911 69.0478
将“销售额[sale]”加入“Depedent”框;“广告形式[ad 加入“Factor List”框。 选择“Normality ….”(正态性检验)
生物统计学 第六章 方差分析

【���������2���
=
���������2��� ������−1
=
(������������−������)���2��� ������−1
���������2��� 为效应方差,������������为处理效应】
方差分析
4.F检验
4.1 F值和F分布 F=������������������������������������=������2+���������2������������2���,自由度������������1 = k − 1, ������������2=������������������=kn-k 在������������1, ������������2确定条件下,F值对应的概率分布称为F 分布, 对应的密度函数为f(F)。������������1, ������������2决定F分布 的形状, 随着自由度的增加,曲线趋向对称。
������������. 各处理观测值之和。
方差分析
自由度的剖分
总自由度dfT=kn-1 处理间自由度dft=k-1 误差自由度 dfe=dfT-dft 均方
试验的总均方、处理间均方、处理内均方分别为:
MST=���������������2���
=
������������������ ������������������
第六章 方差分析
第一节 方差分析的基本原理和步骤
1.基本概念
试验指标 为衡量试验结果的好坏或处理效应 的高低,在试验中具体测定的性状或观测的项 目。
试验因子 试验中所研究的影响试验指标的因素。 当试验中考察的因素只有一个时,称为单因素试 验;若同时研究两个或两个以上的因素对试验指 标的影响时,则称为两因素或多因素试验。试验 因素常用大写字母A、B、C、…等表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
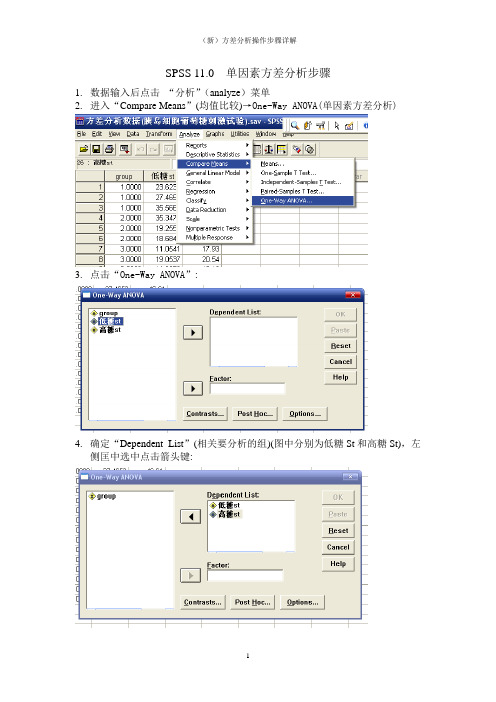
SPSS 11.0 单因素方差分析步骤
1.数据输入后点击“分析”(analyze)菜单
2.进入“Compare Means”(均值比较)→One-Way ANOVA(单因素方差分析)
3.点击“One-Way ANOVA”:
4.确定“Dependent List”(相关要分析的组)(图中分别为低糖St和高糖St),左
侧匡中选中点击箭头键:
5.确定“Factor”(因素)(图中为group):
5. Contrast子对话框:
该对话框有两个用途:对均数的变动趋势进行趋势检验:定义根据研究目的需要进行的某些精确两两比较。
由于该对话框太专业,也较少用,这里只做简单介绍,在综合实例中会结合具体例题讲解。
1). Polynomial:定义是否在方差分析中进行趋势检验,即随着组别的变化,各组均数是否呈现某种变化趋势。
2).Degree下拉列表:和Polynomial复选框配合使用,用于定义需检验的趋势曲线的最高次方项,可选择从线性趋势一直到五次方曲线。
如果你选择了高次方曲线,系统会给出所有相应各低次方曲线的拟合优度检验结果(比如选择3次方曲线时,系统会给出线性、二次方、三次方三个结果),以供你选择。
3).Coefficients框:精确定义某些组间均数的比较。
这里按照分组变量升序给每组一个系数值,注意最终所有系数值相加应为o。
比如说在上例中要对第一、三组进行单独比较,则在这里给三组分配系数为1、0、-1,就会在结果中给出相应的检验内容。
6.点击“Post Hoc…”确定两两比较方法(当各组方差齐时适用):
equal variances assume复选框:方差齐时比较结果有效,根据需要选择,通常选LSD、Tukey 等, 点击“Contimue”返回。
EqualVariancesNotAssumed复选框组:提供了方差不齐时可以采用的两两比较方法,共有四种可以选择,一般认为是Games-Howell法稍好一些,推荐使用。
不过在我看来,由于这方面统计学界尚无定论,建议大家最好在方差不齐时直接使用非参数检验方法,具体的非参数两两比较方法会在相应章节中讲述。
注:
LSD法:即LSD法,实际上就是t检验的变形,只是在变异和自由度的计算上利用了整个样本信息,而不仅仅是所比较两组的信息。
因此它敏感度最高,在比较时仍然存在放大a 水准(一类错误)的问题,但换言之就是总的二类错误非常的小,要是LSD法都没检验出差别,那恐怕是真的没差别。
S-N-K法:即Student Newman Keuls法,是运用最广泛的一种两两比较方法。
它采用StudentRange分布进行所有各组均值间的配对比较。
该方法保证在Ho真正成立时总的a水准等于实际设定值,即控制了一类错误。
Bonferroni法:由LSD法修正而来,通过设置每个检验的a水准来控制总的a水准,该方法的敏感度介于LSD法和Scheffe法之间。
Sidak:也是从t检验修正而釆,和Bonferroni法非常相似,但比Bonferroni法保守。
TUKEY法:即Tukey's honestly significant difference法(Tukey's HSD),同样采用Student-Range 统计量进行所有组间均值的两两比较。
但与S-N-K法不同的是,它控制的是所有比较中最大的一类错误概率值不超过a水准。
Scheffe法:当各组人数不相等,或者想进行复杂的比较时,用此法较为稳妥。
它检验的是各个均数的线性组合,而不是只检验某一对均数间的差异,并控制整体a水准等于0.05。
但正因如此,它相对比较保守,有时候方差分析F值有显著性,用该法两两比较却找不出差异来。
(当方差不齐时应用此检验的数据较可靠)
Dunnett法:将所有的处理组均数分别与指定的对照组均数进行比较,并控制所有比较中最大的一类错误概率值不超过a水准,请注意该方法并不适用于完全两两比较的情况。
选定此方法后会激活下面韵Control Category框,用于设定对照组及单双侧检验。
如何在如此之多的两两比较方法中选出合适的一种是个令人头痛的问题。
以前国内外都以SNK法最为常用,但根据研究,当两两比较的次数极多时,该方法的假阳性非常之高,最终可以达到100%!因此比较次数较多时,包括SPSS和SAS在内的权威统计软件都不再推
荐使用此法。
根据对相关研究的检索结果,除了参照所研究领域的惯例外,一般可以参照如下标准:如果存在明确的对照组,要进行的是验证性研究,即计划好的某两个或几个组间(和对照组)的比较,宜用Bonferroni(LSD)法:若需要进行的是多个均数间的两两比较(糠索性研究),且各组人数相等,适宜用Tukey法:其他情况宜用Scheffe法。
该标准仅供大家参考。
Significance Level 框:定义两两比较时的显著性水平,默认是0.05,一般来说不用更改。
7. 点击“Options”对话框:
Statistcs复选框组:提供了一些可选的统计指标,请注意它们并非可有可无。
Descriptlve:为各组输出常用统计描述指标,如均数、标准差等。
Fixed and random effects:为11.0版新增,按固定效应模型输出标准差、标准误和95%可信区间,同时按随机效应模型输出标准误、95%可信区间和成分间方差。
关于这两种模型的详情请参见一般线性模型部分。
Homogeneity-of-variance:方差齐性检验,这是常常被人忽略的一项重要功能。
Brown-Forsythe:为11.0版新增,采用Brown-Forsythe统计量检验各组均数是否相等,当方差不齐时,该方法要比方差分析更为稳健。
Welch:为11.0版新增,采用Welch统计量检验各组均数是否相等,当方差不齐时,该方法要比方差分析更为稳健。
Mcans plot:用各组均数做图,同时可辅助对均数间趋势做出判断。
通常选择“Homogeneity of variance test”(方差齐性检验),点击“Continue”返回。
Missing Values 单选框组:定义分析中对缺失值的处理方法。
8.按“OK”后开始检验并获得检验结果输出。
双因素方差分析-析因设计(两因素两水平,2×2 ANOV A, Factorial
design)
适用对象:分析两个因素同时作用时是否存在交互作用。
如:动物实验时设四个组:对照、应激、高脂、应激+高脂。
为了观察应激+高脂对动物是否存在交互作用(即协同),可用此分析。
两个因素:应激,高脂饮食
两个固定水平:应激有无(1, 0),高脂饮食有无(1, 0)
分析两个因素对血FFA升高是否有协同作用,数据如下:
应变量:FFA
1.通过线性作图大致观察是否有交互作用(此步与以下分析无关,只
是直观从线性图形观察)
选:Multiple
点击“Define”: 设置“Lines Rwpresent”,“Variable”(血变量),“Category Axis”,“Define Lines by”(注:“Category Axis”和“Define Lines by”可互换,不影响作图)。
点击“OK”:
两条直线不平行,表明可能有交互作用。
如果两条直线几乎平行,则不会有交互作用。
2. 2×2析因分析设置变量及因素:
点击“Model”:
“Specify Model”选“Full factorial”, 点击“Continue”回退后再点击“Options…”:
选中“Descriptive Statistics”(可显示结果均值、标准差)和“Homogeneity Tests”(方差齐性检验)。
点击“Continue”回退后再点击“Plots”:
“Horizontal axis”框:高脂(或应激)
“Separate lined”框:应激(或高脂)
点击“Add”。
注:此项的作用是可以做出因素各种水平组合下的效应图点击“Continue”回退后再点击“OK”:
注:利用本方法也可进行两因素以上的方差分析以检验几种因素间是否存在交互作用。
如三因素二水平(3×2)分析。
此时必须有8组数据(对照,a, b, c, a*b, a*c, b*c, a*b*c)。
