波和粒子
波与粒子

Ua (v)
B
2
A
O
5
10
(1014 Hz )
解: h A eua
hd edua
dቤተ መጻሕፍቲ ባይዱa h
d e
h e dua 6.4 1034 Js
d
( dua tan 2 0.4)
d
5
康普顿效应
一. 康普顿效应 (Compton effect) 1920年起康普顿研究了X射线经物体散射
的实验,发现散射束中除了有与入射束波长相
1. 光强增大----光子数增多-----置换出更多电
子-----光电流增强
2. 频率限制: 只有当 0 时才会发生光电效
应,即
h 0
A0
A h
遏止频率(红限频率)
3. 遏止电势差: 外加反向的电势差恰能阻
碍光电子到达阳极,称为遏止电势差 ua
eua
1 2
mv
m
2
h
1 2
mv
m
2
A
爱因斯坦的光子理论圆满地解释了光电效应
3. 斯特藩---玻尔兹曼定律
总辐出度
MB (T
)
0
M B ( ,T
)d
T
4
式中=5.67 10-8 W/m2.k4 为斯特藩常数
4.维恩位移定律
Tm b
b 2.897 103 m k
MB ( ,T )
2000K 1600K
讨论:上述两定律的意义
m2 m1
例1(1)温度为 20 C 的黑体,其单色辐 出度的峰值所对应的波长是多少?(2)太阳的
单色辐出度的峰值波长 m 483 nm,试由
此估算太阳表面的温度.(3)以上两辐出度 之比为多少?
光子的波粒二象性实验

光子的波粒二象性实验
科学家们借助试验捕获了光的粒子与波同时存在的场景。
主要利用了杨氏双缝实验。
把一支蜡烛放在一张开了一个小孔的纸前面,这样就形成了一个点光源(从一个点发出的光源)。
在纸后面再放一张纸,不同的是第二张纸上开了两道平行的狭缝。
从小孔中射出的光穿过两道狭缝投到屏幕上,就会形成一系列明、暗交替的条纹,这就是众人皆知的双缝干涉条纹。
扩展资料:光的波粒二象性是指光既具有波动特性,又具有粒子特性。
科学家发现光既能像波一样向前传播,有时又表现出粒子的特征。
因此我们称光为“波粒二象性”。
光一直被认为是最小的物质,虽然它是个最特殊的物质,但可以说探索光的本性也就等于探索物质的本性。
历史上,整个物理学正是围绕着物质究竟是波还是粒子而展开的。
光学的任务是研究光的本性,光的辐射、传播和接收的规律;光和其他物质的相互作用(如物质对光的吸收、散射、光的机械作用和光的热、电、化学、生理效应等)以及光学在科学技术等方面的应用。
对波粒二象性的理解与认识

对波粒二象性的理解与认识资料整理:王金诚(资环学院环境09-1)爱因斯坦提出了光电效应的光量子解释,指出光波同时具有波和粒子的双重性质。
电子也会具有干涉和衍射等波动现象,这被后来的电子衍射试验所证实。
关键词:波粒二象性;光电效应;波;粒;电子衍射;电子;波粒二象性是指某物质同时具备波的特质及粒子的特质。
波粒二象性是量子力学中的一个重要概念。
从惠更斯和牛顿的早期光理论开始,中间有费涅尔、麦克斯韦和杨、爱因斯坦和光子、光电效应方程、德布罗意假设、波恩概率波和薛定谔方程,一直都在研究波粒二象性。
到目前为止,有关波粒二象性的研究还在继续。
一、光的波动说与微粒说之争光一直被认为是最小的物质,虽然它是个最特殊的物质,但可以说探索光的本性也就等于探索物质的本性。
在整个科学发展史上,整个物理学正是围绕着物质究竟是波还是粒子而展开的。
(一)笛卡儿提出的两点假说在人们对物理光学的研究过程中,光的本性问题和光的颜色问题成为焦点。
关于光的本性问题,迪卡尔在他《方法论》的三个附录之一《折光学》中提出了两种假说。
一种假说认为,光是类似于微粒的一种物质;另一种假说认为光是一种以“以太”为媒质的压力。
虽然笛卡儿更强调媒介对光的影响和作用,但他的这两种假说已经为后来的微粒说和波动说的争论埋下了伏笔。
(二)格里马第发现了光的衍射现象格里马第设计了一个实验:让一束光穿过一个小孔,让这束光穿过小孔后照到暗室里的一个屏幕上。
他发现光线通过小孔后的光影明显变宽了。
格里马第进行了进一步的实验,他让一束光穿过两个小孔后照到暗室里的屏幕上,这时得到了有明暗条纹的图像。
他认为这种现象与水波十分相像,从而得出结论:光是一种能够作波浪式运动的流体,光的不同颜色是波动频率不同的结果。
格里马第第一个提出了“光的衍射”这一概念,是光的波动学说最早的倡导者。
(三)胡克提出了“光是以太的一种纵向波”英国物理学家胡克重复了格里马第的试验,并通过对肥皂泡膜的颜色的观察提出了“光是以太的一种纵向波”的假说。
粒子加速度和电磁波

粒子加速度和电磁波粒子加速度和电磁波的关系是当一个粒子受到电磁场作用时,会发生运动加速度。
首先,了解什么是粒子加速度。
粒子加速度是指粒子在单位时间内速度的增加量。
它与粒子所受的力有关,根据牛顿第二定律可以得到加速度的表达式为:a = F/m,其中a是加速度,F是作用在粒子上的力,m是粒子的质量。
在粒子加速运动中,加速度方向与力的方向一致。
而电磁波是由电场和磁场交替产生并传播的一种波动现象。
它是由运动带电粒子产生的,当带电粒子在其运动过程中改变速度时,会产生变化的电场和磁场,从而形成电磁波。
电磁波的特点是能够在真空中传播,它的传播速度为光速299792458m/s。
当一个带电粒子进入电磁场时,会受到电场和磁场的作用力。
在静电场中,粒子受到的力由库仑定律决定,即F = qE,其中F是作用在粒子上的力,q是粒子的电荷量,E是电场强度。
而在磁场中,粒子受到的力由洛伦兹力定律决定,即F = q(v× B),其中F是作用在粒子上的力,q是粒子的电荷量,v是粒子的速度,B是磁场强度。
根据以上的原理,可以得出粒子在电磁场中的运动方程。
当只有电场存在时,粒子的运动方程为:m(dv/dt) = qE,即粒子的质量乘以加速度等于电荷量乘以电场强度。
当只有磁场存在时,粒子的运动方程为:m(dv/dt) = q(v × B),即粒子的质量乘以加速度等于电荷量乘以速度和磁场强度的叉积。
而当电场和磁场同时存在时,粒子的运动方程为:m(dv/dt) = qE + q(v × B)。
这就是粒子在电磁场中的洛伦兹运动方程。
根据洛伦兹运动方程,粒子在电磁场中会发生运动加速度,其大小与粒子的电荷量、质量、电场强度和磁场强度有关。
这种运动加速度是粒子在电磁场中受到力的结果。
粒子在电磁场中的加速度可以解释许多现象,例如粒子的轨道曲线、电子在磁场中的旋转、加速器中的粒子加速等。
电磁波和粒子加速度的关系在物理学中有着重要的应用,例如电子加速器中利用电磁波对带电粒子进行加速、粒子物理学中研究带电粒子的运动等。
波与粒子的关系

波与粒子的关系
波与粒子是物理学中的基本概念,它们是研究物质行为的两个方面。
传统观念认为波和粒子是两种对立的存在,而现代物理学则提出
了波粒二象性的概念,使得波和粒子之间的关系变得更加复杂和深刻。
波和粒子是物质的两种不同形式。
波是一种能量传递的形式,具
有传播、干扰和衍射等特征。
在物质的微观世界中,波的一个重要表
现形式是电磁波,它具有光速不变的特点,可以通过电磁场的振荡产生。
而粒子则是物质的基本组成单元,是电子、质子等基本粒子以及
它们的组合体。
尽管波和粒子具有截然不同的特征,但在一些情况下它们却表现
出与众不同的关系。
这就是著名的波粒二象性。
波粒二象性指的是,
在一些实验中,物质既呈现出波的特征,又呈现出粒子的特征。
比如,光子在某些实验中表现出的是粒子性质,而在其他实验中则呈现出波
的特性。
同样,电子、质子等粒子也表现出类似的波粒二象性。
这种
现象对传统物理学提出了挑战,迫使人们重新思考物质的本质和行为。
波粒二象性的影响不仅限于物理学的理论研究,它还为人类社会
带来了许多实际应用。
例如,量子力学中的波粒二象性原理是量子计
算机的理论基础,也是纳米电子学和量子光学的重要研究方向。
此外,波粒二象性的探究也为医学影像学和材料科学提供了新的思路和方法。
总之,波与粒子的内在关系是物理学研究的核心问题之一。
波粒
二象性的概念不仅提高了我们对物质行为的认识,也为未来的科学研
究和技术应用提供了许多有益的思路和方向。
光的波动性与粒子性的关系

光的波动性与粒子性的关系光既有波动性,又有粒子性,这是物理学中一个重要的概念。
在过去的几个世纪里,科学家们通过一系列的实验证明了光的这种双重性质,这对于我们对于光和宇宙的理解有着重要的意义。
本文将从历史背景、实验观测以及量子力学的角度来讨论光的波动性和粒子性的关系。
一、历史背景在19世纪初,科学家们对于光的本质持有不同的观点。
一方面,英国科学家牛顿认为光是由无数微小的粒子组成的,并且这些粒子能够沿直线传播。
另一方面,法国科学家惠更斯认为光是一种波动现象,可以通过干涉和衍射等现象进行解释。
然而,19世纪末到20世纪初的实验观测带来了对于光的本质更深刻的认识。
首先,德国科学家马克斯·普朗克在研究黑体辐射时提出了量子理论,他认为能量是以离散的量子形式存在的。
随后,爱因斯坦在解释光电效应时引入了光子的概念,将光看作是由粒子组成的。
二、实验观测1. 干涉实验干涉实验是观测光的波动性的重要实验之一。
当光通过两个相干光源时,会出现干涉现象。
这可以通过Young双缝实验或干涉仪来实现。
实验结果表明,光的波动性可以解释干涉现象的产生。
2. 衍射实验衍射实验也是观测光的波动性的重要实验之一。
当光通过一个狭缝或物体边缘时,会发生衍射现象,光束会扩散成圆形的波前。
这一现象也可以用波动理论进行解释。
3. 光电效应光电效应实验证明了光的粒子性。
当光照射到金属表面时,会引起电子的逸出。
实验发现,只有当光的频率高于一定阈值时,光电效应才会发生。
这与光的波动性无法解释,而量子理论和光子概念能够提供合理的解释。
三、量子力学的角度在20世纪初,量子力学的发展提供了对光的波动性和粒子性关系的深入理解。
根据德布罗意的假设,粒子也具有波动性,波动和粒子性质是互相转化的。
根据量子力学的核心原理,光既可以看作是由光子构成的粒子流,又可以看作是一种波动传播的电磁波。
根据不同的实验条件和观测方式,光可以展现出不同的性质。
四、结论通过历史背景的回顾、实验观测以及量子力学的角度分析,我们可以得出结论:光既有波动性,又有粒子性。
波-粒相互作用产生的粒子随机加速和扩散过程

波-粒相互作用产生的粒子随机加速和扩散过程在物理学中,波-粒相互作用是指波与粒子之间的相互作用,这种相互作用在许多自然现象和实验中都能够观察到。
其中一个重要的应用就是粒子在波动介质中的随机加速和扩散过程。
在这篇文章中,我们将深入探讨波-粒相互作用产生的粒子随机加速和扩散过程,以及其在物理学和工程领域中的重要应用。
1. 波-粒相互作用的基本原理在自然界中,波与粒子之间存在着复杂的相互作用关系。
波动可以被看作是一个在空间中传播的振荡现象,而粒子则是具有质量和位置的实体。
当波与粒子相互作用时,波动会对粒子产生一定的影响,导致粒子的运动发生变化。
这种相互作用可以通过经典物理学和量子物理学中的相应理论来描述和解释。
2. 粒子在波动介质中的随机加速过程当粒子在波动介质中运动时,由于波-粒相互作用的存在,粒子会受到波动的影响而产生随机加速的现象。
这种随机加速过程可以通过统计物理学中的随机运动模型来描述,其中布朗运动就是一个经典的例子。
在这种过程中,粒子会在短时间内受到波动力的作用而产生微小的随机位移,从而实现在波动介质中的无规则运动。
3. 粒子在波动介质中的扩散过程除了随机加速外,粒子还会在波动介质中产生扩散现象。
这种扩散过程是由于波动介质中的不均匀性和波-粒相互作用导致的。
在扩散过程中,粒子会沿着波动介质中的梯度方向进行无规则的运动,最终实现在空间中的扩散分布。
这种扩散过程在自然界和工程领域中有着广泛的应用,例如扩散现象在化学反应和材料传输中起着重要作用。
4. 波-粒相互作用产生的粒子随机加速和扩散过程的应用波-粒相互作用产生的粒子随机加速和扩散过程在许多领域都有着重要的应用价值。
在物理学中,这种过程可以用来解释粒子在波动介质中的微观运动规律,从而深入理解波-粒相互作用的物理本质。
在工程领域中,粒子随机加速和扩散过程的研究可以为化学反应、材料传输和环境污染等问题提供理论支持和实验依据。
总结与回顾:通过以上内容的介绍,我们可以看到波-粒相互作用产生的粒子随机加速和扩散过程是一个复杂而又普遍存在的现象。
波粒二象性发展

<<从辩证唯物主义观点谈光的波粒二象性>>高中物理课本中“光的波粒二象性”一节中作为对“光的本性”一章的概括性总结,寥寥五百多字将光的本性勾勒得淋漓尽致,不得不让人叹服做作者的物理造诣与文字功力。
但要说服学生接受光既是一种波又是一种粒子无异于在说同一个人既是男人又是女人一样让人难以接受,笔者在从事物理教学过程中曾尝试在概括光的干涉、衍射及光电效应等主要内容的同时,用马克思辨证唯物主义的观点作进一步阐释,收效甚佳。
下面将自己对于光的“波粒二象性”的辨证唯物主义分析的拙见罗列如下,供同行赐教。
一、微粒说和波动说的长期斗争以牛顿为代表的微粒说认为光是微粒流,从光源发生,在均匀介质中遵守力学规律作匀速运动,对于光的反射则用弹性球的反跳来解释,对光的折射则用介质的吸引来阐释,另外牛顿还对光的色散、衍射等现象也作出解释,尽管有些十分牵强,尤其是对光的衍射、色散、干涉的解释。
惠更斯是波动说的代表。
他从波阵面的观点出发,认为将光振动看作在一种特殊介质——“以太”中传播的弹性脉动,而“以太”这种介质则充满了宇宙的全部空间,这便是著名的“惠更斯原理”。
在惠更斯原理中,他未提出波长的概念,因而对光的直线传播的解释十分勉强,而且无法解释偏振现象,对光的色散现象更是束手无策。
牛顿对经典力学的建立作出了空前绝后的贡献,这就很容易使人们用经典力学中机械论的观点去理解光的本性,而惠更斯的波动学说尽管对光的干涉、衍射的解释还比较完美,但其理论构架本身还很粗糙,在许多方面还不够完善,但由于牛顿在物理学界的泰斗地位因而在19世纪长达100多年的时间里,微粒说一直占有主导地位。
值得一提的是,牛顿并未从根本上否定微粒学说,他曾多次提到光可能是一种震动并与声音相类比,他说当光投射到一个物体上时,可能会引起物体中以太粒子的震动,就好象投入水中的石块在水面激起波纹一样,并设想可能正是由于这种波引起干涉现象。
但总的来看,他仍对波动说持否定态度。
波粒二象性的粒子性和波动性

波粒二象性的粒子性和波动性
微观世界的物理现象是综合的,不仅包括粒子性和波动性,而且非常复杂。
粒子和波是现象学研究的两大要素,尤其是物理学家和化学家都强调粒子与波是相互关联,形成了粒子波二象性理论。
粒子性意味着Particles,即在实际实验中可以得到的现象,即它具有以下特性:它们是可以实实在在触碰得到的、占有一定体积的、具有不可分割性的微小实体,这些微小实体可以互相传播力学力和相互作用。
波动性意味着Waves,即指分布在物体空间中的连续变化的现象,它一般具有以下特点:波本身不占据物质空间,它是一种运动状态,可以传播而不消失;它可以耦合物体而发生变化;它可以受到外界场的影响而发生变化。
粒子波二象性强调微观粒子的基本物理现象表现为粒子性和波动性的共存性。
例如,电子具有双重属性:粒子性和波动性。
它既可以像一个实体粒子那样出现在实验中,又可以像一个波那样通过晶体普遍存在,表明它们可以兼具粒子特性和波特性。
粒子波二象性也进一步证实了电磁波的本质:它是一种由粒子组成的波。
粒子波二象性的理解也使得微观世界的科学研究有了更新的思路,在21世纪朝着科学研究和应用的新方向开展实验,探索粒子与波之间的微观世界和现象学连接。
粒子波二象性给物理和其他科学方面的研究和运用带来了新的机遇,而新技术的发展也拓宽了人们对粒子、波以及微观世界的了解,该理念还可以帮助我们更好地研究量子世界。
电子元器件知识普及之波粒二象性
波粒二象性简介标签:电子元器件,IC,波粒二象性波粒二象性(wave-particleduality)是指某物质同时具备波的特质及粒子的特质。
波粒二象性是量子力学中的一个重要概念。
在经典力学中,研究对象总是被明确区分为两类:波和粒子。
前者的典型例子是光,后者则组成了人们常说的“物质。
1905年,爱因斯坦提出了光电效应的光量子解释,人们开始意识到光波同时具有波和粒子的双重性质。
1924年,德布罗意提出“物质波”假说,认为和光一样,一切物质都具有波粒二象性。
根据这一假说,电子也会具有干涉和衍射等波动现象,这被后来的电子衍射试验所证实。
数学关系“波”和“粒子”的数学关系物质的粒子性由能量E和动量p刻划,波的特征则由电磁波频率ν和其波长λ表达,这两组物理量的比例因子由普朗克常数h(h=6.626*10^-34J·s)所联系。
E=hv,E=mc^2联立两式,得:m=hv/c^2(这是光子的相对论质量,由于光子无法静止,因此光子无静质量)而p=mc,则p=hv/c(p为动量)历史介绍波粒二象性在十九世纪末,日臻成熟的原子理论逐渐盛行,根据原子理论的看法,物质都是由微小的粒子—原子构成。
比如原本被认为是一种流体的电,由汤普孙的阴极射线实验证明是由被称为电子的粒子所组成。
因此,人们认为大多数的物质是由粒子所组成。
而与此同时,波被认为是物质的另一种存在方式。
波动理论已经被相当深入地研究,包括干涉和衍射等现象。
由于光在托马斯·杨的双缝干涉实验中,以及夫琅和费衍射中所展现的特性,明显地说明它是一种波动。
不过在二十世纪来临之时,这个观点面临了一些挑战。
1905年由阿尔伯特·爱因斯坦研究的光电效应展示了光粒子性的一面。
随后,电子衍射被预言和证实了。
这又展现了原来被认为是粒子的电子波动性的一面。
这个波与粒子的困扰终于在二十世纪初由量子力学的建立所解决,即所谓波粒二象性。
它提供了一个理论框架,使得任何物质在一定的环境下都能够表现出这两种性质。
世界是由什么构成的,粒子吗,还是能量波呢?

世界是由什么构成的,粒⼦吗,还是能量波呢?某些粒⼦其实就是能量波,或者称之为射线粒⼦。
例如光波其实就是光速移动的光⼦。
如果⾮要选⼀个的话!我们可以认为世界应该是由能量波组成的。
因为能量波给⼈感觉更像是虚⽆,⽽粒⼦给⼈感觉更像是物质!其实能量波和粒⼦都不是最⼩组成,整个宇宙包括空间都是由弦组成的,⽽⼈类的微观观测或者探测程度还远远⽆法探测到弦!所以弦理论也只是具有推论和猜想性质!那么直接解释说的话,物质的多样性,是由能量波或者叫波弦互相纠缠造成的。
纠缠程度不同元素也不同,⼀般都是纠缠程度越⾼需要能量就越⼤,元素质量就越⼤!所以许多⼤质量元素是由⾮常剧烈的宇宙现象造成的。
举个例⼦,就如绳结⼀样,打成的团有⼤有⼩有密有疏。
运动越剧烈拧成的团越⼤!所以组成整个宇宙空间的都是由能量或者准确称之为波弦组成的。
波弦纠缠成各种射线粒⼦。
粒⼦⼜组成夸克,夸克组成质⼦,质⼦加电⼦组成中⼦,中⼦加质⼦组成各种原⼦核,各种原⼦核加电⼦组成各种原⼦,各种原⼦⼜组成各种分⼦。
分⼦组成各种物质,各种⽓态液态固态等离⼦态超固态的物质。
这个世界,除了物质还有真空,还有⼒场磁场等等。
由什么组成?⼀样是波弦组成!真空可以是平衡态的波弦,没有纠缠,现在外太空找不到绝对真空,依然有各种粒⼦和电磁波穿梭其中。
纠缠的波弦会对空间产⽣影响,天体是由⼤量纠缠的波弦组成!所以会使周围平衡态的波弦扭曲,其实就是你有物质的地⽅波弦密集,会造成周围空间的波弦稀疏扭曲,使之对周围同样纠缠的物质互相产⽣引⼒!所以只有弦理论才真正能解释宇宙的本源!⼀个点可以由两个甚⾄成千上万条弦层叠组成!⽽多个这样的点⼜能组成各种线⾯体物质!这些物质⼜互为纠缠,互相有万有引⼒影响!。
什么是波粒二象性

什么是波粒二象性简单来说就是,光在运动的时候可以看成是由光子(粒子)组成的,有粒子性,同时它的运动是按波的方式传播的,有波动性。
更科学,更复杂的说法:波粒二象性第一个肯定光既有波动性又有微粒性的是爱因斯坦。
他认为电磁辐射不仅在被发射和吸收时以能量hv的微粒形式出现,而且在空间运动时,也具有这种微粒形式。
爱因斯坦这一光辉思想是在研究辐射的产生和转化时逐步形成的。
与此同时,实验物理学家也相对独立地提出了同样的看法。
其中有W.H.布拉格和A.H.康普顿(ArthurHollyCompton,1892—1962)。
康普顿证明了,光子与电子在相互作用中不但有能量变换,还有一定的动量交换。
1923年,德布罗意把爱因斯坦的波粒二象性推广到微观粒子,提出物质波假说,论证了微观粒子也具有波动性。
他的观点不久就得到电子衍射等实验的证实。
波粒二象性是人类对物质世界的认识的又一次飞跃,这一认识为波动力学的发展奠定了基础。
§9.1 爱因斯坦的辐射理论早在1905年,爱因斯坦在他提出的光量子假说中,就隐含了波动性与粒子性是光的两种表现形式的思想。
他分析了从牛顿和惠更斯以来,波动说和微粒说之间的长期争论,指出麦克斯韦电磁波理论的局限性,审查了普朗克处理黑体辐射的思路,总结了光和物质相互作用有关的各种现象,认为光在传播过程和与物质相互作用的过程中,能量不是分散的,而是一份一份地以能量子的形式出现的。
1909年1月,爱因斯坦再次撰文讨论辐射问题,9月在萨尔茨堡举行的第81届德国物理学家和医学家会议上作了题为:《论我们关于辐射本质和组成的观点的发展》的演讲。
他利用能量涨落的概念,考察一个挂在空腔中的完全反射性的镜子的运动,空腔中充有温度为T的热辐射。
如果镜子是以一个非零的速度运动,则从它的正面反射出去的具有给定频率v的辐射要比从它的背面反射出去的多一些;因此镜子的运动将会受到阻尼,除非它从辐射涨落获得新的动量。
爱因斯坦利用普朗克的能量分布公式,推导出体积V中频率在v→v+dv,之间的那一部分黑体辐射所具有的能量均方涨落为接着,爱因斯坦对上式两项分别作了说明。
能量量子化及波和粒子 - (学生用)
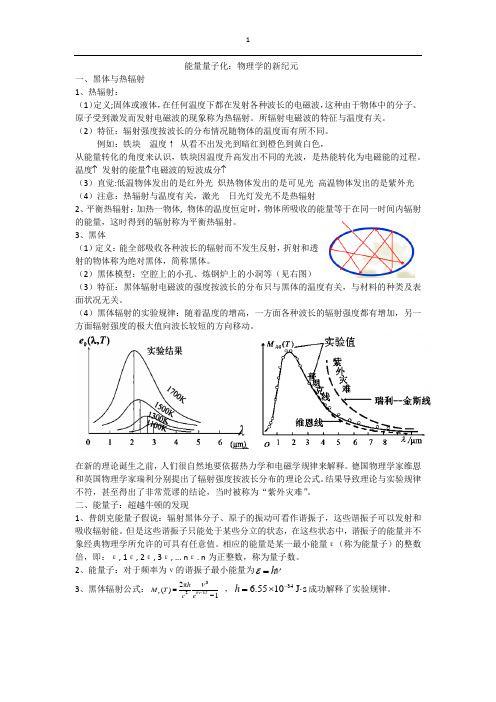
能量量子化:物理学的新纪元 一、黑体与热辐射1、热辐射:(1)定义;固体或液体,在任何温度下都在发射各种波长的电磁波,这种由于物体中的分子、原子受到激发而发射电磁波的现象称为热辐射。
所辐射电磁波的特征与温度有关。
(2)特征:辐射强度按波长的分布情况随物体的温度而有所不同。
例如:铁块 温度↑ 从看不出发光到暗红到橙色到黄白色,从能量转化的角度来认识,铁块因温度升高发出不同的光波,是热能转化为电磁能的过程。
温度↑ 发射的能量↑电磁波的短波成分↑(3)直觉:低温物体发出的是红外光 炽热物体发出的是可见光 高温物体发出的是紫外光(4)注意:热辐射与温度有关,激光 日光灯发光不是热辐射2、平衡热辐射:加热一物体, 物体的温度恒定时,物体所吸收的能量等于在同一时间内辐射的能量,这时得到的辐射称为平衡热辐射。
3、黑体(1)定义:能全部吸收各种波长的辐射而不发生反射,折射和透射的物体称为绝对黑体,简称黑体。
(2)黑体模型:空腔上的小孔、炼钢炉上的小洞等(见右图)(3)特征:黑体辐射电磁波的强度按波长的分布只与黑体的温度有关,与材料的种类及表面状况无关。
(4)黑体辐射的实验规律:随着温度的增高,一方面各种波长的辐射强度都有增加,另一方面辐射强度的极大值向波长较短的方向移动。
在新的理论诞生之前,人们很自然地要依据热力学和电磁学规律来解释。
德国物理学家维恩和英国物理学家瑞利分别提出了辐射强度按波长分布的理论公式。
结果导致理论与实验规律不符,甚至得出了非常荒谬的结论,当时被称为“紫外灾难”。
二、能量子:超越牛顿的发现1、普朗克能量子假说:辐射黑体分子、原子的振动可看作谐振子,这些谐振子可以发射和吸收辐射能。
但是这些谐振子只能处于某些分立的状态,在这些状态中,谐振子的能量并不象经典物理学所允许的可具有任意值。
相应的能量是某一最小能量ε(称为能量子)的整数倍,即:ε, 1ε, 2ε, 3ε, ... n ε. n 为正整数,称为量子数。
波与粒子的关系

波与粒子的关系波与粒子是物质和能量的两种基本表现形式,它们之间的关系一直是物理学中的一个重要课题。
而这种关系的探索,不仅仅是为了满足学术研究的需要,更是为了更好地理解自然界的本质和规律。
在经典物理学中,物质和能量被认为是分离的,物质以粒子的形式存在,而能量则以波的形式传播。
然而,随着科学的发展,特别是在量子力学的研究中,我们逐渐认识到波与粒子的关系并不是如此简单。
让我们来看看波的性质。
波是一种传播的扰动,它具有传递能量和动量的特性。
波可以是机械波,如水波、声波,也可以是电磁波,如光波、无线电波等。
波的传播遵循一定的规律,如波的干涉、衍射等现象。
与此同时,粒子也具有自己的性质。
粒子是物质的基本单位,具有质量和位置,可以相互作用。
粒子的运动是离散的,具有确定的轨迹和动量。
在实际的物理现象中,波与粒子往往并存。
光的行为就是一个很好的例子。
早期的实验观察到光的干涉、衍射等波动性质,因此将光看作是一种波动现象。
然而,在后来的实验中,科学家们也发现了光的粒子性质,这就是光的量子行为。
这种既有波动性质又有粒子性质的现象被称为波粒二象性。
波粒二象性的观念对物理学的发展产生了深远的影响。
它首先打破了经典物理学中物质和能量的分离观念,揭示了物质和能量的统一本质。
其次,波粒二象性的存在也对我们对物质的认识提出了新的挑战。
传统的粒子概念只能描述物质在宏观尺度上的行为,而波动概念适用于宏观和微观尺度。
因此,我们需要用量子力学这样的新理论来描述微观世界的行为。
波粒二象性的发现也引发了许多有趣的思考。
例如,一些物理学家提出了“测量即创造”这样的观点。
根据量子力学的原理,当我们对粒子进行测量时,会导致其波函数坍缩,从而确定其位置或其他性质。
这意味着我们的观察和测量行为会影响粒子的行为,这种观点挑战了我们对客观存在的认识。
尽管波粒二象性的概念在物理学中已经有了很长时间的发展,但我们对于波与粒子的本质仍然存在许多疑问。
例如,我们如何理解波粒二象性的本质?波和粒子之间是否存在某种统一的描述框架?这些问题仍然是科学家们研究的方向。
粒子的波动性

德布罗意假说提出背景
经典物理困境
在经典物理学中,波和粒子是两种完全不同的概念,无法统一解释黑体辐射、光 电效应等现象。
德布罗意假设
为了解释这些现象,德布罗意提出了物质波的概念,认为所有粒子都具有波动性 ,其波长与粒子的动量成反比。
电子衍射等现代实验技术
电子衍射实验
通过电子束照射晶体或非晶态物质, 观察到衍射图案,证明了电子具有波 动性。
量子力学基本原理概述
量子力学是研究微观粒子运动规 律的物理学分支;
量子力学的基本原理包括波粒二 象性、测不准原理、量子态叠加
原理等;
量子力学用波函数来描述粒子的 状态,波函数的模平方给出粒子
在特定位置被发现的概率。
波函数与概率密度解释
波函数是描述粒子状态的复数函数, 其模平方给出粒子在空间的概率分布 ;
04
粒子波动性应用举例
电子显微镜工作原理
01
02
03
波粒二象性
电子具有波粒二象性,其 波动性使得电子可以发生 衍射、干涉等现象,这是 电子显微镜工作的基础。
电子波长
电子的德布罗意波长比可 见光短得多,因此电子显 微镜的分辨率远高于光学 显微镜。
电子枪与电磁透镜
电子显微镜通过电子枪发 射电子,并利用电磁透镜 对电子束进行聚焦和成像 。
重要实验
验证粒子波动性的重要实验包括电子衍射实验、中子干涉实 验、光子反冲实验等。这些实验证实了粒子具有波动性,为 量子力学的发展提供了有力支持。
02
粒子波动性实验证据
光电效应实验介绍
实验原理
光电效应是指光子与物质相互作用, 使得物质吸收光子能量后释放出电子 的现象。
实验装置
实验结果
观察到光照射到物质表面时,物质会 释放出电子,且释放出的电子能量与 光子的频率有关,而与光强无关。
2019-2020学年高中物理 第十七章 波粒二象性 4+5 不确定性关系课件 新人教版选修3-5

3.(多选)根据不确定性关系ΔxΔp≥4hπ,判断下列说法正确的是( ) A.采取办法提高测量Δx精度时,Δp的精度下降 B.采取办法提高测量Δx精度时,Δp的精度上升 C.Δx与Δp测量精度与测量仪器及测量方法是否完备有关 D.Δx与Δp测量精度与测量仪器及测量方法是否完备无关
解析:不确定性关系表明,无论采用什么方法试图确定位置坐标和相应动量中的一 个,必然引起另一个较大的不确定性,这样的结果与测量仪器及测量方法是否完备无 关,无论怎样改善测量仪器和测量方法,都不可能逾越不确定性关系所给出的限 度.故A、D正确. 答案:AD
说明:物质波是一种概率波,但不能将实物粒子的波动性等同于宏观的机械波,更不 能理解为粒子做曲线运动.
[判断辨析] (1)光子通过狭缝后落在屏上的位置是可以确定的.( × ) (2)光子通过狭缝后落在屏上明纹处的概率大些.( √ ) (3)电子通过狭缝后运动的轨迹是确定的.( × )
三、不确定性关系
[特别提醒] (1)在双缝干涉和单缝衍射的暗条纹处也有光子到达,只是光子数量“特别少”,很难 呈现出亮度. (2)要理解统计规律,对统计规律的认识是理解概率波的前提.
[典例1] (多选)物理学家做了一个有趣的实验:在双缝干涉实验中,在光屏处放上照 相底片,若减弱光的强度,使光子只能一个一个地通过狭缝,实验结果表明,如果曝 光时间不太长,底片上只出现一些不规则的点子;如果曝光时间足够长,底片上就出 现了规则的干涉条纹.对这个实验结果有下列认识,其中正确的是( ) A.曝光时间不长时,光子的能量太小,底片上的条纹看不清楚,故出现不规则的点 子 B.单个光子的运动没有确定的轨道 C.干涉条纹中明亮的部分是光子到达机会较多的地方 D.只有大量光子的行为才能表现出波动性
[特别提醒] (1)不确定性关系不是说微观粒子的坐标测不准,也不是说微观粒子的动量测不准,而 是说微观粒子的坐标和动量不能同时测准. (2)普朗克常量是不确定关系中的重要角色,如果h的值可忽略不计,这时物体的位 置、动量可同时有确定的值,如果h不能忽略,这时必须考虑微粒的波粒二象性.普 朗克常量成为划分经典物理学和量子力学的一个界线.
光的波动和粒子性质的计算

光的波动和粒子性质的计算光是一种电磁波,既可以表现出波动性,也可以表现出粒子性。
这一独特的性质在光的计算中起到了至关重要的作用。
本文将探讨光的波动和粒子性质的计算方法,并介绍与之相关的一些重要理论和实验。
一、光的波动性的计算光的波动性可用波动方程来计算。
根据波动理论,光的传播可用以下波动方程来描述:∇^2E - (1/v^2)(∂^2E/∂t^2) = 0其中,E表示电场强度,∇^2是拉普拉斯算子,v是光速。
根据这个波动方程,可以计算出光波在空间中的传播和干涉现象。
例如,当光通过一个狭缝时,可以利用衍射公式计算出光的衍射图样。
此外,光的干涉现象也可以通过波动方程进行计算和解释。
二、光的粒子性质的计算光的粒子性质可用量子力学的理论来计算。
根据量子力学的基本原理,光的粒子性质可以用光子来描述。
光子是光的最小能量单位,其能量公式为:E = hf其中,E为光子的能量,h为普朗克常数,f为光的频率。
根据这个能量公式,可以计算光子的能量和光的频率之间的关系。
此外,光子还具有动量,其动量公式为:p = hf/c其中,p为光子的动量,c为光速。
根据这个动量公式,可以计算光子的动量和光的频率之间的关系。
光的粒子性质还体现在光电效应和康普顿散射等现象中。
这些现象可以通过量子力学的理论进行计算和解释。
三、光的波粒二象性的计算光既可以表现出波动性,也可以表现出粒子性,这种波粒二象性可用波动力学和量子力学的理论进行计算和解释。
在计算光的波粒二象性时,需要综合考虑光的波动性和粒子性特点。
例如,在光的相干和干涉实验中,既可以用波动理论来计算光的干涉图样,也可以用光子的概念来计算光的干涉现象。
此外,还可以利用光的波粒二象性计算其他光学现象,如瑞利散射、拉曼散射等。
这些现象的计算需要综合运用光的波动性和粒子性的特点。
结论光的波动和粒子性质的计算是光学研究中的重要内容。
通过波动方程和量子力学的理论,可以计算光的波动和粒子性质,并解释各种光学现象。
量子力学中的波动性与粒子性的对应关系

量子力学中的波动性与粒子性的对应关系在物理学中,量子力学是一门研究微观粒子行为的学科。
在量子力学中,我们经常会遇到一个有趣的现象,即波动性与粒子性的对应关系。
这个对应关系是量子力学的重要基础之一,也是解释微观粒子行为的重要理论。
本文将探讨波动性与粒子性的对应关系,并且试图给出一些具体的例子来解释这个现象。
首先,我们来看波动性与粒子性的定义。
波动性是指粒子可以表现出波动的性质,例如干涉和衍射。
而粒子性是指粒子具有特定的质量和位置,可以被看作是具有局域性的实物粒子。
在经典物理学中,波动和粒子性是两种互斥的概念,例如光既可以被看作波动,也可以被看作粒子(光子)。
然而,在量子力学中,波动性与粒子性是可以同时存在的。
量子力学中的粒子(例如电子和光子)既可以表现出波动性,也可以表现出粒子性。
这种现象可以通过双缝实验来解释。
在双缝实验中,将只有一个光子或电子的束流通过两个紧密排列在一起的狭缝,观察其在屏幕上的衍射图样。
实验结果显示,光子或电子的分布不是简单地在两个独立的缝洞后面的两个区域上显示,而是出现了干涉图样,表明它们具有波动性。
可以说,量子力学中的波动性与粒子性的对应关系是量子力学的核心之一。
这个对应关系源于量子力学的波动方程——薛定谔方程。
薛定谔方程描述了微观粒子的波函数演化和测量结果的概率性质,它和经典力学中的牛顿方程类似。
根据薛定谔方程,波函数的演化是连续的、平滑的,而测量结果的出现则是不确定的、随机的。
这意味着,当我们试图观测一个微观粒子时,它既可以表现出波动性,也可以表现出粒子性。
在现实世界中,我们可以找到很多关于波动性与粒子性对应关系的例子。
其中一个著名的例子是电子显微镜。
在传统的光学显微镜中,光束通过物体表面并被透镜聚焦,然后通过目镜被观察者观察。
然而,由于光波的衍射极限,光学显微镜的分辨率有限。
相比之下,电子显微镜利用电子束而不是光束,可以获得更高的分辨率。
这是因为电子具有更短的波长,可以绕过光学显微镜的衍射极限。
粒子大小与光波波长

粒子大小与光波波长
粒子大小与光波波长之间存在一种现象称为散射。
当光波与粒子相互作用时,光波会被散射并改变方向。
散射的程度取决于粒子的大小和光波的波长。
如果粒子的尺寸远远大于光波的波长,那么光波会在粒子表面反射或折射,而不会明显散射。
这种情况下,粒子对光波的影响可以忽略不计。
然而,当粒子的尺寸接近或小于光波的波长时,散射效应就会变得显著。
根据散射理论,小于光波波长的粒子会散射出不同波长的光,这被称为Rayleigh散射。
Rayleigh散射导致了天空的蓝色,因为大气中的气体和粒子(如尘埃、水滴等)与太阳光发生散射,而蓝色光的波长比其他颜色的光更短。
总之,粒子大小与光波波长之间的关系会影响光的散射现象。
当粒子的尺寸接近或小于光波的波长时,散射效应会变得显著。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)斯特藩-玻尔兹曼定律
M (T ) M (T )d T
0
4
斯特藩-玻耳ห้องสมุดไป่ตู้曼常量
5.67010 W m K
8 2
4
(2)维恩位移定律
mT b
峰值波长
维恩常量 b 2.898 10 m K
3
二、经典物理解释黑体辐射的困难
由经典物理导出的维恩公式在短波区域与实验 曲线一致,长波区域偏离较大;导出的瑞利 - 金斯公
(2)爱因斯坦光电方程 在光电效应中金属中的电子吸收了光子的能量, 一部分克服电子逸出功W,一部分变为光电子的初动能.
1 2 爱因斯坦方程 h mv W 2
五、光子的性质
1.光子的质量 由相对论光子的质能关系
E mc h
2
光子的质量
m E / c h / c
2
2
由相对论质速关系
( 3 ) 当 > 0 时,光电效应是瞬时的,时间 <10-9s. 当光照射到金属表面上时,几乎立即就有光电子逸出.
3.爱因斯坦光量子理论 (1) “光量子”假设 频率为 的光是由大量光子组成的粒子流,这些
光子沿光的传播方向以光速 c 运动.
光子的能量为
h
一束光的光强为
I nh
式在长波区与实验吻合,而在短波(紫外)区与曲线
偏离 大,当波长变短,辐出度 趋于无穷大.这称为“紫 外灾难”. 由于理论与实验
M (T )
6 5 4 3 2
实验曲线
之间的不可调和性,给
物理学界带来很大困难.
瑞利-金斯 线
1
维恩线 1 2 3 4 5 6
o
三、普朗克能量子假设
在能量子假设的基础上,普朗克从理论上导出了普 朗克公式,与黑体实验规律相符. 普朗克假设: 1.黑体的腔壁由无数带电谐振子组成, 他们不断吸收并 发射电磁波, 与周围电磁场交换能量.
射线外,还有波长 0 的散射线,这种现象称为康普
顿散射或康普顿效应.
2.效应的解释
X 射线视为一些 =h 的光子,与自由电子发生 完全弹性碰撞.
此 碰 撞 过 程 光 入射光子 光子 y p h / c 子 、 电 子 系 统 遵 循 p0 h 0 / c x 能量守恒与动量守 电子 v0 0 恒 . 碰撞时光子将 反冲电子 一部分能量传递给 p mv 电子后, 自身能量减少,波长变长,形成波长大于原入射
1 (u / c) 有 m 0 0 否则 m
光子是一种静止质量为零的粒子.
m
m0
2
2. 光子的动量 根据相对论的能量-动量关系
E p c m c
2 2 2
2 4 0
及其
m0 0
h h p E/c c
六、康普顿效应
1.康普顿效应 X射线被物质散射时,除有与入射波长 0 相同的散
一、黑体辐射
1.热辐射 任何物体在任何温度下都要发射各种波长的电磁
波,这种由于物质中的分子、原子受到热激发而发射
电磁波的现象为热辐射. 2.单色辐出度 描写物体辐射本领的物理量.
dEλ M λ(T) dλ
表示在一定温度T下,单位时间内从物体表面单位
面积上辐射出的波长在附近单位波长间隔内的能量.
12-1 量子论的出现
预习要点
1. 注意黑体这个理想物理模型的特征及黑体辐射的实 验规律.
2. 普朗克量子假说的内容及其意义是什么?
3. 经典物理理论在解释光电效应和康普顿效应实验规 律时遇到了哪些困难?光子理论是如何解释的? 4. 玻尔关于氢原子模型假设的主要内容是什么?它们 是针对哪些问题提出的?
3.黑体 能完全吸收照射到它上面的各种频率的电磁辐射的 物体称为黑体. 可把一个开小孔的不透
光空腔近似看成黑体.
4.黑体辐射实验规律
M (T )
实验中将开有小孔的空
腔视为黑体,如使空腔恒温,
1700 K
测量从小孔中辐射出来的各
种波长范围的单色辐出能与 波长之间的关系.
1500 K
1100 K
o
例: 波长 λ0 3.0 10- 2 nm 的X射线与静止的自由电子 作弹性碰撞, 在与入射角成 900角的方向上观察, 问 (1)散射X射线光子的波长为多少? (2)反冲电子得到多少动能? 解:(1) c (1 cos ) c (1 cos90 ) c
光波长的散射线 . 此外,入射x光子也会与受核束缚紧 密的内层电子碰撞,可看作是与整个原子碰撞,原子质
量远大于光子,碰撞后散射光子能量几乎不变,波长与
入射光相同.
由x光子和自由电子系统的能量守恒和动量守恒可 推导出
h 2 (1 cos ) 2c sin m0c 2
h 2.341012 m 称为康普顿波长 其中 c m0c
第十二章 波和粒子
12-0 教学基本要求
12-1 量子论的出现
12-2 物质波 不确定关系
*12-3 波函数 薛定谔方程及简单应用
教学基本要求
一、了解普朗克能量子假设,爱因斯坦的光子理论对有关 实验规律的解释,理解光的波粒二象性. 了解氢原子光谱的实 验规律,原子核式模型与经典电磁理论说明氢原子的困难,了 解玻尔原子理论及其对氢原子光谱实验规律的解释. 二、了解德布罗意物质波假设及其产生的科学思想方法, 了解描述物质波动性质的物理量和粒子性的物理量之间的关系, 了解物质波的验证实验,了解玻恩对物质波的统计解释及实物 粒子波粒二象性的物理图像. 三、了解不确定关系,并能用于作简单的计算. *四、了解一维自由粒子的波函数,了解波函数必须满足的 条件,了解一维薛定谔方程,了解一维无限深势阱中粒子的 概率分布和能量量子化及驻波解释,了解隧道效应及应用.
2.空腔壁上频率为 的带电谐振子所吸收或发射的能量 是h 的整数倍,即谐振子的能量是量子化的.
nh (n 1,2,3,)
h 6 .626 10 34 J s 称为普朗克常量.
3.谐振子在与周围电磁场交换能量时,能量的改变只能 是最小能量单元 h 的整数倍,称 h 为能量子. 普朗克常数h是界定微观物理与宏观物理的界碑.
四、光电效应和爱因斯坦光量子理论
1.光电效应 当光线照射在金属表面时,金属中有电子逸出,逸 出的电子称为光电子. 这种现象叫光电效应. 2.光电效应实验规律 (1)当入射光频率 < 0 时,无论光强多大也无电子 逸出金属表面,0叫截止频率或红限频率,截止频率与 材料有关与光强无关. (2) 电子初态动能只与光频率 成正比,而与入射光 强无关.
