计算两组数组对应数值平方差之和
平方差公式和完全平方公式计算题

平方差公式和完全平方公式计算题平方差公式是数学中的一个重要公式,通常用于计算求出两个数字的差的平方值。
它是一个有用的公式,可以用来计算多种数学运算,例如计算平均数、标准差和方差。
同样,完全平方公式也是数学中一个重要公式,它可以用来计算两个数字之间的平方根。
平方差公式可以用不同的方式表达,其中最常用的是:(x-y) = x-2xy+y其中,x和y是两个要求差值平方的数字,其中x表示大的数量,y表示小的数量。
换句话说,当x比y大时,这个公式表示(x-y)的值会大于0;相反,当x比y小时,这个公式的值就会小于0。
另外,当x等于y时,这个公式的值也就等于0。
完全平方公式也可以用不同的方式表达,其中最常用的是:x = a + b其中,a和b是要求平方根的数字,其中a小于x,b大于x。
换句话说,此公式表示要求一个数字x的平方根,可以找到两个数字a 和b,使得a + b等于所求数字x的平方。
因此,平方差公式和完全平方公式都是数学运算中重要的公式,可以用来计算数据之间的差值平方和平方根。
熟练掌握平方差公式和完全平方公式,可以帮助你解决诸多数学难题。
要熟练掌握这两个公式,可以采用练习的方式。
首先,应该先熟练掌握上面提到的公式的简单应用,例如计算实数的平方差、完全平方根和其他简单运算。
对于更复杂的数学问题,可以先尝试着用平方差公式和完全平方公式来解决,并加上其他公式来计算或验证答案,这样可以了解数学问题的解法和原理,可以有效地提升自己的数学素养。
另外,精通平方差公式和完全平方公式,还可以结合实际场景,使用更加复杂的运算,以解决实际的科学问题。
例如,结合比例公式和完全平方公式,可以解决实际场景中的面积和体积,从而更好地解决实际问题。
因此,要想在数学学习中取得进步,熟练掌握平方差公式和完全平方公式十分重要。
结合实际场景,通过多加练习和思考,我们可以更好地掌握这两个公式,为解决实际问题提供手段。
两数和差的平方

公式转换法
定义
公式转换法是指利用公式转换, 将两数的和与差的平方表示成其 他数为a和b,则它们的平方 和为(a+b)^2=a^2+b^2+2ab ,差为(a-b)^2=a^2+b^2-2ab 。
例子
利用公式 (a+b)^2=[(a+b)^2+(ab)^2]/2,则 (4+3)^2=[(4+3)^2+(43)^2]/2=41。
两数和差的平方
xx年xx月xx日
目 录
• 引言 • 两数和差的平方的性质 • 两数和差的平方的计算方法 • 两数和差的平方的实例 • 两数和差的平方的应用 • 两数和差的平方的进一步探讨
01
引言
定义和公式
1
两数和差的平方是指两个数的和或差的平方, 具体公式如下
2
(a+b)^2 = a^2 + 2ab + b^2
04
两数和差的平方的实例
整数实例
总结词
整数和差的平方
详细描述
对于两个整数a和b,它们的和差的平方等于(a+b)2-(a-b)2,这个结论 可以通过整数的平方差公式进行验证。例如,两个整数3和5的和差的平方等 于(3+5)2-(3-5)2=160。
分数实例
总结词
分数和差的平方
详细描述
对于两个分数a和b,它们的和差的平方等于(a+b)2-(a-b)2,这个结论可以通过分数的平方差公 式进行验证。例如,两个分数1/2和3/4的和差的平方等于(1/2+3/4)2-(1/2-3/4)2=19/16。
3
(a-b)^2 = a^2 - 2ab + b^2
超全Excel函数大全 含详细教程
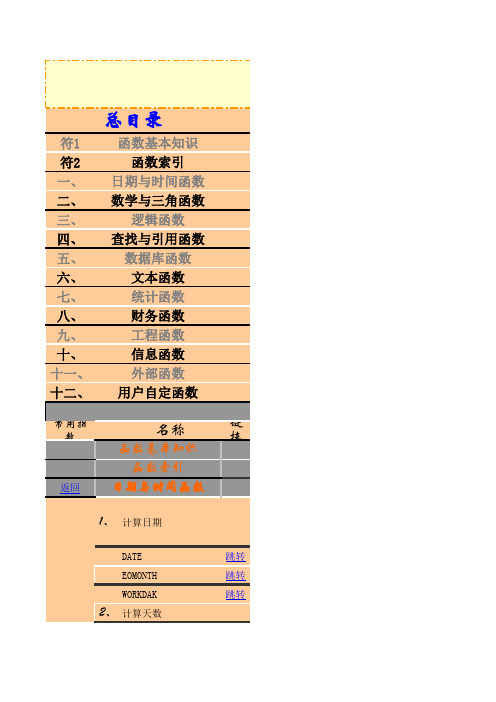
函函 数 大 全链接函数基本知识函数索引日期与时间函数数学与三角函数逻辑函数查找与引用函数数据库函数文本函数统计函数财务函数工程函数信息函数定义返回从开始日期算起的数月之前或之后的序列号.返回指定月份数之前或之后的某月份的最后的日期序列号.返回自开始日期算起相隔指定天数之前或之后(不包括周末和专门指定的假日)的日期的序列号.计算除了周六、日和休息日之外的工作天数计算期间内的年数、月数、天数按一年360天计算两个日期之间的天数计算指定期间占一年的比率计算从1月1日算起的第几个星期从年、月、日来计算日期从表示日期的文本来计算序列号值从时、分、秒来计算出时间的序列号值从表示时间的文本来计算序列号值计算当前的日期计算当前的日期和时间和星期从日期中提取出"年"从日期中提取出"月"从日期中提取出"日"计算出与日期相对应的星期从时间中提取出"时"从时间中提取出"分"从时间中计算出"分"求和计算对满足条件的单元格的数值求和计算满足条件的单元格人个数计算积先计算多个数组的元素之间的乘积再求和计算平方和计算两个数组中对应元素的平方之和计算两个数组中对应元素的平方差之和计算两个数组中对应元素的差的平方之和计算各种总计值将数值向下舍入为最接近的整数根据指定的位数位置向下舍入计算根据指定的位数位置向下舍入根据指定的位数位置向上舍入根据指定的位数位置四舍五入向下舍入为指定的倍数向上舍入为指定的倍数舍入指定值的倍数向上舍入最接近的偶数向上舍入最接近的奇数计算出商的整数部分计算余数倍数计算最大公约数计算绝对值计算正负符号计算阶乘计算双阶倍乘返回从给定元素数目的集合中选取若干元素的排列数计算组合数或二项系数计算多项系数计算幂级数计算平方根计算圆周率的倍数的平方根计算幂乘计算自然对数e的幂乘计算以指定的数值为底的对数计算常用对数计算自然对数计算圆周率的近似值将角度转换为弧度将弧度转换为度计算正弦值计算余弦值计算正切值计算反正弦值计算反正切值计算x-y坐标的反正切值计算双曲正弦值计算双曲余弦值计算比曲正切值计算双曲反正弦值计算双曲反余弦值计算比曲反正切值值计算矩阵行列式的值计算矩阵的逆矩阵计算两数组矩阵的乘积产生大于或等于0且小于1的随机数产生指定数值之间的随机数根据条件满足与否返回不同的值检测所有的条件是否为真检测任意一项条件是否为真对表示条件的参数的逻辑值求反表示总是为真表示总是为假按照垂直方向搜索区域按照水平方向搜索区域(向量形式)搜索单行或单列(数组形式)搜索区域或查找对应值返回搜索值的相对位置计算指定位置的单元格引用(单元格引用方式)返回行和列交差位置的单元格引用(数组形式)返回行和列交叉位置的值间接引用单元格的内容从参数表中选择特定的值位置返回单元格引用或单元格的位置返回序列号返回行序号计算列数返回引用或数组的行数计算指定区域的区域个数行和列的转置创建超链接从支持COM自动化的程序中获取实时的数据将全角字符(双字节字符)转换成半角字符(单字节字符)将半角字符转换成全角字符将所有英文字母转换成大写字母将所有英文字母转换成寂写字母将英文单词的开头字母转换成大写字母将表示数值的文本转换成数值统计文本字符串中字符数目(计算文本的长度)计算文本的字节数将多个字符文本或单元格中的数据连接在一起,显示在一个单元格中从一个文本字符串的第一个字符开始,截取指定数目的字符从一个文本字符串的最后一个字符开始,截取指定数目的字符从一个文本字符串的指定位置开始,截取指定数目的字符根据指定的位置和字节提取字符检索字符位置(区分大小写)检索字节位置(区分大小写)检索字符位置(不区分大小写)检索字节位置(不区分大小写)替换检索的文本替换指定字符数的文本替换指定字节数的文本删除多余的空格字符删除非打印字符返回字符代码返回与字符代码相对的字符给数值添加_符号和千位分隔符给数值附加上美元符号和千位分隔符将数值转换成泰语的货币格式的文本给数值附加千位分隔符和小数分隔符将数值转换成自由的显示格式文本将数值转换成罗马数字检查两文本是否完全相同根据指定次数重复文本只在参数为文本时返回将数值转换成汉字的文本计算日期和数值的个数计算数据的个数计算空白单元格的个数计算数值数据的平均值计算所有数据的平均值剔除异常数据后计算平均值计算几何平均值计算调和平均值计算数据群的为数计算数据群的众数计算数值的最大值计算所有数据的最大值计算数值的最小值计算所有数据的最小值计算从大到小顺序下某一位置的数值计算从小开始指定位置的数值计算位置(排位)计算区间里所含数值的个数计算百分位数计算四分位数计算使用百分率的位置通过数值计算无偏方差通过所有数据计算无偏方差通过数值计算方差通过所有数据计算方差通过数值推测数据集的标准偏差通过数值推测数据集的标准偏差通过数值计算标准偏差通过数值计算标准偏差计算平均偏差计算变动计算标准化变量计算峰度计算偏斜度使用回归曲线进行预测使用重回归分析进行预测计算回归斜线的斜率计算回归斜线的计算截距通过重回归分析计算系数和常数项计算回归曲线的标准误差计算回归曲线的的适合度使用指数回归曲线进行预测计算指数回归曲线的系数和底数计算相关系数计算相关系数计算协方差计算数据集对应的置信区间计算下限值到上限值概率计算二项分布的概率和累积概率计算累积二项概率在基准值以下时的最大值计算负二项分布的概率计算超几何分布的概率计算POISSON分布的概率计算正态分布的概率和累积概率计算累积正态分布的反函数计算标准正态分布的累积概率计算标准正态分布的累积概率的反函数计算对数正态分布的累积概率计算对数正态分布的累积概率反函数计算卡方分布的上侧概率计算卡方分布的上侧概率的反函数进行卡方检验计算t分布的概率计算t分布的反函数进行t检验检验正态数据集的平均值计算F公布的概率计算F公布的反函数进行t检验进行FISHER变换计算FISHER变换的反函数计算指数分布函数的值计算伽玛公布函数的值计算伽玛公布函数的反函数计算伽玛函数的自然对数计算Beta分布的累积函数的值计算Beta分布的累积函数的反函数计算韦伯分布的值计算贷款的还款额和分期储蓄的存款额计算贷款偿还额的本金相应部分计算贷款偿还额的本金相应部分的累计计算贷款偿还额的利息相应部分计算贷款偿还额的利息相应部分的累计计算本金均分偿还时的利息计算当前价格计算将来的价格计算利率变动存款的将来价格计算贷款的偿还时间和分期储蓄的存款时间计算贷款或分期储蓄的利率计算实际年利率计算名目年利率计算定期现金流量的净现值由不定期的现金流量计算净现值由定期的现金流量计算内部利益率由不定期的现金流量计算内部利益率由定期现金流量计算内部利益率函数计算定期付息证券的利率计算定期付息证券的当前价格计算定期付息证券的利息计算之前的付息日计算最近的付息日到成交日的天数计算成交日到下一付息日的天数计算定期成交日到期日的付息次数。
wps表格函数说明大全

wps表格函数说明大全wps表格公式大全数学与三角函数ABS返回数字的绝对值ACOS返回数字的反余弦值ACOSH返回数字的反双曲余弦值ASIN返回数字的反正弦值ASINH返回数字的反双曲正弦值ATAN返回数字的反正切值ATAN2从X和Y坐标返回反正切ATANH返回数字的反双曲正切值CEILING将数字舍入为最接近的整数,或最接近的有效数字的倍数COS返回数字的余弦值COMBIN计算从给定数目的对象集合中提取若干对象的组合数COSH返回数字的双曲余弦值DEGREES将弧度转换为度EVEN将数字向上舍入为最接近的偶型整数EXP返回e的指定数乘幂FACT返回数字的阶乘FACTDOUBLE返回数字的双倍阶乘FLOOR将数字朝着零的方向向下舍入GCD返回最大公约数INT将数字向下舍入为最接近的整数LCM返回整数参数的最小公倍数。
LN返回数字的自然对数LOG返回数字的指定底数的对数LOG10返回数字的常用对数MINVERSE返回数组矩阵的逆距阵MULTINOMIAL返回参数和的阶乘与各参数阶乘乘积的比值MDETERM返回一个数组的矩阵行列式的值MMULT返回两个数组的矩阵乘积MOD返回两数相除的余数MROUND返回一个舍入到所需倍数的数字ODD将数字向上舍入为最接近的奇型整数PI返回PI值POWER返回数的乘幂结果PRODUCT将所有以参数形式给出的数字相乘QUOTIENT返回商的整数部分,该函数可用于舍掉商的小数部分。
RADIANS将度转换为弧度RAND返回0到1之间的随机数RANDBETWEEN返回指定数字之间的随机数ROMAN将阿拉伯数字转换为文本形式的罗马数字ROUND将数字舍入到指定位数ROUNDDOWN将数字朝零的方向舍入ROUNDUP将数朝远离零的方向舍入SERIESSUM返回基于公式的幂级数的和SIGN返回数字的符号SIN返回给定角度的正弦值SINH返回数字的双曲正弦值SQRT返回正平方根SQRPI返回某数与PI的乘积的平方根SUBTOTAL返回数据库清单或数据库中的分类汇总SUM将参数求和SUMIF按给定条件将指定单元格求和SUMIFS在区域中添加满足多个条件的单元格SUMPRODUCT返回相对应的数组部分的乘积和SUMSQ返回参数的平方和SUMX2MY2返回两数组中对应值平方差之和页脚SUMX2PY2返回两数组中对应值的平方和之和SUMXMY2返回两个数组中对应值差的平方和TAN返回数字的正切值TANH返回数字的双曲正切值TRUNC将数字截尾取整日期与时间函数DATE返回特定日期的序列号DATEVALUE将文本格式的日期转换为序列号DATEDIF返回两个日期之间的隔数DAY将序列号转换为月份中的日DAYS360以一年360天为基准计算两个日期间的天数EDATE返回用于表示开始日期之前或之后月数的日期的序列号EOMONTH返回指定月数之前或之后的月份的最后一天的序列号HOUR将序列号转换为小时MINUTE将序列号转换为分钟MONTH将序列号转换为月NETWORKDAYS返回两个日期之间的全部工作日数NOW返回当前日期和时间的序列号SECOND将序列号转换为秒TIME返回特定时间的序列号TIMEVALUE将文本格式的时间转换为序列号TODAY返回今天日期的序列号WEEKDAY将序列号转换为星期几WEEKNUM将序列号转换为一年中相应的周数WORKDAY返回指定的若干个工作日之前或之后的日期的序列号YEAR将序列号转换为年YEARFRAC返回代表start_date和end_date之间整天天数的年分数工程函数BIN2DEC将二进制数转换为十进制数BIN2HEX将二进制数转换为十六进制数CONVERT将数字从一种度量系统转换为另一种度量系统DEC2BIN将十进制数转换为二进制数DEC2HEX将十进制数转换为十六进制数HEX2BIN将十六进制数转换为二进制数HEX2DEC将十六进制数转换为十进制数宏表函数EVALUATE对以文字表示的一个公式或表达式求值,并返回结果统计函数AVEDEV返回数据点与其平均值的绝对偏差的平均值AVERAGE返回参数的平均值AVERAGEA返回参数的平均值,包括数字、文本和逻辑值AVERAGEIF返回区域中满足给定条件的所有单元格的平均值(算术平均值)AVERAGEIFS返回满足多个条件的所有单元格的平均值(算术平均值)BETADIST返回Beta累积分布函数BETAINV返回指定Beta分布的累积分布函数的反函数BINOMDIST返回一元二项式分布概率CHIDIST返回chi平方分布的单尾概率CHIINV返回chi平方分布的反单尾概率CHITEST返回独立性检验值COUNT计算参数列表中数字的个数COUNTA计算参数列表中值的个数COUNTBLANK计算指定单元格区域中空白单元格的个数页脚CONFIDENCE返回总体平均值的置信区间CORREL返回两个数据集之间的相关系数COUNTIF计算区域中满足给定条件的单元格的个数COUNTIFS 计算区域中满足多个条件的单元格的个数COVAR返回协方差,即成对偏移乘积的平均数CRITBINOM返回使累积二项式分布小于等于临界值的最小值DEVSQ返回偏差的平方和EXPONDIST返回指数分布FDIST返回F概率分布FINV返回F概率分布的反函数FISHER返回Fisher变换值FISHERINV返回Fisher变换的反函数FORECAST根据线性趋势返回值FTEST返回F检验的结果FREQUENCY以垂直数组的形式返回频率分布GAMMADIST返回γ分布GAMMAINV返回γ累积分布函数的反函数GAMMALN返回γ函数的自然对数,Γ(x) GEOMEAN返回正数数组或区域的几何平均值GROWTH根据指数趋势返回值HARMEAN返回数据集合的调和平均值HYPGEOMDIST返回超几何分布INTERCEPT返回线性回归线截距KURT返回数据集的峰值LARGE返回数据集中第k个最大值LINEST返回线性趋势的参数LOGINV返回反对数正态分布LOGNORMDIST返回累积对数正态分布函数MAX返回参数列表中的最大值MAXA返回参数列表中的最大值,包括数字、文本和逻辑值MEDIAN返回给定数字的中值MIN返回参数列表中的最小值MINA返回参数列表中的最小值,包括数字、文本和逻辑值MODE返回数据集中出现最多的值间的概率NEGBINOMDIST返回负二项式分布NORMDIST返回正态累积分布NORMINV返回反正态累积分布NORMSDIST返回标准正态累积分布NORMSINV返回反标准正态累积分布PEARSON返回Pearson乘积矩相关系数PERCENTILE返回区域中的第k个百分位值PERCENTRANK返回数据集中值的百分比排位PERMUT返回从给定数目的对象集合中选择的若干对象的排列数POISSON返回Poisson分布PROB返回区域中的数值落在指定区间的对应概率QUARTILE返回数据集的四分位数RANK返回某数在数字列表中的排位RSQ返回Pearson乘积矩相关系数的平方SLOPE返回线性回归直线的斜率SMALL返回数据集中的第k个最小值STANDARDIZE返回正态化数值STDEV基于样本估算标准偏差STDEVA基于样本估算标准偏差,包括数字、文本和逻辑值STDEVP计算基于整个样本总体的标准偏差STDEVPA计算整个样本总体的标准偏差,包括数字、文本和逻辑值TDIST返回学生的t分布页脚TINV返回学生的t分布的反分布TREND返回沿线性趋势的值TRIMMEAN返回数据集的部平均值TTEST返回与学生的t检验相关的概率VAR基于样本估算方差VARA基于样本估算方差,包括数字、文本和逻辑值VARP基于整个样本总体计算方差VARPA基于整个样本总体计算方差,包括数字、文本和逻辑值WEIBULL返回Weibull分布ZTEST返回z检验的单尾概率值财务函数ACCRINTM返回到期付息有价证券的应计利息DB使用固定余额递减法,返回一笔资产在指定期间的折旧值DDB使用双倍余额递减法或其他指定方法,返回一笔资产在指定期间的折旧值FV返回投资的未来值IPMT返回给定期间投资的利息偿还额IRR返回一系列现金流的部收益率ISPMT计算在投资的特定期间支付的利息MIRR返回正负现金流在不同利率下支付的部收益率NPER返回投资的期数NPV基于一系列定期的现金流和贴现率,返回一项投资的净现值PMT返回年金的定期付款额PPMT返回投资在某一给定期间的本金偿还额PV返回投资的现值RATE返回年金的各期利率SLN返回一项资产在一个期间中的线性折旧费SYD返回某项资产按年限总和折旧法计算的指定期间的折旧值VDB使用余额递减法,返回指定期间或部分期间的某项资产折旧值查找与引用函数ADDRESS以文本形式返回对工作表中某个单元格的引用AREAS返回引用中的区域个数CHOOSE从值的列表中选择一个值COLUMN返回引用的列标COLUMNS返回引用中的列数HLOOKUP在数组的首行查找并返回指定单元格的值HYPERLINK 创建一个快捷方式(跳转),用以打开存储在网络服务器、Intranet 或Internet中的文件INDEX使用索引从引用或数组中选择值INDIRECT返回由文本值表示的引用LOOKUP在向量或数组中查找值MATCH在引用或数组中查找值OFFSET从给定引用中返回引用偏移量ROW返回引用的行号ROWS返回引用中的行数TRANSPOSE返回数组的转置Vlookup在数组第一列中查找,然后在行之间移动以返回单元格的值文本函数ASC将字符串的全角(双字节)英文字母或片假名更改为半角(单字节)字符CHAR返回由代码数字指定的字符CLEAN删除文本中所有打印不出的字符CODE返回文本字符串中第一个字符的数字代码CONCATENATE 将若干文本项合并到一个文本项中DOLLAR按$(美元)货币格式将数字转换为文本页脚EXACT检查两个文本值是否完全相同FIND在一文本值查找另一文本值(区分大小写)FINDB在一文本值查找另一文本值(区分大小写)FIXED将数字设置为具有固定小数位的文本格式LEFT返回文本值最左边的字符LEFTB返回文本字符串中的第一个或前几个字符LEN返回文本字符串中的字符个数LENB返回文本字符串中的字符个数LOWER将文本转换为小写形式MID从文本字符串中的指定位置起返回特定个数的字符MIDB从文本字符串中的指定位置起返回特定个数的字符PROPER将文本值中每一个单词的首字母设置为大写REPLACE替换文本的字符REPLACEB替换文本的字符REPT按给定次数重复文本RIGHT返回文本值最右边的字符RIGHTB返回文本串中最后一个或多个字符RMB按¥(RMB)货币格式将数字转换为文本SEARCH在一文本值中查找另一文本值(不区分大小写)SEARCHB在一文本值中查找另一文本值(不区分大小写)SUBSTITUTE在文本字符串中以新文本替换旧文本T将参数转换为文本TEXT设置数字的格式并将数字转换为文本TRIM删除文本中的空格UPPER将文本转换为大写形式VALUE将文本参数转换为数字WIDECHAR将字符串中的半角(单字节)字母转换为全角(双字节)字符逻辑函数AND如果所有参数均为TRUE,则返回TRUEFALSE返回逻辑值FALSEIF指定要执行的逻辑检测IFERROR如果公式的计算结果错误,则返回您指定的值;否则返回公式的结果NOT对参数的逻辑值求反OR如果任一参数为TRUE,则返回TRUETRUE返回逻辑值TRUE信息函数CELL返回有关单元格格式、位置或容的信息ERROR.TYPE返回对应于错误类型的数字ISBLANK如果值为空,则返回TRUEISERR如果值为除#N/A以外的任何错误值,则返回TRUEISERROR如果值为任何错误值,则返回TRUE ISEVEN如果数字为偶数,则返回TRUEISLOGICAL如果值为逻辑值,则返回TRUEISNA如果值为#N/A错误值,则返回TRUE ISNONTEXT如果值不是文本,则返回TRUE ISNUMBER如果值为数字,则返回TRUE ISODD如果数字为奇数,则返回TRUEISREF如果值为一个引用,则返回TRUEISTEXT如果值为文本,则返回TRUEN返回转换为数字的值NA返回错误值#N/ATYPE返回表示值的数据类型的数字页脚。
java 数组字段求方差 极差

java 数组字段求方差极差在Java中,计算数组字段的方差和极差是一个很常见的操作。
方差是一组数据离均值的平方差的平均值,可以衡量数据的分散程度,而极差则是一组数据中最大值和最小值的差。
下面是一些计算数组字段方差和极差的方法:1. 计算数组字段的平均值meandouble[] arr = {1, 2, 3, 4, 5};double sum = 0;for (int i = 0; i < arr.length; i++) {sum += arr[i];}double mean = sum / arr.length;2. 计算数组字段的方差variancedouble[] arr = {1, 2, 3, 4, 5};double sum = 0;for (int i = 0; i < arr.length; i++) {sum += (arr[i] - mean) * (arr[i] - mean);}double variance = sum / arr.length;3. 计算数组字段的极差rangedouble[] arr = {1, 2, 3, 4, 5};double max = arr[0];double min = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}if (arr[i] < min) {min = arr[i];}}double range = max - min;以上是比较简单的计算方法,对于高维数组的操作,需要根据具体情况进行设计和实现。
excel2020常用函数完全手册

excel2020常用函数完全手册函数应用完全手册目录一、函数应用基础 (1)(一)函数和公式 (1)1.什么是函数 (1)2.什么是公式 (1)(二)函数的参数 (1)1.常量 (1)2.逻辑值 (1)3.数组 (1)4.错误值 (1)5.单元格引用 (1)6.嵌套函数 (2)7.名称和标志 (2)(三)函数输入方法 (2)1.“插入函数”对话框 (2)2.编辑栏输入 (3)二、函数速查一览 (3)(一)数据库函数 (3)1.DA VERAGE.( 返回数据库或数据清单中满足指定条件的列中数值的平).. ..... . (3)2.DCOUNT..... (返回数据库或数据清单的指定字段). (3)3.DCOUNTA.( 返回数据库或数据清单指定字段中满足给定条件的非空单元格数目) (3)4.DGET..( 从数据清单或数据库中提取符合指定条件的单个值。
) (3)5.DMAX.( 返回数据清单或数据库的指定列中,满足给定条件单元格中的最大数值) (3)6.DMIN...( 返回数据清单或数据库的指定列中满足给定条件的单元格中的最小数字). (3)7.DPRODUCT..( 返回数据清单或数据库的指定列中,满足给定条件单元格中数值乘积。
) (3)8.DSTDEV...( 估算样本总体的标准偏差) (3)9.DSTDEVP..( 运算总体的标准偏差.) (4)10.DSUM.....( 满足给定条件单元格中的数字之和). (4)11.DV AR......( 估算样本总体的方差.) (4)12.DV ARP....( 运算总体的方差.).. 413.GETPIVOTDATA..( 返回储备在数据透视表报表中的数据) (4)(二)日期与时刻函数 (4)1.DATE.. (返回代表特定日期的序列号。
)....DATE. (4)2.DATEV ALUE....( 返回date_text 所表示的日期的序列号。
1、数组求和

1、数组求和:{=SUM((G12:G21>100)*G12:G21)}[公式说明]:本公式为数组公式,可以对G12:G21区域中大于100的数据进行求和,而排除小于等于100的数据。
输入公式时必须按【Ctrl+Shift+Enter】组合键结束,否则无法得到正确结果。
[使用注意]:1、公式中"G12:G21>100"部分表示求和条件,后跟实际求和区域"G12:G21"。
如果有多个条件,可一并罗列出来。
例如求大于100且小于115的数据之和,公式如下:=SUM(G12:G21>100)*(G12:G21<115)*G12:G21)。
2、此数组公式只适用于单个区域求和,如果有多个区域,只能用多个SUM求和,然后相加。
例如对G12:G21和H12:H21区域中大于100的数汇总,公式如下:=SUM(SUM((G12:G21>100)*G12:G21),SUM((H12:H21>100)*H12:H21))。
3、对于SUM函数的数组公式,可以用SUMPRODUCT函数来代替,从而将数组公式转换成普通公式。
例如本案例的公式用SUMPRODUCT函数后,普通公式如下:=SUMPRODUCT((G12:G21>100)*G12:G21)。
2、数据类型转换求和:=SUM(VALUE(H5),H6:H10,J5:J10,L5:L10);=SUM(--(H5),H6:H10,J5:J10,L5:L10);=SUM((H5)*1,H6:H10,J5:J10,L5:L10);=SUM((H5)/1,H6:H10,J5:J10,L5:L10)[公式说明]:SUM函数用于对单元格区域的数据或者逻辑值、表达式进行求和,它有1-255个参数。
鉴于本题的特殊性,公式也可以改为"=SUM(区域1)",函数会忽略区域中的文本。
[使用注意]:1、SUM函数有1-255个参数。
两数和差的平方

两数和差的平方公式可以应用于二次方程的求解以及不等式 的证明等问题中。例如,在求解二次方程时,可以利用公式 将方程转化为(a+b)^2=c的形式,从而简化计算过程。
公式的扩展及推广
公式的扩展
通过对公式的扩展,可以得到其他类似的公式。例如,对于两数和差的立方公式 ,可以类似地推导得到(a+b)^3=(a-b)^3+3(a-b)ab+3(a-b)ba=(a-b)^3+6(ab)ab。
圆内接矩形对角线乘积之和
总结词
圆内接矩形对角线乘积之和等于两对角线端点所连线 段的平方和的两倍。
详细描述
设圆内接矩形ABCD的对角线AC和BD的长度分别为a 和b,则根据勾股定理,我们有:AB^2 + BC^2 = AC^2,AD^2 + DC^2 = BD^2。将两式相加,得到 :2(AB^2 + BC^2 + AD^2 + DC^2) = a^2 + b^2
符号表示
公式中用到的符号包括加号(+)、减号(-)、平方 符号(²)和括号()。
3
数学模型
公式可以表示为(a+b)²=(a-b)²+4ab,其中a和 b是两个数。
公式推导
推导过程
根据完全平方公式的推导方法,可以将(a+b)²的展开式展开为a²+2ab+b², 同时将(a-b)²的展开式展开为a²-2ab+b²,再结合两者得到(a+b)²=(ab)²+4ab。
05
两数和差的平方的深入研究
公式的深入推导
公式推导的必要性
两数和差的平方公式是数学中的一个 重要公式,对于解决二次方程和不等 式等问题具有关键作用。通过对公式 的深入推导,可以更好地理解其背后 的数学原理,加深对数学知识的掌握 。
公式法——平方差

公式法——平方差公式法,平方差公式法,也称为代数方法或笔算方法,是一种通过使用数学公式和恒等式来解决问题的方法。
它是数学中常用的一种解题方法,适用于各种数学题目,包括代数、几何、微积分等。
其中,平方差是一种常见的公式法问题类型。
平方差是指一个数字的平方与另一个数字的平方之间的差。
解决平方差问题的一种常见方法是使用平方差公式。
平方差公式表示为:(a+b)(a-b)=a^2-b^2这个公式可以将一个数字的平方与另一个数字的平方之间的差表示为两个数字的和与差的乘积。
通过使用这个公式,我们可以简化平方差问题的解决过程。
下面我们将通过几个例子来介绍平方差的求解过程。
例1:求解81的平方与5的平方之差。
解:根据平方差公式,我们有:(81+5)(81-5)=81^2-5^2使用计算器或者手工计算,我们可以得到:(81+5)(81-5)=86×76=6536也就是说,81的平方与5的平方之差为6536例2:求解24的平方与9的平方之差。
解:同样地,根据平方差公式,我们有:(24+9)(24-9)=24^2-9^2计算得到:(24+9)(24-9)=33×15=495所以24的平方与9的平方之差为495除了使用平方差公式,我们还可以运用一些简化技巧来求解平方差问题。
例3:求解64的平方与16的平方之差。
解:在这个问题中,我们可以观察到64和16都是平方数,并且它们之间的关系很特殊。
所以我们可以不使用平方差公式,而是直接计算它们的差。
64^2-16^2=(64+16)(64-16)=80×48=3840通过直接计算,我们得到64的平方与16的平方之差为3840。
在解决平方差问题时,我们还应该注意一些常见的特殊情况。
例4:求解81的平方与-81的平方之差。
解:这个问题中涉及到正负数的平方。
根据平方差公式,我们有:(81+(-81))(81-(-81))=81^2-(-81)^2化简并计算得到:0×162=0所以81的平方与-81的平方之差为0。
两数和(差)的平方课件讲

在解决一些三维图形的体积问题时,如长方体、圆柱体等,利用两数和(差)的平方公式可以快速求出 其体积。特别是对于一些不规则的图形,通过合理地运用该公式,能够大大简化计算过程,提高解题 效率。
线性方程问题
总结词
线性方程问题中经常涉及到平方项的计算,利用两数和(差)的平方公式可以简化计算过 程。
公式证明
证明方法一
利用多项式乘法展开$(a+b)^2$,证明得到$a^2 + 2ab + b^2$。
证明方法二
利用二项式定理展开$(a+b)^2$,证明得到$a^2 + 2ab + b^2$。
02
CHAPTER
两数差的平方公式
公式推导
公式推导方法一
利用多项式展开和代数运算,将两数差的平方表示为单一多 项式。
详细描述
在解决线性方程问题时,如一元二次方程、二元一次方程等,经常会遇到需要计算平方 项的情况。利用两数和(差)的平方公式,可以快速准确地求出方程的解,特别是对于一 些较为复杂的方程,能够大大简化计算过程,提高解题效率。同时,该公式在解决一些
与平方相关的数学问题时也具有广泛的应用。
THANKS
谢谢
03
CHAPTER
两数和与差的混合平方公式
公式推导
01
02
03
公式推导方法一
利用平方差公式和完全平 方公式推导
公式推导方法二
通过代数变形和恒等变换 推导
公式推导方法三
利用几何意义和勾股定理 推导
公式应用
代数运算
在代数运算中,两数和与差的混合平 方公式常用于简化复杂的代数表达式。
几何应用
解决实际问题
该公式在实际问题中也有广泛应用, 如物理学中的位移、速度和加速度的 计算,以及统计学中的数据分析和处 理等。
golang计算数组标准偏差

《Golang中数组标准偏差的计算方法》在Golang中,数组标准偏差的计算方法是一个非常重要的话题。
标准偏差是用来衡量数据的离散程度,对于理解数据分布和质量非常重要。
在本文中,我将介绍如何在Golang中计算数组的标准偏差,并就此展开讨论。
1. 概念介绍让我们简单介绍一下什么是标准偏差。
标准偏差是一组数据的离散程度的度量,它表示数据点相对于其平均值的分散程度。
在统计学上,标准偏差越大,数据的离散程度就越高;标准偏差越小,数据的离散程度就越小。
2. Golang中的数组标准偏差计算方法在Golang中,计算数组的标准偏差需要经过一系列的步骤。
我们需要计算数组的平均值,然后计算每个数据点与平均值的差的平方,并将这些平方差的和除以数据点的个数,最后取平方根即可得到标准偏差。
下面是一个简单的Golang代码示例,用来计算数组的标准偏差:```gopackage mainimport ("fmt""math")func calculateStandardDeviation(data []float64) float64 { // Step 1: 计算平均值var sum float64for _, value := range data {sum += value}mean := sum / float64(len(data))// Step 2: 计算平方差的和var sumOfSquaredDiff float64for _, value := range data {diff := value - meansumOfSquaredDiff += diff * diff}// Step 3: 计算标准偏差standardDeviation := math.Sqrt(sumOfSquaredDiff /float64(len(data)))return standardDeviation}func main() {data := []float64{4, 9, 11, 12, 17, 5, 8, 12, 14}result := calculateStandardDeviation(data)fmt.Println("数组的标准偏差为:", result)}```3. 理解标准偏差的意义计算数组的标准偏差可以帮助我们更好地理解数据的离散程度。
sql server列和列之间的平方差

sql server列和列之间的平方差SQL Server是一款非常强大的关系型数据库管理系统,它提供了众多的数据分析功能,包括列之间的平方差计算。
今天,我们将围绕SQL Server列和列之间的平方差展开讨论。
1. 什么是列和列之间的平方差?列之间的平方差是一种常见的数据分析指标,它用于测量不同列之间的数据差异。
具体来说,它计算每个列的数值与其他列的数值之间的平方差,并将这些平方差求和。
因此,平方差越大,表示列之间的差异越大。
2. 如何计算列和列之间的平方差?在SQL Server中,你可以使用AVG、SUM、COUNT和POWER等函数来计算列之间的平方差。
首先,你需要按照以下步骤准备你的数据:a. 创建一个包含所有需要计算的列的数据表。
b. 将每个列的数值提取出来,并计算它们的平均数。
c. 使用AVG函数计算每个列的平方差。
具体来说,你可以使用以下公式:SELECT AVG(POWER(column1 - avg_column, 2)) AS variance1, AVG(POWER(column2 - avg_column, 2)) AS variance2,AVG(POWER(column3 - avg_column, 2)) AS variance3 FROM yourTable;其中,"column1"、"column2"和"column3"分别代表你需要计算平方差的列的名称;"avg_column"是每个列的平均值。
d. 使用SUM函数将每个列的平方差相加。
具体来说,你可以使用以下公式:SELECT SUM(variance1 + variance2 + variance3) AStotal_variance FROM yourTable;最终,"total_variance"将是所有列之间的平方差之和。
斐波那契数列中的平方和差公式

斐波那契数列是一种非常有趣的数列,它经常被用来表示某一类问题的解决方案。
斐
波那契数列中的“平方和(差)”公式是一个非常重要的公式,它在解决斐波那契数列问题时
非常有用。
公式的基本形式为:a^2 + b^2 = (a+b)^2 -2ab。
在这个公式中,a和b分别表示斐波
那契数列的前两项,而(a+b)^2 -2ab则表示斐波那契数列的下一项。
这个公式可以用来求
解斐波那契数列的前n项,因为它表明斐波那契数列的每一项都可以由前两项的平方和(差)所确定。
斐波那契数列的平方和(差)公式可以用来解决许多有关斐波那契数列的问题,它可以
让研究者更轻松地获得斐波那契数列的任意项值。
同时,它还可以应用到其他数学问题中,用来解决某些类型问题,比如求解三角形面积、求极限等。
总之,斐波那契数列中的“平方和(差)”公式是一个非常重要的公式,它可以用来解决
许多有关斐波那契数列的问题,也可以应用到其他数学问题中,从而帮助我们更轻松地获得正确的答案。
差的平方公式

差的平方公式差的平方公式也称为差平方和公式,是一个关于二次方程的数学公式。
它用于表示两个数相减后进行平方运算的结果。
差的平方公式可以简化数学计算,特别是涉及到对多项式进行因式分解和求解二次方程时。
差的平方公式可以表示为:(a-b)^2 = a^2 - 2ab + b^2其中,a和b为任意实数。
这个公式可以用来展开方程的左侧(a-b)的平方,并将其简化为方程右侧的形式。
为了更好地理解差的平方公式,我们可以通过一个具体的例子进行说明。
假设我们要计算 (3 - 2)^2 的值。
按照差的平方公式:(3 - 2)^2 = 3^2 - 2 × 3 × 2 + 2^2= 9 - 12 + 4= 1因此,(3 - 2)^2 的结果为 1。
除了可以用于计算差的平方,差的平方公式还可以用于因式分解。
当我们碰到需要对一个二次多项式进行因式分解时,差的平方公式可以帮助我们找到一个具有特定形式的因式。
例如,考虑多项式 x^2 - 4x + 4。
我们可以使用差的平方公式来因式分解它。
首先,我们可以将多项式写成完全平方的形式:(x - 2)^2。
然后,我们可以使用差的平方公式将其展开为:(x - 2)^2 = x^2 - 2 × x × 2 + 2^2= x^2 - 4x + 4因此,我们得到了多项式的因式分解结果:x^2 - 4x + 4 = (x - 2)^2。
差的平方公式还可以在求解二次方程的过程中起到重要的作用。
对于一个一般形式的二次方程 ax^2 + bx + c = 0,我们可以使用差的平方公式将其变形为一个完全平方的形式,并通过因式分解来求解它。
例如,考虑方程 x^2 + 4x - 12 = 0。
我们可以将方程变形为:(x + 2)^2 - 16 - 12 = 0然后,我们可以使用差的平方公式将方程进一步变形为:(x + 2)^2 - 28 = 0最后,我们可以通过解方程 (x + 2)^2 - 28 = 0,得到方程的解。
平方相加求和公式

平方相加求和公式
平方相加求和公式是数学中常用的一个公式,用于计算一系列数的平方并求和的结果。
它的表达形式可以简洁明了地表示为:求和符号下方是一个式子,式子中的每个数都要先平方再相加。
这个公式在各个领域都有广泛的应用,尤其在统计学、物理学、工程学等科学领域中经常被用到。
它可以帮助我们对一组数据的平方值进行加总,从而得到一个总体的平方和。
在统计学中,平方相加求和公式可以用来计算方差。
方差是一个衡量数据集中离散程度的指标,而平方相加求和公式正是计算方差的基础。
通过将数据集中的每个数先平方再相加,然后再除以数据的个数,我们就可以得到方差的值。
在物理学中,平方相加求和公式可以用来计算能量。
能量是一个物体的基本属性,它可以用数值来表示。
通过将物体的每个部分的能量先平方再相加,我们就可以得到整个物体的能量。
在工程学中,平方相加求和公式可以用来计算误差。
误差是实际值与理论值之间的差异,它可以用来评估一个系统或者一个模型的精度。
通过将每个测量值与理论值之间的差异先平方再相加,我们就可以得到误差的总和。
总的来说,平方相加求和公式是一个简单而有效的工具,它可以帮助我们对一组数据的平方进行加总,并进一步得到一些重要的统计
指标。
它的应用范围广泛,无论是在学术研究、工程实践还是日常生活中,都能发挥重要的作用。
通过运用这个公式,我们可以更好地理解数据的特征,评估系统的性能,并做出更准确的判断和决策。
两数差的平方公式

两数差的平方公式两数差的平方公式是数学中的一种常见公式,它用来计算两个数之间的差的平方。
这个公式可以解决许多实际问题,让我们来看一些具体的应用。
我们来考虑一个简单的示例。
假设有两个数a和b,我们想要计算它们的差的平方。
根据两数差的平方公式,我们可以得到如下结果:(a - b)² = a² - 2ab + b²这个公式告诉我们,两个数的差的平方等于它们各自的平方减去两倍的乘积再加上另一个数的平方。
通过这个公式,我们可以快速计算出任意两个数之间的差的平方。
接下来,让我们来看一个实际的应用场景。
假设某个城市的温度在一天中的不同时间点有所变化,我们想要计算出这些温度变化的平方差。
我们可以将每个时间点的温度用变量表示,然后利用两数差的平方公式进行计算。
例如,假设某城市的温度在早上8点、中午12点和下午4点分别为20摄氏度、25摄氏度和23摄氏度。
我们可以将这些温度分别用变量a、b和c表示,然后根据两数差的平方公式进行计算。
根据公式,我们可以得到如下结果:(a - b)² = a² - 2ab + b²(20 - 25)² = 20² - 2 * 20 * 25 + 25² = 125(b - c)² = b² - 2bc + c²(25 - 23)² = 25² - 2 * 25 * 23 + 23² = 4(c - a)² = c² - 2ac + a²(23 - 20)² = 23² - 2 * 23 * 20 + 20² = 153通过这些计算,我们可以得到早上8点和中午12点温度的平方差为125,中午12点和下午4点温度的平方差为4,下午4点和早上8点温度的平方差为153。
这些结果可以帮助我们进一步分析温度变化的情况。
