计算机图形学_ 二维图形变换_53 二维图形变换原理及齐次坐标_
计算机图形学实验:二维图形变换

实验三 二维图形变换一、实验任务1. 通过二维几何变换的数学模型,编写缩放、旋转、对称变换; 2. 实现图形变换的交互式操作:缩放、旋转、对称变换等;二、实验内容1. 放大缩小变换放大缩小变换公式为:x’=x..S x , y’=y.S y ; 其中S x , S y 分别为x,y 方向的放缩比例系数。
变换矩阵表达式为: [x’ y’(1)S x =S y = 1.5;等比例放大 (2)S x =S y = 0.5;等比例缩小 2. 对称变换包括以x 轴对称、y 轴对称和原点O 对称三种。
由于屏幕坐标只有第一象限,我们可以将原点平移到(500,240)处。
在第一象限画出一个三角形,然后分别求出三个对称图形。
3. 旋转变换将图形上的点(x ,y )旋转θ角度,得到新的坐标(x’,y’)为:x’=xcos θ-ysin θ, y’=xsin θ+ycos θ;[x’ y’ 4.三、设计思路1. 通过二维几何变换的数学模型,编写缩放、旋转、对称变换;2. 以(500,240)为原点建立图形变换的参考坐标系; 3. 通过键盘按键控制图形的缩放、旋转、对称变换;4. 变换图形设定为以Pt[0](540,220)、Pt[1](670,130)、Pt[2](560,120)为顶点的三角形。
步骤:1.建立Trans工程文件;2.利用Resource View设计菜单,如图所示;3.在CTransView视图类中添加消息映射函数;4.添加自定义的成员变量:CPoint Pt[3]; //三角形定点数组float dAngle; //每一次旋转的角度在视图类CPP文件的构造函数中初始化成员变量Pt[0].x = 540; Pt[0].y = 220;Pt[1].x = 670; Pt[1].y = 130;Pt[2].x = 560; Pt[2].y = 120;dAngle = 0;5.在视图类的OnDraw()函数中加入下列代码,实现视图绘图。
计算机图形学实验3------二维几何变换

实验三图形的二维几何变换一、实验目的了解齐次坐标规范化及矩阵的乘法运算熟悉掌握平移,比例,旋转,错切变换的齐次坐标矩阵掌握基于 Win32、Visual C++环境MFC绘制图形配置过程制过程二、实验原理及思想1.基本几何变换2.齐次坐标给定2D 坐标 (x, y), 引入第3维:[x, y, 1]通常, 一个 2D 坐标点的齐次坐标有如下形式:[x, y, W]两个齐次坐标点 [x, y, W] and [x’, y’, W’] 相同 if x = kx’eg: [2, 3, 6] = [4, 6, 12]y = ky’for some k ≠ 0 where k=2W = kW’因此,任意 [x, y, W] 可归一化:[x/W, y/W, 1]3.三、实验关键代码void C2DChangeView::ClearMatrix(double A[3][3])//清除变换矩阵{for(int i=0;i<3;i++){for(int j=0;j<3;j++)A[i][j]=0;}}void C2DChangeView::Draw(double D[][3],int n)//绘制图形{RedrawWindow();CClientDC dc(this);CPen pen,*pOldpen;pen.CreatePen(PS_SOLID,2,RGB(0,0,0));pOldpen=dc.SelectObject(&pen);for(int i=0;i<n;i++){if(i==0)dc.MoveTo(ROUND(MaxX/2+D[i][0]),ROUND(MaxY/2-D[i][1]));elsedc.LineTo(ROUND(MaxX/2+D[i][0]),ROUND(MaxY/2-D[i][1]));}dc.LineTo(ROUND(MaxX/2+D[0][0]),ROUND(MaxY/2-D[0][1]));dc.SelectObject(pOldpen);pen.DeleteObject();}void C2DChangeView::Calculate(double P0[][3],double T[][3])//两个矩阵相乘{double Ptemp[4][3];KeepMatrix(P,Ptemp);for(int i=0;i<4;i++)for(int j=0;j<3;j++)P[i][j]=Ptemp[i][0]*T[0][j]+Ptemp[i][1]*T[1][j]+Ptemp[i][2]*T[ 2][j];}void C2DChangeView::OnMENUleft()//向左平移{// TODO: Add your command handler code hereTmove(-10,0);}void C2DChangeView::OnMENUright()//向右平移{// TODO: Add your command handler code hereTmove(10,0);}void C2DChangeView::OnMENUup() //向上平移{// TODO: Add your command handler code hereTmove(0,10);}void C2DChangeView::OnMENUdown()//向下平移{// TODO: Add your command handler code hereTmove(0,-10);}void C2DChangeView::OnMENUClockwise()//顺时针旋转{// TODO: Add your command handler code hereTrotate(30);}void C2DChangeView::OnMENUAnticlockwise()//逆时针旋转{// TODO: Add your command handler code hereTrotate(-30);}void C2DChangeView::OnMENUIncrease()//放大比例{// TODO: Add your command handler code hereTscale(2,2);}void C2DChangeView::OnMENUDecrease()//缩小比例{// TODO: Add your command handler code hereTscale(0.5,0.5);}void C2DChangeView::OnMENUXdirectionplus()//X正向错切{// TODO: Add your command handler code hereTreform(0,1);}void C2DChangeView::OnMENUXdirectionneg()//X负向错切{// TODO: Add your command handler code hereTreform(0,-1);}void C2DChangeView::OnMENUITYdirectionplus()//Y正向错切{// TODO: Add your command handler code hereTreform(1,0);}void C2DChangeView::OnMENUYdirectionneg()//Y负向错切{// TODO: Add your command handler code hereTreform(-1,0);}void C2DChangeView::OnMENUReset() //复位{// TODO: Add your command handler code hereif(p3==4){KeepMatrix(OSquare,P);}if(p3==3){KeepMatrix(OTriangle,P);}if(p3==2){KeepMatrix(OLine,P);}Draw(P,p3);}void C2DChangeView::Tmove(double Tx,double Ty)//平移变换矩阵{ClearMatrix(TM);RedrawWindow();TM[0][0]=1;TM[1][1]=1;TM[2][0]=Tx;TM[2][1]=Ty;TM[2][2]=1;Calculate(P,TM);AfxGetMainWnd()->SetWindowText("二维几何变换-平移变换");Draw(P,p3);}void C2DChangeView::Tscale(double Sx,double Sy)//比例变换矩阵{ClearMatrix(TS);RedrawWindow();TS[0][0]=Sx;TS[1][1]=Sy;TS[2][2]=1;Calculate(P,TS);AfxGetMainWnd()->SetWindowText("二维几何变换-比例变换");Draw(P,p3);}void C2DChangeView::Trotate(double thta)//旋转变换矩阵{ClearMatrix(TR);RedrawWindow();TR[0][0]=cos(thta*PI/180);TR[0][1]=sin(thta*PI/180);TR[1][0]=-sin(thta*PI/180);TR[1][1]=cos(thta*PI/180);TR[2][2]=1;Calculate(P,TR);AfxGetMainWnd()->SetWindowText("二维几何变换-旋转变换");Draw(P,p3);}void C2DChangeView::Treflect(double Fx,double Fy)//反射变换矩阵{ClearMatrix(TF);RedrawWindow();TF[0][0]=Fx;TF[1][1]=Fy;TF[2][2]=1;Calculate(P,TF);AfxGetMainWnd()->SetWindowText("二维几何变换-反射变换");Draw(P,p3);}void C2DChangeView::Treform(double b,double c)//错切变换矩阵{ClearMatrix(TC);RedrawWindow();TC[0][0]=1;TC[0][1]=b;TC[1][0]=c;TC[1][1]=1;TC[2][2]=1;Calculate(P,TC);AfxGetMainWnd()->SetWindowText("二维几何变换-错切变换");Draw(P,p3);}void C2DChangeView::KeepMatrix(double Orig[][3],double Dest[][3]){int i,j;for(i=0;i<4;i++)for(j=0;j<3;j++)Dest[i][j]=Orig[i][j];}四、实验结果1. 初始图2 --平移(左移)2 --平移(下移)3 、缩放-——放大3 、缩放-——缩小4 、旋转5 、错切——X负向错切5 、错切——Y正向错切五、心得体会通过这次MFC对计算机图形的编程,进一步掌握了MFC的菜单的实现及其响应函数的实现。
计算机图形学PPT神奇的齐次坐标与二维图形变换

例如:关于X轴对称
P(x,y)
P’(x’,y’)
x’=x
x
y’=-y
2 几何变换
以二维为例:
错切:也称为剪切、错位变换,用于产生弹性物体的变形处理。
y
y
y
(a)原图
x
x
x
(b)沿x方向错切
(c)沿y方向错切
2 几何变换
以二维为例: 错切:也称为剪切、错位变换,用于产生弹性物体的变形处理。
2 几何变换
以二维为例:
平移:指将p点沿直线路径从一个坐标位置移到另一个坐标位置的重定位 过程,是 一种不产生变形而移动物体的刚体变换。
y
P’
PT
Ty
Tx
0
x
P(x,y)
P’(x’,y’)
x’=x+Tx y’=y+Ty
Tx :x方向的平移矢量 Ty :y方向的平移矢量
2 几何变换
以二维为例:
比例:对p点相对于坐标原点沿x方向放缩Sx倍,沿y方向放缩Sy倍。其中Sx 和Sy称 为比例系数。
旋转
x’=xcosθ -ysinθ y’=xsinθ +ycosθ
cos sin 0
sin cos 0
0
0 1
3 齐次坐标的引入
T1
T3
a b p
x' y' 1 x y 1T2D x y 1c d q
l m s
T2
T4
其中:
T1是对图形进行比例、旋转、对称、 错切等变换;
T2是对图形进行平移变换; T3是对图形作投影变换; T4则可以对图形作整体比例变换。
旋转
x’=xcosθ -ysinθ y’=xsinθ +ycosθ
图形变换与齐次坐标

cos sin 0
x'
y'
1 [x
y
1] -sin
cos
0
0 0 1
6. 平移变换
Y
x' x m
y'
y
n
[x' y' 1] [x m y n 1]
1 0 0
x y 10 1
0
m n 1
m P’(x’y’) n
P(x,y) X
变换过程如下:
(x’, y’) θ (x,y)
1 0 0 0
0
1
0
0
0 0 1 0
0 0 0 s
[x y z 1]T = [x y z s]=[x/s y/s z/s 1] 当s>1, 沿三个轴向等比例缩小 当0<s<1, 沿三个轴向等比例放大 (轴向比例变换与全比例变换的关系)
对称变换
在二维变换下,对称变换是以线和点为基准,
在三维变换下,对称变换则是以面、线、点为 基准的。
由于矢量 (0 0 1)绕Y轴旋转θ1 ,再绕Z轴旋转θ2 即 可与ON轴重合。即:
cos1 0 - sin1 0 cos2 sin2 0 0
l m n 1 [0 0 1 1]
0
1
0
0
-
sin 2
cos 2
0
0
sin1 0 cos1 0 0
0 1 0
0
0
0
1
0
0 0 1
[l m n 1] = [sinθ1 cosθ2 sinθ1sinθ2 cosθ1 1]
1 0 0 0
= x
y
z 10
0
1 0
第五章二维图形变换

cosθ 0
0 1
则复合旋转矩阵可表示为:
cos θ 1 T (θ 1 ) ⋅ T (θ 2 ) = − sin θ 1 0 0 cos θ 2 0 ⋅ − sin θ 2 1 0 sin θ 2 cos θ 2 0
0 cos(θ1 + θ 2 ) sin (θ1 + θ 2 ) 0 0 = − sin (θ1 + θ 2 ) cos(θ1 + θ 2 ) 0 1 0 0 1
对于初始点P(x,y)的比例变换是指相对 于坐标原点,其坐标缩放Sx倍,其y坐标缩 放Sy倍,得到变换后的点P′(x′,y′),有:
x′ = x ⋅ S x y′ = y ⋅ S y 变换方程也可以写为矩阵形式:
S x [x′ y′] = [x y] 0 这时的变换矩阵方程T为:
0 Sy
5.2 几何变换的矩阵表示
5.2.1 齐次坐标与平移变换 5.2.2 二维图形齐次坐标变换矩阵
5.2.1 齐次坐标与平移变换
从上一节的内容可以看出,对于除平移变 换之外的几种基本变换都可以通过变换矩 阵T实现:T = a b c d x′ = x + tx 而这种形式却无法实现平移变换:y′ = ty 为了解决这个问题,我们将2×2的变换矩 阵T扩充为3×3的矩阵形式,来把几种二维 几何变换表达为单一的矩阵形式:
[x ′
y ′ 1] = [x
T
y 1] ⋅ T (t x1 , t y1 ) ⋅ T (t x 2 , t y 2 )
, t
y
其中平移变换矩阵为:
(t
x
)=
1 0 t x
计算机图形学课件二维图形变换分解

单位矢量 矢量的夹角
cos
矢量的叉积
U V U V
i U V ux vx
j uy vy
k uz vz
变换的数学基础
矩阵
m n
阶矩阵
n阶方阵
零矩阵 行向量与列向量
单位矩阵
矩阵的加法 矩阵的数乘
有n+1个分量的向量 哑元或标量因子
( x1 , x2 ,..., xn , )
( x1 / , x2 / ,..., xn / )
齐次坐标表示不是唯一的
1 规格化的齐次坐标
5.基本几何变换的齐次坐标表示
平移变换
x
y 1 x
1 y 1 0 Tx
矩阵的乘法
矩阵的转置 矩阵的逆
变换的数学基础
矩阵的含义 矩阵:由m×n个数按一定位置排列的一个 整体,简称m×n矩阵。
A=
a11 a12 ... a1n a 21 a 22 ... a 2 n ... ... ... a m 1 a m 2 ... a mn
(1)沿 x 轴方向关于 y 轴错切
将图形上关于y轴的平行线沿x方向推成θ角的 倾斜线,而保持y坐标不变。
y
几何关系
x' x x y' y 令 a ctg 有 x yctg ay
x ' x ay y' y
△x
x
矩阵形式
x
y 1 x
a b T1 c d
的非对角线元素大多为零,如果c和b不为零,则意味着 对图形进行错切变换。 令b=0可以得到沿x方向的错切变换,c>0是沿x正向的错 切变换,c<0是沿x负向的错切变换. 令c=0可以得到沿 y方向的错切变换,b>0是沿y正向的错切变换,b<0是 沿y负向的错切变换.
计算机图形学二维变换.

P
X’ X
(l,m)
方法A 坐标系不动, 图形变动后坐标值变化
方法B 坐标系变化后 图形在新坐标系中的新值
本课程:变换方法的选择
选择A:坐标系不动,图形变动后坐标值变化
P P’
4.3.1 图形变换的特点 图形变换就是改变图形的几何关系,即改变图形顶点的坐 标,但图形的拓扑关系不变。 最基本的图形变换可以分别用矩阵形式表示为: 平移变换 : P′=P+Tm
P' = P R R(q ) = -sinq cosq 0
0 0 cosq -sinq 0 0 cosq sinq 0 1 0 0 1
(旋转变换矩阵)
R-1 (q ) = sinq cosq
三、对称变换
– 关于x轴的对称变换
1 0 0 SYx 0 1 0 0 0 1
• 包括:
• •
1. 二维、三维图形的平移、旋转、变比、对称等变换; 2. 级联(复合)变换
——相对于某点的比例变换、旋转变换 ——相对于某直线的对称变换
图形变换概述
包括: --几何变换:改变几何形状和位置 --非几何变换:改变图形的颜色、线型等属性
基本几何变换(二维、三维)
几何变换
投影变换(三维)
2. 视区
– 在设备坐标系(屏幕或绘图纸)上指定的矩形区域 , 用来指定窗口内的图形在屏幕上显示的大小及位置。
3. 窗口到视区的变换
“取景器”=窗 口
视区1 视区2 (viewport)
4.1 坐标系、窗口与视区(续)
4.1.4规格化变换 从窗口到视区的变换,称为规格化变换。 (Normalization Transformation) y wyT wyB o wxL wxR x y W(窗口区) (wx,wy) vyB o vx L vxR vyT (vx,vy) x V(视图区)
计算机图形学图形变换

(X0,y0)
绕任意点的旋转
1 0 0
• 用矩阵表示各个过程
T1
0
1 0
x 1y 11 xy1 T 1
x0 y0 1
x 2y 21 x 1y 11 T 2
cos T2 sin
sin cos
0 0
x ' y ' 1 x 2 y 21 T 3
0
0 1
1 0 0
x ' y ' 1 x 2 y 21 T 3
cos
sin
0
TT1T2T3 sin
cos
0
x0(1co)sx0siny0co sy0 1
复合矩阵可以减少计算量
• 不进行矩阵合并 往往在屏幕上划定一个平行于设备坐标轴的矩形区域作为图形显示区。
点P(x,y)在X’轴上的投影可用点乘得到, 常用的方法是在图形坐标系中取一个与x轴、y轴平行的矩形窗口,只显示窗口内的图形内容。
计算机图形学图形 变换
二维图形平移
• 二维图形平移是将图形上任 意一点P(x,y)在x轴方向y轴方 向分别平移距离tx,ty,则变 换后的新坐标
x’=x+tx
ty
y’=y+ty
• 用矩阵表示
1 [x',y'][x,y]0
1 0tx,ty
P’ p
tx
二维图形旋转
• 二维图形旋转是将图形绕圆
点旋转。图形上任意一点
2. 3次变换需要3×9=27次乘法。 这不仅可以节省运算量,还可以明确一个矩阵代表一种变换的概念。
Y’轴的单位方向矢量为(a21,a22) 这不仅可以节省运算量,还可以明确一个矩阵代表一种变换的概念。 复合矩阵可以减少计算量 我们希望将一种变换用一个矩阵来表示,这样就可以用矩阵合并的方法将一系列的简单变换用一个复杂变换来表示。 有时采用活动坐标系模式,是为了更好地理解变换前后两个对应物体之间的坐标关系。 表示变换前的模型上任意一点 仿射变换的特点是变换前的平行线在变换后依然平行。 变换图形、变换关系式和变换矩阵 合并矩阵与一个点向量相乘得到一个点向量,需要9次乘法。 固定坐标系模式:坐标系不变、图形变动。
二维图形变换

由于 所以
T (t x1 , t y1 ) T (t x 2 , t y 2 ) = T (t x1 + t x 2 , t y1 + t y 2 ) P ′ = P T (t x1 + t x 2 , t y1 + t y 2 )
2. 旋转变换 经过两次连续旋转被变换到的位置为: 点P经过两次连续旋转被变换到的位置为 经过两次连续旋转被变换到的位置为
x’=x+tx = +
y’=y+ty = +
(x’, y’)=(x, y)+(tx ,ty) = + 矩阵表示: = + 矩阵表示:P’=P+T
2. 绕原点的旋转变换 在旋转中, 在旋转中,物体绕原点 旋转了 θ 角。 约定:逆时针旋转时角 约定: 度为正; 度为正;顺时针旋转时 角度为负。 角度为负。
1 0 x f 0 1 yf 0 s x 0 0 1 0 0 sy 0 0 1 0 0 1 x f 0 1 yf 0 sx 0 = 0 1 x f (1 s x ) 0 0 sy 0 y f (1 s y ) 1
2.2 坐标变换
本节考虑两个直角坐标系之间的变换。假设在平面上有 本节考虑两个直角坐标系之间的变换。 两个坐标系统oxy和o’x’y’,这时平面上每点 存在两种 两个坐标系统 和 ,这时平面上每点P存在两种 坐标描述(x,y)和(x’,y’)。我们可以认为第二个坐标系统 坐标描述 和 。 o’x’y’是由第一个坐标系统 经过坐标变换得到的。为 是由第一个坐标系统oxy经过坐标变换得到的 经过坐标变换得到的。 是由第一个坐标系统 了将物体的描述从xy坐标变换到 坐标变换到x’y’坐标,我们需要建 坐标, 了将物体的描述从 坐标变换到 坐标 立一个变换,它能够使x’y’轴与 轴重叠一起。具体地, 轴与xy轴重叠一起 立一个变换,它能够使 轴与 轴重叠一起。具体地, 我们通过描述同一点在不同坐标系之下的关系来描述这 种坐标变换。 种坐标变换。 y P (x,y) (x’,y’) y0 o x0 x
二维图形的几何变换

二维图形的几何变换正如我们在附录中提到的那样,用齐次坐标表示点的变换将非常方便,因此在本节中所有的几何变换都将采用齐次坐标进行运算。
二维齐次坐标变换的矩阵的形式是:这个矩阵每一个元素都是有特殊含义的。
形进行平移变换;[g h]是对图形作投影变换;[i]则是对图形整体进行缩放变换。
1)平移变换2)缩放变换3)旋转变换4)对称变换对称变换其实只是a、b、d、e取0、1等特殊值产生的一些特殊效果。
例如:当b=d=0,a=-1,e=1时有x´=-x,y´=y,产生与y轴对称的图形。
当b=d=0,a=-1,e=-1时有x´=x,y´=-y,产生与x轴对称的图形。
当b=d=0,a=e=-1时有x´=-x,y´=-y,产生与原点对称的图形。
当b=d=1,a=e=0时有x´=y,y´=x,产生与直线y=x对称的图形。
当b=d=-1,a=e=0时有x´=-y,y´=-x,产生与直线y=-x对称的图形。
5)错切变换当d=0时,x´=x+by,y´=y,此时,图形的y坐标不变,x坐标随初值(x,y)及变换系数b作线性变化。
当b=0时,x´=x,y´=dx+y,此时,图形的x坐标不变,y坐标随初值(x,y)及变换系数d作线性变化。
6)复合变换如果图形要做一次以上的几何变换,那么可以将各个变换矩阵综合起来进行一步到位的变换。
复合变换有如下的性质:复合平移对同一图形做两次平移相当于将两次的平移两加起来:复合缩放两次连续的缩放相当于将缩放操作相乘:复合旋转两次连续的旋转相当于将两次的旋转角度相加:缩放、旋转变换都与参考点有关,上面进行的各种变换都是以原点为参考点的。
如果相对某个一般的参考点(xf,yf)作缩放、旋转变换,相当于将该点移到坐标原点处,然后进行缩放、旋转变换,最后将(xf,yf)点移回原来的位置。
计算机图形学 第4章 二维图形生成和变换技术

设置初始值
x =x 1; y =y 1;
for(i = l; i<=length; i + + ) { Putpixel(round(x), round(y), l); x = x + increx y = y + increy 求下一 } 点坐标 }
终点控制
将x和y取 整后画点
23
三、 Bresenham法
2)递推公式 由公式可以看出,由于每次要计算两次乘法和一次减法, 所以计算工作量大, 为了简化计算,可设法用前一点的偏 差来推算后一点的走步方向以及走步后的偏差,这种方法 称为递推法。递推公式很容易用计算机实现。
13
递推公式可根据下图用偏差函数判断笔进方向的图例得出 设笔当前位置为 M1(X1,Y1),此时 F1=Y1XA- YAX1<0,应走+Y一步到M2 即X2=X1,Y2=Y1+1,+1表示走一步 M2处的偏差为:F2=Y2XA-YAX2=F1+XA( 用X2=X1,Y2=Y1+1代入得到) 若F2≥0,应走+X一步到M3, 则X3=X2+1,Y3=Y2, M3处的偏差为: F3=Y3XA-YAX3=Y2XA-YAX2-YA=F2-YA
Y
Y
X
X
Z
4
图 4.2 点在二维、三维坐标系统中的表示
二、直线
一条直线是指所有在它上面的点的集合 , 在图形学 中研究的对象是直线段。
已知线段的起点坐标(Xs,Ys)。终点坐标(Xe,Ye )这两点就确定了这条线段,并用线段xe x xs y ye y ys
3)任意象限偏差计算 对于第二、三、四象限的直线,也可类似推出。当直 线段处于第二、三、四象限时,偏差值的计算及走步 方向下表 直线段位 走步方向 偏差值 走步方向 偏差值FK< 置 FK≥0 0 第一象限 +X +Y FK+1= FK+1= 第二象限 -X +Y FK-YA FK+XA
计算机图形学二维图形变换

变换矩阵为:
sx 0 (1 sx ) xr
T复合
0
sy
(1
s
y
)
xy
0 0
1
绕任意点 (x0 , y0 ) 旋转 角
变换步骤:
将旋转中心平移到坐标原点; 绕坐标原点旋转 ; 将旋转中心移回到 (x0 , y0 ) 。
两矩阵相乘
void matrix3x3PreMultiply(Matrix3x3 a,Matrix3x3 b) {
int i,j,k; Matrix3x3 tmp;
for(i=0;i<3;i++) for(j=0;j<3;j++) { tmp[i][j]=0; for(k=0;k<3;k++) tmp[i][j]+=a[i][k]*b[k][j]; }
for(i=0;i<3;i++) for(j=0;j<3;j++) a[i][j]=tmp[i][j];
}
顶点序列变换
void transformPoints() {
int i,j,k;
for(i=0;i<N;i++) for(j=0;j<3;j++) { pt[i][j]=0; for(k=0;k<3;k++) pt[i][j]+=point[i][k]*theMatrix[k][j]; }
0 0 1
关于y轴的对称变换
1 0 0
SYy
计算机图形学实验五:图形变换
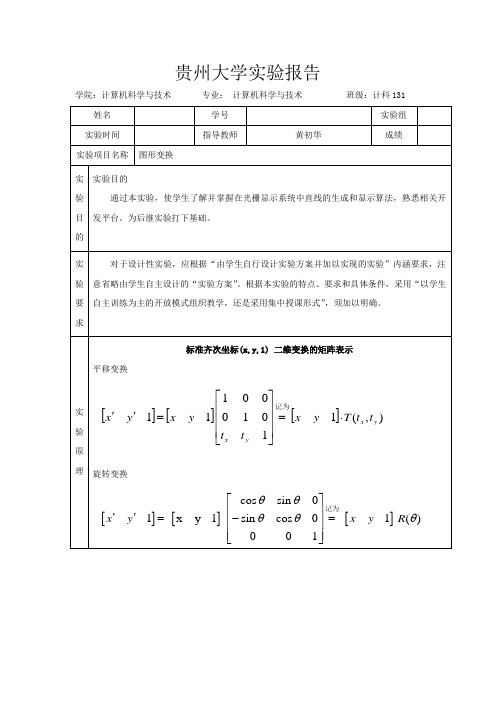
贵州大学实验报告学院:计算机科学与技术专业:计算机科学与技术班级:计科131实验内容#include"stdafx.h"#include<glut.h>#include<stdlib.h>#include<math.h>GLsizei winWidth = 600, winHeight = 600;GLfloat xwcMin = 0.0, xwcMax = 225.0;GLfloat ywcMin = 0.0, ywcMax = 225.0;class wcPt2D{public:GLfloat x, y;};typedef GLfloat Matrix3x3[3][3];Matrix3x3 matComposite;const GLdouble pi = 3.14159;void init(void){glClearColor(1.0, 1.0, 1.0, 0.0);}void matrix3x3SetIdentity(Matrix3x3matIdent3x3){GLint row, col;for (row = 0; row<3; row++)for (col = 0; col<3; col++)matIdent3x3[row][col] = (row == col);//生成{{1,0,0}{0,1,0}{0,0,1}}}void matrix3x3PreMultiply(Matrix3x3m1, Matrix3x3m2){GLint row, col;Matrix3x3 matTemp;for (row = 0; row<3; row++)for (col = 0; col<3; col++)matTemp[row][col] = m1[row][0] * m2[0][col] + m1[row][1] * m2[1][col] + m1[row][2] * m2[2][col];for (row = 0; row<3; row++)for (col = 0; col<3; col++)m2[row][col] = matTemp[row][col];}void translate2D(GLfloat tx, GLfloat ty)//平移{Matrix3x3 matTransl;matrix3x3SetIdentity(matTransl);matTransl[0][2] = tx;matTransl[1][2] = ty;matrix3x3PreMultiply(matTransl, matComposite);}void rotate2D(wcPt2D pivotPt, GLfloat theta)//旋转{Matrix3x3 matRot;matrix3x3SetIdentity(matRot);matRot[0][0] = cos(theta);matRot[0][1] = -sin(theta);matRot[0][2] = pivotPt.x*(1 - cos(theta)) + pivotPt.y*sin(theta);matRot[1][0] = sin(theta);matRot[1][1] = cos(theta);matRot[31][2] = pivotPt.x*(1 - cos(theta)) - pivotPt.y*sin(theta);matrix3x3PreMultiply(matRot, matComposite);}void scale2D(GLfloat sx, GLfloat sy, wcPt2D fixedPt)//缩放{Matrix3x3 matScale;matrix3x3SetIdentity(matScale);matScale[0][0] = sx;matScale[0][2] = (1 - sx)*fixedPt.x;matScale[1][1] = sy;matScale[1][2] = (1 - sy)*fixedPt.y;matrix3x3PreMultiply(matScale, matComposite);}void transformVerts2D(GLint nVerts, wcPt2D * verts)//组合变化后的矩阵{GLint k;GLfloat temp;for (k = 0; k<nVerts; k++){temp = matComposite[0][0] * verts[k].x + matComposite[0][1] * verts[k].y + matComposite[0][2];verts[k].y = matComposite[1][0] * verts[k].x + matComposite[1][1] *verts[k].y + matComposite[1][2];verts[k].x = temp;}}void triangle(wcPt2D*verts){GLint k;glBegin(GL_TRIANGLES);for (k = 0; k<3; k++)glVertex2f(verts[k].x, verts[k].y);glEnd();}void displayFcn(void){GLint nVerts = 3;wcPt2D verts[3] = { { 50.0, 25.0 }, { 150.0, 25.0 }, { 100.0, 100.0 } };wcPt2D centroidPt;GLint k, xSum = 0, ySum = 0;for (k = 0; k<nVerts; k++){xSum += verts[k].x;ySum += verts[k].y;}centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);wcPt2D pivPt, fixedPt;pivPt = centroidPt;fixedPt = centroidPt;GLfloat tx = 0.0, ty = 100.0;GLfloat sx = 0.5, sy = 0.5;GLdouble theta = pi / 2.0;glClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0, 0.0, 1.0);triangle(verts);//三角形matrix3x3SetIdentity(matComposite);scale2D(sx, sy, fixedPt);//缩小transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);triangle(verts);matrix3x3SetIdentity(matComposite);rotate2D(pivPt, theta);//旋转90transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);triangle(verts);matrix3x3SetIdentity(matComposite);translate2D(tx, ty);//平移transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);实验结果。
[课件]计算机图形学--二维几何变换PPT
![[课件]计算机图形学--二维几何变换PPT](https://img.taocdn.com/s3/m/cd1cee150b4c2e3f57276323.png)
连续旋转变换
应用于点P的两个连续旋转,得到的点P’的 坐标可计算为 P’ = R(θ2)[ R(θ1)P]= [R(θ2)R(θ1)]P 可以证明:两个连续旋转是可叠加的 R(θ2)*R(θ1)= R(θ1+θ2) 则P’的坐标可计算为 P’ = R(θ1+θ2)P
Other Transformations
大多数图形软件包中包含了平移、旋转和 缩放这些基本变换。有些软件包还提供一 些有用的其它变换,如反射(Reflection)和 错切(Shear)
2018/12/2
28
Reflection对称变换
对称变换后的图形是原图形关于某一轴线或原点 ty)P
2018/12/2 25
对于绕坐标原点的旋转变换
可简写为:P’ = R(θ)P
2018/12/2 26
对于相对于坐标原点在X和Y方向上的缩放变换
可简写为:P’ =S(sx , sy)P T、R和S分别时平移、旋转、缩放变换距阵
2018/12/2 27
2018/12/2
9
标准的旋转是当基准点在坐标 原点时,即物体绕坐标原点的 旋转。点P绕原点逆时针旋转θ, 得到P’点。则P和P’的坐标之 间的关系,如图,可如下表示 x’=rcos(θ+Ψ) =rcosθcosΨ - rsinθsinΨ y’=rsin(θ+Ψ) =rsinθcosΨ + rcosθsinΨ
P2 M 1 P1 M 2
21
齐次坐标:
是Maxwell.E.A在1946年从几何的角度提出来
的,它的基本思想是把一个n维空间的几何问 题转换到n+1维空间中去, 从形式上来说,就是用一个n+1维的向量表示 一个n维向量的方法,即n+1维向量表示n维空 间中的点。
计算机二维图形变换

下图是矩阵旋转30度的情况,其坐标变换如下:
2 1 1.232 2 1 0.866 0.5 2.232 0.5 0.886 1.232 2 1 2 1 2.232
1.886 0.134 1.866 0.134
各种不同变换。
15
2.二维基本变换的矩阵表示 (1)比例变换 a 0 T 若令变换矩阵 则写成矩阵形式为:
0 d
x
y
a 0 0 d ax dy x' y'
①若取a=3 d=1 对点(2,3)做变换,则
x' y' 2 3
3 0 0 1 6 3
8
(4)对称变换 如果经过变换后所得到的图形与变换前的图形关于 X坐标 轴是对称的,则称此变换为关于X轴的对称变换。经过这 一变换后的坐标点(x',y')与变换前的对应坐标点(x ,y)的关系为: x' = x, y' = -y 与此类似,若变换前后的图形关于 Y轴对称,则称为 关于Y轴的对称变换。这一变换前后点的坐标间的关系: x' = -x,y' = y 当图形对 X 轴和 Y 轴都进行对称变换时,即得相对于原点 的中心对称变换。这一变换前后点的坐标之间的关系为 : x' = -x,y' = -y 对称变换只改变图形方位,不改变其形状和大小。
2 4 2 1.5 0 6 3 2' 0 6 6 3' 3 4 4 1.5 4 2 4 3 6 4'
各点在X,Y两个方向产生相等的比例变换,即变换后 图形和变换前图形相似,相似中心为坐标原点。 若a≠d时,使图形在X和Y两个方向产生不相等比例 变换。下图(b)是a=2,d=1.5时对 (a)中矩阵1234变换 结果。 图 (c)是取a=2,d=0.5对矩阵1234变换结果,变 换后图形在X方向放大,在Y方向缩小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为什么要采用齐次坐标?
在笛卡儿坐标系内,向量(x,y)是位于z=0的平面上的点 ;而向量(x,y,1)是位于z=1的等高平面上的点
对于图形来说,没有实质性的差别,但是却给后面矩阵运 算提供了可行性和方便性
假如变换前的点坐标为(x,y),变换后的点坐标为(x*,y* ),这个变换过程可以写成如下矩阵形式:
x*, y*x,
x* a1x b 1 y c1
y•M
x*, y*x
a1
y
1
b 1
c1
a2 b2 c2
上两式是完全等价的。对于向量(x,y,1),可以在几何意义 上理解为是在第三维为常数的平面上的一个二维向量。
这种用三维向量表示二维向量,或者一般而言,用一个n+1维 的向量表示一个n维向量的方法称为齐次坐标表示法
n维向量的变换是在n+1维的空间进行的,变换后的n维结果 是被反投回到感兴趣的特定的维空间内而得到的。
如n维向量(p1,p2,...,pn)表示为(hp1,hp2,...,hpn,h), 其中h称为哑坐标。 普通坐标与齐次坐标的关系为“一对多”:
变换图形就是要变换图形的几何关系,即改变顶点的坐 标;同时,保持图形的原拓扑关系不变
仿射变换(Affine Transformation或 Affine Map)是一 种二维坐标到二维坐标之间的线性变换 (1)“平直性”。即:直线经过变换之后依然是直线
(2)“平行性”。即:平行线依然是平行线,且直线上 点的位置顺序不变)
采用了齐次坐标表示法,就可以统一地把二维线形变换表示 如下式所示的规格化形式:
x* y* 1x
y
1
a1 b
1
a2 b2
0 0
c1 c2 1
对于一个图形,可以用顶点表来描述图形的几何关系,用连 边表来描述图形的拓扑关系。所以对图形的变换,最后是只 要变换图形的顶点表
二维图形变换
一、图形变换
1、图形变换的用途
图形变换和观察是计算机图形学的基础内容之一,也是 图形显示过程中不可缺少的一个环节
一个简单的图形,通过各种变换(如:比例、旋转、镜象 、错切、平移等)可以形成一个丰富多彩的图形或图案
(1)由一个基本的图案,经过变换组合成另外一个复 杂图形
(2)用很少的物体组成一个场景
(3)可以通过图形变换组合得到动画效果
在计算机动画中,经常有几个物体之间的相对运动,可 以通过平移和旋转这些物体的局部坐标系得到这种动画 效果
2、图形变换的基本原理 图形是根据什么样的原理来实现各种变换的呢?
(1)图形变化了,但原图形的 连边规则没有改变
(2)图形的变化,是因为顶点 位置的改变决定的
x' ax by m
称为二维仿射变换( affine transformation ),其中坐 标x’和y’都是原始坐标x和y的线性函数
参数a,b,c,d,m和n是函数的系数
在几何中把向量看成从一个点到另一个点的位移。向量算 法提供了一种统一面内,我们是用一对坐标值(x,y)来表示一个点 在平面内的确切位置,或着说是用一个向量(x,y)来标定 一个点的位置
