计算机图形学--第八讲 图形的三维几何变换
计算机形学几何变换基础知识全面解析

计算机形学几何变换基础知识全面解析计算机形学几何变换是计算机图形学中一项非常重要的技术,它可以对图像进行平移、旋转、缩放等变换操作,从而实现图像的变形和动画效果。
本文将全面解析计算机形学几何变换的基础知识,包括变换的概念、常见的变换操作及其数学原理等内容。
一、概念介绍计算机形学几何变换是指通过一定的数学变换方法,改变图像或对象的形状、大小和位置。
常用的几何变换包括平移、旋转、缩放和错切等。
以下将逐个介绍这些变换操作的原理及应用。
二、平移变换平移变换是指将一个对象沿着指定方向平行移动一定的距离。
平移变换可以通过对对象中的每个顶点坐标进行相同平移量的加减操作来实现。
设对象的原始坐标为(x,y),平移量为(tx,ty),则平移变换后的新坐标为(x+tx,y+ty)。
三、旋转变换旋转变换是指将一个对象绕着指定的旋转中心点按照一定角度进行旋转。
旋转变换可以通过将对象中的每个顶点坐标绕旋转中心点进行相应角度的旋转来实现。
设对象的原始坐标为(x,y),旋转角度为θ,旋转中心点为(cx,cy),则旋转变换后的新坐标为:x' = (x-cx)*cosθ - (y-cy)*sinθ + cxy' = (x-cx)*sinθ + (y-cy)*cosθ + cy四、缩放变换缩放变换是指将一个对象的大小按照一定比例进行缩放。
缩放变换可以通过将对象中的每个顶点坐标按照指定比例进行缩放来实现。
设对象的原始坐标为(x,y),缩放比例为(sx,sy),缩放中心点为(cx,cy),则缩放变换后的新坐标为:x' = (x-cx)*sx + cxy' = (y-cy)*sy + cy五、错切变换错切变换是指将一个对象的各个顶点坐标按照一定的错切因子进行变换。
错切变换可以分为水平错切和垂直错切两种形式。
水平错切变换可以通过将对象中的每个顶点的y坐标按照指定的错切因子进行变换来实现;垂直错切变换则是将对象中的每个顶点的x坐标按照指定的错切因子进行变换。
三维图形变换

三维图形变换是在二维方法基础上增加了对z坐标的考虑得到的。
与二维变换类似,引入齐次坐标表示,即:三维空间中某点的变换可以表示成点的齐次坐标与四阶的三维变换矩阵相乘。
一、平移变换二.比例变换例如:对长方体进行比例变换,三、旋转变换跟二维的相同四、对称变换有关于坐标平面、坐标轴的对称变换(1)关于坐标平面的对称绕哪个面变换,那个面不变变换矩阵为:其它均类似(2)关于坐标轴变换6.2 投影变换投影变换就是把三维物体投射到投影面上得到二维平面图形两种投影法的本质区别在于:透视投影的投影中心到投影面之间的距离是有限的;而另一个的距离是无限的。
一、中心(透视)投影特点:投影线均通过投影中心,物体的投影视图由计算投影线与观察平面交点而得在投影中心相对投影面确定的情况下,空间的一个点在投影面上只存在唯一一个投影。
透视投影生成真实感视图,但不保证相关比例。
二、平行投影1、把透视投影的中心移至无穷远处,则各投影线称为相互平行的直线,这种投影2、分为正投影和斜投影3、特点:保持物体的有关比例不变三、平面集合投影的分类6.3 三视图一、1、根据投影面与坐标轴的夹角可分为两类:三视图和正轴侧图。
当投影面与某一坐标轴垂直时,得到的投影为三视图,这是投影方向与这个坐标轴的方向一致;否则,得到的投影为正轴侧图2、三视图包括主、侧、俯视图三种,投影面分别于x/y/z轴垂直3、优点:反映形体的实际尺寸,工程制图中常用三视图来测量形体间的距离、角度以及相互位置关系。
4、缺点:三视图上只有物体一个面的投影,只有将三个图放在一起,才能综合物体的空间形状二、三视图的计算1>确定三维物体上个点的位置坐标2>引入齐次坐标,求出所做变换相应的变换矩阵3>将所做变换用矩阵表示,通过运算求得三维物体上各点经变换后的点坐标值4>由变换后得到的二维点绘出三维物体投影后的三视图三、1>主视图:将三维物体xoz面(又称v面)做垂直投影,得到主视图2>俯视图:将三维物体xoy面(又称h面)做垂直投影,得到俯视图为了让其与主视图在一个平面内,让俯视图绕x轴旋转90°。
三维变换

投影线
投影面
A A'
投影中心
B'
B
A'
投影中心在
无穷远处
B'
A B
平行投影
•正投影与斜投影
6.3.2 正投影——三视图的形成
• 将三个投影面画在一个平面上:
(1)V面投影图保持不变(称正投影面,主视图); (2)H面绕OX轴向下翻转90度(称水平投影面,俯视图); (3)W面绕OZ轴向后翻转90度(称侧投影面,左视图); (4)省去投影面的边框和投影轴。见下页。
(x’, y’, z’)
(x’’, y’’, z’’)
1 2
(x, y, z)
x
z
6.2.2 三维几何变换
• 旋转变换
– 绕y轴
y
cos 0 sin 0
Ry
(
)
0
sin
1
0
cos
0 0
0 0 0 1
(x’, y’,
z’)
(x, y, z)
x
z
6.2.2 三维几何变换
• 旋转变换
– 绕z轴
cos
A B
D
x
C
图1
P(2,-2,0)
Y
C(0,2,0)
y
A(2,0,0)
B(2,2,0)
X
图2
随堂练习
4. 假定空间直线AB两端点坐标为A(0,0,0)B(2,2,2),
试写出绕AB轴旋转30度的三维复合变换矩阵。(问:
方向数为??)
Y
1) (毋需)
2)AB绕X轴旋转α角,使之落到ZX平面上;
3)将AB绕Y轴旋转β角,使之与Z轴重合;
数学8三维变换与投影

uz ' u (uz1',uz2 ',uz3')
uy
'
|
u u
ux ux
|
(uy1', uy2
',uy3')
ux ' uy 'uz ' (ux1',ux2 ',ux3')
则所需复合矩阵为
u x1 ' R uy1'
u0z1 '
ux2 ' ux3' 0 uy2 ' uy3 ' 0
uz2 ' 0
x' cos 0 sin 0 x
y'
0
1
0
0
y
z' sin 0 cos 0 z
1
0
0
0
1
1
沿 y 轴 Ry ( )
x' 1 0
0
y'
0
cos
sin
z' 0 sin cos
1
0
0
0
沿 x 轴 Rx ( )
0 x0y0 z11
x' cos sin 0 0 x
b/d c/d
0 0
0 0
0 1
R Ry ( ) Rx ()
d 0 a 0
Ry
(
)
0 a
1 0
0 d
0 0
0 0 0 1
M T 1 Rx ()1 Ry ( )1 Rz ( ) Ry ( ) Rx () T
2020/5/10
12
旋转(二)
得到复合矩阵 R Ry ( ) Rx () 的更快的方法是利用正交矩阵的乘积仍然是正交
计算机图形学--第八讲 图形的三维几何变换

3
变换通式
空间点[x y z] 的四维齐次坐标 [X Y Z H]表示
三维空间点的变换为 [x y z 1] T = [x’ y’ z’ 1]
变换前点的坐标 三维图形的变换矩阵
变换后点的坐标
三维图形变换矩阵通式为4 x 4 方阵
a b c p
T = d
e
5.关于Y轴对称
特点: y 值不变,zx坐标符号改变
[x y z 1] T = [-x y -z 1]
6.关于Z轴对称
特点: z值不变,xy坐标符号改变
[x y z 1] T = [-x -y z 1]
5.3 图形的三维几何变换—三维基本变换(13)
对称变换示意图
17
5.3 图形的三维几何变换—三维基本变换(14)
(x’, y’, z’)
x = xcos −ysin
y = xsin +ycos
z = z
矩阵运算的表达式为
z
cos sin 0 0
x
y
z 1 = x
y
z
1
−
sin
0
cos
0
0
0
1 0
0
0 0 1
y
(x, y, z)
x
10
5.4 图形的三维几何变换-三维基本变换(7)
绕X轴旋转
与二维图形的组合变换一样, 三维立体图形也可通过 三维基本变换矩阵, 按一定顺序依次相乘而得到一个 组合矩阵(称级联), 完成组合变换。
三维组合平移、组合旋转和组合比例变换与二维组合 平移、组合旋转和组合比例变换具有类似的规律。
19
5.3 图形的三维几何变换—三维复合变换(2)
计算机形学三维几何变换

计算机形学三维几何变换计算机形学是计算机科学中的一个重要分支,主要研究计算机图形学中的各类图形的数学描述方法和计算机图形学技术的应用。
其中,三维几何变换是计算机形学中的一项重要内容。
本文将介绍三维几何变换的概念、常见的三维几何变换操作以及其在计算机图形学中的应用。
一、概述三维几何变换是指对三维空间中的图形进行平移、旋转、缩放等操作,从而改变图形的位置和形状的过程。
三维几何变换是计算机图形学中非常常用的操作,可以实现物体的移动、旋转、缩放等效果。
二、三维几何变换的操作1. 平移(Translation)平移是指将图形沿指定的轴方向移动一定距离。
平移操作可以简单地理解为将图形的每一个顶点坐标向指定方向移动相同距离。
平移操作的数学表达式为:\[T(x,y,z) = (x + dx, y + dy, z + dz)\]其中,(x,y,z)表示原始顶点坐标,(dx,dy,dz)表示沿(x,y,z)轴平移的距离。
2. 旋转(Rotation)旋转是指将图形绕指定轴进行旋转。
旋转操作可以用欧拉角、四元数、矩阵等多种方式进行计算。
旋转操作的数学表达式为:\[R(x,y,z) = M(x,y,z)\]其中,(x,y,z)表示旋转前的坐标,M表示旋转变换矩阵。
旋转变换矩阵的计算方式有很多,最常见的是使用旋转角度和旋转轴来计算旋转矩阵。
3. 缩放(Scaling)缩放是指将图形沿各个轴向相应的方向按比例进行扩大或缩小。
缩放操作可以用不同的比例因子对每个顶点坐标进行缩放计算。
缩放操作的数学表达式为:\[S(x,y,z) = (sx, sy, sz)(x,y,z)\]其中,(x,y,z)表示原始顶点坐标,(sx,sy,sz)表示在x轴、y轴和z轴方向的缩放比例。
4. 其他变换操作除了平移、旋转和缩放之外,三维几何变换还可以包括倾斜、翻转、剪切等其他操作。
这些操作都是通过对图形的顶点坐标进行适当的数学计算而实现。
三、三维几何变换的应用三维几何变换在计算机图形学中有广泛的应用。
三维几何变换

三维几何变换利用3×3矩阵,可以实现部分三维变换,如绕X轴、Y轴、Z 轴旋转的变换矩阵为Tx=[1 0 0 ][0 cosθ sinθ][0 -sinθ cosθ]Ty=[cosθ 0 -sinθ][ 0 1 0 ][sinθ 0 cosθ]Tx=[cosθ sinθ 0 ][-sinθ cosθ 0][ 0 0 1]但是,利用齐次坐标变换更方便。
三维空间点[X Y Z]用四维齐次坐标表示为[X Y Z]或[X’Y’ Z’ H],因此三维空间点的变换可写为[X Y Z H]T=[X’ Y’ Z’H]=[X’/H Y’/H Z’/H1]=[X’ Y’ Z’ 1]式中T为变换矩阵,与二维变换矩阵对应,三维变换矩阵为4×4方阵,即T=[a b c|p][d e f|q][h i j|r][-------|-][l m n|s]=[3×3|3×1][----|----][1×3|1×1]此方阵也可以分为4个部分,由二维变换可知,其中3×3矩阵起比例变换,映射变换,错切变换和旋转变换的作用,1×3矩阵起平移变换的作用,3×1矩阵起透视变换的作用,而1×2矩阵起比例变换的作用,下面通过具体图例说明各部分算子的作用,也就是基本三维几何变换。
1、三维比例变换在3×3矩阵中,主对角线上算子a、e、j控制比例变换,令其他算子为零,则三维点[X Y Z]的比例变换写为[X Y Z 1]·S=[X Y Z 1][[a 0 0 0][0 e 0 0][0 0 j 0][0 0 0 1]]=[aX eY jZ 1]=[X* Y* Z* 1]由上式可知,a、e、j分别控制X、Y、Z的比例变换,若令a=e=j=1,则算子S可使整个图形按同一比例放大或缩小。
[X Y Z 1][[1 0 0 0][0 1 0 0][0 0 1 0][0 0 0 1]]=[X Y Z S]=[X/S Y/S Z/S 1]=[X* Y* Z* 1]上式中,若S>1,则整个图形缩小;若S<1,则整个图形放大。
计算机形学中的几何变换与投影算法基础

计算机形学中的几何变换与投影算法基础在计算机图形学中,几何变换与投影算法是实现三维对象表示、变换和可视化的基础。
通过对三维空间中的对象进行变换和投影,可以将其呈现在二维平面上,从而实现更直观的可视化效果。
本文将介绍计算机形学中的几何变换和投影算法的基本概念和应用。
一、几何变换几何变换是指通过对三维对象进行平移、旋转、缩放等操作,改变其在空间中的位置和形状。
在计算机图形学中,常用的几何变换包括平移、旋转、缩放和剪切。
1. 平移平移是指将对象沿着指定方向移动一定的距离。
在计算机图形学中,平移变换可以通过将对象的每个顶点坐标增加一个平移向量来实现。
平移变换公式如下:[x'] = [1 0 0 tx] [x][y'] [0 1 0 ty] [y][z'] [0 0 1 tz] [z][1 ] [0 0 0 1] [1]其中,(tx, ty, tz)表示平移向量。
通过对对象的每个顶点应用上述变换矩阵,可以实现平移效果。
2. 旋转旋转是指将对象绕指定轴进行旋转。
在计算机图形学中,常用的旋转有绕X轴、Y轴和Z轴旋转。
旋转变换可以通过将对象的每个顶点坐标乘以一个旋转矩阵来实现。
旋转变换矩阵的形式如下:[x'] = [1 0 0 0] [x][y'] [0 cosθ -sinθ 0] [y][z'] [0 sinθ cosθ 0] [z][1 ] [0 0 0 1] [1]其中,θ表示旋转角度。
通过对对象的每个顶点应用上述变换矩阵,可以实现旋转效果。
3. 缩放缩放是指改变对象的尺寸大小。
在计算机图形学中,缩放变换可以通过将对象的每个顶点坐标乘以一个缩放因子来实现。
缩放因子分别作用于X、Y和Z轴的坐标,从而改变对象在各个轴上的尺寸。
缩放变换公式如下:[x'] = [sx 0 0 0] [x][y'] [0 sy 0 0] [y][z'] [0 0 sz 0] [z][1 ] [0 0 0 1] [1]其中,(sx, sy, sz)表示缩放因子。
计算机图形学-变换

1 0 Rx ( ) 0 0
d 0 Ry ( ) a 0
0 a 1 0 0 d 0 0
0 0 0 0
42
一般三维旋转--4
cos sin Rz ( ) 0 0 sin cos 0 0 0 0 0 1
0 sy 0 0
0 0 sz 0
0 x 0 y z 0 1 1
45
三维缩放--相对于任意点
平移给定点到原点 使用前面的公式相对于坐标原点缩 放对象 平移给定点回到原始位置
46
三维缩放--相对于任意点
T ( x f , y f , z f ) S (sx , s y , sz ) T (x f , y f ,z f )
P T (t x , t y ) P
10
二维旋转矩阵
x cos y sin 1 0 sin cos 0 0 x 0 y 1 1
P R( ) P
36
一般三维旋转
对于绕与坐标轴不重合的轴进行旋 转的变换矩阵,可以利用平移与坐 标轴旋转的复合而得到 首先将指定旋转轴经移动和旋转变 换到坐标轴之一,然后对该坐标轴 应用适当的旋转矩阵
最后将旋转轴变回到原来位置
37
一般三维旋转
平移对象使得旋转轴通过坐标原点 旋转对象使得旋转轴与某一坐标轴 重合 绕坐标轴完成指定的旋转 利用逆旋转使旋转轴回到原始方向 利用逆平移使旋转轴回
40
一般三维旋转--2
1 0 T 0 0 0 1 0 0 0 x1 0 y1 1 z1 0 0
41
三维变换及三维观察

Y
俯视图
广东工业大学机电学院图学与数字媒体工程系
x
计算机图形学基础——三维变换及三维观察
三维投影变换——平行正投影三视图 侧视图投影矩阵:
立体向YOZ面投影
0 0 0 0
Tyoz
0 0
1 0
0 1
0 0
0 0 0 1
广东工业大学机电学院图学与数字媒体工程系
计算机图形学基础——三维变换及三维观察
0
0
0
1
旋转前后坐标变 换的关系为:
x' x cos z sin
y' y
z' xsin z cos
广东工业大学机电学院图学与数字媒体工程系
计算机图形学基础——三维变换及三维观察
三维几何变换
绕z轴旋转
cos sin 0 0
Tz
sin
0
cos
三维投影变换——平行正投影三视图 俯视图投影矩阵:
立体向XOY面投影
1 0 0 0
Txoy
0 0
1 0
0 0
0 0
0 0 0 1
广东工业大学机电学院图学与数字媒体工程系
计算机图形学基础——三维变换及三维观察
三维投影变换——平行正投影三视图 俯视图投影矩阵:
XOY面绕OX轴向下 旋转90度
T
Txoy TRx
Ttz
0 0
0 0
1 0
0 0
0 0 z0 1
广东工业大学机电学院图学与数字媒体工程系
计算机图形学基础——三维变换及三维观察
三维投影变换——平行正投影三视图
侧视图:获得侧视图是将三维形体往yoz面(侧面W) 作垂直投影。
三维图形几何变换

3.1.2 三维图形几何变换三维几何变换包括平移、旋转和变比。
三维几何变换可以表示为公式,或三维齐次坐标和4×4变换矩阵的乘积。
下面分别以公式,矩阵乘积和简记符号来描述三维几何变换。
并记变换前物体的坐标为x,y,z;变换后物体的坐标为x′,y′,z′。
一、平移设Tx,Ty,Tz是物体在三个坐标方向上的移动量,则有公式:x′=x+T xy′=y+T yz′=z+T z矩阵运算表达为:[x′ y′ z′ 1]=[x y z 1]简记为:T(Tx,Ty,Tz)二、旋转旋转分为三种基本旋转:绕z轴旋转,绕x轴旋转,绕y轴旋转。
在下述旋转变换公式中,设旋转的参考点在所绕的轴上,绕轴转θ角,方向是从轴所指处往原点看的逆时针方向(图3.5(a),(b))。
1 绕z轴旋转的公式为:x′=xcosθ-ysinθy′=xsinθ+ycosθz′=z矩阵运算的表达为:[x′ y′ z 1]=[x y z 1]简记为R z(θ)。
2 绕x轴旋转的公式为:x′=xy′=ycosθ-zsinθz′=ysinθ+zcosθ矩阵运算的表达为:[x′ y′ z′ 1]=[x y z 1]简记为R x(θ)2 绕y轴旋转的公式为:x′=zsinθ+xcosθy′=yz′=zcosθ-xsinθ矩阵的运算表达式为:[x′ y′ z′ 1]=[x y z 1]简记为Ry(θ)。
如果旋转所绕的轴不是坐标轴,而是一根任意轴,则变换过程变显得较复杂。
首先,对物体作平移和绕轴旋转变换,使得所绕之轴与某一根标准坐标轴重合。
然后,绕该标准坐标轴作所需角度的旋转。
最后,通过逆变换使所绕之轴恢复到原来位置。
这个过程须由7个基本变换的级联才能完成。
设旋转所绕的任意轴为p1, p2两点所定义的矢量。
旋转角度为 (图3.6)。
这7个基本变换是:1 T(-x1,-y1,-z1)使p1点与原点重合(图3.6(b));2 R x(α),使得轴p1p2落入平面xoz内(图3.6(c));3 R y(β),使p1p2与z轴重合(图3.6(d));4 R z(θ),执行绕p1p2轴的θ角度旋转(图3.6(e));5 R y(-β),作3的逆变换;6 R x(-α),作2的逆变换;7 T(x1,y1,z1)作1的逆变换。
计算机图形学2010_06三维图形变换
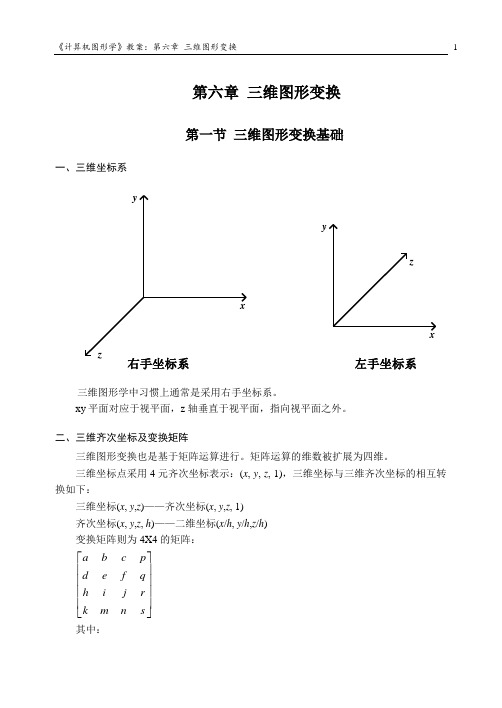
第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。
xy 平面对应于视平面,z 轴垂直于视平面,指向视平面之外。
二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。
矩阵运算的维数被扩展为四维。
三维坐标点采用4元齐次坐标表示:(x , y , z , 1),三维坐标与三维齐次坐标的相互转换如下:三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中:平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种,即绕三个坐标轴的旋转变换。
(1)绕z 轴旋转γ角旋转后z 值不变,x,y 值将发生改变,x,y 值的计算公式与平面旋转相同,即:zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有:)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变,y 和z 的坐标值将改变,相当于在yz 平面上绕平面原点进行旋转变换。
平面转转变换的公式为:ααααcos sin sin cos y x y y x x +='-='对应而来,这里y 对应于x ,z 对应y ,有:ααααcos sin sin cos z y z z y y +='-='则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时,z 对应于x ,x 对应于y 。
计算机图形学几何变换课件

• 平移变换可以用矩阵表示,对于二维平移变换, 矩阵为
平移变换
``` 1 0 tx
0 1 ty
平移变换
``` 其中tx和ty分别表示在x和y轴上的平移距离。对于三维平移变换,矩阵为
平移变换
1 2 3
平移变换
平移变换
```
其中tx、ty和tz分别表示在x、y和z轴上的平移距离。
缩放变换
缩放变换
缩放变换
``` s00 0s0
缩放变换
缩放变换
缩放变换
01 02 03
缩放变换
缩放变换
其中s1、s2和s3分别表示在x、y和z轴 上的缩放比例。
旋转变换
旋转变换
旋转变换
旋转变换
旋转变换
旋转变换
旋转变换
旋转变换
齐次坐标和矩阵表示
03
非线性几何变换
CHAPTER
仿射变换
OpenGL或其他图形库的应用
01
OpenGL
02
DirectX
03
Unity3D
06
课程总结与展望
CHAPTER
本课程的主要内容回顾
矩阵表示法
投影变换
几何变换基础
组合变换
仿射变换
计算机图形学几何变换的未来发展
实时渲染技术 虚拟现实与增强现实 人工智能与几何变换
学生如何进一步深入学习计算机图形学
计算机图形学几何变 换课 件
contents
目录
• 引言 • 线性几何变换 • 非线性几何变换 • 组合几何变换 • 几何变换的计算机实现 • 课程总结与展望
01
引言
CHAPTER
计算机图形学的定义
计算机图形学
计算机图形学中的三维变换与投影算法

计算机图形学中的三维变换与投影算法计算机图形学是研究计算机中图形的表示、生成、处理和显示的学科。
在计算机图形学中,三维变换和投影算法是非常重要的技术,它们可以用来对三维物体进行位置、姿态和尺寸的调整,并将其投影到二维画面上。
三维变换是指通过对三维物体的顶点进行一系列变换操作,来改变物体的位置、形状和方向。
常用的三维变换操作包括平移、旋转和缩放。
平移操作改变物体的位置,旋转操作改变物体的方向,而缩放操作改变物体的尺寸。
通过组合不同的变换操作,可以实现复杂的三维物体的变换。
平移是通过将物体的每个顶点按照指定的距离移动来改变物体的位置。
旋转是通过将物体的每个顶点绕着旋转中心按照指定的角度旋转来改变物体的方向。
缩放是通过将物体的每个顶点按照指定的比例因子进行缩放来改变物体的尺寸。
这些变换操作可以通过矩阵运算来进行计算,从而实现对三维物体的变换。
投影是将三维物体投影到二维画面上的操作。
在计算机图形学中,常用的投影算法有平行投影和透视投影。
平行投影是将物体的每个顶点沿着平行于视线的方向进行投影,得到二维画面上的对应点。
透视投影则考虑到物体离视点的距离,并根据投影面和视点的位置关系而调整投影结果。
通过投影操作,可以将三维物体在计算机屏幕上展示出来,从而实现真实感的图形显示。
在实际应用中,三维变换和投影算法被广泛应用于计算机游戏、虚拟现实、计算机辅助设计等领域。
通过三维变换,可以实现物体的动画效果,使得游戏或虚拟现实场景更加逼真。
而通过投影算法,可以实现对物体的观察和测量,帮助设计师更好地进行产品设计和展示。
总结来说,计算机图形学中的三维变换和投影算法是实现三维物体在计算机中显示和操作的关键技术。
通过对物体进行平移、旋转和缩放等变换操作,可以改变物体的位置、方向和尺寸;而通过投影操作,可以将三维物体投影到二维画面上展示出来。
这些技术在计算机游戏、虚拟现实和计算机辅助设计等领域发挥着重要的作用,推动了计算机图形学的发展。
三维图形的几何变换讲课文档

先平移后旋转
先旋转后平移
第二十三页,共64页。
三、三维图形的几何变换
三维图形的变换是二维图形变换的简单扩展,变换的 原理还是把齐次坐标点(x,y,z,1)通过变换矩阵变换成新 的齐次坐标点(x’,y’,z’,1),即
x ' y ' z '1 x y z 1 T
其中T为三维基本(齐次)变换矩阵:
1 0 0
T1
0
1
0
c / a 0 1
第十四页,共64页。
(2)将直线与平面图形一起按逆时针反向旋转
θ=arctan(-b/a),使直线与轴重合。即作旋转变换。
cos sin 0
T2
sin
cos
0
0
0 1
第十五页,共64页。
(3)将旋转之后的图形对y轴作对称变换,相当于对y轴 进行对称变换。其变换矩阵为:
透视投影的图形与眼睛观察景物的原理及效果是一致的, 因而常用于图形的真实效果显示。由于平行投影后直线 间的平行关系不变,因而它常用于三维图形交互和生成 工程图的视图。
第三十四页,共64页。
投影变换分类:
正交投影 正平行
正等测投影
投影
平行 投影
正轴测 投影
正二测 正三测
斜平行 斜等测
投
投影
影
斜二测
一点透视
1001 0001
1000 窗口
0000
0101 0100
1010 0010 0110
第四十四页,共64页。
对线段的两端点分别进行编码。然后根据线段两端点编 码就能方便地判断出线段相对于窗口的位置关系:
第四十五页,共64页。
计算机图形学三维图形变换

主视图变换矩阵
1 0 0 0 1 0 0 0 1 0 0 0
Tv
0 0
0 0
0 1
0
0
0 0
0
0
பைடு நூலகம்
0
0
1 0 0 0
0 0 0 1 0 0
0
0
0
1
0
0 0 1
0
0 0 1
俯视图变换矩阵
1 0 0 0 1
0
0 0 1 0 0 0
TH
0 0
1 0
0 0
0 0 0 0
cos(90) sin(90)
三维图形变换
基本几何变换
基本几何变换都是相对于原点和坐标
轴进行的几何变换,有平移、缩放和 旋转等。在以下的讲述中,均假设用
p(x, y, z) 表示三维空间上一个未被变 换的点,而该点经过某种变换后得到 的新点用 p'(x', y', z') 表示。
平移变换
平移是指将点沿直线路径从一个坐标位置移动 到另一个坐标位置的一个重定位过程。
0 1
0
0
0 0
0 0 0 1 0 0
0
0
0
1
0
0
0
1
0
0 0 1
0 0 0 0 1 0 0 0
0 1 0 0 0 0 0 1
1 0 0 0
0
Rx ( )
0
c
d b
b
d c
0
0
dd
0 0 0 1
Ry ( )
d 0 a 0
Ry
(
)
0
a
1 0
0 d
图形图像三维变换

视点坐标系
投影变换
设备变换
规格化设备 坐标系
屏幕坐标系
5
三维变换中的各种坐标系
6
场景坐标系和模型变换
几何场景建立于世界坐标系中 场景中的具体物体与局部坐标系相联系
局部坐标系可以简化物体的定义 物体={标准体素,变换}
造型变换:
物体从局部坐标系到世界坐标系的变换 三维线性和非线性变换
二维变换:将定义在视窗中的规格化设备坐 标转换到以像素为单位的屏幕坐标
扫描转换:将连续的几何物体转换为离散的 光栅表示
50
视窗变换
X分量的变换
x xvmin x ' xwmin xvmax xvmin xwmax xwmin
x'
xwmin
xwmax xvmax
xwmin xvmin
V N UP N UP
U VN
得到两个向量 U=(Ux,Uy,Uz) 和V=(Vx,Vy,Vz), 然后单位化。
16
视点坐标系的交互建立
四个矢量C、U、V、N组成了视点坐标系 由世界坐标系到视点坐标系的取景变换:
u Ux Uy Uz 0 1 0 0 Cx x
v
V x
Vy
Vz
0 u
0
v
0 n
0 1
U W
,
V W
,
N W
u n/d
,
v n/d
,
d
up , vp , d
24
关于透视投影
一点透视投影
两点透视投影
三点透视投影
25
规格化设备坐标和设备变换
在投影平面上,有一个矩形区域称为视窗
上图坐标系中vovxvy的矩形和“视域四棱锥” 图中的矩形
计算机图形学(三维几何变换)

有些图形系统,对设备坐标系进行了规范化,将坐标 范围限定在区间{x, y, z | 0≤x≤1, 0≤y≤1, 0≤z≤1}内,称为 标准化设备坐标系
Y
P’(x’,y’,z’) P(x,y,z)
sin cos 0 0 x 0 y (3) 1 z
X
x cos y sin z 0
Z
旋转的图示
2009-2010-2:CG:SCUEC
以图形中心为中心进行缩放的步骤
2009-2010-2:CG:SCUEC
18
以图形中心为中心的缩放变换
以图形中心为中心的缩放 然后再对每一点按照式(*)作变换. 最后再沿x, y和z方向平移xp, yp和zp,把经过缩放 的图形移回原处.
(xp,yp,zp)
以图形中心为中心进行缩放的步骤
2009-2010-2:CG:SCUEC
A
放缩
17
2009-2010-2:CG:SCUEC
以图形中心为中心的缩放变换
为了使缩放变换后的图形仍在原位臵附近,可另 以图形中心为中心的缩放 外定义一个相似中心点(xp,yp,zp). 先把整个图形沿x, y和z方向平移–xp, –yp和–zp, 相似中心就移到了坐标原点.
(xp,yp,zp)
视口
2009-2010-2:CG:SCUEC
8
Yv
世界坐标系
Y
y2 o x y z x2
观察坐标系
y1
X
3d几何变换 形函数 直变弯

3d几何变换形函数直变弯3D几何变换是指在三维空间中对对象进行平移、旋转、缩放等操作,以改变其位置、姿态和大小。
形函数是在有限元方法(Finite Element Method)中使用的数学函数,用于描述和近似结构或物体的形状变化。
直变弯是指将原始对象从直线形状转变为弯曲形状的操作。
下面分别介绍这些概念的具体含义和应用:1.3D几何变换:•平移:在三维空间中,平移是将对象沿着指定的方向和距离移动,使其位置发生改变,而形状和大小保持不变。
•旋转:三维空间中的旋转是通过指定旋转轴和旋转角度,将对象绕轴旋转一定角度,改变对象的姿态和方向。
•缩放:缩放操作改变对象的大小,可以使对象在各个维度上按比例增加或减小。
这些几何变换操作在三维建模、动画制作、虚拟现实等领域得到广泛应用,用于模拟和控制对象的形状、姿态和动作。
2.形函数:在有限元方法中,形函数是一种用于近似和描述结构或物体形状变化的数学函数。
形函数通常是由一系列基函数组合而成,这些基函数用于对结构进行离散化,将其划分为一系列有限元,并以形函数的形式描述其变形和扭曲。
形函数的选择和计算是有限元模拟中的重要步骤,直接影响模拟结果的准确性和精度。
3.直变弯:直变弯是一种操作,将原始对象从直线形状转变为弯曲形状。
在三维建模和动画制作中,直变弯常用于使直线对象变形成曲线、弯曲、扭曲等形状,以创建更加自然和真实的效果。
这在角色动画、建筑设计、工程仿真等领域都有广泛应用。
综上所述,3D几何变换是对三维对象进行位置、姿态和大小改变的操作,形函数是描述和近似物体变形的数学函数,而直变弯是将对象从直线形状转变为弯曲形状的一种操作。
这些概念在三维建模、动画制作、结构仿真等领域具有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23
5.4 图形的三维几何变换—复合变换()
在ZOX 平面上绕Y轴旋转使l与Z轴重合 d n12 n22 n32 1
cos v v
d
sin
n1 d
n1
v
n
R
y
n
v
24
5.4 图形的三维几何变换—复合变换()
Step2:绕Z轴旋转
cos
sin 0 0
Rz
(
)
sin
0
cos
0
同样,我们用齐次坐标来表示三维几何变换矩阵
3
变换通式
空间点[x y z] 的四维齐次坐标 [X Y Z H]表示
三维空间点的变换为 [x y z 1] T = [x’ y’ z’ 1]
变换前点的坐标 三维图形的变换矩阵
变换后点的坐标
三维图形变换矩阵通式为4 x 4 方阵
a b c p
T d
e
f
0 0 1 0 0 0 0 1
5.3 图形的三维几何变换—三维基本变换(12)
反射(对称)变换:关于平面对称
4.关于X轴对称
特点:x 值不变,yz坐标符号改变
[x y z 1] T = [x -y -z 1]
5.关于Y轴对称
特点: y 值不变,zx坐标符号改变
[x y z 1] T = [-x y -z 1]
28
感谢各位同学观看!
29
三维组合平移、组合旋转和组合比例变换与二维组合 平移、组合旋转和组合比例变换具有类似的规律。
19
5.3 图形的三维几何变换—三维复合变换(2)
(1)以P为参考点的比例变换
20
5.3 图形的三维几何变换—三维复合变换(4)
(2)关于任意轴线的三维旋转
直线的单位方向向量n: n n1 n2 n3 n n12 n22 n32 1
将下图的空间四面体连续进行如下变换。写出复合变换矩阵,变 换后图形各点的规范化齐次坐标。 (1)关于点P整体放大2倍 (2)关于Y轴进行对称变换
27
第八讲 作业(2)
2.给定空间任一点P(x,y,z)及任一平面Q: ax+by+cz+d=0,求P对Q的对称点P* (x*,y*,z*)的变换
矩阵。
y y’ y
[x y z 1] T = [x+Tx y+Ty z+Tz 1]
z’ z
z
x x’ x
5
5.3 图形的三维几何变换—三维基本变换(2)
例:一单位立方体,现将它沿x方向移动3单位,y方向移动2单 位,z方向移动3.5单位。
1 0 0 0 T 0 1 0 0
0 0 1 0 3 2 3.5 1
[x y z 1] T = [x y z s]=[x/s y/s z/s 1]
② 轴向比例变换
a 0 0 0
y
T 0 e 0 0
0 0 j 0
0 0 0 1
x
z
[x y z 1] T = [ax ey jz 1]=[x’ y’ z’ 1]
若a=e=j,,则图形三方向的缩放比例相同 若aej,,则图形将产生类似变形
绕任意轴旋转
图 绕任意轴P1P2旋转的前4个步骤
5.3 图形的三维几何变换—三维基本变换(11)
反射(对称)变换:关于平面对称
1 0 0 0
1.对OXY平面的反射
特点:x y 值不变,z坐标符号改变
T 0 1 0 0 0 0 1 0
[x y z 1] T = [x y -z 1]
0 0 0 1
z = zcos xsin
矩阵运算的表达式为
z
cos 0 sin 0
x
y z 1 x
y
z
1
0
sin
1 0
0
cos
0 0
0
0
0 1
y
(x, y, z)
x
12
5.3 图形的三维几何变换—三维基本变换(9)
绕三维坐标轴的旋转变换 绕Y轴旋转90°。
13
5.4 图形的三维几何变换--三维基本变换(10)
5.3 图形的三维几何变换—三维基本变换(4)
绕三维坐标轴的旋转变换
绕Z轴的二维旋转很容易推广到三维:
x' xcos ysin y' xsin y cos
z' z
cos sin 0 0
T sin cos 0 0 0 0 1 0
0
0 0 1
即绕Z轴旋转 角
Z坐标不变 X、Y坐标发生变化
2.对YOZ平面的反射
特点:z y 值不变,x坐标符号改变
[x y z 1] T = [-x y z 1]
1 0 0 0
T
0
1 0 0
0 0 1 0
0
0 0 1
3.对XOZ平面的反射
特点:x z值不变,y坐标符号改变
[x y z 1] T = [x -y z 1]
1 0 0 0 T 0 1 0 0
x = xcos ysin
y = xsin +ycos
z = z
矩阵运算的表达式为
z
cos sin 0 0
x
y
z
1 x
y
z
1
sin
cos
0
0
0
0 1 0
0
0
0 1
y
(x, y, z)
x
10
5.4 图形的三维几何变换-三维基本变换(7)
绕X轴旋转
x = x
y = ycos zsin z = ysin +zcos
基本思想:因任意轴不是坐标轴,应设法旋转该轴,使之与 某一坐标轴重合,然后进行旋转变换,最后按逆过程,恢复 该轴的原始位置。
21
5.3 图形的三维几何变换—三维复合变换(5)
(2)关于任意轴线的三维旋转 Step1:作变换让l与z轴重合。
(1a) 平移,使l 过原点(平移) (1b)绕x轴旋转使l位于 ZOX 平面(绕x轴旋转) (1c)绕y轴旋转使得l 与Z轴重合 (绕y轴旋转)
任课教师: 李陶深教授 tshli@
1
1 变换的数学基础 2 计算机图形处理的过程 3 图形的二维几何变换 4 图形的三维几何变换 5 形体的投影变换
2
5.3 图形的三维几何变换—复合二维变换(10)
三维几何变换可由二维几何变换扩展而来,包括: ►三维平移 ►三维旋转 ►三维比例缩放等
x' x dy gz,d, g 0关于x轴方向有错切
y'
y
bx
hz,b,
h
0关于y轴方向有错切
z'
z cx
f y,c,
f
0关于z轴方向有错切
18
5.3 图形的三维几何变换—三维复合变换(1)
与二维图形的组合变换一样, 三维立体图形也可通过 三维基本变换矩阵, 按一定顺序依次相乘而得到一个 组合矩阵(称级联), 完成组合变换。
y
(x, y, z)
(x’, y’, z’)Leabharlann x矩阵运算的表达式为
z
1 0 0 0
x y z 1 x y z 1 0 cos sin 0
0 sin cos 0
0
0
0 1
11
5.4 图形的三维几何变换-三维基本变换(8)
绕Y轴旋转
(x’, y’, z’)
x = zsin +xcos
y = y
q
h i j r
l
m
n
s
a b c 3x3
d
e
f
h i j
[l m n] 1 x 3
[p q r]T
[s]1x1
比例、反射、旋转、错切
平移 投影变换 总体比例变换
5.3 图形的三维几何变换—三维基本变换(1)
平移变换:
指空间的立体从一个位置移动到另一位置时,其形 状、大小都不发生变换的变换。
6
5.3 图形的三维几何变换—三维基本变换(3)
相对于原点的缩放变换
变换矩阵主对角线上 的元素a、e、j、s的作用是
1 T 0
0 1
0 0
0 0
是图形产生比例变换。
0 0 1 0
① 全比例变换
0
0
0
s
0<S<1,为图形整体放大
S>1,为图形整体缩小 S<0,为对称变换+比例变换 S=1,为恒等变换
0 1
0
0
0
0 0 1
25
5.4 图形的三维几何变换—复合变换()
Step3:旋转轴复位回 原来位置
v 0 n1 0
Ry
(
)
0
n01
1 0 0
0 v 0
0 0 1
1
0
Rx
(
)
0
0
0 n3
v n2
v 0
0 n2
v n3
v 0
0 0
0 1
26
第八讲的作业(1)
1. 已知三角形ABC的各个顶点坐标分别为A(1,2), B(5,2), C(3,5),相 对于直线y-x-1=0作对称变换,请写出变换的步骤和每一步的变换 矩阵。
绕另外两个坐标轴旋转变换公式可由上式坐标参数x,y, z循环替换而得到,即 x y z x
Y
Z
X
X Z
Y X
Z Y
5.3 图形的三维几何变换—三维基本变换(5)
绕三维坐标轴的旋转变换
绕坐标轴的逆时针旋转为正旋转。
9
5.4 图形的三维几何变换-三维基本变换(6)
