有关定积分问题的常见题型解析(全题型)

合集下载

有关定积分问题的常见题型解析(全题型)培训讲学

有关定积分问题的常见题型解析(全题型)有关定积分问题的常见题型解析题型一利用微积分基本定理求积分例1、求下列定积分：（1）()13031x x dx -+⎰ （2）41dx +⎰ （3）⎰--2224x分析：根据求导数与求原函数互为逆运算，找到被积函数得一个原函数，利用微积分基本公式代入求值。

解：（1）因为3221312x x x x x '⎛⎫-+=-+ ⎪⎝⎭，所以()13031x x dx -+⎰=321102x x x ⎛⎫-+ ⎪⎝⎭=32。

（2121x x =+，312222132x x x x '⎛⎫+=+ ⎪⎝⎭，所以 41dx +⎰=3229211454326x x ⎛⎫+= ⎪⎝⎭。

练习：（1）⎰--a a x a 22 （2）⎰--2124x评注：利用微积分基本定理求定积分dx x f ab )(⎰的关键是找出)()(/x f x F =的函数)(x F 。

如果原函数不好找，则可以尝试找出画出函数的图像，图像为圆或者三角形则直接求其面积。

题型二利用定积分求平面图形的面积例2 如图，求直线y=2x+3与抛物线y=x 2所围成的图形面积。

分析：从图形可以看出，所求图形的面积可以转化为一个梯形与一个曲边梯形面积的差，进而可以用定积分求出面积。

为了确定出被积函数和积分和上、下限，我们需要求出两条曲线的交点的横坐标。

解：由方程组⎩⎨⎧=+=232xy x y ，可得3,121=-=x x 。

故所求图形面积为： S ＝()dx x ⎰-+3132－dx x ⎰-312＝（x 2＋3x ）3323113313=---x 。

评注：求平面图形的面积的一般步骤：⑴画图，并将图形分割成若干曲边梯形；⑵对每个曲边梯形确定其存在的范围，从而确定积分上、下限；⑶确定被积函数；⑷求出各曲边梯形的面积和，即各积分的绝对值之和。

关键环节：①认定曲边梯形，选定积分变量；②确定被积函数和积分上下限。

定积分典型例题20例解答

定积分典型例题20例答案例1求33322321lim(2)n n n n n®¥+++．分析将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解将区间[0,1]n 等分，则每个小区间长为1i x n D =，然后把2111n n n =×的一个因子1n乘入和式中各项．于是将所求极限转化为求定积分．即33322321lim (2)n n n n n®¥+++=333112lim ()n n n n n n ®¥+++=13034xdx =ò．例2222x x dx -ò=_________．解法1由定积分的几何意义知，222x x dx -ò等于上半圆周22(1)1x y -+= (0y ³)与x 轴所围成的图形的面积．故222x x dx -ò=2p ．解法2本题也可直接用换元法求解．令1x -=sin t （22t pp-££），则222x x dx -ò=2221sin cos t tdt pp --ò=2221sin cos t tdt p -ò=222cos tdt p ò=2p例3（1）若22()xtxf x e dt -=ò，则()f x ¢=___；（2）若0()()xf x xf t dt=ò，求()f x ¢=___．分析这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ¢¢=-ò．解（1）()f x ¢=422x x xee---；（2）由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =ò，则可得()f x ¢=()()xf t dt xf x +ò．例4 设()f x 连续，且310()x f t dt x -=ò，则(26)f =_________．解对等式31()x f t dt x -=ò两边关于x 求导得32(1)31f x x -×=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =．例5 函数11()(3)(0)x F x dt x t =->ò的单调递减开区间为_________．解 1()3F x x¢=-，令()0F x ¢<得13x >，解之得109x <<，即1(0,)9为所求．为所求．例6 求0()(1)arctan xf x ttdt =-ò的极值点．的极值点．解由题意先求驻点．于是()f x ¢=(1)arctan x x -．令()f x ¢=0，得1x =，0x =．列表如下：如下：故1x =为()f x 的极大值点，0x =为极小值点．为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中处的切线相同，其中 2arcsin0()x tg x e dt -=ò，[1,1]x Î-，试求该切线的方程并求极限3lim()n nf n®¥．分析两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ¢¢=．解由已知条件得由已知条件得2(0)(0)0t f g e dt-===ò，且由两曲线在(0,0)处切线斜率相同知处切线斜率相同知2(arcsin )2(0)(0)11x x ef g x-=¢¢===-．故所求切线方程为y x =．而．而3()(0)3lim ()lim33(0)330n n f f n nf f nn®¥®¥-¢=×==-．例8 求 22sin lim (sin )xx xtdtt t t dt®-òò；分析该极限属于00型未定式，可用洛必达法则．型未定式，可用洛必达法则．解 2200sin lim (sin )xx x tdtt t t dt®-òò=2202(sin )lim (1)(sin )x x x x x x ®-××-=220()(2)lim sin x x x x ®-×-=304(2)lim 1cos x xx ®-×- x(,0)-¥0 (0,1)1 (1,)+¥()f x ¢- 0 ＋ 0 －=2012(2)lim sin x x x®-×=0．注此处利用等价无穷小替换和多次应用洛必达法则．此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b ，使等式221lim 1sin x x tdt x b x a t®=-+ò成立．成立．分析易见该极限属于型的未定式，可用洛必达法则．解 221lim sin x x tdt x b xa t®-+ò=22lim 1cos x xa xb x ®+-=221lim lim 1cos x x xb xa x ®®×-+201lim 11cos x x b xa ®==-，由此可知必有0lim(1cos )0x b x ®-=，得1b =．又由．又由 2012lim 11cosx xx a a ®==-，得4a =．即4a =，1b =为所求．为所求．例10 设sin 20()sin x f x t dt=ò，34()g x x x =+，则当0x ®时，()f x 是()g x 的（的（）． A ．等价无穷小．．等价无穷小． B ．同阶但非等价的无穷小．．同阶但非等价的无穷小． C ．高阶无穷小．．高阶无穷小． D ．低阶无穷小．解法1 由于由于 22300()sin(sin )cos lim lim ()34x x f x x x g x x x ®®×=+ 2200cos sin(sin )lim lim 34x x x x xx ®®=×+ 22011lim 33x xx ®==．故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342xf x t t dt x x =-+=-+ò，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x xx®®®®-+-+===++．例11 计算21||x dx -ò．分析被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -ò＝0210()x dx xdx--+òò＝220210[][]22x x --+＝52．注在使用牛顿－莱布尼兹公式时在使用牛顿－莱布尼兹公式时,,应保证被积函数在积分区间上满足可积条件．如应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=ò，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界积区间内无界. .例12 设()f x 是连续函数，且1()3()f x x f t dt=+ò，则()________f x =．分析本题只需要注意到定积分()baf x dx ò是常数（,a b 为常数）．解因()f x 连续，()f x 必可积，从而1()f t dt ò是常数，记1()f t dt a =ò，则，则()3f x x a =+，且110(3)()x a dx f t dt a+==òò．所以所以211[3]2x ax a +=，即132a a +=，从而14a =-，所以，所以 3()4f x x =-．例13 计算2112211x xdx x-++-ò．分析由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解 2112211x x dx x -++-ò=211112221111xx dx dx x x --++-+-òò．由于22211x x +-是偶函数，而211xx+-是奇函数，有112011xdx x-=+-ò, 于是于是2112211x xdx x -++-ò=2102411x dx x +-ò=22120(11)4x x dx x --ò=11200441dx x dx --òò 由定积分的几何意义可知12014x dx p -=ò, 故2111022444411x x dx dx xp p -+=-×=-+-òò．例14 计算220()xdtf x t dt dx -ò，其中()f x 连续．连续．分析要求积分上限函数的导数，要求积分上限函数的导数，但被积函数中含有但被积函数中含有x ，因此不能直接求导，因此不能直接求导，必须先换必须先换元使被积函数中不含x ，然后再求导．，然后再求导．解由于由于220()xtf x t dt -ò=22201()2xf x t dt -ò．故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以，所以22()xtf x t dt -ò=201()()2x f u du -ò=201()2xf u du ò，故22()xd tf x t dt dx -ò=21[()]2x d f u du dx ò=21()22f x x ×=2()xf x ．错误解答 220()xd tf x t dt dx -ò22()(0)xf x x xf =-=．错解分析这里错误地使用了变限函数的求导公式，公式这里错误地使用了变限函数的求导公式，公式()()()xa d x f t dtf x dx ¢F ==ò中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．导，而应先换元．例15 计算3sin x xdx pò．分析被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解3s i n x x d xpò3(c o s )x d x p=-ò3300[(c o s )](co s )x x x d x p p=×---ò3cos 6xdx pp=-+ò326p=-．例16 计算12ln(1)(3)x dx x +-ò．分析被积函数中出现对数函数的情形，可考虑采用分部积分法．被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-ò=101ln(1)()3x d x +-ò=1100111[ln(1)]3(3)(1)x dx x x x +-×--+ò =101111ln 2()2413dx x x-++-ò 11ln 2ln324=-．例17 计算2sin xe xdx pò．分析被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解由于2sin xe xdx pò2sin x xde p=ò22[sin ]cos xxe x e xdx p p=-ò220cos xe e xdx pp=-ò，（（1）而2cos xe xdx pò2cos xxdep=ò22[cos ](sin )xx e x e x dx pp=-×-ò2sin 1x e xdx p =-ò，（（2）将（将（22）式代入（）式代入（11）式可得）式可得2sin xe xdx pò220[sin 1]xe e xdx pp=--ò,故2sin xe xdx pò21(1)2e p=+．例18 计算1arcsin x xdx ò．分析被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdxò210arcsin ()2x xd =ò221100[arcsin ](arcsin )22x x x d x =×-ò 21021421xdx xp=--ò．（1）令sin x t =，则，则2121xdx x-ò2202sin sin 1sin t d ttp =-ò220sin cos cos t tdt t p=×ò220sin tdt p=ò201cos 22tdt p -==ò20sin 2[]24t t p-4p =．（2）将（将（22）式代入（）式代入（11）式中得）式中得10arcsin x xdx =ò8p．例19设()f x [0,]p 上具有二阶连续导数，()3f p ¢=且[()()]cos 2f x f x xdx p¢¢+=ò，求(0)f ¢．分析分析被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．解由于0[()()]cos f x f x xdx p¢¢+ò00()sin cos ()f x d x xdf x p p¢=+òò[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx pppp¢¢¢=-++òò()(0)2f f p ¢¢=--=．故 (0)f ¢=2()235f p ¢--=--=-．例20 计算2043dxx x +¥++ò．分析该积分是无穷限的的反常积分，用定义来计算．解 2043dx x x +¥++ò=20lim 43t t dx x x ®+¥++ò=0111lim ()213t t dx x x ®+¥-++ò =011lim [ln ]23t t x x ®+¥++=111lim (ln ln )233t t t ®+¥+-+ =ln 32．。

高三数学积分试题答案及解析

高三数学积分试题答案及解析1.．【答案】【解析】=.考点:定积分2.由直线y＝2与函数y＝2cos2(0≤x≤2π)的图象围成的封闭图形的面积为________．【答案】2π【解析】y＝2cos2＝cos x＋1，则所求面积为S＝dx＝(x－sin x)＝2π．3.（e x+2x）dx等于（）A．1B．e﹣1C．e D．e2+1【答案】C1=e+1﹣1=e【解析】（e x+2x）dx=（e x+x2）|故选C．4.设．若曲线与直线所围成封闭图形的面积为，则______．【答案】【解析】．5.已知通过点(1，2)，与有一个交点，交点横坐标为，且．如图所示:设与所围成的面积为S，则S取得最小值为．【答案】【解析】由通过点(1，2)可得，即，由与联立方程组，解得．则与所围成的面积S为．∵由得，由得或，所以当时，S取得极小值，即最小值．此时，最小值．6.设函数，若，则x的值为______．【答案】【解析】，又，∴．7.下列结论中正确命题的序号是（写出所有正确命题的序号）.①积分的值为2；②若，则与的夹角为钝角；③若，则不等式成立的概率是；④函数的最小值为2．【答案】①③【解析】，①正确；时，与的夹角为钝角或为，②不正确；由几何概型概率的计算公式得，时，不等式成立的概率是，③正确；，令在是减函数，在是增函数，所以，函数的无最小值，④不正确；综上知，答案为①③.【考点】定积分，平面向量的数量积，几何概型，指数函数的性质.8.已知，若，则= ( )A．1B．-2C．-2或4D．4【答案】D【解析】，即，解得，（因为），故选D.【考点】定积分基本定理9.．给出下列命题：①已知线性回归方程，当变量增加2个单位，其预报值平均增加4个单位；②在进制计算中，；③若，且，则；④ “”是“函数的最小正周期为4”的充要条件；⑤设函数的最大值为M，最小值为m，则M＋m=4027，其中正确命题的个数是个。

【解析】①由线性回归方程的意义可得结论正确；②，正确③由正态分布函数的性质可知正确；④由定积分的知识得：a=，所以根据周期公式知T=4，正确；⑤根据函数f（x）在单调递增和是一个奇函数，然后进行整体运算.【考点】（1）线性回归方程；（2）正态分布函数；（3）定积分；（4）函数的性质.10.由曲线，直线所围成封闭的平面图形的面积为（）A．B．C．D．【答案】B【解析】如图所示，由曲线与直线的交点为.方法一：则封闭的平面图形的面积为.方法二：.【考点】定积分的简单应用11.已知函数与的图象所围成的阴影部分（如图所示）的面积为，则_____.【答案】【解析】，解得.【考点】定积分的几何意义.12.由曲线xy＝1，直线y＝x，y＝3所围成的平面图形的面积为()A．B．2－ln 3C．4＋ln 3D．4－ln 3【解析】如图所示，所求面积为S＝3－d x－＝8－ln x－4＝4－ln 3，故选D.13.d x＝________.【答案】π【解析】设y＝，则x2＋y2＝4(y≥0)，由定积分的几何意义知d x的值等于半径为2的圆的面积的.∴d x＝×4π＝π.14.________．【答案】1【解析】.【考点】定积分的应用.15.设a＝，b＝，c＝，则下列关系式成立的是()．A．<<B．< <C．D．【答案】C【解析】a＝＝ln x＝ln 2，b＝＝ln x＝ln3，c＝＝ln x＝ln5，所以，，，因为，()6＝32＝9，所以，()10＝25＝32，()10＝52＝25，所以<，即<<，所以16.把函数的图像向左平移后,得到的图像,则与的图像所围成的图形的面积为( )A．4B．C．D．2【答案】D【解析】函数的图像向左平移后，得到，得交点为，，则与的图像所围成的图形的面积为．【考点】三角函数平移变化，定积分．17.若，则f（2016）等于（）A．0B．C．D．【答案】D【解析】，选D.【考点】1、分段函数及函数的周期性；2、定积分.18.= .【答案】0．【解析】因为是奇函数，所以=0．【考点】定积分的计算．19.由曲线与直线所围成的平面图形(图中的阴影部分)的面积是 .【答案】【解析】.【考点】1.积分的运算；2.利用积分求面积.20.已知，，记则的大小关系是（）A．B．C．D．【答案】C．【解析】由已知，联想到定积分的几何意义得：为在上的定积分，即为曲边梯形的面积，而梯形的面积（如图），，故选C．【考点】定积分的几何意义．21.已知为常数，则使得成立的一个充分而不必要条件是 ( )A．B．C．D．【答案】C．【解析】由已知及牛顿-莱布尼茨公式得．由已知要求选项能推出，但不能推出选项．，但不能推出，故选C．【考点】1．定积分的计算；2充分、必要、充要条件的判断．22.在平面直角坐标系中，记抛物线y＝x－与x轴所围成的平面区域为M，该抛物线与直线y ＝kx（k＞0）所围成的平面区域为A，向区域M内随机抛掷一点P，若点P落在区域A内的概率为，则k的值为__________．【答案】【解析】根据题意画出图象如图，则,，则区域的面积，区域的面积为，由题意知，化简得，解得.【考点】定积分的计算.23.已知，直线交圆于两点，则．【答案】．【解析】由定积分的几何意义可知，，圆心到直线的距离．【考点】1．定积分的计算；2．直线与圆（相交弦长公式）．24.由曲线，直线及轴所围成的图形的面积为_______．【答案】【解析】曲线y=，直线y=x-2及y轴所围成的图形如图所示，故：=.【考点】定积分的计算25.曲线，所围成的封闭图形的面积为 .【答案】【解析】曲线，的交点为，所求封闭图形面积为.【考点】曲边梯形面积.26.若，，，则从小到大的顺序为 .【答案】【解析】，，，故.【考点】微积分基本定理.27.＝．【答案】3【解析】，或画出函数的图象，可以求出它在区间与轴围成的面积是3，由定积分的几何意义知答案为3.【考点】定积分的计算、定积分的几何意义.28.曲线和曲线围成的图形面积是．【答案】【解析】解得，或，则所求面积为 .【考点】定积分29.设，则二项式展开式中的第四项为（）A．B．C．D．【答案】A【解析】∵，∴，∴，选A.【考点】微积分基本定理，二项式定理.30.在的展开式中的常数项为p，则 .【答案】11【解析】，令，即，，则.【考点】二项展开式的通项、定积分的运算.31.设函数，其中则的展开式中的系数为（）A．-360B．360C．-60D．60【答案】D【解析】令的系数为【考点】定积分函数导数与二项式定理点评：本题中涉及到的知识点较多，主要有定积分的计算（首要找到被积函数的原函数）函数求导数及二项式定理：的展开式中通项为32.设的展开式中的常数项等于 .【答案】-160【解析】所以常数项为-160.【考点】定积分；二项式定理。

高中高考考点难点常见题型(带答案解析) 定积分与微积分的基本定理(解析版)

简单已测：424次正确率：91.8 %1.定积的值是（）A.B.C.D.考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的概念、微积分基本定理答案：D 解析：，故选：．⼀般已测：3296次正确率：69.9 %2.计算（）A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：定积分的概念、定积分的⼏何意义答案：B解析：选⼀般已测：4642次正确率：87.5 %3.若,,则,,的⼤⼩关系为( )A.B.C.D.考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的基本性质、定积分的常⽤结论答案：B解析：由于,,,且,所以，故选.⼀般已测：3883次正确率：75.3 %4.若,则( )2xdx ∫0212342xdx =x =4∫202∣∣∣∣20D (1−cos x )dx =∫− 2π2ππ+2π−2π−2(1−cos x )dx=(x −sin x )∫− 2π2π =π−2.∣∣∣∣ 2π− 2πB .S = x dx 1∫122S = dx 2∫12x 1S =e dx 3∫12x S 1S 2S 3S <S <S 123S <S <S 213S <S <S 231S <S <S321S = x dx = x ∣ = − = 1∫12231312383137S = dx =lnx ∣ =ln 22∫12x 112S = e dx =e ∣ =e −e 3∫12x x 122ln 2< <e −e 372S <S <S 213B f (x )=x +2 f (x )dx 2∫01 f (x )dx=∫01A.B.C.D.考点：微积分基本定理求定积分、运⽤定积分的相关性质解题知识点：被积函数的原函数、微积分基本定理答案：B解析：令(常数),则,所以,解得,故选:.中等已测：4750次正确率：71.2 %5.在如图所⽰平⾯直⻆坐标系中,正⽅形的边⻓为,曲线是函数图象位于正⽅形内的部分,直线恰好是函数在处的切线,现从正⽅形内任取⼀点,那么点取⾃阴影部分的概率等于（）A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：曲边梯形的⾯积、定积分的⼏何意义答案：D解析：正⽅形的边⻓为,由函数,得,则,得.⼜当时,,可得,曲线的解析式为,阴影部分⾯积.点取⾃阴影部分的概率等于.故选:.−1−31 311f (x )dx =m ∫01f (x )=x +2m 2m = f (x )dx =( x +2mx ) = +2m ∫01313∣∣0131m =− 31B OABC 1m y =a (x −1)+b 2AC y=a (x −1)+b 2x =0P P1213141 61∵OABC 1,∴S =1正方形OABC y =a (x −1)+b 2y =2a (x −1)′y ∣ =−2a =−1′x =0a =21x=0y =a +b =1b = 21∴m y = (x −1)+ 21221∴S = [ (x −1)+ −(−x +1)]dx = x dx = x ∣=∫0121221∫012126130161∴P 61D⼀般已测：4665次正确率：92.6 %6.已知,则⼆项式的展开式中的系数为（）A.B.C.D.考点：利⽤定积分的性质解题、微积分基本定理求定积分知识点：定积分的概念、微积分基本定理答案：C 解析：,的展开式的通项公式为,令得,,展开式中的系数为.⼀般已测：2948次正确率：92.5 %7.实数使得复数是纯虚数,则的⼤⼩关系是（）A.B.C.D.考点：⽤定义求定积分、⽤所求定积分的⼏何意义求定积分知识点：定积分的概念、复数的概念答案：C解析：,它为纯虚数,所以,表⽰单位圆的四分之⼀的⾯积为,所以,应选.中等已测：3726次正确率：56.3 %8.若，则=（）A.B.a = dx ∫ e 1e x1(1− )x a 5x −316080−80−160∵a= dx =lne −ln =2∫ e 1e x 1e 1∴(1−)=(1−)xa 5x25T=C (−2)x r +15r r −r −r=−3r =3∴x −3C (−2)=−80533a1−i a +i b = xdx ,c= dx ∫01∫011−x 2a ,b ,c a <b <c a <c <b b <c <a c <b <a= = 1−i a +i1−i 1+i ()()a +i 1+i ()()2a −1+a +1i ()a =1,b = xdx = ∣ = ,c = dx ∫012x 20121∫011−x 2 4πb <c <a C f x + f x dx =x ()∫01() f x dx ∫01()41 21C.D.考点：⽤定义求定积分、利⽤定积分的性质解题知识点：定积分的基本性质、基本积分公式答案：A 解析：由，则，则，，则，故选A ．⼀般已测：2708次正确率：72.5 %9.⼀个⼈骑⻋以⽶/秒的速度匀速追赶停在交通信号灯前的汽⻋,当他离汽⻋⽶时，交通信号灯由红变绿,汽⻋开始做变速直线⾏驶(汽⻋与⼈的前进⽅向相同),若汽⻋在时刻的速度⽶/秒，那么此⼈（）．A.可在秒内追上汽⻋B.不能追上汽⻋,但其间最近距离为⽶C.不能追上汽⻋,但其间最近距离为⽶D.不能追上汽⻋,但其间最近距离为⽶考点：⼆次函数的单调性、利⽤定积分的⼏何意义解题知识点：微积分基本定理、基本积分公式答案：D解析：设该⼈骑⻋⾏驶距离和汽⻋⾏驶距离的差为，则，所以，所以该⼈不能追上汽⻋，但其间最近距离为⽶⼀般已测：391次正确率：82.7 %10.甲、⼄两⼈从同⼀起点出发按同⼀⽅向⾏⾛，已知甲、⼄⾏⾛的速度与⾏⾛的时间分别为，(如图)，当甲⼄⾏⾛的速度相同(不为零)时刻( )A.甲⼄两⼈再次相遇B.甲⼄两⼈加速度相同12fx +f x dx =x ()∫01()f x =x − f x dx ()∫01() fx dx = x − f x dx dx∫01()∫01(∫01())= xdx − f x dx dx = − f x dx ∫01∫01[∫01()]21∫01()∴ f x dx = − f x dx ∫01()21∫01() f x dx =∫01()41625t v (t )=t 716147S (t )S (t )= 6−t dt =6t −t ∫0t()212S (t ) =S (6)=36−18=18max 7v =甲t v =t 乙2C.甲在⼄前⽅D.⼄在甲前⽅考点：微积分基本定理求定积分、运⽤定积分的相关性质解题知识点：定积分的物理意义、变速运动问题答案：C解析：由，得，解得(舍)，或．由．．所以当甲⼄⾏⾛的速度相同(不为零)时刻甲在⼄前⽅．故选：．中等已测：1818次正确率：73.8 %11.已知，若函数满⾜，则称为区间上的⼀组``等积分''函数，给出四组函数：①②；③；④函数分别是定义在上的奇函数且积分值存在.其中为区间上的“等积分”函数的组数是( )A.B.C.D.考点：利⽤定积分的⼏何意义解题、微积分基本定理求定积分知识点：定积分的基本性质、微积分基本定理答案：C解析：本题是新定义问题，主要考查对定义的理解和定积分的计算.对于①，⽽,所以①是⼀组“等积分”函数；对于②，,⽽,所以②不是⼀组``等积分''函数；对于③，函数的图像是以原点为圆⼼，为半径的半圆，故,⽽,所以③是⼀组``等积分''函数；对于④，由于函数分别是定义在上的奇函数且积分值存在，利⽤奇函数的图像关于原点对称和定积分的⼏何意义，可以求得函数的定积分,所以④是⼀组``等积分''函数.故选.简单已测：3293次正确率：86.3 %12..v =v 甲乙 =t t 2t =0t =1 dt = t ∣ = ∫01t 32 230132 t dt = t ∣= ∫0123130131C a <b f (x ),g (x ) f (x )dx = g (x )dx ∫a b∫a bf (x ),g (x )[a ,b ]f (x )=2∣x ∣,g (x )=x +1;f (x )=sinx ,g (x )=cosx f (x )=,g (x )= πx 1−x 2432f (x ),g (x )[−1,1][−1,1]1234f x dx = 2x dx = 2−x dx + 2xdx =2,∫−11()∫−11∣∣∫−10()∫01g x dx = x +x ∣ =2∫−11()(212)−11 f (x )dx = sinxdx =0∫−11∫−11 g x dx = cos xdx =2sin 1≠0∫−11()∫−11f (x )1 f x dx = dx = ∫−11()∫−111−x 22πg x dx = πx ∣ = ∫−11()413−112πf (x ),g (x )[−1,1] f (x )dx = g x dx =0∫−11∫−11()C (sinx +cosx )dx =∫− 2π2π考点：⽤定义求定积分、微积分基本定理求定积分知识点：定积分的概念、被积函数的原函数答案：解析：；故填.⼀般已测：4543次正确率：94.5 %13..考点：利⽤定积分的⼏何意义解题知识点：定积分的概念、定积分的⼏何意义答案：解析：函数即：，表⽰以为圆⼼，为半径的圆在轴上⽅横坐标从到的部分，即四分之⼀圆，结合定积分的⼏何意义可得．故答案为．⼀般已测：2478次正确率：65.4 %14.⼀辆汽⻋在⾏驶中由于遇到紧急情况⽽刹⻋，以速度⾏驶⾄停⽌，在此期间汽⻋继续⾏驶的距离是.考点：定积分在求⾯积中的应⽤、微积分基本定理求定积分知识点：定积分的物理意义、基本积分公式答案：解析：本题考查定积分的概念.令，化为,⼜,解得.汽⻋继续⾏驶的距离.⼀般已测：4698次正确率：91.6 %15.若正实数满⾜,则的最⼩值为.考点：利⽤基本不等式求最值、利⽤公式求定积分知识点：定积分的基本性质、基本积分公式答案：解析：由题意得;即,所以(当且仅当时等号成⽴).所以,即的最⼩值为.简单已测：1192次正确率：87.8 %16.有⼀⾮均匀分布的细棒，已知其线密度为，棒⻓为，则细棒的质量.考点：⽤定义求定积分、微积分基本定理求定积分2(sinx +cosx )dx =−cosx +sinx ∣ ∫− 2π 2π()−2π2π=1+1=22 ( )dx ∫121−(x −1)2=4πy=1−(x −1)2(x −1)+y =1(x ≥1,y ≥0)22(1,0)1x 12 ( )dx = ×π×1=∫121−(x −1)24124π 4πv (t )=7−3t +1+t 254+25ln 5v (t )=7−3t + =01+t253t −4t −32=02t >0t =4S = (7−3t + )dt =(7t − t +25ln (1+t ))∣ =4+25ln 5∫041+t 2523204m ,n + = (x +)dx m 2n 1∫−22π14−x 2log (m +2n )22(x + )dx = dx = × π×2=2∫−22π14−x 2π1∫−224−x 2π1212 + =2m 2n 1m +2n =(m +2n )( + )= + +2≥2 +2=4m 12n 1m 2n 2n m × m 2n 2n m m =2n log m +2n ≥log 4=22()2log (m +2n )22ρx =x ()32M =(1)(2)知识点：定积分的物理意义、定积分的常⽤结论答案：解析：依题意有：.⼀般已测：3051次正确率：65.2 %17.在区间上给定曲线.试在此区间内确定点的值,使图中的阴影部分的⾯积与之和最⼩,并求最⼩值．考点：导数在最⼤值、最⼩值问题中的应⽤、定积分在求⾯积中的应⽤知识点：利⽤导数求函数的最值、微积分基本定理答案：时,最⼩,且最⼩值为解析：⾯积等于边⻓分别为与的矩形⾯积去掉曲线与轴、直线所围成的⾯积,即.的⾯积等于曲线与轴,,围成的⾯积去掉矩形边⻓分别为,⾯积,即.所以阴影部分的⾯积．令,得或.时,；时,；时,.所以当时,最⼩,且最⼩值为.⼀般已测：401次正确率：92.8 %18.已知．求的单调区间；求函数在上的最值．考点：利⽤导数研究函数的单调性、利⽤导数求闭区间上函数的最值知识点：函数单调性和导数的关系、利⽤导数求函数的最值(1)答案：单调调增区间是,单调递减区间是．解析：依题意得,,定义域是．,令,得或；令得,且函数定义域是,函数的单调增区间是,单调递减区间是．(2)答案：最⼤值是,最⼩值是．解析：由(1)知函数在区间上为减函数,区间上为增函数, 且,在上的最⼤值是,最⼩值是．4x dx= ∣ =4∫0234x 402[0,1]y =x 2t S 1S 2t=21S (t )41S 1t t 2y =x 2x x =t S =t ⋅t − x dx = t 12∫0t 2323S 2y =x 2x x =t x =1t 21−t S = x dx −t (1−t )= t −t + 2∫t 122323231S (t )=S +S = t −t + (0≤t ≤1)12343231S (t )=4t −2t =4t (t − )=0′221t =0t = 21t =0S (t )= 31t = 21S (t )= 41t =1S (t )= 32t = 21S (t )41F (x )= (t +2t −8)dt ,(x >0)∫0x2F (x )F (x )[1,3](2,+∞)(0,2)F (x )= (t +2t −8)dt =( t +t−8t )∣ = x +x −8x ∫0x 231320x 3132(0,+∞)(1)F (x )=x +2x −8′2F (x )>0′x >2x <−4F (x )<0,′−4<x <2(0,+∞)∴F (x )(2,+∞)(0,2)F (3)=−6F (2)=− 328F (x )(0,2)(2,3)F (1)=− ,F (2)=− ,F (3)=−6320328∴F (x )[1,3]F (3)=−6F (2)=− 328(1)(2)中等已测：3275次正确率：52.7 %19.已知⼆次函数，直线，直线(其中，为常数)，若直线,与函数的图象以及,、轴与函数的图象所围成的封闭图形(阴影部分)如图所⽰.求,,的值；求阴影⾯积关于的函数的解析式.考点：求函数解析式的常⽤⽅法、利⽤定积分的⼏何意义解题知识点：⼆次函数的解析式、⼆次函数的图象(1)答案：, , 解析：由图形可知⼆次函数的图象过点，，并且的最⼤值为，则解得，函数的解析式为.(2)答案：解析：由得,,,,直线与的图象的交点坐标为由定积分的⼏何意义知：.f (x )=ax +bx +c 2l :x =21l :y =−t +8t 220≤t ≤2t l 1l 2f (x )l 1l 2y f (x )a b c S t S (t )a=−1b =8c =0(0,0)(8,0)f (x )16 ⎩⎨⎧c =0,a ⋅8+b ⋅8+c =02=164a 4ac −b 2 ⎩⎨⎧a =−1b =8c =0∴f (x )f (x )=−x +8x 2S (t )=− t +10t −16t + 3432340{ y =−t +8t 2y =−x +8x2x −8x −t (t −8)=02∴x =t 1x =8−t 2∵0≤t ≤2∴l 2f (x )(t ,−t +8t )2S (t )= −t +8t −−x +8x dx + [(−x +8x )−(−t +8t )]dx ∫0t [(2)(2)]∫t 222=[(−t +8t )x −(− +4x )]∣ +[(− +4x )−(−t +8t )x ]∣ 23x 320t 3x 322t 2=− t +10t −16t + 3432340。

定积分应用方法总结(经典题型归纳)

定积分复习重点定积分的考查频率不是很高，本讲复习主要掌握定积分的概念和几何意义，使用微积分基本定理计算定积分，使用定积分求曲边图形的面积和解决一些简单的物理问题等． 1.定积分的运算性质1212(1)()()().(2)[()()]()().(3)()()()().bbaab bb aaab c baackf x dx k f x dx k f x f x dx f x dx f x dx f x dx f x dx f x dx =±=±=+⎰⎰⎰⎰⎰⎰⎰⎰为常数其中a<c<b2．微积分基本定理如果()f x 是区间[a ，b]上的连续函数，并且'()()F x f x =，那么()()()baf x dx F b F a =-⎰，这个结论叫微积分基本定理，又叫牛顿—莱布尼兹公式。

3.求定积分的方法（1）利用微积分基本定理就定积分 ①对被积分函数,先简化,再求定积分.例如：230(1-2sin)2d πθθ⎰注：322()3x x '=，(-cos )sin x x '=②分段函数,分段求定积分,再求和.（被积函数中带有绝对值符号时，计算的基本思路就是用分段函数表示被积函数，以去掉绝对值符号，然后应用定积分对积分区间的可加性，分段进行计算）1．计算积分⎰---322|32|dx x x解1. 由于在积分区间]3,2[-上，被积函数可表示为⎩⎨⎧≤<-----≤≤---=--.31,)32(,12,32|32|222x x x x x x x x 所以⎰---322|32|dx x x 13)32()32(312122=-----=⎰⎰---dx x x dx x x .（2）利用定积分的几何意义求定积分如定积分12014x dx π-=⎰，其几何意义就是单位圆面积的14。

（课本P60 B 组第一题） (3)利用被积函数的奇偶性a. 若()f x 为奇函数，则()0aa f x dx -=⎰；b. 若()f x 为偶函数，则0()()a aa f x dx f x dx-=⎰⎰2；其中0a >。

定积分的例题分析及解法

定积分的例题分析及解法本章的基本内容是定积分的概念、计算和应用一、定积分的概念1．定积分是下列和式的极限xi i f dx x f i nba∆∑==→⎰)(lim )(10ξλ其中{}xi ni ∆=≤≤1max λ因此，定积分是一个数，它依赖于被积函数)(x f 和积分区间〔a,b 〕定积分与积分变量用什么字母无关：⎰⎰=babadt t f dx x f )()(定积分的几何意义是曲边梯形的面积（当被积函数0)(≥x f 时）。

2．定积分的性质（1）线性性质[]⎰⎰⎰+=+bab abadx x g k dx x f k dx x g k x f k)()()()(2121（2） ⎰⎰⎰=-=aaabba dx x f dx x f dx x f 0)(,)()( （3） ⎰⎰⎰+=bccaba dx x f dx x f dx x f )()()(（4）若),()(x g x f ≥则⎰⎰≥babadx x g dx x f )()(（5）积分中值定理：设)(x f 在〔a,b 〕上连续，则在〔a,b 〕上至少存在一点ξ，使下式成立),()()(a b f dx x ba-=⎰ξ其中].[b a ∈ξ。

（6）估值定理：若)(x f 在〔a,b 〕上可积，且M x f m ≤≤)(，则有不等式⎰-≤≤-baa b M dx x f a b m )()()(（7）若函数)(x f 在〔a,b 〕上连续，则有⎰=xa x f dt t f dxd )()( 3．广义积分。

二、定积分的计算 1．牛顿—莱布尼茨公式：⎰-=baa Fb F dx x f )()()(2．换元法：注意，在换元的同时不要忘记换积分限 3．分部积分法：⎰⎰-=babab a x du x x x u x d x u )()()()()()(υυυ4．定积分的近似计算：梯形，抛物线法。

三、定积分的应用基本方法是：（1）代公式；（2）微元法1．平面图形的面积（1）直角坐标系。

高中数学试题微积分的应用与题型解析

高中数学试题微积分的应用与题型解析*正文*高中数学试题微积分的应用与题型解析微积分是数学中重要的分支之一，它的应用广泛涉及到各个领域，尤其在高中阶段的教育中，微积分的学习成为了学生的必修内容之一。

本文将探讨高中数学试题中微积分的应用，并对常见的微积分题型进行解析。

一、定积分的应用定积分是微积分中的关键概念之一，它在数学问题的解决中具有重要的应用。

其中，定积分在求解物体的面积、体积、曲线长度等问题中常常发挥着重要作用。

以下是几个常见的应用题型：1. 面积问题题目：已知函数$f(x)$在区间$[a,b]$上连续，其图像与$x$轴围成的图形的面积为$S$，求$S$的表达式。

解析：根据定积分的定义，该题可表示为$\int_a^b |f(x)| dx$。

根据题目中的条件，将函数$f(x)$的图像划分为正负两个部分，分别计算定积分得到的面积，再取绝对值求和即可得到最终答案。

2. 体积问题题目：已知曲线$y=f(x)$在区间$[a,b]$上连续，将其绕$x$轴旋转一周形成一个旋转体，求旋转体的体积。

解析：根据定积分的应用，该题可表示为$\pi\int_a^b [f(x)]^2 dx$。

将曲线$y=f(x)$绕$x$轴旋转一周，可以得到一个旋转体，利用定积分计算旋转体的截面面积，并对其进行累加，最终得到旋转体的体积。

二、无穷积分与级数无穷积分和级数是微积分领域中的另两个重要概念，在高中数学试题中也经常涉及到。

以下是几个常见的应用题型：1. 平面曲线与曲线下的面积题目：已知函数$f(x)$在区间$[a,+\infty)$上连续且大于等于零，求曲线$y=f(x)$与$x$轴所围成的图形的面积。

解析：根据无穷积分的定义，该题可表示为$\int_a^{+\infty} f(x)dx$。

由于区间为无穷大，我们需要先判断积分的收敛性。

若积分收敛，则利用定积分的方法计算出积分的值；若积分发散，则无法计算出面积。

2. 级数求和题目：计算级数$\sum_{n=1}^{+\infty} \frac{1}{n^2}$的和。

专题17：定积分求值(解析版)

专题17：定积分求值（解析版）1．定积分的概念设函数()f x 在区间[,]a b 上连续，则()1()lim nbi an i b af x dx f nξ→∞=-=∑⎰2.用定义求定积分的一般方法是：①分割：n 等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和：1()ni i b a f n ξ=-∑；④取极限：()1()lim n b i a n i b af x dx f n ξ→∞=-=∑⎰ 3.曲边图形面积：()()0,baf x S f x dx ≥=⎰；()()0,ba f x S f x dx <=-⎰在x 轴上方的面积取正，下方的面积取负变速运动路程21()t t S v t dt =⎰；变力做功 ()baW F r dr =⎰4．定积分的性质性质1 ⎰⎰=baba dx x f k dx x kf )()( （其中k 是不为0的常数）性质21212[()()]()()bb baaaf x f x dx f x dx f x dx ±=±⎰⎰⎰性质3 ()()()()b c baacf x dx f x dx f x dxa cb =+<<⎰⎰⎰其中（定积分对积分区间的可加性）5.定理函数()F x 是[,]a b 上()f x 的一个原函数，即()()f x F x '=则()()|()()bb a af x dx F x F b F a ==-⎰一、单选题1．函数()2xf x x e =+在[]01，上的定积分为（） A ．e +2 B ．e +1 C ．e D ．e -1【答案】C 【分析】根据微积分基本定理进行计算可得结果. 【详解】1(2)xx edx +⎰212200()(1)(0)11x x e e e e e =+=+-+=+-=,故选：C2．曲线sin y x =，[0,2]x π与x 轴所围成的面积是（）A ．0B ．2C ．4D ．π【答案】C 【分析】根据积分的几何意义化为求20sin (sin )S xdx x dx πππ=+-⎰⎰可得结果.【详解】曲线sin y x =，[0,2]x π与x 轴所围成的面积20sin (sin )S xdx x dx πππ=+-⎰⎰20cos cos x xπππ=-+(cos cos0)cos 2cos πππ=--+-(11)1(1)=---+-- 4=.故选：C 【点睛】结论点睛：由上下两条连续曲线2()y f x 与1()y f x =及两条直线x a =与x b =()b a >所围成的平面图形的面积为[]21()()baS f x f x dx =-⎰.3．()324xdx +=⎰ （）A ．9B ．12C ．21D ．25【答案】C 【分析】直接利用定积分的运算求解. 【详解】()332333001114434304021333|⎛⎫+=+=⨯+⨯-⨯+⨯= ⎪⎝⎭⎰x dx x x 故选:C 【点睛】本题主要考查定积分的计算，属于基础题.4．计算2cos xdx π⎰的值为（）A ．－1B ．0C ．1D ．π【答案】C 【分析】利用微积分基本定理即可得答案. 【详解】220cos =sin x |=sin-sin 0=12xdx πππ⎰,故选：C 【点睛】本题主要考查了微积分基本定理，属于基础题.5．如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为A ．14B ．15C ．16D ．17【答案】C 【解析】试题分析：由三角形面积为12，312022|33xdx x ==⎰，所以阴影部分面积为211326-=，所求概率为11616P ==考点：定积分及几何概型概率6．如图，抛物线的方程是21y x =-，则阴影部分的面积是（）A ．()221xdx -⎰B ．()221xdx -⎰C ．221x dx -⎰D ．()()12220111xdx x dx ---⎰⎰【答案】C 【分析】微积分基本定理的几何意义可得答案. 【详解】由微积分基本定理的几何意义可得图中阴影部分的面积为122201(1)(1)x dx x dx -+-⎰⎰220|1|x dx =-⎰.故选：C 【点睛】本题考查了微积分基本定理的几何意义，属于基础题. 7．如图，阴影部分的面积是（）A ．3B ．23C ．323D ．353【答案】C 【分析】运用定积分的性质可以求出阴影部分的面积. 【详解】设阴影部分的面积为S，则12321323311132 [(3)2](3)(31)[3(3)(3)(3)]3333 S x x dx x x x--=--=--=---⨯--⨯---=⎰.选C【点睛】考查了定积分在几何学上的应用，考查了数学运算能力.8．224x dx-⎰　＝（）A．πB．2πC．3πD．4π【答案】A【分析】利用定积分的几何意义即可求解．【详解】令24y x=-14圆的面积，故所求定积分的值为2124ππ⨯⨯=【点睛】本题考查定积分的几何意义，属基础题．二、填空题9．()121x dx-+=⎰__________.【答案】23【分析】直接利用微积分的基本定理求解. 【详解】()11230012133|xdx x x ⎛⎫-+=-+= ⎪⎝⎭⎰，故答案为：2310．正弦函数sin y x =在0,3π⎡⎤⎢⎥⎣⎦上的图象与x 轴所围成曲边梯形的面积为______. 【答案】12【分析】由题意可知，30sin S xdx π=⎰，再根据定积分的运算法则求解即可．【详解】解：33001sin cos |cos cos 032S xdx x πππ⎛⎫==-=--= ⎪⎝⎭⎰．故答案为：12．【点睛】本题考查定积分在求不规则图形面积上的应用，熟练掌握定积分的运算法则是解题的关键，考查学生的运算能力，属于基础题．11．11edx x⎰2-+⎰＝________.【答案】21π+ 【分析】根据1(ln )x x'=以及定积分的几何意义可得答案. 【详解】11edx x⎰=ln 1e x ln ln1101e =-=-=，因为2-⎰表示的是圆224x y +=在x 轴及其上方的面积，所以2-⎰21222ππ=⨯⨯=，所以11edx x⎰2224x dx -+-⎰＝12π+.故答案为：21π+. 【点睛】本题考查了定积分的计算，考查了定积分的几何意义，属于基础题.12．设2101()cos 0x x f x x x ⎧⎪-≤≤=⎨<⎪⎩，，，则12()f x dx π-=⎰________.【答案】14π+ 【解析】【分析】由题意得，112022()cos 1f x dx xdx x dx ππ--=+-⎰⎰⎰，根据定积分的几何意义可知，可得1201x dx -⎰表示的是四分之一的圆的面积，再根据微积分基本定理，可求2cos xdx π-⎰，最后相加即可得到结果. 【详解】由题意得，112022()cos 1f x dx xdx x dx ππ--=+-⎰⎰⎰，根据定积分的几何意义可知，1201x dx -⎰表示的是在x 轴上方的半径为1的四分之一圆的面积，如图（阴影部分）：故14π=，又022cos sin |sin 0sin()12xdx x πππ--==--=⎰，所以10022()cos 14f x dx xdx πππ--=+=+⎰⎰.所以本题答案为14π+. 【点睛】本题考查微积分基本定理和定积分的几何意义，利用定积分准确表示封闭图形的面积并正确计算是解答的关键，属基础题.三、解答题13．计算下列定积分：（1）502d x x ⎰；（2）120(2)d x x x -⎰；（3）220(42)(4)d x x x --⎰；（4）22123d x x x x+-⎰．【答案】（1）25；（2）23-；（3）403；（4）73ln 22- 【分析】(1)直接得出其原函数计算定积分可得答案； (2)直接得出其原函数计算定积分可得答案；(3)将积分中的括号展开，可求得其原函数，进而计算定积分可得答案； (4)将积分中分式整理为32x x+-，求出其原函数计算定积分可得答案. 【详解】（1）52500225025x dx x==-=⎰．（2）()11122312100000112221333x x dx x dx x dx x x -=-=-=-=-⎰⎰⎰．（3）()()()222232342000414042416842164323x xdx x xx dx x x x x ⎛⎫--=--+=--+= ⎪⎝⎭⎰⎰．（4）2222211123317223ln 3ln222x x dx x dx x x x x x +-⎛⎫⎛⎫=+-=+-=- ⎪ ⎪⎝⎭⎝⎭⎰⎰．【点睛】本题主要考查的是定积分的简单计算，题型较为简单，在平时的学习中应熟练掌握. 14．（1）求曲线3231y x x =-+在(2,3)-处的切线方程；（2）计算定积分221x e x dx -⎰.【答案】（1）3y =-；（2）273e e --．【分析】（1）求导后根据导数的几何意义求解即可；（2）直接根据定积分的定义求解．【详解】解：（1）∵3231y x x =-+， ∴236y x x '=-， ∴212120x y ==-='， ∴切线平行于x 轴，∴曲线3231y x x =-+在点(2,3)-处的切线方程为3y =-；（2）22231113x x e x dx e x ⎛⎫-=- ⎪⎝⎭⎰22817333e e e e ⎛⎫=---=-- ⎪⎝⎭．【点睛】本题主要考查导数的几何意义与定积分的求法，属于基础题．15．求由抛物线243y x x =-+-与它在点A （0，－3）和点B(3，0)的切线所围成的区域的面积。

有关定积分问题的常见题型解析(全题型)Word版

有关定积分问题的常见题型解析题型一利用微积分基本定理求积分例1、求下列定积分：（1）()13031x x dx -+⎰ （2）()941x x dx +⎰ （3）⎰--2224x分析：根据求导数与求原函数互为逆运算，找到被积函数得一个原函数，利用微积分基本公式代入求值。

解：（1）因为3221312x x x x x '⎛⎫-+=-+ ⎪⎝⎭，所以()13031x x dx -+⎰=321102x x x ⎛⎫-+ ⎪⎝⎭=32。

（2）因为()121x x x x +=+，312222132x x x x '⎛⎫+=+ ⎪⎝⎭，所以()941x x dx +⎰=3229211454326x x ⎛⎫+= ⎪⎝⎭。

练习：（1）⎰--a a x a 22 （2）⎰--2124x评注：利用微积分基本定理求定积分dx x f a b )(⎰的关键是找出)()(/x f x F =的函数)(x F 。

如果原函数不好找，则可以尝试找出画出函数的图像，图像为圆或者三角形则直接求其面积。

题型二利用定积分求平面图形的面积例2 如图，求直线y=2x+3与抛物线y=x 2所围成的图形面积。

分析：从图形可以看出，所求图形的面积可以转化为一个梯形与一个曲边梯形面积的差，进而可以用定积分求出面积。

为了确定出被积函数和积分和上、下限，我们需要求出两条曲线的交点的横坐标。

解：由方程组⎩⎨⎧=+=232x y x y ，可得3,121=-=x x 。

故所求图形面积为：S ＝()dx x ⎰-+3132－dx x ⎰-312＝（x 2＋3x）3323113313=---x 。

关键环节：①认定曲边梯形，选定积分变量；②确定被积函数和积分上下限。

大专院校高等数学课程中定积分概念及微积分基本定理常见题型解析

大专院校高等数学课程中定积分概念及微积分基本定理常见题型解析
摘要: 针对高职院校开设高等数学课程中定积分概念及微积分基本定理常见题型给出了相应的解题思路分析。

关键词: 定积分;常见题型; 解题思路
文献标志码: A
微积分是高职院校高等数学课程中的主要内容，微积分运算能力是学生学习高等数学后
应该具备的一种核心能力，而定积分是微积分中的重要内容。

本文就定积分概念及微积分基本定理常见题型给出了相应的解题思路。

例 1 求数列极限
解本题主要考察的是利用定积分的定义计算数列的极限
将均分成个小区间：.在每一个小区间上，取右端点，求函数在右端点的函数值与区间长度的乘积，并做和式，可得
例2 求定积分的值
解本题主要考察的是定积分的几何意义.
令，因此表示四分之一圆的面积.
=
例3 估计定积分的大小
解因为当时，，由此有
于是估计值为
例4求函数的单调递减开区间．
解，令得，解之得，即为所求．
例5求
解===
==．
参考文献
[1]李继猛．定积分应用中微元分析法探讨［J］．科学技术创新，2021，
19( 4) : 67－68.
[2]李灵晓，黄元元.不定积分概念探析与思考［J］．高等数学研究，2022,25（6）：1-3+29.
[3]刘彩云,蒋诗泉,张涛,汪涛波.高等数学教学中课程思政的探索与思考——以定积分的概念为例［J］．铜陵学院学报，2022，21（05）：115-118.。

高考定积分应用常见题型大全(含答案)

高考定积分应用常见题型大全（含答案）一．选择题（共21小题）1．（2012•福建）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）A．B．C．D．2．（2010•山东）由曲线y=x2，y=x3围成的封闭图形面积为（）A．B．C．D．3．设f（x）=，函数图象与x轴围成封闭区域的面积为（）A．B．C．D．4．定积分的值为（）A．B．3+ln2 C．3﹣ln2 D．6+ln25．如图所示，曲线y=x2和曲线y=围成一个叶形图（阴影部分），其面积是（）A．1B．C．D．6．=（）A．πB．2C．﹣πD．47．已知函数f（x）的定义域为[﹣2，4]，且f（4）=f（﹣2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，则平面区域f（2a+b）＜1（a≥0，b≥0）所围成的面积是（）A．2B．4C．5D．8 8．∫01e x dx与∫01e x dx相比有关系式（）A．∫01e x dx＜∫01e x dx B．∫01e x dx＞∫01e x dxC．（∫01e x dx）2=∫01e x dx D．∫01e x dx=∫01e x dx9．若a=，b=，则a与b的关系是（）A．a＜b B．a＞b C．a=b D．a+b=0 10．的值是（）A．B．C．D．11．若f（x）=（e为自然对数的底数），则=（）A．+e2﹣e B．+eC．﹣e2+eD．﹣+e2﹣e12．已知f（x）=2﹣|x|，则（）A．3B．4C．3.5 D．4.513．设f（x）=3﹣|x﹣1|，则∫﹣22f（x）dx=（）A．7B．8C．7.5 D．6.5 14．积分=（）A．B．C．πa2D．2πa215．已知函数的图象与x轴所围成图形的面积为（）A．1/2 B．1C．2D．3/2A．4B．C．D．2π17．曲线y=x3在点（1，1）处的切线与x轴及直线x=1所围成的三角形的面积为（）A．B．C．D．18．图中，阴影部分的面积是（）A．16 B．18 C．20 D．2219．如图中阴影部分的面积是（）A．B．C．D．20．曲线与坐标轴围成的面积是（）A．B．C．D．21．如图，点P（3a，a）是反比例函y=（k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）A．y=B．y=C．y=D．y=高考定积分应用常见题型大全（含答案）参考答案与试题解析一．选择题（共21小题）1．（2012•福建）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）A．B．C．D．考点：定积分在求面积中的应用；几何概型．专题：计算题．分析：根据题意，易得正方形OABC的面积，观察图形可得，阴影部分由函数y=x与y=围成，由定积分公式，计算可得阴影部分的面积，进而由几何概型公式计算可得答案．解答：解：根据题意，正方形OABC的面积为1×1=1，而阴影部分由函数y=x与y=围成，其面积为∫01（﹣x）dx=（﹣）|01=，则正方形OABC中任取一点P，点P取自阴影部分的概率为=；故选C．点评：本题考查几何概型的计算，涉及定积分在求面积中的应用，关键是正确计算出阴影部分的面积．2．（2010•山东）由曲线y=x2，y=x3围成的封闭图形面积为（）A．B．C．D．考点：定积分在求面积中的应用．专题：计算题．分析：要求曲线y=x2，y=x3围成的封闭图形面积，根据定积分的几何意义，只要求∫01（x2﹣x3）dx即可．解答：解：由题意得，两曲线的交点坐标是（1，1），（0，0）故积分区间是[0，1]所求封闭图形的面积为∫01（x2﹣x3）dx═，故选A．点评：本题考查定积分的基础知识，由定积分求曲线围成封闭图形的面积．3．设f（x）=，函数图象与x轴围成封闭区域的面积为（）考点：分段函数的解析式求法及其图象的作法；函数的图象；定积分在求面积中的应用．专题：计算题；数形结合．分析：利用坐标系中作出函数图象的形状，通过定积分的公式，分别对两部分用定积分求出其面积，再把它们相加，即可求出围成的封闭区域曲边图形的面积．解答：解：根据题意作出函数的图象：根据定积分，得所围成的封闭区域的面积S=故选C点评：本题考查分段函数的图象和定积分的运用，考查积分与曲边图形面积的关系，属于中档题．解题关键是找出被积函数的原函数，注意运算的准确性．4．定积分的值为（）A．B．3+ln2 C．3﹣ln2 D．6+ln2考点：定积分；微积分基本定理；定积分的简单应用．专题：计算题．分析：由题设条件，求出被积函数的原函数，然后根据微积分基本定理求出定积分的值即可．解答：解：=（x2+lnx）|12=（22+ln2）﹣（12+ln1）=3+ln2故选B．点评：本题考查求定积分，求解的关键是掌握住定积分的定义及相关函数的导数的求法，属于基础题．5．如图所示，曲线y=x2和曲线y=围成一个叶形图（阴影部分），其面积是（）考点：定积分；定积分的简单应用．专题：计算题．分析：联立由曲线y=x2和曲线y=两个解析式求出交点坐标，然后在x∈（0，1）区间上利用定积分的方法求出围成的面积即可．解答：解：联立得，解得或，设曲线与直线围成的面积为S，则S=∫01（﹣x2）dx=故选：C点评：考查学生求函数交点求法的能力，利用定积分求图形面积的能力．6．=（）A．πB．2C．﹣πD．4考点：微积分基本定理；定积分的简单应用．专题：计算题．分析：由于F（x）=x2+sinx为f（x）=x+cosx的一个原函数即F′（x）=f（x），根据∫a b f（x）dx=F（x）|a b公式即可求出值．解答：解：∵（x2++sinx）′=x+cosx，∴（x+cosx）dx=（x2+sinx）=2．故答案为：2．点评：此题考查学生掌握函数的求导法则，会求函数的定积分运算，是一道基础题．7．已知函数f（x）的定义域为[﹣2，4]，且f（4）=f（﹣2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，则平面区域f（2a+b）＜1（a≥0，b≥0）所围成的面积是（）考点：定积分的简单应用．分析：根据导函数的图象，分析原函数的性质或作出原函数的草图，找出a、b满足的条件，画出平面区域，即可求解．解答：解：由图可知[﹣2，0）上f′（x）＜0，∴函数f（x）在[﹣2，0）上单调递减，（0，4]上f′（x）＞0，∴函数f（x）在（0，4]上单调递增，故在[﹣2，4]上，f（x）的最大值为f（4）=f（﹣2）=1，∴f（2a+b）＜1（a≥0，b≥0）⇒表示的平面区域如图所示：故选B．点评：本题考查了导数与函数单调性的关系，以及线性规划问题的综合应用，属于高档题．解决时要注意数形结合思想应用．8．∫01e x dx与∫01e x dx相比有关系式（）A．∫01e x dx＜∫01e x dx B．∫01e x dx＞∫01e x dxC．（∫01e x dx）2=∫01e x dx D．∫01e x dx=∫01e x dx考点：定积分的简单应用；定积分．专题：计算题．分析：根据积分所表示的几何意义是以直线x=0，x=1及函数y=e x或y=e x在图象第一象限内圆弧与坐标轴围成的面积，只需画出函数图象观察面积大小即可．解答：解：∫01e x dx表示的几何意义是以直线x=0，x=1及函数y=e x在图象第一象限内圆弧与坐标轴围成的面积，∫01e x dx表示的几何意义是以直线x=0，x=1及函数y=e x在图象第一象限内圆弧与坐标轴围成的面积，如图∵当0＜x＜1时，e x x＞e x，故有：∫01e x dx＞∫01e x dx点评：本题主要考查了定积分，定积分运算是求导的逆运算，解题的关键是求原函数，也可利用几何意义进行求解，属于基础题．9．若a=，b=，则a与b的关系是（）A．a＜b B．a＞b C．a=b D．a+b=0考点：定积分的简单应用．专题：计算题．分析：a==（﹣cosx）=（﹣cos2）﹣（﹣cos）=﹣cos2≈sin24.6°，b==sinx=sin1﹣sin0=sin1≈sin57.3°．解答：解：∵a==（﹣cosx）=（﹣cos2）﹣（﹣cos）=﹣cos2≈﹣cos114.6°=sin24.6°，b==sinx=sin1﹣sin0=sin1≈sin57.3°，∴b＞a．故选A．点评：本题考查定积分的应用，是基础题．解题时要认真审题，仔细解答．10．的值是（）A．B．C．D．考点：定积分的简单应用．专题：计算题．分析：根据积分所表示的几何意义是以（1，0）为圆心，1为半径第一象限内圆弧与抛物线y=x2在第一象限的部分坐标轴围成的面积，只需求出圆的面积乘以四分之一与抛物线在第一象限的部分与x轴和直线x=1围成的图形的面积即可．解答：解；积分所表示的几何意义是以（1，0）为圆心，1为半径第一象限内圆弧与抛物线y=x2在第一象限的部分坐标轴围成的面积，故只需求出圆的面积乘以四分之一与抛物线在第一象限的部分与x轴和直线x=1围成的图形的面积之差．故答案选A点评：本题主要考查了定积分，定积分运算是求导的逆运算，解题的关键是求原函数，也可利用几何意义进行求解，属于基础题11．若f（x）=（e为自然对数的底数），则=（）A．+e2﹣e B．+eC．﹣e2+eD．﹣+e2﹣e考点：定积分的简单应用．专题：计算题．分析：由于函数为分段函数，故将积分区间分为两部分，进而分别求出相应的积分，即可得到结论．解答：解：===故选C．点评：本题重点考查定积分，解题的关键是将积分区间分为两部分，再分别求出相应的积分．12．已知f（x）=2﹣|x|，则（）A．3B．4C．3.5 D．4.5考点：定积分的简单应用．专题：计算题．分析：由题意，，由此可求定积分的值．解答：解：由题意，=+=2﹣+4﹣2=3.5故选C．点评：本题考查定积分的计算，解题的关键是利用定积分的性质化为两个定积分的和．13．设f（x）=3﹣|x﹣1|，则∫﹣22f（x）dx=（）A．7B．8C．7.5 D．6.5考点：定积分的简单应用．专题：计算题．分析：∫﹣22f（x）dx=∫﹣22（3﹣|x﹣1|）dx，将∫﹣22（3﹣|x﹣1|）dx转化成∫﹣21（2+x）dx+∫12（4﹣x）dx，然后根据定积分的定义先求出被积函数的原函数，然后求解即可．解答：解：∫﹣22f（x）dx=∫﹣22（3﹣|x﹣1|）dx=∫﹣21（2+x）dx+∫12（4﹣x）dx=（2x+x2）|﹣21+（4x﹣x2）|12=7 故选A．点评：本题主要考查了定积分，定积分运算是求导的逆运算，同时考查了转化与划归的思想，属于基础题．14．积分=（）考点：定积分的简单应用；定积分．专题：计算题．分析：本题利用定积分的几何意义计算定积分，即求被积函数y=与x轴所围成的图形的面积，围成的图象是半个圆．解答：解：根据定积分的几何意义，则表示圆心在原点，半径为3的圆的上半圆的面积，故==．故选B．点评：本小题主要考查定积分、定积分的几何意义、圆的面积等基础知识，考查考查数形结合思想．属于基础题．15．已知函数的图象与x轴所围成图形的面积为（）A．1/2 B．1C．2D．3/2考点：定积分在求面积中的应用．专题：计算题．分析：根据几何图形用定积分表示出所围成的封闭图形的面积，求出函数f（x）的积分，求出所求即可．解答：解：由题意图象与x轴所围成图形的面积为=（﹣）|01+sinx=+1=故选D．点评：本题考查定积分在求面积中的应用，求解的关键是正确利用定积分的运算规则求出定积分的值，本题易因为对两个知识点不熟悉公式用错而导致错误，牢固掌握好基础知识很重要．16．由函数y=cosx（0≤x≤2π）的图象与直线及y=1所围成的一个封闭图形的面积是（）考点：定积分在求面积中的应用．专题：计算题．分析：由题意可知函数y=cosx（0≤x≤2π）的图象与直线及y=1所围成的一个封闭图形可利用定积分进行计算，只要求∫0（1﹣cosx）dx即可．然后根据积分的运算公式进行求解即可．解答：解：由函数y=cosx（0≤x≤2π）的图象与直线及y=1所围成的一个封闭图形的面积，就是：∫0（1﹣cosx）dx=（x﹣sinx）|0=．故选B．点评：本题考查余弦函数的图象，定积分，考查计算能力，解题的关键是两块封闭图形的面积之和就是上部直接积分减去下部积分．17．曲线y=x3在点（1，1）处的切线与x轴及直线x=1所围成的三角形的面积为（）A．B．C．D．考点：定积分在求面积中的应用．专题：计算题．分析：欲求所围成的三角形的面积，先求出在点（1，1）处的切线方程，只须求出其斜率的值即可，故要利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率，从而问题解决．解答：解：∵y=x3，∴y'=3x2，当x=1时，y'=3得切线的斜率为3，所以k=3；所以曲线在点（1，1）处的切线方程为：y﹣1=3×（x﹣1），即3x﹣y﹣2=0．令y=o得：x=，∴切线与x轴、直线x=1所围成的三角形的面积为：S=×（1﹣）×1=故选B．点评：本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，属于基础题．18．图中，阴影部分的面积是（）A．16 B．18 C．20 D．22考点：定积分在求面积中的应用．专题：计算题．分析：从图象中知抛物线与直线的交点坐标分别为（2，﹣2），（8，4）．过（2，﹣2）作x轴的垂线把阴影部分分为S1，S2两部分，利用定积分的方法分别求出它们的面积并相加即可得到阴影部分的面积．解答：解：从图象中知抛物线与直线的交点坐标分别为（2，﹣2），（8，4）．过（2，﹣2）作x轴的垂线把阴影部分分为S1，S2两部分，分别求出它们的面积A1，A2：A1=∫02[]dx=2 dx=，A2=∫28[]dx=所以阴影部分的面积A=A1+A2==18故选B．点评：本题考查定积分在求面积中的应用，解题是要注意分割，关键是要注意在x轴下方的部分积分为负（积分的几何意义强调代数和），属于基础题．考查学生利用定积分求阴影面积的方法的能力．19．如图中阴影部分的面积是（）A．B．C．D．考点：定积分在求面积中的应用．专题：计算题．分析：求阴影部分的面积，先要对阴影部分进行分割到三个象限内，分别对三部分进行积分求和即可．解答：解：直线y=2x与抛物线y=3﹣x2解得交点为（﹣3，﹣6）和（1，2）抛物线y=3﹣x2与x轴负半轴交点（﹣，0）设阴影部分面积为s，则==所以阴影部分的面积为，故选C．点评：本题考查定积分在求面积中的应用，解题是要注意分割，关键是要注意在x轴下方的部分积分为负（积分的几何意义强调代数和），属于基础题．20．曲线与坐标轴围成的面积是（）A．B．C．D．考点：定积分在求面积中的应用．专题：计算题．分析：先根据题意画出区域，然后依据图形得到积分下限为0，积分上限为，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．解答：解：先根据题意画出图形，得到积分上限为，积分下限为0曲线与坐标轴围成的面积是：S=∫0（﹣）dx+∫dx=∴围成的面积是故选D．点评：本题主要考查了学生会求出原函数的能力，以及考查了数形结合的思想，同时会利用定积分求图形面积的能力，解题的关键就是求原函数．21．如图，点P（3a，a）是反比例函y=（k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）A．y=B．y=C．y=D．y=考点：定积分在求面积中的应用．专题：计算题；数形结合．分析：根据圆的对称性以及反比例函数的对称性可得，阴影部分的面积等于圆的面积的，即可求得圆的半径，再根据P在反比例函数的图象上，以及在圆上，即可求得k的值．解答：解：设圆的半径是r，根据圆的对称性以及反比例函数的对称性可得：πr2=10π解得：r=2．∵点P（3a，a）是反比例函y=（k＞0）与⊙O的一个交点．∴3a2=k且=r∴a2=×（2）2=4．∴k=3×4=12，则反比例函数的解析式是：y=．故选C．点评：本题主要考查反比例函数图象的对称性的知识点，解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系．。

定积分和微积分基本定理知识点及题型归纳总结

定积分和微积分基本定理知识点及题型归纳总结(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--定积分和微积分基本定理知识点及题型归纳总结知识点精讲一、基本概念 1.定积分的极念一般地，设函效()f x 在区间[a ，b]上连续.用分点0121ii ax x x x x n x b 将区间[,]a b 等分成n 个小区间，每个小区间长度为x （b axn），在每个小区间1,i i x x 上任取一点()1,2,,i i n ξ=，作和式：1()n n i i S f x ξ==∆=∑ 1()ni i b af n ξ=-∑，当x 无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分．记为：()baS f x dx =⎰，()f x 为被积函数，x 为积分变量，[,]a b 为积分区间，b 为积分上限，a 为积分下限．需要注意以下几点：（1）定积分()ba f x dx ⎰是一个常数，即n S 无限趋近的常数S （n →+∞时），称为()baf x dx ⎰，而不是n S ．（2）用定义求定积分的一般方法.①分割：n 等分区间,a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和：1()ni i b af nξ=-∑；④取极限：()1()lim nbi an i b af x dx f nξ→∞=-=∑⎰ （3）曲边图形面积：()b aS f x dx =⎰；变速运动路程21()t t S v t dt =⎰；变力做功(x)baS F dx =⎰2．定积分的几何意义从几何上看，如果在区间,a b 上函数()f x 连续且恒有()0f x ≥，那么定积分()ba f x dx ⎰表示由直线,(),0x a x b a b y ==≠=和曲线()yf x 所围成的曲边梯形(如图3-13中的阴影部分所示)的面积，这就是定积分()b af x dx ⎰的几何意义．一般情况下，定积分()b af x dx ⎰的值的几何意义是介于x 轴、函数()f x 的图像以及直线,x a x b 之间各部分面积的代数和，在x 轴上方的面积取正号，在x 轴下方的面积取负号．二、基本性质性质1 1ba dxb a =-⎰.性质2 ()()(0)b baakf x dx k f x dx k =⎰⎰其中是不为的常数（定积分的线性性质）.性质3 1212[()()]()()b b ba aaf x f x dx f x dx f x dx ±=±⎰⎰⎰（定积分的线性性质）.性质4 ()()()()bc baacf x dx f x dx f x dx a c b =+<<⎰⎰⎰其中（定积分对积分区间的可加性）推广1 1212[()()()]()()()bb bbm m a aaaf x f x f x dx f x dx f x dx f x ±±±=±±±⎰⎰⎰⎰推广2 121()()()()kb c c baac c f x dx f x dx f x dx f x dx =+++⎰⎰⎰⎰．三、基本定理设函数()f x 是在区间[,]a b 上连续，且()F x 是()f x 是在[,]a b 上的任意一个原函数，即'()()F x f x =，则()()()b a f x dx F b F a =-⎰，或记为()()ba bf x dx F x a==⎰ ()()F b F a -，称为牛顿—莱布尼兹公式，也称为微积分基本定理．该公式把计算定积分归结为求原函数的问题，只要求出被积函数()f x 的一个原函数()F x ．然后计算原函数()F x 在区间[],a b 上的增量()()F b F a -即可，这一定理提示了定积分与不定积分之间的内在联系．题型归纳及思路提示题型1 定积分的计算思路提示对于定积分的计算问题，若该定积分具有明显的几何意义，如圆的面积等（例及其变式），则利用圆面积计算，否则考虑用牛顿-莱布尼茨公式计算．例计算()12-1sin x x dx +⎰= ．解析 ()123-111112sin =cos cos1cos113333x x dx x x ⎛⎫⎛⎫⎛⎫+-=----= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎰．A. B. C. D.变式1 ()421dx x=⎰ A.-2ln 2 B. 2ln 2 C.-ln2 D. ln 2变式2 ()1(2)x e x dx +=⎰B 1e -. C.e D. +1e变式3 设函数()()20f x ax c a =+≠，若()()()100001f x dx f x x =≤≤⎰，则0x 的值为．变式4 设函数()y f x =的定义域为R, 若对于给定的正数k ，定义函数()()(),(),k k f x k f x f x f x k≤⎧=⎨>⎩，则当函数()1,1f x k x ==时，定积分()214k f x dx ⎰的值为（）A.2ln 22+B. 2ln 21-C.2ln2D. 2ln 21+ 例根据定积分的几何意义计算下列定积分（1）()402x dx -⎰；（2）1-⎰分析根据定积分的几何意义，利用图形的面积求解.解析根据定积分的几何意义，所求的定积分是直线所围成图形（如图3-14所示）的面积的代数和，很显然这是两个面积相等的等腰直角三角形，如图3-14所示，其面积代数和是0，故()4020x dx -=⎰．（2）根据定积分的几何意义，所求的定积分是曲线()2210x y y +=≥和x 轴围成图形（如图3-15所示）的面积，显然是半个单位圆，其面积是2π，故121=2x dx π--⎰．评注定积分()bax dx ⎰的几何意义是函数和直线,x a x b ==以及x 轴所围成的图形面积的代数和，面积是正值,但积分值却有正值和负值之分，当函数时,()0f x >面积是正值，当函数()0f x <时，积分值是负值．变式1 根据定积分的几何几何意义计算下列定积分．（1）()402x dx +⎰；（2）024x dx --⎰；（3）100sin xdx π⎰；（4）344sin xdx ππ-⎰．题型52 求曲边梯形的面积思路提示函数()(),y f x y g x ==与直线(),x a x b a b ==<围成曲边梯形的面积为()()|f g |dx baS x x =-⎰，具体思路是：先作出所涉及的函数图象，确定出它们所围成图形的上、下曲线所对应函数，被积函数左、右边界分别是积分下、上限．例由曲线23,y x y x ==围成的封闭图形的面积为（） A.112 B.14 C.13 D.712解析由23x x =得01,x x ==或则由2y x =和3y x =围成的封闭图形的面积为()1233401111110343412x x dx x x ⎛⎫-=-=-= ⎪⎝⎭⎰，故选A ．变式1（2012湖北理3）已知二次函数()y f x =的图象如图3-16所求，则它与x 轴所围成图形的面积为（） A.25π B.43 C.32 D.2π变式2 由曲线2y x =和直线()20,1,,0,1x x y t t ===∈所围成的图形（如图3-17中阴影部分所示）面积的最小值为（） A.23 B.13 C.12 D.14变式3 求抛物线24y x =与24y x =-围成的平面图形的面积．变式4 求由两条曲线2214,y 4y x x ==和直线4y =所围成的面积．最有效训练题 1.已知函数()223f x x x =--，则()11f x dx -=⎰（）A. -2B.163- D. 1632.定积分())1211x x dx --=⎰（）A,24π- B.12π- C.14π- D. 12π-3.设()[]2,0,12,(1,2]x x f x x x ⎧∈=⎨-∈⎩，则()20f x dx =⎰（）A.34B.45C.56D.不存在 4.222,,sin xa xdxb e dxc xdx ===⎰⎰⎰，则,,a b c 的大小关系是（）A,a c b << B.a b c << C.c b a << D. c a b <<5.曲线sin ,cos y x y x ==与直线0,2x x π==所围成的平面区域的面积为（）A,１ B. ２ C.21 D. )2216.由直线,,033x x y ππ=-==与曲线cos y θ=所围成的平面图形的面积为（）A,12 B.１ C.33 7.抛物线22y x =与直线4y x =-围成的平面图形的面积为．8.已知()f x 是偶函数，且()506f x dx =⎰，则()55f x dx -=⎰ ．9.()22|1x |dx --=⎰ ．1-y xO图3-161110.已知函数()y f x =的图象是折线段ABC ，其中()()10,0,5,1,02A B C ⎛⎫⎪⎝⎭，．函数()()01y xf x x =≤≤的图象与x 轴所围成的图形的面积为．11.根据定积分的几何意义计算下列定积分．（１）11|x|dx -⎰；（２）22411x dx x ⎛⎫+ ⎪⎝⎭⎰；（３）11dx ⎰；（４）20cos 2x dx π⎰；（５）20cos 2cos sin x dx x xπ-⎰ １２．有一条直线与抛物线2y x =相交于Ａ，Ｂ两点，线段ＡＢ与抛物线所围成图形的面积恒等于43，求线段ＡＢ的中点Ｐ的轨迹方程．。

定积分的计算与题型总结

定积分的计算与题型总结本文内容是高等数学中积分相关内容的一个大总结，包括凌乱知识点的总结和一些附带的例子，以及一些常用的和容易出错的细节和结论。

内容主要涉及定积分的计算技巧、结论的运用、定积分的几何和物理应用；多重积分的计算技巧(包括排列和旋转等。

)及其在定积分中的应用；曲线和曲面积分的计算公式和定理总结，各种积分之间的关系，物理和几何的应用。

您现在浏览的内容是此系列的第一篇：定积分的计算与题型总结。

1.定积分的计算(1)直接先计算不定积分，然后使用牛顿-莱布尼茨公式。

这个非常简单，也是最基本的一种方法，不多赘述。

（注意：只适用于所有能简单积分出原函数的题，所以想做好定积分，不定积分首先要过关。

）牛顿-莱布尼茨公式：如果函数 f(x) 在区间 [a, b] 上连续，并且存在原函数 F(x) ，则 \int_{a}^{b} f(x) dx=F(b)-F(a)=F(x)\bigg|_{a} ^{b}(2)利用定义计算。

若函数 f(x) 在区间 [a, b] 上可积，将区间分为 n 等分:\int_{a}^{b} f(x) \mathrm{d} x =\lim _{n\rightarrow\infty} \sum_{i=1}^{n}f\left[a+\frac{i}{n}(b-a)\right] \frac{b-a}{n}特别注意，根据上述表达式有，当 [a, b] 区间恰好为 [0,1] 区间时，则 [0,1] 区间积分表达式为:\int_{0}^{1} f(x) \mathrm{d} x=\lim _{n\rightarrow\infty} \frac{1}{n} \sum_{i=1}^{n}f\left(\frac{i}{n}\right)例1:用定义计算 \int_{0}^{1}x^2\mathrm{d}x解: \int_{0}^{1} x^2 \mathrm{d} x=\lim _{n\rightarrow\infty} \frac{1}{n} \sum_{i=1}^{n}\left(\frac{i}{n}\right)^2=\lim _{n \rightarrow\infty} \frac{1}{n^3} \sum_{i=1}^{n} i^2=\lim _{n\rightarrow\infty}\frac{n(n+1)(2n+1)}{6n^3}=\frac{1}{3}(3)利用奇偶性计算根据定积分的几何意义(图像和横轴围成的有向面积)，奇函数在正负对称区间的积分为0。

考研定积分的各种类型～题型总结

1
x 1 − x2 dx.
√
x
1 − x2
1 −x2
x dx
√ 1 − x2
1 −x2
d(1−x2) = −2x dx
√ x 1 − x2 dx =
√ 1
−
x2
(xdx)
=
−
1 2
√ 1
−
x2
d(1
−
x2)
=
−
1 2
u1/2 du
= − 1 × 2 u3/2
+C
u=1−x2
23
u=1−x2
=
−
1 3
a < 0, b2 − 4ac > 0 a cos t d(a sin t) = a2 cos2 t dt
a2 =
a2 1 + cos 2t dt =
t + sin 2t
a2 + C = (t + sin t cos t) + C
2
2
2
2
=
a2 2
arcsin
x a
+
x 2
√ a2
−
x2
+
C.
11
17
√2x − 1 dx, 1 − x2
√ 2x + 3 dx, −x2 + 6x − 8
(4)
ax
9.
dx 1+ex
.
dx 1 + ex =
exdx ex + e2x =
d(ex) ex + e2x
=
du
u + u2
(
u=ex
(2)
).

有关定积分问题的常见题型解析(全题型)正规版

有关定积分问题的常见题型解析(全题型)(可以直接使用，可编辑优秀版资料，欢迎下载）有关定积分问题的常见题型解析题型一利用微积分基本定理求积分例1、求下列定积分：（1）()13031x x dx -+⎰ （2）()941x x dx +⎰ （3）⎰--2224x分析：根据求导数与求原函数互为逆运算，找到被积函数得一个原函数，利用微积分基本公式代入求值。

评注：利用微积分基本定理求定积分dx x f ab)(⎰的关键是找出)()(/x f x F =的函数)(x F 。

如果原函数不好找，则可以尝试找出画出函数的图像，图像为圆或者三角形则直接求其面积。

题型二利用定积分求平面图形的面积例2 如图，求直线y=2x+3与抛物线y=x 2所围成的图形面积。

分析：从图形可以看出，所求图形的面积可以转化为一个梯形与一个曲边梯形面积的差，进而可以用定积分求出面积。

为了确定出被积函数和积分和上、下限，我们需要求出两条曲线的交点的横坐标。

关键环节：①认定曲边梯形，选定积分变量；②确定被积函数和积分上下限。

知识小结：几种典型的曲边梯形面积的计算方法：（1）由三条直线x=a 、x=b （a ＜b ）、x 轴，一条曲线y=()x f （()x f ≥0）围成的曲边梯形的面积： S ＝()⎰ba dx x f ，如图1。

（2）由三条直线x=a 、x=b （a ＜b ）、x 轴，一条曲线y=()x f （()x f ≤0）围成的曲边梯形的面积： S ＝()()⎰⎰-=b abadx x f dx x f ，如图2。

（3）由两条直线x=a 、x=b （a ＜b ）、两条曲线y=()x f 、y=()x g （()()x g x f ≥）围成的平面图形的面积：S ＝()()⎰-ba dx x g x f ][，如图3。

(常考题)北师大版高中数学高中数学选修2-2第四章《定积分》测试(答案解析)

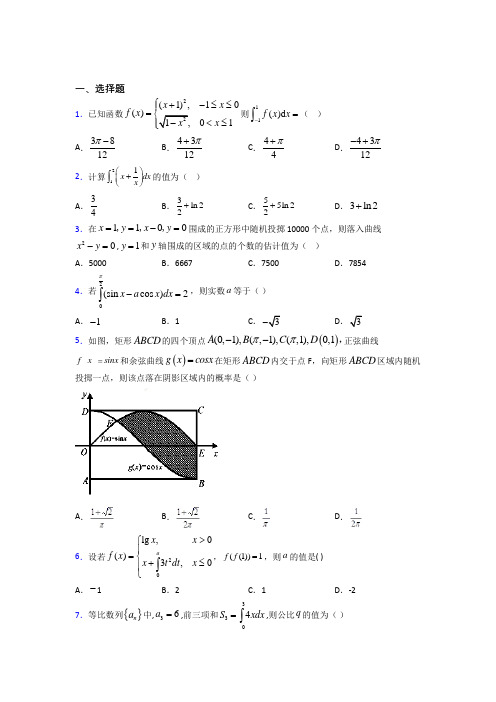
一、选择题1．已知函数22(1),10()1,01x x f x x x ⎧+-≤≤⎪=⎨-<≤⎪⎩则11()d f x x -=⎰（） A ．3812π- B ．4312π+ C ．44π+ D ．4312π-+ 2．计算211x dx x ⎛⎫+ ⎪⎝⎭⎰的值为（）A ．34B ．3ln 22+C ．55ln 22+ D ．3ln 2+3．在1100x y x y ==-=,,,围成的正方形中随机投掷10000个点，则落入曲线20x y -=,1y =和y 轴围成的区域的点的个数的估计值为（）A ．5000B ．6667C ．7500D ．78544．若2(sin cos )2x a x dx π-=⎰，则实数a 等于（）A ．1-B ．1C ．3-D ．35．如图，矩形ABCD 的四个顶点()(0,1),(,1),(,1),0,1A B C D ππ--，正弦曲线f xsinx 和余弦曲线()g x cosx =在矩形ABCD 内交于点F ，向矩形ABCD 区域内随机投掷一点，则该点落在阴影区域内的概率是（）A ．B ．C ．D ．6．设若20lg ,0()3,0ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰，((1))1f f =，则a 的值是( )A ．-1B ．2C ．1D ．-27．等比数列{}n a 中,36a =,前三项和3304S xdx =⎰,则公比q 的值为（）A ．1-或12-B ．1或12-C ．12-D ．18．使函数()322912f x x x x a =-+-图象与x 轴恰有两个不同的交点，则实数a 可能的取值为（） A ．8B ．6C ．4D ．29．由直线y= x - 4，曲线y =x 轴所围成的图形面积为（）A ．15B ．13C ．252D ．40310．由曲线1xy =，直线,3y x y ==所围成的平面图形的面积为（） A ．2ln3- B ．4ln3+C ．4ln3-D ．32911．20sin xdx π=⎰（）A ．4B ．2C ．-2D ．012．已知11em dx x =⎰，函数()f x 的导数()()()f x a x m x a '=++，若()f x 在x a =-处取得极大值，则a 的取值范围是（）A ．1a <B ．10a -<<C ．1a >或0a <D ．01a <<或0a <二、填空题13．(22sin x dx -+=⎰______.14．曲线,,0x y e y e x ===围成的图形的面积S =______15．在直线0x =，1x =，0y =，1y e =+围成的区域内撒一粒豆子，则落入0x =，1y e =+，e 1x y =+围成的区域内的概率为__________．16．若二项式6215x x ⎛⎫+⎪ ⎪⎝⎭的展开式中的常数项为m ，则21mx dx =⎰__________． 17．已知()[](]21,11,1,2x f x x x ∈-=-∈⎪⎩，则()21f x dx -=⎰______．18．设函数2()f x ax b =+（0a ≠），若300()3()f x dx f x =⎰，00x >，则0x =__________．19．若()()4112ax x -+的展开式中2x 项的系数为4，则21aedx x =⎰________________20．若，则的值是__________．三、解答题21．如图所示，抛物线21y x =-与x 轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD 作为工业用地，其中A 、B 在抛物线上，C 、D 在x 轴上已知工业用地每单位面积价值为3a 元()0a >，其它的三个边角地块每单位面积价值a 元．（Ⅰ）求等待开垦土地的面积；（Ⅱ）如何确定点C 的位置，才能使得整块土地总价值最大． 22．已知函数2()11xf x x =++，2()e (0)ax g x x a =<．（1）求函数()f x 的单调区间．（2）若对任意1x ，2[0,2]x ∈，12()()f x g x ≥恒成立，求a 的取值范围．23．设函数()32,0{,0xx x x f x axe x ->=≤，其中0a >. （1）若直线y m =与函数()f x 的图象在(]0,2上只有一个交点，求m 的取值范围；（2）若()f x a ≥-对x ∈R 恒成立，求实数a 的取值范围.24．已知函数()3269f x x x x =-+-．若过点()1,P m -可作曲线()y f x =的切线有三条，求实数m 的取值范围． 25．求曲线6y x =-和8y x =y ＝0围成图形的面积．26．计算由直线4,y x =-曲线2y x =x 轴所围图形的面积S 。

定积分典型例题20例解答

定积分典型例题20例答案例1 求3321lim)n n n →∞+．分析将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解将区间[0,1]n 等分，则每个小区间长为1i x n ∆=，然后把2111n n n=⋅的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即3321lim)n n n →∞+=31lim )n n n n →∞+=34=⎰．例2 0⎰=_________．解法1 由定积分的几何意义知，0⎰等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故0⎰=2π．解法2 本题也可直接用换元法求解．令1x -=sin t （22t ππ-≤≤），则⎰=22tdt ππ-⎰=2tdt =2202cos tdt π⎰=2π 例3 （1）若22()x t xf x e dt -=⎰，则()f x '=___；（2）若0()()xf x xf t dt =⎰，求()f x '=___．分析这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-⎰．解（1）()f x '=422x x xe e ---；（2）由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =⎰，则可得()f x '=0()()xf t dt xf x +⎰．例4 设()f x 连续，且31()x f t dt x -=⎰，则(26)f =_________．解对等式310()x f t dt x -=⎰两边关于x 求导得32(1)31f x x -⋅=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =．例5函数1()(3(0)x F x dt x =>⎰的单调递减开区间为_________．解()3F x '=()0F x '<3>，解之得109x <<，即1(0,)9为所求．例6 求0()(1)arctan xf x t tdt =-⎰的极值点．解由题意先求驻点．于是()f x '=(1)arctan x x -．令()f x '=0，得1x =，0x =．列表如下：故1x =为()f x 的极大值点，0x =为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()xt g x e dt -=⎰，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．分析两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ''=．解由已知条件得2(0)(0)0t f g e dt -===⎰，且由两曲线在(0,0)处切线斜率相同知(0)(0)1f g =''===．故所求切线方程为y x =．而3()(0)3lim ()lim33(0)330n n f f n nf f n n→∞→∞-'=⋅==-．例8 求 22000sin lim(sin )x x xtdtt t t dt→-⎰⎰；分析该极限属于型未定式，可用洛必达法则．解 22000sin lim (sin )x x xtdtt t t dt→-⎰⎰=2202(sin )lim (1)(sin )x x x x x x →-⋅⋅-=220()(2)lim sin x x x x →-⋅-=304(2)lim 1cos x x x→-⋅-=2012(2)lim sin x x x→-⋅=0．注此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b，使等式201lim1sin x x x b x →=-⎰成立．分析易见该极限属于型的未定式，可用洛必达法则．解2001lim sin x x x b x →-⎰=20x →=20lim 1cos x x x b x →→-2011cos x x b x →==-，由此可知必有0lim(1cos )0x b x →-=，得1b =．又由2011cos x x x →=-，得4a =．即4a =，1b =为所求．例10 设sin 20()sin x f x t dt =⎰，34()g x x x =+，则当0x →时，()f x 是()g x 的（）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小．D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→⋅=+ 2200cos sin(sin )lim lim34x x x x x x →→=⋅+ 22011lim 33x x x →==．故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+⎰，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++．例11 计算21||x dx -⎰．分析被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -⎰＝0210()x dx xdx --+⎰⎰＝220210[][]22x x --+＝52．注在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如33222111[]6dx x x --=-=⎰，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界.例12 设()f x 是连续函数，且10()3()f x x f t dt =+⎰，则()________f x =．分析本题只需要注意到定积分()baf x dx ⎰是常数（,a b 为常数）．解因()f x 连续，()f x 必可积，从而10()f t dt ⎰是常数，记1()f t dt a =⎰，则()3f x x a =+，且11(3)()x a dx f t dt a +==⎰⎰．所以2101[3]2x ax a+=，即132a a +=，从而14a =-，所以 3()4f x x =-．例13 计算21-⎰．分析由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解 21-⎰=211--+⎰⎰2是偶函数，而是奇函数，有10-=⎰, 于是21-⎰=214⎰=04⎰=1044dx -⎰⎰由定积分的几何意义可知4π=⎰, 故2114444dx ππ-=-⋅=-⎰⎰．例14 计算220()xd tf x t dt dx -⎰，其中()f x 连续．分析要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解由于220()xtf x t dt -⎰=2221()2x f x t dt-⎰．故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()x tf x t dt -⎰=201()()2x f u du -⎰=201()2x f u du ⎰，故220()x d tf x t dt dx -⎰=201[()]2x d f u du dx ⎰=21()22f x x⋅=2()xf x ．错误解答220()xd tf x t dt dx -⎰22()(0)xf x x xf =-=．错解分析这里错误地使用了变限函数的求导公式，公式()()()xad x f t dt f x dx 'Φ==⎰中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．例15 计算30sin x xdx π⎰．分析被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解30sin x xdx π⎰30(cos )xd x π=-⎰330[(cos )](cos )x x x dx ππ=⋅---⎰30cos 6xdx ππ=-+⎰6π=-．例16 计算120ln(1)(3)x dx x +-⎰．分析被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-⎰=101ln(1)()3x d x +-⎰=1100111[ln(1)]3(3)(1)x dx x x x +-⋅--+⎰ =101111ln 2()2413dx x x-++-⎰11ln 2ln324=-．例17 计算20sin x e xdx π⎰．分析被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解由于2sin xe xdx π⎰20sin xxde π=⎰220[sin ]cos xx e x e xdx ππ=-⎰220cos x e e xdx ππ=-⎰，（1）而20cos xe xdx π⎰20cos xxde π=⎰220[cos ](sin )xx e x e x dx ππ=-⋅-⎰20sin 1x e xdx π=-⎰，（2）将（2）式代入（1）式可得20sin xe xdx π⎰220[sin 1]x e e xdx ππ=--⎰,故20sin xe xdx π⎰21(1)2e π=+．例18 计算1arcsin x xdx ⎰．分析被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdx ⎰210arcsin ()2x xd =⎰221100[arcsin ](arcsin )22x x x d x =⋅-⎰21142π=-⎰．（1）令sin x t =，则21⎰22sin t π=⎰220sin cos cos ttdt t π=⋅⎰220sin tdt π=⎰201cos22t dt π-==⎰20sin 2[]24t t π-4π=．（2）将（2）式代入（1）式中得1arcsin x xdx =⎰8π．例19设()f x [0,]π上具有二阶连续导数，()3f π'=且0[()()]cos 2f x f x xdx π''+=⎰，求(0)f '．分析被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．解由于0[()()]cos f x f x xdx π''+⎰00()sin cos ()f x d x xdf x ππ'=+⎰⎰[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx ππππ'''=-++⎰⎰()(0)2f f π''=--=．故 (0)f '=2()235f π'--=--=-．例20 计算2043dxx x +∞++⎰．分析该积分是无穷限的的反常积分，用定义来计算．解2043dx x x +∞++⎰=20lim 43t t dx x x →+∞++⎰=0111lim ()213t t dx x x →+∞-++⎰ =011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32．。