单样本T检验例题
t检验习题及答案
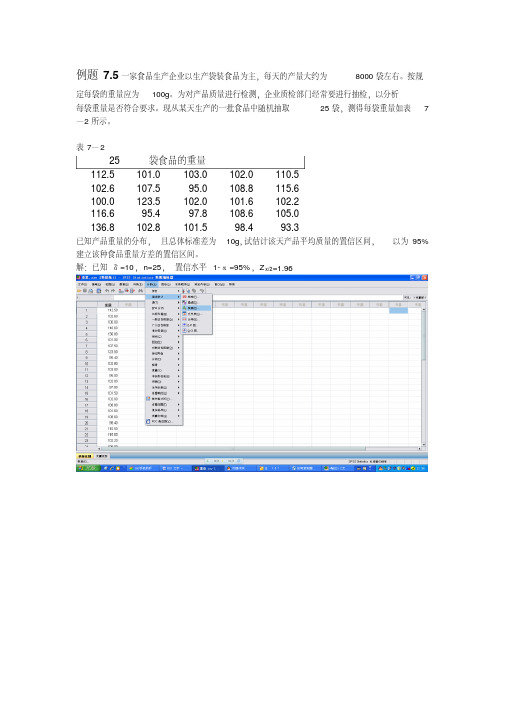
例题7.5一家食品生产企业以生产袋装食品为主,每天的产量大约为8000袋左右。
按规定每袋的重量应为100g。
为对产品质量进行检测,企业质检部门经常要进行抽检,以分析每袋重量是否符合要求。
现从某天生产的一批食品中随机抽取25袋,测得每袋重量如表7—2所示。
表7—225袋食品的重量112.5 101.0 103.0 102.0 110.5102.6 107.5 95.0 108.8 115.6100.0 123.5 102.0 101.6 102.2116.6 95.4 97.8 108.6 105.0136.8 102.8 101.5 98.4 93.3已知产品重量的分布,且总体标准差为10g,试估计该天产品平均质量的置信区间,以为95%建立该种食品重量方差的置信区间。
解:已知δ=10,n=25,置信水平1-α=95%,Z x/2=1.96案例处理摘要案例有效缺失合计N 百分比N 百分比N 百分比重量25 100.0% 0 .0% 25 100.0%描述统计量标准误重量均值105.7600 1.93038 均值的95% 置信区间下限101.7759上限109.74415% 修整均值104.8567中值102.6000方差93.159标准差9.65190极小值93.30极大值136.80范围43.50四分位距9.15偏度 1.627 .464峰度 3.445 .902 重量重量 Stem-and-Leaf PlotFrequency Stem & Leaf1.00 9 . 34.00 9 . 557810.00 10 . 01112222234.00 10 . 57882.00 11 . 02。
单样本t检验例题及答案

单样本t检验例题及答案课题:单样本t检验一、简介单样本T检验,用来检验是否有显著性差异,以及存在什么样的差异。
它假设样本来自正态分布的总体,但是并没有要求两端对称,只要单边有统计显著性就行。
它是实验研究中常用的假设检验方法之一,它将检验样本与某一假设值(通常是总体的平均值、中心假设)之间的偏差作概率分析,判断其是否具有统计学显著性。
二、计算步骤(1)数据准备:我们有一组实验数据,每个受试者吃一顿饭后其血糖指数,我们假设其均在正态分布,计算其均数μ0和标准差σ;(2)计算单样本t值、概率P值:将t值和一定的α(一般α<0.05)的概率值带入t分布概率密度函数中求出概率P值,比较P值能区分做出是否拒绝零假设的结论;(3)最终结果:如果P值<α,则拒绝零假设,说明实验结果有显著性差异,否则,则接受零假设,说明实验结果无显著性差异。
三、示例分析下面为例,20位受试者吃完晚饭后1小时血糖指数测量值:88、86、96、86、75、93、93、78、100、85、86、89、81、85、87、77、90、88、95、94,检验其平均血糖指数和中心假设μ0=80之间是否有显著差异。
(1)数据处理:用上述数据得到均值=87.15,标准差=8.427;(2)计算单样本t值和概率P值:单样本t值为7.349,P值<0.001,α<0.05;(3)最终结果:由于概率P值<α,可以拒绝零假设,说明实验结果有显著性差异,即血糖指数与中心假设μ0=80之间有显著差异。
四、结论从上面的例子可以看出,单样本t检验是一种能够测量统计显著性的方法,用来检验样本数据和中心假设μ0之间的差异,它的特点在于只需要一个样本,就能判断两者间是否存在显著性差异。
t检验法的详细步骤例题

t检验法的详细步骤例题
假设我们想要通过t检验法来判断男生和女生在数学考试成绩上是否存在显著差异。
以下是一个详细步骤的例题:
步骤1: 建立假设(Hypotheses)
- 零假设(H0):男生和女生在数学考试成绩上没有差异,即两个样本的均值相等。
- 对立假设(H1):男生和女生在数学考试成绩上存在差异,即两个样本的均值不相等。
步骤2: 收集样本数据
- 随机抽取一定数量的男生和女生学生作为样本,记录他们在数学考试中的成绩。
步骤3: 计算统计量
- 对于两个独立样本的t检验,统计量t的计算公式为: t = (x1-x2) / sqrt(s1^2/n1 + s2^2/n2)
其中,x1和x2是两个样本的平均值,s1和s2是两个样本的标准差,n1和n2是两个样本的样本容量。
步骤4: 设置显著性水平
- 根据实际情况和问题的重要性,选择一个显著性水平(例如α = 0.05或α = 0.01)。
步骤5: 计算临界值
- 在给定的显著性水平下,查表或使用统计软件来计算临界值。
对于双尾检验,需要计算两侧的临界值。
步骤6: 做出决策
- 比较统计量t与临界值。
如果统计量t的绝对值大于临界值,就拒绝零假设,即表明男生和女生在数学考试成绩上存在显著差异;否则就接受零假设,认为差异不显著。
步骤7: 得出结论
- 根据统计推断的结果,结合具体问题,得出是否拒绝零假设的结论,并解释结果的意义。
43独立对样本t检验例题

【案例1】某医生随机抽取正常人和脑病患者各11例,测定尿中类固醇排出量(mg /d1),结果如下表。
该医生根据此资料算得正常人尿中类固醇排出量的均数1x=4.266mg /d1,标准差s l = 0.985mg /d1;脑病患者尿中类固醇排出量的均数2x=5.732mg /d1,标准差s l = 1.626mg /d1,配对t 检验结果,t =—3.098,P <0.05,故认为脑病患者尿中类固醇排出量高于正常人。
表1 正常人和脑病患者尿中类固醇排出量(mg /d1)测定结果分组 尿中类固醇排出量(mg /d1) 正常人 2.90 5.41 5.48 4.60 4.03 5.10 4.97 4.24 4.37 3.05 2.78 脑病患者 5.28 8.79 3.84 6.46 3.79 6.64 5.89 4.57 7.7l 6.02 4.06 【问题】(1)该资料属于何种设种方案?(2)该医生的统计处理是否正确?为什么?(3)问脑病患者尿中类固醇排出量与正常人有无差别?【案例2】25例糖尿病患者随机分成两组,甲组单纯用药物治疗,乙组采用药物治疗合并饮食疗法,二个月后测空腹血糖(mmol/L)如表5-2 所示,问两种疗法治疗后患者血糖值是否相同?甲组血糖值:8.4,…,15.2,共12例。
乙组血糖值:5.4,…,18.7,共13例。
【案例3】为研究国产新药阿卡波糖胶囊的降血糖效果,某医院用40名II 型糖尿病病人进行同期随机对照试验。
试验者将这些病人随机等分到试验组(用阿卡波糖胶囊)和对照组(用拜唐苹胶囊),分别测得试验开始前和8周后的空腹血糖,算得空腹血糖下降值见下表。
试验组和对照组空腹血糖下降值(mmol/L)试验组X1 -0.70 -5.60 2.00 2.80 0.70 3.50 4.00 5.80 7.10 -0.50 (n1=20) 2.50 -1.60 1.70 3.00 0.40 4.50 4.60 2.50 6.00 -1.40 对照组X2 3.70 6.50 5.00 5.20 0.80 0.20 0.60 3.40 6.60 -1.10 (n2=20) 6.00 3.80 2.00 1.60 2.00 2.20 1.20 3.10 1.70 -2.00【案例3】分别测得15名健康人和13名Ⅲ度肺气肿病人痰中α1抗胰蛋白酶含量(g/L)如下表,问健康人与Ⅲ度肺气肿病人α1抗胰蛋白酶含量是否不同?表2 健康人与Ⅲ度肺气肿患者α1抗胰蛋白酶含量(g/L)健康人 Ⅲ度肺气肿患者 2.7 3.6 2.2 3.4 4.1 3.7 4.3 5.4 2.6 3.6 1.9 6.8 1.7 4.7 0.6 2.9 1.9 4.8 1.3 5.61.5 4.11.7 3.31.3 4.31.31.9为研究国产四类新药阿卡波糖胶囊的降血糖效果,某医院用40名II型糖尿病病人进行同期随机对照试验。
SPSS课件T检验练习

下表.试分析产程(h)与药物及年龄的关系(DATA12-04-
处理02分)组(A) 年龄/岁(B)
第一产程时间/h
用 20~ 3.30
2.65
25~30 5.23
2.75
不用 20~ 5.58
5.45
25~30 10.58
2021/6/7
7.05
3.30 5.30 5.37 4.85 6.65 7.97 6.00 9.88
正常儿童
大 骨 节 病 患儿
X
Y
X
Y
X
Y
13 3.54
10
3.01
11 3.01
9
2.83
9 3.09
11
2.92
6 2.48
12
3.09
8 2.56
15
3.98
10
2.74
10 3.36
16
3.89
15
3.36
12 3.18
8
2.21
13
3.54
2021/6/7 7
2.65
7
2.39
11
3.01
重复测量资料的方差分析
2021/6/7
二、独立样本t检验
(Independent-samples T Test)
例6 以临床试验的数据文件“clinical trial.sav”为例,为了检验随机分组的均 衡性,对治疗前两组的“age”、 “height”、“wt”、“SBP”、“DBP” 、“pulse”做两独立样本比较的t检验。
对高血压患者治疗前后舒张压变化有影响?
病人编号
1
2
3
4
5
6
7
医学统计例题SAS程序

SAS程序 Data ex7; do r=1 to 2; do c=1 to 2; input f@@; output; end; end; cards; 99 5 75 21 ; Proc freq; weight f; tables r*c/chisq expected; Run;
7. 配对四格表资料的 2分析 配对四格表资料的χ
data ex4_2; input x c @@; cards; 3.53 1 2.42 2 2.86 3 0.89 4 4.59 1 3.36 2 2.28 3 1.06 4 4.34 1 4.32 2 2.39 3 1.08 4 2.66 1 2.34 2 2.28 3 1.27 4 3.59 1 2.68 2 2.48 3 1.63 4 3.13 1 2.95 2 2.28 3 1.89 4 3.30 1 2.36 2 3.48 3 1.31 4 4.04 1 2.56 2 2.42 3 2.51 4 3.53 1 2.52 2 2.41 3 1.88 4 3.56 1 2.27 2 2.66 3 1.41 4 3.85 1 2.98 2 3.29 3 3.19 4 4.07 1 3.72 2 2.70 3 1.92 4 1.37 1 2.65 2 2.66 3 0.94 4 3.93 1 2.22 2 3.68 3 2.11 4 2.33 1 2.90 2 2.65 3 2.81 4 2.98 1 1.98 2 2.66 3 1.98 4 4.00 1 2.63 2 2.32 3 1.74 4 3.55 1 2.86 2 2.61 3 2.16 4 2.64 1 2.93 2 3.64 3 3.37 4 2.56 1 2.17 2 2.58 3 2.97 4 3.50 1 2.72 2 3.65 3 1.69 4 3.25 1 1.56 2 3.21 3 1.19 4 2.96 1 3.11 2 2.23 3 2.17 4 4.30 1 1.81 2 2.32 3 2.28 4 3.52 1 1.77 2 2.68 3 1.72 4 3.93 1 2.80 2 3.04 3 2.47 4 4.19 1 3.57 2 2.81 3 1.02 4 2.96 1 2.97 2 3.02 3 2.52 4 4.16 1 4.02 2 1.97 3 2.10 4 2.59 1 2.31 2 1.68 3 3.71 4 ; proc anova; /调用ANOVA过程进行方差分析/ class c; model x=c; means c/lsd; means c/hovtest; run;
T检验例题资料

T检验习题1.按规定苗木平均高达1.60m以上可以出圃,今在苗圃中随机抽取10株苗木,测定的苗木高度如下:1.75 1.58 1.71 1.64 1.55 1.72 1.62 1.83 1.63 1.65假设苗高服从正态分布,试问苗木平均高是否达到出圃要求?(要求α=0.05)解:1)根据题意,提出:无效假设为:苗木的平均苗高为H0=1.6m; 备择假设为:苗木的平均苗高H A>1.6m;2)定义变量:在spss软件中的“变量视图”中定义苗木苗高, 之后在“数据视图”中输入苗高数据;3)分析过程在spss软件上操作分析过程如下:分析——比较均值——单样本T检验——将定义苗高导入检验变量——检验值定义为1.6——单击选项将置信区间设为95%——确定输出如下:表1.1:单个样本统计量表1.2:单个样本检验4)输出结果分析由表1.1数据分析可知,变量苗木苗高的平均值为1.6680m,标准差为0.0843,说明样本的离散程度较小,标准误为0.0267,说明抽样误差较小。
由表1.3数据分析可知,T检验值为2.55,样本自由度为9,t检验的双尾检验值为0.031<0.05,说明差异性显著,因此,否定无效假设H0,取备择假设H A。
根据题意,苗木的苗高服从正态分布,由以上分析知:在显著水平为0.05的水平上检验,苗木的平均苗高大于1.6m,符合出圃的要求。
习题2.从两个不同抚育措施育苗的苗圃中各以重复抽样的方式抽得样本如下:样本1苗高(CM):52 58 71 48 57 62 73 68 65 56样本2苗高(CM):56 75 69 82 74 63 58 64 78 77 66 73设苗高服从正态分布且两个总体苗高方差相等(齐性),试以显著水平α=0.05检验两种抚育措施对苗高生长有无显著性影响。
解:1)根据题意提出:无效假设为H0:两种抚育措施对苗木生长没有显著的影响;备择假设H A:两种抚育措施对苗高生长影响显著;2)在spss中的“变量视图”中定义变量“苗高1”,“抚育措施”,之后在“数据视图”中输入题中的苗高数据,及抚育措施,其中措施一定义为“1”措施二定义为“2”;3)分析过程在spss软件上操作分析过程如下:分析——比较变量——独立样本T检验——将“苗高1变量”导入“检验变量”——将“抚育措施”导入“分组变量”——定义组,其中:组一定义为“1”组二定义为“2”——单击选项将置信区间设为95%——输出分析数据如下;表2.1:组统计量表2.2:独立样本检验4)输出结果分析由上述输出表格分析知:在两种抚育措施下的苗木高度的平均值分别为61.00cm;69.58cm。
3-5--t检验-SPSS-有答案知识讲解

1. 00
16 2.6250 .9270.926763
Independent Samples Test
Levene's Test for Equalit y of Variances t-t est for Equality of Means
F
Sig.
t
血 清 胆 E固 qua 醇 l variances assumed .057 .8141.532
健康者编号 X2
1
2.34
2
6.40
3
2.60
4
3.24
5
6.53
6
5.18
7
5.58
8
3.73
9
4.32
10
5.78
11
3.73
2
2.50
3
1.98
4
1.67
5
1.98
6
3.60
7
2.33
8
3.73
9
4.57
10 4.82
11 5.78
12 4.17
13 4.14
分析步骤
第一步:建立数据文件。它设立两个变 量:group 其取值为1表示甲组,其取值2表 示乙组,取文件名为独立样本t检验。GS表 示血糖值.
Test Variable List框内;在
Test Distribution中 激活“Normal”。 单击OK按钮。 则得出输出结 果。
P1=0.995,P2=0.652,都可认为近似正态分布
One -Sample Kolm ogoro v-Smirnov Te st
GRO UP
1.00
N
Norm al Parameters
t检验试题及详细答案

t检验试题及详细答案一、选择题1. 以下哪种情况最适合使用独立样本t检验?A. 比较两个相关样本的平均值B. 比较两个独立样本的平均值C. 比较一个样本的平均值与总体已知的平均值D. 比较多个样本的平均值答案:B2. 在进行t检验之前,需要满足哪些基本假设?A. 数据应呈正态分布B. 方差齐性C. 数据应随机抽取D. 所有上述答案:D3. 如果两个独立样本的方差不等,应该使用哪种t检验?A. 独立样本t检验B. 配对样本t检验C. Welch's t检验D. 单样本t检验答案:C二、简答题1. 解释什么是t检验,并说明它在统计分析中的应用。
t检验是一种统计检验方法,用于比较两组数据的均值是否存在显著差异。
它广泛应用于社会科学、生物学、经济学等领域,以确定实验处理的效果是否显著,或者两组数据是否来自具有相同均值的总体。
t检验分为单样本t检验、独立样本t检验和配对样本t检验,根据不同的实验设计和数据类型选择适当的t检验。
2. 说明在什么情况下应该使用配对样本t检验。
配对样本t检验用于比较同一组受试者在不同条件下或者在不同时间点的两次测量的平均值。
例如,在医学研究中,可能会对同一组病人在治疗前后的血压进行测量,以确定治疗效果是否显著。
在这种情况下,由于每个受试者的两次测量是相关的,因此使用配对样本t检验来分析数据。
三、计算题一个研究者想要了解音乐训练对儿童注意力的影响。
研究中,20名儿童在进行音乐训练前后的注意力测试分数被记录下来。
训练前的分数平均值为75,标准差为10;训练后的分数平均值为85,标准差为12。
请问音乐训练是否有显著影响?解:使用配对样本t检验来分析这个问题。
t = (M2 - M1) / sqrt((SD2^2 + SD1^2) / n)= (85 - 75) / sqrt((12^2 + 10^2) / 20)= 10 / sqrt((144 + 100) / 20)= 10 / sqrt(244 / 20)= 10 / sqrt(12.2)= 10 / 3.5计算得到t值约为2.86。
T检验答题格式

单样本t检验(计量资料)例:已知野生人参中M物质的含量服从正态分布,总体均值为63.5,今9次测得一批人工培植人参中M物质的含量为40.0、41.0、41.5、41.8、42.4、43.1、43.5、43.8、44.2,推断这批人工培植人参中M物质的含量与野生人参是否相同。
解题步骤:1.正态性检验,分析T描述统计T探索T绘制,带检验的止态图;a. Lilliefors Significance Correction注:如正态性检验无法通过,则不能用单样本t检验,要用单样本秩和检验2.单样本t检验,得出P值。
分析T比较均值T单样本T检验配对样本t检验(计量资料)例:为研究某药的抑瘤效果,将20只小白鼠配成10对,每对中的两只随机分到试验组和对照组,两组都接种肿瘤,试验组在接种肿瘤三天后注射该药液0.5,对照组则注射蒸馏水0.5,结果见表,比较两组瘤体大小是否相同。
解题步骤:1.对配对差值进行正态检验,分析- 非参假设检验-单样本K-S—选择变量f确定单样本a.b.根据数据计算得到。
注:如正态性检验无法通过,则不能用配对样本t检验,要用配对样本秩和检验进行配对样本t检验Mean N Std. Deviation Std. Error Mean Pair 1 对照 4.6600 10 1.00907 .31910 实验 2.5000 10 .93095 .29439Paired DifferencesMeanStd.DeviationStd. ErrorMean95% ConfidenceInterval of theDifferenceLower UpperSig. (2-tailed)2.分析-比较均值 -配对样本T检验Paired Samples Statisticsdf转铁蛋白含量Variancest-test for Equality of MeansSig. (2-Mean Std. Error Sig.t df tailed)DifferenceDifferencethe Difference LowerUpper两独立样本t 检验(计量资料)例:某医师研究转铁蛋白测定对病毒性肝炎诊断的临床意义,测得人和15名病毒性肝炎患者血清转铁蛋白含量的结果如下: 正常人: 265.4、271.5、284.6、291.3、254.8、275.9、281.7、268.6、 、270.8、260.5ph W患者:256.9、235.9、215.4、251.8、224.7、228.3、231.1、253.0、 、233.8、230.9、240.7、260.7、224.4本例为完全随机设计资料,推断转铁蛋白测定对病毒性肝炎诊断的意义。
独立样本T检验

独立样本T检验2027070012 冉垚独立样本T题目:昆明男子立定跳远成绩与怒江男子立定跳远成绩比较一、前提条件:1.昆明男子立定跳远成绩与怒江男子立定跳远成绩均是正太分布或者近似正态分布的连续变量;2.两个样本是独立样本,因为昆明和怒江是两个不同的地区;3.方差齐同与否未知昆明和怒江男子立定跳远成绩样本分别有132个和14个,平均值分别是2.5442米和2.5236米,标准差分别为0.15223米和0.06757米。
2.表2“方差齐同性”分析数据解读:的意义:昆明和怒江男子立定跳远成绩方差齐同;(1)原假设H(2) a=0.05(3)对应的SPSS操作程序:打开昆明和怒江男子立定跳远成绩数据,建立一个新的数据分析库。
分析——比较平均值——独立样本T检验——检验变量修改为男子立地跳远成绩、分组变量为地区、定义级别(组1为昆明,组2为怒江)、显著性水平为95%——确认——确认(4)方差齐同性第5步,比较判断统计结论:F=7.425,p=0.007< p="">专业结论:昆明男子立定跳远成绩和怒江男子立定跳远成绩方差不齐同。
3.“方差齐同性”结果,针对T检验结果的选择公式与SPSS数据结果对应情况说明:(不需要写公式,但是要说明清楚)因此:应该选用短T公式(公式暂不列出),统计结果看的是第二行结果,因为原假设不成立,出现小概率事件,昆明男子和怒江男子立地跳远成绩方差不相等。
4.SPSS数据结果(表2)T检验结果解读(1)表2 T检验的原假设H的含义是:昆明和怒江男子立定跳远成绩成绩存在明显差异(2)公式及检验值(公式用长T还是短T等,不需要写公式,但是要说明清楚)T=0.848,p=0.407>a=0.05,没有出现小概率事件,应该选用的是长T公式。
X Xt=(5)比较判断① 表2 T检验的统计结论是:T=1.317, p=0.407>a=0.05,没有发生小概率事件,支持原假设,差异不显著,无统计学意义。
单样本t检验例题

单样本t检验例题
【案例】例5.1以往通过大规模调查已知某地新生儿出生体重为3.30kg,从该地难产儿中随机抽取35名新生儿作为研究样本,平均出生体重为3.42kg,标准差为0.40kg。
【问题】
1. 用上述信息说明同质、变异、总体、样本、个体、参数和统计量等几个统计学概念。
2. 如何解决此类问题?
3. 新生儿出生体重是什么类型的资料?
4. 该地难产儿出生体重是否与一般新生儿体重不同?
【案例】根据大量调查,一般健康成年男子的平均血红蛋白含量为140.00g/L,现某医生在山区随机测定了25名健康成年男子,其血红蛋白均数为153.64g/L,标准差为24.82g/L,故认为该山区成年男子的血红蛋白均数高于一般健康成年男子的血红蛋白均数。
【问题】(1)该结论是否正确?为什么?(2)如何解决此类问题?(3)问认为该山区成年男子的血红蛋白均数与一般健康成年男子的血红蛋白均数是否有差别?
【案例】以往通过大规模调查已知某地新生儿出生体重为3.30kg,从该地难产儿中随机抽取35名新生儿作为研究样本,平均出生体重为3.42kg,标准差为0.40kg,故认为该地难产儿出生体重低于一般新生儿体重。
【问题】
(1)该结论是否正确?为什么?
(2)如何解决此类问题?
(3)问该地难产儿出生体重是否与一般新生儿体重不同?。
spss操作独立样本T检验格式

例题:对某地区的山地和平原土壤中的磷含量的背景值各取了10个样品,数据如下所示:(单位:10-6),问山地与平原土壤中磷含量是否有显着性差异。
(25分)1、本题中自变量个数等于2,且不是来自于同一组样本,故采用独立样本T检验2、打开spss22.0,在变量视图内定义变量,由题目可知,磷含量为“计量资料”,归类为“度量变量”,地形为计数资料,归类为“名义变量”,并对地形进行赋值,如图输入:3、在数据视图内如下图输入数据:4、独立样本T检验进行的假设:(1)数据必须为连续性数据;(2)方差齐性(可偏不齐,即σ12/σ22<3);(3)每组数据均服从正态分布5、进行验证:(1)由题目可以看出,数据为连续型数据,满足;(2)此检验可于结果中查看;(3)首先,新建spss视图,重新输入变量进行探索队列,如下图所示:将“山地”“平原”选入因变量列表,并于“绘图(T)”中勾选“带检验的正态图”,操作步骤如下图所示:根据正态性检验表的“K-S检验”结果,由于样本内数据数量<30,故看Shapiro-Wilk结果,由于两者的sig均大于0.05,故满足正态分布6、进行独立样本T检验:(1)依次点击“分析”-“比较平均值”-“独立样本T检验”,调出独立样本T检验对话框:(2)将“磷含量”选入检验变量(T),将“地形”选入分组变量,然后定义组,于主页面中点击“确定”,输出结果:7、结果分析:量平原 10 427.10 13.609 4.304独立样本检验列文方差相等性检验平均值相等性的t 检验F显着性t自由度显着性(双尾)平均差标准误差差值差值的95%置信区间 下限上限磷含量已假设方差齐性 9.559.0061.43818.16818.40012.796 -8.482 45.282未假设方差齐性1.438 11.259 .17818.40012.796 -9.684 46.484。
单样本t检验的案例

单样本t检验案例:体重减肥效果研究背景健康和身材一直是现代人关注的焦点,而减肥成为了许多人追求的目标。
然而,不同的减肥方法效果各异,有些方法可能并不适合所有人。
因此,对于某个特定的减肥方法是否有效,需要进行科学的研究和统计分析来验证。
在这个案例中,我们将使用单样本t检验来研究某种特定的减肥方法对体重是否有显著影响。
通过比较减肥前后的体重数据,我们可以判断该减肥方法是否有效。
过程步骤1:收集数据首先,我们需要收集一组参与者在使用该减肥方法前后的体重数据。
为了保证研究结果具有代表性和可靠性,我们需要选择足够数量的参与者,并且要求他们在实施该减肥方法期间保持相对一致的生活习惯。
假设我们选择了100名参与者,并记录了他们在开始使用该减肥方法之前和之后的体重数据。
步骤2:建立假设在进行单样本t检验之前,我们需要建立零假设(H0)和备择假设(H1)。
•零假设(H0):该减肥方法对体重没有显著影响,即参与者的体重在使用该减肥方法前后没有变化。
•备择假设(H1):该减肥方法对体重有显著影响,即参与者的体重在使用该减肥方法前后有变化。
步骤3:计算统计量我们将使用单样本t检验来计算统计量。
单样本t检验用于比较一个样本的均值是否与一个已知的总体均值不同。
在这个案例中,我们将比较参与者在使用该减肥方法前后的平均体重是否有显著差异。
我们可以通过计算样本平均值、样本标准差、样本大小和总体均值来得到统计量。
步骤4:确定显著性水平在进行单样本t检验之前,我们需要确定显著性水平。
显著性水平表示我们愿意接受错误地拒绝零假设的概率。
常见的显著性水平选择是0.05或0.01。
在这个案例中,我们选择显著性水平为0.05,即5%的概率。
步骤5:计算p值通过计算单样本t检验的统计量,我们可以得到一个p值。
p值表示在零假设为真的情况下,观察到样本统计量或更极端情况出现的概率。
在这个案例中,我们将使用统计软件进行计算,得到一个p值。
步骤6:进行假设检验和结果分析根据步骤4和步骤5的结果,我们可以进行假设检验并分析结果。
单样本t检验例题

单样本t检验例题
利用单样本t检验对数据进行检验是统计学中常用的方法,它可以检验两组样本之间是否有显著性差异。
本文通过一个简单的例子来介绍单样本t检验的基本原理和使用方法。
假设有一个包含30个数据的样本,假定这些数据的总体
均值是μ,样本的均值是m,样本的方差是s^
2,则单样本t检验的假设检验形式如下:H0:μ=m,H1:μ≠m,其中H0为零假设,H1为备择假设。
若零假设被接受,则表明样本的均值和总体均值没有显著差异;若零假设被拒绝,则表明样本的均值与总体均值有显著差异。
要进行单样本t检验,首先需要计算样本的均值m,样本
的方差s^2和单样本t检验的t统计量,其计算公式如下:
m=∑x/ns^2=∑(x-m)^2/(n-1)
t=m-μ/√(s^2/n)
其次,根据t统计量的值和自由度,从t分布表中查找临
界值,决定是否拒绝零假设。
若t统计量的值大于临界值,则
说明样本的均值与总体均值有显著差异,可以拒绝零假设;若
t统计量的值小于临界值,则说明样本的均值与总体均值没有
显著差异,可以接受零假设。
综上,单样本t检验是一种检验两组样本之间是否有显著性差异的常用统计学方法,其使用过程包括计算样本的均值和方差,从t分布表中查找临界值,决定是否拒绝零假设。
实验三单样本t检验练习

1 2 3
掌握单样本t检验方法
通过本次实验,我深入理解了单样本t检验的原 理和应用,掌握了其操作步骤和数据分析方法。
培养实验技能
实验过程中,我提高了实验操作能力,学会了如 何设计和实施实验,以及如何处理和分析实验数 据。
增强统计学思维
通过单样本t检验的实践应用,我增强了统计思 维,学会了如何运用统计方法解决实际问题。
确定p值
根据t统计量和自由度,计算p值,并 根据p值判断样本均值与已知值或理 论值之间的差异是否显著。
结果解释与结论
结果解释
根据p值和实际情境,判断样本均值与已知值或理论值之间的差异是否显著,并解释结果的意义。
结论
根据结果解释,得出结论,并提出相应的建议或措施。
05
实验总结与展望
实验收获与体会
实验不足与改进
实验设计需完善
在实验设计阶段,应充分考虑实验的随机性和控 制组的设计,以提高实验的准确性和可靠性。
数据分析需深入
在数据分析阶段,应进一步挖掘数据背后的信息 和规律,以更全面地解释实验结果。
实验操作需规范
在实验操作过程中,应严格按照操作规程进行, 以确保数据的准确性和可靠性。
未来研究方向与实践意义
感谢您的观看
THANKS
显著性水平
在提出假设的同时,我们需要确定显 著性水平,通常选择0.05或0.01。显 著性水平用于判断结果是否具有统计 显著性。
计算t统计量及其对应的自由度
计算t统计量
根据样本数据和样本大小,我们可以使用t分布表或统计软件来计算t统计量。t统计量用于衡量样本均值与已知值 之间的差异程度。
确定自由度
拓展应用领域
单样本t检验在许多领域都有广泛的应用,如医学、生物学、 心理学等。未来可以进一步拓展其应用范围。
t检验经典案例集

1.某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量,结果如下表:某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数男360 4.66 0.58 4.84(1012/L)女255 4.18 0.29 4.33血红蛋白男360 134.5 7.1 140.2(g/L)女255 117.6 10.2 124.7*实用内科学(1976年)所载均数(转为法定单位)请就上表资料:(1)说明女性的红细胞数与血红蛋白的变异程度何者为大?(2)计算男性两项指标的抽样误差。
(3)试估计该地健康成年女性红细胞数的均数。
(4)该地健康成年男、女血红蛋白含量是否不同?(5)该地男性两项血液指标是否均低于上表的标准值(若测定方法相同)?2.一药厂为了解其生产的某药物(同一批次)之有效成份含量是否符合国家规定的标准,随机抽取了该药10片,得其样本均数为103.0mg,标准差为2.22mg。
试估计该批药剂有效成份的平均含量。
3.通过以往大量资料得知某地20岁男子平均身高为1.68米,今随机测量当地16名20岁男子,得其平均身高为1.72米,标准差为0.14米。
问当地现在20岁男子是否比以往高?4.为了解某一新降血压药物的效果,将28名高血压病患者随机分为试验组和对照组,试验组采用新降压药,对照组则用标准药物治疗,测得治疗前后的舒张压(mmHg)如下表。
问:(1)新药是否有效?(2)要比较新药和标准药的疗效是否不同,请用下述两种不同方式分别进行检验:I仅考虑治疗后的舒张压;II考虑治疗前后舒张压之差。
您认为两种方法各有何优缺点?何种方法更好?两种药物治疗前后的舒张压(mmHg)药治疗前102 100 92 98 118 100 102 116 109 116 92 108 102 100 治疗后90 90 85 90 114 95 86 84 98 103 88 100 88 86标准药病人号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 治疗前98 103 110 110 110 94 104 92 108 110 112 92 104 90 治疗后100 94 100 105 110 96 94 100 104 109 100 95 100 855.某医师观察某新药治疗肺炎的疗效,将肺炎病人随机分为新药组和旧药组,得两组的退热天数如下表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R语言、SPSS、EXCEL解决单样本T检验问题。
例:
母猪的怀孕期未114d,今抽测10头母猪的怀孕期分别为116、115、113、112、114、117、115、116、114、113d,试检验所得样本的平均数与总体平均数114d有无显著差异。
SPSS方法:
1)将数据按照列输入:
2)“分析”>“比较均值”>“单样本T检验”
检验变量:G
检验值:114
其他不用改,点击确定。
结果分析:sig(双侧)=0.343 >0.05,因此可知,114与该样本所属总体均数无差异。
R语言方法:
结果:单样本检验(one sample t-test),在95%的置信区间内样本所属均值范围:[113.3689,115.6311]。
114在此区间范围内,因此无差异。
EXCEL方法:
1).将数据按列输入excel表格:
加载excel“数据分析”
打开“数据分析“,选择”描述统计“,点击“确定”。
选定列数据为“输入区域“,分组方式:逐列。
点击输出区域,这个区域为自定义空白区。
然后,点击确定。
结果:算数平均数和置信半径(置信度)分别为114.5 和1.13,在置信度为95%的置信区间内的数值范围:(114.5-1.13)~(114.5+1.13),即:113.37~115.63,该区间包含了114,表明差异不显著,即该样本属总体平均数与114无差异。
