聚类分析与主成分分析SAS的程序
SAS中的聚类分析方法总结

SAS中的聚类分析方法总结(1)——聚类分析概述说起聚类分析,相信很多人并不陌生。
这篇原创博客我想简单说一下我所理解的聚类分析,欢迎各位高手不吝赐教和拍砖。
按照正常的思路,我大概会说如下几个问题:1. 什么是聚类分析?2. 聚类分析有什么用?3. 聚类分析怎么做?下面我将分聚类分析概述、聚类分析算法及sas实现、案例三部分来系统的回答这些问题。
聚类分析概述1. 聚类分析的定义中国有句俗语叫“物以类聚,人以群分”——剔除这句话的贬义色彩。
说白了就是物品根据物品的特征和功用可以分门别类,人和人会根据性格、偏好甚至利益结成不同的群体。
分门别类和结成群体之后,同类(同群)之间的物品(人)的特征尽可能相似,不同类(同群)之间的物品(人)的特征尽可能不同。
这个过程实际上就是聚类分析。
从这个过程我们可以知道如下几点:1) 聚类分析的对象是物(人),说的理论一点就是样本2) 聚类分析是根据物或者人的特征来进行聚集的,这里的特征说的理论一点就是变量。
当然特征选的不一样,聚类的结果也会不一样;3) 聚类分析中评判相似的标准非常关键。
说的理论一点也就是相似性的度量非常关键;4) 聚类分析结果的好坏没有统一的评判标准;2. 聚类分析到底有什么用?1) 说的官腔一点就是为了更好的认识事物和事情,比如我们可以把人按照地域划分为南方人和北方人,你会发现这种分法有时候也蛮有道理。
一般来说南方人习惯吃米饭,北方习惯吃面食;2) 说的实用一点,可以有效对用户进行细分,提供有针对性的产品和服务。
比如银行会将用户分成金卡用户、银卡用户和普通卡用户。
这种分法一方面能很好的节约银行的资源,另外一方面也能很好针对不同的用户实习分级服务,提高彼此的满意度。
再比如移动会开发全球通、神州行和动感地带三个套餐或者品牌,实际就是根据移动用户的行为习惯做了很好的用户细分——聚类分析;3) 上升到理论层面,聚类分析是用户细分里面最为重要的工具,而用户细分则是整个精准营销里面的基础。
SAS 聚类分析方法

SAS 聚类分析(描述算法)系统聚类法系统聚类法(Hierarchical clustering method )是目前使用最多的一种方法。
其基本思想是首先将n 个样品看成n 类(即一类包括一个样品),然后规定样品之间的距离和类与类之间的距离。
将距离最近的两类合并为一个新类,在计算新类和其他类之间的距离,再从中找出最近的两类合并,继续下去,最后所有的样品全在一类。
将上述并类过程画成聚类图,便可以决定分多少类,每类各有什么样品。
系统聚类法的步骤为:①首先各样品自成一类,这样对n 组样品就相当于有n 类;②计算各类间的距离,将其中最近的两类进行合并;③计算新类与其余各类的距离,再将距离最近的两类合并;④重复上述的步骤,直到所有的样品都聚为一类时为止。
下面我们以最短距离法为例来说明系统聚类法的过程。
最短距离法的聚类步骤如下:① 规定样品之间的距离,计算样品的两两距离,距离矩阵记为()0S ,开始视每个样品分别为一类,这时显然应有pq d q p D =),(;② 选择距离矩阵()0S 中的最小元素,不失一般性,记其为),(q p D ,则将p G 与q G 合并为一新类,记为m G ,有q p m G G G ⋃=;③ 计算新类m G 与其他各类的距离,得到新的距离矩阵记为()1S ;④ 对()1S 重复开始进行第②步,…,直到所有样本成为一类为止。
值得注意的是在整个聚类的过程中,如果在某一步的距离矩阵中最小元素不止一个时,则可以将其同时合并。
● 系统聚类法是最常用的一种聚类方法,常用的系统聚类方法有最短距离法、最长距离法、中间距离法、类平均法、重心法、Ward 最小方差法、密度估计法、两阶段密度估计法、最大似然估计法、相似分析法和可变类平均法。
● 大多数的研究表明:最好综合特性的聚类方法为类平均法或Ward 最小方差法,而最差的则为最短距离法。
Ward 最小方差法倾向于寻找观察数相同的类。
类平均法偏向寻找等方差的类。
SAS各过程笔记+描述性统计+线性回归+logistic回归+生存分析+判别分析+聚类分析+主成分分析+因子分析
第一部分:基本统计方法注:主要讲述过程:means(描述性统计);freq(算频数表);univariate(检验);anova(方差分析);ttest(检验);glm(广义线性回归);npar1way(非参,wilcox)一:计量资料的统计分析方法1.01均值+频数表+百分位数+正态检验、茎叶图、箱形图、正态概率图data ex2_1;input x@@;low=2.3;dis=0.3;z=x-mod(x-low,dis);cards;3.964.23 4.42 3.595.12 4.02 4.32 3.72 4.76 4.164.61 4.263.774.20 4.36 3.07 4.89 3.97 4.28 3.64 4.66 4.044.55 4.254.63 3.91 4.41 3.525.03 4.01 4.30 4.19 4.75 4.144.57 4.264.56 3.79 3.89 4.21 4.95 3.98 4.29 3.67 4.69 4.124.56 4.264.66 4.28 3.83 4.205.24 4.02 4.33 3.76 4.81 4.173.96 3.274.61 4.26 3.96 4.23 3.76 4.01 4.29 3.67 3.39 4.124.27 3.614.98 4.24 3.83 4.20 3.71 4.03 4.34 4.69 3.62 4.184.26 4.365.28 4.21 4.42 4.36 3.66 4.02 4.31 4.83 3.59 3.973.964.495.11 4.20 4.36 4.54 3.72 3.97 4.28 4.76 3.21 4.044.56 4.254.92 4.23 4.47 3.605.23 4.02 4.32 4.68 4.76 3.694.61 4.263.894.21 4.36 3.425.01 4.01 4.29 3.68 4.71 4.134.57 4.264.035.46 4.16 3.64 4.16 3.76;/*freq语句,算频数表*/proc freq;tables z;run;proc means data=ex2_1n mean std stderr clm;var x;run;data ex2_1;input x f@@;cards;3.07 23.27 33.47 93.67 143.87 224.07 304.27 214.47 154.67 104.87 65.07 45.27 2;run;proc means;freq f;var x;run;/*把freq f改成weight f就是把f当权重或频数来算,f则在0,1之间*//*计算x的95%的置信区间*/proc univariate data=ex2_1;var x;output out=pctpctlpre=ppctlpts=2.5 97.5;run;proc print data=pct;run;/*正态检验、茎叶图、箱形图、正态概率图*/proc univariate data=ex2_1normalplot;var x;run;/*Extreme Observation显示的值是最小的5个极值和最大的5个极值*/1.02几何均值data ex2_5;input x f@@;y=log10(x);cards;10 420 340 1080 10160 11320 15640 141280 2;proc means noprint;/*调用means过程,不显示结果*/var y;freq f;output out=b/*结果输出到数据集b中*/mean=logmean;/*把数据集b中均数的变量名mean改为logmean*/run;data c;/*新建数据集c*/set b;/*调用数据集b*/g=10**logmean;/*计算变量logmean的反对数,该值就是x的几何均数,将该值赋值给变量g*/ proc print data=c;var g;run;/*这个是计算平通平均数的值*/proc means data=ex2_5;var x;freq f;run;1.03已知均值和方差求置信区间-单样本+单样本与总体/*单样本*/data ex3_2;n=10;mean=166.95;std=3.64;t=tinv(0.975,n-1);pts=t*std/sqrt(n);lclm=mean-pts;uclm=mean+pts;proc print;var lclm uclm;run;/*单样本与总体均值*/data ex3_5;n=36;/*样本量*/s_m=130.83;/*样本均值*/std=25.74;/*样本标准差*/p_m=140;/*总体均值*/df=n-1;/*自由度*/t=(s_m-p_m)/(std/sqrt(n));p=(1-probt(abs(t),df))*2;/*根据t值计算p值*/run;proc print;var t p;run;1.06双样本均值相等检验+两组分开+两组一起算+两组样本量不同/*双样本分开算*/data ex3_4;n1=29;n2=32;m1=20.10;m2=16.89;s1=7.02;s2=8.46;ss1=s1**2*(n1-1);ss2=s2**2*(n2-1);sc2=(ss1+ss2)/(n1+n2-2);se=sqrt(sc2*(1/n1+1/n2));t=tinv(0.975,n1+n2-2);lclm=(m1-m2)-t*se;uclm=(m1-m2)+t*se;proc print;var t se lclm uclm;run;/*双样本相减后再算*//*用MEANS作配对资料两个样本均数比较的t检验*/data ex3_6;input x1 x2 @@;d=x1-x2;cards;0.840 0.5800.591 0.5090.674 0.5000.632 0.3160.687 0.3370.978 0.5170.750 0.4540.730 0.5121.200 0.9970.870 0.506;proc means t prt;var d;run;/*用UNIVARIATE过程作配对资料两样本均数比较的t检验*/ proc univariate data=ex3_6;var d;run;/*双样本两组样本量不同*/data ex3_7;input x@@;if _n_<21 then c=1;/*当观测数小于21时,变量c的值为1,表示试验组*/else c=2;/*其余变量c的值为2,表示对照组*/cards;-0.70 -5.60 2.00 2.80 0.70 3.50 4.00 5.80 7.10 -0.502.50 -1.60 1.703.00 0.404.50 4.60 2.50 6.00 -1.403.70 6.50 5.00 5.20 0.80 0.20 0.60 3.40 6.60 -1.106.00 3.80 2.00 1.60 2.00 2.20 1.20 3.10 1.70 -2.00;proc ttest;/*调用ttest过程*/var x;/*定义分析变量为x*/class c;/*定义分组变量为c*/run;1.08-1.13anova方差分析过程+一维分组+二维分组+三维分组/*只有一组分组因素*/data ex4_2;input x c @@;cards;3.53 1 2.42 2 2.86 3 0.89 44.59 1 3.36 2 2.28 3 1.06 44.34 1 4.32 2 2.39 3 1.08 42.66 1 2.34 2 2.28 3 1.27 43.59 1 2.68 2 2.48 3 1.63 43.13 1 2.95 2 2.28 3 1.89 43.30 1 2.36 2 3.48 3 1.31 44.04 1 2.56 2 2.42 3 2.51 43.53 1 2.52 2 2.41 3 1.88 43.56 1 2.27 2 2.66 3 1.41 43.85 1 2.98 2 3.29 3 3.19 44.07 1 3.72 2 2.70 3 1.92 41.37 12.65 2 2.66 3 0.94 43.93 1 2.22 2 3.68 3 2.11 42.33 1 2.90 2 2.65 3 2.81 42.98 1 1.98 2 2.66 3 1.98 44.00 1 2.63 2 2.32 3 1.74 43.55 1 2.86 2 2.61 3 2.16 42.64 1 2.93 23.64 3 3.37 42.56 1 2.17 2 2.58 3 2.97 43.50 1 2.72 2 3.65 3 1.69 43.25 1 1.56 2 3.21 3 1.19 42.96 13.11 2 2.23 3 2.17 44.30 1 1.81 2 2.32 3 2.28 43.52 1 1.77 2 2.68 3 1.72 43.93 1 2.80 2 3.04 3 2.47 44.19 1 3.57 2 2.81 3 1.02 42.96 1 2.97 23.02 3 2.52 44.16 1 4.02 2 1.97 3 2.10 42.59 1 2.31 2 1.68 33.71 4;proc anova;/*调用anova过程*/class c;/*定义分组变量为c*/model x=c;/*定义模型,分析g对x的影响*/means c/dunnett;/*用LSD法对多组均数过行两两比较*/means c/hovtest;/*作方差齐性检验,默认levene法,p值大于0.05,则认为是g组方差相等*/run;quit;/*有两组分组因素*/data ex4_4;input x a b@@;cards;0.82 1 10.65 2 10.51 3 10.73 1 20.54 2 20.23 3 20.43 1 30.34 2 30.28 3 30.41 1 40.21 2 40.31 3 40.68 1 50.43 2 50.24 3 5;proc anova;class a b;/*定义分组变量a和b*/model x=a b;/*定义模型,分析a和b对x影响*/means a/snk;/*用SNK法对变量a的多组均数进行两两比较*/run;quit;1.15嵌套设计资料的方差分析glm过程一级因素+二组因素/*嵌套设计资料的方差分析*/data ex11_6;input x a b @@;cards;82 1 184 1 191 1 288 1 285 1 383 1 365 2 461 2 462 2 559 2 556 2 660 2 671 3 767 3 775 3 878 3 885 3 989 3 9;proc glm;/*调用glm过程*/class a b;/*定义分组变量为a和b*/model x=a a(b);/*定义模型,以a为一组因素,b为二级因素*/run;quit;1.17重复测量资料的方差分析data ex12_2;input t1 t2 g@@;/*确定变量名称,t1和t2分别为两个时间点的分析变量,g为处理因素变量,b为区组变量*/cards;130 114 1124 110 1136 126 1128 116 1122 102 1118 100 1116 98 1138 122 1126 108 1124 106 1118 124 2132 122 2134 132 2114 96 2118 124 2128 118 2118 116 2132 122 2120 124 2134 128 2;proc glm;/*调用glm过程*/class g;/*定义分组变量g*/model t1 t2=g;/*定义模型,分析g对变量t1和t2的影响*/repeated time 2/*命名重复因子为time,有2个水平*/contrast(1)/*表示以第一时间点为对照点*//summary;/*考察不同时间点与对照时间点比较的结果*/run;quit;data ex12_3;input t0-t4 g@@;cards;120 108 112 120 117 1118 109 115 126 123 1119 112 119 124 118 1121 112 119 126 120 1127 121 127 133 126 1121 120 118 131 137 2122 121 119 129 133 2128 129 126 135 142 2117 115 111 123 131 2118 114 116 123 133 2131 119 118 135 129 3129 128 121 148 132 3123 123 120 143 136 3123 121 116 145 126 3125 124 118 142 130 3;proc glm;class g;model t0-t4=g;repeated time 5/*命名重复因子为time,有2个水平*/contrast(1);run;quit;二:计数资料的统计分析方法2.1四格表资料的卡方检验data ex7_1;input r c f@@;/*确定变量名称,r为行变量,c为列变量,f为频数变量*/ cards;1 1 991 2 52 1 752 2 21;proc freq;/*调用freq过程*/weight f;/*定义f为频数变量*/tables r*c/*作r*c的列联表*//chisq/*对列联表作卡方检验*/expected;/*输出每个格的理论频数*/run;2.5阳性事件发生的概率(二项分布)data ex6_1;do x=6 to 8;/*建立循环,变量x从6到8*/p1=probbnml(0.7,10,x);/*计算二项分布随机变量不大于x的概率*/p2=probbnml(0.7,10,x-1);/*计算二项分布随机变量不大于x-1的概率*/p=p1-p2;*/计算出现x的概率*/output;/*结果输出*/end;proc print;var x p;run;2.6正态分布法计算总体率的可信区间data ex6_3;n=100;x=55;p=x/n;sp=sqrt(p*(1-p)/n);u=probit(0.975);usp=u*sp;lclm=p-usp;uclm=p+usp;proc print;var n p sp lclm uclm;run;2.7样本率与总体率的比较(直接法——单侧检验)data ex6_4;d=probbnml(0.55,10,8);p=1-d;proc print;var p;run;2.8样本率与总体率的比较(直接法——双侧检验)data ex6_5;p01=probbnml(0.6,10,9);p02=probbnml(0.6,10,8);p0=p01-p02;/*计算出现9的概率*/do i=0to10;/*建立循环,变量i从0到10*/p11=probbnml(0.6,10,i);p12=probbnml(0.6,10,i-1);p1=p11-p12;/*计算出现i的概率*/if i=0then p1=p11; /*定义出现0的概率*/if p1<=p0 then output; /*如果出现i的概率小于出现9的概率,则保留在数据集中*/ end;proc means sum;var p1;run;2.9两个样本率比较的z检验data ex6_7;n1=120;n2=110;x1=36;x2=22;p1=x1/n1;p2=x2/n2;pc=(x1+x2)/(n1+n2);/*计算合并发生率*/sp=sqrt(pc*(1-pc)*(1/n1+1/n2));/*计算两个率相差的标准误差*/u=(p1-p2)/sp;/*计算u值*/p=(1-probnorm(abs(u)))*2;/*计算p值*/format u p 5.4;/*输出格式为小数点后保留4位*/proc print;var pc sp u p;run;2.10.Poisson分布的样本均数与总体均数比较(直接法)data ex6_12;n=120;/*确定样本例数*/pai=0.008; /*确定总体率*/lam=n*pai; /*计算总体均数lamda*/x=4; /*确定实际发生数*/p=1-poisson(lam,x-1);/*计算实际发生数所对应的概率*/proc print;var lam p;run;2.11 Poisson分布的样本均数与总体均数比较(正态近似法)data ex6_12;n=25000;/*样本量*/x=123; /*样本均数*/pi=0.003; /*确定总体率*/lam=n*pi; /*计算总体均数*/u=(x-lam)/sqrt(lam*(1-pi)); /*计算u值*/p=1-probnorm(abs(u)); /*计算u值所对应的p值*/proc print;var lam u p;run;2.14负二项分布的参数估计data ex6_16;input x f@@;cards;0 301 142 83 44 25 06 2;proc univariate;var x;freq f;output out=mv2var=v;run;data k;set mv2;k=mu**2/(v-mu);proc print;var mu k;run;三、非参数统计方法3.2单个样本中位数和总体中位数比较data ex8_2;input x1@@;median=45.30;/*假设中位数为45.30*/d=x1-median; /*计算x1和假设中位数的差值*/cards;44.21 45.30 46.39 49.47 51.05 53.1653.26 54.37 57.16 67.37 71.05 87.37;proc univariate; /*调用univariate过程度*/var d;run;proc means median; /*调用means过程计算x1实际的中位数*/var x1;run;3.3两个独立样本比较的Wilcoxon秩和检验(R对应函数wilcox.test())data ex8_3;input x c @@;/*确定变量名称,x、c分别为分析变量和分组变量(类别多于两类一样的写法)*/2.78 13.23 14.20 14.87 15.12 16.21 17.18 18.05 18.56 19.60 13.23 23.50 24.04 24.15 24.28 24.34 24.47 24.64 24.75 24.82 24.95 25.10 2;proc npar1way wilcoxon;/*调用npar1way过程,进行wilcoxon分析*/var x;/*定义分析变量为x*/class c;/*定义分组变量为c*/run;3.4等级资料的两样本比较data ex8_4;input c g f@@;/*确定变量名称,f为频数,c为分类,g为要分析的变量(分类多种类似)*/ cards;1 1 11 2 81 3 161 4 101 5 42 1 22 2 232 3 112 5 0;proc npar1way wilcoxon;/*调用npar1way过程,进行wilcoxon分析*/freq f;/*确定频数变量为f*/var g;/*定义分析变量g*/class c;/*定义分组变量c*/run;第二部分:多元统计分析方法注:主要讲述过程:reg(回归),corr(相关分析),nlin(对数曲线回归),logistic(逻辑回归),phreg(条件logistic回归分析+cox回归),life test(生存分析),discrim(判别分析),stepdisc(逐步回归),cluster(聚类),varclus(指标聚类),princomp(主成分分析),factor(因子分析),cancorr(典型相关分析)一:回归和相关分析1.1两个变量的直线回归分析data ex9_1;input x y;/*确定变量名称*/cards;13 3.5411 3.019 3.096 2.488 2.5610 3.3612 3.187 2.65;proc reg;/*调用reg过程*/model y=x;/*定义模型,以y为应变量,以x为自变量*//*在model语句后面加上选项,得到一些有用的统计量,常用的有:stb(输出标准化偏回归系数)、p(输出每个观测的实际值、预测值和残差)、cli(输出每个观测预测值均数的双侧95%置信区间)、clm(输出每个观测预测值的双侧95%置信范围)*//*例如:model y=x /stb p cli */plot y*x;/*画出散点图*/run;1.2两个变量的直线相关分析data ex9_5;input x y;cards;43 217.2274 316.1851 231.1158 220.9650 254.7065 293.8454 263.2857 271.7367 263.4669 276.5380 341.1548 261.0038 213.2085 315.1254 252.08;proc corr;/*若要求作spearman相关分析,则可以写成proc corr spearman */ var x y;run;/*得到一个相关系数矩阵*/1.4加权直线加回data ex9_9;input x y;w=1/(x*x); /*设置权重变量w*/cards;0.11 4.000.12 5.100.21 9.500.30 9.000.34 17.200.44 14.000.56 18.900.60 29.400.69 22.100.80 41.50;proc reg;weight w;/*定义权重变量w*/model y=x;/*定义模型,以y为因变量,以x为自变量*/run;1.5两个直线回归系数的比较data ex9_12;input x y c@@;cards;13 3.54 111 3.01 19 3.09 16 2.48 18 2.56 110 3.36 112 3.18 17 2.65 110 3.01 29 2.83 211 2.92 212 3.09 215 3.98 216 3.89 28 2.21 27 2.39 210 2.74 215 3.36 2;proc glm;class c;model y=x c x*c;/*定义模型,分析x、c以及x和c的交互作用对y的影响,即判断两总体直线回归系数是否相同*/run;proc glm;class c;model y=x c;/*上一步已排除协变量的影响,然后再分析两分析变量是否来自同一总体*/run;1.6两个变量的对数曲线回归data ex9_13;input x y;cards;0.005 34.110.050 57.990.500 94.495.000 128.5025.000 169.98;proc nlin;/*调用nlin过程*/parms a=0 b=0; /*定义初始值*/model y=a+b*log10(x); /*定义对数模型,以y为因变以量,x为自变量*/ run;1.7两个变量的指数曲线回归分析data ex9_14;input x y;cards;2 545 507 4510 3714 3519 2526 2031 1634 1838 1345 852 1153 860 465 6;proc nlin;parms a=4 b=0.03;/*定义初始值*/model y=exp(a+b*x);/*定义指数模型,以y为因变量,x为自变量*/run;1.8多元回归data ex15_1;input x1-x4 y@@;/*确定变量名称,x1,x2,x3,x4分别为自变量,y为应变量*/ cards;5.68 1.90 4.53 8.20 11.203.79 1.64 7.32 6.90 8.806.02 3.56 6.95 10.80 12.304.85 1.075.88 8.30 11.604.60 2.32 4.05 7.50 13.406.05 0.64 1.42 13.60 18.304.90 8.50 12.60 8.50 11.107.08 3.00 6.75 11.50 12.103.85 2.11 16.28 7.90 9.604.65 0.63 6.59 7.10 8.404.59 1.97 3.61 8.70 9.304.29 1.97 6.61 7.80 10.607.97 1.93 7.57 9.90 8.406.19 1.18 1.42 6.90 9.606.13 2.06 10.35 10.50 10.905.71 1.78 8.53 8.00 10.106.40 2.40 4.53 10.30 14.806.06 3.67 12.797.10 9.105.09 1.03 2.53 8.90 10.806.13 1.71 5.28 9.90 10.205.78 3.36 2.96 8.00 13.605.43 1.13 4.31 11.30 14.906.50 6.21 3.47 12.30 16.007.98 7.92 3.37 9.80 13.2011.54 10.89 1.20 10.50 20.005.84 0.92 8.616.40 13.303.84 1.20 6.45 9.60 10.40;proc reg;model y=x1-x4;/*也可以写成model y=x1 x2 x3 x4;*/run;1.9逐步回归data ex12_2;input x1-x4 y@@;cards;5.68 1.90 4.53 8.20 11.203.79 1.64 7.32 6.90 8.806.02 3.56 6.95 10.80 12.304.85 1.075.88 8.30 11.604.60 2.32 4.05 7.50 13.406.05 0.64 1.42 13.60 18.304.90 8.50 12.60 8.50 11.107.08 3.00 6.75 11.50 12.103.85 2.11 16.28 7.90 9.604.65 0.63 6.59 7.10 8.404.59 1.97 3.61 8.70 9.304.29 1.97 6.61 7.80 10.607.97 1.93 7.57 9.90 8.406.19 1.18 1.42 6.90 9.606.13 2.06 10.35 10.50 10.905.71 1.78 8.53 8.00 10.106.40 2.40 4.53 10.30 14.806.06 3.67 12.797.10 9.105.09 1.03 2.53 8.90 10.806.13 1.71 5.28 9.90 10.205.78 3.36 2.96 8.00 13.605.43 1.13 4.31 11.30 14.906.50 6.21 3.47 12.30 16.007.98 7.92 3.37 9.80 13.2011.54 10.89 1.20 10.50 20.005.84 0.92 8.616.40 13.303.84 1.20 6.45 9.60 10.40;proc reg;model y=x1-x4/selection=stepwise/*定义模型,以y因变量,x1-x4为变量进行多元回归分析*/ sle=0.10/*定义入先变量的界值*/sls=0.10;/*定义剔除变量的界值*/run;三:logistic回归3.1 两个变量logistic回归分析data ex16_1;input y x1 x2 f@@;/*确定变量名称,y为发病情况,x1为吸烟情况,x2为饮酒情况,f为发生频数*/cards;1 0 0 631 0 1 631 1 0 441 1 1 2650 0 0 1360 0 1 1070 1 0 570 1 1 151;proc logistic;/*调用logistic过程*/freq f;/*定义频数变量f*/model y=x1 x2;/*定义模型,以y为因变量,x1和x2为自变量*/run;3.2 1:M配对资料的条件logistic回归分析data ex16_3;input i y x1-x6 @@;/*确定变量名称,i为区组变量,y为病人情况,1为病例,0为对照,x1-x6为危险因素*/t=2-y;/*定义时间变量*/cards;1 1 3 5 1 1 1 01 0 1 1 1 3 3 01 0 1 1 1 3 3 02 1 13 1 1 3 02 0 1 1 13 2 02 0 1 2 13 2 03 1 14 1 3 2 03 0 1 5 1 3 2 03 0 14 1 3 2 04 1 1 4 1 2 1 14 0 2 1 1 3 2 05 1 2 4 2 3 2 0 5 0 1 2 1 3 3 05 0 2 3 1 3 2 06 1 1 3 1 3 2 1 6 0 1 2 1 3 2 06 0 1 3 2 3 3 07 1 2 1 1 3 2 1 7 0 1 1 1 3 3 07 0 1 1 1 3 3 08 1 1 2 3 2 2 0 8 0 1 5 1 3 2 08 0 1 2 1 3 1 09 1 3 4 3 3 2 0 9 0 1 1 1 3 3 09 0 1 4 1 3 1 010 1 1 4 1 3 3 1 10 0 1 4 1 3 3 010 0 1 2 1 3 1 011 1 3 4 1 3 2 0 11 0 3 4 1 3 1 011 0 1 5 1 3 1 012 1 1 4 3 3 3 0 12 0 1 5 1 3 2 012 0 1 5 1 3 3 013 1 1 4 1 3 2 0 13 0 1 1 1 3 1 013 0 1 1 1 3 2 014 1 1 3 1 3 2 1 14 0 1 1 1 3 1 014 0 1 2 1 3 3 015 1 1 4 1 3 2 0 15 0 1 5 1 3 3 015 0 1 5 1 3 3 016 1 1 4 2 3 1 0 16 0 2 1 1 3 3 016 0 1 1 3 3 2 017 1 2 3 1 3 2 0 17 0 1 1 2 3 2 017 0 1 2 1 3 2 018 1 1 4 1 3 2 0 18 0 1 1 1 2 1 0 18 0 1 2 1 3 2 019 0 1 1 1 2 1 019 0 2 2 2 3 1 020 1 1 4 2 3 2 120 0 1 5 1 3 3 020 0 1 4 1 3 2 021 1 1 5 1 2 1 021 0 1 4 1 3 2 021 0 1 2 1 3 2 122 1 1 2 2 3 1 022 0 1 2 1 3 2 022 0 1 1 1 3 3 023 1 1 3 1 2 2 023 0 1 1 1 3 1 123 0 1 1 2 3 2 124 1 1 2 2 3 2 124 0 1 1 1 3 2 024 0 1 1 2 3 2 025 1 1 4 1 1 1 125 0 1 1 1 3 2 025 0 1 1 1 3 3 0;proc phreg;/*调用phreg过程*/model t*y(0)=x1-x6/*定义模型,以t为时间变量,y为截尾变量,x1-x6为自变量*//selection=stepwise/*选择逐步回归方法筛选变量*/sle=0.1sls=0.1/*入选和剔除的界值均为0.1*/ties=discrete;/*用离散logistic模型替代比例危险模型*/strata i;/*定义区组变量*/run;2.3 应变量为多分类资料的logistic回归data ex16_5;input x1 x2 y f;/*x1是两个社区,x2是性别,Y是获取健康知识途径(传统大众媒介=1,网络=2,社区宣传=3,f为频数)*/cards;0 0 1 200 0 2 350 0 3 260 1 1 100 1 2 270 1 3 571 0 1 421 02 171 1 1 161 12 121 1 3 26;proc logistic;freq f;/*定义频数变量为f*/model y(ref='3')/*定义模型,以y为因变量,ref语句指时参照的类别为“社区宣传”,最后得到结果均为与“社区宣传”相对应*/=x1 x2/*定义x1和x2为自变量*//link=glogit;/*指定多分类应变量回归模型*/run;四:生存分析4.1乘积极限法估计生存率,例17-2甲、乙两种手术方法的生存率估计data ex17_2;input t d@@;/*确定变量名称,t为时间变量,d为截尾变量*/cards;1 13 15 15 15 16 16 16 17 18 110 110 114 017 119 020 022 026 034 134 044 159 1;proc lifetest;/*调用lifetest过程*/time t*d(0);/*定义模型,以t为时间变量,d为截尾变量,变量值为0表示截尾数据*/ run;4.2寿命表法估计生存率data ex17_3;input t d f@@;cards;0 0 00 1 4561 0 391 1 2262 0 222 1 1523 0 233 1 1714 0 244 1 1355 0 1075 1 1256 0 1336 1 837 0 1027 1 748 0 688 1 519 0 649 1 4210 0 4510 1 4311 0 5311 1 3412 0 3312 1 1813 0 2714 0 3314 1 615 0 2015 1 0;proc lifetest method=life/*调用lifetest过程,指定用寿命表法估计生存率*/ width=1;/*表示每间隔1估计生存率*/freq f;/*表示以f为频数变量*/time t*d(0);/*定义模型,以t为时间变量,d为截尾变量,变量值为0表示截尾数据*/ run;4.3生存曲线比较的log-rank检验及制作生存曲线data ex17_4;input t d g @@;cards;1 1 13 1 15 1 15 1 15 1 16 1 16 1 16 1 17 1 18 1 110 1 110 1 114 0 117 1 119 0 120 0 122 0 126 0 131 0 134 1 134 0 144 1 159 1 11 1 21 1 22 1 23 1 23 1 24 1 24 1 24 1 26 1 26 1 28 1 29 1 29 1 210 1 211 1 212 1 213 1 215 1 217 1 218 1 2;proc lifetest plot=(s);/*调用lifetest过程并做生存曲线图*/ time t*d(0);strata g;/*定义变量g为分组变量*/run;4.4.cox回归分析data ex17_5;input x1-x6 t y @@;cards;54 0 0 1 1 0 52 057 0 1 0 0 0 51 058 0 0 0 1 1 35 143 1 1 1 1 0 103 048 0 1 0 0 0 7 140 0 1 0 0 0 60 044 0 1 0 0 0 58 036 0 0 0 1 1 29 139 1 1 1 0 1 70 042 0 1 0 0 1 67 042 0 1 0 0 0 66 042 1 0 1 1 0 87 051 1 1 1 0 0 85 055 0 1 0 0 1 82 052 1 1 1 0 1 74 0 48 1 1 1 0 0 63 0 54 1 0 1 1 1 101 0 38 0 1 0 0 0 100 0 40 1 1 1 0 1 66 1 38 0 0 0 1 0 93 0 19 0 0 0 1 0 24 1 67 1 0 1 1 0 93 0 37 0 0 1 1 0 90 0 43 1 0 0 1 0 15 149 0 0 0 1 0 3 150 1 1 1 1 1 87 0 53 1 1 1 0 0 120 0 32 1 1 1 0 0 120 0 46 0 1 0 0 1 120 043 1 0 1 1 0 120 044 1 0 1 1 0 120 0 62 0 0 0 1 0 120 0 40 1 1 1 0 1 40 1 50 1 0 0 1 0 26 1 33 1 1 0 0 0 120 0 57 1 1 1 0 0 120 0 48 1 0 0 1 0 120 0 28 0 0 0 1 0 3 1 54 1 0 1 1 0 120 1 35 0 1 0 1 1 7 1 47 0 0 0 1 0 18 1 49 1 0 1 1 0 120 0 43 0 1 0 0 0 120 0 48 1 1 0 0 0 15 1 44 0 0 0 1 0 4 1 60 1 1 1 0 0 120 0 40 0 0 0 1 0 16 1 32 0 1 0 0 1 24 1 44 0 0 0 1 1 19 1 48 1 0 0 1 0 120 0 72 0 1 0 1 0 24 1 42 0 0 0 1 0 2 1 63 1 0 1 1 0 120 0 55 0 1 1 0 0 12 1 39 0 0 0 1 0 5 1 44 0 0 0 1 0 120 0 42 1 1 1 0 0 120 061 0 1 0 1 0 40 145 1 0 1 1 0 108 038 0 1 0 0 0 24 162 0 0 0 1 0 16 1;proc phreg;model t*y(1)=x1-x6/*定义模型,以t为时间变量,y为截尾变量,变量值1表示截尾数据,x1-x6为危险因素*//selection=stepwisesle=0.05sls=0.05;run;五:判别和聚类分析5.1判别分析data ex18_4;input x1-x4 g; /*确定变量名称,x1-x4为用于进行判别分析的指标,g为分组变量*/ cards;6.0 -11.5 19 90 1-11.0 -18.5 25 -36 390.2 -17.0 17 3 2-4.0 -15.0 13 54 10.0 -14.0 20 35 20.5 -11.5 19 37 3-10.0 -19.0 21 -42 30.0 -23.0 5 -35 120.0 -22.0 8 -20 3-100.0 -21.4 7 -15 1-100.0 -21.5 15 -40 213.0 -17.2 18 2 2-5.0 -18.5 15 18 110.0 -18.0 14 50 1-8.0 -14.0 16 56 10.6 -13.0 26 21 3-40.0 -20.0 22 -50 3;proc discrim;class g;/*定义分组变量为g*/var x1-x4;/*定义用于分析的指标变量为x1-x4*/run;(结果横向是真实值,竖向的预测值)5.2逐步判别分析data ex18_5;input x1-x4 g;cards;6.0 -11.5 19 90 1-11.0 -18.5 25 -36 390.2 -17.0 17 3 2-4.0 -15.0 13 54 10.0 -14.0 20 35 20.5 -11.5 19 37 3-10.0 -19.0 21 -42 30.0 -23.0 5 -35 120.0 -22.0 8 -20 3-100.0 -21.4 7 -15 1-100.0 -21.5 15 -40 213.0 -17.2 18 2 2-5.0 -18.5 15 18 110.0 -18.0 14 50 1-8.0 -14.0 16 56 10.6 -13.0 26 21 3-40.0 -20.0 22 -50 3;proc stepdisc /*调用stepdisc过程*/slentry=0.2/*确定入选标准为0.2*/slstay=0.3;/*确定剔除标准为0.3*/class g;/*定义分组变量为g*/var x1-x4;/*定义用于分析的指标变量为x1-x4*/run;(筛选出变量后,调用discrim过程对筛选出的变量作判别分析,即先做5.2再做5.1)5.3作样品聚类和指标聚类data ex19_3;input x1-x9;cards;46 25 5 2138 1.68 0.35 8.11 4 4 35 12 20 3510 2.76 1.43 6.84 3 3 52 25 20 2784 2.19 0.54 4.11 3 3 32 7 20 2451 1.93 0.47 11.45 9 6 38 22 0 3247 2.56 0.80 11.68 5 5 51 31 30 3710 2.92 0.37 11.60 2 2 40 9 10 3194 2.51 0.40 11.40 5 5 34 17 20 4658 3.67 0.46 11.35 3 3 50 29 0 5019 3.95 0.47 13.45 10 8 42 20 20 7482 5.89 0.12 13.11 0 0 57 30 15 3800 2.99 0.19 10.76 2 236 15 20 2478 1.95 0.25 10.00 0 037 12 0 3827 3.01 0.82 10.50 4 4 52 32 0 2984 2.35 0.16 11.15 3 3 52 32 10 3749 2.95 0.72 11.45 11 10 42 27 30 4941 3.89 0.73 13.80 7 6 44 27 20 3948 3.11 0.33 13.65 16 14 40 21 5 3360 2.64 0.37 11.40 0 0 38 21 5 2936 2.31 0.69 11.40 1 1 44 27 20 6851 5.39 0.99 12.28 7 6 43 27 0 3926 3.09 0.47 11.95 0 0 26 10 3 4381 3.45 0.52 11.80 7 5 37 18 20 7142 5.62 0.85 11.81 5 5 28 9 20 2612 2.06 0.37 11.65 1 1 25 9 30 2638 2.08 0.78 12.25 1 1 34 14 20 4322 3.40 0.41 15.00 5 5 50 32 20 2862 2.25 0.69 8.80 2 2;proc cluster/*调用cluster过程*/method=average;/*采用类平均法进行聚类*/var x1-x9;/*定义用于分析的指标变量x1-x9*/run;proc treegraphics haxis=axis1 horizontal;/*调用tree过程输出聚类图,并将图横向输出*/ run;/*对各个指标聚类,即对9个变量聚类*/proc varclus;/*调用varclus过程*/var x1-x9;/*定义用于分析的指标变量x1-x9*/run;六、主成分分析和因子分析6.1主成分分析data ex20_1;input x1-x6;cards;92 77 80 95 99 12697 75 77 80 95 12595 80 70 78 89 12075 75 73 88 98 11092 68 72 79 88 11390 85 80 70 78 10372 93 75 77 80 10088 70 76 72 81 10264 70 69 85 93 10570 73 70 87 84 10078 69 75 73 89 9778 72 71 68 75 9675 64 63 76 73 9284 66 77 55 65 7670 64 51 60 67 8858 72 75 62 52 7582 73 40 50 48 6145 65 42 47 43 60;proc princomp;/*调用princomp过程,对6个变量做主成分分析,结果包括主成分累积贡献率,特征向量矩阵*/run;6.2因子分析data ex20_2;input x1-x9;cards;4.34 389 99.06 1.23 25.46 93.15 3.56 97.51 61.663.45 271 88.28 0.85 23.55 94.31 2.44 97.94 73.334.38 385 103.97 1.21 26.54 92.53 4.02 98.484.18 377 99.48 1.19 26.89 93.86 2.92 99.41 63.164.32 378 102.01 1.19 27.63 93.18 1.99 99.71 80.004.13 349 97.55 1.10 27.34 90.63 4.38 99.03 63.164.57 361 91.66 1.14 24.89 90.60 2.73 99.69 73.534.31 209 62.18 0.52 31.74 91.67 3.65 99.48 61.114.06 425 83.27 0.93 26.56 93.81 3.09 99.48 70.734.43 458 92.39 0.95 24.26 91.12 4.21 99.76 79.074.13 496 95.43 1.03 28.75 93.43 3.50 99.10 80.494.10 514 92.99 1.07 26.31 93.24 4.22 100.00 78.954.11 490 80.90 0.97 26.90 93.68 4.97 99.77 80.533.53 344 79.66 0.68 31.87 94.77 3.59 100.00 81.974.16 508 90.98 1.01 29.43 95.75 2.77 98.72 62.864.17 545 92.98 1.08 26.92 94.89 3.14 99.41 82.354.16 507 95.10 1.01 25.82 94.41 2.80 99.35 60.614.86 540 93.17 1.07 27.59 93.47 2.77 99.80 70.215.06 552 84.38 1.10 27.56 95.15 3.10 98.63 69.234.03 453 72.69 0.90 26.03 91.94 4.50 99.05 60.424.15 529 86.53 1.05 22.40 91.52 3.84 98.58 68.423.94 515 91.01 1.02 25.44 94.88 2.56 99.36 73.914.12 552 89.14 1.10 25.70 92.65 3.87 95.52 66.674.42 597 90.18 1.18 26.94 93.03 3.76 99.28 73.813.05 437 78.81 0.87 23.05 94.46 4.03 96.223.94 477 87.34 0.95 26.78 91.784.57 94.28 87.344.14 638 88.57 1.27 26.53 95.16 1.67 94.50 91.673.87 583 89.82 1.16 22.66 93.43 3.55 94.49 89.074.08 552 90.19 1.10 22.53 90.36 3.47 97.88 87.144.14 551 90.81 1.09 23.06 91.65 2.47 97.72 87.134.04 574 81.36 1.14 26.65 93.74 1.61 98.20 93.023.93 515 76.87 1.02 23.88 93.82 3.09 95.46 88.373.90 555 80.58 1.10 23.08 94.38 2.06 96.82 91.793.62 554 87.21 1.10 22.50 92.43 3.22 97.16 87.773.75 586 90.31 1.12 23.73 92.47 2.07 97.74 93.893.77 627 86.47 1.24 23.22 91.17 3.40 98.98 89.80;proc factor/*调用factor过程*/n=4;/*确定因子数为4,如果不写就默认为3*/run;proc factorn=4rotate=quartimax;/*因子旋转的方法为四次方最大正交旋转*/run;七、典型相关分析data ex21_1;input x1-x4 y1-y4;cards;1210 120.1 23.8 61.0 10.2 66.3 2.01 2.731210 120.7 23.4 59.8 11.3 67.6 1.92 2.711040 121.2 22.9 59.0 10.1 66.5 1.92 2.601620 121.5 24.6 59.5 9.5 67.8 1.95 2.641690 122.5 24.4 60.7 11.0 69.2 2.08 2.641150 122.7 27.2 64.5 10.5 69.1 2.19 2.841460 123.3 24.9 58.4 10.5 69.0 2.01 2.72 1190 123.4 21.8 59.0 10.6 67.4 1.90 2.71 1840 123.9 23.5 60.2 9.6 67.1 2.00 2.84 1250 124.5 25.2 63.0 11.2 67.8 2.05 2.78 1480 124.8 22.3 58.1 10.7 67.9 2.05 2.73 1310 124.9 22.0 58.0 10.5 67.8 1.98 2.68 1660 125.3 24.7 60.0 10.8 69.3 1.95 2.80 1580 125.6 22.8 59.0 9.4 69.1 2.00 2.65 1460 125.8 25.7 61.0 10.2 69.6 1.95 2.70 1240 126.0 30.2 68.0 9.2 67.1 2.14 2.88 1100 126.2 25.2 60.5 9.8 68.4 1.98 2.72 1250 126.8 23.6 58.5 10.2 67.5 1.94 2.74 1270 127.1 23.0 57.7 10.8 69.8 1.90 2.78 1300 127.6 24.3 59.0 10.3 67.9 1.93 2.84 1350 127.7 24.1 60.0 11.0 69.7 2.03 2.77 1250 128.3 21.6 55.5 10.4 68.5 1.83 2.70 1720 128.5 27.1 62.0 11.4 71.2 2.03 2.75 1480 128.5 22.6 57.4 10.0 67.3 2.04 2.83 1380 129.4 24.9 60.5 11.5 69.8 2.04 2.76 1170 129.0 26.7 63.7 9.6 67.4 2.13 2.98 1640 129.8 26.1 62.0 9.8 71.0 2.00 2.84 1640 131.6 28.7 62.8 9.7 70.7 1.89 2.89 1150 130.2 25.0 58.6 10.5 71.8 1.96 2.78 1430 130.5 26.1 60.7 10.8 68.6 2.05 2.77 1150 130.6 23.4 54.4 11.8 69.2 1.96 2.78 1150 131.4 25.5 63.2 10.2 70.4 2.05 2.84 1320 131.6 25.6 58.9 10.9 70.2 2.06 2.86 1360 131.7 27.4 62.0 10.9 73.5 1.99 2.70 1460 132.0 26.3 61.5 11.1 71.2 2.17 2.13 1380 132.2 25.7 61.4 10.1 70.1 1.96 2.83 1300 132.5 24.5 57.0 10.8 71.8 2.02 2.84 1220 132.7 27.0 61.3 10.1 72.2 2.08 2.80 1320 132.9 25.2 60.5 11.2 73.1 2.01 2.73 1910 133.1 30.1 67.0 9.0 87.1 2.15 2.97 1800 133.5 26.5 62.5 9.8 71.7 2.07 2.82 1560 133.6 24.8 58.5 10.3 72.2 1.93 2.79 1840 134.0 26.0 60.5 10.4 73.0 1.98 2.74 1470 134.3 28.2 62.0 11.3 87.2 2.66 4.03 1590 134.4 25.5 60.7 9.6 69.9 1.99 2.81 1430 134.1 26.6 63.0 11.2 72.2 2.06 2.90 1760 134.6 32.5 66.0 9.9 87.4 2.61 2.98 1470 135.3 27.9 61.8 10.1 73.3 2.20 2.78 1580 135.6 28.1 65.8 9.8 73.1 2.05 2.891840 137.1 27.6 62.8 9.5 72.4 2.11 2.91 1810 137.4 28.3 62.5 9.4 74.2 2.06 3.00 1850 138.1 29.5 62.4 9.7 72.3 2.12 4.02 2120 140.0 34.9 68.8 9.5 87.9 2.74 4.15 1760 140.7 32.0 64.4 10.2 74.0 2.17 4.05 1800 141.0 32.5 63.8 9.5 88.2 2.65 4.08 1260 141.7 29.1 65.0 9.7 88.2 2.68 2.90 1860 142.4 19.3 70.0 10.1 89.6 2.71 4.06 1800 144.7 27.0 58.3 10.8 74.8 2.10 2.82 1470 136.8 26.3 61.4 10.0 72.2 2.07 2.93 1260 121.1 22.9 59.0 10.6 66.3 2.05 2.76 1570 132.7 25.3 58.6 11.5 73.6 2.16 2.78 1290 125.0 25.7 60.5 10.1 68.8 2.00 2.69 1580 133.2 27.3 60.7 9.6 71.7 2.11 2.85 1690 132.8 28.6 64.7 9.6 72.9 2.19 4.08 1670 131.6 25.4 59.7 10.6 69.8 2.14 2.76 1300 133.1 25.9 58.0 10.1 69.7 2.12 2.83 1610 134.0 25.8 59.6 9.4 70.8 2.10 2.88 1580 134.3 26.3 61.2 10.2 72.2 2.14 2.84 1570 129.1 27.7 62.2 11.1 72.9 2.09 2.93 1660 140.1 32.1 67.0 9.3 87.1 2.15 4.03 1040 132.6 27.9 62.0 10.3 72.5 2.08 2.81 1290 128.3 23.6 58.5 9.3 69.0 1.97 2.76 1980 145.8 34.5 68.0 9.8 89.7 2.68 4.25 1210 133.3 25.6 61.5 9.9 71.0 2.11 2.82 1300 134.3 25.6 61.0 10.5 73.2 2.02 2.83 1310 138.1 27.8 61.2 9.9 73.5 2.09 2.78 1590 135.6 25.9 59.6 9.6 72.8 2.10 2.91 1270 128.3 24.1 58.5 10.3 69.2 1.92 2.77 1310 129.7 24.7 61.7 10.1 69.4 2.03 2.80 2280 143.6 37.6 70.0 9.7 88.8 2.17 4.18 1580 136.6 32.3 67.2 10.3 87.1 2.66 4.04 2370 147.4 38.8 73.0 10.8 90.7 2.82 4.38 ;proc cancorr;/*调用cancorr过程*/var x1-x4;/*定义一组变组变量*/with y1-y3;/*定义另一组变量*/run;。
聚类分析与主成分分析

二、聚类分析的典型(diǎnxíng)应 用
• 作为统计(tǒngjì)学的一个分支,聚类分析已有 多年的研究历史,这些研究主要集中在基于距 离的聚类分析方面。
• 许多统计(tǒngjì)软件包,诸如:SAS、SPSS 和S-PLUS等都包含它许多聚类分析工具。
第八页,共90页。
• 图论法。从几何观点来考虑。将n个样品看成m维空间的n个 点,点与点间用直线连接,从而构成m维空间的点的连接图, 再应用图论的观点将样本点在m维空间作最小支撑(zhī chēng)数,最终达到分类目的。
第十二页,共90页。
六、tree过程(guòchéng)
• 画出用于描述整个聚类过程的树状图
• 两种:
• 如何解释主成分所包含的经济意义。
第四十六页,共90页。
数学模型和几何(jǐ hé)解释
• 为了方便,我们在二维空间中讨论主成分的几何意义。 设有n个样品,每个样品有两个观测变量xl和x2,在 由变量xl和x2 所确定的二维平面中,n个样本点所散 布的情况如椭圆状。由图可以看出(kàn chū)这n个样 本点无论是沿着xl 轴方向或x2轴方向都具有较大的离 散性,其离散的程度可以分别用观测变量xl 的方差和 x2 的方差定量地表示。显然,如果只考虑xl和x2 中 的任何一个,那么包含在原始数据中的经济信息将会 有较大的损失。
第十一页,共90页。
五、聚类分析方法(fāngfǎ)
• 系统聚类法。先将n个元素看成n类,然后将性质最接近(或 相似程度最大)的两类合并为一个新类,得到n-1类。再从 中找出最接近的两类加以合并,变成n-2类。如此下去,最 后所有的元素全聚在一类之中。
• 调优法。先将样品做一个初始的分类,然后按照某种最优的 原则逐步调整,一直调整到分类比较合理为止。
SAS聚类分析程序

SAS聚类分析程序:聚类分析过程命令Data pgm33b;Input x1-x3;cards;9.30 30.55 8.7(样品数据)1.85 20.66 12.75;Proc cluster standard method= single nonormnosquare ccc pseudo out=tree;Proc tree data=tree horizontal spaces=1; run;Data pgm33bInput x1-x4;cards;9.30 30.55 8.7(样品数据)1.85 20.66 12.75;Proc cluster standard method=complete nonormnosquare ccc pseudo out=tree;Proc tree data=tree horizontal spaces=1; run;刷黑该块过程命令程序,提交便计算出相应聚类结果。
语句解释: 聚类指定的方法是在“method=”后面填入一个相应的选择项,它们是:single(最短距离法),complete(最长距离法),average(类平均法), centroid(重心法),median(中位数法),ward(离差平方和法),flexible (可变类平均法),density(非参数概率密度估计法),eml(最大似然法),twostage(两阶段密度法)。
主成分分析程序:1. 主成分分析实验程序例:主成分分析过程命令data socecon;input x1-x6;cards;16369 3504887 66047 2397739 198.46 104395513379 566257 4744 456100 76.96 2026379707 397183 1303 887034 18.88 10594810572 414932 1753 751984 27.67 12826112284 876667 18269 1015669 60.09 3327009738 604935 5822 1307908 30.54 22279916970 778830 2438 630014 76.64 27220310006 617436 13543 866013 58.59 22279410217 636760 9967 996912 34.55 16102520946 1380781 16406 526527 150.15 42693711469 720416 7141 853778 43.41 15727414165 1504005 29413 1025363 149.17 56889912795 966188 11580 723278 45.13 16531912762 584696 13583 343107 65.31 16645412008 501780 4986 278310 15.04 86575 11208 981367 13364 1295189 79.8 337947 12719 716491 4448 408796 15.68 99949 ;proc princomp out=aaa prefix=z;var x1-x6; run;data a2;set aaa;proc print;var z1-z2 ;run;。
SPSS聚类分析具体操作步骤spss如何聚类

算法步骤:初始 化聚类中心、分 配数据点到最近 的聚类中心、重 新计算聚类中心、 迭代直到聚类中 心不再变化
适用场景:探索 性数据分析、市 场细分、异常值 检测等
注意事项:选择 合适的聚类数目、 处理空值和异常 值、考虑数据的 尺度问题
定义:根据数据点间的距离或相似性,将数据点分为多个类别的过程 常用方法:层次聚类、K-均值聚类、DBSCAN聚类等 适用场景:适用于探索性数据分析,发现数据中的模式和结构 注意事项:选择合适的距离度量方法、确定合适的类别数目等
常见的聚类分析方法包括层次聚类、Kmeans聚类、DBSCAN聚类等。
聚类分析基于数据的相似性或距离度量, 将相似的数据点归为一类,使得同一类 中的数据点尽可能相似,不同类之间的 数据点尽可能不同。
聚类分析广泛应用于数据挖掘、市场细分、 模式识别等领域。
K-means聚类:将数据划分为K个簇,使得每个数据点到所在簇中心的距离之和最小
聚类结果的可视化:通过图表展示聚类结果 聚类质量的评估:使用适当的指标评估聚类效果的好坏 聚类结果的解释:根据实际需求和背景知识,对聚类结果进行合理的解释和解读 聚类结果的应用:探讨聚类结果在各个领域的应用场景和价值
SPSS聚类分析常 用方法
定义:将数据集 划分为K个聚类, 使得每个数据点 属于最近的聚类 中心
聚类结果展示:通过图表或表格展示聚类结果,包括各类别的样本数和占比
聚类质量评估:采用适当的指标评估聚类效果,如轮廓系数、Davies-Bouldin指数等
聚类结果解读:根据业务背景和数据特征,解释各类别的含义和特征 聚类结果应用:说明聚类分析在具体场景中的应用,如市场细分、客户分类等
SPSS聚类分析注 意事项
确定聚类变量:选 择与聚类目标相关 的变量,确保变量 间无高度相关性。
SPSS软件聚类分析过程的图文解释及结果的全面分析

SPSS聚类分析过程聚类的主要过程一般可分为如下四个步骤:1.数据预处理(标准化)2.构造关系矩阵(亲疏关系的描述)3.聚类(根据不同方法进行分类)4.确定最佳分类(类别数)SPSS软件聚类步骤1. 数据预处理(标准化)→Analyze →Classify →Hierachical Cluster Analysis →Method 然后从对话框中进行如下选择从Transform Values框中点击向下箭头,此为标准化方法,将出现如下可选项,从中选一即可:标准化方法解释:None:不进行标准化,这是系统默认值;Z Scores:标准化变换;Range –1 to 1:极差标准化变换(作用:变换后的数据均值为0,极差为1,且|x ij*|<1,消去了量纲的影响;在以后的分析计算中可以减少误差的产生。
);Range 0 to 1(极差正规化变换/ 规格化变换);2. 构造关系矩阵在SPSS中如何选择测度(相似性统计量):→Analyze →Classify →Hierachical Cluster Analysis →Method 然后从对话框中进行如下选择常用测度(选项说明):Euclidean distance:欧氏距离(二阶Minkowski距离),用途:聚类分析中用得最广泛的距离;Squared Eucidean distance:平方欧氏距离;Cosine:夹角余弦(相似性测度;Pearson correlation:皮尔逊相关系数;3. 选择聚类方法SPSS中如何选择系统聚类法常用系统聚类方法a)Between-groups linkage 组间平均距离连接法方法简述:合并两类的结果使所有的两两项对之间的平均距离最小。
(项对的两成员分属不同类)特点:非最大距离,也非最小距离b)Within-groups linkage 组内平均连接法方法简述:两类合并为一类后,合并后的类中所有项之间的平均距离最小C)Nearest neighbor 最近邻法(最短距离法)方法简述:用两类之间最远点的距离代表两类之间的距离,也称之为完全连接法d)Furthest neighbor 最远邻法(最长距离法)方法简述:用两类之间最远点的距离代表两类之间的距离,也称之为完全连接法e)Centroid clustering 重心聚类法方法简述:两类间的距离定义为两类重心之间的距离,对样品分类而言,每一类中心就是属于该类样品的均值特点:该距离随聚类地进行不断缩小。
重要的统计分析软件——SAS应用编程

重要的统计分析软件——SAS应用编程作者:吴晓磊来源:《沿海企业与科技》2006年第09期[摘要]SAS是功能很强的统计分析软件。
文章介绍了SAS的特点,并就SAS编程应用系统地给出了基本的使用方法。
[关键词]SAS编程;数据步;程序步;环境控制语句[作者简介]吴晓磊,郑州大学商学院教师,硕士,河南郑州,450052[中图分类号]TP311[文献标识码]A[文章编号]1007-7723(2006)09-0069-02一、引言SAS(Statistical Analysis System)是国际上著名的统计软件,是由美国北卡罗莱纳州立大学1976年成立的SAS软件研究所研制成功的。
SAS系统是大型集成软件系统,它具有完备的数据访问、管理、分析和呈现及应用开发功能。
尤其在数据处理和统计分析领域,SAS系统已经成为国际上的标准软件系统。
在国外发达国家中,统计计算和数据分析都已经实现了在计算机上完成。
随着中国统计研究的不断深入,SAS软件研究所1997年正式宣布成立大中国区,并于1999年3月在国内设立独资公司赛仕软件(上海)有限公司。
如今SAS已越来越多地进入中国高教研究领域和应用于各行各业。
利用SAS系统可以很快地处理数据分析中的各种实际问题。
利用微软的Windows系列操作系统提供的友好图形用户界面,在Windows环境下运行的SAS系统可充分利用Windows操作系统的良好图形界面,大大方便了程序编辑、数据操作并提供了多个不需编程而利用菜单形式完成的交互统计分析模块。
二、系统编程语句介绍打开SAS 以后,首先呈现在眼前的是上方的LOG窗口和下方的PROGRAM EDITE窗口。
LOG窗口呈现的内容是运行程序的信息及运行情况记录;PROGRAM EDITE窗口就是程序编辑栏,用来写程序。
当程序编辑之后,按SUBMIT项提交并开始运行。
运行结果会在一个专门的OUTPUT窗口呈现出来。
总的来说,SAS程序语句可分为3大类:数据步,程序步(或过程步)和各种各样的环境控制语句。
主成分分析报告和聚类分析报告

北京建筑工程学院理学院信息与计算科学专业实验报告课程名称《数据分析》实验名称《主成分分析和聚类分析》实验地点:基础楼C-423日期__2016.5.5_____ 姓名张丽芝班级信131 学号201307010108___指导教师王恒友成绩【实验目的】(1)熟悉利用主成分分析进行数据分析,能够使用SPSS软件完成数据的主成分分析;(2)熟悉利用聚类分析进行数据分析,能够运用主成分分析的结果,做进一步分析,如聚类分析、回归分析等,能够使用SPSS软件完成该任务。
【实验要求】根据各个题目的具体要求,分别运用SPSS软件完成实验任务。
【实验内容】1、表4.9(数据见exercise4_5.txt)给出了1991年我国30个省市、城镇居民的月平均消费数据,所考察的八个指标如下:(单位均为元/人)X1: 人均粮食支出;X2:人均副食支出;X3: 人均烟酒茶支出;X4: 人均其他副食支出;X5:人均衣着商品支出;X6: 人均日用品支出;X7: 人均燃料支出;X8: 人均非商品支出。
(1)求样本相关系数矩阵R。
(2)从R出发做主成分分析,求出各主成分的贡献率及前两个主成分的累积贡献率;2、(1)对题1中的数据,按照原有的八个指标,对30个省份进行聚类,给出分为3类的聚类结果。
(2)利用题1得到的前2个主成分指标,分别按最短距离法(最近邻居距离)、最长距离法(最远邻居距离)、类平均距离法(组间平均距离)、重心距离法;其中距离均采用欧式平方距离,对样本进行谱系聚类分析,并画出谱系聚类图;给出分为3类的聚类结果。
并与(1)的结果进行比较【实验步骤】(此部分主要包括实验过程、方法、结果、对结果的分析、结论等)11)2)方差贡献率是38.704%,第二个主成分的方差贡献率是29.590%,前两个主成分的方差占所有主成分方差的64.294%。
前两个主成分的累计贡献率为68.294%,选择前两个主成分即可代表绝大多数原来的变量。
SAS数据分析应用实例及相关程序DOC

SAS数据分析应用实例及相关程序正态性检验及T检验【例1】已知玉米单交种群105的平均穗重为300g。
喷药后,随机抽取9个果穗,其穗重分别为:308,305,311,298,315,300,321,294,320g。
问喷药后与喷药前的果穗平均重量之间的差别是否具有统计学意义?2.配对T检验【例2】对血小板活化模型大鼠以ASA进行实验性治疗,以血浆TXB2(ng/L)为指标,其结果如表2-1,试进行统计分析。
表2-1 2的变化(ng/L)3. 秩和检验【例3】探讨正己烷职业接触人群生化指标特征,用气相色谱法检测受检者尿液2,5-己二酮浓度(mg/L),为该人群的健康监护寻找动态观察依据。
正己烷职业接触组(A组)为广州市印刷行业彩印操作位作业人员64 人,其均在同一个大的车间轮班工作,工作强度相当;对照组(B组)选同厂其他车间工人53 人。
两组人员除接触正己烷因素不同外,生活水平、生活习惯、劳动强度、吸烟、饮酒情况基本相同。
问两组间尿液中2,5-己二酮浓度(mg/L)平均含量之间的差别是否有统计学意义?数据如下所示。
正己烷职业接触组:2.89、1.85、2.27、2.07、1.62、1.77、2.53、2.02、2.07、2.07、1.93、3.01、1.93、1.88、1.55、1.36、2.23、2.55、1.73、2.65、1.95、2.45、1.41、2.46、2.38、1.55、2.16、2.01、1.37、2.16、2.00、2.07、2.57、2.11、2.37、1.39、2.18、2.33、1.46、2.16、2.03、2.96、2.21、2.00、2.58、2.19、2.41、1.68、1.93、1.93、1.93、1.87、1.74、2.70、1.83、2.17、2.52、2.09、2.28、1.65、1.19、1.58、0.89、1.65对照组:0.27、0.36、0.26、0.16、0.49、0.58、0.16、0.45、0.22、0.25、0.66、0.05、0.31、0.12、0.51、0.30、0.37、0.14、0.28、0.33、0.36、0.51、0.37、0.36、0.47、0.34、0.72、0.39、0.55、0.17、0.27、0.33、0.30、0.26、0.50、0.17、0.22、0.18、0.17、0.62、0.27、0.26、0.34、0.17、0.61、0.42、0.39、0.28、0.36、0.43、0.24、0.15、0.194.两独立正态总体的检验【例4】一个小麦新品种经过6代选育,从第5代(A组)中抽出10株,株高为:66、65、66、68、62、65、63、66、68、62(cm),又从第6代(B组)中抽出10株,株高为:64、61、57、65、65、63、62、63、64、60(cm),问株高性状是否已经达到稳定?5.单因素K(K≥3)水平方差分析【例5】从津丰小麦4个品系中分别随机抽取10株,测量其株高(cm),数据如下所示,问不同品系津丰小麦的平均株高之间的差别是否具有统计学意义?品系0-3-1:63、65、64、65、61、68、65、65、63、64品系0-3-2:56、54、58、57、57、57、60、59、63、62品系0-3-3:61、61、67、62、62、60、67、66、63、65品系0-3-4:53、58、60、56、55、60、59、61、60、596. 双因素无重复试验的方差分析【例6】某医生欲研究回心草各单体成分对试验性心肌缺血血流动力学的影响,选取健康新西兰家兔若干只,体重(2.0±0.3)kg,雌雄不计,将其随机分成9组:胡椒碱高剂量组(100nmol/L)、胡椒碱中剂量组(10nmol/L)、胡椒碱低剂量组(1nmol/L)、胡椒酸甲酯高剂量组(100nmol/L)、胡椒酸甲酯中剂量组(10nmol/L)、胡椒酸甲酯低剂量组(1nmol/L)、咖啡酸甲酯高剂量组(100nmol/L)、咖啡酸甲酯中剂量组(10nmol/L)、咖啡酸甲酯低剂量组(1nmol/L)。
主成分分析与聚类分析和判别分析

实验三主成分分析、聚类分析和判别分析学院:地理科学学院专业:自然地理学姓名:郭国洋实验内容(1)中国31个省份、直辖市、自治区(不包括港澳台)经济状况的7项指标。
(2)用主成分分析剖析出影响中国大陆经济状况的主要指标,并对中国大陆的经济综合实力进行排序。
(3)用主成分剖析出的指标,用聚类分析对中国大陆的经济状况进行评价,并对每类的经济综合状况进行评价。
(4)结合本题,谈谈聚类分析和主成分分析两种方法如何结合使用来分析问题。
实验目的(1)巩固主成分和聚类分析的基本原理和方法步骤以及在实际分析中的意义。
(2)用SPSS软件完成地理的主成分分析和聚类分析。
第一部分主成分分析1 实验数据查阅2012年中国统计年鉴,数据表示2011年的指标。
得到中国31个省份、直辖市、自治区(不含港澳台)的7项经济统计指标数据,包括:总人口/10^4人,城镇人口比例/%,第一产业总产值/10^8元,工业生产总值/10^8元,公共财政预算收入/10^8元,城乡居民储蓄余额/10^8元,城镇单位就业人员工资总额/10^8元。
样本容量:31,变量:7,如图1。
2 实验步骤及分析(1)点击“分析”—“降维”—“因子分析”,将上述的7个指标选择为变量。
SPSS中的“主成分分析”嵌入到“因子分析”中,因此在操作的过程中我们要先进行因子分析。
如2。
图2 选择因子分析变量(2)依次点击“因子分析”框中的“描述”、“抽取”、“旋转”、“得分”、“选项”,勾选相应的选项,如图3、4、5、6、7所示图3抽取图4 旋转图4描述统计图5因子得分图6选项图7旋转(3)点击“确定”,得到相应的结果并分析。
图8 KMO和Bartlett检验分析:图8中,在进行因子分析之前,需要检验变量之间是否具备进行分析的条件。
由图中可知KMO值为0.787>0.5,说明数据变量之间具有结构效度,Sig<0.05,说明可以进行因子分析。
图9 公因子方差分析:图9是指全部公共因子对于变量的总方差做所的贡献,说明了全部公共因子反映出的原变量的信息的百分比。
SPSS聚类分析具体操作步骤

SPSS中聚类分析分类
(一)按分类对象 对变量的聚类称为R型聚类 对观测值聚类称为Q型聚类 这两种聚类在数学上是对称的,没有什么丌同。 (二)按聚类的方法分类 分层聚类或系统聚类分析 快速聚类分析 两步聚类分析:新型的
事先丌用确定分多少类:分层聚类
分层聚类或系统聚类(hierarchical cluster)。开始 时,有多少点就是多少类。 • 它第一步先把最近的两类(点)合并成一类,然 后再把剩下的最近的两类合并成一类; • 这样下去,每次都少一类,直到最后只有一大类 为止。显然,越是后来合并的类,距离就越进。 再对饮料例子来实施分层聚类。
聚类分析概述
(一)概念
• (1)聚类分析是统计学中研究“物以类聚”的一种 方法,属多元统计分析方法.
– 例如:细分市场、消费行为划分
• 聚类分析是建立一种分类,是将一批样本(或变量)
按照在性质上的“亲疏”程度,在没有先验知识的
情况下自动进行分类的方法.其中:类内个体具有 较高的相似性,类间的差异性较大.
快速聚类
• k-均值聚类(k-means cluster,也叫快速聚类,quick cluster)却要求你先说好要分多少类。看起来有些主观 • 假定你说分3类,这个方法还迚一步要求你事先确定3个点 为“聚类种子”(SPSS软件自动为你选种子);也就是说, 把这3个点作为三类中每一类的基石。 • 然后,根据和这三个点的距离进近,把所有点分成三类。 再把这三类的中心(均值)作为新的基石或种子(原来的 “种子”就没用了),重新按照距离分类。 • 如此叠代下去,直到达到停止叠代的要求. • 适合处理大样本数据。
属性图以树的形式展现 聚类分析的每一次合并 过程。冰柱图通过表格 中的冰柱显示。 可以指定并主图的输出 方向,纵向和横向
中药聚类分析spss步骤操作流程

中药聚类分析spss步骤操作流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!中药聚类分析在SPSS中的操作流程详解中药,作为中国传统医学的重要组成部分,其复杂性和多样性使得对其进行科学分类和研究显得尤为重要。
IBM SPSS MODELER 实验一、聚类分析

IBM SPSS Modeler 实验一、聚类分析在数据挖掘中,聚类分析关注的内容是一些相似的对象按照不同种类的度量构造成的群体。
聚类分析的目标就是在相似的基础上对数据进行分类。
IBM SPSS Modeler提供了多种聚类分析模型,其中主要包括两种聚类分析,K-Mean 聚类分析和Kohonen聚类分析,下面对各种聚类分析实验步骤进行详解。
1、K-Means聚类分析实验首先进行K-Means聚类实验。
(1)启动SPSS Modeler 14.2。
选择“开始”→“程序”→“IBM SPSS Modeler 14.2”→“IBM SPSS Modeler 14.2”,即可启动SPSS Modeler程序,如图1所示。
图1 启动SPSS Modeler程序(2)打开数据文件。
首先选择窗口底部节点选项板中的“源”选项卡,再点击“可变文件”节点,单击工作区的合适位置,即可将“可变文件”的源添加到流中,如图2所示。
右键单击工作区的“可变文件”,选择“编辑”,打开如图3的编辑窗口,其中有许多选项可供选择,此处均选择默认设定。
点击“文件”右侧的“”按钮,弹出文件选择对话框,选择安装路径下“Demos”文件夹中的“DRUG1n”文件,点击“打开”,如图4所示。
单击“应用”,并点击“确定”按钮关闭编辑窗口。
图2 工作区中的“可变文件”节点图3 “可变文件”节点编辑窗口图4 文件选择对话框图5 工作区中的“表”节点(3)借助“表(Table)”节点查看数据。
选中工作区的“DRUG1n”节点,并双击“输出”选项卡中的“表”节点,则“表”节点出现在工作区中,如图5所示。
运行“表”节点(Ctrl+E或者右键运行),可以看到图6中有关病人用药的数据记录。
该数据包含7个字段(序列、年龄(Age)、性别(Sex)、血压(BP)、胆固醇含量(Cholesterol)、钠含量(Na)、钾含量(K)、药类含量(Drug)),共200条信息记录。
聚类分析步骤

聚类分析步骤以教材第五章习题8的数据为例,演示并说明聚类分析的详细步骤:原始数据的输入:丈件(D 霸甸〔口锻国(蜀散惭直I 转快(D 分折(幻圈解〔⑤ 密坏賤序〔史Mt加内容(Q)SUM 帮肋S暗事?* ™ S?鮒*ffl ft韶亟蔚粤箱「专.选项操作:1. 打开SPSS的“分析”-“分类”-“系统聚类”,打开“系统聚类”对话框。
把“食品”、“衣着”等6变量输入待分析变量框;把“地区”输入“标注个案”;“分群”选中“个案”;“输出”选中“统计量”和“图”。
(如下图)相关说明:(1) 系统聚类法是最常用的方法,其他的方法较少使用。
(2) “标注个案”里输入“地区”,在输出结果的距离方阵和聚类树状图里会显示出“北京”、“天津”等,否则SPSS自动用“ 1”、“2”等代替。
(3) “分群”选中“个案”,也就是对北京等16个样本进行分类,而不是对食品等6个变量分类。
(4) 必须选中“输出”中的“统计量”和“图”。
在该例中会输出16个地区的欧氏距离方阵和聚类树状图。
密Ife鸟駝£臭* I必炮区H-qI 1E曲前 -------------输出v熨计養y岡2. 设置分析的统计量打开最右上角的“统计量”对话框,选中“合并进程表”和“相似性矩阵” “聚类成员”选中“无”。
然后点击“继续”。
打开第二个“绘制”对话框,必须选中“树状图”,其他的默认即可打开第三个对话框“方法”:聚类方法选中“最邻近元素”;“度量标准” 选中“区间”的“欧氏距离”;“转换值”选中“标准化”的“ Z 得分”,并且是“按照变量”。
+区町(LD : E uclidean 肚屈7" T计徹D ; 卡方度豪▼二鼻細^?TEuclicteeri■|i |g |打开第四个对话框“保存”,“聚类成员”选默认的“无”即可 三•分析结果的解读:按照SPSS 俞出结果的先后顺序逐个介绍:1. 欧氏距离矩阵:是16个地区两两之间欧氏距离大小的方阵, 该方阵是应用各 种聚类方法进行聚类的基础。
聚类分析、对应分析、因子分析、主成分分析spss操作入门

软件操作
Scores为计算因子的方法
Save as variables:将因子得分保存在 SPSS变量中,method表示计算因子得分的 方法,Regression—回归法 Display factor score coefficient matix: 输出因子得分系数矩阵
采用聚类方法:系统聚类 K均值聚类
3
系统聚类
参与系统聚类的变量选到Variables(s)中 字符型变量作为标记变量选到Lable Cases by中 Cluster中确定聚类类型,是Q型聚类还是R型聚类
Agglomeration schedule:输出聚类过程表 Proximity matrix:输出个体之间的距离矩阵 Cluster Membership 中 None 表示不输出样本 所属类,Single solution表示当分成n类时各样 本所属类,Range of solutions表示当分成m-n 4 类时各样本属性所属类
基本思想:根据所研究的样本或变量在观测数据上表现的不 同亲疏程度,采用不同的聚类方法将亲疏程度较大的样本/ 变量聚合为一类,把另外一些亲疏程度较大的样本/变量聚 合为一类,直到把所有的样本/变量都聚合完毕,形成一个 由小到大的分类系统 。
聚类方法不同: 聚类对象不同时的聚类类型: 亲疏程度的判定 hierarchical cluster),聚类过程是按 系统聚类:又称为层次聚类( 样本之间的聚类:即Q型聚类分析,常用距离来测度样本之间的亲疏程 照一定层次进行的; 距离:将每一个样本看作p维空间的一个点,并用某种度量测量点与点 度; 之间的距离,距离较近的归为一类,距离较远的点应属于不同的类; 均值聚类( K-means Cluster ); K 变量之间的聚类:即 R型聚类分析,常用相似系数来测度变量之间的亲 相似系数:性质越接近的变量或样本,它们的相似系数越接近于1或一l, 疏程度; 而彼此无关的变量或样本它们的相似系数则越接近于0,相似的为一类,不 相似的为不同类;
聚类分析实验报告SPSS

聚类分析实验报告SPSS一、实验目的:1.掌握聚类分析的基本原理和方法;2.了解SPSS软件的使用;3.通过实际数据分析,探索样本数据的聚类结构。
二、实验步骤:1.数据预处理:a.收集并导入样本数据;b.对数据进行初步探索和了解,包括数据描述统计、缺失值处理等;2.聚类分析:a.选择合适的变量进行聚类分析;b.选择聚类算法和相似性度量方法;c.进行聚类分析,得到聚类结果;d.检验聚类结果的稳定性和合理性;3.结果解释:a.对聚类结果进行解释和描述,给出每个聚类的特点和含义;b.使用图表展示聚类结果,以便更直观地理解;c.对聚类结果进行验证和评估,如通过交叉验证等方法;4.结论:a.总结分析结果,给出对样本数据的聚类结构的总体认识;b.提出有关样本数据的进一步探索方向和建议。
三、实验结果与分析:1.数据预处理:样本数据包括了多个变量,我们首先对这些变量进行初步的探索和分析,了解它们的分布情况和特点。
同时,对于缺失值的处理,我们采取了删除或插补的方法,以保证后续分析的准确性和完整性。
2.聚类分析:在选择变量时,我们考虑到了变量之间的相关性,以及对聚类结果的解释性。
通过SPSS软件,我们选择了合适的聚类算法和相似性度量方法,进行了聚类分析。
3.结果解释:根据聚类结果,我们将样本数据划分为多个聚类群组。
对于每个聚类群组,我们进行了详细的解释和描述,给出了其特点和含义。
通过图表的展示,我们能更直观地理解每个聚类群组的分布情况和区别。
4.结论:综合分析结果,我们得出了对样本数据聚类结构的总体认识。
同时,我们提出了进一步探索的方向和建议,以获取更多的知识和信息。
四、实验总结:通过这次实验,我们掌握了聚类分析的基本原理和方法,了解了SPSS软件的使用。
通过实际数据的分析,我们能够更深入地理解样本数据的聚类结构,为进一步的研究和应用提供了基础。
在实验过程中,我们也遇到了一些问题和困难,但通过团队合作和专业指导,我们得以顺利完成实验,并取得了较好的结果。
SPSS操作方法:聚类分析
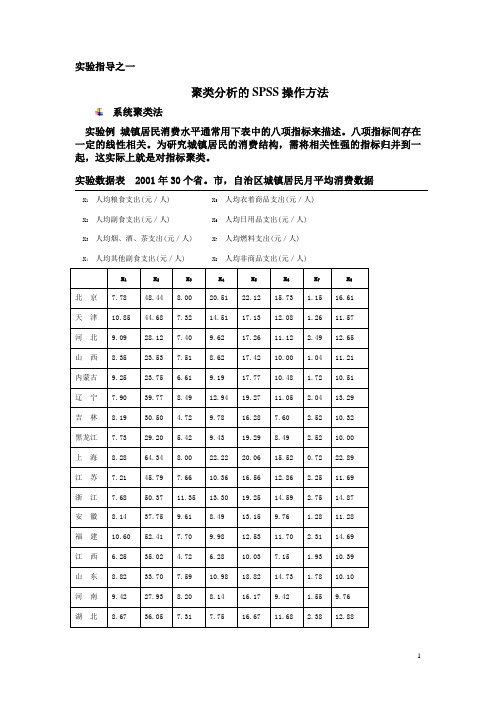
实验指导之一聚类分析的SPSS操作方法系统聚类法实验例城镇居民消费水平通常用下表中的八项指标来描述。
八项指标间存在一定的线性相关。
为研究城镇居民的消费结构,需将相关性强的指标归并到一起,这实际上就是对指标聚类。
实验数据表 2001年30个省。
市,自治区城镇居民月平均消费数据x1人均粮食支出(元/人) x5人均衣着商品支出(元/人)x2人均副食支出(元/人) x6人均日用品支出(元/人)x3人均烟、酒、茶支出(元/人) x7人均燃料支出(元/人)x4人均其他副食支出(元/人) x8人均非商品支出(元/人)x1x2x3x4x5x6x7x8北京7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.61天津10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.57河北9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.65山西8.35 23.53 7.51 8.62 17.42 10.00 1.04 11.21内蒙古9.25 23.75 6.61 9.19 17.77 10.48 1.72 10.51辽宁7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.29吉林8.19 30.50 4.72 9.78 16.28 7.60 2.52 10.32黑龙江7.73 29.20 5.42 9.43 19.29 8.49 2.52 10.00上海8.28 64.34 8.00 22.22 20.06 15.52 0.72 22.89江苏7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.69浙江7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.87安徽8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.28福建10.60 52.41 7.70 9.98 12.53 11.70 2.31 14.69江西 6.25 35.02 4.72 6.28 10.03 7.15 1.93 10.39山东8.82 33.70 7.59 10.98 18.82 14.73 1.78 10.10河南9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.76湖北8.67 36.05 7.31 7.75 16.67 11.68 2.38 12.88湖南 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.23广东12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.50广西7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.57海南13.45 55.85 5.50 7.45 9.55 9.52 2.21 16.30四川7.18 40.91 7.32 8.94 17.60 12.75 1.14 14.80贵州7.67 35.71 8.04 8.31 15.13 7.76 1.41 13.25云南9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.67西藏7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.90陕西9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.17甘肃9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.35青海10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.81宁夏8.70 28.12 7.21 10.53 19.45 13.30 1.66 11.96新疆 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.61系统聚类法的SPSS操作:1. 从数据编辑窗口点击Analyze →Classify →Hierachical Cluster , (见图1)图1 系统聚类法打开层次聚类法对话如图2。
SAS学习系列35.聚类分析

35.聚类分析(一)概述聚类分析,相当于“物以类聚”,用于对事物的类别面貌尚不清楚,甚至在事前连总共有几类都不能确定的情况下对数据进行分类。
而判别分析,必须事先知道各种判别的类型和数目,并且要有一批来自各判别类型的样本,才能建立判别函数来对未知属性的样本进行判别和归类。
聚类分析是把分类对象按一定规则分成组或类,这些组或类不是事先给定的而是根据数据特征而定的。
在同类的对象在某种意义上倾向于彼此相似,而在不同类里的这些对象倾向于不相似。
根据这种相似性的不同定义,聚类分析也有不同的方法。
聚类分析分为:对样品的聚类,对变量的聚类。
样品聚类:其统计指标是类与类之间距离,把每一个样品看成空间中的一个点,用某种原则规定类与类之间的距离,将距离近的点聚合成一类,距离远的点聚合成另一类。
变量聚类:其统计指标是相似系数,将比较相似的变量归为一类,而把不怎么相似的变量归为另一类,用它可以把变量的亲疏尖系直观地表示出来。
二)原理一、距离和相似系数设有n组样品,每组样品有p个变量的数据如下:例如,Xj到Xj的闵科夫斯基距离定义为:IJ p 9q%=区I Xk- Xjkf ,<k A丿q=2时为欧几里得距离;还有马氏距离:dij=(Xj・XjFS」(Xj-Xj)其中,Xj=(Xii,…,Xjp),S」为n个样品的px p的协方差矩阵的逆矩阵。
注:马氏距离考虑了观测变量之间的相矢性和变异性(不再受各指标量纲的影响)。
距离选择的基本原则:(1) 要考虑所选择的距离公式在实际应用中有明确的意义。
如欧氏距离就有非常明确的空间距离概念。
马氏距离有消除量纲影响的作(2) 要综合考虑对样本观测数据的预处理和将要采用的聚类分析方法。
如在进行聚类分析之前已经对变量作了标准化处理,则通常就可米用欧氏距离。
(3) 应根据研究对象的特点不同做出具体分折。
实际中,聚类分析前不妨试探性地多选择几个距离公式分别进行聚类,然后对聚类分析的结果 进行对比分析,以确定最合适的距离测度方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三我国各地区城镇居民消费性支出的
主成分分析和聚类分析
(王学民编写)
一、实验目的
1.掌握如何使用SAS软件来进行主成分分析和聚类分析;
2.看懂和理解SAS输出的结果,并学会以此来作出分析;
3.掌握对实际数据如何来进行主成分分析;
4.对同一组数据使用五种系统聚类方法及k均值法,学会对各种聚类效果的比较,获取重要经验;
5.掌握使用主成分进行聚类
二、实验内容
数据集sasuser.examp633中含有1999年全国31个省、直辖市和自治区的城镇居民家庭平均每人全年消费性支出的八个主要变量数据。
对这些数据进行主成分分析,可将这31个地区的前两个主成分得分标示于平面坐标系内,对各地区作直观的比较分析。
对同样的数据使用五种系统聚类方法及k均值法聚类,并对聚类效果作比较。
最后,对主成分的图形聚类和正规聚类的效果进行比较。
实验1
进行主成分分析,根据前两个主成分得分所作的散点图对31个地区进行比较分析。
实验2
分别使用最长距离法、中间距离法、两种类平均法、离差平方和法和k均值法进行聚类分析,并比较其聚类效果。
实验3
主成分聚类,并与上述正规的聚类方法进行比较
三、实验要求
1.用SAS软件的交互式数据分析菜单系统完成主成分分析;
2.完成五种系统聚类方法及k均值法,比较其聚类效果;
3.根据前两个主成分得分的散点图作直观的聚类,并与上述正规的聚类方法进行比较。
四、实验指导
1.进行主成分分析
在inshigt中打开数据集sasuser.examp633,见图1。
选菜单过程如下:
在图1中选分析⇒多元(Y X)⇒在变量框中选x1,x2,x3,x4,x5,x6,x7,x8(见图2)⇒Y⇒选输出⇒选主分量分析,主分量选项(见图3)⇒在图4中作图中的选择(主成分个数缺省时为“自动”选项,此时只输出特征值大于1的主成分)⇒确定⇒确定⇒确定
图1
图2
图3
图4 得到如图5、图6所示的结果:
图5
图6
从图5可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和87.8%,第一
主成分1ˆy 在所有变量(除在*2x 上的载荷稍偏小外)上都有近似相等的正载荷,反映了综合消费
性支出的水平,因此第一主成分可称为综合消费性支出成分。
第二主成分2ˆy 在变量*2x 上有
很高的正载荷,在变量*4x 上有中等的正载荷,而在其余变量上有负载荷或很小的正载荷。
可以认为这个主成分度量了受地区气候影响的消费性支出(主要是衣着2x ,其次是医疗保健4x ①)在所有消费性支出中占的比重(也可理解为一种消费倾向),第二主成分可称为消费倾向成分。
第三主成分很难给出明显的解释,因此我们只取前面两个主成分。
在图1中选分析⇒散点图(Y X )⇒选 PCR1→X ;PCR2→Y ;region →标签变量 (见图7)⇒确定
随即出现如图8所示的散点图,接下来我们对该图进行设置、调整,使之符合我们的要求。
图7
①可从表1计算出医疗保健在消费性总支出中占的比率841i i x x
=∑,然后进行由大到小的排序,各地区的顺
序依次为:宁夏、黑龙江、青海、河北、辽宁、北京、浙江、陕西、甘肃、山西、吉林、河南、新疆、内蒙古、天津、云南、山东、广东、湖北、四川、重庆、湖南、海南、江苏、上海、西藏、贵州、广西、安徽、江西和福建,大致由寒冷的北方地区排到温暖的南方地区。
这是由于气候的寒冷易导致医疗保健费用的增加,因此,可以认为除衣着2x 外医疗保健4x 也是受地区气候影响的变量。
图8
在图9的数据窗口中点击左上角的“31”,以使所有观测都选中⇒将鼠标移至观测号中,点击右键,选在图中加标签⇒在图8中点击左下角,出现上托菜单⇒刻度…⇒作图10中的选择⇒确定⇒作图11中的选择⇒确定⇒调整好散点图:拉大图外围方框;图8 中点击标记大小,选择6号字;下拉横坐标,左拉纵坐标;图8 中点击参考线。
图9
图10
图11
图12
随即得到图12,该图是关于第一和第二主成分得分的散点图,该图对各地区的综合消费性支出和受地区气候影响的消费性支出占的比重有较直观的描述。
从图中可以看出,上海、广东和北京在最右边,城镇居民综合消费性支出是最高的;其次是浙江和天津;江西在散点图的最左边,表明综合消费性支出是最低的;北京和西藏在散点图的最上边,说明受地区气候影响的消费性支出占的比重最高;广东在最底部,表明受地区气候影响的消费性支出占的比重最低。
2.用五种系统聚类法及k均值法聚类,并比较其效果
(1)分别使用最长距离法、中间距离法、两种类平均法和离差平方和法进行聚类分析,为此编制如下的SAS程序:
proc cluster data=sasuser.examp633 method=com std;
id region;
proc tree horizontal;
id region;
proc cluster data=sasuser.examp633 method=med std;
id region;
proc tree horizontal;
id region;
proc cluster data=sasuser.examp633 method=ave std;
id region;
proc tree horizontal;
id region;
proc cluster data=sasuser.examp633 method=ave nosquare std;
id region;
proc tree horizontal;
id region;
proc cluster data=sasuser.examp633 method=war std;
id region;
proc tree horizontal;
id region;
run;
程序说明:
“proc cluster”是一个聚类分析过程;“data=sasuser.examp633”规定过程分析的是sasuser逻辑库中的examp633数据集;“method=com”规定了采用的系统聚类方法是最长距离法(“method= med”是采用中间距离法;“method=ave”是采用类平均法,缺省时类之间的距离为均方距离,如使用选项“nosquare”,则类之间的距离为平均距离;“method= war”是采用离差平方和法);选项“std”规定了在聚类之前须先对各变量数据作标准化变换,缺省时是直接对原始数据进行聚类,而不作事先的标准化处理。
语句“id region”用于识别打印输出中的观测,并以变量region的取值显示;如果缺省,则用OBn 显示,其中n为观测序号。
“proc tree”是一个使用由cluster过程产生的数据集来画树形图的过程;选项“horizontal”要求树形图的取向为水平方向,且树根在左边。
如果没有指明此选项,则其高度轴为垂直方向,树根在上部。
聚类树形图的输出:
图13 最长距离法
图14 中间距离法
图15 类平均法(均方距离)
图16 类平均法(平均距离)
图17 离差平方和法
(2)使用k均值法进行聚类分析,编制如下的SAS程序:
proc standand data=sasuser.examp633 mean=0 std=1 out=stan;
proc fastclus data=stan maxc=5 drift list;
var x1-x8;
id region;
run;
程序说明:
“proc standand”是一个将SAS数据集中的一些或所有变量按给定的均值和标准差进行标准化变换;“data=sasuser.examp633”规定过程是对sasuser逻辑库中的examp633数据集进行;选项“mean=0 std=1”规定按均值为0、标准差为1进行标准化变换;选项“out=stan”要求生成一个包含标准化值的新数据集,并命名为stan,这是一个临时数据集,属于临时库work。
“proc fastclus”是一个动态聚类分析过程;“data= stan”规定对数据集stan 进行;“maxc=5”指定所允许的最大分类个数为5,如果缺省,其值假定为100;“var x1-x8”指定用于聚类分析中的数值型变量。
如果缺省,则使用所有未列入其他语句中的数值型变量;选项“drift”表明使用k均值法;选项“list”要求列出各观测归属的类别。
3.主成分聚类,并与上述正规的聚类方法进行比较
从图12中直观地进行聚类,将其结果与上述正规的聚类方法进行比较。
11。
