钢管订购和运输论文
钢管订购和运输计划

摘要在钢管的订购和运输汁划中,在第一问中用最短路算法,求解出每个钢厂到站点A2...A15的最小费用(包括运输费和出厂销售价),考虑到在铺设时管道要沿铺设路线离散地卸货,即运货到Aj后,还要在铺设路线上运输,因为不足整公里部分要按照整公里计算,所以我们认为沿管道路线每铺设1公里就要卸下1单位钢管,因此从某点A,向左铺设或向右铺设y时,此段运费应为:丄y(y + l)*O」=0.05y(y + l)2点Aj向右铺设可,从Aw向左铺设yj+i,为了保证合拢,则zj+y j + 1=ai,在这些条件之下,利用/加go软件,求解出总费用最小。
分析模型的销售价灵敏度的时候,将各个钢厂单位钢管的销售价分别增加和减少若干万元,再用弘go求解第一问题的模型,看总费用的变化大小,变化大的就是影响结果比较大的;用同样的方法可以分析生产上限的灵敏度。
第三问得时候,我们利用求解第一问的方式来求解问题。
关键字:最短路算法,lingo ,分别改变同样的条件来对比一,问题重述(略)二,符号说明:a h站点Aj至Aj+i的里程(铺设管道需要的钢管量)Si Si钢厂的最大生产量Xij 从钢厂Sj到Aj的钢管数量c .j 从钢厂si运往心的单位钢材费用最短路,即亮点运输单位钢材所需的最少费用,包括运输费和出厂销价Yj Aj点往左铺设的钢管数量zj Aj点往右铺设钢管的数量f 总费用三,问题分析:(1)对问题一的分析:从钢厂s |向点Aj运输钢管时,为了降低费用,应该走费用最小的路径,从一个工厂si到一个点Aj的路线并不唯一,需要从中找出费用最短的路,相应的最小费用为包括运输费和销售费。
从图我们可以看到,七个钢材厂要到Ai这点必须要经过A2,所以在考虑最低费用路径的时候,可以把Ai和A2看做一个点来考虑“根据图,我们由最短路问题的算法。
例:从s 1到儿最短的铁路为:2 9 02 km,根据1单位钢管的铁路运价表,可知铁路花费为:60+5*20=160万元,公路运费为3*0. 1 =0. 3万元,并且si 钢厂出厂1单位刚窜为16 0万元,所以,总费用二铁路运费+公路运费+销售价即(:耳=160 + 0.3 + 160=32 0.3 (万元):用同样的方法,我们可以得到Aj的最小费用(单位:万元):A AA2 A3 A4 A5 A6A71A8 A9AlA11Al2A131415 162 3S320. 300 25 19 180 3 181 224 5 25 26 28 28 0 1 3 .2 8.6 8 .5 ・1 .2 .2 2 6 6 1.2 8 225 3 3S36 345 32 26 0. 24 22 26 29 0 31 326 3 3 20. 3 .2 6.6 6 5 1 6. 2 9.2 7 1 1 .2 3 473 2 2 26 2 S375. 55. 336. 7 60. 2 24 203. 23 24 256 278 3 3 2 6 6 5 51 1 .2 2 7 1 1 .2 3 7S410395. 376. 31300.29 27 244. 2221 22236.24 254.3 2 6 6 5 1 6. 2 2 2 1 1 2 3 73 3 2 1S 4 0 80. 36 0 85. 27 266. 234 21 8 2 226 22 245 0. 3 2 1.6 1 5 6 2 .2 2 8 06 .2 8 238 3 2 2 2 1 1S 4 0 5. 366. 0 90. 28 271. 23 1 0 9 176 16 76 5.3 2 6 6 5 1 2 4 .2 2 1 5 .2 1 844 3 3 2 1 9 1 1S 25. 05. 386 32 10. 0 91. 259. 23 22 21 8. 8 67 3 2 .6 6 5 1 2 2 6 6 6 2 6 2在铺设时管道要沿铺设路线离散地卸货,即运货到Aj后9还要在铺设路线上运输,因为不足整公里部分要按照整公里计算,所以我们认为沿管道路线每铺设1公里就要卸下1单位钢管,因此从某点Aj向左铺设或向右铺设y时,此段运费应为:+ l)*0.1=0.05y(y + l)设从点Aj向右铺设z j,从Aj+】向左铺设畑,为了保证合拢,则可+ y田=a j, j=l, 2...15.问题的实质是确定从钢厂s,向州运输钢管的数量七,以及从Aj向左, 右铺设的里程(km)数,使总费用最小。
交通运输-钢管的订购及运输优化方案 精品

钢管的订购及运输优化方案承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的的表述方式在正文引用处和中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):吉林省建筑工程学院建筑装饰学院参赛队员(打印并签名) :1. 姜磊2. 魏文超3. 张晓斌指导教师或指导教师组负责人(打印并签名):杨雪日期: 20XX 年 9 月 14 日赛区评阅编号(由赛区组委会评阅前进行编号):20XX高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):摘要:从本题中可以看出我们要解决的问题是钢管怎样订购,怎样运输,才能使得总费用最少。
所以,我们从两个方面着手考虑这个问题,首先我们考虑怎样从钢厂订购货物,接下来我们考虑在订购好货物后我们怎样把货物运输到目的地。
对于这两个问题,从题目可知,订购和运输联系密切,所以,我们必须同时考虑考虑钢管的订购与运输。
再由题中给的钢厂与天然气管道路线分布图可以看出,该问题等同于把起点的信息通过最优路(即就是花费最少的路径)径送到目的地,在送往的途中可以有信息的流失,流失的信息即就是用于铺设道路的货物,但不管流失多少信息,到达目的地时,总还有剩余的信息。
所以,我们就把钢管的运输看成了最小费用最大流问题。
所以,我们通过对线路的标号,我们利用floyd算出最大流问题算出每一个钢厂到每个点的单位最优路径,然后,再算出在运送途中钢管用于铺设管道所花费的费用,我们把这两种费用相加,就得到了总的费用。
钢管的订购及运输优化方案

钢管的订购及运输优化方案钢管是一种常见的工业材料,主要用于建筑、桥梁、机器制造和能源开采等领域。
订购和运输钢管需要考虑多方面因素,如规格、数量、质量、运输距离、运输方式等。
本文将介绍一些钢管订购及运输的优化方案。
一、钢管订购方案1. 确定钢管规格和数量在订购钢管前,首先需要了解工程或项目的具体需求,确定钢管的规格和数量。
不同的工程或项目需要的钢管规格和数量可能会有所不同,选择合适的规格和数量可以避免浪费和损失。
2. 寻找可靠的供应商选择可靠的供应商可以确保钢管的质量和供应稳定性。
可以通过市场调研、参加行业展会或咨询同行业的项目经理、工程师等人员来寻找可靠的供应商。
3. 确定采购合同和交付方式在确定供应商后,需要签订采购合同并确定交付方式。
采购合同要明确规定钢管的规格、数量、价格和交付日期等具体条款,避免误解和纠纷。
交付方式可以选择集装箱运输、散装运输或其他方式,根据具体情况灵活选择。
4. 质量控制为确保钢管的质量,采购方可以要求供应商提供产品质量证明、实际样品或第三方检测报告。
在收到钢管后,可以进行抽检或全检,检查钢管的尺寸、表面状态、壁厚和材质等指标,避免存在不合格品质的钢管进入工程或项目。
二、钢管运输方案1. 选择合适的运输方式钢管的运输可以选择公路运输、铁路运输、水路运输或航空运输等方式。
具体选择哪种方式需要综合考虑运输距离、运输量、运输时间、运输成本及货物安全等各方面因素。
2. 管理运输过程在钢管运输过程中,需要对货车、火车、船舶或飞机等交通工具进行监控,确保运输过程中货物的安全。
可以使用GPS或其他定位技术实时掌握货物的位置和状态,及时处理运输中遇到的问题和风险。
3. 管理卸货和储存在将钢管卸货到工厂、工地或仓库后,需要将其储存到指定位置并标记钢管的规格、数量等信息。
可以采用RFID等智能化技术对钢管进行管理,便于日后的存储和使用。
4. 管理短途运输在项目工期中,可能需要短途运输钢管到具体施工位置。
2000年全国数学建模竞赛B题优秀论文
管道订购与运输问题1 问题重述2 基本假设(1)只考虑订购费用和运输费用,不考虑装卸等其它费用. (2)钢管单价与订购量、订购次数、订购日期无关.(3)订购汁划是指对每个厂商的定货数量;运输方案是指具有如下属性的一批记录:管道区间,供应厂商,具体运输路线.(4)将每一单位的管道所在地看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.3 符号说明M :钢厂总数. n :单位管道总数.:i S 第i 个钢厂 :i S 第i 个钢厂的产量上限。
:i p 第i 个钢厂单位钢管的销售价 i A 管道线上第i 个站点。
i d 管道线上第i 个单位管道的位置。
F :总费用。
:ij C 从钢厂(1,2,,)i S i m =到点(1,2,,)j d j n =的最低单位费用。
4 问题的简化求 S AP 矩阵的基本思路是图的最短路算法 . 由于铁路的运输费用与线路的长度不是线性关系 ,必须对铁路网做一些预处理才能套用图的标准最短路算法 . 下面叙述求 S AP 矩阵的过程:1.利用图的标准最短路算法 ,从铁路网络得出图中任两个点之间的最短路径表 T (如果两个点之间不连通 ,认为它们之间的最短路长度为+ ∞ ) .2.利用题中的铁路运价表将 T 中的每个元素 (即最短距离 )转化为运输费用 ,将运输费用表记为 C.3.将公路的长度换算为运输费用 ,由公路路程图 (包括要沿线铺设管道的公路 )得出公路费用图 G,若 i, j 不连通 ,则令 Gij = + ∞ .4.对于任一组 ( i , j)∈ { 1,… n }× { 1,… m } 如果 Cij <+ ∞ ,且小于 Gij ,那么就在公路费用图中加一条边. 即令 Gij = min{Cij , Gij } .5.利用图的标准最短路算法 ,求公路费用图中任一个 S 点到任一个 A 点的最小费用路径 ,得出 S AP 矩阵. 如表 1所示:SAP 矩阵A123 4 5 6 7 8 9 10 11 12 13 14 15 S1 170716031402986 380 205 31 212 642 920 960 1060 1212 1280 14202 215720531902 1716 1110 955 860 712 1142 1420 1460 1560 1712 1780 19203 230722032002 1816 1210 1055 960 862 482 820 860 960 1112 1180 13204 260725032352 2166 1560 1405 1310 1162 842 620 510 610 762 830 9705 255724532252 2066 1460 1305 1210 1112 792 570 330 510 712 730 8706 265725532352 2166 1560 1405 1310 1212 842 620 510 450 262 110 2807 275726532452 2266 1660 1505 1410 1312 992 760 660 560 382 260 205问题分析运输费用等价转换法则:按单位运费相等原则将任意两点间的最短铁路线转换为公路 线.对于铁路线上的任意两点,i j V V ,用F1oyd 算法找出两点间最短铁路路线的长度ij L 查铁路运价表求得ij L ,对应的铁路单位运费ij f ;又设与该段铁路等费用的公路长度为ij l ,则:0.1ij ij f l =⨯由此,我们就在,i j V V 之间用一条等价的公路线来代替,i j V V 间的最短铁路线.如果,i j V V 之间原来就有公路,就选择新旧公路中较短的一条.这样,我们就把铁路运输网络转换成了公路运输网络.销价等价转换法则:按单位费用相等将任意钢厂的单位销价转换为公路单位运价.对于钢厂S i 的销售单价P i ,我们可以虚设一条公路线,连接钢厂S i 及另一虚拟钢厂'i s ,其长度为i l ,并且满足0.1i i l p =⨯;从而将钢厂的销售单价转换成公路运输单价,而新钢厂'i s 的销售价为0.将铁路和销价转换为公路的过程可以由计算机编程实现. 通过上述的分析,我们可以将原问题化为一个相对简单的产量未定的运输问题,利用115A A 到之间的管道距离和钢厂和站点之间的公路距离建立一个产量未定的运输问题的模型.但是由于1215,A A A ,并不能代表所有的实际需求点(实际需求点是n 个单位管道),因此,我们可以用F1oyd 算法进一步算出7个钢厂到所有实际的n 个需求点(对于问题一,n =5171;对于问题三,n =5903)的最短路径,并由此得出一个具有7个供应点、n 个需求点的产址未定的运输模型.6 模型的建立产量未定的运输模型根据假设4,我们可以将每一单位的管道看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.对每个点,我们可以根据该点的位置和最短等价公路距离,求出各钢厂与该点之间最小单位运输费用ij C (销价已经归人运输费用之中了).设总共有m 个供应点(钢厂),n 个需求点,我们就可以得到一个产量未定的运输模型:有m 个供应点、n 个需求点,每个供应点的供应量{0}{500,}i i u s ∈;每个需求点需要1单位,运输单价矩阵为C ,求使得总运输费用最小的运输方案.其数学规划模型: 11minmnij ij i j F C x ===∑∑11{0}{500,}1,2,,..11,2,01nij i j mij i ij x S i ms tx j n x ==⎧∈=⎪⎪⎪==⎨⎪⎪=⎪⎪⎩∑∑或其中: 1112112n m m mn C C C C CC C ⎛⎫⎪=⎪ ⎪⎝⎭为单位费用矩阵 1112112n m m mn x x x X x x x ⎛⎫⎪=⎪ ⎪⎝⎭为决策矩阵,也为0-1矩阵 代码如下7 模型的求解对于本题,上述0-1规划规模宏大,现有的一些算法不能胜任,我们必须具体问题具体分析,结合本题实际情况,寻找行之有效的算法.(1)初始方案的改进的最小元素法和改进的伏格尔法 *改进的最小元素法改进的最小元素法又称为贪婪法或瞎子爬山法,它的宗旨是每一步都取当前的最优值算法步骤为,对费用矩阵C 作n 次下列循环:①C 中找一个最小值ij C ; ②令1;ij x =③C 的第j 的所有数据改为+∞;④如果1nij i j x s ==∑,第i 个供应点的供应量已达上限,将C 的第i 行数据全改为+∞。
钢管的订购及运输优化方案

钢管的订购及运输优化方案摘要:从本题中可以看出我们要解决的问题是钢管怎样订购,怎样运输,才能使得总费用最少。
所以,我们从两个方面着手考虑这个问题,首先我们考虑怎样从钢厂订购货物,接下来我们考虑在订购好货物后我们怎样把货物运输到目的地。
对于这两个问题,从题目可知,订购和运输联系密切,所以,我们必须同时考虑考虑钢管的订购与运输。
再由题中给的钢厂与天然气管道路线分布图可以看出,该问题等同于把起点的信息通过最优路(即就是花费最少的路径)径送到目的地,在送往的途中可以有信息的流失,流失的信息即就是用于铺设道路的货物,但不管流失多少信息,到达目的地时,总还有剩余的信息。
所以,我们就把钢管的运输看成了最小费用最大流问题。
所以,我们通过对线路的标号,我们利用floyd算出最大流问题算出每一个钢厂到每个点的单位最优路径,然后,再算出在运送途中钢管用于铺设管道所花费的费用,我们把这两种费用相加,就得到了总的费用。
我们通过计算,得出应从哪些钢厂订购多少货物,以怎样的路径进行运送才能使总费用最小。
经过计算我们得出最优解:其最小费用为万元。
在第二问中,我们通过对问题一的精度分析可得:钢厂6S的钢管销价的变化对购运计划和总费用的影响最大;钢管厂1S的钢管产量的上限的变化对总费用的影响最大,钢管厂3S的产量上限的变化对购运计划的影响最大。
对于第三问,我们同样运用问题一的解决办法,先求出每一个钢厂到每段道路的最短路径,然后再求出每一钢厂运送的数量,还有运送途中铺路石所花费的单位费用,最后得出最优解:其最小费用为万元。
问题重述:(略)问题分析:本题看似复杂,但经过分析我们可以看出该问题是求在一个有权图中寻求最优路径的问题,然后再求各个钢厂的运送花费问题,对于运送费用问题,由于我们不知道在哪一个钢厂订货,也不知道定多少,也不知道走哪一条路最合适,所以我们我们利用线性规划中的方法,先利用0—1规划模型,当取0时,我们就认为不在该厂订货,或者说我们不选择某一条路径,这样我们就轻易的将这个复杂的问题分解为线性规划问题。
钢管订购和运输论文(完整)

钢管订购和运输摘要要铺设一条1521A A A →→→ 的输送天然气的主管道,经筛选后可以生产这种主管道钢管的钢厂有721,,S S S ,钢管可由铁路、公路运往铺设地点,需要制定一个主管道钢管的订购和运输计划,使总费用最小。
本文即针对各钢厂生产计划和运输相结合问题建立了相应的最优化问题的数学模型。
首先从从运输问题入手,设1km 主管道钢管称为1单位钢管,根据1单位钢管的铁路运价和公路运输费用以及各钢厂到1521A A A 、、、 的距离,确定各钢厂的生产的钢管运输到哪个铺设点的单价。
经过统计预算,我们将7个钢管生产厂家和14个钢管铺设路段分为两个集合,第一个集合包括钢厂S1、S2、S3和管道路段A12、A23、A34、A45、A56、A67、A78。
第二个集合包括钢厂S4、S5、S6、S7和管道路段A89、A910、A1011、A1112、A1213、A1314、A1415。
针对两个集合,我们分别建立最优化数学模型。
我们将钢厂生产产量的上限和下限以及各铺设点铺设该路段所需的钢管量作为约束条件,建立总费用的方程式,求总费用方程式在约束条件下的极小值,将两个集合计算得到的极小值相加,即得到铺设管道的最低总费用。
接着,进一步考虑哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大。
我们以上述总费用方程式作为目标函数,分别针对第一个集合和第二个集合,计算哪个钢厂的销价和钢管的产量上限的变化对总费用的影响。
对计算钢厂的销价对总费用的影响,采用假定其他钢厂的价格不变,此钢厂价格的变化对总费用的影响。
对钢管的产量上限的变化对总费用的影响,通过问上述最优化数学模型得出的灵敏度分析结果可知。
如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,我们在上述最优化数学模型的基础上,结合该树形网络的情况,分析新增需要铺设的路段,对已建立的最优化数学模型进行修改,即可计算得出树形管道铺设的最低总费用。
钢管定购与运输问题的数学模型与求解的新方法

钢管定购与运输问题的数学模型与求解的新方法一、本文概述钢管作为一种重要的建筑材料,在各类工程项目中具有广泛的应用。
钢管的定购与运输问题涉及到供应链管理、物流优化等多个领域,是工业界和学术界共同关注的重要问题。
随着市场需求的不断变化和物流技术的快速发展,传统的钢管定购与运输方法已经难以满足现代工业的需求。
因此,本文旨在探讨钢管定购与运输问题的数学模型与求解的新方法,以提高钢管供应链的效率和经济性。
本文将首先分析钢管定购与运输问题的特点和难点,包括需求量的不确定性、运输成本的波动性、供应链中的信息不对称等。
在此基础上,建立适用于钢管定购与运输的数学模型,包括需求量预测模型、运输优化模型等。
这些模型将综合考虑市场需求、库存成本、运输费用等多个因素,为钢管的定购与运输提供决策支持。
接下来,本文将介绍求解钢管定购与运输问题数学模型的新方法。
这些方法将结合现代优化算法和计算机技术,对模型进行高效求解。
同时,本文还将探讨如何将这些方法应用于实际钢管供应链管理中,以提高供应链的整体效益。
本文将通过案例分析和仿真实验来验证所提出数学模型和求解方法的有效性和实用性。
这些案例和实验将基于实际钢管供应链数据,对模型和方法进行测试和评估。
通过对比分析不同方案的效果,本文将为钢管定购与运输问题的求解提供新的思路和方法。
本文旨在深入研究钢管定购与运输问题的数学模型与求解的新方法,以提高钢管供应链的效率和经济性。
通过建立适用的数学模型和采用先进的求解方法,本文将为钢管定购与运输问题的优化提供理论支持和实践指导。
二、钢管定购与运输问题的数学模型钢管定购与运输问题是一个涉及供应链管理和物流优化的复杂问题。
为了有效地解决这一问题,首先需要建立一个合适的数学模型。
这个模型需要能够准确地描述钢管的定购、库存、运输以及相关的成本和约束条件。
定购决策:根据预测需求、库存量和供应商条件,决定何时从哪些供应商定购钢管。
运输优化:选择最经济、最高效的运输方式,确保钢管按时送达目的地。
钢管订购与运输论文

钢管订购和运输优化模型关键词:最优化,Floyd 算法;钢管订购与运输;lingo ;摘要本文研究钢管订购与运输问题,该问题给定钢厂生产能力、不同路径长度下运输价格等限制,需要制定使总费用最小的订购运输计划,并分析在生产能力、单位订购价格变化时,对订购及运输计划的影响。
对问题一,我们先将整个网络图简化,利用Floyd 算法通过MATLAB 编程计算出铁路网上,任意两点的最短距离,从而可以知道从每个钢厂S 运往铁路网上各点个单位运输价格,结合公路运输路线,计算出钢管从钢厂i 运往节点j 运输单价ij c 。
设运往节点j ,刚才分别向左右两个方向运输的钢管量分别为j y 、j z ,那么铺设管道过程中的运输费也很容易表示。
我们就可以建立最小费用的优化模型。
再利用lingo 进行求解就可以得出最终结果。
最小总费用为:1278632万元,最终的订购计划为: S1 S2 S3 S4 S5 S6 S7 订购量800800100013211251问题二通过对模型参数的灵敏度分析,我们能得出模型的实际合理性,其中钢厂的产量影响通过问题一的LINGO 求解分析得出答案,而销价对结果的影响要通过自行改变钢厂的销价来实现。
分析结果显示:S1的产量变化对总费用的影响是最大的;S6钢厂销价的变化对总费用的影响是最大的,S4钢厂的销价变化对总费用的影响是最小的。
问题三,相对于问题一管道的铺设路径稍微复杂了一点,我们在问题一的基础上增设管道向第三方运输的运量j m ,再修改问题一的模型,得到本问题模型,再利用lingo 求解,最小总费用为:1404949万元,最终订购计划为: S1 S2 S3 S4 S5S6S7订购量80080010001475.086 1827.914 0最后,我们对模型进行了评价和改进,使模型更加完整和优化。
AbstractIn this paper, we study on the problem of pipe Ordering and Transporting,which Limit steel production capacity and transportation unit price under a different path length, and develop a plan of Pipe ordering and shipping making the minimumcost ,then analyze the production capacity of the unit subscription price changes, see which impacts of the ordering and transportation plans.The first problem, we first simplify the entire network diagram the use MATLAB programs and Floyd algorithm to calculate the shortest distance rail network, between any two points, which can be shipped to know from each steel S-line rail transportation unit price points, combined with road transport routes, calculate the transport unit from steel mills shipped node. Let destined for a node, the amount of steel were just about transport in both directions, respectively, then the process of laying the pipeline transportation costs can easily expressed. We can create the minimum cost optimization model. Reuse lingo for solving the final result can be drawn. The minimum total cost: 12,786,320,000 yuan, the final subscription plan is: S1 S2 S3 S4 S5 S6 S7 subscribe 800 800 1000 0 1321 1251 0 Second problem by sensitivity analysis of the model parameters, we can drawpractical rationality of the model, which yield a steel through problem solving LINGO analysis of the answer, but the selling price impact on the outcome of the change through their own mills the selling price to achieve. Analysis showed: the impact on the total production cost changes S1 is the largest; affect S6 steel selling price changes on the total cost is greatest impact on the selling price changes S4 mills total cost is minimal.Question three, relative to the laying of a pipeline path problem is slightly morecomplicated, we added the issue on the basis of a third-party pipeline to transport the volume, and then modify the problem a model to get the problem model, re-use lingo solved The minimum total cost: 14,049,490,000 yuan, the final subscription plan is:S1S2 S3 S4 S5S6S7subscribe 80080010001475.086 1827.914 0Finally, the model was evaluated and improved to make the model more complete and optimized.一、问题重述1.1问题提出要铺设一条1521A A A →→→ 的输送天然气的主管道,如题中图一所示,图中包括可以生产这种主管道钢管的钢厂有721,,S S S ,钢厂生产的钢管需要通过铁路运输网、公路运输网运到管道铺设处。
钢管运输

221钢管的订购与运输【摘要】 本模型是为了研究如何制定一个主管道钢管的订购和运输计划使得铺设天然气管道费用最小的问题。
由于涉及到钢厂的地理位置和钢厂出厂销价不同等的因素,所以需要综合所有因素来制定订购和运输计划达到最优化使得所需费用最小。
对于问题一制定计划,需要考虑到每个钢厂与铺设管道路径上的车站的相对位置关系和选择从指定钢厂调用多少单位的钢管。
我们可以先确定从钢管生产厂家运输单位钢管到施工站点的费用最小路线,然后设立模型,总费用等于钢厂订购的钢管销价加上所有路线上的花费的总和,建立工程费用的优化模型,采用非线性规划的方法用lingo 软件求解,从中优化出最佳购运方案。
在问题二中,当钢厂钢管销售价格变化时,会对购运计划和总费用造成影响。
为了更好地观察每一个钢厂钢管销售价格所造成的影响,采用比较法,即每次只让一个钢厂钢管的销售价格发生相同的变化,其余钢厂钢管的销售价格不发生变化,同样采用比较法,即每次只让一个钢厂钢管产量的上限的发生相同的变化,其余钢厂钢管产量的上限不发生变化,然后在问题一所设立模型中进行求解,再进行比较便可得出哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大。
问题一结果:购运总费用最小为1406631(万元),具体的购运计划和铺设方案如表4,表5.问题二结果:6S 钢厂销价变化对总费用影响最;56,S S 钢厂钢管的销价的变化对购运计划影响最大,1S 钢厂钢管的产量的上限的变化对总费用影响最大,购运计划影响较小。
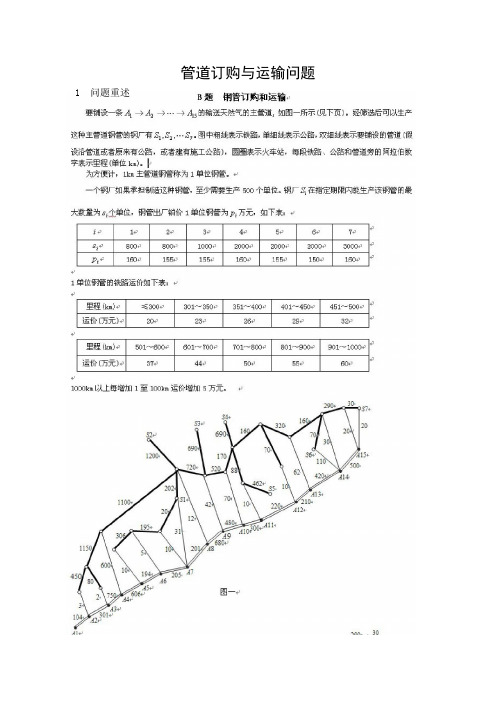
【关键词】 优化 非线性规划一、问题重述和分析222 要铺设4条1215A A A →→→ 、916A A →、1117192021A A A A A →→→→、1718A A →的输送天然气的主管道,如图1所示,经筛选后可以生产这种主管道的钢厂有721,,,S S S . 图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km ).图1为了方便,1km 主管道称为1单位钢管. 一个钢厂如果承担制造这种钢管,至少需要生产500个单位. 钢厂i S 在指定期限内能生产该钢管的最大生产数量为i s 个单位,钢厂出厂销价为i p 万元,如下表:A 132 5 8010103120124270 1088 10 70 6270 30 20 2030450104 301 750 606194205 201 680480 300220210 420500600306195202720 690520170 690462160320160 110 290115011001200A 19130190 260 100A 2A 3 A 4A 5A 6 A 7A 8A 9 A 10A 11A 12A 13 A 14 A 15S 1S 2S 3S 4S 5 S 6 S 7 A 16A 17A 18 A 20(A 21)223表1i 1 2 3 4 5 6 7 i s 800 800 1000 2000 2000 2000 3000 i p1601551551601551501601单位钢管的铁路运价如下表:表2里程(km ) 300≤350~301 351~400 401~450 451~500 运价(万元) 2023 26 29 32 里程(km ) 501~600601~700 701~800 801~900 901~1000 运价(万元) 3744 5055 60 1000km 以上每增加1至100km 运价增加5万元. 公路运输费用为1单位管道每公里0.1万元(不足整公里的按整公里计算). 管道可由铁路、公路运往铺设地点(不只是运到点1521A A A →→→ 、916A A →、1117192021A A A A A →→→→、1718A A →,而是管道全线).问题1. 制定一个主管道钢管的订购和运输计划,使总费用最小,并给出总费用. 问题2. 就(1)的模型进行分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果.二、基本假设1. 在计算运费时,沿管道铺设路线上的公路与其它普通公路相同(1单位钢管每公里0.1万元);2. 订购的钢管数量刚好等于需要铺设的钢管数量;3. 管道可由铁路、公路、管道全线运往铺设地点(不只是运到点1221,,,A A A ); 4. 模型只考虑钢管销价费用和钢管从钢管厂运送到铺设点的钢管运费,而不考虑其它费用,如不计换车、转站的时间和费用,不计装卸费用等;5. 不计运输时由于运输工具出现故障等意外事故引起工期延误造成损失; 6. 销售价和运输价不受市场价格变化的影响.三、符号说明i S : 第i 钢管厂i s :表示i S 的最大生产能力j A : 表示需要铺设管道路径上的车站224 i j x : 从所有i S 运往j A 的钢管数c i j : 表示单位钢管从i S 地运往j A 地的最小费用 i p :从i S 订购钢管的单位价格Q : 订购的所有钢管全部运到(1,2,,21)j A j = 点的总运费 T : 当钢管从钢厂i S 运到点j A 后,钢管向j A 的左右两边运输(铺管道的运输费用Z :用于订购和运输的总费用( jk ): 连接j A 和m A 的边()jm d : 运到j A 地向m A 地铺设钢管的数目d : 单位钢管1公里的公路运输费用()jm A : 表示j m A A 和之间需要铺设的管道长度四、模型的建立与求解问题1.1、 模型的建立钢管的订购和运输方案是直接影响工程费用的主要原因,因此,选取费用最小的路线运送货物,合理的订购计划是决定该工程费用的重要因素,首先利用图论的方法,来确定从钢管生产厂家到施工结点的费用最小路线,然后建立工程费用的优化模型,从中优化出最佳购运方案.对本问题而言,实际上是一个要求制定订购和运输计划,使总费用最小的优化问题. 本模型的总费用包括钢管的销价和运输总的费用. 首先,向某厂订购钢管,然后将在每个厂订购的钢管运往需要铺设的全路段. 欲解决本问题可以按以下方案进行思考:首先,需要确定将货物从i 地运往j 地的最优路线(费用最小);然后,求出向每个钢管厂的订购计划,并确定出运输计划;最后计算将运往j 地的钢管铺到各个管道上的运输费用,我们不妨假设运往以j 为终点的钢管只铺到与j 点相邻的两段管道上. 因此,本问题可以按以下步骤求解.第一步:确定从i 地到j 地的最优路径,从而确定出单位钢管从i 地运往j 地的最小运费.)7,2,1( =i s i 表示钢管厂)7,2,1( =i S i 的最大生产能力,(1,2,,21)j A j = 表示需要铺设钢管路径上的车站. 假设从i S 运往j A 的钢管用于铺设j A 点左右侧的钢管225数为j i x ,单位,单位产品从i S 到j A 地的运费为j i F ,万元,用j i ,c 表示单位钢管从i S 地运往j A 地的最小费用,则:j c min ij i F =(1)第二步:建立从i S 厂运送j ,i x 单位钢管到j A 点的运费的模型:用Q 表示订购的所有钢管全部运到(1,2,,21)j A j = 点的总运费,则:21711Q c i j i j j i x ===∑∑;(2)第三步:将运到j A 处的钢管铺到相邻两段路上的运输费用对于运到j A 的钢管,它向m A 运输的总量为()jm d ,它向m A 运输的总费用为:()()()(1)(2)1jm jm jm d d d d d d d ⨯+-⨯+-⨯⨯=()()()()0.1(12)0.051jm jm jm d d d ⨯+++=+ (万元);用T 表示当钢管从钢厂i S 运到点j A 后,钢管向m A 运输(铺设)管道的运输费用,得()()()211T 0.051jm jm m d d ==+∑(3)()x ij jm d 和之间存在的关系为()()()()721i j i 11x ;(1,2,,21);(,1,2,,21)jm m jm mj jm d j d d A j m ==⎧==⎪⎨⎪+==⎩∑∑ (4)(()jm A 表示j m A A 和之间需要铺设的管道长度)第四步:建立订购费用的模型设W 表示订购管道的总费用,则可建立如下模型:226721, 1j 1W i i j i p x ===∑∑(5)又因为一个钢厂如果承担制造钢管任务,至少需要生产500个单位,钢厂i S 在指定期限内最大生产量为i s 个单位,故212500iji j xs =≤≤∑ 或2120ij j x ==∑ , 用Z 表示订购和运输的总费用,由(2)、(3)、(4)、(5),本问题可建立如下的非线性规划模型:目标函数()()()72121i 111min W Q T ()0.051i i j i j jm jm j m Z p c x d d ====++=+++∑∑∑约束条件()()()()721i j i 11212122x ;(1,2,,21);(,1,2,,21)5000;(1,2,,7)0 1,,7,2,,21jm m jm mj jm ij i ij j j ij d j d d A j m x s x i x i j ====⎧==⎪⎪+==⎪⎪⎨⎪⎪≤≤==⎪⎪≥==⎩∑∑∑∑ 或 (6)其中1 ,+j j A 表示1+j j A A 和之间需要铺设的管道长度.2、模型的求解(1)首先求解 i j c 由于钢管从钢厂i S 运到运输点j A 要通过铁路和公路运输,而铁路运输费用是分段函数,与全程运输总距离有关. 又由于钢厂i S 直接与铁路相连,所以可先求出钢厂i S 到铁路与公路相交点j b 的最短路径. 依据钢管的铁路运价表,算出钢厂i S 到铁路与公路相交点j b 的最小铁路运输费用,并把费用作为边权赋给从钢厂i S 到j b 的边. 再将与j b 相连的公路、运输点i A 及其与之相连的要铺设管道的线路(也是公路)添加到图上,根据单位钢管在公路上的运价规定,得出每一段公路的运费,并把此费用作为边权赋给相应的边. 这样就转换为以单位钢管的运输费用为权的赋权图,再利用E.W.Dijkstra 的最短路算法计算出一个单位钢管从钢厂运到工地的最少费用系数阵()ij c ,MA TLAB 程序(略).227表3 表中对应的值为对应两点最优路径单位钢管运输费用S1 S2 S3 S4 S5 S6 S7 A1170.0 215.7 230.7 260.7 255.7 260.7 275.7 A2 160.3 205.3 220.3 250.3 245.3 250.3 265.3 A3 140.2 190.2 200.2 235.2 225.2 235.2 245.2 A4 98.6 171.6 181.6 216.6 206.6 216.6 226.6 A5 38.0 111.0 121.0 156.0 146.0 156.0 166.0 A6 20.5 95.5 105.5 140.5 130.5 140.5 150.5 A7 3.1 86.0 96.0 131.0 121.0 128.1 141.0 A8 21.2 71.2 86.2 116.2 111.2 116.2 131.2 A9 64.2 114.2 48.2 84.2 79.2 84.2 99.2 A10 92.0 142.0 82.0 62.0 57.0 61.0 76.0 A11 96.0 146.0 86.0 51.0 33.0 47.0 64.0 A12 106.0 156.0 96.0 61.0 51.0 37.0 56.0 A13 121.2 171.2 111.2 76.2 71.2 16.2 38.2 A14 128.0 178.0 118.0 83.0 73.0 11.0 26.0 A15 142.0 192.0 132.0 97.0 87.0 28.0 2.0 A16 60.0 110.0 44.0 80.0 75.0 80.0 95.0 A17 95.0 145.0 85.0 50.0 32.0 46.0 63.0 A18 100.0 150.0 90.0 55.0 45.0 33.0 50.0 A19 105.0 155.0 95.0 60.0 50.0 36.0 55.0 A20 115.0 165.0 105.0 70.0 65.0 10.0 32.0 A21125.0175.0115.080.075.00.026.0(2)根据以上结果, 继续求解非线性规划模型:()()()72121i 111min ()0.051i i j i j jm jm j m Z p c x d d ====+++∑∑∑()()()()721i j i 11212122x ;(1,2,,21);(,1,2,,21).5000;(1,2,,7)0 1,,7,2,,21jm m jm mj jm ij i ij j j ij d j d d A j m s t x s x i x i j ====⎧==⎪⎪+==⎪⎪⎨⎪⎪≤≤==⎪⎪≥==⎩∑∑∑∑ 或 由于不能直接处理约束条件:2121225000;(1,2,,7)iji ij j j xs x i ==≤≤==∑∑ 或,我们可228 先将此条件改为212iji j xs =≤∑,得到如下模型:()()()72121i 111min ()0.051i i j i j jm jm j m Z p c x d d ====+++∑∑∑()()()()721i j i 11212x ;(1,2,,21);(,1,2,,21).;(1,2,,7)0 1,,7,2,,21jm m jm mj jm ij i j ij d j d d A j m s t x s i x i j ===⎧==⎪⎪+==⎪⎪⎨⎪⎪≤=⎪⎪≥==⎩∑∑∑用LINGO 求解(程序略). 分析结果后发现购运方案中钢厂7S 的生产量不足500单位,下面我们采用不让钢厂7S 生产和要求钢厂7S 的产量不小于500个单位两种方法计算:1)不让钢厂7S 生产,程序略.计算结果:1Z =1482890(万元)(此时每个钢厂的产量都满足条件). 2)要求钢厂7S 的产量不小于500个单位,程序略.计算结果:2Z =1406631(万元) (此时每个钢厂的产量都满足条件). 比较这两种情况,得最优解为,121min min(,)Z Z Z Z ===1406631(万元). 所以根据上述的模型,得运输总费用最小为1406631(万元). 具体的购运计划和铺设方案如表4,表5.表4 问题一的订购和调运方案订购量 A 2A 3 A 4 A 5 A 6 A 7 A 8 A 9 A 10 A 11 A 12 A 13 A 14 A 15 S 1 800 0 0 40 295 200 265 0 0 0 0 0 0 0 0 S 2 800 179 0 0 321 0 0 300 0 0 0 0 0 0 0 S 3 1000 0 0 336 0 0 0 0 664 0 0 0 0 0 0 S 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 S 5 1015 0 508 92 0 0 0 0 0 0 415 0 0 0 0 S 6 1556 0 0 0 0 0 0 0 0 351 0 86 333 621 165 S 7表5 问题一的铺设方案y zA1 0.0000000.000000 A2 104.0000 75.00000 A3 226.0000 282.0000 A4468.00000.000000229A5 606.0000 9.500000 A6 184.5000 15.50000 A7 189.5000 76.00000 A8 125.0000 175.0000 A9 505.0000 159.0000 A10 321.0000 30.00000 A11 270.0000 145.0000 A12 75.00000 11.00000 A13 199.0000 134.0000 A14 286.0000 335.0000 A15 165.0000 0.000000问题2. 针对问题一的求解模型,讨论钢厂钢管的销售价格变化对购运计划和总费用影响及钢厂钢管产量的上限变化对购运计划和总费用的影响.定义 方案中运往各点i A 的运输量的变化量的绝对值之和称为运输方案变化量. 1、讨论钢厂钢管的销售价格变化对购运计划和总费用的影响当钢厂钢管销售价格变化时,会对购运计划和总费用造成影响. 为了更好地观察每一个钢厂钢管销售价格所造成的影响,采用比较法,即每次只让一个钢厂钢管的销售价格发生相同的变化,其余钢厂钢管的销售价格不发生变化.我们将各个钢厂单位钢管的销价分别增加1万元和减少1万元,借助LINGO 软件得出相应的总费用、运输方案、订购方案变化情况如表6、表7所示表6 各个钢厂单位钢管的销价分别增加1万元钢厂 总费用 总费用变化量运输方案变化量 订购方案变化量S 1 1279432 800 0 0 S 2 1279432 800 0 0 S 3 1279632 1000 0 0 S 4 1278632 0 0 0 S 5 1279639 1007 40 30 S 6 1279834 1202 712 712 S 7 1278632 0 0 0表7 各个钢厂单位钢管的销价分别减少1万元钢厂 总费用 总费用变化量运输方案变化量 订购方案变化量S 1 1277832 800 0 0 S 2 1277832 800 0 0 S 3 1277632 1000 0 0 S 4 1278632 0 0 0 S 5 1277263 1369 712 712 S 6 1277068 1564 40 30 S 7 1278632 0 0 0由上述表格观察分析可得: 6S 钢厂销价变化对总费用影响最大,56,S S 钢厂钢管的销价的变化对购运计划影响最大.2、讨论钢厂钢管产量的上限的变化对购运计划和总费用的影响同样采用比较法,即每次只让一个钢厂钢管产量的上限的发生相同的变化,其余钢厂钢管产量的上限不发生变化. 将各个钢厂的产量的上限分别增加100个单位和减少100个单位,分别计算,得到购运计划和总费用变化情况如表8、表9所示.表8 各个钢厂钢管的产量的上限分别增加100个单位钢厂总费用总费用变化量运输方案变化量订购方案变化量S1 1268332 10300 218 200S2******* 3500 404 200S3******* 2500 1786 200S4******* 0 0 0S5******* 0 0 0S6******* 0 844 0S7 1278632 0 0 0表9 各个钢厂钢管的产量的上限分别减少100个单位钢厂总费用总费用变化量运输方案变化量订购方案变化量S1 1288932 10300 260 200S2******* 3500 1244 200S3******* 2500 200 200S4******* 0 0 0S5******* 0 0 0S6******* 0 0 0S7 1278632 0 0 0S钢厂钢管的产量的上限的变化对总费用影响最大,由上述表格观察分析可得:1购运计划影响较小.五、模型的评价及改进由于总费用由订购费用和运输费两部分组成,运输费又由一般线路上的运输费和铺设管道上的运输费组成. 利用求网络中最短路径的Dijkstra算法,进行改进得到新的算法,可对含多种权重计算方式的网络进行搜索,得出最小费用路径(最短路径),算出两点之间的最优路径,进而根据非线性规划,借助于Lingo软件求解即可求出相应的结果.1.优点1)本问题中运用了求网络中最短路径的Dijkstra算法的思想,进行改进和修改得到新的算法,可对含多种权重计算方式的网络进行搜索,算出两点之间的最优路径,计算结果准确,从而得出相应的购运单价的矩阵.2)本问题构造出的模型算法较简单,也可以运用相应的其他编程软件来得到比较满意的结果.2303)本模型计算步骤清晰,借助于Lingo软件求解,可靠性较高.2.缺点1)由于题意中不考虑铁路公路间转运的中转费用,也不限制转运次数,因此在算法设计中存在着考虑不周全的缺限,如我们考虑是先通过铁路再通过公路到铺设点,但这不一定是最小费用路径,有可能先通过公路,然后经铁路再经公路运到铺设点,费用更少,这里没有理论证明.2) 问题二要求根据问题一的分析,指出哪家钢厂销价的变化对购运计划和总费用影响最大,哪家钢厂钢管产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果. 这个问题属于规划问题的灵敏度分析,一般来说,应该对于销价的变化△p 和产量上限的变化△s求出相应的总费用的变化△w,但要得到△w关于△p和△s的函数关系,几乎是不可能的,只对每个钢厂进行单独讨论.3.模型改进这个数学模型可以应用于西部开发中"天然气东送”问题,当然,西部开发中"天然气东送”问题远比我们的假设还要复杂的多,但无论如何,他们的本质一样,我们可将本问题运用于时间的变化等范围的推广. 本文还可以把问题1归结为网络最小费用流问题,建立了线性和非线性最小费用流模型,并运用相应的解法和分支定界法求解,简洁,层次分明.参考文献:[1] 甘应爱,田丰等等. 运筹学.清华大学出版社,北京,1994.[2] 袁亚湘.孙文瑜著. 最优化理论与方法.科学出版社,北京,1997.[3] 徐俊明著. 图论及其应用.中国科学技术大学出版社,合肥,1997.[4] 赵静,但琦. 数学建模与数学实验[M].北京:高等教育出版社,2003.图2231。
钢管运输方案

钢管运输方案一、引言钢管是一种重要的建筑材料,广泛应用于工程建设、石油化工等行业。
而钢管的运输则是建设项目中的一个关键环节。
本文将就钢管运输的方案进行讨论,探讨如何提高运输效率、保障运输安全。
二、合理规划运输路线1. 考虑地理条件:在选择运输路线时,应充分考虑地理条件,避免遇到复杂的山川地势或交通瓶颈。
例如,若运输目的地位于山区,应优先选择山地公路运输,而避免选择铁路或水运等无法适应山区道路的方式;2. 考虑运输时间:运输时间是判断运输方案的重要因素。
若时间允许,可以选择较长的航线,通过船运或铁路运输,节约成本的同时确保运输安全;3. 考虑运输成本:根据钢管的运输量和距离选择合适的运输方式,如通过公路运输对于短距离和小批量的钢管运输是最经济、快捷的选择,而对于大规模的钢管运输则可以选择铁路或水运等方式,以降低运输成本。
三、采用合适的运输工具1. 货车运输:对于近距离运输,货车是一种常见且高效的运输工具。
在选用货车运输时,需要注意货车的载重量和尺寸,确保它们能够适应钢管的尺寸和重量,并与货车司机沟通好安全运输的要求;2. 铁路运输:铁路运输具有大容量、避免交通拥堵等特点。
在选择铁路运输时,需考虑到运输路径是否有铁路线路经过,同时还需确认铁路货运车厢的装载容量是否满足需求;3. 水路运输:对于远距离和大批量的钢管运输,水路运输是一种理想的选择。
在选择水路运输时,除了考虑船舶的装载能力,还需关注航道状况、天气情况,确保运输的安全性。
四、保障运输安全1. 钢管包装:在运输前,钢管需要经过包装,以确保其在运输过程中不受损坏。
常见的包装方式有木质箱体、塑料薄膜等,根据钢管的性质和长度进行选择;2. 安全固定:钢管在运输过程中需要固定稳定,以免在行驶中出现晃动和碰撞,造成意外事故。
可以使用绳索、垫块等固定设备,确保钢管牢固地固定在运输工具上;3. 定期检查:运输过程中,应定期检查钢管的运输状态,确保突发情况得到及时处理。
钢管订购和运输计划

钢管订购和运输计划一、引言本文档旨在详细描述钢管订购和运输计划的各个方面,包括订购过程、运输方式、时间安排等内容。
钢管作为建筑、工程和制造业的重要材料之一,对于项目的顺利进行具有重要意义。
因此,钢管的订购和运输需得到合理安排和重视。
二、钢管订购2.1 计算需求量在进行钢管订购之前,首先需要计算所需的钢管数量。
这一计算通常由项目负责人、工程师或建筑师来完成。
计算需求量时,需要考虑以下因素:•项目规模和要求•钢管的类型和规格•使用钢管的位置和用途2.2 选择供应商选择合适的供应商是钢管订购过程中的关键步骤。
在选择供应商时,应考虑以下几个方面:•供应商的信誉和声誉•产品质量和性能•价格和交货时间2.3 发出订单一旦选择了合适的供应商,就需要发出订单。
订单应包括以下信息:•钢管的规格和数量•交货日期和地点•付款方式和条款•其他特殊要求三、钢管运输3.1 运输方式钢管的运输方式多种多样,常见的有以下几种:•公路运输:适合短程或小批量运输,成本较低。
•铁路运输:适合远距离和大批量运输,安全可靠。
•水运:适合长距离和大宗运输,成本相对较低。
•空运:适合迫切需要和紧急情况下的运输,费用较高。
3.2 运输安排在确定运输方式后,需要进行具体的运输安排。
主要包括以下几个方面:•运输时间表:明确每次运输的时间,确保与工程进度相匹配。
•运输车辆或船舶:根据货物的规模和距离选择合适的运输工具。
•路线规划:选择最优的运输路线,考虑效率和安全性。
3.3 运输风险和控制在钢管运输过程中,存在着一定的风险,如交通事故、货物丢失或损坏等。
为了减少这些风险,可以采取以下措施:•选择可靠的运输公司或车队,避免使用低质量的运输工具。
•对货物进行包装和固定,确保在运输过程中不会受到损坏。
•跟踪和监控货物的运输情况,及时处理可能出现的问题。
四、总结本文档详细介绍了钢管订购和运输计划的各个方面。
钢管作为重要的建筑材料,其订购和运输对于项目的进展具有重要意义。
2020年(交通运输)钢管的订购及运输优化方案

(交通运输)钢管的订购及运输优化方案钢管的订购及运输优化方案承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):吉林省建筑工程学院建筑装饰学院参赛队员(打印并签名) :1. 姜磊2. 魏文超3. 张晓斌指导教师或指导教师组负责人(打印并签名):杨雪日期:2009 年9 月14 日赛区评阅编号(由赛区组委会评阅前进行编号):2009高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):摘要:从本题中可以看出我们要解决的问题是钢管怎样订购,怎样运输,才能使得总费用最少。
所以,我们从两个方面着手考虑这个问题,首先我们考虑怎样从钢厂订购货物,接下来我们考虑在订购好货物后我们怎样把货物运输到目的地。
对于这两个问题,从题目可知,订购和运输联系密切,所以,我们必须同时考虑考虑钢管的订购与运输。
再由题中给的钢厂与天然气管道路线分布图可以看出,该问题等同于把起点的信息通过最优路(即就是花费最少的路径)径送到目的地,在送往的途中可以有信息的流失,流失的信息即就是用于铺设道路的货物,但不管流失多少信息,到达目的地时,总还有剩余的信息。
管道运输论文

管道运输论文引言管道运输作为一种高效、经济、环保的物流方式,近年来得到了广泛的应用。
尤其是在石油、天然气等领域,管道运输已成为主要的运输方式之一。
本文将从管道运输的背景、原理、应用、优缺点等方面进行探讨,旨在加深对管道运输的了解。
1. 管道运输的背景管道运输最早可以追溯到公元前4000年的美索不达米亚。
当时,人们就利用竹子、土埋和木头来建造管道,用于引水和输送物料。
随着科学技术的进步,管道运输逐渐发展壮大,成为现代运输体系中不可或缺的一部分。
现如今,特别是在石油和天然气行业,管道运输已经成为主要的输送方式。
2. 管道运输的原理管道运输是通过将物料(如液态或气态的石油、天然气等)置于管道中并利用压力差使其沿着管道输送的一种运输方式。
其原理可以概括为以下几点:•传输媒介:管道可以传输液体、气体和固体颗粒等不同的物质,但具体的管道设计和材料选择需要根据输送物料的性质进行合理的选择。
•压力差驱动:通过压力差,将物料推动到管道的另一端。
压力差可以通过泵站、压缩机或重力等方式产生。
•管道设计:管道设计需要考虑材料的选择、直径的确定、施工方式的选择等因素。
合理的管道设计可以提高运输效率和安全性。
3. 管道运输的应用管道运输在石油、天然气等行业中得到了广泛的应用。
以下是管道运输在不同领域的应用:3.1 石油运输石油管道是管道运输的主要应用之一。
通过管道运输可以将石油从油田输送到加工厂、炼油厂或港口。
石油管道具有输送量大、成本低、运输效率高等优势。
3.2 天然气运输天然气是另一个广泛使用管道运输的领域。
天然气管道的建设可以将天然气从生产地输送到终端用户。
相比于液化天然气运输,管道运输更加经济、环保,并且输送效率更高。
3.3 液化气运输液化气(如液化石油气)也可以通过管道进行运输。
液化气管道具有安全、快速、稳定的特点,适用于长距离运输和大规模供应。
4. 管道运输的优缺点管道运输具有以下优点:•高效性:相比于其他运输方式,管道运输的输送量大,速度快,效率高。
全国数模竞赛优秀论文钢管订购与运输的优化模型(浙江师范大学 胡国英 柯 懿 张惠锋) 精品

(1)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二(见附录一)按(1)的要求给出模型和结果。
(二)问题的分析本题要铺设一条A1~A15的天然气管道,使得总费用最小。
可以这样考虑问题:我们可以先把钢厂生产的钢管运到各个站点Ai(i≠1)再往两边运送,再计算出总的费用使之最小。
事实上我们并不知道每个站点上要运去多少货,所以设每个钢厂运往站点的数量为一变量及站点运往两边的钢管量也为变量,再通过图中已知信息相应的列出一些恒等式和约束条件。
为了使问题便于求解,我们把铁路费用及销价相应转换为公路费用(其简化的图示见附录一的图三),又因为铁路运费为一分段函数,故要对一些点之间加线使运费相当。
转换完毕后再利用赋权图的性质求出厂到站点的最短路。
(其具体数据见附录三)(三)模型的假设(1)运钢管过程中若用火车则可直接把钢管运到公路与铁路交接处,即下了火车不上火车。
(2)假设运输单位可提供足够的火车与汽车。
(3)费用计算时按照钢管数量来算,不考虑其他计费方法及因素。
(4)运费中不足整公里部分按整公里计。
(5)假设向每个钢管厂都订购钢管。
(6)设1Km主管道钢管为1单位钢管。
(7)路中铺设的钢管只允许由其相邻站点提供。
(8)不计各个环节中的装卸费用。
(四)符号说明Si: 表示生产钢管的钢厂(i=1,2…7)。
Ai:表示暂存钢管的站点。
(i=1,2…15)X1,+kk 与X1,-kk:分别表示Ak运往A1+k方向的钢管的数量和Ak运往A1-k方向的钢管的数量。
(其中K=2,3…15 X21=104, X16,15=0)Bk :表示存放在Ak处的钢管数量(k=2,3…15).Yij : 表示从Si->Aj所运的钢管数量。
F(Xij ,Yij): 表示总的费用。
(单位:万元)△Pi :表示钢管销价的变化量。
(五)模型的建立与求解题Ⅰ:为了使问题简化,我们可采取如下原则:(1)总费用公路化原则:就是将铁路运费及钢管销价恰当的转换为公路运费。
钢管的供应链管理和物流配送

钢管的供应链管理和物流配送随着钢管的广泛应用,比如建筑、石油、天然气、水利等行业,市场需求量不断增长。
同时,全球化的经济使得钢管生产和销售变得复杂。
为了满足用户的需求,保证商品质量,降低库存成本,钢管供应链管理和物流配送显得尤为重要。
本文将深入探究钢管的供应链管理和物流配送,以及如何提高这些环节的效率和质量。
一、钢管供应链管理1. 采购环节采购是钢管供应链管理的第一环节,它对钢管质量和价格起着决定性作用。
当采购人员选定合适的供应商后,应该建立长期稳定的合作关系,共同推进口岸、财务、物流等方面的协同管理,提高质量和效率。
2. 生产环节基于二次加工生产的特殊性质,钢管生产延迟的情况难以避免。
生产周期变长可能会导致下游供应商物流配送的质量下降。
因此,及时预估生产时间非常重要。
在钢管生产过程中,应该通过管理系统来进行跟踪,实现生产过程可视化,合并产品加工信息,及时更新状态,避免生产计划出现鸿沟。
3. 仓储环节在钢管仓储过程中,最重要的是确定存储的位置。
只要确保钢管存储的位置得到合理分配,配送就可以得到优化。
配货员将钢管直接拉到提货区,可以减少一些时间和物流成本。
针对某些较大的钢管,因为其存储空间大,应该在仓库中间隔开,便于管理、取出和提货。
二、钢管物流配送1. 物流的重要性物流配送环节,尤其是信息技术和先进的物流管理,可以对钢管的供应链管理起到至关重要的作用。
如果配送环节能够得当,产品的运输时间会大大缩短,使得技术供应商的库存成本降低、顾客的满意度提高。
2. 运输方式对于不同种类的钢管,应该采取不同的运输方式。
例如,短距离运输可以采用交通运输工具,长距离运输可以采用集装箱运输。
钢管不但重而且体积大,应尽量采用全程跟踪和保险服务。
现有的现代化物流体系,可以随时查询货物状态,可以确保物流水平更安全和更可靠。
3. 订单处理订单处理是物流配送环节的细节之一。
钢管供应商应尽快处理客户订单,及时反馈信息,减少交期误差。
钢管运输方案

钢管运输方案摘要:钢管是一种重要的建筑材料,在建筑、能源、化工等行业有广泛应用。
钢管的运输是保证工程顺利进行的关键环节之一。
本文将介绍钢管运输的重要性,目前常见的钢管运输方式,以及钢管运输方案的制定与实施。
引言:随着经济的不断发展,钢管市场的需求不断增加。
无论是大型工程项目还是个体建筑施工,钢管的运输都是一个重要的环节。
钢管的运输方案的选择将直接影响工程的进度和运输成本。
因此,制定一个合理的钢管运输方案对于确保工程质量和安全是至关重要的。
一、钢管运输的重要性钢管作为一种重要的结构材料,其运输环节直接影响到工程的顺利进行。
正确选择合适的运输方式可以降低运输过程中的风险,减少钢管的损坏和浪费,并保证工程进度的及时执行。
同时,合理的钢管运输方案还可以提高物流运输效率,降低运输成本。
二、常见的钢管运输方式1. 铁路运输:铁路运输是一种传统的钢管运输方式。
它具有运输距离长、运输量大、运输速度快等优点,适用于远距离的大型工程项目。
但铁路运输的劣势是需要额外的装卸设备,且受限于铁路线路和站点的限制。
2. 公路运输:公路运输是目前最常见的钢管运输方式。
它具有灵活性高、送货地点多样化的特点,尤其适用于中短距离的小规模项目。
然而,公路运输可能面临交通拥堵、路况不佳等问题,需要合理规划运输路线和时间。
3. 水运运输:水运运输是钢管运输的经济有效方式之一。
大型钢管可通过河流、湖泊或海洋运输,具有运输成本低、负荷能力高的特点。
然而,水运运输需要考虑天气因素以及港口装卸设备的情况。
4. 管道运输:管道运输是一种特殊的钢管运输方式,适用于长距离、大规模项目。
通过运输管道可以实现无缝运输,避免额外的装卸设备和人工操作。
但管道运输需考虑地形地貌和工程施工情况等因素。
三、钢管运输方案的制定与实施制定合理的钢管运输方案需要综合考虑多个因素,如运输距离、运输量、工程进度、运输成本等。
以下是一些常见的制定钢管运输方案的步骤:1. 进行风险评估:根据运输环节中的风险点,评估运输过程中可能发生的问题,如路况拥堵、气候条件、装卸设备等。
钢管订购与运输(西北工业大学)

钢管订购和运输策略段晓军, 俞昌盛, 吴建德指导老师: 张胜贵(西北工业大学,西安 710072)编者按:本文节选的是原沦文中模型的分析与建立以及之前的准备工作部分.该部分通过单位钢管的最小运购费,建立了问题求解的二次规划模型.特点是思路、表述简明、清晰,尤其是第3问的模型具有较强的般性,适用于树形结构的通常情形.值得注意的是.模型中有关铺设费的假设和表达式与常见情形略有不同.摘要:在铺设管道为一条线的情况下.我们建立了解决钢管订购和运输问题的非线性规划模型.由于变量较少.约束条件大都为线性的,口标函数为二次函数.所以利用Lingo 软件.可以很快求得比较满意的订购和运输方案.我们利用Matlab 软件,对所得到的数据进行拟合,得到相应的反映销价变化对总费用影响的曲线,然后比较各个钢厂钢管销价变化对总费用影响的大小.对于钢厂钢管产量上限变化对总费用和购运计划的影响.我们也作了类似的处理.如果要铺设的管道是树形图,我们对树形图的每条边定向,建立了与铺设管道为·—条线时类似的数学模型.从而大大拓广了模刑的使用范围.在论文中.我们还对所建立的模型的优缺点和需要改进的方向进行了讨论.1 符号说明·i s :钢厂i s 在指定期限内钢管的最大产量;·,:i j i j A A ω到,之间铺设管道的里程数;·:ij c :单位钢管从钢厂i S 运到j A ,所需最小订购和运输费用;·:i x 钢厂i S 是否承担制造这种钢管;·:ij y 钢厂i S 运抵A j 点的钢管数量,不含路过A j 的部分;·:j z 运到A i 的所有钢管沿1j j A A +→铺设的数量;·ij z :运抵A i 的所有钢管沿1j j A A +→铺设的数量;·()j d A :树中A j 的度数;·():j d A -树中A j 的入度;·():j d A +树中A j 的出度;·:μ单位钢管1公里的公路运输费用。
钢管订购和运输计划

钢管订购和运输计划钢管是一种广泛应用的建筑材料,其在建筑、制造和其他行业中都有大量的应用需求。
然而,钢管的订购和运输计划并不是一项简单的任务,必须考虑到许多因素,如尺寸、数量、质量、交货时间、成本等因素。
在本文中,将讨论钢管订购和运输计划的关键方面,以便您能够更好地制定计划,满足您的需求。
订购钢管的步骤首先,订购钢管之前应该考虑到需要采购的数量、尺寸、材质、规格等因素,这些都是影响钢管选择和订购的重要因素。
在订购时,应该选择信誉良好、质量可靠的钢管供应商,以确保产品质量。
同时,还需要考虑到交货时间、运输方式、支付条款等因素。
其次,订购钢管之前要确定好计划,包括订购的数量、交货时间、付款方式等,以及产品的相关信息,如材质、规格等。
这些都可以通过与供应商之间进行沟通和协商来确定,以确保您获得最满意的订购计划。
最后,在订购钢管之前,还需要对供应商的信誉度和产品质量进行评估,包括查看其资质、生产能力、技术水平、售后服务等。
只有找到可靠、有信誉的供应商,才能保证订购到质量优良的钢管,满足您的需求。
钢管运输计划运输是钢管订购过程中不可或缺的一环,因为它可以直接影响到订购的成本和交货时间。
以下是一些关于钢管运输计划的关键方面:运送距离:决定了运输成本。
运输方式:运输方式包括海运、铁路运输、公路运输等,选择最佳的运输方式将有助于节约成本和缩短交货时间。
包装方式:钢管通常需要加强包装,以保护产品在运输过程中不被破坏。
运输包装应该符合国际标准,并保证产品不容易损坏。
运输时间:运输时间是关键因素之一,因为它可以影响到交货时间,因此需要尽可能找到最快的运输方式。
交货方式:交货方式包括门到门、门到港口、港口到港口等,选择最适合的交货方式可以有助于节约成本和提高效率。
结论钢管订购和运输计划需要综合考虑许多因素,包括产品尺寸、数量、质量、交货时间、成本、运输方式等。
只有充分了解这些关键因素,才能成功制定好的钢管订购和运输计划。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了全国大学生数学建模的竞赛规则()。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括、电子、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们的参赛(报名)队号为:32参赛组别(研究生或本科):本科参赛队员:兰潇根、柳达强、汪锡平钢管订购和运输摘要:本文拟建立一个最合理的钢管运输与铺设方案模型。
利用离散数学和数据结构中图论相关知识,应用最短路径的floyd算法和灵敏度分析法建立一个以总费用为目标函数的非线性规划模型,对于钢管订购和运输的总费用,分为三部分:购买钢管费用,由钢厂运送到站点的费用以及由站点开始铺设的费用,对于由钢厂运送到站点的费用,用Floyd算法,求出铁路网和公路网的最短路径,然后转化为最少运输费用,之后利用Lingo软件编程,求解分析,解决问题。
关键词:Floyd算法,非线性规划,Lingo一 问题重述要铺设一条1521A A A →→→ 的输送天然气的主管道, 如题图一所示。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对题图二按(1)的要求给出模型和结果。
二 问题分析1.问题一所有的钢管必须通过铁路运送到铺设线路上的站点1521A A A →→→ ,之后再通过公路运输向左或右铺设。
因此,总的费用由三部分组成:一部分为购买所有主管道钢管的总费用,一部分为由钢管厂运送到各个站点时的铁路运费和公路运费的总和,最后一部分为由站点向左右两边铺设时的运输费用。
对于从钢管厂到各个站点的最小运费,由于在铁路和公路上的运费计算方法不同,所以,可以先用Floyd 算法,求出钢管厂到铁路上任意结点的最小距离和路线,得到相应的单位钢管运费,同理再求出各个站点到公路上任意结点的最小距离和路线,得到相应的单位钢管运费,再将两运费求和求出最小值,于是就得到从某钢厂到某铺设地点运输单位钢管的最少运输费用。
2.问题二 题目中“哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大”可以理解为,当该模型达到最优解时,钢管销价或者产量上限变化一个单位时,对购运计划和总费用的影响的大小问题。
可以利用Lingo 编程运行得到结果。
3.问题三要铺设的管道是一个树形图,是题图一的一种延拓,通过观察可知,只有9、11、17站点的铺设方向有三个,其它站点的铺设方向只有左右,因此,可以沿用问题一里的思路,在问题一的基础上再增加一个变量middle (j ),用于表示向第三方向铺设的钢管数量。
三 模型的假设与符号说明1、模型的假设⑴.沿管道或者原来有公路或者建有施工公路。
⑵ 钢管全部由这7个钢厂生产,一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
⑶ 公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
⑷ 由于公路运输费中,不足整公里部分按整公里计算,因此,从站点向左右两边运送钢管时,不应该是边运送边卸下钢管,这样也不符合实际,应当是走一个单位的公路,卸下一个单位的钢管。
2、符号说明四模型的建立与求解(一)、问题一的模型:采用Floyd算法,用matlab编程可以求出单位钢管从i S运输到j A的最小运输费用,数据如下表:目标函数为总费用W ,包括三个部分,购买所有主管道钢管的费用1W ,将钢管从钢厂运到各个站点的费用2W ,将钢管从站点运到铺设地点的费用3W W=1W +2W +3W其中 ),(*711511j i n p W i j i ∑∑===),(*),(cos 711512j i n j i t W i j ∑∑===()()⎥⎦⎤⎢⎣⎡+++=∑=2)()(12)()(1*1.01513j left j left j right j right W j 则目标函数: minW=),(*)(71151j i n i p i j ∑∑==+),(*),(cos 71151j i n j i t i j ∑∑==+()()⎥⎦⎤⎢⎣⎡+++∑=2)()(12)()(1*1.0151j left j left j right j right j 约束条件:1. 钢厂的钢管产量:)(*),()(*500151i c s j i n i c i j ≤≤∑=2. 运到各个站点的钢管刚好用完:)()(),(71j right j left j i n i +=∑=(j=1,2...15) 3. j A 与1j +A 之间的钢管: )()()1(j l j right j left =++, (j=1,2, (14)4. 钢管数量的非负性:n(i,j)≥0 , left(j) ≥0 , right(j) ≥0 (i=1,2,...,7 , j=1,2, (15)5° 钢管数量的整数性:n(i,j)∈N 运用数学软件Lingo 编程求解 问题一的结果最优最小费用1278632=W (万元)(二)、问题二的模型:用Lingo 对问题一求解后,即可根据Lingo 的结果对问题二进行解答。
各钢厂销价的变化:对偶价格表示,在最优解的情况下,各钢厂钢管销价减少一个单位时,对总费用的影响。
根据表中的数据,S(5)钢厂钢管的销价对购运计划和总费用影响最大。
产量上限:对偶价格表示,在最优解的情况下,各钢厂钢管生产上限每增加一个单位时,对总费用的影响。
根据表中的数据,得S(1)钢厂钢管的产量上限的变化对购运计划和总费用的影响最大。
(三)、问题三的模型:采用Floyd 算法,用matlab 编程求出单位钢管从iS 运输到jA 的最小运输费用,数据如下表:由于树形图的出现,发现在站点9、11、17处出现了3条支路的情况。
则模型一中模型的变量left(j),right(j)不再适用,此时可考虑增加一个支路变量middle (j ),相应的增加约束条件,在目标函数中增加相应的从站点运到铺设地点的费用。
目标函数:++=∑∑∑∑====*),(*),(cos ),(*)(min 7121171211j i n j i t j i n i p W i j i j()())20,19,17,17,11,9(21)()(2)(1)m (2)()(12)()(1*1.0212141==⎥⎦⎤⎢⎣⎡+++++++∑∑==n m n right n right m middle middle j left j left j right j right j j )()(约束条件:1. 钢厂的钢管产量: )(*i ),()(*500211i c s j i n i c j )(≤≤∑= )7,...,1(=i 2. 运到各个站点的钢管刚好用完:)()(),(71j right j left j i n i +=∑=(j=1, …,21且j ≠9,11,17))()()(),(71j middle j right j left j i n i ++=∑= (j=9,11,17)3. j A 与1j +A 之间的钢管: )()()1(j l j right j left =++(j=1,2, (14)middle(9)+left(16)=42 middle(11)+middle(17)=10 left(17)+left(18)=130right(17)+left(19)=190 right(19)+left(20)=260 right(20)+left(21)=1004. 钢管数量的非负性:n(i,j)≥0 , left(j) ≥0 ,right(j) ≥0 ,middle(j) ≥0,(i=1,2,…,7 , j=1,2,…,21) 5.钢管数量的整数性:n(i,j)∈N 运用数学软件Lingo 编程求出 问题三的结果:最优最小费用1407149(万元)五 模型优缺点1.该模型通过简化运输网络,采用Floyd 算法,具有技巧性和理论的保障。
2.模型的所有运算均由计算机程序完成,误差只由计算机产生,具有精度高的特点。
3.一般的图均可在该模型的基础上完善得出结果,故该模型具有较好的推广性。
六参考文献[1] 启源、金星《数学模型》(第三版)高等教育2003[2] 《Floyd最短路算法的MATLAB程序》wenku.baidu./view/e5a6e4886529647d272852aa.html七附录问题一:利用Floyd算法求解各钢管厂到各站点的最小费用路线的matlab程序:钢厂到铁路网结点的最短距离:n=24;a=zeros(n);a(1,2)=450;a(2,3)=80;a(2,4)=1150;a(4,8)=1100;a(5,6)=360;a(6,7)=195;a(7,18)=20;a(8,9) =720;a(8,18)=202;a(8,19)=1200;a(9,10)=520;a(9,20)=690;a(10,11)=170;a(11,12)=88;a(11,13)= 160;a(11,21)=690;a(12,22)=462;a(13,14)=70;a(13,15)=320;a(15,16)=160;a(16,17)=290;a(16,2 4)=70;a(17,24)=30;a=a+a';M=max(max(a))*n^2;%M为充分大的正实数a=a+((a==0)-eye(n))*M;path=zeros(n);for k=1:nfor i=1:nfor j=1:nif a(i,j)>a(i,k)+a(k,j)a(i,j)=a(i,k)+a(k,j);path(i,j)=k;endendendenda, path站点到公路网结点的最短距离:n=32;b=zeros(n);b(1,2)=104;b(2,3)=301;b(2,16)=3;b(3,4)=750;b(3,17)=2;b(4,5)=606;b(4,18)=600;b(5,6)=1 94;b(5,19)=10;b(6,7)=205;b(6,20)=5;b(7,21)=10;b(7,22)=31;b(8,23)=12;b(8,9)=680;b(9,10)=480;b(9,24)=42;b(10,1 1)=300;b(10,25)=70;b(11,26)=10;b(12,27)=10;b(13,28)=62;b(14,29)=110;b(14,30)=30;b(15,31)=20;b(15,24)=20;b=b+b';M=mbx(mbx(b))*n^2;%M为充分大的正实数b=b+((b==0)-eye(n))*M;path=zeros(n);for k=1:nfor i=1:nfor j=1:nif b(i,j)>b(i,k)+b(k,j)b(i,j)=b(i,k)+b(k,j);path(i,j)=k;endendendendb,path将最短路程换算成运输费用的程序:b=b*0.1;for k=1:300m1(k)={k};endfor k=1:50m2(k)={300+k};m3(k)={350+k};m4(k)={400+k};m5(k)={450+k};endfor k=1:100m6(k)={500+k};m7(k)={600+k};m8(k)={700+k};m9(k)={800+k};m0(k)={900+k};endfor i=1:24for j=1:24switch D(i,j)case 0a(i,j)=0;case m1a(i,j)=20;case m2a(i,j)=23;case m3a(i,j)=26;case m4a(i,j)=29;case m5a(i,j)=32;case m6a(i,j)=37;case m7a(i,j)=44;case m8a(i,j)=50;case m9a(i,j)=55;case m0a(i,j)=60;otherwisea(i,j)=ceil((a(i,j)-1000)/100)*5+60;endendend各个钢厂到各个站点的最少运输费用的程序for i=1:7for k=1:15for j=8:24if c(i,k)>a(i,j)+b(k,j+8)c(i,k)=a(i,j)+b(k,j+8);endendendendfor i=1:7for k=1:15if c(i,k)>a(i,1)+b(k,33)c(i,k)=a(i,1)+b(k,33);endif c(i,k)>a(i,6)+b(k,34)c(i,k)=a(i,6)+b(k,34);endif c(i,k)>a(i,7)+b(k,35)c(i,k)=a(i,7)+b(k,35);endendendLingo程序:model:sets:!七个生产厂c表示是否运输,p表示单位钢管的售价,s表示规定期限的最大生产能力; sch/1..7/:p,s,c;!十五个站点,left表示某站点向左运输的量,right表示某站点向右运输的量,l表示相邻两个站点的距离;zd/1..15/:left,right,l;!cost表示最小单位运输费用,x表示某厂到某一处站点的运输量;link(sch,zd):cost,n;endsetsdata:s=file('data.txt');cost=file('data.txt');l=file('data.txt');enddata!目标函数;min=sum(link(i,j):n(i,j)*p(i)+n(i,j)*cost(i,j))+0.05*sum(zd(j):left(j)^2+left(j)+right(j)^2+ right(j));!约束条件;!在第一个和第十五个站点分别不能向左和右铺设;left(1)=0;right(15)=0;!c为0-1约束条件;for(sch(i):bin(c(i)));!运输量为整数约束;gin(sum(link(i,j):n(i,j)));!总生产量为铺设管道的长度;sum(link(i,j):n(i,j))=5171;!若生产最低产量为500单位或者不生产,c(i,j)为1,n(i,j)不小于500,c(i,j)为0,n(i,j)为0;for(sch(i):sum(zd(j):n(i,j))>=500*c(i));!各厂最大产量的约束;for(sch(i):sum(zd(j):n(i,j))<=s(i)*c(i));!相邻两站点间管道的铺设量为站点间距;for(zd(j)|j#le#14:right(j)+left(j+1)=l(j));!在某站点的运输量为左右铺设量的总和;for(zd(j):sum(sch(i):n(i,j))=left(j)+right(j));p(1)=160;p(2)=155;p(3)=155;p(4)=160;p(5)=155;p(6)=150;p(7)=160;enddata.txt中的数据:800,800,1000,2000,2000,2000,3000~170.7 160.3 140.2 98.6 38.0 20.5 3.1 21.2 64.2 92.0 96.0 106.0 121.2 128.0 142.0 215.7 205.3 190.2 171.6 111.0 95.5 86.0 71.2 114.2 142.0 146.0 156.0 171.2 178.0 192.0 230.7 220.3 200.2 181.6 121.0 105.5 96.0 86.2 48.2 82.0 86.0 96.0 111.2 118.0 132.0 260.7 250.3 235.2 216.6 156.0 140.5 131.0 116.2 84.2 62.0 51.0 61.0 76.2 83.0 97.0 255.7 245.3 225.2 206.6 146.0 130.5 121.0 111.2 79.2 57.0 33.0 51.0 71.2 73.0 87.0 265.7 255.3 235.2 216.6 156.0 140.5 131.0 121.2 84.2 62.0 51.0 45.0 26.2 11.0 28.0 275.7 265.3 245.2 226.6 166.0 150.5 141.0 131.2 99.2 77.0 66.0 56.0 38.2 26.0 2.0~ 104,301,750,606,194,205,201,680,480,300,220,210,420,500,0~问题三:用Floyd算法求铁路最短距离和公路最短距离,matlab编程与问题一相同,再调用程序转化成费用,求出最小值。
