SOB 问题及解答 -AECOPD(审批版)

合集下载

2023年高考真题英语北京卷解析

年一般高等学校招生全国统一考试英语(北京卷)第一部分：听力理解（共三节：30 分）第二部分：知识运用（共两节，45 分）第一节单项填空（共15 小题；每题 1 分，共15 分）从每题所给旳ABCD 四个选项中，选出可以填入空白处旳最佳选项，并在答题卡上将该项涂黑。

例：It’s so nice to hear from her again. , we last met more than thirty years ago.A. What’s moreB. Tha t’s to sayC. In other wordsD. Believe it or not答案是D。

21. Some animals carry seeds from one place to another, ______ plants can spread to new places.A. soB. orC. forD. but【考点】考察连词辨析【答案】A【解析】本题考察旳连词都是常见旳连词。

So于是（强调上下文因果关系）；or或者；for 由于，由于（起补充阐明作用）;but不过（表达转折）；句意：某些动物把种子从一种地方带到此外一种地方，于是植物就传播到了新旳地方生长了。

上下文之间是因果关系。

故A对旳。

【试题延伸】连词辨析重要考虑上下文之间旳逻辑关系，尤其注意句子构造旳差异。

【举一反三】—Someone wants you on the phone.—_____nobody knows I am here.A. AlthoughB. AndC. ButD. So【答案】C【考点】考察连词使用方法。

【解析】前半句为：有人给你打电话；后半句为：没有人懂得我在这儿，根据句子意思可知前后两句明显为转折关系，因此选C。

22. ---Hi, let’s go skating.[--- Sorry, I’m busy right now. I _______ in an application form for a new job.A. fillB. have filledC. am fillingD. will fill【考点】考察时态【答案】C【解析】句意：—喂，我们五滑冰吧！—对不起，我目前很忙，我正在填写一份新旳工作申请表。

3.4.3反证法

存在唯一的x成立
一、
综合法是“”，而分析法则是“”．它们是截然相反的两种证明方法，分析法便于我们去寻找思路，而综合法便于过程的叙述，两种方法各有所长，在解决具体的问题时，综合运用效果会更好．
二、
1．反证法的概念
在证明数学命题时，要证明的结论要么正确，要么错误，二者必居其一．我们可以先假定命题结论的成立，在这个前提下，若推出的结果与、、相矛盾，或与命题中的已知条件相矛盾，或与假定相矛盾，从而说明命题结论的反面不可能成立，由此断定命题的结论成立，这种证明方法叫作反证法．
二、填空题
7．如果两个正整数之积为偶数，则这两个数是________．
8．将“函数f(x)＝4x2－2(p－2)x－2p2－p＋1在区间[－1,1]上至少存在一个实数c，使f(c)>0”反设，所得命题为__________________________．
9．和两异面直线AB、CD都相交的两条直线的位置关系是________．
知识改变命运，学习成就未来
提示：在证明数学命题时，要证明的结论要么正确，要么错误，二者必居其一，所以命题结论q的反面綈q错误时，q就一定正确．
提示：(1)反证法的原理是否定之否定等于肯定，即在同一过程中，A和非A有且只有一个是对的．
(2)反证法中的“反设”是应用反证法的第一步，也是关键的一步．“反设”的结论将是下一步“归谬”的一个已知条件，“反设”是否正确、全面，将直接影响下一步的证明．做好“反设”应明确：正确分清题设和结论；对结论实施正确的否定；对结论否定后，找出其所有的分类情况．
A.＝B.<C.≥D.＝或<
4．设x，y，z都是正实数，a＝x＋，b＝y＋，c＝z＋，则a，b，c三个数()
A．至少有一个不大于2 B．都小于2 C．至少有一个不小于2 D．都大于2

(好题)初中数学八年级数学上册第五单元《二元一次方程组》测试(含答案解析)(3)

一、选择题1．在长方形ABCD中，放入6个形状大小完全相同的小长方形，所标尺寸如图所示，则小长方形的宽AE的长度为（） cm ．A．1 B．1.6 C．2 D．2.52．如图，一次函数162y x=-+的图象分别交x、y轴于点A、B，与正比例函数y x=的图象交于第一象限内的点C，则OBC的面积为（）A．12 B．24 C．27 D．483．由于今年重庆受到洪水袭击，造成南滨路水电站损害；重庆市政府决定对南滨路水电站水库进行加固．现有4辆板车和5辆卡车一次能运27吨水电站加固材料，10辆板车和3辆卡车一次能运20吨水电站加固材料，设每辆板车每次可运x吨货，每辆卡车每次能运y 吨货，则可列方程组（）A．452710320x yx y+=⎧⎨-=⎩B．45271020x yx y-=⎧⎨+=⎩C．452710320x yx y-=⎧⎨-=⎩D．452710320x yx y+=⎧⎨+=⎩4．我国民间流传的数学名题：“只闻隔壁人分银，不知多少银和人，每人7两少7两，每人半斤多半斤，试问各位善算者，多少人分多少银？（1斤等于10两）”，其大意是：听见隔壁一些人在分银两，每人7两还缺7两，每人半斤则多半斤，问共有多少人？共有多少两银子？设有x个人，共分y两银子，根据题意，可列方程组为（）A．7755x yy x-=⎧⎨=-⎩B．7+755x yy x=⎧⎨-=⎩C．7755y xy x-=⎧⎨-=⎩D．7755x yy x-=⎧⎨-=⎩5．已知24510a ba b+=⎧⎨-=⎩，则+a b等于（）A．8 B．7 C．6 D．56．如图，一次函数y kx b =+与2y x =+的图象相交于点(,4)P m ，则方程组2y x y kx b=+⎧⎪=+⎨⎪⎩的解是（）A ．(2,4)B ．(2,4)-C ．(4,2)D ．(4,2)- 7．已知关于x ，y 的方程组22331x y k x y k +=⎧⎨+=-⎩，以下结论：①当0k =时，方程组的解也是方程24-=-x y 的解；②存在实数k ，使得0x y +=；③不论k 取什么实数，3x y +的值始终不变；④当1y x ->-时，1k >．其中正确的是（）A ．①②③B ．①②④C ．①③④D ．②③④ 8．下列四组数值是二元一次方程26x y -=的解的是（）A ．15x y =⎧⎨=⎩B ．42x y =⎧⎨=⎩C ．24x y =⎧⎨=⎩D ．23x y =⎧⎨=⎩9．下列各组数中①22x y =⎧⎨=⎩； ②21x y =⎧⎨=⎩；③22x y =⎧⎨=-⎩；④16x y ⎧⎨⎩==是方程410x y +=的解的有( )A ．1个B ．2个C ．3个D ．4个10．如图，在两个形状、大小完全相同的大长方形内，分别互不重叠地放入四个如图③的小长方形后得图①、图②，已知大长方形的长为2a ，两个大长方形未被覆盖部分分别用阴影表示，则图①阴影部分周长与图②阴影部分周长的差是（）（用a 的代数式表示）A ．﹣aB ．aC ．12aD ．﹣12a 11．下列方程组的解为31x y =⎧⎨=⎩的是（） A ．224x y x y -=⎧⎨+=⎩ B ．253x y x y -=⎧⎨+=⎩ C ．32x y x y +=⎧⎨-=⎩ D ．2536x y x y -=⎧⎨+=⎩ 12．某校七年级1班学生为了参加学校文化评比买了22张彩色的卡纸制作如下图形（每个图形由两个三角形和一个圆形组成），已知一张彩色卡纸可以剪5个三角形，或3个圆形，要使圆形和三角形正好配套，需要剪三角形的卡纸有x 张，剪圆形的卡纸有y 张，可列式为（）A ．2256x y x y +=⎧⎨=⎩B ．2265x y x y +=⎧⎨=⎩C ．22310x y x y +=⎧⎨=⎩D ．22103x y x y +=⎧⎨=⎩ 二、填空题13．已知直线l 1：y ＝x ＋1与直线l 2：y ＝mx ＋n 相交于点P （2，b ），则关于x ，y 的方程组100x y mx y n -+=⎧⎨-+=⎩的解是______． 14．正比例函数y=kx 的图象经过点(﹣2，4)，则k=__． 15．若方程组41524x y k x y +=-⎧⎨+=⎩的解为x 、y ，且x ＋y ＞0，则k 的取值范围是__________． 16．已知x ，y 满足二元一次方程3x ＋y ＝6，若y ＜0，则x 的取值范围是_____．17．若关于,x y 的二元一次方程组42x y k x y k-=⎧⎨+=⎩的解也是二元一次方程27x y -=-的解；则k 的值是______18．已知24x y -=，用含x 的代数式表示y 为：y =____________．19．若关于x 、y 的二元一次方程组3526x my x ny -=⎧⎨+=⎩，的解是13x y =⎧⎨=⎩，则关于a 、b 的二元一次方程组()()()()3526a b m a b a b n a b ⎧+--=⎪⎨++-=⎪⎩的解是_____． 20．已知x 和y 满足方程组3634x y x y +=⎧⎨+=⎩，则x-y 的值为_____．三、解答题21．某景点的门票价格如下表：购票人数1～5051～100100以上每人门票价2016101）班人数少于50人，（2）班人数多于50人且少于100人，如果两班都以班为单位单独购票，则一共支付1828元，如果两班联合起来作为一个团体购票，则只需花费1020元．（1）两个班各有多少名学生？（2）团体购票与单独购票相比较，两个班各节约了多少元？22．某公司决定从甲、乙、丙三个工厂共购买100件同种产品A，计划从丙厂购买的产品数量是从甲厂购买的产品数量的2倍；从丙厂购买的产品数量的12与从甲厂购买的产品数量之和，刚好等于从乙厂购买的产品数量．（1）设从甲厂购买x件产品A，从乙厂购买y件产品A，请用列方程组的方法求出该公司从三个工厂各应购买多少件产品A；（2）已知这三个工厂生产的产品A的优品率分别为甲：80%；乙：85%；丙：90%，求快乐公司所购买的100件产品A的优品率；（3）在第（2）题的基础上，你认为该公司在购买总数100件不变的情况下，能否通过改变计划，调整从三个工厂购买产品A的数量，使购买产品A的优品率上升2%？若能，请求出所有可能的购买方案；若不能，请说明理由（各厂购买的优品件数是整数）．23．（1）如图1，则∠A、∠B、∠C、∠D之间的数量关系为．（2）如图2，AP、CP分别平分∠BAD、∠BCD．若∠B＝36°，∠D＝14°，求∠P的度数；（3）如图3，CP、AG分别平分∠BCE、∠FAD，AG反向延长线交CP于点P，请猜想∠P、∠B、∠D之间的数量关系．并说明理由．24．解方程：4 34 2312 x yx y⎧+=⎪⎨⎪-=⎩25．解方程组：（1）3 326 x yx y+=-⎧⎨+=⎩（2）0.31 0.20.519x yx y-=⎧⎨-=⎩26．行政区划调整后，某村有两段长度相等的道路需硬化，现分别由甲、乙两个工程队同时开始施工．如图的线段和折线是两队前12天硬化的道路长y y 乙甲、（米）与施工时间x （天）之间的函数图象．根据图象解答下列问题：（1）直接写出y y 乙甲、与x （天）之间的函数关系式：①当012x <≤时，y =甲 _ ；②当04x <≤时，y =乙；当412x <≤时，y =乙；（2）求图中点M 的坐标，并说明点M 的横、纵坐标表示的实际意义；（3）施工过程中，甲队的施工速度始终不变，而乙队在施工12天后，每天的施工速度提高到120米/天，两队将同时完成任务．两队还需要多少天完成任务？【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】设小长方形的长为xcm ，宽为ycm ，则AD=x+3y ，AB=x+y=6+2y ，联立构造方程组求解即可．【详解】设小长方形的长为xcm ，宽为ycm ，则AD=x+3y ，AB=x+y=6+2y 即x-y=6，根据题意，得3146x y x y +=⎧⎨-=⎩，解得62x y =⎧⎨=⎩，即AE=2，故选C ．【点睛】本题考查了二元一次方程组的应用，合理引进未知数，列出正确的方程组是解题的关键． 2．A解析：A【分析】因直线162y x =-+交y 轴于点B ，故可求得点B 的坐标，从而可得OB 的长，又直线162y x =-+与直线y x =相交，故可求得点C 的坐标，从而可得△OBC 的边OB 上的高，因此可求得△OBC 的面积．【详解】对于直线162y x =-+，令0x =，得：6y = ∴6OB = 解方程组162y x y x =⎧⎪⎨=-+⎪⎩，得：44x y =⎧⎨=⎩ 即点C 的坐标为(4,4)∴点C 到y 轴的距离为4 ∴14122OBC SOB =⨯⨯= 故选：A【点睛】本题主要考查了求两直线交点坐标、平面直角坐标系中求直线围成的三角形面积，关键分别求得点B 、点C 的坐标，而求两直线的交点坐标体现了数形结合的思想．3．D解析：D【分析】以每次运送加固材料为等量关系，列方程组即可．【详解】解：根据4辆板车运货量+5辆卡车运货量=27吨，得方程4527x y +=；根据10辆板车运货量+3辆卡车运货量=20吨，得方程10320x y +=．可列方程组为452710320x y x y +=⎧⎨+=⎩．故选D ．【点睛】本题考查了二元一次方程组的应用，解题关键是找准题目数量关系，找到等量关系列方程组．4．D解析：D【分析】根据“每人7两还缺7两，每人半斤则多半斤”，即可得出关于x ，y 的二元一次方程组，此题得解．【详解】解：依题意，得：7755x y y x -=⎧⎨-=⎩．故选：D ．【点睛】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．5．D解析：D【分析】解二元一次方程组再进行计算即可；【详解】24510a b a b +=⎧⎨-=⎩， 10a b -=两边同时乘以2得：2220a b -=，245a b +=减去2220a b -=得：615b =-，解得：52b =-，代入10a b -=得：152a =， ∴155522a b +=-=；故答案选D ．【点睛】本题主要考查了二元一次方程组的求解，结合代数式求值是解题的关键．6．A解析：A【分析】将点P （m 、4）代入2y x =+，求出m 的值，结合图像交点P 的坐标即为二元一次方程组的解．【详解】一次函数y kx b =+与2y x =+的交点为P （m 、4）24m ∴+=解得2m =∴点P 的坐标为（2、4）2y x y kx b =+⎧∴⎨=+⎩的解为：24x y =⎧⎨=⎩故选：A ．【点睛】本题考查了一次函数与二元一次方程组的关系，解题关键是求出点P 坐标，结合图形求解．7．A解析：A【分析】直接利用二元一次一次方程组的解法表示出方程组的解进而分别分析得出答案．【详解】解：①当0k =时，原方程组可整理得：20231x y x y +=⎧⎨+=-⎩，解得：21x y =-⎧⎨=⎩，把21x y =-⎧⎨=⎩代入2x y -得： 2224x y -=--=-，即①正确，②解方程组22331x y k x y k +=⎧⎨+=-⎩得： 321x k y k =-⎧⎨=-⎩，若0x y +=，则(32)(1)0k k -+-=，解得：12k =，即存在实数k ，使得0x y +=，即②正确，③解方程组22331x y k x y k +=⎧⎨+=-⎩得： 321x k y k =-⎧⎨=-⎩， 3323(1)1x y k k ∴+=-+-=，∴不论取什么实数，3x y +的值始终不变，故③正确；④解方程组22331x y k x y k +=⎧⎨+=-⎩得： 321x k y k =-⎧⎨=-⎩，当1y x ->-时，1321k k --+>-，1k ∴<，故④错误，故选：A ．【点睛】本题主要考查解二元一次方程组的能力，熟练掌握解二元一次方程组的技能和二元一次方程的解得定义．8．B解析：B【分析】将各项中x 与y 的值代入方程检验即可．【详解】解：A 、把15x y =⎧⎨=⎩代入方程得：左边=2-5=-3，右边=6，左边≠右边，不符合题意； B 、把42x y =⎧⎨=⎩代入方程得：左边=8-2=6，右边=6，左边=右边，符合题意； C 、把24x y =⎧⎨=⎩代入方程得：左边=4-4=0，右边=6，左边≠右边，不符合题意； D 、把23x y =⎧⎨=⎩代入方程得：左边=4-3=1，右边=6，左边≠右边，不符合题意；故选：B ．【点睛】此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值． 9．B解析：B【详解】解：把①22x y ==⎧⎨⎩代入得左边=10=右边；把②2{1x y ==代入得左边=9≠10；把③2{2x y ==-代入得左边=6≠10；把④1{6x y ==代入得左边=10=右边；所以方程4x +y =10的解有①④2个．故选B ．10．A解析：A【分析】设图③小长方形的长为m ，宽为n ，则由已知可以求得m 、n 关于a 的表达式，从而可以用a 表示出图①阴影部分周长与图②阴影部分周长，然后即可算得二者之差．【详解】解：设图③小长方形的长为m ，宽为n ，则由图①得m=2n ，m+2n=2a ， ∴2a m a n ==，， ∴图①阴影部分周长=22245a n a a a ⨯+=+=，图②阴影部分周长=()2322126n n n n a ++==，∴图①阴影部分周长与图②阴影部分周长的差是：5a-6a=-a ，故选A ．【点睛】本题考查二元一次方程组的几何应用，设图③小长方形的长为m ，宽为n ，并用a 表示出m 和n 是解题关键．11．D解析：D【解析】把31x y =⎧⎨=⎩代入选项A 第2个方程24x y +=不成立，故错误；把31x y =⎧⎨=⎩代入选项B 第2个方程3x y +=不成立，故错误；把31x y =⎧⎨=⎩代入选项C 第1个方程3x y +=不成立，故错误；把31x y =⎧⎨=⎩代入选项D 两个方程均成立，故正确；故选D.12．A解析：A【分析】设需要剪三角形的卡纸有x张，剪圆形的卡纸有y张，根据彩色卡纸的总张数为22张其剪出三角形的数量为圆的2倍，即可得出关于x、y的二元一次方程组，此题得解．【详解】设需要剪三角形的卡纸有x张，剪圆形的卡纸有y张，根据题意得：22 56x yx y+=⎧⎨=⎩．故选：A．【点睛】此题考查由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．二、填空题13．【分析】首先将点P（2b）代入直线l1：y＝x＋1求出b的值进而得到P点坐标再根据两函数图象的交点就是两函数组成的二元一次去方程组的解可得答案【详解】解：∵直线y=x+1经过点P（2b）∴b=2+1解析：23 xy=⎧⎨=⎩【分析】首先将点P（2，b）代入直线l1：y＝x＋1求出b的值，进而得到P点坐标，再根据两函数图象的交点就是两函数组成的二元一次去方程组的解可得答案．【详解】解：∵直线y=x+1经过点P（2，b），∴b=2+1，解得b=3，∴P（2，3），∴关于x的方程组10x ymx y n-+=⎧⎨-+=⎩的解为23xy=⎧⎨=⎩，故答案为：23 xy=⎧⎨=⎩．【点睛】此题主要考查了二元一次去方程组与一次函数的关系，关键是掌握两函数图象的交点就是两函数组成的二元一次去方程组的解．14．-2【分析】将(﹣24)代入正比例函数y=kx的的解析式求出k=-2【详解】∵正比例函数y=kx的图象经过点(﹣24)∴-2k=4解得k=-2故答案为：-2【点睛】此题考查待定系数法求函数解析式正确解析：-2【分析】将(﹣2，4)代入正比例函数y=kx的的解析式，求出k=-2.【详解】∵正比例函数y=kx的图象经过点(﹣2，4)，∴-2k=4，解得k=-2，故答案为：-2.【点睛】此题考查待定系数法求函数解析式，正确理解待定系数法及正确计算是解题的关键. 15．k＞-3【分析】本题可将两式相加得到6x+6y=k+3根据x+y的取值可得出k 的值【详解】两式相加得：6x+6y=k+3∵x+y＞0∴6x+6y=6（x+y）＞0即k+3＞0∴k＞-3故答案为：k＞解析：k＞-3【分析】本题可将两式相加，得到6x+6y=k+3，根据x+y的取值，可得出k的值．【详解】两式相加得：6x+6y=k+3，∵x+y＞0∴6x+6y=6（x+y）＞0，即k+3＞0，∴ k＞-3，故答案为：k＞-3．【点睛】本题考查的是二元一次方程的解的性质，通过化简得到x+y的形式，再根据x+y＞0求得k 的取值．16．x＞2【分析】把x看作已知数求出y根据y＜0求出x的范围即可【详解】方程整理得：y=6-3x由y＜0得到6-3x＜0解得：x＞2故答案为x＞2【点睛】此题考查了二元一次方程的解解一元一次不等式熟练掌解析：x＞2.【分析】把x看作已知数求出y，根据y＜0求出x的范围即可.【详解】方程整理得：y=6-3x，由y＜0，得到6-3x＜0，解得：x＞2.故答案为x＞2.【点睛】此题考查了二元一次方程的解，解一元一次不等式，熟练掌握定义是解本题的关键． 17．-1【分析】把k 看作已知数表示出方程组的解代入已知方程计算即可得到k 的值【详解】①+②得：2x=6k 解得x=3k②-①得2y=-2k 解得：y=-k 代入2x-y=-7得6k+k=-7解得k=-1故答案解析：-1【分析】把k 看作已知数表示出方程组的解，代入已知方程计算即可得到k 的值.【详解】42x y k x y k -=⎧⎨+=⎩①② ①+②得：2x=6k ，解得，x=3k ，②-①得，2y=-2k ，解得：y=-k代入2x-y=-7得，6k+k=-7解得，k=-1．故答案为：-1．【点睛】此题考查了二元一次方程组的解，以及解二元一次方程组．方程组的解即为能使方程组中两方程都成立的未知数的值.18．2x-4【分析】【详解】由2x-y=4得：-y=4-2x ∴y=2x-4故答案为：2x-4 解析：2x-4【分析】【详解】由2x-y=4得：-y=4-2x ，∴ y=2x-4，故答案为：2x-419．【分析】根据已知得出关于ab 的方程组进而得出答案【详解】解：∵关于xy 的二元一次方程组的解是∴方程组中解得：故答案为：【点睛】本题主要考查二元一次方程组的解法关键是根据整体思想及方程组的解法进行求解解析：21a b =⎧⎨=-⎩【分析】根据已知得出关于a ，b 的方程组进而得出答案．【详解】解：∵关于x 、y 的二元一次方程组3526x my x ny -=⎧⎨+=⎩，的解是13x y =⎧⎨=⎩， ∴方程组()()()()3526a b m a b a b n a b ⎧+--=⎪⎨++-=⎪⎩中13a b a b +=⎧⎨-=⎩，解得：21a b =⎧⎨=-⎩．故答案为：21a b =⎧⎨=-⎩．【点睛】本题主要考查二元一次方程组的解法，关键是根据整体思想及方程组的解法进行求解． 20．1【详解】-②可得2x-2y=2即可得x-y=1故答案为1解析：1【详解】3634x y x y +=⎧⎨+=⎩①②， -②可得，2x-2y=2，即可得x-y=1.故答案为1三、解答题21．（1）53人；49人；（2）1班节约了490元，2班节约了318元【分析】（1）设（1）班有x 名学生，（2）班有y 名学生，根据“如果两班都以班为单位单独购票，则一共支付1828元，如果两班联合起来作为一个团体购票，则只需花费1020元”，即可得出关于x ，y 的二元一次方程组，解之即可得出结论；（2）利用节约的钱数=购买每张票节约的钱数×班级人数，即可求出结论．【详解】解：（1）∵1020÷16=6334，6334不为整数， ∴（1）（2）两班的人数之和超过100人．设（1）班有x 名学生，（2）班有y 名学生，依题意得：2016182810()1020x y x y +=⎧⎨+=⎩，解得：4953x y =⎧⎨=⎩．答：（1）班有49名学生，（2）班有53名学生．（2）（1）班节约的钱数为（20-10）×49=490（元），（2）班节约的钱数为（16-10）×53=318（元）．答：团体购票与单独购票相比较，（1）班节约了490元，（2）班节约了318元．【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．22．（1）从甲、乙、丙购买的数量分别为20、40、40；（2）86%；（3）能，方案见解析【分析】（1）根据题意所述的两个等量关系列出方程组，解出即可得出答案；（2）先求出优品数量，然后除以100即可得出优品率；（3）设从甲厂购买x件，从乙厂购买y件，则从丙厂购买（100-x-y）件，根据优品的数量不变，可得出方程，解出即可．【详解】解：（1）由题意得：2100122x x yx x y++=⎧⎪⎨+⨯=⎪⎩，解得：2040 xy=⎧⎨=⎩，所以从甲、乙、丙购买的数量分别为20、40、40；（2）优品率为（80%×20+85%×40+90%×40）÷100=86%；（3）设从甲厂购买x件，从乙厂购买y件，则从丙厂购买（100-x-y）件，80%x+85%y+90%（100-x-y）=100（86%+2%），化简得：2x+y=40因为各厂购买的优品件数是整数，所以45x，1720y要是整数，所以当y=0时，x=20符合；则从甲购20件，乙购0件，丙购80件；当y=20时，x=10符合；则从甲购10件，乙购20件，丙购70件；当y=40时，x=0符合；则从甲购0件，乙购40件，丙购60件．【点睛】本题考查了二元一次方程组的应用，解答此类应用性题目，一定要仔细审题，找到等量关系，然后运用方程思想进行解答．23．（1）∠A+∠B＝∠C+∠D；（2）∠P＝25°；（3）2∠P＝∠B+∠D，理由见解析【分析】（1）根据三角形的内角和定理，结合对顶角的性质可求解；（2）根据角平分线的定义可得∠BAP＝∠DAP，∠BCP＝∠DCP，结合（1）的结论可得2∠P＝∠B+∠D，再代入计算可求解；（3）根据角平分线的定义可得∠ECP＝∠PCB，∠FAG＝∠GAD，结合三角形的内角和定理可得∠P+∠GAD＝∠B+∠PCB，∠P+（180°﹣∠GAD）＝∠D+（180°﹣∠ECP），进而可求解．【详解】解：（1）∵∠AOB+∠A+∠B ＝∠COD+∠C+∠D ＝180°，∠AOB ＝∠COD ，∴∠A+∠B ＝∠C+∠D ，故答案为∠A+∠B ＝∠C+∠D ；（2）∵AP 、CP 分别平分∠BAD 、∠BCD ，∴∠BAP ＝∠DAP ，∠BCP ＝∠DCP ，由（1）可得：∠BAP+∠B ＝∠BCP+∠P ，∠DAP+∠P ＝∠DCP+∠D ，∴∠B ﹣∠P ＝∠P ﹣∠D ，即2∠P ＝∠B+∠D ，∵∠B ＝36°，∠D ＝14°，∴∠P ＝25°；（3）2∠P ＝∠B+∠D ．理由：∵CP 、AG 分别平分∠BCE 、∠FAD ，∴∠ECP ＝∠PCB ，∠FAG ＝∠GAD ，∵∠PAB ＝∠FAG ，∴∠GAD ＝∠PAB ，∵∠P+∠PAB ＝∠B+∠PCB ，∴∠P+∠GAD ＝∠B+∠PCB①，∵∠P+∠PAD ＝∠D+∠PCD ，∴∠P+（180°﹣∠GAD ）＝∠D+（180°﹣∠ECP ），P GAD D ECP ∴∠-∠=∠-∠②∴①+②得：2∠P ＝∠B+∠D ．【点睛】本题考查的是三角形的内角和定理的应用，角平分线的定义，二元一次方程组的解法，掌握以上知识是解题的关键．24．1083x y =⎧⎪⎨=⎪⎩【分析】先将方程组整理为43482312x y x y +=⎧⎨-=⎩，然后利用加减消元法解二元一次方程组．【详解】解：方程组整理得43482312x y x y +=⎧⎨-=⎩①②， ①+②得：660x =，解得：10x =，把10x =代入①得：83y =，则方程组的解为1083x y =⎧⎪⎨=⎪⎩．【点睛】本题考查解二元一次方程组，掌握加减消元法解方程组的计算步骤和计算法则正确计算是解题关键．25．（1）1215x y =⎧⎨=-⎩；（2）370110x y =⎧⎨=⎩【分析】（1）方程组利用加减消元法求出解即可；（2）方程组整理后，利用加减消元法求出解即可．【详解】解：3,32 6.x y x y +=-⎧⎨+=⎩①② ①2⨯，得226x y +=-．③②-③，得12x =．将12x =代入①，得15y =-．∴原方程组的解为12,15.x y =⎧⎨=-⎩（2）0.31,0.20.519.x y x y -=⎧⎨-=⎩①② ①10⨯，得31010x y -=．③②20⨯，得410380x y -=．④④-③，得370x =．将370x =代入③，得110y =．∴原方程组的解为370,110.x y =⎧⎨=⎩ 【点睛】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．26．（1）①100x ；②150x ；50400x +；（2）()8,800M ；工作到第8天时，甲乙两工程队硬化道路的长度相等，均为800m ；（3）10天【分析】（1）根据图像，已知两点的坐标，可根据待定系数法列方程，求函数解析式即可；（2）根据一次函数列出二元一次方程组求出点M 的坐标，即可得出实际意义；（3）设两队还需x 天完成任务，根据速度⨯天数=施工距离，则甲队施工的总距离为1200100x +，乙队施工的总距离为1000120x +，根据总施工道路长相等列出一元一次方程从而求出x 的即可．【详解】（1）① 设=y kx 甲，由图像可知=y kx 甲经过点()12,1200，∴120012k =100k ∴==100y x ∴甲②当04x <≤时，设1=k y x 乙由图像可知1=y k x 乙经过点()4,600∴1600=4k1150k ∴=∴=150y x 乙当412x <≤时，设2=k y x b +乙由图像可知2=k y x b +乙经过点()4,600，点()12,1000224600121000k b k b +=⎧∴⎨+=⎩ 250400k b =⎧∴⎨=⎩=50400y x +乙（2）根据题意可得：10050400y x y x =⎧⎨=+⎩ 解得：8800x y =⎧⎨=⎩M ∴()8,800∴点M 的横、纵坐标的实际意义：工作到第8天时，甲乙两工程队硬化道路的长度相等，均为800m ．()3设两队还需要x 天完成任务，有题意得：10001201200100x x +=+解得：10x =所以两队还需要10天完成任务．【点睛】本题主要考查了用待定系数法求一次函数解析式，用一次函数解决实际问题，解题关键是数形结合读懂图像，找准等量关系列一元一次方程．。

《一元二次方程的解法》(二)配方法—知识讲解(基础 2022人教九年级上册专练

一元二次方程的解法（二）配方法—知识讲解（基础）【学习目标】1．了解配方法的概念，会用配方法解一元二次方程； 2．掌握运用配方法解一元二次方程的基本步骤；3．通过用配方法将一元二次方程变形的过程，进一步体会转化的思想方法，并增强数学应用意识和能力.【要点梳理】知识点一、一元二次方程的解法---配方法 1．配方法解一元二次方程： (1)配方法解一元二次方程：将一元二次方程配成的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法.(2)配方法解一元二次方程的理论依据是公式：.(3)用配方法解一元二次方程的一般步骤： ①把原方程化为的形式；②将常数项移到方程的右边；方程两边同时除以二次项的系数，将二次项系数化为1； ③方程两边同时加上一次项系数一半的平方；④再把方程左边配成一个完全平方式，右边化为一个常数；⑤若方程右边是非负数，则两边直接开平方，求出方程的解；若右边是一个负数，则判定此方程无实数解. 要点诠释：（1）配方法解一元二次方程的口诀：一除二移三配四开方；（2）配方法关键的一步是“配方”，即在方程两边都加上一次项系数一半的平方. （3）配方法的理论依据是完全平方公式2222()a ab b a b ±+=±．知识点二、配方法的应用1．用于比较大小：在比较大小中的应用，通过作差法最后拆项或添项、配成完全平方，使此差大于零（或小于零）而比较出大小.2．用于求待定字母的值：配方法在求值中的应用，将原等式右边变为0，左边配成完全平方式后，再运用非负数的性质求出待定字母的取值．3．用于求最值：“配方法”在求最大（小）值时的应用，将原式化成一个完全平方式后可求出最值． 4．用于证明：“配方法”在代数证明中有着广泛的应用，我们学习二次函数后还会知道“配方法”在二次函数中也有着广泛的应用．要点诠释：“配方法”在初中数学中占有非常重要的地位，是恒等变形的重要手段，是研究相等关系，讨论不等关系的常用技巧，是挖掘题目当中隐含条件的有力工具，同学们一定要把它学好．【典型例题】类型一、用配方法解一元二次方程1.（2020•岱岳区校级模拟）用配方法解方程：2x2+3x﹣1=0．【思路点拨】首先把方程的二次项系数化为1，移项，然后在方程的左右两边同时加上一次项系数一半的平方，左边就是完全平方式，右边就是常数，然后利用平方根的定义即可求解．【答案与解析】解：2x2+3x﹣1=0x2+x2+）x+x1=【点评】一般地，用先配方，再开平方的方法解一元二次方程，应按以下步骤进行：(1)把形如ax2+bx+c=0(a≠0)的方程中二次项的系数化为1；(2)把常数项移到方程的右边；(3)方程的两边都加“一次项系数一半的平方”，配方得形如(x+m)2=n(n≥0)的方程；(4)用直接开平方的方法解此题．举一反三：【变式】用配方法解方程.(1)x2-4x-2=0； (2)x2+6x+8=0.【答案】(1)方程变形为x2-4x=2．两边都加4，得x2-4x+4=2+4．利用完全平方公式，就得到形如(x+m)2=n的方程，即有(x-2)2=6．解这个方程，得x-2=或x-2=-．于是，原方程的根为x=2+或x=2-．(2)将常数项移到方程右边x2+6x=-8．两边都加“一次项系数一半的平方”=32，得 x2+6x+32=-8+32，∴ (x+3)2=1．用直接开平方法，得x+3=±1，∴ x=-2或x=-4．类型二、配方法在代数中的应用2．若代数式221078Ma b a =+-+，2251N a b a =+++，则M N -的值（）Ａ．一定是负数Ｂ．一定是正数Ｃ．一定不是负数Ｄ．一定不是正数【答案】B ；【解析】（作差法）22221078(51)M N a b a a b a -=+-+-+++2222107851a b a a b a =+-+----29127a a =-+291243a a =-++2(32)30a =-+>．故选Ｂ．【点评】本例是“配方法”在比较大小中的应用，通过作差法最后拆项、配成完全平方，使此差大于零而比较出大小.3．（2020•甘肃模拟）用配方法证明：二次三项式﹣8x 2+12x ﹣5的值一定小于0．【答案与解析】解：﹣8x 2+12x ﹣5=﹣8（x 2﹣x ）﹣5=﹣8[x 2﹣x+（）2]﹣5+8×（）2 =﹣8（x ﹣）2﹣， ∵（x ﹣）2≥0， ∴﹣8（x ﹣）2≤0， ∴﹣8（x ﹣）2﹣＜0，即﹣8x 2+12﹣5的值一定小于0．【点评】利用配方法将代数式配成完全平方式后，再分析代数式值的符号. 注意在变形的过程中不要改变式子的值．举一反三：【变式】求代数式 x 2+8x+17的最小值【答案】x 2+8x+17= x 2+8x+42-42+17=（x+4）2+1∵（x+4）2≥0，∴当（x+4）2=0时，代数式 x 2+8x+17的最小值是1.4．已知223730216b aa b -+-+=，求4a b -的值．【思路点拨】解此题关键是把3716拆成91416+ ，可配成两个完全平方式．【答案与解析】将原式进行配方，得2291304216b a a b ⎛⎫⎛⎫-++-+= ⎪ ⎪⎝⎭⎝⎭，即2231024a b ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，∴ 302a -=且104b -=， ∴ 32a =，14b =．∴ 31314422422a b -=-=-=-．【点评】本题可将原式用配方法转化成平方和等于0的形式，进而求出a ．b 的值．《圆》全章复习与巩固—巩固练习（提高）【巩固练习】一、选择题1．如图所示，AB 、AC 为⊙O 的切线，B 和C 是切点，延长OB 到D ，使BD ＝OB ，连接AD ．如果∠DAC ＝78°，那么∠ADO 等于( )．A ．70°B ．64°C ．62°D ．51°2．在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ，S 射向地面的光束呈圆锥形，其轴截面SAB 的顶角为120°(如图所示)，则光源离地面的垂直高度SO 为( )． A ．54m B ．63m C ．93m D ．183m第1题图第2题图第3题图第4题图3．设计一个商标图案，如图所示，在矩形ABCD 中，AB=2BC ，且AB=8cm ，以A 为圆心、AD 的长为半径作半圆，则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24．如图，的半径为5，弦的长为8，点在线段(包括端点)上移动，则的取值范围是( ).A. B. C. D.5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用数学语言可表示为：如图所示，CD为⊙O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，则直径CD的长为( )A．12.5寸 B．13寸 C．25寸D．26寸6．（2020•贵港）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，则线段OM的最小值是（）A．0 B．1 C．2 D．37．一条弦的两个端点把圆周分成4:5两部分，则该弦所对的圆周角为( )．A．80° B．100° C．80°或100° D．160°或200°8．如图所示，AB、AC与⊙O分别相切于B、C两点，∠A＝50°，点P是圆上异于B、C的一动点，则∠BPC的度数是( )．A．65° B．115° C．65°或115° D．130°或50°二、填空题9．如下左图，是的内接三角形，，点P在上移动(点P不与点A、C重合)，则的变化范围是__ ________.第9题图第10题图10．如图所示，EB 、EC 是⊙O 是两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E=46°，∠DCF=32°，那么∠A 的度数是________________. 11．已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2680x x -+= 的两实根，若⊙O 1与⊙O 2的圆心距d =5．则⊙O 1与⊙O 2的位置关系是 __ __ .12．（2020•巴彦淖尔）如图，AB 为⊙O 的直径，AB=AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC ；③AE=2EC ；④劣弧是劣弧的2倍；⑤AE=BC ，其中正确的序号是．13.两个圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是_______ ________. 14.已知正方形ABCD 外接圆的直径为2a ，截去四个角成一正八边形，则这个正八边形EFGHIJLK 的边长为____ ____，面积为_____ ___．15．如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形，分别以它们的各顶点为圆心，以l 为半径画弧与两邻边相交，得到3条弧，4条弧，……(1)图(1)中3条弧的弧长的和为___ _____，图(2)中4条弧的弧长的和为_____ ___； (2)求图(m)中n 条弧的弧长的和为____ ____(用n 表示)．16．如图所示，蒙古包可以近似地看做由圆锥和圆柱组成，如果想用毛毡搭建20个底面积为9πm 2，高为3.5m ，外围高4 m 的蒙古包，至少要____ ____m 2的毛毡．三、解答题17. 如图，⊙O 是△ABC 的外接圆，FH 是⊙O 的切线，切点为F ，FH ∥BC ，连结AF 交BC 于E ，∠ABC 的平分线BD 交AF 于D ，连结BF ．（1）证明：AF 平分∠BAC ；（2）证明：BF ＝FD.18.（2020•南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．19．如图，相交两圆的公共弦长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：①如图(1)，在正△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图(2)，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类似的思想提出了如下命题：③如图(3)，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求：(1)请你从①②③三个命题中选择一个进行证明；(2)请你继续完成下面的探索；①在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)；②如图(4)，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否成立．若成立，请给予证明；若不成立，请说明理由．【答案与解析】一、选择题1．【答案】B；【解析】由AB为⊙O的切线，则AB⊥OD．又BD＝OB，则AB垂直平分OD，AO＝AD，∠DAB＝∠BAO．由AB、AC为⊙O的切线，则∠CAO＝∠BAO＝∠DAB．所以，∠DAB＝∠DAC＝26°．∠ADO＝90°-26°＝64°．本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等．2．【答案】C；【解析】圆锥的高、底面半径与母线组成直角三角形．由题意，SO⊥AB于O，∴∠SOA＝∠SOB＝90°．又SA＝SB，∠ASB＝120°，∴∠SAB＝∠SBA＝180120302=°-?°，设SO＝x m，则AS＝2x m．∵ AO＝27，由勾股定理，得(2x)2-x2＝272，解得93x=(m)．3．【答案】A.；【解析】对图中阴影部分进行分析，可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中，AB=2BC，AB=8cm，∴ AD=BC=4cm，∠DAF=90°，，，又AF=AD=4cm，∴ ，∴.4.【答案】A ；【解析】OM 最长是半径5；最短是OM ⊥AB 时，此时OM=3，故选A. 5．【答案】D ；【解析】因为直径CD 垂直于弦AB ，所以可通过连接OA(或OB)，求出半径即可. 根据“垂直于弦的直径平分弦，并且平分弦所对的两条弧”，知(寸)，在Rt △AOE 中，，即，解得OA=13，进而求得CD=26(寸).故选D. 6．【答案】B.【解析】设OP 与⊙O 交于点N ，连结MN ，OQ ，如图，∵OP=4，ON=2， ∴N 是OP 的中点， ∵M 为PQ 的中点，∴MN 为△POQ 的中位线，∴MN=OQ=×2=1，∴点M 在以N 为圆心，1为半径的圆上，当点M 在ON 上时，OM 最小，最小值为1， ∴线段OM 的最小值为1．故选B ． 7．【答案】C ；【解析】圆周角的顶点在劣弧上时，圆周角为5136010092⨯⨯=°°；圆周角的顶点在优弧上时，圆周角为413608092⨯⨯=°°．注意分情况讨论． 8．【答案】C ；【解析】连接OC 、OB ，则∠BOC ＝360°-90°-90°-50°＝130°．点P 在优弧上时，∠BPC ＝12∠BOC ＝65°；点P 在劣弧上时，∠BPC ＝180°-65°＝115°．主要应用了切线的性质定理、圆周角定理和多边形内角和定理．二、填空题 9．【答案】； 10．【答案】99°；【解析】由EB=EC ，∠E=46°知，∠ECB= 67°，从而∠BCD=180°-67°-32°=81°，在⊙O 中，∠BCD 与∠A 互补，所以∠A=180°-81°=99°. 11．【答案】相交；【解析】求出方程2680x x -+= 的两实根1r 、2r 分别是4、2，则1r -2r <d <1r +2r ,所以两圆相交.12.【答案】①②④；【解析】连接AD ，AB 是直径，则AD ⊥BC ，又∵△ABC 是等腰三角形，故点D 是BC 的中点，即BD=CD ，故②正确； ∵AD 是∠BAC 的平分线，由圆周角定理知，∠EBC=∠DAC=∠BAC=22.5°，故①正确；∵∠ABE=90°﹣∠EBC ﹣∠BAD=45°=2∠CAD ，故④正确； ∵∠EBC=22.5°，2EC ≠BE ，AE=BE ，∴AE ≠2CE ，③不正确； ∵AE=BE ，BE 是直角边，BC 是斜边，肯定不等，故⑤错误．综上所述，正确的结论是：①②④．13.【答案】7或3；【解析】两圆有三种位置关系：相交、相切(外切、内切)和相离(外离、内含).两圆内切时，圆心距，题中一圆半径为5，而d=2，所以有，解得r=7或r=3，即另一圆半径为7或3.14.【答案】(21)a -； 2(222)a -；【解析】正方形ABCD 外接圆的直径就是它的对角线，由此求得正方形边长为a ．如图所示，设正八边形的边长为x ．在Rt △AEL 中，LE ＝x ，AE ＝AL ＝22x ，∴ 222x x a ⨯+=，(21)x a =-，即正八边形的边长为(21)a -．222224[(21)](222)AEL S S S a x a a a =-=-=--=-△正方形正八边形．15.【答案】(1)π； 2π； (2)(n-2)π；【解析】∵ n 边形内角和为(n-2)180°，前n 条弧的弧长的和为(2)1801(2)3602n n -=-个以某定点为圆心，以1为半径的圆周长，∴ n 条弧的弧长的和为121(2)(2)2n n ππ⨯⨯-=-．本题还有其他解法，比如：设各个扇形的圆心角依次为1α，2α，…，n α，则12(2)180n n ααα+++=-…°， ∴ n 条弧长的和为1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-．16.【答案】720π；【解析】∵ S ＝πr 2，∴ 9π＝πr 2，∴ r ＝3．∴ h 1＝4，∴ 2215l h r =+=，∴ 223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱，2036720S ππ=⨯=总．所求面积包括圆锥的侧面积和圆柱的侧面积，不包括底面积．三、解答题17.【答案与解析】（1）连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵F H ∥BC ，∴OF 垂直平分BC∴BF FC =∴AF 平分∠BAC .（2）由（1）及题设条件可知∠1=∠2，∠4=∠3，∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18．【答案与解析】证明：（1）∵四边形ABCD 是⊙O 的内接四边形， ∴∠A+∠BCD=180°， ∵∠DCE+∠BCD=180°， ∴∠A=∠DCE ， ∵DC=DE ，∴∠DCE=∠AEB ， ∴∠A=∠AEB ；（2）∵∠A=∠AEB ，A BCDEO 12345HA BCD EO 12∴△ABE 是等腰三角形， ∵EO ⊥CD ， ∴CF=DF ，∴EO 是CD 的垂直平分线， ∴ED=EC ， ∵DC=DE ， ∴DC=DE=EC ，∴△DCE 是等边三角形， ∴∠AEB=60°，∴△ABE 是等边三角形．19.【答案与解析】解：∵公共弦AB ＝120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=.20. 【答案与解析】 (1)如选命题①．证明：在图(1)中，∵ ∠BON ＝60°，∴ ∠1+∠2＝60°． ∵ ∠3+∠2＝60°，∴ ∠1＝∠3．又∵ BC ＝CA ，∠BCM ＝∠CAN ＝60°， ∴ △BCM ≌△CAN ，∴ BM ＝CM ．如选命题②．证明：在图(2)中，∵∠BON＝90°，∴∠1+∠2＝90°．∵∠3+∠2＝90°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝90°，∴△BCM≌△CDN，∴ BM＝CN．如选命题③．证明：在图(3)中，∵∠BON＝108°，∴∠1+∠2＝108°．∵∠2+∠3＝108°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝108°，∴△BCM≌△CDN，∴ BM＝CN．(2)①答：当∠BON＝(2)180nn°时结论BM＝CN成立．②答：当∠BON＝108°时．BM＝CN还成立．证明：如图(4)，连接BD、CE在△BCD和△CDE中，∵ BC＝CD，∠BCD＝∠CDE＝108°，CD＝DE，∴△BCD≌△CDE．∴ BD＝CE，∠BDC＝∠CED，∠DBC＝∠ECD．∵∠CDE＝∠DEN＝108°，∴∠BDM＝∠CEM．∵∠OBC+∠OCB＝108°，∠OCB+∠OCD＝108°．∴∠MBC＝∠NCD．又∵∠DBC＝∠ECD＝36°，∴∠DBM＝∠ECM．∴△BDM≌△CEN，∴ BM＝CN．。

初中化学实验探究问题分类示例及解题思路教学内容

初中化学实验探究问题分类示例及解题思路化学实验探究问题分类示例及解题思路楚雄市教科室熊文化学实验探究是以化学实验为主要手段，在现实情景中通过发现问题、猜想、设计实验、实验、观察分析、得出结论等几个环节来解决化学问题的一种方法。

实验探究能力的培养是中学化学科重要的教学内容之一，也是中考必须考查的重要内容。

化学实验探究问题往往综合性强，对学生思维敏捷性、严密性、创新性要求较高，有一定难度，对这类问题我们要仔细分析、研究，找出基本解题思路和方法，避免复习陷入“题海”不能自拔。

一、物质性质的实验探究、SO某研究性学习小组收集了某电厂经除尘后的废气样品，主要含有］［例12等，他们对其中的二氧化硫与二氧化碳进行检验，探究过程如下：OCO、、N222［查阅资料］二氧化硫是一种无色、有刺激气味的有毒气体、易溶于水，密度比空气沉，能与石灰水反应生成白色的亚硫酸钙(CaSO))大；能与水反应生成亚硫酸(HSO332淀，能与紫色高锰酸钾溶液反应并使其褪色。

二氧化硫与二氧化碳相似的化学性质有)高锰酸钾溶液中加有硫酸，有利于观察现象［实验］实验装置如下(请帮他们完成下表：简答操作步骤1将各装置按上图连接好并装入化学装置的作用装置的作用装置中的现象2的导管口缓慢连继鼓入经除后的废气样装置中的现象［结论与讨论］通过上述探究实验，该小组获得了检验混合气体中二氧化硫与二氧化碳的方法，该方法是：。

［分析］1.仔细审题，抓住探究目的，找到思路起点。

探究目的：检验混合气体中二氧化硫与二氧化碳的方法2.仔细审题，抓住关键信息，找到解决问题的突破口。

关键信息：SO三个重要性质①与水反应②与石灰水反应生成白色沉淀③能2与高锰酸钾溶液反应并使其褪色。

3.仔细审图，推敲装置作用，最终解决问题。

、CO、O、N)通过A(KMnO) SO?(溶液)→谁会反应SO(废气中主要成分222224溶液)→谁会反应?( SO还有剩余吗?)→B装置作用：判断SOB(KMnO剩余气体再通过242、O、N通过C时，谁会反应?(CO)CO是否已经反应完。

6.3.3余角和补角-(课件)人教版(2024)数学七年级上册

感悟新知
知2－练
解： OE 平分∠BOC. 理由如下：
因为∠DOE=9 0°，
所以∠DOC＋ ∠COE=9 0°.
又因为∠AOB=180°，所以∠AOD＋ ∠BOE=90°.
因为OD平分∠AOC，所以∠AOD= ∠DOC.
所以∠COE= ∠BOE，即OE 平分∠BOC.
感悟新知
4-1.[期末·厦门思明区]如图，∠AOB=90 °， ∠COD=90°，OA 平分∠DOE，若 ∠BOC=20°，求∠AOE 的度数. 解：因为∠AOB＝∠COD＝90°， ∠BOC＋∠AOC＝∠AOB，∠AOD＋ ∠COA＝∠COD，所以∠AOD＝∠BOC ＝20°.因为OA平分∠DOE，所以∠AOE＝∠AOD＝20°.
感悟新知
知1－练
又因为∠AOC＋ ∠BOC=180 °，∠AOC＋ ∠DOE=180 °， ∠DOE＋∠BOC=1 8 0°，所以图中互补的角有7 对，分别是∠1 和∠BOD，∠4 和 ∠AOE，∠3 和∠BOD，∠2 和∠AOE， ∠AOC 和∠BOC，∠AOC 和∠DOE，∠DOE 和∠BOC.
感悟新知
解题秘方：从图中找互余或互补的角，可从两个方面进行：一个方面是从角的度数入手，和为9 0 °的两个角互余，和为180 °的两个角互补；另一个方面是从整体入手，将直角分成两个角，则这两个角互余，将平角分成两个角，则这两个角互补.
感悟新知
知1－练
(1)图中互余的角有几对？分别是哪些？
感悟新知
(3)写出∠COD 的补角. 解：∠COD的补角为∠AOE.
知2－练
感悟新知
知2－练
例 4 如图6.3－25，已知O 是直线AB 上的一点，OC是一条射线，OD平分∠AOC，∠DOE=90 °，OE 平分 ∠BOC 吗？为什么？

PDCA循环在COPD稳定期老年患者呼吸功能锻炼中的应用

PDCA循环在COPD稳定期老年患者呼吸功能锻炼中的应用孙小燕;钱晓云;夏聪聪;谢阳;沈玉【摘要】目的:探讨PDCA循环在慢性阻塞性肺疾病(COPD)稳定期老年患者呼吸功能锻炼中的应用效果.方法:将收治的94例COPD患者按入院先后顺序分为观察组和对照组各47例,对照组采用常规的健康教育方法,观察组运用PDCA循环理论,通过对COPD老年患者呼吸功能锻炼情况进行现状调查,原因分析,制定相应的管理措施,并对措施执行情况进行检查、分析和总结,持续质量改进.出院12周后,比较两组呼吸功能锻炼依从性、呼吸困难的严重程度[采用加州大学圣迭戈呼吸困难问卷(SOBQ)]、COPD自我效能评分[采用COPD自我效能量表(CSES)].结果:出院12周后,两组呼吸功能锻炼依从性评分明显高于护理前(P<0.01),且观察组高于对照组(P<0.01);出院12周后,观察组SOBQ评分低于对照组和同组护理前(P<0.01);出院12周后,观察组CSES高于对照组和同组护理前(P<0.01,P<0.05).结论:PDCA循环的护理质量管理方法有利于提高COPD稳定期老年患者呼吸功能锻炼的依从性,减轻呼吸困难的程度,提高患者的自我效能,值得临床推广.【期刊名称】《齐鲁护理杂志》【年(卷),期】2018(024)021【总页数】5页(P23-27)【关键词】PDCA循环;慢性阻塞性肺疾病;呼吸功能锻炼【作者】孙小燕;钱晓云;夏聪聪;谢阳;沈玉【作者单位】江苏省人民医院江苏南京210029;江苏省人民医院江苏南京210029;江苏省人民医院江苏南京210029;江苏省人民医院江苏南京210029;江苏省人民医院江苏南京210029【正文语种】中文【中图分类】R473.56慢性阻塞性肺疾病(COPD)是一种具有气流受限特征的可以预防和治疗的疾病，气流受限不完全可逆，呈进行性发展[1]。

COPD居我国死亡原因的第三位，可引起肺功能进行性减退，严重影响患者的劳动能力和生活质量。

应用动能定理解决多过程问题-高考物理复习

A级基础对点练 1.(2024·陕西宝鸡高三期末)如图1所示，ABCD是一条长轨道，其中AB段是倾角
为θ的斜面，CD段是水平的，BC段是与AB和CD都相切的一小段圆弧，其长度可以略去不计。一质量为m的滑块(可看作质点)在A点由静止释放，沿轨道滑下，最后停在D点，A点和D点的位置如图所示。现用一方向始终与轨道平行的力推滑块，使它缓慢地由D点推回到A点。滑块与轨道间的动摩擦因数为μ，重力加
g，则滑块经过的总路程是( A )
Байду номын сангаас
A.1μ2gcvo20s θ＋s0tan θ
B.μ12gsvi20n θ＋s0tan θ
C.2μ2gcvo20s θ＋s0tan θ
D.μ12gcvo20s
θ＋tasn0
θ
图4
目录
研透核心考点
解析滑块最终要停在斜面底部，设滑块经过的总路程为 s，对滑块运动的全程应用动能定理得 mgs0sin θ－μmgscos θ＝0－12mv20，解得 s＝μ12gcvo20s θ＋s0tan θ，选项 A 正确。
目录
研透核心考点
1.如图2所示，水平桌面上的轻质弹簧左端固定，右端与静止在O点质量为m＝ 1 kg的小物块接触而不连接，此时弹簧无形变。现对小物块施加F＝10 N的水平向左的恒力，使其由静止开始向左运动。小物块在向左运动到A点前某处速度最大时，弹簧的弹力为6 N，运动到A点时撤去推力F，小物块最终运动到B点静止。图中OA＝0.8 m，OB＝0.2 m，重力加速度取g＝10 m/s2。求小物块： (1)与桌面间的动摩擦因数μ；图2 (2)向右运动过程中经过O点的速度大小； (3)向左运动的过程中弹簧的最大压缩量。
mg(s0＋x)sin θ－μmg(s0＋x)cos θ－Ep＝12mv2m

专题03角(八大类型)(题型专练)-2023-2024学年七年级数学上册

专题03 角（八大类型）【题型1 角的概念及表示】【题型2 钟面角】【题型3 方位角】【题型4 度分秒换算】【题型5 角平分线的定义】【题型6 角的基本运算】【题型7 余角概念及及性质】【题型8 补角及性质】【题型1 角的概念及表示】（2023春•东平县期末）1.下列图形中，能用，，三种方法表示同一个角的是（）A. B.C. D.（2022秋•丰南区校级期末）2.下列四个图中，能用三种方法表示同一个角的是（）A. B.C. D.（2022秋•集贤县期末）3.下列各图中有关角的表示正确的个数有（）A. 1个B. 2个C. 3个D. 4个【题型2 钟面角】（2022秋•铁西区校级期末）4.每天中午11点30分“校园之声”节目都会如约而至，此时时针与分针所夹的的角为（）A. B. C. D.（2023春•肇东市期末）5.一节课45分钟，分针所转过的角度是（）A. B. C. D.（2022秋•武义县期末）6.钟表上从早上6点30分到早上8点10分时针所走的度数为（）A. 45°B. 50°C. 55°D. 60°（2022秋•海港区期末）7.学校早上7：30考试，考试时间为90分钟，则考试结束时时针与分钟的夹角为（）A. 30°B. 45°C. 60°D. 90°【题型3 方位角】（2022秋•龙海市校级月考）8.淘气周末和爸爸妈妈去“水仙花海”游玩，淘气的位置在“水仙花海”大门的西偏南方向处．则淘气该怎样向爸爸妈妈介绍“水仙花海”大门的位置（）A. “水仙花海”大门在淘气的南偏西方向处B. “水仙花海”大门在淘气的东偏北方向处C. “水仙花海”大门在淘气的东偏北方向处D. “水仙花海”大门在淘气的西偏南方向处（2022秋•和平区校级期末）9.如图，下列说法中错误的是（）A. OA方向是北偏东30°B. OB方向是北偏西15°C. OC方向是南偏西25°D. OD方向是东南方向（2022秋•辽阳期末）10.如图，甲、乙两人同时从A 地出发，甲沿北偏东50 方向步行前进，乙沿图示方向步行前进．当甲到达B 地，乙到达C 地时，甲与乙前进方向的夹角∠BAC 为100 ，则此时乙位于A地的( )A. 南偏东30B. 南偏东50C. 北偏西30D. 北偏西50 （2022秋•长春期末）11.如图，OA是点O北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（）A. 北偏西30°B. 北偏西60°C. 东偏北30°D. 东偏北60°（2023春•莱州市期末）12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是【题型4 度分秒换算】（2022秋•天山区校级期末）13.把用度、分、秒表示正确的是（）A. B. C. D.（2022秋•迁安市期末）14.如图，将一个三角板角的顶点与另一个三角板的直角顶点重合，若，则的度数是（）A. B. C. D.（2022秋•榆阳区校级期末）15.若，则用度、分、秒表示为（）A. B. C. D.（2022秋•绥德县期末）16.化为用度表示是（）A. B. C. D.（2022秋•代县期末）17.下列运算正确的是（）A. B.C. D.（2022秋•丛台区校级期末）18.若,,，则下列结论正确的是( )A. B.C. D.（2023•南岗区校级开学）19.计算：．【题型5 角平分线的定义】（2022秋•双阳区期末）20.如图，已知O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，若OC是的平分线，则下列结论正确的是（）A. B. C. D.（2022秋•铜梁区期末）21.如图，点O是直线上一点，射线是的角平分线，若，则的度数是（）A. B. C. D.（2022秋•吴忠期末）22.图，点A、B、O在一条直线上，且∠AOC=50º，OD平分∠AOC，则图中∠BOD= ．（2022秋•栾城区期末）23.如图，点O与量角器中心重合，与零刻度线叠合，与量角器刻度线叠合，是的角平分线，那么．（2022秋•历城区期末）24.如图，是的角平分线，若，则的度数是．（2022秋•绥棱县校级期末）25.已知OC平分∠AOB,若∠AOC=则∠AOB= .【题型6 角的基本运算】（2023秋•衡阳县月考）26.如图，点O在直线上，．若，则的大小为（）A. B. C. D.（2023•姑苏区三模）27.如图，∠AOD－∠AOC等于( )A. ∠AOCB. ∠BOCC. ∠BODD. ∠COD（2022秋•陈仓区期末）28.一副三角板如图摆放，则的度数是（）A. 90°B. 75°C. 60°D. 15°（2022秋•秦淮区期末）29.把两块三角板按如图所示拼在一起，那么的度数是（）A. B. C. D.（2022秋•大竹县校级期末）30.如图，已知直线和相交于点，是直角，平分，，则的大小为( )A. B. C. D.（2022秋•天心区期末）31.如图，O为直线上一点，平分，，，求的度数．（2022秋•铜梁区期末）32.如图所示，点O是直线上一点，以点O为端点分别作射线、射线、射线、射线，若射线平分，且，．（1）求的度数；（2）若，求的度数．（2022秋•丰都县期末）33.如图，已知，是内的一条射线，且．（1）求和的度数；（2）作射线平分，在内作射线，使得，求的度数．（2022秋•南明区校级期中）34.如图所示，是的平分线，是的平分线．（1）如果，，那么是多少度？（2）如果，，那么是多少度？（2022秋•河北区期末）35.如图所示，OB是∠AOC的平分线，OD是∠COE的平分线．（1）如果∠AOB=50°，∠DOE=35°，那么∠BOD是多少度？（2）如果∠AOE=160°，∠COD=25°，那么∠AOB是多少度？【题型7 余角概念及及性质】（2023春•垦利区期末）36.若∠A=35°16′，则其余角的度数为A. 54°44′B. 54°84′C. 55°44′D. 144°44′（2023春•河源期末）37.如果一个角是30°，那么这个角的余角是( )A. 150°B. 40°C. 50°D. 60°（2023•商丘模拟）38.直尺与三角尺按如图所示的方式叠放在一起，在图中所标记的角中，与互余的角有( )A. 2个B. 3个C. 4个D. 5个（2023秋•裕华区期中）39.如图，，且，则（）A. B. C. D.（2022秋•禹城市期末）40.小明将一副三角板摆成如图所示，如果，那么等于（）A. B. C. D.（2023春•垦利区期末）41.将一副三角板按如图所示位置摆放，其中∠α与∠β一定相等的是（）A. B.C. D. （2022秋•亭湖区期末）42.若与互余，且，则的度数为（）A. 132°B. 42°C. 48°D. 138°【题型8 补角及性质】（2023•陇南模拟）43.若，则的补角的大小是（）A. B. C. D. （2023春•闵行区期末）44.如果一个角的补角等于这个角的3倍，那么这个角的度数是（）A. B. C. D. （2023•大兴区一模）45.已知，，，四点的位置如图所示，下列结论正确的是（）A. B. C. 比大D. 与互补（2023春•清远期中）46.已知∠1与∠2互为补角，，则∠2的度数为（）A. 30°B. 40°C. 50°D. 100°（2023•富顺县校级一模）47.若钝角∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系满足（）A. ∠1﹣∠3＝90°B. ∠1+∠3＝90°C. ∠1+∠3＝180°D. ∠1＝∠3（2023•雁塔区校级模拟）48.若与互补，，则的大小是（）A. B. C. D.（2022秋•栾城区校级期末）49.按如下图的方法折纸，下列说法不正确的是（）A. 与互余B.C. 平分D. 与互补（2023•周口一模）50.如图，，垂足为点O，直线经过点O．若，则的度数为（）A. B. C. D.答案1.A【分析】根据角的表示的性质，对各个选项逐个分析，即可得到答案．【详解】A选项中，可用，，三种方法表示同一个角；B选项中，能用表示，不能用表示；C选项中，点A、O、B在一条直线上，∴能用表示，不能用表示；D选项中，能用表示，不能用表示；故选：A．【点睛】本题考查了角的知识；解题的关键是熟练掌握角的表示的性质，从而完成求解．2.B【分析】利用角度的三种表示方法，逐个进行分析即可．【详解】解：A、图中表示的是不同的角，不能表示图中的角，不符合题意；B、图中表示的是同一个角，符合题意；C、图中表示的是同一个角，不能表示图中的角，不符合题意；D、图中表示的是同一个角，表示的是另一个角，不符合题意；故选B．【点睛】本题考查了角的表示方法的应用，角可以用一个大写字母表示，也可以用三个大写字母表示．其中顶点字母要写在中间，唯有在顶点处只有一个角的情况，才可用顶点处的一个字母来记这个角，否则分不清这个字母究竟表示哪个角．3.B【分析】根据角的表示方法，平角、射线、周角的定义分析判断即可．【详解】解：图1中，角的顶点为，应表示为；图2表示正确；图3，射线和周角是两个概念，射线不能表示周角；图4表示正确．所以表示正确的个数为2．故选：B．【点睛】本题主要考查了角的表示方法、平角、射线、周角等知识，理解并掌握相关知识是解题关键．4.C【分析】根据时钟上一大格是进行计算即可解答．【详解】解：由题意得：，∴时针与分针所夹的的角为，故选：C．【点睛】本题考查了钟面角，熟练掌握时钟上一大格是是解题的关键．5.B【分析】利用钟表表盘的特征解答．表盘共被分成60小格，每一小格所对角的度数为．【详解】解：分针经过45分钟，那么它转过的角度是．故选：B．【点睛】关系：分针每转动；两个相邻数字间的夹角为，每个小格夹角为，并且利用起点时间时针和分针的位置关系建立角的图形．6.B【分析】根据时针一分钟走，一共走了100分钟求解即可．【详解】∵从早上6点30分到早上8点10分∴一共走了100分钟∵时针一分钟走∴．∴时针所走的度数为．故选：B．【点睛】此题考查钟面上角度计算，掌握钟面上每个大格的度数及时针与分针在某个时间的位置是解题的关键．7.D【分析】先求解考试结束的时间，再结合钟面被等分成12格，每格组成一个的角，从而可得答案．【详解】解：∵学校早上7：30考试，考试时间为90分钟，∴考试结束时为9点，此时时针指向9，分针指向12，刚好占3格，而钟面被等分成12格，每格组成一个的角，∴考试结束时时针与分钟的夹角为，故选D．【点睛】本题考查的是钟面角的含义，理解钟面被等分成12份是解本题的关键．8.B【分析】根据位置的相对性判断即可．【详解】解：因为淘气的位置在“水仙花海”大门的西偏南方向处，所以“水仙花海”大门在淘气的东偏北方向处，故选B．【点睛】本题考查了利用方向和距离在平面图中确定位置的方法，解题的关键是掌握方向角的意义和相对性．9.A【详解】试题分析：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达成北（南）偏东（西）多少度．根据定义就可以解决．解：A、OA方向是北偏东60°，此选项错误；B、OB方向是北偏西15°，此选项正确；C、OC方向是南偏西25°，此选项正确；D、OD方向是东南方向，此选项正确．错误的只有A．故选A．10.A【分析】直接根据题意得出各角度数，进而结合方向角表示方法得出答案．【详解】解：如图所示：由题意得：∠1=50 ， BAC =100∴∠2=180°-∠1- BAC=180°-50 -100=30故乙位于A地的南偏东30 ．故选：A．【点睛】此题主要考查了方向角，正确掌握方向角的表示方法是解题关键．11.B【分析】首先根据射线OA和OB垂直，得∠AOB=90°，在求出∠BOC得度数，最后判断方位角即可.【详解】因为射线OA和OB垂直，所以∠AOB=90°.因为∠AOC=30°，所以∠BOC=90°-30°=60°，所以OB的方位角是北偏西60°.故选：B.【点睛】本题主要考查了方位角的判断，求出角的度数是解题的关键.12.82【分析】根据方位角的定义可得∠NOA=60°，∠SOB=38°，从而可确定∠AOB的度数．【详解】解：∵OA是表示北偏东60°方向的一条射线，OB是表示南偏东38°方向的一条射线，∴∠NOA=60°，∠SOB=38°，∴∠AOB=180°-60°-38°=82°，故答案是：82°．【点睛】本题考查了方向角的概念及其计算，基础性较强，数形结合准确确定角的度数是本题的解题关键．13.C【分析】本题考查度、分、秒的换算．运用度、分、秒的换算方法运算即可．【详解】解：∵，∴，∵，∴，∴，故选：C．14.C【分析】根据，，求出的度数，再根据，即可求出的度数．【详解】解：，，，，．故选：C ．【点睛】本题主要考查了度分秒的换算，解题的关键是能够正确求出的度数．15.C【分析】根据进行换算，即可得到答案．【详解】解：．故选：C．【点睛】本题考查了角度的换算，熟练掌握是解题关键．16.D【分析】根据度、分、秒之间的进率为进行转化即可．【详解】解：，，∴，故选：D．【点睛】本题考查了度分秒的转化，熟记度分秒之间的进率是解本题的关键．17.B【分析】根据，进行计算即可．【详解】解：、，原计算错误，故此选项不符合题意；、，原计算正确，故此选项符合题意；、，原计算错误，故此选项不符合题意；、，原计算错误，故此选项不符合题意；故选：B．【点睛】本题考查了度分秒的换算，掌握，是解题的关键．18.B【分析】根据小单位化大单位除以进率,可得答案.【详解】解: ∠P=25°12′=25.2°,∠R=25.2°所以B选项是正确的.【点睛】本题考查角的大小比较．关键是将单位统一，即度、分、秒的换算.19.【分析】根据角度计算运算法则求解即可．【详解】解：．故答案为：．【点睛】本题主要考查了角度计算，理解并掌握角度计算法则是解题关键．20.B【分析】先求解利用角平分线的定义再求解从而可得答案.【详解】解：平分故选B【点睛】本题考查的是角的和差运算，角平分线的定义，熟练的运用角的和差关系探究角与角之间的关系是解本题的关键.21.A【分析】先根据角平分线的定义求出的度数，再根据求出的度数，最后相加即可．【详解】∵射线是的角平分线，，∴，∵，∴，∴，故选A．【点睛】本题考查了与角平分线有关的计算，熟练掌握角平分线的定义是解题的关键．22.155°##155度【分析】利用邻补角的定义即可解答．【详解】解：∵∠AOC与∠BOC是邻补角，∴∠AOC＋∠BOC＝180°，∵∠AOC＝50°，∴∠BOC＝180°−50°＝130°，∵OD，∴∠COD∠AOC＝25°，∴∠BOD＝∠BOC＋∠COD＝130°＋25°＝155°．故答案为：155°．【点睛】此题考查了邻补角的定义，理解邻补角的定义是解题的关键．23.##55度【分析】根据角的概念与角平分线的定义解决此题．【详解】解：由题意得，是的角平分线，故答案为：【点睛】本题考查了角、角平分线，解题关键是掌握角的概念以及角平分线的定义．24.【分析】先根据互补的定义可得，再根据角平分线的定义即可得．【详解】，，是的角平分线，，故答案为：．【点睛】本题考查了互补的定义、角平分线的定义，熟练掌握角平分线的定义是解题关键．25.【分析】直接利用角平分线的性质得出∠AOC＝∠BOC,进而得出答案.【详解】OC平分∠AOB,AOC＝∠BOC,∠AOC＝,∠AOB.故答案为: .【点睛】此题主要考查了角平分线的性质以及度分秒的转换，正确掌握角平分线的性质是解题关键.26.C【分析】此题考查了几何图形中角度的计算，首先根据邻补角的性质求出，然后利用角的和差求解即可．正确掌握图形找中各角度的关系是解题的关键．【详解】解：∵，，∴，∵，∴，故选：C．27.D【分析】如果一条射线在一个角的内部，那么射线所分成的两个小角之和等于这个大角．【详解】解：如右图所示，∵∠AOD =∠AOC+∠COD，∴∠AOD－∠AOC=∠COD，故选D．【点睛】本题考查了角的计算．28.B【分析】根据三角板中角度的特点进行求解即可．【详解】解：由题意得，故选B．【点睛】本题主要考查了三角板中角度的计算，熟知三角板中角度的特点是解题的关键．29.C【分析】等于30度角与直角的和，据此即可计算得到．【详解】解：．故选：C．【点睛】本题考查了角度的计算，理解三角板的角的度数是关键．30.A【分析】本题考查角的和差，角平分线的定义、直角的定义等知识；先根据是直角，，求出的度数，再根据平分求出的度数，进而求出的度数，根据对顶角相等即可得出结论．【详解】是直角，，，平分，，，．故选：A．31.【分析】先根据平分求出，进而求出，再根据计算即可．【详解】解：∵平分，，∴，∵，∴，∵，∴【点睛】本题考查了角平分线的有关计算，熟练掌握运算法则是解题的关键．32.（1）；（2）．【分析】（1）利用角平分线的性质求得的度数，再利用互余的性质即可求解；（2）先求得，再根据，进一步计算即可求解．(1)小问详解：解：∵平分，且，∴，∵，∴；(2)小问详解：解：，∵，且，∴，∴．【点睛】本题主要考查角的和差倍分关系，角平分线的定义，数形结合是解题的关键．33.（1）（2）40°【分析】(1)根据比的意义，列式计算即可．(2)根据比的意义，角平分线的意义列式计算即可．(1)小问详解：解：因为，所以．(2)小问详解：解：因为平分，所以．因为∠，所以，所以．【点睛】本题考查了比的意义，角的平分线的意义，熟练掌握角的平分线的意义是解题的关键．34.（1）（2）【分析】（1）可以根据是的平分线，是的平分线，求得的度数，即可求；（2）根据是的平分线，可求的度数，进而可求的度数，再由是的平分线，即可求解．(1)小问详解：解：∵是的平分线，是的平分线，，，∴，，∴；(2)小问详解：解：∵是的平分线，，∴，∵，∴，∵是的平分线，∴．【点睛】本题主要考查了有关角平分线的计算，明确题意，准确得到角与角间的关系是解题的关键．35.（1）85° （2）55°【分析】（1）可以根据角平分线的定义求得∠COD，∠BOC的度数，即可求∠BOD；（2）根据角平分线的定义可求∠COE的度数，进而可求∠AOC的度数，再由角平分线定义即可求解∠AOB．(1)小问详解：解：∵OB是∠AOC的平分线，OD是∠COE的平分线，∴∠COD=∠DOE=35°，∠COB=∠BOA=50°．∴∠BOD=∠COD+∠COB=85°．(2)小问详解：解：∵OD是∠COE的平分线，∴∠COE=2∠COD=2×25°=50°，∴∠AOC=∠AOE-∠COE=160°-50°=110°，又∵OB是∠AOC的平分线，∴∠AOB∠AOC×110°＝55°．【点睛】本题考查了角平分线的定义以及角的和差，根据角平分线定义得出所求角与已知角的关系转化求解．36.A【详解】试题分析：两个角的和等于则这两个角互余，则的余角的度数为故选A考点：余角．37.D【分析】根据余角的概念：若两个角的和为90°，则这两个角互余计算即可．【详解】解：90°﹣30°＝60°，故选D．【点睛】本题考查的是余角的概念，掌握若两个角的和为90°，则这两个角互余是解题的关键．38.B【分析】本题考查了平行线的性质及互余，正确观察图形，熟练掌握平行线的性质和对顶角相等是解题的关键．本题要注意到与互余，并且直尺的两边互相平行，根据平行线的性质以及对顶角即可求解．【详解】直尺的两边平行，(两直线平行，内错角相等)，(对顶角相等)，，，与互余，、也与互余，与互余的角有，，．故选：B．39.A【分析】本题考查了求一个角的余角，几何图形中的角度问题，依题意得出，根据，即可求解．【详解】解：∵，且，∴，∴，故选：A．40.A【分析】先根据角的和差可得，再根据即可得．【详解】解：由题意得：，，，，故选：A．【点睛】本题考查了角的和差，熟练掌握角的和差运算是解题关键．41.B【分析】根据图形中两个角的位置关系依次确定度数关系，从而可得答案．【详解】解：A、，故不符合题意；B、由同角的余角相等可得=，故符合题意；C、∵，，∴与不相等，故不符合题意；D、，，∴与不相等，故不符合题意；故选：B．【点睛】本题考查三角板中角度关系以及计算，熟记三角板中各角度数，根据图形确定两个角的位置关系再进行计算是解题的关键．42.B【分析】互为余角的两个角和为，据此解答．【详解】解：与互余，，故选：B．【点睛】本题考查余角，是基础考点，掌握相关知识是解题关键．43.C【分析】本题考查的是补角的含义，角度的四则运算，掌握“补角的含义以及角的60进位制”是解本题的关键．【详解】解：．故选：C．44.B【分析】设这个角的度数是度，根据互为补角的两个角的和等于表示出它的补角，然后列方程求解即可．【详解】解：设这个角的度数是度，由题意可得：，解得：，故选：B．【点睛】本题考查了余角和补角，熟记概念并列出方程是解题的关键．45.D【分析】分别求出、、、的大小，即可进行判断．【详解】解：由题意可得，，，，，∴选项A、B、C都不正确，，∴选项D正确，故选：D【点睛】此题考查了角的大小和计算，正确求解角的度数是解题的关键．46.B【分析】根据互为补角的两个角的和等于即可出．【详解】解：与互为补角，，．故选：B．【点睛】本题考查了补角和的定义，是基础题，熟记概念是解题的关键．47.A【分析】根据∠1与∠2互补，∠2与∠3互余，先把∠1、∠3都用∠2来表示，再进行运算．【详解】解：∵∠1+∠2＝180°，∴∠2＝180°﹣∠1，又∵∠2+∠3＝90°，∴∠2＝90°﹣∠3，∴180°﹣∠1＝90°﹣∠3，∴∠1﹣∠3＝90°．故选：A．【点睛】本题考查了余角和补角，解决本题的关键是主要记住互为余角的两个角的和为90°，互为补角的两个角的和为180度．48.C【分析】此题考查了补角的定义，解题要根据若两个角互补，则两个角的和等于列出式子是本题的关键．【详解】解：∵与互补，，∴．故选：C．49.C【分析】由折叠易得是平角的一半；组成一个平角，是，那么与互余；与组成一个平角，，即不能平分．【详解】∵，∴，∵，∴，即．故选项B正确；∵∴∠1+∠3=90°，即与互为余角，故选项A正确；∴，即不能平分，故选项C错误；∴，即与互补，故选项D正确；故选：C．【点睛】本题主要考查余角和补角及角的计算，解题的关键是掌握折叠前后对应角相等；相加得90°的角互为余角；相加得180°的角互为补角．50.B【分析】利用邻补角的性质进行计算即可解答．【详解】解：由图得：．∵，∴．故选：B．【点睛】本题主要考查了邻补角的性质，熟练掌握邻补角的性质是解题的关键．。

(必考题)初中数学八年级数学上册第五单元《二元一次方程组》测试(答案解析)(1)

一、选择题1．如图，一次函数162y x=-+的图象分别交x、y轴于点A、B，与正比例函数y x=的图象交于第一象限内的点C，则OBC的面积为（）A．12 B．24 C．27 D．482．已知24510a ba b+=⎧⎨-=⎩，则+a b等于（）A．8 B．7 C．6 D．53．如图，一次函数y kx b=+与2y x=+的图象相交于点(,4)P m，则方程组2y xy kx b=+⎧⎪=+⎨⎪⎩的解是（）A．(2,4)B．(2,4)-C．(4,2)D．(4,2)-4．一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（）（用含有a、b的代数式表示）．A．a-b B．a+b C．ab D．2ab5．在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元购买A，B两种奖品（两种都要买），A种每个15元，B种每个25元，在钱全部用完的情况下，购买方案共有（）A．2种B．3种C．4种D．5种6．使用喷壶在家中喷洒消毒液是预防新冠病毒的有效措施.某同学为了更加合理、科学、节约的喷洒消毒液，做了如下的记录.壶中可装消毒液400ml ，喷洒每次喷出20ml 的水，壶里的剩余消毒液量y (ml)与喷洒次数n (次)有如下的关系：A ．y 随n 的增加而增大B ．喷洒8次后，壶中剩余量为160mlC ．y 与n 之间的关系式为y =400-nD ．喷洒18次后，壶中剩余量为40ml 7．若x m ﹣n ﹣2y m+n ﹣2=2007，是关于x ，y 的二元一次方程，则m ，n 的值分别是（）A ．m=1，n=0B ．m=0，n=1C ．m=2，n=1D ．m=2，n=38．已知关于,x y 的方程组2106x y nx my +=⎧⎨+=⎩和10312mx y nx y -=⎧⎨-=⎩有公共解，则m n -的值为（）A ．1B ．1-C ．2D ．2-9．若关于x y ，的二元一次方程组232320x y kx y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解，则k 的值为（） A ．34-B ．34C ．43D ．43-10．把60个乒乓球分别装在两种不同型号的盒子里（两个盒子必须都装），大盒装6个，小盒装4个，当把乒乓球都装完的时候恰好把盒子都装满，那么不同的装球方法有（）． A ．2种B ．4种C ．6种D ．8种11．已知a b c 、、是ABC 的三边长，其中a b 、是二元一次方程组10216a b a b +=⎧⎨+=⎩的解，那么c 的值可能是下面四个数中的（） A ．2 B ．6 C ．10 D ．1812．将一张面值100元的人民币，兑换成10元或20元的零钱，兑换方案有（） A ．4种 B ．5种 C ．6种 D ．7种二、填空题13．金秋十月，丹桂飘香，重庆市綦江区某中学举行了创新科技大赛，该校初二年级某班共有18人报名参加航海组、航空组和无人机组三个项目组的比赛（每人限参加一项），其中航海组的同学比无人机组的同学的两倍少3人，航空组的同学不少于5人但不超过9人，班级决定为航海组的每位同学购买2个航海模型，为航空组的每位同学购买3个航空模型，为无人机组的每位同学购买若干个无人机模型，已知航海模型75元每个，航空模型98元每个，无人机模型165元每个，若购买这三种模型共需花费6939元，则其中购买无人机模型的费用是_______．14．一笔奖金总额为1092元，分为一等奖、二等奖和三等奖，奖金金额均为整数，每个一等奖的奖金是每个二等奖奖金的2倍，每个二等奖的奖金是每个三等奖奖金的2倍，若把这笔奖金发给6个人，并且要求一等奖的人数不能超过二等奖人数，二等奖人数不能超过三等奖人数，那么三等奖的奖金金额是___________元．15．已知方程组2300x y ax y c -+=⎧⎨-+=⎩的解为11x y =-⎧⎨=⎩，则一次函数y ＝2x ＋3与y ＝ax ＋c 的图象的交点坐标是_____________．16．某风景区有4个相同的出口、4个相同的入口，假设在任何情况下每个入口的人数均是匀速出入，每个出口的人数均是匀速出入，当风景区人数已达到可容纳人数的20%时，若同时开放4个入口和2个出口，则1.6小时刚好达到可容纳人数；若同时开放2个入口和2个出口，则8小时刚好达到可容纳人数．受疫情影响，2020年五一期间，该风景区游览人数只允许达到平时可容纳人数的60%，当风景区人数已达到平时可容纳人数的10%时，若同时开放3个入口和2个出口，则经过__________小时刚好达到平时可容纳人数的60%．17．已知一个两位数，它的十位上的数字与个位上的数字和是3，若颠倒个位数字与十位数字的位置，得到的新数比原数小9，求这个两位数是_____． 18．若关于x 、y 的二元一次方程组3526x my x ny -=⎧⎨+=⎩，的解是13x y =⎧⎨=⎩，则关于a 、b 的二元一次方程组()()()()3526a b m a b a b n a b ⎧+--=⎪⎨++-=⎪⎩的解是_____．19．已知x 和y 满足方程组3634x y x y +=⎧⎨+=⎩，则x-y 的值为_____．20．如图，已知点A 坐标为(6,0)，直线()0y x b b =+>与y 轴交于点B ，与x 轴交于点C ，连接AB ，43AB =，则OC 的长为______．三、解答题21．着中国传统节日“端午节”的临近，永旺超市决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买1盒甲品牌粽子和2盒乙品牌粽子需230元：打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．（1）打折前甲、乙两种品牌粽子每盒分别为多少元？（2）阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？ 22．阅读下列材料：在数学的解题中，我们把一个式子中比较复杂的数学部分，用一个新的未知数（元）去代替它，原式被改造得更简化，问题更易于解决，这种方法称为换元法．换元可以达到降次、或化分式为整式等目的换元法可以运用于数式计算、分解因式、解方程（组）等方面．下面举例说明例，计算11111111111111111111234523456234562345⎛⎫⎛⎫⎛⎫⎛⎫----++++------+++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭23．A ，B ，C 三个村庄依次在一条笔直的公路旁，甲从A 村庄出发沿着这条公路匀速去B 村庄，乙从C 村庄出发沿着这条公路匀速去A 村庄，当其中一人到达目的地时，另一人也随之停止运动．甲、乙与B 村庄的距离y ，y 2，与甲的行驶时间t 之间的函数关系如图所示．请根据所给图象解答下列问题：（1）填空：A ，B 两村庄之间的距离为____km ，乙比甲晚出发____h ；乙的速度为____km/h ，甲的速度为____km/h ；（2）求乙从C 村庄到B 村庄的行驶过程中，与B 村庄的距离y 2与甲行驶的时间t 之间的函数关系式；（3）请直接写出当t 为何值时，甲与乙相遇．24．某化肥厂把化肥送到甲、乙两个村庄，先后送了两次．每次的运量和运费如下表：次序甲村运量/t乙村运量/t共计运费/元第1次 6 5 270 第2次811490（2）试问两个村庄各负担运费多少元？25．已知点(4,0)A 及在第一象限的动点(,)P x y ，且6x y +=，设OPA 的面积为S ．（1）用含x 的式子表示S ，并写出自变量x 的取值范围；（2）求S 9=时P 点坐标；（3）在（2）的基础上，设点Q 为y 轴上一动点，当PQ AQ +的值最小时，求点Q 坐标．26．关于x 、y 的方程组2564x y mx ny +=-⎧⎨-=⎩．与关于x 、y 的方程组35168x y nx my -=⎧⎨+=-⎩的解相同，求2021(2)m n +【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】因直线162y x =-+交y 轴于点B ，故可求得点B 的坐标，从而可得OB 的长，又直线162y x =-+与直线y x =相交，故可求得点C 的坐标，从而可得△OBC 的边OB 上的高，因此可求得△OBC 的面积．【详解】对于直线162y x =-+，令0x =，得：6y = ∴6OB =解方程组162y xy x =⎧⎪⎨=-+⎪⎩，得：44x y =⎧⎨=⎩ 即点C 的坐标为(4,4) ∴点C 到y 轴的距离为4∴14122OBCSOB =⨯⨯= 故选：A本题主要考查了求两直线交点坐标、平面直角坐标系中求直线围成的三角形面积，关键分别求得点B 、点C 的坐标，而求两直线的交点坐标体现了数形结合的思想．2．D解析：D 【分析】解二元一次方程组再进行计算即可；【详解】24510a b a b +=⎧⎨-=⎩， 10a b -=两边同时乘以2得：2220a b -=， 245a b +=减去2220a b -=得：615b =-，解得：52b =-，代入10a b -=得：152a =， ∴155522a b +=-=；故答案选D ．【点睛】本题主要考查了二元一次方程组的求解，结合代数式求值是解题的关键．3．A解析：A 【分析】将点P （m 、4）代入2y x =+，求出m 的值，结合图像交点P 的坐标即为二元一次方程组的解．【详解】一次函数y kx b =+与2y x =+的交点为P （m 、4）24m ∴+= 解得2m =∴点P 的坐标为（2、4）2y x y kx b =+⎧∴⎨=+⎩的解为：24x y =⎧⎨=⎩故选：A ．【点睛】本题考查了一次函数与二元一次方程组的关系，解题关键是求出点P 坐标，结合图形求解．4．C【分析】设小正方形的边长为x ，大正方形的边长为y ，列方程求解，用大正方形的面积减去4个小正方形的面积即可．【详解】解：设小正方形的边长为x ，大正方形的边长为y ，则：22x y ay x b+=⎧⎨-=⎩ ，解得：42a b x a b y -⎧=⎪⎪⎨+⎪=⎪⎩， ∴阴影面积=（2a b +）2﹣4×（4a b -）22222224444a ab ba ab b ab ++-+=-=＝ab ．故选C ．【点睛】本题考查了整式的混合运算，求得大正方形的边长和小正方形的边长是解题的关键．5．A解析：A 【分析】设A 种买x 个，B 种买y 个，据题意列二元一次方程，找出这二元一次方程的正整数解的个数就是购买方案的种类数．【详解】解：设A 种买x 个，B 种买y 个，依题意得1525200x y += 得4035xy -=，由于x 、y 只取正整数，所以需使(403)x -被5整除且(403)x -为正数，所以x 只能取5、10，对应的y 为5、2，∴1525200x y +=的正整数解有两组510,52x x y y ==⎧⎧⎨⎨==⎩⎩．所以购买方案共有2种．故选：A ．【点睛】此题考查二元一次方程的应用，会求解二元一次方程的正整数解是关键．6．D解析：D 【分析】先利用待定系数法求出y 与n 之间的函数关系式，再根据一次函数的性质逐项判断即可得．【详解】由表格可知，y 与n 之间的函数关系式为一次函数，设y 与n 之间的函数关系式为y kn b =+，将点(1,380),(2,360)代入得：3802360k b k b +=⎧⎨+=⎩，解得20400k b =-⎧⎨=⎩，则y 与n 之间的函数关系式为20400y n =-+，选项C 错误；由一次函数的性质可知，y 随n 的增大而减小，选项A 错误；当8n =时，208400240y =-⨯+=，选项B 错误；当18n =时，201840040y =-⨯+=，选项D 正确；故选：D ．【点睛】本题考查了利用待定系数法求一次函数的解析式、一次函数的性质等知识点，熟练掌握待定系数法是解题关键．7．C解析：C 【分析】根据二元一次方程的定义，列出关于m 、n 的方程组，然后解方程组即可．【详解】解：根据题意，得121m n m n -=⎧⎨+-=⎩，解得21m n =⎧⎨=⎩．故选：C ． 8．A解析：A 【分析】联立不含m 与n 的两个方程组成方程组，求出x 与y 的值，进而求出m 与n 的值，代入m-n ，计算即可．【详解】解：联立得：210312x y x y +=⎧⎨-=⎩①②，①×3+②得：7x=42，解得：x=6，把x=6代入②得：y=-2，把62x y =⎧⎨=-⎩ 代入得：6266210n m m n -=⎧⎨+=⎩，解得：m=3，n=2，则m-n=3-2=1．故选A ．【点睛】本题考查了二元一次方程组的解：一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解．利用两个方程组有公共解得出x ，y 的值是解题关键．9．B解析：B 【分析】首先解关于x 的方程组，求得x ，y 的值，然后代入方程2x ＋3y ＝6，即可得到一个关于k 的方程，从而求解．【详解】解232320x y k x y k +=⎧⎨-=⎩得72x ky k=⎧⎨=-⎩，由题意知2×7k ＋3×（−2k ）＝6，解得k ＝34．故选：B 【点睛】此题考查了解二元一次方程组，二元一次方程组的解，能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解．解题的关键是要知道两个方程组之间解的关系．10．B解析：B 【分析】结合题意，列二元一次方程，再根据x 和y 均为正整数，通过解二元一次方程，即可得到答案．【详解】假设大盒有x 个，小盒有y 个根据题意得：6460x y += 结合题意，x 和y 均为正整数当1x =时，60613.54y -==，不符合题意当2x =时，6012124y -==，符合题意当3x =时，601810.54y -==，不符合题意当4x =时，602494y -==，符合题意当5x =时，60307.54y -==，不符合题意当6x =时，603664y -==，符合题意当7x =时，60424.54y -==，不符合题意当8x =时，604834y -==，符合题意当9x =时，60541.54y -==，不符合题意当10x =时，606004y -==，不符合题意 ∴共有4种装球方法故选：B ．【点睛】本题考查了二元一次方程的知识；解题的关键是熟练掌握二元一次方程的性质并运用到实际问题中，从而完成求解．11．B解析：B 【分析】先解二元一次方程组求出a,b 的值，然后再根据三角形三边之间的关系确定c 的值．【详解】解：由题意可知：10(1)216(2)a b a b +=⎧⎨+=⎩，(2)-(1)式得：a =6，代回(1)中，解得b =4，根据三角形两边之和大于第三边，两边之差小于第三边可知， 6-4<c<6+4，即：2<c<10，故选：B ．【点睛】本题考查了二元一次方程组的解法及三角形三边之间的关系，熟练掌握二元一次方程组的解法是解决本题的关键．12．C解析：C 【分析】设兑换成10元x 张，20元的零钱y 元，根据题意可得等量关系：10x 张+20y 张=100元，根据等量关系列出方程求整数解即可．【详解】解：设兑换成10元x 张，20元的零钱y 元，由题意得：10x+20y=100，整理得：x+2y=10，方程的整数解为：方程的整数解为：246810x0,,,,,,432105 x x x x xy y y y y y======⎧⎧⎧⎧⎧⎧⎨⎨⎨⎨⎨⎨======⎩⎩⎩⎩⎩⎩因此兑换方案有6种，故选C．【点睛】此题主要考查了二元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．二、填空题13．4125元【分析】设无人机组有x个同学航空组有y个同学根据人数为18列出二元一次方程根据航空组的同学不少于5人但不超过9人得到xy的解再代入模型费用进行验证即可求解【详解】设无人机组有x个同学航空组解析：4125元．【分析】设无人机组有x个同学，航空组有y个同学，根据人数为18列出二元一次方程，根据航空组的同学不少于5人但不超过9人，得到x,y的解，再代入模型费用进行验证即可求解．【详解】设无人机组有x个同学，航空组有y个同学，则航海组有(2x-3)个同学，依题意得x+2x-3+y=18，解得x=21=733y y --，∵航空组的同学不少于5人但不超过9人，x，y为正整数，y为3的倍数，故方程的解为，56xy=⎧⎨=⎩，49xy=⎧⎨=⎩，设为无人机组的每位同学购买a个无人机模型，当56xy=⎧⎨=⎩时，依题意得5a×165+2×7×75+6×3×98=6939解得a=4125=5825，符合题意，故购买无人机模型的费用是4125元；当49xy=⎧⎨=⎩时，依题意得4a×165+2×5×75+9×3×98=6939解得a=3543660，不符合题意；综上，答案为4125元．故答案为：4125元．【点睛】此题主要考查二元一次方程的应用，解题的关键是根据题意列出方程，再分类讨论进行求解．14．【分析】获一等奖人获二等奖人获三等奖由之间的关系结合均为整数即可得出的值设三等奖的奖金金额为x 元则二等奖的奖金金额为2x 元一等奖的奖金金额为4x 元根据奖金的总额为1092元即可得出关于x 的一元一次方解析：78【分析】获一等奖a 人，获二等奖b 人，获三等奖c ，由,,a b c 之间的关系结合,,a b c 均为整数，即可得出,,a b c 的值，设三等奖的奖金金额为x 元，则二等奖的奖金金额为2x 元，一等奖的奖金金额为4x 元，根据奖金的总额为1092元，即可得出关于x 的一元一次方程，解之即可得出结论（取其为整数的值）．【详解】解：获一等奖a 人，获二等奖b 人，获三等奖c ，根据题意=6a b c ++0a b c <≤≤且,,a b c 均为整数，∴114a b c =⎧⎪=⎨⎪=⎩，123a b c =⎧⎪=⎨⎪=⎩，222a b c =⎧⎪=⎨⎪=⎩．设三等奖的奖金金额为x 元，则二等奖的奖金金额为2x 元，一等奖的奖金金额为4x 元，依题意，得：4x+2x+4x=1092，4x+2×2x+3x=1092，2×4x+2×2x+2x=1092，解得：x=109.2（不合题意，舍去），x=99311（不合题意，舍去），x=78．故答案为： 78．【点睛】本题考查了三元一次方程整数解和一元一次方程的应用，掌握三元一次方程的整数解的求法，和一元一次方程解应用题的方法与步骤，找准等量关系，正确列出一元一次方程是解题的关键． 15．【分析】函数图象交点坐标为两函数解析式组成的方程组的解据此即可求解【详解】解：∵关于xy 的二元一次方程组的解为∴一次函数y ＝2x ＋3与y ＝ax ＋c 的图象的交点坐标为（-11）故答案为：（-11）【点解析：()1,1-【分析】函数图象交点坐标为两函数解析式组成的方程组的解，据此即可求解．【详解】解：∵关于x ，y 的二元一次方程组2300x y ax y c -+=⎧⎨-+=⎩的解为11x y =-⎧⎨=⎩， ∴一次函数y ＝2x ＋3与y ＝ax ＋c 的图象的交点坐标为（-1，1）．故答案为：（-1，1）．【点睛】本题考查了一次函数与二元一次方程组，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．16．【分析】设每个入口每小时可进可容纳人数的每个出口每小时可出可容纳人数的根据当风景区人数已达到可容纳人数的20时若同时开放4个入口和2个出口则16小时刚好达到可容纳人数；若同时开放2个入口和2个出口则解析：53【分析】设每个入口每小时可进可容纳人数的%x ，每个出口每小时可出可容纳人数的%y ，根据“当风景区人数已达到可容纳人数的20%时，若同时开放4个入口和2个出口，则1.6小时刚好达到可容纳人数；若同时开放2个入口和2个出口，则8小时刚好达到可容纳人数”，即可得出关于,x y 的二元一次方程组，解之即可得出,x y 的值，再将其代入60%10%3%2%x y --即可求出结论．【详解】解：设每个入口每小时可进可容纳人数的%x ，每个出口每小时可出可容纳人数的%y ，依题意，得： 1.64 1.62100208282=10020x y x y ⨯-⨯=-⎧⎨⨯-⨯-⎩，解得：2015x y =⎧⎨=⎩， ∴60%10%50%53%2%320%215%3x y -==-⨯-⨯．故答案为：53．【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键． 17．21【分析】设这个两位数十位数字为x 个位数字为y 根据题意可得：据此列方程组求解【详解】解：设这个两位数十位数字为x 个位数字为y 由题意得：解得：则这个两位数为21故答案为：21【点睛】本题主要考查了二【分析】设这个两位数十位数字为x，个位数字为y，根据题意可得：10(10)93x y y xx y+-+=⎧⎨+=⎩据此列方程组求解．【详解】解：设这个两位数十位数字为x，个位数字为y，由题意得：10(10)93x y y xx y+-+=⎧⎨+=⎩解得：21 xy=⎧⎨=⎩则这个两位数为21．故答案为：21．【点睛】本题主要考查了二元一次方程的应用，理解题意从中找出相应的等量关系列出二元一次方程组是解题的关键．18．【分析】根据已知得出关于ab的方程组进而得出答案【详解】解：∵关于xy的二元一次方程组的解是∴方程组中解得：故答案为：【点睛】本题主要考查二元一次方程组的解法关键是根据整体思想及方程组的解法进行求解解析：21 ab=⎧⎨=-⎩【分析】根据已知得出关于a，b的方程组进而得出答案．【详解】解：∵关于x、y的二元一次方程组3526x myx ny-=⎧⎨+=⎩，的解是13xy=⎧⎨=⎩，∴方程组()()()()3526a b m a ba b n a b⎧+--=⎪⎨++-=⎪⎩中13a ba b+=⎧⎨-=⎩，解得：21 ab=⎧⎨=-⎩．故答案为：21 ab=⎧⎨=-⎩．【点睛】本题主要考查二元一次方程组的解法，关键是根据整体思想及方程组的解法进行求解．19．1【详解】-②可得2x-2y=2即可得x-y=1故答案为1解析：13634x y x y +=⎧⎨+=⎩①②， -②可得，2x-2y=2，即可得x-y=1.故答案为120．【分析】根据勾股定理求得OB 即可求得b 的值得到直线解析式令y=0求得x 的值即可求得OC 的值【详解】解：∵点A 坐标为（60）∴OA=6∵AB=4∴OB=∴b=OB=2∴直线的解析式为y=x+2令y=0解析：【分析】根据勾股定理求得OB ，即可求得b 的值，得到直线解析式，令y=0，求得x 的值，即可求得OC 的值．【详解】解：∵点A 坐标为（6，0），∴OA=6，∵∴=∴∴直线的解析式为令y=0，则∴C （0），∴故答案为【点睛】本题考查一次函数图象上点的坐标特征，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．三、解答题21．（1）甲品牌粽子每盒70元，乙品牌粽子每盒80元；（2）3120元【分析】（1）设打折前甲品牌粽子每盒x 元，乙品牌粽子每盒y 元，根据“打折前，买1盒甲品牌粽子和2盒乙品牌粽子需230元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元”，即可得出关于x 、y 的二元一次方程组，解之即可得出结论；（2）根据节省钱数=甲品牌粽子节省的钱数+乙品牌粽子节省的钱数，即可求出节省的钱数．解：（1）设打折前甲品牌粽子每盒x 元，乙品牌粽子每盒y 元，题意得：2230500.8400.755200x y x y +=⎧⎨⨯+⨯=⎩，解得：7080x y =⎧⎨=⎩， ∴甲品牌粽子每盒70元，乙品牌粽子每盒80元．（2）80×70×（1-80%）+100×80×（1-75%）=3120（元）．答：打折后购买这批粽子比不打折节省了3120元．【点睛】本题考查了二元一次方程组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据数量关系，列式计算．22．（1）见解析；（2）14；（3）16【分析】（1）根据整式的混合运算法则计算即可；（2）设x +3y =m ，3x +y =n ，则方程组变形为3261323m n m n -=⎧⎪⎨+=⎪⎩①②，然后利用加减消元法求出m 即可；（3）设a =95，则m 2=（a -2）•a •（a +2）•（a +4）+k =（a 2+2a ）2-8（a 2+2a ）+k ，然后利用完全平方公式得到k 的最小值．【详解】解：（1）原式11(1)166a a a a ⎛⎫⎛⎫=-+--- ⎪ ⎪⎝⎭⎝⎭ =22111666a a a a a a +---++ =16；（2）设x +3y =m ，3x +y =n ，方程组3261323m n m n -=⎧⎪⎨+=⎪⎩①②，由②得3m +2n =78③，①+③得6m =84，解得m =14，所以x +3y =14；故答案为14；（3）设a =95，则m 2=93×95×97×99+k =（a -2）•a •（a +2）•（a +4）+k=（a2+2a-8）（a2+2a）+k=（a2+2a）2-8（a2+2a）+k≥（a2+2a-4）2=（a2+2a）2-8（a2+2a）+16当93959799k⨯⨯⨯+为正整数m的平方，k的最小值为16．【点睛】本题考查了解二元一次方程组和完全平方公式，利用代入消元法或加减消元法解二元一次方程组．也考查了整体的思想．由于题目中，11112345+++，在各个因式中重复出现，可以令11112345a+++=原式11 (1)166a a a a⎛⎫⎛⎫=-+---⎪ ⎪⎝⎭⎝⎭=．．．请解决下列问题：（1）完成例中未完成的部分；（2）在方程组3(3)2(3)6331323x y x yx y x y+-+=⎧⎪++⎨+=⎪⎩中，求3x y+的值；（3）已知正整数k，使93959799k⨯⨯⨯+是一个正整数m的平方，求k的最小值．23．（1）240,1,80,60；（2）()22000178028012tyt t⎧≤<⎪=⎨⎛⎫-+≤≤⎪⎪⎝⎭⎩；（3）267t=【分析】（1）根据函数图象直接得到A，B两村庄之间的距离为240km，乙比甲晚出发1h，根据7200(1)2÷-=80km/h，求出乙的速度；根据甲行驶的路程及时间求出甲的速度为2404÷=60km/h；（2）由图象可分0≤t＜1与712t≤≤两种情况，结合图象和待定系数法求解即可；（3）由题意得，甲从A村庄到B村庄的行驶过程中的函数解析式为y=240-60t，设乙从B村庄到A村庄行驶过程中的函数解析式为y2=mt+n，将点（72，0），（4,40）代入求出y2=80t-280，根据y=y2得到240-60t=80t-280，求出t即可．【详解】解：（1）根据函数图象得，A，B两村庄之间的距离为240km，乙比甲晚出发1h，乙的速度为7200(1)2÷-=80km/h，甲的速度为2404÷=60km/h，故答案为：240,1,80,60；（2）当0≤t＜1时，y2=200；当712t ≤≤时，设2y 与t 之间的函数关系式为：2y kt b =+．由（1）知，乙的速度为80km/h ，∴80k =-．将(1,200)代入280y t b =-+，得280b =，∴乙从C 村庄到B 村庄的行驶过程中，与B 村庄的距离2y 与甲行驶的时间t 之间的函数关系式为()22000178028012t y t t ⎧≤<⎪=⎨⎛⎫-+≤≤ ⎪⎪⎝⎭⎩．（3）由题意得，甲从A 村庄到B 村庄的行驶过程中的函数解析式为y=240-60t ，设乙从B 村庄到A 村庄行驶过程中的函数解析式为y 2=mt+n ，∵乙的行驶速度为80km/h ， ∴780(4)402⨯-=，∴y 2=mt+n 过点（72，0），（4,40）， ∴702440t n t n ⎧+=⎪⎨⎪+=⎩，解得80280t n =⎧⎨=-⎩， ∴y 2=80t-280，当y=y 2时，240-60t=80t-280，解得267t =．当267t =时，甲与乙相遇．【点睛】此题考查一次函数的实际应用，待定系数法求函数解析式，一次函数图象交点，解题的关键是正确理解函数图象，掌握路程、时间、速度的关系．24．（1）把化肥送到甲、乙两个村庄每吨化肥分别需要20元，30元；（2）甲、乙两个村庄各负担运费分别为280元，480元【分析】（1）根据题意列出二元一次方程组并且求解即可；（2）将（1）求出的值直接代入68x x +和511y y +进行求值即可；【详解】（1）解：设把化肥送到甲、乙两个村庄每吨化肥分别需要x 元，y 元．依题意，得：65270811490x y x y +=⎧⎨+=⎩，解得2030x y =⎧⎨=⎩．答：把化肥送到甲、乙两个村庄每吨化肥分别需要20元，30元．（2）甲村需负担运费：68620820280x x +=⨯+⨯=（元）乙村需负担运费：5115301130480y y +=⨯+⨯=（元）答：甲、乙两个村庄各负担运费分别为280元，480元．【点睛】本题考查了二元一次方程组的应用，重点要找到题中的等量关系进行求解即可；25．（1）122S x =-；06x <<；（2）P 15,5(4)..；（3）Q 360,11⎛⎫ ⎪⎝⎭【分析】（1）首先把x+y=6，变形成y=6-x ，再利用三角形的面积求法：底×高÷2=S ，可以得到S 关于x 的函数表达式；P 在第一象限，故x ＞0，再利用三角形的面积S ＞0，可得到x 的取值范围；（2）把S=9代入函数解析式即可；（3）根据题意画出图象，作出A 的对称点A′，连接PA′，此时PA′与y 轴交于点Q ，此时PQ+AQ 的值最小，进而求出即可．【详解】（1）∵6x y +=∴6y x =-，∴()462S x =-÷即：122S x =-∵1220x ->∴6x <∴06x <<；（2）∵9s =∴9122x =-解得： 1.5x =，∴61545y =-=.. ∴当9s =时，P 点坐标15,5(4)..；（3）如图所示：作出A 的对称点A '，连接PA '，此时PA '与y 轴交于点Q ，此时PQ AQ +的值最小．∵A 点坐标为()4,0，∴()4,0A '-，∴将()4,0-，15,5(4)..代入y kx b =+， 401545k b k b -+=⎧⎨+=⎩．．得：解得：9113611k b ⎧=⎪⎪⎨⎪=⎪⎩∴9361111y x =+，∴0x =，时，3611y = ∴当PQ AQ +的值最小时，Q 点坐标为：360,11⎛⎫ ⎪⎝⎭．【点睛】此题主要考查了待定系数法求函数解析式以及画一次函数的图象和最短路线求法，解题时一定要注意自变量的取值范围．26．1【分析】由题意，根据方程组的解相同得到2563516x y x y +=-⎧⎨-=⎩，从而得到22x y =⎧⎨=-⎩，再代入计算，求出m 、n 的值，即可得到答案．【详解】解：根据题意，由2563516x y x y +=-⎧⎨-=⎩，解得：22x y =⎧⎨=-⎩，代入48mx ny nx my -=⎧⎨+=-⎩，得224228m n n m +=⎧⎨-=-⎩，解得：31m n =⎧⎨=-⎩；则20212021(2)(32)1m n +=-=；【点睛】本题考查了解二元一次方程组，解题的关键是掌握解二元一次方程组的方法进行解题．。

sob工作流程

sob工作流程Sob工作流程Sob工作流程是一种高效的项目管理方法，它可以帮助团队协作完成复杂的任务。

Sob是“Specify（需求确定）- Organize（组织计划）- Build（实施）”的缩写，它包含了三个主要的阶段。

下面将详细介绍Sob工作流程的每个阶段。

一、需求确定（Specify）在Sob工作流程中，需求确定是项目的第一个关键步骤。

在这个阶段，团队需要明确项目的目标和要求，以便为后续的计划和实施提供指导。

需求确定包括以下几个步骤：1.1 确定项目目标：明确项目的整体目标和预期结果，以便在后续的工作中有一个明确的方向。

1.2 收集需求：与项目相关的各方进行沟通，了解他们的需求和期望，确保项目的设计和实施符合他们的要求。

1.3 确定约束条件：明确项目的约束条件，如时间、资源和预算等，以确保项目可以在可接受的范围内完成。

1.4 制定项目计划：根据项目目标和约束条件，制定详细的项目计划，包括工作分解结构（WBS）、里程碑和时间表等。

二、组织计划（Organize）在需求确定阶段完成后，团队需要进行组织计划，以明确项目的详细实施步骤和资源分配。

组织计划包括以下几个步骤：2.1 制定工作分解结构（WBS）：将项目目标分解为可管理的工作包，以便更好地组织和控制项目进展。

2.2 确定关键路径：通过网络图或甘特图等工具，确定项目的关键路径和关键活动，以便优化项目进度和资源分配。

2.3 分配资源：根据项目计划和工作包的需求，合理分配资源，确保项目能够按时、按质完成。

2.4 制定沟通计划：确定项目团队成员之间的沟通方式和频率，以及与项目相关方的沟通方式，确保信息流通畅。

三、实施（Build）在组织计划完成后，团队开始进行项目的实施阶段，这是项目最关键的阶段之一，要确保按照计划和需求进行实施。

实施阶段包括以下几个步骤：3.1 开展工作：根据项目计划和工作分解结构，团队成员开始按照任务和时间表进行工作。

3.2 监控进展：定期监控项目的进展情况，比较实际进展与计划进展的差异，及时调整和处理项目中的问题和风险。

沪科版数学七年级上册综合训练50题(含答案)

沪科版数学七年级上册综合训练50题（填空、解答题）一、填空题1．用正三角形、正四边形和正六四边形按如图所示的规律拼图案，则第n 个图案中正三角形的个数为_____．2．数轴上表示－2的点先向右移动3个单位，再向左移动5个单位，则此时该点表示的数是___.3．一个角是 25°30′，则它的补角为____________度． 4．若13n ab +-与143m a b -的和仍是单项式，则m n =_______．5．关于x 的一元一次方程（2m ﹣6）x ﹣2＝0 ，x ＝1是一元一次方程的解，则m ＝_____．6．下列各数：12，﹣（﹣3），﹣|﹣4|，0，﹣22，﹣0.01，（﹣1）3，属于负数的有_________个．7．近似数7.2765精确到0.01是______．8．若α与β互余，且α=35°18′，则β=___________． 9．单项式3223a x π-的系数是__________，次数是__________．10．若是同类项，则= ，= ．11．有下列判断：①两点确定一条直线，①直线上任意两点都可以表示这条直线；①三点确定一条直线；①过一点有无数条直线，其中错误的是_____（填序号）12．已知x ，y 满足方程345254x y x y +=⎧⎨+=⎩，则x -y 的值为_______；13．在CCTV “开心辞典”栏目中，主持人问这样一道题目：“a 是最小的正整数，b 是最大的负整数，c 是绝对值最小的有理数，请问：a ，b ，c 三数之和是____________．”14．若单项式12m xy +与单项式2313n x y -是同类项，则m n -=__________．15．为了了解5000件商品的质量问题，从中任意抽取100件商品进行试验在这个问题中，样本容量是__________．16．有一个密码系统,其原理为下面的框图所示当输出为-3时,则输入的x=______.17．已知132n x y +-与34y x 是同类项，则n 的值是__________．18．已知代数式22a a -的值是3，则代数式2542a a +-的值为__________． 19．若a ，b 互为相反数，且0ab ≠，c 、d 互为倒数，m 是数轴上到原点的距离为2的点表示的数，则322()3b a b cd m a ⎛⎫++-+ ⎪⎝⎭的值为___________．20．如图所示，点A 在点O 的北偏东50°方向，点B 在点O 的南偏东30°方向上，则AOB ∠=______．21．如图，在长方形ABCD 中，8cm AB =，9cm BC =，点E 是AD 上一点，2AE DE =，点P 从点B 出友，以1cm/s 的速度从点B —C —D —E 匀速运动，设点P运动的时间为ts ，当PCE 的面积为6cm 2时，则t ＝________．22．大于133-而小于2的所有整数的和是__________．23．规定符号⊗的意义为2a b ab a ⊗=-，那么34-⊗=_________. 24．若13x 2y m 与2x n y 6是同类项，则m+n=______．25．明明带了a 元去书店买了一套《四大名著》，每本名著售价b 元，一套有4本，还剩_______元．如果150a =，36.45b =元，还剩_______元． 26．用“＞”或“＜”或“＝”填空：（1）﹣|﹣9|_____﹣（﹣9）；（2）34-_____78-．27．用“①”定义一种新运算：对于任意有理数a 和b ，规定23a b ab a =+☆．如：213133112=⨯+⨯=☆，则()32-=☆_________．28．长为4，宽为2的矩形绕其一边旋转构成一个圆柱的最大体积为___ (结果保留π). 29．下图是一个无盖的长方体盒子的展开图（重叠部分不计），根据图中数据，则该无盖长方体盒子的容积为__．二、解答题30．化简并求值：2(3)4(31)4a b b a ---+--．其中53a b +=． 31．计算：（1（2）｜13.32．我们定义一种新运算：*2a b a b ab =-+（等号右边为通常意义的运算）：（1）计算()2*3-的值；（2）解方程：132x x *=*． 33．解方程组：2201160x y z x y z x y ++=-⎧⎪-+=⎨⎪+=⎩．34．为了了解学校图书馆上个月借阅情况，管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计，并绘制了下列不完整的统计图，请根据图中信息解答下列问题：（1）上个月借阅图书的学生有多少人？扇形统计图中“经济”部分的圆心角度数是多少？（2）把条形统计图补充完整；（3）从借阅情况分析，如果要添置这四类图书3600册，请你估算“科普”类图书应添置多少册合适？35．先化简，再求值：()22222232324x y xy x y xy xy xy ⎡⎤+---+-⎣⎦，其中2x =，=3y -．36．先化简，再求值：（1）﹣a 2b +（ab 2﹣3a 2b ）﹣2（ab 2﹣2a 2b ），其中a ＝2，b ＝1；（2）2（a 2﹣b ）+3a 2﹣2（a 2+12b ），其中（a 2+m ﹣1）2+|b +m +2|＝0．37．有20筐白菜，以每筐25千克为标准，超过或不足的数分别用正、负数来表示．记录如下：（1）这20筐中，最重的一筐比最轻的一筐重 _____千克（2）与标准重量比较，总计超过或不足多少千克？（3）若售价1.8元，则出售这筐可卖多少元？38．八年级（1）班的学习委员亮亮对本班每位同学每天课外完成数学作业的时间进行了一次统计，并根据收集的数据绘制了如图的统计图（不完整），请你根据图中提供的信息，解答下面的问题：（注：每组数据包括最大值，不包括最小值．）（1）这个班的学生人数为______人；（2）将图①中的统计图补充完整；（3）完成课外数学作业的时间的中位数在______时间段内；（4）如果八年级共有学生500名，请估计八年级学生课外完成数学作业时间超过1.5小时的有多少名？39．在做解方程练习时，有一个方程“y 125-=y +■”，题中■处不清晰，李明问老师，老师只是说：“■是一个有理数，该方程的解与当x ＝2时整式5（x ﹣1）﹣2（x ﹣2）﹣4的值相同．”依据老师的提示，请你帮李明找到“■”这个有理数，并求出方程的解． 40．计算：(1)514166÷×÷8357⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭； (2)－3－3510.225⎡⎤⎛⎫-+-⨯÷- ⎪⎢⎥⎝⎭⎣⎦；(3)114332⎛⎫- ⎪⎝⎭ ×(－2)－221÷32⎛⎫- ⎪⎝⎭；(4)2711150(6)9126⎡⎤⎛⎫--+⨯- ⎪⎢⎥⎝⎭⎣⎦÷(－7)2.41．解方程组：32823154x y y z x y z -=⎧⎪+=⎨⎪+-=-⎩．42．10个互不相等的有理数，每9个的和都是“分母为22的既约真分数（分子与分母无公约数的真分数）”，则这10个有理数的和为___．43．先化简再求值：22223[22( 1.5)]3,3,2x y xy xy x y xy xy x y ---++=-=-其中 44．计算：（1）111410233535⎛⎫-+-- ⎪⎝⎭；（2）()12524236⎛⎫-⨯-+ ⎪⎝⎭．45．在机器人大赛中，机器人沿一条直线爬行．规定向右爬行为正，向左爬行为负，机器人爬行5次，爬行的路程依次为：（单位：厘米）8,4,12,5,10--+-+．（1）机器人最后离出发点多少厘米？在出发点的左边还是右边？（2）若机器人爬行的速度不变，共用了8分钟，问机器人的爬行的速度是多少？ 46．如图，438624,AOB BOC '∠=︒∠=,，OD 为AOC ∠的平分线，求BOD ∠的度数47．（1）计算：()535112 2.5147⎛⎫---÷-- ⎪⎝⎭（2）如图，OD 平分AOC ∠，75BOC ∠=︒，15BOD ∠=︒．求AOB ∠的度数．48．解下列方程: (1)13(2)5x x --=- (2)213136x x---=-.参考答案：1．42n +##24n +【分析】由题意可知：每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个，由此规律得出答案即可．【详解】解：第一个图案正三角形个数为624+＝；第二个图案正三角形个数为244224+++⨯＝；第三个图案正三角形个数为2244234+⨯++⨯＝； …；第n 个图案正三角形个数为21442442n n n +⨯+++（﹣）＝＝．故答案为：42n +．【点睛】此题考查图形的变化规律，找出图形之间的数字运算规律，得出规律，解决问题． 2．－4【详解】试题分析：在数轴上向右移动几个单位则加上几个单位，向左移动几个单位则减去几个单位. －2+3－5=－4. 考点：数轴上点的表示 3．154.5【分析】利用补角的意义“两角之和等于180°，那么这两个角互为补角，其中一个角叫做另一个角的补角”．直接列式计算即可．【详解】1802530'15430'154.5︒-︒=︒=︒．故答案为：154.5．【点睛】本题考查了补角的概念，如果两个角的和等于180°，就说这两个角互为补角． 4．9【分析】根据同类项的定义可得11m -=，14n +=，解方程可得m 、n 的值，再代入代数式m n 求值即可．【详解】由题意得：11m -=，14n +=，解得：2m =，3n =，把2m =，3n =代入m n 中得：239=，故答案为：9．【点睛】本题考查了单项式的定义、同类项等知识，关键是掌握同类项的定义． 5．4【分析】将x ＝1代入原方程求解即可．【详解】解：将x ＝1代入（2m ﹣6）x ﹣2＝0，2620m --=，解得：4m =，故答案为：4．【点睛】本题考查一元一次方程的解，熟练掌握解一元一次方程是解题关键． 6．4【分析】根据正负数的定义便可直接解答，即大于0的数为正数，小于0的数为负数，0既不是正数也不是负数．【详解】解：12是正数，﹣（﹣3）＝3是正数，﹣|﹣4|＝﹣4是负数，0既不是正数也不是负数，﹣22＝﹣4是负数，﹣0.01是负数，（﹣1）3＝﹣1是负数，负数共4个．故答案为：4【点睛】此题考查了正数与负数，解答此题的关键是：正确理解正、负数的概念，区分正、负数的关键就是看它的值是大于0还是小于0，不能只看前面是否有负号． 7．7.28【分析】利用四舍五入法解答，即可求解．【详解】解：近似数7.2765精确到0.01是7.28．故答案为：7.28【点睛】本题主要考查运用“四舍五入”法求一个数的近以数，解题的关键是要看清精确到哪一位，就根据它的下一位上数是否满5，再进行四舍五入． 8．5442'︒【分析】根据互为余角的两个角的和等于90°列式计算即可得解．【详解】①α与β互余，且α=35°18′， ①9035185442β=︒-︒=︒''．故答案为：5442︒'．【点睛】本题考查了余角和补角，熟记余角的概念是解题的关键．9．23π-5【分析】根据单项式系数、次数的定义来求解．单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．【详解】根据单项式定义得：单项式3223a xπ-的系数是23π-，次数是5．故答案为：23π-；5．【点睛】本题考查了单项式．确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．10．3；1【详解】试题分析：解：因为是同类项，所以n＝1，3m＝9，所以n＝1，m＝3.考点：同类项的定义点评：本题主要考查了同类项的定义.我们把所含字母相同，相同字母的指数也相等的项叫做同类项.11．①．【分析】根据直线的性质，相交线的定义对各选项分析判断后利用排除法求解．【详解】①两点确定一条直线，故正确；②直线上任意两点都可以表示这条直线，故正确；③三点确定一条直线或三条直线，故错误；④过一点可以作无数条直线，故正确．故答案为③．【点睛】本题考查了直线的性质，熟记两点确定一条直线是解题的关键．12．1【分析】方程组中两个方程相加即可求出x-y的值.【详解】345254x yx y+=⎧⎨+=⎩中的第一个方程减去第二个方程得：x-y=1，故答案为1.【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两个方程都成立的未知数的值. 13．0【分析】先求出a ，b ，c 的值，再把它们相加即可．【详解】解：由题意，得：a =1，b =-1，c =0，故a +b +c =1-1+0=0．故答案为：0．【点睛】此题主要考查的是绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0． 14．1-【分析】所含字母相同，并且相同字母的指数也相同的项叫做同类项．【详解】①单项式12m xy +与单项式2313n x y -是同类项①2113n m -=⎧⎨+=⎩，解得32n m =⎧⎨=⎩ ①231m n -=-=-．故答案为：1-．【点睛】本题考查了同类项的概念．注意同类项与字母的顺序无关． 15．100【分析】一个样本包括的个体数量叫做样本容量．【详解】解：要了解5000件商品的质量问题，从中任意抽取100件商品进行试验，在这个问题中，样本包括的个体数量是100，所以样本容量是100. 故答案为100．【点睛】考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．样本容量是样本中包含的个体的数目，不能带单位． 16．-4.5【分析】根据题意得到式子2x+6=-3即可求解. 【详解】根据题意得2x+6=-3 解得x=-4.5 故填：-4.5.【点睛】此题主要考查代数式求值，解题的关键是根据题意列出式子求解.17．3【分析】根据同类项的概念可得关于n 的一元一次方程，求解方程即可得到n 的值．【详解】解：①132n x y +-与34y x 是同类项，①n ＋1＝4，解得，n ＝3，故答案为：3．【点睛】本题考查了同类项，解决本题的关键是判断两个项是不是同类项，只要两看，即一看所含有的字母是否相同，二看相同字母的指数是否相同．18．-1【分析】由已知条件得到（a 2-2a ）的值后，代入代数式求值．【详解】223a a -=，∴原式()2522a a =--561=-=-，故答案为1-．【点睛】本题考查了整式的运算，要会把a 2-2a 看作一个整体，然后整体代入计算． 19．0【分析】根据题意得出012a b cd m +===，，或2m =-，然后整体代入代数式求解即可．【详解】解：①a ，b 互为相反数，且0ab ≠，c 、d 互为倒数，m 是数轴上到原点的距离为2的点表示的数，①012a b cd m +===，，或2m =-， ①1b a=-， ①322()3b a b cd m a ⎛⎫++-+ ⎪⎝⎭()324103-=+-+ 0=，故答案为：0．【点睛】题目主要考查相反数、倒数的定义及数轴上的点到原点的距离，求代数式的值等，理解题意，综合运用这些基础知识点是解题关键．20．100°．【分析】直接利用方位角结合平角的性质得出答案．【详解】解：如图所示：因为点A在点O的北偏东50°方向所以①NOA=50°；因为点B在点O的南偏东30°方向上所以①SOB=30°则①AOB=180°-①NOA-①SOB=100°．故答案为：100°．【点睛】题考查了方位角的意义和角的和差．用方位角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边．21．152或13或372【分析】分三种情况：当点P在BC边上时，当点P在CD边上时，当点P在DE边上时，分别利用三角形面积公式求解即可．【详解】解：①长方形ABCD，①AD=BC=9cm，CD=AB=8cm，①AE=2DE，①AE=6cm，DE=3cm，当点P在BC边上时，如图，S△PCE=12PC AB＝12(9-t)×8=6，解得：t=152；当点P在CD边上时，S△PCE=12PC DE⋅=12(t-9)×3=6，解得：t=13；当点P在DE边上时，S△PCE=12PE CD⋅=12(9+8+3-t)×8=6，解得：t=372；综上，当PCE的面积为6cm2时，则点P运动的时间为152s或13s或372s．故答案为：152或13或372【点睛】本题考查长方形的性质，三角形面积，一元一次方程的应用，分类讨论思想的应用是解题的关键．22．-5【分析】找出绝对值大于133-而小于2的所有的整数，求出之和即可．【详解】大于133-而小于2的所有的整数为-3，-2，-1，0，1，则所有整数之和为-3-2-1+0+1=-5．故答案为：-5．【点睛】此题考查了有理数的加法，以及绝对值，熟练掌握运算法则是解本题的关键． 23．-21【详解】解：34-⊗=-3×4-（-3）2=-21．故答案为：-2124．8【详解】①13x 2y m 与2x n y 6是同类项， ①n =2，m =6.①n +m =8.故答案为8.25． 4a b - 4.2【分析】用总钱数减去买名著的钱数就是剩下的钱数，然后把a=150，b=36.45，代入含有字母的式子，即可求出还剩下的钱数．【详解】解：根据题意，则买完一套名著剩下的钱为：4a b -；当150a =，36.45b =元时，①4150436.45 4.2a b -=-⨯=（元）；故答案为：4a b -；4.2；【点睛】做这类用字母表示数的题目时，解题关键是根据已知条件，把未知的数用字母正确的表示出来，然后根据题意列式计算即可得解．26． < >【分析】（1）先化简绝对值、去括号，再根据有理数的大小比较法则即可得；（2）根据有理数的大小比较法则即可得．【详解】（1）99--=-，()99--=，则()99--<--；（2）346788=<，则8347->-；故答案为：<，>．【点睛】本题考查了绝对值、去括号、有理数的大小比较法则，熟练掌握有理数的大小比较法则是解题关键．27．21.【分析】根据新定义，用3和-2分别代替公式中的a,b 正确计算即可.【详解】①对于任意有理数a 和b ，规定23a b ab a =+☆，①()32-=☆3×2(2)-+3×3=21，故应该填21.【点睛】本题考查了新定义知识，准确理解新定义公式的意义是解题的关键.28．32π【分析】分情况讨论，分绕长为2或是4的边旋转，再根据圆柱的体积公式即可解【详解】由题意，旋转构成一个圆柱的体积为π×22×4=16π或π×24×2=32π，故答案为32π【点睛】圆柱的体积公式是底面积与高的积．29．6000cm 3【分析】根据图形找出长方体的长宽高即可解题.【详解】解：由图可知长方体的长为30cm,宽为20cm,高为10cm,①长方体的容积=302010⨯⨯=6000 cm 3.【点睛】本题考查了立体图形的体积,中等难度,读图能力,由平面图形找到长方体的长宽高是解题关键.30．102a b --，6-．【分析】先去括号，再计算整式的加减，然后将53a b +=代入求值即可得．【详解】解：原式2641244a b b a =-+-+-102a b =--，将53a b +=代入得：原式2(5)236a b =-+=-⨯=-．【点睛】本题考查了整式加减中的化简求值，熟练掌握整式的加减运算法则是解题关键． 31．（1）4（2）-4a =(a≥0)a ，3a =，和绝对值的意义计算.解：（1=2-(-2)=4.（2）｜13=-4.32．（1）1；（2）2x =-【分析】（1）由题中所给定义新运算可直接代入求解；（2）根据题中所给定义新运算可列出方程，然后求解即可．【详解】解：（1）由题意得：()()()2*3223231-=⨯--+⨯-=；（2）由题意得：16312x x x x -+=-+ 移项，得13162x x x x -++-=-，合并同类项，得552x =-，系数化为1，得2x =-．【点睛】本题主要考查一元一次方程的解法，熟练掌握一元一次方程的解法是解题的关键．33．6113x y z =⎧⎪=-⎨⎪=⎩．【分析】①﹣①得出2y ＝－22，求出y ＝﹣11，把y ＝﹣11代入①，即可求得x ＝6，再把x ＝6，y ＝－11代入①进而求得z ＝3即可．【详解】解：2201160x y z x y z x y ++=-⎧⎪-+=⎨⎪+=⎩①②③ ①－①得，2y ＝－22，解得y ＝－11．把y ＝－11代入①中，得11x ＋6×(－11)＝0，解得x ＝6．把x ＝6，y ＝－11代入①中，得6－11＋z ＝－2，解得z ＝3．①原方程组的解为6113x y z =⎧⎪=-⎨⎪=⎩．【点睛】本题考查了三元一次方程组的解法，利用了消元的思想，解决本题的关键是消元，消元的方法有：代入消元法与加减消元法．34．（1）240人、60º；（2）40人，图见解析；（3）600册【分析】(1)、用借“生活”类的书的人数除以它所占的百分比即可得到调查的总人数；然后用360°乘以借阅“经济”的人数所占的百分比得到“经济”部分的圆心角度；(2)、先计算出借阅“科普”的学生数，然后补全条形统计图；(3)、利用样本估计总体，用样本中“科普”类所占的百分比乘以3600即可．【详解】解：(1)、上个月借阅图书的学生总人数为60÷25%=240（人）；扇形统计图中“经济”部分的圆心角度数=360°×40240=60°； (2)、借阅“科普”的学生数=240﹣100﹣60﹣40=40（人），条形统计图为：(3)、3600×40240=600（册），估计“科普”类图书应添置600册合适．【点睛】本题考查了条形统计图，扇形统计图，用样本估计总体，读懂统计图，从不同的统计图中得到必要的信息是解题关键．35．22106x y xy xy --+，-204【分析】先根据整式的加减：合并同类项化简整式，再将x 、y 的值代入求解即可．【详解】()22222232324x y xy x y xy xy xy ⎡⎤+---+-⎣⎦()22222232324x y xy x y xy xy xy =+-+-+-2222223644x y xy x y xy xy xy =+--+-22106x y xy xy =--+当2x =，=3y -时原式()()()22231023623=-⨯--⨯⨯-+⨯⨯- 1218036=--204=-．【点睛】本题考查了整式的化简求值，熟记整式的加减法则是解题关键．36．（1）-2；（2）9【分析】（1）先根据整式的混合运算顺序和运算法则化简原式，再将a 、b 的值代入计算可得；（2）先根据整式的混合运算顺序和运算法则化简原式，再由非负数性质得出a 2＝1﹣m ，b ＝2﹣m ，代入计算可得．【详解】解：（1）原式＝﹣a 2b +ab 2﹣3a 2b ﹣2ab 2+4a 2b＝﹣ab 2；当a ＝2，b ＝1时，原式＝-2×12=﹣2．（2）原式＝2a 2﹣2b +3a 2﹣2a 2﹣b＝3a 2﹣3b ，①（a 2+m ﹣1）2+|b +m +2|＝0，①a 2+m ﹣1＝0，b +m +2＝0①3a 2﹣3b ＝3（1﹣m ）﹣3（﹣m ﹣2）＝9．【点睛】此题主要考查整式的运算，解题的关键是熟知整式的加减运算法则.37．（1）5.5（2）10千克（3）918元【详解】试题分析：（1）根据正负数的意义列式计算即可得解；（2）根据图表数据列出算式，然后计算即可得解；（3）求出20筐白菜的质量乘以单价，计算即可得解．试题解析：（1）最轻的是-3，最重的是2.5，2.5-（-3）=2.5+3=5.5（千克）答：最重的一筐比最轻的一筐重5.5千克；故答案为5.5．（2）（-3）×1+（-2）×4+（-1.5）×2+0×1+1×4+2.5×8=-3-8-3+0+4+20=-14+24=10（千克）答：与标准重量比较，20筐白菜总计超过10千克；（3）25×20+10=500+10=510（千克），510×1.8=918（元）．故出售这20筐白菜可卖918元．考点：正数和负数．38．（1）40；（2）补图见解析；（3）1～1.5；（4）125名．【分析】（1）利用1～1.5小时的频数和百分比即可求得总数；（2）根据总数可计算出时间在0.5～1小时的人数，从而补全图形；（3）根据中位数的定义得到完成作业时间的中位数是第20个数和第21个数的平均数，而0.5-1有12人，1-1.5有18人，即可得到中位数落在1-1.5h内；（4）用七年级共有的学生数乘以完成作业时间超过1.5小时的人数所占的百分比即可．【详解】解：（1）（1）根据题意得：该班共有的学生是：1845%=40（人）；这个班的学生人数为40人；（2）0.5～1小时的人数是：40×30%=12（人），如图：（3）共有40名学生，完成作业时间的中位数是第20个数和第21个数的平均数，即中位数在1-1.5小时内；（4）①超过1.5小时有10人，占总数的1025% 40=．①25%500125⨯=答：估计八年级学生课外完成数学作业时间超过1.5小时的有125名．【点睛】本题考查了条形统计图：条形统计图反映了各小组的频数，并且各小组的频数之和等于总数．也考查了扇形统计图、中位数的概念．39．“■”这个有理数为65-，方程的解为：y＝1【分析】利用“该方程的解与当x＝2时整式5（x−1）−2（x−2）−4的值相同”求出方程的解；再将方程的解代入y125-=y+■中求得■．【详解】解：当x＝2时，整式5（x−1）−2（x−2）−4＝5×（2−1）−2×（2−2）−4＝1．①方程的解与当x＝2时整式5（x−1）−2（x−2）−4的值相同，①方程的解为：y＝1．当y＝1时，y125-=y+■．①1125-=+■解得：■＝65 -．答：“■”这个有理数为65-，方程的解为：y＝1．【点睛】本题主要考查了一元一次方程的解，求代数式的值．利用方程的解的意义，将方程的解去替换未知数的值是解题的关键．40．(1)－12；(2) 11425；(3) 323；(4)1.【分析】根据有理数混合运算法则即可解题.【详解】解：（1）514166÷×÷8357⎛⎫⎛⎫⎛⎫---⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=53167×÷81456⎛⎫⎛⎫⎛⎫-⨯--⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=1 2 -;（2）－3－3510.225⎡⎤⎛⎫-+-⨯÷-⎪⎢⎥⎝⎭⎣⎦=-3-221 5252 -+⨯（）=-3-（-5+1125）=-3+5-1125=2-1125=14 125;（3）114332⎛⎫-⎪⎝⎭×(－2)－221÷32⎛⎫-⎪⎝⎭=（13732-）×(－2)823-⨯-（）=53-+163=113=323; (4)()271115069126⎡⎤⎛⎫--+⨯- ⎪⎢⎥⎝⎭⎣⎦÷(－7)2 =[50-(79)36⨯+(1112)36⨯-(16)36⨯]÷49 =(50-28+33-6)÷49 =49÷49=1.【点睛】本题考查了有理数的混合运算,属于简单题,熟悉有理数运算法则和运算优先级是解题关键.41．211x y z =⎧⎪=-⎨⎪=⎩【分析】由①+①×3可得31711x y +=-④，再由由①-①可得1y =-，然后把1y =-分别代入①，①，即可求解．【详解】解： 32823154x y y z x y z -=⎧⎪+=⎨⎪+-=-⎩①②③ 由①+①×3得：31711x y +=-④，由①-①得：1919y -=，解得：1y =-，把1y =-代入①得：2x =，把1y =-，代入①得：1z =，所以原方程组的解为211x y z =⎧⎪=-⎨⎪=⎩【点睛】本题主要考查了解三元一次方程组，熟练掌握三元一次方程组的解法是解题的关键．42．59【分析】这10个有理数，每9个相加，一共得出另外10个数，由于原10个有理数互不相等，可以轻易得出它们相加后得出的另外10个数也是互不相等的，而这10个数根据题意都是分母22的既约真分数，而满足这个条件的真分数正好有10个，分别是13579131517192122222222222222222222、、、、、、、、、，它们每一个都是原来10个有理数其中9个相加的和，那么，如果再把这10个以22为分母的真分数相加，得出来的结果必然是原来的10个有理数之和的9倍，即可求出10个有理数之和．【详解】解：由题意得：分母为22的既约真分数有13579131517192122222222222222222222、、、、、、、、、 ①135791315171921522222222222222222222+++++++++= ①10个有理数之和为5599÷= 故答案为：59．【点睛】本题主要考查来了有理数的加法和除法，准确地理解题意，得出正确的数量关系是求解的关键．43．2xy xy +，6-【分析】先利用乘法分配率计算小括号，然后再算中括号，最后合并得到最简结果，将x 与y 的值代入计算，即可求出值．【详解】解：()2222322 1.53x y xy xy x y xy xy ⎡⎤⎣⎦---++()222232233x y xy xy x y xy xy =--+++222232233x y xy xy x y xy xy =--++- 2xy xy =+当3,2x y =-=-时原式()()()()23232+=---- 126=-+6=-；【点睛】此题考查了整式的加减混合运算、去括号法则，合并同类项法则和代数式求值，熟练掌握公式及法则是解本题的关键．44．（1）4；（2）16-．【分析】（1）利用有理数加减法的交换律与结合律进行计算即可得；（2）利用有理数乘法的分配律进行计算即可得．【详解】（1）原式111410323355⎛⎫=+--- ⎪⎝⎭， 111410323355⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭， 73=-，4=；（2）原式()()()125242424236=-⨯--⨯+-⨯， 121620=-+-，420=-，16=-．【点睛】本题考查了有理数加减法的交换律与结合律、有理数乘法的分配律，熟练掌握有理数的运算法则和运算律是解题关键．45．（1）机器人最后离出发点5厘米，在出发点的右边；（2）4.875（厘米/分）【分析】（1）直接把5次爬行的数据相加，再根据有理数的加减混合运算规则计算出结果即可；（2）求出各数据的绝对值的和，再根据速度=路程÷时间解答．【详解】（1）-8-412-5105++=，所以机器人最后离出发点5厘米，在出发点的右边；（2）机器人爬行的总路程为841251039++++=厘米，所以速度为39÷8=4.875（厘米/分）【点睛】本题主要考查有理数的加减运算，第二问要利用爬行过的路程的绝对值的和求解，这是学生容易出错的地方．46．21°42′【分析】首先求得①AOC 的度数，根据角平分线的定义求得①AOD ，然后根据①BOD=①AOD-①AOB 求解．【详解】①①AOB=43°，①BOC=86°24′，①①AOC=43°+86°24′=129°24′，①OD 平分①AOC ，①①AOD=12①AOC=129°24′÷2=64°42′， ①①BOD=①AOD- ①AOB=64°42′-43°=21°42′．【点睛】本题考查了角度的计算，正确理解角平分线的定义，求得①AOD 是关键． 47．（1）9-；（2）45︒．【分析】（1）先计算有理数的乘方、将除法转化为乘法、小数化为分数，再计算有理数的乘法与加减法即可得；（2）先根据角的和差可得60COD ∠=︒，再根据角平分线的定义可得60AOD COD ∠=∠=︒，然后根据角的和差即可得．【详解】（1）解：()535112 2.5147⎛⎫---÷-- ⎪⎝⎭ ()55187142=---⨯-- 55922=-+- 9=-；（2）解：75BOC ∠=︒，15BOD ∠=︒，751560COD BOC BOD ∴∠=∠-∠=︒-︒=︒，①OD 平分AOC ∠，①60AOD COD ∠=∠=︒，①601545AOB AOD BOD ∠=∠-∠=︒-︒=︒．【点睛】本题考查了含乘方的有理数混合运算、与角平分线有关的角度计算，熟练掌握各运算法则和角平分线的定义是解题关键．48．（1）3x =；（2）15x =- 【分析】(1) 根据解一元一次方程的步骤求解即可；(2)根据解一元一次方程的步骤求解即可.【详解】（1）去括号得：1365x x -+=-，移项得：3561x x --=---，合并同类项得：412x -=-，系数化为1得：3x =（2）去分母得：()()22136x x ---=-，去括号得：4236x x --+=-，移项、合并同类项得：5=1x -，系数化为1得：1=5x -. 【点睛】此题考查了解一元一次方程，解题的关键是熟练掌握解一元一次方程的步骤.。

高中数学解三角形解题方法

高中数学解三角形解题方法高中数学解三角形的开放型题型的解法研究也是很重要的只有解决了解三角形的难题，数学成绩才会整体上升，高考成绩也会有所提高。

下面是小编为大家整理的关于高中数学解三角形解题方法，希望对您有所帮助。

欢迎大家阅读参考学习!1高中数学解三角形解题方法解三角形，要求记忆三角函数公式，不仅要熟练记忆，牢牢掌握解三角形的解题技巧，还要能够将已经掌握的知识灵活运用。

开放型题型更是需要结合题目要求开拓新思路，以一个全新的思考方式去思考解决问题，这也就是开放型题型的新颖之处，也是开放型题型的难点。

一般开放型题型在题目阅读中增加了难度，相应来说，解题的难度就会减少，那么只要能够读懂题目，了解题目要求，理清楚解题的思路就可以轻松的完成三角函数题目的解答。

但是对于高中生来说对于解三角形函数的了解已经很深入了，只是高中生一般就掌握了解三角形的基本解题思路，对照相应的题型进行练习解答，这么一来，高中生也就变成了解题机器，只会一种思路，一种思考方式，不会变通，如果在这时候遇到了开放型题型，就会完全傻了眼。

这时候，在大形势趋向于开放型题型，高中生只能在自己掌握的知识基础上，多练练开放型题型，运用自己了解的三角函数知识根据开放型题型的题目要求去解答问题。

高中生对于三角函数的知识已经掌握的很熟练了，只是对于这些开放型题型就是缺少练习，多找一些开放型题型来练习，增加高中生对开放型题型题目的理解程度，因为题目要求难度增加，对应的解题难度就会减少，这样一来只要能够多练习开放型题型，熟练掌握解题思路，能够读懂题目要求，就会很简单的解答这方面的问题。

2高中数学解三角形的技巧正弦定理●教学目标。

知识与技能：通过对任意三角形边长和角度关系的探索，掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。

过程与方法：让学生从已有的几何知识出发，共同探究在任意三角形中，边与其对角的关系，引导学生通过观察，推导，比较，由特殊到一般归纳出正弦定理，并进行定理基本应用的实践操作。

PPQP 培训ppt课件

Agreement to Build Gate Review
Part Approval at Supplier
评审小组批准零件
Team Approves
Part
小组代表签署
质保书
Yes
TeaYmes
representative
sign-off quality
warrant sheet
发运零件及相关文件
制造现场 Build Floor
首辆样车供应商现场支持 Supplier at PPO for 1st Build
12
流程简介——非关键零件
Process introduction——Non-Critical parts
-9 SOB
-2 SOB
IVBR Virtual Build
供应商生产零件 Supplier Manufactures Parts (Week -11 TO -2 SOB)
PPQP流程培训
PPQP Process training
Contact information: PPO Yao Wei 28941986
Wei Yao/test/PATAC/SGM
wei_yao@
February, 2009
1
培训内容
Training Outline
PPQP流程背景及简介
长期措施：进一步优化RASIC，完善执行细则 Long term solution: Optimize RASIC, and complete detailed rules for PPQP
8
流程简介
Process Introduction
PPQP对试制零件的检查、验证及发运的过程进行了定义。

专练04 填空题-基础(30题)-2020~2021学年七年级数学上学期期末考点(解析版)

专练04 填空题-基础（30题）1．（2020·河北七年级期末）如图所示，是一个立体图形的展开图，这个立体图形是______________．【答案】圆锥因为圆锥的展开图为一个扇形和一个圆形，故这个立体图形是圆锥．故填：圆锥．【点睛】本题考查了几何体的展开图，熟悉圆锥的展开图特点，是解答此题的关键．2．（2020·湖北七年级期末）如图是一个正方体的展开图，把展开图折叠成正方体后，有“弘”字一面的相对面上的字是________．【答案】文这是一个正方体的平面展开图，共有六个面，其中面“扬”与“统”相对，面“弘”与面“文”相对，“传”与面“化”相对．故答案为：文．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．3．（2018·山东九年级期末）如图所示为一机器零件的三视图．若俯视图中三角形为正三角形，那么请根据图中所标的尺寸，计算这个几何体的表面积为_____．【答案】3【解析】∵△ABC 是正三角形，又∵CD ⊥AB ，CD =2， ∴AC ==4，∴S 表面积=4×2×3+2×4××2， =24+8．故答案为：24+8．4．（2018·甘肃九年级期末）上图是由一些相同的小正方体构成的几何体的三视图,在这个几何体中,小正方体的个数是_______个.【答案】5【解析】根据三视图，主视图以及俯视图都是相同的，可以得出底层有4个小正方体，然后第2层有1个小正方体，故共5个小正方体．解：综合三视图，这个几何体中，底层有3+1=4个小正方体，第二层有1个小正方体，因此小正方体的个数为4+1=5个．故答案为5．5．（2020·黑龙江七年级期末）已知：2a -=，||6b =，且a b >，则a b +=__．【答案】8-．解：2a -=，||6b =，且a b >，2a ∴=-，6b =-，2(6)8a b ∴+=-+-=-，故答案为：8-．【点睛】本题考查了有理数的加法，绝对值的性质，熟练掌握运算法则是解题的关键．6．（2020·内蒙古七年级期末）某种零件，标明要求是()200.02φ±mm ，(φ表示直径），经检查，一个零件的直径是19.9mm ，该零件_______．(填“合格”或“不合格”）【答案】不合格解：由题意得零件的合格范围是：φ19.98mm —20.02mm ，19.9mm 不在合格范围内．故答案为：不合格【点睛】本题考查了正数和负数，利用有理数的加减法得出合格范围是解题关键．7．（2020·江苏八年级期末）我国首艘国产航母山东舰于2019年12月17日下午4时交付海军，山东舰的排水量达到65000吨，请将65000精确到万位，并用科学记数法表示______．【答案】4710⨯65000≈70000，70000=7×104．故答案为：7×104．【点睛】本题主要考查了用科学记数法和近似数．一般形式为a×10n ，其中1≤|a|＜10，确定a 与n 的值是解题的关键．8．（2019·浙江七年级期末）把数轴上的点A 移动3个单位，恰好与表示10-的点重合，则点A 表示的数为_____．【答案】－13或－7解：由题意可知，点A 和表示10-的点的距离为3，∴点A 表示的数为－13或－7，故答案为：－13或－7.【点睛】本题考查了数轴，熟知在数轴上与某一点距离相等的点有两个是解题的关键.9．（2020·山东七年级期末）珠穆朗玛峰高出海平面的高度约为8844.43m ，记为+8844.43m ；吐鲁番盆地低于海平面155m ，记为______．【答案】-155m∵高出海平面的高度约为8844.43m ，记为+8844.43m ，∴低于海平面155m ，记为-155m ．故答案为：-155m ．【点睛】本题主要考查了相反意义的量，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示． 10．（2019·湖北七年级期末）比较大小：﹣23______﹣25. 【答案】<解：∵|-23|＝23，|-25|＝25， 23＞25， ∴-23＜-25. 【点睛】本题主要考查两个负数的大小比较，两个负数比较大小，应先算出两个负数的绝对值，比较两个绝对值，绝对值大的反而小.11．（2020·江苏七年级期末）若单项式12m a b -与212n a b 的和仍是单项式，则m n 的值是__________．【答案】8解：由题意得：单项式12m a b -与212n a b 是同类项， ∴3,2m n ==，∴328m n ==；故答案为8．【点睛】本题主要考查同类项，熟练掌握同类项的概念是解题的关键．12．（2020·宁夏七年级期末）若34x y -=-，那么326x y +-的值是_______．【答案】-5．解：当34x y -=-时，326x y +-32(3)x y =+-32(4)=+⨯-38=-5=-，故答案为：5-．【点睛】本题主要考查代数式的求值，解题的关键是熟练掌握整体代入思想的运用．13．（2020·广西七年级期末）化简3[2()]a a a b b ---+，结果是__________．【答案】4a b -化简得：[]3[2()]=3223224a a a b b a a a b b a a a b b a b ---+--++=-+-+=-，故答案为：4a b -.【点睛】本题主要考查了整式的加减，熟练运用去括号，合并同类项等运算知识是解决本题的关键.14．（2020·山东七年级期末）在代数式:①2a π；②-3x 3y ；③-4+3x 2；④0；⑤2019mn ；⑥212x -中，是单项式的有________(只填序号）．【答案】①②④⑤①2aπ，①-3x 3y ，①0，①2019mn 是单项式； ①-4+3x 2，①212x -是多项式．故答案为：①①①①．【点睛】本题考查了单项式的概念，不含有加减运算的整式叫做单项式，单独的一个数或一个字母也是单项式． 15．（2020·江西七年级期末）一个角的余角是5134'，这个角的补角是__________．【答案】14134' ①一个角的余角是5134'，所以这个角是9051343826''︒-︒=︒，∴这个角的补角为180382614134''︒-︒=︒；故答案是14134'︒．【点睛】本题主要考查了余角和补角的性质，准确利用度分秒计算是解题的关键．16．（2019·河北七年级期末）用度、分、秒表示:54.26=_______________________．【答案】541536'"54.26=541536'"故答案为：541536'"．【点睛】此题主要考查度数的换算，解题的关键是熟知度、分、秒的换算方法．17．（2020·黑龙江七年级期末）计算：52353246''︒-︒=______°______′．【答案】19 49原式51953246''=︒-︒，1949'=︒，故答案为：19，49．【点睛】本题考查了角度的四则运算，熟记运算法则是解题关键．18．（2019·台州市白云学校七年级期末）如图所示，点A 在点O 的北偏东50°方向，点B 在点O 的南偏东30°方向上，则AOB ∠=______．【答案】100°．解：如图所示：因为点A 在点O 的北偏东50°方向所以∠NOA=50°；因为点B 在点O 的南偏东30°方向上所以∠SOB=30°则∠AOB=180°-∠NOA-∠SOB=100°．故答案为：100°．【点睛】题考查了方位角的意义和角的和差．用方位角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边．19．（2020·江西七年级期末）若方程的解23x -=-也是方程6314x k +=的解，则常数k =__________．【答案】20323x -=-1x ∴=-把1x=-代入方程6314x k +=中，得6314k -+=203k ∴= 故答案为：203k =．【点睛】本题考查一元一次方程的解等知识，是基础考点，难度较易，掌握相关知识是解题关键．20．（2019·山西七年级期末）已知方程(1)30m x ++=是关于x 的一元一次方程，则m 的取值范围是____________．【答案】1m ≠-∵方程(1)30m x ++=是关于x 的一元一次方程，∴10m +≠，解得：1m ≠-．故答案为：1m ≠-．【点睛】本题主要考查了一元一次方程的一般形式，只含有一个未知数，且未知数的指数是1，一次项系数不是0．21．（2020·吉林七年级期末）一件定价为150元的商品，若按九折销售仍可获利25%，设这种商品的进价为x 元，则可列出方程是______________________．【答案】()15090%125%x ⨯=+解：设商品的进价为x 元，根据题意得，()15090%125%x ⨯=+故答案为：()15090%125%x ⨯=+．【点睛】本题考查一元一次方程的应用，解决本题的关键是得到商品的售价的等量关系，利润问题是一元一次方程的重点题型．22．（2020·陕西七年级期末）若关于x 的方程360x +=与关于y 的方程5216y m +=的解互为相反数，则m =__________．【答案】3解：解方程360x +=，解得2x =-，∵这两个方程的解互为相反数，∴2y =是方程5216y m +=的解，将2y =代入原方程，得到10216m +=，解得3m =．故答案是：3．【点睛】本题考查一元一次方程的解和相反数的定义，解题的关键是理解什么是方程的解和掌握解一元一次方程的方法．23．（2020·辽宁七年级期末）某商品的标价为800元，四折销售后仍可赚60元，则该商品的进价为__________元【答案】260解：设商品的进价为x元，则：800×40%-x=60，解得：x=260．故答案为：260．【点睛】本题考查一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程再求解．24．（2020·黑龙江七年级期末）已知13xy=⎧⎨=⎩是方程21kx y-=的解，则k的值为_______．【答案】2将13xy=⎧⎨=⎩代入方程21kx y-=得：2k－3=1解得：k=2故答案为：2．【点睛】本题考查求解一元一次方程，注意本题是关于k的一元一次方程．25．（2019·江苏七年级期末）把方程3x＋y＝6写成用含有x的代数式表示y的形式为：y＝____．【答案】6－3x解：∵3x＋y＝6，∴y＝6−3x，故答案为：6−3x．【点睛】本题考查了解二元一次方程，能正确根据等式的性质进行变形是解此题的关键．26．（2020·河南七年级期末）代数21a+与2a互为相反数，则a=__________．【答案】1 4 -解：根据题意得：21a++2a=0解得：14 a=-故答案为：1 4 -【点睛】此题考查了解一元一次方程，以及相反数，熟练掌握运算法则是解本题的关键．27．（2018·山西七年级期末）如图是光明中学七年级（1）班学生最喜爱的电视节目扇形统计图，由图可以了解该班学生喜欢娱乐类电视节目的人数在扇形中所占圆心角为___________°．【答案】144喜欢娱乐类电视节目的人数在扇形统计图中对应的扇形所占的圆心角的度数：36040%144︒⨯=︒，故答案为：144．【点睛】本题考查扇形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．28．（2020·湖北七年级期末）某班学生参加环保知识竞赛，已知竞赛得分都是整数，把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图(如图所示)，根据图中的信息可得，成绩不及格(低于60分)的学生占全班参赛人数的百分率是_______．【答案】20%原创精品资源学科网独家享有版权，侵权必究！11解：∵全班的总人数为3+6+12+11+7+6=45人，其中成绩低于60分的学生有3+6=9人，∴成绩低于60分的学生占全班参赛人数的百分率是9100%=20% 45故答案为：20%．【点睛】本题主要考查频数分布直方图，根据频数分布直方图明确各分组人数是解题的关键．29．（2020·北京人大附中八年级期末）将七年级一班分成五个组，各组人数在频数分布直方图中的小长方形高的比依次为1：2：5：3：1，人数最多的一组有25人，则该班共有_____________人．【答案】60∵各组人数在频数分布直方图中的小长方形高的比依次为1∶2∶5∶3∶1，人数最多的有25人∴各组人数人数为5人、10人、25人、15人、5人，∴总人数＝5＋10＋25＋15＋5＝60人故答案为：60【点睛】本题主要考查频数分布直方图中的知识点，关键要掌握频数分布直方图中的小长方形的高的比就是各组频数之比．30．（2020·北京人大附中八年级期末）为了解某市4万名学生平均每天读书的时间，请你运用所学的统计知识，将统计的主要步骤进行排序：①从4万名学生中随机抽取400名学生，调查他们平均每天读书的时间；②分析数据；③得出结论，提出建议；④利用统计图表将收集的数据整理和表示．合理的排序是_____．(只填序号)【答案】①④②③【解析】根据数据的调查的步骤，可知合理的排序为：①④②③.故答案为①④②③.点睛：此题主要考查了调查收集数据的过程和方法，正确进行数据的调查，掌握调查的步骤是解题关键.。

煤矸石堆积问题

1/ 3 2/ 3
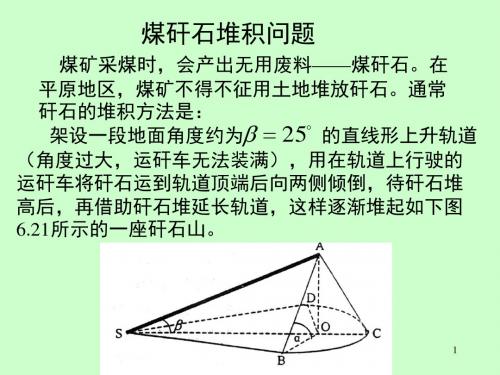
当p=0.1 时，h(20)=162(m)， S(20)=102(亩)。 3）征地计划因为地价年涨幅 10%高于贷款利率 5% ，所以应在开始时一次性将用地全部购入，所缺经费向银行贷款。当P=0.1时，征地费为 Q 8 102 816(万元)
2．堆积矸石的电费
1）运矸车机械效率设运矸车坡道行程为L ，则 L x / sin ( x为高度 )
(4)
6
由（3）、（4）式可得矸石高度与t的关系
0.784h 1.5qt 10
3
2/ 3
1/ 3 即 h(t ) 124.1(qt) (m) (5) （5）代入（2）得t年后占地面积为
S (t ) 59.77(qt) (亩)
(6)
7
这样，可得20年后矸石山高与占地面积分别为
h(20) 337.1q (m), S(20) 440.4q (亩)
（7）煤矿设计原煤产量为300万吨/年；（8）煤矿设计寿命为20年；（9）采矿出矸率（矸石占全部采出的百分比）一般为7%~10%。（10）为保护耕地，煤矿堆矸石地应比实际占地多征用10%。现在煤矿设计中用于处理矸石的经费（只计征地费及堆积时运矸车用的电费）为100万元/年，这笔钱是否够用？试制订合理的年度征地计划，并对不同的出矸率预测处理矸石的最低费用。
煤矸石堆积问题
煤矿采煤时，会产出无用废料——煤矸石。在平原地区，煤矿不得不征用土地堆放矸石。通常矸石的堆积方法是：架设一段地面角度约为 25 的直线形上升轨道（角度过大，运矸车无法装满），用在轨道上行驶的运矸车将矸石运到轨道顶端后向两侧倾倒，待矸石堆高后，再借助矸石堆延长轨道，这样逐渐堆起如下图 6.21所示的一座矸石山。

2024届陕西省韩城市苏山分校数学高一下期末学业质量监测模拟试题含解析2

2024届陕西省韩城市苏山分校数学高一下期末学业质量监测模拟试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．已知()f x 为定义在R 上的函数，其图象关于y 轴对称，当0x ≥时，有(1)()f x f x +=-，且当[0,1)x ∈时，2()log (1)=+f x x ，若方程()0f x kx -=（0k >）恰有5个不同的实数解，则k 的取值范围是（） A ．11[,)74B ．11[,)64C ．11[,)65D ．11[,)752．已知底面半径为1，体积为3π的圆柱，内接于一个高为23圆锥（如图），线段AB 为圆锥底面的一条直径，则从点A 绕圆锥的侧面到点B 的最短距离为（）A ．8B ．3C ．42D ．43．已知等差数列{}n a 中，34568a a a a +-+=, 则7S =（） A ．8 B ．21 C ．28D ．354．设函数21(0)()lg (0)xx f x x x ⎧+≤⎪=⎨>⎪⎩，若关于x 的方程2()()20f x af x -+=恰有6个不同的实数解，则实数a 的取值范围为（） A ．(2,22B ．()22,3C ．()3,4D ．()22,45．在ABC ∆中，3AB =，3C π=，O 为ABC ∆的外接圆的圆心，则CO =（）A 3B ．23C ．3D ．66．已知数列{}n a 的通项公式()2019112n n n a -⎧-⎪=⎨⎛⎫⎪ ⎪⎝⎭⎩120192020n n ≤≤≥，前n 项和为n S ，则关于数列{}n a 、{}n S 的极限，下面判断正确的是（） A ．数列{}n a 的极限不存在，{}n S 的极限存在 B ．数列{}n a 的极限存在，{}n S 的极限不存在 C ．数列{}n a 、{}n S 的极限均存在，但极限值不相等 D ．数列{}n a 、{}n S 的极限均存在，且极限值相等7．已知数列}{n a 满足111,1n n a a a +=-=，则10a =（） A ．10B ．20C ．100D ．2008．在△ABC 中, sin?B sin?CsinA cos?B cosC+=+,则△ABC 为( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形9．执行如图的程序框图，则输出的λ是( )A ．-2B ．-4C ．0D ．-2或010．已知ππ042βα<<<<，且π10sin 410α⎛⎫-= ⎪⎝⎭，π4sin 45β⎛⎫+= ⎪⎝⎭，则()sin αβ+=( )A ．1010B ．1010-C ．31010D ．31010-二、填空题：本大题共6小题，每小题5分，共30分。

sob工作流程

SOB工作流程一、什么是SOB工作流程？SOB工作流程是指一种管理和执行任务的方法和过程，通过将任务划分为不同的阶段和活动，以确保任务的顺利进行和高效完成。

SOB，即Situation（情况）、Objective（目标）和Background（背景），是指在每个阶段进行细致的分析和计划，以确保任务的成功。

二、SOB工作流程的步骤1. 了解情况了解情况是SOB工作流程的第一步，它包括以下活动： - 收集相关信息和资料，包括任务的背景、目标和相关的约束条件。

- 确定任务的需求和期望，以及任务的重要性和紧急性。

- 分析任务的相关方面，包括任务的范围、关键要素和可能的风险。

2. 设定目标设定目标是SOB工作流程的第二步，它包括以下活动： - 确定任务的具体和可测量的目标，以便能够评估任务的完成情况。

- 设定任务的时间表，包括任务的起止时间、关键里程碑和可行性评估。

- 确定任务的预算，包括资源需求和资金的分配。

3. 制定计划制定计划是SOB工作流程的第三步，它包括以下活动： - 制定详细的工作计划，包括任务的分解、活动的安排和资源的分配。

- 确定任务的执行顺序和依赖关系，以确保任务的合理推进。

- 评估任务的风险和问题，并提供相应的解决方案和备选方案。

4. 执行任务执行任务是SOB工作流程的第四步，它包括以下活动： - 分配任务给相应的人员或团队，并确保他们具备执行任务所需的能力和资源。

- 监督任务的执行情况，包括任务的进度、质量和成本控制。

- 处理任务的问题和风险，及时调整计划并采取必要的措施。

5. 评估结果评估结果是SOB工作流程的最后一步，它包括以下活动： - 检查任务的完成情况，与设定的目标进行比较和评估。

- 分析任务的效率和效果，寻找改进的空间和机会。

- 提供任务的总结和反馈，包括任务的成功因素和不足之处。

三、SOB工作流程的优势1.全面性：SOB工作流程提供了一种全面的方法来分析和处理任务，确保任务的各个方面得到充分考虑和满足。

2022-2023学年福建省福州市闽侯县大义中学高三物理联考试题含解析

2022-2023学年福建省福州市闽侯县大义中学高三物理联考试题含解析一、选择题：本题共5小题，每小题3分，共计15分．每小题只有一个选项符合题意1. （单选）如图所示，质量均为m的小物块A、B，在水平恒力F的作用下沿倾角为37°固定的光滑斜面加速向上运动．A、B之间用与斜面平行的形变可忽略不计的轻绳相连，此时轻绳张力为F T=0.8mg，下列说法错误的是（已知sin37°=0.6）（）解：A、以A为研究对象，根据牛顿第二运动定律可得：F T﹣mgsin37°=ma，解得：a=0.2g，小车A、B的加速度均为0.2g，故A正确；B、以A、B整体为研究对象：Fcos37°﹣2mgsin37°=2ma，解得：F=2mg，故B正确；C、撤掉F的瞬间，绳子上的拉力立刻消失了，小物块A的加速度方向变为向下，故C错误、D正确．本题选错误的，故选：C．2.（单选）均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场．如图所示，在半球面AB上均匀分布正电荷，总电荷量为q，球面半径为R，CD为通过半球顶点与球心O的轴线，在轴线上有M、N两点，OM=ON=2R．已知M点的场强大小为E，则N点的场强大小为（）．﹣E B．C．﹣ED．+E解：若将带电量为2q的球面放在O处，均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场．则在M、N点所产生的电场为E==，由题知当半球面如图所示产生的场强为E，则N点的场强为E′=﹣E，故选A．本题解题关键是抓住对称性，找出两部分球面上电荷产生的电场关系．A．做匀速直线运动的物体，一定不受外力的作用B．相互作用的两物体之间，弹力或摩擦力总是成对出现的C．沿粗糙平面运动的物体一定受到滑动摩擦力的作用D．一个物体受到几个不同性质的共点力的作用，这几个共点力可以合成一个力；一个力也可以分解成几个不同性质的力参考答案：B4. （多选题）一理想变压器原、副线圈的匝数比为10：1，原线圈输入电压的变化规律如图甲所示，副线圈所接电路如图乙所示，P为滑动变阻器的触头．下列说法正确的是（）A．副线圈输出电压的频率为50HzB．副线圈输出电压的有效值为31VC．P向右移动时，变压器的输出功率增加D．P向右移动时，原、副线圈的电流比减小参考答案：AC【分析】从图中读出原线圈输入电压的最大值和周期，计算出频率，根据变压器的电压之比等于匝数之比计算出副线圈的电压有效值，P滑动，结合电路动态分析知识分析输出功率的变化．【解答】解：A、从图中可知原线圈的输入电压的周期T为2×10﹣2s，则频率f=，变压器原副线圈的电压频率相同，则副线圈输出电压的频率为50Hz，A正确；B、从图中可知原线圈的输入电压最大值为310V，原、副线圈的匝数比为10：1，则副线圈副线圈输出电压的最大值为31V，不是有效值，B错误；C、P向右滑动，滑动变阻器的接入电阻变小，则副线圈的电流增大，副线圈电压不变，则副线圈的总功率即输出功率增加，C正确；D、原副线圈的电流比与原副线圈匝数成反比，匝数没变，则原副线圈的电流比不变，与P向右移动无关，D错误；故选：AC．5. （多选题）如图所示，人在岸上拉船，已知船的质量为m，水的阻力大小恒为f，当轻绳与水平面的夹角为θ时，船的速度为v，此时人的拉力大小为F，则（）A．人拉绳行走的速度为vcosθB．人拉绳行走的速度为C．船的加速度为D．船的加速度为参考答案：AD解：A、船运动的速度是沿绳子收缩方向的速度和绕定滑轮的摆动速度的合速度．如右上图所示根据平行四边形定则有，v人=vcosθ．故A正确，B错误．C、对小船受力分析，如左下图所示，则有Fcosθ﹣f=ma，因此船的加速度大小为a=，故C错误，D正确；故选：AD．二、填空题：本题共8小题，每小题2分，共计16分6. 假设太阳与地球之间充满了水而不是真空，那么光从太阳到达地球要多花的时间是▲s。

《切线长定理—知识讲解》同步 2022人教九年级上册专练

切线长定理—知识讲解（基础）【学习目标】1.了解切线长定义；理解切线的判定和性质；理解三角形的内切圆及内心的定义；2.掌握切线长定理；利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线的判定定理和性质定理1．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.要点诠释：切线的判定方法：（1）定义：直线和圆有唯一公共点时，这条直线就是圆的切线；（2）定理：和圆心的距离等于半径的直线是圆的切线；（3）判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.（切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可）.2．切线的性质定理：圆的切线垂直于过切点的半径.要点诠释：切线的性质：（1）切线和圆只有一个公共点；（2）切线和圆心的距离等于圆的半径；（3）切线垂直于过切点的半径；（4）经过圆心垂直于切线的直线必过切点；（5）经过切点垂直于切线的直线必过圆心.要点二、切线长定理1．切线长：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长.要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段. 2．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角. 要点诠释：切线长定理包含两个结论：线段相等和角相等.3．圆外切四边形的性质：圆外切四边形的两组对边之和相等.要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S 为三角形的面积，P 为三角形的周长，r 为内切圆的半径).(3) 三角形的外心与内心的区别：名称确定方法图形性质外心(三角形外接圆的圆心)三角形三边中垂线的交点(1)OA=OB=OC ；(2)外心不一定在三角形内部内心(三角形内切圆的圆心)三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA 、OB 、OC 分别平分 ∠BAC 、∠ABC 、∠ACB ； (3)内心在三角形内部.【典型例题】类型一、切线长定理1．如图，PA 、PB 、DE 分别切⊙O 于A 、B 、C ，⊙O 的半径长为6 cm ，PO ＝10 cm ，求△PDE 的周长．【答案与解析】连结OA ，则OA ⊥AP ．在Rt △POA 中，PA ＝22OA OP -＝22610-＝8（cm ）．由切线长定理，得EA ＝EC ，CD ＝BD ，PA ＝PB ， ∴ △PDE 的周长为PE ＋DE ＋PD ＝PE ＋EC ＋DC ＋PD ，＝PE ＋EA ＋PD ＋DB ＝PA ＋PB ＝16（cm ）．【总结升华】本题考查切线长定理、切线的性质、勾股定理．注意：在有关圆的切线长的计算中，往往利用切线长定理进行线段的转换．2．（2020•柳州）如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，边CD与⊙O相交于点E，连接AE，BE．（1）求证：AB=AC；（2）若过点A作AH⊥BE于H，求证：BH=CE+EH．【思路点拨】（1）根据弦切角定理和圆周角定理证明∠ABC=∠ACB，得到答案；（2）作AF⊥CD于F，证明△AEH≌△AEF，得到EH=EF，根据△ABH≌△ACF，得到答案．【答案与解析】证明：（1）∵AD与△ABC的外接圆⊙O恰好相切于点A，∴∠ABE=∠DAE，又∠EAC=∠EBC，∴∠DAC=∠ABC，∵AD∥BC，∴∠DAC=∠ACB，∴∠ABC=∠ACB，∴AB=AC；（2）作AF⊥CD于F，∵四边形ABCE是圆内接四边形，∴∠ABC=∠AEF，又∠ABC=∠ACB，∴∠AEF=∠ACB，又∠AEB=∠ACB，∴∠AEH=∠AEF，在△AEH和△AEF中，，∴△AEH≌△AEF，∴EH=EF，∴CE+EH=CF，在△ABH和△ACF中，，∴△ABH≌△ACF，∴BH=CF=CE+EH．【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质，运用性质证明相关的三角形全等是解题的关键，注意圆周角定理和圆内接四边形的性质的运用．举一反三：【变式】（2020•青海）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．（1）求证：AM=AC；（2）若AC=3，求MC的长．【答案】（1）证明：连接OA，∵AM是⊙O的切线，∴∠OAM=90°，∵∠B=60°，∴∠AOC=120°，∵OA=OC，∴∠OCA=∠OAC=30°，∴∠AOM=60°，∴∠M=30°，∴∠OCA=∠M，∴AM=AC；（2）作AG⊥CM于G，∵∠OCA=30°，AC=3，∴AG=，由勾股定理的，CG=，则MC=2CG=3．类型二、三角形的内切圆3．已知：如图，△ABC的三边BC=a，CA=b，AB=c，它的内切圆O的半径长为r．求△ABC的面积S．【答案与解析】设内切圆与三角形的三边AB 、AC 、BC 分别交于D 、E 、F ，连接OE 、 OF 、OD 、AO 、BO 、CO.∴△ABC=△AO B +△AO C +△BO C=12r(a+b+c). 【总结升华】考虑把△ABC 的面积分割成3个以圆的半径为高的三角形面积的和，从而求出△ABC 的面积. 举一反三：【变式】已知如图，△ABC 中，∠C=90°，BC=4，AC=3，求△ABC 的内切圆⊙O 的半径r.【答案】连结OA 、OB 、OC ，∵△ABC 中，∠C=90°，BC=4，AC=3，∴AB=5. 则S △AOB +S △COB +S △AOC =S △ABC ，即11115+4+3=34=12222r r r r ⨯⨯⨯⨯⨯，类型三、与相切有关的计算与证明4．如图，平行四边形ABCD 中，以A 为圆心，AB 为半径的圆交AD 于F ，交BC 于G ，延长BA 交圆于E .（1）若ED 与⊙A 相切，试判断GD 与⊙A 的位置关系，并证明你的结论；（2）在（1）的条件不变的情况下，若GC ＝CD ＝5，求AD 的长.G FEDCBA【答案与解析】（1）结论：GD 与O 相切证明：连接AG ∵点G 、E 在圆上， ∴AG AE =∵四边形ABCD 是平行四边形， ∴AD BC ∥ ∴123B ∠=∠∠=∠，∵AB AG =，∴3B ∠=∠，∴12∠=∠1F E在AED ∆和AGD ∆12AE AG AD AD =⎧⎪∠=∠⎨⎪=⎩∴AED AGD ∆∆≌，∴AED AGD ∠=∠ ∵ED 与A 相切∴90AED ∠=︒，∴90AGD ∠=︒ ∴AG DG ⊥∴GD 与A 相切（2）∵5GC CD ==，四边形ABCD 是平行四边形 ∴AB DC =，45∠=∠，5AB AG ==∵AD BC ∥，∴46∠=∠，∴1562B ∠=∠=∠∴226∠=∠ ，∴630∠=︒ ∴10AD =.【总结升华】本题虽然是圆和平行四边形的位置关系问题，但是依然考察的是如何将所有条件放在最基本的三角形中求解的能力.判断出DG 与圆相切不难，难点在于如何证明.第二问则不难，重点在于如何利用角度的倍分关系来判断直角三角形中的特殊角度，从而求解.《圆》全章复习与巩固—巩固练习（提高）【巩固练习】一、选择题1．如图所示，AB 、AC 为⊙O 的切线，B 和C 是切点，延长OB 到D ，使BD ＝OB ，连接AD ．如果∠DAC ＝78°，那么∠ADO 等于( )．A ．70°B ．64°C ．62°D ．51°2．在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ，S 射向地面的光束呈圆锥形，其轴截面SAB 的顶角为120°(如图所示)，则光源离地面的垂直高度SO 为( )． A ．54m B．．．第1题图第2题图第3题图第4题图3．设计一个商标图案，如图所示，在矩形ABCD中，AB=2BC，且AB=8cm，以A为圆心、AD的长为半径作半圆，则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24．如图，的半径为5，弦的长为8，点在线段(包括端点)上移动，则的取值范围是( ).A. B. C. D.5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用数学语言可表示为：如图所示，CD为⊙O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，则直径CD的长为( )A．12.5寸 B．13寸 C．25寸D．26寸6．（2020•贵港）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，则线段OM的最小值是（）A．0 B．1 C．2 D．37．一条弦的两个端点把圆周分成4:5两部分，则该弦所对的圆周角为( )．A．80° B．100° C．80°或100° D．160°或200°8．如图所示，AB、AC与⊙O分别相切于B、C两点，∠A＝50°，点P是圆上异于B、C的一动点，则∠BPC的度数是( )．A．65° B．115° C．65°或115° D．130°或50°二、填空题 9．如下左图，是的内接三角形，，点P 在上移动(点P 不与点A 、C 重合)，则的变化范围是__ ________.第9题图第10题图10．如图所示，EB 、EC 是⊙O 是两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E=46°，∠DCF=32°，那么∠A 的度数是________________. 11．已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2680x x -+= 的两实根，若⊙O 1与⊙O 2的圆心距d =5．则⊙O 1与⊙O 2的位置关系是 __ __ .12．（2020•巴彦淖尔）如图，AB 为⊙O 的直径，AB=AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC ；③AE=2EC ；④劣弧是劣弧的2倍；⑤AE=BC ，其中正确的序号是．13.两个圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是_______ ________. 14.已知正方形ABCD 外接圆的直径为2a ，截去四个角成一正八边形，则这个正八边形EFGHIJLK 的边长为____ ____，面积为_____ ___．15．如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形，分别以它们的各顶点为圆心，以l 为半径画弧与两邻边相交，得到3条弧，4条弧，……(1)图(1)中3条弧的弧长的和为___ _____，图(2)中4条弧的弧长的和为_____ ___； (2)求图(m)中n 条弧的弧长的和为____ ____(用n 表示)．16．如图所示，蒙古包可以近似地看做由圆锥和圆柱组成，如果想用毛毡搭建20个底面积为9πm 2，高为3.5m ，外围高4 m 的蒙古包，至少要____ ____m 2的毛毡．三、解答题17. 如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．（1）证明：AF平分∠BAC；（2）证明：BF＝FD.18.（2020•南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．19．如图，相交两圆的公共弦长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：①如图(1)，在正△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图(2)，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类似的思想提出了如下命题：③如图(3)，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求：(1)请你从①②③三个命题中选择一个进行证明；(2)请你继续完成下面的探索；①在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)；②如图(4)，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否成立．若成立，请给予证明；若不成立，请说明理由．【答案与解析】一、选择题1．【答案】B；【解析】由AB为⊙O的切线，则AB⊥OD．又BD＝OB，则AB垂直平分OD，AO＝AD，∠DAB＝∠BAO．由AB、AC为⊙O的切线，则∠CAO＝∠BAO＝∠DAB．所以，∠DAB＝∠DAC＝26°．∠ADO＝90°-26°＝64°．本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等．2．【答案】C；【解析】圆锥的高、底面半径与母线组成直角三角形．由题意，SO⊥AB于O，∴∠SOA＝∠SOB＝90°．又SA＝SB，∠ASB＝120°，∴∠SAB＝∠SBA＝180120302=°-?°，设SO＝x m，则AS＝2x m．∵ AO＝27，由勾股定理，得(2x)2-x2＝272，解得93x=．3．【答案】A.；【解析】对图中阴影部分进行分析，可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中，AB=2BC，AB=8cm，∴ AD=BC=4cm，∠DAF=90°，，，又AF=AD=4cm，∴，∴.4.【答案】A；【解析】OM最长是半径5；最短是OM⊥AB时，此时OM=3，故选A.5．【答案】D；【解析】因为直径CD垂直于弦AB，所以可通过连接OA(或OB)，求出半径即可.根据“垂直于弦的直径平分弦，并且平分弦所对的两条弧”，知(寸)，在Rt△AOE中，，即，解得OA=13，进而求得CD=26(寸).故选D.6．【答案】B.【解析】设OP与⊙O交于点N，连结MN，OQ，如图，∵OP=4，ON=2，∴N是OP的中点，∵M为PQ的中点，∴MN为△POQ的中位线，∴MN=OQ=×2=1，∴点M在以N为圆心，1为半径的圆上，当点M在ON上时，OM最小，最小值为1，∴线段OM的最小值为1．故选B．7．【答案】C；【解析】圆周角的顶点在劣弧上时，圆周角为5136010092⨯⨯=°°；圆周角的顶点在优弧上时，圆周角为413608092⨯⨯=°°．注意分情况讨论．8．【答案】C；【解析】连接OC、OB，则∠BOC＝360°-90°-90°-50°＝130°．点P在优弧上时，∠BPC＝12∠BOC＝65°；点P在劣弧上时，∠BPC＝180°-65°＝115°．主要应用了切线的性质定理、圆周角定理和多边形内角和定理．二、填空题9．【答案】； 10．【答案】99°；【解析】由EB=EC ，∠E=46°知，∠ECB= 67°，从而∠BCD=180°-67°-32°=81°，在⊙O 中，∠BCD 与∠A 互补，所以∠A=180°-81°=99°. 11．【答案】相交；【解析】求出方程2680x x -+= 的两实根1r 、2r 分别是4、2，则1r -2r <d <1r +2r ,所以两圆相交.12.【答案】①②④；【解析】连接AD ，AB 是直径，则AD ⊥BC ，又∵△ABC 是等腰三角形，故点D 是BC 的中点，即BD=CD ，故②正确； ∵AD 是∠BAC 的平分线，由圆周角定理知，∠EBC=∠DAC=∠BAC=22.5°，故①正确；∵∠ABE=90°﹣∠EBC ﹣∠BAD=45°=2∠CAD ，故④正确； ∵∠EBC=22.5°，2EC ≠BE ，AE=BE ，∴AE ≠2CE ，③不正确； ∵AE=BE ，BE 是直角边，BC 是斜边，肯定不等，故⑤错误．综上所述，正确的结论是：①②④．13.【答案】7或3；【解析】两圆有三种位置关系：相交、相切(外切、内切)和相离(外离、内含).两圆内切时，圆心距，题中一圆半径为5，而d=2，所以有，解得r=7或r=3，即另一圆半径为7或3.14.【答案】21)a ； 2(222)a ；【解析】正方形ABCD 外接圆的直径就是它的对角线，由此求得正方形边长为a ．如图所示，设正八边形的边长为x ．在Rt △AEL 中，LE ＝x ，AE ＝AL ＝2x ，∴ 22x x a +=，21)x a =，即正八边形的边长为21)a ．222224[(21)](222)AEL S S S a x a a a =-=-=-=△正方形正八边形．15.【答案】(1)π； 2π； (2)(n-2)π；【解析】∵ n 边形内角和为(n-2)180°，前n 条弧的弧长的和为(2)1801(2)3602n n -=-个以某定点为圆心，以1为半径的圆周长，∴ n 条弧的弧长的和为121(2)(2)2n n ππ⨯⨯-=-．本题还有其他解法，比如：设各个扇形的圆心角依次为1α，2α，…，n α，则12(2)180n n ααα+++=-…°，∴ n 条弧长的和为1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-．16.【答案】720π；【解析】∵ S ＝πr 2，∴ 9π＝πr 2，∴ r ＝3．∴ h 1＝4，∴ 2215l h r =+=，∴ 223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱，2036720S ππ=⨯=总．所求面积包括圆锥的侧面积和圆柱的侧面积，不包括底面积．三、解答题17.【答案与解析】（1）连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ，∴OF 垂直平分BC∴BF FC =∴AF 平分∠BAC .（2）由（1）及题设条件可知∠1=∠2，∠4=∠3，∠5=∠2 ∴∠1+∠4=∠2+∠3A DO 1234A BCDEO 12∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18．【答案与解析】证明：（1）∵四边形ABCD 是⊙O 的内接四边形， ∴∠A+∠BCD=180°， ∵∠DCE+∠BCD=180°， ∴∠A=∠DCE ， ∵DC=DE ，∴∠DCE=∠AEB ， ∴∠A=∠AEB ；（2）∵∠A=∠AEB ， ∴△ABE 是等腰三角形， ∵EO ⊥CD ， ∴CF=DF ，∴EO 是CD 的垂直平分线， ∴ED=EC ， ∵DC=DE ， ∴DC=DE=EC ，∴△DCE 是等边三角形， ∴∠AEB=60°，∴△ABE 是等边三角形．19.【答案与解析】解：∵公共弦AB ＝120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=.20. 【答案与解析】(1)如选命题①．证明：在图(1)中，∵∠BON＝60°，∴∠1+∠2＝60°．∵∠3+∠2＝60°，∴∠1＝∠3．又∵ BC＝CA，∠BCM＝∠CAN＝60°，∴△BCM≌△CAN，∴ BM＝CM．如选命题②．证明：在图(2)中，∵∠BON＝90°，∴∠1+∠2＝90°．∵∠3+∠2＝90°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝90°，∴△BCM≌△CDN，∴ BM＝CN．如选命题③．证明：在图(3)中，∵∠BON＝108°，∴∠1+∠2＝108°．∵∠2+∠3＝108°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝108°，∴△BCM≌△CDN，∴ BM＝CN．(2)①答：当∠BON＝(2)180nn°时结论BM＝CN成立．②答：当∠BON＝108°时．BM＝CN还成立．证明：如图(4)，连接BD、CE在△BCD和△CDE中，∵ BC＝CD，∠BCD＝∠CDE＝108°，CD＝DE，∴△BCD≌△CDE．∴ BD＝CE，∠BDC＝∠CED，∠DBC＝∠ECD．∵∠CDE＝∠DEN＝108°，∴∠BDM＝∠CEM．∵∠OBC+∠OCB＝108°，∠OCB+∠OCD＝108°．∴∠MBC＝∠NCD．又∵∠DBC＝∠ECD＝36°，∴∠DBM＝∠ECM．∴△BDM≌△CEN，∴ BM＝CN．。

SOB 问题及解答 -AECOPD(审批版)

2023年高考真题英语北京卷解析

3.4.3反证法

(好题)初中数学八年级数学上册第五单元《二元一次方程组》测试(含答案解析)(3)

《一元二次方程的解法 》(二)配方法—知识讲解(基础 2022人教九年级上册专练

初中化学实验探究问题分类示例及解题思路教学内容

6.3.3余角和补角-(课件)人教版(2024)数学七年级上册

PDCA循环在COPD稳定期老年患者呼吸功能锻炼中的应用

应用动能定理解决多过程问题-高考物理复习

专题03角(八大类型)(题型专练)-2023-2024学年七年级数学上册

(必考题)初中数学八年级数学上册第五单元《二元一次方程组》测试(答案解析)(1)

sob工作流程

沪科版数学七年级上册综合训练50题(含答案)

高中数学解三角形解题方法

PPQP 培训ppt课件

专练04 填空题-基础(30题)-2020~2021学年七年级数学上学期期末考点(解析版)

煤矸石堆积问题

2024届陕西省韩城市苏山分校数学高一下期末学业质量监测模拟试题含解析2

sob工作流程

2022-2023学年福建省福州市闽侯县大义中学高三物理联考试题含解析

《切线长定理—知识讲解 》同步 2022人教九年级上册专练

《一元二次方程的解法》(二)配方法—知识讲解(基础 2022人教九年级上册专练

《切线长定理—知识讲解》同步 2022人教九年级上册专练