统计学第3章作业参考答案知识讲解
统计学第三章课后作业参考答案

统计学第三章课后作业参考答案1、统计整理在统计研究中的地位如何?答:统计整理在统计研究中的地位:统计整理实现了从个别单位标志值向说明总体数量特征的指标过度,是人们对社会经济现象从感性认识上升到理性认识的过度阶段,为统计分析提供基础,因而,它在统计研究中起了承前启后的作用。
2、什么是统计分组?为会么说统计分组的关键在于分组标志的选择?答:1)统计分组是根据统计研究任务的要求和现象总体的内在特点,把统计总体按照某一标志划分为若干性质不同而又有联系的几个部分。
2)因为分组标志作为现象总体划分为各处不同性质的给的标准或根据,选择得正确与否,关系到能否正确地反映总体的性质特征、实现统计研究的目的的任务。
分组标志一经选取定,必然突出了现象总体在此标志下的性质差异,而掩盖了总体在其它标志下差异。
缺乏科学根据的分组不但无法显示现象的根本特征,甚至会把不同性质的事物混淆在一起,歪曲了社会经济的实际情况。
所以统计分组的关键在于分组的标志选取择。
3、统计分组可以进行哪些分类?答:统计分组可以进行以下分类1)按其任务和作用的不同分为:类型分组、结构分组、分析分组2)按分组标志的多少分为:简单分组、复合分组3)按分组标志性质分为:品质分组、变量分组5单项式分组和组距式分组分别在什么条件下运用?答:单项式分组运用条件:变量值变动范围小的离散变量可采取单项式分组组距式分组运用条件:变量值变动很大、变量值的项数又多的离散变量和连续变量可采取组距式分组8、什么是统计分布?它包括哪两个要素?答:1)在分组的基础上把总体的所有单位按组归并排列,形成总体中各个单位在各组分布,称为统计分布,是统计整理结果的重要表现形式。
2)统计分布的要素:一、是总体按某一标志分的组,二、是各组所占有的单位数——次数10、频数和频率在分配数列中的作用如何?答:频数和频率的大小表示相应的标志值对总体的作用程度,即频数或频率越大则该组标志值对全体标志水平所起作用越大,反之,频数或频率越小则该组标志值对全体标志水平所起作用越小11、社会经济现象次数分布有哪些主要类型?分布特征?答:1) 社会经济现象次数分布有以下四种主要类型:钟型、U 型 、J 型、洛伦茨分布 2)分布特征如下:钟型分布:正态分布,两头小,中间大U 型分布:两头大,中间小J 型分布:次数随变量值增大而增多;倒J 型分布:次数随变量值增大而减少 洛伦茨分布:各组标志比重随着各组单位数比重(频率)增加而增加;17、有27个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3 试编制分配数列18、某车间同工种40名工人完成个人生产定额百分数如下 :97 88 123 115 119 158 112 146 117 108 105 110 107 137 120 136 125 127 142 118 103 87115 114 117 124 129 138 100 103 92 95 113 126 107 108 105 119 127 104根据上述资料,试编制分配数列错例:下面解法几个地方错?19、1993年某出口创汇大户出口实绩(万美元)列举如下:1011 1052 865 721 2032 1218 1046 721 546 623 2495 1015 1113 1104 1084 707 878 678 2564 620 575 943 828 2035 2375 4342 751 505 798 728 1103 1285 2856 3200 518第九章时间序列分析一、单项选择题二、多项选择题三、判断题四、填空题1、时间序列 指标数值2、总量指标时间数列 相对指标时间数列 平均指标时间数列 总量指标时间数列3、简单 na a ∑=间断 连续 间隔相等 间隔不等4、逐期 累计 报告期水平–基期水平 逐期 累计5、环比 定基基期水平报告期水平环比 定基 环比6、水平法 累计法 水平 nx x ∏=或nna a x 0= 累计 032a a x x x x n∑=++++7、26 26 8、79、)-(y y ˆ∑ = 0)-(y y ˆ∑2为最小 10、季节比率 1200% 400% 五、简答题(略) 六、计算题1、4月份平均库存 = 3053008370122505320⨯+⨯+⨯+⨯= 302(辆)2、第一季度平均人数917301024927217270302751026424258++++⨯+⨯+⨯+⨯+⨯=(人)3、第一季度平均库存额142434405408240012221-+++=-+++=n a a a a n = 410(万元) 同理,第二季度平均库存额1424184384262434-+++= 430(万元)上半年平均库存额1724184384264344054082400-++++++= 420(万元)或 2430410+= 420(万元)4、年平均增加的人数 =516291678172617931656++++= 1696.4(万人)5、某酿酒厂成品库1998年的平均库存量12111232121222---+++++++++=n n n n f f f f a a f a a f a a a=121124084122233533012330326+++⨯+++⨯++⨯+=124620= 385(箱)6、列计算表如下:该柴油机厂全年的平均计划完成程度指标为.346004.47747==∑∑b bc c = 138.0% 7、列计算表如下:该企业第一季度生产工人数占全部职工人数比重232003100320023000225602356249622250++++++==b a c = 77.2% 8、①填写表中空格:②第一季度平均职工人数 =3= 268. 33(人)③第一季度工业总产值 = + + = 83.475(万元) 第一季度平均每月工业总产值 =3475.83=27.825(万元) ④第一季度劳动生产率 =33.268834750=3110.91(元/人)第一季度平均月劳动生产率 =33.26891.3110=1036.97(元/人)或 =33.268278250=1036.97(元/人)9、煤产量动态指标计算表:第①、②与③的要求,计算结果直接在表中; ④平均增长量=552.2=(万吨) ⑤水平法计算的平均发展速度=554065.120.672.8== 107.06% 平均增长速度= 107.06%-100%=7.06% 10、以1991年为基期的总平均发展速度为 62306.105.103.1⨯⨯= 104.16% 11、每年应递增:535.2=118.64%以后3年中平均每年应递增:355.135.2=114.88% 12、计算并填入表中空缺数字如下:(阴影部分为原数据)平均增长量为:3266.39÷6 = 544.40(万台) 平均发展速度为:66556.3= 124.12% 平均增长速度为:124.12%-1=%13、设在80亿元的基础上,按8 %的速度递增,n 年后可达200亿元,即n80200= 108% → n 1 → n = 08.1log 5.2log按8 %的速度递增,约经过年该市的国民收入额可达到200亿元。
统计学 第三章练习题答案及解析

3%1%2%5.1++453025453025++++统计学第三章出题优课后习题答案原多项选择第三题D 选项解释有误,现在已经重新更改。
一、单项选择题1. 某商场某月商品销售额为1200万元,月末商品库存额为400万元,这两个总量指标( )。
A. 是时期指标B. 前者是时期指标,后者是时点指标C. 是时点指标2. 国民总收入与国内生产总值之间相差一个( )。
A. 出口与进口的差额B. 固定资产折旧C. 来自国外的要素收入净额3. 有三批产品,废品率分别为1.5%、2%、1%,相应的废品数量为25件、30件、45件,则这三批产品平均废品率的计算式应为( )。
A. B.C. D.4. 下列各项中,超额完成计划的有( )。
A. 利润计划完成百分数103.5%B. 单位成本计划完成百分数103.5%C. 建筑预算成本计划完成百分数103.5%5. 某厂某种产品生产量1月刚好完成计划,2月超额完成2%,3月超额完成4%,则该厂该年一季度各月平均超额完成计划的计算方法是( )。
A. 2%+4%=6%B. (2%+4%)÷2=3%C. (2%+4%)÷3=2%453025%1%2%5.1++++3%1%2%5.1⨯⨯6. 甲、乙两组工人的平均日产量分别为18件和15件。
若甲乙两组工人的平均日产量不变,但是甲组工人数占两组工人总数的比重下降,则两组工人总平均日产量( )。
A. 上升B. 下降C. 不变D.可能上升,也可能下降7. 当各个变量值的频数相等时,该变量的()。
A. 众数不存在B. 众数等于均值C. 众数等于中位数8. 如果你的业务是提供足球运动鞋的号码,那么哪一种平均指标对你更有用?( )A. 算术平均数B. 几何平均数9. 某年年末某地区城市和乡村平均每人居住面积分别为30.3和33.5平方米,标准差分别12.8和13.1平方米,则居住面积的差异程度( )。
A. 城市大B. 乡村大10. 下列数列的平均数都是50,在平均数附近散布程度最小的数列是( )。
统计学教材部分参考答案(第三版)
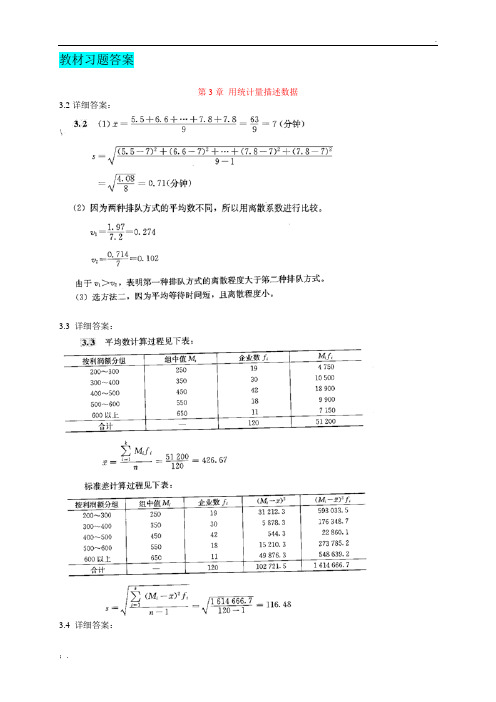
教材习题答案第3章用统计量描述数据3.2详细答案:3.3 详细答案:3.4 详细答案:通过计算标准化值来判断,,,说明在A项测试中该应试者比平均分数高出1个标准差,而在B项测试中只高出平均分数0.5个标准差,由于A项测试的标准化值高于B项测试,所以A项测试比较理想。
3.5详细答案:3方法B 方法C方法A平均165.6 平均128.73 平均125.53中位数165 中位数129 中位数126众数164 众数128 众数126标准差 2.13 标准差 1.75 标准差 2.77峰度-0.13 峰度0.45 峰度11.66偏度0.35 偏度-0.17 偏度-3.24极差8 极差7 极差12离散系数0.013 离散系数0.014 离散系数0.022最小值162 最小值125 最小值116最大值170 最大值132 最大值128(1)从集中度、离散度和分布的形状三个角度的统计量来评价。
从集中度看,方法A 的平均水平最高,方法C最低;从离散度看,方法A的离散系数最小,方法C最大;从分布的形状看,方法A和方法B的偏斜程度都不大,方法C则较大。
(2)综合来看,应该选择方法A,因为平均水平较高且离散程度较小。
第5章参数估计5.3详细答案:第6章假设检验6.3详细答案:,,,不拒绝,没有证据表明该企业生产的金属板不符合要求。
6.4 详细答案:,,,拒绝,该生产商的说法属实。
6.6详细答案:设,。
,=1.36,,不拒绝,广告提高了平均潜在购买力得分。
第7章方差分析与实验设计第8章一元线性回归8.1详细答案:(1)散点图如下:产量与生产费用之间为正的线性相关关系。
(2)。
检验统计量,,拒绝原假设,相关系数显著。
8.4 详细答案:(1)方差分析表中所缺的数值如下:方差分析表变差来源df SS MS F Significance F回归 1 1422708.6 1422708.6 354.277 2.17E-09残差10 40158.07 4015.807 ——总计11 1642866.67 ———(2)。
《统计学概论》第三章课后练习题答案

《统计学概论》第三章课后练习题答案一、思考题1.什么是统计整理,统计整理的对象是什么?P612.什么是统计分组,它可以分为哪几种形式?P633.简述编制变量数列的一般步骤。
P70-754.统计表分为哪几种?P785.什么是统计分布,它包括哪两个要素?P686.单项式分组和组距公式分组分别在什么情况下运用?P667.如何正确选择分组标志?P658.为什么要进行统计分组?其主要作用是什么?P63(2009.01)二、判断题1.统计整理只能对统计调查所得到的原始资料进行加工整理。
(×)P61 【解析】统计整理分为两情况:一种是对原始资料进行整理,另一种是对次级资料即已加工过的现成资料进行在整理。
2.对一个既定总体而言,合理的分组标志只有一个。
(×)P67【解析】复合分组就是对同一总体选择两个或两个以上标志进行的分组。
3.在异距数列中,计算次数密度主要是为了消除组距因素对次数分布的影响。
(√ )P744.组中值是指各组上限和下限之中点数值,故在任何情况下它都能代表各组的一般水平。
(×)P72【解析】当组×)(2010.01)P71【解析】变量数列的分组可分为等距分组和异距分组,只有在等距分组的情况下,组数等于全距除以组距。
6.统计分组的关键问题是确定组数和组距。
(×)(2009.10)P65【解析】统计分组的关键问题是选择恰当的分组标志。
7.按数量标志分组的目的,就是要区分各组在数量上的差别。
(×)P66 【解析】按数量标志分组的目的,并不是单纯确定各组在数量上的差别,而是要通过数量上的变化来区分各组的不同类型和性质。
8.连续型变量可以作单项式分组或组距式分组,而离散型变量只能作组距式分组。
(×)P72【解析】对于连续型变量,一般只能编制组距式变量数列;对于离散型变量,如果变量值个数较多,并且变动幅度较大时,应该编制组距式变量数列,对于变量值较少的离散型数据,一般编制单项式变量数列。
统计学原理第三章(统计资料整理)习题答案解析

第三章统计资料整理一.判断题部分1:对统计资料进行分组的目的就是为了区分各组单位之间质的不同。
(×)2:统计分组的关键问题是确定组距和组数。
(×)3:组中值是根据各组上限和下限计算的平均值,所以它代表了每一组的平均分配次数。
(×)3:分配数列的实质是把总体单位总量按照总体所分的组进行分配。
(∨)4:次数分配数列中的次数,也称为频数。
频数的大小反映了它所对应的标志值在总体中所起的作用程度。
(∨)5:某企业职工按文化程度分组形成的分配数列是一个单项式分配数列。
(×)6:连续型变量和离散型变量在进行组距式分组时,均可采用相邻组组距重叠的方法确定组限。
(∨)7:对资料进行组距式分组,是假定变量值在各组内部的分布是均匀的,所以这种分组会使资料的真实性受到损害。
(∨)8:任何一个分布都必须满足:各组的频率大于零,各组的频数总和等于1 或100%。
(×)9:按数量标志分组形成的分配数列和按品质标志分组形成的分配数列,都可称为次数分布。
( ∨ )10:按数量标志分组的目的,就是要区分各组在数量上的差异。
(×)11:统计分组以后,掩盖了各组内部各单位的差异,而突出了各组之间单位的差异。
(∨)12:分组以后,各组的频数越大,则组的标志值对于全体标志水平所起的作用也越大;而各组的频率越大,则组的标志值对全体标志水平所起的作用越小。
(×)二.单项选择题部分1:统计整理的关键在( B )。
A、对调查资料进行审核B、对调查资料进行统计分组C、对调查资料进行汇总D、编制统计表2:在组距分组时,对于连续型变量,相邻两组的组限( A )。
A、必须是重叠的B、必须是间断的C、可以是重叠的,也可以是间断的D、必须取整数3:下列分组中属于按品质标志分组的是( B )。
A、学生按考试分数分组B、产品按品种分组C、企业按计划完成程度分组D、家庭按年收入分组4:有一个学生考试成绩为70分,在统计分组中,这个变量值应归入( B )。
第三章统计学课后习题答案

第三章统计学课后习题答案第三章统计学课后习题答案统计学是一门研究数据收集、分析和解释的学科,它在各个领域都有广泛的应用。
在学习统计学的过程中,做课后习题是非常重要的一部分,它可以帮助我们巩固所学的知识,提高解决实际问题的能力。
本文将为大家提供第三章统计学课后习题的答案,希望对大家的学习有所帮助。
1. 什么是样本调查?与全面普查有什么区别?样本调查是指通过对一部分个体进行调查和观察,从而推断出整个总体的特征和规律的方法。
与样本调查相对应的是全面普查,全面普查是指对总体中的每一个个体进行调查和观察。
样本调查相对于全面普查来说,具有成本低、效率高的优势。
通过合理选择和处理样本,可以在保证统计结果的准确性的同时,节省调查成本和时间。
2. 什么是抽样误差?如何减小抽样误差?抽样误差是指样本统计量与总体参数之间的差异。
在样本调查中,由于样本的随机性,样本统计量与总体参数之间会存在一定的差异。
为了减小抽样误差,可以采取以下措施:- 增大样本容量:样本容量越大,样本统计量与总体参数之间的差异越小,抽样误差也就越小。
- 采用分层抽样:将总体划分为若干个层次,然后在每个层次上进行抽样,可以减小抽样误差。
- 采用整群抽样:将总体划分为若干个群体,然后随机选择一部分群体进行调查,可以减小抽样误差。
3. 什么是抽样分布?如何描述抽样分布?抽样分布是指在同样的抽样条件下,重复进行样本调查,得到的样本统计量的分布。
抽样分布的特点是:在样本容量足够大的情况下,抽样分布的形状逐渐接近正态分布。
根据中心极限定理,当样本容量足够大时,样本均值的抽样分布近似服从正态分布。
抽样分布可以通过描述统计量来进行描述。
常用的描述统计量有样本均值、样本方差、样本比例等。
通过计算样本统计量的平均值和标准差,可以对抽样分布进行描述。
4. 什么是置信区间?如何计算置信区间?置信区间是指通过样本统计量对总体参数进行估计的区间。
置信区间的计算方法根据不同的参数类型有所不同。
高等职业教育“十一五”规划教材《统计学》第三章课后习题及答案

高等职业教育“十一五”规划教材《统计学》第三章课后习题及答案高等职业教育“十一五”规划教材《统计学》第三章课后习题及答案一.判断题1.对于连续变量,根据“排除上限”的原则总结其组限。
对。
所谓“上组限不在内”的原则,是对连续变量分组采用重合组限时,习惯上规定一般只包括本组下限变量值的单位,而当个体的变量值恰为组的上限是时,不包括在本组。
2.统计资料的整理不仅是对原始资料的整理,而且还包括对次级资料的整理。
对。
3.确定组限时,最大组上限必须大于最大变量值,最小组下限必须小于最小变量值。
错,这意味着你也可以在封闭的小组中尝试。
4.对统计总体进行分组是由于总体各单位的“同质性”所决定的。
错,将原始数据按照某种标准化分成不同的组别。
5.对连续变量进行分组时,它们的分组极限可以用“不重叠”的形式表示。
对二.单项选择题a组的中值是550组的下限,B组的中值是550组的下限a.550b.650c.700d.750因为它是一个连续变量,所以变量的值是连续的。
由于最后一组的起始下限大于相邻组的中值,请注意这是一个递减变量序列。
一个组的最小值叫做下限。
所以这里的下限实际上是相邻群的上限。
因此,最后一组的下限=相邻组的上限,因此相邻组的上限也为600。
另一个相邻组的组中值为550,因此可以确定相邻组的组距离为100。
重新使用公式:无上限开放组的中值=下限+相邻组的组距离/2,最后一组的中值为650。
2.对一个总体选择三个标志做复合分组,按各个标志所分的组数分别为3、4、5,则所分的全部组数为(a)a、 60b。
12c。
30天。
六3.某小区居民人均月收入最高为5500元,最低为2500元,据此分为6组,形成等距数列,其组距应为(a)a、 500b。
600摄氏度。
550d。
6504.整理统计数据的主要环节是(c)a.编制统计报表b.审核汇总资料c.审核原始资料d.设计整理方案5.对于一年的收入变量序列,分组为10万元以下、10万-20万元、20万-30万元和30万元以上,则为(c)a、10万元应归入第一组b、20万元应归入第二组c、20万元应归入第三组d、30万元应归入第三组6.组号与组距的关系为(a)a.组数越多,组距越小b.级数越多,组距越大c.组数与组距无关d.组数越少,组距越小三.简答题1.简要说明统计排序的意义和内容统计整理,首先要搞清楚教材当中关于统计整理的内容,通常理解的统计整理包括制作次数分布、或者给出排秩、等级的结果,有些还可能包括对数据的类型的判别、编码和对原始数据的必要转换等.有些人认为描述统计也可以视为统计整理的内容,或者是汇总统计的内容.根据统计整理的内容再来回答其意义.主要是可以在正式的描述统计和推断统计之前,预先了解和掌握数据的大致状况,尤其是其分布和次数特征,以便根据数据的类型选择适当的统计方法(不论是描述统计还是推断统计,很重要的一点是依据数据的类型来选择统计法).有些时候,需要对数据进行必要的转换,也是为了便于后继的统计,如由量表原始数据转换成量表得分,原始数据转换成标准分数,或者转换成可统计的某种指标等.简而言之,数据整理就是服务于后续的统计过程,使原始测量数据满足统计方法的需要,为统计方法的选择提供依据。
统计学教程答案第三章

统计学教程 第三章 正态分布22五、习题答题要点(一)单项选择题 1.A 2.C 3. D 4. D 5. A (二)名词解释 1.正态曲线:正态曲线(normal curve)是函数 )2()(2221)(σµπσ−−=X e X f , +∞<<∞−X对应的曲线。
此曲线呈钟型,两头低中间高,左右对称。
2.正态分布:若指标X 的频率曲线对应于数学上的正态曲线,则称该指标服从正态分布(normal distribution)。
通常用记号),(2σµN 表示均数为µ,标准差为σ的正态分布。
3.标准正态分布:均数为0、标准差为1的正态分布被称为标准正态分布(standard normal distribution),通常记为2(0,1)N 。
4.标准化变换:σµ−=X u ,此变换有特性:若X 服从正态分布),(2σµN ,则u 就服从标准正态分布,故该变换被称为标准化变换(standardized transformation)。
(二)简答题 1.医学中常把绝大多数正常人的某指标范围称为该指标的参考值范围,也叫正常值范围。
所谓“正常人”不是指完全健康的人,而是指排除了所研究指标的疾病和有关因素的同质人群。
制定参考值范围的一般步骤: (1)定义“正常人”,不同的指标“正常人”的定义也不同。
(2)选定足够数量的正常人作为研究对象。
(3)用统一和准确的方法测定相应的指标。
(4)根据不同的用途选定适当的百分界限,常用95%。
(5)根据此指标的实际意义,决定用单侧范围还是双侧范围。
(6)根据此指标的分布决定计算方法,常用的计算方法:正态分布法、百分位数法。
2. 三种分布均为连续型随机变量的分布。
正态分布、标准正态分布均为对称分布,对数正态分布是不对称的,其峰值偏在左边。
标准正态分布是一种特殊的正态分布(均数为0,标准差为1)。
统计学第三章习题答案

统计学第三章习题答案1. 描述性统计量:在描述一组数据时,我们通常使用均值、中位数、众数、方差和标准差等统计量。
例如,如果一组数据为 {2, 4, 4, 4, 5, 5, 7, 9},其均值为 (2+4+4+4+5+5+7+9)/8 = 5,中位数为4.5(因为数据是偶数个,所以取中间两个数的平均值),众数为4(出现次数最多),方差为 (1/8) * [(2-5)^2 + ... + (9-5)^2] = 8.5,标准差为方差的平方根,即√8.5。
2. 频率分布表:将数据分组并计算每个组的频数或频率。
例如,如果数据是年龄分布,可以创建如下的频率分布表:| 年龄区间 | 频数 | 频率 || | - | - || 20-25 | 10 | 0.2 || 26-30 | 15 | 0.3 || ... | ... | ... |3. 直方图和箱线图:直方图用于显示数据的分布情况,箱线图则提供了数据的最小值、第一四分位数、中位数、第三四分位数和最大值的快速视图。
例如,对于上述年龄数据,可以绘制相应的直方图和箱线图来观察数据的分布和集中趋势。
4. 概率分布:在统计学中,我们经常使用正态分布来描述数据的分布。
正态分布的数学表达式为N(μ, σ^2),其中μ是均值,σ^2是方差。
例如,如果一个随机变量X服从正态分布N(50, 25),那么X的均值是50,方差是25。
5. 中心极限定理:无论原始数据的分布如何,当样本量足够大时,样本均值的分布将趋近于正态分布。
这个定理是推断统计的基础之一。
6. 假设检验:假设检验是统计推断的一部分,用于确定一个统计假设是否成立。
例如,如果我们要检验一个样本均值是否显著不同于总体均值,可以使用t检验。
具体步骤包括提出原假设和备择假设,选择适当的检验统计量,确定显著性水平,计算p值,并作出结论。
7. 置信区间:置信区间提供了一个范围,我们可以在这个范围内估计总体参数的值。
例如,如果我们有一个样本均值和样本标准差,我们可以计算95%置信区间来估计总体均值的范围。
统计学第三章习题答案

统计学第三章习题答案统计学第三章习题答案统计学是一门研究数据收集、分析和解释的学科,它在各个领域都有广泛的应用。
第三章是统计学中的重要章节,涵盖了概率论和概率分布的基本概念。
本文将为读者提供统计学第三章习题的答案,帮助读者更好地理解和掌握这一章节的内容。
1. 问题:某公司的员工平均年龄为35岁,标准差为5岁。
假设年龄服从正态分布,求年龄在30岁到40岁之间的员工所占的比例。
答案:由于年龄服从正态分布,可以使用标准正态分布表来计算概率。
首先,将年龄转化为标准正态分布,即计算Z值。
Z = (X - μ) / σ,其中X为年龄,μ为平均年龄,σ为标准差。
对于年龄30岁,Z = (30 - 35) / 5 = -1,对应的标准正态分布概率为0.1587。
对于年龄40岁,Z = (40 - 35) / 5 = 1,对应的标准正态分布概率为0.8413。
年龄在30岁到40岁之间的员工所占的比例为0.8413 - 0.1587 = 0.6826,即68.26%。
2. 问题:某商品的销售量服从泊松分布,平均每天销售10件。
求一天销售量不超过5件的概率。
答案:泊松分布是一种描述稀有事件发生次数的概率分布。
对于泊松分布,概率函数为P(X=k) = (λ^k * e^(-λ)) / k!,其中λ为平均发生率。
对于该问题,λ = 10。
我们需要计算一天销售量不超过5件的概率,即P(X<=5)。
可以通过计算P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)来得到答案。
P(X=0) = (10^0 * e^(-10)) / 0! = 0.000045P(X=1) = (10^1 * e^(-10)) / 1! = 0.000453P(X=2) = (10^2 * e^(-10)) / 2! = 0.002266P(X=3) = (10^3 * e^(-10)) / 3! = 0.007553P(X=4) = (10^4 * e^(-10)) / 4! = 0.018883P(X=5) = (10^5 * e^(-10)) / 5! = 0.037767P(X<=5) = 0.000045 + 0.000453 + 0.002266 + 0.007553 + 0.018883 + 0.037767 = 0.067967,即6.80%。
统计学简明教程(第2版)习题答案3.3第三章习题详解

3.3.第三章习题详解一、选择题:1.今有N辆汽车在同一距离的公路上行驶的速度资料,确定汽车平均每小时行驶速度的平均数公式是:( C )A.xN∑B.∑∑fxfC.1Nx∑D.∑∑xmm2.权数对加权算术平均数的影响,取决于( A.B )A. 权数所在组标志值的大小;B. 权数的大小;C. 各组单位数的多少;D. 总体单位数的多少3.是非标志不存在变异时,意味着:( B、C )A. 各标志值遇到同样的成数;B. 所有单位都只具有某属性C. 所计算的方差为0;D. 所计算的方差为0.254.能够综合反映总体各个单位标志值的差异,对总体标志变异程度作全面客观评定的指标有( A、C )A.方差B.算术平均数C.标准差D.全距二、判断题1.甲乙两地,汽车去程时速20公里,回程时速30公里,其平均速度为25公里。
答:错。
这里不能简单地将两个速度加以平均。
因为来去速度不一样,花费的时间不同。
应采用调和平均数的形式计算。
其结果为24公里/小时。
1.权数起作用的前提是各组的变量必须互有差异。
答:正确。
如果变量值没有差异不必加权计算。
只要观察其中一个数值即可。
3.变量同减某个数再同除于另一数然后求其方差,其方差等于原方差乘于除数的平方。
答:正确。
4.与平均数相比,中位数比较不受极端值的影响。
答:正确。
因为确定中位数时,并不考虑极端值。
三、计算题1.甲乙两企业生产三种产品的单位成本和总成本资料如下表,试比较哪个企业的平均成本高,并分析其原因。
解:甲企业平均单位成本=1500/303000/202100/15150030002100++++=19.41元乙企业平均单位成本=1500/301500/203255/15150015003255++++=18.29元从以上结果可以看出,甲企业的平均成本较高。
其主要原因在于甲企业生产的单位成本较低的A 产品数量少于乙企业,单位成本较高的B 产品数量则比乙企业更多。
2.甲、乙两市场农产品价格及成交量资料如下表,试比较哪个市场的平均价格高,并分析其原因。
统计学第三章习题答案

7:30
4
8:00
4
8:30
7
9:00
2
总计
20
(2)
第三章
7
第三章
7、 (1)、
(2)
8
第三章
8、 (1)
(2)
(3)
9
第三章
9、 (1)
接收 29 39 49 59 69 79 89
合计
(2)
频率% 10 16 12 16 20 12 4 100
累积 % 10.00 26.00 38.00 64.00 84.00 96.00 100.00 -
多少,其宽度(表示类别)则是固定的;直方图是用面积表示各组频数的多少,矩形的
高度表示每一组的频数或频率,宽度则表示各组的组距,因此其高度与宽度均有意义。
其次,由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开
排列。最后,条形图主要用于展示分类数据,而直方图则主要用于展示数值型数据。
Stem width: 10.00
Each leaf:
1 case(s)
5、
(1) VAR00003 Stem-and-Leaf Plot
Frequency Stem & Leaf
1.00 2.00 1.00 2.00 2.00
11 . 6 12 . 02 12 . 8 13 . 04 13 . 56
Frequency Stem & Leaf
2.00 6.00 8.00 11.00 9.00 7.00 4.00 2.00 1.00
6. 7. 8. 9. 10 . 11 . 12 . 13 . 14 .
89 233566 01123456 12224556788 002466678 2355899 4678 24 1
统计学 第三章习题参考答案(书上习题)向蓉美

第三章习题参考答案1.数据分布特征可以从集中趋势、离中趋势及分布形态三个方面进行描述。
平均指标是在反映总体的一般水平或分布的集中趋势的指标。
测定集中趋势的平均指标有两类:位置平均数和数值平均数。
位置平均数是根据变量值位置来确定的代表值,常用的有:众数、中位数。
数值平均数就是均值,它是对总体中的所有数据计算的平均值,用以反映所有数据的一般水平,常用的有算术平均数、调和平均数、几何平均数和幂平均数。
变异指标是用来刻画总体分布的变异状况或离散程度的指标。
测定离中趋势的指标有极差、平均差、四分位差、方差和标准差、以及离散系数等。
标准差是方差的平方根,即总体中各变量值与算术平均数的离差平方的算术平方根。
离散系数是根据各离散程度指标与其相应的算术平均数的比值。
矩、偏度和峰度是反映总体分布形态的指标。
矩是用来反映数据分布的形态特征,也称为动差。
偏度反映指数据分布不对称的方向和程度。
峰度反映是指数据分布图形的尖峭程度或峰凸程度。
2.三批产品的平均废品率为:x̅=25+30+45251.5%+302%+451%=1.3%(因为题目给了废品的数量和废品率,可以计算出总的产品数,所以用废品数除以总产品数得到平均废品率)3.该月这批产品的平均废品率为:x̅=100%−√(100%−1.5%)×(100%−2%)×(100%−2.5%)×(100%−1%) 4=1.75%(这道题错的比较多,首先应该选择几何平均(教材P54:几何平均数常用于总量等于各个数据之积的现象求平均数,如发展速度、某些比率的平均),然后不能直接将废品率进行几何平均(教材P55:计算几何平均数的前提是各个变量值的乘积有经济意义,废品率*废品率是没有经济意义的),应该先计算平均合格率(因为经过连续工序的产品的总合格率=每道工序的合格率之积,这是有经济意义的),再用100%减去平均合格率得到平均废品率)4.先对数据做一个从小到大的排序:186 188 190 199 202 207 208 211 213 215 217 218 219 221 222 223 224 226 228 230 231 234 241 242 245 247 251 253 260 272(1)均值:224.1中位数:222.5众数:不存在(2)切尾均值:223.73(3)下四分位数Q1的位置是:30+14=7.75=734第7个数是208,第8个数是211所以下四分位数Q1=208+34×(211−208)=210.25同理,上四分位数Q2的位置是:3(30+1)4=23.25=2314第23个数是241,第24个数是242所以上四分位数Q2=241+14×(211−208)=241.25极差=272-186=86;四分位差=241.25-210.25=31(4)平均差AD=∑|x−x̅|n=16.4467方差σ2=∑(x−x̅)2n=433.4233标准差σ=√∑(x−x̅)2n=20.81885.因为是定序数据,集中趋势应该选择众数和中位数(教材P58:算数平均数只适用于定量数据,中位数适用于定量和定序数据,众数适用于定量、定序和定类数据);离中趋势应该选择异众比率(教材P63:以上的变异指标均只适用于定量数据,对于定性数据,可以计算“异众比率”来衡量集中趋势值众数的代表性)①从中位数来看,甲城市为“一般”,乙城市为“不满意”,甲城市优于乙城市。
《统计学概论》第三章课后练习题答案

《统计学概论》第三章课后练习题答案一、思考题1.什么是统计整理,统计整理的对象是什么?P612.什么是统计分组,它可以分为哪几种形式?P633.简述编制变量数列的一般步骤。
P70-754.统计表分为哪几种?P785.什么是统计分布,它包括哪两个要素?P686.单项式分组和组距公式分组分别在什么情况下运用?P667.如何正确选择分组标志?P658.为什么要进行统计分组?其主要作用是什么?P63(2009.01)二、判断题1.统计整理只能对统计调查所得到的原始资料进行加工整理。
(×)P61【解析】统计整理分为两情况:一种是对原始资料进行整理,另一种是对次级资料即已加工过的现成资料进行在整理。
2.对一个既定总体而言,合理的分组标志只有一个。
(×)P67【解析】复合分组就是对同一总体选择两个或两个以上标志进行的分组。
3.在异距数列中,计算次数密度主要是为了消除组距因素对次数分布的影响。
(√)P74 4.组中值是指各组上限和下限之中点数值,故在任何情况下它都能代表各组的一般水平。
(×)P72【解析】当组内标志值分布均匀时,组中值能代表各组的一般水平(平均水平),当组内标志值分布不均匀时,组中值不能代表各组的一般水平(平均水平)。
5.在变量数列中,组数等于全距除以组距。
(×)(2010.01)P71【解析】变量数列的分组可分为等距分组和异距分组,只有在等距分组的情况下,组数等于全距除以组距。
6.统计分组的关键问题是确定组数和组距。
(×)(2009.10)P65【解析】统计分组的关键问题是选择恰当的分组标志。
7.按数量标志分组的目的,就是要区分各组在数量上的差别。
(×)P66【解析】按数量标志分组的目的,并不是单纯确定各组在数量上的差别,而是要通过数量上的变化来区分各组的不同类型和性质。
8.连续型变量可以作单项式分组或组距式分组,而离散型变量只能作组距式分组。
统计学原理第三章习题答案

第三章统计资料整理一.判断题部分1 :对统计资料进行分组的目的就是为了区分各组单位之间质的不一样。
(×)2:统计分组的重点问题是确立组距和组数。
(×)3:组中值是依据各组上限和下限计算的均匀值,因此它代表了每一组的均匀分派次数。
(× )3 :分派数列的本质是把整体单位总量依据整体所分的组进行分派。
(∨)4:次数分派数列中的次数,也称为频数。
频数的大小反应了它所对应的标记值在整体中所起的作用程度。
(∨ )5:某公司员工按文化程度分组形成的分派数列是一个单项式分派数列。
(×)6:连续型变量和失散型变量在进行组距式分组时,均可采纳相邻组组距重叠的方法确立组限。
(∨ )7:对资料进行组距式分组,是假设变量值在各组内部的散布是均匀的,因此这类分组会使资料的真切性遇到伤害。
(∨ )8:任何一个散布都一定知足:各组的频次大于零,各组的频数总和等于 1 或 100%。
(×)9:按数目标记分组形成的分派数列和按质量标记分组形成的分派数列,都可称为次数散布。
( ∨ )10:按数目标记分组的目的,就是要区分各组在数目上的差别。
(×)11:统计分组此后,掩饰了各组内部各单位的差别,而突出了各组之间单位的差别。
(∨ )12:分组此后,各组的频数越大,则组的标记值关于全体标记水平所起的作用也越大;而各组的频次越大,则组的标记值对全体标记水平所起的作用越小。
(×)二.单项选择题部分1:统计整理的重点在(B)。
A 、对换查资料进行审查B、对换查资料进行统计分组C 、对换查资料进行汇总D、编制统计表2:在组距分组时,关于连续型变量,相邻两组的组限(A)。
A、一定是重叠的B、一定是中断的C、能够是重叠的,也能够是中断的D、一定取整数3:以下分组中属于按质量标记分组的是(B)。
A 、学生按考试分数分组B、产品按品种分组C 、公司按计划达成程度分组D、家庭按年收入分组4 :有一个学生考试成绩为70分,在统计分组中,这个变量值应纳入(B)。
统计学第三章课后答案
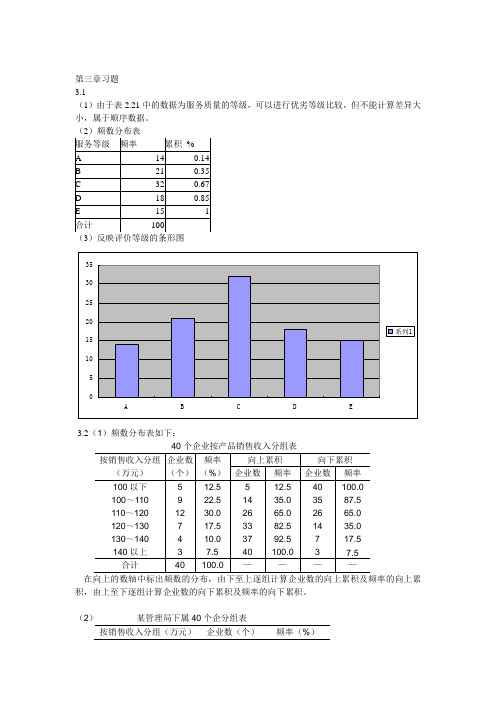
第三章习题 3.1(1)由于表2.21中的数据为服务质量的等级,可以进行优劣等级比较,但不能计算差异大小,属于顺序数据。
(2)频数分布表 服务等级 频率 累积 % A 14 0.14 B 21 0.35 C 32 0.67 D 18 0.85 E151合计100 (3)反映评价等级的条形图5101520253035ABCDE系列13.2(1)频数分布表如下:40个企业按产品销售收入分组表按销售收入分组 (万元) 企业数 (个) 频率 (%) 向上累积 向下累积 企业数 频率 企业数 频率 100以下 100~110 110~120 120~130 130~140 140以上 5 9 12 7 4 3 12.5 22.5 30.0 17.5 10.0 7.5 5 14 26 33 37 40 12.5 35.0 65.0 82.5 92.5 100.0 40 35 26 14 7 3 100.0 87.5 65.0 35.0 17.5 7.5 合计40100.0————在向上的数轴中标出频数的分布,由下至上逐组计算企业数的向上累积及频率的向上累积,由上至下逐组计算企业数的向下累积及频率的向下累积。
(2) 某管理局下属40个企分组表按销售收入分组(万元) 企业数(个)频率(%)先进企业 良好企业 一般企业 落后企业 11 11 9 9 27.5 27.5 22.5 22.5 合计40100.03.3频数分布表如下某百货公司日商品销售额分组表按销售额分组/万元频数/天 频率/% 25~30 30~35 35~40 40~45 45~50 4 6 15 9 6 10.0 15.0 37.5 22.5 15.0 合计40100.03.4茎叶图如下:茎 叶数据个数 1 8 8 9 3 2 0 1 1 3 3 6 8 8 8 9 9 9 12 3 1 3 5 6 9 5 4 1 2 3 6 6 7 6 512743.5(2)频数分布表如下:100只灯泡使用寿命非频数分布按使用寿命分组/小时灯泡个数/只频率/% 650~660 2 2 660~670 5 5 670~680 6 6 680~690 14 14 690~700 26 26 700~710 18 18 710~720 13 13 720~730 10 10 730~740 3 3 740~75033合计100 100(3)直方图(4)茎叶图如下茎叶65 1 866 1 4 5 6 867 1 3 4 6 7 968 1 1 2 3 3 3 4 5 5 5 8 8 9 969 0 0 1 1 1 1 2 2 2 3 3 4 4 5 5 6 6 6 7 7 8 8 8 8 9 970 0 0 1 1 2 2 3 4 5 6 6 6 7 7 8 8 8 971 0 0 2 2 3 3 5 6 7 7 8 8 972 0 1 2 2 5 6 7 8 9 973 3 5 674 1 4 73.6(1)频数分布表如下按重量分组频率/包40~42 242~44 344~46 746~48 1648~50 1752~52 1052~54 2054~56 856~58 1058~60 460~62 3合计100(2)直方图:(3)食品重量的分布基本上是对称的。
统计学第五版第三章课后习题答案

3.5(1)
11
3.5(2)
12
3.5(3)
灯泡使用寿命大 都在690-700小 时,占所有测试 灯泡的26%, 18%在700-710 小时,在680730小时内的灯 泡占所有灯泡的 81%。
13
681-729
3.5(4) 茎叶图:
的映中茎 更的区叶 为状域图 直况为反 观比 映 详频 了 细数 灯 。分 泡
布小使 直时用 方内寿 图,命 反所的 映反集
14
3.6 (1)频数分布表:
15
(2)频数分布直方图:
(3)袋装食品每 袋重量大多分布在 45-55之间,其中 在45-50内的数量 最多,占37%,在 50-55内的食品占 34%,55-60的占 18%,40-45的占 8%,分布在60-65 内的所占比例最小, 占3%。
30
3.14 (1)国内生产总值线图:
31
(2)第一、二、三产业国内生产总值线图:
32
(3)2004年的国内生产总值及其构成数据 饼图:
我国国内生产总值从 1995年到2004年逐年 递增,其中第二产业增 速较快,其次是第三产 业,第一产业增速最慢。 我国2004年国内生产 总值第二产业所占比重 最大,达到53%,第 三产业其次,占32%; 第一产业所占比重最小, 只有15%。
33
3.15 箱线图:
34
如图所示:这几个城市中,相对湿度最低的 为长春,在40以下;相对湿度最高的为广 州,在85以上。平均相对湿度最高的为广 州,达到80以上;最低的为兰州,只有50。 平均相对湿度在60以下的城市有北京、长 春和兰州;在60到70之间的有郑州和西安; 平均相对湿度在70以上的城市有南京、武 汉、广州、成都和昆明。
统计学第三章课后题及答案解析

第三章一、单项选择题1.统计整理的中心工作是()A.对原始资料进行审核 B.编制统计表C.统计汇总问题 D.汇总资料的再审核2.统计汇总要求资料具有()A.及时性 B.正确性C.全面性 D.系统性3.某连续变量分为五组:第一组为40—50,第二组为50—60,第三组为60—70,第四组为70—80,第五组为80以上,依习惯上规定()A.50在第一组,70在第四组 B.60在第二组,80在第五组C.70在第四组,80在第五组 D.80在第四组,50在第二组4.若数量标志的取值有限,且是为数不多的等差数值,宜编制()A.等距式分布数列 B.单项式分布数列C.开口式数列 D.异距式数列5.组距式分布数列多适用于()A.随机变量 B.确定型变量C.连续型变量 D.离散型变量6.向上累计次数表示截止到某一组为止()A.上限以下的累计次数 B.下限以上的累计次数C.各组分布的次数 D.各组分布的频率7.次数分布有朝数量大的一边偏尾,曲线高峰偏向数量小的方向,该分布曲线属于()A.正态分布曲线 B.J型分布曲线C.右偏分布曲线 D.左偏分布曲线8.划分连续变量的组限时,相临组的组限一般要()A.交叉 B.不等C.重叠 D.间断二、多项选择题1.统计整理的基本内容主要包括()A.统计分组 B.逻辑检查C.数据录入 D.统计汇总E.制表打印2.影响组距数列分布的要素有()A.组类 B.组限C.组距 D.组中值E.组数据3.常见的频率分布类型主要有()A.钟型分布 B.χ型分布C.U型分布 D.J型分布E.F型分布4.根据分组标志不同,分组数列可以分为()A.组距数列 B.品质数列C.单项数列 D.变量数列E.开口数列5.下列变量一般是钟型分布的有()A.粮食平均产量的分布 B.零件公差的分布C.大学生身高的分布 D.商品市场价格的分布E.学生成绩的分布6.下列变量呈J型分布的有()A.投资额按利润率的分布 B.60岁以上人口按年龄分组的分布C.经济学中的供给曲线 D.不同年龄人口的死亡率分布E.经济学中的需求曲线三、填空题1.分布在各组的_______叫次数(频数)。
统计学习题第三章答案

统计学习题第三章答案第三章统计数据的概括性描述班级:_________________ 姓名:_________________ 学号:___________________注意:答案请做在下面表格中!一、单项选择题1.数据筛选的主要目的是A.发现数据的错误B.对数据进行排序C.找出所需要的某类数据D.纠正数据中的错误2.落在某一特定类别或族中的数据个数称为A.频数B.频数分布C.频率D.累积频数3.把各个类别及落在其中的相应频数全部列出,并用表格形式表现出来,称为A.频数B.频数分布C.频率D.累积频数4.一个样本或总体中各个部分的数据与全部数据之比称为A.频数B.频率C.比例D.比率5.样本或总体中各不同类别数值之间的比值称为A.频数B.频率C.比例D.比率6.将比例乘以100得到的数值称为A.频率B.百分数C.比例D.比率7.将各有序类别或组的频数逐渐累加起来得到的频数称为A.频率B.累积频数C.比例D.比率8.组中值是A.一个组的上限与下限之差B.一个的上限与下线的中点值C.一个组的最小值D.一个组的最大值9.下面的图形中最适合于描述一组数据分布的图形是A.条形图B.箱线图C.直方图D.饼图10.对于大批量的数据,最适合于描述其分布的图形是A.条形图B.茎叶图C.直方图D.饼图11.由一组数据的最大值,最小值,中位数和两个四分位数5个特征值绘制而成的,反映原始数据分布的图形,称为A.条形图B.茎叶图C.直方图D.箱线图12.下面的哪个图形不适合描述分类数据A.条形图B.饼图C.环形图D.茎叶图13.累积频数分布图适合于描述A.分类数据B.顺序数据C.数值型数据D.品质数据14.将某企业职工的月收入一次分为2000元以下,2000元—3000元,3000元—4000元,4000元—5000元,5000元以上几个组。
第一组的组中值近似为A.2000 B.1000 C.1500 D.250015. 将某企业职工的月收入一次分为2000元以下,2000元—3000元,3000元—4000元,4000元—5000元,5000元以上几个组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章作业参考答案
一、单项选择
1、直接反映总体规模大小的统计指标是(A)
A、总量指标
B、相对指标
C、平均指标
D、变异指标
2、计算结构相对指标时,总体各部分数值与总体数值对比求得的比重之和
(C)
A、小于100%
B、大于100%
C、等于100%
D、小于或大于100%
3、权数对于算术平均数的影响作用,实质上取决于(D)
A、标志值本身的大小
B、标志值数量的多少
C、各组标志值占总体标志总量比重的大小
D、各组单位数占总体单位总数比重的大小
4、对于不同水平的总体其平均指标代表性的测定,往往是用(D)来进行的
A、全距
B、四分位差
C、标准差
D、离散系数
5、某企业的总产值计划比上年提高4%,执行结果提高5%,则总产值计划完成提高程度为(C)A、5%-4% B、5%÷4%
C、(105%÷104%)-100%
D、(104%÷105%)-100%
6、甲、乙两数列的平均数分别为100和14.5,它们的标准差分别为12.8和3.7,则(A)
A、甲数列平均数的代表性高于乙数列
B、乙数列平均数的代表性高于甲数列
C、两数列平均数的代表性相同
D、两数列平均数的代表性无法比较
7、某企业按照计划规定单位成本应比上年下降10%,实际比计划少完成5%,则同上年相比单位成本(B)
A、下降14.5%
B、下降5.5%
C、提高14.5%
D、提高5%
8、分配数列中各组标志值不变,每组次数均增加20%,则加权算术平均数的数值(C)
A、增加20%
B、减少20%
C、没变化
D、无法判断
9、某市某年零售商业网密度=1179000÷10019=108人/个,该指标是(C)
A、总量指标
B、强度相对正指标
C、强度相对逆指标
D、无法判断
10、假定标志值所对应的权数都缩小1/10,则算术平均数(A)
A、不变
B、无法判断
C、缩小百分之一
D、扩大十倍
二、多项选择
1、国内生产总值是(BCE)
A.时点指标
B.时期指标
C.数量指标
D.质量指标
E.价值指标
2、下列属于时点指标的有(ABD)
A.商品库存额
B.在校学生数
C.利税总额
D.全国从业人口数
E.婴儿出生率
3、在相对指标中,子项和母项可以互换的指标有(BCD)
A.结构相对指标
B.比较相对指标
C.比例相对指标
D.强度相对指标
E.计划完成相对指标
4、下列指标中,属于结构相对指标的有(AB)
A.大学生占全部学生的比重
B.某年第三产业增加值在国内生产总值中占比
C.某年人均消费额
D.某企业今年的销售额是去年的125%
E.某年积累额与消费额之比
5、下列有关众数的陈述,错误的有(ACD)
A.是总体中出现最多的次数
B.根据标志值出现的次数决定的
C.易受极端变量值的影响
D.当各组次数分布均匀时为零
E.总体一般水平的代表值
三、计算题
1
2
3
甲市场的平均价格比乙市场要高,其原因在于价格较高的乙、丙品种的销售量占总销售量的比重甲市场(占75%)要高于乙市场(占50%)。
4、今有甲单位职工的平均工资为1050元,标准差为112元;乙单位职工人数及
②计算乙单位职工的平均工资;
总的流通费用率。
(1)平均计划完成程度:
(2)总的流通费用率:
有代表性。
甲单位职工平均工资更乙甲∴〈σσV V
6、某公司一共进行了五期短期国债投资,每期收益继续投资,各期的年收益率分别为3%、2.3%、2%、4%和3.1%,计算这5期的平均年收益率。
