数学竞赛中的三角函数问题
一道三角函数竞赛题的多种解法

一道三角函数竞赛题的多种解法《华罗庚数学奥林匹克竞赛集训教材》第169页有这样一道竞赛题: 求满足下式的锐角x :4sin 347cos 1215=-+-x x由于此题较难,所以笔者将它作为我校高二竞赛培训中的一道压轴考试题,但考试结果较好。
笔者收集了几种颇具代表性的解答,供竞赛教练和同学参考。
解法1:考虑构造余弦定理(此法与教程相同)。
因4)90cos(3432cos 31223123222=-︒-++⨯-+x x在ABC Rt ∆中,设3 =CE ,x ACD =∠,则x BCD -︒=∠90。
如图,||4|||AB BE AE ≥=+,又4412||=+=AB 所以点E 、D 重合。
设y AD =||,于是)]90sin(2sin 32[32132x x S S S BCD ACD ABC -︒+⨯=+==∆∆∆ ︒=⇒︒+=⇒60)30sin(1x x解法2:运用柯西不等式。
因≥⎥⎦⎤⎢⎣⎡-+-⨯⎥⎦⎤⎢⎣⎡+2222sin 347cos 4513x x2sin 3471cos 453⎥⎦⎤⎢⎣⎡-⨯+-⨯≥x x 16sin 347cos 12152=⎥⎦⎤⎢⎣⎡-+-=x x 当且仅当xx sin 3471cos 453-=-,即4cos sin 33=-x x ,因x x x f cos sin 33)(-=在⎪⎭⎫⎝⎛2 ,0π上递增,又4)3(==πf ,则3π=x 。
解法3:分子有理化巧妙化简。
因4sin 347cos 1215=-+-x x ① 则⇒=------4sin 347cos 1215)sin 347()1215(xx x cocxx x x x sin 3cos 32sin 347cos 1215+-=--- ②由(①+②2)整理得:04)sin 3(cos 4)sin 3(cos 2=++-+x x x x则2sin 3cos =+x x ,从而︒=60x .1232CABD E解法4:朴素的化简运算。
奥数挑战三角函数的高级运算

奥数挑战三角函数的高级运算在奥数竞赛中,三角函数的高级运算一直是考察的重点之一。
掌握三角函数的高级运算,不仅可以帮助我们更好地理解数学知识,还能够提高解题的效率和准确性。
在本文中,我将为大家介绍奥数中的三角函数高级运算,并给出一些例题进行详细讲解。
一、三角函数的基本概念在开始介绍三角函数的高级运算之前,我们首先需要明确三角函数的基本概念。
常见的三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。
这些函数可以通过对应的特殊角度值来确定,如0度、30度、45度、60度等。
同时,三角函数也可以表示为一个周期性函数,其取值范围在区间[-1, 1]之间。
二、三角函数的高级运算1. 复合角的三角函数运算复合角是由两个角度相加、相减或相乘而成的新角。
在奥数中,我们经常会遇到复合角的运算,这需要灵活运用三角函数的运算性质。
以sin(A + B)为例,我们可以利用三角函数的加法公式进行计算:sin(A + B) = sinAcosB + cosAsinB同样地,我们还可以利用其他三角函数的加法公式计算cos(A + B)和tan(A + B)。
需要注意的是,复合角的三角函数运算可以通过套用不同的公式来实现,所以我们需要灵活选择适合的公式。
2. 幂函数与三角函数的运算在奥数竞赛中,我们常常需要处理幂函数与三角函数的运算。
例如,我们需要计算sin²x、cos²x和tan²x等。
这时候,我们可以利用三角函数的平方公式进行计算:sin²x = 1/2(1 - cos2x)cos²x = 1/2(1 + cos2x)tan²x = (1 - cos2x) / (1 + cos2x)通过利用这些公式,我们可以将幂函数与三角函数的运算转化为幂函数与幂函数的运算,从而更容易求解。
3. 倍角、半角和三角恒等式倍角、半角和三角恒等式是三角函数的高级运算中常见的一类题型。
初中数学竞赛:锐角三角函数(附练习题及答案)

初中数学竞赛:锐角三角函数古希腊数学家和古代中国数学家为了测量的需要,他们发现并经常利用下列几何结论:在两个大小不同的直角三角形中,只要有一个锐角相等,那么这两个三角形的对应边的比值一定相等.正是古人对天文观察和测量的需要才引起人们对三角函数的研究,1748年经过瑞士的著名数学家欧拉的应用,才逐渐形成现在的sin 、cos 、tg 、ctg 的通用形式.三角函数揭示了直角三角形中边与锐角之间的关系,是数形结合的桥梁之一,有以下丰富的性质: 1.单调性;2.互余三角函数间的关系; 3.同角三角函数间的关系. 平方关系:sin 2α+cos 2α=1; 商数关系:tg α=ααcos sin ,ctg α=ααsin cos ; 倒数关系:tg αctg α=1. 【例题求解】【例1】 已知在△ABC 中,∠A 、∠B 是锐角,且sinA =135,tanB=2,AB=29cm , 则S △ABC = .思路点拨 过C 作CD ⊥AB 于D ,这样由三角函数定义得到线段的比,sinA=135=AC CD ,tanB=2=BDCD,设CD=5m ,AC =13m ,CD =2n ,BD =n ,解题的关键是求出m 、n 的值.注:设△ABC 中,a 、b 、c 为∠A 、∠B 、∠C 的对边,R 为△ABC 外接圆的半径,不难证明:与锐角三角函数相关的几个重要结论:(1) S △ABC =C ab B ac A bc sin 21sin 21sin 21==;(2)R CcB b A a 2sin sin sin ===. 【例2】 如图,在△ABC 中.∠ACB =90°,∠ABC =15°,BC=1,则AC=( ) A .32+ B .32- C .0.3D .23-思路点拨 由15°构造特殊角,用特殊角的三角函数促使边角转化.注:(1)求(已知)非特角三角函数值的关是构造出含特殊角直角三角形.(2)求(已知)锐角角函数值常根据定转化为求对应线段比,有时需通过等的比来转换.【例3】 如图,已知△ABC 是等腰直角三角形,∠ACB =90°,过BC 的中点D 作DE ⊥AB 于E ,连结CE ,求sin ∠ACE 的值.思路点拨 作垂线把∠ACE 变成直角三角形的一个锐角,将问题转化成求线段的比.【例4】 如图,在△ABC 中,AD 是BC 边上的高,tanB=cos ∠DAC , (1)求证:AC =BD ; (2)若sinC=1312,BC=12,求AD 的长. 思路点拨 (1)把三角函数转化为线段的比,利用比例线段证明;(2) sinC=ACAD=1312,引入参数可设AD=12k ,AC =13k .【例5】 已知:在Rt △ABC 中,∠C=90°,sinA 、sinB 是方程02=++q px x 的两个根. (1)求实数p 、q 应满足的条件;(2)若p 、q 满足(1)的条件,方程02=++q px x 的两个根是否等于Rt △ABC 中两锐角A 、B 的正弦?思路点拨 由韦达定理、三角函数关系建立p 、q 等式,注意判别式、三角函数值的有界性,建立严密约束条件的不等式,才能准确求出实数p 、q 应满足的条件.专题训练1.已知α为锐角,下列结论①sin α+cos α=l ;②如果α>45°,那么sin α>cos α;③如果cos α>21,那么α<60°; ④αsin 11)-(sin 2-=α.正确的有 .2.如图,在菱形ABCD 中,AE ⊥BC 于E ,BC=1,cosB135,则这个菱形的面积为 . 3.如图,∠C=90°,∠DBC=30°,AB =BD ,利用此图可求得tan75°= .4.化简(1)263tan 27tan 22-+ = .(2)sin 2l °+sin 22°+…+sin 288°+sin 289°= .5.身高相等的三名同学甲、乙、丙参加风筝比赛.三人放出风筝线长、线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )A .甲的最高B .丙的最高C .乙的最低D .丙的最低6.已知 sin αcos α=81,且0°<α<45°则co α-sin α的值为( )A .23 B .23- C .43 D .43-7.如图,在△ABC 中,∠C =90°,∠ABC =30°,D 是AC 的中点,则ctg ∠DBC 的值是( ) A .3 B .32 C .23 D .43 8.如图,在等腰Rt △ABC 中.∠C =90°,AC =6,D 是AC 上一点,若tan ∠DBA=51,则AD的长为( )A .2B .2C . 1D .229.已知关于x 的方程0)1(242=++-m x m x 的两根恰是某直角三角形两锐角的正弦,求m 的值.10.如图,D 是△ABC 的边AC 上的一点,CD=2AD ,AE ⊥BC 于E ,若BD =8,sin ∠CBD=43,求AE 的长. 11.若0°<α<45°,且sin αcon α=1673,则sin α= .12.已知关于x 的方程0)cos 1(2sin 423=-+⋅-ααx x 有两个不相等的实数根,α为锐角,那么α的取值范围是 .13.已知是△ABC 的三边,a 、b 、c 满足等式))((4)2(2a c a c b -+=,且有035=-c a ,则sinA+sinB+sinC 的值为 .14.设α为锐角,且满足sin α=3cos α,则sin αcos α等于( ) A .61 B .51 C .92 D .10315.如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( ) A .2 B .23C .1D .2116.如图,在△ABC 中,∠A =30°,tanB=23,AC=32,则AB 的长是( ) A .33+ B .322+ C .5 D .29 17.己在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,且c=35,若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根,又方程0sin 5)sin 10(22=+-A x A x 的两实根的平方和为6,求△ABC 的面积.18.如图,已知AB=CD=1,∠ABC =90°,∠CBD °=30°,求AC 的长.19.设 a 、b 、c 是直角三角形的三边,c 为斜边,n 为正整数,试判断n n b a +与n c 的关系,并证明你的结论.20.如图,已知边长为2的正三角形ABC 沿直线l 滚动.(1)当△ABC 滚动一周到△A l B 1C 1的位置,此时A 点所运动的路程为 ,约为 (精确到0.1,π=3.14)(2)设△ABC 滚动240°,C 点的位置为C ˊ,△ABC 滚动480°时,A 点的位置在A ˊ,请你利用三角函数中正切的两角和公式tan(α+β)=(tan α+tan β)÷(1-tan α·tan β),求出∠CAC ˊ+∠CAA ˊ的度数.参考答案。
专题探究课二--中学生数学竞赛中三角函数问题的热点题型

专题探究课二--中学生数学竞赛中三角函数问题的热点题型三角函数是中学数学中的重要内容之一,也是中学生数学竞赛中经常涉及的题型之一。
本文将探讨中学生数学竞赛中三角函数问题的热点题型,以帮助学生更好地应对这类题目。
1. 正弦函数与余弦函数问题1.1 角度转换在数学竞赛中,经常出现要求将弧度转换为角度或者将角度转换为弧度的问题。
考生需要熟悉如何使用正弦函数和余弦函数的定义来进行转换,并灵活运用。
1.2 函数图像理解正弦函数和余弦函数的函数图像是解题的关键。
考生需要熟悉函数图像的特点,如振幅、周期、相位等,并能利用这些特点解决各种类型的问题。
1.3 同角三角函数的关系正弦函数、余弦函数与其他三角函数之间存在一定的关系,如正切函数、余切函数等。
考生需要了解这些关系,并能够利用它们简化计算、求解方程等。
2. 三角恒等式与方程2.1 基本恒等式三角函数的基本恒等式是解题中常用的工具,如正弦函数的和差公式、倍角公式、半角公式等。
考生需要熟悉这些恒等式的推导和应用,并能够利用它们求解各类三角函数方程。
2.2 复杂方程与恒等式的转化在数学竞赛中,有时会出现较为复杂的三角函数方程或者恒等式,考生需要能够灵活运用恒等式的性质将其转化为较为简单的形式,从而更好地解决问题。
2.3 解三角形三角函数的性质可以用来解决三角形相关的问题,如求解三角形的边长、角度等。
考生需要了解三角形的基本概念和性质,并能够运用三角函数解决各类三角形问题。
3. 应用题型数学竞赛中的应用题目常常涉及到三角函数的应用,如航空、导航、建筑等领域。
考生需要能够理解问题背景,灵活运用三角函数的概念和性质解决实际问题,并能够给出合理的解释和推理过程。
总结中学生数学竞赛中三角函数问题是较为常见的题型,要解决这类问题,考生需要熟悉正弦函数和余弦函数的性质,掌握三角函数的基本恒等式和转化方法,并能够灵活应用于各类题目中。
通过不断练习和探索,考生将能够在数学竞赛中取得更好的成绩。
高一三角函数竞赛题(含答案)

竞赛试题选讲:三角函数一1.已知锐角α终边上一点A 的坐标为(2sin3,-2cos3),则角α的弧度数为的弧度数为( )A .3 B .π-3 C .3-2p D . 2p-3 2.若f (sin x )=cos2x ,则(cos )f x 等于(等于( ). A .-cos2xB .cos2xC .-sin2xD .sin2x答.A ∵f (sin x )=cos2x ,∴(cos )=(sin())=cos2()=cos(2)=cos 222f x f x x x x p pp ----3.已知:集合þýüîíìÎ-==Z k k x x P ,3)3(sin |p ,集合,集合þýüîíìÎ--==Z k ky y Q ,3)21(sin |p ,则P 与Q 的关系是 ( ).A .P ÌQ B .P ÉQ C .P=Q D .P ∩Q=φ 答.C∵(21)(3)(3)sinsin[8]sin333k k k pp p p ----=-+=,∴P=Q,∴P=Q4.化简sin(2)cos(2)tan(24)p p -+---所得的结果是(所得的结果是( ))A.2sin 2 B.0B.0 C.2sin 2- D.-1D.-1答.C答.C sin(2)cos(2)tan(24)=sin 2(cos 2)tan 22sin 2p p -+---+-=- 5.设99.9,412.721-==a a ,则21,a a 分别是第分别是第 象限的角象限的角若集合一、二若集合一、二 07.4122,2pp <-<得1a 是第一象限角;是第一象限角;9.994,2pp p <-+<得2a 是第二象限角是第二象限角6.|,3A x k x k k Z pp p p ìü=+££+Îíýîþ,{}|22B x x =-££,则B A =___[2,0][,2]3p-7.某时钟的秒针端点A 到中心点O 的距离为5cm ,秒针均匀地绕点O 旋转,当时间0t =时,点A 与钟面上标12的点B 重合,将,A B 两点的距离()d cm 表示成()t s 的函数,则d =π10sin60t,其中[0,60]t Î。
高中数学竞赛历年真题三角函数部分及答案

C
)
A 焦点在x轴上的椭圆
B 焦点在x轴上的双曲线
C 焦点在y轴上的椭圆
D 焦点在y轴上的双曲线
12,(2005年)设, , 满足0 2 ,若对于任意的 x R
4
cosx cosx cosx 0,则 = 3 。
提示:令 f x cosx cosx cosx 0 ,则f f f 0 ,可解得:
解:原不等式变形为 cos2 x 1 acos x a2 0 对任意的 x R 恒成立。运用换元法,令t=cosx,则
g1 0
可得到
gt t2 1 at a2
0
对任意的
t 1,1 恒成立。只需要
g1 0
即可,又因为a为负数,
所以 a 2
6,(2003年)若
x
5 12
,
3
,则
2
所以
AA1 cos
A 2
2sin B
A cos 2
A 2
sin
B
sinA
B
sin
B
sin C
同理 BB1 sin A sin C,CC1 sin A sin B ,所以原式=2
11,(2005年 )方程 sin
x2 2 sin
3 cos
y2 2 cos
3 1 表示的曲线是(
y
tan
x
2 3
tan x cos x 6 6
的最大值是(
C
)
A 12 2
5
B
11 2 6
C 11 3
6
D 12 3
5
解:
y
tan x 2 tan x 3
cost sin t cost sin t cost
三角函数及解直角三角形竞赛试题
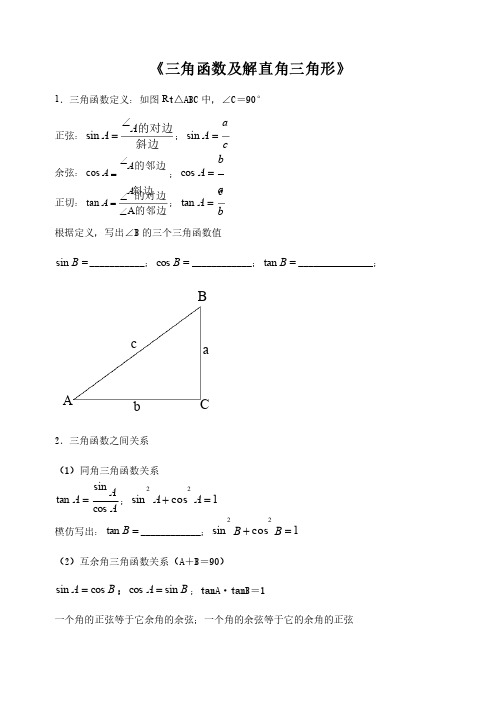
《三角函数及解直角三角形》1.三角函数定义:如图R t △ABC 中,∠中,∠C C =9090°°正弦:斜边的对边A A Ð=sin ;c aA =sin余弦:斜边的邻边A A Ð=cos ;c b A =cos正切:的邻边的对边A tan ÐÐ=A A ;ba A =tan根据定义,写出∠根据定义,写出∠B B 的三个三角函数值的三个三角函数值=B sin ______________________;;=B cos ________________________;;=B tan ______________________________;;cabBCA2.三角函数之间关系.三角函数之间关系 (1)同角三角函数关系)同角三角函数关系AAA cos sintan =;1cos sin 22=+A A模仿写出:=B tan ________________________;;1cos sin 22=+B B (2)互余角三角函数关系()互余角三角函数关系(A A +B =9090))B A cos sin =;B A sin cos =;tanA tanA··tanB tanB==1一个角的正弦等于它余角的余弦;一个角的余弦等于它的余角的正弦3.特殊角的三角函数值3030°、°、°、454545°、°、°、606060°°三角函数三角函数 3030°° 4545°° 6060°° a sina cos a tan4.会设计并根据三角函数关系计算15°、°、757575°角的三角函数°角的三角函数°角的三角函数DC BA5.根据表格中数据总结正弦、余弦、正切的增减性.根据表格中数据总结正弦、余弦、正切的增减性 当0°≤a ≤9090°时,°时,°时,sin a 随a 的增大而的增大而_____________________;;cos a 随a 的增大而的增大而_____________________;;tan a 随a 的增大而的增大而_______ _______6.已知一个三角函数值,求其他三角函数值。
【高中数学竞赛专题大全】 竞赛专题3 三角函数(50题竞赛真题强化训练)解析版+原卷版

【高中数学竞赛专题大全】 竞赛专题3 三角函数 (50题竞赛真题强化训练)一、单选题1.(2018·吉林·高三竞赛)已知()sin 2cos xf x x=+,则对任意x ∈R ,下列说法中错误的是( ) A .()1sin 3f x x ≥B .()f x x ≤C .()f x ≤D .()()0f x f x ππ++-=【答案】A 【解析】 【详解】由()1sin 3f x x ≥得sin (1cos 01cos 0x x x ),-≥-≥,所以该式不一定成立,sinx 有可能是负数,所以选项A 错误; ()sin sin 2cos x f x x x x =≤≤+.所以选项B 正确;()sin 2cos x f x x=+=sin 0||cos (2)x x ---表示单位圆上的点和(-2,0)所在直线的斜率的绝对值,数形结合观察得到()f x ≤C 正确; ()()f x f x ππ++-=sin sin 002-cos 2-cos 2-cos x x x x x-+==,所以选项D 正确.故答案为A2.(2018·四川·高三竞赛)函数()()()sin 1cos 12sin 2x x y x R x--=∈+的最大值为( ).A .2B .1C .12+D【答案】B 【解析】 【详解】因为()sin cos sin cos 122sin cosxx x x x y x ⋅-++=+⋅,令sin cos 4t x x x π⎛⎫⎡=+=+∈ ⎪⎣⎝⎭, 则()21sin cos 12x x t ⋅=-,于是()()22211112.2121t t t y t t --+==-++- 令()(21t g t t t =+,则()()22211t g t t '-=+. 由()0g t '=知1t =-或1.因为(()()111,1,22g g g g =-=-==()g t 的最小值是()112g -=-,所以y 的最大值是11122⎛⎫--= ⎪⎝⎭.故答案为:B3.(2019·全国·高三竞赛)函数[][]sin cos sin cos y x x x x =⋅++的值域为( )([]x 表示不超过实数x 的最大整数). A .{}2,1,0,1,2-- B .{}2,1,0,1-- C .{}1,0,1- D .{}2,1,1--【答案】D 【解析】 【详解】1sin224y x x π⎤⎡⎤⎛⎫=++ ⎪⎥⎢⎥⎣⎦⎝⎭⎦..下面的讨论均视k Z ∈. (1)当222k x k πππ≤≤+时,1y =; (2)当32224k x k ππππ+<≤+时,1y =-; (3)当3224k x k ππππ+<<+时,2y =-; (4)当2x k ππ=+或322k ππ+时,1y =-;(5)当3222k x k ππππ+<<+时,2y =-; (6)当372224k x k ππππ+<<+时,2y =-; (7)当72224k x k ππππ+≤<+时,1y =-. 综上,{}2,1,1y ∈--. 故答案为D4.(2010·四川·高三竞赛)已知条件43p =和条件4:sin cos 3q αα+=.则p 是q 的( ). A .充分但不必要条件 B .必要但不充分条件 C .充要条件 D .既不充分也不必要条件【答案】C 【解析】 【详解】sin cos αα+,所以,p 是q 的充要条件.5.(2018·全国·高三竞赛)在ABC ∆中,A B C ∠≤∠≤∠,sin sin sin cos cos cos A B CA B C++=++则B 的取值范围是( ).A .,32ππ⎛⎫ ⎪⎝⎭B .0,2π⎛⎫ ⎪⎝⎭C .3π D .,43ππ⎛⎫ ⎪⎝⎭【答案】C 【解析】 【详解】由条件有)sin sin sin cos cos cos A B C A B C ++=++2sincos sin 22A C A C B +-⇒︒+ 2cos cos cos 22A C A C B +-⎫=︒+⎪⎭2sin cos222A C A C A C ++-⎛⎫⇒- ⎪⎝⎭ sin B B =. 利用辅助角公式有2sin cossin 3223A C A C B ππ+-⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭2sin cos 262B A C π-⎛⎫⇒- ⎪⎝⎭ 2sin cos 2626B B ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭60602sin cos cos 0222B A C B -︒--︒⎛⎫⇒-= ⎪⎝⎭606060sinsin sin 0244B AC B B A C -︒-+-︒-+-︒⇒︒︒=, 所以,600B ∠-︒=或者600A C B ∠-∠+∠-︒=或者600B A C ∠-∠+∠-︒=, 即60B ∠=︒或者60C ∠=︒或者60A ∠=︒,亦即A B C ∠∠∠、、中有一个为60︒.若60B ∠<︒,则60A B ∠≤∠<︒,所以,只能60C ∠=︒,此时,180A B C ∠+∠+∠<︒,矛盾; 若60B ∠>︒,则60C B ∠≥∠>︒,所以,只能60A ∠=︒,从而,180A B C ∠+∠+∠>︒,亦矛盾. 选C. 二、填空题6.(2018·江西·高三竞赛)若三个角x 、y 、z 成等差数列,公差为π3,则tan tan tan tan tan tan x y y z z x ++=______.【答案】3- 【解析】 【详解】 根据π3x y =-,π3z y =+,则tan x =tan z =所以tan tan x y tan tan y z 22tan 3tan tan 13tan y z x y -=-. 则229tan 3tan tan tan tan tan tan 313tan y x y y z z x y-++==--. 故答案为-37.(2018·广东·高三竞赛)已知△ABC 的三个角A 、B 、C 成等差数列,对应的三边为a 、b 、c ,且a 、c成等比数列,则2:ABC S a ∆=___________.【解析】 【详解】因为A 、B 、C 成等差数列,2B A C =+,3180B A B C =++=︒,因此60B =︒.又因为a 、c成等比数列,所以c qa =,b =由正弦定理()sin sin 120a qa A A ==︒-,整理得22sin A q =221A q q=-,()()232235420q q q q ⎡⎤-+++-=⎣⎦. 所以2q =,1sin 2A =,30A =︒,90C =︒.故212ABC S ab ∆==,所以2:ABC S a ∆=8.(2019·全国·高三竞赛)设锐角α、β满足αβ≠,且()()22cos cos 1tan tan 2αβαβ++⋅=,则αβ+=__________. 【答案】90 【解析】 【详解】由已知等式得()()()()22222tan tan 1tan tan 21tan 1tan αβαβαβ+++⋅=++,()()2tan tan tan tan 10αβαβ-⋅-=.但锐角αβ≠,故tan tan 10αβ⋅-=()cos 090αβαβ⇒+=⇒+=︒.故答案为909.(2021·全国·高三竞赛)函数sin 1tan tan 2x y x x ⎛⎫=+⋅ ⎪⎝⎭的最小正周期为____________.【答案】2π 【解析】 【详解】解析:当=2,x k k Z π∈时,sin 1tan tan 02x y x x ⎛⎫=+⋅= ⎪⎝⎭,当2,x k k Z π≠∈时,sin 1cos sin 1tan cos sin x x y x x x x -⎛⎫=+⋅= ⎪⎝⎭,其中2x k ππ≠+且2x k ππ≠+,画出图象可得函数周期为2π.故答案为:2π.10.(2021·浙江金华第一中学高三竞赛)设()()πcos 2243x f x x x =++为定义在R 上的函数.若正整数n 满足()12021nk f k ==∏,则n 的所有可能值之和为______.【答案】12121 【解析】 【详解】()cos cos cos 2222()41(1)(3)xxxf k k k k k πππ=++=++,111()(11)(13)(21)(23)nk f k --==++++⨯∏00(431)(433)m m ⨯-+-+11(421)(423)m m --⨯-+-+0011(411)(413)(41)(43)m m m m ⨯-+-+++,考虑cos2x π的周期为4,分四种情况考虑(1)当43k m =-(m 为正整数)时,4311111001()(21)(23)(41)(43)(443)(431)(433)m k f k m m m ---==++++⨯-+-+-+∏13(41)2021m -=⨯-=,所以416063,436061m n m -==-=;(2)当42k m =-时,42111()3(41)2021m k f k m ---==⨯+=∏,无正整数解;(3)当41k m =-时,41111()3(41)2021m k f k m ---==⨯+=∏,无正整数解;(4)当4k m =时,41111()3(43)2021m k f k m --==⨯+=∏,此时46060n m ==,综上,6060n =或6061n =, 故答案为:12121.11.(2021·全国·高三竞赛)在ABC 中,1155,tantantan222AC AC B =+-=,则+BC AB 的值为__________. 【答案】7 【解析】 【详解】解析:记ABC 中A 、B 、C 所对的边分别是a 、b 、c , 如图,设内切圆的半径为r ,则tan22A r b c a =+-,tan 22C r a b c =+-,tan 22B r a c b =+-,故5()b c a a b c a c b +-++-=+-,故()57a c b +=, 即7a c +=, 故答案为:712.(2021·全国·高三竞赛)已知ABC 满足2sin sin 2sin A B C +=,则59sin sin A C+的最小值是_______. 【答案】16 【解析】【详解】解析:2sin sin 2sin sin 2(sin sin )A B C B C A +=⇒=-2sincos 4sin cos 2222A C A C C A A C ++-+⇒⋅=⋅sin 2sin tan 3tan 2222A C C A C A+-⇒=⇒=. 令tan 2A t =,则222259595527326sin sin 22191t t t t A C t t t t +++=+=+++216416t t +=≥=.当113,tan ,tan 22222A C t ===时,tan02A C+>,所以180A C +<︒, 故min5916sin sin A C ⎛⎫+= ⎪⎝⎭. 故答案为:1613.(2020·浙江·高三竞赛)已知,,0,2παβγ⎡⎤∈⎢⎥⎣⎦,则cos 2cos cos cos()2cos()αβγαγβγ++-+-+的最大值为___________.【答案】【解析】 【详解】()cos cos 2sin sin 2sin 222γγγααγα⎛⎫-+=+≤ ⎪⎝⎭,同理()cos cos 2sin2γββγ-+≤,故cos 2cos cos cos()6sin22cos()cos αβγαγβγγγ++-+-++≤,而22cos 2sin 3116sin 6sin 12sin 222222γγγγγ⎛⎫+++=--+ -⎪=⎝⎭,因为0sin 2γ≤≤23112sin 222γ⎛⎫--+≤ ⎪⎝⎭当且仅当,24ππγαβ===时,各等号成立,故答案为:14.(2021·全国·高三竞赛)已知三角形ABC 的三个边长a b c 、、成等比数列,并且满足a b c ≥≥.则A ∠的取值范围为___________.【答案】2[,)33ππ【解析】 【详解】由条件2b ac =,结合余弦定理222cos 2a c b B ac+-=,则有11cos (1)22a c B c a =+-≥,从而(0,]3B π∈,而A 是最大角,从而2,33A ππ⎡⎫∈⎪⎢⎣⎭.故答案为:2,33ππ⎡⎫⎪⎢⎣⎭. 15.(2021·全国·高三竞赛)设02πθ<<,且333cos sin 1(cos sin 1)m θθθθ++=++,则实数m 的取值范是___________.【答案】14⎫⎪⎣⎭ 【解析】 【详解】解析:333cos sin 1(cos sin 1)m θθθθ++=++ ()223(cos sin )cos cos sin sin 1(cos sin 1)θθθθθθθθ+-++=++.令cos sin x θθ=+,则4x πθ⎛⎫=+∈ ⎪⎝⎭,且21sin cos 2x θθ-=, 于是2323321112232231(1)2(1)2(1)2(1)2(1)2x x x x x x x m x x x x x ⎛⎫--+ ⎪+-+--⎝⎭=====-+++++, 为然m是上的减函数,所以()(1)f f m f ≤<,即14m ⎫∈⎪⎣⎭.故答案为:41,24⎡⎫⎪⎢⎣⎭. 16.(2021·浙江·高三竞赛)在ABC 中,30B C ∠=∠=︒,2AB =.若动点P ,Q 分别在AB ,BC 边上,且直线PQ 把ABC 的面积等分,则线段PQ 的取值范围为______.【答案】 【解析】 【分析】【详解】如图所示,设,BP x BQ y ==,所以113sin 30222BPQBBCSxy S ︒===,所以23xy =由余弦定理可得,2222222312266PQ x y xy x y x x=+-=+-=+-, 易得[1,2]x ∈,所以2[1,4]x ∈, 所以2367PQ ≤≤,则PQ 的取值范围为[436,7]-. 故答案为:[436,7]-.17.(2021·浙江·高三竞赛)若π3,π44x ⎛⎫∈- ⎪⎝⎭,则函数4sin cos 3sin cos x x y x x +=+的最小值为______.【答案】22【解析】 【分析】 【详解】令(sin cos 224t x x x π⎛⎫=+=+∈ ⎪⎝⎭, ()22213211222t t y t tt t-++===+≥当且仅当12t t =即2t =.故答案为:2218.(2021·全国·高三竞赛)已知等腰直角PQR 的三个顶点分别在等腰直角ABC 的三条边上,记PQR 、ABC 的面积分别为PQR S、ABCS,则PQR ABCS S的最小值为__________.【答案】15【解析】 【分析】 【详解】(1)当PQR 的直角顶点在ABC 的斜边上,如图1所示,则P ,C 、Q ,R 四点共圆,180APR CQR BQR ∠=∠=︒-∠,所以sin sin APR BQR ∠=∠.在APR △、BQR 中分别应用正弦定理得,sin sin sin sin PR AR QR BRA APRB BQR==∠∠. 又45,A B PR QR ∠=∠=︒=,故AR BR =,即R 为AB 的中点. 过R 作RH AC ⊥于H ,则12PR RH BC ≥=, 所以22221124PQR ABCBC SPR SBC BC ⎛⎫ ⎪⎝⎭=≥=,此时PQR ABCS S 的最小值为14.(2)当PQR 的直角顶点在ABC 的直角边上,如图2所示.设1,(01),02BC CR x x BRQ παα⎛⎫==≤≤∠=<< ⎪⎝⎭,则90CPR PRC BRQ α∠=︒-∠=∠=. 在Rt CPR 中,sin sin CR xPR αα==,在BRQ 中, 31,,sin 4x BR x RQ PR RQB QRB B ππαα=-==∠=-∠-∠=-, 由正弦定理,11sin 3sin sin sin cos 2sin sin sin 44x RQ RB x x B RQB απαααπα-=⇔=⇔=∠+⎛⎫- ⎪⎝⎭,因此222111122sin 2cos 2sin PQRx SPR ααα⎛⎫⎛⎫=== ⎪ ⎪+⎝⎭⎝⎭. 这样,()()2222111cos 2sin 512cos sin PQR ABCS Sαααα⎛⎫=≥= ⎪+++⎝⎭,当且仅当arctan 2α=时取等号,此时PQR ABCS S的最小值为15.故答案为:15.19.(2021·全国·高三竞赛)满足方程223cos cos 22cos cos2cos4,[0,2]4x x x x x x π+-=∈的实数x 构成的集合的元素个数为________. 【答案】14 【解析】 【分析】 【详解】将方程变形为,1cos2cos44cos cos2cos42x x x x x +-=-.两边同乘2sin x ,运用积化和差和正弦的倍角公式,得:(sin3sin )(sin5sin3)sin8sin x x x x x x -+--=-,即sin5sin8x x =,故58(21),x x k k π+=+∈Z 或852,x x k k π=+∈Z , 即21,13k x k π+=∈Z 或2,3k x k π=∈Z . 又因为在方程两边同时乘sin x 时,所以引入了增根,x k k π=∈Z (代入原方程检验可得). 再结合[0,2]xπ,得所求结果为14.故答案为:14.20.(2021·全国·高三竞赛)设ABC 的三内角A 、B 、C 所对的边长分别为a 、b 、c ,若2b c a +-=,则2222sin sin 2sin sin sin 22222C B A B Cb c bc +-值为_________. 【答案】1 【解析】 【分析】 【详解】2222sin sin 2sin sin sin 22222C B A B Cb c bc +- 2211(1cos )(1cos )12(cos cos cos 1)22b Cc B bc A B C =-+--++- 22(2)(cos cos 1114)(cos cos 22)b c bc b C b c B c c B b C =++-+-+221(2cos )4b c bc A ++-22221111(2)()142242b c a b c bc ba ca a +-=++--+==. 故答案为:1.21.(2021·全国·高三竞赛)ABC 中,A 、B 、C 的对边分别为a 、b 、c ,O 是ABC 的外心,点P 满足OP OA OB OC =++,若3B π=,且4BP BC ⋅=,则ABC 的面积为_________.【答案】【解析】 【分析】 【详解】由OP OA OB OC =++,得OP OA OB OC -=+,即AP OB OC =+. 注意到()OB OC BC +⊥,所以AP BC ⊥. 同理,BP AC ⊥,所以P 是ABC 的垂心, ()BP BC BA AP BC BA BC ⋅=+⋅=⋅,所以cos 4ac B =,8ac =,所以1sin 2ABC S ac B ==△故答案为:22.(2021·全国·高三竞赛)设ABC 的三个内角分别为A 、B 、C ,并且sin cos sin A B C 、、成等比数列,cos sin cos A B C 、、成等差数列,则B 为____________. 【答案】23π【解析】 【分析】 【详解】依题意,2sin sin cos ,cos cos 2sin A C B A C B =+=, 前一式积化和差可得2cos()2cos cos A C B B -=-,后一式和差化积可得cos2cos 22A C B-=, 所以22cos()2cos18cos 14cos 322A CB AC B --=-=-=+,联立两式得1cos 2B =-或3(舍去),所以23B π=. 故答案为:23π. 23.(2021·全国·高三竞赛)如果三个正实数x y 、、z 满足2225x xy y ++=,22144y yz z ++=,22169z zx x ++=,则xy yz zx ++=_________.【答案】【解析】 【分析】 【详解】易知三个等式可化为2222222222cos1205,2cos12012,2cos12013.x y xy y z yz z x zx ⎧+-︒=⎪+-︒=⎨⎪+-︒=⎩构造Rt ABC ,其中13,5,12AB BC CA ===.设P 为ABC 内一点,使得,,,120PB x PC y PA z BPC CPA APB ===∠=∠=∠=︒. 因BPCCPAAPBABCSSSS++=,则11()sin12051222xy yz zx ++︒=⨯⨯,所以xy yz zx ++=故答案为:24.(2021·全国·高三竞赛)设()cos ()cos 30xf x x =︒-,则()()()1260f f f ︒+︒++︒=_________.【解析】 【分析】 【详解】 因为()cos ()cos 30xf x x =︒-,所以:()()()()cos 60cos ()60cos 30cos 30x xf x f x x x ︒-+︒-=+︒--︒()()()()cos cos 602cos30cos 30cos 30cos 30x x x x x +︒-︒-︒===-︒-︒令:()()()1259s f f f =︒+︒++︒,① ()()()()595821s f f f f =︒+︒++︒+︒,②①+②得::()()()()()()2159258591s f f f f f f =︒+︒+︒+︒++︒+︒=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦所以s =()()()59312592f f f +++=.又()()1cos6060cos 3060f ︒︒==︒=︒-,则()()()()125960f f f f ︒+︒++︒+︒==. 25.(2021·全国·高三竞赛)已知cos cos 1x y +=,则sin sin xy -的取值范围是________. 【答案】⎡⎣【解析】 【分析】 【详解】设sin sin x y t -=,易得2cos in sin 1cos s 2y x y t x --=,即21cos()2t x y -+=. 由于()1cos 1x y -≤+≤,所以21112t --≤≤,解得t≤故答案为:⎡⎣.26.(2020·全国·高三竞赛)在ABC中,6,4AB BC ==,边AC 66sin cos 22A A+的值为_______. 【答案】211256. 【解析】【分析】由中线长公式计算出AC 的长度,然后运用余弦定理计算出cos A 的值,化简后即可求出结果. 【详解】记M 为AC 的中点,由中线长公式得()222242BM AC AB BC +=+,可8AC ==.由余弦定理得2222228647cos 22868CA AB BC A CA AB +-+-===⋅⋅⋅,所以66224224sin cos sin cos sin sin cos cos 22222222A A A A A A A A ⎛⎫⎛⎫+=+-+ ⎪⎪⎝⎭⎝⎭22222sin cos 3sin cos 2222A A A A ⎛⎫=+- ⎪⎝⎭231sin 4A =-213211cos 44256A =+=. 故答案为:211256【点睛】关键点点睛:解答本题关键是能够熟练运用中线长公式、余弦定理、倍角公式等进行计算,考查综合能力.27.(2019·江苏·高三竞赛)已知函数()4sin 23cos 22sin 4cos f x x x a x a x =+++的最小值为-6,则实数a 的值为________ .【答案】【解析】 【详解】令sin 2cos x x t +=,则[t ∈, ∴224sin 23cos 25t x x =++,∴2()()225,[f x g t t at t ==+-∈,当2a-≤a ≥函数的最小值为:(((22256g a =⨯+⨯⨯-=-,解得:a =当2a-a ≤-函数的最小值为:22256g a =⨯+⨯⨯-=-,解得:a =,不合题意,舍去;当2a-<a -< 函数的最小值为:22256222a a a g a ⎛⎫⎛⎫⎛⎫-=⨯-+⨯-⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得:a =.故答案为:28.(2019·福建·高三竞赛)在△ABC中,若AC =AB =25tan 12π=,则BC =____________ .【解析】 【详解】5tan 12π=,得2sin 56tan 122cos 6A A πππ⎛⎫+ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭,即5tan tan 612A ππ⎛⎫+= ⎪⎝⎭,所以5,612A k k πππ+=+∈Z . 结合0A π<<,得5,6124A A πππ+==. 所以由余弦定理,得:2222cos BC AC AB AC AB A =+-⋅⋅⋅22222cos4π=+-⋅2=所以BC29.(2018·全国·高三竞赛)设 A B C ∠∠∠、、是ABC 的三个内角.若sin ,A a =cos B b =,其中,a >0,0b >,且221a b +≤,则tan C =______.【解析】 【详解】因为cos 0B b =>,所以,B ∠为锐角,sin B又221a b +≤,则sin sin A a B =≤. 于是()sin sin A B π-≤. 若A ∠为钝角,则A π-∠为锐角.又B ∠为锐角,则A B A B ππ-∠≤∠⇒∠+∠≥矛盾.从而,A ∠为锐角,且cos A .故sin tan cos A A A ==sin tan cos B B B ==则tan tan tan tan tan 1A B C A B +==⋅-30.(2018·全国·高三竞赛)在ABC ∆中,已知a 、b 、c 分别是A ∠、B 、C ∠的对边.若4cos a b C b a +=,()1cos 6A B -=,则cos C ______. 【答案】23【解析】 【详解】由题设及余弦定理知222222422a b a b c a b c b a ab+-+=⋅⇒+=()()2221cos21cos22sin sin sin 1cos cos 22A BC A B A B A B --⇒=+=+=-+⋅-()2111cos 1cos 21cos 66C C C =+⇒+=-2cos 3C ⇒=或34-. 而()3cos cos 2sin sin 0cos 4C A B A B C ++=⋅>⇒=-(舍去).因此,2cos 3C =. 31.(2018·全国·高三竞赛)若对任意的ABC ∆,只要()+p q r p q R 、+=∈,就有222sin sin sin p A q B pq C +>,则正数r 的取值范围是______.【答案】01r <≤ 【解析】 【详解】设的三边长分别为a 、b 、c . 则222sin sin sin p A q B pq C +>①22211a b c q p⇔+>. 若1r ≤,则()22221111a b q p a b q p qp ⎛⎫+≥++ ⎪⎝⎭ ()22a b c ≥+>;若1r >,令2rp q ==. 当a b =,C π∠→时,2221 22a b rc +→<,式①不成立.综上,01r <≤.32.(2018·全国·高三竞赛)在锐角ABC ∆中,cos cos sin sin A B A B +--的取值范围是______. 【答案】()2,0- 【解析】 【详解】由02A B C π<∠∠∠<、、 22A B AB πππ⇒<∠+∠⇒∠-∠,2B A π∠>-∠.则0cos sin 1A B <<<,0cos sin 1B A <<<故2cos cos sin sin 0A B A B -<+--<. 所以取值范围是()2,0-.33.(2019·全国·高三竞赛)已知单位圆221x y +=上三个点()11,A x y ,()22,B x y ,()33,C x y满足1231230x x x y y y ++=++= .则222222123123x x x y y y ++=++=__________.【答案】32【解析】 【详解】设1cos x α=,2cos x β=,3cos x γ=,1sin y α=,2sin y β= 3sin y γ=. 由题设知ABC ∆的外心、重心、垂心重合,其为正三角形.故()222313cos cos cos cos2cos2cos2222αβγαβγ++=+++=, ()222313sin sin sin cos2cos2cos2222αβγαβγ++=-++=. 故答案为3234.(2021·全国·高三竞赛)在ABC 中,2cos 3cos 6cos A B C +=,则cos C 的最大值为_______________.【解析】 【分析】 【详解】令cos ,cos ,cos A x B y C z ===,则236x y z +=,即223y z x =-. 因为222cos cos cos 2cos cos cos 1A B C A B C +++=, 所以22222212233x z x z x z x z ⎛⎫⎛⎫+-+=-- ⎪ ⎪⎝⎭⎝⎭,整理得222134********z x z z x z ⎛⎫⎛⎫-+-+-= ⎪ ⎪⎝⎭⎝⎭,()2228134Δ44510393z z z z ⎛⎫⎛⎫=----≥ ⎪ ⎪⎝⎭⎝⎭,化简得2413(1)(1)4039z z z z ⎛⎫+-+-≥ ⎪⎝⎭, 于是24134039z z +-≤,得z ≤ 所以cos C.16. 35.(2021·全国·高三竞赛)已知正整数n p 、,且2p ≥,设正实数12,,,n m m m 满足1111npi im ==+∑,则12n m m m 的最小值为_______.【答案】(1)mp n - 【解析】 【分析】【详解】令2tan ,0,,1,2,,2p i i i m x x i n π⎛⎫=∈= ⎪⎝⎭.由题设可得22212cos cos cos 1n x x x +++=,于是:2222121cos cos cos sin n n x x x x -+++=,222221221cos cos cos cos sin n n n x x x x x --++++=,……2222231cos cos cos sin n x x x x +++=,将上述各式利用均值不等式得:2221(1)cos sin n n n x x --≤, 22221(1)cos sin n n n x x ---≤,……2231(1)cos sin n n x x -≤,再把上述n 个不等式相乘,得()2222221212(1)cos cos cos sin sin sin n n n n x x x x x x -≤,即22212tan tan tan (1)n n x x x n ≥-.由于2tan ,1,2,,p i i m x i n ==,故12(1)n pn m mm n ≥-,当且仅当1(1)p i m n =-时上式等号成立.故答案为:(1)mp n -.36.(2021·全国·高三竞赛)设锐角ABC 的三个内角、、A B C ,满足sin sin sin A B C =⋅,则tan tan tan A B C ⋅⋅的最小值为_______.【答案】163【解析】 【分析】 【详解】由题设可知,0,,2A B C π<<,则cos 0,cos 0B C >>.又由A B C π++=及sin sin sin A B C =⋅ 得()()sin sin sin B C B C π-+=⋅, 即()sin sin sin B C B C +=⋅,则sin cos cos sin sin sin B C B C B C +=⋅, ① 由cos 0,cos 0B C >>,①式两边同时除以cos cos B C ⋅, 可得tan tan tan tan B C B C +=⋅. 设tan tan B C s +=,则tan tan B C s ⋅=, 由0,2B C π<<知,tan 0,tan 0B C >>,则0s >. 于是有()tan tan B s B s ⋅-=,故2tan tan 0B s B s -+=,从而有22(tan )(4)244s s sB s s -=-=-.又2(tan )02s B -≥,得(4)04s s -≥,而0s >.所以4s ≥.故4s ≥.tan tan tan tan(())tan tan A B C B C B C π⋅⋅=-+⋅⋅2tan tan tan tan 1tan tan 1B C s B C B C s +=-⋅⋅=-⋅-. 因为4s ≥,于是求tan tan tan A B C ⋅⋅的最小值转化为求函数2()(4)1x f x x x =≥-的最小值.考虑函数221()(4),()(1)2(4)111x x f x x f x x x x x x =≥==-++≥---,即()f x 在[)4,+∞上单调递增,从而()()4,4x f x f ≥≥. 因此()f x 的最小值在4x =时取得,为2416(4)413f ==-. 由tan tan tan tan 4B C B C +=⋅=得,tan tan 2B C ==,从而4tan 3A =, 故当4tan 3A =,tan tan 2BC ==时,tan tan tan A B C ⋅⋅取得最小值163. 故答案为:163. 37.(2019·贵州·高三竞赛)在△ABC 中,0,0GA GB GC GA GB ++=⋅=.则(tan tan )tan tan tan A B CA B+⋅=____________ .【答案】12 【解析】 【详解】设△ABC 中角A 、B 、C 所对的边分别为a 、b 、c .由0,0GA GB GC GA GB ++=⋅=,知G 为△ABC 的重心. 又GA ⊥GB ,所以22222222211221122GA GB c GA GB a GB GA b ⎧⎪+=⎪⎪⎪⎛⎫⎛⎫+=⎨ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎛⎫⎛⎫⎪+= ⎪ ⎪⎪⎝⎭⎝⎭⎩.得到2225a b c +=.故:(tan tan )tan (sin cos cos sin )sin tan tan sin sin cos A B C A B A B C A B A B C++=⋅2sin sin sin cos C A B C =()22222abc ab a b c =+-2222212c a b c ==+-. 故答案为:12.38.(2019·江西·高三竞赛)△ABC 的三个内角A 、B 、C 满足:A =3B =9C ,则cos cos A B +cos cos cos cos B C C A +=____________ .【答案】14-【解析】 【详解】设,3,9C B A θθθ===,由39θθθπ++=得13πθ=,所以cos cos cos cos cos cos S A B B C C A =++9339coscos cos cos cos cos 131313131313ππππππ=++112642108cos cos cos cos cos cos 2131313131313ππππππ⎡⎤⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 注意括号中的诸角度构成公差为213π的等差数列,两边同乘4sin 13π,得到 246810124sin2sincos cos cos cos cos cos 1313131313131313S ππππππππ⎛⎫⋅=+++++⎪⎝⎭35375sin sin sin sin sin sin 131313131313ππππππ⎛⎫⎛⎫⎛⎫=-+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭971191311sin sin sin sin sin sin 131313131313ππππππ⎛⎫⎛⎫⎛⎫-+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ sin13π=-.所以,14S =-.故答案为:14-.三、解答题39.(2021·全国·高三竞赛)在ABC 中,三内角A 、B 、C 满足tan tan tan tan tan tan A B B C C A =+,求cos C 的最小值.【答案】23【解析】 【分析】 【详解】由tan tan tan tan tan tan A B B C C A =+,得: sin sin sin sin sin sin cos cos cos cos cos cos A B B C C AA B B C C A =+sin (sin cos sin cos )cos cos cos C B A A B A B C +=sin sin()cos cos cos C A B A B C+=2sin cos cos cos C A B C=, 所以2sin sin cos sin A B C C =.由正余弦定理,得22222a b c abc ab+-=, 所以2222222sin 223,cos sin sin 333C c a b ab a b c C A B ab ab ab ++====≥=, 当且仅当a b =时等号成立,所以cos C 的最小值为23.40.(2021·全国·高三竞赛)解关于实数x 的方程:{}202020201arctan k x x k==∑(这里{}[][],x x x x =-为不超过实数x 的最大整数) 【答案】{}0 【解析】 【分析】 【详解】(1)当0x <时,{}202020201arctan 0(1,2,,2020),arctan 0k x x k x k k =<=<≤⋅⋅⋅∑,此时原方程无解.(2)当0x =时,有{}202020001arctan0k x x k===∑. (3)当01x <<时,令arct ()1)2an (0x xf x x =-<<,则211()0(01)12f x x x '=-><<+, 故()f x 在()0,1上递增.有()()00f x f >=,即arctan 2x x > 于是,此时{}202020204202020201111125arctan 2224k k k x x x xx x x k k k =====>>=>∑∑∑,即1x >,矛盾.故无解.(4)当1≥x 时,注意到111123tan(arctan arctan )112316++==-, 且由110arctan arctan arctan1arctan1232π<+<+=,知11arctan arctan 234+=π.则{}20202020202011111arctan arctan arctan1arctan arctan 1232k k x x k k π===≥>++=>∑∑,与{}202001x <<,矛盾.故此时无解.由(1)(2)(3)(4),知原方程的解集为{}0.41.(2021·全国·高三竞赛)已知点(2cos ,sin ),(2cos ,sin ),(2cos ,sin )A B C ααββγγ,其中,,[0,2)αβγπ∈,且坐标原点O 恰好为ABC 的重心,判断ABCS是否为定值,若是,求出该定值;若不是,请说明理由.【答案】三角形ABC【解析】 【分析】 【详解】先证明一个引理:若()()1122,,,,(0,0)A x y B x y C ,则122112ABCS x y x y =-. 因为()()1122,,,CA x y CB x y ==, 所以21cosCA CB C CA CBx⋅==⨯所以sin C ==所以:1sin 2ABCSCACB C =⋅⋅ 12211122x y x y ==-回到原题,连结OA 、OB 、OC ,则: ABCOABOBCOACSSSS=++112cos sin 2sin cos 2cos sin 2sin cos 22αβαββγβγ=-+- 12cos sin 2sin cos 2αγαγ+- sin()sin()sin()αββγαγ=-+-+-.由三角形的重心为原点得sin sin sin 0,2cos 2cos 2cos 0.αβγαβγ++=⎧⎨++=⎩即sin sin sin ,cos cos cos .αβγαβγ+=-⎧⎨+=-⎩ 所以两式平方相加可得1cos()2αβ-=-,所以sin()αβ-=,同理sin()sin()βγαγ-=-=, 所以sin()sin()sin()3ABCSαββγαγ=-+-+-==故三角形ABC 42.(2019·上海·高三竞赛)已知,0,2A B π⎛⎫∈ ⎪⎝⎭,且sin sin A B =()sin A B +,求tanA 的最大值.【答案】43【解析】 【详解】由题设等式可得sin sin (sin cos cos sin )A B A B A B =+, 所以tan sin (tan cos sin )A B A B B =+. 令tan t A =,则2sin cos sin t t B B B =+,于是2sin 21cos2t t B B =+-,21)t B θ--, 这里θ是锐角,sin θ=.所以2|21|1t t -+,注意到t >0,可得43t. 当413arctan ,arcsin 3225A B π⎛⎫==+ ⎪⎝⎭时,题设等式成立.所以,tanA 的最大值为43.43.(2018·全国·高三竞赛)在ABC ∆中,证明:coscos cos cos cos cos 222222cos cos cos 222B C C A A BA B C ⋅⋅⋅++≥ABC ∆为正三角形时,上式等号成立.【答案】见解析 【解析】 【详解】如图,对ABC ∆,作其相伴111A B C ∆. 则11cos 2B E B B O =,111cos 2C G C A C =,111cos 2C G A B C =. 故11111111111111coscos 22cos2B E C G B C B O A C B E B C A C G B O A C B C ⋅⋅⋅==⋅. 由O 、E 、1C 、F 四点共圆得11111B E B C B O B F ⋅=⋅则111cos cos 22cos 2B C B F A AC ⋅=.类似地,111coscos 22cos 2B C C G A A B ⋅=,111cos cos 22cos2B C A E A B C ⋅= 记111A B C ∆的三边111111B C C A A B 、、分别为111a b c 、、,相应边上的高111A E B F C G 、、分别为123h h h 、、,且其面积为S 、则312222222111111111cos cos 222111222cos2B C h h h S S S S A a b c a b c a b c ⋅⎛⎫∑=++=++=++ ⎪⎝⎭.其中,“∑”表示轮换对称和.由熟知的不等式222111111334a b c S++≥,得coscos 33222cos 2B CA ⋅∑≥. 当且仅当ABC ∆为正三角形时,上式等号成立.44.(2019·全国·高三竞赛)在△ABC 中,若cos cos 2sin sin A BB A+=,证明:∠A +∠B =90° 【答案】见解析 【解析】 【详解】由sin cos sinB sin sin sin sinB 0A A cosB A B A ⇒⋅+⋅-⋅-⋅=()()sin cos sin sinB cosB sinA 0A A B ⇒-+-=()()sinA sin 90sinB sinB sin 90sinA 0A B ⎡⎤⎡⎤⇒︒--+︒--=⎣⎦⎣⎦909090902sinA cossin 2sin cos sin 2222A B A B B A B AB ︒-+︒--︒-+︒--⇒⋅⋅+⋅⋅ 902sin sin cos 45?sin cos 450222A B A B A B A B ⎡⎤︒----⎛⎫⎛⎫⎛⎫⇒⋅︒-+⋅︒+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=0902A B ︒--⎛⎫⇒ ⎪⎝⎭sin cos sin sin cos sin 02222A B A B A B A B A B ⎡⎤----⎛⎫⎛⎫++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.()()90cos sin sin sin sin sin 0222A B A B A B A B A B ︒----⎛⎫⎡⎤⇒++-= ⎪⎢⎥⎝⎭⎣⎦222cos sin 2sin cos 02222A B A B A B A B -+-+⋅+⋅>sin cos sin sin cos sin 02222A B A B A B A B A B ⎡⎤----⎛⎫⎛⎫++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. 90sin 02A B ︒--⎛⎫⇒= ⎪⎝⎭ 90A B ⇒∠+∠=︒()10A a a a ⎛⎫> ⎪⎝⎭,. 45.(2018·全国·高三竞赛)已知ABC 的三个内角满足2A C B ∠+∠=∠,cos cos A C +=cos 2A C -的值.【解析】 【详解】由题设知60,B ∠= 120A C ∠+∠=︒. 设2A Cα∠-∠=,则2A C α∠-∠=,于是,60,60A C αα∠=+∠=-. 故()()cos cos cos 60cos 602cos60cos cos A C αααα+=++-=⋅=.()()()260cos 6032cos2cos120cos cos604αααα+⋅-⎫==+︒=-⎪⎭.故223cos cos 2cos 04αααα⎫=--⇒+-=⎪⎭()(32cos 0αα⇒+=.若3cos 1αα+⇒=<-舍,从而,2cos 0cos αα=⇒=. 46.(2018·全国·高三竞赛)已知函数()()()3333sin cos sin cos f x x x m x x =+++在0,2x π⎡⎤∈⎢⎥⎣⎦有最大值2.求实数m 的值.【答案】1m =- 【解析】 【详解】注意到,()()233sin cos sin cos sin cos 3sin cos x x x x x x x x ⎡⎤+=++-⋅⎣⎦()()()223sin cos sin cos sin cos 12x x x x x x ⎧⎫⎡⎤=++-+-⎨⎬⎣⎦⎩⎭.令sin cos 4t x x x π⎛⎫⎡=+=+∈ ⎪⎣⎝⎭. 则()()()223333931222f x t t t mt m t t g t ⎡⎤⎛⎫=--+=-+∆ ⎪⎢⎥⎣⎦⎝⎭.由()233322g t m t ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦',有以下两种情形.(1)32m ≥. 由()0g t '>,知()max 92322g t g m ⎫==-+=⎪⎭ 230m ⇒-<,矛盾.(2)32m <. 若32132m -<-,即0m <时,()()max 1321g t g m m ==+=⇒=-;若32132m -≤≤-3012m ⎛≤≤ ⎝⎭时, ()max271523248g t g m m ==⇒=-⇒=-,矛盾;若3232m ->-33122m ⎛<< ⎝⎭时,()max 3 222g t g m ⎫==+=⎪⎭34m ⇒=-. 综上,1m =-.47.(2019·全国·高三竞赛)求(),f xy =【答案】42 【解析】 【详解】注意到,2cos472cos 26x x +=+ ()2222cos 16x =-+ ()428cos cos 1x x =-+,同理,()42cos478cos cos 1y y y +=-+,而22cos4cos48sin sin 6x y x y +-⋅+ ()()22cos47cos478sin sin 8x x x y =+++-⋅-()428cos cos 1x x =-++ ()428cos cos 1y y -+- ()()2281cos 1cos 8x y ---()44228cos cos 8cos cos x y x y =+-⋅,()()42424422,8cos cos 1cos cos 1cos cos cos cos f x y x x y y x y x y =-++-+++-⋅,如图,作边长为1的正SAB ∆、SBC ∆、SCD ∆,在SB 、SC 上分别取点X 、Y 使得2cos SX x =,2cos SY y =,联结AX 、AY ,则(),f x y ()8AX XY YD =++,其最小值就是线段ASD 的长度,即当2x y π==时,min 2842f ==.48.(2021·全国·高三竞赛)求证:对任意的n +∈N ,都有21111arctan arctan arctanarctan 37114n n n π++++=+++.【答案】证明见解析. 【解析】 【详解】由于1111tan arctan 1412111n n n n n π-⎛⎫+-== ⎪++⎝⎭+⨯+,只需证: 2111arctan arctan arctanarctan 3712nn n n +++=+++.设*(),2nf n n n =∈+N ,注意到:21()(1)12111()(1)1121n n f n f n n n n n f n f n n n n n ----++==-+-+++⋅++,即21tan[arctan ()arctan (1)]tan arctan 1f n f n n n ⎛⎫--= ⎪++⎝⎭, 又由于()f n 、(1)f n -、211n n ++均大于0,则21[arctan ()arctan (1)],,arctan 0,2212f n f n n n πππ⎛⎫⎛⎫--∈-∈ ⎪ ⎪++⎝⎭⎝⎭, 从而21arctanarctan ()arctan (1)1f n f n n n =--++. 所以2111arctan arctan arctan371n n +++=++arctan ()arctan (0)arctan 2nf n f n -=+,所以对任意的n +∈N ,都有21111arctan arctan arctanarctan 37114n n n π++++=+++.49.(2021·全国·高三竞赛)设αβγ、、是锐角,满足αβγ+=,求证:cos cos cos 1αβγ++-≥【答案】证明见解析 【解析】 【详解】2cos cos cos 12coscos2sin 222αβαβγαβγ+-++-=⋅- 2cos cos sin sin 2222γαβγαβ-+⎛⎫=⋅-⋅ ⎪⎝⎭.由于0,224αβγπ+⎛⎫=∈ ⎪⎝⎭,所以cos cos cos sin 2222αβαβγγ-+>=>. 由恒等式()()222222()()ac bd ad bc a b c d ---=--可知,如果0a b >>且0c d >>,则ac bd -≥cos cossinsin2222γαβγαβ-+⋅≥-⋅===所以cos cos cos 1αβγ++-≥50.(2019·河南·高二竞赛)锐角三角形ABC 中,求证:cos()cos()cos()8cos cos cos B C C A A B A B C ---.【答案】证明见解析 【解析】 【详解】 原不等式等价于cos()cos()cos()8cos cos cos B C C A A B A B C---.在三角形ABC 中,tan tan tan tan tan tan A B C A B C ++=, cos()sin sin cos cos cos sin sin cos cos B C B C B C A B C B C -+=-tan tan 1tan tan 1B C B C +=-tan (tan tan 1)tan tan A B C B C +=+2tan tan tan tan tan A B CB C++=+.令tan tan tan tan tan tan A B xB C y C A z+=⎧⎪+=⎨⎪+=⎩,则原不等式等价于()()()8z x y z x y yxz +++. 而上式左边228zx yxz⋅=,故原不等式得证【高中数学竞赛专题大全】 竞赛专题3 三角函数 (50题竞赛真题强化训练)一、单选题1.(2018·吉林·高三竞赛)已知()sin 2cos xf x x=+,则对任意x ∈R ,下列说法中错误的是( ) A .()1sin 3f x x ≥B .()f x x ≤C .()f x ≤D .()()0f x f x ππ++-=2.(2018·四川·高三竞赛)函数()()()sin 1cos 12sin 2x x y x R x--=∈+的最大值为( ).A .2B .1C .12+D3.(2019·全国·高三竞赛)函数[][]sin cos sin cos y x x x x =⋅++的值域为( )([]x 表示不超过实数x 的最大整数). A .{}2,1,0,1,2-- B .{}2,1,0,1-- C .{}1,0,1-D .{}2,1,1--4.(2010·四川·高三竞赛)已知条件43p =和条件4:sin cos 3q αα+=.则p 是q 的( ). A .充分但不必要条件 B .必要但不充分条件 C .充要条件D .既不充分也不必要条件5.(2018·全国·高三竞赛)在ABC ∆中,A B C ∠≤∠≤∠,sin sin sin cos cos cos A B CA B C++=++则B 的取值范围是( ).A .,32ππ⎛⎫ ⎪⎝⎭B .0,2π⎛⎫ ⎪⎝⎭C .3π D .,43ππ⎛⎫ ⎪⎝⎭二、填空题6.(2018·江西·高三竞赛)若三个角x 、y 、z 成等差数列,公差为π3,则tan tan tan tan tan tan x y y z z x ++=______.。
高中数学竞赛与强基计划试题专题:三角函数

高中数学竞赛与强基计划试题专题:三角函数一、单选题1.(2021·北京·高三强基计划)已知O 为ABC 的外心,,AB AC 与OBC △的外接圆分别交于点D ,E .若DE OA =,则OBC ∠=()A .30︒B .45︒C .60︒D .以上答案都不对2.(2020·北京·高三强基计划)设等边ABC 的边长为1,过点C 作以AB 为直径的圆的切线交AB 的延长线于点D ,AD BD >,则BCD △的面积为()ABCD .前三个答案都不对3.(2020·北京·高三强基计划)()AB.CD .前三个答案都不对4.(2020·北京·高三校考强基计划)使得sin115cos1n >+成立的最小正整数n 的值为()A .3B .4C .5D .65.(2020·北京·高三校考强基计划)在ABC中,90,1,A AB AC ∠=︒==点P 满足0||||||PA PB PCPA PB PC ++=,则()A .120APC ∠=︒B .120APB ∠=︒C .||2||PB PA =D .||2||PC PB = 6.(2020·北京·高三校考强基计划)设,αβ为锐角,且sin cos()sin ααββ+=,则tan α的最大值为()本号资*料全部来源于微信公众号:数学第六感A.4BC .1D7.(2020·北京·高三校考强基计划)212lim arctan nn k k →∞==∑()A .3π4B .πC .5π4D .3π28.(2020·北京·高三校考强基计划)sin arctan1⎛+= ⎝⎭()A .1BCD .22二、多选题9.(2020·北京·高三校考强基计划)设ABC 的三边长a ,b ,c 都是整数,面积是有理数,则a 的值可以为()A .1B .2C .3D .410.(2022·贵州·高二统考竞赛)如图,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复上述操作(其中123∠∠∠==),得到四个小正方形,,,A B C D ,记它们的面积分别为,,,A B C D S S S S ,则以下结论正确的是()A .A DBC S S S S +=+B .AD B C S S S S ⋅=⋅C .2A D B S S S + D .2D A CS S S +<11.(2020·湖北武汉·高三统考强基计划)设ABC 的内角,,A B C 的对边分别为,,a b c .若{3cos (sin 1)0a cb Cc b C +=+-=),则()A .3B π=B .4B π=C .ABC 3316D .ABC 332三、填空题12.(2021·北京·高三强基计划)在锐角ABC 中,tan tan 2tan tan 3tan tan A B B C C A ++的最小值是_________.13.(2022·江苏南京·高三强基计划)设0,2x π⎛⎫∈ ⎪⎝⎭,则函数2sin cos y x x =的最大值为___________.14.(2022·江苏南京·高三强基计划)在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知2cos cos sin sin sin a C b A a A B c A -=-,则tan A 的值为___________.15.(2022·江苏南京·高三强基计划)函数4153y x x =--___________.16.(2021·全国·高三竞赛)设02πθ<<,且333cos sin 1(cos sin 1)m θθθθ++=++,则实数m 的取值范围是___________.17.(2020·浙江·高三竞赛)已知,,0,2παβγ⎡⎤∈⎢⎥⎣⎦,则cos 2cos cos cos()2cos()αβγαγβγ++-+-+的最大值为___________.18.(2021·全国·高三竞赛)函数sin 1tan tan 2x y x x ⎛⎫=+⋅ ⎪⎝⎭的最小正周期为____________.19.(2021·全国·高三竞赛)已知ABC 满足2sin sin 2sin A B C +=,则59sin sin A C+的最小值是_______.20.(2021·全国·高三竞赛)在ABC 中,1155,tantantan222AC A C B =+-=,则+BC AB 的值为__________.21.(2021·浙江·高三竞赛)若π3,π44x ⎛⎫∈- ⎪⎝⎭,则函数4sin cos 3sin cos x x y x x +=+的最小值为______.22.(2022·福建·高二统考竞赛)已知α,β,()0,γπ∈,且,则cos cos sin 2αβγ++的最大值为___________.23.(2022·浙江·高二竞赛)已知锐角ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且cos 2b aC a-=,则角A 的取值范围是______.24.(2022·北京·高三校考强基计划)在ABC 中,()2ABC cS a b =- ,其外接圆半径2R =,且())224sin sin sin A B b B -=-,则sinsin 22A B C-+=___________.25.(2022·北京·高三校考强基计划)在梯形ABCD 中,,AD BC M ∥在边CD 上,有ABM CBD BCD ∠∠∠==,则AMBM取值范围为___________.26.(2022·北京·高三校考强基计划)若ABC 三边长为等差数列,则cos cos cos A B C ++的取值范围是___________.27.(2021·全国·高三竞赛)在ABC 中,2cos 3cos 6cos A B C +=,则cos C 的最大值为_______________.四、解答题28.(2021·全国·高三竞赛)求证:对任意的n +∈N ,都有21111arctan arctan arctan arctan 37114n n n π++++=+++ .29.(2022·新疆·高二竞赛)直角三角形DEF 的三个顶点分别在等边三角形ABC 的边,,AB BC CA 上,且=90,=30DEF EDF ∠∠︒︒,求DEFABCS S 的最小值.30.(2019·河南·高二校联考竞赛)锐角三角形ABC 中,求证:cos()cos()cos()8cos cos cos B C C A A B A B C --- .高中数学竞赛与强基计划试题专题:三角函数答案一、单选题1.(2021·北京·高三强基计划)已知O 为ABC 的外心,,AB AC 与OBC △的外接圆分别交于点D ,E .若DE OA =,则OBC ∠=()A .30︒B .45︒C .60︒D .以上答案都不对【答案】B【分析】利用圆周角和圆心角的关系可求OBC ∠的大小.【详解】如图,连结BE .由于DE OA OB OC ===,于是弧BO 分别与弧DE 、弧OC 相等,进而可得弧BD 与弧OE 相等、弧OD 与弧CE 相等,进而190902EBC OBD AOB ECB ∠=∠=︒-∠=︒-∠,从而90BEC ∠=︒,因此BC 是OBC △外接圆的直径,进而45OBC ∠=︒.2.(2020·北京·高三强基计划)设等边ABC 的边长为1,过点C 作以AB 为直径的圆的切线交AB 的延长线于点D ,AD BD >,则BCD △的面积为()A .16-B .16-C .16D .前三个答案都不对【答案】C【分析】利用射影定理可求4OD =,故可求BCD △的面积.【详解】如图,设题中圆的圆心为O ,CD 与圆O 切于点T ,连结,CO TO ,则12OC OT ==,于是OD =,从而1112242216BCD S BD OC ⎛⎫=⋅⋅=⨯-⨯= ⎪⎝⎭△.3.(2020·北京·高三强基计划)222323cos cos 523cos cos 4sin θθθθθ++-++()A 23B .223C 223D .前三个答案都不对【答案】D【分析】利用基本不等式可求代数式的最大值.【详解】题中代数式为223cos 123cos 10(3cos 1)10(3cos 1)33θθθ+++-++-++111033≤+21023+=210(3cos 1)103cos 3cos 123θθθ-+=⇒+103.4.(2020·北京·高三校考强基计划)使得sin115cos1n >+成立的最小正整数n 的值为()A .3B .4C .5D .6【答案】C【分析】先证明3,1s π02in 6x x x x ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝-⎭>成立,再结合2()1f x x x =+-21151sin1sin 1+-n 的值.【详解】根据题意,有21151sin1sin 1n >+-记2()1f x x x =+-,则函数()f x 在(1,)+∞上是单调递增函数.设()31sin 6g x x x x =-+,则:()2222sin 2sin sin 11cos 12222222g x x x xx x x x x ⎛⎫⎛⎫=-=-+ ⎪⎪⎝⎭+⎝=-⎭',当0,2x π⎛⎫∈ ⎪⎝⎭时,有sin 22x x >,故()0g x '>,故()g x 为0,2π⎛⎫⎪⎝⎭上的增函数,故()()30100sin 6g x g x x x >=⇔->+.接下来利用当0,2x π⎛⎫∈ ⎪⎝⎭时,31sin 6x x x >-以及正弦函数的单调性估计sin1.511sin1sin 663π=-<<<有16661045sin15553f f f ⎛⎫⎛⎫<=<<=++< ⎪ ⎪⎝⎭⎝⎭,因此使得不等式成立的最小正整数n 的值为5.5.(2020·北京·高三校考强基计划)在ABC 中,90,1,A AB AC ∠=︒==点P 满足0||||||PA PB PCPA PB PC ++=,则()A .120APC ∠=︒B .120APB ∠=︒C .||2||PB PA =D .||2||PC PB = 【答案】ABCD【分析】根据题设条件可得P 为ABC 的费马点,如图,以,AB BC 为边作等边三角形,ABE BCD ,可证,PAB BAD △∽△PBC BEC △∽△,故可判断各项的正误.【详解】根据题意,,,PA PB PC方向上的单位向量之和为零向量,因此120APB BPC CPA ∠=∠=∠=︒,进而P 为ABC 的费马点.如图,以,AB BC 为边作等边三角形,ABE BCD ,则60BPD BCD ∠=∠=︒,故,,,B P C D 四点共圆,故PBC PDC ∠=∠,故D PBA A B ∠=∠,故12PA BA PAB BAD PB BD ⇒==△∽△,同理,12PB BE PBC BEC PC BC ⇒==△∽△,因此所有选项均正确.6.(2020·北京·高三校考强基计划)设,αβ为锐角,且sin cos()sin ααββ+=,则tan α的最大值为()A .4B C .1D 【答案】A【分析】利用基本不等式可求最大值.【详解】解法一:由sin cos()sin ααββ+=得2cos cos sin sin sin sin αββαβα-=,所以2cos sin tan sin tan ββαβα-=.因为,αβ均为锐角,所以22cos sin tan 1tan 11sin 12tan 42tan tan βββαββββ===≤+++,当且仅当tan β=tan α的最大值是4.解法二:由sin cos()sin ααββ+=得:1cos()sin sin [sin(2)sin ]sin 2αββααβαα+=⇒+-=,于是11sin sin(2)33ααβ=+≤,等号当111arcsin ,arccos 323αβ==时取得,因此tan α的最大值为1tan arcsin 34=.7.(2020·北京·高三校考强基计划)212lim arctan nn k k →∞==∑()A .3π4B .πC .5π4D .3π2【答案】A【分析】利用裂项相消法可求数列的和,再根据基本极限可求题设中数列的极限.【详解】根据题意,有22(1)(1)arctanarctan arctan(1)arctan(1)1(1)(1)k k k k k k k +--==+--++-,于是211]2lim arctan lim arctan(1)arctan(1)nnn n k k k k k →∞→∞===+--∑∑()()lim arctan 1arctan arctan1arctan 0n n n ∞→=++--3π4=.8.(2020·北京·高三校考强基计划)sin arctan1arcsin arccos 510⎛++= ⎝⎭()A .1B.10C.5D.2【答案】A【分析】利用复数的乘法可求3个角的和的正弦值.【详解】arctan1,arcsin510分别是复数1i,2i,3i +++的辐角,于是题中代数式为复数(1i)(2i)(3i)10i z =+++=的辐角的正弦值,为1.二、多选题9.(2020·北京·高三校考强基计划)设ABC 的三边长a ,b ,c 都是整数,面积是有理数,则a 的值可以为()A .1B .2C .3D .4【答案】CD【分析】由特例可得a 的值可以取3,4,再利用整数的性质可判断a 的值不可能为1,2,故可得正确的选项.【详解】取三边为3,4,5的三角形,其面积为6,此时a 的值可以取3,4.当1a =时,有||||a b c a b c b -<<+⇒=,此时ABC 2413(mod 4)b -≡,不为完全平方数,因此ABC 的面积不可能是有理数.当2a =时,不妨设2b c ≤≤,有||||a b c a b c b -<<+⇒=或1c b =+.情形一若c b =,则ABCp q=,其中p ,q 为互质的正整数,则()2221q b p -=,于是21b -为完全平方数,而正整数的完全平方数的最小间隔为22213-=,因此该情形不成立.情形二若1c b =+,则2222(1)23cos 44b b b C b b+-+-+==,于是面积为有理数,等价于sin C =2121293(mod 4)b b +-≡,因此ABC 的面积不可能是有理数.综上所述,a 的值不可能为1,2,可能为3,4.故选:CD.10.(2022·贵州·高二统考竞赛)如图,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复上述操作(其中123∠∠∠==),得到四个小正方形,,,A B C D ,记它们的面积分别为,,,A B C D S S S S ,则以下结论正确的是()A .A DBC S S S S +=+B .AD B C S S S S ⋅=⋅C .2A D B S S S + D .2D A CS S S +<【答案】BC【详解】设123α∠=∠=∠=,最大正方形的边长为1,小正方形,,,A B C D 的边长分别为a b c d ,,,.∵2cos ,sin cos a b ααα==,2sin cos ,sin c d ααα==,4422sin cos 2sin cos A D S S αααα+=+≥,22sin cos B C S S αα==,2A D B S S S +≥,所以C 正确;4444sin sin ,sin sin A D B C S S S S αααα==,所以A D B C S S S S =,所以B 正确,故选:BC.11.(2020·湖北武汉·高三统考强基计划)设ABC 的内角,,A B C 的对边分别为,,a b c .若{cos (sin 1)0a cbc b C ++-=),则()A .3B π=B .4B π=C .ABCD .ABC 【答案】AC【分析】利用正弦定理结合两角和的正弦公式以及基本不等式化简即可。
高中数学竞赛0710试题之三角函数教师版

高中数学竞赛(07-10年)试题分类汇总——三角、向量一、选择题1.(07全国)设函数f (x )=3sin x +2cos x +1。
若实数a 、b 、c 使得af (x )+bf (x−c )=1对任意实数x 恒成立,则acb cos 的值等于( ) A. 21- B. 21 C. −1 D. 1解:令c=π,则对任意的x ∈R ,都有f (x )+f (x−c )=2,于是取21==b a ,c=π,则对任意的x ∈R ,af (x )+bf (x−c )=1,由此得1cos -=acb 。
一般地,由题设可得1)sin(13)(++=ϕx x f ,1)sin(13)(+-+=-c x c x f ϕ,其中20π<<ϕ且32tan =ϕ,于是af (x )+bf (x−c )=1可化为1)sin(13)sin(13=++-+++b a c x b x a ϕϕ,即0)1()cos(sin 13cos )sin(13)sin(13=-+++-+++b a x c b c x b x a ϕϕϕ,所以 0)1()cos(sin 13)sin()cos (13=-+++-++b a x c b x c b a ϕϕ。
由已知条件,上式对任意x ∈R 恒成立,故必有⎪⎩⎪⎨⎧=-+==+)3(01)2(0sin )1(0cos b a c b c b a , 若b =0,则由(1)知a =0,显然不满足(3)式,故b≠0。
所以,由(2)知sin c =0,故c=2kπ+π或c=2kπ(k ∈Z )。
当c=2kπ时,cos c =1,则(1)、(3)两式矛盾。
故c=2kπ+π(k ∈Z ),cos c =−1。
由(1)、(3)知21==b a ,所以1cos -=ac b 。
2.(08全国)ABC ∆中,边,,a b c 成等比数列,则sin cot coscos A C A B+的取值范围是( C)A. (0,)+∞B.C. D. )+∞[解] 设,,a b c 的公比为q ,则2,b aq c aq ==,而sin cot cos sin cos cos sin sin cot cos sin cos cos sin A C A A C A CB C B B C B C++=++ sin()sin()sin sin()sin()sin A C B B bq B C A A aππ+-=====+-.因此,只需求q 的取值范围.因,,a b c 成等比数列,最大边只能是a 或c ,因此,,a b c 要构成三角形的三边,必需且只需a b c +>且b c a +>.即有不等式组22,a aq aq aq aq a ⎧+>⎪⎨+>⎪⎩即2210,10.q q q q ⎧--<⎪⎨+->⎪⎩解得q q q <<⎨⎪><⎪⎩从而1122q <<,因此所求的取值范围是. 3.(08江苏)如果111C B A ∆的三个内角的余弦值分别是222C B A ∆的三个内角的正弦值,那么 答:[B]A. 111C B A ∆与222C B A ∆都是锐角三角形B. 111C B A ∆是锐角三角形,222C B A ∆是钝角三角形C. 111C B A ∆是钝角三角形,222C B A ∆是锐角三角形D. 111C B A ∆与222C B A ∆都是钝角三角形解 两个三角形的内角不能有直角;111C B A ∆的内角余弦都大于零,所以是锐角三角形;若222C B A ∆是锐角三角形,则不妨设cos 1A =sin 2A =cos ⎪⎭⎫⎝⎛-12A π, cos 1B =sin 2B =cos ⎪⎭⎫ ⎝⎛-22A π, cos 1C =sin 2C =cos ⎪⎭⎫⎝⎛-12C π.则212A A -=π,212B B -=π,212C C -=π,即 )(23222111C B A C B A ++-=++π,矛盾. 选B. 4.(08河北)已知cos cos 1x y +=,则sin sin x y -的取值范围是( ).A []11-,B []2-,2C 0⎡⎣ D⎡⎣答案:D .解:设sin sin x y t -=,易得21cos cos sin sin 2t x y x y --=,即()21cos 2t x y -+=.由于()1cos 1x y -≤+≤,所以21112t --≤≤,解得t ≤ 5.(08湖南)设)2008sin(sin 0=a ,)2008sin(cos 0=b ,)2008cos(sin 0=c ,)2008cos(cos 0=d ,则d c b a ,,,的大小关系是( )A.d c b a <<< B.c d a b <<< C.a b d c <<< D.b a c d <<<解:因为00002818036052008++⨯=,所以,0)28sin(sin )28sin sin(00<-=-=a ;0)28sin(cos )28cos sin(00<-=-=b ; 0)28cos(sin )28sin cos(00>=-=c ;0)28cos(cos )28cos cos(00>=-=d .又0028cos 28sin <,故.c d a b <<<故选B.6.(08江西)若对所有实数x ,均有sin sin cos cos cos 2kkkx kx x kx x ⋅+⋅=,则k =( ). A 、6; B 、5; C 、4; D 、3. 解:记()sin sin cos cos cos 2k k k f x x kx x kx x =⋅+⋅- ,则由条件,()f x 恒为0,取2x π=,得()sin12k k π=-,则k 为奇数,设21k n =-,上式成为sin 12n ππ⎛⎫-=- ⎪⎝⎭,因此n 为偶数,令2n m =,则41k m =-,故选择支中只有3k =满足题意.二、填空题1.(08江西)0sin 20sin 40sin80⋅⋅= .解:()0000008sin 20sin 40sin804cos 20cos60sin80⋅⋅=-()0004sin80cos202sin802sin100sin 602sin80=-=+-02sin 60==所以0sin 20sin 40sin 80⋅⋅=. 2.(08湖北)设集合⎭⎬⎫⎩⎨⎧-∈==)34,3(,21|sin |ππx x x E ,则E 的真子集的个数为 15 3.(08湖北)若1|lg |<ϕ,则使函数)cos()sin()(ϕϕ-+-=x x x f 为奇函数的ϕ的个数为 3 .4.(08湖北)在△ABC 中,已知B ∠的平分线交AC 于K .若BC =2,CK =1,223=BK ,则△ABC 的面积为16715.5.(08湖北)已知a OA =,b OB =,过O 作直线AB 的垂线,垂足为P .若3||,3||==,6π=∠AOB ,y x +=,则=-y x -2 .6.(07全国)在△ABC 和△AEF 中,B 是EF 的中点,AB =EF =1,BC =6,33=CA ,若2=⋅+⋅AF AC AE AB ,则EF 与BC 的夹角的余弦值等于________解:因为2=⋅+⋅AF AC AE AB ,所以2)()(=+⋅++⋅BF AB AC BE AB AB ,即22=⋅+⋅+⋅+。
竞赛中的三角函数例题选讲附答案

竞赛中的三角函数例题选讲【内容综述】 一.三角函数的性质 1.正,余弦函数的有界性对任意角,,2.奇偶性与图象的对称性正弦函数,正切函数和余切函数都是奇函数,它们的图象关于原点对称,并且y=sinx 的图象还关于直线对称:余弦函数是偶函数,从而y=cosx 的图象关于y轴对称,并且其图象还关于直线对称 3.单调性 y=sinx 在上单调递增,在上单调递减:y=cosx 在上单调递增,在上单调递减;y=tanx 在上都是单调递增的;y=cotx 在上都是单调递减的。
4.周期性y=sinx 与y=cosx 的最小正周期是2π,y=tanx 与y=cosxr 的最小正周期是π。
【例题分析】例1 已知圆222k y x =+至少覆盖函数的一个最大值点与一个最小值点,求实数k 的取值范围。
解 因为是一个奇函数,其图象关于原点对称,而圆222k y x =+也关于原点对称,所以,图222k y x =+只需覆盖的一个最值点即可。
令,可解得的图象上距原点最近的一个最大值点,依题意,此点到原点的距离不超过|k|,即综上可知,所求的K 为满足的一切实数。
例2 已知,且求 cos(x+2y)的值。
解原方程组可化为因为所以令,则在上是单调递增的,于是由得 f(x)=f(-2y)得 x=-2y即 x+2y=0例3 求出(并予以证明)函数解首先,对任意,均有这表明,是函数f(x)的一个周期其次,设,T是f(x)的一个周期,则对任意,均有在上式中,令x=0,则有。
两边平方,可知即sin2T=0,这表明,矛盾。
综上可知,函数的最小正周期为。
例3 求证:在区间内存在唯一的两个数,使得sin(cosc)=c, cos(sind)=d证,构造函数f(x)=cos(sinx)-xf(x)在区间内是单调递减的,由于f(0)=cos(sin0)-0=1>0.故存在唯一的,使f(d)=0,即cos(sind)=d对上述两边取正弦,并令c=sind,有sin(cos(sind))=sindsin(cosc)=c显然,由于y=sinx在是单调递增的,且d是唯一的,所以c也是唯一的,且例4 已知对任意实数x,均有求证:证首先,f(x)可以写成①其中是常数,且,在①式中,分别令和得②③②+③,得又在①式中分别令,得④⑤由④+⑤,得【能力训练】(A组)1.求函数的单调递增区间2.已知是偶函数,,求3.设,,试比较的大小。
高中奥数举一反三 三角函数问题

高中奥数举一反三三角函数问题高中奥数举一反三:三角函数问题介绍三角函数是数学中重要的概念,广泛应用于各个领域。
在高中奥数竞赛中,三角函数问题常常出现,考察学生对三角函数的理解和运用能力。
本文将重点讨论高中奥数中的三角函数问题,以便帮助学生更好地准备竞赛。
正文1. 三角函数的基本概念三角函数包括正弦、余弦和正切等基本函数。
其中,正弦函数(sin)表示一个角的正弦值,余弦函数(cos)表示一个角的余弦值,正切函数(tan)表示一个角的正切值。
这些函数与角的边长比例相关。
2. 三角函数的性质- 正弦函数和余弦函数是周期函数,周期为360度或2π弧度。
- 正弦函数在0度和180度时取最大值1,在90度时取最小值-1。
- 余弦函数在0度和360度时取最大值1,在180度时取最小值-1。
- 正切函数在0度和180度时无定义,其他角度的正切值可能是正数、负数或无穷大。
3. 常见的三角函数问题类型在高中奥数竞赛中,三角函数问题的形式多种多样,但常见的类型包括:- 求角度:已知三角函数值,求对应角度。
- 求三角函数值:已知角度,求对应的三角函数值。
- 利用三角函数的性质解题:根据已知条件,运用三角函数的性质求解。
4. 解决三角函数问题的方法解决三角函数问题的关键是要熟悉三角函数的定义和性质,并掌握解决不同类型问题的方法。
以下是一些解题策略:- 使用特殊角度的三角函数值,如30度、45度和60度等。
- 利用三角函数的定义和性质进行变形、代入和联立方程等运算。
- 利用三角恒等式简化复杂的三角函数表达式。
- 结合图形进行推理和解题。
5. 案例分析以下是一个三角函数问题的案例:已知正弦函数sin(x)在90度时取最小值-1,求角度x的值。
解答:根据问题中给出的信息,我们知道sin(90度) = -1。
由此可知,角度x为90度。
结论通过研究和讨论高中奥数中的三角函数问题,我们深入了解了三角函数的基本概念和性质,掌握了解决不同类型问题的方法。
竞赛三角函数训练题

三角函数竞赛训练题1.(2011湖北联赛)已知R α∈,如果集合{sin ,cos 2}{cos ,sin 2}αααα=,则所有符合要求的角α构成的集合为 .2.(2011湖北联赛)满足方程28sin()160x x xy ++=(R,[0,2)x y π∈∈)的实数对(,)x y 的个数为 .3.设向量)cos sin ,cos sin 2(),,3(θθθθβαa a x x +=+=满足对任意R x ∈和θ∈[0, π2], 2||≥+βα恒成立. 则实数a 的取值范围是 .4.(2005全国联赛)设α、β、γ满足πγβα20<<<<,若对于任意++++∈)cos()cos(,βαx x R x ,0)cos(=+γx 则=-αγ .5.(2007一试4)已知函数)4541(2)cos()sin()(≤≤+-=x xπx πx x f ,则f (x )的最小值为 .6.(2008一试)设ABC ∆的内角A B C ,,所对的边,,a b c 成等比数列,则sin cot cos sin cot cos A C AB C B++的取值范围是 .7.设111sin cos tan tan sin cos y x x x x x x=+++++,则||y 的最小值为 .8.(2007年全国联赛)函数()3sin 2cos 1f x x x =++,若实数,,a b c 使得af(x)+bf(x −c)=1对任意实数x 恒成立,则acb cos 的值等于 .9.设,0πα<<,2πβπ<<若对任意的R x ∈,等式)sin()cos(βα+++x x +0cos 2=x 恒成立,试求α、β的值。
10.已知当x ∈[0,1]时,不等式x 2cos θ-x (1-x )+(1-x ) 2sin θ>0恒成立,试求θ的取值范围。
11.(2010北大自主招生)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.12.已知函数,72sin 3|)cos ||sin (|)(--+=x x x a x f 其中a 为实数,求所有的数对(,)a n ()n N +∈,使得函数)(x f y =在区间),0(πn 内恰好有2011个零点.13.(2010北大自主招生)向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ 在0t 时取得最小值,问当0105t <<时,夹角的取值范围.14.(2012北大自主招生)设点A 、B 、C 分别在边长为1的正三角形的三边上,求222AB BC CA ++的最小值.15(2012北大自主招生)若关于x 的方程sin4sin2sin sin3x x x x a -=在[0,)π有唯一解的实数a 的范围三角函数竞赛训练题1.(2011湖北联赛)已知R α∈,如果集合{sin ,cos 2}{cos ,sin 2}αααα=,则所有符合要求的角α构成的集合为{|2,}k k Z ααπ=∈.2.(2011湖北联赛)满足方程28sin()160x x xy ++=(R,[0,2)x y π∈∈)的实数对(,)x y 的个数为 . 83.设向量)cos sin ,cos sin 2(),,3(θθθθβαa a x x +=+=满足对任意R x ∈和θ∈[0, π2], 2||≥+βα恒成立. 则实数a 的取值范围是 .解:令,cos sin t =+θθ则]2,1[∈t ,,1cos sin 22-=t θθ),2(2at x x t +++=+βα,因2222222)2(21)2(21)()2(+-=--++≥++++at t at x x t at x x t ,所以,2||≥+βα2)()2(222≥++++⇔at x x t 对任意R x ∈恒成立⇔02)2(21222≥-⇔≥+-at t at t 或t a at t ≤⇔≤+-042或t t a 4+≥对任意 ]2,1[∈t 恒成立1≤⇔a 或5≥a .4.(2007一试4)已知函数)4541(2)cos()sin()(≤≤+-=x xπx πx x f ,则f (x )的最小值为 .【解析】实际上)4541(2)4sin(2)(≤≤+-=x xππx x f ,设 )4541)(4sin(2)(≤≤-=x ππx x g ,则g (x )≥0,g (x )在]43,41[上是增函数,在]45,43[上是减函数,且y =g (x )的图像关于直线43=x 对称,则对任意]43,41[1∈x ,存在]45,43[2∈x ,使g (x 2)=g (x 1)。
数学竞赛专题练习-三角函数

数学竞赛专题练习-三角函数一、单选题1.已知αβγπ++=,β为锐角,tan 3tan αβ=,则11tan tan γα+的最小值为( ) A .12B .43C .32D .34【答案】A 【分析】由已知结合诱导公式及两角和的正切公式,先进行化简,然后代入到所求式子后,结合基本不等式即可求出最值,即可得出答案. 【详解】解:∵αβγπ++=, ∴2tan tan 4tan tan tan()1tan tan 13tan αββγαβαββ+=-+=-=---,22113tan 119tan 1tan tan 4tan 3tan 12tan ββγαβββ-+∴+=+=31321tan 49tan 432ββ⎛⎫=+≥⨯= ⎪⎝⎭, 当且仅当1tan 9tan ββ=即1tan 3β=时取等号, 所以11tan tan γα+的最小值为12.故选:A. 【点睛】本题考查三角函数的恒等变换以及基本不等式的运用,涉及诱导公式、两角和的正切公式,考查化简计算能力.第II 卷(非选择题)请点击修改第II 卷的文字说明二、解答题2.如图所示,某人为“花博会”设计一个平行四边形园地,其顶点分别为i A (1,2,3,4i =),1230A A =米,214120A A A ∠=,D 为对角线24A A 和13A A 的交点.他以2A 、4A 为圆心分别画圆弧,一段弧与12A A 相交于1A 、另一段弧与34A A 相交于3A,这两段弧恰与24A A 均相交于D .设12A A D θ∠=.(1)若两段圆弧组成“甬路”L (宽度忽略不计),求L 的长(结果精确到1米); (2)记此园地两个扇形面积之和为1S ,其余区域的面积为2S .对于条件(1)中的L ,当11320.12S LA A S -<时,则称其设计“用心”,问此人的设计是否“用心”?并说明理由. 【答案】(1)36米;(2)此人的设计是“用心”的;答案见解析. 【分析】(1)在△124A A A 中,根据正弦定理求出142arcsin 4A A A ∠=,再根据弧长公式可求出结果;(2)利用余弦定理求出1A D ,可得13A A ,利用三角形面积公式和扇形的面积公式求出1S ,2S ,可得1132||S LA A S -,再通过近似计算可得答案. 【详解】(1)根据题设条件,可得在△124A A A 中,24122A A A A =.由正弦定理,得2412214142sin sin A A A A A A A A A A =∠∠,即14212sin sin 23A A A π∠==.所以142arcsinA A A ∠=3πθ=-,所以12260L A A θθ=⋅==60arcsin3π⎛⋅-⎝⎭≈36米. 答:甬路L 的长约为36米.(2)由(1)得60L θ=,在△12A A D 中,由余弦定理,得21221800180303023030c cos 0os A D θθ=+-⨯⨯⨯=-,所以1A D = 故13A A=,所以13LA A=2112002930S θθ==⨯⨯,2914303000(2s )sin 90n 0i 2S θθθθ=⨯⨯⨯-=-,故122sin S S θθθ=-,当3πθ=-0.11810.122sin θθθ-≈<-.所以此人的设计是“用心”的. 【点睛】关键点点睛:利用正弦定理、余弦定理、弧长和扇形的面积公式、三角形的面积公式求解是解题关键.3.已知定义在区间2π[π]3-,上的函数()y f x =的图象关于直线π6x =-对称,当π2π[,]63x ∈-时,函数()sin()f x A x ωϕ=+(A >0,ω>0,π2-<ϕ<π2)的图象如图所示.(1)求函数()y f x =在2π[π,]3-上的表达式; (2)求方程()f x =. 【答案】(1)πsin ,[π,],6()ππ2πsin(),(,].363x x f x x x ⎧-∈--⎪⎪=⎨⎪+∈-⎪⎩;(2)2π3-,π3-,0,π3.【分析】(1)根据图象可得1A =,1ω=,根据最高点的坐标可得3πϕ=,由此可得π2π[,]63x ∈-时,π()sin()3f x x =+,再根据函数()y f x =的图象关于直线π6x =-对称,可求得当π[π,]6x ∈--时,()sin f x x =-,从而可得函数()y f x =在2π[π,]3-上的表达式;(2)当2[,]63x ππ∈-时,解方程sin()3x π+=,可得0x =或π3x =,再根据对称性可得[,)6x ππ∈--上的解为23x π=-或3x π=-.【详解】(1)由图象可知1A =,24362T πππ=-=,所以2T π=,所以21Tπω==, 由sin(1)16πϕ⨯+=,得62k ππϕπ+=+,k Z ∈,得3k πϕπ=+,k Z ∈,因为ππ22ϕ-<<,所以3πϕ=, ∴π2π[,]63x ∈-时,π()sin()3f x x =+.因为函数()y f x =的图象关于直线π6x =-对称, 所以当π[π,]6x ∈--时,2[,]363x πππ--∈-, 所以()2()6f x f x π⎡⎤=⨯--⎢⎥⎣⎦()3f x π=--sin()sin()sin 33x x x ππ=--+=-=-.综上,πsin ,[π,),6()ππ2πsin(),[,].363x x f x x x ⎧-∈--⎪⎪=⎨⎪+∈-⎪⎩(2)∵()f x =则在区间π2π[,]63-上有:ππ33x +=或π2π33x +=,∴0x =,π3x =.又()y f x =关于π6x =-对称, ∴π3x =-,2π3x =-也是方程的解.∴()f x =2π3-,π3-,0,π3.【点睛】本题考查了由图象求解析式,考查了根据函数图象的对称性求解析式,考查了简单的三角方程的解法,属于中档题.4.在△ABC 中,BC =a ,CA =b ,AB =c .若b 是a 与c 的等比中项,且sin A 是sin(B -A )与sin C 的等差中项,求cos B 的值.【分析】根据等比中项和等差中项,结合正弦和余弦定理,即可求得2q ,进而由余弦定理,即可求得cosB . 【详解】因b 是a 、c 的等比中项,故存在q >0,满足2,b qa c q a ==.① 因sin A 是sin(B -A ),sin C 的等差中项,故2sin sin()sin A B A C =-+sin()sin()B A B A =-++2sin cos B A =.结合正、余弦定理,得222sin cos sin 2a A b c a A b B bc+-===,即2222b c a ac +-=. 将①代入并化简,可知24212q q q +-=,即421q q =+,所以212q =.进而222422211cos 22c a b q q B ac q q +-+-====. 【点睛】本题考查等差中项、等比中项的应用,涉及正余弦定理,属综合中档题.5.锐角三角形ABC 中,求证:cos()cos()cos()8cos cos cos B C C A A B A B C ---. 【答案】证明见解析 【详解】 原不等式等价于cos()cos()cos()8cos cos cos B C C A A B A B C---.在三角形ABC 中,tan tan tan tan tan tan A B C A B C ++=,cos()sin sin cos cos cos sin sin cos cos B C B C B C A B C B C -+=-tan tan 1tan tan 1B C B C +=-tan (tan tan 1)tan tan A B C B C +=+2tan tan tan tan tan A B C B C++=+.令tan tan tan tan tan tan A B xB C y C A z+=⎧⎪+=⎨⎪+=⎩,则原不等式等价于()()()8z x y z x y yxz +++.而上式左边228zx yxz⋅=,故原不等式得证6.如图,在平面上,直线12l l ,A ,B 分别是1l ,2l 上的动点,C 是1l ,2l 之间的一定点,C 到1l 的距离CM =1,C 到2l 的距离CN =ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a b >,且cos cos b B a A =.(1)判断ABC 的形状; (2)记ACM θ∠=,()11f b aθ=+,求()f θ的最大值.【答案】(1)ABC 是直角三角形.(2. 【分析】(1)由正弦定理及二倍角公式化简即可得sin 2sin 2B A =,根据边的大小及诱导公式可求2C π=(2)由正弦定理化为关于θ的三角函数,求最值即可.【详解】(1)由正弦定理及cos cos b B a A =, 得sin 2sin 2B A =. 因为a b >, 所以A B >, 所以22A B π+=, 所以2C π=,所以ABC 是直角三角形. (2)由(1)得2BCN πθ∠=-,则1cos b θ=,a =()11cos 6f b a πθθθθ⎛⎫=+==- ⎪⎝⎭.所以当6πθ=时,()fθ【点睛】本题主要考查了正弦定理,三角恒等变换,三角函数的最值,属于中档题.7.求arcsin arctan713-等的值. 【答案】3π 【解析】 【分析】先把反三角函数用角度arcsin7和arctan 13用,αβ表示,再通过正弦两角和与差的运算算出sin()αβ-,即可得出αβ-的值,就是arcsin -的值. 【详解】解:设α=则02πα<<且sin α=,1cos 7α=.设13arctanβ=,则02πβ<<,且tan β=sin β=1314cos β=.又因,22ππαβ⎛⎫-∈- ⎪⎝⎭,sin()sin cos cos sin αβαβαβ-=-=3παβ∴-=,即arcsin 3π-=. 故答案为3π 【点睛】本题考查反三角函数的计算,要转化为三角函数来计算,借助正弦函数两角和差公式来运算.8.在锐角ABC ∆,证明:()()()()()()sin sin sin sin sin sin 0sin 2sin 2sin 2A B A C B A B C C A C B ABC-⋅--⋅--⋅-++≥.【答案】见解析 【解析】 【详解】 证法1:注意到()()sin sin sin2A B A C A-⋅-()()sin cos sin sin cos sin 2sin cos A B A C B A A C A A⋅⋅--⋅⋅-=⋅()()cos sin cos cos sin sin sin cos cos sin 2cos 2sin B A C A C B A C A C A A ⋅-⋅⋅-⋅=-cos cos sin cos sin sin cos sin sin cos 2cos 222sin B C A B C B C B C AA A⋅⋅⋅⋅⋅⋅=--+()sin cos cos sin sin sin cos 2cos 22sin B C B C A B C AA A +⋅⋅⋅⋅=-+cos cos sin sin sin sin cos 2cos 22sin B C A A B C AA A⋅⋅⋅⋅=-+.同理,()()sin sin sin2B A B C B-⋅- cos cos sin sin sin sin cos 2cos 22sin C A B B C A BB B⋅⋅⋅⋅=-+,()()sin sin sin2C A C B C-⋅- cos cos sin sin sin sin cos 2cos 22sin A B C C A B CC C⋅⋅⋅⋅=-+.因此,所证不等式化为sin sin cos cos cos sin sin cos A B C A B C C C ⋅⋅⋅⋅⎛⎫+ ⎪⎝⎭sin sin cos cos cos sin sin cos B C A B C A A A ⋅⋅⋅⋅⎛⎫++ ⎪⎝⎭sin sin cos cos cos sin sin cos C A B C A B B B ⋅⋅⋅⋅⎛⎫++ ⎪⎝⎭sin sin sin A B C ≥++. ①令cot x A =,cot y B =,cot z C =.则x 、y 、z R +∈,1xy yz zx ++=. 因此,sin sin cos cos cos sin sin cos A B C A B CC C⋅⋅⋅⋅+1z z=2=同理,sin sin cos cos cos sin sin cos B C A B C A A A ⋅⋅⋅⋅+2=sin sin cos cos cos sin sin cos C A B C A B B B ⋅⋅⋅⋅+2=222+≥②又()()221x xy yz zx x x y x z +=+++=++,()()221y xy yz zx y x y y z +=+++=++, ()()221z xy yz zx z x z y z +=+++=++,故式②222. 上式关于x 、y 、z 对称,故设x y z ≥≥.22x x y z yz -++x y x z --=,2y z y x --=2z x z y --=,即要证:x y x z y z y x z x z y ------≥. ③x y x z --≥,y z y x z x z y ----()y z⎛⎫=--(0y z=-≥,所以,式③成立.因此结论得证.证法2:据对称性,不妨设A B C ∠≥∠≥∠.则6090A ︒≤∠<︒,90B C ∠+∠>︒,45B A ︒<∠≤∠.所以,()sin2sin 802A A =︒- ()sin 1802sin2B B ≤︒-=,()()()()sin sin sin sin sin2sin2A B B C A B B C AB-⋅---≥.则()()()()sin sin sin sin sin2sin2B A B C B A B C BA-⋅--⋅-≥.故()()()()sin sin sin sin sin2sin2A B A C B A B C AB-⋅--⋅-+()()()()sin sin sin sin 0sin2sin2A B A C B A B C AA-⋅--⋅-≥+≥.因()()sin sin 0sin2C A C B C-⋅-≥,所以,()()()()()()sin sin sin sin sin sin 0sin2sin2sin2A B A C B A B C C A C B ABC-⋅--⋅--⋅-++≥.三、填空题9.2221x xy y ++=,则222x xy y ++的最小值为______.【分析】根据条件等式可设sinx y θ==-辅助角公式化简,根据三角函数的性质可求出最值. 【详解】2221x xy y ++=,则2227144x x xy y +++=,即22122x y ⎛⎫⎛⎫++= ⎪ ⎪ ⎪⎝⎭⎝⎭,cos ,sin 2x y θθ=+=,则sin x y θ==∴22222sin 2sin x xy y θθ⎛⎛++=-+ ⎝⎝224cos 2sin 7θθ=+41cos 21cos 272θθ+⎛⎫=- ⎪⎝⎭592cos 277θθ=-+()9277θϕ=++,其中ϕ是辅助角,且tan ϕ= 当()sin 21θϕ+=-.故答案为:97-+. 【点睛】本题考查条件等式求最值,解题的关键是设sin x y θ==恒等变换化简可求出. 10.如果方程组1212sin sin sin 0sin 2sin sin 2019n n x x x x x n x ++⋅⋅⋅+=⎧⎨++⋅⋅⋅+=⎩有实数解,则正整数n 的最小值是___【答案】90【分析】当90n <时,用方程(2)减去方程(1)的45倍,然后利用三角函数的有界性,发现矛盾,故从90n =开始分析,当90n =,我们可以取9120,,,x x x 使sin 1(1,2,,45)i x i =-=,sin 1(46,47,,90)j x j ==得出方程组的实数解,进而可得正整数n 的最小值.【详解】如果90n <,对于方程组1212sin sin sin 0(1)sin 2sin sin 2019(2)n n x x x x x n x ⎧++⋅⋅⋅+=⎨++⋅⋅⋅+=⎩ 用方程(2)减去方程(1)的45倍,得1444624744sin 43sin sin sin 2sin (45)sin 2019n x x x x x n x ----++++-=(3) (3)式的左端的绝对值不大于(44431)21980++⋯+⨯=,因此(3)式不可能成立,故原方程组当90n <时无解;∴从90n =开始分析,当90n =,我们可以取9120,,,x x x 使sin 1(1,2,,45)i x i =-= sin 1(46,47,,90)j x j ==12max (sin 2sin sin )123454647902025n x x n x ++⋅⋅⋅+=----⋅⋅⋅-+++⋅⋅⋅+= 则12sin 2sin sin 1234243044045460470n x x n x ++⋅⋅⋅+=----⋅⋅⋅--⨯-⨯-+⨯+⨯+4849902019++⋅⋅⋅+=时,min 90n =故答案为:90.【点睛】本题考查三角函数有界性的应用,关键时要发现90n <时,原方程组无解,考查了学生计算能力和分析能力,本题难度较大.。
挑战奥数的三角函数计算

挑战奥数的三角函数计算在奥数竞赛中,三角函数计算是一个常见且关键的题型,其涉及到三角函数的基本概念、性质以及计算方法。
掌握三角函数的计算技巧,能够帮助我们在解题过程中更加高效、准确地求解。
本文将介绍一些挑战奥数的三角函数计算知识和技巧。
一、角度和弧度的转换在三角函数计算中,角度和弧度是常见的两种单位。
角度是我们日常生活中常用的度量单位,弧度则是数学中常用的度量单位。
为了在计算中灵活使用三角函数,我们需要掌握角度和弧度之间的转换关系。
1. 角度转弧度:一圆的周长为2π,一个完整的角度为360°,所以可以得出转换公式:1° = π/180。
2. 弧度转角度:根据转换公式可以得出:1弧度= 180/π°。
二、基本三角函数的计算1. 正弦函数(sin):对于给定角度θ,正弦函数的计算公式为:sinθ = 对边/斜边。
2. 余弦函数(cos):对于给定角度θ,余弦函数的计算公式为:cosθ = 邻边/斜边。
3. 正切函数(tan):对于给定角度θ,正切函数的计算公式为:tanθ = 对边/邻边。
三、常用角度值的三角函数计算在奥数竞赛中,往往会遇到一些特殊的角度值,例如30°、45°、60°等。
这些角度值的三角函数计算是需要我们熟练掌握的。
1. 30°的三角函数计算:sin30° = 1/2,cos30° = √3/2,tan30° = 1/√3。
2. 45°的三角函数计算:sin45° = √2/2,cos45° = √2/2,tan45° = 1。
3. 60°的三角函数计算:sin60° = √3/2,cos60° = 1/2,tan60° = √3。
四、三角函数的运算性质在奥数竞赛中,三角函数的运算性质是经常会涉及到的。
掌握三角函数的运算性质能够帮助我们简化计算过程和提高解题效率。
初中数学竞赛:三角函数

初中数学竞赛:三角函数直角三角形中有两条直角边和一条斜边,从这三条边中适当取两条边可以得到不同的比,这些比值的大小显然只与直角三角形中锐角的大小有关,这佯便定义了直角三角形中锐角的三角函数(如图3-14),常用的有:利用比例的变形并且结合勾股定理,可以从三角函数定义中推出同角三角函数间的关系式:(1)倒数关系tgα·ctgα=1;(2)商的关系(3)平方关系sin2α+cos2α=1.这些同角三角函数关系式对任意锐角都成立,它们在求值、化简以及三角式的变形中有着重要的应用.如图3-15所示,在直角三角形ABC中,∠A与∠B互为余角,根据三角函数定义不难得到互为余角的三角函数之间的关系:sinB=sin(90°-A)=cosA,cosB=cos(90°-A)=sinA,tgB=tg(90°-A)=ctgA,ctgB=ctg(90°-A)=tgA.上述四个公式可以概括为:一个锐角的余角的三角函数值,等于该锐角相应的余函数的函数值由图3-16可以看到,在直角三角形ABC中,如果斜边长度不变,当锐角A 增大时,sinA与tgA的值也随之增大,而cosA与ctgA的值随之减小.特别地,当A=0时,sin0=0,tg0=0,cos0=1,ctg0值不存在;当A=90°时,sin90°=1,tg90°值不存在,cos90°=0,ctg90°=0.由于一个角的正弦或余弦值等于直角边与斜边的比,而直角三角形的斜边总是大于直角边,所以,当α为锐角时,总有0<sinα<1,0<cosα<1.我们利用以上锐角三角函数的定义及性质,可以解决一些求值、化简以及等式证明等问题.例1 不查表,求15°的四种三角函数值.分析 30°,45°,60°这些特殊角的三角函数值,我们可以利用含有这些特殊角的直角三角形的几何性质及勾股定理直接推出.同样,15°角的三角函数值,也可以利用直角三角形的性质将其推出.解如图3-17所示.在△ABC中,∠C=90°,∠ABC=30°,延长CB到D,使BD=BA,则所以所以说明将15°角的三角函数求值问题,通过构造适当的三角形,将它转化为30°角的三角函数问题,这种将新的未知问题通过一定途径转化为旧的已解决了的问题的方法,是我们研究解决新问题的重要方法.根据互余三角函数关系式,我们很容易得到75°角的四种三角函数值.例2 比较下列各组三角函数值的大小:(1)sin19°与cos70°;(2)ctg65°与cos40°;(3)cos1°,tg46°,sin88°和ctg38°.分析 (1)利用互余角的三角函数关系式,将cos70°化为sin20°,再与sin19°比大小.(2)余切函数与余弦函数无法化为同名函数,但是可以利用某些特殊再将ctg65°,cos40°分别与ctg60°,cos45°比大小.(3)tg45°=1,显然cos1°,sin88°均小于1,而tg46°,ctg38°均大于1.再分别比较cos1°与sin88°,以及tg46°与ctg38°的大小即可.解 (1)因为cos70°=cos(90°-20°)=sin20°,而sin19°<sin20°,所以sin19°<cos70°.(2)因为所以 ctg60°<cos45°,所以 ctg65°<cos40°.(3)因为ctg38°=ctg(90°-52°)=tg52°,所以tg52°>tg46°>tg45°=1.因为cos1°=cos(90°-89°)=sin89°,所以sin88°<sin89°<1,所以ctg38°>tg46°>cos1°>sin88°.说明比较三角函数值的大小,一般分为三种类型:(1)同名的两个锐角三角函数值,可直接利用三角函数值随角变化的规律,通过比较角的大小来确定三角函数值的大小.(2)互为余函数的两锐角三角函数值,可利用互余角的三角函数关系式化为同名三角函数,比较其大小.(3)不能化为同名的两个三角函数,可通过与某些“标准量”比大小,间接判断它们的大小关系,常选择的标准量有:0,1以及其他一些特殊角如30°,45°,60°的三角函数值.例3 化简求值:(1)tg1°·tg2°·tg3°·…·tg89°;分析 (1)因为tg89°=tg(90°-1°)=ctg1°,而tg1°·ctg1°=1,所以,可将连乘积中的第一个因式与倒数第一个因式相乘,结果为1.同样方法,将第二个因式与倒数第二个因式相乘,其积也是1.依次类推.(3)利用同角三角函数关系将正切函数化为正弦函数与余弦函数,再进一步化简求值.(4)将被开方式化为完全平方的形式,即1-2sin11°·cos11°=sin211°-2sin11°·cos11°+cos211°=(sin11°-cos11°)2.因为sin1l°<cos11°,所以根式化简后得cos11°-sin11°.(5)根据tgα=3,求出sinα与cosα的值.也可以将所求分式的分子、分母同除以cos2α,将其化为用tgα表示的分式.解 (1)原式=tg1°·tg2°·tg3°·…·tg44°·tg45°·ctg44°·ctg43°·…·ctg3°·ctg2°·ctg1°=(tg1°·ctg1°)·(tg2°·ctg2°)·…·(tg44°·ctg44°)·tg45°=1·1·…·1=1.说明同角三角函数关系式以及互余两角三角函数关系式,在三角式变形、化简、求值及证明中是重要的依据.例4 设α是锐角,若求以tgα,ctgα为两根的一元二次方程.分析根据韦达定理,以tgα,ctgα为两根的一元二次方程是x2-(tgα+ctgα)x+tgα·ctgα=0,因此,解决问题的关键是求出tgα+ctgα的值.解由已知条件可得所以(1)当sinα=cosα时,tgα=ctgα=1,所求方程为x2-2x+1=0,所求方程为即4x2-9x+4=0.说明这是一道一元二次方程与三角函数相结合的综合题,应注意运用分析法、综合法,寻求解题途径.例5 设x2+y2=1,且x≠-1,y≠-2,求证:分析本题如果直接用代数方法,通过代数式的运算证明等式成立,比较复杂.根据已知条件x2+y2=1,联想到sin2α+cos2α=1,因此可设x=sinα,y=cos α,则将代数式转化为三角式,利用三角函数有关公式进行变形,这样会简便一些.证设x=sinα,y=cosα,则说明在一些代数等式的证明中,如果已知条件x2+y2=1或x2+y2=a(a>0),则可设从而将代数式转化为三角等式的证明问题,我们称这种转化为三角代换法.由于三角函数的公式较多,因此化为三角式后,运算化简常比较方便.练习十一3.求值:sin6α+cos6α+3sin2α·cos2α+4.4.求证:(1)sin(90°-A)ctg(90°-A)=sinA;(2)sinAcos(90°-A)+cosAsin(90°-A)=1;5.化简下列各式,并求出它们的值:(1)(sinA+cosA)2+(sinA-cosA)2;6.证明:sin2A·tgA+cos2A·ctgA+2sinA·cosA=tgA+ctgA.。
三角函数竞赛试题与方法

三角函数竞赛试题与方法二、方法与例题 1.结合图象解题。
例1 求方程s inx =lg |x |的解的个数。
【解】在同一坐标系内画出函数y =s inx 与y =lg |x |的图象(见图),由图象可知两者有6个交点,故方程有6个解。
2.三角函数性质的应用。
例2 设x ∈(0, π), 试比较co s(s inx )与s in (co s x )的大小。
【解】 若⎪⎭⎫⎢⎣⎡∈ππ,2x ,则co s x ≤1且co s x >-1,所以co s ⎥⎦⎤ ⎝⎛-∈0,2πx ,所以s in (co s x ) ≤0,又0<s inx ≤1, 所以co s(s inx )>0,所以co s(s inx )>s in (co s x ). 若⎥⎦⎤⎝⎛-∈2,0πx ,则因为s inx +co s x =2cos 22sin 222=⎪⎪⎭⎫ ⎝⎛+x x (s inxco s 4π+s in 4πco s x )=2s in (x +4π)≤2<2π, 所以0<s inx <2π-co s x <2π, 所以co s(s inx )>co s(2π-co s x )=s in (co s x ).综上,当x ∈(0,π)时,总有co s(s inx )<s in (co s x ).例3 已知α,β为锐角,且x ·(α+β-2π)>0,求证:.2sin cos sin cos <⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛xxαββα【证明】 若α+β>2π,则x >0,由α>2π-β>0得co s α<co s(2π-β)=s in β,所以0<βαsin cos <1,又s in α>s in (2π-β)=co s β, 所以0<αβsin cos <1,所以.2sin cos sin cos sin cos sin cos 0=⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛αββααββαxx若α+β<2π,则x <0,由0<α<2π-β<2π得co s α>co s(2π-β)=s in β>0, 所以βαsin cos >1。
数维杯2023题目

数维杯2023题目
数维杯是一个非常重要的数学竞赛,反映了当前数学领域中的热
点问题和难点。
2023年的数维杯题目难度较高,需要学生具备一定的数学基础和思维能力。
下面是数维杯2023的题目内容:
正文:
一、几何与三角函数
1.证明:向量AB=(2,3)和向量BC=(5,-4)的模长之和等于3。
2.解方程组:x^2+4xy-8y^2=0和2x^2+5xy-7y^2=0。
3.求函数f(x)=x^3+3xx^2+2x^1+x^0的最小值。
拓展:
几何与三角函数是数学中非常重要的分支,涉及到许多实际问题,如建筑、机械、物理和工程等。
在数维杯竞赛中,这些问题需要学生
运用几何和三角函数的知识进行分析和求解,对学生的数学基础和思
维能力提出了较高的要求。
除了几何与三角函数,还有一些其他的问题,如代数方程、微积分、线性代数等,这些问题需要学生掌握一定的代数和微积分知识,并能
够运用这些知识解决实际问题。
数维杯竞赛的题目难度较高,需要学生具备扎实的数学基础和思
维能力,能够运用所学的数学知识进行分析和解决实际问题。
通过参
加数维杯竞赛,学生可以不断提高自己的数学水平和思维能力,为今
后的学习和职业发展打下坚实的基础。
竞赛中的三角函数问题

;
① tan A + tan B + tan C = tan A ・ tan B ・ tan C; ②sin A + sin B + sin C = 4co s
A
2
co s
B
2
co s sin
C
3 sin B , 则 2 sin A + sin C + sin A co s C + co s A sin C = 3sin B ,
x
π 论 f ( x) 在 [ 0 , ]上的最值 . 2 π 当 x ∈[ 0 , ]时 , f ( x) = sin x + sin4 2 x + co s x. 2 π π π ∵f ( + x) = sin ( x + ) + sin4 ( 2 x + ) + 4 4 2 π π π π co s ( x + ) = co s ( - x ) + sin4 ( - 2 x ) + sin ( 4 4 2 4
tan
A A B B C C
பைடு நூலகம்
2
・ tan
2
+ tan
2
・tan
2
+ tan
2
・
2
= 1.
助角 ; ( 7) 升幂与降幂 ; ( 8) 利用万能公式转化为代数 问题 ; ( 9) 积化和差与和差化积 ; ( 10) 裂项求和 ; ( 11 ) 三角代换 . 应注意熟悉以下常用结论 : π ( 1) 当 0 < x < 时 , sin x < x < tan x ; 2
π π 2 2 ) + sin (α) = 0; 3 3 π π 2 2 3 ) + sin2 (α) = ; 3 3 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
条件中的角度变换为结论中所要的角度 .
) = 5sinβ, 得 证明 由已知 sin ( 2α+ β ) + α] = 5sin [ (α+ β ) - α] , 于是 sin [ (α+ β ) cos α+ cos (α+ β ) sinα sin (α+ β ) cos α- 5cos (α+ β ) sinα, = 5sin (α+ β ) sinα= 2sin (α+ β ) cos α. 整理得 3cos (α+ β
) ( cos2α + sec2α ) 思考题 8 证明 : ( sin2α + csc2α
思路分析 :容易发现 , 结论中的角度 α,α + β与
) - α, 条件中的角度β, 2α + β 有关系式β = (α + β ) + β, 因此对条件变形时应考虑先将 2α+ β= (α+ β
π ,α= arctan 2 时 , 原不等式等号 4
a - b , 即原式 = a- b
3 3
三角式的化简和求值是三角变换的基础 . 一般 说来 , 角变换是三角变换的主线 , 侧重于函数的有 “化杂为弦” “ , 化为互为倒数的函数” “ , 化异名为同 名” 等等 , 侧重于运算的有 “弦函数升降幂” “ , 和积互 化” 以及纯代数运算的各种变换 .
2004 年第 14 ,16 期 数学通讯
85
= 5 + tan2α+ 4cot 2α
) 2 + 4tan・ = 5 + ( tanα- 2cotα cotα
α 2sinα cos sinα = α( 1 - cosα ) 1 - cos α 2cos α 1 + cos = = 右边 . sinα tanα sinα tanα+ sinα 思考题 6 证明 α = . tan - sinα tanα sinα ) = 5sinβ 例6 已知 sin ( 2α+ β .
). 例3 化简 sin2α+ sin2β+ 2sinα sinβ cos (α+ β
可 看 作 a2 + ab + b2 =
sin3 10° - cos3 40° 3 3 , 而 sin 10° , cos 10° 可利用公式: sin10° - cos40°
α 来降 sin3α= 3sinα - 4sin3α, cos3α = 4cos3α - 3cos 幂. 即 sin3α=
) . 于是 + cos3α
1 ( 1 ( ) , cos3α = α 3sinα - sin3α 3cos 4 4
分析 1 注意到式中有三种角 :α,β,α + β, 我 β, 后一项中的 们可考虑将前两项降幂并化积成 α± β, 以尽量造成同角 , sinα sinβ可由积化和差造出α± 于是便有下面的解法 1 :
=
). 求证 :3tanα= 2tan (α+ β
≥ 5+4=9 若 ( 1) 等号成立 , 则 sin2β= 1 , 即 β=
( 2)
π . 4 若 ( 2) 等号成立 , 则 tanα= 2cotα, 即 tan2α= 2 , 故 α= arctan 2 . 所以 , 当 β= 成立 . 由例 7 的证明可以看到 , 在三角不等式的证明 过程中 , 一般要对已知或求证的不等式作各种巧妙 的三角变换和代数变形 , 具有很大的灵活性和技巧 性.
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
84
2 3 ( a - 1) ; 当 a >
数 学 通 讯 2004 年第 14 ,16 期 β+ cosα )2 = ( sinα cos sinβ
). = sin2 (α+ β
7 1 +3a 时 , y 有最小值 . 3 2 7 综上 , 当 1 < a ≤ 时 , f ( θ) 有 最 小 值 3 7 2 3 ( a - 1) + a + 2 ; 当 a > 时 , f (θ) 有 最 小 值 3 1 +3a 5 +5a + a+2= . 2 2
0<
y
2
≤ 2,
Δ = y2 - 12 ( a - 1) ≥ 0.
4. 3 ( a - 1) ≤y ≤
y
2
>2,
g ( 2) = - 2 y + 3 a + 1 ≤ 0, y >4且 y ≥
1 +3a . 2 7 . 而当 a > 3
3 ( a - 1) ≤4 得 1 < a ≤
7 1 +3a 7 时, > 4 , 故当 1 < a ≤ 时 , y 有最小值 3 2 3
思考题 4 化简
3 - 4cos2α+ cos4α . 3 + 4cos2α+ cos4α
例4 求 sin2 10° + cos2 40° + sin10° cos40° 的值 . 分析 1 我们侧重于角来考虑 , 设法化成同角或 者特殊角 . 由于 40° = 30° + 10° , 故可化为 30° 和 10° 的三角函数 . 解法 1 sin2 10° + cos2 40° + sin10° cos40°
1 1 ( 1 - cos2α ) + ( 1 - cos2β ) 2 2 ) - cos (α- β ) ]cos (α+ β ) - [ cos (α+ β
解法 2
1 (3sin10° ) - sin30° - 3cos40° - cos120° 4 sin10° - cos40° 3 = . 4 思考题 5 ( 1991 年全国高中数学联赛试题 ) 求
2
三角等式的证明分恒等式与条件等式的证明两 大类型 . 证明过程一般是将等式较繁的一边通过化 简后等于另一边 . 如果等式左右两边都很繁杂时 , 则 将左右两边分别化简为同一式子 .
sin2α 例 5 证 明 : ( α α- 1) ( sinα- cosα+ 1) sin + cos α 1 + cos = . sinα sin2α 证明 左边 = 2 α- 1 sin α- cos2α+ 2cos α 2sinα cos = α- 1 1 - 2cos2α+ 2cos
(B) cos (α+ β ) < cos α+ cos β . ( C) cos (α+ β ) > sinα+ sinβ .
( )
g ( 2) = - 2 y + 3 a + 1 ≤ 0 时 , 方程 ( 1) 在 ( 0 , 2 ]内至少有一实根 .
由 解得 2 由 解得 再由 2
原式 =
解法 1 原式 =
) cos (α - β ) - cos2 (α + β ) + cos (α + = 1 - cos (α+ β
cos2 10° + cos2 50° - sin40° sin80° 的值 . 3 三角等式和不等式的证明
β )・ ) cos (α- β
). = sin (α+ β
= sin2α ( 1 - sin2β) + sin2β ( 1 sin2α) +
α β 2sinα cos sinβ cos α β+ sin2α = sin2α cos2β+ 2sinα cos sinβ cos cos2α
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
) + sin10° ) = sin2 10° + cos2 ( 30° + 10° cos ( 30° + 10°
这里 , 我们利用正弦函数的有界性将求最小值 的问题化归为讨论二次函数的有关问题来解决 . 利用三角函数的有界性 , 可以用来解决某些三 角函数的最值和证明某些三角不等式的问题 . 思考题 2 已知函数 y = cos2 x + 2 p sin x + q 的 值域为 [ 7 , 10 ] , 试求 p , q 之值 . 思考题 3 对所有的实数 x , y , 有不等式
1 三角函数的性质及其应用
( D) cos (α+ β ) < sinα+ sinβ .
例 2 设 a > 1 , a ,θ 均为实数 , 试求当 θ 变化 时 , 函数
) = f (θ ( a + sinθ ) ( 4 + sin θ )
1 + sinθ
2
的最小值 .
π 内 , 且满足 cosα 2 β ) = β, cos ( sinγ ) = γ, 试比较 α,β,γ 的 = α, sin ( cos 例1 设 α,β,γ在区间 0 , 大小 . α, 由余弦函数在 0 , 解 若 β≥ 可知 π β≤ α= α< 0 < cos cos , 2 β= sin ( cos β ) < cos β≤ α= α. cos 这与假设矛盾 , 故有 β< α. α, 再由余弦函数在 0 , 若 γ≤ 不等式 α< 0 < sinγ < γ ≤ π , 2 π 的单调性及 2 π 的单调性 2
θ+ ( 4 + a) sinθ+ 4 a 1 + sinθ 3 ( a - 1) ) + = ( 1 + sinθ + a + 2. 1 + sinθ 令 1 + sinθ= x , 由于 - 1 ≤ sinθ≤ 1 , 1 + sinθ≠ 0,
