椭圆函数滤波器

椭圆函数滤波器
维基百科，自由的百科全书
跳转到：导航, 搜索
椭圆滤波器（Elliptic filter）又称考尔滤波器（Cauer filter），是在通带和阻带等波纹的一种滤波器。

椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下有着最小的通带和阻带波动。

它在通带和阻带的波动相同，这一点区别于在通带和阻带都平坦的巴特沃斯滤波器，以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。

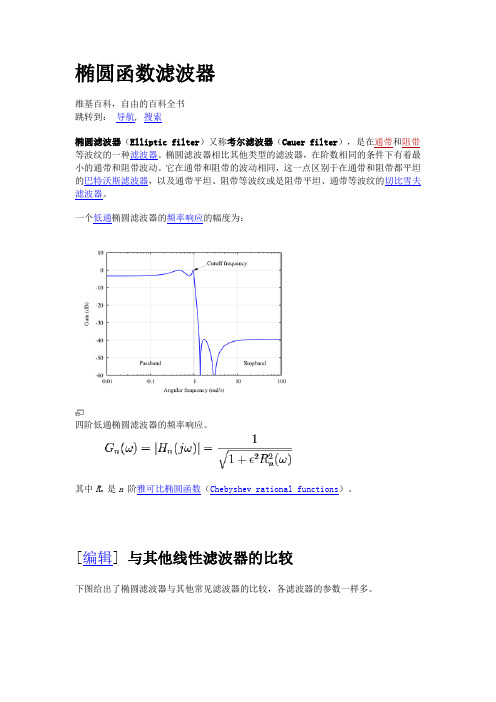
一个低通椭圆滤波器的频率响应的幅度为：
四阶低通椭圆滤波器的频率响应。

其中R n是n阶雅可比椭圆函数（Chebyshev rational functions）。

[编辑]与其他线性滤波器的比较
下图给出了椭圆滤波器与其他常见滤波器的比较，各滤波器的参数一样多。

由图可见，椭圆滤波器比其他滤波器更陡，因此在选择滤波器的时候，椭圆滤波器能够以较低的阶数获得较窄的过渡带宽，但是它在通带和阻带上都有波动。

椭圆滤波器(考尔滤波器)

椭圆滤波器（考尔滤波器）
特点：幅值响应在通带和阻带内都是等波纹的，对于给定的阶数和给定的波纹要求，椭圆滤波器能获得较其它滤波器为窄的过渡带宽，就这点而言，椭圆滤波器是最优的，其振幅平方函数为
式中，RN（Ω，L）为雅可比椭圆函数，L是一个表示波纹性质的参量。

由图可见，在归一化通带内（-1≤Ω≤1），在（0，1）间振荡，而超过ΩL后，在L2和间振荡。

L越大，ΩL也变大。

这一特点使滤波器同时在通带和阻带具有任意衰减量。

下图为典型的椭园滤波器振幅平方函数：
图中ε和A的定义与切比雪夫滤波器相同。

当Ωc、Ωs、ε和A确定后，阶次N的确定方法为：
上面讨论了三种最常用模拟低通滤波器的特性和设计方法，设计时按照指标要求，合理选用。

一般，椭圆滤波器的阶次可最低，切比雪夫次之，巴特沃兹最高，参数的灵敏度则恰恰相反。

椭圆函数带通滤波器

椭圆函数带通滤波器首先基于椭圆函数的微波带通滤波器设计，首先，由要求的技术指标确定滤波器阶数；其次，通过已成熟的滤波器理论查表确定相应低通原型滤波器各元件的参数，并根据频率变换得到所需带通滤波器的电路模型；然后，借助微波电路设计的首选工程软件ADS2008对其原理图进行仿真，得到所设计的椭圆函数微波带通滤波器的21S和11S的数据显示图；最后通过分析数据图并不断优化设计方案以达到所设计的技术指标要求，并综合比较得到最佳的原理图及相应的元件值。

分析数据结果可得到所设计的滤波器达到了设计指标要求，表明设计设计方案可行微波滤波器的意义在无线通信技术飞速发展的近几年来，滤波器作为一种二端口网络,具有让某些频率的信号顺利通过,而对另外一些频率的信号加以阻隔和衰减的频率选择特性，而目前在通信、雷达、广播、微波等领域，多频率工作应用越来越普遍,对分隔频率的要求也相应地提高了。

因此,滤波器在这些领域被广泛运用,是微波,毫米波系统中不可缺少的器件,其性能的优劣往往直接影响整个通信系统的质量。

尤其是在通信系统的接收机前端，带通滤波器性能的优劣会直接影响到整个接收机性能的好坏。

因此,无线通信系统对滤波器的性能指标提出了越来越高的要求。

特别是在移动通信基站双工器和多工器中使用的滤波器,除了高选择性、小尺寸、通带内低插入损耗的要求以外,对滤波器通带内的群延迟和通带外的衰减都提出了十分苛刻的要求。

面对这些要求,传统的滤波器比如最大平坦和切比雪夫滤波器很难胜任,因为普通结构的滤波器只有通过增加阶数来满足要求,而这样却会增加滤波器的插损,而且生产出来的滤波器的重量和体积都会非常大,不满足现代通信的需求。

而椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下有着最小的通带和阻带波动，具有良好的选择性，但实现起来却比较困难。

带通滤波器是滤波器中应用最多、最重要也是较难设计的一种滤波器。

目前射频微波电路的高度集成，尤其是单片微波集成芯片(MMIC)的发展，使得用微带线来实现高频信号在电路板上传输更为普遍。

语音信号的数字滤波处理十一——椭圆函数(hanning窗)滤波器

语音信号的数字滤波处理十一——椭圆函数（hanning窗）滤波器数字信号处理课程设计语音信号的数字滤波处理(十一)题目：——椭圆函数（hanning窗）滤波器学生姓名：学号：班级:专业：指导教师：实习起止时间: 2015年6月29日至2015年7月3日题目数字信号处理——语音信号的数字滤波处理(十一)学生姓名：学号：班级：所在院(系):指导教师：摘要本次设计的内容为切比雪夫及hanning低通、高通、带通滤波器，并利用MATLAB平台进行设计。

首先通过声音处理语句得到声音信号的时域数据，利用FFT变换可得到频域数据，以此进行频率分析。

然后对原语音信号进行加噪处理，得到被污染信号。

最后将被污染信号通过设计的滤波器，实现滤波功能，得到滤波后的语音信号。

滤波器分别用切比雪夫II型和hanning窗设计，间接法设计IIR滤波器采用双线性变换法，滤波器设计指标由频谱分析得到。

通过声音播放语句进行语音播放，可观察声音的变化；通过图形处理语句和FFT得到时域图和频谱图，可分析得到滤波器对频率的滤波功能。

关键词：切比雪夫；声音处理；hanning；MATLAB；FFT目录1 绪论 (2)1.1 课题背景 (2)1.2 课题目的 (2)2 课程设计预习与原理 (3)2.1 课程设计预习 (3)2.1.1 卷积运算的演示 (3)2.2.2 采样定理的演示 (9)2.2 课程设计原理 (11)2.2.1 频谱分析原理 (11)2.2.2 IIR设计原理 (12)2.2.3 FIR设计原理 (12)3 课程设计步骤和过程 (15)3.1 IIR设计步骤和过程 (15)3.2 FIR设计步骤和过程 (15)4 设计程序的调试和运行结果 (16)4.1切比雪夫低通滤波器程序的调试和运行结果 (16)4.2切比雪夫高通滤波器程序的调试和运行结果 (18)4.3切比雪夫带通滤波器程序的调试和运行结果 (20)4.4 hamming滤波器程序的调试和运行结果 (23)5 总结 (25)参考文献 (27)附录 (28)附录 A (28)附录 B (33)1 绪论1.1 课题背景随着软硬件技术的发展，仪器的智能化与虚拟化已成为未来实验室及研究机构的发展方向。

用MAX264构成椭圆函数滤波器的设计

用M AX264构成椭圆函数滤波器的设计山东大学电子工程系(250100)　刘立国摘　要:叙述了用开关电容有源滤波器M A X264构成椭圆函数滤波器的设计方法,并且给出了设计实例,该滤波器具有参数可调、滤波性能良好等特点。

关键词:开关电容有源滤波器M A X264　椭圆函数滤波器1　M A X264概述开关电容有源滤波器M A X264由完全相同的两个二阶滤波器组成,其中心频率、Q值及工作模式均可通过相应的引脚连接到V+或V-任意选择,中心频率的选择范围为1H Z～140kH z,外加时钟源或由晶振供芯片工作,时钟频率范围为40H Z～4M H Z,Q值选择范围为0.5～64,其工作模式设有四种,除外加时钟源或晶振外,无须外接其他元件即可实现带通、低通、高通、陷波、全通滤波,外加少许阻容元件可构成多反馈型滤波器,外加有源器件和阻容元件可构成频率可调的陷波器。

12M A X264内部结构如图1所示。

图1(接上页) (3)写“1”子程序W1W1:　CL R　P1.2 SETB　P1.4CL R P1.4SETB P1.2SETB P1.5R ET(4)发送地址子程序LA。

地址高8位在单片机内RAM中20H,低8位在21H。

LA:M OV R0,#20HM OV R1,#00HLA1:M OV B,#08HM OV A1,@R0LA2:CL R P1.2CL R P1.4RCL AM OV P1.5,CSETB P1.4SETB P1.2DJN Z B,LA2I N C R1DJN Z R1,#2,LA3I N C R0A JM P LA1LA3:R ET(5)读1字节子程序RBY。

读出数据在A中。

RBY:A CALL RD ;读;A CALL W Z;写“0”;A CALL RD;读;A CALL LA;发送16位地址;M OV B,#8;设置读数据位数;RBY1:CL R P1.2;选通X84041;CL R P1.3;发出读信号;M OV C,P1.5;数据读入C;RL C A;C中数据移位到A;SETB P1.3;结束读信号;SETB P1.2;结束选通X84041信号;DJN Z B,RBY1;1字节未完循环;R ET;1字节读结束返回。

椭圆函数低通滤波器

GOAL
Goal OptimGoal2 Expr="dB(S(2,1))" SimInstanceName="SP1" Min= Max=-65 Weight= RangeVar[1]="freq" RangeMin[1]=240MHz RangeMax[1]=250MHz
0 -20
dB(S(2,1)) dB(S(1,1))
（七）低通滤波器的设计步骤
根据设计指标在ADS设计向导中建模仿真； ADS设计向导中建模仿真 1、根据设计指标在ADS设计向导中建模仿真；对电路进行优化； 2、对电路进行优化；电容换成标称值，对电感进行优化； 3、电容换成标称值，对电感进行优化；最后对电感用专门软件计算； 4、最后对电感用专门软件计算；画版图加工； 5、画版图加工；安装调试； 5、安装调试；
几种常见滤波器的比较
滤波器类型 LC滤波器微带滤波器腔体滤波适用频率插损 3GHz以下 3～ 30GHz 3～ 30GHz 较小较大很小体积接口小小 SMA SMA
较大波导
（六）低通滤波器的设计指标
1、工作频率：DC～200MHz 工作频率：DC～ 2、插损 ≤1.5dB 纹波≤ 3、纹波≤1dB 带外抑制：@250MHz衰减衰减≥ 4、带外抑制：@250MHz衰减≥60dB 5、驻波≤1.5 驻波≤ 接头：SMA-506、接头：SMA-50-K
-40 -60 -80 -100 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
freq, GHz
低通滤波器电路版图
（八）低通滤波器的调试步骤 1、根据指标要求对网络分析仪校准；根据指标要求对网络分析仪校准； 2、对电感进行调试；对电感进行调试； 3、改变电感线圈间距来微调电感，间距变大，电感变小；改变电感线圈间距来微调电感，间距变大，电感变小； 4、重点调试滤波器通带内的驻波比。重点调试滤波器通带内的驻波比。特别注意：特别注意：线圈要绕正确； 1、线圈要绕正确； 2、装配要规范；装配要规范； 3、主要的问题是电容和电感值偏离仿真值。主要的问题是电容和电感值偏离仿真值。

椭圆函数LC带通滤波器的应用设计

椭圆函数LC带通滤波器的应用设计
滤波器类型的选择可根据滤波器设计的带宽等指标和具体的应用场合来选择。

相对带宽在20%以下的为窄带滤波器，应选用窄带滤波器的设计方法来设计；相对带宽在40%以上的为宽带滤波器，应选用宽带滤波器的设计方法来设计；而介于两者之间的为中等带宽滤波器。

由上面的指标可以看出本滤波器是窄带带通滤波器。

采用巴特沃斯滤波器来设计可以使通带内具有最大平坦的幅频响应；而切比雪夫滤波器的好处是：带外抑制好，但是带内有一定的波动；本文设计的滤波器要求带外近端抑制良好（可以用切比雪夫滤波器或椭圆函数滤波器来实现，但是从后面的分析看要使用LC滤波器，而用LC滤波器的话，使用切比雪夫形式电路元件的值过于小，很难实现，这个可以用软件仿真来说明），以此可以看出，用椭圆函数滤波器更适合。

微带滤波器通过采用不同的衬底材料可以在很大的频率范围内应用（从几百MHz到几十GHz）；同轴滤波器由于其微小的尺寸，制作精度很难达到；波导滤波器在小信号电平上，它的频率基本是8~100 GHz;陶瓷介质滤波器体积大，形状因子与品质因数较小；LC滤波器适用于本滤波器频段，且较容易制作和调试。

椭圆函数低通滤波器设计

椭圆函数低通滤波器设计引言椭圆函数低通滤波器是一种常用的滤波器，在信号处理中起着重要的作用。

它具有较为复杂的设计和计算方法，但可以实现较为精确的滤波效果。

本文将介绍椭圆函数低通滤波器的设计原理和步骤，并给出具体的实例。

设计原理椭圆函数低通滤波器的设计基于椭圆函数（或称Chebyshev函数）的性质。

椭圆函数具有特殊的振幅响应特性，可以实现更为陡峭的滤波特性。

在椭圆函数低通滤波器设计中，需要指定截止频率、通带波纹和阻带衰减等参数。

通过调整这些参数，可以灵活地设计出满足特定需求的低通滤波器。

设计步骤椭圆函数低通滤波器的设计步骤如下：1.确定滤波器的截止频率。

根据具体应用需求，选择适当的截止频率。

截止频率是指滤波器开始对信号进行衰减的频率。

2.确定通带波纹和阻带衰减。

通带波纹是指通过滤波器的信号波形的最大波动幅度，阻带衰减是指滤波器对截止频率之后的频率的衰减程度。

3.根据截止频率、通带波纹和阻带衰减等参数，计算滤波器的阶数。

阶数是指滤波器的阶数，即滤波器的复杂度。

较高的阶数可以实现更陡峭的滤波特性，但也会增加滤波器的计算和设计难度。

4.根据计算的阶数，使用椭圆函数逼近方法计算椭圆函数的极点和零点。

极点和零点是滤波器设计中重要的参数，它们的位置决定了滤波器的频率响应特性。

5.根据计算得到的极点和零点，构造椭圆函数低通滤波器的传递函数。

传递函数描述了滤波器的输入输出关系。

6.对传递函数进行归一化处理，以确保滤波器的增益在通带为1。

7.根据得到的传递函数，设计数字滤波器的巴特沃斯原型。

8.使用数字滤波器设计中的双线性变换方法将巴特沃斯原型转换为数字滤波器。

实例演示以一个实例来演示椭圆函数低通滤波器的设计过程。

假设我们需要设计一个截止频率为1 kHz，通带波纹为0.5 dB，阻带衰减为40 dB的椭圆函数低通滤波器。

根据设计步骤，首先确定截止频率为1 kHz。

然后根据通带波纹和阻带衰减，选择滤波器的阶数为4。

椭圆滤波器设计的公式

椭圆滤波器设计的公式椭圆滤波器是一种常用于信号处理和通信系统中的数字滤波器。

与其他滤波器相比，椭圆滤波器具有更为复杂的频率响应特性，可以更精确地滤除或增强特定频率范围内的信号。

椭圆滤波器的设计基于椭圆函数，其频率响应特性可以通过椭圆函数的参数来控制。

椭圆滤波器的设计目标一般是在给定的频率范围内实现最小的幅度失真和最小的相位失真。

椭圆滤波器的设计过程可以分为两个步骤：规格化和设计。

规格化是指将滤波器的频率响应特性转化为对应的规格化频率响应，这样可以将设计问题简化为一个标准化的问题。

设计是指根据规格化的频率响应特性，选择合适的椭圆函数参数，并计算出滤波器的系数。

在椭圆滤波器的设计中，有两个重要的参数需要确定：通带和阻带的边界频率，以及通带和阻带的最大允许衰减。

通带是指滤波器允许通过的频率范围，阻带是指滤波器需要抑制的频率范围。

边界频率是通带和阻带的分界点，最大允许衰减是指滤波器需要在阻带中实现的最小衰减。

根据给定的规格化频率响应特性，可以使用椭圆函数的参数来确定椭圆滤波器的频率响应。

常用的椭圆函数有零阶椭圆函数、一阶椭圆函数和二阶椭圆函数。

根据设计要求和滤波器的阶数，选择合适的椭圆函数进行设计。

在椭圆滤波器的设计中，需要进行参数优化和系数计算。

参数优化是指根据设计要求和椭圆函数的参数，通过迭代计算得到最优的滤波器参数。

系数计算是指根据最优的滤波器参数，计算出滤波器的系数，以实现所需的频率响应。

椭圆滤波器设计的公式较为复杂，可用于计算滤波器的各个参数和系数。

通过公式计算，可以得到滤波器的频率响应、阶数、通带和阻带的边界频率等信息。

这些信息对于滤波器的设计和性能评估非常重要。

总结起来，椭圆滤波器是一种常用的数字滤波器，其设计基于椭圆函数。

通过选择合适的椭圆函数参数，计算滤波器的系数，可以实现所需的频率响应特性。

椭圆滤波器的设计公式可以帮助工程师快速计算和设计滤波器，提高滤波器设计的效率和准确性。

椭圆滤波器传递函数

椭圆滤波器传递函数
椭圆滤波器是数字信号处理中经常使用的一种滤波器，其具有优秀的滤波性能和高效的计算能力，可以广泛应用于音频、图像等领域中。

椭圆滤波器的传递函数是其设计中的核心部分，它决定了滤波器的滤波特性和实际运行效果。

在进行椭圆滤波器设计时，我们需要先确定其传递函数，然后再求解相应的滤波器参数。

椭圆滤波器的传递函数是一个复数函数，通常表示成下面的形式：
H(z) = K * F(z)
其中，K是一个常数因子，F(z)是一个有理函数，可以写成分子和分母的形式：
其中，B(z)和A(z)都是多项式函数，分别表示椭圆滤波器的分子和分母部分。

椭圆滤波器的传递函数是如何得出的呢？其实，在进行椭圆滤波器设计时，我们通常会先选择一种标准的滤波器特性，比如低通、高通、带通或带阻特性，然后通过一系列的计算和参数调整，得出相应的传递函数。

这一过程通常是一个迭代优化的过程，需要不断调整参数，直至得出满足要求的传递函数。

1. 具有截止频率，可以实现滤波器的截止特性；
2. 在截止频率处的滤波器幅频响应具有最小的过渡带宽度，可以实现高效的滤波效果；
3. 具有很高的滚降率，可以在截止频率之外快速地减小功率；
4. 由于其复杂的多项式函数形式，椭圆滤波器的传递函数通常难以精确计算，需要使用近似方法进行处理。

基于上述特点，椭圆滤波器在数字信号处理中被广泛应用，特别是在需要高效、精确滤波的领域中，如音频处理、图像处理等。

但也需要注意，椭圆滤波器由于其复杂的计算过程和高阶多项式表达式，其在实际使用中也存在一定的限制和不足，需要根据实际情况进行选用和调整。

基于准椭圆函数的高温超导滤波器设计

基于准椭圆函数的高温超导滤波器设计
一、引言
高温超导材料的发现和应用，使得超导滤波器在微波通信领域中得到了广泛的应用。

其中准椭圆函数是一种重要的数学工具，在设计高性能滤波器时起着关键作用。

二、准椭圆函数简介
准椭圆函数是指解析式为 $sn(u,k)$ 的特殊函数，其中 $k$ 为模量，$u$ 为自变量。

它们可以看做是 Jacobi 椭圆函数的变形，并且具有许多优秀的性质，如周期性、对称性等。

三、基于准椭圆函数设计高温超导滤波器
1. 高通滤波器设计：利用几何平均法将两个低通滤波器级联即可实现一个高通滤波器。

通过选择适当的参数值和阶数，可以获得所需频率响应。

2. 带通/带阻滤波器设计：采用直接合成法或者间接合成法来构造带通/带阻滤波器。

其中直接合成法需要先求出理想频率响应再进行近似处理；而间接合成法则是根据给定条件反推出所需频率响应。

3. 多段式抽头线型低通/带阻混合型微带线过渡结构：这种结构常见于集总元件电路中，在使用时需要考虑其尺寸限制以及与其他元件之间的匹配问题。

四、总结
基于准椭圆函数设计高温超导滤波器已经被广泛地研究和应用。

在实际工程中，我们需要综合考虑各种因素并灵活运用不同方法来完成所需任务。

未来随着技术水平不断提升，相信这方面会有更多新进展产生。

椭圆、切比雪夫、巴特沃斯、贝塞尔滤波器理解和实现

椭圆、切比雪夫、巴特沃斯、贝塞尔滤波器是数字信号处理中常用的滤波器类型，它们在频域滤波中具有重要的应用。

本文将对这几种滤波器进行深入的理解和实现。

一、椭圆滤波器1. 椭圆滤波器简介椭圆滤波器是数字信号处理中常用的一种频域设计滤波器，其特点是具有最小的幅度波动和最快的衰减速度。

椭圆滤波器在通信系统、雷达信号处理等领域有着广泛的应用。

2. 椭圆滤波器的设计原理椭圆滤波器的设计依托于椭圆函数的性质，通过对椭圆函数的特定变换和调节参数，可以实现对滤波器的频率响应进行精确的设计。

3. 椭圆滤波器的实现方法椭圆滤波器的实现方法通常包括传统的基于频率采样的设计方法和现代的最优化设计方法。

基于频率采样的设计方法通过对频率响应进行离散采样，从而得到滤波器的截止频率和通带波动等参数；而最优化设计方法则通过数学优化算法来求解滤波器的设计参数，以实现更加精确的频率响应设计。

二、切比雪夫滤波器1. 切比雪夫滤波器简介切比雪夫滤波器是一种具有等波纹特性的滤波器，在通信系统、图像处理等领域有着广泛的应用。

切比雪夫滤波器的特点是在通带和阻带波动上都具有等波纹特性，可以实现更加灵活的频率响应设计。

2. 切比雪夫滤波器的设计原理切比雪夫滤波器的设计依托于切比雪夫多项式的性质，通过调节切比雪夫多项式的阶数和系数，可以实现对滤波器的频率响应进行灵活的设计。

3. 切比雪夫滤波器的实现方法切比雪夫滤波器的实现方法通常包括频域采样方法和参数优化方法。

其中，频域采样方法可以通过对频率响应进行离散采样来得到滤波器的设计参数；而参数优化方法则通过数学优化算法来寻找滤波器的最优参数。

三、巴特沃斯滤波器1. 巴特沃斯滤波器简介巴特沃斯滤波器是一种具有平坦通带和陡峭阻带的滤波器，其特点是在通带和阻带的过渡区域都具有平坦的频率响应。

巴特沃斯滤波器在无线通信系统、生物医学信号处理等领域有着广泛的应用。

2. 巴特沃斯滤波器的设计原理巴特沃斯滤波器的设计原理是基于布特沃斯多项式的特性，通过调节巴特沃斯多项式的阶数和系数，可以实现对滤波器的频率响应进行设计。

滤波器设计中的自适应椭圆滤波器

滤波器设计中的自适应椭圆滤波器自适应滤波器是数字信号处理中常用的一种滤波器类型，它能够根据输入信号的特征动态地调整滤波器参数，以达到最佳的滤波效果。

其中，椭圆滤波器作为一种常见的滤波器设计方法，在多个领域中得到广泛应用。

本文将介绍滤波器设计中的自适应椭圆滤波器原理及其应用。

一、自适应滤波器简介自适应滤波器是一种根据输入信号的特性动态地调整滤波器参数的滤波器。

与传统固定滤波器相比，自适应滤波器能够通过自我学习和自我调整的方式，实现对不同信号的有效滤波处理。

其中，椭圆滤波器是自适应滤波器的一种重要形式。

二、椭圆滤波器原理椭圆滤波器的设计基于椭圆函数的特性以及信号的频域表示。

椭圆函数是一类具有特殊对称性质的函数，其在频域表示中具有较为复杂的频率响应特征。

椭圆滤波器通过调整椭圆函数的参数，实现对不同频率成分的滤波。

与其他滤波器相比，椭圆滤波器具有更好的滤波特性，能够实现更高的阻带衰减和更低的过渡带宽。

三、自适应椭圆滤波器设计方法自适应椭圆滤波器的设计方法主要包括参数估计和参数更新两个步骤。

在参数估计阶段，通过分析输入信号的特征，确定椭圆滤波器的初值参数。

然后，在参数更新阶段，根据滤波器的误差性能，使用最优化算法来调整椭圆滤波器的参数，以使滤波器的输出更加接近于期望信号。

四、自适应椭圆滤波器的应用自适应椭圆滤波器在信号处理领域有着广泛的应用。

例如，在通信系统中，自适应椭圆滤波器可用于抑制噪声、消除多径信道干扰等；在图像处理中，自适应椭圆滤波器可用于图像去噪、边缘增强等。

此外，在雷达、声音处理等领域中，自适应椭圆滤波器也发挥着重要的作用。

五、总结自适应椭圆滤波器作为数字信号处理中的一种重要滤波器类型，具有良好的滤波特性和适应能力。

通过动态地调整滤波器参数，自适应椭圆滤波器能够实现对不同信号的最佳滤波处理。

在实际应用中，我们可以根据具体需求和信号特点选择合适的自适应椭圆滤波器设计方法，并进行参数调整和优化，以实现更好的滤波效果。

椭圆滤波器算法通带截止频率

椭圆滤波器算法通带截止频率
椭圆滤波器是一种常用的数字滤波器，其特点是具有截止频率可调的通带和阻带。

本文将介绍椭圆滤波器的算法以及如何根据通带截止频率来设计椭圆滤波器。

椭圆滤波器的设计是一种最优化问题，旨在使滤波器在通带内尽可能平坦，而在阻带内尽可能陡峭。

通常情况下，椭圆滤波器的通带和阻带都是以分贝为单位来衡量的，常见的通带截止频率有3dB和6dB两种。

设计椭圆滤波器的算法可以分为两个步骤：首先是确定滤波器的阶数，即滤波器的复杂度；然后是确定滤波器的系数，即滤波器的具体形状。

对于阶数的确定，可以根据滤波器的要求来选择。

阶数越高，滤波器的复杂度越高，但滤波器的性能也越好。

一般来说，通带截止频率越低，阶数就需要越高。

确定了阶数之后，接下来就是确定滤波器系数的过程。

在椭圆滤波器中，可以通过调整通带和阻带的边界来实现对滤波器系数的控制。

通带截止频率越低，滤波器的通带边界就需要越靠近截止频率，从而使得通带的响应更加平坦。

通过调整通带和阻带的边界，可以得到不同截止频率的椭圆滤波器。

在确定了滤波器系数之后，可以通过离散化的方式将滤波器应用到
实际的信号处理中。

一般来说，可以使用差分方程来表示滤波器的响应，然后使用数字信号处理的方法来实现滤波器的运算。

总结一下，椭圆滤波器是一种常用的数字滤波器，可以根据通带截止频率来设计。

设计椭圆滤波器的算法包括确定滤波器的阶数和确定滤波器的系数两个步骤。

通带截止频率越低，滤波器的阶数就需要越高，通过调整通带和阻带的边界可以得到不同截止频率的椭圆滤波器。

最后，可以使用离散化的方式将滤波器应用到实际的信号处理中。

椭圆滤波器原理 -回复

椭圆滤波器原理-回复椭圆滤波器（Elliptical Filter）是一种常用于信号处理和通信系统中的数字滤波器，它在频域上具有非常灵活的滤波特性。

椭圆滤波器是一种有限脉冲响应（FIR）滤波器，可以实现高阶滤波，具有较为陡峭的衰减特性和较小的相位失真。

本文将一步步解析椭圆滤波器的原理。

第一步：了解滤波器的基本原理在讨论椭圆滤波器之前，我们需要先了解滤波器的基本原理。

滤波器是一种可以改变信号频谱特性的系统，可以用于增强或减弱信号中的特定频率成分。

在数字信号处理中，滤波器可以通过对输入信号的离散时间序列施加权重来实现。

传统的滤波器根据其频率响应特性可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。

低通滤波器允许低频信号通过并削弱高频信号，高通滤波器则允许高频信号通过并削弱低频信号，带通滤波器则滤波指定的频段内的信号，而带阻滤波器则削弱指定的频段内的信号。

第二步：了解椭圆滤波器的定义及特性椭圆滤波器是一种基于信号频域特性设计的滤波器，它是一种无限脉冲响应（IIR）滤波器，也被称为Cauer滤波器。

与传统的低通、高通、带通、带阻滤波器不同，椭圆滤波器在滤波器频率响应曲线上具有非常灵活的特点。

椭圆滤波器不但具有窄带宽、阻带宽、过渡带宽和衰减比等通常用于IIR 滤波器的参数，还有一些额外的参数，如最大允许的振荡次数和相位特性等。

这些参数可以通过设计椭圆曲线来实现。

第三步：椭圆滤波器的设计方法椭圆滤波器的设计方法主要分为两种：模拟滤波器到数字滤波器的转化和频域方法。

在模拟滤波器到数字滤波器转化的方法中，首先设计一种与所需的椭圆滤波器频响相似的模拟滤波器，然后将其转换为数字滤波器。

这种方法的主要优点是设计思路简单，但是需要进行反变换来将模拟滤波器转换为数字滤波器，可能引入一定的误差。

在频域方法中，首先根据椭圆滤波器的设计规范在频域上设计一条满足要求的椭圆曲线，然后通过傅里叶变换将这个频域描述转换为时域的冲激响应，进而得到滤波器的权值系数。

有源低通椭圆函数滤波器的设计

2010届电子信息工程专业毕业设计（论文）前言经过D/A转换获得模拟信号在现代社会生活中比比皆是，如声卡中的语音合成输出、合成信号发生器等，为了滤除谐波干扰，获得高精度的模拟信号，大多采用衰减特性陡峭的椭圆低通滤波器进行滤波。

基于上述原因，文章提出了一种有源椭圆函数滤波器的设计，椭圆滤波器在通带和阻带内都是等波纹的逼近方式，是滤波器阶数N 已给定的情况下的最好的逼近方式。

对于同样的性能要求，它比巴特沃思、切比雪夫滤波器所需用的阶数都低，而且它的过渡带比较窄。

滤波器设计是比较成熟的技术，根据设计要求，首先确定滤波器的曲线和类型，以及滤波器的阶数，根据设计参数确定具体曲线和归一化的元件值，再根据实际去归一化得到实际的元件值。

这样得到的设计参数完全是计算得到的，往往与实际有一定的出入，修正也比较繁锁。

现在EDA技术的应用可以大大简化了设计过程，特别是设计过程中进行仿真，确保设计的一次成功率。

本文以语音和波形合成中常用的椭圆低通滤波器为例说明滤波器的设计过程和EDA技术在其中的应用。

目录摘要 (I)ABSTRACT ................................................................ I I 第1章绪论 (1)1.1滤波器的发展 (1)1.1.1早期的情况 (1)1.1.2 发展时期 (1)1.1.3 现代的滤波器 (2)1.2滤波器的功能 (3)1.3滤波器的分类 (4)1.3.1按所处理的信号 (4)1.3.2按所通过信号的频段 (4)1.3.3按所采用的元器件 (4)1.4文章所做工作 (5)第2章滤波器综合技术基础 (7)2.1现代网络理论 (7)2.1.1极-零点的概念 (7)2.1.2 由多项式综合滤波器 (9)2.2频率响应的归一化 (11)2.2.1频率和阻抗标度 (11)2.2.2低通滤波器的归一化 (14)2.3椭圆函数滤波器 (15)第3章方案设计及仿真 (19)3.1滤波器的逼近 (19)3.1.1滤波器的实现形式选择 (19)3.1.2滤波器的阶数确定 (20)3.2电路实现 (21)3.2.1 实现方式选择 (21)3.2.2 元件值的计算 (22)3.3仿真 (24)3.3.1 EDA技术的概念 (24)3.3.2 EDA常用软件 (25)3.3.3电子电路设计与仿真工具 (25)3.3.4 multisim10 仿真实现 (26)3.3.5仿真结果 (30)第4章调试与测试结果 (31)4.1测试仪器表 (31)4.2对安装好的电路进行调整和测试 (31)4.3实际电路遇到的问题及解决方法 (31)4.4测试结果和幅频图分析 (32)第5章结论 (35)5.1结论 (35)5.2感想和收获 (35)5.3展望 (36)参考文献 (37)致谢 (38)附录 (39)附录一：电路板 (39)附录二：元器件清单 (40)2010届电子信息工程专业毕业设计（论文）摘要分析信号频谱时为了提高系统的频率分辨率，需要设计性能优良的模拟滤波器。

椭圆函数滤波器响应

低通原型滤波器器件参数的确定
最平坦响应的低通原型滤波器至15阶时的衰减曲线如下：
低通原型滤波器器件参数的确定
对于等波纹响应的低通原型滤波器，至10阶的滤波器参数值列表如下(带内波纹0.01dB)：
LAr = 0.01dB
n g1
g2
g3
g4
g5
g6
g7
g8
g9
g10
g11
1 0.0960 1.0000
Rejection: it is parameter according to the specification of a filter
Qulity factor Q: Another parameter describing filter selectivity
Q = f0 / BW
微波网络综合法设计滤波器
• 一般先设计低通原型滤波器，实际的低通高通带通带阻滤波器可由低通原型变换得到。
• 微波网络综合法设计滤波器时，将整个滤波器看成是多级二端口网络的级联，实际中这些二端口网络是串连电感并联电容。
微波网络综合法设计滤波器
• 由转移参量可以得到整个滤波器的频率响应特性。
A C
B D
1 0
RG 1
with ripple of 1dB
100 100
1
10
1
10
Comparison of Frequency response between Butterworht and Chebyshev Filters
典型滤波器响应
椭圆滤波器（elliptic filter）是利用椭圆函数（elliptic function）的双周期函数性质设计的。

椭圆滤波器

椭圆滤波器（考尔滤波器）
特点：幅值响应在通带和阻带内都是等波纹的，对于给定的阶数和给定的波纹要求，椭圆滤波器能获得较其它滤波器为窄的过渡带宽，就这点而言，椭圆滤波器是最优的，其振幅平方函数为
式中，R
N
（Ω，L）为雅可比椭圆函数，L是一个表示波纹性质的参量。

图 N=5时的特性曲线
由图可见，在归一化通带内（-1≤Ω≤1），在（0，1）间振荡，而
超过Ω
L 后，在L2和间振荡。

L越大，Ω
L
也变大。

这一特点使滤波器同时
在通带和阻带具有任意衰减量。

下图为典型的椭园滤波器振幅平方函数：
图椭圆滤波器的振幅平方函数
图中ε和A的定义与切比雪夫滤波器相同。

、ε和A确定后，阶次N的确定方法为：
当Ωc、Ω
s
式中K(k)=为第一类完全椭圆积分。

上面讨论了三种最常用模拟低通滤波器的特性和设计方法，设计时按照指标要求，合理选用。

一般，椭圆滤波器的阶次可最低，切比雪夫次之，巴特沃兹最高，参数的灵敏度则恰恰相反。