A寻路算法
浅谈游戏中自动寻路算法的实现与应用

浅谈游戏中自动寻路算法的实现与应用作者:蒋恺来源:《中国新通信》 2018年第2期在信息技术的支持下,互联网进入了迅猛发展期,各种网游、页游大量出现,受到不同玩家的喜爱与青睐。
当然为了逐步扩大受众群,需要不断的优化游戏,满足玩家对游戏的需求,其中自动寻路算法就是十分关键的技术之一,提升了游戏角色在虚拟游戏环境中的灵活性,更利于对游戏角色的控制,是判断游戏质量的重要标准之一”1。
一、关于自动寻路算法的概述1.1自动寻路算法的原理在自动寻路算法中最常用的为A*算法,这属于启发式的算法,被广泛应用于游戏中的路径搜索【21。
主要是节点的设置,具有记录、搜索进度的功能,通过节点在游戏地图中移动,当搜寻到目标位置时就结算,否则会进一步搜索记录目标位置周围相邻的位置。
举例而言,游戏角色最初的位置就是开始节点,将要到达的目标位置设置为目标节点,在两者之间存在一定的障碍物和可以顺利通行的路径,黑色部分为障碍物,白色部分为可通行路径,具体如下图1所示:在设计A*算法时采用的基本原理,其实为最短路径算法,在整个游戏地图中,从起始节点到目标节点的路径多种多样,将这些全部读入到开放式列表中,再通过与目标节点距离最近的节点进行对比,从而找到最优路径”1。
将上图1中的起始节点设置为A,目标节点力B,在计算最优路径节点C时需要在考虑几何距离基础上使用计算公式:(A—C)2+fB—C)2在A*算法中通过对各个不同节点的计算,从而找出路径最短最优的节点,但这一算法具有一定的缺陷,很可能要将整个地图上的节点都计算完了才能得出结果,当游戏场景复杂且节点数量过多的话,会大大增加游戏设计制作中的寻路算法的费用。
为此,就要对A*算法进行优化改进,以便扩大应用范围,满足玩家的游戏需求。
1.2自动寻路算法的实现为了最快的找到游戏地图中的最优路径,需要将游戏场景进行网格划分,让每个网路成为大小相同的正方形,成为游戏中的导航网格,就可以选择一个节点起始位置,进行目标节点位置的广度搜索,在确定区域后在计算最佳路径。
a星算法的原理

a星算法的原理A*算法的原理A*算法是一种常用的寻路算法,用于在图形化的环境中找到从起点到目标点的最短路径。
它结合了Dijkstra算法和贪心算法的优点,能够高效地找到最佳路径。
A*算法的核心思想是通过启发式函数来评估每个节点的价值,以选择下一个要探索的节点。
这个启发式函数通常被称为估价函数,它用来估计从当前节点到目标节点的距离。
A*算法会维护一个开放列表和一个关闭列表,来存储待探索的节点和已经探索过的节点。
A*算法的具体步骤如下:1. 初始化:将起点加入开放列表,并将其G值(起点到起点的实际代价)设置为0。
2. 进入循环:如果开放列表不为空,则继续执行循环。
3. 寻找最佳节点:从开放列表中选择估价函数值最小的节点作为当前节点,并将其移出开放列表,加入关闭列表。
4. 判断是否达到目标:如果当前节点是目标节点,则路径已找到,终止算法。
5. 遍历相邻节点:遍历当前节点的所有相邻节点。
6. 更新节点:计算每个相邻节点的G值和H值(估价函数值)。
如果该节点不在开放列表中,则将其加入开放列表,并更新其父节点为当前节点。
7. 重新排序开放列表:按照节点的F值(G值加上H值)重新排序开放列表,以便下一次循环时选择估价函数值最小的节点。
8. 继续循环:回到步骤2,继续执行循环。
9. 生成路径:当目标节点被加入关闭列表时,路径已找到。
通过回溯每个节点的父节点,从目标节点到起点生成最短路径。
A*算法的优势在于它能够根据启发式函数快速找到接近最佳路径的节点,从而减少了搜索的时间和空间复杂度。
启发式函数的选择对算法的性能影响很大,一个好的启发式函数能够提高算法的效率。
然而,A*算法也存在一些限制。
首先,如果启发式函数不是一致的(也称为单调的),则无法保证找到的路径是最短路径。
其次,A*算法在遇到图形中存在大量障碍物或者复杂的地形时,可能会产生大量的节点扩展,导致算法效率下降。
为了解决这些问题,研究者们提出了各种改进的A*算法,例如IDA*算法、Jump Point Search算法等。
astar寻路算法原理

astar寻路算法原理
A(A星)寻路算法是一种常用的启发式搜索算法,用于在图中
找到从起点到终点的最短路径。
它结合了Dijkstra算法和启发式搜
索的优点,具有较高的搜索效率。
A算法基于图的搜索,其中每个节点表示一个状态,边表示从
一个状态到另一个状态的转移。
算法使用两个函数来评估每个节点
的重要性,g(n)表示从起点到节点n的实际代价,h(n)表示从节点
n到终点的估计代价。
A算法通过综合考虑这两个函数来选择下一个
要扩展的节点。
具体来说,A算法通过维护一个开放列表和一个关闭列表来进
行搜索。
它首先将起点加入开放列表,然后重复以下步骤直到找到
终点或者开放列表为空:
1. 从开放列表中选择f(n)=g(n)+h(n)最小的节点n进行扩展。
2. 将节点n从开放列表中移入关闭列表。
3. 对节点n的相邻节点进行检查,更新它们的g值和f值,并
将它们加入开放列表中。
A算法的关键在于如何选择合适的启发函数h(n)以及如何高效地维护开放列表和关闭列表。
合适的启发函数可以大大提高搜索效率,而高效的列表维护可以减少搜索时间。
总的来说,A算法是一种高效的寻路算法,能够在图中找到最短路径,并且可以通过调整启发函数来适应不同的问题。
A星算法

很早以前就写过A*算法,现在把概念写出来供参考寻路一般主要有深度优先和广度优先及启发式探索算法。
a. 深度优先:一般是深度优先是按照一定的顺序前查找完一个分支,再查找另一个分支,直到找到目标或到达步数为止。
b.广度优先一般是找周围所有点记录下来,然后在对每个点找它们周围所有未找过的点,然后再如此循环下去直到找到目标为止。
c. 启发式启发式搜索一般是对每个搜索位置进行评估,找到最好的位置,再从这个位置如此循环进行搜索直到目标。
启发中的估价是用估价函数表示的:f(n) = g(n) + h(n)其中f(n) 是节点n的估价函数,g(n)是从初始点到n结点的实际代价,h(n)是从n结点到目标点最佳路径的估价。
如果公式中的h(n)总是=0, 也即不进行估价,那么就是广度优先,现在的A*算法一般都使用了启发式函数,对于普通的A*算法通常使用当前结点到目标结点的距离来计算h。
关于启发式要考虑的启发因素还有类似于一些地形属性如泥士地走慢点等也可考虑在内。
晕死, 后来发现原来我早之前已经写过这个文章, 见我旧blog:/blog/cns!8E578E7901A88369!444.entry内容如下:寻路备忘录寻路备忘录一.深度优先搜索(DFS)按照一定顺序(如左上右下)能走则走(这就是深度两字的来源),就象一个瞎子走迷宫一样:1.选定一个方向一直走2.碰壁后退一步,再重复1的步骤.缺点:a.在很少障碍的空地图上若跨出的第一步顺序不对时寻路挺费时;b.找到的不一定是最短路径优点:算法所用内存较少.二.广度优先搜索(BFS)1.先在开始位置测试周围一格所能走的路,并记录周围的通路格子;2.然后依次选择周围的通路格子位置重复1步骤.这就象一个水波扩散一样,这就是广度两字的来源.缺点:寻路所用内存较大优点:能保证找到最短路径三.启发式搜索:A*就是常用的一种启发式算法.作法如下:1.选路,这会用到一个叫估价函数的东东F(X),其中F(X)=G(X)+H(X);式中的G(X)一般是已经搜索的步数,而H(X)则是一个从当前节点到目标节点估计函数,一般可用当前节点到目标节点的距离来作比较.2.走路,碰到不通路时,在所有所记录的通路中重新选择一条路来走,即重复1.优点:速度快并且所占内存不多。
浅谈寻路A算法范文

浅谈寻路A算法范文寻路算法(Pathfinding)是计算机中常用的一种算法,通过图形结构中两个节点之间的最佳路径,解决了很多实际问题,如游戏中的NPC寻路、自动驾驶的路径规划等。
其中,A*算法(A-star algorithm)被广泛应用于寻路算法中,本文将对A*算法进行详细介绍。
A*算法是通过启发式算法(Heuristic Search)实现的一种寻路算法,根据估算函数(Heuristic Function)对节点进行评估,并选择具有最小开销的节点进行扩展。
A*算法的核心思想是综合考虑节点的实际开销(G 值)和预估的目标开销(H值),并选择最优节点进行。
在A*算法中,节点的开销是通过计算路径上节点的实际开销和预估开销得到的。
实际开销是指从起始节点到当前节点的移动开销,通常是节点间的距离或代价。
预估开销是通过估算函数对当前节点到目标节点的距离进行评估,常用的估算函数有欧几里得距离、曼哈顿距离等。
A*算法的具体步骤如下:1. 创建一个开启列表(Open List)和一个关闭列表(Closed List),起始节点放入开启列表。
2.从开启列表中选出具有最小开销的节点作为当前节点,并将其放入关闭列表中。
3.对当前节点的所有相邻节点进行遍历,如果该节点不可通过或者在关闭列表中,则忽略。
4.计算相邻节点的实际开销和预估开销,更新节点的G值和H值。
5.如果相邻节点不在开启列表中,将其加入开启列表,并将当前节点设置为该节点的父节点。
6.如果相邻节点已经在开启列表中,比较当前节点作为父节点时的G 值和之前的G值,如果小于之前的G值,更新节点的父节点为当前节点。
7.重复2-6步骤,直到达到目标节点或者开启列表为空。
8.如果达到目标节点,从目标节点开始回溯父节点,得到最佳路径。
A*算法的优势在于通过使用估算函数,能够快速找到目标节点,而且能够保证找到的路径是最佳路径。
同时,A*算法可以通过调整估算函数的权重来权衡的速度和路径的质量。
a算法计算

a*算法关于A*算法网上介绍的有很多,我只是看了之后对这个算法用c写了一下,并测试无误后上传以分享一下,欢迎指正!下面是我找的一个介绍,并主要根据这个实现的。
寻路算法不止A* 这一种, 还有递归, 非递归, 广度优先, 深度优先, 使用堆栈等等, 有兴趣的可以研究研究~~简易地图如图所示简易地图, 其中绿色方块的是起点(用A 表示), 中间蓝色的是障碍物, 红色的方块(用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.寻路步骤1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.3. 从"开启列表"中删除起点A, 并将起点A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格图中浅绿色描边的方块表示已经加入"开启列表" 等待检查. 淡蓝色描边的起点A 表示已经放入"关闭列表" , 它不需要再执行检查.从"开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式F=G+H 来计算.F =G + HG 表示从起点A 移动到网格上指定方格的移动耗费(可沿斜方向移动).H 表示从指定的方格移动到终点B 的预计耗费(H 有很多计算方法, 这里我们设定只可以上下左右移动).我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算FGH, 图中方块的左上角数字表示F, 左下角表示G, 右下角表示H. 看看是否跟你心里想的结果一样?从"开启列表" 中选择F 值最低的方格C (绿色起始方块A 右边的方块), 然后对它进行如下处理:4. 把它从"开启列表" 中删除, 并放到"关闭列表" 中.5. 检查它所有相邻并且可以到达(障碍物和"关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在"开启列表" 里的话, 将它们加入"开启列表", 计算这些方格的G, H 和 F 值各是多少, 并设置它们的"父方格" 为C.6. 如果某个相邻方格D 已经在"开启列表" 里了, 检查如果用新的路径(就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的"父方格" 改为目前选中的方格C, 然后重新计算它的 F 值和G 值(H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的G 值比较高, 就说明经过C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.如图, 我们选中了C 因为它的F 值最小, 我们把它从"开启列表" 中删除, 并把它加入"关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到"关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的G 是14, 如果通过 C 到达它的话, G将会是10 + 10, 这比14 要大, 因此我们什么也不做.然后我们继续从"开启列表" 中找出F 值最小的, 但我们发现C 上面的和下面的同时为54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进"开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从"方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)就这样, 我们从"开启列表" 找出F 值最小的, 将它从"开启列表" 中移掉, 添加到"关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...那么什么时候停止呢? ——当我们发现"开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.如何找回路径如上图所示, 除了起始方块, 每一个曾经或者现在还在"开启列表" 里的方块, 它都有一个"父方块", 通过"父方块" 可以索引到最初的"起始方块", 这就是路径.以上转自/technology/archive/2011/05/26/2058842.html下面是我的代码(c):一共三个文件:Apath.h 、Apath.c 、main.c 代码中有详细注释。
A算法的实现原理及应用

A算法的实现原理及应用算法是计算机科学中重要的概念,其本质是一种数学思想,是一系列求解问题的方法和步骤。
A算法,也称为A*算法,是一种常见的寻路算法,被广泛应用于游戏开发、人工智能、机器人控制等领域。
本文将介绍A算法的实现原理及其应用。
一、A算法的实现原理A算法是一种搜索算法,其目标是在搜索图中找到从起点到终点的最短路径。
A算法基于一种启发式搜索策略,即优先考虑最有可能通向终点的节点。
下面是A算法的基本实现步骤:1. 初始化开始节点和结束节点,并把开始节点加入到开启列表中。
2. 从开启列表中选出具有最小f值(f值是节点的启发值和代价值之和)的节点作为当前节点。
3. 把当前节点从开启列表中删除,并将其加入到关闭列表中。
4. 遍历当前节点的相邻节点,如果相邻节点不可通过或者已经在关闭列表中,就忽略。
5. 对于未被遍历过的相邻节点,计算它的f值、g值和h值。
其中,g值表示从起点到该节点的代价,h值表示该节点到终点的启发值,即估算到终点的实际代价。
6. 如果相邻节点已经在开启列表中,比较新的g值和原先的g值,如果新的g值更小,就更新g值和f值。
如果相邻节点不在开启列表中,将其加入到开启列表中,并计算其f、g、h值。
7. 重复步骤2到步骤6,直到找到终点或者开启列表为空。
二、A算法的应用A算法是一种高效的寻路算法,其应用非常广泛。
下面列举几个例子:1. 游戏开发在游戏开发中,A算法被广泛用于计算游戏场景中的敌人或角色行走的最佳路径。
游戏场景通常被表示为一个二维数组,A算法可以根据玩家角色的位置和目标位置,在场景图中寻找最短路径,并输出路径。
2. 人工智能A算法是人工智能领域中常用的算法之一,可以被用于求解最优路径问题。
例如,在机器人路径规划中,A算法可以根据机器人的当前位置和目标位置,搜索机器人的最短路径,并输出路径。
3. 网络路由A算法也被广泛应用于网络路由领域。
当网络中出现路由选择问题时,A算法可以根据网络拓扑结构和路由代价,寻找到源节点到目标节点的最短路径。
简易的A星算法自动寻路(C#)

简易的A星算法⾃动寻路(C#)路径计算⽅式(详见参考:堪称最好最全的A*算法详解(译⽂)):1. 曼哈顿距离,横向和纵向直线距离,仅限于横向纵向移动2. 对⾓线距离,对⾓线 + 直线,可以横向、纵向、对⾓线⽅向移动3. 欧⼏⾥得距离,任意⾓度直线,任意⽅向移动using System.Collections;using System.Collections.Generic;using UnityEngine;using System.Linq;public class AStartTest{AStarNode[,] nodeMap = new AStarNode[10, 10];void CheckAndFindPath(AStarNode startNode, AStarNode endNode){//计算路径List<AStarNode> pathNodes = FindNodePath(startNode, endNode, nodeMap);if (pathNodes == null || pathNodes.Count == 0)return;//计算路径折点List<AStarNode> pathPoints = GetPathPoint(pathNodes);}//计算路径折点List<AStarNode> GetPathPoint(List<AStarNode> path){List<AStarNode> tmpPointList = new List<AStarNode>();//⽆折点if (path.Count <= 2)return tmpPointList;//当前节点与前⼀节点的位置关系(X坐标相同或Y坐标相同)bool lastDirIsX = path[1].pos.x == path[0].pos.x;//计算折点for (int i = 2; i < path.Count; i++){//若与前⼀节点X坐标相同if (path[i].pos.x == path[i - 1].pos.x){//前两个节点时Y坐标相同,即为折点if (!lastDirIsX){//记录折点,记录当前节点关系tmpPointList.Add(path[i - 1]);lastDirIsX = true;}}else{if (lastDirIsX){tmpPointList.Add(path[i - 1]);lastDirIsX = false;}}}//路径最后节点也视为折点tmpPointList.Add(path[path.Count - 1]);//return tmpPointList;}#region --- A*算法 ---//计算最短有效路径List<AStarNode> openList = new List<AStarNode>();List<AStarNode> closeList = new List<AStarNode>();List<AStarNode> aroundNodes;List<AStarNode> FindNodePath(AStarNode startNode, AStarNode endNode, AStarNode[,] allNodes) {//计算范围内的节点openList.Clear();//不在计算范围内的节点closeList.Clear();//添加起点openList.Add(startNode);AStarNode curNode;//从起点开始循环判断while (openList.Count > 0){//初始当前位置curNode = openList[0];//计算最优当前位置for (int i = 0; i < openList.Count; i++){//F:从起点到⽬标点的移动步数//H:从当前位置到⽬标位置的移动步数if (openList[i].CostF < curNode.CostF && openList[i].costH < curNode.costH){curNode = openList[i];}}//锁定当前位置节点openList.Remove(curNode);closeList.Add(curNode);////已经计算到⽬标点//if (curNode.Equals(endNode))//{// //返回最优路径// return GetPathWithNode(startNode, endNode);// }//未计算到⽬标点, 继续//获取当前点的周围节点, 在周围节点中查找下⼀步的最优节点aroundNodes = GetAroundNodes(curNode, allNodes);for (int i = 0; i < aroundNodes.Count; i++){//计算到⽬标点if (aroundNodes[i].Equals(endNode)){//设置上⼀节点aroundNodes[i].lastNode = curNode;//返回最优路径return GetPathWithNode(startNode, endNode);}//不是⽬标点, 继续计算, 剔除周围节点不可通过、在不可计算范围内的节点if (!aroundNodes[i].isWall && !closeList.Contains(aroundNodes[i])){//计算 G H F//F:从起点到⽬标点的移动步数//G:从起点到当前位置的移动步数int newCostG = curNode.costG + GetNodesDistance(curNode, aroundNodes[i]);if (newCostG <= aroundNodes[i].costG || !openList.Contains(aroundNodes[i])){//刷新赋值aroundNodes[i].costG = newCostG;//H:从当前位置到⽬标位置的移动步数aroundNodes[i].costH = GetNodesDistance(aroundNodes[i], endNode);//设置上级节点aroundNodes[i].lastNode = curNode;//添加到计算范围内if (!openList.Contains(aroundNodes[i])){openList.Add(aroundNodes[i]);}}}}}return null;}//计算距离int GetNodesDistance(AStarNode startNode, AStarNode endNode){return Mathf.Abs(startNode.pos.x - endNode.pos.x) + Mathf.Abs(startNode.pos.y - endNode.pos.y);}//周围节点只取上下左右四个, 不取对⾓线(根据实际需求设置周围节点)Vector2Int[] aroundPos = { new Vector2Int(0, 1), new Vector2Int(0, -1), new Vector2Int(1, 0), new Vector2Int(-1, 0) }; //获取周围NodeList<AStarNode> tmpAroundList = new List<AStarNode>();List<AStarNode> GetAroundNodes(AStarNode curNode, AStarNode[,] allNodes){tmpAroundList.Clear();for (int i = 0; i < aroundPos.Length; i++){//计算周围节点坐标int x = curNode.pos.x + aroundPos[i].x;int y = curNode.pos.y + aroundPos[i].y;//剔除不在取值范围内的数据if (x >= 0 && x < allNodes.GetLength(0) && y >= 0 && y < allNodes.GetLength(1)){if (allNodes[x, y] != null)tmpAroundList.Add(allNodes[x, y]);}}return tmpAroundList;}//获取路径(包含起点)List<AStarNode> tmpNodePath = new List<AStarNode>();List<AStarNode> GetPathWithNode(AStarNode startNode, AStarNode endNode){tmpNodePath.Clear();if (endNode != null){//逆向查找路径AStarNode temp = endNode;while (temp != startNode){tmpNodePath.Add(temp);temp = stNode;}tmpNodePath.Add(startNode);//路径数据反向tmpNodePath.Reverse();}return tmpNodePath;}#endregion}public class AStarNode{//A*算法节点类//是否能通过public bool isWall;//位置坐标public Vector2Int pos;//上个节点public AStarNode lastNode;//从起点到当前位置的移动步数public int costG;//从当前位置到⽬标位置的移动步数public int costH;//从起点到⽬标点的移动步数public int CostF{get { return costG + costH; }}public AStarNode(bool _isWall, Vector2Int _pos) {isWall = _isWall;pos = _pos;}//重写Equalspublic override bool Equals(object obj){if (obj is AStarNode){AStarNode objNode = (AStarNode)obj;return objNode.pos == pos;}return false;}public override int GetHashCode(){return base.GetHashCode();}}。
astar寻路算法原理 -回复

astar寻路算法原理-回复A*寻路算法原理及步骤一、简介A*(A-Star)寻路算法是一种常用的路径规划算法,用于找到两个点之间的最短路径。
它综合了Dijkstra算法和贪心算法的优点,既考虑了每个节点的代价,也考虑了每个节点到目标节点的预估代价。
本文将一步一步详细介绍A*寻路算法的原理和步骤。
二、原理A*算法的核心思想是使用一个估算函数来预测从起始节点到目标节点的代价,并在遍历过程中选择最小代价节点来进行扩展。
该算法综合了代价函数和启发函数的信息,以更快地找到最短路径。
其具体步骤如下:1. 初始化将起始节点添加到一个开放列表(open list)中,开放列表存放待扩展的节点。
同时,创建一个空的闭合列表(closed list),用于存放已扩展过的节点。
2. 循环操作进入循环操作,直到开放列表为空或找到目标节点。
在每次循环中,选择开放列表中代价最小的节点进行扩展。
3. 节点扩展取开放列表中代价最小的节点,将其从开放列表中删除,并加入到闭合列表中。
然后,获取该节点的相邻节点,计算它们的代价和预估代价,并更新它们的代价值和路径。
4. 判断相邻节点对于每个相邻节点,判断它们是否在开放列表或闭合列表中。
若在闭合列表,则跳过该节点;若在开放列表,比较新路径与旧路径的代价,若新路径更好,则更新代价和路径;否则,不做任何操作。
5. 添加新节点对于不在开放列表中的相邻节点,将它们添加到开放列表中,并计算它们的代价和预估代价。
6. 重复操作重复步骤2至5,直到开放列表为空或找到目标节点。
若开放列表为空,则无法找到路径;若找到目标节点,则回溯路径,回到起始节点。
三、关键要点在上述步骤中,有几个关键要点需要注意:1. 代价函数代价函数用于计算节点到起始节点的实际代价,包括走过的距离、障碍物等影响因素。
根据具体情况,可以自定义代价函数。
2. 启发函数启发函数用于估算节点到目标节点的代价,即预测代价。
常见的启发函数有曼哈顿距离、欧几里得距离等,根据实际情况选择合适的启发函数。
java 利用a算法寻找最优路径 实验步骤

java 利用a算法寻找最优路径实验步骤实验:利用A*算法寻找最优路径引言:A*算法是一种常用的寻找最优路径的算法,它结合了Dijkstra算法的广度优先搜索和Greedy Best-First Search算法的贪心思想,能够在实际操作中有效地优化路径的选择。
本实验将通过Java语言编写代码,展示如何使用A*算法在一个图形环境中寻找最优路径。
步骤一:创建图形界面和渲染基本场景首先,在Java中创建一个图形界面,并添加一个画布用于渲染基本场景。
在画布中,我们可以使用不同的形状和颜色表示不同的地形和障碍物。
这些地形和障碍物将构成我们的路径搜索环境。
步骤二:定义节点和边的数据结构接下来,我们需要定义节点和边的数据结构。
节点是图形环境中的一个位置,边是将两个节点连接起来的路径。
每个节点都有一个唯一的标识符,并且存储其在画布中的位置、与其他节点相邻的边以及其他有关信息。
步骤三:实现A*算法的估价函数A*算法的核心是估价函数,它用来评估路径的优劣。
在我们的实验中,我们可以使用欧几里得距离作为估价函数。
给定两个节点A(x1, y1)和B(x2,y2),欧几里得距离可以通过以下公式计算:distance = sqrt((x2-x1)^2 + (y2-y1)^2)。
我们可以通过这个函数来评估两个节点之间的距离。
步骤四:实现A*算法的启发函数启发函数用于预测节点到目标节点的成本。
在我们的实验中,我们可以使用欧几里得距离作为启发函数。
给定一个节点A(x, y)和目标节点B(tx, ty),启发函数可以通过以下公式计算:heuristic = sqrt((tx-x)^2 + (ty-y)^2)。
我们可以通过这个函数来预测节点到目标节点的成本。
步骤五:实现A*算法的搜索过程现在,我们可以开始实现A*算法的搜索过程。
首先,我们需要创建一个开放列表和一个关闭列表。
开放列表用于存储待处理的节点,关闭列表用于存储已经处理过的节点。
A星寻路算法

此文档由网络搜集而来。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。
取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。
你尽可以用任意的计算机程序语言实现它。
如你所愿,我在文章的末尾包含了一个指向例子程序的链接。
压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。
让我们从头开始。
序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1,从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
3DA星寻路算法实现

3DA星寻路算法实现图1旱桥的寻路(粉红⾊块为路径)图2螺旋楼梯的寻路(粉红⾊块为路径)当场景的碰撞使⽤3D以后相关的寻路也应该具有3D寻路功能,由于引擎中的碰撞格分为多层,所以在开启⼀个节点的时候就需要将每⼀层进⾏判断,判断条件主要是2个a碰撞格不能为红⾊b⾼度差不能超过⼀定的范围,为了寻路更有效率,增加了⼀个⾼度⽅向的启发值,当两个节点在平⾯⽅向与⽬标距离相等,但⾼度⽅向有区别那么与⽬标⾼度相差较⼩的节点优先遍历,其它的过程与2D的a*寻路算法没什么区别。
我的寻路算法中使⽤了⼆叉堆管理Open表,代码如下,供⼤家参考,SOpenMask是节点的结构定义,AddOpenMask函数功能是将⼀个节点放⼊Open表中,GetMinOpenMask函数是从Open表中取出具有最⼩权值的节点,上图是3d a*寻路算法的结果演⽰。
struct SOpenMask{::SOpenMask *pFather;SOpenMask *pLeft;SOpenMask *pRight;};int CAStarTrace::AddOpenMask( SOpenMask* pOpenMask, SOpenMask* pHead ){if( pHead == NULL ){m_pOpenHead = pOpenMask;return 0;}if( pHead->nDistance <= pOpenMask->nDistance ){if( pHead->pRight == NULL ){pHead->pRight = pOpenMask;pOpenMask->pFather = pHead;}elseAddOpenMask( pOpenMask, pHead->pRight );}else{if( pHead->pLeft == NULL ){pHead->pLeft = pOpenMask;pOpenMask->pFather = pHead;}elseAddOpenMask( pOpenMask, pHead->pLeft );}return 0;}SOpenMask* CAStarTrace::GetMinOpenMask( SOpenMask* pHead ) {if( pHead == NULL )return NULL;if( pHead->pLeft == NULL ){SOpenMask * pMinNode = pHead;if( pHead->pFather == NULL ){m_pOpenHead = pHead->pRight;if( m_pOpenHead )m_pOpenHead->pFather = NULL;}else{pHead->pFather->pLeft = pHead->pRight;if( pHead->pRight )pHead->pRight->pFather = pHead->pFather;}return pMinNode;}elsereturn GetMinOpenMask( pHead->pLeft );}。
寻路算法
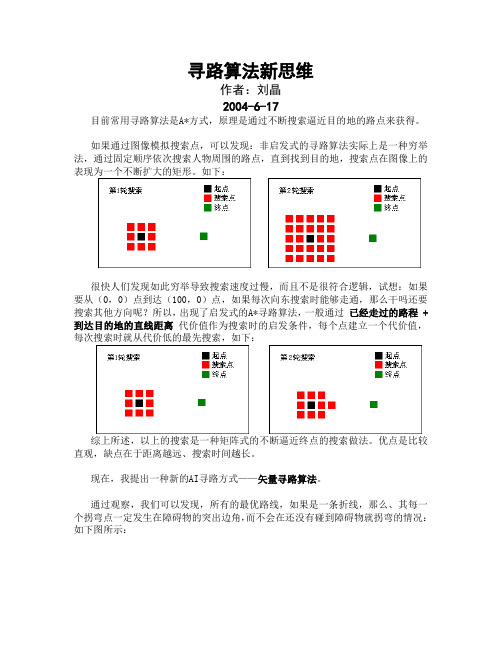
寻路算法新思维作者:刘晶2004-6-17目前常用寻路算法是A*方式,原理是通过不断搜索逼近目的地的路点来获得。
如果通过图像模拟搜索点,可以发现:非启发式的寻路算法实际上是一种穷举法,通过固定顺序依次搜索人物周围的路点,直到找到目的地,搜索点在图像上的表现为一个不断扩大的矩形。
如下:很快人们发现如此穷举导致搜索速度过慢,而且不是很符合逻辑,试想:如果要从(0,0)点到达(100,0)点,如果每次向东搜索时能够走通,那么干吗还要搜索其他方向呢?所以,出现了启发式的A*寻路算法,一般通过已经走过的路程 + 到达目的地的直线距离代价值作为搜索时的启发条件,每个点建立一个代价值,每次搜索时就从代价低的最先搜索,如下:综上所述,以上的搜索是一种矩阵式的不断逼近终点的搜索做法。
优点是比较直观,缺点在于距离越远、搜索时间越长。
现在,我提出一种新的AI寻路方式——矢量寻路算法。
通过观察,我们可以发现,所有的最优路线,如果是一条折线,那么、其每一个拐弯点一定发生在障碍物的突出边角,而不会在还没有碰到障碍物就拐弯的情况:如下图所示:我们可以发现,所有的红色拐弯点都是在障碍物(可以认为是一个凸多边形)的顶点处,所以,我们搜索路径时,其实只需要搜索这些凸多边形顶点不就可以了吗?如果将各个顶点连接成一条通路就找到了最优路线,而不需要每个点都检索一次,这样就大大减少了搜索次数,不会因为距离的增大而增大搜索时间。
这种思路我尚未将其演变为算法,姑且提出一个伪程序给各位参考:1.建立各个凸多边形顶点的通路表TAB,表示顶点A到顶点B是否可达,将可达的顶点分组保存下来。
如: ( (0,0) (100,0) ),这一步骤在程序刚开始时完成,不要放在搜索过程中空耗时间。
2.开始搜索A点到B点的路线3.检测A点可以直达凸多边形顶点中的哪一些,挑选出最合适的顶点X1。
4.检测与X1相连(能够接通)的有哪些顶点,挑出最合适的顶点X2。
5.X2是否是终点B?是的话结束,否则转步骤4(X2代入X1)如此下来,搜索只发生在凸多边形的顶点,节省了大量的搜索时间,而且找到的路线无需再修剪锯齿,保证了路线的最优性。
A星及路标寻路算法

一劳永逸的固定寻路平时我尽我所能,以避免可能被解释为一个在行业中的其他游戏或开发的批评说的事情。
但在这种情况下,我不得不做出一个异常的位。
我要谈谈我们与寻路面临的一些问题。
为了证明,这些问题仍然存在,我觉得有必要使这个视频... ...在幽默和轻松愉快的精神,它的目的是,希望在采取所有这些片段在上周录得最新,最最近修补的每场比赛的版本。
正如你可以看到,我们仍然是一个强大的寻路全线长的路要走... ...它甚至在一些万元的单位销售,AAA级质量职称的问题。
它不一定是一个普遍性的问题。
许多现代游戏有高品质的寻路,寻路经常在这里显示的一些游戏。
但仍有太多的游戏,寻路,游戏在20世纪90年代,以同样的方式。
(注:只是你看到大量的PC角色扮演游戏的唯一原因归结到便利,这些都是我当时安装的游戏,问题是不特定的任何类型或任何发挥想象力的平台。
有类似的问题,大量的游戏机游戏)。
据我所知,这些游戏大多使用寻路航点图。
我认为这几个寻路的问题,您在这个视频中看到,许多我们在整个行业面临的寻路问题的原因。
我相信航点图现在已经过时。
这篇文章解释了航点图方法的局限性,并勾画出了一个更好的方法五点的说法。
曾经有一段时间,这是有意义的,使用寻路航点。
早在20世纪80年代和90年代,我们的工作受到严重的技术限制,我们不得不削减了很多弯道。
但是我们现在一个多亿美元的产业。
我们的目标平台多内核和日益增加的大量的内存,我们可以做不起寻路正确。
有一个行业AI开发中说:“寻路是解决了。
”我们每一个寻路的问题,面临着现代游戏的好方法。
我们只是不经常使用它们。
我们没有理由不寻路,在每场比赛,每次。
打跳了详细的解释。
为什么航点对于寻路让我告诉你什么是一个典型的航点图看起来。
下面是一个在魔兽世界暴风城的小片:图1。
魔兽世界暴风城的一部分,下面是一个典型的航点图可能看起来在这方面想。
图2。
同一地区的一个航点图注释还有另一种方式做到这一点,它涉及使用凸多边形来描述AI角色可以旅行。
A星寻路算法流程

A*算法流程图
1.初始化起点和终点的节点,并将起点节点加入开放列表。
2.对于开放列表中的每个节点,计算它到终点的预估代价(通常使用欧几里得距离或曼哈顿距离)和它到起点的实际代价。
3.选择开放列表中预估代价加实际代价最小的节点,将其加入封闭列表。
4.对于当前节点的每个相邻节点,计算它们到起点的实际代价,并更新它们的父节点为当前节点。
5.如果终点节点被加入封闭列表,说明找到了一条最优路径,结束搜索。
6.如果开放列表为空,说明无法到达终点节点,搜索失败。
7.否则,返回步骤3,继续搜索。
在实现A* 算法时,还需要注意以下几点:
1.使用一个优先队列来存储开放列表中的节点,以便在每次选择节点时,选择预估代价加实际代价最小的节点。
2.在计算预估代价时,应该使用一个启发函数来估算节点到终点的距离,以便能够在搜索过程中优先考虑离终点更近的节点。
3.要在更新节点时记录每个节点的父节点,以便在搜索结束后能够回溯找到最优路径。
总之,A算法是一种常用的寻路算法,能够在图形化游戏中广泛应用。
理解A 算法的流程和实现细节,能够帮助开发者更加高效地实现游戏寻路功能。
astarpathfinding 简书

astarpathfinding 简书A*寻路算法简介导语:A*寻路算法是一种常用的路径规划算法,它可以在图形地图中找到最短路径。
本文将介绍A*寻路算法的原理、应用以及优缺点。
一、A*寻路算法的原理A*寻路算法是一种基于启发式搜索的路径规划算法。
它通过综合考虑已经走过的路径和预估的剩余路径来选择下一步的移动方向,从而找到从起点到终点的最短路径。
具体来说,A*算法使用了两个重要的评估函数:g(n)和h(n)。
其中,g(n)表示从起点到达当前节点n的实际代价,h(n)表示从当前节点n到达目标节点的估计代价。
A*算法的核心思想是选择f(n)=g(n)+h(n)值最小的节点作为下一步的移动方向。
二、A*寻路算法的应用A*寻路算法在许多领域都有广泛的应用。
其中最常见的应用是在游戏开发中用于NPC的路径规划。
NPC需要在地图中找到最短路径来实现自主移动,而A*算法正是解决这个问题的有效工具。
A*寻路算法也被应用于机器人导航、交通路线规划以及迷宫求解等领域。
它能够高效地找到最短路径,减少了搜索空间,大大提高了路径规划的效率。
三、A*寻路算法的优缺点1. 优点:- A*算法能够找到最短路径,并且在大多数情况下具有较高的效率。
- 算法的可扩展性较好,适用于不同规模的地图。
- A*算法能够避开障碍物,寻找到可行的路径。
2. 缺点:- A*算法在处理复杂地图时可能会陷入局部最优解,无法找到全局最优解。
- 算法的计算复杂度较高,对于大规模地图可能消耗较多的计算资源。
- A*算法对于地图中频繁变动的情况需要重新计算路径,效率较低。
四、总结A*寻路算法是一种常用的路径规划算法,它通过综合考虑已经走过的路径和预估的剩余路径来选择下一步的移动方向。
在游戏开发、机器人导航、交通路线规划等领域都有广泛的应用。
虽然A*算法在处理复杂地图时可能存在局部最优解的问题,但它仍然是一种高效的路径规划算法,能够找到最短路径并避开障碍物。
同时,A*算法也具有一定的计算复杂度和计算资源消耗,需要根据实际情况进行权衡和优化。
最优寻路算法公式

最优寻路算法公式寻路算法,这听起来是不是有点高大上?别急,让我慢慢给您讲讲这其中的门道。
您知道吗?就像我们每天出门找路去上班、上学或者去玩耍一样,在计算机的世界里,程序也得“找路”。
比如说,在一个游戏里,角色怎么从 A 点走到 B 点,走哪条路最快、最省事儿,这就得靠寻路算法来帮忙啦。
先来说说最简单的一种寻路算法,叫深度优先搜索。
这就好比您走进了一个迷宫,啥也不想,先一条道走到黑,走不通了再回头换条路。
听起来有点笨是不是?但有时候还真能管用。
我想起之前玩一个解谜游戏,里面的小角色就得靠这种简单的算法来找路。
那个场景是在一个古老的城堡里,到处都是弯弯绕绕的通道和紧闭的门。
我控制的小角色就这么闷着头往前走,有时候走进死胡同,那叫一个郁闷。
但当它终于找到出路的时候,那种惊喜感简直难以言表。
再说说广度优先搜索算法。
这个就像是您在探索迷宫的时候,一层一层地往外扩,把周围能走的路都先看一遍,再决定下一步往哪走。
这种算法相对更全面一些,不容易错过好的路线。
有一次我设计一个小程序,要让一个小机器人在一个虚拟的地图上找宝藏。
我一开始用了深度优先搜索,结果小机器人老是迷路。
后来换成广度优先搜索,嘿,它很快就找到了通往宝藏的最佳路径,那感觉就像我自己找到了宝藏一样兴奋。
然后咱们来聊聊 A* 算法。
这可是寻路算法里的大明星!它综合考虑了距离和预估的代价,就像是您出门前不仅知道距离有多远,还能大概猜到路上会不会堵车、好不好走。
我曾经参与过一个物流配送的项目,要给送货的车规划最优路线。
用了 A* 算法之后,送货的效率大大提高,司机师傅们都夸这个算法厉害,省了不少油钱和时间。
还有 Dijkstra 算法,它总是能找到从起点到所有点的最短路径。
这就像是您有一张超级详细的地图,能清楚地知道去任何地方的最短距离。
在实际应用中,选择哪种寻路算法可不是随便拍拍脑袋就能决定的。
得看具体的情况,像地图的大小、复杂程度,还有对时间和资源的限制等等。
易语言摇杆寻路算法

易语言摇杆寻路算法易语言摇杆寻路算法可以使用A*算法实现。
A*算法是一种基于启发式搜索的寻路算法,通过在地图上搜索最短路径,即从起点到终点的最短路径。
下面是使用易语言编写的A*算法的摇杆寻路示例程序:pascal判断一个点是否在地图范围内func InMap(x, y, map_width, map_height) {return x >= 0 && x < map_width && y >= 0 && y < map_height; }计算两点之间的曼哈顿距离func ManhattanDistance(x1, y1, x2, y2) {return x2 - x1 + y2 - y1 ;}A*算法寻路函数func AStar(start_x, start_y, end_x, end_y, map_width, map_height,map_data) {创建开放列表和关闭列表open_list = [[start_x, start_y]];close_list = [];创建用于记录父节点和G、H、F值的辅助数组parent_nodes = [[[start_x, start_y], -1, -1]]; 父节点、G值、H值、F 值创建移动方向的数组directions = [[-1, 0], [1, 0], [0, -1], [0, 1], [-1, -1], [-1, 1], [1, -1], [1, 1]];开始循环直到找到路径或者无法找到路径while !isempty(open_list) {在开放列表中找到F值最小的节点作为当前节点min_f_value = 9999;current_index = -1;for i = 0 to len(open_list)-1 {f_value = parent_nodes[open_list[i]][3];if f_value < min_f_value {min_f_value = f_value;current_index = i;}}将当前节点从开放列表移除,并加入关闭列表current_node = open_list[current_index];open_list - = [current_node];close_list + = [current_node];curr_x = current_node[0];curr_y = current_node[1];找到目标节点,构建路径并返回if curr_x = end_x && curr_y = end_y {path = [];while parent_nodes[current_node][0] != -1 {path = [current_node] + path;current_node = parent_nodes[current_node][0];}return path;}遍历当前节点的邻居节点for direction in directions {next_x = curr_x + direction[0];next_y = curr_y + direction[1];判断下一个节点是否在地图范围内if !InMap(next_x, next_y, map_width, map_height) { continue;}判断下一个节点是否为障碍物if map_data[next_x][next_y] = 1 {continue;}计算下一个节点的G、H、F值G_value = parent_nodes[current_node][1] + 1;H_value = ManhattanDistance(next_x, next_y, end_x, end_y); F_value = G_value + H_value;判断下一个节点是否已经在关闭列表中if [next_x, next_y] in close_list {continue;}如果下一个节点已经在开放列表中,判断是否更新G值和F值if [next_x, next_y] in open_list {if G_value < parent_nodes[[next_x, next_y]][1] {parent_nodes[[next_x, next_y]][0] = current_node;parent_nodes[[next_x, next_y]][1] = G_value;parent_nodes[[next_x, next_y]][3] = F_value;}} else {将下一个节点加入开放列表open_list + = [[next_x, next_y]];parent_nodes + = [[current_node, G_value, H_value, F_value]];}}}无法找到路径,返回空路径return [];}使用示例定义地图数据,0表示可以通过的路径,1表示障碍物map_data = [[0, 0, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 0, 0],[0, 1, 1, 1, 0],[0, 0, 0, 0, 0]];从(0, 0)点到(4, 4)点寻路start_x = 0;start_y = 0;end_x = 4;end_y = 4;path = AStar(start_x, start_y, end_x, end_y, len(map_data),len(map_data[0]), map_data);print("Path:", path);输出结果:Path: [[0, 0], [0, 1], [0, 2], [0, 3], [0, 4], [1, 4], [2, 4], [3, 4], [4, 4]]以上就是使用易语言编写的A*算法的摇杆寻路示例程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A*寻路算法原文出处:A* Pathfinding for Beginners译者序很久以前就知道了A*算法,但是从未认真读过相关的文章,也没有看过代码,只是脑子里有个模糊的概念。
这次决定从头开始,研究一下这个被人推崇备至的简单方法,作为学习人工智能的开始。
这篇文章非常知名,国内应该有不少人翻译过它,我没有查找,觉得翻译本身也是对自身英文水平的锻炼。
经过努力,终于完成了文档,也明白的A*算法的原理。
毫无疑问,作者用形象的描述,简洁诙谐的语言由浅入深的讲述了这一神奇的算法,相信每个读过的人都会对此有所认识(如果没有,那就是偶的翻译太差了--b)。
以下是翻译的正文。
(由于本人使用ultraedit编辑,所以没有对原文中的各种链接加以处理(除了图表),也是为了避免未经许可链接的嫌疑,有兴趣的读者可以参考原文。
会者不难,A*(念作A星)算法对初学者来说的确有些难度。
这篇文章并不试图对这个话题作权威的陈述。
取而代之的是,它只是描述算法的原理,使你可以在进一步的阅读中理解其他相关的资料。
最后,这篇文章没有程序细节。
你尽可以用任意的计算机程序语言实现它。
如你所愿,我在文章的末尾包含了一个指向例子程序的链接。
压缩包包括C++和Blitz Basic两个语言的版本,如果你只是想看看它的运行效果,里面还包含了可执行文件。
我们正在提高自己。
让我们从头开始......序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1.从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
2.寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。
也把他们加入开启列表。
为所有这些方格保存点A作为“父方格”。
当我们想描述路径的时候,父方格的资料是十分重要的。
后面会解释它的具体用途。
3.从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
在这一点,你应该形成如图的结构。
在图中,暗绿色方格是你起始方格的中心。
它被用浅蓝色描边,以表示它被加入到关闭列表中了。
所有的相邻格现在都在开启列表中,它们被用浅绿色描边。
每个方格都有一个灰色指针反指他们的父方格,也就是开始的方格。
[图2]接着,我们选择开启列表中的临近方格,大致重复前面的过程,如下。
但是,哪个方格是我们要选择的呢?是那个F值最低的。
路径评分选择路径中经过哪个方格的关键是下面这个等式:F =G + H这里:∙G = 从起点A,沿着产生的路径,移动到网格上指定方格的移动耗费。
∙H = 从网格上那个方格移动到终点B的预估移动耗费。
这经常被称为启发式的,可能会让你有点迷惑。
这样叫的原因是因为它只是个猜测。
我们没办法事先知道路径的长度,因为路上可能存在各种障碍(墙,水,等等)。
虽然本文只提供了一种计算H的方法,但是你可以在网上找到很多其他的方法。
我们的路径是通过反复遍历开启列表并且选择具有最低F值的方格来生成的。
文章将对这个过程做更详细的描述。
首先,我们更深入的看看如何计算这个方程。
正如上面所说,G表示沿路径从起点到当前点的移动耗费。
在这个例子里,我们令水平或者垂直移动的耗费为10,对角线方向耗费为14。
我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号2(别怕),或者约1.414倍。
为了简化,我们用10和1 4近似。
比例基本正确,同时我们避免了求根运算和小数。
这不是只因为我们怕麻烦或者不喜欢数学。
使用这样的整数对计算机来说也更快捷。
你不就就会发现,如果你不使用这些简化方法,寻路会变得很慢。
既然我们在计算沿特定路径通往某个方格的G值,求值的方法就是取它父节点的G值,然后依照它相对父节点是对角线方向或者直角方向(非对角线),分别增加14和10。
例子中这个方法的需求会变得更多,因为我们从起点方格以外获取了不止一个方格。
H值可以用不同的方法估算。
我们这里使用的方法被称为曼哈顿方法,它计算从当前格到目的格之间水平和垂直的方格的数量总和,忽略对角线方向。
然后把结果乘以10。
这被成为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数,在那里你不能沿对角线方向穿过街区。
很重要的一点,我们忽略了一切障碍物。
这是对剩余距离的一个估算,而非实际值,这也是这一方法被称为启发式的原因。
想知道更多?你可以在这里找到方程和额外的注解。
F的值是G和H的和。
第一步搜索的结果可以在下面的图表中看到。
F,G和H的评分被写在每个方格里。
正如在紧挨起始格右侧的方格所表示的,F被打印在左上角,G在左下角,H则在右下角。
[图3]现在我们来看看这些方格。
写字母的方格里,G = 10。
这是因为它只在水平方向偏离起始格一个格距。
紧邻起始格的上方,下方和左边的方格的G值都等于10。
对角线方向的G值是14。
H值通过求解到红色目标格的曼哈顿距离得到,其中只在水平和垂直方向移动,并且忽略中间的墙。
用这种方法,起点右侧紧邻的方格离红色方格有3格距离,H值就是30。
这块方格上方的方格有4格距离(记住,只能在水平和垂直方向移动),H值是40。
你大致应该知道如何计算其他方格的H值了~。
每个格子的F值,还是简单的由G和H相加得到继续搜索为了继续搜索,我们简单的从开启列表中选择F值最低的方格。
然后,对选中的方格做如下处理:4.把它从开启列表中删除,然后添加到关闭列表中。
5.检查所有相邻格子。
跳过那些已经在关闭列表中的或者不可通过的(有墙,水的地形,或者其他无法通过的地形),把他们添加进开启列表,如果他们还不在里面的话。
把选中的方格作为新的方格的父节点。
6.如果某个相邻格已经在开启列表里了,检查现在的这条路径是否更好。
换句话说,检查如果我们用新的路径到达它的话,G值是否会更低一些。
如果不是,那就什么都不做。
另一方面,如果新的G值更低,那就把相邻方格的父节点改为目前选中的方格(在上面的图表中,把箭头的方向改为指向这个方格)。
最后,重新计算F和G的值。
如果这看起来不够清晰,你可以看下面的图示。
好了,让我们看看它是怎么运作的。
我们最初的9格方格中,在起点被切换到关闭列表中后,还剩8格留在开启列表中。
这里面,F值最低的那个是起始格右侧紧邻的格子,它的F值是40。
因此我们选择这一格作为下一个要处理的方格。
在紧随的图中,它被用蓝色突出显示。
[图4]首先,我们把它从开启列表中取出,放入关闭列表(这就是他被蓝色突出显示的原因)。
然后我们检查相邻的格子。
哦,右侧的格子是墙,所以我们略过。
左侧的格子是起始格。
它在关闭列表里,所以我们也跳过它。
其他4格已经在开启列表里了,于是我们检查G值来判定,如果通过这一格到达那里,路径是否更好。
我们来看选中格子下面的方格。
它的G值是14。
如果我们从当前格移动到那里,G值就会等于20(到达当前格的G值是10,移动到上面的格子将使得G值增加10)。
因为G值20大于14,所以这不是更好的路径。
如果你看图,就能理解。
与其通过先水平移动一格,再垂直移动一格,还不如直接沿对角线方向移动一格来得简单。
当我们对已经存在于开启列表中的4个临近格重复这一过程的时候,我们发现没有一条路径可以通过使用当前格子得到改善,所以我们不做任何改变。
既然我们已经检查过了所有邻近格,那么就可以移动到下一格了。
于是我们检索开启列表,现在里面只有7格了,我们仍然选择其中F值最低的。
有趣的是,这次,有两个格子的数值都是54。
我们如何选择?这并不麻烦。
从速度上考虑,选择最后添加进列表的格子会更快捷。
这种导致了寻路过程中,在靠近目标的时候,优先使用新找到的格子的偏好。
但这无关紧要。
(对相同数值的不同对待,导致不同版本的A*算法找到等长的不同路径。
)那我们就选择起始格右下方的格子,如图。
[图5]这次,当我们检查相邻格的时候,发现右侧是墙,于是略过。
上面一格也被略过。
我们也略过了墙下面的格子。
为什么呢?因为你不能在不穿越墙角的情况下直接到达那个格子。
你的确需要先往下走然后到达那一格,按部就班的走过那个拐角。
(注解:穿越拐角的规则是可选的。
它取决于你的节点是如何放置的。
)这样一来,就剩下了其他5格。
当前格下面的另外两个格子目前不在开启列表中,于是我们添加他们,并且把当前格指定为他们的父节点。
其余3格,两个已经在关闭列表中(起始格,和当前格上方的格子,在表格中蓝色高亮显示),于是我们略过它们。
最后一格,在当前格的左侧,将被检查通过这条路径,G值是否更低。
不必担心,我们已经准备好检查开启列表中的下一格了。
我们重复这个过程,知道目标格被添加进开启列表,就如在下面的图中所看到的。
[图6]注意,起始格下方格子的父节点已经和前面不同的。
之前它的G值是28,并且指向右上方的格子。
现在它的G值是20,指向它上方的格子。
这在寻路过程中的某处发生,当应用新路径时,G值经过检查变得低了-于是父节点被重新指定,G和F值被重新计算。
尽管这一变化在这个例子中并不重要,在很多场合,这种变化会导致寻路结果的巨大变化。
那么,我们怎么确定这条路径呢?很简单,从红色的目标格开始,按箭头的方向朝父节点移动。
这最终会引导你回到起始格,这就是你的路径!看起来应该像图中那样。
从起始格A移动到目标格B只是简单的从每个格子(节点)的中点沿路径移动到下一个,直到你到达目标点。
就这么简单。
[图7]A*方法总结好,现在你已经看完了整个说明,让我们把每一步的操作写在一起:1.把起始格添加到开启列表。
2.重复如下的工作:a) 寻找开启列表中F值最低的格子。
我们称它为当前格。
b) 把它切换到关闭列表。
