热学第二版习题答案
化工热力学(郑丹星)_第二版课后习题答案

pr 0.08664 0.0454 0.005383 Tr 0.7307 Z Z (Z )
对于水蒸汽,
Z 1 q
利用 Z 1 的初值进行迭代,收敛结果为 Z 0.962
Vm
ZRT 0.962 8.314 473 3.78 103 m3 mol 1 6 p 1.0 10
Tr
473 0.7307 647.3
pr
1.0 0.0454 22.05
q
3 / 2 0.42748 Tr 0.7307 3 / 2 4.3332 0.08664
pr 0.08664 0.0454 0.1720 Tr 0.7307 Z Z (Z )
4)L-K 方程
Z Z 0 Z 1
查表 Z 0.9624
0
Z 1 0.03661
0.344
Z 0.950
Vm
ZRT 3.74 103 mol 1 p
3 3 1
查水蒸气表,473K,1.0MPa 下水蒸汽(过热蒸汽)的摩尔体积为 3.71 10 m mol
pc 3.799MPa
0.193
Vc 255cm3 mol 1
则 Tr
T 0.9246 Tc
pr
p 0.5791 pc
Rackett 方程
(1Tr ) V Vc Z c
0.2857
137.37 103 m3 kmol 1
RK 方程
q
3 / 2 0.42748 Tr 0.73073 / 2 5.5494 0.08664
b y1b1 y 2 b2 64 .4705 cm 3 mol 1
热工学第二版课后题答案

第一章思考题1. 平衡状态与稳定状态有何区别?热力学中为什幺要引入平衡态的概念?答:平衡状态是在不受外界影响的条件下,系统的状态参数不随时间而变化的状态。
而稳定状态则是不论有无外界影响,系统的状态参数不随时间而变化的状态。
可见平衡必稳定,而稳定未必平衡。
热力学中引入平衡态的概念,是为了能对系统的宏观性质用状态参数来进行描述。
2. 表压力或真空度能否作为状态参数进行热力计算?若工质的压力不变,问测量其压力的压力表或真空计的读数是否可能变化?答:不能,因为表压力或真空度只是一个相对压力。
若工质的压力不变,测量其压力的压力表或真空计的读数可能变化,因为测量所处的环境压力可能发生变化。
3.当真空表指示数值愈大时,表明被测对象的实际压力愈大还是愈小?答:真空表指示数值愈大时,表明被测对象的实际压力愈小。
4. 准平衡过程与可逆过程有何区别?答:无耗散的准平衡过程才是可逆过程,所以可逆过程一定是准平衡过程,而准平衡过程不一定是可逆过程。
5. 不可逆过程是无法回复到初态的过程,这种说法是否正确?答:不正确。
不可逆过程是指不论用任何曲折复杂的方法都不能在外界不遗留任何变化的情况下使系统回复到初态,并不是不能回复到初态。
6. 没有盛满水的热水瓶,其瓶塞有时被自动顶开,有时被自动吸紧,这是什幺原因?答:水温较高时,水对热水瓶中的空气进行加热,空气压力升高,大于环境压力,瓶塞被自动顶开。
而水温较低时,热水瓶中的空气受冷,压力降低,小于环境压力,瓶塞被自动吸紧。
7. 用U形管压力表测定工质的压力时,压力表液柱直径的大小对读数有无影响?答:严格说来,是有影响的,因为U型管越粗,就有越多的被测工质进入U型管中,这部分工质越多,它对读数的准确性影响越大。
第二章思考题绝热刚性容器,中间用隔板分为两部分,左边盛有空气,右边为真空,抽掉隔板,空气将充满整个容器。
问:⑴ 空气的热力学能如何变化?⑵ 空气是否作出了功?⑶ 能否在坐标图上表示此过程?为什么?答:(1)空气向真空的绝热自由膨胀过程的热力学能不变。
热学第二版-秦允豪-第四章答案

第四章热力学第一定律(题号有所不同)5-1.0.020Kg的氦气温度由升为,若在升温过程中:(1)体积保持不变;(2)压强保持不变;(3)不与外界交换热量,试分别求出气体内能的改变,吸收的热量,外界对气体所作的功,设氦气可看作理想气体,且,解:理想气体内能是温度的单值函数,一过程中气体温度的改变相同,所以内能的改变也相同,为:热量和功因过程而异,分别求之如下:(1)等容过程:V=常量A=0由热力学第一定律,(2)等压过程:由热力学第一定律,负号表示气体对外作功,(3)绝热过程Q=0由热力学第一定律5-2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半;(1)等温过程;(2)绝热过程;(3)等压过程,试分别求出在这些过程中气体内能的改变,传递的热量和外界对气体所作的功,设氮气可看作理想气体,且,解:把上述三过程分别表示在P-V图上,(1)等温过程理想气体内能是温度的单值函数,过程中温度不变,故由热一、负号表示系统向外界放热(2)绝热过程由或得由热力学第一定律另外,也可以由及先求得A(3)等压过程,有或而所以===由热力学第一定律,也可以由求之另外,由计算结果可见,等压压缩过程,外界作功,系统放热,内能减少,数量关系为,系统放的热等于其内能的减少和外界作的功。
5-3 在标准状态下的0.016Kg的氧气,分别经过下列过程从外界吸收了80cal的热量。
(1)若为等温过程,求终态体积。
(2)若为等容过程,求终态压强。
(3)若为等压过程,求气体内能的变化。
设氧气可看作理想气体,且解:(1)等温过程则故(2)等容过程(3)等压过程5-4 为确定多方过程方程中的指数n,通常取为纵坐标,为横坐标作图。
试讨论在这种图中多方过程曲线的形状,并说明如何确定n。
解:将两边取对数或比较知在本题图中多方过程曲线的形状为一直线,如图所示。
直线的斜率为可由直线的斜率求n。
或即n可由两截距之比求出。
5-5 室温下一定量理想气体氧的体积为,压强为。
热学第二版课后习题答案

热学第二版课后习题答案热学第二版课后习题答案热学是物理学中的一门重要学科,研究热量的传递、热力学规律以及热力学系统的性质等。
在学习热学的过程中,课后习题是检验学生对知识掌握程度的重要手段。
下面将为大家提供热学第二版课后习题的答案。
第一章:热力学基础1. 什么是热力学第一定律?它的数学表达式是什么?热力学第一定律是能量守恒定律的推广,它表明能量可以从一种形式转化为另一种形式,但总能量守恒。
数学表达式为ΔU = Q - W,其中ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统对外界做功。
2. 什么是热容?如何计算物体的热容?热容是物体吸收或释放单位温度变化时所需的热量。
计算物体的热容可以使用公式C = Q/ΔT,其中C表示热容,Q表示吸收或释放的热量,ΔT表示温度变化。
3. 什么是等容过程?等容过程的特点是什么?等容过程是指在恒定体积条件下进行的热力学过程。
在等容过程中,系统对外界做功为零,因为体积不变。
等容过程的特点是内能变化等于吸收的热量,即ΔU = Q。
第二章:理想气体的热力学性质1. 理想气体的状态方程是什么?它的含义是什么?理想气体的状态方程是PV = nRT,其中P表示气体的压强,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的温度。
这个方程表示了理想气体的状态与其压强、体积、物质量和温度之间的关系。
2. 理想气体的内能与温度有何关系?理想气体的内能与温度成正比,即U ∝ T。
当温度升高时,理想气体的内能也会增加。
3. 理想气体的等温过程与绝热过程有何区别?等温过程是指在恒定温度条件下进行的热力学过程,绝热过程是指在没有热量交换的情况下进行的热力学过程。
在等温过程中,气体的温度保持不变,而在绝热过程中,气体的内能保持不变。
第三章:热力学第二定律1. 热力学第二定律的表述是什么?它有哪些等效表述?热力学第二定律的表述是热量不会自发地从低温物体传递到高温物体。
它有三个等效表述:卡诺定理、克劳修斯不等式和熵增原理。
化工热力学第二版答案

化工热力学第二版答案马沛生【篇一:马沛生主编化工热力学第四章习题解答】是否题4-1 对于理想溶液的某一容量性质m,则mi?mi。
解:否4-2 在常温、常压下,将10cm3的液体水与20 cm3的液体甲醇混合后,其总体积为 30 cm3。
解:否4-3 温度和压力相同的两种纯物质混合成理想溶液,则混合过程的温度、压力、焓、gibbs自由能的值不变。
解:否4-4 对于二元混合物系统,当在某浓度范围内组分2符合hey规则,则在相同的浓度范围内组分1符合lewis-randall规则。
解:是4-5 在一定温度和压力下的理想溶液的组分逸度与其摩尔分数成正比。
解:是4-6 理想气体混合物就是一种理想溶液。
解:是4-7 对于理想溶液,所有的混合过程性质变化均为零。
解:否4-8 对于理想溶液所有的超额性质均为零。
解:否4-9 理想溶液中所有组分的活度系数为零。
解:否4-10 系统混合过程的性质变化与该系统相应的超额性质是相同的。
解:否4-11理想溶液在全浓度范围内,每个组分均遵守lewis-randall定则。
解:否4-12 对理想溶液具有负偏差的系统中,各组分活度系数?i均大于1。
解:否4-13 wilson方程是工程设计中应用最广泛的描述活度系数的方程。
但它不适用于液液部分互溶系统。
解:是二、计算题4-14 在一定t、p下,二元混合物的焓为h?ax1?bx2?cx1x2其中,a=15000,b=20000,c = - 20000 单位均为j?mol-1,求 (1) 组分1与组分2在纯态时的焓值h1、h2;(2) 组分1与组分2在溶液中的偏摩尔焓h1、h2和无限稀释时的偏摩尔焓h1?、h2?。
j?molj?mol?1解:(1)h1?limh?a?15000x1?1h2?limh?b?20000x2?1?1(2)按截距法公式计算组分1与组分2的偏摩尔焓,先求导: dhdx1??ddx1ddx1?ax1?bx2?cx1x2???ax1?b?1?x1??cx1?1?x1????a?b?c?2cx1将dh代入到偏摩尔焓计算公式中,得dx1h1?h??1?x1?dhdx1?ax1?bx2?cx1x2?(1?x1)?a?b?c?2cx1??ax1?b?1?x1??cx1?1?x1??a?b?c?2cx1?x1?a?b?c?2cx1? ?a?c?1?x1??a?cx2h2?h?x122dhdx1?ax1?bx2?cx1x2?x1?a?b?c?2cx1??ax1?b?1?x1??cx1?1?x1??x1?a?b?c?2cx1??b?cx12无限稀释时的偏摩尔焓h1?、h2?为:h1?limh1?lim?a?cx2??15000?20000?35000?2x1?0x2?1j?molj?mol-1h??limh2?lim?b?cxx2?0x1?121??20000?20000?40000-14-15 在25℃,1atm以下,含组分1与组分2的二元溶液的焓可以由下式表示:h?90x1?50x2?x1x2(?6x1?9x2)式中h 单位为cal?mol-1,x1、x2分别为组分1、2的摩尔分数,求 (1) 用x1表示的偏摩尔焓h1和h2的表达式; (2) 组分1与2在纯状态时的h1、h2;(3) 组分1与2在无限稀释溶液的偏摩尔焓h1?、h2?;(5) x1=0.5 的溶液中的h1和h2值及溶液的?h值。
化工热力学第二版夏清干燥答案

第5章 干燥的习题解答1.已知湿空气的总压强为50Pa,温度为60℃,相对湿度为40%,试求:1湿空气中水汽的分压; 2湿度; 3湿空气的密度;解:1湿空气的水汽分压,V S p P ϕ=由附录查得60C 时水的饱和蒸汽压19.92S p KPa = 2 湿度 (1) 密度32.27m =湿空气/kg 绝干气 密度 3110.1180.493/2.27H H H kg m v ρ++==湿空气 2.在总压下,已知湿空气的某些参数,利用湿空气的H-I 图查出本题附表中空格内的数值,并给出序号4中各数值的求解过程示意图;习题2附表解: CCC上表中括号内的数据为已知,其余值由图H I -查得; 分题4的求解示意图如附图所示,其中A 为状态点;3.干球温度为20℃、湿度为0.009kg 水/kg 绝干气的温空气通过预热器加热到50℃后,再送至常压干燥器中,离开干燥器时空气的相对温度为80%,若空气在干燥器中经历等焓干燥过程,试求:11m 3原温空气在预热过程中始的变化; 21m 3原温空气在干燥器中获得的水分量; 解:131m 原湿空气在预热器中焓的变化当0020,0.009/t C H kg kg ==绝干气时,由H I -图查出043/I KJ kg =绝干气; 当01050,0.009/t C H H kg kg ===绝干气时,由H I -图查出1kg 绝干空气在预热器中焓的变化为:原湿空气的比容为30.84m =湿空气/kg 绝干气31m 原湿空气的焓变为 33136.9/0.84H I KJ m v ∆==湿空气 231m 原湿空气在干燥器中获得的水分当01050,0.009/t C H H kg kg ===绝干气时,在H I -图上确定空气的状态点,由该点沿等焓线向右下方移动与80%ϕ=的线相交,交点即为离开干燥器时空气的状态点;由该点读出空气离开干燥器时的湿度20.018H =/kg kg 绝干气 故31m 原湿空气在干燥器中获得的水分3210.0180.0090.0107/0.84H H H kg m v --==原湿空气 4..将t 0=25℃、0ϕ=40%的常压新鲜空气,与由干燥器排出的t 2=50℃、2ϕ=80%的常压废气混合,两者中绝干气的质量比为1:3;试求:1混合气体的温度和焓;2现需将此混合温空气的相对湿度降至10%后用于干燥湿物料,应将空气的温度升至多少度;解:1对混合气列湿度和焓的衡算,得0234m H H H += 10234m I I I += 2由附录查得025t C =时,水的饱和蒸汽压,3168.4o S p Pa = 050t C =时,水的饱和蒸汽压2,12340S p Pa = 当025t C =,050%ϕ=时,空气的湿度和焓分别为 当250t C =,280%ϕ=时,空气的湿度和焓分别为 将以上数据代入式子1、2,即分别解得 0.0529m H =/kg kg 绝干气由(1.01 1.88)2490m m m m I H t H =+⨯+并代如m H 及m I 的值解得44.15m t C = 2加热到相对湿度为10%时,空气湿度不变 水汽分压不变,则110.6220.0529101.3P P =-,解得 17.94p KPa =由 17.970.01SP ϕ==, 解得 79.7S P KPa = 查水的饱和蒸汽压表,得对应的温度为093.1t C =5.采用如图所示的废气循环系统干燥湿物料,已知数据标于本题附图中;假设系统热损失可忽略,干燥操作为等始干燥过程;试求:1新鲜空气的耗量;2进入干燥器的湿空气的温度及焓;3预热器的加热量;解:1新鲜空气消耗量蒸发水量 12()800(0.250.05263)157.9W G X X kg =-=⨯-=水/h 绝干空气用量 20()L H H W -=新鲜空气用量 0(1)2760.5 1.012788L H kg h +=⨯=新鲜空气/ (1) 由于干燥过程为等焓过程,故进出干燥器的空气的焓相等即:1(1.01 1.88)2490224.1m m H t H +⨯+=将0.0529m H =/kg kg 绝干气代入上式,解出 183.26t C =m H 的值在第4题中已解出所以,进入干燥器的湿蒸汽的温度为83.26C ,焓为224.1/KJ Kg 绝干气 (2) 预热器的加热量其中 442760.611042m L L kg ==⨯=绝干气/h所以 511042(224.1180.7) 4.7910/133.1P Q KJ h KW =⨯-=⨯=6. 干球温度t 0=26℃、湿球温度t w0=23℃的新鲜空气,预热到t l =95℃后送至连续逆流干燥器内,离开干燥器时温度t 2=85℃;湿物料初始状态为:温度1θ=25℃、含水量1w =15%;终了时状态为:温度2θ=25℃、含水量2w =%;每小时有9200kg 温物料加入干燥器内;绝干物料的比热容c s =kg 绝干料·℃;干燥器内无输送装置,热损失为580KJ/kg 汽化的水分;试求:1单位时间内获得的产品质量;2写出干燥过程的操作线方程,在H-I 图上画出操作线; 3单位时间内消耗的新鲜空气质量; 4干燥器的热效率;解:操作流程示意图见本题附图11单位时间内获得的产品质量 绝干物料流量 干燥产品流量 2干燥过程的操作线由250,t C =23wo t C =查出066/I KJ kg =绝干气,求出00.0157/H kg kg =绝干气 由195,t C =100.0157/H H kg kg ==绝干气,求出1138.6/I KJ kg =绝干气 热损失速度 580119.969542/L Q KJ h =⨯= 由焓的定义可计算出干燥器的焓分别为同理'2222 1.8434.50.02 4.18734.563.8/S W I C X C KJ kg θθ=+=⨯+⨯⨯=绝干物料 对干燥器作水分衡算,得或 2(0.0157)119.9L H -= 1 再对干燥器做物料衡算,得或 2(138.2)9602(63.847.6)69542L I -=⨯-+ 2 联立1、2解得 4225.55100.0928H I -+⨯= 3上式为本题干燥操作的操作线方程;经过本题附图2的点B ,故任意设一H 值,如0.02H =,由式3求得131.5/I kJ kg =绝干气;据此在附图2上标出点D ,过点D 及点B 的直线即为干燥过程的操作线;该线与265t C =的线交于点C ,点C 为空气离开干燥器的状态点,由点C 读出20.023/H kg kg =绝干气,2126/I kJ kg =绝干气3单位时间内消耗新鲜空气的质量 由式1得 2119.9119.9171280.01570.0230.0157L kg H ===--绝干气/h新鲜空气消耗量 00(1)17100(10.0157)17403/L L H kg h =+=⨯+=新鲜空气 (3) 干燥器的热效率其中 610()17128(138.666) 1.24310/P Q Q L I I kJ h ==-=⨯-=⨯7.在一常压逆流转筒干燥器中,干燥某种晶状物料;温度t 0=25℃、相对湿度0ϕ=55%的新鲜空气经过预热器使温度升至t 1=85℃后送入干燥器中,离开干燥器时温度t 2=30℃;湿物料初始温度1θ=24℃、湿基含水量1w =,干燥完毕后温度升到2θ=60℃、湿基含水量降为2w =;干燥产品流量G 2=1000kg/h;绝干物料比热容c s =kg 绝干料·℃;转筒干燥器的直径D=1.3m,长度Z=7m;干燥器外壁向空气的对流—辐射传热系数为35KJ/m 2·h·℃;试求绝干空气流量和预热器中加热蒸汽消耗量;加热蒸汽的绝对压强为180KPa; 解:1绝干空气流量绝干空气流量 22(1)1000(10.002)998G G w kg =-=⨯-=绝干物料/h 水分蒸发量 12()998(0.03840.002)36.33W G X X kg =-=⨯-=水/h 由附录查出25C 时水的饱和蒸汽压为Pa ,故湿度为 对干燥器作水分的物料衡算,取1h 为基准,得2(0.0109)36.33L H -= 1对干燥器做物料衡算,得其中1111(1.01 1.88)2490I H t H =+⨯+ 题给 1.507/()S C KJ kg C =绝干物料 题给235/()a KJ m h C α=所以 120()()2L a a t tQ S t DL t ααπ+=∆=-将以上各值代入热量衡算式,得2114.799840(30.32546)99890.932520L H L +⨯=++⨯+ 2 联立式1、2,解得2预热器中加热蒸气消耗量加热蒸气压强为180KPa ,由附录查出相应的汽化热为/KJ kg ,116.6T C =,预热器中消耗热量的速度为其中 0(1.01 1.880.0109)2524900.010952.9/I KJ kg =+⨯⨯+⨯=绝干气/h 所以 3102(114.752.9)191700/53.25P Q KJ h KW =⨯-==加热蒸气消耗量19170086.6/2214.3kg h =8.在恒定干燥条件下进行间歇干燥实验;已知物料的干燥面积为0.2m 2,绝干物料质量为15kg;测得的实验数据列于本例附表中;试标绘干燥速率曲线,并求临界含水量X c 及平衡含水量X ;习题8附表解:以表中第1、2组数据为例计算如下:开始时物料的干基湿含量 44.1151.94/15X kg kg -==绝干物料, 终了时 37151.47/15X kg kg -==绝干物料蒸发的水份量 3744.17.1/W kg h ∆=-=- 干燥时间的增量 0.200.2h τ∆=-= 干燥速度 27.1177.5/()0.20.2W u kg m h S τ∆-===-∆⨯ 与干燥速率对应的物料的平均湿含量为 由上法计算的数据列于下表以X 为横坐标,u 为纵坐标绘图,从图中读出临界含水量 1.24C X =/kg kg 绝干物料 平衡含水量 *0.13X =/kg kg 绝干物料9.某湿物料经过进行恒定干燥操作;物料含水量由X 1=0.35kg/kg 绝干料降至X 2=0.1kg/kg 绝干料;若在相同条件下,要求将物料含水量由X 1=0.35kg/kg 绝干料降至X '2=g/kg 绝干料;试求新情况下的干燥时间;物料的临界含水量Xc=g/kg 绝干料、平衡含水量X=0.04kg/kg 绝干料;假设在降速阶段中干燥速率与物料的自由含水量X-X 成正比. 解:恒速干燥的干燥时间为 11'()C CG X X Su τ=- 降速干燥阶段,干燥速率与物料的自由含水量*()X X -成正比; 因此, *()C X C u k X X =-降速干燥的干燥时间为 ***2**22''ln ln C C C C X X X X X X X G G S u X X Sk X X τ---==-- 总干燥时间为 *112**2'(ln )CC X C X X X X G Sk X X X X τττ--=+=+--将第一次干燥实验的数据代入,得 于是'2.27XG Sk = 第二次干燥时间由于第二次干燥实验的条件与第一次相同,即所有定性的参数均不变,所以10.对lOkg 某温物料在恒定干燥条件下进行间歇干燥,物料平铺在0.8m×lm 的浅盘中,常压空气以2m/s 的速度垂直穿过物料层;空气t=75℃,H =0.018kg/kg 绝干气,物料的初始含水量为X 1=025Kukg 绝干料;此干燥条件下物料的X c =0.1kg/kg 绝干料,r=0;假设阵速段干燥速率与物料含水量呈线性关系;试求:1将物料干燥至含水量为0.02kg/kg 绝干料所需的总干燥时问:2空气的t 、H 不变,而流速加倍,此时将物料由含水量0.25kg/kg 绝干料干燥至0.02kg/kg 绝干料需,求此干燥条件下的X e ; 解:1恒速段干燥速率由空气75,0.018/t C H kg kg ==绝干气,查H I -图得34w t C =相应水的汽化热2416/tw r KJ kg =,空气对物料的对流传热系数湿空气的质量速度 '3600H L μρ= 湿空气密度 1H HHv ρ+=湿空气的比容 273101.3(0.772 1.244)273H t v H P+=+⨯⨯降速干燥阶段时间降速段u X -为线性关系,故降速段干燥时间 因为 *0X =,所以总干燥时间为 120.07850.840 1.625h τττ=+=+= 2空气流速加倍后 '2u u = 恒速干燥时间为 '11''()C CG X X Su τ=- 降速干燥时间为 ''2'2'ln C C C X G X Su X τ=总干燥时间为 ''121'2'()(ln )C C C C X G X X X Su X τττ=+=-+即 '''3101.43600()(0.25ln )0.688100.2C C C X X X -⨯=-+⨯ 解得 '0.121CX =/kg kg 绝干物料 11.在常压间歇操作的厢式干燥器内干燥某种温物料;每批操作处理湿基含水量为159毛的湿物料500kg 物料提供的总干燥面积为40㎡;经历4h 后干燥产品中的含水量可达到要求;操作属于恒定干燥过程;由实验测得物料的临界含水量及平衡含水量分别为0.11kg 水/kg 绝干料及0.002kg 水/kg 绝干料;临界点的干燥速率为1kg 水/㎡-h,降速阶段干燥速率线为直线;每批操作装卸物料时间为10min,求此干燥器的生产能力,以每昼夜24h 获得的干燥产品质量计;解:一批物料中的绝干空气流量 恒速干燥阶段时间为 11'()C CG X X Su τ=- 降速阶段干燥速率线为直线,所以降速段干燥时间为总干燥时间为 **121*2'()()ln C C C XX X G X X X X Sk X X τττ⎡⎤-=+=-+-⎢⎥-⎣⎦代入已知数据得 20.110.002410.625(0.1760.11)(0.110.002)ln 0.002X ⎡⎤-=⨯-+-⎢⎥-⎣⎦解得 20.00809X kg =水/kg 绝干物料干燥一批物料的干燥产品量 22'(1)425 1.00809428.4G G X kg +=⨯==干燥一批物料所用时间 104 4.166760h += 因此,生产能力为 428.42424684.1667kg ⨯=干燥产品/昼夜12.在常压并流操作的干燥器中,用热空气将每种物料由初含水量X 1=1kg/kg 绝干料干燥到最终含水量X 2=kg 绝干料;空气进干燥器的温度为135℃、湿度为0.01kg/kg 绝干气;离开干燥器的温度为60℃;空气在干燥器内经历等熔过程;根据实验得出的干燥速率表达式为:干燥第一阶段)(30,H H d dXw t s -=-τ 干燥第二阶段X d dX2.1=-τ式中τd dX -——干燥速度,㎏/㎏绝干料h试计算完成上述干燥任务所需要的干燥时间;解:本题为变动干燥操作,但给出了本题特定条件下的干燥速率微分式;根据11135,0.01/t C H kg kg ==绝干气,在H I -图上确定空气的状态点,由该点沿等焓线向右下方移动与260t C =的线相交,读出交点处的20.039H =/kg kg 绝干气;与100%ϕ=的饱和空气线相交,由交点读出初始状态空气的饱和湿度,0.048S tw H =/kg kg 绝干气;对干燥器作水分衡算,得在临界点处的干燥速率应既满足干燥第一阶段,也满足干燥第二阶段的速度,将题给的两个求干燥速率的式子均应用于临界点,得,3030() 1.2(0.048) 1.2251.2C S tw C C C C C dX H H X X H H d τ-=-=⇒=-=- 1 在空气进入干燥器与临界点处列水分方程衡算式111310.01C C C C X X X L G H H X --===-- 2 联立1、2解得 0.018/C H kg kg =绝干气 20.743X kg =/kg 绝干物料 干燥第一阶段的时间为11110,3030()C C X X X X S tw dX dX d H H H τττ--===∆-⎰⎰⎰ 3 在离开干燥器的微元长度内列水分的衡算式,有将以上关系代入式3,并将式中积分上下限换成相应的H ,即 干燥第二阶段的时间为总干燥时间为 120.255 1.67 1.925h τττ=+=+=。
热学答案第二版(完整版)解析-李椿-章立源等著

第一章温度1-1在什么温度下,下列一对温标给出相同的读数:(1)华氏温标和摄氏温标;(2)华氏温标和热力学温标;(3)摄氏温标和热力学温标?解:(1)当时,即可由,解得故在时(2)又当时则即解得:故在时,(3)若则有显而易见此方程无解,因此不存在的情况。
1-2 定容气体温度计的测温泡浸在水的三相点槽内时,其中气体的压强为50mmHg。
(1)用温度计测量300K的温度时,气体的压强是多少?(2)当气体的压强为68mmHg时,待测温度是多少?解:对于定容气体温度计可知:(1)(2)1-3 用定容气体温度计测得冰点的理想气体温度为273.15K,试求温度计内的气体在冰点时的压强与水的三相点时压强之比的极限值。
解:根据已知冰点。
1-4用定容气体温度计测量某种物质的沸点。
原来测温泡在水的三相点时,其中气体的压强;当测温泡浸入待测物质中时,测得的压强值为,当从测温泡中抽出一些气体,使减为200mmHg时,重新测得,当再抽出一些气体使减为100mmHg时,测得.试确定待测沸点的理想气体温度.解:根据从理想气体温标的定义:依以上两次所测数据,作T-P图看趋势得出时,T约为400.5K亦即沸点为400.5K.题1-4图1-5铂电阻温度计的测量泡浸在水的三相点槽内时,铂电阻的阻值为90.35欧姆。
当温度计的测温泡与待测物体接触时,铂电阻的阻值为90.28欧姆。
试求待测物体的温度,假设温度与铂电阻的阻值成正比,并规定水的三相点为273.16K。
解:依题给条件可得则故1-6在历史上,对摄氏温标是这样规定的:假设测温属性X随温度t做线性变化,即,并规定冰点为,汽化点为。
设和分别表示在冰点和汽化点时X的值,试求上式中的常数a和b。
解:由题给条件可知由(2)-(1)得将(3)代入(1)式得1-7水银温度计浸在冰水中时,水银柱的长度为4.0cm;温度计浸在沸水中时,水银柱的长度为24.0cm。
(1)在室温时,水银柱的长度为多少?(2)温度计浸在某种沸腾的化学溶液中时,水银柱的长度为25.4cm,试求溶液的温度。
《热学》期末复习用 各章习题+参考答案

(
29 × 10 3
)
485������
(4) 空气分子的碰撞频率为
√2������ ������
√2
6 02 × 10 × 22 4 × 10
3 3
×
(3
7 × 10−10)
× 485
(5) 空气分子的平均自由程为
7 9 × 109
������
485 7 9 × 109
6 1 × 10 8������
(������ + ������ )������������ ������ ������������ + ������ ������������
(4)
联立方程(1)(2)(3)(4)解得
������ + ������
������
2
������ ������ ������ (������ ������ + ������ ������ ) (������ + ������ )
������ (������ + ∆������) ������
������
������
(������ + ∆������) ������
������
ln
������������ ������
ln ������
������ + ∆������
ln
Hale Waihona Puke 133 101000ln
2
2
+
20 400
269
因此经过 69 × 60 40 后才能使容器内的压强由 0.101MPa 降为 133Pa.
1-7 (秦允豪 1.3.6) 一抽气机转速������ 400������ ∙ ������������������ ,抽气机每分钟能抽出气体20������.设 容器的容积������ 2 0������,问经过多长时间后才能使容器内的压强由 0.101MPa 降为 133Pa.设抽 气过程中温度始终不变.
数值传热学陶文铨主编第二版习题答案
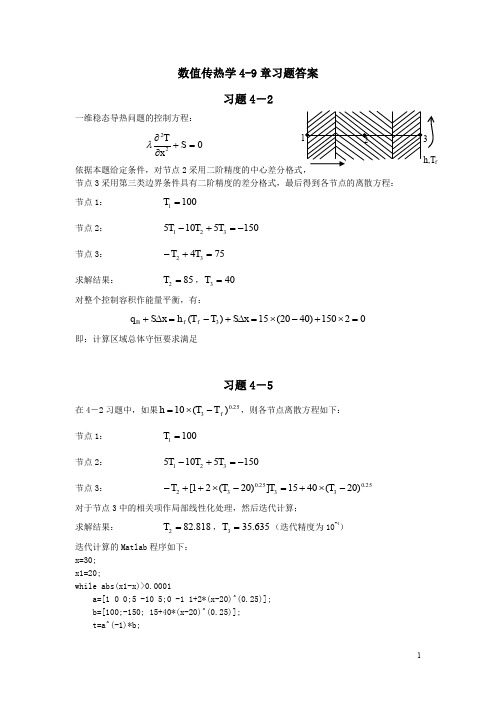
依据本题给定条件,对节点 2 采用二阶精度的中心差分格式, 节点 3 采用第三类边界条件具有二阶精度的差分格式,最后得到各节点的离散方程: 节点 1: 节点 2: 节点 3: 求解结果:
T1 100
5T1 10T2 5T3 150 T2 4T3 75
T2 85 , T3 40
习题 4-12 的 Matlab 程序
%代数方程形式 AiTi=CiTi+1+BiTi-1+Di mdim=10;%计算的节点数 x=linspace(1,3,mdim);%生成 A、C、B、T 数据的基数; A=cos(x);%TDMA 的主对角元素 B=sin(x);%TDMA 的下对角线元素 C=cos(x)+exp(x); %TDMA 的上对角线元素 T=exp(x).*cos(x); %温度数据 %由 A、B、C 构成 TDMA coematrix=eye(mdim,mdim); for n=1:mdim coematrix(n,n)=A(1,n); if n>=2 coematrix(n,n-1)=-1*B(1,n); end if n<mdim coematrix(n,n+1)=-1*C(1,n); end end %计算 D 矢量 D=(coematrix*T')'; %由已知的 A、B、C、D 用 TDMA 方法求解 T %消元 P(1,1)=C(1,1)/A(1,1); Q(1,1)=D(1,1)/A(1,1); for n=2:mdim P(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1)); Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end %回迭 Tcal(1,mdim)=Q(1,mdim); for n=(mdim-1):-1:1 Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n); end Tcom=[T;Tcal]; %绘图比较给定 T 值和计算 T 值 plot(Tcal,'r*') hold on plot(T)
热力学第二定律练习题及答案

热力学第二定律练习题一、是非题,下列各题的叙述是否正确,对的画√错的画×1、热力学第二定律的克劳修斯说法是:热从低温物体传给高温物体是不可能的 ( )2、组成可变的均相系统的热力学基本方程 d G =-S d T +V d p +d n B ,既适用于封闭系统也适用于敞开系统。
( )3、热力学第三定律的普朗克说法是:纯物质完美晶体在0 K 时的熵值为零。
( )4、隔离系统的熵是守恒的。
( )5、一定量理想气体的熵只是温度的函数。
( )6、一个系统从始态到终态,只有进行可逆过程才有熵变。
( )7、定温定压且无非体积功条件下,一切吸热且熵减少的反应,均不能自发发生。
( )8、系统由状态1经定温、定压过程变化到状态2,非体积功W ’<0,且有W ’>G 和G <0,则此状态变化一定能发生。
( );9、绝热不可逆膨胀过程中S >0,则其相反的过程即绝热不可逆压缩过程中S <0。
( ) 10、克-克方程适用于纯物质的任何两相平衡。
( ) 11、如果一个化学反应的r H不随温度变化,则其r S 也不随温度变化, ( )12、在多相系统中于一定的T ,p 下物质有从化学势较高的相自发向化学势较低的相转移的趋势。
( ) 13、在10℃, kPa 下过冷的H 2O ( l )凝结为冰是一个不可逆过程,故此过程的熵变大于零。
( ) 14、理想气体的熵变公式只适用于可逆过程。
( )15、系统经绝热不可逆循环过程中S = 0,。
( )二、选择题1 、对于只做膨胀功的封闭系统的(A /T )V 值是:( )(1)大于零 (2) 小于零 (3)等于零 (4)不确定…2、 从热力学四个基本过程可导出VU S ∂⎛⎫⎪∂⎝⎭=( )(1) (2) (3) (4) T p S pA H U G V S V T ∂∂∂∂⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭3、1mol 理想气体(1)经定温自由膨胀使体积增加1倍;(2)经定温可逆膨胀使体积增加1倍;(3)经绝热自由膨胀使体积增加1倍;(4)经绝热可逆膨胀使体积增加1倍。
热学第二版习题答案

热学第二版习题答案热学第二版习题答案【篇一:热工测试课后练习答案】1-1、测量方法有哪几类,直接测量与间接测量的主要区别是什么?(p1-2) 答:测量的方法有:1、直接测量;2、间接测量;3、组合测量。
直接测量与间接测量的主要区别是直接测量中被测量的数值可以直接从测量仪器上读得,而间接测量种被测量的数值不能直接从测量仪器上读得,需要通过直接测得与被测量有一定函数关系的量,然后经过运算得到被测量的数值。
1-2、简述测量仪器的组成与各组成部分的作用。
(p3-4) 答:测量仪器由感受器、中间器和效用件三个部分组成。
1、感受器或传感器:直接与被测对象发生联系(但不一定直接接触),感知被测参数的变化,同时对外界发出相应的信号;2、中间器或传递件:最简单的中间件是单纯起“传递”作用的元件,它将传感器的输出信号原封不动地传递给效用件;3、效用件或显示元件:把被测量信号显示出来,按显示原理与方法的不同,又可分模拟显示和数字显示两种。
1-3、测量仪器的主要性能指标及各项指标的含义是什么?(p5-6)答:测量仪器的主要性能指标有:精确度、恒定度、灵敏度、灵敏度阻滞、指示滞后时间等。
1、精确度:表示测量结果与真值一致的程度,它是系统误差与随机误差的综合反映;2、恒定度:仪器多次重复测试时,其指示值的稳定程度,通常以读数的变差来表示;3、灵敏度:以仪器指针的线位移或角位移与引起这些位移的被测量的变化值之间的比例来表示。
4、灵敏度阻滞:又称感量,是以引起仪器指针从静止到作极微小移动的被测量的变化值。
5、指示滞后时间:从被测参数发生变化到仪器指示出该变化值所需的时间。
1-4、说明计算机测控系统基本组成部分及其功能。
(p6-7)答:计算机测控系统基本组成部分有:传感器、信号调理器、多路转换开关、模/数(a/d)和数/模(d/a)转换及微机。
1、信号调理器:完成由传感器输出信号的放大、整形、滤波等,以保证传感器输出信号成为a/d转换器能接受的信号;2、实现多路信号测量,并由它完成轮流切换被测量与模/数转换器的连接;3、采样保持器:保证采样信号在a/d转换过程中不发生变化以提高测量精度;4、a/d转换器:将输入的模拟信号换成计算机能接受的数字信号;5、d/a转换器:将输入的数字信号换成计算机能接受的模拟信号。
基础化学李保山第二版-化学热力学基础习题标准答案

基础化学李保山第二版-化学热力学基础习题答案————————————————————————————————作者:————————————————————————————————日期:2884 化学热力学基础习题解答(p87-89)思考题1.解:(1) ⨯ 原因见(3)(2) ⨯ 原因见(3)(3) √ 确切地说,应为:恒压过程中,系统的焓变等于恒压反应热。
(4) ⨯ H 是状态函数,任何过程都有∆H ,不是只有恒压过程才有∆H 。
(5) ⨯ 原因见(7) (6) ⨯ 原因见(7)(7) √ 应为:在某温度和标准压力下,最稳定的纯态单质的标准生成焓等于零。
(8) ⨯ 由于CaCO 3的生成焓为负值,但不是由于它的分解是吸热的。
(9) ⨯ 热化学方程式的系数影响反应的焓变值。
2.解:(1)、(2)、(5)单质的标准生成焓不等于零。
3.解:(1) 不同,因为二反应方程式中各物质前的系数不同; (2) 不同,因为二反应中Br 2的状态不同。
4.解:书写热化学方程式应注意:(1) 注明各物质前的计量系数−表明物质的量。
(2) 标明物质所处的状态(l 、g 、s)和晶形;对于溶液中的反应,还要注明物种的浓度,以aq 代表水溶液。
(3) 注明温度。
(4) 标明反应热(焓变)。
5. 解:(1) ∆S > 0 ; (2) ∆S > 0 ; (3) ∆S > 0 ; (4) ∆S < 0 ; (5) ∆S < 0 ; (6) ∆S < 0 6. 解:(1) ∆S < 0 ; (2) ∆S > 0 ; (3) ∆S > 0 ; (4) ∆S < 0 ; (5) ∆S > 0习题1.解:(1) ∆U = Q + W = 100 – 540 = - 440 J(2) ∆U = Q + W = – 100 + 635 = 535 J2.解:(1) W = – p 外∆V = – 100( 0.040 – 0.015 ) = - 2.5 kJ(2) 中间平衡态时,气体的体积为V = 33025.010200298314.80.2m p nRT =⨯⨯⨯= W = – p 外,1∆V 1 + (– p 外,2∆V 2) = - 200(0.025-0.015) - 100(0.040-0.025) = - 3.5 kJ3.解:此过程为: )()(22l O H g O H =解法1:恒压过程:∆H = Q = - 2.26 ⨯ 450 = -1017 kJ∆U = ∆H – (∆n)RT = -1017 – ( 0 - 18450)⨯ 8.314 ⨯ (100 + 273.15) ⨯ 10-3 = -939.4 kJW = ∆U – Q = -939.4 – (-1017) = 77.6 kJ9 9解法2:33311m 76480Pa 103101mol Kg 100218K 15373K mol J 3148Kg 450 0218450../....V RT .pV nRT pV =⨯⋅⨯⋅⋅⋅⋅=⇒=⇒=--- 所以77.5KJ 7648.0103.101W 33=⨯⨯=m PaKJ 1017g 450KJ/g 26.2-=⨯-=Q由于为恒压过程,KJ 1017Q -==∆p H-939.5KJ 77.5KJ KJ 1017U =+-=+=∆W Q4.解:方程式 (1) – (2) 得2N 2(g) + 2O 2(g) = 4NO(g) ∆H θ = 360 kJ ⋅mol -1所以11904360),(--⋅=⋅=mol kJ mol kJ g NO H m f θ∆5.解:反应)()(2)(42g CH g H s C =+可由 (1) + 2 ⨯ (2) – (3) 得到,所以123123935228588900753.(.)(.).r m r r r H H H H kJ mol θθθθ-∆=∆+⨯∆-∆==-+⨯---=-⋅6.解:① N 2H 4(l)生成反应为:N 2(g) + 2H 2(g) → N 2H 4(l)由反应[(2) ⨯ 3 + (3) – (1) – (4)]/4 得 N 2(g) + 2H 2(g) → N 2H 4(l)② N 2H 4(l)的)]4()1()3()2(3[41θθθθθm r m r m r m r m f H H H H H ∆-∆-∆+∆=∆16.50)]8.285()5.1011()143()3.317(3[41-⋅=-----+-⨯=mol kJ7.解:由反应(1) – 2 ⨯ (2) – 2 ⨯ (3)得N 2H 4 (l) + 2H 2O 2 (l) → N 2 + 4H 2O(l) 故此反应的12.818)5.51(25.14922.622)3(2)2(2)1(-⋅-=-⨯-⨯--=∆⨯-∆⨯-∆=∆mol kJ H H H H m r m r m r m r θθθθ8.解:(1) 反应NH 3(g) + HCl(g) = NH 4Cl(s) 的4313144461923176 (,)(,)(,).(.)(.)r m f m r m f mH H NH Cl s H NH g H HCl g kJ mol θθθθ-∆=∆-∆-∆=-----=-⋅故2.0mol HCl (g)与2.0mol NH 3 (g)反应生成NH 4Cl (s)放出的热量为2 ⨯ 176 kJ = 352 kJ ;(2) 由于HCl (g) → HCl (aq)12.73-⋅-=∆mol kJ H m r θ1010NH 3 (g) → NH 3 (aq)12.35-⋅-=∆mol kJ H m r θNH 3 (aq) + HCl (aq) = NH4Cl (aq) 1602.r mH kJ mol θ-∆=-⋅ 故1.0mol HCl (g)和1.0mol NH 3 (g)同时溶解于水中NH 3 (g) + HCl (g) = NH4Cl (aq) (i) 的热效应为7323526021686.(.)(.).r mH kJ mol θ-∆=-+-+-=-⋅(3) (i)过程的热效应),(),(),(34g HCl H g NH H aq Cl NH H H m f m r m f mr θθθθ∆-∆-∆=∆ 4)3.92()1.46(),(=----∆=aq Cl NH H m f θ可求出),(4aq Cl NH H m f θ∆=-307.0 kJ ⋅mol -1(4) 用反应NH 3(g) + HCl(g) = NH 4Cl(aq)减去NH 3(g) + HCl(g) = NH 4Cl(s)得 NH 4Cl(s) = NH 4Cl(aq)此过程的热效应为14.7)176(6.168-⋅=--=∆mol kJ H m r -θ,所以NH 4Cl (s)溶解是吸热过程。
(完整版)数值传热学陶文铨主编第二版习题答案

数值传热学4-9章习题答案习题4-2一维稳态导热问题的控制方程:022=+∂∂S xTλ依据本题给定条件,对节点2节点3采用第三类边界条件具有二阶精度的差分格式,最后得到各节点的离散方程:节点1:1001=T 节点2:1505105321-=+-T T T 节点3:75432=+-T T 求解结果:,852=T 403=T 对整个控制容积作能量平衡,有:2150)4020(15)(3=⨯+-⨯=∆+-=∆+x S T T h x S q f f B 即:计算区域总体守恒要求满足习题4-5在4-2习题中,如果,则各节点离散方程如下:25.03)(10f T T h -⨯=节点1:1001=T 节点2:1505105321-=+-T T T 节点3:25.03325.032)20(4015])20(21[-⨯+=-⨯++-T T T T 对于节点3中的相关项作局部线性化处理,然后迭代计算;求解结果:,(迭代精度为10-4)818.822=T 635.353=T 迭代计算的Matlab 程序如下:x=30;x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b;x1=x;x=t(3,1);endtcal=t习题4-12的Matlab程序%代数方程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数x=linspace(1,3,mdim);%生成A、C、B、T数据的基数;A=cos(x);%TDMA的主对角元素B=sin(x);%TDMA的下对角线元素C=cos(x)+exp(x); %TDMA的上对角线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif n<mdimcoematrix(n,n+1)=-1*C(1,n);endend%计算D矢量D=(coematrix*T')';%由已知的A、B、C、D用TDMA方法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图比较给定T值和计算T值plot(Tcal,'r*')hold onplot(T)n gin th a r e 结果比较如下,由比较可知两者值非常切合(在小数点后8位之后才有区别):习题4-14充分发展区的温度控制方程如下:)(1rTr r r x T uc p ∂∂∂∂=∂∂λρ对于三种无量纲定义、、进行分析如下w b w T T T T --=Θ∞∞--=ΘT T T T w ww T T T T --=Θ∞1)由得:wb wT T T T --=Θww b T T T T +Θ-=)(由可得:T x T x T x T T T x T w b w w b ∂∂Θ-+∂∂Θ=∂+Θ-∂=∂∂)1(])[(rT r T T r T T T r T w w b w w b ∂∂Θ-+∂Θ∂-=∂+Θ-∂=∂∂)1()(])[(由与无关、与无关以及、的表达式可知,除了均匀的情况外,该无量b T r Θx x T ∂∂rT∂∂w T 纲温度定义在一般情况下是不能用分离变量法的;2)由得:∞∞--=ΘT T T T w ∞∞+Θ-=T T T T w )(由可得:T xT x T T T x T w w ∂∂Θ=∂+Θ-∂=∂∂∞∞])[(rT r T T r T T T r T w w w ∂∂Θ+∂Θ∂-=∂+Θ-∂=∂∂∞∞∞)(])[(由与无关、与无关以及、的表达式可知,在常见的四种边界条件中除了b T r Θx x T ∂∂rT ∂∂轴向及周向均匀热流的情况外,有,则该无量纲温度定义是可以用分const q w =0=∂∂rT w离变量法的;3)由得:wwT T T T --=Θ∞ww T T T T +Θ-=∞)(由可得:T xT x T T T x T w w w ∂∂Θ-=∂+Θ-∂=∂∂∞)1(])[(r T T r T T T r T w w w -+∂Θ∂-=∂+Θ-∂=∂∂∞∞1()(])[(同2)分析可知,除了轴向及周向均匀热流const q w =温度定义是可以用分离变量法的;习题4-181)采用柱坐标分析,写出统一的稳态柱坐标形式动量方程:S r r r r r r x x w r v r r r u x +∂∂∂∂+∂∂∂∂+∂∂∂∂=∂∂+∂∂+∂∂(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ、和分别是圆柱坐标的3个坐标轴,、和分别是其对应的速度分量,其中x r θu v w 是管内的流动方向;x 对于管内的层流充分发展有:、,;0=v 0=w 0=∂∂xu并且方向的源项:x x pS ∂∂-=方向的源项:r r pS ∂∂-=方向的源项:θθ∂∂-=pr S 1由以上分析可得到圆柱坐标下的动量方程:方向:x 0)(1)(1=∂∂-∂∂∂∂+∂∂∂∂x pu r r r u r r r θλθλ方向:r 0=∂∂r p 方向:θ0=∂∂θp 边界条件:,R r =0=u ,;对称线上,0=r 0=∂∂r u 0=∂∂θu 不考虑液体的轴向导热,并简化分析可以得到充分发展的能量方程为:)(1(1θλθλρ∂∂∂∂+∂∂∂∂=∂∂Tr r r T r r r x T uc p 边界条件:,;,R r =w q r T =∂∂λ0=r 0=∂∂rT,πθ/0=0=∂∂-θλT2)定义无量纲流速:dxdp R uU 2-=λ并定义无量纲半径:;将无量纲流速和无量纲半径代入方向的动量方程得:R r /=ηx 0))1((1)1((122=∂∂-∂-∂∂∂+∂-∂∂∂xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得:011(1(1=+∂∂∂∂+∂∂∂∂θηθηηηηηU U 边界条件:,1=η0=U ,;对称线上,0=η0=∂∂ηU 0=∂∂θU定义无量纲温度:λ/0R q T T b-=Θ其中,是折算到管壁表面上的平均热流密度,即:;0q Rq q wπ=0由无量纲温度定义可得:bT Rq T +Θ=λ0将表达式和无量纲半径代入能量方程得:T η(1)(100θληλθηηλληηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂R q R R R R q R R R x T uc b p 化简得:(1))1(1)(10θηθηηηηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂x T u c q R b p 由热平衡条件关系可以得:mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T uc 020221221)(===∂∂=∂∂ππρρρ将上式代入式(1)可得:)1(1)(12θηθηηηηη∂Θ∂∂∂+∂Θ∂∂∂=m U U 边界条件:,;,0=η0=∂Θ∂η1=ηR q q w πη10==∂Θ∂,;,0=θ0=∂Θ∂θπθ=0=∂Θ∂θ单值条件:由定义可知: 且: 0/0=-=ΘλR q T T b b b ⎰⎰Θ=ΘAAb UdAUdA 即得单值性条件:=Θ⎰⎰AA UdAUdA 3)由阻力系数及定义有:f Re 228)(21/Re ⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=D D U D u u dx dp D f e m e m me νρ且:m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5-21.一维稳态无源项的对流-扩散方程如下所示: (取常物性)xx u 22∂∂Γ=∂∂φφρ边界条件如下:LL x x φφφφ====,;,00上述方程的精确解如下: 11)/(00--=--⋅Pe L x Pe L e e φφφφΓ=/uL Pe ρ2.将分成20等份,所以有:L ∆=P Pe 20 1 2 3 4 5 6……………………… 17 18 19 20 21对于中心差分、一阶迎风、混合格式和QUICK 格式分别分析如下:1)中心差分中间节点: 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ20,2 =i 2)一阶迎风中间节点: ∆-∆++++=P P i i i 2)1(11φφφ20,2 =i 3)混合格式当时,中间节点: 1=∆P 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ 20,2 =i 当时,中间节点: 10,5=∆P 1-=i i φφ20,2 =i 4)QUICK 格式*12111)35(8122121⎥⎦⎤⎢⎣⎡---++++++=+--∆∆-∆∆+∆i i i i i i i P P P P P φφφφφφφ2≠i*1111)336(8122121⎥⎦⎤⎢⎣⎡--++++++=+-∆∆-∆∆+∆i i i i i i P P P P P φφφφφφ2=i 数值计算结果与精确解的计算程序如下:%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solutiony=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')y1=subs(y1,'-(y0-yL)/L*x','(-y0+yL)*X')%grid Pe number tt=[1 5 10];%dimensionless length m=20;%mdim is the number of inner node mdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculation y0=1;yL=2;%cal exact solution for n=1:size(tt,2) t=m*tt(1,n); if t==0 yval1(n,:)=eval(y1); else yval1(n,:)=eval(y); end end%extra treatment because max number in MATLAB is 10^308if max(isnan(yval1(:))) yval1=yval1'; yval1=yval1(:);indexf=find(isnan(yval1)); for n=1:size(indexf,1) if rem(indexf(n,1),size(X,2))==0 yval1(indexf(n),1)=yL; else yval1(indexf(n),1)=y0; endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';end%CD solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt);title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt);title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt);title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1,nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt(1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL);elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)));endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));a n d A l l t h i n g s i n t h ei r b e i n g a r e g 13精确解与数值解的对比图,其中边界条件给定,。
《热力学第二定律》习题及答案

《热力学第二定律》习题及答案选择题1.ΔG=0 的过程应满足的条件是(A) 等温等压且非体积功为零的可逆过程 (B) 等温等压且非体积功为零的过程 (C) 等温等容且非体积功为零的过程(D) 可逆绝热过程 答案:A2.在一定温度下,发生变化的孤立体系,其总熵(A )不变 (B)可能增大或减小(C)总是减小(D)总是增大答案:D 。
因孤立系发生的变化必为自发过程,根据熵增原理其熵必增加。
3.对任一过程,与反应途径无关的是(A) 体系的内能变化 (B) 体系对外作的功 (C) 体系得到的功 (D) 体系吸收的热 答案:A 。
只有内能为状态函数与途径无关,仅取决于始态和终态。
4.下列各式哪个表示了偏摩尔量: (A),,j i T p n U n ⎛⎫∂ ⎪∂⎝⎭ (B) ,,j i T V n H n ⎛⎫∂ ⎪∂⎝⎭ (C) ,,j i T V n A n ⎛⎫∂ ⎪∂⎝⎭ (D) ,,ji i T p n n μ⎛⎫∂ ⎪∂⎝⎭ 答案:A 。
首先根据偏摩尔量的定义,偏导数的下标应为恒温、恒压、恒组成。
只有A和D 符合此条件。
但D 中的i μ不是容量函数,故只有A 是偏摩尔量。
5.氮气进行绝热可逆膨胀ΔU=0 (B) ΔS=0 (C) ΔA =0 (D) ΔG=0答案:B 。
绝热系统的可逆过程熵变为零。
6.关于吉布斯函数G, 下面的说法中不正确的是(A)ΔG ≤W'在做非体积功的各种热力学过程中都成立(B)在等温等压且不做非体积功的条件下, 对于各种可能的变动, 系统在平衡态的吉氏函数最小(C)在等温等压且不做非体积功时, 吉氏函数增加的过程不可能发生(D)在等温等压下,一个系统的吉氏函数减少值大于非体积功的过程不可能发生。
答案:A 。
因只有在恒温恒压过程中ΔG ≤W'才成立。
7.关于热力学第二定律下列哪种说法是错误的(A)热不能自动从低温流向高温(B)不可能从单一热源吸热做功而无其它变化(C)第二类永动机是造不成的(D 热不可能全部转化为功答案:D 。
热力学第二版习题答案(全)

PD
F-
XC
h a n g e Vi e
w
F-
XC
h a n g e Vi e
w
er
er
!
O W
N
y
bu
to
m
w
.d o
c u -tr
. ack
c
w
o
.d o
c u -tr a c k
.c
习题: 2-1.为什么要研究流体的 pVT 关系? 答:在化工过程的分析、研究与设计中,流体的压力 p、体积 V 和温度 T 是流体最基本的性 质之一,并且是可以通过实验直接测量的。而许多其它的热力学性质如内能 U、熵 S、Gibbs 自由能 G 等都不方便直接测量, 它们需要利用流体的 p –V –T 数据和热力学基本关系式进行 推算;此外,还有一些概念如逸度等也通过 p –V –T 数据和热力学基本关系式进行计算。因 此,流体的 p –V –T 关系的研究是一项重要的基础工作。 2-2.理想气体的特征是什么? 答:假定分子的大小如同几何点一样,分子间不存在相互作用力,由这样的分子组成的气体 叫做理想气体。严格地说,理想气体是不存在的,在极低的压力下,真实气体是非常接近理 想气体的,可以当作理想气体处理,以便简化问题。 理想气体状态方程是最简单的状态方程:
pV RT
2-3.偏心因子的概念是什么?为什么要提出这个概念?它可以直接测量吗? 答:纯物质的偏心因子 是根据物质的蒸气压来定义的。实验发现,纯态流体对比饱和蒸 气压的对数与对比温度的倒数呈近似直线关系,即符合:
1 log p 1 T r
s r
ps 其中, p pc
迭代结果为: V 3.39m 3 kmol 1 (2) 压缩功 W pdV
工程热力学(朱明善)第二版答案

3.6 103 24 N 3.6 103 24 25000 276000kg /日 276吨/日 q0 29000 0.27 276000 (2) b 0.46kg / ( kW h) 0.46kg / 度 24 25000
故 B
4
1-10 解:
5 t / F 32 设 t / C t / F t 9 5 5 则有 t 1 32 9 9 5 解上式有 t 32 40 4
按关系式 t / C 可见可出现相同数值的情况,其温度为-40
1-11 解:由已知条件有:
h液体钠
1-2 解:由 pE = pb H 2O g hm l g hl 代入数据有
pE = 1.01 105 1005 9.81 0.54 - 900 9.81 0.15
1.0499 105 Pa 787.7 mmHg
1-3 解: p pb Hg g hc sin15 Hg g hv H 2O g hH 2O
电机发热功率60000053157890951kg空气可带走的热量552035kjkg为维持电机正常工作至少需空气流量31578990325003536030007320741073207374400300kjkgkjkg0857170007374360119144kjkg2502871071775kjkg071775170036096179kjkg可见按平均比热容表数据计算要偏大239这是因为当时已远远偏离071775kjkgkjkg也可以看出与定比热相去甚远
如果循环为 ACBA,则(被做功)
W'
提示:有些同学分开计算每段的做功然后相加,其中 AB 段要用到积分,较为繁琐。简单的办法是根据做 功的定义 W
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热学第二版习题答案【篇一:热工测试课后练习答案】1-1、测量方法有哪几类,直接测量与间接测量的主要区别是什么?(p1-2) 答:测量的方法有:1、直接测量;2、间接测量;3、组合测量。
直接测量与间接测量的主要区别是直接测量中被测量的数值可以直接从测量仪器上读得,而间接测量种被测量的数值不能直接从测量仪器上读得,需要通过直接测得与被测量有一定函数关系的量,然后经过运算得到被测量的数值。
1-2、简述测量仪器的组成与各组成部分的作用。
(p3-4) 答:测量仪器由感受器、中间器和效用件三个部分组成。
1、感受器或传感器:直接与被测对象发生联系(但不一定直接接触),感知被测参数的变化,同时对外界发出相应的信号;2、中间器或传递件:最简单的中间件是单纯起“传递”作用的元件,它将传感器的输出信号原封不动地传递给效用件;3、效用件或显示元件:把被测量信号显示出来,按显示原理与方法的不同,又可分模拟显示和数字显示两种。
1-3、测量仪器的主要性能指标及各项指标的含义是什么?(p5-6)答:测量仪器的主要性能指标有:精确度、恒定度、灵敏度、灵敏度阻滞、指示滞后时间等。
1、精确度:表示测量结果与真值一致的程度,它是系统误差与随机误差的综合反映;2、恒定度:仪器多次重复测试时,其指示值的稳定程度,通常以读数的变差来表示;3、灵敏度:以仪器指针的线位移或角位移与引起这些位移的被测量的变化值之间的比例来表示。
4、灵敏度阻滞:又称感量,是以引起仪器指针从静止到作极微小移动的被测量的变化值。
5、指示滞后时间:从被测参数发生变化到仪器指示出该变化值所需的时间。
1-4、说明计算机测控系统基本组成部分及其功能。
(p6-7)答:计算机测控系统基本组成部分有:传感器、信号调理器、多路转换开关、模/数(a/d)和数/模(d/a)转换及微机。
1、信号调理器:完成由传感器输出信号的放大、整形、滤波等,以保证传感器输出信号成为a/d转换器能接受的信号;2、实现多路信号测量,并由它完成轮流切换被测量与模/数转换器的连接;3、采样保持器:保证采样信号在a/d转换过程中不发生变化以提高测量精度;4、a/d转换器:将输入的模拟信号换成计算机能接受的数字信号;5、d/a转换器:将输入的数字信号换成计算机能接受的模拟信号。
1-5、试述现代测试技术及仪器的发展方向。
(p6、p9)答:计算机、微电子等技术迅速发展,推动了测试技术的进步,相继出现了智能测试仪、总线仪器、pc仪器、虚拟仪器、网络化仪器等微机化仪器及自动化测试系统。
随着计算机网络技术、多媒体技术、分布式技术等手段的迅速发展,测试技术与计算机相结合已成为当前测试技术的主流,测试技术的虚拟化和网络化的时代已经不远了。
第二章2-1、试述测量仪器的动态特性的含意和主要研究内容,它在瞬变参数测量中的重要意义。
(p11、p16) 答:测量仪器或测量系统的动态特性的分析就是研究动态测量时所产生的动态误差,它主要用以描述在动态测量过程中输入量与输出量之间的关系,或是反映系统对于随机时间变化的输入量响应特性。
从而能够选择合适的测量系统并于所测参数相匹配,使测量的动态误差限制在试验要求的允许范围内,这便是动态测量技术中的重要研究课题。
在瞬变参数动态测量中,要求通过测量系统所获得的输出信号能准确地重现输入信号的全部信息,而测量系统的动态响应正是用来评价系统正确传递和显示输入信号的重要指标。
2-2、测量系统的输出量与输入量之间的关系可采用传递函数表示,试说明串联环节、并联环节及反馈环节的传递函数的表示方法。
(p13-14)答:串联环节:t(s)z(s)y(s)h(s)???h1(s)h2(s)x(s)x(s)z(s)并联环节: y(s)y1(s)?y2(s)h(s)???h1(s)?h2(s)x(s)x(s)正反馈环节: ha(s)y(s)h(s)??x(s)1?ha(s)hb(s)负反馈环节:ha(s)y(s)h(s)??x(s)1?ha(s)hb(s)2-3、试述常用的一、二阶测量仪器的传递函数及它的典型实例。
(p15-16)答:y(s)1h(s)??常用的一阶测量系统的传递函数:x(s)?s?1以热电偶突然放入温度为t0 的介质为例,每一瞬间介质传递给热电偶节点的热量dq为dq?ha(t0?t)dt式中,t为热电偶瞬间温度;h为热接点表面传热系数;a为热接点表面积。
在不考虑导热及热辐射损失的情况下,介质传给热接点的热量即为热电偶的储热量。
若热电偶吸收热量dq后,温度上升dt,于是dq?cpmdt式中,为热电偶热接点的比定压热容;m为热接点的质量。
cp根据热平衡可得ha(t0?t)dt?cpmdt经简化后可得dt??t?t0dt? 称为测量系统的时间常数。
式中,cpm???ha上式是热电偶(测温传感器)数学模型的一阶线性微分方程,这类传感器称为一阶测量系统,该系统的传递函数为t(s)1h(s)??t0(s)?s?12?ny(s)常用的二阶测量系统的传递函数:h(s)??22x(s)s?2??s??nn以测振仪为例,描述质量m的运动微分方程为d2ydym2?c?ky?f(t)dtdt式中,c为阻尼;k为弹性系数;f(t)为干扰力。
d2ydy上式是一个单质量强迫阻尼振动微分方程。
将其与a22?a1?a0y?b0xdtdt比较可得a2?m,a1?c,a0?k,b0?1,f(t)相当于x。
用k除以两端可得md2ycdyx??y?kdt2kdtkd2ydy将上式与a22?a1?a0y?b0x相比,其传递函数有相同形式。
这时,dtdt1/k为系统的柔性系数,??c/2km为系统?n?k/m为系统的固有频率,的阻尼比。
因而,测振仪属二阶测量系统。
2-4、试述测量系统的动态响应的含意、研究方法及评价指标。
答:含义:在瞬态参数动态测量中,要求通过系统所获得的输出信号能准确地重现输入信号的全部信息,而测量系统的动态响应正是用来评价系统正确传递和显示输入信号的重要指标。
研究方法:对测量系统施加某些已知的典型输入信号,包括阶跃信号、正弦信号、脉冲信号、斜升信号,通常是采用阶跃信号和正弦信号作为输入量来研究系统对典型信号的响应,以了解测量系统的动态特性,依此评价测量系统。
评价指标:稳定时间ts、最大过冲量ad。
2-5、试述常用的一、二阶测量仪器的频率响应及内容。
答:一阶测量系统的频率响应函数为h(j?)?1,一阶测量系统的副频特性1?j???n1h(?)??22(j?)?2??(j?)??nn [1?()2?j2??n?n??0.6~0.8范围的原因。
2-6、试说明二阶测量系统通常取阻尼比 ??0.6~0.8,这样能减少动态误差,系统能以较短的答:对于二阶系统应使时间进入偏离稳态不到2%~5%的范围内,是系统的动态响应好,当系统的阻尼比?在0.8左右时幅频特性近似常数的频率范围最宽,而相频特性曲线也最接近直??0.6~0.8可获得较小的误差和较宽的工作频率范围,相位失真线。
因而去也很小,使系统具有较好的稳定性。
而且,此时提高系统的固有频率会使响应速率变得更快。
2-7、某一力传感器拟定为二阶系统,其固有频率为800hz,阻尼比为0.14。
问使用改传感器作频率为400hz正弦变化的外力测试时,其振幅和相位角各位多少?解:a????????1???????n????21?????4?2?????n?2?????212??400?2?400??2???4??0.14????1??800800????????2?1.31????400?2??2?0.14???????800n??????10.6???????arctg??arctg22????400?1????1?????800???n?2-8、用一阶系统对100hz的正弦信号进行测量时,如果要求振幅误差在10%以内,时间常数应为多少?如果用该系统对50hz的正弦信号进行测试时,幅值和相位误差各为多少?解:(1)?a(?)?1?a(?)?1?则 ??7.71?10?4s1?(??)2?1?1?(100?2??)2?10%(2)?a(?)?1?a(?)?1?1?(??)2?1?1?(50?2??7.71?10)?42?2.81%?(?)??arctg????arctg(50?2??7.71?10?4)2??13.622-9、用传递函数为1/(0.0025s+1)的一阶装置进行周期信号测量,若将幅值误差限制在5%以下,试求所能测量的最高频率成分,此时相位差是多少?解:??0.0025s,?a(?)?1?a(?)?1?1?(??)2?1?1?(0.0025?)2?5%则??131.5(rad/s)或f??/2??20.9hz)??18.2? 相位差:?(?)??arctg????arctg(131.5?0.00252-10、某一阶测量装置的传递函数为1/(0.04s+1),若用它测量频率0.5hz,1hz,2hz的正弦信号,试求其幅值误差。
解:??0.04s,?a(?)?1?a(?)?1?(1)当f=0.5hz时, ?a(?)?1?a(?)?1?(2)当f=1hz时, ?a(?)?1?a(?)?1?(3)当f=2hz时,1?(??)2?1?1?(2?f?)121?(??)1?(??)22?1??(2??0.5?0.04)1?(2??1?0.04)122?0.78%?1??3.02%?a(?)?1?a(?)?1?1?(??)2?1??(2??2?0.04)2?10.56%2-11、对某二阶系统进行动态标定时,测量最大过冲量ad?1.5以及在响应曲线上由n个周期取平均值的衰减周期试求该系统的阻尼比及系统固有td?2s。
频率。
解:【篇二:热力学习题答案- 第2章】的气体,在气缸活塞机构中由初态p1=0.7mpa、v1=0.02m3,准静膨胀到v2=0.04m3.试确定下列各过程中气体完成的功量及比功量:(1)定压过程;(2)pv2=常数。
解:(1)因为=pdv 又p=0.7mpapdv=p(v1-v2)=0.7x106pax0.02m3=14kj所以w=则w=w/m=14kj/0.5kg=28kj/kg (2)=pdv可知pv2=p1v22=常数 w=pdv=pv21/v2dv=p1v12(1/v12-1/v22)=7kj则w=w/m=7kj/0.5kg=14kj/kg2-3,气体在某一过程中吸入热量少?解:因为12kcal,同时热能力学能增加20kcal,问此过程是膨胀过程还是压缩过程?对外交换的功量是多得:w=12kcal-20kcal=-8kcal 则可知此过程为压缩过程2-5,闭系中实施某过程,试填补表中空缺的数据:2-7,如图2-18所示,某封闭系统沿a-c-b途径由状态a变化到状态 b时,吸入热量84kj,对外做功32kj。
