高等代数(相似标准形)
高等代数_矩阵的相抵合同相似

( A1 , A2 ,
于是
An ) (1 ,2 , n ) B, , n )] X ( A1 , A 2 ,
( A1 ,A 2 , An ) A ( 1 , 2 ,n A ) [(1 , 2 , [ A(1 , 2 ,
(1 , 2 ,
D ( ( 及D 都是首一的多项式,因此必有 D 。证毕 ( ( D i ) i ) i ) i )
定理 3 两个复数对称矩阵合同的充要条件是它们的秩相同。 证明: 由于任意一个复系数的二次型经过一适当的非退化线性替换 可以变成规范形,且规范形是唯一的。换个说法既是,任一复数的对 称矩阵合同于一个形式为
代入〈5〉式经整理得:
R( A) ( B ) [N (1 ) Q ( ) ( A
)〈 ] 7〉
〈7〉式的左边是一次的矩阵多项式,因此〈7〉式中括号内的部分必 须是零次的,也即必是一个常数矩阵,设为 P 。于是
R( A) ( B) P
〈8〉式又可整理为 ( R P) RA BP
M ( )( A) N ( ) B
〈4〉
其中 M ( ) 与 N ( ) 都是有限个初等矩阵之积,因而都是可逆阵。因 此可将〈4〉式写为:
M ( )( A) ( B) N ( )1
又可设
〈5〉 〈6〉
M ( ) ( B ) Q ( ) R
' ' ' ' '' ' '
易看出矩阵 C AC 也是对称的,事实上 (C AC ) C AC C AC 由此,即得 B C AC
'
这就是前后两个二次型的矩阵的关系,与之相应,我们引入 定义 4
高等代数第八章 7第七节 矩阵的有理标准形

返回
上页
下页
定义8 对数域 上的一个多项式 对数域P上的一个 上的一个多项式 定义 d(λ)=λn+a1λn-1+…+an 称矩阵 0 0 L 0 − an 1 0 L 0 − a n −1 (1) A = 0 1 L 0 − an− 2 M M M M 0 0 L 1 − a1 多项式d(λ)的伴侣阵 为多项式 的伴侣阵. 容易证明, 的不变因子(即 - 的不变因子)是 容易证明,A的不变因子 即λE-A的不变因子 是 1 , 1 ,L , 1 , d ( λ ) (见习题 见习题3
下页
引理 (2)中矩阵的不变因子为 中矩阵的不变因子为 中矩阵的不变因子 1,1, …,1, d1(λ),d2(λ),…,ds(λ) , 其中 1 的个数等于 d1(λ), d2(λ), …, ds(λ) 的次数之和 n减去 减去s. 减去 证明 因为
λE1 − A1 λE − A =
第七节*
矩阵的有理标准形
前一节中证明了复数域上任一矩阵 都可 都可相似 前一节中证明了复数域上任一矩阵A都可相似 复数域 一个若当形矩阵 这一节将对任意数域P来 若当形矩阵. 于一个若当形矩阵 这一节将对任意数域 来讨论 类似的问题. 我们证明P上任一矩阵必相似于 必相似于一个 类似的问题 我们证明 上任一矩阵必相似于一个 有理标准形矩阵. 有理标准形矩阵.
返回
上页
下页
矩阵A的初等因子为 例 设3×3矩阵 的初等因子为(λ-1)2, (λ-1) ,则它 × 矩阵 不变因子是 它的有理标准形 有理标准形为 的不变因子是1, (λ-1), (λ-1)2 ,它的有理标准形为 A1
1 0 0 0 0 − 1 0 1 2
高等代数 教学大纲

教学大纲一.课程的教学目的和要求通过这门课的学习,使学生掌握高等代数的基本知识,基本方法,基本思路,为进一步学习专业课打下良好的基础,适当地了解代数的一些历史,一些背景。
要突出传授数学思想和数学方法,让学生尽早地更多地掌握数学的思想和方法。
突出高等代数中等价分类的思想,分解结构的思想,同构对应的思想,揭示课程内部的本质的有机联系。
二.课程的主要内容:代数学是研究代数对象的结构理论与表示方法的一门学科。
代数对象是在一个集合上定义若干运算,且满足若干公理所构成的代数系统,线性空间则是数学类专业本科生所接触和学习的第一个代数对象。
本课程力求突出代数学的思想和方法。
《高等代数》分为两个部分主要内容。
一部分是基本工具性质的,包括多项式,行列式,矩阵初步,二次型。
既然是工具性质的,因而除了多项式内容外,也是数学专业以外的理科、工科、经管类《线性代数》的内容,以初等变换为灵魂的矩阵理论是这部分内容的核心。
另外一部分是研究线性空间的结构,这是研究代数结构的起点和模型,也是《高等代数》有别于《线性代数》之所在。
《高等代数》从三个角度进行研究。
从元素的角度看,研究向量间的线性表示,线性相关性,基向量;从子集角度看,研究子空间的运算和直和分解;从线性空间之间的关系来研究线性空间结构,就是线性映射,线性变换,线性映射的像与核,Jordan 标准形对应的空间分解。
而欧氏空间则是具体的研究空间的例子。
在研究线性空间中,始终贯穿着几何直观和矩阵方法的有机结合,矩阵的相似标准形和对应的线性空间分解则是这种有机结合的生动体现和提升,因而是本课程的精华内容。
本课程力求突出几何直观和矩阵方法的对应和互动。
我们强调矩阵理论,把握简洁和直观的代数方法,同时重视线性空间和线性映射(变换)的主导地位和分量,从几何观点理解和把握课程内容。
三.课程教材和参考书:教材:林亚南编著,高等代数,高等教育出版社,第一版参考书:1. 姚慕生编著,高等代数(指导丛书),复旦大学出版社,第二版2. 北京大学数学系编,高等代数,高等教育出版社,北京(1987)3. 张禾瑞、郝炳新,高等代数,高等教育出版社,北京(1999)4. 樊恽、郑延履、刘合国,线性代数学习指导,科学出版社,北京(2003)5. 林亚南编:高等代数方法选讲,2002年,见厦门大学精品课程“高等代数”网站四.课程内容及学时分配本课程开课时间:一学年(共两学期),共170学时,其中课堂讲授122学时,习题讨论课42学时,考试6学时。
(完整版)高等代数知识点归纳

1122,,0,.i j i j in jn A i j a A a A a A i j ⎧=⎪++=⎨≠⎪⎩L==()mn A O A A O A BO BO BBO A AA B B O B O*==**=-1(1)211212112111()n n nnn n n n n n n a Oa a a a a a a Oa O---*==-K N N 1范德蒙德行列式:()1222212111112n i j nj i nn n n nx x x x x x x x x x x ≤<≤---=-∏L L L M M M L111代数余子式和余子式的关系:(1)(1)i j i j ij ijij ij M A A M ++=-=-分块对角阵相乘:11112222,A B A B A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭⇒11112222A B AB A B ⎛⎫= ⎪⎝⎭,1122nn n A A A ⎛⎫= ⎪⎝⎭分块矩阵的转置矩阵:TTT TT A B A C C D BD ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭()1121112222*12n Tn ijn n nn A A A A A A A A A A A ⎛⎫ ⎪ ⎪== ⎪⎪⎝⎭LL M M M L ,ij A 为A 中各个元素的代数余子式. **AA A A A E ==,1*n A A -=, 11A A --=.分块对角阵的伴随矩阵:***A BA B AB ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭111A B BA---⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭ 1231111213a a a a a a -⎛⎫⎛⎫ ⎪ ⎪=⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭3211111213a a a a a a -⎛⎫⎛⎫⎪⎪=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭矩阵的秩的性质:① ()A O r A ≠⇔≥1; ()0A O r A =⇔=;0≤()m n r A ⨯≤min(,)m n④ ()(),,()0m n n s r A r B n A B r AB B Ax ⨯⨯+≤⎧=⇒⎨=⎩若若0的列向量全部是的解⑤ ()r AB ≤{}min (),()r A r B⑥ 若P 、Q 可逆,则()()()()r A r PA r AQ r PAQ ===; 即:可逆矩阵不影响矩阵的秩.⑦ 若()()()m n Ax r AB r B r A n AB O B O A AB AC B C ο⨯⇔=⎧⎪=⎧⎪=⎨⎪⇒=⇒=⎧⎨⎪⎨⎪⎪=⇒=⎩⎩⎩ 只有零解在矩阵乘法中有左消去律;若()()()n s r AB r B r B n B ⨯=⎧=⇒⎨⎩ 在矩阵乘法中有右消去律.⑧ ()rr E O E O r A r A A OO OO ⎛⎫⎛⎫=⇒⎪ ⎪⎝⎭⎝⎭若与唯一的等价,称为矩阵的等价标准型. ⑨ ()r A B ±≤()()r A r B +, {}max (),()r A r B ≤(,)r A B ≤()()r A r B +⑩ ()()A O O A r r A r B O B B O ⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭, ()()A C r r A r B O B ⎛⎫≠+ ⎪⎝⎭①n 个n 维线性无关的向量,两两正交,每个向量长度为1. ③(,)0αβ=. 记为:αβ⊥④21ni i a α====∑⑤1α==. 即长度为1的向量.内积的性质:① 正定性② 对称性③ 线性性12n A λλλ=L 1ni A λ=∑tr ,A tr 称为矩阵A 特征值与特征向量的求法(1) 写出矩阵A 的特征方程0A E λ-=,求出特征值i λ. (2) 根据()0i A E x λ-=得到 A 对应于特征值i λ的特征向量.设()0i A E x λ-=的基础解系为 12,,,i n r ξξξ-L 其中()i i r r A E λ=-. 则A 对应于特征值i λ的全部特征向量为1122,i i n r n r k k k ξξξ--+++L 其中12,,,in r k k k -L 为任意不全为零的数.3. ①1P AP B -= (P 为可逆矩阵)②1P AP B -= (P 为正交矩阵)③A 与对角阵Λ相似.(称Λ是A 7. 矩阵对角化的判定方法① n 阶矩阵A 可对角化 (即相似于对角阵) 的充分必要条件是A 有n 个线性无关的特征向量. 这时,P 为A 的特征向量拼成的矩阵,1P AP -为对角阵,主对角线上的元素为A 的特征值. 设i α为对应于i λ的线性无关的特征向量,则有:121n P AP λλλ-⎛⎫⎪⎪= ⎪ ⎪⎝⎭O .② A 可相似对角化⇔()i i n r E A k λ--=,其中i k 为i λ的重数⇔A 恰有n 个线性无关的特征向量.○注:当iλ=0为A 的重的特征值时,A 可相似对角化⇔i λ的重数()n r A =-=Ax ο=基础解系的个数.③ 若n 阶矩阵A 有n 个互异的特征值⇒A 可相似对角化. 正交矩阵 T AA E =③ 正交阵的行列式等于1或-1; ⑤ 两个正交阵之积仍是正交阵;⑥ A 的行(列)向量都是单位正交向量组.施密特正交规范化 123,,ααα线性无关,112122111313233121122(,)(,)(,)(,)(,)(,)βααββαβββαβαββαββββββ=⎧⎪⎪⎪=-⎨⎪⎪=--⎪⎩正交化单位化:111βηβ= 222βηβ= 333βηβ=1. ① 二次型 11121121222212121112(,,,)(,,,)n n n n Tn ij i j n i j n n nn n a a a x a a a x f x x x a x x x x x x Ax a a a x ==⎛⎫⎛⎫ ⎪⎪⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑L L L L L L L L L L其中A 为对称矩阵,12(,,,)T n x x x x =L② A 与B 合同 TC AC B =. (,,A B C 为实对称矩阵为可逆矩阵)求C (A I)→(B C^T) 这个变换先进行行变换 再进行一致的列变换 最后 求得C 和C^T③ 正惯性指数 二次型的规范形中正项项数p 负惯性指数二次型的规范形中负项项数r p - ④ 两个矩阵合同⇔它们有相同的正负惯性指数⇔他们的秩与正惯性指数分别相等. ⑤ 两个矩阵合同的充分条件是:A 与B 等价 ⑥ 两个矩阵合同的必要条件是:()()r A r B =2. 12(,,,)Tn f x x x x Ax =L 经过合同变换可逆线性变换x Cy = 化为21ni i f d y =∑标准形.① 正交变换法② 配方法(1)若二次型含有i x 的平方项,则先把含有i x 的乘积项集中,然后配方,再对其余的变量同样进行, 直到都配成平方项为止,经过非退化线性变换,就得到标准形;(2) 若二次型中不含有平方项,但是0ij a ≠ (i j ≠), 则先作可逆线性变换()1,2,,,i i j j i jkk x y y x y y k n k i j x y=-⎧⎪=+=≠⎨⎪=⎩L 且,3.12,,,n x x x L 不全为零,12(,,,)n f x x x >L 0.正定二次型对应的矩阵.4. ()Tf x x Ax =为正定二次型⇔(之一成立): (1) x ο∀≠ ,Tx Ax >0; (2)A 的特征值全大于0; (3)f 的正惯性指数为n ; (4)A 的所有顺序主子式全大于0;(5)A 与E 合同,即存在可逆矩阵C 使得TC AC E =; (6)存在可逆矩阵P ,使得TA P P =;(),nT A r A n A A Ax x Ax A Ax A A A E οοοββ==⇔∀≠≠≠⇔∀∈=≅可逆的列(行)向量线性无关 的特征值全不为0 只有零解 ,0总有唯一解 是正定矩阵 R 12,s iA p p p p nB AB E AB E⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪=⋅⋅⋅⎪==⎪⎩ 是初等阵存在阶矩阵使得 或 ()A r A n A A A Ax A ολ<=⇔==不可逆 0的列(行)向量线性相关 0是的特征值 有非零解,其基础解系即为关于0的⎧⎪⎪⎪⎨⎪⎪⎪⎩特征向量。
高等代数 第9章矩阵的标准型 9.6 若当标准型

T
再由第三个方程解出一个特解为
,那么所求相似变换矩阵为
0 4 1 P X 1, X 2 , X 3 1 3 0 0 2 0
例 2 求方阵
1 2 6 A 1 0 3 1 1 4
J 0 3 1 0 0 3
或
3 1 0 J 0 3 0 0 0 1
例 2 用矩阵秩的方法求出矩阵
1 0 A 0 0
的Jordan标准形。
2 1 0 0
3 2 1 0
4 3 2 1
解:首先求出其特征值,显然其特征多项式为
矩阵的Jordan标准形 定义: 称 n 阶矩阵
ai Ji
1 ai
1 1 ai ni ni
为Jordan块。设 J1, J 2 ,, J s 为Jordan块, 称准对角形矩阵
J1 J
J2
Js
X 3 2, 0, 1
T
T
再由第三个方程解出一个特解为
,那么所求相似变换矩阵为
1 2 2 P X 1, X 2 , X 3 1 1 0 0 1 1
从而有
1 0 0 1 P AP 0 1 1 0 0 1
故 A 的Jordan标准形为
0 0 0 J 0 0 0 0 0 2
或
0 0 0 J 0 2 0 0 0 0
求Jordan标准形的另一种方法:特征矩阵秩 的方法. 具体操作步骤: (1)先求出该矩阵的特征多项式及其特征 值 A (2)其Jordan标准形的主对角线上都是 i 在主对角线上出 的特征值,并且特征值 现的次数等于 i 作为特征根的重数。对于每 i ,求出以它为主对角元的各级 个特征值 Jordan 块的数目N (i ) ,首先求出
高等代数第八章 6第六节 Jordan标准形的理论推导

(1)
(其中 1,λ2,…,λs可能有相同的,指数k1,k2,…,ks也可 其中λ 可能有相同的,指数 其中 能有相同的). 每一个初等因子 能有相同的 每一个初等因子 ( λ − λi ) k 对应于一
i
个若当块
返回 上页 下页
λ0 1 Ji = 0 M 0
返回
上页
下页
例2 求矩阵
− 1 − 2 6 A = − 1 0 3 − 1 − 1 4
若当标准形. 的若当标准形 解 先求 -A的初等因子: 先求λE- 的初等因子:
0 − λ + 1 − λ2 + 3λ − 2 λ +1 2 − 6 r1-(λ+1)3 +1)r +1) λE − A = 1 λ − 3 → 0 λ −1 −λ +1 1 r2-r3 1 1 λ − 4 λ−4 1
返回 上页 下页
应该指出,若当形矩阵包括对角矩阵作为特殊 应该指出,若当形矩阵包括对角矩阵作为特殊 包括对角矩阵 情形,那就是由一级若当块构成的若当形矩阵, 情形,那就是由一级若当块构成的若当形矩阵,由 此即得 定理12 复数矩阵 与对角矩阵相似的<=>是A的 复数矩阵A与对角矩阵相似 相似的 = 是 的 定理 初等因子全为一次的. 初等因子全为一次的 证明留给大家作练习. 证明留给大家作练习 根据若当形的作法 可以看出矩阵A的 根据若当形的作法,可以看出矩阵 的最小多 若当形的作法, 项式就是 就是A的最后一个不变因子d 项式就是 的最后一个不变因子 n(x). 因此有 定理13 复数矩阵 与对角矩阵相似的<=>是A的 复数矩阵A与对角矩阵相似 相似的 = 是 的 定理 不变因子都没有重根 都没有重根. 不变因子都没有重根
高等代数_若当标准形
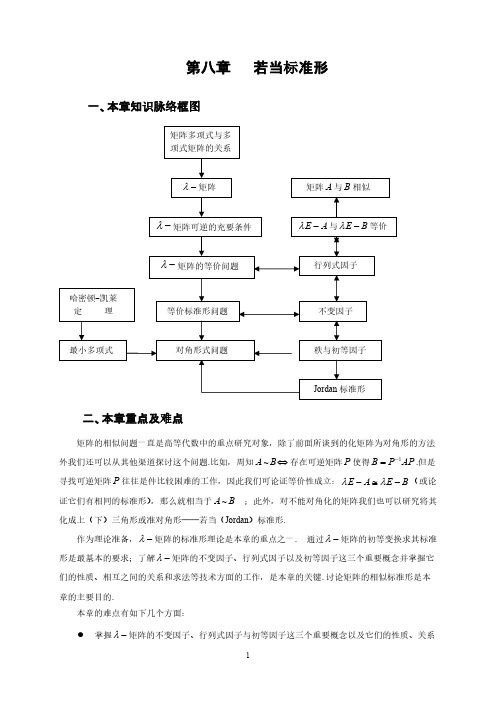
第八章 若当标准形一、本章知识脉络框图二、本章重点及难点矩阵的相似问题一直是高等代数中的重点研究对象,除了前面所谈到的化矩阵为对角形的方法外我们还可以从其他渠道探讨这个问题.比如,周知~存在可逆矩阵使得.但是A ⇔B P 1B P AP -=寻找可逆矩阵往往是件比较困难的工作,因此我们可论证等价性成立:(或论P E A E B λλ-≅-证它们有相同的标准形),那么就相当于~ ;此外,对不能对角化的矩阵我们也可以研究将其A B 化成上(下)三角形或准对角形──若当(Jordan )标准形.作为理论准备,矩阵的标准形理论是本章的重点之一. 通过矩阵的初等变换求其标准-λ-λ形是最基本的要求;了解矩阵的不变因子、行列式因子以及初等因子这三个重要概念并掌握它-λ们的性质、相互之间的关系和求法等技术方面的工作,是本章的关键.讨论矩阵的相似标准形是本章的主要目的. 本章的难点有如下几个方面:掌握矩阵的不变因子、行列式因子与初等因子这三个重要概念以及它们的性质、关系-λ和求法;●理解并掌握两个数字矩阵与相似的充分必要条件,以及数字矩阵与对角矩阵相似A B A 的充分必要条件;●充分发挥最小多项式的性质在讨论矩阵的相似标准形中的作用;●掌握矩阵的Jordan 标准形的求法、性质及其应用.三、本章的基本知识要点 (一)矩阵的概念和性质λ-1.设是一个数域,是一个文字,如果矩阵的每个元素都是的多项式,即 F λn m ⨯()A λλ=,那么,就是一个关于的多项式矩阵,简称为矩阵.如果 ,()A λ(())ij m n a λ⨯()A λλ-λn m =则称为阶矩阵.()A λn -λ2. 如果在矩阵中,有一个阶子式不为零,一切阶子式(如果存在)全-λ()A λ(1)r r ≥1r +为零,则称的秩为,记为.()A λr (())r A r λ=注意:① ;(())0r A λ=⇔()0A λ=② 若是一个数字阶矩阵,则必有.A n ()r E A n λ-=3. 设是阶矩阵,若存在阶矩阵使得()A λn -λn -λ()B λ ()()()()A B B A E λλλλ==则称是可逆的,并称是的逆矩阵,记为.()A λ()B λ()A λ1()()B A λλ-=4.注意:(1)一个阶矩阵是可逆的充要条件为行列式:.n -λ()A λ()0A c λ=≠(2)若是可逆时,则有,其中是伴随矩阵.()A λ)(|)(|1)(*1λλλA A A =-()A λ*()A λ(3)在数字矩阵中,阶矩阵是可逆的充分必要条件是行列式(即是满秩矩阵),但n A ||0A ≠A 对于矩阵来说,当矩阵的行列式时,矩阵未必是可逆的,即满秩的矩阵未-λ|()|0A λ≠()A λ-λ必是可逆的. (二)初等矩阵λ-1、由阶单位矩阵经过一次矩阵的初等变换得到的阶矩阵称为初等矩阵.其n E -λn -λ-λ有三种不同的类型,分别是、与,而且都是可逆矩阵,且逆矩阵仍是(,)P i j (())P i k (,(()))P i j ϕλ同类的初等矩阵.-λ2、对的矩阵进行一次初等行变换,相当于在的左边乘上相应的阶初等m n ⨯()A λ()A λm 矩阵;而对进行一次初等列变换,就相当于在的右边乘上相应的阶初等矩阵.-λ()A λ()A λn -λ3.矩阵可逆的充分必要条件是可表成一系列初等矩阵的乘积. -λ()A λ()A λ-λ4.注意:(1) 由于在矩阵的第二类型的初等变换中,不允许用一个非常数的多项式去乘或除矩-λ()ϕλ阵的某一行(列),这导致了矩阵的初等变换与数字矩阵的初等变换在性质上有些区别,这请读λ-者充分注意.(2) 等价的矩阵具有相同的秩、行列式因子、不变因子和初等因子.-λ(三)矩阵的标准形λ-1.矩阵不变因子λ-设的矩阵的秩为,那么可经过一系列的初等变换化成对角矩阵m n ⨯-λ()A λr ()A λ, ()11()()(),,(),0,,000r r d d diag d d λλλλ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ()*即存在阶可逆矩阵和阶可逆矩阵,使m ()P λn ()Q λ,()()()P A Q λλλ=()1(),,(),0,,0r diag d d λλ= 其中是首一多项式,且()i d λ(1,2,,)i r = .1()(),(1,2,,1)j j d d j r λλ+=- 并称※式为矩阵的标准形.其中称为的不变因子.-λ()A λ12(),(),,()r d d d λλλ ()A λ注意:若是一个阶数字矩阵,则的特征多项式必有A n A (1);12()()()()A n f E A d d d λλλλλ=-= (2)所有不变因子的次数之和.1(())n i i d n λ=∂==∑2、矩阵的行列式因子λ-(1)设的矩阵的秩为,那么对于正整数的全部阶子式m n ⨯-λ()A λr ,1,k k r ≤≤()A λk 的首项系数为1的最大公因式,称为的阶行列式因子,记为.()A λk ()k D λ(2)不变因子与行列式因子之间的关系是:12(),(),,()r d d d λλλ 12(),(),,()r D D D λλλ ,,……, (I )11()()D d λλ=212()()()D d d λλλ=12()()()()r r D d d d λλλλ= (3)两个矩阵等价的充分必要条件是它们具有相同的不变因子或相同的各阶行列式因子.-λ(4)阶可逆矩阵的各阶行列式因子是,进一步,n -λ()A λ12()()()1n D D D λλλ====的不变因子是()A λ,12()()()1n d d d λλλ==== 从而知道矩阵的标准形是单位矩阵.即可逆的矩阵的标准形是单位矩阵,反过来,如果()A λE -λ矩阵与单位矩阵等价,那么一定是一个可逆矩阵.-λ()A λ()A λ3. 矩阵的初等因子与阶数字矩阵的初等因子λ-n (1)把矩阵的每个次数大于零的不变因子分解成互不相同的一次因式的方幂的乘积,-λ()A λ所有这些一次因式的方幂(相同的必须按出现的次数计算),称为的初等因子.()A λ特别地,如果为阶数字矩阵,的特征矩阵的初等因子习惯上称为的初等因子.A n A E A λ-A (2)设为阶数字矩阵,若特征矩阵等价于下列的对角形矩阵(不一定是标准形)A n E A λ-,1()()()n h B h λλλ⎛⎫ ⎪= ⎪ ⎪⎝⎭ 其中都是首一多项式. 那么将分解成互不相同的一次因式的方幂(相同的必须按出现的()i h λ()i h λ次数计算)就是的全部初等因子.A 4. 不变因子、行列式因子与初等因子之间的关系矩阵的不变因子、行列式因子与初等因子之间存在有密切关系,它们之间可以互相-λ()A λ导出.(1)如果已知不变因子,直接使用定义可得到初等因子,利用上面的12(),(),,()r d d d λλλ 关系式(I )可导出行列式因子.12(),(),,()r D D D λλλ (2)如果已知行列式因子,同样可以利用关系式(I )导出不变因子12(),(),,()r D D D λλλ ,从而得出初等因子.12(),(),,()r d d d λλλ (3)如果已知矩阵的秩及其初等因子,这时可以将全部初等因子按不可约因子的方幂()A λr 降幂排列,同一个不可约因子的方幂排成一行.如果不可约因子的方幂的个数不足个,则在后面r 用1补足,这时全体不可约因子的方幂排成下列的形式:11121212221211122212(),(),,(),(),(),,(),0(1,2,,)(),(),,(),r r s s sr t t t t t t i i ir t t t s s s P P P P P P t t t i s P P P λλλλλλλλλ≥≥≥≥= 那么,矩阵的不变因子是()A λ,12112()()()()sr r r t t t s d P P P λλλλ= ,11121212()()()()s r r r tt t s d P P P λλλλ---= ……………… 1112112()()()()s t t t r s d P P P λλλλ= 依此就可以得到矩阵的行列式因子.12(),(),,()r D D D λλλ 下图列出了矩阵及其标准形,不变因子,行列式因子以及秩与初等因子之间的关系.在计算过程中,读者可以根据具体情况采用适当的步骤进行.(四)矩阵的等价、数字方阵相似和对角化的条件λ-1.设与都是的矩阵,那么有下列等价条件:()A λ()B λm n ⨯-λ(1)与等价与有相同的标准形; ()A λ()B λ⇔()A λ()B λ(2)与等价与有相同的不变因子;()A λ()B λ⇔()A λ()B λ(3)与等价与有相同的行列式因子;()A λ()B λ⇔()A λ()B λ(4)与等价与有相同的秩和初等因子;()A λ()B λ⇔()A λ()B λ(5)与等价存在一系列初等矩阵和使得()A λ()B λ⇔-λ12,,,s P P P 12,,,t Q Q Q ;1212()()s t PP P A Q Q Q B λλ= (6)与等价存在可逆矩阵和使得.()A λ()B λ⇔-λ()P λ()Q λ()()()()P A Q B λλλλ=注意:两个阶数一样的矩阵仅是初等因子相同时,不能保证它们等价.例如矩阵-λ如的初等因子相同,但它们不等价.10()01A λλλ-=+⎛⎫ ⎪⎝⎭(1)(1)0()00B λλλ-+=⎛⎫ ⎪⎝⎭2.设都是阶数字矩阵,那么有下列关于矩阵相似的等价条件:,A B n (1)~与等价;A ⇔B E A λ-E B λ-(2)~与有相同的标准形;A ⇔B E A λ-E B λ-(3)~与有相同的不变因子;A ⇔B E A λ-E B λ-(4)~与有相同的行列式因子;A ⇔B E A λ-E B λ-(5)~与有相同的初等因子(或者与有相同的初等因子);A ⇔B E A λ-E B λ-A B (6)~与有相同的若当标准形.A ⇔B A B 3.设是阶数字复矩阵,那么有下列等价条件:A n (1)与对角矩阵相似的充分必要条件是的不变因子没有重根;A E A λ-(2)与对角矩阵相似的充分必要条件是的初等因子都是一次的;A A (3)与对角矩阵相似的充分必要条件是的最小多项式没有重根;A A (4)与对角矩阵相似的充分必要条件是每个特征根的代数重数等于几何重数.A A (五)数字矩阵的若当标准形与有理标准形 从前面所谈论的化矩阵为对角形矩阵可知,并不是所有的阶数字矩阵都能相似对角化,虽然n 如此,但对于实数域上的阶对称矩阵,即实对称矩阵是一定与一个实对角矩阵相似的.于R n A A 是,我们自然会提出这样一个有待解决的重要问题:当一个矩阵不与对角矩阵相似时,能否退而求其次,使相似于一个比对角矩阵稍为复杂,但仍能给计算和研究带来便利的某种标准形呢?这就A 是我们下面要介绍的矩阵的若当标准形与有理标准形.1.矩阵的若当标准形(1)设是一个复数,形式为0λ0000000001000(,)00100001t tJ t λλλλλ⨯⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ 的矩阵称为若当(Jordan )块. 而由若干个若当块组成的准对角矩阵(分块对角矩阵)(,)i i J t λ1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 称为若当形矩阵,其中参数可以是相等,也可以是不相等.12,,,s λλλ (2)由于若当块的特征矩阵的各阶行列式因子是0(,)J t λ0(,)E J t λλ-,1210()()()1,()()t t t D D D D λλλλλλ-=====- 因此,它的不变因子是.1210()()()1,()()t t t d d d d λλλλλλ-=====- 由此即得,的初等因子是,也就是若当块的初等因子.由于若当块0(,)E J t λλ-0()t λλ-0(,)J t λ完全被它的级数与主对角线上的元素所刻划,而这两个数都反映在它的初等因子0(,)J t λt 0λ中.因此,若当块是由它的初等因子唯一决定的.0()t λλ-(3)类似地,我们可以求得若当形矩阵1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 的初等因子是.1212(),(),,()s t t t s λλλλλλ--- 也就是说,每个若当形矩阵的全部初等因子是由它的全部若当块的初等因子构成的.而每个若当块是由其初等因子来决定的,由此可见,若当形矩阵除去其中的若当块排列的次序外,是被它的初等因子唯一决定的.(4)若当形矩阵的主要结论是:复数域上任一个阶矩阵都相似于一个若当形矩阵C n A ,1122(,)(,)(,)s s J t J t J J t λλλ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 这个若当形矩阵称为的若当标准形.A (5)设是一个阶矩阵,是的若当标准形,那么A n J A ●存在可逆矩阵,使得;T 1T AT J -=●与有相同的秩与行列式;A J ●与有相同的特征多项式与最小多项式;A J ●特征矩阵与有相同的行列式因子;E A λ-E J λ-●与(或者与)有相同的不变因子与初等因子.E A λ-E J λ-A J (6)对于复数域上的维线性空间的任一个线性变换,在中必存在有一组基C n V σV ,使得在此基下的矩阵是一个若当形的.12,,,n ααα σ(7)每个阶的复数矩阵都与一个下(或上)三角形矩阵相似,其主对角线上的元素刚好n A 是矩阵的全部特征值. 即存在可逆矩阵,使A T (下三角形矩阵),110*n T AT λλ-⎛⎫ ⎪= ⎪ ⎪⎝⎭ 其中是矩阵的全部特征值.如果是一个多项式,则的全部特征值是1,,n λλ A ()g λ()g A,即1(),,()n g g λλ .11()0()*()n g T g A T g λλ-⎛⎫ ⎪= ⎪ ⎪⎝⎭ 2.矩阵的有理标准形在上面我们讨论了复数域上任何一个阶矩阵可相似于一个若当形矩阵,下面我们将在任意C n 一个数域上来讨论类似的问题,而且证明了上任意一个阶矩阵必相似于一个有理标准形矩F F n 阵.(1)对于数域上的一个多项式F ,12121(),1n n n n n f a a a a n λλλλλ---=+++++≥ 称矩阵122100001000010000100001n n n a a a A a a ---⎛⎫ ⎪- ⎪ ⎪-= ⎪ ⎪ ⎪- ⎪ ⎪-⎝⎭ 是多项式的伴侣阵.()f λ多项式的伴侣阵的不变因子(即是的不变因子)是()f λA E A λ-,.121()()()1n d d d λλλ-==== ()()n d f λλ=(2)设阶矩阵的不变因子是n A 121,,1,(),(),,()k k n d d d λλλ++ 其中的次数大于等于1,并且假设分别是的()k i d λ+12,,,n k N N N - 12(),(),,()k k n d d d λλλ++ 伴侣阵,这时我们称分块对角矩阵12n k N N F N -⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭是矩阵的有理标准形.A (3)数域上的任意一个阶矩阵必相似于它的有理标准形(因为它们具有相同的初等因F n A 子).注意:若当标准形在复数域上是一定存在的,而有理标准形在任何数域上都是存在的.(六)最小多项式及其性质 1.零化多项式与最小多项式设是一个数域,是上的阶数字矩阵,如果数域上的多项式使得,F A F n F ()f x ()0f A =则称以为根或为的零化多项式.()f x A ()f x A 在以为根的多项式中,次数最低且首一的多项式称为的最小多项式,记为.A A ()A m λ2、哈密顿─凯莱定理设是一个数域,是上的阶数字矩阵,记的特征多项式为F A F n A12121()n n n A n n f E A a a a a λλλλλλ---=-=+++++ 那么 12121()0n n n A n n f A A a A a A a A a E ---=+++++= 即的特征多项式是的零化多项式.同时,还有A A *12231211211()()()()n n n n n n E A A a A a a A a a E λλλλλλ-------=++++++++++ 3、最小多项式的性质设是数域上的阶数字矩阵,为的最小多项式.A F n ()A m λA (1)最小多项式是唯一的;(2)设,则的充分必要条件是;特别地,矩阵的最小()[]g F λλ∈()0g A =()()A m g λλA 多项式是的特征多项式的一个因式.()A m λA ()A f E A λλ=-(3)若是一个阶数字矩阵,且的特征多项式为A n A 12()()()()A n f E A d d d λλλλλ=-= 那么;()()A n m d λλ=1()()A n f D λλ-=(4)的特征根都是根.A ()A m λ(5)设都是阶数字矩阵,如果相似,即~;,AB n ,A B A ⇔B ()()A B m m λλ=(6)设是准对角形,且分别是的最小多项式,那么1s A A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭ ()i m λi A ;()A m λ12[(),(),,()]s m m m λλλ= (7)阶若当块t0000000001000(,)00100001t t J t λλλλλ⨯⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ 的最小多项式.0()()t J m λλλ=-(六)主要定理与结论定理1 假设都是阶数字矩阵,如果存在阶数字矩阵满足,A B n n 00,P Q 00()E A P E B Q λλ-=-则矩阵与相似.A B 作为矩阵多项式,矩阵也有下列的带余除法定理.-λ定理2 设是数域上的两个阶矩阵,其中(),()A B λλF n -λ1011(),(),0,1,,.m m m m i n B B B B B B M F i m λλλλ--=++++∈= 如果可逆,则存在矩阵及,满足0B -λ(),()L L Q R λλ(),()R R Q R λλ,,()()()()L L A B Q R λλλλ=+()()()()R R A Q B R λλλλ=+其中分别是零或者,且满足上述条件的(),()L R R R λλ(())(()),(())(())L R R B R B λλλλ∂<∂∂<∂及是唯一的.表示矩阵中所有元素的最高次数.(),()L L Q R λλ(),()R R Q R λλ(())A λ∂()A λ如果把定理2的矩阵分别改成数字矩阵的特征矩阵,那么定理2变成下列的()B λA E A λ-定理.定理3 对于任何不是零的阶数字矩阵,以及矩阵与,一定存在矩阵n A -λ()U λ()V λ-λ与以及数字矩阵与使得()Q λ()R λ0U 0V ,.0()()()U E A Q U λλλ=-+0()()()V R E A V λλλ=-+定理3的一个常用推论是下面的定理4 设,则存在唯一的矩阵使得()[],()n f F A M F λλ∈∈-λ()Q λ.()()()()()()()f E E A Q f A Q E A f A λλλλλ=-+=-+证明:存在性的验证. 假设多项式1011()m m m m f c c c c λλλλ--=++++ 那么,1011()m m m m f E c E c E c E c E λλλλ--=++++ 1011()m m m m f A c A c A c A c E--=++++ 取120121()m m m m Q D D D D λλλλ----=++++ 其中10110,0,1,, 1.kk i k k k i k k i D c A c A c A c A c k m ---===++++=-∑ 代入定理中,可以验证等式成立.唯一性的证明. 假设还存在有另一个矩阵使得-λ1()Q λ11()()()()()()()f E E A Q f A Q E A f A λλλλλ=-+=-+只要把两个等式相减,可以得到11(()())(()())Q Q A Q Q λλλλλ-=-再通过比较等式两边的次数,即可得到.■λ1()()Q Q λλ=定理5 阶数字矩阵的最大不变因子等于的所有初等因子的最小公倍式.n A ()n d λA 证明: 因为,将矩阵全部初等因子按不可约因子的方幂降幂排列,同一()r E A n λ-=A 个不可约因子的方幂排成一行,不足个的在后面用1补足. 排列的形式如下:n 11112221221*********(),(),,(),(),(),,(),0(1,2,,)(),(),,(),n n s s sn t t t t t t i i in t t t s s s P P P P P P t t t i s P P P λλλλλλλλλ≥≥≥≥=那么,不变因子 ,也就是等于所有初等因子的最小公倍式. ■1112112()()()()s tt t n s d P P P λλλλ= 定理6设阶矩阵的最小多项式为,证明:,其中是n A ()m λ()()n m d λλ=()n d λ的最后一个不变因子.E A λ-证明:设的全部初等因子是A 1111211121111112112(),(),,(),(),(),,(),r sr s s s sn n n rn n n s s s s s sr n n n n n n λλλλλλλλλλλλ⎧---≤≤≤⎪⎪⎨⎪---≤≤≤⎪⎩其中两两不同.这时 .12,,,s λλλ 121212()()()()sr r r sn n n n s d λλλλλλλ=--- 其次,由于相似于若当标准形A ,1112srs n n n J J J J ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭1,1,2,,.1,2,,.1ij i i n s i J i s j r λλλ⎛⎫ ⎪⎪=== ⎪ ⎪⎝⎭ 由于对角分块矩阵的最小多项式等于各分块矩阵最小多项式的最小公倍式,而且相似矩阵有相同的最小多项式,所以1111111()(),,(),,(),,()sr r s s n nn n s s m λλλλλλλλλ⎡⎤=----⎣⎦.■111()()()sr r s n ns n d λλλλλ=--= 定理7设是准对角形,且分别是的最小多项式,证明:1s A A A ⎛⎫⎪= ⎪ ⎪⎝⎭()i m λi A ,其中表示的最小公倍式.()A m λ1[(),,()]s m m λλ= 1[(),,()]s m m λλ 1(),,()s m m λλ 证明:因为 ,所以,,1()()0()A A A s m A m A m A ⎛⎫⎪== ⎪ ⎪⎝⎭1()()0A A s m A m A === 即是矩阵零化多项式,因此,故是()A m λ1,,s A A )(|)(,,)(|)(1λλλλA s A m m m m ()A m λ的一个公倍式.1(),,()s m m λλ 另一方面,任取的一个公倍式,则有,1(),,()s m m λλ )(λh 1()()0()s h A h A h A ⎛⎫⎪== ⎪ ⎪⎝⎭可见是矩阵的一个零化多项式,所以,. 再因为的首项系数为1,因)(λh A ()|()A m h λλ()A m λ此. ■()A m λ1[(),,()]s m m λλ= 定理8 相似矩阵具有相同的最小多项式.证明:设阶矩阵与相似,即存在可逆矩阵,使得.又设分n A B T 1B T AT -=12(),()m m λλ别是矩阵,的最小多项式,且设A B 12110()s s s m b b b λλλλ--=++++ 那么,我们有121100()s s s m B B b B b B b E--==++++ 1111102()().s s s T A b A b A b E T T m A T ----=++++= 所以,,是的零化多项式,而是的最小多项式,因此,2()0m A =2()m λA 1()m λA .12()|()m m λλ类似可以证明,.再从的首项系数为1,即可得到.■21()|()m m λλ12(),()m m λλ12()()m m λλ=四、基本例题解题点击1.矩阵的基本概念与计算λ-【例1】设有矩阵,-λ2222123(),()1253A B λλλλλλλλλλλ⎛⎫-⎛⎫== ⎪ ⎪++++⎝⎭⎝⎭计算:(1);(2).()2()A B λλ-()()A B λλ⋅【提示及点评】矩阵的运算法则与数字矩阵的运算法则相同.-λ【例2】设,求.21()12A λλλλλ⎛⎫=⎪+++⎝⎭1()A λ-【提示及点评】可以按数字矩阵求逆的方法进行计算.【例3】设,求.00()1001A λλλλ=⎛⎫ ⎪ ⎪ ⎪⎝⎭()nA λ【解】因为00100000()1001010001001010A EB λλλλλλ==+=+⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭而,所以可以应用牛顿二项式定理来进行计算.EB BE B ==0111222()()n nnk n k k n n n n n n n k A E B C E B C E C B C B λλλλλλ---==+=⋅=++∑. ■1(1)21200nn nn n n n n n n λλλλλλ----⎛⎫⎪= ⎪ ⎪⎝⎭【知识扩展提示】题目可以扩充为对任意阶数的若当块,0000000001000(,)00100001t tJ t λλλλλ⨯⎛⎫⎪⎪ ⎪=⎪⎪ ⎪⎝⎭求.0(,)nJ t λ【例4】设有矩阵-λ2221211111()2211,()2131221023A B λλλλλλλλλλλλλλλλ-+-+-+--+=-+++=---+---⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭试求矩阵使得(),()L L Q R λλ,()()()()L L A B Q R λλλλ=+其中或者.()0L R λ=(())(())L R B λλ∂<∂【提示及点评】此例子主要介绍矩阵的带余除法定理.-λ【解】首先把矩阵表示成矩阵多项式的形式:(),()A B λλ22012100120111()010121211002101012A A A A λλλλλ---=++-=++--⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭01101111()010*********B B B λλλ--=+--=+--⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭然后借助于多项式除以多项式的运算,我们有01B B λ+2012A A A λλ++100()L Q B A λλ-=210100A B B A λλ-+1101100()B A B B A --+-111002()A B B A A λ--+1111100101100()()A B B A B B A B B A λ----+-112101100()()L R A B B A B B A λ--=--所以,,1110001100211()()134002L Q B A B A B B A λλλλλ-----⎛⎫ ⎪=+-=-+ ⎪ ⎪+⎝⎭.■112101100250()()169205L R A B B A B B A λ--⎛⎫ ⎪=--= ⎪ ⎪-⎝⎭【知识扩展提示】题目如果是求矩阵使得,则在-λ(),()R R Q R λλ()()()()R R A Q B R λλλλ=+做多项式除法的时候,注意矩阵与相乘时的左右方向即可.01B B λ+()R Q λ2.求矩阵的标准形、行列式因子、不变因子与初等因子λ-(1)行列式因子的计算方法一:直接使用行列式因子的定义进行计算.【例5】设有矩阵-λ,2221211()2211122A λλλλλλλλλλλ⎛⎫-+-+- ⎪=-+++ ⎪ ⎪-+-⎝⎭试求其行列式因子.【解】由于矩阵的元素中含有非零常数1,所以一阶行列式因子.或者是由于下列()A λ1()1D λ=所有多项式{}2221,21,1,2,21,1,,1,22λλλλλλλλλλ-+-+--+++-+-的最大公因式是1,所以.1()1D λ=对于二阶行列式因子. 由于的2阶子式一共有9个,一一计算比较麻烦,我们只2()D λ()A λ要找出特别的几个出来,看它们是否互素即行. 由于2阶子式与22211λλλλ-++-2211211λλλλ-+-+++是互素的,即最大公因式是1,所以二阶行列式因子.2()1D λ=最后计算三阶行列式因子,由于矩阵的3阶子式只有1个,所以3()D λ()A λ. ■65432311()|()|(2338385)2D A a λλλλλλλλ==++--+-【注意】由于使用定义的方法求行列式因子的计算过程比较麻烦,因此一般很少用,除非是矩阵比较简单.()A λ方法二:先用初等变换化简矩阵,一般情况是化简成为标准形或者对角形,再对简化后的-λ矩阵求行列式因子.-λ【例6】设有矩阵-λ111()2131023B λλλλλ+--+=----⎛⎫⎪ ⎪ ⎪⎝⎭试求其行列式因子.【解】由于(1)(3)1111023()2132131023111B λλλλλλλλλ↔+--+--=------+--+⎛⎫⎛⎫ ⎪ ⎪−−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭32100010002447λλλ-→→--+-⎛⎫⎪ ⎪ ⎪⎝⎭因此,所求的行列式因子是,. ■12()()1D D λλ==3237()222D λλλλ=-+-方法三:对于特殊类型的矩阵(如对角形、上下三角形等等),可以先求出阶数大的行列-λ式因子,再利用的关系,求出阶数低的行列式因子.1()|()k k D D λλ-【例7】设有下列矩阵-λ①;②1221000100010()0000001n n n a a a A a a λλλλλλ--⎛⎫ ⎪- ⎪⎪-= ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭31104101()0021001A λλλλλ--⎛⎫ ⎪+ ⎪= ⎪+- ⎪⎝⎭试求它们的行列式因子.【解】① 由于矩阵的行列式()A λ12121|()|n n n n nA a a a a λλλλλ---=+++++ 所以,,12121()n n n n n n D a a a a λλλλλ---=+++++ 又由于在中有一个阶的子式,故,于是,()A λ1n -110001(1)0000001n λλλ---=--1()1n D λ-=.231()()()1n n D D D λλλ--==== ② 显然,2243121()(1)(1)411D λλλλλλλ--+-==-++又其中的一个3阶子式,11010123021λλλ-+=++-由于三阶行列式因子并且还有,因此可见,于是3()|(23)D λλ+34()|()D D λλ3()1D λ=. ■21()()1D D λλ==(2)矩阵的标准形、不变因子与初等因子的计算-λ方法一:直接使用矩阵的初等变换,求矩阵的标准形,进而可以得到不变因子.-λ【例8】用初等变换求下列矩阵的标准形、不变因子与初等因子.-λ.222223222213()2322A λλλλλλλλλλλλλλλλλ⎛⎫- ⎪=--+-- ⎪ ⎪+++⎝⎭【提示及点评】在使用初等变换来求矩阵的标准形时,第一步应将矩阵左上角的元素变成-λ能够整除矩阵的所有元素,第二步才能消去矩阵的第一行与第一列的其余元素,重复这个过程即可把矩阵化其标准形. 关键的一步是在矩阵的所有元素中直接找出一个或者经过加减运算后找出-λ一个元素,使其能够整除矩阵的所有元素.【解】2222222322232(1)(2)(1)2222212112()23222322022A λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ+⋅-⎛⎫⎛⎫-- ⎪ ⎪=--+--−−−−→--+-- ⎪ ⎪⎪ ⎪+++++⎝⎭⎝⎭1000(1)000(1)(1)λλλλλ⎛⎫⎪→→+ ⎪⎪+-⎝⎭于是,的不变因子,从而得出矩阵的初()A λ123()1,()(1),()(1)(1)d d d λλλλλλλλ==+=+-等因子是.■,,1,1, 1.λλλλλ++-方法二:对于一些形如上(下)三角形、对角形等特殊的矩阵,可以先求其行列式因子-λ(或者初等因子),再利用不变因子与行列式因子的关系,求出不变因子,进而得到矩阵的标准形.【例9】求下列矩阵的标准形与不变因子.-λ①;②21000210()00210002A λλλλλ+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭22220(1)00(1)000()000100(1)0A λλλλλλλλ⎛⎫+ ⎪- ⎪= ⎪- ⎪ ⎪+⎝⎭【解】① 显然,行列式因子,而且矩阵有一个3阶子式44()|()|(2)D A λλλ==+)(λA ,所以有,故的不变因子是 1002101021λλ+=+321()()()1D D D λλλ===)(λA ,,即的标准形是. 123()()()1d d d λλλ===44()(2)d λλ=+)(λA 410000100001000(2)λ⎛⎫⎪⎪⎪ ⎪+⎝⎭② 虽然矩阵不是对角形,但可用初等变换化成对角形:)(λA 220(1)00(1)000λλλλ⎛⎫⎛⎫+-由此可得矩阵的初等因子是,而矩阵的)(λA 222,,,(1),(1),1,1,1λλλλλλλλ+++--秩=4,据此可知不变因子是,2123()1,()(1),()(1)(1)d d d λλλλλλλλ==+=+-,故矩阵的标准形是224()(1)(1)d λλλλ=+- . ■22210000(1)0000(1)(1)0000(1)(1)λλλλλλλλ⎛⎫ ⎪+ ⎪ ⎪+- ⎪+-⎝⎭(3)有关数字矩阵的初等因子的计算【例10】求下列数字矩阵的初等因子(以及不变因子,相应特征矩阵的行列式因子)...308316205A ⎛⎫⎪=- ⎪ ⎪--⎝⎭【提示及点评】对于计算数字矩阵的初等因子,其实其过程与求矩阵的若当标准形一样. 计算方法与求一般矩阵的初等因子是一样的.-λ【解】因为(2)(3)1308308316111205205E A λλλλλλλλ+⋅----⎛⎫⎛⎫ ⎪ ⎪-=-+-−−−−→-+- ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭210002(1)000(1)/2λλ-⎛⎫⎪→→+ ⎪⎪-+⎝⎭因此,所求的初等因子是,不变因子是,2(1),1λλ++2123()1,()1,()(1)d d d λλλλλ==+=+行列式因子是. ■3123()1,()1,()(1)D D D λλλλλ==+=+3.有关矩阵等价的判断与证明λ-【例11】判断下列两个矩阵是否等价?,010001()000000A λαλαλλαλα+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭010100()000000B λαλαλλαλα+⎛⎫ ⎪+ ⎪= ⎪+ ⎪+⎝⎭【提示及点评】利用矩阵等价的6个方法之一进行判断.-λ【解】易见,矩阵与的行列式因子都是)(λA )(λB 241234()()1,()(),()()D D D D λλλλαλλα===+=+因此,矩阵与是等价的. ■)(λA )(λB 【例12】对于任意的阶矩阵,证明与等价.n -λ)(λA )(λA )(/λA 【提示及点评】可以证明它们有相同的行列式因子或者有相同的标准形.【解】假设矩阵的标准形是)(λA ()1()(),,(),0,,0r D diag d d λλλ= 因此,存在可逆矩阵使得,两边取转置得到)(,)(λλQ P )()()()(λλλλD Q A P =,从而知道与有相同的标准形,所以与)()()()()(////λλλλλD D P A Q ==)(λA )(/λA )(λA 等价.■)(/λA 4.有关数字矩阵的特征矩阵(特征多项式、凯莱定理)的应用A E A λ-【例13】设有矩阵,求,其中是正整数.130240121A -=---⎛⎫ ⎪ ⎪ ⎪⎝⎭nA n 【提示及点评】利用哈密顿-凯莱定理及带余除法进行计算.【解】设是矩阵的特征多项式,那么计算可得()||f E A λλ=-A 322()452(2)(1)f λλλλλλ=-+-=--再根据计算的要求,取多项式,并令(带余除法)nA ()ng λλ=2()()()n g f q a b cλλλλλλ==+++分别把代入,得到 .又因为是特征多项式2,1λλ==422,1na b c a b c ++=++=1λ=的2重根,所以,对上式两边求导后有()f λ///1()()()()()2n g f q f q a b n λλλλλλλ-=+++=再代入得到,.求解上面关于的联立方程组,我们可以得到1λ=2a b n +=,,a b c 121,223,22n n n a n b n c n+=--=-+=-因此,.■12323(12)02(12)23206(12)799271n n n n n n n A aA bA cE n n +⎛⎫--+ ⎪=++=--+-+⋅ ⎪ ⎪-+--⋅+⎝⎭【注意】关键是如何利用矩阵A 的特征值,找到关于的联立方程组.,,a b c 【例14】设有矩阵,及多项式,求130240121A -⎛⎫ ⎪=- ⎪ ⎪--⎝⎭119653()461f λλλλλλλ=-+--+-.1()f A -【提示及点评】利用哈密顿-凯莱定理及带余除法进行计算.【解】因为特征多项式,再由带余除法得到32()||452g E A λλλλλ=-=-+-2()()()(759933)f g q λλλλλ=+-+-因此,由哈密顿—凯莱定理得到,22433780()75993325238703997779f A A A E -⎛⎫ ⎪=-+-=- ⎪ ⎪--⎝⎭再求其逆,得到. ■43141354512811355511469113513590()0f A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭【注意】此题型的计算量比较大,关键是掌握其计算的方法与技巧.【例15】如果是一个阶可逆矩阵,导出使用哈密顿—凯莱定理求逆矩阵的公式.A n 1-A 【解】假定矩阵的特征多项式是A 12121()||n n n n nf E A a a a a λλλλλλ---=-=+++++ 则由凯莱定理知道,121210n n n n n A a A a A a A a E ---+++++= 而,因此,(1)||0n na A =-≠1231211()n n n n nA A a A a A a E E a -----⋅++++= 即矩阵的逆矩阵A . ■11231211()n n n n nA A a A a A a E a ------=++++ 【知识扩展提示】题目可以改成:证明存在一个实系数多项式,使得.)(x g )(1A g A=-【例16】设是任意一个阶矩阵,且A n 12121()||n n n n nf E A a a a a λλλλλλ---=-=+++++ 证明:的伴随矩阵是的多项式,并且A *A A .*1123121(1)()n n n n n A A a A a A a E -----=-++++ 【证明】由上例知道,123121(1)()n n n n n A A a A a A a E a E----⋅-++++= 而,代入上述,可以得到||(1)||nn a A A =-=-1123121(1)()||n n n n n A A a A a A a E A E-----⋅-++++=所以,.■*1123121(1)()n n n n n A A a A a A a E -----=-++++ 5.相似矩阵的判断与证明【例16】判断下列矩阵3253212610,222123365A B --⎛⎫⎛⎫ ⎪ ⎪=-=- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭是否相似.【提示及点评】要判断两个矩阵是否相似,通常的方法是先求出它们的不变因子(或行列式因子、或初等因子),如果它们相同,则相似,否则不相似.当然,如果两个矩阵的秩,行列式,特征多项式或最小多项式有一个不相等,则它们一定不相似.要注意的是,即使它们的秩,行列式,特征多项式或最小多项式都相等,仍然不能确定它们是否相似.许多学生往往根据两个矩阵的特征多项式相同,就断定这两个矩阵相似,这是初学者常犯的一个错误,请读者给予充分的注意.【解】由于2325100261002012300(2)E A λλλλλλ--⎛⎫⎛⎫ ⎪ ⎪-=--→→- ⎪ ⎪⎪ ⎪--+-⎝⎭⎝⎭ 232110022202036500(2)E B λλλλλλ--⎛⎫⎛⎫ ⎪ ⎪-=-+-→→- ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭ 从而,与有相同的不变因子,故与相似.■A B A B 【例17】假设多项式有个不同的根12121()n n n n n f a a a a λλλλλ---=+++++ n ,证明矩阵12,,,n λλλ 与 相似.1210000100001000001n n n a a A a a ---⎛⎫⎪- ⎪ ⎪=- ⎪⎪ ⎪-⎝⎭12n B λλλ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 【提示及点评】验证两个矩阵的不变因子相同即行.■【例18】下列形式的矩阵1100a b ⎛⎫⎪(其中称为上对角元素)称为海森伯格矩阵.试证明:两个上对角元素全非零的海森伯格矩阵相j b 似的充分必要条件是它们有相同的特征多项式.【提示及点评】计算特征矩阵的行列式因子,再依此进行证明.H E -λ【证明】由于特征矩阵112231000*n n a b a b E H a b a λλλλλ---⎛⎫⎪--⎪⎪-=- ⎪- ⎪ ⎪-⎝⎭如果,由于有一个阶的子式0(1,2,,1)jb j n ≠=- H E -λ1-n 1221121100(1)0n n n b a b b b b b λ------=-≠- 所以的行列式因子.由此得,的行列式因子是H E -λ1()1n D λ-=H E -λ.121()()()1,()()||n n H D D D D f E H λλλλλλ-======- 于是,两个上对角元素全非零的海森伯格矩阵相似于与有相同的1H 2H ⇔1H E -λ2H E -λ行列式因子. ■⇔)()(21λλH H f f =6.求矩阵的Jordan 标准形和有理标准形【例19】求下列数字矩阵的若当(Jordan )标准形和有理标准形.(1); (2).308316205A ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭230002000042013A ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭【提示及点评】可以先求出矩阵的初等因子,然后由初等因子写出矩阵的若当标准形及有理标准形.【解】(1)由于2308308100316112401020520500(1)E A λλλλλλλλλλ----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=-+-→++→+ ⎪ ⎪ ⎪⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭所以,初等因子是,因此矩阵的若当标准形与有理标准形分别是21,(1)λλ++A J F,.100010011J -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭100001012F -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭(2)容易算得,矩阵的初等因子是,所以,若当标准形与有理标A 25,2,(2)λλλ---J 准形分别是F ,. ■52212J ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭520414F ⎛⎫⎪⎪= ⎪ ⎪-⎝⎭【知识扩展提示】从上面的例子可以看出,矩阵的若当标准形 = 有理标准形的充分必要A J F 条件是:矩阵的初等因子都是一次的.A 【例20】设. 求可逆矩阵,使得成为若当标准形.308316205A ⎛⎫⎪=- ⎪ ⎪--⎝⎭T 1T AT -【提示及点评】这是求相似变换矩阵的问题. 可先求出若当标准形,然后通过求解线性方程组来求可逆矩阵.T 【解】由例19知道,矩阵的若当标准形是A .100010011J -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭设有可逆矩阵,使得,则.令,其中是列T 1T AT J -=AT TJ =()123,,T ααα=123,,ααα向量组,那么1122333,,,A A A ααααααα=-=-+=-所以,是的属于特征值的特征向量,且满足.13,ααA 1λ=-23,αα23()A E αα+=下面先求向量,因,所以是齐次线性方程组2α223()()0A E A E αα+=+=2α2()0A E X +=的非零解,并且满足()0A E X +≠又因为,所以每一个非零向量都是的非零解. 取2()0A E +=2()0A E X +=,则()/21,1,1α=/32()(12,9,6)0.A E αα=+=-≠再从齐次线性方程组()0A E X +=求出一个属于特征值的特征向量,此时取矩阵1λ=-/1(2,0,1)α=-()1232112,,019116T ααα-==-⎛⎫ ⎪ ⎪ ⎪⎝⎭则可逆,且T ■1100010011.T AT J --==--⎛⎫ ⎪ ⎪ ⎪⎝⎭7.矩阵最小多项式的计算及在证明中的应用求阶方阵的最小多项式,通常采用如下三种方法:n A ()A m λ方法一试探法:首先求出的特征多项式,然后写出中包含的所A ()||f E A λλ=-()f λA 有互异特征值的因式,最后验证这些因子是否是的零化多项式,其中次数最低的首一多项式即是A .()A m λ方法二 求出的若当标准形,再利用A 1212()()()()tr r r A t m λλλλλλλ=--- 其中是的若当标准形中以为对角元的若当块的最高阶数.i r A J i λ方法三 当的阶行列式因子易于求得,利用求最小多项式.A 1-n 1()n D λ-1()()()A n f m D λλλ-=【例21】求下列矩阵的最小多项式.(1); (2);(3)2300020000420013A ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭2123021200210002A ⎛⎫⎪⎪=⎪ ⎪⎝⎭308316205A ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭【解】(1)因为,其包含的所有互异的特征值的因式有:3()||(2)(5)f E A λλλλ=-=--A ,直接计算有23(2)(5),(2)(5),(2)(5)λλλλλλ------,(2)(5)0A E A E --≠2(2)(5)0A E A E --=从而的最小多项式.A 2()(2)(5)A m λλλ=--(2) 显然可以求得的三阶行列式因子,而特征多项式,所E A λ-3()1D λ=4()(2)f λλ=-以最小多项式.443()()()(2)()A f m d D λλλλλ===-(3) 由例19知道,矩阵的不变因子是,所以最小A 2123()1,()1,()(1)d d d λλλλλ==+=+多项式是.■2()(1)A m λλ=+【例22】求指定的数字矩阵的最小多项式A (1) 4阶矩阵的元素均是1;A (2) ;123331313;3;31333J J J ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3) 已知3阶矩阵的特征值分别是1,-1,2,B 325A B B =-(4) 的充分必要条件是什么?()()A A f m λλ=(5) 若的特征值都是单根,那么对吗?A ()()A A f m λλ=【解】(1)由于,而计算知道,所以最小多项式是3()||(4)A f E A λλλλ=-=-(4)0A E A -=.()(4)A m λλλ=-【知识扩展提示】题目可扩充为如果阶矩阵的所有元素都是且不为零,求其最小多项式.n A a (2) 可以把矩阵看作若当标准形矩阵,其最小多项式由各个若当块的最小多项式的最小公倍式组成. 因此,3个矩阵的最小多项式分别是;;1()[3,3,3]3J m λλλλλ=---=-222()[(3),3](3)J m λλλλ=--=-333()[(3)](3)J m λλλ=-=-(3) 由于,而且矩阵的特征值分别是1,-1,2,由此,可以求得矩阵的特325A B B =-B A 征值分别是-4,-6,-12.故的特征多项式,由此得到的最小多A ()(4)(6)(12)A f λλλλ=+++A 项式是.()(4)(6)(12)A m λλλλ=+++(4)对于阶数字矩阵,的充分必要条件是的行列式因子n A ()()A A f m λλ=E A λ-. 这可从计算公式得到.1()1n D λ-=1()()()A n f m D λλλ-=(5) 若的特征值都是单根,那么矩阵与一对角矩阵相似,从而知道最小多项式没A A ()A m λ有重根,再根据特征多项式与含有相同的的特征值,因此有. ■()A f λ()A m λA ()()A A f m λλ=【例23】求矩阵的全体零化多项式集.2300020000420013A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭【提示及点评】求一个矩阵的零化多项式集,其实是求矩阵的最小多项式,再转化成一种零化。
幂等矩阵的相似标准型与分解形式

幂等矩阵的相似标准型与分解形式董庆华;王成伟【摘要】利用线性变换的方法研究了幂等矩阵的相似标准型, 并在此基础上推导出了幂等矩阵的秩恰好等于它的迹, 证明了任意 n阶矩阵都可以分解为一个可逆矩阵与一个幂等矩阵的乘积, 任意一个幂等矩阵都可以分解为两个对称矩阵的乘积.【期刊名称】《大庆师范学院学报》【年(卷),期】2010(030)006【总页数】3页(P43-45)【关键词】幂等矩阵;矩阵秩;相似标准型;分解形式【作者】董庆华;王成伟【作者单位】北京服装学院,基础教学部,北京,100029;北京服装学院,基础教学部,北京,100029【正文语种】中文【中图分类】O150 引言在计量经济学中对于大多数经济现象进行比较静态分析的结果, 都可以合理地归结为一个线性经济模型Ax=b, 其中的系数矩阵A往往是一个幂等矩阵。
为此,有必要对幂等矩阵展开理论方面的深入研究。
定义1:设有n阶方阵A满足A2=A, 则称方阵A为幂等矩阵。
显然,n阶零矩阵和单位矩阵都是幂等矩阵。
关于幂等矩阵,目前已有一些结论, 我们选择其中三个作为性质列举如下:1) 设有全矩阵I=(1)n×n, 则是一个幂等矩阵[1];2) 若方阵B是幂等矩阵, 则BT和E-B也是幂等矩阵[2];3)若n阶方阵A为幂等矩阵,则它的秩满足R(A)+R(E-A)=n[3]。
我们将首先以线性变换的方法来构造幂等矩阵的相似标准型,然后在此基础上研究幂等矩阵的秩和迹之间的关系,以及幂等矩阵在矩阵分解中的重要作用。
1 主要研究内容与结果1.1 幂等矩阵的相似标准型对角矩阵可以认为是形式最简单的一种矩阵, 对角矩阵的特征值就是其主对角线上的全部元素, 对角矩阵的秩就等于主对角线上非零元素的个数。
接下来我们以幂等矩阵的特征值为线索,探求幂等矩阵的具有对角形式的相似标准型。
定理1:若n阶方阵A为幂等矩阵, 并且A的秩R(A)=r,则存在可逆矩阵P使得P-1AP=(Er000)(1)证明:在n维线性空间V中任取一组基(ε1,ε2,…εn), 定义线性变换σ在基(ε1,ε2,…εn)下的矩阵为A, 即σ(ε1,ε2,…εn)=(ε1,ε2,…εn)A假设Ax=λ,其中x≠0,则由λx=Ax=A2x=λ2x,得λ2=λ,所以幂等矩阵特征值为1或0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、设
⎛ − 3 − 4 − 4⎞ ⎟ ⎜ A=⎜ 4 5 4 ⎟ ⎜ − 2 − 2 −1⎟ ⎠ ⎝
计算 A 的特征值和特征向量,并求可
−1 P 逆矩阵 ,使得 P AP 为对角矩阵。
解: A 的特征多项式
f (λ ) = λE − A = (λ + 1)(λ − 1)
2
进而得到特征值 λ1 = −1, λ2,3 = 1 。 解方程组 (λ1E − A)x = 0 可得 λ1 = −1 的 特征向量 x = ( 2, −2,1) 。
T 2
所以属于 λ2 = 2 的全部特征向量为:
Vλ2 = {kx2 Ax2 = λ2 x2 , k ∈ R}
我们记
⎛1 2⎞ ⎟ P = ( x1 , x2 ) = ⎜ ⎜ −1 − 3⎟ ⎝ ⎠
则有பைடு நூலகம்
AP = A( x1 , x2 ) = ( Ax1 , Ax2 ) = (λ1 x1 , λ2 x2 ) =
T 1
解方程组 (λ2 E − A)x = 0 可得 λ2 = 1 的特 征向量 x2 = (1,0, −1) 和 x3 = (1, −1,0) 。
T T
所以取
⎛ 2 ⎜ P = ( x1 , x 2 , x 3 ) = ⎜ − 2 ⎜ 1 ⎝ 1 ⎞ ⎟ − 1⎟ −1 0 ⎟ ⎠ 1 0
则有:
命题 1 相似的矩阵有相同的特征多项式。
证明:设矩阵 A, B 相似,即存在可逆矩 阵 P ,使得 A = P BP 。 因此,利用行列式性质可得:
λ E − A = P −1 (λ E ) P − P −1 BP
= P (λ E − B ) P
−1 −1
−1
= P
λE − B P
= λE − B
λE − A = 0 。 而 λE − A 是关于 λ
的多项式, 称为 A 的特征多项式,记作 f A ( λ ) 或 f ( λ ) ,其根称
为特征值或特征根。
若 λ 是方阵 A 的特征值,则
Vλ = {x Ax = λx}称为特征值 λ 的特征子空间。
由于每一个线性变换 σ 都对应于一个
矩阵 A ,把 f A (λ ) 也称为线性变换 σ 的特征 多项式。 特征多项式的根的重数称为该特征值 的代数重数。
从右边乘上面
各式,得到:
⎧ B0 A = A ⎪ n −1 n n −1 ⎪ B1 A − B0 A = a1 A n−2 n−2 n −1 ⎪ ⎪ B2 A − B1 A = a2 A ⎨ """"" ⎪ ⎪ Bn −1 A − Bn − 2 A2 = an −1 A ⎪ − Bn −1 A = an E ⎪ ⎩
f ( λ ) = λ n + a 1 λ n −1 + " + a n −1 λ + a n
, 由 于
B ( λ )( λ E − A ) = f ( λ ) E ,则有
( λ n −1 B 0 + λ n − 2 B1 + " + λ B n − 2 + B n −1 )( λ E − A )
= λ n E + a1 λ n −1 E + " + a n −1 λ E + a n E
⎛−1 0 ⎜ −1 P AP = ⎜ 0 1 ⎜ 0 0 ⎝
0⎞ ⎟ 0⎟ ⎟ 1⎠
⎛ 1 1⎞ ⎟ A=⎜ ⎜ 4、设 ⎝ 0 1⎟ ,问是否存在可逆矩阵 ⎠
P ,使得矩阵 A 相似于一个对角阵?
解: A 的特征多项式
f (λ ) = λE − A = (λ − 1)
2
所以 A 特征值是 λ1,2 = 1 。
⎛−1 − 2⎞ ⎟ A=⎜ ⎜ 1、设 ⎝ 3 4 ⎟ ⎠ ,计算
例题
A 的特征值和特
−1 P P AP 为 使得 征向量, 并求可逆矩阵 ,
对角矩阵。 解: 因为 A 的特征多项式为
f (λ ) =
λ +1
−3
2
λ −4
= ( λ − 1)( λ − 2 )
所以得到特征方程 ( λ − 1)( λ − 2) = 0 因此 A 的特征值为 λ1 = 1 , λ2 = 2 。
由此我们可以得到计算对称矩阵
A 的正交合同(相似)标准形的步骤 如下(或者说求一个正交矩阵 O ,使
得 O AO 为对角矩阵) : (1) 计算对称矩阵 A 的特征值及特征 向量;
−1
(2)利用 Gram-Schmidt 正交化方法 把属于同一特征值的特征向量正交 化; (3)把所有求出的特征向量单位化; (4)求出正交变换的矩阵 O ,使得
2、设
⎛ −1 − 2⎞ ⎟ A=⎜ ⎜3 4⎟ ⎝ ⎠
计算 A 和 A 。
10
n
解:由例 1 知道,对于矩阵 A ,如果 我们取矩阵
−1
⎛1 2⎞ P=⎜ ⎟ ⎜ − 1 − 3⎟ ⎠ ⎝
则有:
⎛1 0⎞ P AP = ⎜ ⎟ ⎜0 2⎟ ⎠ ⎝
因此 计算可知
⎛1 0⎞ ( P AP) = ⎜ ⎜0 2⎟ ⎟ ⎝ ⎠
几何重数是
r 。 取 Vλ 的 一 组 基
0
α1,α2 ,",αr , 并 扩 充 为 V 的 一 组 基
α1,α2 ,",αn ,则 σ 在基 α1,α2 ,",αn 下的矩
阵的形式是:
⎛ λ0 E ⎜ ⎜ 0 ⎝
r
A1 ⎞ ⎟ ⎟ A2 ⎠
此矩阵的特征多项式是:
f (λ ) = (λ − λ0 ) λE − A2
由此可知,λ0 的几何重数 ≤ λ0 的代数 重数。
注意: 由前面的命题和定理我们得到, 判定 一个 n 阶矩阵 A 能否对角化的方法及步 骤是: (1)先计算 A 的特征值和特征向量;
(2)如果 A 的特征值的几何重数等于 它的代数重数,则 A 可以对角化,即就 是一定存在一个可逆矩阵 P ,使得
即 A, B 的特征多项式相同。
问题 计算矩阵
⎛1 0⎞ I =⎜ ⎟ ⎝0 1⎠
⎛ 1 1⎞ A=⎜ ⎟ 0 1 ⎝ ⎠
的特征多项式。考虑一下命题 1,你有 什么结论?
显然,这两个矩阵的特征多项式一 样,从而其特征值也一样,都是两个 1。 按命题 1 我们可以得到下列结果: (1)若 n 阶矩阵 A 相似一个单位矩阵, 则这个矩阵的特征值是 n 个 1; (2)若 n 阶矩阵 A 相似一个对角矩阵, 则这个矩阵的特征值就是对角矩阵的对 角线上的元素。
n n
相加即得结果:
f ( A) = A n + a1 A n −1 + " + a n −1 A + a n E = 0
推论 1
线性变换 σ 的特征多项式是
f ( x) ,则 f (σ ) = 0 。
注意 这里 f (σ ) 是一个线性变换。
定理 2 设 n 阶方阵 A 的特征多项式是
O AO 成为对角形矩阵。
T
由于实二次型所对应的矩阵是 一个实对称矩阵,所以利用上述方法 可以求出一个正交相似变换,把此实 二次型化为标准形。其过程是: (1) 写出实二次型所对应的对称矩 阵 A;
(2)按上述方法计算正交矩阵 O; (3)利用正交矩阵 O,写出正交相似 变换: X =OY (4)写出实二次型化成的标准形(标 准形中的系数是 A的特征值) 。
( λE − A) x = 0 的解空间的维数。我们
把 λ 作为 f (λ ) = λ E − A = 0 的根的重数 称为 λ 的代数重数。
在例 3 中, − 1 的几何重数和代 数重数均为 1 ; 1 的几何重数和代数 重数均为 2。在例 4 中,1 的几何重 数是 1,而代数重数是 2。
定理 1 几何重数 ≤ 代数重数。 证明:设线性变换 σ 的特征值 λ0 的
10 10
⎛ −2045 −2046 ⎞ =⎜ ⎟。 3070 ⎠ ⎝ 3069
同理,可得对自然数 n ,有
⎛1 0⎞ −1 ⎛ − 2 + 3 − 2 + 2⎞ ⎜ ⎟ ⎟ A = P⎜ P = ⎜ 0 2⎟ ⎜ 3×2n − 3 3×2n − 2⎟ ⎝ ⎠ ⎝ ⎠
n+1 n+1 n n
问题 在一个二维线性空间 V 中,选定 一组基 α1 、 α 2 ,作一个线性变换 σ , 使得:
比较等式两端 λ 的各次幂的系数,可得:
B0 = E ⎧ ⎪ B1 − B0 A = a1E ⎪ B2 − B1A = a2E ⎪ ⎨ " " " " " ⎪ ⎪ B n −1 − B n − 2 A = a n −1 E ⎪ − B n −1 A = a n E ⎩
依次用
A n , A n −1 , " , A , E
解方程组 (λ1E − A)x = 0 ,可得 λ1 = 1的特 征向量 x1 = (1, −1)
T
所以属于 λ1 = 1的全部特征向量为:
Vλ1 = {kx1 Ax1 = λ1 x1 , k ∈ R}
解方程组 (λ2 E − A)x = 0 , 可得 λ2 = 2 的 特征向量 x = ( 2, −3) 。
相似标准形
北京科技大学应用学院数力系 卫宏儒 Weihr168@
本章主要内容
一、特征值和特征向量的计算 二、对称矩阵的标准形的计算 三、特征多项式和最小多项式
一、特征值和特征向量的计算
在第五章中, 我们给出了线性变换的特 征值和特征向量概念, 同时引入了方阵 A 的 特征值和特征向量。若 λ 是方阵 A 的特征 即方程组 ( λE − A) x = 0 有 值, 则必有 Ax = λx , 非零解。因此, λE − A 的行列式为零,也即
