点到直线的距离公式应用
点到直线之间的距离公式

点到直线之间的距离公式
点到直线之间的距离公式是一个重要的几何概念,它用于计算一个点到直线的
最短距离。
这个公式在数学、物理学和工程学中都有广泛的应用。
设直线的方程为Ax + By + C = 0,点的坐标为(x0, y0)。
要计算点到直线的距离,我们可以利用点到直线的垂直距离公式。
点到直线的距离公式可以通过以下步骤来推导:
1. 首先,我们找到直线上的一个任意点P(x1, y1)。
这可以通过令x = 0或y = 0
来使方程简化。
2. 然后,我们计算点P与点O(x0, y0)之间的欧几里德距离d = √((x1 - x0)² + (y1 - y0)²)。
3. 接下来,我们求解点P到直线的垂直距离。
我们通过将点P代入直线的方程Ax + By + C = 0,求解出P点在直线上的投影点Q(x2, y2)的坐标。
4. 最后,我们计算点O和点Q之间的距离d' = √((x2 - x0)² + (y2 - y0)²)。
根据直角三角形的性质,我们知道d就是点到直线的最短距离。
总结一下,点到直线之间的距离可以通过以下公式来计算:
d = √((x1 - x0)² + (y1 - y0)²),其中(x1, y1)是直线上的任意一点,(x0, y0)是点的
坐标。
这个公式在解决实际问题时非常有用,例如在测量中确定点到线的最短距离,
或者在几何建模中计算点到平面的距离。
它为我们提供了一个可靠和准确的计算方法。
点到直线的距离公式 高等数学

点到直线的距离公式高等数学
高等数学中,点到直线的距离公式是十分重要的,它可以帮助我们精确地计算
出一个点到一条直线的距离。
在数学中,一个点P(x,y)到一条直线ax+by+c=0的
距离公式为:
距离=|ax_0+by_0+c|/√(a^2+b^2)
其中x_0, y_0为点P(x_0, y_0)的坐标。
作为一项重要的概念,点到直线的距离公式有着广泛的应用,它常被用于积分,微分,函数等复杂科学问题的求解中。
比如当我们要求出某个几何边界上的点的坐标时,就可以用点到直线的距离公式来解决这些复杂的函数极值问题。
另外,它也可以应用于计算机图形学,机器人技术和模拟实验中。
归纳而论,点到直线的距离公式在高等数学中起着极其重要的作用,不仅可以
用于求解复杂的函数极值问题,而且还可以用于计算机图形学,机器人技术和模拟实验等多个领域。
但是要注意,点到直线的距离公式求解需要先确认直线的一般式方程,因此,理解一般式的概念对于熟练的使用点到直线的距离公式至关重要。
点到直线的距离公式解析几何

点到直线的距离公式解析几何在解析几何中,点到直线的距离可以使用以下公式进行计算:假设直线方程为Ax + By + C = 0,点的坐标为(x0, y0)。
1. 首先,计算直线上任意一点P(x1, y1)到点的距离d,公式为:d = |Ax1 + By1 + C| / √(A^2 + B^2)2. 然后,将直线上任意一点P(x1, y1)替换为点(x0, y0):d = |Ax0 + By0 + C| / √(A^2 + B^2)即为点到直线的距离。
该公式的推导过程如下:点P到直线的距离可以看作点P到直线的垂足H的距离。
将垂足H的坐标设为(xh, yh)。
由于直线上的任意一点P(x1, y1)满足Ax1 + By1 + C = 0,所以垂足H的坐标应满足Axh + Byh + C = 0。
由于垂足H在直线上,所以垂足H到点P的向量与直线的方向向量垂直,即向量HP与直线的法向量垂直。
向量HP为(Px - xh, Py - yh),直线的法向量为(A, B)。
根据向量的垂直关系,有:(A, B) · (Px - xh, Py - yh) = 0化简得:A(Px - xh) + B(Py - yh) = 0展开得:APx - Axh + BPy - Byh = 0移项得:APx + BPy = Axh + Byh对比直线方程Ax + By + C = 0,可知:Axh + Byh = -C代入上式,得:APx + BPy = -C由于点P的坐标为(x0, y0),所以有:APx0 + BPy0 = -C展开得:Ax0 + By0 + C = 0移项得:Ax0 + By0 + C = 0取绝对值,得:|Ax0 + By0 + C| = 0所以,点到直线的距离为:d = |Ax0 + By0 + C| / √(A^2 + B^2)即为所求公式。
点到直线的距离公式应用举例

点到直线的距离公式应用举例1. 引言在几何学中,我们经常需要计算点到直线的距离。
这个问题在实际生活中有许多应用,例如测量物体的位置、判断点与直线的关系等。
本文将介绍点到直线的距离公式,并通过举例说明其应用。
2. 点到直线的距离公式假设有一个点P(x₀, y₀)和一条直线L,直线L可以用一般式方程 Ax + By + C = 0 表示。
那么,点P到直线L的距离d可以通过以下公式计算:d = |Ax₀ + By₀ + C| / √(A² + B²)其中,|x| 表示x的绝对值。
3. 举例1:点到直线的距离计算我们通过一个简单的例子来演示如何利用点到直线的距离公式计算点P到直线L的距离。
假设有一点P(2, 3)和一条直线L,直线L的一般式方程为3x - 4y - 5 = 0。
现在我们要计算点P到直线L的距离。
根据距离公式,我们可以得到:A = 3,B = -4,C = -5, x₀ = 2, y₀ = 3d = |3*2 - 4*3 - 5| / √(3² + (-4)²)= |6 - 12 - 5| / √(9 + 16)= |-11| / √25= 11 / 5≈ 2.2因此,点P(2, 3)到直线L的距离约为2.2。
4. 举例2:判断点与直线的位置关系除了计算点到直线的距离,我们还可以利用距离公式判断点与直线的位置关系。
假设有一点P(4, 6)和一条直线L,直线L的一般式方程为2x + y - 8 = 0。
现在我们要判断点P与直线L的位置关系。
首先,我们计算点P到直线L的距离:A = 2,B = 1,C = -8, x₀ = 4, y₀ = 6d = |2*4 + 1*6 - 8| / √(2² + 1²)= |8 + 6 - 8| / √(4 + 1)= 6 / √5≈ 2.68由于点P到直线L的距离为正数,所以点P不在直线L上。
接下来,我们可以观察点P与直线L的位置关系:•如果点P在直线L的上方,点P到直线L的距离将为正数;•如果点P在直线L的下方,点P到直线L的距离将为负数。
点到直线的距离公式应用

点与直线问题(1)点P(x0,y)到直线Ax+By+C=0的距离(运用本公式要把直线方程变为一般式)(2)两条平行线之间的距离(运用此公式时要注意把两平行线方程 x、y前面的系数变为相同的)(3)点 P(x,y)关于Q(a,b)的对称点为P'(2a-x,2b-y)(4)直线关于点对称:在已知直线上任取两点A、B,再分别求出A、B关于P点的对称点A′、B′,然后由两点式可得所求直线方程.(5)点关于直线的对称点,要抓住“垂直”和“平分”设 P(x0,y),l:Ax+By+C=0(A2+B2≠0),若P关于l的对称点的坐标Q为(x,y),则l是PQ的垂直平分线,即①PQ⊥l;②PQ的中点在l上,解方程组可得 Q点的坐标例1求点P = (–1,2 )到直线3x = 2的距离解:例2已知点A(1,3),B(3,1),C(–1,0),求三角形ABC的面积.解:设AB边上的高为h,则AB边上的高h就是点C到AB的距离.AB边所在直线方程为即x + y– 4 = 0.点C到x + y– 4 = 0的距离为h ,因此,例3 求两平行线l1:2x + 3y– 8 = 0l2:2x + 3y– 10 =0的距离.解法一:在直线l1上取一点P(4,0),因为l1∥l2,所以P到l2的距离等于l1与l2的距离,于是解法二:直接由公式例 4、求直线3x-y-4=0关于点P(2,-1)对称的直线l的方程解析:设直线 l上任一点为(x,y),关于P(2,1)对称点(4-x,-2-y)在直线3x-y-4=0上.∴ 3(4-x)-(-2-y)-4=0∴ 3x-y-10=0∴所求直线 l的方程3x-y-10=0例5. 等腰直角三角形ABC的直角顶点C和顶点B都在直线2x + 3y– 6 = 0上,顶点A的坐标是(1,–2).求边AB、AC所在直线方程.(AC的直线方程为:3x– 2y– 7 = 0 AB的直线方程为:x– 5y– 11 = 0或5x + y– 3 = 0.)1. 分别求点()2,3P -到下列直线l 的距离:(1)2390x y +-=; (2)7x =; (3)3y =; 2. 若点(),3P a 到直线4310x y -+=的距离等于4,求a 的值;3. 若直线1:220l ax y ++=与直线2:320l x y --=平行,求两直线的距离;4. 已知ABC ∆中,()()3,2,1,5,A B C -点在直线330x y -+=上,若ABC ∆的面积为10,求点C 的坐标;5. 若直线l 通过直线75240x y +-=和直线0x y -=的交点,并且点()5,1到直线l ,求直线l 的方程;6. 已知一个三角形的顶点为()()()2,3,4,1,4,1A B C --,直线//l AB ,且l 将ABC ∆的面积分成相等的两部分,求l 的方程;7. 求点()4,0关于直线54210x y ++=的对称点的坐标;8.如图,一次函数与正比例函数的图象交于点A ,且与轴交于点B.(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥轴于点C ,过点B 作直线l∥轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形若存在,求t 的值;若不存在,请说明理由。
点到直线的距离公式应用

点到直线的距离公式应用点到直线的距离公式是数学中常用的一个公式,它可以用来计算点到直线的最短距离。
这个公式对于几何学和物理学的许多问题都有着重要的应用。
在本文中,我们将探讨这个公式的起源、推导过程以及如何应用它来解决一些实际问题。
起源与推导我们从直线的一般方程开始推导。
一般方程的形式为Ax+By+C=0,其中A、B、C是直线方程的系数。
我们假设有一个点P(x₁,y₁)并且有一条直线L,我们想要计算点P到直线L的最短距离。
我们如何找到这条直线上的另一个点Q(x₂,y₂)?我们可以通过直线上的两个点构成的线段来找到这个点。
让我们设P₁(x₁',y₁')为由x₁轴和y₁轴交点组成的点。
由于L上的任意一点必然与P₁共线,我们可以利用斜率公式推导出Q的坐标。
斜率的定义是两点之间的纵向变化量与横向变化量的比值。
斜率m可以通过以下公式来计算:m=(y₂-y₁')/(x₂-x₁')我们可以将该公式变形得到x₂的表达式:x₂=(m*x₁'-y₁+y₁'+m*x₁)/m根据上述公式,我们可以得到Q点的坐标(x₂,y₂)。
然后,我们可以使用两点之间的距离公式来计算点P到点Q的距离。
两点之间的距离可以通过以下公式计算:d=√((x₂-x₁)²+(y₂-y₁)²)应用1.在三角形中,我们可以使用点到直线的距离公式来计算垂直边的高度。
设三角形的底边为L,且L方程为Ax+By+C=0。
如果我们有一个顶点为P(x₁,y₁),我们可以使用点到直线的距离公式来计算垂直边的高度,即点P到直线L的最短距离。
2.在物理学中,点到直线的距离公式可以被应用于计算运动物体的轨迹。
假设一个运动物体的位置可以由直线方程描述,我们可以使用点到直线的距离公式来计算物体离轨迹最近点的距离。
3.在计算机图形学中,点到直线的距离公式经常被用来解决一些问题,比如计算点到直线的最近距离。
这可以用于图像处理中的边缘检测等应用。
点到直线的距离公式及其应用

点到直线的距离公式及其应用山东 孙天军一、知识要点1.点00()P x y ,到直线x a =的距离0d x a =-;点00()P x y ,到直线y b =的距离0d y b =-;2.点00()P x y ,到直线l :0Ax By C ++=的距离d =; 3.点00()P x y ,到直线l ':y kx b =+的距离d = 4.利用点到直线的距离公式,可求得两平行线11:0l Ax By C ++=与2212:0()l Ax By C C C ++=≠间的距离d =.推导方法如下:由于A B ,不同时为零,不妨设0A ≠,令0y =,得直线1l 与x 轴的交点10C P A ⎛⎫- ⎪⎝⎭,,点P 到直线2l的距离d =即为两平行线间的距离;当0A =时,公式d =也成立.二、解题指导1.求距离例1 已知(23)A --,,(21)B -,,(02)C ,,求ABC △的面积.分析:欲求ABC △的面积,可先求出直线AB 的方程,再求点C 到直线AB 的距离. 解:由两点式,可求出直线AB 的方程为:240x y --=,点C 到直线AB 的距离等于ABC △中AB 边上的高h,h ==AB = ∴182ABC S AB h ==△. 2.求点的坐标例2 求直线:220l x y --=上到直线:230l x y '+-=的距离为的点的坐标.解:设()P a b ,为直线l 上到l '220a b --=,22b a =-,所以点P 的坐标为(22)a a -,.=∴125a =或25. ∴所求点的坐标为121455⎛⎫⎪⎝⎭,,或为2655⎛⎫- ⎪⎝⎭,. 3.求方程利用点到直线的距离可确定直线方程中的参数,从而求得直线方程;利用点到直线的距离列方程可求动点的轨迹方程.例3 点()P x y ,到定点M的距离与到直线3x =2,求点()P x y ,的轨迹方程.2=. 化简,得所求的轨迹方程为2244x y +=.4.求最值(创新应用型)例4 已知51260x y +=的最小值.解:∵的最小值是点(40)P ,到直线51260x y +=的距离4013d ==, ∴ 所求最小值为4013. 三、感悟与体验点到直线的距离公式是解析几何常用的基本公式之一.解析几何中的轨迹问题、最值问题、曲线与直线的位置关系等都与点到直线的距离有关,应用点到直线的距离公式能够解决许多重要问题.。
点到直线的距离公式。

点到直线的距离公式。
点到直线的距离公式是一种常见的几何计算方法,它是指将点P(x,y)投影
到直线AX + By + C = 0上,计算点P到直线距离的实际方法。
点到直线距离公式
如下:
d=|Ax+By+C|√(A^2+B^2)
其中A,B,C是直线AX + BY + C = 0上的参数,x,y是点P(x,y)的坐标。
这个公式可以把任何一个平面中的点到直线的距离都可以正确计算出来。
应用点到直线距离公式到实际中,不仅可以用来计算出点到直线的距离,还可以应用到各种计算机图形处理等工程应用上,帮助我们计算出形状中位置、大小、形状等信息。
在可视化设计图形艺术研究中,这一公式也可以帮助我们分析图形的比例、坐标,以及绘制出美观精致的图形。
从上面这个公式我们可以得出的结论就是,只要把点的坐标和直线的参数带入这个点到直线距离公式中,就可以准确的计算出点到直线的距离,节约计算的麻烦,提高精度和可靠性。
点到直线的距离公式应用

点与直线问题(1)点P (x 0,y 0)到直线Ax +By +C=0的距离(运用本公式要把直线方程变为一般式)(2)两条平行线之间的距离(运用此公式时要注意把两平行线方程 x 、y 前面的系数变为相同的)(3)点 P (x ,y )关于Q (a ,b )的对称点为P'(2a -x ,2b -y )(4)直线关于点对称:在已知直线上任取两点A 、B,再分别求出A 、B 关于P 点的对称点A′、B′,然后由两点式可得所求直线方程.(5)点关于直线的对称点,要抓住“垂直”和“平分”设 P (x 0,y 0),l :Ax +By +C=0(A 2+B 2≠0),若P 关于l 的对称点的坐标Q 为(x ,y ),则l 是PQ 的垂直平分线,即①PQ ⊥l ;②PQ 的中点在l 上,解方程组可得 Q 点的坐标例1求点P = (–1,2 )到直线3x = 2的距离 解:22|3(1)2|5330d ⨯--==+例2 已知点A (1,3),B (3,1),C (–1,0),求三角形ABC 的面积.解:设AB 边上的高为h ,则221||2||(31)(13)22ABC S AB h AB =⋅=-+-=AB 边上的高h 就是点C 到AB 的距离. AB 边所在直线方程为311331y x --=--即x + y – 4 = 0.点C 到x + y – 4 = 0的距离为h2|104|112h -+-==+,因此,122522S ABC =⨯⨯= 例3 求两平行线l 1:2x + 3y – 8 = 0l 2:2x + 3y – 10 =0的距离. 解法一:在直线l 1上取一点P (4,0),因为l 1∥l 2,所以P 到l 2的距离等于l 1与l 2的距离,于是222131323d ==+ 解法二: 直接由公式22|8(10)|2131323d ---==+例 4、求直线3x -y -4=0关于点P (2,-1)对称的直线l 的方程解析: 设直线 l 上任一点为(x ,y ),关于P (2,1)对称点(4-x ,-2-y )在直线3x -y -4=0上.∴ 3(4-x)-(-2-y)-4=0∴ 3x -y -10=0 ∴ 所求直线 l 的方程3x -y -10=0例5. 等腰直角三角形ABC 的直角顶点C 和顶点B 都在直线2x + 3y – 6 = 0上,顶点A 的坐标是(1,–2).求边AB 、AC 所在直线方程.(AC 的直线方程为:3x – 2y – 7 = 0 AB 的直线方程为:x – 5y – 11 = 0或5x + y – 3 = 0.)1. 分别求点()2,3P -到下列直线l 的距离:(1)2390x y +-=; (2)7x =; (3)3y =; 2. 若点(),3P a 到直线4310x y -+=的距离等于4,求a 的值;3. 若直线1:220l ax y ++=与直线2:320l x y --=平行,求两直线的距离;4. 已知ABC ∆中,()()3,2,1,5,A B C -点在直线330x y -+=上,若ABC ∆的面积为10,求点C 的坐标;5. 若直线l 通过直线75240x y +-=和直线0x y -=的交点,并且点()5,1到直线l,求直线l 的方程;6. 已知一个三角形的顶点为()()()2,3,4,1,4,1A B C --,直线//l AB ,且l 将ABC ∆的面积分成相等的两部分,求l 的方程;7. 求点()4,0关于直线54210x y ++=的对称点的坐标;8.如图,一次函数7y x =-+与正比例函数43y x =的图象交于点A ,且与x 轴交于点B. (1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒. ①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由。
点到直线的距离公式及其应用

点到直线的距离公式及其应用设直线L的方程为ax + by + c = 0,点P(x0, y0)为平面上的一个点,点P到直线L的距离公式可以表示为:d = ,ax0 + by0 + c,/ √(a^2 + b^2)其中,d为点P到直线L的距离,ax0 + by0 + c,表示点P到直线L 的有向距离(即沿着垂直于直线L的方向),√(a^2 + b^2)为直线L的斜率的模。
应用一:点到直线的距离应用二:点到直线的位置关系判断1. 如果ax0 + by0 + c > 0,则点P在直线L的上方;2. 如果ax0 + by0 + c < 0,则点P在直线L的下方;3. 如果ax0 + by0 + c = 0,则点P在直线L上。
应用三:点到直线的垂线点到直线的距离公式还可以用于构造点到直线的垂线。
具体而言,给定一个点P(x0, y0)和一个直线L的方程ax + by + c = 0,我们可以通过找到直线L的垂直于它且通过点P的直线L1的斜率k1来构造。
斜率k1可以通过点到直线的距离公式计算得到:k1=-a/b这样,我们就可以得到直线L1的方程为y-y0=k1(x-x0)。
应用四:点到直线的投影点到直线的距离公式还可以用于计算点在直线上的投影点。
给定一个点P(x0, y0)和一个直线L的方程ax + by + c = 0,我们可以通过找到直线L上距离点P最近的点Q(x1, y1)来计算。
这个点Q就是点P在直线L上的投影点。
具体而言,我们可以通过点到直线的距离公式求解出点Q 的坐标:x1 = x0 - (ax0 + by0 + c)a / (a^2 + b^2)y1 = y0 - (ax0+ by0 + c)b / (a^2 + b^2)。
一个点到直线的距离公式

一个点到直线的距离公式点到直线的距离是一种几何问题,非常有用且广泛应用的公式。
在解决这类问题时,我们常常使用以下点到直线的距离公式:设直线的方程为Ax+By+C=0,点的坐标为(x0,y0),点到直线的距离为d。
这个距离公式的由来可以通过几何推导得到。
首先我们从点(x0,y0)引一条垂直于直线的线段,设交点为P。
因为P在直线上,所以P的坐标一定满足直线的方程,即有:A*x+B*y+C=0由于P点在直线上,所以直线上任意一点(x1,y1)也应该满足这个方程。
我们可以根据两个点的坐标(x0,y0)和(x1,y1)代入直线的方程,得到:A*x0+B*y0+C=0(1)A*x1+B*y1+C=0(2)我们可以将(1)式减去(2)式,得到:A*(x0-x1)+B*(y0-y1)=0这个式子表示直线上的两个点的向量之差与(0,0)向量垂直,因此直线的法向量为(n,m)=(A,B)。
我们可以将法向量与P点到直线上其中一点的向量相乘,即(x0-x1,y0-y1)和(A,B)的点积为0,可以得到:A*(x0-x1)+B*(y0-y1)=0我们可以将这个方程稍微变换一下:A*x0+B*y0-A*x1-B*y1=0这个方程表示直线上的两个点P(x0,y0)和(x1,y1)到直线的距离为0。
我们可以将这个方程稍微改写为:A*x0+B*y0+C=0(3)这个方程依然表示点P(x0,y0)到直线的距离为0,因此点P一定在直线上。
这意味着我们可以将点(x0,y0)代入方程(3)来计算点到直线的距离。
为了得到点到直线的距离,我们使用了线代中的点积的性质,即两个向量之间的点积为零,表示这两个向量垂直。
在这个推导中,我们使用了点的坐标和直线的法向量,将点的坐标表示为(x0,y0),直线的法向量表示为(n,m)=(A,B)。
将这两个向量点乘结果为零,可以得到点到直线的距离。
所以,我们可以通过公式d=,A*x0+B*y0+C,/√(A²+B²)来计算点到直线的距离。
点到直线的距离公式 两点式

点到直线的距离公式两点式
点到直线的距离公式可以使用两点式来表示。
假设直线的方程
为Ax + By + C = 0,点P(x₁, y₁)为平面上的任意一点,那么点
P到直线的距离可以使用以下公式来计算:
d = |Ax₁ + By₁ + C| / √(A² + B²)。
其中,d表示点P到直线的距离,|Ax₁ + By₁ + C|表示点P
带入直线方程后的结果取绝对值,√(A² + B²)表示A和B的平方
和的平方根。
这个公式的推导可以通过向量的方法来进行,也可以通过点到
直线的垂直距离的几何性质来进行推导。
无论哪种方法,最终得到
的公式都是上述形式的点到直线的距离公式。
使用这个公式,我们可以轻松计算任意一点到给定直线的距离,这在几何学和工程学中都有着重要的应用。
需要注意的是,这个公
式要求直线不是平行于坐标轴,因为在这种情况下A或B会为0,
导致分母为0,公式无法使用。
如果直线是平行于坐标轴的情况,
可以使用其他方法来计算点到直线的距离。
点到直线的距离公式

点到直线的距离公式直线是平面几何中的基本概念,我们可以通过两点来确定一条直线。
而点到直线的距离是指从给定点到直线上最近的点之间的距离。
一、向量法设直线的方程为Ax+By+C=0,点P(x0,y0)离直线的距离为d,直线上任意一点Q(x1,y1)离点P的向量为v。
过点P的垂线与直线相交于点Q,向量v与直线垂线的向量w垂直,所以v·w=0。
(其中·表示向量的点乘)点P在直线上,所以Ax0+By0+C=0,所以垂线的方程为Bx-Ay+Bx0-Ay0=0,即Bx-Ay+D=0(其中D=Bx0-Ay0)。
根据向量的表达式,可以得到点Q相对于P的向量v=(x1-x0)i+(y1-y0)j。
(其中i和j分别为x方向和y方向的单位向量)直线垂线的向量w=Ai+Bj。
所以v·w=(x1-x0)A+(y1-y0)B=0。
解得A(x1-x0)+B(y1-y0)=0,即Ax1+By1+C=0,所以点Q也在直线上。
因此,直线上任意一点Q与向量v相乘的结果为0,即v·w=0。
展开等式可得(A(x1-x0)+B(y1-y0))-AD-BD=0,所以(A(x0-x1)+B(y0-y1))=AD+BD。
根据向量的定义可得,A(x0-x1)+B(y0-y0),=,D(A^2+B^2)^(1/2),即,Ax0+By0+C,/√(A^2+B^2)=d。
所以点到直线的距离公式为:d=,Ax0+By0+C,/√(A^2+B^2)。
二、坐标法设直线的方程为y = mx + n,点P的坐标为(x0, y0)。
点P到直线的距离可以通过点到直线的垂线和点到垂足的距离来表示。
直线的斜率为m,所以垂线的斜率为-1/m。
过点P的直线的方程为y - y0 = (-1/m)(x - x0),即mx + y0 = x0 + y。
垂线和直线相交的点的坐标为(x1,y1),代入垂线的方程可以得到y1=(-1/m)x1+(x0/m+y0)。
点到直线的距离公式的推导过程及其应用
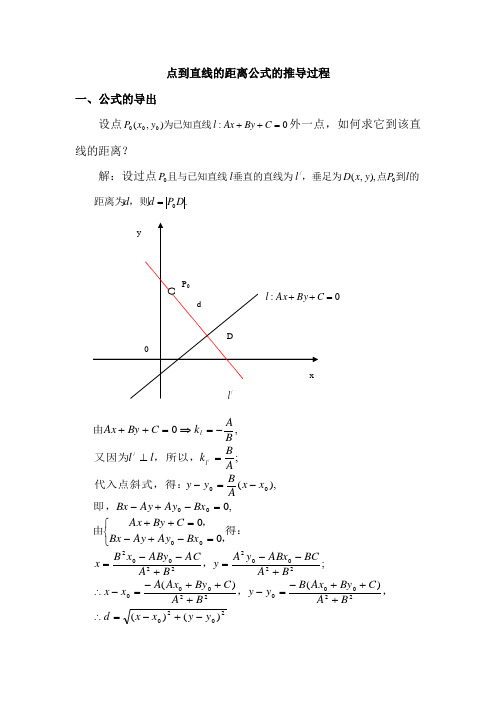
点到直线的距离公式的推导过程一、公式的导出设点0:),(000=++C By Ax l y x P 为已知直线外一点,如何求它到该直线的距离?解:设过点的到点,垂足为垂直的直线为且与已知直线l P y x D l l P 0/0),,(.0D P d d =,则距离为202022000220002200222002000000/)()()()(;00,0),(;,0/y y x x d B A C By Ax B y y B A C By Ax A x x B A BC ABx y A y B A AC ABy x B x Bx Ay Ay Bx C By Ax Bx Ay Ay Bx x x ABy y A Bk l l B A k C By Ax l l -+-=∴+++-=-+++-=-∴+--=+--=⎩⎨⎧=-+-=++=-+--=-=⊥-=⇒=++,,,得:,,由即,代入点斜式,得:,所以,又因为由.)()()(2200222002220022200BA C By AxB AC By Ax B A C By Ax B B A C By Ax A +++=+++=⎥⎦⎤⎢⎣⎡+++-+⎥⎦⎤⎢⎣⎡+++-=即,直线外一已知点0P 到已知直线l 的距离公式为:.2200BA CBy Ax d +++=二、公式的应用(一)求点到直线的距离:例1、)到下列直线的距离:,(求点21-P⑴ 0543=+-y x ; ⑵ 53=x ; ⑶.1-=y分析:应用点到直线的距离公式时应该把直线方程化为一般式.解 ⑴式,得根据点到直线的距离公: .56)4(3524)1(322=-++⨯--⨯=d ⑵,得:将直线方程化为一般式.053=-x 式,得根据点到直线的距离公:.3803520)1(322=+-⨯+-⨯=d ⑶,得:将直线方程化为一般式.01=+y 式,得根据点到直线的距离公:.310121)1(022=++⨯+-⨯=d评析:当已知直线与x(或y)轴平行时,用几何意义来解会更简洁.(二)求两平行直线间的距离:例2、之间的距离.和求两平行直线04320632=--=+-y x y x 分析:因为两平行直线间的距离处处相等,所以,我们可以在其中的某条直线上任取一点P (一般是取其与坐标轴的交点),则两平行直线间的距离即为点P 到另外那条直线的距离.解:在直线),则:,(轴的交点上取其与020432P x y x =--.131310)3(26032222=-++⨯-⨯=d(三)证明两平行直线的距离为:与AA2001=++=++C By x C By x .2221B A C C d +-=证明:如图所示,设(),,,122222D l P l y x P 作垂线,垂足为向过点∈.2d D P 距离的长即为两平行线间的则,垂线段,即d d ∴∴=三、课堂练习1、求点(2,1)到直线0543=+-y x 的距离.2、求点(1,-2)到直线的距离.3=-y x3、求直线0742=++y x 和直线之间的距离.62=+y x附答案:1、57=d ; 2、0=d ;3、.10519=d四、课后练习1、求下列点到直线的距离:⑴ 01243)23(=++-y x A ,,; ⑵ 033)11(=-+y x B ,,; ⑶ .,0)2,1(=--y x C 2、求下列各平行线间距离:⑴016320632=++=-+y x y x 与; ⑵.与02230423=+-=--y x y x3、在y 轴上,求与直线的点.的距离等于1031x y =附答案:1、⑴511; ⑵ 21; ⑶ .223 2、⑴131322; ⑵ 13136. 3、 .,和,⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-310100310100 五、课后作业练习册距离公式》.之练习七《点到直线的21P(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
点到直线的距离公式例子

点到直线的距离公式例子
1. 你看啊,比如说在一个平面上,有一个点(3,4),然后有一条直线
y=2x+1,那它们的距离咋算呢?就可以用点到直线的距离公式呀!这不就
派上用场啦!
2. 想象一下,你在地图上有个位置,然后有一条公路,你要算你到公路的最短距离,嘿,点到直线的距离公式就能帮上忙啦!比如点是(5,6),直线是
x-y=0,是不是很有意思呀!
3. 嘿,你想想,课堂上老师出了个题,已知点(-2,3)和直线 3x+4y-5=0,
让你们算距离,这时点到直线的距离公式不就是大功臣嘛!
4. 假如你在玩一个游戏,游戏里有个点和一条线,你得知道它们的距离,哇,这时候点到直线的距离公式不就闪亮登场啦!像点(1,-2)和直线 2x-y+3=0 这样的。
5. 哎呀呀,要是你在街上看到一个公交站和一条公交线路,想知道你离公交站有多远,这不就跟点到直线的距离差不多嘛!比如点是(0,0),直线是
4x+3y-12=0 呢!
6. 你说神奇不神奇,点(4,-5)和直线 5x+12y+3=0 的距离,就能用点到直
线的距离公式轻松搞定呀,是不是很厉害呢?
7. 举个例子呗,你有个好朋友在某个位置,而你和他之间隔着一条虚拟的线,你要知道你俩的距离,这不正需要点到直线的距离公式嘛!就像点(6,-1)和
直线 x+2y-3=0 这样。
8. 哇哦,如果在一个数学谜题里,出现了点(2,-3)和直线 3x-2y+4=0,那解决问题的关键肯定就是点到直线的距离公式呀!
9. 你想想看,在好多地方都能用到点到直线的距离公式呢,它可真是个实用的好东西呀!所以说,它真的超级重要呀!。
点到直线y=kx+b的距离公式

点到直线y=kx+b的距离公式点到直线y=kx+b的距离公式可以通过以下步骤推导出来:1. 假设点P(x1, y1)为直线上一点,直线的斜率为k,截距为b。
2. 首先,我们可以计算出直线的方程:y = kx + b。
3. 接下来,我们可以计算出点P到直线的距离d。
4. 由于点P(x1, y1)到直线的距离d可以表示为点P到直线的垂直线段的长度,我们需要找到直线上一点A(x, y)使得点A到点P的向量与直线的斜率垂直。
5. 假设点A(x, y)为直线上一点,则直线上的任意向量都可以表示为向量AP = (x1 - x, y1 - y)。
6. 由于直线的斜率为k,所以直线的法向量为直线的斜率的负倒数向量,即向量n = (1, -k)。
7. 根据向量的垂直关系,向量AP与向量n的内积为0,即(x1 - x, y1 - y) · (1, -k) = 0。
8. 展开上述等式,我们可以得到以下方程:(x1 - x) + (-k)(y1 - y) = 0。
9. 将直线的方程代入上述方程,我们可以得到以下方程:(x1 - x) + (-k)(y1 - kx - b) = 0。
10. 继续展开上述方程,我们可以得到以下方程:x1 - x - ky1 + k^2x + kb = 0。
11. 整理上述方程,我们可以得到以下方程:(1 + k^2)x - x1 - ky1 + kb = 0。
12. 将上述方程表示为x的形式,我们可以得到以下方程:x = (ky1 - kb + x1) / (1 + k^2)。
13. 将直线的方程代入上述方程,我们可以得到以下方程:y = k(ky1 - kb + x1) / (1 + k^2) + b。
14. 将点P(x1, y1)代入上述方程,我们可以得到点A的横坐标x。
15. 将点A的横坐标x代入直线的方程,我们可以得到点A的纵坐标y。
16. 最后,点P到直线的距离d可以表示为点P到点A的欧几里得距离,即d = sqrt((x1 - x)^2 + (y1 - y)^2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点与直线问题
(1)点P (x 0,y 0)到直线Ax +By +C=0
的距离
(运用本公式要把直线方程变为一般
式)
(2)两条平行线
之
间的距离
(运用此公式时要注意把两平行线方程 x 、y 前面的系数变为相同的)
(3)点 P (x ,y )关于Q (a ,b )的对称点为P'(2a -x ,2b -y )
(4)直线关于点对称:在已知直线上任取两点A 、B,再分别求出A 、B 关于P 点的对称点A ′、B ′,然后由两点式可得所求直线方程. (5)点关于直线的对称点,要抓住“垂直”和“平分”
设 P (x 0,y 0),l :Ax +By +C=0(A 2+B 2≠0),若P 关于l 的对称点的坐标Q 为(x ,y ),则l 是PQ 的垂直平分线,即①PQ ⊥l ;②PQ 的中点在l 上,
解方程组可得 Q 点的坐标
例1
求点P = (–1,2 )到直线3x = 2的距离 解:2
2
|3(1)2|53
30
d ⨯--=
=
+
例2 已知点A (1,3),B (3,1),C (–1,
0),求三角形ABC 的面积. 解:设AB 边上的高为h ,则
221
||2
||(31)(13)22
ABC S AB h AB =
⋅=-+-=V
AB 边上的高h 就是点C 到AB 的距离.
AB 边所在直线方程为
31
1331
y x --=
-- 即x + y – 4 = 0.
点C 到x + y – 4 = 0的距离为h
2|104|5
112
h -+-=
=
+, 因此,15
225
22S ABC =⨯⨯=V 例3 求两平行线
l 1:2x + 3y – 8 = 0
l 2:2x + 3y – 10 =0的距离.
解法一:在直线l 1上取一点P (4,0),因为l 1∥l 2,所以P 到l 2的距离等于l 1与l 2的距离,于是
22
|243010|
2
1313
23d ⨯+⨯-=
=+ 解法二: 直接由公式22
|8(10)|21313
23d ---=
=
+
例 4、求直线3x -y -4=0关于点P (2,-1)对称的直线l 的方程
解析: 设直线 l 上任一点为(x ,y ),关于P (2,1)对称点(4-x ,-2-y )在直线3x -y -4=0上.
∴ 3(4-x)-(-2-y)-4=0∴ 3x -y -10=0 ∴ 所求直线 l 的方程3x -y -10=0
例5. 等腰直角三角形ABC 的直角顶点C 和顶点B 都在直线2x + 3y – 6 = 0上,顶点A 的坐标是(1,–2).求边AB 、AC 所在直线方程.
(AC 的直线方程为:3x – 2y – 7 = 0 AB 的直线方程为:x – 5y – 11 = 0或5x + y – 3 = 0.)
1. 分别求点()2,3P -到下列直线l 的距离:
(1)2390x y +-=; (2)7x =; (3)3y =; 2. 若点(),3P a 到直线4310x y -+=的距离等于4,求a 的值;
3. 若直线1:220l ax y ++=与直线2:320l x y --=平行,求两直线的距离;
4. 已知ABC ∆中,()()3,2,1,5,A B C -点在直线330x y -+=上,若ABC ∆的面积为10,求点C 的坐标;
5. 若直线l 通过直线75240x y +-=和直线0x y -=的交点,并且点()5,1到直线l 的距离为10,求直线l 的方程;
6. 已知一个三角形的顶点为()()()2,3,4,1,4,1A B C --,直线//l AB ,且l 将
ABC ∆的面积分成相等的两部分,求l 的方程;
7. 求点()4,0关于直线54210x y ++=的对称点的坐标;
8.如图,一次函数7y x =-+与正比例函数4
3
y x =
的图象交于点A ,且与x 轴交于点B. (1)求点A 和点B 的坐标;
(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.
①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?
②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由。
l
R
P
C A
B
O
y
x
9.如图,在平面直角坐标系中,O 是坐标原点,点A 的坐标是(﹣4,0),点B 的坐标是(0,b )(b >0).P 是直线AB 上的一个动点,作PC ⊥x 轴,垂足为C .记点P 关于y 轴的对称点为P ´(点P ´不在y 轴上),连接PP ´,P ´A ,P ´C .设点P 的横坐标为a . (1)当b =3时,
①求直线AB 的解析式;
②若点P ′的坐标是(﹣1,m ),求m 的值; (2)若点P 在第一象限,记直线AB 与P ´C 的交点为D .当P ´D :DC=1:3时,求a 的值;
(3)是否同时存在a ,b ,使△P ´CA 为等腰直角三角形?若存在,请求出所有满足要求的a ,b 的值;若不存在,请说明理由.
【思路点拨】(1)①利用待定系数法考虑。
②把(﹣1,m )代入函数解析式即可。
(2)证明△PP ′D ∽△ACD ,根据相似三角形的对应边的比成比例求解。
(3)分P 在第一,二,三象限,三种情况进行讨论。
10.已知直线3
+=kx y (k <0)分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB 于点C ,设运动时间为t 秒.
(1)当1
-=k 时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度 同时出发,当点P 到达点A 时两点同时停止运动(如图1). ① 直接写出t =1秒时C 、Q 两点的坐标;
② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值.
(2)当4
3-=k 时,设以C 为顶点的抛物线n
m x y ++=2
)(与直线AB 的另一交点为D (如图2), ① 求CD 的长;
② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大?
【思路点拨】(1)②分两种情形讨论。
(2)①过点D 作DE ⊥CP 于点E ,证明△DEC ∽△AOB 。
②先求得三角形COD 的面积为定值,又由Rt △PCO ∽Rt △OAB ,在比例线段中求出t 值为多少时,h 最大。
Welcome To Download !!!
欢迎您的下载,资料仅供参考!。
