SPC控制图判异准则制定依据 判异准则顺口溜
SPC“控制图”的分析与判定

SPC“控制图”的分析与判定控制图(Control Chart)又叫管制图,是对过程质量特性进行测定、记录、评估,从而监察过程是否处于控制状态的一种用统计方法设计的图。
图上有三条平行于横轴的直线:中心线(CL,Central Line)、上控制线(UCL,Upper Control Line)和下控制线(LCL,Lower Control Line),并有按时间顺序抽取的样本统计量数值的描点序列。
UCL、CL、LCL统称为控制线(Control Line),通常控制界限设定在±3标准差的位置。
根据控制图使用目的不同,控制图可分为:分析用控制图和控制用控制图。
根据统计数据的类型不同,控制图可分为:计量控制图和计数控制图(包括计件控制图和计点控制图)。
计量型控制图平均数与极差控制图( -X-R Chart )平均数与标准差控制图( -X-S Chart )中位数与极差控制图( ~X-R Chart )个別值与移动极差控制图( X-Rm Chart )计数值控制图不良率控制图(P chart)不良数控制图(nP chart,又称 np chart 或 d chart)缺点数控制图(C chart)单位缺点数控制图(U chart)控制图种类及应用场合:控制图的分析与判定应用控制图的目的,就是要及时发现过程中出现的异常,判断异常的原则就是出现了“小概率事件”,为此,判断的准则有两类。
第一类:点子越出界限的概率为0.27% 。
准则1属于第一类。
第二类:点子虽在控制界限内,但是排列的形状有缺陷。
准则2-8属于第二类。
控制图八大判异准则(口诀)2/3A (连续3点中有2点在中心线同一侧的B区外<即A 区内>4/5C (连续5点中有4点在中心线同一侧的C区以外)6连串(连续6点递增或递减,即连成一串)8缺C (连续8点在中心线两侧,但没有一点在C区中)9单侧(连续9点落在中心线同一侧)14交替(连续14点相邻点上下交替)15全C (连续15点在C区中心线上下,即全部在C区内1界外(1点落在A区以外)▶2/3A (连续3点中有2点在中心线同一侧的B区外<即A区内>)判读:1 . 控制过严;2 . 材料品质有差异;3 . 检验设备或方法之大不相同;4 . 不同制程之资料绘于同一控制图上;5 . 不同品质材料混合使用。
spc控制图判异标准

X
C C B
LCL
A
LCL
A
准则3
连续6点递增或递减
准则 Criteria 3 UCL UCL
准则4
连续14点相邻点上
下交替
准则 Criteria 4
A B
A B
X
C C B
X
C C B
LCL
A
LCL
A
天马行空官方博客:/tmxk_docin ;QQ:1318241189;QQ群:175569632
准则5
连续3点中有2点落在中
准则6
连续5点中有4点落
心线同一侧的B区以外
准则 Criteria 5 UCL
UCL
在中心线同一侧的 C区以外
准则 Criteria 6
A B
A B
X
C C B
X
C C B
LCL
A
LCL
A
准则7
连续15点C区
准则8
但无一在C区中
准则 Criteria 8 UCL
175569632连续3点中有2点落在中心线同一侧的b区以外连续5点中有4点落在中心线同一侧的c区以外准则criterialclucl准则criterialclucl连续15点c区中心线上下连续8点在中心线两侧但无一在c区中准则criterialclucl准则criterialclucl第一
SPC-控制图判异准则
连续8点在中心线两侧,
中心线上下
准则 Criteria 7 UCL
A B
A B
X
C C B A
X
C C B
LCL
LCL
A
控制图在贯彻预防原则中的作用
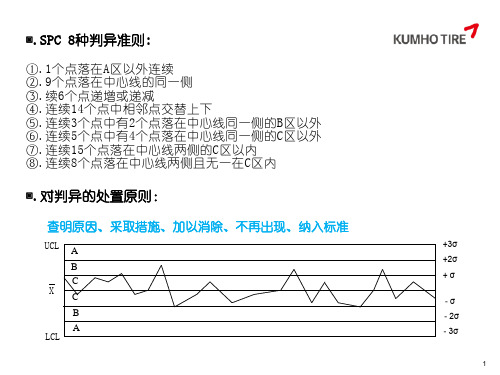
SPC_8种判异准则

SPC_8种判异准则SPC(统计过程控制)是一种结合统计和数据分析的质量管理方法,用于监控过程的稳定性和控制产品的质量。
为了有效地判断一个过程是否发生了变化,并且有助于及时采取纠正措施,SPC中有八种常用的判异准则。
1. 极差判异准则(Range Test):极差是指一组数据中最大值和最小值之间的差异,当一些样本的极差超过了设定的极差上限或下限时,就发生了极差异常。
极差过大可能是因为操作方法改变、设备故障或材料变异导致。
2. 一致性判异准则(Run Test):一致性是指一组数据连续出现的相同结果,当同一个符号连续出现的次数超过设定的限制时,就发生了一致性异常。
一致性的出现可能是由于操作员的错误或机器的固有问题导致。
3. 均值判异准则(Mean Test):均值是指一组数据的平均值,在SPC中常常用于判断处理过程中是否存在平均偏移。
当一个样本的均值超过设定的均值上限或下限时,就发生了均值异常。
均值异常可能是由于原材料的变化、机器调整不当、操作员技术水平等问题引起。
4. 均值差异判异准则(Mean Difference Test):均值差异是指两组数据的均值之间的差异,在SPC中常常用于不同运营条件或不同设备之间的比较。
当两组数据的均值差异超过设定的差异上限或下限时,就发生了均值差异异常。
均值差异异常可能是由于不同设备或运营条件导致的。
5. 中位数判异准则(Median Test):中位数是指一组有序数据中处于中间位置的数值,中位数判异准则用于判断一组数据是否存在异常,当一个样本的中位数超过设定的中位数上限或下限时,就发生了中位数异常。
中位数异常可能是由于样本中存在极端值或其他偏倚导致。
6. 偏度判异准则(Skewness Test):偏度是指一组数据分布的不对称程度,正偏表示分布右侧比左侧更重,负偏表示分布左侧比右侧更重。
偏度判异准则用于判断一组数据的偏度是否超过设定的阈值,一旦发生偏度异常,可能是由于采样偏差或数据收集错误导致。
SPC判异准则及异常处理方法
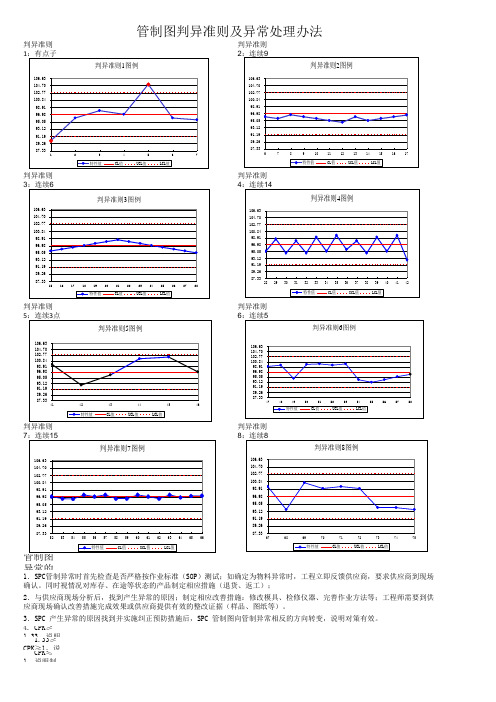
判异准则1:有点子落在界外。
判异准则2:连续9点落在中心线同一侧。
判异准则3:连续6点递增或递减。
判异准则4:连续14点相邻点上下交替。
判异准则5:连续3点中有2点落在中心线同一侧的B 区以外。
判异准则6:连续5点中有4点在中心线同一侧的C 区以外。
判异准则7:连续15点在C 区中心线上下。
判异准则8:连续8点在中心线两侧。
但无一在C 区中。
管制图异常的处理:
4. CPK≥1.33,说明制程能力较好,需继续保持; 1.33≥CPK≥1,说明制程能力一般,须改进加强; CPK≤1,说明制程能力较差,急需改进。
管制图判异准则及异常处理办法
1.SPC管制异常时首先检查是否严格按作业标准(SOP)测试;如确定为物料异常时,工程立即反馈供应商,要求供应商到现场确认。
同时视情况对库存、在途等状态的产品制定相应措施(退货、返工);
2.与供应商现场分析后,找到产生异常的原因;制定相应改善措施:修改模具、检修仪器、完善作业方法等;工程师需要到供应商现场确认改善措施完成效果或供应商提供有效的整改证据(样品、图纸等)。
3.SPC 产生异常的原因找到并实施纠正预防措施后,SPC 管制图向管制异常相反的方向转变,说明对策有效。
SPC控制图判异准则制定依据判异准则顺口溜

SPC控制图判异准则制定依据判异准则顺口溜Revised by BLUE on the afternoon of December 12,2020.SPC控制图判异准则制定依据过程控制图包含2种.一种是“分析用控制图”.另一种是“控制用控制图”。
分析用控制图,主要作以下2点用途:①所分析的过程是否为稳态:②过程能力指数是否满足要求。
这种把能力抬数满足要求称作技术稳态。
分析用控制图的调整过程即质址不断改进的过程。
控制用控制图,、”I过程达到我们所确定的“统计稳态“和技术稳态”后.才能将分析用控制图的控制线延长作为控制用控制图°这种延长的控制线相当于生产立法,便进入日常管理。
故从数埋统讣的角度來看,分析用控制图阶级就是过程参数未知阶段,而控制用控制图阶段则是过程参数已知阶段。
在由分析用控制图向控制用控图转化前,需嬰对过程判读.这时就需要用到:判稳准则和判异原则。
1)判稳准则的思路对于判井來说.“点出界就判界” O虽不百发百中,也是干发九九七中.很可靠.但在控制图上有一点未出界. 可否判稳这可能存在2种可能:①过程木來就稳定:②异常漏报c故出现一点未出界不能立即判稳。
但接连出现m(m»l)个点子未出界,则情况大不相同。
这时整个点子系列的0总要比个别点子的0小得筝,可以忽略不讣。
那么仅有一种可能.即过程稳定。
如果接连在控制界内的点子更女.即使有个别个点子偶然出界.过程仍可看作是稳态的。
这就是判稳准则的思路。
判稳准则,在点子随机排列的情况下,符合下列各原则之一就判稳:连续25个点.界外点数d=0;其概率P二al连续35个点•界外点数dWl;其概率P二a 2连续100个点,界外点数dW2;其概率P二a 3尽管在上述判稳原则下,对于出界点也应十加以排査。
用概率统计如下•假设过程正常:P (连续35 点,dWl) = ( ) 35 ( ) 0+ ( ) 31 ( ) 1= =a2故,P (连续35 点,d>l) = 1 - = =a2同理,al = : a2 = : a3 = •可见al与a2和a 3明显不相称。
SPC-8种判异准则

对判异的处置原则:查明原因,采取措施,加以消除,不再 出现,纳入标准
UCL A
+3σ
+2σ
B
C
+σ
X
C
-σ
B
- 2σ
LCL A
- 3σ
1
判异准则1
任何 1个点落在A区以外
x
UCL A
B C
C B A
LCL
x
Test 1. One Point Beyond Zone A
异常原因一般为: • 新操作人员,方法不对,机器故障,原料不合格 • 检验方法或标准变化 • 计算错误,测量误差
2
判异准则2,5, 6:
Test 2. Nine Points in a Row on One Side of the Center Line
2: 连续9个点落在中心线的同一侧;
UCL
A
5: 连续3个点中有2个点落在中心线同一侧的B 区以外;
B
6: 连续5个点中有4个点落在中心线同一侧的C
C
区以外
B
x
A
LCL
3
判异准则3 连续6个点递增或递减
Test 3. 6 Points in a Row Steadily Increasing or Decreasing
UCL
A
x
B
C
C
B A
LCL
x
异常原因一般为:
• 工具逐渐磨损,维护水平逐渐降低,操作人员技能逐渐提高
4
判异准则4
连续14个点中相邻点交替上下
异常原因一般为:
• 数据有假,计算错误;分层不够
6
判异准则8
连续8个点落在中心线两侧且无一在C区内
SPC控制图判异准则制定依据判异准则顺口溜精选文档

S P C控制图判异准则制定依据判异准则顺口溜精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-SPC控制图判异准则制定依据过程控制图包含2种,一种是“分析用控制图”,另一种是“控制用控制图”。
分析用控制图,主要作以下2点用途:①所分析的过程是否为稳态;②过程能力指数是否满足要求。
这种把能力指数满足要求称作技术稳态。
分析用控制图的调整过程即质量不断改进的过程。
控制用控制图,当过程达到我们所确定的“统计稳态“和技术稳态”后,才能将分析用控制图的控制线延长作为控制用控制图。
这种延长的控制线相当于生产立法,便进入日常管理。
故从数理统计的角度来看,分析用控制图阶级就是过程参数未知阶段,而控制用控制图阶段则是过程参数已知阶段。
在由分析用控制图向控制用控图转化前,需要对过程判读,这时就需要用到:判稳准则和判异原则。
1)判稳准则的思路对于判异来说,“点出界就判异”。
虽不百发百中,也是千发九九七中,很可靠,但在控制图上有一点未出界,可否判稳?这可能存在2种可能:①过程本来就稳定;②异常漏报。
故出现一点未出界不能立即判稳。
但接连出现m (m>>1)个点子未出界,则情况大不相同。
这时整个点子系列的β总=βm要比个别点子的β小得多,可以忽略不计。
那么仅有一种可能,即过程稳定。
如果接连在控制界内的点子更多,即使有个别个点子偶然出界,过程仍可看作是稳态的。
这就是判稳准则的思路。
判稳准则,在点子随机排列的情况下,符合下列各原则之一就判稳:连续25个点,界外点数d=0;其概率P = α1连续35个点,界外点数d≤1; 其概率P = α2连续100个点,界外点数d≤2; 其概率P = α3尽管在上述判稳原则下,对于出界点也应当加以排查。
用概率统计如下,假设过程正常:P(连续35点,d≤1)=(0.9973)35(0.0027)0+(0.9973)34(0.0027)1= 0.9959 =α2故, P(连续35点,d>1)= 1 - 0.9959 = 0.0041 =α2同理,α1 = 0.0654;α2 = 0.0041;α3 = 0.0026,可见α1 与α2 和α3明显不相称。
SPC控制图判断标准

SPC控制图判断标准SPC控制图判断标准⼀:判稳准则在点⼦随机排列的情况下,符合下列个点之⼀就判稳:(1)连续25个点,界外点数d=0;(2)连续35个点,界外点数d≤1;(3)连续100个点,界外点数d≤2。
⼆:判异准则SPC的基准是稳态,如若过程出现显著偏离稳态则为异态。
异态出可分为异常好与异常坏两类。
判异准则:(1)点出界就判异;(2)界内点排列不随机判异。
2.1判异准则1⼀点落在A区以外。
出现该情况可能因素:计算错误、测量误差、原材料不合格、设备故障等。
点排布如下图2-1所⽰:图2-1 准则1判异图2.2判异准则2出现连续9点落在中⼼线⼀侧。
原因:分布的a减⼩。
点排布如下图2-2所⽰:图2-2 准则2判异图2.3判异准则3连续6点递增或递减。
产⽣趋势可能因素:⼯具逐渐磨损、维修⽔平逐渐降低、操作⼈员技能逐渐降低等。
点排布如下图2-3所⽰:图2-3 准则3判异图2.4判异准则4连续14点中相邻点上下交替。
产⽣趋势可能因素:轮流使⽤两台设备、两位⼈员轮流操作。
点排布如下图2-4所⽰:图2-4 准则4判异图2.5判异准则5连续3点落在中⼼线同⼀侧的B区以外。
产⽣趋势可能因素:参数u发⽣了变化。
点排布如下图2-5所⽰:图2-5准则5判异图2.6判异准则6连续5点中有4点落在中⼼线同⼀侧的C区以外。
表明参数u发⽣了变化。
点排布如下图2-6所⽰:图2-6准则6判异图2.7判异准则715点在C区中⼼线上下。
可能原因:①是否应⽤了假数据,弄虚作假;②是否数据分层不够。
点排布如下图2-7所⽰:图2-7准则7判异图2.8判异准则88点在中⼼线两侧,但⽆⼀在C区中。
原因:数据分层不够。
点排布如下图2-8所⽰:图2-8准则8判异图。
SPC8种判异准则(新2018)
异常原因一般为:
• • • 新操作人员,方法不对,机器故障,原料不合格 检验方法或标准变化 计算错误,测量误差
4
▣.判异准则: ⑥.连续5个点中有4个点落在中心线同一侧的C区以外
UCL
A
B C C
x
B
A
LCL
x
Test 6. 4 Out of 5 Points in a Row in Zone B and Beyond
7
▣.判异准则: ⑦.连续15个点落在中心线两侧的C区以内
UCL
A B C C B A
x
LCL
Test 7. 15 Points in a Row in Zone C (Above and Below CL)
ห้องสมุดไป่ตู้
异常原因一般为: • 数据有假,计算错误;分层不够
8
▣.判异准则: ⑧.连续8个点落在中心线两侧且无一在C区内
▣.SPC 8种判异准则:
①.1个点落在A 区以外连续 ②.9个点落在中心线的同一侧 ③.续6个点递增或递减 ④.连续14个点中相邻点交替上下 ⑤.连续3个点中有 2个点落在中心线同一侧的 B区以外 ⑥.连续5个点中有 4个点落在中心线同一侧的 C区以外 ⑦.连续15个点落在中心线两侧的 C区以内 ⑧.连续8个点落在中心线两侧且无一在 C区内
异常原因一般为:
• • • 新操作人员,方法不对,机器故障,原料不合格 检验方法或标准变化 计算错误,测量误差
2
▣.判异准则: ②.连续9个点落在中心线的同一侧;
UCL
A B
C
C B A
LCL
x
Test 2. Nine Points in a Row on One Side of the Center Line
spc控制图判定准则

spc控制图判定准则准则编辑稳态是生产过程追求的目标。
那么如何用控制图判断过程是否处于稳态?为此,需要制定判断稳态的准则。
判稳准则:在点子随机排列的情况下,符合下列各点之一就认为过程处于稳态:(1)连续25个点子都在控制界限内;(2)连续35个点子至多1个点子落在控制界限外;(3)连续100个点子至多2个点子落在控制界限外。
在讨论控制图原理时,已经知道点子出界就判断异常,这是判断异常的最基本的一条准则。
为了增加控制图使用者的信心,即使对于在控制界限内的点子也要观察其排列是否随机。
若界内点排列非随机,则判断异常。
判断异常的准则:符合下列各点之一就认为过程存在异常因素:(1)点子在控制界限外或恰在控制界限上;(2)控制界限内的点子排列不随机;(3)链:连续链,连续9点排列在中心线之下或之上;间断链,大多数点在一侧(4)多数点屡屡靠近控制界限(在2一3倍的标准差区域内出现)连续3个点至少有2点接近控制界限。
连续7个点至少有3点接近控制界限。
连续10个点至少有4点接近控制界限。
(5)倾向性(连续不少于6点有上升或下降的倾向)与周期性。
(6)连续14点中相邻点交替上下。
(7)点子集中在中心线附近。
(原因:数据不真实;数据分层不当)为了方便记忆,下面总结了控制图判异的八个准则:准则1:1个点子落在A区以外(点子越出控制界限)准则2:连续9点落在中心线同一侧准则3:连续6点递增或递减准则4:连续14点中相邻点子总是上下交替准则5:连续3点中有2点落在中心线同一侧B区以外准则6:连续5点中有4点子落在中心线同一侧C区以外准则7:连续15点落在中心线同两侧C区之内准则8:连续8点落在中心线两侧且无1点在C区中。
SP控制图判异准则制定依据判异准则顺口溜

题,选择 14 点是通过统计模拟试验而得出的,其 准则五,连续 3 点中有 2 点在 A 区
α 大体与准则一, α0 =0.0027 相当。
过程平均值的变化通常可由本准则判定,它对于变异的增加也较灵敏。这里要补充的是任何两点,至于第三点在何处,
甚至可以根本不存在。由于点子落在中心线一侧
2-3 σ 个标准差间的概率 =0.0214, 故 α 0 =2 ×3×0.02143×( 0.9973-
控制图八大判异准则-精简顺口溜版
本人因记性差,对八大判异准则总记不下,所以就想到用把内容精简提练后,编成顺口溜。这样好记一些, 再也不会忘记了。大家提提意见,觉得怎么样?
控制图八大判异准则-精简顺口溜版口决:(就三句,很简单吧!只要记住以下兰色部分的三句话就行了, 不过第一次要对照下面附件中的图看才明白。)
P( 6 点倾向) = α 5 = 0.00273 P( 7 点倾向) = α 7 = 0.00039 显然, 6 点倾向最接近准则一, α0 =0.0027 ,故其判异是合适的。 准则四,连续 14 点上下交替。 出现这种现象是由于轮流使用两台设备或两位操作人员轮流操作而引起的系统效应。实际上这是一个数据分层不够的问
控制图。这种延长的控制线相当于生产立法,便进入日常管理。
故从数理统计的角度来看,分析用控制图阶级就是过程参数未知阶段,而控制用控制图阶段则是过程参数已知阶段。
在由分析用控制图向控制用控图转化前,需要对过程判读,这时就需要用到:判稳准则和判异原则。
1)判稳准则的思路 对于判异来说,“点出界就判异”。虽不百发百中,也是千发九九七中,很可靠,但在控制图上有一点未出界,可否判
SPC控制图判异准则制定依据
过程控制图包含 2 种,一种是 “分析用控制图”,另一种是“控制用控制图”。
判异准则

原则1: 原则 : 一点在A区之外 一点在 区之外 UCL X LCL
A B C C B A
原则2: 原则 : 连续9点落在中心线同一侧 点落在中心线同一侧; 连续 点落在中心线同一侧; UCL X LCL
A B C C B A
原则3: 原则
X-R图 图
SPC的判异准则 的判异准则
1.一点落在A 1.一点落在A区以外 一点落在 2.连续6 2.连续6点递增或递减 连续 3.连续9点在中心线的同一侧 3.连续9 连续 4.连续14点交替上下 4.连续14点交替上下 连续14 5.连续3点中有2点落在中心线同一侧的B 5.连续3点中有2点落在中心线同一侧的B区以外 连续 6.连续5点中有4点落在中心线同一侧的C 6.连续5点中有4点落在中心线同一侧的C区以外 连续 7.连续15点落在中心线的C 7.连续15点落在中心线的C区以内 连续15点落在中心线的 8.连续8点落在中心线两侧,且无一在C 8.连续8点落在中心线两侧,且无一在C区内 连续
A B C C B A
原则4: 原则 : 连续14点呈上下交替 连续 点呈上下交替 UCL X LCL
A B C C B A
原则5: 原则 : 连续3中点有 点落在A区 中点有2点落在 连续 中点有 点落在 区 UCL X LCL
A B C C B A
原则6: 原则 : 连续5点中有 点在 连续 点中有4点在 区 点中有 点在B区 UCL X LCL
A B C C B A
原则7: 原则 : 连续15点在 点在C区中心线上下 连续 点在 区中心线上下 UCL X LCL
A B C C B A
原则8: 原则 : 连续8点在中心线两侧 点在中心线两侧A、 区内 连续 点在中心线两侧 、B区内 UCL X LCL
SPC 8种判异准则

6
判异准则8 判异准则 连续8个点落在中心线两侧且无一在C区内
Test 8. 8 Points in a Row on Both Sides of CL with None in Zone C
UCL
A B C C B A
x
LCL
异常原因一般为: • 数据分层不够
7
对判异的处置原则:查明原因,采取措施,加以消除,不再 对判异的处置原则:查明原因,采取措施,加以消除, 出现, 出现,纳入标准
UCL X LCL
A B C C B A
+3σ +2σ +σ -σ - 2σ - 3σ
1
判异准则1 判异准则 任何 1个点落在A区以外
UCL
x
A B C C B A
LCL
x
UCL
A B C C B A
x
LCL
x
异常原因一般为: • 工具逐渐磨损,维护水平逐渐降低,操作人员技能逐渐提高
4
判异准则4 判异准则 连续14个点中相邻点交替上下
Test 4. 14 Points in a Row Alternating Up and Down
UCL
A B C C B A
x
LCL
Test 5. 2 Out of 3 Points in a Row in Zone A or Beyond x x
Test 2. Nine Points in a Row on One Side of the Center Line
UCL
A B C C B A
x
LCL
UCL
A B C C B A
x
异常原因一般为: • 轮流使用两台设备或有两个操作员工轮流操作,使得数据分 层不够
【口诀】三句话记住控制图八大判异准则

【口诀】三句话记住控制图八大判异准则
展开全文
控制图八大判异准则-精简顺口溜版口决:
就三句,很简单吧!
只要记住以下蓝色部分的三句话就行了,不过第一次要对照下面附件中的图看才明白。
23456,AC连串串(连增或连减);
81 514,缺C全C交替转;
9单侧,一点在外。
控制图八大判异准则提练(口决、图片对应项目):
1、2/3A(连续3点中有2点在中心线同一侧的B区外即A区内>)
2、4/5C(连续5点中有4点在中心线同一侧的C区以外)
3、6连串(连续6点递增或递减,即连成一串)
4、8缺C(连续8点在中心线两侧,但没有一点在C区中)
5、9单侧(连续9点落在中心线同一侧)
6、14交替(连续14点相邻点上下交替)
7、15全C(连续15点在C区中心线上下,即全部在C区内)
8、1界外(1点落在A区以外)
解说:
23456,AC连串串(连增或连减);
---2/3、4/5、6分别对应A、C、连串串;即2/3A;4/5C;6连串。
81514,缺C全C交替转
---8、15、14分别对应缺C、全C、交替转;即8缺C;15全C;14上下交替。
9单侧,一点在外
---9点在同一侧;一点出A区外。
【作者:waywang2006 】。
控制图判异准则
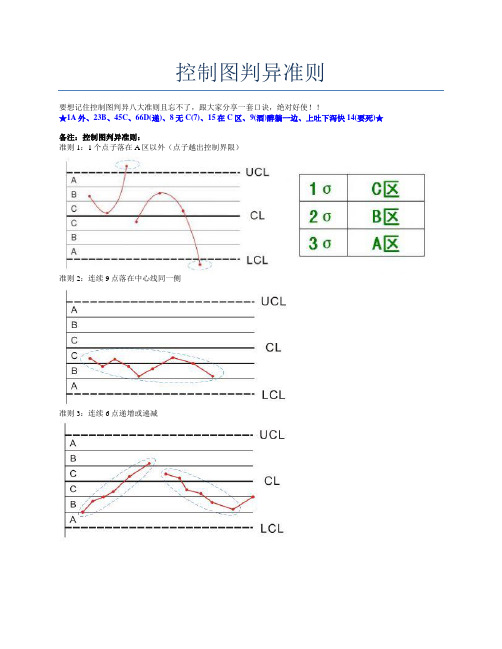
控制图判异准则
要想记住控制图判异八大准则且忘不了,跟大家分享一套口诀,绝对好使!!
★1A外、23B、45C、66D(递)、8无C(7)、15在C区、9(酒)醉躺一边、上吐下泻快14(要死)★
备注:控制图判异准则:
准则1:1个点子落在A区以外(点子越出控制界限)
准则2:连续9点落在中心线同一侧
准则3:连续6点递增或递减
准则4:连续14点中相邻点子总是上下交替
准则5:连续3点中有2点落在中心线同一侧B区以外准则6:连续5点中有4点子落在中心线同一侧C区以外
准则7:连续15点落在中心线同两侧C区之内
准则8:连续8点落在中心线两侧且无1点在C区中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPC控制图判异准则制定依据
过程控制图包含2种,一种是“分析用控制图”,另一种是“控制用控制图”。
分析用控制图,主要作以下2点用途:①所分析的过程是否为稳态;②过程能力指数是否满足要求。
这种把能力指数满足要求称作技术稳态。
分析用控制图的调整过程即质量不断改进的过程。
控制用控制图,当过程达到我们所确定的“统计稳态“和技术稳态”后,才能将分析用控制图的控制线延长作为控制用控制图。
这种延长的控制线相当于生产立法,便进入日常管理。
故从数理统计的角度来看,分析用控制图阶级就是过程参数未知阶段,而控制用控制图阶段则是过程参数已知阶段。
在由分析用控制图向控制用控图转化前,需要对过程判读,这时就需要用到:判稳准则和判异原则。
1)判稳准则的思路
对于判异来说,“点出界就判异”。
虽不百发百中,也是千发九九七中,很可靠,但在控制图上有一点未出界,可否判稳?这可能存在2种可能:①过程本来就稳定;②异常漏报。
故出现一点未出界不能立即判稳。
但接连出现m (m>>1)个点子未出界,则情况大不相同。
这时整个点子系列的β总=βm要比个别点子的β小得多,可以忽略不计。
那么仅有一种可能,即过程稳定。
如果接连在控制界内的点子更多,即使有个别个点子偶然出界,过程仍可看作是稳态的。
这就是判稳准则的思路。
判稳准则,在点子随机排列的情况下,符合下列各原则之一就判稳:
连续25个点,界外点数d=0;其概率P = α1
连续35个点,界外点数d≤1; 其概率P = α2
连续100个点,界外点数d≤2; 其概率P = α3
尽管在上述判稳原则下,对于出界点也应当加以排查。
用概率统计如下,假设过程正常:
P(连续35点,d≤1)=(0.9973)35(0.0027)0+(0.9973)34(0.0027)1= 0.9959 =α2
故, P(连续35点,d>1)= 1 - 0.9959 = 0.0041 =α2
同理,α1 = 0.0654;α2 = 0.0041;α3 = 0.0026,可见α1 与α2 和α3明显不相称。
故有专家认为应取消第①条,但体哈特控制图的国际标准ISO8258:1991仍然保留了这条原则,显然有经济因素考虑。
判异准则,我们知道SPC的基准为统计控制状态,若过程偏离这种状态就称为异常。
因此,所以异常就会存在异常的好和异常的坏。
判异准则有2类:
点出界就判异;
界内点排不随机就判异。
由于点子数量未加以界定,其模式可能有无穷多,但现场能保留下来继续使用的只有明显物理意义的若干种,在控制图中要注意加以识别。
准则一,一点在A区外
准则一可对参数μ与σ变化给出信号,还可对过程单个失控作出反应,如计算错误,测量误差,原材料不合格,设备故障等,犯第一种错误的概率,称为显著水平,记α0 =0.0027
准则二,连续9点在C区或其外排成一串
此准则作为准则一而补充的,以提高控制图的灵敏度,选择9点是为了使其犯第一种错误的概率α与准则一的α0 =0.0027大体相仿.在控制线一侧连续出现的点称为链,下列点数链长的α为:
P(中心线一侧出现长为7的链)= α7 = 2(0.9973/2)7 = 0.0153
P(中心线一侧出现长为8的链)= α8 = 2(0.9973/2)8 = 0.0076
P(中心线一侧出现长为9的链)= α9 = 2(0.9973/2)9 = 0.0038
P(中心线一侧出现长为10的链)= α10 = 2(0.9973/2)10 = 0.0019
可见,α9 与准则一的α0 相当,若长=7判异,比α0 大的多。
以往采用不着7点,而目前改为9点判异。
这主要是因为推行SPC一般采用电脑进行,从而使得整个系统的α总概率增大,不难
证明:α总≈∑αi为减少α总,就得使每条判异准则各自的αi
准则三,连续6点递增或递减。
此条准则针对过程平均值的倾向性而设计的,它判定过程平均值的较小倾向要比准则一更为灵敏。
其产生原因可能是工具损坏,或作业员技能改进等。
P(n倾向)= αi = 2/ni(0.9973/2)n ,于是有:
P(5点倾向)= α5 = 0.01644
P(6点倾向)= α5 = 0.00273
P(7点倾向)= α7 = 0.00039
显然,6点倾向最接近准则一,α0 =0.0027,故其判异是合适的。
准则四,连续14点上下交替。
出现这种现象是由于轮流使用两台设备或两位操作人员轮流操作而引起的系统效应。
实际上这是一个数据分层不够的问题,选择14点是通过统计模拟试验而得出的,其α大体与准则一,α0 =0.0027相当。
准则五,连续3点中有2点在A区
过程平均值的变化通常可由本准则判定,它对于变异的增加也较灵敏。
这里要补充的是任何两点,至于第三点在何处,甚至可以根本不存在。
由于点子落在中心线一侧2-3σ个标准差间的概率=0.0214,故α0 =2×3×0.02143×(0. 9973-0.0214)=0.00268,这与准则一很接近。
准则六,连续5点中有4点在B区。
此准则与准则五类似,这第5点可在任何地方。
本准则对于过程平均值的偏移也灵敏。
由于点子在 1-2σ之间的概率=φ(1)-φ(2)= 0.15886-0.02275 = 0.13591,故有P(5点中有4点在B区)= 2×C5×0.135914×(0.997 3-0.13591)=0.0029与准则一α0 =0.0027相当。
准则七,连续15点在C区中心线上下
对于本准则的现象,不要被它良好现象所迷惑,而应注意它的非随机性。
造成这种现象的原因有2种:数据虚假或数据分层不够。
我们知道点在C区的概率=0.68268
连续14点在C区,α14 = 0.6826814 = 0.00478
连续15点在C区,α15 = 0.6826815 = 0.00326
连续16点在C区,α16 = 0.6826816 = 0.00223
其中, α15= 0.00326与准则一α0 =0.0027较近,故有准则七.从表面上看, α16 = 0.00223与准则一α0 = 0.0027更接近点,16个点子比15个点子应用起来不如15个点子方便.
准则八,8点在中心线两侧,但无1点在C区
造成此现象的原因为数据分层不够。
由于点子落在1-3σ之间的概率=φ(1)-φ(3)= 0.15886-0.00135 = 0.15 731,故有
α8 = 2×(C1×C2×C3×C4×C5×C6×C7×C8)×0.157318 = 0.0002,类似地可算出:
α7 =0.0006,α6 =0.0019,α5 =0.006。
据此计算,显然α8 = 0.0002较之α0 =0.0027过小,而α6 =0.001 9与之较接近,故建议准则8改为:6点在中心线两侧,而无1点在C区。
综合上述,不论是判稳还是判异原则,都是以是否服从正态分布为出发点,以休哈特定制的3σ为管理限度为类比参照。
控制图八大判异准则-精简顺口溜版
本人因记性差,对八大判异准则总记不下,所以就想到用把内容精简提练后,编成顺口溜。
这样好记一些,再也不会忘记了。
大家提提意见,觉得怎么样?
控制图八大判异准则-精简顺口溜版口决:(就三句,很简单吧!只要记住以下兰色部分的三句话就行了,不过第一次要对照下面附件中的图看才明白。
)
23456,AC连串串(连增或连减);
81 514,缺C全C交替转;
9单侧,一点在外。
控制图八大判异准则提练(口决、图片对应项目):
1、2/3A(连续3点中有2点在中心线同一侧的B区外<即A区内>)
2、4/5C(连续5点中有4点在中心线同一侧的C区以外)
3、6连串(连续6点递增或递减,即连成一串)
4、8缺C(连续8点在中心线两侧,但没有一点在C区中)
5、9单侧(连续9点落在中心线同一侧)
6、14交替(连续14点相邻点上下交替)
7、15全C(连续15点在C区中心线上下,即全部在C区内)
8、1界外(1点落在A区以外)
解说:
23456,AC连串串(连增或连减);
---2/3、4/5、6分别对应A、C、连串串;即2/3A;4/5C;6连
串。
81514,缺C全C交替
转
---8、15、14分别对应缺C、全C、交替转;即8缺C;15全C;14上下交
替。
9单侧,一点在
外
---9点在同一侧;一点出A区外。
