接触问题的有限元分析
有限元法在分析接触问题中的应用

∑ 0 :
( d 7 ( Ac s c s 一 c4 oo)ia r A+ d a)o (L s ̄s +  ̄ o c n
t ( As a)ia t (As a)oa 0 r d n s +r d n c s = i n y i
求 正应 力 的极值 :
正应 力 的最 大值 和最 小值 是
可 知 ,它 只 能 度 取 决 于接 触 区 的 接 触 尺 寸 和
其 求 解 几 何 形 状 非 接 触 区的 单元 尺 寸 , 中接 触 区的单 元 尺 寸是 最 大 的 影 响 因素 。 过粗 的单 元 尺 寸可 能 比较 简单 , 边 但 将 界 条 件 比较 规 导 致 收 敛 问 题 , 过 细 的 单 元 尺 寸 , 会延 长分 析 时 间 , 范 的 接 触体 问 甚至会得不到分析结果 ,所 以在接触问题分析 中要有合
社 ,0 3 20 .
在 划 分 网格 模 型 的基 础 上建 立 解 除对 ,并 对模 型 进 行 加载 , 图 3中拾取 四分 之一 的截 面上 施 加 对称 约 束 。 在
[ 2] 谭 建国 . 使用 A S S . 行有限元 分析 [ . N Y 60进 M] 北京 : 北京大学
r (As a)oa o ( Acs s a 0 d n cs — - d )i = i y o n
根 据 不 同的 分 网模 型 进 行 分析 得 到 不 同精 度 的分 析结 果 , 分析模 型结果变形 情况 如 图 6
所示 。 由图 6可 知 , 形 的最 大 变 位置 发 生在 两 者接 触 部分 , 即盘 的 内 圈面 与轴 的外 圈 面接 触 处 。
出 版社 ,0 2 20 .
[] 刘鸿文 . 3 材料力学 [ . M]北京 : 高等教育 出版社 , 0 . 2 9 0
有限元 接触 有限滑移 小滑移

有限元接触有限滑移小滑移简介有限元方法是一种基于数值计算的工程分析方法,用于求解连续介质力学问题。
接触问题是指两个或多个物体之间存在接触并产生相互作用的情况。
在接触问题中,有时会出现滑移现象,即两个物体之间存在相对滑动。
而小滑移是指在接触问题中,滑动幅度相对较小的情况。
本文将详细介绍有限元方法在接触问题中的应用,以及如何考虑有限滑移和小滑移现象。
有限元方法在接触问题中的应用有限元方法通过将结构离散化为一个个小单元,利用单元间的节点连接关系建立整个结构的数学模型,并通过求解该模型得到结构的应力、位移等信息。
在接触问题中,可以使用有限元方法来模拟物体之间的接触行为。
常见的接触问题包括刚性-刚性接触和刚性-弹性接触。
刚性-刚性接触指两个刚体之间存在接触,并且不考虑变形;而刚性-弹性接触则考虑了至少一个物体的弹性变形。
在有限元方法中,接触问题可以通过引入接触算法来处理。
常用的接触算法包括节点投影法、增广拉格朗日法和无网格法等。
这些算法能够考虑接触面上的力、位移和形状等信息,并将其应用于有限元模型中进行求解。
有限滑移和小滑移现象在接触问题中,当两个物体之间存在相对滑动时,就产生了滑移现象。
有时候,滑动幅度很小,被称为小滑移。
小滑移是一种常见的现象,在许多工程领域都有应用。
有限滑移是指在有限元分析中考虑接触问题时引入的一种特殊技术。
通过引入摩擦系数和界面力来模拟物体之间的摩擦行为,并考虑相对位移导致的接触力变化。
在实际工程中,小滑移和有限滑移现象常常同时存在。
因此,在进行有限元分析时需要同时考虑这两种情况,并合理选择适当的模型和参数。
如何考虑有限滑移和小滑移现象要考虑有限滑移和小滑移现象,可以采取以下步骤:1.定义接触面和接触区域:首先需要确定物体之间的接触面和接触区域,在有限元模型中进行建模。
2.引入摩擦系数:根据实际情况,选择适当的摩擦系数来模拟物体之间的摩擦行为。
摩擦系数可以是常数,也可以是与位移或速度相关的函数。
第18章接触问题有限元分析技术

第18章接触问题的有限元分析技术第1节基本知识接触问题是一种高度非线性行为,需要较大的计算资源,为了进行准确而有效的计算,理解问题的特性和建立合理的模型是很重要的。
接触问题存在两个较大的难点:其一,在求解问题之前,不知道接触区域,表面之间是接触或分开是未知的、突然变化的,这些随载荷、材料、边界条件和其它因素而定;其二,大多数的接触问题需要计算摩擦,有几种摩擦和模型可供挑选,它们都是非线性的,摩擦使问题的收敛性变得困难。
一、接触问题分类接触问题分为两种基本类型:刚体─柔体的接触和半柔体─柔体的接触。
在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体,(与它接触的变形体相比,有大得多的刚度),一般情况下,一种软材料和一种硬材料接触时,问题可以被假定为刚体─柔体的接触,许多金属成形问题归为此类接触;另一类,柔体─柔体的接触,是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有近似的刚度)。
ANSYS支持三种接触方式:点─点、点─面和平面─面。
每种接触方式使用的接触单元适用于某类问题。
二、接触单元为了给接触问题建模,首先必须认识到模型中的哪些部分可能会相互接触,如果相互作用的其中之一是一点,模型的对立应组元是一个节点。
如果相互作用的其中之一是一个面,模型的对应组元是单元,例如梁单元,壳单元或实体单元。
有限元模型通过指定的接触单元来识别可能的接触匹对,接触单元是覆盖在分析模型接触面之上的一层单元。
下面分类详述ANSYS使用的接触单元和使用它们的过程。
1.点─点接触单元点─点接触单元主要用于模拟点─点的接触行为,为了使用点─点的接触单元,需要预先知道接触位置,这类接触问题只能适用于接触面之间有较小相对滑动的情况(即使在几何非线性情况下)。
如果两个面上的节点一一对应,相对滑动又以忽略不计,两个面挠度(转动)保持小量,那么可以用点─点的接触单元来求解面─面的接触问题,过盈装配问题是一个用点─点的接触单元来模拟面─与的接触问题的典型例子。
第8章 接触问题的有限元法

18
小滑动和有限滑动 当选用小滑动公式时,ABAQUS从模拟开始就
建立从属表面和主控表面的关系。ABAQUS确定主 控表面的哪个部分与从属表面的每一个节点发生关 系。这种关系在整个分析中保持不变。如果分析包 括几何非线性,小滑动公式需要考虑主控表面的任 何转动与变形对接触力的影响。如果不包括几何非 线性问题,可忽略主控表面的任何转动和变形,认 为加载路径是固定的。
一对接触面的法线方向应该相反,如果法线方向 错误,ABAQUS理解为过盈接触,因此无法收敛。
17
从属表面和主控表面
ABAQUS采用主控—从属接触算法:从属表面 的节点不能穿透主控表面的任何部分。这种算法对 主控表面没有限制,它可以穿透从属表面。为了获 得接触模拟的最好结果,必须认真和准确地定义从 属和主控表面:
力引起的等效节点力向量
和罚系数有关的矩阵
F 'k+1 = −Λ'T T N cd c − Λ'd '
整体坐标系下接触力等效节点力向量
对称阵 F k+1 = −(N c )T T Λ'T T N cd c − (N c )T T Λ'd '
F k+1 = −Kcd c + F̃ k+1 --系统的等效节点接触力向量
采用有限元法分析接触问题时,需要分别对接触 物体进行有限元网格剖分,并规定在初始接触面上, 两个物体对应节点的坐标位置相同,形成接触对。整 体和局部坐标系下,两个物体由于接触载荷引起的等 效节点力矢量分别记为
3
{ } F Ι = F1Ι , F2Ι , F3Ι T
滚动轴承接触问题数值计算及有限元分析

节点单 元 ,采 用 C wt4 o a 8单 元 进 行 分 析 ,有 限元 模 型如 图 2 示 。然后对 轴承进行 约束 ,在 Y方 向施加 所 了 ~0 0 5mm的位 移约束 ,并且施 加 载荷进 行 求解 。 . 0
图 3为模 型 的网格划 分 ,图 4为 Y方 向的应力 图 ,图 5为其等 效应力 图 。
M A e W n
( c n lg n e fTay a a yM a hneyGr u ., d. Tay a 0 2 Chn ) Te h oo yCe tro iu n He v c i r o p Co Lt , iu n03 0 4, ia
Ab ta t sr c :Th te so h o lr b a i g i r s a c e t h h o y o r z o u i g o h y e o o l g b a i g 6 0 .Th e s r s ft er l e rn s e e r h d wi t e t e r fHe t ,f c sn n t e t p f r l n e rn 2 6 e h i e d f rf t n o h ol g b a i g a d t eb g e ts r s o n n h ieo h o t c r a u d r t e c ra n l a r ac lt d eo r a i ft er l n e rn n h i g s te sp i ta d t e sz ft e c n a t a e n e h e t i o d a e c lu a e . o i W i r sc n a t h o y h s p p rb i st emo e f h o l g b a i g i t He t o t c e r ,t i a e u l h d l er i n e r ANS n a c l ts c n a tp o l ms h t d o t i n n YS a d c l u a e o t c r b e ,me n i , a wh l e
滚动轴承接触问题的有限元分析

滚动轴承接触问题的有限元分析马士垚张进国(哈尔滨工业大学(威海)机械工程系,威海264209)Contact analysis on rolling bearing by finite element methodMA Shi-yao ,ZHANG Jin-guo(Department of Mechanical Engineering ,Harbin Institute of Technology ,Weihai 264209,China )文章编号:1001-3997(2010)09-0008-02【摘要】基于ANSYS 有限元分析软件,建立了滚动轴承接触分析的三维有限元模型,分析得到了轴承滚动体的径向位移、滚动体与内外圈的接触应力云图,并将接触应力结果与Hertz 理论计算的结果对比,计算两者的接近度,进而说明该法分析的可行性,也为轴承的进一步研究提供了理论基础。
关键词:ANSYS ;滚动轴承;有限元;接触分析【Abstract 】A three-dimensional model is first established for rolling bearing based on an FEA soft -ware as ANSYS .The bearing ’s radial displacement 、the contact stress between rolling elements and inner and outer ring is pared the contact stress results of ANSYS with the Hertz results ,see the difference between each other ,so that the feasibility of this method is proved ,also provides theoretical principle for further research.Key words :ANSYS ;Rolling bearing ;Finite element ;Contact analysis中图分类号:TH133.33文献标识码:A*来稿日期:2009-11-131前言轴承是机械传动部分中的重要组成部分,在对轴承的设计与分析中,经常要计算轴承的承载能力、寿命、变形等问题,由于传统的赫兹接触理论在实际应用中存在局限性,只能得到轴承接触应力的近似解,而且求解方法繁琐,利用有限元分析软件ANSYS 对轴承进行接触问题的分析,可以解决所有的赫兹接触问题,方法简洁,易于程式化,结果可视性强,对轴承的分析有一定的指导作用。
Hertz接触问题的有限元分析

link appraisement
喻 琴 马咪娜 李 刚
庆安集团有限公司
;
最大接触应力:
坐标原点位于两圆柱体初始接触点处,X 半接触长度:,其中,,材料
图1 两圆柱体接触
图2 几何模型
图3 平面应变设置
图4 有限元模型
有限元模型
采用4节点四边形单元对两圆柱体接触模型进行网格划
分,由于本文的目的是为了研究两圆柱体之间的Hertz
应力分布情况,故为了提高计算效率并保证计算结果的精度,
对上、下两矩形面网格划分粗一些,对两圆柱体特别是接触
部位网格划分细一些。
经过多次的试算确定计算结果收敛到
稳定的数值,此时单元数为79884,节点数为240960,两
圆柱体接触有限元模型如图4所示。
材料属性
两圆柱体的材料参数为:弹性模量为E1=4000N/
,E=4000N/mm2,泊松比为υ=0.3,υ=0.3。
矩
图5 接触设置
图8 接触应力云图
图6 约束与载荷
图9 穿透量云图
的基础上,仅将两圆柱体之间的接触由无摩擦改为摩擦,并
分别取摩擦系数为0.2、0.5进行计算,其余设置均不变,
图7 约束反力
2.7×10-9mm,可以忽略,说明计算结果是合理的。
参数分析
(1)接触行为分为对称接触和非对称接触两种,确定
接触行为后,再选择支持此行为的接触算法。
为了对两种接
触行为进行对比,在原计算文件的基础上,仅将非对称行
为改为对称行为,相应地将接触算法改为支撑对称行为的。
基于ANSYS的球轴承赫兹接触问题有限元分析

Ab t a t s r c :He t ea t o tc r be o e t r s alb a i g i a a y e s a x mp e i h s p p r b e n s f r r lsi c n a t o lm ft h u t l e r s n l z d a n e a l n ti a e a d o ot e z c p h b n s wa ANS S C n a t u cin a d F M ul i g t c n q e o h o t r r n r d c d Y . o tc n t n E b i n e h i u ft e s f f o d wae ae i to u e .Ma i m o tc t s n eo ma xmu c n a ts e s a d d fr - r t n r o y u i gfe i l — o f x b e s ra e t — u fe o t c lme t o e s f a e n c mp rs n w t h e u t i s a e g t s x b e t — e i l u f c — o s ra e c n a t e n s ft ot r .I o aio i t e r s s o b n l l e h w h l
9 6 x1 q m 8=7 4 9 x1 一m 。 2 8 0r / 。 .2 5 0
的性能与配置要求较高。
浅谈结构有限元分析中的接触问题
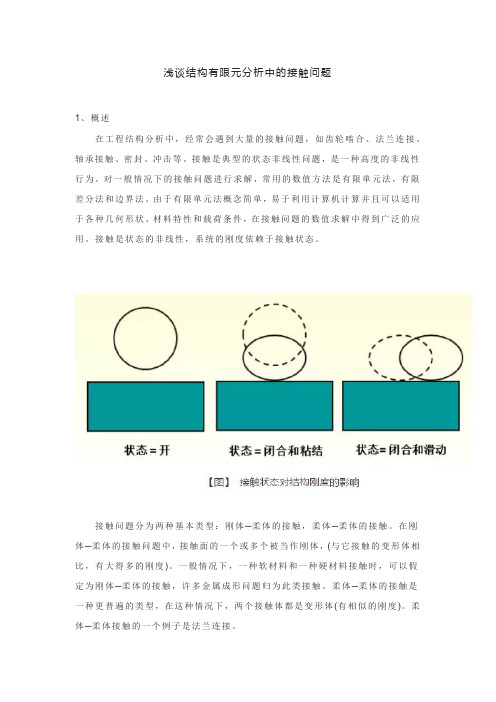
浅谈结构有限元分析中的接触问题1、概述在工程结构分析中,经常会遇到大量的接触问题,如齿轮啮合、法兰连接、轴承接触、密封、冲击等。
接触是典型的状态非线性问题,是一种高度的非线性行为。
对一般情况下的接触问题进行求解,常用的数值方法是有限单元法,有限差分法和边界法。
由于有限单元法概念简单,易于利用计算机计算并且可以适用于各种几何形状、材料特性和载荷条件,在接触问题的数值求解中得到广泛的应用。
接触是状态的非线性,系统的刚度依赖于接触状态。
接触问题分为两种基本类型:刚体─柔体的接触,柔体─柔体的接触。
在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体,(与它接触的变形体相比,有大得多的刚度)。
一般情况下,一种软材料和一种硬材料接触时,可以假定为刚体─柔体的接触,许多金属成形问题归为此类接触。
柔体─柔体的接触是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有相似的刚度)。
柔体─柔体接触的一个例子是法兰连接。
2、接触算法介绍接触问题可描述为求区域内位移场U,使得系统的势能在接触边界条件的约束下达到最小,即式中K、U、F分别为通常有限元位移法中的刚度矩阵、未知结点位移向量和结点荷载向量,为两物体间的穿透量。
接触约束算法就是通过对接触边界约束条件的适当处理,将上式所示的约束优化问题转化为无约束优化问题求解。
根据无约束优化方法的不同,主要可分为罚函数方法、Lagrange乘子法及增广Lagrange乘子法等。
(1)罚函数法数学上要求有限的穿透量在交界面处产生接触力。
保持系统平衡需要此接触力。
为了平衡,必须大于零。
然而,实际的接触体相互不穿透。
因此,为了最高的精度,应使发生在接触界面处的穿透量最小,这意味着,理想的接触刚度应该是个非常大的值。
然而,值太大会引起收敛困难。
如果接触刚度太大,一个微小的穿透将会产生一个过大的接触力,在下一次迭代中可能会将接触面推开,用太大的接触刚度通常会导致收敛振荡,并且常会发散。
第8章 接触问题的有限元法

T T 4
d = {u
c
T P
u
T 1
u
T 2
u
T 3
u
}
Ni = Ni I 3×3
i = 1, 2, 3, 4
为方便引入接触条件,引入局部坐标系
' ' uP uQ = T T (uP uQ ) = T T N c d c
10
二,有限元方程
粘结接触状态 由罚函数法有,局部坐标系下一个接触点对的接触 力引起的等效节点力向量 和罚系数有关的矩阵
间隙
F2 ' Ι = F2 ' ∏ = ± F3' Ι sin α
'
其中: --滑动方向与 x1 轴间的夹角. α 滑动方向与
5
二,接触判定条件
接触求解的迭代过程首先假定可能接触区内各接 触点对的接触状态,根据相应的接触定解条件求解. 但是,一般来说,开始假定的接触状态并不符合实 际,如何确定三种接触状态的分界点是接触问题处 理中最基本的,在有限元中,这一问题可以归结为 确定积分界限的问题.而这一问题只有通过迭代过 程才能求解,每次迭代必须逐个检查接触点对的接 触状态是否需要修改. 接触点对状态判定条件只能用于分析滑动量较 小的情况.对于接触间有较大相对滑动的情况,须 用点-线,点-面或面-面接触条件.这些判定条 件要比点对判定条件复杂得多.
18
小滑动和有限滑动 当选用小滑动公式时,ABAQUS从模拟开始就 建立从属表面和主控表面的关系.ABAQUS确定主 控表面的哪个部分与从属表面的每一个节点发生关 系.这种关系在整个分析中保持不变.如果分析包 括几何非线性,小滑动公式需要考虑主控表面的任 何转动与变形对接触力的影响.如果不包括几何非 线性问题,可忽略主控表面的任何转动和变形,认 为加载路径是固定的. 小滑移有两种算法:点对面和面对面.面对面 小滑移有两种算法:点对面和面对面 点对面和面对面.面对面 算法的应力的计算结果的精度比较高,并且可以考 虑板壳和膜初始厚度.
ansys有限元接触分析体会

在ansys 中,有专门的接触单元用于解决各种不同的接触问题。
对于点对点接触问题有二维点对点接触单元CONTAC12 、三维点对点接触单元CONTAC52 和CONTAC178 。
为了能够使用这些点对点接触单元,需要预先知道明确的接触位置,即使在几何非线性的情况下,接触面之间也只能允许有较小的相对滑动。
对于面对点接触问题,常用的有用来模拟柔性点对刚性面接触单元CONTAC26 、二维点对面接触单元CONTAC48 、三维点对面接触单元CONTAC49 、CONTAC175. 这类接触单元,不需要预先知道确切的接触位置,二期接触面之间也不需要保持一致的网格,同时允许有大的变形和相对滑动。
对于面对面接触问题,有二维 2 节点的低阶线接触单元CONTAC171 、3 节点的高阶抛物线接触单元CONTAC172 、三维4 节点的缔结四边形接触单元CONTAC173 、8 节点的高阶四边形接触单元CONTAC174. 由于面跟面之间的相互接触,有一个目标面和接触面的问题,因此使用这些接触单元必须同时使用配对单元(用来模拟目标面和目标单元)。
同CONTAC171 和CONTAC172 配对的是二维目标单元TARGET169 ,同CONTAC173 和CONTAC174 配对的是三维目标单元TARGET170. 面对面单元比点对面单元具有更好的性能、对接触的位置、范围要求更宽,但是接触的求解结果却更好。
三大类接触单元的使用并不是限制的很死,只要对问题的本质理解清楚,就能灵活运用。
比如两个面上的节点一一对应,相对滑动又可忽略不计,两个面的挠度、转动保持小量,那么就可以用点对点接触单元来模拟面对面的接触问题。
又如能通过一组节点来定义接触面,生成多个单元,那么就可以用点对面的对接触单元来模拟面对面的接触问题。
接触单元就像皮肤一样覆盖在下面的有限元模型上,会自动跟踪整个变形过程。
对于点对点的接触情况,只要对节点赋予点对点接触单元即可。
有限元接触分析

第五章接触问题的非线性有限元分析5.1引言在工程结构中,经常会遇到大量的接触问题。
火车车轮与钢轨之间,齿轮的啮合是典型的接触问题。
在水利和土木工程中,建筑物基础与地基,混凝土坝分缝两侧,地下洞室衬砌与围岩之间,岩体结构面两侧都存在接触问题。
对于具有接触面的结构,在承受荷载的过程中,接触面的状态通常是变化的,这将影响接触体的应力场。
而应力场的改变反过来又影响接触状态,这是一个非线性的过程。
由于接触问题对工程实践的重要性,本章将作为专门问题进行研究。
最早对接触问题进行系统研究的是H. Hertz,他在1882年发表了《弹性接触问题》一书中,提出经典的Hertz弹性接触理论。
后来Boussinesg 等其他学者又进一步发展了这个理论。
但他们都是采用一些简单的数学公式来研究接触问题,因而只能解决形状简单(如半无限大体)、接触状态不复杂的接触问题。
二十世纪六十年代以后,随着计算机和计算技术的发展,使应用数值方法解决复杂接触问题成为可能。
目前,分析接触问题的数值方法大致可分为三类:有限元法、边界元法和数学规划法。
数学规划法是一种优化方法,求解接触问题时,根据接触准则或变分不等式建立数学模型,然后采用二次规划或罚函数方法给出解答。
边界元方法也被用来求解接触问题,1980年和1981年,Anderson先后发表两篇文章,用于求解无摩擦弹性接触和有摩擦弹性接触问题。
近年来虽有所发展,但仍主要用于解决弹性接触问题。
就目前的发展水平来看,数学规划法和边界元法只适合于解决比较简单的弹性接触问题。
对于相对复杂的接触非线性问题,如大变形、弹塑性接触问题,还是有限元方法比较成熟、比较有效。
早在1970年,Wilson和Parsons提出一种位移有限元方法求解接触问题。
Chan和Tuba,Ohte等进一步发展了这类方法。
它的基本思想是假定接触状态,求出接触力,检验接触条件,若与假定的接触状态不符,则重新假定接触状态,直至迭代计算得到的接触状态与假定状态一致为止。
第8章 接触问题的有限元法

一、接触面的连接条件
在有限元位移法中,借助于恰当的选择位移模式 和形函数可以保证连续体中单元内部的连续性和跨单 元的连续性,而无需增加其他条件。但在接触问题中, 除了各相互接触物体内部变形的协调性以外,还必须 保证各接触物体之间在接触边界上变形的协调性,不 可相互侵入。同时还包括摩擦条件---称为接触面的连 接条件。
小滑移有两种算法:点对面和面对面。面对面 算法的应力的计算结果的精度比较高,并且可以考 虑板壳和膜初始厚度。
19
有限滑动接触公式要求确定主控表面的哪一部分 与从属表面的哪些节点保持接触。这是很复杂的计算, 特别是两个表面都在变化的时候。两个变形表面间的 有限滑动仅应用于二维问题---平面应力、平面应变和 轴对称问题。
一个刚性面和一个变形面间的接触的有限滑动 相对简单,在主控表面是刚性的情况下,有限滑动 可应用于三维问题。
对于有限滑移,在整个分析过程中,尽量不要 让从属面上的节点落到主控表面的外面,特别是, 不能落到主控表面的背面。
小滑移问题的接触压强总是根据未变形时的接 触面积来计算,有限滑移问题的接触压强则是根据 变化的接触面积来计算。
接触点对状态判定条件只能用于分析滑动量较 小的情况。对于接触间有较大相对滑动的情况,须 用点-线、点-面或面-面接触条件。这些判定条 件要比点对判定条件复杂得多。
6
接触判定条件
7
第二节 接触问题的罚函数法
产生接触的两个物体必须满足无穿透约束条件, 数学上施加无穿透约束的方法有拉格朗日乘子法, 罚函数法以及直接约束法。用拉格朗日乘子法、罚 函数法或增广拉格朗日乘子法将接触约束条件引入 到系统的总泛函中,再根据变分原理或虚功原理得 到系统的总体平衡方程,求解的迭代过程实际上是 一个搜索接触状态的过程。ABAQUS/Standard中 应用的是罚函数法—将约束条件引入势能泛函分析。
接触问题的显式与隐式有限元方法研究

接触问题的显式与隐式有限元方法研究接触问题是固体力学中的一个重要问题,它在机械、航空航天、汽车制造等领域都有着广泛的应用。
有限元方法是解决接触问题的一种有效手段,其中显式方法和隐式方法是两种常见的有限元方法。
显式方法指的是在求解过程中,通过显式地列出接触条件和摩擦力,从而求解接触问题。
显式方法的优点是计算过程简单,易于实现,且能够考虑接触面间的摩擦力。
但是,显式方法也存在一些缺点,例如难以处理复杂的接触形状和非线性材料性质,此外,显式方法还需要对摩擦系数进行假设,否则无法求解。
隐式方法指的是在求解过程中,通过隐式地考虑接触条件和摩擦力,从而求解接触问题。
隐式方法的优点是能够自适应地计算接触面间的摩擦力,且能够处理复杂的接触形状和非线性材料性质。
但是,隐式方法的计算过程比较复杂,需要对材料性质和接触面进行精确的建模,此外,隐式方法还需要对摩擦系数进行假设,否则无法求解。
为了验证显式方法和隐式方法的有效性,我们通过实例进行了计算。
我们选取了一个简单的接触问题,即两个平行的金属板之间的接触问题,其中一个金属板的长度为 100mm,宽度为 50mm,厚度为 1mm,另一个金属板的长度为 100mm,宽度为 50mm,厚度为 2mm。
两个金属板之间的接触面为 50mm×50mm。
我们分别采用了显式方法和隐式方法进行计算,并比较了计算结果。
显式方法的计算过程如下:我们首先建立有限元模型,然后列出接触条件和摩擦力,最后求解得到接触压力和摩擦力。
显式方法的计算结果如下:接触压力为 999.5N,摩擦力为 29.1N。
隐式方法的计算过程如下:我们首先建立有限元模型,然后采用隐式方法计算接触面间的摩擦力,最后求解得到接触压力和摩擦力。
隐式方法的计算结果如下:接触压力为 999.5N,摩擦力为 29.1N。
通过比较计算结果,我们可以发现,显式方法和隐式方法都能够准确地计算接触问题,但是,隐式方法的计算结果更加准确,能够考虑接触面间的摩擦力,而显式方法需要对摩擦系数进行假设,否则无法求解。
有限元分析接触类问题

有限元接触分析
题目条件:由两个厚壁圆筒组成的组合圆筒,材料为Q235钢,弹性模量E=2.1e11Pa,泊松比μ=0.3。
内筒半径为r1=0.1m,r2=0.1505m,外筒半径r2=0.1495m,r3=0.2m,两筒长为0.8m,承受内压p=10MPa。
所求问题:试用有限元方法分析组合圆筒的受载情况。
解题步骤:
1 建模及计算
设置单元类型:选择单元类型为plane42和solid45。
建立同心圆面,用三边形网格划分两面,网格大小为0.05m。
创建放样直线,如图1
图1 初步模型
使用Extrude Areas Alone Lines建立模型,如图2:
图2 模型及网格划分
对划分好的模型设置接触对,接触对设置情况如图3,设置完需要检查接触对是否闭合,否则模型将会无法实现接触。
图3 接触对设置
加载边界条件,模型需要固定起来,所以可以在两断面加对称约束,使其无刚体位移。
约束加载如图4所示。
图4 边界条件的加载
施加载荷。
载荷大小为10MPa,作用与组合圆筒的内壁。
加载情况如图5所示。
设置材料参数及载荷步
设置材料弹性模量为2.1e11,泊松比为0.3,摩擦系数为0.05。
设置步长为1,子步为30。
计算并保存结果。
图5 添加载荷
2 结果分析
观察米塞斯应力分布图6,最大米塞斯应力为22.3MPa,而且还是位于载荷添加处,所以比较可知满足第四强度理论。
圆筒符合安全性要求。
图6 米塞斯应力分布图。
接触问题的有限元分析

U
1 2
λT
E
p
1
λ
6.1 接触边界的有限元算法
(2)接触约束算法
2) Lagrange 乘子法与增广Lagrange 乘子法
U
1 2
λT
E p
1
λ
min
U,
λ
1 2
UT
K
U
UT
F
g
U
T
λ
1 2
λT
Ep
λ
U
1 2
λT
Ep
1
λ
解收敛于
min U, λ 1 UT K UUT F g U T λ 解
虚力法:用沿边界的虚拟等效压力来模拟接触状态, 这样在每次迭代中并不重新形成刚度矩阵,所做的只是 回代工作。
有限元混合法:以结点位移和接触力为未知量,并 采用有限元形函数插值,将接触区域的位移约束条件和 接触力约束条件均反映到刚度矩阵中去,构成有限元混 合法控制方程
6.1 接触边界的有限元算法
(1)直接迭代法
惩罚函数法对接触约束条件的处理是通过在势能泛函中
增加一个惩罚势能。
p
U
1 2
P T
EP
P
惩罚因子
嵌入深度,是节点位移的函数
接触问题就等价于无约束优化问题:
min U U p U
K K U FF
p
p
6.1 接触边界的有限元算法
(2)接触约束算法
1)罚函数方法
K K U FF
p
6.1 接触边界的有限元算法
(2)接触约束算法 2) Lagrange 乘子法与增广Lagrange 乘子法
min U, λ 1 UT K UUT F g U T λ
有限元基础理论课件第7章接触分析
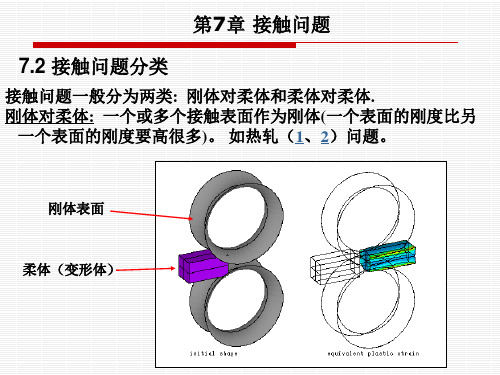
TARGE169 - 2-D Target Segment TARGE170 - 3-D Target Segment
第7章 接触问题
7.4 接触分析步骤
只有面-面接触单元上能提取接触应力 接触面一般是柔性面(刚度较低的面),目标面一般是刚 度较大。接触面和目标面合称“接触对”,通过相同的单 元实常数来识别和定义“接触对”。
面-面 :接触区域未知, 并且允许大滑动,能提取接触应力(常用)
CONTA17urface Contact CONTA172 - 2-D 3-Node Surface-to-Surface Contact CONTA173 - 3-D 4-Node Surface-to-Surface Contact CONTA174 - 3-D 8-Node Surface-to-Surface Contact
第7章 接触问题
7.3 接触单元(conta)与目标单元(targe)
接触单元: 节点-节点 : 接触的最终位置事先是知道的,不能提取接触应力.
CONTAC12 - 2-D Point-to-Point Contact CONTAC52 - 3-D Point-to-Point Contact CONTA178 - 3-D Node-to-Node Contact
面-面(柔-柔)接触分析步骤:
➢建立模型,划分网格(全部划分); ➢定义刚性目标面(也变形,只不过刚度较大或形状简单点); ✓定义柔性接触面; ✓设置接触单元的实常数; ✓设置边界条件; ✓设置求解选项和载荷步(非必须); ✓求解; ✓查看结果。
柔-柔接触分析例题与步骤
(1)面-面(刚-柔)接触分析步骤:
✓建立模型,将柔体划分网格(刚体不划分); ✓定义刚性目标面(可同时定义pilot); ✓定义柔性接触面; ✓设置接触单元的实常数; ✓设置边界条件; ✓设置求解选项和载荷步(非必须); ✓求解; ✓查看结果。
橡胶接触的有限元分析

圆球与橡胶垫接触的有限元分析一、问题描述分别模拟钢球以及橡胶球在以=0.95F N 的垂向载荷挤压硅橡胶(PDMS )垫时的变形情况。
钢球直径1=12.7mm Φ,硅橡胶圆盘直径2=50mm Φ,厚度d=5mm .已知硅橡胶杨氏模量 1.0363E MPa =,泊松比0.499σ=,为超弹性材料。
分别模拟小球为刚性材料和为橡胶材料时两种情况下硅橡胶垫的变形情况。
二、有限元分析由于橡胶本构关系的非线性化,以及橡胶制品在应用时的大变形、接触非线性边界条件使其工程模拟变的非常困难。
模拟的准确性与采用的本构关系模型以及模型中材料常数测试的准确性有密切关系。
本次分析以橡胶中常用的Mooney-Rivlin 材料作为橡胶的本构模型。
1、 材料参数的确定Mooney-Rivlin 模型的基本理论不赘述,通过查阅相关文献得知Mooney-Rivlin 模型中材料常数与材料弹性模量有如下关系:10016()E C C =+并且有经验公式:01100.25C C =可以计算Mooney-Rivlin 模型中材料常数1001138173,34543C C ==,用于有限元分析中定义材料。
2、 钢球与硅橡胶盘接触由于钢球与硅橡胶接触时钢球变形可以忽略,可以把钢球看做刚体(Rigid body ),建有限元模型如下:图1 刚性球接触时的有限元模型分析结果如下:图2 刚性球接触时圆盘变形云图最大变形为图中红色部分,为42.82100.282y m mm-∆=⨯=3、橡胶球与硅橡胶圆盘接触将球划分网格,并定义为可变性体(Deformable body)有限元模型如下:图3 橡胶球与硅橡胶圆盘接触时的有限元模型将球看做可变性体,与圆盘赋相同的材料进行分析,圆盘变形云图如下:图4 橡胶球接触时圆盘变形云图最大变形为图中红色部分,为41.62100.162z m mm -∆=⨯=。
有限元法在分析轴承接触问题中的应用

寸很重要 " 从上 面 的 分 析 结 果 和 相 应 参 考 资 料 可 以 得出 ! 非接触区的单元尺寸一般可以确定为整体尺寸 的十分之一以下 ! 接触区的单元尺寸一般定在理论计 算得到的接触区尺寸的五分之一以下 ! 这样得到的分 析结果具有一定的可靠性 ! 和理论值的误差在 @a 以 内 " 这个结论对于分析复杂的接触问题同样适用 " # $ 一般 来 说 ! @ 4’ = > =分析结果随着分网等级 的提高而收敛 于 真 值 ! 所 以 在 对 分 析 结 果 的 判 定 上! 可以通过对上一 次 分 析 模 型 的 细 化 ! 重 新 分 析! 比较 前后两次结果相拟和的程度 ! 来确定所分析的接触问 题的真实解的大小和范围 " 参考文献 #
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
增广Lagrange 乘子法:最直接的一种方法是构造修 正的势能泛函:
U U p U c U
6.1 接触边界的有限元算法
(2)接触约束算法 2) Lagrange 乘子法与增广Lagrange 乘子法
U U p U c U
相应的控制方程为:
K Kp
G
GT 0
U
λ
F Fp
U
1 2
λT
E
p
1
λ
6.1 接触边界的有限元算法
(2)接触约束算法
2) Lagrange 乘子法与增广Lagrange 乘子法
U
1 2
λT
E p
1
λ
min
U,
λ
1 2
UT
K
U
UT
F
g
U
T
λ
1 2
λT
Ep
λ
U
1 2
λT
Ep
1
λ
解收敛于
min U, λ 1 UT K UUT F g U T λ 解
惩罚函数法对接触约束条件的处理是通过在势能泛函中
增加一个惩罚势能。
p
U
1 2
P T
EP
P
惩罚因子
嵌入深度,是节点位移的函数
接触问题就等价于无约束优化问题:
min U U p U
K K U FF
p
p
6.1 接触边界的有限元算法
(2)接触约束算法
1)罚函数方法
K K U FF
p
接触问题基本类型:刚体─柔体接触,柔体─柔体接 触。
在刚体─柔体的接触中,接触面的一个或多个被当作 刚体(与它接触的变形体相比,有大得多的刚度),一般情 况下,一种软材料和一种硬材料接触时,问题可以被假定 为刚体─柔体的接触,许多金属成形问题归为此类接触;
而柔体─柔体的接触,是一种更普遍的类型,在这种 情况下,两个接触体都是变形体(有近似的刚度)。
2
系统的控制方程写为:
K GT E p
G
U F GT E p
g0
U
6.1 接触边界的有限元算法
(2)接触约束算法
3) 数学规划法 基于势能或余能原理,并利用变分不等式等现代数学方
法而导出,最初该方法是针对无摩擦接触问题提出,它利用 了无摩擦接触问题的非穿透条件和互补条件:
un 0 pn 0
6.1 接触边界的有限元算法
(1)直接迭代法 在用有限元位移法求解接触问题时,首先假设初始
接触状态形成系统刚度矩阵,求得位移和接触力后,根 据接触条件不断修改接触状态,重新形成刚度矩阵求解, 反复迭代直至收敛。
每次迭代都要重新形成刚度矩阵,求解控制方程, 而实际上接触问题的非线性主要反映在接触边界上,因 此,通常采用静力凝聚技术,使得每次迭代只是对接触 点进行, 大大提高了求解效率。
6.1 接触边界的有限元算法
(2)接触约束算法 2) Lagrange 乘子法与增广Lagrange 乘子法
min U, λ 1 UT K UUT F g U T λ
2
代入
g
U
g0
U
g U U
U
g0
U
GU
K GT U F
G
0
λ
g0
U
Lagrange 乘子法中 接触约束条件可以精 确满足
6.1 接触边界的有限元算法
(2)接触约束算法
1)罚函数方法 障碍函数法假设接触面之间充满某虚拟物质,在未接触
时其刚度趋于零,不影响物体的自由运动,在接触时其刚度 变得足够大,能阻止接触物体之间的相互嵌入。
常用的间隙元等方法均属于此类,该方法处理简单,编 程方便,只是在传统有限元分析中增加一种单元模式而已;
g0
U
考虑Lagrange 乘子的物理意义,可将其用接触对的接 触应力代替,通过迭代计算得到问题的正确解。
在迭代过程中,接触应力作为已知量出现,这样既吸
收了罚函数方法和Lagrange 乘子法的优点,又不增加系统 的求解规模,而且收敛速度也比较快。
另一种增广Lagrange 乘子法主要是为了弥补 Lagrange 乘子法中控制矩阵存在零主元的弱点:
《有限元基本理论及应用》
接触问题的有限元分析
接触问题存在两个较大的难点: 1)在求解问题之前,接触区域不确定,表面之间是否接 触或分开是未知的、瞬时变化的,它由载荷、材料、边界 条件和其它因素而定; 2)大多的接触问题需要计算摩擦,有多种摩擦及其模型 可供挑选,但它们都是非线性的,摩擦使问题的收敛性变 得困难。
p
n
u n
0
经有限元离散后,无摩擦接触问题被归结为二次规划
( 线性互补) 问题求解。把摩擦条件可以写成如下带导数的
互补形式:
wT
pT 0
0
0
6.1 接触边界的有限元算法
(2)接触约束算法
3) 数学规划法 对摩擦条件的另一种处理方法是引进惩罚因子,然后仿
照塑性力学将摩擦接触条件表示成有惩罚因子的互补形式:
pT
ET u T
g pT
v 0
v 0
v 0
0
有了上述摩擦接触条件的互补关系,就可以利用参
变量变分原理或虚功原理建立摩擦接触问题的有限元二 次规划(线性互补)模型。
(2)接触约束算法
min
U
1 2
UT
K
U
UT
F
s.t. g U 0
接触约束算法就是通过对接触边界约束条件的适当
处理,将约束优化问题转化为无约束优化问题求解。
根据无约束优化方法的不同,可分为罚函数方法和
Lagrange 乘子法。
1)罚函数方法
将接触非线性问题转化为材料非线性问题。分为障
碍函数法和惩罚函数法
虚力法:用沿边界的虚拟等效压力来模拟接触状态, 这样在每次迭代中并不重新形成刚度矩阵,所做的只是 回代工作。
有限元混合法:以结点位移和接触力为未知量,并 采用有限元形函数插值,将接触区域的位移约束条件和 接触力约束条件均反映到刚度矩阵中去,构成有限元混 合法控制方程
6.1 接触边界的有限元算法
(1)直接迭代法
K
L
J 0
U C
F
0
对弹塑性接触问题,在求解过程中接触非线性和材料 非线性都需要迭代求解。
通常是利用系统刚度矩阵的变化来反映材料非线性的 影响,在每次塑性修正迭代过程中都要结合对接触状态的 判断进行接触迭代计算,并且,荷载增量更是受到不允许 在一个增量步中出现两种非线性的限制。
6.1 接触边界的有限元算法
p
其中
K
p
P
T
U
E p
P
U
K
p
P
T
U
E p
P
0
由于人为假设了很大 的罚因子,可能引起 方程的病态。
2) Lagrange 乘子法与增广Lagrange 乘子法
c
U
1 2
g
U
T
λ
min
U
1 2
UT
K
U
U T
F
s.t. g U 0
约束最小化问题转化 为无约束最小化问题
