环境规划与管理计算题
环境管理与规划复习题答案

环境管理与规划复习题答案一、名词解释1.市场价格法:直接根据物品或服务的价格,利用因环境质量变化引起的产量和利润的变化来计量环境质量变化的经济效益或经济损失。
2.机会成本法:是指把一定的资源用在生产某种产品时,所放弃的对其他产品生产中所能获得的最大效益。
3.防护费用法:环境资源破坏时带来的经济损失,可以通过为防护该环境资源不受破坏所支付的费用来推断。
4.水环境规划:对某一时期内的水环境保护目标和措施所作出的统筹安排和设计。
5.耗氧有机物的水环境容量:水环境所能容纳的耗氧有机物的最大容许量。
该容量即通常所说的水环境容量。
6.空间结构理论:研究人类活动空间分布及组织优化的科学。
7.大气环境质量预测:为了了解未来一定时期的经济、社会活动对大气环境带来的影响,以便采取改善大气环境质量的措施。
8.社区:指居住在某一个特定区域内的、共同实现多元目标的人所构成的群体。
9.环境预测:指根据人类过去和现在已掌握的信息、资料经验和规律,运用现代科技手段和方法,对未来的环境状况和环境发展趋势及其主要污染物和污染源的动态变化进行描述和分析。
10.环境规划指标:是直接反映环境现象以及相关的事物,并用来描述环境规划内容的总体数量和质量的特征值。
11.环境容量:是一个复杂的反映环境净化能力的量,其数值应能表征污染物在环境中的物理、化学变化及空间机械运动性质。
12.规划协调型预测:指通过一定手段,使环境与经济协调发展所能达到的环境状况。
13.环境规划目标:是环境规划的核心内容,是对规划对象未来某一阶段环境质量状况的发展方向和发展水平所作的规定。
14.环境评价:是在环境调查分析的基础上,运用数学方法,对环境质量、环境影响进行定性和定量的评述,旨在获取各种信息、数据和资料。
15.总量控制:就是依据某一区域的环境容量确定该区域内污染物容许排放总量,再按照一定原则分配给区域内的各个污染源,同时制定出一系列政策和措施,以保证区域内污染物排放总量不超过区域容许排放总量。
环境规划与管理期末考试重点(含题目和答案)【重点修改版】

§1 环境规划与管理概述1 P.19 1什么是环境管理?如何理解其内涵?答:环境管理是对损害人类自然环境质量的人的活动(特别是损害大气、水和陆地外貌的质量的人的活动)施加影响。
环境管理的内涵是规范和限制人类的观念和行为。
2 P。
19 2什么是环境规划,如何理解其内涵?答:环境规划是国民经济和社会发展的有机组成部分,是环境管理的首要职能,是环境决策在时间、空间上的具体安排,是规划管理者对一定时期内环境保护目标和措施作出的具体规定,是一种带有指令性的环境保护方案,其目的是在发展经济的同时保护环境,使经济与社会协调发展。
环境规划的实质是一种克服人类经济社会活动和环境保护活动盲目和主观随意性的科学决策活动。
3 P.19 3简述环境规划与环境管理的关系。
答:规划职能是环境管理的首要职能。
环境目标是环境规划与环境管理的共同核心。
环境规划与管理具有共同的理论基础.4 P。
19 8简述环境规划与管理的基本任务.答:环境管理的基本任务应该是:转变人类社会的基本观念和调整人类社会的行为。
文化决定着人类的行为,只有转变了过去那种视环境为征服对象的文化,才能从根本上去解决环境问题。
从这个意义上来讲,环境文化的建设是环境规划与管理的一项长期的根本的任务。
人类的社会行为分为政府行为、市场行为和公众行为三种。
这三种行为都可能会对环境产生不同程度的影响。
因此,调整人类社会行为,提倡环境友好型行为是环境规划与管理的基本任务。
5 P。
19 10说明环境规划与管理的主要内容,并归纳本书的基本框架。
答:1 环境规划的内容(1)环境规划的基本内容:包括环境规划的原则和程序、环境目标和指标体系、环境评价和预测、环境功能区划、环境规划方案的设计和比较以及环境规划的实施。
(2)流域水环境规划:包括水环境功能区划、水环境容量和水环境保护目标、水环境质量目标、流域水环境控制规划等。
(3)城市环境规划:包括城市大气污染控制规划、城市水环境规划、固体废物规划管理、噪声污染控制规划等。
环保工程环境规划与管理考核试卷

B.提高就业
C.降低环境质量
D.提升环保水平
20.以下哪项不属于循环经济的核心原则?()
A.资源减量化
B.资源循环利用
C.污染物排放最小化
D.资源消耗最大化
二、多选题(本题共20小题,每小题1.5分,共30分,在每小题给出的四个选项中,至少有一项是符合题目要求的)
1.环境规划的主要内容包括()
D.资源消耗最大化
三、填空题(本题共10小题,每小题2分,共20分,请将正确答案填到题目空白处)
1.环境规划的基本任务是____________________。
2.环保工程主要包括____________________、____________________和____________________等方面的内容。
B.加强环境监测与执法
C.放宽环保政策
D.减少环保投资
8.以下哪种方法不属于噪声污染防治措施?()
A.噪声源控制
B.噪声传播途径控制
C.噪声受体控制
D.增加噪声污染源
9.生态保护的主要目标是()
A.保护生物多样性
B.加速资源开发
C.破坏生态环境
D.降低生态质量标准
10.以下哪项不属于绿色发展的基本原则?()
B.开发新能源
C.增加化石能源消费
D.减少工业废弃物排放
5.下列哪种污染物是大气污染的主要来源?()
A.二氧化硫
B.氧气
C.氮气
D.二氧化碳
6.水污染防治的主要措施是()
A.提高工业用水重复利用率
B.增加污水排放量
C.降低污水处理标准
D.减少水资源开发
7.以下哪项属于环保法律法规的主要内容?()
《环境规划和管理》试题卷

切勿让任何老师知道《环境规划与管理》试题一、不定向选择题1.环境规划的基本原理是使得在保证环境目标(环境质量)或不超过环境容量的前提下,( D )。
P8或者P3A.环境效益达到最大B.社会效益达到最大C.环境污染降到最低 D. 使得所有的效益和损失的总和为最大2.环境规划与国民经济和社会发展规划关系最密切的有(ABCD )。
P4A.人口与经济部分B.生产力的布局和产业结构C.因经济发展产生的污染D.国民经济能够给环境保护提供多少资金3.城市总体规划和城市环境规划的相互关联主要有(ABD )。
P6A.城市人口与经济B.城市的生产力和布局C.城市规模D.城市的基础设施建设4.限期治理的对象主要包括(BD )。
百度A.“十五小”企业 B.对环境造成严重污染的排污单位 C.没有按时缴纳排污费的企业 D.在特别保护区域内的工业生产设施超标排放污染物的单位5.环境规划的作用是( ABCD )。
P3A.合理分配排污削减量、约束排污者的行为 B.以最小的投资获取最佳的环境效益C.实行环境管理目标的基本依据 D.保障环境保护活动纳入国民经济和社会发展计划6.下列那一种废物最有可能为危险废物( C )。
A.生活垃圾 B.包装垃圾 C.电镀污泥 D.生活污水处理厂的污泥7.环境规划的特征有( ABCD )。
P6~7A.区域性B.动态性C.政策性强D.信息密集8.环境规划的原则有(ABCD )。
P9~10A.经济建设、城乡建设和环境建设同步原则B.预防为主,防治结合的原则C.强化环境管理的原则 D.遵循生态规律,合理利用环境资源的原则9.按照环境要素,环境规划可以划分为(ABD )。
P12A.大气污染控制规划B.水污染控制规划C.自然保护规划D.固体废物污染控制规划10.环境规划从性质上可分为(AB )。
P14A.污染综合防治规划B.生态规划C.部门环境规划D.专题规划11.固体废物能否用焚烧法处理的最重要依据是( B )。
环境规划与管理考试试题

环境规划与管理考试试题一、选择题1.环境规划的目的是什么?A.保护环境资源B.提高经济发展速度C.增加污染排放量D.扩大城市规模2.环境管理的基本原则包括哪些?A.盲目开发B.可持续发展C.资源浪费D.环境破坏3.以下哪项可以促进环境管理的实施?A.政府监管缺失B.企业盲目追求利润C.公众参与和监督D.环境法律法规的缺失4.环境影响评价的主要内容是什么?A.评价环境友好性B.分析环境问题C.规划环境改善方案D.监督环境施工过程5.环境规划与管理中的“3R”原则是指什么?A.减少、重复、复制B.减少、回收、重复C.减少、回收、重复利用D.减少、获取、再利用二、问答题1.请简要说明环境规划的概念及其意义。
2.环境管理的基本内容包括哪些方面?请结合实际案例进行说明。
3.简要介绍环境影响评价的程序及其重要性。
4.请列举三种常见的环境污染物,并说明对人类健康及环境造成的影响。
5.如何提高公众对环境规划与管理的认知和参与度?请提出具体建议。
三、综合题某城市规划部门计划开展城市环境规划与管理工作,请你作为规划师,针对以下问题提出具体解决方案:1.城市绿地空间不足,导致城市热岛效应严重,如何规划和设计城市绿地系统以缓解热岛效应?2.市区污染物排放量较大,空气质量较差,如何制定有效的污染物控制计划并监督执行?3.市区垃圾处理能力不足,垃圾分类率低,如何设计垃圾处理设施并制定提高市民垃圾分类率的政策和措施?请结合理论知识及实践经验,分析问题并提出完整的解决方案。
本试卷总分100分,考试时间120分钟,请务必认真作答,祝你顺利通过考试!。
环境规划与管理计算题

- 1 0 0 0 0
不 综 合 利 用 0
1
2020/1/16
试 验 △ - 3 0 0 0
不 试 验 b
1
好 2 4 0 0 0
概 率 为 0 . 6
不 好 概 率 为 0 . 4
0
综 合 利 用
1 2 0 0 0
27
• 3.计算状态点①的期望值:24000×0.6+ 0×0.4=14400
• 4.在决策1作出决策。
2020/1/16
8
2020/1/16
12
2020/1/16
13
2020/1/16
14
2020/1/16
15
2020/1/16
16
2020/1/16
17
2020/1/16
18
2020/1/16
19
2020/1/16
20
例题
• 用狄克逊法判断下列测试数据(40.02,40.15 , 40.20,40.13,40.16)中的40.02是否应舍 弃?
• 图示
河流 化工厂1
例题一
化工厂2
湖 泊
化工厂3
思考题
• 1、工业污染源和生活污染源调查的主要内容分别 有哪些?
• 2、常用河流水质模型的各自的适用条件是什么?
人的生产 人的生产
环境质量
商品
物质生产
废弃物 自然资源
环境生产
2020/1/16
6
2020/1/16
7
已知某县 2005 年工农业生产的总产值是 300 万元, COD 排放总量是 250吨,2010 年工农业生产的总产 值是 400 万元,COD 排放总量是 275 吨;若到 2020 年工农业生产的总产值实现翻一番,用弹性系数法求 那时 COD 的年排放总量是多少吨?
《环境规划与管理》—习题库

《环境规划与管理》试题库一、名词解释1、环境管理2、环境规划3、环境容量4、环境承载力5、环境标准6、环境影响评价制度7、环境管理信息系统8、环境统计9、环境标准管理模式10、生命周期评价(LCA)11、环境管理政策12、环境管理制度13、环境管理体制14、环境预测15、环境民事责任16、三同时制度17、环境绩效管理18、环境审计19、绿色管理模式20、有毒有害固体废物21、工业企业环境管理22、环境管理方针23、环境预测24、污染预防25、环境审计26、限期治理污染制度27、环境绩效管理28、环境规划指标29、绿色管理模式30、环境功能分区31、A-P值法32、排污收费制度33、末端治理34、公众参与35、清洁生产36、循环经济37、自然资源38、生物多样性39、管理职能40、三同步三统一方针41、环境保护目标责任制、42、环境纠纷43、环境民事责任44、无过失责任45、举证责任转移46、生态红线47、生态敏感性评价二、填空题1、环境管理具有、、等特点。
2、环境管理的基本任务包括:一是,二是。
3、环境经济学的基本理论包括:、、、、。
4、常规的环境监测包括和。
5、环境标准包括、和。
6、环境管理的手段有:、、、、。
7、环境统计的分析方法有:、和。
8、环境保护许可证分为:,和。
9、工业固体废物实行、、管理对策和的处理原则。
10、环境影响评价的形式分为:、和。
11、环境管理的要素包括、和。
12、环境管理的技术支撑包括:、、、、、、。
13、特殊目的监测包括、和。
14、政府对企业的环境管理包括三个方面的内容:、和。
15、环境管理的手段有:、、、、。
16、环境统计的分析方法有:、和。
17、环境审计包括、、。
18、工业固体废物实行、、管理对策。
19、我国环境管理的基本政策包括:、和。
20、我国环境管理的八项基本制度包括:、、、、、、、。
21、环境管理的对象包括:、、、、。
22、管理基本职能包括、和。
23、我国环境管理体制的三个特征为:、和。
《环境规划与管理》考点

题型结构:1、名词解释15 5×3;2、选择20 20×1;3、简答题30 6×5;4、计算题25 9+8+8;5、论述题10 1×10。
第一章选择1、管理手段包括法律、经济、行政、技术和教育五种手段,人类行为包括自然、经济、社会三种基本行为。
2、环境管理的核心是对人的管理。
3、人是各种行为的实施主体,是产生各种环境问题的根源。
4、大力发展清洁生产和推广“三废”综合利用,将污染消灭在生产过程中,积极采用适宜规模的、先进的、经济的治理技术。
5、对于资源,有狭义和广义的两种理解,狭义的主要指自然资源(如水、气候、生物、土地、矿物、天然风景等);广义的则包括社会资源(如男女劳动力数量、年龄构成、就业比重、劳动技能、文化教育水平等)和经济资源(指在这一地区积累的物质财富,包括工农业生产、交通运输、水利、城镇建设等物质技术基础)。
6、观念的转变是根本.7、人类的社会行为,从行为主体来说,还可以分为政府行为、市场行为和公众行为三种。
8、环境管理按管理范围分类:(简答)(1)流域环境管理;(2)区域环境管理;(3)行业环境管理;(4)部门环境管理。
9、环境管理按管理性质分类:(1)资源环境管理;(2)环境质量管理;(3)环境技术管理。
10、俄罗斯的环境保护规划属于协调型的环境保护规划。
11、复合生态系统具有生产、生活、还原三个功能。
12、人地系统ds〉0的人地冲突型:包括E,F,G三种状态,冲突最厉害的状态为G(ds人〉0,ds地〉0),表现为经济发展衰退,地理环境恶化,可视为人地冲突的最终状态。
13、人地系统是一个开放的复杂巨系统,或称为开放的复杂的人工生态系统.对这一系统进行研究,仅靠常规方法(如模型方法、空间规划方法)是不见效的,其正确而又有效的方法目前只能是综合集成法。
所以综合集成法必然要成为环境规划与管理的有效方法和途径.14、社会亚系统包括人的物质生活与精神生活的各个方面.15、自然亚系统包括人类赖以生存的基本物质环境.16、按横向原则进行分类的环境政策,有环境经济政策、环境保护技术政策和环境管理政策。
最新环境规划与管理试题库

《环境规划与环境管理》试题1级资源环境与城乡规划管理专业本专科《环境规划与环境管理》考试卷课程号(2630160)一、名词解释(每小题4分,计20分)1、环境规划:2、环境质量评价:3、基本环境容量:4、环境管理:5、“一控双达标”:二、简答题(每小题8分,计40分)1、污染物在环境介质中的运动变化形式和特点是什么?2、工业污染源调查有哪些主要内容?3、环境管理的任务和基本职能分别是什么?4、区域环境规划方案制定的中心工作主要包括哪些方面?5、环境规划编制程序。
三、理论分析计算题(每小题8分,计40分)1、已知某县1995 年工农业生产的总产值是300 万元,COD 排放总量是250吨,2000 年工农业生产的总产值是400 万元,COD 排放总量是275 吨;若到2010年工农业生产的总产值实现翻一番,用弹性系数法求那时COD 的年排放总量是多少吨?、某造纸厂使用矩形排水渠排水,现测得水渠宽度0.6m,水深是0.7m,平均流速0.12m/s,COD浓度145mg/L(g/m3),求该厂年排放COD总量。
、S-P模型的基本方程为:请回答S-P模型的假设是什么。
4、下表是高斯模式的浓度扩散公式汇总。
请填写出其适用条件。
5、污水处理厂的位置规划某城市有 3 个工厂排放污水,拟集中于污水处理厂进行污水处理。
已知工厂的污水排放量,输送每一方污水的每公里费用Ci,试决定污水处理厂的坐标位置,使总输水投资最小。
项目食品厂酿造厂造纸厂Qi污水量(m3/d) 420 350 750Xi 20 80 90Yi 30 100 10Ci($/km.m3) 1.2 1.5 0.8表污水处理厂位置求解的表格形式和结果求解结果:污水处理厂位置的坐标:6.7108,3.6036时,使总输水投资为最小,年输水费7899元。
《环境规划与环境管理》试题2级资源环境与城乡规划管理专业本专科《环境规划与环境管理》考试卷课程号(2630160)一、名词解释(每小题4分,计20分)1、环境质量:2、环境:3、环境质量影响评价4、环境规划指标:5、环境质量指数:二、简答题(第1小题4分,第5小题10分,其余小题8分,计40分)1、中国环境管理八项制度是哪些制度?2、环境规划管理的工作程序3、环境规划必须依据哪些预测做出?4、环境影响报告书的内容5、请说明大气环境影响评价技术工作程序。
环境管理与规划(成考专升本考期末真题与答案,可直接复制)

环境管理与规划(成考专升本考试题与答案)一、单选题1.“以新带老”的原则就是____A以新建项目管理带动老污染治理B以新技术改造带动老产品更新C以新管理对策代替老管理对策正确答案A2.环境管理的核心是对__的管理。
A物B人C技术D资金正确答案B3.环保部门在海洋建设项目管理方面具有__权。
A执法监督B执法C监督D管理正确答案C4. 粒径分别为16 um及8 um的两种颗粒在同一旋风分离器中沉降,则两种颗粒的离心沉降速度之比为__ (降在斯托克斯区) ( )。
A2 B4 C1 D1/2正确答案B5. 下列叙述中那些不属于环境因素( )A粉尘排放B电能消耗C煤气泄漏D锅炉燃烧正确答案D6. 相关方是指哪些团体或个人( )A组织附近的居民和单位B关注组织的环境行为的团体和个人C受组织的环境行为影响的团体和个人 D B和C正确答案D7. 层流与湍流的本质区别是( )。
A湍流流速大于层流流速B湍流的流动阻力大,层流的流动阻力小C湍流的雷诺数大于层流的雷诺数: D层流无径向脉动而湍流有径向脉动。
正确答案D8. 环境管理主要是针对___而言的一种管理活动A 环境污染B原生环境问题C次生环境问题D生态破坏正确答案C9. 环境管理学的基本理论:三种生产理论、界面活动理论、冲突协同理论A对B错正确答案A10. 具有中国特色的环境政策是。
A预防为主B谁污染谁治理C强化管理正确答案C二、多选题1. 当前产业结构调整正在向“三化”方向发展。
“三化”指的是__A资源利用合理化B生产过程无害化C废物产生最小化D资源利用最大化正确答案ABC2. ___是依据国家环境法律规定落实地方政府环境责任的行政管理制度。
A环境保护目标责任制B污染限期治理C城市环境综合整治定量考核D污染强制淘汰制度正确答案AC3. 建设项目环境管理包括三个阶段,其中第二阶段属于施工___审批阶段,第三阶段属于___A竣工验收B施工C立项正确答案AB4. 环境总是相对于某个_________而言的,因此说环境是一个______________概念。
环境规划题目汇总--删减第二版

1、什么是环境容量?答:在人类生存和自然生态不致受害的前提下,某环境所能容纳污染物的最大负荷量。
2、什么是环境承载力?答:某时刻环境系统所能承受的人类社会、经济活动的极限值(阈值)。
环境承载量:某时刻环境系统所承受的人类系统(对他)的作用量3、简述环境承载力理论答:环境承载量在一定时空条件下是有限度的,社会、经济的发展不应超越环境承载力,否则将造成生态破坏和环境污染,应通过规划不断提高环境承载力,在环境承载力范围内制定社会经济发展的最优方案。
4、人地系统遵循熵方程?人地系统协调共生状态的熵变类型?(可参考课本P45的答案)答:熵变方程:ds=d i s+d e sd i s---人地系统内部相互作用过程产生的熵。
根据热力学第二定律:d i s≧0(可逆过程=0,不可逆>0)d e s---人地系统和外界的熵交换(可正、可负、可零)ds---人地系统的熵变,可以衡量人地关系状态的变化ds<0 熵值降低---稳定、有序---协调共生ds>0 熵增---混乱、无序---人地冲突ds=0 熵值不变---维持原有状态---警戒协调ds=? 熵变无规律---方向不定---混沌1、确定环境规划目标应遵守哪些原则?(1)以规划区环境特征、性质和功能为基础(2)以经济社会发展的战略思想为依据(3)应当满足人们生存发展对环境质量的基本要求(4)应满足现有技术经济条件(5)能作时空分解和定量化3、什么叫环境功能区划?依据社会经济发展需要和不同地区在环境结构、环境状态和使用功能上的差异,对区域进行合理划分。
4、设计环境规划方案应该遵循哪些原则?(1)善用信息,紧指目标(2)以提高资源利用率为根本途经(3)遵循国家或地区有关的政策法规第三章(李俊杰、张亦楠)1、环境规划指标体系的类型?类型:环境质量指标、污染物总量控制指标、环境规划措施与管理指标、相关指标(经济指标、社会指标、生态指标)2、环境规划实施的基本措施是什么?1.采取协调和审议的措施:(1)规划部门内部的协调和调整(2)与有关部门进行协调和调整(3)与区域周围邻近地区间的协调和调整(4)与国家办事机构的协调和调整2.组织管理方面的措施(1)制定资源利用开发标准(2)统计报表制度(3)依法控制保证规划的实施3.科学研究方面的措施(1)协调发展规划方法的研究(2)生态工程工艺的研究3、环境预测的主要内容由:社会和经济发展预测、环境容量和资源预测、环境污染预测、环境治理和投资预测、生态环境预测名词解释4、环境功能区划环境功能区划依据社会经济发展需要和不同地区在环境结构、环境状态和使用功能上的差异,对区域进行合理区划。
《环境规划与管理》期末考试复习题及参考答案.docx

环境规划与管理复习题(课程代码272331)一、选择题1.宏观环境管理的实施主体并对区域环境质量负责的是(B)。
A.环保部门B.地方政府C.行业主管部门2.城市环境综合整治定量考核制度是考核(D)。
A.国家B国务院 C.环保局 D.市政府3.一般说来,三种生产的共同界面是(B)=A.自然资源B.废弃物C.商品D.环境质量4.环境管理对象是(D)。
A.自然要素B.社会关系C.企业D.人类的社会行为5.首创“三同时"制度的国家是(D)。
A.美国B.日本C.俄罗斯D.中国6.依据国家环境法律规定落实地方政府环境责任的行政管理制度是(A) oA.环境保护目标责任制B.污染限期治理C.城市环境综合整治定量考核D.污染强制淘汰制度7.下面哪一项不是ISO 14000的审核准则?(D)。
A.ISO14001标准B.适用于组织的环境法律、法规及其它要求C.组织的环境管理体系文件D.国家环保法律法规8.我国《自然保护区条例》规定,自然保护区内保存完好的天然状态的生态系统以及珍稀、源危动植物的集中分布地,应当划为(C) oA.缓冲区B.实验区C.核心区D.外围保护地带9.地表水环境质量标准分为(C) oA.3级B.4级C.5级D.6级10.按环境与经济的辩证关系分环境规划的类型不包括(C)。
A.经济制约型B.协调型C.持续型D.环境制约型11.环境规划按时间分可分为短期、中期、长期,其中中期的年度范围为(B) oA.3-5 年B.5-10 年C.10-15 年D.15-20 年12.处理解决多阶段最优化问题的数学方法为(B)。
A非线性规划 B.动态规划 C.线性规划 D.多目标规划13.环境管理主要是针对的对象是(C)。
A.环境污染B.原生环境问题C.次生环境问题D.生态破坏14. 一般说来, 物资生产和环境生产之间的界面是(C)。
A.自然资源B.废弃物C.商品D.环境质量15.一般说来, 人口生产和物资生产之间的界面是(B) oA.自然资源B.环境质量C.商品D.废弃物16,建设项目对环境可能造成轻度影响的,应当编制(B)。
(环境管理)环境规划与管理复习题

一、单项选择题(本大题共10小题,每小题1分,共10分)1.环境问题产生的根源在于人类思想深处的不正确自然观和(A)A.人——地关系观 B.价值观C.消费观D.科学观2.环境管理思想与方法演变大致经历了三个阶段。
其中第三个阶段管理手段是(D)A.经济刺激B.污染治理C.环境评价D.协调经济发展与环境保护关系3.环境在自然力作用下消纳污染和产生出自然资源的总过程称为(C)A.物质生产B.自然净化C.环境生产D.资源再生4.制订环境质量标准的首要原则是(B )A.考虑环境效益B.保障人体健康C.保障经济发展D.保障可持续发展5.环境管理的基本任务是转变人类社会的一系列基本观念和调整人类社会的(D)A.状态B.思想C.生活方式D.行为6.在环境管理手段中,行政手段具有(D)A.强制性B.权威性C.规范性D.①、②和③7.我国环境审计的主体是(D)A.国家审计机关B.社会审计机构C.国际审计机构D.①、②8.清洁生产被联合国环境规划署首次提出的年份是(B)A.1972 B.1989 C.1992 D.20009.俄罗斯环境规划的突出特点是(C)A.保护人体健康重于经济发展B.环境规划中的防治重点突出C.属于协调型环境规划D.将“标准”作为基本的规划目标和规划手段10.下列不是按性质划分的环境规划类型是(A)A.环境制约型规划B.生态规划C.污染综合防治规划D.自然保护规划11.下列不是按环境与经济的辩证关系分的环境规划类型是(D )A.经济制约型B.协调型C.环境制约型D.自然保护规划12. 下列不属于日本环境规划特点的是(C )A.保护人体健康重于经济发展B.环境规划中的防治重点突出C.属于协调型环境规划D.将“标准”作为基本的规划目标和规划手段。
13.下列不属于复合生态系统功能的是:(B )A.生产B.能量流动C.还原D.信息传递14. 根据热力学第二定律,人地系统遵循熵方程:dS=dSi+ dSe 下列属于环境系统严重恶化的熵变类型是(B )A.dS<0 B.dS>0 C.dS=0 D.dS不确定15.大气环境功能区划中特定工业区执行的大气质量标准是:(C )A.一级B.二级C.三级D.四级16.地表水域环境功能区划中一般工业用水区及人体非直接接触的娱乐用水区执行的地表水环境质量标准是:(D )A.Ⅰ类B.Ⅱ类C.Ⅲ类D.Ⅳ类E.Ⅴ类17.噪声功能区划中以居住、文教机关为主的区域执行声环境质量标准是:(B)A.0类B.1类C.2类D.3类E.4类18. 决策问题结构良好,可用数学模型刻画;有明确的目标和判断准则;可借助计算机处理的决策属于:(A)A.结构化决策B.非结构化决策C.半结构化决策D.非程序化决策19.处理解决多阶段最优化问题的数学方法为(B)A.非线性规划B.动态规划C.线性规划D.多目标规划20.目标函数或约束条件中,至少存在一个决策变量为非线性函数的规划属于(A)A.非线性规划B.动态规划C.线性规划D.多目标规划21.风廓线是指( C )。
环境规划与管理作业答案

环境规划与管理第四章、环境规划与管理的数学基础1、计算下面数据的各种平均值、标准差、算术平均误差和级差。
0.83,0.76,0.89,0.73,0.92,0.81,0.92,0.75,0.88,0.79,0.90,0.84 解:算数平均值: 加权平均值: 几何平均值: 调和平均值: 标准差:0676.0)835.084.0()935.090.0()835.079.0()835.088.0()835.075.0()835.92.0()835.081.0()835.092.0()835.073.0()835.089.0()835.076.0()835.083.0(1121)(1122222222222212=-+-+-+-+-+-+-+-+-+-+-+--=--=∑=-o x x n s ni i 算数平均误差: 级差:2、对某合金中铜的含量进行测定,不同的人员测定的数据为56.91,57.13,57.21,57.36,57.41,58.49,58.56,59.11,59.76,60.31,试用格拉布斯准则检验是否有应舍去的数据。
解:算术平均值: 标准差:取显着水平05.0=∂得616.22.118.2)10,,05.0(=⨯=λ 偏差最大的数60.31,检验该数 所以没有应舍去的数据。
3、有一组3因子数据:x 1=(1,3,4,5),x 2=(0.2,0.3,0.4),x 3=(32,35,36),试对它们进行标准化处理。
解:)5,4,3,1(1=x ,计算得:71.1,25.311==-s x由iiij ij s x x u --=得:同理:所以,标准化处理后得:4、某建筑材料预制厂生产a 、b 两种绿色环保产品,现有两种原料,第一种有72m 3,第二种56m 3,假设生产每种产品都需要用两种材料。
生产每件产品所需原料如下表所示,每生产一件a 产品可获利60元,生产一件b 产品可获利100元,问预制厂在现有原料的条件下,啊a 、b 各生产多少,才使获得利润最大?解:设a 、b 各生产想x 、y ,可获得利润最大。
环境规划复习重点计算题.docx
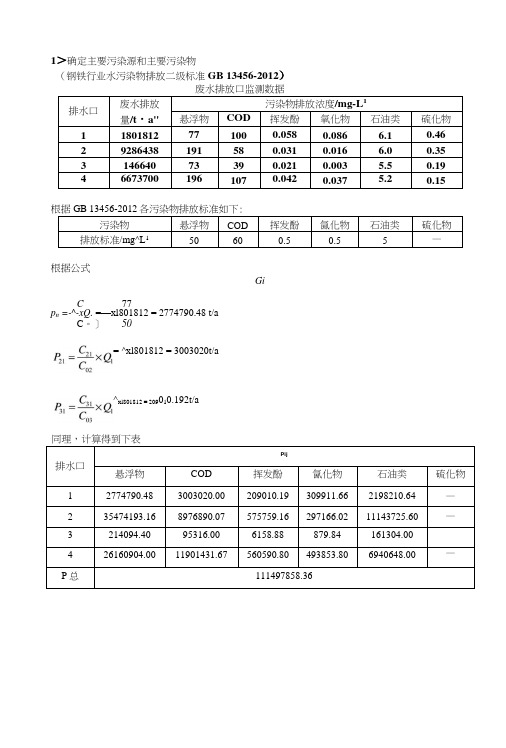
1>确定主要污染源和主要污染物(钢铁行业水污染物排放二级标准GB 13456-2012)废水排放口监测数据排水口废水排放量/t・a"污染物排放浓度/mg-L1悬浮物COD挥发酚氧化物石油类硫化物11801812771000.0580.086 6.10.46 29286438191580.0310.016 6.00.35 314664073390.0210.003 5.50.19 466737001961070.0420.037 5.20.15根据GB 13456-2012各污染物排放标准如下:污染物悬浮物COD 挥发酚氤化物石油类硫化物排放标准/mg^L150 60 0.5 0.5 5 —根据公式GiC77p n =-^-xQ. =—xl801812 = 2774790.48 t/aC。
]50^xl801812 = 209010.192t/a同理,计算得到下表排水口Pij悬浮物COD 挥发酚氤化物石油类硫化物1 2774790.48 3003020.00 209010.19 309911.66 2198210.64 —2 35474193.16 8976890.07 575759.16 297166.02 11143725.60 —3 214094.40 95316.00 6158.88 879.84 161304.004 26160904.00 11901431.67 560590.80 493853.80 6940648.00 —P总111497858.36= ^xl801812 = 3003020t/a根据表格可知:对于污染源K2〉K4>K1>K3,所以主要污染源为第2污染源;对于污染物K1>K2>K5>K3>K4,所以主耍污染物为悬浮物。
2、某水域经五次监测溶解氧的浓度:5.6mg/L, 6.1mg/L, 4.5mg/L, 4.8mg/L, 5.8mg/L,用内梅罗法计算溶解氧的统计浓度值是4・95mg/LPn亦=4.5加g/厶(由于溶解氧越高,水体越干净,因此选择溶解氧最低值作为Pn和)(5・6 + 6・1 + 4・5 + 4・8 + 5・8)徳/厶=5.36卿/厶方法一:根据地表水环境质量标准(GB 3838-2002),选用溶解氧第II类标准5. = 6mg / L导专“75max5 晋二晋= 0.8931内=J«nJ2+(U)2 = J0.8932; 0.752 = ° 825p内=1内xSj = 0.825 x 6加g IL- 4.9 5 mg / L即:溶解氧的统计浓度为4.95mg / L方法二卩内=(竝J+(几_w_ LxD408 50x5000t / m 2 • d408X1X106 50x5000x24x3600g / m 2 •s = 0.0189g / m 2c = c° +QLuH0.0189x50 >2x750 )= 0.0116m 5 / L3、试按下表给定的数据计算某处的大气质量指数,分别采用单因子环境质量指 数,均值型,加评价因子 飘尘so 2NO X CO 日均浓度/mg*m 30.22 0.32 0.13 5.20 评价标准 0.25 0.25 0.15 6.70 计权系数0.20.50.2 0.1飘尘2豊嚨加(2)均值型综合质量指数:1 "1/均=—工厶=—(0.88 + 1.28 + 0.87 + 0.78) = 0.9525ni=\ 4 (3)加权型综合质量指数:/=£ 比厶=0.2x0.88 + 0.5x1.28 + 0.2x0.87 + 0」x0.78 = 1.068 /=! (4)内梅罗多因子环境质量指数:G = I 均=0.9525= 1.1284、已知某工业位于一山谷地区,计算的混合高度h=750m,该地区长50m,宽 5km,上风向风速为2m/s, SO2的本地浓度为0.011mg/L o 该地区建成后的计划 燃煤量为8000t/d,煤的含硫量约为3%, SO?的转化率为85%,试用单箱模型估 计该地区的S02浓度。
环境管理与规划复习题答案

环境管理与规划复习题答案一、名词解释1.市场价格法:直接根据物品或服务的价格,利用因环境质量变化引起的产量和利润的变化来计量环境质量变化的经济效益或经济损失。
2.机会成本法:是指把一定的资源用在生产某种产品时,所放弃的对其他产品生产中所能获得的最大效益。
3.防护费用法:环境资源破坏时带来的经济损失,可以通过为防护该环境资源不受破坏所支付的费用来推断。
4.水环境规划:对某一时期内的水环境保护目标和措施所作出的统筹安排和设计。
5.耗氧有机物的水环境容量:水环境所能容纳的耗氧有机物的最大容许量。
该容量即通常所说的水环境容量。
6.空间结构理论:研究人类活动空间分布及组织优化的科学。
7.大气环境质量预测:为了了解未来一定时期的经济、社会活动对大气环境带来的影响,以便采取改善大气环境质量的措施。
8.社区:指居住在某一个特定区域内的、共同实现多元目标的人所构成的群体。
9.环境预测:指根据人类过去和现在已掌握的信息、资料经验和规律,运用现代科技手段和方法,对未来的环境状况和环境发展趋势及其主要污染物和污染源的动态变化进行描述和分析。
10.环境规划指标:是直接反映环境现象以及相关的事物,并用来描述环境规划内容的总体数量和质量的特征值。
11.环境容量:是一个复杂的反映环境净化能力的量,其数值应能表征污染物在环境中的物理、化学变化及空间机械运动性质。
12.规划协调型预测:指通过一定手段,使环境与经济协调发展所能达到的环境状况。
13.环境规划目标:是环境规划的核心内容,是对规划对象未来某一阶段环境质量状况的发展方向和发展水平所作的规定。
14.环境评价:是在环境调查分析的基础上,运用数学方法,对环境质量、环境影响进行定性和定量的评述,旨在获取各种信息、数据和资料。
15.总量控制:就是依据某一区域的环境容量确定该区域内污染物容许排放总量,再按照一定原则分配给区域内的各个污染源,同时制定出一系列政策和措施,以保证区域内污染物排放总量不超过区域容许排放总量。
环境规划与管理作业答案,DOC

环境规划与管理第四章、环境规划与管理的数学基础1、计算下面数据的各种平均值、标准差、算术平均误差和级差。
0.83,0.76,0.89,0.73,0.92,0.81,0.92,0.75,0.88,0.79,0.90,0.84s56.91,57.13,57.21,57.36,57.41,58.49,58.56,59.11,59.76,60.31,试用格拉布斯准则检验是否有应舍去的数据。
解:算术平均值:标准差:取显著水平05.0=∂得616λ.0(==10,,05⨯).22.118.2偏差最大的数60.31,检验该数所以没有应舍去的数据。
3、有一组3因子数据:x1=(1,3,4,5),x2=(0.2,0.3,0.4),x3=(32,35,36),试对它们进行标准化处理。
解:设a、b各生产想x、y,可获得利润最大。
目标函数:y=max+60Z100x约束条件:⎪⎩⎪⎨⎧>>≤+≤+0,0563.01.0721.02.0y x y x y x5、某城镇为防止附近河流富营养化,需消减其排放到河流中污水的含磷量。
按环境标准,该城镇每年排磷总量要求控制在1000kg 。
现该城三个污水处理厂磷排放每天各为1000kg 、500kg 和2000kg 。
所以得:xlg+=.2-y lg593945.8将题中的x值代入式中得y’值:作业2某地区有甲、乙、丙三个工厂,年废水排放量与污染物监测结果如表所示。
若废水排入城市二级污水处理厂,污染物最高允许排放浓度为:悬浮物250mg/L,BOD560mg/L,酚2.0mg/L,石油类20mg/L。
试确定该地区的主要污染物和主要污染源。
主要污染源是:甲厂,主要污染物是:BOD 5 第七章、流域水环境规划 作业3有一河段长x =2km ,流量Q P =3.4m 3/s ,C P =1mg/L ,断面平均点进行入河有机污染物的消减,4个污水口基本情况如图所示,河流规划,目标预定BOD 5最高5mg/L ,Do 最高6mg/L 。
环境规划与管理题型

环境规划与管理一、名词解释1、环境行政责任:是指违反环境法和国家行政法规中有关环境行政义务的规定者所应当承担的法律责任。
2、环境民事责任:是指公民、法人因污染或破坏环境而侵害公共财产或他人人身权、财产权或合法环境权益所应当承担的民事方面的法律责任。
3、环境刑事责任:是指行为人因违反环境法,造成或可能造成严重的环境污染或生态破坏,构成犯罪时,应当依法承担的以刑罚为处罚方式的法律后果。
4、环境统计:用数字反映并计量人类活动引起的环境变化和环境变化对人类的影响。
5、环境审计:对特定项目的环境保护情况,包括组织机构、管理、生产及环保设施运转与排污等情况进行系统的、有文字记录的、定期的、客观的评定。
6、末端控制(又称末端治理或末端处理):是指在生产过程的终端或者是在废弃物排放到自然界之前,采取一系列措施对其进行物理、化学或生物过程的处理,以减少排放到环境中的废物量。
7、源头控制:针对末端控制而提出的一项控制方式,是指在源头削减或消除污染物,即尽量减少污染物的产生量,实施源削减。
8、产品生态设计系:指将环境因素纳入设计之中,在产品生命周期的每一环节都考虑其可能带来的环境影响,通过设计改进,使产品的环境影响降为最低,最终引导产生一个更具有可持续性的生产和消费系统。
9、环境管理体系:指全面管理体系的一个组成部分,包括制定、实施、评审和保持环境方针所需的组织机构、规划活动、职责、惯例、程序、过程和资源。
10、环境审核:客观地获取审核证据并予以评价,以判断一个组织的环境管理体系是否符合该组织所规定的环境管理体系审核准则的一个以文件支持的系统化验证过程,并将这一过程的结果呈报管理者。
11、环境绩效:指一个组织基于其环境方针、目标、指标,控制其环境因素所取得的可测量的环境管理体系成效。
12、水环境自净容量:指由于沉降、生化、吸附等物理、化学和生物作用,给定水域达到水质目标所能自净的污染物量。
13、水环境稀释容量:指在给定水域的本底污染物浓度低于水质目标时,依靠稀释作用达到水质目标所能承纳的污染物量。
环境规划计算题

计算值 公式:()()n ncn n b r 1r 1+=+=C PV B PV ,式中PV b 为效益现值;PV c 为费用现值;B n 、C n 为发生在第n 年的效益、费用;(第一年的n 值为0,第二年n=1,依次类推)公式:()()iin0i c i i n0i b r 1r 1+=+=∑∑==C PV B PV , 式中,B i 为发生在第i 年的效益;C i 为发生在第i 年的费用;n 为计算期;r 为社会贴现率。
解:费用:101.0110r 10n n 2011=+=+=)()(C PV C 亿元; 64.131.0115r 11n n 2012=+=+=)()(C PV C 亿元; 53.161.0120r 12n n 2013=+=+=)()(C PV C 亿元; 78.181.0115r 13n n 2014=+=+=)()(C PV C 亿元; 49.201.0115r 14n n 2015=+=+=)()(C PV C 亿元。
效益: 21.012r 10n n 2011b =+=+=)()(B PV 亿元; 64.31.014r 11n n 2012b =+=+=)()(B PV 亿元; 96.41.0115r 12n n 2013b =+=+=)()(B PV 亿元; 01.61.018r 13n n 2014b =+=+=)()(B PV 亿元; 83.61.0110r 14n n 2015b =+=+=)()(B PV 亿元。
总费用: 44.7949.2078.1853.1664.1310r 1iini =++++=+=∑=)(C PV C 亿元;44.2383.601.696.464.32r 1iini b =++++=+=∑=)(B PV 亿元。
2. 扬州新建设电厂排气筒高度为20m ,除尘效率90%,颗粒物容许排放指标100kg/(h.m 2),计算烟尘容许排放量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 0 0 0 0
不 综 合 利 用 0
1
2020/7/14
试 验 △ - 3 0 0 0
不 试 验 b
1
好 2 4 0 0 0
概 率 为 0 . 6
不 好 概 率 为 0 . 4
0
综 合 利 用
1 2 0 0 0
26
• 3.计算状态点①的期望值:24000×0.6+ 0×0.4=14400
• 4.在决策1作出决策。
• 图示
河流 化工厂1
例题一
化工厂2
湖 泊
化工厂3
思考题
• 1、工业污染源和生活污染源调查的主要内容分别 有哪些?
• 2、常用河流水质模型的各自的适用条件是什么?
人的生产 人的生产
环境质量
商品
物质生产
废弃物 自然资源
环境生产
2020/7/14
5
2020/7/14
6
已知某县 2005 年工农业生产的总产值是 300 万元, COD 排放总量是 250吨,2010 年工农业生产的总产 值是 400 万元,COD 排放总量是 275 吨;若到 2020 年工农业生产的总产值实现翻一番,用弹性系数法求 那时 COD 的年排放总量是多少吨?
• 5.最后得出整个问题的决策序列为:不作实 验、直接综合利用,收入期望值为12000元 。
2020/7/14
27
2020/7/14
28
2020/7/14
29
2020/7/14
31
2020/7/14
32
2020/7/14
33
2020/7/14
34
2020/7/14
35
2020/7/14
• 根据图中给出之数据求解。决策树采用逆顺序计算法。
2020/7/14
23
1.计算事件点②、③、④的期望值
试验
1
1
好 2
概率为0.6
-3000
综合利用 2
-10000
产品成功概率为0.85 产品不成功概率为0.15
不综合利用
40000 0 0
不试验 --决策点
不好 3
概率为0.4 4
综合利用 3
-10000
2020/7/14
7
2020/7/14
11
2020/7/14
12
2020/7/14
13
2020/7/14
14
2020/7/14
15
2020/7/14
16
2020/7/14
17
2020/7/14
18
2020/7/14
19
例题
• 用狄克逊法判断下列测试数据(40.02,40.15 , 40.20,40.13,40.16)中的40.02是否应舍 弃?
• 解:将数据排列,取 α =0.05
*
• 0.611<0.642
• 所以40.02应保留。
2020/7/14
20
2020/7/14
21
2020/7/14
22
决策树例题
• 有一石油化工企业,对一批废油渣进行综合利用。它可以先 作实验,然后决定是否综合利用;也可以不作实验,只凭经 验决定是否综合利用。作实验的费用每次为3000元,综合利 用费每次为10000元。若做出产品,可收入40000元;作不 出产品,没有收入。各种不同情况下的产品成功概率均已估 计出来,都标在图1上。试问欲使收益期期望值为最大,企 业应如何作出决策。
产品成功概率为0.1 产品不成功概率为0.9
不综合利用
40000 0 0
综合利用 4
-10000
产品成功概率为0.55 产品不成功概率为0.45
不综合利用
40000 0 0
2020- /7/- 14决策(事件)点;
--支出符号
24
②40000×0.85+0×0.15=34000 ③40000×0.10+0×0.90=4000 ④40000×0.55+0×0.45=22000 • 原决策树根据以上算出的期望值可简化为(图2a): 2.在决策点2、3、4作出决策 2 按max[(34000-10000),0]=24000,决定综合利用。 3 按max[(4000-10000),0]=0,决定不综合利用。 4 按max[(22000-10000),0]=12000,决定综合利用。 • 决策树继续简化为(图2b)
例题
• 有三个化工厂①②③每天分别排放氰化物760kg、110kg 、250kg到河流,要求进入湖泊的氰化物不超过 315kg/d。已知三个化工厂排放的氰化物到入湖口时的降 解率分别为45%、30%、40%;三个化工厂氰化物处理 费用分别为1.25万元/kg、2.0万元/kg、1.75万元/kg。 写出既能达到湖泊污染物控制要求,又使总处理费用最小 的线性规划模型的标准型。
2020/7/14
25
试 验
△ 3 0 0 0
好 概 率 为 0 . 6
综 合 利 用
△
3 4 0 0 0
- 1 0 0 0 0
不 综 合 利 用 0
不 好 3
概 率 为 0 . 4
综 合 利 用
△
4 0 0 0
- 1 0 0 0 0
不 综 合 利 用 0
不 试 验 a
4
综 合 利 用
△
2 2 0 0 0
36
2020/7/14
37
2020/7/14
38
2020/7/14
39
2020/7/14
40
2020/7/14
41
2020/7/14
42
2020/7/14
43
2020/7/14
44
2020/7/14
45
2020/7/14
46
2020/7/14
47
2020/7/14
48
2020/7/14
49
2020/7/14
50
2020/7/14
51
2020/7/14
52
