晶体的结构的周期性1讲解

v a1 (a2 a3 )
等于晶体中每个格点平均所占据的体积。 —— 原胞是体积最小的结构单元。
2、 维格纳 – 赛茨原胞： 原胞的选取不是唯一的，也不一定是平行六面体， 只要求它是体积最小的结构单元即可。
以任意格点为中心作它与最近邻（有时也包括次近邻等 各格点）连线的垂直平分面，由这些面所围成的最小的封闭 多面体，也满足原胞的要求。 —— 维格纳 – 赛茨原胞。 ① 每个维格纳 – 赛茨原胞只含一个格点且位于原胞中心。 ② 维格纳 – 赛茨原胞外形的对称性高于平行六面体原胞。 它是一种对称性原胞，它具有晶体所属点阵点群的全部对称性。 一切保持点阵不变的旋转、 反映和反演操作都将保持 W-S原胞不变。
具有NaCl 结构的化合物如：LiF、LiCl、NaF、NaBr、 MgO、CaO、BaO、MnO、FeO、NiO 等。
2、CsCl 结构： CsCl结构是由两个简立方的子晶格彼此沿立方体空间对 角线位移1／2 的长度套构而成。
基元：取相邻的一对Cs+和Cl-作为组成CsCl晶体的基元。 结点：取基元中的Cs+所在的点为结点。显然这些基元的代表 点（即结点）构成的是简单立方的晶格 具有CsCl 结构的化合物如：CsBr、CsI、TlCl、TlBr 等。
原胞体积
=
a3
0.5a3
= 2 = 晶胞中所包含的格点数
(3) 面心立方的晶胞与原胞:
关于晶胞：
a ˆ ˆ a1 ( j k ) 2 ˆ k 基矢 a ˆ ˆ a2 (i k ) a a2 1 2 a ˆ ˆ ˆ j a a ( i j ) 3 原胞体积 3 2 ˆ i 1 3 v0 a1 (a2 a3 ) a 面心立方的晶胞与原胞 4
关于原胞： 晶胞的点阵常数 = a Ni ----- 晶胞内的阵点数=0 晶胞內的格点数 : Nf ----- 晶胞面上的阵点数=6 N f Nc Nc ----- 晶胞顶角上的阵点数=8 NN
i
a
2
8
晶胞的体积 原胞体积
=
a3 0.25a3
对面心立方晶胞 N=4
= 4 = 晶胞中所包含的格点数
§2 典型的晶体结构
一、NaCl 与 CsCl 结构： 1、NaCl 结构：
钠 离 子 构 成 面 心 立 方 格 子
氯 离 子 构 成 面 心 立 方 格 子
基元：取相邻的一对Na+和Cl-作为组成NaCl晶体的基元。 结点：取基元中的Na+所在的点为结点。显然这些基元的代 表点（即结点）构成的是面心立方的晶格
二、钙钛矿 结构：
由5个相同的简立方结构子 晶格套构而成 BaTiO3的基元由 Ba、Ti、 OI、OII、OIII这五个不等价 的原子构成。 结点：取基元中的Ba+所在 的点为结点。显然这些基元的 代表点（即结点）构成的是简 单立方的晶格
具有CaTiO3 结构的化合物如： LiNbO3、PbZrO3、BaTiO3 等。 这类化合物的化学式为ABO3， 其中A和B为金属离子。 氧八面体基团, 是钙钛矿型 晶体结构的特点。
(3) 具有六方密堆结构的金属: 金属Be、Mg、Zn、Cd、Ti、Zr等，都是六方密堆结构。 这种结构的配位数 = 12 3、简单晶格与复式晶格： 基元中的原子数n = 1的晶格为简单晶格，它就是布喇菲晶格。 基元中的原子数n ≥ 2的晶格为复式晶格。 复式晶格可看成是由两个或多个简单晶格套构而成，其中 每个简单晶格的形式与布喇菲晶格相同。如NaCl 的结构就是复 式晶格。
—— 原胞中只包含一个原子
关于晶胞： 晶胞的晶格常数 = a 晶胞的体积 = a3
晶胞內的格点数 :
Ni ----- 晶胞内的阵点数 = 1 Nf ----- 晶胞面上的阵点数 = 0 Nc ----- 晶胞顶角上的阵点数 = 8
a
Nc N Ni 2 8
晶胞的体积
晶体的结合
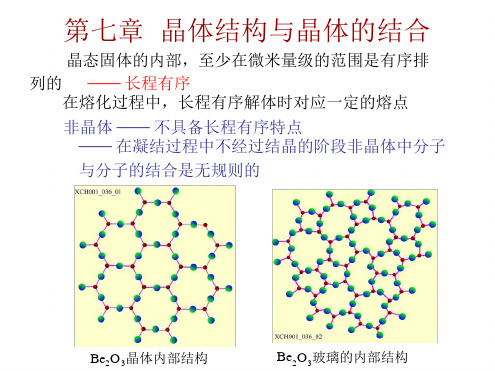
晶态固体的内部，至少在微米量级的范围是有序排 列的 —— 长程有序 在熔化过程中，长程有序解体时对应一定的熔点 非晶体 —— 不具备长程有序特点 —— 在凝结过程中不经过结晶的阶段非晶体中分子 与分子的结合是无规则的
Be2O3晶体内部结构
Be2O3玻璃的内部结构
§1、在实空间中对晶体结构周期性的描述
A
C B C A A B C A A B C A B C A
A
B C A
B A
B A
B C A
B A
B A
B C A
B C A
A
B A
二、布喇菲晶格：
1、基元： 是由一种或多种原子组成的构成晶体的基本结构单元。 基元可以是晶体中的原子 , 分子 , 离子或原子集团 .基元 在晶体中呈有规则 , 周期性的排列 . ① 基元的构成: 必要条件：基元中所包含的原子必定是不等价的。 ② 基元的特点： 基元所含的原子的种类、 数量和空间分布，可以反 映晶体的组成成分。 ③ 结点与空间点阵 ： 表示晶体基元质心所在位置 的点 ------ 结点 , 基元与结点示意图 结点的总体被称为空间点阵。
一、晶体中原子排列的一些具体形式举例：
1 简单立方晶格： ① 原子球在一个平面内呈现为正方排列 ②平面的原子层叠加起来得到简单立方格子
用圆点表示原子的位置 —— 得到简单立方晶格结构
2 体心立方晶格
A B A B A
A B
A B A A B B A A B B A
A A
A
A
A A
B
A 体心立方晶格结构的金属 A
晶胞內的格点数 : N f Nc Ni ----- 晶胞内的阵点数 = 0 N Ni 2 8 Nf ----- 晶胞面上的阵点数 = 0 Nc ----- 晶胞顶角上的阵点数 = 8 对简单立方晶胞 N = 1
(2) 体心立方的晶胞与原胞 : 关于原胞： 由立方体的中心到三个顶点引三个基矢
这一整数正是晶胞中所包含的格点数
(1) 简单立方的晶胞与原胞是相同的: 关于原胞： 原胞体积 基矢
v0 a1 (a2 a3 ) a3
原胞中只包含一个原子 关于晶胞： 晶胞的晶格常数 = a
ˆ a1 ai a2 aˆ j ˆ a3 ak
a3
a2
a1
晶胞的体积 = a3
线的垂直平分面割去八面体的 六个角，形成的14面体 八个面是正六边形， 六个面是正四边形
3、晶胞： 周期性和对称性是晶体结构的两大特点，原胞能很好 的描述晶体结构的周期性，但有时不能兼顾对称性
原胞是只考虑点阵周期性的最小重复单元，而晶胞是同 时计及周期性和对称性的最小重复单元
根据不同的对称性，有的布喇菲格子的原胞与晶胞相同； 有的形状有明显的差别，但后者的体积为前者的整数倍
a1 , a2 , a3
a1 (a / 2)( i j k )
基矢
a2 (a / 2)(i j k )
a3 (a / 2)(i j k ) 3 (a / 2)(i j k )
原胞体积
v0 a1 ( a2 a3 ) 1 3 a 2
三、金刚石与闪锌矿结构：
1、闪锌矿（ZnS）的晶胞： 立方系的ZnS —— S和Zn分 别组成面心立方结构的子晶格 沿空间对角线位移 1／4 的长 度套构而成。 基元：取0处的Zn ˆ) ˆ ˆ 原子和 (a / 4)(i jk 处的S原子作为组成 ZnS晶体的基元。 结点：取基元中的Zn原子 所在的点为结点。显然这些基 元的代表点（即结点）构成的 是面心立方的晶格
简单立方情况下的 维格纳 — 塞茨原胞： 原点和6个近邻格点连线的 垂直平分面围成的立方体。
面心立方晶格情况下的维格纳—塞茨原胞： 原点和12个近邻格点连线的垂直平分面围成的正十二面体
面心立方结构配位数示意图
体心立方情况下的维格纳
—塞茨原胞：
原点和8个近邻格点连线的 垂直平分面围成的正八面体，
和沿立方轴的6个次近邻格点连
2、金刚石的晶胞： 碳1位置 碳2位置 基元：取0处的C1 ˆ) ˆ ˆ 原子和 (a / 4)(i jk 处的C2原子作为组成 金刚石晶体的基元。 结点：取基元中的C1原子 所在的点为结点。显然这些基 元的代表点（即结点）构成的 是面心立方的晶格 沿对角线的位移为
结论：金刚石与闪锌矿结构的基元均含两个原子，其布 喇菲晶格为面心立方格子。
如 : Fe(<910°C) , Fe(>1400°C) , 钒 , 铌 , 鉭 , 钼 , 钡 , 钨等30多种金属具有这种晶体结构 .
3 面心立方晶格
——六角密排的情况之一
六角密排是指：全同小圆球平铺在平面上，任一个球都 与6个球相切每三个相切的球的中心构成一等边三角形
Fe , Cu , Ni , Al , Ag等20多种金属具有这种晶体结构 。
基元 + 布喇菲晶格 = 晶体结构
2、布喇菲晶格： 结点的总体称为布喇菲点阵或布喇菲晶格，它可以反 映晶体结构的几何性质。 ① 布喇菲晶格的判断标准：在布喇菲晶格中，每个格 点在几何上必定是完全等价的，这是判断一个晶格是否为 布喇菲晶格的标准。 ② 同一种原子组成的布喇菲晶格：如果晶体由完全相 同的一种原子组成，这种原子所组成的网格就是布喇菲晶 格。 ③ 复式格子：如果晶体的基元中包含两种或两种以上 的原子，则每个基元中，相应的同种原子各构成和结点相 同的网格，由于这些网格之间相对地有位移从而形成复式 格子。------复式格子是由若干相同的布喇菲格子相互位移 套构而成。
3、布喇菲晶格的数学表示：
以任意一个格点为原点，沿 三个不共面的方向连接最近的格 点，作矢量a1、a2、a3，矢量长 度为该方向的格点周期，则任意 一个格点的位置矢量R都可以表 示为：
R n1a1 n2a2 n3a3