瑞典条分法计算
瑞典圆弧条分法

x
0 1.100969 2.226749 3.375967 4.547224
y
0 -0.73012 -1.42138 -2.07292 -2.68397
分条计算
总宽度
分条宽度
59.29437977 0.592943798
分条上端 x 坐标 y 分条下端 x 坐标 y 求面积 三角形面积
矩形面积 圆弧面积 p
41.97366 41.97366 41.97366 41.97366 41.97366 41.97366 41.97366 41.97366 41.97366
求面积
三角形面积 矩形面积 圆弧面积
p
a
b c 分条面积m2
底面倾角 条重Wi(KN/m)
Wisinβi
Wicosβi
总滑动力矩 总抗滑力矩
0 0.418348 0.836696 1.255044 1.673392 0 0.7246 1.4492 2.1738 2.8984 0 0.418348 0.836696 1.255044 1.673392 0 -0.01252 -0.02087 -0.02504 -0.02505 0.151567431 0.151567 0.151567 0.151567 0.151567 0.154186514 0.461687 0.767441 1.071451 1.373716 0.000254735 0.000255 0.000254 0.000254 0.000254 42.18292504 42.18287 42.18284 42.18283 42.18284
2.09174 2.510088 2.928436 3.346783 3.765131 4.183479 4.601827 5.020175 5.438523 -0.02089 -0.01255 -4.5E-05 0.016641 0.037509 0.062565 0.091818 0.125276 0.162948 0.151567 0.151567 0.151567 0.151567 0.151567 0.151567 0.151567 0.151567 0.151567 1.674237 1.973012 2.27004 2.56532 2.858848 3.150623 3.440641 3.728897 4.015387 0.000255 0.000255 0.000255 0.000255 0.000256 0.000256 0.000257 0.000257 0.000258 42.18287 42.18292 42.183 42.18309 42.18321 42.18334 42.1835 42.18368 42.18388
瑞典条分法的具体步骤

瑞典条分法的具体步骤
嘿,咱今儿就来聊聊瑞典条分法的具体步骤哈!这瑞典条分法啊,就像是搭积木,一块一块地把复杂的问题给拼凑清楚。
首先呢,咱得把要研究的土体划分成一条条的小块儿,就跟切蛋糕似的,可别切得乱七八糟哦!这每一条小块都有它自己的作用呢。
然后呢,就得考虑这些小块之间的作用力啦。
想象一下,它们就像是一群小伙伴,互相之间有着各种牵扯和影响。
要仔细分析它们之间的摩擦力、重力啥的,可不能马虎。
接下来呀,计算每一条土条的重量。
这可不能算错喽,不然整个分析可就都错啦。
就好像走路,一步错步步错呀!
再之后呢,根据那些力呀重量呀,来计算整个土体的稳定性。
这就像是给土体做个全面的“体检”,看看它到底稳不稳固。
接着说哈,还得反复调整那些土条的划分和参数,就跟调整收音机的频道似的,直到找到最合适的那个状态。
咱再想想啊,这瑞典条分法不就是个厉害的工具嘛,能帮咱搞清楚土体的各种情况。
就好比你有一把神奇的钥匙,能打开土体秘密的大门。
你说,要是没有这瑞典条分法,咱咋能这么清楚地了解土体呀?它就像是黑暗中的一盏明灯,给咱指引方向呢!而且呀,学会了它的具
体步骤,咱就像是掌握了一门独特的技能,在工程领域里那可就能大
显身手啦!
咱可别小瞧了这瑞典条分法的每一个步骤哦,每一步都得认真对待,就像对待宝贝似的。
要是有一步出了差错,那后果可不堪设想啊!
总之呢,瑞典条分法的具体步骤虽然有点复杂,但只要咱用心去学,去理解,就一定能掌握得牢牢的。
到时候,咱就能在土体分析的世界
里自由驰骋啦,哈哈!。
边坡稳定性计算方法

一、边坡稳定性计算方法在边坡稳定计算方法中,通常采用整体的极限平衡方法来进行分析。
根据边坡不同破裂面形状而有不同的分析模式。
边坡失稳的破裂面形状按土质和成因不同而不同,粗粒土或砂性土的破裂面多呈直线形;细粒土或粘性土的破裂面多为圆弧形;滑坡的滑动面为不规则的折线或圆弧状。
这里将主要介绍边坡稳定性分析的基本原理以及在某些边界条件下边坡稳定的计算理论和方法。
(一)直线破裂面法所谓直线破裂面是指边坡破坏时其破裂面近似平面,在断面近似直线。
为了简化计算这类边坡稳定性分析采用直线破裂面法。
能形成直线破裂面的土类包括:均质砂性土坡;透水的砂、砾、碎石土;主要由内摩擦角控制强度的填土。
图 9 - 1 为一砂性边坡示意图,坡高 H ,坡角β,土的容重为γ,抗剪度指标为c、φ。
如果倾角α的平面AC面为土坡破坏时的滑动面,则可分析该滑动体的稳定性。
沿边坡长度方向截取一个单位长度作为平面问题分析。
已知滑体ABC重 W,滑面的倾角为α,显然,滑面 AC上由滑体的重量W= γ(Δ ABC)产生的下滑力T和由土的抗剪强度产生的抗滑力Tˊ分别为:T=W · sina和则此时边坡的稳定程度或安全系数可用抗滑力与下滑力来表示,即为了保证土坡的稳定性,安全系数F s 值一般不小于 1.25 ,特殊情况下可允许减小到 1.15 。
对于C=0 的砂性土坡或是指边坡,其安全系数表达式则变为从上式可以看出,当α =β时,F s 值最小,说明边坡表面一层土最容易滑动,这时图9-1 砂性边坡受力示意图当 F s =1时,β=φ,表明边坡处于极限平衡状态。
此时β角称为休止角,也称安息角。
此外,山区顺层滑坡或坡积层沿着基岩面滑动现象一般也属于平面滑动类型。
这类滑坡滑动面的深度与长度之比往往很小。
当深长比小于 0.1时,可以把它当作一个无限边坡进行分析。
图 9-2表示一无限边坡示意图,滑动面位置在坡面下H深度处。
取一单位长度的滑动土条进行分析,作用在滑动面上的剪应力为,在极限平衡状态时,破坏面上的剪应力等于土的抗剪强度,即得式中N s =c/ γ H 称为稳定系数。
《瑞典条分法》课件

该方法由瑞典工程师 K.E.Petterson在20世纪30年代提 出,后来得到了进一步完善和发 展。
主要特点
考虑土压力分布
简化计算
该方法考虑了土压力沿土坡高度的分 布,能够更准确地分析土坡的稳定性 。
相对于其他数值分析方法,瑞典条分 法计算过程相对简单,易于理解和应 用。
应力-应变关系
利用土体的应力-应变关系来描述土体 的变形和破坏,能够更准确地预测土 坡的失稳模式和滑坡的滑动面。
加强与实际工程的结合,不断优 化和完善瑞典条分法,提高其在 解决实际工程问题中的实用性和
可靠性。
THANKS
感谢观看
计算步骤
01
02
03
04
确定滑坡体的几何参数和物理 参数,如滑坡体的尺寸、土的 容重、内摩擦角、粘聚力等。
将滑坡体划分为若干个竖向土 条,并计算各土条的重力、水
压力和地震力等作用。
计算各土条的抗滑力和下滑力 ,判断滑坡体的稳定性。
根据计算结果,提出相应的治 理措施和建议。
公式推导
瑞典条分法的公式推导基于极限平衡 理论,通过力的平衡条件和土的极限 平衡条件,推导出各土条的抗滑力和 下滑力的计算公式。
实例二:水库大坝安全评估
总结词
确保大坝稳定与安全
详细描述
瑞典条分法在水库大坝安全评估中发挥了关键作用。通过对大坝的应力、应变、 位移等参数进行监测和分析,评估大坝的稳定性和安全性,及时发现和解决潜在 的安全隐患,确保水库的正常运行和下游人民群众的生命财产安全。
实例三:海岸防护工程
总结词
保护沿海地区免受蚀
简化复杂问题
对于非常复杂的地形和土壤条件,单独使用瑞典条分法可 能面临较大的困难。结合其他方法可以简化计算过程,提 高计算效率,并更好地处理复杂问题。这种综合方法有助 于更有效地解决实际工程中的土压力问题。
岩土专业考试滑坡体计算常用条分法总结
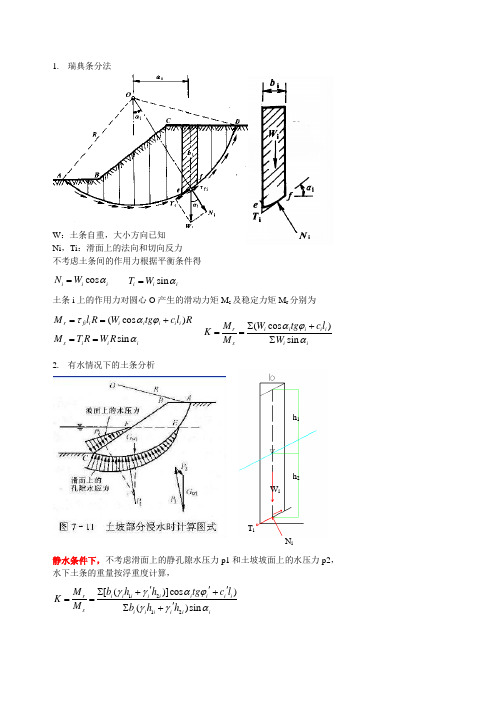
1212[()]cos )()sin i i i i i i i i i r s i i i i i i b h h tg c l M K M b h h γγαϕγγα'''∑++=='∑+(cos )r fi i i i i i i M l R W tg c l R ταϕ==+(cos )sin i i i i i r s i i W tg c l M K M W αϕα∑+==∑sin i i i T W α=cos ii i N W α=sin s i i i M T R W R α==1. 瑞典条分法W :土条自重,大小方向已知 Ni ,Ti :滑面上的法向和切向反力不考虑土条间的作用力根据平衡条件得土条i 上的作用力对圆心O 产生的滑动力矩M s 及稳定力矩M r 分别为2. 有水情况下的土条分析静水条件下,不考虑滑面上的静孔隙水压力p1和土坡坡面上的水压力p2, 水下土条的重量按浮重度计算,h 1W ih 2T iN isin i α=123123[()]cos )()sin i i i i i i i i i i i r s i i i sati i i i i b h h h tg c l M K M b h h h γγγαϕγγγα''''∑+++=='∑++2sin i w i iJ b h γα=∑['(cos )tan ']sin i i i i i i i s i i c l W u L F W αϕα+-=∑∑由荷载引起的超静孔隙水压力条件下(有效应力法) 当有超静孔隙水压力时,超静孔隙水压力作用在滑面上, 减小土条的有效法向应力由渗流引起的超静孔隙水压力条件下(代替法)流线平行坡面时, 用浸润线以下,坡外水位以上 所包围的同体积的水重对滑动圆心的力矩代替渗流力对 圆心的滑动力矩。
用瑞典条分法计算土坡的稳定安全系数

用瑞典条分法计算土坡的稳定安全系数
瑞典条分法(Bishop Method)是一种常用的土体稳定分析方法,具体步骤如下:
1. 确定土体受力状态:包括土体内部角度(黏聚力)和外部角度(摩擦角),以及土体所受的重力和附加力。
2. 确定土体的滑动面和翻转面:根据土坡形状和地形情况,确定可能出现滑动面和翻转面的位置和形状。
3. 计算土体的承载力和抗剪强度:根据土体的受力状态,使用适当的力学模型计算土体的承载力和抗剪强度。
4. 计算土体的稳定安全系数:根据所选用的稳定准则(例如平衡法、弹性理论等),将土体的各个受力因素代入公式中,计算出土体的稳定安全系数。
以平衡法为例,其稳定准则要求土坡能够保持平衡状态,不出现任何变形和位移,稳定安全系数(FS)的计算公式如下:FS = 其中,W是土体重力所受的作用力,L是土坡滑动面的长度,N是土坡滑动面所处的法向力, T是土坡滑动面所受的切向力,φ是土体的外部角度,c是土体的黏聚力。
通过以上步骤,可以使用瑞典条分法计算土坡的稳定安全系数。
瑞典条分法计算

滑面倾角 α (° ) 50 48 46 44 42 40 38 36 34 32
滑面长度 L (m) 10.00 12.00 14.00 16.00 18.00 20.00 22.00 24.00 26.00 28.00
Ⅰ
Ⅱ
1 2 3 4 5 6 7 8 9 10
25.00 25.00 25.00 25.00 25.00 25.00 25.00 25.00 25.00 25.00
3.425 -0.320 147.372 0.975 -1.575 15.671 1.581 -6.764 6.017 1.497
1.10 1.10 1.10 1.10 1.10 1.10 1.10 1.10 1.10 1.10
379.18 -977.48 -830.64 17.32 -1600.12 -1718.34 -343.91 -2099.63 -2384.83 -641.08
-558.59 220.52 836.89 134.96 942.14 1848.07 1130.39 1805.93 2918.38 2416.12
-163.10 -525.05 693.83 132.77 -736.61 716.09 597.05 -981.99 752.05 1128.63
-163.10 -688.15 5.68 138.44 -598.16 117.93 714.98 -267.00 485.05 1613.68
20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00 20.00
18.00 18.00 18.00 18.00 18.00 18.00 18.00 18.00 18.00 18.00
瑞典条分法ppt课件

16
186.60
W icosi 11.0 32.1 48.5 59.41 58.33 36.62 12.67
258.6314
四、泰勒图表法
土坡的稳定性相关因素:
泰勒(Taylor,D.W, 1937)用图表表达影 响因素的相互关系
抗剪强度指标c和、 重度 、土坡的尺寸
坡角 和坡高H
稳定数
土坡的临界高 度或极限高度
根据不同的 绘出 与Ns的关系曲线
泰勒图表法适宜解决简单土坡稳定分析的问题:
①已知坡角及土的指标c、、,求稳定的坡高H
②已知坡高H及土的指标c、、,求稳定的坡角
③已知坡角、坡高H及土的指标c、、,求稳定安全系数F15
五、例题分析 【例】一简单土坡=15°,c =12.0kPa, =17.8kN/m3,
6
最危险滑动面圆心的确定
O β2 A R
β1 β
B
对于均质粘性土 土坡,其最危险 滑动面通过坡脚
=0 F
s
β1 β
B
>0
圆心位置在EO
的延长线上
圆心位置由β1, β2确定
O β2 A
H 2H
4.5H
E
7
二、条分法
O
对于外形复杂、 >0的粘性
土土坡,土体分层情况时,要
R
βi
d c
B
C 确定滑动土体的重量及其重心 位置比较困难,而且抗剪强度 的分布不同,一般采用条分法
H 分析
i A
ab
滑动土体 分为若干 垂直土条
土坡稳定 安全系数
各土条对滑弧 圆心的抗滑力 矩和滑动力矩
瑞典条分法边坡稳定安全系数的定义

瑞典条分法边坡稳定安全系数的定义瑞典条分法边坡稳定安全系数的定义近年来,随着现代化建设不断推进,边坡工程越来越常见。
其中,如何确保边坡的稳定与安全一直是工程师们所关注的问题。
而瑞典条分法边坡稳定安全系数又成为了衡量边坡稳定性的有效工具。
本文将介绍瑞典条分法的定义、计算公式、使用注意事项等方面,帮助读者了解该方法。
I. 瑞典条分法的定义瑞典条分法又称“葛弗斯坦法”,是由瑞典工程师葛弗斯坦于1951年提出的一种边坡稳定性评估方法。
其核心思想是基于材料的强度与边坡的深度,通过计算边坡的稳定安全系数来判断边坡的稳定性。
II. 瑞典条分法的计算公式瑞典条分法的计算公式如下:Fs = χ [(Nc + b×Nq + γ×Nγ) F1 F2]/F3其中,Fs为边坡稳定安全系数,χ为修正系数,Nc、Nq、Nγ分别为某种特定材料的有效地应力系数。
而b、γ则是边坡的深度与单位重力。
F1、F2、F3是结构和边坡几何因素的校正系数。
III. 使用瑞典条分法的注意事项使用瑞典条分法需要注意以下问题:1. 材料特性与边坡几何形状应准确测定,并根据实际情况修正系数。
2. 边坡内部存在水文地质因素时,应对水压力进行计算。
3. 瑞典条分法具有明显的线性特性,因此只适用于边坡稳定性较好的情况下使用。
4. 该方法因受到许多严格的限制条件而不易适用于较为复杂的边坡工程中,应结合其他方法综合分析。
IV. 结论总而言之,瑞典条分法作为一种边坡稳定安全系数评估工具,因其简单、可靠的核心思想以及使用方法被工程界广泛认可与采用。
我们相信,在未来的技术发展中,它将会有更加广泛的应用。
用瑞典条分法计算锚固边坡的稳定性

用瑞典条分法计算锚固边坡的稳定性
F.0.1锚固土质边坡或呈现碎裂结构、散体结构的岩质边坡的稳定性可按图F.0.1进行分析。
边
坡稳定安全系数K可按下式计算(图F.0.1):
图F.0.1锚固土质边坡或呈现软弱碎裂结构、散体结构的岩质边坡稳定性分析简图
Fl 191 Jt
/(∑∆G w+∑TM)+∑c∙∆L
K=— --------------------------------------------- (F.0.1)
∑∆G tf-∑T dv
1-1 >-1
式中:K——边坡稳定安全系数;
△G ni—作用于第i条滑动面上的岩土体的垂直分力(kN);
△G ti一作用于第i条滑动面上的岩土体的切向分力(kN);
△f、c——岩土体的摩擦系数标准值与粘聚力标准值(kPa);
△1.——第i条滑动面圆弧段长度(m);
Tdnj——第j根预应力锚杆受拉承载力设计值作用于滑动面上的垂直分量(kN);
Tdt j——第j根预应力锚杆受拉承载力设计值作用于滑动面上的切向分量(kN)。
瑞典条分法

假定滑动面为圆柱面, 截面为圆弧,利用土 体极限平衡条件下的 受力情况:
Fs M M
f
C
f LR f LR LR Wd
W 饱和粘土,不排水 剪条件下,u=0, τf =cu 滑动面上的最 大抗滑力矩与 滑动力矩之比
Fs cu LR Wd
瑞典圆弧滑动法的应用条件
cos tan sin w sin
三、例题分析 【例】均质无粘性土土坡,其饱和重度 sat=20.0kN/m3, 内摩擦角 =30°,若要求该土坡的稳定安全系数为1.20,
在干坡情况下以及坡面有顺坡渗流时其坡角应为多少度?
干坡或完全浸水情况 T T
Ns
土坡的稳定性相关因素:
抗剪强度指标c和、 重度 、土坡的尺寸 坡角 和坡高H
H cr
c
土坡的临界高 度或极限高度
Fs H
cr
稳定数
根据不同的 绘出 与Ns的关系曲线
H
泰勒图表法适宜解决简单土坡稳定分析的问题:
①已知坡角及土的指标c、、,求稳定的坡高H
②已知坡高H及土的指标c、、,求稳定的坡角 ③已知坡角、坡高H及土的指标c、、,求稳定安全系数F
二、有渗流作用时的无粘性土土坡分析
T J T W N
Fs T T J
w
稳定条件:T>T+J
顺坡出流情况:
T T J
J
sin
坡面有顺坡渗 流作用时,无 粘性土土坡稳 定安全系数将 近降低一半
tan sat tan
/ sat≈1/2,
Fs
W cos tan W sin J
用瑞典条分法excel

用瑞典条分法excel(原创实用版)目录1.瑞典条分法的概念和应用范围2.瑞典条分法在 Excel 中的操作方法3.使用瑞典条分法进行数据分析的实际案例4.瑞典条分法的优点和局限性正文1.瑞典条分法的概念和应用范围瑞典条分法(Swedish Method)是一种用于解决多元非线性规划问题的数值计算方法。
它是 20 世纪 50 年代由瑞典数学家 Gunnar Kvalsheim 提出的,主要应用于经济学、工程学等领域的优化问题。
这种方法通过迭代计算,逐步寻找到满足约束条件的最优解。
在实际应用中,瑞典条分法广泛应用于资源配置、生产计划、投资决策等问题。
2.瑞典条分法在 Excel 中的操作方法要在 Excel 中使用瑞典条分法,可以通过以下步骤进行操作:(1)首先,在 Excel 中输入决策变量和相关约束条件。
例如,假设有一个生产问题,需要确定生产 A、B 两种产品的数量以最大化总利润。
在这个例子中,决策变量是生产 A、B 两种产品的数量,约束条件是生产能力和成本。
(2)然后,在 Excel 中输入目标函数。
目标函数描述了决策者希望达到的目标。
在这个例子中,目标函数是利润函数。
(3)接下来,使用 Excel 的“数据”菜单中的“排序”功能,对目标函数进行排序。
这将帮助我们找到最优解。
(4)最后,根据排序结果,得出满足约束条件的最优解。
在这个例子中,最优解是生产 A、B 两种产品的最佳数量,以实现最大利润。
3.使用瑞典条分法进行数据分析的实际案例假设有一个企业需要确定生产 A、B 两种产品的最佳数量,以实现最大利润。
已知生产 A 产品的成本是 20 元/件,生产 B 产品的成本是 30 元/件;销售 A 产品的价格是 40 元/件,销售 B 产品的价格是 60 元/件。
假设企业有 1000 小时的生产能力,生产 A、B 两种产品分别需要 4 小时/件和 6 小时/件。
根据上述信息,我们可以使用瑞典条分法在 Excel 中进行计算。
瑞典条分法计算边坡稳定性

说明:
1、本边坡计算采用瑞典条分法计算;
2、以边坡坡脚为圆心建立坐标系;
3、本边坡计算,需要输入的基本参数有:边坡高度、边坡角度、滑动圆弧圆心坐标、土层重度、土的有效粘聚力、内摩擦角,水头高、各土层厚度、附加荷载情况等;
4、其他计算因子可根据实际工程情况调整;
5、土条宽度建议采用(0.05——0.1)R(滑动圆半径);本人经验在一般土条宽度越小,Ks值也会偏小;本边坡计算只作为计算范本,实际计算时应按要求调整;
6、有效内摩擦角:考虑地下水;当通过不同地层时,按土条中线位置在相应的土层来确定的;
7、有效粘聚力:考虑地下水;当通过不同地层时,按土条中线位置在相应的土层来确定的;
8、地下水水头高h wi 取土条中点数值,故水压U i=γw h wi b i。
瑞典条分法

土坡稳定 安全系数
各土条对滑弧 圆心的抗滑力 矩和滑动力矩
条分法分析步骤I
O
R
βi
d
c
i A
da b
c
Pi+1Xi+1
Wi
Xi
Pi
b
a Ti Ni
li
C B
H
假设两组合力 (Pi,Xi)= (Pi +1,Xi+1)
静力平衡
1.按比例绘出土坡剖面
2.任选一圆心O,确定
滑动面,将滑动面以上 土体分成几个等宽或不 等宽土条 3.每个土条的受力分析
=0 F
s
β1 β
B
>0
圆心位置在EO
的延长线上
圆心位置由β1, β2确定
O β2 A
H 2H
4.5H
E
二、条分法
O
对于外形复杂、 >0的粘性
土土坡,土体分层情况时,要
R
βi
d c
B
C 确定滑动土体的重量及其重心 位置比较困难,而且抗剪强度 的分布不同,一般采用条分法
H 分析
i A
ab
滑动土体 分为若干 垂直土条
如果能准确知道土中孔隙水压力分布,采用有效应力法比较合 理。重要的工程应采用有效强度指标进行核算。对于控制土坡稳 定的各个时期,应分别采用不同试验方法的强度指标
四、安全系数的选用
影响安全系数的因素很多,如抗剪强度指标的选用,计算方 法和计算条件的选择等。工程等级愈高,所需要的安全系数愈大。
目前,对于土坡稳定的安全系数,各个部门有不同的规定。
i
Ni li
1 li
Wi
cos i
i
Ti li
瑞典条分法在深基坑支护稳定性分析中的应用

瑞典条分法在深基坑支护稳定性分析中的应用【摘要】根据瑞典条分法的基本原理和稳定性验算,探讨了建筑深基坑支护设计的方法、思路。
通过工程实例,采用瑞典条分法进行建筑深基坑支护、山体滑坡支护等是可行、有效的,值得推广应用。
【关键词】瑞典条分法;基坑支护;滑动土体;稳定性验算【abstract 】according to Sweden slice method and the basic principle and stability checking, probes into the construction of the deep foundation pit supporting design method, the thinking. Through engineering examples, the article Sweden on building method runs deep foundation pit supporting, landslides bracing is feasible and effective, popularization.【key words 】Sweden slice method; Foundation pit supporting; Sliding the soil; Stability checking随着城市建设和改造的迅猛发展,都市建筑通常设计地下室,但是,由于建筑场地狭窄,常常给地下室开挖造成很大的困难。
因此,基坑支护结构的设计与施工,已成为当前现代建筑深基坑支护的热点和难点,成为影响整个工程造价和进度的关键。
目前用于基坑支护稳定性分析的新技术、新方法很多,其中,瑞典条分法作为传统而古老的极限平衡分析法, 在边坡稳定分析中是一种最常用、最重要的方法,常被工程设计人员所采用,其主要特点是:概念清晰,容易被工程人员理解和掌握,同时通过瑞典条分法不仅给出了深基坑边坡土体极限平衡条件下的受力情况,还直接给出反映边坡稳定安全系数值的计算分析,因此,该方法力学概念明确,适应范围较广,安全系数计算合理,在建筑工程领域得到广泛应用。
传统方法

瑞典圆弧滑动面条分法,首先假定滑动面为圆柱面,截面为圆弧,然后将假定滑动面以上的土体分成n个垂直土条,对作用于各土条上的力进行力和力矩平衡分析,求出在极限平衡状态下土体稳定的安全系数。
该法由于忽略土条之间的相互作用力的影响,因此是条分法中最简单的一种方法。
运用瑞典条分法的边坡的滑动面形状如下图所示:
图1 瑞典条分法
圆心半径(m):(-0.720,13.800),R=13.819。
安全系数F s=0.948。
简化毕肖普法是建立在圆弧滑裂面基础上的,在计算中假定土条侧向垂直面上的切向剪力为零,只考虑土条之间水平作用力的影响,根据圆弧滑裂面的极限平衡即可求得简化毕肖普法的安全系数。
图2 简化Bishop法
圆心半径(m):(-1.800,15.800),R=15.902。
安全系数F s=0.985。
Janbu法(普遍条分法)也是提前假定滑动面,但其形状不一定是圆弧状,计算前需要假定作用力的位置,可以得到整体和单个土条的平衡。
图3 Janbu法
圆心半径(m):(-1.960,16.000),R=16.120。
安全系数Fs=0.987。
强度折减法不需要提前假定滑动面的形状,可以考虑土内部的应力-应变关系,而且可以根据判别失稳依据直接得到安全系数。
图4 强度折减法
安全系数F s=0.989。
瑞典条分法计算过程

瑞典条分法计算过程
瑞典条分法是一种计算罚款金额的方法,它的计算方式如下:
1. 首先确定被罚款人的收入净额。
2. 根据违法行为的严重程度给出相应的“日罚金数”,即罚款金额的基数。
这个数值通常是在50 到1500 瑞典克朗(SEK) 之间。
3. 然后将被罚款人的收入净额除以730,得出日收入净额。
4. 将日收入净额与“日罚金数”相乘即可得出每日罚款金额。
5. 最后,将每日罚款金额乘以违法行为的持续时间,得出总罚款金额。
例如,假设某人违反了交通规则,根据违法行为的严重程度,每日罚金数为100 SEK。
他的收入净额为10000 SEK,日收入净额为13.7 SEK。
如果违法行为持续了10 天,那么他需要支付的罚款金额就是:
每日罚款金额= 13.7 SEK ×100 SEK = 1370 SEK
总罚款金额= 1370 SEK ×10 天= 13700 SEK
因此,该被罚款人需要支付13700 瑞典克朗的罚款。
用瑞典条分法excel

用瑞典条分法excel摘要:1.瑞典条分法简介2.使用Excel 进行瑞典条分法计算3.步骤详解a.准备数据b.创建公式c.计算结果d.分析与解读4.注意事项5.结论正文:瑞典条分法(Swedish Logic)是一种基于逻辑回归的分类方法,它通过一系列的问题对数据进行逐步分类,最终得到一个简洁明了的二分类或者多分类模型。
在实际应用中,瑞典条分法常常被用于金融、医疗、教育等领域的风险评估、信用评级等任务。
使用Excel 进行瑞典条分法计算,可以借助Excel 内置的数据分析和公式功能,轻松完成计算过程。
下面我们将详细介绍如何使用Excel 进行瑞典条分法计算。
1.准备数据首先,需要将数据整理成适合进行瑞典条分法计算的格式。
通常情况下,数据需要包括特征(自变量)和目标变量(因变量)两大部分。
例如,在进行信用评级时,特征可能包括年龄、收入、婚姻状况等,目标变量则是信用评级(如优质、一般、较差等)。
2.创建公式在Excel 中,我们可以通过创建公式来实现瑞典条分法的计算。
具体操作步骤如下:- 在一个空白单元格中,输入以下公式:`=IF(AND(条件1, 条件2, ...), 结果1, 结果2)`- 将公式向下填充,直至覆盖所有可能的条件组合。
需要注意的是,在创建公式时,应确保每个条件都与前面的条件组合逻辑相容。
例如,在信用评级任务中,如果某个特征只有两种状态(如已婚和未婚),那么在创建公式时,应确保已婚和未婚的公式结果互斥。
3.计算结果在创建完所有公式后,我们可以通过Excel 的“数据”选项卡中的“求和”功能,计算各个结果的频次。
这一步可以帮助我们了解各个条件组合在整体数据中所占的比例。
4.分析与解读根据计算结果,我们可以分析各个特征对目标变量的影响程度,从而找出对分类贡献最大的特征。
此外,我们还可以通过观察各个条件组合的频次,来了解不同特征组合对目标变量的影响。
需要注意的是,在解读结果时,应结合实际情况进行判断。
