高考数学专题复习例题习题及答案解析:线面垂直
线面垂直判定(解答题)
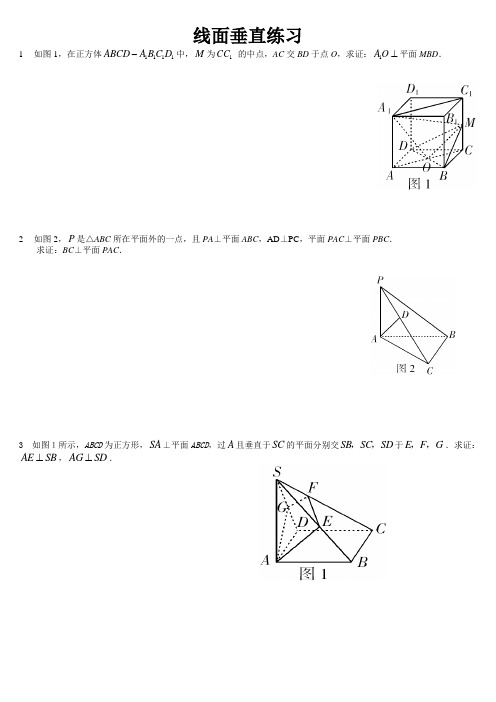
线面垂直练习1 如图1,在正方体1111ABCD A BC D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD .2 如图2,P 是△ABC 所在平面外的一点,且PA ⊥平面ABC ,AD ⊥PC ,平面PAC ⊥平面PBC .求证:BC ⊥平面PAC .3 如图1所示,ABCD 为正方形,SA ⊥平面ABCD ,过A 且垂直于SC 的平面分别交SB SC SD ,,于E F G ,,.求证:AE SB ⊥,AG SD ⊥.4 如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,F 是AB 中点, 作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .5 如图3,AB 是圆O的直径,C是圆周上一点,PA 平面ABC .若AE ⊥PC ,E为垂足,F是PB 上任意一点,求证:平面AEF ⊥平面PBC .6. 空间四边形ABCD 中,若AB ⊥CD ,BC ⊥AD ,求证:AC ⊥BDD7. 证明:在正方体ABCD -A 1B 1C 1D 1中,A 1C ⊥平面BC 1DAC证明:连结ACBD AC ⊥AC 为A 1C 在平面AC 上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面8. 如图,PA ⊥平面ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中点,求证:MN AB ⊥C. 证:取PD 中点E ,则EN DC //12C⇒ENAM// ∴AE MN//又平面平面平面 CD AD PA AC CD PAD AE PAD ⊥⊥⎫⎬⎭⇒⊥⊂⎫⎬⎭ ⇒⊥⎫⎬⎪⎭⎪⇒⊥CD AE CD AB AE MN MN AB////9如图在ΔABC 中, AD ⊥BC , ED=2AE , 过E 作FG ∥BC , 且将ΔAFG 沿FG 折起,使∠A 'ED=60°,求证:A 'E ⊥平面A 'BC分析:弄清折叠前后,图形中各元素之间的数量关系和位置关系。
立体几何线面垂直-题型全归纳(解析版)

立体几何线面垂直-题型全归纳题型一利用等腰三角形“三线合一”例题1、如图,在正三棱锥P-ABC中,E,F,G分别为线段PA,PB,BC的中点,证明:BC⊥平面PAG。
证明:在正三棱锥P-ABC中,AB=AC,G是BC的中点,∴AG⊥BC,又 PB=PC,G是BC的中点,∴PG⊥BC,PG⋂AG=G,PG,AG⊂平面PAG,∴BC⊥平面PAG,解题步骤(1)根据线段的中点,找出相应的等腰三角形;(2)格式“因为D是BC的中点,且AB=AC,所以AD⊥BC”;(3)依据“三线合一”得到线线垂直。
变式训练1、已知四面体ABCD中,AB=AC,BD=CD,E为棱BC的中点,求证:AD⊥BC证明:连接DE,AB=AC,E是BC的中点,∴AE⊥BC,又 BD=CD,E是BC的中点,∴DE⊥BC,AE⋂DE=E,AE,DE⊂平面ADE,∴BC⊥平面ADE,AD⊂平面ADE,∴AD⊥BC变式训练2、在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥.求证:PC AB ⊥证明:取AB的中点O,连接OP,OC, AP=BP,O是AB的中点,∴PE⊥AB,又 AC=BC,O是AB的中点,∴OC⊥AB,PO⋂CO=O,PO,CO⊂平面POC,∴AB⊥平面POC,PC⊂平面POC,∴AB⊥PC。
变式训练3、如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,E为CD的中点,060=∠ABC ,求证:AB⊥平面PAE。
证明: 底面ABCD是菱形,060=∠ABC ,∴AE⊥CD,又 AB//CD,∴AB⊥AE,又PA⊥平面ABCD,AB⊂平面ABCD,∴AB⊥PA,AP⋂AE=A,AP,AE⊂平面PAE,∴AB⊥平面PAE。
A CB P题型二利用勾股定理逆定理例题2、如图,在正方体1111D C B A ABCD -中,M 为棱1CC 的中点,AC 交BD 于点O ,求证:BDM1平面⊥O A 证明:连接OM,M A 1,11C A ,设正方体的棱长为2,则6222222121=+=+=AO A A O A 32122222=+=+=OC CM OM 91)22(222121121=+=+=M C C A M A 21221M A OM O A =+∴即:OM⊥OA 1又 在正方体1111D CB A ABCD -中,∴BD⊥OA 1 OM,BD⊂平面BDM,∴BDM1平面⊥O A 解题步骤(1)根据题干给出的线段长度(没有长度的可以假设),标示在图形上,找出相应的三角形;(2)把线段的长度分别求平方,判断能否构成“222c b a =+”;(3)根据平方关系得到线线垂直。
专练06 空间线面的垂直(解析版)

专练06 空间线面的垂直一、基础强化1. 设l 是直线,α,β是两个不同的平面,则下列命题正确的是 ( )A.若l ∥α,l ∥β,则α∥βB.若l ∥α,l ⊥β,则α⊥βC.若α⊥β,l ⊥α,则l ⊥βD.若α⊥β,l ∥α,则l ⊥β 【答案】B【解析】对于A 选项,设α∩β=a ,若l ∥a ,且l ⊄α,l ⊄β,则l ∥α,l ∥β,此时α与β相交,即A 选项错误;对于B 选项,若l ∥α,l ⊥β,则存在直线a ⊂α,使得l ∥a ,此时a ⊥β,由平面与平面垂直的判定定理得α⊥β,即B 选项正确;对于C 选项,若α⊥β,l ⊥α,则l ∥β或l ⊂β,即C 选项错误;对于D 选项,若α⊥β,l ∥α,则l 与β的位置关系不确定,即D 选项错误.故选B.2. (2019·山东潍坊月考)已知平面α和直线a ,b ,若a ∥α,则“b ⊥a”是“b ⊥α”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】B【解析】根据空间中直线与平面之间的位置关系,由a ∥α,b ⊥α,可得b ⊥a ,反之不成立,可能b 与α相交或平行.∴“b ⊥a”是“b ⊥α”的必要不充分条件.故选B.3. 已知在直四棱柱ABCD A 1B 1C 1D 1中,AB =2,AD =2,BD =6,AA 1=1,则异面直线A 1B 与B 1D 1所成角的大小为( )A .π6B .π3C . π4D .π2【答案】C 【解析】如图所示:在直四棱柱ABCD A 1B 1C 1D 1中,AB =2,AD =2,AA 1=1.所以D 1C =3,B 1C = 3.且易知D 1C ∥A 1B ,所以∠B 1D 1C(或其补角)即为所求.在△B 1D 1C 中,D 1C =3,B 1C =3,BD =6,所以∠D 1CB 1=π2,∠B 1D 1C=π4.故选C. 4. 如图,PA 垂直于矩形ABCD 所在的平面,则图中与平面PCD 垂直的平面是( )A .平面ABCDB .平面PBC C .平面PAD D .平面PAB【答案】C【解析】由PA ⊥平面ABCD 得PA ⊥CD ,由四边形ABCD 为矩形得CD ⊥AD ,从而有CD ⊥平面PAD ,所以平面PCD ⊥平面PAD. 故选C.5.在直三棱柱ABC A 1B 1C 1中,∠BAC =π2,AB =AC =2AA 1,则异面直线AC 1与A 1B 所成角的余弦值为( )A .15B .-15C .55D .-55【答案】A【解析】将三棱柱补为长方体ABDCA 1B 1D 1C 1,异面直线AC 1与A 1B 所成的角即为∠AC 1D ,设AA 1=1,则AC =CD =2,AC 1=DC 1=5,AD =2 2. 由题意知cos ∠AC 1D =5+5-82×5×5=15.故选A.6. 在三棱锥P -ABC 中,点P 在平面ABC 上的射影为点O ,若PA ⊥PB ,PB ⊥PC ,PC ⊥PA ,则点O 是△ABC 的 心. 【答案】垂【解析】如图∵PC ⊥PA ,PB ⊥PC ,PA∩PB=P ,∴PC ⊥平面PAB ,又AB ⊂平面PAB ,∴PC ⊥AB ,又AB ⊥PO ,PO∩PC=P ,∴AB ⊥平面PGC ,又CG ⊂平面PGC ,∴AB ⊥CG ,即CG 为AB 边上的高.同理可证BD ,AH 分别为AC 边,BC 边上的高,则O 为△ABC 的垂心.7. 如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.【答案】2【解析】取圆柱下底面弧AB的另一中点D,连接C1D,AD,因为C是圆柱下底面弧AB的中点,所以AD∥BC,所以直线AC1与AD所成角等于异面直线AC1与BC 所成角.因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD,因为圆柱的轴截面ABB1A1是正方形,所以C1D=2AD,所以直线AC1与AD所成角的正切值为2,所以异面直线AC1与BC所成角的正切值为 2.8. 正方体ABCD-A1B1C1D1的棱和六个面的对角线共24条,其中与体对角线AC1垂直的有条.【答案】6【解析】如图,连接AC,则BD⊥AC.在正方体ABCD-A1B1C1D1中,∵C1C⊥平面BCD,BD⊂平面BCD,∴C1C⊥BD,又AC∩CC1=C,∴BD⊥平面ACC1,∵AC1⊂平面ACC1,∴AC1⊥BD.同理A 1B ,A 1D ,B 1D 1,CD 1,B 1C 都与AC 1垂直. 正方体ABCD -A 1B 1C 1D 1的棱中没有与AC 1垂直的棱, 故与体对角线AC 1垂直的有6条.9.如图,点M ,N 分别是正方体ABCD A 1B 1C 1D 1的棱BB 1和B 1C 1的中点,则MN 和CD 1所成角的大小是________.【答案】60°【解析】因为MN ∥BC 1,CD 1∥A 1B ,所以∠A 1BC 1就是MN 和CD 1所成角,而△A 1BC 1是等边三角形,所以∠A 1BC 1=60°.10.已知长方体1111ABCD A B C D -的外接球体积为32π3,且12AA BC ==,则1A C 与平面11BB C C 所成的角为 。
2021高中数学线线,线面,面面垂直的证明(含解析)
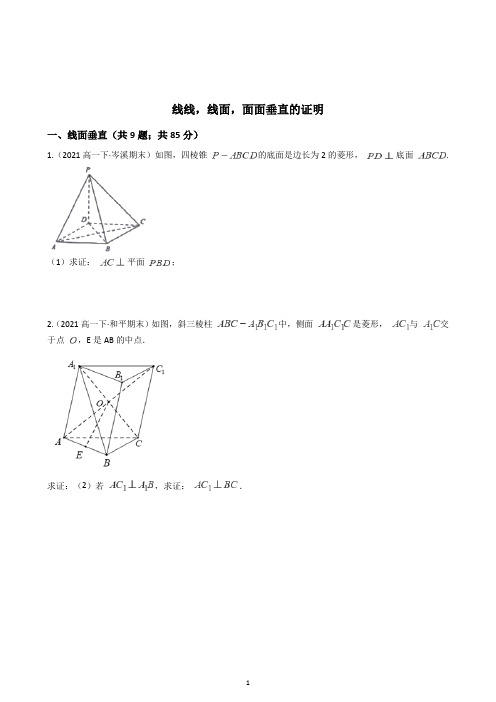
线线,线面,面面垂直的证明一、线面垂直(共9题;共85分)1.(2021高一下·岑溪期末)如图,四棱锥的底面是边长为2的菱形,底面.(1)求证:平面;2.(2021高一下·和平期末)如图,斜三棱柱中,侧面是菱形,与交于点,E是AB的中点.求证:(2)若,求证:.3.(2021高一下·宁波期末)已知三棱锥,平面,是以为斜边的等腰直角三角形,是以为斜边的直角三角形,为上一点,为上一点,且.(Ⅰ)现给出两个条件:① ;② 为中点.从中任意选一个条件为已知条件,求证:平面;4.(2021高一下·怀化期末)如图,在正方体中.(1)求证:面;5.(2021高一下·绍兴期末)如图,四棱台的底面是矩形,,,,.(Ⅰ)证明:平面;6.(2021高二下·二道期末)如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD是正三角形,侧面底面ABCD,M是PD的中点.(1)求证:平面PCD;7.(2021高一下·长春期末)如图,AB是的直径,PA垂直于所在的平面,C是圆周上不同于A,B的一动点.8.(2021高一下·河北期末)如图,在正四棱锥中,点E,F分别在棱PB,PD上,且.(1)证明:平面PAC.9.(2021高一下·天津期末)如图,在四棱锥中,平面,底面是菱形,(2)求证:直线平面二、线线垂直(共7题;共70分)10.(2021高一下·海南期末)如图所示,三棱柱中,,,,.(1)证明:;11.(2021·全国甲卷)已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.(1)证明:BF⊥DE;12.(2021·全国甲卷)已知直三棱柱中,侧面为正方形.分别为和的中点,.(2)已知为棱上的点,证明:.13.(2021·新高考Ⅰ)如图,在三棱锥A-BCD中.平面ABD丄平面BCD,AB=AD.O为BD的中点.(1)证明:OA⊥CD:14.(2021高一下·广东期末)如图,在三棱锥中,,点是线段的中点,平面平面.(2)求证:.15.(2021高二下·湖北期末)中国是风筝的故乡,南方称“鹞”,北方称“鸢”,如图,某种风筝的骨架模型是四棱锥,其中于,,,平面.(1)求证:;16.(2021·浙江)如图,在四棱锥中,底面是平行四边形,,M,N分别为的中点,.(1)证明:;三、面面垂直(共9题;共105分)17.(2021·新高考Ⅱ卷)在四棱锥中,底面是正方形,若.(1)证明:平面平面;18.(2021高一下·滨海新期末)如图,在三棱柱中,平面,,是的中点.(2)求证:平面平面;19.(2021高一下·和平期末)如图,在四棱锥中,平面平面,四边形为矩形,,,为的中点.(2)求证:平面平面;20.(2021高一下·龙岩期末)如图,是圆锥的顶点,是底面圆的直径,为底面圆周上异于的点,为的中点.(1)求证:平面平面21.(2021高一下·东丽期末)如图,三棱柱,底面,且为正三角形,,为中点.(2)求证:平面平面.22.(2021高一下·湖北期末)如图,在三棱台中,上底面为等腰直角三角形,,,,在上,.(1)证明:平面平面;23.(2021高一下·重庆期末)如图1,在平行四边形ABCD中,,,,将沿折起,使得平面平面,如图2.(1)证明:平面平面BCD;24.(2021高一下·河北期末)如图,在三棱柱中,,点为的中点,,.(1)证明:平面平面ABC.25.(2021·全国乙卷)如图,四棱锥P-ABCD的底面是矩形,PD 底面ABCD,M为BC的中点,且PB AM.(1)证明:平面PAM 平面PBD;线线,线面,面面垂直的证明参考答案一、线面垂直(共9题;共85分)1.(2021高一下·岑溪期末)如图,四棱锥的底面是边长为2的菱形,底面.(1)求证:平面;【答案】(1)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PD⊥平面ABCD,平面ABCD,所以PD⊥AC,又,AC⊥平面PBD2.(2021高一下·和平期末)如图,斜三棱柱中,侧面是菱形,与交于点,E是AB的中点.求证:(2)若,求证:.(2)∵侧面是菱形∴∵,,平面,平面∴平面∵平面∴.3.(2021高一下·宁波期末)已知三棱锥,平面,是以为斜边的等腰直角三角形,是以为斜边的直角三角形,为上一点,为上一点,且.(Ⅰ)现给出两个条件:① ;② 为中点.从中任意选一个条件为已知条件,求证:平面;【答案】解:(Ⅰ)若选①证明:∵平面,平面,∴,又,,∴平面.又平面,∴.又,,∴平面.又平面,∴.又,,∴平面.若选② 为中点证明:∵平面,平面,∴.又,,∴平面.又平面,∴.又,,∴平面.又平面,∴.又为等腰直角三角形斜边中点,则,,∴平面.4.(2021高一下·怀化期末)如图,在正方体中.(1)求证:面;【答案】(1)证明:因为为正方体,所以ABCD为正方形,所以,又因为平面ABCD,平面ABCD,故,又,平面,所以平面.5.(2021高一下·绍兴期末)如图,四棱台的底面是矩形,,,,.(Ⅰ)证明:平面;【答案】解:(Ⅰ)证明:因为底面是矩形,所以,又,,所以平面,又因为,所以平面.6.(2021高二下·二道期末)如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD是正三角形,侧面底面ABCD,M是PD的中点.(1)求证:平面PCD;【答案】(1)在正方形ABCD中,,又侧面底面ABCD,侧面底面,所以平面PAD,平面PAD,所以,是正三角形,M是PD的中点,所以,又,所以平面PCD.7.(2021高一下·长春期末)如图,AB是的直径,PA垂直于所在的平面,C是圆周上不同于A,B的一动点.(1)证明:BC⊥面PAC;【答案】(1)证明见解析PA垂直于所在的平面PA⊥BCAB是的直径AC⊥BCBC⊥面PAC8.(2021高一下·河北期末)如图,在正四棱锥中,点E,F分别在棱PB,PD上,且.(1)证明:平面PAC.【答案】(1)证明:如图,连接,记,连接PO,由题意可得四边形ABCD是正方形,,则O为AC的中点,且,因为,所以,因为平面,面,且,所以平面,因为,所以,则平面PAC;9.(2021高一下·天津期末)如图,在四棱锥中,平面,底面是菱形,(2)求证:直线平面【答案】(2)因为四边形是菱形,所以又因为平面平面所以又因为所以平面二、线线垂直(共7题;共70分)10.(2021高一下·海南期末)如图所示,三棱柱中,,,,.(1)证明:;【答案】(1)∵,,.∴,∴.∵,,∴.又∵,平面,∴平面.∵平面,∴.11.(2021·全国甲卷)已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.(1)证明:BF⊥DE;【答案】法一法2(1)因为三棱柱是直三棱柱,所以底面,所以因为,,所以,又,所以平面.所以两两垂直.以为坐标原点,分别以所在直线为轴建立空间直角坐标系,如图.所以,.由题设().因为,所以,所以.12.(2021·全国甲卷)已知直三棱柱中,侧面为正方形.分别为和的中点,.(2)已知为棱上的点,证明:.(2)由(1)的结论可将几何体补形为一个棱长为2的正方体,如图所示,取棱的中点,连结,正方形中,为中点,则,又,故平面,而平面,从而.13.(2021·新高考Ⅰ)如图,在三棱锥A-BCD中.平面ABD丄平面BCD,AB=AD.O为BD的中点.(1)证明:OA⊥CD:【答案】(1),为中点,,面,面面且面面,面,.14.(2021高一下·广东期末)如图,在三棱锥中,,点是线段的中点,平面平面.(2)求证:.【答案】(2)证明:∵,∴,∴,∵平面平面,且平面平面,平面,∴平面,∵平面,∴.15.(2021高二下·湖北期末)中国是风筝的故乡,南方称“鹞”,北方称“鸢”,如图,某种风筝的骨架模型是四棱锥,其中于,,,平面.(1)求证:;【答案】(1)证明:∵平面,平面,∴,又,,平面,平面,∴平面,又平面.∴.16.(2021·浙江)如图,在四棱锥中,底面是平行四边形,,M,N分别为的中点,.(1)证明:;【答案】(1)证明:在中,,,,由余弦定理可得,所以,.由题意且,平面,而平面,所以,又,所以三、面面垂直(共9题;共105分)17.(2021·新高考Ⅱ卷)在四棱锥中,底面是正方形,若.(1)证明:平面平面;【答案】(1)取的中点为,连接.因为,,则,而,故.在正方形中,因为,故,故,因为,故,故为直角三角形且,因为,故平面,因为平面,故平面平面.18.(2021高一下·滨海新期末)如图,在三棱柱中,平面,,是的中点.(2)求证:平面平面;【答案】(2)∵,是的中点,∴,∵三棱柱中,平面,∴平面∵AD 平面,∴,又、BC是平面内的两条相交直线∴平面∵AD 平面∴平面平面19.(2021高一下·和平期末)如图,在四棱锥中,平面平面,四边形为矩形,,,为的中点.(2)求证:平面平面;【答案】(2)因为平面平面,平面平面,,所以平面,因为平面,所以,又, 平面,所以平面,又平面,所以,又,所以,又平面,所以平面,又平面,所以平面平面;20.(2021高一下·龙岩期末)如图,是圆锥的顶点,是底面圆的直径,为底面圆周上异于的点,为的中点.(1)求证:平面平面【答案】(1)由圆锥的性质可知,底面圆∵在底面圆上,∴,∵在圆上,为直径,∴,又点分别为的中点,∴∴又,且平面,∴平面,又平面,∴平面平面.21.(2021高一下·东丽期末)如图,三棱柱,底面,且为正三角形,,为中点.(2)求证:平面平面.【答案】(2)∵面,面,∴.又,,∴,面,∴面.又面,∴面面.22.(2021高一下·湖北期末)如图,在三棱台中,上底面为等腰直角三角形,,,,在上,.(1)证明:平面平面;【答案】(1)因为三棱台中,因为,所以,由,所以,所以,又由,所以,因为,且平面,所以平面,又因为平面,所以平面平面.23.(2021高一下·重庆期末)如图1,在平行四边形ABCD中,,,,将沿折起,使得平面平面,如图2.(1)证明:平面平面BCD;【答案】(1)在中,因为,,,由余弦定理得,所以,所以,所以如图所示:作于点,因为平面平面,平面平面,所以平面,所以,又因为,所以平面,因为平面,所以,又由,所以平面.所以平面平面BCD;24.(2021高一下·河北期末)如图,在三棱柱中,,点为的中点,,.(1)证明:平面平面ABC.【答案】(1)证明:因为,所以,,在三棱柱中,,所以,又因为,所以平面ABC,又因为平面,所以平面平面ABC;25.(2021·全国乙卷)如图,四棱锥P-ABCD的底面是矩形,PD 底面ABCD,M为BC的中点,且PB AM.(1)证明:平面PAM 平面PBD;【答案】(1)因为底面,平面,所以,又,,所以平面,而平面,所以平面平面.。
线面垂直练习题及答案

线面垂直练习题及答案线面垂直是立体几何中的一个重要概念,它指的是一条直线与一个平面垂直。
在解决线面垂直问题时,我们通常需要利用相关的定理和性质来进行证明和计算。
以下是一些线面垂直的练习题及答案。
练习题1:已知直线AB与平面α垂直,点C在平面α内,求证:直线AC垂直于平面α。
答案1:由于直线AB垂直于平面α,根据线面垂直的性质定理,直线AB与平面α内的所有直线都垂直。
因此,直线AC作为平面α内的一条直线,必然与直线AB垂直。
根据线面垂直的定义,直线AC也垂直于平面α。
练习题2:在长方体ABCD-EFGH中,求证:直线BF垂直于平面ABEF。
答案2:由于长方体的对角线BF是连接两个相对顶点的直线,根据长方体的性质,对角线BF垂直于底面ABCD和顶面EFGH。
因此,直线BF垂直于平面ABEF内的任意直线,满足线面垂直的定义。
练习题3:已知直线l与平面α相交于点P,且直线m垂直于平面α,求证:直线m与直线l垂直。
答案3:由于直线m垂直于平面α,根据线面垂直的性质,直线m与平面α内的所有直线都垂直。
由于直线l与平面α相交于点P,我们可以将直线l投影到平面α上,得到一个与l平行的直线。
由于直线m垂直于平面α,它也垂直于平面α内的任何直线,包括l的投影。
因此,直线m与直线l垂直。
练习题4:在三棱锥P-ABC中,若PA⊥平面ABC,且AB⊥AC,求证:平面PAB垂直于平面PAC。
答案4:由于PA垂直于平面ABC,根据线面垂直的性质,PA也垂直于平面ABC 内的所有直线,包括AB和AC。
由于AB垂直于AC,根据面面垂直的判定定理,如果一个平面内的两条相交直线都垂直于另一个平面,则这两个平面垂直。
因此,平面PAB垂直于平面PAC。
练习题5:已知直线a与平面α垂直,直线b在平面α内,且直线a与直线b 相交于点O,求证:点O是直线a上的垂足。
答案5:由于直线a垂直于平面α,根据线面垂直的性质,直线a与平面α内的所有直线都垂直。
线面垂直练习题及答案

线面垂直练习题及答案线面垂直是几何学中的一项基本概念,用于描述线段、射线、直线和平面之间的垂直关系。
理解线面垂直的概念对于解决几何问题至关重要。
本文将为读者提供一些线面垂直练习题及答案,帮助读者巩固对该概念的理解。
练习题一:1. AB为一条线段,m是一平面。
如果AB与m垂直,判断下列命题的真假:a) 线段AB垂直于平面mb) 平面m垂直于线段ABc) 线段AB平行于平面m2. P是平面XYZ的内点,AP的延长线与平面XYZ有几个交点?练习题二:1. 给出下列命题的定义:a) 垂线b) 垂直平分线c) 垂直平面2. 在平面上画一条线段AB和一条直线l,求证:若线段AB与直线l垂直,则直线l过点A和点B的垂直平分线。
1. 已知直线l与平面P垂直,直线m过l上一点,那么直线m与平面P的关系是什么?2. 在长方形ABCD中,线段AC和线段BD相交于点O。
求证:线段AC与平面ABCD垂直。
答案及解析:练习题一:1. a) 假,线段AB无法垂直于平面m,因为线段只有两个端点而不是无限延伸。
b) 真,平面m可以垂直于线段AB。
c) 假,线段和平面不可能平行。
2. AP的延长线与平面XYZ有且只有一个交点。
练习题二:1. a) 垂线是与给定线段或直线垂直的线段或直线。
b) 垂直平分线是将给定线段或直线垂直平分的线段或直线。
c) 垂直平面是与给定平面垂直的平面。
2. 假设直线l过点A和点B的垂直平分线交线段AB于点M,则根据垂直平分线的定义,我们可以得出线段AM和线段BM的长度相等,且直线l与线段AM和线段BM都垂直。
1. 直线m与平面P平行。
2. 连接线段AC的中点和线段BD的中点,设为点O'。
根据长方形的性质,线段OO'相等且垂直于两个平行线段AC和BD。
因此,线段OO'垂直于平面ABCD,而线段OO'与线段AC相等,所以线段AC与平面ABCD垂直。
通过以上练习题及答案,我们可以加深对线面垂直概念的理解。
线面垂直判定(解答题)
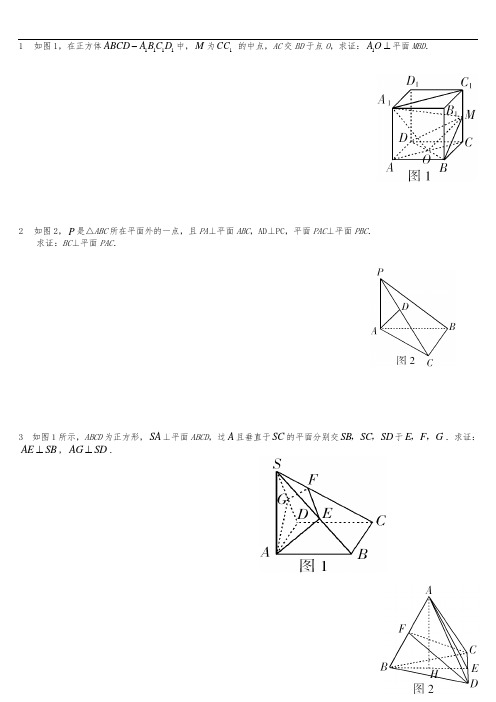
1如图1,在正方体1111ABCD A B C D-中,M为1CC的中点,AC交BD于点O,求证:1A O⊥平面MBD.2如图2,P是△ABC所在平面外的一点,且PA⊥平面ABC,AD⊥PC,平面PAC⊥平面PBC.求证:BC⊥平面PAC.3 如图1所示,ABCD为正方形,SA⊥平面ABCD,过A且垂直于SC的平面分别交SB SC SD,,于E F G,,.求证:AE SB⊥,AG SD⊥.4 如图2,在三棱锥A-BCD中,BC=AC,AD=BD,F是AB中点,作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.5 如图3,AB是圆O的直径,C是圆周上一点,PA 平面ABC.若AE⊥PC,E为垂足,F是PB上任意一点,求证:平面AEF⊥平面PBC.6. 空间四边形ABCD中,若AB⊥CD,BC⊥AD,求证:AC⊥BDADB OC7. 证明:在正方体ABCD -A 1B 1C 1D 1中,A 1C ⊥平面BC 1DAC证明:连结ACBD AC ⊥AC 为A 1C 在平面AC 上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面8. 如图,PA ⊥平面ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中点,求证:MN AB ⊥C. 证:取PD 中点E ,则EN DC //12C⇒EN AM //∴AE MN //又平面平面平面 CD AD PA AC CD PAD AE PAD ⊥⊥⎫⎬⎭⇒⊥⊂⎫⎬⎭⇒⊥⎫⎬⎪⎭⎪⇒⊥CD AE CD AB AE MN MN AB ////9如图在ΔABC 中, AD ⊥BC , ED=2AE , 过E 作FG ∥BC , 且将ΔAFG 沿FG 折起,使∠A'ED=60°,求证:A'E ⊥平面A'BC分析:弄清折叠前后,图形中各元素之间的数量关系和位置关系。
解: ∵FG ∥BC ,AD ⊥BC∴A'E ⊥FG∴A'E ⊥BC设A'E=a ,则ED=2a 由余弦定理得:A'D 2=A'E 2+ED 2-2•A'E •EDcos60°=3a2∴ED 2=A'D 2+A'E 2∴A'D ⊥A'E∴A'E ⊥平面A'BC10如图, 在空间四边形SABC 中, SA 平面ABC , ABC = 90, AN SB 于N , AM SC 于M 。
线面垂直练习题及答案

线面垂直练习题及答案线面垂直是几何学中一个重要的概念,它涉及到直线和平面之间的关系。
在几何学中,我们经常需要判断线和平面是否垂直,以及如何确定它们的垂直关系。
为了帮助大家更好地理解和掌握线面垂直的概念,本文将介绍一些线面垂直的练习题及答案。
1. 练习题:判断线段和平面是否垂直题目:已知线段AB的两个端点分别为A(1, 2, 3)和B(4, 5, 6),平面P的法向量为(2, -1, 3),判断线段AB是否垂直于平面P。
解答:要判断线段AB是否垂直于平面P,只需判断线段AB的方向向量是否与平面P的法向量垂直。
线段AB的方向向量为AB = B - A = (4, 5, 6) - (1, 2, 3) = (3, 3, 3)。
两个向量的点积为3*2 + 3*(-1) + 3*3 = 9,不等于0。
因此,线段AB不垂直于平面P。
2. 练习题:确定两平面之间的垂直关系题目:已知平面P1的法向量为(1, 2, -1),平面P2的法向量为(2, -1, 3),判断平面P1和平面P2之间的垂直关系。
解答:两个平面垂直的条件是它们的法向量垂直,即两个法向量的点积为0。
计算两个法向量的点积为1*2 + 2*(-1) + (-1)*3 = 0,等于0。
因此,平面P1和平面P2垂直。
3. 练习题:求垂直平面上的直线题目:已知平面P的方程为2x + 3y - z = 6,求过点A(1, 2, 3)且垂直于平面P的直线的方程。
解答:垂直于平面P的直线的方向向量应该与平面P的法向量垂直。
由平面P的方程可知,平面P的法向量为(2, 3, -1)。
因此,过点A(1, 2, 3)且垂直于平面P 的直线的方向向量为(2, 3, -1)。
直线的方程可以表示为x = 1 + 2t,y = 2 + 3t,z = 3 - t,其中t为参数。
4. 练习题:判断直线和平面是否垂直题目:已知直线L的方程为x = 1 + 2t,y = 2 + 3t,z = 3 - t,平面P的方程为2x + 3y - z = 6,判断直线L是否垂直于平面P。
高考数学专题20 立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨:证明直线与平面的平行与垂直问题,一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
直线与平面的平行有两种方法:一是在面内找线;二是通过面面平行转化。
直线与平面垂直关键是找两条相交直线例1、(2021南通、泰州、扬州一调〕如图,在四棱锥PABCD中,M,N分别为棱PA,PD的中点.侧面PAD⊥底面ABCD,底面ABCD是矩形,DA=DP.求证:(1)MN∥平面PBC;MD⊥平面PAB.【证明】(1)在四棱锥P-ABCD中,M,N分别为棱PA,PD的中点,所以MN∥AD.(2分)又底面ABCD是矩形,所以BC∥AD.所以MN∥BC.(4分)又BC⊂平面PBC,MN⊄平面PBC,所以MN∥平面PBC. (6分)(2)因为底面ABCD是矩形,所以AB⊥AD.又侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,AB⊂底面ABCD,所以AB⊥侧面PAD.(8分)又MD⊂侧面PAD,所以AB⊥MD.(10分)因为DA=DP,又M为AP的中点,从而MD⊥PA. (12分)又PA,AB在平面PAB内,PA∩AB=A,所以MD⊥平面PAB.(14分)例2、(2021扬州期末〕如下图,在三棱柱ABCA1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.(1) 求证:EF∥平面ABC;(2) 求证:BB1⊥AC.标准解答(1)在三棱柱ABCA1B1C1中,四边形AA1B1B,四边形BB1C1C均为平行四边形,E,F分别是侧面AA1B1B,BB1C1C对角线的交点,所以E,F分别是AB1,CB1的中点,所以EF∥AC.(4分)因为EF⊄平面ABC,AC⊂平面ABC,所以EF∥平面ABC.(8分)(2)因为四边形AA1B1B为矩形,所以BB1⊥AB.因为平面AA1B1B⊥平面ABC,且平面AA1B1B∩平面ABC=AB,BB1⊂平面AA1B1B,所以BB1⊥平面ABC.(12分)因为AC⊂平面ABC,所以BB1⊥AC.(14分)例3、(2021南京、盐城二模〕如图,在三棱柱ABCA1B1C1中,AB=AC,A1C⊥BC1,AB1⊥BC1,D,E 分别是AB1和BC的中点.求证:(1)DE∥平面ACC1A1;(2)AE⊥平面BCC1B1.标准解答(1)连结A1B,在三棱柱ABCA1B1C1中,AA1∥BB1且AA1=BB1,所以四边形AA1B1B是平行四边形.又因为D是AB1的中点,所以D也是BA1的中点.(2分)在△BA1C中,D和E分别是BA1和BC的中点,所以DE∥A1C.又因为DE⊄平面ACC1A1,A1C⊂平面ACC1A1,所以DE∥平面ACC1A1.(6分)(2)由(1)知DE∥A1C,因为A1C⊥BC1,所以BC1⊥DE.(8分)又因为BC1⊥AB1,AB1∩DE=D,AB1,DE⊂平面ADE,所以BC1⊥平面ADE.又因为AE⊂平在ADE,所以AE⊥BC1.(10分)在△ABC中,AB=AC,E是BC的中点,所以AE⊥BC.(12分)因为AE⊥BC1,AE⊥BC,BC1∩BC=B,BC1,BC⊂平面BCC1B1,所以AE⊥平面BCC1B1. (14分)例4、(2021苏锡常镇调研〕如图,三棱锥DABC中,AC⊥BC,AC⊥DC,BC=DC,E,F分别为BD,CD的中点.求证:(1) EF∥平面ABC;(2) BD⊥平面ACE..标准解答(1)三棱锥DABC中,因为E为DB的中点,F为DC的中点,所以EF∥BC,(3分)因为BC⊂平面ABC,EF⊄平面ABC,所以EF∥平面ABC.(6分)(2)因为AC⊥BC,AC⊥DC,BC∩DC=C,BC,DC⊂平面BCD所以AC⊥平面BCD,(8分)因为BD⊂平面BCD,所以AC⊥BD,(10分)因为DC=BC,E为BD的中点,所以CE⊥BD,(12分)因为AC∩CE=C,AC,CE⊂平面ACE,所以BD⊥平面ACE.(14分)例5、(2021苏州三市、苏北四市二调〕如图,在直三棱柱ABCA1B1C1中,侧面BCC1B1为正方形,A1B1⊥B1C1.设A1C与AC1交于点D,B1C与BC1交于点E.求证:(1) DE∥平面ABB1A1;(2) BC1⊥平面A1B1C.标准解答(1)因为三棱柱ABCA1B1C1为直三棱柱,所以侧面ACC1A1为平行四边形.又A1C与AC1交于点D,所以D为AC1的中点,同理,E为BC1的中点.所以DE∥AB.(3分)又AB⊂平面ABB1A1,DE⊄平面ABB1A1,所以DE∥平面ABB1A1.(6分)(2)因为三棱柱ABCA1B1C1为直三棱柱,所以BB1⊥平面A1B1C1.又因为A1B1⊂平面A1B1C1,所以BB1⊥A1B1.(8分)又A1B1⊥B1C1,BB1,B1C1⊂平面BCC1B1,BB1∩B1C1=B1,所以A1B1⊥平面BCC1B1.(10分)又因为BC1⊂平面BCC1B1,所以A1B1⊥BC1.(12分)又因为侧面BCC1B1为正方形,所以BC1⊥B1C.又A1B1∩B1C=B1,A1B1,B1C⊂平面A1B1C,所以BC1⊥平面A1B1C.(14分)例6、(2021苏北四市一模〕如图,在正三棱柱ABCA1B1C1中,D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:(1) 直线A1E∥平面ADC1;(2) 直线EF⊥平面ADC1.标准解答(1) 证法1 连结ED,因为D,E分别为BC,B1C1的中点,所以B1E∥BD且B1E=BD,所以四边形B1BDE是平行四边形,(2分)所以BB1∥DE且BB1=DE.又BB1∥AA1且BB1=AA1,所以AA1∥DE且AA1=DE,所以四边形AA1ED是平行四边形,所以A1E∥AD.(4分)又因为A1E⊄平面ADC1,AD⊂平面ADC1,所以直线A1E∥平面ADC1.(7分)证法2 连结ED ,连结A 1C ,EC 分别交AC 1,DC 1于点M ,N ,连结MN ,那么因为D ,E 分别为BC ,B 1C 1的中点,所以C 1E ∥CD 且C 1E =CD ,所以四边形C 1EDC 是平行四边形,所以N 是CE 的中点.(2分) 因为A 1ACC 1为平行四边形,所以M 是A 1C 的中点,(4分) 所以MN ∥A 1E .又因为A 1E ⊄平面ADC 1,MN ⊂平面ADC 1,所以直线A 1E ∥平面ADC 1.(7分) (2) 在正三棱柱ABCA 1B 1C 1中,BB 1⊥平面ABC . 又AD ⊂平面ABC ,所以AD ⊥BB 1.又△ABC 是正三角形,且D 为BC 的中点,所以AD ⊥BC .(9分) 又BB 1,BC ⊂平面B 1BCC 1,BB 1∩BC =B , 所以AD ⊥平面B 1BCC 1,又EF ⊂平面B 1BCC 1,所以AD ⊥EF .(11分)又EF ⊥C 1D ,C 1D ,AD ⊂平面ADC 1,C 1D ∩AD =D , 所以直线EF ⊥平面ADC 1.(14分)题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题,一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
线面垂直判定定理测试题(含答案)
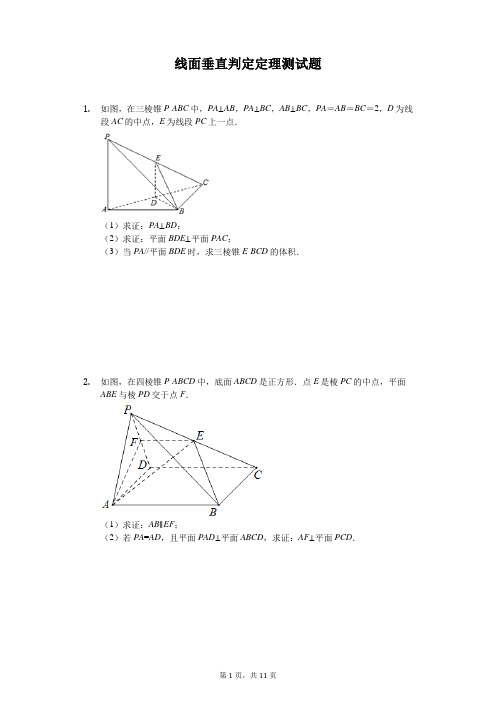
线面垂直判定定理测试题1.如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA//平面BDE时,求三棱锥E-BCD的体积.2.如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.(1)求证:AB∥EF;(2)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.3.如图,已知AF⊥面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=1,AB=2(1)求证:AF∥面BCE;(2)求证:AC⊥面BCE;(3)求三棱锥E-BCF的体积.4.如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.5.如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD=√3.(1)求证:CD⊥平面ADS;(2)求AD与SB所成角的余弦值;(3)求二面角A-SB-D的余弦值.6.如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:(1)MN∥平面PAB;(2)AM⊥平面PCD.7.如图所示四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4,E为PD的中点,F为PC中点.(Ⅰ)求证:CD⊥平面PAC;(Ⅱ)求证:BF∥平面ACE;(Ⅲ)求直线PD与平面PAC所成的角的正弦值.答案和解析1.【答案】(1)证明:由PA ⊥AB ,PA ⊥BC ,AB ⊂平面ABC ,BC ⊂平面ABC ,且AB ∩BC =B ,可得PA ⊥平面ABC ,由BD ⊂平面ABC ,可得PA ⊥BD ;(2)证明:由AB =BC ,D 为线段AC 的中点,可得BD ⊥AC ,由PA ⊥平面ABC ,PA ⊂平面PAC ,可得平面PAC ⊥平面ABC ,又平面PAC ∩平面ABC =AC ,BD ⊂平面ABC ,且BD ⊥AC ,即有BD ⊥平面PAC ,BD ⊂平面BDE ,可得平面BDE ⊥平面PAC ;(3)解:PA //平面BDE ,PA ⊂平面PAC ,且平面PAC ∩平面BDE =DE ,可得PA //DE ,又D 为AC 的中点,可得E 为PC 的中点,且DE =12PA =1,由PA ⊥平面ABC ,可得DE ⊥平面ABC ,可得S △BDC =12S △ABC =12×12×2×2=1, 则三棱锥E -BCD 的体积为13DE •S △BDC =13×1×1=13.【解析】本题考查空间的线线、线面和面面的位置关系的判断,主要是平行和垂直的关系,注意运用线面平行的性质定理以及线面垂直的判定定理和性质定理,面面垂直的判定定理和性质定理,同时考查三棱锥的体积的求法,考查空间想象能力和推理能力,属于中档题.(1)运用线面垂直的判定定理可得PA⊥平面ABC,再由性质定理即可得证;(2)要证平面BDE⊥平面PAC,可证BD⊥平面PAC,由(1)运用面面垂直的判定定理可得平面PAC⊥平面ABC,再由等腰三角形的性质可得BD⊥AC,运用面面垂直的性质定理,即可得证;(3)由线面平行的性质定理可得PA//DE,运用中位线定理,可得DE的长,以及DE⊥平面ABC,求得三角形BCD的面积,运用三棱锥的体积公式计算即可得到所求值.2.【答案】解:(1)证明:∵底面ABCD是正方形,∴AB∥CD ,又∵AB⊄平面PCD,CD⊂平面PCD,∴AB∥平面PCD ,又∵A,B,E,F四点共面,且平面ABEF∩平面PCD=EF,∴AB∥EF ;(2)证明:在正方形ABCD中,CD⊥AD ,又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,CD⊂平面ABCD,CD⊄平面PAD∴CD⊥平面PAD ,又∵AF⊂平面PAD ,∴CD⊥AF ,由(1)可知,AB∥EF,又∵AB∥CD,C,D,E,F在同一平面内,∴CD∥EF ,∵点E是棱PC中点,∴点F是棱PD中点,在△PAD中,∵PA=AD,∴AF⊥PD ,又∵PD∩CD=D,PD、CD⊂平面PCD,∴AF⊥平面PCD.【解析】(1)证明AB∥平面PCD,即可得AB∥EF;(2)利用平面PAD⊥平面ABCD,证明CD⊥AF,PA=AD,所以AF⊥PD,即可证明AF⊥平面PCD;本题考查线面平行的性质,平面与平面垂直的性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.3.【答案】(1)证明:∵四边形ABEF为矩形,∴AF∥BE,∵AF⊄平面BCE,BE⊄平面BCE,∴AF∥面BCE.(2)证明:∵AF⊥面ABCD,四边形ABEF为矩形,∴BE⊥平面ABCD,∵AC⊂平面ABCD,∴AC⊥BE,∵四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=1,AB=2 ∴AC=BC=√12+12=√2,∴AC2+BC2=AB2,∴AC⊥BC,∵BC∩BE=B,∴AC⊥面BCE.(3)解:三棱锥E-BCF的体积:V E-BCF=V C-BEF=13×S△BEF×AD=1 3×12×BE×EF×AD=1 3×12×1×2×1=13.【解析】本题考查线面平行、线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、转化化归思想,考查数据处理能力和运用意识,是中档题.(1)推导出AF∥BE,由此能证明AF∥面BCE.(2)推导出AC⊥BE,AC⊥BC,由此能证明AC⊥面BCE.(3)三棱锥E-BCF的体积V E-BCF=V C-BEF,由此能求出结果.4.【答案】证明:(1)取AC中点O,连结DO、BO,∵△ABC是正三角形,AD=CD,∴DO⊥AC,BO⊥AC,∵DO∩BO=O,∴AC⊥平面BDO,∵BD⊂平面BDO,∴AC⊥BD.(2)解:连结OE,由(1)知AC⊥平面OBD,∵OE⊂平面OBD,∴OE⊥AC,设AD=CD=√2,则OC=OA=1,EC=EA,∵AE⊥CE,AC=2,∴EC2+EA2=AC2,∴EC=EA=√2=CD,∴E是线段AC垂直平分线上的点,∴EC=EA=CD=√2,由余弦定理得:cos∠CBD=BC2+BD2−CD22BC⋅BD =BC2+BE2−CE22BC⋅BE,即4+4−22×2×2=4+BE2−22×2×BE,解得BE=1或BE=2,∵BE<BD=2,∴BE=1,∴BE=ED,∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,∵BE=ED,∴S△DCE=S△BCE,∴四面体ABCE与四面体ACDE的体积比为1.【解析】本题考查线线垂直的证明,考查两个四面体的体积之比的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.(1)取AC中点O,连结DO、BO,推导出DO⊥AC,BO⊥AC,从而AC⊥平面BDO,由此能证明AC⊥BD.(2)连结OE,设AD=CD=,则OC=OA=1,由余弦定理求出BE=1,由BE=ED,四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,S△DCE=S△BCE,由此能求出四面体ABCE与四面体ACDE的体积比.5.【答案】解:(I)证明:∵ABCD是矩形,∴CD⊥AD又SD⊥AB,AB∥CD,则CD⊥SD(2分)AD⊥SD∴CD⊥平面ADS(II)矩形ABCD,∴AD∥BC,即BC=1,∴要求AD与SB所成的角,即求BC与SB所成的角在△SBC中,由(1)知,SD⊥面ABCD.∴Rt△SDC中,SC=√(√3)2+22=√7∴CD是CS在面ABCD内的射影,且BC⊥CD,∴SC⊥BCtan∠SBC=SCCB =√71=√7cos∠SBC=√24从而SB与AD的成的角的余弦为√24.(III)∵△SAD中SD⊥AD,且SD⊥AB∴SD⊥面ABCD.∴平面SDB⊥平面ABCD,BD为面SDB与面ABCD的交线.∴过A作AE⊥DB于E∴AE⊥平面SDB又过A作AF⊥SB于F,连接EF,从而得:EF⊥SB∴∠AFB为二面角A-SB-D的平面角在矩形ABCD中,对角线∵√12+22=√5BD=√5∴在△ABD中,AE=AB⋅CDBD =1⋅2√5=2√55由(2)知在Rt△SBC,SB=√(√7)2+12=√8.而Rt△SAD中,SA=2,且AB=2,∴SB2=SA2+AB2,∴△SAB为等腰直角三角形且∠SAB为直角,∴AF=√22AB=√2∴sin∠AFE=AEAF =2√55√2=√105所以所求的二面角的余弦为√155【解析】(1)要证CD⊥平面ADS,只需证明直线CD垂直平面ADS内的两条相交直线AD、SD即可;(2)要求AD与SB所成的角,即求BC与SB所成的角,解三角形可求AD与SB所成角的余弦值;(3)过A作AE⊥DB于E 又过A作AF⊥SB于F,连接EF,说明∠AFB为二面角A-SB-D的平面角,解三角形可求二面角A-SB-D的余弦值.本题考查直线与平面垂直的判定,二面角的求法,异面直线所成的角,考查学生逻辑思维能力,计算能力,是中档题.6.【答案】证明:(1)因为M、N分别为PD、PC的中点,所以MN∥DC,又因为底面ABCD是矩形,所以AB∥DC.所以MN∥AB,又AB⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)因为AP=AD,P为PD的中点,所以AM⊥PD.因为平面PAD⊥平面ABCD,又平面PAD∩平面ABCD=AD,CD⊥AD,CD⊂平面ABCD,所以CD⊥平面PAD,又AM⊂平面PAD,所以CD⊥AM.因为CD、PD⊂平面PCD,CD∩PD=D,∴AM⊥平面PCD.【解析】(1)推导出MN∥DC,AB∥DC.从而MN∥AB,由此能证明MN∥平面PAB.(2)推导出AM⊥PD,CD⊥AD,从而CD⊥平面PAD,进而CD⊥AM,由此能证明AM⊥平面PCD.本题考查线面平行、线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.7.【答案】(Ⅰ)证明:因为PA⊥底面ABCD,CD⊂面ABCD,所以PA⊥CD,又因为直角梯形ABCD中,AC=2√2,CD=2√2,所以AC2+CD2=AD2,即AC⊥CD,又PA∩AC=A,所以CD⊥平面PAC;(Ⅱ)解法一:如图,连接BD,交AC于O,取PE中点G,连接BG,FG,EO,则在△PCE中,FG∥CE,又EC⊂平面ACE,FG⊄平面ACE,所以FG∥平面ACE,因为BC∥AD,所以BOOD =GEED,则OE∥BG,又OE⊂平面ACE,BG⊄平面ACE,所以BG∥平面ACE,又BG∩FG=G,所以平面BFG∥平面ACE,因为BF⊂平面BFG,所以BF∥平面ACE.解法二:如图,连接BD,交AC于O,取PE中点G,连接FD交CE于H,连接OH,则FG∥CE,在△DFG中,HE∥FG,则GEED =FHHD=12,在底面ABCD中,BC∥AD,所以BOOD =BCAD=12,所以FHHD =BOOD=12,故BF∥OH,又OH⊂平面ACE,BF⊄平面ACE,所以BF∥平面ACE.(Ⅲ)由(Ⅰ)可知,CD⊥平面PAC,所以∠DPC为直线PD与平面PAC所成的角,在Rt△PCD中,CD=2√2,PD=√PA2+AD2=2√5,所以sin∠DPC=CDPD =2√22√5=√105,所以直线PD与平面PAC所成的角的正弦值为√105.【解析】本题考查线面垂直、线面平行,考查线面角,解题的关键是掌握线面垂直、线面平行的判定方法,正确找出线面角.(Ⅰ)证明CD⊥平面PAC,证明PA⊥CD,AC⊥CD即可;(Ⅱ)解法一:连接BD,交AC于O,取PE中点G,连接BG,FG,EO,证明平面BFG∥平面ACE,即可证得BF∥平面ACE;解法二:如图,连接BD,交AC于O,取PE中点G,连接FD交CE于H,连接OH,则证明BF∥OH,即可证得BF∥平面ACE;(Ⅲ)确定∠DPC为直线PD与平面PAC所成的角,在Rt△PCD中,即可求得直线PD与平面PAC所成的角的正弦值.第11页,共11页。
2023高考数学复习专项训练《空间中直线与平面的位置关系》(含解析)

2023高考数学复习专项训练《空间中直线与平面的位置关系》一、单选题(本大题共12小题,共60分)1.(5分)设m,n为两条不同的直线,α,β为两个不同的平面,给出下列命题:①若m⊥α,m⊥β,则α//β②若m//α,m//β,则α//β③若m//α,n//α,则m//n④若m⊥α.n⊥α,则m//n上述命题中,所有真命题的序号是()A. ①④B. ②③C. ①③D. ②④2.(5分)直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,下列命题正确的是:A. l与l1,l2都不相交B. l与l1,l2都相交C. l至多与l1,l2中的一条相交D. l至少与l1,l2中的一条相交3.(5分)已知α、β是不同的平面,m、n是不同的直线,则下列命题不正确的是()A. 若m⊥α,m//n,n⊂β,则α⊥βB. 若m//α,α∩β=n,,则m//nC. 若m//n,m⊥α,则n⊥αD. 若m⊥α,m⊥β,则α//β4.(5分)已知两条直线m、n,两个平面α、β,给出下面四个命题:①m//n,m⊥α⇒n⊥α①α//β,m⊂α,n⊂β⇒m//n①m//n,m//α⇒n//α①α//β,m//n,m⊥α,⇒m⊥β其中正确命题的序号是()A. ①①B. ①①C. ①①D. ①①5.(5分)已知α,β是两个不同的平面,下列四个条件中能推出α//β的是()①存在一条直线m,m⊥α,m⊥β;②存在一个平面γ,γ⊥α,γ⊥β;③存在两条平行直线m,n,m⊂α,n⊂β,m//β,n//α;④存在两条异面直线m,n,m⊂α,n⊂β,m//β,n//α.A. ①①B. ①①C. ①①D. ①①6.(5分)棱柱的一条侧棱所在的直线与不含这条侧棱的侧面所在平面的位置关系是()A. 平行B. 相交C. 平行或相交D. 不相交7.(5分)若α,β是两个不同的平面,m,n,l是三条不同的直线,则下列命题错误的是()A. 若m⊂α,l∩α=A,且A∉m,则l与m不共面B. 若m,l是异面直线,l//α,m//α,且n⊥l,n⊥m,则n⊥αC. 若l⊂α,m⊂α,l∩m=A,l//β,m//β,则α//βD. 若l//α,m//β,α//β,则l//m8.(5分)已知平面α⊥平面β,α∩β=n,直线l⊂α,直线m⊂β,则下列说法正确的个数是()①若l⊥n,l⊥m,则l⊥β;②若l//n,则l//β;③若m⊥n,l⊥m,则m⊥α.A. 0B. 1C. 2D. 39.(5分)已知a,b为两条不同直线,α、β为两个不同平面.下列命题中正确的是()A. 若a//α,b//α,则a与b共面B. 若a⊥α,α//β,则a⊥βC. 若a⊥α,α⊥β,则a//βD. 若α//b,β//b,则α//β10.(5分)若直线l平行于平面α,则()A. α内所有直线与l平行B. 在α内不存在直线与l垂直C. α内存在唯一的直线与l平行D. α内存在无数条直线与l成60°角11.(5分)在空间中,设l是一条直线,α,β是两个不同的平面.下列结论正确的是()A. 若l//α,l//β,则α//βB. 若l⊥α,l⊥β,则α//βC. 若l//α,α//β,则l//βD. 若l//α,α⊥β,则l⊥β12.(5分)直线l⊂平面α,直线m⊄平面α,命题p:“若直线m⊥α,则m⊥l”的逆命题、否命题、逆否命题中真命题的个数为()A. 0B. 1C. 2D. 3二、填空题(本大题共5小题,共25分)13.(5分)设l,m,n是空间三条不同的直线,α,β是空间两个不重合的平面,给出下列四个命题:①若l与m异面,m//n,则l与n异面;②若l//α,α//β,则l//β;③若α⊥β,l⊥α,m⊥β,则l⊥m;④若m//α,m//n,则n//α.其中正确命题的序号有 ______ .(请将你认为正确命题的序号都填上)14.(5分)作直线a、b和平面α,则下列小组内两个事件互为对立事件的有 ______组(请填写个数).A组:“a//b”和“a⊥b”;B组:“a、b为异面直线”和“a⊥b”;C组:“a//α或a⊂α”和“a与α相交”.15.(5分)已知关于空间两条不同直线m,n,两个不同平面α,β,有下列四个命题:①若m//α且n//α,则m//n;②若m⊥β且m⊥n,则n//β;③若m⊥α且m//β,则α⊥β;④若n⊂α且m不垂直于α,则m不垂直于n.其中正确命题的序号为______.16.(5分)若α、β是两个相交平面,则在下列命题中,真命题的序号为______.(写出所有真命题的序号)①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线.②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直.③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线.④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.17.(5分)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为√3,那么P到平面ABC的距离为________.三、解答题(本大题共6小题,共72分)18.(12分)如图,四棱锥P−ABCD中,AD//BC,AB=BC=1AD,E,F,H分别为线段AD,PC,CD的中点,AC2与BE交于O点,G是线段OF上一点.(1)求证:AP//平面BEF;(2)求证:GH//平面PAD.19.(12分)用符号语表示图中点、直线、平面的位置关系.20.(12分)如图,在正三棱柱ABC−A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为√29,设这条最短路线与CC1的交点为N,求:(I)该三棱柱的侧面展开图的对角线长(II)PC和NC的长(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)21.(12分)如图,正方体ABCD−A1B1C1D1中,M,N分别是AB,A1D1的中点.判断直线MN与平面BB1D1D的位置关系,并说明理由.22.(12分)如图,在棱长为a的正方体ABCD−A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2BF。
线面垂直及应用(习题及答案)

线面垂直及应用(习题)➢例题示范例1:如图,在正三棱柱ABC-A1B1C1 中,AB=AA1=1,则点C 到平面ABC1 的距离为()A.42 6B.3C.217D.2 37思路分析:思路一:观察特征,考虑采用构造垂面法,取AB 的中点E ,易证平面C1CE⊥平面ABC1,过点C 作CF⊥C1E,则CF 的长即为所求距离,接着在直角三角形中研究边角关系,求解.思路二:采用等体积法,VC -ABC =VC -ABC,建立等式,求解.1 1解题过程:方法一:如图,取AB 的中点E,连接CE,C1E,过点C 作CF⊥C1E 于点F.在正三棱柱ABC-A1B1C1 中,CC1⊥平面ABC,则AB⊥CC1,∵△ABC 是等边三角形,∴AB⊥CE,又CE CC1=C,∴AB⊥平面CC1E,∴平面C1CE⊥平面ABC1,∴CF⊥平面ABC1,则CF 的长即为所求距离.在Rt△CEC1 中,CC1=1,CE = 3AB =3,∴C1E =2 2 =7.2由等面积得,CF =CC1 ⨯CE=C1E21,7即点C 到平面ABC1 的距离为21.71CC12 +CE 22 1 37方法二:在正三棱柱ABC-A1B1C1 中,CC1⊥平面ABC,AB=BC=AC=CC1=1,易得AC1=BC1=,S△ ABC =4,在△ABC1 中,AC1=BC1= ,AB=1,∴ S△ ABC =4,∵VC -A BC=V C -ABC ,设点 C 到平面ABC1 的距离为d,1 1则1⨯7⨯d =1⨯3⨯1 ,解得d =21.3 4 3 4 7例2:如图,∠BAC 在平面α内,点P 在α外,PE⊥AB,PF⊥AC,PO⊥α,垂足分别为E,F,O,且PE=PF,求证:∠BAO=∠CAO.思路分析:根据特征,有线面垂直、平面的斜线与平面内直线垂直,根据三垂线定理的逆定理处理.解题过程:∵PO⊥α,PE⊥AB,PF⊥AC,∴OE⊥AB,OF⊥AC,∵PE⊥AB,PF⊥AC,PE=PF,∴Rt△PAE≌Rt△PAF,∴AE=AF,∴Rt△AOE≌Rt△AOF,∴∠BAO=∠CAO.2232 3323➢巩固练习1.如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,PA⊥底面ABCD,PA=AB=2,则点C 到平面PBD 的距离为()A.B.C.D.1第1 题图第2 题图2.如图,在四棱锥P-ABCD 中,底面ABCD 是直角梯形,PA⊥底面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=2,AD=4,则点A 到平面PCD 的距离为()A.63B.2C.26D.233.如图,在四棱锥P-ABCD 中,底面ABCD 是直角梯形,PA⊥底面ABCD,AD∥BC,∠BAD=90°,BC=2,PA=AB=1,则点D 到平面PBC 的距离为()A.22B.1C.12 3D.33第3 题图第4 题图4.如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E 是BC 的中点,则点B1 到平面AEC1 的距离为()A.B.4 3C.3D.623665.下列命题:①若a 是平面α的斜线,直线b 垂直于a 在平面α内的射影,则a⊥b;②若a 是平面α的斜线,平面β内的直线b 垂直于a 在平面α内的射影,则a⊥b;③若a 是平面α的斜线,直线b⊂α且b 垂直于a 在另一平面β内的射影,则a⊥b;④若a 是平面α的斜线,直线b∥α且b 垂直于a 在平面α内的射影,则a⊥b.其中正确的有()A.0 个B.1 个C.2 个D.3 个6.如图,PA⊥矩形ABCD,则下列结论中不正确的是()A.PD⊥BD B.PD⊥CDC.PB⊥BC D.PA⊥BD7.如图,下列四个正方体中,l 是正方体的一条对角线,M,N,P 分别为其所在棱的中点,能得出直线l⊥平面MNP 的图形是()①②③④A.①④B.①②C.②④D.①③48.直接利用三垂线定理证明下列各题:(1)已知:PA⊥正方形ABCD 所在平面,O 是BD 的中点,求证:PO⊥BD,PC⊥BD.(2)已知:PA⊥平面PBC,PB=PC,M 是BC 的中点,求证:BC⊥AM.59.如图,在直三棱柱ABC-A1B1C1 中,∠ACB=90°,AC=BC=a,AA1 2a ,D,E,M 分别为棱AB,BC,AA1的中点.(1)求证:A1B1⊥C1D;(2)求点C 到平面MDE 的距离.10.如图,在直三棱柱ABC-A1B1C1 中,AB=4,AC=AA1=2,∠ACB=90°.(1)求证:A1C⊥B1C1;(2)求点B1 到平面A1BC 的距离.62 【参考答案】 1.B 2.C 3.A 4.B 5.B 6.A 7.A 8. 证明略.9. (1)证明略; (2)点 C 到平面 MDE 的距离为 6a .610. (1)证明略;(2)点 B 1 到平面 A 1BC 的距离为 .7。
【小初高学习】高考数学一轮复习 名校尖子生培优大专题 高频考点分析之关于线线、线面及面面垂直的问题

四、关于线线、线面及面面垂直的问题:典型例题:例1.已知矩形ABCD ,1AB =,BC =ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中,【 】A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直 【答案】B 。
【考点】空间中直线与直线之间的位置关系。
【解析】 如图,AE ⊥BD ,CF ⊥BD ,依题意,1AB =,BC =AE =CF3BE EF FD ===。
A ,若存在某个位置,使得直线AC 与直线BD 垂直,则∵BD ⊥AE ,∴BD ⊥平面AEC ,从而BD ⊥EC ,这与已知矛盾,排除A ;B ,若存在某个位置,使得直线AB 与直线CD 垂直,则CD ⊥平面ABC ,平面ABC ⊥平面BCD 。
取BC 中点M ,连接ME ,则ME ⊥BD ,∴∠AEM 就是二面角A BD C --的平面角,此角显然存在,即当A 在底面上的射影位于BC 的中点时,直线AB 与直线CD 垂直,故B 正确;C ,若存在某个位置,使得直线AD 与直线BC 垂直,则BC ⊥平面ACD ,从而平面ACD ⊥平面BCD ,即A 在底面BCD 上的射影应位于线段CD 上,这是不可能的,排除C ;D ,由上所述,可排除D 。
故选 B 。
例2.如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
【答案】解:(I)证明:∵由题设,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,∴BC⊥CC 1,BC⊥AC,CC 1AC=C ,∴BC⊥平面ACC 1A 1。
线面垂直面面垂直知识点总结经典例题及解析高考题练习及答案

直线、平面垂直的判定与性质【考纲说明】1、能够认识和理解空间中线面垂直的有关性质和判定定理。
2、能够运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题。
【知识梳理】一、直线与平面垂直的判定与性质 1、直线与平面垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直,记作l ⊥α,直线l 叫做平面α的垂线,平面α叫做直线l 的垂面。
如图,直线与平面垂直时,它们唯一公共点P 叫做垂足。
(2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
结论:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,记作.//a b b a αα⎫⇒⊥⎬⊥⎭(3)性质定理:垂直于同一个平面的两条直线平行。
即,//a b a b αα⊥⊥⇒.由定义知:直线垂直于平面内的任意直线。
2、直线与平面所成的角平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角。
一条直线垂直于平面,该直线与平面所成的角是直角;一条直线和平面平行,或在平面内,则此直线与平面所成的角是00的角。
3、二面角的平面角从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
如果记棱为l ,那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则两射线所构成的角叫做叫做二面角的平面角。
其作用是衡量二面角的大小;范围:000180θ<<.二、平面与平面垂直的判定与性质1、定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直.2、判定:一个平面过另一个平面的垂线,则这两个平面垂直。
简述为“线面垂直,则面面垂直”,记作l l βαβα⊥⎫⇒⊥⎬⊂⎭.3、性质:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直,记作l m m m lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭I .【经典例题】【例1】(2012浙江文)设l 是直线,a,β是两个不同的平面 ( ) A .若l ∥a,l ∥β,则a∥β B .若l ∥a,l ⊥β,则a⊥β C .若a⊥β,l ⊥a,则l ⊥β D .若a⊥β,l ∥a,则l ⊥β 【答案】B【解析】利用排除法可得选项B 是正确的,∵l ∥a,l ⊥β,则a⊥β.如选项A:l ∥a,l ∥β时,a⊥β或a∥β;选项C:若a⊥β,l ⊥a,l ∥β或l β⊂;选项D:若若a⊥β,l ⊥a,l ∥β或l ⊥β.【例2】(2012四川文)下列命题正确的是 ( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行 【答案】C【解析】若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A 错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B 错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D 错;故选项C 正确.【例3】(2012山东)已知直线m 、n 及平面α,其中m∥n ,那么在平面α内到两条直线m 、n 距离相等的点的集合可能是:①一条直线;②一个平面;③一个点;④空集.其中正确的是( )A .①②③B .①④C .①②④D .②④ 【答案】C【解析】如图1,当直线m 或直线n 在平面α内时有可能没有符合题意的点;如图2,直线m 、n 到已知平面α的距离相等且所在平面与已知平面α垂直,则已知平面α为符合题意的点;如图3,直线m 、n 所在平面与已知平面α平行,则符合题意的点为一条直线,从而选C.【例4】(2012四川理)如图,在正方体1111ABCD A B C D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成的角的大小是____________.【答案】90o【解析】方法一:连接D 1M,易得DN⊥A 1D 1,DN⊥D 1M,所以,DN⊥平面A 1MD 1,又A 1M ⊂平面A 1MD 1,所以,DN⊥A 1D 1,故夹角为90o方法二:以D 为原点,分别以DA,DC,DD 1为x,y,z 轴,建立空间直角坐标系D —xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A 1(2,0,2)故,),(),(2,121,2,01-== N MB 1A 1C 1D 1BD C所以,cos<|MA ||DN |111MA DN MA DN •=〉〈,=0,故DN⊥D 1M,所以夹角为90o【例5】(2012大纲理)三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,则异面直线1AB 与1BC 所成角的余弦值为_____________. 【答案】66【解析】设该三棱柱的边长为1,依题意有1111,AB AB AA BC AC AA AB =+=+-u u u r u u u r u u u r u u u u r u u u r u u u r u u u r,则22221111||()222cos603AB AB AA AB AB AA AA =+=+⋅+=+︒=u u u r u u u r u u u r u u u r u u u r u u u r u u u r而1111()()AB BC AB AA AC AA AB ⋅=+⋅+-u u u r u u u u r u u u r u u u r u u u r u u u r u u u r【例6】(2011·福建)如图,正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上,若EF∥平面AB 1C ,则线段EF 的长度等于________. 【答案】【解析】∵EF∥面AB 1C ,∴EF∥AC .又E 是AD 的中点,∴F 是DC 的中点. ∴EF =AC =.【例7】(2012年山东文)如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =⊥. (1)求证:BE DE =;(2)若∠120BCD =︒,M 为线段AE 的中点, 求证:DM ∥平面BEC .【解析】(1)设BD 中点为O ,连接OC ,OE ,则由BC CD =知CO BD ⊥,又已知CE BD ⊥,所以BD ⊥平面OCE .所以BD OE ⊥,即OE 是BD 的垂直平分线,所以BE DE =.(2)取AB 中点N ,连接,MN DN ,∵M 是AE 的中点,∴MN ∥BE , ∵△ABD 是等边三角形,∴DN AB ⊥.由∠BCD =120°知,∠CBD =30°, 所以∠ABC =60°+30°=90°,即BC AB ⊥,所以ND ∥BC ,所以平面MND ∥平面BEC ,又DM ⊂平面MND ,故DM ∥平面BEC . 另证:延长BC AD ,相交于点F ,连接EF.因为CB=CD,090=∠ABC . 因为△ABD 为正三角形,所以0090,60=∠=∠ABC BAD ,则030=∠AFB ,所以AF AB 21=,又AD AB =, 所以D 是线段AF 的中点,连接DM,又由点M 是线段AE 的中点知EF DM //,而⊄DM 平面BEC ,⊂EF 平面BEC ,故DM ∥平面BEC .【例8】(2011天津)如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形∠ADC =45°,AD =AC =1,O 为AC 的中点,PO ⊥平面ABCD ,PO =2,M 为PD 的中点. (1)证明:PB∥平面ACM ; (2)证明:AD ⊥平面PAC ;(3)求直线AM 与平面ABCD 所成角的正切值. 【解析】(1)证明:连接BD ,MO ,在平行四边形ABCD 中,因为O 为AC 的中点,所以O 为BD 的中点.又M 为PD 的中点,所以PB∥MO .因为PB ?平面ACM ,MO ?平面ACM ,所以PB∥平面ACM .(2)证明:因为∠ADC =45°,且AD =AC =1,所以∠DAC =90°,即AD ⊥AC ,又PO ⊥平面ABCD ,AD ?平面ABCD ,所以PO ⊥AD .而AC ∩PO =O ,所以AD ⊥平面PAC . (3)取DO 中点N ,连接MN ,AN .因为M 为PD 的中点,所以MN∥PO ,且MN =PO =1.由PO ⊥平面ABCD ,得MN ⊥平面ABCD ,所以∠MAN 是直线AM 与平面ABCD 所成的角,在Rt△DAO 中,AD =1,AO =,所以DO =,从而AN =DO =.在Rt△ANM 中,tan∠MAN ===,即直线AM 与平面ABCD 所成角的正切值为.【例9】(2012湖南文)如图,在四棱锥P-ABCD 中,PA⊥平面ABCD,底面ABCD 是等腰梯形,AD∥BC,AC⊥BD. (1)证明:BD⊥PC;(2)若AD=4,BC=2,直线PD 与平面PAC 所成的角为30°,求四棱锥P-ABCD 的体积. 【解析】(1)因为,,.PA ABCD BD ABCD PA BD ⊥⊂⊥平面平面所以又,,AC BD PA AC ⊥是平面PAC 内的两条相较直线,所以BD ⊥平面PAC, 而PC ⊂平面PAC,所以BD PC ⊥.(2)设AC 和BD 相交于点O,连接PO,由(Ⅰ)知,BD ⊥平面PAC, 所以DPO ∠是直线PD 和平面PAC 所成的角,从而DPO ∠30=o . 由BD ⊥平面PAC,PO ⊂平面PAC,知BD PO ⊥. 在Rt POD V 中,由DPO ∠30=o ,得PD=2OD.因为四边形ABCD 为等腰梯形,AC BD ⊥,所以,AOD BOC V V 均为等腰直角三角形, 从而梯形ABCD 的高为111(42)3,222AD BC +=⨯+=于是梯形ABCD 面积 在等腰三角形AOD 中,2,22,2OD AD == 所以22242, 4.PD OD PA PD AD ===-=故四棱锥P ABCD -的体积为11941233V S PA =⨯⨯=⨯⨯=.【例10】(2012新课标理)如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,BD DC ⊥1 (1)证明:BC DC ⊥1(2)求二面角11C BD A --的大小.【解析】(1)在Rt DAC ∆中,AD AC =得:45ADC ︒∠=同理:1114590A DC CDC ︒︒∠=⇒∠=得:111,DC DC DC BD DC ⊥⊥⇒⊥面1BCD DC BC ⇒⊥ (2)11,DC BC CC BC BC ⊥⊥⇒⊥面11ACC A BC AC ⇒⊥ 取11A B 的中点O ,过点O 作OH BD ⊥于点H ,连接11,C O C H1111111AC B C C O A B =⇒⊥,面111A B C ⊥面1A BD 1C O ⇒⊥面1A BD 1OH BD C H BD ⊥⇒⊥得:点H 与点D 重合且1C DO ∠是二面角11C BD A --的平面角设AC a =,则12C O =,111230C D C O C DO ︒==⇒∠= 既二面角11C BD A --的大小为30︒【课堂练习】.(2012浙江理)已知矩形ABCD ,AB =1,BC将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直 .(2012四川理)下列命题正确的是 ( )A .若两条直线和同一个平面所成的角相等,则这两条直线平行B .若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C .若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D .若两个平面都垂直于第三个平面,则这两个平面平行3.(2011重庆)到两互相垂直的异面直线的距离相等的点( )A .只有1个B .恰有3个C .恰有4个D .有无穷多个4.(2012上海)已知空间三条直线l ,m ,n 若l 与m 异面,且l 与n 异面,则 ( ) A .m 与n 异面. B .m 与n 相交. C .m 与n 平行. D .m 与n 异面、相交、平行均有可能. 5.(2011烟台)已知m ,n 是两条不同的直线,α,β为两个不同的平面,有下列四个命题:①若m ⊥α,n ⊥β,m ⊥n ,则α⊥β;②若m∥α,n∥β,m ⊥n ,则α∥β;③若m ⊥α,n∥β,m ⊥n ,α•AB•β则α∥β;④若m ⊥α,n∥β,α∥β,则m ⊥n . 其中正确命题的个数为( ) A .1 B .2 C .3 D .4 6.(2011潍坊)已知m 、n 是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是( )A .若α⊥γ,α⊥β,则γ∥βB .若m∥n ,m ?α,n ?β,则α∥βC .若m∥n ,m∥α,则n∥αD .若n ⊥α,n ⊥β,则α∥β7.(2010全国卷文)直三棱柱111ABC A B C -中,若90BAC ∠=︒,1AB AC AA ==,则异面直线1BA 与1AC 所成的角等于()A .30°B.45°C.60°D.90°8.(2010全国卷)正方体ABCD-1111A B C D 中,B 1B 与平面AC1D 所成角的余弦值为()AB.23D 9.(2010全国Ⅱ卷理)已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为()A .1B .2D .310.(2010全国Ⅰ卷)已知在半径为2的球面上有A .B .C .D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为()ABC.11.(2010江西理)过正方体1111ABCD A B C D -的顶点A 作直线L ,使L 与棱AB ,AD ,1AA 所成的角都相等,这样的直线L 可以作() A .1条B .2条C .3条D .4条12.(2012大纲)已知正方形1111ABCD A B C D -中,,E F 分别为1BB ,1CC 的中点,那么异面直线AE 与1D F 所成角的余弦值为____.13.(2010上海文)已知四棱椎P ABCD -的底面是边长为6的正方形,侧棱PA ⊥底面ABCD ,且8PA =,则该四棱椎的体积是.14.(2010四川卷)如图,二面角l αβ--的大小是60°,线段AB α⊂.B l ∈,AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是.15.(江西卷文)长方体1111ABCD A B C D -的顶点均在同一个球面上,11AB AA ==,2BC =,则A ,B 两点间的球面距离为16.(2010湖南理)如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点。
线面垂直练习题及答案

线面垂直练习题及答案线面垂直的证明中的找线技巧通过计算,运用勾股定理寻求线线垂直M为CC1 的中点,AC交BD于点O,求证:1 如图1,在正方体ABCD?A1BC11D1中,AO?平面MBD. 1A1M,∵DB⊥A1A,DB⊥AC,A1A?AC?A,∴DB⊥平面A?平面A1ACC1 ∴DB⊥AO1ACC1,而AO1. 1 323222设正方体棱长为a,则A1O?a,MO?a.2492222AM?a.∵AO 在Rt△AC中,,∴AOM?OM?MO2?AM111111 4∩DB=O,∴ AO1⊥平面MBD.证明:连结MO,?.∵OM评注:在证明垂直关系时,有时可以利用棱长、角度大小等数据,通过计算来证明.利用面面垂直寻求线面垂直如图2,P是△ABC所在平面外的一点,且PA⊥平面ABC,平面PAC⊥平面PBC.求证:BC⊥平面PAC.证明:在平面PAC内作AD⊥PC交PC于D.因为平面PAC⊥平面PBC,且两平面交于PC,AD?平面PAC,且AD⊥PC,由面面垂直的性质,得AD⊥平面PBC.又∵BC?平面PBC,∴AD⊥BC.∵PA⊥平面ABC,BC?平面ABC,∴PA⊥BC.∵AD∩PA=A,∴BC⊥平面PAC..评注:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直?线面垂直?线线垂直.判定性质判定性质????线面垂直???????面面垂直.这三者一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直?????之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理.同学们应当学会灵活应用这些定理证明问题.下面举例说明.如图1所示,ABCD为正方形,SA⊥平面ABCD,过A且垂直于SC的平面分别交SB,SC,SD于E,F,G.求证:AE?SB,AG?SD.证明:∵SA?平面ABCD,∴SA?BC.∵AB?BC,∴BC?平面SAB.又∵AE?平面SAB,∴BC?AEAE?平面SBC.∴AE?SB.同理可证AG?SD..∵SC?平面AEFG,∴SC?AE.∴评注:本题欲证线线垂直,可转化为证线面垂直,在线线垂直与线面垂直的转化中,平面起到了关键作用,同学们应多注意考虑线和线所在平面的特征,从而顺利实现证明所需要的转化.如图2,在三棱锥A-BCD中,BC=AC,AD =BD,作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.证明:取AB的中点F,连结CF,DF.∵AC?BC,∴CF?AB.∵AD?BD,∴DF?AB.又CF?DF?F,∴AB?平面CDF.∵CD?平面CDF,∴CD?AB.又CD?BE,BE?AB?B,∴CD?平面ABE,CD?AH.∵AH?CD,AH?BE,CD?BE?E,∴AH?平面BCD.评注:本题在运用判定定理证明线面垂直时,将问题转化为证明线线垂直;而证明线线垂直时,又转化为证明线面垂直.如此反复,直到证得结论.如图3,AB是圆O的直径,C是圆周上一点,PA?平面ABC.若AE⊥PC ,E为垂足,F是PB上任意一点,求证:平面AEF⊥平面PBC.证明:∵AB是圆O的直径,∴AC∵PA∴PA??BC.?平面ABC,BC?平面ABC,BC.∴BC?平面APC.∵BC?平面PBC,∴平面APC⊥平面PBC.∵AE⊥PC,平面APC∩平面PBC=PC,∴AE⊥平面PBC.∵AE?平面AEF,∴平面AEF⊥平面PBC.评注:证明两个平面垂直时,一般可先从现有的直线中寻找平面的垂线,已知条件出发寻找线线垂直的关系.6. 空间四边形ABCD中,若AB⊥CD,BC⊥AD,求证:AC⊥BD即证线面垂直,而证线面垂直则需从D证明:过A作AO⊥平面BCD于O?AB?CD,?CD?BO 同理BC⊥DO ∴O为△ABC的垂心 . 证明:在正方体ABCD-A1B1C1D1中,A1C⊥平面BC1D 于是BD?CO?BD?ACAC证明:连结AC?BD?ACAC为A1C在平面AC上的射影?BD?A1C???A1C?平面BC1D同理可证A1C?BC1?8. 如图,PA?平面ABCD,ABCD是矩形,M、N分别是AB、PC的中点,求证:MN?ABC1EN//DC2. 证:取PD中点E,则C?EN?AE///AM/MN9如图在ΔABC中,AD⊥BC, ED=2AE,过E作FG∥BC,且将ΔAFG沿FG折起,使∠A’ED=60°,求证:A’E⊥平面A’BC分析:A’C弄清折叠前后,图形中各元素之间的数量关系和位置关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面垂直的证明中的找线技巧◆通过计算,运用勾股定理寻求线线垂直1 如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD . 证明:连结MO ,1A M ,∵DB ⊥1A A ,DB ⊥AC ,1A AAC A =,∴DB ⊥平面11A ACC ,而1AO ⊂平面11A ACC ∴DB ⊥1A O . 设正方体棱长为a ,则22132A O a =,2234MO a =. 在Rt △11A C M 中,22194A M a =.∵22211A O MO A M +=,∴1AO OM ⊥. ∵OM ∩DB =O ,∴ 1A O ⊥平面MBD .评注:在证明垂直关系时,有时可以利用棱长、角度大小等数据,通过计算来证明.◆利用面面垂直寻求线面垂直2 如图2,P 是△ABC 所在平面外的一点,且PA ⊥平面ABC ,平面PAC ⊥平面PBC .求证:BC ⊥平面PAC .证明:在平面PAC 内作AD ⊥PC 交PC 于D .因为平面PAC ⊥平面PBC ,且两平面交于PC ,AD ⊂平面PAC ,且AD ⊥PC , 由面面垂直的性质,得AD ⊥平面PBC . 又∵BC ⊂平面PBC ,∴AD ⊥BC .∵PA ⊥平面ABC ,BC ⊂平面ABC ,∴PA ⊥BC . ∵AD ∩PA =A ,∴BC ⊥平面PAC .评注:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理.同学们应当学会灵活应用这些定理证明问题.下面举例说明.3 如图1所示,ABCD 为正方形,SA ⊥平面ABCD ,过A 且垂直于SC 的平面分别交SB SC SD ,,于E F G ,,.求证:AE SB ⊥,AG SD ⊥. 证明:∵SA ⊥平面ABCD ,∴SA BC ⊥.∵AB BC ⊥,∴BC ⊥平面SAB .又∵AE ⊂平面SAB ,∴BC AE ⊥.∵SC ⊥平面AEFG ,∴SC AE ⊥.∴AE ⊥平面SBC .∴AE SB ⊥.同理可证AG SD ⊥.评注:本题欲证线线垂直,可转化为证线面垂直,在线线垂直与线面垂直的转化中,平面起到了关键作用,同学们应多注意考虑线和线所在平面的特征,从而顺利实现证明所需要的转化. 4 如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD . 证明:取AB 的中点F,连结CF ,DF . ∵AC BC =,∴CF AB ⊥.∵AD BD =,∴DF AB ⊥.又CF DF F =,∴AB ⊥平面CDF . ∵CD ⊂平面CDF ,∴CD AB ⊥. 又CD BE ⊥,BE AB B =,∴CD ⊥平面ABE ,CD AH ⊥.∵AH CD ⊥,AH BE ⊥,CD BE E =,∴ AH ⊥平面BCD .评注:本题在运用判定定理证明线面垂直时,将问题转化为证明线线垂直;而证明线线垂直时,又转化为证明线面垂直.如此反复,直到证得结论.5 如图3,AB 是圆O的直径,C是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,E为垂足,F是PB 上任意一点,求证:平面AEF ⊥平面PBC .证明:∵AB 是圆O的直径,∴AC BC ⊥. ∵PA ⊥平面ABC ,BC ⊂平面ABC , ∴PA BC ⊥.∴BC ⊥平面APC . ∵BC ⊂平面PBC , ∴平面APC ⊥平面PBC .∵AE ⊥PC ,平面APC ∩平面PBC =PC , ∴AE ⊥平面PBC .∵AE ⊂平面AEF ,∴平面AEF ⊥平面PBC .评注:证明两个平面垂直时,一般可先从现有的直线中寻找平面的垂线,即证线面垂直,而证线面垂直则需从已知条件出发寻找线线垂直的关系.10如图, 在空间四边形SABC 中, SA ⊥平面ABC , ∠ABC = 90︒, AN ⊥SB 于N , AM ⊥SC 于M 。
求证: ①AN ⊥BC; ②SC ⊥平面ANM 分析:①要证AN ⊥BC , 转证, BC ⊥平面SAB 。
②要证SC ⊥平面ANM , 转证, SC 垂直于平面ANM 内的两条相交直线, 即证SC ⊥AM , SC ⊥AN 。
要证SC ⊥AN , 转证AN ⊥平面SBC , 就可以了。
证明:①∵SA ⊥平面ABC ∴SA ⊥BC 又∵BC ⊥AB , 且AB SA = A ∴BC ⊥平面SAB ∵AN 平面SAB ∴AN ⊥BC ②∵AN ⊥BC , AN ⊥SB , 且SB BC = B ∴AN ⊥平面SBC ∵SCC 平面SBC ∴AN ⊥SC 又∵AM ⊥SC , 且AM AN = A ∴SC ⊥平面ANM[例2]如图9—40,在三棱锥S —ABC 中,SA ⊥平面ABC ,平面SAB ⊥平面SBC .图9—40(1)求证:AB ⊥BC ;(1)【证明】作AH ⊥SB 于H ,∵平面SAB ⊥平面SBC .平面SAB ∩平面SBC=SB ,∴AH ⊥平面SBC , 又SA ⊥平面ABC ,∴SA ⊥BC ,而SA 在平面SBC 上的射影为SB ,∴BC ⊥SB ,又SA ∩SB=S , ∴BC ⊥平面SAB .∴BC ⊥AB .[例3]如图9—41,PA ⊥平面ABCD ,四边形ABCD 是矩形,PA=AD=a ,M 、N 分别是AB 、PC 的中点.(1)求平面PCD 与平面ABCD 所成的二面角的大小;(2)求证:平面MND ⊥平面PCD (1)【解】PA ⊥平面ABCD ,CD ⊥AD ,∴PD ⊥CD ,故∠PDA 为平面ABCD 与平面PCD 所成二面角的平面角,在Rt △PAD 中,PA=AD , ∴∠PDA=45°(2)【证明】取PD 中点E ,连结EN ,EA ,则EN 21CDAM ,∴四边形ENMA 是平行四边形,∴EA ∥MN .∵AE ⊥PD ,AE ⊥CD ,∴AE ⊥平面PCD ,从而MN ⊥平面PCD ,∵MN ⊂平面MND ,∴平面MND ⊥平面PCD . 【注】 证明面面垂直通常是先证明线面垂直,本题中要证MN ⊥平面PCD 较困难,转化为证明AE ⊥平面PCD 就较简单了.另外,在本题中,当AB 的长度变化时,可求异面直线PC 与AD 所成角的范围.[例4]如图9—42,正方体ABCD —A 1B 1C 1D 1中,E 、F 、M 、N 分别是A 1B 1、BC 、C 1D 1、B 1C 1的中点.图9—42(1)求证:平面MNF ⊥平面ENF .(2)求二面角M —EF —N 的平面角的正切值.(1)【证明】∵M 、N 、E 是中点,∴M C NC N B EB 1111===∴︒=∠=∠45MNC ENB 11∴︒=∠90MNE 即MN ⊥EN ,又NF ⊥平面A 1C 1,11C A MN 平面⊂∴MN ⊥NF ,从而MN ⊥平面ENF .∵MN ⊂平面MNF ,∴平面MNF ⊥平面ENF .(2)【解】过N 作NH ⊥EF 于H ,连结MH .∵MN ⊥平面ENF ,NH 为MH 在平面ENF 内的射影,∴由三垂线定理得MH ⊥EF ,∴∠MHN 是二面角M —EF —N 的平面角.在Rt △MNH 中,求得MN=22a ,NH=33a , ∴tan ∠MHN=26=NHMN ,即二面角M —EF —N 的平面角的正切值为26.4.如图9—45,四棱锥P —ABCD 的底面是边长为a 的正方形,PA ⊥底面ABCD ,E 为AB 的中点,且PA=AB .图9—45(1)求证:平面PCE ⊥平面PCD ;(2)求点A 到平面PCE 的距离. (1)【证明】PA ⊥平面ABCD ,AD 是PD 在底面上的射影,又∵四边形ABCD 为矩形,∴CD ⊥AD ,∴CD ⊥PD ,∵AD ∩PD=D ∴CD ⊥面PAD ,∴∠PDA 为二面角P —CD —B 的平面角,∵PA=PB=AD ,PA ⊥AD ∴∠PDA=45°,取Rt △PAD 斜边PD 的中点F ,则AF ⊥PD ,∵AF ⊂面PAD ∴CD ⊥AF ,又PD ∩CD=D ∴AF ⊥平面PCD ,取PC 的中点G ,连GF 、AG 、EG ,则GF21CD 又AE 21CD ,∴GF AE ∴四边形AGEF 为平行四边形∴AF ∥EG ,∴EG ⊥平面PDC 又EG ⊂平面PEC ,∴平面PEC ⊥平面PCD .(2)【解】由(1)知AF ∥平面PEC ,平面PCD ⊥平面PEC ,过F 作FH ⊥PC 于H ,则FH ⊥平面PEC ∴FH 为F 到平面PEC 的距离,即为A 到平面PEC 的距离.在△PFH 与 △PCD 中,∠P 为公共角,而∠FHP=∠CDP=90°,∴△PFH ∽△PCD .∴PC PFCDFH =,设AD=2,∴PF=2,PC=324822=+=+CD PD ,∴FH=362322=⋅∴A 到平面PEC 的距离为36.【拓展练习】 一、备选题1.如图,AB 是圆O 的直径,C 是圆周上一点,PA ⊥平面ABC . (1)求证:平面PAC ⊥平面PBC ;(2)若D 也是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.(1)【证明】∵C 是AB 为直径的圆O 的圆周上一点,AB 是圆O 的直径 ∴BC ⊥AC ;又PA ⊥平面ABC ,BC ⊂平面ABC , ∴BC ⊥PA ,从而BC ⊥平面PAC . ∵BC ⊂平面PBC ,∴平面PAC ⊥平面PBC .(2)【解】平面PAC ⊥平面ABCD ;平面PAC ⊥平面PBC ;平面PAD ⊥平面PBD ;平面PAB ⊥平面ABCD ;平面PAD ⊥平面ABCD .2.ABC —A ′B ′C ′是正三棱柱,底面边长为a ,D ,E 分别是BB ′,CC ′上的一点,BD =21a ,EC =a .(1)求证:平面ADE ⊥平面ACC ′A ′; (2)求截面△ADE 的面积.(1)【证明】分别取A ′C ′、AC 的中点M 、N ,连结MN , 则MN ∥A ′A ∥B ′B ,∴B ′、M 、N 、B 共面,∵M 为A ′C ′中点,B ′C ′=B ′A ′,∴B ′M ⊥A ′C ′,又B ′M ⊥AA ′且AA ′∩A ′C ′=A ′∴B ′M ⊥平面A ′ACC ′. 设MN 交AE 于P ,∵CE =AC ,∴PN =NA =2a.又DB =21a ,∴PN =BD .∵PN ∥BD , ∴PNBD 是矩形,于是PD ∥BN ,BN ∥B ′M , ∴PD ∥B ′M .∵B ′M ⊥平面ACC ′A ′,∴PD ⊥平面ACC ′A ′,而PD ⊂平面ADE , ∴平面ADE ⊥平面ACC ′A ′.(2)【解】∵PD ⊥平面ACC ′A ′,∴PD ⊥AE ,而PD =B ′M =23a ,AE =2a .∴S △ADE =21×AE ×PD =21×246232aa a =⨯.。
