二阶电路的动态响应实验报告
二阶动态电路响应的研究

U0
U0
U0
0
ωt 0
ωt
0
ωt
欠阻尼波形
过阻尼波形 临界阻尼波形
当电路参数R 、L 、C取值不同时,
8
如何用示波器测量输出波形,并计算出衰减系数
调节R ,使示波器荧光屏上呈现稳定的欠 阻尼响应波形,定量测定此时电路的衰 减常数α 和振荡频率ω d。
U0
uo = K e-? t sin(wdt + b)
五、实验报告
? 1. 根据观测结果,在方格纸上描绘二阶电路过 阻尼、 临界阻尼和欠尼的响应波形。绘坐标图 时,绘出1.5 ~ 2个周期的波形即可。在波形图
旁标出R、L、C的取值。
? 2. 测算欠阻尼振荡曲线上的 ? 与ωd 。 ? 3. 归纳、总结电路元件参数的改变对响应变化
趋势的影响。 。
R,分别使电路工作在过阻尼,欠阻尼和 衰减振荡状态,测量出输出波形。并进行 数据计算,求出衰减系数 ? 、振荡角频率
ωd 。结果填入下表 10-1。
表10-1
L=10mH C = 0.022 μ F f0 = 1.5KHz
?= R
2L
ω =d w02 - ? 2
电路状态
R1=51Ω
R2=1kΩ
R3=3kΩ
波形
? 2 测量不同参数下的衰减系数和波形
? 保证电路一直处于欠阻尼状态,取三个不同 阻值的电阻,用示波器测量输出波形,并计 算出衰减系数?,= R 将波形和数据填入表10-2。
2L
改为R1=51 R2=100 R3=200
? 3. 测量临界电阻值
? 将图10-4所示的接线图中的R改为实验箱上 的20K电位器RP,调节RP,波形出现临界状 态时,在断电情况(拔掉相连电线)下用万用表 测出此时的电位器RP值,即为临界电阻值。 与理论值进行如图所示衰减振荡波形看出,若测得第一个波峰出现的时间为
二阶响应实验报告

二阶响应实验报告二阶响应实验报告引言:在控制系统中,二阶响应是一种常见的动态特性。
通过研究二阶响应的实验,我们可以更好地理解控制系统的动态行为,并且能够对系统进行更精确的调节。
本次实验旨在通过实际操作和数据分析,探索二阶响应的特性并得出相关结论。
实验目的:1. 了解二阶响应的特点和表现形式;2. 掌握二阶系统的参数调节方法;3. 分析实验数据,验证理论模型。
实验步骤:1. 准备实验装置:搭建一个简单的二阶控制系统,包括一个电机、一个位置传感器、一个控制器和一个计算机;2. 设计实验方案:确定实验所需的参数,包括控制器增益、位置传感器灵敏度等;3. 进行实验:根据实验方案进行实验操作,记录数据;4. 数据分析:利用实验数据,绘制二阶响应曲线,并进行参数拟合;5. 结果讨论:根据实验结果,分析二阶响应的特性,并与理论模型进行对比。
实验结果与分析:通过实验,我们得到了二阶响应曲线,并进行了参数拟合。
根据实验数据和拟合结果,我们可以得出以下结论:1. 二阶响应的特点:在初始阶段,系统的响应会有一个较大的超调量,随后逐渐趋于稳定。
此外,二阶响应还具有一定的振荡频率和阻尼比。
2. 参数调节方法:根据实验结果,我们可以通过调节控制器增益和位置传感器灵敏度来改变二阶系统的动态特性。
增大控制器增益可以减小超调量,但会增加系统的振荡频率;增大位置传感器灵敏度可以提高系统的稳定性。
3. 理论模型验证:通过与理论模型进行对比,我们可以验证实验结果的准确性。
如果实验数据与理论模型吻合良好,则说明实验操作和参数拟合的准确性较高。
结论:通过本次实验,我们深入了解了二阶响应的特性和参数调节方法,并通过实际操作和数据分析验证了理论模型的准确性。
掌握了二阶响应的相关知识后,我们能够更好地设计和调节控制系统,提高系统的稳定性和性能。
进一步研究:在实验过程中,我们发现二阶响应的特性受到多种因素的影响,如系统的惯性、控制器的类型等。
因此,可以进一步研究这些因素对二阶响应的影响,并探索更精确的参数调节方法,以提高控制系统的性能。
一阶电路和二阶电路的动态响应

实验四 一阶电路和二阶电路的动态响应一、 实验目的(1) 理解零输入响应、零状态响应和完全响应 (2) 理解欠阻尼、临界和过阻尼的意义和条件 二、 实验原理用二阶微分方程描述的动态电路称为二阶电路。
图所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:s 2U 2=++c c c u dt du RC dtu d LC 1. 零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图6.2所示,设电容已经充电,其电压为U 0,电感的初始电流为0。
(1) CL R 2>,响应是非振荡性的,称为过阻尼情况。
电路响应为:图6.2 RLC 串联零输入响应电路图6.3 二阶电路的过阻尼过程u Lt mU 0)()()()()(212112012120t P t P t P t P C e e P P L U t i e P e P P P U t u ---=--=响应曲线如图6.3所示。
可以看出:u C (t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值, 且当2112lnP P P P t m -=时,电流有极大值。
(2)CL R 2=,响应临界振荡,称为临界阻尼情况。
电路响应为tt c te LUt i e t U t u ααα--=+=00)()1()( t ≥0响应曲线如图6.4所示。
图6.4 二阶电路的临界阻尼过程(3) CL R 2<,响应是振荡性的,称为欠阻尼情况。
电路响应为t e LU t i t e U t u d td d t dC ωωβωωωααsin )(),sin()(000--=+==t ≥0其中衰减振荡角频率 2220d 2L R LC 1⎪⎭⎫ ⎝⎛-=-=αωω ,αωβdarctan= 响应曲线如图6.5所示。
U 0t图6.5 二阶电路的欠阻尼过程 图6.6 二阶电路的无阻尼过程(4)当R =0时,响应是等幅振荡性的,称为无阻尼情况。
二阶动态电路设计 实验报告(含数据处理)

实验二十一 二阶动态电路设计
一、实验内容
已知RLC 串联电路, 输入为单位阶跃信号, 设计元件参数, 要求电容负载输出电压的超调量约为20%, 调节时间0.003秒。
先进行理论设计和仿真分析, 连接好电路后, 再通过示波器观察实际输入和输出曲线。
二、实验原理图和理论分析
)()()()()(22t t u t u dt t du RC dt
t u d LC S C C C ε==++ 二阶电路的阶跃响应为)sin(1)(0βωωωδ++
=-t e t u t C 超调量为21%ζζπ
σ--==e
M P 调节时间为n s t ζω3=
(5%稳态范围)
,
, C
L n ⋅=21ω L R n ⋅⋅=ωζ2 选用电容C=4.7
F, 由以上推导得L=44.2mH, R=88.4
三、实验设备
函数信号发生器
KTDG-4可调式电感箱0~100mH
可调式电阻箱0~99999.9Ω
交流电压表, 交流电流表
双踪示波器
四、仿真实验
利用EWB 软件, 仿真模型图如下
运行结果如下
电容电阻电感在实验台上连接好电
路, 测量结果如下。
电压有效值
电流有效值
利用示波器观测输入电压和输出电容上电压曲线:
六、数据处理和实验结论
略。
二阶电路响应实验报告

二阶电路响应实验报告二阶电路响应实验报告引言:二阶电路是电路理论中的重要内容之一,它由两个储能元件(电感和电容)和一个耗能元件(电阻)组成。
在实际应用中,二阶电路广泛用于滤波器、振荡器等电子设备中。
本次实验旨在通过对二阶电路的响应特性进行实验研究,深入理解二阶电路的工作原理和特性。
实验目的:1. 了解二阶电路的基本结构和工作原理;2. 掌握二阶电路的频率响应特性;3. 通过实验数据分析,验证理论模型的准确性。
实验器材和仪器:1. 信号发生器;2. 双踪示波器;3. 电压表;4. 电流表;5. 二阶电路实验箱。
实验步骤:1. 搭建二阶低通滤波器电路,并连接信号发生器和示波器;2. 调节信号发生器的频率,记录输入信号和输出信号的幅值;3. 改变输入信号频率,重复步骤2,记录数据;4. 换用高通滤波器电路,重复步骤2和3。
实验结果与分析:在实验中,我们记录了不同频率下输入信号和输出信号的幅值,并绘制了频率响应曲线。
通过观察和分析实验数据,我们得出以下结论:1. 低通滤波器的频率响应特性:在低频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢;在高频段,输出信号的幅值随频率的增加而迅速下降。
这表明低通滤波器对低频信号有较好的传递性能,但对高频信号有较强的衰减能力。
2. 高通滤波器的频率响应特性:与低通滤波器相反,高通滤波器在低频段对信号的传递能力较差,输出信号的幅值较小;而在高频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢。
这说明高通滤波器对高频信号有较好的传递性能,但对低频信号有较强的衰减能力。
3. 实验数据与理论模型的比较:将实验数据与理论模型进行比较,发现它们之间存在一定的偏差。
这可能是由于实验中存在的误差,例如电路元件的参数与理论值之间的差异,以及仪器的测量误差等。
然而,总体上实验数据与理论模型仍然具有较好的一致性,验证了理论模型的准确性。
结论:通过本次实验,我们深入了解了二阶电路的工作原理和频率响应特性。
二阶系统阶跃响应实验报告
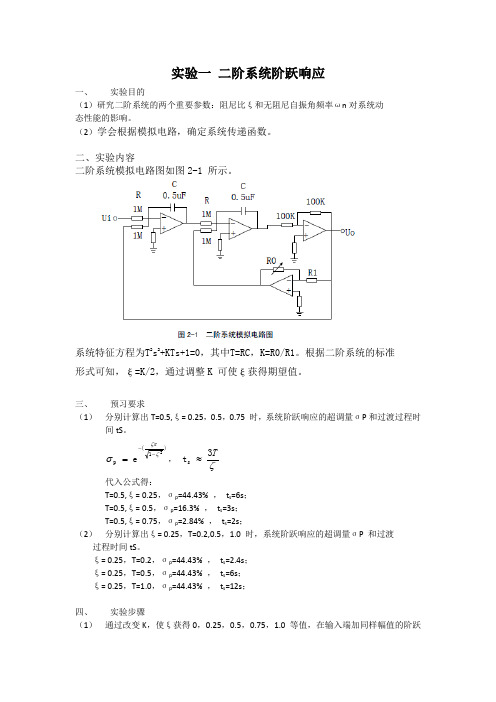
实验一 二阶系统阶跃响应一、 实验目的(1)研究二阶系统的两个重要参数:阻尼比ξ和无阻尼自振角频率ωn 对系统动 态性能的影响。
(2)学会根据模拟电路,确定系统传递函数。
二、实验内容二阶系统模拟电路图如图2-1 所示。
系统特征方程为T 2s 2+KTs+1=0,其中T=RC ,K=R0/R1。
根据二阶系统的标准 形式可知,ξ=K/2,通过调整K 可使ξ获得期望值。
三、 预习要求(1) 分别计算出T=0.5,ξ= 0.25,0.5,0.75 时,系统阶跃响应的超调量σP 和过渡过程时间tS 。
)1(p 2e ζζπσ--=, ζT3t s ≈代入公式得:T=0.5,ξ= 0.25,σp =44.43% , t s =6s ; T=0.5,ξ= 0.5,σp =16.3% , t s =3s ; T=0.5,ξ= 0.75,σp =2.84% , t s =2s ;(2) 分别计算出ξ= 0.25,T=0.2,0.5,1.0 时,系统阶跃响应的超调量σP 和过渡过程时间tS 。
ξ= 0.25,T=0.2,σp =44.43% , t s =2.4s ; ξ= 0.25,T=0.5,σp =44.43% , t s =6s ; ξ= 0.25,T=1.0,σp =44.43% , t s =12s ;四、 实验步骤(1) 通过改变K ,使ξ获得0,0.25,0.5,0.75,1.0 等值,在输入端加同样幅值的阶跃信号,观察过渡过程曲线,记下超调量σP 和过渡过程时间tS,将实验值和理论值进行比较。
(2)当ξ=0.25 时,令T=0.2 秒,0.5 秒,1.0 秒(T=RC,改变两个C),分别测出超调量σP 和过渡过程tS,比较三条阶跃响应曲线的异同。
五、实验数据记录与处理:阶跃响应曲线图见后面附图。
原始数据记录:(2)ξ=0.25,改变C的大小改变T值理论值与实际值比较:对误差比较大,比如T=0.5,ξ=0.75时,超调量的相对误差为30%左右。
实验十四二阶动态电路响应及其测试

实验十四二阶动态电路响应及其测试1实验目的1.学会用示波器观测二阶电路的响应曲线,加深对二阶电路的认识。
2.了解电路元件的参数对响应的影响。
3.学会用实验的方法测量二阶电路的衰减系数和振荡频率。
2实验器材1.QY-DT01电源控制屏2.QY-DG02仪器仪表模块I3.函数信号发生器4.QY-DG05通用电路实验模块5.示波器3实验原理1.原理图图1二阶动态电路响应测试原理图二阶电路由二阶微分方程描述,本实验中的二阶电路由电阻、电容、电感元件串联而成,由于电容和电感为动态元件,所以当激励信号发生突变时,电路会经历一个过渡过程,当R、L、C的参数值不同时,过渡过程也不完全相同,在本实验中,我们只以u C的波形作为二阶电路的响应来进行研究。
根据R 、L 、C 取值不同,电路的过渡过程会出现三种情况:当C L R 2>时,电路工作于过阻尼状态;当C L R 2<时,电路工作于欠阻尼状态;当CLR 2=时,电路工作于临界阻尼状态。
当为该电路施加一个脉冲激励时,即能观察到电容电压的波形变化曲线,即电路的零状态响应和零输入响应。
2.预习内容衰减系数的计算公式:LR 2=δ 振荡频率的计算公式:LC10=ω电路的三种过渡情况:(1) 当CLR 2>,即0ωδ>时,响应为非振荡性质,称为过阻尼状态,波形如图16-2所示;图2过阻尼响应曲线(2) 当C LR 2=,即0ωδ=时,响应仍属于非振荡性质,称为临界阻尼状态,临界阻尼响应曲线与过阻尼相同;(3) 当C LR 2<,即0ωδ<时,响应为振荡性质,称为欠阻尼状态,欠阻尼响应曲线如图3所示。
图3欠阻尼响应曲线当R=0时,称为无阻尼状态。
振荡频率和衰减系数的测量方法:调节电路中元件参数,使其工作于欠阻尼振荡状态,用示波器观察电容电压u C 的波形如图4所示:图4欠阻尼响应曲线T10=ω , m m u u T 21ln 1=δ (T=t 2-t 1)4 实验内容在RLC 的串联和并联实验中,我们研究的是二阶电路的稳态响应,但由于电路中存在电容和电感这些动态元件,使得电路从上电开始带进入稳态之间会经历一个过渡过程。
二阶电路地动态响应实验报告材料

实验二:二阶电路的动态响应学号:0928402012 姓名:王畑夕 成绩:一、 实验原理及思路图6.1 RLC 串联二阶电路用二阶微分方程描述的动态电路称为二阶电路。
图6.1所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:s 2U 2=++c c c u dt du RC dtu d LC (6-1) 初始值为CI C i dtt du U u L t c c 000)0()()0(===-=--求解该微分方程,可以得到电容上的电压u c (t )。
再根据:dtdu ct i cc =)( 可求得i c (t ),即回路电流i L (t )。
式(6-1)的特征方程为:01p p 2=++RC LC 特征值为:20222,11)2(2p ωαα-±-=-±-=LCL R L R (6-2)定义:衰减系数(阻尼系数)LR 2=α 自由振荡角频率(固有频率)LC10=ω 由式6-2 可知,RLC 串联电路的响应类型与元件参数有关。
1.零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图6.2所示,设电容已经充电,其电压为U 0,电感的初始电流为0。
(1) CL R 2>,响应是非振荡性的,称为过阻尼情况。
电路响应为:)()()()()(212112012120t P t P t P t P C e e P P L U t i e P e P P P U t u ---=--=响应曲线如图6.3所示。
可以看出:u C (t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值, 且当2112lnP P P P t m -=时,电流有极大值。
(2)CL R 2=,响应临界振荡,称为临界阻尼情况。
电路响应为tt c te LUt i e t U t u ααα--=+=00)()1()( t ≥0响应曲线如图6.4所示。
二阶电路响应的研究实验报告

二阶电路响应的研究实验报告摘要:本实验通过对二阶电路的响应进行研究,以深入了解二阶电路的工作原理和性质。
实验中通过利用示波器观察RC电路和RLC电路的频率响应曲线、计算共振频率和带宽等参数。
数据结果表明,当电路达到共振频率时,电路在谐振时的电压幅度最大,而带宽与电路的阻抗相关。
本次实验结论将有助于加深学生对于二阶电路的认识和理解,进一步提高本专业同学对于微电子学科的综合素质。
关键词:二阶电路;共振频率;带宽;频率响应曲线Introduction:二阶电路是指电路中包含了两个存储元件的线性电路。
存储元件可以是电容、电感或共同组成的电容电感(LC)元件,具有强烈的共振特性。
二阶电路在电子工程学科中具有重要意义,可以广泛应用于无线电、通信和信号处理等各种领域。
深入了解二阶电路的工作原理和性质是非常重要的。
本实验旨在通过研究二阶电路的响应,通过实验数据结果对二阶电路进行深入的分析,包括共振频率、带宽等参数。
实验结果将有助于加深学生对于二阶电路的认识和理解。
Experimental content:在实验中,我们分别通过示波器对RC电路和RLC电路进行了测量,计算了两个电路的共振频率和带宽。
在RC电路中,我们通过更改电阻和电容的数值,观察了频率响应曲线的变化。
在RLC电路中,我们将电路带入谐振状态并观测该状态下的电压幅度。
详细实验步骤如下:1. RC电路的实验:步骤1.1:所需器材:函数发生器、示波器、电阻器、电容器。
步骤1.2:根据电路图连cct,将电路接上函数发生器和示波器,以观察RC电路的响应曲线,并进行录像记录。
步骤1.3:逐渐调整函数发生器的频率,观测并记录RC电路的响应曲线,包括电压和相位。
记录下不同电容值对响应曲线的影响。
步骤1.4:通过观察响应曲线,计算出RC电路的共振频率和带宽。
步骤2.4:通过观察响应曲线,将RLC电路带入谐振状态,并记录下谐振状态下电压幅度的大小。
Results and analysis:实验结果表明,在RC电路中,随着电容值的不断增大,电路的共振频率也随之而增大。
一阶、二阶电路的动态响应

一阶电路和二阶电路的动态响应学号:1028401083 姓名:赵静怡一、实验目的1、掌握用Multisim研究一阶电路的动态响应特性测试方法2、掌握用Multisim软件绘制电路原理图3、掌握用Multisim软件进行瞬态分析4、深刻理解和掌握零输入响应、零状态响应和完全响应5、深刻理解欠阻尼、临界、过阻尼的意义6、研究电路元件参数对二阶电路动态响应的影响二、实验原理⑴一阶电路含有一个独立储能元件,可以用一阶微分方程来描述的电路,称为一阶电路。
一阶RC电路零输入响应:当U s=0时,电容的初始电压U c(0+)=U0时,电路的响应称为零输入响应。
RCt c U t u -=0)((t>=0)零状态响应:当电容电压的初始值U c (0+)=0时,而输入为阶跃电压u s =U S u(t)时,电路的响应称为零状态响应。
)()1()(t u eU t u RCts c --=⑵二阶电路用二阶微分方程描述的动态电路称为二阶电路。
RLC 串联二阶电路如上图就是一个典型的二阶电路,可以用下述二阶线性常系数微分方程来描述:s c cc U u dt du RC dtu d LC =++22 衰减系数(阻尼系数)LR2=α 自由振荡角频率(固有频率)LCw o 1=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=<=>,称为无阻尼情况,响应是等幅振荡性的0伟欠阻尼情况,响应是振荡性的,陈2临界阻尼情况,响应临界振荡,称为2为过阻尼情况响应是非振荡性的,称,2RCLR CLR CLR三、实验内容:1.用Multisim研究一阶电路的动态响应(1)实验电路(a) (b) (c)(2)初始条件如图所示,t=0电路闭合,分别仿真出电容上电压(从零时刻开始)的波形,说明各属于什么响应?三种情况下分别测量电容电压达到3v所用的时间。
①图(a)为零状态相应,电容上电压的波形如下图:由上图可知,电容电压达到3v所用的时间约为91.6146μm②图(b)为零输入相应,电容上电压的波形如下图:由上图可知,电容电压达到3v所用的时间为51.1196μm ③图(c)为全响应,电容上电压的波形如下图:由上图可知,电容电压达到3v 所用的时间为40.6082μm(3)写出三种情况下电容电压随时间的函数表达式,并分别计算出电容电压为3V 时的时间。
multisim二阶动态电路响应的研究实验报告思考题

multisim二阶动态电路响应的研究实验报告思考题二阶电路动态响应实验报告二阶电路动态的响应 11微电子黄跃学号:一实验目的1.深刻理解和掌握零输入响应和零状态响应以及全响应; 2.深刻理解欠阻尼,临界,过阻尼的意义; 3.研究电路元件参数对二阶电路动态响应的影响; 4.掌握Multisim软件绘制电路原理图; 5.掌握Multisim软件中的Transient Analysis等SPICE 仿真分析方法; 6.掌握Multisim软件中的函数发生器,示波器的方使用法。
二实验原理用二阶微分方程描述的动态电路称为二阶电路。
图6.1所示的线性RLC串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:(6-1)初始值为求解该微分方程,可以得到电容上的电压uc(t)。
再根据:可求得ic(t),即回路电流iL(t)。
式(6-1)的特征方程为:特征值为:(6-2) 定义:衰减系数(阻尼系数)自由振荡角频率(固有频率)由式6-2 可知,RLC串联电路的响应类型与元件参数有关。
零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路6.2所示,设电容已经充电,其电压为U0,电感的初始电流为0。
(1) ,响应是非振荡性的,称为过阻尼情况。
电路响应为:响应曲线6.3所示。
可以看出:uC(t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值,且当时,电流有极大值。
(2),响应临界振荡,称为临界阻尼情况。
电路响应为t≥0 响应曲线6.4所示。
图6.4 二阶电路的临界阻尼过程 (3) ,响应是振荡性的,称为欠阻尼情况。
电路响应为t≥0 其中衰减振荡角频率,响应曲线6.5所示。
图6.5 二阶电路的欠阻尼过程图6.6 二阶电路的无阻尼过程(4)当R=0时,响应是等幅振荡性的,称为无阻尼情况。
电路响应为响应曲线6.6所示。
理想情况下,电压、电流是一组相位互差90度的曲线,由于无能耗,所以为等幅振荡。
二阶动态电路响应的研究实验报告

二阶动态电路响应的研究实验报告二阶动态电路响应的研究实验报告引言:在电路研究中,二阶动态电路是一种常见的电路结构,它具有较为复杂的响应特性。
本实验旨在通过实际的电路搭建和测量,研究二阶动态电路的响应特性,并探讨其在实际应用中的意义。
实验原理:二阶动态电路是由两个电容和两个电感组成的电路结构,其基本原理是通过电容和电感的相互作用,实现信号的放大、滤波和频率选择。
在本实验中,我们将搭建一个基于二阶动态电路的低通滤波器,通过调节电容和电感的数值,研究其对输入信号的响应。
实验步骤:1. 搭建电路:根据实验原理,我们按照电路图搭建了一个二阶动态电路。
电路包括两个电容、两个电感和一个电阻,其中电容和电感的数值可以根据实验需求进行调节。
2. 输入信号:我们选择了一个正弦波作为输入信号,并将其连接到电路的输入端口。
3. 测量输出:通过连接示波器,我们可以实时观察到电路的输出信号,并记录下其振幅、频率和相位等参数。
4. 调节电容和电感:在测量输出信号的过程中,我们逐步调节电容和电感的数值,观察其对输出信号的影响,并记录下相应的参数变化。
5. 数据分析:通过实验数据的统计和分析,我们可以得到二阶动态电路的响应特性曲线,并探讨其在不同频率下的变化规律。
实验结果:通过实验测量和数据分析,我们得到了二阶动态电路的响应特性曲线。
在低频信号下,电路对输入信号的放大倍数较大,且相位变化较小;而在高频信号下,电路对输入信号的放大倍数逐渐减小,且相位变化较大。
这一结果与我们的预期相符,说明二阶动态电路在频率选择和信号放大方面具有较好的性能。
讨论与应用:二阶动态电路的研究在电路设计和信号处理领域具有重要的意义。
通过研究其响应特性,我们可以了解电路对不同频率信号的处理能力,从而优化电路设计和信号处理算法。
此外,二阶动态电路还广泛应用于音频信号处理、通信系统和控制系统等领域,对于提高系统性能和抑制干扰具有重要作用。
结论:通过本次实验,我们研究了二阶动态电路的响应特性,并探讨了其在实际应用中的意义。
二阶电路的动态响应
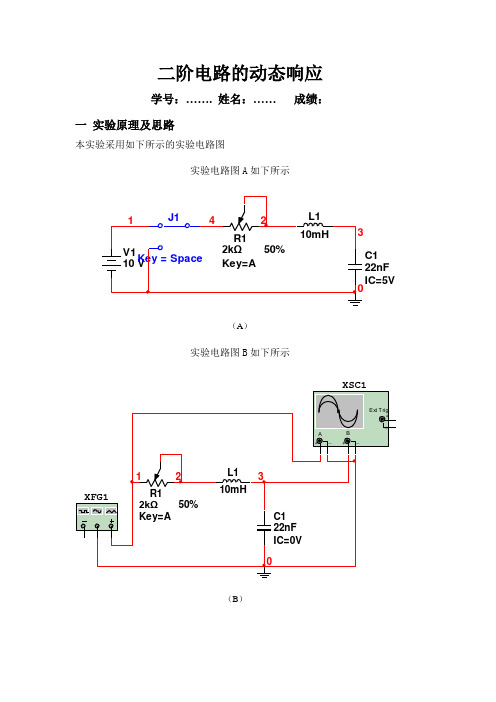
二阶电路的动态响应学号:……. 姓名:……成绩:一实验原理及思路本实验采用如下所示的实验电路图实验电路图A如下所示C122nFIC=5V(A)实验电路图B如下所示(B)实验电路图C如下所示W(C)用二阶微分方程描述动态电路称为二阶电路。
上图所示的线性RLC串联电路是一个典型的二阶电路。
1、零输入响应动态电路在没有外施激励时,由动态原件的初始储能引起的响应,称为零输入相应当R>2√(L/C)时,响应是非振荡性的,称为过阻尼情况;当R=2√(L/C)时,响应临界振荡,称为临界阻尼情况;当R<2√(L/C)时,响应是振荡性的,称为欠阻尼情况;当R=0时,响应是等幅荡性的,称为无阻尼情况;2、零状态响应动态电路的初始储能为零,由外施激励引起的电路响应,称为零状态响应。
与零输入响应相类似,电压电流的变化规律取决于电路的结构、电路参数,可分为难过阻尼、欠阻尼、临界阻尼等三种充电过程。
二实验内容及结果1.Multisim仿真欠阻尼R=100Ω;临界阻尼R=1348.4Ω;过阻尼R=2000ΩC122nF IC=5V红:欠阻尼 蓝:临界阻尼 绿:过阻尼欠阻尼R=100欧临界阻尼R=1348.4欧过阻尼R=2000欧2.在电路板上焊接实验电路(R=100ΩL=10mH C=47nF)各状态下的波形图如下所示:欠阻尼临界阻尼过阻尼1.当L、C增大时,振荡周期Td会增大,响应变化趋势会变得缓慢。
2.当R增大时,响应的变化会由欠阻尼图像到临界阻尼图像到过阻尼图像。
一阶二阶动态电路实验报告

一阶二阶动态电路实验报告实验目的:1、学习串联与并联一阶电路的响应特性;2、掌握求解一阶电路的重要参数;3、学会利用示波器分析电路响应,并用频域图分析电路特性;4、学习二阶电路的响应特性及其电路稳定条件;5、练习利用示波器分析二阶电路响应,体验相位响应和幅频响应的相互作用。
实验原理:一阶电路有两种基本形式,串联和并联,它们的特点均在于对信号时间常数t=rC的响应。
其中r为电路中电阻器的电阻,C为电容器的电容。
在外加电压U0下电路的响应可以由基尔霍夫定律表达出来。
串联电路的电压状态方程为:Uc + UR = U0C dUc/dt + Uc/R = U0/RdUc/dt + Uc/(RC) = U0/(RC)t=R*C 表示电路响应的时间常数。
并联电路的电压状态方程为:Uc = I * RC dI/dt + I/R = 0dI/dt + I/(RC) = 0同样t=R*C为响应时间常数。
二阶电路由一个电容和两个电感组成,电等效可以看作一个阻尼振荡器。
为了保证电路的稳定性,我们定义电路的品质因数Q:Q = 2pi * f0 * R * C_L其中f0为振荡器的谐振频率,C_L为负载电容器的电容量。
Q越大表示电路谐振的削减效果越弱,电路的稳态响应时间也越长。
另一个表征电路稳定的量是阻尼系数a=R/(2L)*sqrt(C/L)。
实验中我们会接触两种阻尼振荡器的形式:无阻尼振荡器和过阻尼振荡器。
无阻尼振荡器表示an=0, 此时电路振荡渐进不会消失,一阶上升较快,二阶下降趋势相对平坦,折返特点也非常明显。
过阻尼振荡器an<1,振荡不会消失,响应时间也较长,调节电路特性时需注意an<1而不是an=1。
实验装置:1. 1个函数信号发生器2. 2个示波器3. 1个二阶低通电路电路板4. 1个一阶低通电路电路板5. 量表,接线,信号装置实验内容、步骤及数据记录:1. 测量并记录一阶电路的时间常数。
电路基本参数:R=10K, C=0.1uFa. 连接串联电路,使输出信号为阶跃状,并使用示波器监控输出电压;b. 调节信号发生器使输入信号幅值约为1V;c. 测量信号的主要电压,记录t0,t1,t2,t3等关键时间,建立电路时间响应曲线,并测量电路时间响应曲线的渐近斜率;d. 完成数据拟合,计算电路的时间常数并确定其可靠误差范围。
二阶电路实验报告

二阶电路实验报告二阶电路实验报告引言:二阶电路是电路学中的重要内容,它由两个电感、电容和电阻组成,具有较为复杂的响应特性。
本次实验旨在通过实际搭建二阶电路并观察其响应,进一步加深对二阶电路的理解和应用。
一、实验目的:1. 理解二阶电路的基本原理和响应特性;2. 学会搭建二阶电路并进行实际测量;3. 分析二阶电路的频率响应曲线。
二、实验仪器和材料:1. 函数发生器2. 双踪示波器3. 电感、电容、电阻等元件4. 电路连接线等三、实验步骤:1. 搭建二阶低通RC电路:将一个电容和一个电阻串联,再并联一个电感,形成一个二阶低通RC电路。
2. 搭建二阶高通RLC电路:将一个电感和一个电阻串联,再并联一个电容,形成一个二阶高通RLC电路。
3. 将函数发生器连接到电路输入端,设置为正弦波信号。
4. 将示波器连接到电路输出端,观察和记录电路的响应波形。
5. 改变函数发生器的频率,观察电路的频率响应曲线。
四、实验结果和分析:1. 二阶低通RC电路:在实验中,我们观察到当输入正弦波频率较低时,输出波形基本保持与输入信号一致;当频率逐渐增加时,输出波形逐渐变形,幅值减小,相位滞后。
这是因为在低频情况下,电容对电路的影响较小;而在高频情况下,电容开始起到滤波作用,导致输出信号的幅值减小和相位滞后。
2. 二阶高通RLC电路:在实验中,我们观察到当输入正弦波频率较低时,输出波形基本保持与输入信号一致;当频率逐渐增加时,输出波形逐渐变形,幅值增大,相位超前。
这是因为在低频情况下,电容对电路的影响较大,起到滤波作用;而在高频情况下,电容对电路的影响减小,导致输出信号的幅值增大和相位超前。
五、实验总结:通过本次实验,我们深入了解了二阶电路的基本原理和响应特性。
通过搭建二阶低通RC电路和二阶高通RLC电路,并观察其响应波形和频率响应曲线,我们进一步加深了对二阶电路的理解。
在实际应用中,我们可以根据需要选择合适的二阶电路来实现信号的滤波、放大或延时等功能。
二阶电路的动态响应实验报告

二阶电路的动态响应实验报告一、实验目的:1. 学习用实验的方法来研究二阶动态电路的响应。
2. 研究电路元件参数对二阶电路动态响应的影响。
3. 研究欠阻尼时,元件参数对α和固有频率的影响。
4. 研究RLC 串联电路所对应的二阶微分方程的解与元件参数的关系。
二、实验原理:图1.1 RLC 串联二阶电路用二阶微分方程描述的动态电路称为二阶电路。
图1.1所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:s 2U 2=++c c c u dt du RC dt u d LC (1-1)初始值为CI C i dtt du U u L t c c 000)0()()0(===-=--求解该微分方程,可以得到电容上的电压u c (t )。
再根据:dtdu c t i cc =)( 可求得i c (t ),即回路电流i L (t )。
式(1-1)的特征方程为:01p p 2=++RC LC 特征值为:20222,11)2(2p ωαα-±-=-±-=LCL R L R(1-2)定义:衰减系数(阻尼系数)LR 2=α自由振荡角频率(固有频率)LC10=ω 由式1-2 可知,RLC 串联电路的响应类型与元件参数有关。
1. 零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图1.2所示,设电容已经充电,其电压为U 0,电感的初始电流为0。
图1.2 RLC 串联零输入电路(1) CLR 2>,响应是非振荡性的,称为过阻尼情况。
电路响应为:)()()()()(212112012120t P t P t P t P C e e P P L U t i e P e P P P U t u ---=--=图1.3 RLC 串联零输入瞬态分析响应曲线如图1.3所示。
可以看出:u C (t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
“二阶动态电路的响应测试”实验报告

“二阶动态电路的响应测试”实验报告实验名称:二阶动态电路的响应测试
实验目的:
1.了解二阶动态电路的响应特性。
2.学习使用示波器和信号发生器进行实验。
3.训练实验操作和数据处理能力。
实验原理:
二阶动态电路是指由两个电容和两个电感构成的LC电路,具有自然频率和阻尼系数两个参数。
当外加一个脉冲信号时,电路会产生一定的响应,其中包括欠阻尼、临界阻尼和过阻尼三种响应模式。
通过观察和记录响应波形,可以对电路的自然频率、阻尼系数和响应特性进行分析和计算。
实验设备:
示波器、信号发生器、RLC电路板等。
实验步骤:
1.按照图示连接电路板,设置合适的R、L、C元件。
2.使用信号发生器产生单位阶跃信号,并将其输入到电路板上。
3.将示波器分别接在电路板的两个端口上,并观察并记录电压随时间的变化波形。
4.根据波形记录,计算电路的自然频率、阻尼系数和响应模式。
5.将电路参数和波形结果进行汇总和分析,撰写实验报告。
实验结果:
通过观察示波器记录的波形,我们得到了RLC电路在接收单位阶跃信号时的响应特性。
通过计算波形图中的振动周期、振幅减衰系数等指标,我们得到了电路的自然频率和阻尼系数,并对其响应模式进行了分析和解释。
由于实验数据和具体步骤过多,这里不再赘述,附上完整的实验报告供参考。
二阶动态电路响应的研究实验报告

二阶动态电路响应的研究实验报告嘿,大家好!今天咱们聊聊一个让人兴奋的话题——二阶动态电路响应。
听上去是不是有点深奥?别担心,我来给你们揭开这个神秘的面纱。
这就像是一个电路在回应我们的“指令”,就像小狗听到主人的口令一样,乖乖地反应。
不过呢,这种反应可不是简单的坐下、转圈圈,而是复杂得多。
想象一下,我们把电路看成是一位艺术家,二阶动态电路就像是他用来创作的画笔。
这画笔的灵敏度、反应速度,还有画出的每一笔,每一划,都是我们研究的重点。
二阶动态电路有两个能量储存元件——电感和电容,它们就像是电路里的双胞胎,一起工作,互相影响。
你可能会问,这双胞胎到底有多厉害?嘿,这可得看看它们的“化学反应”了。
在我们的实验中,我们设置了一些有趣的场景,让电路在不同条件下进行“表演”。
想象一下,你调高音量,看看电路是怎么回应的。
嘿,瞬间,你就能看到电压和电流的波动,简直像是在看一场电气交响乐!这些变化就像是电路在告诉你,它感受到了什么。
就像人在舞台上跳舞,随着音乐的节奏而舞动。
我们称这些反应为“响应”,就像小猫看到鱼一样,立刻就能“扑”上去。
我们还得提到一个小秘密,那就是“自然频率”。
这是电路的“特色”,就像每个人都有自己独特的声音。
当我们施加一个信号,电路就会在这个频率上表现得特别活跃。
想想看,就像一个歌手在高音区时,整个气氛都被点燃了。
我们通过实验观察到,电路在自然频率附近的反应特别明显,像个兴奋的小孩子,跃跃欲试,恨不得马上就来个大展示。
实验中也不乏一些小插曲。
我们的电路表现得不太“听话”,比如出现了过冲和下冲,就像小孩闹脾气一样。
这个时候,我们就得耐心点,调整电路的参数,试图让它回到正常的“轨道”上。
你要知道,电路就像一个情绪丰富的孩子,有时候需要些耐心和引导,才能让它表现得更好。
咱们得聊聊数据分析。
这部分虽然有点严肃,但其实也挺有趣的。
我们用一些图表来展示电路的响应情况,就像是在看运动会的成绩单。
每一条曲线、每一个数据点,都是电路表演的证据。
二阶电路动态响应实验报告材料

二阶电路动态的响应11微电子 黄跃学号:1117426021一 实验目的1.深刻理解和掌握零输入响应和零状态响应以及全响应;2.深刻理解欠阻尼,临界,过阻尼的意义;3.研究电路元件参数对二阶电路动态响应的影响;4.掌握Multisim 软件绘制电路原理图;5.掌握Multisim 软件中的Transient Analysis 等SPICE 仿真分析方法;6.掌握Multisim 软件中的函数发生器,示波器的方使用法。
二 实验原理用二阶微分方程描述的动态电路称为二阶电路。
图6.1所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:s2U 2=++c cc u dt du RC dt ud LC (6-1)初始值为CI C i dtt du U u L t c c 000)0()()0(===-=--求解该微分方程,可以得到电容上的电压uc(t)。
再根据:dtdu ct i cc =)(可求得ic(t),即回路电流iL(t)。
式(6-1)的特征方程为:01p p 2=++RC LC 特征值为:20222,11)2(2p ωαα-±-=-±-=LC L R L R (6-2)定义:衰减系数(阻尼系数)L R2=α自由振荡角频率(固有频率)LC 10=ω由式6-2 可知,RLC 串联电路的响应类型与元件参数有关。
零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图6.2所示,设电容已经充电,其电压为U0,电感的初始电流为0。
(1)CL R 2>,响应是非振荡性的,称为过阻尼情况。
电路响应为:响应曲线如图6.3所示。
可以看出:uC(t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值, 且当图6.2 RLC 串联零输入响应电路图6.3 二阶电路的过阻尼过程u Lt mU 02112lnP P P P tm -=时,电流有极大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二阶电路的动态响应实验报告
一、实验目的:
1. 学习用实验的方法来研究二阶动态电路的响应。
2. 研究电路元件参数对二阶电路动态响应的影响。
3. 研究欠阻尼时,元件参数对α和固有频率的影响。
4. 研究RLC 串联电路所对应的二阶微分方程的解与元件参数的关系。
二、实验原理:
图1.1 RLC 串联二阶电路
用二阶微分方程描述的动态电路称为二阶电路。
图1.1所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:
s 2
U 2=++c c c u dt du RC dt
u d LC (1-1) 初始值为
C
I C i dt
t du U u L t c c 0
00
)0()()0(==
=-=--
求解该微分方程,可以得到电容上的电压u c (t )。
再根据:dt
du c
t i c
c =)( 可求得i c (t ),即回路电流i L (t )。
式(1-1)的特征方程为:01p p 2
=++RC LC 特征值为:2
0222,11)2(2p ωαα-±-=-±-
=LC
L R L R (1-2)
定义:衰减系数(阻尼系数)L
R 2=
α 自由振荡角频率(固有频率)LC
1
0=
ω 由式1-2 可知,RLC 串联电路的响应类型与元件参数有关。
1. 零输入响应
动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图1.2所示,设电容已经充电,其电压为U 0,电感的初始电流为0。
图1.2 RLC 串联零输入电路
(1) C
L
R 2
>,响应是非振荡性的,称为过阻尼情况。
电路响应为:
)
()
()()
()(2
1
2
1
120
121
20
t P t P t P t P C e e P P L U t i e P e P P P U t u ---=
--=
图1.3 RLC 串联零输入瞬态分析
响应曲线如图1.3所示。
可以看出:u C (t)由两个单调下降的指数函数组成,为非振荡的
过渡过程。
整个放电过程中电流为正值, 且当2
11
2ln
P P P P t m -=时,电流有极大值。
(2)C
L
R 2
=,响应临界振荡,称为临界阻尼情况。
电路响应为
t
t c te L
U
t i e t U t u ααα--=+=00)()1()( t ≥0
响应曲线如图1.3所示。
(3) C
L
R 2
<,响应是振荡性的,称为欠阻尼情况。
电路响应为
t e L
U t i t e U t u d t
d d t d
C ωωβωωωααsin )(),sin()(000
--=
+==t ≥0
其中衰减振荡角频率 2
2
2
0d 2L R LC 1⎪⎭⎫
⎝⎛-=
-=αωω , α
ωβd arctan = 响应曲线如图1.3所示。
图1.3 二阶电路零输入响应
(4)当R =0时,响应是等幅振荡性的,称为无阻尼情况。
电路响应为
t L
U t i t U t u C 000
00sin )(cos )(ωωω=
= 响应曲线如图1.6所示。
理想情况下,电压、电流是一组相位互差90度的曲线,由于无能耗,所以为等幅振荡。
等幅振荡角频率即为自由振荡角频率0ω,
注:在无源网络中,由于有导线、电感的直流电阻和电容器的介质损耗存在,R 不可能为零,故实验中不可能出现等幅振荡。
2. 零状态响应
动态电路的初始储能为零,由外施激励引起的电路响应,称为零输入响应。
过阻尼 临界阻尼 欠阻尼
电路如图1.4所示,设电容已经放电,其电压为0V ,电感的初始电流为0。
图1.4 RLC 串联零状态电路
根据方程1-1,电路零状态响应的表达式为:
)
()()t ()t (212112121
2t p t p S
t p t p S
S C e e p p L U i e p e p p p U U u ---=---
=)(0t ≥
与零输入响应相类似,电压、电流的变化规律取决于电路结构、电路参数,可以分为过阻尼、欠阻尼、临界阻尼等三种充电过程。
响应曲线如图1.5所示。
图1.5 二阶电路零状态响应
3. 全响应
动态电路的初始储能不为零,和外施激励一起引起的电路响应,称为全响应。
电路如图1.6所示,设电容已经充电,其电压为5V ,电压源电压10V 。
欠阻尼 临界阻尼 过阻尼
图1.6 RLC 串联全响应电路
响应曲线如图1.7所示。
图1.7 二阶电路全响应
4.状态轨迹
对于图1.1所示电路,也可以用两个一阶方程的联立(即状态方程)来求解:
L U L t Ri L t u dt
t di C
t i dt t du s
L C L L c ---==)()()
()
()( 初始值为
00
)0()0(I i U u L c ==--
其中,)(t u c 和)(t i L 为状态变量,对于所有t ≥0的不同时刻,由状态变量在状态平面上所确定的点的集合,就叫做状态轨迹。
三、实验设备与器件
1. 低频信号发生器
2. 交流毫伏表
3. 双踪示波器
4.
万用表
欠阻尼
临界阻尼
过阻尼
5. 可变电阻
6. 电阻、电感、电容 (电阻100Ω,电感10mH, 电容47n F),可变电阻(5k Ω)。
四、实验内容(multisim 仿真)
1. 按图1.8所示电路接线(R 1=100Ω L =10mH C =47nF )
画出仿真图,如下,调节R2阻值,使电容两端电压分别出现欠阻尼、临界阻尼、过阻尼状态。
仿真图
L
R 2
R 1
C
信号发生器
示波器 图6.8 二阶电路实验接线图
图1.8 二阶电路实验接线图
欠阻尼状态
临界阻尼状态
过阻尼状态
2.在电路板上按图1.8焊接实验电路。
实际测量值:R1=97.8Ω,C1=42.2nF,(R L1=54.3Ω)
波形R L C 震荡周期T d第一波峰峰值h1第二波峰峰值h2
97.8 10m 42.2n 150μs 2.2V 0.2V
理论值测量值震荡衰减角频率ωd46076.57 41887.90
衰减系数α5200 15985.96 六.实验结论分析与总结
在欠阻尼状态下.
R增大,ωd不变,α减小
L增大,ωd减小,α减小
C增大,ωd减小,α不变。
