勤学早七年级下期中专题———综合题
七年级数学下册专题08 期中-几何综合大题必刷(压轴题)(原卷版)
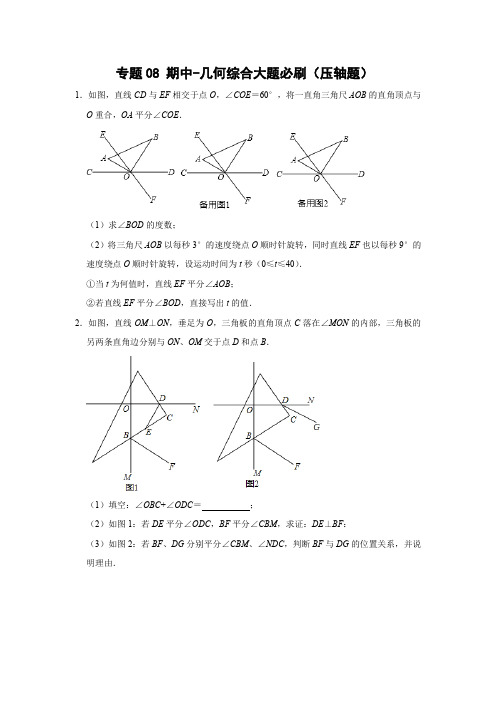
专题08 期中-几何综合大题必刷(压轴题)1.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.(1)求∠BOD的度数;(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).①当t为何值时,直线EF平分∠AOB;②若直线EF平分∠BOD,直接写出t的值.2.如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.(1)填空:∠OBC+∠ODC=;(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:(3)如图2:若BF、DG分别平分∠CBM、∠NDC,判断BF与DG的位置关系,并说明理由.3.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM 时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC 与边ON互相垂直.(直接写出答案)4.【学科融合】物理学中把经过入射点O并垂直于反射面的直线ON叫做法线,入射光线与法线的夹角i叫做入射角,反射光线与法线的夹角r叫做反射角(如图①).由此可以归纳出如下的规律:在反射现象中,反射光线、入射光线和法线都在同一平面内;反射光线、入射光线分别位于法线两侧;反射角等于入射角.这就是光的反射定律(reflection law).【数学推理】如图1,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:∠1=∠2,∠3=∠4.在这样的条件下,求证:AB∥CD.【尝试探究】两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD.(1)如图2,光线AB与CD相交于点E,则∠BEC=;(2)如图3,光线AB与CD所在的直线相交于点E,∠BED=β,则α与β之间满足的等量关系是.5.已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG =30°,求∠MGN+∠MPN的度数;(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.6.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B 射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.7.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.8.如图1,MN∥EF,C为两直线之间一点.(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系:.9.(1)【问题】如图1,若AB∥CD,∠BEP=25°,∠PFC=150°.求∠EPF的度数;(2)【问题迁移】如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;(3)【联想拓展】如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.10.如图,已知直线AB∥射线CD,∠CEB=100°.P是射线EB上一动点,过点P作PQ ∥EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧.①求∠PCG的度数;②若∠EGC﹣∠ECG=40°,求∠CPQ的度数.(2)在点P的运动过程中,是否存在这样的情形,使?若存在,求出∠CPQ 的度数;若不存在,请说明理由.11.如图,AB∥CD,∠ABE=120°.(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.12.已知:AB∥CD,点E在直线AB上,点F在直线CD上.(1)如图(1),∠1=∠2,∠3=∠4.①若∠4=36°,求∠2的度数;②试判断EM与FN的位置关系,并说明理由;(2)如图(2),EG平分∠MEF,EH平分∠AEM,试探究∠GEH与∠EFD的数量关系,并说明理由.13.已知M、N分别为直线AB,直线CD上的点,且AB∥CD,E在AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,P是CD上一点,连PM,作MQ∥EN,若∠QMP=∠BME.试探究∠E与∠AMP的数量关系,并说明理由;(3)在(2)的条件下,作NG⊥CD交PM于G,若MP平分∠QME,NF平分∠ENG,若∠MGN=m°,∠MFN=n°,直接写出m与n的数量关系.14.如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.(1)试说明:∠BAG=∠BGA;(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.15.已知:如图,直线PQ∥MN,点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.(1)若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1,∠2之间的数量关系.(2)若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,给出下列两个结论:①的②∠GEN﹣∠BDF的值不变.其中只有一个是正确的,你认为哪个是正确的?并求出不变的值是多少.16.已知AB∥CD,解决下列问题:(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.(2)如图②,若∠ABP=∠ABE,∠CDP=∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=∠ABE,∠CDP=∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).17.如图1,AM∥CN,点B为平面内一点,AB⊥BC于B,过B作BD⊥AM.(1)求证:∠ABD=∠C;(2)如图2,在(1)问的条件下,分别作∠ABD、∠DBC的平分线交DM于E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,①求证:∠ABF=∠AFB;②求∠CBE的度数.18.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,连接PM、PN、PQ,PQ平分∠MPN,如图①.(1)若∠PMA=α、∠PQC=β,求∠NPQ的度数(用含α,β的式子表示);(2)过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F,如图②,请你判断EF与PQ的位置关系,并说明理由;(3)在(2)的条件下,连接EN,如图③,若∠NEF=∠PMA,求证:NE平分∠PNQ.19.如图1,AB∥CD,G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2,若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.20.如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.(1)如图1,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠EIH的度数.(2)如图2,点G在点E的右侧,点H也在点F的右侧,若∠AEF=α,∠CHG=β,其他条件不变,求∠EIH的度数.(3)如图3,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG 的平分线EJ于点J.其他条件不变,若∠AEF=α,∠CHG=β,求∠EJH的度数.21.如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD(1)求证:∠EMF=90°.(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.22.已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.(1)如图1,点G在CH的延长线上时,①若∠GAB=36°,则∠MCD=.②猜想:∠GAB与∠MCD之间的数量关系是.(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.23.已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.(1)如图1,∠BME,∠E,∠END的数量关系为;(直接写出答案)(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数.(用含m的式子表示)(3)如图3点G为CD上一点,∠BMN=n•∠EMN,∠GEK=n•∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)24.如图1,AB∥CD,P为AB、CD之间一点(1)若AP平分∠CAB,CP平分∠ACD.求证:AP⊥CP;(2)如图(2),若∠BAP=∠BAC,∠DCP=∠ACD,且AE平分∠BAP,CF平分∠DCP,猜想∠E+∠F的结果并且证明你的结论;(3)在(1)的条件下,当∠BAQ=∠BAP,∠DCQ=∠DCP,H为AB上一动点,连HQ并延长至K,使∠QKA=∠QAK,再过点Q作∠CQH的平分线交直线AK于M,问当点H在射线AB上移动时,∠QMK的大小是否变化?若不变,求其值;若变化,求其取值范围.25.如图1,AB∥CD.G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2.若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系;并证明你的结论.26.已知,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,此时∠EOC的度数等于(直接写出答案即可);(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求此时∠OCA度数.27.如图1,AB∥CD,点E、F分别在AB、CD上,点O在直线AB、CD之间,且∠EOF =80°.(1)求∠BEO+∠OFD的值;(2)如图2,直线MN分别交∠BEO、∠OFC的角平分线于点M、N,直接写出∠EMN ﹣∠FNM的值(3)如图3,EG在∠AEO内,∠AEG=m∠OEG;FH在∠DFO内,∠DFH=m∠OFH,直线MN分别交EG、FH分别于点M、N,且∠FMN﹣∠ENM=80°,直接写出m的值.28.已知,两直线AB,CD,且AB∥CD,点M,N分别在直线AB,CD上,放置一个足够大的直角三角尺,使得三角尺的两边EP,EQ分别经过点M,N,过点N作射线NF,使得∠ENF=∠ENC.(1)转动三角尺,如图①所示,当射线NF与NM重合,∠FND=45°时,求∠AME的度数;(2)转动三角尺,如图②所示,当射线NF与NM不重合,∠FND=60°时,求∠AME 的度数.(3)转动直角三角尺的过程中,请直接写出∠FND与∠AME之间的数量关系.29.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∥CD;(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.30.如图1,BC⊥AF于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.31.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.(1)如图1,求证:EF∥GH;(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.32.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF 交CD于点M,且∠FEM=∠FME.(1)判断直线AB与直线CD是否平行,并说明理由;(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.①当点G在点F的右侧时,若β=56°,求α的度数;②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.33.如图1,G,E是直线AB上两点,点G在点E左侧,过点G的直线GP与过点E的直线EP交于点P.直线PE交直线CD于点H,满足点E在线段PH上,∠PGB+∠P=∠PHD.(1)求证:AB∥CD;(2)如图2,点Q在直线AB,CD之间,PH平分∠QHD,GF平分∠PGB,点F,G,Q在同一直线上,且2∠Q+∠P=120°,求∠QHD的度数;(3)在(2)的条件下,若点M是直线PG上一点,直线MH交直线AB于点N,点N 在点B左侧,请直接写出∠MNB和∠PHM的数量关系.(题中所有角都是大于0°且小于180°的角)34.已知,DE平分∠ADB交射线BC于点E,∠BDE=∠BED.(1)如图1,求证:AD∥BC;(2)如图2,点F是射线DA上一点,过点F作FG∥BD交射线BC于点G,点N是FG 上一点,连接NE,求证:∠DEN=∠ADE+∠ENG;(3)如图3,在(2)的条件下,连接DN,点P为BD延长线上一点,DM平分∠BDE 交BE于点M,若DN平分∠PDM,DE⊥EN,∠DBC﹣∠DNE=∠FDN,求∠EDN的度数.35.综合应用题:如图,有一副直角三角板如图①放置(其中∠D=45°,∠C=30°),P A、PB与直线MN重合,且三角板P AC,三角板PBD均可以绕点P逆时针旋转.(1)∠DPC=;(2)如图②,若三角板PBD保持不动,三角板∠P AC绕点P逆时针旋转,转速为10°/秒,转动一周三角板P AC就停止转动,在旋转的过程中,当旋转时间为多少时,有PC ∥DB成立;(3)如图③,在图①基础上,若三角板P AC的边P A从PN.处开始绕点P逆时针旋转,转速为3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/秒,(当PC转到与PM重合时,两三角板都停止转动),在旋转过程中,当∠CPD=∠BPM,求旋转的时间是多少?36.已知E,F分别是AB、CD上的动点,P也为一动点.(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.37.“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)若两灯同时开始转动,两灯射出的光束交于点C,且∠ACB=120°,则在灯B射线到达BQ之前,转动的时间为秒.38.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成图中的填空部分)证明:过点G作直线MN∥AB,又∵AB∥CD,∴∥CD∵MN∥AB,∴∠=∠MGA.∵MN∥CD,∴∠D=()∴∠AGD=∠AGM+∠DGM=∠A+∠D.(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.(3)【应用拓展】如图3,AH平分∠GAE,DH交AH于点H,且∠GDH=2∠HDF,∠HDF=22°,∠H=32°,直接写出∠DGA的度数为°.39.如图1,直线AB、CD被直线EF截,分别交AB于点G,交CD于点H,∠AGE与∠EHC互补.(1)求证:AB∥CD;(2)如图2,点P在直线AB、CD内部直线EF上,点M、N分别在直线AB、CD上,连接PM、PN,点K在∠PMB的角平分线上,连接KN,若∠MKN=180°∠MPN,求证:∠PNK=∠CNK;(3)如图3,在(2)的条件下,点O为AB上一点,连接ON、MN,MN平分∠PNO,若∠MNK:∠PMK=2:7,2∠MKN﹣∠PNO=180°,求∠NOM的度数.40.已知,AB∥CD,点F、G分别在AB、CD上,且点E为射线FG上一点.(1)如图1:当点E在线段FG上时,连接AE、DE,易得∠AED=∠EAF+∠EDG.小明给出的理由是:如图1,过E作EH∥AB,∵AB∥CD,∴AB∥CD∥EH,(平行于同一条直线的两条直线互相平行)∴∠EAF=∠AEH,∠EDG=∠DEH,(依据1)∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(依据2)填空:依据1:.依据2:.(2)如图2,当点E在FG延长线上时,求证:∠EAF=∠AED+∠EDG;(3)如图3,AI平分∠BAE,DI交AI于点I,交AE于点K,且∠EDI:∠CDI=2:1,∠AED=20°,∠I=30°,求∠EKD的度数.41.如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠P AC=50°,∠ADC=30°,AE平分∠P AD,CE平分∠ACD,AE与CE相交于E.(1)求∠AEC的度数;(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠P AC=50°,∠A1D1C=30°,求∠A1EC 的度数.(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.42.阅读下面材料:小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是.参考小亮思考问题的方法,解决问题:(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,作∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M=(直接用含α的式子表示).。
3_《勤学早》七下学用1-138

&'!&统计调查 &'% 第&课时统计调查& &'% 第!课时统计调查! &'" &'!!直方图 &&& 章末复习单元核心考点归纳 &&$
方法技巧专题!巧用槡!%!%(&的双重非负性解题 '-
0!'!实数 '. !第#课时!实数%#& '. !第&课时!实数%&& /* #回归教材二!平方根在实际问题中的应用 /# $章末复习单元核心考点归纳 /&
第!课时一元一次不等式的应用 "# "!$一元一次不等式组 "% 第&课时一元一次不等式组的解法 "% 重点强化专题解一元一次不等式组 "" 重点强化专题一元一次不等式组的综合应用 &'' 第!课时一元一次不等式组的应用 &'& 重点强化专题实际问题与一元一次不等式组 &'$ 回归教材五用作差法比较大小 &'( 章末复习单元核心考点归纳 &'#
第二部分期中练)期末练
期 末 重 点 强 化 基 础 题 ) 中 档 题
期末重点强化!相交线所成的角度计算 &&# 期末重点强化"平行线的判定 &&* 期末重点强化#平行线的性质 &&% 期末重点强化$实数 &&+ 期末重点强化%平面直角坐标系&坐标与图形面积 &&" 期末重点强化&平面直角坐标系!用坐标表示平移 &!' 期末重点强化'解二元一次方程组 &!& 期末重点强化(二元一次方程组的应用 &!! 期末重点强化)实际问题与二元一次方程组& &!$ 期末重点强化!*实际问题与二元一次方程组! &!( 期末重点强化!!解一元一次不等式组 &!# 期末重点强化!" 实际问题与不等式组&方案问题 &!* 期末重点强化!# 实际问题与不等式组!与方程组的结合 &!% 期末重点强化!$统计调查 &!+
七下语文勤学早期末模拟卷4答案

七下语文勤学早期末模拟卷4答案第一部分积累与运用(50分)(一)基础知识(20分)1、下列加点字的注音全部正确的一项是( B )A、校(jiào)正归省(xǐng) 头晕目眩(xuàn) 咀嚼(jiáo)B、伺(sì)机蹊跷(qiāo) 酣(hān)然入梦吞噬(shì)C、摇曳(yè) 洗濯(zhuó) 削(xiāo)足适履后裔(yì)D、栖(xī)息弥散(sàn) 木椽(chuán) 翱(áo)翔2、下列词语中,没有错别字的一项是(B )A、撺掇故弄弦虚怒不可遏浩瀚B、自矜余音绕梁推推搡搡萦绕C、白蓬船不屑一顾风尘仆仆步履蹒跚D、山坳遥无消息坚忍不拔义无反顾3、横线中填入的词语正确的一项是(B )在农村这片的土地上,袁隆平凭借执着的精神,培育出杂交水稻,让农民摆脱了,解决了我们这个大国的吃饭问题。
A、疮痍贫穷B、贫瘠贫穷C、疮痍贫瘠D、贫穷贫瘠4、“改了国籍,不等于就改了民族感情;没有一个民族像我们这么依恋故土的”句式变换正确的一项是(C )A、难道改了国籍,就不等于就改了民族感情吗?有哪一个民族像我们这么依恋故土的?B、难道改了国籍,就等于就改了民族感情吗?难道没有一个民族像我们这么依恋故土的吗?C、改了国籍,难道就等于就改了民族感情吗?有哪一个民族像我们这么依恋故土的?D、改了国籍,难道就不等于就改了民族感情吗?怎么没有一个民族像我们这么依恋故土的?5、下列表述中,不正确的一项是(D )A、白妞、黑妞都是清代谴责小说家刘鹗《老残游记》中的人物。
B、天后赫拉是希腊奥林匹斯主神之一,她是宙斯的妻子,代表了女性的美德和尊严。
C、《伤仲永》的作者王安石和《卖油翁》的作者欧阳修同属于唐宋八大家之一,以文见长。
D、“乐天”即唐代诗人白居易,号香山居士,人称“诗豪”。
(二)默写:(21分)6、为人性癖耽佳句,语不惊人死不休。
人教版2020七年级数学下册期中综合复习培优训练题4(附答案详解)

人教版2020七年级数学下册期中综合复习培优训练题4(附答案详解)1.在如图所示的单位正方形网格中,ABC ∆经过平移后得到111A B C ∆,已知在AC 上一点()2.4,2P 平移后的对应点为1P ,则1P 点的坐标为( )A .(1.4,-1)B .(-1.5,2)C .(-1.6,-1)D .(-2.4,1)2.在数学课上,同学们在练习过点B 作线段AC 所在直线的垂线段时,有一部分同学画出下列四种图形,正确的是( )A .B .C .D . 3.在下列实数中:0,2.5,﹣3.1415,29,4,227,1π-,0.4343343334……(相邻两个4之间3的个数逐次加1),无理数有( )A .1个B .2个C .3个D .4个 4.在实数:3.14159,,1.010010001…(每相隔1个就多1个0),,中,无理数的个数有( )A .1个B .2个C .3个D .4个 5.已知点A (1,0),B (0,3),点P 在x 轴上,且三角形P AB 的面积为3,则点P 的坐标是( )A .(﹣1,0)B .(3,0)C .(﹣1,0)或(3,0)D .(0,9)或(0,﹣3)6.如图,在△ABC 中,∠A=90°,点D 在AC 边上,DE//BC ,若∠1=155°,则∠B 的度数为( )A .55°B .65°C .45°D .75°7.点P 在第二象限内,P 到x 轴的距离是4,到y 轴的距离是3,那么点P 的坐标为( )A .(43)-,B .(34)--,C .(34)-,D .(34)-,8.在坐标平面内,若点P (x-3,x+2)在第二象限,则x 的取值范围是( )A .x >3B .x <3C .x >-2D .-2<x <39.如图,在∠1、∠2、∠3、∠4中,内错角是( )A .1∠与4∠B .2∠与4∠C .1∠与3∠D .2∠与3∠10.有一个数值转换器,原理如图:当输入的x 为﹣83时,输出的y 是_____.11.在平面直角坐标系中,将点A (-2,6)向右平移2个单位,得到A’点的坐标是_______ 12.如图,直线AB ,CD 相交于点O ,已知∠AOD =3x °,∠BOC =2x °+40°,则∠BOC=________°.13.新定义:aUb=(a 2b+ab+ab 2)÷ab ,其中a,b 都不为零,则3U (2U4)=_____14.写出一个比4大的无理数:____________.15._____数和数轴上的点一一对应.16.在实数①73-,②0.010010001,③22,④227,⑤2π-中,有理数是_____(填序号).17.如果a 22a +1,那么整数a =______.18.我们用符号[x ]表示一个不大于实数x 的最大的整数,如:[2.78]=2,[﹣0.23]=﹣1,则按这个规律,[﹣17]=_____.19.如图,已知m n ∕∕,1105∠=︒,2140∠=︒则a ∠=________.20.如图,已知AB ∥CD ,点E 是直线AB 上一个定点,点F 在直线CD 上运动,设∠CFE =α,在线段EF 上取一点M ,射线EA 上取一点N ,使得∠ANM =160°.(1)当∠AEF =2a 时,α= ; (2)当MN ⊥EF 时,求α;(3)作∠CFE 的角平分线FQ ,若FQ ∥MN ,直接写出α的值: .21.如图所示,//AB CD ,点E 为两条平行线外部一点,F 为两条平行线内部一点,G H 、分别为AB CD 、上两点,GB 平分EGF ∠,HF 平分EHD ∠,且2F ∠与E ∠互补,求EGF ∠的大小.22.两条平行线被第三条直线所截,试说明:内错角的角平分线互相平行.23.将一副三角板的直角重合放置,如图1所示,(1)图1中∠BED 的度数为 ;(2)三角板△AOB 的位置保持不动,将三角板△COD 绕其直角顶点O 顺时针方向旋转: ①当旋转至图2所示位置时,恰好OD ∥AB ,求此时∠AOC 的大小;②若将三角板△COD 继续绕O 旋转,直至回到图1位置,在这一过程中,是否会存在△COD 其中一边能与AB 平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.24.如图所示,在象棋盘上建立平面直角坐标系,使使“马”位于点(2,2),“炮”位于点(﹣1,2),写出“兵”所在位置的坐标.25.已知AB ∥DE ,∠ABC =800,∠CDE =1400.请你探索出一种(只须一种)添加辅助线求出∠BCD 度数的方法,并求出∠BCD 的度数.26.(1)计算:32564|12|-+-.(2)解不等式2223x x x +--<,并把解集在数轴上表示出来.(3)解方程组:521123x y y x +⎧⎪-⎨-⎪⎩==. 27.“联片办学”在近几年的教育教学中取得了丰硕的成绩,右图是我们第四片区六所兄弟学校的大致位置,其中点O 表示西站十字,点A 表示牵头学校五十五中,点B 表示八十三中,点C 表示三十四中,点D 表示三十六中,点E 表示九中,点F 表示三十一中.以西站十字为坐标原点,向右向上分别为X 、Y 轴的正方向,结合图解答下列问题:(1)分别写出表示六所学校的点的坐标;(2)试确定△OEF的形状;(3)求△ADE的面积.28.阅读下面材料:小伟遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O.若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积.小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).参考小伟同学的思考问题的方法,解决下列问题:如图3,△ABC的三条中线分别为AD,BE,CF.(1)在图3中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹);(2)若△ABC 的面积为1,则以AD ,BE ,CF 的长度为三边长的三角形的面积等于_____. 29.如图,180∠=︒,2100∠=︒,C D ∠=∠.(1)判断BC 与DE 的位置关系,并说明理由;(2)若35A ∠=︒,求F ∠的度数.参考答案1.C【解析】【分析】根据平移的性质得出,△ABC的平移方向以及平移距离,即可得出P1坐标.【详解】解:∵A点坐标为:(2,4),A1(-2,1),∴点P(2.4,2)平移后的对应点P1为:(-1.6,-1),故选:C.【点睛】此题主要考查了平移的性质,根据已知得出平移距离是解题关键.2.A【解析】【分析】满足两个条件:①经过点B.②垂直AC;由此即可判断.【详解】解:根据垂线段的定义可知,图①线段BE,是点B作线段AC所在直线的垂线段,故选:A.【点睛】本题考查作图-复制作图,垂线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.3.C【解析】【分析】开方开不尽的数,含π的式子,无限不循环的数均为无理数,据此来判断即可.【详解】解:在实数0,2.5,﹣3.1415,227,1π-,0.4343343334……(相邻两个4之间3的个数逐次加1)中,,1π-,0.4343343334……(相邻两个4之间3的个数逐次加1)为无理数,共3个.【点睛】本题考查无理数的概念,掌握无理数的几种形式是解答此题的关键.4.B【解析】【分析】根据无理数的定义对题中各数进行判断即可得出答案.【详解】解:3.14159,,1.010010001…(每相隔1个就多1个0),,中,无理数有:1.010010001…(每相隔1个就多1个0),,故选:B.【点睛】本题考查了无理数的定义:无限不循环小数叫无理数.是基础题,熟记概念是解题的关键.5.C【解析】【分析】根据题意画出图像,由三角形的面积公式即可求解判断.【详解】解:如图,设P(m,0),由题意:12•|1﹣m|•3=3,∴m=﹣1或3,∴P(﹣1,0)或(3,0),故选C.【点睛】此题主要考查直角坐标系的图形,解题的关键是根据题意作出直角坐标系,再进行求解. 6.B【分析】先根据补角的定义求出∠CDE的度数,再由平行线的性质求出∠C的度数,根据余角的定义即可得出结论.【详解】解:∵∠1=155°,∴∠CDE=180°-155°=25°.∵DE∥BC,∴∠C=∠CDE=25°.∵∠A=90°,∴∠B=90°-25°=65°.故选:B.【点睛】本题考查的是平行线的性质,以及余角的性质,解题的关键是掌握两直线平行,内错角相等.7.C【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.【详解】解:∵点P在第二象限内,点P到x轴的距离是4,到y轴的距离是3,∴点P的横坐标是-3,纵坐标是4,∴点P的坐标为(-3,4).故选C.【点睛】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度是解题的关键.8.D【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.【详解】∵点P(x-3,x+2)在第二象限,∴3020xx-⎧⎨+⎩<①>②,解不等式①得,x<3,解不等式②得,x>-2,所以,不等式组的解集是-2<x<3,即x的取值范围是-2<x<3.故选D.【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式组,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).9.D【解析】【分析】根据内错角的定义找出即可.【详解】解:根据内错角的定义,∠2与∠3是内错角,故选:D.【点睛】本题考查“三线八角”问题,确定三线八角的关键是从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.10【解析】【分析】将x的值代入数值转化器计算即可得到结果.【详解】将x=﹣838,将x=﹣82,将x=﹣2则输出y【点睛】此题考查了立方根和无理数的概念,熟练掌握立方根和无理数的定义是解本题的关键.11.(0,6)【解析】【分析】利用点平移的坐标规律,把点A的横坐标加2,纵坐标不变即可得到A′的坐标.【详解】解:将点A(-2,6)向右平移2个单位长度,得到点A′,则点A′的坐标是(-2+2,6),即A′(0,6).故答案为:(0,6).【点睛】本题考查坐标与图形变化-平移,掌握平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.12.120【解析】【分析】根据对顶角相等得出∠AOD=∠BOC,可得到关于x的方程,解方程即可得x的度数,即可求出∠BOC的度数.【详解】∵∠AOD=∠BOC(对顶角相等),∠AOD=3x°,∠BOC=2x°+40°,∴3x°=2x°+40°,解得x=40,∴∠BOC=2x°+40°=120°.故答案为:120.【点睛】本题考查对顶角的性质,对顶角相等.13.11【解析】【分析】首先理解aUb=(a2b+ab+ab2)÷ab,然后计算2U4,其中2对应a,4对应b,根据定义的运算法则即可求出结果7,然后根据法则计算3U7即可【详解】解:∵aUb=(a2b+ab+ab2)÷ab,∴2U4=(16+8+32)÷8=7;∴3U(2U4)=3U7=(63+21+147)÷21=11故答案为:11【点睛】此题主要考查了有理数的混合运算,解题关键是正确理解定义的运算法则,能够根据运算法则计算解决问题.14【解析】【分析】无理数是指无限不循环小数,根据定义和实数的大小比较法则写出一个即可.【详解】一个比4.【点睛】本题考查了估算无理数的大小,实数的大小比较的应用,能估算无理数的大小是解此题的关键,此题是一道开放型的题目,答案不唯一.15.实【解析】【分析】根据数轴上的点表示全体实数解答即可.【详解】∵数轴上的点表示全体实数,∴实数和数轴上的点一一对应.故答案为:实【点睛】本题比较简单,考查的是数轴的特点,即数轴上的点和实数是一一对应的.16.①②④【解析】【分析】根据有理数包括整数与分数,其中有限小数与无限不循环小数也属于分数进行判断即可.【详解】①73-,②0.010010001,④227,以上三个数都是分数,所以都是有理数;而③2,⑤2π-是无限不循环小数,属于无理数.所以答案为①②④.【点睛】本题主要考查了有理数与无理数的判断,熟练掌握相关概念是解题关键.17.4【解析】【分析】a 的值即可.【详解】解:∴4<5,∵a <a+1,∴整数a=4.故答案为:4.【点睛】本题考查了估算无理数的大小,其常见的思维方法:用有理数逼近无理数,求无理数的近似值.18.-4【解析】【分析】直接利用7的取值范围得出﹣4<﹣1﹣7<﹣3,进而得出答案.【详解】解:∵2<7<3,∴﹣4<﹣1﹣7<﹣3,∴[﹣1﹣7]=﹣4.故答案为:﹣4.【点睛】此题主要考查了估算无理数的大小,正确得出7的取值范围是解题关键.19.65°【解析】【分析】根据两直线平行,同旁内角互补求出∠3,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】∵m∥n,∠1=105°,∴∠3=180°−∠1=180°−105°=75°∴∠α=∠2−∠3=140°−75°=65°故答案为:65°.【点睛】此题考查平行线的性质,解题关键在于利用同旁内角互补求出∠3.20.(1)α=120°;(2)α=110°;(3)α=40°.【解析】【分析】(1)根据平行线的性质即可得到结论;(2)如图1所示,过点M 作直线PM ∥AB ,由平行公理推论可知:AB ∥PM ∥CD .根据平行线的性质即可得到结论;(3)如图2,根据角平分线的定义和平行线的性质即可得到结论.【详解】解:(1)∵AB ∥CD ,∴∠AEF +∠CFE =180°,∵∠CFE =α,∠AEF =2α, ∴α+2α=180°, ∴α=120°;(2)如图所示,过点M 作直线PM ∥AB ,由平行公理推论可知:AB ∥PM ∥CD . ∵∠ANM =160°,∴∠NMP =180°﹣160°=20°,又∵NM ⊥EF ,∴∠NMF =90°,∠PMF =∠NMF ﹣∠NMP =90°﹣20°=70°.∴α=180°﹣∠PMF =180°﹣70°=110°;(3)如图2,∵FQ 平分∠CFE ,∴∠QFM =2α, ∵AB ∥CD ,∴∠NEM =180°﹣α,∵MN ∥FQ ,∴∠NME =2α, ∵∠ENM =180°﹣∠ANM =20°,∴20°+2α+180°﹣α=180°, ∴α=40°.故答案为120°,40°.【点睛】本题考查了平行线的性质,角平分线定义,熟练掌握平行线的性质定理是解题的关键.平行线的性质:①两直线平行同位角相等,②两直线平行内错角相等,③两直线平行同旁内角互补.21.120EGF ∠=︒.【解析】【分析】先设EGB x ∠=,EHF y ∠=,则BGF x ∠=,FHD y ∠=,由题意及平行线的性质得F BGF DHF ∠=∠+∠,EGB E EHD ∠=∠+∠,得到F x y ∠=+,2x E y =∠+,由于2F ∠与E ∠互补,得到222180x y x y ++-=︒,最终得出120EGF x x ∠=+=︒【详解】设EGB x ∠=,EHF y ∠=,则BGF x ∠=,FHD y ∠=由侧M 图BGFCD 可知:F BGF DHF ∠=∠+∠,由鸟嘴图AGEHC 可知:EGB E EHD ∠=∠+∠,即F x y ∠=+,2x E y =∠+,2F ∠与E ∠互补222180x y x y ∴++-=︒306018x x ︒∴=∴=︒120EGF x x ∴∠=+=︒.【点睛】本题考查平行线的性质,解题的关键是设EGB x ∠=,EHF y ∠=,且由题意得到x ,y 的关系.22.见解析【解析】【分析】利用平行线性质及角平分线性质解题即可【详解】已知:AB ∥CD ,MG 平分∠AGH ,HN 平分∠GHD ,求证:MG ∥HN∵AB ∥CD∴∠AGH=∠GHD (两直线平行,内错角相等)∵MG 平分∠AGH ,HN 平分∠GHD∴∠MGH=12∠AGH ,∠GHN=12∠GHD ∴∠MGH=∠GHN∴MG ∥HN (内错角相等,两直线平行)∴两条平行线被第三条直线所截,内错角的角平分线互相平行.【点睛】熟练掌握平行线性质及角平分线性质是解题关键23.(1)15°;(2)①30°;②120°,165°,30°,150°,60°,15°. 【解析】【分析】(1)根据三角形的外角性质和对顶角的性质求出∠BED 的度数;(2)①由OD ∥AB 可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC 的度数;②根据题意作图,可分6种情况进行分析求解.【详解】(1)∵∠CEA=∠BAO-∠C=60°-45°=15°,∴∠BED=∠CEA=15°,(2)①∵OD ∥AB,∴∠BOD=∠B=30°又∠BOD+∠BOC=90°和∠AOC+∠BOC=90°∴∠AOC=∠BOD=30°;②存在,如图1,∵AB∥CO,∴∠AOC=∠AOB+∠BOC=∠AOB+∠B=120°;如图2,延长AO交CD于E,∵AB∥DC,∴∠DEO=∠A=60°,又∠C=45°,∴∠COE=∠DEO-∠C=15°,∴∠AOC=180°-∠COE=165°;如图3,∵AB∥DO,∴∠A+∠AOD=180°,∵∠A=60°∴∠AOD=120°∴∠AOC=∠AOD-∠COD=30°;如图4,∵AB∥DO,∴∠AOC=∠AOD+∠COD=∠BAO+∠COD=60°+90°=150°如图5,∵AB∥CO,∴∠AOC=∠BAO =60°如图6,设AO与CD相交于点M∵AB∥CD,∴∠DMO=∠A=60°∴∠AOD=180°-45°-60°=75°,∴∠AOC=90°-∠AOD =15°.【点睛】此题主要考查三角形的角度计算,解题的关键是熟知三角形的外角性质及平行线的判定与性质.24.“兵”所在位置的坐标(﹣2,3).【解析】【分析】以“马”的位置向左2个单位,向下2个单位为坐标原点建立平面直角坐标系,然后写出兵的坐标即可.【详解】解:“马”的位置向下平移两个单位是x轴,再向左平移两个单位是y轴,得“兵”所在位置的坐标(﹣2,3).【点睛】此题考查坐标确定位置,解题关键在于掌握平移的性质.25.∠BCD=40°【解析】【分析】过点C作FG∥AB,根据平行线的传递性得到FG∥DE,根据平行线的性质得到∠B=∠BCF,∠CDE+∠DCF=180°,根据已知条件等量代换得到∠BCF=80°,由等式性质得到∠DCF=40°,于是得到结论.【详解】解:过C作CF∥DE∵CF∥DE(作图)AB∥DE(已知)∴AB∥DE∥CF(平行于同一条直线的两条直线平行)∴∠BCF=∠B=80°(两直线平行,内错角相等)∠DCF+∠D=180°(两直线平行,同旁内角互补)又∵∠D=140°(已知)∴∠DCF=40°(等量代换)又∵∠BCD=∠BCF-∠DCF(角的和差定义)∴∠BCD=80°-40°(等量代换)即∠BCD=40°【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,26.(12;(2)x<2,(3)12 xy==⎧⎨-⎩【解析】【分析】(1)根据实数的运算法则计算即可;(2)去分母、去括号、移项、合并同类项、系数化为1即可得答案;再按照不等式解集的表示方法在数轴上表示即可;(3)先把②两边同时乘以6可得6x-2y=10③,再利用加减消元法解方程即可求出x的值,代入①求出y值即可得答案. 【详解】(1)原式22;(2)去分母,得6x-3(x+2)<2(2-x),去括号,得6x-3x-6<4-2x,移项,合并得5x<10,系数化为1,得x<2,不等式的解集在数轴上表示如下:(3)521123x yyx+⎧⎪⎨--⎪⎩=①=②②×6得:6x-2y=10③,①+③得:11x=11,即x=1,将x=1代入①,得y=-2,则方程组的解为12 xy==⎧⎨-⎩.【点睛】本题考查了实数的运算、解一元一次不等式及解二元一次方程组,熟练掌握实数的运算法则及一元一次不等式、二元一次方程组的解法是解题关键.27.(1)A(0,﹣1),B(2,﹣3),C(﹣5,0),D(8,﹣6),E(﹣4,﹣4),F(﹣4,4);(2)△OEF为等腰直角三角形;(3)△ADE的面积=22.【解析】【分析】(1)先根据题意找出原点并画出坐标轴即可得出答案;(2)根据第一问得出的坐标,利用两点间距离公式分别计算三条边的长度即可得出答案;(3)根据割补法即可得出答案.【详解】解:(1)以西站十字为坐标原点,向右向上分别为x、y轴的正方向建立平面直角坐标系,∴A(0,﹣1),B(2,﹣3),C(﹣5,0),D(8,﹣6),E(﹣4,﹣4),F(﹣4,4);(2)∵OF2=42+42=32;OE2=42+42=32;EF2=82=64;∴OF2+OE2=32+32=64=EF2∴△OEF为直角三角形,又∵OF=OE=4∴△OEF为等腰直角三角形;(3)△ADE的面积=12×5﹣12×8×5﹣12×4×3=22.【点睛】本题主要考查的是平面直角坐标系,需要掌握两点间的距离公式以及割补法求面积.28.(1)见解析;(2)34.【解析】【分析】根据平移可知,△ADC≌△ECD,且由梯形的性质知△ADB与△ADC的面积相等,即△BDE 的面积等于梯形ABCD的面积.(1)分别过点F、C作BE、AD的平行线交于点P,得到的△CFP即是以AD、BE、CF的长度为三边长的一个三角形.(2)由平移的性质可得对应线段平行且相等,对应角相等.结合图形知以AD,BE,CF的长度为三边长的三角形的面积等于△ABC 的面积的34. 【详解】△BDE 的面积等于1. (1)如图.以AD 、BE 、CF 的长度为三边长的一个三角形是△CFP .(2)平移AF 到PE ,可得AF ∥PE ,AF=PE ,∴四边形AFEP 为平行四边形,∴AE 与PF 互相平分,即M 为PF 的中点,又∵AP ∥FN ,F 为AB 的中点,∴N 为PC 的中点,∴E 为△PFC 各边中线的交点,∴△PEC 的面积为△PFC 面积的 13连接DE ,可知DE 与PE 在一条直线上∴△EDC 的面积是△ABC 面积的14所以△PFC 的面积是1×14×3=34∴以AD 、BE 、CF 的长度为三边长的三角形的面积等于34.29.(1)BC DE ∕∕,见解析;(2)35F ∠=︒.【解析】【分析】(1)根据平行四边形的判定和性质证明即可;(2)由(1)知BC DE ∕∕,根据两直线平行,内错角相等即可求出F ∠的度数.【详解】解:(1)BC DE ∕∕∵180,2100∠=︒∠=︒∴1280100180∠+∠=︒+︒=︒∴BD CE ∕∕∴CEF D ∠=∠∵C D ∠=∠∴CEF C ∠=∠∴BC DE ∕∕(3)由(1)可知:BC DE ∕∕,即AC DF ∕∕∵AC DF ∕∕∴A F ∠=∠∵35A ∠=︒∴35F ∠=︒答:F ∠的度数是35︒【点睛】本题是平形线的性质与判定的综合应用,灵活应用其判定和性质是解题的关键.。
七年级下册数学 勤学早大培优与必刷题

七年级下册数学勤学早大培优与必刷题
勤学早大培优与必刷题七年级下册数学,这本书是为了帮助学生们更好地掌握数学知识和提高数学思维能力而设计的。
以下是一些可能在这本书中出现的主题和概念:
1. 整式的加减:学习如何进行整式的加、减、乘、除等运算,包括幂的运算和因式分解等。
2. 分式:了解分式的性质和运算,包括约分、通分和分式的加减等。
3. 三角形:掌握三角形的性质、分类和全等条件,了解等腰三角形和直角三角形的特点。
4. 变量与函数:学习变量的概念、函数的定义和表示方法,理解一次函数和反比例函数的性质和应用。
5. 平面直角坐标系:了解平面直角坐标系的概念和表示方法,掌握点的坐标和图形的平移、对称等变换。
6. 解方程:学习一元一次方程、二元一次方程组的解法和实际应用。
7. 概率初步知识:了解概率的基本概念和计算方法,以及在生活中的应用。
通过这些主题和概念的学习,学生们可以更好地掌握数学的基本知识和技能,提高数学思维能力,为以后的学习打下坚实的基础。
勤学早七年级下数学试卷

一、选择题(每题3分,共30分)1. 下列数中,不是有理数的是()A. -2.5B. √4C. 0D. √-12. 已知a、b是实数,且a + b = 0,那么a和b的关系是()A. a > bB. a < bC. a = bD. a和b无关系3. 下列各组数中,成等差数列的是()A. 2, 5, 8, 11B. 3, 6, 9, 12C. 4, 8, 12, 16D. 5, 10, 15, 204. 一个等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的周长是()A. 20cmB. 22cmC. 24cmD. 26cm5. 下列图形中,是轴对称图形的是()A. 正方形B. 等腰三角形C. 长方形D. 梯形6. 若x² - 5x + 6 = 0,则x的值为()A. 2B. 3C. 2或3D. 无法确定7. 下列各数中,是质数的是()A. 31B. 30C. 32D. 338. 已知函数y = 2x - 1,当x = 3时,y的值为()A. 5B. 4C. 3D. 29. 下列各式中,不是同类项的是()A. 3x²B. 5x²C. 2x²D. 4x10. 一个圆的半径增加了2cm,其面积增加了()A. 4πcm²B. 8πcm²C. 12πcm²D. 16πcm²二、填空题(每题5分,共20分)11. 已知一个数的平方是25,则这个数是______。
12. 在直角坐标系中,点A(-3,4)关于x轴的对称点是______。
13. 一个等腰三角形的底边长为8cm,腰长为10cm,则其高为______cm。
14. 若a² + b² = 100,且a - b = 6,则ab的值为______。
15. 一个长方体的长、宽、高分别为5cm、3cm、2cm,则其体积为______cm³。
勤学早语文七年级下册人教版答案2022

勤学早语文七年级下册人教版答案20221、1“寒舍”一般用于对自己住处的谦称。
[判断题] *对(正确答案)错2、袅娜中的娜读作()[单选题] *nānǎnuó(正确答案)nuò3、1妻子对酒驾的丈夫说:“你想死,别带上我。
”妻子的表达是得体的。
[判断题] *对(正确答案)错4、下列语句不是出自《红楼梦》的一项是( ) [单选题] *A.字字看来皆是血,十年辛苦不寻常。
B.女儿是水作的骨肉,男人是泥作的骨肉,我见了女儿,我便清爽:见了男子,便觉浊臭逼人。
C.话说天下大势,分久必合,合久必分。
(正确答案)D.世人都晓神仙好,惟有功名忘不了!5、“阡陌”“纤维”“纤夫”中的“阡”“纤””“纤”的读音各不相同。
[判断题] *对(正确答案)错6、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、偏僻(piān)杜撰(zhuàn)B、稀罕(gàn)溺爱(ruò)(正确答案)C、辜负(gū)风骚(sāo)D、愚蠢(chǔn)纨绔(kù)7、22.下列词语中加点字的注音,不完全正确的一项是()[单选题] *A.着落(zhuó)粗犷(guǎng)字帖(tiè)屏息敛声(bǐng)B.瞭望(liáo)稽首(qī)侍候(shì)浮光掠影(nüè)(正确答案)C.麾下(huī)睥睨(pì)鲜妍(yán)战战兢兢(jīng)D.一霎(shà)翌日(yì)箴言(zhēn)刨根问底(páo)8、37. 下列表述不正确的一项是()[单选题] *A.陶渊明,东晋诗人。
名潜,字元亮。
私谥靖节,因宅边有五棵柳树,又自号“五柳先生”。
B.《诗经》是我国最早一部诗歌总集,收录了从西周到战国时期的诗歌305篇,也称《诗》或《诗三百》。
(正确答案)C.鲁迅,原名周树人,字豫才,伟大的文学家、思想家、革命家。
勤学早系列测试卷语文七年级下册小综合卷(七)的答案

勤学早系列测试卷语文七年级下册小综合卷(七)的答案一、选择题(30分)1.下列注音都正确的是( )。
A.无垠(yín) 羸弱(yíng) 哀悼(dào ) 冻饿之虞(yú )B.沮丧(jǔ) 斫痕(zhuó) 梨铧(huà) 聊以自慰(liáo)C.吞噬(shì) 遗孀(shuānɡ) 砭骨(biān) 怏怏不乐(yàng)D.疲惫(beì) 阴霾(mái) 虫豸(zhì) 白雪皑皑(kái)2.选择书写无误的一项是( )。
A. 坚持不懈精疲力竭养精蓄锐孜孜不倦B. 忧心仲仲迫不急待梦寐以求芸芸众生C. 珊珊来迟耀武扬威不可思议闷闷不乐D. 郑重其是语无伦次齐心协力不毛之地3.下列加点词语运用正确的一项是( )。
A.这个家伙深知罪恶深重,内心十分恐慌,却从容不迫地擦着鼻子。
B.晚会结束前,他献上一曲《烛光里的妈妈》,唱得栩栩如生。
C.同学们经常向老师请教,这种不耻下问的精神值得提倡。
D.王老师没有偏见,对基础较差的学生也能够一视同仁。
4.下列句子标点符号使用正确的一项是( )。
A.“哎呀。
真是太美了!”张老师说:“我非常满意!”B.在中国传统教育典籍里,大家一致认为最重要的是《四书五经》。
C.怎么可能这样?你说的?没搞错吧?有没有再调查?D.贵州的黄果树、龙宫、重庆的武隆、四川的乐山均是旅游胜地。
5.依次填入下面句子括号处的词语,最恰当的一项是( )。
我们的视野,因着美丽的存在而开阔;我们的心灵,因着( )的情感而生动;我们的成长,因着彼此的关照而( )......为此,我们感恩,感恩我们拥有的一切。
向父母感恩生命的赐予,向生活感恩色彩的绚丽,向自然感恩山水的( ),向经典感恩智慧的精彩,向世界感恩万物的( )......A.细腻茁壮博大灵动B.丰富温暖开阔茁壮C.温暖丰富美妙博大D.细腻茁壮灵动博大6.下列各句中没有语病的是( )。
勤学早七下语文期中测试卷

一、选择题(每题2分,共20分)1. 下列词语中,加点字的注音完全正确的一项是()A. 稀疏(shū)沉默(mò)拘泥(nì)B. 疲惫(bèi)拈轻怕重(niān)腼腆(tiǎn)C. 气瘁(cuì)稳如磐石(pán)憾事(hàn)D. 摧枯拉朽(xiǎo)青翠欲滴(cuì)沉鱼落雁(diàn)2. 下列句子中,没有语病的一项是()A. 为了保护环境,我们应该少用一次性筷子。
B. 随着科技的不断发展,人们的生活水平得到了极大的提高。
C. 面对困难,我们要有坚定的信念和顽强的毅力。
D. 他的学习成绩一直名列前茅,这是他勤奋努力的结果。
3. 下列各句中,没有错别字的一项是()A. 水天相接,碧波荡漾,令人心旷神怡。
B. 在这美好的时光里,我们要珍惜每一分每一秒。
C. 他的眼神中透露出一丝不安,似乎有什么事情要发生。
D. 这本书的内容丰富多彩,让我受益匪浅。
4. 下列各句中,加点的词语使用不正确的一项是()A. 这个问题很复杂,非得动一番脑筋才能解决。
B. 他虽然年纪轻轻,但已经取得了不少成就。
C. 面对挫折,我们要保持乐观的心态,勇敢面对。
D. 他的成绩一直名列前茅,可见他的勤奋程度。
5. 下列各句中,句式使用不恰当的一项是()A. 他不但学习成绩好,而且积极参加各种社会活动。
B. 为了实现自己的梦想,他付出了很多努力。
C. 在这美好的时光里,我们要珍惜每一分每一秒。
D. 他的声音洪亮,仿佛在告诉我们一个道理。
二、填空题(每题2分,共20分)6. 下列词语中,加点字的解释不正确的一项是()A. 沉默(沉默寡言,不善于说话)B. 拘泥(固执己见,不知变通)C. 憾事(令人遗憾的事情)D. 沉鱼落雁(形容女子美丽动人)7. 下列各句中,加点字的用法不正确的一项是()A. 他不仅学习好,而且品德高尚。
B. 我们要珍惜今天的时光,为美好的未来努力奋斗。
七年级下册期中复习专题资料

七年级下册期中复习专题一.选择题(共1小题)1.(2015春•蠡县期中)在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定;正方形内部不包括边界上的点,如果如图所示的中心在原点,一边平行于x轴的正方形,边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整数点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内的整点个数为()A.42 B.40 C.36 D.49二.填空题(共4小题)2.(2015•曲靖二模)如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2015的坐标为.3.(2008•黄陂区校级自主招生)将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数.如数12对应的坐标为(2,1),则数2008对应的坐标是.4.(2013•湖州一模)如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,3),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为3n(n为正整数)时,m=(用含n的代数式表示).5.(2015•甘孜州)如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为.三.解答题(共13小题)6.(2015春•崆峒区期末)完成下面推理过程:如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:∵∠1=∠2(已知),且∠1=∠CGD(),∴∠2=∠CGD(等量代换).∴CE∥BF().∴∠=∠C().又∵∠B=∠C(已知),∴∠=∠B(等量代换).∴AB∥CD().7.(2014春•济南校级期末)在括号内填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(),∴AB∥CD ()∴∠B=∠DCE()又∵∠B=∠D(),∴∠DCE=∠D ()∴AD∥BE()∴∠E=∠DFE()8.(2013春•冠县校级期末)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.∵∠1=∠2,∠2=∠3,∠1=∠4()∴∠3=∠4()∴∥,(),∴∠C=∠ABD()∵∠C=∠D()∴∠D=∠ABD()∴DF∥AC().9.如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q代表河流b上的桥梁.请你画图回答下列问题,并说明理由.(1)从公共汽车站P到桥梁Q怎么走路程最近?(2)从公共汽车站P到河流岸边b怎么走路程最近?(3)从桥梁Q到公路a怎么走路程最近?10.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A、B 的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.11.如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(﹣6,a),(1)求△ABC三个顶点A、B、C的坐标;(2)连接PA、PB,并用含字母a的式子表示△PAB的面积(a≠2);(3)在(2)问的条件下,是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.12.如图1,以长方形ABCD的中心O为原点,平行于BC的直线为x轴建立平面直角坐标系,若点D的坐标为(6,3).(1)直接写出A、B、C的坐标;(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的,求点M的坐标;(3)如图2,若点P从C点出发向CB方向匀速移动(不超过点B),点Q从B点出发向BA方向匀速移动(不超过点A),且点Q的速度是P的一半,P、Q两点同时出发,已知当移动时间为t秒时,B点的横坐标为6﹣2t,此时①CP=,AQ=(用含t的式子表示).②在点P、Q移动过程中,四边形PBQD的面积是否发生变化?若不变,求其值;若变化,求其变化范围.13.(2015春•蠡县期中)如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+=0.(1)求a,b的值;(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积恒成立?若存在,请直接写出符合条件的点M的坐标.15.(2015春•鞍山期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.16.(2015春•微山县期中)将一副三角板如图所示位置摆放.(1)直接写出∠AOC与∠BOD的大小关系,不需证明;(2)图1中的△AOB不动,将△COD绕点O旋转至CO∥AB(如图2),判断DO与AB的位置关系,并证明.(3)在(2)的条件下,△COD绕点O旋转的过程中,能否使CD⊥AB?若能,求出此时∠AOC的度数;若不能,请说明理由.18.(2015春•荣昌县校级期中)小明在学习了平面直角坐标系后,突发奇想,画出了这样的图形(如图),他把图形与x轴正半轴的交点依次记作A1(1,0),A2(5,0),…A n,图形与y轴正半轴的交点依次记作B1(0,2),B2(0,6),…B n,图形与x轴负半轴的交点依次记作C1(﹣3,0),C2(﹣7,0),…C n,图形与y轴负半轴的交点依次记作D1(0,﹣4),D2(0,﹣8),…D n,发现其中包含了一定的数学规律.请根据你发现的规律完成下列题目:(1)请分别写出下列点的坐标:A3,B3,C3,D3;(2)请分别写出下列点的坐标:A n,B n,C n,D n;(3)请求出四边形A5B5C5D5的面积.七年级下册期中复习专题一.选择题(共1小题)1.(2015春•蠡县期中)在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定;正方形内部不包括边界上的点,如果如图所示的中心在原点,一边平行于x轴的正方形,边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整数点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内的整点个数为()A.42 B.40 C.36 D.49【解答】解:设边长为8的正方形内部的整点的坐标为(x,y),x,y都为整数.则﹣4<x<4,﹣4<y<4,故x只可取﹣3,﹣2,﹣1,0,1,2,3共7个,y只可取﹣3,﹣2,﹣1,0,1,2,3共7个,它们共可组成点(x,y)的数目为7×7=49(个).故选:D.二.填空题(共4小题)2.(2015•曲靖二模)如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),…,那么点A2015的坐标为(1007,0).【解答】解:∵2015÷4=503 (3)∴A2015的坐标是(503×2+1,0),即(1007,0).故答案为:(1007,0).3.(2008•黄陂区校级自主招生)将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数.如数12对应的坐标为(2,1),则数2008对应的坐标是(5,﹣22).【专题】规律型.【解答】解:观察图的结构,发现所有奇数的平方数都在第四象限的角平分线上.452=2025,由2n+1=45得n=22,所以2025的坐标为(22,﹣22).图中纵坐标为﹣22的数共有45个,2008=2025﹣17,22﹣17=5,所以2008的坐标是(5,﹣22).故答案为(5,﹣22).4.(2013•湖州一模)如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,3),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为3n(n为正整数)时,m=3n﹣2(用含n的代数式表示).【专题】规律型.【解答】解:如图,n=1,即点B的横坐标为3时,整点个数为1,n=2,即点B的横坐标为6时,整点个数为4,n=3,即点B的横坐标为9时,整点个数为7,n=4,即点B的横坐标为12时,整点个数为10,…,所以,点B的坐标为3n时,整点个数为3n﹣2.故答案为:3n﹣2.5.(2015•甘孜州)如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为(5,﹣5).【专题】压轴题.【解答】解:∵=5,∴A20在第四象限,∵A4所在正方形的边长为2,A4的坐标为(1,﹣1),同理可得:A8的坐标为(2,﹣2),A12的坐标为(3,﹣3),∴A20的坐标为(5,﹣5),故答案为:(5,﹣5).三.解答题(共13小题)6.(2015春•崆峒区期末)完成下面推理过程:如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:∵∠1=∠2(已知),且∠1=∠CGD(对顶角相等),∴∠2=∠CGD(等量代换).∴CE∥BF(同位角相等,两直线平行).∴∠BFD=∠C(两直线平行,同位角相等).又∵∠B=∠C(已知),∴∠BFD=∠B(等量代换).∴AB∥CD(内错角相等,两直线平行).7.(2014春•济南校级期末)在括号内填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知),∴AB∥CD (同旁内角互补,两直线平行)∴∠B=∠DCE(两直线平行,同位角相等)又∵∠B=∠D(已知),∴∠DCE=∠D (等量代换)∴AD∥BE(内错角相等,两直线平行)∴∠E=∠DFE(两直线平行,内错角相等)8.(2013春•冠县校级期末)如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.∵∠1=∠2,∠2=∠3,∠1=∠4(对顶角的性质)∴∠3=∠4(等量代换)∴BD∥CE,(内错角相等两直线平行),∴∠C=∠ABD(两直线平行,同位角相等)∵∠C=∠D(已知)∴∠D=∠ABD(等量代换)∴DF∥AC(内错角相等,两直线平行).9.(2015春•微山县期中)如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q代表河流b上的桥梁.请你画图回答下列问题,并说明理由.(1)从公共汽车站P到桥梁Q怎么走路程最近?(2)从公共汽车站P到河流岸边b怎么走路程最近?(3)从桥梁Q到公路a怎么走路程最近?【解答】解:画图如图所示:(1)连接PQ,从公共汽车站到桥梁沿线段PQ走最近;理由:两点之间线段最短;(2)作PF⊥b于点F,从公共汽车站到河流沿垂线段PF走最近.理由:垂线段最短;(3)作QE⊥a于点E,从桥梁到公路沿垂线段QE走最近.理由:垂线段最短.10.(2015春•吴忠校级期中)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A、B 的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.【解答】解:(1)C(0,2),D(4,2),四边形ABCD的面积=(3+1)×2=8;(2)假设y轴上存在P(0,b)点,则S△PAB=S四边形ABDC∴|AB|•|b|=8,∴b=±4,∴P(0,4)或P(0,﹣4).11.(2015春•哈尔滨校级期中)如图,已知在平面直角坐标系中,点A在y轴上,点B、C在x轴上,S△ABO=8,OA=OB,BC=10,点P的坐标是(﹣6,a),(1)求△ABC三个顶点A、B、C的坐标;(2)连接PA、PB,并用含字母a的式子表示△PAB的面积(a≠2);(3)在(2)问的条件下,是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.【解答】解:(1)∵S△ABO=OA•OB,∵OA=OB,∴OA2=8,解得OA=4,∴OB=OA=4,∴OC=BC﹣OB=10﹣4=6,∴A(0,﹣4),B(﹣4,0),C(6,0);(2)当点P在第二象限,即a>0,作PH⊥y轴于H,如图,S△PAB=S△AOB+S梯形BOHP﹣S△PBH=8+(4+6)•a﹣•6•(a+4)=2a﹣4;当点P在第三象限,即a<0,作PH⊥x轴于H,如图,S△PAB=S梯形OHPA﹣S△PBH﹣S△OAB=(﹣a+4)•6﹣•(6﹣4)•(﹣a)﹣8=4﹣2a;(3)S△ABC=×10×4=20,当2a﹣4=20,解得a=12.此时P点坐标为(﹣6,12);当4﹣2a=24,解得a=﹣10.此时P点坐标为(﹣6,﹣10).综上所述,点P的坐标为(﹣6,12)或(﹣6,﹣10).12.(2015春•广州校级期中)如图1,以长方形ABCD的中心O为原点,平行于BC的直线为x轴建立平面直角坐标系,若点D的坐标为(6,3).(1)直接写出A、B、C的坐标;(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的,求点M的坐标;(3)如图2,若点P从C点出发向CB方向匀速移动(不超过点B),点Q从B点出发向BA方向匀速移动(不超过点A),且点Q的速度是P的一半,P、Q两点同时出发,已知当移动时间为t秒时,B点的横坐标为6﹣2t,此时①CP=2t,AQ=6﹣t(用含t的式子表示).②在点P、Q移动过程中,四边形PBQD的面积是否发生变化?若不变,求其值;若变化,求其变化范围.【解答】解:(1)A、B、C的坐标分别为(﹣6,3)、(﹣6,﹣3)、(6,﹣3);(2)由题意得E点的坐标为(0,3),设M点坐标为(0,a),则×|a﹣3|×6=×12×6解得:a=﹣1或a=7,M点坐标为(0,﹣1)或(0,7).(3)∵B点的横坐标为6﹣2t=﹣6,∴t=6,则点P的运动速度为12÷6=2,点Q的运动速度为2÷2=1,①CP=12﹣2t,AQ=6﹣t;②不变.理由:∵四边形PBQD的面积=12×6﹣(6﹣t)×12﹣×2t×6=36,∴四边形PBQD的面积不发生变化.13.(2015春•蠡县期中)如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+=0.(1)求a,b的值;(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积恒成立?若存在,请直接写出符合条件的点M的坐标.【解答】解:(1)由题意得,a+2=0,b﹣3=0,解得:a=﹣2,b=3;(2)①∵a=﹣2,b=3,C(﹣1,2),∴AB=3﹣(﹣2)=5,点C到AB的距离为2,∴OM•2=××5×2,解得:OM=2.5,∵点M在x轴正半轴上,∴M的坐标为(2.5,0);②存在.点M在x轴负半轴上时,点M(﹣2.5,0),点M在y轴上时,OM•1=××5×2,解得OM=5.所以点M的坐标为(0,5)或(0,﹣5).综上所述,存在点M的坐标为(0,5)或(﹣2.5,0)或(0,﹣5).15.(2015春•鞍山期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.【解答】解:(1)依题意,得C(0,2),D(4,2),∴S四边形ABDC=AB×OC=4×2=8;(2)在y轴上是否存在一点P,使S△PAB=S四边形ABDC.理由如下:设点P到AB的距离为h,S△PAB=×AB×h=2h,由S△PAB=S四边形ABDC,得2h=8,解得h=4,∴P(0,4)或(0,﹣4).16.(2015春•微山县期中)将一副三角板如图所示位置摆放.(1)直接写出∠AOC与∠BOD的大小关系,不需证明;(2)图1中的三角板AOB不动,将三角板COD绕点O旋转至CO∥AB(如图2),判断DO与AB的位置关系,并证明.(3)在(2)的条件下,三角板COD绕点O旋转的过程中,能否使CD⊥AB?若能,求出此时∠AOC的度数;若不能,请说明理由.理由是:∵∠DOC=∠AOB=90°,∴∠DOC﹣∠AOD=∠AOB﹣∠AOD,∴∠AOC=∠BOD;(2)如图2,DO⊥AB,证明:∵CO∥AB,∠COD=90°,∴∠NMD=∠COD=90°,∴DO⊥AB;(3)如图3,解:能使CD⊥AB,理由是:∵CD⊥AB,∴∠ANQ=90°,∵∠A=30°,∴∠AQN=180°﹣90°﹣30°=60°,∴∠CQO=∠AQN=60°,∵∠C=45°,∴∠AOC=180°﹣∠CQO﹣∠C=180°﹣60°﹣45°=75°.18.(2015春•荣昌县校级期中)小明在学习了平面直角坐标系后,突发奇想,画出了这样的图形(如图),他把图形与x轴正半轴的交点依次记作A1(1,0),A2(5,0),…A n,图形与y轴正半轴的交点依次记作B1(0,2),B2(0,6),…B n,图形与x轴负半轴的交点依次记作C1(﹣3,0),C2(﹣7,0),…C n,图形与y轴负半轴的交点依次记作D1(0,﹣4),D2(0,﹣8),…D n,发现其中包含了一定的数学规律.请根据你发现的规律完成下列题目:(1)请分别写出下列点的坐标:A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12);(2)请分别写出下列点的坐标:A n(4n﹣3,0),B n(0,4n﹣2),C n(﹣4n+1,0),D n(0,﹣4n);(3)请求出四边形A5B5C5D5的面积.【解答】解:(1)A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).(2)A n(4n﹣3,0),B n(0,4n﹣2),C n(﹣4n+1,0),D n(0,﹣4n).(3)∵A5(17,0),B5(0,18),C5(﹣19,0),D5(0,﹣20).∴四边形A5B5C5D5的面积=+++=×17×18+×18×19+×19×20+×20×17=684.故答案为:A3(9,0),B3(0,10),C3(﹣11,0),D3(0,﹣12).A n(4n﹣3,0),B n(0,4n﹣2),C n(﹣4n+1,0),D n(0,﹣4n).。
2023年湖南省七年级数学下册精练精析:期中综合检测(2)

湖南省七年级下数学期中综合检测(120分钟120分)一、选择题(每小题3分,共30分)1.(·巴中中考)下列计算正确的是( )A.a2+a3=a2B.a3+a2=a3C.a3+a2=a5D.(a4)3=a122.下列各式中,是二元一次方程的是( )①x+=7;②a-3b;③4x=3y;④y=x2;⑤=1;⑥xy=x+y;⑦x2-y2;⑧4(x+y)=5(x-y)+1.A.①③B.②⑥C.④⑧D.③⑧3.下列多项式能进行因式分解的是( )A.x2-yB.x2+1C.x2+y+y2D.x2-4x+44.(·咸宁中考)下列运算正确的是( )A.a6÷a2=a3B.3a2b-a2b=2C.(-2a3)2=4a6D.(a+b)2=a2+b25.(·晋江中考)计算:2x3·x2等于( )A.2B.x5C.2x5D.2x66.解方程组以下解法中不正确的是( )A.由①、②消去z,再由①、③消去zB.由①、②消去z,再由②、③消去zC.由①、③消去y,再由①、②消去yD.由①、②消去z,再由①、③消去y7.计算(a+m)的结果中不含有关于字母a的一次项,那么m等于( )A.2B.-2C.D.-8.如果方程组的解也是方程3x+my-8=0的一个解,则m的值为( )A.1B.2C.3D.49.甲、乙两人练习跑步,如果乙先跑10m,甲跑5s就可追上乙;如果乙先跑2s,甲跑4s就可追上乙.设甲的速度为xm/s,乙的速度为ym/s,则可列方程组为( ) A. B.C. D.10.对于任何整数m,多项式(4m+5)2-9都能( )A.被8整除B.被m整除C.被(m-1)整除D.被(2m-1)整除二、填空题(每小题3分,共24分)11.方程3x+2y=15在自然数范围内的解共有对.12.(1)(·宜宾中考)因式分解:am2-4an2= .(2)(·北京中考)因式分解:ab2-4ab+4a= .(3)(·黔西南州中考)因式分解2x4-2= .13.在代数式x2+ax+b中,当x=2时,它的值为3;当x=-2时,它的值为19,则代数式a-b的值为.14.计算:4×1752-100×25= .15.把4x2+1加上一个单项式,使其成为一个完全平方式.请你写出所有符合条件的单项式.16.已知a+b=2,则a2-b2+4b的值为.17.(·孝感中考)因式分解:ax2+2ax-3a= .18.观察下列等式:12-3×1=1×(1-3);22-3×2=2×(2-3);32-3×3=3×(3-3);42-3×4=4×(4-3);…,则第n个等式可表示为.三、解答题(共66分)19.(6分)计算:(1)3x2y·(-2xy)3.(2)2a2(3a2-5b).(3)(5x+2y)(3x-2y).20.(8分)解下列方程组:(1)(·汕头中考)(2)21.(6分)给出三个多项式:x2+2x-1,x2+4x+1,x2-2x.请把任意的两个多项式进行加法运算,并把结果因式分解.22.(9分)我们知道(x+a)(x+b)=x2+(a+b)x+ab,把此等式倒过来,便得到x2+(a+b)x+ab=(x+a)(x+b).即对于二次三项式x2+px+q,若能找到两个常数a,b,使a+b=p,ab=q,则x2+px+q=x2+(a+b)x+ab=(x+a)(x+b).这样便把形如x2+px+q的二次三项式分解了,试用上述方法分解下列各式:(1)x2+5x-6.(2)a2b2-ab-12.(3)x4-7x2-18.23.(8分)观察下列式子:1×8+1=9=32;3×16+1=49=72;7×32+1=225=152;…你得出了什么结论?你能说明这个结论吗?24.(12分)在一次联欢会上,节目主持人让大家做一个猜数的游戏,游戏的规则是:主持人让观众每人在心里想好一个除0以外的数,然后按以下顺序计算:(1)把这个数加上2后平方.(2)然后再减去4.(3)再除以原来所想的那个数,得到一个商.最后把你所得到的商是多少告诉主持人,主持人便立即知道你原来所想的数是多少,你能解释其中的奥妙吗?25.(8分)(·长沙中考)为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线、2号线每千米的平均造价分别是多少亿元?(2)除1、2号线外,长沙市政府规划到2022年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?26.(9分)阅读材料并回答问题:我们知道,完全平方式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)或图(2)等图形的面积表示.(1)请写出图(3)所表示的代数恒等式: .(2)试画一个几何图形,使它的面积表示为(a+b)(a+3b)=a2+4ab+3b2.(3)请仿照上述方法另写一个含有a,b的代数恒等式,并画出与它对应的几何图形.答案解析1.【解析】选D.(a4)3=a4×3=a12.2.【解析】选D.含有两个未知数,未知数的次数是1,方程两边都是关于未知数的整式的方程叫二元一次方程,故只有③和⑧为二元一次方程.3.【解析】选D.选项A,B,C中的多项式均没有公因式,且不能利用公式法分解,而x2-4x+4=x2-2·x·2+22=(x-2)2.故选项D中的多项式可以进行因式分解.4.【解析】选C.因为a6÷a2=a4故A错;3a2b-a2b=2a2b,故B错;(a+b)2=a2+2ab+b2,故D错,所以选C.5.【解析】选C.2x3·x2=2x3+2=2x5.6.【解析】选D.解三元一次方程组时应通过两次消元,消去同一个未知数,得到二元一次方程组,而选项D的解法没有达到消元的目的.7.【解析】选D.(a+m)=a2+a+ma+m=a2+a+m.因为原式的结果中不含有关于字母a的一次项,所以+m=0,得m=-.8.【解析】选 B.解方程组得把代入3x+my-8=0,得6+m-8=0,所以m=2.9.【解析】选C.本题的两个相等关系:甲跑5s的路程=乙跑5s的路程+10甲跑4s的路程=乙跑6s的路程.故选C.10.【解析】选A.(4m+5)2-9=(4m+5)2-32=(4m+8)·(4m+2)=8(m+2)(2m+1),因为m 是整数,而(m+2)和(2m+1)都是随着m的变化而变化的数,所以该多项式肯定能被8整除.11.【解析】由3x+2y=15得3x=15-2y,所以x=5-y.所以当y=0时,x=5,当y=3时,x=3,当y=6时,x=1,故3x+2y=15在自然数范围内的解有或或共3对.答案:312.【解析】(1)am2-4an2=a(m2-4n2)=a(m+2n)(m-2n).(2)原式=a(b2-4b+4)=a(b-2)2.(3)原式=2(x4-1)=2(x2+1)(x2-1)=2(x2+1)(x+1)(x-1).答案:(1)a(m+2n)(m-2n)(2)a(b-2)2(3)2(x2+1)(x+1)(x-1)13.【解析】由题意知解得所以a-b=-4-7=-11.答案:-1114.【解析】4×1752-100×25=4×1752-4×252=4×(1752-252)=4×(175+25)(175-25)=4×200×150=120XX0.答案:120XX015.【解析】因为4x2+1±4x=(2x±1)2;4x2+1+4x4=(2x2+1)2;4x2+1-1=(±2x)2;4x2+1-4x2=(±1)2.所以加上的单项式可以是±4x,4x4,-4x2,-1.答案:±4x,4x4,-4x2,-116.【解析】方法一:a2-b2+4b=a2-(b2-4b+4)+4=a2-(b-2)2+4=(a-b+2)(a+b-2)+4, 又a+b=2,所以原式=(a-b+2)(2-2)+4=4.方法二:a2-b2+4b=(a+b)(a-b)+4b=2(a-b)+4b=2a-2b+4b=2a+2b=2(a+b)=2×2=4. 答案:417.【解析】ax2+2ax-3a=a(x2+2x-3)=a(x+3)(x-1).答案:a(x+3)(x-1)18.【解析】因为12-3×1=1×(1-3);22-3×2=2×(2-3);32-3×3=3×(3-3);42-3×4=4×(4-3);…所以第n个等式可表示为n2-3n=n(n-3).答案:n2-3n=n(n-3)19.【解析】(1)原式=3x2y·(-8x3y3)=-24x5y4.(2)原式=2a2·3a2-2a2·5b=6a4-10a2b.(3)原式=15x2-10xy+6xy-4y2=15x2-4xy-4y2.20.【解析】(1)方法一:将x=y+1代入到2x+y=8中,得2(y+1)+y=8,解得y=2, 所以x=3,因此原方程组的解为方法二:对①进行移项,得x-y=1③,②+③得3x=9,解得x=3,将x=3,代入①中,得y=2,所以原方程组的解为(2)原方程组化为①×3+②×2得17m=306,得m=18.把m=18代入①得54+2n=78,得n=12.所以原方程组的解为21.【解析】①+=x2+6x=x(x+6).②+=x2-1=(x+1)(x-1).③+=x2+2x+1=(x+1)2.22.【解析】(1)x2+5x-6=x2+(6-1)x+(+6)×(-1)=(x+6)(x-1).(2)a2b2-ab-12=(ab)2-ab-12=(ab-4)(ab+3).(3)x4-7x2-18=(x2)2-7x2-18=(x2+2)(x2-9)=(x2+2)(x+3)(x-3).23.【解析】结论:(2n-1)·2n+2+1=(2n+1-1)2.说明:(2n-1)·2n+2+1=22n+2-2n+2+1=(2n+1)2-2×2n+1+1=(2n+1-1)2. 24.【解析】设这个数为x,据题意得,[(x+2)2-4]÷x=(x2+4x+4-4)÷x=x+4.如果把这个商告诉主持人,主持人只需减去4就知道这个数是多少.25.【解析】(1)设1号线每千米平均造价为x亿元,2号线每千米平均造价y亿元.根据题意得:解得答:1号线、2号线每千米的平均造价分别为6亿元,5.5亿元.(2)91.8×1.2×6=660.96(亿元).26.【解析】(1)(2a+b)(a+2b)=2a2+5ab+2b2.(2)(答案不唯一)如图:(3)恒等式是(a+2b)(a+b)=a2+3ab+2b2(答案不唯一),如图所示.。
语文勤学早直播课堂七年级下册答案2022

语文勤学早直播课堂七年级下册答案20221、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、点缀(zhuì)聆听(línɡ)B、伫立(zhù)蹒跚(pán)C、徘徊(huái)褶皱(zhě)D、婀娜(nà)颔首(hán)(正确答案)2、1演讲又称演说或讲演。
它是指演讲者面对听众,就某一个问题系统地阐述自己的观点和主张的社会活动。
[判断题] *对(正确答案)错3、1学习老舍写的《我的母亲》一文,我们会由衷敬佩母亲坚忍、善良、宽容、勤俭和好客的品性,也会为儿子子欲养而亲不待的痛悔之情感动不已。
[判断题] *对(正确答案)错4、下列各句中加点词的解释,有误的一项是()[单选题] *A.便可白公姥,及时相遣归。
白:告诉,禀告。
B.令尹子兰闻之,大怒,卒使上官大夫短屈原于顷襄王。
短:进谗言,说坏话。
C.上官大夫与之同列,争宠而心害其能。
害:妨碍,不利。
(正确答案)D.臣具以表闻,辞不就职。
闻:使知道,报告给……知道。
5、1著名元杂剧《西厢记》是白朴的代表作。
[判断题] *对(正确答案)错6、1“说”是古代的一种议论文体。
[判断题] *对错(正确答案)7、对《红楼梦》中的情节概述不准确的一项是( ) [单选题] *A.史湘云醉眠芍药裀B.王熙凤大闹宁国府C.薛宝钗重建桃花社(正确答案)D.贾探春兴利除宿弊8、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、收敛(liǎn)贪婪(lán)谆谆教诲(zhūn)B、荫庇(pì)云霄(xiāo)自怨自艾(ài)(正确答案)C、涎水(xián)富饶(ráo)惟妙惟肖(xiào)D、汲取(jí)谄媚(chǎn)一哄而散(hòng)9、1豪放派和婉约派是宋代词坛上的两大流派。
豪放派代表词人有李清照、柳永等,婉约派的代表词人有苏轼、辛弃疾等。
2022七年级下册语文勤学早答案

2022七年级下册语文勤学早答案1、下列各句中加点词的解释,有误的一项是()[单选题] *A.召有司案图,指从此以往十五都予赵。
案:通“按”,用手压住。
(正确答案)B.秦时与臣游,项伯杀人,臣活之。
游:交往。
C.他日趋庭,叨陪鲤对。
趋:小步快走。
D.触柱,折辕,劾大不敬。
劾:弹劾,判罪。
2、下面选项中加着重号字的注音正确的一项是()[单选题] *A、颇多pō外壳ké淤泥yū睥睨pì(正确答案)B、旖旎qí嫌弃xián 招惹rě赐名cìC、洋溢yì萌芽méng 赋予fǔ耀眼yàoD、抗御yù观摩mó堕落duǒ吸吮yǔn3、1《我的母亲》中“母亲笑了。
及至听说我还须回校,她愣住了。
半天,她才叹出一口气来。
”这句话运用了动作、神态描写,生动形象地写出了母亲对儿子回家过年的喜悦,得知儿子即刻就要返校的惊讶及无奈。
[判断题] *对(正确答案)错4、“脍炙人口”中“炙”的读音是“jiǔ”。
[判断题] *对错(正确答案)5、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、埋怨(mán)目睹(dǔ)对峙(zhì)B、弊病(bì)栖息(qī)烘托(hōng)C、绷带(bēng)骤然(zhòu)哽咽(yè)D、吹嘘(xū)浮躁(cào)停滞(dài)(正确答案)6、1《劝学》是《荀子》开篇之作。
在《劝学》里,荀子主要论述了后天的学习对人的品性具有决定的意义。
[判断题] *对(正确答案)错7、1著名元杂剧《西厢记》是白朴的代表作。
[判断题] *对(正确答案)错8、1议论文中论据与论点的关系是证明与被证明的关系。
[判断题] *对(正确答案)9、1公司号召大家为贫困山区的孩子捐款,作为公司秘书的你说:“在座的不是董事长,就是总经理,现在请大家出钱出物,为国家尽匹夫之责。
语文勤学早七年级下册答案2022

语文勤学早七年级下册答案20221、1公司号召大家为贫困山区的孩子捐款,作为公司秘书的你说:“在座的不是董事长,就是总经理,现在请大家出钱出物,为国家尽匹夫之责。
”你的表述是得体的。
[判断题] *对错(正确答案)2、1“人生是多么奇怪,多么变幻无常呵,极细小的一件事可以败坏你,也可以成全你!”这句话从一个侧面表明了在当时资本主义社会金钱万能、尔虞我诈的竞争中,小资产阶级生活的艰难,命运的无奈。
[判断题] *对(正确答案)错3、下列语句不是出自《红楼梦》的一项是( ) [单选题] *A.字字看来皆是血,十年辛苦不寻常。
B.女儿是水作的骨肉,男人是泥作的骨肉,我见了女儿,我便清爽:见了男子,便觉浊臭逼人。
C.话说天下大势,分久必合,合久必分。
(正确答案)D.世人都晓神仙好,惟有功名忘不了!4、修辞手法选择:有的石头错落成桥。
[单选题] *夸张拟人未用修辞比喻(正确答案)5、14.下面各组词语中加点字的注音,完全正确的一项是()[单选题] *A.渲染(xuàn)抽噎(yè)逞能(chěnɡ)自惭形秽(huì)B.迸溅(bènɡ)荣膺(yīnɡ)褶皱(zhě)气冲斗牛(dǒu)(正确答案)C.殷红(yīn)阔绰(chuò)惩戒(chéng)戛然而止(jiá)D.缄默(jiān)追溯(sù)栈桥(zhàn)鲜为人知(xiān)6、1人们常用唐诗、宋词、元曲、明清小说概括唐、宋、元、明、清这几个时期突出的文学形式。
[判断题] *对(正确答案)错7、补全句子:荡胸()层云[单选题] *升生(正确答案)盛胜8、下列选项中加着重号字注音正确的一项是()[单选题] *A、冠冕miǎn脑髓suǐ吝啬lìB、自诩xǔ蹩进bié鱼鳍qí(正确答案)C、国粹cù譬如pì磕头kēD、孱头càn 摩登mó给予gěi9、下列句子中加括号成语使用不正确的一项是()[单选题] *A.近日,国务院大督查第二批核查问责不作为情况又公之于众,不断加大的问责力度让为官不为者(如坐针毡),推动着工作的真落实,让群众真正受益。
数学勤学早试卷七年级下册

一、选择题(每题3分,共30分)1. 已知一个等差数列的前三项分别是2,5,8,则这个数列的公差是()A. 1B. 2C. 3D. 42. 在直角坐标系中,点A(-2,3)关于原点的对称点是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,-3)3. 若a^2 + b^2 = 1,则(a + b)^2的最大值为()A. 1B. 2C. 3D. 44. 已知一个三角形的三边长分别为3,4,5,则这个三角形是()A. 等腰三角形B. 直角三角形C. 等边三角形D. 梯形5. 若x + y = 5,x^2 + y^2 = 23,则xy的值为()A. 6B. 7C. 8D. 96. 在平面直角坐标系中,点P(2,3)关于x轴的对称点是()A.(2,-3)B.(-2,3)C.(-2,-3)D.(2,-3)7. 已知一个等比数列的前三项分别是2,6,18,则这个数列的公比是()A. 2B. 3C. 6D. 98. 在直角坐标系中,点A(1,2)关于y轴的对称点是()A.(1,-2)B.(-1,2)C.(-1,-2)D.(1,-2)9. 若a^2 + b^2 = 2,则(a - b)^2的最小值为()A. 0B. 1C. 2D. 310. 已知一个三角形的三边长分别为5,6,7,则这个三角形是()A. 等腰三角形B. 直角三角形C. 等边三角形D. 梯形二、填空题(每题5分,共25分)11. 等差数列{an}的前n项和为Sn,若S10 = 55,公差d = 2,则第10项an = _______。
12. 已知点A(2,3)和B(-3,4),则线段AB的中点坐标为 _______。
13. 若x^2 + 2x + 1 = 0,则x的值为 _______。
14. 在直角坐标系中,点P(-2,1)到原点的距离为 _______。
15. 已知一个等比数列的前三项分别是3,6,12,则这个数列的公比是 _______。
勤学早数学试卷七年级下

一、选择题(每题4分,共40分)1. 下列数中,是偶数的是()A. 2.5B. 0.3C. 4D. 3.62. 下列各数中,绝对值最小的是()A. -2B. -3C. 0D. 13. 如果 |a| = 5,那么 a 的值为()A. ±5B. 5C. -5D. 04. 在数轴上,表示 -3 的点在表示 3 的点的()A. 左边B. 右边C. 正中间D. 无法确定5. 下列各式中,正确的是()A. (-5)² = 5B. (-3)² = -9C. (4)² = 16D. (-2)² = -46. 下列图形中,是轴对称图形的是()A. 正方形B. 长方形C. 等腰三角形D. 平行四边形7. 已知 a = 3,b = -2,那么a² + b² 的值为()A. 7B. 5C. 13D. 18. 下列代数式中,正确的是()A. a + b = abB. a - b = abC. a × b = abD. a ÷ b = ab9. 若 a > b,那么下列不等式中正确的是()A. a + c > b + cB. a - c < b - cC. ac > bcD. ac < bc10. 下列图形中,面积最大的是()A. 正方形B. 长方形C. 等腰三角形D. 平行四边形二、填空题(每题4分,共40分)1. -8 的倒数是 _______。
2. 2 的平方根是 _______。
3. 若 |x| = 4,则 x 的值为 _______。
4. 下列数中,负数是 _______。
5. 若 a = 3,b = -2,那么 a - b 的值为 _______。
6. 若 a > b,那么 a + 1 > b + 1。
7. 下列图形中,是轴对称图形的是 _______。
8. 若 a = 3,b = -2,那么a² + b² 的值为 _______。
七下语文勤学早试卷电子版

七下语文勤学早试卷电子版1、袅娜中的娜读作()[单选题]nānǎnuó(正确答案)nuò2、1杜甫的诗歌反映现实的深广度是空前的,因此,其诗被后人称为“诗史”。
[判断题]对(正确答案)错3、13.下列各组词语中,加点字的读音全都正确的一组是()[单选题]A.滑稽(jī)宽宥(yǒu)菡萏(hán)殚精竭虑(dān)B.门槛(kǎn)缄默(jiān)胸脯(pú)间不容发(fà)(正确答案) C.坍塌(tān)锃亮(zèng)怯懦(ruò)信手拈来(diān)D.盘桓(yuán)褴褛(lǚ)拾级(hè)舳舻相接(zhóu)4、下列加括号词语使用正确的一项是()[单选题]A。
王立同学对这道数学题冥思苦想,终于(妙手偶得),有了答案。
B。
盛夏又至,万物蓬勃,(油然而生)的秧苗已然开花抽穗。
C。
喜剧演员贾玲言语幽默,动作滑稽,令人(忍俊不禁)。
(正确答案)D。
歌曲《我和我的祖国》陶醉了每一个炎黄子孙,真是(哗众取宠)啊!5、1侍坐是《论语》中比较罕见的完整段落,生动地再现了孔子和学生一起畅谈理想的情形。
子路的轻率急躁、冉求的谦虚、公西华的委婉曲致、曾皙的高雅宁静,给人留下了极其深刻的印象。
[判断题]对错(正确答案)6、下列对有关名著的说明,不正确的一项是()[单选题]A。
宝玉神志不清,贾府决定给宝玉娶亲冲喜。
袭人得知是宝钗要做宝二奶奶,怕宝玉承受不了,便把宝玉和黛玉交往的情形告诉了王夫人。
贾府感到为难,王熙凤献了个掉包儿计,在贾府公开宣扬宝玉要娶黛玉。
洞房之夜宝玉虽然不太高兴,但婚后身体还是逐渐恢复过来。
(正确答案) B。
《红楼梦》是一部百科全书式的长篇小说,它以一个贵族家庭为中心展开了一幅广阔的社会历史图景,社会的各阶级和阶层都得到了生动的描写。
C。
《红楼梦》中别号“蕉下客”的贾探春是个大气、具有男子性格的女性,她发起组织了大观园里的诗社活动,但是“才自精明志自高,生于末世运偏消”,她想用“兴利除弊”的微小来挽回这个封建大家庭的颓势,却注定无济于事。
勤学早七年级下数学

勤学早七年级下数学一.填空题:1、长方体货仓1个,长50米,宽30米,高5米,这个长方体货仓最多可容纳8立方米的正方体货箱()个。
2、有一根20厘米长的铁丝,用它围成一个对边都是4厘米的四边形,这个四边形可能是()。
3、一项工程,甲乙两队合作20天完成,已知甲乙两队的工作效率之比为4:5,甲队单独完成这项工程需要()天。
4、一座钟的时针长3厘米,它的尖端在一昼夜里走过的路程是()厘米。
5、在一块长10分米,宽6分米的长方形铁板上,最多能截取()个直径是2分米的圆形铁板。
6、3/4吨可以看作3吨的(/ ),也可以看作9吨的(/ )。
7、两个正方体的棱长比为1∶3,这两个正方体的表面积比是()∶(),体积比是()∶()。
8、一个三角形的底角都是45度,它的顶角是()度,这个三角形叫做()三角形。
9、棱长1厘米的小正方体至少需要()个拼成一个较大的正方体,需要()个可以拼成一个棱长1分米的大正方体。
如果把这些小正方体依次排成一排,可以排成()米。
10、一个数的20%是100,这个数的3/5是()。
11、六(1)班今天出勤48人,有2人因病请假,这天的出勤率是()%。
12、A除B的商是2,则A∶B=()∶()。
13、甲数的5/8等于乙数的5/12,甲数∶乙数=()∶()。
14、把4∶15的前项加上2.5,为了要使所得的比值不变,比的后项应加上()。
15、6/5吨:350千克,化简后的比是(),比值是()。
16、把甲班人数的1/8调入乙班后两班人数相等,原来甲、乙两班人数比是()。
17、甲走的路程是乙的4/5,乙用的时间是甲的4/5,甲、乙速度比是()。
18、一个数由500个万,8个千,40个十组成,这个数写作(),改写成万为单位的数写作()万,省略万后面的尾数写作()万。
19、50以内只含有质因数2的数有()。
20、一根绳子长4米,把它平均分成5段,每段是这根绳子的(),长()米,等于1米的()。
21、3/8的单位是(),要添上()个这样的单位是87.5%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学第二学期期中迎考小专题---综合题
1.如图,直线GC∥HD,EF交CG、HD于A、B,三条直线把EF右侧的平面分成①、②、③三个
30角区域,(规定:直线上各点不属于任何区域).将一个透明的直角三角尺放置在该图中,使得0 30)的两边分别经过点A、B,当点P落在某个区域时,连接P A、PB,得到∠PBD、∠(即∠P=0
P AC两个角.
(1) 如图(1),当点P落在第②区域时,求∠P AC+∠PBD的度数;
(2) 如图(2),当点P落在第③区域时,写出∠P A C ∠PBD=_______度(不证明);
(3) 如图(3),当点P落在第①区域时,写出∠P AC、∠PBD之间的等量关系并写出解答过程.
2.如图,一只甲虫在55⨯的方格(每小格边长为1)上沿着网格线运动.它从A 处出发去看望
B 、
C 、
D 处的其它甲虫(A ,B ,C ,D 都在格点上).规定:向上向右走为正,向下向左走为负,如果从A 到B 记为:A →B (+1,+4),从B 到A 记为:B →A (-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1) 填空:图中A →C ( ),B →C ( ),C →D ( );
(2) 若这只甲虫的行走路线为A →B →C →D ,则该甲虫走过的路程是_______________;
(3) 若这只甲虫从A 处去甲虫P 处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P 的位置.
(4) 若图中另有两个格点M 、N ,且M →A (a -3,4-b ),M →N (a -5,2-b ),则N →A 应记为什么?
3.已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.
(1) 如图1,AB∥EF,BC∥DE. ∠1与∠2的大小关系是:________________;
(2) 如图2,AB∥EF,BC∥DE. ∠1与∠2的数量关系是:_________________;
(3) 经过上述证明,我们可以得到一个真命题:如果__________________________________,
那么____________________________________.
30,则这两个角分别是多少度?
(4) 若两个角的两边互相平行,且一个角比另一个角的2倍少0
4.已知长方形OABC的长AB=5,宽BC=3,将它的顶点O落在平面直角坐标系的原点上,顶点A,C两点分别落在x,y轴上,点B在第一象限内,根据下列图示回答问题:
(1) 如图1,写出下列各点的坐标:A ( ),B ( ),C ( );
(2) 如图2,若过点C 的直线CD 交AB 于D ,且把长方形OABC 的周长分为3:1两部分,求点D 的坐标;
(3) 如图3,将(2)中的线段CD 向下平移2个单位,得到D C '',计算四边形C D OA ''的面积.
5.阅读并探究下列问题
(1) 如图1,将长方形纸片剪两刀,其中AB //CD ,则∠2与∠1、∠3有何关系?写出你的结论并证明;
(2) 如图2,将长方形纸片剪四刀,其中AB //CD ,则∠2+∠4与∠1+∠3+∠5有何关系?写出你的结论并证.
(3) 如图3,直线AB ∥CD ,∠EF A =030,∠FGH =090,∠HMN =030,∠CNP =0
50,求∠GHM 的度数.
6.在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,连接AC 、BD .
(1) 直接写出图中相等的线段、平行的线段;
(2) 已知A (-3,0)、B (-2,-2),点C 在y 轴的正半轴上,点D 在第一象限内,且5=∆ACD S ,求点C 、D 的坐标;
(3) 如图②,在平面直角坐标系中,已知一定点M (1,0),两个动点E (a ,12+a )、F (b ,32+-b ),请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM .若存在,求以点D 、M 、E 、F 为顶点的四边形的面积,若不存在,请说明理由.。
