(完整版)利用导数求曲线的切线和公切线
公切线知识点

公切线知识点一、公切线的定义公切线是指在几何学中,一条直线与两个曲线相切于同一点的情况。
这个点被称为切点,而直线则被称为公切线。
公切线有着重要的几何性质和应用,它在数学、物理和工程等领域中都有广泛的应用。
二、公切线的性质1.公切线与曲线的切点处的切线方向相同。
2.公切线与曲线的切点处的切线斜率相同。
3.公切线与曲线的其他交点处,切线方向与曲线的切线方向相同。
三、公切线的求解方法1. 利用导数求解对于给定的曲线,我们可以通过求解曲线的导数来找到公切线的方程。
具体步骤如下:1.求解曲线的导函数。
2.找到曲线上与切点处的横坐标相同的点,计算该点处的斜率。
3.利用切线斜率和切点坐标,得到切线方程。
2. 利用几何性质求解对于一些简单的曲线,我们可以通过利用几何性质来求解公切线。
例如,对于圆和直线的公切线,我们可以利用圆的半径和切点构成的直角三角形来求解公切线。
四、公切线的应用公切线在数学和实际应用中有着广泛的应用。
以下是一些常见的应用场景:1. 几何问题公切线在解决几何问题中起着关键作用。
例如,求解两个曲线的公切线可以帮助我们确定曲线之间的关系以及切点的位置。
2. 物理问题在物理学中,公切线可以用来描述曲线运动的轨迹。
例如,当一个物体沿着曲线运动时,其速度矢量与曲线在切点处的切线方向相同。
3. 工程应用在工程学中,公切线可以用来解决各种实际问题。
例如,在设计道路转弯处时,需要确定车辆行驶路线和转弯半径,公切线可以帮助我们确定最佳的转弯半径和车辆行驶路线。
五、总结公切线是几何学中一个重要的概念,它有着广泛的应用。
通过求解公切线,我们可以了解曲线的性质,解决各种几何、物理和工程问题。
掌握公切线的知识和求解方法对于理解和应用几何学和曲线运动学有着重要的意义。
希望本文能够帮助读者更好地理解和应用公切线的知识。
高考数学热点必会题型第4讲 导数求切线及公切线归类(原卷版)

高考数学热点必会题型第4讲 导数求切线及公切线归类 ——每天30分钟7天轻松掌握一、重点题型目录【题型】一、零点存在定理法判断函数零点所在区间 【题型】二、方程法判断函数零点个数 【题型】三、数形结合法判断函数零点个数 【题型】四、转化法判断函数零点个数 【题型】五、利用函数的零点或方程有根求参数 【题型】六、利用函数的交点或交点个数求参数 【题型】七、一元二次不等式恒成立问题 【题型】八、一元二次不等式能成立问题 二、题型讲解总结第一天学习及训练【题型】一、求曲线切线的斜率与倾斜角例1.(2023·全国·高三专题练习)函数()ln f x x x =+在1x =处的切线的斜率为( ) A .2B .-2C .0D .1例2.(2023·全国·高三专题练习)函数()f x 的导函数为()f x ',若已知()f x '的图像如图,则下列说法正确的是( )A .()f x 一定存在极大值点B .()f x 有两个极值点C .()f x 在(),a -∞单调递增D .()f x 在x =0处的切线与x 轴平行例3.(2023·全国·高三专题练习)若函数()()ln 2f x x x =+,则( ) A .()f x 的定义域是()0,∞+ B .()f x 有两个零点C .()f x 在点()()1,1f --处切线的斜率为1-D .()f x 在()0,∞+递增【题型】二、求在曲线上一点处的切线方程或斜率例4.(2023·上海·高三专题练习)2(5)3lim2,(3)32x f x f x →--==-,()f x 在(3,(3))f 处切线方程为( ) A .290x y ++= B .290x y +-= C .290x y -++=D .290x y -+-=例6.(2023·全国·高三专题练习)在平面直角坐标系xOy 中,抛物线2:2(0)C x py p =>的焦点为,F P 是C 上位于第一象限内的一点,若C 在点P 处的切线与x 轴交于M 点,与y 轴交于N 点,则与PF 相等的是( ) A .MNB .FNC .PMD .ON例7.(2023·江苏南京·高三阶段练习)已知双曲线C :224x y -=,曲线E :2y ax x b =++,记两条曲线过点()1,0的切线分别为1l ,2l ,且斜率均为正数,则( ) A .若=0a ,1b =,则C 与E 有一个交点B .若=1a ,=0b ,则C 与E 有一个交点C .若0a b ,则1l 与E 夹角的正切值为7-D .若==1a b ,则1l 与2l 例8.(2023·江苏·苏州中学高三阶段练习)已知函数()()e e x xf x x -=- ,则( )A .()f x 在()0,∞+单调递增B .()f x 有两个零点C .()=y f x 在点()()ln 2,ln 2f 处切线的 斜率为35ln 222+D .()f x 是奇函数第二天学习及训练【题型】三、利用导数求直线的倾斜角或倾斜角范围例9.(2023·全国·高三专题练习)已知()()2cos 0cos 2f x x f x π⎛⎫=-+ '⎪⎝⎭,则曲线()y f x =在点33,44f ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线的斜率为( )A B .C .D .-例10.(2023·全国·高三专题练习)已知点M 是曲线()22ln 5f x x x x =+-上一动点,当曲线在M 处的切线斜率取得最小值时,该切线的倾斜角为( ) A .4πB .3π C .23π D .34π 例11.(2022·江西省定南中学高二阶段练习(理))若()ln f x x x =,则()f x 图像上的点的切线的倾斜角α满足( ) A .一定为锐角B .一定为钝角C .可能为0︒D .可能为直角例12.(2022·全国·高三专题练习)已知函数()()ln 0sin 0x x f x x x ⎧-<=⎨≥⎩,,, ()020x kx x g x x >⎧=⎨≤⎩,,,若x 1、x 2、x 3,x 4是方程()()f x g x =仅有的4个解,且x 1<x 2<x 3<x 4,则( ) A .0<x 1x 2<1 B .x 1x 2>1 C .43πtan π2x ,⎛⎫∈ ⎪⎝⎭D .4πtan π2x ,⎛⎫∈ ⎪⎝⎭【题型】四、求在过一点的切线方程例13.(2023·全国·高三专题练习)过点()0,P b 作曲线e x y x =的切线,当240e b -<<时,切线的条数是( ) A .0B .1C .2D .3例14.(2023·全国·高三专题练习)若过点(,)a b 可以作曲线ln y x =的两条切线,则( ) A .ln a b <B .ln b a <C .ln b a <D .ln a b <例15.(2023·全国·高三专题练习)过曲线()3:C f x x ax b =-+外一点1,0A 作C 的切线恰有两条,则( ) A .a b =B .1a b -=C .1b a =+D .2a b =例16.(2023·江西·赣州市赣县第三中学高三期中(理))已知定义域为R 的奇函数()f x 满足:()()ln ,0121,1x x x f x f x x <≤⎧=⎨->⎩,若方程()12f x kx =-在[]1,2-上恰有三个根,则实数k 的取值范围是________.例17.(2023·全国·高三专题练习)若过点()1,P t 可作出曲线3y x =的三条切线,则实数t 的取值范围是___________第三天学习及训练【题型】五、利用导数值求出参数值例18.(2023·上海·高三专题练习)已知P 是曲线)2:ln C y x x a x =++上的一动点,曲线C 在P 点处的切线的倾斜角为θ,若32ππθ≤<,则实数a 的取值范围是( )A .)⎡⎣B .)⎡⎣C .(,-∞D .(-∞例19.(2023·全国·高三专题练习)若曲线()ln a xf x x=在点(1,f (1))处的切线方程为1y x =-,则a =( ) A .1B .e2C .2D .e例20.(2023·全国·高三专题练习)首钢滑雪大跳台是冬奥史上第一座与工业旧址结合再利用的竞赛场馆,它的设计创造性地融入了敦煌壁画中飞天的元素,建筑外形优美流畅,飘逸灵动,被形象地称为雪飞天.中国选手谷爱凌和苏翊鸣分别在此摘得女子自由式滑雪大跳台和男子单板滑雪大跳台比赛的金牌.雪飞天的助滑道可以看成一个线段PQ 和一段圆弧QM 组成,如图所示.假设圆弧QM 所在圆的方程为22:(25)(2)162C x y ++-=,若某运动员在起跳点M 以倾斜角为45且与圆C 相切的直线方向起跳,起跳后的飞行轨迹是一个对称轴在y 轴上的抛物线的一部分,如下图所示,则该抛物线的轨迹方程为( )A .232(1)y x =--B .21364y x =-- C .232(1)x y =--D .2364x y =-+例21.(2023·全国·高三专题练习)已知奇函数()()()()220f x x x ax b a =-+≠在点()(),a f a处的切线方程为()y f a =,则b =( )A .1-或1B .C .2-或2D .例22.(2023·上海·高三专题练习)设函数()ln f x x x =,()1x g x x =+. (1)若直线12y x b =+是曲线()f x 的一条切线,求b 的值; (2)证明:①当01x <<时,()()()112g x f x x x ⋅>-; ②0x ∀>,()()2e-<g x f x .(e 是自然对数的底数,e 2.718≈) 【题型】六、已知切线的斜率求参数方程例23.(2023·江苏南京·高三阶段练习)已知函数()2e ,<1=e ,1x x x f x x -≥⎧⎨⎩若方程()0f x x a --=有三个不同的解,则a 的取值范围是( ) A .()0,1B .()1,e 1-C .()1,eD .()e 1,e -例24.(2023·江西·赣州市赣县第三中学高三期中(理))已知0a >,0b >,直线2e y x b-=+与曲线ln y x a =-相切,则11a b+的最小值是( ) A .16B .12C .8D .4例25.(2023·全国·高三专题练习)若函数()ln bf x a x x=-在点(1,f (1))处的切线的斜率为1,则22a b +的最小值为( )A .12B C D .34例26.(2023·全国·高三专题练习)已知点P 是曲线23ln y x x =-上任意的一点,则点P 到直线2230x y ++=的距离的最小值是( )A .74B .78C .2D例27.(2023·全国·高三专题练习)设函数()e 2xf x x =-,直线=+y ax b 是曲线()=y f x 的切线,则2a b +的最大值是__________第四天学习及训练【题型】七、两条切线平行、垂直、重合公切线问题例28.(2023·全国·高三专题练习)对于三次函数()f x ,若曲线()y f x =在点(0,0)处的切线与曲线()y xf x =在点(1,2)处点的切线重合,则(2)f '=()A .34-B .14-C .4-D .14例29.(2023·全国·高三专题练习)若直线l 与曲线e x y =和ln y x =都相切,则直线l 的条数有( ) A .0B .1C .2D .无数条例30.(2023·全国·高三专题练习)若直线l 与函数()e x f x =,()ln g x x =的图象分别相切于点()()11,A x f x ,()()22,B x g x ,则1212x x x x -+=( ) A .2-B .1-C .1D .2例31.(2023·全国·高三专题练习)已知函数()ln f x a x =,()e x g x b =,若直线()0y kx k =>与函数()f x ,()g x 的图象都相切,则1a b+的最小值为( )A .2B .2eC .2eD 例32.(2023·全国·高三专题练习)若两曲线ln 1y x =-与2y ax =存在公切线,则正实数a 的取值范围是( ) A .(]0,2eB .31e ,2-⎡⎫+∞⎪⎢⎣⎭C .310,e 2-⎛⎤⎥⎝⎦D .[)2e,+∞例33.(2023·全国·高三专题练习)若函数()()22ln 12x axf x x -=++的图象上,不存在互相垂直的切线,则a 的值可以是( )A .-1B .3C .1D .2【题型】八、已知某点处的导数求参数或自变量例34.(2023·全国·高三专题练习)已知曲线()40y x x x=+<在点P 处的切线与直线310x y -+=垂直,则点P 的横坐标为( )A .1B .1-C .2D .2-例35.(2023·全国·高三专题练习)已知函数()sin f x m x b =+在6x π=处的切线方程为1y x =+,则实数b 的值为( )A .12B C .1 D 例36.(2023·全国·高三专题练习)若实数a ,b ,c ,d 满足ln ,1a b c d =+=,则()()22a cb d -+-的最小值为______.。
利用导数的几何意义求切线方程

利用导数的几何意义求切线方程江南中教研组曲线y f x =()在点x 0的导数)( 0x f '就是曲线在该点的切线的斜率,我们通常用导数的这个几何意义来研究一些与曲线的切线有关的问题。
对于利用导数的几何意义求切线方程我们要把握三个等量关系:1. 曲线y f x =()在点x 0的导数)( 0x f '就是曲线在该点的切线的斜率,有)(0x f k '=;2.切点在曲线y f x =()上,有)(00x f y = 3. 切点在切线上,有切线方程)(00x x k y y -=-最基础的题型就是已知切点求斜率、切线方程。
例一:曲线221y x =+在x=1的切线方程为 ; 解析:直接利用等量关系得到切点的坐标、切线的斜率;由题意可知,切点的坐标为(1,5)又∵x y 4=',∴切线的斜率为4,∴切线的方程为y -5 = 4(x -1),即y=4x +1。
利用导数的几何意义求切线方程的关键是要理解导数的几何意义,熟悉等量关系。
另有一种题型是先知道切线的斜率,求切点坐标、切线方程。
例二:曲线2y x =的一条切线的斜率是4-,求切线方程。
解析:先设出切点的坐标,再利用等量关系由待定系数法求出切点坐标,进而求切线方程;设切点的坐标为(200,x x )∵x y 2=',∴切线的斜率为02x ,∴02x = -4,∴20-=x ∴切点的坐标为(-2,4)∴切线的方程为y =-4x -4解这种题型的关键问题就是不能忽视切点在曲线上的这个关系。
再有一种题型求过曲线外一点的切线的方程。
例三:曲线2x y -=的切线过点(0,4)求切线的方程。
解析:同样设切点坐标,充分利用等量关系,由待定系数法求出切点坐标,进而求切线方程;设切点坐标为()00y x P ,,∵x y 2-='则在点P 处的切线方程为:()0002x x x y y --=-∵过点()4,0P ,且200x y -=()002002)(4x x x --=--∴ 20=∴x 或20-=x当20=x 时,切点为)4,2(-,此时切线方程为y=-4x +4,当20-=x 时,切点为()4,2--P ,此时切线方程为y=4x +4,∴过点(0,4)的切线方程为: y=-4x +4, y=4x +4。
导数中的公切线问题--2024年新高考数学一轮复习题型归纳与方法总结 解析版
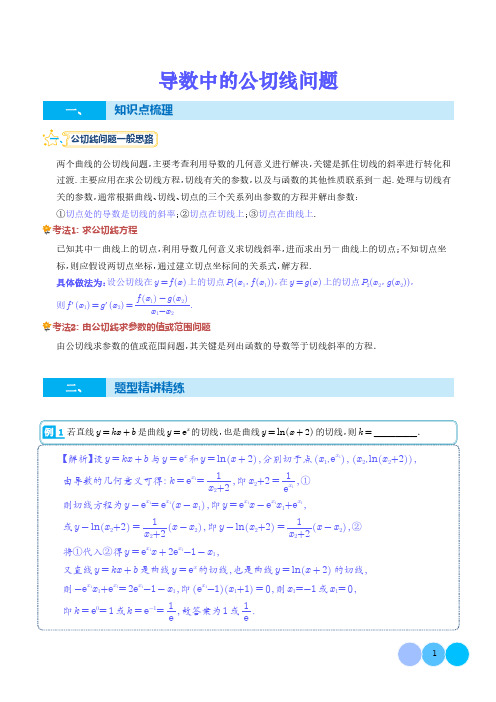
导数中的公切线问题知识点梳理一、公切线问题一般思路两个曲线的公切线问题,主要考查利用导数的几何意义进行解决,关键是抓住切线的斜率进行转化和过渡.主要应用在求公切线方程,切线有关的参数,以及与函数的其他性质联系到一起.处理与切线有关的参数,通常根据曲线、切线、切点的三个关系列出参数的方程并解出参数:①切点处的导数是切线的斜率;②切点在切线上;③切点在曲线上.考法1:求公切线方程已知其中一曲线上的切点,利用导数几何意义求切线斜率,进而求出另一曲线上的切点;不知切点坐标,则应假设两切点坐标,通过建立切点坐标间的关系式,解方程.具体做法为:设公切线在y =f (x )上的切点P 1(x 1,f (x 1)),在y =g (x )上的切点P 2(x 2,g (x 2)),则f ′(x 1)=g ′(x 2)=f x 1 -g x 2x 1-x 2.考法2:由公切线求参数的值或范围问题由公切线求参数的值或范围问题,其关键是列出函数的导数等于切线斜率的方程.题型精讲精练1若直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则k =______.【解析】设y =kx +b 与y =e x 和y =ln x +2 ,分别切于点x 1,e x 1,x 2,ln x 2+2 ,由导数的几何意义可得:k =e x 1=1x 2+2,即x 2+2=1ex 1,①则切线方程为y -e x 1=e x 1x -x 1 ,即y =e x 1x -e x 1x 1+e x 1,或y -ln x 2+2 =1x 2+2x -x 2 ,即y -ln x 2+2 =1x 2+2x -x 2 ,②将①代入②得y =e x 1x +2e x 1-1-x 1,又直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则-e x 1x 1+e x 1=2e x 1-1-x 1,即e x 1-1 x 1+1 =0,则x 1=-1或x 1=0,即k =e 0=1或k =e -1=1e ,故答案为1或1e.2已知直线y =kx +b 与函数y =e x 的图像相切于点P x 1,y 1 ,与函数y =ln x 的图像相切于点Q x 2,y 2 ,若x 2>1,且x 2∈n ,n +1 ,n ∈Z ,则n =______.【解析】依题意,可得e x 1=k =1x 2y 1=e x 1=kx 1+by 2=ln x 2=kx 2+b,整理得x 2ln x 2-ln x 2-x 2-1=0令f x =x ln x -ln x -x -1x >1 ,则f x =ln x -1x在1,+∞ 单调递增且f 1 ⋅f 2 <0,∴存在唯一实数m ∈1,2 ,使f m =0f x min =f m <f 1 <0,f 2 =ln2-3<0,f 3 =2ln3-4<0,f 4 =3ln4-5<0,f 5 =4ln5-6>0,∴x 2∈4,5 ,故n =4.【题型训练】1.求公切线方程一、单选题1(2023·全国·高三专题练习)曲线y =1x与曲线y =-x 2的公切线方程为()A.y =-4x +4B.y =4x -4C.y =-2x +4D.y =2x -4【答案】A【分析】画出图象,从而确定正确选项.【详解】画出y =1x,y =-x 2以及四个选项中直线的图象如下图所示,由图可知A 选项符合.故选:A2(2023·全国·高三专题练习)对于三次函数f (x ),若曲线y =f (x )在点(0,0)处的切线与曲线y =xf (x )在点(1,2)处点的切线重合,则f ′(2)=()A.-34B.-14C.-4D.14【答案】B【分析】由f(0)=0得d=0,然后求得f (x),由f (0)=2-01-0求得c=2,设g(x)=xf(x),由g(1)=2得f(1)=2及a+b=0,再由g (1)=2得3a+2b+2=0,解得a,b后可得f (2).【详解】设f(x)=ax3+bx2+cx+d(a≠0),∵f(0)=d=0,∴f(x)=ax3+bx2+cx,∴f′(x)=3ax2+2bx+c∴f′(0)=c=2-01-0=2,设g(x)=xf(x),则g(1)=f(1)=a+b+2=2,即a+b=0⋯⋯①又∵g′(x)=f(x)+xf′(x),∴g′(1)=f(1)+f′(1)=2,∴f′(1)=0,即3a+2b+2=0⋯⋯②由①②可得a=-2,b=2,c=2,∴f′(2)=-14.故选:B.3(2023·全国·高三专题练习)已知函数f x =x ln x,g x =ax2-x.若经过点A1,0存在一条直线l与曲线y=f x 和y=g x 都相切,则a=()A.-1B.1C.2D.3【答案】B【分析】先求得f(x)在A(1,0)处的切线方程,然后与g x =ax2-x联立,由Δ=0求解【详解】解析:∵f x =x ln x,∴f x =1+ln x,∴f 1 =1+ln1=1,∴k=1,∴曲线y=f x 在A1,0处的切线方程为y=x-1,由y=x-1y=ax2-x得ax2-2x+1=0,由Δ=4-4a=0,解得a=1.故选:B4(2023·全国·高三专题练习)已知函数f(x)=x2-4x+4,g(x)=x-1,则f(x)和g(x)的公切线的条数为A.三条B.二条C.一条D.0条【答案】A【分析】分别设出两条曲线的切点坐标,根据斜率相等得到方程8n3-8n2+1=0,构造函数f x =8x3-8x2+1,f x =8x3x-2,研究方程的根的个数,即可得到切线的条数.【详解】设公切线与f x 和g x 分别相切于点m,f m,n,f n,f x =2x-4,g x =-x -2,gn =fm =g n -f m n -m ,解得m =-n -22+2,代入化简得8n 3-8n 2+1=0,构造函数f x =8x 3-8x 2+1,f x =8x 3x -2 ,原函数在-∞,0 ↗,0,23 ↘,23,+∞ ↗,极大值f 0 >0,极小值,f 23<0故函数和x 轴有交3个点,方程8n 3-8n 2+1=0有三解,故切线有3条.故选A .【点睛】这个题目考查了利用导数求函数在某一点处的切线方程;步骤一般为:一,对函数求导,代入已知点得到在这一点处的斜率;二,求出这个点的横纵坐标;三,利用点斜式写出直线方程.考查了函数零点个数问题,即转化为函数图像和x 轴的交点问题.5(2023·全国·高三专题练习)已知函数f x =x 2-2m ,g x =3ln x -x ,若y =f x 与y =g x在公共点处的切线相同,则m =()A.-3B.1C.2D.5【答案】B【分析】设曲线y =f x 与y =g x 的公共点为x 0,y 0 ,根据题意可得出关于x 0、m 的方程组,进而可求得实数m 的值.【详解】设函数f x =x 2-2m ,g x =3ln x -x 的公共点设为x 0,y 0 ,则f x 0 =g x 0 f x 0 =g x 0 ,即x 20-2m =3ln x 0-x 02x 0=3x 0-1x 0>0,解得x 0=m =1,故选:B .【点睛】本题考查利用两函数的公切线求参数,要结合公共点以及导数值相等列方程组求解,考查计算能力,属于中等题.6(2023·全国·高三专题练习)函数f (x )=ln x 在点P (x 0,f (x 0))处的切线与函数g (x )=e x 的图象也相切,则满足条件的切点的个数有A.0个B.1个C.2个D.3个【答案】C【分析】先求直线l 为函数的图象上一点A (x 0,f (x 0))处的切线方程,再设直线l 与曲线y =g (x )相切于点(x 1,e x 1),进而可得ln x 0=x 0+1x 0-1,根据函数图象的交点即可得出结论.【详解】解:∵f (x )=ln x ,∴f ′(x )=1x ,∴x =x 0,f ′(x 0)=1x 0,∴切线l的方程为y-ln x0=1x0(x-x0),即y=1x0x+ln x0-1,①设直线l与曲线y=g(x)相切于点(x1,e x1),∵g (x)=e x,∴e x1=1x0,∴x1=-ln x0.∴直线l也为y-1x0=1x0(x+ln x0)即y=1x0x+ln x0x0+1x0,②由①②得ln x0=x0+1 x0-1,如图所示,在同一直角坐标系中画出y=ln x,y=x+1x-1的图象,即可得方程有两解,故切点有2个.故选:C二、填空题7(2023·吉林长春·长春吉大附中实验学校校考模拟预测)与曲线y=e x和y=-x24都相切的直线方程为.【答案】y=x+1【分析】分别设出直线与两曲线相切的切点,然后表示出直线的方程,再根据切线是同一条直线建立方程求解.【详解】设直线与曲线y=e x相切于点x1,e x1,因为y =e x,所以该直线的方程为y-e x1=e x1x-x 1,即y=e x1x+e x11-x1,设直线与曲线y=-x24相切于点x2,-x224,因为y =-x2,所以该直线的方程为y+x224=-x22x-x2,即y=-x22x+x224,所以e x1=-x22e x11-x1=x224,解得x1=0,x2=-2,所以该直线的方程为y=x+1,故答案为:y=x+1.8(2023·全国·高三专题练习)已知f x =e x-1(e为自然对数的底数),g x =ln x+1,请写出f x 与g x 的一条公切线的方程.【答案】y=ex-1或y=x【分析】假设切点分别为m,e m-1,n,ln n+1,根据导数几何意义可求得公切线方程,由此可构造方程求得m,代入公切线方程即可得到结果.【详解】设公切线与f x 相切于点m,e m-1,与g x 相切于点n,ln n+1,∵f x =e x,g x =1x,∴公切线斜率k=e m=1n;∴公切线方程为:y-e m+1=e m x-m或y-ln n-1=1nx-n,整理可得:y=e m x-m-1e m-1或y=1nx+ln n,∴e m=1nm-1e m+1=-ln n,即m=-ln nm-1e m +1=-ln n,∴m-1e m+1-m=m-1e m-1=0,解得:m=1或m=0,∴公切线方程为:y=ex-1或y=x.故答案为:y=ex-1或y=x.9(2023春·安徽·高三合肥市第六中学校联考开学考试)已知直线l与曲线y=e x、y=2+ln x都相切,则直线l的方程为.【答案】y=x+1或y=ex【分析】分别求出两曲线的切线方程是y=e x1x+e x11-x1和y=1x2x+1+ln x2,解方程e x1=1x2,e x11-x1=1+ln x2,即得解.【详解】解:由y=e x得y =e x,设切点为x1,e x1,所以切线的斜率为e x1,则直线l的方程为:y=e x1x+e x11-x1;由y =2+ln x 得y =1x ,设切点为x 2,2+ln x 2 ,所以切线的斜率为1x 2,则直线l 的方程为:y =1x 2x +1+ln x 2.所以e x 1=1x 2,e x 11-x 1 =1+ln x 2,消去x 1得1x 2-11+ln x 2 =0,故x 2=1或x 2=1e,所以直线l 的方程为:y =x +1或y =ex .故答案为:y =x +1或y =ex 10(2023春·浙江金华·高三浙江金华第一中学校考阶段练习)已知直线y =kx +b 是曲线y =ln 1+x 与y =2+ln x 的公切线,则k +b =.【答案】3-ln2【分析】分别设两条曲线上的切点,写出切线方程,建立方程组,解出切点,计算k +b .【详解】设曲线y =ln 1+x 上切点A x 1,ln 1+x 1 ,y =11+x,切线斜率k =11+x 1,切线方程y -ln 1+x 1 =11+x 1x -x 1 ,即y =11+x 1x -x 11+x 1+ln 1+x 1同理,设曲线y =2+ln x 上切点B x 2,2+ln x 2 ,y =1x,切线斜率k =1x 2,切线方程y -2+ln x 2 =1x 2x -x 2 ,即y =1x 2x +1+ln x 2,所以11+x 1=1x 2-x11+x 1+ln (1+x 1)=1+ln x 2,解得x 1=-12x 2=12,所以k =2,b =1-ln2,k +b =3-ln2.故答案为:3-ln2.2.公切线中的参数问题一、单选题1(2023·陕西渭南·统考一模)已知直线y =ax +b (a ∈R ,b >0)是曲线f x =e x 与曲线g x =ln x +2的公切线,则a +b 等于()A.e +2B.3C.e +1D.2【答案】D【分析】由f x 求得切线方程,结合该切线也是g x 的切线列方程,求得切点坐标以及斜率,进而求得直线y =ax +b ,从而求得正确答案.【详解】设t ,e t 是f x 图象上的一点,f x =e x ,所以f x 在点t ,e t 处的切线方程为y -e t =e t x -t ,y =e t x +1-t e t ①,令g x =1x=e t ,解得x =e -t ,g e -t=ln e -t+2=2-t ,所以2-t -e te -t-t=e t ,1-t =1-t e t ,所以t =0或t =1(此时①为y =ex ,b =0,不符合题意,舍去),所以t =0,此时①可化为y -1=1×x -0 ,y =x +1,所以a +b =1+1=2.故选:D2(2023·陕西榆林·校考模拟预测)若直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,与曲线y =x +32也相切,切点为N x 2,y 2 ,则2x 1-x 2的值为()A.-2B.-1C.0D.1【答案】B【分析】根据导数求出切线的斜率,得到切线方程,根据两切线方程即可得解.【详解】因为直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,可知直线l 的方程为y =e x 1x -x 1 +e x 1=e x 1x +1-x 1 e x 1,又直线l 与曲线y =x +3 2也相切,切点为N x 2,y 2 ,可知直线l 的方程为y =2x 2+3 x -x 2 +x 2+3 2=2x 2+3 x -x 22+9,所以e x 1=2x 2+3 1-x 1 e x 1=-x 22+9,两式相除,可得21-x 1 =3-x 2,所以2x 1-x 2=-1.故选:B3(2023春·河南·高三校联考阶段练习)已知曲线y =x 在点x 0,x 0 0<x 0<14处的切线也与曲线y =e x 相切,则x 0所在的区间是()A.0,14e 4B.14e 4,14e 2C.14e 2,14eD.14e ,14【答案】C【分析】设切线l与曲线y=e x的切点为m,e m,通过导数分别写出切线方程,由两条切线重合得出方程,再通过此方程有解得出结果.【详解】设该切线为l,对y=x求导得y =12x,所以l的方程为y-x0=12x0x-x0,即y=12x0x+x02.设l与曲线y=e x相切的切点为m,e m,则l的方程又可以写为y-e m=e m x-m,即y=e m x+1-me m.所以e m=12x0,x02=1-me m.消去m,可得x0=1+ln2x0,0<x0<1 4,令t=2x0∈0,1,则ln t-t24+1=0.设h t =ln t-t24+1,当0<t<1时,h t =1t-t2>0,所以h t 在0,1上单调递增,又h1e=-14e2<0,h1e=12-14e>0,所以t0=2x0∈1e,1e,所以x0∈14e2,14e.故选:C.4(2023·全国·高三专题练习)若函数f x =2a ln x+1与g x =x2+1的图像存在公共切线,则实数a的最大值为()A.eB.2eC.e22D.e2【答案】A【分析】分别设公切线与g x =x2+1和f(x)=2a ln x+1的切点x1,x21+1,x2,2a ln x2+1,根据导数的几何意义列式,再化简可得a=2x22-2x22ln x2,再求导分析h(x)=2x2-2x2⋅ln x(x >0)的最大值即可【详解】g x =2x,f x =2a x,设公切线与g x =x2+1的图像切于点x1,x21+1,与曲线f(x)=2a ln x+1切于点x2,2a ln x2+1,所以2x1=2ax2=2a ln x2+1-x21+1x2-x1=2a ln x2-x21x2-x1,故a=x1x2,所以2x1=2x1x2ln x2-x21x2-x1,所以x1=2x2-2x2⋅ln x2,因为a=x1x2,故a=2x22-2x22ln x2,设h(x)=2x2-2x2⋅ln x(x>0),则h (x)=2x(1-2ln x),令h (x)=0⇒x=e当h (x)>0时,x∈(0,e),当h (x)<0时,x∈(e,+∞),所以h x 在(0,e)上递增,在(e,+∞)上递减,所以h(x)max=h(e)=e,所以实数a的最大值为e,故选:A.5(2023·湖南郴州·统考模拟预测)定义:若直线l与函数y=f x ,y=g x 的图象都相切,则称直线l为函数y=f x 和y=g x 的公切线.若函数f x =a ln x a>0和g x =x2有且仅有一条公切线,则实数a的值为()A.eB.eC.2eD.2e【答案】C【分析】设直线与g x =x2的切点为x1,x21,然后根据导数的几何意义可推得切线方程为y=2x1x-x21,y=ax2x+a ln x2-1.两条切线重合,即可得出a=4x22-4x22ln x2有唯一实根.构造h x =4x2-4x2ln x x>0,根据导函数得出函数的性质,作出函数的图象,结合图象,即可得出答案.【详解】设直线与g x =x2的切点为x1,x21,因为g x =2x,根据导数的几何意义可知该直线的斜率为2x1,即该直线的方程为y-x21=2x1x-x1,即y=2x1x-x21.设直线与f x =a ln x的切点为(x2,a ln x2),因为f x =ax,根据导数的几何意义可知该直线的斜率为ax2,即该直线的方程为y-a ln x2=ax2x-x2,即y=ax2x+a ln x2-1.因为函数f x =a ln x a>0和g x =x2有且只有一条公切线,所以有2x1=ax2a ln x2-1=-x21 ,即a=4x22-4x22ln x2有唯一实根.令h x =4x2-4x2ln x x>0,则h x =8x-8x ln x-4x=4x1-2ln x.解h x =0,可得x= e.当4x1-2ln x>0时,0<x<e,所以h x 在0,e上单调递增;当4x1-2ln x<0时,x>e,所以h x 在e,+∞上单调递减.所以h x 在x=e处取得最大值h e=4e-4e×12=2e.当x→0时,h x →0,h e =4e2-4e2ln e=0,函数h x 图象如图所示,因为a>0,a=4x2-4x2ln x有唯一实根,所以只有a=2e.故选:C6(2023春·广东汕头·高三汕头市潮阳实验学校校考阶段练习)已知函数f x =2+ln x,g x = a x,若总存在两条不同的直线与函数y=f x ,y=g x 图象均相切,则实数a的取值范围为()A.0,1B.0,2C.1,2D.1,e【答案】B【分析】设函数y=f x ,y=g x 的切点坐标分别为x1,2+ln x1,x2,a x2,根据导数几何意义可得a2=4ln x1+4x1,x1>0,即该方程有两个不同的实根,则设h x =4ln x+4x,x>0,求导确定其单调性与取值情况,即可得实数a的取值范围.【详解】解:设函数f x =2+ln x上的切点坐标为x1,2+ln x1,且x1>0,函数g x =a x 上的切点坐标为x2,a x2,且x2≥0,又f x =1x,g x =a2x,则公切线的斜率k=1x1=a2x2,则a>0,所以x2=a24x21,则公切线方程为y-2+ln x1=1x1x-x1,即y=1x1x+ln x1+1,代入x 2,a x 2 得:a x 2=1x 1x 2+ln x 1+1,则a 22x 1=1x 1⋅a 24x 21+ln x 1+1,整理得a 2=4ln x 1+4x 1,若总存在两条不同的直线与函数y =f x ,y =g x 图象均相切,则方程a 2=4ln x 1+4x 1有两个不同的实根,设h x =4ln x +4x,x >0,则h x =4x⋅x -4ln x +4x2=-4ln xx,令h x =0得x =1,当x ∈0,1 时,h x >0,h x 单调递增,x ∈1,+∞ 时,h x <0,h x 单调递减,又h x =0可得x =1e,则x →0时,h x →-∞;x →+∞时,h x →0,则函数h x 的大致图象如下:所以a >00<a 2<4,解得0<a <2,故实数a 的取值范围为0,2 .故选:B .【点睛】本题考查了函数的公切线、函数方程与导数的综合应用,难度较大.解决本题的关键是,根据公切线的几何意义,设切点坐标分别为x 1,2+ln x 1 ,且x 1>0,x 2,a x 2 ,且x 2≥0,可得k =1x 1=a 2x 2,即有x 2=a 24x 21,得公切线方程为y =1x 1x +ln x 1+1,代入切点x 2,a x 2 将双变量方程a x 2=1x 1x 2+ln x 1+1转化为单变量方程a 22x 1=1x 1⋅a 24x 21+ln x 1+1,根据含参方程进行“参变分离”得a 2=4ln x 1+4x 1,转化为一曲一直问题,即可得实数a 的取值范围.7(2023·全国·高三专题练习)若曲线y =ln x +1与曲线y =x 2+x +3a 有公切线,则实数a 的取值范围()A.2ln2-36,3-ln22B.1-4ln212,3-ln22C.2ln2-36,+∞ D.1-4ln212,+∞【答案】D【分析】分别求出两曲线的切线方程,则两切线方程相同,据此求出a 关于切点x 的解析式,根据解析式的值域确定a 的范围.【详解】设x 1,y 1 是曲线y =ln x +1的切点,设x 2,y 2 是曲线y =x 2+x +3a 的切点,对于曲线y =ln x +1,其导数为y =1x ,对于曲线y =x 2+x +3a ,其导数为y =2x +1,所以切线方程分别为:y -ln x 1+1 =1x 1x -x 1 ,y -x 22+x 2+3a =2x 2+1 x -x 2 ,两切线重合,对照斜率和纵截距可得:1x 1=2x 2+1ln x 1=-x 22+3a,解得3a =ln x 1+x 22=ln 12x 2+1+x 22=-ln 2x 2+1+x 22x 2>-12 ,令h x =-ln 2x +1 +x 2x >-12,hx =-22x +1+2x =4x 2+2x -22x +1=2x +1 2x -1 2x +1=0,得:x =12,当x ∈-12,12时,h x <0,h x 是减函数,当x ∈12,+∞时,h x >0,h x 是增函数,∴h min x =h 12 =14-ln2且当x 趋于-12时,,h x 趋于+∞;当x 趋于+∞时,h x 趋于+∞;∴3a ≥14-ln2,∴a ≥1-4ln212;故选:D .8(2023·河北·统考模拟预测)若曲线f (x )=3x 2-2与曲线g (x )=-2-m ln x (m ≠0)存在公切线,则实数m 的最小值为()A.-6eB.-3eC.2eD.6e【答案】A【分析】求出函数的导函数,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,即可得到m =-6x 1x 2,则x 1=0或x 1=2x 2-x 2ln x 2,从而得到m =12x 22ln x 2-12x 22,在令h x =12x 2ln x -12x 2,x >0 ,利用导数求出函数的最小值,即可得解;【详解】因为f (x )=3x 2-2,g (x )=-2-m ln x (m ≠0),所以f (x )=6x ,g (x )=-mx,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,所以6x 1=-m x 2=-2-m ln x 2-3x 21-2 x 2-x 1=-m ln x 2-3x 21x 2-x 1,所以m =-6x 1x 2,所以6x 1=6x 1x 2ln x 2-3x 21x 2-x 1,所以x 1=0或x 1=2x 2-x 2ln x 2,因为m ≠0,所以x 1≠0,所以x 1=2x 2-x 2ln x 2,所以m =-62x 2-x 2ln x 2 x 2=12x 22ln x 2-12x 22,令h x =12x 2ln x -12x 2,x >0 ,则h x =12x 2ln x -1 ,所以当0<x <e 时h x <0,当x >e 时h x >0,所以h x 在0,e 上单调递减,在e ,+∞ 上单调递增,所以h x min =h e =-6e ,所以实数m 的最小值为-6e.故选:A【点睛】思路点睛:涉及公切线问题一般先设切点,在根据斜率相等得到方程,即可找到参数之间的关系,最后构造函数,利用导数求出函数的最值.二、多选题9(2023·湖北·统考模拟预测)若存在直线与曲线f x =x 3-x ,g x =x 2-a 2+a 都相切,则a 的值可以是()A.0B.-24C.log 27D.e π+πe【答案】ABC【分析】设该直线与f x 相切于点x 1,x 31-x 1 ,求出切线方程为y =3x 21-1 x -2x 31,设该直线与g x 相切于点x 2,x 22-a 2+a ,求出切线方程为y =2x 2x -x 22-a 2+a ,联立方程组,得到-a 2+a =94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,讨论h x 的单调性,从而得到最值,则可得到-a 2+a ≥-1,解出a 的取值范围,四个选项的值分别比较与区间端点比较大小即可判断是否在区间内.【详解】设该直线与f x 相切于点x 1,x 31-x 1 ,因为f x =3x 2-1,所以f x 1 =3x 21-1,所以该切线方程为y -x 31-x 1 =3x 21-1 x -x 1 ,即y =3x 21-1 x -2x 31.设该直线与g x 相切于点x 2,x 22-a 2+a ,因为g x =2x ,所以g x 2 =2x 2,所以该切线方程为y -x 22-a 2+a =2x 2x -x 2 ,即y =2x 2x -x 22-a 2+a ,所以3x 21-1=2x 2-2x 31=-x 22-a 2+a ,所以-a 2+a =x 22-2x 31=3x 21-122-2x 31=94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,∴h x =9x 3-6x 2-3x ,所以当x ∈-∞,-13 ∪0,1 时,hx <0;当x ∈-13,0 ∪1,+∞ 时,h x >0;∴h x 在-∞,-13和0,1 上单调递减;在-13,0 和1,+∞ 上单调递增;又h -13 =527,h 1 =-1,所以h x ∈-1,+∞ ,所以-a 2+a ≥-1,解得1-52≤a ≤1+52,所以a 的取值范围为1-52,1+52,所以A 正确;对于B ,-24-1-52=25-2+2 4>0,所以1-52<-24<0,所以B 正确;对于C ,因为0<log 27<log 222=32<1+52,所以C 正确;对于D ,因为e π+πe>2e π⋅πe=2>1+52,所以D 不正确.故选:ABC10(2023·全国·高三专题练习)函数f x =ln x +1,g x =e x -1,下列说法正确的是( ).(参考数据:e 2≈7.39,e 3≈20.09,ln2≈0.69,ln3≈1.10)A.存在实数m ,使得直线y =x +m 与y =f x 相切也与y =g x 相切B.存在实数k ,使得直线y =kx -1与y =f x 相切也与y =g x 相切C.函数g x -f x 在区间23,+∞ 上不单调D.函数g x -f x 在区间23,+∞上有极大值,无极小值【答案】AB【分析】对AB ,设直线与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,利用点在线上及斜率列方程组,解得切点即可判断;对CD ,令h x =g x -f x ,由二阶导数法研究函数单调性及极值.【详解】对AB ,设直线l 与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,f x =1x,gx =ex,则有y1=f x1=ln x1+1y2=g x2=e x2-1y1-y2x1-x2=1x1=e x2⇒ln x1+1-e x2-1x1-x2=e x2⇒-x2+1-e x2-11e x2-x2=e x2⇒e x2-1x2-1=0,解得x2=0或x2=1.当x2=0,则y2=0,x1=1,y1=1,公切线为y=x,此时存在实数m=0满足题意;当x2=1,则y2=e-1,x1=1e,y1=0,公切线为y=e x-1e=ex-1,此时存在实数k=1满足题意,AB对;对CD,令h x =g x -f x =e x-ln x-2,x∈0,+∞,则m x =h x =e x-1 x,由m x =e x+1x2>0得h x 在0,+∞单调递增,由h23=e23-32=e2-278e232+32e23+94>0得,x∈23,+∞时,h x >0,h x 单调递增,CD错.故选:AB.三、填空题11(2023·全国·高三专题练习)若曲线y=ax2与y=ln x有一条斜率为2的公切线,则a= .【答案】1ln2e【分析】根据导数的几何意义以及切线方程的求解方法求解.【详解】设公切线在曲线y=ax2与y=ln x上的切点分别为A(x1,y1),B(x2,y2),由y=ln x可得y =1x,所以1x2=2,解得x2=12,所以y2=ln x2=-ln2,则B12,-ln2 ,所以切线方程为y+ln2=2x-1 2,又由y=ax2,可得y =2ax,所以2ax1=2,即ax1=1,所以y1=ax21=x1,又因为切点A(x1,y1),也即A(x1,x1)在切线y+ln2=2x-1 2上,所以x1+ln2=2x1-1 2,解得x1=ln2+1,所以a =1x 1=1ln2+1=1ln2e .故答案为:1ln2e.12(2023·河北唐山·统考三模)已知曲线y =ln x 与y =ax 2a >0 有公共切线,则实数a 的取值范围为.【答案】12e,+∞【分析】设公切线与曲线的切点为x 1,ln x 1 ,x 2,ax 22 ,利用导数的几何意义分别求y =ln x 和y =ax 2上的切线方程,由所得切线方程的相关系数相等列方程求参数关系,进而构造函数并利用导数研究单调性求参数范围.【详解】设公切线与曲线y =ln x 和y =ax 2的切点分别为x 1,ln x 1 ,x 2,ax 22 ,其中x 1>0,对于y =ln x 有y =1x ,则y =ln x 上的切线方程为y -ln x 1=1x 1x -x 1 ,即y =xx 1+ln x 1-1 ,对于y =ax 2有y =2ax ,则y =ax 2上的切线方程为y -ax 22=2ax 2x -x 2 ,即y =2ax 2x -ax 22,所以1x 1=2ax 2ln x 1-1=-ax 22,有-14ax21=ln x 1-1,即14a=x 21-x 21ln x 1x 1>0 ,令g x =x 2-x 2ln x ,g x =x -2x ln x =x 1-2ln x ,令gx =0,得x =e 12,当x ∈0,e12时,g x >0,g x 单调递增,当x ∈e 12,+∞ 时,g x <0,g x 单调递减,所以g x max =g e12=12e ,故0<14a ≤12e ,即a ≥12e.∴正实数a 的取值范围是12e,+∞.故答案为:12e,+∞.13(2023·浙江金华·统考模拟预测)若存在直线l 既是曲线y =x 2的切线,也是曲线y =a ln x 的切线,则实数a 的最大值为.【答案】2e【分析】设切线与两曲线的切点分别为(n ,n 2),(m ,a ln m ),根据导数的几何意义分别求出切线方程,可得a4m2=1-ln m,由题意可知a4=m2(1-ln m)有解,故令g(x)=x2(1-ln x),(x>0),利用导数求得其最值,即可求得答案.【详解】由题意知两曲线y=x2与y=a ln x,(x>0)存在公切线,a=0时,两曲线y=x2与y=0,(x>0),不合题意;则y=x2的导数y =2x,y=a ln x的导数为y =a x,设公切线与y=x2相切的切点为(n,n2),与曲线y=a ln x相切的切点为(m,a ln m),则切线方程为y-n2=2n(x-n),即y=2nx-n2,切线方程也可写为y-a ln m=am(x-m),即y=amx-a+a ln m,故2n=am-n2=-a+a ln m,即a24m2=a-a ln m,即a4m2=1-ln m,即a4=m2(1-ln m)有解,令g(x)=x2(1-ln x),(x>0),则g (x)=2x(1-ln x)+x2-1 x=x(1-2ln x),令g (x)=0可得x=e,当0<x<e时,g (x)>0,当x>e时,g (x)<0,故g(x)在(0,e)是增函数,在(e,+∞)是减函数,故g(x)的最大值为g(e)=e 2,故a4≤e2,所以a≤2e,即实数a的最大值为2e,故答案为:2e。
用导数求切线方程的步骤

导数的切线方程怎么求
先求出函数在(x0,y0)点的导数值导数值就是函数在X0点的切线的斜率值。
之后代入该点坐标(x0,y0),用点斜式就可以求得切线方程。
当导数值为0,改点的切线就是y=y0;当导数不存在,切线就是x=x0;当在该点不可导,则不存在切线。
切线方程:切线方程是研究切线以及切线的斜率方程,涉及几何、代数、物理向量、量子力学等内容。
是关于几何图形的切线坐标向量关系的研究。
导数:导数是函数的局部性质。
一个函数在某一点的导数描述了这个函数在这一点附近的变化率。
如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
导数的本质是通过极限的概念对函数进行局部的线性逼近。
例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
导数专题:导数与曲线切线问题的6种常见考法(解析版)

导数专题:导数与曲线切线问题的6种常见考法一、求曲线“在”与“过”某点的切线1、求曲线“在”某点处的切线方程步骤第一步(求斜率):求出曲线在点()()00,x f x 处切线的斜率0()f x '第二步(写方程):用点斜式000()()()y f x f x x x '-=-第三步(变形式):将点斜式变成一般式。
2、求曲线“过”某点处的切线方程步骤(此类问题的点不一定是切点)第一步:设切点为()()00,Q x f x ;第二步:求出函数()y f x =在点0x 处的导数0()f x ';第三步:利用Q 在曲线上和0()PQ f x k '=,解出0x 及0()f x ';第四步:根据直线的点斜式方程,得切线方程为000()()()y f x f x x x '-=-.二、公切线问题研究曲线的公切线,一般是分别设出两切点,写出两切线方程,然后再使用这两个方程表示同一条直线,但要注意以下两个方面:(1)两个曲线有公切线,且切点是同一点;(2)两个曲线有公切线,但是切点不是同一点。
三、切线条数问题求曲线的切线条数一般是设出切点()(),t f t ,由已知条件整理出关于t 的方程,把切线问条数问题转化为关于t 的方程的实根个数问题。
四、已知切线求参数问题此类问题常见的考查形式有两种,一是判断符合条件的切线是否存在,二是根据切线满足条件求参数的值或范围。
常用的求解思路是把切线满足条件转化为关于斜率或切点的方程或函数,再根据方程的根的情况或函数性质去求解。
题型一“在”点求切线问题【例1】函数2()ln 2f x x x x =++在点()()1,1f 处的切线方程为()A.33y x =-B.3y x =C.31y x =+D.33y x =+【答案】B【解析】因为2()ln 2f x x x x =++,所以()1ln 2f x x x=++'()13f '∴=,又()13f =,∴曲线()y f x =在点()()1,1f 处的切线方程为33(1)y x -=-,即3y x =.故选:B.【变式1-1】已知函数()f x 满足()()3211f x x f x =-'⋅+.(1)求()1f '的值;(2)求()f x 的图象在2x =处的切线方程.【答案】(1)()11f '=;(2)8110x y --=【解析】(1)因为()()3211f x x f x =-'⋅+,则()()2321f x x f x ''=-,所以,()()1321f f ''=-,解得()11f '=.(2)由(1)可知()321f x x x =-+,则()232f x x x '=-,则()25f =,()28f '=,因此,()f x 的图象在2x =处的切线方程为()582y x -=-,即8110x y --=.【变式1-2】若曲线2y x ax b =++在点(0,)P b 处的切线方程为10x y -+=,则a ,b 的值分别为()A.1,1B.1-,1C.1,1-D.1-,1-【答案】A【解析】因为2y x a '=+,所以0|x y a='=曲线2y x ax b =++在点(0,)b 处的切线10x y -+=的斜率为1,1a ∴=,又切点(0,)b 在切线10x y -+=上,010b ∴-+=1b ∴=.故选:A.【变式1-3】已知函数()2ln f x a x x =+的图象在1x =处的切线方程为30x y b -+=,则a b +=()A.2-B.1-C.0D.1【答案】B【解析】因为()2ln f x a x x =+,所以()2af x x x'=+.又()f x 的图象在1x =处的切线方程为30x y b -+=,所以()123f a '=+=,解得1a =,则()2ln f x x x =+,所以()11f =,代入切线方程得310b -+=,解得2b =-,故1a b +=-.故选:B.题型二“过”点求切线问题【例2】(多选)已知曲线()()3211f x x =++,则曲线过点()0,3P 的切线方程为()A.630x y +-=B.630x y -+=C.5260x y -+=D.3260x y -+=【答案】BD【解析】设切点坐标为()()300,211x x ++,()()261f x x '=+,∴切线斜率为()()20061k f x x '==+切线方程为()()()2003012161y x x x x ⎤=+-++⎦-⎡⎣曲线过点()0,3P ,代入得()()()20030362111x x x ⎡⎤++⎣=--⎦+可化简为()()032001113x x x +-+=,即3020023x x -=-,解得00x =或032x =-则曲线过点()0,3P 的切线方程为630x y -+=或3260x y -+=故选:BD【变式2-1】过原点的直线,m n 与分别与曲线()e xf x =,()lng x x =相切,则直线,m n 斜率的乘积为()A.-1B.1C.eD.1e【答案】B【解析】设()(),f x g x 的切点分别为()()1122,e ,,ln xx x x ,由题意可得()e xf x '=,()1g x x'=,所以()f x 在1x x =处的切线为()111e e x xy x x -=-,()g x 在2x x =处的切线为()2221ln y x x x x -=-,又因为两条切线过原点,所以()()1112220e e 010ln 0x x x x x x ⎧-=-⎪⎨-=-⎪⎩,解得121e x x =⎧⎨=⎩,所以直线,m n 斜率的乘积为()()1121e 1ef xg x ''=⨯=,故选:B【变式2-2】设点P 是曲线e e e ex xx x y ---=+上任意一点,直线l 过点P 与曲线相切,则直线l 的倾斜角的取值范围为______.【答案】π0,4⎛⎤⎥⎦⎝【解析】设直线l 的倾斜角为α2e e e e 4(e e e e e e x x x x x x x x x x y y -------''=∴=+++=()0e e 1x x y -≥∴≤<'+2][]tan (0,1,0,ααπ∴∈∈π0,4α⎛⎤∴∈ ⎥⎦⎝【变式2-3】过点()1,0作曲线e x y =的两条切线,则这两条切线的斜率之和为______.【答案】2e 1-【解析】0x >时,e x y =,设切点()11,ex x ,则11e ,e x xy k==',切线()1111:e e x xl y x x -=-过()1,0,()111e e 1x x x ∴-=-,2112,e x k ∴==,0x ≤时,e x y -=,切点()22,e xx -,22e ,e x x y k --=-=-',切线()2222:ee x x l y x x ---=--过()1,0,()222e e 1x x x --∴-=--,220,1x k ∴==-,故212e 1k k +=-.故答案为:2e 1-.题型三切线的条数问题【例3】若过点()0,(0)b b >只可以作曲线e xxy =的一条切线,则b 的取值范围是__________.【答案】24,e ∞⎛⎫+⎪⎝⎭【解析】函数e x x y =的定义域为R ,则1e x x y -'=,设切点坐标为000,e x x x ⎛⎫ ⎪⎝⎭,则切线斜率为001e x x k -=,故切线方程为:()000001e e x x x x y x x --=-,又切线过点()0,(0)b b >,则()000200001e e e x x x x x x b x b --=-⇒=,设()2ex x h x =,则()()20e xx x h x -'==得,0x =或2x =,则当(),0x ∈-∞时,()0h x '<,函数()h x 单调递减,当()0,2x ∈时,()0h x '>,函数()h x 单调递增,当()2,x ∈+∞时,()0h x '<,函数()h x 单调递减,所以()()2400,2e h h ==,又x →-∞时,()h x →+∞,x →+∞时,()0h x →,所以02ex x b =有且只有一个根,且0b >,则24e b >,故b 的取值范围是24,e ∞⎛⎫+ ⎪⎝⎭.故答案为:24,e ∞⎛⎫+⎪⎝⎭.【变式3-1】若曲线(2)e x y x a =-有两条过坐标原点的切线,则实a 的取值范围为______.【答案】(,0)(8,)-∞⋃+∞【解析】设切点坐标为:00(,)x y ,(22)e x y x a '=+-,所以切线斜率为00(22)e x k x a =+-,即切线方程为0000(2)e (22)e ()x xy x a x a x x --=+--,又切线过坐标原点,所以00000(2)e (22)e (0)x x x a x a x --=+--,整理得20020x ax a -+=,又曲线有两条过坐标原点的切线,所以该方程有两个解,所以280a a ∆=->,解得(,0)(8,).a ∈-∞⋃+∞故答案为:(,0)(8,).-∞⋃+∞【变式3-2】已知过点(),0A a 可以作曲线()2e xy x =-的两条切线,则实数a 的取值范围是()A.()2,+∞B.()(),e 2,∞∞--⋃+C.()(),22,∞∞--⋃+D.()(),12,-∞-+∞【答案】C【解析】设切点是()00,P x y ,0R x ∈,即()0002e x y x =-,而()1exy x '=-故切线斜率()001e x k x =-,切线方程是()()()00002e 1e x xy x x x x --=--,又因为切线经过点(),0A a ,故()()()00002e 1e x xx x a x --=--,显然01x ≠,则()0000021111x a x x x x -=+=-+--,在01x ≠上有两个交点,令01x x =-,设()1,0h x x x x =+≠,则()222111x h x x x-=-=',令()0h x '=得11x =-,21x =,所以当(),1x ∈-∞-时,()0h x '>,()h x 单调递增,当()1,0x ∈-时,()0h x '<,()h x 单调递减,当()0,1x ∈时,()0h x '<,()h x 单调递减,当()1,x ∈+∞时,()0h x '>,()h x 单调递增,又()12h -=-,()12h =,且x →-∞时,()h x →-∞,0x -→时,()h x →-∞,0x +→时,()h x →+∞,x →+∞时,()h x →+∞,所以()a h x =有两个交点,则2a >或2a <-,故实数a 的取值范围是()(),22,∞∞--⋃+.故选:C.【变式3-3】已知函数()326f x x x =-,若过点()1,P t 可以作出三条直线与曲线()f x 相切,则t 的取值范围是()A.()5,4--B.()4,3--C.()3,2--D.()2,1--【答案】A【解析】设过点()1,P t 的切线与()f x 相切于点()32,6m m m -,()2312f x x x '=-,()2312f m m m '∴=-,则切线方程为:()()()3226312y m m m m x m --=--,又切线过点()1,P t ,()()()23232312162912t m m m m m m m m ∴=--+-=-+-,令()322912g m m m m =-+-,则问题等价于y t =与()g m 有三个不同的交点,()()()261812612g m m m m m '=-+-=---,∴当()(),12,m ∈-∞+∞时,()0g m '<;当()1,2m ∈时,()0g m '>;()g m ∴在()(),1,2,-∞+∞上单调递减,在()1,2上单调递增,又()15g =-,()24g =-,由此可得()g m 图象如下图所示,由图象可知:当()5,4t ∈--时,y t =与()g m 有三个不同的交点,即当()5,4t ∈--时,过点()1,P t 可以作出三条直线与曲线()f x 相切.故选:A.题型四两曲线的公切线问题【例4】若直线1:2l y kx b k ⎛⎫=+> ⎪⎝⎭与曲线1()e x f x -=和()ln(1)g x x =+均相切,则直线l 的方程为___.【答案】y x=【解析】设()f x ,()g x 上的切点分别为()111,ex A x -,()()22,ln 1B x x+,由()1e xf x -'=,()11g x x '=+,可得1121e 1x k x -==+,故()f x 在A 处的切线方程为()()1111111111ee e e 1x x x x y x x y x x -----=-⇒=+-,()g x 在B 处的切线方程为()()()222222211ln 1ln 1111x y x x x y x x x x x -+=-⇒=++-+++,由已知()()()111122121221e 1ln 11e 1ln 11x x x x x x x x x --⎧=⇒-=+⎪+⎪⎨⎪-=+-⎪+⎩,所以()()()22222222221ln 1ln 1ln 11111x x x x x x x x x x ⎛⎫+=+-⇒=+ ⎪++++⎝⎭,故20x =或()2ln 11x +=,而()222111ln 111e 1e 2x x x +=⇒+=⇒=<+,不合题意舍去,故20x =,此时直线l 的方程为y x =.故答案为:y x =.【变式4-1】已知函数()e xf x =与函数()lng x x b =+存在一条过原点的公共切线,则b =________.【答案】2【解析】设该公切线过函数()e xf x =、函数()lng x x b =+的切点分别为()11,ex x ,()22,ln b x x +.因为()e xf x '=,所以该公切线的方程为()1111111e e e e ex x x x x y x x x x =-+=+-同理可得,该公切线的方程也可以表示为()2222211ln ln 1y x x x b x x b x x =-++=⋅++-因为该公切线过原点,所以()112121e e 10ln 10x x xx x b ⎧=⎪⎪⎪-=⎨⎪+-=⎪⎪⎩,解得1211,e ,2x x b ===.故答案为:2【变式4-2】函数()bf x ax x =+的图象在点(1,3)处的切线也是抛物线213x y =的切线,则a b -=()A.1B.3C.6D.2【答案】C【解析】()bf x ax x =+,则2()b f x a x '=-,则在点(1,3)处的切线的斜率为12(1)1bk f a a b '==-=-,213x y =,则6y x '=,则在点(1,3)处的切线的斜率为26k =,函数()bf x ax x =+的图象在点(1,3)处的切线也是抛物线213x y =的切线,则12k k =,即6a b -=,故选:C.【变式4-3】若曲线e x y a =与曲线y ==a __________.【解析】令()e x f x a =,()g x ()e xf x a '=,()g x '=设()f x 与()g x 的公共点为()00,x y ,()f x 与()g x 在公动点处有相同的切线,()()()()0000f x g x f x g x '⎧=∴'⎪⎨=⎪⎩,即00e e x x a a ⎧=⎪⎨⎪=⎩=012x =,12e a ∴=a ==题型五切线平行、垂直问题【例5】若曲线ln x ay x+=在点()1,a 处的切线与直线:250l x y -+=垂直,则实数=a ().A.12B.1C.32D.2【答案】C 【解析】因为21ln x ay x --'=,所以曲线ln x ay x+=在点()1,a 处的切线的斜率为()111k f a ='=-,直线l 的斜率22k =,由切线与直线l 垂直知121k k =-,即()211a -=-,解得32a =.故选:C.【变式5-1】已知曲线y =y x =--24垂直的曲线的切线方程为_________.【答案】2250x y -+=【解析】设切点为(),m n ,因为y =y '=,因为曲线的切线与直线y x =--24垂直,()21-=-,解得25m =,又点(),m n在曲线y =25n ==,所以切点坐标为()25,25,所以曲线y =y x =--24垂直的切线方程为:()125252y x -=-,即2250x y -+=,故答案为:2250x y -+=.【变式5-2】若曲线s n e i =+x y x a 存在两条互相垂直的切线,则a 的取值范围是________.【答案】()(),00,∞-+∞U 【解析】由题知,令()e sin x f x a x =+,则()e cos xf x a x '=+.若函数曲线存在两条互相垂直的切线则可得1x ∃,2x ,()()121f x f x ''⋅=-.当0a =时,()21e 0,xx x f x '=>⇒∀,()()120f x f x ''>,与题目矛盾;当0a ≠时,由()e 0,xy =∈+∞,cos y a x a=≥-可得()f x '的值域是(),a -+∞故12,x x ∃,使得()()1,0f x a '∈-,()210,f x a ⎛⎫'∈ ⎪ ⎪⎝⎭,()()121f x f x ''⋅=-.故答案为:()(),00,∞-+∞U .【变式5-3】曲线33y x x =-+在点P 处的切线平行于直线21y x =-,则点P 的坐标为______.【答案】()1,3或()1,3-【解析】由已知得231y x '=-,令2y '=,则2312x -=,解得1x =或=1x -,所以()1,3P 或()1,3P -.经检验,点()1,3P 与()1,3P -均符合题意.故答案为:()1,3或()1,3-【变式5-4】若曲线()21ln 2f x x x ax =++存在与直线50x y -=平行的切线,则实数a 的最大值为______.【答案】3【解析】()()10f x x a x x=++>,因为曲线()21ln 2f x x x ax =++存在与直线50x y -=平行的切线,所以15x a x ++=在()0,∞+有解.即15a x x ⎛⎫=-+ ⎪⎝⎭在()0,∞+有解.设()15g x x x⎛⎫=-+ ⎪⎝⎭,()0,x ∈+∞,则()1553g x x x ⎛⎫=-+≤-= ⎪⎝⎭,当且仅当1x x=,即1x =时等号成立,即()3g x ≤.所以3a ≤,即a 的最大值为3.故答案为:3题型六与切线有关的最值问题【例6】若动点P 在直线1y x =+上,动点Q 在曲线22x y =-上,则|PQ |的最小值为()A.14B.4C.22D.18【答案】B【解析】设与直线1y x =+平行的直线l 的方程为y x m =+,∴当直线l 与曲线22x y =-相切,且点Q 为切点时,P ,Q 两点间的距离最小,设切点()00,Q x y ,22x y =-,所以212y x =-,y x ∴'=-,0011x x ∴-=⇒=-,012y ∴=-,∴点11,2Q ⎛⎫-- ⎪⎝⎭,∴直线l 的方程为12y x =+,,P Q ∴两点间距离的最小值为平行线12y x =+和1y x =+间的距离,,P Q ∴24=.故选:B .【变式6-1】在平面直角坐标系xOy 中,P 是曲线24x y =上的一个动点,则点P 到直线40x y ++=的距离的最小值是_____.【答案】2【解析】设直线0x y b ++=与214y x =相切,则切线的斜率为1-且12y x '=,令112y x '==-,则2x =-,即切点的横坐标为2-,将2x =-,代入214y x =,可得1y =,即切点坐标为()2,1-,所以点P 到直线40x y ++=的距离的最小值即为()2,1-到直线的距离,即2d =,故答案为:【变式6-2】已知P 为直线210x y +-=上的一个动点,Q 为曲线423242210x x y x x --++=上的一个动点,则线段PQ 长度的最小值为______.【解析】直线210x y +-=可化为:1122y x =-+.对于曲线423242210x x y x x --++=.当0x =时,代入10=不成立,所以0x ≠.所以423242210x x y x x --++=可化为22112122y x x x =-++,导数为31142y x x -'=-所以线段PQ 的最小值即为与1122y x =-+平行的直线与423242210x x y x x --++=相切时,两平行线间的距离.设切点(),Q m n .由题意可得:322111422112122m m n m m m ⎧--=-⎪⎪⎨⎪=-++⎪⎩,即32214112122m m n m m m ⎧=⎪⎪⎨⎪=-++⎪⎩,解得:234m n ⎧=⎪⎪⎨⎪=-⎪⎩或234m n ⎧=-⎪⎪⎨⎪=+⎪⎩.当Q ⎝⎭时,PQ当,324Q ⎛-+ ⎝⎭时,PQ =综上所述:线段PQ.【变式6-3】点P 是曲线2ln y x x =-上任意一点,且点P 到直线y x a =+的距离的a 的值是__________.【答案】2-【解析】由题设12y x x '=-且0x >,令0'>y ,即22x >;令0'<y ,即202x <<,所以函数2ln y x x =-在0,2⎛⎝⎭上单调递减,在,2⎫+∞⎪⎪⎝⎭上单调递增,且12|ln 022x y ->,如图所示,当P 为平行于y x a =+并与曲线2ln y x x =-相切直线的切点时,距离最近.令1y '=,可得12x =-(舍)或1x =,所以1|1x y ==,则曲线上切线斜率为1的切点为(1,1)P ,=2a =(舍去)或2-,故答案为:2-.。
导数第一讲:求导、切线、单调性、极值、最值(解析版)

导数第一讲:求导、切线、单调性、极值、最值例1.(1)求曲线21xy x =-,在点()1,1处的切线方程;(2)求过点()2,3的抛物线2y x =的切线方程.解:(1)()2121y x '=--,可知所求切线的斜率1k =-故所求切线的方程为()11y x -=--,即20x y +-=.(2)设切点坐标为()200,x x ,2y x '=,可知所求切线的斜率022k x =∵切线过点()2,3和点()200,x x ,∴2000322x x x -=-,解得01x =或03x =,∴切线的斜率为2或6故所求切线的方程为()322y x -=-或()362y x -=-,即210x y --=或690x y --=.练习1.已知函数()3233f x x x bx c =-++在=0x 处取得极大值1.(1)求函数()y f x =的图象在=1x -处的切线方程;(2)求过点()1,1-与曲线()y f x =相切的直线方程.解:(1)()3233f x x x bx c =-++,则()2363f x x x b '=-+,由题意可得()()03001f b f c ⎧'==⎪⎨==⎪⎩,解得01b c =⎧⎨=⎩,即()3231f x x x =-+,()236f x x x '=-,令()0f x ¢>,解得2x >或0x <,故()f x 在()(),0,2,-∞+∞上单调递增,在()0,2上单调递减,则()f x 在=0x 处取得极大值1,即0,1b c ==符合题意.∵()()13,19f f '-=--=,则切点坐标为()1,3--,切线斜率9k =,∴函数()y f x =的图象在=1x -处的切线方程为()391y x +=+,即960x y -+=.(2)由(1)可得:()3231f x x x =-+,()236f x x x '=-,设切点坐标为()32000,31x x x -+,切线斜率20036k x x =-,则切线方程为()()()322000003136y x x x x x x --+=--,∵切线过点()1,1-,则()()()32200000131361x x x x x ---+=--,整理得()3010x -=,即01x =,∴切线方程为()131y x +=--,即320x y +-=.例2.函数32()(1)31f x x a x x =+--+.(1)当1a =时,求函数()f x 的单调区间;(2)若过原点O 可作三条直线与()f x 的图像相切,求实数a 的取值范围.解:(1)当1a =时,3()31,R f x x x x =-+∈.由2()33f x x '=-,令()0f x '>,解得1x <-或1x >;令()0f x '<,解得11x -<<.所以()f x 的单调递增区间为(,1)-∞-和(1,)+∞,单调递减区间为(1,1)-.(2)易知原点O 不在函数()f x 的图像上,设切点为(,())(0)t f t t ≠.求导得2()32(1)3f x x a x =+--',则()()f t f t t =',即322(1)3132(1)3t a t t t a t t +--+=+--,整理得322(1)10t a t +--=,所以2112a t t -=-,令21()2(0)g t t t t =-≠,则32()2g t t =+',令()0g t '>,解得0t >或1t ≤-;令()0g t '<,解得10t -<<,所以函数()g t 在区间(,1)-∞-上单调递增,在(1,0)-上单调递减,在(0,)+∞上递增,故当0t <时,max ()(1)3g t g =-=-;当t →-∞时,()g t →-∞;0t →时,()g t →-∞,当0t >时,()g t 的取值范围为R .而过原点O 可作三条直线与()f x 的图像相切,则()()f t f t t='有三个不相等的实数根,也就是直线1y a =-与函数()y g t =的图象有三个交点,则有13a -<-,即4a >.练习2.已知函数()f x =e x ,()ln g x x =.()f x 的图象与()g x 的图象是否存在公切线?如果存在,有几条公切线,请证明你的结论.解:曲线y =f (x ),y =g (x )公切线的条数是2,证明如下:设公切线与g (x )=lnx ,f (x )=ex 的切点分别为(m ,lnm ),(n ,en ),m ≠n ,∵g ′(x )1x =,f ′(x )=ex ,可得11nne mlnm e m n m ⎧=⎪⎪⎨-⎪=⎪-⎩,化简得(m ﹣1)lnm =m +1,当m =1时,(m ﹣1)lnm =m +1不成立;当m ≠1时,(m ﹣1)lnm =m +1化为lnm 11m m +=-,由lnx 11x x +==-121x +-,即lnx ﹣121x =-.分别作出y =lnx ﹣1和y 21x =-的函数图象,由图象可知:y =lnx ﹣1和y 21x =-的函数图象有两个交点,可得方程lnm 11m m +=-有两个实根,则曲线y =f (x ),y =g (x )公切线的条数是2条.例3.已知函数()()()21ln 1R 2f x x ax a x a =+-+∈.(1)当2a =时,求函数()y f x =的极值;(2)求当0a >时,函数()y f x =在区间[1,e]上的最小值()Q a .解:(1)当2a =时,函数2()ln 3(0)f x x x x x =+->.1(21)(1)()23x x f x x x x--'=+-=,令()0f x '=,得1x =或12x =,当1(0,)2x ∈时,()0f x '>,()f x 在1(0,)2上单调递增,当1(,1)2x ∈时,()0f x '<,()f x 在1(,1)2上单调递减,当(1,)x ∈+∞时,()0f x '>,()f x 在(1,)+∞上单调递增,则()f x 在12x =处取得极大值,在1x =处取得极小值.极大值为15()ln 224f =--,极小值为(1)2f =-.(2)函数()f x 的定义域是[1,e],1()(1)1()(1)(0)a x x a f x ax a a x x--'=+-+=>.当0a >时,令()0f x '=有两个解,1x =或1x a=.当10ea <≤,即1e a ≥时,()0f x '≤,()f x ∴在[1,e]上单调递减,()f x ∴在[1,e]上的最小值是(e)f 211e (1)e 2a a =+-+,当11ea <<,即11e a <<时,当1(1,)x a ∈时,()0f x '<,()f x ∴在1(1,)a上单调递减,当1(,e)x a ∈时,()0f x '>,()f x ∴在1(,e)a 上单调递增,()f x ∴在[1,e]上的最小值是11()ln 12f a a a=---,当1a ≥,即101a<≤时,[1,e]x ∈,()0f x '≥,()f x ∴在[1,e]上单调递增,()f x ∴在[1,e]上的最小值是(1)f 112a =--.综上,2111e (1)e,02e 11()ln 1,12e 11,12a a a Q a a a a a a ⎧+-+<≤⎪⎪⎪=---<<⎨⎪⎪--≥⎪⎩.练习3.已知()()2,R f x x x c c =-∈.(1)若()f x 在2x =处有极大值,求c 的值;(2)若03c <<,求()f x 在区间[1]2,上的最小值.解:(1)由题知,()()()3f x x c x c =--',由题意,()()()2260f c c '=--=,得2c =或6c =,当2c =时,在()2,,2,3⎛⎫-∞+∞ ⎪⎝⎭上()0f x ¢>,在2,23⎛⎫ ⎪⎝⎭上()0f x '<,此时,()f x 在2x =处有极小值,不符题意;当6c =时,在()(),2,6,-∞+∞上()0f x ¢>,在()2,6上()0f x '<,此时,()f x 在2x =处有极大值,符合题意.综上,6c =.(2)令()0f x '=,得3cx =或x c =,由03c <<,则在(),,,3c c ∞∞⎛⎫-+ ⎪⎝⎭上()0f x ¢>,在,3c c ⎛⎫⎪⎝⎭上()0f x '<,即()f x 在(),,,3c c ∞∞⎛⎫-+ ⎪⎝⎭上单调递增,在,3c c ⎛⎫⎪⎝⎭上单调递减.由题意,13c <,当23c ≤<时,()f x 在区间[]1,2上单调递减,则()2min ()22(2)f x f c ==-,当12c <<时,()f x 在区间()1,c 上单调递减,在(),2c 上单调递增,则()min ()0f x f c ==,当01c <≤时,()f x 在区间[]1,2上单调递增,则()2min ()1(1)f x f c ==-,综上,()()()2min21,010,1222,23c c f x c c c ⎧-<≤⎪⎪=<<⎨⎪-≤<⎪⎩.例4.已知函数()()22ln f x x x a x a =-+∈R .(1)若()f x 的单调递减区间为13,44⎡⎤⎢⎥⎣⎦,求a 的值;(2)若0x 是()f x 的极大值点,且()2002f x x a <-恒成立,求a 的取值范围.解:(1)由题可知()f x 的定义域为()0,∞+,()22222a x x af x x x x-+'=-+=.()f x 的单调递减区间为13,44⎡⎤⎢⎥⎣⎦等价于()0f x '≤的解集为13,44⎡⎤⎢⎥⎣⎦,即2220x x a -+≤的解集为13,44⎡⎤⎢⎥⎣⎦.所以方程2220x x a -+=的两个根分别为14,34,由根与系数的关系可得13244a =⨯,所以38a =.(2)若0x 是()f x 的极大值点,定义域为()0+∞,,则()0f x '=至少有一正根,即方程2220x x a -+=至少有一正根.若0a =,则方程2220x x a -+=的正根为1x =,因为当01x <<时()0f x '<,当1x >时()0f x ¢>,所以此时()f x 只有极小值点1,不符合题意.若0<a ,则方程2220x x a -+=有一正根和一负根,设为α,β,且0α>,0β<,则()()2222x x a x x αβ-+=--.因为当0x α<<时,()0f x '<,当x α>时,()0f x ¢>,所以此时()f x 只有极小值点α,不符合题意.若0a >,由题可知方程2220x x a -+=应有两个不等的正根,设为1x ,2x ,其中12x x <,则Δ48002a a =->⎧⎪⎨>⎪⎩解得102a <<.所以()()()212222x x x x x x a f x x x ---+'==.列表如下:x()10,x 1x ()12,x x 2x ()2,x +∞()f x '+-+()f x 单调递增极大值单调递减极小值单调递增所以1x 是极大值点,2x 是极小值点,则01x x =.由120x x <<,且121x x =+,得110x 2<<.由题可知()22000002ln 2f x x x a x x a =-+<-,即00ln 220a x x a -+<当0102x <<时恒成立.令()ln 22h x a x x a =-+,102x <<,则()222a x a x h x x x ⎛⎫- ⎪-⎝⎭'==.因为102a <<,所以1024a <<.所以当02a x <<时,()0h x '>,当2ax >时,()0h x '<,所以()max ln 022a a h x h a a ⎛⎫==+< ⎪⎝⎭,解得20e a <<,又102a <<,所以此时a 的取值范围是10,2⎛⎫⎪⎝⎭.综上,实数a 的取值范围是102⎛⎫⎪⎝⎭,.练习4.设函数21()3ln ,2af x x x a R x=+-∈.(1)若函数()f x 是增函数,求实数a 的取值范围;(2)是否存在实数a ,使得1x =是()f x 的极值点?若存在,求出a ;若不存在,请说明理由.解:(1)23()a f x x x x=--',∵()f x 是增函数,∴23()0a f x x x x=--≥'对0x ∀>恒成立,∴()3min3a x x ≤-,令32()3,()33g x x x g x x '=-=-,令()01g x x '=⇒=且当01x <<时,()0g x '<,()g x 单调递减;当1x >时,()0g x '>,()g x 单调递增.∴min ()(1)2g x g ==-,∴2a ≤-,即a 的取值范围为(,2]-∞-.(2)若1x =是()f x 的极值点,则必有(1)1302f a a =--=⇒=-'(必要性)当2a =-时,322222332(1)(2)()0x x x x f x x x x x x -+-+=+-='=≥∴()f x 在(0,)+∞上单调递增,()f x 无极值点,故假设不成立,即不存在这样的a .练习5.已知函数()()=ln 3R f x a x ax a --∈(1)求函数()f x 的单调区间;(2)若函数()f x 的图像在点()()2,2f 处的切线斜率为12,设()()m g x f x x=-,若函数()g x 在区间[]1,2内单调递增,求实数m 的取值范围.解:(1)(1)()(0)a a x f x a x x x-=-=>'当0a >时,()f x 的单调增区间为()0,1,减区间为()1,+∞;当0a <时,()f x 的单调增区间为(1,)+∞,减区间为()0,1;当=0a 时,()f x 不是单调函数.(2)∵1(2)2f '=,∴12122a -⋅=,解得1a =-,∴()ln 3f x x x =-+-()()()ln 30m m g x f x x x x x x =-=-+-->,又()221()10m x g x x x x x x m-+'=-++=>()g x 要在区间[1,2]上单调递增,只需()0g x '≥在[]1,2上恒成立,即20x x m -+≥在[]1,2上恒成立,即()2maxm x x≥-,又在[1,2]上()2maxx x-=∴0m ≥.练习6.已知函数()(ln 1),R f x x x k k =--∈.(1)当1x >时,求函数()f x 的单调区间和极值;(2)若对于任意2e,e x ⎡⎤∈⎣⎦,都有()4ln f x x <成立,求实数k 的取值范围;解:(1)由题知,()()ln 1,R f x x x k k =--∈,所以1()ln 1ln ,0f x x k x x k x x'=--+⋅=->,当0k ≤时,因为1x >,所以()ln 0f x x k '=->,所以()f x 的单调增区间是(1,)+∞,无单调减区间,无极值,当0k >时,令ln 0x k -=,解得e k x =,当1e k x <<时,()0f x '<,当e k x >时,()0f x '>,所以()f x 的单调减区间是()1,e k ,单调增区间是()e ,k ∞+,极小值为()()e e 1e k k kf k k =⋅--=-,无极大值.(2)因为对于任意2e,e x ⎡⎤∈⎣⎦,都有()4ln f x x <成立,所以()4ln 0f x x -<,即问题转化为(4)ln (1)0x x k x --+<,对于2e,e x ⎡⎤∈⎣⎦恒成立,即(4)ln 1x x k x -+>,对于2e,e x ⎡⎤∈⎣⎦恒成立,令(4)ln ()x x g x x -=,所以24ln 4()x x g x x +-'=,令()24ln 4,e,e t x x x x ⎡⎤=+-∈⎣⎦,所以4()10t x x'=+>,所以()t x 在区间2e,e ⎡⎤⎣⎦上单调递增,所以()()min e e 44e 0t x t ==-+=>,所以()0g x '>,所以()g x 在区间2e,e ⎡⎤⎣⎦上单调递增,所以函数()()22max 8e 2eg x g ==-,要使(4)ln 1x x k x -+>,对于2e,e x ⎡⎤∈⎣⎦恒成立,只要max 1()k g x +>,所以2812e k +>-,即281e k >-,所以实数k 的取值范围为281,e ∞⎛⎫-+ ⎪⎝⎭;备选1.设a 为实数,已知函数()()32211932f x x a x =-++(1)讨论()f x 的单调性(2)若过点()0,10有且只有两条直线与曲线()32111132y x a x ax =-+++相切,求a 的值.解:(1)因为()()32211932f x x a x =-++,则()()221f x x a x '=-+,由()0f x '=可得10x =,212a x +=,①当102a +=时,即当1a =-时,对任意的x ∈R ,()0f x '≥且()f x '不恒为零,此时,函数()f x 的增区间为(),-∞+∞,无减区间;②当102a +<时,即当1a <-时,由()0f x '<可得102a x +<<,由()0f x ¢>可得12a x +<或0x >,此时,函数()f x 的减区间为1,02a +⎛⎫⎪⎝⎭,增区间为1,2a +⎛⎫-∞ ⎪⎝⎭、()0,∞+;③当102a +>时,即当1a >-时,由()0f x '<可得102a x +<<,由()0f x ¢>可得0x <或12a x +>,此时,函数()f x 的减区间为10,2a +⎛⎫ ⎪⎝⎭,增区间为(),0∞-、1,2a +⎛⎫+∞⎪⎝⎭.综上所述,当1a =-时,函数()f x 的增区间为(),-∞+∞,无减区间;当1a <-时,函数()f x 的减区间为1,02a +⎛⎫⎪⎝⎭,增区间为1,2a +⎛⎫-∞ ⎪⎝⎭、()0,∞+;当1a >-时,函数()f x 的减区间为10,2a +⎛⎫ ⎪⎝⎭,增区间为(),0∞-、1,2a +⎛⎫+∞⎪⎝⎭.(2)解:设切点为()3211,1132t t a t at ⎛⎫-+++ ⎪⎝⎭,对函数()32111132y x a x ax =-+++求导得()21y x a x a '=-++,所以,切线方程为()()()3221111132y t a t at t a t a x t ⎡⎤⎡⎤--+++=-++-⎣⎦⎢⎥⎣⎦,将点()0,10的坐标代入切线方程整理可得()322119032t a t -++=,即()0f t =,故关于t 的方程()0f t =有两个不等的实根,①当1a =-时,函数()f t 在R 上单调递增,则方程()0f t =至多一个实根,不合乎题意;②当1a <-时,则()()090f t f ==>极小值,故当12a t +>时,()0f t >,此时方程()0f t =至多一个实根,不合乎题意;③当1a >-时,则()()090f t f ==>极大值,则()()311910224a f t f a +⎛⎫==-+= ⎪⎝⎭极大值,解得5a =,合乎题意.综上所述,5a =.备选2.已知函数()22ln 2x af x x x-=-.(1)若()f x 在()0,∞+上单调递减,求实数a 的取值范围;(2)若1a =,试问过点()0,1向曲线()y f x =可作几条切线?解:(1)依题意,因为()22ln 2x af x x x-=-,所以()f x 的定义域为()0,∞+,()()()22222222112142x x x a x a f x x x x ⨯----+-'=-=,若()f x 在()0,∞+上单调递减,则有()0f x '≤在()0,∞+上恒成立,即()21120x a --+-≤恒成立,所以()22111a x ≥--+≥,解得12a ≥,所以实数a 的取值范围为:1,2⎡⎫+∞⎪⎢⎣⎭.(2)当1a =时,()22ln 2x f x x x -=-且点()0,1不在()f x 上,所以()()22112x f x x---'=,设切线方程的斜率为k ,切点为()00,P x y ,根据导数的几何意义,则有()2020112x k x---=,又切线过点()0,1,所以切线方程可设为1y kx =+,则有001y kx =+,200002ln 2x y x x -=-,所以()2002020002112ln 21x x x x x x --=---⨯+,整理得000ln 220x x x -+=,令()ln 22g x x x x =-+()0x >,则()ln 1g x x '=-,所以在x ∈()0,e 时,()0g x '<,()g x 单调递减;在()e,x ∈+∞,()0g x '>,()g x 单调递增;所以()g x 在e x =处取得最小值,又()10g =,所以()g x 在()0,e 有一零点,又因为()0e e 2g =-<,()2222eeln e 2e 220g =-+=>,由零点存在性定理可知,在()2e,e x ∈必有一个根0x ,使得000ln 220x x x -+=成立,综上,方程000ln 220x x x -+=有两个解,所以过点()0,1向曲线()y f x =可作2条切线.备选3.已知函数1()2ln f x a x x x ⎛⎫=-- ⎪⎝⎭,其中a R ∈.(1)若()f x 是定义在(0,)+∞上的单调函数,求实数a 的取值范围;(2)当0a >时,判断()f x 与()2g x x =的图象在其公共点处是否存在公切线?若存在,求满足条件的a 值的个数;若不存在,请说明理由.解:(1)222122()1ax x a f x a x x x -+⎛⎫'=+-= ⎪⎝⎭.当0a ≤时,()0f x '<,故()f x 在(0,)+∞上单调递减,满足题意;当0a >时,要使得()f x 在(0,)+∞上单调,则恒有()0f x '≥.∴2440a ∆=-≤,解得:1a ≥.综上,1a ≥或0a ≤(2)假设()f x ,()g x 的图象在其公共点()00,x y 处存在公切线,则()()()()2000200000200002212ln ax x ax x f x g x f x g x a x x x x ⎧-+=⎪⎧=⎪⎪⇒⎨⎨=⎛⎫⎪⎩⎪--= '⎪'⎪⎝⎭⎩①②由①可得:()()32200000220120x ax x a x x a -+-=⇔+-=,∴002x a=>.将02a x =代入②,则222ln 2224a a a --=,即:28ln 82a a-=.令28()182x xh x n -=-,则11()4h x x x '=-,故()h x 在()0,2上单调递减,在(2,)+∞上单调递增.又1(2)02h =-<,且当0x →,()h x →+∞;当x →+∞,()h x →+∞∴()h x 在(0,)+∞有两个零点,即方程28ln 82a a-=在(0,)+∞有两个不同的解.所以,()f x 与2()g x x =的图象在其公共点处存在公切线,满足条件的a 值有2个。
第5讲利用导数研究函数的公切线问题 高考数学

试卷讲评课件
练2
若曲线f x = acosx与曲线g x = x 2 + bx + 3在交点 0, m 处有
6
公切线,则a + b + m =___.
【分析】若曲线 与曲线 在交点 , 处有公切线,则切点的
坐标相等且切线的斜率(切点处的导函数值)均相等,由此构造关于,
当 , 不是 的切点时,
设切点为 , − + ≠ ,
则 ′ = − + ,
试卷讲评课件
− +
所以
= − + ,得 = ,
所以
= − ,所以直线的方程为 = − .
=
+
= .
故选:
− = + − +
,则
= +
,即
试卷讲评课件
例2
已知f x =1 lnx,g x = x a ,若f x 与g x 的图象在交点处的切
−1
/e
线重合,则a =______.
e
【分析】设 与 的图象交点为 , ,再根据导数的几何意义
第5讲 利用导数求解函数的切线(3)
主讲人:某某某老师
某某学校
知识点一 利用导数求解公切线问题
知识点二 与公切线有关的参数问题
知识点一 利用导数求解公切线问题
试卷讲评课件
例1
若直线y = kx + b是曲线y = lnx + 2的切线,也是曲线
y = ln x + 1 的切线,则k =(
用导数求切线方程的四种类型

用导数求切线方程的四种类型求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点00()P x y ,及斜率,其求法为:设00()P x y ,是曲线()y f x =上的一点,则以P 的切点的切线方程为:000()()y y f x x x '-=-.若曲线()y f x =在点00(())P x f x ,的切线平行于y 轴(即导数不存在)时,由切线定义知,切线方程为0x x =.下面例析四种常见的类型及解法.类型一:已知切点,求曲线的切线方程此类题较为简单,只须求出曲线的导数()f x ',并代入点斜式方程即可. 例1 曲线3231y x x =-+在点(11)-,处的切线方程为( ) A.34y x =-B.32y x =-+ C.43y x =-+D.45y x =-解:由2()36f x x x '=-则在点(11)-,处斜率(1)3k f '==-,故所求的切线方程为(1)3(1)y x --=--,即32y x =-+,因而选B.类型二:已知斜率,求曲线的切线方程此类题可利用斜率求出切点,再用点斜式方程加以解决.例2 与直线240x y -+=的平行的抛物线2y x =的切线方程是( ) A.230x y -+= B.230x y --= C.210x y -+=D.210x y --=解:设00()P x y ,为切点,则切点的斜率为0022x x y x ='==|. 01x =∴.由此得到切点(11),.故切线方程为12(1)y x -=-,即210x y --=,故选D. 评注:此题所给的曲线是抛物线,故也可利用∆法加以解决,即设切线方程为2y x b =+,代入2y x=,得220x x b --=,又因为0∆=,得1b =-,故选D.类型三:已知过曲线上一点,求切线方程过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.例3 求过曲线32y x x =-上的点(11)-,的切线方程. 解:设想00()P x y ,为切点,则切线的斜率为02032x x y x ='=-|.∴切线方程为2000(32)()y y x x x -=--. 320000(2)(32)()y x x x x x --=--.又知切线过点(11)-,,把它代入上述方程,得3200001(2)(32)(1)x x x x ---=--. 解得01x =,或012x =-.故所求切线方程为(12)(32)(1)y x --=--,或13112842y x ⎛⎫⎛⎫⎛⎫--+=-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,即20x y --=,或5410x y +-=.评注:可以发现直线5410x y +-=并不以(11)-,为切点,实际上是经过了点(11)-,且以1728⎛⎫- ⎪⎝⎭,为切点的直线.这说明过曲线上一点的切线,该点未必是切点,解决此类问题可用待定切点法.类型四:已知过曲线外一点,求切线方程此类题可先设切点,再求切点,即用待定切点法来求解. 例4 求过点(20),且与曲线1y x=相切的直线方程.解:设00()P x y ,为切点,则切线的斜率为021x x y x ='=-|.∴切线方程为0021()y y x x x -=--,即02011()y x x x x -=--. 又已知切线过点(20),,把它代入上述方程,得0211(2)x x x -=--.解得000111x y x ===,,即20x y +-=.评注:点(20),实际上是曲线外的一点,但在解答过程中却无需判断它的确切位置,充分反映出待定切点法的高效性.例5 已知函数33y x x =-,过点(016)A ,作曲线()y f x =的切线,求此切线方程.解:曲线方程为33y x x =-,点(016)A ,不在曲线上. 设切点为00()M x y ,,则点M 的坐标满足30003y x x =-. 因200()3(1)f x x '=-,故切线的方程为20003(1)()y y x x x -=--.点(016)A ,在切线上,则有32000016(3)3(1)(0)x x x x --=--. 化简得308x =-,解得02x =-.所以,切点为(22)M --,,切线方程为9160x y -+=. 评注:此类题的解题思路是,先判断点A 是否在曲线上,若点A 在曲线上,化为类型一或类型三;若点A 不在曲线上,应先设出切点并求出切点.。
利用导数求曲线的切线和公切线以及切线条数专题总结.doc

导数中的切线问题专题总结一、求切线方程1.过曲线上一点求切线方程的三个步骤:求斜率)T求出曲线在点(椀,/(劭))处切线的斜率/'(%)] ZIZ写方程)一函氐斜式厂八城月(孙)(”』)写出切线方程):变形式)~{¥后可式变为二,般式[2.求过曲线y=f(x)外一点尸(如必)的切线方程的六个步骤⑴设切点(靛,£(%)).⑵利用所设切点求斜率k =及+Ax - f %A x '(3)用(xo, P(毛, %)表示斜率.(4)根据斜率相等求得知然后求得斜率无(5)根据点斜式写出切线方程.(6)将切线方程化为一般式.例1.已知曲线尸士X(1)求曲线在点尸(1, D处的切线方程;(2)求曲线过点0(1, 0)处的切线方程.(1)显侏1.1)是曲歧上的点•所以〃为切点,所求切圾斜率为函数■在点p( 1,1)的导致,即A=r(D = 一】・所以曲馒在P( 1,1)处的切线方程为y — 1 = 一(X 一1),即为y= 一工+2.(2)显传Q(】,0)不在曲线y=}上,则可设过该点的切线的切点为那么该切段<4率为k = f(a) = --y. a则切线方程为y- - = - -① a a将Q(1,0)代入方程:0 —,= 一上(1-a)・ a a将得a =;,代入方程①整理可得切发方程为y= - 41+4.例2.已知曲线y=±⑴求曲线在点尸(1,1)处的切线方程;(2)求曲线过点0(1,0)处的切线方程.3. (2016全国卷HD 已知f(x)为偶函数,当xVO 时,f(x)=f (-X)+3x,线y=f (x)在点(1, -3)处的切线方程是1 1则曲二、求切点坐标【小结】求切点坐标可以按以下步骤进行⑴设出切点坐标;(2)利用导数或斜率公式求出斜率;(3)利用斜率关系列方程,求出切点的横坐标;(4)把横坐标代入曲线或切线方程,求出切点纵坐标例1.已知抛物线 .21+1分别满足下列条件,请求出切点的坐标.⑴切线的倾斜角为45° .(2)切线平行于直线4LX-2=0.⑶切线垂直于直线升8L3=0.变式练习直线2:升升a(�)和曲线G y=y-x2+1相切,则a的值为切点坐标为.三、求两个函数公切线公切线问题:切点相同。
导数公切线问题

导数公切线问题
导数部分,曲线的切线问题是高考常考的知识点,如果仅仅是单个切线,问题比较好处理,例如已知切线方程求参数的值,一般都是根据以下两个等量关系来解题:1、根据导数的几何意义,切线的斜率k等于导函数在切点处的函数值;2、根据切点在切线上,又在曲线上列等式。
如果是考察公切线问题,稍微复杂一点,其实理解了一样简单,只需要分开来考虑,先解决切线和第一条曲线相切,然后再解决切线和第二条切线相切即可;用的方法及解题思维还是上面的两个等量关系。
导数专题:导数与曲线切线问题(6大题型)(解析版)

第1页共14页
导数与曲线切线问题
一、求曲线“在”与“过”某点的切线
1、求曲线“在”某点处的切线方程步骤
第一步(求斜率):求出曲线在点()()00,x f x 处切线的斜率0()
f x '第二步(写方程):用点斜式000()()()
y f x f x x x '-=-第三步(变形式):将点斜式变成一般式。
2、求曲线“过”某点处的切线方程步骤(此类问题的点不一定是切点)
第一步:设切点为()()00,Q x f x ;
第二步:求出函数()y f x =在点0x 处的导数0()f x ';
第三步:利用Q 在曲线上和0()PQ f x k '=,解出0x 及0()f x ';
第四步:根据直线的点斜式方程,得切线方程为000()()()y f x f x x x '-=-.
二、切线条数问题
求曲线的切线条数一般是设出切点()(),t f t ,由已知条件整理出关于t 的方程,把切线问条数问题转化为关于t 的方程的实根个数问题。
三、公切线问题
研究曲线的公切线,一般是分别设出两切点,写出两切线方程,然后再使用这两个方程表示同一条直线,但要注意以下两个方面:
(1)两个曲线有公切线,且切点是同一点;
(2)两个曲线有公切线,但是切点不是同一点。
四、已知切线求参数问题
此类问题常见的考查形式有两种,一是判断符合条件的切线是否存在,二是根据切线满足条件求参数的值或范围。
常用的求解思路是把切线满足条件转化为关于斜率或切点的方程或函数,再根据方程的
根的情况或函数性质去求解。
用导数求切线方程的四种类型知识讲解

用导数求切线方程的四种类型用导数求切线方程的四种类型浙江 曾安雄求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点00()P x y ,及斜率,其求法为:设00()P x y ,是曲线()y f x =上的一点,则以P 的切点的切线方程为:000()()y y f x x x '-=-.若曲线()y f x =在点00(())P x f x ,的切线平行于y 轴(即导数不存在)时,由切线定义知,切线方程为0x x =.下面例析四种常见的类型及解法. 类型一:已知切点,求曲线的切线方程此类题较为简单,只须求出曲线的导数()f x ',并代入点斜式方程即可. 例1 曲线3231y x x =-+在点(11)-,处的切线方程为( ) A.34y x =- B.32y x =-+ C.43y x =-+D.45y x =-解:由2()36f x x x '=-则在点(11)-,处斜率(1)3k f '==-,故所求的切线方程为(1)3(1)y x --=--,即32y x =-+,因而选B.类型二:已知斜率,求曲线的切线方程此类题可利用斜率求出切点,再用点斜式方程加以解决.例2 与直线240x y -+=的平行的抛物线2y x =的切线方程是( ) A.230x y -+=B.230x y --=C.210x y -+=D.210x y --=解:设00()P x y ,为切点,则切点的斜率为0022x x y x ='==|.01x =∴.由此得到切点(11),.故切线方程为12(1)y x -=-,即210x y --=,故选D.评注:此题所给的曲线是抛物线,故也可利用∆法加以解决,即设切线方程为2y x b =+,代入2y x =,得220x x b --=,又因为0∆=,得1b =-,故选D.类型三:已知过曲线上一点,求切线方程过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法. 例3求过曲线32y x x =-上的点(11)-,的切线方程. 解:设想00()P x y ,为切点,则切线的斜率为02032x x y x ='=-|.∴切线方程为2000(32)()y y x x x -=--.320000(2)(32)()y x x x x x --=--.又知切线过点(11)-,,把它代入上述方程,得3200001(2)(32)(1)x x x x ---=--. 解得01x =,或012x =-.故所求切线方程为(12)(32)(1)y x --=--,或13112842y x ⎛⎫⎛⎫⎛⎫--+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,即20x y --=,或5410x y +-=.评注:可以发现直线5410x y +-=并不以(11)-,为切点,实际上是经过了点(11)-,且以1728⎛⎫- ⎪⎝⎭,为切点的直线.这说明过曲线上一点的切线,该点未必是切点,解决此类问题可用待定切点法.类型四:已知过曲线外一点,求切线方程此类题可先设切点,再求切点,即用待定切点法来求解. 例4 求过点(20),且与曲线1y x=相切的直线方程. 解:设00()P x y ,为切点,则切线的斜率为0201x x y x ='=-|. ∴切线方程为00201()y y x x x -=--,即020011()y x x x x -=--. 又已知切线过点(20),,把它代入上述方程,得020011(2)x x x -=--. 解得000111x y x ===,,即20x y +-=. 评注:点(20),实际上是曲线外的一点,但在解答过程中却无需判断它的确切位置,充分反映出待定切点法的高效性.例5 已知函数33y x x =-,过点(016)A ,作曲线()y f x =的切线,求此切线方程.解:曲线方程为33y x x =-,点(016)A ,不在曲线上. 设切点为00()M x y ,,则点M 的坐标满足30003y x x =-. 因200()3(1)f x x '=-,故切线的方程为20003(1)()y y x x x -=--.点(016)A ,在切线上,则有32000016(3)3(1)(0)x x x x --=--. 化简得308x =-,解得02x =-.所以,切点为(22)M --,,切线方程为9160x y -+=.评注:此类题的解题思路是,先判断点A 是否在曲线上,若点A 在曲线上,化为类型一或类型三;若点A 不在曲线上,应先设出切点并求出切点.在初中数学中,曲线的切线没有一般的定义。
利用导数求曲线的切线和公切线以及切线条数专题总结.doc

导数中的切线问题专题总结一、求切线方程1.过曲线上一点求切线方程的三个步骤2.求过曲线y =f (x )外一点P (x 1,y 1)的切线方程的六个步骤(1)设切点(x 0,f (x 0)).(2)利用所设切点求斜率k =f ′(x 0)=li m Δx →0f x 0+Δx-f x 0Δx .(3)用(x 0,f (x 0)),P (x 1,y 1)表示斜率.(4)根据斜率相等求得x 0,然后求得斜率k .(5)根据点斜式写出切线方程.(6)将切线方程化为一般式.例1.已知曲线y =1x .(1)求曲线在点P (1,1)处的切线方程;(2)求曲线过点Q (1,0)处的切线方程.例2.已知曲线y=1 x .(1)求曲线在点P(1,1)处的切线方程;(2)求曲线过点Q(1,0)处的切线方程.3.(2016全国卷Ⅲ)已知f(x)为偶函数,当x<0时,f(x)=f(-x)+3x,则曲线y=f(x)在点(1,-3)处的切线方程是二、求切点坐标【小结】求切点坐标可以按以下步骤进行(1)设出切点坐标;(2)利用导数或斜率公式求出斜率;(3)利用斜率关系列方程,求出切点的横坐标;(4)把横坐标代入曲线或切线方程,求出切点纵坐标例1.已知抛物线y =2x 2+1分别满足下列条件,请求出切点的坐标.(1)切线的倾斜角为45°.(2)切线平行于直线4x -y -2=0.(3)切线垂直于直线x +8y -3=0..变式练习直线l :y =x +a (a ≠0)和曲线C :y =x 3-x 2+1相切,则a 的值为___________,切点坐标为____________.三、求两个函数公切线公切线问题:切点相同。
()()00x g x f =()()00''x g x f =切点不同。
()()()()k x g x f mkx x g m kx x f ==+=+=212211'',例1、 已知直线b kx y +=是曲线2ln +=x y 的切线,也是曲线x e y =的切线,求k 和b 的值解析:例2.若直线b kx y +=是曲线2ln +=x y 的切线,也是y =ln(x +1)的切线,求b 的值例3.已知函数f (x )=lnx ,g (x )=2﹣(x >0)(1)试判断当f (x )与g (x )的大小关系;(2)试判断曲线 y=f (x )和 y=g (x )是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;变式练习1.两曲线y =x 2−1和y =alnx −1存在公切线,则正实数a 的取值范围变式练习2.若曲线y =12e x 2与曲线y =alnx 在它们的公共点P (s,t )处有公切线,则实数a =变式练习 3.已知函数()()1263,1163223++=--+=x x x g ax x ax x f 和直线m:9+=kx y ,又()01'=-f ,是否存在k,使直线m 既是曲线()x f y =的切线,又是曲线()x g y =的切线?如果存在,求出k 的值四、切线条数切线的条数问题====以切点0x 为未知数的方程的根的个数例1.已知函数32()f x ax bx cx =++在点0x 处取得极小值-4,使其导数'()0f x >的x 的取值范围为(1,3),求:(1)()f x 的解析式;(2)若过点(1,)P m -可作曲线()y f x =的三条切线,求实数m 的取值范围.例2.已知函数f (x )=2x 3﹣3x+1,g (x )=kx+1﹣lnx .(1)设函数,当k <0时,讨论h (x )零点的个数;(2)若过点P (a ,﹣4)恰有三条直线与曲线y=f (x )相切,求a 的取值范围.变式练习.已知函数f (x )=x 2+2(1﹣a )x ﹣4a ,g (x )=﹣(a+1)2,则f (x )和g (x )图象的公切线条数的可能值是 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用导数求曲线的切线和公切线一.求切线方程【例1】.已知曲线f(x)=x3-2x2+1.(1)求在点P(1,0)处的切线l1的方程;(2)求过点Q(2,1)与已知曲线f(x)相切的直线l2的方程.提醒:注意是在某个点处还是过某个点!二.有关切线的条数【例2】.(2014•北京)已知函数f(x)=2x3﹣3x.(Ⅰ)求f(x)在区间[﹣2,1]上的最大值;(Ⅱ)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;(Ⅲ)问过点A(﹣1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)【解答】解:(Ⅰ)由f(x)=2x3﹣3x得f′(x)=6x2﹣3,令f′(x)=0得,x=﹣或x=,∵f(﹣2)=﹣10,f(﹣)=,f()=﹣,f(1)=﹣1,∴f(x)在区间[﹣2,1]上的最大值为.(Ⅱ)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y),则y0=2﹣3x,且切线斜率为k=6﹣3,∴切线方程为y﹣y0=(6﹣3)(x﹣x),∴t﹣y0=(6﹣3)(1﹣x),即4﹣6+t+3=0,设g(x)=4x3﹣6x2+t+3,则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,等价于“g(x)有3个不同的零点”.∵g′(x)=12x2﹣12x=12x(x﹣1),∴g(0)=t+3是g(x)的极大值,g(1)=t+1是g(x)的极小值.∴g(0)>0且g(1)<0,即﹣3<t<﹣1,∴当过点过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(﹣3,﹣1).(Ⅲ)过点A(﹣1,2)存在3条直线与曲线y=f(x)相切;过点B(2,10)存在2条直线与曲线y=f(x)相切;过点C(0,2)存在1条直线与曲线y=f(x)相切.【例3】.已知函数f(x)=lnax(a≠0,a∈R),.(Ⅰ)当a=3时,解关于x的不等式:1+e f(x)+g(x)>0;(Ⅱ)若f(x)≥g(x)(x≥1)恒成立,求实数a的取值范围;(Ⅲ)当a=1时,记h(x)=f(x)﹣g(x),过点(1,﹣1)是否存在函数y=h(x)图象的切线?若存在,有多少条?若不存在,说明理由.【解答】解:(I)当a=3时,原不等式可化为:1+e ln3x+>0;等价于,解得x,故解集为(Ⅱ)∵对x≥1恒成立,所以,令,可得h(x)在区间[1,+∞)上单调递减,故h(x)在x=1处取到最大值,故lna≥h(1)=0,可得a=1,故a的取值范围为:[1,+∞)(Ⅲ)假设存在这样的切线,设切点T(x,),∴切线方程:y+1=,将点T坐标代入得:即,①设g(x)=,则∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,故g(x)极大=g(1)=1>0,故g(x)极,小=g(2)=ln2+>0,.又g()=+12﹣6﹣1=﹣ln4﹣3<0,由g(x)在其定义域上的单调性知:g(x)=0仅在(,1)内有且仅有一根,方程①有且仅有一解,故符合条件的切线有且仅有一条.【作业1】.(2017•莆田一模)已知函数f (x )=2x 3﹣3x+1,g (x )=kx+1﹣lnx . (1)设函数,当k <0时,讨论h (x )零点的个数;三.切线与切线之间的关系 【例4】.(2018•绵阳模拟)已知a ,b ,c ∈R ,且满足b 2+c 2=1,如果存在两条互相垂直的直线与函数f (x )=ax+bcosx+csinx 的图象都相切,则a+c的取值范围是 .23a b c ++=则23b c +,∵b 2+c 2=1,∴sin ,cos b a ββ==设,∴235sin()b c βϕ+=+,故a+c ∈[﹣,],【例5】.已知函数f (x )=lnx ﹣a (x ﹣1),g (x )=e x ,其中e 为自然对数的底数. (Ⅰ)设,求函数t (x )在[m ,m+1](m >0)上的最小值;(Ⅱ)过原点分别作曲线y=f (x )与y=g (x )的切线l 1,l 2,已知两切线的斜率互为倒数,求证:a=0或.【解答】(Ⅰ)解:,令t'(x)>0得x>1,令t'(x)<0得x<1,所以,函数t(x)在(0,1)上是减函数,在(1,+∞)上是增函数,∴当m≥1时,t(x)在[m,m+1](m>0)上是增函数,∴当0<m<1时,函数t(x)在[m,1]上是减函数,在[1,m+1]上是增函数,∴t(x)min=t(1)=e.(Ⅱ)设l2的方程为y=k2x,切点为(x2,y2),则,∴x2=1,y2=e∴k2=e.由题意知,切线l1的斜率,∴切线l1的方程为,设l1与曲线y=f(x)的切点为(x1,y1),∴,∴,,又y1=lnx1﹣a(x1﹣1),消去y1,a后整理得,令,则,∴m(x)在(0,1)上单调递减,在(1,+∞)上单调递增,若x1∈(0,1),∵,,∴,而,在单调递减,∴.若x1∈(1,+∞),∵m(x)在(1,+∞)上单调递增,且m(e)=0,∴x1=e,∴综上,a=0或.【作业2】.(2017•黄山二模)已知函数f(x)=(ax2+x﹣1)e x+f'(0).(1)讨论函数f(x)的单调性;(2)若g(x)=e﹣x f(x)+lnx,h(x)=e x,过O(0,0)分别作曲线y=g(x)与y=h(x)的切线l1,l2,且l1与l2关于x轴对称,求证:﹣<a <﹣.四.求公切线的方程【例6】.(2018•安阳一模)已知函数,g(x)=3elnx,其中e为自然对数的底数.(Ⅰ)讨论函数f(x)的单调性.(Ⅱ)试判断曲线y=f(x)与y=g(x)是否存在公共点并且在公共点处有公切线.若存在,求出公切线l的方程;若不存在,请说明理由.【解答】解:(Ⅰ)由,得,令f′(x)=0,得.当且x≠0时,f′(x)<0;当时,f′(x)>0.∴f(x)在(﹣∞,0)上单调递减,在上单调递减,在上单调递增;(Ⅱ)假设曲线y=f(x)与y=g(x)存在公共点且在公共点处有公切线,且切点横坐标为x>0,则,即,其中(2)式即.记h(x)=4x3﹣3e2x﹣e3,x∈(0,+∞),则h'(x)=3(2x+e)(2x﹣e),得h(x )在上单调递减,在上单调递增,又h(0)=﹣e3,,h(e)=0,故方程h(x0)=0在(0,+∞)上有唯一实数根x=e,经验证也满足(1)式.于是,f(x0)=g(x)=3e,f′(x)=g'(x)=3,曲线y=g(x)与y=g(x)的公切线l的方程为y﹣3e=3(x﹣e),即y=3x.【作业3】.已知函数f (x)=lnx,g(x)=2﹣(x>0)(1)试判断当f(x)与g(x)的大小关系;(2)试判断曲线 y=f(x)和 y=g(x)是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;(3)试比较(1+1×2)(1+2×3)…(1+2012×2013)与 e4021的大小,并写出判断过程.五.与公切线有关的参数取值范围问题【例7】.已知函数f(x)=blnx,g(x)=ax2﹣x(a∈R).(Ⅰ)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;(Ⅱ)当b=1时,若曲线f(x)与g(x)在公共点P处有相同的切线,求证:点P唯一;(Ⅲ)若a>0,b=1,且曲线f(x)与g(x)总存在公切线,求正实数a的最小值.【解答】解:(Ⅰ)f′(x)=,g'(x)=2ax﹣1.∵曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,∴,解得a=b=1.(Ⅱ)设P(x0,y),则由题设有lnx=ax2﹣x…①,又在点P有共同的切线,∴f′(x0)=g′(x),∴,∴a=,代入①得lnx0=x,设h(x)=lnx ﹣+x,则h′(x)=+(x>0),则h′(x)>0,∴h(x)在(0,+∞)上单调递增,所以 h(x)=0最多只有1个实根,从而,结合(1)可知,满足题设的点P只能是P(1,0).(Ⅲ)当a>0,b=1时,f(x)=lnx,f′(x)=,f(x)在点(t,lnt)处的切线方程为y﹣lnt=(x﹣t),即y=x+lnx﹣1.与y=ax2﹣x,联立得ax2﹣(1+)x﹣lnt+1=0.∵曲线f(x)与g(x)总存在公切线,∴关于t(t>0)的方程△=+4a(lnt﹣1)=0,即=4a(1﹣lnt)(*)总有解.若t>e,则1﹣lnt<0,而>0,显然(*)不成立,所以 0<t<e,从而,方程(*)可化为4a=.令H(t)=(0<t<e),则H′(t)=.∴当0<t<1时,h'(t)<0;当1<t<e时,h'(t)>0,即 h(t)在(0,1)上单调递减,在(1,e)上单调递增.∴h(t)在(0,e)上的最小值为h(1)=4,∴要使方程(*)有解,只须4a≥4,即a≥1.∴正实数a的最小值为1.【例8】.(2017•韶关模拟).已知函数f(x)=ae x(a≠0),g(x)=x2(Ⅰ)若曲线c1:y=f(x)与曲线c2:y=g(x)存在公切线,求a最大值.(Ⅱ)当a=1时,F(x)=f(x)﹣bg(x)﹣cx﹣1,且F(2)=0,若F(x)在(0,2)内有零点,求实数b的取值范围.【解答】解:(Ⅰ)设公切线l与c1切于点(x1,a)与c2切于点(x2,),∵f′(x)=ae x,g′(x)=2x,∴,由①知x2≠0,①代入②:=2x2,即x2=2x1﹣2,由①知a=,设g(x)=,g′(x)=,令g′(x)=0,得x=2;当x<2时g′(x)>0,g(x)递增.当x>2时,g′(x)<0,g(x)递减.∴x=2时,g(x)max =g(2)=,∴amax=.(Ⅱ)F(x)=f(x)﹣bg(x)﹣cx﹣1=e x﹣bx2﹣cx﹣1,∵F(2)=0=F(0),又F(x)在(0,2)内有零点,∴F(x)在(0,2)至少有两个极值点,即F′(x)=e x﹣2bx﹣c在(0,2)内至少有两个零点.∵F″(x)=e x﹣2b,F(2)=e2﹣4b﹣2c﹣1=0,c=,①当b≤时,在(0,2)上,e x>e0=1≥2b,F″(x)>0,∴F″(x)在(0,2)上单调增,F′(x)没有两个零点.②当b≥时,在(0,2)上,e x<e2≤2b,∴F″(x)<0,∴F″(x)在(0,2)上单调减,F′(x)没有两个零点;③当<b<时,令F″(x)=0,得x=ln2b,因当x>ln2b时,F″(x)>0,x<ln2b时,F″(x)<0,∴F″(x)在(0,ln2b)递减,(ln2b,2)递增,所以x=ln2b时,∴F′(x)最小=F′(ln2b)=4b﹣2bln2b﹣+,设G(b)=F′(ln2b)=4b﹣2bln2b﹣+,令G′(b)=2﹣2ln2b=0,得2b=e,即b=,当b<时G′(b)>0;当b>时,G′(b)<0,当b=时,G(b)最大=G()=e+﹣<0,∴G(b)=f′(ln2b)<0恒成立,因F′(x)=e x﹣2bx﹣c在(0,2)内有两个零点,∴,解得:<b <,综上所述,b 的取值范围(,).【作业4】.已知函数f(x)=a(x ﹣)﹣blnx(a,b∈R),g(x)=x2.(1)若a=1,曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,求b的值;(2)若b=2,试探究函数f(x)与g(x)在其公共点处是否有公切线,若存在,研究a的个数;若不存在,请说明理由.六.公切线的条数问题【例9】.已知函数f(x)=lnx,g(x)=e x.(1)确定方程f(x)=实数根的个数;(2)我们把与两条曲线都相切的直线叫作这两条曲线的公切线,试确定曲线y=f (x),y=g(x)公切线的条数,并证明你的结论.【解答】解:(1)由题意得lnx==1+,即lnx﹣1=.分别作出y=lnx﹣1和y=的函数图象,由图象可知:y=lnx﹣1和y=的函数图象有两个交点,∴方程f(x)=有两个实根;(2)解:曲线y=f(x),y=g(x)公切线的条数是2,证明如下:设公切线与f(x)=lnx,g(x)=e x的切点分别为(m,lnm),(n,e n),m≠n,∵f′(x)=,g′(x)=e x,∴,化简得(m﹣1)lnm=m+1,当m=1时,(m﹣1)lnm=m+1不成立;当m≠1时,(m﹣1)lnm=m+1化为lnm=,由(1)可知,方程lnm=有两个实根,∴曲线y=f(x),y=g(x)公切线的条数是2条.【作业5】.已知函数f(x)=x2+2(1﹣a)x﹣4a,g(x)=﹣(a+1)2,则f (x)和g(x)图象的公切线条数的可能值是.【作业1解答】解:(1)f′(x)=(2x+1)(x﹣1)2=0,x=﹣或1,∴x=﹣是h(x)的零点;∵g′(x)=k﹣,k<0,g′(x)<0,g(x)在[1,+∞)上单调递减,g(x)的最大值为g(1)=k+1.k<﹣1,g(1)<0,g(x)在[1,+∞)上无零点;k=﹣1,g(1)=0,g(x)在[1,+∞)上有1个零点;﹣1<k<0,g(1)>0,g(e1﹣k)=ke1﹣k+k<0,g(x)在[1,+∞)上有1个零点;综上所述,k<﹣1时,h(x)有1个零点;﹣1≤k<0时,h(x)有两个零点;(2)设切点(t,f(t)),f′(x)=6x2﹣6x,∴切线斜率f′(t)=6t2﹣6t,∴切线方程为y﹣f(t)=(6t2﹣6t)(x﹣t),∵切线过P(a,﹣4),∴﹣4﹣f(t)=(6t2﹣6t)(a﹣t),∴4t3﹣3t2﹣6t2a+6ta﹣5=0①由题意,方程①有3个不同的解.令H(t)=4t3﹣3t2﹣6t2a+6ta﹣5,则H′(t)=12t2﹣6t﹣12at+6a=0.t=或a.a=时,H′(t)≥0,H(t)在定义域内单调递增,H(t)不可能有两个零点,方程①不可能有两个解,不满足题意;a时,在(﹣),(a,+∞)上,H′(t)>0,函数单调递增,在(,a)上,H′(t)<0,函数单调递减,H(t)的极大值为H(),极小值为H (a);a时,在(﹣∞,a),(,+∞)上,H′(t)>0,函数单调递增,在(a,)上,H′(t)<0,函数单调递减,H(t)的极大值为H(a),极小值为H ();要使方程①有三个不同解,则H()H(a)<0,即(2a﹣7)(a+1)(2a2﹣5a+5)>0,∴a>或a<﹣1.【作业2解答】解:由已知得f'(x)=[ax2+(2a+1)x]e x,f'(0)=0,所以f (x)=(ax2+x﹣1)e x.(1)f'(x)=[ax2+(2a+1)x]e x=[x(ax+2a+1)]e x.①若a>0,当或x>0时,f'(x)>0;当时,f'(x)<0,所以f(x)的单调递增区间为;单调递减区间为.②若a=0,f(x)=(x﹣1)e x,f'(x)=xe x,当x>0时,f'(x)>0;当x<0时,f'(x)<0,所以f(x)的单调递增区间为(0,+∞);单调递减区间为(﹣∞,0).③若,当或x<0时,f'(x)<0;当时,f'(x)>0,所以f(x)的单调递增区间为;单调递减区间为.④若,故f(x)的单调递减区间为(﹣∞,+∞).⑤若,当或x>0时,f'(x)<0;当时,f'(x)>0,所以f(x)的单调递增区间为;单调递减区间为.当a>0时,f(x)的单调递增区间为;单调递减区间为.当a=0时,f(x)的单调递增区间为(0,+∞);单调递减区间为(﹣∞,0).,当时,f(x)的单调递增区间为;单调递减区间为.当时,f(x)的单调递减区间为(﹣∞,+∞);当时,f(x)单调递增区间为;单调递减区间为,(0,+∞);(2)证明:g(x)=e﹣x f(x)+lnx=﹣e﹣x(ax2+x﹣1)e x+lnx=ax2+x﹣1+lnx,设l2的方程为y=k2x,切点为(x2,y2),则,所以x2=1,y2=e,k2=e.由题意知k1=﹣k2=﹣e,所以l1的方程为y=﹣ex,设l1与y=g(x)的切点为(x1,y1),则.又,即,令,在定义域上,u'(x)>0,所以(0,+∞)上,u(x)是单调递增函数,又,所以,即,令,则,所以,故.【作业3解答】解:(1)证明:设F(x)=f(x)﹣g(x),则F′(x)=﹣,由F'(x)=0,得x=3,当0<x<3时,F'(x)<0,当x>3时F'(x)>0,可得F(x)在区间(0,3)单调递减,在区间(3,+∞)单调递增,所以F(x)取得最小值为F(3)=ln3﹣1>0,∴F(x)>0,即f(x)>g(x);(2)假设曲线f(x)与g(x)有公切线,切点分别为P(x0,lnx)和Q(x1,2﹣).因为f′(x)=,g′(x)=,所以分别以P(x0,lnx)和Q(x1,2﹣)为切线的切线方程为y=+lnx﹣1,y=+2﹣.令,即2lnx1+﹣(3+ln3)=0.令h(x)=2lnx1+﹣(3+ln3).所以由h′(x)=﹣=0,得x1=3.显然,当0<x1<3时,h'(x)<0,当x1>3时,h'(x)>0,所以h(x)min=ln3﹣1>0,所以方程2lnx1+﹣(3+ln3)=0无解,故二者没有公切线.所以曲线y=f(x)和y=g(x)不存在公切线;(3)(1+1×2)(1+2×3)•…•(1+2012×2013)>e4021.理由:由(1)可得lnx>2﹣(x>0),可令x=1+n(n+1),可得ln(1+n(n+1))>2﹣>2﹣=2﹣3(﹣),则ln(1+1×2)+ln(1+2×3)+…+ln(1+2012×2013)>2×2012﹣3(1﹣+﹣+…+﹣)=4024﹣3+>4021.即有(1+1×2)(1+2×3)…(1+2012×2013)>e4021.【作业4解答】解:(Ⅰ)∵f(x)=x﹣﹣blnx,∴f′(x)=1+﹣,由于曲线y=f(x)在点(1,f(1))处的切线垂直于y轴,故该切线斜率为0,即f′(1)=0,即1+1﹣b=0,∴b=2;(2)假设f(x),g(x)的图象在其公共点(x0,y)处存在公切线,由f(x)=a(x﹣)﹣2lnx,得f′(x)=,g′(x)=2x,由f′(x0)=g′(x),得=2x,即2x3﹣ax2+2x﹣a=0,即(x02+1)(2x﹣a)=0,则x=,又函数的定义域为(0,+∞),当a≤0时,x0=≤0,则f(x),g(x)的图象在其公共点(x,y)处不存在公切线;当a>0时,令f()=g(),﹣2ln﹣2=,即=ln,令h(x)=﹣ln(x>0),h′(x)=x﹣=,则h(x)在(0,2)递减,(2,+∞)递增.且h(2)=﹣<0,且当x→0时,h(x)→+∞;当x→+∞时,h(x)→+∞,∴h(x)在(0,+∞)有两个零点,∴方程=ln在(0,+∞)解的个数为2.综上:当a≤0时,函数f(x)与g(x)的图象在其公共点处不存在公切线;当a>0时,函数f(x)与g(x)的图象在其公共点处存在公切线,a的值有2个.在导数的练习中,常见这一类题型:已知含有的一个不等式,以及的一些其他性质,让解不等式或者比较大小。
