离散数学(双语) - 第九章答案(高辉)
离散数学(刘任任版)第9章答案

d
abcdea = c 1 ,Q c1 = 5(奇数) ∴至少要用3种颜色
由对称性可考虑 3种色的任一种方案, 如图.于是联结内外两 个回路的五条边(af , bg , ch, di, ej )也就随之确定了它们的颜 色, 如图。从而必有if着α色, 而fg不能着α、β和γ .故只有着 颜色δ .
2011-5-27 10
p2 k ≥ 2 p − 2q
2
2011-5-27
2. 证明: χ ( K 1 ) = 1 ,且 χ ( K 1 − v ) = 0 < 1 。故 K 1 是 1 临 (1) 界图。反之 , 设 G 是 1临界图 , 若 | V ( G ) |> 1,则 G 是零图。 但 χ ( G − V ) = χ ( G ) = 1, 即 G 不是临界图,故 从而 | V ( G ) |= 1,故 G = K 1 ( 2 ) χ ( K 2 ) = 2,且 χ ( K 2 − v ) = 1 < χ ( K 2 ). 故 K 2 是 2临界图 .。 反之,设 G 是 2临界图,即 χ ( G ) = 2。于是可划分 成两个极大独立集 V 1 和 V 2 ( 二分图 )。若 | V 1 |> 1,则任 | V 2 |= 1。 取 u ∈ V ,有 χ ( G − u ) = 2 = χ ( G )。此与 G 是 2临界图矛盾, 故 | V 1 |= 1。同理可证 设 V 1 = {u }, V 2 = { v },显然 uv ∈ E ( G ),故 G = K 2。
2011-5-27 14
= t (t − 3t + 2)(t − 4t + 5)
2 2
= (t 5 − 3t 2 + 2t )(t 2 − 4t + 5) = t − 4t + 5t − 3t + 12t − 15t + 2t − 8t + 10t
离散数学--第九章--作业答案
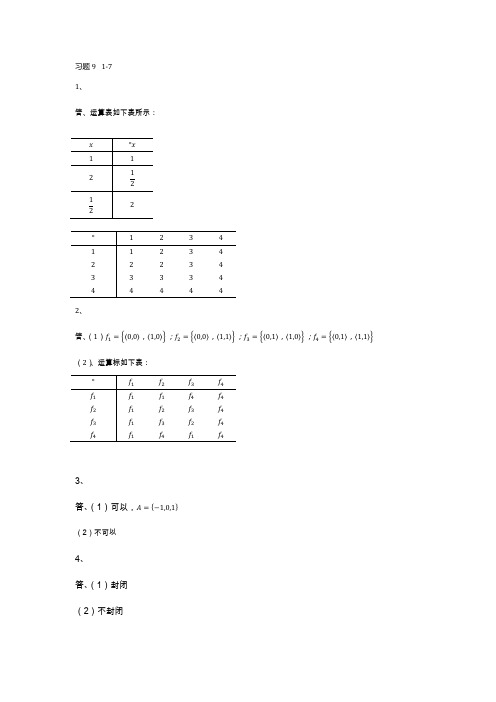
习题9 1-71、答、运算表如下表所示:2、答、(1),;,;,;,(2)、运算标如下表:3、答、(1)可以,(2)不可以4、答、(1)封闭(2)不封闭(3)加法、乘法都封闭(4)加法不封闭,乘法封闭(5)不封闭(6)加法、乘法都封闭(7)封闭(8)加法不封闭,乘法封闭(9)加法不封闭,乘法封闭(10)加法不封闭,乘法封闭5、答、(1)没有交换律、结合律,对于一个运算不能考虑分配率(3)加法满足交换律、结合律,乘法满足结合律,乘法对加法满足分配率(4)乘法满足结合律(6)加法和乘法都满足交换律、结合律,乘法对加法满足分配率(7)满足结合律(8)乘法满足交换律、结合律(9)乘法满足交换律、结合律(10)乘法满足交换律、结合律6、答、(1)没有单位元、零元,没有可逆元素(3)n阶全0矩阵是加法单位元,也是乘法的零元;n阶单位矩阵是乘法单位元;加法没有零元。
任意n阶矩阵M对于加法都是可逆元素,其逆元为-M;只有n阶可你矩阵(行列式不为0)对乘法是可逆元素,其逆元为(4)乘法单位元为n阶单位矩阵,没有零元。
每个矩阵M都是逆元(6)加法单位元0,没有零元,每个元素x都可逆,其逆元是它的相反数-x,当n=1时,乘法有单位元1,只有两个可逆元素:,。
当>时乘法没有单位元和可逆元素。
(7)没有单位元和零元,也没有可逆元素(8)乘法单位元为1,只有1是可逆元素,(9)乘法单位元为1,只有1是可逆元素,,乘法零元是0(10)乘法没有单位元、零元以及可逆元素7、答、(1)4*6=4,7*3=3(2)满足交换律、结合律、幂等律(3)没有单位元,1是零元,没有可逆元素。
离散数学习题答案解析

离散数学习题答案解析(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p:李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语∧解:设p:王强学过法语;q:刘威学过法语;则命题符号化的结果是p q(9)只有天下大雨,他才乘班车上班→解:设p:天下大雨;q:他乘班车上班;则命题符号化的结果是q p (11)下雪路滑,他迟到了解:设p:下雪;q:路滑;r:他迟到了;则命题符号化的结果是()∧→p q r 15、设p:2+3=5.q:大熊猫产在中国.r:太阳从西方升起.求下列复合命题的真值:(4)()(())∧∧⌝↔⌝∨⌝→p q r p q r解:p=1,q=1,r=0,∧∧⌝⇔∧∧⌝⇔,p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型:(2)()→⌝→⌝p p q解:列出公式的真值表,如下所示:由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值: (4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值: (2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式, 所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式, 所以成假赋值为100。
离散数学答案 第九章 特殊代数系统

第九章 特殊的代数系统习题9.11.解 ⑴是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,,,,N c b a ∈∀有(){}{}c b a c b a c b a ,,max ,max == ,而(){}{}c b a c b a c b a ,,m ax ,m ax == ,因此,()()c b a c b a =,所以,运算“ ”满足结合律的,故>< ,N 是半群;⑵是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,N c b a ∈∀,,,有()c c b c b a == ,而()c c a c b a == ,则()()c b a c b a =,所以,运算“ ”满足结合律,故><,N 是半群;⑶是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,N c b a ∈∀,,,有()abc c ab c ab c b a 4)2(2)2(=== ,()()abc bc a bc a c b a 422)2(=== ,即()()c b a c b a = ,所以,运算“ ”满足结合律,故>< ,N 是半群。
⑷不是半群。
虽然,二元运算“ ”在N 上是封闭的,即>< ,N 是一个代数系统,但是 对于5,3,6,因为,()4635635635=--=-= ,而2635635)63(5=--=-= ,即())63(5635 ≠,所以,运算“ ”不满足结合律,故>< ,N 不是半群。
2.解 ⑴正确。
因为,运算显然封闭。
⑵正确。
abc bc ac ab c b a c ab b a c b a ++++++=++= )()(, bc ac ab c b a bc c b a c b a +++++=++=)()( ,即是()()c b a c b a =,所以︒满足结合律。
离散数学课后答案

离散数学课后答案1. 集合论1.1. 集合的基本概念•问题1:什么是集合?如何表示一个集合?集合是由一些确定的元素构成的整体。
可以使用以下方式表示一个集合:–列举法:将集合的所有元素逐一列举出来,并用大括号{}包括起来。
–描述法:使用一种公式或条件来描述集合中的元素的特点,并用大括号{}包括起来。
–空集:不包含任何元素的集合,用符号∅表示。
•问题2:集合的关系有哪些?集合的关系有以下几种:–包含关系(⊆):集合A的所有元素都属于集合B,则称集合A是集合B的子集,表示为A⊆B。
–真包含关系(⊂):集合A是集合B的子集,且A≠B,则称集合A是集合B的真子集,表示为A⊂B。
–并集(∪):将两个集合中的所有元素合并在一起,去除重复元素。
–交集(∩):将两个集合中共有的元素提取出来。
–差集(-):从一个集合中去掉与另一个集合中相同的元素。
–互斥关系:两个集合没有共同的元素,即交集为空集。
1.2. 集合的运算•问题1:集合的运算有哪些?集合的运算有以下几种:–并集运算(∪):将两个集合中的所有元素合并在一起,去除重复元素。
–交集运算(∩):将两个集合中共有的元素提取出来。
–差集运算(-):从一个集合中去掉与另一个集合中相同的元素。
–补集运算(C):对于给定的全集U,集合A 在U中的补集就是U中除去集合A中的所有元素所构成的集合,表示为A’。
–笛卡尔积(×):将两个集合的元素按照有序对的形式进行组合,构成一个新的集合。
•问题2:集合运算的性质有哪些?集合运算的性质有以下几种:–交换律:A∪B = B∪A,A∩B = B∩A。
–结合律:(A∪B)∪C = A∪(B∪C),(A∩B)∩C = A∩(B∩C)。
–分配律:A∪(B∩C) = (A∪B)∩(A∪C),A∩(B∪C) = (A∩B)∪(A∩C)。
–吸收律:A∪(A∩B) = A,A∩(A∪B) = A。
–互补律:A∪A’ = U,A∩A’ = ∅。
离散数学第四版课后答案(第9章)

第9章 习题解答9.1 有5片树叶.分析 设T 有x 个1度顶点(即树叶).则T 的顶点数Tx x n ,523+=++=的边数.41x n m +=-=由握手定理得方程.∑=+=⋅+⨯+⨯==+=ni ix x vd x m 1.1312233)()4(22由方程解出.5=x所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.分析 设T 中有x 个3度顶点,则T 中的顶点数,7x n +=边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122由方程解出x=5.所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.要析 设T 中有x 个3度顶点,则T 中的顶点数x n +=7,边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122.由此解出5=x ,即T 中有5个3度顶.T 的度数列为1,1,1,1,1,1,1,3,3,3,3,3.由于T 中只有树叶和3度顶点,因而3度顶点可依次相邻,见图9.7所示. 还有一棵与它非同构的树,请读者自己画出.9.3 加1-k 条新边才能使所得图为无向树.分析 设具有k 个连通分支的森林为G,则G 有k 个连通分支i K T T TT ,,,21全为树,.,,2,1k i =加新边不能在i T 内部加,否则必产生回路.因而必须在不同的小树之间加新边. 每加一条新边后,所得到的森林就减少一个连通分支. 恰好加1-k 条新边,就使得图连通且无回路,因而是树.在加边过程中,只需注意,不在同一人连通分支中加边. 下面给出一种加边方法,取iv 为iT 中顶点,加新边1,,2,1),(1-=+k i vv i i,则所得图为树,见图9.8 给出的一个特例.图中虚线边为新加的边.9.4 不一定.分析 n 阶无向树T 具有1-n 条边,这是无向树T 的必要条件,但不是充公条件.例如, 阶圈(即1-n 个顶点的初级回路)和一个孤立点组成无向简单图具有1-n 条边, 但它显然不是树.9.5 非同构的无向树共有2棵,如图 9.9所示.分析由度数列1,1,1,1,2,2,4不难看出,唯一的4度顶点必须与2度顶点相邻,它与1个2度顶点相邻,还是与两个2度顶点都相邻,所得树是非同构的,再没有其他情况.因而是两棵非同构的树.9.6 有两棵非同构的生成树,见图9.10所示.分析图9.10 是5阶图(5个顶点的图), 5阶非同构的无向树只有3棵,理由如下. 5阶无向树中,顶点数5=n,边数4=m,各顶点度数之和为8,度数分配方案有3种,分别为①1,1,1,1,4;②1,1,1,2,3;③1,1,2,2.2.每种方案只有一棵非同构的树.图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种,也就是说,它至多有3棵非同构的生成树, 但由于图中无4度顶点,所示,不可能有度数列为①的生成树,于是该图最多有两棵非同构的生成树. 但在图9.10 中已经找出了两个非同构的生成树,其中(1)的度数列为③,(2) 的度数列为②,因而该图准确地有两棵非同构的生成树.9.7 基本回路为: .,,,hfab C gfa C ead C cbad C h g e c====基本回路系统为}.,,,{h g e cC C C C基本割集为:},,{},,{},,,{},,,,,{h g f Sc ed S h c b S h g ce a S fd b a ====基本回路系统为},,,{f d b aS S S S.分析 1°注意基本回路用边的序列表示,而基本割集用边的集合表示.2° 基本回路中,只含一条弦,其余的边全为树枝,其求法是这样的: 设弦),(j iv ve =,则jiv v,在生成树T 中,且在T 中,ji v v ,之间存在唯一的路径ji ,Γ与),(j iv ve =组成的回路为G 中对应弦e 的基本回路.3° 基本割集中,只含一条树枝,其余的边都是弦,其求法是这样的:设树枝),(j iv ve =,则e 为T 中桥,于是eT-(将e 从T中支掉),产生两棵小树1T 和2T ,则}|{21'''中和的两端点分别在中且在T T e G e e S e =e S 为树枝e 对应的基本割集. 显然ee S S e ,∈中另外的边全是弦. 注意,两棵小树1T 和2T ,中很可能有平凡的树(一个顶点).aT -得两棵小树如图9.11中(1) 所示. G 中一个端点在i T 中,另一个端点在2T 中的边为a(树枝), h g c e ,,,,它们全是弦,于是},,,,{h g c e a Sa=bT - 得两棵小树如图9.11中(2) 所示, 其中有一棵为平凡树. G 中一个端点在1T 中,另一个端点在2T 中的边数除树枝b 外,还有弦,,h c 所以, },,{h c b Sb=dT -产生的两棵小树如图9.11中(3) 所示 . G 中一个端点在1T 中,另中一个端点在2T 中的边,除树枝d 外,还有两条弦e c ,,所示, },,{e c d Sd=fT -产生的两棵小树如图9.11中(4) 所示. 由它产生的基本割集为},,{h g f Sf=9.8 按Kruskal 求最小生成树的算法,求出的图9.3(1)的最小生成树T 为图9.12中(1) 所示, 其7)(=T W .(2) 的最小生成树T 为图9.12中(2)所示,其.11)(=T W9.9 421,,B B B为前缀码.分析 在421,,B B B中任何符号串都不是另外符号串的前串,因而它们都是前缀码.而在3B 中, 1是11,101的前缀,因而3B不是前缀码. 在5B 中,,a 是ac aa ,等的前缀,因而5B 也不是前缀码.9.10 由图9.4 (1) 给出的2元前缀码.}11,011,01010,0100,00{1=B由(2) 给出的3元前缀码为.}.2,1,022,0202,0201,0200,01,00{2=B分析 1B 是2元树产生的2元前缀码(因为码中的符号串由两个符号0,1组成),类似地,2B 是由3元树产生的3元前缀码(因为码中符号串由3个符号0,1,2组成).一般地,由r 元树产生r 元前缀码.9.11 (1) 算式的表达式为ji h g f e d c b a *)*()()*)*((((++÷-+.由于使其成为因而可以省去一些括号优先于,,,*,-+÷ji h g f e d c b a **)()*)*((++÷-+.(2) 算式的波兰符号法表达式为.****hij fg bcde a ++-÷+(3) 算式的逆波兰符号法表达式为.****+÷+-+jI hi fg e d abc9.12 答案 A:①; B ②; C:④; D:⑨.分析 对于每种情况都先求出非同构的无向树,然后求出每棵非同构的无向树派生出来的所有非同构的根树.图9.13 中,(1),(2),(3),(4)分别画出了2阶,3阶,4阶,5阶所有非同构的无向树,分别为1棵,1棵,2棵和3棵无向树.2阶无向树只有1棵,它有两个1度顶点,见图9.13中(1)所示,以1个顶点为树根,1个顶点为树叶,得到1棵根树.3阶非同的无向树也只有1棵,见图9.13中(2)所示.它有两个1度顶点,1个2度顶点,以1度顶点为根的根树与以2度顶点为根的树显然是非同构的根树,所以2个阶非同构的根树有两棵.4阶非同构的无向树有两棵,见图9.13中(3)所示. 第一棵树有3片树叶,1个3度顶点, 以树叶为根的根树与以3度顶点为根的树非同构.所以,由第一棵树能生成两个非同构的根树, 见图9.14 中(1)所示. 第二棵树有两片树叶,两个2度顶点,由对称性,以树叶为根的根树与2度顶点为根的根树非同构,见图9.14中(2) 所示. 所以,4阶非同构的根树有4棵.5阶非同构的无向树有3棵,见图9.13中(4)所示. 由第一棵能派生两棵非同构的根树, 由第二棵能派生4棵非同构的根树,由第三棵能派生3棵非同构的根树,所以,5阶非同构的根树共有9棵,请读者将它们都画出来.9.13 答案 A:②; B:②; C:③; D:③; E:③;F:④; G: ④; H:③.分析 将所有频率都乘100,所得结果按从小到大顺序排列:.35,20,15,10,10,5,5=======a b c d e f g w w w w w w w以以上各数为权,用Huffman 算法求一棵最优树,见图9.15所示.对照各个权可知各字母的前缀码如下:a ——10,b ——01,c ——111,d ——110,e ——001,f ——0001,g ——0000.于是,a,b 的码长为e d c ,,,2的码长为g f ,,3的码长为4. W(T)=255(各分支点的权之和),W(T)是传输100按给定频率出现的字母所用的二进制数字,因则传输104个按上述频率出现的字母要用25500⨯个二进制数字..24=1055最后还应指出一点,在画最优树叶, 由于顶点位置的不同,所得缀码可能不同,即有些字母的码子在不同的最优树中可能不同,但一般说来码长不改变.特别是,不同的最优树,它们的权是固定不变的.9.14 答案 A:②; B:④分析用2元有序正则树表示算式,树叶表示参加运算的数,分支点上放运算符,并将被减数(被除数)放在左子树上,所得2元树如图9.16所示.用前序行遍法访问此树,得波兰符号表示法为abc-++de-*.**ghf用后序行遍法访问此树,得逆波兰符号表示法为dec*fghab--++**。
大学_《离散数学》课后习题答案

《离散数学》课后习题答案《离散数学》简介1、集合论部分:集合及其运算、二元关系与函数、自然数及自然数集、集合的基数2、图论部分:图的基本概念、欧拉图与哈密顿图、树、图的矩阵表示、平面图、图着色、支配集、覆盖集、独立集与匹配、带权图及其应用3、代数结构部分:代数系统的基本概念、半群与独异点、群、环与域、格与布尔代数4、组合数学部分:组合存在性定理、基本的计数公式、组合计数方法、组合计数定理5、数理逻辑部分:命题逻辑、一阶谓词演算、消解原理离散数学被分成三门课程进行教学,即集合论与图论、代数结构与组合数学、数理逻辑。
教学方式以课堂讲授为主,课后有书面作业、通过学校网络教学平台发布课件并进行师生交流。
《离散数学》学科内容随着信息时代的到来,工业革命时代以微积分为代表的连续数学占主流的地位已经发生了变化,离散数学的重要性逐渐被人们认识。
离散数学课程所传授的思想和方法,广泛地体现在计算机科学技术及相关专业的诸领域,从科学计算到信息处理,从理论计算机科学到计算机应用技术,从计算机软件到计算机硬件,从人工智能到认知系统,无不与离散数学密切相关。
由于数字电子计算机是一个离散结构,它只能处理离散的或离散化了的数量关系,因此,无论计算机科学本身,还是与计算机科学及其应用密切相关的现代科学研究领域,都面临着如何对离散结构建立相应的数学模型;又如何将已用连续数量关系建立起来的数学模型离散化,从而可由计算机加以处理。
离散数学是传统的逻辑学,集合论(包括函数),数论基础,算法设计,组合分析,离散概率,关系理论,图论与树,抽象代数(包括代数系统,群、环、域等),布尔代数,计算模型(语言与自动机)等汇集起来的一门综合学科。
离散数学的应用遍及现代科学技术的诸多领域。
离散数学也可以说是计算机科学的基础核心学科,在离散数学中的有一个著名的典型例子-四色定理又称四色猜想,这是世界近代三大数学难题之一,它是在1852年,由英国的一名绘图员弗南西斯格思里提出的,他在进行地图着色时,发现了一个现象,“每幅地图都可以仅用四种颜色着色,并且共同边界的国家都可以被着上不同的颜色”。
离散数学第九章图的道路与连通习题答案

P PT=
abcdefg a 1111000 b 1111000 c 1111000 d 1111000 e 0000100 f 0000011 g 0000011
a
b
g
e
d
c
f
所以强分图有:
{a,b,c,d},{e},{f,g}
2021/4/9
10
感谢您的阅读收藏,谢谢!
2021/4/9
11
m=n(n-1)/4,一个图为自补图的最低条件可设为结 点数须为4k或4k+1。 例如:当k=1时:
2021/4/9
5
习题十 10
判别图中两图是否同构,并说明理由。
解:
两图不同构。因为如果同构,两图中唯一的3度结点 应对应,但左图3度点的邻接结点度数分布是2,1, 1,而右图的为2,2,1,不对应。
a 0101000
b 0010100
解:
c 1100100
邻接矩阵A= d 0 0 1 0 0 0 0
e 0000000
f 0000101
g 0000110
abcdefg
a 1111100 b 1111100 c 1111100
可达矩阵P= d 1 1 1 1 1 0 0
e 0000000 f 0000111 g 0000111
Cn2 。 其次,当G是完全图时,每对结点间都有一条边,
即m =Cn2 , 反之亦然。
2021/4/9
Байду номын сангаас
1
证明:在不少于2人的一群人中,至少有2个人这群人中有相 同数目的朋友。
证明:
可转化为图论问题,以人为结点,如果2人是朋友关系,就 对应的2个结点之间连一条边。
离散数学-第9章 图

例9.2.2 分析
分析 由于V中有5个结点,因此要用5个小圆圈 分别表示这5个结点,点的具体摆放位置可随意 放。而对E中的6条边,圆括号括起的结点对表示 无向边,直接用直线或曲线连接两个端点,尖括 号括起的结点对表示有向边,前一个是始点,后 一个始终点,用从始点指向终点的有向直线或曲 线连接。
ai
j
1 , 0 ,
若 ( vi,vj ) 否则
E
或
vi,vj
E
i,j 1,2,3, ,n
2023/11/27
例9.2.4
试写出下图所示图G的邻接矩阵。
分解析 若首结先点将排图序中为的v16v个2v结3v4点v5排v6,序则, v1 然其邻后接利矩用v1阵定v义2 9.v23.2写v4出其v5邻接v6矩阵。 初按结学vv点时21 0排可1 序先01标在上0矩01结阵1 点的000,行0若与1第01列i1前行01分前别的 v5 结在否则可邻点则vvvv标接到为6543 记矩第00011。A如阵jG列若下0001的前结:第11100的点0111i10000行结排第点序111100111j有为11100列边v11000元00111v相2素11100v连30111为v4,v15则,v6,
2023/11/27
例9.2.5
试写出下图所示图G的所有结点的邻接点、所有边
的邻接边,并指出所有的孤立结点和环。
v3
v4
v5
e4 e5 v2
e6 e1
e2 v6 e7
v1 e3
2023/11/27
例9.2.5 分析
根据定义9.2.4,如果两个结点间有边相连,那 么它们互为邻接点;如果两条边有公共结点,那 么它们互为邻接边。需要注意的是,只要当一个 结点处有环时,它才是自己的邻接点;由于一条 边有两个端点,在计算邻接边时要把这两个端点 都算上,例如e2和e4都是e1的邻接边。所有边都 是自己的邻接边。
离散数学答案英文版

P.161.14.f) If I did not buy a lottery ticket this week, then I did not win the million dollar jackpot on Friday.g) I did not buy a lottery ticket this week, and I did not win the million dollar jackpot on Friday.h ) Either I did not buy a lottery ticket this week, or else I did buy one and won the million dollar jackpot on Friday.10.a) r ∧┐q b) p ∧ q∧ r c)r → pd) p ∧┐q ∧ r e) (p ∧q) → r f) r↔ ( q ∨ p)20.a) If I am to remember to send you the address, then you will have to send me ane-mail message.(This has been slightly reworded so that the tenses make more sense.)b) If you were born in the United States, then you are a citizen of this country.c) If you keep your textbook, then it will be a useful reference in your future courses.(The word "then" is understood in English, even if omitted.)d) If their goaltender plays well, then the Red Wings will win the Stanley Cup.e) If you get the job, then you had the best credentials.f) If there is a storm, then the beach erodes.g) If you log on to the server, then you have a valid password.h) If you don’t begin your climb too late, then you will reach the summit.33.c)P.261.28.a) Kwame will not take a job in industry and he will not go to graduate school.b) Yoshiko doesn’t know Java or she doesn’t know calculus.c) James is not young or he is not strong.d) Rita will not move to Oregon and she will not move to Washington.10.a)c)12.a) Assume the hypothesis is true. Then p is false. Since p∨q is true, we conclude that q must be true.Here is a more "algebraic" solution:[┐p∧(p ∨q)]→q <=> ┐[┐p∧(p ∨q)]∨q <=> ┐┐p∨┐(p∨q)∨q <=> p∨┐(p∨q)∨q <=> (p ∨q)∨┐(p∨q) <=> Tc) Assume the hypothesis is true. Then p is true, and since the second part of the hypothesis is ture, we conclude that q is also true, as desired.51.((p ↓ p) ↓ q )↓((p ↓ p) ↓ q )7.The graph is planar.20.The graph is not homeomorphic to K3,3, since by rerouting the edge between a and h we seethat it is planar.22.Replace each vertex of degree two and its incident edges by a single edge. Then the result isK3,3 : the parts are {a,e,i} and {c,g,k}. Therefore this graph is homeomorphic to K3,3.23.The graph is planar.25. The graph is not planar.9.83. 3F E8. 310.417. time slot 1: Math 115, Math 185; time slot 2: Math 116, CS 473;time slot 3: Math 195, CS 101; time slot 4: CS 102time slot 5: CS 273P.461.33. a) true b) false c) false d) false5. a) There is a student who spends more than 5 hours every weekday in class.b) Every student spends more than 5 hours every weekday in class.c) There is a student who does not spend more than 5 hours every weekday in class.d) No student spends more than 5 hours every weekday in class.9. a) x(P(x)∧Q(x)) b) x(P(x)∧﹁Q(x))c) x(P(x)∨Q(x)) d) x﹁(P(x)∨Q(x))16. a) true b) false c) true d) false24. Let C(x) be the propositional function “x is in your class.”a)x P(x) and x(C(x)→P(x)), where P(x) is “x has a cellular phone.”b) x F(x) and x(C(x)∧F(x)), where F(x) is “x has seen a foreign movie.”c)x﹁S(x) and x(C(x)∧﹁S(x)), where S(x) is “x can swim.”d)x E(x) and x(C(x)→E(x)), where E(x) is “x can solve quad ratic equations.”e)x﹁R(x) and x(C(x)∧﹁R(x)), where R(x) is “x wants to be rich.”62.a) x (P(x)→﹁S(x)) b)x(R(x)→S(x))c) x (Q(x)→P(x))d)x(Q(x)→﹁R(x))e) Yes. If x is one of my poultry, then he is a duck (by part(c)), hence not willing to waltz (part (a)). Since officers are always willing to waltz (part (b)), x is not an officer.1.412.d)x┐C(x, Bob)h)x y (I(x) ∧((x≠y) →┐ I(y)))k)x y( I(x) ∧┐C(x, y))n)x y z ((x≠y) ∧┐ (C(x, z) ∧ C(y, z)))14.a) x H(x), where H(x) is “x can speak Hindi”and the universe of the discourse consists of all students in this class.b) x y P(x, y), where P(x, y) is “x plays y.” and the universe of the discourse for x consists of all students in this class, and the universe of the discourse for y consists of all sports.c) x A(x) ∧┐H(x) , where A(x) is “x has visited Alaska.” , H(x) is “x has visited Hawaii” and the universe of the discourse for x consists of all students in this class.d) x y L(x, y), where L(x, y) is “x has learned programming language y” and the universe of the discourse for x consists of all students in this class, and the universe of the discourse for y consists of all programming languages.e) x z y (Q(y,z) →P(x, y)), where P(x, y) is“x has taken course y.”, Q(y, z) is “course y is offered by department z.”, and the universe of the discourse for x consists of all students in this class, the universe of the discourse for y consists of all courses in this school, and the universe of the discourse for z consists of all departments in this school.f)x y z ( (x≠y) ∧P(x, y)∧ ((x≠y≠z) →┐P(x, z))), where P(x, y) is “x and y grew up in the same town.” and the universe of the discourse for x, y, z consists of all students in this class.g) x y z C(x, y) ∧G(y, z), where C(x, y) is “x has chatted with y”, G(y, z) is “y is in chat group z”, the universe of the discourse for x, y consists of all students in this class, and the universe of the discourse for z consists of all chat group in this class.a) There is an additive identity for the real numbers.d) The product of two nonzero numbers is nonzero for the real numbers.38.b) There are no students in this class who have never seen a computer.d) There are no students in this class who have taken been in at least one room of every building on campus.1.5(1)(┐r∧(q→p))→(p→(q∨r)) <=> ┐(┐r∧(┐q∨p))∨(┐p∨(q∨r)) <=>(q∧┐p)∨(┐p∨q∨r)<=> (┐p∨q∨r∨q)∧(┐p∨q∨r∨┐p) <=> (┐p∨q∨r) <=> ∏3 <=> ∑0,1,2,4,5,6,7 (2) P.726. Let r be the proposition "It rains", let f be the proposition "It is foggy", let s be the proposition "The sailing race will be held", let l be the proposition "The lifesaving demonstration will go on", and let t be the proposition "The trophy will be awarded". We are given premises (┐r∨┐f)→(s∧l), s→t, and ┐t. We want to conclude r. We set up the proof in two columns, with reasons. Note that it is valid to replace subexpressions by other expressions logically equivalent to them.Step Reason1. ┐t Hypothesis2. s→t Hypothesis3. ┐s Modus tollens using Steps 1 and 24. (┐r∨┐f)→(s∧l) Hypothesis5. (┐(s∧l))→┐(┐r∨┐f) Contrapositive of step 46. (┐s∨┐l)→(r∧f) De Morgan's law and double negative7. ┐s∨┐l Addition, using Step 38. r∧f Modus ponens using Step 6 and 79. r Simplification using Step 8First, using the conclusion of Exercise 11, we should show that the argument form with premises (p ∧t) → (r ∨s), q→ (u ∧t), u→p, ┐s, q, and conclusion r is valid. Then, we use rules of inference from Table 1.Step Reason1. q Premise2. q→ (u ∧t)P remise3. u ∧t Modus ponens using Steps 1 and 24. u Simplification using Step 35. u→p Premise6. p Modus ponens using Steps 3 and 47. t Simplification using Step 38. p ∧t Conjunction using Steps 6 and 79. (p ∧t) → (r ∨s) Premise10. r ∨s Modus ponens using Steps 8 and 911. ┐s Premise12. r Disjunctive syllogism using Steps 10 and 11 14.b)Let R(x) be “x is one of the five roommates,” D(x) be “x has taken a course in discrete mathematics,” and A(x) be “x can take a course in algorithms.” The premises are x (R(x) → D(x)), x (D(x) → A(x)) and R(Melissa). Using the first premise and Universal Instantiation, R(Melissa) → D(Melissa) follows. Using the third premise and Modus Ponens, D(Melissa) follows. Using the second premise and Universal Instantiation, A(Melissa) follows. So do the other roommates.d) Let C(x) be “x is in the class,”F(x) be “x has been to France,” and L(x) be “x has visited Louvre.” The premises are x(C(x) ∧F(x)) and x (F(x) → L(x)). From the first premise and Existential Instantiation imply that C(y) ∧F(y) for a particularperson y. Using Simplification, F(y) follows. Using the second premise and Universal Instantiation F(y) → L(y) follows. Using Modus Ponens, L(y) follows. Using Existential Generalization, x(C(x) ∧L(x)) follows.24. The errors occur in steps (3), (5) and (7).For steps (3) and (5), we cannot assume, as is being done here, that the c that makes P(x) true is the same as the c that makes Q(x) true at the same time. For step (7), it is not a conjunction and there is no such disjunction rule.29.Step Reason1. x ┐P(x) Premise2. ┐P(c) Existential instantiation from (1)3. x (P(x) ∨Q(x)) Premise4. P(c) ∨Q(c) Universal instantiation from (3)5. Q(c) Disjunctive syllogism from (2) and (4)6. x (┐Q(x) ∨S(x)) Premise7. ┐Q (c) ∨S(c) Universal instantiation from (6)8. S(c) Disjunctive syllogism from (5) and (7)9. x (R(x) →┐S(x)) Premise10. R(c) →┐S(c) Universal instantiation from (9)11. ┐R(c) Modus tollens from (8) and (10)12. x ┐R(x) Existential generalization from (11)P.861.637.Suppose that P1→P4→P2→P5→P3→P1. To prove that one of these propositions implies any of the others, just use hypothetical syllogism repeatedly.P.1031.713.a) This statement asserts the existence of x with a certain property. If we let y=x, then we see that P(x) is true. If y is anything other than x, then P(x) is not true. Thus, x is the unique element that makes P true.b) The first clause here says that there is an element that makes P true. The second clause says that whenever two elements both make P true, they are in fact the same element. Together these say that P is satisfied by exactly one element.c) This statement asserts the existence of an x that makes P true and has the further property that whenever we find an element that makes P true, that element is x. In other words, x is the unique element that makes P true.P.1202.19.T T F T T F16. Since the empty set is a subset of every set, we just need to take a set B that contains Φ as an element. Thus we can let A = Φ and B = {Φ} as the simplest example.20 .The union of the sets in the power set of a set X must be exactly X. In other words, we can recover X from its power set, uniquely. Therefore the answer is yes.22.a) The power set of every set includes at least the empty set, so the power set cannot be empty. Thus Φ is not the power set of any set.b) This is the power set of {a}c) This set has three elements. Since 3 is not a power of 2, this set cannot be the power set of any set.d) This is the power set of {a,b}.28.a) {(a,x,0), (a,x,1), (a,y,0), (a,y,1), (b,x,0), (b,x,1), (b,y,0), (b,y,1), (c,x,0), (c,x,1), (c,y,0), (c,y,1)}c) {(0,a,x), (0,a,y), (0,b,x), (0,b,y), (0,c,x), (0,c,y), (1,a,x), (1,a,y), (1,b,x), (1,b,y), (1,c,x), (1,c,y)}P.1302.214. Since A = (A - B)∪(A∩B), we conclude that A = {1,5,7,8}∪{3,6,9} ={1,3,5,6,7,8,9}. Similarly B = (B - A)∪(A ∩ B) = {2,10}∪{3,6,9} = {2,3,6,9,10}.24. First suppose x is in the left-hand side. Then x must be in A but in neither B nor C. Thus x∈A - C, but x B - C, so x is in the right-hand side. Next suppose that x is in the right-hand side. Thus x must be in A - C and not in B - C. The first of these implies that x∈A and x C. But now it must also be the case that x B, since otherwise we would have x∈B - C. Thus we have shown that x is in A but in neither B nor C, which implies that x is in the left-hand side.40. This is an identity; each side consists of those things that are in an odd number of the sets A,B,and C.P147.2.335a) This really has two parts. First suppose that b is in f(S∪T). Thus b=f(a) for somea∈S∪T. Either a ∈S, in which case b∈f(S), or a∈T, in which case b∈f(T). Thus in either case b∈ f(S) ∪f(T). This shows that f(S∪T) ⊆f(S) ∪f(T), Conversely, suppose b∈f(S) ∪f(T). Then either b∈f(S) or b∈f(T). This means either that b=f(a) for some a∈S or that b=f(a) for some a ∈T. In either case, b=f(a) for some a∈S∪T, so b∈f(S∪T). This shows that f(S) ∪f(T) ⊆f(S∪T), and our proof is complete. b)Suppose b∈f(S∩T). Then b=f(a) for some a∈S∩T. This implies that a∈S anda∈T , so we have b∈f(S) and b∈f(T). Therefore b∈f(S)∩f(T), as desired.52In some sense this question is its own answer—the number of integers between a and b, inclusive, is the number of integers between a and b, inclusive. Presumably we seek an express involving a, b, and the floor and/or ceiling function to answer this question. If we round a up and round b down to integers, then we will be looking at the smallest and largest integers just inside the range of the integers we want to count, respectively. These values are of course ⎡⎤a and ⎣⎦b, respectively. Then the answer isb-+1 (just think of counting all the integers between these two values, ⎣⎦⎡⎤aincluding both ends—if a row of fenceposts one foot apart extends for k feet, then there are k +1 fenceposts). Note that this even works when, for example, a=0.3 and b=0.7 .P1622.434.a) This is countable. The integers in the set are ±1,±2,±4,±5,±7,andso on. We can listthese numbers in the order 1, -1 , 2, -2, 4, -4,…, thereby establishing the desired correspondence. In other words, the correspondence is given by 1↔1,2↔-1,3↔2,4↔-2,5↔4,and so on.b) This is similar to part(a);we can simply list the elements of the set in order ofincreasing absolute value, listing each positive term before its correspondingnegative:5,-5,10,-10,15,-15,20,-20,30,-30,40,-40,45,-45,50,-50,……c) This is countable but a little tricky. We can arrange the numbers in a 2-dimensionaltable as follows:1..1 0.11 0.111 0.1111 0.11111 ……1.1 1 1.1 1.11 1.111 1.1111 ……1.1111 11.1 11.11 11.111 11.1111 ……1111.111 111.1 111.11 111.111 111.1111 ……………………………………d) This set is not countable. We can prove it by the same diagonalization argument aswas used to prove that the set of all reals is uncountable in Example 21.All we need to do is choose d i=1 when d ii=9 and choose d i=9 when d ii=1 or d ii is blank(if the decimal expansion is finite)46.We know from Example 21 that the set of real numbers between 0 and 1 is uncountable. Let us associate to each real number in this range(including 0 but excluding 1) a function from the set of positive integers to the set {0,1,2,3,4,5,6,7,8,9} as follows: If x is a real number whose decimal representation is 0.d1d2d3…(with ambiguity resolved by forbidding the decimal to end with an infinite string of9's),then we associate to x the function whose rule is given by f(n)=d n. clearly this is a one-to-one function from the set of real numbers between 0 and 1 and a subset of the set of all functions from the set of positive integers the set {0,1,2,3,4,5,6,7,8,9}.Two different real numbers must have different decimal representations, so the corresponding functions are different.(A few functions are left out, because of forbidding representations such as 0.239999…)Since the set of real numbers between 0 and 1 is uncountable, the subset of functions we have associated with them must be uncountable. But the set of all such functions has at least this cardinality, so it, too, must be uncountable.P1913.21. The choices of C and k are not unique.a) Yes C = 1, k = 10 b) Yes C = 4, k = 7 c) Nod) Yes C = 5, k = 1 e) Yes C = 1, k = 0 f) Yes C = 1, k = 29. x2+4x+17 ≤ 3x3 for all x>17, so x2+4x+17 is O(x3), with witnesses C = 3, k=17. However, if x3 were O(x2+4x+17), then x3≤C(x2+4x+17) ≤ 3Cx2for some C, for all sufficiently large x, which implies that x≤ 3C, for all sufficiently large x, which is impossible.P2093.419.a) no b) no c) yes d) no31.a) GR QRW SDVV JRb) QB ABG CNFF TBc) QX UXM AHJJ ZXP2183.513.a) Yes b) No c) Yes d) Yes17a) 2 b) 4 c) 12P2804.122.A little computation convinces us that the answer is that n2 ≤ n! for n= 0, 1, and all n≥ 4. (clearly the inequality doesn’t hold for n=2 or n=3) We will prove by mathematical induction that the inequality holds for all n≥ 4. The base case is clear, since 16 ≤ 24. Now suppose that n2 ≤ n! for a given n≥ 4. We m ust show that (n+1)2≤ (n+1)!. Expanding the left-hand side, applying the inductive hypothesis, and then invoking some valid bounds shows this:n2 + 2n+ 1 ≤ n! + 2n + 1≤ n! + 2n + 1 = n! + 3n≤ n! + n·n≤ n! + n·n!≤ (n+1)n! = (n+1)!P2934.231.Assume that the well-ordering property holds. Suppose that P(1) is true and that the conditional statement [P(1)∧P(2) ∧···∧P(n)] →P(n+1) is true for every positive integer n. Let S be the set of positive integers n for which P(n) is false. We will show S=Ø. Assume that S≠Ø, then by the well-ordering property there is a least integer m in S. We know that m cannot be 1 because P(1) is true. Because n=m is the least integer such that P(n) is false, P(1), P(2),…,P(m-1) are true, and m-1 ≥1. Because [P(1)∧P(2) ∧···∧P(m-1)] →P(m) is true, it follows that P(m) must also be true, which is a contradiction. Hence, S= Ø.P3084.310.The base case is that S m(0)=m. The recursive part is that S m(n+1) is the successor of S m(n)(i.e., S m(n)+1)12.The base case n=1 is clear, since f12=f1f2=1. Assume the inductive hypothesis. Thenf12+f22+…+f n2+f n+12 = f n+12+f n f n+1= f n+1(f n+1+f n)= f n+1f n+2, as desired.31.If x is a set or variable representing set, then x is well-formed formula. if x and y are all well-formed formulas, then x, (x∪y), (x∩y) and (x-y) are all well-formed formulas.50.Let P(n) be “A(1, n) = 2n .”BASIC STEP: P(1) is true, because P(1) = A(1, 1) = 2 = 21.INDCUTIVE STEP: Assume that P(m) is true, that is A(1, m) = 2m and m≥1. Then P(m+1) = A(1, m+1) = A(0, A(1, m))= A(0, 2m)=2·2m=2m+1.So A(1, n) = 2n whenever n≥159.b) Not well defined. F(2) is not defined since F(0) isn’t.Also, F(2) is ambiguous.d) Not well defined. The definition is ambiguous about n=1.P3445.13.a) 104b) 10512.We use the sum rule, adding the number of bit strings of each length up to 6. If we include the empty string, then we get 20 + 21 + 22 + 23 + 24 + 25 + 26= 27–1=12720.a) Every seventh number is divisible by 7. Therefore there are 999 / 7=142such numbers. Note that we use the floor function, because the k th multiple of 7 does not occur until the number 7k has been reached.b) For solving this part and the next four parts, we need to use the principle of inclusion-exclusion. Just as in part(a), there are 999/11=90 numbers in our range divisible by 11, and there are 999/77=12 numbers in our range divisible by both 7 and 11 (the multiples of 77 are the numbers we seek). If we take these 12 numbers are away from the 142 numbers divisible by 7, we see that there are 130 numbers in our range divisible by 7 but not by 11.c) as explained in part(b), the answer is 12.d) By the principle of inclusion-exclusion, the answer, using the data from part (b), is 142+90-12=220.e) If we subtract from the answer to part(d) the number of numbers divisible by neither of them; so the answer is 220-12=208.f) If we subtract the answer to part(d) from the total number of positive integers less than 1000, we will have the number of numbers divisible by exactly one of them; so the answer is 999-220=779.g) If we assume that numbers are written without leading 0s, then we should break the problem down into three cases-one-digit numbers, two-digit numbers. Clearly there are 9 one-digit numbers, and each of them has distinct digits. There are 90 two-digit numbers (10 through 99), and all but 9 of them have distinct digits. An alternativeway to compute this is to note that the first digit must be 1 through 9 (9 choices) and the second digit must be something different from the first digit (9 choices out of the 10 possible digits), so by the product rule, we get 9*9=81 choices in all. This approach also tells us that there are 9*9*8=648 three-digit numbers with distinct digits (again, work from left to right-in the ones place, one 8 digits are left to choose from). 80 the final answer is 9+81+648=738.h) It turns out to be easier to count the odd numbers with distinct digits and subtract from our answer to part(g), so let us proceed that way. There are 5 odd one-digit numbers. For two-digit numbers, first choose the one digit (5 choices), then choose the tens digits (8 choices), since neither the ones digit value not 0 is available); therefore there are 40 such two-digit numbers. (Note that this is not exactly half of 81.) For the three-digit numbers, first choose the ones digit (5 choices), then the hundreds digit (8 choices), then the tens digit (8 choices), giving us 320 in all. So there are 5+40+320=365 odd numbers with distinct digits. Thus the final answer is 738-365=373.35.a) 若n=1, 为2;若n=2, 为2; 若n>=3, 为0b) 对于n>1, 为22 n;若n=1, 为1;c) 2(n-1) (注:n可映射到0,1两种可能)44.First we count the number of bit strings of length 10 that contain five consecutive 0’s. We will base the count on where the string of five or more consecutive 0’s starts. If it starts in the first bit, then the first five bits are all 0’s, but there is free choice for the last five bits; therefore there are 25 = 32 such strings. If it starts in the second bit, then the first bit must be a 1, the next five bits are all 0’s, but there is free choice for the last four bits; therefore there are 24 = 16 such strings. If it starts in the third bit, then the second bit must be a 1 but the first bit and the last three bits are arbitrary; therefore there are 24= 16 such strings. Similarly, there are 16 such strings that have the consecutive 0’s starting in each of positions four, five ,and six. This gives us a total of 32+5×16=112 strings that contain five consecutive 0’s. Symmetrically, there are 112 strings that contain five consecutive 1’s. Clearly there are exactly two strings that contain both (0000011111,1111100000). Therefore by the inclusion-exclusion principle, the answer is 2*(112)-2=222.52.We draw the tree, with its root at the top. We show a branch for each of the possibilities 0 and 1, for each bit in order, except that we do not allow three consecutive 0’s. Since there are 13 leaves, the answer is 13.second bitthird bitfourth bitP3535.26.There are only d possible remainders when an integer is divided by d, namely 0, 1, …, d-1. By the pigeonhole principle, if we have d+1 remainders, then at least two must be the same.10.The midpoint of the segment whose endpoints are (a,b) and (c,d) is ( ( a + c ) / 2, ( b + d ) / 2). We are concerned only with integer values of the original coordinates. Clearly the coordinates of these fractions will be integers as well if and only if a and c have the same parity (both odd or both even) and b and d have the same parity. Thus what matters in this problem is the parities of coordinates. There are four possible pairs of parities: (odd,odd), (odd, even), (even, even) and (even,odd). Since we are given five points, the pigeonhole principle guarantees that at least two of them will have the same pair of parties. The midpoint of the segment joining these two points will therefore have integer coordinates.38.a) T b) Tc) T1 ≤a1< a2 < …< a75≤ 125 , and 26 ≤a1 + 25 < a2 + 25 < …< a75 + 25 ≤ 150.Now either of these 150 numbers are precisely all the number from 1 to 150, or else by the pigeonhole principle we get, as in Exercise 37, a i = a j + 25 for some i and j and we are done. In the former case, however, since each of the number a i + 25 is greater than or equal to 26, the numbers 1, 2, … , 25 must all appear among the a i’s. But since the a i’s are increasing, the only way this can happen is if a1=1, a2 =2 , …, a25=25. Thus there were exactly 25 matches in the first25 hours.d) TWe need a different approach for this part, an approach, incidentally, that works for many numbers besides 30 in this setting. Let a1, a2 , …a75 be as before, and note that 1 ≤a1< a2 < …< a75≤ 125. By the pigeonhole principle two of the numbers among a1, a2 , …a 31 are congruent modulo 30. If they differ by 30, then we have our solution. Otherwise they differ by 60 or more, so a 31 ≥ 61. Similarly, among a 31through a 61 ,either we find a solution, or two numbers must differ by 60 or more; therefore we assume that a 61 ≥ 121. But this means that a 66 ≥ 126, a contradiction.注:38题d 因为30大于25,不能用解决a,b,c的方法解决,所以适用一种新的方法(这种方法对前面3问同样适用的)。
(完整版)《离散数学》试题及答案解析,推荐文档

4. 设 I 是如下一个解释:D = {2, 3},
a
b
f (2) f (3)
3
2
3
2
试求 (1) P(a, f (a))∧P(b, f (b));
WORD 整理版
一、填空题 1 设集合 A,B,其中 A={1,2,3}, B= {1,2}, 则 A - B=____________________;
(A)
- (B)= __________________________ . 2. 设有限集合 A, |A| = n, 则 |(A×A)| = __________________________. 3. 设集合 A = {a, b}, B = {1, 2}, 则从 A 到 B 的所有映射是 __________________________ _____________, 其中双射的是
专业资料学习参考
WORD 整理版
0 1 1 1 1
15. 设图 G 的相邻矩阵为 1 0 1 0 0 ,则 G 的顶点数与边数分别为(
).
1 1 0 1 1
1 0 1 0 1
1 0 1 1 0
(A)4, 5 (B)5, 6 三、计算证明题
(C)4, 10
(D)5, 8.
1.设集合 A={1, 2, 3, 4, 6, 8, 9, 12},R 为整除关系。
则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是( ).
离散数学第9章习题答案

习题91. 设G 是一个(n ,m)简单图。
证明:,等号成立当且仅当G 是完全图。
证明:(1)先证结论:因为G 是简单图,所以G 的结点度上限 max(d(v)) ≤ n-1, G 图的总点度上限为 max(Σ(d(v)) ≤ n ﹒max(d(v)) ≤ n(n-1) 。
根据握手定理,G 图边的上限为 max(m) ≤ n(n-1)/2,所以。
(2) =〉G 是完全图 因为G 具有上限边数,假设有结点的点度小于n-1,那么G 的总度数就小于上限值,边数就小于上限值,与条件矛盾。
所以,G 的每个结点的点度都为n-1,G 为完全图。
G 是完全图 =〉 因为G 是完全图,所以每个结点的点度为n-1, 总度数为n(n-1),根据握手定理,图G 的边数 。
■2. 设G 是一个(n ,n +1)的无向图,证明G 中存在顶点u ,d (u )≥3。
证明:反证法,假设,则G 的总点度上限为max(Σ(d(u)) ≤2 n ,根据握手定理,图边的上限为max(m) ≤ 2n/2=n 。
与题设m = n+1,矛盾。
因此,G 中存在顶点u ,d (u )≥3。
■3.确定下面的序列中哪些是图的序列,若是图的序列,画出一个对应的图来: (1)(3,2,0,1,5); (2)(6,3,3,2,2) (3)(4,4,2,2,4); (4)(7,6,8,3,9,5)解:除序列(1)不是图序列外,其余的都是图序列。
因为在(1)中,总和为奇数,不满足图总度数为偶数的握手定理。
可以按如下方法构造满足要求的图:序列中每个数字ai 对应一个点,如果序列数字是偶数,那么就在对应的点上画ai/2个环,如果序列是奇数,那么在对应的点上画(ai-1)/2个环。
最后,将奇数序列对应的点两两一组,添加连线即可。
下面以(2)为例说明:(6 , 3, 3, 2, 2 ) 对应图G 的点集合V= { v 1,v 2,v 3,v 4,v 5}每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)将奇数3,3 对应的结点v 2,v 3一组,画一条连线其他序列可以类式作图,当然大家也可以画图其它不同的图形。
离散数学第9章习题解答

第9章习题解答9.1 有5片树叶.分析设T有x个1度顶点(即树叶).则T的顶点数的边数由握手定理得方程.由方程解出所求无向树T的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T中有5个3度顶点.分析设T中有个3度顶点,则T中的顶点数边数,由握手定理得方程.由方程解出x=5.所求无向树T的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T中有5个3度顶点.要析设T中有x个3度顶点,则T中的顶点数,边数,由握手定理得方程..由此解出,即T中有5个3度顶.T的度数列为1,1,1,1,1,1,1,3,3,3,3,3.由于T中只有树叶和3度顶点,因而3度顶点可依次相邻,见图9.7所示. 还有一棵与它非同构的树,请读者自己画出.9.3 加条新边才能使所得图为无向树.分析设具有个连通分支的森林为G,则G有个连通分支全为树,加新边不能在内部加,否则必产生回路.因而必须在不同的小树之间加新边. 每加一条新边后,所得到的森林就减少一个连通分支. 恰好加条新边,就使得图连通且无回路,因而是树.在加边过程中,只需注意,不在同一人连通分支中加边. 下面给出一种加边方法,取为中顶点,加新边,则所得图为树,见图9.8 给出的一个特例.图中虚线边为新加的边.9.4 不一定.分析 n阶无向树T具有条边,这是无向树T的必要条件,但不是充公条件.例如, 阶圈(即个顶点的初级回路)和一个孤立点组成无向简单图具有条边, 但它显然不是树.9.5 非同构的无向树共有2棵,如图 9.9所示.分析由度数列1,1,1,1,2,2,4不难看出,唯一的4度顶点必须与2度顶点相邻,它与1个2度顶点相邻,还是与两个2度顶点都相邻,所得树是非同构的,再没有其他情况.因而是两棵非同构的树.9.6 有两棵非同构的生成树,见图9.10所示.分析图9.10 是5阶图(5个顶点的图), 5阶非同构的无向树只有3棵,理由如下. 5阶无向树中,顶点数,边数,各顶点度数之和为8,度数分配方案有3种,分别为①1,1,1,1,4;②1,1,1,2,3;③1,1,2,2.2.每种方案只有一棵非同构的树.图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种,也就是说,它至多有3棵非同构的生成树, 但由于图中无4度顶点,所示,不可能有度数列为①的生成树,于是该图最多有两棵非同构的生成树. 但在图9.10 中已经找出了两个非同构的生成树,其中(1)的度数列为③,(2) 的度数列为②,因而该图准确地有两棵非同构的生成树.9.7 基本回路为:基本回路系统为基本割集为:基本回路系统为.分析1°注意基本回路用边的序列表示,而基本割集用边的集合表示.2° 基本回路中,只含一条弦,其余的边全为树枝,其求法是这样的: 设弦,则在生成树T中,且在T中,之间存在唯一的路径与组成的回路为G中对应弦的基本回路.3° 基本割集中,只含一条树枝,其余的边都是弦,其求法是这样的:设树枝,则为T中桥,于是(将从T中支掉),产生两棵小树和,则为树枝对应的基本割集. 显然中另外的边全是弦. 注意,两棵小树和,中很可能有平凡的树(一个顶点).得两棵小树如图9.11中(1) 所示. G中一个端点在中,另一个端点在中的边为(树枝),,它们全是弦,于是得两棵小树如图9.11中(2) 所示, 其中有一棵为平凡树. G中一个端点在中,另一个端点在中的边数除树枝外,还有弦所以,产生的两棵小树如图9.11中(3) 所示 . G中一个端点在中,另中一个端点在中的边,除树枝外,还有两条弦,所示,产生的两棵小树如图9.11中(4) 所示. 由它产生的基本割集为.9.8 按Kruskal求最小生成树的算法,求出的图9.3(1)的最小生成树T为图9.12中(1) 所示, 其.(2) 的最小生成树T为图9.12中(2)所示,其9.9为前缀码.分析在中任何符号串都不是另外符号串的前串,因而它们都是前缀码.而在中, 1是11,101的前缀,因而不是前缀码. 在中,是等的前缀,因而也不是前缀码.9.10 由图9.4 (1) 给出的2元前缀码.由(2) 给出的3元前缀码为.分析是2元树产生的2元前缀码(因为码中的符号串由两个符号0,1组成),类似地,是由3元树产生的3元前缀码(因为码中符号串由3个符号0,1,2组成).一般地,由元树产生元前缀码.9.11 (1) 算式的表达式为.由于.(2) 算式的波兰符号法表达式为(3) 算式的逆波兰符号法表达式为9.12 答案A:①; B②; C:④; D:⑨.分析对于每种情况都先求出非同构的无向树,然后求出每棵非同构的无向树派生出来的所有非同构的根树.图9.13 中,(1),(2),(3),(4)分别画出了2阶,3阶,4阶,5阶所有非同构的无向树,分别为1棵,1棵,2棵和3棵无向树.2阶无向树只有1棵,它有两个1度顶点,见图9.13中(1)所示,以1个顶点为树根,1个顶点为树叶,得到1棵根树.3阶非同的无向树也只有1棵,见图9.13中(2)所示.它有两个1度顶点,1个2度顶点,以1度顶点为根的根树与以2度顶点为根的树显然是非同构的根树,所以2个阶非同构的根树有两棵.4阶非同构的无向树有两棵,见图9.13中(3)所示. 第一棵树有3片树叶,1个3度顶点, 以树叶为根的根树与以3度顶点为根的树非同构.所以,由第一棵树能生成两个非同构的根树, 见图9.14 中(1)所示. 第二棵树有两片树叶,两个2度顶点,由对称性,以树叶为根的根树与2度顶点为根的根树非同构,见图9.14中(2) 所示. 所以,4阶非同构的根树有4棵.5阶非同构的无向树有3棵,见图9.13中(4)所示. 由第一棵能派生两棵非同构的根树, 由第二棵能派生4棵非同构的根树,由第三棵能派生3棵非同构的根树,所以,5阶非同构的根树共有9棵,请读者将它们都画出来.9.13 答案A:②; B:②; C:③; D:③; E:③;F:④; G: ④; H:③.分析将所有频率都乘100,所得结果按从小到大顺序排列:以以上各数为权,用Huffman算法求一棵最优树,见图9.15所示.对照各个权可知各字母的前缀码如下:a——10, b——01, c——111, d——110,e——001, f——0001,g——0000.于是,a,b的码长为的码长为的码长为4.W(T)=255(各分支点的权之和),W(T)是传输100按给定频率出现的字母所用的二进制数字,因则传输104个按上述频率出现的字母要用个二进制数字.最后还应指出一点,在画最优树叶, 由于顶点位置的不同,所得缀码可能不同,即有些字母的码子在不同的最优树中可能不同,但一般说来码长不改变.特别是,不同的最优树,它们的权是固定不变的.9.14 答案 A:②; B:④分析用2元有序正则树表示算式,树叶表示参加运算的数,分支点上放运算符,并将被减数(被除数)放在左子树上,所得2元树如图9.16所示.用前序行遍法访问此树,得波兰符号表示法为用后序行遍法访问此树,得逆波兰符号表示法为。
离散数学第四版 课后答案

离散数学第四版课后答案第1章习题解答1.1 除(3),(4),(5),(11)外全是命题,其中,(1),(2),(8),(9),(10),(14),(15)是简单命题,(6),(7),(12),(13)是复合命题。
分析首先应注意到,命题是陈述句,因而不是陈述句的句子都不是命题。
本题中,(3)为疑问句,(5)为感叹句,(11)为祈使句,它们都不是陈述句,所以它们都不是命题。
其次,4)这个句子是陈述句,但它表示的判断结果是不确定。
又因为(1),(2),(8),(9),(10),(14),(15)都是简单的陈述句,因而作为命题,它们都是简单命题。
(6)和(7)各为由联结词“当且仅当”联结起来的复合命题,(12)是由联结词“或”联结的复合命题,而(13)是由联结词“且”联结起来的复合命题。
这里的“且”为“合取”联结词。
在日常生活中,合取联结词有许多表述法,例如,“虽然……,但是……”、“不仅……,而且……”、“一面……,一面……”、“……和……”、“……与……”等。
但要注意,有时“和”或“与”联结的是主语,构成简单命题。
例如,(14)、(15)中的“与”与“和”是联结的主语,这两个命题均为简单命题,而不是复合命题,希望读者在遇到“和”或“与”出现的命题时,要根据命题所陈述的含义加以区分。
1.2 (1)p: 2是无理数,p为真命题。
(2)p:5能被2整除,p为假命题。
(6)p→q。
其中,p:2是素数,q:三角形有三条边。
由于p与q都是真命题,因而p→q为假命题。
(7)p→q,其中,p:雪是黑色的,q:太阳从东方升起。
由于p为假命题,q为真命题,因而p→q为假命题。
(8)p:2000年10月1日天气晴好,今日(1999年2月13日)我们还不知道p的真假,但p的真值是确定的(客观存在的),只是现在不知道而已。
(9)p:太阳系外的星球上的生物。
它的真值情况而定,是确定的。
1(10)p:小李在宿舍里. p的真值则具体情况而定,是确定的。
离散数学答案英文版

离散数学答案英⽂版P.161.14.f) If I did not buy a lottery ticket this week, then I did not win the million dollar jackpot on Friday.g) I did not buy a lottery ticket this week, and I did not win the million dollar jackpot on Friday.h ) Either I did not buy a lottery ticket this week, or else I did buy one and won the million dollar jackpot on Friday.10.a) r ∧┐q b) p ∧ q∧ r c)r → pd) p ∧┐q ∧ r e) (p ∧q) → r f) r? ( q ∨ p)20.a) If I am to remember to send you the address, then you will have to send me ane-mail message.(This has been slightly reworded so that the tenses make more sense.)b) If you were born in the United States, then you are a citizen of this country.c) If you keep your textbook, then it will be a useful reference in your future courses.(The word "then" is understood in English, even if omitted.)d) If their goaltender plays well, then the Red Wings will win the Stanley Cup.e) If you get the job, then you had the best credentials.f) If there is a storm, then the beach erodes.g) If you log on to the server, then you have a valid password.h) If you don’t begin your climb too late, then you will reach the summit.33.c)P.261.28.a) Kwame will not take a job in industry and he will not go to graduate school.b) Yoshiko doesn’t know Java or she doesn’t know calculus.c) James is not young or he is not strong.d) Rita will not move to Oregon and she will not move to Washington.10.a)c)12.a) Assume the hypothesis is true. Then p is false. Since p∨q is true, we conclude that q must be true.Here is a more "algebraic" solution:[┐p∧(p ∨q)]→q <=> ┐[┐p∧(p ∨q)]∨q <=> ┐┐p∨┐(p∨q)∨q <=> p∨┐(p∨q)∨q <=> (p ∨q)∨┐(p∨q) <=> Tc) Assume the hypothesis is true. Then p is true, and since the second part of the hypothesis is ture, we conclude that q is also true, as desired.51.((p ↓ p) ↓ q )↓((p ↓ p) ↓ q )7.The graph is planar.20.The graph is not homeomorphic to K3,3, since by rerouting the edge between a and h we see that it is planar.22.Replace each vertex of degree two and its incident edges by a single edge. Then the result is K3,3 : the parts are {a,e,i} and {c,g,k}. Therefore this graph is homeomorphic to K3,3.23.The graph is planar.25. The graph is not planar.9.83. 3F E8. 310.417. time slot 1: Math 115, Math 185; time slot 2: Math 116, CS 473;time slot 3: Math 195, CS 101; time slot 4: CS 102time slot 5: CS 273P.461.33. a) true b) false c) false d) false5. a) There is a student who spends more than 5 hours every weekday in class.b) Every student spends more than 5 hours every weekday in class.c) There is a student who does not spend more than 5 hours every weekday in class.d) No student spends more than 5 hours every weekday in class.9. a) x(P(x)∧Q(x)) b) x(P(x)∧﹁Q(x))c) x(P(x)∨Q(x)) d) x﹁(P(x)∨Q(x))16. a) true b) false c) true d) false24. Let C(x) be the propositional function “x is in your class.”a)x P(x) and x(C(x)→P(x)), where P(x) is “x has a cellular phone.”b) x F(x) and x(C(x)∧F(x)), where F(x) is “x has seen a foreign movie.”c)x﹁S(x) and x(C(x)∧﹁S(x)), where S(x) is “x can swim.”d)x E(x) and x(C(x)→E(x)), where E(x) is “x can solve quad ratic equations.”e)x﹁R(x) and x(C(x)∧﹁R(x)), where R(x) is “x wants to be rich.”62.a) x (P(x)→﹁S(x)) b)x(R(x)→S(x))c) x (Q(x)→P(x))d)x(Q(x)→﹁R(x))e) Yes. If x is one of my poultry, then he is a duck (by part(c)), hence not willing to waltz (part (a)). Since officers are always willing to waltz (part (b)), x is not an officer.1.412.d)x┐C(x, Bob)h)x y (I(x) ∧((x≠y) →┐ I(y)))k)x y( I(x) ∧┐C(x, y))n)x y z ((x≠y) ∧┐ (C(x, z) ∧ C(y, z)))14.a) x H(x), where H(x) is “x can speak Hindi”and the universe of the discourse consists of all students in this class.b) x y P(x, y), where P(x, y) is “x plays y.” and the universe of the discourse for x consists of all students in this class, and the universe of the discourse for y consists of all sports.c) x A(x) ∧┐H(x) , where A(x) is “x has visited Alaska.” , H(x) is “x has visited Hawaii” and the universe of the discourse for x consists of all students in this class.d) x y L(x, y), where L(x, y) is “x has learned programming language y” and the universe of the discourse for x consists of all students in this class, and the universe of the discourse for y consists of all programming languages.e) x z y (Q(y,z) →P(x, y)), where P(x, y) is“x has taken course y.”, Q(y, z) is “course y is offered by department z.”, and theuniverse of the discourse for x consists of all students in this class, the universe of the discourse for y consists of all courses in this school, and the universe of the discourse for z consists of all departments in this school.f)x y z ( (x≠y) ∧P(x, y)∧ ((x≠y≠z) →┐P(x, z))), where P(x, y) is “x and y grew up in the same town.” and the universe of the discourse for x, y, z consists of all students in this class.g) x y z C(x, y) ∧G(y, z), where C(x, y) is “x has chatted with y”, G(y, z) is “y is in chat group z”, the universe of the discourse for x, y consists of all students in this class, and the universe of the discourse for z consists of all chat group in this class. a) There is an additive identity for the real numbers.d) The product of two nonzero numbers is nonzero for the real numbers.38.b) There are no students in this class who have never seen a computer.d) There are no students in this class who have taken been in at least one room of every building on campus.1.5(1)(┐r∧(q→p))→(p→(q∨r)) <=> ┐(┐r∧(┐q∨p))∨(┐p∨(q∨r)) <=>(q∧┐p)∨(┐p∨q∨r)<=> (┐p∨q∨r∨q)∧(┐p∨q∨r∨┐p) <=> (┐p∨q∨r) <=> ∏3 <=> ∑0,1,2,4,5,6,7 (2) P.726. Let r be the proposition "It rains", let f be the proposition "It is foggy", let s be the proposition "The sailing race will be held", let l be the proposition "The lifesaving demonstration will go on", and let t be the proposition "The trophy will be awarded". We are given premises (┐r∨┐f)→(s∧l), s→t, and ┐t. We want to conclude r. We set up the proof in two columns, with reasons. Note that it is valid to replace subexpressions by other expressions logically equivalent to them.Step Reason1. ┐t Hypothesis2. s→t Hypothesis3. ┐s Modus tollens using Steps 1 and 24. (┐r∨┐f)→(s∧l) Hypothesis5. (┐(s∧l))→┐(┐r∨┐f) Contrapositive of step 46. (┐s∨┐l)→(r∧f) De Morgan's law and double negative7. ┐s∨┐l Addition, using Step 38. r∧f Modus ponens using Step 6 and 79. r Simplification using Step 8First, using the conclusion of Exercise 11, we should show that the argument form with premises (p ∧t) → (r ∨s), q→ (u ∧t), u→p, ┐s, q, and conclusion r is valid. Then, we use rules of inference from Table 1.Step Reason1. q Premise2. q→ (u ∧t)P remise3. u ∧t Modus ponens using Steps 1 and 24. u Simplification using Step 35. u→p Premise6. p Modus ponens using Steps 3 and 47. t Simplification using Step 38. p ∧t Conjunction using Steps 6 and 79. (p ∧t) → (r ∨s) Premise10. r ∨s Modus ponens using Steps 8 and 911. ┐s Premise12. r Disjunctive syllogism using Steps 10 and 11 14.b)Let R(x) be “x is one of the five roommates,” D(x) be “x has taken a course in discrete mathematics,” and A(x) be “x can take a course in algorithms.” The premises are x (R(x) → D(x)), x (D(x) → A(x)) and R(Melissa). Using the first premise and Universal Instantiation, R(Melissa) → D(Melissa) follows. Using the third premise and Modus Ponens, D(Melissa) follows. Using the second premise and Universal Instantiation, A(Melissa) follows. So do the other roommates.d) Let C(x) be “x is in the class,”F(x) be “x has been to France,” and L(x) be “x has visited Louvre.” The premises are x(C(x)∧F(x)) and x (F(x) → L(x)). From the first premise and Existential Instantiation imply that C(y) ∧F(y) for a particularperson y. Using Simplification, F(y) follows. Using the second premise and Universal Instantiation F(y) → L(y) follows. Using Modus Ponens, L(y) follows. Using Existential Generalization, x(C(x) ∧L(x)) follows.24. The errors occur in steps (3), (5) and (7).For steps (3) and (5), we cannot assume, as is being done here, that the c that makes P(x) true is the same as the c that makes Q(x) true at the same time. For step (7), it is not a conjunction and there is no such disjunction rule.29.Step Reason1. x ┐P(x) Premise2. ┐P(c) Existential instantiation from (1)3. x (P(x) ∨Q(x)) Premise4. P(c) ∨Q(c) Universal instantiation from (3)5. Q(c) Disjunctive syllogism from (2) and (4)6. x (┐Q(x) ∨S(x)) Premise7. ┐Q (c) ∨S(c) Universal instantiation from (6)8. S(c) Disjunctive syllogism from (5) and (7)9. x (R(x) →┐S(x)) Premise10. R(c) →┐S(c) Universal instantiation from (9)11. ┐R(c) Modus tollens from (8) and (10)12. x ┐R(x) Existential generalization from (11)P.861.637.Suppose that P1→P4→P2→P5→P3→P1. To prove that one of these propositions implies any of the others, just use hypothetical syllogism repeatedly.P.1031.713.a) This statement asserts the existence of x with a certain property. If we let y=x, then we see that P(x) is true. If y is anythingother than x, then P(x) is not true. Thus, x is the unique element that makes P true.b) The first clause here says that there is an element that makes P true. The second clause says that whenever two elements both make P true, they are in fact the same element. Together these say that P is satisfied by exactly one element.c) This statement asserts the existence of an x that makes P true and has the further property that whenever we find an element that makes P true, that element is x. In other words, x is the unique element that makes P true.P.1202.19.T T F T T F16. Since the empty set is a subset of every set, we just need to take a set B that contains Φ as an element. Thus we can letA = Φ andB = {Φ} as the simplest example.20 .The union of the sets in the power set of a set X must be exactly X. In other words, we can recover X from its power set, uniquely. Therefore the answer is yes.22.a) The power set of every set includes at least the empty set, so the power set cannot be empty. Thus Φ is not the power set of any set.b) This is the power set of {a}c) This set has three elements. Since 3 is not a power of 2, this set cannot be the power set of any set.d) This is the power set of {a,b}.28.a) {(a,x,0), (a,x,1), (a,y,0), (a,y,1), (b,x,0), (b,x,1), (b,y,0), (b,y,1), (c,x,0), (c,x,1), (c,y,0), (c,y,1)}c) {(0,a,x), (0,a,y), (0,b,x), (0,b,y), (0,c,x), (0,c,y), (1,a,x), (1,a,y), (1,b,x), (1,b,y), (1,c,x), (1,c,y)}P.1302.214. Since A = (A - B)∪(A∩B), we conclude that A = {1,5,7,8}∪{3,6,9} ={1,3,5,6,7,8,9}. Similarly B = (B - A)∪(A ∩ B) = {2,10}∪{3,6,9} = {2,3,6,9,10}.24. First suppose x is in the left-hand side. Then x must be in A but in neither B nor C. Thus x∈A - C, but x B - C, so x is in the right-hand side. Next suppose that x is in the right-hand side. Thus x must be in A - C and not in B - C. The first of these implies that x∈A and x C. But now it must also be the case that x B, since otherwise we would have x∈B - C. Thus we have shown that x is in A but in neither B nor C, which implies that x is in the left-hand side.40. This is an identity; each side consists of those things that are in an odd number of the sets A,B,and C.P147.2.335a) This really has two parts. First suppose that b is in f(S∪T). Thus b=f(a) for somea∈S∪T. Either a ∈S, in which case b∈f(S), or a∈T, in which case b∈f(T). Thus in either case b∈ f(S) ∪f(T). This shows that f(S∪T) ?f(S) ∪f(T), Conversely, suppose b∈f(S) ∪f(T). Then either b∈f(S) or b∈f(T). This means either that b=f(a) for somea∈S or that b=f(a) for some a ∈T. In either case, b=f(a) for some a∈S∪T, so b∈f(S∪T). This shows that f(S) ∪f(T) ?f(S∪T), and our proof is complete. b)Suppose b∈f(S∩T). Then b=f(a) for some a∈S∩T. This implies that a∈S anda∈T , so we have b∈f(S) and b∈f(T). Therefore b∈f(S)∩f(T), as desired.52In some sense this question is its own answer—the number of integers between a and b, inclusive, is the number of integers between a and b, inclusive. Presumably we seek an express involving a, b, and the floor and/or ceiling function to answer this question. If we round a up and round b down to integers, then we will be looking at the smallest and largest integers just inside the range of the integers we want to count, respectively. These values are of course ??a and ??b, respectively. Then the answer isb-+1 (just think of counting all the integers between these two values, aincluding both ends—if a row of fenceposts one foot apart extends for k feet, then there are k +1 fenceposts). Note that this even works when, for example, a=0.3 and b=0.7 .P1622.434.a) This is countable. The integers in the set are ±1,±2,±4,±5,±7,andso on. We can listthese numbers in the order 1, -1 , 2, -2, 4, -4,…, thereby establishing the desired correspondence. In other words, the correspondence is given by 1?1,2?-1,3?2,4?-2,5?4,and so on.b) This is similar to part(a);we can simply list the elements of the set in order ofincreasing absolute value, listing each positive term before its correspondingnegative:5,-5,10,-10,15,-15,20,-20,30,-30,40,-40,45,-45,50,-50,……c) This is countable but a little tricky. We can arrange the numbers in a 2-dimensionaltable as follows:1..1 0.11 0.111 0.1111 0.11111 ……1.1 1 1.1 1.11 1.111 1.1111 ……1.1111 11.1 11.11 11.111 11.1111 ……1111.111 111.1 111.11 111.111 111.1111 ……………………………………d) This set is not countable. We can prove it by the same diagonalization argument aswas used to prove that the set of all reals is uncountable in Example 21.All we need to do is choose d i=1 when d ii=9 and choose d i=9 when d ii=1 or d ii is blank(if the decimal expansion is finite)46.We know from Example 21 that the set of real numbers between 0 and 1 is uncountable. Let us associate to each real number in this range(including 0 but excluding 1) a function from the set of positive integers to the set {0,1,2,3,4,5,6,7,8,9} as follows: If x is a real number whose decimal representation is 0.d1d2d3…(with ambiguity resolved by forbidding the decimal to end with an infinite string of9's),then we associate to x the function whose rule is given by f(n)=d n. clearly this is a one-to-one function from the set of real numbers between 0 and 1 and a subset of the set of all functions from the set of positive integers the set{0,1,2,3,4,5,6,7,8,9}.Two different real numbers must have different decimal representations, so the corresponding functions are different.(A few functions are left out, because of forbidding representations such as 0.239999…)Since the set of real numbers between 0 and 1 is uncountable, the subset of functions we have associated with them must be uncountable. But the set of all such functions has at least this cardinality, so it, too, must be uncountable.P1913.21. The choices of C and k are not unique.a) Yes C = 1, k = 10 b) Yes C = 4, k = 7 c) Nod) Yes C = 5, k = 1 e) Yes C = 1, k = 0 f) Yes C = 1, k = 29. x2+4x+17 ≤ 3x3 for all x>17, so x2+4x+17 is O(x3), with witnesses C = 3, k=17. However, if x3 were O(x2+4x+17), thenx3≤C(x2+4x+17) ≤ 3Cx2for some C, for all sufficiently large x, which implies that x≤ 3C, for all sufficiently large x, which is impossible.P2093.419.a) no b) no c) yes d) no31.a) GR QRW SDVV JRb) QB ABG CNFF TBc) QX UXM AHJJ ZXP2183.513.a) Yes b) No c) Yes d) Yes17a) 2 b) 4 c) 12P2804.122.A little computation convinces us that the answer is that n2 ≤ n! for n= 0, 1, and all n≥ 4. (clearly the inequality doesn’t hold for n=2 or n=3) We will prove by mathematical induction that the inequality holds for all n≥ 4. The base case is clear, since 16 ≤24. Now suppose that n2 ≤ n! for a given n≥ 4. We m ust show that (n+1)2≤ (n+1)!. Expanding the left-hand side, applying the inductive hypothesis, and then invoking some valid bounds shows this:n2 + 2n+ 1 ≤ n! + 2n + 1≤ n! + 2n + 1 = n! + 3n≤ n! + n·n≤ n! + n·n!≤ (n+1)n! = (n+1)!P2934.231.Assume that the well-ordering property holds. Suppose that P(1) is true and that the conditional statement [P(1)∧P(2)∧···∧P(n)] →P(n+1) is true for every positive integer n. Let S be the set of positive integers n for which P(n) is false. We will show S=?. Assume that S≠?, then by the well-ordering property there is a least integer m in S. We know that m cannot be 1 because P(1) is true. Because n=m is the least integer such that P(n) is false, P(1), P(2),…,P(m-1) are true, and m-1 ≥1. Because [P(1)∧P(2) ∧···∧P(m-1)] →P(m) is true, it follows that P(m) must also be true, which is a contradiction. Hence, S= ?. P3084.310.The base case is that S m(0)=m. The recursive part is that S m(n+1) is the successor of S m(n)(i.e., S m(n)+1)12.The base case n=1 is clear, since f12=f1f2=1. Assume the inductive hypothesis. Thenf12+f22+…+f n2+f n+12 = f n+12+f n f n+1= f n+1(f n+1+f n)= f n+1f n+2, as desired.31.If x is a set or variable representing set, then x is well-formed formula. if x and y are all well-formed formulas, then x, (x∪y), (x∩y) and (x-y) are all well-formed formulas.50.Let P(n) be “A(1, n) = 2n .”BASIC STEP: P(1) is true, because P(1) = A(1, 1) = 2 = 21.INDCUTIVE STEP: Assume that P(m) is true, that is A(1, m) = 2m and m≥1. Then P(m+1) = A(1, m+1) = A(0, A(1, m))= A(0, 2m)=2·2m=2m+1.So A(1, n) = 2n whenever n≥159.b) Not well defined. F(2) is not defined since F(0) isn’t.Also, F(2) is ambiguous.d) Not well defined. The definition is ambiguous about n=1.P3445.13.a) 104b) 10512.We use the sum rule, adding the number of bit strings of each length up to 6. If we include the empty string, then we get 20 + 21 + 22 + 23 + 24 + 25 + 26= 27–1=12720.a) Every seventh number is divisible by 7. Therefore there are 999 / 7=142such numbers. Note that we use the floor function, because the k th multiple of 7 does not occur until the number 7k has been reached.b) For solving this part and the next four parts, we need to use the principle of inclusion-exclusion. Just as in part(a), there are 999/11=90 numbers in our range divisible by 11, and there are 999/77=12 numbers in our range divisible by both 7 and 11 (the multiples of 77 are the numbers we seek). If we take these 12 numbers are away from the 142 numbers divisible by 7, we see that there are 130 numbers in our range divisible by 7 but not by 11.c) as explained in part(b), the answer is 12.d) By the principle of inclusion-exclusion, the answer, using the data from part (b), is 142+90-12=220.e) If we subtract from the answer to part(d) the number of numbers divisible by neither of them; so the answer is 220-12=208.f) If we subtract the answer to part(d) from the total number of positive integers less than 1000, we will have the number of numbers divisible by exactly one of them; so the answer is 999-220=779.g) If we assume that numbers are written without leading 0s, then we should break the problem down into three cases-one-digit numbers, two-digit numbers. Clearly there are 9 one-digit numbers, and each of them has distinct digits. There are 90 two-digit numbers (10 through 99), and all but 9 of them have distinct digits. An alternativeway to compute this is to note that the first digit must be 1 through 9 (9 choices) and the second digit must be something different from the first digit (9 choices out of the 10 possible digits), so by the product rule, we get 9*9=81 choices in all. This approach also tells us that there are 9*9*8=648 three-digit numbers with distinct digits (again, work from left to right-in the ones place, one 8 digits are left to choose from). 80 the final answer is 9+81+648=738.h) It turns out to be easier to count the odd numbers with distinct digits and subtract from our answer to part(g), so let us proceed that way. There are 5 odd one-digit numbers. For two-digit numbers, first choose the one digit (5 choices), then choose the tens digits (8 choices), since neither the ones digit value not 0 is available); therefore there are 40 such two-digit numbers. (Note that this is not exactly half of 81.) For the three-digit numbers, first choose the ones digit (5 choices), then the hundreds digit (8 choices), then the tens digit (8 choices), giving us 320 in all. So there are 5+40+320=365 odd numbers with distinct digits. Thus the final answer is 738-365=373.35.a) 若n=1, 为2;若n=2, 为2; 若n>=3, 为0b) 对于n>1, 为22 n;若n=1, 为1;c) 2(n-1) (注:n可映射到0,1两种可能)44.First we count the number of bit strings of length 10 that contain five consecutive 0’s. We will base the count on where the string of five or more consecutive 0’s starts. If it starts in the first bit, then the first five bits are all 0’s, but there is free choice for the last five bits; therefore there are 25 = 32 such strings. If it starts in the second bit, then the first bit must be a 1, the next five bits are all 0’s, but there is free choice for the last four bits; therefore there are 24 = 16 such strings. If it starts in the third bit, then the second bit must be a 1 but the first bit and the last three bits are arbitrary; therefore there are 24= 16 such strings. Similarly, there are 16 such strings that have the consecutive 0’s starting in each of positions four, five ,and six. This gives us a total of 32+5×16=112 strings that contain five consecutive 0’s. Symmetrically, there are 112 strings that contain five consecutive 1’s. Clearly there are exactly two strings that contain both (0000011111,1111100000). Therefore by the inclusion-exclusion principle, the answer is 2*(112)-2=222.52.We draw the tree, with its root at the top. We show a branch for each of the possibilities 0 and 1, for each bit in order, except that we do not allow three consecutive 0’s. Since there are 13 leaves, the answer is 13.second bitthird bitfourth bitP3535.26.There are only d possible remainders when an integer is divided by d, namely 0, 1, …, d-1. By the pigeonhole principle, if wehave d+1 remainders, then at least two must be the same.10.The midpoint of the segment whose endpoints are (a,b) and (c,d) is ( ( a + c ) / 2, ( b + d ) / 2). We are concerned only with integer values of the original coordinates. Clearly the coordinates of these fractions will be integers as well if and only if a and c have the same parity (both odd or both even) and b and d have the same parity. Thus what matters in this problem is the parities of coordinates. There are four possible pairs of parities: (odd,odd), (odd, even), (even, even) and (even,odd). Since we are given five points, the pigeonhole principle guarantees that at least two of them will have the same pair of parties. The midpoint of the segment joining these two points will therefore have integer coordinates.38.a) T b) Tc) T1 ≤a1< a2 < …< a75≤ 125 , and 26 ≤a1 + 25 < a2 + 25 < …< a75 + 25 ≤ 150.Now either of these 150 numbers are precisely all the number from 1 to 150, or else by the pigeonhole principle we get, as in Exercise 37, a i = a j + 25 for some i and j and we are done. In the former case, however, since each of the number a i + 25 is greater than or equal to 26, the numbers 1, 2, … , 25 must all appear among the a i’s. But since the a i’s are increasing, the only way this can happen is if a1=1, a2 =2 , …, a25=25. Thus there were exactly 25 matches in the first25 hours.d) TWe need a different approach for this part, an approach, incidentally, that works for many numbers besides 30 in this setting. Let a1, a2 , …a75 be as before, and note that 1 ≤a1< a2 < …< a75≤ 125. By the pigeonhole principle two of the numbers among a1, a2 , …a 31 are congruent modulo 30. If they differ by 30, then we have our solution. Otherwise they differ by 60 or more, so a 31 ≥ 61. Similarly, among a 31through a 61 ,either we find a solution, or two numbers must differ by 60 or more; therefore we assume that a 61 ≥ 121. But this means that a 66 ≥ 126, a contradiction.注:38题d 因为30⼤于25,不能⽤解决a,b,c的⽅法解决,所以适⽤⼀种新的⽅法(这种⽅法对前⾯3问同样适⽤的)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.1:P595
Ex2: a) Simple graph b) Multigraph c) Pseudograph
Ex20:Team four beat the vertices to which there are edges from team four, namely only team three. The other teams —team one, team two, team five and team six —all beat team four.
9.2:P608
Ex4 For the graph in exercise 1 the sum is 12, there are 6 edges; For the pseudograph in exercise 2, the sum is 26, there are 13 edges; For the pseudograph in exercise 3, the sum is 24, there are 12 edges;
Ex8: in this directed multigraph there are 4 vertices and 8 edges. The degrees are deg -(a)=2,deg +(a)=2; deg -(b)=3,deg +(b)=4; deg -(c)=2,deg +(c)=1; deg -(d)=1,deg +(d)=1;
Ex20 f) We take two copies of Q3 and joining corresponding vertices.
Ex22: This graph is bipartite, with bipartition {a,c} and {b,d,e}
9.3:P618
Ex2: the list is as follows
Vertex adjacent vertices
a b,d
b a,d,e
c d,e
d a,b,c
e b,c
Ex8
0101010111011001
000100101⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
Ex16: Because of the numbers larger than 1, we need multiple edges in this graph.
Ex36: These graphs are not isomorphic. The second has a vertex of degree 4, whereas the first
9.4:P629
Ex2: a) a path of length 4; b) a path of length 4; c) not a path; d) not a path
Ex12 b) Notice that the sequence a,b,c,d,e,f,a provides a path from every vertex to every other vertex , so this graph is strongly connected.
Ex20: The two graphs are isomorphic: u1↔v2, u2↔v1, u3↔v3, u4↔v4, u5↔v8, u6↔v7, u7↔v5,u8↔v6.
Ex24(a) to find the number of paths of length 2, we need to look at A 2, which is
3121221413222130311
30312223141221213⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
Since the (3,4)th entry is 0, so there are no paths of length 2.
9.5:P643
Ex4: The graph has no Euler circuit, since the degree of vertex c is odd. There is an Euler path between the two vertices of odd degree. One such path is f,a,b,c,d,e,f,b,d,a,e,c
Ex30:
This graph can have no Hamilton circuit because of the cut edge {c,f}.
9.6:P655
Ex2: the length of a shortest path is 7.
Ex12: In theory, we can use Dijkstra ’s algorithm.
a) the path through Chicago is the fastest.
b) The path via New York is the cheapest.
c) The path via Denver (or the path Via Los Angeles) is the fastest.
d) The path via Dallas( or the path via Chicago) is the fastest.
Ex14:Here we simply assign the weight of 1 to each edge.
9.7:P665
Ex5: This is K 3,3,with parts {a,d,f} and {b,c,e}, therefore it is not planar.
Ex20: this graph is not homeomorphic to K 3,3, since by rerouting the edge between a and h we see that it is planar.
Ex8: Since there is a triangle, at least 3 colors are needed. The coloring in which b and c are blue, a and f are red, and d and e are green shows that 3 colors suffice.。
