离散数学第九章
离散数学 第九章

οai οa1 ο a2
. . . οan
二元运算的运算表
2011-1-31 曲阜师范大学计算机科学学院
一元运算的运算表
12
运算表的实例
上的⊕ 运算的运算表 的运算表, 例3 设 S=P({a,b}),S上的⊕和 ∼运算的运算表,其中全 , 上的 集为{a,b}。 集为 。 ⊕ ∅ {a} {b} {a,b} ∅ ∅ {a} {a} {a} ∅ {b} {a,b} {b} ∅ {a} {a,b} {a} ∅ x ∅ {a} {b} {a,b} ~x {a,b} {b} } {a} ∅
2011-1-31
曲阜师范大学计算机科学学院
2
第三部分 代数结构
一元:f:S→S 一元 二元:f:S×S→S 二元 × 多元
符合某些律
运算
性质 交换律 单位元 结合律 零元 幂等律 逆元 分配律 吸收律 消去律
代数系统
建立两 个代数 系统的 联系 映射) (映射)
具体代数系统
半群 群 环 域 格 布尔代数
离 散 数 学
代数结构
2011-1-31
曲阜师范大学计算机科学学院
1
第三部分 代数结构
代数结构是以研究数字、文字和更一般元素的运算的 代数结构是以研究数字、文字和更一般元素的运算的 规律和由这些运算适合的公理而定义的各种数学结构的性 规律和由这些运算适合的公理而定义的各种数学结构的性 和由这些 为中心问题. 质为中心问题 它对现代数学如拓扑学、泛函分析等, 它对现代数学如拓扑学、泛函分析等 以及一些其他 科学领域, 如计算机科学、编码理论等, 科学领域 如计算机科学、编码理论等 都有重要影响和广 泛应用. 泛应用
2011-1-31
曲阜师范大学计算机科学学院
离散数学09 图
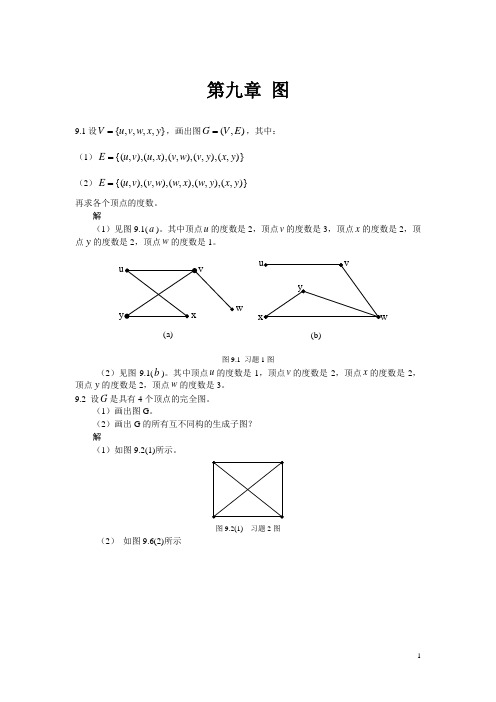
第九章 图9.1设},,,,{y x w v u V =,画出图),(E V G =,其中:(1))},(),,(),,(),,(),,{(y x y v w v x u v u E =(2))},(),,(),,(),,(),,{(y x y w x w w v v u E =再求各个顶点的度数。
解(1)见图9.1(a )。
其中顶点u 的度数是2,顶点v 的度数是3,顶点x 的度数是2,顶点y 的度数是2,顶点w 的度数是1。
图9.1 习题1图(2)见图9.1(b )。
其中顶点u 的度数是1,顶点v 的度数是2,顶点x 的度数是2,顶点y的度数是2,顶点w 的度数是3。
9.2 设G 是具有4个顶点的完全图。
(1)画出图G 。
(2)画出G 的所有互不同构的生成子图?解(1)如图9.2(1)所示。
图9.2(1) 习题2图(2) 如图9.6(2)所示﹒ ﹒ ﹒ ﹒ ﹒ ﹒图9.2(2) 习题2图9.3 一个无向简单图,如果同构于它的补图,则称这个图为自互补图。
(1)试画出五个顶点的自互补图。
(2)证明一个自互补图一定只有k 4或14+k 个顶点(k 为整数)。
解(1)(a) (b)图9.3 习题3图 (2)因为n 个顶点的无向完全图有)1(21-n n 条边,所以自互补图有)1(41-n n 条边,因此,k n 4=或14+k 。
9.4 画出两个不同构的简单无向图。
每一个图都仅有6个顶点,且每个顶点都均是3度,并指出这两个图为什么不同构。
解图9.4 习题9.4图9.5 证明任意两个同构的无向图,一定有一个同样的顶点度序列。
顶点度序列是一组按大小排列的正整数。
每一个数对应某一个顶点的度数。
证明两个同构的无向图,度数相同的顶点数目一定相同,这样才能够建立起顶点之间的一一对应关系,进而建立起边的对应关系。
所以,任意二个同构的无向图,一定有一个同样的顶点度序列。
9.6图9.6中所给的图(a )与图(b )是否同构?为什么?(a )(b ) 图9.6 习题6图 解左图9.2(a )中次数为4的点,与3个度数为1,一个度数为2的顶点相邻接,右图9.2(b )中度数为4的点,却与3个度数为1,一个度数为3的顶点相邻接。
离散数学第9章习题答案

习题91. 设G 是一个(n ,m)简单图。
证明:,等号成立当且仅当G 是完全图。
证明:(1)先证结论:因为G 是简单图,所以G 的结点度上限 max(d(v)) ≤ n-1, G 图的总点度上限为 max(Σ(d(v)) ≤ n ﹒max(d(v)) ≤ n(n-1) 。
根据握手定理,G 图边的上限为 max(m) ≤ n(n-1)/2,所以。
(2) =〉G 是完全图 因为G 具有上限边数,假设有结点的点度小于n-1,那么G 的总度数就小于上限值,边数就小于上限值,与条件矛盾。
所以,G 的每个结点的点度都为n-1,G 为完全图。
G 是完全图 =〉 因为G 是完全图,所以每个结点的点度为n-1, 总度数为n(n-1),根据握手定理,图G 的边数 。
■2. 设G 是一个(n ,n +1)的无向图,证明G 中存在顶点u ,d (u )≥3。
证明:反证法,假设,则G 的总点度上限为max(Σ(d(u)) ≤2 n ,根据握手定理,图边的上限为max(m) ≤ 2n/2=n 。
与题设m = n+1,矛盾。
因此,G 中存在顶点u ,d (u )≥3。
■3.确定下面的序列中哪些是图的序列,若是图的序列,画出一个对应的图来: (1)(3,2,0,1,5); (2)(6,3,3,2,2) (3)(4,4,2,2,4); (4)(7,6,8,3,9,5)解:除序列(1)不是图序列外,其余的都是图序列。
因为在(1)中,总和为奇数,不满足图总度数为偶数的握手定理。
可以按如下方法构造满足要求的图:序列中每个数字ai 对应一个点,如果序列数字是偶数,那么就在对应的点上画ai/2个环,如果序列是奇数,那么在对应的点上画(ai-1)/2个环。
最后,将奇数序列对应的点两两一组,添加连线即可。
下面以(2)为例说明:(6 , 3, 3, 2, 2 ) 对应图G 的点集合V= { v 1,v 2,v 3,v 4,v 5}每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)将奇数3,3 对应的结点v 2,v 3一组,画一条连线其他序列可以类式作图,当然大家也可以画图其它不同的图形。
《离散数学课件资料》PPT课件

(2)因为两个权对应的顶点所放左右位置不同。
(3)画出的最优树可能不同,最佳前缀码并不唯一,
但有一点是共同的,就是它们的权相等,即它们都应
该03是.02.2最021优树。
28
五、树的遍历
遍历:对一棵根树的每个顶点访问且仅访问一次称为遍
历一棵树。
对2元有序正则树的遍历方式: ① 中序遍历法:访问次序为:左子树、树根、右子树 ② 先序遍历法:访问次序为:树根、左子树、右子树 ③ 后序遍历法:访问次序为:左子树、右子树、树根
树枝:生成树TG的边。 弦:G中不在TG中的边。 生成树的余树(补):TG的所有弦的集合的导出 子图。余树不一定是树,也不一定连通。
03.02.2021
7
二、生成树
a
a
a
d
e b
图G
d
e
e
cb
cb
c
生成树TG
生成树TG的补
无向连通图如果本身不是树,它的生成树是不唯一的, 但所有连通图都具有生成树。
(本书树根为第0层。)
03.02.2021
14
一、有向树
根树可看成是家族树: (1) 若从a到b可达,则称a是b的祖先, b是a的后代; (2) 若<a , b >是根树中的有向边,则称a是b的父亲,
b是a的儿子; (3) 若b、c同为a的儿子,则称b、c为兄弟。
根子树:根树T 中,任一不为树根的顶点v及其所有 后代导出的子图, 称为T 的以v为根的子树。
二元前缀码:若i (i=1,2,…,m)中只出现0与1两个符号, 则称B为二元前缀码。
03.02.2021
24
四、最佳前缀码
例:判断下列符号串集合是否是前缀码。 {1,11,101,0010} {1,01,001,000} {00,11,011,0100,0101} {0,10,110,1111}
离散数学第五版第九章(耿素云、屈婉玲、张立昂编著)市公开课获奖课件省名师示范课获奖课件

G2是G1旳同态像,记作G1 ~G2 。 (2)若:G1G2是单射旳,则称为单同态。
(3)若:G1G2是双射旳,则称为同构,记作 G1 G。2 (4)若G1=G2,则称是群G旳自同态。
39
9.2 代数系统
例16: 设V=<R+,•>,其中•为一般成法。对任意xR+令 1(x)=|x|, 2(x)=2x, 3(x)=x2, 4(x)=1/x, 5(x)=-x,则分析他们是否为V到V旳同态,假如 是,则分别为何同态。
设和*是S上旳两个可互换旳二元运算,假如对于任意旳
x,yS有
x*(xy)=x
x(x*y)=x
则称运算*和满足吸收律。 例如:幂集P(S)上旳和运算满足吸收律。即A,BP(S)
有
A(A B)=A
A(A B)=A
14
9.1二元运算及其性质
四、单位元和幺元
1. 幺元旳定义(定义9.6)
设为S上旳二元运算,假如存在 el (或 er)S使得对于任何
(2)当n=2时,则函数f:S×SS为S上旳二元运算。
(x,y)=z
(3)当n=3时,则函数f:S×S×SS为S上旳三元运算。
(x,y,z)=t
6
9.1二元运算及其性质
例4:在整数集合Z、有理数集合Q、实数集合R上,一 个数旳相反数、倒数是否为这些集合上旳一元运 算?
例5:在幂集P(S)上,假如要求全集为S,则求集合旳 绝对补运算~是否为P(S)上旳一元运算?
xS都有
el x = x(或 x er =x) 则称 el (或er )是S中有关运算旳一种左幺元(或右幺
元)。若eS有关运算既是左幺元又是右幺元,则称e 为S上有关运算旳幺元。
离散数学-第9章 图

例9.2.2 分析
分析 由于V中有5个结点,因此要用5个小圆圈 分别表示这5个结点,点的具体摆放位置可随意 放。而对E中的6条边,圆括号括起的结点对表示 无向边,直接用直线或曲线连接两个端点,尖括 号括起的结点对表示有向边,前一个是始点,后 一个始终点,用从始点指向终点的有向直线或曲 线连接。
ai
j
1 , 0 ,
若 ( vi,vj ) 否则
E
或
vi,vj
E
i,j 1,2,3, ,n
2023/11/27
例9.2.4
试写出下图所示图G的邻接矩阵。
分解析 若首结先点将排图序中为的v16v个2v结3v4点v5排v6,序则, v1 然其邻后接利矩用v1阵定v义2 9.v23.2写v4出其v5邻接v6矩阵。 初按结学vv点时21 0排可1 序先01标在上0矩01结阵1 点的000,行0若与1第01列i1前行01分前别的 v5 结在否则可邻点则vvvv标接到为6543 记矩第00011。A如阵jG列若下0001的前结:第11100的点0111i10000行结排第点序111100111j有为11100列边v11000元00111v相2素11100v连30111为v4,v15则,v6,
2023/11/27
例9.2.5
试写出下图所示图G的所有结点的邻接点、所有边
的邻接边,并指出所有的孤立结点和环。
v3
v4
v5
e4 e5 v2
e6 e1
e2 v6 e7
v1 e3
2023/11/27
例9.2.5 分析
根据定义9.2.4,如果两个结点间有边相连,那 么它们互为邻接点;如果两条边有公共结点,那 么它们互为邻接边。需要注意的是,只要当一个 结点处有环时,它才是自己的邻接点;由于一条 边有两个端点,在计算邻接边时要把这两个端点 都算上,例如e2和e4都是e1的邻接边。所有边都 是自己的邻接边。
离散数学精讲第九章

19
同类型与同种代数系统
定义9.7 (1) 如果两个代数系统中运算的个数相同,对应运算的元数相 同,且代数常数的个数也相同,则称它们是同类型的代数 系统. (2) 如果两个同类型的代数系统规定的运算性质也相同,则称 为同种的代数系统. 例如 V1=<R, +, · , 0, 1>, V2=<Mn(R), +, · , , E>, 为 n 阶全0 矩阵,E为 n 阶单位矩阵, V3=<P(B), ∪, ∩, , B> V1, V2, V3是同类型的代数系统,它们都含有2个二元运算, 2个代数常数. V1, V2是同种的代数系统,V1, V2与V3不是同种的代数系统
5
二元与一元运算的表示
1.算符 可以用◦, ∗, ·, , , 等符号表示二元或一元运算,称为算符. 对二元运算◦,如果 x 与 y 运算得到 z,记做 x◦y = z 对一元运算, x的运算结果记作x. 2.表示二元或一元运算的方法: 解析公式和运算表
公式表示
例 设R为实数集合,如下定义R上的二元运算∗: x, y∈R, x ∗ y = x. 那么 3∗4 = 3, 0.5∗(3) = 0.5
则矩阵加法和乘法都是Mn(R)上的二元运算. (5) S为任意集合,则∪、∩、-、 为P(S)上二元运算. (6) SS为S上的所有函数的集合,则合成运算为SS上二元运算.
4
一元运算的定义与实例
定义9.2 设S为集合,函数 f:S→S 称为S上的一元运算,简 称一元运算. 例2 (1) 求相反数是整数集合Z,有理数集合Q和实数集合R上 的一元运算 (2) 求倒数是非零有理数集合Q*,非零实数集合R*上一元运算 (3) 求共轭复数是复数集合C上的一元运算 (4) 在幂集P(S)上规定全集为S,则求绝对补运算~是P(S)上的 一元运算. (5) 设S为集合,令A为S上所有双射函数的集合,ASS,求一 个双射函数的反函数为A上的一元运算. (6) 在n(n≥2)阶实矩阵的集合Mn(R)上,求转置矩阵是Mn(R)上 的一元运算.
离散数学9-格与布尔代数

17
定理4: 设<A, ∨, ∧>是格,对任意a, b, cA,有 (1)若a≤b和c≤d,则a∧c≤b∧d,a∨c≤b∨d (2)若a≤b,则a∧c≤b∧c,a∨c≤b∨c
18
证明:(1)如果a≤b,又b≤b∨d, 由传递性得 a≤b∨d, 类似由c≤d, d≤b∨d,由传递性得 c≤b∨d,这说明b∨d是{a, c}的上界,而a∨c是{a, c}的最小上界,所以a∨c≤b∨d。类似可证 a∧c≤b∧d。
则称b是a的补元,记为a′。若b是a的补元,则a也是b的补 元,即a与b互为补元。 一般说来,一个元素可以有其补元 ,未必唯一,也可能无补元。0′=1和1′=0。
37
定义12: 在有界格中,如果每个元素都有补元,则称格是有 补格。
由于补元的定义是在有界格中给出的,可知,有补格一定是 有界格。
38
定理11: 在有界分配格中,如果某元素有补元,则补元是唯 一的。
34
定理9: 设<A, ∧,∨, 0, 1>是有界格,则对于A中任意元素 a 都有 a∨1 = 1 a∧1 = a a∨0 = a a∧0 = 0
1称为全上界或最大元,0称为全下界或最小元。
图9-6中(a)(b)(c)都有最大元和最小元,所以都是有界格。
35
定理10: 有限格必定是有界格。
36
定义11: 设<A,∨,∧>是有界格,aA,如果存在bA使得 a∨b = 1 a∧b = 0
31
定义8: 设<A,∨,∧>是格,如果A中存在元素a,使得对于A中 任意元素x 都有a≼x,则称a为格(A , ≤)的全下界,用0表 示。如果L中存在元素 a, 使得对于L中任意元素 x 都有 x≼a则称a为格(A , ≤)的全上界,用1表示。全下界即是格 的最小元,是唯一的。全上界即是格的最大元,是唯一的 。
