物理化学 第十章
第五版物理化学第十章习题答案

第十章界面现象请回答下列问题:(1)常见的亚稳定状态有哪些?为什么会产生亚稳定状态?如何防止亚稳定状态的产生?解:常见的亚稳定状态有:过饱和蒸汽、过热或过冷液体和过饱和溶液等。
产生亚稳定状态的原因是新相种子难生成。
如在蒸气冷凝、液体凝固和沸腾以及溶液结晶等过程中,由于要从无到有生产新相,故而最初生成的新相,故而最初生成的新相的颗粒是极其微小的,其表面积和吉布斯函数都很大,因此在系统中产生新相极其困难,进而会产生过饱和蒸气、过热或过冷液体和过饱和溶液等这些亚稳定状态,为防止亚稳定态的产生,可预先在系统中加入少量将要产生的新相种子。
(2)在一个封闭的钟罩内,有大小不等的两个球形液滴,问长时间恒温放置后,会出现什么现象?解:若钟罩内还有该液体的蒸气存在,则长时间恒温放置后,出现大液滴越来越大,小液滴越来越小,并不在变化为止。
其原因在于一定温度下,液滴的半径不同,其对应的饱和蒸汽压不同,液滴越小,其对应的饱和蒸汽压越大。
当钟罩内液体的蒸汽压达到大液滴的饱和蒸汽压时。
该蒸汽压对小液滴尚未达到饱和,小液滴会继续蒸发,则蒸气就会在大液滴上凝结,因此出现了上述现象。
(3)物理吸附和化学吸附最本质的区别是什么?解:物理吸附与化学吸附最本质的区别是固体与气体之间的吸附作用力不同。
物理吸附是固体表面上的分子与气体分子之间的作用力为范德华力,化学吸附是固体表面上的分子与气体分子之间的作用力为化学键力。
(4)在一定温度、压力下,为什么物理吸附都是放热过程?解:在一定温度、压力下,物理吸附过程是一个自发过程,由热力学原理可知,此过程系统的ΔG<0。
同时气体分子吸附在固体表面,有三维运动表为二维运动,系统的混乱度减小,故此过程的ΔS<0。
根据ΔG=ΔH-TΔS可得,物理吸附过程的ΔH<0。
在一定的压力下,吸附焓就是吸附热,故物理吸附过程都是放热过程。
在K及下,把半径为1×10-3m的汞滴分散成半径为1×10-9m小汞滴,试求此过程系统的表面吉布斯函数变为多少?已知汞的表面张力为·m-1。
物理化学第十章表面现象

消;在垂直方向上的分力为 γ cosα 。 因此在垂直于截面方向上这些分力的合力为 : F = 2πr `γ cosα r' cos α = r F = 2πr ' 2γ / r §10-3 弯曲液面的附加压力和毛细现象 在弯曲液面上垂直作用于单位截面上的力,即为附加压力,用 F 2γ 来表 该公 式就是拉普拉斯方程。 P P= P P = 外 内 得出: ⑴对指定的液体而言(即 γ 为一定值),附加压力与表面曲率 半径成 反比。曲率半径越大,附加压力越小。 ⑵对于凸液面来说 r > 0 , ∴ P > 0 方向 为指向液体内部。 对于凹液面来说 r < 0 , ∴ P < 0 方向指向气体。 对于水平液 面来说 r → ∞ , ∴ P = 0 。 ⑶对于不同液体而言,液面的曲率相同时,附加压 力与表面张力 成正比。 ⑷从上面推导的过程来看,拉普拉斯方程适用于曲率半径为 定值 的小液滴或液体中小气泡的附加压力的计算; ⑸而对于球形液膜,例如空气中 的肥皂泡,有内、外两个球形表 面,外表面是凸液面,内表面是凹液面,产生的附加 压力均指向 液泡中心,所以液泡内气体的压力大于泡外气体的压力,其附加 4γ 压 力 。 P = r πr '2 = r §10-3 弯曲液面的附加压力和毛细现象 三、毛细现象 把一根毛细管插入到液体中,管中液面会出 现两种现象: ⑴若 该液体能润湿毛管管管壁 (例如水),管中的液面呈凹开,曲面受到 一向上的附加 压力;此时曲面下的液体对表 面层的压力P应当小于大气压Pg,液面会上升 一定高度 。 ⑵若该液体不能润湿毛管管管壁(例如汞), 管中的液面呈现凸形,曲面受到一 向下的附 图10-10 毛细管现象 加压力,此时曲面下的液体所受到的压力P 应当大于 大气压Pg ,因而液面会下降。 利用毛细现象,可以来测定液体的表面张力,以毛细 管中液体上 升为例: 设毛细管半径为r ,管内液面可以近似看作球形的一部分,并 设 2γ 方向向上,致使管 该球面的曲率半径为R ,则附加压 力 P = 内的液柱上升 一定高度, R §10-3 弯曲液面的附加压力和毛细现象 当达到平衡时,向上的附加压力 P 与高出液面的那部分液柱的静 2γ P = ρg h = 压力 ρgh 相等,即: R 而一般测量时R不容易测定,转化 成毛细球面的曲率半 径 r。 r cos θ = 从图10-10上可知: R ρghR ρghr = γ= 因而液体的表面张力 : (10-17) 2 2 cos θ 式中 ρ--为液体与气体的密度差(或直接表示成液体的密度 ) g--为重力加速度 θ--为液体与毛细管壁的接触角 若已知液体的表面张力 γ 和 接触角θ,则可以求得弯曲液面上升的 2γ 高度h: h= cos θ ρgr (10-18) 由式 10-18可知:在一定温度下( γ 不变)毛细管愈细,液体的密 度愈小,液体对管壁 润湿得愈好(越小),液体在毛细管中上升得 愈高。 cos 当液体不能润湿管壁时, > 90 0 , θ < 0 ,h为负值,表示管内凸液 θ 面下降的高度。 §10-4 分散度对系统性质的影响 一、微小液滴的饱和蒸气压——开尔文公式( kelvin) 在一定温度与外压下,纯液体有一定的饱和蒸气压 但这“ 饱和蒸气压, 在一定温度与外压下,纯液体有一定的饱和蒸气压,但这“饱和 蒸 气压”指的是, 平面液体的 气压”指的是,平面液体的。 实验表明,微小液滴的饱和蒸气压高于平 面液体的饱和蒸气压, 高于平面液体的饱和蒸气压 实验表明,微小液滴的饱和蒸气 压高于平面液体的饱和蒸气压, 这说明,蒸气压不但与温度,压力与物质本性有关, 这说明,蒸气压不但与温度,压力与物质本性有关,还与液滴的 大小,即其曲率半 径有关。如图10- 所示 所示: 大小,即其曲率半径有关。如图 -11所示: 恒温下 将1mol液体(平液面) 分散成半径为的小液滴,可 按两种途径来进行如下所示:
物理化学第十章 胶体化学

3. 沉降与沉降平衡
多相分散系统中的粒子,因受重力作用而下 沉的过程,称为沉降。沉降与扩散为一对矛盾 的两个方面
沉降 扩散 分散相分布
真溶液
粗分散系统 胶体系统 平衡
均相
沉于底部 形成浓度梯度
贝林(Perrin)导出沉降平衡时粒子浓度随高度的分布:
o c2 Mg ln 1 ( h2 h1 ) c1 RT
胶核 可滑动面
胶粒
{[AgI]m nI-(n-x)K+}x- xK+ 胶团结构
K+
K+
I-
K+
(AgI)m
I-
I-
K+
特点:
1) 胶核:首先吸附过量的成核离子,然后吸附反离子; 2) 胶团整体为电中性
I-
§10.5
溶胶的稳定与聚沉
Derjaguin&Landau(1941)
1. 溶胶的经典稳定理论DLVO理论
溶胶粒子间的作用力:
Verwey &Overbeek(1948) van der Waals 吸引力:EA -1/x2
势 能 ER
双电层引起的静电斥力:ER ae-x 总作用势能:E = ER + EA
E
EA 曲线的形状由粒子本
性决定,不受电解质影响;
Emax
0 x 第二最小值 EA 第一最小值
势 能 ER 电解质浓度: c1 < c2 < c3 ,
0EAc3源自c2c1E电解质浓度,ER,E,
溶胶稳定性。在 c3 以后, 引力势能占绝对优势,分散 相粒子一旦相碰,即可聚合。
41
电解质对溶胶的聚沉规律:
(i)反离子的价数起主要作用
物理化学 第十章

精品PPT
水滴为什么是圆 形而不是方形
精品PPT
它们为什么可以 漂在水面上
精品PPT
水在毛细管中为
什么会上升
水
(shàngshēng)
精品PPT
界面(Interface)
界面(jièmiàn)是相与相 之间的交界所形成的物理 区域 界面相是一个准三维区 域,其广度(guǎngdù)无 限,而厚度约为几个分 子的线度 体系性质在体相为常数, 界面的结构和性质与相邻 两侧的体相都不相同。
1. 弯曲液面的附加压力——Laplace方程
在凸液面上
pg
由于液面是弯曲的,则
沿AB的周界上的表面张力 f 不是水平的,作用于边界的
AB
p
f
力将有一指向(zhǐ xiànɡ)液
体内部所的有合的力点产生的合力和
pl
为△p ,称为附加(fùjiā)压
力凸面上受的总压力为:
pl pg p
精品PPT
在凹液面上
精品PPT
2. 热力学公式 (gōng单sh相ì)多组分系统:
对需要考虑表面层的系统,由于多了一个(yī ɡè)表面相 ,在体积功之外,还要增加表面功,若系统内只有一个 (yī ɡè)相界面,且两相T、p相同 ,则基本公式为:
精品PPT
考虑了表面(biǎomiàn)功的热力学基本公式 为
同样(tóngyàng)推导可得
精品PPT
恒T、p、 、恒组分下积分,有:
全微分得:
可知(kě zhī)自发降低界面吉布斯函数有两种途径: 降低(jiàngdī)表面 降积低表面张力
精品PPT
精品PPT
3. 界面张力及其影响因素
(1) 物质的本性 分子间相互作用力越大, 越大
物理化学(第五版傅献彩)第10_电解与极化作用

无电流
ϕ可逆
= ϕy Ag+ |Ag
−
RT F
ln
1 aAg+
有电流
ϕ不可逆
= ϕy Ag+ |Ag
−
RT F
ln
1 aAg+ , e
η阴
= ϕ可逆
− ϕ不可逆
=
RT F
ln aAg+ aAg+ , e
>0
aAg+ , e < aAg+ ϕ不可逆 < ϕ可逆
阳极上的情况类似,但 ϕ不可逆 > ϕ可逆
的金属先在阴极析出,这在电镀工业上很重要 例如,利用氢的超电势,控制溶液的pH,实
现镀 Zn,Sn,Ni,Cr 等
25
阴极上发生还原反应
发生还原 (1) 金属离子 的物质: (2) 氢离子 (中性水溶液 aH+ = 10−7 ) 判断在阴极上首先析出何种物质,应把各 种可能还原的物质的电极电势求出来(气 体要考虑超电势,金属可不考虑超电势)
2H+ + 2e- = H2
ϕ可逆
=ϕΟ H+ |H2
− RT 2F
ln
pH2 / p Ο a2
H+
= −0.059pH = −0.414V
ϕ不可逆 = ϕ可逆 −η = −0.414V − 0.584V = −0.998V
Zn2+ + 2e- = Zn
ϕ可逆
=ϕΟ Zn2+ |Zn
− RT 2F
1 ln
=−
RT 2F
ln
aH2 a2
H+
−ηH2
设 pH2 = p Ο
10-物理化学第十章 界面现象

ln
Pr Ps
2 M r RT
凸(液滴)~ “+” 凹(气泡)~ “–”
凸(液滴,固体粉末 or r > 0)— Pr>Ps 凹(气泡 or r < 0 )— Pr<Ps
水平液面(r→∞)— Pr=Ps
❖ 亚稳状态和新相的生成 ——分散度对系统性质的影响
亚稳状态
——热力学不稳定态,一定条件下能相对 稳定的存在。
杨氏方程
cos
s l
sl
润湿条件 s sl 铺展条件 s sl l
❖ 应用
毛细管内液面
凹: 润湿
凸: 不润湿
§10–3 弯曲液面下的附加压
由此产生毛细现象,并影响饱和蒸气压
10·3·1 弯曲液面产生附加压
附加压 △P= P心-P外
➢ 杨-拉普拉斯方程
曲面— P 2 膜— P 4
第十章 界面现象
讨论界面性质对系统的影响
新的系统—多相,小颗粒系统
非体积功—表面功
❖ 需考虑界面影响的系统 界面所占比例大的系统
比表面——
aS
AS m
❖ 本章内容 表面张力
① 表面现象的成因 表面现象的总成因
与AS↓有关 ② 各类现象分析
与γ↓有关
§10–1 表面现象的成因 10·1·1 表面张力 ❖ 表面张力 γ 定义—作用于单位边界上的表面紧缩力 方向—总指向使表面积减小的方向
为降低表面张力而产生 吸附剂 —— 起吸附作用的 吸附质 —— 被吸附的
§10–4 固体表面的吸附 固体对气体的吸附
10·4·1 吸附的产生
固体特点—有大的比表面,不稳定。 通过吸附其它分子间力较小的物质,形成 新的表面能较低的界面。
两个相对的过程——吸附和解吸 吸附量——一定T、P下,吸附和解吸达平 衡时,吸附气体的量。
物理化学第六版第十章界面现象课后思考题

物理化学第六版第十章界面现象课后思考题
(原创版)
目录
1.物理化学第六版第十章界面现象概述
2.课后思考题解答
正文
一、物理化学第六版第十章界面现象概述
物理化学第六版第十章主要讲述了界面现象,界面现象是指发生在两种不同相(如固相与液相、液相与气相等)之间的物理化学现象。
在这一章中,我们学习了界面张力、表面能、润湿现象等相关知识。
通过学习这些内容,我们可以更好地理解不同相之间的相互作用,从而为实际应用提供理论基础。
二、课后思考题解答
课后思考题 1:请简述界面张力的概念及其对界面现象的影响。
答:界面张力是指作用在液体界面上的力,使得液体表面有缩小的趋势。
界面张力的大小取决于液体的性质以及液体之间的相互作用。
界面张力对界面现象有重要影响,它决定了液体滴的形成、液滴的合并以及液体在固体表面的展开等过程。
课后思考题 2:请举例说明表面能的概念,并分析其在实际应用中的意义。
答:表面能是指在标准状态下,将一个物质的表面从完美晶体变为实际表面所需要的能量。
表面能可以通过吉布斯吸附等温线来测量。
在实际应用中,表面能对材料的润湿性、腐蚀性以及催化活性等方面具有重要意义。
课后思考题 3:请简述润湿现象及其分类。
答:润湿现象是指液体在固体表面上的展开过程。
根据液体在固体表面上的行为,润湿现象可分为三种类型:附着润湿、铺展润湿和毛细润湿。
润湿现象对涂料、粘合剂等材料的性能有重要影响。
通过学习物理化学第六版第十章界面现象,我们可以深入了解不同相之间的相互作用,为实际应用提供理论基础。
物理化学知识点chap 10

Pa
2.356
103
kPa
【10.5】水蒸气迅速冷却至298.15K时可达到过饱和状态。已
知该温度下水的表面张力为71.97×10-3 N·m -1 ,密度为997
kg·m-3。 当过饱和水蒸气压力为平液面水的饱和蒸气压的4
倍时,计算: (1)开始形成水滴的半径;(2)每个水滴中
所含水分子的个数。
m
= 7.569 ? 10- 10m
(2)每个水滴的体积
( ) V 水滴=
4 3
pr
3
=
4 创3.14 3
7.569 ? 10- 10 3 m 3
1.815 ? 10- 27m 3
每个水分子的体积
V 水分子=
M rL
=
骣 琪 琪 琪 桫997
创
0.018 6.022
m 3 = 3.00 ? 10- 29m 3 1023
分析: 利用拉普拉斯方程
p 2
r
解: (1)和(2)两种情况下均只存在一个气-液界面, 其附加压力相同。根据拉普拉斯方程
p
2
r
2 58.91103 0.1106
Pa
1.178
103
kPa
(3)空气中存在的气泡,有两个气-液界面,其附加压力 为
p
4
r
4
58.91103 0.1106
•
pg
••
•
气
•
p
• •
pl
(a)
pg
• 气 p • •
液•
pl (b)
附加压力方向示意图
•
•
气•
•
•
• •
p=• 0
物理化学第六版第十章界面现象课后思考题

物理化学第六版第十章界面现象课后思考题摘要:1.物理化学第六版第十章界面现象概述2.课后思考题解答正文:一、物理化学第六版第十章界面现象概述物理化学第六版第十章主要讲述了界面现象,这是物理化学中的一个重要内容。
界面现象是指两种或多种物质相互接触时,由于它们之间的相互作用力不同,会发生的一系列现象。
这些现象包括表面张力、接触角、界面电荷等。
本章主要通过讲述这些现象,使读者了解并掌握界面现象的基本概念和相关知识。
二、课后思考题解答1.问题一:请简述表面张力的概念及其产生原因。
答:表面张力是指液体分子之间的相互作用力。
当液体与气体接触时,液体表面层的分子受到气体分子的吸引,使液体表面层的分子间距大于液体内部分子间距,从而使液体表面形成一个收缩的趋势。
这种使液体表面有收缩趋势的力称为表面张力。
2.问题二:请解释接触角的概念,并举例说明。
答:接触角是指液体与固体接触时,液体与固体的界面形成的角度。
接触角可以用来判断液体与固体的亲水性或疏水性。
当接触角小于90°时,液体与固体呈亲水性;当接触角大于90°时,液体与固体呈疏水性。
例如,水滴在玻璃板上时,水滴与玻璃板接触角大于90°,说明水与玻璃呈疏水性。
3.问题三:请简述界面电荷的概念及其产生原因。
答:界面电荷是指在两种介质接触的界面上,由于介质的极性不同,会产生电荷分布的现象。
当两种介质接触时,如果它们的极性不同,就会在接触界面上产生正负电荷。
这些电荷称为界面电荷。
例如,当金属与非金属接触时,由于金属表面的电子与非金属表面的电子互相转移,会在接触界面上产生界面电荷。
通过以上解答,我们可以更好地理解物理化学第六版第十章界面现象的相关知识。
《物理化学》第十章 电解与极化作用PPT课件

(1)电解时那种物质先析出,初始电压是多少?
(2)当第二种金属析出时,电压应为多少?此时 溶液中第一种金属的残余浓度是多少?
(3) 当电压加到多大时,H2开始析出?
已知H2在Cu上的超电势为1V,在Zn上的超电势 为1.3V, 在 Pt上的超电势可忽略不计。
氢析出超电势较大, 且在不同金属上超电势不
同, 不能忽略. 由于超电势存在, 氢析出电势向负向
移动.
例1 电解 AgNO3(a± = 1) 水溶液. 解: 在阴极上析出反应:
Ag (a 1) e Ag(s)
Ag,析
θ Ag
0.799V
H (a
10-7 )
e
1 2
H2(
pθ )
H2 ,析 0.414V H2
2 1
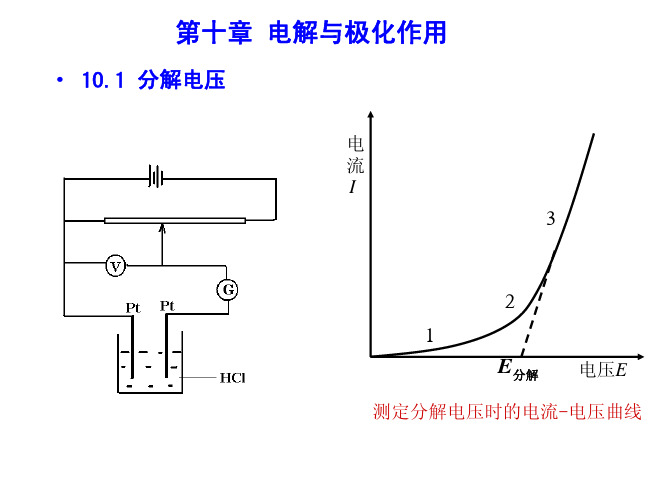
E分解 电压E
测定分解电压时的电流-电压曲 线
实际分解电压
要使电解池顺利地进行连续反应,除了克服作 为原电池时的可逆电动势外,还要克服由于极化在 阴、阳极上产生的超电势(阴) 和(阳) ,以及克服电 池电阻所产生的电位降 IR。这三者的加和就称为实 际分解电压。
E(分解) E(可逆) E(不可逆) IR
§10.2 极化作用
例如电解一定浓度的硝酸银溶液
阴极反应
Ag+ (mAg+ ) e Ag(s)
电解时
可逆
Ag |Ag
RT F
ln
1 aAg+
不可逆
Ag |Ag
RT F
ln
1 ae,Ag
阴 (可逆 不可逆)阴 RT ln aAg
F
ae,Ag
> ae,Ag < aAg 可逆
不可逆
阳极上有类似的情况,但 可逆 < 不可逆
物化第十章习题

板上,滴上一小滴水,再在水上覆盖上油,这时
水对毛细管的润湿角为,如习题 10.7 图图(b)所
示。油和水的密度分别用O 和W 表示,AA/为油水界面,油层的深度为 h/。请导出水在毛细管中 上升的高度 h 与油-水界面张力WO 之间的定量关
系。
解:因为在油中水可以润湿玻璃管,在玻璃毛细管中油-水界面为凹面,毛细管半径
பைடு நூலகம்
题 10.8 图示
10.9 已知在 273.15K 时,用活性炭吸附 CHCl3,其饱和吸附量为 93.8dm3kg-1, 若 CHCl3 的分压力为 13.375kPa,其平衡吸附量为 82.5dm3kg-1,试求:
(1) 朗谬尔吸附等温式中的 b 值;
(2) CHCl3 的分压力为 6.6672kPa 时,平衡吸附量为若干?
解:(1)因为
Va
Vma
bp 1 bp
依题意 V a=93.8dm3kg-1, Vma=82.5dm3kg-1 p=13.375kPa 代入上式得 b=[82.5/13.375×(93.8-82.5)] kPa-1= 0.5459 kPa-1
(2)当 p=6.6672kPa 时
V
a
Vma
bp 1 bp
答:亚稳态是热力学不完全稳定的状态,常见的亚稳态有过饱和蒸气、过热液体、 过冷液体、过饱和溶液。产生的原因是在新的相生成时,颗粒极其微小,其比表面积和表 面吉布斯函数都很大,因此在系统中产生新相极为困难而造成亚稳态的产生。防止亚稳 态产生的方法一般是引入“种子”,使之形成结晶或凝聚或气化核心。
(2)在一个封闭的钟罩内,有大小不等的两个球形液滴,问长时间恒温放置后,会 出现什么现象?
解:对方程 V a=kpn 取对数可得:
物理化学第十章 胶体化学

+++++++++++++++ –––––––––––––––
+
–
首
页
上一页
+++++++++++++++ –––––––––––––––
电渗
下一页 末 页 17
第三节
溶胶的稳定与聚沉
一 溶胶的稳定性
溶胶的聚结不稳定性:
溶胶的动力稳定性:
1)分散相粒子的布朗运动:在重力场中不易沉降
2)扩散电势(ζ电势):稳定剂的存在使胶团形成
双电层结构,ζ电势越大,越不易聚沉。
首
页
上一页
下一页
末
页
18
二
1
溶胶的聚沉
电解质对聚沉的影响 少量电解质的存在对溶胶起稳定作用;
过量电解质的存在对溶胶起破坏作用(聚沉) 1)聚沉值: 使一定量溶胶在一定时间内完全聚沉所需最小电
解质的物质的量浓度。
2)反离子起聚沉作用,聚沉值与价数有关,聚沉值: 1 1 1 舒尔采(Schulze) 100 : 1.6 : 0.14 6 : 6 : 6 1 2 3 ——哈迪(Hardy)规则
+ ++ ++ + ++ + +
+ + -
-
+ + + -
热力学电势φ 0 斯特恩电势φ 电动电势ζ:
固体表面 斯特恩面 滑动面
+ +
物理化学第10章界面现象ppt课件

在1913—1942年期间,美国科学家Langmuir在界面 科学领域做出了杰出的贡献,特别是对吸附、单分 子膜的研究尤为突出。他于1932年获诺贝尔奖,被 誉为界面化学的开拓者。 界面化学的统计力学研 究是从范德华开始的。1893年,范德华认识到在界 面层中密度实际上是连续变化的。他应用了局部
与一般体系相比,小颗粒的分散体系有很大的表 面积,它对系统性质的影响绝对不可忽略。
首 页 刚看的页 上一页 下一页 结 束
物质的分散度用比表面积 as 表示,它的定义为 物质的表面
积 As 与质量 m 的比:
as
As m
10.0.1 单位:m2·kg-1
对于以上水滴的例子,若近似认为其在室温下密度为 1g ·cm-3,则以上两种情况,比表面积 as 分别约为:6 cm2 ·g1 及600 m2 ·g-1 。
αB
4.2.7
首 页 刚看的页 上一页 下一页 结 束
dU TdS pdV μB (α)dnB (α) 4.2.8
αB
dH TdS Vdp μB (α)dnB (α) 4.2.9
αB
dA SdT pdV μB (α)dnB (α) 4.2.10
αB
当体系作表面功时,G 还是面积A的函数
界面现象是自然界普遍存在的现象。胶体指的是 具有很大比表面的分散体系。对胶体和界面现象 的研究是物理化学基本原理的拓展和应用。从历 史角度看,界面化学是胶体化学的一个最重要的 分支,两者间关系密切。而随着科学的发展,现 今界面化学已独立成一门科学,有关“界面现象” 或“胶体与界面现象”的专著在国内外已有多种 版本。本课程主要介绍与界面现象有关的物理化 学原理及应用。它包括各种相界面和表面活性剂 的相关特性,界面上的各种物理化学作用,实验 的和理论的研究方法及其重要应用。对于准备考 研的同学,还应将其作为物理化学课程的一部分。
物理化学第十章课件

若再在水中加入少许NaCl,管中液位又如何变化?
例2:如图,四支内径相同的玻璃毛细管垂直插入水中,a中水面 升高h,则其它三支中水位(面)如何变化?c、d中水能否溢出?
h
a
2013-11-15
b
c
d
界面现象
―永动机”能否实现?
20
例3:用同一支滴管分别滴取1cm3 纯水和1cm3 NaCl 稀水溶液, 何者滴数较少?
解: 体积/m3 半径 水滴个数 表面积/m2
大水滴
小水滴
1×10-6
1×10-6
0.62 cm
1 nm
1
2.39×1020
4.83×10-4
3.01×103
ΔG = γ ΔAs = 0.07275×3.01×103 = 219 J
2013-11-15
界面现象
6
系统比表面越大,能量越高,越不稳定。 空气中的尘埃就是高度分散的固体微粒,表面能很高,很不稳定, 容易和氧结合,释放大量的能量,甚至发生爆炸—粉尘爆炸. 某些物质的爆炸极限: 淀粉/硫磺 7,面粉/糖粉 10,煤粉 17(单位:mg/L空气)。 聚四氟乙烯(PTFE,“塑料王”)是已知固体中表面能最小的, 即任何东西都不能粘附在其表面上,可用于制造热交换器(不粘 水垢)、“不粘锅”表面涂层。另外,它耐腐蚀、不吸湿、不燃 烧、耐候性特别好,摩擦系数极低(用作摩擦密封材料)。
2013-11-15
界面现象
8
任意形状 自由移动
张开成圆 (膜面积最小)
水黾(mĭn)
某些昆虫可以在水面上自由行走,主要 就是由于表面张力的缘故(还有就是脚 部的超疏水微结构纤毛)。 硬币如小心放也可以停在水面而不下沉。 比表面吉布斯能、表面张力两者物理意 义、单位不同,但数值、量纲都相同。
第十章界面现象物理化学

严格讲表面应是液体和固体与其饱和蒸气之间 的界面,但习惯上把液体或固体与空气的界面称为 液体或固体的表面。
常见的界面有:气-液界面,气-固界面,液-液 界面,液-固界面,固-固界面。
表面和界面(surface and interface)
表面张力(surface tension)
如果在金属线框中间系一线圈,
一起浸入肥皂液中,然后取出,上
面形成一液膜。
(a)
由于以线圈为边界的两边表面张 力大小相等方向相反,所以线圈成 任意形状可在液膜上移动,见(a)图。
如果刺破线圈中央的液膜,线 圈内侧张力消失,外侧表面张力立 (b) 即将线圈绷成一个圆形,见(b)图, 清楚的显示出表面张力的存在。
剖 面 图
附加压力示意图
杨-拉普拉斯公式
1805年Young-Laplace导出了附加压力与曲率半 径之间的关系式:
根据数学上规定,凸面的曲率半径取正值,凹 面的曲率半径取负值。所以,凸面的附加压力指向 液体,凹面的附加压力指向气体,即附加压力总是 指向球面的球心。
附加压力与毛细管中液面高度的关系
表面张力(surface tension)
如果在活动边框上挂一重物,
使重物质量W2与边框质量W1所产生 的重力F(F=(W1+W2)g)与总的 表面张力大小相等方向相反,则金 属丝不再滑动。
这时
F 2g l
l是滑动边的长度,因膜有两个
面,所以边界总长度为2l,g 就是作
用最小的趋势,并 使表面层显示出一些独特性质,如表面张力、表面吸 附、毛细现象、过饱和状态等。
比表面(specific surface area)
物理化学 (11)

表面活性剂的实际应用
润湿、去污、助磨、乳化、破乳(消泡) 等等。
例: 去污作用
水(W) 油(O)
水(W) 油(O)
固(S) 洗涤前
洗涤后
固(S)
本章小结
本章主要介绍了界面的特殊物理化学性质。 由于界面上的分子受力不对称,产生了界面张 力,进而引起了一系列界面现象,如:弯曲液 面上的附加压力、小液滴上的饱和蒸气压、亚 稳态现象、吸附现象、润湿现象等等。
开始形成胶束所需表面活性剂的最低浓 度称为临界胶团浓度cmc。
表面活性剂的基本性质 临界胶束浓度(cmc)和亲水亲油平衡 (HLB) 临界胶束浓度
表面活性剂的许多性质在cmc处发生转折, 例如电导率,渗透压、去污能力、增溶作用等。
表 面 活 性 剂 溶 液 的 性 质
c
HLB—亲水亲油平衡(hydrophile-lipophile balance) 表示表面活性剂的亲水性,数值越大,
第十章 界面现象
表面活性物质和表面活性剂
表面活性物质
通常我们把凡是能使溶液表面张力降低 的物质,称为表面活性物质。 表面活性物质在表面层的定向排列
一般情况下,表面活性物质的 Γ - c 曲线如 下图
Γm:饱和吸附量,在单位表面上定向排列呈 单分子层吸附时溶质的物质的量。
Γ
Γm
1
kc kc
1 = 1 + 1 1 Γ Γm Γmk c
表面活性剂的结构 分子间同时含有亲水的极性基团和憎水的
非极性碳链或环。
结构: 亲油的长链非极性基团 亲水的极性基团
表面活性剂的分类
按结构分,可分为离子型与非离子型的表 面活性剂。
为什么溶液的表面张力会随表面活性剂浓度 的变化出现这样的现象?
物理化学第十章 电解与极化作用
3、析出电势 :
ϕ阳,不可逆 = ϕ阳,析出 = ϕ阳,可逆 + η阳 ϕ阴,不可逆 = ϕ阴,析出 = ϕ阴,可逆 − η阴
三、极化曲线-超电势的测定 1、测定超电势的装置
2、电解池中两电极的极化曲线
j(电流密度)
阴极曲线
阳极曲线
E可逆+ΔE不可逆
E可逆
η阴
η阳
电
−ϕ
+ϕ
电解池中两电极的极化曲线
正极: 负极:
LiCoO 2 , LiNiO 2 , LiMn 2 O 2
石墨,焦炭
2
正极反应: L i C o O
+
充 + Z Z Z X L i C o O + x L i + YZ Z Z 1 -x 2 放 −
充 ZZZ X Li C 负极反应: C+xLi + xe YZZ Z x 放
总反应:
Ag + (a ) Ag ( s ) Ag + (a ) + e − → Ag ( s ) RT 没有电流通过时 : ϕ Ag + / Ag (可逆) = ϕ + + ln a Ag + Ag / Ag F RT θ 有电流通过时:ϕ Ag + / Ag (不可逆) =ϕ + + ln a’ + Ag / Ag Ag F 扩散速度小于电极反应速度,a’ + < a Ag +
3、原电池中两电极的极化曲线
η阳
j(电流密度)
E可逆 -ΔE不可
η阴
负 极 曲 线 E可逆
正 3;ϕ
电解池中两电极的极化曲
4、氢超电势
物理化学:第十章 电化学反应的热力学与动力学

该式叫离子独立运动定律。
⑶弱电解质的m∞ :
可直接查表: m∞ =λ+∞ +λ-∞
可通过测强电解质的m∞求得:
例如:Λ( m HAc)=Λ( H+)+Λ( Ac-)
=[Λ( H+)Λ( Cl-)]+[Λ( Ac-)Λ( Na+)] -[Λ( Cl-)Λ( Na+)]
在两相或数相间存在电势差的系统叫电化学系统。
电化学系统研究
电化学系统的热力学; 电化学系统的动力学。
①电化学系统的热力学
主要研究电化学系统中没有电流通过时系统的性质,亦 即有关电化学反应平衡的规律。
②电化学系统的动力学 主要研究电化学系统中有电流通过时系统的性质,亦即有 关电化学反应速率的规律。
二. 电化学系统的研究方法
Λ
m
HCl
Λ
m
C
2
H
5
COONa
Λ
m
NaCl
=(42.616+8.592-12.665)103S·m2·mol1 =38.543103S·m2·mol1
10.5 离子的平均活度、平均活度因子
一.电解质和离子的化学势
电解质溶液中,
溶质(
即电解质)
的化学势
B
def
G nB
T
,
p,
nA
根据电解质电离度大小分类:
电解质分为
强电解质 弱电解质
在溶剂中全部电离; 在溶剂中部分电离。
强弱电解质的划分除与电解质本身性质有关外,还取决于
溶剂性质。例如,CH3COOH在水中部分电离属弱电解质,而 在液氨中则全部电离,属强电解质。
根据电解质的结合键类型分类:
电解质分为 真正电解质 潜在电解质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dp=0, dnB=0时,
TTc(临界温度)时, =0(气液相界面消失)。
临界状态下,由于_____,所以液体的表面张力_______。
(4) 压力
a.表面分子受力不对称的程度 ↓ b.气体分子可被表面吸附 c.气体分子溶于液相
↓1mN/m,例:
P↑
↓
一般:p↑10atm,
1atm 10atm
恒温、恒压下的可逆非体积功等于系统的吉布 斯函数变 即:
:恒温恒压下,增加单位表面时系统所增加的
吉布斯函数。 单位:J· m-2。
三者物理意义不同,但量值和量纲等同, 单位均可化为: N· m-1
在定温定压条件下将10ml水的表面积迅速增大2倍, 功为W,水的吉布斯函数变为ΔG,则: A ΔG<W B ΔG =W C ΔG>W D 无法确定
(1)液体的表面张力
从宏观层面来看,液 体表面仿佛存在一层 紧绷的液膜,在膜内 处处存在的使膜紧绷 的力即为表面张力 表面张力的存在解释 了针为什么可以漂在 水面上
在两相(特别是气-液)界面上,处处存在着 一种张力,这种力垂直于表面的边界,指向液 体方向并与表面相切。 把作用于单位边界线上的这种力称为表面张 力,用 表示。 表面张力的单位是: Nm-1
弯曲液面上的附加压力: A 恒大于零 B 恒小于零 C 恒等于零 D 无法确定
x+dx x r
dr
r
——Laplace方程 ① 该形式的Laplace公式只适用于球形液面。 ②曲面内(凹)的压力大于曲面外(凸)的压力, Δp>0。 ③ r 越小,Δp越大;r越大,Δp越小。 平液面:r →∞,Δp→0,(并不是 = 0) ④ 永远指向球心。
3. 亚稳状态及新相的生成
(1) 过饱和蒸气 原因:液滴小,饱和蒸 气压大,新相难成而导 致过冷。 解决办法:引入凝结核 心如人工降雨用的AgI 或干冰。 这种在正常相平衡条件下应该凝结而未凝结的 蒸气,称为过饱和蒸气。
(2) 过热液体
液体内部产生气泡所需压力:
pi = p大+ p静+Δp
由此所需的温度: Ti >T正常 因此很容易产生暴沸。
如右图,将装有液体的毛细 管水平放置,在其右端加热, (a) 则管内液体将(a): (b): A 向右移动 B 向左移动 (b) C 不动 D 以上都有可能
毛细现象 由于附加压力而引起的液面与管外液面有高 度差的现象 ' ''
p p
p0
M
H 2O
Hg
N
毛细管内液柱上升(或下降)的高度可近似用 如下的方法计算
表面张力一般随压力的增加而下降,但影响一般不大
10.2 弯曲液面的附加压力及其后果
在平液面上
对一小面积AB,沿 AB的四周每点的两边 都存在表面张力,大小 相等,方向相反,所以 没有附加压力 设向下的大气压力为 pg,向上的反作用力也为 pl ,附加压力△p等于零。
pg
f
A
B
f
pl
p pg pl 0
Va
1) 低压时:bp << 1,1+bp 1
V
a a = Vm bp
2) 高压时:bp >> 1,1+bp bp
T1 <T2
lg(p/[p])
斜率 n 截距 k
4. 朗缪尔单分子层吸附理论及吸附等温式
四个基本假设:
Ⅰ、气体在固体表面上单分子层吸附;
Ⅱ、固体表面是均匀的(吸附热为常数, 与θ无关) Ⅲ、被吸附在固体表面上的分子相互之 间无作用力 ; Ⅳ、吸附平衡是动态平衡 。
覆盖率 θ=
被吸附质复盖的固体表面积 = 固体总的表面积
液体的表面张力总是力图缩小液体的表面积。 液体表面张力的方向总是与液面垂直。
2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l
= 2 l
F =W2 g
W2
这时重物质量W所产生的重力 F与总的表面张力大小相等方向 相反,金属丝不再滑动。
溶液浓度已超过饱和 液体,但仍未析出晶体的 溶液称为过饱和溶液。
由于小颗粒物质的表面特殊性,造成新相难以 生成,从而形成四种不稳定状态(亚稳态): 过饱和蒸气、过热液体、过冷液体、过饱和溶液
10.3 固体表面
固体表面的气体与液体有在固体表面自动 聚集,以求降低表面能的趋势。
在相界面上,某物质的浓度与体相浓度不同 的现象称为吸附。
p较低时,p↑,θ↑,平衡吸附量 ↑ p足够高时,θ→1 ,饱和吸附量 A(g) + M(表面)
k1 k-1
AM
(N:具有吸附能力的总的位置数)
吸附平衡时:v吸附= v解吸,有:
——Langmuir吸附等温式
b=k1/k-1:吸附系数或吸附平衡常数
以1/Va对1/p作图,截距、斜率 Vam 和 b
应用:干燥剂、防毒面具、脱色剂、色谱、 污水处理、催化剂、… 吸附剂:具有吸附能力的固体物质 吸附质:被吸附的物质 吸附(adsorption):气体停留在固体表面 吸收(absorption):气体进入到固体内部
吸附量:当吸附平衡时,单位质量吸附剂所吸附 吸附质的物质的量或其在标准状况下所 占有的体积(气体)。
在一定的T,p下,将一个大水滴分散为很多个小水 滴, 基本不变的性质是: A 表面吉布斯函数 B 饱和蒸气压 C 弯曲液面下的附加压力 D 表面张力
在三通活塞两端涂上肥皂液,关闭右端,在左端吹一 大泡,关闭左端,在右端吹一小泡,然后使左右两端 相通,将会出现什么现象? A 大泡变小,小泡变大 B 小泡变小,大泡变大 C 两泡大小保持不变 D 不能确定
Kelvin公式也可以表示两种不同大小颗粒的(a)难 溶物值溶解度之比或(b)分解压之比。
颗粒总是凸面, r 取正值, r 越小,小颗粒的饱 和溶液的浓度越大,溶解度越大。
无机盐的结晶中常用到陈化处理,在陈化过程中: A 晶粒变大,晶粒数减小 B 晶粒变小,晶粒数增多 C 晶粒大小和数目均保持不变 D 大小晶粒尺寸趋于相等,晶粒数保持不变
即:
或:
n
a
n = m
单位:molkg-1 单位: m3kg-1
V
a
V = m
V: 被吸附的气体在0 oC, 101.325kPa下的体积
1. 物理吸附与化学吸附
性质 吸附力 吸附层数 吸附热 物理吸附 范德华力 单层或多层 小(近于液化热) 化学吸附 化学键力 单层 大(近于反应热)
选择性
可逆性 吸附平衡
第十章
水滴为什么是圆 形而不是方形
它们为什么可以 漂在水面上
水在毛细管中为 什么会上升
水
界面(Interface)
界面是相与相之间的交界 所形成的物理区域
界面相是一个准三维区 域,其广度无限,而厚 度约为几个分子的线度 体系性质在体相为常数, 界面的结构和性质与相邻 两侧的体相都不相同。
H H
h/2 h h a b c d
最大气泡压力法测表面张力
下列关于最大泡压法测定液体表面 张力实验的说法中,错误的是: A 毛细管壁必须洁净 B 毛细管口必须平整 C 毛细管必须垂直放置 D 毛细管须插入液体内部一定深度
当r气泡=r毛细管时,r最小,p有最大值
2. 微小液滴的饱和蒸汽压-Kelven公式
例:水滴分散成微小水滴
分成1018个
直 径:1cm 表面积:3.1416 cm2
直 径:10nm 表面积:314.16 m2
表面积是原来的106倍
一些多孔物质如:硅胶、活性炭等,也 具有很大的比表面积。
10.1 界面张力
1.液体的表面张力,表面功及表面吉布斯函数
表面现象的微观成因: 表面相分子受力不均匀, 其分子有被拉入液相的 趋势。 液体表面有自动收缩的倾 向,扩展表面要作功。 这解释了为什么液滴会 以球形的形态存在。
原因:
Kelvin公式
Kelvin公式也可以表示为两种不同曲率半径的液
滴或蒸气泡的蒸气压之比
对凸面,r取正值,r越小,液滴的蒸气压越高; 对凹面,r取负值,|r|越小,小气泡中的蒸气压越低。
在潮湿的空气中,放有三只粗细不等的毛细管,其半径大 小顺序为:r1>r2>r3,则毛细管内水蒸气凝结的顺序是: A 1,2,3 B 2,3,1 C 3, 2, 1 D 无法判断
1. 弯曲液面的附加压力——Laplace方程
在凸液面上 由于液面是弯曲的,则 沿AB的周界上的表面张力不 f 是水平的,作用于边界的力 将有一指向液体内部的合力
所有的点产生的合力和 为△p ,称为附加压力 凸面上受的总压力为:
pg
A
p
B
f
pl
pl pg p
在凹液面上
由于液面是凹面,沿 AB的周界上的表面张力 不能抵消,作用于边界的 力有一指向凹面中心的合 力 所有的点产生的合力 和为△p ,称为附加压力 凹面上受的总压力为:
2. 热力学公式
单相多组分系统:
对需要考虑表面层的系统,由于多了一个表面相, 在体积功之外,还要增加表面功,若系统内只有一 个相界面,且两相T、p相同 ,则基本公式为:
考虑了表面功的热力学基本公式为
同样推导可得
恒T、p、 、恒组分下积分,有: 全微分得:
可知自发降低界面吉布斯函数有两种途径:
降低表面积 降低表面张力
H
H2
H
H H
Air H2O
H
H2O
Ni
Glass
Hg
H2O Hg
Fe Cu
表面(Surface)
表面:凝聚态物质相对于其纯气相的界面。 S-g、L-g界面算作表面 也常将两个不同体相间的界面称为表面
