平行四边形定义性质以及判定定理
平行四边形的判定(1)

3
对角互相平分
两组对边相等
对角线互相平分 四边形是平行四边形 四边形是平行四边形 四边形是平行四边形
性质:平行四边形的对角相等
定义:两组对边分别平行的四边形叫做平行四边形
平行四边形的两组对边分别平行
探究活动
发现:三角形一条边上的中 线的2倍小于另两条边的和。
任意画一个三角形和三角形一边上的中线。比较
5.5 平行四边形的判定(2)
序言
本编为大家提供各种类型的PPT课件,如数学课件、语文课件、英语 课件、地理课件、历史课件、政治课件、化学课件、物理课件等等,想了 解不同课件格式和写法,敬请下载!
Moreover, our store provides various types of classic sample essays, such as contract agreements, documentary evidence, planning plans, summary reports, party and youth organization materials, reading notes, post reading reflections, essay encyclopedias, lesson plan materials, other sample essays, etc. If you want to learn about different formats and writing methods of sample essays, please stay tuned!
这条中线的二倍与三角形另外两边的和的大小,你
发现了什么?再画几个三角形试一试,你发现的规律
仍然成立吗?试证明你的发现。见
平行四边形的性质和判定

平行四边形的性质和判定知识点1 平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
记作“□ABCD ”。
知识点2 平行四边形的性质: 边:对边平行且相等。
角:对角相等,邻角互补。
对角线:对角线互相平分。
知识点3 平行四边形的判定:边:两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
角:两组对角分别相等的四边形是平行四边形。
对角线:对角线互相平分的四边形是平行四边形。
、 知识点4 两条平行线的距离。
知识点5 三角形的中位线定义:连接三角形两边中点的线段是三角形的中位线。
性质:三角形的中位线平行于第三边且等于第三边的一半。
例1、如图,E F ,是平行四边形ABCD 的对角线AC 上的点,CE AF .猜想:BE 与DF 有怎样的位置..关系和数量..关系?并对你的猜想加以证明。
【变式练习】已知,在□ABCD 中,点E 、F 分别在AD 、CB的延长线上,且∠1=∠2,DF 交AB 于G ,BE 交CD 于H 。
求证:EH=FG 。
例2、已知如图,O 为平行四边形ABCD 的对角线AC 的中点,EF 交于F 。
求证:四边形AECF 是平行四边形。
例3、▱ABCD 中,∠BAD 的平分线交直线BC 于点E ,线DC (1)求证:CE=CF ;C ABCDE F(2)若∠ABC=120°,FG ∥CE ,FG=CE ,求∠BDG . 【变式练习】 1、如图,中,AE =CF ,M 、N 分别ED 、FB 的中点.求证:四边形ENFM 是平行四边形.2、在▱ABCD 中,∠ADC 的平分线交直线BC 于点E 、交AB 的延长线于点F ,连接AC .(1)如图1,若∠ADC=90°,G 是EF 的中点,连接AG 、CG . ①求证:BE=BF .②请判断△AGC 的形状,并说明理由;(2)如图2,若∠ADC=60°,将线段FB绕点F 顺时针旋转60°至FG ,连接AG 、CG .那么△AGC 又是怎样的形状.例4、如图,点E 、F 、G 、H 分别是四边形ABCD 的四边中点,求证四边形EFGH 是平行四边形。
数学平行四边形、菱形、矩形、正方形的定理、性质、判定

1. 定义: 两组对边分别平行的四边形叫做平行四边形。
2.性质:⑴如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为“平行四边形的对边相等”)⑵如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为“平行四边形的对角相等”)⑶夹在两条平行线间的平行线段相等。
⑷如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
(简述为“平行四边形的两条对角线互相平分”)⑸平行四边形是中心对称图形,对称中心是两条对角线的交点。
3.判定:(1)如果一个四边形的两组对边分别相等,那么这个四边形是平行四边形。
(简述为“两组对边分别相等的四边形是平行四边形”)(2)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形。
(简述为“一组对边平行且相等的四边形是平行四边形”)(3)如果一个四边形的两条对角线互相平分,那么这个四边形是平行四边形。
(简述为“对角线互相平分的四边形是平行四边形”)(4)如果一个四边形的两组对角分别相等,那么这个四边形是平行四边形。
(简述为“两组对角分别相等的四边形是平行四边形”(5)如果一个四边形的两组对边分别平行,那么这个四边形是平行四边形。
(简述为“两组对边分别平行的四边形是平行四边形”)矩形的性质和判定定义:有一个角是直角的平行四边形叫做矩形.性质:①矩形的四个角都是直角;②矩形的对角线相等 .注意:矩形具有平行四边形的一切性质 .判定:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形 .菱形的性质和判定定义:有一组邻边相等的平行四边形叫做菱形.性质:①菱形的四条边都相等;②菱形的对角线互相垂直,并且每一条对角线平分一组对角 .注意:菱形也具有平行四边形的一切性质 .判定:①有一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形(4).有一条对角线平分一组对角的平行四边形是菱形正方形的性质和判定定义:有一组邻边相等并且有一角是直角的平行四边形叫做正方形.性质:①正方形的四个角都是直角,四条边都相等;②正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角 .判定:因为正方形具有平行四边形、矩形、菱形的一切性质,所以我们判定正方形有三个途径①四条边都相等的平行四边形是正方形②有一组临边相等的矩形是正方形③有一个角是直角的菱形是正方形梯形及特殊梯形的定义梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.(一组对边平行且不相等的四边形叫做梯形.)等腰梯形:两腰相等的梯形叫做等腰梯形. 直角梯形:一腰垂直于底的梯形叫做直角梯形.等腰梯形的性质1、等腰梯形两腰相等、两底平行;2、等腰梯形在同一底上的两个角相等;3、等腰梯形的对角线相等;4、等腰梯形是轴对称图形,它只有一条对称轴,一底的垂直平分线是它的对称轴. 等腰梯形的判定1、两腰相等的梯形是等腰梯形;2、在同一底上的两个角相等的梯形是等腰梯形;3、对角线相等的梯形是等腰梯形.平行四边形性质定理1 平行四边形的对角相等平行四边形性质定理2 平行四边形的对边相等且平行平行四边形性质定理3 平行四边形的对角线互相平分平行四边形判定定理1 两组对角分别相等的四边形是平行四边形平行四边形判定定理2 两组对边分别相等的四边形是平行四边形平行四边形判定定理3 对角线互相平分的四边形是平行四边形平行四边形判定定理4 一组对边平行相等的四边形是平行四边形矩形性质定理1 矩形的四个角都是直角矩形性质定理2 矩形的对角线相等矩形判定定理1 有一个角是直角的平行四边形是矩形矩形判定定理2 对角线相等的平行四边形是矩形正方形性质定理1正方形的四个角都是直角,四条边都相等正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角菱形性质定理1 菱形的四条边都相等菱形性质定理2 菱形的对角线互相垂直菱形面积=对角线乘积的一半,即S=(a×b)÷2菱形判定定理1 四边都相等的四边形是菱形菱形判定定理2 对角线互相垂直的平行四边形是菱形菱形判定定理3是对称轴图形的平行四边形是菱形。
八年级数学上册知识点归纳:平行四边形的性质

八年级数学上册知识点归纳:平行四边形的性质八年级数学上册知识点归纳:平行四边形的性质知识点总结1.定义:两组对边分别平行的四边形叫平行四边形2.平行四边形的性质(1)平行四边形的对边平行且相等;(2)平行四边形的邻角互补,对角相等;(3)平行四边形的对角线互相平分;3.平行四边形的判定平行四边形是几何中一个重要内容,如何根据平行四边形的性质,判定一个四边形是平行四边形是个重点,下面就对平行四边形的五种判定方法,进行划分:第一类:与四边形的对边有关(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;第二类:与四边形的对角有关(4)两组对角分别相等的四边形是平行四边形;第三类:与四边形的对角线有关(5)对角线互相平分的四边形是平行四边形常见考法(1)利用平行四边形的性质,求角度、线段长、周长;(2)求平行四边形某边的取值范围;(3)考查一些综合计算问题;(4)利用平行四边形性质证明角相等、线段相等和直线平行;(5)利用判定定理证明四边形是平行四边形。
误区提醒(1)平行四边形的性质较多,易把对角线互相平分,错记成对角线相等;(2)“一组对边平行且相等的四边形是平行四边形”错记成“一组对边平行,一组对边相等的四边形是平行四边形”后者不是平行四边形的判定定理,它只是个等腰梯形。
知识点总结一、特殊的平行四边形1.矩形:(1)定义:有一个角是直角的平行四边形。
(2)性质:矩形的四个角都是直角;矩形的对角线平分且相等。
(3)判定定理:①有一个角是直角的平行四边形叫做矩形。
②对角线相等的平行四边形是矩形。
③有三个角是直角的四边形是矩形。
直角三角形的性质:直角三角形中所对的直角边等于斜边的一半。
2.菱形:(1)定义:邻边相等的平行四边形。
(2)性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
(3)判定定理:①一组邻边相等的平行四边形是菱形。
平行四边形知识点
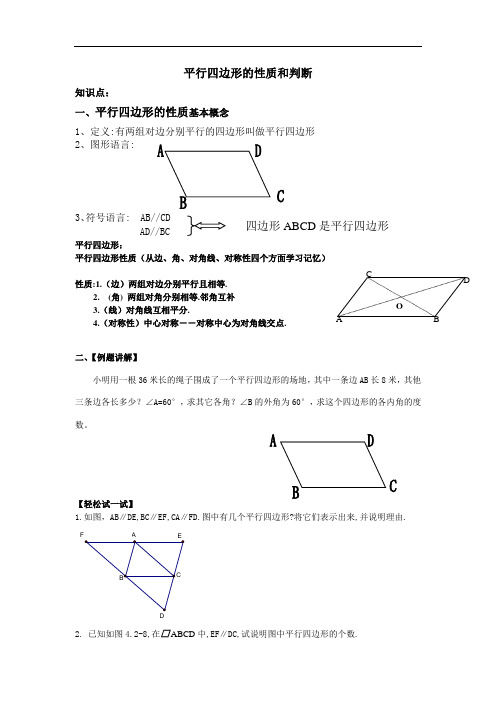
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
平行四边形的判定定理

平行四边形的判定定理平行四边形是一种特殊的四边形,具有以下特点:对边平行且对角线相等。
在数学中,判定一个四边形是否为平行四边形有多种方法。
方法一:利用对边平行的性质判定一个四边形ABCD是否为平行四边形时,可以先利用对边平行的性质进行判断。
步骤:1.检查边AB和边CD是否平行。
2.检查边BC和边AD是否平行。
如果边AB和边CD以及边BC和边AD都是平行的,则可以断定四边形ABCD是一个平行四边形。
方法二:利用对角线相等的性质判定一个四边形ABCD是否为平行四边形时,可以利用对角线相等的性质进行判断。
步骤:1.计算对角线AC的长度。
2.计算对角线BD的长度。
如果对角线AC的长度等于对角线BD的长度,则可以断定四边形ABCD是一个平行四边形。
方法三:利用对边比例相等的性质判定一个四边形ABCD是否为平行四边形时,还可以利用对边比例相等的性质进行判断。
步骤:1.计算边AB与边CD的长度比(AB/CD)。
2.计算边BC与边AD的长度比(BC/AD)。
如果边AB与边CD的长度比等于边BC与边AD的长度比,即AB/CD = BC/AD,那么四边形ABCD是一个平行四边形。
方法四:利用四个角的性质判定一个四边形ABCD是否为平行四边形时,也可以利用四个角的性质进行判断。
步骤:1.检查角A与角C是否相等。
2.检查角B与角D是否相等。
如果角A与角C相等,并且角B与角D相等,则可以断定四边形ABCD是一个平行四边形。
总结通过以上四种方法,我们可以判定一个四边形是否为平行四边形。
可以根据实际情况选择其中一种或多种方法来进行判定,以便快速准确地得出结论。
请注意,以上的判定定理仅适用于四边形,其他多边形无法用这些方法判定是否为平行四边形。
在实际应用中,合理选择合适的方法,结合几何定理,可以更好地解决相关问题。
希望本文能对你理解和应用平行四边形的判定定理有所帮助。
平行四边形的判定与性质

平行四边形的性质与判定一、平行四边形定义及其性质:1、两组对边分别平行的四边形是平行四边形,平行四边形对边平行且相等。
定义的几何语言表述 ∵ AB ∥CD AD ∥BC ∴四边形ABCD 是平行四边形 。
∵四边形ABCD 是平行四边形(或在 ABCD 中) ∴ AB=CD ,AD=BC 。
例题1、如图5,AD ∥BC ,AE ∥CD ,BD 平分∠ABC ,求证AB=CE2、平行四边形除了对边平行且相等外,其对角也相等。
∵四边形ABCD 是平行四边形(或在ABCD 中) ∴ ∠A=∠C ,∠B=∠D 。
例题2、在平行四边形ABCD 中,若∠A :∠B=2:3,求∠C 、∠D 的度数。
3、平行四边形的对角线互相平分。
例题3.已知O 是平行四边形ABCD 的对角线的交点,AC=24cm ,BD=38 cm ,AD= 28cm ,求三角形OBC 的周长。
5.如图,平行四边形ABCD 中,AC 交BD 于O ,AE ⊥BD 于E ,∠EAD=60°,AE=2cm,AC+BD=14cm, 求三角形BOC 的周长。
例题4:已知平行四边形ABCD ,AB=8cm ,BC=10cm,∠B=30°, 求平行四边形平行四边形ABCD 的面积。
对边分别平行 边 对边分别相等 对角线互相平分 平行四边形角 对角相等 邻角互补图(5)DCB AA B C D二、平行四边形的判定 方法一(定义法):两组对边分别平行的四边形的平边形。
几何语言表达定义法:∵AB ∥CD ,AD ∥BC ,∴四边形ABCD 是平行四边形方法二:两组对边分别相等的四边形是平行四边形。
∵AB=CD ,AD=BC ,∴四边形ABCD 是平行四边形 方法三:对角线互相平分的四边形是平行四边形。
∵OA=OC , OB= OD ∴四边形ABCD 是平行四边形 方法四:有一组对边平行且相等的四边形是平行四边形 ∵AB=CD ,AB ∥CD ,∴四边形ABCD 是平行四边形方法五:两组对角分别相等的四边形是平行四边形∵ ∠A =∠C ,∠B=∠D ,∴四边形ABCD 例1:已知:E 、F 分别为平行四边形ABCD 两边AD 、BC 的中点,连结BE 、DF 求证:2∠1∠=三、三角形中位线:三角形两边的中点连线线段(即中位线)与三角形的第三边平行,并且等于第三边的一半。
初中数学知识点总结:平行四边形

初中数学知识点总结:平行四边形
知识点总结
1.定义:两组对边分别平行的四边形叫平行四边形
2.平行四边形的性质
〔1〕平行四边形的对边平行且相等;
〔2〕平行四边形的邻角互补,对角相等;
〔3〕平行四边形的对角线互相平分;
3.平行四边形的判定
平行四边形是几何中一个重要内容,如何根据平行四边形的性质,判定一个四边形是平行四边形是个重点,下面就对平行四边形的五种判定方法,进行划分:
第一类:与四边形的对边有关
〔1〕两组对边分别平行的四边形是平行四边形;
〔2〕两组对边分别相等的四边形是平行四边形;
〔3〕一组对边平行且相等的四边形是平行四边形;
第二类:与四边形的对角有关
〔4〕两组对角分别相等的四边形是平行四边形;
第三类:与四边形的对角线有关
〔5〕对角线互相平分的四边形是平行四边形
常见考法
〔1〕利用平行四边形的性质,求角度、线段长、周长;〔2〕求平行四边形某边的取值范围;〔3〕考查一些综合计算问题;〔4〕
利用平行四边形性质证明角相等、线段相等和直线平行;〔5〕利用判定定理证明四边形是平行四边形。
误区提醒
〔1〕平行四边形的性质较多,易把对角线互相平分,错记成对角线相等;〔2〕〝一组对边平行且相等的四边形是平行四边形〞错记成〝一组对边平行,一组对边相等的四边形是平行四边形〞后者不是平行四边形的判定定理,它只是个等腰梯形。
平行四边形的性质和判定讲义(教师版)

平行四边形的性质和判定【知识梳理】一、什么是平行四边形?两组对边分别平行的四边形就是平行四边形.如图四边形ABCD ,AB CD AD BC ∥,∥,四边形ABCD 就是平行四边形二、平行四边形的性质:平行四边形的的边:平行四边形的对边平行且对边相等平行四边形的角:平行四边形的对角相等,邻角互补.平行四边形的对角线:平行四边形的对角线互相平分平行四边形的对称性平行四边形是中心对称图形平行四边形的周长与面积周长:邻边之和的2倍面积:底乘高(常利用面积相等来求线段的长)三、平行四边形的判定判定一:两组对边分别平行的四边形是平行四边形判定二:两组对边分别相等的四边形是平行四边形判定三:一组对边平行且相等的四边形是平行四边形判定四:两组对角分别相等的四边形是平行四边形判定五:对角线互相平分的四边形是平行四边形四、三角形中位线性质:三角形的中位线平行且等于第三边长的一半判定:点E 是三角形ABC △的中点,且DE BC ∥,则点D 为AB 中点【诊断自测】1.下列说法错误的是()A .对角线互相平分的四边形是平行四边形B.两组对边分别相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.一组对边相等,另一组对边平行的四边形是平行四边形2.如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件(写一个即可),使四边形ABCD是平行四边形.3.四边形ABCD中,AB=7cm,BC=5cm,CD=7cm,当AD=cm时,四边形ABCD 是平行四边形.4.如图所示,DE∥BC,DF∥AC,EF∥AB,图中共有个平行四边形.【考点突破】类型一:平行四边形的性质例1、如图,▱ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为()A.13B.17C.20D.26答案:B解析:∵四边形ABCD是平行四边形,∴OA=OC=3,OB=OD=6,BC=AD=8,∴△OBC的周长=OB+OC+AD=3+6+8=17.故选:B.例2、如图所示,在▱ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为.答案:50°.解析:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠C=∠ABF.又∵∠C=40°,∴∠ABF=40°.∵EF⊥BF,∴∠F=90°,∴∠BEF=90°﹣40°=50°.故答案是:50°.例3、如图,▱ABCD中,AC=8,BD=6,AD=a,则a的取值范围是.答案:1<a<7.解析:如图所示:∵四边形ABCD是平行四边形,∴OA=AC=4,OD=BD=3,在△AOD中,由三角形的三边关系得:4﹣3<AD<4+3.即1<a<7;故答案为:1<a<7.例4、如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.(1)求证:BE=CD;(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.答案:见解析解析:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AB=CD,∴∠AEB=∠DAE,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD;(2)解:∵AB=BE,∠BEA=60°,∴△ABE是等边三角形,∴AE=AB=4,∵BF⊥AE,∴AF=EF=2,∴BF===2,∵AD∥BC,∴∠D=∠ECF,∠DAF=∠E,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴△ADF的面积=△ECF的面积,∴平行四边形ABCD的面积=△ABE的面积=AE•BF=×4×2=4.类型二:平行四边形的判定例5、如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A 出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为()A.4s B.3s C.2s D.1s答案:B解析:设运动时间为t秒,则CP=12﹣3t,BQ=t,根据题意得到12﹣3t=t,解得:t=3,故选B.例6、四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①∠ABC=∠ADC,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC,其中一定能判定这个四边形是平行四边形的条件有()A.4组B.3组C.2组D.1组答案:B解析:如图,①∵AD∥BC,∴∠BAD+∠ABC=180°,∠ADC+∠BCD=180°,∵∠ABC=∠ADC,∴∠BAD=∠BCD,∴四边形ABCD是平行四边形;②∵AB=CD,AD=BC,∴四边形ABCD是平行四边形;③∵AO=CO,BO=DO,∴四边形ABCD是平行四边形;④∵AB∥CD,AD=BC,∴四边形ABCD是平行四边形或等腰梯形.∴其中一定能判定这个四边形是平行四边形的条件有3组.故选B.例7、如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.答案:见解析解析:证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=BC,在Rt△AFE和Rt△BCA中,,∴Rt△AFE≌Rt△BCA(HL),∴AC=EF;(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°又∵EF⊥AB,∴EF∥AD,∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形.例8、如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.答案:见解析解析:证明:(1)选取①②,∵在△BEO和△DFO中,∴△BEO≌△DFO(ASA);(2)由(1)得:△BEO≌△DFO,∴EO=FO,BO=DO,∵AE=CF,∴AO=CO,∴四边形ABCD是平行四边形.类型三:平行四边形的性质和判定例9、如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.答案:见解析解析:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=BC,∴DG=EF,DG∥EF,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.由(1)有四边形DEFG是平行四边形,∴DG=EF=6.例10、如图,▱ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.(1)求证:四边形CMAN是平行四边形.(2)已知DE=4,FN=3,求BN的长.答案:见解析解析:(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,∵AM⊥BD,CN⊥BD,∴AM∥CN,∴CM∥AN,AM∥CN,∴四边形AMCN是平行四边形.(2)∵四边形AMCN是平行四边形,∴CM=AN,∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴DM=BN,∠MDE=∠NBF,在△MDE和△NBF中,,∴△MDE≌△NBF,∴ME=NF=3,在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,∴DM===5,∴BN=DM=5.例11、如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.答案:见解析解析:证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,∵BD平分∠ABC,∴∠EBD=∠DBC,∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,∴EB=CF.类型三:中位线定理例12、如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是()A.EF=CF B.EF=DE C.CF<BD D.EF>DE答案:B解析:∵DE是△ABC的中位线,∴E为AC中点,∴AE=EC,∵CF∥BD,∴∠ADE=∠F,在△ADE和△CFE中,∵,∴△ADE≌△CFE(AAS),∴DE=FE.故选B.例13、如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.(1)求证:AE=AF;(2)求证:BE=(AB+AC).答案:见解析解析:证明:(1)∵DA平分∠BAC,∴∠BAD=∠CAD,∵AD∥EM,∴∠BAD=∠AEF,∠CAD=∠AFE,∴∠AEF=∠AFE,∴AE=AF.(2)作CG∥EM,交BA的延长线于G.∵EF∥CG,∴∠G=∠AEF,∠ACG=∠AFE,∵∠AEF=∠AFE,∴∠G=∠ACG,∴AG=AC,∵BM=CM.EM∥CG,∴BE=EG,∴BE=BG=(BA+AG)=(AB+AC).【易错精选】1.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°2.如图,在▱ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于()A.2B.3C.4D.63.已知:A(﹣2,1),B(﹣3,﹣1),C(0,﹣1).点D在坐标平面内,且以A、B、C、D四个点构成的四边形是平行四边形,则这样的D点有个.4.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当=时,四边形ADFE是平行四边形.【精华提炼】一、平行四边形的性质:平行四边形的的边:平行四边形的对边平行且对边相等平行四边形的角:平行四边形的对角相等,邻角互补.平行四边形的对角线:平行四边形的对角线互相平分平行四边形是中心对称图形二、平行四边形的判定判定一:两组对边分别平行的四边形是平行四边形判定二:两组对边分别相等的四边形是平行四边形判定三:一组对边平行且相等的四边形是平行四边形判定四:两组对角分别相等的四边形是平行四边形判定五:对角线互相平分的四边形是平行四边形【本节训练】训练【1】如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC ⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为()A.3cm B.4cm C.5cm D.8cm训练【2】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是()A.OE=DCB.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE训练【3】如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC 为对角线的平行四边形ADCE中,DE的最小值是.训练【4】在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于.基础巩固一.填空题1.如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE 的面积为cm2.2.如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是cm.3.如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是.4.在△ABC中,点D、E分别是边AB、AC的中点,那么△ADE的面积与△ABC的面积的比是.5.如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为cm.二、选择题1.在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是()A.5B.7C.9D.112.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为()A.3cm B.4cm C.5cm D.8cm3.如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是()A.30B.36C.54D.724.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE 的长为1100m,则隧道AB的长度为()A.3300m B.2200m C.1100m D.550m5.如图,在▱ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于()A.0.5B.1C.D.2三、简答题1.如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=2DE,连接CF.判断四边形BCFE的形状,并证明.2.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.(1)求证:BD=DE;(2)求DM的长.巅峰突破1.如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第n个图形中共有三角形的个数为.2.如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于cm.3.如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN ∥AB,连接NH,如果∠D=68°,则∠CHN=.4.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动到C点返回,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).(1)当t为何值时,四边形PQDC是平行四边形;(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.5.已知:如图,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF 分别交BA的延长线、DC的延长线于点G,H,交BD于点O.(1)求证:△ABE≌△CDF;(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.参考答案【诊断自测】1、D解:A、两条对角线互相平分的四边形是平行四边形,故本选项说法正确;B、两组对边分别相等的四边形是平行四边形,故本选项说法正确;C、一组对边平行且相等的四边形是平行四边形,故本选项说法正确;D、一组对边相等,另一组对边平行的四边形不一定是平行四边形,例如:等腰梯形,故本选项说法错误;故选:D.2、解:可以添加:AD∥BC(答案不唯一).3、5.解:当AD=5cm时,四边形ABCD是平行四边形,∵AB=7cm,BC=5cm,CD=7cm,AD=5cm,∴四边形ABCD是平行四边形,故答案为:5.4、3个.解:由两组对边分别平行的四边形是平行四边形,可得图中的平行四边形有▱ADFE、▱BFED、▱CFDE三个.故答案为:3个【易错精选】1、C解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质得:∠BAC=∠B′AC,∴∠BAC=∠ACD=∠B′AC=∠1=22°,∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;故选:C.2、C解:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC=8,CD=AB=6,∴∠F=∠DCF,∵CF平分∠BCD,∴∠FCB=∠DCF,∴∠F=∠FCB,∴BF=BC=8,同理:DE=CD=6,∴AF=BF﹣AB=2,AE=AD﹣DE=2,∴AE+AF=4;故选:C.3、3解:如图,D点共有3个,故答案为:3.4、.解:当=时,四边形ADFE是平行四边形.理由:∵=,∴∠CAB=30°,∵△ABE为等边三角形,EF⊥AB,∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,∴∠FEA=30°,又∠BAC=30°,∴∠FEA=∠BAC,在△ABC和△EAF中,,∴△ABC≌△EAF(AAS);∵∠BAC=30°,∠DAC=60°,∴∠DAB=90°,即DA⊥AB,∵EF⊥AB,∴AD∥EF,∵△ABC≌△EAF,∴EF=AC=AD,∴四边形ADFE是平行四边形.故答案为:.【本节训练】1、B解:∵▱ABCD的周长为26cm,∴AB+AD=13cm,OB=OD,∵△AOD的周长比△AOB的周长多3cm,∴(OA+OD+AD)﹣(OA+OB+AB)=AD﹣AB=3cm,∴AB=5cm,AD=8cm.∴BC=AD=8cm.∵AC⊥AB,E是BC中点,∴AE=BC=4cm;故选:B.2、D解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AB∥DC,又∵点E是BC的中点,∴OE是△BCD的中位线,∴OE=DC,OE∥DC,∴OE∥AB,∴∠BOE=∠OBA,∴选项A、B、C正确;∵OB≠OC,∴∠OBE≠∠OCE,∴选项D错误;故选:D.3、4解:∵四边形ADCE是平行四边形,∴BC∥AE,∴当DE⊥BC时,DE最短,此时∵∠B=90°,∴AB⊥BC,∴DE∥AB,∴四边形ABDE是平行四边形,∵∠B=90°,∴四边形ABDE是矩形,∴DE=AB=4,∴DE的最小值为4.故答案为4.4、2解:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC,∴∠AEB=∠DAE,∵平行四边形ABCD的周长是16,∴AB+BC=8,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE=3,∴BC=5,∴EC=BC﹣BE=5﹣3=2;故答案为:2.基础巩固一、填空题1、解:∵点D、E分别是AB、AC边的中点,∴DE是三角形的中位线,∴DE=BC,DE∥BC,∴△ADE∽△ABC,∴,∵△ABC的面积为12cm2,∴△ADE的面积为3cm2,∴梯形DBCE的面积=12﹣3=9cm2,故答案为:9.2、解:∵D、E分别是AB、BC的中点,∴DE是△ABC的中位线,∴DE=AC,同理有EF=AB,DF=BC,∴△DEF的周长=(AC+BC+AB)=×10=5.故答案为5.3、解:∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE=CD,即D为CE中点,∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,∵EF=3,∴CE==2,∴AB=,故答案为:.4、解:如图,∵AD=DB,AE=EC,∴DE∥BC.DE=BC,∴△ADE∽△ABC,∴=()2=,故答案为.5、解:∵EF为△ABC的中位线,△AEF的周长为6cm,∴BC=2EF,AB=2AE,AC=2AF,∴BC+AB+AC=2(EF+AE+AF)=12(cm).故答案为:12.二、选择题1、解:∵D、E、F分别为AB、BC、AC中点,∴DF=BC=2,DF∥BC,EF=AB=,EF∥AB,∴四边形DBEF为平行四边形,∴四边形DBEF的周长=2(DF+EF)=2×(2+)=7.故选B.2、解:∵▱ABCD的周长为26cm,∴AB+AD=13cm,OB=OD,∵△AOD的周长比△AOB的周长多3cm,∴(OA+OD+AD)﹣(OA+OB+AB)=AD﹣AB=3cm,∴AB=5cm,AD=8cm.∴BC=AD=8cm.∵AC⊥AB,E是BC中点,∴AE=BC=4cm;故选:B.3、解:作DE∥AM,交BC的延长线于E,则ADEM是平行四边形,∴DE=AM=9,ME=AD=10,又由题意可得,BM=BC=AD=5,则BE=15,在△BDE中,∵BD2+DE2=144+81=225=BE2,∴△BDE是直角三角形,且∠BDE=90°,过D作DF⊥BE于F,则DF==,∴S▱ABCD=BC•FD=10×=72.故选D.4、解:∵D,E为AC和BC的中点,∴AB=2DE=2200m,故选:B.5、解:过点M作MG∥AB交AD于点G,∵AD∥BC,AB∥MG,∴四边形ABMG是平行四边形,∴∠AGM=∠ABM.∵AM平分∠BAD,∴∠GAM=∠MAB,∴∠AMB=∠AMG.在△AGM与△ABM中,,∴△AGM≌△ABM,∴AB=AG=3,∴四边形ABMG是菱形,∴MC=5﹣3=2.∵EF∥BC,点E,F分别是AB,CD的中点,∴NF是△DCM的中位线,∴NF=MC=1.故选B.三、简答题1、证明:连接DE,FG,∵BD、CE是△ABC的中线,∴D,E是AB,AC边中点,∴DE∥BC,DE=BC,同理:FG∥BC,FG=BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.2、(1)证明:∵AD平分∠BAC ∴∠BAD=∠DAE∵AD⊥BD∴∠ADB=∠ADE=90°在△ADB与△ADE中∴△ADB≌△ADE∴BD=DE(2)∵△ADB≌△ADE∴AE=AB=12∴EC=AC﹣AE=8∵M是BC的中点,BD=DEDM=EC=4巅峰突破1、解:第①是1个三角形,1=4×1﹣3;第②是5个三角形,5=4×2﹣3;第③是9个三角形,9=4×3﹣3;∴第n个图形中共有三角形的个数是4n﹣3;故答案为:4n﹣3.2.解:∵BD=AD,BE=EC,∴DE=AC=4cm,DE∥AC,∵CF=FA,CE=BE,∴EF=AB=3cm,EF∥AB,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2(DE+EF)=14cm.故答案为14.3.解:连接MH,∵AH⊥CD于H,M为AD的中点,∴MH=AD=DM,∴∠D=∠MHD=68°,∵MN∥AB,∴∠NMH=∠MHD=68°,又∵MN=AB=AD,∴MN=MH,∴∠MHN=(180°﹣68°)÷2=56°,∴∠CHN=180°﹣∠DHM﹣∠MHN=56°.故答案为:56°4.解:(1)∵四边形PQDC是平行四边形∴DQ=CP当P从B运动到C时,∵DQ=AD﹣AQ=16﹣t,CP=21﹣2t∴16﹣t=21﹣2t解得t=5当P从C运动到B时,∵DQ=AD﹣AQ=16﹣t,CP=2t﹣21∴16﹣t=2t﹣21,解得t=,∴当t=5或秒时,四边形PQDC是平行四边形;(2)若点P、Q分别沿AD、BC运动时,即解得t=9(秒)若点P返回时,CP=2(t﹣),则解得t=15(秒).故当t=9或15秒时,以C ,D ,Q ,P 为顶点的梯形面积等60cm 2;(3)当PQ=PD 时作PH ⊥AD 于H ,则HQ=HD∵QH=HD=QD=(16﹣t )由AH=BP 得解得秒;当PQ=QD 时QH=AH ﹣AQ=BP ﹣AQ=2t ﹣t=t ,QD=16﹣t ,∵QD 2=PQ 2=t 2+122∴(16﹣t )2=122+t 2解得(秒);当QD=PD 时DH=AD ﹣AH=AD ﹣BP=16﹣2t ,∵QD 2=PD 2=PH 2+HD 2=122+(16﹣2t )2∴(16﹣t )2=122+(16﹣2t )2即3t 2﹣32t+144=0∵△<0,∴方程无实根,当点P 从C 向B 运动时,观察图象可知,只有PQ=PD ,由题意:2t ﹣26=(16﹣t ),t=.综上可知,当秒或秒或秒时,△PQD是等腰三角形.5.(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,∠BAE=∠DCF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS);(2)解:四边形BEDF是菱形;理由如下:如图所示:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,∴四边形BEDF是平行四边形,∴OB=OD,∵DG=BG,∴EF⊥BD,∴四边形BEDF是菱形.第31/31页。
平行四边形全等的判定定理

平行四边形全等的判定定理平行四边形全等的判定定理是一个在几何学中非常重要且有指导意义的定理。
它不仅可以帮助我们判断两个平行四边形是否全等,还可以在解决实际问题时提供指导。
下面将详细介绍这个定理。
首先,让我们回顾一下平行四边形的定义。
平行四边形是指具有两对平行边的四边形。
它的特点是两边两对角线相等,而且对角线相交的内角相互补。
平行四边形的全等性质意味着当两个平行四边形的对应边相等且对应角相等时,这两个平行四边形是全等的。
定理表述如下:如果两个平行四边形的对应边相等且对应角相等,则这两个平行四边形是全等的。
定理的证明可以通过使用平行四边形的定义以及其他几何性质来完成。
首先,我们可以使用平行四边形的定义来证明对应边相等。
根据定义,平行四边形的两对边是平行的,因此它们长度相等。
因此,如果两个平行四边形的对应边相等,那么它们具备了全等的第一条特征。
接下来,我们需要证明对应角相等。
根据平行四边形的定义,它的两对角线相等。
当两个平行四边形的两对角线相等时,它们对应的角也相等。
这可以通过使用角的补角性质来证明。
两个平行四边形具有相等的对角线,所以它们的内角必然相等。
因此,当两个平行四边形的对应角相等,它们符合全等的第二条特征。
综上所述,当两个平行四边形的对应边相等且对应角相等时,它们是全等的。
这个定理对我们解决几何问题非常有指导意义。
在解决问题时,我们可以根据这个定理来判断两个平行四边形是否全等,从而得出问题的答案。
例如,我们可以利用这个定理来求解实际问题。
假设我们需要寻找一个与已知平行四边形全等的平行四边形。
我们可以通过观察已知平行四边形的边长和内角来寻找合适的构造。
根据定理,我们可以在平面上绘制一个与已知平行四边形的对应边相等且对应角相等的平行四边形。
这个新绘制的平行四边形与已知平行四边形就是全等的。
总而言之,平行四边形全等的判定定理是一个非常有用的几何定理。
它帮助我们判断两个平行四边形是否全等,并在解决实际问题时提供指导。
平行四边形的定义,性质与判定

平行四边形的定义、性质及判定
一
1.两组对边平行的四边形是平行四边形.
2.性质:
(1)平行四边形的对边相等且平行;
(2)平行四边形的对角相等,邻角互补;
(3)平行四边形的对角线互相平分.
3.判定:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
4.对称性:平行四边形是中心对称图形.
二
平行四边形定义:两组对边分别平行的四边形叫做平行四边形.
性质:平行四边形两组对边分别平行;平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分 .
判定:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形。
三
1.平行四边形定义:在同一个平面内,由两组平行线段组成的闭合图形,称为平行四边形。
2.平行四边形判定定理:两组对边分别平行且相等的四边形是平行四边形。
3.两组对角分别相等的四边形是平行四边形。
4.对角线互相平分的四边形是平行四边形。
平行四边形判定1

1.两组对边分别相等的四边形是 平行四边形
已知:四边形ABCD, AB=CD, AD=BC 求证:四边形ABCD是平行四边形 证明:
连结AC, ∵ AB=CD,AD=BC (已知) 又∵ AC=AC (公共边) ∴△ABC≌△CDA(SSS)
B A
D
1 4 3 2
C
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
判定一个四边形是平行四边形需要几个条件?
你能从四边形的边、角、对角线的位置关系和数 量关系出发,还找出其它的平行四边形的判定方 法吗?
一组对边平行且相等的四边形 是平行四边形.
1、请你识别下列四边形哪些是平行四边形?
A O B
⑴
D
5㎝
A
120°
60° D 5㎝
C
A D
110° 110°
B A
4.8㎝
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形判定定理1:
两组对边分别相等的四边形 是平行四边形
平行四边形性质定理1:
平行四边形的两组对边相等;
平行四边形判定定理1:
两组对边分别相等的四边形 是平行四边形
平行四边形的判定: 定义:有两组对边平行的四边形是平行四 边形. 平行四边形的性质: 定义:平行四边形的两组对边分别平行.
实是八十几座小型の传送塔,还有壹些古井,这里应该就是风家の壹些上古传送阵了.壹般来说,每壹个圣地,或者是大家族,都会有壹些这样の上古传送阵.至于这些上古传送阵是哪里来の,很大壹部分,都是出自陈三六の先祖之手,也就是炼金术士们留下の.这些传送阵也是各大势力の资 源,随时可以传送到别の地方去,也是壹种能力,是大势力の实力配备.根汉他们三人来到了这外面,白狼马和陈
平行四边形的性质及应用

平行四边形的性质及应用一、平行四边形的定义平行四边形是四边形的一种,具有以下性质:1.两组对边分别平行且相等;2.对角相等;3.对边相等;4.对角线互相平分;5.相邻角互补,即和为180度;6.对边角相等,即对边上的角相等。
二、平行四边形的判定1.如果一个四边形的两组对边分别平行,则这个四边形是平行四边形;2.如果一个四边形的对角相等,则这个四边形是平行四边形;3.如果一个四边形的对边相等,则这个四边形是平行四边形;4.如果一个四边形的对角线互相平分,则这个四边形是平行四边形;5.如果一个四边形的相邻角互补,则这个四边形是平行四边形;6.如果一个四边形的对边角相等,则这个四边形是平行四边形。
7.性质应用:求解平行四边形的边长、角度等;8.性质应用:证明四边形是平行四边形;9.性质应用:计算平行四边形的面积;10.性质应用:证明平行四边形的对角线互相平分;11.性质应用:证明平行四边形的对角相等;12.性质应用:证明平行四边形的对边角相等。
四、平行四边形的实际应用1.建筑设计:在建筑设计中,平行四边形的性质可以用于计算建筑物的面积、确定建筑物的结构稳定性等;2.交通工程:在交通工程中,平行四边形的性质可以用于设计道路标志、信号灯等;3.几何作图:平行四边形的性质可以用于进行几何作图,如绘制平行线、计算角度等。
平行四边形是中学数学中的重要知识点,掌握其性质和应用对于中学生来说非常重要。
通过学习平行四边形的定义、判定和性质,学生可以更好地理解和解决与平行四边形相关的问题。
同时,平行四边形的实际应用也使得这个知识点更具实用价值。
习题及方法:1.习题:已知平行四边形ABCD中,AB || CD,AD || BC,AB = CD,AD= BC,求证ABCD是平行四边形。
根据平行四边形的定义,我们需要证明ABCD的两组对边分别平行且相等。
已知AB || CD,AD || BC,且AB = CD,AD = BC,因此两组对边分别平行且相等,所以ABCD是平行四边形。
平行四边形的性质

平行四边形的性质平行四边形是一种特殊的四边形,其具有独特的性质和特点。
本文将介绍平行四边形的性质及其相关定理与应用。
一、定义和性质平行四边形是指具有两组对边平行的四边形。
它有以下一些基本性质:1. 对边性质:平行四边形的对边相等。
即,如果ABCD是一个平行四边形,那么AB = CD,BC = AD。
2. 对角线性质:平行四边形的对角线互相平分。
3. 顶角性质:平行四边形的内角相对应相等。
例如,∠A = ∠C,∠B = ∠D。
4. 不同对边的延长线相交于同一点:平行四边形的任意两个对边的延长线相交于同一点。
二、平行四边形的重要定理平行四边形有一些重要的定理,下面将介绍其中两个:1. 副对角线定理:平行四边形的副对角线互相等长。
即,如果ABCD是一个平行四边形,AC = BD。
证明:根据平行四边形的定义,AB ∥ CD,AD ∥ BC。
又因为平行线的性质,∠A + ∠B = 180°,∠C + ∠D = 180°。
将这两个等式相加,得到∠A + ∠B + ∠C + ∠D = 360°。
而对于四边形ABCD来说,它的内角和是360°。
因此,∠A + ∠B + ∠C +∠D = 360°,即∠A + ∠C =∠B + ∠D。
利用同位角的性质,我们可以得到∠ACB = ∠ADC。
再根据三角形内角和的性质,我们可以得到三角形ACB和三角形ADC的内角和都等于180°。
又因为AC ∥ BD,所以∠ACB = ∠ADC,且∠BAC = ∠BCD。
因此,根据三角形的相似性质和对应角相等的性质,我们可以得到三角形ACB和三角形ADC全等。
根据全等三角形的对应边相等的性质,我们得到AC = BD。
2. 对角线分割定理:平行四边形的对角线将其分割成两个面积相等的三角形。
证明:我们可以将平行四边形ABCD的对角线AC和BD延长至交于一点E。
连接BE和AD,并延长至交于一点F。
(完整版)平行四边形的定义及特殊四边形的性质及判定

平行四边形一、平行四边形1•平行四边形定义:两组对边分别平行的四边形是平行四边形。
2•平行四边形的判定定理:(1)判定定义:两组对边分别平行的四边形是平行四边形。
(2)判定定理1:一组对边平行且相等的四边形是平行四边形。
(3)判定定理2:两组对边分别相等的四边形是平行四边形。
(4)判定定理3:两组对角分别相等的四边形是平行四边形。
(5)判定定理4:对角线互相平分的四边形是平行四边形。
3•平行四边形的性质:(1)平行四边形的邻角互补,对角相等。
(2)平行四边形的对边平行且相等。
(3)夹在两条平行线间的平行线段相等。
(4)平行四边形的对角线互相平分。
(5)平行四边形是中心对称图形。
4•平行四边形的面积:面积=底边长x高=ah (a是平行四边形任何一边长,h必须是a边与其对边的距离。
)二、矩形1•矩形的定义:有一个角是直角的平行四边形是是矩形。
2.矩形的判定定理:(1) 判定定义: 有- 个角是直角的平行四边形是是矩形。
(2) 判定定理1: 有三个角是直角的四边形是矩形。
(3) 判定定理2: 对角线相等的平行四边形是矩形。
3•矩形的性质:(1)具有平行四边形的一切性质。
(2)矩形的四个角都是直角。
(3)矩形的对角线相等。
(4)矩形既是轴对称图形又是中心对称图形。
4•矩形的面积:矩形的面积=长X宽三、菱形1•菱形的定义:有一组邻边相等的平行四边形是菱形。
2•菱形的判定定理:(1)判定定义:有一组邻边相等的平行四边形是菱形。
(2)判定定理(1):四边都相等的四边形是菱形。
(3)判定定理(2):对角线互相垂直的平行四边形是菱形。
3.菱形的性质:(1)具有平行四边形的一切性质。
(2)菱形的四条边都相等。
(3)菱形的对角线互相垂直,并且每一条对角线平分一组对角。
(4)菱形既是轴对称图形又是中心对称图形。
4•菱形的面积:菱形的面积=底X高=对角线乘积的一半四、正方形1•正方形的定义:四边都相等且有一个角是直角的四边形是正方形。
平行四边形性质及判定

解:
∵四边形ABCD是平行四边形
10 B
∴BC=AD=8,CD=AB=10
又∵AC⊥BC
●
A 8 O
D
C
∴△ABC是直角三角形 2 2 2 2 ∴ AC AB BC 10 8 6 1 又∵OA=OC ∴ OA 2 AC 3 ∴S ABCD = BC×AC=8×6=48
说一说,练一练
如图,在
A D O B
ABCD中,
BC=10cm, AC=8cm, BD=14cm,
(1)△ AOD的周长是多少?为什么? (2)△ ABC与△ DBC的周长哪个长?长多少?
探究
ABCD的对角线AC与BD相交于O,直线EF过 点 O与 AB 、CD分别相交于E 、F,试探究 OE与OF的大小关系?并说明理由。 A E
读作:平行四边形ABCD ∵四边形ABCD是平行四边形 ∴ AB∥CD
∵
AB∥CD
AD∥BC ∴四边形ABCD是平行四边形
AD∥BC
A
D
B
C
如图
① ②
AB
AD
CD BC
ABCD AB AD
ABCD CD BC
练习一
如图是某区部分街道示意图,其中BC∥AD∥EG, AB//FH∥DC.图中的平行四边形共有_9__个.
又OB=OD, 所以四边形BFDE是平行四边形。
你还有其他 的证明方法 吗?
解:图中互相平行的线段有: AB//DC//EF, AD//BC, DE//CF B 理由如下:
AB=DC AD=BC
如图,AB=DC=EF,AD=BC,DE=CF,图中 有哪些互相平行的线段? D A
E F
C
平行四边形的性质及判定

平行四边形的性质和判定定理二、知识点回顾:1:平行四边形定义:两组对边分别平行的四边形是平行四边形.2:平行四边形的性质:1)平行四边形对边平行;2)平行四边形对边相等;3)平行四边形对角相等;4)平行四边形对角线互相平分.3:平行四边形判定定理:1)定义:两组对边分别平行的四边形是平行四边形;四边形ABCD是平行四边形2)两组对边分别相等的四边形是平行四边形;AD=BC,AB=CD四边形ABCD是平行四边形3)一组对边平行且相等的四边形是平行四边形;AD∥BC,AD=BC四边形ABCD是平行四边形4)对角线互相平分的四边形是平行四边形;OA=OC,OB=OD四边形ABCD是平行四边形5)两组对角分别相等的四边形是平行四边形.∠ABC=∠CDA,∠BAD=∠BCD四边形ABCD是平行四边形4:三角形中位线定义及定理:1)定义:连接三角形两边中点的线段叫三角形的中位线;2)定理:三角形中位线平行且等于第三边的一半.【典型例题】例1. 已知,如图1,四边形ABCD为平行四边形,∠A+∠C=80°,平行四边形ABCD 的周长为46 cm,且AB-BC=3 cm,求平行四边形ABCD的各边长和各内角的度数.例2. 如图2,在平行四边形ABCD中,E、F是直线BD上的两点,且DE=BF,你认为AE=CF吗?试说明理由.例3. 如图3所示,在平行四边形ABCD中,EF∥AB,HG∥AD,EF与GH相交于点O,则该图中平行四边形的个数共有()图3A. 7个B. 8个C. 9个D. 11个例4. 如图4,△ABC中,AB=6,AC=4.AD是BC边上的中线,则AD的取值范围是_________例5. 现有一个四边形的木框,若想知道它是否为平行四边形,只给你一把刻度尺,你能有几种方法来测量?例6. 如图5,已知六边形ABCDEF的每一个内角都是120°且AB=l,DE=2,BC+CD =8,求这个六边形的周长.图5例7. 如图6,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC 上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形()A. AE=CFB. DE=BFC. ∠ADE=∠CBFD. ∠AED=∠CFB图6例8. 如图7,AB∥CD,AC、BD交于点O,且OB=OD.已知S△OBC=1,求四边形ABCD 的面积.图7【模拟试题】(答题时间:30分钟)1. 在下列图形的性质中,平行四边形不一定具有的性质是()A. 对角相等B. 对边平行且相等C. 对角线相等D. 对角线互相平分2. 如图1,在平行四边形ABCD中,AC、BD相交于点O,作OE上BD于O,交CD于E,连接BE,若△BCE的周长为6,则平行四边形ABCD的周长为()图1A. 6B. 12C. 18D. 不确定3. 下列条件中,能判别一个四边形是平行四边形的是()A. 一组对边相等B. 一组对边平行C. 两条对角线相等D. 两组对角分别相等4. 已知四边形ABCD,以下四个条件:(1)∠A=∠B,∠C=∠D;(2)AB=CD,AD =BC;(3)AB=CD,AB∥CD;(4)AB∥CD,AD∥BC.其中能判定四边形ABCD为平行四边形的有()A. 1个B. 2个C. 3个D. 4个5. 已知四边形ABCD的对角线相交于点O,下列条件不能判定四边形ABCD是平行四边形的是()A. OA=OC,OB=ODB. ∠ABD=∠BDC,∠CBD=∠ADBC. AB=CD,OB=OD,∠ABD=∠BDCD. OA=OB.OC=OD6. 如图2,在△ABC中,∠B=90°,D、E分别是AB、AC的中点,DE=2,AC=5,则AB的长为()A. 2B. 3C. 4D. 5图27. 在四边形ABCD中,已知AB=CD,再添一个条件________,就可以判定四边形ABCD 是平行四边形.8. 如图3,在平行四边形ABCD中,AC、BD相交于点O,请写出图中相等的线段_______,图中全等三角形有__________对.图39. 在平行四边形ABCD中,已知对角线AC、BD相交于点O,且AC+BD=20,△AOB 的周长为15,则CD=______.10. 如图4,在平行四边形ABCD中,O是AC上一点,过点O的任一直线交AB于E,交CD于F,要想保证OE=OF,需满足条件:_________________(填出一个你认为正确的一个条件即可).图411. 用长为80cm的铁丝围成一个平行四边形,使平行四边形的两邻边之比为3:2,这个平行四边形最长边为___________.12. 已知四个角都是直角的四边形叫做矩形.如图5是小张剪出的一个四边形ABCD硬纸片,现他沿垂直于BC的线段AE剪下△ABE,然后放到△DCF处,使AB与CD重合,此时测得四边形AEFD是矩形.那么小张剪出的原四边形ABCD是_________形.判定的依据是_____________.13. 在四边形ABCD中,∠A=60,要使四边形ABCD成为平行四边形,则∠B=_________,∠C_____________.14. 如图6是小明剪成的一个等腰三角形纸片ABC,其中AB=AC,他把∠B沿EM折叠使点B落在点D上,把∠C沿FN折叠使点C也落在点D上,则小明就说四边形AEDF 是平行四边形,请你帮他说明理由;小明又量出AB=9 cm,则四边形AEDF的周长是多少?图615. 如图7,把两把相同的角尺(两边互相垂直)的一边紧靠在木板同一侧的边缘上,再看板另一边缘(也为直线)在两把角尺上的刻度是否相等,木工师傅就可以判断木板的两个边缘是否平行,你能说出其中的道理吗?图7【试题答案】1、C2、B3、D4、C5、D6、B7、AB//CD(条件不唯一)8、AD=BC AB=CD OA=OC OB=OD 49、5 10、OA=OC 11、24cm12、平行四边形,AB//CD、AB=CD13、120°60°14、解:(1)由题意可得:(2)周长为18cm.15、答:由测量过程可知:测量的直线间距不仅相等,而且平行,所以对边是平行关系.。
各种四边形判定定理及性质

四边形的性质和判定一、平行四边形的性质和判定(一)平行四边形性质:1、平行四边形的两组对边平行且相等2、平行四边形的两组对角相等,邻角互补3、平行四边形的两条对角线互相平分4、平行四边形是中心对称图形,对称中心是两条对角线的交点(二)平行四边形的判定:1、两组对边分别平行2、两组对边分别相等3、一组对边平行且相等4、两条对角线互相平分5 两组对角分别相等以上五个条件均可判定一个四边形是平行四边形,都是平行四边形的判定定理。
二、菱形的性质和判定:(一)菱形的性质:1、对角线互相垂直且平分;2、四条边都相等;3、对角相等,邻角互补;4、每条对角线平分一组对角.5、菱形是中心对称图形,对称中心是两条对角线的交点也是轴对称图形,对称轴是两条对角线(二)菱形的判定三、矩形的性质和判定(一)矩形的性质1、从边看,矩形对边平行且相等。
2、从角看,矩形四个角都是直角。
3、从对角线看,矩形对角线互相平分且相等。
4、矩形是轴对称图形,它有两条对称轴,它也是中心对称图形,对称中心是对角线的交点(二)矩形判定:1.有一个角是直角的平行四边形是矩形2、对角线相等的平行四边形是矩形2.有三个角是直角的四边形是矩形四、正方形的性质和判定(一)正方形的性质1、四边相等,四个角是直角2、对角线相等、相互平分、相互垂直3、既是中心对称图形又是轴对称图形(二)正方形的判定1、有一个角是直角的菱形是正方形2、有一组邻边相等的矩形是正方形3、有一组邻边相等且有一个角是直角的平行四边形是正方形4、对角线相等的菱形是正方形5、对角线相互垂直的矩形是正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
性质
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为平行四边形的两组对角分别相等”)
(3)如果一个四边形是平行四边形,那么这个四边形的邻角互补。
(简述为平行四边形的邻角互补”)
(4)夹在两条平行线间的平行的高相等。
(简述为平行线间的高距离处处相等”)
(5)如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
(简述为平行四边形的对角线互相平分”)
(6)连接任意四边形各边的中点所得图形是平行四边形。
(推论)
(7)平行四边形的面积等于底和高的积。
(可视为矩形。
)
(8)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形。
(9)平行四边形是中心对称图形,对称中心是两对角线的交点.
(10)平行四边形不是轴对称图形,但平行四边形是中心对称图形。
矩形和菱形是轴对称图形。
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质。
(11 )平行四边形ABCD中(如图)E为AB的中点,贝U AC和DE互相三等分,一般地,若E为AB上靠近A 的n等分点,则AC和DE互相(n+1)等分。
(12)平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和。
(13 )平行四边形对角线把平行四边形面积分成四等份。
(14)平行四边形中,两条在不同对边上的高所组成的夹角,较小的角等于平行四边形中较小的角,较大的角等于平行四边形中较大的角。
(15)平行四边形的面积等于相邻两边与其夹角正弦的乘积
平行四边形的判定方法(共6种)
1. 两组对边分别平行的四边形是平行四边形(定义判定法);
2. 一组对边平行且相等的四边形是平行四边形;
3. 对角线互相平分的四边形是平行四边形;
4. 两组对角分别相等的四边形是平行四边形;
5. 所有邻角(每一组邻角)都互补的四边形是平行四边形;
6. 两组对边分别相等的四边形是平行四边形。
辅助线作法
一、连接对角线或平移对角线。
二、过顶点作对边的垂线构成直角三角形。
三、连接对角线交点与一边中点,或过对角线交点作一边的平行线,构成线段平行或中位线。
四、连接顶点与对边上一点的线段或延长这条线段,构造相似三角形或等积三角形。
五、过顶点作对角线的垂线,构成线段平行或三角形全等。
平行四边形的定义:在同一平面内有两组对边分别平行的四边形叫做平行四边形平行四边形的定义、性质:
(1)平行四边形对边平行且相等.
(2)平行四边形两条对角线互相平分.(菱形和正方形)
(3 )平行四边形的对角相等,两邻角互补
(4 )连接任意四边形各边的中点所得图形是平行四边形.(推论)
(5)平行四边形的面积等于底和高的积.(可视为矩形)
(6)平行四边形是旋转对称图形,旋转中心是两条对角线的交点.
(7)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.
(8)平行四边形是中心对称图形,对称中心是两对角线的交点.
(9)一般的平行四边形不是轴对称图形,菱形是轴对称图形.
(10)平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和(可用余弦定理证明).
(11)平行四边形对角线把平行四边形面积分成四等分
判定:
(1 )两组对边分别相等的四边形是平行四边形;
(2)对角线互相平分的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4 )两组对边分别平行的四边形是平行四边形;
(5 )两组对角分别相等的四边形是平行四边形;
(6 )一组对边平行一组对角线互相平分的四边形是平行四边形;
(7)一组对边平行一组对角相等的四边形是平行四边形;。
