《平行四边形》的性质与判定 专题练习题 含答案
平行四边形练习题及答案

平行四边形练习题及答案1. 判断题:平行四边形的对角线是否一定相等?- 答案:错误。
只有矩形和正方形的对角线相等。
2. 选择题:下列哪个选项不是平行四边形的性质?- A. 对边相等- B. 对角相等- C. 对角线互相平分- D. 邻角互补- 答案:B。
平行四边形的对角不一定相等,这是矩形和正方形的特殊性质。
3. 计算题:如果一个平行四边形的一边长为10厘米,且相邻的两边夹角为60度,求对边的长度。
- 答案:由于平行四边形的邻角互补,所以另一个角也是60度。
这意味着平行四边形是一个菱形。
在菱形中,所有边长相等,所以对边的长度也是10厘米。
4. 证明题:证明平行四边形的对角线互相平分。
- 答案:设平行四边形为ABCD,对角线AC和BD相交于点E。
由于AB平行于CD,根据平行线的性质,∠BAC=∠DCA,同理∠ABC=∠BCD。
因此,△ABC和△CDA是相似三角形。
根据相似三角形的性质,我们可以得出AE/EC = BE/ED。
同理,我们可以证明AE/EC = BD/DC。
因此,AE = EC且BE = ED,证明了对角线互相平分。
5. 应用题:一个平行四边形的面积是64平方厘米,已知一边长为8厘米,求另一边的长度。
- 答案:平行四边形的面积公式是底乘以高。
设另一边的长度为x厘米,高为h厘米。
根据面积公式,8h = 64,解得h = 8厘米。
由于平行四边形的对边相等,另一边的长度也是8厘米。
练习题答案解析通过这些练习题,学生可以检验自己对平行四边形性质的理解,并通过计算和证明题来加深对平行四边形几何特性的认识。
这些题目覆盖了平行四边形的基本性质、面积计算以及证明题,有助于培养学生的逻辑推理能力和空间想象能力。
希望这些练习题和答案能够帮助学生更好地掌握平行四边形的相关知识。
在解决实际问题时,学生应该灵活运用所学知识,结合图形的特点进行分析和计算。
平行四边形的性质习题(有答案)

平行四边形的性质测试题一、选择题(每题3分共30分)1.下面的性质中,平行四边形不一定具备的是( )A .对角互补B .邻角互补C .对角相等D .内角和为360° 2.在中,∠A :∠B :∠C :∠D 的值可以是( )A .1:2:3:4B .1:2:1:2C .1:1:2:2D .1:2:2:1 3.平行四边形的对角线和它的边可以组成全等三角形( ) A .3对 B .4对 C .5对 D .6对 4.如图所示,在中,对角线AC 、BD 交于点O ,•下列式子中一定成立的是( )A .AC ⊥BDB .OA=OC C .AC=BD D .AO=OD 5.如图所示,在中,AD=5,AB=3,AE 平分∠BAD 交BC边于点E ,则线段BE 、EC 的长度分别为( )A .2和3B .3和2C .4和1D .1和4 6.的两条对角线相交于点O ,已知AB=8cm ,BC=6cm ,△AOB 的周长是18cm ,那么△AOD 的周长是( ) A .14cm B .15cm C .16cm D .17cm7.平行四边形的一边等于14,它的对角线可能的取值是( )A .8cm 和16cmB .10cm 和16cmC .12cm 和16cmD .20cm 和22cm 8.如图,在中,下列各式不一定正确的是( )A .∠1+∠2=180°B .∠2+∠3=180C .∠3+∠4=180°D .∠2+∠4=180° 9.如图,在中,∠ACD=70°,AE ⊥BD 于点E ,则∠ABE 等于( )A 、20°B 、25°C 、30°D 、35°10.如图,在△MBN 中,BM=6,点A 、C 、D 分别在MB 、NB 、MN 上,四边形ABCD 为平行四边形,∠NDC=∠MDA ,那么的周长是( )A .24B .18C .16D .12ODCBA EDC BA二、填空题(每题3分共18分)11.在中,∠A:∠B=4:5,则∠C=______.12.在中,AB:BC=1:2,周长为18cm,则AB=______cm,AD=_______cm.13.在中,∠A=30°,则∠B=______,∠C=______,∠D=________.14.如图,已知:点O是的对角线的交点,•AC=•48mm,•BD=18mm,AD=16mm,那么△OBC的周长等于_______mm.15.如图,在中,E、F是对角线BD上两点,要使△ADF≌△CBE,还需添加一个条件是________.16.如图,在中,EF∥AD,MN∥AB,那么图中共有_______•个平行四边形.三、解答题17.已知:如图,在中,E、F是对角线AC•上的两点,AE=CF.BE与DF的大小有什么关系,并说明理由。
专题 平行四边形的性质和判定(原卷版)
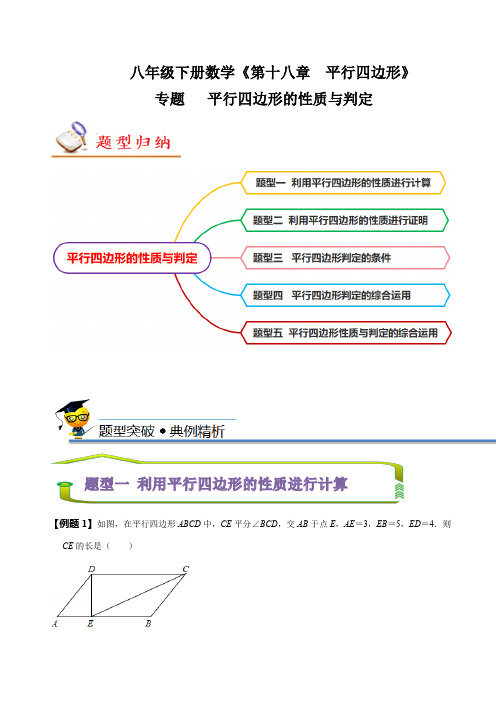
八年级下册数学《第十八章 平行四边形》专题 平行四边形的性质与判定【例题1】如图,在平行四边形ABCD 中,CE 平分∠BCD ,交AB 于点E ,AE =3,EB =5,ED =4.则CE 的长是( )A .2√2B .6√2C .5√5D .4√5【变式1-1】如图,在平行四边形ABCD 中,AB =5,AD =7,AE 平分∠BAD 交BC 于点E ,作DG ⊥AE 于点G 并延长交BC 于点F ,则线段EF 的长为( )A .2B .52C .3D .2√6【变式1-2】如图,在▱ABCD 中,O 为对角线AC 与BD 的交点,AC ⊥AB ,E 为AD 的中点,并且OF ⊥BC ,∠D =53°,则∠FOE 的度数是( )A .143°B .127°C .53°D .37°【变式1-3】如图,将平行四边形OABC 放置在平面直角坐标系xOy 中,O 为坐标原点,若点C 的坐标是(1,3),点A 的坐标是(5,0),则点B 的坐标是( )A .(5,3)B .(4,3)C .(6,3)D .(8,1)【变式1-4】如图,在平行四边形ABCD 中P 是CD 边上一点,且AP 和BP 分别平分∠DAB 和∠CBA ,若AD =5,AP =8,则△APB 的周长是( )A.18B.24C.23D.14【变式1-5】如图,在平行四边形ABCD中,∠B=60°,AE平分∠BAD交BC于点E,若∠AED=80°,则∠ACE的度数是()A.30°B.35°C.40°D.45°【变式1-6】▱ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是()A.3≤AB≤4B.2<AB<14C.1<AB<7D.1≤AB≤7【变式1-7】在平行四边形ABCD中,∠A的角平分线把边BC分成长度为4和5的两条线段,则平行四边形ABCD的周长为()A.13或14B.26或28C.13D.无法确定【变式1-8】如图,▱ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.(1)求证:OE=OF;(2)若EF⊥AC,△BEC的周长是10,求▱ABCD的周长.【例题2】(2022•南京模拟)如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=EF =FC.(1)求证:DE∥BF;(2)若BE⊥BC,DE=6,求对角线AC的长.【变式2-1】(2022春•西吉县校级月考)如图.已知四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,求证:BE=DF.【变式2-2】(2022•泉山区校级三模)已知,如图,在平行四边形ABCD中,点E、F分别在AB、CD的延长线上,BE=DF,连接EF,分别交BC、AD于G、H.求证:EG=FH.【变式2-3】(2022秋•北碚区校级期末)如图,平行四边形ABCD中,CB=2AB,∠DCB的平分线交BA 的延长线于点F.(1)求证:DE=AE;(2)若∠DAF=70°,求∠BEA的度数.【变式2-4】(2022秋•道里区校级月考)在平行四边形ABCD中,点E在CD边上,点F在AB边上,连接AE、CF、DF、BE,∠DAE=∠BCF.(1)如图1,求证:DE=BF;(2)如图2,设AE交DF于点G,BE交CF于点H,连接GH,若E是CD边的中点,在不添加任何辅助线的情况下,请直接写出图中以G为顶点并且与△EHC全等的所有三角形.【变式2-5】(2021春•九龙坡区校级期中)在▱ABCD中,∠ABC=45°,过A作AE⊥CD于E,连接BE,延长EA至F,使CE=AF,连接DF.(1)求证:DF=BE;(2)若DF=√34,AD=3√2,求四边形ADEB的周长.【变式2-6】(2022春•济南期中)如图,将▱ABCD的边BC延长到点E,使BE=CD,连接AE交CD 于点F.(1)求证:AE平分∠BAD;(2)已知BC=CE=3,EF=4,FG⊥AB,求FG的长.【例题3】如图,平行四边形ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是()A.CE=AF B.BE=DF C.∠DAF=∠BCE D.AF∥CE【变式3-1】在下列条件中,能够判定一个四边形是平行四边形的有()①一组对边平行,另一组对边相等②一组对边平行,一条对角线平分另一条对角线③一组对边平行,一组对角相等④一组对角相等,一条对角线平分另一条对角线A.1个B.2个C.3个D.4个【变式3-2】下列条件能判定四边形ABCD是平行四边形的是()A.∠A=∠B,∠C=∠D B.AB=AD,BC=CDC.AB=CD,AD=BC D.AB∥CD,AD=BC【变式3-3】四边形ABCD中,对角线AC,BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB∥CD,∠BAD=∠BCD;③AO=CO,BO=DO;④AB∥CD,AD=BC.一定能判定四边形ABCD 是平行四边形的条件有()A.1组B.2组C.3组D.4组【变式3-4】如图,在△ABC中,D,F分别是AB,AC上的点,且DF∥BC.点E是射线DF上一点,若再添加下列其中一个条件后,不能判定四边形DBCE为平行四边形的是()A.∠ADE=∠E B.∠B=∠E C.DE=BC D.BD=CE【变式3-5】如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是()A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF【变式3-6】如图,在▱ABCD中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是(写出一个即可).【变式3-7】平行四边形ABCD中,E、F是对角线BD上不同的两点,写出一个能使四边形AECF一定为平行四边形的条件.(用题目中的已知字母表示)【例题4】(2021•江华县一模)如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.(1)求证:△ACD≌△CBF;(2)点D在线段BC上何处时,四边形CDEF是平行四边形且∠DEF=30°.【变式4-1】如图,点B、C、E、F在同一直线上,BE=CF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)四边形ABED是平行四边形.【变式4-2】如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,求证:四边形BDEF是平行四边形.【变式4-3】(2021秋•海阳市期末)如图,在△ABC中,AD是BC边的中线,F是AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,试分析当点G在何位置时,四边形AFDG为平行四边形?【变式4-4】(2022春•顺义区校级月考)如图,四边形ABCD中,BD垂直平分AC,垂足为点F、E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.(1)求证:四边形ABDE是平行四边形;(2)如果DA平分∠BDE,AB=3,AD=4,求AC的长.【变式4-5】(2021春•西安期末)如图,在△AFC中,∠F AC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD,求证:四边形ABCD是平行四边形.【变式4-6】(2022春•礼泉县期末)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)求证:△AEF≌△BAC;(2)四边形ADFE是平行四边形吗?请说明理由.【例题5】如图,在▱ABCD 中,要在对角线BD 上找两点E 、F ,使A 、E 、C 、F 四点构成平行四边形,现有①,②,③,④四种方案,①只需要满足BE =DF ;②只需要满足AE ⊥BD ,CF ⊥BD ;③只需要满足AE ,CF 分别平分∠BAD ,∠BCD ,④只需要满足AE =CF .则对四种方案判断正确的是( )A .①②③B .①③④C .①②④D .②③④【变式5-1】如图,在▱ABCD 中,E 、F 分别为边AB 、DC 的中点,连接AF 、CE 、DE 、BF 、EF ,AF 与DE 交于点G ,CE 与BF 交于点H ,则图中共有平行四边形( )A .3个B .4个C .5个D .6个【变式5-2】如图,已知△ABC 是边长为6的等边三角形,点D 是线段BC 上的一个动点(点D 不与点B ,C 重合),△ADE 是以AD 为边的等边三角形,过点E 作BC 的平行线,分别交线段AB ,AC 于点F ,G ,连接BE 和CF .则下列结论中:①BE =CD ;②∠BDE =∠CAD ;③四边形BCGE 是平行四边形;④当CD =2时,S △AEF =23,其中正确的有( )A .4个B .3个C .2个D .1个【变式5-3】(2022春•南海区月考)如图,在▱ABCD 中,点E 是BC 边的中点,连接AE 并延长与DC的延长线交于F.(1)求证:四边形ABFC是平行四边形;(2)若AF平分∠BAD,∠D=60°,AD=8,求▱ABCD的面积.【变式5-4】(2022春•重庆月考)已知,如图,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.【变式5-5】(2022春•南湖区校级期中)如图,在平行四边形ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.(1)求证:四边形AFCE是平行四边形.(2)若AD=13cm,AE=12cm,AB=20cm,求四边形AFCE的面积.【变式5-6】(2021春•南昌期中)如图,点O是平行四边形ABCD对角线的交点,过点O的直线交AD,BC于P,Q两点,交BA,DC的延长线于M,N两点.(1)求证:AP=CQ;(2)连接DM,BN,求证:四边形BNDM是平行四边形.【变式5-7】(2022春•温州校级月考)在Rt△ABC中,∠ACB=90°,D是斜边AB上的一点,作DE ⊥BC,垂足为E,延长DE到F,连结CF,使∠A=∠F.(1)求证:四边形ADFC是平行四边形.(2)连接CD,若CD平分∠ADE,CF=10,CD=12,求四边形ADFC的面积.【变式5-8】(2022春•锦江区校级期中)如图,在等边△ABC中,D、E两点分别在边BC、AC上,BD =CE,以AD为边作等边△ADF,连接EF,CF.(1)求证:△CEF为等边三角形;(2)求证:四边形BDFE为平行四边形;(3)若AE=2,EF=4,求四边形BDFE的面积.。
平行四边形的判定练习题(含答案)

平行四边形的判定练习题(含答案)(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.()(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.()(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.()(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.()(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.()(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.()5.已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件________.6.如图所示,∠1=∠2,∠3=∠4,问四边形ABCD是不是平行四边形.7.如图所示,在四边形ABCD中,AB=CD,BC=AD,E,F 为对角线AC上的点,且AE=CF,求证:BE=DF.8.如图所示,D为△ABC的边AB上一点,DF交AC于点E,且AE=CE,FC∥AB.求证:CD=AF.9.如图所示,已知四边形ABCD是平行四边形,在AB 的延长线上截取BE=•AB,BF=BD,连接CE,DF,相交于点M.求证:CD=CM.10.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC•交EB于F,求证:EF=FB.知能点2 三角形的中位□线11.如图所示,已知E为□ABCD中DC边的延长线上的一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF,求证:AB=2OF.12.如图所示,在ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF•交于点M,连接CF,DE交AD.于点N,求证:MN∥AD且MN=1213.如图所示,DE是△ABC的中位线,BC=8,则DE=_______.14.如图所示,在□ABCD中,对角线AC,BD交于点O,OE∥BC交CD•于E,•若OE=3cm,则AD的长为(). A.3cm B.6cm C.9cm D.12cm 15.如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,•则四边形EFGH是平行四边形吗?为什么?16.如图所示,在△ABC中,AC=6cm,BC=8cm,AB=10cm,D,E,F分别是AB,BC,CA的中点,求△DEF的面积.规律方法应用17.如图所示,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,•并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离是多少?18.如图所示,在□ABCD中,AB=2AD,∠A=60°,E,F 分别为AB,CD的中点,EF=1cm,那么对角线BD的长度是多少?你是怎样得到的?19.如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.•(BC-AC).试说明:(1)DE∥BC.(2)DE=12开放探索创新20.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD•于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.中考真题实战21.(长沙)如下左图所示,在四边形ABCD中,AB∥CD,要使四边形ABCD•为平行四边形,则应添加的条件是________.(添加一个即可)22.(呼和浩特)如上右图所示,已知E,F,G,H是四边形ABCD各边的中点,•则S四边形EFGH :S四边形ABCD的值是_________.23.(南京)已知如图19-1-55所示,在Y ABCD中,E,F分别是AB,CD的中点.求证:(1) △AFD≌△CEB.(2)四边形AECF是平行四边形.答案:1.C 2.C 3.D4.(1)× (2)× (3)∨ (4)∨ (5)∨ (6)×5.AD=BC或AB∥CD6.解:∵∠1=∠2,∴AD∥BC.又∵∠3=∠4,∴AB∥CD.∴四边形ABCD是平行四边形.7.证明:∵AB=CD,BC=AD,∴四边形ABCD是平行四边形.∴AB∥CD,∴∠BAE=∠DCF.又∵AE=CE,∴△ABE≌△CDF(SAS),∴BE=EF.8.证明:∵FC∥AB,∴∠DAC=∠ACF,∠ADF=∠DFC.又∵AE=CE,∴△ADE≌△CFE(AAS),∴DE=EF.∵AE=CE,∴四边形ADCF为平行四边形.∴CD=AF.9.证明:∵四边形ABCD是平行四边形.∴AB//DC.又∵BE=AB,∴BE//DC,∴四边形BDCE是平行四边形.∵DC∥BF,∴∠CDF=∠F.同理,∠BDM=∠DMC.∵BD=BF,∴∠BDF=∠F.∴∠CDF=∠CMD,∴CD=CM.10.证明:过点B作BG∥AD,交DC的延长线于G,连接EG.∵DC∥AB,∴ABGD是平行四边形,∴BG// AD.在□ACED中,AD//CE,∴CE//BG.∴四边形BCEG为平行四边形,∴EF=FB.11.证明:∵四边形ABCD是平行四边形,∴AB//CD,AD=BC.∵CE=CD,∴AB//CE,∴四边形ABEC为平行四边形.∴BF=FC,∴OF//1AB,即AB=2OF.212.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.又∵EF∥AB,∴EF∥CD.∴四边形ABEF,ECDF均为平行四边形.又∵M,N分别为Y ABEF和Y ECDF对角线的交点.∴M为AE的中点,N为DE的中点,即MN为△AED的中位线.∴MN∥AD且MN=12AD.13.4 14.B15.解:EFGH是平行四边形,连接AC,在△ABC中,∵EF是中位线,∴EF//12AC.同理,GH//12AC.∴EF//GH,∴四边形EFGH为平行四边形.16.解:∵EF,DE,DF是△ABC的中位线,∴EF=12AB,DE=12AC,DF=12BC.又∵AB=10cm,BC=8cm,AC=6cm,∴EF=5cm,DE=3cm,DF=4cm,而32+42=25=52,即DE2+DF2=EF2.∴△EDF为直角三角形.∴S△EDF =12DE·DF=12×3×4=6(cm2).17.解:∵M,N分别是AC,BC的中点.∴MN是△ABC的中位线,∴MN=12AB.∴AB=2MN=2×20=40(m).故A,B两点间的距离是40m.18.解:连接DE.∵四边形ABCD是平行四边形,∴AB//CD.∵DF=12CD,AE=12AB,∴DF//AE.∴四边形ADFE是平行四边形.∴EF=AD=1cm.∵AB=2AD,∴AB=2cm.∵AB=2AD,∴AB=2AE,∴AD=AE.∴∠1=∠4.∵∠A=60°,∠1+∠4+∠A=180°,∴∠1=∠A=∠4=60°.∴△ADE是等边三角形,∴DE=AE.∵AE=BE,∴DE=BE,∴∠2=∠3.∵∠1=∠2+∠3,∠1=60°,∴∠2=∠3=30°.∴∠ADB=∠3+∠4=90°.=cm).19.解:延长AD交BC于F.(1)∵AD⊥CD,∴∠ADC=∠FDC=90°.∵CD平分∠ACB,∴∠ACD=∠FCD.在△ACD与△FCD中,∠ADC=∠FDC,DC=DC,∠ACD=∠FCD.∴△ACD≌△FCD,∴AC=FC,AD=DF.又∵E为AB的中点,∴DE∥BF,即DE∥BC.(2)由(1)知AC=FC,DE=12BF.∴DE=12(BC-FC)=12(BC-AC).20.解:AE=CF.理由:过E作EG∥CF交BC于G,∴∠3=∠C.∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.∴∠C=∠BAD,∴∠3=∠BAD.又∵∠1=∠2,BE=BE,∴△ABE≌△GBE(AAS),∴AE=GE.∵EF∥BC,EG∥CF,∴四边形EGCF是平行四边形,∴GE=CF,∴AE=CF.21.答案不唯一,如AB=CD或AD∥BC.22.1223.解:(1)在□ABCD中,AD=CB,AB=CD,∠D=∠B.∵E,F分别为AB,CD的中点,∴DF=12CD,BE=12AB,∴DF=BE,∴△AFD≌△CEB.(2)在□ABCD中,AB=CD,AB∥CD.由(1)得BE=DF,∴AE=CE,∴四边形AECF是平行四边形.。
(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)
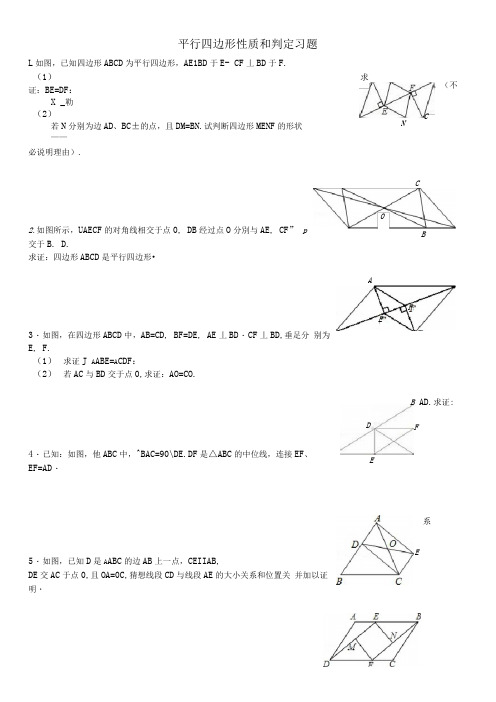
平行四边形性质和判定习题L如图,已知四边形ABCD为平行四边形,AE1BD于E- CF丄BD于F.(1)求证:BE=DF:X _勒(2)若N分别为边AD、BC±的点,且DM=BN.试判断四边形MENF的形状——必说明理由).2.如图所示,UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证:四边形ABCD是平行四边形•3・如图,在四边形ABCD中,AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.(1)求证J A ABE=A CDF:(2)若AC与BD交于点0,求证:AO=CO.4・已知:如图,他ABC中,^BAC=90\DE.DF是△ABC的中位线,连接EF、EF=AD・5・如图,已知D是A ABC的边AB上一点,CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。
(不CNCBAFED FE系E6・如图,已知,UABCD中,AE=CF, M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形•7・如图,平行四边形ABCD, E 、F 两点在对角线BD 上,且BE=DF,连接AE. EG CF, FA ・求证:四边形AECF 是平行四边形•& 在UABCD 中,分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证:四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点,求证:BC=DE ・2如图,在梯形ABCD 中,ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动,到D 点Q 自点C 向B 以2cm/s 的速度运动,到B点即停止,直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发,几秒后其中一个四边形为平行四边形?IL 如图:已知D 、E 、F 分别是A ABC 各边的中点, 求证:AE 仃DF 互相平分.如图所示, 9・ED13.如图,已知四边形ABCD中,点E, F. G, H分别是AB、CD、AC. BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分・14.如图J oABCD 中,MNIIAC.试说明MQ=NP.15.已知:如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证:四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH. 连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,尖余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在A ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证J AF=CE:(2)如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形,并证明你的结论・18,如图平行四边形ABCD 中.mBC=6(几 点E 、F 分別在CD.BC 的延长线上,AE||BD ・ EEhBB 垂足为点F, DF=2 (1) 求证:D 是EC 中点; (2) 求FC 的长.19.如图,已知A ABC 是等边三角形,点D 、F 分别在线段BC 、AB 匕 厶EFB=60。
部编数学八年级下册平行四边形的性质与判定大题专练(分层培优30题,八下册人教)2023复习备考含答案

2022-2023学年八年级数学下学期复习备考高分秘籍【人教版】专题2.5平行四边形的性质与判定大题专练(分层培优30题,八下人教)A卷基础过关卷(限时50分钟,每题10分,满分100分)1.如图,▱ABCD的对角线AC与BD相交于点O,AC+BD=24,∠ABC=70°,△ABO的周长是20.(1)求∠ADC的度数;(2)求AB的长.【分析】(1)根据平行四边形对角相等即可得答案;(2)根据平行四边形对角线互相平分可得AO+BO的长,进而可求出AB.【解析】(1)∵四边形ABCD是平行四边形,∴∠ADC=∠ABC=70°;(2)∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∴AO+BO=(AC+BD)=12,∴AO+BO+AB=20,∴AB=8.2.已知,如图,E,F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.【分析】连接BD,与AC交于点O,由平行四边形的对角线互相平分得到OA=OC,OB=OD,进而得到OE=OF,利用对角线互相平分的四边形是平行四边形即可得证.【解答】证明:如图,连接BD,与AC交于点O,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OA﹣AE=OC﹣CF,即OE=OF,又OB=OD,∴四边形DEBF是平行四边形.3.如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.(1)求证:AF=DE;(2)若AC=6,BC=10,求四边形AEDF的周长.【分析】(1)根据三角形中位线定理、直角三角形的性质证明四边形DEAF是平行四边形,根据平行四边形的性质证明;(2)由(1)的结论计算即可.【解答】(1)证明:∵D,E分别为AB,BC的中点,∴DE∥AC,DE=AC,∵∠BAC=90°,E为BC的中点,∴EA=EB,∴∠EAB=∠B,又∠FDA=∠B,∴∠FDA=∠EAB,∴EA∥DF,∴四边形DEAF是平行四边形,∴AF=DE;(2)解:∵∠BAC=90°,E为BC的中点,∴EA=BC=5,∵D,E分别为AB,BC的中点,∴DE=AC=3,∴四边形AEDF的周长=2×(3+5)=16.4.如图,AC,BD相交于点O,AB∥CD,AD∥BC,E,F分别是OB,OD的中点,求证:四边形AFCE 是平行四边形.【分析】由条件AB∥CD,AD∥BC可证到四边形ABCD是平行四边形,根据平行四边形的性质可得OA =OC,OB=OD,要证四边形AFCE是平行四边形,只需证OE=OF即可.【解答】证明:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵E,F分别是OB,OD的中点,∴OE=OB,OF=OD,∴OE=OF,∴四边形AFCE是平行四边形.5.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC =∠B,(1)CF=DE成立吗?试说明理由.(2)若AC=6cm,AB=10cm,求四边形DCFE的面积.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=BD,再根据等边对等角可得∠B=∠DCE,然后求出∠FEC=∠DCE,根据等腰三角形三线合一的性质可得∠CED=90°,然后求出∠CED=∠ECF=90°,再利用“角边角”证明△CDE和△ECF全等,根据全等三角形对应边相等证明即可.(2)由三角形的中位线定理得到DE的长度,再由平行四边形的面积公式求得.【解析】(1)证明:∵∠ACB=90°,点D是AB的中点,∴CD=BD,∴∠B=∠DCE,∵∠FEC=∠B,∴∠FEC=∠DCE,∵点E是BC的中点,∴∠CED=90°,∴∠CED=∠ECF=90°,在△CDE和△ECF中,∴△CDE≌△ECF(ASA),∴CF=DE;(2)在Rt△ABC中,∠ACB=90°,∴BC==8,∵点D、E分别是AB、BC的中点,∴DE=AC=3,CE=,=3×4=12.∴S四边形DCFE6.如图,在平行四边形ABCD中,E为AD上一点,F为BC上一点,EF与对角线BD交于点O.有以下三个条件:①AE=CF;②EO=OF;③O为BD中点.从中选取一个作为题设,余下的两个作为结论,组成一个正确的命题,并加以证明.【分析】利用已知结合全等三角形的判定与性质得出DE=BF进而得出答案.【解析】答案不唯一,例如:已知②EO=OF;③O为BD中点,结论:①AE=CF.理由:在△DOE和△BOF中,∴△DOE≌△BOF(SAS),∴DE=BF,∵四边形ABCD是平行四边形,∴AD=BC,∴AE=FC.7.如图,在▱ABCD中,点E是CD的中点,点F是BC边上的一点,且EF⊥AE.求证:AE平分∠DAF.李华同学读题后有一个想法,延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.请你参考李华的想法,完成此题的证明.【分析】通过倍长中线可证△EDM≌△ECF,进而可得EM=EF,即可得△AMF是等腰三角形.【解答】证明:延长AD,FE交于M.在平行四边形ABCD中,AD∥BC,∴∠MDE=∠FCE,∠EMD=∠EFC,又E是CD的中点,∴DE=CE,∴△EDM≌△ECF(AAS),∴EM=EF,又∵EF⊥AE,∴AF=AM,即△AMF是等腰三角形,∴AE平分∠DAF.8.在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, ② (填写序号).求证:BE=DF.【分析】由四边形ABCD是平行四边形得BO=DO,加上条件OE=OF,从而得出四边形BEDF为平行四边形,从而有BE=DF.【解析】选②,如图,连接BF,DE,∵四边形ABCD是平行四边形,∴BO=DO,∵OE=OF,∴四边形BEDF为平行四边形,∴BE=DF.故选择:②(答案不唯一).9.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.(1)求证:四边形AFHD为平行四边形;(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.【分析】(1)由平行四边形的性质得出AD=BC,AD∥BC;证明BC是△EFG的中位线,得出BC∥FG,BC=FG,证出AD∥FH,AD=FH,由平行四边形的判定方法即可得出结论;(2)由平行四边形的性质得出∠BCE=50°,再由等腰三角形的性质得出∠CBE=∠CEB,根据三角形内角和定理即可得出结果.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=FG,∵H为FG的中点,∴FH=FG,∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,∴四边形AFHD是平行四边形;(2)解:∵∠BAE=80°,∴∠BCD=80°,∵∠DCE=30°,∴∠BCE=80°﹣30°=50°,∵CB=CE,∴∠CBE=∠CEB=(180°﹣50°)=65°.10.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB 上,EF∥BC.(1)求证:四边形BDEF是平行四边形;(2)若AB=10,AC=4,求BF的长.【分析】(1)证明△AGE≌△ACE,根据全等三角形的性质可得到GE=EC,再利用三角形的中位线定理证明DE∥AB,再加上条件EF∥BC可证出结论;(2)先证明BF=DE=BG,再证明AG=AC,可得到BF=(AB﹣AG)=(AB﹣AC).【解答】(1)证明:延长CE交AB于点G,∵AE⊥CE,∴∠AEG=∠AEC=90°,在△AEG和△AEC中,,∴△AGE≌△ACE(ASA).∴GE=EC.∵BD=CD,∴DE为△CGB的中位线,∴DE∥AB.∵EF∥BC,∴四边形BDEF是平行四边形.(2)解:∵四边形BDEF是平行四边形,∴BF=DE.∵D、E分别是BC、GC的中点,∴BF=DE=BG.∵△AGE≌△ACE,∴AG=AC,∴BF=(AB﹣AG)=(AB﹣AC)=(10﹣4)=3.B卷能力提升卷(限时60分钟,每题10分,满分100分)11.如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.(1)求证:CD=CE;(2)若点E是BC的中点,∠C=108°,求∠DAE的度数.【分析】(1)由AD//BC可得∠ADE=∠DEC,再由∠ADE=∠EDC,从而可得∠DEC=∠EDC,继而可证得CD=CE;(2)由题意可得AD//BC,AB=CD,继而可求得∠BAD的度数,AB=BE,从而可求得∠BAE的度数,由此即可求得∠DAE的度数.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD//BC,∴∠ADE=∠DEC,∵DE平分∠ADC,∴∠ADE=∠EDC,∴∠DEC=∠EDC,∴CD=CE;(2)解:∵四边形ABCD是平行四边形,∴AD//BC,AB=CD,∴∠B+∠BAD=180°,∵∠C=108°,∴∠B=180°﹣108°=72°,∵BE=CE,CE=CD,∴AB=BE,∴∠BAE=∠BEA=(180°﹣72°)÷2=54°,∴∠DAE=∠BAD﹣∠BAE=108°﹣54°=54°.12.如图,在▱ABCD中,AE平分∠BAD交对角线BD于点E,CF平分∠DCB交对角线BD于点F,连接AF,CE.(1)若∠BCF=50°,求∠ADC的度数;(2)求证:四边形AECF为平行四边形.【分析】(1)由四边形ABCD是平行四边形得出∠ADC+∠DCB=180°,再根据角平分线的定义得出∠DCB的度数即可求解;(2)由ASA证明△ABE≌△CDF得出AE=CF,∠AEB=∠DFC,再根据平行线的判定得出AE∥CF即可得出结论.【解答】(1)解:∵四边形ABCD是平行四边形,∴∠ADC+∠DCB=180°,∵CF平分∠DCB,∴∠DCF=∠BCF=50°,∴∠ADC=180°﹣∠DCF﹣∠BCF=180°﹣50°﹣50°=80°;(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠BAD=∠DCB,∴∠ABE=∠CDF,∵AE平分∠BAD,CF平分∠DCB,∴∠BAE=,,∴∠BAE=∠DCF,∴△ABE≌△CDF(ASA),∴AE=CF,∠AEB=∠DFC,∴∠AEF=∠CFE,∴AE∥CF,∴四边形AECF为平行四边形.13.如图,以平行四边形ABCD的边AB、CD为边,作等边△ABE和等边△CDF,连接DE,BF.求证:四边形BFDE是平行四边形.【分析】由平行四边形的性质得出AB=CD,AD=BC,∠BAD=∠DCB,由等边三角形的性质得出BE=AE=AB=CD=CF=DF,∠BAE=∠DCF=60°,证明△ADE≌△CBF(SAS),得出DE=BF,则可得出结论.【解答】证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠BAD=∠DCB,∵△ABE和△CDF是等边三角形,∴BE=AE=AB=CD=CF=DF,∠BAE=∠DCF=60°,∴∠DCB﹣∠DCF=∠DAB﹣∠BAE,即∠DAE=∠FCB,在△ADE和△CBF中,,∴△ADE≌△CBF(SAS),∴DE=BF,又∵BE=DF,∴四边形BFDE为平行四边形.14.如图,平行四边形ABCD中AB∥CD,AD∥BC,AB=CD,AD=BC,CB=2AB,∠DCB的平分线交BA的延长线于点F.(1)求证:DE=AE;(2)若∠DAF=70°,求∠BEA的度数.【分析】(1)根据平行四边形的性质证明A为BF的中点,然后证明△DEC≌△AEF(AAS),进而得出结论;(2)由平行四边形的对边平行证出∠CBF=∠DAF=70°,∠BEA=∠EBC,由等腰三角形的性质得出∠CBE=∠ABE,即可得出答案.【解答】(1)证明:∵CE是∠DCB的平分线,∴∠DCE=∠BCF,∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC,∴∠DCE=∠CFB,∴∠BCF=∠CFB,∴BC=BF,∵BC=2AB,∴BF=2AB,∴A为BF的中点,∴AB=AF,∴AB=DC=AF,在△DEC和△AEF中,,∴△DEC≌△AEF(AAS),∴DE=AE;(2)解:∵四边形ABCD是平行四边形,∴DA∥CB,∴∠CBF=∠DAF=70°,∠BEA=∠EBC,∵△DEC≌△AEF,∴CE=EF,∵BC=BF,∴∠EBC=∠FBE=CBF=35°,∴∠BEA=35°.15.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上一点,且CF=3BF,连接DB,EF.若∠ACB=90°,AC=12,DE=4.(1)求证:DE=BF;(2)求四边形DEFB的周长.【分析】(1)根据三角形中位线定理得到DE∥BC,DE=BC,根据题意得到BF=BC,等量代换证明结论;(2)根据勾股定理求出DB,证明四边形DBFE为平行四边形,根据平行四边形的周长公式计算即可.【解答】(1)证明:∵点D,E分别是AC,AB的中点,∴DE为△ABC的中位线,∴DE∥BC,DE=BC,∵CF=3BF,∴BF=BC,∴DE=BF;(2)解:∵点D是AC的中点,AC=12,∴CD=6,∵DE=4,∴BC=8,由勾股定理得:DB===10,∵DE=BF,DE∥BC,∴四边形DBFE为平行四边形,∴四边形DEFB的周长=2×(4+10)=28.16.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC.(1)求证:①△AOE≌△COF;②四边形ABCD为平行四边形;(2)过点O作EF⊥BD,交AD于点E,交BC于点F,连接BE,若∠BAD=100°,∠DBF=32°,求∠ABE的度数.【分析】(1)①由平行线的性质得出∠OAD=∠OCB,可证明△AOE≌△COF(ASA);②证得AD=CB,再由AD∥BC,即可得出结论;(2)由全等三角形的性质得出OE=OF,证出BE=BF,由等腰三角形的性质得出∠OBF=∠OBE=32°,求出∠ABC=116°,则可得出答案.【解答】(1)①证明:∵AD∥BC,∴∠OAD=∠OCB,在△AOE和△COF中,,∴△AOE≌△COF(ASA);②同理可证△AOD≌△COB,∴AD=CB,又∵AD∥BC,∴四边形ABCD为平行四边形;(2)解:∵△AOE≌△COF,∴OE=OF,∵EF⊥BD,∴BE=BF,∴∠OBF=∠OBE=32°,∴∠EBF=64°,∵AD∥BC,∴∠ABC=180°﹣∠BAD=180°﹣100°=80°,∴∠ABE=∠ABC﹣∠EBF=80°﹣64°=16°.17.如图,在▱ABCD中,O是对角线AC、BD的交点,延长边CD到点F,使DF=DC,过点F作EF∥AC,连接OF、EC.(1)求证△ODC≌△EDF.(2)连接AF,已知 ② .(从以下两个条件中选择一个作为已知,填写序号),请判断四边形OCEF 的形状,并证明你的结论.条件①:AF=FC且AC=2DC;条件②:OD=DC且∠BEC=45°.【分析】(1)由DF=DC,EF∥AC,可以证明△ODC≌△EDF;(2)由△ODC≌△EDF推出四边形OCEF是平行四边形,再由OD=DC证明四边形OCEF是矩形,最后由∠BEC=45°即可证明四边形OCEF是正方形.【解答】(1)证明:∵EF∥AC,∴∠EFC=∠DCO,∠FED=∠DOC,∵DF=DC,∴△ODC≌△EDF(AAS);(2)选择②,四边形OCEF是正方形,证明:∵△ODC≌△EDF(AAS),∴OD=DE,CD=DF,∴四边形OCEF是平行四边形,∵OD=DC,∴OD=DE=CD=DF,∴四边形OCEF是矩形,∵∠BEC=45°,∴∠EOC=45°,∴∠OEC=∠EOC,∴OC=CE,∴四边形OCEF是正方形,18.如图所示,平行四边形ABCD的对角线AC与BD交于点O,若AB=,AC=2,BD=4.(1)猜想∠BAO= 90° ,并证明你的猜想.(2)求平行四边形ABCD的周长.(3)求点A到BC边的距离.【分析】(1)先根据平行四边形的性质可得,再利用勾股定理的逆定理即可得出结论;(2)先利用勾股定理可得,再根据平行四边形的周长公式即可得;=BC⋅AE=AB⋅AC即可得.(3)过点A作AE⊥BC于点E,根据S平行四边形ABCD【解析】(1)猜想∠BAO=90°,证明如下:∵四边形ABCD是平行四边形,且AC=2,BD=4,∴,∵,∴OA2+AB2=4=OB2,∴△AOB是直角三角形,且∠BAO=90°,故答案为:90°;(2)∵,∴,则平行四边形ABCD的周长为;(3)如图,过点A作AE⊥BC于点E,∵,=BC⋅AE=AB⋅AC,即,∴S平行四边形ABCD解得,即点A到BC边的距离为.19.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,∠ABC=90°.(1)求证:AC=BD;(2)若点E、F分别为线段AB、AO的中点,连接EF,,BC=6,求AB的长及四边形ABCD的面积.【分析】(1)证明四边形ABCD是矩形,即可解决问题;(2)利用矩形的性质,根据勾股定理可得AB=8,然后利用矩形的面积公式即可解决问题.【解答】(1)证明:∵平行四边形ABCD,∠ABC=90°,∴四边形ABCD是矩形,∴AC=BD;(2)解:∵E,F分别为AB、AO的中点,∴OB=2EF=5;∵四边形ABCD是矩形,∴AC=BD=2OB=10,∵BC=6,∠ABC=90°,∴AB==8,所以矩形ABCD的面积=AB•BC=6×8=48.20.如图,在▱ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG =CE,连接FG,点H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:四边形AFHD为平行四边形.【分析】(1)由平行四边形的性质和平行线的判定和性质得出答案即可;(2)由平行四边形的性质得出AD=BC,AD∥BC;证明BC是△EFG的中位线,得出BC∥FG,BC=FG,证出AD∥FH,AD∥FH,进而解答即可.【解答】(1)解:∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∥BC,∵∠DCE=20°,AB∥CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=FG,∵H为FG的中点,∴FH=FG,∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,∴四边形AFHD是平行四边形.C卷培优压轴卷(限时70分钟,每题10分,满分100分)21.在平行四边形ABCD中,点H,G分别在AD,BC上,且AH=BG,点P是线段GH上一点,过点P 作直线EF交AB于E,交CD于F,且∠BEP=∠BGH.(1)如图1,求证:四边形HPFD是平行四边形;(2)如图2,当点P在对角线BD上时,请直接写出图中所有面积相等的四边形.【分析】(1)由平行四边形的性质和已知条件得出EF∥BC∥AD,由平行线的性质得出∠HPF+∠PHD=180°,证出∠D+∠PHD=180°,得出PH∥FD,即可得出结论;(2)证出四边形BGPE是平行四边形,由平行四边形的性质得出△ABD的面积=△BCD的面积,△BEP 的面积=△BGP的面积,△BDH的面积=△PDF的面积,因此四边形AEPH的面积=四边形PGCF的面积,得出四边形ABGH的面积=四边形BCFE的面积,四边形AEFD的面积=四边形GHDC的面积即可.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∵EF∥BC,∴EF∥BC∥AD,∴∠HPF+∠PHD=180°,∵∠HPF=∠D,∴∠D+∠PHD=180°,∴PH∥FD,∴四边形HPFD是平行四边形;(2)解:四边形AEPH的面积=四边形PGCF的面积,四边形ABGH的面积=四边形BCFE的面积,四边形AEFD的面积=四边形GHDC的面积;理由如下:∵AB∥CD,PH∥FD,∴AB∥GH∥CD,∴四边形BGPE是平行四边形,∵△ABD的面积=△BCD的面积,△BEP的面积=△BGP的面积,△BDH的面积=△PDF的面积,∴四边形AEPH的面积=四边形PGCF的面积,∴四边形ABGH的面积=四边形BCFE的面积,四边形AEFD的面积=四边形GHDC的面积.22.如图,▱ABCD的对角线AC、BD相交于点O,点F在CD上,连接FO并延长,交AB于点E,交CB 的延长线于点M.(1)求证:OE=OF;(2)若AD=3,AB=,BM=1,直接写出BE的长为 .【分析】(1)通过ASA证明△AOE≌△COF即可得出结论;(2)过点O作ON∥BC交AB于N,由△AON∽△ACB得出ON=,BN=,再由△ONE∽△MBE得出等式求出BE即可.【解答】(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,BC=AD,∴∠OAE=∠OCF,在△AOE与△COF中,,∴△AOE≌△COF(ASA),(2)解:过点O作ON∥BC交AB于N,则△AON∽△ACB,∵OA=OC,∴ON=,BN=,∵ON∥BC,∴△ONE∽△MBE,∴,即,∴BE=,故答案为:.23.如图1,平行四边形ABCD,E、F为AB、DC中点,连接DE、CE、AF、BF,交点分别为G、H.(1)如图1,求证:四边形EGFH是平行四边形;(2)如图2,若∠BAD=90°时,请直接写出图中所有直角三角形.【分析】(1)根据平行四边形的性质得出AB=DC,AB∥DC,求出AE=CF=BE=DF,根据平行四边形的判定得出四边形AFCE和四边形BFDE都是平行四边形,根据平行四边形的性质得出AF∥CE,DE(2)根据矩形的判定得出四边形ABCD是矩形,根据矩形的性质得出∠BAD=∠ADC=∠BCD=∠ABC =90°,根据全等三角形的判定得出△EAD≌△EBC,求出∠AED=∠BEC=45°,求出∠DEC=90°,得出四边形EGFH是矩形,再得出答案即可.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC,∵E、F分别为AB、DC的中点,∴AE=BE=AB,DF=CF=DC,∴AE=CF=BE=DF,∴四边形AFCE和四边形BFDE都是平行四边形,∴AF∥CE,DE∥BF,即GF∥EH,EG∥HF,∴四边形EGFH是平行四边形;(2)解:直角三角形有△ADE,△BCE,△ADF,△CBE,△AGE,△AGD,△DGF,△CFH,△BHC,△BHE.24.如图,四边形ABCD是平行四边形,分别以AD,BC为边向外构造等边△ADE和等边△BCF,连接BE,DF,BD.(1)求证:四边形BFDE是平行四边形.(2)若AD与BE交于点G,且AD=BD,∠DFB=45°,,求△BDG的面积.【分析】(1)根据平行四边形的性质和等边三角形的性质证得DE=BF,∠EDB=∠DBF即DE∥BF,进而利用平行四边形的判定即可得证;(2)先求得∠DBF=∠EDB=90°,进而求得∠ADB=∠DBC=30°,∠DEB=∠DBE=45°,过G 作GH⊥BD于H,利用等腰直角三角形的性质和含30°角的直角三角形的性质求得BH、GH、DH,进而求得BD即可得所求面积.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC,∵等边△ADE和等边△BCF,∴DE=AD,BC=BF,∠EDA=∠CBF=60°,∴DE=BF,∠EDB=∠DBF,∴DE∥BF,∴四边形BFDE是平行四边形;(2)解:∵AD=BD,AD=DE=BF,∴DE=BD=BF,又∵∠DFB=45°,∴∠DBF=180°﹣2∠DFB=90°=∠EDB,∴∠DBC=∠DBF﹣∠CBF=30°,∠DEB=∠DBE=45°,∴∠ADB=∠DBC=30°,过G作GH⊥BD于H,在Rt△GHB中,,∠HBG=45°,BG2=GH2+HB2,∴,在Rt△GHD中,∠GDH=30°,GH=1,∴DG=2GH=2,∴,∴,∴△BDG的面积为=.25.如图,在四边形ABCD中,E,F分别是AD,BC的中点.(1)若AB=10,CD=24,∠ABD=30°,∠BDC=120°,求EF的长.(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.【分析】(1)取BD的中点P,连接EP、FP,由三角形中位线定理得PE∥AB,且PE=5,PF∥CD,且PF=12,再证∠EPF=90°,然后由勾股定理即可得出结论;(2)由三角形中位线定理得PE∥AB,且,PF∥CD,且,再证∠EPF=90°,然后由勾股定理即可得出结论.【解答】(1)解:如图,取BD的中点P,连接EP、FP,∵E,F分别是AD、BC的中点,AB=10,CD=24,∴PE是△ABD的中位线,PF是△BCD的中位线,∴PE∥AB,且,且,∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=180°﹣120°=60°,∴∠EPF=∠EPD+∠DPF=90°,在Rt△EPF中,由勾股定理得:,即EF的长为13;(2)证明:由(1)可知,PE是△ABD的中位线,PF是△BCD的中位线,∴PE∥AB,且,PF∥CD,且,∴∠EPD=∠ABD,∠DPF=180°﹣∠BDC.∵∠BDC﹣∠ABD=90°,∴∠BDC=90°+∠ABD,∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,∴,∴AB2+CD2=4EF2.26.如图,在平行四边形ABCD内有一点E,且∠CBE=∠CDE=90°.(1)请在下面三个结论中,选出一个正确的结论并证明:①∠BED=2CABE;②∠BED﹣∠ABE=90°;③∠BED﹣∠CBD=90°.(2)若BD平分∠CDE,求证:BC=BE.【分析】(1)根据平行四边形的性质可得正确的结论为②∠BED﹣∠ABE=90°,证明即可;(2)在DC上截取DF=DE,证明△BDE≌△BDF(SAS),可得BE=BF,∠BED=∠BFD,进而可以解决问题.【解答】(1)解:正确的结论为:②∠BED﹣∠ABE=90°,证明过程如下:∵四边形ABCD是平行四边形,∴AB∥DC,∴∠C+∠ABC=180°,∵∠CBE=∠CDE=90°,∴∠BED+∠C=180°,∴∠BED=∠ABC,∴∠BED﹣∠ABE=∠ABC﹣∠ABE=∠CBE=90°;(2)证明:如图,在DC上截取DF=DE,∵BD平分∠CDE,∴∠BDE=∠BDF,在△BDE和△BDF中,,∴△BDE≌△BDF(SAS),∴BE=BF,∠BED=∠BFD,由(1)知:∠BED+∠C=180°,∠BFD+∠BFC=180°,∴∠BFC=∠C,∴BF=BC,∴BC=BE.27.在等边△ABC中,D,E,F分别是边AB,BC,CA上的动点,满足DE=EF,且∠DEF=60°.作点E 关于AC的对称点G,连接CG,DG.(1)当点D,E,F在如图1所示的位置时,请在图1中补全图形,并证明四边形DBCG是平行四边形;(2)当AD<BD,AB=DE时,求∠BDE的度数.【分析】(1)根据题意即可补全图形;然后证明△BDE≌△CEF可得CE=BD,进而可以解决问题;(2)根据题意证明△DEF是等边三角形,可得DE=DF,由点E,点G关于AC对称,可得EF=GF,∠FEC=∠FGC,所以DF=GF,进而可以解决问题.【解析】(1)如图1,即为补全的图形,证明:在等边△ABC中,∠A=∠B=∠ACB=60°,∵点E,点G关于AC对称,∴∠ACG=∠ACB=60°,CE=CG,∴∠A=∠ACG,∴AB∥CG,即BD∥CG,∵∠DEF=60°,∠BED+∠CEF+∠DEF=180°,∴∠BED+∠CEF=120°,在△BDE中,∠BDE+∠BED=180°﹣∠B=120°,∴∠BDE=∠CEF,在△BDE与△CEF中,,∴△BDE≌△CEF(AAS),∴CE=BD,∴CG=CE=BD,∵BD∥CG,∴四边形DBCG是平行四边形;(2)∵四边形DBCG是平行四边形,∴BC=DG,∠DGC=∠B=60°,∵BC=AB,AB=DE,∴DG=DE,∵DE=EF,∠DEF=60°,∴△DEF是等边三角形,∴DE=DF,∵点E,点G关于AC对称,∴EF=GF,∠FEC=∠FGC,∴DF=GF,∴DG=DF=GF,在△DFG中,DG2=DF2+GF2,∴∠DFG=90°,∵DF=GF,∴∠FDG=∠FGD=45°,∴∠CGF=∠CGD﹣∠FGD=15°,∴∠BDE=∠CEF=∠CGF=15°.28.如图1,在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)当∠ABC=90°时,G是EF的中点,联结DB,DG(如图2),请直接写出∠BDG的度数(2)当∠ABC=120°时,FG∥CE,且FG=CE,分别联结DB、DG(如图3),求∠BDG的度数.【分析】(1)根据∠ABC=90°,G是EF的中点可直接求得;(2)延长AB、FG交于H,连接HD.易证平行四边形AHFD为菱形,进而可得△ADH,△DHF为全等的等边三角形,再证明△BHD≌△GFD,所以可得∠BDH=∠GDF,然后即可求得答案.【解析】(1)连接GC、BG,∵四边形ABCD为平行四边形,∠ABC=90°,∴四边形ABCD为矩形,∵AF平分∠BAD,∴∠DAF=∠BAF=45°,∵∠DCB=90°,DF∥AB,∴∠DFA=45°,∠ECF=90°∴△ECF为等腰直角三角形,∵G为EF中点,∴EG=CG=FG,CG⊥EF,∵△ABE为等腰直角三角形,AB=DC,∴BE=DC,∵∠CEF=∠GCF=45°,∴∠BEG=∠DCG=135°,在△BEG与△DCG中,,∴△BEG≌△DCG(SAS),∴BG=DG,∵CG⊥EF,∴∠DGC+∠DGA=90°,又∵∠DGC=∠BGA,∴∠BGA+∠DGA=90°,∴△DGB为等腰直角三角形,∴∠BDG=45°;(2)延长AB、FG交于H,连接HD.∵AD∥GF,AB∥DF,∴四边形AHFD为平行四边形,∵∠ABC=120°,AF平分∠BAD,∴∠DAF=30°,∠ADC=120°,∠DFA=30°,∴△DAF为等腰三角形,∴AD=DF,∴CE=CF,∴平行四边形AHFD为菱形,∴△ADH,△DHF为全等的等边三角形,∴DH=DF,∠BHD=∠GFD=60°.∵FG=CE,CE=CF,CF=BH,∴BH=GF.在△BHD与△GFD中,,∴△BHD≌△GFD(SAS),∴∠BDH=∠GDF,∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.29.在平行四边形ABCD中,∠C=45°,AD=BD,点P为边CD上的动点(点P不与点D重合),连接AP,过点P作EP⊥AP交直线BD于点E.(1)如图①,当点P为线段CD的中点时,求证:PA=PE;(2)如图②,当点P在线段CD上时,求证:DE﹣DA=DP.【分析】(1)连接PB,根据题意可得△BDC是等腰直角三角形,再证明△ADP≌△EBP,即可;(2)过点P作PF⊥CD交DE于点F,可得∠DPA=∠FPE,再结合平行四边形的性质可得△ADP≌△EFP,可得AD=EF,再由勾股定理可得,即可.【解答】证明:(1)如图,连接PB,∵四边形ABCD是平行四边形,∴AD=CB,AD∥BC,∵AD=BD,∴BC=BD,∵∠C=45°,∴∠BDC=∠C=45°,∴△BDC是等腰直角三角形,∵点P为线段CD的中点,∴DP=BP,∠CPB=90°,∵AD∥BC,∴∠ADP=∠PBE=135°,∵EP⊥AP,∴∠APE=∠DPB=90°,∴∠APD=∠BPE,∴△ADP≌△EBP(ASA),∴PA=PE;(2)证明:如图,过点P作PF⊥CD交DE于点F,∵PF⊥CD,EP⊥AP,∴∠DPF=∠APE=90°,∴∠DPA=∠FPE,∵四边形ABCD是平行四边形,∴∠C=∠DAB=45°,AB∥CD,∵AD=BD,∴∠DAB=∠DBA=∠C=∠CDB=45°,∴∠ADB=∠DBC=90°,∴∠PFD=45°,∴∠PFD=∠PDF=45°,∴PD=PF,∴∠PDA=∠PFE=135°,∴△ADP≌△EFP(ASA),∴AD=EF,∵PD=PF,∠PFD=∠PDF=45°,∴△PDF是等腰直角三角形,∴,∵DE=DF+EF,∴DE=DF+DA,∴.30.如图,在▱ABCD中,已知AD=15cm,点P在AD上以1cm/s的速度从点A向点D运动,点Q在BC 上以4cm/s的速度从点C出发往返运动,两点同时出发,当点P到达点D时停止运动(同时点Q也停止),设运动时间为t(s)(t>0).(1)当点P运动t秒时,线段PD的长度为 (15﹣t) cm;当点P运动2秒时,线段BQ的长度为 7 cm;当点P运动5秒时,线段BQ的长度为 5 cm;(2)若经过t秒,以P、D、Q、B四点为顶点的四边形是平行四边形.请求出所有t的值.【分析】(1)由路程=速度×时间,可求解;(2)分四种情况讨论,由平行四边形的性质,列出等式可求解.【解析】(1)∵点P在AD上以1cm/s的速度从点A向点D运动,∴AP=tcm,∴PD=(15﹣t)cm,当点P运动2秒时,CQ=2×4=8cm,∴BQ=15﹣8=7cm,当点P运动5秒时,CQ=4×5=20cm,∴BQ=20﹣15=5cm,故答案为:(15﹣t);7;5;(2)∵P在AD上运动,∴t≤15÷1=15,即0<t≤15,∵以点P、D、Q、B为顶点的平行四边形,已有PD∥BQ,还需满足DP=BQ,①当点Q的运动路线是C﹣B时,BQ=15﹣4t,由题意得:15﹣t=15﹣4t,t=0 不合题意,②当点Q的运动路线是C﹣B﹣C时,BQ=4t﹣15,由题意得:15﹣t=4t﹣15,解得:t=6;③当点Q的运动路线是C﹣B﹣C﹣B时,BQ=45﹣4t,由题意得:15﹣t=45﹣4t,解得:t=10;④当点Q的运动路线是C﹣B﹣C﹣B–C时,BQ=4t﹣45,由题意得:15﹣t=4t﹣45,解得:t=12;综上所述,t的值为6或10或12.。
平行四边形的性质与判定(练习)

E DCBA 平行四边形的性质与判定(练习)【知识点】:1. 平行四边形的定义:2.平行四边形性质:⑴边: ;⑵角: ; ⑶对角线: ;(3)对称性:___________________________. 3.平行四边形判定:边:①___________________ ___②_____________ ___________③ ; 角: ; 对角线: ; 【基础训练】一.填空题 (3分×10 = 30分)1.在□ABCD 中,如果∠A +∠C =120°,那么∠B = °.2.已知平行四边形的周长为56㎝,两邻边之比为3:1,则四边形较长的边长为 . 3.已知□ABCD 中,AB = 6,BC 、AB 边上的高分别为6、4,则BC 边长为 . 4.已知□ABCD 中,∠A =60°,AB = 4㎝,AD = 6㎝,则□ABCD 的面积为 . 5.已知□ABCD 中,若∠B 的2倍与∠A 的补角的和为90°,则∠B = 度.6.已知□ABCD 的周长为20cm ,对角线相交于点O ,且△BOC 的周长比△AOB 的周长多2cm ,则AB = cm .7.如图1,已知□ABCD 中,AE =CF ,则图中有 对全等三角形.8.如图2,已知□ABCD 中,BC =12,AB =10,AE ⊥BC 于点E ,且AE =8,则AB 与CD 两边之间的距离为 .9.如图3,已知□ABCD 中,AB =6,AD =8,AE 平分∠BAD 交BC 于E ,则EC = .图1 图2 图310.在四边形ABCD 中,AB =CD ,要使这个四边形成为平行四边形,则可添加的一个条件可以是 . 二.选择题 (3分×6 = 18分)E DCB A1.平行四边形是 ( )(A )轴对称图形 (B )既是轴对称图形,又是中心对称图形 (C )中心对称图形 (D )既不是轴对称图形,也不是中心对称图形2.用两个全等的三角形(三边互不相等)拼成不同的四边形,其中不同的平行四边形的个数是 ( ) (A )1个 (B )2个 (C )3 个 (D )4个 3.下列条件中,能判断四边形是平行四边形的条件是( ) (A )一组对边平行 (B )四条边相等 (C )一组对边平行,另一组对边相等 (D )两条对角线相等4.已知□ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 长为( ) (A )5cm (B )15cm (C )6cm (D )16cm 5.如图4,已知四边形ABCD 和CEFG 都是平行四边形, 则下列等式中正确的是( )(A )∠1+∠8=1800(B )∠1+∠5=180° (C )∠4+∠6=180° (D )∠2+∠8=180°6.已知P 为□ABCD 的边AB 上的任一点,则△PCD 与 图4□ABCD 的面积的比S △PCD :S □ABCD 为( )(A )1:2 (B )1:3 (C )1:4 (D )不能确定 三、几何证明1.已知:如图,D 、F 分别是ΔABC 的边BC 、AC 的中点,点E 在线段DF 的延长线上,FE =DF 。
平行四边形的判定练习题(有答案)

平行四边形的判定练习题(有答案)平行四边形的判定练题1.用边长为2cm,3cm,4cm的两个全等三角形拼成四边形,可以拼成6个四边形,其中3个为平行四边形。
2.在四边形ABCD中,若AB=CD且AD=BC,则四边形ABCD为平行四边形。
3.延长△ABC的中线AD至E,使DE=AD,连接BE,CE,则有AB=CE,AC=BE。
4.若四边形ABCD中,AC,BD相交于点O,要判定它为平行四边形,从角的关系看应满足相邻角之和为180度,从对角线的关系看应满足对角线互相平分。
5.四边形EFGH为平行四边形,且其边长分别为AB,BC,CD,DA的中点E,F,G,H。
6.能识别四边形ABCD是平行四边形的题设是AB∥CD,AD=BC。
7.选法有6种。
8.正确的结论是一组对边平行且一组对角相等的四边形是平行四边形。
9.不能判定四边形ABCD是平行四边形的条件是AB=CD,AD∥BC。
10.添加条件①或②可以使四边形AFCE为平行四边形。
11.正确的说法有3个,即DE∥AF,FD∥CE,EF∥BD。
12.在四边形ABCD中,点E和F分别在BD上,且BF=DE。
证明四边形AECF是平行四边形,可以使用两种方法。
14.在四边形ABCD中,对角线AC和BD相交于点O。
过点O作两条直线分别与AB、BC、CD、AD相交于点G、F、H、E。
证明四边形EGFH是平行四边形。
15.在△ABC中,以BC、AC、AB为边长分别作等边三角形ABD、BCE、ACF,连接DE和EF。
证明四边形ADEF是平行四边形。
16.在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E和F,点G和H分别为AD和BC的中点。
证明EF和GH互相平分。
17.在△ABC中,P是内部任意一点。
过点P作EF∥AB分别交AC和BC于点E和F,作GH∥BC分别交AB和AC于点G和H,作MN∥AC分别交AB和BC于点M和N。
猜想EF+GH+MN的值是多少,并说明理由。
八年级平行四边形专题练习(含答案)

中考专题复习平行四边形知识考点:理解并掌握平行四边形的判定和性质 精典例题:【例1】已知如图:在四边形ABCD 中,AB =CD ,AD =BC ,点E 、F 分别在BC 和AD 边上,AF =CE ,EF 和对角线BD 相交于点O ,求证:点O 是BD 的中点。
分析:构造全等三角形或利用平行四边形的性质来证明BO =DO 略证:连结BF 、DE在四边形ABCD 中,AB =CD ,AD =BC ∴四边形ABCD 是平行四边形 ∴AD ∥BC ,AD =BC 又∵AF =CE∴FD ∥BE ,FD =BE ∴四边形BEDF 是平行四边形∴BO =DO ,即点O 是BD 的中点。
【例2】已知如图:在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形EFGH 是平行四边形。
分析:欲证四边形EFGH 是平行四边形,根据条件需从边上着手分析,由E 、F 、G 、H 分别是各边上的中点,可联想到三角形的中位线定理,连结AC 后,EF 和GH 的关系就明确了,此题也便得证。
(证明略)变式1:顺次连结矩形四边中点所得的四边形是菱形。
变式2:顺次连结菱形四边中点所得的四边形是矩形。
变式3:顺次连结正方形四边中点所得的四边形是正方形。
变式4:顺次连结等腰梯形四边中点所得的四边形是菱形。
变式5:若AC =BD ,AC ⊥BD ,则四边形EFGH 是正方形。
变式6:在四边形ABCD 中,若AB =CD ,E 、F 、G 、H 分别为AD 、BC 、BD 、AC 的中点,求证:EFGH 是菱形。
娈式6图娈式7图变式7:如图:在四边形ABCD 中,E 为边AB 上的一点,△ADE 和△BCE 都是等边三角形,P 、Q 、M 、N 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形PQMN 是菱形。
例1图 O F E D CB A 例2图探索与创新:【问题】已知如图,在△ABC 中,∠C =900,点M 在BC 上,且BM =AC ,点N 在AC 上,且AN =MC ,AM 和BN 相交于P ,求∠BPM 的度数。
(完整版)平行四边形的性质练习题及答案

(完整版)平⾏四边形的性质练习题及答案平⾏四边形的性质、课中强化(10分钟训练)1?如图3,在平⾏四边形 ABCD 中,下列各式不⼀定正确的是()A. / 1 + Z 2=180 °B. / 2+ / 3=180 °C. / 3+Z 4=180的周长为()3. 如图5,」ABCD 中,EF 过对⾓线的交点 O,如果AB=4 cm,AD=3 cm,OF=1 cm,则四边形 BCFE 的周长为 ____________________ .4. 如图6,已知在平⾏四边形 ABCD 中,AB=4 cm , AD=7 cm , / ABC 的平分线交 AD 于点E ,5. 如图7,在平⾏四边形 ABCD 中,点E 、F 在对⾓线6. 如图 8,在 ABCD 中,AE 丄BC 于 E,AF 丄 CD 于 F,BE=2 cm,DF=3 cm, / EAF=60° ,试求 CF 的长.D. /2+ /4=180O , OE 丄AC 交AD 于丘,则⼛DCEA.4 cmB.6 cmC.8 cmD.10 cm交CD 的延长线于点 F ,贝U DF= _____________cm.BD 上,且 BE=DF ,求证:AE=CF.图32?如图4,⼆ABCD 的周长为图5图6图7图8三、课后巩固(30分钟训练)1?⼆ABCD中,/A⽐/ B⼤20。
,则/ C的度数为()A.60 °B.80 °C.100 °D.120 2?以A、B、C三点为平⾏四边形的三个顶点,作形状不同的平⾏四边形,⼀共可以作(A.0个或3个B.2个C.3个D.4个3?如图9 所⽰,在—ABCD 中,对⾓线AC、BD交于点0,下列式⼦中⼀定成⽴的是()A.AC 丄BDB.OA=OCC.AC=BDD.AO=OD4?如图10,平⾏四边形ABCD中,对⾓线AC、BD相交于点O ,将⼛AOD平移⾄△ BEC的位置,则图中与OA相等的其他线段有()A.1条B.2条C.3条D.4条5?如图11,在平⾏四边形ABCD中,EF // AB , GH // AD , EF与GH交于点O,则该图中的平⾏四边形的个数共有()6?如图12,平⾏四边形ABCD中,AE丄BD , CF丄BD,垂⾜分别为E、F,求证:/ BAE= / DCF.7、如图13所⽰,已知平⾏四边形ABCD中,E、F分别是BC和AD上的点,且BE=DF.求证:△ ABE CDF.A.7个B.8个C.9个D.11 个图12图138?如图14,已知四边形ABCD是平⾏四边形,/ BCD的平分线CF交边AB于F,/ ADC的平分线DG交边AB于G.⑴求证:AF=GB ;(2)请你在已知条件的基础上再添加⼀个条件,使得△EFG是等腰直⾓三⾓形,并说明理由?19.1.2平⾏四边形的判定⼆、课中强化(10分钟训练)1?如图3,在ABCD中,对⾓线AC、BD相交于点O,E、F是对⾓线AC上的两点,当E、F满⾜下列哪个条件时,四边形DEBF不⼀定是平⾏四边形()A.AE=CFC.Z ADE= / CBFD. / AED= / CFB,使四边形AECF是平⾏四边形.4. 如图6,AD=BC,要使四边形ABCD是平⾏四边形,还需补充的⼀个条件是:__________________5. 如图,在,ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN也是平⾏四边形.2.如图4,AB 喪DC ,DC=EF=10 ,DE=CF=8,则图中的平⾏四边形有,理由分别是图4 图53.如图5,E、F是平⾏四边形ABCD对⾓线BD上的两点,B.DE=BF图14三、课后巩固(30分钟训练)1?以不在同⼀直线上的三个点为顶点作平⾏四边形最多能作()是平⾏四边形的是()4?已知四边形 ABCD 的对⾓线 AC 、BD 相交于点② OA=OC :③ AB=CD ;④/ BAD= / DCB :⑤ AD // BC.(1)从以上5个条件中任意选取 2个条件,能推出四边形 ABCD 是平⾏四边形的有(⽤序号表⽰): _____________________________ :(2)对由以上5个条件中任意选取 2个条件,不能推出四边形请选取⼀种情形举出反例说明平⾏四边形?6?如图,E 、F 是四边形ABCD 的对⾓线 AC 上的两点,AF=CE , DF=BE , DF // BE. 求证:⑴△AFD ◎△ CEB;(2)四边形ABCD 是平⾏四边形A.4个B.3个C.2个D.1个2?下⾯给出了四边形 ABCD 中/A 、/ B 、/ C 、/ D 的度数之⽐,其中能判定四边形 ABCDA.1 : 2 : 3 : 4B. 2 : 2 : 3 : 3C. 2 : 3 : 3 : 2D. 2 : 3 : 2 : 33?九根⽕柴棒排成如右图形状,图中 ____ 个平⾏四边形 ,你判断的根据是O ,给出下列 5个条件:①AB // CD ;5?若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对⾓线 ABCD 是平⾏四边形的,,另17?如图,已知DC // AB,且DC= — AB , E为AB的中点.2(1) 求证:△ AED ◎△ EBC ;(2) 观察图形,在不添加辅助线的情况下,除△EBC⼣⼘,请再写出两个与△ AED的⾯积相等的三⾓形(直接写出结果,不要求证明): ___________________________8?如图,已知⼆ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平⾏四边形9?如图,已知■ ABCD中,E、F分别是AB、CD的中点?求证:(1) △ AFD ◎△ CEB;(2) 四边形AECF是平⾏四边形?⼆、课中强化(10 分钟训练)1 答案:D2. 解析:因为四边形ABCD 是平⾏四边形,所以OA=OC. ⼜0E丄AC , 所以EA=EC.贝U △ DCE 的周长=CD+DE+CE=CD+DE+EA=CD+AD. 在平⾏四边形ABCD 中,AB=CD ,AD=BC ,且AB+BC+CD+AD=16 cm ,所以CD+AD=8 cm.答案:C3?解析:0E=0F=1,其周长=BE+BC+CF+EF=CD+BC+EF=AD+AB+2DF=8(cm).答案:8 cm4?解析:由平⾏四边形的性质AB // DC,知/ ABE= / F,结合⾓平分线的性质/ ABE= / EBC,得/ EBC= / F,再根据等⾓对等边得到BC=CF=7 ,再由AB=CD=4 , AD=BC=7 得到DF=DE=AD-AE=3.答案:35?答案:证明:四边形ABCD是平⾏四边形,AB // CD , AB=CD./ ABE= / CDF.AB CD,在⼛ABE和⼛CDF中,ABE CDF ,BE DF .△ ABE ◎△ CDF.AE=CF.6. 解:/ EAF=60°AE 丄BC,AF 丄CD, C=120°. B=60°「./ BAE=30° .AB=2BE=4(cm). CD=4(cm). CF=1(cm).三、课后巩固(30 分钟训练)1 答案:C2. 解析:分两种情况,A、B、C三点共线时,可作0个当点A、B、C不在同⼀直线上时,可作3 个. 答案:A3. 解析:平⾏四边形对⾓线互相平分,所以OA=OC. 答案:B4. 解析:由平⾏四边形的对⾓线互相平分知OA=OC;再由平移的性质:经过平移,对应线段平⾏且相等可得OA=BE.答案:B5?解析:本题借助于平⾏四边形的定义,按照从左到右,从⼩到⼤的顺序,可找到下列的平⾏四边形:DEOH,.HOFC,. DEFC, EAGO,OGBF,EABF,■ DAGH,■ HGBC,⼆ABCD.答案:C6?答案:证明:四边形ABCD是平⾏四边形,AB // CD , AB=CD. /-Z ABE= / CDF ?/ AE 丄BD , CF 丄BD ,「./ AEB= / CFD=90 .△ABE ◎△ CDF. /.Z BAE= Z DCF.7、答案:证明:四边形ABCD是平⾏四边形,AB=CD, Z B= Z D.在⼛ABE和⼛CDF中,AB CD,B D, ?/△ ABE 也⼛CDF.BE DF.8?答案:(1)证明:四边形ABCD是平⾏四边形,? AB // CD. AGD= Z CDG.vZ ADG= Z CDG,/?/ ADG= Z AGD. ? AD=AG ?同理,BC=BF.⼜四边形ABCD 是平⾏四边形,? AD=BC,AG=BF. ? AG-GF=BF-GF ,即AF=GB.(2)解:添加条件EF=EG.理由如下:1 1由(1)证明易知Z AGD= Z ADG= Z ADC , Z BFC= Z BCF= Z BCD.2 2/ AD // BC,/?/ ADC+ Z BCD=180 ./Z AGD+ Z BFC=90 ./Z GEF=90 .⼜v EF=EG ,?△ EFG为等腰直⾓三⾓形.⼆、课中强化(10分钟训练)1. 解析:当E、F满⾜AE=CF时,由平⾏四边形的对⾓线相等知OB=OD,OA=OC , 故OE=OF.可知四边形DEBF是平⾏四边形.当E、F满⾜Z ADE= Z CBF 时,因为AD // BC,所以Z DAE= Z BCF.⼜AD=BC,可证出⼛ADE ◎△ CBF,所以DE=BF , Z DEA= Z BFC.故Z DEF= Z BFE.因此DE // BF,可知四边形DEBF是平⾏四边形.类似地可说明D也可以.。
平行四边形判定专项练习30题

平行四边形的判定专项练习30题(有答案)1.如图,四边形ABCD中,AD∥BC,ED∥BF,AF=CE,求证:ABCD是平行四边形.2.如图,四边形ABCD中,∠BAC=90°,AB=11﹣x,BC=5,CD=x﹣5,AD=x﹣3,AC=4.求证:四边形ABCD为平行四边形.3.已知四边形ABCD的对角线AC与BD交于点O,现给出四个条件:①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.请你从中选择两个,推出四边形ABCD为平行四边形,并写出你的推理过程.(1)从以上4个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示)_________ .(2)从(1)中选出一种情况,写出你的推理过程.4.如图,已知:点B、E、F、D在一条直线上,DF=BE,AE=CF.请从下列三个条件中选择一个合适的条件,添加到已知条件中,使四边形ABCD是平行四边形,并说明理由,供选择的三个条件(请从其中选择一个):①AB=DC;②BC=AD;③∠AED=∠CFB.5.如图,在▱ABCD中,AC交BD于点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的位置关系和数量关系,并说明你的结论.6.如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF 是什么四边形,试证明你的结论.7.如图,已知BE⊥AD,CF⊥AD,且BE=CF.求证:(1)AD是△ABC的中线;(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.8.如图,矩形ABCD的两条对角线AC和BD相交于点O,E、F是BD上的两点,且∠AEB=∠CFD.求证:四边形AECF 是平行四边形.9.如图:在四边形ABCD中,AD∥BC,AB=CD,E是BC上一点,DE=AB.求证:四边形ABED是平行四边形.10.如图,已知 AB∥DC,E是BC的中点,AE,DC的延长线交于点F;(1)求证:△ABE≌△FCE;(2)连接AC,BF.则四边形ABFC是什么特殊的四边形?请说明理由.11.等边△ABC中,点D在BC上,点E在AB上,且CD=BE,以AD为边作等边△ADF,如图.求证:四边形CDFE是平行四边形.12.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.若∠BAC=30°,EF⊥AB,垂足为F,连结DF.求证:(1)△ABC≌△EAF;(2)四边形ADFE是平行四边形.13.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:四边形DFGE是平行四边形.14.如图所示:在四边形ABCD中,AD∥BC、BC=18cm,CD=15cm,AD=10cm,AB=12cm,动点P、Q分别从A、C同时出发,点P以2cm/秒的速度由A向D运动,点Q以3cm/秒的速度由C向B运动.(1)几秒钟后,四边形ABQP为平行四边形?并求出此时四边形ABQP的周长(2)几秒钟后,四边形PDCQ为平行四边形?并求出此时四边形PDCQ的周长.15.求证:顺次连接四边形各边中点所得的四边形是平行四边形.16.△ABC中,中线BE、CF相交于O,M是BO的中点,N是CO的中点,求证:四边形MNEF是平行四边形.17.如图,AD=DB,AE=EC,FG∥AB,AG∥BC.(1)证明:△AGE≌△CFE;(2)说明四边形ABFG是平行四边形;(3)研究图中的线段DE,BF,FC之间有怎样的位置关系和数量关系.18.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB.(1)求证:△ABE≌△ACD;(2)求证:四边形EFCD是平行四边形.19.已知在△ABC中,D、E分别是AB、AC的中点,点F在DE的延长线上,且EF=DE,图中有几个平行四边形?请说明你的理由.20.如图,在△ABC中,AD是中线,点E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF.求证:四边形AFBD是平行四边形.21.如图:在四边形ABCD中,AD∥BC,E是BC的中点,BC=2AD.找出图中所有的平行四边形,并选择一个说明它是平行四边形的理由.22.求证:两组对角分别相等的四边形是平行四边形.23.已知:如图,A、B、C、D在同一条直线上,且AB=CD,AE∥DF,AE=DF.求证:四边形EBFC是平行四边形.24.如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.图中的四边形BFCE 是平行四边形吗?为什么?25.已知点E、F、G、H分别为四边形ABCD四边的中点,试问四边形EFGH的形状并说明理由.26.如图,已知四边形ABCD中AD=BC,点A、B、E在同一条直线上,且∠B=∠EAD,试说明四边形ABCD是平行四边形.27.如图,AD∥BC,ED∥BF,且AE=CF,求证:四边形ABCD是平行四边形.28.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.29.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.30.已知:在四边形ABCD中,AD∥BC,且AB=DC=5,AC=4,BC=3.求证:四边形ABCD为平行四边形.平行四边形的判定30题参考答案:1.∵AD∥BC,∴∠DAE=∠BCF,∵ED∥BF,∴∠DEF=∠BFE,∴∠AED=∠CFB,又∵AF=CE,∴AE=CF,在△ADE和△CBF中:∵∠DAE=∠BCF,∠AED=∠CFB,AE=CF,∴△ADE≌△CBF(AAS),∴AD=CB,即:AD∥CB,AD=CB,∴四边形ABCD是平行四边形,2.∵∠BAC=90°,AB=11﹣x,BC=5,AC=4.∴(11﹣x)2+42=52,解得:x1=8,x2=14>11(舍去),当x=8时,BC=AD=5,AB=CD=3,∴四边形ABCD为平行四边形.3.(1)解:能推出四边形ABCD是平行四边形的有①④、③④;故答案是:①④、③④;(2)以①④为例进行证明.如图,在四边形ABCD中,OA=OC,AD∥BC.证明:∵AD∥BC,∴∠DAO=∠BCO.∴在△AOD与△COB中,,∴△AOD≌△COB(ASA),∴AD=BC,∴在四边形ABCD中,AD BC,∴四边形ABCD为平行四边形.4.选择①,∵DF=BE,AE=CF,AB=CD,∴△ABE≌△CDF(sss),∴∠ABE=∠CDF,∴四边形ABCD是平行四边形.5. BE=DF,BE∥DF因为ABCD是平行四边形,所以OA=OC,OB=OD,因为E,F分别是OA,OC的中点,所以OE=OF,所以BFDE是平行四边形,所以BE=DF,BE∥DF 6.四边形ADEF是平行四边形.连接ED、EF,∵△ABD、△BCE、△ACF分别是等边三角形,∴AB=BD,BC=BE,∠DBA=∠EBC=60°.∴∠DBE=∠ABC.∴△ABC≌△DBE.同理可证△ABC≌△FEC,∴AB=EF,AC=DE.∵AB=AD,AC=AF,∴AD=EF,DE=AF.∴四边形ADEF是平行四边形7.(1)∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD.∵∠BDE=∠CDF,BE=CF,∴△BED≌△CFD.∴BD=CD.∴AD是△ABC的中线.(2)四边形BECF是平行四边形,由(1)得:BD=CD,ED=FD.∴四边形BECF是平行四边形8.∵四边形ABCD是矩形∴AB∥CD,AB=CD,∴∠ABE=∠CDF,又∵∠AEB=∠CFD,∴△ABE≌△CDF,∴BE=DF,又∵四边形ABCD是矩形,∴OA=OC,OB=OD,∴OB﹣BE=OD﹣DF,∴OE=OF,∴四边形AECF是平行四边形9.∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴∠B=∠C,∵DE=AB,∴∠DEC=∠B,∴AB∥DE,∴四边形ABED是平行四边形.10.(1)证明:∵AB∥DC,∴∠1=∠2,∠FCE=∠EBA,∵E为BC中点,∴CE=BE,∵在△ABE和△FCE中,∠1=∠2,∠FCE=∠EBA,CE=BE,∴△ABE≌△FCE;(2)四边形ABFC是平行四边形;理由:由(1)知:△ABE≌△FCE,∴EF=AE,∵CE=BE,∴四边形ABFC是平行四边形11.连接BF,∵△ADF和△ABC是等边三角形,∴AF=AD=DF,AB=AC=BC,∠ABC=∠ACD=∠CAB=∠FAD=60°,∴∠FAD﹣∠EAD=∠CAB﹣∠EAD,∴∠FAB=∠CAD,在△FAB和△DAC中,∴△FAB≌△DAC(SAS),∴BF=DC,∠ABF=∠ACD=60°,∵BE=CD,∴BF=BE,∴△BFE是等边三角形,∴EF=BE=CD,在△ACD和△CBE中∵,∴△ACD≌△CBE(SAS),∴AD=CE=DF,∵EF=CD,∴四边形CDFE是平行四边形.12.(1)∵△ABE为等边三角形,EF⊥AB,∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,在△ABC和△EAF中,,∴△ABC≌△EAF(AAS);(2)∵∠BAC=30°,∠DAC=60°,∴∠DAB=90°,即DA⊥AB,∵EF⊥AB,∴AD∥EF,∵△ABC≌△EAF,∴EF=AC=AD,∴四边形ADFE是平行四边形13.在△ABC中,∵AD=BD,AE=CE,∴DE∥BC且DE=BC.在△OBC中,∵OF=FB,OG=GC,∴FG∥BC且FG=BC.∴DE∥FG,DE=FG.∴四边形DFGE为平行四边形14.(1)x秒后,四边形ABQP为平行四边形.则2x=18﹣3x,解得x=3.6.3.6秒钟后,四边形ABQP为平行四边形,此时四边形ABQP的周长是3.6×2×2+12×2=38.4cm.(2)y秒后,四边形PDCQ为平行四边形.10﹣2y=3y,解得y=2.2秒钟后,四边形PDCQ为平行四边形,此时四边形PDCQ的周长是3.6×2×2+15×2=43.2cm.15.:连接BD,∵E、F为AD,AB中点,∴FE BD.又∵G、H为BC,CD中点,∴GH BD,故GH FE.同理可证,EH FG.∴四边形FGHE是平行四边形16.∵BE,CF是△ABC的中线,∴EF∥BC且EF=BC,∵M是BO的中点,N是CO的中点,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.17.(1)证明:∵AG∥BC(已知)∴∠G=∠EFC(两直线平行,内错角相等)∵∠AEG=∠FEC(对顶角相等),又AE=EC(已知)∴△AGE≌△CFE(AAS);(2)说明:∵FG∥AB,AG∥BC(已知)∴四边形ABFG是平行四边形(平行四边形的定义);(3)解:线段DE,BF,FC之间的位置关系是DE∥BF,DE∥FC,数量关系是DE=BF=FC,理由:由(1)可知△AGE≌△CFE∴AG=FC,FE=EG(全等三角形的对应边相等),∴E是FG的中点,又∵AD=DB(已知)∴DE为三角形ABC的中位线,∴DE=BC,DE∥BC,即DE∥BF,DE∥FC,由(2)可知四边形ABFG是平行四边形∴AG=BF,∴BF=FC=BC,∴DE=BF=FC,即线段DE,BF,FC之间的位置关系是DE∥BF,DE∥FC,数量关系是DE=BF=FC.18.(1)∵△ABC和△ADE都是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°,∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,即:∠EAB=∠DAC,∴△ABE≌△ACD(SAS);(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,又∵BF=DC,∴BE=BF.∵△ABC是等边三角形,∴∠DCA=60°,∴△BEF为等边三角形.∴∠EFB=60°,EF=BF∵△ABC是等边三角形,∴∠ABC=60°,∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,∴四边形EFCD是平行四边形19.平行四边形ADCF和平行四边形DBCF.理由:(1)∵D、E分别是AB、AC边的中点,∴DE∥BC ,.又∵EF=DE,∴DF=BC,∴四边形DBCF是平行四边形;(2)在四边形ADCF中,∵EF=DE,又∵E是AC边的中点,∴EA=EC,∴四边形ADCF是平行四边形20.∵E为AD中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DCE,在△AEF和△CED中∵,∴△AEF≌△CED(AAS),∴AF=DC,∵AD是△ABC的中线,∴BD=DC,∴AF=BD,即AF∥BD,AF=BD,故四边形AFBD是平行四边形21.图中有两个平行四边形:▱ABED、▱AECD.∵,∴AD=BE,∵AD∥BC,∴四边形ABED是平行四边形.22.已知:四边形ABCD,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形,证明:∵∠A=∠C,∠B=∠D,∠A+∠B+∠C+∠D=360°,∴2∠A+2∠B=360°,∴∠A+∠B=180°,∴AD∥BC,同理AB∥CD,∴四边形ABCD是平行四边形.在△ABE和△DCF中∴△ABE≌△DCF(SAS),∴EB=FC,∠ABE=∠DCF,∵∠ABE+∠EBC=180°,∠DCF+∠FCB=180°,∴∠EBC=∠FCB,∴BE∥FC,∵BE=FC,∴四边形EBFC是平行四边形24.∵CE∥BF,BD=CD,∴△BDF≌△CDE,∴BF=CE,∴四边形BFCE是平行四边形.25.四边形EFGH是平行四边形证明:连接AC、BD∵E、F、G、H分别为四边形ABCD四边的中点∴EH=BD,FG=BD,HG=AC,EF=AC∴EH=FG,EF=HG∴四边形EFGH是平行四边形.26.∵∠B=∠EAD,∴AD∥BC,∵AD=BC,∴四边形ABCD是平行四边形.27.∵AD∥BC,∴∠EAD=∠FCB,又ED∥BF,∴∠FED=∠EFB,∠AED=180°﹣∠FED,∠CFB=180°﹣∠EFB,∴∠AED=∠CFB,又已知AE=CF,∴△AED≌△CFB,∴AD=BC,∴四边形ABCD是平行四边形.28.∵AD∥BC,∴∠EAD=∠FCB,又ED∥BF,∴∠FED=∠EFB,∠AED=180°﹣∠FED,∠CFB=180°﹣∠EFB,∴∠AED=∠CFB,又已知AE=CF,∴△AED≌△CFB,∴AD=BC,∴四边形ABCD是平行四边形.29.∵△ABE、△BCF为等边三角形,∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.∴∠FBE=∠CBA,在△FBE和△CBA中,,∴△FBE≌△CBA(SAS).∴EF=AC.又∵△ADC为等边三角形,∴CD=AD=AC.∴EF=AD.同理可得AE=DF.∴四边形AEFD是平行四边形30.∵AB=5,AC=4,BC=3∴AB2=AC2+BC2∴∠BCA=90°∵AD∥BC∴∠DAC=∠BCA=90°∵DC=5,AC=4,∴AD2=DC2﹣AC2=9∴AD=BC=3∴四边形ABCD为平行四边形.。
平行四边形性质和判定测试

一、选择题1、平行四边形的两邻边分别为3、4,那么其对角线必()A.大于1B.小于7C.大于1且小于7D.小于7或大于12、在ABCD中,M为CD的中点,如DC=2AD,则AM、BM夹角度数是()A.90°B.95°C.85°D.100°3、如图,四边形ABCD是平行四边形,∠D=120°,∠CAD=32°.则∠ABC、∠CAB的度数分别为()A.28°,120°B.120°,28°C.32°,120°D.120°,32°4、在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是()A.1∶2∶3∶4B.1∶2∶2∶1C.1∶1∶2∶2D.2∶1∶2∶15、平行四边行的两条对角线把它分成全等三角形的对数是()A.2B.4C.6D.86、在□ABCD中,∠A、∠B的度数之比为5∶4,则∠C等于()A.60°B.80°C.100°D.120°7、A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有()A.3种B.4种C.5种D.6种8、能够判别一个四边形是平行四边形的条件是()A.一组对角相等B.两条对角线互相垂直且相等C.两组对边分别相等D.一组对边平行9、下列条件中不能确定四边形ABCD是平行四边形的是()A.AB=CD,AD∥BCB.AB=CD,AB∥CDC.AB∥CD,AD∥BCD.AB=CD,AD=BC10.已知在平行四边形ABCD中,AB=6,BC=4,若∠B=45°,则平行四边形ABCD的面积为()A.8 B.122C.162D.2411.将一张平行四边形纸片折一次,使得折痕平分这个平行四边形的面积,•则这样的折纸方法有()A.1种B.2种C.3种D.无数种12.在平行四边形ABCD中,∠A的平分线交BC于点E,若CD=10,AD=16,则EC为()A.10 B.16 C.6 D.13二、填空题1、以不在一条直线上的三点A、B、C为顶点的平行四边形共有个3、ABCD中,若∠A∶∠B=1∶3,那么∠A=________,∠B=________,∠C=________,∠D=________.4、平行四边形的周长等于56 cm,两邻边长的比为3∶1,那么这个平行四边形较长的边长为_______.5.□ABCD的周长为80cm,对角线AC、BD相交于O,若△OAB的周长比△OBC的周长小8cm,则AB= cm.6.一个四边形的边长依次为a,b,c,d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是 .7. 如图,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=200,∠ACB=600,则∠FEG=.三、解答题1、如图,四边形ABCD是平行四边形,BD⊥AD,求BC,CD及OB的长.2..如图,平行四边形ABCD中,M、N分别为AD、BC的中点,连结AN、DN、BM、CM,且AN、BM交于点P,CM、DN交于点Q.证明:四边形MGNP是平行四边形3、已知如图:在ABCD中,延长AB到E,延长CD到F,使BE=DF,证明:线段AC与EF是否互相平分5.已知E为平行四边形ABCD边的延长线上的一点,且CE=DC,连结AE,分别交BC、BD于F、G,连结AC 交BD于O点,连AF。
北师大版八年级数学下册 平行四边形的性质与判定 专题(附答案)

北师大版八年级数学下册平行四边形的性质与判定专题(附答案)综合滚动练:平行四边形的性质与判定一、选择题(每小题4分,共32分)1.在平行四边形ABCD中,若∠A+∠C=120°,则∠A 的度数是()。
A。
100° B。
120° C。
80° D。
60°2.如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,下列结论错误的是()。
A。
AB∥CD B。
AB=CD C。
AC=BD D。
OA=OC3.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的值可以是()。
A。
4∶3∶3∶4 B。
7∶5∶5∶7 C。
4∶3∶2∶1 D。
7∶5∶7∶54.平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是()。
A。
(-2,1) B。
(-2,-1) C。
(-1,-2) D。
(-1,2)5.如图,在平行四边形ABCD中,点E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为()。
A。
BE=DF B。
BF=DE C。
AE=CF D。
∠1=∠26.如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,CE平分∠BCD交AD于点E。
若AB=6,EF=2,则BC的长为()。
A。
8 B。
10 C。
12 D。
147.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于E,CF∥AE交AD于F,则∠BCF等于()。
A。
40° B。
50° C。
60° D。
80°8.(2017·龙东中考)在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是()。
A。
22 B。
20 C。
22或20 D。
18二、填空题(每小题4分,共24分)9.已知AB∥CD,添加一个条件使得四边形ABCD为平行四边形。
(完整版)平行四边形练习题及答案(DOC).doc

20.1平行四边形的判定一、选择题1 .四边形ABCD,从( 1)AB∥CD;( 2)AB=CD;( 3)BC∥AD;( 4) BC=AD这四个条件中任选两个,其中能使四边形ABCD是平行四边形的选法有()A . 3 种B.4种C.5种D.6种2.四边形的四条边长分别是a, b, c,d,其中 a,b 为一组对边边长, c,d?为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是()A .任意四边形B.平行四边形C.对角线相等的四边形 D .对角线垂直的四边形3.下列说法正确的是()A.若一个四边形的一条对角线平分另一条对角线,则这个四边形是平行四边形B.对角线互相平分的四边形一定是平行四边形C.一组对边相等的四边形是平行四边形D.有两个角相等的四边形是平行四边形二、填空题4 .在□ ABCD中,点 E, F 分别是线段A D, BC上的两动点,点 E 从点 A 向 D 运动,点 F从 C?向 B 运动,点 E 的速度边形.m与点F 的速度n 满足 _______关系时,四边形BFDE为平行四5.如图 1 所示,平行四边形ABCD中, E, F 分别为AD,BC边上的一点,连结EF,若再增加一个条件_______,就可以推出BE=DF.图 1图 26 .如图 2 所示, AO=OC,BD=16cm,则当 OB=_____cm时,四边形ABCD是平行四边形.三、解答题7.如图所示,四边形 ABCD中,对角线 BD=4,一边长 AB=5,其余各边长用含有未知数 x的代数式表示,且 AD⊥BD于点 D,BD⊥BC 于点 B.问:四边形 ABCD?是平行四边形吗?为什么?四、思考题8.如图所示,在□ABCD中, E,F 是对角线 AC上的两点,且 AF=CE,?则线段 DE?与 BF的长度相等吗?参考答案一、 1. B 点拨:可选择条件(1)(3)或(2)( 4)或( 1)( 2)或( 3)(4).故有 4 种选法.2. B 点拨: a2+b 2+c2+d2=2ab+2cd 即( a-b)2+( c-d )2=0,即( a-b )2=0 且( c-d )2=0.所以 a=b, c=d,即两组对边分别相等,所以四边形为平行四边形.3. B 点拨:熟练掌握平行四边形的判定定理是解答这类题目的关键.二、 4.相等点拨:利用“一组对边平行且相等的四边形是平行四边形”来确定.5 .AE=CF 点拨:本题答案不惟一,只要增加的条件能使四边形EBFD?是平行四边形即可.6. 8 点拨:根据对角线互相平分的四边形为平行四边形来进行判别.三、 7.解:如图所示,四边形ABCD是平行四边形.理由如下:在 Rt△BCD 中,根据勾股定理,得BC2+BD 2=DC 2,即( x-5 )2+42=( x-3 )2,解得 x=8.所以 AD=11-8=3, BC=x-5=3, DC=x-3=8-3=5 ,所以 AD=BC, AB=DC.所以四边形ABCD是平行四边形.点拨:本题主要告诉的是线段的长度,故只要说明AD=BC, AB=DC即可,本题也可在Rt△ABD中求 x 的值.四、 8.解:线段DE与BF 的长度相等;连结BD交AC于O点,连结DF, BE,如图所示.在ABCD中, DO=OB, AO=OC,又因为 AF=EC,所以 AF-AO=CE-OC,即 OF=OE,所以四边形 DEBF是平行四边形,所以DE=BF.点拨:本题若用三角形全等,也可以解答,但过程复杂,学了平行四边形性质后,要学会应用.20.2 矩形的判定一、选择题1 .矩形具有而一般平行四边形不具有的性质是()A .对角相等B .对边相等C .对角线相等D .对角线互相垂直2 .下列叙述中能判定四边形是矩形的个数是()①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.A . 1B . 2C . 3D . 43.下列命题中,正确的是()A.有一个角是直角的四边形是矩形 B .三个角是直角的多边形是矩形C .两条对角线互相垂直且相等的四边形是矩形D .有三个角是直角的四边形是矩形二、填空题4.如图 1 所示,矩形 ABCD中的两条对角线相交于点O,∠ AOD=120°, AB=4cm,则矩形的对角线的长为 _____.D E CF OA B图 1 图 25.若四边形 ABCD的对角线 AC, BD相等,且互相平分于点 O,则四边形 ABCD?是_____ 形,若∠ AOB=60°,那么AB:AC=______.6.如图 2 所示,已知矩形ABCD周长为 24cm,对角线交于点O,OE⊥DC 于点 E,于点 F, OF-OE=2cm,则 AB=______, BC=______.三、解答题7.如图所示,□ABCD的四个内角的平分线分别相交于E, F, G,H 两点,试说明四边形EFGH是矩形.四、思考题8.如图所示,△ABC 中, CE, CF分别平分∠ACB和它的邻补角∠ACD.AE⊥CE 于 E,AF⊥CF 于F,直线EF分别交AB, AC于 M, N 两点,则四边形AECF是矩形吗?为什么?参考答案一、 1. C点拨:A与B都是平行四边形的性质,而D是一般矩形与平行四边形都不具有的性质.2 .B点拨:③是矩形的判定定理;④中对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形,故④能判定矩形,应选B.3. D 点拨:选项 D 是矩形的判定定理.二、 4. 8cm5.矩; 1: 2 点拨:利用对角线互相平分来判定此四边形是平行四边形,再根据对角线相等来判定此平行四边形是矩形.由矩形的对角线相等且互相平分,?可知△ AOB 是等腰三角形,又因为∠ AOB=60°,所以AB=AO=1AC.26 . 8cm; 4cm三、 7.解:在□ABCD中,因为AD∥BC,所以∠ DAB+∠CBA=180°,又因为∠ HAB= 1∠DAB,∠ HBA=1∠CBA.2 2所以∠ HAB+∠HBA=90°,所以∠ H=90°.所以四边形EFGH是矩形.点拨:由于“两直线平行,同旁内角的平分线互相垂直”,所以很容易求出四边形EFGH 的四个角都是直角,从而求得四边形EFGH是矩形.四、 8.解:四边形AECF是矩形.理由:因为CE平分∠ ACB, ?CF?平分∠ ACD, ?所以∠ ACE=1∠ACB,∠ ACF=1∠ACD.所以∠ ECF=1(∠ ACB+∠ACD)=90°.22 2又因为 AE⊥CE,AF⊥CF, ?所以∠ AEC=∠AFC=90°,所以四边形AECF是矩形.点拨: ?本题是通过证四边形中三个角为直角得出结论.还可以通过证其为平行四边形,再证有一个角为直角得出结论.20.3菱形的判定一、选择题1.下列四边形中不一定为菱形的是()A .对角线相等的平行四边形B.每条对角线平分一组对角的四边形C.对角线互相垂直的平行四边形D.用两个全等的等边三角形拼成的四边形2.四个点 A, B, C,D 在同一平面内,从① AB∥CD;② AB=CD;③ AC⊥BD;④ AD=BC;5 个条件中任选三个,能使四边形ABCD是菱形的选法有().A . 1 种B.2种C.3种D.4种3 .菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是()A.8cm和 4 3 cm B.4cm和83 cm C.8cm和83 cm D.4cm和43 cm二、填空题4.如图 1 所示,已知□ABCD,AC,BD相交于点O,?添加一个条件使平行四边形为菱形,添加的条件为 ________.(只写出符合要求的一个即可)图 1图 25.如图 2 所示, D, E,F 分别是△ ABC 的边 BC, CA,AB 上的点,且 DE∥AB,DF∥CA,要使四边形 AFDE是菱形,则要增加的条件是 ________.(只写出符合要求的一个即可)6 .菱形 ABCD的周长为48cm,∠ BAD:∠ ABC=1:?2,?则 BD=?_____,?菱形的面积是______.7.在菱形ABCD中, AB=4, AB 边上的高DE垂直平分边AB,则 BD=_____,AC=_____.三、解答题8.如图所示,在四边形ABCD中, AB∥CD, AB=CD=BC,四边形 ABCD是菱形吗? ?说明理由.四、思考题9.如图,矩形 ABCD的对角线相交于点 O,PD∥AC,PC∥BD, PD,PC相交于点 P,四边形 PCOD是菱形吗?试说明理由.参考答案一、 1. A点拨:本题用排除法作答.2. D 点拨:根据菱形的判定方法判断,注意不要漏解.3. C点拨:如图所示,若∠ ABC=60°,则△ABC为等边三角形,?所以 AC=AB=1×32=8( cm), AO=1AC=4cm.4 2因为 AC⊥BD,在 Rt△AOB中,由勾股定理,得OB= 2 2 2 2AB OA 8 4 =43 (cm ? ),所以 BD=2OB=8 3 cm.二、 4. AB=BC 点拨:还可添加AC⊥BD 或∠ ABD=∠CBD等.5.点 D 在∠ BAC的平分线上(或 AE=AF)26. 12cm; 723 cm点拨:如图所示,过 D 作 DE⊥AB 于 E,因为 AD∥BC, ?所以∠ BAD+∠ABC=180°.又因为∠ BAD:∠A BC=1:2,所以∠ BAD=60°,因为 AB=AD,所以△ ABD 是等边三角形,所以BD=AD=12cm.所以 AE=6cm.在Rt△AED 中,由勾股定理,得 AE 2+ED 2=AD 2, 62+ED 2=12 2,所以 ED 2=108 ,所以 ED=6 3 cm,所以S菱形ABCD=12×63=72 3 (cm2).7. 4;4 3 点拨:如图所示,因为DE垂直平分 AB,又因为 DA=AB,所以 DA=DB=4.所以△ ABD 是等边三角形,所以∠ BAD=60°,由已知可得AE=2.在 Rt△AED中,2 2 2 2 2 2 2?AE +DE=AD,即 2 +DE=4 ,所以 DE=12,所以 DE=2 3 ,因为1AC·BD=AB·DE,即1AC·4=4×2 3 ,所以AC=4 3 .2 2三、 8.解:四边形ABCD是菱形,因为四边形ABCD中, AB∥CD,且AB=CD,所以四边形ABCD是平行四边形,又因为AB=BC,所以Y ABCD是菱形.点拨:根据已知条件,不难得出四边形ABCD为平行四边形,又AB=BC,即一组邻边相等,由菱形的定义可以判别该四边形为菱形.四、 9.解:四边形PCOD是菱形.理由如下:因为 PD∥OC,PC∥OD, ?所以四边形P COD是平行四边形.又因为四边形ABCD是矩形,所以OC=OD,所以平行四边形PCOD是菱形.20.4正方形的判定一、选择题1.下列命题正确的是()A.两条对角线互相平分且相等的四边形是菱形B.两条对角线互相平分且垂直的四边形是矩形C.两条对角线互相垂直,平分且相等的四边形是正方形D.一组邻边相等的平行四边形是正方形2.矩形四条内角平分线能围成一个()A.平行四边形B.矩形C.菱形 D .正方形二、填空题3.已知点 D, E,F 分别是△ ABC 的边 AB, BC, CA的中点,连结 DE, EF, ?要使四边形ADEF是正方形,还需要添加条件_______.4.如图 1 所示,直线L 过正方形ABCD的顶点 B,点 A, C 到直线 L?的距离分别是 1 和2,则正方形ABCD的边长是 _______.图 1图2图 35.如图 2 所示,四边形 ABCD是正方形,点 E 在 BC的延长线上, BE=BD且 AB=2cm,则∠E的度数是 ______, BE 的长度为 ____.6.如图 3 所示,正方形 ABCD的边长为 4,E 为 BC上一点, BE=1,F?为 AB?上一点,AF=2, P 为 AC上一动点,则当 PF+PE取最小值时, PF+PE=______.三、解答题7.如图所示,在 Rt△ABC中, CF为∠ ACB的平分线, FD⊥AC 于 D,FE⊥BC于点 E,试说明四边形 CDFE是正方形.BEF四、思考题8.已知如图所示,在正方形 ABCD中, E,F 分别是(1) AF 与 DE相等吗?为什么?(2) AF 与 DE是否垂直?说明你的理由.C D A AB,BC边上的点,且 AE=BF,?请问:参考答案一、 1. C点拨:对角线互相平分的四边形是平行四边形,?对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形一定是正方形,故选 C.2. D 点拨:由题意画出图形后,利用“一组邻边相等的矩形是正方形”来判定.二、 3.△ ABC是等腰直角三角形且∠ BAC=90°点拨:还可添加△ ABC 是等腰三角形且四边形ADEF是矩形或∠ BAC=90°且四边形ADEF 是菱形等条件.4.5点拨:观察图形易得两直角三角形全等,由全等三角形的性质和勾股定理得正方形的边长为 22 12 = 5.5. 67. 5°; 2 2 cm点拨:因为BD是正方形ABCD的对角线,所以∠ DBC=45°, AD=?AB=2cm.在Rt△BAD中,由勾股定理得 AD 2+AB 2=BD 2,即 22+22=BD 2,所以 BD=2 2 cm,所以 BE=BD=2 2( cm),又因为BE=BD,所以∠ E=∠EDB= 1(180°- 45°)=67. 5°.26.17 点拨:如图所示,作 F 关于AC的对称点G.连结EG交AC于P,则PF+?PE=PG+PE=GE为最短.过 E 作 EH⊥AD.在Rt△GHE中,HE=4,HG=AG-AH=AF-BE=1,所以 GE= 4212 = 17,?即 PF+PE= 17.三、 7.解:因为∠ FDC=∠FEC=∠BCD=90°,所以四边形CDFE是矩形,因为 CF?平分∠ ACB,FE⊥BC,FD⊥AC,所以FE=FD,所以矩形CDFE是正方形.点拨:本题先说明四边形是矩形,再求出有一组邻边相等,?还可以先说明其为菱形,再求其一个内角为90°.四、 8.解:( 1)相等.理由:在△ ADE 与△ BAF 中, AD=AB,∠ DAE=∠ABF=90°, AE=BF,所以△ ADE≌△ BAF( S. A. S.),所以 DE=AF.( 2) AF 与 DE垂直.理由:如图,设DE与 AF 相交于点O.因为△ ADE≌△ BAF, ?所以∠ AED=∠BFA.又因为∠ BFA+∠EAF=90°,所以∠ AEO+∠EAO=90°,所以∠ EOA=90°,所以DE⊥AF.20.5等腰梯形的判定1 A C 一、选择题.下列结论中,正确的是(.等腰梯形的两个底角相等.一组对边平行的四边形是梯形)BD.两个底角相等的梯形是等腰梯形.两条腰相等的梯形是等腰梯形2.如图所示,等腰梯形ABCD的对角线 AC,BD相交于点O,则图中全等三角形有()A. 2 对B.3对C.4对D.5对3.课外活动课上, ?老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和至少为()A . 30 2 cm B.30cm C.60cm D.60 2 cm二、填空题4.等腰梯形上底,下底和腰分别为 4,?10,?5,?则梯形的高为 _____,?对角线为 ______.5.一个等腰梯形的上底长为5cm,下底长为 12cm,一个底角为 60°,则它的腰长为____cm,周长为 ______cm.6.在四边形 ABCD中, AD∥BC,但 AD≠BC,若使它成为等腰梯形,则需要添加的条件是__________ (填一个正确的条件即可).三、解答题7.如图所示,AD是∠ BAC的平分线, DE∥AB, DE=AC,AD≠EC.求证: ?四边形 ADCE是等腰梯形.四、思考题8.如图所示,四边形ABCD中,有 AB=DC,∠ B=∠C,且AD<BC,四边形 ABCD是等腰梯形吗?为什么?参考答案一、 1. D点拨:梯形的底角分为上底上的角和下底上的角,?因此在等腰梯形的性质和判别方法中必须强调同一底上的两个内角(?指上底上的两个内角或下底上的两个内角),否则就会出现错误,因此A, B 选项都不正确,而 C 选项中漏掉了限制条件另外一组对边不平行,若平行该四边形就形成了平行四边形了,因此应选D.2. B点拨:因为△ ABC≌△DCB,△ BAD≌△CDA,△ AOB≌△DOC,所以共有 3 对全等的三角形.3. C点拨:设该等腰梯形对角线长为Lcm,因为两条对角线互相垂直,?所以梯形面积为122L =450,解得 L=30,所以所用竹条长度之和至少为2L=2× 30=60(cm).二、 4. 4:65点拨:如图所示,连结BD,过 A,D 分别作 AE⊥BC,DF⊥BC,垂足分别为E, F.易知△ BAE≌△ CDF,在四边形 AEFD为矩形,所以BE=CF=3, AD=EF=4.在Rt△CDF 中, FC2+DF 2=CD 2,即 32+DF 2=52,所以 DF=4 ,在 Rt △BFD 中, BF2+DF 2=BD 2,即 72+42=BD 2,所以 BD=65 .5. 7;31点拨:如图所示,过点D作 DE∥AB 交 BC于 E.因为ABED是平行四边形.所以 BE=AD=5(cm), AB=DE.又因为 AB=CD,所以 DE=?DC,又因为∠ C=60°,所以△ DEC 是等边三角形,所以 DE=DC=EC=7( cm),所以周长为5+?12+7+7=31(cm).6. AB=CD(或∠ A=∠D,或∠ B=∠C,或 AC=BD,或∠ A+∠C=180°,或∠B+∠D=180°)三、 7.证明:因为 AB∥ED,所以∠ BAD=∠ADE.又因为 AD是∠ BAC的平分线,所以∠ BAD=∠CAD,所以∠ CAD=∠ADE,所以 OA=OD.又因为AC=DE,所以 AC-OA=DE-OD即 OC=OE, ?所以∠ OCE=∠OEC,又因为∠ AOD=∠COE,所以∠ CAD=∠OCE.所以AD∥CE,而 AD≠CE,故四边形ADCE是梯形.又因为∠ CAD=∠ADE, AD=DA, AC=DE,所以△ DAC≌△ ADE,所以DC=?AE,所以四边形ADCE是等腰梯形.点拨:证明一个四边形是等腰梯形时,应先证其是梯形而后再证两腰相等或同一底上的两个角相等.四、 8.解:四边形ABCD是等腰梯形.理由:延长BA, CD,相交于点 E,如图所示,由∠ B=∠C,可得EB=EC.又AB=DC,所以 EB-AB=EC-DC,即 AE=DE,所以∠ EAD=∠EDA.因为∠ E+∠EAD+∠EDA=180°,∠ E+∠B+∠C=180°,所以∠ EAD=∠B.故 AD∥BC. ?又 AD<BC,所以四边形 ABCD是梯形.又AB=DC,所以四边形 ABCD是等腰梯形.点拨:由题意可知,只要推出 AD∥BC,再由 AD<BC就可知四边形 ABCD为梯形,再由AB=DC,即可求得此四边形是等腰梯形,由∠ B=∠C联想到延长 BA,CD,即可得到等腰三角形,从而使AD∥BC.华东师大版数学八年级(下)第 20 章平行四边形的判定测试(答卷时间: 90 分钟,全卷满分: 100 分)姓名得分 ____________一、认认真真选,沉着应战!(每小题 3 分,共 30 分)1. 正方形具有菱形不一定具有的性质是()(A )对角线互相垂直(B)对角线互相平分(C)对角线相等(D)对角线平分一组对角2.如图 (1),EF 过矩形 ABCD 对角线的交点 O,且分别交 AB 、CD 于 E、 F,那么阴影部分的面积是矩形ABCD 的面积的()(A )A 1 1 1( D )3A5(B )( C)104 3D E FFEB C D HB C(1)(2)(3)3.在梯形ABCD 中, AD ∥ BC ,那么 A : B : C : D 可以等于()( A )4:5:6:3(B)6:5:4:3(C)6:4:5:3(D)3:4:5:64.如图 (2) ,平行四边形ABCD 中,DE ⊥ AB 于 E,DF⊥ BC 于 F,若Y ABCD的周长为48,DE = 5, DF= 10,则Y ABCD的面积等于 ()( A )87.5(B)80(C)75(D)72.55. A 、 B、 C、 D 在同一平面内,从① AB∥CD;② AB=CD;③ BC∥AD;④ BC=AD这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有()( A )3种(B)4种(C)5种(D)6种6.如图 (3) ,D、E、F分别是VABC各边的中点,AH 是高,如果 ED5cm ,那么 HF的长为()( A ) 5cm(B)6cm(C)4cm(D)不能确定7.如图( 4):E 是边长为 1 的正方形 ABCD 的对角线 BD 上一点,且 BE = BC, P 为 CE 上任意一点, PQ⊥BC 于点 Q, PR⊥ BE 于点 R,则 PQ+PR 的值是()2 13 2( A )2 ( B)2 ( C)2 ( D)38.如图( 5),在梯形ABCD 中, AD ∥ BC , AB CD , C 60 , BD 平分ABC ,如果这个梯形的周长为30,则AB的长()( A )4 ( B )5 ( C )6 ( D )7A DA DERPB C( 5)B( 4)Q C9.右图是一个利用四边形的不稳定性制作的菱形晾衣架.A B C 已知其中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉 A 、 B 之间的距离为20 3 cm,则∠1等于()1)( A ) 90°(B) 60°(C) 45°(D) 30°10.某校数学课外活动探究小组,在老师的引导下进一步研究了完全平方公式.结合实数的性质发现以下规律:对于任意正数a、 b,都有 a+b ≥ 2 ab 成立.某同学在做一个面积为3600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来做对角线用的竹条至少需要准备xcm.则 x 的值是()(A) 1202(B) 602(C) 120(D) 60二、仔仔填,自信!( 每小 2 分,共20 分)11.一个四形四条次是a、b、c、d,且a2 b 2 c 2 d 2 2ac 2bd,个四形是 _______________ .12.在四形ABCD中,角AC、BD交于点O,从(1)AB CD ;(2) AB ∥CD ;(3)OA OC;(4)OB OD ;(5) AC ⊥ BD ;(6) AC 平分 BAD 六个条件中,取三个推出四形ABCD 是菱形.如( 1)( 2)( 5)ABCD 是菱形,再写出符合要求的两个:ABCD 是菱形;ABCD 是菱形.13. 如,已知直l 把 Y ABCD 分成两部分,要使两部分的面相等,直l 所在位置需足的条件是____________________. (只需填上一个你合适的条件)lA DB C(第 13 )(第 16 )14.梯形的上底 6cm ,上底的一点引一腰的平行,与下底相交,所构成的三角形周 21cm ,那么梯形的周_________ cm。
中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图在四边形ABCD中AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是()A.CF=AE B.OE=OFC.△CDE为直角三角形D.四边形ABCD是平行四边形2.如图四边形ABCD中AB∥CD,∥B=∥D点E为BC延长线上一点,连接AE,AE交CD于点H,∥DCE的平分线交AE于点G.若AB=2AD=10,点H为CD的中点,HE=6,则AC的值为()A.9B.√97C.10D.3 √103.如图在Rt∥ABC中∥ACB=90°,分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE,连结DE,CA的延长线交DE于点F,则与线段AF相等的是()A.AC B.AB C.BC D.AB4.如图在菱形ΑΒCD中∠Α=60∘,AD=8,F是ΑΒ的中点.过点F作FΕ⊥ΑD,垂足为Ε.将ΔΑΕF沿点Α到点Β的方向平移,得到ΔΑ′Ε′F ′.设Ρ、Ρ′分别是ΕF、Ε′F ′的中点,当点Α′与点Β重合时,四边形ΡΡ′CD的面积为()A.28√3B.24√3C.32√3D.32√3−85.下列说法中错误的是()A.平行四边形的对角线互相平分B.对角线互相垂直的四边形是菱形C.菱形的对角线互相垂直D.对角线互相平分的四边形是平行四边形6.如图.若要使平行四边形ABCD成为菱形.则需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD7.如图点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∥ABC+∥ADC=120°,则∥A的度数是()A.100°B.110°C.120°D.125°8.如图在∥ABC中AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则∥BED与∥DFC的周长的和为()A.34B.32C.22D.209.如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4),当四边形ABCD 的周长最小时,则m 的值为().A.√2B.32C.2D.310.如图分别在四边形ABCD的各边上取中点E,F,G,H,连接EG,在EG上取一点M,连接HM,过F作FN∥HM,交EG于N,将四边形ABCD中的四边形①和②移动后按图中方式摆放,得到四边形AHM′G′和AF′N′E,延长M′G′,N′F′相交于点K,得到四边形MM′KN′.下列说法中错误的是()A.S四边形MM′KN′=S四边形ABCD B.HM=NFC.四边形MM′KN′是平行四边形D.∠K=∠AHM′11.如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为()A.2B.3C.4D.512.如图P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若S四边形AHPE=3,S四边形PFCG=5,则S∥PBD为()A.0.5B.1C.1.5D.2二、填空题13.如图在平行四边形ABCD中点E,F分别在BC,AD上,请添加一个条件,使四边形AECF是平行四边形(只填一个即可).14.如图在Rt△ABC中AC=2√3,BC=2,点P是斜边AB上任意一点,D是AC的中点,连接PD并延长,使DE=PD.以PE,PC为边构造平行四边形PCQE,则对角线PQ的最小值为.15.如图▱ABCD中∥BAD=120°,E、F分别在CD和BC的延长线上,AE∥BD,EF∥BC,EF=5√3,则AB的长是16.如图在∥ABC中∥ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= 13BD,连接DM、DN、MN.若AB=6,则DN=.17.若AC=10,BD=8,那么当AO=DO=时,四边形ABCD是平行四边形。
《平行四边形》专题练习(含答案)

平行四边形专题练习一、选择题1. (2018·宜宾)在ABCD Y 中,若BAD Ð与CDA Ð的平分线交于点E ,则AED Ð的形状是() A.锐角三角形锐角三角形 B.直角三角形直角三角形 C.钝角三角形钝角三角形 D.不能确定不能确定2. (2018·黔西南州)如图,在ABCD Y 中,4AC =cm.若ACD D 的周长为13 cm ,则AB C D Y的周长为( ) A. 26 cm B. 24 cm C. 20 cmD. 18 cm3. (2018·海南)如图ABCD Y 的周长为36,对角线,AC BD 相交于点O ,E 是CD 的中点,12BD =,则DOE D 的周长为() A.15 B. 18 C. 21D. 24 4. ( 2018·台州)如图,在ABCD Y 中,2,3AB BC ==.以点C 为圆心,适当长为半径画弧,交BC 于点P ,交CD 于点Q ,再分别以点,P Q 为圆心,大于12PQ 的长为半径画弧,两弧相交于点N ,射线CN 交BA 的延长线于点E ,则AE 的长是( ) A.12B. 1C. 65D. 325. (2018·东营)如图,在四边形ABCD 中,E 是BC 边的中点,连接DE 并延长,交AB 的延长线于点F ,AB BF =.添加一个条件使四边形ABCD 是平行四边形,你认为下列四个条件中可选择的是( ) A. AD BC = B. CD BF = C. A C Ð=Ð D. F CDF Ð=Ð 6. (2018·安徽)在ABCD Y 中,,E F 是对角线BD 上不同的两点.下列条件中,不能得出四边形AECF 一定为平行四边形的是() A. BE DF = B. AE CF = C. //AF CED. BAE DCF Ð=Ð 7. (2018·玉林)在四边形ABCD 中:①//AB CD ;②//AD BC ;③AB CD =;④AD BC =,从以上选择两个条件使四边形ABCD 为平行四边形的选法共有() A. 3种 B. 4种 C. 5种D. 6种8. (2018·呼和浩特)顺次连接平面上,,,A B C D 四点得到一个四边形,从①//AB CD ;②BC AD =;③A C Ð=Ð;④B D Ð=Ð四个条件中任取其中两个,可以得出‘“四边形ABCD 是平行四边形”这一结论的情况共有() A. 5种 B. 4种 C. 3种D. 1种 9. (2018·眉山)如图,在ABCD Y 中,2CD AD =,BE AD ^于点E ,F 为DC 的中点,连接,EF BF ,下列结论:①2ABC ABF Ð=Ð;②EF BF =;③2EFBDEBCS SD =四边形;④3CFE DEF Ð=Ð.其中正确的结论共有() A.1个 B. 2个 C. 3个D. 4个10. (2018·通辽)如图,ABCD Y 的对角线,AC BD 交于点O ,DE 平分ADC Ð交AB 于点E ,60BCD Ð=°,12AD AB =,连接OE .下列结论:①ABCDS AD BD =Y g ; ②DB 平分CDE Ð; ③AO DE =;④5ADEOFES SD D =.其中正确的有( ) A. 1个 B. 2个 C. 3个 D. 4个 二、填空题11. (2018·常州)如图,在ABCD Y 中,70A Ð=°,DC DB =,则CDB Ð=.12. (2018·十堰)如图,ABCD Y 的对角线,AC BD 相交于点O ,且8AC =,10BD =,5AB =,则OCD D 的周长为的周长为 . 13. (2018·泰州)如图,在ABCD Y 中,,AC BD 相交于点O .若6,16AD AC BD =+=,则BOC D 的周长为的周长为. 14. (2018·衡阳)如图,ABCD Y 的对角线相交于点O ,且A D C D ¹,过点O 作OM AC ^,交AD 于点M .如果CDM D 的周长为8,那么ABCD Y 的周长是的周长是.15.(2018·临沂)如图,在ABCD Y 中,10,6AB AD ==,AC BC ^,则BD 的长为. 16. (2018·东营)如图,(3,3)B -,(5,0)C ,以,OC CB 为边作OABC Y ,则经过点A 的反比例函数的解析式为比例函数的解析式为. 17. (2018·株洲)如图,在ABCD Y 中,连接BD ,且BD CD =,过点A 作AM BD ^于点M ,过点D 作DN AB ^于点N ,且32DN =,在DB 的延长线上取一点P ,满足ABD MAP PAB Ð=Ð+Ð,则AP 的长为的长为.18.(导学号78816053)(2018·无锡)如图,60XOY Ð=°,点A 在边OX 上,2OA =.过点A作AC OY ^于点C ,以AC 为一边在XOY Ð内作等边三角形ABC ,P 是ABC D 围成的区域(包括各边)内的一点,过点P 作//PD OY 交OX 于点D ,作//PE OX 交OY于点E .设,OD a OE b ==,则2a b +的取值范围是的取值范围是 . 三、解答题19. (2018·无锡)如图,在A B C D Y 中,,E F 分别是边,B C A D 的中点.求证:ABF CDE Ð=Ð.20. (2018·衢州)如图,在ABCD Y 中,AC 是对角线,BE AC ^,DF AC ^,垂足分别为E ,F .求证:AE CF =.21. (2018·大连)如图,ABCD Y 的对角线,AC BD 相交于点O ,点,E F 在AC 上,且AF CE =.求证:BE DF =.22. (2018·福建)如图,ABCD Y 的对角线,AC BD 相交于点O ,EF 过点O 且与,AD BC分别相交于点,E F .求证:OE OF =.23. (2018·宿迁)如图,在ABCD Y 中,点,E F 分别在边,CB AD 的延长线上,且BE DF =,EF 分别与,AB CD 交于点,G H .求证:AG CH =.24. (2018·曲靖)如图,在ABCD Y 的边,AB CD 上截取,AF CE ,使得AF CE =,连接,,EF M N 是线段EF 上两点,且EM FN =,连接,AN CM .(1)求证: AFN CEM D @D ;(2)若107CMF Ð=°,72CEM Ð=°,求NAF Ð的度数.25. (2018·岳阳)如图,在ABCD Y 中,AE CF =.求证:四边形BFDE 是平行四边形.26. (2018·孝感)如图,,,,B E C F 在一条直线上,已知//,//,AB DE AC DF BE CF =,连接AD 求证:四边形ABED 是平行四边形.27. (2018·陕西)如图,//AB CD ,,E F 分别为,AB CD 上的点,且//EC BF ,连接AD ,分别与,EC BF 相交于点,G H ,若AB CD =,求证:AG DH =.28. (2018·巴中)如图,在ABCD Y 中,过点B 作BM AC ^于点E ,交CD 于点M ,过点D 作DN AC ^于点F ,交AB 于点N .(1)求证:四边形BMDN 是平行四边形;(2)已知12,5AF EM ==,求AN 的长.29. (2018·江西)如图,在四边形ABCD 中,//AB CD ,2AB CD =,E 为AB 的中点,请仅用无刻度的直尺分别按下面的要求画图.(保留画图痕迹)(1)在图①中,画出ABD D 的BD 边上的中线; (2)在图②中,若BA BD =,画出ABD D 的AD 边上的高.30. (2018·黄冈)如图,在ABCD Y 中,分别以边,BC CD 作等腰三角形BCF 、等腰三角形CDE ,使,BC BF CD DE ==,CBF CDE Ð=Ð,连接,AF AE .(1)求证: ABF EDA D @D ;(2)延长AB 与CF ,相交于点G ,若AF AE ^,求证: BF BC ^.31. (2018·永州)如图,在ABC D 中,90ACB Ð=°,30CAB Ð=°,以线段AB 为边向外作等边三角形ABD ,E 是线段AB 的中点,连接CE 并延长交线段AD 于点F .(1)求证:四边形BCFD 为平行四边形;(2)若6AB =,求BCFD Y 的面积.32. (2018·重庆)如图,在ABCD Y 中,O 是对角线AC 的中点,E 是BC 上一点,且AB AE =,连,连 接EO 并延长交AD 于点F .过点B 作AE 的垂线,垂足的垂线,垂足 为H ,交AC 于点G .(1)若3,1AH HE ==,求ABE D 的面积;(2)若45ACB Ð=°,求证:2DF CG =.参考答案参考答案一、1. B 2. D 3. A 4. B 5. D 6. B 7. B 8. C9. D10. B 二、填空题二、填空题11. 40° 12. 1413. 14 14. 16 15. 41316. 6y x= 17. 618. 225a b £+£ 三、三、19. 点拨:证明()ABF CDE SAS D @D ,即可得ABF CDE Ð=Ð. 20. 点拨:证明()ABE CDF AAS D @D ,即可得AE CF =. 21. 点拨:证明()BEO DFO SAS D @D ,即可得BE DF =. 22. 点拨:证明()AOE COF ASA D @D ,即可得OE OF =. 23. 点拨:证明()AGF CHE ASA D @D ,即可得AG CH =.24. (1)点拨:由FN EM AFN CEM AF CE =ìïÐ=Ðíï=î,得到AFN CEM D @D(2) 35NAF Ð=°25. 点拨:由//BF DEBF DF ìí=î,得到四边形BFDE 是平行四边形是平行四边形26. 点拨:证明()ABC DEF ASA D @D ,得到AB DE =, 又∵//AB DE ,∴四边形ABED 是平行四边形.27. 点拨:证明()AEG DFH ASA D @D ,得到AG DH =.28. (1) 点拨:由////CD ABDN BM ìíî,得到四边形BMDN 是平行四边形;(2)13AN = 29. (1)如图①,连接CE ,交BD 于点F ,连接AF ,线段AF 即为所求即为所求 (2)如图②,连接CE ,交BD 于点F ,连接AF ,DE 交于点G ,连接BG ,并延长BG ,交AD 于点H ,线段BH 即为所求即为所求30. (1) 点拨:由BF DA ABF EDA AB DE=ìïÐ=Ðíï=î,得到ABF EDA D @D(2) 点拨:由90CBF EAF Ð=Ð=°,得到BF BC ^ 31. (1) 点拨:由////BC DFCF BD ìíî,得到四边形BCFD 为平行四边形; (2) 93BCFD S =Y 32. (1) 27ABE S D =(2) 点拨:AOF COE D @D ,得到AF CE =, ∵AD BC =, ∴DF BE =.AME BNG D @D ,得到ME NG =,∴22BE ME NG ==在Rt GNC D 中,45GCN Ð=°,∴2CG NG =,∴22CG NG =, ∴2DF CG =。
初中平行四边形试题及答案

初中平行四边形试题及答案一、选择题1. 平行四边形的对边相等,其对角线互相平分,以下哪个选项不是平行四边形的性质?A. 对边相等B. 对角线互相平分C. 相邻角互补D. 对角相等答案:C2. 如果一个平行四边形的对角线长度相等,那么这个平行四边形是:A. 矩形B. 平行四边形C. 菱形D. 梯形答案:A二、填空题1. 平行四边形的对角线将平行四边形分成四个________的三角形。
答案:全等2. 如果一个平行四边形的一组对边平行且相等,那么这个平行四边形是________。
答案:矩形三、判断题1. 平行四边形的对角线相等。
()答案:错误2. 平行四边形的对角线互相垂直。
()答案:错误四、简答题1. 请简述平行四边形的性质。
答案:平行四边形的性质包括:对边平行且相等;对角相等;对角线互相平分;邻角互补;对角线互相平分且将平行四边形分成四个全等的三角形。
2. 如何证明一个四边形是平行四边形?答案:证明一个四边形是平行四边形的方法包括:两组对边分别平行;两组对边分别相等;一组对边平行且相等;两组对角分别相等;对角线互相平分。
五、计算题1. 如图所示,平行四边形ABCD中,AB=4cm,BC=5cm,∠A=60°,求平行四边形ABCD的面积。
答案:由于∠A=60°,且AB=4cm,BC=5cm,根据30°-60°-90°三角形的性质,我们可以知道这是一个等边三角形,所以AD=5cm。
平行四边形的面积等于底乘以高,这里的底可以是AB或BC,高是另一条边的高。
由于∠A=60°,高等于边长的一半,即2cm。
所以平行四边形ABCD的面积是5cm×2cm=10cm²。
六、证明题1. 已知平行四边形ABCD中,AB=CD,AD=BC,证明ABCD是矩形。
答案:由于AB=CD,AD=BC,根据平行四边形的性质,我们知道AB∥CD,AD∥BC。
平行四边形性质及判定练习题及答案

平行四边形性质及判定练习题及答案1、已知平行四边形ABCD中,AE⊥BC,AF⊥CD,E,F分别是BC,CD的中点,则2、已知平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是多少?3、已知平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,求AB的长。
4、下列哪些命题是正确的:(1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形。
5、已知平行四边形ABCD中,AB=6,AC=4,E,D,F 分别是AB,BC,CA的中点,求四边形AEDF的周长。
6、已知平行四边形ABCD的对角线AC、BD相交于点O,下列哪个结论不正确:(A)DC∥AB;(B)OA=OC;(C)AD=BC;(D)DB平分∠ADC。
7、已知平行四边形ABCD中,AB=4,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,求BC的长。
8、已知平行四边形ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF,若EF=3,则CD的长为多少?9、已知平行四边形ABCD中,对角线AC、BD相交于点O,点E是BC的中点,OE=3,求AB的长。
10、已知平行四边形ABCD中,AB=8,AD=5,E,F分别是AB,AD的中点,连接EF,求四边形CDEF的周长。
11、已知平行四边形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,OE=3,求AD的长。
12、已知平行四边形ABCD中,AB=5,BC=7,对角线AC,BD相交于点O,点E是BC的中点,求AE的长。
13、已知平行四边形ABCD中,AB=4,BC=6,BC边上的高AE=2,求DC边上的高AF的长度。
14、在平行四边形ABCD中,AB=2cm,BC=3cm,∠B、∠C的平分线分别交AD于F、E,求EF的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学八年级下册第十八章平行四边形平行四边形的性质与判定专题练习题1.在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各
点中不能作为平行四边形顶点坐标的是()
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
2.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有▱ADCE中,DE最小的值是()
A.2 B.3 C.4 D.5
3.如图,E是▱ABCD内任意一点,若平行四边形的面积是6,则阴影部分的面积为____.4.如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_______.
5.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
6.如图,在▱ABCD中,E是BC的中点,AE=9,BD=12,AD=10.
(1)求证:AE⊥BD;
(2)求▱ABCD的面积.
7 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求▱ABCD的面积
8. 如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
9. 如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′的位置,则四边形ACE′E的形状是_____________.10. 如图,已知点E,C在线段BF上,BE=CE=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)试判断四边形AECD的形状,并证明你的结论.
11. 如图1,在▱ABCD中,点O是对角线AC的中点,EF过点O与AD,BC分别相交于点E,F,GH过点O与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有的平行四边形.(四边形AGHD除外)
12.如图,△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
答案:
1. A
2. B
3. 3
4. 25°
5. 解:(1)∵四边形ABCD是平行四边形,∴BC=AD,BC∥AD,∴∠EAD=∠AEB,∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,∴△ABC≌△EAD(SAS)(2)∵AE平分∠DAB,∴∠DAE=∠BAE,又∵∠DAE=∠AEB,AB=AE,∴∠BAE=∠AEB=∠B,∴△ABE 为等边三角形,∴∠BAE=60°,∵∠EAC=25°,∴∠BAC=85°,∵△ABC≌△EAD,∴∠AED=∠BAC=85°
6. 解:(1)过点D作DF∥AE交BC的延长线于点F,∵AD∥BC,∴四边形AEFD为
平行四边形,∴EF=AD=10,DF=AE=9,∵E是BC的中点,∴BF=1
2AD+AD=15,∴BD
2
+DF2=122+92=225=BF2,∴∠BDF=90°,即BD⊥DF,∵AE∥DF,∴AE⊥BD(2)过点
D作DM⊥BF于点M,∵BD·DF=BF·DM,∴DM=9×12
15=
36
5,∴S▱ABCD=BC·DM=72
7. 分析:(1)证AB=BE,AB=CD,即可得到结论;(2)将▱ABCD的面积转化为△ABE的面积求解即可.
解:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD∥BE,∴∠DAE=∠E,∵∠BAE =∠DAE,∴∠BAE=∠E,∴AB=BE,∴BE=CD(2)∵AB=BE,BF⊥AE,∴AF=FE,又∵∠DAF=∠CEF,∠AFD=∠EFC,∴△AFD≌△EFC(ASA),∴S▱ABCD=S
△ABE
,∵AB=
BE,∠BEA=60°,∴△ABE是等边三角形,由勾股定理得BF=23,∴S△ABE=1
2AE·BF=
43,∴S▱ABCD=4 3
8. 分析:可通过证BE綊CF来得到结论.
解:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,∴BE∥CF,∵AB∥CD,∴∠A=∠D,又∵AE=DF,∴△AEB≌△DFC(ASA),∴BE=CF,∴四边形BECF是平行四边形
9. 平行四边形
10. 解:(1)∵AB∥DE,∴∠B=∠DEF,∵BE=EC=CF,∴BC=EF,又∵∠ACB=∠F,∴△ABC≌△DEF(ASA)(2)四边形AECD是平行四边形.证明:∵△ABC≌△DEF,∴AC =DF,∵∠ACB=∠F,∴AC∥DF,∴四边形ACFD是平行四边形,∴AD∥CF,AD=CF,∵EC=CF,∴AD∥EC,AD=CE,∴四边形AECD是平行四边形
11. 解:(1)∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EAO=∠FCO,又∵OA=OC,∠AOE=∠COF,∴△OAE≌△OCF(ASA),∴OE=OF,同理OG=OH,∴四边形EGFH是平行四边形
(2)▱GBCH,▱ABFE,▱EFCD,▱EGFH
12. 解:(1)∵△ABC是等边三角形,∴∠ABC=60°,又∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥BC,又∵DC=EF,∴四边形EFCD是平行四边形(2)连接BE,∵∠EFB=60°,BF =EF,∴△BEF为等边三角形,∴BE=BF=EF,∠ABE=60°,∵CD=EF,∴BE=CD,又∵△ABC为等边三角形,∴AB=AC,∠ACD=60°,∴∠ABE=∠ACD,∴△ABE≌△ACD(SAS),∴AE=AD。
