用matlab绘制各种数字信号中的函数-还有分段函数及翻褶-平移
MATLAB常用的基本数学函数解读
MATLAB常用的基本数学函数解读基本运算与函数下表即为MATLAB 常用的基本数学函数及三角函数:小整理:MATLAB 常用的基本数学函数abs(x:纯量的绝对值或向量的长度angle(z:复数 z 的相角 (Phase anglesqrt(x:开平方real(z:复数 z 的实部imag(z:复数 z 的虚部conj(z:复数 z 的共轭复数round(x:四舍五入至最近整数fix(x:无论正负,舍去小数至最近整数floor(x:地板函数,即舍去正小数至最近整数 ceil(x:天花板函数,即加入正小数至最近整数 rat(x:将实数 x 化为分数表示rats(x:将实数 x 化为多项分数展开sign(x:符号函数 (Signum function。
当 x<0时, sign(x=-1;当 x=0时, sign(x=0;当 x>0时, sign(x=1。
> 小整理 :MATLAB 常用的三角函数sin(x:正弦函数cos(x:馀弦函数tan(x:正切函数asin(x:反正弦函数acos(x:反馀弦函数atan(x:反正切函数atan2(x,y:四象限的反正切函数sinh(x:超越正弦函数cosh(x:超越馀弦函数tanh(x:超越正切函数asinh(x:反超越正弦函数acosh(x:反超越馀弦函数 atanh(x:反超越正切函数其他函数:sy msum(f(x , n,a, b 求级数sum(x :sum([1:10],运行结果一定是 55sum(A 的用法,是对矩阵 A ,按列计算,得到每一列的和工具箱函数汇总Ⅰ .1统计工具箱函数表Ⅰ -1概率密度函数函数名对应分布的概率密度函数betapd f 贝塔分布的概率密度函数binopd f 二项分布的概率密度函数chi2pd f 卡方分布的概率密度函数exppd f 指数分布的概率密度函数fpd f f 分布的概率密度函数gampd f 伽玛分布的概率密度函数geopd f 几何分布的概率密度函数hygepd f 超几何分布的概率密度函数normpd f 正态(高斯分布的概率密度函数lognpd f 对数正态分布的概率密度函数nbinpd f 负二项分布的概率密度函数ncfpd f 非中心 f 分布的概率密度函数nctpd f 非中心 t 分布的概率密度函数ncx2pd f 非中心卡方分布的概率密度函数poisspd f 泊松分布的概率密度函数raylpd f 雷利分布的概率密度函数tpd f 学生氏 t 分布的概率密度函数 uni d pd f 离散均匀分布的概率密度函数unifpd f 连续均匀分布的概率密度函数weibpd f 威布尔分布的概率密度函数表Ⅰ -2 累加分布函数函数名对应分布的累加函数betacd f 贝塔分布的累加函数binocd f 二项分布的累加函数chi2cd f 卡方分布的累加函数expcd f 指数分布的累加函数fcd f f 分布的累加函数gamcd f 伽玛分布的累加函数geocd f 几何分布的累加函数hygecd f 超几何分布的累加函数logncd f 对数正态分布的累加函数 nbincd f 负二项分布的累加函数ncfcd f 非中心 f 分布的累加函数 nctcd f 非中心 t 分布的累加函数 ncx2cd f 非中心卡方分布的累加函数 normcd f 正态(高斯分布的累加函数 poisscd f 泊松分布的累加函数raylcd f 雷利分布的累加函数tcd f 学生氏 t 分布的累加函数uni d cd f 离散均匀分布的累加函数 unifcd f 连续均匀分布的累加函数 weibcd f 威布尔分布的累加函数表Ⅰ -3 累加分布函数的逆函数函数名对应分布的累加分布函数逆函数betainv 贝塔分布的累加分布函数逆函数binoinv 二项分布的累加分布函数逆函数chi2inv 卡方分布的累加分布函数逆函数expin v 指数分布的累加分布函数逆函数finv f 分布的累加分布函数逆函数gaminv 伽玛分布的累加分布函数逆函数geoinv 几何分布的累加分布函数逆函数hygeinv 超几何分布的累加分布函数逆函数logninv 对数正态分布的累加分布函数逆函数nbininv 负二项分布的累加分布函数逆函数ncfinv 非中心 f 分布的累加分布函数逆函数 nctinv 非中心 t 分布的累加分布函数逆函数 ncx2inv 非中心卡方分布的累加分布函数逆函数 icd fnorminv 正态(高斯分布的累加分布函数逆函数poissinv 泊松分布的累加分布函数逆函数raylinv 雷利分布的累加分布函数逆函数tinv 学生氏 t 分布的累加分布函数逆函数uni d inv 离散均匀分布的累加分布函数逆函数 unifin v 连续均匀分布的累加分布函数逆函数 weibin v 威布尔分布的累加分布函数逆函数表Ⅰ -4 随机数生成器函数函数对应分布的随机数生成器betarnd 贝塔分布的随机数生成器binornd 二项分布的随机数生成器chi2rnd 卡方分布的随机数生成器exprnd 指数分布的随机数生成器frnd f分布的随机数生成器gamrnd 伽玛分布的随机数生成器geornd 几何分布的随机数生成器hygernd 超几何分布的随机数生成器 lognrnd 对数正态分布的随机数生成器nbinrnd 负二项分布的随机数生成器 ncfrnd 非中心 f 分布的随机数生成器 nctrnd 非中心 t 分布的随机数生成器 ncx2rnd 非中心卡方分布的随机数生成器normrnd 正态(高斯分布的随机数生成器poissrnd 泊松分布的随机数生成器raylrnd 瑞利分布的随机数生成器trnd 学生氏 t 分布的随机数生成器uni d rnd 离散均匀分布的随机数生成器 unifrnd 连续均匀分布的随机数生成器weibrnd 威布尔分布的随机数生成器表Ⅰ -5 分布函数的统计量函数函数名对应分布的统计量betastat 贝塔分布函数的统计量binostat 二项分布函数的统计量chi2stat 卡方分布函数的统计量expstat 指数分布函数的统计量fstat f 分布函数的统计量gamstat 伽玛分布函数的统计量geostat 几何分布函数的统计量hygestat 超几何分布函数的统计量lognstat 对数正态分布函数的统计量 nbinstat 负二项分布函数的统计量ncfstat 非中心 f 分布函数的统计量nctstat 非中心 t 分布函数的统计量ncx2stat 非中心卡方分布函数的统计量 normstat 正态(高斯分布函数的统计量poisstat 泊松分布函数的统计量续表函数名对应分布的统计量raylstat 瑞利分布函数的统计量tstat 学生氏 t 分布函数的统计量uni d stat 离散均匀分布函数的统计量 unifstat 连续均匀分布函数的统计量weibstat 威布尔分布函数的统计量表Ⅰ -6 参数估计函数函数名对应分布的参数估计betafit 贝塔分布的参数估计betalike 贝塔对数似然函数的参数估计 binofit 二项分布的参数估计expfit 指数分布的参数估计gamfit 伽玛分布的参数估计gamlike 伽玛似然函数的参数估计mle 极大似然估计的参数估计normlike 正态对数似然函数的参数估计 normfit 正态分布的参数估计poissfit 泊松分布的参数估计unifit 均匀分布的参数估计weibfit 威布尔分布的参数估计weiblike 威布尔对数似然函数的参数估计表Ⅰ -7统计量描述函数函数描述bootstrap 任何函数的自助统计量cov 协方差crosstab 列联表geomean 几何均值grpstats 分组统计量har mmean 调和均值iqr 内四分极值kurtosis 峰度mad 中值绝对差mean 均值med ian 中值moment 样本模量nanmax 包含缺失值的样本的最大值续表函数描述Nanmean 包含缺失值的样本的均值nanmed ian 包含缺失值的样本的中值nanmin 包含缺失值的样本的最小值 nanstd 包含缺失值的样本的标准差 nansum 包含缺失值的样本的和 prctile 百分位数range 极值sk ewness 偏度std 标准差tabulate 频数表trimmean 截尾均值var 方差表Ⅰ -8 统计图形函数函数描述cd fplot 指数累加分布函数图errorbar 误差条图fsurfht 函数的交互等值线图gline 画线gname 交互标注图中的点gpl otmatrix 散点图矩阵gscatter 由第三个变量分组的两个变量的散点图lsline 在散点图中添加最小二乘拟合线 normplot 正态概率图pareto 帕累托图qqplot Q-Q 图rcoplot 残差个案次序图refcurve 参考多项式曲线refline 参考线surfht 数据网格的交互等值线图weibp lot 威布尔图表Ⅰ -9 统计过程控制函数函数描述capable 性能指标capaplot 性能图ewmaplot 指数加权移动平均图续表函数描述histfit 添加正态曲线的直方图normspec 在指定的区间上绘正态密度schart S图xbarplot x 条图表Ⅰ -10 聚类分析函数函数描述cluster 根据 lin kage 函数的输出创建聚类 cluster d ata 根据给定数据创建聚类cophenet Cophenet相关系数dend rogram 创建冰柱图inconsistent 聚类树的不连续值linkage 系统聚类信息pd ist 观测量之间的配对距离 squareform 距离平方矩阵zscore Z分数表Ⅰ -11线性模型函数函数描述anova1单因子方差分析anova2 双因子方差分析anovan 多因子方差分析aoctool 协方差分析交互工具dummyvar 拟变量编码friedman Friedman 检验gl mfit 一般线性模型拟合kruskalwallis Kruskalwallis 检验 leverage 中心化杠杆值lscov 已知协方差矩阵的最小二乘估计 manova1 单因素多元方差分析manovacluster 多元聚类并用冰柱图表示 multcompare 多元比较多项式评价及误差区间估计polyfit 最小二乘多项式拟合polyval 多项式函数的预测值polyconf 残差个案次序图regress 多元线性回归regstats 回归统计量诊断续表函数描述Ri d ge 岭回归rstool 多维响应面可视化robustfit 稳健回归模型拟合stepwise 逐步回归x2fx 用于设计矩阵的因子设置矩阵表Ⅰ -12 非线性回归函数函数描述nlinfit 非线性最小二乘数据拟合(牛顿法 nlintool 非线性模型拟合的交互式图形工具 nlparci 参数的置信区间nlpred ci 预测值的置信区间nnls 非负最小二乘表Ⅰ -13 试验设计函数函数描述cord exch D-优化设计(列交换算法 daugment 递增 D-优化设计dcovary 固定协方差的 D-优化设计ff2n 二水平完全析因设计fracfact 二水平部分析因设计fullfact 混合水平的完全析因设计 hadamard Hadamar d 矩阵(正交数组 rowexch D-优化设计(行交换算法表Ⅰ -14 主成分分析函数函数描述barttest Barttest检验pcacov 源于协方差矩阵的主成分pcares 源于主成分的方差princomp 根据原始数据进行主成分分析表Ⅰ -15 多元统计函数函数描述classify 聚类分析mahal 马氏距离manova1 单因素多元方差分析manovacluster 多元聚类分析表Ⅰ -16 假设检验函数函数描述ranksum 秩和检验si gnrank 符号秩检验si gntest 符号检验ttest 单样本 t 检验ttest2 双样本 t 检验ztest z检验表Ⅰ -17分布检验函数函数描述jbtest 正态性的 Jar que-Bera 检验kstest 单样本K olmogorov -Smirnov 检验kstest2 双样本K olmogorov -Smirnov 检验表Ⅰ -18 非参数函数函数描述friedman Friedman 检验kruskalwallis Kruskalwallis 检验ranksum 秩和检验si gnrank 符号秩检验si gntest 符号检验表Ⅰ -19 文件输入输出函数函数描述caseread 读取个案名casewrite 写个案名到文件tblread 以表格形式读数据tblwrite 以表格形式写数据到文件td fread 从表格间隔形式的文件中读取文本或数值数据表Ⅰ -20 演示函数函数描述aoctool 协方差分析的交互式图形工具disttool 探察概率分布函数的 GUI 工具gl md emo 一般线性模型演示rand tool 随机数生成工具polytool 多项式拟合工具rsmd emo 响应拟合工具robustd emo 稳健回归拟合工具Ⅰ .2 优化工具箱函数表Ⅰ -21最小化函数表fgoalattain 多目标达到问题fminbnd 有边界的标量非线性最小化 fmincon 有约束的非线性最小化 fminimax 最大最小化fminsearch, fminunc 无约束非线性最小化 fseminf 半无限问题linprog 线性课题quad prog 二次课题表Ⅰ -22 方程求解函数表函数描述\ 线性方程求解fsolve 非线性方程求解fzero 标量非线性方程求解表Ⅰ -23 最小二乘函数表函数描述\ 线性最小二乘lsqlin 有约束线性最小二乘lsqcurvefit 非线性曲线拟合lsqnonlin 非线性最小二乘lsqnonneg 非负线性最小二乘表Ⅰ -24 实用函数表函数描述optimset 设置参数optimget 获取参数表Ⅰ -25 大型方法的演示函数表circustent 马戏团帐篷问题—二次课题molecule 用无约束非线性最小化进行分子组成求解optd eblur用有边界线性最小二乘法进行图形处理表Ⅰ -26 中型方法的演示函数表函数描述bandemo 香蕉函数的最小化dfild emo 过滤器设计的有限精度goal d emo 目标达到举例optd emo 演示过程菜单tutd emo 教程演示Ⅰ .3 样条工具箱函数表Ⅰ -27三次样条函数函数描述csapi 插值生成三次样条函数csape 生成给定约束条件下的三次样条函数csaps 平滑生成三次样条函数cscvn 生成一条内插参数的三次样条曲线getcurve 动态生成三次样条曲线表Ⅰ -28 分段多项式样条函数函数描述pplst 显示关于生成分段多项式样条曲线的 M 文件 ppmak 生成分段多项式样条函数ppual 计算在给定点处的分段多项式样条函数值表Ⅰ -29 B样条函数splst 显示生成 B 样条函数的 M 文件spmak 生成 B 样条函数spcrv 生成均匀划分的 B 样条函数spapi 插值生成 B 样条函数spap2 用最小二乘法拟合生成 B 样条函数spaps 对生成的 B 样条曲线进行光滑处理spcol 生成 B 样条函数的配置矩阵表Ⅰ -30 有理样条函数函数描述rpmak 生成有理样条函数rsmak 生成有理样条函数表Ⅰ -31操作样条函数函数描述fnval 计算在给定点处的样条函数值fmbrk 返回样条函数的某一部分(如断点或系数等fncmb 对样条函数进行算术运算fn2fm 把一种形式的样条函数转化成另一种形式的样条函数fnd er 求样条函数的微分 (即求导数fnd ir 求样条函数的方向导数fnint 求样条函数的积分fnjmp 在间断点处求函数值fnplt 画样条曲线图。
matlabplot函数详解
matlabplot函数详解plot函数是MATLAB中最重要和最常用的绘图函数之一、它可以绘制多种类型的图形，如折线图、散点图、柱状图等。
在本文中，我们将详细介绍plot函数的用法和参数，以及一些实例演示。
plot函数的一般用法为：plot(x, y, LineSpec)，其中x和y分别是要绘制的数据点的横坐标和纵坐标，LineSpec是一个可选参数，用于指定线条的样式和颜色。
1.绘制简单的折线图首先，我们来绘制一个简单的折线图，假设我们有一个数据集x和一个对应的函数y = sin(x)。
我们可以使用以下代码绘制这个折线图：x = linspace(0, 2*pi, 100); % 生成0到2π之间的100个等间距点y = sin(x); % 计算对应的sin值plot(x, y) % 绘制折线图运行以上代码，我们就能得到一个以x为横轴，以y为纵轴的折线图。
2.指定线条样式和颜色我们可以使用LineSpec参数来指定线条的样式和颜色。
LineSpec是一个由3个部分组成的字符串，分别表示线条类型、标记类型和颜色。
例如，我们可以使用红色实线和圆形标记来绘制折线图，代码如下所示：plot(x, y, 'r-o')其中，'r'表示红色，'-'表示实线，'o'表示圆形标记。
运行以上代码，我们可以得到红色实线和圆形标记的折线图。
3.绘制多条曲线plot函数可以同时绘制多条曲线。
我们只需要将不同的数据点传递给x和y，然后用逗号分隔开即可。
例如，我们可以绘制一个由两条正弦曲线构成的图形，代码如下所示：y1 = sin(x);y2 = sin(2*x);plot(x, y1, x, y2)运行以上代码，我们将得到两条正弦曲线组成的图形。
title('折线图示例')xlabel('x')ylabel('y')5.修改坐标轴范围有时候，我们希望修改坐标轴的范围，以更好地展示数据。
matlab 阶梯函数
matlab 阶梯函数阶梯函数，也被称为单位阶跃函数，是一种常见的数学函数。
它在数学和工程领域中有着广泛的应用。
阶梯函数的定义如下：当输入x小于0时，阶梯函数的值为0；当输入x大于等于0时，阶梯函数的值为1。
阶梯函数的图像呈现出一种“台阶”的形状，因此得名阶梯函数。
在Matlab中，我们可以使用函数stepfun(x,a)来定义阶梯函数。
这个函数的参数x是一个向量，表示输入的取值范围；参数a是一个数值，表示阶梯函数的值。
stepfun函数会返回一个与x相同大小的向量，其中元素的值满足阶梯函数的定义。
阶梯函数在信号处理和控制系统中有着重要的应用。
在信号处理中，阶梯函数可以用来表示离散信号的开始和结束时间点。
在控制系统中，阶梯函数可以用来描述系统的输入或输出信号。
下面我们来看一个具体的例子，来说明阶梯函数在Matlab中的应用。
假设我们要绘制一个阶梯信号，它的起始时间是0秒，结束时间是10秒。
在0秒到5秒的时间段内，信号的幅值为0；在5秒到10秒的时间段内，信号的幅值为1。
我们可以使用Matlab来实现这个功能。
我们需要定义时间范围。
在这个例子中，时间范围是从0秒到10秒，以0.1秒为步长。
我们可以使用Matlab的linspace函数来生成一个包含这个时间范围的向量。
```matlabt = linspace(0, 10, 101);```接下来，我们可以使用stepfun函数来定义阶梯信号。
在0秒到5秒的时间段内，阶梯信号的值为0；在5秒到10秒的时间段内，阶梯信号的值为1。
```matlaby = stepfun(t, 5);```我们可以使用plot函数来绘制阶梯信号的图像。
```matlabplot(t, y);```运行以上代码，我们可以得到一个阶梯信号的图像。
在0秒到5秒的时间段内，信号的幅值为0；在5秒到10秒的时间段内，信号的幅值为1。
通过这个图像，我们可以清楚地看到阶梯信号的特点。
MATLAB程序设计-关于常用绘图函数的运用方法及说明
MATLAB程序设计作业陈杰杰2013090302072014-11-3MATLAB具有强大的图形处理功能。
下面给出了3个m脚本文件，请在MA TLAB环境下运行，观察其输出。
要求根据每个m文件输出的图形（共18个），用中文翻译并解释产生每个输出图形的函数具体是什么？其功能是什么？文件1：clear all %清除工作区间所有的变量clf %清除图形窗口的内容mfilename('fullpath') %返回当前正在运行的函数所在文件的文件名（全部路径）echo on %显示M文件执行的每一条命令subplot(2,3,1) %使（2*3）幅子图中第一个子图成为当前图t = 0:0.1:10; %将以0为起点、以10为终点、以0.1为步长的一维矩阵赋值给t z = impulse(1, [1 1 1], t); %动力系统的脉冲响应数据，以时间t步长0.1为单位stairs(t(1:5:end),z(1:5:end)) %绘制阶梯状图,从第1行开始，间隔5行取1行，到最后1行为止hold on %保持当前坐标轴和图形，并接受下一次绘制plot(t,z,'r') %用红线绘制横轴为t、纵轴为z的二维函数图plot([0 t(end)], [0 0], 'k:') %用黑色虚线绘制函数图像，要求经过原点平行于横轴、取值范围为0到t的最后一个值title('Impulse Response - (STAIRS)') %将此图命名为Impulse Response - (STAIRS)（脉冲响应-（阶梯图））subplot(2,3,2) %使（2*3）幅子图中第二个子图成为当前图theta = 2*pi*(0:74)/75; %将以0为起点、以2*pi*74/75为终点、2*pi/75为步长的一维矩阵赋值给thetax = cos(theta); %计算cos(theta)的值，并赋给xy = sin(theta); %计算sin(theta)的值，并赋给yz = abs(fft(ones(10,1), 75))'; %ones(10,1)生成十行一列的全一矩阵；fft(ones(10,1), 75)进行快速傅里叶变换；z = abs(fft(ones(10,1), 75))'取幅值并转置stem3(x, y, z) %绘制三维杆状图title('Polar FFT - (STEM3)') %将此图命名为Polar FFT - (STEM3)（极坐标下快速傅里叶变换-（三维针状图））subplot(2,3,3) %使（2*3）幅子图中第二个子图成为当前图[X,Y,Z] = peaks(-2:0.25:2); %产生-2为起点、2为终点、0.25为步长的guassian分布矩阵，返回峰函数的三个坐标轴空间上的数值，X表示在x轴，Y表示在y轴，Z表示在z轴，这样每个点就对应一个（X，Y，）[U,V] = gradient(Z, 0.25); %返回二维数值梯度的U、V部分，这里的0.25指定了沿着梯度的方向取点的间隔为0.25contour(X,Y,Z,10); %绘制矩阵Z的等高线，绘制的等高线被限定在由X、Y指定的区域内，等高线条数为10hold on %保持当前坐标轴和图形，并接受下一次绘制quiver(X,Y,U,V); %使用箭头来直观的显示矢量场，该调用格式表示通过在(X, Y)指定的位置绘制小箭头来表示以该点为起点的向量(U,V)title('Surface Gradient - (CONTOUR & QUIVER)') %将此图命名为Surface Gradient - (CONTOUR & QUIVER)（表面梯度-（等高线图和矢量场图））theta = 0:0.1:4*pi; %将以0为起点、以4*pi为终点、0.1为步长的一维矩阵赋值给theta[x,y] = pol2cart(theta(1:5:end), theta(1:5:end)); %把极坐标(theta(1:5:end), theta(1:5:end))转换为对应的二维笛卡尔坐标(x,y),theta(1:5:end)表示从第一行到最后一行，每五行取一行subplot(2,3,4) %使（2*3）幅子图中第四个子图成为当前图polar(theta,theta) %绘制极坐标图像，第一个theta是用弧度制表示的角度，第二个theta是对应的半径axis([-13 13 -12.5 14.5]) %横坐标范围为-13到13，纵坐标范围为-12.5到14.5title('Spiral Plot - (POLAR)') %将此图命名为Spiral Plot - (POLAR)（螺旋图-极坐标图）subplot(2,3,5) %使（2*3）幅子图中第五个子图成为当前图compass(x,y) %绘制罗盘图axis([-13 13 -12.5 14.5]) %横坐标范围为-13到13，纵坐标范围为-12.5到14.5title('Direction Vectors - (COMPASS)') %将此图命名为Direction Vectors - (COMPASS)（方向矢量-罗盘图）subplot(2,3,6) %使（2*3）幅子图中第六个子图成为当前图feather(x(1:19),y(1:19)) %绘制羽状图，其中x、y表示一组向量，x是向量的横坐标（x分量），y是向量的纵坐标（y分量）。
matlab大m法分段函数
matlab大m法分段函数MATLAB大M法是解决非线性规划问题的一种常用方法，也称为“大M惩罚因子法”或“人工变量法”。
该方法的基本思想是通过引入人工变量和一个大的正的M值，将原问题转化为一个辅助问题，然后通过寻找辅助问题的最优解来近似原问题的最优解。
具体来说，MATLAB大M法可以用于求解如下形式的非线性规划问题：最小化f(x)约束g(x)≤0h(x)=0lb ≤ x ≤ ub其中，f(x)为目标函数，g(x)≤0为不等式约束条件，h(x)=0为等式约束条件，lb和ub为变量x的下界和上界。
MATLAB大M法的基本步骤如下：1. 将目标函数和约束条件转化为标准形式：将不等式约束条件g(x)≤0和变量x的上下界lb≤x≤ub转化为等式约束条件：g(x)+s=0，其中s为松弛变量；lb - x = 0，其中x为原变量，lb为下界；x - ub = 0，其中x为原变量，ub为上界。
2.引入人工变量和大M值：对于每个不等式约束条件g(x)≤0，引入人工变量a和大的正的M值，得到约束条件：g(x)+s-Ma≤0；a≥0。
3.构建辅助问题：将目标函数加上大M值乘以人工变量，构造辅助问题：最小化f(x)+Ma4.求解辅助问题：使用MATLAB等工具求解辅助问题，得到辅助问题的最优解x*和人工变量的最优解a*。
5.判断辅助问题的最优解：若辅助问题的最优解中a*>0，则说明原问题无可行解，结束算法；否则，继续进行下一步。
6.去除人工变量：在原问题中去除人工变量a，即将约束条件g(x)+s-Ma≤0中的人工变量a去除。
7.求解原问题：使用MATLAB等工具求解去除人工变量后的原问题，得到原问题的最优解x*。
通过以上步骤，可以利用MATLAB大M法求解非线性规划问题。
需要注意的是，在设置大M值时需要选择一个足够大的值以确保人工变量a总是为0，同时又不至于导致数值问题或算法收敛困难。
另外，该方法适用于一般的非线性规划问题，但对于特定的问题可能存在更有效的求解方法。
Matlab中常见数学函数的使用
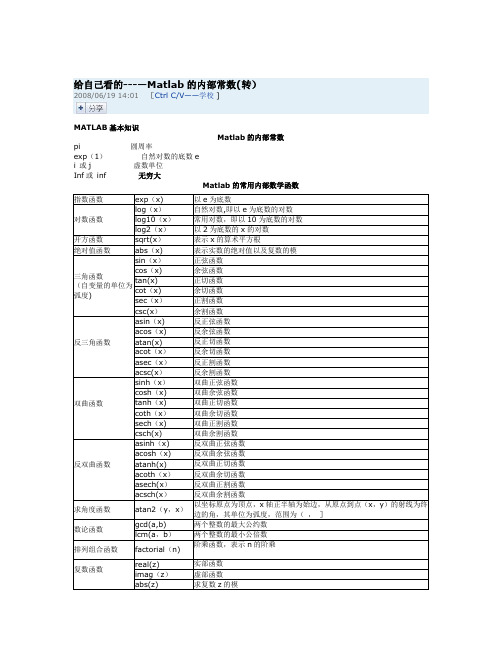
给自己看的---—Matlab的内部常数(转）2008/06/19 14:01［Ctrl C/V——学校 ]MATLAB基本知识Matlab的内部常数pi 圆周率exp（1）自然对数的底数ei 或j 虚数单位Inf或inf 无穷大Matlab的常用内部数学函数我们也可在matlab中调用maple的命令进行多项式的运算,调用格式如下:maple（’maple中多项式的运算命令')如何用matlab进行分式运算发现matlab只有一条处理分式问题的命令，其使用格式如下：[n，d］=numden（f）把符号表达式f化简为有理形式，其中分子和分母的系数为整数且分子分母不含公约项，返回结果n为分子，d为分母。
注意：f必须为符号表达式不过我们可以调用maple的命令，调用方法如下：maple（'denom（f）’）提取分式f的分母maple（’numer（f）’）提取分式f的分子maple(’normal（f）’ ）把分式f的分子与分母约分成最简形式maple(’expand（f）’）把分式f的分子展开,分母不变且被看成单项.maple（’factor（f)'）把分式f的分母和分子因式分解,并进行约分。
如何用Matlab进行因式分解syms 表达式中包含的变量factor(表达式）如何用Matlab展开syms 表达式中包含的变量expand(表达式）如何用Matlab进行化简syms 表达式中包含的变量simplify（表达式)如何用Matlab合并同类项syms 表达式中包含的变量collect（表达式,指定的变量）如何用Matlab进行数学式的转换调用Maple中数学式的转换命令，调用格式如下:maple（‘Maple的数学式转换命令’）即：maple(‘convert(表达式，form)'）将表达式转换成form的表示方式maple(‘convert(表达式,form, x)’）指定变量为x，将依赖于变量x的函数转换成form的表示方式(此指令仅对form为exp与sincos的转换式有用）如何用Matlab进行变量替换syms 表达式和代换式中包含的所有变量subs(表达式,要替换的变量或式子，代换式）如何用matlab进行复数运算a+b*i 或 a +b＊j表示复数a+bi 或a+bjreal(z）求复数z的实部imag（z）求复数z的虚部abs（z）求复数z的模angle（z）求复数z的辐角，conj（z）求复数z的共轭复数exp（z）复数的指数函数,表示e^z如何在matlab中表示集合[a, b, c,…］表示由a，b, c,…组成的集合（注意：元素之间也可用空格隔开）unique（A) 表示集合A的最小等效集合（每个元素只出现一次）也可调用maple的命令，格式如下:maple（’{a, b，c，…}’)表示由a，b, c,…组成的集合下列命令可以生成特殊的集合：maple（‘｛seq(f(i),i=n。
matlab平移函数
matlab平移函数Matlab是一种非常强大的数学软件，它有着丰富的函数库可以完成各种各样的数学运算和图像处理。
其中一个非常常用的函数就是平移函数，在图像处理中经常被用到。
本文将介绍Matlab中的平移函数及其用法。
平移函数是一种对图像进行平移操作的函数，可以将图像在水平和垂直方向上进行平移。
在Matlab中，平移函数的基本语法如下：```matlabB = imtranslate(A, tform)```其中，A表示原始图像，tform表示平移的参数，B表示平移后的图像。
在平移函数中，tform参数可以是一个二维平移向量或一个仿射变换矩阵。
二维平移向量表示图像在水平和垂直方向上的平移距离，可以用[x,y]表示。
仿射变换矩阵是一个2x3的矩阵，表示了图像在平移、旋转和缩放等操作下的变化。
使用平移函数进行图像平移非常简单。
下面是一个示例：```matlabA = imread('image.jpg'); % 读取原始图像tform = affine2d([1 0 50; 0 1 100; 0 0 1]); % 创建一个平移矩阵，向右平移50个像素，向下平移100个像素B = imtranslate(A, tform); % 对图像进行平移操作imshow(B); % 显示平移后的图像```上述示例代码中，首先使用imread函数读取了一张原始图像，然后通过affine2d函数创建了一个平移矩阵tform，该矩阵表示了图像向右平移50个像素，向下平移100个像素。
最后，使用imtranslate函数对图像进行平移操作，并使用imshow函数显示平移后的图像。
除了平移矩阵，平移函数还可以接受一个二维平移向量作为参数。
下面是一个使用二维平移向量进行图像平移的示例：```matlabA = imread('image.jpg'); % 读取原始图像tform = [50 100]; % 创建一个二维平移向量，向右平移50个像素，向下平移100个像素B = imtranslate(A, tform); % 对图像进行平移操作imshow(B); % 显示平移后的图像```上述示例代码中，创建了一个二维平移向量tform，该向量表示了图像向右平移50个像素，向下平移100个像素。
利用Matlab绘制各类特殊图形的实例代码
利⽤Matlab绘制各类特殊图形的实例代码Matlab绘图介绍强⼤的绘图功能是Matlab的特点之⼀，Matlab提供了⼀系列的绘图函数，⽤户不需要过多的考虑绘图的细节，只需要给出⼀些基本参数就能得到所需图形，这类函数称为⾼层绘图函数。
此外，Matlab还提供了直接对图形句柄进⾏操作的低层绘图操作。
这类操作将图形的每个图形元素（如坐标轴、曲线、⽂字等）看做⼀个独⽴的对象，系统给每个对象分配⼀个句柄，可以通过句柄对该图形元素进⾏操作，⽽不影响其他部分。
Matlab绘制特殊图形1. 绘制极坐标图说明：使⽤polarplot函数绘制极坐标图，每组数据表⽰⼀条闭合曲线，共有20条曲线构成20条封闭同⼼曲线。
t = linspace(0,2*pi,500);y = 1+0.3*sin(20*t)+0.1*sin(30*t)+0.1*sin(40*t);polarplot(t,y,t,1.1*y,t,1.2*y,t,1.3*y,t,1.4*y,t,1.5*y,t,1.6*y,t,1.7*y,t,1.8*y,t,1.9*y,...t,2.0*y,t,2.1*y,t,2.2*y,t,2.3*y,t,2.4*y,t,2.5*y,t,2.6*y,t,2.7*y,t,2.8*y,t,2.9*y,'linewidth',1.5);2. 单条曲线绘制分段函数（反⽐例函数y=1/x）说明：反⽐例函数在x接近于0时，趋近于奇异（1/0 趋近于⽆穷⼤），使⽤nan⾮数对图形进⾏镂空，可以实现⼀条曲线绘制y=1/x的整个定义域。
x = linspace(-3,3,500);f = @(x) 1./x;y = f(x);for ii = 1:length(x)if abs(x(ii))<0.03x(ii) = nan;y(ii) = nan;endendplot(x,y)legend('y=1/x')3. 正⽅体内绘制随机分布的颜⾊⽚图说明：使⽤plot3绘制正⽅体12条边，使⽤fill3函数绘制颜⾊⽚，颜⾊⽚位置和填充颜⾊随机⽣成。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《数字信号处理》（一）实验目的使用stem绘图函数分别画出离散时间信号在指定范围内的图形。
画图时使用xlabel,ylabel,title,legend等函数进行注释。
复习MATLAB的基本应用，如：函数的定义、画图……并巩固理论知识中的多种离散时间信号及其图形，以及延迟与翻褶的函数变换等。
（二）程序的运行与截图1)用stem绘制单位阶跃序列u（n）clear all;close all;clc;%清除所有变量n=0:50;%取值范围y=(n>=0);%n>=0,y=1;n<0,y=0stem(n,y);%显示出当0<=n<=50 时，函数u(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y=u(n)');%对纵轴进行注释title('y=u(n)的图形');%对图像的标题进行注释legend('y=u(n)',2);%对图中曲线进行注释，标注在第二象限2)用stem绘制单位抽样（冲激）序列δ（n）clear all;close all;clc; %清除所有变量n=0:50; %取值范围y=(n==0);%n=0,y=1;n!=0,y=1stem(n,y);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y=δ(n)');%对纵轴进行注释title('y=δ(n)的图形');%对图像的标题进行注释legend('y=δ(n)',2);%对图中曲线进行注释，标注在第二象限3）用stem绘制矩形序列Rn（n）clear all;close all;clc; %清除所有变量n=0:50; %取值范围R10=((n>=0)&(n-9)<=0);%0<=n<=10,y=1;n>10,y=0stem(n,R10);%显示出当0<=n<=50 时，函数Rn（n）的取值范围xlabel('n');%对横轴进行注释ylabel(' y=R10（n）');%对纵轴进行注释title('y=R10（n）的图形');%对图像的标题进行注释legend('y=R10（n）',2);%对图中曲线进行注释，标注在第二象限4）用stem绘制nu(n)序列clear all;close all;clc; %清除所有变量n=0:50; %取值范围y=n;%函数关系stem(n,y);%显示出当0<=n<=50 时，函数nu(n)的取值xlabel('n');%对横轴进行注释ylabel('y=nu(n)');%对纵轴进行注释title('y=nu(n)的图形');%对图像的标题进行注释legend('y=nu(n)',2);%对图中曲线进行注释，标注在第二象限5)用stem绘制1.1^n*u（n）序列clear all;close all;clc; %清除所有变量n=0:50; %取值范围y=1.1.^n;%函数关系stem(n,y);%显示出当0<=n<=50 时，函数1.1^n*u（n）的取值范围xlabel('n');%对横轴进行注释ylabel('y=1.1.^n u(n)');%对纵轴进行注释title('y=1.1.^nu(n)的图形');%对图像的标题进行注释legend(‘y=1.1.^nu(n)’,2);%对图中曲线进行注释，标注在第二象限6）用stem绘制sin(0.1*n)序列clear all;close all;clc;%清除所有变量n=0:100;%取值范围y=sin(0.1*n);%函数关系stem(n,y); %显示出当0<=n<=100 时，函数sin(0.1*n)的取值范围xlabel('n');%对横轴进行注释ylabel('y=sin(0.1*n)');%对纵轴进行注释title('y=sin(0.1*n)的图形');%对图像的标题进行注释legend('y=sin(0.1*n)',2);%对图中曲线进行注释，标注在第二象限7）用stem绘制sin(0.1*pi*n)序列clear all;close all;clc;%清除所有变量n=0:100;%取值范围y=sin(0.1*pi*n);%函数关系stem(n,y);%显示出当0<=n<=100 时，函数sin(0.1*pi*n)的取值范围xlabel('n');%对横轴进行注释ylabel('y=sin(0.1*pi*n)');%对纵轴进行注释title('y=sin(0.1*pi*n)的图形');%对图像的标题进行注释legend('y=sin(0.1*pi*n)',2);%对图中曲线进行注释，标注在第二象限由此题结果得到的结论：（1）如实验6和实验7可以看出：当采样点间隔相同（如图都为1时），两者的周期不同；（2）当函数的角频率由0.1变为0.1*π时，包络的形状压缩为原来的1/π，反之则拉伸为原来的π倍；（3）y=sin(0.1*n)的周期并不是包络的周期；而y=sin(0.1*π*n)则是周期函数，周期为20。
8)分段函数x(m)1）用stem绘图函数画出x(n)：clear all;close all;clc; %清除所有变量n=-10:10; %取值范围y=(2*n+10).*(-10<=n&n<=-1)+6.*(0<=n&n<=10) stem(n,y);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y=x(n)');%对纵轴进行注释title('y=x(n)的图形');%对图像的标题进行注释legend('y=x(n)',2);%对图中曲线进行注释，标注在第二象限程序运行结果图结果分析：当-10<=n<=-1时，y=2*n+10的图像如图所示；当0<=n<=10时，y=6；其它的为0。
令)1(2)(1-=n x n y ，画出)(1n y 的图形，并说明由此题结果得到什么结论？2）用stem 绘图函数画出y1(n)：clear all;close all;clc; %清除所有变量n=-10:10; %取值范围y1=2*(2*(n-1)+10).*(-10<=(n-1)&(n-1)<=-1)+6.*(0<=(n-1)&(n-1)<=10)stem(n,y1);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y1=2*x(n-1)');%对纵轴进行注释title(' 2*x(n-1)');%对图像的标题进行注释legend('y1=2*x(n-1)',2);%对图中曲线进行注释，标注在第二象限结论：在-10<=n<=10相同的范围内，本题是将y=x(n)的图象右移一个单位，变为y=x(n-1)，再把幅度变为原来的2倍y=2*x(n-1)。
图形基本没有变化，只是x,y轴的坐标变为：x 轴坐标向左平移一个单位，y轴坐标扩大一倍。
令)2(3)(2+=n x n y ，画出)(2n y 的图形，并说明由此题结果得到什么结论？3） 用stem 绘图函数画y2(n)：clear all;close all;clc; %清除所有变量n=-10:10; %取值范围y2=3*((2*(n+2)+10).*(-10<=(n+2)&(n+2)<=-1)+6.*(0<=(n+2)&(n+2)<=10));stem(n,y2);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y2=3*x(n+2)');%对纵轴进行注释title('3*x(n+2)');%对图像的标题进行注释legend('y2=3*x(n+2)',2);%对图中曲线进行注释，标注在第二象限结论：在-10<=n<=10相同的范围内，本题是将y=x(n)的图象左移两个单位，即y=x(n+2)，再把幅度变为原来的3倍即y=3*x(n+2)。
可容易看出图形的大体形状没有变化，只是x,y轴的坐标变为：x轴坐标向右平移2个单位，y轴坐标扩大为原来3倍。
将)(n x 延迟4个单位再以y 轴翻转，得到)(3n y ，画出)(3n y 的图形，并说明由此题结果得到什么结论？ 4） 用stem 绘图函数画y3(n)：clear all;close all;clc; %清除所有变量n=-10:10; %取值范围y3=(2*(-(n+4))+10).*(-10<=(-(n+4))&(-(n+4))<=-1)+6.*(0<=(-(n+4))&(-(n+4))<=10);stem(n,y3);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y3=x(-(n+4))');%对纵轴进行注释title('x(-(n+4))');%对图像的标题进行注释legend('y3=x(-(n+4))',2);%对图中曲线进行注释，标注在第二象限结论：本题是先将y=x(n) 左延迟4个单位变为y=x(n+4)，然后再把（n+4）当做一个整体以y轴翻转，即在（n+4）前加一个负号，变为y=x(-（n+4）)。
可以看出图形大体形状没有发生变化，只是x,y轴的坐标发生变化：x轴坐标右移4个单位然后再以y轴翻转，y轴坐标没有改变。
将)(n x 以y 轴翻转再延迟4个单位再得到)(4n y ，画出)(4n y 的图形，并说明由此题结果得到什么结论？5） 用stem 绘图函数画y4(n)：clear all;close all;clc; %清除所有变量n=-10:10; %取值范围y4=(2*(-n+4)+10).*(-10<=(-n+4)&(-n+4)<=-1)+6.*(0<=(-n+4)&(-n+4)<=10); stem(n,y4);%显示出当0<=n<=50 时，函数δ(n)的取值范围xlabel('n');%对横轴进行注释ylabel('y4=x(-n+4)');%对纵轴进行注释title('x(-n+4)');%对图像的标题进行注释legend('y4=x(-n+4)',2);%对图中曲线进行注释，标注在第二象限结论：本题先将y=x(n)右延迟4个单位，然后将n-4作为一个整体以y轴翻转，即将（n-4）变为（4-n）,则变成变为x(-n+4)。