勾股
常用勾股数表

常用勾股数表什么是勾股数?勾股数又称毕达哥拉斯数,是指满足勾股定理的三个正整数a、b和c的组合。
根据勾股定理,当a、b和c满足以下关系时,它们就是一个勾股数:a² + b² = c²其中,c为斜边的长度,而a和b为直角边的长度。
例如,3、4和5就是一个常见的勾股数,因为3² + 4² = 5²。
常见的勾股数在学习和应用数学中,我们经常会遇到一些常见的勾股数。
下面是一些常见的勾股数及其对应的直角边长度:•3、4、5•5、12、13•8、15、17•7、24、25•9、40、41这些常见的勾股数在实际生活中有广泛的应用,特别是在几何学和物理学领域。
勾股数组成规律除了上述列举的常见勾股数之外,还存在其他很多不同组合的勾股数。
通过观察这些组合可以发现一些规律。
首先,我们可以发现勾股数中的直角边长度一般为奇数和偶数的组合。
例如,3、4、5中有一个奇数(3)和一个偶数(4)。
其次,两个直角边的长度之间一般存在一定的倍数关系。
例如,3、4、5中每个数都可以乘以2得到6、8和10,也满足勾股定理。
此外,我们还可以通过一些公式来生成勾股数。
例如,欧拉公式给出了生成无穷多个勾股数的方法:a = m² - n²b = 2mnc = m² + n²其中m和n为任意正整数,并且m > n。
勾股数在实际应用中的意义勾股数在几何学和物理学等领域有着广泛的应用。
下面列举了一些使用勾股数的实际应用场景:1. 测量距离在测量距离时,常常会使用勾股定理来计算两点之间的直线距离。
根据两点坐标计算它们之间的距离时,可以利用勾股定理快速求解。
2. 建筑设计在建筑设计中,常常需要考虑角度和长度之间的关系。
勾股数可以帮助建筑师计算角度和长度之间的关系,从而保证建筑的结构稳定。
3. 电子工程在电子工程中,勾股数被广泛应用于电路设计和信号处理。
勾股数

1. 下列几组数能否作为直角三角形的三边长? 下列几组数能否作为直角三角形的三边长? 说说你的理由. 说说你的理由
(1)9,12,15 ( √ ) ) , , (2)15,36,39 ( √ ) ) , , (3)12,18,22 ( × ) ) , ,
做一做: 做一做:
李叔叔想要检测雕塑底座正 面的AD边和 边和BC边是否分别 面的 边和 边是否分别 垂直于底边AB,但他随身只 垂直于底边 , 带了卷尺, 带了卷尺,
【例 4】在△ABC中,a=15, b=17, 】 中 c=8,求此三角形的面积。 求此三角形的面积 解:在△ABC中 中 C ∵a2+c2= 152+ 82=225+64=289 =289 ∴a2+c2=b2 ∴△ABC是Rt三角形 是 三角形 ∠B=900 ∴S△ABC=15×8÷2=60 × ÷ b2=172
52 =25
3 C 5
∴32+42=52 ∴∠C=900
4
∴这是个Rt三角形 这是个 三角形
例2:一个零件的形状如图所示 按 :一个零件的形状如图所示,按 规定这个零件中∠ 和 都应为直角,工人师 规定这个零件中∠A和∠DBC都应为直角 工人师 都应为直角 傅量得这个零件各边的尺寸如图所示,你说这个零 傅量得这个零件各边的尺寸如图所示 你说这个零 件符合要求吗? 件符合要求吗 解:在△ABD中 中 解:在△BCD中 中 13
4.如图,有一个长方体的长、宽、高分别是6、4、4, 如图,有一个长方体的长、 如图 高分别是 、 、 , 在底面A处有一只蚂蚁 它想吃到长方体上面与A 处有一只蚂蚁, 在底面 处有一只蚂蚁,它想吃到长方体上面与 相对的B点处的食物 点处的食物, 相对的 点处的食物,需要爬行的最短路程是 10 ________.
关于“勾股定理”的60种证法
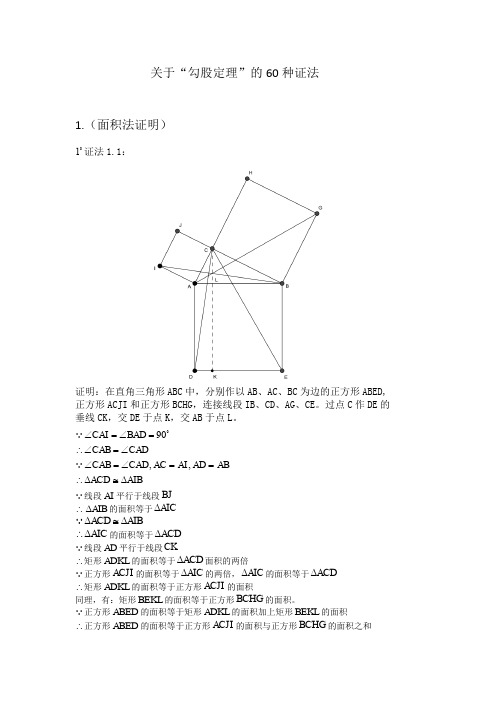
关于“勾股定理”的60种证法1.(面积法证明)1 证法1.1:证明:在直角三角形ABC 中,分别作以AB 、AC 、BC 为边的正方形ABED,正方形ACJI 和正方形BCHG ,连接线段IB 、CD 、AG 、CE 。
过点C 作DE 的垂线CK ,交DE 于点K ,交AB 于点L 。
90,,CAI BAD CAB CADCAB CAD AC AI AD AB ACD AIB∠=∠=∴∠=∠∠=∠==∴∆≅∆线段AI 平行于线段BJ ∴AIB ∆的面积等于AIC ∆ACD AIB ∆≅∆AIC ∴∆的面积等于ACD ∆ 线段AD 平行于线段CK∴矩形ADKL 的面积等于ACD ∆面积的两倍正方形ACJI 的面积等于AIC ∆的两倍,AIC ∆的面积等于ACD ∆ ∴矩形ADKL 的面积等于正方形ACJI 的面积同理,有:矩形BEKL 的面积等于正方形BCHG 的面积。
正方形ABED 的面积等于矩形ADKL 的面积加上矩形BEKL 的面积∴正方形ABED 的面积等于正方形ACJI 的面积与正方形BCHG 的面积之和即222AC BC AB +=.Remark :此为欧几里得(Euclid,约公元前330年-公元前275年)在几何原本中的证明方法。
2 证法1.2:证明:在上图中,整个正方形的面积为2()a b +,又等于四个直角三角形的面积加上里面的小正方形的面积,等于22ab c +。
因此,22()2a b ab c +=+,此即:222a b c +=。
Remark :此证法据Bretschneider 和Hankel 的推测,为毕达哥拉斯(Pythagoras ,约公元前580~约前500)的证法。
3 证法1.3(总统证明法)如图,三角形ABC 与三角形BDE 完全相等,易证三角形ABE 为等腰直角三角形。
整个直角梯形ACDE 的面积为21()2a b +,又等于两个直角三角形的面积加上等腰直角三角形ABE 的面积,等于212ab c +,故2211()22a b ab c +=+。
勾股定理方法大全

勾股定理方法大全勾股定理是数学中的重要定理之一,它是描述直角三角形边长关系的定理。
下面将介绍一些常见的求解直角三角形边长的方法,使用勾股定理。
1.利用勾股定理求直角三角形的斜边长给定直角三角形的两条直角边a和b,求斜边c的长度,可以使用勾股定理c^2=a^2+b^2进行求解。
首先将a和b的值代入公式,然后进行开方运算,即可得到c的长度。
2.利用勾股定理判断三条边是否构成直角三角形给定三条边长a、b和c,判断它们是否能够构成直角三角形,可以利用勾股定理判断。
如果c^2=a^2+b^2成立,则说明三条边构成直角三角形;反之,如果该等式不成立,则说明不构成直角三角形。
3.利用勾股定理求解直角三角形的未知边已知直角三角形的一条直角边a和斜边c的长度,求另一条直角边b的长度。
可以利用勾股定理b^2=c^2-a^2进行求解。
首先将c和a的值代入公式,然后进行开方运算,即可得到b的长度。
4.利用勾股定理判断三角形的形状给定一个三角形的边长a、b和c,判断该三角形是锐角三角形、直角三角形还是钝角三角形。
可以利用勾股定理进行判断,如果c^2<a^2+b^2,则为锐角三角形;如果c^2=a^2+b^2,则为直角三角形;如果c^2>a^2+b^2,则为钝角三角形。
5.利用勾股定理求解实际问题勾股定理不仅可以用于求解理论数学问题,也可以应用于求解实际问题。
例如,给定一个直角梯形的底边长a和顶边长b,以及斜边c的长度,可以利用勾股定理求解梯形的高h。
首先利用勾股定理求解出两条腰长的平方和,即(a^2+h^2)+(b^2+h^2)=c^2;然后进行整理和求解,即可得到梯形的高h的长度。
6.利用勾股定理计算直角三角形的面积给定直角三角形的两条直角边a和b,可以利用勾股定理求解三角形的斜边c的长度。
然后利用三角形面积公式S=1/2*a*b,即可得到三角形的面积。
勾股定理

勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方。
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉斯定理”或者“百牛定理“(毕达哥拉斯发现了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”),法国、比利时人又称这个定理为“驴桥定理”。
他们发现勾股定理的时间都比我国晚,我国是最早发现这一几何宝藏的国家。
目前初二学生学,教材的证明方法采用赵爽弦图。
勾股定理是一个基本的几何定理,它是用代数思想解决集几何问题的最重要的工具之一,是数形结合的纽带之一。
勾股定理指出:直角三角形两直角边(即“勾”“股”短的为勾,长的为股)边长平方和等于斜边(即“弦”)边长的平方。
也就是说,设直角三角形两直角边为a和b,斜边为c,那么a的平方+b的平方=c的平方a^2+b^2=c^2周髀算经》记载了勾股定理的公式与证明,相传是在商代由商高发现,故又有称之为商高定理;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,又给出了另外一个证明[1]。
法国和比利时称为驴桥定理,埃及称为埃及三角形。
我国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦。
我国是发现和研究勾股定理最古老的国家之一。
我国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理。
在公元前1000多年,据记载,商高(约公元前1120年)答周公曰“故折矩,以为句广三,股修四,径隅五。
既方之,外半其一矩,环而共盘,得成三四五。
两矩共长二十有五,是谓积矩。
”因此,勾股定理在我国又称“商高定理”。
在公元前7至6世纪一中国学者陈子,曾经给出过任意直角三角形的三边关系即“以日下为勾,日高为股,勾、股各乘并开方除之得邪至日。
在法国和比利时,勾股定理又叫“驴桥定理”。
还有的国家称勾股定理为“平方定理”。
西欧对此定理戏称为“笨蛋的难关(Asses' Bridge)”,照原文直译,就是“驴桥”,因此,我国也有将此命题译作“驴桥定理”的。
勾股定理的方程式

勾股定理的方程式勾股定理是一种数学定理,用于计算直角三角形的边长关系。
它描述了直角三角形中,直角边的平方等于两个其他边的平方和。
勾股定理的方程式可以表示为:a²+b²=c²。
在这个方程式中,a和b代表直角三角形的两条边,c代表斜边。
根据勾股定理,当直角三角形的两条直角边的长度分别为a和b时,斜边的长度为c。
勾股定理可以用来解决各种与直角三角形相关的问题,比如求解未知边长、计算角度等。
通过应用勾股定理,我们可以准确地计算出直角三角形的各个边长,从而解决与直角三角形相关的数学和物理问题。
勾股定理的原理可以通过几何图形来理解。
假设有一个直角三角形ABC,其中∠C是直角。
我们可以将三角形ABC放在一个正方形格子中,使得直角顶点C位于格子的一个角落,直角边a和b分别与格子的两条边平行。
然后,我们可以用格子的单位长度来表示直角边a和b的长度,即a和b的长度为整数个格子单位。
我们可以将直角边a和b的长度分别表示为a个和b个格子单位。
根据直角三角形的性质,我们可以将斜边c的长度表示为a个格子单位加上b个格子单位。
当我们把a个格子单位和b个格子单位的长度相加时,正好可以得到斜边c的长度。
这就是勾股定理的基本原理。
通过勾股定理,我们可以解决各种与直角三角形相关的问题。
比如,当我们已知直角三角形的两条边a和b的长度时,可以通过勾股定理求解斜边c的长度。
勾股定理还可以用来计算直角三角形的角度。
通过知道三角形的两个边长,我们可以计算出与这两条边相关的角度。
这在导航和测量等领域中非常有用。
总结起来,勾股定理是一种用于计算直角三角形边长关系的数学定理。
它通过描述直角三角形的两条直角边的平方和等于斜边的平方,提供了一种解决与直角三角形相关问题的方法。
勾股定理在数学和物理等领域有着广泛的应用,可以帮助我们解决各种与直角三角形相关的计算和测量问题。
勾股定理

勾股定理勾股定理又叫商高定理、毕氏定理,或称毕达哥拉斯定理(Pythagor as Theorem).在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和。
如果直角三角形两直角边分别为a、b,斜边为c,那么a²+b²=c²据考证,人类对这条定理的认识,少说也超过 4000 年!中国最早的一部数学著作——《周髀算经》的第一章,就有这条定理的相关内容:周公问:“窃闻乎大夫善数也,请问古者包牺立周天历度。
夫天不可阶而升,地不可得尺寸而度,请问数安从出?”商高答:“数之法出于圆方,圆出于方,方出于矩,矩出九九八十一,故折矩以为勾广三,股修四,径隅五。
既方其外,半之一矩,环而共盘。
得成三、四、五,两矩共长二十有五,是谓积矩。
故禹之所以治天下者,此数之所由生也。
”就是说,矩形以其对角相折所称的直角三角形,如果勾(短直角边)为3,股(长直角边)为4,那么弦(斜边)必定是5。
从上面所引的这段对话中,我们可以清楚地看到,我国古代的人民早在几千年以前就已经发现并应用勾股定理这一重要的数学原理了。
在西方有文字记载的最早的证明是毕达哥拉斯给出的。
据说当他证明了勾股定理以后,欣喜若狂,杀牛百头,以示庆贺。
故西方亦称勾股定理为“百牛定理”。
遗憾的是,毕达哥拉斯的证明方法早已失传,我们无从知道他的证法。
实际上,在更早期的人类活动中,人们就已经认识到这一定理的某些特例。
除上述两个例子外,据说古埃及人也曾利用“勾三股四弦五”的法则来确定直角。
但是,这一传说引起过许多数学史家的怀疑。
比如说,美国的数学史家M·克莱因教授曾经指出:“我们也不知道埃及人是否认识到毕达哥拉斯定理。
我们知道他们有拉绳人(测量员),但所传他们在绳上打结,把全长分成长度为3、4、5的三段,然后用来形成直角三角形之说,则从未在任何文件上得证实。
”不过,考古学家们发现了几块大约完成于公元前2000年左右的古巴比伦的泥板书,据专家们考证,其中一块上面刻有如下问题:“一根长度为 30个单位的棍子直立在墙上,当其上端滑下6个单位时,请问其下端离开墙角有多远?”这是一个三边为为3:4:5三角形的特殊例子;专家们还发现,在另一块泥板上面刻着一个奇特的数表,表中共刻有四列十五行数字,这是一个勾股数表:最右边一列为从1到15的序号,而左边三列则分别是股、勾、弦的数值,一共记载着15组勾股数。
勾股定理16种证明方法

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2.∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c , ∴ ABEG 是一个边长为c 的正方形∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴ 222c b a =+. 【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形,所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得= 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+. 【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a cb -=, ∴ 222c b a =+. 【证法12】在Rt ΔABC 中,设直角边BC . 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+. 【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c .∵ EM = EH + HM = b + a , ED = a , ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a ,∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理知识点总结

第18章 勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: 方法一:4EFGHS S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c =b,a = ②知道直角三角形一边,可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题c b aH G F ED CB Abacbac cabcab a bcc baE D CBA5、利用勾股定理作长为的线段作长为、、的线段。
10种勾股定理的证明方法

10种勾股定理的证明方法1什么是勾股定理勾股定理,又称勾股论,是基督教神学家和物理学家第乌里希(Pythagoras)在公元前6世纪提出的一个名言:在给定一个直角三角形中,直角两边的平法相加,等于直角边的平方。
也就是说,在一个直角三角形中,腰边的平方等于两个斜边的平方和。
2勾股定理的表示形式勾股定理可以用一下式子表示:a²+b²=c²,其中a和b是直角三角形的两个斜边,c是这个直角三角形的直角腰边。
3关于勾股定理的10种证明方法1.构造法:构造带有两个相等斜边a和b的两个直角三角形,以证明a²+b²=c²。
2.投影定理:利用投影定理将这些斜边投影,使两个三角形等同,从而证明勾股定理。
3.物理四边形法:采用正方形,梯形和菱形将这三角形组合成一个完整的四边形,证明了勾股定理。
4.三角不等式:根据直角三角形的三角不等式来证明a²+b²>c²。
5.毕达哥拉斯定理:该定理指出,在给定一个直角三角形时,斜边的平方和等于两个斜边相乘再乘以直角边的任何一个数字。
6.幂法:将a²+b²和c²都改写成几次幂的形式,然后将两个完整的当作可以对等的数字比较,从而证明勾股定理。
7.等差数列法:分别建立一个等差数列和一个等比数列,将它们相加,可以得到勾股定理的完整证明。
8.泰勒公式:根据勾股定理,a²+b²=c²,用泰勒公式解析勾股定理,就能得出正确的结论。
9.三角函数法:将勾股定理表示为正弦、余弦和正切的函数关系,根据不同的三角函数的关系证明勾股定理。
10.几何图表法:将斜边a、b、c绘制成一个两个直角三角形的示意图,并且两个三角形的直角边的和是刚好相等的,可以读出完整的证明。
4结论勾股定理是一个经典的定理,已被证明是绝对正确的,而证明它的方法也分多种。
从上面这10种证明方法中,我们可以看出,勾股定理可以通过计算、构造、投影和其它几何变换理论来证明。
第10讲 勾股定理

第10讲 勾股定理〖学习目标〗1.知道勾股定理及其逆定理的联系与区别,能用这两个定理解决一些简单的实际问题.2.初步认识勾股定理及其逆定理的重要意义,会用这两个定理解决一些几何问题. ※考情分析勾股定理是解决直角三角形三边关系的重要工具,在几何证明和几何计算中有着重要的应用,不过这一知识点在中考试卷中直接考查一般比较容易,以填空选择为主,分值一般控制在3分以内,但如果作为解决其它问题的工具,它有可能出现在解答题甚至压轴题中.〖基础知识·轻松学〗一、勾股定理1.定义:如果直角三角形的两直角边长分别为a ,b ,斜边为c ,那么222a b c +=. 即直角三角形两直角边的平方和等于斜边的平方. 精讲:(1)勾股定理几种表达式在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,则222c a b =+,222a c b =-,222b c a =-;22c a b =+,22a c b =-,22b c a =-.(2)需要注意的是,勾股定理只有在直角三角形中才适用,如果不是直角三角形,那么三条边之间就没有这种关系.应用勾股定理的时候,一定要弄清哪两条边是直角边,哪条边是斜边.二、面积法与勾股定理的证明勾股定理证明常用的方法是面积法,即几何图形经过割补拼接后,只要没有重叠,没有空隙,面积就不会改变,再利用面积公式进行计算论证,这种割补法是验证勾股定理的有效方法.精讲:两种著名的证法 1.赵爽弦图(如图10-1)BDEAb (股)a (勾)c (弦)C图10-1图10-2aacc CDEAB证明思路:S 正方形ABDE =214()2ab b a ⨯+-,S 正方形ABDE =2c .所以2214()2ab b a c ⨯+-=.化简便得:a 2+b 2=c 2,即22c a b =+. 2.美国总统加菲尔德的证法(如图10-2) 证明思路:根据梯形的面积计算公式,得211()()()22S a b a b a b =++=+梯形, 又因为梯形由三个直角三角形组成,得2211222S ab c ab c =⨯+=+梯形. 所以2211()22a b ab c +=+,整理,得222a b c +=. 三、勾股定理的逆定理如果一个三角形的三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形. 精讲:1.判断判定一个三角形是直角三角形的步骤 ①首先确定最大的边(设为c );②验证2c 与22a b +是否具有相等关系,若2c =a 2+b 2,那么△ABC 是以∠C 为直角的直角三角形;若2c ≠22a b +,那么△ABC 不是直角三角形。
勾股定理判定条件

勾股定理判定条件一、什么是勾股定理?勾股定理是数学中的一条基本定理,描述了直角三角形三条边之间的关系。
它的表述如下:在直角三角形中,设直角边为a、b,斜边为c,则有a² + b² = c²。
勾股定理是古希腊数学家毕达哥拉斯所发现的,因此也被称为毕达哥拉斯定理。
二、勾股定理的判定条件在解决实际问题中,我们经常需要判断一个三元组是否满足勾股定理。
下面是勾股定理判定条件的详细说明:1. 条件一:三边长度满足勾股定理勾股定理判定条件的第一个条件是,三边的长度满足勾股定理的关系式。
即对于给定的三边长度a、b、c,如果满足a² + b² = c²,则该三元组满足勾股定理。
2. 条件二:满足直角三角形的定义勾股定理判定条件的第二个条件是,三边的长度满足直角三角形的定义。
直角三角形的定义是:其中一个角为直角,即90度。
3. 条件三:满足三角形的三边关系勾股定理判定条件的第三个条件是,三边的长度满足三角形的三边关系。
三角形的三边关系是:任意两边之和大于第三边。
即对于给定的三边长度a、b、c,必须满足a + b > c、a + c > b、b + c > a。
三、勾股定理判定条件的应用勾股定理判定条件在实际问题中有着广泛的应用。
下面是一些常见的应用场景:1. 判断三边长度是否构成直角三角形通过勾股定理判定条件,我们可以判断给定的三边长度是否构成直角三角形。
只需要验证三边长度是否满足勾股定理的关系式a² + b² = c²,并且其中一个角是否为直角(即是否为90度)。
2. 解决与直角三角形相关的实际问题勾股定理判定条件还可以应用于解决与直角三角形相关的实际问题。
例如,通过已知的两条边长度,可以使用勾股定理判定条件求解第三条边的长度。
或者通过已知的两条边长度,可以使用勾股定理判定条件求解三角形的面积。
3. 辅助测量和设计勾股定理判定条件在测量和设计领域也有着重要的应用。
勾股定理

勾股定理:在任何一个直角三角形中,两 勾股定理:在任何一个直角三角形中, 条直角边长的平方之和一定等于斜边长的 平方。这个定理在中国又称为“ 平方。这个定理在中国又称为“商高定 在外国称为“毕达哥拉斯定理” 理”,在外国称为“毕达哥拉斯定理”。 勾股定理(又称商高定理, 勾股定理(又称商高定理,毕达哥拉 斯定理)是一个基本的几何定理,早在中 斯定理)是一个基本的几何定理, 国商代就由商高发现。 国商代就由商高发现。据说毕达哥拉斯发 现了这个定理后,即斩了百头牛作庆祝, 现了这个定理后,即斩了百头牛作庆祝, 因此又称“百牛定理” 因此又称“百牛定理”。
伽菲尔德证明勾股定理的故事
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人 年一个周末的傍晚,在美国首都华盛顿的郊外, 年一个周末的傍晚 正在散步,欣赏黄昏的美景, 正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽 菲尔德。他走着走着,突然发现附近的一个小石凳上, 菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正 在聚精会神地谈论着什么,时而大声争论,时而小声探讨。 在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇 心驱使,伽菲尔德循声向两个小孩走去, 心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干 什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。 什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。 于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说: 于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问 先生,如果直角三角形的两条直角边分别为3和 , 先生,如果直角三角形的两条直角边分别为 和4,那么斜边长为多少 伽菲尔德答道: 小男孩又问道: 呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边 呀 分别为5和 ,那么这个直角三角形的斜边长又是多少? 分别为 和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不 加思索地回答到: 那斜边的平方一定等于5的平方加上 的平方. 的平方加上7的平方 加思索地回答到:“那斜边的平方一定等于 的平方加上 的平方.” 小男孩说: 先生,你能说出其中的道理吗? 伽菲尔德一时语塞, 小男孩说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞, 无法解释了,心里很不是滋味。,伽菲尔德不再散步,立即回家, 。,伽菲尔德不再散步 无法解释了,心里很不是滋味。,伽菲尔德不再散步,立即回家,潜 心探讨小男孩给他出的难题。他经过反复思考与演算, 心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其 中的道理,并给出了简洁的证明方法。 中分 别为A,B,斜边为C,那么 a²+b²=c²;; 即直角三角形两直 角边长的平方和等于斜边长的平 方。 如果三角形的三条边A,B,C满 足a²+b²=c²;,还有变形公式: AB=根号( a²+b²=c² ),如: 一条直角边是a,另一条直角边 是b,如果a的平方与b的平方和 等于斜边c的平方那么这个三角 形是直角三角形。(称勾股定理 的逆定理)
勾股定理9种证明(有图)

勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF.∵∠AEH+∠AHE=90o,∴∠AEH+∠BEF=90o. ∴∠HEF=180o ―90o=90o.∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c2.∵Rt ΔGDH ≌Rt ΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90o, ∴∠EHA+∠GHD=90o. 又∵∠GHE=90o,∴∠DHA=90o+90o=180o.∴ABCD 是一个边长为a+b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+.∴222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c.把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P. ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt ∴∠EGF=∠BED , ∵∠EGF+∠GEF=90°,∴∠BED+∠GEF=90°,∴∠BEG=180o ―90o=90o. 又∵AB=BE=EG=GA=c ,∴ABEG 是一个边长为c 的正方形.∴∠ABC+∠CBE=90o.∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC=∠EBD.∴∠EBD+∠CBE=90o. 即∠CBD=90o.又∵∠BDE=90o ,∠BCP=90o ,BC=BD=a.∴BDPC 是一个边长为a 的正方形.同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b(b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵∠BCA=90o ,QP ∥BC ,∴∠MPC=90o ,∵BM ⊥PQ , ∴∠BMP=90o ,∴BCPM 是一个矩形,即∠MBC=90o.∵∠QBM+∠MBA=∠QBA=90o ,∠ABC+∠MBA=∠MBC=90o , ∴∠QBM=∠ABC ,又∵∠BMP=90o ,∠BCA=90o ,BQ=BA=c , ∴Rt ΔBMQ ≌Rt ΔBCA.同理可证Rt ΔQNF ≌Rt ΔAEF.从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD.过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵AF=AC ,AB=AD ,∠FAB=∠GAD , ∴ΔFAB ≌ΔGAD ,∵ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴矩形ADLM 的面积=2a . 同理可证,矩形MLEB 的面积=2b .∵正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 ∴222b a c +=,即222c b a =+. 【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b(b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R.过B 作BP ⊥AF ,垂足为P.过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵∠BAD=90o ,∠PAC=90o ,∴∠DAH=∠BAC.又∵∠DHA=90o ,∠BCA=90o , AD=AB=c , ∴Rt ΔDHA ≌Rt ΔBCA.∴DH=BC=a ,AH=AC=b.由作法可知,PBCA 是一个矩形, 所以Rt ΔAPB ≌Rt ΔBCA.即PB= CA=b ,AP=a ,从而PH=b ―a.∵Rt ΔDGT ≌Rt ΔBCA, Rt ΔDHA ≌Rt ΔBCA.∴Rt ΔDGT ≌Rt ΔDHA.∴DH=DG=a ,∠GDT=∠HDA. 又∵∠DGT=90o ,∠DHF=90o ,∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90o , ∴DGFH 是一个边长为a 的正方形.∴GF=FH=a.TF ⊥AF ,TF=GT ―GF=b ―a.∴TFPB 是一个直角梯形,上底TF=b ―a ,下底BP=b ,高FP=a+(b ―a ).用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438=ab b 212-, 985S S S +=,∴824321S ab b S S --=+=812SS b --.② 把②代入①,得=922S S b ++=22a b +.∴222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c.做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上.用数字表示面积的编号(如图).∵∠TBE=∠ABH=90o , ∴∠TBH=∠ABE. 又∵∠BTH=∠BEA=90o ,BT=BE=b , ∴Rt ΔHBT ≌Rt ΔABE. ∴HT=AE=a. ∴GH=GT ―HT=b ―a.又∵∠GHF+∠BHT=90o ,∠DBC+∠BHT=∠TBH+∠∴∠GHF=∠DBC.∵DB=EB ―ED=b ―a ,∠HGF=∠BDC=90o , ∴Rt ΔHGF ≌Rt ΔBDC.即27S S =.过Q 作QM ⊥AG ,垂足是M.由∠BAQ=∠BEA=90o ,可知∠ABE =∠QAM ,而AB=AQ=c ,所以Rt ΔABE ≌Rt ΔQAM.又Rt ΔHBT ≌ Rt ΔABE.所以Rt ΔHBT ≌Rt ΔQAM.即58S S =.由Rt ΔABE ≌Rt ΔQAM ,又得QM=AE=a ,∠AQM=∠BAE.∵∠AQM+∠FQM=90o ,∠BAE+∠CAR=90o ,∠AQM=∠BAE , ∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90o ,QM=AR=a ,∴Rt ΔQMF ≌Rt ΔARC.即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ,即222c b a =+.【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC=a ,AC=b ,斜边AB=c (如图).过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙, ∵AB=DC=c ,AD=BC=a , AC=BD=b ,∴222AC BC AB +=,即222b a c +=, ∴222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知AD AB AC ∙≠2,或者BD AB BC ∙≠2.即AD :AC ≠AC :AB ,或者BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵∠A=∠A ,∴若AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵∠B=∠B , ∴若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵∠ACB=90o ,∴∠ADC ≠90o ,∠CDB ≠90o.这与作法CD ⊥AB 矛盾.所以,222AB BC AC ≠+的假设不能成立. ∴222c b a =+.【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c.作边长是a+b 的正方形ABCD.把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+=22c ab +.∴22222c ab ab b a +=++, ∴222c b a =+.。
股市勾股定理

股市勾股定理什么是勾股定理?勾股定理是数学中的一条基本定理,也被称为毕达哥拉斯定理。
它描述了直角三角形中的关系,即直角边的平方和等于斜边的平方。
勾股定理的数学表达式为:a^2 + b^2 = c^2其中,a和b代表直角边的长度,c代表斜边的长度。
股市与勾股定理的关系你可能会想,股市和勾股定理有什么关系?事实上,股市中也存在一种类似于勾股定理的关系。
这个关系是指股票的价格、盈利和市值之间的关系。
在股市中,股票的价格是指股票在市场上的交易价格。
盈利是指公司在一定时间内所实现的利润。
市值是指公司的总市值,即公司的股票数量乘以股票价格。
在这个关系中,我们可以将股票的价格看作是直角边a,盈利看作是直角边b,市值看作是斜边c。
根据勾股定理,我们可以得到以下关系:价格^2 + 盈利^2 = 市值^2这个关系告诉我们,在股市中,股票的价格、盈利和市值是相互关联的。
当我们知道其中两个变量时,可以通过勾股定理求解第三个变量。
如何应用股市勾股定理?股市勾股定理的应用可以帮助投资者更好地理解股市中的价格、盈利和市值之间的关系,从而做出更明智的投资决策。
1. 价格与盈利的关系根据股市勾股定理,当我们知道股票的价格和盈利时,可以通过勾股定理计算出市值。
这可以帮助投资者评估公司的估值是否合理。
如果市值远大于根据价格和盈利计算得出的市值,那么这个股票可能被高估,投资者应该谨慎购买。
2. 盈利与市值的关系通过股市勾股定理,我们可以通过已知的股票价格和市值计算出盈利。
这可以帮助投资者评估公司的盈利能力。
如果公司的盈利远低于根据股票价格和市值计算得出的盈利,那么这个股票可能存在风险,投资者应该谨慎投资。
3. 价格与市值的关系股市勾股定理还可以帮助投资者评估股票价格的合理性。
通过已知的盈利和市值,可以计算出股票的价格。
如果公司的盈利稳定增长,而市值相对较低,那么这个股票可能被低估,投资者可以考虑购买。
实例分析为了更好地理解股市勾股定理的应用,下面我们以某公司为例进行实例分析。
勾股定理

勾股定理勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
[1]中文名勾股定理外文名Pythagoras theorem 别称商高定理、毕达哥拉斯定理、百牛定理表达式a²+b²=c²提出者毕达哥拉斯赵爽商高提出时间公元前551年应用学科几何学适用领域范围数学,几何学适用领域范围数学,几何学中国记载著作《周髀算经》《九章算术》外国记载著作《几何原本》限制条件直角三角形在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。
如果设直角三角形的两条直角边长度分别是和,斜边长度是,那么可以用数学语言表达:勾股定理是余弦定理中的一个特例。
推导赵爽弦图《九章算术》中,赵爽描述此图:“勾股各自乘,并之为玄实。
开方除之,即玄。
案玄图有可以勾股相乘为朱实二,倍之为朱实四。
以勾股之差自相乘为中黄实。
加差实亦成玄实。
以差实减玄实,半其余。
以差为从法,开方除之,复得勾矣。
加差于勾即股。
凡并勾股之实,即成玄实。
或矩于内,或方于外。
形诡而量均,体殊而数齐。
勾实之矩以股玄差为广,股玄并为袤。
而股实方其里。
减矩勾之实于玄实,开其余即股。
倍股在两边为从法,开矩勾之角即股玄差。
加股为玄。
以差除勾实得股玄并。
以并除勾实亦得股玄差。
令并自乘与勾实为实。
倍并为法。
所得亦玄。
勾实减并自乘,如法为股。
什么是勾股定理

什么是勾股定理
一·勾股定理及其逆定理
1·勾股定理:直角三角形两直角边的平方和等于斜边的平方。
2·勾股定理的逆定理:有两边的平方和等于第三边的平方的三角形是直角三角形。
【注意】
1·勾股定理是直角三角形的一条重要性质,具有广泛的应用,另外勾股定理因其结构简单,形式优美而被公认为最美定理之一。
2·勾股定理的证明方法非常多,诸如内弦图、外弦图、总统法、火柴合法、欧几里德法等等,感兴趣的可自行查询,此处从略。
3·为了解题迅速,记住常用的勾股数(3,4,5),(6,8,10),(5,12,13)。
二·直角三角形的性质
1·角的性质:直角三角形的两锐角互余。
2·边的性质:
(1)直角三角形中,两直角边的平方和等于斜边的平方,此即为勾股定理。
(2)直角三角形中,三十度所对的边等于斜边的一半。
(3)直角三角形中,斜边上的中线等于斜边的一半。
【注意】
两个常用的结论:
(1)三十度、六十度、九十度的直角三角形对应边之比为1:根号3:2。
(2)四十五度、四十五度、九十度的直角三角形对应边之比为1:1:根号2。
三·典型题目分析
勾股定理在中考中常出现的题型包括:(1)毕氏树模型;(2)梯子模型;(3)折叠模型;(4)最短距离模型等,下面分别举例说明。
1·毕氏树模型:
2·梯子模型:
3·折叠模型:
4·最短距离模型。
什么是勾股定理

什么是勾股定理
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。
如果设直角三角形的两条直角边长度分别是a和b,斜边长度是C,那么可以用数学语言表达:
a²+b²=c²
勾股定理是余弦定理中的一个特例。
勾股定理-讲义

勾股定理一、知识梳理1.勾股定理(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.(2)勾股定理应用的前提条件是在直角三角形中.(3)勾股定理公式a2+b2=c2的变形有:a2=c2﹣b2,b2= c2﹣a2及c2=a2+b2.(4)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.2. 直角三角形的性质(1)有一个角为90°的三角形,叫做直角三角形.(2)直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质:性质1:直角三角形两直角边的平方和等于斜边的平方(勾股定理).性质2:在直角三角形中,两个锐角互余.性质3:在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.性质5:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半;在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.3.勾股定理的应用(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.4.平面展开-最短路径问题(1)平面展开﹣最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.(2)关于数形结合的思想,勾股定理及其逆定理它们本身就是数和形的结合,所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型.二、经典例题+基础练习1. 勾股定理.【例1】已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为()A.21 B.15 C.6 D.以上答案都不对.练1.在△ABC中,AB=15,AC=13,BC上的高AD长为12,则△ABC的面积为()A.84 B.24 C.24或84 D.42或84练2.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=()A.1 B. C. D.2 2. 等腰直角三角形.【例2】已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的面积是()A.2n﹣2 B.2n﹣1 C.2n D.2n+1练3.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是()A. B. C. D.3.等边三角形的性质;勾股定理.【例3】以边长为2厘米的正三角形的高为边长作第二个正三角形,以第二个正三角形的高为边长作第三个正三角形,以此类推,则第十个正三角形的边长是()A.2×()10厘米 B.2×()9厘米C.2×()10厘米 D.2×()9厘米练4.等边三角形ABC的边长是4,以AB边所在的直线为x轴,AB边的中点为原点,建立直角坐标系,则顶点C的坐标为.4.勾股定理的应用.【例4】工人师傅从一根长90cm的钢条上截取一段后恰好与两根长分别为60cm、100cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为()A.80cm B. C.80cm或 D.60cm 练5.现有两根铁棒,它们的长分别为2米和3米,如果想焊一个直角三角形铁架,那么第三根铁棒的长为()A.米B.米C.米或米 D.米5.平面展开-最短路径问题.【例5】如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D 出发沿着圆柱的表面爬行到点C的最短路程大约是()A.6cm B.12cm C.13cm D.16cm 练6.如图是一个长4m,宽3m,高2m的有盖仓库,在其内壁的A处(长的四等分)有一只壁虎,B处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为()m.A.4.8 B. C.5 D.三、课堂练习1.已知两边的长分别为8,15,若要组成一个直角三角形,则第三边应该为()A.不能确定 B. C.17 D.17或2.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若∠A:∠B:∠C=1:2:3.则a:b:c=()A.1::2 B.:1:2 C.1:1:2 D.1:2:33.直角三角形的两边长分别为3厘米,4厘米,则这个直角三角形的周长为()A.12厘米 B.15厘米 C.12或15厘米 D.12或(7+)厘米4.有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的.5.如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为m.6.在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且大于AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处,到达C处需要走的最短路程是米.(精确到0.01米)四、能力提升1.若一个直角三角形的三边长分别为3,4,x,则满足此三角形的x值为()A.5 B. C.5或 D.没有2.已知直角三角形有两条边的长分别是3cm,4cm,那么第三条边的长是()A.5cm B.cm C.5cm或cm D.cm3.已知Rt△ABC中的三边长为a、b、c,若a=8,b=15,那么c2等于()A.161 B.289 C.225 D.161或2894.一个等腰三角形的腰长为5,底边上的高为4,这个等腰三角形的周长是()A.12 B.13 C.16 D.185.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.6.如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用秒钟.7.如图,一个长方体盒子,一只蚂蚁由A出发,在盒子的表面上爬到点C1,已知AB=5cm,BC=3cm,CC1=4cm,则这只蚂蚁爬行的最短路程是cm.8.如图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.9.如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:cm),在上盖中开有一孔便于插吸管,吸管长为13cm,小孔到图中边AB距离为1cm,到上盖中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为hcm,则h的最小值大约为cm.(精确到个位,参考数据:≈1.4,≈1.7,≈2.2).10.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为mm.勾股定理的逆定理一、知识点梳理1.勾股定理的逆定理(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.说明:①勾股定理的逆定理验证利用了三角形的全等.②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.(2)运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角.然后进一步结合其他已知条件来解决问题.注意:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.2.勾股定理的应用(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.3.平面展开-最短路径问题(1)平面展开﹣最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.(2)关于数形结合的思想,勾股定理及其逆定理它们本身就是数和形的结合,所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型.4.方向角(1)方位角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.(2)用方位角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方位角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)(3)画方位角以正南或正北方向作方位角的始边,另一边则表示对象所处的方向的射线.5.三角形的面积(1)三角形的面积等于底边长与高线乘积的一半,即S△=×底×高.(2)三角形的中线将三角形分成面积相等的两部分.6.作图—复杂作图复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.7.坐标与图形性质1、点到坐标轴的距离与这个点的坐标是有区别的,表现在两个方面:①到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.2、有图形中一些点的坐标求面积时,过已知点向坐标轴作垂线,然后求出相关的线段长,是解决这类问题的基本方法和规律.3、若坐标系内的四边形是非规则四边形,通常用平行于坐标轴的辅助线用“割、补”法去解决问题.二、经典例题+基础练习1.勾股定理的逆定理.【例1】下列四组线段中,能组成直角三角形的是()A.a=1,b=2,c=3 B.a=2,b=3,c=4 C.a=2,b=4,c=5 D.a=3,b=4,c=5练1.下列各组线段能构成直角三角形的一组是()A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6练2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A.,,B.1,,C.6,7,8 D.2,3,42. 勾股定理的应用.【例2】如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行()A.8米B.10米C.12米D.14米练3.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)为()A.12m B.13m C.16m D.17m 3.平面展开-最短路径问题.【例3】如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是()A.13cm B.2cm C.cm D.2cm练4.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为.4.勾股定理的应用:方向角.【例4】已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是km;若A地在C地的正东方向,则B地在C 地的方向.练5.如图,小明从A地沿北偏东60°方向走2千米到B地,再从B地正南方向走3千米到C地,此时小明距离A地千米(结果可保留根号).5.坐标与图形性质;勾股定理的逆定理.【例5】在平面直角坐标系中有两点A(﹣2,2),B(3,2),C是坐标轴上的一点,若△ABC 是直角三角形,则满足条件的点共有()A.1个 B.2个 C.4个 D.6个练6.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,且△ABC是直角三角形,则满足条件的点C有个.三、课堂练习1.如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行米.2.如图,小聪用一块有一个锐角为30°的直角三角板测量树高,已知小聪和树都与地面垂直,且相距3米,小聪身高AB为1.7米,则这棵树的高度= 米.3.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果精确到0.1米,参考数据:=1.41,=1.73).4.在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为cm.(结果保留π)5.如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.四、能力提升1.下列四组线段中,可以构成直角三角形的是()A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3 2.若a、b、c为三角形三边,则下列各项中不能构成直角三角形的是()A.a=7,b=24,c=25 B.a=5,b=13,c=12C.a=1,b=2,c=3 D.a=30,b=40,c=503.以下各组数为边长的三角形中,能组成直角三角形的是()A.3、4、6 B.9、12、15 C.5、12、14 D.10、16、25 4.工人师傅从一根长90cm的钢条上截取一段后恰好与两根长分别为60cm、100cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为()A.80cm B. C.80cm或 D.60cm5.现有两根铁棒,它们的长分别为2米和3米,如果想焊一个直角三角形铁架,那么第三根铁棒的长为()A.米 B.米 C.米或米 D.米6.现有两根木棒的长度分别为40厘米和50厘米,若要钉成一个直角三角形框架,那么所需木棒的长一定为()A.30厘米 B.40厘米 C.50厘米 D.以上都不对7.如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A.6cm B.12cm C.13cm D.16cm8.如图所示,是一个圆柱体,ABCD是它的一个横截面,AB=,BC=3,一只蚂蚁,要从A 点爬行到C点,那么,最近的路程长为()A.7 B. C. D.59.有一长、宽、高分别是5cm,4cm,3cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为()A.5cm B.cm C.4cm D.3cm 10.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB 的距离为4,且△ABC是直角三角形,则满足条件的点C有个.11.设a>b,如果a+b,a﹣b是三角形较小的两条边,当第三边等于时,这个三角形为直角三角形.12.有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的.13.如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为m.14.“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)15.校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:=1.41,=1.73)16.如图,一根长6米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.(1)求OB的长;(2)当AA′=1米时,求BB′的长.勾股定理中的折叠问题一、经典例题例1.如图,在矩形ABCD 中,AB =6,BC =8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股数
勾股数又名毕氏三元数。
勾股数就是可以构成一个直角三角形三边的一组正整数。
勾股定理:直角三角形两条直角边
a、b的平方和等于斜边c的平方(a²+b²=c²)
表达式
a²+b²=c²,a,b,c∈N
常用套路
简介
所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(例如a,b,c)。
即a^2+b^2=c^2,a,b,c∈N
又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
关于这样的数组,比较常用也比较实用的套路有以下两种:[1]
第一套路
当a为大于1的奇数2n+1时,b=2n^2+2n, c=2n^2+2n+1。
实际上就是把a的平方数拆成两个连续自然数,例如:
n=1时(a,b,c)=(3,4,5)
n=2时(a,b,c)=(5,12,13)
n=3时(a,b,c)=(7,24,25)[1]
... ...
这是最经典的一个套路,而且由于两个连续自然数必然互质,所以用这个套路得到的勾股数组全部都是互质的。
[1]第二套路
2、当a为大于4的偶数2n时,b=n^2-1, c=n^2+1
也就是把a的一半的平方分别减1和加1,例如:
n=3时(a,b,c)=(6,8,10)
n=4时(a,b,c)=(8,15,17)
n=5时(a,b,c)=(10,24,26)
n=6时(a,b,c)=(12,35,37)[1]
... ...
这是第二经典的套路,当n为奇数时由于(a,b,c)是三个偶数,所以该勾股数组必然不是互质的;而n为偶数时由于b、c是两个连续奇数必然互质,所以该勾股数组互质。
所以如果你只想得到互质的数组,这条可以改成,对于a=4n (大于等于2), b=4n²-1, c=4n²+1,例如:
n=2时(a,b,c)=(8,15,17)
n=3时(a,b,c)=(12,35,37)
n=4时(a,b,c)=(16,63,65)[1]
... ...
公式证明
证明
a=2mn
b=m²-n²
c=m²+n²
证:
假设a²+b²=c²,这里研究(a,b)=1的情况(如果不等于1则(a,b)|c,两边除以(a,b)即可)
如果a,b均奇数,则a² + b² = 2(mod 4)(奇数mod4余1),而2不是模4的二次剩余,矛盾,所以必定存在一个偶数。
不妨设a=2k
等式化为4k² = (c+b)(c-b)
显然b,c同奇偶(否则右边等于奇数矛盾)
作代换:M=(c+b)/2, N=(c-b)/2,显然M,N为正整数
往证:(M,N)=1
如果存在质数p,使得p|M,p|N, 那么p|M+N(=c),
p|M-N(=b), 从而p|c, p|b, 从而p|a,这与(a,b)=1矛盾所以(M,N)=1得证。
依照算术基本定理,k² = p1^a1 * p2^a2 * p3^a3 * ...,其中a1,a2...均为偶数,p1,p2,p3...均为质数
如果对于某个pi,M的pi因子个数为奇数个,那N对应的pi因子必为奇数个(否则加起来不为偶数),从而pi|M,
pi|N,(M,N)=pi>1与刚才的证明矛盾所以对于所有质因子,pi²|M, pi²|N,即M,N都是平方数。
设M = m², N = n²
从而有c+b = 2m², c-b = 2n²,解得c=m²+n², b=m²-n², 从而a=2mn[1]
推广形式
关于勾股数的公式还是有局限的。
勾股数公式可以得到所有的基本勾股数,但是不可能得到所有的派生勾股数。
比如3,4,5;6,8,10;9,12,15...,就不能全部有公式计算出来。
[1]
但可以采用同乘以任意整数的形式来获取所有解!
其中规定m>n>0(两负数相乘可抵消固不考虑),(m,n)=1,m和n必须为一奇一偶,t为正整数
完全公式
公式
a=m,b=(m^2 / k - k) / 2,c=(m^2 / k + k) / 2 ①
其中m ≥3
⒈当m确定为任意一个≥3的奇数时,k={1,m^2的所
有小于m的因子}
⒉当m确定为任意一个≥4的偶数时,k={m^2 / 2的所有小于m的偶数因子}
基本勾股数与派生勾股数可以由完全一并求出。
例如,当m确定为偶数432时,因为k={432^2 / 2的所有小于432
的偶数因子}= {2,4,6,8,12,16,18,24,32,36,48,54,64,72,96,108,128,144,162,192,216,288,324,384},将m=432及24组不同k值分别代入b=(m^2 / k - k) / 2,c=(m^2 / k + k) / 2;即得直角边a=432时,具有24组不同的另一直角边b和斜边c,基本勾股数与派生勾股数一并求出。
而勾股数的组数也有公式能直接得到。
[1]
组数N
算术基本定理:一个大于1的正整数n,如果它的标准分解式为n=p1^m1×p2^m2×……×pr^mr,那么它的正因数个数为N=(m1+1)×(m2+1)×……×(mr+1);依据定理,易得以下结论
当a给定时,不同勾股数组a,b,c的组数N等于①式中k的可取值个数
⒈取奇数a=p1^m1×p2^m2×……×pr^mr,其中k={1,a^2的所有小于a的因子},则k的可取值个数:N=[(2m1+1)×(2m2+1)×……×(2mr+1)-1]/2
⒉取偶数a=2^m0×p1^m1×p2^m2×……×pr^mr,其中
k={a^2 / 2的所有小于a的偶数因子},则k的可取值个数:
N=[(2m0-1)×(2m1+1)×(2m2+1)×……×(2mr+1)-1]/2 其中,p1,p2,……,pr为互不相同的奇素数,m0,m1,……,mr为幂指数。
[1]
常见组合
3,4,5 :勾三股四弦五
5,12,13 :5·12记一生(13)
6,8,10:连续的偶数
8,15,17 :八月十五在一起(17)
特殊组合
连续的勾股数只有3,4,5
连续的偶数勾股数只有6,8,10
20以内
3 4 5;5 12 13;6 8 10;8,15,17;9 12 15
20-130
7 24 25;9 40 41;10 24 26;11 60 61;12 16 20;12 35 37;
13 84 85;14 48 50;15 20 25;15 36 39;15 112 113;
16 30 34;16 63 65;18 24 30;18 80 82;20 21 29;20 48 52;20 99 101;21 28 35;21 72 75;22 120 122;24 32 40;
24 45 51;24 70 74;25 60 65;27 36 45;28 45 53;30 40 50;30 72 78;32 60 68;33 44 55;33 56 65;35 84 91;
36 48 60;36 77 85;39 52 65;39 80 89;40 42 58;40 75 85;40 96 104;42 56 70;45 60 75;48 55 73 ;48 64 80 ;48 90 102 ;51 68 85 ;54 72 90 ;56 90 106 ;
57 76 95 ;60 63 87 ;60 80 100 ;60 91 109 ;63 84 105 ;65 72 97 ;66 88 110 ;69 92 115 ;72 96 120 ;
75 100 125 ;80 84 116。
三个数都在100以内共有52组。
其他公式
三个任意半径的圆相互外切,其半径两两相加,分别是以三个圆的圆心为顶点的三角形的三个边长。
如图:设一直角三角形斜边为a+n,另两个直角边分别是a+b和b+n。
a、b 都是正整数,且a>b。
以勾股定理得
,展开并化简得:
,即
,按图中步骤得
,将任意两个不相等的正整数数带入上式,注意a>b,即可得到一组勾股数。
不过得到的勾股数可能不互质,要除以三个数的最大公因数,就可得到一组互质的勾股数。
