频率分布表与图
合集下载
7.4频数分布表和频数分布直方图

(2)视力在4.9及4.9以
上的同学占调查学生的比
频 60
数
()
例为_3_/8__ ;
名 50
(3)如果视力在第1,2,3 40
组范围内均属视力不良,那 30
么该校约共有_1_25_0_名学 20
生视力不良,应给予治疗、 矫正。
10
第3组
第2组 第1组
第4组 第5组 视力
3.95 4.25 4.55 4.85 5.15 5.45
()
才艺展示
1.一次统计七年级若干名学生每分跳绳次数的频数分布直方图如图. 请根据这个直方图回答下面的问题:
(1)参加测试的总人数是多少? 15人
(2)自左至右最后一组的频数、频率分别是多少?
频数是3
频率是0.2
(3)数据分组时,组距是多少?
组距是25次
频
数
七年级若干名学生每分跳绳次数的频数分布 直方图
合计
20 ___2_5__
30 10 5 100
3.每年的6月6日是全国的爱眼日,让我们行动起来, 爱护我们的眼睛!某校为了做好全校2000名学生的眼 睛保健工作,对学生的视力情况进行一次抽样调查, 如图,是利用所得数据绘制的频数分布直方图。请你 根据此图提供的信息,回答下列问题:
(1)本次调查共抽测了__16_0 _名学生;
82.5; 82.5~87.5; 87.5~92.5)
解: 20名学生每分脉搏跳动次数的频数分布表
组别(次) 67.5~72.5 72.5~77.5 77.5~82.5 82.5~87.5 87.5~92.5
频数 2 4 9 3 2
20名学生每分脉搏跳动次数的频数分布直方图
频
数 10
频率分布表与频率分布直方图

大部分同学处于哪个分数段? 成绩的整体分布情况怎样?
制作频数分布表
先将成绩按10分的距离分段,统计每个分数 段学生出现的频数,填入表20.1.2.
表 20.1.2
根据频数分布表绘制直方图
79.5分到89.5分 这个分数段的学 生数最多
表 20.1.2
根据频数分布表绘制直方图
90分以上 的同学较 少
频数 8 6 4 2 0 22.5 24.5 26.5 28.5 30.5 32.5 数据
1、一个样本含有20个数据:35,31,33,35,37,39, 35,38,40,39,36,34,35,37,36,32,34,35,36,34.
在列频数~34.5这组的频数为_____
数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组 内的频数为高,画出一个个矩形。
例题:已知一个样本:27,23,25,27,29,
31,27,30,32,23,28,26,27,29, 28,24,26,27,28,30。 列出频数分布表, 并绘出频数分布直方图和频数折线图。
根据频数分布表绘制直方图
不及格的 学生数最 少!!!
绘制频数折线图
将直方图中每个小 长方形上面一条边 的中点顺次连结起 来,即可得到频数 折线图
画频数分布直方图的一般步骤:
(1) 计算最大值与最小值的差(极差).
极差:
(2) 决定组距与组数:
注意:一般情况
极差/组距=_______ 数据分成_____组.
解:(1)计算最大值与最小值的差: 32-23=9 (2)决定组距为2, 因为9/2=4.5,所以组数为5 (3)决定分点: 22.5~24.5,24.5~26.5, 26.5~28.5,28.5~30.5,30.5~32.5.
制作频数分布表
先将成绩按10分的距离分段,统计每个分数 段学生出现的频数,填入表20.1.2.
表 20.1.2
根据频数分布表绘制直方图
79.5分到89.5分 这个分数段的学 生数最多
表 20.1.2
根据频数分布表绘制直方图
90分以上 的同学较 少
频数 8 6 4 2 0 22.5 24.5 26.5 28.5 30.5 32.5 数据
1、一个样本含有20个数据:35,31,33,35,37,39, 35,38,40,39,36,34,35,37,36,32,34,35,36,34.
在列频数~34.5这组的频数为_____
数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组 内的频数为高,画出一个个矩形。
例题:已知一个样本:27,23,25,27,29,
31,27,30,32,23,28,26,27,29, 28,24,26,27,28,30。 列出频数分布表, 并绘出频数分布直方图和频数折线图。
根据频数分布表绘制直方图
不及格的 学生数最 少!!!
绘制频数折线图
将直方图中每个小 长方形上面一条边 的中点顺次连结起 来,即可得到频数 折线图
画频数分布直方图的一般步骤:
(1) 计算最大值与最小值的差(极差).
极差:
(2) 决定组距与组数:
注意:一般情况
极差/组距=_______ 数据分成_____组.
解:(1)计算最大值与最小值的差: 32-23=9 (2)决定组距为2, 因为9/2=4.5,所以组数为5 (3)决定分点: 22.5~24.5,24.5~26.5, 26.5~28.5,28.5~30.5,30.5~32.5.
频数分布表与直方图

THANKS
感谢观看
均匀分布
数据在各个区间内的频数或频 率大致相等,表示数据分布较 为均匀。
双峰分布
数据呈现两个明显的峰值,表 示数据可能存在两个不同的集
中区域。
03
频数分布表与直方图关系
数据呈现方式比较
频数分布表
通过表格形式展示数据分布情况,横 轴为数据分组,纵轴为频数或频率。
直方图
通过图形形式展示数据分布情况,横 轴为数据分组,纵轴为频数或频率, 各矩形面积总和表示所有数据点的数 量。
可以是水平的。
数据表示Βιβλιοθήκη 02直方图用矩形的面积表示频数或频率,而条形图的条形长度直
接表示数据值。
数据间隔
03
直方图的矩形通常是连续的,没有间隔,而条形图的条形之间
通常有间隔。
常见直方图形状解读
钟型分布
数据呈现中间高、两边低的形 状,类似于钟的轮廓,表示数
据分布较为集中。
偏态分布
数据分布偏向一侧,可能是左 偏或右偏,表示数据在某个方 向上存在较多的极端值。
调整柱子形状
可以选择不同的柱子形状,如矩形、圆形等,以更好地展示数据 分布。
调整柱子颜色
可以通过调整柱子颜色来区分不同的数据组,使得直方图更加直 观易懂。
添加图例
为不同的数据组添加图例,以便读者更好地理解直方图。
添加标题、坐标轴标签等元素
添加标题
为直方图添加标题,简要说明数据的来源和含义。
添加坐标轴标签
05
直方图制作步骤及注意事 项
根据频数分布表绘制直方图
确定组数
根据数据的分布规律,选择合适的组数,通常组数选择在5-15之 间。
确定组距
根据数据的范围和组数,计算合适的组距,使得数据能够均匀地分 布在各个组中。
频率分布表

闭右开区间,最后一组取闭区间;
(3)登记频数,计算频率,列出频率分布表.
12.5,15.5,3; 15.5,18.5,8; 18.5,21.5,9; 21.5 1.5,9; 21.5,24.5,11; 24.5,27.5,10; 27.5,30.5,4.
由此估计,不大于27.5的数据约为总 体的 ( A ) A.91% B.92% C.95% D.30%
[177.5,1Βιβλιοθήκη 0.5)(3)从第一组 [150.5,153.5) 开始分别 统计各组的频数,再计算各组的频率, 列频率分布表:
频率分布表
频率分布表
一般地编制频率分布表的步骤如下: (1)求全距,决定组数和组距;全距是指整个
取值区间的长度,组距是指分成的区间的长度;
(2)分组,通常对组内的数值所在的区间取左
建构数学
频率分布表:
一般地:当总体很大或不便获取 时,用样本的频率分布估计总体的 频率分布。把反映总体频率分布的 表格称为频率分布表.
数学运用
例1.从某校高一年级的1002名新生中用系统抽样的 方法抽取一个容量为100的身高样本,如下(单 位:cm).作出该样本的频率分布表.
频率分布表
解:(1)在全部数据中找出最大值180 与最小值151,它们相差(极差)29,确 定全距为30,决定组距为3; (2)将区间 [150.5,180.5] 分成10组;分 别是 [150.5,153.5),[153.5,156.5) ,…,
(2)有一个容量为45的样本数据,分 组后各组的频数如下:
(3)一个容量为20的样本数据,数据的 分组及各组的频数如下: (10,20),2;(20,30),3;(30, 40),4;(40,50),5;(50, 60),4;(60,70),2 则样本在区间(-∞,50)上的频率为( B ) A.0.5 B.0.7 C.0.25 D.0.05
(3)登记频数,计算频率,列出频率分布表.
12.5,15.5,3; 15.5,18.5,8; 18.5,21.5,9; 21.5 1.5,9; 21.5,24.5,11; 24.5,27.5,10; 27.5,30.5,4.
由此估计,不大于27.5的数据约为总 体的 ( A ) A.91% B.92% C.95% D.30%
[177.5,1Βιβλιοθήκη 0.5)(3)从第一组 [150.5,153.5) 开始分别 统计各组的频数,再计算各组的频率, 列频率分布表:
频率分布表
频率分布表
一般地编制频率分布表的步骤如下: (1)求全距,决定组数和组距;全距是指整个
取值区间的长度,组距是指分成的区间的长度;
(2)分组,通常对组内的数值所在的区间取左
建构数学
频率分布表:
一般地:当总体很大或不便获取 时,用样本的频率分布估计总体的 频率分布。把反映总体频率分布的 表格称为频率分布表.
数学运用
例1.从某校高一年级的1002名新生中用系统抽样的 方法抽取一个容量为100的身高样本,如下(单 位:cm).作出该样本的频率分布表.
频率分布表
解:(1)在全部数据中找出最大值180 与最小值151,它们相差(极差)29,确 定全距为30,决定组距为3; (2)将区间 [150.5,180.5] 分成10组;分 别是 [150.5,153.5),[153.5,156.5) ,…,
(2)有一个容量为45的样本数据,分 组后各组的频数如下:
(3)一个容量为20的样本数据,数据的 分组及各组的频数如下: (10,20),2;(20,30),3;(30, 40),4;(40,50),5;(50, 60),4;(60,70),2 则样本在区间(-∞,50)上的频率为( B ) A.0.5 B.0.7 C.0.25 D.0.05
2.1 频率分布表与频率分布图

26~ 28~30 合计
频数 (2)
1 3 6 8 12 20 27 18 12 8 4 1 120
频率(%) (3) 0.83 2.50 5.00 6.67 10.00 16.67 22.50 15.00 10.00 6.67 3.33 0.83
100.00
累计频数 (4) 1 4 10 18 30 50 77 95 107 115 119 120 —
100.0
累计频率(%) (5) 4.2 11.5 22.9 36.5 63.5 87.5 100.0
4
频率分布 图
30 频 率 25 (%)
20
15
10
5
0
0
1
2
3
4
5 >5
产前检查次数
图21 某地96名妇女产前检查次率分布
横坐标:产前检查次数; 纵坐标:频率, 检查k次的妇女 所占的比例(%) 等宽矩形长条:高度为检查次 数的频率
试编制血清含量的频率分布表。
6
编 制 步 骤 : 2
计 算 全 距 (range,R),又 称 极 差
(1)找• 出R = 最最大 值小-值最=小7值.4=229.647.42 = 22.22
3
确 定 组 段 数最与大组值距 = 29.64
•组 段 数 一 般 在 10 左 右 下 限 : 组 段 的 左 端 点
第二章 定量资料的统计描述
一、频率分布表与频率分布图
定
义
当变量值个数较多时,对各变量值出现的频率列表即为频 率分布表(frequency distribution table),简称频率表。
频率分布表的图形表示即为频率分布图。
2
1、离散型定量变量的频率分布
频数 (2)
1 3 6 8 12 20 27 18 12 8 4 1 120
频率(%) (3) 0.83 2.50 5.00 6.67 10.00 16.67 22.50 15.00 10.00 6.67 3.33 0.83
100.00
累计频数 (4) 1 4 10 18 30 50 77 95 107 115 119 120 —
100.0
累计频率(%) (5) 4.2 11.5 22.9 36.5 63.5 87.5 100.0
4
频率分布 图
30 频 率 25 (%)
20
15
10
5
0
0
1
2
3
4
5 >5
产前检查次数
图21 某地96名妇女产前检查次率分布
横坐标:产前检查次数; 纵坐标:频率, 检查k次的妇女 所占的比例(%) 等宽矩形长条:高度为检查次 数的频率
试编制血清含量的频率分布表。
6
编 制 步 骤 : 2
计 算 全 距 (range,R),又 称 极 差
(1)找• 出R = 最最大 值小-值最=小7值.4=229.647.42 = 22.22
3
确 定 组 段 数最与大组值距 = 29.64
•组 段 数 一 般 在 10 左 右 下 限 : 组 段 的 左 端 点
第二章 定量资料的统计描述
一、频率分布表与频率分布图
定
义
当变量值个数较多时,对各变量值出现的频率列表即为频 率分布表(frequency distribution table),简称频率表。
频率分布表的图形表示即为频率分布图。
2
1、离散型定量变量的频率分布
《频数分布表与直方图》PPT课件

直方图是为了把表中的结果直观地表示出来,它
们是频数分布的“数”与“形”的两种不同形式,
互相补充.
(来自《点拨》)
知2-练
1 某学校八年级共有你n名男生. 现测量他们的身高 (单位:cm. 结果精确到1 cm),依据数据绘制的 频数分布直方图如图所示(为了避免有些数据落 在分组的界限上,对作为分点的数保留一位小数).
的学生为正常,试求身高正常的学生的百分比.
知2-讲
导引知:先识确点定最大值与最小值的差为180-140=40(cm),故可
将数据按组距为5进行分组,可分40÷5=8(组). 解:(1)计算这组数据的最大值与最小值的差为180-140=
40(cm). 确定组数与组距,将数据按组距为5进行分组,可分 为40÷5=8(组),即每个小组的范围分别是140≤x< 145,145≤x<150,150≤x<155,155≤x<160,160≤ x<165,165≤x<170,170≤x<175,175≤x≤180. 其中x为学生身高.
C.8组
D.10组
导引:因为这组数据的最大值是187,最小值是140,最 大值与最小值的差是47,且 47 7 5 ,所以应 66 分为8组. 答案:C
总结
知1-讲
确定组数的方法:若最大值与最小值的差除 以组距所得的商是整数,则这个商即为组数;若 最大值与最小值的差除以组距所得的商是小数, 则这个商的整数部分+1即为组数.
知2-讲
知2-讲
例2 某中学部分同学参加全国初中数学竞赛,取得了优异的成
绩,指导老师统计了所有参赛同学的成绩(成绩都是整数, 试题满分120分),并且绘制了如图所示的频数分布直方图 (每组中含最低分数,但不含最高分数),请回答: (1)该中学参加本次数学竞
频率分布表

• 这样得出一系列的矩形,每个矩形的面积恰好是 该组上的频率,这些矩形就构成了频率分布直方 图。
例2、为了了解一大片经济林的生长情况,随机测量其中的100株的 底部周长,得到如下数据表(长度单位:cm):
135 98 102 110 99 121 110 96 100 103 125 97 117 113 110 92 102 109 104 112 109 124 87 131 97 102 123 104 104 128 105 123 111 103 105 92 114 108 104 102 129 126 97 100 115 111 106 117 104 109 111 89 110 121 80 120 121 104 108 118 129 99 90 99 121 123 107 111 91 100 99 101 116 97 102 108 101 95 107 101 102 108 117 99 118 106 119 97 126 108 123 119 98 121 101 113 102 103 104 108
合计
பைடு நூலகம்
100 1
频率分布表的制作
1、计算数据中最大值与最小值的差,
即全距。据此,决定组数和组距。
组距
全距 组数
2、分组:通常对组内数据所在区间取 左闭右开区间,最后一组取闭区间。
3、登记频数,计算频率,列出频率分 布表
练习1
1. 某电子元件厂生产一批同型号的电子元件,今 从中随机地抽取40个测得其电阻值如下:
168 165 171 167 170 165 170 152 175 174 165 170 168 169 171 166 164 155 164 158 170 155 166 158 155 160 160 164 156 162 160 170 168 164 174 171 165 179 163 172 180 174 173 159 163 172 167 160 164 169 151 168 158 168 176 155 165 165 169 162 177 158 175 165 169 151 163 166 163 167 178 165 158 170 169 159 155 163 153 155 167 163 164 158 168 167 161 162 167 168 161 165 174 156 167 166 162 161 164 166
例2、为了了解一大片经济林的生长情况,随机测量其中的100株的 底部周长,得到如下数据表(长度单位:cm):
135 98 102 110 99 121 110 96 100 103 125 97 117 113 110 92 102 109 104 112 109 124 87 131 97 102 123 104 104 128 105 123 111 103 105 92 114 108 104 102 129 126 97 100 115 111 106 117 104 109 111 89 110 121 80 120 121 104 108 118 129 99 90 99 121 123 107 111 91 100 99 101 116 97 102 108 101 95 107 101 102 108 117 99 118 106 119 97 126 108 123 119 98 121 101 113 102 103 104 108
合计
பைடு நூலகம்
100 1
频率分布表的制作
1、计算数据中最大值与最小值的差,
即全距。据此,决定组数和组距。
组距
全距 组数
2、分组:通常对组内数据所在区间取 左闭右开区间,最后一组取闭区间。
3、登记频数,计算频率,列出频率分 布表
练习1
1. 某电子元件厂生产一批同型号的电子元件,今 从中随机地抽取40个测得其电阻值如下:
168 165 171 167 170 165 170 152 175 174 165 170 168 169 171 166 164 155 164 158 170 155 166 158 155 160 160 164 156 162 160 170 168 164 174 171 165 179 163 172 180 174 173 159 163 172 167 160 164 169 151 168 158 168 176 155 165 165 169 162 177 158 175 165 169 151 163 166 163 167 178 165 158 170 169 159 155 163 153 155 167 163 164 158 168 167 161 162 167 168 161 165 174 156 167 166 162 161 164 166
统计学中的频数分布与频率分布

统计学中的频数分布与频率分布统计学是一门研究数据收集、分析和解释的学科,而频数分布与频率分布是统计学中常用的数据展示方法。
它们能够帮助我们更好地理解数据的特征和分布规律。
一、频数分布频数分布是将数据按照不同数值进行分类,并统计每个数值出现的次数,从而得到一个数据表。
以下是一个关于某班级学生考试成绩的频数分布表:成绩范围频数60-69 570-79 880-89 1290-100 10通过这个表格,我们可以直观地看到学生在各个成绩范围内的分布情况。
例如,在80-89分数段内,有12个学生获得了这个分数范围内的成绩。
频数分布表不仅可以展示数据的分布情况,还能帮助我们计算各个分数段内学生人数的百分比。
二、频率分布频率分布是通过统计每个数值出现的次数,然后将次数转化为频率(占总数的比例),得到一个数据表。
以下是使用相同数据的频率分布表:成绩范围频率60-69 0.2570-79 0.480-89 0.690-100 0.5与频数分布表相比,频率分布表更加直观地展示了各个成绩范围内学生所占的比例。
例如,在80-89分数段内的学生占总人数的0.6,即60%。
频数分布和频率分布都能够帮助我们更好地理解数据的特征和分布规律。
它们的选择取决于我们想要表达的信息。
如果我们更关注每个数值出现的次数,那么使用频数分布表更为合适;如果我们更关注各个数值所占的比例,那么使用频率分布表更为合适。
总结起来,频数分布和频率分布是统计学中常用的数据展示方法。
通过这些分布表,我们可以更加直观地了解数据的特征和分布规律,从而做出更准确的统计和分析。
在实际应用中,我们可以根据具体情况选择合适的分布表来展示数据。
频率分布表

B、1/14
C、0.03
D、3/14
3、将一个容量为50的样本数据分组后,组距和频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9; [21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),6; [30.5,33.5],3.
则估计小于30的数据大约占总体的( A)
161
165
174
156
167
166
162
161
164
166
168
165
171
167
170
165
170
152
175
174
165
170 160 180 151 177 178 167 161
170
155 170 174 168 158 165 163 165
168
166 168 173 158 175 158 164 174
练习1
1. 某电子元件厂生产一批同型号的电子元件,今 从中随机地抽取40个测得其电阻值如下:
101 101 107 92 99 97 102 98 99 113 93 106 103 101 90 87 95 99 98 103 102 96 94 100 94 97 110 103 99 103 108 102 102 100 94 105 98 97 107 101
问题情境
为了了解7月25日至8月24日北京地区的气温分布状况, 我们对以往年份此段时间的日最高气温进行抽样,得到如 下样本(单位:C )
7月25 日至8 月10 日
41.9 37.5 35.7 35.4 37.2 38.1 34.7 33.7 33.3 32.5 34.6 33.0 30.8 31.0 28.6 31.5 28.8 28.6 31.5 28.8 33.2 32.5 30.3 30.2 29.8 33.1 32.8 29.4 25.6 24.7 30.0 30.1 29.5 30.3
频率分布表和频率分布直方图课件

人口普查
在人口普查中,需要收集大量的人口数据。频率分布表和频率分布直方
图可以用于分析人口数据的分布情况,了解人口结构、年龄分布、性别
比例等情况。
05 练习与巩固
基础练习题
基础练习题1
根据给出的数据,制作频率分布表和 频率分布直方图。
基础练习题2
根据频率分布表和频率分布直方图, 计算各组的频数、频率和累计频率。
联系与区别
联系
频率分布表和频率分布直方图都是用于描述数据分布特征的 工具,它们都可以展示数据的频数、频率和分布情况。
区别
频率分布表是表格形式,可以提供更详细的数据信息,包括 频数、频率等,而频率分布直方图则更直观地展示数据的分 布形态,可以观察数据的集中趋势、离散程度和分布形态。
转换方法
将频率分布表转换为频率分布直方图
制作方法
数据分组
将数据按照一定的范围 进行分组,确定每个组 的上界和下界。
统计频数
统计每个组内的数据个 数,即频数。
计算频率
频率是频数与数据总数 的比值,用于表示该组 数据出现的相对频率。
制作表格
将分组情况、频数和频 率等信息整理成表格形 式。
实例分析
数据来源 数据分组 统计频数 计算频率 制作表格
在进行数据分析时,首先需要对数据进行探索性分析,以 了解数据的分布、变化规律和特征。频率分布表和频率分 布直方图是数据探索阶段的重要工具。
数据可视化
频率分布直方图是一种有效的数据可视化方法,可以直观 地展示数据的分布情况,帮助分析人员更好地理解数据。
比较分析
通过比较不同数据集的频率分布表和频率分布直方图,可 以分析它们之间的相似性和差异性,进而进行比较分析。
根据频数和频率数据,在坐标系中绘制条形图或直方图,每个条形或柱子的高度 代表该组的频数或频率。
2.2.1频率分布表和频率分布直方图

2.2 用样本估计总体
第一课时
知识探究(一):频率分布表
【问题】 我国是世界上严重缺水的国家 之一,某市政府为了节约生活用水,计 划在本市试行居民生活用水定额管理, 即确定一个居民月用水量标准a,用水量 不超过a的部分按平价收费,超出a的部 分按议价收费.通过抽样调查,那么标准a 制定为多少较合理呢?为了较为合理的 确定出这个标准,需要做哪些工作 ?
频率 组距 0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
频率分布表.
分组
[0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5] 合计
频数
频数 4 8 15 22 25 14 6 4 2
思考: 频率分布直方图中
小长方形的高
频率 组距
小长方形的面积表示什么?
小长方形的面积表示该组的频率.
所有小长方形的面积和=?
所有小长方形的面积和=1.
知识探究(二):频率分布直方图
思考:频率分布直方图非常直观地表明了 样本数据的分布情况,你能根据上述频率 分布直方图指出居民月均用水量的一些数 据特点吗?
2
0.02
100 1.00
知识探究(一):频率分布表
思考:如果市政府希望85%左右的居民每 月的用水量不超过标准,根据上述频率分 布表,你对制定居民月用水量标准(即a的 取值)有何建议?
知识探究(一):频率分布表
思考:如果市政府希望85%左右的居民每 月的用水量不超过标准,根据上述频率分 布表,你对制定居民月用水量标准(即a的 取值)有何建议?
优点:直观地表明了样本数据的分布情况,清楚 的看出数据分布的总体态势。 缺点:从直方图本身得不出原始的数据内容,造 成原有数据信息的丢失。
第一课时
知识探究(一):频率分布表
【问题】 我国是世界上严重缺水的国家 之一,某市政府为了节约生活用水,计 划在本市试行居民生活用水定额管理, 即确定一个居民月用水量标准a,用水量 不超过a的部分按平价收费,超出a的部 分按议价收费.通过抽样调查,那么标准a 制定为多少较合理呢?为了较为合理的 确定出这个标准,需要做哪些工作 ?
频率 组距 0.5 0.4 0.3 0.2 0.1
O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量/t
频率分布表.
分组
[0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5] 合计
频数
频数 4 8 15 22 25 14 6 4 2
思考: 频率分布直方图中
小长方形的高
频率 组距
小长方形的面积表示什么?
小长方形的面积表示该组的频率.
所有小长方形的面积和=?
所有小长方形的面积和=1.
知识探究(二):频率分布直方图
思考:频率分布直方图非常直观地表明了 样本数据的分布情况,你能根据上述频率 分布直方图指出居民月均用水量的一些数 据特点吗?
2
0.02
100 1.00
知识探究(一):频率分布表
思考:如果市政府希望85%左右的居民每 月的用水量不超过标准,根据上述频率分 布表,你对制定居民月用水量标准(即a的 取值)有何建议?
知识探究(一):频率分布表
思考:如果市政府希望85%左右的居民每 月的用水量不超过标准,根据上述频率分 布表,你对制定居民月用水量标准(即a的 取值)有何建议?
优点:直观地表明了样本数据的分布情况,清楚 的看出数据分布的总体态势。 缺点:从直方图本身得不出原始的数据内容,造 成原有数据信息的丢失。
频率分布直方图如下
(1)解:如图:茎为成绩的整环数,叶为小数点后的数字
甲
乙
85 2 74
7
1
8
57
4
9
112 78
8751
10
11
(2)乙成绩大致对称,甲成绩的中位数为9.05, 乙成绩的中位数为9.15,所以乙成绩较甲好, 乙成绩较集中于峰值,甲成绩分散
所以乙发挥的稳定性好,甲波动大
练习2:课本71页练习第三题
作业:课本71页练习1,上面的练习1和2。
优化设计
小结:1.什么是频率折线图
2.什么是总体密度曲线及其意义 3.1)认识茎叶图,如何做茎叶图 2)分析茎叶图,3)茎叶图的优缺点
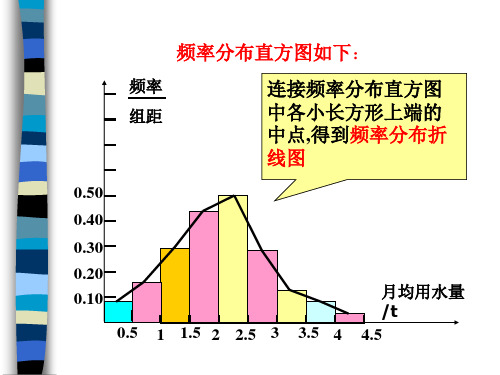
频率分布直方图如下:
频率
连接频率分布直方图
组距
中各小长方形上端的
中点,得到频率分布折
线图
0.50
0.40
0.30
0.20
0.10
月均用水量
/t
0.5 1 1.5 2 2.5 3 3.5 4 4.5
利用样本频率分布对总体分布进行相应估计
(1)上例的样本容量为100,如果增至1000, 其频率分布直方图的情况会有什么变化?假如增 至10000呢?
26
思考: 数据大于俩位数的整数时又如何选茎,叶?
数据为小数时又如何选茎,叶?
结论:1>当数据为整数时:通常个位数字在叶上, 其他位数在茎上(一位数时,茎为0)
2>当数据为小数时:通常小数部分在叶上, 整数部分在茎上
甲的茎叶图画法
也可以画一组数据的茎叶图,竖线左边为茎,
右边为叶。
茎
叶
08
1 364
甲的中位数为26,乙的中位数为36,所以乙较甲成绩要好, 另,乙的叶较甲的更集中于峰值附近,所以乙较甲发挥 更稳定
频数分布表和频率分布直方图课件

医学数据分析
在医学领域,频数分布表和频率分布直方图可以用于分析病例数据 、药物疗效等,为医学研究和临床诊断提供支持。
05
制作频数分布表和频率分布直方图 的注意事项
数据来源的可靠性
确保数据来源可靠
在制作频数分布表和频率分布直 方图时,应确保所使用数据的来 源可靠,避免使用不准确或过时
的数据。
验证数据准确性
作用
方便地展示数据的分布情况,帮助我们了解数据的集中趋势、离散程度以及分布形态等特征,为进一步的数据 分析提供基础。
制作步骤
01
02
03
04
收集数据
首先需要收集需要分析的数据 。
数据分组
将数据按照一定的分类标准进 行分组,分组的方法可以根据
实际需求进行选择。
统计频数
统计每组数据的数量,即频数 。
制作表格
应用场景
频数分布表
适用于需要详细了解数据各组频数的场景,如人口普查、销 售数据统计等。
频率分布直方图
适用于需要直观展示数据分布的场景,如市场调研、产品质 量检测等。
实例对比
频数分布表
一个班级的考试成绩统计,可以得出各分数段的学生人数。
频率分布直方图
同个班级的考试成绩分布图,可以直观地看出成绩的集中区域和离散程度。
数据收集
收集需要分析的数据,并进行必要的整理 和筛选,确保数据的质量和准确性。
添加图表元素
在直方图中添加必要的图表元素,如坐标 轴、标题、图例等,以便更好地解释和展 示数据。
数据分组
将数据按照一定的规则进行分组,分组的 方法可以根据实际需求选择,常见的分组 方式有等距分组和等频分组等。
绘制直方图
根据频数和频率数据,绘制条形图来表示 每个数据组的分布情况,பைடு நூலகம்形图的高度代 表频率,宽度代表组距。
在医学领域,频数分布表和频率分布直方图可以用于分析病例数据 、药物疗效等,为医学研究和临床诊断提供支持。
05
制作频数分布表和频率分布直方图 的注意事项
数据来源的可靠性
确保数据来源可靠
在制作频数分布表和频率分布直 方图时,应确保所使用数据的来 源可靠,避免使用不准确或过时
的数据。
验证数据准确性
作用
方便地展示数据的分布情况,帮助我们了解数据的集中趋势、离散程度以及分布形态等特征,为进一步的数据 分析提供基础。
制作步骤
01
02
03
04
收集数据
首先需要收集需要分析的数据 。
数据分组
将数据按照一定的分类标准进 行分组,分组的方法可以根据
实际需求进行选择。
统计频数
统计每组数据的数量,即频数 。
制作表格
应用场景
频数分布表
适用于需要详细了解数据各组频数的场景,如人口普查、销 售数据统计等。
频率分布直方图
适用于需要直观展示数据分布的场景,如市场调研、产品质 量检测等。
实例对比
频数分布表
一个班级的考试成绩统计,可以得出各分数段的学生人数。
频率分布直方图
同个班级的考试成绩分布图,可以直观地看出成绩的集中区域和离散程度。
数据收集
收集需要分析的数据,并进行必要的整理 和筛选,确保数据的质量和准确性。
添加图表元素
在直方图中添加必要的图表元素,如坐标 轴、标题、图例等,以便更好地解释和展 示数据。
数据分组
将数据按照一定的规则进行分组,分组的 方法可以根据实际需求选择,常见的分组 方式有等距分组和等频分组等。
绘制直方图
根据频数和频率数据,绘制条形图来表示 每个数据组的分布情况,பைடு நூலகம்形图的高度代 表频率,宽度代表组距。
频数,频率,频数分布表

12.3频数,频率,频数分布表
常熟市新港中学
生活中的数据
确定调研的问题 收集数据 抽样调查 折线统计图 扇形统计图 条形统计图
统计图
整理数据
普查
发布数据
提供合理的建议
抽样调查时:
样本容量要合适 样本要具有代表性
画统计图时:
要根据调研的问题考虑 用合适的统计图来表示
折线统计图
利润(万元)
20 15 10 5 0 1 2 3 4 5 6
探索新知识
频数,总数,频率 频数分布表
本节课要了解的重要的观念:
1。什么叫频数?什么叫频率? 2。频数,总数,频率之间的关系? 3。频数分布表
看下面的例题:
某班40名学生一次数学测验成绩如下: 63,84,91,53,69,81,61,69,91, 78,75,81,80,67,76,81,79,94, 61,69,89,70,70,87,81,86,90, 88,85,67,71,82,87,75,87,95, 53,65,74,77.
(2)小龙和小燕在各自的班级竞选班长, 小龙得39票,小燕得37票,可以断言小龙在 班级受欢迎的程度比小燕高.
课堂思考题: 在等式x+y=10中,已知x、y均为自然 数,试求x、y同时为正整数的频率。
小结与回顾
1.某个对象出现的次数称为频数. 2.出现的频数与总次数的比称为频率. 频 数 频数 总 次 数 = 频率 = 总次数 频 率
90~99
2
2÷40 =5%
9
9÷40 =22.5%
14
14÷40 =35%
5
5÷40 =12.5%
频率
1.在统计中,某个对象出现的次数称为频数
2.频数与总次数的比值称为频率.
常熟市新港中学
生活中的数据
确定调研的问题 收集数据 抽样调查 折线统计图 扇形统计图 条形统计图
统计图
整理数据
普查
发布数据
提供合理的建议
抽样调查时:
样本容量要合适 样本要具有代表性
画统计图时:
要根据调研的问题考虑 用合适的统计图来表示
折线统计图
利润(万元)
20 15 10 5 0 1 2 3 4 5 6
探索新知识
频数,总数,频率 频数分布表
本节课要了解的重要的观念:
1。什么叫频数?什么叫频率? 2。频数,总数,频率之间的关系? 3。频数分布表
看下面的例题:
某班40名学生一次数学测验成绩如下: 63,84,91,53,69,81,61,69,91, 78,75,81,80,67,76,81,79,94, 61,69,89,70,70,87,81,86,90, 88,85,67,71,82,87,75,87,95, 53,65,74,77.
(2)小龙和小燕在各自的班级竞选班长, 小龙得39票,小燕得37票,可以断言小龙在 班级受欢迎的程度比小燕高.
课堂思考题: 在等式x+y=10中,已知x、y均为自然 数,试求x、y同时为正整数的频率。
小结与回顾
1.某个对象出现的次数称为频数. 2.出现的频数与总次数的比称为频率. 频 数 频数 总 次 数 = 频率 = 总次数 频 率
90~99
2
2÷40 =5%
9
9÷40 =22.5%
14
14÷40 =35%
5
5÷40 =12.5%
频率
1.在统计中,某个对象出现的次数称为频数
2.频数与总次数的比值称为频率.
(课件1)18.3频数分布表与频数分布图

我们根据频率分布表以每小组的组距宽.频数 为高画出频率条形图, 从而画出频率分布直方图
我们根据频率分布表以每小组的组距为宽.频数 为高画出频率条形图,从而画出频率分布直方
图
分数段的最大值与最小值的差是‘组距’分数段的个数 是‘组数’ 每个小组所有数据的个数称为这个组的频数 频数
15
注意: ① 各长方形长条的宽度要相同 ②相邻长条的间距要适当。 ③长方形长条的高度 表示取各值的频率。
25.43 25.40 25.38 25.37 25.44 25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37 25.35 25.32 25.45 25.40 25.27
25.43 25.54 25.39 25.45 25.43 25.40 25.43 25.44 25.41
正
正正 T 正正正下 正正正正正 正正正一 正正下 TT T
5
12 18 25 16 13 4 2
0.05
0.12 0.18 0.25 0.16 0.13 0.04 0.02
0.08
0.20 0.38 0.67 0.79 0.92 0.96 0.98
[25.535,25.565)
合计
T
2
100
0.02
对这次成绩我们能统计出的数据是:
最高分 优秀率 最低分 极差 平均分 标准差 及格率
我们还希望知道这次成绩更具体的分布.如,哪个分数段 的人数最多,哪个分数段的人数最少,分别占人数的 百分比是多少,等等.
1.数据的分组整理
要解决这个问题,就需要统计各分数段的人数, 先划分出分数段 .再统计各分数段的分数个数
四.列出频率分布表
分 组 个数累计
频率分布直方图

1
频数直方图(频数条形图) 件数
8
6
4
件数2Βιβλιοθήκη 0 一二三四五频率分布表 频率分布直方图
分组 频数 频率
频率
一 6 0.35
0.4
二2
0.12 0.3
三3
0.18 0.2
频率
四5
0.29 0.1
五 1 0.06 0
合计 17 1
一二三四五
频率分布直方图的特征: (1)从频率分布直方图可以清楚的 看出数据分布的总体趋势. (2)从频率分布直方图得不出原始 的数据内容,把数据表示成直方图后, 原有的具体数据信息就被抹掉了.
频率分布折线图 在频率分布直方图中,取相邻矩形上底边 的中点顺次连结起来,就得到频率分布折 线图(简称频率折线图)如图:
密度曲线
如果样本容量取得足够大,分组的组距取 得足够小,则相应的频率折线图将趋于一 条光滑的曲线,称这条光滑的曲线为总体 的密度曲线.
直方图与密度曲线
下表是某学校一个星期中收交来的失物数, 5天中收交来的失物件数如下,请作出频率 分布表,更直观的图示?
星期 一 二 三 四 五 件数 6 2 3 5 1 累计 6 8 11 16 17
频率分布表
分组 一 二 三 四 五 合计
频数 6 2 3 5 1 17
频率 0.35 0.12 0.18 0.29 0.06
频数直方图(频数条形图) 件数
8
6
4
件数2Βιβλιοθήκη 0 一二三四五频率分布表 频率分布直方图
分组 频数 频率
频率
一 6 0.35
0.4
二2
0.12 0.3
三3
0.18 0.2
频率
四5
0.29 0.1
五 1 0.06 0
合计 17 1
一二三四五
频率分布直方图的特征: (1)从频率分布直方图可以清楚的 看出数据分布的总体趋势. (2)从频率分布直方图得不出原始 的数据内容,把数据表示成直方图后, 原有的具体数据信息就被抹掉了.
频率分布折线图 在频率分布直方图中,取相邻矩形上底边 的中点顺次连结起来,就得到频率分布折 线图(简称频率折线图)如图:
密度曲线
如果样本容量取得足够大,分组的组距取 得足够小,则相应的频率折线图将趋于一 条光滑的曲线,称这条光滑的曲线为总体 的密度曲线.
直方图与密度曲线
下表是某学校一个星期中收交来的失物数, 5天中收交来的失物件数如下,请作出频率 分布表,更直观的图示?
星期 一 二 三 四 五 件数 6 2 3 5 1 累计 6 8 11 16 17
频率分布表
分组 一 二 三 四 五 合计
频数 6 2 3 5 1 17
频率 0.35 0.12 0.18 0.29 0.06
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如下样本是随机抽取近年来北京地区 7月25日至8月24日的日最高气温
问题:怎样通过上表中的数据,分析比较
两时间段内的高温( 33 C )状况?
1
分析上面两样本的高温天数的频率用下表 表示:
由此可得:近年来北京地区7月25日至8 月10日的高温天气的频率明显高于8月8 日至8月24日.
2
频率分布表:
合计
频数累计 4 12 20 31 53 72 86 93 97 100
频数 4 8 8 11 22 19 14 7 4 3 100
频率 0 .04 0 .08 0 .08 0.11 0 .22 0 .19 0 .14 0 .07 0 .04 0.03 1
9
解 1 先制作频
率分布表 , 然后作
频率/组距 0.08
距取得足够小 ,
则相应的频率 折线图将趋于
150
155
160
一条光滑曲线 , 我们称这条光滑曲线为
165
170
175
180 身高/cm
总体分布的 密度曲线 .
13
Байду номын сангаас
例 3 为了了解
一大片经济 林 135 98 102 110 99 121 110 96 100 103
的生长情况 ,随 125 97 117 113 110 92 102 109 104 112
次连,再 结将矩形的,得 边频 去率 除折线图. 如 作图时取值区间 须两 分端 别点 向外沿伸 距,并 半个
取此组距x轴 上上 在的点与折线 分的 别首 相. 尾 连
12
频率折线图的 优点是它反映 了数据的变化
频率/组距 0.08
趋势 .如果把样
0.06
本容量取得足
0.04
够大 , 分组的组
0.02
一般地:当总体很大或不便获取 时,用样本的频率分布估计总体的 频率分布.把反映总体频率分布的表 格称为频率分布表.
3
例1.从某校高一年级的1002名新生中用系统抽样的 方法抽取一个容量为100的身高样本,如下(单 位:cm).作出该样本的频率分布表.
4
5
一般地编制频率分布表的步骤如下: (1)求全距,决定组数和组距;全距是指整个
80 ,85 开始 , 将
各组的频数、 频率和 频率 填
组距 入表中 .
7
解:(1)样本频率分布表如下:
分组 [122,126) [126,130) [130,134) [134,138) [138,142) [142,146) [146,150) [150,154) [154,158)
合计
频数 5 8 10 22 33 20 11 6 5 120
频率 (2)由样本频率
直角坐标系
, 以横
0.06
轴表示身高
, 纵轴
0.04
表示频率 / 组距 ; 0.02
2在 横轴上标上
15.5,015.5,315.5,6 150.5153.5156.5159.5162.5165.5168.5171.5174.5177.5180.5 身高/cm
,18.50 表示(为 的方 点便 ,起起 始 1见 5.点 50可适当 ); 前
0.04 分布表可知身高小
0.07 于134cm 的男孩出
0.08 现的频率为
0.18 0.28
0.04+0.07+0.08
0.17 =0.19,所以我们估
0.09 计身高小于134cm
0.05 的人数占总人数的
0.04 19%.
1 8
分组
150 .5 ,153 .5 153 .5 ,156 .5 156 .5 ,159 .5 159 .5 ,162 .5 162 .5 ,165 .5 165 .5 ,168 .5 168 .5 ,171 .5 171 .5 ,174 .5 174 .5 ,177 .5 177 .5 ,180 .5
11
如果将频率分
频率/组距
布直方图中各
0.08
相邻的矩形的
0.06
上底边的中点 顺序连结起来
0.04
,
就得到 频率分 0.02
布折线图 ,简称 频率折线图 .
149 152 155 158 161 164 167 170 173 176 179 182 身高/cm
例1的 频 率 直,方 取图 各中 相 邻 矩 形中的点上并底
3在上面标 ,分 出 别 各 以 点 连 中 结 线相 条邻 为两 ,底
高等于该 /组 组 .距 的频率
至此 ,就得到了这组 率数 分据 布的 直 ,如 频 方 上图 图.所示
10
一般地,作频率分布直方图的法方为: 把横轴分成若干段,每一线段对应一个组的组距, 然后以此线段为底作一个矩形,它的高等于该组 的组 频距 率,这样得出一系列矩形,每个矩形的面积 恰好是该组上的频率.这些矩形就构成了频率分 布直方图.
布直方图 ;
3 估计该经济林中底部周 长小于 100 cm 的树木约占多少 ,周长
不小于 120 cm 的树木约占多少 .
14
解 1 从 表中
可以看出 , 这组 数 据 的 最大值 为 135 , 最 小 值 为 80 , 故全距为 55 , 可将其分为 11 组 , 组距为 5 .
2 从第一组
机测量其中的
109 124 87 131 97 102 123 104 104 128
100 株 的 底部 周长 ,得到如下 数据表 ( 长度单 位 : cm ) :
1 编制频率分
布表 ;
2 绘制频率分
105 123 111 103 105 92 114 108 104 102 129 126 97 100 115 111 106 117 104 109 111 89 110 121 80 120 121 104 108 118 129 99 90 99 121 123 107 111 91 100 99 101 116 97 102 108 101 95 107 101 102 108 117 99 118 106 119 97 126 108 123 119 98 121 101 113 102 103 104 108
取值区间的长度,组距是指分成的区间的长度;
(2)分组,通常对组内的数值所在的区间取左
闭右开区间,最后一组取闭区间;
(3)登记频数,计算频率,列出频率分布表.
6
例2.下表给出了某校500名12岁男孩中用 随机抽样得出的120人的身高(单位:cm)
(1)列出样本频率分布表﹔ (2)估计身高小于134cm的人数占总人数的百分 比。
问题:怎样通过上表中的数据,分析比较
两时间段内的高温( 33 C )状况?
1
分析上面两样本的高温天数的频率用下表 表示:
由此可得:近年来北京地区7月25日至8 月10日的高温天气的频率明显高于8月8 日至8月24日.
2
频率分布表:
合计
频数累计 4 12 20 31 53 72 86 93 97 100
频数 4 8 8 11 22 19 14 7 4 3 100
频率 0 .04 0 .08 0 .08 0.11 0 .22 0 .19 0 .14 0 .07 0 .04 0.03 1
9
解 1 先制作频
率分布表 , 然后作
频率/组距 0.08
距取得足够小 ,
则相应的频率 折线图将趋于
150
155
160
一条光滑曲线 , 我们称这条光滑曲线为
165
170
175
180 身高/cm
总体分布的 密度曲线 .
13
Байду номын сангаас
例 3 为了了解
一大片经济 林 135 98 102 110 99 121 110 96 100 103
的生长情况 ,随 125 97 117 113 110 92 102 109 104 112
次连,再 结将矩形的,得 边频 去率 除折线图. 如 作图时取值区间 须两 分端 别点 向外沿伸 距,并 半个
取此组距x轴 上上 在的点与折线 分的 别首 相. 尾 连
12
频率折线图的 优点是它反映 了数据的变化
频率/组距 0.08
趋势 .如果把样
0.06
本容量取得足
0.04
够大 , 分组的组
0.02
一般地:当总体很大或不便获取 时,用样本的频率分布估计总体的 频率分布.把反映总体频率分布的表 格称为频率分布表.
3
例1.从某校高一年级的1002名新生中用系统抽样的 方法抽取一个容量为100的身高样本,如下(单 位:cm).作出该样本的频率分布表.
4
5
一般地编制频率分布表的步骤如下: (1)求全距,决定组数和组距;全距是指整个
80 ,85 开始 , 将
各组的频数、 频率和 频率 填
组距 入表中 .
7
解:(1)样本频率分布表如下:
分组 [122,126) [126,130) [130,134) [134,138) [138,142) [142,146) [146,150) [150,154) [154,158)
合计
频数 5 8 10 22 33 20 11 6 5 120
频率 (2)由样本频率
直角坐标系
, 以横
0.06
轴表示身高
, 纵轴
0.04
表示频率 / 组距 ; 0.02
2在 横轴上标上
15.5,015.5,315.5,6 150.5153.5156.5159.5162.5165.5168.5171.5174.5177.5180.5 身高/cm
,18.50 表示(为 的方 点便 ,起起 始 1见 5.点 50可适当 ); 前
0.04 分布表可知身高小
0.07 于134cm 的男孩出
0.08 现的频率为
0.18 0.28
0.04+0.07+0.08
0.17 =0.19,所以我们估
0.09 计身高小于134cm
0.05 的人数占总人数的
0.04 19%.
1 8
分组
150 .5 ,153 .5 153 .5 ,156 .5 156 .5 ,159 .5 159 .5 ,162 .5 162 .5 ,165 .5 165 .5 ,168 .5 168 .5 ,171 .5 171 .5 ,174 .5 174 .5 ,177 .5 177 .5 ,180 .5
11
如果将频率分
频率/组距
布直方图中各
0.08
相邻的矩形的
0.06
上底边的中点 顺序连结起来
0.04
,
就得到 频率分 0.02
布折线图 ,简称 频率折线图 .
149 152 155 158 161 164 167 170 173 176 179 182 身高/cm
例1的 频 率 直,方 取图 各中 相 邻 矩 形中的点上并底
3在上面标 ,分 出 别 各 以 点 连 中 结 线相 条邻 为两 ,底
高等于该 /组 组 .距 的频率
至此 ,就得到了这组 率数 分据 布的 直 ,如 频 方 上图 图.所示
10
一般地,作频率分布直方图的法方为: 把横轴分成若干段,每一线段对应一个组的组距, 然后以此线段为底作一个矩形,它的高等于该组 的组 频距 率,这样得出一系列矩形,每个矩形的面积 恰好是该组上的频率.这些矩形就构成了频率分 布直方图.
布直方图 ;
3 估计该经济林中底部周 长小于 100 cm 的树木约占多少 ,周长
不小于 120 cm 的树木约占多少 .
14
解 1 从 表中
可以看出 , 这组 数 据 的 最大值 为 135 , 最 小 值 为 80 , 故全距为 55 , 可将其分为 11 组 , 组距为 5 .
2 从第一组
机测量其中的
109 124 87 131 97 102 123 104 104 128
100 株 的 底部 周长 ,得到如下 数据表 ( 长度单 位 : cm ) :
1 编制频率分
布表 ;
2 绘制频率分
105 123 111 103 105 92 114 108 104 102 129 126 97 100 115 111 106 117 104 109 111 89 110 121 80 120 121 104 108 118 129 99 90 99 121 123 107 111 91 100 99 101 116 97 102 108 101 95 107 101 102 108 117 99 118 106 119 97 126 108 123 119 98 121 101 113 102 103 104 108
取值区间的长度,组距是指分成的区间的长度;
(2)分组,通常对组内的数值所在的区间取左
闭右开区间,最后一组取闭区间;
(3)登记频数,计算频率,列出频率分布表.
6
例2.下表给出了某校500名12岁男孩中用 随机抽样得出的120人的身高(单位:cm)
(1)列出样本频率分布表﹔ (2)估计身高小于134cm的人数占总人数的百分 比。
