2019年北京市高考数学试卷
2019年高考真题理科数学(北京卷)含解析

2019 年普通高等学校招生全国统一考试(北京卷)
理科数学
本试卷共 5 页,150 分。考试时长 120 分钟。考生务必将答案答在答题卡上, 在试卷上作答无效。考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共 40 分) 一、选择题共 8 小题,每小题 5 分,共 40 分。在每小题列出的四个选项中,选 出符合题目要求的一项。 1.已知复数 z=2+i,则 z z
点到坐标原点距离的最值和范围,利用图形的对称性和整点的坐标可确定图形面积的范围.
【
详
解
】
由
x2 y2 1 x y
得,
y2
x
y
1
x2
,
y
|
x | 2 2
1
3x2 4
,1
3x2 4
0, x2
4 3
,
所以 x 可为的整数有 0,-1,1,从而曲线 C : x2 y2 1 x y 恰好经过
(0,1),(0,-1),(1,0),(1,1), (-1,0),(-1,1)六个整点,结论①正确.
(2)根据 y<120 、 y 120 分别探究.
【详解】(1)x=10,顾客一次购买草莓和西瓜各一盒, 需要支付(60+80)-10=130 元. (2)设顾客一次购买水得到的金额为 y×80%,符合要求.
y 120 元时,有(y-x)×80%≥y×70%成立,
a 的取值范围.
【详解】若函数 f x ex aex 为奇函数,则 f x f x , ex aex ex aex , a 1 ex ex 0 对任意的 x 恒成立.
若函数 f x ex aex 是 R 上的增函数,则 f ' x ex aex 0 恒成
2019年北京卷文数高考试题 Word版含答案

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合A={x|–1<x<2},B={x|x>1},则A∪B=(A)(–1,1)(B)(1,2)(C)(–1,+∞)(D)(1,+∞)(2)已知复数z=2+i,则z z⋅=(A)3(B)5(C)3 (D)5(3)下列函数中,在区间(0,+∞)上单调递增的是(A)12y x=(B)y=2x-(C)12logy x=(D)1yx=(4)执行如图所示的程序框图,输出的s值为(A)1 (B)2 (C)3 (D)4(5)已知双曲线2221xya-=(a>05a=(A )6 (B )4(C )2 (D )12(6)设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(7)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为k m 的星的亮度为k E (k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为 (A )1010.1(B )10.1(C )lg10.1(D )10.110-(8)如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β.图中阴影区域的面积的最大值为(A )4β+4cos β (B )4β+4sin β (C )2β+2cos β (D )2β+2sin β第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2019北京卷理科数学高考真题

⎧5(B )4(A ) 15(D ) 67m2019 年普通高等学校招生全国统一考试数 学(理)(北京卷)本试卷共 5 页,150 分。
考试时长 120 分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共 40 分)一、选择题共 8 小题,每小题 5 分,共 40 分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知复数 z =2+i ,则 z ⋅ z =(A ) 3(B ) 5 (C )3 (D )5(2)执行如图所示的程序框图,输出的 s 值为(A )1 (B )2 (C )3 (D )4(3)已知直线 l 的参数方程为 ⎨x = 1 +3t, ⎩ y = 2 + 4t (t 为参数),则点(1,0)到直线 l 的距离是25(C )5(4)已知椭圆 x 2 y 2+ a 2 b 21 = 1 (a >b >0)的离心率为 ,则2(A )a 2=2b 2(B )3a 2=4b 2 (C )a =2b (D )3a =4b(5)若 x ,y 满足 | x |≤ 1- y ,且 y ≥−1,则 3x+y 的最大值为(A )−(B )1 (C )5 (D )7(6)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足 m 2− 1= 5 2Elg 1 ,E2r其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是−26.7,天狼星的星等是−1.45,则太阳与天狼星的亮度的比值为(A)1010.1(B)10.1(C)lg10.1(D)10−10.1uuur uu u uuur uuur uuur(7)设点A,B,C不共线,则“AB与AC的夹角为锐角”是“|AB+AC|>|BC|”的(A)充分而不必要条件(C)充分必要条件(B)必要而不充分条件(D)既不充分也不必要条件(8)数学中有许多形状优美、寓意美好的曲线,曲线C:x2+y2=1+|x|y就是其中之一(如图).给出下列三个结论:①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C上任意一点到原点的距离都不超过2;③曲线C所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是(A)①(B)②(C)①②(D)①②③第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
2019年高考理科数学北京卷理数(附参考答案和详解)

绝密★启用前 6月7日15:00-17:002019年普通高等学校招生全国统一考试(北京卷)数学(理工农医类)总分:150分考试时间:120分钟★祝考试顺利★注意事项:1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证条形码粘贴在答题卡的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:选出每小题答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸、答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,写在试题卷、草稿纸、答题卡上的非答题区域均无效。
4、考试结束后,将本试卷和答题卡一并上交。
第I卷一、选择题:本题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2019北京卷·理)已知复数2iz=+,则z z⋅=()A.3B.5C.3D.5【解析】因为2iz z⋅=+⋅-=.故选D.z=+,所以2iz=-,所以(2i)(2i)5【答案】D2.(2019北京卷·理)执行如图所示的程序框图,输出的s值为()A.1B.2C.3D.4【解析】1,1k s ==;第一次循环:2s =,判断3,2k k <=;第二次循环:2s =,判断3,3k k <=;第三次循环:2s =,判断3k =.故输出2,故选B. 【答案】B3.(2019北京卷·理)已知直线l 的参数方程为13,24x t y t=+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是( )A.15B.25C.45D.65【解析】由题意可知直线l 的普通方程为4320x y -+=,由点到直线的距离公式可得点(1,0)到直线l的距离65d ==.故选D. 【答案】D4.(2019北京卷·理)已知椭圆22221(0)x y a b a b+=>>的离心率为12,则( )A.222a b =B.2234a b =C.2a b =D.34a b =【解析】因为椭圆的离心率为12c e a ==,所以224a c =.又222a b c =+,所以2234a b =.故选B. 【答案】B5.(2019北京卷·理)若x ,y 满足||1x y ≤-,且1y ≥-,则3x y +的最大值为( )A.7-B.1C.5D.7【解析】由||1x y ≤-,且1y ≥-,得10,10,1.x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩作出可行域如图阴影部分所示.设3z x y =+,则3y x z =-+,作直线0:3l y x =-,并进行平移.显然当0l 经过点(2,1)A -时,z 取得最大值,max 3215z =⨯-=.故选C. 【答案】C6.(2019北京卷·理)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足12125lg2E m m E -=,其中星等为k m 的星的亮度为(1,2)k E k =.已知太阳的星等是26.7-,天狼星的星等是 1.45-,则太阳与天狼星的亮度的比值为( )A.10.110B.10.1C.lg10.1D.10.110-【解析】由题意知,126.7m =-,2 1.45m =-,代入所给公式得1251.45(26.7)lg 2EE ---=,所以12lg10.1E E =,所以10.11210EE =.故选A. 【答案】A7.(2019北京卷·理)设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“AB AC BC +>”的( ) A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解析】因为设点A ,B ,C 不共线,由向量加法的三角形法则,可知BC AC AB =-,所以||||AB AC BC +>等价于||||AB AC AC AB +>-,因模为正,故不等号两边平方得22222||||cos 2||||cos AB AC AB AC AC AB AC AB θθ++⋅⋅>+-⋅⋅(θ为AB 与AC 的夹角),整理得4||||cos 0AB AC θ⋅⋅>,故cos 0θ>,即θ为锐角.又以上推理过程可逆,所以“AB 与AC 的夹角为锐角”是“AB AC BC +>”的充分必要条件.故选C. 【答案】C8.(2019北京卷·理)数学中有许多形状优美、寓意美好的曲线,曲线22:1||C x y x y +=+就是其中之一(如图).给出下列三个结论: ①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C③曲线C 所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是( )A.①B.②C.①②D.①②③【解析】由221||x y x y +=+,当0x =时,1y =±;当0y =时,1x =±;当1y =时,01x =±,.故曲线C 恰好经过6个整点:(0,1)A ,(0,1)B -,(1,0)C ,(1,1)D ,(1,0)E -,(1,1)F -,所以①正确.由基本不等式,当0y >时,22221||1||12x y x y x y xy ++=+=+≤+,所以222x y +≤222x y +≤②正确.如图,由①知矩形CDFE 的面积为2,△BCE 的面积为1,所以曲线C 所围成的“心形”区域的面积大于3,故③错误.故选C. 【答案】C第Ⅱ卷二、填空题:本题共6小题,每小题5分。
2019年北京高考数学试卷

2019年北京高考数学试卷第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)(A (B (C )3(D )5(2)执行如图所示的程序框图,输出的s 值为(A )1(B )2(C )3(D )4(3)已知直线l 的参数方程为x =1+3t y =2+4tìíî(t 为参数),则点(1,0)到直线l 的距离是(A )15(B )25(C )45(D )65(4)已知椭圆2x 2a +2y 2b=1(a>b>0)的离心率为12,则(A )a 2=2b 2.(B )3a 2=4b 2.(C )a=2b (D )3a=4b (5)若x ,y 满足的最大值为(A )-7(B )1(C )5(D )7(6)在天文学中,天体的明暗程度可以用星等或亮度来描述。
两颗星的星等与亮度满足m 2-m 1=52lg E 1E 2,其中星等为m k 的星的亮度为E k (k =1,2)。
已知太阳的星等为-26.7,天狼星的星等为-1.45,则太阳与天狼星的亮度的比值为(A)1010.1(B)10.1(C)lg10.1(D)10-10.1(7)设点A,B,C不共线,则”是的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(8)数学中有许多形状优美、寓意美好的曲线,曲线C:x2+y2=1+x y就是其中之一(如图)。
给出下列三个结论:①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C上任意一点到原点的距离都不超过2;③曲线C所围城的“心形”区域的面积小于3.其中,所有正确结论的序号是(A)①(B)②(C)①②(D)①②③第二部分(非选择题共10分)二、填空题共6小题,每小题5分,共30分。
(9)函数f(x)=sin22x的最小正周期是________。
(10)设等差数列{a n}的前n项和为S n,若a2=-3,S5=-10,则a3=________.S n的最小值为_______。
高中-数学-高考-2019年普通高等学校招生全国统一考试数学(文)(北京卷)

2019年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1、已知集合A={x|–1<x<2},B={x|x>1},则A∪B=()A. (–1,1)B. (1,2)C. (–1,+∞)D. (1,+∞)2、已知复数z=2+i,则z z⋅=()A. 3B. 5C. 3D. 53、下列函数中,在区间(0,+∞)上单调递增的是()A.12y x= B. y=2x- C. 12logy x= D. 1yx=4、执行如图所示的程序框图,输出的s值为()A. 1B. 2C. 3D. 45、已知双曲线2221xya-=(a>05则a=()A. 6B. 4C. 2D. 1 26、设函数f(x)=cosx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的()A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7、在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为( )A. 1010.1B. 10.1C. lg 10.1D. 10-10.1 8、如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β.图中阴影区域的面积的最大值为( )A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
2019年高考数学真题-北京卷(文)答案

2019年普通高等学校招生全国统一考试(北京卷)数学(文)参考答案一、选择题(共8小题,每小题5分,共40分)(1)C (2)D (3)A (4)B (5)D(6)C(7)A(8)B二、填空题(共6小题,每小题5分,共30分)(9)8(10)–3 1 (11)22(1)4x y −+=(12)40(13)若,l m l α⊥⊥,则m αP .(答案不唯一) (14)130 15三、解答题(共6小题,共80分) (15)(共13分)解:(Ⅰ)由余弦定理2222cos b a c ac B =+−,得2221323()2b c c =+−⨯⨯⨯−.因为2b c =+,所以2221(2)323()2c c c +=+−⨯⨯⨯−. 解得5c =. 所以7b =. (Ⅱ)由1cos 2B =−得3sin 2B =. 由正弦定理得33sin sin 14a A Bb ==. 在ABC △中,B C A +=π−. 所以33sin()sin 14B C A +==. (16)(共13分)解:(Ⅰ)设{}n a 的公差为d .因为110a =−,所以23410,102,103a d a d a d =−+=−+=−+. 因为23410,8,6a a a +++成等比数列, 所以()()()23248106a a a +=++. 所以2(22)(43)d d d −+=−+. 解得2d =.所以1(1) 212n a a n d n =+−=−. (Ⅱ)由(Ⅰ)知,212n a n =−.所以,当7n ≥时,0n a >;当6n ≤时,0n a ≤. 所以,n S 的最小值为630S =−. (17)(共12分)解:(Ⅰ)由题知,样本中仅使用A 的学生有27+3=30人,仅使用B 的学生有24+1=25人, A ,B 两种支付方式都不使用的学生有5人.故样本中A ,B 两种支付方式都使用的学生有100–30–25–5=40人. 估计该校学生中上个月A ,B 两种支付方式都使用的人数为401000400100⨯=. (Ⅱ)记事件C 为“从样本仅使用B 的学生中随机抽取1人,该学生上个月的支付金额大于2 000元”,则1()0.0425P C ==. (Ⅲ)记事件E 为“从样本仅使用B 的学生中随机抽查1人,该学生本月的支付金额大于2 000元”. 假设样本仅使用B 的学生中,本月支付金额大于2 000元的人数没有变化,则由(II )知,()P E =0.04. 答案示例1:可以认为有变化.理由如下:()P E 比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月支付金额大于2000元的人数发生了变化.所以可以认为有变化. 答案示例2:无法确定有没有变化.理由如下:事件E 是随机事件,()P E 比较小,一般不容易发生,但还是有可能发生的.所以无法确定有没有变化.(18)(共14分)解:(Ⅰ)因为PA⊥平面ABCD,所以PA BD⊥.又因为底面ABCD为菱形,所以BD AC⊥.所以BD⊥平面PAC.(Ⅱ)因为PA⊥平面ABCD,AE⊂平面ABCD,所以PA⊥AE.因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.所以AB⊥AE.所以AE⊥平面PAB.所以平面PAB⊥平面PAE.(Ⅲ)棱PB上存在点F,使得CF∥平面PAE.取F为PB的中点,取G为PA的中点,连结CF,FG,EG.则FG∥AB,且FG=12 AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12 AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.因为CF⊄平面PAE,EG⊂平面PAE,所以CF ∥平面PAE . (19)(共14分)解:(I )由题意得,b 2=1,c =1. 所以a 2=b 2+c 2=2.所以椭圆C 的方程为2212x y +=.(Ⅱ)设P (x 1,y 1),Q (x 2,y 2), 则直线AP 的方程为1111y y x x −=+. 令y =0,得点M 的横坐标111M x x y =−−. 又11y kx t =+,从而11||||1M x OM x kx t ==+−.同理,22||||1x ON kx t =+−.由22,12y kx t x y =+⎧⎪⎨+=⎪⎩得222(12)4220k x ktx t +++−=. 则122412kt x x k +=−+,21222212t x x k−=+. 所以1212||||||||11x x OM ON kx t kx t ⋅=⋅+−+−()12221212||(1)(1)x x k x x k t x x t =+−++−22222222212||224(1)()(1)1212t k t kt k k t t k k−+=−⋅+−⋅−+−++12||1t t+=−. 又||||2OM ON ⋅=,所以12||21tt+=−. 解得t =0,所以直线l 经过定点(0,0). (20)(共14分)解:(Ⅰ)由321()4f x x x x =−+得23()214f x x x '=−+. 令()1f x '=,即232114x x −+=,得0x =或83x =.又(0)0f =,88()327f =,所以曲线()y f x =的斜率为1的切线方程是y x =与88273y x −=−,即y x =与6427y x =−.(Ⅱ)令()(),[2,4]g x f x x x =−∈−.由321()4g x x x =−得23()24g'x x x =−. 令()0g'x =得0x =或83x =.(),()g'x g x 的情况如下:x 2−(2,0)−8(0,)3 838(,4)34()g'x+−+()g x6− Z]6427−Z所以()g x 的最小值为6−,最大值为0. 故6()0g x −≤≤,即6()x f x x −≤≤. (Ⅲ)由(Ⅱ)知,当3a <−时,()(0)|(0)|3M F g a a a ≥=−=−>; 当3a >−时,()(2)|(2)|63M F a g a a ≥−=−−=+>; 当3a =−时,()3M a =. 综上,当()M a 最小时,3a =−.。
2019年北京市高考数学试卷(理科)以及答案解析

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试(北京卷)理科数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.(5分)已知复数z=2+i,则z•=()A.B.C.3D.52.(5分)执行如图所示的程序框图,输出的s值为()A.1B.2C.3D.43.(5分)已知直线l的参数方程为(t为参数),则点(1,0)到直线l的距离是()A.B.C.D.4.(5分)已知椭圆+=1(a>b>0)的离心率为,则()A.a2=2b2B.3a2=4b2C.a=2b D.3a=4b5.(5分)若x,y满足|x|≤1﹣y,且y≥﹣1,则3x+y的最大值为()A.﹣7B.1C.5D.76.(5分)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2﹣m1=lg,其中星等为m k的星的亮度为E k(k=1,2).已知太阳的星等是﹣26.7,天狼星的星等是﹣1.45,则太阳与天狼星的亮度的比值为()A.1010.1B.10.1C.lg10.1D.10﹣10.17.(5分)设点A,B,C不共线,则“与的夹角为锐角”是“|+|>||”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件8.(5分)数学中有许多形状优美、寓意美好的曲线,曲线C:x2+y2=1+|x|y就是其中之一(如图).给出下列三个结论:①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C上任意一点到原点的距离都不超过;③曲线C所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是()A.①B.②C.①②D.①②③二、填空题共6小题,每小题5分,共30分。
2019年高考真题——理科数学(北京卷)附答案

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试数 学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知复数z =2+i ,则z z ⋅= (A 3(B 5(C )3(D )5(2)执行如图所示的程序框图,输出的s 值为(A )1 (B )2 (C )3 (D )4(3)已知直线l 的参数方程为13,24x t y t =+=+⎧⎨⎩(t 为参数),则点(1,0)到直线l 的距离是(A )15(B )25(C )45(D )65(4)已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则(A )a 2=2b 2(B )3a 2=4b2(C )a =2b (D )3a =4b(5)若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为(A )−7 (B )1 (C )5 (D )7(6)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2−m 1=52lg 21E E ,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是−26.7,天狼星的星等是−1.45,则太阳与天狼星的亮度的比值为 (A )1010.1(B )10.1 (C )lg10.1 (D )10−10.1(7)设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(8)数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 2; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是 (A )①(B )②(C )①②(D )①②③第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2019年高考北京卷理科数学真题(含答案)

绝密★启用前2019年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知复数z=2+i,则z z⋅=5 C. 3 D. 5【答案】D【解析】【分析】题先求得z,然后根据复数的乘法运算法则即得.=+⋅=+-=故选D.【详解】∵z2i,z z(2i)(2i)5【点睛】本容易题,注重了基础知识、基本计算能力的考查.2.执行如图所示的程序框图,输出的s值为A. 1B. 2C. 3D. 4【答案】B根据程序框图中的条件逐次运算即可.【详解】运行第一次, =1k ,2212312s ⨯==⨯- ,运行第二次,2k = ,2222322s ⨯==⨯- ,运行第三次,3k = ,2222322s ⨯==⨯- ,结束循环,输出=2s ,故选B .【点睛】本题考查程序框图,属于容易题,注重基础知识、基本运算能力的考查.3.已知直线l 的参数方程为13,24x t y t =+⎧⎨=+⎩(t 为参数),则点(1,0)到直线l 的距离是A.15B.25 C.45D.65【答案】D 【解析】 【分析】首先将参数方程化为直角坐标方程,然后利用点到直线距离公式求解距离即可. 【详解】直线l 的普通方程为()()41320x y ---=,即4320x y -+=,点()1,0到直线l 的距离65d ==,故选D. 【点睛】本题考查直线参数方程与普通方程转化,点到直线的距离,属于容易题,注重基础知识、基本运算能力的考查.4.已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则A. a 2=2b 2B. 3a 2=4b 2C. a =2bD. 3a =4b【答案】B由题意利用离心率的定义和,,a b c 的关系可得满足题意的等式. 【详解】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =, 故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.5.若x ,y 满足|1|x y ≤-,且y ≥−1,则3x+y 的最大值为 A. −7 B. 1C. 5D. 7【答案】C 【解析】 【分析】首先画出可行域,然后结合目标函数的几何意义确定其最值即可.【详解】由题意1,11yy x y-≤⎧⎨-≤≤-⎩作出可行域如图阴影部分所示.设3,3z x y y z x =+=-, 当直线0:3l y z x =-经过点()2,1-时,取最大值5.故选C.【点睛】本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知识、基本技能的考查.6.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg Em m E =,其中星等为m 1的星的亮度为E 2(k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为 A. 1010.1B. 10.1C. lg10.1D. 10–10.1【答案】D 【解析】 【分析】 先求出12lgE E ,然后将对数式换为指数式求12E E 再求12E E【详解】两颗星的星等与亮度满足12125lg 2E m m E -= , 令21.45m =- ,126.7m =- ,()1212221g( 1.4526.7)10.155E m m E =-=-+=, 10.110.112211010E EE E -=⋅= , 故选D.【点睛】考查考生的数学应用意识、信息处理能力、阅读理解能力以及指数对数运算.7.设点A ,B ,C 不共线,则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C 【解析】 【分析】由题意结合向量的减法公式和向量的运算法则考查充分性和必要性是否成立即可.【详解】∵A 、B 、C 三点不共线,∴|AB +AC |>|BC |⇔|AB +AC |>|AB -AC |⇔|AB +AC |2>|AB -AC |2AB ⇔•AC >0AB ⇔与AC的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C. 【点睛】本题考查充要条件的概念与判断、平面向量的模、夹角与数量积,同时考查了转化与化归数学思想.8.数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 2;③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是 A. ① B. ②C. ①②D. ①②③【答案】C 【解析】 【分析】将所给方程进行等价变形确定x 的范围可得整点坐标和个数,结合均值不等式可得曲线上的点到坐标原点距离的最值和范围,利用图形的对称性和整点的坐标可确定图形面积的范围.详解】由221x y x y +=+得,221y x y x -=-,2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭厔, 所以x 可为的整数有0,-1,1,从而曲线22:1C x y x y +=+恰好经过(0,1),(0,-1),(1,0),(1,1),(-1,0),(-1,1)六个整点,结论①正确.由221x y x y +=+得,222212x y x y +++…,解得222x y +≤,所以曲线C 上任意一点到原点的距. 结论②正确.如图所示,易知()()()()0,1,1,0,1,1,,0,1AB C D -,四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=,很明显“心形”区域的面积大于2ABCD S ,即“心形”区域的面积大于3,说法③错误.故选C.【点睛】本题考查曲线与方程、曲线的几何性质,基本不等式及其应用,属于难题,注重基础知识、基本运算能力及分析问题解决问题的能力考查,渗透“美育思想”.第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2019年北京市高考数学试卷(文科)以及答案解析

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试(北京卷)文科数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.(5分)已知集合A={x|﹣1<x<2},B={x|x>1},则A∪B=()A.(﹣1,1)B.(1,2)C.(﹣1,+∞)D.(1,+∞)2.(5分)已知复数z=2+i,则z•=()A.B.C.3D.53.(5分)下列函数中,在区间(0,+∞)上单调递增的是()A.y=x B.y=2﹣x C.y=log x D.y=4.(5分)执行如图所示的程序框图,输出的s值为()A.1B.2C.3D.45.(5分)已知双曲线﹣y2=1(a>0)的离心率是,则a=()A.B.4C.2D.6.(5分)设函数f(x)=cos x+b sin x(b为常数),则“b=0”是“f(x)为偶函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m2﹣m1=lg,其中星等为m k的星的亮度为E k(k=1,2).已知太阳的星等是﹣26.7,天狼星的星等是﹣1.45,则太阳与天狼星的亮度的比值为()A.1010.1B.10.1C.lg10.1D.10﹣10.18.(5分)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β,图中阴影区域的面积的最大值为()A.4β+4cosβB.4β+4sinβC.2β+2cosβD.2β+2sinβ二、填空题共6小题,每小题5分,共30分。
2019年高考理数北京卷(附答案与解析)
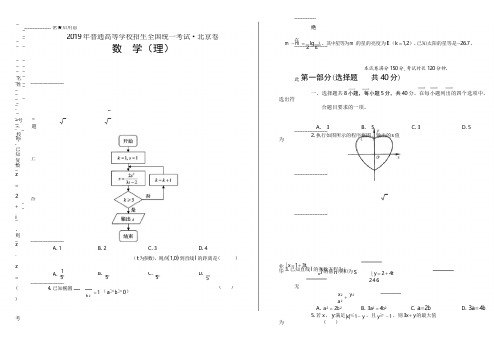
---------------- 密★启用前 2019 年普通高等学校招生全国统一考试·北京卷数学(理)m - m = lg 1 ,其中星等为 m 的星的亮度为 E (k = 1,2).已知太阳的星等是 -26.7 ,2 E_ -------------------- __ __ ___号 卷__ 生 __ __ 上___ 答 __ ___ --------------------A .1B .2C .3D .4( t 为参数),则点 (1,0) 到直线 l 的距离是()A . 15B .5C .5D .5--------------------b 2 = 1 ( a >b >0 )4.已知椭圆( )n }的前 n 项和为 S_ __ __1.已知复数 z = 2 + i ,则 z ⋅ z =()考__ __ __ _ _ _ _ _ _ _ _ _ _ _ _ 名 __ 姓 _ _ _ __ __ __ _ 题校 学 -------------绝在--------------------本试卷满分 150 分,考试时长 120 分钟.此 第一部分(选择题 共 40 分)一、选择题共 8 小题,每小题 5 分,共 40 分。
在每小题列出的四个选项中,选出符合题目要求的一项。
A . 3B . 5C .3D .5--------------------2.执行如图所示的程序框图,输出的 s 值为 ( )----------------------------------------业 ⎧ x = 1 + 3t,毕 3.已知直线 l 的参数方程为 ⎨ ⎩ y = 2 + 4t2 4 6无x 2 y 2a 2 +A . a 2 = 2b 2B . 3a 2 = 4b 2C . a = 2bD . 3a = 4b 5.若 x , y 满足 |x|≤1 - y ,且 y ≥ - 1 ,则 3x + y 的最大值为 ( )|A . -7B .1C .5D .7 6.在天文学中,天体的明暗程度可以用星等或亮度来描述 .两颗星的星等与亮度满足 5 E2 1 k k 2天狼星的星等是 -1.45 ,则太阳与天狼星的亮度的比值为下列说法中,正确的是( )A .1010.1B .10.1C . lg10.1D .10 -10.1 7.设点 A , B , C 不共线,则“ AB 与 AC 的夹角为锐角”是“| AB + AC | > B C | ”的 ( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件8.数学中有许多形状优美、寓意美好的曲线,曲线 C : x 2 + y 2 = 1+ | x | y 就是其中之一(如图).给出下列三个结论:①曲线 C 恰好经过 6 个整点(即横、纵坐标均为整数的点);②曲线 C 上任意一点到原点的距离都不超过 2 ; ③曲线 C 所围成的“心形”区域的面积小于 3.其中,所有正确结论的序号是 ( )A .①B .②C .①②D .①②③第二部分(非选择题 共 110 分)二、填空题共 6 小题,每小题 5 分,共 30 分。
2019年北京卷数学(文)高考真题(选择题和填空题)详解版

绝密★本科目考试启用前2019年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合A={x|–1<x<2},B={x|x>1},则A∪B=(A)(–1,1)(B)(1,2)(C)(–1,+∞)(D)(1,+∞)考点:考查集合的基本性质概念:解析:此题考查集合的基本性质。
将集合A、集合B表示在数轴(如下图所示)上。
数轴那么{A∪B=x|x>−1}答案:C(2)已知复数z=2+i,则z z⋅=(A(B(C)3 (D)5考点:复数的基本概念及其四则运算概念:①i2=−1;②两个实部相等,虚部互为相反数的复数互为共轭复数解析:因为z=2+i所以 z̅=2+i所以z ⋅⎺z = (2+i) (2-i)=22-i2=4-(-1)=5,答案:D(3)下列函数中,在区间(0,+∞)上单调递增的是(A)12y x=(B)y=2x-(C)12logy x=(D)1yx=考点:考查函数的概念与性质概念:解析:A为幂函数y=x a(a>0,且a≠1),在区间(0,+ ∞)单调递增。
B为指数函数y=a x(0<a<1),在区间(0,+ ∞)单调递减。
C为对数函数y=loga x(0<a<1),在区间(0,+ ∞)单调递减。
D为典型的反比例函数,在区间(0,+ ∞)单调递减。
答案:A(4)执行如图所示的程序框图,输出的s 值为(A )1 (B )2 (C )3 (D )4考点:考查程序框图的应用,考查学生逻辑推理能力、运算求解能力 解析:解决此类问题最常用的方法就是代入求值法。
当k =1,s =1时,s =2×123×1−2=2,不满足k ≥3,进入循环; 当k =2,s =2时,s =2×223×2−2=2,不满足k ≥3,进入循环;当k =3,s =2时,s =2×223×2−2=2, 满足k ≥3,退出循环; 输出s =2; 答案:B(5)已知双曲线2221x y a-=(a >0a =(A(B )4(C )2(D )12考点: 考查双曲线的性质 概念:双曲线x 2a2−y 2b 2=1(a >0,b >0)的离心率为e =c a=√a 2+b 2a解析:根据题意可知e =√a 2+12a=√5,推出a =12答案:D(6)设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件考点: 考查函数的性质 概念:解析:当b =0时,f (x )=cosx ,则f(x)是偶函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年北京市高考数学试卷(理科)一、选择题 共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知复数2z i =+,则(z z =g )A .3B .5C .3D .52.执行如图所示的程序框图,输出的s 值为( ) A .1 B .2 C .3 D .43.已知直线l 的参数方程为13,(24x t t y t=+⎧⎨=+⎩为参数),则点(1,0)到直线l 的距离是( ) A .15 B .25 C .45 D .654.已知椭圆22221(0)x y a b a b +=>>的离心率为12,则( ) A .222a b = B .2234a b = C .2a b = D .34a b =5.若x ,y 满足||1x y -„,且1y -…,则3x y +的最大值为( )A .7-B .1C .5D .76.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足121252E m m lg E -=,其中星等为k m 的星的亮度为(1,2)k E k =.已知太阳的星等是26.7-,天狼星的星等是 1.45-,则太阳与天狼星的亮度的比值为( )A .10.110B .10.1C .10.1lgD .10.110- 7.设点A ,B ,C 不共线,则“AB u u u r 与AC u u u r 的夹角为锐角”是“||||AB AC BC +>u u u r u u u r u u u r ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件8.数学中有许多形状优美、寓意美好的曲线,曲线22:1||C x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C 2③曲线C 所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是( )A .①B .②C .①②D .①②③二、填空题 共6小题,每小题5分,共30分。
9.函数2()sin 2f x x =的最小正周期是 .10.设等差数列{}n a 的前n 项和为n S ,若23a =-,510S =-,则5a = ,n S 的最小值为 .11.某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为l ,那么该几何体的体积为 .12.已知l ,m 是平面α外的两条不同直线.给出下列三个论断:①l m ⊥;②//m α;③l α⊥.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: .13.设函数()(x x f x e ae a -=+为常数).若()f x 为奇函数,则a = ;若()f x 是R 上的增函数,则a 的取值范围是 .14.李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x 元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.①当10x =时,顾客一次购买草莓和西瓜各1盒,需要支付 元;②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x 的最大值为 .三、解答题 共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程。
15.(13分)在ABC ∆中,3a =,2b c -=,1cos 2B =-. (Ⅰ)求b ,c 的值;(Ⅱ)求sin()B C -的值.16.(14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,//AD BC ,2PA AD CD ===,3BC =.E 为PD 的中点,点F 在PC 上,且13PF PC =. (Ⅰ)求证:CD ⊥平面PAD ;(Ⅱ)求二面角F AE P --的余弦值;(Ⅲ)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由. 17.(13分)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A ,B 两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A ,B 两种支付方式都不使用的有5人,样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下:支付金额(元) 支付方式(0,1000] (1000,2000]大于2000 仅使用A 18人 9人 3人仅使用B 10人 14人 1人 (Ⅱ)从样本仅使用A 和仅使用B 的学生中各随机抽取1人,以X 表示这2人中上个月支付金额大于1000元的人数,求X 的分布列和数学期望;(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A 的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化说明理由.18.(14分)已知抛物线2:2C x py =-经过点(2,1)-.(Ⅰ)求抛物线C 的方程及其准线方程;(Ⅱ)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线1y =-分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.19.(13分)已知函数321()4f x x x x =-+. (Ⅰ)求曲线()y f x =的斜率为l 的切线方程;(Ⅱ)当[2x ∈-,4]时,求证:6()x f x x -剟;(Ⅲ)设()|()()|()F x f x x a a R =-+∈,记()F x 在区间[2-,4]上的最大值为M (a ).当M (a )最小时,求a 的值.20.(13分)已知数列{}n a ,从中选取第1i 项、第2i 项、⋯、第m i 项12()m i i i <<⋯<,若12m i i i a a a <<⋯<,则称新数列1i a ,2i a ,⋯,m i a 为{}n a 的长度为m 的递增子列.规定:数列{}n a 的任意一项都是{}n a 的长度为1的递增子列.(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;(Ⅱ)已知数列{}n a 的长度为p 的递增子列的末项的最小值为0m a ,长度为q 的递增子列的末项的最小值为0n a .若p q <,求证:00m n a a <;(Ⅲ)设无穷数列{}n a 的各项均为正整数,且任意两项均不相等.若{}n a 的长度为s 的递增子列末项的最小值为21s -,且长度为s 末项为21s -的递增子列恰有12s -个(1s =,2,)⋯,求数列{}n a 的通项公式.2019年北京市高考数学试卷(理科)参考答案与试题解析一、选择题 共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知复数2z i =+,则(z z =g )A .3B .5C .3D .5【思路分析】直接由2||z z z =g 求解. 【解析】:2z i =+Q ,2222||(21)5z z z ∴==+=g .故选:D .【归纳与总结】本题考查复数及其运算性质,是基础的计算题.2.执行如图所示的程序框图,输出的s 值为( )A .1B .2C .3D .4【思路分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量s 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解析】:模拟程序的运行,可得1k =,1s =2s =不满足条件3k …,执行循环体,2k =,2s =不满足条件3k …,执行循环体,3k =,2s =此时,满足条件3k …,退出循环,输出s 的值为2.故选:B .【归纳与总结】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.3.已知直线l 的参数方程为13,(24x t t y t =+⎧⎨=+⎩为参数),则点(1,0)到直线l 的距离是( ) A .15 B .25 C .45 D .65【思路分析】消参数t 化参数方程为普通方程,再由点到直线的距离公式求解.【解析】:由13(24x t t y t =+⎧⎨=+⎩为参数),消去t ,可得4320x y -+=. 则点(1,0)到直线l 的距离是22654(3)d ==+-. 故选:D .【归纳与总结】本题考查参数方程化普通方程,考查点到直线距离公式的应用,是基础题.4.已知椭圆22221(0) x ya ba b+=>>的离心率为12,则()A.222a b=B.2234a b=C.2a b=D.34a b=【思路分析】由椭圆离心率及隐含条件222a b c=+得答案.【解析】:由题意,12ca=,得2214ca=,则22214a ba-=,22244a b a∴-=,即2234a b=.故选:B.【归纳与总结】本题考查椭圆的简单性质,熟记隐含条件是关键,是基础题.5.若x,y满足||1x y-„,且1y-…,则3x y+的最大值为()A.7-B.1 C.5 D.7【思路分析】由约束条件作出可行域,令3z x y=+,化为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解析】:由||11x yy-⎧⎨-⎩„…作出可行域如图,联立110yx y=-⎧⎨+-=⎩,解得(2,1)A-,令3z x y=+,化为3y x z=-+,由图可知,当直线3y x z=-+过点A时,z有最大值为3215⨯-=.故选:C.【归纳与总结】本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.6.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足121252Em m lgE-=,其中星等为km的星的亮度为(1,2)kE k=.已知太阳的星等是26.7-,天狼星的星等是 1.45-,则太阳与天狼星的亮度的比值为()A.10.110B.10.1 C.10.1lg D.10.110-【思路分析】把已知熟记代入121252Em m lgE-=,化简后利用对数的运算性质求解.【解析】:设太阳的星等是126.7m=-,天狼星的星等是21.45m=-,由题意可得:1251.45(26.7)2ElgE---=,∴1250.510.15ElgE==,则10.11210EE=.故选:A.【归纳与总结】本题考查对数的运算性质,是基础的计算题.7.设点A,B,C不共线,则“ABu u u r与ACu u u r的夹角为锐角”是“||||AB AC BC+>u u u r u u u r u u u r”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【思路分析】“AB u u u r 与AC u u u r 的夹角为锐角” ⇒ “||||AB AC BC +>u u u r u u u r u u u r ”,“ ||||AB AC BC +>u u u r u u u r u u u r ” ⇒ “AB u u u r 与AC u u u r 的夹角为锐角”,由此能求出结果.【解析】:点A ,B ,C 不共线, “AB u u u r 与AC u u u r 的夹角为锐角” ⇒ “||||AB AC BC +>u u u r u u u r u u u r ”, “||||AB AC BC +>u u u r u u u r u u u r ” ⇒ “AB u u u r 与AC u u u r 的夹角为锐角”, ∴设点A ,B ,C 不共线,则“AB u u u r 与AC u u u r 的夹角为锐角”是“||||AB AC BC +>u u u r u u u r u u u r ”的充分必要条件.故选:C .【归纳与总结】本题考查充分条件、必要条件、充要条件的判断,考查向量等基础知识,考查推理能力与计算能力,属于基础题.8.数学中有许多形状优美、寓意美好的曲线,曲线22:1||C x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C 上任意一点到原点的距离都不超过2;③曲线C 所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是( )A .①B .②C .①②D .①②③【思路分析】将x 换成x -方程不变,所以图形关于y 轴对称,根据对称性讨论y 轴右边的图形可得.【解析】:将x 换成x -方程不变,所以图形关于y 轴对称,当0x =时,代入得21y =,1y ∴=±,即曲线经过(0,1),(0,1)-;当0x >时,方程变为2210y xy x -+-=,所以△224(1)0x x =--…,解得(0x ∈23, 所以x 只能取整数1,当1x =时,20y y -=,解得0y =或1y =,即曲线经过(1,0),(1,1), 根据对称性可得曲线还经过(1,0)-,(1,1)-,故曲线一共经过6个整点,故①正确.当0x >时,由221x y xy +=+得222212x y x y xy ++-=„,(当x y =时取等), 222x y ∴+„,∴222x y +„C 上y 2,根据对称性可得:曲线C 2在x 轴上图形面积大于矩形面积122=⨯=,x 轴下方的面积大于等腰直角三角形的面积12112=⨯⨯=,因此曲线C 所围成的“心形”区域的面积大于213+=,故③错误. 故选:C .【归纳与总结】本题考查了命题的真假判断与应用,属中档题.二、填空题共6小题,每小题5分,共30分。
