二次函数与相似三角形结合问题
类型五 二次函数与三角形全等、相似(位似)有关的问题(解析版)

类型五二次函数与三角形全等、相似(位似)有关的问题【典例1】如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.(1)求抛物线的解析式;(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.【答案】(1)y=﹣2x2+4x+6;(2)S△PBC=﹣3m2+9m(0<m<3);(3)M(1,8),N(0,17 2)或M(74,558),N(0,838)或M(94,398),N(0,38)或M(3,0),N(0,﹣32)【解析】【分析】(1)根据点A、B的坐标利用待定系数法即可求出抛物线的解析式;(2)过点P作PF∥y轴,交BC于点F,利用二次函数图象上点的坐标特征可得出点C的坐标,根据点B、C的坐标利用待定系数法即可求出直线BC的解析式,设点P的坐标为(m,﹣2m2+4m+6),则点F的坐标为(m,﹣2m+6),进而可得出PF的长度,利用三角形的面积公式可得出S△PBC=﹣3m2+9m,配方后利用二次函数的性质即可求出△PBC面积的最大值;(3)分两种不同情况,当点M位于点C上方或下方时,画出图形,由相似三角形的性质得出方程,求出点M,点N的坐标即可.【详解】(1)将A (﹣1,0)、B (3,0)代入y =ax 2+bx+6, 得:609360a b a b -+=⎧⎨++=⎩,解得:24a b =-⎧⎨=⎩,∴抛物线的解析式为y =﹣2x 2+4x+6.(2)过点P 作PF ∥y 轴,交BC 于点F ,如图1所示.当x =0时,y =﹣2x 2+4x+6=6, ∴点C 的坐标为(0,6). 设直线BC 的解析式为y =kx+c ,将B (3,0)、C (0,6)代入y =kx+c ,得:306k c c +=⎧⎨=⎩,解得:26k c =-⎧⎨=⎩, ∴直线BC 的解析式为y =﹣2x+6.设点P 的坐标为(m ,﹣2m 2+4m+6),则点F 的坐标为(m ,﹣2m+6), ∴PF =﹣2m 2+4m+6﹣(﹣2m+6)=﹣2m 2+6m , ∴223273931224PBCSPF OB m m m ⎛⎫=-+=--+ ⎪⎝⎭=, ∴当32m =时,△PBC 面积取最大值,最大值为274. ∵点P (m ,n )在平面直角坐标系第一象限内的抛物线上运动, ∴0<m <3.(3)存在点M 、点N 使得∠CMN =90°,且△CMN 与△OBC 相似.如图2,∠CMN =90°,当点M 位于点C 上方,过点M 作MD ⊥y 轴于点D ,∵∠CDM =∠CMN =90°,∠DCM =∠NCM , ∴△MCD ∽△NCM ,若△CMN 与△OBC 相似,则△MCD 与△NCM 相似, 设M (a ,﹣2a 2+4a+6),C (0,6), ∴DC =﹣2a 2+4a ,DM =a ,当3162DM OB CD OC === 时,△COB ∽△CDM ∽△CMN , ∴21242a a a =-+ ,解得,a =1, ∴M (1,8),此时1122ND DM ==, ∴N (0,172),当12CD OB DM OC ==时,△COB ∽△MDC ∽△NMC , ∴22412a a a +=﹣ ,解得74a =, ∴M (74,558),此时N (0,838). 如图3,当点M 位于点C 的下方,过点M 作ME ⊥y 轴于点E , 设M (a ,﹣2a 2+4a+6),C (0,6), ∴EC =2a 2﹣4a ,EM =a ,同理可得:21224a a a -=或2242a a a-=,△CMN 与△OBC 相似,解得94a =或a =3, ∴M (94,398)或M (3,0),此时N 点坐标为,N (0,38)或N (0,﹣32).综合以上得,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),,N (0,38)或M (3,0),N (0,﹣32),使得∠CMN =90°,且△CMN 与△OBC 相似.【典例2】如图,抛物线212y x bx c =++与x 轴交于A 、B 两点(点A 在点B 左边),与y 轴交于点C .直线122y x =-经过B 、C 两点.(1)求抛物线的解析式;(2)点P 是抛物线上的一动点,过点P 且垂直于x 轴的直线与直线BC 及x 轴分别交于点D 、M .PN BC ⊥,垂足为N .设(),0M m .①点P 在抛物线上运动,若P 、D 、M 三点中恰有一点是其它两点所连线段的中点(三点重合除外).请直接写出符合条件的m 的值;②当点P 在直线BC 下方的抛物线上运动时,是否存在一点P ,使PNC △与AOC △相似.若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)213222y x x =--;(2)-2,12-,1;(3)存在,(3,-2) 【解析】 【分析】 (1)根据直线122y x =-经过B 、C 两点求出B 、C 两点的坐标,将B 、C 坐标代入抛物线212y x bx c =++可得答案; (2)①由题意得P (m ,213222m m --),D (m ,122m -);根据P 、D 、M 三点中恰有一点是其它两点所连线段的中点列式计算即可求得m 的值;②先证明CBO AOC △∽△,得出ACO=ABC ∠∠,再根据PNC △与AOC △相似得出ACO=PCN ∠∠,则ABC=PCN ∠∠,可得出AB//PC ,求出点P 的纵坐标,代入抛物线213222y x x =--,即可求得点P 的横坐标. 【详解】解:(1)由直线122y x =-经过B 、C 两点得B (4,0),C (0,-2) 将B 、C 坐标代入抛物线得2840c b c =-⎧⎨++=⎩,解得322b c ⎧=-⎪⎨⎪=-⎩, ∴抛物线的解析式为:213222y x x =--; (2)①∵PN BC ⊥,垂足为N . (),0M m ∴P (m ,213222m m --),D (m ,122m -), 分以下几种情况:M 是PD 的中点时,MD=PM ,即0-(122m -)=213222m m -- 解得12m =-,24m =(舍去);P 是MD 的中点时,MD=2MP ,即122m -=2(213222m m --) 解得112m =-,24m =(舍去);D 是MP 的中点时,2MD=MP ,即213222m m --=2(122m -) 解得11m =,24m =(舍去); ∴符合条件的m 的值有-2,12-,1;②∵抛物线的解析式为:213222y x x =--, ∴A (-1,0),B (4,0),C (0,-2) ∴AO=1,CO=2,BO=4, ∴AO CO=CO BO,又AOC=COB ∠∠=90°, ∴AOC COB △∽△, ∴ACO=ABC ∠∠, ∵PNC △与AOC △相似 ∴ACO=PCN ∠∠, ∴ABC=PCN ∠∠, ∴ AB//PC ,∴点P 的纵坐标是-2,代入抛物线213222y x x =--,得 2322122x x --=- 解得:10x =(舍去),23x =, ∴点P 的坐标为:(3,-2) 【典例3】如图,抛物线215:324L y x x =--与x 轴正半轴交于点A ,与y 轴交于点B .(1)求直线AB 的解析式及抛物线顶点坐标;(2)如图1,点P 为第四象限且在对称轴右侧抛物线上一动点,过点P 作PC x ⊥轴,垂足为C ,PC 交AB 于点D ,求PD BD +的最大值,并求出此时点P 的坐标;(3)如图2,将抛物线215:324L y x x =--向右平移得到抛物线L ',直线AB 与抛物线L '交于M ,N 两点,若点A 是线段MN 的中点,求抛物线L '的解析式.【答案】(1)直线AB 的解析式为334y x =-,抛物线顶点坐标为5121,432⎛⎫- ⎪⎝⎭;(2)当134x =时,PD BD +的最大值为16932; 1357,432P ⎛⎫- ⎪⎝⎭;(3)21133242y x x =-+. 【解析】 【分析】(1)先根据函数关系式求出A 、B 两点的坐标,设直线AB 的解析式为y kx b =+,利用待定系数法求出AB 的解析式,将二次函数解析式配方为顶点式即可求得顶点坐标;(2)过点D 作DE y ⊥轴于E ,则//DE OA .求得AB=5,设点P 的坐标为2155,34244x x x x ⎛⎫⎛⎫--<< ⎪⎪⎝⎭⎝⎭,则点D 的坐标为3,34x x ⎛⎫- ⎪⎝⎭,ED=x ,证明BDE BAO ∽,由相似三角形的性质求出54BD x =,用含x 的式子表示PD ,配方求得最大值,即可求得点P 的坐标;(3)设平移后抛物线L '的解析式21121()232y x m =--,将L ′的解析式和直线AB 联立,得到关于x 的方程,设()()1122,,,M x y N x y ,则12,x x 是方程2232520416x m x m ⎛⎫-++-= ⎪⎝⎭的两根,得到12324x x m ⎛⎫+=+ ⎪⎝⎭,点A 为MN 的中点,128x x +=,可求得m 的值,即可求得L ′的函数解析式.【详解】(1)在215324y x x =--中, 令0y =,则2153024x x --=,解得123,42x x =-=,∴(4,0)A .令0x =,则3y =-,∴()0,3B -.设直线AB 的解析式为y kx b =+,则403k b b +=⎧⎨=-⎩,解得:343k b ⎧=⎪⎨⎪=-⎩,∴直线AB 的解析式为334y x =-. 2215151213242432y x x x ⎛⎫=--=--⎪⎝⎭, ∴抛物线顶点坐标为5121,432⎛⎫-⎪⎝⎭(2)如图,过点D 作DE y ⊥轴于E ,则//DE OA . ∵4,3OA OB ==,∴5AB ===, 设点P 的坐标为2155,34244x x x x ⎛⎫⎛⎫--<< ⎪⎪⎝⎭⎝⎭,则点D 的坐标为3,34x x ⎛⎫- ⎪⎝⎭, ∴ED x =. ∵//DE OA ,∴BDE BAO ∽,∴BD EDBA OA =, ∴54BD x=, ∴54BD x =.而2231513324242PD x x x x x ⎛⎫=----=-+ ⎪⎝⎭, ∴22215113113169224242432PD BD x x x x x x ⎛⎫+=-++=-+=--+⎪⎝⎭, ∵102-<,544x <<,由二次函数的性质可知:当134x =时,PD BD +的最大值为16932.2235313513573344444432x x ⎛⎫--=⨯-⨯-=- ⎪⎝⎭, ∴1357,432P ⎛⎫-⎪⎝⎭.(3)设平移后抛物线L '的解析式21121()232y x m =--,联立23341121()232y x y x m ⎧=-⎪⎪⎨⎪=--⎪⎩,∴2311213()4232x x m -=--, 整理,得:2232520416x m x m ⎛⎫-++-= ⎪⎝⎭, 设()()1122,,,M x y N x y ,则12,x x 是方程2232520416x m x m ⎛⎫-++-= ⎪⎝⎭的两根, ∴12324x x m ⎛⎫+=+ ⎪⎝⎭.而A 为MN 的中点,∴128x x +=, ∴3284m ⎛⎫+= ⎪⎝⎭,解得:134m =. ∴抛物线L '的解析式2211312111332432242y x x x ⎛⎫=--=-+ ⎪⎝⎭.【典例4】在平面直角坐标系中,已知抛物线()24460y ax ax a a =++->与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为点D .(1)当6a =时,直接写出点A ,B ,C ,D 的坐标:A ______,B ______,C ______,D ______;(2)如图1,直线DC 交x 轴于点E ,若4tan 3AED =∠,求a 的值和CE 的长; (3)如图2,在(2)的条件下,若点N 为OC 的中点,动点P 在第三象限的抛物线上,过点P 作x 轴的垂线,垂足为Q ,交AN 于点F ;过点F 作FH DE ⊥,垂足为H .设点P 的横坐标为t ,记f FP FH =+.①用含t 的代数式表示f ;②设()50t m m -<≤<,求f 的最大值.【答案】(1)()3,0-,()1,0-,()0,18,()2,6--;(2)23;256;(3)①228433f t t =--+;②263.【解析】 【分析】(1)求出0y =时,x 的值可得点A 、B 的坐标,求出0x =时,y 的值可得点C 的坐标,将二次函数的解析式化为顶点式即可得点D 的坐标;(2)先求出顶点D 的坐标,从而可得DK 、OK 的长,再利用正切三角函数可得EK 、OE 、OC 的长,从而可得出点C 的坐标,然后将点C 的坐标代入二次函数的解析式可得a 的值,利用勾股定理可求出CE 的长;(3)①如图,先利用待定系数法求出直线AN 的解析式,从而可得点F 的坐标,由此可得出PF 的长,再利用待定系数法求出直线CE 的解析式,从而可得点J 的坐标,由此可得出FJ 的长,然后根据相似三角形的判定与性质可得FH FJOE CE=,从而可得FH 的长,最后根据f 的定义即可得;②先将f 的表达式化为顶点式,从而得出其增减性,再利用二次函数的性质即可得. 【详解】(1)当6a =时,262418y x x =++当0y =时,2624180x x ++=,解得1x =-或3x =-则点A 的坐标为(3,0)A -,点B 的坐标为(1,0)B - 当0x =时,18y = 则点C 的坐标为(0,18)C将262418y x x =++化成顶点式为26()62y x =+- 则点D 的坐标为(2,6)D --故答案为:()3,0-,()1,0-,()0,18,()2,6--; (2)如图,作DK x ⊥轴于点K将2446y ax ax a =++-化成顶点式为2(2)6y a x =+-则顶点D 的坐标为(2,6)D -- ∴6DK =,2OK = 在Rt DKE 中,tan DK AED EK ∠=,即643EK = 解得92EK =95222K OE EK O =--=∴= 在Rt COE △中,tan OC AED OE=∠,即4532OC =解得103OC =10(0,)3C ∴-,2222105()()32256CE OC OE =+=+= 将点10(0,)3C -代入2446y ax ax a =++-得:10463a -=- 解得23a =;(3)①如图,作FP 与ED 的延长线交于点J由(2)可知,23a =,100,3C ⎛⎫- ⎪⎝⎭∴22810333y x x =+- 当0y =时,228100333x x +-=,解得5x =-或1x = ∴()5,0A -,()10B , N 为OC 的中点∴50,3N ⎛⎫- ⎪⎝⎭设直线AN 的解析式为11y k x b =+将点()5,0A -,50,3N ⎛⎫- ⎪⎝⎭代入得:1115053k b b -+=⎧⎪⎨=-⎪⎩,解得111353k b ⎧=-⎪⎪⎨⎪=-⎪⎩则直线AN 的解析式为1533y x =-- ∵22810,333P t t t ⎛⎫+-⎪⎝⎭∴15,33F t t ⎛⎫-- ⎪⎝⎭∴2215281025()33333333PF t t t t t =---+-=--+ 由(2)知,25OE =∴5,02E ⎛⎫ ⎪⎝⎭,100,3C ⎛⎫- ⎪⎝⎭设直线CE 的解析式为22y k x b =+将点5,02E ⎛⎫ ⎪⎝⎭,100,3C ⎛⎫- ⎪⎝⎭代入得:222502103k b b ⎧+=⎪⎪⎨⎪=-⎪⎩,解得2243103k b ⎧=⎪⎪⎨⎪=-⎪⎩则直线CE 的解析式为41033y x =-∴410,33J t t ⎛⎫-⎪⎝⎭∴1541055()333333FJ t t t =----=-+ ∵FH DE ⊥,//JF y 轴∴90FHJ EOC ∠=∠=︒,FJH ECO ∠=∠ ∴FJH ECO ~∴FH FJOE CE=,即553226535t FH -+= 解得1FH t =-+∴()2253133f PF FH t t t =+=--++-+ 即228433f t t =--+; ②将228433f t t =--+化成顶点式为()2226333t f =-++由二次函数的性质可知,当3t <-时,f 随t 的增大而增大;当3t ≥-时,f 随t 的增大而减小()50t m m -<≤<50m ∴-<<因此,分以下两种情况: 当53m -<<-时在5t m -<≤内,f 随t 的增大而增大 则当t m =时,f 取得最大值,最大值为()2226333m -++ 又当53m -<<-时,()20233m -+< ()2226263333m -++<∴ 当30m -≤<时在53t -<<-内,f 随t 的增大而增大;在3t m -≤≤内,f 随t 的增大而减小则当3t =-时,f 取得最大值,最大值为263综上,f 的最大值为263.【典例5】如图①,直线l 经过点(4,0)且平行于y 轴,二次函数y =ax 2﹣2ax +c (a 、c 是常数,a <0)的图象经过点M (﹣1,1),交直线l 于点N ,图象的顶点为D ,它的对称轴与x 轴交于点C ,直线DM 、DN 分别与x 轴相交于A 、B 两点.(1)当a =﹣1时,求点N 的坐标及ACBC的值; (2)随着a 的变化,ACBC的值是否发生变化?请说明理由; (3)如图②,E 是x 轴上位于点B 右侧的点,BC =2BE ,DE 交抛物线于点F .若FB =FE ,求此时的二次函数表达式.【答案】(1)N (4,﹣4),AC BC =32;(2)不变,理由见解析;(3)y =﹣7568x 2+7534x +29368或y =﹣568x 2+534x +8368.【解析】 【分析】(1)证明△DME ∽△DAC ,△DCB ∽△DFN ,则ME DE AC DC =,BC DC FN DF=,求出AC =52,BC=53,即可求解;(2)点D(1,1﹣4a),N(4,1+5a),则ME=2,DE=﹣4a,由(1)的结论得:AC=142aa--,BC=143aa--,即可求解;(3)利用△FHE∽△DCE,求出F(53﹣512a,16﹣23a),即可求解.【详解】解:(1)分别过点M、N作ME⊥CD于点E,NF⊥DC于点F,∵ME∥FN∥x轴,∴△DME∽△DAC,△DCB∽△DFN,∴ME DEAC DC=,BC DCFN DF=,∵a=﹣1,则y=﹣x2+2x+c,将M(﹣1,1)代入上式并解得:c=4,∴抛物线的表达式为:y=﹣x2+2x+4,则点D(1,5),N(4,﹣4),则ME=2,DE=4,DC=5,FN=3,DF=9,∴245,539BCAC==,解得:AC=52,BC=53,∴ACBC=32;(2)不变,理由:∵y=ax2﹣2ax+c过点M(﹣1,1),则a+2a+c=1,解得:c=1﹣2a,∴y=ax2﹣2ax+(1﹣3a),∴点D(1,1﹣4a),N(4,1+5a),∴ME=2,DE=﹣4a,由(1)的结论得:AC=142aa--,BC=143aa--,∴ACBC=32;(3)过点F作FH⊥x轴于点H,则FH∥l,则△FHE∽△DCE,∵FB=FE,FH⊥BE,∴BH=HE,∵BC=2BE,则CE=6HE,∵CD=1﹣4a,∴FH=146a -,∵BC=41 3aa-,∴CH=54×413aa-=20512aa-,∴F(53﹣512a,16﹣23a),将点F的坐标代入y=ax2﹣2ax+(1﹣3a)=a(x+1)(x﹣3)+1得:16﹣23a =a (53﹣512a +1)(53﹣512a ﹣3)+1,解得:a =﹣7568或﹣568,故y =﹣7568x 2+7534x +29368或y =﹣568x 2+534x +8368.【典例6】若一次函数33y x =--的图象与x 轴,y 轴分别交于A ,C 两点,点B 的坐标为()3,0,二次函数2y ax bx c =++的图象过A ,B ,C 三点,如图(1).(1)求二次函数的表达式;(2)如图(1),过点C 作//CD x 轴交抛物线于点D ,点E 在抛物线上(y 轴左侧),若BC 恰好平分DBE ∠.求直线BE 的表达式;(3)如图(2),若点P 在抛物线上(点P 在y 轴右侧),连接AP 交BC 于点F ,连接BP ,BFPBAFSmS=.①当12m =时,求点P 的坐标; ②求m 的最大值.【答案】(1)223y x x =--;(2)113y x =-;(3)①点(2,3)P -或(1,4)-P ;②916m =最大值 【解析】 【分析】(1)先求的点A 、C 的坐标,再用待定系数法求二次函数的解析式即可; (2)设BE 交OC 于点M .由(3,0),(0,3)B C -可得OB OC =,45OBC OCB ︒∠=∠=.再由//CD AB ,根据平行线的性质可得45BCD ︒∠=,所以OCB BCD ∠=∠.已知BC 平分DBE ∠,根据角平分线的定义可得EBC DBC ∠=∠.利用AAS 证得MBC DBC ≌.由全等三角形的性质可得CM CD =. 由此即可求得点M 的坐标为(0,-1).再由(3,0)B ,即可求得直线BE 解析式为113y x =-; (3)①由12BFPBAF SS =可得12PF AF =.过点P 作//PN AB 交BC 于点N ,则ABF PNF ∽.根据相似三角形的性质可得2AB NP =.由此即可求得2NP =.设()2,23P t t t --,可得2233N t t x --=-.所以22N x t t =-.由此即可得()22PN t t t =--=2,解得122,1t t ==.即可求得点(2,3)P -或(1,4)-P ;②由①得4PN m =.即()22213442169t t t m t --⎛⎫==--+ ⎪⎝⎭.再根据二次函数的性质即可得916m =最大值. 【详解】(1)解:令330x --=,得1x =-.令0x =时,3y =-. ∴(1,0),(0,3)A C --. ∵抛物线过点(0,3)C -, ∴3c =-.则23y ax bx =+-,将(1,0),(3,0)A B -代入得03,093 3.a b a b =--⎧⎨=+-⎩解得1,2.a b =⎧⎨=-⎩∴二次函数表达式为223y x x =--.(2)解:设BE 交OC 于点M .∵(3,0),(0,3)B C -,∴OB OC =,45OBC OCB ︒∠=∠=.∵//CD AB ,∴45BCD ︒∠=.∴OCB BCD ∠=∠.∵BC 平分DBE ∠,∴EBC DBC ∠=∠.又∵BC BC =,∴MBC DBC ≌.∴CM CD =.由条件得:(2,3)D -.∴2CD CM ==.∴321OM =--.∴(0,1)M -.∵(3,0)B ,∴直线BE 解析式为113y x =-.(3)①12BFP BAF S S =,∴12PF AF =. 过点P 作//PN AB 交BC 于点N ,则ABF PNF ∽. ∴2AB NP =.∵4AB =,∴2NP =.∵直线BC 的表达式为3y x =-,设()2,23P t t t --,∴2233N t t x --=-.∴22N x t t =-.∴()22PN t t t =--,则()222t t t --=,解得122,1t t ==. ∴点(2,3)P -或(1,4)-P .②由①得:4PN m =. ∴()()222222331391344442442916t t t t t t t m t t ----⎡⎤-+⎛⎫⎛⎫====⨯--+=--+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦. ∴m 有最大值,916m =最大值.。
二次函数与相似三角形问题(含答案 完美打印版)

综合题讲解 函数中因动点产生的相似三角形问题例题 如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;(用顶点式...求得抛物线的解析式为x x 41y 2+-=) ⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似若存在,求出P 点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. 函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
y xEQ PC B OA 例题2:如图,已知抛物线y=ax 2+4ax+t (a >0)交x 轴于A 、B 两点,交y 轴于点C ,抛物线的对称轴交x 轴于点E ,点B 的坐标为(-1,0). (1)求抛物线的对称轴及点A 的坐标;(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ,你能判断四边形ABCP 是什么四边形并证明你的结论;(3)连接CA 与抛物线的对称轴交于点D ,当∠APD=∠ACP 时,求抛物线的解析式.练习1、已知抛物线2y ax bx c =++经过5330P E ⎫⎪⎪⎝⎭,,,及原点(00)O ,.(1)求抛物线的解析式.(由一般式...得抛物线的解析式为225333y x x =-+) (2)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似若存在,求出Q 点的坐标;若不存在,说明理由.(3)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系为什么练习2、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,将边BC 折叠,使点B 落在边OA 的点D处。
2023年中考数学高频压轴题突破——二次函数与相似三角形

2023年中考数学高频压轴题突破——二次函数与相似三角形1.在平面直角坐标系xOy中(如图),已知点A在x轴的正半轴上,且与原点的距离为3,抛物线y=ax2﹣4ax+3(a≠0)经过点A,其顶点为C,直线y=1与y轴交于点B,与抛物线交于点D(在其对称轴右侧),联结BC、CD.(1)求抛物线的表达式及点C的坐标;(2)点P是y轴的负半轴上的一点,如果△PBC与△BCD相似,且相似比不为1,求点P的坐标;(3)将∠CBD绕着点B逆时针方向旋转,使射线BC经过点A,另一边与抛物线交于点E(点E在对称轴的右侧),求点E的坐标.2.如图,在平面直角坐标系中,将抛物线平移,使平移后的抛物线C2经过点A (﹣3,0),B(1,0),与y轴的交点为E.(1)求抛物线C2的函数解析式;(2)点P(m,n)(﹣3<m<0)是抛物线C2上的动点,设四边形OAPE的面积为S,求S与m的函数关系式,并求四边形OAPE的面积的最大值;(3)若y=x2与平移后的抛物线对称轴交于D点,在抛物线C2的对称轴上,是否存在一点M,使得以M,O,D为顶点的三角形与△BOD相似?若存在,求点M的坐标;若不存在,说明理由.3.如图,在直角坐标系中,直线y=﹣x﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.(1)求抛物线的解析式;(2)在线段AB上是否存在一点P,使以A,D,P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;如果不存在,请说明理由;(3)若点Q在第三象限内,且tan∠AQD=2,线段CQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.4.已知直线y=﹣x+2与x轴、y轴分别交于点A、C,抛物线y=﹣+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作DE⊥AC于点E.(1)求抛物线的表达式;(2)求△ACD面积的最大值;(3)若△CED与△COB相似,求点D的坐标.5.如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y =﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.(1)求抛物线的解析式.(2)求△ABE面积的最大值.(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.6.如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.(1)求该函数的表达式;(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.①求线段PQ的最大值;②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.7.如图所示,抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,(1)求cos∠CAO的值;(2)求直线AC的函数关系式;(3)如果有动点P是y轴上,且△OP A与△OAC相似,求P点坐标.8.如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.(1)求二次函数的解析式;(2)若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E 的坐标,并求出四边形ABEC的最大面积;(3)若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M 为顶点的三角形与△AOC相似,求点M的坐标.9.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的解析式;(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q 的坐标;若不存在,说明理由.10.如图,已知二次函数y=ax2﹣4x+c的图象与x轴交于点A(﹣1,0)、点C,与y轴交于点B(0,﹣5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标,并求出△ABP周长的最小值;(3)在线段AC上是否存在点E,使以C、P、E为顶点的三角形与三角形ABC相似?若存在写出所有点E的坐标;若不存在,请说明理由.11.已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB 上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.(1)求这个二次函数的解析式;(2)设点P的横坐标为x,求线段PE的长(用含x的代数式表示);(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.12.如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点M,连接AC.(1)求该抛物线的解析式;(2)抛物线对称轴上存在一点H,连接AH、CH,当△AHC周长最小时,求此时点H 坐标.(3)设对称轴与x轴交于点E,在对称轴上是否存在点G,使以B、E、G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.13.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+8与x轴相交于A,B两点,与y 轴相交于点C,OA=4,OB=2,点D是抛物线上一动点,且在y轴的左侧,连接AD,BC,AC,CD.(1)求抛物线的解析式;(2)已知直线m:y=kx+8(不经过点B),同时与x轴和y轴相交,若直线m与x轴和y轴围成的三角形与△BCO相似,求k的值;(3)连接OD,若△ACD的面积是△ABC的面积的时,求△DOC的面积.14.如图,抛物线y=a(x﹣2)2+1与x轴交于点A(1,0),B(3,0),与y轴交于点C,顶点为D.(1)求抛物线的解析式及点C的坐标;(2)点E是直线BC上一动点,求出△ADE周长的最小值;(3)点P,M分别是抛物线和直线BC上的动点,是否存在以P,M,C为顶点的三角形与△AOC相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.15.如图,点A(0,2),B(1,0),连接AB并将线段AB绕点B顺时针旋转90°,点A 转到点C处.一抛物线经过C、B两点,与x轴交于另一点D(3.5,0).(1)求点C的坐标和抛物线的解析式.(2)在BC上方抛物线上是否存在一点P,使得四边形PBDC的面积最大?若存在,求出P的坐标及最大面积;若不存在,请说明理由.(3)连接CD,①求证:CD∥AB;②直线CD上是否存在一点M,使得△MBC与△AOB相似?若存在,求出点M的坐标;若不存在,请说明理由.16.如图,抛物线与坐标轴交于A,B,C三点,且4CO=2BO=OA=4,点D是线段AB 上的动点,过点D作DF⊥x轴,交x轴于点F,交抛物线于点E.(1)求抛物线的解析式;(2)当点D的坐标是多少时,DE最长,最长是多少?(3)当DE最长时,在直线DE上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似,若存在,直接写出点P的坐标,若不存在,说明理由.17.已知抛物线与直线AC相交于A、C两点,且A(﹣2,0)、C(4,3).(1)填空:b=,c=;(2)长度为的线段DE在线段AC上移动,点G与点F在上述抛物线上,且线段DG 与EF始终平行于y轴.①连接FG,求四边形DEFG的面积的最大值,并求出对应点D的坐标;②CH⊥AB,垂足为点H,线段DE在移动的过程中,是否存在点D,使△DEG与△ACH相似?若存在,请求出此时点D的坐标;若不存在,试说明理由.18.如图1,抛物线y=ax2+bx+4的顶点为(1,),抛物线交x轴于A,B两点(A在B 的左边),交y轴于C.(1)求抛物线的解析式;(2)如图2,沿射线AC方向平移抛物线y=ax2+bx+4,分别记A、C两点的对应点为E、F,在平移过程中,是否存在以A,E,B为顶点的三角形与△ABF相似,若存在,请求出此时平移后的E的横坐标;若不存在,请简要说明理由;(3)如图3,点N在y轴负半轴上,点A绕点N顺时针旋转,恰好落在第四象限的抛物线上点M处,且∠ANM+∠ACM=180°,求N点坐标.19.如图,二次函数y=a(x+1)(x﹣3)(a>0)的图象与x轴交于点A,B(A在B的左边),与y轴交于点C,点P是二次函数图象上一动点.(1)若点C的坐标为(0,﹣3),求二次函数及直线BC的函数关系式.(2)如图①,在(1)的条件下,若点P在第四象限,过P作PQ∥AC,交直线BC于点Q,求线段PQ长的最大值.(3)如图②,若点P在第一象限,且△ABP有△ABC相似,求点P的坐标.20.如图,若抛物线y=﹣x2+bx+c与x轴相交于A(﹣1,0),B两点,与y轴相交于点C,直线y=﹣x+3经过点B,C.(1)求抛物线的解析式;(2)点P为抛物线位于第二象限上的一点,连接BP交线段AC于点Q,若△AQB与△AOC相似,求点P的坐标;(3)若点D为抛物线位于第一象限上的一点,过点D作x轴的垂线,垂足为F,直线DF交直线BC于点E,若△CDE为等腰三角形,请直接写出点D的坐标.参考答案:1.【分析】(1)把点A的坐标代入抛物线的解析式中可得:a的值,从而得抛物线的解析式,配方得顶点C的坐标;(2)根据∠DBC=∠PBC=45°,且相似比不为1,所以只能△CBP∽△DBC,列比例式可得BP的长,从而得点P的坐标;(3)连接AC,过E作EH⊥BD于H,先根据勾股定理的逆定理证明△ABC是直角三角形,且∠ACB=90°,由等角三角函数得tan∠ABC=tan∠EBD==,设EH=m,则BH=2m,表示E(2m,m+1),代入抛物线的解析式,可得结论.【解答】解:(1)∵点A在x轴的正半轴上,且与原点的距离为3,∴A(3,0),把A(3,0)代入抛物线y=ax2﹣4ax+3中得:0=9a﹣12a+3,∴a=1,∴抛物线的表达式为:y=x2﹣4x+3,y=x2﹣4x+3=(x﹣2)2﹣1,∴C(2,﹣1);(2)当y=1时,x2﹣4x+3=1,解得:x1=2﹣,x2=2+,由题意得:D(2+,1),∵B(0,1),C(2,﹣1),∴BC==2,BD=2+,∵∠DBC=∠PBC=45°,且相似比不为1,只能△CBP∽△DBC,∴,即,∴BP=8﹣4,∴P(0,4﹣7);(3)连接AC,过E作EH⊥BD于H,由旋转得:∠CBD=∠ABE,∴∠EBD=∠ABC,∵AB2=32+12=10,BC2=22+22=8,AC2=12+12=2,∴AB2=BC2+AC2,∴△ABC是直角三角形,且∠ACB=90°,∴tan∠ABC==,∴tan∠EBD==,设EH=m,则BH=2m,∴E(2m,m+1),∵点E在抛物线上,∴(2m)2﹣4×2m+3=m+1,4m2﹣9m+2=0,解得:m1=2,m2=(舍),∴E(4,3).2.【分析】(1)设抛物线C2的函数解析式为y=x2+bx+c,把A、B的坐标代入上式,即可求解;(2)S=S△OAP+S△OEP=(﹣m2﹣2m+3)+×3(﹣m)即可求解;(3)分、,两种情况分别求解即可.【解答】解:(1)设抛物线C2的函数解析式为y=x2+bx+c,把A、B的坐标代入得,解得:,故抛物线C2的函数解析式为y=x2+2x﹣3;(2)连接OP,作PH⊥x轴,作PQ⊥y轴,把P(m,n)代入y=x2+2x﹣3得n=m2+2m ﹣3,由抛物线y=x2+2x﹣3得:点E(0,﹣3),则S=S△OAP+S△OEP=(﹣m2﹣2m+3)+×3(﹣m)=﹣(m+)2+,所以四边形OAPE的面积最大值是;(3)由y=x2+2x﹣3得对称轴是直线x=﹣1,所以D(﹣1,1),则DF=OF=1,则△DOF为等腰直角三角形,∴∠DOF=∠ODF=45°,OD=,BD=,∠BOD=135°,∴点M只能在点D上方,∵∠BOD=∠ODM=135°,∴当时,以M、O、D为顶点的三角形与△BOD相似.①,则解得DM=2,此时点M坐标为(﹣1,3);②若,则解得DM=1,此时点M坐标为(﹣1,2);综上,点M坐标为(﹣1,3)或(﹣1,2).3.【分析】(1)利用对称性和待定系数法求函数关系式;(2)分类讨论三角形相似情况即可;(3)由已知,满足条件的Q点在以A、D、F(﹣1,﹣1)的圆E在第三象限的部分,连接CE交圆于Q,则CQ最小.【解答】解:(1)由已知,点A坐标为(﹣3,0)∵直线x=﹣1为对称轴∴点C坐标为(1,0)∴抛物线解析式为:y=(x+3)(x﹣1)=x2+2x﹣3(2)存在由已知点D坐标为(﹣1,0)设点P的横坐标为(a,﹣a﹣1)当△AOB∽△ADP时∴a=﹣1点P坐标为(﹣1,)当△AOB∽△APD时过点P作PE⊥x轴于点E则△APE∽△APDE∴PE2=AE•ED∴(﹣a﹣1)2=(a+3)(﹣a﹣1)解得a1=﹣3(舍去),a2=﹣∴点P坐标为(﹣,﹣)(3)存在,CQ最小值为如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,﹣)为圆心.∵tan∠AFD=2∴(A、D除外)上的点都是满足条件的Q点.连CE交⊙E于点Q,则CQ为满足条件的最小值此时CE=,⊙E半径为∴CQ最小值为4.【分析】(1)根据题意求得点A、C的坐标,将它们分别代入函数解析式,列出关于系数b、c的方程组,通过解方程组求得它们的值;(2)如图1,过点D作DG⊥x轴于点G,交AC于点F.利用三角形的面积公式得到二次函数关系式,由二次函数最值的求法解答;(3)需要分类讨论:①当∠DCE=∠BCO时,∠DCE=∠OAC;②当∠DCE=∠CBO 时,∠DCE=∠OCA.根据相似三角形的对应边成比例求得相关线段的长度,从而得到点D的坐标.【解答】解:(1)∵直线y=﹣x+2与x轴、y轴分别交于点A、C,∴A(4,0),C(0,2),OA=4,OC=2,(1分)将A(4,0),C(0,2)分别代入y=﹣+bx+c中,解得,∴y=﹣+x+2;(2)如图1,过点D作DG⊥x轴于点G,交AC于点F,设D(t,﹣t2+t+2),其中0<t<4,则F(t,﹣t+2)∴DF=﹣t2+t+2﹣(﹣t+2)=﹣t2+2tS△ACD=S△CDF+S△ADF=DF•OG+DF•AG=DF•(OG+AG)=DF•OA=×4×(﹣t2+2t)=﹣(t﹣2)2+4.∴当t=2时,S△ACD最大=4.(3)设y=0,则﹣t2+t+2=0,解得x1=4,x2=﹣1,∴B(﹣1,0),OB=1∵tan∠OCB==,tan∠OAC===∴∠OCB=∠OAC∴∠OCA=∠OBC;①当∠DCE=∠BCO时,∠DCE=∠OAC,∴CD∥OA,点D的纵坐标与点C纵坐标相等,令y=2,则﹣t2+t+2=2,解得x1=0,x2=3,∴D1(3,2);②如图2,当∠DCE=∠CBO时,∠DCE=∠OCA,将△OCA沿AC翻折得△MCA,点O的对称点为点M,过点M作MH⊥y轴于点H,AN⊥MH于点N,则CM=CO=2,AM=AO=4,设HM=m,MN=HN﹣HM=OA﹣HM=4﹣m,由∠AMC=∠AOC=∠ANM=∠MHC=90°易证△CHM∽△MNA,且相似比=,∴AN=2MH=2m,CH=MN=2﹣m,在Rt△CMH中,由勾股定理得:m2+(2﹣m)2=22,解得m1=0,m2=∴MH=,OH=,M(,).设直线CM的表达式为y=kx+n,则,解得,∴y=x+2,由解得,∴D2(,)综上所述,点D的坐标为D1(3,2)、D2(,).5.【分析】(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;(2)设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),从而得出OC=﹣m、OF=﹣m2﹣3m+4、BF=﹣m2﹣3m,根据S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF 得出S=﹣2(m+2)2+8,据此可得答案;(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.【解答】解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,∴A(﹣4,0),B(0,4).∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,∴,解得:b=﹣3,c=4,∴抛物线的解析式为:y=﹣x2﹣3x+4.(2)如图,连接AE、过点E作EF⊥y轴于点F,设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),则OC=﹣m,OF=﹣m2﹣3m+4,∵OA=OB=4,∴BF=﹣m2﹣3m,则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF=×(﹣m+4)(﹣m2﹣3m+4)﹣×4×4﹣×(﹣m)×(﹣m2﹣3m).=﹣2m2﹣8m=﹣2(m+2)2+8,∵﹣4<m<0,∴当m=﹣2时,S取得最大值,最大值为8.即△ABE面积的最大值为8.(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD=OC=﹣m,则D(m,4+m).∵△ACD为等腰直角三角形,△DBE和△DAC相似∴△DBE必为等腰直角三角形.i)若∠BED=90°,则BE=DE,∵BE=OC=﹣m,∴DE=BE=﹣m,∴CE=4+m﹣m=4,∴E(m,4).∵点E在抛物线y=﹣x2﹣3x+4上,∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,∴D(﹣3,1);ii)若∠EBD=90°,则BE=BD=﹣m,在等腰直角三角形EBD中,DE=BD=﹣2m,∴CE=4+m﹣2m=4﹣m,∴E(m,4﹣m).∵点E在抛物线y=﹣x2﹣3x+4上,∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,∴D(﹣2,2).综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).6.【分析】(1)设交点式y=a(x+1)(x﹣4),再展开可得到﹣4a=2,解得a=﹣,然后写出抛物线解析式;(2)①作PN⊥x轴于N,交BC于M,如图,先利用待定系数法求出直线BC的解析式为y=﹣x+2,设P(t,﹣t2+t+2),则M(t,﹣t+2),用t表示出PM=﹣t2+2t,再证明△PQM∽△BOC,利用相似比得到PQ=﹣t2+t,然后利用二次函数的性质解决问题;②讨论:当∠PCQ=∠OBC时,△PCQ∽△ABC,PC∥x轴,利用对称性可确定此时P点坐标;当∠CPQ=∠OBC时,△CPQ∽△ABC,则∠CPQ=∠MPQ,所以△PCM为等腰三角形,则PC=PM,利用两点间的距离公式得到t2+(﹣t2+t+2﹣2)2=(﹣t2+2t)2,然后解方程求出t得到此时P点坐标.【解答】解:(1)抛物线解析式为y=a(x+1)(x﹣4),即y=ax2﹣3ax﹣4a,则﹣4a=2,解得a=﹣,所以抛物线解析式为y=﹣x2+x+2;(2)①作PN⊥x轴于N,交BC于M,如图,BC==2,当x=0时,y=﹣x2+x+2=2,则C(0,2),设直线BC的解析式为y=mx+n,把C(0,2),B(4,0)得,解得,∴直线BC的解析式为y=﹣x+2,设P(t,﹣t2+t+2),则M(t,﹣t+2),∴PM=﹣t2+t+2﹣(﹣t+2)=﹣t2+2t,∵∠NBM=∠NPQ,∴△PQM∽△BOC,∴=,即PQ=,∴PQ=﹣t2+t=﹣(t﹣2)2+,∴当t=2时,线段PQ的最大值为;②当∠PCQ=∠ABC时,△PCQ∽△ABC,此时PC∥OB,点P和点C关于直线x=对称,∴此时P点坐标为(3,2);当∠CPQ=∠OBC时,△CPQ∽△ABC,∵∠OBC=∠NPQ,∴∠CPQ=∠MPQ,而PQ⊥CM,∴△PCM为等腰三角形,∴PC=PM,∴t2+(﹣t2+t+2﹣2)2=(﹣t2+2t)2,解得t=,此时P点坐标为(,),综上所述,满足条件的P点坐标为(3,2)或(,).7.【分析】(1)根据抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,可以求得A、B、C三点的坐标,从而可以求得OA、OC、AC的长,进而可以得到cos∠CAO 的值;(2)根据点A、C两点的坐标,可以求得直线AC的函数关系式;(3)根据第三问的条件,可知符合要求的三角形OP A存在三种情况,然后分别画出相应的图形,即可求得点P的坐标.【解答】解:(1)∵抛物线y=x2﹣4x+3与x轴分别交于A、B两点,交y轴于点C,∴x2﹣4x+3=0,得x=1或x=3,x=0时,y=3,∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3),∴OA=1,OC=3,∴,∴cos∠CAO=;(2)设直线AC的解析式为:y=kx+b,∵点A的坐标为(1,0),点C的坐标为(0,3),∴解得k=﹣3,b=3.即直线AC的解析式为:y=﹣3x+3;(3)如果有动点P是y轴上,且△OP A与△OAC相似,则有如下三种情况,第一种情况如下图1所示,当∠OP A=∠OCA,∠AOC=∠AOP时,△OP A∽△OAC,∴,∵点C的坐标为(0,3),∴OP=OC=3,∴点P的坐标为(0,﹣3);第二种情况如下图2所示,点P位于y轴正半轴,当∠OP A=∠OAC,∠AOC=∠AOP时,△OP A∽△OAC,∴,∵点C的坐标为(0,3),点A的坐标为(1,0),∴OA=1,OC=3,即点P的坐标为(0,);第三种情况如下图3所示,点P位于y轴负半轴,当∠OP A=∠OAC,∠AOC=∠AOP时,△OP A∽△OAC,∴,∵点C的坐标为(0,3),点A的坐标为(1,0),∴OA=1,OC=3,∴,即点P的坐标为(0,﹣).由上可得,点P的坐标为:(0,﹣3),(0,),(0,﹣).8.【分析】(1)根据题意把点A(﹣1,0),B(2,0)代入二次函数解析式,得到b和c 的二元一次方程组,求出b和c的值即可;(2)设E(a,b),且a>0,b>0,首先用a和b表示出S四边形ABEC,再结合点E在二次函数的图象上,得到S四边形ABEC=﹣a2+2a+3,即可求解;(3)首先画出图形,以C,D,M为顶点的三角形与△AOC相似,得到,或,根据n的取值范围求出m的值即可.【解答】解:(1)∵二次函数y=﹣x2+bx+c的图象与x轴相交于点A(﹣1,0),B(2,0),∴,∴二次函数的解析式为y=﹣x2+x+2.(2)如图1.∵二次函数的解析式为y=﹣x2+x+2与y轴相交于点C,∴C(0,2).设E(a,b),且a>0,b>0.∵A(﹣1,0),B(2,0),∴OA=1,OB=2,OC=2.则S四边形ABEC==1+a+b,∵点E(a,b)是第一象限的抛物线上的一个动点,∴b=﹣a2+a+2,∴S四边形ABEC=﹣a2+2a+3=﹣(a﹣1)2+4,当a=1时,b=2,∴当四边形ABEC的面积最大时,点E的坐标为(1,2),且四边形ABEC的最大面积为4.(3)如图2.设M(m,n),且m>0.∵点M在二次函数的图象上,∴n=﹣m2+m+2.∵⊙M与y轴相切,切点为D,∴∠MDC=90°.∵以C,D,M为顶点的三角形与△AOC相似,∴,或.①当n>2时,或,解得m1=0(舍去),m2=,或m3=0(舍去),m4=﹣1(舍去).②同理可得,当n<2时,m1=0(舍去),m2=,或m3=0(舍去),m4=3.综上,满足条件的点M的坐标为(,),(,),(3,﹣4).9.【分析】(1)把点A、B的坐标代入二次函数解析式,利用待定系数法求二次函数解析式解答;(2)先求出点C的坐标,再利用待定系数法求出直线AC的解析式,然后判断出平行于AC的直线与二次函数图象只有一个交点时△ACP的面积最大,再联立直线与二次函数解析式,消掉y,利用根的判别式Δ=0时方程只有一个根求解即可;(3)设点E的横坐标为c,表示出BE、QE,然后根据相似三角形对应边成比例,分OA 和BE,OA和QE是对应边两种情况列出比例式求解即可.【解答】解:(1)∵二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,∴,解得,∴二次函数的解析式为y=﹣x2﹣x+2;(2)令x=0,则y=2,∴点C(0,2),设直线AC的解析式为y=kx+m(k≠0),则,解得,∴直线AC的解析式为y=x+2,由三角形的面积可知,平行于AC的直线与二次函数图象只有一个交点时△ACP的面积最大,此时设过点P的直线为y=x+n,联立,消掉y得,﹣x2﹣x+2=x+n,整理得,2x2+6x﹣6+3n=0,△=62﹣4×2×(﹣6+3n)=0,解得n=,此时x1=x2=﹣=﹣,y=×(﹣)+=,∴点P(﹣,)时,△ACP的面积最大;(3)存在点Q(﹣2,2)或(﹣,)使以点B、Q、E为顶点的三角形与△AOC 相似.理由如下:设点E的横坐标为c,则点Q的坐标为(c,﹣c2﹣c+2),BE=1﹣c,①OA和BE是对应边时,∵△BEQ∽△AOC,∴=,即=,整理得,c2+c﹣2=0,解得c1=﹣2,c2=1(舍去),此时,﹣×(﹣2)2﹣×(﹣2)+2=2,点Q(﹣2,2);②OA和QE是对应边时,∵△QEB∽△AOC,∴=,即=,整理得,4c2﹣c﹣3=0,解得c1=﹣,c2=1(舍去),此时,﹣×(﹣)2﹣×(﹣)+2=,点Q(﹣,),综上所述,存在点Q(﹣2,2)或(﹣,)使以点B、Q、E为顶点的三角形与△AOC相似.10.【分析】(1)利用A(﹣1,0)、点B(0,﹣5)代入解析式求出即可;(2)利用轴对称图形的性质得出P点位置,进而得出直线BC的解析式,进而求出P点坐标;(3)利用相似三角形的性质利用对应边不同分别得出E点坐标即可.【解答】解:(1)根据题意,得,解得,故二次函数的表达式为y=x2﹣4x﹣5;(2)令y=0,得二次函数y=x2﹣4x﹣5的图象与x轴的另一个交点坐标C(5,0).由于P是对称轴x=2上一点,连接AB,由于AB==,要使△ABP的周长最小,只要P A+PB最小.由于点A与点C关于对称轴x=2对称,连接BC交对称轴于点P,则P A+PB=BP+PC=BC,根据两点之间,线段最短,可得P A+PB的最小值为BC=5,故△ABP的周长最小值为:+5.因为BC与对称轴x=2的交点P就是所求的点.设直线BC的解析式为y=kx+b,根据题意,可得:,解得,所以直线BC的解析式为y=x﹣5.因此直线BC与对称轴x=2的交点坐标是方程组的解,解得,所求的点P的坐标为(2,﹣3).(3)存在.∵A(﹣1,0),C(5,0),∴AC=6,∵P(2,﹣3),C(5,0),∴PC=3,∵B(0,﹣5),C(5,0),∴BC=5,当△PEC∽△ABC,∴=,∴=,解得:EC=5,∴E(0,0);当△EPC∽△ABC,∴=,∴=,解得:EC=3.6,∴OE=5﹣3.6=1.4,故E点坐标为:(1.4,0),综上所述:以C、P、E为顶点的三角形与三角形ABC相似,点E的坐标为:(0,0),(1.4,0).11.【分析】(1)首先设二次函数的解析式为y=a(x﹣1)2﹣2,由A点坐标为(3,0),则可将A点的坐标代入函数解析式,利用待定系数法即可求得这个二次函数的解析式;(2)首先利用待定系数法求得直线AB的解析式,然后由P在直线上,将x代入直线方程,即可求得P的纵坐标,又由E在抛物线上,则可求得E的纵坐标,它们的差即为PE 的长;(3)分别从当∠EDP=90°时,△AOB∽△EDP与当∠DEP=90°时,△AOB∽△DEP 两种情况去分析,注意利用相似三角形的对应边成比例等性质,即可求得答案,注意不要漏解.【解答】解:(1)设二次函数的解析式为y=a(x﹣1)2﹣2,∵A(3,0)在抛物线上,∴0=a(3﹣1)2﹣2∴a=,∴y=(x﹣1)2﹣2,(2)抛物线与y轴交点B的坐标为(0,),设直线AB的解析式为y=kx+m,∴,∴,∴直线AB的解析式为y=x﹣.∵P为线段AB上的一个动点,∴P点坐标为(x,x﹣).(0<x<3)由题意可知PE∥y轴,∴E点坐标为(x,x2﹣x﹣),∵0<x<3,∴PE=(x﹣)﹣(x2﹣x﹣)=﹣x2+x,(3)由题意可知D点横坐标为x=1,又D点在直线AB上,∴D点坐标(1,﹣1).①当∠EDP=90°时,△AOB∽△EDP,∴.过点D作DQ⊥PE于Q,∴x Q=x P=x,y Q=﹣1,∴△DQP∽△AOB∽△EDP,∴,又OA=3,OB=,AB=,又DQ=x﹣1,∴DP=(x﹣1),∴,解得:x=﹣1±(负值舍去).∴P(﹣1,)(如图中的P1点);②当∠DEP=90°时,△AOB∽△DEP,∴.由(2)PE=﹣x2+x,DE=x﹣1,∴,解得:x=1±,(负值舍去).∴P(1+,﹣1)(如图中的P2点);综上所述,P点坐标为(﹣1,)或(1+,﹣1).12.【分析】(1)运用待定系数法把点A、B、C的坐标代入求解即可;(2)连接BC与对称轴的交点即为点H,此时AH+CH=BH+CH=BC最小,故△AHC 周长最小,运用待定系数法求得直线BC的解析式为y=﹣x+3,即可求得答案;(3)当以B、E、G为顶点的三角形与△AOC相似时,分两种情况:①△BEG∽△AOC,②△GEB∽△AOC,分别利用相似三角形性质建立方程求解即可.【解答】解:(1)∵抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,∴,解得:,∴该抛物线的解析式为y=﹣x2+2x+3;(2)∵y=﹣x2+2x+3,∴抛物线的对称轴为直线x=﹣=1,∵点A(﹣1,0)和点B(3,0)关于抛物线的对称轴对称,∴连接BC与对称轴的交点即为点H,此时AH+CH=BH+CH=BC最小,如图,∴AC+AH+CH=AC+BH最小,即△AHC周长最小,设直线BC的解析式为y=kx+d,则,解得:,∴直线BC的解析式为y=﹣x+3,∵当x=1时,y=﹣1+3=2,∴点H的坐标为(1,2);(3)存在.理由如下:由题意得:OA=1,OC=3,∵抛物线对称轴为直线x=1,∴E(1,0),设G(1,m),则EG=|m|,∵B(3,0),∴BE=3﹣1=2,当以B、E、G为顶点的三角形与△AOC相似时,①△BEG∽△AOC,∴=,即=,∴|m|=6,解得:m=±6,∴点G的坐标为(1,6)或(1,﹣6);②△GEB∽△AOC,∴=,即=,∴|m|=,解得:m=±,∴点G的坐标为(1,)或(1,﹣);综上所述,以B、E、G为顶点的三角形与△AOC相似时,点G的坐标为(1,6)或(1,﹣6)或(1,)或(1,﹣).13.【分析】(1)由OA和OB的长得到点A和点B的坐标,然后用待定系数法求得抛物线的解析式;(2)先求得点C的坐标得到OC的长,然后求得直线m与坐标轴的两个交点的坐标,最后利用相似三角形的性质分类讨论求得k的值;(3)先求得直线AC的解析式,过点D作DE⊥x轴,交AC于点E,设点D的坐标得到点E的坐标,从而表示出△ACD的面积,再求得△ABC的面积,从而列出方程求得点D 的坐标,最后求得△COD的面积.【解答】(1)解:∵OA=4,OB=2,∴A(﹣4,0),B(2,0),将点A和点B的坐标代入y=ax2+bx+8,得,解得:,∴抛物线的解析式为y=﹣x2﹣2x+8.(2)对y=﹣x2﹣2x+8,令x=0,得y=8,∴点C的坐标为(0,8),∴OC=8,对直线y=kx+8,当x=0时,y=8,当y=0时,x=﹣,∴直线y=kx+8与y轴的交点为点C(0,8),与x轴的交点为(﹣,0),记为点M,∴OM=|﹣|,如图1,当△MOC∽△BOC时,∴=1,∴MO=BO=2,∴M1(﹣2,0),代入y=kx+8中,得﹣2k+8=0,解得:k=4;当△MOC∽△COB时,,∴==4,∴MO=32,∴M2(﹣32,0),M3(32,0),分别代入y=kx+8中,得﹣32k+8=0或32k+8=0,解得:k=或k=﹣;综上所述,k=4或k=或k=﹣.(3)设直线AC的解析式为y=kx+b,则,解得:,∴直线AC的解析式为y=2x+8,如图2,当点D在AC之间的抛物线上时,过点D作DE⊥x轴,交AC于点E,设点D的坐标为(x,﹣x2﹣2x+8),则点E的坐标为(x,2x+8),∴DE=﹣x2﹣2x+8﹣(2x+8)=﹣x2﹣4x,∴S△ACD=S△AED+S△ECD==,∴S△ACD==﹣2x2﹣8x,∵OA=4,OB=2,OC=8,∴S△ABC==24,又∵S△ACD=S△ABC,∴﹣2x2﹣8x=×24,解得:x=﹣2+或x=﹣2﹣,∵S△COD=,∴S△COD==8﹣4或S△COD==8+4;如图3,当点D在点A左侧抛物线上时,过点D作DE⊥x轴,交AC于点E,设点D的坐标为(x,﹣x2﹣2x+8),则点E的坐标为(x,2x+8),∴DE=2x+8﹣(﹣x2﹣2x+8)=x2+4x,∴S△ACD=S△ECD﹣S△AED==,∴S△ACD==2x2+8x,∵OA=4,OB=2,OC=8,∴S△ABC==24,又∵S△ACD=S△ABC,∴2x2+8x=×24,解得:x=﹣2﹣或x=﹣2+(舍),∵S△COD=,∴S△COD==8+4;综上所述,△COD的面积为8﹣4或8+4或8+4.14.【分析】(1)把A(1,0)代入y=a(x﹣2)2+1即可求解;(2)作A点关于直线BC的对称点A',连接A'D交BC于点E,连接AE,A'B,当A'、D、E三点共线时,△ADE的周长最小,求出A'(3,﹣2),再求A'D=,AD=,即可求解;(3)分三种情况讨论:①当∠CMP=90°时,过点M作MG⊥y轴交于点G,过点P作PH⊥y轴交于点H,可得△GCM∽△HPC,设M(t,t﹣3),当∠CPM=∠ACO时,=,则P(3t,﹣3﹣3t),可求P(5,﹣8);当∠CMP=∠ACO时,=3,可求P(5,﹣8);②当∠CMP=90°时,过点M作EF∥x轴,交y轴于点E,过点P作PF ⊥EF交于点F,证明△ECM∽△FMP,设M(t,t﹣3),则P(4t,﹣2t﹣3),可求P (,﹣);当∠CMP=∠OCA时,=3,则P(t,t﹣3),可求P(,﹣);③当∠CPM=90°时,过点P作KL⊥y轴交于点L,过点M作MK⊥LK交于K 点,证明△CLP∽△PKM,设P(m,﹣m2+4m﹣3),则M(3m2﹣11m,﹣m2+7m﹣3),可求P(,﹣);当∠MCP=∠OCA时,=3,M(m2﹣m,﹣m2+m﹣3),可求P(,﹣).【解答】解:(1)把A(1,0)代入y=a(x﹣2)2+1得:a+1=0,∴a=﹣1,∴抛物线的解析式为y=﹣(x﹣2)2+1=﹣x2+4x﹣3,在y=﹣x2+4x﹣3中,令x=0得y=﹣3,∴C(0,﹣3);(2)设直线BC的解析式为y=kx+b,∴,∴,∴y=x﹣3,作A点关于直线BC的对称点A',连接A'D交BC于点E,连接AE,A'B,∴AE+DE+AD=A'E+DE+AD≥A'D+DE,当A'、D、E三点共线时,△ADE的周长最小,∵OB=OC,∴∠OBC=45°,∴∠ABA'=90°,∵AB=A'B,∴A'(3,﹣2),∵D(2,1),∴A'D=,AD=,∴△ADE周长的最小值为+;(3)存在以P,M,C为顶点的三角形与△AOC相似,理由如下:∵A(1,0),C(0,﹣3),∴OA=1,OC=3,∴tan∠OCA=,①当∠CMP=90°时,过点M作MG⊥y轴交于点G,过点P作PH⊥y轴交于点H,∴∠GCM+∠HCP=90°,∵∠GCM+∠GMC=90°,∴∠HCP=∠GMC,∴△GCM∽△HPC,∴==,设M(t,t﹣3),∴GM=t,GC=t,当∠CPM=∠ACO时,=,∴CH=3t,HP=3t,∴P(3t,﹣3﹣3t),∴﹣3﹣3t=﹣9t2+12t﹣3,解得t=0(舍)或t=,∴P(5,﹣8);当∠CMP=∠ACO时,=3,∴CH=t,HP=t,∴P(t,﹣3﹣t),∴﹣3﹣t=﹣t2+t﹣3,解得t=0(舍)或t=15,∴P(5,﹣8);②当∠CMP=90°时,过点M作EF∥x轴,交y轴于点E,过点P作PF⊥EF交于点F,∴∠EMC+∠FMP=90°,∵∠EMC+∠ECM=90°,∴∠FMP=∠ECM,∴△ECM∽△FMP,∴==,设M(t,t﹣3),∴EM=EC=t,当∠CPM=∠OCA时,=,∴MF=FP=3t,∴P(4t,﹣2t﹣3),∴﹣2t﹣3=﹣16t2+16t﹣3,解得t=0(舍)或t=,∴P(,﹣);当∠CMP=∠OCA时,=3,∴MF=FP=t,∴P(t,t﹣3),∴﹣t﹣3=﹣t2+t﹣3,解得t=0(舍)或t=,∴P(,﹣);③如图3,当∠CPM=90°时,过点P作KL⊥y轴交于点L,过点M作MK⊥LK交于K点,∴∠CPL+∠MPK=90°,∵∠CPL+∠PCL=90°,∴∠MPK=∠PCL,∴△CLP∽△PKM,∴==,设P(m,﹣m2+4m﹣3),∴LP=m,CL=m2﹣4m,当∠CMP=∠OCA时,=,∴MK=3m,PK=3m2﹣12m,∴M(3m2﹣11m,﹣m2+7m﹣3),∴﹣m2+7m﹣3=3m2﹣11m﹣3,解得m=0(舍)或m=,∴P(,﹣);当∠MCP=∠OCA时,=3,∴MK=m,PK=m2﹣m,∴M(m2﹣m,﹣m2+m﹣3),∴﹣m2+m﹣3=m2﹣m﹣3,解得m=0(舍)或m=,∴P(,﹣);综上所述:P点坐标为(5,﹣8)或(,﹣)或(,﹣)或(,﹣)或(,﹣).15.【分析】(1)过点C作CE⊥x轴于点E,先求得点C的坐标,然后由点B和点D的坐标设函数的交点式,再将点C的坐标代入求得函数的解析式即可;(2)过点P作PH⊥x轴,交BC于点H,先求得直线BC的解析式,再设点P的坐标,得到点H的坐标,然后求得△PBC的面积,结合点B、C、D求得△BCD的面积,从而求得四边形PBDC的面积,最后由二次函数的性质求得四边形PBDC的面积最大值,及点P的坐标;(3)①分别求得tan∠ABO和tan∠CDE的大小,从而得到∠ABO=∠CDE,然后得证CD∥AB;②由∠ABO=∠CDE,∠ABC=90°得到BC⊥CD,即∠BCD=90°,由旋转得BC=AB,然后分情况讨论,(i)△BCM∽△AOB;(ii)△BCM∽△BOA,先由相似三角形的性质求得CM的长,再求得直线CD的解析式,设点M的坐标,借助两点间的距离公式求得点M的坐标即可.【解答】(1)解:如图1,过点C作CE⊥x轴于点E,则∠BEC=∠AOB=90°,由旋转得,∠ABC=90°,AB=CB,∴∠ABO+∠CBE=90°,∵∠ABO+∠OAB=90°,∴∠CBE=∠OAB,∴△AOB≌△BEC(AAS),∴BE=AO,CE=OB,∵点A(0,2),B(1,0),∴BE=2,CE=1,∴点C的坐标为(3,1),由点B(1,0),点D(3.5,0)可设函数的解析式为y=a(x﹣1)(x﹣3.5),将点C(3,1)代入,得a(3﹣1)×(3﹣3.5)=1,解得:a=﹣1,∴抛物线的解析式为y=﹣(x﹣1)(x﹣3.5)=﹣x2+x﹣.(2)解:过点P作PH⊥x轴,交BC于点H,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=x﹣,设点P的坐标为(x,﹣x2+x﹣),则点H的坐标为(x,x﹣),∴PH=﹣x2+x﹣﹣x+=﹣x2+4x﹣3=﹣(x﹣2)2+1,∵S△PBC=S△PBH+S△PCH=,∴S△PBC=×2×[﹣(x﹣2)2+1]=﹣(x﹣2)2+1,∵B(1,0),C(3,1),D(3.5,0),∴BD=2.5,CE=1,∴S△BCD==,∴S四边形PBDC=S△PBC+S△BCD=﹣(x﹣2)2+1+=﹣(x﹣2)2+,∴当x=2时,四边形PBDC的面积最大值为,此时,点P的坐标为(2,).(3)①证明:由(1)得,AO=BE=2,BO=CE=1,BD=2.5,∴tan∠ABO=,ED=BD﹣BE,2.5﹣2=0.5,∴tan∠CDE==2,∴∠ABO=∠CDE,∴CD∥AB.②解:∵∠ABC=90°,∴∠ABO+∠CBD=90°,由①得,∠ABO=∠CDB,∴∠CBD+∠CDB=90°,∴∠BCD=90°,由旋转得,BC=AB==,设直线CD的解析式为y=mx+n,则,解得:,∴直线CD的解析式为y=﹣2x+7,设点M(x,﹣2x+7),则CM=,如图2,(i)当△BCM∽△AOB时,,∴,∴CM=,∴=,解得:x1=,x2=,∴点M1(,2),M2(,0);(ii)当△BCM∽△BOA时,,∴,∴CM=2,∴=2,解得:x3=1,x4=5,∴点M3(1,5),M4(5,﹣3);综上所述,当点M的坐标为(,2)或(,0)或(1,5)或(5,﹣3)时,△MBC 与△AOB相似.16.【分析】(1)根据线段关系求出A点、B点、C点的坐标,用待定系数法求出解析式即可;(2)求出直线AB的解析式,设出D点坐标,得出DE的表达式,根据二次函数的性质求出最大值即可;(3)根据(2)设出P点的坐标,分请款根据线段比例关系求出P点的坐标即可.【解答】解:(1)∵4CO=2BO=OA=4,∴OA=4,OB=2,OC=1,即A(4,0),B(0,2),C(﹣1,0),设抛物线的解析式为y=ax2+bx+c,∵抛物线与坐标轴交于A,B,C三点,∴,解得,∴抛物线的解析式为y=﹣x2+x+2;(2)由(1)知A(4,0),B(0,2),设直线AB的解析式为y=kx+d,∴,解得,∴直线AB的解析式为y=﹣x+2,设D(t,﹣t+2),则E(t,﹣t2+t+2),∴DE=﹣t2+t+2﹣(﹣t+2)=﹣t2+2t=﹣(t﹣2)2+2,∴当t=2时DE有最大值,最大值为2,即D点坐标为(2,1)时,DE有最大值为2;(3)存在,由(2)知F点和P点的横坐标为2,OA=4,OB=2,OC=1,∴F(2,0),AB==2,BC==,AC=4+1=5,。
二次函数背景下的相似三角形问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数

模型介绍在坐标系中确定点,使得由该点及其他点构成的三角形与其他三角形相似,即为“相似三角形存在性问题”.【相似判定】判定1:三边对应成比例的两个三角形是相似三角形;判定2:两边对应成比例且夹角相等的两个三角形是相似三角形;判定3:有两组角对应相等的三角形是相似三角形.以上也是坐标系中相似三角形存在性问题的方法来源,根据题目给的已知条件选择恰当的判定方法,解决问题.【题型分析】通常相似的两三角形有一个是已知的,而另一三角形中有1或2个动点,即可分为“单动点”类、“双动点”两类问题.【思路总结】根据相似三角形的做题经验,可以发现,判定1基本是不会用的,这里也一样不怎么用,对比判定2、3可以发现,都有角相等!所以,要证相似的两个三角形必然有相等角,关键点也是先找到一组相等角.然后再找:思路1:两相等角的两边对应成比例;思路2:还存在另一组角相等.事实上,坐标系中在已知点的情况下,线段长度比角的大小更容易表示,因此选择方法可优先考虑思路1.一、如何得到相等角?二、如何构造两边成比例或者得到第二组角?搞定这两个问题就可以了.例题精讲【例1】.如图,抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,点M是第一象限内抛物线上一点,过点M作MN⊥x轴于点N.若△MON与△BOC相似,求点M的横坐标.解:∵抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,∴当y=0时,0=﹣x2+x+2,解得x1=﹣1,x2=4,∴OB=4,当x=0时,y=2,∴OC=2,∵点M是第一象限内抛物线上一点,∴设M(m,﹣m2+m+2),∵MN⊥x轴,∴ON=m,MN=﹣m2+m+2,∠ONM=90°,∵∠BOC=90°,∴∠BOC=∠ONM,∵△MON与△BOC相似,∴或,∴=或=,∴m=或m=﹣1+(负值舍去),∴点M的横坐标为或﹣1+.变式训练【变1-1】.如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,(1)求出此抛物线的解析式、对称轴以及B点坐标;(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.解:(1)由x=0得y=0+4=4,则点C的坐标为(0,4);由y=0得x+4=0,解得x=﹣4,则点A的坐标为(﹣4,0);把点C(0,4)代入y=x2+kx+k﹣1,得k﹣1=4,解得:k=5,∴此抛物线的解析式为y=x2+5x+4,∴此抛物线的对称轴为x=﹣=﹣.令y=0得x2+5x+4=0,解得:x1=﹣1,x2=﹣4,∴点B的坐标为(﹣1,0).(2)∵A(﹣4,0),C(0,4),∴OA=OC=4,∴∠OCA=∠OAC.∵∠AOC=90°,OB=1,OC=OA=4,∴AC==4,AB=OA﹣OB=4﹣1=3.∵点D在y轴负半轴上,∴∠ADC<∠AOC,即∠ADC<90°.又∵∠ABC>∠BOC,即∠ABC>90°,∴∠ABC>∠ADC.∴由条件“以A、C、D为顶点的三角形与△ABC相似”可得△CAD∽△ABC,∴=,即=,解得:CD=,∴OD=CD﹣CO=﹣4=,∴点D的坐标为(0,﹣).【例2】.如图,抛物线y=x2+bx+c与x轴交于A(1,0),B两点,与y轴交于点C(0,3).(1)求该抛物线的表达式;(2)过点B作x轴的垂线,在该垂线上取一点P,使得△PBC与△ABC相似,请求出点P的坐标.解:(1)把C(0,3)代入y=x2+bx+c,得c=3,∴y=x2+bx+3,把A(1,0)代入y=x2+bx+3,得1+b+3=0,解得b=﹣4,∴该抛物线的表达式为y=x2﹣4x+3.(2)当点P在点B上方时,如图1,PB=AB,∵PB⊥x轴,∴∠ABP=90°,抛物线y=x2﹣4x+3,当y=0时,则x2﹣4x+3=0,解得x1=1,x2=3,∴B(3,0),∴OB=OC=3,PB=AB=3﹣1=2,∵∠BOC=90°,∴∠OBC=∠OCB=45°,∴∠PBC=∠ABC=45°,∵==1,∴△PBC∽△ABC,此时点P的坐标为(3,2);如图2,△PBC∽△CBA,且∠CBP=∠ABC=45°,∠BCP=∠BAC,∴=,∵BC2=OB2+OC2=32+32=18,BA=2,∴BP===9,此时点P的坐标为(3,9);当点P在点B下方时,∠PBC=135°,∠BAC=∠AOC+∠ACO=90°+∠ACO<135°,此时△PBC与△ABC不相似,综上所述,点P的坐标为(3,2)或(3,9).变式训练【变2-1】.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.(3)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标.解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设点P(m,m2﹣2m﹣3),①当点P在第三象限时,设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S△POD=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,②当点P在第四象限时,设PD交y轴于点M,=×OM(x D﹣x P)=﹣m2+m+3,同理可得:S△POD=﹣m2+m+3,综上,S△POD有最大值,当m=时,其最大值为;∵﹣1<0,故S△POD(3)∵OB=OC=3,∴∠OCB=∠OBC=45°,∵∠ABC=∠OBE,故△OBE与△ABC相似时,分为两种情况:①当∠ACB=∠BOQ时,AB=4,BC=3,AC=,过点A作AH⊥BC于点H,S△ABC=×AH×BC=AB×OC,解得:AH=2,则sin∠ACB==,则tan∠ACB=2,则直线OQ的表达式为:y=﹣2x…②,联立①②并解得:x=或﹣,故点Q(,﹣2)或(﹣,2),②∠BAC=∠BOQ时,tan∠BAC==3=tan∠BOQ,则点Q(n,﹣3n),则直线OQ的表达式为:y=﹣3x…③,联立①③并解得:x=,故点Q(,)或(,);综上,当△OBE与△ABC相似时,Q的坐标为:(,﹣2)或(﹣,2)或(,)或(,).1.抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.(1)求平移后的抛物线的解析式和点D的坐标;(2)∠ACB和∠ABD是否相等?请证明你的结论;(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4);(2)∠ACB与∠ABD相等,理由如下:如图,∵y=﹣x2+2x+3,∴点x=0时,y=3,即C点坐标为(0,3),又∵B(3,0),∠BOC=90°,∴OB=OC,∠OBC=∠OCB=45°.在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,∴BC2+CD2=BD2,∴∠BCD=90°,∴tan∠CBD===,∵在△AOC中,∠AOC=90°,∴tan∠ACO==,∴tan∠ACO=tan∠CBD,∴∠ACO=∠CBD,∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD;(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,∴可设P点的坐标为(1,n).∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形,∴n<4,即点P只能在点D的下方,又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:①如果△CDP∽△ABC,那么=,即=,解得n=,∴P点的坐标为(1,);②如果△CDP∽△CBA,那么=,即=,解得n=,∴P点的坐标为(1,).综上可知P点的坐标为(1,)或(1,).2.如图,已知△ABC中,∠ACB=90°,以AB所在直线为x轴,过c点的直线为y轴建立平面直角坐标系.此时,A点坐标为(﹣1,0),B点坐标为(4,0)(1)试求点C的坐标;(2)若抛物线y=ax2+bx+c过△ABC的三个顶点,求抛物线的解析式;(3)点D(1,m)在抛物线上,过点A的直线y=﹣x﹣1交(2)中的抛物线于点E,那么在x轴上点B的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE相似?若存在,求出P点坐标;若不存在,说明理由.解:(1)在Rt△ABC中,∠ACB=90°,OC⊥AB,由射影定理,得:OC2=OA•OB=4,即OC=2,∴C(0,2);(2)∵抛物线经过A(﹣1,0),B(4,0),C(0,2),可设抛物线的解析式为y=a(x+1)(x﹣4)(a≠0),则有:2=a(0+1)(0﹣4),a=﹣,∴y=﹣(x+1)(x﹣4)=﹣x2+x+2;(3)存在符合条件的P点,且P(,0)或(﹣,0).根据抛物线的解析式易知:D(1,3),联立直线AE和抛物线的解析式有:,解得,,∴E(6,﹣7),∴tan∠DBO==1,即∠DBO=45°,tan∠EAB==1,即∠EAB=45°,∴∠DBA=∠EAB,若以P、B、D为顶点的三角形与△ABE相似,则有两种情况:①△PBD∽△BAE;②△PBD∽△EAB.易知BD=3,EA=7,AB=5,由①得:,即,即PB=,OP=OB﹣PB=,由②得:,即,即P′B=,OP′=OB﹣BP′=﹣,∴P(,0)或(﹣,0).3.如图已知直线y=x+与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣),交x轴正半轴于D点,抛物线的顶点为M.(1)求抛物线的解析式;(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.解:(1)将点B(4,m)代入y=x+,∴m=,将点A(﹣1,0),B(4,),C(0,﹣)代入y=ax2+bx+c,解得a=,b=﹣1,c=﹣,∴函数解析式为y=x2﹣x﹣;(2)设P(n,n2﹣n﹣),则经过点P且与直线y=x+垂直的直线解析式为y=﹣2x+n2+n﹣,直线y=x+与其垂线的交点G(n2+n﹣,n2+n+),∴GP=(﹣n2+3n+4),当n=时,GP最大,此时△PAB的面积最大,∴P(,﹣),∵AB=,PG=,∴△PAB的面积=××=;(3)∵M(1,﹣2),A(﹣1,0),D(3,0),∴AM=2,AD=4,MD=2,∴△MAD是等腰直角三角形,∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,设N(t,t2﹣t﹣)①如图1,当MQ⊥QN时,N(3,0);②如图2,当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,∵QN=MN,∠QNM=90°,∴△MNS≌△NMS(AAS)∴t﹣1=﹣t2+t+,∴t=±,∴t>1,∴t=,∴N(,1﹣);③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点M作MR ∥x轴,与过Q点的垂线分别交于点S、R;∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),∴SQ=QR=2,∴t+2=1+t2﹣t﹣,∴t=5,∴N(5,6);④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,∴t2﹣t﹣=t﹣1,∴t=2±,∵t>1,∴t=2+,∴N(2+,1+);综上所述:N(3,0)或N(2+,1+)或N(5,6)或N(,1﹣).4.如图,已知抛物线经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)直接写出:b=2,c=1;(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP 的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.解:(1)将点A(0,1),B(﹣9,10)代入,∴,解得,∴抛物线的解析式为,∴b=2,c=1,故答案为:2,1;(2)∵AC∥x轴,A(0,1),∴,∴x1=﹣6,x2=0,∴C(﹣6,1),∵A(0,1),B(﹣9,10),∴直线AB的解析式为y=﹣x+1,设点,则E(m,﹣m+1),∴,∵AC⊥EP,AC=6,=S△AEC+S△APC∴S四边形AECP=×AC×EF+=×AC×(EF+PF)=×AC×PE=×6×(﹣m2﹣3m)=﹣m2﹣9m=﹣(m+)2+,∵﹣6<m<0,当时,四边形AECP的面积的最大值是,此时点;(3)存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,理由如下:∵,∴P(﹣3,﹣2),∴PF=y F﹣y P=3,CF=x F﹣x C=3,∴PF=CF,∴∠PCF=45°.同理可得:∠EAF=45°,∴∠PCF=∠EAF,∴在直线AC上存在满足条件的Q,设Q(t,1),∵A(0,1),B(﹣9,10),C(﹣6,1),∴,AC=6,,以C,P,Q为顶点的三角形与△ABC相似,①当△CPQ∽△ABC时,∴,∴,∴t=﹣4,∴Q(﹣4,1);②当△CQP∽△ABC时,∴,∴,∴t=3,∴Q(3,1);综上所述:Q点坐标为(﹣4,1)或(3,1).5.已知抛物线经过点A(﹣2,0),B(0,﹣4),与x轴交于另一点C,连接BC.(1)求抛物线的解析式;=S△PBC,求直线AP的表达式;(2)如图,P是第一象限内抛物线上一点,且S△PBO(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请直接写出点D的坐标;若不存在,请说明理由.解:(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=x2+bx+c中得:,解得:,∴抛物线的解析式为:y=x2﹣x﹣4;(2)当y=0时,x2﹣x﹣4=0,解得:x=﹣2或4,∴C(4,0),如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,=S△PBC,∵S△PBO∴,∴OE=CF,易得△OEG≌△CFG,∴OG=CG=2,设P(x,x2﹣x﹣4),过P作PM⊥y轴于M,tan∠PBM===,∴BM=2PM,∴4+x2﹣x﹣4=2x,x2﹣6x=0,x1=0(舍),x2=6,∴P(6,8),∴AP的解析式为:y=x+2,BC的解析式为:y=x﹣4,∴AP∥BC;(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC 和△BCE,①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,∵∠BAE=∠BAC,∠ABE≠∠ABC,∴∠ABE=∠ACB=45°,∴△ABE∽△ACB,∴,∴,∴AE=,OE=﹣2=∴E(,0),∵B(0,﹣4),∴BE:y=3x﹣4,则x2﹣x﹣4=3x﹣4,x1=0(舍),x2=8,∴D(8,20);②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,此时E在C的左边,∵∠BEA=∠BEC,∴当∠ABE=∠BCE时,△ABE∽△BCE,∴==,设BE=2m,CE=4m,Rt△BOE中,由勾股定理得:BE2=OE2+OB2,∴,3m2﹣8m+8=0,(m﹣2)(3m﹣2)=0,m1=2,m2=,∴OE=4m﹣4=12或,∵OE=<2,∠AEB或∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,∴E(﹣12,0);同理得BE的解析式为:y=﹣x﹣4,﹣x﹣4=x2﹣x﹣4,x=或0(舍)∴D(,﹣);同理可得E在C的右边时,△ABE∽△BCE,∴=,设AE=2m,BE=4m,Rt△BOE中,由勾股定理得:BE2=OE2+OB2,∴,3m2+2m﹣5=0,(m+)(3m﹣)=0,m1=﹣,m2=,∴OE=﹣12(舍)或,∵OE=<4,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,综上,点D的坐标为(8,20)或(,﹣6.如图,已知抛物线y =ax 2+bx +6经过两点A (﹣1,0),B (3,0),C 是抛物线与y 轴的交点.(1)求抛物线的解析式;(2)点P (m ,n )在平面直角坐标系第一象限内的抛物线上运动,直线CP 与x 轴交于点Q ,当∠BQC =∠BCO 时,求此时P 点坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得∠CNM =90°,且△CMN 与△OBC 相似,如果存在,请求出点M 和点N 的坐标.解:(1)把A(﹣1,0),B(3,0)代入y=ax2+bx+6得:,解得,∴抛物线的解析式为y=﹣2x2+4x+6;(2)由y=﹣2x2+4x+6得C(0,6),∴OC=6,当Q在x轴正半轴,如图:∵∠BQC=∠BCO,且∠COB=∠QOC,∴△COB∽△QOC,∴=,即=,∴OQ=12,∴Q(12,0),设直线CQ解析式为y=kx+6,则0=12k+6,∴k=﹣,即直线CQ为y=﹣x+6,由得(与C重合,舍去)或,∴P(,),当Q在x轴负半轴,如图:同理可得:△BOC∽△BCQ,∴=,即BC2=OB•BQ,而OC=6,OB=3,∴BC=3,∴(3)2=3×BQ,∴BQ=15,∴Q(﹣12,0),设直线CQ为y=mx+6,则0=﹣12m+6,解得m=,∴直线CQ为y=x+6,由得(舍去)或,∴P(,),综上所述,P点坐标为(,)或(,),(3)设M(t,﹣2t2+4t+6),则N(0,﹣2t2+4t+6),∴MN=|t|,CN=|2t2﹣4t|,∵OC=6,OB=3,∴OC=2OB,∵△CMN与△OBC相似,∴MN=2CN或CN=2MN,①MN=2CN时,如图:∴|t|=2|2t2﹣4t|,解得t=或t=或t=0(舍去),∴M(,),N(0,)或M(,),N(0,);②CN=2MN时,如图:∴|2t2﹣4t|=2|t|,解得t=0(舍去)或t=3(M与B重合,舍去)或t=1,∴M(1,8),N(0,8),综上所述,M(,),N(0,)或M(,),N(0,)或M(1,8),N(0,8).7.如图,抛物线与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为点C,D,.(1)求b,c的值;(2)求直线CD的函数解析式;(3)求∠ADB的度数;(4)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,当△ABD与△BPQ 相似时,请直接写出所有满足条件的点Q的坐标.解:(1)∵点A,B分别位于原点的左、右两侧,BO=3AO=3,∴A(﹣1,0),B(3,0),把A(﹣1,0),B(3,0)代入y=x2+bx+c,得,解得:,∴b=﹣,c=﹣;(2)如图1,过点D作DE⊥AB于E,则∠DEB=∠COB=90°,∴DE∥OC,∴=,∵BC=CD,OB=3,∴=,∴OE=,∴点D横坐标为﹣,当x=﹣时,y=×(﹣)2﹣×(﹣)﹣=+1,∴点D坐标为(﹣,+1),设直线BD的函数解析式为y=kx+n,把B(3,0),D(﹣,+1)代入,得,解得:,∴直线BD的函数解析式为y=﹣x+;(3)如图2,连接AC,∵直线BD的函数解析式为y=﹣x+,∴C(0,),∵A(﹣1,0),D(﹣,+1),∴AC2=OA2+OC2=12+()2=4,则AC=2,BC2=OB2+OC2=32+()2=12,则BC=2,∴AB=3﹣(﹣1)=4,∴AC2+BC2=AB2,∴∠ACB=90°,∴∠ACD=180°﹣90°=90°,∵BC=CD,∴CD=2,∴tan∠ADB===1,∴∠ADB=45°;(4)在△ABD中,tan∠ABD==,∴∠ABD=30°,∵∠ADB=45°,∴∠BAD=180°﹣(∠ABD+∠ADB)=180°﹣(30°+45°)=105°,∵CD=2,BC=CD=2,∴BD=BC+CD=2+2,由(3)知:AC=CD=2,∠ACD=90°,AB=4,∴AD=2,∵y=x2﹣x﹣,∴对称轴为直线x=1.∵点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,∴∠PBQ<90°,∴分两种情况:①当∠PBQ=∠ABD=30°时,如图3,设对称轴与x轴交于点M,则M(1,0),∴BM=3﹣1=2,∴PM=BM•tan∠PBQ=2×tan30°=,∵点P在抛物线的对称轴上且在x轴下方,∴P(1,﹣),BP===,∵△ABD与△BPQ相似,且∠PBQ=∠ABD,∴=或=,∴=或=,∴BQ=或BQ=,∴Q(,0)或(,0);②当∠PBQ=∠ADB=45°时,如图4,∵PM=BM•tan∠PBQ=2tan45°=2,∴P(1,﹣2),∴BP=2,∵△ABD与△BPQ相似,且∠PBQ=∠ADB,∴=或=,∴=或=,∴BQ=2﹣2或2+2,∴Q(5﹣2,0)或(1﹣2,0);综上所述,点Q的坐标为Q(,0)或Q(,0)或Q(5﹣2,0)或Q(1﹣2,0).8.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).(1)求抛物线的函数表达式;(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求的最大值;(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为y=a(x+1)(x﹣4).将C(0,﹣2)代入得:﹣4a=﹣2,解得a=,∴抛物线的解析式为y=(x+1)(x﹣4),即y=x2﹣x﹣2.(2)过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K,∴AK∥DG,∴△AKE∽△DFE,∴=.设直线BC的解析式为y=kx+b1,∴,解得,∴直线BC的解析式为y=x﹣2,∵A(﹣1,0),∴y=﹣﹣2=﹣,∴AK=,设D(m,m2﹣m﹣2),则F(m,m﹣2),∴DF=m﹣2﹣m2+m+2=﹣m2+2m.∴==﹣(m﹣2)2+.∴当m=2时,有最大值,最大值是.(3)符合条件的点P的坐标为(,)或(,).∵l∥BC,∴直线l的解析式为y=x,设P(a1,),①当点P在直线BQ右侧时,如图2,过点P作PN⊥x轴于点N,过点Q作QM⊥直线PN于点M,∵A(﹣1,0),C(0,﹣2),B(4,0),∴AC=,AB=5,BC=2,∵AC2+BC2=AB2,∴∠ACB=90°,∵△PQB∽△CAB,∴==,∵∠QMP=∠BNP=90°,∴∠MQP+∠MPQ=90°,∠MPQ+∠BPN=90°,∴∠MQP=∠BPN,∴△QPM∽△PBN,∴===,∴QM=,PM=(a1﹣4)=a1﹣2,∴MN=a1﹣2,ON﹣QM=a1﹣=a1,∴Q(a1,a1﹣2),将点Q的坐标代入抛物线的解析式得×(a1)2﹣×a1﹣2=a1﹣2,解得a1=0(舍去)或a1=.∴P(,).②当点P在直线BQ左侧时,由①的方法同理可得点Q的坐标为(a1,2).此时点P的坐标为(,).综上所述,符合条件的点P的坐标是(,)或(,).9.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;(3)将抛物线在0≤x≤3之间的部分记为图象L,将图象L在直线y=t上方部分沿直线y=t翻折,其余部分保持不动,得到一个新的函数图象,记这个函数的最大值为a,最小值为b,若a﹣b≤3,请直接写出t的取值范围.解:(1)将(3,0)代入y=﹣x+c得0=﹣2+c,解得c=2,∴y=﹣x+2.将x=0代入y=﹣x+2得y=2,∴点B坐标为(0,2).将(3,0),(0,2)代入y=﹣x2+bx+c得,解得,∴y=﹣x2+x+2.(2)如图,当BM∥AM时满足题意,点B,N关于抛物线对称轴对称,∵y=﹣x2+x+2,∴抛物线对称轴为直线x=﹣=,∴点N坐标为(,2),∴点M坐标为(,0).如图,当∠NBP=90°时符合题意,作NC⊥y轴于点C,则N(m,﹣m2+m+2),∵∠NBC+∠ABO=∠ABO+∠BAO=90°,∴∠NBC=∠BAO,∴△BCN∽△AOB,∴=,即,解得m=,∴点M坐标为(,0).综上所述,点M坐标为(,0)或(,0).(3)∵y=﹣x2+x+2=﹣(x﹣)2+,∴抛物线顶点坐标为(,),∴翻折后顶点坐标为(,2t﹣),当点A为最低点时,t﹣0≤3,解得t≤3,令t﹣(2t﹣)=3,解得t=,∴≤t≤3.10.如图所示,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴相交于点C,B、C两点的坐标分别为(1,0)、(0,﹣3),直线y=kx+3k经过点A,与y轴交于点D.(1)求抛物线的函数表达式;(2)点E是抛物线上一动点(不与点C重合),连接AE,过点E作EF⊥x轴,垂足为F,若△AEF是等腰直角三角形,求点E的坐标;(3)在(2)的条件下,若在直线y=kx+3k上存在一点G使得△DFG与△AOC相似,求出k的值.解:(1)∵直线y=kx+3k经过点A,则点A的坐标为(﹣3,0),将点A、B、C的坐标代入抛物线表达式得:,解得,故抛物线的表达式为y=x2+2x﹣3;(2)设点E的坐标为(x,x2+2x﹣3),则AF=|x+3|,EF=|x2+2x﹣3|,∵△AEF是等腰直角三角形,∴AF=EF,∴|x2+2x﹣3|=|x+3|,∴x=﹣3(舍去)或x=0(舍去)或x=2,故点E的坐标为(2,5);(3)∵CO=BO=3,故△AOC为等腰直角三角形,当△DFG与△AOC相似时,则△DFG为等腰直角三角形,显然∠DFG不可能为直角,∵直线y=kx+3k与y轴交于点D,则点D(0,3k),由(2)知,点F(2,0),①当∠FDG为直角时,∵点G在直线AD上,故在∠FDG的前提下,总能找到GD=DF,故只需要DF⊥AD即可,在等腰Rt△FDG中,由直线AD的表达式为:y=kx+3k,则tan∠DOA=k,而tan∠DFO====,解得k=±;②当∠FGD为直角时,如下图,过点G作MN∥y轴,交x轴于点N,交过点D与x轴的平行线于点M,则DG=GF,设点G的坐标为(t,kt+3k),则MD=﹣t,MG=3k﹣tk﹣3k=﹣kt;GN=kt+3k,FN=2﹣t,∵∠MGD+∠FGN=90°,∠FGN+∠GFN=90°,∴∠MGD=∠GFN,∵∠GMD=∠FNG=90°,GD=FG,∴△GMD≌△FNG(AAS),∴MD=GN,MG=NF,即﹣t=kt+3k且﹣kt=2﹣t,解得k=2或﹣;当∠DFG=90°时,过点G作GH⊥x轴于H,则△ODF≌△HFG,∴GH=OF=2,HF=OD=3k,∵y=﹣2时,﹣2=kx+3k,∴x=,∴2+=3k,解得k=2或﹣综上,k=±或2或﹣.11.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N 的坐标,若不存在,请说明理由.解:(1)把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣1,得解得∴抛物线解析式为:y=∴抛物线对称轴为直线x=﹣(2)存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,﹣1)关于直线x=1的对称点C′(2,﹣1),连C′O与直线x=1的交点即为P点.设过点C′、O直线解析式为:y=kx∴k=﹣∴y=﹣则P点坐标为(1,﹣)(3)当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,﹣a﹣1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,﹣)∵N为DM中点∴点M坐标为(2a,)把M代入y=,解得a=0(舍去)或a=4∴a=4则N点坐标为(4,﹣3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点M由(2)M为(2,﹣1)∴由相似CN=,MN=由面积法求N到MC距离为则N点坐标为(,﹣)∴N点坐标为(4,﹣3)或(,﹣)12.抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.(1)求出抛物线L的解析式;(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D,F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点,若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.解:(1)由题意知,解得:,∴抛物线L的解析式为y=﹣x2+2x+1;(2)如图1,∵y=kx﹣k+4=k(x﹣1)+4,∴当x=1时,y=4,即该直线所过定点G坐标为(1,4),∵y=﹣x2+2x+1=﹣(x﹣1)2+2,∴点B(1,2),则BG=2,=1,即S△BNG﹣S△BMG=BG•(x N﹣1)﹣BG•(x M﹣1)=1,∵S△BMN∴x N﹣x M=1,由得x2+(k﹣2)x﹣k+3=0,解得:x==,则x N=、x M=,由x N﹣x M=1得=1,∴k=±3,∵k<0,∴k=﹣3;(3)如图2,设抛物线L 1的解析式为y =﹣x 2+2x +1+m ,∴C (0,1+m )、D (2,1+m )、F (1,0),设P (0,t ),①当△PCD ∽△FOP 时,,∴,∴t 2﹣(1+m )t +2=0①;②当△PCD ∽△POF 时,,∴,∴t =(m +1)②;(Ⅰ)当方程①有两个相等实数根时,Δ=(1+m )2﹣8=0,解得:m =2﹣1(负值舍去),此时方程①有两个相等实数根t 1=t 2=,方程②有一个实数根t =,∴m =2﹣1,此时点P 的坐标为(0,)和(0,);(Ⅱ)当方程①有两个不相等的实数根时,把②代入①,得:(m +1)2﹣(m +1)2+2=0,解得:m =2(负值舍去),此时,方程①有两个不相等的实数根t 1=1、t 2=2,方程②有一个实数根t =1,∴m=2,此时点P的坐标为(0,1)和(0,2);综上,当m=2﹣1时,点P的坐标为(0,)和(0,);当m=2时,点P的坐标为(0,1)和(0,2).13.设抛物线y=ax2+bx﹣2与x轴交于两个不同的点A(﹣1,0)、B(m,0),与y轴交于点C,且∠ACB=90度.(1)求m的值和抛物线的解析式;(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P 在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;(3)在(2)的条件下,△BDP的外接圆半径等于或.解:(1)令x=0,得y=﹣2,∴C(0,﹣2),∵∠ACB=90°,CO⊥AB,∴△AOC∽△COB,∴OA•OB=OC2∴OB=,∴m=4,将A(﹣1,0),B(4,0)代入y=ax2+bx﹣2,得,∴抛物线的解析式为y=x2﹣x﹣2.(2)D(1,n)代入y=x2﹣x﹣2,得n=﹣3,由,得,,∴E(6,7),过E作EH⊥x轴于H,则H(6,0)∴AH=EH=7∴∠EAH=45°过D作DF⊥x轴于F,则F(1,0)∴BF=DF=3∴∠DBF=45°∴∠EAH=∠DBF=45°∴∠DBH=135°,90°<∠EBA<135°则点P只能在点B的左侧,有以下两种情况:①若△DBP1∽△EAB,则∴BP1===∴OP1=4﹣=,∴P1(,0).②若△DBP2∽△BAE,则∴BP2===∴OP2=﹣4=∴P2(﹣,0).综合①、②,得点P的坐标为:P1(,0)或P2(﹣,0).(3)或.如图所示:先作△BPD的外接圆,过P作直径PM,连接DM,作DF⊥x轴于F.∵∠PMD=∠PBD,∠DFP=∠PDM,∴△PMD和△FBD相似,∴,∴PD===,DF=3,BD==3,∴PM==,∴△BPD的外接圆的半径=;同理可求出当P点在x轴的负半轴上时,△BPD的外接圆的半径=.14.如图1,在平面直角坐标系中,抛物线y=x2+x﹣与x轴交于点A、B(点A在点B右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.(1)求点A、B、D的坐标;(2)求证:四边形BFCE是平行四边形;(3)如图2,过顶点D作DD1⊥x轴于点D1,点P是抛物线上一动点,过点P作PM⊥x轴,点M为垂足,使得△PAM与△DD1A相似(不含全等).①求出一个满足以上条件的点P的横坐标;②直接回答这样的点P共有几个?解:(1)令x2+x﹣=0,解得x1=1,x2=﹣7.∴A(1,0),B(﹣7,0).由y=x2+x﹣=(x+3)2﹣2得,D(﹣3,﹣2);(2)证明:∵DD1⊥x轴于点D1,∴∠COF=∠DD1F=90°,∵∠D1FD=∠CFO,∴△DD1F∽△COF,∴=,∵D(﹣3,﹣2),∴D1D=2,OD1=3,∵AC=CF,CO⊥AF∴OF=OA=1∴D1F=D1O﹣OF=3﹣1=2,∴=,∴OC=,∴CA=CF=FA=2,∴△ACF是等边三角形,∴∠AFC=∠ACF,∵△CAD绕点C顺时针旋转得到△CFE,∴∠ECF=∠AFC=60°,∴EC∥BF,∵EC=DC==6,∵BF=6,∴EC=BF,∴四边形BFCE是平行四边形;(3)∵点P是抛物线上一动点,∴设P点(x,x2+x﹣),①当点P在B点的左侧时,∵△PAM与△DD1A相似,∴或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣11或x1=1(不合题意舍去)x2=﹣;当点P在A点的右侧时,∵△PAM与△DD1A相似,∴=或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣(不合题意舍去);当点P在AB之间时,∵△PAM与△DD1A相似,∴=或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣;综上所述,点P的横坐标为﹣11或﹣或﹣;②由①得,这样的点P共有3个.15.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,①求点M的坐标;②在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵B(2,t)在直线y=x上,∴t=2,∴B(2,2),把A、B两点坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=2x2﹣3x;(2)如图1,过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点F,∵点C是抛物线上第四象限的点,∴可设C(t,2t2﹣3t),则E(t,0),D(t,t),∴OE=t,BF=2﹣t,CD=t﹣(2t2﹣3t)=﹣2t2+4t,=S△CDO+S△CDB=CD•OE+CD•BF=(﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∴S△OBC∵△OBC的面积为2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);(3)①设MB交y轴于点N,如图2,∵B(2,2),∴∠AOB=∠NOB=45°,在△AOB和△NOB中,∴△AOB≌△NOB(ASA),∴ON=OA=,∴N(0,),∴可设直线BN解析式为y=kx+,把B点坐标代入可得2=2k+,解得k=,∴直线BN的解析式为y=x+,联立直线BN和抛物线解析式可得,解得(舍去)或,∴M(﹣,),②∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=2,OC=,∵△POC∽△MOB,∴==2,∠POC=∠BOM,当点P在第一象限时,如图3,过M作MG⊥y轴于点G,过P作PH⊥x轴于点H,∵∠COA=∠BOG=45°,∴∠MOG=∠POH,且∠PHO=∠MGO,∴△MOG∽△POH,∴===2,。
二次函数中三角形问题(含问题详解)

二次函数中的三角形一.与三角形面积例1:如图,已知在同一坐标系中,直线22k y kx =+-与y 轴交于点P ,抛物线k x k x y 4)1(22++-=与x 轴交于)0,(),0,(21x B x A 两点。
C 是抛物线的顶点。
(1)求二次函数的最小值(用含k 的代数式表示); (2)若点A 在点B 的左侧,且021<⋅x x 。
①当k 取何值时,直线通过点B ;②是否存在实数k ,使ABC ABP S S ∆∆=?如果存在,请求出此时抛物线的解析式;如果不存在,请说明理由。
例2:已知抛物线)1(3)4(2-+---=m x m x y 与x 轴交于A 、B 两点,与y 轴交于C 点, (1)求m 的取值范围;(2)若0<m ,直线1-=kx y 经过点A ,与y 轴交于点D ,且25=⋅BD AD ,求抛物线的解析式; (3)若A 点在B 点左边,在第一象限内,(2)中所得的抛物线上是否存在一点P ,使直线P A 平分ACD ∆的面积?若存在,求出P 点的坐标;若不存在,请说明理由。
例3.已知矩形ABCD 中,AB =2,AD =4,以AB 的垂直平分线为x 轴,AB 所在的直线为y 轴,建立平面直角坐标系(如图)。
(1)写出A 、B 、C 、D 及AD 的中点E 的坐标;(2)求以E 为顶点、对称轴平行于y 轴,并且经过点B 、C 的抛物线的解析式; (3)求对角线BD 与上述抛物线除点B 以外的另一交点P 的坐标;(4)△PEB 的面积S △PEB 与△PBC 的面积S △PBC 具有怎样的关系?证明你的结论。
A BC DO E x y(第25题图)例4.如图1,已知直线12y x =-与抛物线2164y x =-+交于AB ,两点. (1)求A B ,两点的坐标;(2)求线段AB 的垂直平分线的解析式;(3)如图2,取与线段AB 等长的一根橡皮筋,端点分别固定在A B ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动,动点P 将与A B ,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.二.与三角形形状例5. 如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.图2图1例 6.如图①,在平面直角坐标系中,点A 的坐标为(12),,点B 的坐标为(31),,二次函数2y x =的图象记为抛物线1l .(1)平移抛物线1l ,使平移后的抛物线过点A ,但不过点B ,写出平移后的一个抛物线的函数表达式: (任写一个即可).(2)平移抛物线1l ,使平移后的抛物线过A B ,两点,记为抛物线2l ,如图②,求抛物线2l 的函数表达式.(3)设抛物线2l 的顶点为C ,K 为y 轴上一点.若ABK ABC S S =△△,求点K 的坐标.(4)请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ,使ABP △为等腰三角形.若存在,请判断点P 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.x 图①x 图②x 图③例7. 已知:如图,抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点. (1)求抛物线的函数关系式;(2)若过点C 的直线y kx b =+与抛物线相交于点E (4,m ),请求出△CBE 的面积S 的值; (3)在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标;(4)除(3)中所求的0P 点外,在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形?若存在,请求出一共有几个满足条件的点P (要求简要说明理由,但不证明);若不存在这样的点P ,请说明理由.例8.如图,在直角坐标系中,点A 的坐标为(-2,0),连接OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由;(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方, 那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB 的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)(第25题图)三.二次函数与三角形相似 例9:已知一次函数1243--=x y 的图象分别交x 轴、y 轴于A 、C 两点, (1)求出A 、C 两点的坐标;(2)在x 轴上找出点B ,使ACB ∆∽AOC ∆,若抛物线过A 、B 、C 三点,求出此抛物线的解析式; (3)在(2)的条件下,设动点P 、Q 分别从A 、B 两点同时出发,以相同速度沿AC 、BA 向C 、A 运动,连结PQ ,使m AP =,是否存在m 的值,使以A 、P 、Q 为顶点的三角形与ABC ∆相似,若存在,求出所有m 的值;若不存在,请说明理由。
2023年中考数学压轴题专题04 二次函数与相似问题-【含答案】

专题4二次函数与相似问题函数中因动点产生的相似三角形问题一般有三个解题途径①求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
相似三角形常见的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.判定定理“两边及其夹角法”是常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分AB DEAC DF=和AB DFAC DE=两种情况列方程.应用判定定理“两角法”解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理“三边法”解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【例2】.(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【例3】.(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y 轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.7.(2022•祥云县模拟)如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),交y轴于点C(0,3),点M是该抛物线上第一象限内的一个动点,ME垂直x轴于点E,交线段BC于点D,MN∥x轴,交y轴于点N.(1)求抛物线y=ax2+bx+c的表达式;(2)若四边形MNOE是正方形,求该正方形的边长;(3)连结OD,AC,抛物线上是否存在点M,使得以C,O,D为顶点的三角形与△ABC相似,若存在,请求出点M的坐标,若不存在,请说明理由.8.(2022•松江区校级模拟)如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.(1)求抛物线的解析式以及顶点坐标;(2)连接BC,CD,DB,求∠CBD的正切值;(3)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BE,直线BE与对称轴交于点M,在(2)的条件下,点P是抛物线对称轴上的一点,是否存在点P使△CDB和△BMP相似,若存在,求点P坐标,若不存在,请说明理由.9.(2022•平江县一模)如图,抛物线y=ax2+bx+8与x轴交于A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求该抛物线的函数表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,设四边形PBOC和△AOC的面积分别为S四边形PBOC ,记S=S四边形PBOC﹣S△AOC,求S最大值点P的坐标及S的最大值;和S△AOC(3)点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△BOC相似?若存在,求点M的坐标;若不存在,请说明理由.10.(2022•莱州市一模)如图①,在平面直角坐标系中,抛物线y=x2+c经过点A(4,3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,﹣2)且垂直于y轴的直线,连接PO.(1)求抛物线的表达式,并求出顶点B的坐标;(2)试证明:经过点O的⊙P与直线l相切;(3)如图②,已知点C的坐标为(1,2),是否存在点P,使得以点P,O及(2)中的切点为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.11.(2022•巩义市模拟)已知,二次函数y=ax2+bx﹣3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于C点,点A的坐标为(﹣1,0),且OB=OC.(1)求二次函数的解析式;(2)当0≤x≤4时,求二次函数的最大值和最小值分别为多少?(3)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC 与PO是对应边?若存在,求出点P的坐标;若不存在,请说明理由.12.(2022•澄迈县模拟)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求该抛物线的函数表达式及顶点C的坐标;(2)设该抛物线上一动点P的横坐标为t.①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;③在图3中,若P是y轴左侧该抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.13.(2022•丰南区二模)如图①、②,在平面直角坐标系中,一边长为2的等边三角板CDE恰好与坐标系中的△OAB重合,现将三角板CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C′ED的位置.(1)直接写出C′的坐标,并求经过O、A、C′三点的抛物线的解析式;(2)点P在第四象限的抛物线上,求△C′OP的最大面积;(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,抛物线上是否存在一点M,使得△BOF与△AOM相似?若存在,请求出点M的坐标;若不存在,请说明理由.14.(2022•莱芜区三模)如图,在平面直角坐标系中,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=x2+bx+c的图象经过A和点C(0,﹣3).(1)求二次函数的表达式;(2)如图1,平移线段AC,点A的对应点D落在二次函数在第一象限的图象上,点C的对应点E落在直线AB上,直接写出四边形ACED的形状,并求出此时点D的坐标;(3)如图2,在(2)的条件下,连接CD,交x轴于点M,点P为直线CD下方抛物线上一个动点,过点P作PF⊥x轴,交CD于点F,连接PC,是否存在点P,使得以点P,C,F为顶点的三角形与△COM相似?若存在,求出线段FP的长度;若不存在,请说明理由.15.(2022•临清市三模)如图,抛物线y=﹣x2+bx+c的顶点D坐标为(1,4),且与x轴相交于A,B两点(点A在点B的左侧,与y轴相交于点C,点E在x轴上方且在对称轴左侧的抛物线上运动,点F在抛物线上并且和点E关于抛物线的对称轴对称,作矩形EFGH,其中点G,H都在x轴上.(1)求抛物线解析式;(2)设点F横坐标为m,①用含有m的代数式表示点E的横坐标为(直接填空);②当矩形EFGH为正方形时,求点G的坐标;③连接AD,当EG与AD垂直时,求点G的坐标;(3)过顶点D作DM⊥x轴于点M,过点F作FP⊥AD于点P,直接写出△DFP与△DAM相似时,点F 的坐标.16.(2022•成都模拟)如图①,已知抛物线y=﹣(x﹣1)2+k交x轴于A,B两点,交y轴于点C,P是抛物线上的动点,且满足OB=3OA.(1)求抛物线的解析式;(2)若点P在第一象限,直线y=x+b经过点P且与直线BC交于点E,设点P的横坐标为t,当线段PE 的长度随着t的增大而减小时,求t的取值范围;(3)如图②,过点A作BC的平行线m,与抛物线交于另一点D.点P在直线m上方,点Q在线段AD 上,若△CPQ与△AOC相似,且点P与点O是对应点,求点P的坐标.17.(2022•东莞市校级一模)在平面直角坐标系xOy中,已知抛物线y=﹣x2+2kx+2k2+1与x轴的左交点为A,右交点为B,与y轴的交点为C,对称轴为直线l,对于抛物线上的两点(x1,y1),(x2,y2)(x1<k<x2),当x1+x2=2时,y1﹣y2=0恒成立.(1)求该抛物线的解析式;(2)点M是第二象限内直线AC上方的抛物线上的一点,过点M作MN⊥AC于点N,求线段MN的最大值,并求出此时点M的坐标;(3)点P是直线l右侧抛物线上的一点,PQ⊥l于点Q,AP交直线l于点F,是否存在这样的点P,使△PQF与△ACO相似?若存在,请求出点P的坐标,若不存在,请说明理由.18.(2022•碑林区校级模拟)如图,Rt△ABC中,∠ACB=90°,AB=8,AC=4,以AB所在直线为x轴建立平面直角坐标系,若C(0,2).(1)请直接写出A、B的坐标;(2)求经过A、B、C三点的抛物线表达式;(3)l为抛物线对称轴,P是直线l右侧抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△ABC全等,求满足条件的点P,点E的坐标.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【分析】(1)直接利用待定系数法,即可求出解析式;(2)先求出点C的坐标,然后证明Rt△DPE∽Rt△AOC,再由二次函数的最值性质,求出答案;(3)根据题意,可分为两种情况进行分析:当△AOC∽△APD时;当△AOC∽△DAP时;分别求出两种情况的点的坐标,即可得到答案.【解析】(1)将A(0,3)和B(,﹣)代入y=﹣x2+bx+c,,解得,∴该抛物线的解析式为y=﹣x2+2x+3;(2)设直线AB的解析式为y=kx+n,把A(0,3)和B(,﹣)代入,,解得,∴直线AB的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得:x=2,∴C点坐标为(2,0),∵PD⊥x轴,PE∥x轴,∴∠ACO=∠DEP,∴Rt△DPE∽Rt△AOC,∴,∴PE=PD,∴PD+PE=PD,设点P的坐标为(a,﹣a2+2a+3),则D点坐标为(a,﹣a+3),∴PD=(﹣a2+2a+3)﹣(﹣a+3)=﹣(a﹣)2+,∴PD+PE=﹣(a﹣)2+,∵﹣<0,∴当a=时,PD+PE有最大值为;(3)①当△AOC∽△APD时,∵PD⊥x轴,∠DPA=90°,∴点P纵坐标是3,横坐标x>0,即﹣x2+2x+3=3,解得x=2,∴点D的坐标为(2,0);∵PD⊥x轴,∴点P的横坐标为2,∴点P的纵坐标为:y=﹣22+2×2+3=3,∴点P的坐标为(2,3),点D的坐标为(2,0);②当△AOC∽△DAP时,此时∠APG=∠ACO,过点A作AG⊥PD于点G,∴△APG∽△ACO,∴,设点P的坐标为(m,﹣m2+2m+3),则D点坐标为(m,﹣m+3),则,解得:m=,∴D点坐标为(,1),P点坐标为(,),综上,点P的坐标为(2,3),点D的坐标为(2,0)或P点坐标为(,),D点坐标为(,1).【例2】(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)令x=0和翻折的性质可得C(0,2),令y=0可得点A、B的坐标,利用待定系数法即可求出图象W的解析式;(2)利用数形结合找出当y=﹣x+b经过点C或者y=﹣x+b与y=x2﹣x﹣2相切时,直线y=﹣x+b与新图象恰好有三个不同的交点,①当直线y=﹣x+b经过点C(0,2)时,利用一次函数图象上点的坐标特征,即可求出b值;②当y=﹣x+b与y=x2﹣x﹣2相切时,联立一次函数解析式和抛物线解析式,利用根的判别式Δ=0,即可求出b值.综上即可得出结论;(3)先确定△BOC是等腰直角三角形,分三种情况:∠CNM=90°或∠MCN=90°,分别画图可得结论.【解析】(1)当x=0时,y=﹣2,∴C(0,2),当y=0时,x2﹣x﹣2=0,(x﹣2)(x+1)=0,∴x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),设图象W的解析式为:y=a(x+1)(x﹣2),把C(0,2)代入得:﹣2a=2,∴a=﹣1,∴y=﹣(x+1)(x﹣2)=﹣x2+x+2,∴图象W位于线段AB上方部分对应的函数关系式为:y=﹣x2+x+2(﹣1<x<2);(2)由图象得直线y=﹣x+b与图象W有三个交点时,存在两种情况:①当直线y=﹣x+b过点C时,与图象W有三个交点,此时b=2;②当直线y=﹣x+b与图象W位于线段AB上方部分对应的函数图象相切时,如图1,﹣x+b=﹣x2+x+2,x2﹣2x+b﹣2=0,Δ=(﹣2)2﹣4×1×(b﹣2)=0,∴b=3,综上,b的值是2或3;(3)∵OB=OC=2,∠BOC=90°,∴△BOC是等腰直角三角形,如图2,CN∥OB,△CNM∽△BOC,∵PN∥y轴,∴P(1,0);如图3,CN∥OB,△CNM∽△BOC,当y=2时,x2﹣x﹣2=2,x2﹣x﹣4=0,∴x1=,x2=,∴P(,0);如图4,当∠MCN=90°时,△OBC∽△CMN,∴CN的解析式为:y=x+2,∴x+2=x2﹣x﹣2,∴x1=1+,x2=1﹣(舍),∴P(1+,0),综上,点P的坐标为(1,0)或(,0)或(1+,0).【例3】(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【分析】(1)由y=﹣x2+3x+4可得A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,可知四边形CC'QP是平行四边形,及得CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,而B,Q,C'共线,故此时CP+PQ+BQ最小,最小值为BC'+PQ的值,由勾股定理可得BC'=5,即得CP+PQ+BQ最小值为6;(3)由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),知BN=,QN=t,PM=,CM=|t﹣3|,①当=时,=,可解得Q(,)或(,);②当=时,=,得Q(,).【解析】(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,∴A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,如图:∵CC'=PQ,CC'∥PQ,∴四边形CC'QP是平行四边形,∴CP=C'Q,∴CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,∵B,Q,C'共线,∴此时CP+PQ+BQ最小,最小值为BC'+PQ的值,∵C(0,4),CC'=PQ=1,∴C'(0,3),∵B(4,0),∴BC'==5,∴BC'+PQ=5+1=6,∴CP+PQ+BQ最小值为6;(3)如图:由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),∵B(4,0),C(0,4);∴BN=,QN=t,PM=,CM=|t﹣3|,∵∠CMP=∠QNB=90°,∴△CPM和△QBN相似,只需=或=,①当=时,=,解得t=或t=,∴Q(,)或(,);②当=时,=,解得t=或t=(舍去),∴Q(,),综上所述,Q的坐标是(,)或(,)或(,).【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.【分析】(1)把点B(2,0)代入y=﹣2x2+bx+c中,再由对称轴是直线x=列方程,两个方程组成方程组可解答;(2)当△POD是等边三角形时,点P在OD的垂直平分线上,所以作OD的垂直平分线与抛物线的交点即为点P,计算OD≠PD,可知△POD不可能是等边三角形;(3)分种情况:①当PC∥x轴时,△CPM∽△BHM时,根据PH的长列方程可解答;②②如图3,△PCM ∽△BHM,过点P作PE⊥y轴于E,证明△PEC∽△COB,可得结论.【解析】(1)由题意得:,解得:,∴抛物线的解析式为:y=﹣2x2+2x+4;(2)△POD不可能是等边三角形,理由如下:如图1,取OD的中点E,过点E作EP∥x轴,交抛物线于点P,连接PD,PO,∵C(0,4),D是OD的中点,∴E(0,1),当y=1时,﹣2x2+2x+4=1,2x2﹣2x﹣3=0,解得:x1=,x2=(舍),∴P(,1),∴OD≠PD,∴△POD不可能是等边三角形;(3)设点P的坐标为(t,﹣2t2+2t+4),则OH=t,BH=2﹣t,分两种情况:①如图2,△CMP∽△BMH,∴∠PCM=∠OBC,∠BHM=∠CPM=90°,∴tan∠OBC=tan∠PCM,∴====2,∴PM=2PC=2t,MH=2BH=2(2﹣t),∵PH=PM+MH,∴2t+2(2﹣t)=﹣2t2+2t+4,解得:t1=0,t2=1,∴P(1,4);②如图3,△PCM∽△BHM,则∠PCM=∠BHM=90°,过点P作PE⊥y轴于E,∴∠PEC=∠BOC=∠PCM=90°,∴∠PCE+∠EPC=∠PCE+∠BCO=90°,∴∠BCO=∠EPC,∴△PEC∽△COB,∴=,∴=,解得:t1=0(舍),t2=,∴P(,);综上,点P的坐标为(1,4)或(,).1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.【分析】(1)运用待定系数法将A(4,0),B(﹣1,0)代入y=ax2+bx+4,解方程组即可求得答案;(2)根据题意,当S1=S2+5,即S△ABD=S△ABC+5,设D(x,y),表示出△ABD和△ABC的面积,列方程求解即可;(3)分情况讨论,列出三角形相似的三种情况,画出相应图形,设M(m,4),则N(m,﹣m2+3m+4),运用相似三角形性质,建立方程求解即可.【解析】(1)∵抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,∴,解得:,∴y=﹣x2+3x+4;(2)∵抛物线y=﹣x2+3x+4与y轴交于点C,令x=0,则y=4,∴C(0,4),∵S1=S2+5,∴S1+S△AEB=S2+S△AEB+5,=S△ABC+5,即S△ABD∵A(4,0),B(﹣1,0),∴AB=5,设D(x,y),∴×5×y=×5×4+5,∴y=6,∴﹣x2+3x+4=6,解得:x1=1,x2=2,∴D1(1,6),D2(2,6);(3)设M(m,4),则N(m,﹣m2+3m+4),①如图2,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);②如图3,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=﹣1,经检验,m=﹣1是原方程的解,∴M(﹣1,4);③如图4,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);④如图5,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=7,经检验,m=7是原方程的解,∴M(7,4);综上所述,点M的坐标为(,4)或(﹣1,4)或(,4)或(7,4).2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.【分析】(1)在抛物线解析式中,令y=0则可求得A、B的坐标;(2)证明△AOP∽△AED,根据相似三角形面积的比等于对应边的比的平方列比例式可得AE=2,从而得点D的横坐标为3,代入抛物线的解析式可得点D的坐标;(3)如图2所示,若以Q,A,M为顶点的三角形与△QNA相似,有两种情况,但是∠QAM与∠QAN不可能相等,所以最后只存在一种情况:△AQM∽△NQA,列比例式可得结论.【解析】(1)当y=0时,x2﹣3x+=0,解得:x1=1,x2=5,∴A(1,0),B(5,0);(2)∵DE⊥x轴,∴∠AED=90°,∴∠AOP=∠AED=90°,∵∠OAP=∠DAE,∴△AOP∽△AED,∴==,∴=,∵OA=1,∴AE=2,∴OE=3,当x=3时,y=﹣3×3+=﹣2,∴D(3,﹣2);(3)如图2,设Q(0,m),当x=0时,y=,∴F(0,),∵点Q是线段OF上的动点,∴0≤m≤,当y=m时,x2﹣3x+=m,x2﹣6x+5﹣2m=0,x=3,∴x1=3+,x2=3﹣,∴QM=3﹣,QN=3+,在Rt△AOQ中,由勾股定理得:AQ=,∵∠AQM=∠AQN,∴当△AQM和△AQN相似只存在一种情况:△AQM∽△NQA,∴,∴AQ2=NQ•QM,即1+m2=(3+)(3﹣),解得:m1=﹣1+,m2=﹣1﹣(舍),∴Q(0,﹣1+).3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.【分析】(1)根据点A、B的坐标,利用待定系数法即可求出该抛物线的函数关系式;(2)根据点P是直线BC下方抛物线上一动点,其横坐标为m,表示PH的长,根据三角形的面积列方程解出即可得出结论;(3)先根据两三角形相似判断出∠CED=∠BMD=90°或∠DCE=∠DMB=90°,进而分两种情况讨论即可得出结论.【解析】(1)把点B(6,0)和点C(0,﹣3)代入得:,解得:,∴抛物线的解析式为;(2)设直线BC的解析式为:y=ax+n,由点B(6,0)和C(0,﹣3)得:,解得:,∴直线BC的解析式为,如图1,过点P作y轴的平行线交BC于点H,∵点P的坐标为(m,),PH∥y轴,∴点H的坐标为(m,),∴PH=y H﹣y P=﹣()=﹣,x B﹣x C=6﹣0=6,=PH×6=(﹣)×6=﹣=,∵S△PBC解得:m1=1,m2=5,∴m值为1或5;(3)如图2,∵∠CDE=∠BDM,△CDE与△BDM相似,∴∠CED=∠BMD=90°或∠DCE=∠DMB=90°,设M(x,0),①当∠CED=∠BDM=90°,∴CE∥AB,∵C(0,﹣3),∴点E的纵坐标为﹣3,∵点E在抛物线上,∴x2﹣x﹣3=﹣3.∴x=0(舍)或x=5,∴M(5,0);②当∠DCE=∠DMB=90°,∵OB=6,OC=3,∴BC==3,由(2)知直线BC的关系式为y=x﹣3,∴OM=x,BM=6﹣x,DM=3﹣x,由(2)同理得ED=﹣+3x,∵DM∥OC,∴,即,∴CD=,∴BD=BC﹣CD=﹣x,∵△ECD∽△BMD,∴,即=,∴=x(3﹣x)2,x(6﹣x)(1﹣x)=0,x1=0(舍),x2=6(舍),x3=1,∴M(1,0);综上所述:点M的坐标为(5,0)或(1,0).4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.【分析】(1)将抛物线配方后可得顶点A的坐标,将抛物线和一次函数的解析式联立方程组,解出可得B 和C的坐标;(2)先根据两点的距离计算AB、BC、AC的长,根据勾股定理的逆定理可得:∠ABC=90°,最后根据两边的比相等且夹角为90度得两三角形相似;(3)存在,设M(x,0),则P(x,x2+2x),表示OM=|x|,PM=|x2+2x|,分两种情况:有=或=,根据比例式代入可得对应x的值,计算点P的坐标即可.【解答】(1)解:y=x2+2x=(x+1)2﹣1,∴顶点A(﹣1,﹣1);由,解得:或∴B(﹣2,0),C(1,3);(2)证明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),∴AB==,BC==3,AC==2,∴AB2+BC2=AC2,==,∴∠ABC=90°,∵OD=1,CD=3,∴=,∴,∠ABC=∠ODC=90°,∴△ODC∽△ABC;(3)存在这样的P点,设M(x,0),则P(x,x2+2x),∴OM=|x|,PM=|x2+2x|,当以O,P,M为顶点的三角形与△ABC相似时,有=或=,由(2)知:AB=,CB=3,①当=时,则=,当P在第二象限时,x<0,x2+2x>0,∴,解得:x1=0(舍),x2=﹣,当P在第三象限时,x<0,x2+2x<0,∴=,解得:x1=0(舍),x2=﹣,②当=时,则=3,同理代入可得:x=﹣5或x=1(舍),综上所述,存在这样的点P,坐标为(﹣,﹣)或(﹣,)或(﹣5,15).5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.【分析】(1)①函数的对称轴为:x=﹣=,故点M(,),即可求解;②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,即可求解;③四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,即可求解;(2)分∠DBP为直角、∠BDP为直角两种情况,分别求解即可.【解析】(1)①函数的对称轴为:x=﹣=,故点M(,),当x=时,y=﹣2x+4=3,故点N(,3);②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,将R、B的坐标代入一次函数表达式:y=kx+b并解得:直线RB的表达式为:y=4x+4,当x=时,y=6,故点Q(,6);③不存在,理由:设点P(x,﹣2x+4),则点D(x,﹣2x2+2x+4),MN=﹣3=,四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,故不存在点P,使四边形MNPD为菱形;(2)当点P的横坐标为1时,则其坐标为:(1,2),此时点A、B的坐标分别为:(2,0)、(0,4),①当∠DBP为直角时,以B、P、D为顶点的三角形与△AOB相似,则∠BAO=∠BDP=α,tan∠BAO==2=tanα,则sinα=,PA=,PB=AB﹣PA=2﹣=,则PD==,故点D(1,);②当∠BDP为直角时,以B、P、D为顶点的三角形与△AOB相似,则BD∥x轴,则点B、D关于抛物线的对称轴对称,故点D(1,4),综上,点D的坐标为:(1,4)或(1,),将点A、B、D的坐标代入抛物线表达式:y=ax2+bx+c并解得:y=﹣2x2+2x+4或y=﹣x2+3x+4.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.。
二次函数与相似三角形综合题
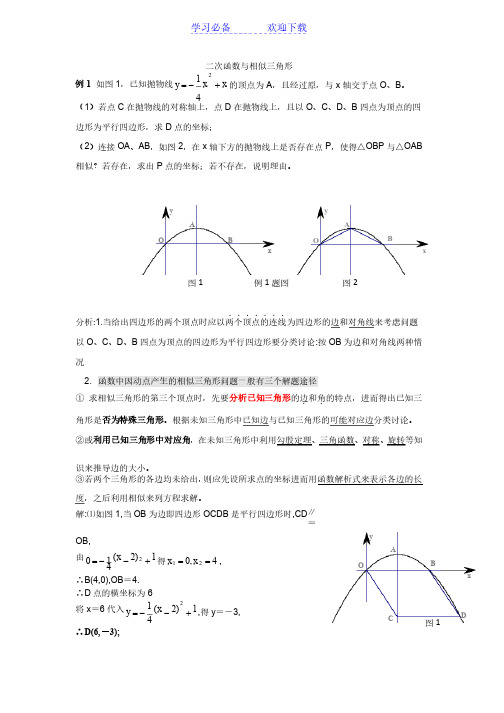
二次函数与相似三角形二次函数与相似三角形例1 如图1,已知抛物线x x 41y 2+-=的顶点为A ,且经过原,与x 轴交于点O 、B 。
(1)若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;点的坐标;(2)连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似?若存在,求出P 点的坐标;若不存在,说明理由。
点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. . 函数中因动点产生的相似三角形问题一般有三个解题途径函数中因动点产生的相似三角形问题一般有三个解题途径函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、在未知三角形中利用勾股定理、三角函数、三角函数、三角函数、对称、对称、旋转等知识来推导边的大小。
识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
度,之后利用相似来列方程求解。
解:⑴如图1,当OB 为边即四边形OCDB 是平行四边形时,CD ∥=OB, 由1)2x (4102+--=得4x ,0x 21==, ∴B(4,0),OB =4. ∴D 点的横坐标为6 将x =6代入1)2x (41y 2+--=,得y =-3, ∴D(6,-3); 例1题图题图 图1 OAByxOAByx图2 COABDyx图1 13E A'OAB Py x图2 (2)先根据A 、C 的坐标,用待定系数法求出直线AC 的解析式,进而根据抛物线和直线AC 的解析式分别表示出点P 、点M 的坐标,即可得到PM 的长;(3)由于∠PFC 和∠AEM 都是直角,F 和E 对应,则若以P 、C 、F 为顶点的三角形和△AEM 相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m 的代数式表示出AE 、EM 、CF 、PF 的长,根据相似三角形对应边的比相等列出比例式,求出m 的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM 的形状.解答:解:(1)∵抛物线y=ax 2﹣2ax+c (a≠0)经过点A (3,0),点C (0,4), ∴,解得,∴抛物线的解析式为y=﹣x 2+x+4; (2)设直线AC 的解析式为y=kx+b , ∵A(3,0),点C (0,4), ∴,解得,∴直线AC 的解析式为y=﹣43x+4.∵点M 的横坐标为m ,点M 在AC 上,∴M 点的坐标为(m ,﹣43m+4), ∵点P 的横坐标为m ,点P 在抛物线y=﹣x 2+x+4上,∴点P 的坐标为(m ,﹣ m 2+m+4), ∴PM=PE﹣ME=(﹣m 2+m+4)﹣(﹣43m+4)=﹣m 2+73m ,即PM=﹣m 2+73m (0<m <3); (3)在(2)的条件下,连结PC ,在CD 上方的抛物线部分存在这样的点P ,使得以P 、C 、F 为顶点的三角形和△AEM 相似.理由如下:由题意,可得AE=3﹣m ,EM=﹣m+4,CF=m ,PF=﹣m 2+m+4﹣4=﹣m 2+m . 若以P 、C 、F 为顶点的三角形和△AEM 相似,分两种情况:①若△PFC∽△AEM,则PF :AE=FC :EM ,即(﹣m 2+m ):(3﹣m )=m :(﹣ m+4), ∵m≠0且m≠3, ∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME, ∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF 中,∵∠CMF+∠MCF=90°, ∴∠PCF+∠MCF=90°,即∠PCM=90°, ∴△PCM 为直角三角形;②若△CFP∽△AEM,则CF :AE=PF :EM ,即m :(3﹣m )=(﹣m 2+m ):(﹣m+4), ∵m≠0且m≠3,yxEQP C B OA ∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME, ∵∠AME=∠CMF,∴∠CPF=∠CMF. ∴CP=CM,∴△PCM 为等腰三角形.综上所述,存在这样的点P 使△PFC 与△AEM 相似.此时m 的值为或1,△PCM 为直角三角形或等腰三角形.点评:此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解. 练习1、已知抛物线225333y x x =-+经过53(33)02P E æöç÷ç÷èø,,,及原点(00)O ,. (1)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似?若存在,求出Q 点的坐标;若不存在,说明理由.点的坐标;若不存在,说明理由.(2)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系?为什么?之间存在怎样的关系?为什么?(1)存在.)存在.设Q 点的坐标为()m n ,,则225333n m m =-+, 要使,BQ PB OCP PBQ CP OC =△∽△,则有3333n m --=,即2253333333m m m +--=解之得,12232m m ==,.当123m =时,2n =,即为Q 点,所以得(232)Q ,要使,BQ PB OCP QBP OC CP =△∽△,则有3333n m --=,即2253333333m m m +--=解之得,12333m m ==,,当3m =时,即为P 点,点, 当133m =时,3n =-,所以得(333)Q -,. 故存在两个Q 点使得OCP △与PBQ △相似.相似.Q 点的坐标为(232)(333)-,,,.(2)在Rt OCP △中,因为3tan 3CP COP OC Ð==.所以30COP Ð=. 当Q 点的坐标为(232),时,30BPQ COP Ð=Ð=. 所以90OPQ OCP B QAO Ð=Ð=Ð=Ð=.因此,OPC PQB OPQ OAQ ,,,△△△△都是直角三角形.都是直角三角形.又在Rt OAQ △中,因为3tan 3QA QOA AO Ð==.所以30QOA Ð=. 即有30POQ QOA QPB COP Ð=Ð=Ð=Ð=. 所以OPC PQB OQP OQA △∽△∽△∽△, 又因为QP OP QA OA ,⊥⊥30POQ AOQ Ð=Ð=,所以OQA OQP △≌△.2.在平面直角坐标系xOy 中,已知二次函数223y x x =-++的图象与x 轴交于A B ,两点(点A 在点B 的左边),与y 轴交于点C .(1)若直线:(0)l y kx k =¹与线段BC 交于点D (不与点B C ,重合),则是否存在这样的直线l ,使得以B O D ,,为顶点的三角形与BAC △相似?若存在,求出该直线的函数表达式及点D 的坐标;若不存在,请说明理由;(10)(30),(03)A B C -,,,, (2)若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角PCO Ð与ACO Ð的大小(不必证明),并写出此时点P 的横坐标p x 的取值范围.的取值范围.(1)假设存在直线:(0)l y kx k =¹与线段BC 交于点D (不与点B C ,重合),使得以B O D ,,为顶点的三角形与BAC △相似.相似.在223y x x =-++中,令0y =,则由2230x x -++=,解得1213x x =-=,(10)(30)A B \-,,,. 令0x =,得3y =.(03)C \,. 设过点O 的直线l 交BC 于点D ,过点D 作DE x ⊥轴于点E .yCl xB A 1x = 练习3图yx B E A OC D1x =l点B的坐标为(30),,点C的坐标为(03),,点A的坐标为(10)-,.4345.AB OB OC OBC\===Ð=,,223332BC\=+=.要使BOD BAC△∽△或BDO BAC△∽△,已有B BÐ=Ð,则只需BD BOBC BA=,①或.BO BDBC BA=②成立.成立.若是①,则有3329244BO BCBDBA´===.而45OBC BE DEÐ=\=,.\在Rt BDE△中,由勾股定理,得222229224BE DE BE BDæö+===ç÷ç÷èø.解得解得94BE DE==(负值舍去).93344OE OB BE\=-=-=.\点D的坐标为3944æöç÷èø,.将点D的坐标代入(0)y kx k=¹中,求得3k=.\满足条件的直线l的函数表达式为3y x=.[或求出直线AC的函数表达式为33y x=+,则与直线AC平行的直线l的函数表达式为3y x=.此时易知BOD BAC△∽△,再求出直线BC的函数表达式为3y x=-+.联立33y x y x==-+,求得点D的坐标为3944æöç÷èø,.]若是②,则有342232BO BABDBC´===.而45OBC BE DEÐ=\=,.\在Rt BDE △中,由勾股定理,得222222(22)BE DE BE BD +===.解得解得2BE DE ==(负值舍去).321OE OB BE \=-=-=.\点D 的坐标为(12),. 将点D 的坐标代入(0)y kx k =¹中,求得2k =.∴满足条件的直线l 的函数表达式为2y x =.\存在直线:3l y x =或2y x =与线段BC 交于点D (不与点B C ,重合),使得以B O D ,,为顶点的三角形与BAC △相似,且点D 的坐标分别为3944æöç÷èø,或(12),.(2)设过点(03)(10)C E ,,,的直线3(0)y kx k =+¹与该二次函数的图象交于点P . 将点(10)E ,的坐标代入3y kx =+中,求得3k =-. \此直线的函数表达式为33y x =-+.设点P 的坐标为(33)x x -+,,并代入223y x x =-++,得250x x -=. 解得1250x x ==,(不合题意,舍去).512x y \==-,.\点P 的坐标为(512)-,.此时,锐角PCO ACO Ð=Ð.又二次函数的对称轴为1x =,\点C 关于对称轴对称的点C ¢的坐标为(23),. \当5px>时,锐角PCO ACO Ð<Ð;当5p x =时,锐角PCO ACO Ð=Ð; 当25p x <<时,锐角PCO ACO Ð>Ð.OxBEA O C1x =PC ¢ ·3.如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C ,过点A 作AP ∥CB 交抛物线于点P . 在x 轴上方的抛物线上是否存在一点M ,过M 作MG ^x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与D PCA 相似.若存在,请求出M 点的坐标;否则,请说明理由.否则,请说明理由. 解:解: 假设存在假设存在A (1,0)-B (1,0)C (0,1)- ∵ÐPAB=ÐBAC =45 ∴P A ^AC ∵MG ^x 轴于点G , ∴ÐMGA=ÐPAC =90 在Rt △AOC 中,OA=OC=1 ∴AC=2 在Rt △PAE 中,AE=PE=3 ∴AP= 32 设M 点的横坐标为m ,则M 2(,1)m m - ①点M 在y 轴左侧时,则1m <-(ⅰ) 当D AMG ∽D PCA 时,有AG PA =MG CA∵AG=1m --,MG=21m -即211322m m ---=解得11m =-(舍去)(舍去) 223m =(舍去)(舍去)(ⅱ) 当D MAG ∽D PCA 时有AG CA =MGPA即 211232m m ---=解得:1m =-(舍去)(舍去) 22m =- ∴M (2,3)-② 点M 在y 轴右侧时,则1m > (ⅰ) 当D AMG ∽D PCA 时有AG PA =MGCA∵AG=1m +,MG=21m -G M 图3 C B y P A oxG M 图2 C B y P A ox图1 C P B y A ox∴211322m m +-=解得11m =-(舍去)(舍去) 243m =∴M 47(,)39(ⅱ) 当D MAG ∽D PCA 时有AG CA =MGPA即211232m m +-=解得:11m =-(舍去)(舍去) 24m = ∴M (4,15)∴存在点M ,使以A 、M 、G 三点为顶点的三角形与D PCA 相似相似M 点的坐标为(2,3)-,47(,)39,(4,15)4.4.(2013•曲靖压轴题)如图,在平面直角坐标系(2013•曲靖压轴题)如图,在平面直角坐标系xOy 中,直线y=x+4与坐标轴分别交于A 、B 两点,过A 、B 两点的抛物线y=﹣x 2﹣3x+4..点D 为线段AB 上一动点,过点D 作CD⊥x 轴于点C ,交抛物线于点E .(1)当DE=4时,求四边形CAEB 的面积.的面积. (2)连接BE BE,,是否存在点D ,使得△DBE 和△DAC 相似?若存在,求此点D 坐标;若不存在,说明理由.说明理由.考点: 二次函数综合题. 分析: (1)首先求出点A 、B 的坐标,然后利用待定系数法求出抛物线的解析式;(2)设点C 坐标为(m ,0)(m <0),根据已知条件求出点E 坐标为(m ,8+m );由于点E 在抛物线上,则可以列出方程求出m 的值.在计算四边形CAEB 面积时,利用S 四边形CAEB =S △A CE +S 梯形OCEB ﹣S △BCO ,可以简化计算;(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.解答:解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,∴A(﹣4,0),B(0,4).∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,∴,解得:b=﹣3,c=4,∴抛物线的解析式为:y=﹣x 2﹣3x+4.(2)设点C坐标为(m,0)(m<0),则OC=﹣m,AC=4+m.∵OA=OB=4,∴∠BAC=45°,∴△ACD为等腰直角三角形,∴CD=AC=4+m,∴CE=CD+DE=4+m+4=8+m,∴点E坐标为(m,8+m).∵点E在抛物线y=﹣x 2﹣3x+4上,∴8+m=﹣m2﹣3m+4,解得m=﹣2.∴C(﹣2,0),AC=OC=2,CE=6,S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO=×2×6+(6+4)×2﹣×2×4=12.(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD=OC=﹣m,则D(m,4+m).∵△ACD为等腰直角三角形,△DBE和△DAC相似∴△DBE必为等腰直角三角形.i)若∠BED=90°,则BE=DE,∵BE=OC=﹣m,∴DE=BE=﹣m,∴CE=4+m﹣m=4,∴E(m,4).∵点E在抛物线y=﹣x2﹣3x+4上,∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,∴D(﹣3,1);ii)若∠EBD=90°,则BE=BD=﹣m,在等腰直角三角形EBD中,DE=BD=﹣2m,∴C E=4+m﹣2m=4﹣m,∴E(m,4﹣m).∵点E在抛物线y=﹣x2﹣3x+4上,∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,∴D(﹣2,2).综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).点评:本题考查了二次函数与一次函数的图象与性质、函数图象上点的坐标特征、待定系数法、相似三角形、等腰直角三角形、图象面积计算等重要知识点.第(3)问需要分类讨论,这是本题的难点.5.5.(2013•绍兴压轴题)抛物线(2013•绍兴压轴题)抛物线y=y=((x ﹣3)(x+1x+1))与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,点D 为顶点.为顶点.(1)求点B 及点D 的坐标.的坐标.(2)连结BD BD,,CD CD,抛物线的对称轴与,抛物线的对称轴与x 轴交于点E .①若线段BD 上一点P ,使∠DCP=∠BDE,求点P 的坐标.的坐标.②若抛物线上一点M ,作MN⊥CD,交直线CD 于点N ,使∠CMN=∠BDE,求点M 的坐标.的坐标.考点: 二次函数综合题.3718684分析: (1)解方程(x ﹣3)(x+1)=0,求出x=3或﹣1,根据抛物线y=(x ﹣3)(x+1)与x轴交于A ,B 两点(点A 在点B 左侧),确定点B 的坐标为(3,0);将y=(x ﹣3)(x+1)配方,写成顶点式为y=x 2﹣2x ﹣3=(x ﹣1)2﹣4,即可确定顶点D 的坐标;(2)①根据抛物线y=(x ﹣3)(x+1),得到点C 、点E 的坐标.连接BC ,过点C 作CH⊥DE 于H ,由勾股定理得出CD=,CB=3,证明△BCD 为直角三角形.分别延长PC 、DC ,与x 轴相交于点Q ,R .根据两角对应相等的两三角形相似证明△BCD∽△QOC,则==,得出Q 的坐标(﹣9,0),运用待定系数法求出直线CQ 的解析式为y=﹣x ﹣3,直线BD 的解析式为y=2x ﹣6,解方程组,即可求出点P 的坐标;②分两种情况进行讨论:(Ⅰ)当点M 在对称轴右侧时.若点N 在射线CD 上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G,先证明△MCN∽△DBE,由相似三角形对应边成比例得出MN=2CN.设CN=a,再证明△CNF,△MGF均为等腰直角三角形,然后用含a的代数式表示点M的坐标,将其代入抛物线y=(x﹣3)(x+1),求出a的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠KCN<45°,所以点M不存在.解答:解:(1)∵抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),∴当y=0时,(x﹣3)(x+1)=0,解得x=3或﹣1,∴点B的坐标为(3,0).∵y=(x﹣3)(x+1)=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点D的坐标为(1,﹣4);(2)①如右图.∵抛物线y=(x﹣3)(x+1)=x2﹣2x﹣3与与y轴交于点C,∴C点坐标为(0,﹣3).∵对称轴为直线x=1,∴点E的坐标为(1,0).连接BC,过点C作CH⊥DE于H,则H点坐标为(1,﹣3),∴CH=DH=1,∴∠CDH=∠BCO=∠BCH=45°,∴CD=,CB=3,△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.∵∠BDE=∠DCP=∠QCR,∠CDB=∠CDE+∠BDE=45°+∠DCP,∠QCO=∠RCO+∠QCR=45°+∠DCP,∴∠CDB=∠QCO,∴△BCD∽△QOC,∴==,∴OQ=3OC=9,即Q(﹣9,0).∴直线CQ的解析式为y=﹣x﹣3,直线BD的解析式为y=2x﹣6.由方程组,解得.∴点P的坐标为(,﹣);②(Ⅰ)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G.∵∠CMN=∠BDE,∠CNM=∠BED=90°,∴△MCN∽△DBE,∴==,∴MN=2CN.设CN=a,则MN=2a.∵∠CDE=∠DCF=45°,∴△CNF,△MGF均为等腰直角三角形,∴NF=CN=a,CF=a,∴MF=MN+NF=3a,∴MG=FG=a,∴CG=FG﹣FC=a,∴M(a,﹣3+a).代入抛物线y=(x﹣3)(x+1),解得a=,∴M(,﹣);若点N在射线DC上,如备用图2,MN交y轴于点F,过点M作MG⊥y轴于点G.∵∠CMN=∠BDE,∠CNM=∠BED=90°,∴△MCN∽△DBE,∴==,∴MN=2CN.设CN=a,则MN=2a.∵∠CDE=45°,∴△CNF,△MGF均为等腰直角三角形,∴NF=CN=a,CF=a,∴MF=MN﹣NF=a,∴MG=FG=a,点评: 本题是二次函数的综合题型,其中涉及到的知识点有二次函数图象上点的坐标特征,二次函数的性质,运用待定系数法求一次函数、二次函数的解析式,勾股定理,等腰直角三角形、相似三角形的判定与性质,综合性较强,有一定难度.(2)中第②问进行分类讨论及运用数形结合的思想是解题的关键.6.6.(2013•恩施州压轴题)如图所示,直线(2013•恩施州压轴题)如图所示,直线l :y=3x+3与x 轴交于点A ,与y 轴交于点B .把△AOB 沿y 轴翻折,点A 落到点C ,抛物线y=y=x x 2﹣4x+3过点B 、C 和D (3,0). (1)若BD 与抛物线的对称轴交于点M ,点N 在坐标轴上,以点N 、B 、D 为顶点的三角形与△MCD 相似,求所有满足条件的点N 的坐标.的坐标. (2)在抛物线上是否存在点P ,使S △PBD =6=6?若存在,求出点?若存在,求出点P 的坐标;若不存在,说明理由.由.考点: 二次函数综合题.分析: (1)由待定系数法求出直线BD 和抛物线的解析式;(2)首先确定△MCD 为等腰直角三角形,因为△BND 与△MCD 相似,所以△BND 也是等腰直角三角形.如答图1所示,符合条件的点N 有3个;(3)如答图2、答图3所示,解题关键是求出△PBD 面积的表达式,然后根据S △PBD =6的已知条件,列出一元二次方程求解.解答: (1)抛物线的解析式为:y=x 2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).直线BD :y=﹣x+3与抛物线的对称轴交于点M ,令x=2,得y=1,∴M(2,1).设对称轴与x 轴交点为点F ,则CF=FD=MN=1,∴△MCD 为等腰直角三角形.∵以点N 、B 、D 为顶点的三角形与△MCD 相似,∴△BND 为等腰直角三角形.如答图1所示:(I )若BD 为斜边,则易知此时直角顶点为原点O ,∴N 1(0,0);(II )若BD 为直角边,B 为直角顶点,则点N 在x 轴负半轴上,∵OB=OD=ON 2=3,∴N 2(﹣3,0);(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,∵OB=OD=ON3=3,∴N3(0,﹣3).∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).(2)假设存在点P,使S△PBD=6,设点P坐标为(m,n).(I)当点P位于直线BD上方时,如答图2所示:过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=(3+n)•m﹣×3×3﹣(m﹣3)•n=6,化简得:m+n=7 ①,∵P(m,n)在抛物线上,∴n=m2﹣4m+3,代入①式整理得:m2﹣3m﹣4=0,解得:m1=4,m2=﹣1,∴n1=3,n2=8,∴P1(4,3),P2(﹣1,8);(II)当点P位于直线BD下方时,如答图3所示:过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.S△PBD=S梯形PEOD+S△BOD﹣S△PBE=(3+m)•(﹣n)+×3×3﹣(3﹣n)•m=6,化简得:m+n=﹣1 ②,∵P(m,n)在抛物线上,∴n=m 2﹣4m+3,代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.故此时点P不存在.综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).点评:本题是中考压轴题,综合考查了二次函数的图象与性质、待定系数法、相似三角形的判定与性质、图形面积计算、解一元二次方程等知识点,考查了数形结合、分类讨论的数学思想.第(2)(3)问均需进行分类讨论,避免漏解.。
中考压轴题--二次函数与相似三角形的综合

中考数学压轴题——二次函数与相似三角形的综合例题:(2014衡阳)已知某二次函数的图象与x 轴分别相交于点()30A -,和点()10B ,,与y 轴相交于点()()030C m m ->,,顶点为点D 。
⑴求该二次函数的解析式(系数用含m 的代数式表示);⑵如图①,当2m =时,点P 为第三象限内抛物线上的一个动点,设APC ∆的面积为S ,试求出S 与点P 的横坐标x 之间的函数关系式及S 的最大值;⑶如图②,当m 取何值时,以A 、D 、C 三点为顶点的三角形 与OBC ∆相似? 解:⑴∵该二次函数的图象与x 轴分别相交于点()30A -,和点()10B ,,∴设该二次函数的解析式为()()31y a x x =+-∵该二次函数的图象与y 轴相交于点()03C m -,,∴()313a m -=-,故a m =∴该二次函数的解析式为()()23123y m x x mx mx m =+-=+-⑵当2m =时,点C 的坐标为()06-,,该二次函数的解析式为2246y x x =+- ∵点A 的坐标为()30-,,点C 的坐标为()06-,∴直线AC 的解析式为136x y +=--,即26AC y x =-- 过点P 作PE x ⊥轴于点E ,交AC 于点F∵点P 为第三象限内抛物线上的一个动点且点P 的横坐标为x ()30x -<< ∴点P 的坐标为()2246x x x +-,,点E 的坐标为()0x ,,点F 的坐标为()26x x --,∴()()()()()11333322222P F P F F P S OA PF PE EF y y y y y y ==⨯⨯-=-=---=-⎡⎤⎣⎦ ()()()()()2222222333262462624626222393273933332424x x x x x x x x x x x x x x ⎡⎤=---+-=----+=--⎣⎦⎡⎤⎛⎫⎛⎫=--=-+=-+-=-++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦∴当32x =-时,S 有最大值274; 另解:()()221133324626246262222P F S OA PF y y x x x x x x ==⨯⨯-=+----=+-++ 22233926333224x x x x x ⎛⎫=+=+=+- ⎪⎝⎭ ∵30x -<<,∴333222x -<+<,∴23924x ⎛⎫+< ⎪⎝⎭,∴239024x ⎛⎫+-< ⎪⎝⎭, 图① 图②⑶∵()()()()()22231231414y m x x m x x m x m x m ⎡⎤=+-=+-=+-=+-⎣⎦,∴点D 的坐标为()14m --, ∴()()()()()()2222222230033399A C A C AC x x y y m m m =-+-=--+--=-+=+⎡⎤⎣⎦()()()()()()22222222310424416A D A D AD x x y y m m m =-+-=---+--=-+=+⎡⎤⎡⎤⎣⎦⎣⎦ ()()()()22222201341C D C D CD x x y y m m m =-+-=--+---=+⎡⎤⎡⎤⎣⎦⎣⎦ ∵OBC ∆是直角三角形,∴欲使以A 、D 、C 三点为顶点的三角形与OBC ∆相似,必有Rt ACD ∆①若在ACD ∆中,90ACD =∠,则222AC CD AD +=,即()()222991416m m m +++=+ 化简整理得:21m =,∵0m >,∴1m =(舍去负值)90且AC CD ②若在ACD ∆中,90ADC =∠,则222AD CD AC +=,即()()222416199m m m +++=+ 90,但是时,以A练习:(2013辽宁营口)如图,抛物线与x 轴交于A ()0,1 、)03(,-B 两点,与y 轴交于点C (),3,0设抛物线的顶点为D .(1)求该抛物线的解析式与顶点D 的坐标.(2)试判断△BCD 的形状,并说明理由.(3)探究坐标轴上是否存在点P ,使得以C A P 、、为顶点的三角形与△BCD 相似?若存在,请直接写出点P答案:(1)抛物线的解析式为-=x y (2) △BCD 是直角三角形. 理由略(3)坐标轴上存在点P ,使得以C A P 、、为顶点的三角形与△BCD 相似.符合条件的点P 的坐标为:)09(),310(),00(321,,,--P P P .。
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)(含简单答案)
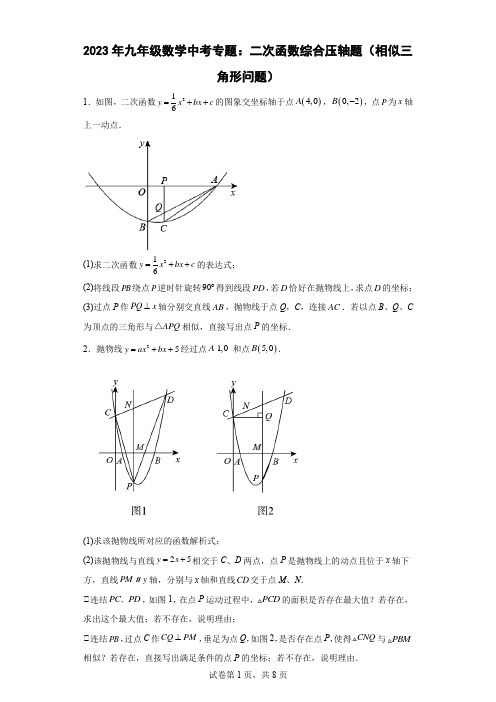
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)1.如图,二次函数216y x bx c =++的图象交坐标轴于点()4,0A ,()0,2B -,点P 为x 轴上一动点.(1)求二次函数216y x bx c =++的表达式; (2)将线段PB 绕点P 逆时针旋转90︒得到线段PD ,若D 恰好在抛物线上,求点D 的坐标; (3)过点P 作PQ x ⊥轴分别交直线AB ,抛物线于点Q ,C ,连接AC .若以点B 、Q 、C 为顶点的三角形与APQ △相似,直接写出点P 的坐标. 2.抛物线25y ax bx =++经过点1,0A 和点()5,0B .(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线25y x =+相交于C 、D 两点,点P 是抛物线上的动点且位于x 轴下方,直线PM y ∥轴,分别与x 轴和直线CD 交于点M 、N .①连结PC PD 、,如图1,在点P 运动过程中,PCD 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;①连结PB ,过点C 作CQ PM ⊥,垂足为点Q ,如图2,是否存在点P ,使得CNQ 与PBM 相似?若存在,直接写出满足条件的点P 的坐标;若不存在,说明理由.3.已知抛物线24y ax ax b =-+与x 轴交于A ,B 两点,(A 在B 的左侧),与y 轴交于C ,若OB OC =,且03C (,).(1)求抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标; (3)在抛物线上是否存在一点M ,过M 作MN x ⊥轴于N ,以A 、M 、N 为顶点的三角形与AOC ∆相似,若存在,求出所有符合条件的M 点坐标,若不存在,请说明理由. 4.如图.在平面直角坐标系中.抛物线212y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C .点A 的坐标为()1,0-,点C 的坐标为()0,2-.已知点(),0E m 是线段AB 上的动点(点E 不与点A ,B 重合).过点E 作PE x ⊥轴交抛物线于点P ,交BC 于点F .(1)求该抛物线的表达式;(2)若:1:2EF PF =,请求出m 的值;(3)是否存在这样的m ,使得BEP △与ABC 相似?若存在,求出此时m 的值;若不存在,请说明理由;(4)当点E 运动到抛物线对称轴上时,点M 是x 轴上一动点,点N 是抛物线上的动点,在运动过程中,是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,请直接写出点M 的坐标.5.如图,二次函数212y x bx c =-++图像交x 轴于点A ,B (A 在B 的左侧),与y 轴交于点(0,3)C ,CD y ⊥轴,交抛物线于另一点D ,且5CD =,P 为抛物线上一点,PE y轴,与x 轴交于E ,与BC ,CD 分别交于点F ,G .(1)求二次函数解析式;(2)当P 在CD 上方时,是否存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,若存在,求出CPG △与FBE 的相似比,若不存在,说明理由.(3)点D 关于直线PC 的对称点为D ,当点D 落在抛物线的对称轴上时,此时点P 的坐标为________.6.如图,抛物线22y ax bx =++与x 轴交于点A ,B ,与y 轴交于点C ,已知A ,B 两点坐标分别是(1,0)A ,(4,0)B -,连接,AC BC .(1)求抛物线的表达式;(2)将ABC ∆沿BC 所在直线折叠,得到DBC ∆,点A 的对应点D 是否落在抛物线的对称轴上?若点D 在对称轴上,请求出点D 的坐标;若点D 不在对称轴上,请说明理由;(3)若点P 是抛物线位于第二象限图象上的一动点,连接AP 交BC 于点Q ,连接BP ,BPQ ∆的面积记为1S ,ABQ ∆的面积记为2S ,求12S S 的值最大时点P 的坐标. 7.已知,二次函数23y ax bx =+-的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于C 点,点A 的坐标为()1,0-,且OB OC =.(1)求二次函数的解析式;(2)当04x ≤≤时,求二次函数的最大值和最小值分别为多少?(3)设点C '与点C 关于该抛物线的对称轴对称.在y 轴上是否存在点P ,使PCC '△与POB 相似,且PC 与PO 是对应边?若存在,求出点P 的坐标;若不存在,请说明理由.8.已知菱形OABC 的边长为5,且点(34)A ,,点E 是线段BC 的中点,过点A ,E 的抛物线2y ax bx c =++与边AB 交于点D ,(1)求点E 的坐标;(2)连接DE ,将BDE △沿着DE 翻折痕.①当B 点的对应点B '恰好落在线段AC 上时,求点D 的坐标;①连接OB ,BB ',若BB D '△与BOC 相似,请直接写出此时抛物线二次项系数=a ______. 9.如图,抛物线22(0)y ax x c a =-+≠与x 轴交于A 、()3,0B 两点,与y 轴交于点()0,3C -,抛物线的顶点为D .(1)求抛物线的解析式;(2)已知点M 是x 轴上的动点,过点M 作x 轴的垂线交抛物线于点G ,是否存在这样的点M ,使得以点A 、M 、G 为顶点的三角形与BCD △相似,若存在,请求出点M 的坐标;若不存在,请说明理由.(3)在直线BC 下方抛物线上一点P ,作PQ 垂直BC 于点Q ,连接CP ,当CPQ 中有一个角等于ACO ∠时,求点P 的坐标.10.如图,抛物线顶点D 在x 轴上,且经过(0,3)-和(4,3)-两点,抛物线与直线l 交于A 、B 两点.(1)直接写出抛物线解析式和D 点坐标;(2)如图1,若()03A ,-,且 94ABDS =,求直线l 解析式; (3)如图2,若90ADB ∠=︒,求证:直线l 经过定点,并求出定点坐标.11.如图1,已知抛物线2=23y x x --与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接BC ,点P 是线段BC 下方抛物线上一动点,过点P 作∥PE BC ,交x 轴于点E ,连接OP 交BC 于点F .(1)直接写出点A ,B ,C 的坐标以及抛物线的对称轴; (2)当点P 在线段BC 下方抛物线上运动时,求BFPE取到最小值时点P 的坐标; (3)当点P 在y 轴右边抛物线上运动时,过点P 作PE 的垂线交抛物线对称轴于点G ,是否存在点P ,使以P 、E 、G 为顶点的三角形与①AOC 相似?若存在,来出点P 的坐标;若不存在,请说明理由.12.如图,抛物线212ax ax b =-+y 经过()1,0A -,32,2C ⎛⎫⎪⎝⎭两点,与x 轴交于另一点B .(1)求此抛物线的解析式;(2)若抛物线的顶点为M ,点P 为线段OB 上一动点(不与点B 重合),点Q 在线段MB 上移动,且2PM MQ MB =⋅,设线段OP x =,2MQ y =,求2y 与x 的函数关系式,并直接写出自变量x 的取值范围;并直接写出PM APPQ BQ-的值;(3)在同一平面直角坐标系中,两条直线x m =,x n =分别与抛物线交于点E ,G ,与(2)中的函数图象交于点F ,.H 问四边形EFHG 能否为平行四边形?若能,求m ,n 之间的数量关系;若不能,请说明理由.13.已知抛物线213222y x x =-++交x 轴于A 、B 两点,A 在B 的左边,交y 轴于点C .(1)求抛物线顶点的坐标;(2)如图1,若10,2E ⎛⎫- ⎪⎝⎭,P 在抛物线上且在直线AE 上方,PQ AE ⊥于O ,求PQ 的最大值;(3)如图2,点(),3D a (32a <)在抛物线上,过A 作直线交抛物线于第四象限另一点F ,点M 在x 轴上,以M 、B 、D 为顶角的三角形与AFB △相似,求点M 的坐标. 14.如图,抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ,与y 轴交于点C ,联结AC 、BC .(1)求该抛物线的表达式及顶点D 的坐标;(2)如果点P 在抛物线上,CB 平分ACP ∠,求点P 的坐标:(3)如果点Q 在抛物线的对称轴上,DBQ 与ABC 相似.求点Q 的坐标.15.如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45︒得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式; (2)当点D 在第二象限且34DE EO =时,求点D 的坐标; (3)当ODF △为直角三角形时,请直接写出点D 的坐标.16.如图①,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,3),顶点为D (4,-1),对称轴与直线BC 交于点E ,与x 轴交于点F .(1)求二次函数的解析式;(2)点M 在第一象限抛物线的对称轴上,若点C 在BM 的垂直平分线上,求点M 的坐标; (3)如图①,过点E 作对称轴的垂线在对称轴的右侧与抛物线交于点H ,x 轴上方的对称轴上是否存在一点P ,使以E ,H ,P 为顶点的三角形与EFB △相似,若存在,求出P点坐标;若不存在,请说明理由.17.如图,在平面直角坐标系xOy 中,已知抛物线2y ax x c =++经过()2,0A -,()0,4B 两点,直线3x =与x 轴交于点C .(1)求a ,c 的值;(2)经过点O 的直线分别与线段AB ,直线3x =交于点D ,E ,且BDO △与OCE △的面积相等,求直线DE 的解析式;(3)P 是抛物线上位于第一象限的一个动点,在线段OC 和直线3x =上是否分别存在点F ,G ,使B ,F ,G ,P 为顶点的四边形是以BF 为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.18.如图1,抛物线2y ax bx c =++与x 轴交于A ,B (点A 在点B 左侧),与y 轴负半轴交于C ,且满足2OA OB OC ===.(1)求抛物线的解析式;(2)如图2,D 为y 轴负半轴上一点,过D 作直线l 垂直于直线BC ,直线l 交抛物线于E ,F 两点(点E 在点F 右侧),若3DF DE =,求D 点坐标; (3)如图3,点M 为抛物线第二象限部分上一点,点M ,N 关于y 轴对称,连接MB ,P 为线段MB 上一点(不与M 、B 重合),过P 点作直线x t =(t 为常数)交x 轴于S ,交直线NB 于Q ,求QS PS -的值(用含t 的代数式表示).参考答案:1.(1)211266y x x =-- (2)()3,1D -或()8,10D -(3)点P 的坐标为()011-,或()10,.2.(1)265y x x =-+ (2)37,24⎛⎫- ⎪⎝⎭或()3,4-3.(1)243y x x =-+ (2)()2,2P 或()2,2-(3)存在符合条件的M 点,且坐标为:110(3M ,7)9-,()26,15M ,38(3M ,5)9-4.(1)213222y x x =--; (2)2m =;(3)存在,m 的值为0或3;(4)存在,M 点的坐标为()7,0或()1,0M 或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭.5.(1)215322y x x =-++;(2)存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,CPG △与FBE 的相似比为2或25;(3)P 点横坐标55.6.(1)213222y x x =--+(2)点D 不在抛物线的对称轴上, (3)(2,3)-7.(1)2=23y x x --(2)函数的最大值为5,最小值为4- (3)存在,(0,9)P -或9(0,)5P -8.(1)13(2)2E , (2)①11(4)2D ,或23(4)6D ,;①47-9.(1)2=23y x x --(2)()0,0,()6,0,8,03⎛⎫ ⎪⎝⎭,10,03⎛⎫⎪⎝⎭(3)57,24⎛⎫- ⎪⎝⎭或者315,24⎛⎫- ⎪⎝⎭10.(1)()2324y x =--,()2,0D (2)334y x =-或1534y x =- (3)证明见解析,定点坐标为423⎛⎫- ⎪⎝⎭,11.(1)A (﹣1,0),B (3,0),C (0,﹣3),对称轴为直线x =1(2)当t =32时,BF PE 最小,最小值为47,此时P (32,﹣154).(3)存在,点P 的坐标为(2,﹣3)12.(1)211322y x x =-++(2)22150322y x x x =-+≤<(),PM AP PQ BQ -的值为0 (3)m 、n 之间的数量关系是2(1)m n m +=≠13.(1)(32,258)答案第3页,共3页(3)(2,0)或(-5,0)或13,07⎛⎫ ⎪⎝⎭或2205⎛⎫- ⎪⎝⎭,14.(1)2=+43y x x --,(21)D , (2)111639⎛⎫ ⎪⎝⎭,- (3)(2,−2)或12,3⎛⎫ ⎪⎝⎭15.(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)(3,4)-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭16.(1)21234y x x =-+(2)(4,3(3)存在P 1)或(4,1),使以E ,H ,P 为顶点的三角形与EFB △相似,17.(1)12a =-,4c = (2)23y x =- (3)存在这样的点F ,点F 的坐标为(2,0)或18.(1)2122y x =- (2)()0,1D -或190,8D ⎛⎫- ⎪⎝⎭, (3)24QS PS t -=-+。
二次函数中的三角形相似

二次函数中的三角形相似三角形相似是中学数学重要数学工具之一,是我们必须掌握的内容,学习了二次函数后,与三角形相似相结合的题型成为了中考的热点,下面给大家列举一下相关的题型。
一、 求关系式型例1、 如图1所示,在边长为a 的正方形ABCD 的BC 边上任取一点E ,作EF ⊥AE ,交CD 于点F ,如果BE=x ,CF=y ,那么x 与y 的函数关系式 为()A 、21y x x a =-+B 、2x y x a =-C 、2x y x a =-+D 、2x y x a=+ 分析:欲求x 与y 的函数关系式,发现它们分别处在Rt ΔABE 和Rt ΔECF 中,由EF ⊥AE ,易求Rt ΔABE 和Rt ΔECF 相似,根据对应边比例关系即可求出。
解:在正方形ABCD 中,∠B=∠C=90º,∵EF ⊥AE ,∴∠AEB+∠CEF=90º,又∵∠AEB+∠BAE=90º,∴∠CEF=∠BAE∴Rt ΔABE ∽ Rt ΔECF ,AB BE EC CF =,a x a x y =-,∴21y x x a=-+,选A. 例2、 如图2所示,等腰Rt ΔABC 的斜边AB 所在的直线上有点E 、F ,且∠E+∠F=45º,AE=3,设AB=x,BF=y ,则y 关于x 的函数关系式为 。
分析:由等腰Rt ΔABC 及∠E+∠F=45º,利用外角的 知识,易得∠E=∠BCF ,∠ECA=∠F ,从而证得ΔEAC ∽ ΔCBF ,根据对应边比例关系即可求出。
解:在等腰Rt ΔABC 中,AB=x ,得∠CAB=∠ABC=45º,AC BC x ==,又因为∠CAB=∠E+∠ECA ,∠E+∠F=45º,得∠ECA=∠F ,同理可得∠E=∠BCF ,所以,ΔEAC ∽ ΔCBF ,EA AC CB BF =22y=,∴216y x =. 二、 求面积最大型例3、如图3所示,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m 长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长为xm , ⑴要使鸡场面积最大,鸡场的长应为多少?⑵如果中间有n (n 是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少? 分析:长方形的长为xm ,则可以把它的宽表示出来,再根据长方形的面积公式得出关系式,C D E y F 图1C EA B F图2 图3根据最大值去求出即可。
重难点02二次函数中相似三角形问题(原卷版)

重难点02 二次函数中相似三角形问题二次函数背景下的相似三角形考点分析:1.先求函数的解析式,然后在函数的图像上探求符合几何条件的点;2.简单一点的题目,就是用待定系数法直接求函数的解析式;3.复杂一点的题目,先根据图形给定的数量关系,运用数形结合的思想,求得点的坐标,继而用待定系数法求函数解析式;4.还有一种常见题型,解析式中由待定字母,这个字母可以根据题意列出方程组求解;5.当相似时:一般说来,这类题目都由图像上的点转化到三角形中的边长的问题,再由边的数量关系转化到三角形的相似问题;6.考查利用几何定理和性质或者代数方法建立方程求解的方法。
一、单选题1.(2022·浙江绍兴·九年级期末)如图,已知点()16,0A ,O 为坐标原点,P 是线段OA 上任意一点(不含端点O ,A ),过P ,O 两点的二次函数1y 和过P ,A 两点的二次函数2y 的图象开口均向下,它们的顶点分别为B ,C ,射线OB 与AC 相交于点D ,当10OD AD ==时,这两个二次函数的最大值之和等于( )A .10B .8C .6D .4二、填空题 2.(2022·浙江宁波·九年级期末)已知过点()4,1B 的抛物线21522y x x c =-+与坐标轴交于点A ,C 如图所示,连结AC ,BC ,AB ,第一象限内有一动点M 在抛物线上运动,过点M 作AM MP ⊥交y 轴于点P ,当点P 在点A 上方,且AMP 与ABC 相似时,点M 的坐标为______.三、解答题能力拓展技巧方法3.(2022·浙江丽水·三模)定义:对于抛物线()2240y ax bx c b ac =++->,把它在x 轴下方的部分图形作关于x 轴的轴对称图形,所得的图形称为2y ax bx c =++的“W 型曲线”.如图为242y mx x =-+的“W 型曲线”,与x 轴的交点为A ,B ,与y 轴的交点为C ,与对称轴的交点为P ,有CP x ∥轴.(1)求m 的值.(2)若直线y x n =+与242y mx x =-+的“W 型曲线”有且只有三个公共点,求n 的值.(3)在242y mx x =-+的“W 型曲线”是否存在点Q ,使得1tan 2POQ ∠=,若存在,求点Q 的横坐标;若不存在,说明理由.4.(2022·浙江湖州·中考真题)如图1,已知在平面直角坐标系xOy 中,四边形OABC 是边长为3的正方形,其中顶点A ,C 分别在x 轴的正半轴和y 轴的正半轴上,抛物线2y x bx c =-++经过A ,C 两点,与x 轴交于另一个点D .(1)①求点A ,B ,C 的坐标;②求b ,c 的值.(2)若点P 是边BC 上的一个动点,连结AP ,过点P 作PM ⊥AP ,交y 轴于点M (如图2所示).当点P 在BC 上运动时,点M 也随之运动.设BP =m ,CM =n ,试用含m 的代数式表示n ,并求出n 的最大值.5.(2022·浙江金华·二模)如图1,已知等腰ABC ∆中,10,12,AB AC BC AD BC ===⊥,垂足为点D ,动点P 从点A 出发,以1.5个单位每秒速度,沿AB 方向运动,同时,点Q 从点B 出发,以1个单位每秒速度,沿BC 方向运动,当点P 到达点B 时,点Q 即停止运动,设运动时间为t 秒,过点P 作PR AD ⊥,垂足为R ,连结,QR PQ ,作PQR ∆关于QR 的对称MQR ∆.(1)如图2,当PQ AB ⊥时,求PQ 的长度.(2)求PBQ ∆与PQR ∆面积差的最大值.(3)当点M 落在ABC ∆的边上时,求t 的值.6.(2022·浙江宁波·九年级期末)如图1,已知二次函数()2416133y x =-++的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 是抛物线的顶点.(1)求点A ,点C 的坐标;(2)如图2,连结AC ,DC ,过点C 作CE AB ∥交抛物线于点E .求证:∠DCE =∠CAO ;(3)如图3,在(2)的条件下,连结BC ,在射线EC 上有点P ,使以点D ,E ,P 为顶点的三角形与△ABC 相似,求EP 的长.7.(2022·浙江湖州·九年级期中)抛物线23y ax bx =++过点A (-1,0),点B (3,0),顶点为C .(1)求抛物线的表达式及点C的坐标;(2)如图1,点P在抛物线上,连接CP并延长交x轴于点D,连接AC,若△DAC是以AC为底的等腰三角形,求点P的坐标;(3)如图2,在(2)的条件下,点E是线段AC上(与点A,C不重合)的动点,连接PE,作PEF CAB∠=∠,边EF交x轴于点F,当AF的长度最大时,求点E的坐标.8.(2021·浙江金华·一模)如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求抛物线的函数表达式;(2)当△PMN的周长是△AOB周长的35时,求m的值;(3)如图2,在(2)的条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E′A、E′B,在平面直角坐标系内找一点Q,使△AOE′∽△BOQ,并求出点Q的坐标.9.(2021·浙江温州·九年级期末)如图,y=ax22ax+a4与x轴负半轴交于A,交y轴于B,过抛物线顶点C作CD y轴,垂足为D,四边形AOCD是平行四边形.(1)求抛物线的对称轴以及二次函数的解析式;(2)作BE x∥轴交抛物线于另一点E,交OC于F,求EF的长;(3)该二次函数图象上有一点G(m,n)若点G到y轴的距离小于2,则n的取值范围为___.10.(2022·浙江·嘉兴一中一模)如图,抛物线y=1-x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与2y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与△OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.11.(2022·浙江金华·一模)如图,把两个全等的Rt AOB 和Rt COD 分别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点()2,4A ,过A 、C 两点的直线分别交x 轴、y 轴于点E 、F ,抛物线2y ax bx c =++经过O 、A 、C 三点.(1)求该抛物线的函数解析式;(2)点G 为抛物线上位于线段OC 所在直线上方部分的一动点,求G 到直线OC 的最大距离和此时点G 的坐标;(3)点P 为线段OC 上一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 的边AM 与边BP 相等?若存在,求出此时点P 的坐标;若不存在,请说明理由.12.(2022·浙江绍兴·九年级期末)在平面直角坐标系xOy 中,如果抛物线()20y ax bx c a =++≠上存在一对点P 和P ',且它们关于坐标原点O 对称,那么我们把点P 和P '叫做这条抛物线的成对点.(1)已知点()2,P m -与P '是抛物线224y x x =--的成对点,求P '的坐标.(2)如图,已知点A 与C 为抛物线22y x x c =--+的成对点,且A 为该抛物线的顶点.①求c 的值.②若这条抛物线的对称轴与x 轴交于点B ,连结AC ,BC ,点D 是射线AB 上一点.如果∠ADC =∠ACB ,求点D 的坐标.13.(2021·浙江·天台县赤城中学一模)如图,抛物线y =ax 2+bx +c 交x 轴于点A ,B ,其中点A (﹣1,0),交y 轴于点C (0,2),对称轴交x 轴于点M (32,0).(1)求抛物线的解析式;(2)作点C关于点M的对称点D,顺次连接A,C,B,D,判断四边形ACBD的形状,并说明理由;(3)在该抛物线的对称轴上是否存在点P,使△BMP与△BAD相似?若存在,求出所有满足条件的P点的坐标;若不存在,请说明理由.14.(2022·浙江金华·九年级期末)已知抛物线:y=ax2﹣6ax﹣16a(a>0)与x轴交点为A,B(A在B的左侧),与y轴交于点C,点G是AC的中点.(1)求点A ,B 的坐标及抛物线的对称轴.(2)直线y =﹣32x 与抛物线交于点M 、N ,且MO =NO ,求抛物线解析式. (3)已知点P 是(2)中抛物线上第四象限内的动点,过点P 作x 轴的垂线交BC 于点E ,交x 轴于点F .若以点C ,P ,E 为顶点的三角形与△AOG 相似,求点P 的坐标.15.(2022·浙江宁波·九年级期末)如图,抛物线213222y x x =--与x 轴交于点A ,B ,与y 轴交于点C .点P 是线段BC 上的动点(点P 不与点B ,C 重合),连结AP 并延长AP 交抛物线于另一点Q ,连结CQ ,BQ ,设点Q 的横坐标为x x .(1)①写出A ,B ,C 的坐标:A ( ),B ( ),C ( );②求证:ABC 是直角三角形;(2)记BCQ △的面积为S ,求S 关于x 的函数表达式;(3)在点P 的运动过程中,PQ AP是否存在最大值?若存在,求出的最大值;若不存在,请说明理由.16.(2021·浙江金华·九年级期末)已知抛物线()()12y x x m m =+-与x 轴负半轴交于点A ,与x 轴正半轴交于点B ,与y 轴交于点C ,点P 为抛物线上一动点(点P 不与点C 重合).(1)当ABC为直角三角形时,求ABC的面积轴于点Q,求BQ的长.(2)如图,当AP BC∥时,过点P作PQ x(3)当以点A,B,P为顶点的三角形和ABC相似时(不包括两个三角形全等),求m的值.。
中考总复习专题:二次函数与相似的结合

二次函数与相似的结合题型一:动点在线段上如图,平面直角坐标系xOy 中,已知(1,0)B -,一次函数5y x =-+的图像与x 轴、y 轴分别交于点A 、C 两点,二次函数2y x bx c =-++的图像经过点A 、点B ;(1)求这个二次函数的解析式;(2)点P 是该二次函数图像的顶点,求△APC 的面积;(3)如果点Q 在线段AC 上,且△ABC 与△AOQ 相似,求点Q 的坐标;如图,抛物线22y ax ax c =++(0)a >与x 轴交于(3,0)A -、B 两点(A 在B 的左侧),与y 轴交于点(0,3)C -,抛物线的顶点为M ;(1)求a 、c 的值; (2)求tan MAC ∠的值;(3)若点P 是线段AC 上一个动点,联结OP ;问是否存在点P ,使得以点O 、C 、P 为顶点的三角形与△ABC 相似?若存在,求出P 点坐标;若不存在,请说明理由; 如图,已知抛物线2y ax x c =-+的对称轴为直线x =1,与x 轴的一个交点为A (-1,0),顶点为B . 点C (5,m )在抛物线上,直线BC 交x 轴于点E . (1) 求抛物线的表达式及点E 的坐标; (2) 联结AB ,求∠B 的正切值;(3) 点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标. 【参考答案】24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)解:(1)∵抛物线2y ax x c =-+的对称轴为直线x =1,∴12a =. ∵抛物线与x 轴的一个交点为A (-1,0),∴32c =-. ∴抛物线的表达式为21322y x x =--.………………………………………………(2分) ∴顶点B (1,-2).…………………………………………………………………(1分) ∵点C (5,m )在抛物线上,∴6m =. ∴C 点坐标为(5,6). 设直线BC 的表达式为y =kx +b (k ≠0),xyAB EC O (第24题图)则652k b k b=+⎧⎨-=+⎩,∴2,4.k b =⎧⎨=-⎩即BC 的表达式为y =2x -4.∴E (2,0).……………………………………………………………………………(1分)(2)作CH ⊥x 轴,垂足为H ,作BP ⊥x 轴,垂足为P , ∵C (5,6),A (-1,0),∴CH =6=AH . ∴∠CAH=45°. ∵B (1,-2),A (-1,0),∴BP =2=AP .∴∠BAP=45°. ∴∠CAB=90°. …………………………………………………………………………(1分)∵CH =6=AH ,CH ⊥x 轴,∴AC =∵BP =2=AP ,BP ⊥x 轴,∴AB =∴tan 3.ACB AB∠==…………………………………………………………………(2分) (3)∵∠CAB=90°,∴∠B +∠ACB =90°. ∵GM ⊥BC ,∴∠CGM +∠ACB =90°.∴∠CGM =∠B . ………………………………(1分) ∵△CGM 与△ABE 相似,∴∠BAE =∠CMG 或∠BAE =∠MCG . 情况1:当∠BAE =∠CMG 时, ∵∠BAE =45°,∴∠CMG =45°. ∵GM ⊥BC ,∴∠MCE =45°.∴∠MCE =∠EAB .∵∠AEB =∠CEM ,∴△ABE ∽△CME . ……………………………………………(1分)∴BE AEEM CE =.即EM =∴EM =5. ∴M (7,0). ……………………………(1分) 情况2:当∠BAE =∠MCG 时,∵∠BAE =∠CAM ,∴∠MCG =∠CAM .∴MC =MA . ………………………………(1分) 设M (x ,0),∵C (5,6),A (-1,0),∴222(1)(5)6.x x +=-+∴x=5.∴M (5,0). …………………………………………………………………………(1分) 题型二:动点在线段的延长线上如图7,已知抛物线32++-=bx x y 与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C ,且OC OB =,点D 是抛物线的顶点,直线AC 和BD 交于点E 。
二次函数与相似三角形结合专题练习

二次函数与相似三角形结合专题练习1.如图,已知直线y=2x+2与x轴交于点C,与y轴交于点B,抛物线y=ax2-2ax+c过点C 且与直线y=2x+2交于点A(5,12).(1)求该抛物线的解析式;(2)D为x轴上方抛物线上一点,若△DCO与△DBO的面积相等,求D点的坐标;(3)在线段AB上是否存在点P,过P作x轴的垂线交抛物线于E点,使得以P、B、E为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.2.已知抛物线y=ax2-2x+c与x轴交于A(-1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=- 1/3x+1交y轴于点D.(1)求抛物线的解析式;(2)求证:△BCE∽△BOD;(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE 的面积?3.如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C(1)求抛物线的函数解析式.(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE 是平行四边形,求点D的坐标.(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.4.如图1,抛物线y=-x2+bx+c经过A(-1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.(1)求抛物线的表达式;(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.5.已知抛物线y=a(x+3)(x-1)(a≠0),与x轴从左至右依次相交于A、B两点,与y 轴相交于点C,经过点A的直线y=-√3x+b与抛物线的另一个交点为D.(1)若点D的横坐标为2,求抛物线的函数解析式;(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒2√3/3个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?6.如图,已知二次函数y=-x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m >0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).7.如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.(1)求抛物线的解析式及顶点D的坐标;(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;(3)点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似?若存在,请求出所有符合条件的点N 的坐标;若不存在,请说明理由.8.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.(1)求抛物线的解析式及点C的坐标;(2)求证:△ABC是直角三角形;(3)若点N 为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.9.如图,直线y=-x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c 与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.(1)求该抛物线的解析式;(2)连接PB、PC,求△PBC的面积;(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.10.如图,抛物线与x轴交于点A(-1/3,0)、点B(2,0),与y轴交于点C(0,1),连接BC.(1)求抛物线的函数关系式;(2)点N为抛物线上的一个动点,过点N作NP⊥x 轴于点P,设点N的横坐标为t(-1/3<t<2),求△ABN的面积S与t的函数关系式;(3)若-1/3<t<2且t≠0时△OPN∽△COB,求点N的坐标.11.如图,在平面直角坐标系xOy中,直线y=1/2x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-3/2且经过A、C两点,与x轴的另一交点为点B.(1)①直接写出点B的坐标;②求抛物线解析式.(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.12.如图,已知抛物线y=ax2+bx+3与y轴交于点A,与x轴交于点B(-1,0)和点C(3,0).(1)求抛物线的表达式和对称轴;(2)设抛物线的对称轴与直线AC交于点D,连接AB、BD,求△ABD的面积;(3)点M为抛物线上一动点,过点M作y轴的平行线M N,与直线AC 交于点N.问在抛物线上是否存在点M,使得以D、N、M为顶点的三角形与△ACO相似?若存在,求点M的坐标;若不存在,请说明理由。
中考数学二次函数与相似三角形有关的问题知识解读

二次函数与相似三角形有关的问题知识解读【专题说明】二次函数与相似三角形是中考数学的压轴题,具有一定的难度,也是中考考频比较高的,本节未同学们提供解题途径,希望能够助同学们轻松解题。
【解题思路】关于函数与相似三角形的问题一般三个解决途径:(1)求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形.根据未知三角形中已知边与已知三角形的可能对应边分类讨论;(2)利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数来推导边的大小;(3)若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解.【典例分析】【典例1】(2019•娄底)如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标.【解答】解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)∵OB=OC=3,∴∠OCB=∠OBC=45°,∵∠ABC=∠OBE,故△OBE与△ABC相似时,分为两种情况:①当∠ACB=∠BOQ时,AB=4,BC=3,AC=,过点A作AH⊥BC于点H,S△ABC=×AH×BC=AB×OC,解得:AH=2,则sin∠ACB==,则tan∠ACB=2,则直线OQ的表达式为:y=﹣2x…②,联立①②并解得:x=或﹣,故点Q(,﹣2)或(﹣,2),②∠BAC=∠BOQ时,tan∠BAC==3=tan∠BOQ,则点Q(n,﹣3n),则直线OQ的表达式为:y=﹣3x…③,联立①③并解得:x=,故点Q(,)或(,);综上,当△OBE与△ABC相似时,Q的坐标为:(,﹣2)或(﹣,2)或(,)或(,).【变式1-1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【解答】解:(1)将A(0,3)和B(,﹣)代入y=﹣x2+bx+c,,解得,∴该抛物线的解析式为y=﹣x2+2x+3;(3)①当△AOC∽△DP A时,∵PD⊥x轴,∠DP A=90°,∴点P纵坐标是3,横坐标x>0,即﹣x2+2x+3=3,解得x=2,∴点D的坐标为(2,0);∵PD⊥x轴,∴点P的横坐标为2,∴点P的纵坐标为:y=﹣22+2×2+3=3,∴点P的坐标为(2,3),点D的坐标为(2,0);②当△AOC∽△DAP时,此时∠APG=∠ACO,过点A作AG⊥PD于点G,∴△APG∽△ACO,∴,设点P的坐标为(m,﹣m2+2m+3),则D点坐标为(m,﹣m+3),则,解得:m=,∴D点坐标为(,1),P点坐标为(,),综上,点P的坐标为(2,3),点D的坐标为(2,0)或P点坐标为(,),D 点坐标为(,1).【变式1-2】(2022•绵阳)如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°,若存在,求出点P的坐标,若不存在,请说明理由;(3)过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与△ADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.【解答】解:(1)∵顶点D的横坐标为1,∴抛物线的对称轴为直线x=1,∵A(﹣1,0),∴B(3,0),∴设抛物线的解析式为:y=a(x+1)(x﹣3),将C(0,3)代入抛物线的解析式,则﹣3a=3,解得a=﹣1,∴抛物线的解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)存在,P(0,﹣1),理由如下:∵∠APB+∠ACB=180°,∴∠CAP+∠CBP=180°,∴点A,C,B,P四点共圆,如图所示,由(1)知,OB=OC=3,∴∠OCB=∠OBC=45°,∴∠APC=∠ABC=45°,∴△AOP是等腰直角三角形,∴OP=OA=1,∴P(0,﹣1).(3)存在,理由如下:由(1)知抛物线的解析式为:y=﹣x2+2x+3,∴D(1,4),由抛物线的对称性可知,E(2,3),∵A(﹣1,0),∴AD=2,DE=,AE=3.∴AD2=DE2+AE2,∴△ADE是直角三角形,且∠AED=90°,DE:AE=1:3.∵点M在直线l下方的抛物线上,∴设M(t,﹣t2+2t+3),则t>2或t<0.∴EF=|t﹣2|,MF=3﹣(﹣t2+2t+3)=t2﹣2t,若△MEF与△ADE相似,则EF:MF=1:3或MF:EF=1:3,∴|t﹣2|:(t2﹣2t)=1:3或(t2﹣2t):|t﹣2|=1:3,解得t=2(舍)或t=3或﹣3或(舍)或﹣,∴M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).综上,存在点M,使以M,F,E三点为顶点的三角形与△ADE相似,此时点M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).【典例2】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.【解答】解:(1)由题意得:,解得:,∴抛物线的解析式为:y=﹣2x2+2x+4;(2)设点P的坐标为(t,﹣2t2+2t+4),则OH=t,BH=2﹣t,分两种情况:①如图2,△CMP∽△BMH,∴∠PCM=∠OBC,∠BHM=∠CPM=90°,∴tan∠OBC=tan∠PCM,∴====2,∴PM=2PC=2t,MH=2BH=2(2﹣t),∵PH=PM+MH,∴2t+2(2﹣t)=﹣2t2+2t+4,解得:t1=0,t2=1,∴P(1,4);②如图3,△PCM∽△BHM,则∠PCM=∠BHM=90°,过点P作PE⊥y轴于E,∴∠PEC=∠BOC=∠PCM=90°,∴∠PCE+∠EPC=∠PCE+∠BCO=90°,∴∠BCO=∠EPC,∴△PEC∽△COB,∴=,∴=,解得:t1=0(舍),t2=,∴P(,);综上,点P的坐标为(1,4)或(,).【变式2-1】(2022•辽宁)抛物线y=ax2﹣2x+c经过点A(3,0),点C(0,﹣3),直线y=﹣x+b经过点A,交抛物线于点E.抛物线的对称轴交AE于点B,交x轴于点D,交直线AC于点F.(1)求抛物线的解析式;(2)如图,连接CD,点Q为平面内直线AE下方的点,以点Q,A,E为顶点的三角形与△CDF相似时(AE与CD不是对应边),请直接写出符合条件的点Q的坐标.【解答】解:(1)将A(3,0),点C(0,﹣3)代入y=ax2﹣2x+c,∴,解得,∴y=x2﹣2x﹣3;(2)∵C(0,﹣3),D(1,0),F(1,﹣2),∴CD=,CF=,DF=2,∵E(﹣2,5),A(3,0),∴AE=5,设Q(x,y),①当△CDF∽△QAE时,==,∴==,∴AQ=5,EQ=5,∴,解得或(舍去),∴Q(﹣7,5);②当△CDF∽△AQE时,==,∴==,∴AQ=5,QE=10,∴,解得(舍去)或,∴Q(﹣12,5);③当△CDF∽△EQA时,==,∴==,∴EQ=5,AQ=10,∴,解得或(舍去),∴Q(3,﹣10);④当△CDF∽△QEA时,==,∴==,∴EQ=5,AQ=5,∴,解得或(舍去),∴Q(3,﹣5);综上所述:Q点坐标为(﹣7,5)或(﹣12,5)或(3,﹣10)或(3,﹣5).【变式2-2】(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ (点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【解答】解:(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,∴A(﹣1,0),B(4,0),C(0,4);(2)如图:由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),∵B(4,0),C(0,4);∴BN=,QN=t,PM=,CM=|t﹣3|,∵∠CMP=∠QNB=90°,∴△CPM和△QBN相似,只需=或=,①当=时,=,解得t=或t=,∴Q(,)或(,);②当=时,=,解得t=或t=(舍去),∴Q(,),综上所述,Q的坐标是(,)或(,)或(,).【变式2-3】(2021•黑龙江)如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,连接BC,与抛物线的对称轴交于点E,顶点为点D.(1)求抛物线的解析式;(2)点P是对称轴左侧抛物线上的一个动点,点Q在射线ED上,若以点P、Q、E为顶点的三角形与△BOC相似,请直接写出点P的坐标.【解答】解:(1)∵抛物线y=ax2+bx+3过点A(1,0),B(﹣3,0),∴,解得,∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)令x=0,y=3,∴OC=OB=3,即△OBC是等腰直角三角形,∵抛物线的解析式为:y=﹣x2﹣2x+3,∴抛物线对称轴为:x=﹣1,∵EN∥y轴,∴△BEN∽△BCO,∴,∴,∴EN=2,①若△PQE∽△OBC,如图所示,过点P作PH⊥ED垂足为H,∴∠PEH=45°,∴∠PHE=90°,∴∠HPE=∠PEH=45°,∴PH=HE,∴设点P坐标(x,﹣x﹣1+2),∴代入关系式得,﹣x﹣1+2=﹣x2﹣2x+3,整理得,x2+x﹣2=0,解得,x1=﹣2,x2=1(舍),∴点P坐标为(﹣2,3),②若△EPQ∽△OCB,如图所示,设P(x,2),代入关系式得,2=﹣x2﹣2x+3,整理得,x2+2x﹣1=0,解得,(舍),∴点P的坐标为(﹣1﹣,2),综上所述点P的坐标为(﹣1﹣,2)或(﹣2,3)。
二次函数背景下的三角形相似(全等) (解析版)

备战2020年中考数学压轴题之二次函数专题07 二次函数背景下的三角形相似(全等)【方法综述】三角形全等是三角形相似的特殊情况。
三角形的全等和相似是综合题中的常见要素,解答时注意应用全等三角形和相似的判定方法。
另外,注意题目中“≅”与全等表述、“~”和相似表述的区别。
全等和相似的符号,标志着三角形全等(相似)的对应点的一一对应关系。
解答时,对于确定的对应边角可以直接利用于解题。
而全等、相似的语言表述,标志着对应点之间的组合关系,解答时,要进行对应边的分类讨论。
【典例示范】类型一确定的全等三角形条件的判定应用例1:如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D 的坐标分别为(-2,0),(6,-8).(1)求抛物线的解析式,并分别求出点B和点E的坐标;(2)试探究抛物线上是否存在点F,使△FOE≌△FCE.若存在,请直接写出点F的坐标;若不存在,请说明理由.【答案】(1) y=12x2-3x-8;(2)点F的坐标为(3+17,-4)或(3-17,-4).【思路引导】(1)根据待定系数法求出抛物线解析式即可求出点B坐标,求出直线OD解析式即可解决点E 坐标.(2)抛物线上存在点F使得△FOE≌△FCE,此时点F纵坐标为-4,令y=-4即可解决问题.【解析】(1)∵抛物线y=ax2+bx-8经过点A(-2,0),D(6,-8),∴4280 {36688a ba b--+--==解得1 {23 ab==∴抛物线的函数表达式为y=12x2−3x−8;∵y=12x2−3x−8=12(x−3)2−252,∴抛物线的对称轴为直线x=3.又抛物线与x轴交于A,B两点,点A的坐标为(-2,0).∴点B的坐标为(8,0),设直线L的函数表达式为y=kx.∵点D(6,-8)在直线L上,∴6k=-8,解得k=-43,∴直线L的函数表达式为y=-43 x,∵点E为直线L和抛物线对称轴的交点,∴点E的横坐标为3,纵坐标为-43×3=-4,∴点E的坐标为(3,-4);(2)抛物线上存在点F,使△FOE≌△FCE.∵OE=CE=5,∴FO=FC,∴点F在OC的垂直平分线上,此时点F的纵坐标为-4,∴12x2-3x-8=-4,解得,∴点F的坐标为(3-4)或(-4).【方法总结】本题考查二次函数综合题、一次函数的性质、待定系数法,等腰三角形的判定和性质等知识,解题的关键是学会分类讨论,不能漏解,学会用方程的思想思考问题,属于中考压轴题针对训练1.综合与探究:已知二次函数y=﹣12x2+32x+2的图象与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C.(1)求点A ,B ,C 的坐标;(2)求证:△ABC 为直角三角形;(3)如图,动点E ,F 同时从点A 出发,其中点E 以每秒2个单位长度的速度沿AB 边向终点B 运动,点F AC 方向运动.当点F 停止运动时,点E 随之停止运动.设运动时间为t 秒,连结EF ,将△AEF 沿EF 翻折,使点A 落在点D 处,得到△DEF .当点F 在AC 上时,是否存在某一时刻t ,使得△DCO ≌△BCO ?(点D 不与点B 重合)若存在,求出t 的值;若不存在,请说明理由.【答案】(1)点A 的坐标为(4,0),点B 的坐标为(﹣1,0),点C 的坐标为(0,2);(2)证明见解析;(3)t =34. 【解析】 (1)解:当y =0时,﹣21322x +x +2=0, 解得:x 1=1,x 2=4,∴点A 的坐标为(4,0),点B 的坐标为(﹣1,0),当x =0时,y =2,∴点C 的坐标为(0,2);(2)证明:∵A (4,0),B (﹣1,0),C (0,2),∴OA =4,OB =1,OC =2.∴AB =5,AC ===BC =,∴AC 2+BC 2=25=AB 2,∴△ABC 为直角三角形;(3)解:由(2)可知△ABC 为直角三角形.且∠ACB =90°,∵AE =2t ,AF ,∴AF AB AE AC ==, 又∵∠EAF =∠CAB ,∴△AEF ∽△ACB ,∴∠AEF =∠ACB =90°,∴△AEF 沿EF 翻折后,点A 落在x 轴上点 D 处,由翻折知,DE =AE ,∴AD =2AE =4t ,当△DCO ≌△BCO 时,BO =OD ,∵OD =4﹣4t ,BO =1,∴4﹣4t =1,t =34, 即:当t =34秒时,△DCO ≌△BCO .2.如图,已知抛物线y =√32x 2+bx +6√3与x 轴交于A 、B 两点,其中点A 的坐标为(2,0),抛物线的顶点为P .(1)求b 的值,并求出点P 、B 的坐标;(2)在x 轴下方的抛物线上是否存在点M ,使△AMP ≌△AMB ?如果存在,请直接写出点M 的坐标;如果不存在,试说明理由.【答案】(1)(6,0)(2)存在,(163,−10√39) 【解析】(1)∵抛物线y =√32x 2+bx +6√3经过A(2,0), ∴√32×22+2b +6√3=0,解得:b =−4√3,∴抛物线的表达式为y =√32x 2−4√3x +6√3. ∵y =√32x 2+bx +6√3=√32(x −4)2−2√3, ∴点P 的坐标为(4,−2√3).令y =0得:√32x 2+bx +6√3=0,解得x =2或x =6,∴B 的坐标为(6,0).(2)存在,点M(163,−10√39). 如图:过点P 作PC ⊥x 轴,垂足为C ,连接AP 、BP ,作∠PAB 的平分线,交PB 与点N ,交抛物线与点M ,连接PM 、BM .∵A(2,0),B(6,0),P(4,−2√3),∴AB =4,AP =√(4−2)2+(−2√3)2=4,BP =√(4−6)2+(−2√3)2=4,∴△ABP 是等边三角形,∵∠APB =∠ABP ,AP =AB .∴AM ⊥PB ,PN =BN ,∠PAM =∠BAM .在△AMP 和△AMB 中,{AP =AB∠PAM =∠BAM AM =AM,∴△AMP ≌△AMB .∴存在这样的点M ,使得△AMP ≌△AMB .∵B(6,0),P(4,−2√3),点N 是PB 的中点,∴N(5,−√3).设直线AM 的解析式为y =kx +b ,将点A 和点N 的坐标代入得:{2k +b =05k +b =−√3 ,解得:{k =−√33b =2√33, ∴直线AM 的解析式为y =−√33x +2√33.将y =−√33x +2√33代入抛物线的解析式得:√32x 2−4√3x +6√3=−√33x +2√33,解得:x =163或x =2(舍去), 当x =163时,y =−10√39, ∴点M 的坐标为(163,−10√39). 类型二 全等三角形的存在性探究例2.如图,抛物线y=ax 2+bx+c 与x 轴的交点分别为A (﹣6,0)和点B (4,0),与y 轴的交点为C (0,3).(1)求抛物线的解析式;(2)点P 是线段OA 上一动点(不与点A 重合),过P 作平行于y 轴的直线与AC 交于点Q ,点D 、M 在线段AB 上,点N 在线段AC 上.①是否同时存在点D 和点P ,使得△APQ 和△CDO 全等,若存在,求点D 的坐标,若不存在,请说明理由; ②若∠DCB=∠CDB ,CD 是MN 的垂直平分线,求点M 的坐标.【答案】(1)y=﹣18x 2﹣14x+3;(2)①点D 坐标为(﹣32,0);②点M (32,0). 【分析】(1)应用待定系数法问题可解;(2)①通过分类讨论研究△APQ 和△CDO 全等②由已知求点D 坐标,证明DN ∥BC ,从而得到DN 为中线,问题可解【解析】(1)将点(-6,0),C (0,3),B (4,0)代入y=ax 2+bx+c ,得{36a −6b +c =016a +4b +c =0c =0,解得:{a =−18b =−14c =3 , ∴抛物线解析式为:y=-18x 2-14x+3;(2)①存在点D,使得△APQ和△CDO全等,当D在线段OA上,∠QAP=∠DCO,AP=OC=3时,△APQ和△CDO全等,∴tan∠QAP=tan∠DCO,OC OA =ODOC,∴36=OD3,∴OD=32,∴点D坐标为(-32,0).由对称性,当点D坐标为(32,0)时,由点B坐标为(4,0),此时点D(32,0)在线段OB上满足条件.②∵OC=3,OB=4,∴BC=5,∵∠DCB=∠CDB,∴BD=BC=5,∴OD=BD-OB=1,则点D坐标为(-1,0)且AD=BD=5,连DN,CM,则DN=DM,∠NDC=∠MDC,∴∠NDC=∠DCB,∴DN∥BC,∴ANNC =ADDB=1,则点N为AC中点.∴DN 时△ABC 的中位线,∵DN=DM=12BC=52, ∴OM=DM -OD=32∴点M (32,0)【点评】本题是二次函数综合题,考查了二次函数待定系数法、三角形全等的判定、锐角三角形函数的相关知识.解答时,注意数形结合 针对训练1.如图,在平面直角坐标系中,以点M (2,0)为圆心的⊙M 与y 轴相切于原点O ,过点B (﹣2,0)作⊙M 的切线,切点为C ,抛物线y =−√33x 2+bx +c 经过点B 和点M .(1)求这条抛物线解析式;(2)求点C 的坐标,并判断点C 是否在(1)中抛物线上;(3)动点P 从原点O 出发,沿y 轴负半轴以每秒1个单位长的速度向下运动,当运动t 秒时到达点Q 处.此时△BOQ 与△MCB 全等,求t 的值.【答案】(1)y =﹣√33x 2+4√33;(2)点C 在(1)的抛物线上;(3)t =2√3.【解析】(1)将点M (2,0)、B (﹣2,0)代入 y =−√33x 2+bx +c 中,得: {−4√33+2b +c =0−4√33−2b +c =0解得:{b =0c =4√33∴抛物线的解析式:y =−√33x 2+4√33. (2)连接MC ,则MC ⊥BC ;过点C 作CD ⊥x 轴于D ,如图,在Rt △BCM 中,CD ⊥BM ,CM =2,BM =4,则:DM =CM 2BM =224=1,CD =√CM 2−DM 2=√22−1=√3,OD =OM ﹣DM =1,∴C (1,√3).当x =1时,y =−√33x 2+4√33=√3,所以点C 在(1)的抛物线上.(3)△BCM 和△BOQ 中,OB =CM =2,∠BOQ =∠BCM =90°,若两三角形全等,则:OQ =BC =√BM 2−CM 2=√42−22=2√3,∴当t =2√3时,△MCB 和△BOQ 全等.2.(广西田阳县实验中学2019届九年级中考一)如图所示,抛物线y =−(x −√3m)2(m >0)的顶点为A ,直线l:y =√33x −m 与y 轴的交点为点B.(1)求出抛物线的对称轴及顶点A 的坐标(用含m 的代数式表示);(2)证明点A 在直线l 上,并求∠OAB 的度数;(3)动点Q 在抛物线对称轴上,问:抛物线上是否存在点P ,使以点P 、Q 、A 为顶点的三角形与△OAB 全等?若存在,求出m 的值,并写出所有符合上述条件的点P 的坐标;若不存在,请说明理由.【答案】(1)抛物线的对称轴为直线x =√3m ,顶点A 的坐标为(√3m ,0);(2)∠OAB=30°;(3)存在,①m =13时, P1(0,-13),P 2(23√3,-13);②m =√3时,P 3(3-√3,-3),P 4(3+√3,-3);③m =2时, P 5(√3,-3),P 6(√33,-3);④m =23时, P 7(√33,-13),P 8(√3,-13).【解析】(1)对称轴:x=√3m ;顶点:A (√3m ,0).(2)将x=√3m 代入函数y=√33x -m ,得y=√33×√3m -m=0∴点A (√3m ,0)在直线l 上.当x=0时,y=-m ,∴B (0,-m )tan ∠OAB=√3m =√33, ∴∠OAB=30度.(3)以点P 、Q 、A 为顶点的三角形与△OAB 全等共有以下四种情况: ①当∠AQP=90°,PQ=√3m ,AQ=m 时,如图1,此时点P 在y 轴上,与点B 重合,其坐标为(0,-m ),代入抛物线y=-(x -√3m )2得-m=-3m 2,∵m >0,∴m=13 这时有P 1(0,-13) 其关于对称轴的对称点P 2(2√33,- 13)也满足条件. ②当∠AQP=90°,PQ=m ,AQ=√3m 时 点P 坐标为(√3m -m ,-√3m ),代入抛物线y=-(x -√3m )2得√3m=m 2,∵m >0, ∴m=√3这时有P 3(3-√3,-3)还有关于对称轴的对称点P 4(3+√3,-3). ③当∠APQ=90°,AP=√3m ,PQ=m 时点P 坐标为(√32m ,−32m ),代入抛物线y=-(x -√3m )2得32m=34m 2, ∵m >0, ∴m=2这时有P 5(√3,-3)还有关于对称轴的对称点P 6(3√3,-3).④当∠APQ=90°,AP=m ,PQ=√3m 时 点P 坐标为(√32m ,−12m ), 代入抛物线y=-(x -√3m )2 得12m=34m 2, ∵m >0, ∴m=23这时有P 7(√33,-13)还有关于对称轴对称的点P 8(√3,-13). 所以当m=13时,有点P 1(0,-13),P 2(2√33,-13);当m=√3时,有点P 3(3-√3,-3),P 4(3+√3,-3); 当m=2时,有点P 5(√3,-3),P 6(3√3,-3); 当m=23时,有点P 7(√33,-13),P 8(√3,-13).3.如图1,抛物线y 1=ax 2﹣12x+c 与x 轴交于点A 和点B (1,0),与y 轴交于点C (0,34),抛物线y 1的顶点为G ,GM ⊥x 轴于点M .将抛物线y 1平移后得到顶点为B 且对称轴为直线l 的抛物线y 2.(1)求抛物线y 2的解析式;(2)如图2,在直线l 上是否存在点T ,使△TAC 是等腰三角形?若存在,请求出所有点T 的坐标;若不存在,请说明理由;(3)点P 为抛物线y 1上一动点,过点P 作y 轴的平行线交抛物线y 2于点Q ,点Q 关于直线l 的对称点为R ,若以P ,Q ,R 为顶点的三角形与△AMG 全等,求直线PR 的解析式. 【答案】(1)y 2=-14x 2+12x -14;(2)存在;(3)y=﹣12x+34或y=﹣12x −14.【解析】(1)由已知,c=34,将B (1,0)代入,得:a ﹣12+34=0, 解得a=﹣14,抛物线解析式为y 1=14x 2-12 x+34,∵抛物线y 1平移后得到y 2,且顶点为B (1,0), ∴y 2=﹣14(x ﹣1)2,即y 2=-14x 2+12 x -14; (2)存在,如图1:抛物线y 2的对称轴l 为x=1,设T (1,t ), 已知A (﹣3,0),C (0,34), 过点T 作TE ⊥y 轴于E ,则 TC 2=TE 2+CE 2=12+(34)2=t 2﹣32t+2516,TA 2=TB 2+AB 2=(1+3)2+t 2=t 2+16, AC 2=15316,当TC=AC 时,t 2﹣32t+2516=15316,解得:t 1=3+√1374,t 2=3−√1374;当TA=AC 时,t 2+16=15316,无解; 当TA=TC 时,t 2﹣32t+2516=t 2+16, 解得t 3=﹣778;当点T 坐标分别为(1,3+√1374),(1,3−√1374),(1,﹣778)时,△TAC 为等腰三角形;(3)如图2:设P (m ,−14m 2−12m +34),则Q (m ,−14m 2+12m −14), ∵Q 、R 关于x=1对称∴R (2﹣m ,−14m 2+12m −14), ①当点P 在直线l 左侧时, PQ=1﹣m ,QR=2﹣2m , ∵△PQR 与△AMG 全等,∴当PQ=GM 且QR=AM 时,m=0, ∴P (0,34),即点P 、C 重合, ∴R (2,﹣14),由此求直线PR 解析式为y=﹣12x+34,当PQ=AM 且QR=GM 时,无解; ②当点P 在直线l 右侧时, 同理:PQ=m ﹣1,QR=2m ﹣2, 则P (2,﹣54),R (0,﹣14), PQ 解析式为:y=﹣12x −14;∴PR 解析式为:y=﹣12x+34或y=﹣12x −14.类型三 确定的相似三角形条件的判定应用例3:如图,已知二次函数22y x x m =-+的图象与x 轴交于点A 、B ,与y 轴交于点C ,直线AC 交二次函数图象的对称轴于点D ,若点C 为AD 的中点.(1)求m 的值;(2)若二次函数图象上有一点Q ,使得tan 3ABQ ∠=,求点Q 的坐标;(3)对于(2)中的Q 点,在二次函数图象上是否存在点P ,使得QBP ∆∽COA ∆?若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)3m =-;(2)()4,21Q -或()2,3Q -;(3)不存在,理由见解析. 【思路引导】(1)设对称轴与x 轴交于点E ,如图1,易求出抛物线的对称轴,可得OE 的长,然后根据平行线分线段成比例定理可得OA 的长,进而可得点A 的坐标,再把点A 的坐标代入抛物线解析式即可求出m 的值; (2)设点Q 的横坐标为n ,当点Q 在x 轴上方时,过点Q 作QH ⊥x 轴于点H ,利用tan 3ABQ ∠=可得关于n 的方程,解方程即可求出n 的值,进而可得点Q 坐标;当点Q 在x 轴下方时,注意到tan 3BAC ∠=,所以点Q 与点C 关于直线1x =对称,由此可得点Q 坐标;(3)当点Q 为x 轴上方的点时,若存在点P ,可先求出直线BQ 的解析式,由BP ⊥BQ 可求得直线BP 的解析式,然后联立直线BP 和抛物线的解析式即可求出点P 的坐标,再计算此时两个三角形的两组对应边是否成比例即可判断点P 是否满足条件;当点Q 取另外一种情况的坐标时,再按照同样的方法计算判断即可. 【解析】解:(1)设抛物线的对称轴与x 轴交于点E ,如图1,∴y 轴//ED ,∴::1AC CD AO OE ==, ∵抛物线的对称轴是直线212x -=-=,∴OE =1,∴1AO OE ==,∴()1,0A - ∴将点()1,0A -代入函数表达式得:120m ++=,∴3m =-;(2)设()2,23Q n n n --,①点Q 在x 轴上方时,0n <,如图2,过点Q 作QH ⊥x 轴于点H ,∵tan 3ABQ ∠=,∴22333n n n--=-,解得:4n =-或3n =(舍),∴()4,21Q -;②点Q 在x 轴下方时,∵OA =1,OC =3,∴tan 3BAC ∠=,∵tan 3ABQ ∠=,∴点Q 与点C 关于直线1x =对称,∴()2,3Q -;(3)①当点Q 为()4,21-时,若存在点P ,使QBP ∆∽COA ∆,则∠PBQ =∠COA =90°, 由B (3,0)、Q ()4,21-可得,直线BQ 的解析式为:39y x =-+,所以直线PB 的解析式为:113y x =-,联立方程组:211323y x y x x ⎧=-⎪⎨⎪=--⎩,解得:1130x y =⎧⎨=⎩,2223119x y ⎧=-⎪⎪⎨⎪=-⎪⎩,∴211,39P ⎛⎫-- ⎪⎝⎭, ∵:1:3OA OC =,:1:3BP BQ =≠, ∴::BP BQ OA OC ≠,∴P 不存在;②当点Q 为()2,3-时,如图4,由B (3,0)、Q ()2,3-可得,直线BQ 的解析式为:39y x =-,所以直线PB 的解析式为:113y x =-+, 联立方程组:211323y x y x x ⎧=-+⎪⎨⎪=--⎩,解得:1130x y =⎧⎨=⎩,2243139x y ⎧=-⎪⎪⎨⎪=⎪⎩,∴413,39P ⎛⎫- ⎪⎝⎭,∵:1:3OA OC =,:1:3BP BQ =≠, ∴::BP BQ OA OC ≠,∴P 不存在.综上所述,不存在满足条件的点P ,使QBP ∆∽COA ∆. 【方法总结】本题考查了平行线分线段成比例定理、二次函数图象上点的坐标特征、一元二次方程的解法、相似三角形的判定和性质、锐角三角函数和两个函数的交点等知识,综合性强、具有相当的难度,熟练掌握上述知识、灵活应用分类和数形结合的数学思想是解题的关键.针对训练1.如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a ,b ,c ]称为“抛物线系数”. (1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;(3)若一条抛物线系数为[-1,2b ,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式; (4)在(3)的前提下,该抛物线的顶点为A ,与x 轴交于O ,B 两点,在抛物线上是否存在一点P ,过P 作PQ ⊥x 轴于点Q ,使得△BPQ ∽△OAB ,如果存在,求出P 点坐标,如果不存在,请说明理由. 【答案】(1)假;(2)2√2;(3)y =-x 2+2x 或y =-x 2-2x ;(4)P (1,1)或P (-1,-3)或P (1,-3)或(-1,1).【解析】(1)当△>0时,抛物线与x 轴有两个交点,此时抛物线才有“抛物线三角形”,故此命题为假命题; (2)由题意得:y =x 2−2,令y =0,得:x =±√2,∴ S =12×2√2×2=2√2; (3)依题意:y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0); 当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形.∵y=-x2+2bx=−(x−b)2+b2,∴顶点为(b,b2),由直角三角形斜边上的中线等于斜边的一半得到:b2=12×|2b|,∴b2=|b|,解得:b=0(舍去)或b=±1,∴y=-x2+2x 或y=-x2-2x.(4)①当抛物线为y=-x2+2x 时.∵△AOB为等腰直角三角形,且△BPQ∽△OAB,∴△BPQ为等腰直角三角形,设P(a,-a2+2a),∴Q((a,0),则|-a2+2a|=|2-a|,即|a(a−2)|=|a−2|.∵a-2≠0,∴|a|=1,∴a=±1,∴P(1,1)或(-1,-3).②当抛物线为y=-x2-2x 时.∵△AOB为等腰直角三角形,且△BPQ∽△OAB,∴△BPQ为等腰直角三角形,设P(a,-a2-2a),∴Q((a,0),则|-a2-2a|=|2+a|,即|a(a+2)|=|a+2|.∵a+2≠0,∴|a|=1,∴a=±1,∴P(1,-3,)或(-1,1).综上所述:P(1,1)或P(-1,-3)或P(1,-3,)或(-1,1).2.如图1,一次函数y=﹣x+3的图象交x轴于点A,交y轴于点D,抛物线y=ax2+bx+c(a≠0)的顶点为C,其图象过A、D两点,并与x轴交于另一个点B(B点在A点左侧),若ABAD =√23;(1)求此抛物线的解析式;(2)连结AC、BD,问在x轴上是否存在一个动点Q,使A、C、Q三点构成的三角形与△ABD相似.如果存在,求出Q点坐标;如果不存在,请说明理由.(3)如图2,若点P是抛物线上一动点,且在直线AD下方,(点P不与点A、点D重合),过点P作y轴的平行线l与直线AD交于点M,点N在直线AD上,且满足△MPN∽△ABD,求△MPN面积的最大值.【答案】(1)y=x2﹣4x+3;(2)见解析;(3)△MPN的面积的最大值为:24364.【解析】(1)当x=0时,y=﹣x+3=3,则D(3,0);当y=0时,﹣x+3=0,解得x=3,则A(3,0),∵OD=OA,∴△OAD为等腰直角三角形,∴AD=3√2,∵ABAD =√23,∴AB=2,∴B(1,0),设抛物线解析式为y=a(x﹣1)(x﹣3),把D(0,3)代入得a•(﹣1)•(﹣3)=3,解得a=1,∴抛物线解析式为y=(x﹣1)(x﹣3),即y=x2﹣4x+3;(2)作CH⊥x轴,如图1,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴C(2,﹣1)∴AH=CH=1,∴△ACH为等腰直角三角形,∴∠CAH=45°,AC=√2,∵△OAD为等腰直角三角形,∴∠DAO=45°,∵∠CAQ=∠DAB,∴当AQAD =ACAB时,△AQC∽△ADB,即3√2=√22,解得AQ=3,此时Q(0,0);当AQAB =ACAD时,△AQC∽△ABD,即AQ2=√23√2,解得AQ=23,此时Q(73,0);综上所述,Q点的坐标为(0,0)或(73,0);(3)作PE⊥AD于E,如图2,∵△MPN∽△ABD,∴MNAD =MPAB,∴MN =3√22MP , 设P (x ,x 2﹣4x+3),则M (x ,﹣x+3),∴MP =﹣x+3﹣(x 2﹣4x+3)=﹣x 2+3x =﹣(x ﹣32)2+94,当x =32时,MP 有最大值94,∴MN 的最大值为3√22×94=27√28, ∵∠PME =45°,∴PE =√22PM ,∴PE 的最大值为√22×94=9√28,∴△MPN 的面积的最大值为12×27√28×9√28=24364 .3.如图,抛物线y=ax 2+bx+c 过原点O 、点A (2,﹣4)、点B (3,﹣3),与x 轴交于点C ,直线AB 交x 轴于点D ,交y 轴于点E .(1)求抛物线的函数表达式和顶点坐标;(2)直线AF ⊥x 轴,垂足为点F ,AF 上取一点G ,使△GBA ∽△AOD ,求此时点G 的坐标;(3)过直线AF 左侧的抛物线上点M 作直线AB 的垂线,垂足为点N ,若∠BMN=∠OAF ,求直线BM 的函数表达式.【答案】(1)y=x 2-4x ;(2,-4);(2)G (2, −83);(3)y=−13x −2或y=-3x+6. 【解析】(1)解:将原点O (0,0)、点A (2,﹣4)、点B (3,﹣3),分别代入y=ax 2+bx+c ,得,解得 ,∴y=x 2-4x=, ∴顶点为(2,-4). (2)解:设直线AB 为y=kx+b ,由点A (2,-4),B (3,-3),得解得,∴直线AB 为y=x -6.当y=0时,x=6,∴点D (6,0).∵点A (2,-4),D (6,0),B (3,-3),∴OA= ,OD=6,AD= ,AF=4,OF=2,DF=4,AB= , ∴DF=AF ,又∵AF ⊥x 轴,∴∠AD0=∠DAF=45°,∵△GBA ∽△AOD ,∴ ,∴, 解得 ,∴FG=AF -AG=4- ,∴点G (2,). (3)解:如图1,∵∠BMN=∠OAF,,∴∠MBN=∠AOF,设直线BM与AF交于点H,∵∠ABH=∠AOD,∠HAB=∠ADO,∴∴,则,解得AH= ,∴H(2,).设直线BM为y=kx+b,∵将点B、G的坐标代入得,解得.∴直线BM的解析式为y= ;如图2,BD=AD -AB= .∵∠BMN=∠OAF ,∠GDB=∠ODA ,∴△HBD ∽△AOD .∴ ,即 ,解得DH=4.∴点H 的坐标为(2,0).设直线BM 的解析式为y=kx+b .∵将点B 和点G 的坐标代入得:,解得k=-3,b=6.∴直线BM 的解析式为y=-3x+6.综上所述,直线MB 的解析式为y=或y=-3x+6. 类型四 相似三角形存在性探究例4.在平面直角坐标系中,已知抛物线L :经过点A (-3,0)和点B (0,-6),L 关于原点O 对称的抛物线为.(1)求抛物线L 的表达式;(2)点P 在抛物线上,且位于第一象限,过点P 作PD ⊥y 轴,垂足为D.若△POD 与△AOB 相似,求符合条件的点P 的坐标.()2y ax c a x c =+-+L 'L '【答案】(1) y =-x 2-5x -6;(2)符合条件的点P 的坐标为(1,2)或(6,12)或(,)或(4,2)。
二次函数与三角形相似问题

二次函数与三角形相似问题二次函数是初中数学中的重要内容,而三角形相似问题是初中几何中的重点难点。
在解决一些复杂的几何问题时,我们常常需要将二次函数和三角形相似问题结合起来进行思考。
本文将从几个方面探讨二次函数与三角形相似问题的关系和应用。
一、二次函数的解析式与三角形的边长关系在解决与三角形相似的二次函数问题时,我们需要先确定三角形的边长关系。
例如,已知一个直角三角形的两条直角边分别为3和4,那么这个直角三角形的斜边长为5。
如果以这个直角三角形的斜边为底边构造一个新的直角三角形,那么它的另一条直角边就是原来直角三角形的斜边的一半,即2.5。
因此,我们可以得出以下结论:当一个直角三角形的一条直角边与另一个直角三角形的斜边相等时,这两个直角三角形是相似的。
二、二次函数的最大值与最小值与三角形的高线关系在解决与三角形相似的二次函数问题时,我们还需要考虑二次函数的最大值和最小值与三角形的高线的关系。
例如,已知一个抛物线的顶点坐标为(0,2),对称轴为y轴。
如果以这个抛物线的顶点为原点构造一个新的抛物线,那么它的顶点坐标就是原来的顶点坐标加上或减去某个常数c。
因此,我们可以得出以下结论:当一个抛物线的顶点与另一个抛物线的顶点之间的距离等于它们到某个固定点的距离之差时,这两个抛物线是相似的。
三、二次函数的对称性与三角形的对称性关系在解决与三角形相似的二次函数问题时,我们还需要考虑二次函数的对称性和三角形的对称性之间的关系。
例如,已知一个抛物线的对称轴为x=1,如果以这个抛物线的对称轴为中心构造一个新的抛物线,那么它的对称轴就是原来的对称轴加上或减去某个常数d。
因此,我们可以得出以下结论:当一个抛物线的对称轴与另一个抛物线的对称轴之间的距离等于它们到某个固定点的距离之和时,这两个抛物线是相似的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
琢玉教育个性化辅导讲义
教师姓名学科上课时间年月日学生姓名年级讲义序号
课题名称
教学目标1.会根据题目条件求解相关点的坐标和线段的长度;
2.掌握用待定系数法求解二次函数的解析式;
3.能根据题目中的条件,画出与题目相关的图形,继而帮助解题;
教学重点难点1.体会利用几何定理和性质或者代数方法建立方程求解的方法;
2.会应用分类讨论的数学思想和动态数学思维解决相关问题。
课前检查上次作业完成情况:优□良□中□差□建议_______________________________
教学内容知识结构:
一.二次函数知识点梳理:下图中0
a≠二.特殊的二次函数:下图中0
a≠
3
4
y x
=与BC边交于D点.
(1)求D点的坐标;
(2)若抛物线2
y ax bx
=+经过A、D两点,求此抛物线的表达式;
(3)设(2)中的抛物线的对称轴与直线OD交于点M,点P是对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求出符合条件的点P.
方法总结:
1.已知:如图,在平面直角坐标系xOy中,二次函数c
bx
x
y+
+
-
=2
3
1
的图像经过点
A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.二次函数背景下相似三角形的解题方法和策略:
1.根据题意,先求解相关点的坐标和相关线段的长度;
2.待定系数法求解相关函数的解析式;
3.相似三角形中,注意寻找不变的量和相等的量(角和线段);
4.当三角形的三边不能用题目中的未知量表示时,注意利用相似三角形的转化求解;
5.根据题目条件,注意快速、正确画图,用好数形结合思想;
6.注意利用好二次函数的对称性;
7.利用几何定理和性质或者代数方法建立方程求解都是常用方法。
(1)求这个二次函数的解析式和它的对称轴;(4分)
(2)求证:∠ABO=∠CBO;(4分)
(3)如果点P在直线AB上,且△POB与△BCD相似,求点P的坐标.(6分)
2.如图,抛物线2
15
2
22
y x x
=-+-与x轴相交于A、B,与y轴相交于点C,过点C作CD ∥x轴,交抛物线于点D。
点P是直线CD上一点,且△PAC与△ABC相似,求符合条件的点P坐标。
【参考教法】:
一.你能求出题目中点A B C D
、、、的坐标吗?(让学生独立计算求解)
二.点P的运动有什么特征吗?提示:点P的不同位置相似的情况不一样。
三.当△PAC与△ABC相似时:
1.需要讨论吗?提示:需要,根据点P的不同位置讨论
2.怎么讨论?根据点P的位置,分两大类讨论:
(1)当点P在C的左侧,由题意有PCA BAC
∠=∠,则分2类讨论:
①当△PAC∽△BAC时:
AC AC
PC AB
=,即
55
3
PC
=;
②当△PAC∽△ABC时:,
AC AB
PC AC
=,即
53
5
PC
=。
(2)点P在C的左侧,由题意有ACP ABC ACB CAB
∠≠∠≠∠≠∠,不存在。
3.情况分好了,那怎么计算呢?你算一下。
提示:让学生计算。
4题目分析完了吧!你算一下每一个情况看看!
5以后做题,可以把分类的情况先写下来,之后再计算求解。
6.根据本题的求解你有什么想法没?提示:
①二次函数中当点的坐标已知时,注意计算各线段的长度;
②注意及时画图,体会数形结合的思想。
y
x
O
A
B
1
1
-1
-1
【满分解答】:
当点P在C的左侧,由题意有PCA BAC
∠=∠,分两类讨论:
若
AC AC
PC AB
=,即
55
3
PC
=时,△PAC∽△BAC,此时CP=3,P(-3,-2); ------2 若
AC AB
PC AC
=,即
53
5
PC
=时,△PAC∽△ABC;此时CP=
5
3
,P(-
5
3
,-2).---2 当点P在C的左侧,由题意有ACP ABC ACB CAB
∠≠∠≠∠≠∠,不存在。
3.如图,在平面直角坐标系中,二次函数2
y ax bx c
=++的图像经过()
3,0
A-、()
1,0
B、()
0,3
C-三点,没该二次函数图像的顶点为D.(★★★)
(1)求这个二次函数的解析式及其图像的顶点D的坐际;
(2)在线段AC上是否存在点M,使△AOM∽△ABC,其中坐标轴的原点O对应点B,点M的对应点为C?若存在,求出点M的坐标;若不存在,请说明理由。
【解法点拨】:
1.二次函数经过三点,可以根据待定系数法求解函数解析式;(让学生自己计算)
2.当△AOM∽△ABC时,字母已经对应好,无需分类讨论,则由△AOM∽△ABC得OA AM
AB AC
=,所以
9
2
4
AM=。
又因为点M在线段AC上,且AC的解析式是:3
y x
=--,则可直接计算出点M的坐标。
3.注意及时画图,体会数形结合的思想。
【满分解答】:(1)由题意得:
930
3
a b c
a b c
c
-+=
⎧
⎪
++=
⎨
⎪=-
⎩
解得:
1
2
3
a
b
c
=
⎧
⎪
=
⎨
⎪=-
⎩
∴二次函数的解析式为223
y x x
=+-
顶点G的坐标是()
1,4
--。
