质量控制图
质量控制图

质量控制图质量控制图的概念与用处如果要系统地介绍,可能要从质量管理(Quality Management,QM)开始,从传统的质量管理七工具,到全面质量管理阶段的6σ管理,这里不去展开,只介绍质量控制图。
质量控制图,简称控制图(Control Chart),是质量管理七工具之一,由美国的贝尔电话实验所的休哈特(W.A.Shewhart)博士在1924年首先提出,因此也称为“休哈特控制图”。
最初的应用当然是在生产领域,使用抽样的方式检验产品的质量是否处于控制状态。
一般而言,指标的波动受随机因素和系统因素的影响,如果指标只受到随机因素的影响,那么在正常情况下指标的变化状态是稳定的、可控的,但如果发生某种系统性的变化就会使指标超出原先可控的波动范围,处于失控状态,所以控制图就是帮助我们及时发现这种失控状态,从而进行及时的调整。
质量控制图通过统计上均值μ和标准差σ的状况来衡量指标是否在稳定状态,同时选择3σ来确定一个正常波动的上下限范围(根据正态分布的结论,指标的特征值落在μ±3σ之间的概率是99.73%),使用均值μ作为控制图的中心线(Center Line, CL),用μ+3σ作为控制上限(Upper Control Limit, UCL),用μ-3σ作为控制下限(Lower Control Limit, LCL),如图。
根据衡量的指标数值类型的差异,质量控制图主要分为两类:计数型控制图和计量型控制图,下面分别介绍其中的一种:质量控制图具体用法因为生产制造业和互联网行业存在着较大差异,所以这里只介绍适合用于网站分析的2个控制图。
其中计数型控制图中主要介绍P控制图,主要用于定类型变量,即符合二项分布检验“是否”的变量,如用户是否完成交易、用户是否为新用户……这类指标一般会以比率的形式出现,如转化率、新用户比例等,而P控制图正是衡量这些比率是否出现异常(在生产行业通常用于不合格率等);另外的计量型控制图主要用于一些关键的数值度量,如每个订单的消费额、每个用户的下载次数等,这类指标在网站分析中通常计算全部数据的均值来观察波动情况,其实计量型控制图最常用的是均值-极差(X-R )和均值-标准差(X-S )控制图,但两者都是通过取样的方式实现的,并且每次取样的样本数最好能保持相等,所以这类抽样统计不太适合于上述网站分析中的指标,这里介绍个相对能够普遍适用并且计算也没有那么复杂的图——单值-移动极差(X-MR )控制图。
质量管理学控制图课件.ppt

• 计算统计量的中心值和控制界限。
x 图:
中心值CL=
= =x29.86(g)
UCL= =x+ A2 R ≈ 45.69(g)
LCL=
= x—
A2
R
≈
14.03(g)
注:A2为随着样本容量n而变化的系数,可由控制图系数选用表中选取。
第13页,共35页。
R 图:
中心值 CL= R=27.44(g) UCL= D4 R≈ 58.04(g)
• 在质量改进方面,可以用来确认某过程是否得到了改进。
第5页,共35页。
二、应用控制图的步骤
应用步骤如下:
选择控制图拟控制的质量特性,如重量、不合格品数等;
选用合适的控制图种类; 确定样本容量和抽样间隔;
收集并记录至少20~ 25个样本的数据,或使用以前所记录的数据; 计算各个样本的统计量,如样本平均值、样本极差、样本标准差等;
• 在不对该过程做任何调整的同时,继续用同样的方法对 多装量抽样、观察和打点。如果在继续观察时,控制图 显示出存在异常原因,则应进一步分析具体原因,并采 取措施对过程进行调整。
第16页,共35页。
四、控制图的观察与分析
点子没有超出控制线(在控制线上的点子按出超出处理),
控制界限内的点子排列无缺陷,反映工序处于控制状态,生 产过程稳定,不必采取措施。 控制图上的点子出现下列情形之一时,即判断生产过程异常:
34.2
25
24
28
27
22
32
54
163
32.6
32
25
42
34
15
29
21
141
23.2
27
累计
746.6
工程质量控制图
监理工程师质量控制的方法
1、建立质量检验工作制度; 2、制订质量检验工作程序; 3、严格把好事前技术报告审批关; 4、现场跟踪检查; 5、严把工程质量验收关。
质量标准
质量控制措施
施工图纸提供或设计变更
工 程 质 量 控 制 程 序 框 图
设计文件签发
意见或建议
设计单位对设计 文件进行修改 施工单位修改 后重新报送
质量检验签证审核
ok
监理过程完备性审核
NO
ok
支付量测 支付单价审核
签发支付证书 报请业主单位支付
索 赔 程 序 流 程 图
索赔事件发生
28天内 简 单 28 索 赔 天 事 内 件 提出索赔要求意向 承包商 正式提出索赔材料 承包商
连件次后 续每直 影隔至 响 28 事 索天件 赔报终 事一了
监理机构详 细记录事件 过程的范围
合同进度控制总目标
设计供图计划
协助业主编制控制性进度计划 资金供应计划 采购计划
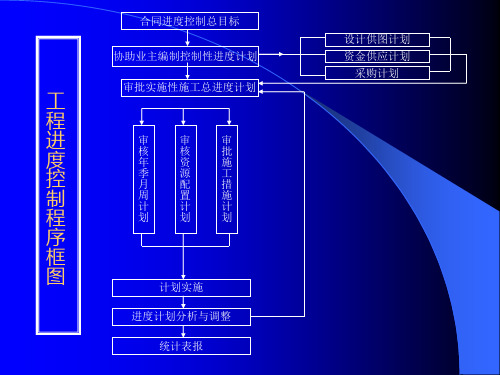
工 程 进 度 控 制 程 序 框 图
审批实施性施工总进度计划
审 核 年 季 月 周 计 划
审 核 资 源 配 置 计 划
审 批 施 工 措 施 计 划
计划实施 进度计划分析与调整 统计表报
进度实施
干扰
项 目 进 度 监 测 系 统 过 程 图
不 同 意 请事议评审组
同 意
执行
仲裁或诉讼
执行
执行
协助业主编制招标文件
施 工 招 标 阶 段 监 理 工 作 程 序 框 图
协助业主发招标公告(或邀请通知) 协助业主审查投标单位资质 协助业主召开标前会议和组织现场查勘 协助业主组织开标评标
协助业主发出中标通知
如何理解质量控制图

如何理解质量控制图质量控制图现代质量管理强调以预防为主。
要求在质量形成的整个⽣产过程中,尽量少出或不出不合格品,这就需要研究两个问题:⼀是如何使⽣产过程具有保证不出不合格品的能⼒;⼆是如何把这种保证不出不合格品的能⼒保持下去,⼀旦这种保证质量的能⼒不能维持下去,应能尽早发现,及时得到情报,查明原因,采取措施,使这种保证质量的能⼒继续稳定下来,保持下去,真正做到防患于未然。
前⼀个问题⼀般称为⽣产过程中的⼯序能⼒分析,后⼀个问题⼀般称为⽣产过程的控制。
这两个问题都与控制图有着密切的联系。
控制图是画有控制界限的⼀种图。
它是⽤来区分质量波动究竟是偶然原因引起的还是由于系统原因引起的,可以提供系统原因存在的信息,从⽽判断⽣产过程是否处于稳定状态的图。
从这个意义上讲,控制图是发现系统原因的“信号图”、“温度计”。
控制图的主要⽤途有:①分析质量形成过程的状态,看⼯序或质量形成过程是否处于稳定。
如不稳定,应找出其原因,采取措施,控制4M1E,使⼯序或过程达到稳定。
②预防不良品的产⽣等。
⼀、质量波动及其原因分析1.质量特性值的波动性某个⼯⼈,⽤同⼀批原材料在同⼀台机器设备上所⽣产出来的同⼀种零件,其质量特性值不会完全⼀样。
这就是我们常说的产品质量特性值有波动(或称分散、差异)的现象。
这种现象反映了产品质量具有“波动性”这个特点。
2.引起质⼰被动的4M1E造成产品质量的波动的原因主要有五个⽅⾯:①⼈(Man)操作者对质量的认识、技术熟练程度、⾝体状况等;②机器(Machine)机器设备、⼯夹具的精度和维护保养状况等;③材料(Material)材料的成分、物理性能和化学性能等;④⽅法(Method)这⾥包括加⼯⼯艺、⼯装选择、操作规程、测量⽅法等;⑤环境(Enviromen)⼯作地的温度、湿度、照明和清洁条件等;由于这五个因素的英⽂名称的第⼀个字母是M和E,所以常简称为4M1E。
3.偶然性原因和系统性原因从过程质量控制的⾓度来看,通常⼜把上述造成质量波动的五⽅⾯的原因归纳为偶然性原因和系统性原因。
质量控制图原理.pptx

• 在± 3s之外,出现的概率为: 100%-99.73%=0.27%,
即检验1000个样品,可能有997个落在±3s之 内,而在±3s之外的检验结果不会超过3个。
• 确切地说,大于μ+3s或小于μ-3s概率为 0.27%/2=0.135%≈0.1%。
• 因此,在控制图中,测定值超出μ+3s或μ- 3s界限只有0.1%,即小概率事件实际上不发 生的原理。如果发生了,就判为异常。
• 啤酒中双乙酰含量在第311页0/共-410页000ug/L,属痕量
30
• 由于痕量分析标准偏差较大,偏差的大小和方 法本身有关,包括实验条件如样品处理过程、 进样系统、检测器的种类等,我们必须采用适 当的方法对分析过程加以控制,以保证检测处 于正常的工作状态下,避免系统误差的产生并 尽量减少偶然误差。
• ③ 如果各次分析的时间间隔较长,在此期间
可能由于气温波动较大而影响测定结果,必 12 第13页/共40页
• 分析数据的运算:当质量分析样品的分析数
据累积至20个以上时,即可按下列公式计算 出总均X 值 、标准偏差S、平均R极差 等。
X X1 X2 , X
X ,
2
n
S
( Xi X )2
24
第25页/共40页
(二)非控制状态的判定
标准1:有一个点在控制界限外。 标准2:9个点均在中心线的同一侧。 标准3:6个点连续上升或下降。 标准4:14个点交替上升下降。 标准5:连续三点中,有2个点在区域2 σ~ 3 σ
或在控制界限外。 标准6:连续5点中,有4个点在区域1 σ~ 2 σ
或落到该区域之外。 标准7:连续15点都在区域CL~ 1σ中。 标准8:连续8点都落在区域CL~ 1σ之外。
质量控制图的正确理解和应用

质量控制图的正确理解与应用众所周知,目前定量检测室内质控的主要工具为质量控制图。
工作中经常遇到对质量控制图的理解与应用问题,下面谈一些基本认识,供同道们参考。
一、“事后检查”与“予防为主”日常工作中,当每批检验结果出来后,都会对检验结果进行复核,检查有无漏项、填错结果等等,并对一些异常结果的可信度进行评估,显然这对保证检验结果是否正确无误有重要作用,但也不能否认,这种复核制度有许多局限性,例如患者间的结果各不相同,检测结果出来前,无法知道每一患者测定值应该是多少,有怀疑时经常进行重复检查,但重复检查也只是检查重复性,如存在系统误差,复查也发现不了问题。
大家知道,质控图法是从工业中引进临床实验室的。
1924年W.A.Shewhart发明了质量控制图,直到1951年Levey-Jennings才将Shewhart质控图引入临床实验室,将临床实验室的质量控制推向了一个新阶段,质控图也成为临床实验室内质控的主要方法。
但临床检验与企业生产有许多不同,工业生产中,每一批产品的不管数量多大,其规格是事先规定了的,而且都是一致的,但由于临床标本某一成分的含量事先并不知道,检测结果是否正确的评估就带有一定主观性、评估的结果也带有一定不确定性。
分析阶段的质量控制是通过检测过程的控制来保证检验质量的。
其基本思路是检测条件得到控制,其检验结果的准确性(与真值或理想值的偏倚)及精密度是满足临床要求的话,则检测过程如果是在控制条件下进行的,那么检验结果就应该是可靠的,反之如果检测过程失控,检验结果将是不可靠的。
所以质控图法是通过对检测过程是否在控的判断,来推论检验结果是否可靠,这是总体上的判断。
这是一个重要的思想,但总体上的判断不能完全代替“个体的判断。
”因为一批检验结果中,难免有个别非常“异常”、难以解释的结果,这就需要“个别对待、个别处理”;同时质控图法用来判断检测过程是否在控,并作出该批结果可否发出时,还有一个前提:即送检标本的质量必须是合格的。
质量控制流程图

3 139
1
323 221
3
1
2
2
7 4 10
6 2 26 2
3 1 2 2
2 24
52 61
13
25
1
3
23
1 10 22 1
133
155
124
68
69
269
3
75
98
60
3
2 2
4
57 10 2
2
6
8
持续改善,消除浪费
实施QCPC – 案例
统计并展示FPY数据,每个车间,具体到每个产品每条拉
Process Yield Wk1 Wk2 First Pass Yield 90.6% 0.0%
数据
持续改善,消除浪费
实施QCPC – 分析
定义
测量
分析
改进
控制
使用QCPC核查表上的折返数据,制作已观察到的“折返率”的巴累托图形
计算
折返 率
=
折返数 进入流程的件数
持续改善,消除浪费
实施QCPC – 分析
计算工序层面的折返率
流程 OP 10
折返数 35
OP 20
101
OP 30
77
OP 40
20000 18000 16000 14000 12000 10000
8000 6000 4000 2000
0
120%
17264
13987
8100%0% 69%
72%
76%
80%
83%
86%
89%
91%
93%
95%
96% 97% 98% 99%
质量管理工程中的质量控制图分析方法解析

质量管理工程中的质量控制图分析方法解析在质量管理领域中,质量控制图是一种常用的工具,用于监控和分析过程的稳定性和性能。
通过质量控制图,我们可以及时发现过程中的异常情况,并采取相应的措施进行改进和调整。
本文将对质量控制图的分析方法进行解析,探讨其在质量管理工程中的应用。
一、质量控制图的基本原理质量控制图是基于统计学原理的一种图形化工具。
其基本原理是将过程的数据按照时间顺序绘制在图表上,通过观察数据的变化趋势,判断过程是否处于稳定状态。
常用的质量控制图包括均值图、范围图、标准差图等。
二、均值图的分析方法均值图是一种用于监控过程平均水平的质量控制图。
其分析方法主要包括以下几个步骤:1. 收集过程数据:收集过程中的样本数据,并按照时间顺序记录。
2. 计算过程平均值:根据收集到的数据,计算每个样本的平均值,并绘制在均值图上。
3. 绘制控制限:根据统计学原理,计算出均值图的上下控制限,并绘制在图表上。
4. 分析数据变化:观察均值图中的数据点是否在控制限范围内,如果出现超出控制限的情况,则表示过程出现异常,需要进行进一步分析和改进。
三、范围图的分析方法范围图是一种用于监控过程离散程度的质量控制图。
其分析方法如下:1. 收集过程数据:同样需要收集过程中的样本数据,并按照时间顺序记录。
2. 计算样本范围:对于每个样本,计算其最大值和最小值之间的范围,并绘制在范围图上。
3. 绘制控制限:根据统计学原理,计算出范围图的上下控制限,并绘制在图表上。
4. 分析数据变化:观察范围图中的数据点是否在控制限范围内,如果出现超出控制限的情况,则表示过程出现异常,需要进行进一步分析和改进。
四、标准差图的分析方法标准差图是一种用于监控过程离散程度的质量控制图,其分析方法与范围图类似,但在计算标准差时,使用的是样本标准差而不是样本范围。
标准差图的分析方法如下:1. 收集过程数据:同样需要收集过程中的样本数据,并按照时间顺序记录。
2. 计算样本标准差:对于每个样本,计算其标准差,并绘制在标准差图上。
质量控制工程图

7、产品的磁性能、耐温状况。
8、产品的规格牌号、标识
1、产品的尺寸。
2、产品的密度.
3、产品的表磁.
4、产品的磁性能。
5、产品的耐温。
6、规格牌号是否相符
7、标识是否清楚
1、目视
2、真空计
3、卡尺
4、无芯磨
5、高斯计
6、磁通计
7、磁测仪
8、密度计
1、按工艺要求
2、两极偏差≤300Gs
2、品管部检验员
压
制
1、环境温、湿度。
2、投料重量
3、压制尺寸
4、大小头
5、有无开裂
6、坯件防护
7、规格牌号是否相符
8、充磁电流
1、环境温、湿度。
2、投料重量
3、压制尺寸
4、大小头
5、有无开裂
6、标识
7、充磁电流
பைடு நூலகம்1、温湿度计
2、电子秤
3、卡尺
4、目视
1、温度不超过22℃,湿度不超过70%。
2、粉重按工艺单偏差≤0。5%
6、产品防护.
7、煮料或烤料有无过头现象
8、规格牌号是否相符
1、加工尺寸公差。
2、产品垂直度。
3、表面刀丝。
4、平面不平度。
5、外观缺角。
6、产品有无煮或烤氧化现象。
1、千分尺
2、角度尺
3、目视
4、塞尺
1、尺寸公差符合工艺要求
2、产品不垂直度≤0。10mm
3、表面无明显刀丝印痕
4、平面不平度≤0。02mm
镀
1、电镀产品尺寸公差、电镀过程参数控。
2、表面镀层色泽一致性.
3、镀层结合力、耐腐蚀程度。
质量控制图

目
录
质量控制图的原理 一、质量控制图的原理 二、质量控制图的种类 三、质量-极差控制图 六、质量控制图的分析 七、质量控制图在啤酒分析中的应用 八、质量控制图对于仪器分析工作的指导作用
4
一、 质量控制图的原理
质量控制图是假设分析测试处于受控状 质量控制图是假设分析测试处于受控状 态时, 态时,总体分析数据的质量特性呈正态分布 N(μ 其图形来自于正态分布曲线图。 N(μs2 )。其图形来自于正态分布曲线图。 当将正态分布图按顺时针方向旋转90 90° 当将正态分布图按顺时针方向旋转90°,再 上下翻转180 180° 即成为图1的质控基本图 上下翻转180°时,即成为图1的质控基本图 由正态分布性质可知, 形。由正态分布性质可知,质量指标值落在 3s以外的概率只有0.27%,这是一个小概 以外的概率只有0.27%, ±3s以外的概率只有0.27%,这是一个小概 按照小概率事件原理, 率。按照小概率事件原理,在一次实践中超 3s的范围的小概率事件几乎是不会发 出±3s的范围的小概率事件几乎是不会发 生的。 生的。
11
这五条线是通过搜集过去在测试稳定状态下 某一段时间的数据计算出来的。使用时, 某一段时间的数据计算出来的。使用时,定时抽 取样本, 取样本,把所测得的质量特性数据用点子一一描 在图上。根据点子是否超越 是否超越上 在图上。根据点子是否超越上、下控制线和点子 的排列情况来判断测试过程是否处于正常的控制 状态。 状态。
17
18
19
(2)计算各组平均值和极差 x = ∑ xi , R = xmax − xmin (3)计算 x的平均值和R
20
16.652 x= = = 0.833 k 20 (4)计算UCL、CL和LCL
第5章质量控制图

Range
x-图与R-图实例: x -图
X-Bar Chart
10.9 10.85
10.8 10.75
10.7 10.65
10.6 10.55
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Sample Number
按时间顺序确定 的样本号
3、多个点接近边界
连续3点中有2点接近边界;连续7点中有3点接近边界 连续10点中有4点接近边界
质量 特性 数据 或统 计量
UCL
CL LCL
1 2 3 4 5 6 7 8 9 10
按时间顺序确定 的样本号
4、连续7点出现按次序上升或下降 的趋势
质量 特性 数据 或统 计量
应用时需 具体化 对总体参数(u ,σ)进行估计
注意 规格界限不能作为控制界限线
六、控制图的种类
1、按对象分
控制图
名称
X —R
~ X
—R
X —RS
均值—极差控制图
中位数—极差控制图 单值—移动极差控制图
计量值数据 计数值数据
X —S 均值—标准偏差控制图 Pn 不合格品数控制图. p 不合格品率控制图 C 缺陷数控制图 U 缺陷率控制图
10.78 10.591 10.693 10.749 10.791 10.744 10.769 10.718 10.787 10.622 10.657 10.806
10.66
观察 2 10.689
10.86 10.667 10.727 10.708 10.714 10.713 10.779 10.773 10.671 10.821 10.802 10.822 10.749 10.681
质量控制图的原理和作用

质量控制图的原理和作用
质量控制图是质量管理中常用的工具,用于监控和控制过程的稳定性和一致性。
它基于统计原理,帮助团队识别和分析过程中的变异,并提供及时的反馈,以便采取适当的措施来改进和控制质量。
质量控制图的原理是建立在统计过程控制的概念上。
它通常基于数据采集和样本检验,并与预期的标准进行比较。
以下是几个常见的质量控制图和其原理:
1. 控制图:控制图是一种统计工具,用于检测过程中的常规变异和特殊因素引起的非常规变异。
它基于样本数据的变异性,并通过设置上下控制限来标识正常变异范围。
当样本数据超出控制限时,表示过程发生了特殊因素,需要进一步调查和纠正。
2. 均值图:均值图用于监控过程的中心线(平均值)是否在可接受的范围内稳定。
它计算每个样本的平均值,并绘制在控制图上。
如果平均值超出控制限,表示过程存在偏差,需要进行调整和改进。
3. 范围图:范围图用于监控过程的变异性。
它计算每个样本的范围(最大值与最小值之差),并绘制在控制图上。
范围图可以帮助识别过程中的非常规变异,并检测出偶然误差或特殊因素的存在。
4. Cp/Cpk图:Cp(过程能力指数)和Cpk(过程能力指数对称性)图用于评
估过程的能力和一致性。
它们基于过程的规格限制和测量数据的变异性,提供了关于过程能力。
质量控制图

谢谢!
六、质量的控制图受控状态的分析
3.失控状态
(1)若点子在控制界限外恰在控制界限上,则分析 过程处于失控状态 (2)在点子基本上随机排列的情况下,有下列情况 出现,则判断有异常:
质量控制图
六、质量的控制图受控状态的分析
3.失控状态
(1)若点子在控制界限外恰在控制界限上,则分析过程处 于失控状态 (2)在点子基本上随机排列的情况下,有下列情况出现, 则判断有异常
质量控制图
五、质量控制图的参数计算与作图
表1 质量控制图的基本参数计算公式
质量控制图
五、质量控制图的参数计算与作图
计算3σ控制限的系数 :
当样本大小相同时,即各组由相同数目的观测值组成时,系数 A1和A2;B3和B4;D3和D4的数值列于表2
表2 计算3σ控制限的系数
★
五、质量控制图的参数计算与作图
② 当有连续不少于7点的上升或下降的倾向(点子逐渐上升或下降的状态称为倾 向)时,则判断有异常
质量控制图
六、质量的控制图受控状态的分析
3.失控状态
(2)在点子基本上随机排列的情况下,有下列情况出现,则判断有异常:
③ 中心线一侧点子连续出现下列情况:连续11点中,至少10点在一侧;连续14 点中,至少12点在一侧;连续17点中,至少14点在一侧;连续20点中,至少16 点在一侧,应判 断有异常
质量控制图
二、质量控制图的作用
(1)可以对被控过程作出估计。如用极差或标准偏差控制图可以估 计例行测量过程变动性 (2) 对例行检验工作中决定检验数据取舍的最好标准和依据 (3) 是检验各实验室间数据是否一致的有效方法 (4) 可检验测量过程是否有明显的系统偏差,并能指出偏差的方向 (5) 可以及时、直观地展示出分析检测过程是否处于统计控制中 (6)当控制图表示出失控时,它能指出在什么时间、什么位置及多大 置信水平下发生了问题,它还能指出问题的性质,如平均值单向 变化趋势、突然的漂移、变动性的增大等情况
绘制常用分析质量控制图

五、质量控制图重新绘制
出现一些情形,质量控制图重新绘制
当操作人员更换或通过学习操作水平显著提高 仪器设备更新 采用新的分析方法后其它试剂 改变实验环境或条件时 经过相当长时间使用后应重新制作控制图(一般以20对数据为
一个单元) 在使用均值—极差控制图中,如极差值R稳步下降逐次变小,
逐次变小以至于R≈D3 R(n>7)已接近下控制限时,表明精密度有
存在系统误差,需查明原因
四、质量控制图的判断
质量控制图是对过程质量特性值进行测定、记录、评估, 从而检查过程是否处于控制状态。
利用质量控制图建立可靠的数据置信限:一组数据的控 制图不能真正反映出测量系统的精度,由此而建立的置信 限也不算十分可靠,但是随着测定次数的增加,通常把以 前的数据和现在的数据合并后再做新的质控图,依次进行 下去,平均值变化不大,标准偏差S变小,即警戒限和控制 限逐渐变窄,这样确定的置信限,才是测量系统长期的测 量情况和特性的反映,所以才比较可靠。
0.29
0.29)
0.51
上警告限:
R
2 3
(D
4
R
R)
0.29
2 (3.27 3
0.29
0.29)
0.73
上控制限: D 4 R 3.27 0.29 0.95
下控制限: D3R 0 0.29 0
三、质控图的绘制
三、质控图的绘制
图5 粗蛋白—质控样均数-极差控制图
三、质控图的绘制
n
x i1 xi x1 x2 xn
n
n
一、质量控制图基本概念
4、标准偏差:一种量度数据分布的分散程度之标准,用以衡量数 据值偏离算术平均值的程度。
贝塞尔公式:
质量控制图

质量控制图近年来质量控制图愈来愈多地被用来控制与评估分析测试的质量。
质量控制图建立在实验数据分布接近于正态分布(高斯分布)的基础上,把分析数据用图表形式表现出来,纵坐标为测量值,横坐标为测量值的次序(次数)。
过去人们采用假定是精确的分析方法来检查样品的变异性,评估分析测试的结果。
目前,则是用组成均匀、稳定的与试样基体相似的标准物质来检查分析方法的变异性,评估与控制分析测试的质量。
质量控制图的作用(一)质量控制图有三个作用:(1)它是分析系统性能的系统图表记录,可用来证实分析系统是否处于统计控制状态之中,并可以找出质量变化的趋势;(2)是对分析系统中存在的问题找出原因的有效方法;(3)可积累大量的数据,从而得到比较可靠的置信限。
(二)质量控制图的分类质量控制图的形式有x(测量值)质量控制图、(平均值)质量控制图和R(极差)质量控制图等。
(1)x质量控制图:这种控制图的纵坐标为测量值,横坐标为测量值的次序。
中线可以是以前测量的平均值,也可以是标准物质的标准值(即总体平均值)μ。
其警戒限和控制限分别为:警戒限(线):警戒上限(线)x+ 2s(或2σ)警戒下限(线)x- 2s(或2σ)控制限(线):控制上限(线)+ 3s(或2σ)控制下限(线)x- 3s(或2σ)注:s为标准偏差。
σ为总体标准偏差。
分析测试中测量值的平均值x与标准物质的标准值μ之间为完全相等,这是正常的。
但两者之间的差异不能太大。
如果标准物质的标准值落在平均值与警戒限之间一半高度以外去了,即︱x–μ ︳>1s时,说明分析系统存在明显的系统误差,这是不能允许的,此时的控制图不予成立。
应该重新检查方法、试剂、器皿、操作、校准等各个方面,找出误差原因之后,采取纠正措施,使平均值尽可能地接近标准物质的给出值。
为了画好一张质量控制图,首先必须要有稳定、均匀、具有与分析试样相似基体的标准物质标样。
通常标准物质价格较高,而且为了确保标准物质的稳定性,还必须保存在低温、惰性气体、避光或湿度控制的条件下。
质量控制图

质量控制图质量控制图的概念与用处如果要系统地介绍,可能要从质量管理(Quality Management,QM)开始,从传统的质量管理七工具,到全面质量管理阶段的6σ管理,这里不去展开,只介绍质量控制图。
质量控制图,简称控制图(Control Chart),是质量管理七工具之一,由美国的贝尔电话实验所的休哈特(W.A.Shewhart)博士在1924年首先提出,因此也称为“休哈特控制图”。
最初的应用当然是在生产领域,使用抽样的方式检验产品的质量是否处于控制状态。
一般而言,指标的波动受随机因素和系统因素的影响,如果指标只受到随机因素的影响,那么在正常情况下指标的变化状态是稳定的、可控的,但如果发生某种系统性的变化就会使指标超出原先可控的波动范围,处于失控状态,所以控制图就是帮助我们及时发现这种失控状态,从而进行及时的调整。
质量控制图通过统计上均值μ和标准差σ的状况来衡量指标是否在稳定状态,同时选择3σ来确定一个正常波动的上下限范围(根据正态分布的结论,指标的特征值落在μ±3σ之间的概率是99.73%),使用均值μ作为控制图的中心线(Center Line, CL),用μ+3σ作为控制上限(Upper Control Limit, UCL),用μ-3σ作为控制下限(Lower Control Limit, LCL),如图。
根据衡量的指标数值类型的差异,质量控制图主要分为两类:计数型控制图和计量型控制图,下面分别介绍其中的一种:质量控制图具体用法因为生产制造业和互联网行业存在着较大差异,所以这里只介绍适合用于网站分析的2个控制图。
其中计数型控制图中主要介绍P控制图,主要用于定类型变量,即符合二项分布检验“是否”的变量,如用户是否完成交易、用户是否为新用户……这类指标一般会以比率的形式出现,如转化率、新用户比例等,而P控制图正是衡量这些比率是否出现异常(在生产行业通常用于不合格率等);另外的计量型控制图主要用于一些关键的数值度量,如每个订单的消费额、每个用户的下载次数等,这类指标在网站分析中通常计算全部数据的均值来观察波动情况,其实计量型控制图最常用的是均值-极差(X-R)和均值-标准差(X-S)控制图,但两者都是通过取样的方式实现的,并且每次取样的样本数最好能保持相等,所以这类抽样统计不太适合于上述网站分析中的指标,这里介绍个相对能够普遍适用并且计算也没有那么复杂的图——单值-移动极差(X-MR)控制图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制图的标题
质量特性 x
公差上限Tu
控制上限UCL
Upper Control Limit
3σ
中心线CL
Central Limit
3σ
控制下限LCL
Lower Control Limit
公差下限TL
样品编号(或取样时间)
控制图的基本模式
2005.03.10
抽取样本
对策措施
检验
制程正常
原因分析
绘制管制图
Ri
0.06
0.07 0.06 0.07 0.11 0.12 0.10 0.06 0.12 0.09 0.11 0.06 0.07 0.10
样 本
xi1 xi 5
xi
49.490
49.504 49.510 49.506 49.510 49.502 49.516 49.502 49.502 49.500 49.524 1237.66 9 49.5068
CL= 0.08
例-第六步
7、分析生产过程是否处于统计控制状态; 利用分析用控制图的判断规则,分析生产过程 是否处于统计控制状态。本例经分析,生产过程 处于统计控制状态。
例-第七步
8、计算过程能力指数;
1) 求 C p值
T T 0.20 Cp 0.97 6 6 R / d 2 (n) 6 0.08 / 2.326
制程异常 No
制程是 否
异常
Yes
控制图的实施循环
正态性假定
3σ准则
小概率原理 反证法思想
控制图的设计原理
正态性假定:
任何生产过程生产出来的产品,其质量特性值 总会存在一定程度的波动,当过程稳定或者说受控 时,这些波动主要是由5MIE的微小变化造成的随机 误差。此时,绝大多数质量特性值均服从或近似服 从正态分布。这一假定,称之为正态性假定。
★
计数值控制图
x-R图是x图(均值控制图)和R图(极差控制图)联合使 用的一种控制图。 x图主要用于判断生产过程的均值是否处于或保持在所要 求的受控状态; R图用于判断生产过程的标准差是否处于或保持在所要求 的受控状态;
x- R图通常在样本大小n ≤ 10时使用,是一种最常用的计 量值控制图;
X-R图(均值-极差控制图)
式中d2(n)查控制图系数表,n = 5时,d2(n)=2.326 2) 求修正系数k
K=
Tm
T /2
x Tm T /2
49.5068 49.50 0.20 / 2
0.068
例-第八步
8、计算过程能力指数;
1) 求修正后的过程能力指数Cpk
Cpk = (1- k) Cp = (1 – 0.068 )×0.97= 0.90
控制图的用途
控制图的基本格式包括两个部分: 1、标题部分;
Ø Æ ¿ Ö Í ¼ à û ³ Æ £ º XXX¿ Ø Ö Æ Í ¼ ú Æ ² ·Ã û ³ Æ Ê Á Ö ¿ Ì Ø Ð Ô Û ² ¹ â · ½ · ¨ æ · ¹ ¶ ½ ç Ï Þ ¨» £ ò Ò ª Ç ó £ © æ · ¹ ¶ ± à º Å ú ² É ú ¹ ý ³ Ì Ö Ê Á ¿ Ò ª Ç ó
质量管理原则(澳大利亚)
使用正确的过程控制技术,可使得质量提高而成本降低。 25~40% 10~25%
预防 检验 核对
差额25% 预防
检验
核对 故障
故障
采用七项质量管理原则之前
消除浪费
采用七项质量管理原则之后
质量成本(以占生产成本的百分比计算 2000.8.25
1977年3月27日,两架波音747飞机在Canary Islands的机场 的跑道上相撞,583人丧生。
3σ准则
小概率原理
所谓小概率原理,即认为小概率事件一般是不会发 生的。 由准则可知,若X服从正态分布,则X的可能值超 出控制界限的可能性只有0.27%。因此,一般认为不 会超出控制界限。 小概率原理又称为实际推断原理,当然运用小概率 原理也可能导致错误,但犯错误的可能性恰恰就是此 小概率。
小概率原理
2、控制图部分;
¤× ¹ ÷Á î ± à º Å µ ¼ ³ ä æ ¶ ¹ ¨È Õ ² ú Á ¿ ä ô ¼ ¸ é Ñ ³ ù ý ¿ Ê Á Û ² ¹ â Ò Ç ± à º Å
Õ ¼ Ê ¯ Ê ý ¾ Ý Æ Ú ¼ ä è ± É ¸ ± à º Å Ù × ² ÷Ô ± ì Ñ ¼ é Ô ±
p 2 3C p (1 k ) 3C p (1 k )
例-第九步
分析用控制图用于分析生产过程是否处于统计控 制状态。分以下四点考虑: 1. 若经分析后,生产过程处于统计控制状态且满足质量 要求,则把分析用控制图转为控制用控制图; 2. 若经分析后,生产过程处于非统计控制状态,则应查找 过程失控的异常原因,并加以消除,去掉异常数据点, 重新计算中心线和控制界限线; 3. 若异常数据点比例过大,则应改进生产过程,再次收集 数据,计算中心线和控制界限线;
1 R Ri 0.0800 k i 1
例-第三步
k
4、计算控制线;
UCL x A2 R 49.5068 0.577 0.0800 49.5530 x 图CL x 49.5068 LCL x A2 R 49.5068 0.577 0.0800 49.4606
系数A(n)数值表
n A(n) D3(n) D4(n) 2 1.881 3.267 3 1.023 2.575 4 0.729 2.282 5 0.577 2.115 6 0.483 2.004
上 式 中 A2,D4,D3 均 从 控 制图系数表中查得:当 n=5时,A2=0.577 D3<0 D4=2.115
Ri
0.09
0.05 0.07 0.06 0.05 0.08 0.10 0.06 0.09 0.05 0.11 2.00 0.080
1
2 3 4 5 6 7 8 9 10 11 12
15
16 17 18 19 20 21 22 23 24 25
平 均
单位 mm
13 14
表(某零件长度值数据表)
数据
5MIE:
人、机器、原材料、工艺方法、测量及生产环境
正态性假定
3σ准则
在生产过程中,仅有偶然性误差存在时,质量 2 ),则据正态分布的概 特性X服从正态分布N( µ , 率性质,有
P{µ - 3 σ < X< µ + 3 σ }=99.73 %
也即( µ - 3 σ , µ + 3 σ )是X的实际取值范围。
例-第五步
6、描点;
49.56 49.54 49.52 49.5 49.48 49.46 49.44
x图
UCL= 49.553 CL= 49.5068
LCL= 49.4606
0.2 0.18 0.16 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0
R图
UCL= 0.1692
3
2
预防检查能力不足的系统
含铅汽油
无铅汽油
三芯电源插头只能以唯 一的位置插入三芯插座
防止将含铅汽油加入适 用无铅汽油的车辆
预防为基础的系统
研发费用占国民生产总值的百分 比与生产力之间的关系(55-64年)
过程控制应当以预防为目的,而不是简单地在发现问题后返工。
如果输入符合规范,且过程变量被控制在一定的范围内, 则输出就是正确的。
2、计算每组的样本均值和样本极差;
1 xi x i j n j 1
n
i =1,2,…,k
Ri max xi
1 j n
j
minx
1 j n i j
例-第二步
样 本
xi1 xi 5
xi
49.485
49.516 49.500 49.496 49.530 49.506 49.504 49.502 49.506 49.526 49.500 49.512 49.494 49.526
倘若过程质量要求为过程能力指数不小于1,则显然不满足要 求,于是不能将分析用控制图转化为控制用控制图,应采取措施, 提高加工精度。
据过程平均不合格品率P与过程能力指数的关系,计算P 值如下:
2 3 0.97 (1 0.068) 3 0.97(1 0.068) 2 (2.71) (3.11) 2 0.9966 0.9991 0.43%
检验还是预防?
以预防为主的系统,我们应着重减少变化,并避免浪费。
检验还是预防?
1、分析判断生产过程的稳定性,从而使生产过程处于统 计控制状态; 2、及时发现生产过程中的异常现象和缓慢变异,预防不 合格品发生; 3、查明生产设备和工艺装备的实际精度,以便作出正确 的技术决定; 4、为评定产品质量提供依据;
某厂生产一种零件,其长度要求为49.50±0.10 ( mm ), 生产过程质量要求为过程能力指数不小 于1,为对该过程实施连续监控,试设计x-R图;
例
1、收集数据并加以分组 在5MIE充分固定,并标准化的情况下,从生产 过程中收集数据。 本例每隔2h,从生产过程中抽取5个零件,测量 其长度值,组成一个大小为5的样本,一共收集25 个样本. 一般来说,制作-R图,每组样本大小 n≤ 10 , 组数k≥ 25. 例-第一步
本章主要要求
1924年,美国的休哈特(W.A.Sheuhart)首先提出用控制 图进行工序控制,起到直接控制生产过程,稳定生产过程
的质量达到预防为主的目的。
在现场直接研究质量数据随时间变化的统计规律 的动态方法; 控制图是判别生产过程是否处于控制状态的一种 手段,利用它可以区分质量波动是由偶然原因引 起的还是由系统原因引起的。 控制图由来
