《极坐标系》导学案
高中数学《极坐标系》导学案 (2)

§1.2极坐标系1. 理解空间向量的概念,掌握其表示方法;2. 会用图形说明空间向量加法、减法及它们的运算律;3. 能用空间向量的运算意义及运算律解决简单的立体几何中的问题.【重点、难点】\教学重点:空间向量的加减与数乘运算及运算律.教学难点:应用向量解决立体几何问题.二、学习过程【情景创设】1.平面直角坐标系中的点与其直角坐标(x,y)之间是一一对应的,那么极坐标系中的点与其极坐标(ρ,θ)之间是一一对应的吗?提示:不是一一对应的.若已知点的极坐标(ρ,θ),则点是确定的,反之,若已知点,则其极坐标不确定.2.在极坐标系中,点批的位置是否是确定的?提示:是确定的.点M的位置位于∠xOM的终边上,其中∠xOM= ,|OM|=3(O为极点).3.在极坐标系中,极轴上一点P距离极点的距离为1,那么点P的极坐标惟一吗?提示:不惟一.点P的极坐标为无数个有序数对(1,2kπ),k∈Z.【导入新课】1.极坐标系的建立1)取极点:平面内取一个______.(2)作极轴:自极点引一条射线Ox.(3)定单位:选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).2.点的极坐标(1)定义:有序数对(ρ,θ)叫做点M的极坐标,记为__________.(2)意义:ρ______,即极点O与点M的距离(ρ≥0).θ=______,即以极轴Ox为始边,射线OM为终边的角.三 、典例分析1,在极坐标系中,求点 (2,)3P π 到极轴的距离.2.在极坐标系中,极轴的反向延长线上一点M 与极点的距离为2,则点M 的极坐标的下列表示:①(2,0);②(2,π);③(2,-π);④(2,2k π)(k ∈Z).其中,正确表示的序号为------------------------.3,在极坐标系中,点O 为极点,已知点 (6,)3A π,2(6,)3B π 求|AB|的值.【变式拓展】在极坐标系中,若△ABC 的三个顶点为 5(5,)2A π,5(8,)6B π,7(3,)6C π 判断三角形的形状.四、总结反思确定点的极坐标的方法点P 的极坐标的一般形式为(ρ,θ+2k π),k ∈Z ,则(1)ρ为点P 到极点的距离,是个定值.(2)极角为满足θ+2k π,k ∈Z 的任意角,不惟一,其中θ是始边在极轴上,终边过OP 的任意一个角,一般取绝对值较小的角.五、随堂检测1,已知在极坐标系中,O 为极点, (3,)6A π, B(ρ,θ),OA ⊥OB ,|AB|=5,ρ≥0,θ∈[0,2π),求点B 的极坐标.,2,在极坐标系中,已知点A (4,1), (3,1)2B π+ 则线段AB 的长度是()A.1 C.7 D.5。
极坐标系的概念(学案)444

选修4-4《1.2极坐标系》导学案引导老师:高朝孟学习目标:1.学会建立极坐标系。
2.掌握极坐标系中坐标与点的对应关系。
学习过程:一、问题情境,导入新课:情境1:钓鱼岛问题:中国海监船如何确定日本渔船?二、讲解新课:1、合作探究,概念形成。
(1)读教材P8-P10页,归纳极坐标系的建立。
定义新知1:极坐标的概念1、如右图,在平面内取一个定点O,叫做, 自极点O引一条射线Ox,叫做;再选定一个,一个(通常取)及其(通常取方向),这样就建立了一个。
极坐标系中点该如何表示M到极点的距离记做,以OX为始边,OM为终边所成的角叫极角。
有序数对叫做点M的,记作。
2、思考:建立极坐标系有几要素?),(θρM●ρθOx3、典型例题例1 写出下图中各点的极坐标A ( )B ( )C ( )D ( )E ( )F ( )G ( )变式训练.在极坐标系里描出下列各点(3,0),(6,2),4(3,)(5,),235(3,),(4,)65(6,)3A B C D E F G ππππππ合作探究1:点M 的极坐标是什么?惟一吗?这些极坐标之间有何异同?点M 的极坐标统一表达式是什么?答:合作探究2:怎样使得平面内的点和极坐标一一对应呢?答:探究3:一个极坐标是否对应惟一的一点呢?答:课堂练习已知极坐标M (5,34π),下列所给出的不能表示点M 的坐标的是( ))38,5(,)3,5(),32,5(),310,5(ππππ--- D C B A三、课堂小结通过这节课的学习,我们有哪些收获?四、分层作业,发展深化:必做题:12P 习题1.2第1、2题选做题:1,已知)3,2(πQ ,分别按下列条件求出点P 的极坐标。
(1) P 是点Q 关于极点O 的对称点;(2) P 是点Q 关于直线2πθ=的对称点;(3) P 是点Q 关于极轴的对称点。
广东省广州市番禺区石碁中学高二数学《极坐标系》导学案

一、学习目标:1、可以把点的直角坐标转化为极坐标;2、可以把点的极坐标转化为直角坐标;二、学习内容:【预习案】教材助读:阅读选修4-4第9页完成:1、建立一个极坐标系(画图,标名称)2、有序数对(,)ρθ叫做点的极坐标,其中ρ叫做 ,表示θ叫做 ,表示 阅读选修4-4第11页完成:3、把极坐标(,)ρθ化为直角坐标用公式:4、把直角坐标(,)x y 化为极坐标用公式:【探究案】例1:(1)点33,π⎛⎝ ⎫⎭⎪的直角坐标为(2)点()22-,的极坐标为例2:若A 33,π⎛⎝ ⎫⎭⎪,B ⎪⎭⎫ ⎝⎛-64π,,则|AB|=___________,S AOB ∆=___________。
(其中O 是极点)【训练案】教材第12页:3,4,5作业:1、已知下列点的极坐标,求它们的直角坐标。
2、已知点的直角坐标, 求它们的极坐标.石碁中学高二年级数学科“以学定教、分层渗透”导学稿极坐标系(二)一、学习目标: 1、可以把直线和圆的极坐标方程转化为直角坐标方程;2、可以把直线和圆的直角坐标方程转化为极坐标方程。
二、学习内容:(3,)6A π(2,)2B π(1,)2C π-3(,)24D π3(2,)4Eπ(3,A(1B (5,0)C (0,2)D -【探究案】例1:把极坐标方程()cos sin 2ρθθ+=化为直角坐标方程例2:求圆心为C 36,π⎛⎝ ⎫⎭⎪,半径为3的圆的极坐标方程。
小结:把极坐标方程化为直角坐标方程用公式:把直角坐标方程化为极坐标方程用公式:【训练案】1、在极坐标系中,点()1,0到直线()cos sin 2ρθθ+=的距离为2、把极坐标方程cos()16πρθ-=化为直角坐标方程是6、在极坐标系中,过点)6,4(π,并且和极轴平行的直线的极坐标方程是___________________. 7、在极坐标系中,圆心在)4A(1,π,半径为1的圆的极坐标方程是_______________________.。
高中高三数学《极坐标系》教案、教学设计

3.教师巡回指导,针对每个小组的讨论情况进行点评,引导学生深入思考。
(四)课堂练习
1.设计具有代表性的练习题,涵盖本节课的知识点,让学生在练习中巩固所学。
2.分层次布置练习题,使每个学生都能在适合自己的练习中提高。
3.及时批改反馈,针对学生存在的问题,给予个性化指导。
高中高三数学《极坐标系》教案、教学设计
一、教学目标
(一)知识与技能
1.理解极坐标系的概念,掌握极坐标与直角坐标之间的转换方法,能够熟练运用互化公式进行坐标变换。
2.掌握极坐标系下点的表示方法,能够准确地绘制极坐标图形,并解决相关几何问题。
3.熟练运用极坐标系解决实际问题,如极坐标下的直线、圆等图形的方程求解,以及极坐标系在物理学、工程学中的应用。
1.基础题:完成课本第十五章的习题1、2、3,要求学生熟练掌握极坐标系的基本概念和转换方法。
2.提高题:解答课本第十五章习题4、5,培养学生运用极坐标系解决几何问题的能力。
3.应用题:结合实际案例,设计一道与极坐标系相关的应用题,要求学生运用所学知识分析问题、解决问题。
4.研究性学习:分组进行课题研究,选择与极坐标系相关的科学问题或实际应用场景,深入探讨并撰写研究报告。
作业布置要求:
1.学生在完成作业时,要认真思考,独立完成,切勿抄袭。
2.对于基础题,要求学生掌握基本概念,注意运算过程的准确性。
3.提高题和应用题旨在培养学生的解题策略和实际应用能力,鼓励学生多角度思考问题。
4.研究性学习要注重团队合作,充分发挥每个成员的作用,提高学生的综合素质。
5.教师在批改作业时,要关注学生的解题思路和过程,给予针对性的评价和建议。
导学案1:极坐标系

4.1.2 极坐标系学习目标:复习直角坐标系;理解极坐标系的建立及相关概念,掌握点的极坐标表示方法及点的直角坐标与极坐标的互相转化。
一、极坐标系实例引入:凸轮控制机器的传动;军舰在海面上如何确定目标的位置;例1中,各顶点如何用距离和方向来确定。
1.极坐标系的建立2.坐标系,极点,极轴,极径,极角的概念。
由极径的意义可知0≥ρ。
当极角的取值 范围是[)π2,0时,平面上的点(除去极点)就与及坐标()()0,≠ρθρ建立了一一对应的关系。
约定:极点的极坐标是极径0=ρ,极角可取任意角。
例1 写出图中各点的极坐标为了研究方便,在极坐标系中,极径允许取负值,极角也可以取任意的正角或负角。
当0<ρ时,点),(θρM 位于极角终边的反向延长线上,且ρ=OM 。
一般地,如果),(θρ是点M 的极坐标,那么))()12(,()2,(Z k k k ∈++-+πθρπθρ或都可以作为点M 的坐标。
但这样建立的极坐标系,平面上的点与它的极坐标之间的关系就不是一一对应关系。
例2在极坐标系中,(1)已知两点),4,1(),45,5(ππQ P 求线段PQ 的长度;(2)已知M 点的极坐标为),(θρ,且,,3R ∈=ρπθ说明满足上述条件的点M 的位置。
例3已知点),(θρQ ,分别按下列要求求出点P 的坐标。
(1)点P 是Q 关于极点O 的对称点;(2)P 是点Q 关于直线2πθ=的对称点。
3.点的直角坐标与极坐标的相互转化(1)转化的意义;(2)转化的公式例4、(1)把点M 的极坐标)32,8(π化为直角坐标;(2)把点P 的直角坐标)2,6(-化为极坐标。
《极坐标系》导学案

第2课时极坐标系1.通过实例了解极坐标系的建立,会用极坐标表示极坐标系内的点,掌握极坐标的应用.2.理解极坐标与直角坐标间的相互转化,掌握转化公式,并运用公式实现极坐标与直角坐标间的相互转化.李先生是个外地人,他想到市教育局去,却不知道该怎么去.于是他向路人询问去市教育局如何走?路人说市教育局就在我们现在的位置东南方3公里处.请问路人的回答,能让李先生找到目的地吗?“在我们现在的位置东南方3公里处”是一个确定的位置吗?问题1:极坐标系的建立在平面内取一个定点O,叫作极点;自极点O引一条射线Ox,叫作;再选定一个长度单位和角的正方向(通常取方向),这样就建立了一个平面极坐标系,简称为.问题2:对于平面内任意一点M,用ρ表示点M到极点O的距离,用θ表示以Ox为始边,以OM为终边的角度,其中ρ叫作,θ叫作,有序数对(ρ,θ)就叫作点M 的,记为.问题3:将点M的极坐标(ρ,θ)化为直角坐标(x,y)的关系式为.问题4:将点M的直角坐标(x,y)化为极坐标(ρ,θ)的关系式为.1.在极坐标系中,点M(-2,π)的位置,可按如下规则确定( ).6,再在射线OP上取点M,使|OM|=2A.作射线OP,使∠xOP=π6,再在射线OP上取点M,使|OM|=2B.作射线OP,使∠xOP=7π6,再在射线OP的反向延长线上取点M,使|OM|=2C.作射线OP,使∠xOP=7π6D.作射线OP,使∠xOP=-π6,再在射线OP上取点M,使|OM|=22.若ρ1+ρ2=0,θ1+θ2=π,则点M1(ρ1,θ1)与点M2(ρ2,θ2)的位置关系是( ).A.关于极轴所在的直线对称B.关于极点对称C.关于过极点且垂直于极轴的直线对称D.关于过极点且与极轴成π4的直线对称3.点P的直角坐标为(-√2,√2),那么它的极坐标可表示为.4.在极坐标系中作下列各点,并说明每组中各点的位置关系.(1)A(2,0)、B(2,π6)、C(2,π4)、D(2,π2)、E(2,3π2)、F(2,5π4)、G(2,11π6);(2)A(0,π4)、B(1,π4)、C(2,5π4)、D(3,5π4)、E(3,π4).化极坐标为直角坐标分别把下列点的极坐标化为直角坐标.(1)(2,π6);(2)(3,π2);(3)(4,2π3);(4)(4,-π12).极坐标的概念已知极坐标系中点A(2,π2),B(√2,3π4),O(0,0),则△AOB为( ).A.等边三角形B.顶角为钝角的等腰三角形C.顶角为锐角的等腰三角形D.等腰直角三角形极坐标与直角坐标间的互化在极坐标系中,点P(2,π3)和点Q(4,5π6)之间的距离为.把下列各点的极坐标化为直角坐标,并判断所表示的点在第几象限.(1)(2,4π3);(2)(2,2π3);(3)(2,-π3);(4)(2,-2).在极坐标系中,已知△ABC的三个顶点的极坐标分别为A(2,π3),B(2,π),C(2,5π3).(1)判断△ABC的形状;(2)求△ABC的面积.极坐标平面内两点P(4,3π2)、Q(ρ,-π4)之间的距离为√10,则ρ= .1.在极坐标系中,若点A、B的坐标分别是(2,π3)、(3,-π6),则△AOB为( ).A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形2.将极坐标(6,4π3)化为直角坐标为( ).A.(-3√3,3)B.(-3√3,-3)C.(-3,-3√3)D.(-3,3√3)3.在极坐标系中,已知两点A、B的极坐标分别为(3,π3)、(4,π6),则△AOB(其中O为极点)的面积为.4.在极坐标系中,已知三点M(2,5π3),N(2,0),P(2√3,π6).(1)将M、N、P三点的极坐标化为直角坐标;(2)判断M、N、P三点是否在一条直线上.在极坐标系中,已知两点A(2,π4),B(2,5π4),且△ABC为等腰直角三角形,求直角顶点C的极坐标与该三角形的面积.考题变式(我来改编):第2课时 极 坐 标 系知识体系梳理问题1:极轴 逆时针 极坐标系 问题2:极径 极角 极坐标 M(ρ,θ) 问题3:{x =ρcosθ,y =ρsinθ问题4:{ρ2=x 2+y 2,tanθ=yx(x ≠0)基础学习交流1.B 当ρ<0时,点M(ρ,θ)的位置按下列规定确定:作射线OP,使∠xOP=θ,在OP 的反向延长线上取|OM|=|ρ|,则点M 就是坐标(ρ,θ)的点,故选B.2.A 因为点(ρ,θ)关于极轴所在的直线对称的点为(-ρ,π-θ),由点M 1(ρ1,θ1)和M 2(ρ2,θ2)满足ρ1+ρ2=0,θ1+θ2=π,可知点M 1与M 2关于极轴所在的直线对称.3.(2,3π4)(答案不唯一) 直接利用极坐标与直角坐标的互化公式求解,即ρ=√(-√2)2+(√2)2=2,tan θ=-1.因为点P 在第二象限,所以可取一个极角为3π4.4.解:(1)所有点都在以极点为圆心,半径为2的圆上.点B 、G 关于极轴对称,点D 、E 关于极轴对称,点C 、F 关于极点对称.(2)所有点都在倾斜角为π4,且过极点的直线上.点D 、E 关于极点对称.重点难点探究探究一:【解析】(1)∵x=ρcos θ=2cos π6=√3,y=ρsinθ=2sin π6=1.∴点(2,π6)的直角坐标为(√3,1).(2)∵x=ρcos θ=3cos π2=0,y=ρsin θ=3sin π2=3.∴点(3,π2)的直角坐标为(0,3).(3)∵x=ρcos θ=4cos 2π3=-2,y=ρsin θ=4sin 2π3=2√3.∴点(4,2π3)的直角坐标为(-2,2√3).(4)∵cos π12=√1+cos π62=√1+√322=√6+√24,sin π12=√1-cos π62=√1-√322=√6-√24,∴x=ρcos θ=4cos(-π12)=4cosπ12=√6+√2,y=ρsin θ=4sin(-π12)=-4sin π12=√-√6.∴点(4,-π12)的直角坐标为(√+√6,√-√6).【小结】严格按照{x =ρcosθ,y =ρsinθ进行转化,注意准确计算.探究二:【解析】显然OA=2,OB=√,∠AOB=π4,由余弦定理得AB=√OA 2+OB 2-2OA·OB·cos∠AOB =√2,故OB=AB,∠ABO=π2,即△AOB为等腰直角三角形.【答案】D【小结】极坐标中的ρ和θ分别表示到极点的距离和极轴逆时针转过的角度.探究三:【解析】(法一)由公式{x =ρcosθ,y =ρsinθ ,得点P(2,π3)和点Q(4,5π6)的直角坐标分别为P(1,√3)和Q(-2√3,2),由两点间的距离公式得|PQ|=√(1+2√3)2+(√3-2)2=2√5.(法二)在极坐标系中,已知点P(2,π3)和点Q(4,5π6),故∠POQ=π2,所以|PQ|=2+42√5.【答案】2√【小结】如果极坐标系中的两点确定,那么它们之间的距离也确定,可以把各点极坐标转化为直角坐标,在平面直角坐标系中计算,也可以利用极径、极角的定义和余弦定理在三角形中计算. 思维拓展应用应用一:(1)由题意知x=2cos4π3=2×(-12)=-1,y=2sin4π3=2×(-√32)=-√3,即点(2,4π3)的直角坐标为(-1,-√3),是第三象限内的点. (2)由题意知x=2cos 2π3=-1,y=2sin 2π3=√3,即点(2,2π3)的直角坐标为(-1,√3),是第二象限内的点.(3)由题意知x=2cos(-π3)=1,y=2sin(-π3)=-√3,即点(2,-π3)的直角坐标为(1,-√3),是第四象限内的点.(4)由题意知x=2cos(-2)=2cos 2<0(π2<2<π),y=2sin(-2)=-2sin2<0,即点(2,-2)的直角坐标为(2cos 2,-2sin 2),是第三象限点. 应用二:(1)画图可知,A 、B 、C 三点都在以极点为圆心,2为半径的圆上,且所对的圆心角均为23π,∴|AB|=|AC|=|BC|,∴△ABC 为正三角形.(2)由(1)知12|AB|=2sin π3,∴|AB|=2√3,∴△ABC 的面积为S=12×2√3×2√3×√32=3√3.应用三:√2或3√2 根据x=ρcos θ,y=ρsin θ,得P 、Q 的直角坐标分别为P(0,-4)、Q(√22ρ,-√22ρ).∴|PQ|=√(0-√22ρ)2+(-4+√22ρ)2=√10,解得ρ=√2或ρ=3√2. 基础智能检测1.B 由题意知∠AOB=π3-(-π6)=π2,故选B.2.C 由公式{x =ρcosθ,y =ρsinθ,得{x =6×(-12)=-3,y =6×(-√32)=-3√3,所以直角坐标为(-3,-3√3),选择C.3.3 结合图形,△AOB 的面积S=12OA ·OB ·sin(π3-π6)=3.4.解:(1)将三点坐标代入公式{x =ρcosθ,y =ρsinθ,可知点M 的直角坐标为(1,-√3),点N 的直角坐标为(2,0),点P 的直角坐标为(3,√3). (2)∵k MN =√32-1=√3,k NP =√3-03-2=√3,∴k MN =k NP ,∴M 、N 、P 三点在同一条直线上. 全新视角拓展(法一)利用坐标转化.点A(2,π4)的直角坐标为(√2,√2),点B(2,5π4)的直角坐标为(-√2,-√2),设点C 的直角坐标为(x,y).由题意得AC ⊥BC,|AC|=|BC|.∴AC ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0,|AC|2=|BC|2,于是(x-√2,y-√2)·(x+√2,y+√2)=0,即x 2+y 2=4. ①(x-√2+(y-√)2=(x+√)2+(y+√2,即y=-x. ② 将②代入①得x 2=2,解得x=±√2,∴{x =√2,y =-√2或{x =-√2,y =√2,∴点C 的直角坐标为(√√)或(-√,√).∴ρ=√2+2=2,tan θ=-1,θ=7π4或3π4,∴点C 的极坐标为(2,3π4)或(2,7π4).S △ABC =12|AC|·|BC|=12|AC|2=12×8=4.(法二)设点C 的极坐标为(ρ,θ)(ρ>0,0≤θ<2π),∵|AB|=2|OA|=4,∠C=π2,|AC|=|BC|,∴|A C|=|BC|=2√根据余弦定理可得{ρ2+22-2×2ρcos(θ-π4)=8, ①ρ2+22-2×2ρcos(θ-5π4)=8, ②①+②化简得ρ2=4,由ρ>0得ρ=2,代入①得cos(θ-π4)=0,∴θ-π4=π2+kπ,k∈Z,即θ=3π4+kπ,k∈Z,又∵0≤θ<2π,令k=0,1,得θ=3π4或7π4,∴点C的极坐标为(2,3π4)或(2,7π4),S△ABC=12|AC|·|BC|=12|AC|2=12×8=4.精品文档。
河北省承德市平泉县蒙古族高级中学高中数学极坐标系导学案1(无答案)新人教A版选修4_4

(1)P是点Q关于极点O的对称点;
(2)P是点Q关于直线 的对称点;
(3)P是点Q关于极轴的对称点。
变式训练
1.在极坐标系中,与点 关于极点对称的点的一个坐标是( )
2.已知点M的极坐标为 ,下列所给出的四个坐标中不能表示点M的坐标的是()
【课堂小结】本节课的主要内容是:
你还学会了哪些思想ABC的两个顶点是 、 ,那么顶点C的坐标可能是()
2.在极坐标系内,点 关于直线 的对称点坐标为()
A(3,0)
3.若 是极坐标系中的一点, 四点中与P重合的点有()A.1个B 2个C 3个D 4个
M(,)也可以表示为
【探究应用】
探究一极坐标系中点的坐标
例1写出下图中各点的极坐标
A(4,0)B(2)C()D()
E()F()G()
思考:
1平面上一点的极坐标是否唯一?
2若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式
约定:极点的极坐标是 =0, 可以取任意角。
特别强调:由极径 的意义可知0;当极角的取值范围是[0, 2 )时,平面上的点(除去极点)就与极坐标(,)建立一一对应的关系.们约定,极点的极坐标是极径=0,极角是任意角.
3、负极径的规定
在极坐标系中,极径允许取负值,极角也可以去任意的正角或负角
当<0时,点M( ,)位于极角终边的反向延长线上,且OM= 。
课题
极坐标系(1)
课型
新授课
学习目标
1.认识极坐标系
2.能够在极坐标系中用极坐标刻画点的位置,体会在极坐标系和直角坐标系中刻画点的区别,能进行极坐标和直角坐标的互化。
数学4-4(极坐标系)导学案

数学4-4(极坐标系)导学案本卷须知1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2、选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3、请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4、保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
课题:极坐标系〔两课时〕【一】三维目标知识与技能:认识极坐标,能在极坐标系中用极坐标刻画点的位置;体会极坐标系与平面直角坐标系的区别,能进行极坐标和直角坐标间的互化。
过程与方法:通过生活中的实例,让学生认识到学习极坐标系的必要性,从而引出极坐标系与极坐标的概念;根据极坐标与直角坐标的特点和三角函数的概念,实现极坐标和直角坐标间的互化情感态度价值观:通过学习,体会数学知识的产生与发展源于生活又服务于生活,体会数学的应用价值,激发学生的学习数学的热情。
【二】教学重难点重点:理解并能用极坐标刻画点的位置,能进行极坐标与直角坐标的互化。
难点:理解用极坐标刻画点的位置的基本思想;点与极坐标之间的对应关系的认识。
【三】学法指导:认真阅读教材P8—10,结合实例,理解极坐标的建立、点与极坐标的对应;结合任意角的三角函数的定义,理解极坐标和直角坐标间的互化。
【四】知识链接:1、回顾自己在为人指路时常用的方法2举一个生活中用“距离”和“角度”刻画位置的例子【五】学习过程:【一】极坐标系的概念1、引入:阅读课本P9页的“思考”,并回答提出的问题答1〕:答2〕:2、你是否注意到在以上问题中,用“距离”和“角度”刻画位置时,总是先固定一个位置作为,并以某个方向作为参照。
3极坐标系的概念:1〕在平面内取一个定点O,叫做极点;自极点O引一条射线OX,叫做极轴;再选定一个长度单位,一个角度单位〔通常用弧度〕及其正方向〔通常取逆时针方向〕,这样就建立了一个极坐标系.ρ;2〕如图:设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为以极轴OX为始边,射线OM为终边的角XOM叫做点M的极角,记为θ;有序实数对〔,ρθ〕叫做点M 的极坐标,记为(,)M ρθ;注:一般地,不做特殊说明时,我们认为0,ρθ≥∈R4例题例1.如图,在极坐标系中,写出点A ,B ,C的极坐标,并标出点D 〔2,6π〕,E 〔4,34π〕,F〔3.5,53π〕所在的位置。
选讲44极坐标系导学案(全).pdf

以极轴 Ox 为始边,射线 OM 为终边的角 xOM 叫做点 M 的________,记为 。则 有序数对 (, ) 叫做点 M 的__________,记为___________.
【注】①.一般地,不作说明时, 0, 取任意实数。
②.极坐标 (, ) 与 (, + 2k )(k Z) 表示同一个点。
4.在直角坐标系 xOy 中,圆 C1 : x2 + y 2 = 4 ,圆 C2 : (x − 2)2 + y 2 = 4 ,求出圆
C1,C2 的焦点坐标(用极坐标表示)
1
3
3
2.已知点的极坐标分别为 (3, ), (2, 2 ), (4, ), ( 3 , ) ,求他们的直角坐标。 4 3 22
3. 已知点的直角坐标分别为( 3, 3 ),( 0,− 5 ),求它们的极坐标。 3
(三 )达标检测
1.写出图中 A,B,C,D,E,F,G 各点的极坐标( 0,0 2 )。
在平面内取一个定点 O ,叫做________;以 O 为端点作射线 Ox ,叫做_______;
再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(逆时针方向),这 样就建立了一个__________.
(2)极坐标
个性笔 记
设 M 是平面内一点,极点 O 与点 M 的距离 OM 叫做点 M 的_______,记为 ;
边位置),以便正确地求出[0,2 ) 内的角 。
D(2, ) , E(4, 3 ) , F (3.5, 5 ) 所在的位置。
6
4
3
2.将点 M 的极坐标 (5, 2 ) 化成直角坐标。 3
3. 将点 M 的直角坐标 (− 3,−1) 化成极坐标。
选讲44极坐标系导学案(全)(2020年整理).pdf
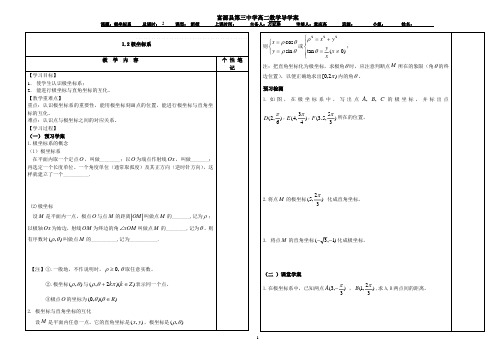
再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(逆时针方向),这 样就建立了一个__________.
个性笔 记
则
x
y
= =
cos sin
或
2 = tan
x2 + y = y (x
姓名:
3
课题:极坐标系 总课时: 2 课型: 新授
富源县第三中学高二数学导学案
上课时间:
主备人:万亚琳
审核人:章应高
班级:
小组:
姓名:
1.2 极坐标系
教学内容
【学习目标】 1. 使学生认识极坐标系; 2. 能进行极坐标与直角坐标的互化。 【教学重难点】 重点:认识极坐标系的重要性,能用极坐标刻画点的位置,能进行极坐标与直角坐 标的互化。 难点:认识点与极坐标之间的对应关系。 【学习过程】 (一) 预习学案 1.极坐标系的概念 (1)极坐标系
上课时间:
主备人:万亚琳
审核人:章应高
班级:
小组:
2. 写出 1 题中 A,B,C,D,E,F,G 各点的直角坐标。
姓名:
3. 已知点的直角坐标分别为( 3, 3 ),( 0,− 5 ),求它们的极坐标。 3
(三 )达标检测
1.写出图中 A,B,C,D,E,F,G 各点的极坐标( 0,0 2 )。
(二 )课堂学案
1.在极坐标系中,已知两点 A(3,− ) , B(1, 2 ) ,求 A,B 两点间的距离。
3
3
1
课题:极坐标系 总课时: 2 课型: 新授
2.已知点的极坐标分别为 (3, ), (2, 2 ), (4, ), ( 3 , ) ,求他们的直角坐标。 4 3 22
河北省承德市平泉县蒙古族高级中学高中数学 极坐标系导学案2(无答案)新人教A版选修4-4

极坐标系(2)
课型
新授课
学习目标
1.认识极坐标系
2.能够在极坐标系中用极坐标刻画点的位置,体会在极坐标系和直角坐标系中刻画点的区别,能进行极坐标和直角坐标的互化。
重点难点
认识极坐标系的重要性,能用极坐标刻画点的位置,能进行极坐标与直角坐标的互化。
导学过程
备注
【自主导学】
1.极坐标系和点的极坐标
极点、极轴、长度单位、角度单位和它的方向构成极坐标系的四要素,缺一不可。
规定:当点M在极点时,它的极坐标 可以取任意值。
2.平面直角坐标与极坐标的区别
在平面直角坐标系内,点与有序实数对(x,y)是一一对应的,可是在极坐标系中,虽然一个有序实数对 只能与一个点P对应,但一个点P却可以与个有序实数对对应 ,极坐标系中的点与有序实数对极坐标 不是一一对应的。
3.极坐标系中,点M 的极坐标统一表达式 。
例3化下列方程为直角坐标方程,并说明表示的曲线.
(1) ,(
(2)
【课堂检测】
1.极坐标方程 表示的曲线是()
A余弦曲线B两条相交直线C一条射线D两条射线
2.极坐标系中,点A的极坐标是 ,则(1)点A关于极轴对称的点是_______.
(2)点A关于极点对称的点的极坐标是___.
(3)点A关于直线 的对称点的极坐标是________.(规定:
3.点 ,则它的极坐标是()A. B. C. D.
4.极坐标方程 表示的曲线是()A.双曲线B.椭圆C.抛物线D.圆
5.圆 的圆心坐标是()A. B. C. D.
6.在坐标系中,与圆 相切的一条直线方程为()
A. B. C. D.
7、已知点 则 为()
A、正三角形B、直角三角形C、锐角等腰三角形D、直角等腰三角形
吉林省长市实验中学高中数学《极坐标系》导学案 新人教A版选修44

吉林省长春市实验中学高中数学《极坐标系》导学案 【学习目标】 1、理解极坐标的概念;2、能在极坐标系中刻画极坐标的位置,体会极坐标与平面直角坐标刻画点位置的区别。
【重点难点】重点:理解极坐标的概念难点:能在极坐标中找到点的位置【自主学习】阅读教材108P P -,将重点内容画在书上,并回答下面的问题1、 如何建立极坐标2、 如何在极坐标下确定点得坐标阅读教材11P ,将重点内容在书中画下来,【合作释疑】例1、 写出下图中各点的极坐标A (4,0)B (2 )C ( )D ( )E ( )F ( )G ( )① 平面上一点的极坐标是否唯一?② 若不唯一,那有多少种表示方法?③坐标不唯一是由谁引起的?④不同的极坐标是否可以写出统一的表达式?例2、在极坐标系中,(1)已知两点P (5,45π),Q )4,1(π,求线段PQ 的长度; (2)已知M 的极坐标为(ρ,θ)且θ=3π,ρR ∈,说明满足上述条件的点M 的位置。
例3、 已知Q (ρ,θ),分别按下列条件求出点P 的极坐标。
(1) P 是点Q 关于极点O 的对称点;(2) P 是点Q 关于直线2πθ=的对称点; (3) P 是点Q 关于极轴的对称点。
【巩固训练,整理提高】1、.已知5,3M π⎛⎫ ⎪⎝⎭,下列所给出的能表示该点的坐标的是( ) A .⎪⎭⎫ ⎝⎛-3,5π B .⎪⎭⎫ ⎝⎛34,5π C .⎪⎭⎫ ⎝⎛-32,5π D .55,3π⎛⎫- ⎪⎝⎭ 2、在极坐标系中,与(ρ,θ)关于极轴对称的点是( )A 、),(θρB 、),(θρ-C 、),(πθρ+D 、),(θπρ-3、设点P 对应的复数为-3+3i ,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P 的极坐标为( ) A.(23,π43) B. (32,π45) C. (3,π45) D. (3,π43) 4、求极坐标系中,与点)6,8(π-关于极点对称的点的一个坐标?5、在极坐标系中,如果等边ABC ∆的两个顶点是),45,2(),4,2(B A π求第三个顶点C 的坐标。
极坐标系导学案

第2课时极坐标系1.通过实例了解极坐标系的建立,会用极坐标表示极坐标系的点,掌握极坐标的应用.2.理解极坐标与直角坐标间的相互转化,掌握转化公式,并运用公式实现极坐标与直角坐标间的相互转化.先生是个外地人,他想到市教育局去,却不知道该怎么去.于是他向路人询问去市教育局如何走?路人说市教育局就在我们现在的位置东南方3公里处.请问路人的答复,能让先生找到目的地吗?“在我们现在的位置东南方3公里处〞是一个确定的位置吗?问题1:极坐标系的建立在平面取一个定点O,叫作极点;自极点O引一条射线Ox,叫作;再选定一个长度单位和角的正方向(通常取方向),这样就建立了一个平面极坐标系,简称为.问题2:对于平面任意一点M,用ρ表示点M到极点O的距离,用θ表示以Ox为始边,以OM为终边的角度,其中ρ叫作,θ叫作,有序数对(ρ,θ)就叫作点M的,记为.问题3:将点M的极坐标(ρ,θ)化为直角坐标(x,y)的关系式为.问题4:将点M的直角坐标(x,y)化为极坐标(ρ,θ)的关系式为.1.在极坐标系中,点M(-2,)的位置,可按如下规那么确定( ).A.作射线OP,使∠xOP=,再在射线OP上取点M,使|OM|=2B.作射线OP,使∠xOP=,再在射线OP上取点M,使|OM|=2C.作射线OP,使∠xOP=,再在射线OP的反向延长线上取点M,使|OM|=2D.作射线OP,使∠xOP=-,再在射线OP上取点M,使|OM|=22.假设ρ1+ρ2=0,θ1+θ2=π,那么点M1(ρ1,θ1)与点M2(ρ2,θ2)的位置关系是( ).A.关于极轴所在的直线对称B.关于极点对称C.关于过极点且垂直于极轴的直线对称D.关于过极点且与极轴成的直线对称3.点P的直角坐标为(-,),那么它的极坐标可表示为.4.在极坐标系中作以下各点,并说明每组中各点的位置关系.(1)A(2,0)、B(2,)、C(2,)、D(2,)、E(2,)、F(2,)、G(2,);(2)A(0,)、B(1,)、C(2,)、D(3,)、E(3,).化极坐标为直角坐标分别把以下点的极坐标化为直角坐标.(1)(2,);(2)(3,);(3)(4,);(4)(4,-).极坐标的概念极坐标系中点A(2,),B(,),O(0,0),那么△AOB为( ).A.等边三角形B.顶角为钝角的等腰三角形C.顶角为锐角的等腰三角形D.等腰直角三角形极坐标与直角坐标间的互化在极坐标系中,点P(2,)和点Q(4,)之间的距离为.把以下各点的极坐标化为直角坐标,并判断所表示的点在第几象限. (1)(2,);(2)(2,);(3)(2,-);(4)(2,-2).在极坐标系中,△ABC的三个顶点的极坐标分别为A(2,),B(2,π),C(2,).(1)判断△ABC的形状;(2)求△ABC的面积.极坐标平面两点P(4,)、Q(ρ,-)之间的距离为,那么ρ=.1.在极坐标系中,假设点A、B的坐标分别是(2,)、(3,-),那么△AOB为( ).A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形2.将极坐标(6,)化为直角坐标为( ).A.(-3,3)B.(-3,-3)C.(-3,-3)D.(-3,3)3.在极坐标系中,两点A、B的极坐标分别为(3,)、(4,),那么△AOB(其中O为极点)的面积为.4.在极坐标系中,三点M(2,),N(2,0),P(2,).(1)将M、N、P三点的极坐标化为直角坐标;(2)判断M、N、P三点是否在一条直线上.在极坐标系中,两点A(2,),B(2,),且△ABC为等腰直角三角形,求直角顶点C的极坐标与该三角形的面积.考题变式(我来改编):第2课时极坐标系知识体系梳理问题1:极轴逆时针极坐标系问题2:极径极角极坐标M(ρ,θ)问题3:问题4:根底学习交流1.B 当ρ<0时,点M(ρ,θ)的位置按以下规定确定:作射线OP,使∠xOP=θ,在OP的反向延长线上取|OM|=|ρ|,那么点M就是坐标(ρ,θ)的点,应选B.2.A 因为点(ρ,θ)关于极轴所在的直线对称的点为(-ρ,π-θ),由点M1(ρ1,θ1)和M2(ρ2,θ2)满足ρ1+ρ2=0,θ1+θ2=π,可知点M1与M2关于极轴所在的直线对称.3.(2,)(答案不唯一) 直接利用极坐标与直角坐标的互化公式求解,即ρ==2,tan θ=-1.因为点P在第二象限,所以可取一个极角为.4.解:(1)所有点都在以极点为圆心,半径为2的圆上.点B、G关于极轴对称,点D、E关于极轴对称,点C、F关于极点对称.(2)所有点都在倾斜角为,且过极点的直线上.点D、E关于极点对称. 重点难点探究探究一:【解析】(1)∵x=ρcos θ=2cos=,y=ρsin θ=2sin=1.∴点(2,)的直角坐标为(,1).(2)∵x=ρcos θ=3cos=0,y=ρsin θ=3sin=3.∴点(3,)的直角坐标为(0,3).(3)∵x=ρcos θ=4cos=-2,y=ρsin θ=4sin=2.∴点(4,)的直角坐标为(-2,2).(4)∵cos===,sin===,∴x=ρcos θ=4cos(-)=4cos=+,y=ρsin θ=4sin(-)=-4sin=-.∴点(4,-)的直角坐标为(+,-).【小结】严格按照进展转化,注意准确计算.探究二:【解析】显然OA=2,OB=,∠AOB=,由余弦定理得AB==,故OB=AB,∠ABO=,即△AOB 为等腰直角三角形.【答案】D【小结】极坐标中的ρ和θ分别表示到极点的距离和极轴逆时针转过的角度.探究三:【解析】(法一)由公式得点P(2,)和点Q(4,)的直角坐标分别为P(1,)和Q(-2,2),由两点间的距离公式得|PQ|==2.(法二)在极坐标系中,点P(2,)和点Q(4,),故∠POQ=,所以|PQ|==2.【答案】2【小结】如果极坐标系中的两点确定,那么它们之间的距离也确定,可以把各点极坐标转化为直角坐标,在平面直角坐标系中计算,也可以利用极径、极角的定义和余弦定理在三角形中计算.思维拓展应用应用一:(1)由题意知x=2cos=2×(-)=-1,y=2sin=2×(-)=-,即点(2,)的直角坐标为(-1,-),是第三象限的点.(2)由题意知x=2cos =-1,y=2sin =,即点(2,)的直角坐标为(-1,),是第二象限的点.(3)由题意知x=2cos(-)=1,y=2sin(-)=-,即点(2,-)的直角坐标为(1,-),是第四象限的点.(4)由题意知x=2cos(-2)=2cos 2<0(<2<π),y=2sin(-2)=-2sin 2<0,即点(2,-2)的直角坐标为(2cos 2,-2sin 2),是第三象限点.应用二:(1)画图可知,A、B、C三点都在以极点为圆心,2为半径的圆上,且所对的圆心角均为π,∴|AB|=|AC|=|BC|,∴△ABC为正三角形.(2)由(1)知|AB|=2sin ,∴|AB|=2,∴△ABC的面积为S=×2×2×=3.应用三:或3根据x=ρcos θ,y=ρsin θ,得P、Q的直角坐标分别为P(0,-4)、Q(ρ,-ρ).∴|PQ|==,解得ρ=或ρ=3.根底智能检测1.B 由题意知∠AOB=-(-)=,应选B.2.C 由公式得所以直角坐标为(-3,-3),选择C.3.3 结合图形,△AOB的面积S=OA·OB·sin(-)=3.4.解:(1)将三点坐标代入公式可知点M的直角坐标为(1,-),点N的直角坐标为(2,0),点P的直角坐标为(3,).(2)∵k MN==,k NP==,∴k MN=k NP,∴M、N、P三点在同一条直线上.全新视角拓展(法一)利用坐标转化.点A(2,)的直角坐标为(,),点B(2,)的直角坐标为(-,-),设点C的直角坐标为(x,y).由题意得AC⊥BC,|AC|=|BC|.∴·=0,|AC|2=|BC|2,于是(x-,y-)·(x+,y+)=0,即x2+y2=4. ①(x-)2+(y-)2=(x+)2+(y+)2,即y=-x. ②将②代入①得x2=2,解得x=±,∴或∴点C的直角坐标为(,-)或(-,).∴ρ==2,tan θ=-1,θ=或,∴点C的极坐标为(2,)或(2,).S△ABC=|AC|·|BC|=|AC|2=×8=4.(法二)设点C的极坐标为(ρ,θ)(ρ>0,0≤θ<2π),∵|AB|=2|OA|=4,∠C=,|AC|=|BC|,∴|AC|=|BC|=2, 根据余弦定理可得①+②化简得ρ2=4,由ρ>0得ρ=2,代入①得cos(θ-)=0,∴θ-=+kπ,k∈Z,即θ=+kπ,k∈Z,又∵0≤θ<2π,令k=0,1,得θ=或,∴点C的极坐标为(2,)或(2,),S△ABC=|AC|·|BC|=|AC|2=×8=4.。
高中数学选修4-4极坐标系导学案.doc

极坐标系导学案心学习目标1、能在极坐标系中用极坐标刻画点的位置。
2、体会在极坐标系和平面直角坐标系屮刻画点的位置的区别。
3、掌握直角坐标与极坐标的相互转化。
一、极坐标的概念(预习教材,找出疑惑之处)情境1:军舰巡逻在海面上,发现前方有一群水雷,如何确定它们的位置以便将它们引爆?情境2:如图为某校园的平面示意图,假设某同学在教学楼处。
(1)他向东偏60°方向走120M后到达什么位置?该位置唯一-确定吗?(2)如呆有人打听体冇馆和办公楼的位置,他应如何描述?问题1:为了简便地表示上述问题中点的位置,应创建怎样的坐标系呢?问题2:如何刻1師这些点的位置?定义新知1:极坐标的概念1>如右图,在平面内取一个定点O,叫做____________ ;自极点O引一条射线Ox ,叫做_____________ ;再选定_个___________ , _个 __________ (通常取)及其_______ (通常取 _________ 方向),这样就建立了一个__________ O2、设M是平而内一点,极点0与M的距离I0MI叫做点M的 ____________ ,记为____ ;以极轴Or为始边,射线0M为终边的角xOM叫做点M的________ ,记为 _____ 有序数对_______ 叫做点M的________ ,记作________________ o3、思考:直角坐标系与极坐标系有何异同?♦应用示例例题1:⑴写出图中A, B, C, D, E, F, G 各点的极坐标(°〉0,05&<2兀).(2):思考下列问题,给出解答。
① 平面上一点的极坐标是否唯一? ② 若不唯一,那有多少种表示方法?③ 坐标不唯一是由谁引起的?④ 不同的极处标是否可以写出统一表达式?⑤ 本题点G 的极坐标统一表达式。
二、与直角坐标的转化直角坐标系的原点0为极点,兀轴的正半轴为极轴,月•在两 坐标系中取相同的t 度单位。
《极坐标系》导学案

《极坐标系》导学案【基础知识导学】1.极坐标系和点的极坐标极点、极轴、长度单位、角度单位和它的方向构成极坐标系的四要素,缺一不可。
规定:当点M 在极点时,它的极坐标θρ,0=可以取任意值。
2.平面直角坐标与极坐标的区别在平面直角坐标系内,点与有序实数对(x ,y )是一一对应的,可是在极坐标系中,虽然一个有序实数对),(θρ只能与一个点P 对应,但一个点P 却可以与无数多个有序实数对对应),(θρ,极坐标系中的点与有序实数对极坐标 ),(θρ不是一一对应的。
3.极坐标系中,点M ),(θρ的极坐标统一表达式Z k k ∈+),2,(θπρ。
4.如果规定πθρ20,0<≤>,那么除极点外,平面内的点可用唯一的极坐标),(θρ表示,同时,极坐标),(θρ表示的点也是唯一确定的。
5.极坐标与直角坐标的互化(1) 互化的前提:①极点与直角坐标的原点重合;②极轴与X 轴的正方向重合;③两种坐标系中取相同的长度单位。
(2) 互化公式⎩⎨⎧==θρθρsin cos y x ,⎪⎩⎪⎨⎧≠=+=0,tan 222x x y y x θρ。
【知识迷航指南】【例1】 在极坐标系中,描出点)3,2(πM ,并写出点M 的统一极坐标。
X【点评】点)3,2(πM 的统一极坐标表示式为)32,2(ππ+k ,如果允许0<ρ,还可以表示为)3)12(,2(ππ++-k 。
【例2】已知两点的极坐标)6,3(),2,3(ππB A ,则|AB|=______,AB 与极轴正方向所成的角为________.解:根据极坐标的定义可得|AO|=|BO|=3,∠AOB=600,即∆AOB 为等边三角形,所以|AB|=|AO|=|BO|=3, ∠ACX=65π 【点评】在极坐标系中我们没有定义两点间的距离,我们只要画出图形便可以得到结果.【例3】化下列方程为直角坐标方程,并说明表示的曲线. (1)43πθ=,()R ∈ρ (2)θθρcos 2sin +=【解】(1)根据极坐标的定义,因为x y xy -==即,43tan π,所以方程表示直线. (2)因为方程给定的ρ不恒为0,用ρ同乘方程的两边得:θρθρρcos 2sin 2+=化为直角坐标方程为,222x y y x +=+即45)21()1(22=-+-y x ,这是以(1,21)为圆心,半径为25的圆.ρ这一条件,则方程表示一条射线.【点评】①若没有R∈②极坐标方程化为直角坐标方程,方程两边同乘ρ,使之出现ρ2是常用的方法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时极坐标系1.通过实例了解极坐标系的建立,会用极坐标表示极坐标系内的点,掌握极坐标的应用.2.理解极坐标与直角坐标间的相互转化,掌握转化公式,并运用公式实现极坐标与直角坐标间的相互转化.李先生是个外地人,他想到市教育局去,却不知道该怎么去.于是他向路人询问去市教育局如何走?路人说市教育局就在我们现在的位置东南方3公里处.请问路人的回答,能让李先生找到目的地吗?“在我们现在的位置东南方3公里处”是一个确定的位置吗?问题1:极坐标系的建立在平面内取一个定点O,叫作极点;自极点O引一条射线Ox,叫作;再选定一个长度单位和角的正方向(通常取方向),这样就建立了一个平面极坐标系,简称为.问题2:对于平面内任意一点M,用ρ表示点M到极点O的距离,用θ表示以Ox为始边,以OM为终边的角度,其中ρ叫作,θ叫作,有序数对(ρ,θ)就叫作点M 的,记为.问题3:将点M的极坐标(ρ,θ)化为直角坐标(x,y)的关系式为.问题4:将点M的直角坐标(x,y)化为极坐标(ρ,θ)的关系式为.1.在极坐标系中,点M(-2,π6)的位置,可按如下规则确定().A.作射线OP,使∠xOP=π6,再在射线OP上取点M,使|OM|=2B.作射线OP,使∠xOP=7π6,再在射线OP上取点M,使|OM|=2C.作射线OP,使∠xOP=7π6,再在射线OP的反向延长线上取点M,使|OM|=2D.作射线OP,使∠xOP=-π6,再在射线OP上取点M,使|OM|=22.若ρ1+ρ2=0,θ1+θ2=π,则点M1(ρ1,θ1)与点M2(ρ2,θ2)的位置关系是().A.关于极轴所在的直线对称B.关于极点对称C.关于过极点且垂直于极轴的直线对称D.关于过极点且与极轴成π4的直线对称3.点P的直角坐标为(-√2,√2),那么它的极坐标可表示为.4.在极坐标系中作下列各点,并说明每组中各点的位置关系.(1)A(2,0)、B(2,π6)、C(2,π4)、D(2,π2)、E(2,3π2)、F(2,5π4)、G(2,11π6);(2)A(0,π4)、B(1,π4)、C(2,5π4)、D(3,5π4)、E(3,π4).化极坐标为直角坐标分别把下列点的极坐标化为直角坐标.(1)(2,π6);(2)(3,π2);(3)(4,2π3);(4)(4,-π12).极坐标的概念已知极坐标系中点A(2,π2),B(√2,3π4),O(0,0),则△AOB为().A.等边三角形B.顶角为钝角的等腰三角形C.顶角为锐角的等腰三角形D.等腰直角三角形极坐标与直角坐标间的互化在极坐标系中,点P(2,π3)和点Q(4,5π6)之间的距离为.把下列各点的极坐标化为直角坐标,并判断所表示的点在第几象限.(1)(2,4π3);(2)(2,2π3);(3)(2,-π3);(4)(2,-2).在极坐标系中,已知△ABC的三个顶点的极坐标分别为A(2,π3),B(2,π),C(2,5π3).(1)判断△ABC的形状;(2)求△ABC的面积.极坐标平面内两点P(4,3π2)、Q(ρ,-π4)之间的距离为√10,则ρ=.1.在极坐标系中,若点A、B的坐标分别是(2,π3)、(3,-π6),则△AOB为().A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形2.将极坐标(6,4π3)化为直角坐标为().A.(-3√3,3)B.(-3√3,-3)C.(-3,-3√3)D.(-3,3√3)3.在极坐标系中,已知两点A、B的极坐标分别为(3,π3)、(4,π6),则△AOB(其中O为极点)的面积为.4.在极坐标系中,已知三点M(2,5π3),N(2,0),P(2√3,π6).(1)将M、N、P三点的极坐标化为直角坐标;(2)判断M、N、P三点是否在一条直线上.在极坐标系中,已知两点A(2,π4),B(2,5π4),且△ABC为等腰直角三角形,求直角顶点C的极坐标与该三角形的面积.考题变式(我来改编):第2课时 极 坐 标 系知识体系梳理问题1:极轴 逆时针 极坐标系 问题2:极径 极角 极坐标 M(ρ,θ) 问题3:{x =ρcosθ,y =ρsinθ问题4:{ρ2=x 2+y 2,tanθ=yx(x ≠0)基础学习交流1.B 当ρ<0时,点M(ρ,θ)的位置按下列规定确定:作射线OP,使∠xOP=θ,在OP 的反向延长线上取|OM|=|ρ|,则点M 就是坐标(ρ,θ)的点,故选B.2.A 因为点(ρ,θ)关于极轴所在的直线对称的点为(-ρ,π-θ),由点M 1(ρ1,θ1)和M 2(ρ2,θ2)满足ρ1+ρ2=0,θ1+θ2=π,可知点M 1与M 2关于极轴所在的直线对称.3.(2,3π4)(答案不唯一) 直接利用极坐标与直角坐标的互化公式求解,即ρ=√(-√2)2+(√2)2=2,tan θ=-1.因为点P 在第二象限,所以可取一个极角为3π4.4.解:(1)所有点都在以极点为圆心,半径为2的圆上.点B 、G 关于极轴对称,点D 、E 关于极轴对称,点C 、F 关于极点对称.(2)所有点都在倾斜角为π4,且过极点的直线上.点D 、E 关于极点对称.重点难点探究探究一:【解析】(1)∵x=ρcos θ=2cos π6=√3,y=ρsinθ=2sin π6=1.∴点(2,π6)的直角坐标为(√3,1).(2)∵x=ρcos θ=3cos π2=0,y=ρsin θ=3sin π2=3.∴点(3,π2)的直角坐标为(0,3).(3)∵x=ρcos θ=4cos 2π3=-2,y=ρsin θ=4sin 2π3=2√3.∴点(4,2π3)的直角坐标为(-2,2√3).(4)∵cos π12=√1+cos π62=√1+√322=√6+√24,sin π12=√1-cos π62=√1-√322=√6-√24,∴x=ρcos θ=4cos(-π12)=4cosπ12=√6+√2,y=ρsin θ=4sin(-π12)=-4sin π12=√2-√6.∴点(4,-π12)的直角坐标为(√2+√6,√2-√6).【小结】严格按照{x =ρcosθ,y =ρsinθ进行转化,注意准确计算.探究二:【解析】显然OA=2,OB=√2,∠AOB=π4,由余弦定理得AB=√OA 2+OB 2-2OA ·OB ·cos∠AOB =√2,故OB=AB,∠ABO=π2,即△AOB 为等腰直角三角形.【答案】D【小结】极坐标中的ρ和θ分别表示到极点的距离和极轴逆时针转过的角度.探究三:【解析】(法一)由公式{x =ρcosθ,y =ρsinθ ,得点P(2,π3)和点Q(4,5π6)的直角坐标分别为P(1,√3)和Q(-2√3,2),由两点间的距离公式得|PQ|=√(1+2√3)2+(√3-2)2=2√5.(法二)在极坐标系中,已知点P(2,π3)和点Q(4,5π6),故∠POQ=π2,所以|PQ|=√22+42=2√5.【答案】2√5【小结】如果极坐标系中的两点确定,那么它们之间的距离也确定,可以把各点极坐标转化为直角坐标,在平面直角坐标系中计算,也可以利用极径、极角的定义和余弦定理在三角形中计算. 思维拓展应用应用一:(1)由题意知x=2cos4π3=2×(-12)=-1,y=2sin4π3=2×(-√32)=-√3,即点(2,4π3)的直角坐标为(-1,-√3),是第三象限内的点. (2)由题意知x=2cos 2π3=-1,y=2sin 2π3=√3,即点(2,2π3)的直角坐标为(-1,√3),是第二象限内的点.(3)由题意知x=2cos(-π3)=1,y=2sin(-π3)=-√3,即点(2,-π3)的直角坐标为(1,-√3),是第四象限内的点.(4)由题意知x=2cos(-2)=2cos 2<0(π2<2<π),y=2sin(-2)=-2sin2<0,即点(2,-2)的直角坐标为(2cos 2,-2sin 2),是第三象限点. 应用二:(1)画图可知,A 、B 、C 三点都在以极点为圆心,2为半径的圆上,且所对的圆心角均为23π,∴|AB|=|AC|=|BC|,∴△ABC 为正三角形.(2)由(1)知12|AB|=2sin π3,∴|AB|=2√3,∴△ABC 的面积为S=12×2√3×2√3×√32=3√3.应用三:√2或3√2 根据x=ρcos θ,y=ρsin θ,得P 、Q 的直角坐标分别为P(0,-4)、Q(√22ρ,-√22ρ).∴|PQ|=√(0-√22ρ)2+(-4+√22ρ)2=√10,解得ρ=√2或ρ=3√2. 基础智能检测1.B 由题意知∠AOB=π3-(-π6)=π2,故选B.2.C 由公式{x =ρcosθ,y =ρsinθ,得{x =6×(-12)=-3,y =6×(-√32)=-3√3,所以直角坐标为(-3,-3√3),选择C.3.3 结合图形,△AOB 的面积S=12OA·OB·sin(π3-π6)=3.4.解:(1)将三点坐标代入公式{x =ρcosθ,y =ρsinθ,可知点M 的直角坐标为(1,-√3),点N 的直角坐标为(2,0),点P 的直角坐标为(3,√3). (2)∵k MN =√32-1=√3,k NP =√3-03-2=√3,∴k MN =k NP ,∴M、N 、P 三点在同一条直线上.全新视角拓展(法一)利用坐标转化.点A(2,π4)的直角坐标为(√2,√2),点B(2,5π4)的直角坐标为(-√2,-√2),设点C 的直角坐标为(x,y).由题意得AC⊥BC,|AC|=|BC|.∴AC ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0,|AC|2=|BC|2,于是(x-√2,y-√2)·(x+√2,y+√2)=0,即x 2+y 2=4. ①(x-√2)2+(y-√2)2=(x+√2)2+(y+√2)2,即y=-x. ② 将②代入①得x 2=2,解得x=±√2,∴{x =√2,y =-√2或{x =-√2,y =√2,∴点C 的直角坐标为(√2,-√2)或(-√2,√2).∴ρ=√2+2=2,tan θ=-1,θ=7π4或3π4,∴点C 的极坐标为(2,3π4)或(2,7π4).S △ABC =12|AC|·|BC|=12|AC|2=12×8=4.(法二)设点C 的极坐标为(ρ,θ)(ρ>0,0≤θ<2π),∵|AB|=2|OA|=4,∠C=π2,|AC|=|BC|,∴|A C|=|BC|=2√2,根据余弦定理可得{ρ2+22-2×2ρcos (θ-π4)=8, ①ρ2+22-2×2ρcos (θ-5π4)=8, ② ①+②化简得ρ2=4,由ρ>0得ρ=2,代入①得cos(θ-π4)=0,∴θ-π4=π2+kπ,k∈Z,即θ=3π4+kπ,k∈Z,又∵0≤θ<2π,令k=0,1,得θ=3π4或7π4,∴点C 的极坐标为(2,3π4)或(2,7π4),S △ABC =12|AC|·|BC|=12|AC|2=12×8=4.。
