全等三角形的性质及判定(习题及答案)
全等三角形的性质及判定(经典讲义)

全等三角形的性质及判定知识要点1、全等三角形概念:两个能完全重合的三角形叫做全等三角形.2、全等三角形性质:(1)两全等三角形的对应边相等,对应角相等.(2)全等三角形的对应边上的高相等,对应边上的中线相等, 对应角的平分线相等.(3)全等三角形的周长、面积相等.3、全等三角形判定方法:(1)全等判定一:三条边对应相等的两个三角形全等(SSS )(2)全等判定二:两角和它们的夹边对应相等的两个三角形全等(ASA ) (3)全等判定三:两角及其中一个角的对边对应相等的两个三角形全等(AAS) (4)全等判定四:两边和它们的夹角对应相等的两个三角形全等(SAS )专题一、全等图形的性质——全等图形的对应边(对应中线、角平分线、高线)、对应角、对应周长、对应面积相等例题1:下列说法,正确的是( )A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形 例题2:如图1,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD=7cm ,DM=5cm ,∠DAM=39°,则AN =____cm ,NM =____cm ,NAB ∠= .【仿练1】如图2,已知ABC ADE ∆≅∆,AB AD =,BC DE =,那么与BAE ∠相等的角是 . 【仿练2】如图3,ABC ADE ∆≅∆,则AB= ,∠E= _.若∠BAE=120°,∠BAD=40°,则∠BAC= .、图4EDCB A图2 图3M DA NBC 图1三角形全等的判定一(SSS )相关几何语言考点∵AE=CF ∵CM 是△的中线∴_____________( )∴____________________∴__________( ) 或 ∵AC=EF∴____________________∴__________( )AB=AB ( )在△ABC 和△DEF 中∵⎪⎩⎪⎨⎧___________________________ ∴△ABC ≌△DEF ( )例1.如图,AB =AD ,CB =CD .△ABC 与△ADC 全等吗?为什么?例2.如图,C 是AB 的中点,AD =CE ,CD =BE .求证△ACD ≌△CBE .BFECAFE DCB ACMBA B A例3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证∠A=∠D.练习1..如图,AB=CD,AD=CB,那么下列结论中错误的是()A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD2、如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定()A.△ABD≌△ACD B.△BDE≌△CDEC.△ABE≌△ACE D.以上都不对3.如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是()A.SSS B.SAS C.AASD.HL4.如图,AB=AC,D为BC的中点,则△ABD≌_________.5.如图,已知AB=DE,BC=EF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:.6.如图,AB=AC,BD=DC,∠BAC=36°,则∠BAD的度数是°.7、.如图,AB=AE,AC=AD,BD=CE,求证:△ABC≌ADE。
三角形全等的判定证明题-(含答案)
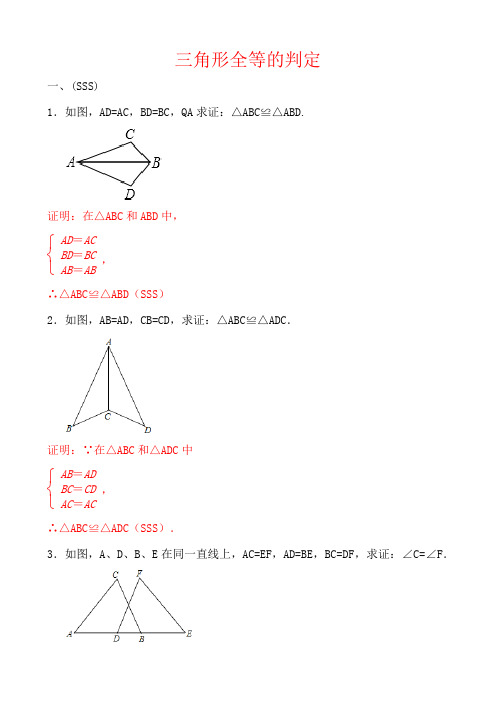
三角形全等的判定一、(SSS)1.如图,AD=AC ,BD=BC ,QA 求证:△ABC≌△ABD .证明:在△ABC 和ABD 中,⎩⎨⎧ AD =ACBD =BCAB =AB ,∴△ABC≌△ABD(SSS )2.如图,AB=AD ,CB=CD ,求证:△ABC≌△AD C .证明:∵在△ABC 和△ADC 中⎩⎨⎧ AB =ADBC =CDAC =AC,∴△ABC≌△ADC(SSS ).3.如图,A 、D 、B 、E 在同一直线上,AC=EF ,AD=BE ,BC=DF ,求证:∠C=∠F.证明:∵AD=BE∴AD+DB=BE+DB,即:AB=DE ,在△ABC 和△DEF 中,⎩⎨⎧ AC =EFAB =DEBC =DF ,∴△ABC≌△DEF(SSS ),∴∠C=∠F.4.如图,已知线段AB 、CD 相交于点O,AD 、CB 的延长线交于点E,OA=OC,EA=EC,请说明∠A=∠C.解:连结OE 在△EAC 和△EBC 中OA OC EA EC OE OE ⎧⎪⎨⎪⎩===(已知)(已知)(公共边)∴△EAC ≌△EBC (SSS )∴∠A =∠C (全等三角形的对应角相等)二、(SAS )5.已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .6.如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB ,∴∠DCA+∠ACE=∠BCE+∠ACE ,∴∠DCE=∠ACB ,∵在△DCE 和△ACB 中,∴△DCE ≌△ACB (SAS )∴DE=AB .7. 已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .8. 如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB,∴∠DCA+∠ACE=∠BCE+∠ACE,∴∠DCE=∠ACB,∵在△DCE和△ACB中,∴△DCE≌△ACB(SAS)∴DE=AB.三、(ASA)(AAS)9.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.证明:∵FB=CE,∴BC=EF.∵AB∥ED,∴∠B=∠E∵AC∥EF,∴∠ACB=∠DFE.在△ABC和△DEF中{∠B=∠EBC=EF∠ACB=∠DFE∴△ABC≌△DEF(ASA).∴AC=DF.10. 如图,在△AEC和△DFB中,∠E=∠F,点A,B,C,D在同一直线上,AE∥DF,AB=CD,求证:CE=BF。
《全等三角形的判定》练习(含答案)

全等三角形的判定一、选择题1.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )A .①B .②C .③D .①和②【答案】C .【解析】解带③去可以利用“角边角”得到全等的三角形.故选C .2.如图,已知:∠A=∠D ,∠1=∠2,下列条件中能使△ABC ≌△DEF 的是()A .∠E=∠B B .ED=BC C .AB=EFD .AF=CD【答案】D .【解析】添加AF=CD ,∵AF=CD ,∴AF+FC=CD+FC ,∴AC=FD ,在△ABC 和△DEF 中12A DAC DF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DEF (ASA ),故选D .3.下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③有两角和其中一个角的对边对应相等的两个三角形全等;④有两边和一个角对应相等的两个三角形全等.正确的说法个数是( )A .1个B .2个C .3个D .4个【答案】B .【解析】①不正确,因为判定三角形全等必须有边的参与;②正确,符合判定方法SSS ;③正确,符合判定方法AAS ;④不正确,此角应该为两边的夹角才能符合SAS .所以正确的说法有两个.故选B .4.在△ABC 和△A ˊB ′C ′中,已知∠A=∠A ′,AB=A ′B ′,在下面判断中错误的是( )A .若添加条件AC=A ′C ′,则△ABC ≌△A ′B ′C ′B .若添加条件BC=B ′C ′,则△ABC ≌△A ′B ′C ′C .若添加条件∠B=∠B ′,则△ABC ≌△A ′B ′C ′D .若添加条件∠C=∠C ′,则△ABC ≌△A ′B ′C ′【答案】B.【解析】A ,正确,符合SAS 判定;B ,不正确,因为边BC 与B ′C ′不是∠A 与∠A ′的一边,所以不能推出两三角形全等;C ,正确,符合AAS 判定;D ,正确,符合ASA 判定;故选B .5.如图,在等腰△ABC 中,AB=AC ,∠A=20°,AB 上一点D 使AD=BC ,过点D 作DE ∥BC 且DE=AB ,连接EC ,则∠DCE 的度数为( )A .80°B .70°C .60°D .45°【答案】B.【解析】如图所示,连接AE .∵AE=DE,∴∠ADE=∠DAE,∵DE∥BC,∴∠DAE=∠ADE=∠B,∵AB=AC,∠BAC=20°,∴∠DAE=∠ADE=∠B=∠ACB=80°,在△ADE 与△CBA 中,DAE ACB AD BCADE B ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴AE=AC,∠AED=∠BAC=20°,∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°,∴△ACE 是等边三角形,∴CE=AC=AE=DE,∠AEC=∠ACE=60°,∴△DCE 是等腰三角形,∴∠CDE=∠DCE,∴∠DEC=∠AEC﹣∠AED=40°,∴∠DCE=∠CDE=(180﹣40°)÷2=70°.故选B .6.如图:AB=AC ,∠B=∠C,且AB=5,AE=2,则EC 的长为( )A .2B .3C .5D .2.5【答案】B.【解析】在△ABE 与△ACF 中,∵A AAB AC B C∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABE≌△ACF(ASA ),∴AC=AB=5∴EC=AC﹣AE=5﹣2=3,故选B.二、填空题.7.如图,AB=AC ,要使△ABE≌△ACD,依据ASA ,应添加的一个条件是 .【答案】∠C=∠B .【解析】添加∠C=∠B,在△ACD 和△ABE 中,A AAB AC C B∠=∠⎧⎪=⎨⎪∠=∠⎩,8.如图,AB∥CF,E 为DF 中点,AB=20,CF=15,则BD= 5 .【答案】5.【解析】∵AB∥FC,∴∠ADE=∠EFC,∵E 是DF 的中点,∴DE=EF,在△ADE 与△CFE 中,ADE EFC DE EFAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ADE≌△CFE,∴AD=CF,∵AB=20,CF=15,∴BD=AB﹣AD=20﹣15=5.9.如图,∠1=∠2,∠3=∠4,BC=5,则BD= .【答案】5. 【解析】∵∠ABD+∠3=180°∠ABC+∠4=180°,且∠3=∠4,∴∠ABD=∠ABC在△ADB 和△ACB 中,1=2AB ABABD ABC ∠∠⎧⎪=⎨⎪∠=∠⎩, ∴△ADB≌△ACB(ASA ),∴BD=BC=5.10.如图,要测量一条小河的宽度AB 的长,可以在小河的岸边作AB 的垂线 MN ,然后在MN 上取两点C ,D ,使BC=CD ,再画出MN 的垂线DE ,并使点E 与点A ,C 在一条直线上,这时测得DE 的长就是AB 的长,其中用到的数学原理是: .【答案】ASA ,全等三角形对应边相等 .【解析】∵AB⊥MN,DE⊥MN,∴∠ABC=∠EDC=90°,在△ABC 和△EDC 中,ABC EDC BC DCACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC≌△EDC(ASA ),∴DE=AB.11.如图,在四边形ABCD 中,AB∥DC,AD∥BC,对角线AC 、BD 相交于点O ,则图中的一对全等三角形为 .(写出一对即可)【答案】△ABC ≌△ADC.【解析】△ABC≌△ADC,理由如下:∵AB∥DC,AD∥BC,∴∠BAC=∠DCA,∠DAC=∠BCA,在△ABC 与△ADC 中,BAC DCA AC CADAC BCA ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC≌△ADC(ASA ),∴AB=DC,BC=DA ,在△ABO 与△CDO 中,BAO DCO AOB COD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABO≌△CDO(AAS ),同理可得:△BCO≌△DAO,三、解答题12.如图,点A ,B ,C ,D 在同一条直线上,AB=FC ,∠A=∠F,∠EBC=∠FCB.求证:BE=CD .【答案】证明见解析.【解析】∵∠EBC=∠FCB,∠EBC+∠ABE=180°,∠FCB+∠FCD=180°,∴∠ABE=∠FCD,在△ABE 与△FCD 中,A F AB FCABE FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE≌△FCD(ASA ),∴BE=CD.13.如图,点D 在AB 上,DF 交AC 于点E ,CF∥AB,AE=EC .求证:AD=CF .【答案】答案见解析.【解析】∵CF∥AB,∴∠A=∠ACF,∠ADE=∠CFE.在△ADE 和△CFE 中,A ACF ADE CFE AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△CFE(AAS ).∴AD=CF.14. 如图,锐角△ABC 中,∠BAC=60°,O 是BC 边上的一点,连接AO ,以AO 为边向两侧作等边△AOD 和等边△AOE,分别与边AB ,AC 交于点F ,G .求证:AF=AG .【答案】答案见解析.【解析】∵△AOD 和△AOE 是等边三角形,∴∠E=∠AOF=60°,AE=AO ,∠OAE=60°,∵∠BAC=60°,∴∠FAO=∠EAG=60°﹣∠CAO, 在△AFO 和△AGE 中, FAO EAG AO AEAOF E ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFO≌△AGE(ASA ), ∴AF=AG.。
全等三角形的概念和性质及判定一-教师版

1 / 22【例1】 下列说法正确的是()A .全等三角形是指形状相同的三角形B .全等三角形是指面积相等的三角形C .全等三角形的周长和面积都相等D .所有的等边三角形都全等 【难度】★ 【答案】C【解析】A 错,形状相同,大小也要相同;B 错,面积相等不一定全等,反例同底等高 的三角形;D 错,大小不一定相等. 【总结】本题主要考查全等三角形的概念.【例2】 直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是( )A .形状相同B .周长相等C .面积相等D .全等【难度】★ 【答案】C【解析】等底同高,所以面积相等.【总结】本题主要考查同底等高的两个三角形的面积相等的运用.【例3】 如图所示,△ABC ≌△CDA ,且AB =CD ,则下列结论错误的是() A .∠1=∠2 B .AC =CA C .∠B =∠D D .AC =BC【难度】★ 【答案】D【解析】全等三角形对应角相等,对应边相等. 【总结】考察学生对全等三角形性质的理解及运用.【例4】 下列各条件中,不能作出唯一的三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边 【难度】★ 【答案】C【解析】C 选项是边边角,不能作为全等的判定条件. 【总结】考查全等三角形的判定定理的运用.例题解析21ABCD【例5】 练习画出下列条件的三角形:(1) 画,ABC ∆使40,45,4A B AB cm ∠=︒∠=︒=; (2) 画,ABC ∆使6,8,10AB cm BC cm AC cm ===; (3) 画,ABC ∆使4,3,45AB cm AC cm A ==∠=︒; (4) 画,ABC ∆使8,5,50AB cm AC cm B ==∠=︒. 【难度】★ 【答案】略 【解析】略.【例6】 下列说法:①形状相同的两个图形是全等形;②面积相等的两个三角形是全等三角形;③全等三角形的周长相等,面积相等;④在△ABC 和△DEF 中,若∠A =∠D ,∠B =∠E ,∠C =∠F ,AB =DE ,BC =EF ,AC =DF ,则两个三角形的关系,可记作△ABC ≌△DEF ,其中说法正确的是( ) A .1个 B .2个C .3个D .4个【难度】★★ 【答案】B【解析】(1)错,大小不一定相等;(2)面积相等不一定全等,反例同底等高;(3)对; (4)对,故选B .【总结】考察学生对全等三角形的概念及性质的理解. 【例7】 下列说法中错误的是()A .全等三角形的公共角是对应角,对顶角也是对应角B .全等三角形的公共边也是对应边C .全等三角形的公共顶点是对应顶点D .全等三角形中相等的边所对应的角是对应角,相等的角所对的边是对应边 【难度】★★ 【答案】C【解析】全等三角形的公共顶点不一定是对应顶点,两个全等三角形任意放置,使得三 角形的一个顶点与另一个三角形的不对应的顶点重合.【总结】考察学生对全等三角形的概念的辨析能力,以及正确的举反例.【例8】 如图所示,ABE ADC ABC ∆∆∆和是分别沿着AB AC 、边翻折形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( ) A .80°B .100°C .60°D .45°【难度】★★α321ABCDEP3 / 22【答案】A【解析】设1=28x ∠,25x ∠=,33x ∠=,则36180x =,解得:5x =. 1140∴∠=︒,225∠=︒,315∠=︒, 22ABC ACB ∴∠∂=∠+∠212280=∠+∠=︒.【总结】考察学生对全等三角形的应用以及翻折知识的理解及运用.【例9】 如图,在矩形ABCD 中,AE 平分∠DAB 交DC 于点E ,连接BE ,过E 作EF ⊥BE交AD 于F .(1)∠DEF 和∠CBE 相等吗?请说明理由;(2)请找出图中与ED 相等的线段(不另添加辅助线和字母),并说明理由. 【难度】★★【答案】(1)相等;(2)ED BC AD ==.【解析】(1)90DEF CEB ∠+∠=︒,90CBE CEB ∠+∠=︒, DEF CBE ∴∠=∠(同角的余角相等) (2)AE 平分DAB ∠, 45DAE ∴∠=︒,DE AD ∴=.AD BC =, DE AD BC ∴==.【总结】考察学生对图形的理解和掌握,能够迅速的根据图形发现同角的余角相等,再 利用特殊的角度45得出等腰直角三角形,从而解题.【例10】 如图所示,30255ADF BCE B F BC cm ∆≅∆∠=︒∠=︒=,,,,14CD cm DF cm ==,.求:(1)1∠的度数;(2)AC 的长. 【难度】★★【答案】(1)1=55∠°;(2)4AC cm =. 【解析】(1)ADF BCE ≅,30A B ∴∠=∠=︒,AD BC =,155A F ∴∠=∠+∠=︒; (2)ADF BCE ≅,AD BC ∴=, 514AC AD CD cm ∴=-=-=.【总结】考察学生对全等三角形对应边相等,对应角相等的掌握,并且学会正确运用.【例11】 如图,在△ABC 中,∠A :∠B :∠ACB =2:5:11,若将△ABC 绕点C 逆时针旋转,试旋转前后的△A ’B ’C ’中的顶点B ’在原三角形的边AC 的延长线上,求∠BCA ’的度数. 【难度】★★ 【答案】40︒.【解析】设2A x ∠=,5B x ∠=,11ACB x ∠=,1ABC DEFABCA’B ’则18180x =, 解得:10x =, ∴110BCA ∠=,70BCB '∠=.110A CB ''∠=, 40BCA '∴∠=.【总结】考察学生对旋转的理解,注意利用全等三角形的性质进行解题.【例12】 如图,已知△ABC ≌△ADE ,BC 的延长线交AD 于点F ,交AE 的延长线于G ,∠ACB =1050,∠CAD =100,∠ADE =250,求∠DFB 和∠AGB 的度数. 【难度】★★【答案】∠DFB =85︒,∠AGB =45︒. 【解析】证明:ABC ADE ≅, 25ADE ABC ∴∠=∠=︒,50CAB EAD ∠=∠=︒, 10502585DFB ∴∠=︒+︒+︒=︒, 1801102545AGB ∠=︒-︒-︒=︒.【总结】本题主要考察学生对全等三角形的性质及三角形外角性质和内角和定理的综合 运用.【例13】 如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时.(1)写出图中一对全等的三角形,并写出它们的所有对应角;(2)设∠AED 的度数为x , ∠ADE 的度数为y ,那么∠1,∠2的度数分别是多少?(用含有x 或y 的代数式表示)(3)∠A 与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律. 【难度】★★★【答案】(1)AED A ED '≅,A A '∠=∠, AED A ED '∠=∠,ADE A DE '∠=∠; (2)11802x ∠=-,21802y ∠=-; (3)()1122A ∠=∠+∠. 【解析】(3)证明:∵()180A x y ∠=-+,1+2=3602()x y ∠∠-+, ∴()1122A ∠=∠+∠. 【总结】本题一方面考查翻折的性质,另一方面考查全等三角形的性质及三角形内角和 定理的运用.ABC DEF G 21AB C DEA ’【例14】 如图(1)所示,把△ABC 沿直线BC 移动线段BC 那样长的距离可以变到△ECD的位置;如图(2)所示,以BC 为轴把△ABC 翻折180°,可以变到△DBC 的位置;如图(3)所示,以点A 为中心,把△ABC 旋转180°,可以变到△AED 的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换,问题:如图(4),△ABC ≌△DEF ,B 和E 、C 和F 是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.ABC DE(1)ABCD(2)A BCDE(3)ABC(4)DEF【难度】★★★【答案】翻折变换,平移变换或旋转变换,平移变换. 【解析】AB ED =,BC EF =,AC DF =.【总结】考察学生对图形的运动的理解和掌握,需要学生进行一定的空间想象.【例15】 如图,已知∠B =∠D ,∠1=∠2,AC =AE ,说明△ABC ≌△ADE 的理由. 【难度】★★ 【答案】见解析.【解析】证明:12∠=∠,12DAC DAC ∴∠+∠=∠+∠,即BAC DAE ∠=∠. 在ABC 和DAE 中,B D BAC DAE AC AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△ADE (A.A.S ).【总结】考察学生对全等三角形的判定条件的掌握.【例16】 如图,已知∠C =∠E ,BE =CD ,说明△ABE 与△ADC 全等的理由,AB 与AD相等吗?为什么? 【难度】★ 【答案】见解析.【解析】证明:在ABE 和ADC 中,A A C E BE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,ABE ADC ∴≅(A.A.S ), AB AD ∴=.【总结】考察学生对全等三角形的判定及性质的综合运用.ABCDEF21AB CDE【例17】 如图,已知AD =BC ,AE =BE .说明AC =BD ,∠C =∠D 的理由. 【难度】★ 【答案】见解析. 【解析】证明:AD BC =,AE BE =,DE CE ∴=.在ACE 和BDE 中,AE BE = AEC BED ∠=∠, CE DE =ACE BDE ∴≅(S.A.S )AC BD ∴=,C D ∠=∠(全等三角形的对应边相等,对应角相等)【总结】考察学生对全等三角形的判定及性质的综合运用.【例18】 如图,已知AB =CD ,AD =BC ,说明∠A =∠C 的理由. 【难度】★ 【答案】见解析. 【解析】证明:连接BD 在ABD 和CDB 中,AB CD AD BC BD DB =⎧⎪=⎨⎪=⎩, (..)ABD CDB S S S ∴≅ A C ∴∠=∠(全等三角形的对应角相等)【总结】考察学生对全等三角形的判定及性质的综合运用.【例19】 如图,已知BD 是△ABC 的中线,B 、D 、E 、F 在一条直线上,且AE ∥CF ,说明△ADE 与△CDF 全等的理由. 【难度】★★ 【答案】见解析. 【解析】//AE CF , E EFC ∴∠=∠.∵BD 是△ABC 的中线, ∴AD CD =.在ADE 和CDF 中,E EFCADE FDC AD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ADE CDF ∴≅(A.A.S ). 【总结】考察学生对全等三角形的判定条件的掌握.ABCDEABCDEFAB CD【例20】 如图,已知AC ∥BD ,AC =BD ,(1)说明△AOC 与△BOD 全等的理由;(2)说明EO =FO 的理由. 【难度】★★ 【答案】见解析. 【解析】证明:(1)//AC BD ,C D ∴∠=∠.在AOC 和BOD 中,C DAOC BOD AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, AOC BOD ∴≅(A.A.S ); (2)AOC BOD ≅, CO DO ∴=.在CEO 和DFO 中,C D CO DOCOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()CEO DFO ASA ∴≅, EO FO ∴=.【总结】考察学生对全等三角形的判定及性质的综合运用.【例21】 如图,CD ⊥AB 于D ,BE ⊥AC 于E ,OD =OE ,说明AB =AC 的理由. 【难度】★★ 【答案】见解析.【解析】CD AB BE AC ⊥⊥,, 90BDC DEC ∴∠=∠=︒. 在BDO 和CEO 中,BDC BEC DO EODOB COE ∠=∠⎧⎪=⎨⎪∠=∠⎩, (..)BDO CEO A S A ∴≅. DO EO ∴=,B C ∠=∠,BO CO =, BE CD ∴=.在ABE 和ACD 中,A A BE CDBC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABE ≌ACD (A.S.A ), AB AC ∴=(全等三角形的对应边相等)【总结】本题主要考察学生对全等三角形的判定条件的掌握,注意利用多次全等.ABCDEFOABCDEO【例22】 如图,已知AD ∥BC ,BF ∥DE ,AE =CF .(1) △ADE 与△CBF 全等吗,为什么? (2) 说明AB =CD 的理由; (3) 图中有哪几对全等三角形? 【难度】★★ 【答案】见解析. 【解析】证明:(1)全等, //AD BC , DAC ACB ∴∠=∠.//BF DE ,DEF BFE ∴∠=∠, AED BFC ∴∠=∠.在AED 和BFC 中,DAC ACB AE CF AED BFC ∠=∠⎧⎪=⎨⎪∠=∠⎩, (..)ADE CBF A S A ∴≅; (2)ADE CBF ≅, AD BC ∴=.在ABC 和ADC 中AD BC DAC ACB AC AC =⎧⎪∠=∠⎨⎪=⎩,(..)ABC ADC S A S ∴≅, AB CD ∴=(全等三角形的对应边相等);(3)AED CFB ≅;DEC BFA ≅;ABC CDA ≅. 【总结】本题主要考察全等三角形的判定与性质的综合运用.【例23】 如图,已知AB =CD ,BM =CM ,AC =BD ,说明AM =DM 的理由. 【难度】★★ 【答案】见解析.【解析】在ABC 和BCD 中,AB CDAC BD BC BC =⎧⎪=⎨⎪=⎩, (..)ABC DCB S S S ∴≅, ABC BCD ∴∠=∠, 在ABM 和DCM 中,AB CD ABC BCD BM CM =⎧⎪∠=∠⎨⎪=⎩,(..)ABM DCM S A S ∴≅, AM DM ∴=. 【总结】本题主要考察全等三角形的判定与性质的综合运用,利用多次全等进行证明.AB CDMABCDEF【例24】 如图,∠1=∠2,AC =BD ,E 、A 、B 、F 在同一条直线上,说明:∠CAD =∠DBC 的理由. 【难度】★★ 【答案】见解析.【解析】12∠=∠, CAB DBA ∴∠=∠.在CAB 和DBA 中,AC BD CAB DBA AB AB =⎧⎪∠=∠⎨⎪=⎩, (..)CAB DBA S A S ∴≅, CBA DAB ∴∠=∠,又CAB DBA ∠=∠,CAD DBC ∴∠=∠.【总结】本题主要考察全等三角形的判定与角的和差的综合运用.【例25】 如图所示,AB =AC ,CE =BE ,连结AE 并延长交BC 于D ,说明AD ⊥BC 的理由. 【难度】★★ 【答案】见解析【解析】证明:在ABE 和ACE 中,AB AC BE CE AE AE =⎧⎪=⎨⎪=⎩,(..)ABE ACE S S S ∴≅, BAD CAD ∴∠=∠.在ABD 和ACD 中,AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩, (..)ABD ACD S A S ∴≅, 90ADB ADC ∴∠=∠=, AD BC ∴⊥.【总结】本题主要考查全等三角形的判定的综合运用,通过多次全等得到垂直.21ABC DEFABCDE【例26】 如图所示,BE 、CD 相交于O ,AB =AC ,AD =AE ,说明OD =OE 的理由. 【难度】★★ 【答案】见解析.【解析】证明:在ADC 和AEB 中, AD AE A A AB AC =⎧⎪∠=∠⎨⎪=⎩, ∴(..)ADC AEB S A S ≅ B C ∴∠=∠(全等三角形的对应角相等) AB CA =,AD AE =,BD CE ∴=.在BDO 和CEO 中,DOB COE ∠=∠ B C ∠=∠ BD CE =(..)BDO CEO A A S ∴≅, OD OE ∴=(全等三角形的对应边相等)【总结】本题主要考查全等三角形的判定的综合运用,注意对全等的多次运用.【例27】 如图,已知AB ⊥BD ,DE ⊥BD ,AB =CD ,BC =DE .试说明:AC ⊥CE ,若将CD 沿CB 方向平移得到图(2)(3)(4)(5)的情形,其余的条件不变, 结论AC 1⊥C 2E 还成立吗?请说明理由. 【难度】★★★ 【答案】见解析. 【解析】证明:(1)AB BD ⊥,DE BD ⊥, 90B D ∴∠=∠=︒在ABC 和CDE 中,AB CDB D BC DE =⎧⎪∠=∠⎨⎪=⎩, (..)ABC CDE S A S ∴≅, A ECD∴∠=∠.90A ACB ∠+∠=,90ACB ECB ∴∠+∠=, 即AC CE ⊥.ABCD EMAB C 2D EC 1AB C 1D EM AB C 2 DEM C 1MAB C 1D EC 2ABCDEO(2)12ABC C ED ≅, 2A E CD ∴∠=∠.190A AC B ∠+∠=,2190EC D AC B ∴∠+∠=, 1290C MC ∴∠=, 12AC C E ∴⊥.【总结】本题主要考察全等三角形的判定及垂直的综合运用,说理时注意分析.【例28】 如图,线段BE 上有一点C ,以BC 、CE 为边分别在BE 的同侧作等边三角形ABC 、DCE ,连结AE 、BD ,分别交CD 、CA 于Q 、P .(1)找出图中的一组相等的线段(等边三角形的边长相等除外),并说明你的理由; (2)取AE 的中点M 、BD 的中点N ,连结MN ,试判断△CMN 的形状. 【难度】★★★【答案】(1)BD AE =,(2)等边三角形. 【解析】(1)∵等边三角形ABC 和 等边三角形DCE , ∴BC AC =,CD CE =, BCA DCE ∠=∠=60°.BCA ACD DCE ACD ∴∠+∠=∠+∠,即BCD ACE ∠=∠.在BCD 和ACE 中,BC ACBCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩, BCD ACE ∴≅(S.A.S ),BD AE ∴=(全等三角形的对应边相等); (2)BCD ACE ≅, DBE EAC ∴∠=∠.M 、N 分别为BD 、AE 的中点, BN ND ∴=,AM ME =,BD AE =, BN AM ∴=.在BCN 和ACM 中,BC ACCBN CAM BN AM =⎧⎪∠=∠⎨⎪=⎩, BCN ACM ∴≅(S.A.S ),CM CN ∴=,BCN ACM ∠=∠,60NCM BCA ∴∠==︒, CM CN =, ∴△CMN 是等边三角形.【总结】考察学生对全等三角形的判定条件的掌握,注意在复杂的图形中准确的找出全 等三角形及其对应条件.2121A BCDEQP ABCDEMNPQ【例29】 如图,△ABC 是等腰直角三角形,其中CA =CB ,四边形CDEF 是正方形,连接AF 、BD .(1)观察图形,猜想AF 与BD 之间有怎样的关系,并证明你的猜想;(2)若将正方形CDEF 绕点C 按顺时针方向旋转,使正方形CDEF 的一边落在△ABC 的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由. 【难度】★★★【答案】(1)AF BD =,AF BD ⊥;(2)成立.【解析】证明:(1)△ABC 是等腰直角三角形,四边形CDEF 是正方形,CF CD ∴=,AC BC =,90DCF ACB ∠=∠=, FCA DCB ∴∠=∠.在FCA 和DCB 中,CF CD FCA DCB AC CB=⎧⎪∠=∠⎨⎪=⎩,()FCA DCB SAS ∴≅.AF DB ∴=,DBC FAC ∠=∠.90DBC ABD BAC ∠+∠+∠=, 90FAC ABD BAC ∴∠+∠+∠=,AF BD ∴⊥.(2)成立,证明过程同(1).【总结】考察学生对全等三角形的判定条件的掌握,注意根据旋转图形的不变性进行解 题.【习题1】 下列命题中正确的是 ( )A .全等三角形的高相等B .全等三角形的中线相等C .全等三角形的角平分线相等D .全等三角形对应角的平分线相等【难度】★ 【答案】D【解析】A 错,全等三角形对应边上的高相等;B 错,全等三角形对应边上的中线相等; C 错,全等三角形对应角的平分线相等;D 对. 【总结】考察学生对全等三角形的相关概念的理解.随堂检测ABC D E F【习题2】 如图,△ABD ≌△CDB ,且AB 、CD 是对应边;下面四个结论中不正确的是( )A .△ABD 和△CDB 的面积相等 B .△ABD 和△CDB 的周长相等C .∠A +∠ABD =∠C +∠CBD D .AD ∥BC ,且AD =BC 【难度】★ 【答案】C【解析】C 错,正确答案是∠A +∠ABD =∠C +∠CDB ,A ,B ,D 均对. 【总结】主要考察学生对全等三角形的概念的理解.【习题3】 如图,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD =7厘米,DM =5厘米,∠DAM =390,则AN =______厘米,NM =___________厘米,∠NAB =_______. 【难度】★【答案】7;5;12°.【解析】由翻折的性质,可得:ADM ANM ≅, 则7AN AD ==厘米,5MN DM ==厘米,39MAN MAD ∠=∠=, 故9023912NAB ∠=-⨯=.【总结】本题主要考查翻折性质与全等三角形性质的综合运用.【习题4】 尺规作图作AOB ∠的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得OCP ODP △≌△的根据是( ) A .SAS B .ASA C .AAS D .SSS【难度】★ 【答案】D【解析】∵AC AD =,PC PD =,OP OP =,(..)DCP ODP S S S ∴≅【总结】根据画图考察学生对画图过程中不变性的理解和掌握.A BCDA BC DM NABCDPO【习题5】如图,CE⊥AB,DF⊥AB,垂足分别为E、F,(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据_________;(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据_________;(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据_________;(4)若AC=BD,AE=BF,CE=DF.则△ACE≌△BDF,根据_________.【难度】★★【答案】(1)A.A.S;(2)A.S.A;(3)S.A.S;(4)S.S.S.【解析】//AC BD,A B∴∠=∠,C D∠=∠,则(1)、(2)、(3)、(4)分别得证.【总结】考察学生对全等三角形的判定条件的熟练掌握.【习题6】如图,已知△ABC≌△ADE, ∠CAD=150,∠DFB=900,∠B=250.求∠E和∠DGB的度数.【难度】★★【答案】105E∠=︒,65DEG∠=︒.【解析】AD BG⊥,90AFB∴∠=︒(垂直的意义)15DAC∠=︒,75FCA∴∠=︒(互余的意义)105ACB∴∠=︒(邻补角的意义)ACB AED≅,105E ACB∴∠=∠=︒,25B D∠=∠=︒902565DGB∴∠=︒-︒=︒(互余的意义)【总结】考察学生对全等三角形的性质的理解,并且对邻补角和互余等知识点要熟练掌握并应用.【习题7】如图:A、E、F、C四点在同一条直线上,AE=CF,过E、F分别作BE⊥AC、DF⊥AC,且AB∥CD,AB=CD.试说明:BD平分EF.【难度】★★【答案】见解析.【解析】//AB CD,A C∴∠=∠,ABD CDB∠=∠在ABG和CDG中,ABD CDBAB CDA C∠=∠⎧⎪=⎨⎪∠=∠⎩,()ABG CGD ASA∴≅,AG CG∴=,AE CF=,EG GF∴=,BD∴平分EF.【总结】考察学生对全等三角形的性质及判定的理解及运用.ABCEDFA BCDEFGABDE FG【习题8】 如图所示,△ABC 绕顶点A 顺时针旋转,若∠B =40°,∠C =30°,(1)顺时针旋转多少度时,旋转后的△AB 'C '的顶点C '与原三角形的顶点B 和A 在同一直线上?(原△ABC 是指开始位置)(2)再继续旋转多少度时,点C 、A 、C '在同一直线上? 【难度】★★【答案】(1)110︒;(2)70︒.【解析】(1)1803040110CAB ∠=︒-︒-︒=︒; (2)18011070︒-︒=︒.【总结】考察学生对旋转的理解,注意旋转过程中的不变性.【习题9】 已知:如图,△ABC 是等边三角形,过AB 边上的点D 作DG ∥BC ,交AC于点G ,•在GD 的延长线上取点E ,使DE =DB ,连结AE 、CD . 试说明:△AGE ≌△DAC . 【难度】★★ 【答案】见解析. 【解析】ABC 是等边三角形.AB AC BC ∴==,60BAC ACB B ∠=∠=∠=(等边三角形的性质) //DG BC ,60ADG B ∴∠=∠=°,60AGD ACB ∠=∠=°, ADG AGD ∴∠=∠.ED DB =,又DG AD =, DE DG DB AD ∴+=+,即AB EG =.AB AC =,AC EG ∴=.在ADG 和ADC 中,AG ADAGE DAC EG AC =⎧⎪∠=∠⎨⎪=⎩,(..)AGE DAC S A S ∴≅∠.【总结】考察学生对全等三角形的判定的掌握和应用以及等边三角形的性质综合运用.ABCDE FG【习题10】 在∠O 的两边上分别取点A 、D 和B 、C ,连接AC 、BD 相交于P .(1)若∠A =∠B ,P A =PB ,试说明OA =OB 的理由; (2)若OA =OB ,P A =PB ,试说明PC =PD 的理由. 【难度】★★★ 【答案】见解析.【解析】(1)在ADP 和BCP 中,A BPA PBDPA CPB ∠=∠⎧⎪=⎨⎪∠=∠⎩, (..)ADP BCP A S A ∴≅,DP CP ∴=(全等三角形对应边相等). AP BP =, AC BD ∴=(等式性质). 在OAC 和ODB 中,O OA B AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,(..)AOC BOD A A S ∴≅,AO BO ∴=(全等三角形的对应边相等); (2)连接OP在AOP 和BOP 中,OA OBPA PB OP OP =⎧⎪=⎨⎪=⎩,(..)AOP BOP S S S ∴≅,A B ∴∠=∠,AP = BP (全等三角形的对应角相等、对应边相等). 在ADP 和PCB 中,A BAP PB APD CPB ∠=∠⎧⎪=⎨⎪∠=∠⎩(..)ADP PCB A S A ∴≅,PC PD ∴=(全等三角形的对应边相等). 【总结】考察学生对全等三角形的性质及判定的理解和掌握,注意多次全等的综合运用.ABCDP OABCDP O【习题11】 如图,△ABC 、△ADE 都是等腰直角三角形,绕着顶点A 旋转后位置如下:(1) 当C 、A 、D 在同一直线上,说明CE 与BD 有何关系?为什么?(2) 当△ADE 再继续旋转到(2)、(3)、(4)的位置后,CE 与BD 又有何关系. 【难度】★★★【答案】(1)CE BD =,CE BD ⊥;(2)CE BD =,CE BD ⊥.【解析】(1)证明:△ABC 、△ADE 都是等腰直角三角形,AD AE ∴=,AC AB =,90BAD CAB ∠=∠=︒(等边三角形的性质)在ADB 和AEC 中,AD AEDAE CAE AB AC =⎧⎪∠=∠⎨⎪=⎩,(..)ADB AEC S A S ∴≅,CE BD ∴=,ACE ABD ∠=∠(全等三角形的对应边相等,对应角相等)90ACE BCE CBE ∠+∠+∠=, 90ABD BCE CBE ∴∠+∠+∠=,CE BD ∴⊥.(2)CE BD =,CE BD ⊥,证明过程同上.【总结】本题主要考查等腰直角三角形的性质与全等三角形的判定和性质的综合运用, 注意认真分析题目中的条件.【作业1】 如图,△ABC ≌△ABD ,C 和D 是对应顶点,若AB =6cm ,AC =5cm ,BC =4cm ,则AD 的长为_________cm . 【难度】★ 【答案】5【解析】全等三角形的对应边相等,5AD AC ==. 【总结】本题主要考查全等三角形的性质.课后作业A BCDE(1)(2)ABDCE(3) (4)AB CE DABCDE ABCD【作业2】 如图,给出下列四组条件:①AB DE BC EF AC DF ===,,; ②AB DE B E BC EF ===∠∠,,; ③B E BC EF C F ===∠∠∠∠,,; ④AB DE AC DF B E ===∠∠,,.其中,能使ABC DEF △≌△的条件共有 ( ) A .1组B .2组C .3组D .4组【难度】★ 【答案】C【解析】(1)S.S.S ;(2)S.A.S ;(3)A.S.A ;(4)S.S.A 不符合,所以正确答案 是(1)、(2)、(3),故选C .【总结】考察学生对全等三角形的判定定理的掌握.【作业3】 下列各条件中,不能作出唯一三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边 【难度】★ 【答案】C【解析】边边角不能作为全等三角形的判定条件.【作业4】 已知△ABC ≌△DEF ,若△ABC 的周长为32,AB =8,BC =12,DE =_______,DF =_______,EF = _______. 【难度】★★ 【答案】8;12;12. 【解析】△ABC ≌△DEF ,8DE AB ∴==,3212812DF AC ==--=,12EF BC ==. 【总结】本题主要考察全等三角形的性质的运用.ABCDEF【作业5】 如图△ACE ≌△DBF ,AE =DF ,CE =BF ,AD =8,BC =2.(1)求AC 的长度;(2)说明CE ∥BF 的理由. 【难度】★★【答案】(1)5;(2)见解析. 【解析】(1)△ACE ≌△DBF ,AC BD ∴=(全等三角形对应边相等)AB BC CD BC ∴+=+(等式性质),即AB CD =. 8AD =,2BC =,3AB CD ∴==, 5AC ∴=;(2)△ACE ≌△DBFECA DBF ∴∠=∠(全等三角形的对应角相等) //CE BF ∴(内错角相等,两直线平行)【总结】考察学生对全等三角形的性质的掌握及运用.【作业6】 如图,已知△ABC ≌△AED ,AE =AB ,AD =AC ,∠D -∠E =200,∠BAC =600,求∠C 的度数. 【难度】★★ 【答案】70︒.【解析】设E x ∠=,20D x ∠=+,△ABC ≌△AED , 60BAC EAD ∴∠=∠=︒,C D ∠=∠2060180x x ∴+++=︒,50x ∴=,70D ∴∠=︒, 70C ∴∠=︒.【总结】考察学生对全等三角形的性质的理解和运用,注意利用设未知数解题.【作业7】 如图,△DAC 和△EBC 均是等边三角形,点C 在线段AB 上,AE 、BD 分别与CD 、CE 交于点M 、N ,有如下结论①△ACE ≌△DCB ;②CM =CN ;③AC =DN .其中正确的结论是_______________,证明正确的结论. 【难度】★★ 【答案】①和②正确.【解析】①△DAC 和△EBC 均是等边三角形, ∴AC DC =,BC EC =,60ACD BCE ∠=∠=︒, ACE DCB ∴∠=∠.在ACE 和DCB 中,AC CD ACE DCB EC BC =⎧⎪∠=∠⎨⎪=⎩, (..)ACE DCB S A S ∴≅;ABCDA BCD EMNABCDEF(2)ACE DCB≅,CAE CDB∴∠=∠(全等三角形的对应角相等)60ACD BCE∠=∠=︒,60DCE ACD∴∠=∠=︒.在ACM和DCN中,AC DCACD DCECAE BDC=⎧⎪∠=∠⎨⎪∠=∠⎩,ACM DCN∴≅(A.A.S)CM CN∴=(全等三角形的对应边相等)【总结】考察学生对全等三角形的性质及判定的理解和运用.【作业8】如图,AD⊥AB,AC⊥AE,且AD=AB,AC=AE.试说明:DC=BE,DC⊥BE.【难度】★★【答案】见解析.【解析】AD⊥AB,AC⊥AE,90DAB EAC∴∠=∠=︒(垂直的意义)DAC BAE∴∠=∠(等式性质)在DAC和BAE中,AD ABDAC BAEAC AE=⎧⎪∠=∠⎨⎪=⎩,(..)DAC ABE S A S∴≅DC BE∴=,B D∠=∠(全等三角形的对应角相等,对应边相等)设BE与DC交于点F,DGA BGC∠=∠,90D DGA∠+∠=,90B BGC∴∠+∠=,90BFG∴∠=︒,DC BE∴⊥(垂直的意义).【总结】考察学生对全等三角形的性质及判定及三角形内角和定理的综合运用,注意归纳总结证明垂直的方法.ABCDEFGE【作业9】 如图,已知AE =CF ,∠DAF =∠BCE ,AD =CB . (1)问△ADF 与△CBE 全等吗?请说明理由;(2)如果将△BEC 沿CA 边方向平行移动,可有图中3幅图,如上面的条件不变, 结论仍成立吗?请选择一幅图说明理由. 【难度】★★ 【答案】(1)全等; (2)成立,全等. 【解析】(1)AE CF =,AE EF CF EF ∴-=-,即AF CE =(等式性质).在ADF 和BCE 中,AF CEA C AD BC =⎧⎪∠=∠⎨⎪=⎩, (..)ADF BCE S A S ∴≅;(2)成立,证明过如(1).【总结】考察学生对全等三角形的性质及判定的理解和运用.【作业10】 如图,以△ABC 的边AB 、AC 为边向外作等边△ABD 和等边△ACE ,BE与CD 相交于点F .(1)请说明△ABE ≌△ADC 的理由; (2)求∠1的度数. 【难度】★★★【答案】(1)见解析;(2)1120∠=︒.【解析】(1)证明:在等边△ABD 和等边△ACE 中,AD AB =,AC AE =,60DAB CAE ∠=∠=︒,DAB BAC CAE BAC ∴∠+∠=∠+∠, DAC BAE ∠=∠即.在ABE 和DAC 中,AD ABDAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩, ∴(..)ABE ADC S A S ≅;(2)ABE ADC ≅, DCA BEA ∴∠=∠(全等三角形对应角相等)1DCE BEC ∠=∠+∠, 又DCA BEA ∠=∠ 1ACE AEB BEC ∴∠=∠+∠+∠6060120=︒+︒=︒.【总结】考察学生对全等三角形的性质及判定的理解和掌握,综合性较强,注意利用外 角进行适当的转化,把未知的角度转化为和题目有关的已知角,从而进行解题.ABCD EF A BCD E FAB CDEFC (A )BD。
三角形全等的判定(含例题)

1.判定两个三角形全等的基本事实:边边边(SSS)(1)基本事实:三边分别相等的两个三角形全等,简写成“__________”或“SSS”.(2)这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.2.判定两个三角形全等的基本事实:边角边(SAS)(1)基本事实:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“__________”.(2)此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.3.判定两个三角形全等的基本事实:角边角(ASA)(1)基本事实:两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“__________”.(2)用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.4.判定两个三角形全等的基本事实:角角边(AAS)(1)基本事实:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“__________”.(2)这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.5.直角三角形全等的判定方法:斜边、直角边(HL)(1)基本事实:斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“________”.(2)“HL ”定理是直角三角形所独有的,对于一般三角形不成立. 【归纳】判定两个三角形全等常用的思路方法如下: HL SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎪⎩一直角边一斜边—已知两边找夹角—找另一边—边为角的对边—找任一角—找夹角的另一边—已知一边一角边为角的邻边找夹边的另一角—找边的对角—找夹边—已知两角找任一角的对边—K 知识参考答案:1.(1)边边边2.(1)SAS 3.(1)ASA4.(1)AAS5.(1)HLK —重点 三角形全等的判定K —难点 三角形全等的判定和性质的综合运用 K —易错三角形全等的判定一、用边边边(SSS )证明三角形全等明确要证明全等的两个三角形,在书写两个三角形全等时,“≌”左边三角形的三边与“≌”右边三角形的三边的前后顺序要保持一致.【例1】如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可判定A .ABD △≌ACD △B .ABE △≌ACE △△D.以上答案都不对C.BDE△≌CDE【答案】B二、用边角边(SAS)证明三角形全等此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【例2】如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC【答案】C【解析】∵AB=AC(已知),∠A=∠A(公共角),∴只需要AE=AD,∴△ABE≌△ACD,故选C.三、用角边角、角角边(ASA、AAS)证明三角形全等1.不能说“有两角和一边分别相等的两个三角形全等”,这是因为:假设这条边是两角的夹边,则根据角边角可知正确;假设一个三角形的一边是两角的夹边,而与另一个三角形相等的边是其中一等角的对边,则两个三角形不一定全等.2.有三个角对应相等的两个三角形不一定全等.【例3】如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是A.SSS B.SASC.SAA D.ASA【答案】D【解析】∵BF⊥AB,DE⊥BD,∴∠ABC=∠BDE.又∵CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA).故选D.【例4】如图,已知点B、C、F、E在同一直线上,∠A=∠D,BF=EC,AB∥DE,若∠1=80°,求∠BFD 的度数.四、用斜边、直角边(HL)证明直角三角形全等1.当证明两个直角三角形全等时,若不适合应用“HL”,也可考虑用“SAS”“ASA”或“AAS”来证明.2.在用一般方法证明时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可,在实际证明中可根据条件灵活选用不同的方法.【例5】如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌△Rt△DCF,则还需要添加一个条件是A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC【答案】D五、全等三角形的判定和性质的综合寻找解决问题的思路方法可以从求证的结论出发,结合已知条件,逐步寻求解决问题所需要的条件.同时要注意对图形本身隐含条件的挖掘,如对顶角、公共角、公共边等.【例6】如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为A.50°B.30°C.80°D.100°【答案】B【解析】∵OA=OC,OD=OB,∠AOD=∠COB,∴△AOD≌△COB(SAS),∴∠D=∠B=30°.故选B.【例7】如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.【解析】∵∠CAB=∠DBA,∠CBD=∠DAC,∴∠DAB=∠CBA.在△ADB与△BCA中,CAB DBA AB ABDAB CBA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADB≌△BCA(ASA),∴BC=AD.。
初中数学全等三角形判定及性质练习题(附答案)

初中数学全等三角形判定及性质练习题一、单选题1 •如图,将厶ABC沿BC方向平移2cm得到ZXDEF,若厶ABC的周长为16cm,则四边形ABFD的周长为()A.16 CInB. 18 CmC. 20 CmD. 22 Cm2.如图,在RtZXABC中,ZC = 90o, AC = 12cm, BC = GCn一条线段PQ = AB, P,0两点分别在线段AC和AC的垂线AX上移动,若AABC和AAPQ全等•则AP的值为()A. 6 CmB.12cmC.12cm 或6cmD.以上都不对3•如图,ΛACB=ΛA f CB∖ ZBCB' = 32。
,则ZACA'的度数为()A.30oB.32C.35oD.45o4.如图,AB,CD表示两根长度相等的铁条,若O为AB.CD的中点,经测≡AC = 15c m,则容器内径为()A. 12 cmB. 13 CmC. 14 CmD. 15 Cm5. 如图,ZACB = 90°, AC = BC, AD 丄 CE, BE 丄 CE ,垂足分别是点 D,E,AD = 3,BE = I,则 DE 的长是()6•在△ ABC 中,若AD 是ZXABC 的中线,AB = 39 AC = 5,则AD 的长度可以是(C.57. 在正方形网格中,OoB 的位宜如图所示,到ZAoB 两边距离相等的点是()A.M 点 B ・N 点 C.P 点 D.Q 点8. 如图,AB = AC, BE 丄AC 于点E 、CF 丄AB 于点F, BE,CF 相交于点D,则① △ABE =ΛACF ,②厶BDF ≡∆CDE ;③点、D 在ZBAC 的平分线上•以上结论正确的有()2 D .√ΓOA.®B•② C.①② D.①②®9.已知ZXABC 与ZXDEF全等,ZA = ZD = 90o,ZB = 25° ,则ZE 的度数是()A.25oB.65oC.25o或55°D. 25°或65°10.如图,在Z∖PAB中,ZA = ZEM,N, K分别是PA.PB. AB ±的点,且AM=BK.BN = AK,若ZMKN = 44°,则ZP的度数为()A.44oB.66oC.88oD.92o二、解答题11 •如图所示,EF分别为线段AC上的两个点,且DE丄AC于点E.BF丄Ae于点F,若AB = CD、AE = CF、BD交AC 于点M.(1)试猜想£>£与3尸的关系,并证明你的结论;⑵求HE:MB = MD・D12.如图,点P是△/!BC内一点,EF分别是边Ae,BC上的两点,连接PE, PF,且PE = PF,点D 为AC延长线上一点,连接PD,且DE=BF,ZAEP+ ZBFP = 180。
(完整版)全等三角形的性质及判定

全等三角形第 1 节全等三角形的性质和判断【知识梳理】1、全等图形:能够完整重合的两个图形就是全等图形.2、全等三角形的观点与表示:能够完整重合的两个三角形叫作全等三角形.能够互相重合的极点、边、角分别叫作对应极点、对应边、对应角.全等符号为“≌”.3、全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角均分线相等,面积相等.4、全等三角形的判断方法:(1)边角边定理 ( SAS) :两边和它们的夹角对应相等的两个三角形全等.(2)角边角定理 ( ASA) :两角和它们的夹边对应相等的两个三角形全等.(3)边边边定理 ( SSS) :三边对应相等的两个三角形全等.(4)角角边定理 ( AAS ) :两个角和此中一个角的对边对应相等的两个三角形全等.(5)斜边、直角边定理 ( HL ) :斜边和一条直角边对应相等的两个直角三角形全等.【诊疗自测】1、假如ABC≌Δ DBC,则 AB的对应边是_____,AC的对应边是_____,∠DBC的对应角是_____,∠ DCB的对应角是_____.2、如图,已知△ABE≌△ DCE, AE=2 cm, BE=1.5 cm,∠ A=25°,∠ B=48°;那么 DE=_____cm,EC= _____cm,∠C= _____°;∠D= _____°.C 和点E,点 B 和点D 分别是对应点,则另一3、假如△ABC和△ DEF这两个三角形全等,点组对应点是,对应边是,对应角是,表示这两个三角形全等的式子是.【考点打破】种类一:全等形例 1、由同一张底片冲刷出来的两张五寸照片的图案 _____全等图案,而由同一张底片冲刷出来的五寸照片和七寸照片 ____全等图形。
(填“是”或许“不是”)种类二:全三角形的定义和性质例 2、如图,点 E,F 在线段 BC 上,△ ABF 与△ DCE 全等,点 A 与点 D ,点 B 与点 C 是对应极点, AF 与 DE 交于点 M ,则∠ DCE= ()A .∠B B.∠ A C.∠ EMF D .∠ AFB例 3、如图,△ ABE 和△ ADC 是△ ABC 分别沿着AB 、AC 边翻折 180°形成的,若∠ BAC :∠ABC :∠ BCA=28 : 5: 3,则∠α的度数为()A . 90° B. 85° C. 80° D. 75°种类三:全等三角形的判断(SSS)例 4、用直尺和圆规作一个角等于己知角的作图印迹如下图,则作图的依照是()A . SSS B. SAS C. ASA D. AAS例 5、已知:如图 2- 1,△ RPQ 中, RP= RQ, M 为 PQ 的中点.求证: RM 均分∠ PRQ.剖析:要证 RM 均分∠ PRQ,即∠ PRM= ______,只需证 ______≌ ______证明:∵M 为 PQ 的中点(已知),∴______= ______在△ ______和△ ______中,RP RQ(已知 ),PM ______,______ ______(),∴______≌ ______().∴∠ PRM = ______( ______).即 RM.例 6.已知:如图, AD =BC. AC= BD .试证明:∠ CAD =∠ DBC .种类四:全等三角形的判断(SAS)例 7. 已知:如图3-1,AB、CD订交于O点,AO=CO,OD=OB.求证:∠ D=∠ B.剖析:要证∠ D=∠ B,只需证 ______≌ ______证明:在△ AOD 与△ COB 中,AO CO ( ),______ ______( ),OD ______( ),∴△ AOD ≌△ ______ ().∴∠D=∠ B ( ______).例8、小红家有一个小口瓶(如下图),她很想知道它的内径是多少?可是尺子不可以伸在里边直接测,于是她想了想,唉!有方法了.她拿来了两根长度同样的细木条,而且把两根长木条的中点固定在一同,木条能够绕中点转动,这样只需量出AB 的长,就能够知道玻璃瓶的内径是多少,你知道这是为何吗?请说明原因.(木条的厚度不计)例 9、如图,将两个一大、一小的等腰直角三角尺拼接∠ABC= ∠ EBD=90 °),连结 AE 、 CD,试确立 AE 结论.(A 、B、D 三点共线,AB=CB ,EB=DB ,与 CD 的地点与数目关系,并证明你的种类五:全等三角形的判断(AAS和 ASA)例 10、某同学把一块三角形的玻璃打坏成了 3 块,现要到玻璃店去配一块完整同样的玻璃,同学小明知道只需带③ 去就行了,你知道此中的道理是()A . SAS B. SSA C. ASA D. HL例 11.如图,已知△ ABC的六个元素,则以下甲、乙、丙三个三角形中和△ABC 全等的图形是例 12、已知:如图,PM = PN,∠ M=∠ N.求证: AM= BN.剖析:∵ PM= PN,∴要证AM=BN,只需证PA= ______,只需证 ______≌ ______.证明:在△ ______与△ ______中,______ ______( ),______ ______( ),______ ______( ),∴△ ______≌△ ______ ().∴ PA= ______ ().∵PM=PN (),∴PM - ______= PN- ______,即 AM = ______.例 13、已知: AB ⊥ AE ,AD ⊥ AC ,∠ E=∠ B, DE=CB .求证: AD=AC ..例 14、如图,在△ ABC中,∠ ACB=90°, AC=BC,BE⊥CE于点 E. AD⊥CE于点D.求证:△ DEC≌△ CDA.种类六:全等三角形的判断(HL)例 15. 已知在△ ABC和△ DEF中 , ∠ A=∠D=90°, 则以下条件中不可以判断△ABC和△DEF全等的是 ( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠ F,BC=EF例 16、如下图,在△ ABC中,∠ C=90°, DE⊥AB 于点 D, BD=BC,若 AC=6,则AE+DE=_____BDAE C【易错优选】1、如下图,△ABC ≌△ DEC,则不可以获得的结论是()A . AB=DEB .∠ A= ∠ D C. BC=CD D .∠ ACD= ∠ BCE2、如图,梯形 ABCD中,AD∥BC,点 M是 AD的中点,且 MB=MC,若 AD=4,AB=6,BC=8,则梯形 ABCD的周长为()A.22 B.24 C.26 D. 283、如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度 DF 相等,则∠ ABC+∠ DFE=__________度【精髓提炼】判断三角形全等的基本思路:找夹角SAS已知两边 SS找直角HL找另一边SSS边为角的对边→找随意一角→AAS找这条边上的另一角→ASA已知一边一角 SA边就是角的一条边找这条边上的对角→AAS找该角的另一边→ SAS找两角的夹边ASA已知两角 AA找随意一边AAS备注:找寻对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边 ( 或最大角 ) 是对应边 ( 或对应角 ) ,一对最短边 ( 或最小角 ) 是对应边 ( 或对应角 ) .要想正确地表示两个三角形全等,找出对应的元素是重点.全等三角形的图形概括起来有以下几种典型形式:⑴ 平移全等型⑵ 对称全等型⑶ 旋转全等型【本节训练】训练【 1】如图, E 为线段 BC 上一点, AB ⊥BC,△ ABE ≌△ ECD ,判断 AE 与 DE 的关系,并证明你的结论.训练【 2】如图,点A、F、C、D在同向来线上,点 B 和点 E 分别在直线 AD的双侧,且 AB=DE,∠ A=∠ D,AF= DC.求证: BC∥EF.训练【 3】已知图中的两个三角形全等,则∠ 1 等于度.【训练 4】.如图,∠ BAC= ∠DAE ,∠ ABD= ∠ ACE ,AB=AC .求证: BD=CE .基础稳固一、选择题1、以下说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;④有一条边相等的两个等腰直角三角形全等.此中正确的有().A、1 个B、2 个C、3 个D、4 个DE=BC,以D、 E 为两个极点作地点不一样的三2、如图,△ABC是不等边三角形,角形,使所作三角形与△ABC全等,这样的三角形最多能够画出[ ] .A.2 个B.4 个C.6 个D.8 个3、以下说法正确的选项是()A、全等三角形是指周长和面积都同样的三角形;B、全等三角形的周长和面积都同样;C、全等三角形是指形状同样的两个三角形;D、全等三角形的边都相等4、以下两个三角形中,必定全等的是()A.两个等边三角形B.有一个角是 40°,腰相等的两个等腰三角形C.有一条边相等,有一个内角相等的两个等腰三角形D.有一个角是 100°,底相等的两个等腰三角形5、如图,△ ABC与△ BDE都是等边三角形, AB<BD,若△ ABC不动,将△ BDE绕点CD的大小关系为( )B 旋转,则在旋转过程中,AE与A.AE=CD B . AE>CD C.AE<CD D.没法确立ECA B D6、如图,已知 AB=AD,那么增添以下一个条件后,仍没法判断△ABC≌△ ADC的是()A.CB=CD B .∠ BAC=∠DAC C.∠ BCA=∠ DCA D.∠ B=∠D=90°二、填空题6、如图,在△ ABC 中,AD⊥ BC 于 D,BE⊥ AC 于 E,AD 与 BE 订交于点F,若 BF=AC,则∠ ABC=_______7、如图,等腰直角三角形ABC的直角极点 B 在直线 PQ上,AD⊥ PQ于 D,CE⊥PQ 于 E,且 AD=2cm,DB=4cm,则梯形 ADEC的面积是 _____ .8、(着手操作实验题)如下图是小明自制对顶角的“小仪器”表示图:(1)将直角三角板 ABC的 AC边延伸且使 AC固定;(2)另一个三角板 CDE?的直角极点与前一个三角板直角极点重合;(3)延伸 DC,∠PCD与∠ ACF就是一组对顶角,已知∠ 1=30°,∠ ACF为多少?三、简答题9、如图,已知AB=AC ,∠ 1=∠ 2,AD=AE ,求证:∠ C=∠ B.10、如图,在△ ABC中, AD是∠ BAC的均分线, DE、DF分别是△ ABD和△ ACD的高线,求证: AD⊥EF。
2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)知识回顾1.三角形的三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
三角形的三边一旦确定,这三角形就固定了,这是三角形具有稳定性。
2.三角形的内角和定理:三角形的三个内角之和等于180°。
3.三角形的外角定理:三角形的一个外角等于它不相邻的两个内角之和。
大于它不相邻的任意一个内角。
4.全等三角形的性质:若两个三角形全等,则他们的对应边相等;对应角相等;对应边上的中线相等,高线相等,角平分线也相等;且这两个三角形的周长和面积均相等。
5.全等三角形的判定:①边边边(SSS):三条边分别对应性相等的两个三角形全等。
②边角边(SAS):两边及其这两边的夹角对应相等的两个三角形全等。
③角边角(ASA):两角及其这两角的夹边对应相等的两个三角形全等。
④角角边(AAS):两角及其其中一角的对边对应相等的两个三角形全等。
⑤直角三角形判定(HL):直角三角形中斜边与其中任意一直角边分别对应相等的两个直角三角形全等。
全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件。
在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形。
专项练习题(含答案解析)1.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.【分析】根据邻补角的定义得出∠ACB=∠ACD,利用ASA证明△ACB≌△ACD,根据全等三角形的性质即可得解.【解答】证明:∵∠3=∠4,∴∠ACB=∠ACD,在△ACB和△ACD中,,∴△ACB≌△ACD(ASA),∴AB=AD.2.如图,△ABC是等腰三角形,点D,E分别在腰AC,AB上,且BE=CD,连接BD,CE.求证:BD=CE.【分析】根据等腰三角形的性质得出∠EBC=∠DCB,进而利用SAS证明△EBC与△DCB全等,再利用全等三角形的性质解答即可.【解答】证明:∵△ABC∴∠EBC=∠DCB,在△EBC与△DCB中,,∴△EBC≌△DCB(SAS),∴BD=CE.3.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.【分析】由∠BAD=∠EAC可得∠BAC=∠EAD,根据SAS可证△BAC≌△EAD,再根据全等三角形的性质即可求解.【解答】解:∵∠BAD=∠EAC,∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD,在△BAC与△EAD中,,∴△BAC≌△EAD(SAS),∴∠D=∠C=50°.4.如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为B,D.(1)求证:△ABC≌△ADC;(2)若AB=4,CD=3,求四边形的面积.【分析】(1)由AC平分∠BAD,得∠BAC=∠DAC,根据CB⊥AB,CD⊥AD,得∠B=90°=∠D,用AAS 可得△ABC≌△ADC;(2)由(1)△ABC≌△ADC,得BC=CD=3,S△ABC=S△ADC,求出S△ABC=AB•BC=6,即可得四边形ABCD的面积是12.【解答】(1)证明:∵AC平分∠BAD,∴∠BAC=∠DAC,∵CB⊥AB,CD⊥AD,∴∠B=90°=∠D,在△ABC和△ADC中,,∴△ABC≌△ADC(AAS);(2)解:由(1)知:△ABC≌△ADC,∴BC=CD=3,S△ABC=S△ADC,∴S△ABC=AB•BC=×4×3=6,∴S△ADC=6,∴S四边形ABCD=S△ABC+S△ADC=12,答:四边形ABCD的面积是12.5.如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.【分析】利用平行线的性质得∠EDC=∠B,再利用ASA证明△CDE≌△ABC,可得结论.【解答】证明:∵DE∥AB,∴∠EDC=∠B,在△CDE和△ABC中,,∴△CDE≌△ABC(ASA),∴DE=BC.6.如图,在等边三角形ABC中,点M为AB边上任意一点,延长BC至点N,使CN=AM,连接MN交AC于点P,MH⊥AC于点H.(1)求证:MP=NP;(2)若AB=a,求线段PH的长(结果用含a的代数式表示).【分析】(1)过点M作MQ∥BC,交AC于点Q,根据等边三角形的性质以及平行线的性质可得∠AMQ=∠AQM=∠A=60°,可得△AMQ是等边三角形,易证△QMP≌△CNP(AAS),即可得证;(2)根据等边三角形的性质可知AH=HQ,根据全等三角形的性质可知QP=PC,即可表示出HP的长.【解答】(1)证明:过点M作MQ∥BC,交AC于点Q,如图所示:在等边△ABC中,∠A=∠B=∠ACB=60°,∵MQ∥BC,∴∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N,∴△AMQ是等边三角形,∴AM=QM,∵AM=CN,∴QM=CN,在△QMP和△CNP中,,∴△QMP≌△CNP(AAS),∴MP=NP;(2)解:∵△AMQ是等边三角形,且MH⊥AC,∴AH=HQ,∵△QMP≌△CNP,∴QP=CP,∴PH=HQ+QP=AC,∵AB=a,AB=AC,∴PH=a.7.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF.有下列三个条件:①AC=DF,②∠ABC =∠DEF,③∠ACB=∠DFE.(1)请在上述三个条件中选取一个条件,使得△ABC≌△DEF.你选取的条件为(填写序号)(只需选一个条件,多选不得分),你判定△ABC≌△DEF的依据是(填“SSS”或“SAS”或“ASA”或“AAS”);(2)利用(1)的结论△ABC≌△DEF.求证:AB∥DE.【分析】(1)根据SSS ABC≌△DEF,即可解决问题;(2)根据全等三角形的性质可得∠A=∠EDF,再根据平行线的判定即可解决问题.【解答】(1)解:在△ABC和△DEF中,,∴△ABC≌△DEF(SSS),∴在上述三个条件中选取一个条件,使得△ABC≌△DEF,选取的条件为①,判定△ABC≌△DEF的依据是SSS.故答案为:①,SSS;(答案不唯一).(2)证明:∵△ABC≌△DEF.∴∠A=∠EDF,∴AB∥DE.8.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.(1)如图1,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图2.若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.【分析】(1)证明△BCD≌△FCE(SAS),由全等三角形的性质得出∠DBC=∠EFC,证出BD∥EF,则可得出结论;(2)由题意画出图形,延长BC到F,使CF=BC,连接AF,EF,由(1)可知BD∥EF,BD=EF,证出∠AEF=90°,得出∠DHE=90°,由直角三角形的性质可得出结论.【解答】(1)证明:在△BCD和△FCE中,,∴△BCD≌△FCE(SAS),∴∠DBC=∠EFC,∴BD∥EF,∵AF⊥EF,∴BD⊥AF;(2)解:由题意补全图形如下:CD=CH.证明:延长BC到F,使CF=BC,连接AF,EF,∵AC⊥BF,BC=CF,∴AB=AF,由(1)可知BD∥EF,BD=EF,∵AB2=AE2+BD2,∴AF2=AE2+EF2,∴∠AEF=90°,∴AE⊥EF,∴BD⊥AE,∴∠DHE=90°,又∵CD=CE,∴CH=CD=CE.9.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,且点D在线段BC上,连CE.(1)求证:△ABD≌△ACE;(2)若∠EAC=60°,求∠CED的度数.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠ACE=∠ABD,利用等腰直角三角形的性质可求得∠ACE=∠ABD=∠AED =45°,再根据三角形的内角和定理可求解∠AEC的度数,进而可求可求解【解答】(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵△ABD≌△ACE,∴∠ACE=∠ABD,∵△ABC和△ADE都是等腰直角三角形,∴∠ACE=∠ABD=∠AED=45°,∵∠EAC=60°,∴∠AEC=180°﹣∠ACE﹣∠EAC=180°﹣45°﹣60°=75°,∴∠CED=∠AEC﹣∠AED=75°﹣45°=30°.10.如图,在△ABC中(AB<BC),过点C作CD∥AB,在CD上截取CD=CB,CB上截取CE=AB,连接DE、DB.(1)求证:△ABC≌△ECD;(2)若∠A=90°,AB=3,BD=2,求△BCD的面积.【分析】(1)由CD∥AB得∠ABC=∠ECD,而CD=CB,CE=AB,即可根据全等三角形的判定定理“SAS”证明△ABC≌△ECD;(2))由∠A=90°,根据全等三角形的对应角相等证明∠BED=∠CED=∠A=90°,设BE=x,由BD2﹣BE2=CD2﹣EC2=DE2,列方程(2)2﹣x2=(3+x)2﹣32,解方程求得符合题意的x的值为2,则BC =5,再根据勾股定理求出DE的长,即可求出△BCD的面积.【解答】(1)证明:∵CD∥AB,CD=CB,CE=AB,∴∠ABC=∠ECD,在△ABC和△ECD中,,∴△ABC≌△ECD(SAS).(2)解:∵∠A=90°,∴∠CED=∠A=90°,∴∠BED=180°﹣∠CED=90°,设BE=x,∵EC=AB=3,BD=2,∴CD=BC=3+x,∵BD2﹣BE2=CD2﹣EC2=DE2,∴(2)2﹣x2=(3+x)2﹣32,整理得x2+3x﹣10=0,解得x1=2,x2=﹣5(不符合题意,舍去),∴BE=2,BC=3+2=5,∴DE===4,∴S△BCD=BC•DE=×5×4=10,∴△BCD的面积为10.11.如图,在Rt△ABC中,∠BAC=90°,AB=AC=1,D是BC边上的一点,以AD为直角边作等腰Rt △ADE,其中∠DAE=90°,连接CE.(1)求证:△ABD≌△ACE;(2)若∠BAD=22.5°时,求BD的长.【分析】(1)由“SAS”可证△ACE;(2)由等腰三角形三角形的性质可得BC的长,由角度关系可求∠ADC=67.5°=∠CAD,可得AC=CD =1,即可求解.【解答】(1)证明:∵∠BAC=90°=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵∠BAC=90°,AB=AC=1,∴BC=,∠B=∠ACB=45°,∵∠BAD=22.5°,∴∠ADC=67.5°=∠CAD,∴AC=CD=1,∴BD=﹣1.12.如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB沿AC对折到△ACE的位置,AE和CD交于点F.(1)求证:△CEF≌△ADF;(2)求tan∠DAF的值(用含x的式子表示).【分析】(1)根据矩形的性质得到∠B=∠D=90°,BC=AD,根据折叠的性质得到BC=CE,∠E=∠B =90°,等量代换得到∠E=∠D=90°,AD=CE,根据AAS证明三角形全等即可;(2)设DF=a,则CF=8﹣a,根据矩形的性质和折叠的性质证明AF=CF=8﹣a,在Rt△ADF中,根据勾股定理表示出DF的长,根据正切的定义即可得出答案.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=AD,根据折叠的性质得:BC=CE,∠E=∠B=90°,∴∠E=∠D=90°,AD=CE,在△CEF与△ADF中,,∴△CEF≌△ADF(AAS);(2)解:设DF=a,则CF=8﹣a,∵四边形ABCD是矩形,∴AB∥CD,AD=BC=x,∴∠DCA=∠BAC,根据折叠的性质得:∠EAC=∠BAC,∴∠DCA=∠EAC,∴AF=CF=8﹣a,在Rt△ADF中,∵AD2+DF2=AF2,∴x2+a2=(8﹣a)2,∴a=,∴tan∠DAF==.13.如图,△ABC和△DEF,点E,F在直线BC上,AB=DF,∠A=∠D,∠B=∠F.如图①,易证:BC+BE =BF.请解答下列问题:(1)如图②,如图③,请猜想BC,BE,BF之间的数量关系,并直接写出猜想结论;(2)请选择(1)中任意一种结论进行证明;(3)若AB=6,CE=2,∠F=60°,S△ABC=123,则BC=,BF=.【分析】(1)根据图形分别得出答案;(2)利用AAS证明△ABC≌△DFE,得BC=EF,再根据图形可得结论;(3)首先利用含30°角的直角三角形的性质求出BH和AH的长,从而得出BC,再对点E的位置进行分类即可.【解答】解:(1)图②:BC+BE=BF,图③:BE﹣BC=BF;(2)图②:∵AB=DF,∠A=∠D,∠B=∠F,∴△ABC≌△DFE(ASA),∴BC=EF,∵BE=BC+CE,∴BC+BE=EF+BC+CE=BF;图③:∵AB=DF,∠A=∠D,∠B=∠F,∴△ABC≌△DFE(ASA),∴BC=EF,∵BE=BF+EF,∴BE﹣BC=BF+EF﹣BC=BF+BC﹣BC=BF;(3)当点E在BC上时,如图,作AH⊥BC于H,∵∠B=∠F=60°,∴∠BAH=30°,∴BH=3,∴AH=3,∵S△ABC=12,∴=12,∴BC=8,∵CE=2,∴BF=BE+EF=8﹣2+8=14;同理,当点E在BC延长线上时,如图②,BF=BC+BE=8+10=18,故答案为:8,14或18.14.△ABC和△ADE都是等边三角形.(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有P A+PB =PC(或P A+PC=PB)成立(不需证明);(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接P A,猜想线段P A、PB、PC 之间有怎样的数量关系?并加以证明;(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接P A,猜想线段P A、PB、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论;(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.【解答】解:(2)PB=P A+PC,理由如下:如图②,在BP上截取BF=PC,连接AF,∵△ABC、△ADE都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAC+∠CAD=∠CAD+∠DAE,即∠DAB=∠EAC,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵AB=AC,BF=CP,∴△BAF≌△CAP(SAS),∴AF=AP,∠BAF=∠CAP,∴∠BAC=∠P AF=60°,∴△AFP是等边三角形,∴PF=P A,∴PB=BF+PF=PC+P A;(3)PC=P A+PB,理由如下:如图③,在PC上截取CM=PB,连接AM,同理得:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵AB=AC,PB=CM,∴△AMC≌△APB(SAS),∴AM=AP,∠BAP=∠CAM,∴∠BAC=∠P AM=60°,∴△AMP是等边三角形,∴PM=P A,∴PC=PM+CM=P A+PB.15.【情境再现】甲、乙两个含45°角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处.将甲绕点O 顺时针旋转一个锐角到图②位置.按图②作出示意图,并连接AG,BH,如图③所示,AB交HO于E,AC 交OG于F,通过证明△OBE≌△OAF,可得OE=OF.请你证明:AG=BH.【迁移应用】延长GA分别交HO,HB所在直线于点P,D,如图④,猜想并证明DG与BH的位置关系.【拓展延伸】小亮将图②中的甲、乙换成含30°角的直角三角尺如图⑤,按图⑤作出示意图,并连接HB,AG,如图⑥所示,其他条件不变,请你猜想并证明AG与BH的数量关系.【分析】【情境再现】由△OBE≌△OAF,得BE=AF,OE=OF,∠BEO=∠AFO,可证明△BHE≌△AGF (SAS),得BH=AG;【迁移应用】由△BHE≌△AGF,得∠BHE=∠AGF,可得∠AGF+∠GPO=90°,从而∠BHE+∠HPD=90°,∠HDP=90°,故DG⊥BH;【拓展延伸】设AB交OH于T,OG交AC于K,根据△ABC,△HOG是含30°角的直角三角形,AO⊥BC,可得OB=AO,∠OBA=∠OAC=30°,∠BOT=90°﹣∠AOT=∠AOK,即得△BOT∽△AOK,有===,∠BTO=∠AKO,又OH=GO,可得==,故△BTH∽△AKG,即得==,BH=AG.【解答】【情境再现】证明:由阅读材料知△OBE≌△OAF,∴BE=AF,OE=OF,∠BEO=∠AFO,∴∠BEH=∠AFG,∵OH=OG,∴OH﹣OE=OG﹣OF,即EH=GF,在△BHE和△AGF中,,∴△BHE≌△AGF(SAS),∴BH=AG;【迁移应用】解:猜想:DG⊥BH;证明如下:由【情境再现】知:△BHE≌△AGF,∴∠BHE=∠AGF,∵∠HOG=90°,∴∠AGF+∠GPO=90°,∴∠BHE+∠GPO=90°,∵∠GPO=∠HPD,∴∠BHE+∠HPD=90°,∴∠HDP=90°,∴DG⊥BH;【拓展延伸】解:猜想:BH=AG,证明如下:设AB交OH于T,OG交AC于K,如图:由已知得:△ABC,△HOG是含30°角的直角三角形,AO⊥BC,∴∠AOB=90°,∴OB=AO,∠OBA=∠OAC=30°,∠BOT=90°﹣∠AOT=∠AOK,∴△BOT∽△AOK,∴===,∠BTO=∠AKO,∴OT=OK,BT=AK,∠BTH=∠AKG,∵OH=GO,∴HT=OH﹣OT=GO﹣OK=(GO﹣OK)=KG,∴==,∴△BTH∽△AKG,∴==,∴BH=AG19。
(完整版)全等三角形知识总结和经典例题

全等三角形复习[ 知识要点 ]一、全等三角形1.判定和性质一般三角形直角三角形边角边( SAS)、角边角( ASA)具备一般三角形的判定方法判定斜边和一条直角边对应相等( HL )角角边( AAS)、边边边( SSS)对应边相等,对应角相等性质对应中线相等,对应高相等,对应角平分线相等注:①判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等.2.证题的思路:找夹角( SAS)已知两边找直角( HL )找第三边( SSS)若边为角的对边,则找任意角( AAS)找已知角的另一边(SAS)已知一边一角边为角的邻边找已知边的对角(AAS)找夹已知边的另一角(ASA)找两角的夹边(ASA)已知两角找任意一边(AAS)性质1、全等三角形的对应角相等、对应边相等。
2、全等三角形的对应边上的高对应相等。
3、全等三角形的对应角平分线相等。
4、全等三角形的对应中线相等。
5、全等三角形面积相等。
6、全等三角形周长相等。
( 以上可以简称 : 全等三角形的对应元素相等)7、三边对应相等的两个三角形全等。
(SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS)9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用 SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测等距离。
以及等角,用于工业和军事。
有一定帮助。
5、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。
全等三角形全套练习题

全等三角形一、全等三角形1、定义:能够完全重合的两个三角形叫做全等三角形。
特征:形状相同、大小相等、完全重合。
一个三角形经过平移、翻折、旋转可以得到它的全等形。
平移、翻折、旋转前后的图形全等。
2、全等三角形的表示:“全等”用“≌”表示,“∽”表示两图形的形状相同,“=”表示大小相等,读作“全等于”。
注意:记两三角形全等时,通常把表示对应顶点的字母写在对应位置上。
全等三角形的对应元素:对应顶点,对应边,对应角3、全等三角形的性质(1)全等三角形的对应边相等、对应角相等.(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
4、全等三角形的判定(1)边边边:三边对应相等的两个三角形全等(可简写成“SSS”)(2)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)(3(4(551、2、(判定)角的内部到角的两边的距离相等的点在角的平分线上。
三、学习全等三角形应注意的问题(1)要正确区分“对应边”与“对边”,“对应角"与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。
FE DCBA1.如图,AB =AD ,CB =CD .△ABC 与△ADC 全等吗?为什么?2.如图,C 是AB 的中点,AD =CE ,CD =BE .求证△ACD ≌△CBE .3.如图,点B ,E ,C ,F 在一条直线上,AB=DE,AC=DF ,BE=CF .求证∠A=∠D .4.已知,如图,AB=AD ,DC=CB .求证:∠B=∠D.5.如图,AD =BC ,AB =DC ,DE =BF 。
求证:BE =DF.CA B A C E AD C B1.如图,AC 和BD 相交于点O ,OA=OC ,OB=OD .求证DC ∥AB .2.如图,△ABC ≌△A B C ''',AD,A D ''分别是△ABC,△A B C '''的对应边上的中线,AD 与A D ''有什么关系?证明你的结论.3.如图,已知AC ⊥AB ,DB ⊥AB ,AC =BE,AE =BD,试猜想线段CE 与DE 的大小与位置关系,并证明你的结论.4.已知:如图,AD ∥BC ,AD=CB,求证:△ADC ≌△CBA .5.已知:如图AD ∥BC ,AD=CB ,AE=CF 。
最新人教版数学八年级上册第十二章-全等三角形(含答案)

第十二章 --全等三角形一、基本概念1.全等的图形必须满足:(1)形状相同的图形;(2)大小相等的图形;(3)能够完全重合的三角形叫做全等三角形2.全等三角形的表示两个三角形全等用“≌”符号表示;例如:△ABC与△DEF全等,那么我们可以表示为:△ABC≌△DEF。
3.全等三角形的基本性质(1)全等三角形对应边相等;(2)全等三角形对应角相等4.全等三角形的判定方法(1)三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)例:在如图所示的三角形中,AB=AC,AD是△ABC的中线,求证△ABD≌△ACD.AB D C(2)两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)例:如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一点C不经过池塘可以直接到达点A和B。
连接AC并延长到点D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离。
为什么?(3)两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)例:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C。
求证AD=AE.AD EB C(4)两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).例:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证△ABC≌△DEF(5)斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)例:如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.5.角平分线的性质及判定性质:角平分线上的点到角两边的距离相等判定:到一个角的两边距离相等的点在这个角的平分线上。
二、灵活运用定理1.判定两个三角形全等的定理中,必须具备三个条件,且至少要有一组边对应相等,因此在寻找全等的条件时,总是先寻找相等的可能性。
(1)已知条件中有两角对应相等,可找:①夹边相等(ASA)②任一组等角的对边相等(AAS)(2)已知条件中有两边对应相等,可找①夹角相等(SAS)②第三组边也相等(SSS)(3)已知条件中有一边一角对应相等,可找①任一组角相等(AAS或ASA)②夹等角的另一组边相等(SAS)三、常见考法(1)利用全等三角形的性质:①证明线段(或角)相等;②证明两条线段的和差等于另一条线段;③证明面积相等(2)利用判定公理来证明两个三角形全等练习题1.(2015•莆田)如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC2.(2015•茂名)如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为()A.6 B.5 C.4 D.33.(2015•贵阳)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE 4.(2015•青岛)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=()A.B.2 C.3 D.+25.(2015•启东市模拟)如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组6.(2015•杭州模拟)用直尺和圆规作已知角的平分线的示意图如右,则说明∠CAD=∠DAB 的依据是()A.SSS B.SAS C.ASA D.AAS 7.(2015•滕州市校级模拟)如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC8.(2015•奉贤区二模)如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是()A.∠B=45°B.∠BAC=90°C.BD=AC D.AB=AC 9.(2015•西安模拟)如图所示,AB∥EF∥CD,∠ABC=90°,AB=DC,那么图中的全等三角形有()A.4对B.3对C.2对D.1对10.(2015春•泰山区期末)如图,△A BC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是()A.1个B.2个C.3个D.4个二.填空题(共10小题)11.(2015春•沙坪坝区期末)如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为.12.(2015春•张家港市期末)如图,已知Rt△ABC≌Rt△ABCDEC,连结AD,若∠1=20°,则∠B的度数是.13.(2015春•苏州校级期末)如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=°.14.(2015春•万州区期末)如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=60°,则∠CAE=.15.(2015•黔东南州)如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件,使△ABD≌△CDB.(只需写一个)16.(2014秋•曹县期末)如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是.17.(2015•盐亭县模拟)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE 的度数是度.18.(2014秋•腾冲县校级期末)如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=度.19.(2015•聊城)如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是.20.如图,在△A BC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是.三.解答题(共7小题)21.如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB 延长线上一点.(1)求∠EBG的度数.(2)求CE的长.22.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系请证明你的结论.23.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.24.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.25.如图,为了测量一池塘的宽AB,在岸边找到一点C,连接AC,在AC的延长线上找一点D,使得DC=AC,连接BC,在BC的延长线上找一点E,使得EC=BC,测出DE=60m,试问池塘的宽AB为多少请说明理由.练习题参考答案一.选择题(共10小题)1.A 2.A 3.B 4.C 5.C 6.A 7.D 8.D 9.B 10.C 二.填空题(共10小题)11.4 12.70°13.30 14.30°15.AB=CD 16.AC=DE 17.60 18.90 19. 20.4三.解答题(共7小题)21.解:(1)∵△ABE≌△ACD,∴∠EBA=∠C=42°,∴∠EBG=180°﹣42°=138°;(2)∵△ABE≌△ACD,∴AC=AB=9,AE=AD=6,∴CE=AC﹣AE=9﹣6=3.22.证明:(1)∵AB=AC,∴∠B=∠ACD,∵AE∥BC,∴∠EAC=∠ACD,∴∠B=∠EAC,∵AD是BC边上的中线,∴AD⊥BC,∵CE⊥AE,∴∠ADC=∠CEA=90°在△ABD和△CAE中∴△ABD≌△CAE(AAS);(2)AB=DE,AB∥DE,如右图所示,∵AD⊥BC,AE∥BC,∴AD⊥AE,又∵CE⊥AE,∴四边形ADCE是矩形,∴AC=DE,∵AB=AC,∴AB=DE.∵AB=AC,∴BD=DC,∵四边形ADCE是矩形,∴AE∥CD,AE=DC,∴AE∥BD,AE=BD,∴四边形ABDE是平行四边形,∴AB∥DE且AB=DE.23.证明:(1)∵AD⊥BC,CE⊥AB,∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,∴∠CFD=∠B,∵∠CFD=∠AFE,∴∠AFE=∠B在△AEF与△CEB中,,∴△AEF≌△CEB(AAS);(2)∵AB=AC,AD⊥BC,∴BC=2CD,∵△AEF≌△CEB,∴AF=BC,∴AF=2CD.24.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC,∵在Rt△DCF和Rt△DEB中,,∴Rt△CDF≌Rt△EBD(HL).∴CF=EB;(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴CD=CE.在△ADC与△ADE中,∵∴△ADC≌△ADE(HL),∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+E B=AF+2EB.25.解:AB=60米.理由如下:∵在△ABC和△DEC中,,∴△ABC≌△DEC(SAS),∴AB=DE=60(米),则池塘的宽AB为60米.。
【人教版】八年级上小专题(4)全等三角形的性质与判定同步练习及答案

小专题(四) 全等三角形的性质与判定1.如图所示,D、E是△ABC中BC边上的点,AD=AE,∠ADC=∠AEB,EB=DC,那么∠1和∠2之间是什么关系?说你的理由.2.已知:如图,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB.求证:AE =CE.3.已知:如图,AB,CD交于点O,E,F为AB上两点,OA=OB,OE=OF,∠A=∠B,∠ACE=∠BDF.求证:△ACE≌△BDF.4.如图,已知AC交BD于点O,AB=DC,∠A=∠D.(1)请写出符合上述条件的五个结论(并且不再添加辅助线,对顶角除外);(2)从你写出的5个结论中,任选一个加以证明.5.如图,点C,F在线段BE上,BF=EC,∠1=∠2.请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)6.如图,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9 cm,AN=2 cm,求△ABC的周长.7.如图所示,要测量湖中小岛E距岸边A和D的距离,作法如下:(1)任作线段AB,取中点O;(2)连接DO并延长使DO=CO;(3)连接BC;(4)用仪器测量E,O在一条线上,并交CB 于点F,要测量AE,DE,只需测量BF,CF即可,为什么?8.两个大小不同的等腰直角三角板如图1所示方式放置,图2是由它抽象出的几何图形,B,C,E在同一直线上,连接DC.(1)请找出图2中的全等三角形,并予以证明;(2)求证:DC⊥BE.9.如图,在Rt△ABC中,∠BAC=90°,点D、E在边BC上,∠CAE=∠B,E是CD的中点,且AD平分∠BAE,试问:BD与AC相等吗?请说说你的理由.10.(1)如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC、∠DEF 都是钝角,求证:△ABC≌△DEF.(2)在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC、∠DEF都是锐角,请你用尺规在图2中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)参考答案1.在△ADC 和△AEB 中,⎩⎨⎧AD =AE ,∠ADC =∠AEB,DC =EB ,所以△ADC≌△A EB(SAS). 所以∠DAC=∠EAB.因为∠EAB-∠DAE=∠DAC-∠DAE, 所以∠1=∠2.2.证明:∵FC∥AB,∴∠ADE =∠CFE.在△ADE 和△CFE 中,⎩⎨⎧∠ADE=∠CFE,DE =FE ,∠AED =∠CEF,∴△ADE ≌△CFE(ASA). ∴AE=CE.3.证明:∵OA=OB ,OE =OF ,∴OA -OE =OB -OF ,即AE =BF.在△ACE 和△BDF 中,⎩⎨⎧∠A=∠B,∠ACE =∠BDF,AE =BF ,∴△ACE ≌△BDF(AAS).4.(1)五个结论:OB =OC ;OA =OD ;AC =DB ;∠ABO=∠DCO;∠ABC=∠DCB.(2)选证OB =OC.在△ABO 和△DCO 中,⎩⎨⎧∠AOB=∠DOC,∠A =∠D,AB =DC ,∴△ABO ≌△DCO(AAS). ∴OB=OC.5.答案不唯一,可以是∠E=∠B,∠D =∠A,FD =CA ,AB ∥ED 等.以DF =AC 加以证明.∵BF=EC , ∴BF -CF =EC -CF ,即BC =EF.在△ABC 和△DEF 中,⎩⎨⎧BC =EF ,∠1=∠2,CA =FD ,∴△ABC ≌△DEF(SAS).6.因为MN 平分∠AMC,所以∠AMN=∠CMN, 因为MN⊥AC,所以∠MNA=∠MNC=90°.在△AMN 和△CMN 中,⎩⎨⎧∠AMN=∠CMN,MN =MN ,∠MNA =∠MNC,所以△AMN≌△CMN(ASA). 所以AN =NC ,AM =CM.因为AN =2 cm ,所以AC =2AN =4 cm. 又因为△ABM 的周长为9 cm , 所以△ABC 的周长为9+4=13(cm). 7.由条件可知,△AOD ≌△BOC ,∴BC =AD.又∠A=∠B,∠AOE =∠BOF,AO =BO ,故△AOE≌△BOF. ∴AE=BF. ∴DE=CF.因此只要测出BF ,CF 即可知AE ,DE 的长度了. 8.(1)图2中△ABE≌△ACD.证明:∵△ABC 和△AED 都是等腰直角三角形, ∴AB =AC ,AE =AD ,∠BAC =∠EAD=90°.∴∠BAC +∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD. ∴△ABE≌△AC D(SAS).(2)证明:由(1)知△ABE≌△ACD,∴∠ACD =∠B=45°. 又∵∠ACB=45°,∴∠BCD =∠ACB+∠ACD=90° .∴DC ⊥BE.9.BD =AC ,理由如下:过D 点作AC 的平行线交AE 的延长线于F ,则∠CAE=∠F. 又∵∠AEC=∠DEF,E 是CD 的中点, ∴CE =DE.∴△AEC≌△FED. ∴AC=FD.又∵AD 平分∠BAE, ∴∠DAE =∠BAD.又∵∠B=∠F,AD 为公共边, ∴△ABD ≌△AFD. ∴BD =DF. ∴BD=AC.10.(1)证明:过点C 作CG⊥AB 交AB 的延长线于G ,过点F 作FH⊥DE 交DE 的延长线于H , ∵∠ABC =∠DEF,且∠ABC、∠DEF 都是钝角, ∴180°-∠ABC=180°-∠DEF,即∠CBG=∠FEH.在△CBG 和△FEH 中,⎩⎨⎧∠G=∠H=90°,∠CBG =∠FEH,BC =EF ,∴△CBG ≌△FEH(AAS).∴CG=FH.在Rt △ACG 和Rt △DFH 中,⎩⎨⎧AC =DF ,CG =FH ,∴Rt △ACG ≌Rt △DFH(HL). ∴∠A =∠D.在△ABC 和△DEF 中,⎩⎨⎧∠ABC=∠DEF,∠A =∠D,AC =DF ,∴△ABC ≌△DEF(AAS). (2)略。
全等三角形的性质及判定(习题及答案)

全等三角形的性质及判断(习题)例题示范例 1:已知:如图, C 为 AB 中点, CD=BE,CD∥BE.求证:△ ACD≌△ CBE.A【思路剖析】① 读题标明:DA CB EDCB E② 梳理思路:要证全等,需要三组条件,此中一定有一组边相等.由已知得, CD=BE;依据条件 C 为 AB 中点,得 AC=CB;这样已经有两组条件都是边,接下来看第三边或已知两边的夹角.由条件 CD∥BE,得∠ ACD=∠B.发现两边及其夹角相等,所以由SAS可证两三角形全等.【过程书写】先准备不可以直接用的两组条件,再书写全等模块.过程书写中需要注意字母对应.证明:如图∵C为 AB中点∴ AC=CB∵CD∥BE∴∠ ACD=∠B在△ ACD和△ CBE中AC= CB(已证)ACD= B (已证)CD = BE(已知)∴△ ACD≌△ CBE(SAS)稳固练习1.如图,△ ABC≌△ AED,有以下结论:①AC=AE;②∠ DAB=∠EAB;③ED=BC;④∠ EAB=∠DAC.此中正确的有()A.1 个B.2 个C.3 个D.4 个EA A1F EB C2BD C D第1 题图第2 题图2.如图, B, C, F,E 在同向来线上,∠ 1=∠2,BF=EC,要使△ABC≌△ DEF,还需要增添一组条件,这个条件能够是,原因是;这个条件也能够是,原因是;这个条件还能够是,原因是.3.如图, D 是线段 AB 的中点,∠ C=∠E,∠ B=∠A,找出图中的一对全等三角形是,原因是.A C AGD FE CHB E B D第3 题图第4 题图4.如图, AB=AD,∠ BAE=∠DAC,要使△ ABC≌△ ADE,还需要增添一组条件,这个条件能够是,原因是;这个条件也能够是,原因是;这个条件还能够是,原因是.5.如图,将两根钢条 AA' ,BB' 的中点连在一同,使 AA' ,BB' 能够绕着中点O 自由旋转,这样就做成了一个丈量工具,A'B'的长等于内槽宽 AB.此中判断△ OAB≌△OA'B' 的原因是()A. SAS B.ASA C.SSS D.AASAAOB'B A'BC DFE第5 题图第6题图6.要丈量河两岸相对的两点A,B 的距离,先在AB 的垂线BF上取两点 C,D,使 CD=BC,再定出 BF 的垂线 DE,使 A,C,E 在一条直线上(如下图),能够说明△ EDC≌△ ABC,得ED=AB,所以测得 ED的长就是 AB 的长.判断△ EDC≌△ABC最适合的原因是()A. SAS B.ASA C.SSS D.AAA7.已知:如图, M 是AB 的中点,∠ 1=∠2,∠ C=∠D.求证:△ AMC≌△ BMD.C D【思路剖析】① 读题标明:② 梳理思路:要证全等,需要由已知得:依据条件所以,由【过程书写】证明:如图12A M B组条件,此中一定有一组相等.=,=.,得=.可证两三角形全等.8. 已知:如图,点 B, F, C, E 在同一条直线上,且 BC=EF,AB∥DE,AB=DE.A求证:△ ABC≌△ DEF.【思路剖析】B F① 读题标明:② 梳理思路:要证全等,需要组条件,此中一定有一组由已知得:=,=依据条件,得=所以,由可证两三角形全等.【过程书写】证明:如图CED相等...思虑小结1.两个三角形全等的判断有,, _,,此中 AAA,SSA不可以证明三角形全等,请举反例进行说明.2.如图, A,B 两点分别位于一个池塘的两头,小明想用绳索丈量A,B 间的距离,但绳索不够长,一个叔叔帮他出了这样一个想法:先在地上取一个能够直接抵达 A 点和 B 点的点 C,连结 AC 并延伸到 D,使 CD=CA;连结 BC并延伸到 E,使CE=CB,连结 DE 并丈量出它的长度, DE 的长度就是 A,B 间的距离.你能说明此中的道理吗A ECB D【参照答案】稳固练习1. B2.AC=DF,SAS;∠ B=∠ E, ASA;∠ A=∠D,AAS3.△BCD≌△ AED,AAS4.AC=AE,SAS;∠ B=∠ D,ASA;∠ C=∠E,AAS5. A6. B7.①略②3,边∠1,∠ 2;∠ C,∠ DM 是 AB的中点, AM,BMAAS【过程书写】证明:如图,∵M 是 AB的中点∴AM=BM在△ AMC 和△ BMD中 C= D (已知)1 = 2(已知)AM = BM (已证)∴△ AMC≌△ BMD(AAS)8.①略②3,边BC,EF, AB,DEAB∥DE,∠ B,∠E SAS【过程书写】证明:如图,∵AB∥ DE∴∠ B=∠E在△ ABC和△ DEF中AB = DE (已知)B = E(已证)BC= EF(已知)∴△ ABC≌△ DEF(SAS)思虑小结1.SAS,SSS,ASA,AASAAA 反例:大小三角板SSA反例:作图略2.证明:如图,在△ ABC和△ DEC中AC = DC (已知)ACB= DCE(对顶角相等)BC= EC(已知)∴△ ABC≌△ DEC( SAS)∴AB=DE(全等三角形对应边相等)即DE的长度就是 A,B 间的距离。
全等三角形的的性质与判定难题50道(含详细答案)

全等三角形的的性质与判定难题50道1.边长为a 的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),⋯,按此方式依次操作,则第6个正六边形的边长为( )A .511()32a ⨯B .511()23a ⨯C .611()32a ⨯D .611()23a ⨯2.如图,在等边ABC ∆中,点D ,E 分别在边BC ,AC 上,且//DE AB ,过点E 作EF DE ⊥,交BC 的延长线于点F ,(1)求F ∠的度数;(2)若3CD =,求DF 的长.3.数学课上,李老师出示了如下的题目:“在等边三角形ABC 中,点E 在AB 上,点D 在CB 的延长线上,且ED EC =,如图,试确定线段AE 与DB 的大小关系,并说明理由”. 小敏与同桌小聪讨论后,进行了如下解答: (1)特殊情况,探索结论当点E 为AB 的中点时,如图1,确定线段AE 与DB 的大小关系,请你直接写出结论:AEDB (填“>”,“ <”或“=” ). (2)特例启发,解答题目解:题目中,AE 与DB 的大小关系是:AE DB (填“>”,“ <”或“=” ).理由如下:如图2,过点E 作//EF BC ,交AC 于点F .(请你完成以下解答过程) (3)拓展结论,设计新题在等边三角形ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED EC =.若ABC ∆的边长为1,2AE =,求CD 的长(请你直接写出结果).4.如图,过等边ABC ∆的边AB 上一点P ,作P E A C ⊥于E ,Q 为BC 延长线上一点,且PA CQ =,连PQ 交AC 边于D . (1)求证:PD DQ =;(2)若ABC ∆的边长为1,求DE 的长.5.如图所示,已知等边ABC ∆的边长为a ,P 是ABC ∆内一点,//PD AB ,//PE BC ,//PF AC ,点D 、E 、F 分别在BC 、AC 、AB 上,猜想:PD PE PF ++= ,并证明你的猜想.6.如图,已知ABC ∆和CDE ∆均为等边三角形,且点B 、C 、D 在同一条直线上,连接AD 、BE ,交CE 和AC 分别于G 、H 点,连接GH .(1)请说出AD BE =的理由; (2)试说出BCH ACG ∆≅∆的理由;(3)试猜想:CGH ∆是什么特殊的三角形,并加以说明.7.如图,已知ABC ∆是边长为6cm 的等边三角形,动点P ,Q 同时从A 、B 两点出发,分别沿AB 、BC 方向匀速运动,其中点P 运动的速度是1/cm s ,点Q 运动的速度是2/cm s ,当点Q 运动到点C 时,P ,Q 都停止运动.(1)出发后运动2s 时,试判断BPQ ∆的形状,并说明理由;那么此时PQ 和AC 的位置关系呢?请说明理由;(2)设运动时间为t ,BPQ ∆的面积为S ,请用t 的表达式表示S .8.已知:在等边ABC ∆中,点D 、E 、F 分别为边AB 、BC 、AC 的中点,点G 为直线BC 上一动点,当点G 在CB 延长线上时,有结论“在直线EF 上存在一点H ,使得DGH ∆是等边三角形”成立(如图①),且当点G 与点B 、E 、C 重合时,该结论也一定成立. 问题:当点G 在直线BC 的其它位置时,该结论是否仍然成立?请你在下面的备用图②③④中,画出相应图形并证明相关结论.9.已知点C 为线段AB 上一点,分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆,且CA CD =,CB CE =,ACD BCE ∠=∠,直线AE 与BD 交于点F ,(1)如图1,若60ACD ∠=︒,则AFB ∠= ;如图2,若90ACD ∠=︒,则AFB ∠= ;如图3,若120ACD ∠=︒,则AFB ∠= ;(2)如图4,若ACD α∠=,则AFB ∠= (用含α的式子表示);(3)将图4中的ACD ∆绕点C 顺时针旋转任意角度(交点F 至少在BD 、AE 中的一条线段上),变成如图5所示的情形,若ACD α∠=,则AFB ∠与α的有何数量关系?并给予证明.10.如图1,ABC ∆为等边三角形,面积为S .1D 、1E 、1F 分别是ABC ∆三边上的点,且11112AD BE CF AB ===,连接11D E 、11E F 、11F D ,可得△111D E F 是等边三角形,此时△11AD F 的面积114S S =,△111D E F 的面积114S S =. (1)当2D 、2E 、2F 分别是等边ABC ∆三边上的点,且22213AD BE CF AB ===时如图2,①求证:△222D E F 是等边三角形;②若用S 表示△22AD F 的面积2S ,则2S = ;若用S 表示△222D E F 的面积2S ',则2S '= .(2)按照上述思路探索下去,并填空:当n D 、n E 、n F 分别是等边ABC ∆三边上的点,11n n n AD BE CF AB n ===+时,(n 为正整数)△n n n D E F 是 三角形;若用S 表示△n n AD F 的面积n S ,则n S = ;若用S 表示△n n n D E F 的面积n S ',则n S '= .11.如图,在等边ABC ∆的三边上分别取点D 、E 、F ,使AD BE CF ==. (1)试说明DEF ∆是等边三角形;(2)连接AE 、BF 、CD ,两两相交于点P 、Q 、R ,则PQR ∆为何种三角形?试说明理由.12.如图所示,一个六边形的六个内角都是120︒,其中连续四边的长依次是1、9、9、5.求这个六边形的周长.13.如图,已知D 是ABC ∆的边BC 上的一点,CD AB =,BDA BAD ∠=∠,AE 是ABD ∆的中线.(1)若60B ∠=︒,求C ∠的值; (2)求证:AD 是EAC ∠的平分线.14.如图,ABC ∆为等边三角形,BD 平分ABC ∠交AC 于点D ,//DE BC 交AB 于点E . (1)求证:ADE ∆是等边三角形.(2)求证:12AE AB =.15.如图.在等边ABC ∆中,ABC ∠与ACB ∠的平分线相交于点O ,且//OD AB ,//OE AC . (1)试判定ODE ∆的形状,并说明你的理由;(2)线段BD 、DE 、EC 三者有什么关系?写出你的判断过程.16.如图,ABC ∆是等边三角形,DF AB ⊥,DE CB ⊥,EF AC ⊥,求证:DEF ∆是等边三角形.17.用三根火柴棒可以搭成一个等边三角形,你能用9根火柴搭出5个等边三角形吗? 18.如图,ABC ∆是等边三角形,AD 是高,并且AB 恰好是DE 的垂直平分线. 求证:ADE ∆是等边三角形.19.如图,60AOB ∠=︒,OC 平分AOB ∠,C 为角平分线上一点,过点C 作CD OC ⊥,垂足为C ,交OB 于点D ,//CE OA 交OB 于点E . (1)判断CED ∆的形状,并说明理由;(2)若3OC=,求CD的长.20.如图,在ABC∆中,AB AC=,120BAC∠=︒,D、F分别为AB、AC的中点,且DE AB⊥,FG AC⊥,点E、G在BC上,18BC cm=,求线段EG的长.(提示:需要添加辅助线)21.已知,如图,ABC∆是正三角形,D,E,F分别是各边上的一点,且AD BE CF==.请你说明DEF∆是正三角形.22.如图所示,DEF∆是等边三角形,且123∠=∠=∠,试问:ABC∆是等边三角形吗?请说明理由.23.如图,ABC∆为等边三角形,BD平分ABC∠,//DE BC.(1)求证:ADE∆是等边三角形;(2)求证:12AE AB=.24.如图ABC∆是等边三角形(1)如图①,//∆是等边三角形;DE BC,分别交AB、AC于点D、E.求证:ADE(2)如图②,ADE∆仍是等边三角形,点B在ED的延长线上,连接CE,判断BEC∠的度数及线段AE、BE、CE之间的数量关系,并说明理由.25.如图,E是AOB⊥,C、D是垂足,连接CD ∠的平分线上一点,EC OB⊥,ED OA交OE于点F,若60∠=︒.AOB(1)求证:OCD∆是等边三角形;(2)若5EF=,求线段OE的长.26.如图,ABCBCD CBE∠=∠=︒,BAC∆中,60∠=︒,点D、E分别在AB、AC上,30 BE、CD相交于点O,OG BC+=.OE OD OG⊥于点G,求证:227.如图,在ABC∠=∠=︒,EBC E∠,60∆中,AB AC=,D、E是ABC∆内两点,AD平分BAC若30=,则BC=cm.DE cmBE cm=,228.如图,已知ABC=,∆为等边三角形,D为BC延长线上的一点,CE平分ACD∠,CE BD 求证:ADE∆为等边三角形.29.如图,ABC∆∠=︒,DE与ABC ∆为等边三角形,D为BC边上一点,以AD为边作60ADE的外角平分线CE交于点E,连接AE,且CE BD∆是等边三角形.=.求证:ADE30.如图,在ABC+=.求ABD∠=︒,BD DC AB ∆中,AB AC=,D是三角形外一点,且60证:60∠=︒.ACD31.如图,在等边ABCOD AB,//OE AC.∠与ACB∠的平分线相交于点O,且//∆中,ABC(1)求证:ODE∆是等边三角形.(2)线段BD、DE、EC三者有什么数量关系?写出你的判断过程.(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)32.已知:如图,在ABC∠=︒,BD是中线,延长BC至点E,使C E C D=.A=,60∆中,AB AC求证:DB DE=.33.如图,ABD∆和BCD∆均是边长为2的等边三角形,E、F分别是AD、CD上的两个动点,且满足2+=.AE CF(1)求证:BDE BCF∆≅∆;(2)判断BEF∆的形状,并说明理由.34.已知:如图,四边形ABCD中,AB BC CD DA a∠=︒,M为BC上====,120BAD的点(M不与B、C重合),若AMN∆有一角等于60︒.(1)当M 为BC 中点时,则ABM ∆的面积为 (结果用含a 的式子表示); (2)求证:AMN ∆为等边三角形;(3)设AMN ∆的面积为S ,求出S 的取值范围(结果用含a 的式子表示).35.如图,点O 是等边ABC ∆内一点,110AOB ∠=︒,BOC α∠=,将B O C ∆绕点C 按顺时针方向旋转60︒得ADC ∆,连接OD . (1)COD ∆是什么三角形?说明理由;(2)若21AO n =+,21AD n =-,2(OD n n =为大于1的整数),求α的度数; (3)当α为多少度时,AOD ∆是等腰三角形?36.已知:如图,ABC ∆、CDE ∆都是等边三角形,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点. (1)求证:AD BE =; (2)求DOE ∠的度数;(3)求证:MNC ∆是等边三角形.37.已知:在AOB ∆和COD ∆中,OA OB =,OC OD =.(1)如图①,若60AOB COD ∠=∠=︒,求证:①AC BD =②60APB ∠=︒.(2)如图②,若A O B C O D α∠=∠=,则AC 与BD 间的等量关系式为 ,APB ∠的大小为 (直接写出结果,不证明)38.如图,ABC ∆是等边三角形,D 是AC 上一点,BD CE =,12∠=∠,试判断ADE ∆形状,并证明你的结论.39.等边ABC ∆边长为6,P 为BC 上一点,含30︒、60︒的直角三角板60︒角的顶点落在点P 上,使三角板绕P 点旋转.(1)如图1,当P 为BC 的三等分点,且PE AB ⊥时,判断EPF ∆的形状;(2)在(1)问的条件下,FE 、PB 的延长线交于点G ,如图2,求EGB ∆的面积; (3)在三角板旋转过程中,若2CF AE ==,()CF BP ≠,如图3,求PE 的长.40.为了使同学们更好地解答本题,我们提供了思路点拨,你可以依照这个思路填空,并完成本题解答的全过程,当然你也可以不填空,只需按照解答的一般要求,进行解答即可. 如图,已知AB AD =,60BAD ∠=︒,120BCD ∠=︒,延长BC ,使C E C D =,连接DE ,求证:BC DC AC +=. 思路点拨:(1)由已知条件AB AD=,60BAD∠=︒,可知:ABD∆是三角形;(2)同理由已知条件120BCD∠=︒得到DCE∠=,且CE CD=,可知;(3)要证BC DC AC+=,可将问题转化为两条线段相等,即=;(4)要证(3)中所填写的两条线段相等,可以先证明⋯.请你完成证明过程:41.已知ABC∆是等边三角形,点P是AC上一点,PE BC⊥于点E,交AB于点F,在CB 的延长线上截取BD PA=,PD交AB于点I,PA nPC=.(1)如图1,若1n=,则EBBD=,FIED=;(2)如图2,若60EPD∠=︒,试求n和FIED的值;(3)如图3,若点P在AC边的延长线上,且3n=,其他条件不变,则EBBD=.(只写答案不写过程)42.如图ABC∆为等边三角形,直线//a AB,D为直线BC上任一动点,将一60︒角的顶点置于点D处,它的一边始终经过点A,另一边与直线a交于点E.(1)若D恰好在BC的中点上(如图1)求证:ADE∆是等边三角形;(2)若D为直线BC上任一点(如图2),其他条件不变,上述(1)的结论是否成立?若成立,请给予证明;若不成立,请说明理由.43.如图,在等边ABC=,点P从点C出发沿CB边向点B点以2/cm s的速AB cm∆中,9度移动,点Q点从B点出发沿BA边向A点以5/cm s速度移动.P、Q两点同时出发,它们移动的时间为t秒钟.(1)你能用t表示BP和BQ的长度吗?请你表示出来.(2)请问几秒钟后,PBQ∆为等边三角形?(3)若P、Q两点分别从C、B两点同时出发,并且都按顺时针方向沿ABC∆三边运动,请问经过几秒钟后点P与点Q第一次在ABC∆的哪条边上相遇?44.如图:在ABC⊥于Q.==,AE CD∆中,AB BC AC=,AD与BE相交于点P,BQ AD求证:①ADC BEA∆≅∆;②2=.BP PQ45.如图1,点B是线段AD上一点,ABC∆分别是等边三角形,连接AE和CD.∆和BDE(1)求证:AE CD=;(2)如图2,点P、Q分别是AE、CD的中点,试判断PBQ∆的形状,并证明.46.如图:已知ABC∆是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN FM=,连接DM、MN、DN.(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断DMN∆是怎样的特殊三角形(不要求证明);(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.47.如图,ABC∆是等边三角形,点D、E、F分别是线段AB、BC、CA上的点,(1)若AD BE CF∆是等边三角形吗?试证明你的结论;==,问DEF(2)若DEF∆是等边三角形,问AD BE CF==成立吗?试证明你的结论.48.如图,已知ABC=,连∆为等边三角形,延长BC到D,延长BA到E,并且使AE BD 接CE,DE.求证:EC ED=.49.如图,已知ABC ∆与ACD ∆都是边长为2的等边三角形,如图有一个60︒角的三角板绕着点A 旋转分别交BC 、CD 于点P 、Q 两点(不与端点重合). (1)试说明:PAQ ∆是等边三角形; (2)求四边形APCQ 的面积;(3)填空:当BP = 时,APQ S ∆最小.50.如图,A 、B 、C 三点在同一直线上,ABM ∆和BCN ∆是正三角形,P 是AN 中点,Q 是CM 中点.求证:BPQ ∆是正三角形.全等三角形的的性质与判定难题50道参考答案与试题解析一.选择题(共1小题)1.边长为a 的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),⋯,按此方式依次操作,则第6个正六边形的边长为( )A .511()32a ⨯B .511()23a ⨯C .611()32a ⨯D .611()23a ⨯【解答】解:连接AD 、DF 、DB . 六边形ABCDEF 是正六边形,ABC BAF AFE ∴∠=∠=∠,AB AF =,120E C ∠=∠=︒,EF DE BC CD ===, 30EFD EDF CBD BDC ∴∠=∠=∠=∠=︒, 120AFE ABC ∠=∠=︒, 90AFD ABD ∴∠=∠=︒,在Rt ABD ∆和RtAFD 中 AF ABAD AD =⎧⎨=⎩Rt ABD Rt AFD(HL)∴∆≅∆, 1120602BAD FAD ∴∠=∠=⨯︒=︒,60120180FAD AFE ∴∠+∠=︒+︒=︒, //AD EF ∴,G 、I 分别为AF 、DE 中点,////GI EF AD ∴,60FGI FAD ∴∠=∠=︒,六边形ABCDEF 是正六边形,QKM ∆是等边三角形, 60EDM M ∴∠=︒=∠,ED EM ∴=,同理AF QF =, 即AF QF EF EM ===, 等边三角形QKM 的边长是a ,∴第一个正六边形ABCDEF 的边长是13a ,即等边三角形QKM 的边长的13,过F 作FZ GI ⊥于Z ,过E 作EN GI ⊥于N , 则//FZ EN , //EF GI ,∴四边形FZNE 是平行四边形,13EF ZN a ∴==,11112236GF AF a a ==⨯=,60FGI ∠=︒(已证), 30GFZ ∴∠=︒,11212GZ GF a ∴==,同理112IN a =, 1111123122GI a a a a ∴=++=,即第二个等边三角形的边长是12a ,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是1132a ⨯;同理第第三个等边三角形的边长是1122a ⨯,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是111322a ⨯⨯;同理第四个等边三角形的边长是111222a ⨯⨯,第四个正六边形的边长是11113222a ⨯⨯⨯;第五个等边三角形的边长是11112222a ⨯⨯⨯,第五个正六边形的边长是1111132222a ⨯⨯⨯⨯;第六个等边三角形的边长是1111122222a ⨯⨯⨯⨯,第六个正六边形的边长是111111322222a ⨯⨯⨯⨯⨯, 即第六个正六边形的边长是511()32a ⨯,故选:A .二.解答题(共49小题)2.如图,在等边ABC ∆中,点D ,E 分别在边BC ,AC 上,且//DE AB ,过点E 作EF DE ⊥,交BC 的延长线于点F ,(1)求F ∠的度数;(2)若3CD =,求DF 的长.【解答】解:(1)ABC ∆是等边三角形,60B ∴∠=︒, //DE AB ,60EDC B ∴∠=∠=︒,EF DE ⊥,90DEF ∴∠=︒,9030F EDC ∴∠=︒-∠=︒;(2)60ACB ∠=︒,60EDC ∠=︒,EDC∴∆是等边三角形.∴==,ED DC3∠=︒,F90∠=︒,30DEF∴==.DF DE263.数学课上,李老师出示了如下的题目:“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED EC=,如图,试确定线段AE与DB的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE =DB(填“>”,“<”或“=”).(2)特例启发,解答题目解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作//EF BC,交AC于点F.(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED EC∆的边=.若ABC 长为1,2AE=,求CD的长(请你直接写出结果).【解答】解:(1)故答案为:=.(2)过E作//EF BC交AC于F,等边三角形ABC,∴∠=∠=∠=︒,AB AC BC==,ABC ACB A60AFE ACB∴∠=∠=︒,60∠=∠=︒,AEF ABC60即60∠=∠=∠=︒,AEF AFE A∴∆是等边三角形,AEFAE EF AF ∴==,60ABC ACB AFE ∠=∠=∠=︒,120DBE EFC ∴∠=∠=︒,60D BED FCE ECD ∠+∠=∠+∠=︒,DE EC =,D ECD ∴∠=∠,BED ECF ∴∠=∠,在DEB ∆和ECF ∆中DEB ECF DBE EFC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,DEB ECF ∴∆≅∆,BD EF AE ∴==,即AE BD =,故答案为:=.(3)解:1CD =或3,理由是:分为两种情况:①如图1过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,则//AM EN ,ABC ∆是等边三角形,1AB BC AC ∴===,AM BC ⊥, 1122BM CM BC ∴===, DE CE =,EN BC ⊥,2CD CN ∴=,//AM EN ,AMB ENB ∴∆∆∽, ∴AB BM BE BN=, ∴11221BN=-, 12BN ∴=, 13122CN ∴=+=, 23CD CN ∴==;②如图2,作AM BC ⊥于M ,过E 作EN BC ⊥于N ,则//AM EN ,ABC ∆是等边三角形,1AB BC AC ∴===,AM BC ⊥,1122BM CM BC ∴===, DE CE =,EN BC ⊥,2CD CN ∴=,//AM EN , ∴AB BM AE MN=, ∴1122MN=, 1MN ∴=,11122CN ∴=-=,21CD CN ∴==,即3CD =或1.4.如图,过等边ABC ∆的边AB 上一点P ,作P E A C ⊥于E ,Q 为BC 延长线上一点,且PA CQ =,连PQ 交AC 边于D .(1)求证:PD DQ =;(2)若ABC ∆的边长为1,求DE 的长.【解答】(1)证明:如图,过P 做//PF BC 交AC 于点F ,AFP ACB ∴∠=∠,FPD Q ∠=∠,PFD QCD ∠=∠ABC ∆为等边三角形,60A ACB ∴∠=∠=︒,60A AFP ∴∠=∠=︒,APF ∴∆是等边三角形;AP PF =,AP CQ =,PF CQ ∴=PFD QCD ∴∆≅∆,PD DQ ∴=.(2)APF ∆是等边三角形,PE AC ⊥,AE EF ∴=,PFD QCD ∆≅∆,CD DF ∴=,12DE EF DF AC =+=, 1AC =,12DE =. 5.如图所示,已知等边ABC ∆的边长为a ,P 是ABC ∆内一点,//PD AB ,//PE BC ,//PF AC ,点D 、E 、F 分别在BC 、AC 、AB 上,猜想:PD PE PF ++= a ,并证明你的猜想.【解答】解:PD PE PF a ++=.理由如下:如图,延长EP 交AB 于G ,延长FP 交BC 于H ,//PE BC ,//PF AC ,ABC ∆是等边三角形,60PGF B ∴∠=∠=︒,60PFG A ∠=∠=︒,PFG ∴∆是等边三角形,同理可得PDH ∆是等边三角形,PF PG ∴=,PD DH =,又//PD AB ,//PE BC ,∴四边形BDPG是平行四边形,∴=,PG BD∴++=++==.PD PE PF DH CH BD BC a故答案为a.6.如图,已知ABC∆均为等边三角形,且点B、C、D在同一条直线上,连接AD、∆和CDEBE,交CE和AC分别于G、H点,连接GH.(1)请说出AD BE=的理由;(2)试说出BCH ACG∆≅∆的理由;(3)试猜想:CGH∆是什么特殊的三角形,并加以说明.【解答】解:(1)ABC∆均为等边三角形∆和CDE=∴=,EC DCAC BC∠=∠=︒ACB ECD60∴∠=∠ACD ECBACD BCE∴∆≅∆∴=;AD BE(2)ACD BCE∆≅∆∴∠=∠CBH CAGACB ECD∠=∠=︒,点B、C、D在同一条直线上60∴∠=∠=∠=︒ACB ECD ACG60又AC BC=ACG BCH∴∆≅∆;(3)CGH∆是等边三角形,理由如下:ACG BCH∆≅∆∴=(全等三角形的对应边相等)CG CH又60∠=︒ACG∴∆是等边三角形(有一内角为60度的等腰三角形为等边三角形);CGH7.如图,已知ABC∆是边长为6cm的等边三角形,动点P,Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1/cm s,cm s,点Q运动的速度是2/当点Q运动到点C时,P,Q都停止运动.(1)出发后运动2s时,试判断BPQ∆的形状,并说明理由;那么此时PQ和AC的位置关系呢?请说明理由;(2)设运动时间为t,BPQ∆的面积为S,请用t的表达式表示S.【解答】解:(1)BPQ∆是等边三角形,//PQ AC,(2分)运动至2s时,2AP=,4BQ=,BP AB AP BQ∴=-==(4分)4又ABC∆是边长为6cm的等边三角形∴∠=︒B60∴∆是等边三角形(6分)BPQ∴∠=∠=︒60BPQ A∴.//PQ AC(2)过Q作QH AB⊥于H,=,30∠=︒,BQHBQ t2∴=,QH=.(10分)BH t=-BP t6213(6)3(6)2S t t t t ∴=-=-=+. (12分)8.已知:在等边ABC ∆中,点D 、E 、F 分别为边AB 、BC 、AC 的中点,点G 为直线BC上一动点,当点G 在CB 延长线上时,有结论“在直线EF 上存在一点H ,使得DGH ∆是等边三角形”成立(如图①),且当点G 与点B 、E、C 重合时,该结论也一定成立. 问题:当点G 在直线BC 的其它位置时,该结论是否仍然成立?请你在下面的备用图②③④中,画出相应图形并证明相关结论.【解答】证明:连接DE 、EF 、DF .(1)当点G 在线段BE 上时,如图①,在EF 上截取EH 使EH BG =.D 、E 、F 是等边ABC ∆三边中点,DEF ∴∆、DBE ∆也是等边三角形且12DE AB BD ==. 在DBG ∆和DEH ∆中,60DB DE DBG DEH BG EH =⎧⎪∠=∠=︒⎨⎪=⎩,()DBG DEH SAS ∴∆≅∆,DG DH ∴=.BDG EDH ∴∠=∠.60BDE GDE BDG ∠=∠+∠=︒,60GDH GDE EDH ∴∠=∠+∠=︒∴在直线EF 上存在点H 使得DGH ∆是等边三角形.(2)当点G 在射线EC 上时,如图②,在EF 上截取EH 使EH BG =.由(1)可证DBG DEH ∆≅∆.DG DH ∴=,BDG EDH ∠=∠.60BDE BDG EDG ∠=∠-∠=︒,60GDH EDH EDG ∴∠=∠-∠=︒.∴在直线EF 上存在点H 使得DGH ∆是等边三角形.(3)当点G 在BC 延长线上时,如图③,与(2)同理可证,结论成立.综上所述,点G 在直线BC 上的任意位置时,该结论成立.9.已知点C 为线段AB 上一点,分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆,且CA CD =,CB CE =,ACD BCE ∠=∠,直线AE 与BD 交于点F ,(1)如图1,若60ACD ∠=︒,则AFB ∠= 120︒ ;如图2,若90ACD ∠=︒,则AFB ∠= ;如图3,若120ACD ∠=︒,则AFB ∠= ;(2)如图4,若ACDα∠=(用含α的式子表示);∠=,则AFB(3)将图4中的ACD∆绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若ACDα∠与α的有何数量关系?并给予∠=,则AFB证明.【解答】解:(1)如图1,CA CD∠=︒,ACD=,60所以ACD∆是等边三角形.∠=∠=︒,ACD BCE=,60CB CE所以ECB∆是等边三角形.AC DC∠=∠+∠,BCD BCE DCE∠=∠+∠,=,ACE ACD DCE又ACD BCE∠=∠,∴∠=∠.ACE BCDAC DC=,=,CE BC∴∆≅∆.ACE DCB∴∠=∠.EAC BDC∠是ADFAFB∆的外角.∴∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒AFB ADF FAD ADC CDB FAD ADC EAC FAD ADC DAC120.如图2,AC CD=,∠=∠=︒,EC CBACE DCB=,90∴∆≅∆.ACE DCB∴∠=∠,AEC DBC又FDE CDB∠=︒,DCB∠=∠,9090EFD ∴∠=︒.90AFB ∴∠=︒.如图3,ACD BCE ∠=∠,ACD DCE BCE DCE ∴∠-∠=∠-∠.ACE DCB ∴∠=∠.又CA CD =,CE CB =,ACE DCB ∴∆≅∆.EAC BDC ∴∠=∠.180180(180)120BDC FBA DCB ACD ∠+∠=︒-∠=︒--∠=︒, 120FAB FBA ∴∠+∠=︒.60AFB ∴∠=︒.故填120︒,90︒,60︒.(2)ACD BCE ∠=∠,ACD DCE BCE DCE ∴∠+∠=∠+∠.ACE DCB ∴∠=∠.CAE CDB ∴∠=∠.DFA ACD ∴∠=∠.180180180AFB DFA ACD α∴∠=︒-∠=︒-∠=︒-.(3)180AFB α∠=︒-;证明:ACD BCE α∠=∠=,则ACD DCE BCE DCE ∠+∠=∠+∠, 即ACE DCB ∠=∠.在ACE ∆和DCB ∆中AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,则()ACE DCB SAS ∆≅∆.则CBD CEA ∠=∠,由三角形内角和知EFB ECB α∠=∠=. 180180AFB EFB α∠=︒-∠=︒-.10.如图1,ABC ∆为等边三角形,面积为S .1D 、1E 、1F 分别是ABC ∆三边上的点,且。
全等三角形的判定和性质(一)(人教版)(含答案)

A.SSS B.SAS
C.AAS D.HL
答案:D
解题思路:
1.思路点拨:
三角板说明∠PMO=∠PNO=90°,结合OM=ON,OP=OP,故判定三角形全等的方法是“HL”.
C.(4)(6)(1) D.(2)(3)(4)
答案:D
解题思路:
1.思路点拨:判定两个三角形是否全等,必须依据全等三角形的五种判定方法;且全等三角形的判定方法中必有一条边相等.
2.解题过程:
根据全等三角形的判定方法,对照图形和选项,注意验证:
选项A:符合判定方法SAS;
选项B:符合判定方法SSS
选项C:符合判定方法AAS;
A.AAS B.SAS
C.ASA D.SSS
答案:B
解题思路:
1.思路点拨:
等边三角形存在边相等,可以证全等.
2.解题过程:
∵△ABD和△ACE均为等边三角形,且∠DAB=∠CAE=60°
∴DA=BA,AC=AE,∠DAB+∠BAC=∠CAE+∠BAC
在△ADC和△AEB中
∴△ADC≌△ABE(SAS)
A.50° B.60°
C.62° D.64°
答案:B
解题思路:
1.思路点拨:
①把∠BDC看成△ACD的外角,只需求∠ACD;
②利用全等的性质,得到 ;求出 即可.
2.解题过程:
∵∠ACB=90°,∠A=20°
∴∠CBA=70°
∵
∴ , ,
∴
∵
∴
∴∠BDC=∠A+∠ACD=20°+40°=60°,
中考数学每日一练:全等三角形的判定与性质练习题及答案_2020年解答题版

中考数学每日一练:全等三角形的判定与性质练习题及答案_2020年解答题版答案答案答案答案2020年中考数学:图形的性质_三角形_全等三角形的判定与性质练习题~~第1题~~(2020嘉兴.中考模拟) 如图,在▱ABCD 中,对角线 AC ,BD 相交于点 O ,过点 O 的一条直线分别交 AD ,BC于点 E ,F .求证:AE=CF .考点: 全等三角形的判定与性质;平行四边形的性质;~~第2题~~(2020温州.中考模拟) 如图,等腰直角△ABC 中,CA=CB ,点E 为△ABC 外一点,CE=CA ,且CD 平分∠ACB 交AE 于D ,且∠CDE=60°.(1) 求证:△CBE 为等边三角形;(2) 若AD=5,DE=7,求CD 的长.考点: 全等三角形的判定与性质;等边三角形的判定与性质;~~第3题~~(2019陕西.中考模拟) 如图,点B 、F 、C 、E 在一条直线上,FB=CE ,AB ∥ED ,AC ∥FD ,AD 交BE于O .求证:AD 与BE 互相平分.考点: 全等三角形的判定与性质;平行四边形的判定与性质;~~第4题~~(2019山西.中考真卷) (2019·山西) 已知:如图,点B ,D 在线段AE 上,AD=BE ,AC ∥EH,∠C=∠H.求证:BC=DH.考点:全等三角形的判定与性质;~~第5题~~(2019大连.中考真卷) 如图,点,在 上, , , ,求证: .考点:全等三角形的判定与性质;答案2020年中考数学:图形的性质_三角形_全等三角形的判定与性质练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
全等三角形的性质及判定(讲义及答案)

15. 已知:如图,点 D 在 AB 上,点 E 在 AC 上,AB=AC,∠B=∠C.
求证:△ADC≌△AEB. A
第 6 题图 第 7 题图
7. 如图,某同学把一块三角形的玻璃打碎成 3 块,现要到玻璃店去配一块完
全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
C
第 11 题图 第 12 题图
12. 如图,点 B,E,C,F 在同一直线上,在△ABC 与△DEF 中,AB=DE,
2. _____________________的两个三角形叫做全等三角形,全等用符号
“_________”表示.全等三角形的__________相等,____________相等.
3. 全等三角形的判定定理:______________________________.
精讲精练
C
B
D
3. 如图,△ABC≌△DEC,对应边___________,__________,___________,
对应角_______________,_______________,
______________. A
D
知识点睛
1. 不在同一直线上,首尾顺次相接,△
2. 能够完全重合,≌,对应边,对应角
16. 已知:如图,AB=CD,AB∥CD.求证:△ABD≌△CDB.
A D
B C
A 2
B C
第 8 题图 第 9 题图
9. 如图,∠1=∠2,若加上一个条件_______________________,
O
B D
11. 如图,AB=AD,∠1=∠2,如果要使△ABC≌△ADE,还需要添加一个条
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的性质及判定(习题)
➢ 例题示范
例1:已知:如图,C 为AB 中点,CD =BE ,CD ∥BE .
求证:△ACD ≌△CBE . 【思路分析】 ① 读题标注:
A
B
C D
E
② 梳理思路:
要证全等,需要三组条件,其中必须有一组边相等. 由已知得,CD =BE ;
根据条件C 为AB 中点,得AC =CB ;
这样已经有两组条件都是边,接下来看第三边或已知两边的 夹角.
由条件CD ∥BE ,得∠ACD =∠B .
发现两边及其夹角相等,因此由SAS 可证两三角形全等. 【过程书写】
先准备不能直接用的两组条件,再书写全等模块.过程书写中需要注意字母对应. 证明:如图 ∵C 为AB 中点 ∴AC =CB ∵CD ∥BE ∴∠ACD =∠B 在△ACD 和△CBE 中
AC CB ACD B CD BE =⎧⎪
∠=∠⎨⎪=⎩
(已证)(已证)
(已知) ∴△ACD ≌△CBE (SAS )
➢ 巩固练习
1. 如图,△ABC ≌△AED ,有以下结论:
①AC =AE ;②∠DAB =∠EAB ;③ED =BC ;④∠EAB =∠DAC .
E
D
C B
A
其中正确的有( ) A .1个
B .2个
C .3个
D .4个
E
D
B
A
2
1
F E
D
C
B
A
第1题图 第2题图
2. 如图,B ,C ,F ,E 在同一直线上,∠1=∠2,BF =EC ,要使△ABC ≌△DEF ,
还需要添加一组条件,
这个条件可以是_______________,理由是_____________;这个条件也可以是_____________,理由是_____________;这个条件还可以是_____________,理由是_____________.
3. 如图,D 是线段AB 的中点,∠C =∠E ,∠B =∠A ,找出图中的一对全等三角
形是_______________,理由是_________.
H G F
E
D
C
B
A
E
C
B
A
第3题图 第4题图
4. 如图,AB =AD ,∠BAE =∠DAC ,要使△ABC ≌△ADE ,还需要添加一组条件,
这个条件可以是_______________,理由是_____________;这个条件也可以是_____________,理由是_____________;这个条件还可以是_____________,理由是_____________.
5. 如图,将两根钢条AA',BB'的中点连在一起,使AA',BB'可以绕着中点O
自由旋转,这样就做成了一个测量工具,A'B'的长等于内槽宽AB .其中判定△OAB ≌△OA'B'的理由是( ) A .SAS
B .ASA
C .SSS
D .AAS
B'
A'
O
B
A
F
E
D C B A
第5题图 第6题图
6. 要测量河两岸相对的两点A ,B 的距离,先在AB 的垂线BF 上取两点C ,D ,
使CD =BC ,再定出BF 的垂线DE ,使A ,C ,E 在一条直线上(如图所示),可以说明△EDC ≌△ABC ,得ED =AB ,因此测得ED 的长就是AB 的长.判定△EDC ≌
△ABC 最恰当的理由是( ) A .SAS
B .ASA
C .SSS
D .AAA
7. 已知:如图,M 是AB 的中点,∠1=∠2,∠C =∠D .
求证:△AMC ≌△BMD . 【思路分析】 ① 读题标注: ② 梳理思路:
要证全等,需要______组条件,其中必须有一组_____相等. 由已知得:_______=_______,_______=_______. 根据条件_________________,得_______=_______. 因此,由________可证两三角形全等. 【过程书写】 证明:如图
8. 已知:如图,点B ,F ,C ,E 在同一条直线上,且BC =EF ,AB ∥DE ,AB =DE .
求证:△ABC ≌△DEF .
【思路分析】 ① 读题标注: ② 梳理思路:
2
1M
D
C
B
A F
E
D
C
B
A
要证全等,需要_____组条件,其中必须有一组____相等.
由已知得:_______=_______,_______=_______.
根据条件_________________,得_______=_______.
因此,由__________可证两三角形全等.
【过程书写】
证明:如图
➢思考小结
1.两个三角形全等的判定有_____,_____,_____,_____,其中AAA,SSA
不能证明三角形全等,请举反例进行说明.
2.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距
离,但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B 间的距离.你能说明其中的道理吗?
【参考答案】
➢巩固练习
1. B
2.AC=DF,SAS;∠B=∠E,ASA;∠A=∠D,AAS
3.△BCD≌△AED,AAS
4.AC=AE,SAS;∠B=∠D,ASA;∠C=∠E,AAS
5. A
6. B
7.①略
②3,边
∠1,∠2;∠C,∠D
M是AB的中点,AM,BM
AAS
【过程书写】 证明:如图, ∵M 是AB 的中点 ∴AM =BM
在△AMC 和△BMD 中 1 2 C D AM BM ∠=∠⎧⎪
∠=∠⎨⎪=⎩
(已知)(已知)(已证) ∴△AMC ≌△BMD (AAS ) 8. ①略
②3,边
BC ,EF , AB ,DE AB ∥DE ,∠B ,∠E SAS
【过程书写】 证明:如图, ∵AB ∥DE ∴∠B =∠E
在△ABC 和△DEF 中 AB DE B E BC EF =⎧⎪
∠=∠⎨⎪=⎩
(已知)(已证)
(已知) ∴△ABC ≌△DEF (SAS )
➢ 思考小结
1. SAS ,SSS ,ASA ,AAS AAA 反例:大小三角板 SSA 反例:作图略
2. 证明:如图,
在△ABC 和△DEC 中 AC DC ACB DCE BC EC =⎧⎪
∠=∠⎨⎪=⎩
(已知)(对顶角相等)
(已知) ∴△ABC ≌△DEC (SAS )
∴AB =DE (全等三角形对应边相等) 即DE 的长度就是A ,B 间的距离。
