高等钢结构理论-第二讲
高等钢结构理论-第二章

(a)压杆控制设计 (b)拉杆控制设计 网架荷载-挠度曲线
第二章 钢结构稳定问题概述
2.2 失稳的类别
第二章 钢结构稳定问题概述 早期钢结构稳定问题的分类
1. 平衡分岔(分支点)失稳(第一类稳定问题)
2.2 失稳的类别
二
对于理想的轴心压杆,在临界状态时,构件(结构)从初始的平衡位形 突变到与其邻近的另一平衡位形,表现出平衡位形的分岔现象。
第二章 钢结构稳定问题概述
2.5 稳定设计的几项原则
二
结构的整体布置须考虑整体和部分的稳定性要求
1
计算假定应与设计对象一致
2
细部构造应与稳定计算相互配合
3
The END
THANKS
二
稳定分岔屈曲
第二章 钢结构稳定问题概述 弹性稳定的分类
2. 不稳定分岔屈曲(有限干扰屈曲)
2.2 失稳的类别
二
超越临界状态后,只能在比临界荷载低的荷载下维持平衡位形。
承受轴向荷载的圆柱壳、承受均匀外压的圆球壳、缀条柱、薄壁型钢 方管等。
不稳定分岔屈曲
第二章 钢结构稳定问题概述 弹性稳定的分类
3. 跃越屈曲
平衡分岔(分支点)失稳
第二章 钢结构稳定问题概述 早期钢结构稳定问题的分类
2. 极值点失稳(第二类稳定问题)ຫໍສະໝຸດ 2.2 失稳的类别二
有缺陷的轴心受压构件和偏心受压构件发生的弹塑性失稳。
极值点失稳
第二章 钢结构稳定问题概述 弹性稳定的分类
1. 稳定分岔屈曲
超越临界状态后,荷载还能进一步增加。
2.2 失稳的类别
增大
临界力增大
第二章 钢结构稳定问题概述
2.4 稳定计算中的整体观点
桥梁高等钢结构理论(ch1)PPT课件

如果采用数学表达式描述结构设计准则,为:
S R
(1-1)
如果结构设计准则中的内力和变形以及抗力或限值都是确定性的,则所进行的计算
和验算将是比较简单的。
然而,影响结构功能的因素如结构上的作用、材料性能、构件几何参数、连接(构 造细部)类型、施工质量、计算模型、试验方法及设备等,很多都是具有随机性的 非确定值。因此,在设计中如何合理地考虑S这 些R 因素,使设计方法更接近于实际情 况,是长期以来钢结构设计方法发展演变所要达到的目的。
然而,无论是极限荷载法还是容许应力法,所采用的安全系数实际上是凭借 工程经验笼统地确定一个定值,这样各种构件的可靠度将不能保证具有比较一致 的水平,这是因为,结构的可靠性(安全性、适用性、耐久性)受各种随机因素 的影响,不能事先确定,只能用概率方S法 来R描述。
(2)半概率极限状态法
半概率极限状态法特点是明确了两种极限状态的概念:承载能力极限状态和变形极 限状态。我国的《钢结构设计规范》(TJ17-74)就是采用这样的设计方法编制的。 尽管该设计方法仍采用了容许应力法的表达方式,但其安全系数则分成了荷载系数 K1,材料系数K2和调整系数K3。是按承载力极限状态经多系数分析得到的。
1.1.2 基于强度的钢结构设计方法发展概述
基于强度的钢结构设计方法大致分为: 容许应力法和极限荷载法、半概率极限状态法、概率极限状态法。
(1)容许应力法和极限荷载法(最大荷载法)
容许应力法
S R
设计原则:结构构件的实际应力小于或等于所给定的容许应力,即:
f
[] y
K
(1-2)
优点:简单、明确,有大量工程数据S,R特 别是应力均匀的构件; 缺点:单一安全系数,保守(受弯构件);
不能合理反映结构设计的目的(经济性+适当的可靠度)。
高等钢结构

总势能为极大值,平衡 状态是不稳定的;
不稳定平衡
(3)总势能保持不变,则为中性平衡
d 2 d 2 0
还要看总势能的高阶导 数是大于零、小于零还 是等于零才能判断
随遇平衡 (中性平衡)
弹性应变能U是外力作用下储藏在体系内 的能量,意味着外力去除后回复到原来状态的 能力。变形后应变能增加,因而始终为正值;
因此该折线平衡状态不稳定。
屈曲后的荷载--位移曲线:
0, P kl cos ;
, P 0;
2
二、不对称分枝现象(稳定性)
变形时杆上端荷 载点从A移到B, 弹簧压缩了 FB
斜向弹簧支撑刚性杆件
几何关系 :
EB l sin
FB l(sin cos 1) 2 OD l(sin cos ) 2 对O点弯矩平衡: P l sin kl2 (sin cos 1)(sin cos ) 2 0
解为两个:
(1) 0 (2) Pl 4k sin
可由能量和静力两个途径得到,如由静力
弹簧力矩: 2 k
轴力对C点力矩:
Pl 2
sin
平衡方程:
4k Pl sin 0
讨论两种平衡状态稳定性
(1)当 0 ,即杆系处于直线平衡状态时,
d 2
d 2
杆系的总势能为
U V 2k 2 P(l 1-cos)
总势能对角位移的导数为
d 4k Pl sin d
d 2
d 2
4k
Pl
cos
d 3
d 3
Pl
sin
由 d d 0
高等钢结构理论第二讲

2、焊接或型钢构件极限状态:
毛截面屈服: f y A
r
净截面拉断后果严重:
fu
r ru A n
规范规定: = (1 0 .5 n 1 ) N f
n An
= N 高等f钢结构理论第二讲
A
初始弯曲和残余应力对有孔、 无孔拉杆影响没有区别; 孔旁应力集中不影响杆的 强度。
净截面的效率 影响净截面的效率的因素: = A e / A n
=1 a/l
材料塑性:塑性越高,净截面 效率越高
制孔方式:冲成的栓孔,净截 面效率需再乘0.85
紧固件排列:孔的行距与孔径 的比值(应变的不均匀性), 行距大效率低
行距较大时,有效净截
面一般不超过0.85 ~0.9的
毛截面
对无孔拉杆(如焊接时)存在
同样问题。剪切滞后
高等钢结构理论第二讲
单角钢拉杆
N y )
<
N
2 y
y s2
=0
高等钢结构理论第二讲
单轴对称构件
k = 1 ( y s / r0 ) 2
失稳形式(应用)
塔架单角钢主肢的设计:
高等钢结构理论第二讲
几何缺陷对整体的影响
初始弯曲:使轴压构件的失稳性质发生质变 无缺陷弹性范围: 平衡分岔问题 无缺陷非弹性分析: 切线模量与折算模量(Shanley理论) 有缺陷非弹性分析: 极限承载力问题
N A r
扭转屈曲和弯扭屈曲的计算
压杆的计算长度 杆端约束
高等钢结构理论第二讲
桁架和塔架杆件计算长度
3. 钢结构基本构件:压杆(续)
3.2 压杆(续)
格构式压杆 剪力对格构柱稳定的影响:换算长细比法 几何及力学缺陷对单肢的影响(实际上与一般实腹式不同) 单肢验算: 缀材计算 垫板式组合压杆
钢结构基本原理(第2章)

σ
f0.2
S E
0 0.2
ε
图2.4 高强度钢的应力-应变曲线
第2章 钢结构的材料
钢
结 构 钢材在单向受压时(短试件) ,抗压强度与单向受拉时相同。钢材受扭转 基 时的应力-应变曲线也与受拉时相似,但剪切屈服点和抗剪强度低于fy和fu;
本 剪变模量G也低于弹性模量E。钢材和铸钢件的弹性模量、剪变模量、线膨胀
理 法、环境温度有关。冲击韧性由冲击试验
( 黄
冲击韧性:测α定k 。AA(kN•m/cm2)
呈
伟 主 编
式中:AK—试验机的冲击功(N•m); A—缺口处净截面面积(cm2)。
)
55 1
10
1
1-1
10
2
2
R=1 U 形缺口 R=0.25
45°
图2.6 冲击韧性试验
第2章 钢结构的材料
钢 2.1.4 可焊性
黄 呈 伟
冷弯试验是鉴定钢材质量的一种良好方法, 常作为静力拉伸试验和冲击试验的一种补充试
主 验,是一项衡量钢材力学性能的综合指标。
编 )
a
d
a
d+2.1a
图2.5 冷弯1800试件
第2章 钢结构的材料
钢
结 构
2.1.3 冲击韧性
基 本 原
冲击韧性是衡量钢材强度、塑性及材 质的一项综合指标。钢材的韧性与轧制方
本
原 理
σ
fu
B
D
(
fy
C
F
fe
E
黄
fp A
呈
伟
l0
主 编 )
d0
0 0.1 0.15
2.5
ε/%
《高等钢结构理论》课件

钢结构的连接与构造
拼接方式和连接材料
详细说明几种典型的钢结构拼 接方式和各种连接材料的特点 以及使用方法。
节点构造和细节设计
讲解钢结构的节点构造和细节 设计,包括节点类型、强度验 算和防腐措施等。
构造验收和质量控制
结束语
本课程旨在帮助工程师更深入地了解钢结构的理论和实践,为未来钢结构领域的发展提供参考和支持。
谢谢观看!
钢材的分类和性能
概述常见的钢材分类和性 能参数,以及每种钢材在 钢结构中的应用。
钢结构设计的基本原理
讲解钢结构设计的基本原 理,包括力学分析、结构 优化和验算等。
钢结构载荷分析
1
荷载的分类和作用原理
2
详细说明荷载的分类和作用原理,包 括静态荷载、动态荷载和温度荷载等。
3
受力特点
介绍钢结构受力的基本特点,包括受 力形式、受力方向和受力损伤等。
《高等钢结构理论》PPT课件
一个实用性强的高等钢结构理论课件,包含钢结构基础、载荷分析、连接与 构造、设计和施工等多个部分,可为钢结构工程师提供参考。
前言
本课程将深入介绍钢结构的基础知识和设计流程,旨在为钢结构工程师提供 帮助和指导。
钢结构基础
定义和特点
介绍钢结构的定义、特点 以及与其他建筑结构的比 较。
介绍钢结构的构造验收标准和 质量控制要点,确保钢结构工 程施工质量。
钢结构的设计与施工
1 设计的步骤和流程
详细讲解钢结构设计的 步骤和流程,帮助工程 师高效完成设计工作。
2 施工的注意事项和
方法
讲解钢结构施工的注意 事项和方法,包括施工 流程、安全防范和质量 控制等。
3 安全管理和维护措施
钢结构基本原理课件:第二章

硫S:降低钢材的塑性、韧性、可焊性和疲劳强度, 在高温时,使钢材变脆,称之为热脆。含量 应不超过0.045%。(有害成分) 磷P:降低钢材的塑性、韧性、可焊性和疲劳强度, 在低温时,使钢材变脆,称之为冷脆。含量 应不超过0.045%。可以提高强度和抗锈蚀 性。 (有害成分) 氧O:降低钢材的塑性、韧性、可焊性和疲劳强度, 在高温时,发生热脆。含量应不超过0.008%。 (有害成分) 氮N:降低钢材的塑性、韧性、可焊性和疲劳强度, 在低温时,发生冷脆。含量应不超过0.008%。 (有害成分)
碳C :含量增加,钢材强度提高,而塑性、韧性和 疲劳强度低。同时焊接性能和抗腐蚀性恶 化。一般在碳素结构钢中不应超过0.22 % ; 在焊接结构中还应低于0.2 %。 硅Si:含Si适量使强度提高,其它影响不大,有益元素, 碳素结构钢中应控制≤0.3 %, 在低合金高强 度钢中硅的含量可达0.55 %。 锰Mn:含Mn适量使强度提高,降低S、O的热脆影 响,改善热加工性能,对其它性能影响不大, 有益。在碳素结构钢中锰的含量为0.3 %~0.8 % ,在低合金高强度钢中锰的含量可达1.0 % ~1.6%。 钒和钛:是钢中的合金元素,能提高钢的强度和 抗腐蚀性能,又不显著降低钢的塑性。
材质量的综合指标。
图2.4 钢材冷弯试验示意图
2.3.3 冲击韧性
冲击韧性:在动力荷载作用下,材料吸收能量的能力。 韧性是钢材抵抗冲击荷载的能力,它用材料在断裂时所吸 收的总能量来量度(Cv) 摆锤 h1 h2 韧性是钢材强度和塑性的综合指标。
图2.5 冲击韧性试验
2.4
各种因素对钢材性能的影响
4、气孔:浇注时氧化铁和 碳作用生成的CO气体未充 分逸出。
图2.10 层间撕裂
2.4.3 钢材的硬化
钢结构基本原理》第2章 钢结构的材料幻灯片PPT

有一向为异号应力,且同号两个应力相差又较大, 破坏为塑性。
钢结构基本原理
平面应力状态
eq 1 22 21 2
σ eq σ x 2 σ2 y σ xσy 3 τx 2y
普通梁
σeq σ23τ2
名义应力低于屈服点、材料处于弹性阶段,当 荷载循环到达一定次数后,钢材会发生突然脆性断 裂破坏,疲劳计算方法详见第9章。
(二)低周疲劳破坏
反复应力高于屈服强度、材料处于弹塑性阶段, 反复荷载会使钢材的剩余应变逐渐增长,最后产生 突然破坏。
钢结构基本原理
出版社 科技分社
(三)包辛格〔Bauschinger〕效应
对于没有缺陷和剩余应力 影响的试件,可认为钢材是图 2-3所示理想弹-塑性体,经历 两个阶段,即假定钢材应力小 于fy时是完全弹性的,应力超 过fy后那么是完全塑性的。设 计时,取fy作为强度限值,而 取fu作为材料的强度储藏。
图2-3 理想弹-塑性 应力-应变曲线图
钢结构基本原理
出版社 科技分社
钢结构基本原理
本章内容
出版社 科技分社
第一节 钢材的工作性能 第二节 钢构造对钢材性能的要求 第三节 影响钢材性能的主要因素 第四节钢材的种类、规格和选用原那么
钢结构基本原理
出版社 科技分社
第一节 钢材的工作性能
一、钢材静力单向均匀拉伸时的性能 钢材的主要强度指标和变形性能根据常温〔20
±5°〕、静载条件下标准试件一次拉伸试验确定。 常温静载条件下,图2-1所示低碳钢标准试件
单向一次拉伸试验得到的简化光滑应力-应变曲线如 图2-2所示,钢材历经五个阶段 :
高等钢结构理论专题2
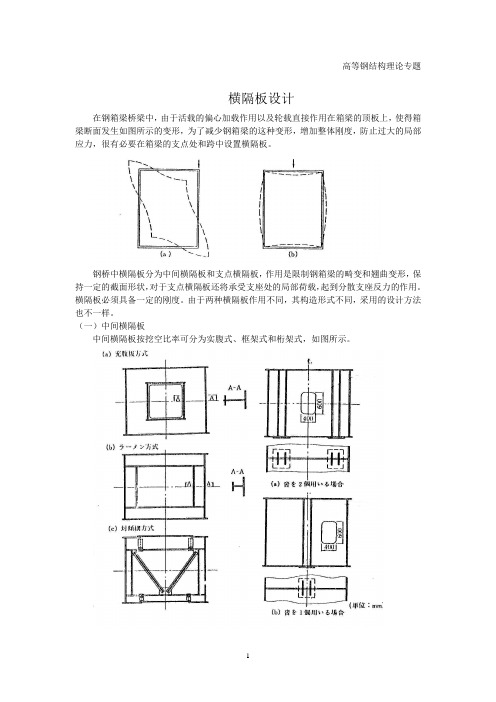
高等钢结构理论专题横隔板设计在钢箱梁桥梁中,由于活载的偏心加载作用以及轮载直接作用在箱梁的顶板上,使得箱梁断面发生如图所示的变形,为了减少钢箱梁的这种变形,增加整体刚度,防止过大的局部应力,很有必要在箱梁的支点处和跨中设置横隔板。
钢桥中横隔板分为中间横隔板和支点横隔板,作用是限制钢箱梁的畸变和翘曲变形,保持一定的截面形状,对于支点横隔板还将承受支座处的局部荷载,起到分散支座反力的作用。
横隔板必须具备一定的刚度。
由于两种横隔板作用不同,其构造形式不同,采用的设计方法也不一样。
(一)中间横隔板中间横隔板按挖空比率可分为实腹式、框架式和桁架式,如图所示。
这里定义开口率BH bh A A =='ρ,当4.0≤ρ时,横隔板可视为实腹式,主要考虑剪应力,当8.0≥ρ,为桁架式,可简化为仅受轴力的杆件,在8.04.0<<ρ范围内,横隔板受力性质介于实腹式和桁架式之间,作为框架处理,考虑轴力和抗弯。
实腹式横隔板适用于尺寸较小的钢箱梁,制作简单,应用最广,桁架式适用于较大的箱子,受力简化为拉压杆,能以较小的自重提供较大的刚度。
中间横隔板的设计需要确定横隔板间距L D 和横隔板刚度K 。
1.横隔板间距L D 的确定对于横隔板间距L D 一般依据经验,各国规范及常规做法不一样。
日本偏安全,以下是日本的经验公式:⎩⎨⎧>≤-≤≤≤)50(20114.0)50(6u u Du D L L L L L 且 (式1) 其中L u 桥梁单跨长,单位m这个公式只适用于200m 以内跨径的钢箱梁桥,这个公式的来源见下图,根据偏心活载作用下,限制翘曲应力与容许应力的比值在0.02~0.06之间,得到横隔板间距与跨径的关系。
对于大于200m 的跨径,公式就不适用了,日本人多采用桁架式,间距一般取为6m ,中国也比较保守,上海的卢浦桥中隔板间距取为4m ,欧洲一般取为20m ,但是多为实腹式的厚钢板。
2.横隔板刚度K 的确定钢箱梁中间横隔板的刚度K 需要满足下面的公式:320DDW L EI K ≥ (式2)其中I Dw 是箱梁的断面抗扭惯矩,根据箱梁的截面尺寸形式由下式算得:⎭⎬⎫⎩⎨⎧+-++++=)(2)21()21(22212122222121ααααααFh Bl b Fl Bu b Fu I DW (式3) 其中Fu 是箱梁上顶板截面积,Fl 是箱梁下底版截面积,Fh 是一个腹板的截面积。
钢结构基本原理优秀课件

手册(见附表1.1)。弹性设计时,构件的应力不能大于f值。
抗拉强度fu在实际构件中是不允许达到的,钢材的抗拉强 度fu值高,可以增加结构的安全保障。
伟
主
编 )
第2章 钢结构的材料
钢 另外,Q235钢材在屈服
结 构 基 本 原 理
图2.3 理想弹-塑性的应力-应变曲线
第2章 钢结构的材料
钢 结
高强度钢材没有明显的屈服
构 台阶,这类钢的屈服点是根据
σ
基 实验分析结果人为规定的,称 f0.2 S
本 原 理
为条件屈服(用f0.2表示,定 义为试件卸载后其残余应变为
E
( 2%时所对应的应力)。这类
黄 钢材在设计中不宜利用塑性。 呈 伟 主 编 )
伟 主
度比常温拉伸试验的强度低得多,应另行测定“强度”。
编 耐疲劳性:钢结构或构件在长期连续的交变荷载或重复荷
) 载作用下,应力虽低于fy也会发生破坏,称为“疲劳破坏”。
呈 良好方法,常作为静力拉伸试验和
伟 主 编
冲击试验的一种补充试验,是一项 衡量钢材力学性能的综合指标。
)
a
d
a
d+2.1a
图2.5 冷弯1800试件
第2章 钢结构的材料
钢
2.1.3 冲击韧性
结
构 冲击韧性是衡量钢材强度、
基 塑性及材质的一项综合指标。
本 钢材的韧性与轧制方法、环境
原 温度有关。冲击韧性由冲击试
0 0.2
ε
图2.4 高强度钢的应力-应变曲线
第2章 钢结构的材料
钢 结 构 钢材在单向受压时(短试件) ,抗压强度与单向受拉时 基 相同。钢材受扭转时的应力-应变曲线也与受拉时相似,但 本 剪切屈服点和抗剪强度低于fy和fu;剪变模量G也低于弹性模 原 量E。钢材和铸钢件的弹性模量、剪变模量、线膨胀系数α 理 和质量密度ρ列于表2.1。
高等钢结构理论教学大纲

《高等钢结构理论》教学大纲
课程编号:
英文名称:Advanced Steel Structure Theory
课程类别:选修课学时:40 学分:2
适用专业:结构工程
预修课程:钢结构设计原理、结构力学、材料力学、弹性力学
课程内容:
本课程开设目的是为了加深学生钢结构理论知识,为今后钢结构方向的研究打下坚实基础。
具体内容为:钢材的两种破坏方式;脆性破坏的特点;常幅疲劳、变幅疲劳的概念、区别、验算方法。
焊接应力、焊接变形的产生原因;焊接应力对结构性能的影响;减少焊接应力、焊接变形的措施。
高强度螺栓抗拉连接的工作性能。
屈曲的分类;轴心压杆的弹性弯曲屈曲;初始几何缺陷、残余应力对轴心压杆极限承载力的影响;轴心压杆的非弹性弯曲屈曲。
受弯构件的弹性弯扭屈曲;受弯构件的弹塑性弯扭屈曲;压弯构件平面内的稳定承载力;稳定计算的能量法、瑞利——里兹法、伽辽金法;稳定计算的有限单元法。
教材:
王国周,瞿履谦. 钢结构原理与设计. 北京:清华大学出版社,1993
参考书目:
1. 陈绍藩. 钢结构设计原理. 北京:科学出版社,1998
2. 陈骥. 钢结构稳定理论与设计. 北京:科学出版社,2001
考核方式与要求:
读书报告或论文
19。
高等钢结构2

框架有水平荷载,又有竖向荷载, 则弯矩放大系数有两个:一个是竖向荷 载作用下的弯矩及对应按无侧移模式计 算的弯矩放大系数;另一个是水平力产 生的弯矩及对应的弯矩放大系数。
我国《规范》为了简化计算, 对纯框架没有区分两种荷载产生的 弯矩,统一按照有侧移失稳的计算 长度系数来计算弯矩放大系数,并 且等效弯矩系数取为1.0。
M BA
取
s4 c2
随着柱子轴力增加,柱子抗弯刚度减小, 梁刚度没有变化,因此梁将分配到更多弯 矩,而柱端弯矩减小。 当 P PE 0.3 时, s 3.588,
M AB
c 2.109
19.190 M A 6.327 M B 0.4924M A 0.1624 M B 38.954
2
按不带轴力转角位移方程计算弯矩
M
' AB
HL 2
带轴力与不带轴力弯矩比 (即弯矩放大系数m):
m M AB ' M AB
12 K tan(u 2) m 6 Ku u 2 tan u 2
临界荷载
2 EI c 7.5K 2 2 K Pcr 7.5K 2 8K 1.52 L2
取 m 1.0 偏于安全
•
两端铰支跨中集中力压弯杆:
M max
1 0.18 P
PE M 0
1 P PE
1 0.25 P
PE M eq
1 P PE
1 0.18 P PE P m 1 0.43 1 0.25 P PE PE
P 《规范》GB 5007-2003取 m 1 0.2 PE
M BA
如果, ib ic , 则:
M AB 3s s 2 c 2 M A 3cM B 2 3 s c2 3s s 2 c 2 M B 3cM A 2 3 s c2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计屈服点高 于标准屈服点
欧洲钢结构协会(ECCS)的曲线背景 残余应力分布: =0 .5 f
r y
a曲线
b曲线
c曲线
试验比较:
轧制工字钢IPE160弱轴屈曲试验与b 曲线的比较
中国规范的曲线 特点:
结合国情,重点放在 H型钢和双角钢组合 截面上。其他截面如 工字型和钢管也做了 分析。 三条曲线,无 从 0~0.2的水平段。 《高层钢结构设计与 施工规程》中的d曲 线: t > 40mm的H型 或箱型钢 常用的双角钢T形截面、焰割 边焊接工字形截面以及格构式 截面都归入b曲线。b曲线是 设计中用得最多的曲线。
塔架杆件计算长度:塔架腹杆
塔架腹杆: 单系腹杆:几何长度。 交叉腹杆:具体问题具体考虑。
残余应力对整体的影响
改变残余应力分布来加固构件, 加焊盖板或堆焊焊珠
翼缘加盖板
确定曲线的方法
方法1:采用切线模量理论,Et按残余应力的分布决定,初始弯曲的不利作用 在安全系数范围内考虑。
方法2:采用极限承载力理论,同时计入初始弯曲和残余应力的效应。
部分人认为端部约束可抵消初始弯曲的不利影响,倾向于保留切线模量理论。
杆端约束(梁柱连接)
确定原则:非完善弹塑性杆模型 构造实际情况、几何缺陷及力学缺陷 Step1
Step2
考虑因素: 侧向支撑状态 失稳模式:长细比 构造(半刚性) 缺陷
Step3
桁架和塔架杆件计算长度:各国并不一致
桁架和塔架的稳定设计原则:
目前一般通过每根构件考虑相关构件的约束的稳定来保证。由计算长度体现。 基本假定:节点铰接(当腹杆考虑两端约束时,端部连接需承担一般塑性弯矩 除短而粗桁架外,一般不必考虑次弯矩效应:(塑性好) 对稳定的有利影响: 发展:整体稳定分析
Байду номын сангаас
螺纹拉杆:
因自重的下垂(预应力):杆端螺纹、花篮螺丝等调整 D 2 (1 k p )2 净截面(规范)与有效截面: A e =
4 D
3. 钢结构基本构件:压杆
3.2 压杆
轴心压杆的极限状态:失稳 失稳形式:弯曲失稳、扭转失稳、弯扭失稳(单轴弯曲、双轴弯 曲) 缺陷的影响:
几何缺陷:初始弯曲、初始扭曲、初始偏心等
A =N / ( f )
3. 钢结构基本构件:压杆(续)
3.2 压杆(续)
压杆的支撑:减小计算长度,提高承载力 单个柱的支撑 柱列的支撑 支撑设计中的扭转问题 总结: 稳定理论在结构设计中的应用
轴心受压构件的荷载—挠度曲线
考虑稳定系数的准则:
岔屈曲荷载为准则:
截面边缘纤维屈服: 构件的极限荷载:
8.1 塑性设计
第五讲 第六讲
8.2 抗震钢结构
8.3 箱形梁 8.4 受扭构件 第七讲
8.5 设计中的试验工作
8.6 钢结构加固设计
3. 钢结构基本构件:拉杆
3.1 拉杆
拉杆的极限状态: 无孔拉杆 有孔拉杆 净截面的效率 : 杆件截面能否发挥作用? 角钢拉杆: 单角钢拉杆 双角钢拉杆 桁架中单角钢腹杆的布置
扭转屈曲和弯扭屈曲的计算 基本策略:
弯曲失稳(直变弯):
N
E
N fy < =f A r
<N
= EI / l
2
2
几何缺陷及力学缺陷不可忽略 非弹性 一般较弯曲失稳大,无计算规定 较小时通过意板件局部稳定避免 必要时转化弯曲失稳分析
扭转失稳(直变扭):
2 E I / l2) <N = 2 ( G J + N r0
4 2
1) ,则 N0
l 0 =0 .5 l
当两杆均受压时,应取 N0 N
(2) 拉杆 l0 =l (3) 交叉杆单角钢杆件斜平面长细比时 ,l0 取节点中心到交叉点的距离
规范:
塔架杆件计算长度:塔架主杆
塔架主杆: 中国:随腹杆体系的布置而不同。 欧洲:下图
主杆每节点两个面内均有腹杆
高等钢结构 理论
1. 钢结构基本性能及特点
1.1 钢材生产对材性的影响 1.2 钢材加工(施工) 对构件性能的影响 1.3 外界作用对钢结构性能的影响
2. 钢结构的几个特殊问题
目 录
2.1 残余应力及其影响 2.2 钢结构的稳定问题 2.3 钢结构的断裂问题 2.4 钢结构的疲劳问题
第一讲
3. 钢结构基本构件
弯曲失稳(直变弯): 扭转失稳(直变扭):
N
E
= 2 EI / l 2 <N 1 r
2 0
N =
( G J + 2 E I / l 2 ) <N
E
两端铰支无翘 曲约束
弯扭失稳(两端铰支无翘曲约束):
r02 ( N
y
N
y
)( N N
fy A
An
r
fu
r ru
0 .5 规范规定: =(1
n1 N f ) n An
=
N f A
初始弯曲和残余应力对有孔、 无孔拉杆影响没有区别; 孔旁应力集中不影响杆的 强度。
净截面的效率
影响净截面的效率的因素: =A e / A n
1、构件截面上材料相对于节点板的 分布情况;材料贴于节点板并和 节点板相连的部分占的比重越大越接近1. 连接方式: 全部直接连接与部 分直接连接 构件截面上材料相 对于节点板的分布 (偏心距)
(2)扭转失稳
构件整体失稳时只发生扭转变形,十字形截面轴心受压构件的失稳属于这 种情况。
(3)弯扭失稳
构件整体失稳时既发生弯曲变形又发生扭转变形,单轴对称截面轴心受压 构件绕对称轴失稳以及无对称轴截面轴心受压构件的失稳属于这种情况。
弯曲失稳
扭转失稳 构件失稳时截面位移投影图
弯扭失稳
失稳形式(整体失稳)
桁架平面外计算长度
弦杆: 节点板在桁架平面外约束刚度不大,一般取侧向支撑的间距 当弦杆轴心压力在侧向支撑点间有变化时:
l 0 = l1 ( 0 .7 5 +0 .2 5 N2 ) N1
受压腹杆:
规范:k =1 .0 交叉斜腹杆: 考虑自身及 相交叉杆的 拉压性质及 节点构造, 采用不同公 式。
规范:桁架平面外,当两交叉杆长度相等时
fy
扭转屈曲和弯扭屈曲的计算
双角钢组合T型截面:残余应力低(0.25fy),抗扭刚度好,不必采用换算 的长细比(但新规范考虑了) 焊接T型截面: 采用换算的长细比 规范:仅考虑初弯曲的换算的长细比方法 开口冷弯薄壁型钢截面:单轴对称时,绕对称轴的弯扭失稳要进一步考虑
扭转失稳:无具体规定,可采用换算的长细比方法
桁架结构(平面):
平面内计算长度:上弦杆、受压腹杆 平面外计算长度:取决与支撑布置情况 规范
塔架结构(空间桁架):塔架主杆、腹杆
桁架平面内计算长度
上弦杆: 理论分析:
k= 15 4n
规范:k =1
受压腹杆: 较弦杆有利: 端部弦杆约束大。
规范:k = 0 .8(支座处除外)
交叉斜腹杆: 分析模型 规范:AB、BC段几何长度
3 N0 0.5l 4) 相交杆受拉,受拉杆在交叉点节点板处中断 l0 =l 1 4N
5) 相交杆受拉,在交叉点处不中断,而计算压杆中断
2
若 N 0 N ,或拉杆的 EI y (
l 为桁架节点中心间距离,交叉点不作为节点考虑 N 为所计算的压杆的内力,取绝对值;N0 为相交杆的内力,取绝对值
y
) < N
2 y
y s2 =0
单轴对称构件
k =1 ( y s / r0 ) 2
失稳形式(应用)
塔架单角钢主肢的设计:
几何缺陷对整体的影响
初始弯曲:使轴压构件的失稳性质发生质变 无缺陷弹性范围: 平衡分岔问题 无缺陷非弹性分析: 切线模量与折算模量(Shanley理论)
力学缺陷:截面屈服点的非均匀性、残余应力等
N A
r
扭转屈曲和弯扭屈曲的计算
压杆的计算长度
杆端约束 桁架和塔架杆件计算长度
3. 钢结构基本构件:压杆(续)
3.2 压杆(续)
格构式压杆 剪力对格构柱稳定的影响:换算长细比法 几何及力学缺陷对单肢的影响(实际上与一般实腹式不同) 单肢验算: 缀材计算 垫板式组合压杆 压杆的截面尺寸 板件宽厚比限值 截面尺寸的确定:
有缺陷非弹性分析: 极限承载力问题
初始扭曲:
产生初始扭矩和剪应力,使杆件提前屈服
但初始扭曲值较小,一般不考虑
初始偏心: 类似初始弯曲
残余应力对整体的影响
取决于残余应力的分布、变化情况、分布宽度、截面上位置等 不仅对不同截面形式和不同生产条件的影响不同,同一杆件不同屈曲轴影响也不同
经过退火处理,受压承载力可较大提高
十字形截面(四角钢组成十字形截面):与板件局部屈曲等稳定考虑
其他:具体分析:对板件宽厚比大而翼缘又窄者需多加注意
杆端约束
(铰非铰、刚非刚)
杆端约束(轻型柱脚)
柱:H型W150*30 底板:200*13 L=5.5m L=50mm
加拿大试验研究:
L=25mm
性能接近嵌固 如上端为不动铰 ky=0.82 ky=0.90
注:高260mm的一种 焊接H型钢曲线 初始弯曲: 1/1000 小长细比范围内 线模量理论的 值低(切线模 量理论得到的是 承载力的下限)
欧洲钢结构协会(ECCS)的曲线 特点:
几何缺陷、屈服应力及残余应力的数据均由试验资料统计分析得到 试件1067根,包括工字型、H型、T型、圆管和方管等,长细比:55、75、 95、130、160 承载力取试验平均值减去两倍标准差(与拉杆在安全度上协调一致)
净截面的效率
影响净截面的效率的因素: =A e / A n
